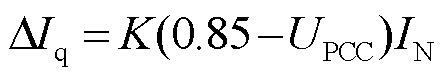 (1)
(1)
摘要 大量分布式电源(DG)的接入使有源配电网拓扑结构与故障特征越加复杂,特别是逆变型DG的弱故障特征、不可测分支负荷的T型接入使得传统差动保护在有源配电网中的灵敏性下降。对此,该文提出了一种能量积分型无功电流差动保护,通过挖掘暂态过程中无功差动电流的非线性能量积分在区内外故障时的差异特征,构造了能量积分型保护判据,正常运行或区外故障时无功差动电流的能量积分为0,而区内故障时能够灵敏地感知无功差动电流幅值、频率的变化,无功差动电流的能量积分远大于0。所提方法降低了区内故障穿越性电流对差动保护灵敏度的影响,解决了不可测分支负荷引起的不平衡电流与故障电流辨识困难的问题。仿真结果表明所提方法能够可靠地识别区内外故障,具有一定的抗同步误差能力。最后,开发了具备5G通信功能的智能终端样机,通过RTDS闭环测试进一步验证了该方法的有效性。
关键词:差动保护 无功电流 能量积分 不可测分支负荷 保护样机 5G通信
为推动实现“双碳”目标,构建以新能源为主体的新型电力系统,风电、光伏等新能源得以迅猛发展。大量清洁能源以逆变型分布式电源(Inverter-Based Distributed Generator, IBDG)的形式接入配电网,IBDG的助增、外汲、反向作用劣化了配电网原有三段式电流保护的性能[1-4]。
针对有源配电网继电保护问题,国内外学者提出了许多新保护原理。文献[5]根据正序电压、正序电流计算保护安装处正序测量阻抗,构造了积标制动式正序阻抗纵联保护。文献[6]将被保护线路两侧测量阻抗和、差分别定义为差动阻抗与制动阻抗,提出了一种阻抗差动保护,但该方法在含T接分支馈线中存在不正确动作风险。文献[7]利用高频电压、电流计算高频差动阻抗与高频制动阻抗,仅需故障后2.5 ms数据且适用于含T接分支场景。考虑到有源配电网非有效接地、分布式电源多点接入等问题,文献[8]将能量方向纵联保护引入有源配电网,提出了一种基于故障超前相的改进能量方向纵联保护。文献[9]提出了一种基于正序故障分量的能量方向纵联保护,能够避免T接分支负荷频繁投切引起的误动作。但上述保护方法需要电压信息,应用场景存在局限性。现有文献基于IBDG的故障特征构造保护方案,保护灵敏性与IBDG出力大小相关。文献[10]利用光伏故障电流的波形畸变率构造方向判据,光伏并网容量越大,保护灵敏性越高。文献[11]通过修改IBDG的控制策略,使其在故障后主动向配电网注入特征信号,实现控保协同。然而,光伏等IBDG的出力具有间歇性,在夜间光伏IBDG退出运行后,一些基于IBDG故障特征的保护方法均存在灵敏度下降甚至失效的风险。因此,引入输电线路电流差动保护一直是有源配电网保护的研究热点。文献[12]利用正序电流工频变化量构造差动保护判据,与传统电流差动保护相比,减少了2/3的通信量。文献[13]利用正序电流故障分量的幅值比、相位差分别构造差动保护的动作量与制动量。文献[14]提出了基于派克变换的新型电流差动保护,利用d轴电流实现差动保护。文献[15]利用d、q轴电流故障分量的矢量合成电流构造差动保护,在不对称故障下具有比文献[12]更高的灵敏度。上述方法改进了构造差动保护所使用的电流量,但仍沿用传统差动保护的动作判据,通过比较差动电流与制动电流实现区内外故障判别。然而,传统差动保护设计思路基于输电线路的故障特征,通常采用比率制动型动作判据,由于被保护线路两侧均为同步机电源,在区内故障两侧电流幅值、相位相同时具有最高的灵敏度。然而在有源配电网中,受低电压穿越(Low Voltage Ride Through, LVRT)、限电流等控制策略影响,IBDG提供的短路电流幅值受限、相位受控,当过渡电阻较高时故障区段将流过由系统电源提供的穿越性电流,此时传统差动保护灵敏度下降甚至拒动。
另外,配电系统拓扑结构复杂,主馈线往往存在分支线路,若分支具备电流互感器(Current Transformer, CT)与通信条件,可以配置多端差动保护[16-17];然而,一些容量较小的负荷T型接入主馈线时,通常不具备通信条件,此时基于双端信息的传统差动保护从原理上即不适用。对此,文献[18]提出了一种幅值差动保护,利用自适应的动作特性曲线规避分支的影响,但仅针对电机类分布式电源。文献[19]利用负序电流相位差构造适用于含不可测分支线路的保护判据,但仅适用于不对称故障。解决含不可测分支线路保护问题的另一种思路是推算分支线路的电气量,构造虚拟多端纵联保护。文献[20]利用被保护线路两端电压、电流信息推算分支线路的功率,构造多端功率差动保护;文献[21]利用被保护线路两端电压、电流信息推算不可测分支的电流相量,提出了虚拟三端差动保护;文献[22]利用对端正序电压、电流推算本端正序电流,正常运行或区外故障时,正序电流计算值与测量值相同,而区内故障时则存在较大差异,据此构造的纵联保护方案能够适应含有T接IBDG的馈线,但该类方法均依赖电压信息。
针对上述问题,本文提出了一种能量积分型无功电流差动保护。首先推导了IBDG动态无功电流的时域表达式,其在暂态过程中包含衰减的工频分量,即区内故障时无功差动电流的幅值与频率时变。其次,利用非线性能量算子表征无功差动电流的能量,仅当无功差动电流的幅值或频率为0时,该能量算子计算结果为0,故正常运行或区外故障时无功差动电流能量为0,区内故障时无功差动电流能量非0。据此,构造了能量积分型无功电流差动保护判据。另外,正常运行时不可测分支负荷引起的不平衡电流的无功分量为直流量,其频率为0,故能量为0,而故障电流的无功分量,即无功差动电流能量非0,利用非线性能量算子与无功差动电流的故障特征解决了不平衡电流与故障电流辨识困难的问题。最后,搭建PSCAD仿真模型与RTDS硬件在环测试平台,对所提保护方法的有效性进行了验证。
配电网发生短路故障后,IBDG公共连接点(Point of Common Coupling, PCC)电压跌落,根据《光伏发电系统接入配电网技术规定》[23],故障期间IBDG应具备低电压穿越能力,输出动态无功电流支撑电网电压,其动态无功电流增量为
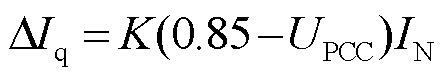 (1)
(1)
式中,ΔIq为IBDG的动态无功电流增量;K为动态无功电流比例系数;UPCC为PCC电压标幺值;IN为IBDG的额定电流。
考虑到不对称故障情况下,并网点电压存在负序分量,经Park变换后将变为附加的二倍频分量,使得实际电流难以无误差地跟踪参考电流,从而影响输出电流的波形质量。故IBDG通常以并网点正序分量电压为基准电压,假设故障后PCC正序分量电压为
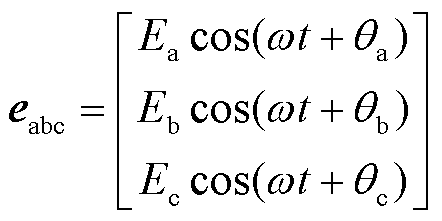 (2)
(2)
式中,Ex、θx分别为x相电压幅值、初相位,x=a,b,c;eabc为PCC电压;ω为工频角频率。PCC电压、逆变器输出电流输入逆变器控制回路后,产生dq轴电流参考值,其简化控制环路如图1所示。
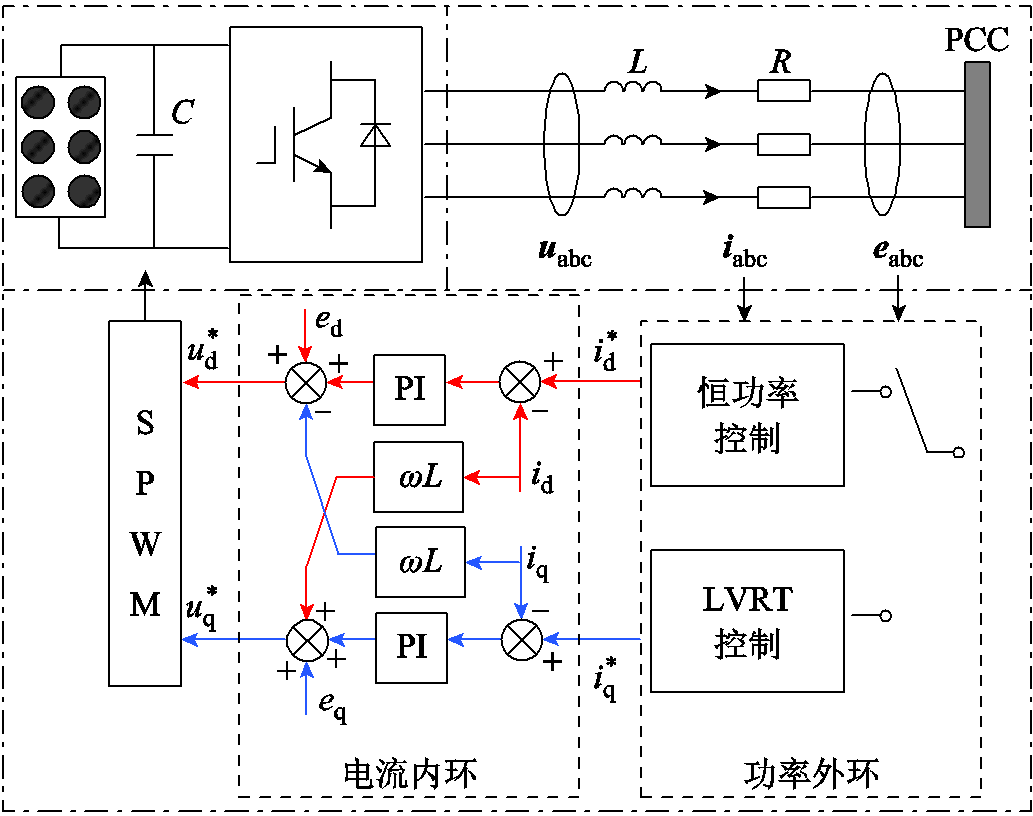
图1 逆变器控制简化示意图
Fig.1 Simplified schematic diagram of inverter control
图1中,uabc为逆变器端口电压,iabc为逆变器输出电流;R、L分别为逆变器端口到PCC的等效电阻、等效电感,C为直流母线电容,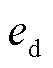 、
、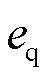 分别为PCC电压的dq轴分量,id、iq与
分别为PCC电压的dq轴分量,id、iq与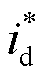 、
、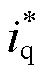 分别为dq轴电流的实际值与参考值,
分别为dq轴电流的实际值与参考值,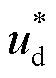 、
、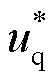 为电压参考值。IBDG的控制策略包括恒功率控制与LVRT控制,当检测到PCC电压低于0.9(pu)时,控制策略即由恒功率控制切换为LVRT控制。
为电压参考值。IBDG的控制策略包括恒功率控制与LVRT控制,当检测到PCC电压低于0.9(pu)时,控制策略即由恒功率控制切换为LVRT控制。
经功率外环得到电流参考值后输入电流内环生成电压参考值,逆变器控制方程[24]为
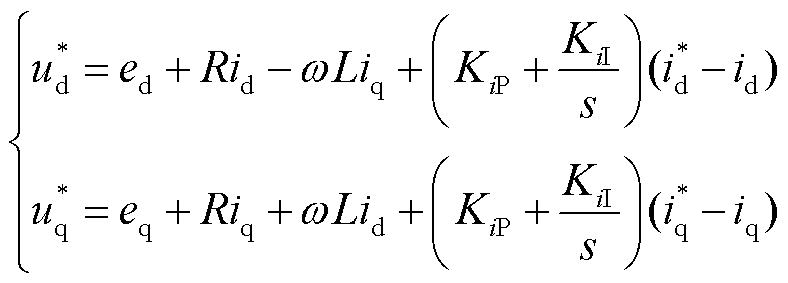 (3)
(3)
式中,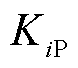 、
、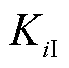 分别为比例、积分系数;s为拉普拉斯算子。为得到PCC电压的dq轴分量ed、eq,对式(2)进行Park变换,则ed、eq分别为
分别为比例、积分系数;s为拉普拉斯算子。为得到PCC电压的dq轴分量ed、eq,对式(2)进行Park变换,则ed、eq分别为
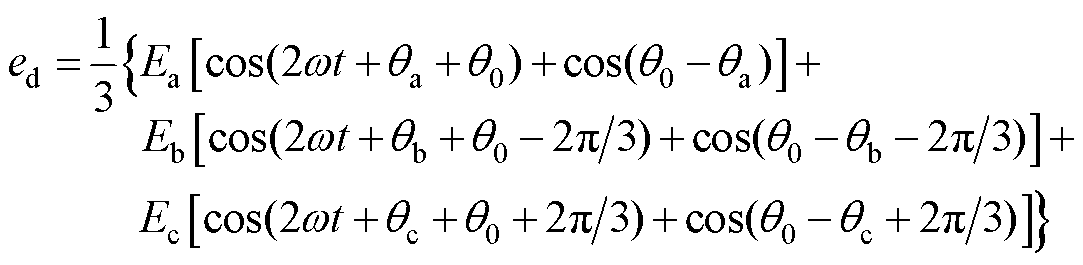 (4)
(4)
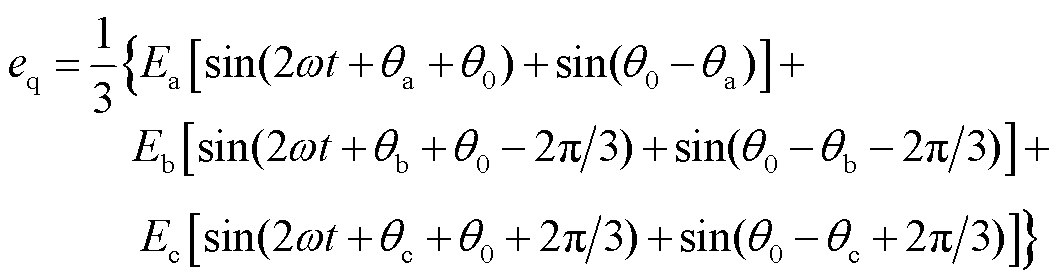 (5)
(5)
式中,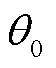 为Park变换矩阵中的参考相位。将式(4)、式(5)代入式(3),在忽略逆变器控制响应时间的前提下,认为电压、电流实际值能够快速跟踪指令值,得到逆变器端口电压的dq轴分量ud、uq为
为Park变换矩阵中的参考相位。将式(4)、式(5)代入式(3),在忽略逆变器控制响应时间的前提下,认为电压、电流实际值能够快速跟踪指令值,得到逆变器端口电压的dq轴分量ud、uq为
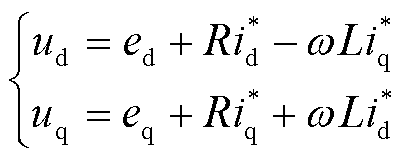 (6)
(6)
对式(6)进行反变换可以得到逆变器端口三相电压为
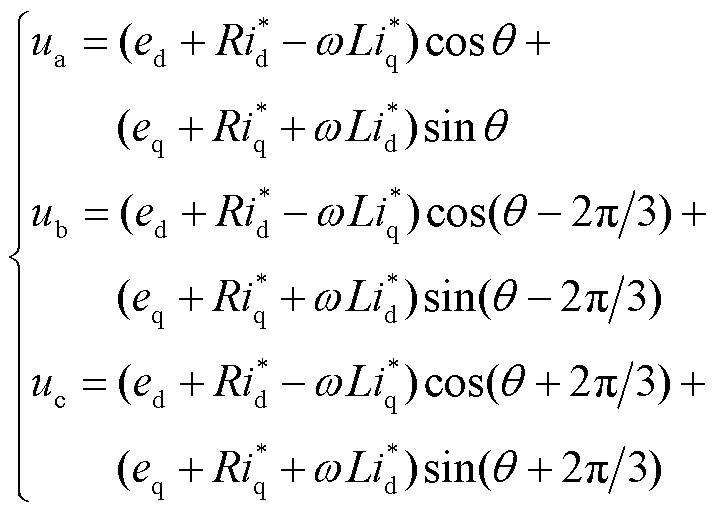 (7)
(7)
式中,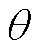 为Park变换矩阵中的旋转角度。
为Park变换矩阵中的旋转角度。
逆变器端口到PCC之间可以建立起关于逆变器输出电流iabc的一阶微分方程,即
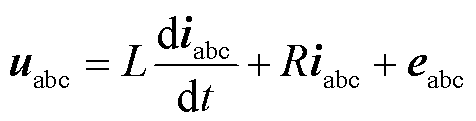 (8)
(8)
通过求解式(8)即可得到逆变器输出电流为
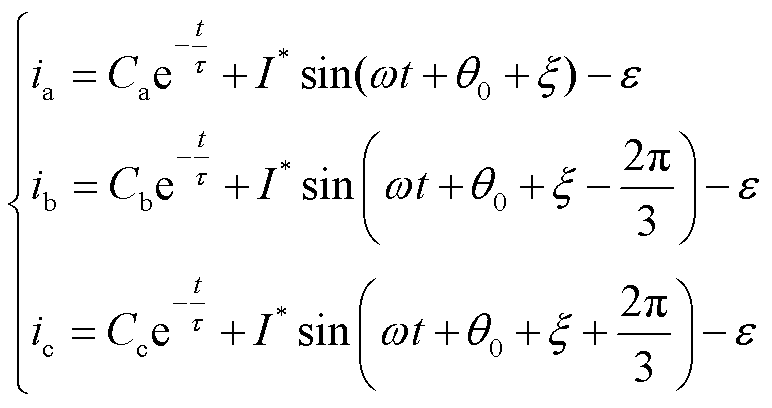 (9)
(9)
式中,Ca、Cb、Cc为常数,取决于各相微分方程的初始条件;时间常数t=L/R;I*、x、e的表达式分别为
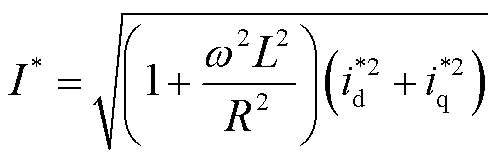 (10)
(10)
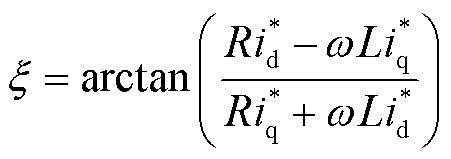 (11)
(11)
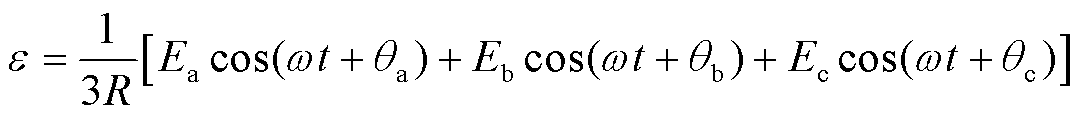 (12)
(12)
由式(9)~式(12)可知,逆变器输出电流工频分量的幅值I*、相位均与电流参考值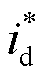 、
、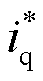 相关,其输出的电流的暂态故障特征取决于LVRT控制策略,故障穿越期间电流参考值与电压跌落程度的关系为
相关,其输出的电流的暂态故障特征取决于LVRT控制策略,故障穿越期间电流参考值与电压跌落程度的关系为
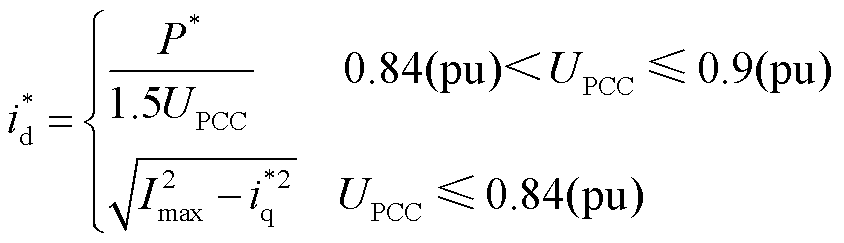 (13)
(13)
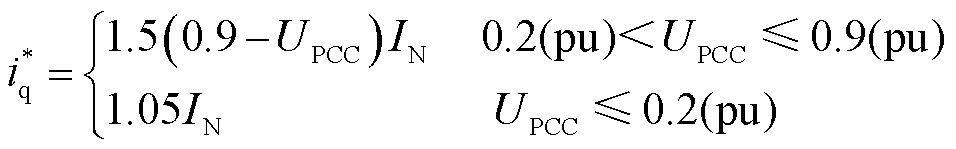 (14)
(14)
式中,P*为有功功率参考值;Imax为IBDG限流幅值。
式(1)与式(14)均表明,故障穿越期间,电网电压支撑需求以及短路电流限幅策略使得逆变器输出的无功电流随着PCC电压跌落程度的加深而增加。将故障穿越期间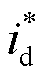 、
、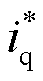 的表达式(13)、式(14)代入式(9),即为故障穿越期间逆变器输出电流的解析表达式,此处不再赘述。进一步对式(9)进行Park变换,得到逆变器输出无功电流为
的表达式(13)、式(14)代入式(9),即为故障穿越期间逆变器输出电流的解析表达式,此处不再赘述。进一步对式(9)进行Park变换,得到逆变器输出无功电流为
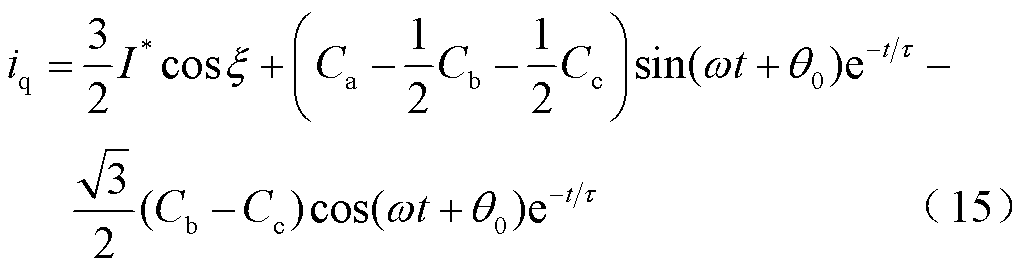
分析式(15)可知,逆变器输出无功电流由三部分组成,第一项为恒定的直流分量,后两项为衰减的工频分量。由于衰减工频分量的存在,暂态过程中逆变器输出无功电流的幅值、频率时变。
为构造差动保护判据,以图2所示的简化有源配电网为例,分析无功差动电流的故障特征。图2中RM、RN代表母线M、N处保护装置;k1、k2分别代表区内、外故障点;IqM、IqN、Iqf分别为M侧电流、N侧电流、故障电流的无功分量。规定电流正方向由母线指向线路,定义无功差动电流为
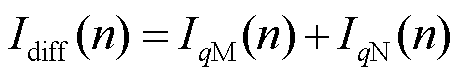 (16)
(16)
式中,IqM(n)、IqN(n)分别为M、N侧第n个采样点的无功电流;Idiff(n)为第n个采样点的无功差动电流。
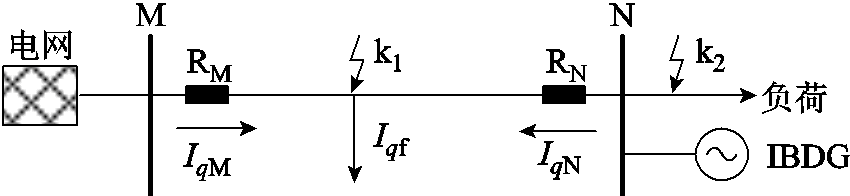
图2 简化有源配电网示意图
Fig.2 Diagram of a simplified ADN
1)正常运行或区外k2点短路时,无功差动电流满足
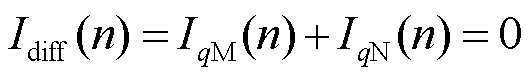 (17)
(17)
利用非线性能量算子表征无功差动电流能量,即
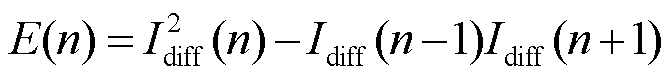 (18)
(18)
式中,E(n)为无功差动电流能量值。式(18)用于计算输入信号(Idiff)的能量,该式为Teager-Kaiser能量算子,由于能够灵敏识别突变量,常被用于识别高阻接地故障[25]。由于无功差动电流为0,故此时无功差动电流的能量也为0。
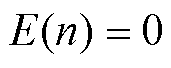 (19)
(19)
2)当区内k1点短路时,无功差动电流为
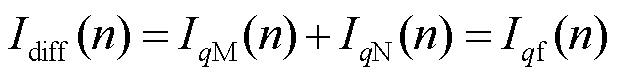 (20)
(20)
为说明非线性能量算子的性质,此处假设输入信号为
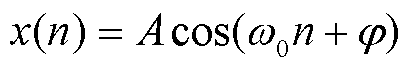 (21)
(21)
式中,A、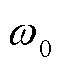 、φ分别为输入信号的幅值、频率、相位。将式(21)代入式(18)可得
、φ分别为输入信号的幅值、频率、相位。将式(21)代入式(18)可得
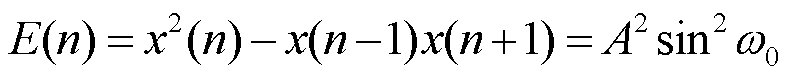 (22)
(22)
根据式(22),无功差动电流的能量仅与其幅值A、频率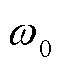 相关,当无功差动电流的幅值或频率为0时(对应正常运行或区外故障),E(n)=0。当发生区内短路故障时,由1.1节分析,无功差动电流包含衰减的工频分量,认为其幅值与频率时变,故暂态过程中无功差动电流的能量E(n)满足
相关,当无功差动电流的幅值或频率为0时(对应正常运行或区外故障),E(n)=0。当发生区内短路故障时,由1.1节分析,无功差动电流包含衰减的工频分量,认为其幅值与频率时变,故暂态过程中无功差动电流的能量E(n)满足
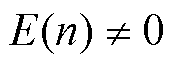 (23)
(23)
根据正常运行或区外故障时E(n)=0而区内故障时E(n)≠0,可以构造能量积分型无功差动电流保护判据。
为提高保护的灵敏性,本文构造能量积分型保护判据,首先对无功差动电流能量E(n)进行积分,有
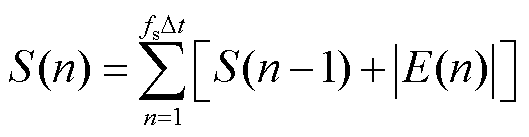 (24)
(24)
式中,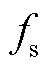 为采样频率;
为采样频率;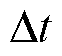 为积分时间。正常运行或区外故障时,无功差动电流的能量|E(n)|=0;区内故障时,能量值
为积分时间。正常运行或区外故障时,无功差动电流的能量|E(n)|=0;区内故障时,能量值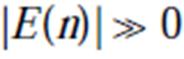 。考虑到非对称故障下无功差动电流包含负序分量引起的二倍频分量,选取故障后5 ms数据窗计算S(n)即可正确反映区内外故障,即
。考虑到非对称故障下无功差动电流包含负序分量引起的二倍频分量,选取故障后5 ms数据窗计算S(n)即可正确反映区内外故障,即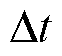 =5 ms。当故障后第5 ms时刻的能量积分值S(
=5 ms。当故障后第5 ms时刻的能量积分值S(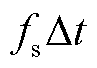 )超过整定阈值时,判断发生区内短路,即
)超过整定阈值时,判断发生区内短路,即
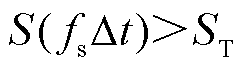 (25)
(25)
式中,ST为保护动作阈值。理论上,正常运行或区外短路时能量积分S(n)始终为0,ST取稍大于0的值即可准确识别区内、外短路。综合考虑噪声影响、耐过渡电阻能力、采样与计算误差,本文将阈值ST整定为300。综上所述,保护流程如图3所示。
当被保护线路含有不可测分支负荷时,以图4为例,正常运行时无功差动电流为
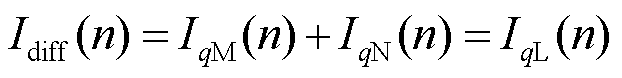 (26)
(26)
式中,IqL(n)为不可测分支负荷电流的无功分量。
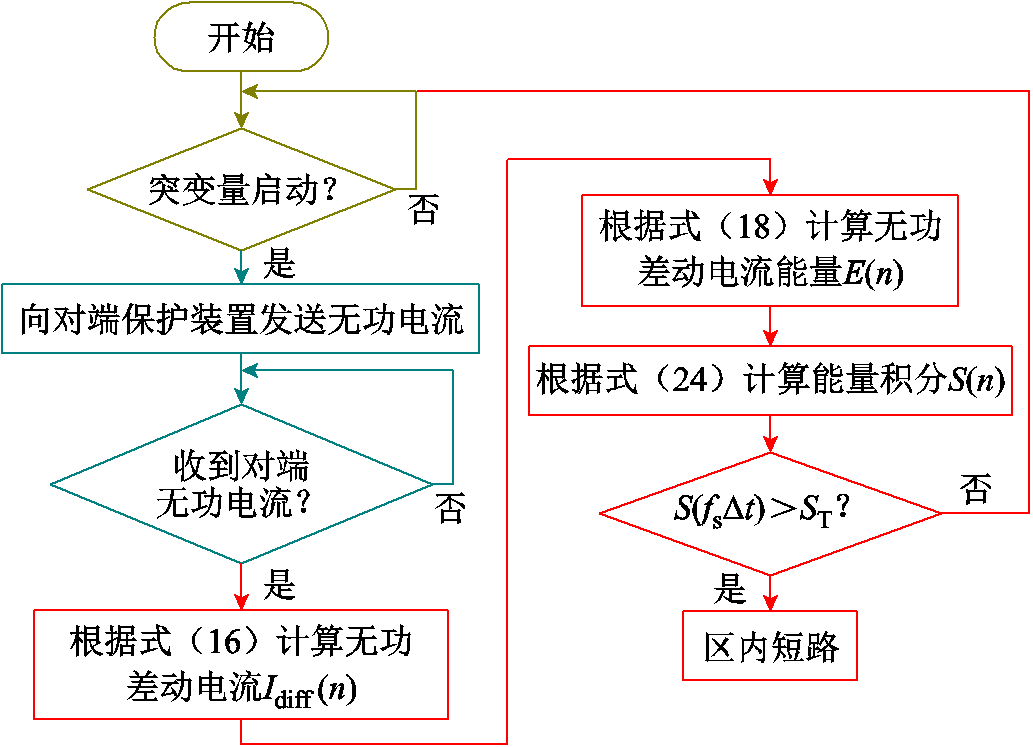
图3 能量积分型无功电流差动保护流程
Fig.3 Flow chart of energy integral based reactive current differential protection
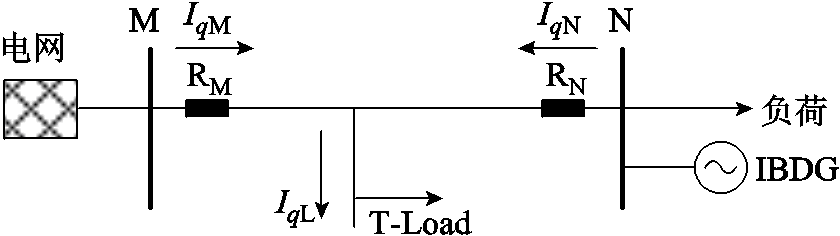
图4 含不可测分支负荷馈线示意图
Fig.4 Diagram of feeder with unmeasured branch load
式(26)表明,若被保护线路含有不可测分支负荷,则正常运行时无功差动电流不再为0,存在正常不平衡电流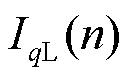 与故障电流
与故障电流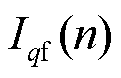 辨识困难的问题。然而,正常运行时分支负荷电流
辨识困难的问题。然而,正常运行时分支负荷电流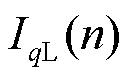 的无功分量为直流量[14],其频率为0,由式(22)可知,此时正常不平衡电流IqL(n)的能量E(n)=0;而区内故障时,无功差动电流的能量E(n)≠0(分析同1.2节)。
的无功分量为直流量[14],其频率为0,由式(22)可知,此时正常不平衡电流IqL(n)的能量E(n)=0;而区内故障时,无功差动电流的能量E(n)≠0(分析同1.2节)。
因此,利用非线性能量算子计算无功差动电流的能量时,正常不平衡电流的能量E(n)=0,而故障电流的能量E(n)≠0,解决了正常不平衡电流与故障电流难以辨识的问题。被保护线路含有不可测分支负荷时的故障特征同1.2节一致,沿用图3所示保护流程即可正确区分区内外故障。
若IBDG退出运行,短路电流的无功分量仅由系统电源提供。馈线发生对称故障时,以a相为例,系统电源提供短路电流为
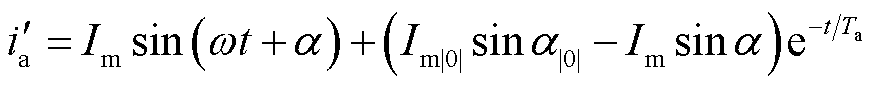 (27)
(27)
式中,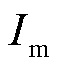 为相电流幅值;
为相电流幅值;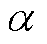 为相电流初相位;
为相电流初相位;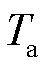 为衰减时间常数;含下标“
为衰减时间常数;含下标“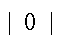 ”代表短路前物理量。b、c两相电流满足幅值相等、相位依次滞后120°。对三相短路电流进行Park变换,系统电源提供的短路电流无功分量为
”代表短路前物理量。b、c两相电流满足幅值相等、相位依次滞后120°。对三相短路电流进行Park变换,系统电源提供的短路电流无功分量为
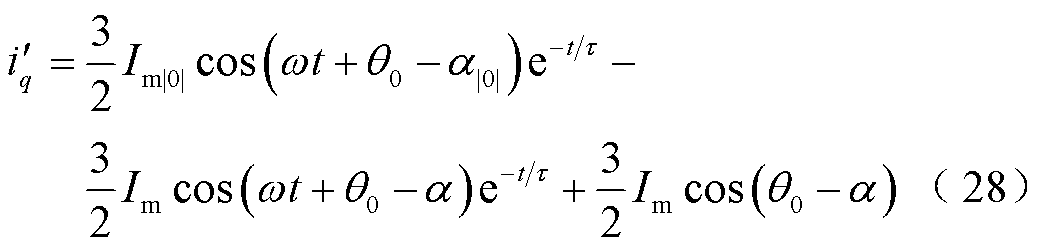
式中,前两项为衰减工频分量,末项为恒定的直流分量。当发生对称故障时,无功差动电流存在系统电源提供的衰减工频分量;发生非对称短路故障时,系统电源输出短路电流的负序分量经Park变换后变为二倍频分量。综上所述,由于系统电源所提供衰减工频分量或二倍频分量的存在,区内故障时无功差动电流的能量E(n)总是不为0的,即IBDG退出运行后所提保护原理仍有效。由此推知,当配电网中接入同步型分布式电源(Synchronous-Based Distributed Generator, SBDG)时,SBDG的故障特征同上,所提保护原理仍适用。
在PSCAD搭建如图5所示有源配电网仿真模型,系统频率为50 Hz,保护采样频率为10 kHz。图5中,R1~R10为保护装置;f1~f5代表各区段中点的短路故障;CB为常开联络开关;IBDG采用恒功率、LVRT与限流控制策略;区段5用于测试所提方法在含不可测分支负荷场景中的性能,其中Lub为不可测分支负荷,设置于该区段中点处;各负荷、IBDG容量及线路参数见表1;保护判据式(25)中的动作阈值整定为300。
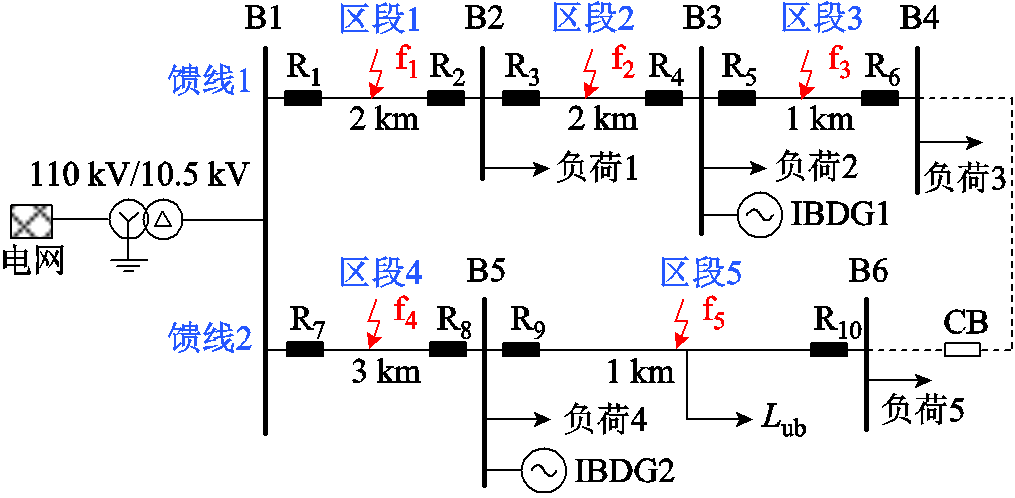
图5 有源配电网仿真模型
Fig.5 Simulation model for ADN
表1 仿真模型参数
Tab.1 Parameters of simulation model

参数数值参数数值 负荷1/(MV·A)1+j0.54Lub/(MV·A)0.27+j0.13 负荷2/(MV·A)3+j1.32IBDG1/MW2 负荷3/(MV·A)3+j2.19IBDG2/MW2 负荷4/(MV·A)1+j0.52线路正序阻抗/(Ω/km)0.17+j0.32 负荷5/(MV·A)2+j0.66线路零序阻抗/(Ω/km)0.32+j1.12
为验证理论分析无功差动电流Idiff故障特征的正确性,在馈线1上f2点处2 s时刻设置金属性三相短路、AB两相短路故障,分别代表典型对称、非对称故障,保护R3、R4处Idiff的波形如图6a、图6b所示。根据1.2节分析,无功差动电流包含衰减的工频分量,发生对称故障时,由图6a可知,无功差动电流包含衰减的工频分量与恒定的直流分量;发生非对称故障时,由图6b可知,无功差动电流包含衰减的工频分量与二倍频分量(由系统电源输出的负序电流引起)。
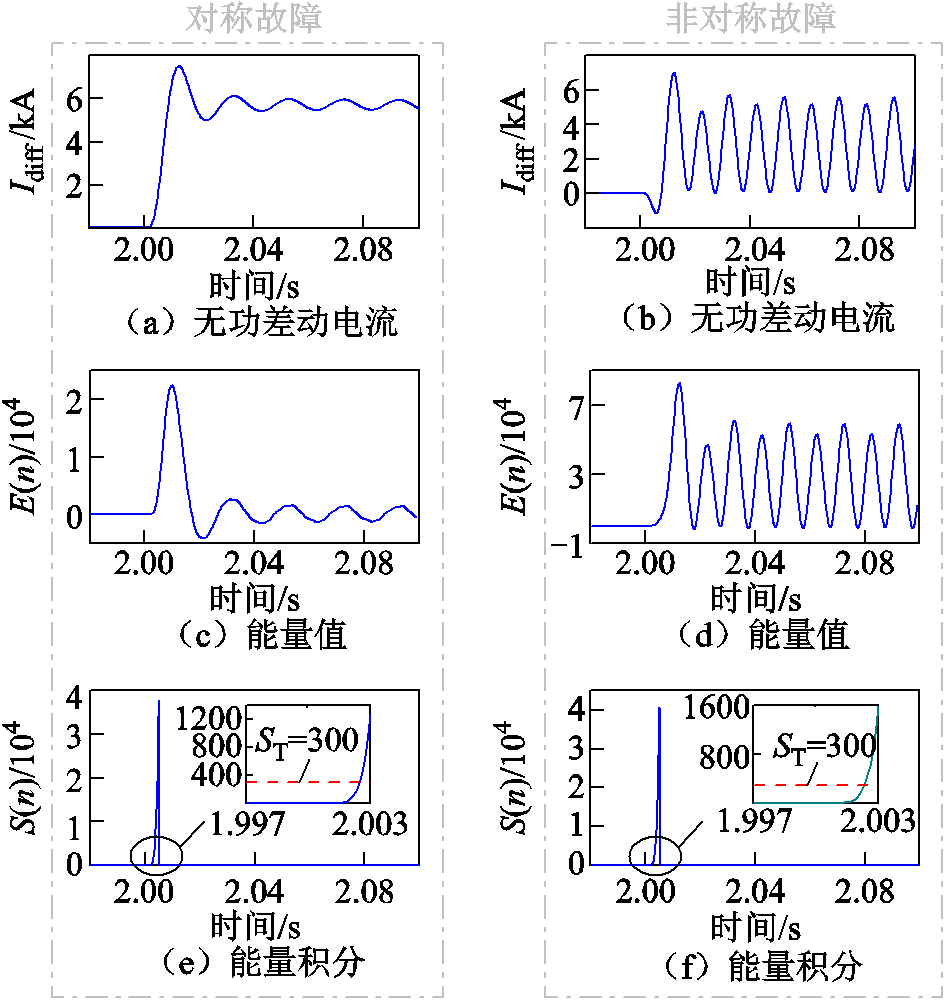
图6 区内故障下的仿真波形
Fig.6 Waveforms under internal faults
发生区内故障时,由于无功差动电流Idiff的幅值、频率不为0(如图6a、图6b所示),其能量E(n)亦不为0(如图6c、图6d所示),因此能量积分S(n)在故障后3 ms内超过设定阈值(如图6e、图6f所示),所提方法能够灵敏地识别区内故障。
在馈线2中f4、f5点处分别设置不同类型的短路故障,f4点故障为区段4的区内短路,f5点故障为区段5的区内短路。仿真结果如图7所示,S(n)代表故障后第5 ms时的能量积分值(即图6e中t=2.005 s时刻的S(n))。由图7a可知,当区段4中f4点发生区内短路故障时,区段4的S(n)远大于动作阈值,而区段5的S(n)远小于动作阈值,即故障区段能够可靠动作而非故障区段不误动;当区段5中f5点故障时同理。
值得注意的是,对于含不可测分支负荷的区段5而言,当发生区外短路故障时,由图7a可知,其能量积分S(n)不超过15,远小于动作阈值;而发生区内短路故障时,由图7b可知,其能量积分S(n)远大于动作阈值。换言之,不可测分支负荷引起的正常不平衡电流与区内故障时短路电流的能量积分S(n)存在数量级上的显著差异,本文提出的能量积分型无功电流差动保护在含不可测分支负荷的线路中能够正确地识别区内外故障,有效地解决了不平衡电流与故障电流的辨识问题。
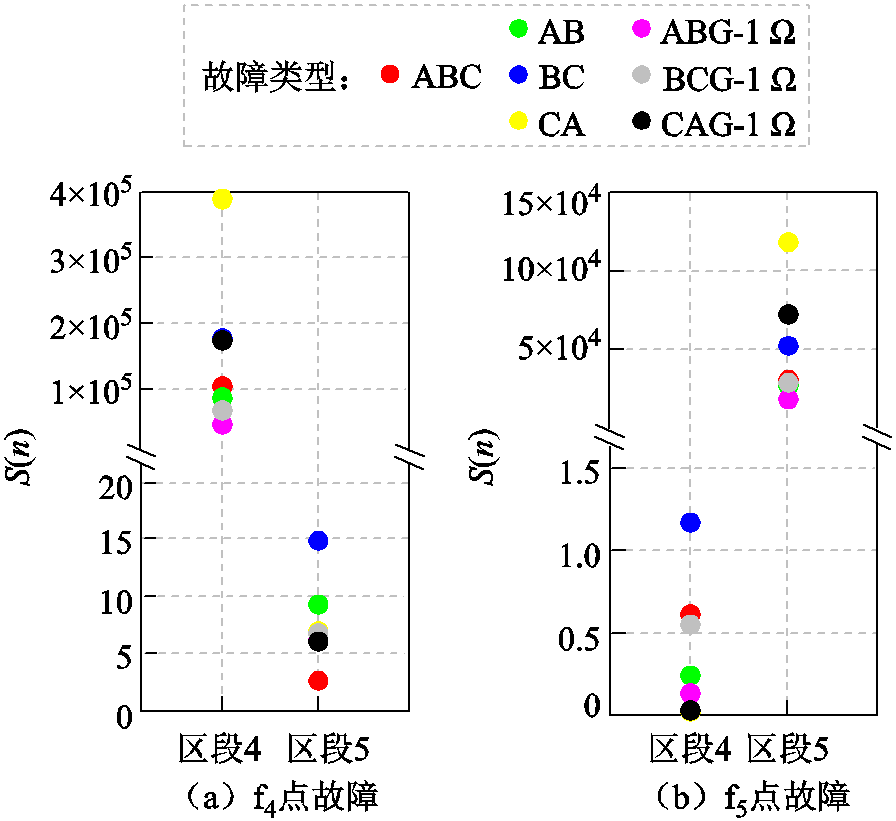
图7 馈线2中发生短路故障时的仿真结果
Fig.7 Simulation results when faults occur at feeder 2
为验证本文方法在IBDG退出运行时性能,断开IBDG1与IBDG2,模拟光伏夜间退出运行的场景,在f1、f2、f4、f5点设置短路故障,仿真结果如图8所示。其中,区段1、2、4、5的位置已在图5中标注,故障点f1、f2、f4、f5依次位于区段1、2、4、5中。由于系统采用中性点不接地运行方式,故障工况1~7考虑了除单相接地外所有故障类型,依次为:ABC、AB、BC、CA、ABG-1 Ω、BCG-1 Ω、CAG-1 Ω。图8中,S(n)代表故障后第5 ms时的能量积分值。
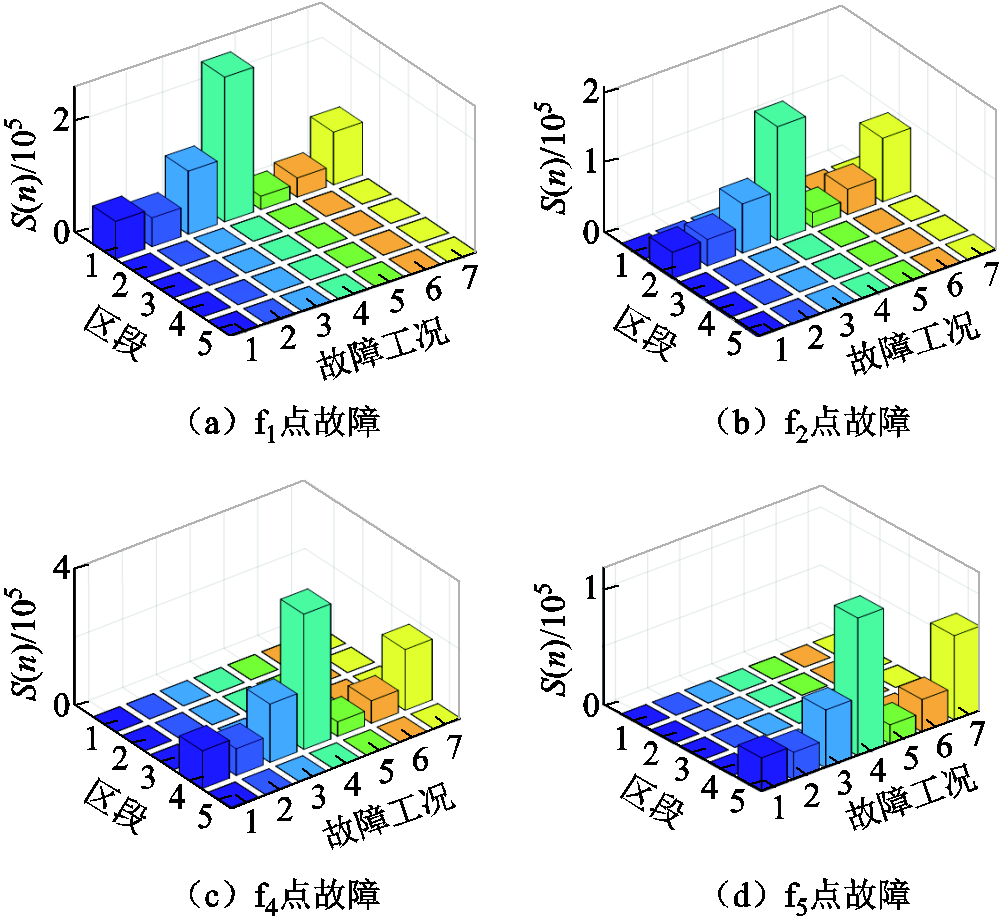
图8 IBDG退出运行时的仿真结果
Fig.8 Simulation results when IBDGs exit
以图8a为例对仿真结果进行说明,当故障发生在区段1的f1点时,区段1的能量积分S(n)在各种故障类型下均超过整定值;而区段2~区段5的能量积分S(n)在各种故障类型下均小于整定阈值。分析图8可知,当IBDG退出运行时,所提保护原理仍能灵敏地识别区内外故障。
差动保护正确动作的前提是双端数据的同步。为测试所提方法的耐同步误差能力,在区段3中设置含10 Ω过渡电阻的AB两相接地故障,在此工况下设置了步长为1.8°、范围为0°~162°的同步误差,测试区段3中本文所提差动保护与文献[13]中基于正序故障分量的差动保护的动作情况,绘制不同数据同步误差下两种差动保护的动作曲线如图9所示。
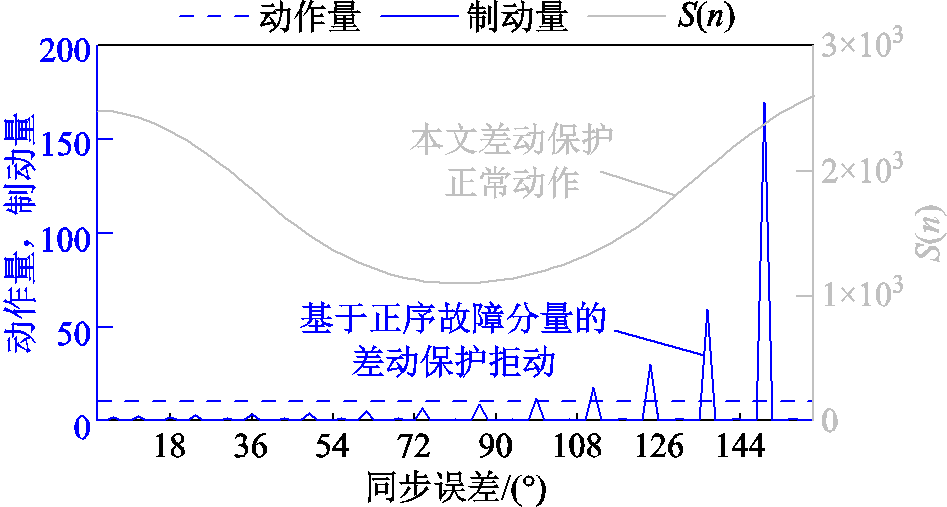
图9 不同同步误差下本文方法与文献[9]方法的仿真结果
Fig.9 Simulation results of proposed method and the method in Ref.[9] under different synchronization errors
文献[13]分别利用正序故障分量电流的幅值比与相位差构造差动保护的动作量与制动量,分别如图9中蓝色虚线、蓝色实线所示。随着同步误差的增加,基于幅值比构造的动作量不受影响,均为10.21,而基于相位差构造的制动量随着同步误差的增加而增加,同步误差大于99°后出现拒动情况。
分析图9可知,本文所提差动保护的能量积分S(n)随着同步误差的增加先减小后增大,但均超过本文设定的动作阈值300,所提出的差动保护在0°~162°的数据同步误差下均能正确动作,故具备一定的耐同步误差能力。
由于IBDG提供短路电流能力有限,故障区段可能出现由系统电源提供的穿越性电流,导致传统差动保护的灵敏度下降。在区段2的f2点设置含20 Ω过渡电阻的AB两相接地短路故障,测试采样点差动保护、文献[14]中直轴电流差动保护与本文所提无功差动保护的动作情况,仿真结果如图10所示。
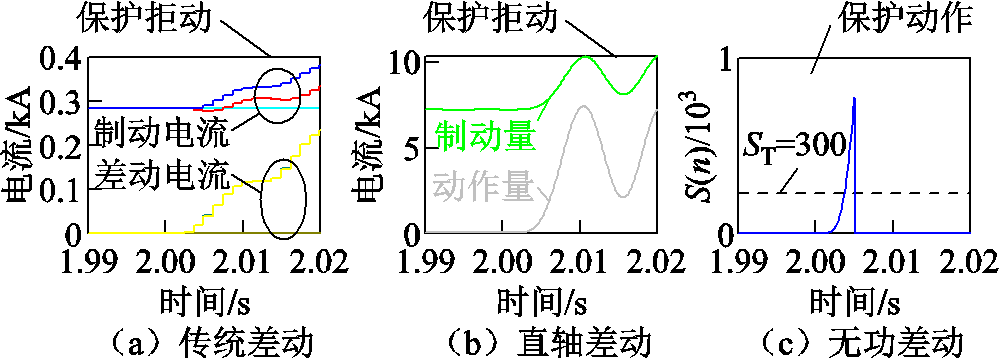
图10 不同电流差动保护方法的仿真结果
Fig.10 Simulation results of different current differential protection methods
根据图10a、图10b,传统差动保护的差动电流小于制动电流、文献[14]中方法的动作量小于制动量,两种方法均拒动。而本文所提出的能量积分型无功电流差动保护如图10c所示,故障后5 ms的能量积分S(n)超过整定值300,保护正确动作,所提方法具有更高的灵敏度。
保护算法耐受过渡电阻能力受配电网拓扑、线路参数、故障位置、分布式电源类型等诸多因素影响,在本文所搭建的配电网模型、线路参数下,本节探究所提保护原理在不同类型分布式电源接入时的耐过渡电阻能力,同时验证不同类型分布式电源接入时所提保护原理的适应性。设置三种场景进行仿真,依次为:①分布式电源均为IBDG;②分布式电源均为SBDG(容量同为2 MW);③分布式电源退出运行。三种场景下均在区段2的f2点设置不同大小的过渡电阻进行仿真,本文所提方法在不同类型分布式电源接入、不同故障类型下所能耐受的最大过渡电阻值见表2。由于仿真模型采用中性点不接地运行方式,未考虑单相接地故障。
表2 所提方法在不同类型DG接入、不同故障类型下所能耐受最大过渡电阻值
Tab.2 The proposed method can withstand the maximum transition resistance value under different types of DG connections and fault types

场景故障类型耐受过渡电阻值/Ω 分布式电源均为IBDG三相短路24 两相相间短路100 两相短路接地50
(续)

场景故障类型耐受过渡电阻值/Ω 分布式电源均为SBDG三相短路30 两相相间短路109 两相短路接地51 分布式电源退出运行三相短路23 两相相间短路105 两相短路接地53
根据表2,所提保护在接入IBDG、SBDG或DG退出运行时均有效,不同场景下的耐受过渡电阻能力不同。在DG退出运行时,以区段2发生含80 Ω过渡电阻的CA两相相间短路故障为例,高阻故障时保护R3、R4处的三相电流波形分别如图11a、图11b所示,利用离散傅里叶变换计算故障后20 ms的三相电流相量,此故障工况下的三相电流相量图如图11c所示,保护R3、R4处的同名相电流的相位差接近180°,故障区段流过穿越性电流。此时区段2两端保护装置R3、R4处的故障相电流分别为: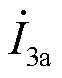 = (-440.6-j196.8)A,
= (-440.6-j196.8)A,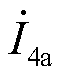 =(333.3+j148.1)A,
=(333.3+j148.1)A,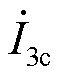 = (405.9-j176.6)A,
= (405.9-j176.6)A,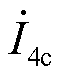 =(-298.6+j225.3)A。a相差动电流与制动电流分别为117.8、847.2 A,c相差动电流与制动电流分别为117.8、811.1 A,即使将制动电流乘以制动系数0.5,传统差动保护亦无法动作。在此故障工况下所提保护方法的仿真结果如图12所示,故障后能量积分S(n)超过整定阈值,所提保护方法在高阻故障(穿越性电流存在)时仍能正确动作。
=(-298.6+j225.3)A。a相差动电流与制动电流分别为117.8、847.2 A,c相差动电流与制动电流分别为117.8、811.1 A,即使将制动电流乘以制动系数0.5,传统差动保护亦无法动作。在此故障工况下所提保护方法的仿真结果如图12所示,故障后能量积分S(n)超过整定阈值,所提保护方法在高阻故障(穿越性电流存在)时仍能正确动作。
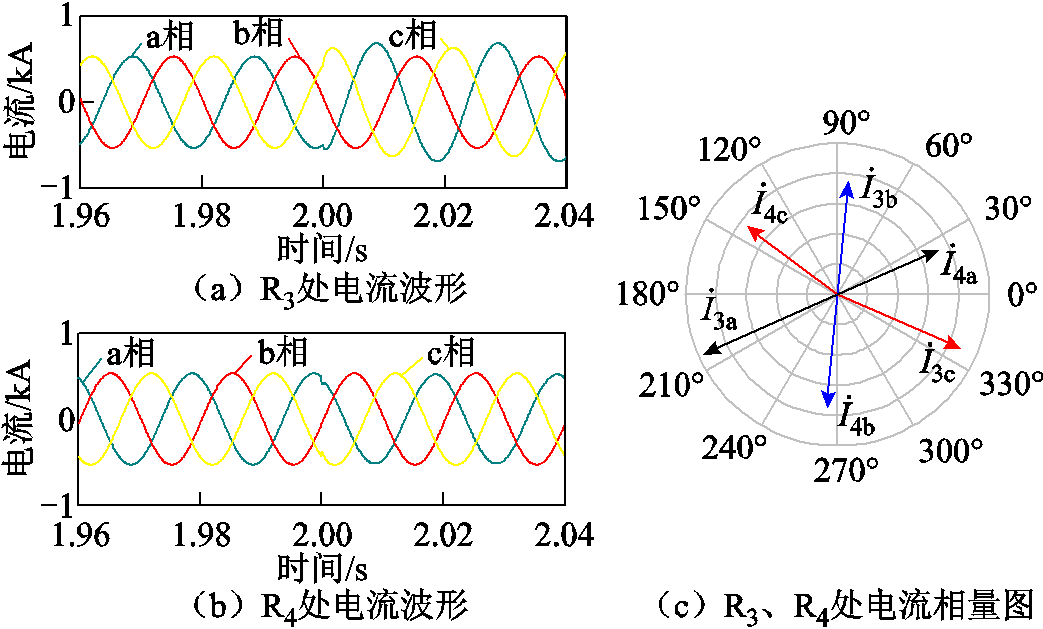
图11 区段2发生含80 Ω过渡电阻CA两相相间短路故障时保护R3、R4处电流波形及相量图
Fig.11 Current waveform and phasor diagrams of protection R3 and R4 in case of a phase-C-to-phase-A short circuit fault with a 80 Ω transition resistance
为进一步验证所提方法的有效性,开发了具备所提保护原理的智能终端样机,样机采样频率为10 kHz。基于RTDS搭建如图13所示的闭环测试平台对样机进行测试。在RSCAD的Runtime界面设置短路故障,RTDS将仿真的数字信号转换为模拟信号经过功率放大器输入保护样机,保护样机根据保护算法判断区内外故障并输出跳闸信号,最终通过Runtime界面观察断路器动作情况。考虑当前配电网通信条件,两台保护样机之间采用5G进行通信[26]。
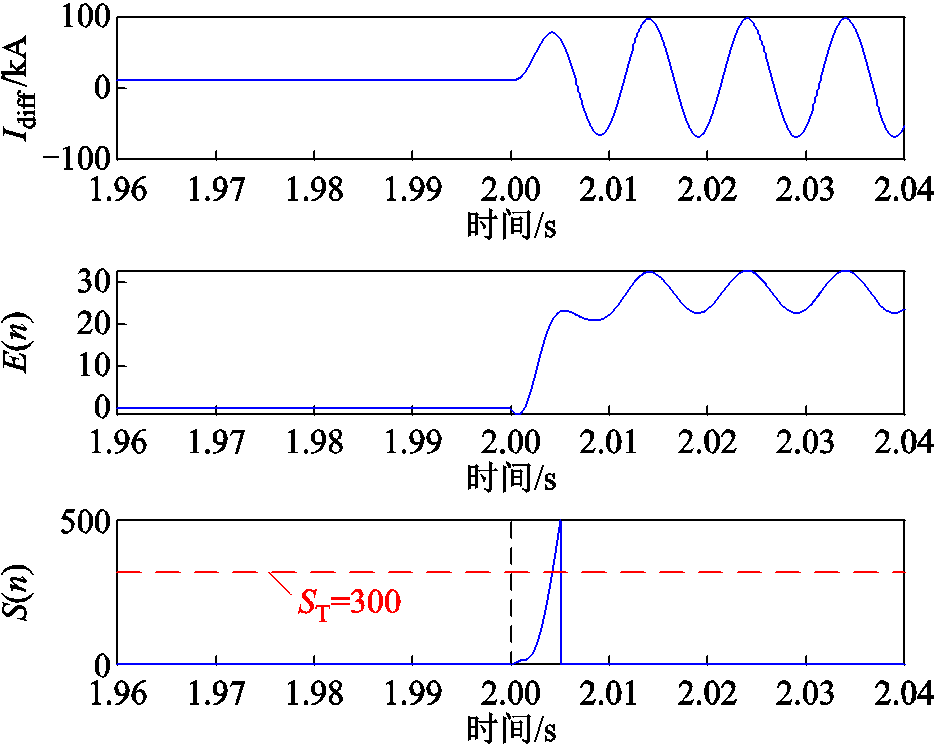
图12 区段2发生含80 Ω过渡电阻CA两相相间短路故障时所提保护方法的仿真结果
Fig.12 Simulation results of proposed method in case of a phase-C-to-phase-A short circuit fault with a 80 Ω transition resistance

图13 RTDS闭环测试系统
Fig.13 RTDS Closed loop testing system
在RSCAD中搭建的“手拉手”馈线模型如图14所示,线路参数已在图中标注。其中IBDG为2 MW光伏,CB1、CB2为站出线开关,S11、S12、S13…为环网箱进线开关与馈线开关,SLL为常开联络开关。两台样机分别控制S12与S21的开合,保护动作阈值仍整定为300。在F1点设置不同类型的区内短路故障,每种类型的短路故障各测试5次,S12与S21处保护装置动作时间如图15所示。
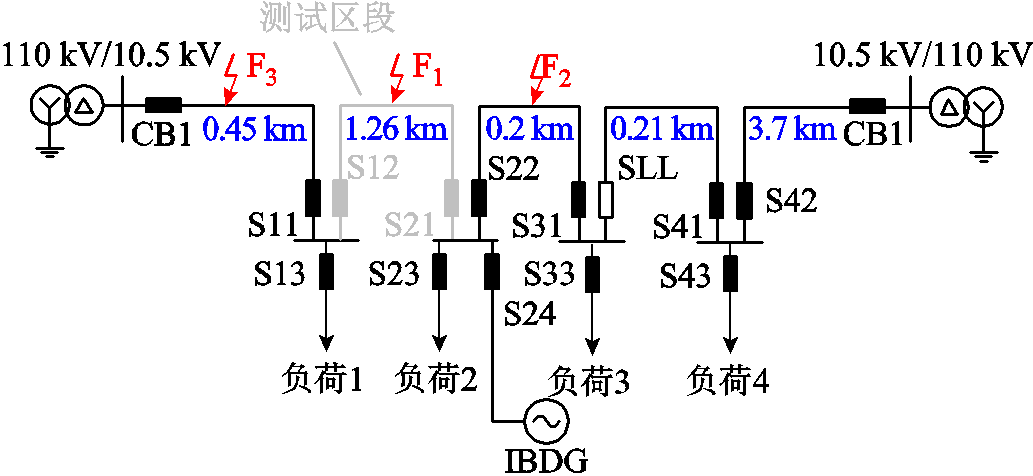
图14 RSCAD测试模型
Fig.14 Simulation model in RSCAD

图15 保护样机动作时间
Fig.15 Protection prototype trip time
故障工况1~10依次为:ABC、AB、BC、CA、ABG-1 Ω、BCG-1 Ω、CAG-1 Ω、ABG-20 Ω、BCG-20 Ω、CAG-20 Ω。保护样机动作时间范围为64.6~79.2 ms,平均动作时间为71.837 ms,包括保护算法延时、5G通信延时以及其他延时。其中,保护算法仅需故障后5 ms数据,5G模组采用传输控制协议(Transmission Control Protocol, TCP)进行通信,公网环境下5G通信延时平均为41 ms。另外,在F2、F3点处均设置了大量区外短路进行仿真。测试结果表明,在通信有效的前提下,保护样机识别区内外故障准确率为100%。
本文提出了一种能量积分型无功电流差动保护方法,利用非线性能量算子表征无功差动电流的能量,根据故障后5 ms内的能量积分是否超过整定阈值判断是否发生区内短路。测试结果表明,所提方法能够正确识别区内外故障,适用于含不可测分支负荷的场景,在IBDG退出运行时仍具有较高的灵敏性。与传统差动保护方法相比,不受穿越性电流的影响,耐过渡电阻能力更强。
然而,当被保护线路存在不可测IBDG时,IBDG出力的间歇性可能使所提保护原理灵敏度下降甚至失效,如何实现含不可测IBDG时的高可靠保护将作为下一阶段的研究重点。
参考文献
[1] 韦明杰, 王聪博, 余越, 等. 适用高比例分布式光伏接入的配电网多级保护优化配置方案[J]. 电力系统自动化, 2023, 47(22): 55-65.
Wei Mingjie, Wang Congbo, Yu Yue, et al. Optimal configuration scheme of multi-staged protection in distribution network for integration of high proportion of distributed photovoltaic[J]. Automation of Electric Power Systems, 2023, 47(22): 55-65.
[2] 乔一达, 吴红斌, 吴通华, 等. 含逆变型分布式电源的配电网分区域电流保护[J]. 电工技术学报, 2022, 37(增刊1): 134-144.
Qiao Yida, Wu Hongbin, Wu Tonghua, et al. A partitioned current protection scheme of distribution network with inverter interfaced distributed generator [J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 134-144.
[3] 李君, 何敏, 黄守道, 等. 基于相位差的小电阻接地有源配电网接地故障保护算法[J]. 电工技术学报, 2024, 39(23): 7418-7429.
Li Jun, He Min, Huang Shoudao, et al. Grounding fault protection algorithm of small resistance earthing active distribution network based on phase difference [J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7418-7429.
[4] 李宗博, 崔一嘉, 王昊晴, 等. 含逆变型分布式电源的配电网馈线终端告警信息校正及故障定位方法[J]. 电工技术学报, 2025, 40(4): 1268-1286.
Li Zongbo, Cui Yijia, Wang Haoqing, et al. Method of alarm information correction and fault location for distribution network with inverter-interfaced distributed generation[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1268-1286.
[5] 徐萌, 邹贵彬, 高磊, 等. 含逆变型分布式电源的配电网正序阻抗纵联保护[J]. 电力系统自动化, 2017, 41(12): 93-99.
Xu Meng, Zou Guibin, Gao Lei, et al. Pilot protection of positive sequence impedance for distribution network with inverter-based distributed generator[J]. Automation of Electric Power Systems, 2017, 41(12): 93-99.
[6] Chen Guobin, Liu Yiqing, Yang Qifan. Impedance differential protection for active distribution network [J]. IEEE Transactions on Power Delivery, 2020, 35(1): 25-36.
[7] 晁晨栩, 郑晓冬, 高飘, 等. 含高比例光伏配电网的高频阻抗差动保护[J]. 中国电机工程学报, 2021, 41(20): 6968-6979.
Chao Chenxu, Zheng Xiaodong, Gao Piao, et al. High frequency impedance differential protection with high proportion of photovoltaic power distribution network [J]. Proceedings of the CSEE, 2021, 41(20): 6968-6979.
[8] 徐萌, 邹贵彬, 陈宁, 等. 基于故障超前相的有源配电网能量方向纵联保护方法[J]. 电力自动化设备, 2017, 37(1): 58-64.
Xu Meng, Zou Guibin, Chen Ning, et al. Energy-directional pilot protection based on leading-phase for active distribution network[J]. Electric Power Automation Equipment, 2017, 37(1): 58-64.
[9] Zhou Chenghan, Zou Guibin, Zhang Shuo, et al. Energy-based directional pilot protection for distribution networks with IBDGs considering unmeasured load switching[J]. CSEE Journal of Power and Energy Systems, 2024, 10(1): 139-150.
[10] 和敬涵, 王语然, 李猛, 等. 基于电流波形畸变特征的高比例光伏配电网故障方向判别原理[J]. 电网技术, 2023, 47(12): 4856-4867.
He Jinghan, Wang Yuran, Li Meng, et al. New fault direction identification based on current distortion characteristics in high proportion PV distribution system[J]. Power System Technology, 2023, 47(12): 4856-4867.
[11] 戴志辉, 吴桐, 何静远, 等. 基于控保协同的有源配网主动注入式保护方法[J]. 电力系统保护与控制, 2024, 52(3): 94-103.
Dai Zhihui, Wu Tong, He Jingyuan, et al. An active distribution network active injection protection method based on control-protection coordination[J]. Power System Protection and Control, 2024, 52(3): 94-103.
[12] Gao Houlei, Li Juan, Xu Bingyin. Principle and implementation of current differential protection in distribution networks with high penetration of DGs[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 565-574.
[13] 周成瀚, 邹贵彬, 杜肖功, 等. 基于正序电流故障分量的有源配电网纵联保护[J]. 中国电机工程学报, 2020, 40(7): 2102-2112, 2390.
Zhou Chenghan, Zou Guibin, Du Xiaogong, et al. A pilot protection method based on positive sequence fault component current for active distribution networks[J]. Proceedings of the CSEE, 2020, 40(7): 2102-2112, 2390.
[14] Zang Lindong, Zou Guibin, Zhou Chenghan, et al. A d-axis based current differential protection scheme for an active distribution network[J]. Protection and Control of Modern Power Systems, 2022, 7(1): 23.
[15] Joshua A M, Vittal K P. Superimposed current based differential protection scheme for AC microgrid feeders[J]. Applied Energy, 2023, 341: 121079.
[16] Li Botong, Chen Fahui, Li Bin, et al. A multi-terminal current differential protection setting method for fully weak-infeed distribution networks based on restricted enumeration method[J]. IEEE Transactions on Smart Grid, 2024, 15(3): 2570-2585.
[17] 袁通, 高厚磊, 彭放, 等. 免疫同步误差的有源配电网多端纵联保护方法[J]. 电网技术, 2023, 47(12): 4847-4861.
Yuan Tong, Gao Houlei, Peng Fang, et al. Multiterminal pilot protection for active distribution networks immune to synchronization error[J]. Power System Technology, 2023, 47(12): 4847-4861.
[18] 王子璇, 马啸, 杨勇, 等. 计及不可测分支负荷电源助增效应的有源配网幅值差动保护新判据[J]. 中国电机工程学报, 2020, 40(增刊1): 56-68.
Wang Zixuan, Ma Xiao, Yang Yong, et al. A new criterion for amplitude differential protection of active distribution network considering the boosting effect of unmeasurable branch load power supply[J]. Proceedings of the CSEE, 2020, 40(S1): 56-68.
[19] 肖澍昱, 林湘宁, 魏繁荣, 等. 面向含不可测分支配电线路不对称故障可靠辨识的负序电流比相保护判据[J]. 电工技术学报, 2023, 38(9): 2435-2447.
Xiao Shuyu, Lin Xiangning, Wei Fanrong, et al. Phase comparison protection of negative sequence current for distribution lines with unmeasurable branches[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2435-2447.
[20] 罗国敏, 谭颖婕, 吴梦宇, 等. 考虑电压跌落差异的有源配电网功率差动保护[J]. 电工技术学报, 2025, 40(4): 1287-1306.
Luo Guomin, Tan Yingjie, Wu Mengyu, et al. Power differential protection for active distribution networks considering voltage drop differences[J]. Transactions ofChina Electrotechnical Society, 2025, 40(4): 1287-1306.
[21] 梁伟宸, 王泽众, 周成瀚, 等. 考虑不可测T接负荷的配电网虚拟三端电流差动保护[J]. 电力系统保护与控制, 2024, 52(15): 81-90.
Liang Weichen, Wang Zezhong, Zhou Chenghan, et al. Virtual three-terminal current differential protection for distribution networks considering unmeasurable T-connected loads[J]. Power System Protection and Control, 2024, 52(15): 81-90.
[22] 戴志辉, 何静远, 王文卓, 等. 适用于逆变型分布式电源T接的配电网线路纵联保护方案[J]. 电力自动化设备, 2024, 44(5): 88-94, 119.
Dai Zhihui, He Jingyuan, Wang Wenzhuo, et al. Line pilot protection scheme for distribution network with inverter-interfaced distributed generation in T-connection mode[J]. Electric Power Automation Equipment, 2024, 44(5): 88-94, 119.
[23] 国家市场监督管理总局, 国家标准化管理委员会. 光伏发电系统接入配电网技术规定: GB/T 29319—2024[S]. 北京: 中国标准出版社, 2024.
[24] 郑涛, 邹芃蓥, 王子鸣. 计及锁相环动态响应特性的光伏并网系统故障电流解析计算[J]. 电网技术, 2022, 46(12): 4656-4667.
Zheng Tao, Zou Pengying, Wang Ziming. Fault current analysis of photovoltaic grid-connected system considering dynamic response characteristics of PLL[J]. Power System Technology, 2022, 46(12): 4656-4667.
[25] Dubey K, Jena P. A novel high-impedance fault detection technique in smart active distribution systems[J]. IEEE Transactions on Industrial Electronics, 2024, 71(5): 4861-4872.
[26] 麻秀范, 张乐萱, 于琨澎, 等. 考虑5G基站备用储能优化调控的配电网重构双层优化方法[J]. 电工技术学报, 2024, 39(16): 5028-5041.
Ma Xiufan, Zhang Lexuan, Yu Kunpeng, et al. A two-layer optimization approach for distribution network reconfiguration considering optimal regulation of 5G base station backup energy storage[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5028-5041.
Abstract A significant amount of renewable energy is integrated into the distribution network in the form of inverter-based distributed generators (IBDGs), which transform the traditional distribution networks into active distribution networks. The integration of numerous distributed generators (DGs) has increased the complexity of topology and fault characteristics in active distribution networks. Specifically, the weak fault current contribution of IBDGs and T-connected unmeasurable branch loads have reduced the sensitivity of traditional current differential protection in active distribution networks, sometimes even causing maloperation. To address these issues, an energy integral based reactive current differential protection method is proposed.
Firstly, the reactive differential current is defined as the sum of the reactive components of fault currents at both sides of the protected feeder. Based on the distinct characteristics of nonlinear energy integral value of reactive differential currents during internal and external faults, an energy integral based reactive current differential protection criterion is established. The nonlinear energy integral value is sensitivity to the amplitude and frequency variations of reactive differential current. The energy value is zero when either amplitude or frequency becomes zero. Under normal operation or external faults, the reactive differential current remains zero or consists of a DC component (the frequency of DC components is zero), resulting in an energy integral value equaling zero. However, during internal faults, the reactive differential current contains decaying power frequency components or double power frequency components, leading to significantly large energy integral values. The unbalanced reactive differential current caused by unmeasurable T-connected branch loads manifests as a DC component, and its energy integral value equals zero. In contrast, the reactive differential current resulting from internal short-circuit faults contains decaying power frequency components or double power frequency components, yielding a significantly large energy integral value. This distinction enables the proposed method to be applicable to feeders with unmeasurable T-connected branch loads while requiring only current information from both ends of the feeder.
Subsequently, a 10 kV active distribution network simulation model was built in PSCAD. The simulation results show that the proposed method effectively mitigates the impact of crossing currents on current differential protection during internal high-impedance faults. Additionally, it addresses the challenges of distinguishing unbalanced currents caused by unmeasurable T-connected branch loads from fault currents due to internal short-circuits. This approach reliably discriminates internal and external faults and exhibits certain ability to withstand data synchronization errors. Furthermore, two smart terminal prototypes with 5G communication capabilities were developed, and a RTDS closed-loop testing system was established for hardware-in-the-loop validation. The experimental results demonstrate that the fault clearance time of the prototype ranges from 64.6 ms to 79.2 ms. With effective communication, the prototypes achieved 100% accuracy in short-circuit faults identification.
The simulations and hardware-in-the-loop experiments yield the following conclusions: (1) The proposed method only requires current information from both sides of the protected feeder and is applicable to feeders with unmeasurable T-connected branch loads while accurately identifying all types of internal and external short-circuit faults. (2) Compared with traditional current differential protection, the proposed method demonstrates superior ability to withstand transition resistance and reliably identifies high-impedance faults even when crossing currents exist in the protected feeder. (3) The method remains effective regardless of power source characteristics, showing consistent sensitivity in identifying short-circuit faults in active distribution networks with IBDGs, synchronous-based DGs (SBDGs), or even without DGs integration.
Keywords:Differential protection, reactive current, energy integral, unmeasured branch loads, protection prototype, 5G communication
郑新铖 男,1999年生,博士研究生,研究方向为有源配电网保护与控制。
E-mail:zxc425148@163.com
邹贵彬 男,1971年生,教授,博士生导师,研究方向为交直流电力系统保护与控制等。
E-mail:guibinzou@sdu.edu.cn(通信作者)
中图分类号:TM77
DOI: 10.19595/j.cnki.1000-6753.tces.250119
山东省电力公司科技项目(520604230003)和广西电网公司科技项目(046000KK52230003)资助。
收稿日期 2025-01-17
改稿日期 2025-05-08
(编辑 赫 蕾)