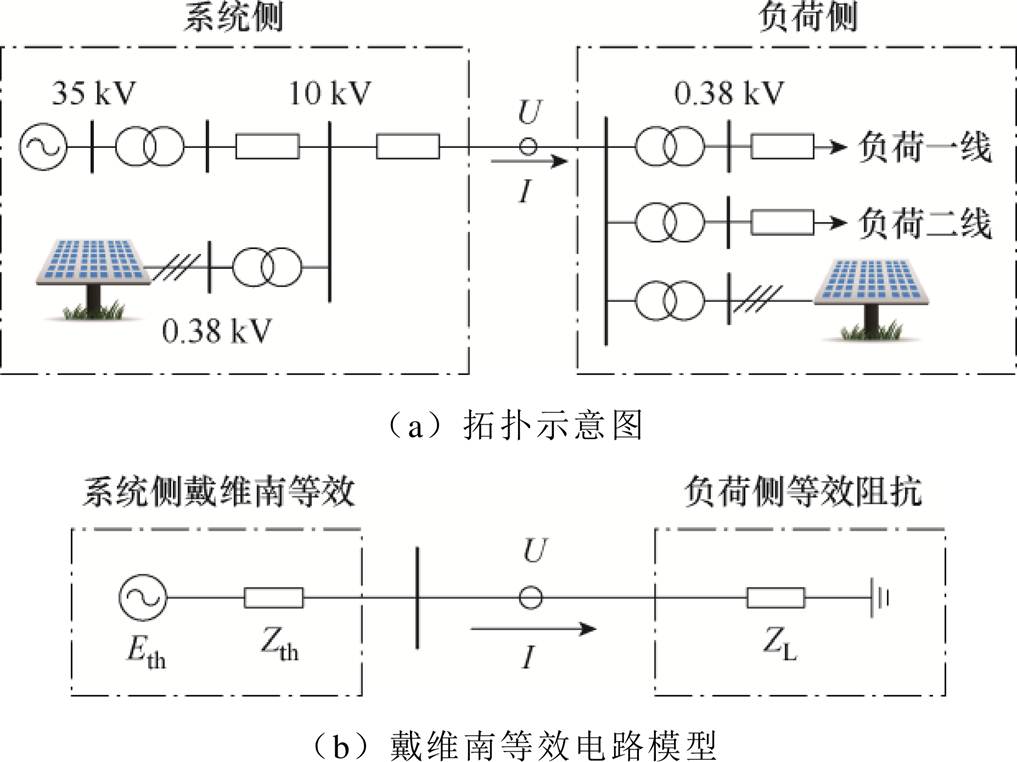
图1 戴维南等效电路研究算例
Fig.1 Thevenin equivalent circuit research example
摘要 根据系统运行等效阻抗大小变化而实时调整保护定值的自适应保护,是解决高比例新能源接入配电网保护适应性问题的重要手段。其中,准确的系统等效阻抗辨识技术是其中的关键。然而,传统辨识方法在系统内部发生扰动时会对辨识结果产生较大的误差,从而影响辨识精度。针对该问题,该文提出了基于波动特性解析的阻抗辨识方法。该方法将系统等效电动势分解为稳态值与波动值的叠加,建立了新的考虑系统侧等效电动势扰动的数学模型,利用波动特性对模型进行求解。在此基础上,进一步提出改进遗忘因子法,相较于传统方法,系统运行方式的等效阻抗辨识最大误差降低了78%,增强了辨识方法在不同工况下的适应性。最后,搭建硬件在环测试平台进行测试,所提阻抗辨识方法的平均误差均小于5%,验证了所提方法的准确性。
关键词:阻抗辨识 系统扰动 波动特性 改进遗忘因子法
近年来,为实现国家“双碳”目标,持续推进我国绿色能源低碳转型,高比例分布式电源接入电网[1-2]。然而,随着分布式电源接入电网,传统的单辐射网络变为源荷互动的多源网络,系统运行方式发生大范围变化,导致基于单电源故障特征的阶段式电流保护面临巨大挑战[3-5]。为此,有学者研究根据系统运行方式变化的自适应保护[6]解决保护适应性问题。其中不同运行方式下系统等效阻抗辨识方法是研究关键。
现有电网运行方式等效阻抗辨识方法按照其量测信息的获取方式,分为基于网络信息的辨识方法和基于本地信息的辨识方法。
基于网络信息的辨识方法主要是通过获取全局网络的基本情况,根据系统节点导纳矩阵或节点阻抗矩阵对所需网络进行阻抗辨识。文献[7]通过补偿法求解等效节点开路电压和短路电流,随后用两者之比求取等效阻抗。文献[8]首先对网络节点导纳矩阵进行修正,随后求逆得出节点阻抗矩阵,等效节点的阻抗即为该节点的自阻抗,而文献[9]则直接利用阻抗矩阵对等效节点进行辨识。然而这些方法往往涉及电网的安全,无法直接获取正确的信息,并且当配电网的拓扑发生变化时,需要修改的节点导纳/阻抗矩阵的计算量太大,导致难以在线应用。
相比于基于网络信息的辨识方法,基于本地信息的辨识方法不需要获知全网的拓扑情况,只需要通过相量测量单元(Phasor Measurement Unit, PMU)对需要的辨识点进行信息采集,随后利用不同算法计算等效阻抗即可。常见的算法有最小二乘法和协方差法。
基于本地测量的戴维南等效参数辨识计算方法[10]采用的是利用最小二乘法进行计算,该方法假设相邻采样时刻内等效阻抗和电动势都不发生改变,运用多个时间断面的电气测量信息,对系统进行等效。在此基础上,为提高最小二乘法处理突变的能力,文献[11]提出了扰动事件复位算法。由于PMU采集的信息都是利用计算机进行处理和计算,可能会因其内部处理舍入误差引起发散问题,文献[12]为解决该问题提出了平方根最小二乘算法。文献[13]结合电力系统实际的运行情况,提出了一种基于改进的递推最小二乘法,避免了参数漂移问题。由于电网中的频率一直在改变,不同时间点的等效电源相角不相等,文献[10]的假设条件过于绝对,而文献[14-15]则认为戴维南等效电动势幅值不变而相角可变,弱化了假设条件。然而当系统内部发生扰动时,这些方法由于假设条件失效而导致辨识不准确,此时最小二乘法的辨识误差很大。
基于统计量的协方差法[16-19]是最小二乘法之外的补充手段。文献[16]利用等效电动势与负荷阻抗之间波动不相关性,利用协方差法计算等效阻抗。在文献[16]的基础上,文献[17-18]添加了滤波效果,使辨识结果更加精确。当协方差法中系统侧电动势与负荷侧阻抗之间的不相关性假设难以满足时[19],协方差法会因误差太大而失效。文献[20]提出利用遗忘因子法对辨识结果进行滤波处理,但是该方法的本质是通过调节辨识结果的比例来达到滤波的效果,并不能很好地从算法本身对所产生的误差进行消除。
综上所述,针对传统辨识方法在系统内部发生扰动时会对辨识结果产生较大误差的问题,本文提出基于波动特性解析的系统阻抗辨识方法,通过将系统等效电动势分解为稳态值与波动值,建立新的考虑系统侧等效电动势扰动的数学模型,利用波动特性对模型进行求解。本文提出用改进遗忘因子法对辨识结果进行滤波,该滤波方法能够消除算法本身所带来的误差影响,相较于传统遗忘因子法,效果更优。最后搭建测试平台,硬件在环实验结果验证了所提算法的准确性。
本文根据南方电网某地部分拓扑凝练成如图1a所示研究对象。线路PMU装置安装位置位于负荷侧降压变压器的高压母线处,所测参数为线路线电压U和电流I。

图1 戴维南等效电路研究算例
Fig.1 Thevenin equivalent circuit research example
图1b所示为戴维南等效电路模型,Eth和Zth分别为系统侧戴维南等效电动势和等效阻抗,ZL为负荷侧的等效阻抗。
由图1b中的拓扑结构,根据电气量关系,有
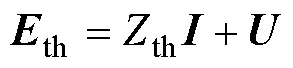 (1)
(1)
在系统进行戴维南参数辨识的过程中,Eth和Zth的辨识结果很有可能处于一个动态变化状态,假设在很小的Dt跨度范围内,等效阻抗Zth保持不变,而等效电动势Eth可写为
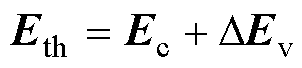 (2)
(2)
式中,Ec为等效电动势稳态值;DEv为等效电动势波动值。
将式(2)中等效电动势稳态值Ec,以及式(1)中的相量及阻抗实部、虚部分离,得到
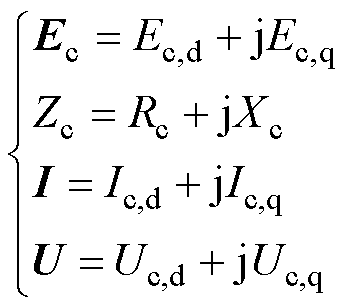 (3)
(3)
将式(1)用矩阵形式表示为
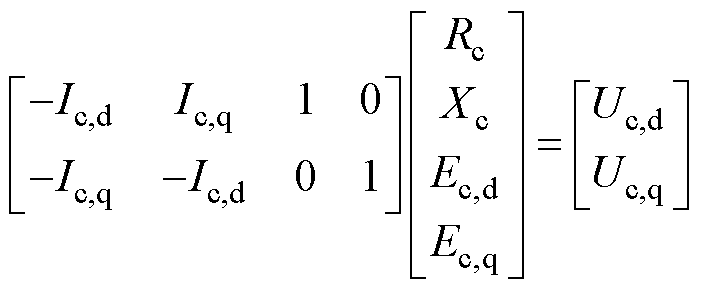 (4)
(4)
式中,下标d与q分别表示实部和虚部;下标c表示基于等效电动势稳态值的计算值。
利用Dt时间内的N组电气量数据进行估计,则式(4)可以改写为
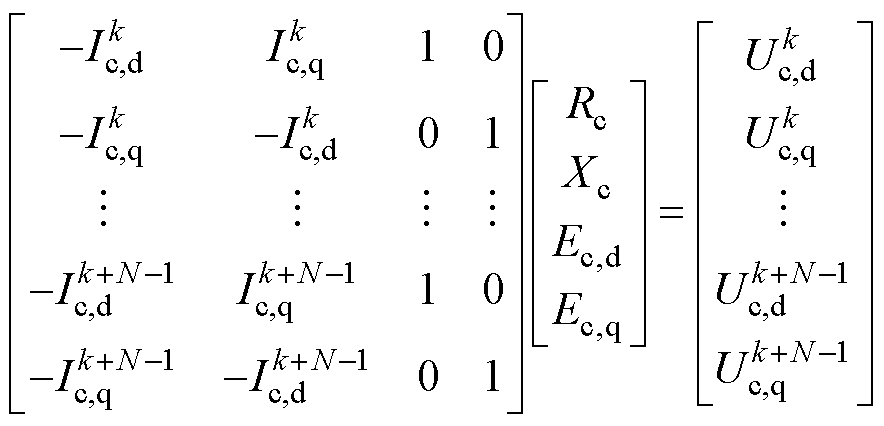 (5)
(5)
式中,上标k表示第k次的计算值。
对式(5)进行求解,用偏移平均值的波动量表示为
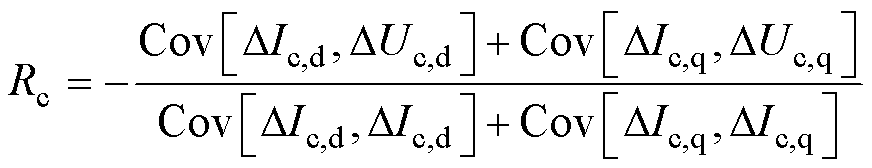 (6)
(6)
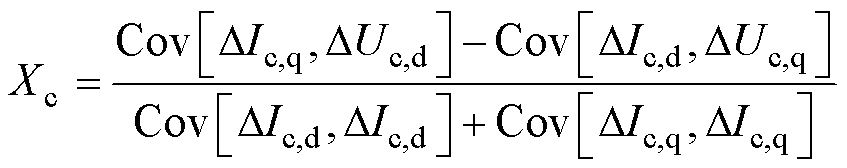 (7)
(7)
式(6)和式(7)推导过程可见附录。若将式(6)与式(7)合并,则有
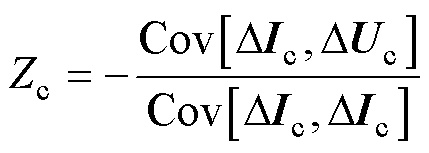 (8)
(8)
对于式(2)中等效电动势波动值DEv,有关系式
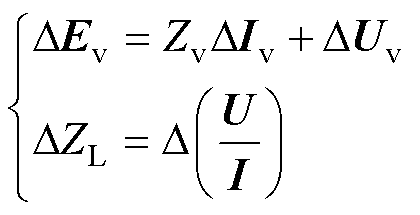 (9)
(9)
式中,下标v表示基于等效电动势波动值的计算值。
将式(9)中负荷阻抗波动量与戴维南等效电动势波动量作复数协方差,得到
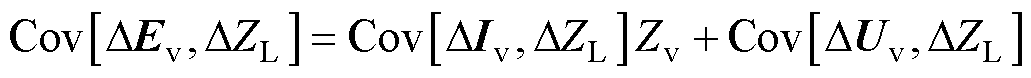 (10)
(10)
基于“源-荷”波动不相关原理,假设负荷阻抗波动量DZL与戴维南等效电动势波动量DEv相互独立,可表示为
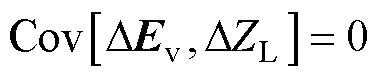 (11)
(11)
将式(11)代入式(10),可以推导出等效阻抗Zv为
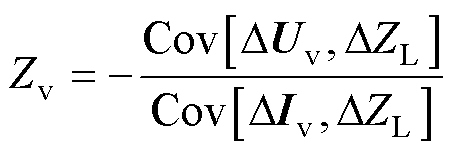 (12)
(12)
根据式(8)与式(12)计算出各自的等效阻抗,随后利用控制系数l把两者联系起来,得到
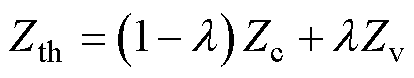 (13)
(13)
根据式(13),只需确定控制系数l,即可计算出等效阻抗的大小。基于等效电动势稳态值及波动值辨识的阻抗表达式形式一致,但是两者所利用的波动参数不一样。为了进一步说明两者的区别,下文将对两者进行波动特性分析,以便更好地确定控制系数。
基于等效电动势稳态值Ec进行阻抗辨识,基于等效电动势波动值DEv进行阻抗辨识,两者都是利用电气量波动进行求解,但是两者所针对的波动特性并不相同。前者运用的是每组数据内偏离期望值的波动量,具体形式如图2所示。图2中红框部分是进行一次戴维南等效所需要用的N组电压和电流样本数据,将红框部分进行详细展示,Di表示电压和电流实部虚部偏离期望的波动量。随后利用电压电流波动量,根据式(6)和式(7),对该组数据进行一次戴维南等效,计算出等效阻抗。而后者运用的是后一组数据与前一组数据的波动量,具体形式如图3所示。图3中上层数据是电压、电流和阻抗的样本数据,下层是每次等效所需要的波动数据。将上层每组对应位置的数据作差得到下层电压、电流和阻抗的波动量。随后根据式(12)对该组数据进行戴维南等效,计算出等效阻抗。
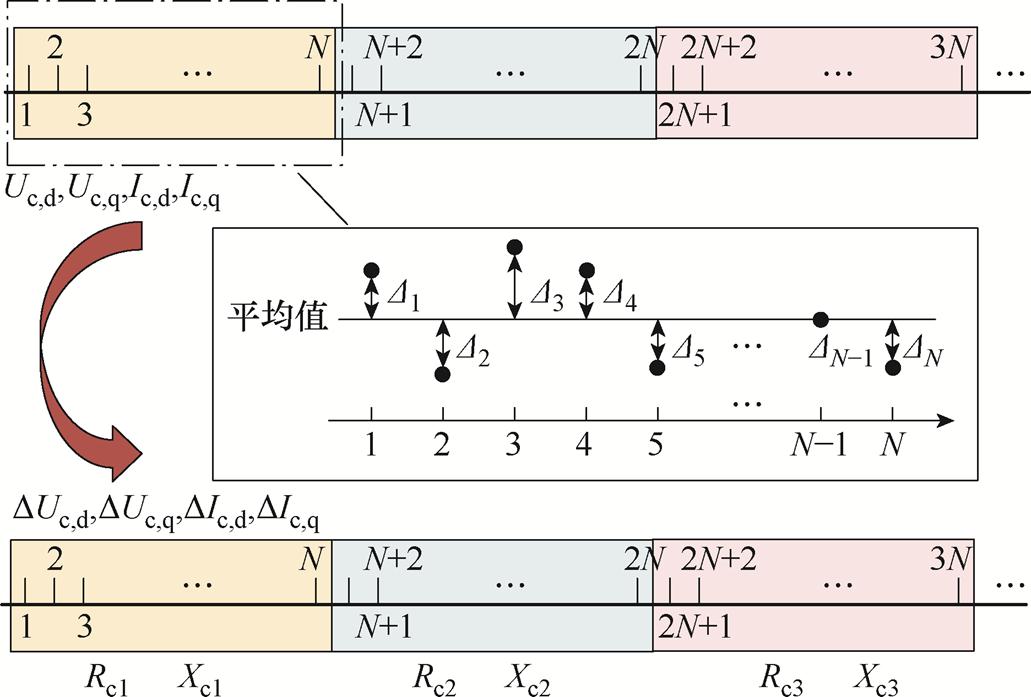
图2 基于稳态值的波动解析图
Fig.2 Fluctuation analytic diagram based on steady-state value
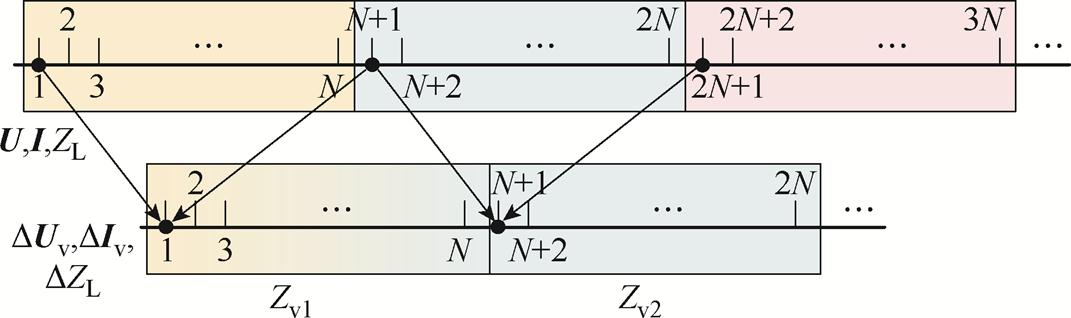
图3 基于波动值的波动解析图
Fig.3 Fluctuation analytic diagram based on fluctuation value
根据上文分析可知,基于等效电动势稳态值求解等效阻抗仅用了一组样本值,而基于等效电动势波动值求解等效阻抗利用了两组样本值,利用样本数量是前者的一倍。由于基于等效电动势稳态值求解需要大量样本数据,当每次等效所用样本数量很少时,该方法辨识误差较大。而此时基于等效电动势波动值求解利用相邻的样本数据,扩大了样本数量,辨识结果更加准确。但随着样本数量的增加,基于等效电动势波动值辨识阻抗中所假设的“源-荷”波动不相关原理将会失效[19],此时会产生一个误差d,即
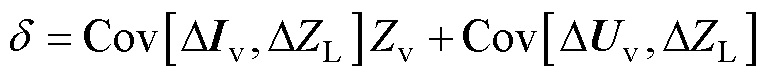 (14)
(14)
等效阻抗的表达式为
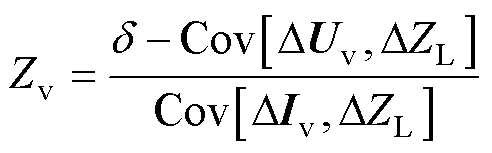 (15)
(15)
根据式(15),误差d的数量级与分子和分母协方差的数量级之间的关系直接影响戴维南等效阻抗,应该加以重视。若误差d的数量级大于或等于协方差的数量级,则基于等效电动势波动值计算戴维南等效阻抗距离真值的误差将会很大;若误差d的数量级小于协方差的数量级,则计算戴维南等效阻抗距离真值的误差在接受的范围内。在文献[21]中,作者指出两个互不相关复数随机变量序列的协方差不恒等于0,误差d本质上是一个复数的随机变量。所以可以通过限制d的相对大小,从而使得等效阻抗具有较高的准确性。
基于等效电动势波动值的阻抗辨识方法,一次等效所需要的数据依赖两组数据的电压、电流、负荷阻抗相量值。对于第i次和第i-1次等效,有以下关系式
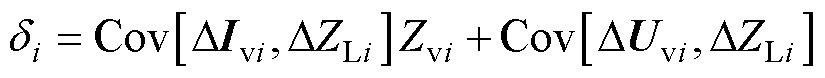 (16)
(16)
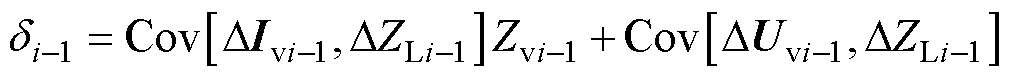 (17)
(17)
在阻抗辨识过程中,连续两次阻抗辨识结果有关系式
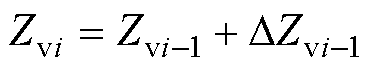 (18)
(18)
把式(18)代入式(16)并化简得
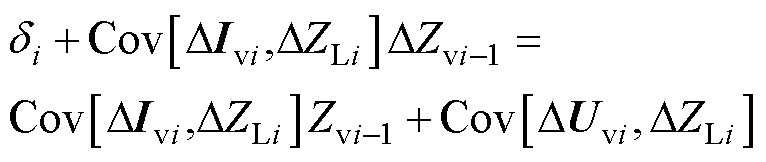 (19)
(19)
等式左侧Cov[DIvi, DZLi]的数量级很小,并且两时刻所等效的阻抗近似相等,即DZvi-1≈0,将两者相乘之后,此时认为误差di的数量级远大于两者乘积Cov[DIvi, DZLi]DZvi-1,所以忽略后一项有
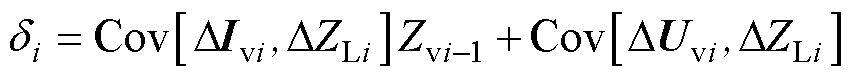 (20)
(20)
为了更直观地体现误差对等效阻抗结果所带来的影响,进一步引入波动系数ei,即
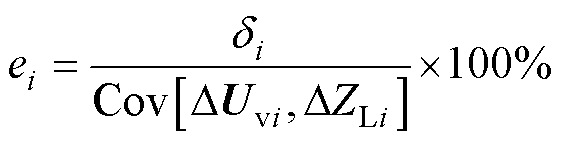 (21)
(21)
波动系数ei本质由第i-1、i、i+1组样本数据决定。通过第i-1和i组样本,两组样本作差得到第i-1组波动量,通过式(17)得出第i-1次等效阻抗,随后利用第i、i+1组样本数据得出第i组波动量,通过式(20)计算出第i次等效的误差di,根据式(21)得出第i组的波动系数ei,由此看出ei表示的是两次等效阻抗之间波动量比率。若波动系数ei很小,则基于等效电动势波动值进行戴维南等效的效果很好,相对应的控制系数li可以占比很大;若波动系数ei很大,则说明在第i相邻时刻的样本值变化很大,调节控制系数li使其占比减小。
根据以上分析,本文的控制系数l选取为
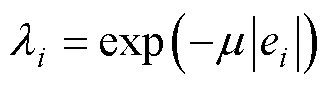 (22)
(22)
式中,m为衰减系数。
至此,本文所提阻抗辨识的表达式为
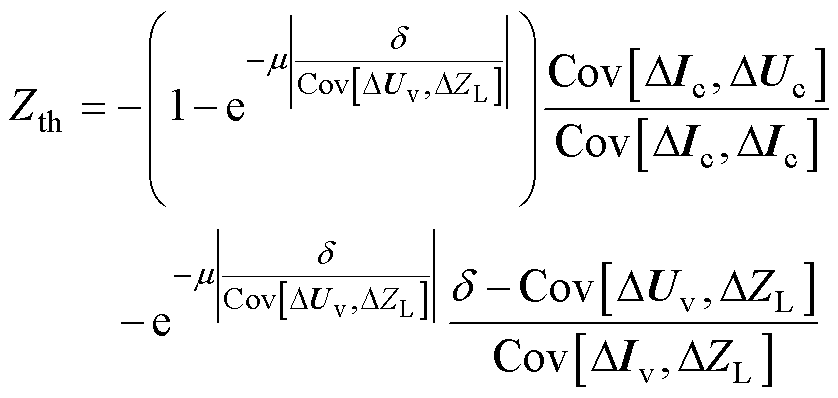 (23)
(23)
本文根据波动系数的值,利用指数函数衰减特性,合理调节控制系数。当波动系数很大时,基于等效电动势波动值的等效阻抗受相邻样本影响大,导致辨识阻抗不准确,此时调节控制系数,使其阻抗占比减小,减小了误差所带来的影响;当波动系数很小时,充分利用更多数据,从而在样本数量少的情况下保持更佳的辨识效果。
由于在实际电网中,测点处的电压和电流受噪声影响,会使测量数据有一定的偏差,以至于辨识阻抗会出现幅度较大的波动。为了使辨识方法更具实用性,本节通过协方差法阻抗辨识结果,提出了一种策略来提高结果的可靠性。将该策略结合1.1节所提辨识法,使等效结果更准确。
本文在文献[20]的基础上提出改进遗忘因子法,以基于等效电动势波动值的辨识结果为例介绍本文所提滤波方法。
对于每次等效结果,有
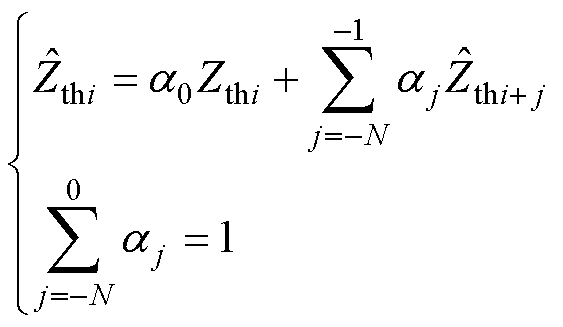 (24)
(24)
式中,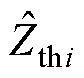 为当前第i组Zth的估计值;
为当前第i组Zth的估计值;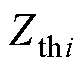 为当前第i组Zth的计算值;aj 为第j时刻的遗忘因子。
为当前第i组Zth的计算值;aj 为第j时刻的遗忘因子。
对于每次等效计算值
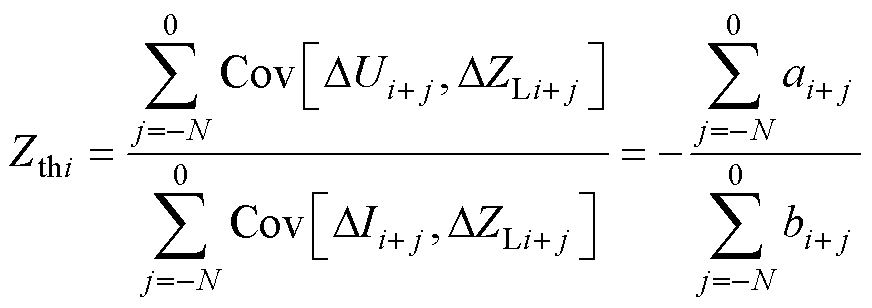 (25)
(25)
式中,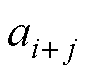 为电压波动量与负荷阻抗波动量的协方差;
为电压波动量与负荷阻抗波动量的协方差;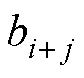 为电流波动量与负荷阻抗波动量的协方差。
为电流波动量与负荷阻抗波动量的协方差。
基于等效电动势稳态值的等效形式与基于等效电动势波动值的等效形式类似,不再赘述。以后者为例,证明改进遗忘因子法与传统遗忘因子法相比具有良好的适用性。为了使得证明结论更具普适性,假设遗忘因子相等,对误差波动进行处理,通过式(25)与传统遗忘因子法进行比较,证明该方法能减小误差,使结果更接近真值。传统遗忘因子法如式(26)所示。
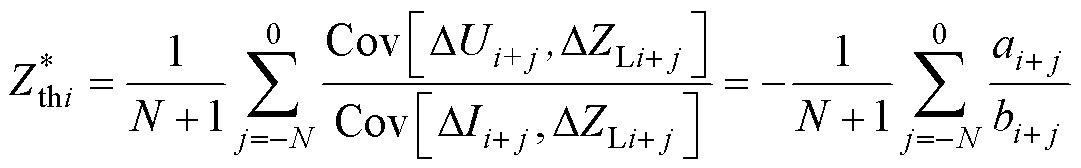 (26)
(26)
此时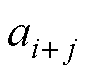 与
与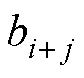 都是计算值,若用真值与扰动量可表示为
都是计算值,若用真值与扰动量可表示为
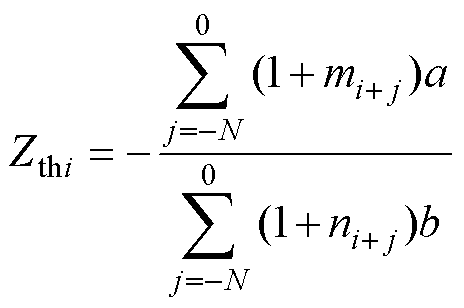 (27)
(27)
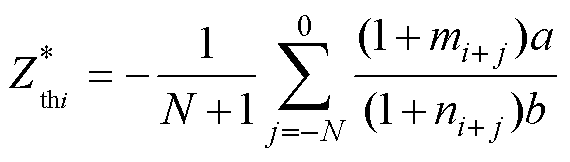 (28)
(28)
式中,a为分子真值;m为分子的扰动量;b为分母真值;n为分母的扰动量。
若扰动量是均匀分布,则两种方法的期望为
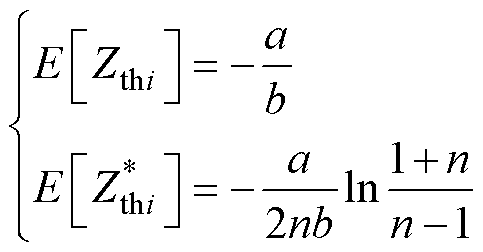 (29)
(29)
由式(29)可知,只有当分母扰动量n趋近于0时,传统遗忘因子法的期望才是真值,而改进法不管分子分母扰动量为多少,其期望一直都是真值。
若扰动量是正态分布,则两种方法的期望为
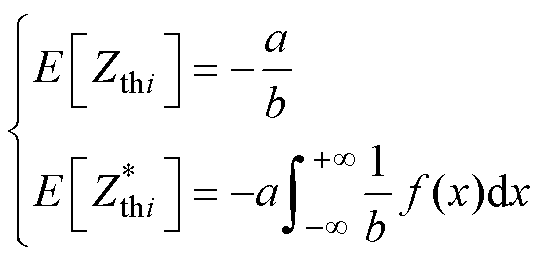 (30)
(30)
式中,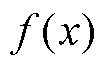 为正态分布的概率密度。
为正态分布的概率密度。
由式(30)可知,改进法的期望一直都是真值,而传统法的期望受分母扰动影响,使其在真值附近波动。由此可见,本文所提的改进法有利于抑制波动,提高辨识准确度。
为验证本文所提基于波动特性解析的配电系统阻抗辨识方法的有效性,在硬件在环平台上搭建拓扑结构如图1所示的10 kV配电系统,硬件在环实验设备如图4所示,具体参数见附表1。

图4 硬件在环实验设备
Fig.4 Hardware-in-the-loop experimental equipment
实际情况中,负荷侧和系统侧都会存在波动,因此需要探究在不同波动场景下本文所提算法的适应性。在进行辨识过程中,文本的衰减系数m取值为2,在实际系统中,衰减系数的取值可以根据情况进行调整。
波动场景设置负荷阻抗以±5%的幅度进行随机波动保持不变,而系统侧等效电动势波动分别以±0.2%、±0.4%、±0.6%等随机波动进行变化。将本文所提方法与传统方法1(基于最小二乘的阻抗辨识法[10])和方法2(基于协方差的阻抗辨识法[16])进行对比分析。
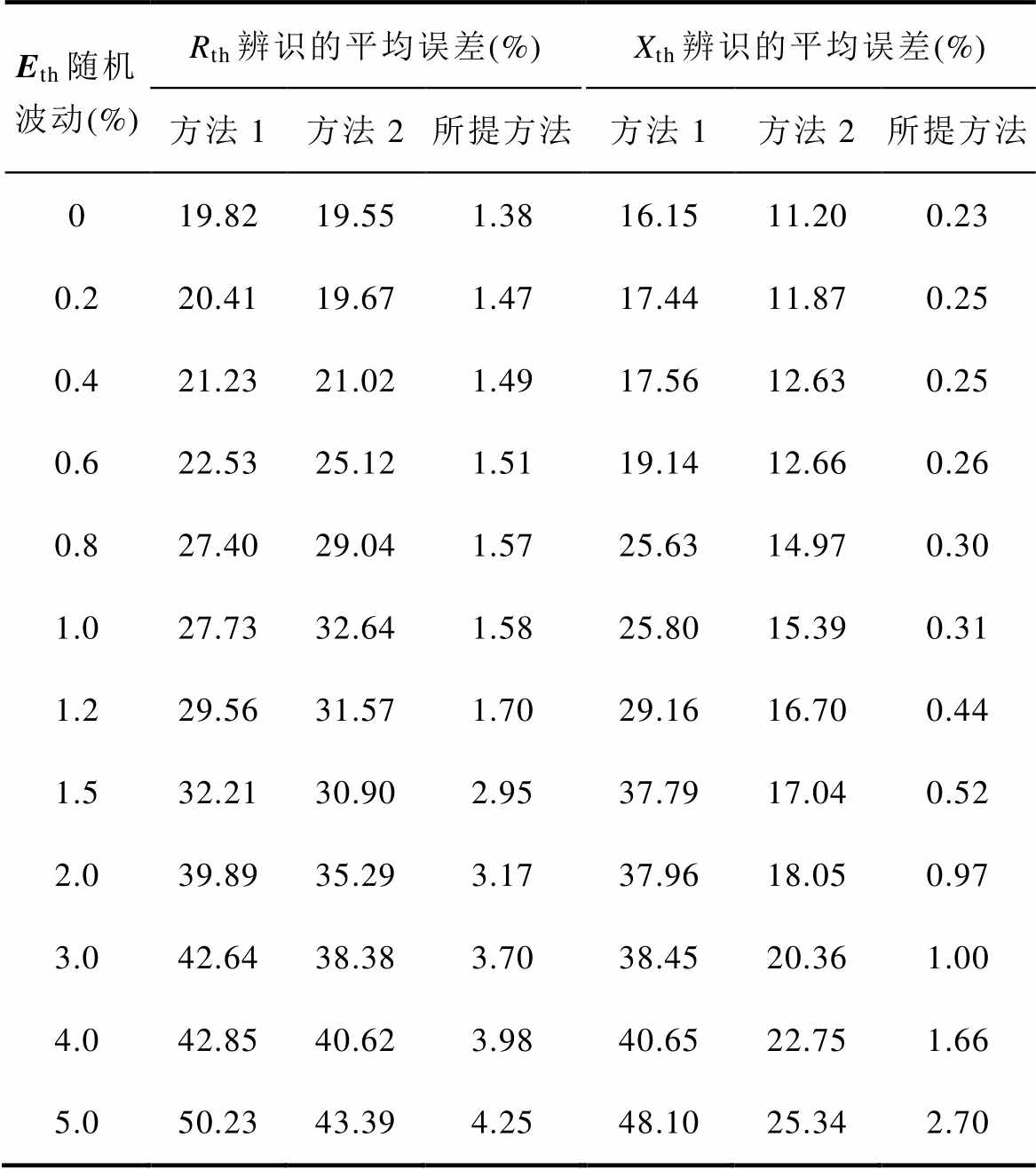
选取不同电动势波动场景与现有方法进行对比分析,得到不同场景下的阻抗辨识误差见表1。由表1可知,传统方法1、方法2的阻抗辨识平均误差都会随着系统等效电动势随机波动的增大而增加,这是由于方法1基于电源电动势不波动假设失效、方法2基于源-荷波动不相关假设失效导致。而本文所提方法不基于以上任何假设,考虑电源电动势波动以及误差d 所带来的影响。
表1 不同场景下的阻抗辨识误差
Tab.1 Impedance identification error in different scenarios
Eth随机波动(%)Rth辨识的平均误差(%)Xth辨识的平均误差(%) 方法1方法2所提方法方法1方法2所提方法 019.8219.551.3816.1511.200.23 0.220.4119.671.4717.4411.870.25 0.421.2321.021.4917.5612.630.25 0.622.5325.121.5119.1412.660.26 0.827.4029.041.5725.6314.970.30 1.027.7332.641.5825.8015.390.31 1.229.5631.571.7029.1616.700.44 1.532.2130.902.9537.7917.040.52 2.039.8935.293.1737.9618.050.97 3.042.6438.383.7038.4520.361.00 4.042.8540.623.9840.6522.751.66 5.050.2343.394.2548.1025.342.70
实验数据表明,无论电源电动势波动幅度多大,所提方法电阻平均误差在5%以内,电抗平均误差在3%以内,能够精准辨识出系统侧的等效阻抗大小。
当系统侧的网络结构发生改变时,戴维南等效阻抗也会相应发生改变。所以有必要进一步说明所提方法对等效阻抗发生改变时的跟踪能力验证。本文所提方法与传统方法1、方法2的阻抗辨识效果如图5所示。在中间运行时刻改变系统侧等效阻抗。
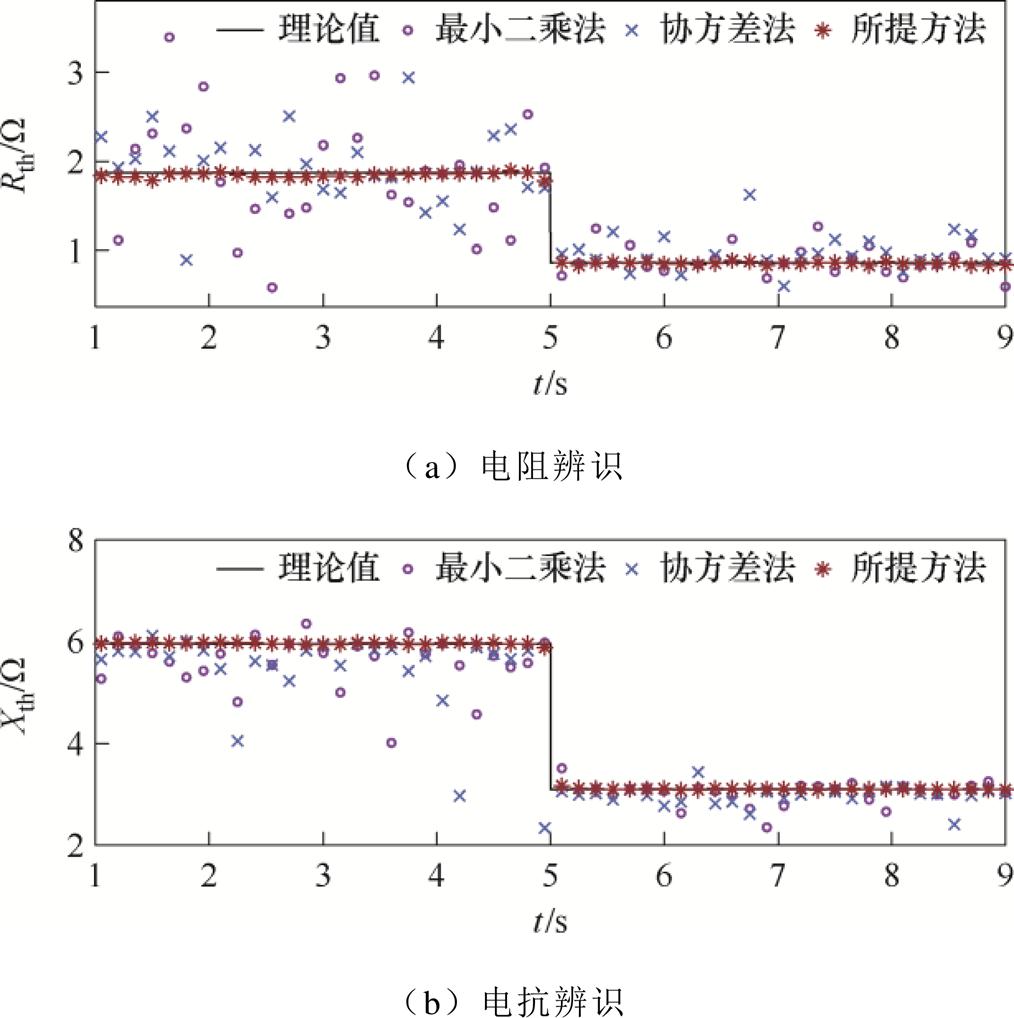
图5 仿真结果
Fig.5 Simulation results
如图5所示,所提方法阻抗辨识结果与理论值曲线契合度较高,电阻辨识最大误差与平均误差为4.34%、1.47%,电抗辨识最大误差与平均误差为1.08%、0.29%,辨识效果尤其显著。无论是电阻还是电抗的辨识结果,所提方法在辨识效果上均优于传统方法,当系统阻抗发生变化时,对系统阻抗辨识依旧具有较高的准确性。
在实际工程应用中,不仅系统侧接入了分布式发电设备,负荷侧也同样可能包含分布式电源[22],甚至负荷侧的分布式电源输出可能与系统侧分布式电源产生耦合效应。为此,本文在系统侧及负荷侧都接入了容量为2 600 kW的光伏模型,以进一步验证所提方法的适用性。
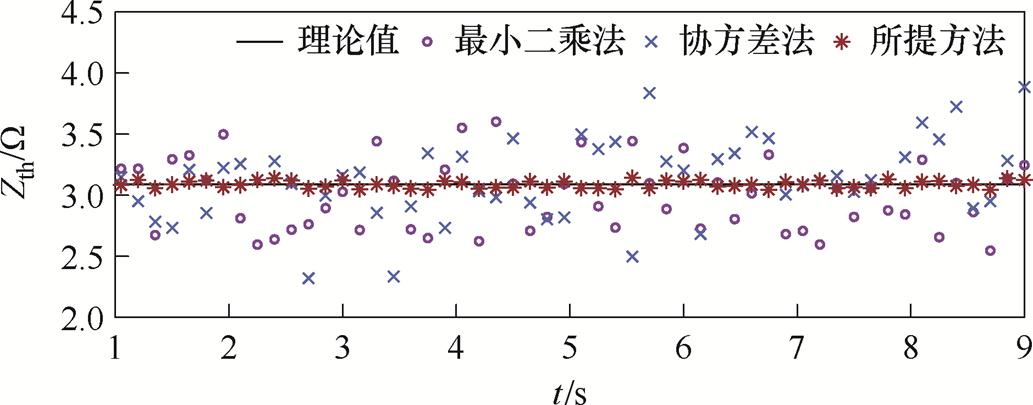
图6 分布式电源接入辨识图
Fig.6 Distributed power access identification diagram
由图6可知,方法1受系统侧波动影响较大,其平均辨识误差高达15.87%。此外,系统侧光伏受负荷侧光伏耦合的影响,系统侧光伏出力与负荷侧光伏所等效的阻抗之间存在一定的映射关系,导致方法2基于“源-荷”波动不相关假设进一步失效,从而影响阻抗辨识准确度,其平均辨识误差为17.21%。相比之下,所提方法在建模过程中充分考虑了电源电动势波动特性及“源-荷”波动不相关假设失效的影响。因此即使在负荷侧接入分布式电源的情况下,该方法仍能保持较高的适用性,其平均辨识误差为0.92%,相较于传统方法1和方法2,大幅度提升了辨识精度。
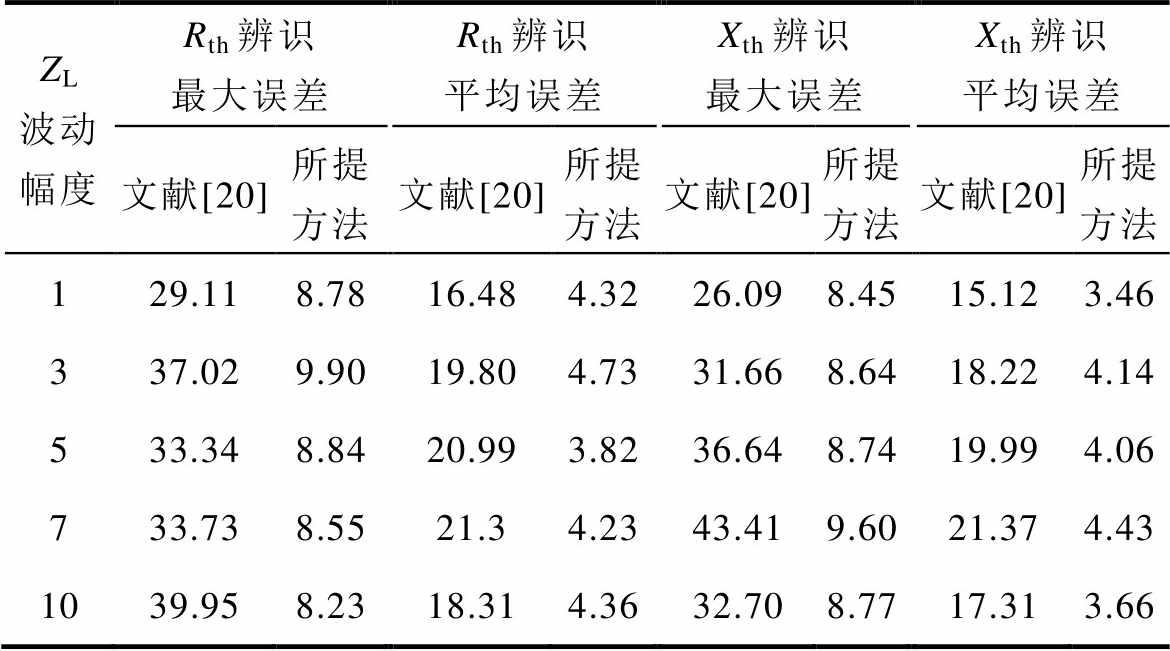
在改进遗忘因子方法中,所有的计算值实际都是来自负荷阻抗波动量,所以本文在负荷阻抗波动幅度为1%、3%、5%、7%、10%五种情况下,利用协方差法对系统侧阻抗进行辨识,比对传统滤波 法[20]与本文所提改进遗忘因子法的辨识误差。
由表2可知,文献[20]滤波法的阻抗辨识最大误差达到40%以上,而本文所提改进法的阻抗辨识最大误差在10%以内,相较于文献[20]最大误差减小了78%。此外,无论负荷阻抗波动幅度为多少,本文所提方法的平均误差皆小于5%,电阻、电抗辨识平均误差最低可至3.82%、3.46%。本文方法在各种负荷阻抗波动下都有很好的适应性。
表2 所提滤波法的阻抗辨识误差
Tab.2 Impedance identification error of the proposed filtering method (%)
ZL波动幅度Rth辨识最大误差Rth辨识平均误差Xth辨识最大误差Xth辨识平均误差 文献[20]所提方法文献[20]所提方法文献[20]所提方法文献[20]所提方法 129.118.7816.484.3226.098.4515.123.46 337.029.9019.804.7331.668.6418.224.14 533.348.8420.993.8236.648.7419.994.06 733.738.5521.34.2343.419.6021.374.43 1039.958.2318.314.3632.708.7717.313.66
本文研究了阻抗辨识算法的波动特性,提出了基于波动特性解析的阻抗辨识算法,并得出了以下结论:
1)传统最小二乘辨识法不考虑系统侧波动,一旦系统侧电源电动势发生波动,无法保证能准确地辨识其等效阻抗;传统协方差辨识法依赖“源-荷”波动不相关假设,而当该假设失效将会导致辨识结果不准确。
2)考虑系统侧电源电动势波动,建立了新的考虑系统侧等效电动势扰动的数学模型。该模型可以准确地对系统侧阻抗进行辨识,且不依赖任何假设。并提出了基于波动特性解析的阻抗辨识算法,该方法将系统等效电动势分解为稳态值与波动值的叠加,随后进行阻抗辨识,最后利用改进遗忘因子法对辨识结果进行滤波,相较于传统滤波法,系统运行方式的等效阻抗辨识最大误差降低了78%,增强了辨识方法在不同工况下的适应性。最后通过硬件在环实验验证了所提方法的准确性,所提阻抗辨识方法的平均误差均小于5%。
附 录
式(5)中,令电流系数矩阵为A,等效阻抗及电动势矩阵为X,电压系数矩阵为B,表达式分别为
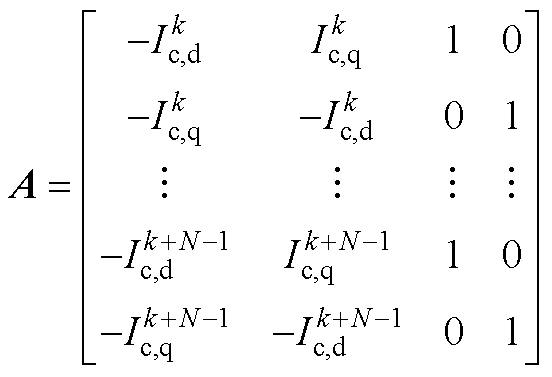 (A1)
(A1)
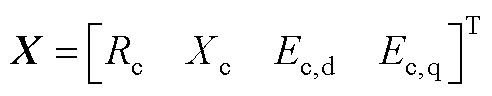 (A2)
(A2)
 (A3)
(A3)
利用最小二乘法对式(5)求解,得到
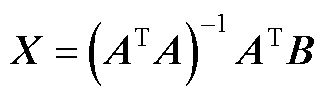 (A4)
(A4)
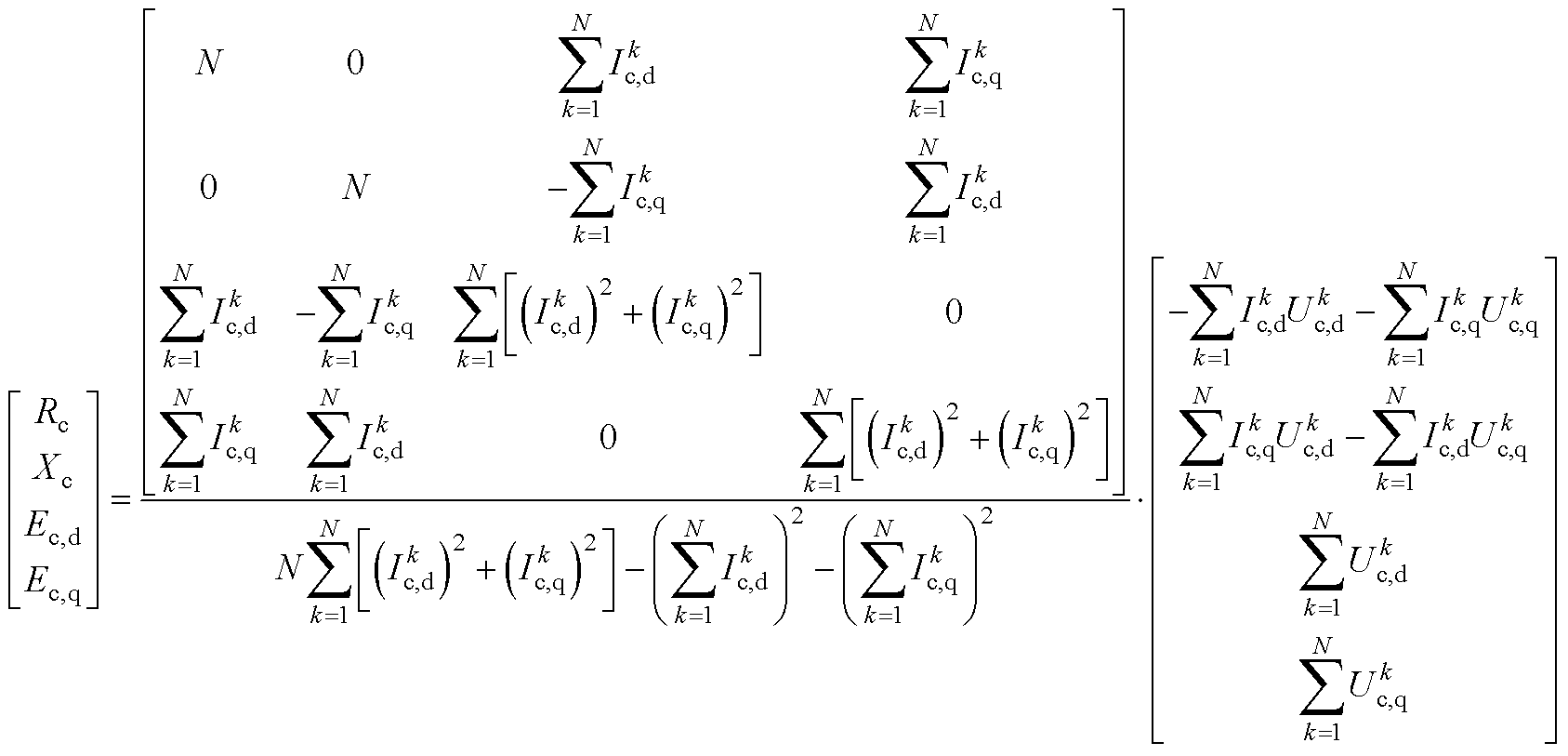 (A5)
(A5)
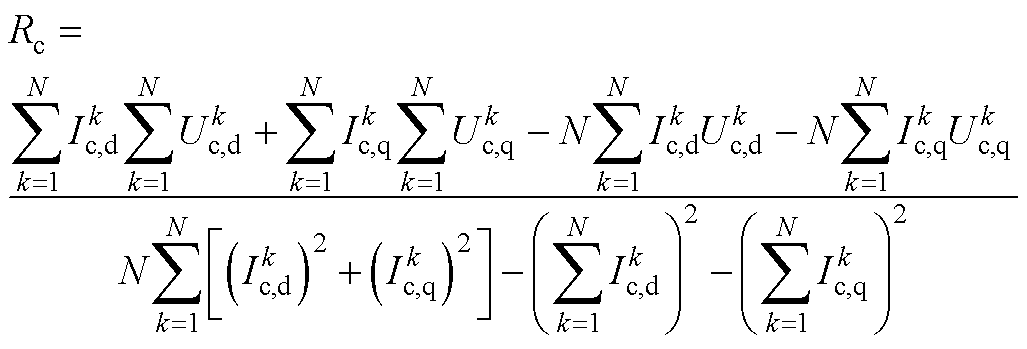 (A6)
(A6)
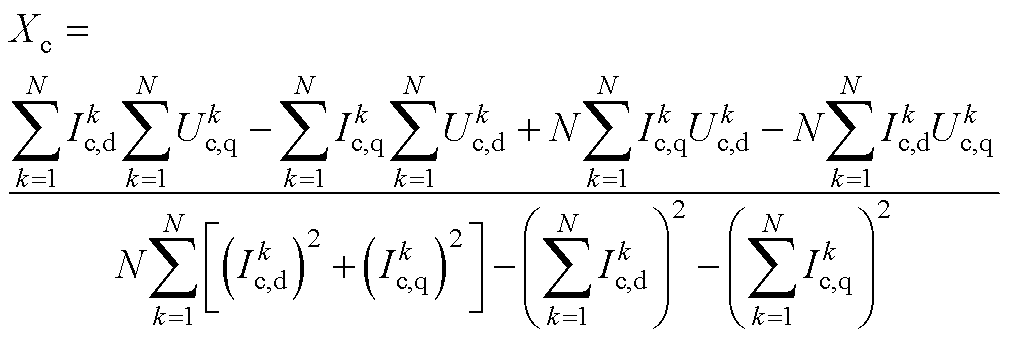 (A7)
(A7)
电流和电压的期望为
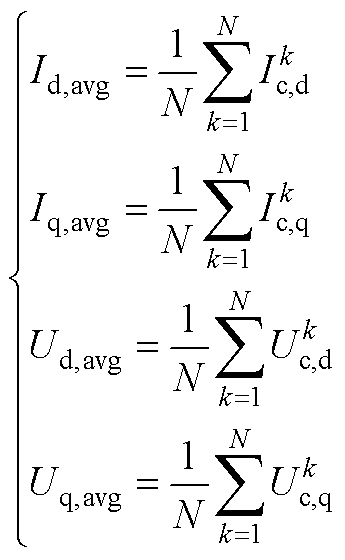 (A8)
(A8)
则该组电流量测和电压量测可以用期望值与波动量表示为
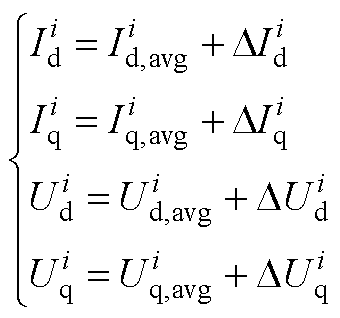 (A9)
(A9)
将式(A9)代入式(A6)和式(A7)得
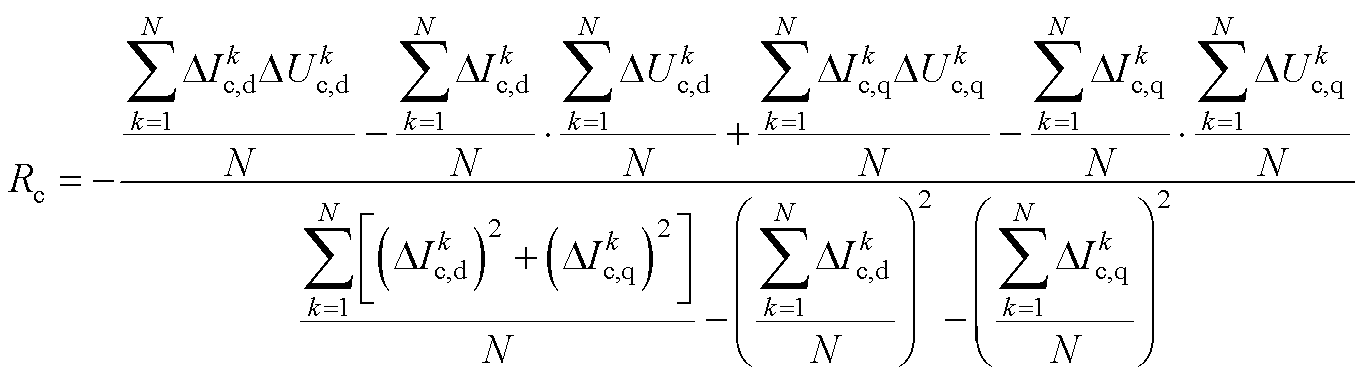 (A10)
(A10)
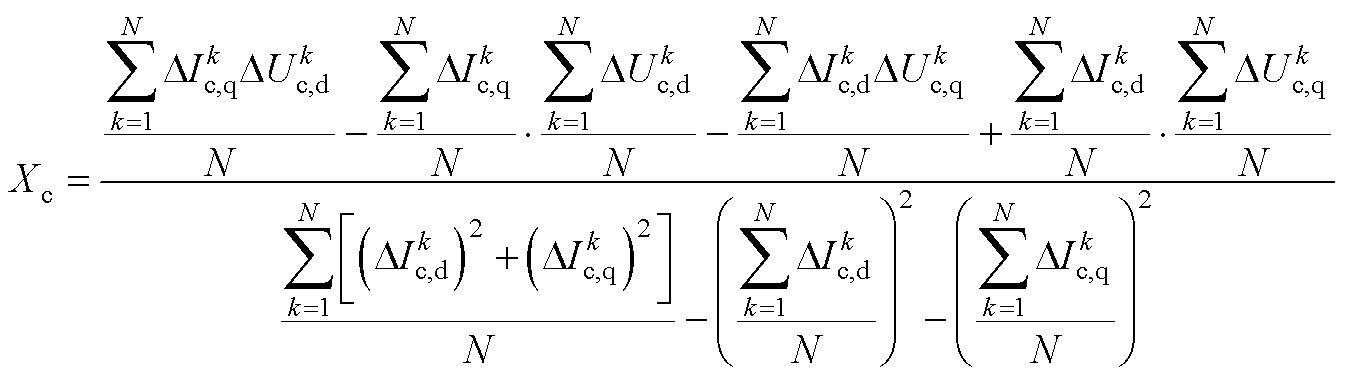 (A11)
(A11)
根据协方差的定义,等效阻抗的表达式为
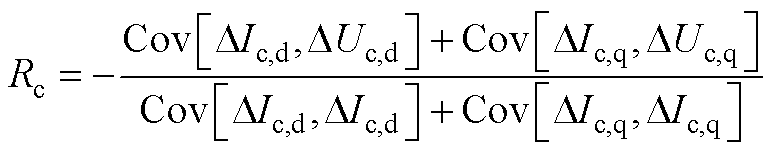 (A12)
(A12)
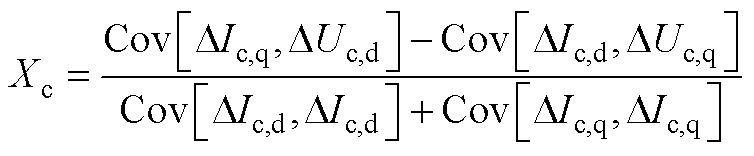 (A13)
(A13)
附表1 线路和负荷阻抗等其他参数
App.Tab.1 Other parameters of the model
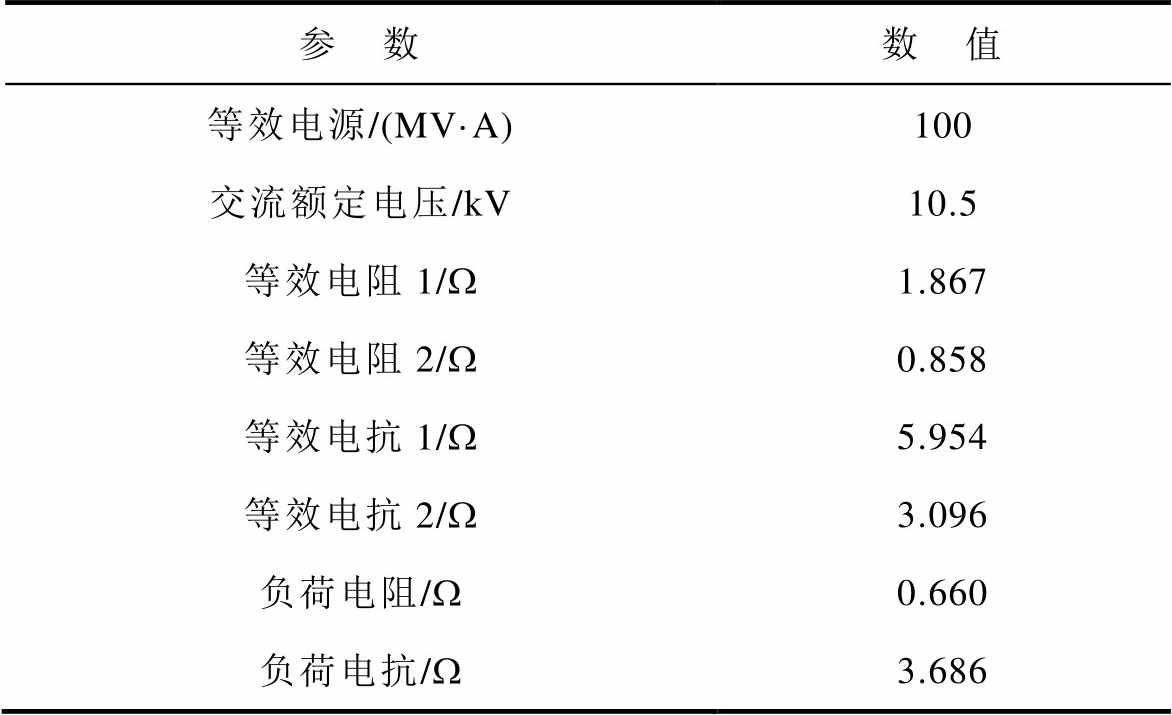
参 数数 值 等效电源/(MV·A)100 交流额定电压/kV10.5 等效电阻1/W1.867 等效电阻2/W0.858 等效电抗1/W5.954 等效电抗2/W3.096 负荷电阻/W0.660 负荷电抗/W3.686
参考文献
[1] 王守相, 尹孜阳, 赵倩宇. 考虑多供电层级耦合的中低压配电网分布式光伏承载力一体化精细评估方法[J]. 电工技术学报, 2025, 40(6): 1930-1944.
Wang Shouxiang, Yin Ziyang, Zhao Qianyu. A precise distributed PV hosting capability evaluation method for MV and LV distribution network conside- ring the coupling of multiple power supply layers[J]. Transactions of China Electrotechnical Society, 2025, 40(6): 1930-1944.
[2] 孔宇, 张恒旭, 施啸寒, 等. 基于多时间尺度分层协同的电力系统开放式推演框架[J]. 电工技术学报, 2025, 40(7): 2063-2077.
Kong Yu, Zhang Hengxu, Shi Xiaohan, et al. Open evolution simulation framework for power system based on multi-time scale hierarchical coordination[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2063-2077.
[3] 戴志辉, 牛宝仪, 李铁成, 等. 基于控保协同的三端混合直流输电系统线路保护[J]. 电工技术学报, 2025, 40(1): 108-121.
Dai Zhihui, Niu Baoyi, Li Tiecheng, et al. Line protection method of three-terminal hybrid DC transmission system based on control and protection coordination[J]. Transactions of China Electrotech- nical Society, 2025, 40(1): 108-121.
[4] 贾科, 李昱霖, 毕天姝, 等. 基于早期故障判别的直流并网系统主动保护[J]. 电工技术学报, 2025, 40(5): 1427-1439.
Jia Ke, Li Yulin, Bi Tianshu, et al. Incipient fault identification based active protection of DC collection line[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1427-1439.
[5] 李君, 何敏, 黄守道, 等. 基于相位差的小电阻接地有源配电网接地故障保护算法[J]. 电工技术学报, 2024, 39(23): 7418-7429.
Li Jun, He Min, Huang Shoudao, et al. Grounding fault protection algorithm of small resistance earthing active distribution network based on phase difference [J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7418-7429.
[6] 武岳, 范开俊, 徐丙垠, 等. 配合防孤岛保护的配电网时限自适应重合闸方法[J]. 电力系统自动化, 2024, 48(3): 122-132.
Wu Yue, Fan Kaijun, Xu Bingyin, et al. Time-limited adaptive reclosing method for distribution networks in coordination with anti-islanding protection[J]. Automation of Electric Power Systems, 2024, 48(3): 122-132.
[7] 付正鑫, 卢继平, 乔梁, 等. 基于戴维南参数等值的电压稳定性分析[J]. 中国电力, 2014, 47(5): 44-47.
Fu Zhengxin, Lu Jiping, Qiao Liang, et al. Voltage stability analysis based on thevenin equivalent parameters[J]. Electric Power, 2014, 47(5): 44-47.
[8] Moghimi Haji M, Xu W. Online determination of external network models using synchronized phasor data[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 635-643.
[9] Abdi P, Hamedani-Golshan M E, Alhelou H H, et al. A PMU-based method for on-line Thévenin equivalent estimation[J]. IEEE Transactions on Power Systems, 2022, 37(4): 2796-2807.
[10] Vu K, Begovic M M, Novosel D, et al. Use of local measurements to estimate voltage-stability margin[J]. IEEE Transactions on Power Systems, 1999, 14(3): 1029-1035.
[11] Begovic M, Milosevic B, Novosel D. A novel method for voltage instability protection[C]//Proceedings of the 35th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 2002: 802-811.
[12] 闫常友, 刘建飞, 杨奇逊, 等. 基于平方根滤波的网络等值算法[J]. 继电器, 2006, 34(3): 41-46.
Yan Changyou, Liu Jianfei, Yang Qixun, et al. Research on real-time equivalent based on square-root algorithm[J]. Relay, 2006, 34(3): 41-46.
[13] 常鲜戎, 王建文, 崔赵俊. 基于戴维南等值模型的静稳极限在线监视[J]. 电测与仪表, 2015, 52(16): 11-16.
Chang Xianrong, Wang Jianwen, Cui Zhaojun. Static stability limit online monitoring based on Thevenin equivalent model[J]. Electrical Measurement & Instrumentation, 2015, 52(16): 11-16.
[14] Zhou Ning, Trudnowski D J, Pierre J W, et al. Electromechanical mode online estimation using regularized robust RLS methods[J]. IEEE Transactions on Power Systems, 2008, 23(4): 1670-1680.
[15] 刘明松, 张伯明, 姚良忠, 等. 基于PMU和改进戴维南等值模型的电压稳定在线监视[J]. 电力系统自动化, 2009, 33(10): 6-10.
Liu Mingsong, Zhang Boming, Yao Liangzhong, et al. On-line voltage stability monitoring based on PMU and improved thevenin equivalent model[J]. Automa- tion of Electric Power Systems, 2009, 33(10): 6-10.
[16] Ojaghi M, Sudi Z, Faiz J. Implementation of full adaptive technique to optimal coordination of overcurrent relays[J]. IEEE Transactions on Power Delivery, 2013, 28(1): 235-244.
[17] Shen Shaofei, Lin Da, Wang Huifang, et al. An adaptive protection scheme for distribution systems with DGs based on optimized thevenin equivalent parameters estimation[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 411-419.
[18] Shen Shaofei, Wang Huifang, Hu Peijun, et al. A nonparametric denoising approach for thevenin equivalent parameters estimation based on taut-string- multiresolution algorithm[C]//2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 2017: 1-5.
[19] 张森, 王慧芳, 叶睿恺. 基于分层估计的戴维南等值阻抗在线计算方法[J]. 电力系统保护与控制, 2023, 51(12): 90-98.
Zhang Sen, Wang Huifang, Ye Ruikai. Thevenin equivalent impedance online calculation method based on hierarchical estimation[J]. Power System Protection and Control, 2023, 51(12): 90-98.
[20] Burchett S M, Douglas D, Ghiocel S G, et al. An optimal Thévenin equivalent estimation method and its application to the voltage stability analysis of a wind hub[J]. IEEE Transactions on Power Systems, 2018, 33(4): 3644-3652.
[21] 沈绍斐. 基于就地和区域信息的自适应保护研究[D]. 杭州: 浙江大学, 2018.
Shen Shaofei. Research on the local and regional area information-based adaptive protection[D]. Hangzhou: Zhejiang University, 2018.
[22] 刘洪波, 刘珅诚, 盖雪扬, 等. 高比例新能源接入的主动配电网规划综述[J]. 发电技术, 2024, 45(1): 151-161.
Liu Hongbo, Liu Shencheng, Gai Xueyang, et al. Overview of active distribution network planning with high proportion of new energy access[J]. Power Generation Technology, 2024, 45(1): 151-161.
Abstract With the continuous promotion of low-carbon transformation of green energy, a high proportion of distributed power sources are connected to the power grid, and the traditional single-radiation network becomes a source-load interactive multi-source network. The system operation mode changes in a wide range, resulting in a huge challenge for the staged current protection based on single-source fault characteristics. Although the existing adaptive protection technology improves flexibility by adjusting the protection setting value in real time, its core depends on accurate system equivalent impedance identification. However, the traditional identification method has significant errors under complex conditions such as new energy output fluctuation, multi-source coupling and internal disturbance of the system. Especially when the load side interacts with the distributed power supply on the system side, the failure of traditional assumptions leads to a sharp decline in identification accuracy. Aiming at the above problems, this paper proposes an impedance identification method based on fluctuation characteristic analysis. By reconstructing the mathematical model, optimizing the algorithm framework and multi-scenario verification, the system solves the problem of protection adaptability of high-proportion new energy distribution network.
Traditional impedance identification methods can be divided into two categories based on network information and local information. The former relies on global topological parameters and has defects such as complex calculation and difficulty in online application. Although the latter uses local measurement information, the least square method, covariance method and other algorithms increase the error due to ignoring the potential fluctuation component and coupling effect in the new energy disturbance scenario. This paper innovatively proposes to decompose the equivalent potential of the system into a superposition model of steady-state value and fluctuation value, which breaks through the limitations of traditional methods on the assumption of constant potential or single variable. By analyzing the dynamic correlation between the fluctuation component and the system impedance, the impedance identification equation considering the coupling of multi-source disturbances is established, and the improved forgetting factor algorithm is used to dynamically adjust the weight of historical data, which effectively suppresses the influence of the algorithm itself.
In the scenario of system-side potential fluctuation of ±0.2% and ±0.4% and load-side impedance disturbance of ±5%, the method in this paper stabilizes the resistance and reactance identification errors within 5% and 3% respectively through the potential steady-wave decoupling model, which is more than 50% lower than the traditional method. For the sudden change of system impedance, the maximum tracking error of resistance and reactance of the proposed algorithm is only 4.34% and 1.08%. Aiming at the two-way coupling problem caused by the penetration of distributed power supply on the load side, a test scenario with 2 600 kW load side photovoltaic is constructed. The traditional method leads to an error of more than 15% due to source-load coupling, while the phase decoupling strategy in this paper reduces the average error to 0.92%. When the load impedance fluctuation is 10%, the maximum error of the improved forgetting factor method is reduced from 50% to 14%, and the average error is less than 5%. Experiments show that the proposed method meets the national standard requirements in the scenarios of new energy fluctuation, topology change and multi-source coupling, and provides high-precision parameter support for adaptive protection.
Keywords:Impedance identification, system perturbation, wave characteristics, improved forgetting factor method
邓 邦 男,2000年生,硕士研究生,研究方向为面向自适应保护需求的配电系统等值阻抗辨识计算等。
E-mail: dengbang@ncepu.edu.cn
贾 科 男,1986年生,教授,博士生导师,研究方向为电力系统保护与控制、新型配电网保护与故障定位等。
E-mail: ke.jia@ncepu.edu.cn(通信作者)
中图分类号:TM711
DOI: 10.19595/j.cnki.1000-6753.tces.250014
国家自然科学基金青年科学基金项目(52322703)和国家自然科学基金面上项目(52277097)资助。
收稿日期 2025-01-02
改稿日期 2025-03-04
(编辑 郭丽军)