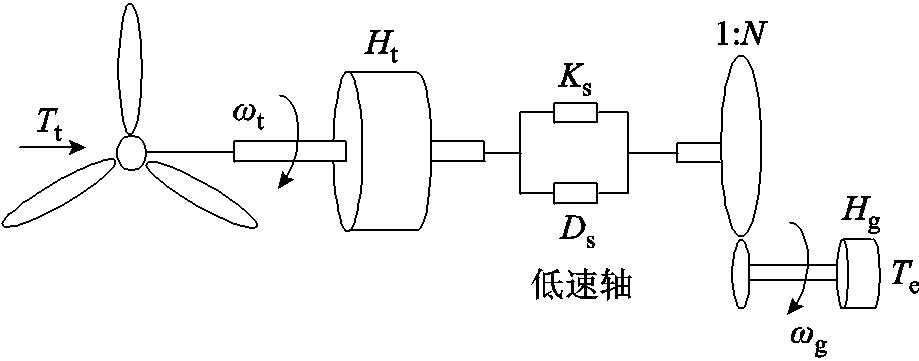
图1 双馈风电机组轴系二质量块模型
Fig.1 Model of two-mass blocks of drive-chain of DFIG
摘要 为了减少双馈风电机组参与调频导致轴系疲劳载荷累积而发生的轴系断裂风险,该文首先针对风机传动链模型推导了发电机电磁转矩对传动链扭角速度的传递函数,分析了其幅频特性曲线,利用构建的风电机组疲劳载荷灵敏度模型,揭示了传动链轴转矩波动与功率波动的关系;其次设计了风储分频段响应策略,利用风机虚拟惯量和下垂控制计算实时调频功率,以轴转矩波动和储能出力为优化目标,并考虑负荷波动因素,实时调整避开轴系自然振荡频率的滤波器参数,分配风机和储能系统的调频功率;最后搭建Matlab/Simulink-GH Bladed联合仿真平台进行仿真验证。结果表明,所提方法可在保证快速调频响应的同时,显著降低风机轴系的扭矩与扭角波动幅度,大幅降低轴系的等效疲劳载荷。
关键词:双馈风电机组 疲劳载荷 传动链 一次调频 储能
近年来,风电的大规模并网大幅降低了电力系统的频率稳定性[1-3]。为保障电力系统的安全稳定运行,参与电网的风电机组被要求积极参与一次调频,提供有效的频率支撑[4-7]。然而,电网频率的频繁波动会引起发电机电磁转矩的频繁波动,风机敏感的机械结构导致其承受更大的疲劳载荷,严重影响机组的安全运行,缩短设备的使用寿命[8-9]。因此,研究风电机组在参与一次调频过程中如何缓解轴系疲劳载荷具有重要意义。
为改善电力系统的动态频率特性并提升整体稳定性,储能系统被广泛应用[10-11]。通过其快速响应和调节能力,储能能够有效地辅助电力系统应对频率波动[12-14]。在此背景下,分频段响应的方法逐渐受到关注。文献[15]提出了一种分频系统,从而自动确定风储火的有功出力,提高了系统的调频速度与质量。文献[16]设计了基于滤波时间常数的模糊自适应指令分解方法,实现了对电网频率的灵活响应。文献[17]提出了一种基于多尺度分解的风火储协同调频控制策略,通过小波包分解频率偏差指令,实现了风电、火电和储能的协同互补,有效地改善了电网的频率特性。
目前针对风电机组在参与一次调频过程中所面临的疲劳载荷累积问题[18-19]已有一定研究。文献[20]提出了一种基于扭矩波动状态反馈的传动链扭矩阻尼控制,对传动系统的振动频率进行有针对性的抑制,实现了对传动链的降载。文献[21]通过设置调频死区来控制风储系统的调频参与时机和调频深度,在频率偏差较小时,风机主动参与调频;随着偏差增大,逐步由储能系统接管调频,从而避免风机过度频繁参与而造成的机械疲劳。文献[22]通过调整转子转速和桨距角来预留调频所需功率裕度,实现了风电机组静调差系数的整定,验证了所提策略能有效降低机组疲劳载荷。文献[23]定义了风电机组疲劳载荷对功率参考的灵敏度,推导了疲劳载荷灵敏度的显式解析方程,并将其引入公式化最优功率调度问题中。文献[24]提出了一种改进的疲劳载荷灵敏度计算方法,通过考虑轴和塔架的双质量模型及风速变化对疲劳载荷的影响,减少主轴扭矩和塔架弯曲力矩的波动,以提高系统频率的稳定性。文献[25]建立了疲劳载荷与有功出力变化之间的关系,以风电场总疲劳载荷及其站内分布最小为优化目标,在保证风电场调频性能的同时降低风电机组的疲劳载荷。
综上所述,上述研究集中于基于频率偏差信号或频率信号的分频段响应策略,旨在提升电力系统对频率变化的响应能力,并没有考虑风电机组在调频过程中可能面临的疲劳载荷问题。同时,目前关于风电机组在调频过程中的疲劳载荷缓解的研究,主要集中于风电场内部及机组自身的出力调整和调节策略,意在通过优化风机之间的协作或者风机本身运行参数来提升系统的动态响应性能。这些方法虽然在一定程度上减轻了机组的疲劳荷载并增强了整体调频能力,但研究普遍较少考虑储能系统在缓解风电机组轴系疲劳方面的应用潜力。
基于此,本文提出了一种分频段响应的风储联合调频控制策略。首先利用风机虚拟惯量和下垂控制计算实时调频功率,以轴转矩波动和储能出力为优化目标,通过序列二次规划算法得到最优决策量;其次考虑负荷波动因素,实时调整避开轴系自然振荡频率的滤波器参数,采用低通滤波、相位和幅值补偿对调频功率信号进行频段划分,分配给风机和储能;最后,搭建Matlab/Simulink-GH Bladed联合仿真平台进行仿真验证。
为了缓解风电机组调频过程中的轴系疲劳载荷,选取轴系二质量块模型作为研究对象,如图1所示。相比于三质量块或六质量块模型,简化后的二质量块模型聚焦于传动链中主要动力学特征,能够以更低的复杂度有效反映轴系的扭振动态特性。

图1 双馈风电机组轴系二质量块模型
Fig.1 Model of two-mass blocks of drive-chain of DFIG
将风电机组发电机转子高速轴侧的参量折算至风电机组低速轴侧,将折算后的各参数和变量仍用折算前的符号表示,则双馈风电机组轴系二质量块方程为
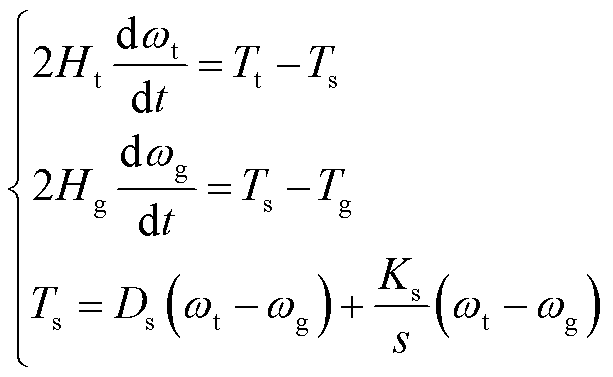 (1)
(1)
式中,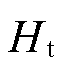 为风轮惯性时间常数;
为风轮惯性时间常数;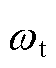 为风轮转速;
为风轮转速;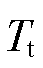 为风轮机械转矩;
为风轮机械转矩;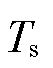 为传动链轴系转矩;
为传动链轴系转矩;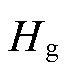 为发电机惯性时间常数;
为发电机惯性时间常数;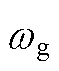 为发电机转速;
为发电机转速;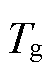 为发电机电磁转矩;
为发电机电磁转矩;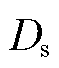 为传动链阻尼系数;
为传动链阻尼系数;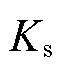 为传动链刚度系数。
为传动链刚度系数。
根据式(1)所示的轴系二质量块模型,得到传动链扭转角度的二阶常系数线性齐次微分方程为
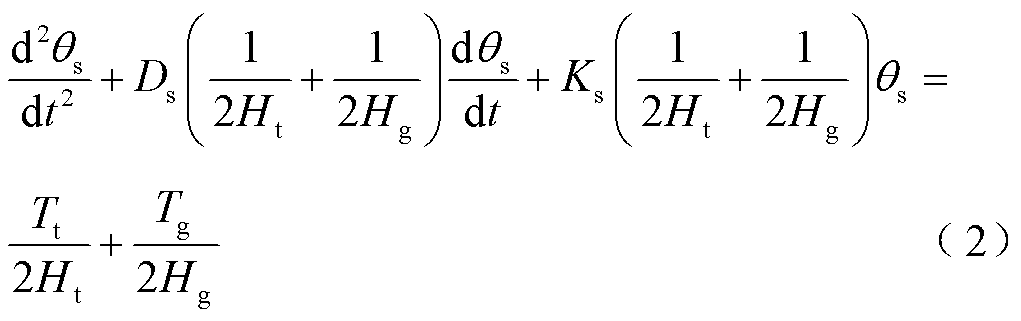
式中,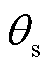 为传动链扭转角度。
为传动链扭转角度。
根据式(2),可以得到传动链的自然振荡角频率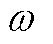 和阻尼比
和阻尼比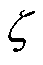 为
为
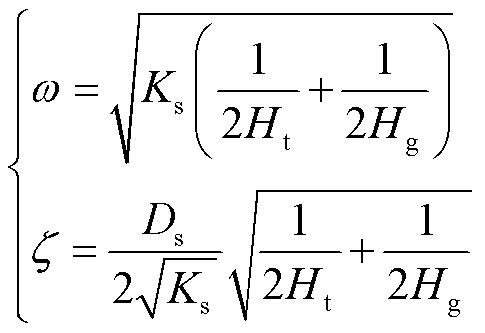 (3)
(3)
本文中风机传动链参数为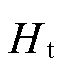 =2.45 s,
=2.45 s,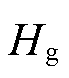 = 0.19 s,
= 0.19 s,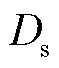 =0.355,
=0.355,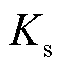 =75.35。根据式(3)计算得
=75.35。根据式(3)计算得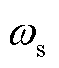 =14.79 rad/s,
=14.79 rad/s,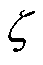 =0.035,自然振荡角频率换算为频率f=2.35 Hz,阻尼比计算结果为0.035,远小于1,则系统为典型的欠阻尼系统,容易引起轴系扭振。
=0.035,自然振荡角频率换算为频率f=2.35 Hz,阻尼比计算结果为0.035,远小于1,则系统为典型的欠阻尼系统,容易引起轴系扭振。
根据式(2)可以看出,电磁转矩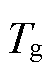 和机械转矩
和机械转矩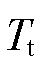 的波动均可能引起轴系的扭振反应。本文研究风电机组参与一次调频过程中的轴系载荷问题,而电磁转矩
的波动均可能引起轴系的扭振反应。本文研究风电机组参与一次调频过程中的轴系载荷问题,而电磁转矩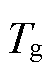 的扰动主要受电网侧的频率波动影响,因此可基于传动链模型构建从电磁转矩
的扰动主要受电网侧的频率波动影响,因此可基于传动链模型构建从电磁转矩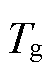 到扭振响应特征量的传递函数。衡量轴系扭振响应特性的关键参数之一为传动链扭转角速度
到扭振响应特征量的传递函数。衡量轴系扭振响应特性的关键参数之一为传动链扭转角速度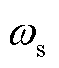 ,电磁转矩
,电磁转矩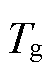 到传动链扭转角速度
到传动链扭转角速度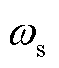 的传递函数为
的传递函数为
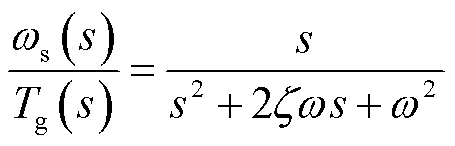 (4)
(4)
式(4)对应的幅频特性曲线如图2所示。可以看出,在轴系的自然振荡频率点附近的增益最高,电磁转矩容易激发轴系的扭振,从而导致轴系疲劳载荷增大,影响风机寿命。
风力机轴上输出的机械功率为
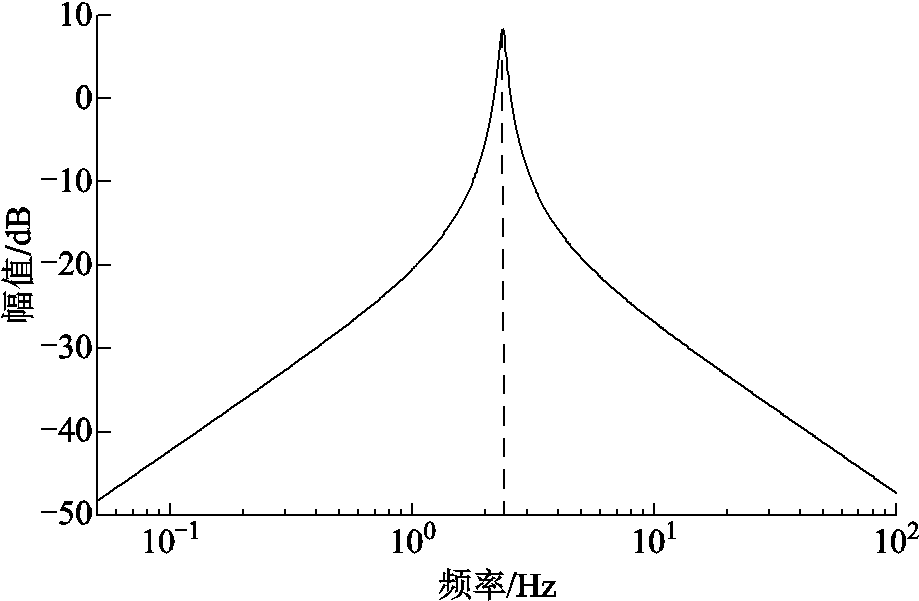
图2 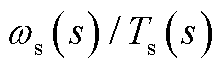 幅频特性曲线
幅频特性曲线
Fig.2 Amplitude-frequency curve of 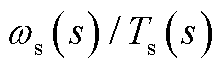
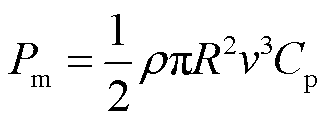 (5)
(5)
式中,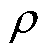 为空气密度;
为空气密度;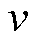 为上游风速;
为上游风速;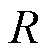 为风轮半径;
为风轮半径;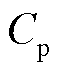 为风能利用系数。
为风能利用系数。
风轮机械转矩为
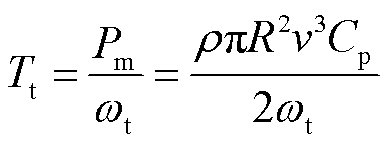 (6)
(6)
风能利用系数理论计算方法为
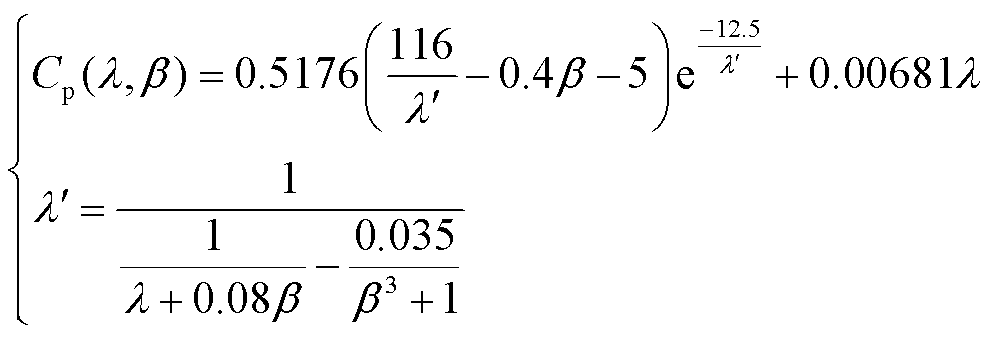 (7)
(7)
式中,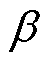 为桨距角;
为桨距角;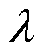 为叶尖速比。
为叶尖速比。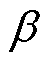 和
和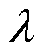 计算式为
计算式为
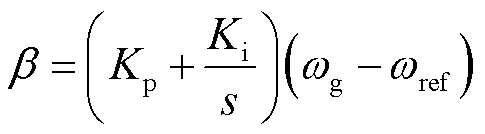 (8)
(8)
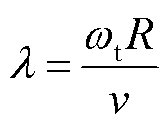 (9)
(9)
式中,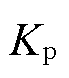 为变桨系统比例系数;
为变桨系统比例系数;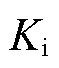 为变桨系统积分系数;
为变桨系统积分系数;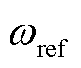 为转速参考值。
为转速参考值。
发电机电磁转矩为
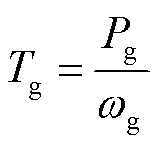 (10)
(10)
式中,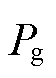 为风机电磁功率。
为风机电磁功率。
根据式(6)得到风轮机械转矩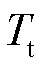 的增量形式[23]为
的增量形式[23]为
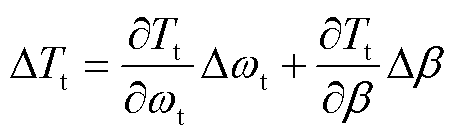 (11)
(11)
风轮机械转矩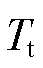 对风轮转速
对风轮转速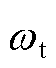 和桨距角β的偏导计算式为
和桨距角β的偏导计算式为
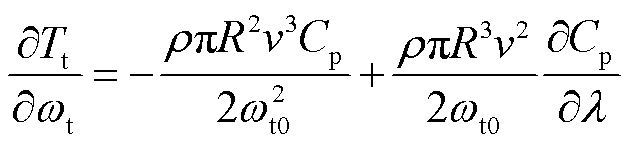 (12)
(12)
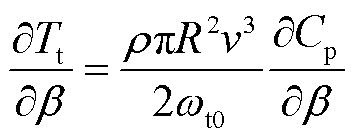 (13)
(13)
式中,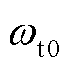 为当前采样时刻下的风轮转速。
为当前采样时刻下的风轮转速。
根据式(10)得到发电机转矩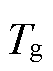 增量形式为
增量形式为
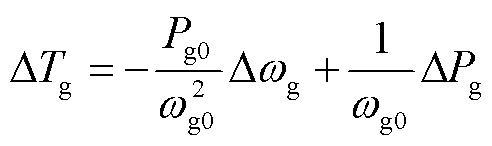 (14)
(14)
式中,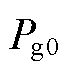 为当前采样时刻下的有功功率;
为当前采样时刻下的有功功率;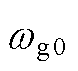 为当前采样时刻下的发电机转速。
为当前采样时刻下的发电机转速。
根据式(8)得到桨距角β的增量形式为
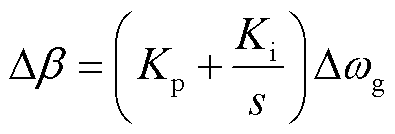 (15)
(15)
根据式(1)得到风轮转速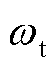 、发电机转速
、发电机转速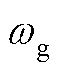 和传动链轴系转矩
和传动链轴系转矩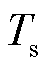 增量形式为
增量形式为
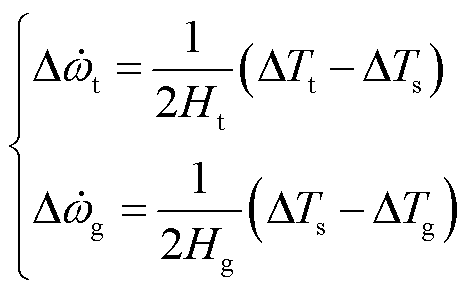 (16)
(16)
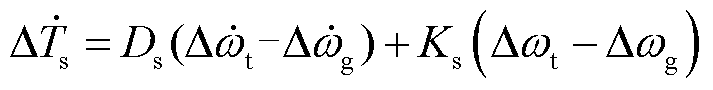 (17)
(17)
根据式(11)~式(17)可建立连续状态空间方程为
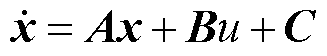 (18)
(18)
其中
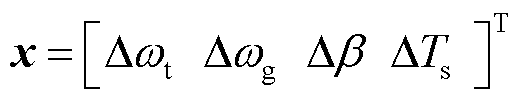 (19)
(19)
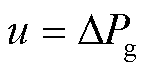 (20)
(20)
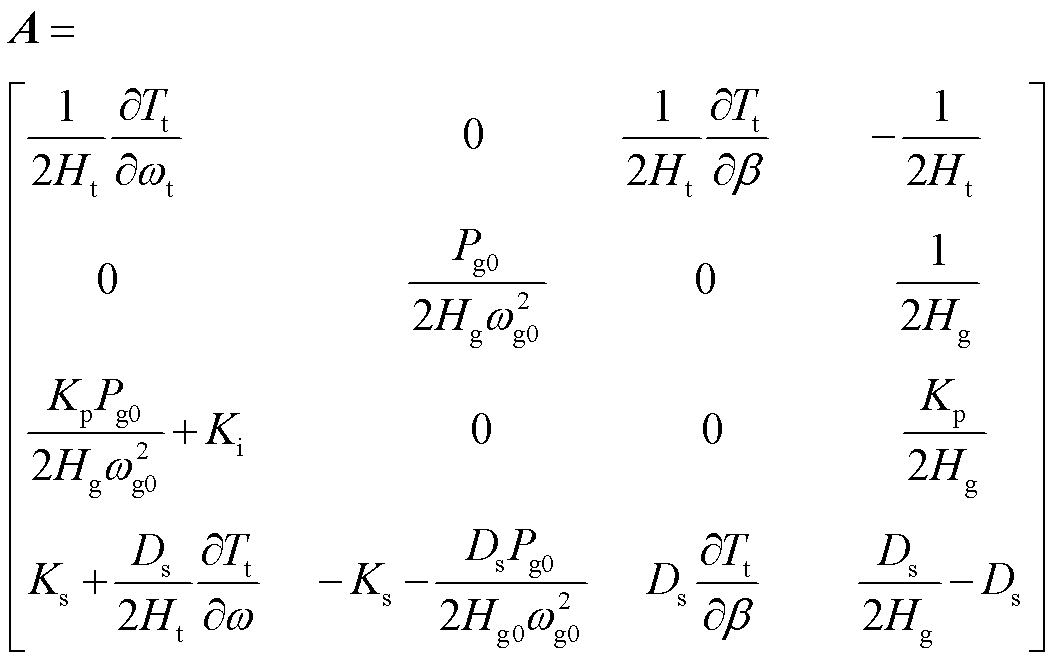 (21)
(21)
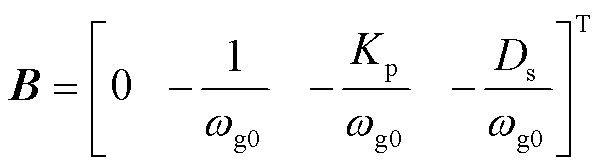 (22)
(22)
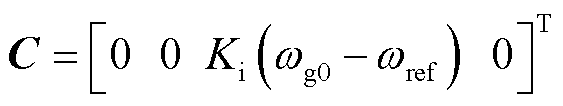 (23)
(23)
经采样周期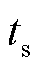 对式(18)离散化后得到离散状态空间表达式为
对式(18)离散化后得到离散状态空间表达式为
 (24)
(24)
其中
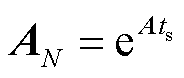 (25)
(25)
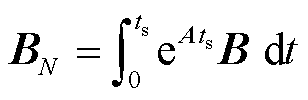 (26)
(26)
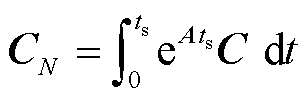 (27)
(27)
则轴转矩波动与有功功率波动变化的关系为
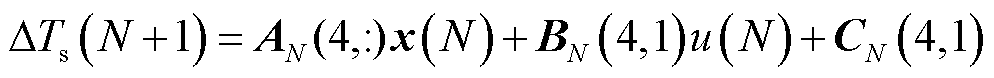 (28)
(28)
在实际的调频过程中,通过负荷波动以及风电机组各参量的观测值计算得到轴转矩波动情况,以此为优化目标对风电机组功率分配进行调整。
当调频功率信号的频率分量接近风机轴系的自然振荡频率时,会引发较大的轴转矩波动,导致轴系疲劳载荷累积加速。因此,为实现对轴系疲劳的有效控制,必须设计调频策略以合理分配频率分量,同时避免共振点及附近的影响。
风储参与一次调频是一个实时动态的过程,系统需要对频率变化做出快速而准确的响应。低通滤波器简单、计算效率高,适合实时性要求高的场景,因此选择低通滤波器作为频率分解的方法。
低通滤波器可表示为
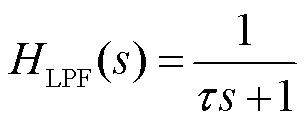 (29)
(29)
式中,τ为滤波器的时间常数。
输入的信号经过低通滤波器之后,得到的输出会有一定的相位滞后。为弥补低通滤波器所造成的相位滞后,增加一个相位补偿器,其表达式为
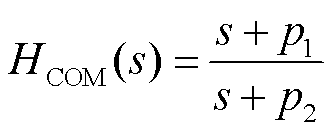 (30)
(30)
式中,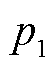 与零点相关,确保相位补偿器能基本弥补低通滤波器造成的相位延迟;
与零点相关,确保相位补偿器能基本弥补低通滤波器造成的相位延迟;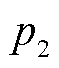 与极点相关,限制高频范围的增益和相位响应。
与极点相关,限制高频范围的增益和相位响应。
经过相位补偿器之后,会给低频范围信号的幅值造成一定的衰减。为了弥补衰减,设置幅值补偿器,其表达式为
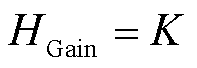 (31)
(31)
式中,K为增益系数,维持系统幅值响应保持稳定。
将低通滤波器、相位补偿和幅值补偿结合,得到综合传递函数,其表达式为
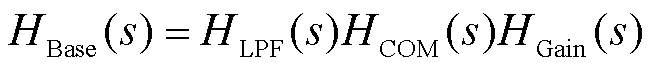 (32)
(32)
综合传递函数同时考虑了幅值响应和相位响应,既能有效地滤除高频分量,避免机械共振,又能够在低频范围内保持调节任务的快速性和精度。
在分频响应策略中,合理调整频率分点可以优化风机与储能系统的任务分配。为了适应不同负荷波动的动态变化,本文提出了一种频率分点动态调整方法。
2.2.1 序列二次规划算法
储能系统能够快速地响应负荷波动,但其过度的充放电会影响寿命。同时风电机组轴扭矩波动是疲劳载荷累积的主要因素,因此确定优化目标为最小化轴转矩波动,同时限制储能的过度充放电,则目标函数为
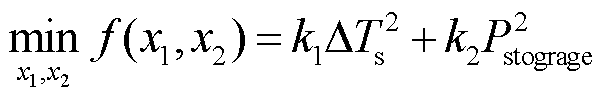 (33)
(33)
式中, 为实际储能出力;
为实际储能出力;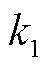 、
、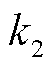 为优化目标的权重;
为优化目标的权重;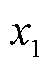 为风机功率;
为风机功率;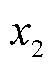 为储能功率。
为储能功率。
为确保调频目标的实现,风机和储能输出的总功率必须满足功率需求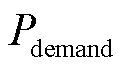 ,等式约束为
,等式约束为
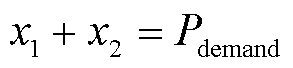 (34)
(34)
同时风机和储能的出力控制在其上下限出力范围内,不等式约束为
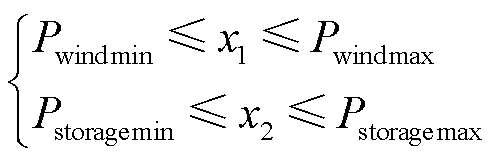 (35)
(35)
式中,Pwindmin和Pwindmax分别为风电机组最小和最大可输出功率;Pstoragemin和Pstoragemax分别为储能最小和最大可输出功率。
当前优化问题需要在调频控制期间实时进行,并且具有非线性目标函数以及线性约束的特性,同时决策量较少(仅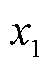 、
、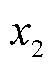 ),所以选择采用序列二次规划算法(Sequential Quadratic Programming, SQP)。SQP利用目标函数和约束条件构造增广目标函数,借此将约束最优化问题转换为无约束最优化问题。该方法收敛性好、计算效率高、边界搜索能力强,当功率需求
),所以选择采用序列二次规划算法(Sequential Quadratic Programming, SQP)。SQP利用目标函数和约束条件构造增广目标函数,借此将约束最优化问题转换为无约束最优化问题。该方法收敛性好、计算效率高、边界搜索能力强,当功率需求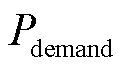 发生变化时,SQP优化可以快速响应,重新分配风机和储能的调节任务。
发生变化时,SQP优化可以快速响应,重新分配风机和储能的调节任务。
2.2.2 数据归一化处理
负荷发生波动后,通过SQP算法实时优化得到了理论上最优的风机和储能出力。在本文提到的方法中,频率分点决定了最终风机和储能的出力分配。因此,频率分点应根据优化结果动态调整,以适应系统的实时运行需求。
优化分配的结果包含风机功率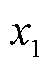 和储能功率
和储能功率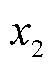 ,将其转换为归一化指标,即
,将其转换为归一化指标,即
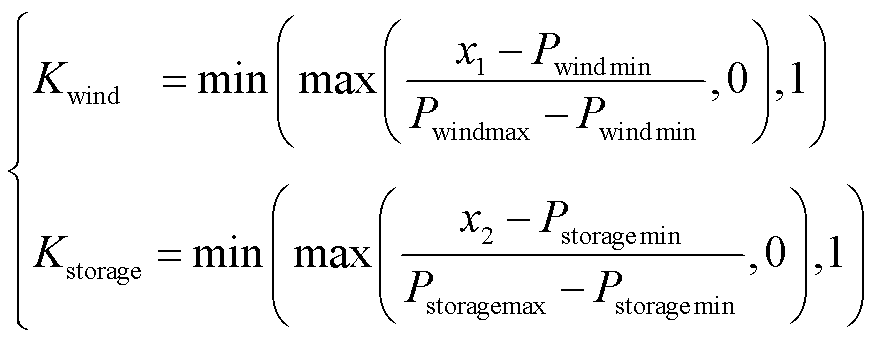 (36)
(36)
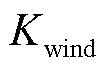 和
和 仅反映风机和储能在当前时刻承担的调节任务比例,无法反映当前系统调节压力的变化趋势。如果负荷突然增加,只考虑当前归一化值可能忽略了负荷波动对调节任务的整体影响。系统可能需要在负荷增加时更主动地降低分频点。引入
仅反映风机和储能在当前时刻承担的调节任务比例,无法反映当前系统调节压力的变化趋势。如果负荷突然增加,只考虑当前归一化值可能忽略了负荷波动对调节任务的整体影响。系统可能需要在负荷增加时更主动地降低分频点。引入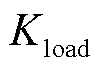 可以将风机和储能的任务分配与系统负荷波动直接关联,避免调频策略与实际负荷需求脱节,有
可以将风机和储能的任务分配与系统负荷波动直接关联,避免调频策略与实际负荷需求脱节,有
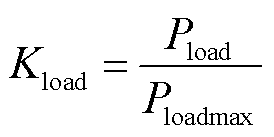 (37)
(37)
式中,Pload为系统负荷波动大小;Ploadmax为允许系统负荷波动最大值。
虽然归一化可以将指标限制在0~1,但数值的变化与实际状态的影响相关,输入的微小变化会导致输出的频率分点也发生线性变化。
为了频率分点的调整过程更加平滑和鲁棒,避免因小扰动引发的频繁调整,同时保证系统在面对大扰动时的灵敏响应能力,引入Sigmoid函数,它是一种S型非线性映射函数,其数学形式为
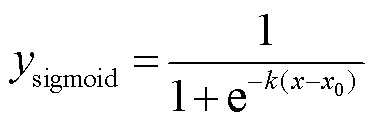 (38)
(38)
式中,k为灵敏度系数,通过调节k可以根据系统需求优化响应速度和平滑度;x0为中心位置,当输入x接近中心位置时,函数变化较为缓慢。
对于微小的输入波动,Sigmoid函数输出变化较小,可有效抑制小噪声对频率分点的影响。系统在面对小幅度扰动时,频率分点调整更平滑,避免频繁调节。对大幅度变化具备灵敏的响应能力,保证系统能够及时进行频率分点的有效调整。在面对较大负荷波动或储能/风机出力变化时,能够快速进行合理的分频点调整。归一化后的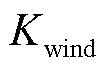 、
、 和
和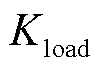 作为输入,通过Sigmoid函数得到
作为输入,通过Sigmoid函数得到 、
、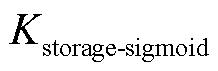 和
和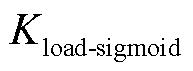 ,可以动态平稳地反映系统的实时状态,避免直接使用导致剧烈波动。
,可以动态平稳地反映系统的实时状态,避免直接使用导致剧烈波动。
2.2.3 频率分点计算
根据负荷波动的方向,确定不同的频率分点调整策略。当系统负荷增加时,风机和储能出力任务同步增大,系统面临更高的调频需求。此时,频率分点的调整依据为
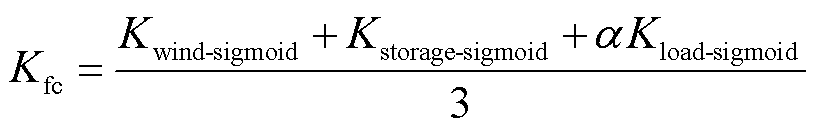 (39)
(39)
式中,α为负荷增加权重因子。三个指标加权平均,确保频率分点根据系统状态动态调整。
当系统负荷减少时,调频需求相对降低,此时,频率分点的调整依据为
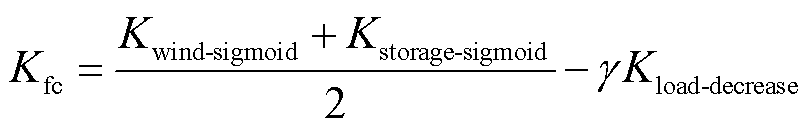 (40)
(40)
式中,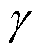 为负荷减少权重因子,通过参数
为负荷减少权重因子,通过参数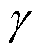 调节负荷减少时对频率分点的影响程度;
调节负荷减少时对频率分点的影响程度; 为负荷减少时的归一化指标。此时,负荷的直接影响作为负项引入,有效抑制频率分点的过度降低,避免系统在低负荷条件下频繁切换任务分配。
为负荷减少时的归一化指标。此时,负荷的直接影响作为负项引入,有效抑制频率分点的过度降低,避免系统在低负荷条件下频繁切换任务分配。
根据频率分点的调整因子,基于线性插值原理,通过式(41)动态计算最终的频率分点。
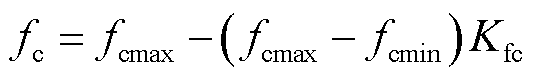 (41)
(41)
式中,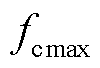 为频率分点上边界;
为频率分点上边界;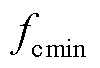 为频率分点下边界。
为频率分点下边界。
通过这种动态计算方法控制频率分点始终保持在预定的有效范围内,同时确保了频率分点平滑调整,频率分点动态调整流程如图3所示。
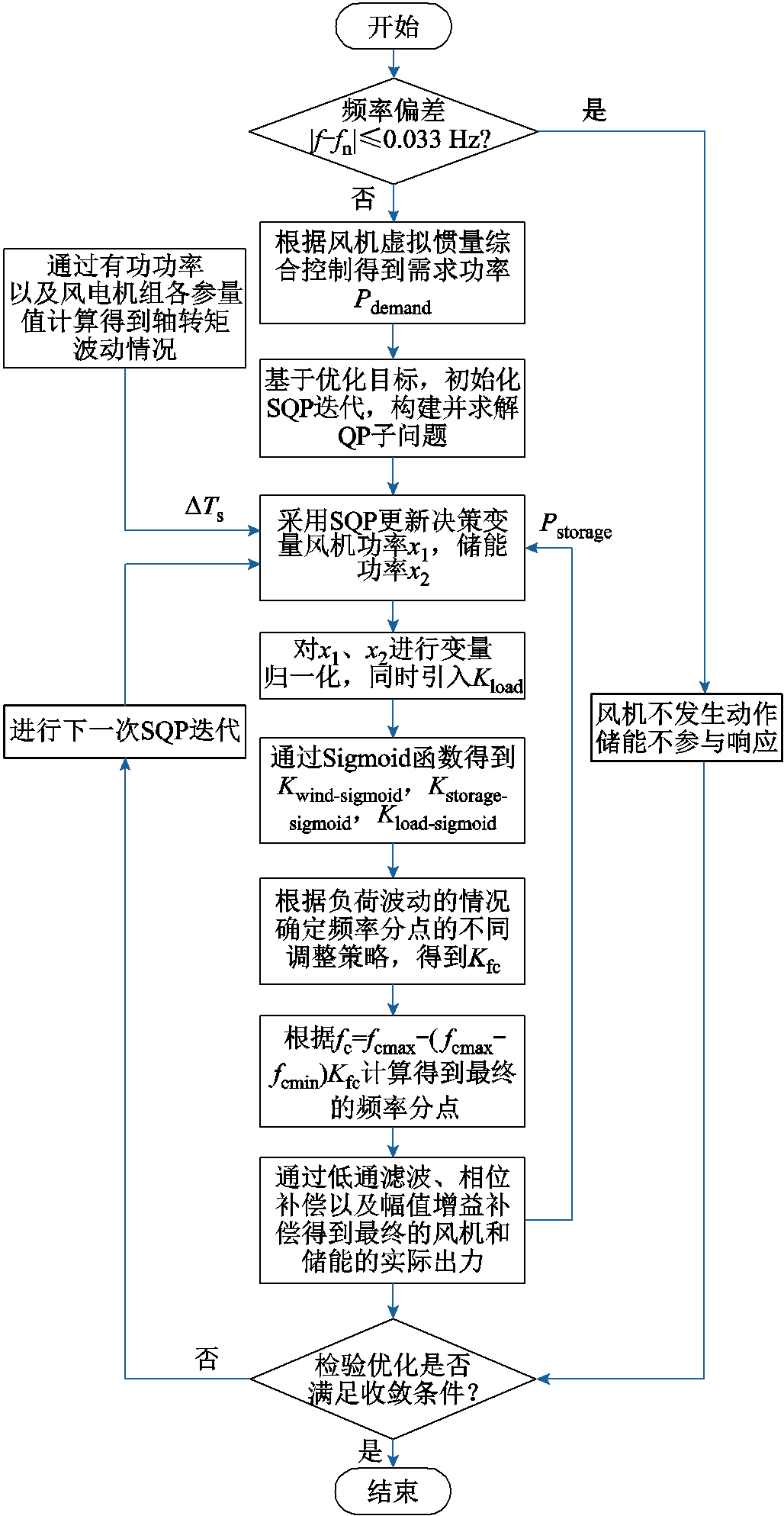
图3 风储分频段响应流程
Fig.3 Flow chart of frequency-domain response for wind-storage
本文以2 MW双馈风力发电机组作为对象,在Bladed搭建其机械模型,在Matlab/Simulink中搭建风电机组系统频率响应模型,通过标幺化将单台风机等效为200 MW风电场(100台风机),系统总容量为1 000 MW,风电渗透率为20%。储能装置选择超级电容器,额定功率为0.2MW,额定容量为0.001 6 MW·h,对应于标幺化后的数值。通过搭建Matlab-GH Bladed联合仿真平台,对本文所提策略进行仿真验证。
设置恒定风速10 m/s,当仿真运行到55 s时,负荷突增0.12(pu),频率分点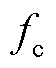 为0.05 Hz。通过两种对比策略验证所提策略的有效性:策略一是仅风机转子动能参与调频,用以验证储能参与调频对风机轴系疲劳载荷的减缓效果;策略二是风储按固定比例参与调频,控制其与本文策略在调频时间内的总平均出力一致,确保对比的公平性,从而排除累积出力对轴系疲劳载荷的影响;本文所提策略为策略三。不同策略的仿真结果如图4所示。
为0.05 Hz。通过两种对比策略验证所提策略的有效性:策略一是仅风机转子动能参与调频,用以验证储能参与调频对风机轴系疲劳载荷的减缓效果;策略二是风储按固定比例参与调频,控制其与本文策略在调频时间内的总平均出力一致,确保对比的公平性,从而排除累积出力对轴系疲劳载荷的影响;本文所提策略为策略三。不同策略的仿真结果如图4所示。
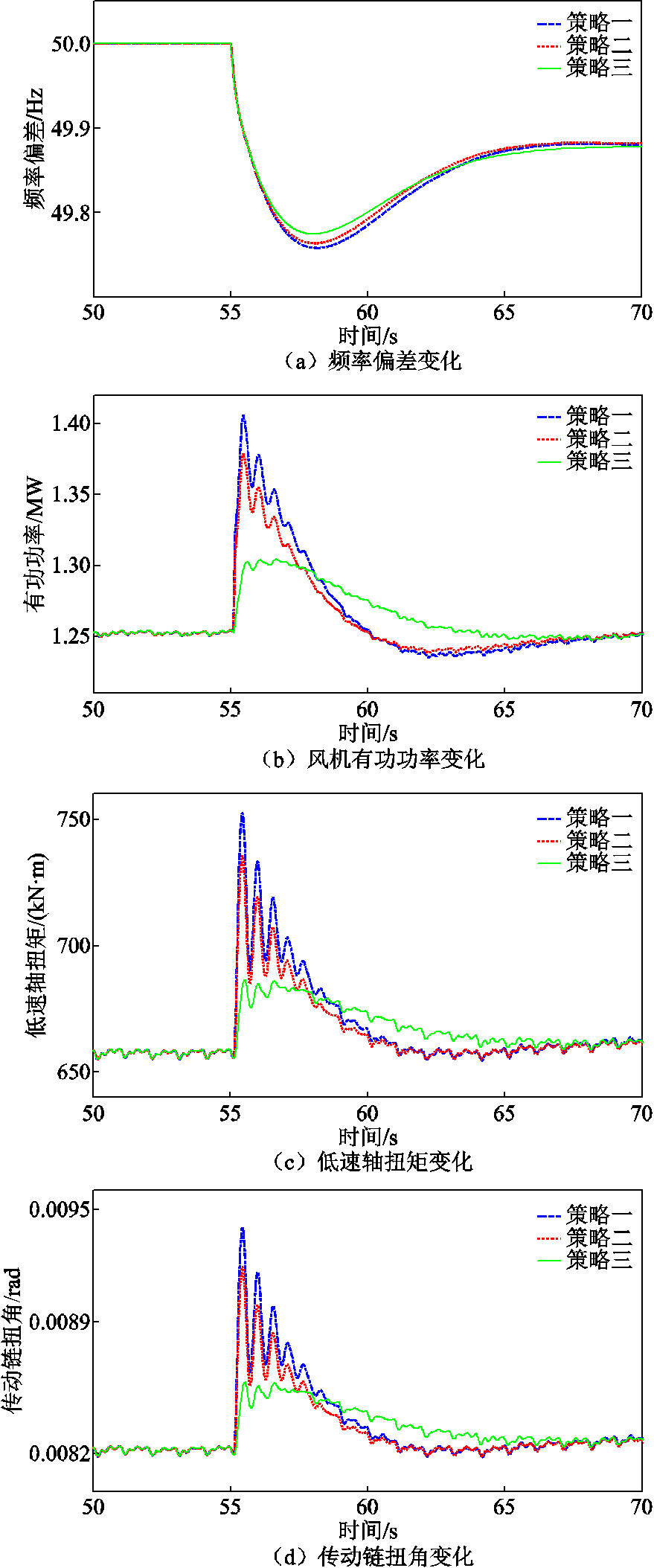
图4 不同策略下仿真变化曲线
Fig.4 Simulation curves under different strategies
如图4所示,图4a给出了三种策略下系统频率变化,最大功率点追踪(Maximum Power Point Tracking, MPPT)运行状态下最大频率偏差为-0.36Hz策略一、策略二和策略三各自的最大频率偏差为-0.225、-0.235和-0.242Hz。图4b给出了三种策略下风机有功出力变化,负荷突变后,策略三中风电机组有功输出的峰值小于策略二中风电机组有功输出峰值,但其衰减速度远小于策略二。在负荷突变3 s左右,策略三中的风机有功输出超过策略二中的风机有功输出。最终两种策略中的风机有功输出在同一时间趋于稳定,保证了平均出力大小相同。图4c和图4d分别给出了三种策略下风机传动链扭角和低速轴扭矩的变化曲线,相较于其他两个策略,策略三中的低速轴扭矩和传动链扭角的大小和波动程度都大幅降低。
根据工况一仿真运行结果,计算得到了不同策略下低速轴转矩数据,以及经雨流计数后不同策略下低速轴等效疲劳载荷情况,计算结果见表1。
表1 工况一不同策略下低速轴等效疲劳载荷及转矩特性对比
Tab.1 Comparison of equivalent fatigue loads and torque characteristics of low-speed shafts under different strategies in operating condition 1

调频策略等效疲劳载荷/(kN·m)等效疲劳载荷减少百分比(%)平均转矩/(kN·m)动态波动峰峰值/(kN·m)波动标准差/(kN·m) 策略一39.920661.6798.047.81 策略二32.8417.74661.8981.016.35 策略三13.0967.2661.2732.074.54
策略一、策略二和策略三中的低速轴等效疲劳载荷分别为39.92、32.84、13.09 kN·m;以策略一作为参考,策略二中的低速轴等效疲劳载荷减少了17.8%,而策略三中的低速轴等效疲劳载荷减少了67.2%,更大程度上缓解了轴系上的载荷负担。同时以策略一、二作为对比,策略三中低速轴转矩的动态波动峰峰值和波动标准差最小,更显著地抑制了轴系扭振的瞬时冲击和波动。
由图2可知0.1 Hz以下的幅频增益已经远小于-40 dB,此频段内的电磁转矩对轴系扭振的激励作用影响较小,同时需求功率的频谱特性分析表明,其主要能量分布集中在0.1 Hz以下的低频段,所以将0.1 Hz作为分频点的初始值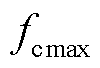 ,设定0.01 Hz作为分频点的下界
,设定0.01 Hz作为分频点的下界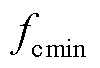 。为了验证动态频率分点调整策略,仿真工况设置风速为湍流风速,平均风速为10 m/s,其纵向、横向和垂直湍流强度分别为2%、2%和1%。仿真运行到50 s时,负荷连续变化,每12 s变化一次。不同策略的仿真结果如图5、图6所示。
。为了验证动态频率分点调整策略,仿真工况设置风速为湍流风速,平均风速为10 m/s,其纵向、横向和垂直湍流强度分别为2%、2%和1%。仿真运行到50 s时,负荷连续变化,每12 s变化一次。不同策略的仿真结果如图5、图6所示。
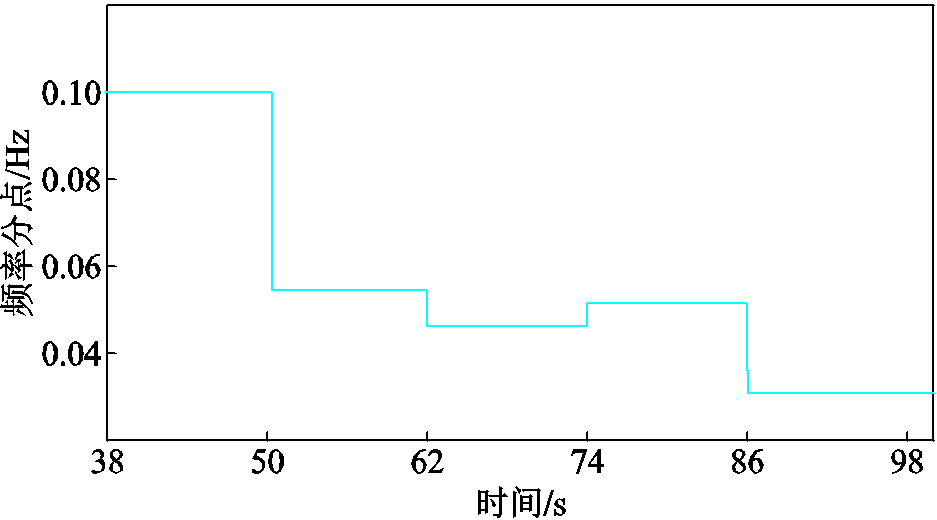
图5 频率分点变化曲线
Fig.5 Curve of frequency modulation variation
图5给出了连续负荷波动下频率分点的变化。根据频率分点的调整依据,在负荷相对增加的时候,频率分点降低;在负荷相对减小的时候,频率分点升高或者不动。结合图中频率变化以及功率变化,所得频率分点符合调整依据。
图6a和图6b为三种策略下系统频率和有功功率变化情况,相较于其他两策略,策略三相对减少了最大频率偏差和有功功率的输出峰值。图6c和图6d给出了对应的三种策略下储能SOC变化以及储能出力变化情况,可以看出,策略二和策略三中的SOC值在仿真时间100 s左右时段相同,表明两种策略在负荷连续波动的时段内,平均出力是相同的。图6e和图6f给出了三种策略下低速轴扭矩和传动链扭角的变化情况,对比于其他两种策略,策略三中的低速轴扭矩和传动链扭角的大小和波动程度都大幅降低。
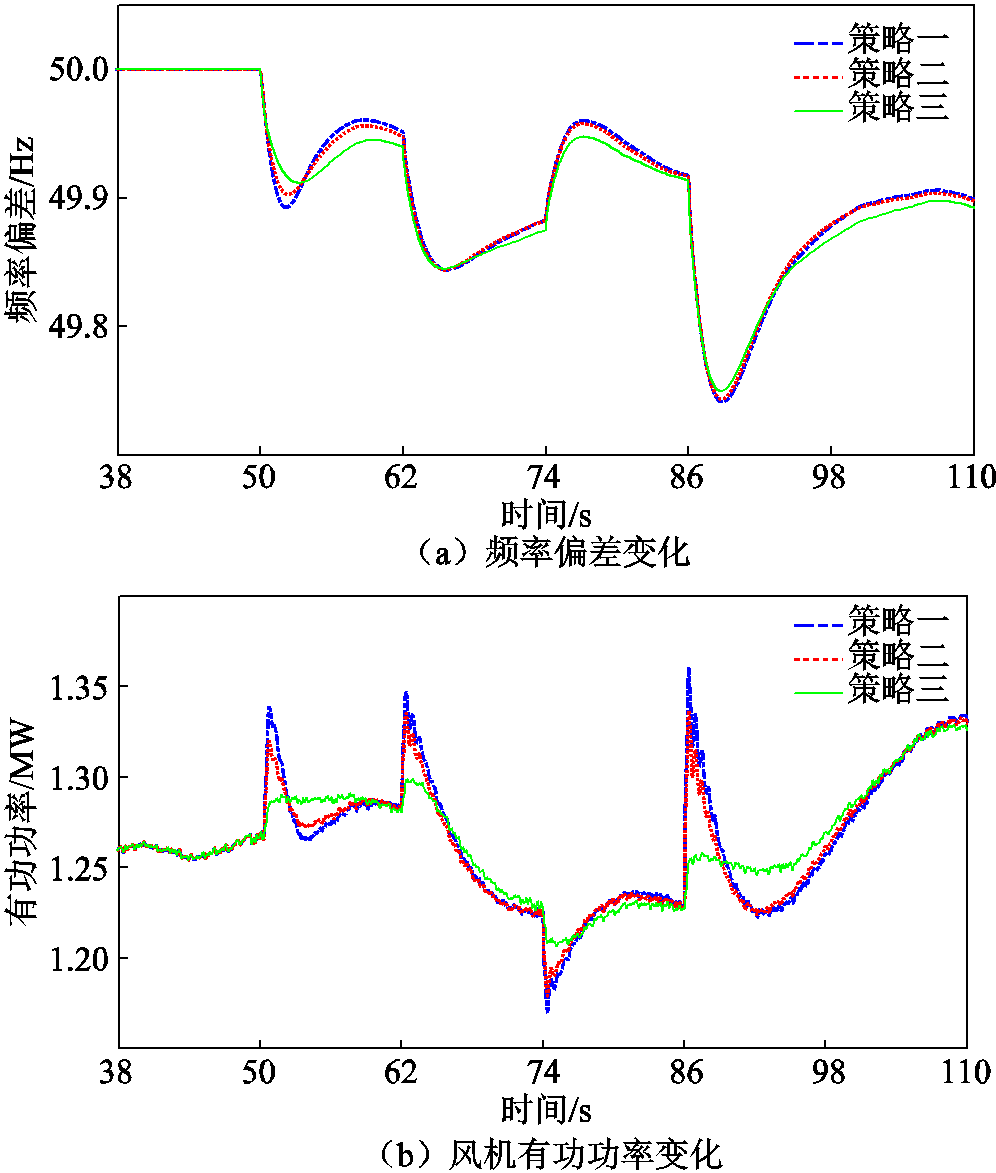
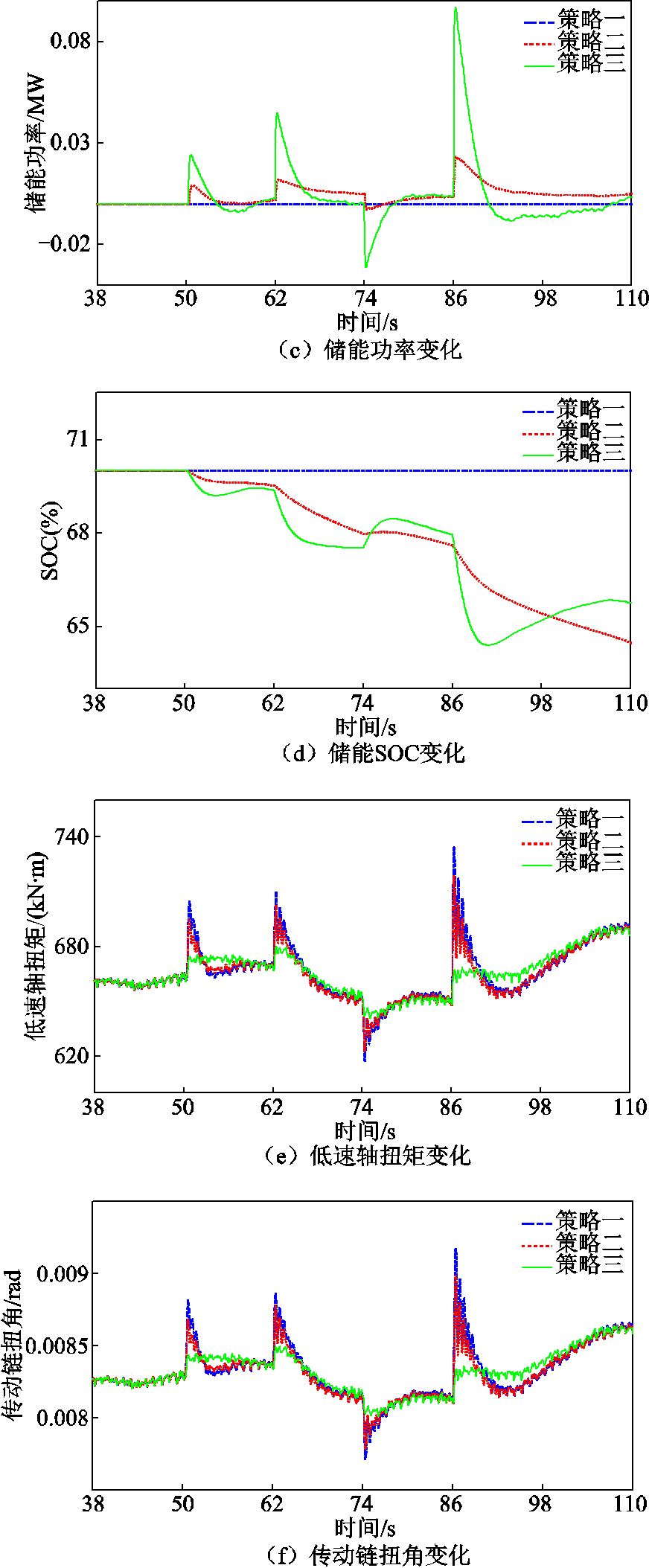
图6 不同策略下仿真变化曲线
Fig.6 Simulation curves under different strategies
根据工况二仿真运行结果,计算得到了不同策略下低速轴转矩数据,以及经雨流计数后不同策略下低速轴等效疲劳载荷情况,计算结果见表2。
表2 工况二不同策略下低速轴等效疲劳载荷及转矩特性对比
Tab.2 Comparison of equivalent fatigue loads and torque characteristics of low-speed shafts under different strategies in operating condition 2

调频策略等效疲劳载荷/(kN·m)等效疲劳载荷减少百分比(%)平均转矩/(kN·m)动态波动峰峰值/(kN·m)波动标准差/(kN·m) 策略一48.790667.18117.5215.38 策略二40.4617.07666.8996.6914.51 策略三23.2152.43666.7655.3713.37
策略一、策略二和策略三中的低速轴等效疲劳载荷分别为48.79、40.46、23.21 kN·m;以策略一作为参考,策略二中的低速轴等效疲劳载荷减少了17.07%,而策略三中的低速轴等效疲劳载荷减少了52.43%。同时以策略一、二作为对比,策略三中低速轴转矩的动态波动峰峰值和波动标准差最小。
为了缓解风电机组参与调频过程中的疲劳载荷累积问题,本文分析了传动链轴系的扭振特性,构建了传动链疲劳载荷灵敏度模型,提出了一种基于分频段响应的风储联合调频控制方法,动态调整滤波器参数,同时避免自然振荡频率附近的功率信号对轴系的影响。通过建模与联合仿真验证,得出以下结论:
1)通过风机传动链二阶方程,推导了发电机电磁转矩对传动链扭角速度的传递函数。结果表明,以电磁转矩作为输入对传动链扭转角速度的影响在自然振荡频率附近最大。基于此,设计风储分频段响应方法,调频功率信号通过低通滤波、相位和幅值补偿进行频段划分后分配给风机和储能系统。
2)通过构建风电机组疲劳载荷灵敏度模型,明确了传动链轴转矩波动与有功功率波动之间的关系。以轴转矩波动和储能出力为优化目标,提出了一种动态频率分点调整方法,通过分频响应方法,能够对优化结果进行处理,从而在实时状态下得到最优的风机和储能出力分配方案。
3)搭建Matlab/Simulink-GH Bladed联合仿真平台验证本文策略。以仅风机转子动能出力和风储按比例出力作为对比策略,仿真过程中控制风储平均出力,避免累积出力的影响。分别在平均风速与单次负荷变化和湍流风速与连续负荷波动下对分频策略和动态分频策略进行验证。仿真结果表明,在保证快速调频响应的同时,所提方法显著降低了风机轴系的扭矩与扭转角波动幅度,大幅降低了轴系的等效疲劳载荷。
参考文献
[1] 张丽英, 叶廷路, 辛耀中, 等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报, 2010, 30(25): 1-9.
Zhang Liying, Ye Tinglu, Xin Yaozhong, et al. Problems and measures of power grid accommodating large scale wind power[J]. Proceedings of the CSEE, 2010, 30(25): 1-9.
[2] 胡正阳, 高丙团, 张磊, 等. 风电机组双向支撑能力分析与自适应惯量控制策略[J]. 电工技术学报, 2023, 38(19): 5224-5240.
Hu Zhengyang, Gao Bingtuan, Zhang Lei, et al. Bidirectional support capability analysis and adaptive inertial control strategy of wind turbine[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5224-5240.
[3] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[4] 张祥宇, 邵孜建, 付媛. 风储并网发电系统的虚拟多段协同调速与频率安全支撑技术[J]. 电工技术学报, 2025, 40(15): 4677-4693.
Zhang Xiangyu, Shao Zijian, Fu Yuan. Virtual multi-stage coordinated speed regulation and frequency safety support technology of wind-storage grid-connected power generation system[J]. Transactions of China Electrotechnical Society, 2025, 40(15): 4677-4693.
[5] 钱敏慧, 张建胜, 秦文萍, 等. 高比例风电联网背景下风电机组快速频率支撑研究综述[J]. 太阳能学报, 2025, 46(10): 714-726.
Qian Minhui, Zhang Jiansheng, Qin Wenping, et al. Rewiew of fast frequency support of WTGS under background of high proportion wind power interconnection[J]. Acta Energiae Solaris Sinica, 2025, 46(10): 714-726.
[6] 高海淑, 张峰, 丁磊. 风电机组两分段下垂调频控制策略及参数整定方法[J]. 电力系统自动化, 2023, 47(18): 111-121.
Gao Haishu, Zhang Feng, Ding Lei. Two-segment droop frequency regulation control strategy and parameter setting method for wind turbines[J]. Automation of Electric Power Systems, 2023, 47(18): 111-121.
[7] 张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑[J]. 电工技术学报, 2024, 39(3): 672-685.
Zhang Xiangyu, Hu Jianfeng, Fu Yuan, et al. Virtual inertia demand and collaborative support of wind power and energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 672-685.
[8] 赵洪山, 李自立. 风电机组轴系的剩余寿命预估[J]. 电力自动化设备, 2020, 40(6): 70-75, 99.
Zhao Hongshan, Li Zili. Prognosis of remaining lifetime of wind turbine unit shafting[J]. Electric Power Automation Equipment, 2020, 40(6): 70-75, 99.
[9] Zhang Xiaojie, He Wei, Hu Jiabing. Impact of inertia control of DFIG-based WT on torsional vibration in drivetrain[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2525-2534.
[10] 林莉, 林雨露, 谭惠丹, 等. 计及SOC自恢复的混合储能平抑风电功率波动控制[J]. 电工技术学报, 2024, 39(3): 658-671.
Lin Li, Lin Yulu, Tan Huidan, et al. Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 658-671.
[11] 缪雅慧, 焦燕, 徐浩. 含储能的多能互补系统功率控制方案[J]. 电气技术, 2024, 25(5): 75-80.
Miao Yahui, Jiao Yan, Xu Hao. Power control scheme of multi-energy complementary system with energy storage[J]. Electrical Engineering, 2024, 25(5): 75-80.
[12] 颜湘武, 孙雪薇, 崔森, 等. 基于转子动能与超级电容器储能的双馈风电机组惯量和一次调频改进控制策略[J]. 电工技术学报, 2021, 36(增刊1): 179-190.
Yan Xiangwu, Sun Xuewei, Cui Sen, et al. Improved control strategy for inertia and primary frequency regulation of doubly fed induction generator based on rotor kinetic energy and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 179-190.
[13] 马德智, 栗文义, 温彩凤, 等. 基于双馈发电机组调频参与度的风/储协调一次调频控制策略[J]. 电网技术, 2023, 47(3): 968-979.
Ma Dezhi, Li Wenyi, Wen Caifeng, et al. Wind/storage coordinated primary frequency regulation control strategy based on participation level of DFIG units[J]. Power System Technology, 2023, 47(3): 968-979.
[14] 张冠锋, 杨俊友, 王海鑫, 等. 基于虚拟同步机技术的风储系统协调调频控制策略[J]. 电工技术学报, 2022, 37(增刊1): 83-92.
Zhang Guanfeng, Yang Junyou, Wang Haixin, et al. Coordinated frequency modulation control strategy of wind farm-storage system based on virtual synchronous generator technology[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 83-92.
[15] 曲彤, 苏小林, 阎晓霞, 等. 基于分频原理和区域控制的风储火联合调频策略[J]. 电测与仪表, 2018, 55(20): 122-129, 147.
Qu Tong, Su Xiaolin, Yan Xiaoxia, et al. Frequency combination modulation strategy of wind power, energy storage and thermal power unit system based on frequency division and regional control principle [J]. Electrical Measurement & Instrumentation, 2018, 55(20): 122-129, 147.
[16] 陈彪, 王玮, 高嵩, 等. 基于模糊自适应指令分解的飞轮-火电一次调频控制策略[J]. 电力系统自动化, 2023, 47(19): 128-137.
Chen Biao, Wang Wei, Gao Song, et al. Primary frequency regulation control strategy for flywheel-thermal power joint system based on fuzzy adaptive command decomposition[J]. Automation of Electric Power Systems, 2023, 47(19): 128-137.
[17] 陈鹏, 王玮, 杨建青, 等. 基于多尺度分解的风火储协同调频控制策略[J]. 太阳能学报, 2024, 45(3): 428-435.
Chen Peng, Wang Wei, Yang Jianqing, et al. Cooperative frequency regulation control strategy of wind-thermal-storage system based on multi-scale decomposition[J]. Acta Energiae Solaris Sinica, 2024, 45(3): 428-435.
[18] 杨伟峰, 文云峰, 张武其, 等. 基于风-储联合的双层频率响应控制策略[J]. 电力系统自动化, 2022, 46(12): 184-193.
Yang Weifeng, Wen Yunfeng, Zhang Wuqi, et al. Bi-level frequency response control strategy based on wind power and energy storage[J]. Automation of Electric Power Systems, 2022, 46(12): 184-193.
[19] 王中权, 刘维斌, 孙枭雄, 等. 限功率工况风电场一次调频与疲劳抑制协调优化控制研究[J]. 电网与清洁能源, 2023, 39(2): 114-121.
Wang Zhongquan, Liu Weibin, Sun Xiaoxiong, et al. A study on coordinated optimal control for primary frequency regulation and fatigue suppression of wind farms under limited power condition[J]. Power System and Clean Energy, 2023, 39(2): 114-121.
[20] 孙涵. 风电机组参与一次调频疲劳载荷特征分析及降载控制方法[D]. 哈尔滨: 哈尔滨工业大学, 2023.
Sun Han. Analysis of fatigue load characteristics of wind turbine participating in primary frequency regulation and load reduction control method[D]. Harbin: Harbin Institute of Technology, 2023.
[21] 杨德健, 王鑫, 严干贵, 等. 计及调频死区的柔性风储联合频率控制策略[J]. 电工技术学报, 2023, 38(17): 4646-4656.
Yang Dejian, Wang Xin, Yan Gangui, et al. Flexible frequency regulation scheme of DFIG embed battery energy storage system considering deadbands[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4646-4656.
[22] 彭海涛, 何山, 袁至, 等. 基于改进转子转速和桨距角协调控制的变速风电机组一次调频策略[J]. 电力自动化设备, 2023, 43(9): 87-94.
Peng Haitao, He Shan, Yuan Zhi, et al. Primary frequency regulation strategy for variable-speed wind turbines based on improved coordinated control of rotor speed and pitch angle[J]. Electric Power Automation Equipment, 2023, 43(9): 87-94.
[23] Zhao Haoran, Wu Qiuwei, Huang Shaojun, et al. Fatigue load sensitivity-based optimal active power dispatch for wind farms[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1247-1259.
[24] Wang Yingwei, Guo Yufeng, Zhang Dongrui. Optimal ancillary control for frequency regulation of wind turbine generator based on improved fatigue load sensitivity[J]. International Journal of Electrical Power & Energy Systems, 2022, 137: 107751.
[25] 潘沈恺, 高丙团, 毛永恒, 等. 考虑机组疲劳载荷的风电场快速有功功率分配方法[J]. 电力系统自动化, 2024, 48(15): 112-121.
Pan Shenkai, Gao Bingtuan, Mao Yongheng, et al. Fast active power distribution method for wind farms considering fatigue loads of wind turbines[J]. Auto-mation of Electric Power Systems, 2024, 48(15): 112-121.
Abstract The large-scale integration of wind power into the grid has significantly reduced the frequency stability of the power system. To ensure the safe and stable operation of the power system, wind turbines participating in the grid are required to actively engage in primary frequency control and provide effective frequency support. However, the frequent fluctuations in grid frequency can cause frequent variations in the electromagnetic torque of the generators, and their sensitive mechanical structures may bear greater fatigue loads. The accumulation of these fatigue loads poses a threat to the safe and stable operation of the units and shortens the lifespan of the equipment.
In order to reduce the risk of shaft fracture due to the accumulation of fatigue loads in the shaft system caused by the participation of doubly-fed induction generator (DFIG) in frequency modulation, this paper proposes a frequency-segmented response-based coordinated frequency modulation control strategy for wind and energy storage systems. Firstly, a transfer function from the electromagnetic torque of the generator to the angular velocity of the transmission chain is derived through the wind turbine drive train model, and the amplitude-frequency characteristic curve is analyzed. Using the constructed fatigue load sensitivity model for wind turbines, the relationship between the fluctuations in the transmission chain shaft torque and power fluctuations is revealed. Secondly, a frequency-segmented response strategy for wind and energy storage is designed. The virtual inertia of the wind turbine and droop control are used to calculate the real-time frequency modulation power. The optimization objectives are the fluctuations in shaft torque and energy storage output. The optimal decision variables are obtained through a sequential quadratic programming algorithm, taking into account load fluctuation factors, and real-time adjustments are made to the filter parameters to avoid the natural oscillation frequency of the shaft system, thus distributing the frequency modulation power between the wind turbine and the energy storage system. Finally, a joint simulation platform of Matlab/Simulink-GH Bladed is built, and simulation validation is conducted.
Using only the output of the wind turbine rotor kinetic energy and the proportional output of wind storage as a comparison strategy, the simulation process controls the average output of wind storage to avoid the impact of accumulated output. The frequency division strategy and dynamic frequency division strategy are verified under varying average wind speeds and single load variations, as well as turbulent wind speeds and continuous load fluctuations. The simulation results under different working conditions indicate that the proposed strategy ensures a rapid response in frequency and significantly reduces the torque and angular fluctuation amplitude of the wind turbine shaft system, greatly lowering the equivalent fatigue load on the shaft system.
Based on the analysis and simulation verification, the main conclusions obtained are as follows: (1) By deducing the transmission chain’s second-order equations for a generator’s electromagnetic torque, the transfer function of the electromagnetic torque affecting the transmission chain's twist speed was derived. Results indicate that the effect of the electromagnetic torque acting as an input on the transmission chain’s twist velocity is maximum around the natural oscillation frequency. Therefore, considering that the modulated power signal should be divided into frequency bands after passing through low-pass filtering, phase and amplitude compensation, it is allocated to both the fan and the energy storage system. (2) By constructing a fatigue load sensitivity model for wind turbines, it was clearly elucidated that fluctuations in drive chain torque corresponded to variations in active power. Based on this relationship, an optimized dynamic frequency shifting method was proposed, with torque fluctuations and energy storage output as the optimization targets. (3) Simulation results indicate that, in ensuring rapid frequency response, the proposed method significantly reduces the torque and angular fluctuation of the rotor shaft system as well as significantly lowers its equivalent fatigue load.
Keywords:Doubly-fed induction generator (DFIG), fatigue load, drive chain, primary frequency modulation, energy storage
董 清 男,1970年生,副教授,研究方向为电力系统分析与控制。
E-mail:dq.d@163.com
颜湘武 男,1965年生,教授,博士生导师,研究方向为新能源电力系统稳定与控制、分布式发电并网与系统特性分析等。
E-mail:xiangwuy@ncepu.edu.cn(通信作者)
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.250056
国家自然科学基金资助项目(52207102)。
收稿日期 2025-01-09
改稿日期 2025-03-09
(编辑 赫 蕾)