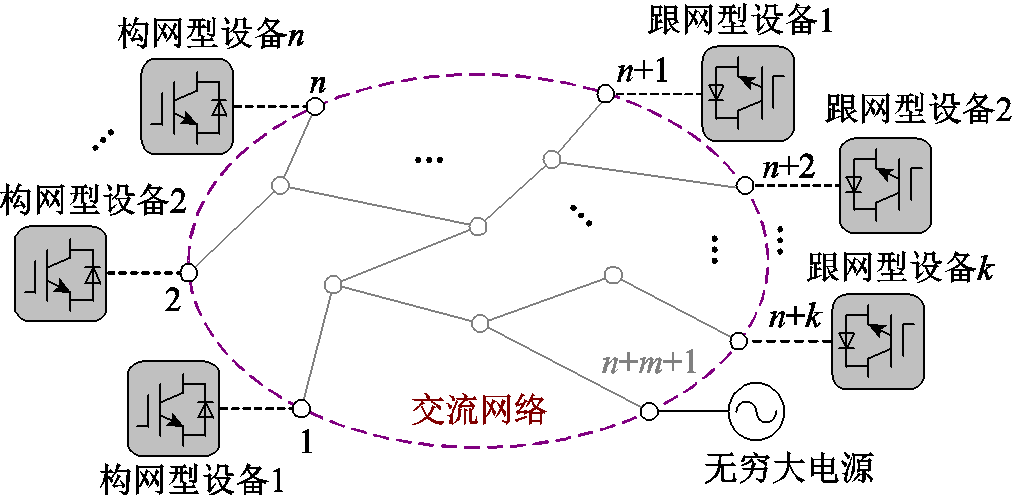
图1 含跟网型设备和构网型设备混联多馈入系统示意图
Fig.1 Diagram of hybrid multi-infeed system with GFMDs and GFLDs
摘要 未来电力系统将呈现大量跟网型与构网型设备混联并网新特征。然而,强电网背景下系统存在构网型设备引发的低频振荡问题,构网型设备异构特性以及跟网型与构网型设备交互作用如何影响该类低频振荡问题目前尚不清楚。为此,该文首先构建了适用于低频振荡分析的构网型和跟网型设备的简化模型;其次,基于矩阵摄动理论,分别针对考虑异构特性的构网型设备多馈入系统以及跟网型和构网型混联多馈入系统,构造了近似反映原系统低频主导模态的等效同构系统,保留了原系统网架结构特征,并得到了能反映原系统低频主导模态的特征子系统;然后,从系统强度的视角提出了考虑异构特性的系统低频段稳定性评估指标,并揭示了构网型设备异构特性以及跟网型设备动态对系统低频段稳定性的作用机理;最后,通过仿真算例说明了所提分析方法的有效性。
关键词:跟网型设备 构网型设备 低频振荡 特征子系统 系统强度
在能源转型和科技进步的推动下,中国电网逐渐演变为含高比例新能源和高比例电力电子设备的新型电力系统[1]。这些新能源设备或电力电子设备大多采用变流器作为接口,直接与交流电网相连。目前,实际工程中应用的变流器大多采用跟网型控制架构(简称跟网型设备,Grid-Following Device, GFLD),即通过锁相环(Phase-Locked Loop, PLL)实现变流器与电网之间的同步[2]。然而,已有研究表明跟网型设备对外呈现电流源特性,不具备电压、频率支撑能力,难以主动支撑电网运行[3]。此外,随着新能源占比的增加,双高电力系统电压支撑强度逐渐减弱,跟网型设备之间及其与电网间交互作用变强,容易引发PLL主导的次超同步振荡问题[4]。因此,新能源场站内全部机组采用跟网型控制难以适应电力系统未来弱电网化的趋势。
相比于跟网型设备的并网特性,采用构网型控制架构的变流器(简称构网型设备,Grid-Forming Device, GFMD)可以为电网提供电压和频率主动支撑,进而提升系统的电压支撑强度(简称系统强度),且在弱电网下具有较好的稳定性[5]。研究表明:在跟网型设备并网系统中增加少量构网型设备,可以改善原并网系统在弱电网条件下的小扰动稳定性[6-7]。由于存在上述优势,构网型设备在未来的电力系统中将得到广泛应用,未来高比例新能源电力系统将会是大量跟网型与构网型设备并存的复杂混联多馈入电力系统。
然而,已有研究表明构网型设备在高短路比强电网背景下存在低频振荡的风险[8]。例如,2023年4月,考艾岛电网出现了构网型设备交互引发的 1 Hz左右低频振荡问题[9],这种振荡失稳机制目前尚不清楚。由于新能源出力的强随机性,极端场景下系统可能出现电网新能源占比低的高短路比强电网场景,容易引发构网型设备主导的低频振荡问题。因此,探究强电网背景下构网型设备间交互作用引发的低频振荡作用机理,特别是分析跟网型设备接入如何影响该类型振荡问题,具有重要的工程应用价值。
现有的研究大多关注跟网型设备在弱电网下存在的次同步振荡问题。例如,文献[10]基于阻抗法,推导出系统多输入多输出阻抗模型,并采用舒尔补变换得到系统降阶后的单输入单输出传递函数,结合奈奎斯特判据判稳,利用降阶后的单输入单输出传递函数幅值或相角裕度评估系统稳定裕度。然而,舒尔补过程中可能引入右半平面极点,导致裕度评估结果误判[11]。文献[12]直接利用装备和网络的阻抗模型得到两者的回比矩阵,并结合广义奈奎斯特判据判稳。但分析过程较为复杂,相比于奈奎斯特判据不够直观。以上研究主要针对单新能源并网系统。针对由跟网型设备构成的多馈入系统,文献[13]提出了基于系统强度的小干扰稳定性分析方法,用于量化分析弱电网下跟网型设备中PLL主导的次/超同步频段主导模态的稳定裕度。其中,系统强度由表征电网电压支撑能力的广义短路比(generalized Short-Circuit Ratio, gSCR)和反映设备固有特性的临界短路比两部分构成。与此同时,构网型设备在强电网下存在的低频振荡问题也逐渐受到关注。例如,文献[14]表明,强电网条件下交流电网与风电机组控制耦合作用引入的负阻尼分量将变大,从而增加构网型变流器产生振荡的风险。文献[15]采用特征模式分析方法,分析了两台构网型设备并列运行时并网系统中设备之间的控制相互作用及主导低频失稳模式稳定性,结果表明虚拟同步控制参数对系统稳定性有重要影响,但是上述分析方法难以推广至多机系统。文献[16]将系统强度的概念扩展至分析构网型设备多馈入系统的低频段主导模态稳定性,但是仅关注了构网型设备外特性相同的同构多馈入系统(简称同构系统),对于设备外特性存在一定差异的构网型设备多馈入系统(简称异构系统)在强电网下存在的低频振荡问题缺少深入研究。
此外,部分文献[17-19]探究了跟网型设备与构网型设备相互作用如何影响系统的低频段稳定性。文献[17]提出用自/互影响分量来量化弱电网下构网型与跟网型设备之间相互作用强度的分析方法,研究发现构网型与跟网型设备之间的相互作用程度增强将有利于系统稳定性。文献[18]建立了跟网型光伏和构网型储能混联系统的单输入单输出等效阻抗模型,基于正阻尼判据深入分析了影响该系统稳定性的关键因素,研究发现在跟网型光伏并网系统中接入构网储能可以有效地提升混联系统在弱电网条件下的稳定性,但同时会导致其在强电网条件下的稳定性变差。文献[19]构建了含跟网型光伏及构网型储能并网系统的综合阻抗模型,采用阻抗分析法,实现了弱电网条件下稳定性的准确评估,研究发现构网型设备在弱电网下可改善并联系统的稳定性。但这些研究主要聚焦于弱电网背景下系统存在的次超同步振荡问题,未涉及强电网背景下混联并网系统中构网型设备主导的低频振荡问题;此外,上述研究仅适用于小规模互联系统,难以推广到大系统中。综上所述,强电网背景下关于构网型与跟网型设备交互作用如何影响含跟网型设备和构网型设备混联多馈入系统(简称混联多馈入系统)的低频段稳定性的相关研究尚不完善。
为此,本文从系统强度的视角,提出了混联多馈入系统低频段主导模态稳定性分析方法,适用于分析混联多馈入系统中构网型变流器引发的低频振荡问题。首先,为简化分析,构建了适用于低频振荡分析的跟网型设备、构网型设备的简化动态模型;其次,分别针对考虑异构场景的构网型设备多馈入系统以及考虑跟网型设备接入场景的混联多馈入系统,构造了能近似反映原系统低频主导模态的特征子系统;然后,从系统强度的视角提出了原复杂多馈入系统的低频振荡稳定性评估指标,并揭示了构网型设备的异构特性以及跟网型设备与构网型设备间交互作用对系统低频振荡的作用机理;最后,通过算例验证了所提方法及推论的正确性。
考虑图1所示的含k台跟网型设备和n台构网型设备的混联多馈入系统。其中,节点1~n连接构网型设备,节点n+1~n+k连接跟网型设备,n+m+1为无穷大节点,剩余节点为无源节点。本文考虑的跟网型设备和构网型设备的控制框图如图2所示,跟网型设备采用基于PLL的矢量控制策略[16],构网型设备采用虚拟同步机控制策略[16]。其中,Iabc和Ioabc分别为流过滤波电感和流入外电网的三相电流,Vabc为并网公共连接点(Point of Common Coupling, PCC)的三相电压,Lf、Cf分别为滤波电感、滤波电容,下标d、q分别表示电气量在dq旋转坐标系下的d轴和q轴分量。为不失一般性,假设网络线路电阻R和电感L之比为定值(令τ=R/L,其中τ为常数),且忽略网络中电容的影响[20]。此外,本文主要考虑新能源设备运行在额定工况的情况。

图1 含跟网型设备和构网型设备混联多馈入系统示意图
Fig.1 Diagram of hybrid multi-infeed system with GFMDs and GFLDs
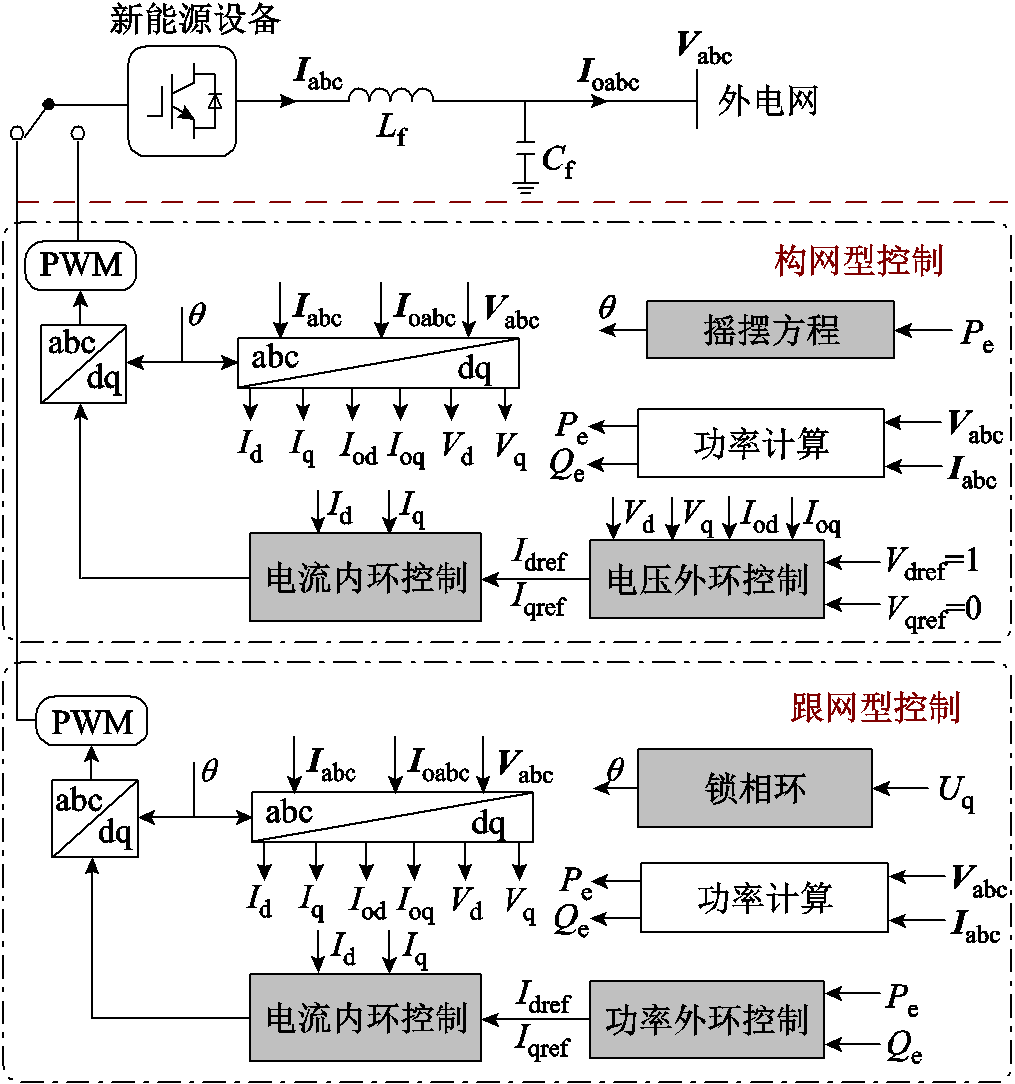
图2 构网型设备与跟网型设备控制框图
Fig.2 Control block diagram of a GFMD/GFLD
为分析混联多馈入系统的低频段稳定性,可在全局坐标系下,建立图1所示系统线性化后的频域动态模型。该模型分为装备侧传递函数矩阵YGm(s)和网络侧传递函数矩阵Ynetm(s)[21],可表示为如图3所示的多变量反馈系统形式。其中,ΔVxy和∆Ixy分别为各设备端口电压和电流微增量构成的列向量,系统对应的闭环特征方程可表示为
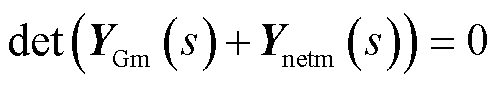 (1)
(1)
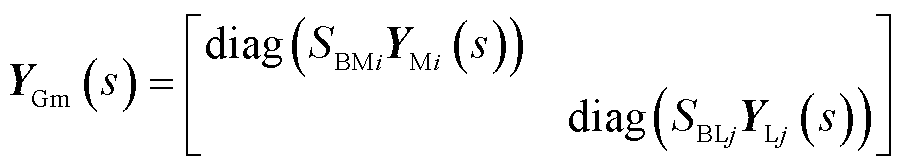 (2)
(2)
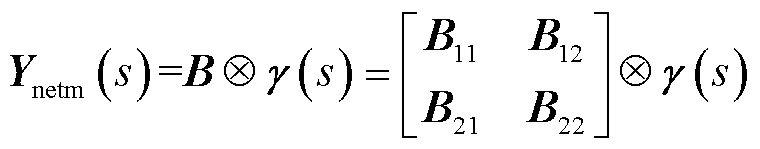 (3)
(3)
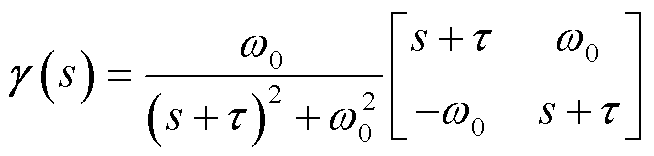 (4)
(4)
式中,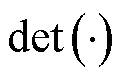 表示求矩阵的行列式;
表示求矩阵的行列式;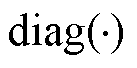 为对角矩阵;
为对角矩阵; 表示矩阵的Kronecker积;SBMi(i=1, 2,
表示矩阵的Kronecker积;SBMi(i=1, 2, , n)为第i台构网型设备经系统基准容量标幺后的自身额定容量;SBLj(j=n+1, n+2,
, n)为第i台构网型设备经系统基准容量标幺后的自身额定容量;SBLj(j=n+1, n+2, , n+m)为第j台跟网型设备经系统基准容量标幺后的自身额定容量,当节点j未接入跟网型设备时,SBLj=0;YMi(s)和YLj(s)分别为基于自身容量基准的第i台构网型设备和第j台跟网型设备的导纳传递函数矩阵;s为拉普拉斯算子; w0为系统额定角速度;B为网络结构保持的导纳矩阵[22];B11ÎRn´n,B12ÎRn´m,B21ÎRm´n, B22ÎRm´m;τ=Rij/Lij, Rij、Lij分别为线路的电阻和电感。
, n+m)为第j台跟网型设备经系统基准容量标幺后的自身额定容量,当节点j未接入跟网型设备时,SBLj=0;YMi(s)和YLj(s)分别为基于自身容量基准的第i台构网型设备和第j台跟网型设备的导纳传递函数矩阵;s为拉普拉斯算子; w0为系统额定角速度;B为网络结构保持的导纳矩阵[22];B11ÎRn´n,B12ÎRn´m,B21ÎRm´n, B22ÎRm´m;τ=Rij/Lij, Rij、Lij分别为线路的电阻和电感。
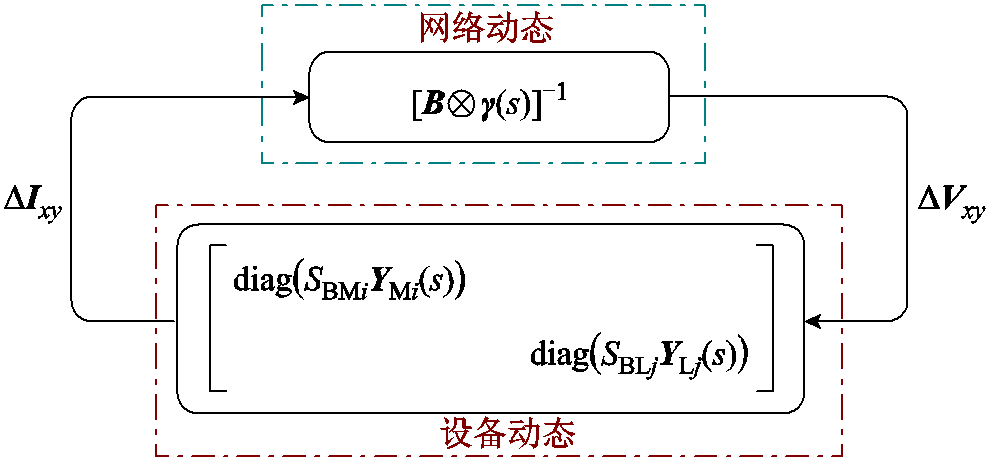
图3 混联多馈入系统的闭环动态特性
Fig.3 The closed-loop dynamic characteristics of the hybrid multi-infeed system
将式(2)和式(3)代入式(1),得到可用于低频段稳定性分析的系统闭环特征方程为
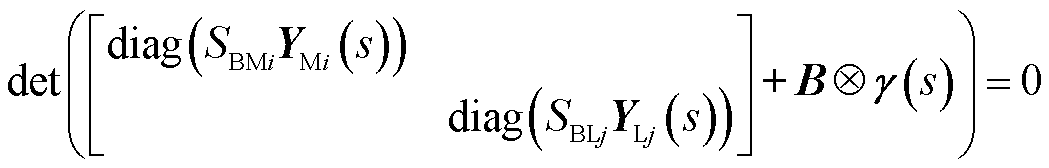 (5)
(5)
求解式(5)中s值,得到系统模态,进而可分析混联多馈入系统的稳定性。观察式(5)可知,跟网型设备和构网型设备通过网络存在复杂的耦合作用,难以直接求解式(5)中的s值,特别是对于系统中含大量新能源设备的场景。此外,当新能源设备为“黑箱”模型时,式(5)也难以解析s值。因此,如何分析跟网与构网间的相互作用对系统低频段稳定性的影响是个难题。
为解决上述难题,需要一种更为简便的方法来研究该混联多馈入系统的低频段稳定性。为此,本文拟回答如下两个问题:
1)考虑构网型设备异构时,如何评估强电网背景下构网型设备多馈入系统低频段稳定性,以及如何分析设备异构特性对系统低频段稳定性的影响。
2)考虑跟网型设备接入时,如何分析跟网型设备与构网型设备相互作用对系统低频段稳定性的影响。
由于本文重点关注构网型设备引发的低频振荡问题,为分析方便,下文将对构网型设备和跟网型设备进行简化处理。其中,网络忽略线路的动态,采用代数模型表示,具体可参考文献[23]。此外,构网型设备和跟网型设备简化模型如图4所示,具体介绍如下。
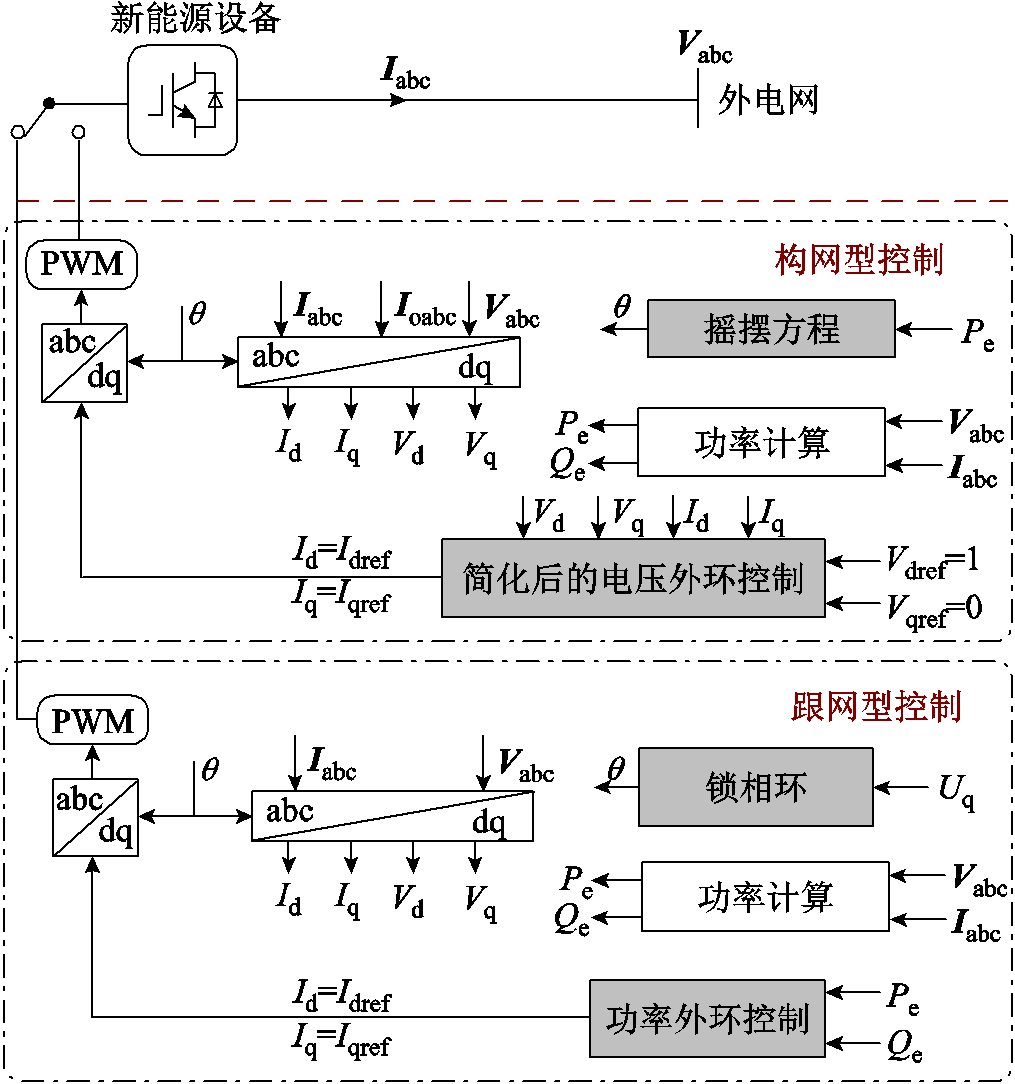
图4 用于分析低频振荡的构/跟网型设备简化模型示意图
Fig.4 The diagram of a simplified model of a GFMD/GFLD for analyzing low-frequency oscillations
为了简化分析,本节对构网型设备做以下简化:①忽略电流内环动态。通常电流内环响应速度较快,对应的控制时间尺度接近100 Hz,对于低频问题可近似忽略其动态过程。②忽略滤波电容和滤波电感。由于电流内环(或电压外环)的前馈wLf(或wCf)抵消了滤波电感Lf(或滤波电容Cf)的影响,因此可近似忽略两者的影响。
基于上述简化,构网型设备主要包括摇摆方程和电压外环控制的动态,其导纳模型可表示为
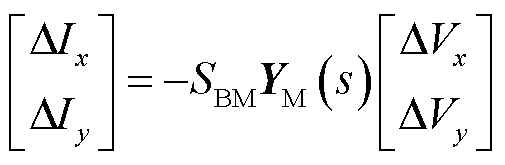 (6)
(6)
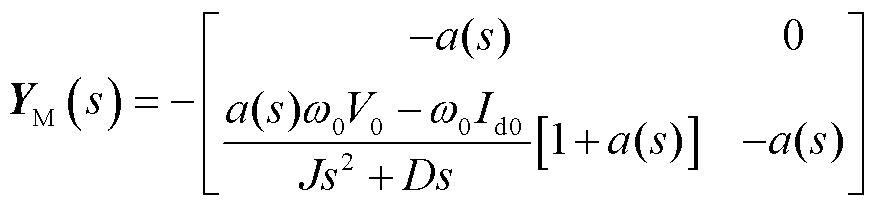 (7)
(7)
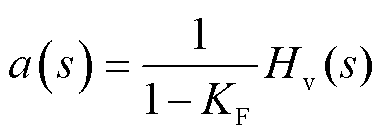 (8)
(8)
式中,YM(s)为基于自身容量基准的构网型设备导纳传递函数矩阵;Δ为变量的微增量;下标“0”表示平衡点处的值;Hv(s)为交流电压外环中PI调节器的传递函数;J为虚拟惯量;D为虚拟阻尼;KF为电流前馈系数;SBM为构网型设备容量。详细推导过程参考附录第2节。
对于跟网型设备,本文进行了如下简化:①忽略电流内环的动态。类似于2.1节的讨论,对于低频振荡问题,电流内环的动态足够快,可近似忽略。②忽略滤波电感和滤波电容的动态。由于电流内环含有电流前馈可抵消滤波电感的影响,故可以忽略滤波电感的动态。此外,滤波电容数值较小,相当于很大的负电抗接地,强电网背景下(电网线路电抗很小)可近似看成断路,故滤波电容动态也可忽略。
基于上述简化,跟网型设备主要包括PLL和功率外环的动态。对于跟网型设备,有功环考虑了直流电压控制和恒有功功率控制两种模式,无功环考虑了恒无功功率控制和恒交流电压控制两种模式。跟网型设备的导纳模型可表示为
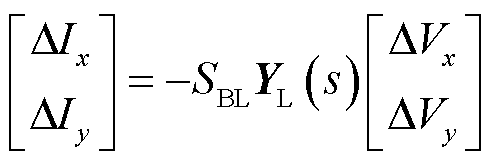 (9)
(9)
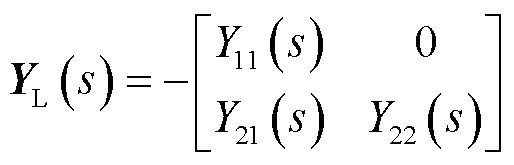 (10)
(10)
其中
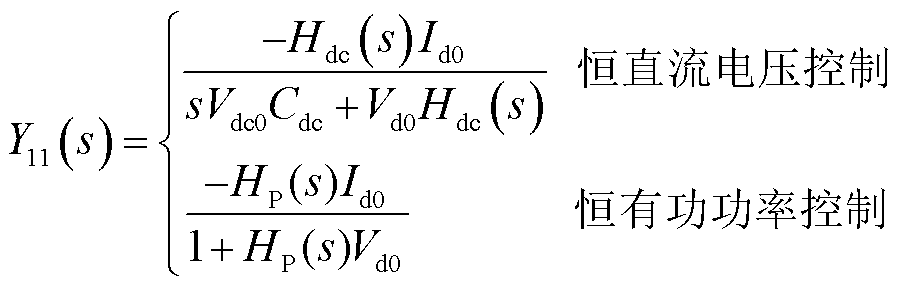 (11)
(11)
 (12)
(12)
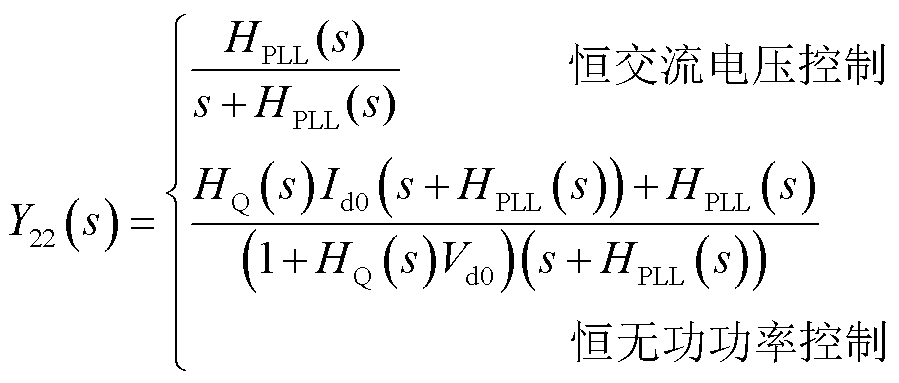 (13)
(13)
式中,YL(s)为基于自身容量基准的跟网型设备导纳传递函数矩阵;SBL为跟网型设备容量;Hdc(s)和Hp(s)分别为直流电压外环和有功功率外环中PI调节器的传递函数;Hvc(s)和HQ(s)分别为交流电压外环和无功功率外环中PI调节器的传递函数;HPLL(s)为PLLPI调节器的传递函数。具体推导参考附录第3节。
针对第1节所提第1个问题,本节主要分析构网型设备异构时,如何评估构网型设备多馈入系统的低频段稳定性,以及构网型设备异构特性对系统低频段稳定性的影响。
对于构网型设备多馈入系统,当考虑设备异构时,参考式(5)并结合第2节的简化模型,系统的特征方程可以表示为
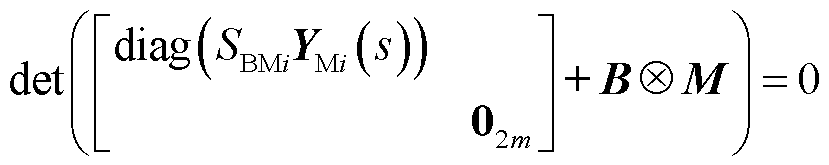 (14)
(14)
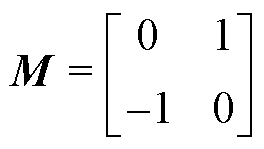 (15)
(15)
式中,02m为零矩阵。
用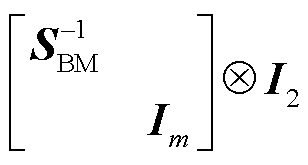 和
和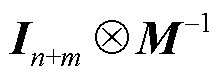 分别左乘和右乘式(14),其中SBM为各构网型设备容量构成的对角矩阵,SBM=diag(SBM1,SBM2,…,SBMn)。原构网型设备多馈入系统(
分别左乘和右乘式(14),其中SBM为各构网型设备容量构成的对角矩阵,SBM=diag(SBM1,SBM2,…,SBMn)。原构网型设备多馈入系统(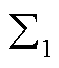 )的特征方程可等价变换为
)的特征方程可等价变换为
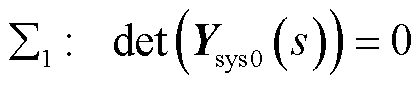 (16)
(16)
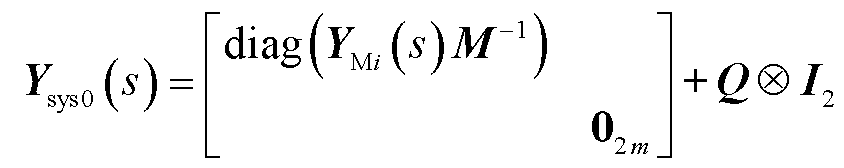 (17)
(17)
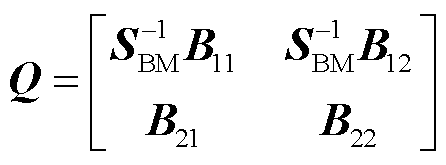 (18)
(18)
式中,Ysys0(s)为系统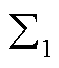 的闭环传递函数矩阵;I为单位阵,下标表示单位阵的阶数。
的闭环传递函数矩阵;I为单位阵,下标表示单位阵的阶数。
由文献[16]可知,当构网型设备同构时,系统的低频段稳定性问题可分解为n个构网型设备单馈入系统的低频段稳定性问题,其中短路比最大的单馈入系统代表了原系统稳定性,可称为表征原系统稳定性的特征子系统[24]。进一步地,参考跟网型设备多馈入系统中基于广义短路比的电网强度定义[21],文献[16]将特征子系统的短路比定义为反映构网型设备主导低频段稳定性的广义短路比gSCRGFM,用于量化电网强度,其具体表达式为
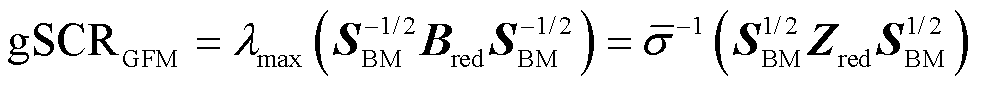 (19)
(19)
式中,gSCRGFM为构网型设备多馈入系统的广义短路比,代表了原多馈入系统的电网强度;Bred为中间节点消去后的导纳矩阵,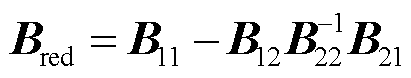 ;
;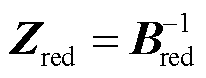 ;
;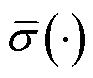 和
和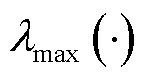 分别为求解矩阵的最小奇异值和最大特征值。
分别为求解矩阵的最小奇异值和最大特征值。
为进一步厘清式(19)中gSCRGFM的物理意义,参考文献[13],可以得到n个构网型设备接入节点的电流增量对电压增量的放大倍数h满足
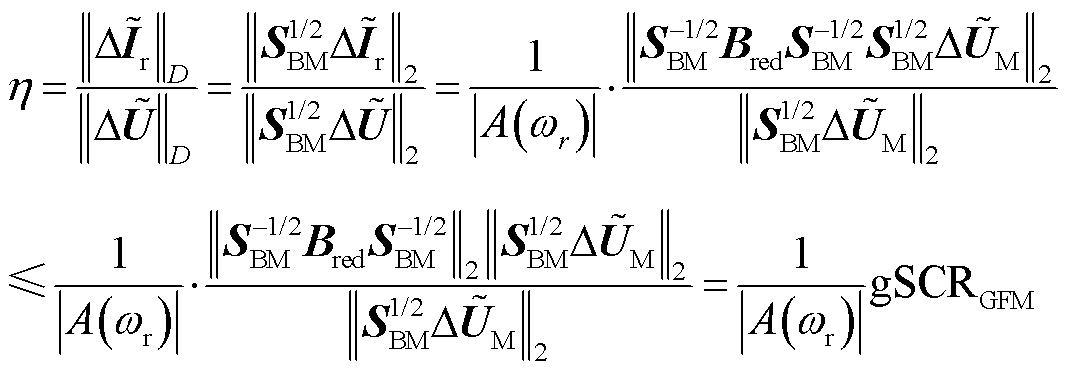 (20)
(20)
式中,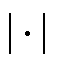 表示取模;
表示取模;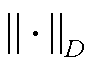 表示D范数[13];
表示D范数[13];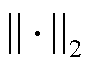 表示2范数;
表示2范数;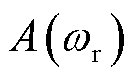 、
、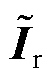 、
、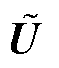 具体表达式参考文献[13],
具体表达式参考文献[13],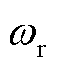 为关注的扰动频率。
为关注的扰动频率。
不等式(20)可进一步表示为
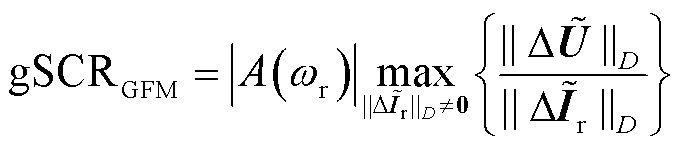 (21)
(21)
式中,max表示取最大值。
由式(21)可知,gSCRGFM反映了交流网络中电流对电压的最大灵敏度,物理上可理解为一种网络连接强度指标。非工频下,最大灵敏度与扰动频率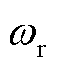 呈线性关系,因此静态指标gSCRGFM可用于分析系统的动态稳定性。对于构网型设备,放大倍数h越大,其输出电流对端电压的波动越敏感,系统越容易发生低频振荡问题。
呈线性关系,因此静态指标gSCRGFM可用于分析系统的动态稳定性。对于构网型设备,放大倍数h越大,其输出电流对端电压的波动越敏感,系统越容易发生低频振荡问题。
需要指出的是,不同于跟网型设备中PLL主导的次同步振荡问题,网络强度反映设备馈入节点的电压对电流或无功功率最大灵敏度,本文主要聚焦构网型设备主导低频振荡问题,网络强度反映设备馈入节点电流对电压的最大灵敏度。
当考虑设备异构时,式(16)难以解耦,难以得到代表原系统低频段稳定性的特征子系统。为此,本小节首先构造一个能近似代表原异构多馈入系统低频段稳定性的等效同构系统(令为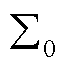 ),进而结合文献[24]的分析,可以得到近似代表原异构多馈入系统低频段稳定性的特征子系统。具体地,构造所得等效同构系统
),进而结合文献[24]的分析,可以得到近似代表原异构多馈入系统低频段稳定性的特征子系统。具体地,构造所得等效同构系统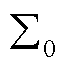 的特征方程可表示为
的特征方程可表示为
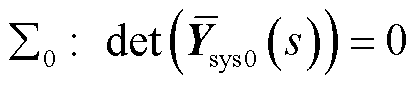 (22)
(22)
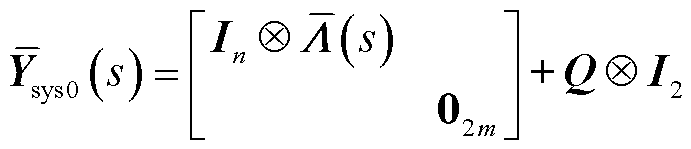 (23)
(23)
其中
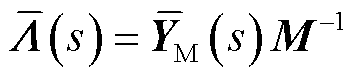 (24)
(24)
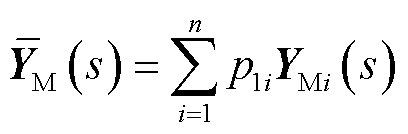 (25)
(25)
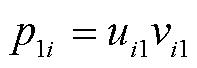 (26)
(26)
式中,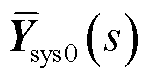 为系统
为系统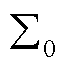 的闭环传递函数矩阵;
的闭环传递函数矩阵;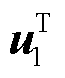 和
和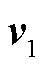 分别为
分别为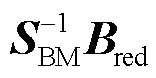 最大模态归一化后的左、右特征向量;
最大模态归一化后的左、右特征向量;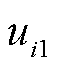 和
和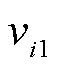 分别为
分别为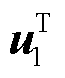 和
和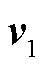 的第i个元素,归一化后满足
的第i个元素,归一化后满足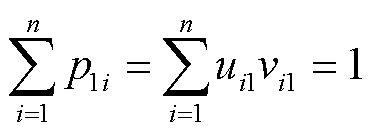 。
。
令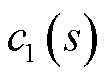 和
和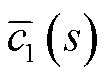 分别为
分别为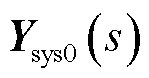 (属于系统
(属于系统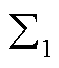 )和矩阵
)和矩阵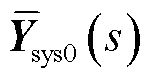 (属于系统
(属于系统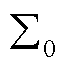 )关于矩阵
)关于矩阵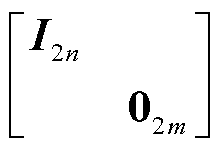 的主导广义特征值(因为与s有关,所以后文称广义特征函数;此外,这里“主导”的意思是指系统的主导模态为广义特征函数
的主导广义特征值(因为与s有关,所以后文称广义特征函数;此外,这里“主导”的意思是指系统的主导模态为广义特征函数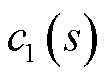 或
或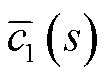 的解)。此外,将
的解)。此外,将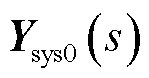 看成对
看成对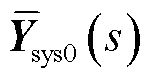 的摄动,参考文献[21]可知,
的摄动,参考文献[21]可知,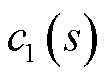 和
和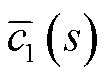 满足
满足
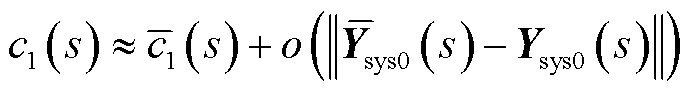 (27)
(27)
式中,矩阵的广义特征值定义见文献[25];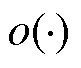 为高阶无穷小量。
为高阶无穷小量。
由式(27)可知,系统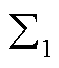 和
和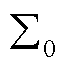 的主导广义特征函数存在一阶近似相等的关系。因此,结合文献[24]分析可知,当构网型设备异构特性差异不大时,通过等效同构系统解耦得到的特征子系统(令为
的主导广义特征函数存在一阶近似相等的关系。因此,结合文献[24]分析可知,当构网型设备异构特性差异不大时,通过等效同构系统解耦得到的特征子系统(令为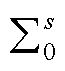 )可以近似反映原异构系统
)可以近似反映原异构系统 的低频段稳定性,简化了原复杂系统的分析。由图5可知,特征子系统为单机无穷大系统,由构网型设备动态等效加权与等效线路构成,其中,特征子系统
的低频段稳定性,简化了原复杂系统的分析。由图5可知,特征子系统为单机无穷大系统,由构网型设备动态等效加权与等效线路构成,其中,特征子系统 对应的特征方程为
对应的特征方程为
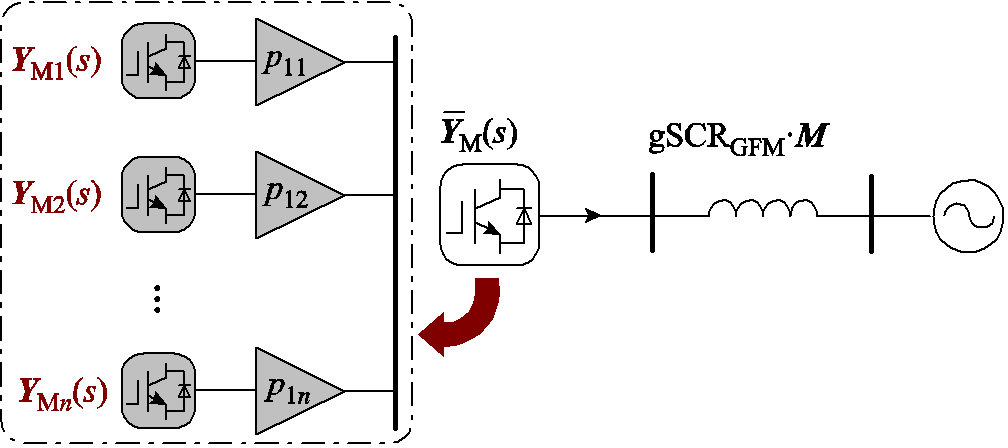
图5 特征子系统 的示意图
的示意图
Fig.5 Diagram of the eigen-subsystem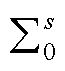
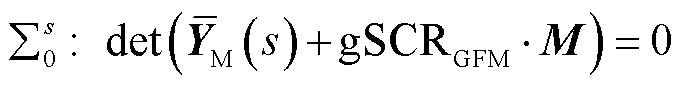 (28)
(28)
式中,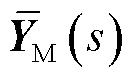 参考式(25)。
参考式(25)。
根据3.1节可知,考虑设备异构的构网型设备多馈入系统低频段稳定性可由特征子系统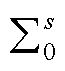 表示。而对于构网型设备单馈入系统,当设备控制参数给定时,系统低频段稳定性与短路比存在负相关性,即短路比越大,系统稳定性越差。因此,该短路比存在上临界值[16],具体来说,反映原构网型设备多馈入系统临界稳定的CgSCRGFM的定义如下:
表示。而对于构网型设备单馈入系统,当设备控制参数给定时,系统低频段稳定性与短路比存在负相关性,即短路比越大,系统稳定性越差。因此,该短路比存在上临界值[16],具体来说,反映原构网型设备多馈入系统临界稳定的CgSCRGFM的定义如下:
定义1:构网型设备多馈入系统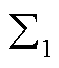 的CgSCRGFM定义为特征子系统
的CgSCRGFM定义为特征子系统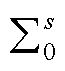 在额定工况下达到临界稳定状态或给定性能要求时的短路比(简称临界短路比),其具体表达式为
在额定工况下达到临界稳定状态或给定性能要求时的短路比(简称临界短路比),其具体表达式为
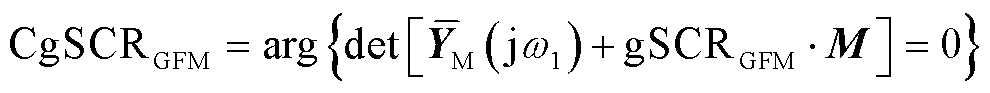 (29)
(29)
式中,arg为求解系统临界稳定时gSCRGFM对应的数值;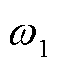 为系统临界稳定时主导模态对应的振荡频率。
为系统临界稳定时主导模态对应的振荡频率。
针对考虑设备异构的构网型设备多馈入系统,可基于系统的gSCRGFM及其临界值给出系统低频段稳定裕度指标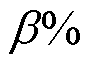 ,定义为
,定义为
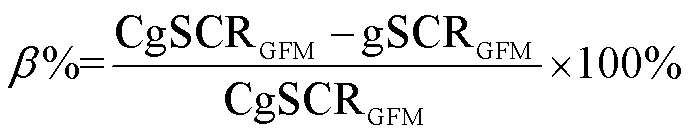 (30)
(30)
基于以上分析,给出异构系统的低频段稳定性评估方法:当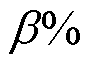 >0时,系统稳定;当
>0时,系统稳定;当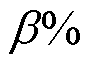 =0时,系统处于临界稳定;当
=0时,系统处于临界稳定;当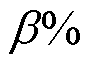 <0时,系统不稳定,此时会出现低频振荡问题。此外,
<0时,系统不稳定,此时会出现低频振荡问题。此外,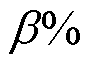 的数值代表系统的稳定裕度,
的数值代表系统的稳定裕度,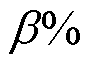 越大,系统越稳定;反之,
越大,系统越稳定;反之,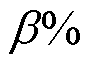 越小,系统稳定性越差,系统越容易出现低频振荡问题。
越小,系统稳定性越差,系统越容易出现低频振荡问题。
结合式(19)、式(29)和文献[22]可知,在网络参数与设备容量不变的情况下,改变设备的外特性并不会改变系统的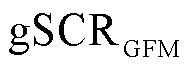 ,只会改变系统的CgSCRGFM,因此设备的异构特性可以认为是改变了原系统的CgSCRGFM,进而改变了原系统的低频段稳定性。
,只会改变系统的CgSCRGFM,因此设备的异构特性可以认为是改变了原系统的CgSCRGFM,进而改变了原系统的低频段稳定性。
针对第1节所提第2个问题,本节主要考虑跟网型设备接入时,如何分析跟网型设备与构网型设备的相互作用对系统低频段稳定性的影响。
对于混联多馈入系统,当考虑设备异构时,参考3.1节分析可得混联多馈入系统(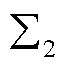 )的特征方程为
)的特征方程为
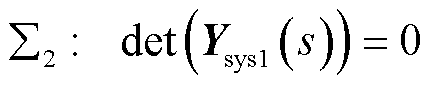 (31)
(31)
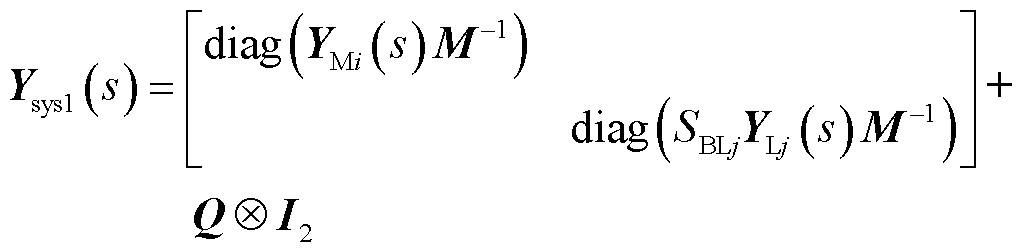 (32)
(32)
式中,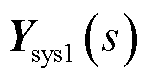 为系统
为系统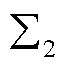 的闭环传递函数矩阵。
的闭环传递函数矩阵。
值得一提的是,当考虑跟网型设备接入时,研究发现低频段下等容量跟网型设备导纳外特性要小于构网型设备导纳外特性。为此,可以将跟网型设备的接入近似看成对构网型设备动态的摄动,具体讨论参考附录第4节。因此,可以参考3.1节的分析,构造一个低维的特征子系统代表原含跟网型和构网型设备混联多馈入系统的低频段稳定性。进而将混联多馈入系统的低频段稳定性问题转换为gSCRGFM及其临界值的计算问题。具体地,构造的等效同构系统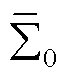 特征方程可表示为
特征方程可表示为
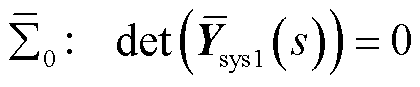 (33)
(33)
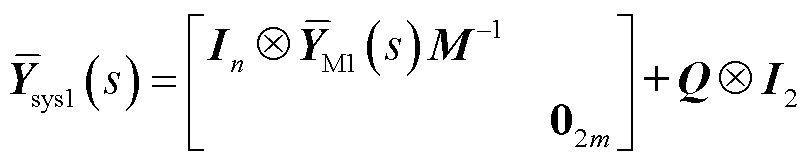 (34)
(34)
其中
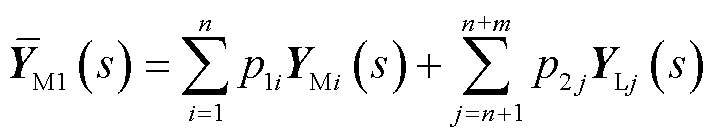 (35)
(35)
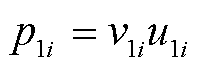 (36)
(36)
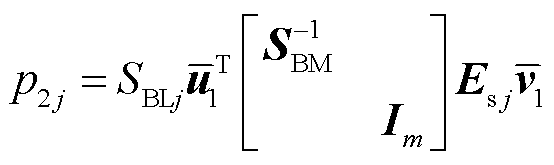 (37)
(37)
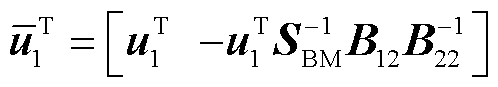 (38)
(38)
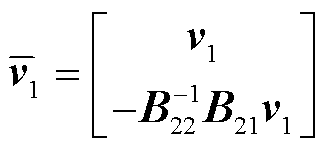 (39)
(39)
式中,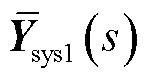 为系统
为系统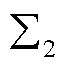 的闭环传递函数矩阵;
的闭环传递函数矩阵;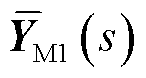 为等效设备xy坐标系导纳矩阵;p1i为节点i的构网型设备的权重系数;p2j为节点j接入的跟网型设备的权重系数;Esj为仅第j个对角元素为1、其余元素为0的方阵。
为等效设备xy坐标系导纳矩阵;p1i为节点i的构网型设备的权重系数;p2j为节点j接入的跟网型设备的权重系数;Esj为仅第j个对角元素为1、其余元素为0的方阵。
类似于3.1节分析,可以证明系统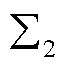 和系统
和系统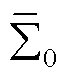 的主导广义特征函数存在一阶近似相等的关系,相关证明过程可以参考文献[22]。事实上,上述证明关键步骤是利用了混联多馈入系统
的主导广义特征函数存在一阶近似相等的关系,相关证明过程可以参考文献[22]。事实上,上述证明关键步骤是利用了混联多馈入系统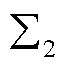 和同构系统
和同构系统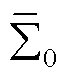 的主导广义特征函数近似相等这一结论,它们都等于特征子系统
的主导广义特征函数近似相等这一结论,它们都等于特征子系统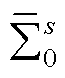 的主导广义特征函数。上述推理过程如图6所示。
的主导广义特征函数。上述推理过程如图6所示。
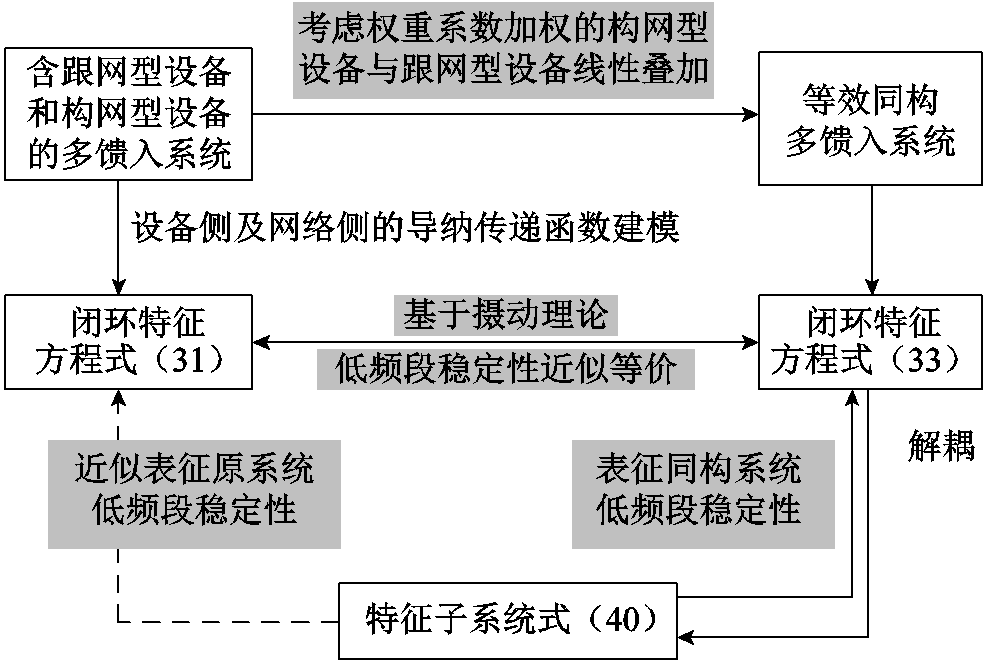
图6 原系统对应特征子系统导出思路
Fig.6 The derivation methodology for the eigen-subsystem corresponding to the original system
基于上述分析可知,原系统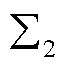 的低频段稳定性分析问题可简化为特征子系统(令其为
的低频段稳定性分析问题可简化为特征子系统(令其为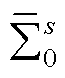 ,参考图7)低频段稳定性分析问题。具体来说,所构造的特征子系统
,参考图7)低频段稳定性分析问题。具体来说,所构造的特征子系统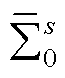 的闭环特征方程表示为
的闭环特征方程表示为
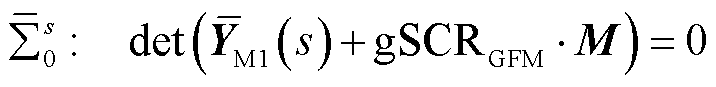 (40)
(40)
此外,当新能源设备控制参数和控制结构给定时,系统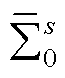 或系统
或系统 的稳定性主要由gSCRGFM及其临界值的差值决定。这里给出混联多馈入系统gSCRGFM临界值的定义。
的稳定性主要由gSCRGFM及其临界值的差值决定。这里给出混联多馈入系统gSCRGFM临界值的定义。
定义2:混联多馈入系统 的CgSCRGFM定义为特征子系统
的CgSCRGFM定义为特征子系统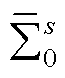 在额定工况下达到临界稳定状态或给定性能要求所需时的最大短路比,即临界短路比,其具体表达式为
在额定工况下达到临界稳定状态或给定性能要求所需时的最大短路比,即临界短路比,其具体表达式为
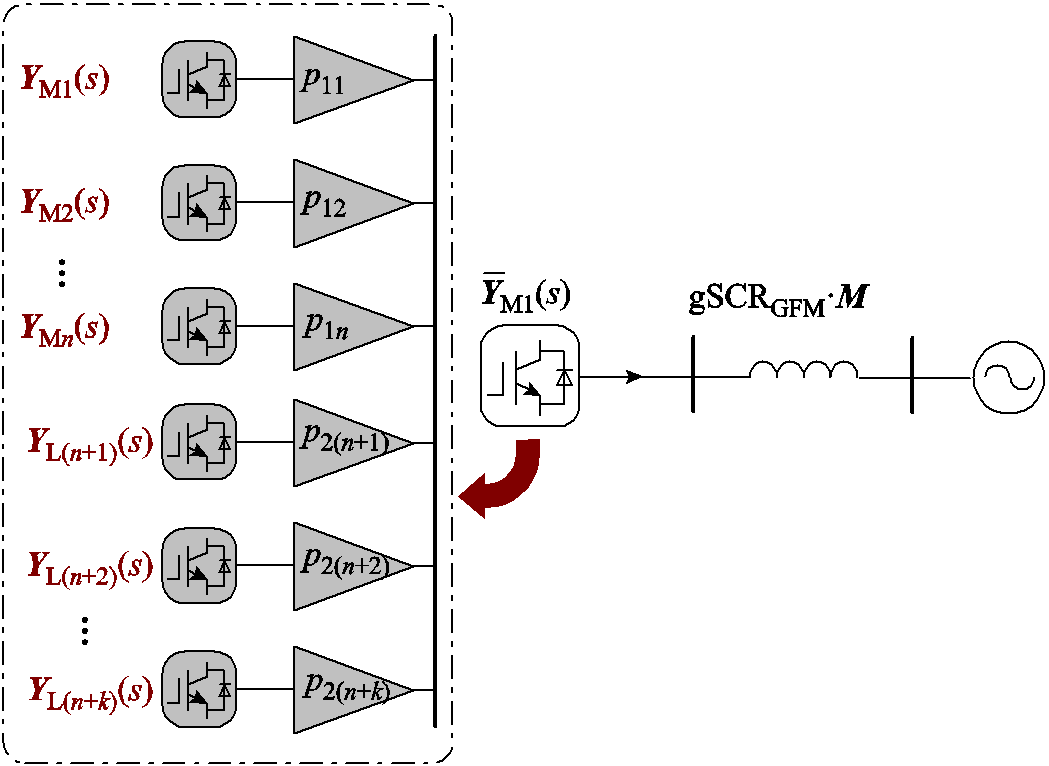
图7 特征子系统动态模型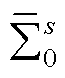 示意图
示意图
Fig.7 Diagram of the eigen-subsystem 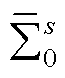
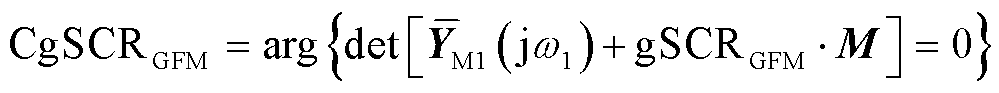 (41)
(41)
综合以上分析可知,针对混联多馈入系统的低频段稳定性,同样可以用式(30)中的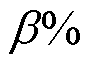 来评估,只需将式(41)解析计算所得的gSCRGFM临界值替换(30)中CgSCRGFM即可。具体来说,
来评估,只需将式(41)解析计算所得的gSCRGFM临界值替换(30)中CgSCRGFM即可。具体来说,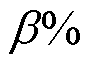 越大,系统越稳定;反之,
越大,系统越稳定;反之,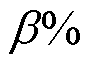 越小,系统稳定性越差,系统越容易出现低频振荡问题。
越小,系统稳定性越差,系统越容易出现低频振荡问题。
值得一提的是,等效设备动态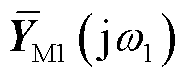 为原系统中跟网型和构网型设备的加权求和,具体表达式参考式(35)。其中,加权系数p1i或p2j(其中,i=1,…,n,j=n+1,…,n+k)反映了各个设备对系统低频段稳定性的相对影响程度;从系统强度的视角,加权系数可以理解为对系统临界短路比CgSCRGFM的相对影响程度(参考式(25)、式(29)、式(35)和式(41));此外,加权系数也可理解为设备与其余设备之间的相互作用程度。具体地,加权系数越大,表明该设备与其余设备间的交互作用加剧,且该设备对系统CgSCRGFM或低频段稳定性的影响程度越大;反之,加权系数越小,表明该设备与其余设备间的交互作用程度减小,且该设备对系统CgSCRGFM或低频段稳定性影响程度越小。具体论述参考附录第5节。
为原系统中跟网型和构网型设备的加权求和,具体表达式参考式(35)。其中,加权系数p1i或p2j(其中,i=1,…,n,j=n+1,…,n+k)反映了各个设备对系统低频段稳定性的相对影响程度;从系统强度的视角,加权系数可以理解为对系统临界短路比CgSCRGFM的相对影响程度(参考式(25)、式(29)、式(35)和式(41));此外,加权系数也可理解为设备与其余设备之间的相互作用程度。具体地,加权系数越大,表明该设备与其余设备间的交互作用加剧,且该设备对系统CgSCRGFM或低频段稳定性的影响程度越大;反之,加权系数越小,表明该设备与其余设备间的交互作用程度减小,且该设备对系统CgSCRGFM或低频段稳定性影响程度越小。具体论述参考附录第5节。
基于上述分析可知:①考虑接入跟网型设备前后,网络结构保持的导纳传函矩阵不变,等效同构系统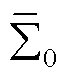 的gSCRGFM与跟网型设备未接入时多馈入系统的gSCRGFM相同;②考虑接入跟网型设备后,等效同构系统
的gSCRGFM与跟网型设备未接入时多馈入系统的gSCRGFM相同;②考虑接入跟网型设备后,等效同构系统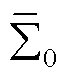 设备动态为构网型设备动态与跟网型设备动态的加权平均。
设备动态为构网型设备动态与跟网型设备动态的加权平均。
因此,跟网型设备的接入可理解为原构网型多馈入系统的设备侧动态发生了改变,跟网型设备接入前后系统gSCRGFM不变,但gSCRGFM的临界值发生了变化。换句话说,跟网型设备的作用可等效为改变了原构网型多馈入并网系统所需的满足最大gSCRGFM条件,从而改变了系统的低频段稳定性。此外,由于式(40)只是说明跟网型设备的加入可以等价为构网型设备的动态特性发生改变,但是否提升稳定性及提升程度与跟网型设备的实际控制策略有关(跟网型设备可能让系统变得更稳定,也可能恶化系统稳定性)。因此,如何通过修正跟网型设备的控制策略使系统稳定性提升成为可能,这将是未来需要进一步开展的研究。
综合以上分析,考虑跟网型设备接入以及不接入两种情况下系统低频段稳定性评估问题可以转换为gSCRGFM及其临界值的计算两个子问题,计算流程如图8所示。
具体计算步骤如下:
1)根据网络信息,得到中间节点消去后的导纳矩阵Bred。
2)结合构网型设备容量信息计算gSCRGFM(式(19))。
3)当考虑跟网型设备未接入时,需要计算构网型设备权重系数p1i(式(26)),并构造等效同构系统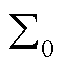 (式(22)),再通过计算特征子系统
(式(22)),再通过计算特征子系统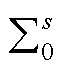 的CgSCRGFM(式(29)),进而得到系统
的CgSCRGFM(式(29)),进而得到系统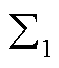 的CgSCRGFM。
的CgSCRGFM。
4)当考虑跟网型设备接入时,需要结合跟网型设备落点位置和容量信息SBsj,计算构网型设备权重系数p1i(式(36))和跟网型设备权重系数p2j(式(37));再结合各构网型设备动态以及跟网型设备动态,构造等效同构系统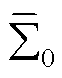 (式(33)),通过计算特征子系统
(式(33)),通过计算特征子系统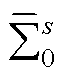 的CgSCRGFM(式(41)),进而得到系统
的CgSCRGFM(式(41)),进而得到系统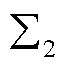 的CgSCRGFM。
的CgSCRGFM。
5)计算稳定裕度指标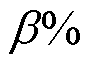 (式(30))。
(式(30))。
gSCRGFM临界值的计算可分为两种情况考虑:①当跟网型设备和构网型设备参数已知时,可根据式(40)解析计算得到CgSCRGFM;②当跟网型设备和构网型设备的控制参数未知时,可在实验平台搭建单馈入系统式(40),并通过控制器在环的半实物仿真得到临界值。
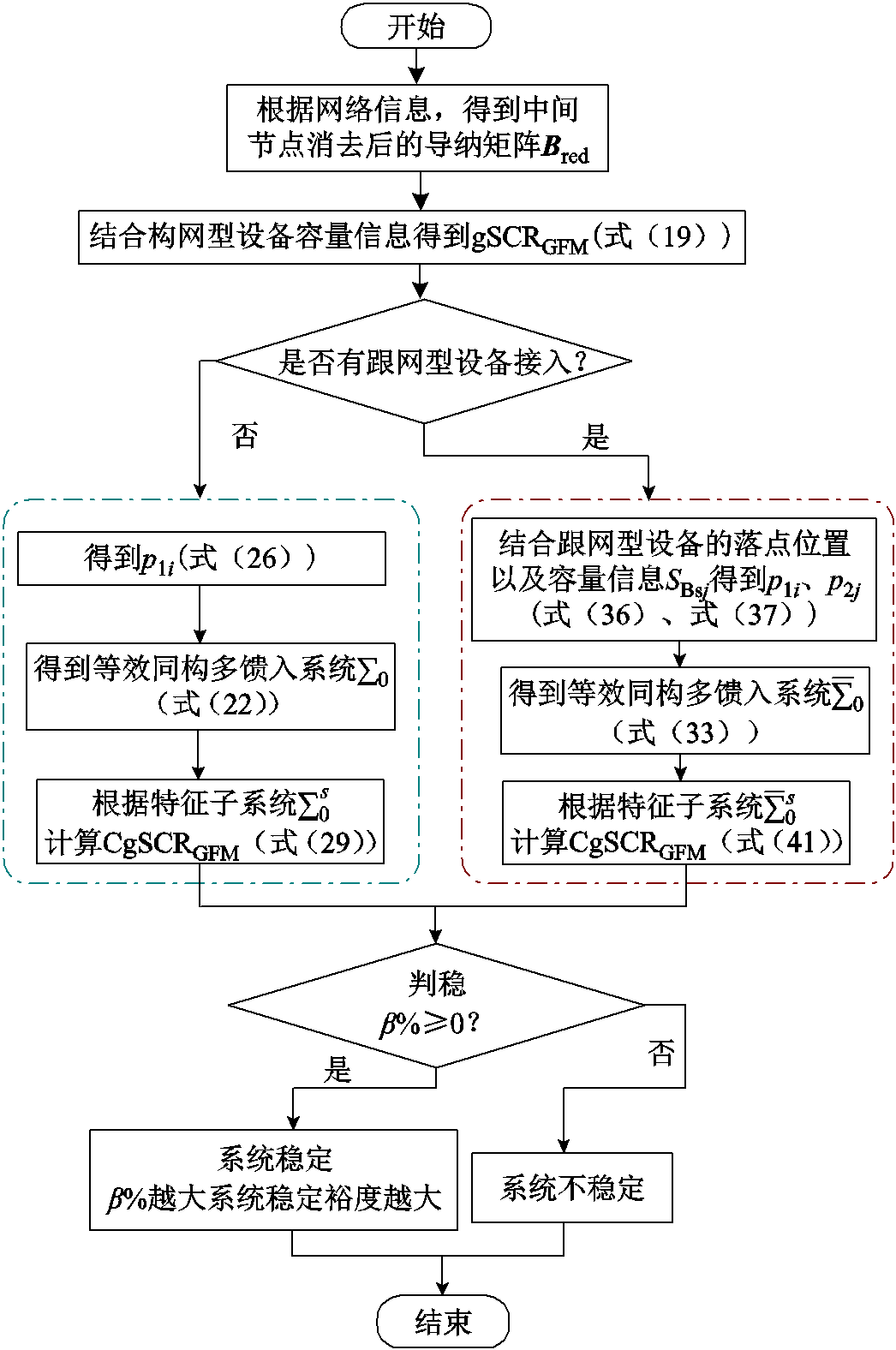
图8 考虑跟网型设备接入以及不接入两种情况下系统稳定性分析流程
Fig.8 Flow chart for the stability analysis of system considering both scenarios with and without GFLDs
为便于理解,本节首先基于简单的三机系统介绍所提特征子系统构造的详细流程以及系统强度计算和分析的详细流程,并验证该特征子系统近似反映原混联多馈入系统低频段稳定性的有效性;其次,基于改进的39节点并网系统,验证广义短路比指标gSCRGFM量化混联多馈入系统低频段稳定性的有效性,并分析跟网型设备不同控制方式及控制参数对系统低频段稳定性的影响规律。
本节基于简单三机系统介绍了所提特征子系统构造的详细流程以及系统强度计算和分析的详细流程。需要说明的是,限于篇幅,下文仿真中仅考虑跟网型设备接入情况下的算例分析。含两台构网型设备和单台跟网型设备的三机并网系统示意图如图9所示,三台设备经PCC汇集并通过线路电感接入无穷大电源。图9中,节点1、节点2连接构网型设备,节点3连接跟网型设备,节点4为无源节点,节点5为无穷大节点;Lf、Cf分别为滤波电感、滤波电容;构网型设备1和构网型设备2均采用虚拟同步控制,但控制参数存在一定差异,其中构网型设备1的电压外环Hvc(s)比例、积分参数分别为4.5、25,虚拟惯量J与虚拟阻尼D参数分别为3.5、58;构网型设备2的外环电压外环Hvc(s)比例、积分参数分别为4、21,虚拟惯量J与虚拟阻尼D参数分别为4、59,其余控制参数均相同,具体参考附表1;跟网型设备采用Udc控制,除外环控制以外的其他参数参考附表2,外环参数参考附表3中的设备1;X1、X2、X3为线路电抗标幺值,Xg为电网电抗标幺值,令初始的网络参数为X1=0.14(pu)、X2=0.05(pu)、X3=0.04(pu)和Xg=0.1(pu);构网型设备的容量均为1.0(pu);跟网型设备的容量为2.0(pu)。
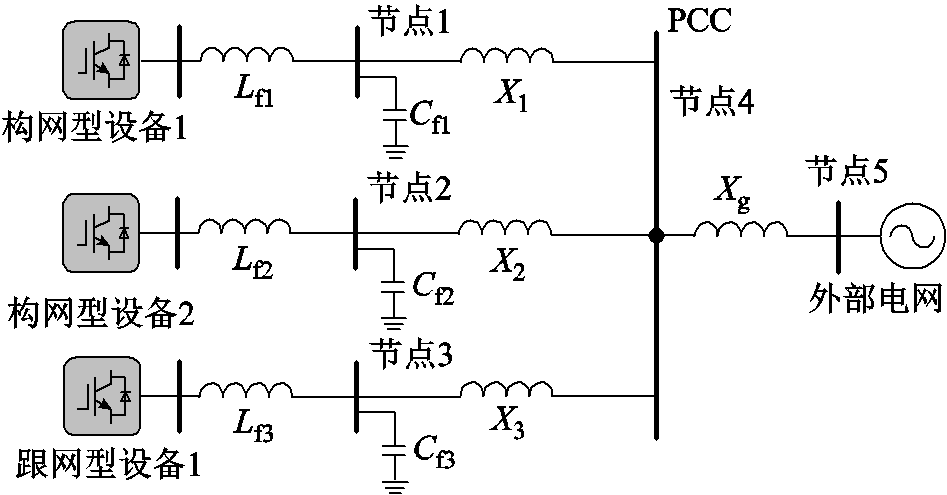
图9 含两台构网型设备和单台跟网型设备的三机并网系统示意图
Fig.9 The diagram of a three-infeed system with two GFMDs and a GFLD
首先,为说明在构造特征子系统过程中,跟网型设备动态可近似看成构网型设备摄动,考虑跟网型设备四种不同的控制策略,附录第4节给出了跟网型设备和构网型设备导纳传递函数矩阵等容量下在低频段奇异值比值图。由附图2可知,跟网型设备导纳外特性动态在低频段要小于构网型设备。因此,在低频段,可以近似将跟网型设备动态看成构网型设备的摄动。
其次,介绍代表原系统低频段稳定性的特征子系统构造流程。
1)结构保持下网络的导纳矩阵可表示为
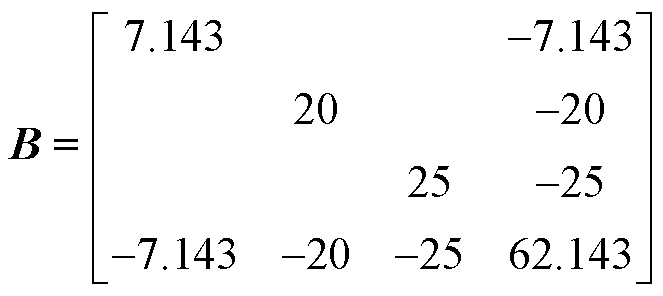 (42)
(42)
2)基于式(42),通过Schur补计算,得到仅保留构网型设备节点的网络节点压缩导纳矩阵为
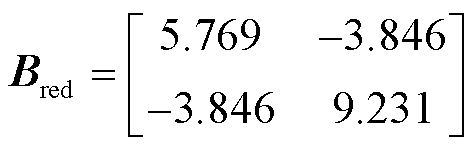 (43)
(43)
3)计算等效子系统的gSCRGFM为
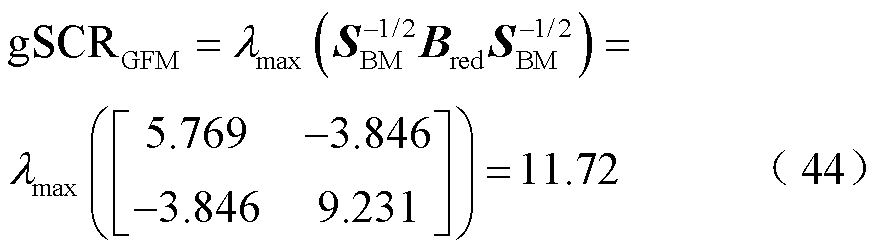
此外,构网型设备1和2的加权系数分别为
 (45)
(45)
式中,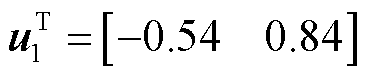 ,
,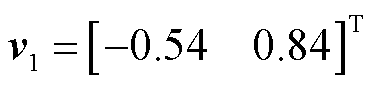 。
。
跟网型设备1的加权系数为
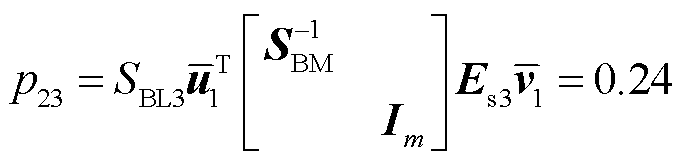 (46)
(46)
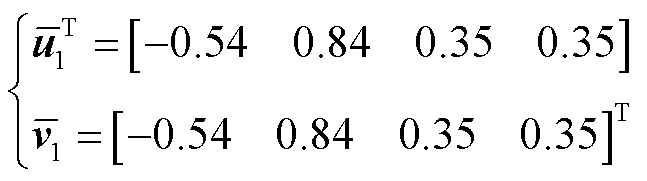 (47)
(47)
4)计算等效子系统的等效设备导纳矩阵为
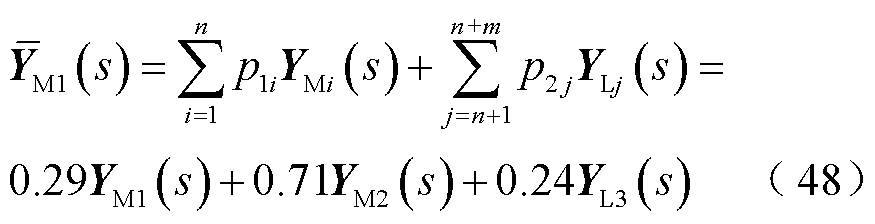
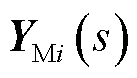 和
和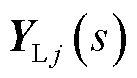 的加权系数反映了各自设备对系统稳定性影响的相对大小,以及设备与其余设备的相互作用程度。具体讨论参考附录第5节。
的加权系数反映了各自设备对系统稳定性影响的相对大小,以及设备与其余设备的相互作用程度。具体讨论参考附录第5节。
5)结合式(44)和式(48)得到特征子系统的闭环特征方程为
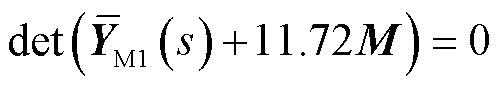 (49)
(49)
最后,介绍基于系统强度的混联型多馈入系统低频段稳定性分析流程。
1)基于特征子系统计算系统的CgSCRGFM为
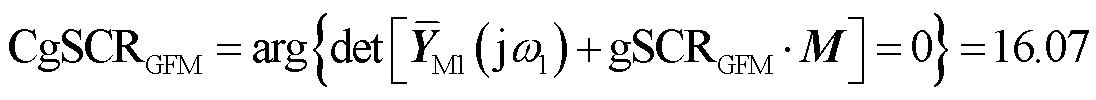 (50)
(50)
2)计算稳定裕度指标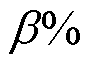 ,根据
,根据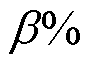 的大小判断系统稳定及其稳定裕度,具体参考3.2节分析。
的大小判断系统稳定及其稳定裕度,具体参考3.2节分析。
为验证所构造特征子系统的有效性,引入缩放系数k1用于等比例缩放所有网络线路的电感。图10给出了当k1从1减小到0.68时,三种情况下的系统主导模态轨迹对比:情况1为基于简化模型的混联多馈入系统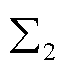 ;情况2为特征子系统
;情况2为特征子系统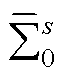 ;情况3为基于详细电磁模型的混联多馈入系统。由图10可知,当参数k1从1减小到0.68时,三种情况下的系统主导模态轨迹的主导模态近似,说明用系统
;情况3为基于详细电磁模型的混联多馈入系统。由图10可知,当参数k1从1减小到0.68时,三种情况下的系统主导模态轨迹的主导模态近似,说明用系统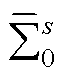 近似反映原混联多馈入系统
近似反映原混联多馈入系统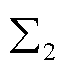 低频段稳定性的思路是可行的;同时验证了本文所提简化模型的合理性。
低频段稳定性的思路是可行的;同时验证了本文所提简化模型的合理性。
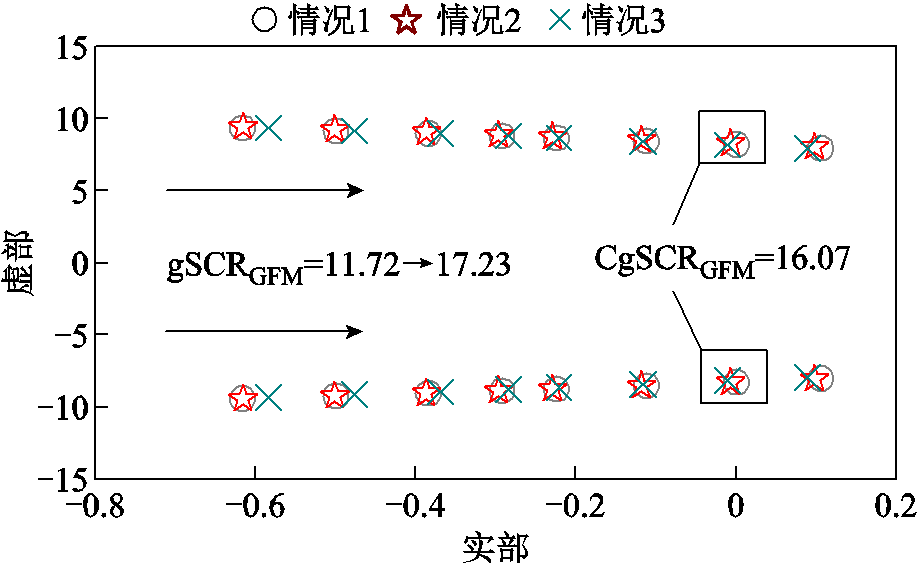
图10 系数k1变化时系统主导模态轨迹对比
Fig.10 Comparison of dominant root loci in systems with varying k1
搭建图11所示39节点并网系统的电磁暂态仿真模型,考虑接入6个构网型设备及3个跟网型设备。其中,构网型变流器电压环、虚拟惯量J、虚拟阻尼D参数存在一定差异,跟网型变流器外环参数存在一定差异,参数分别见附表3和附表4。构网型设备和跟网型设备的其他控制参数分别见附表1和附表2,其中跟网型设备的直流电压参考值为1.0(pu),无功功率参考值为0(pu),构网型设备容量见附表5,跟网型设备的容量均为10(pu),网络参数参考文献[20]。
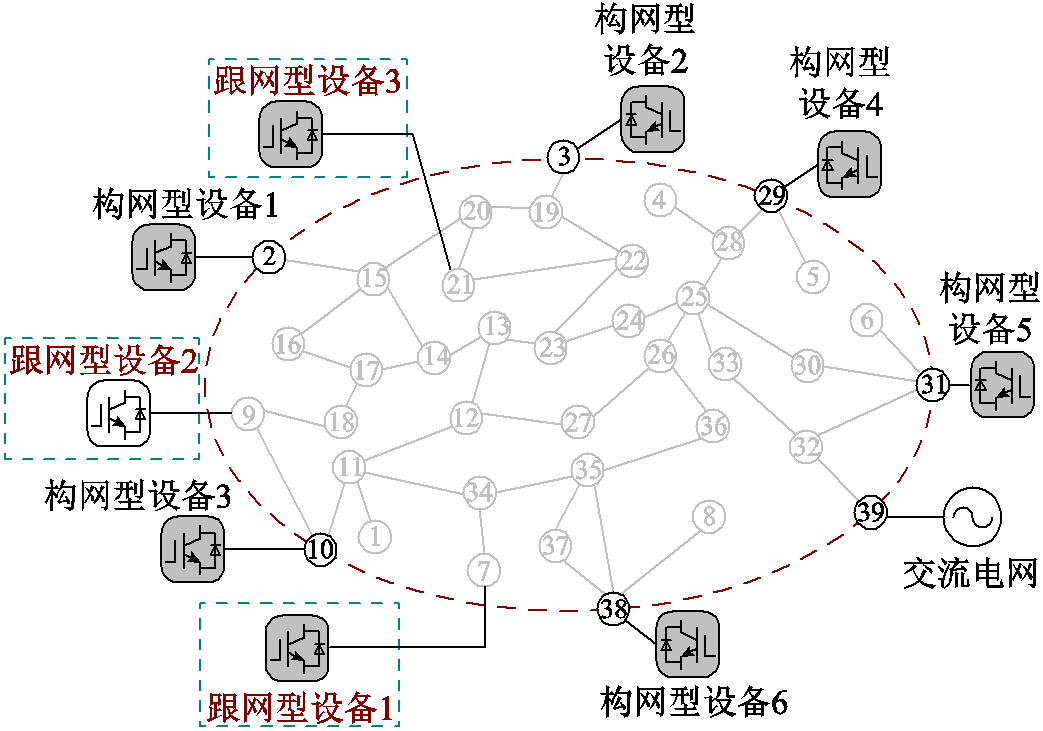
图11 39节点系统示意图
Fig.11 The diagram of 39-node system
具体地,从时域角度说明基于gSCRGFM的分析方法是有效的。同样引入缩放系数k1用于等比例缩放所有网络线路的电感,针对三种情况(k1=1、0.711、0.65)做相同的小扰动实验:设备1的有功功率参考值在t =0.3 s时发生持续0.05 s的0.1(pu)跌落。上述三种情况下,构网型设备1及跟网型设备1输出有功功率的振荡波形如图12所示。
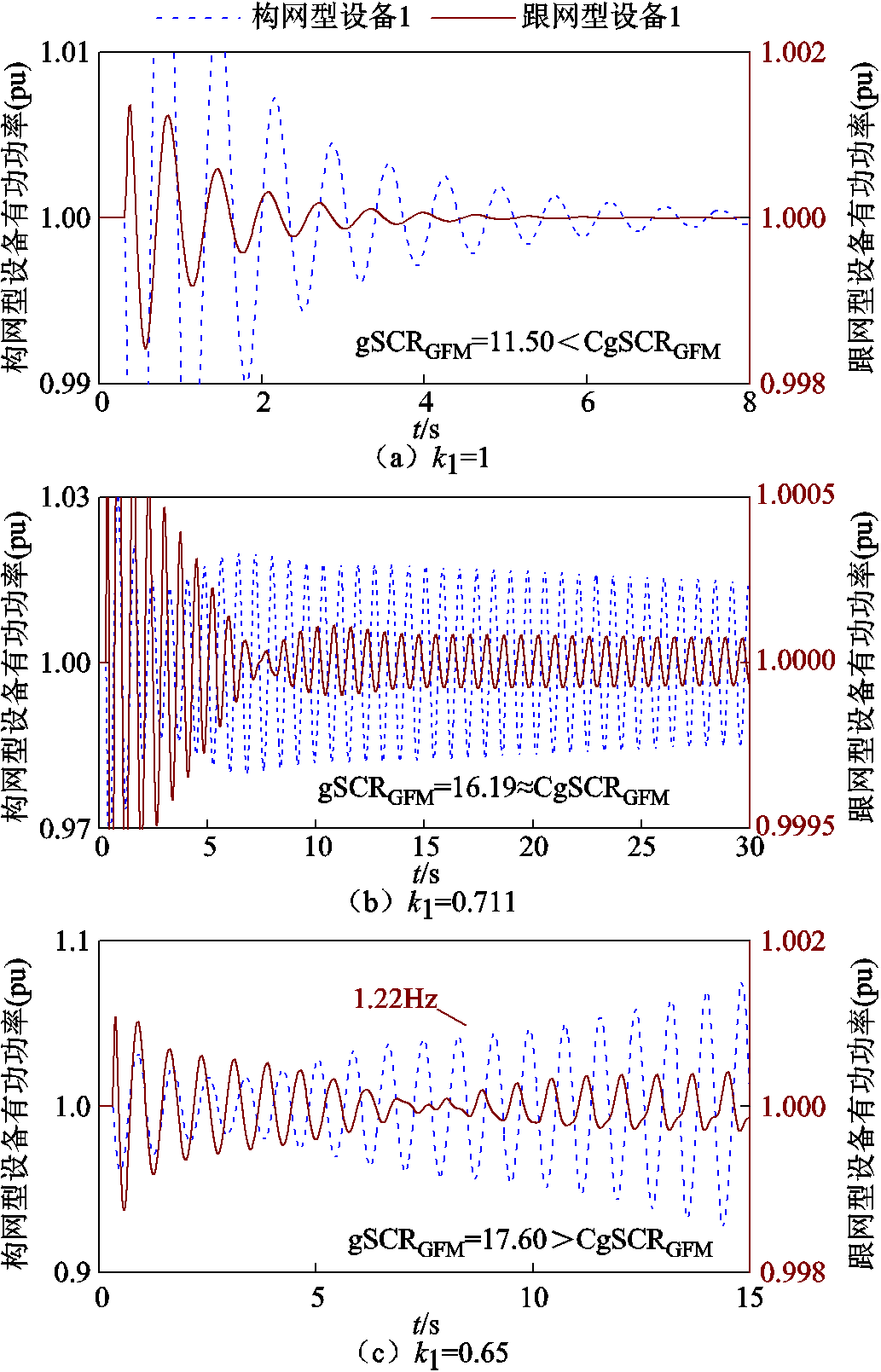
图12 不同系数k1下39节点系统中各设备功率振荡波形
Fig.12 Time-domain responses of active power outputs of all devices in the 39-node system under different coefficients k1
由图12可知,当系数k1=1时,构网型设备1及跟网型设备1输出有功功率曲线振荡收敛,这说明系统稳定,而该工况下,gSCRGFM=11.50<CgSCRGFM(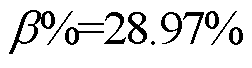 >0),说明系统处于稳定状态并且具有一定的稳定裕度。当系数k1=0.711时,各设备输出有功功率曲线近似等幅振荡,系统处于临界稳定状态,而该工况下gSCRGFM=16.19≈CgSCRGFM(
>0),说明系统处于稳定状态并且具有一定的稳定裕度。当系数k1=0.711时,各设备输出有功功率曲线近似等幅振荡,系统处于临界稳定状态,而该工况下gSCRGFM=16.19≈CgSCRGFM(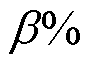 = 0),说明系统是临界稳定的。当系数k1=0.65时,各设备输出有功功率曲线振荡发散,系统处于不稳定状态,而该工况下gSCRGFM=17.60>CgSCRGFM(
= 0),说明系统是临界稳定的。当系数k1=0.65时,各设备输出有功功率曲线振荡发散,系统处于不稳定状态,而该工况下gSCRGFM=17.60>CgSCRGFM(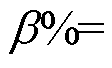
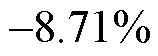 <0),说明系统不稳定。综上所述,从时域角度说明了所提基于系统强度的混联多馈入系统小干扰稳定性分析方法是有效的。
<0),说明系统不稳定。综上所述,从时域角度说明了所提基于系统强度的混联多馈入系统小干扰稳定性分析方法是有效的。
本节考察了不同控制方式及不同参数下跟网型设备接入对原构网型多馈入系统稳定性的影响。针对图11所示39节点系统(k1=1),分别考虑如下五个算例。
算例1:跟网型设备未接入。
算例2:所有的跟网型设备均采用Udc、Q控制,参数采用附表6中参数①以及参数②。
算例3:所有的跟网型设备均采用PQ控制,参数采用附表6中参数①以及参数②。
算例4:所有的跟网型设备均采用Udc、V控制,参数采用附表6中参数①以及参数②。
算例5:所有的跟网型设备均采用PV控制,参数采用附表6中参数①以及参数②。
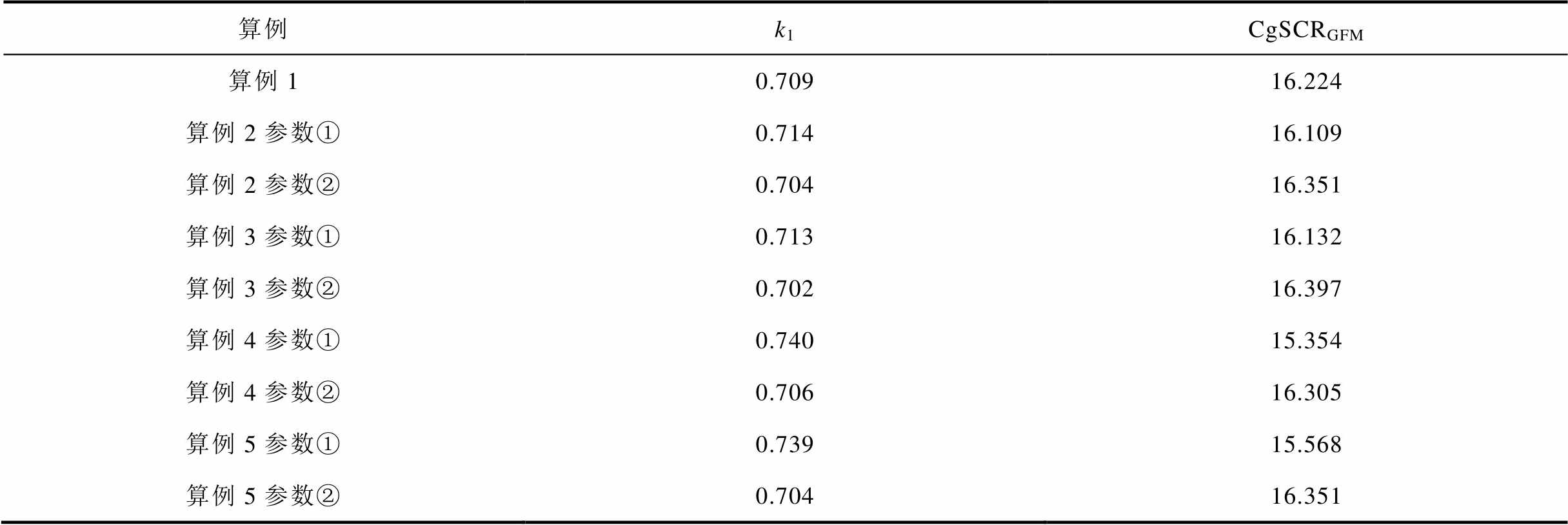
表1分析了考虑不同参数下的跟网型设备接入对构网型多馈入系统gSCRGFM临界值的影响,通过增加系数k1直至系统临界稳定,给出这五个算例临界稳定时对应的系数k1大小以及系统CgSCRGFM。
表1 不同跟网型设备参数下39节点系统CgSCRGFM
Tab.1 CgSCRGFM of 39-node system with different parameters of GFLD
算例k1CgSCRGFM 算例10.70916.224 算例2参数①0.71416.109 算例2参数②0.70416.351 算例3参数①0.71316.132 算例3参数②0.70216.397 算例4参数①0.74015.354 算例4参数②0.70616.305 算例5参数①0.73915.568 算例5参数②0.70416.351
由表1可以看出,对比算例1(跟网型设备未接入),在算例2~5中,当跟网型设备采用参数①时,CgSCRGFM减小,根据系统的稳定裕度表达式(30)可知,此时系统的稳定裕度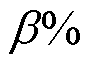 减小,说明跟网型设备的接入恶化了系统的稳定性。当跟网型设备采用参数②时,CgSCRGFM增大,此时系统的稳定裕度
减小,说明跟网型设备的接入恶化了系统的稳定性。当跟网型设备采用参数②时,CgSCRGFM增大,此时系统的稳定裕度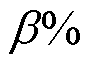 增大,说明此时跟网型设备的接入有利于系统的稳定性。因此跟网型设备在同一控制方式、不同的控制参数下对系统稳定性的影响不同;此外,在相同控制参数下,不同的控制方式对系统稳定性的影响也不同。比较表1算例2~5采用参数①时的CgSCRGFM可知,跟网型设备采用Udc、V控制对应的CgSCRGFM最小,说明在所给参数下跟网型设备采用Udc、V控制对原系统稳定性恶化程度最大;比较表1算例2~5采用参数②时的CgSCRGFM可知,跟网型设备采用P、Q控制对应的CgSCRGFM最大,说明在所给参数下跟网型设备采用PQ控制对原系统稳定性提升程度最大。
增大,说明此时跟网型设备的接入有利于系统的稳定性。因此跟网型设备在同一控制方式、不同的控制参数下对系统稳定性的影响不同;此外,在相同控制参数下,不同的控制方式对系统稳定性的影响也不同。比较表1算例2~5采用参数①时的CgSCRGFM可知,跟网型设备采用Udc、V控制对应的CgSCRGFM最小,说明在所给参数下跟网型设备采用Udc、V控制对原系统稳定性恶化程度最大;比较表1算例2~5采用参数②时的CgSCRGFM可知,跟网型设备采用P、Q控制对应的CgSCRGFM最大,说明在所给参数下跟网型设备采用PQ控制对原系统稳定性提升程度最大。
综上所述,从系统强度的视角可以阐释如下机理:当跟网型设备的接入导致系统gSCRGFM减小时,系统的稳定裕度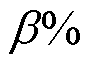 随之减小,意味着跟网型设备的接入恶化了原构网多馈入系统的稳定性,进而增加了系统遭受低频振荡风险的可能性;相反,当跟网型设备的接入导致系统CgSCRGFM增大时,系统的稳定裕度
随之减小,意味着跟网型设备的接入恶化了原构网多馈入系统的稳定性,进而增加了系统遭受低频振荡风险的可能性;相反,当跟网型设备的接入导致系统CgSCRGFM增大时,系统的稳定裕度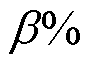 随之增大,意味着跟网型设备的接入提升了原构网型多馈入系统的稳定性。
随之增大,意味着跟网型设备的接入提升了原构网型多馈入系统的稳定性。
本文围绕跟网型和构网型设备混联多馈入系统潜在的低频振荡问题,提出了一种基于系统强度的低频段主导模态稳定性分析方法,并通过频域模态分析以及电磁暂态仿真验证了所提方法及推论的正确性。主要结论如下:
1)本文所提跟网型与构网型设备的简化模型适用于混联多馈入系统的低频段稳定性分析;所构造的特征子系统可以近似反映原混联多馈入系统的低频段稳定性。
2)从系统强度的视角,跟网型设备的接入并未改变原构网型设备多馈入系统的电网强度。因此,跟网型设备的接入对系统低频振荡稳定的影响可等效为改变了原多构网型设备并网系统所需满足的最大gSCRGFM要求,从而影响了系统的低频段稳定性,且改变程度与跟网型设备的控制结构与控制参数有关(跟网型设备的加入可能使原系统变得更稳定,也可能会恶化系统的稳定性)。
上述结论为深入理解混联多馈入系统的低频振荡特性及其稳定性分析提供了新的视角和方法。如何设计跟网型设备的控制策略及控制参数,进而提升混联多馈入系统低频段的稳定性将需要进一步开展研究。此外,考虑到传统同步机组存在低频振荡失稳问题,未来将进一步研究考虑传统同步机组接入的混联多馈入系统低频段小干扰稳定性分析。
附 录
1. 仿真算例模型参数
附表1 构网型设备自身基准容量下控制参数
App.Tab.1 Control parameters of GFMD based on its capacity

参数数值 滤波电感Lf(pu)0.05 滤波电容Cf(pu)0.05 电流内环Hi(s)比例、积分参数1, 10 电压前馈GFF(s)滤波时间常数0.001 电流前馈KF0.1 无功电流指令Iqref(pu)0 有功功率参考值Pref1
附表2 跟网型设备自身基准容量下控制参数
App.Tab.2 Control parameters of GFLD based on its capacity(pu)

参数数值 直流电容Cdc、滤波电容Lf和电感Cf0.038, 0.05, 0.05 电流内环Hi(s)比例、积分参数1, 10 PLLHPLL(s)比例、积分参数50, 7 500 电压前馈GFF(s)滤波时间常数0.001 直流电压、无功电流参考值Udcref, Iqref1, 0 直流母线输入功率Pr1
附表3 39节点并网系统各跟网型设备的直流电压外环和无功功率外环参数
App.Tab.3 Hdc(s) and HQ(s) of all GFLDs in 39-node system
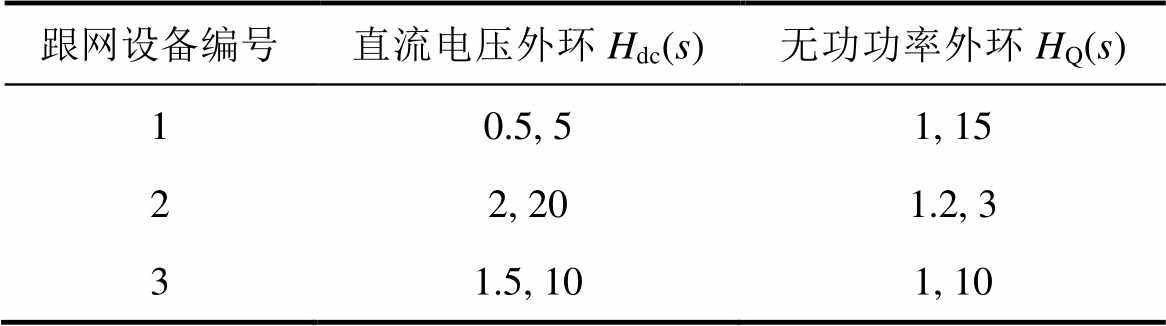
跟网设备编号直流电压外环Hdc(s)无功功率外环HQ(s) 10.5, 51, 15 22, 201.2, 3 31.5, 101, 10
附表4 39节点并网系统各构网型设备的J, D及电压外环参数
App.Tab.4 J, D,Hv(s) of all GFMDs in 39-node system

构网设备编号JD电压外环Hv(s) 1和64.5574.2, 19 2和43.5513.7, 17 3和54534, 20
附表5 39节点并网系统构网型设备容量
App.Tab.5 capacity of all GFMDs in 39-node system

设备编号容量(pu) 15.48 25.32 34.43 44.81 510.06 63.2
2. 构网型设备导纳矩阵的详细推导
式(7)详细推导过程如下。
1)构网型设备摇摆方程的动态可表示为
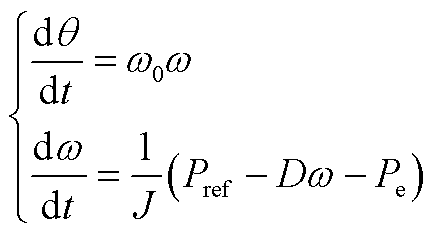 (A1)
(A1)
式中,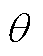 为摇摆方程输出相角;ω为虚拟角速度;Pref为有功功率参考值;Pe为输出有功功率;J和D分别为虚拟惯量和虚拟阻尼。
为摇摆方程输出相角;ω为虚拟角速度;Pref为有功功率参考值;Pe为输出有功功率;J和D分别为虚拟惯量和虚拟阻尼。
附表6 算例2~5中跟网型设备控制参数
App.Tab.6 Control parameters for GFLD in Case 2~5
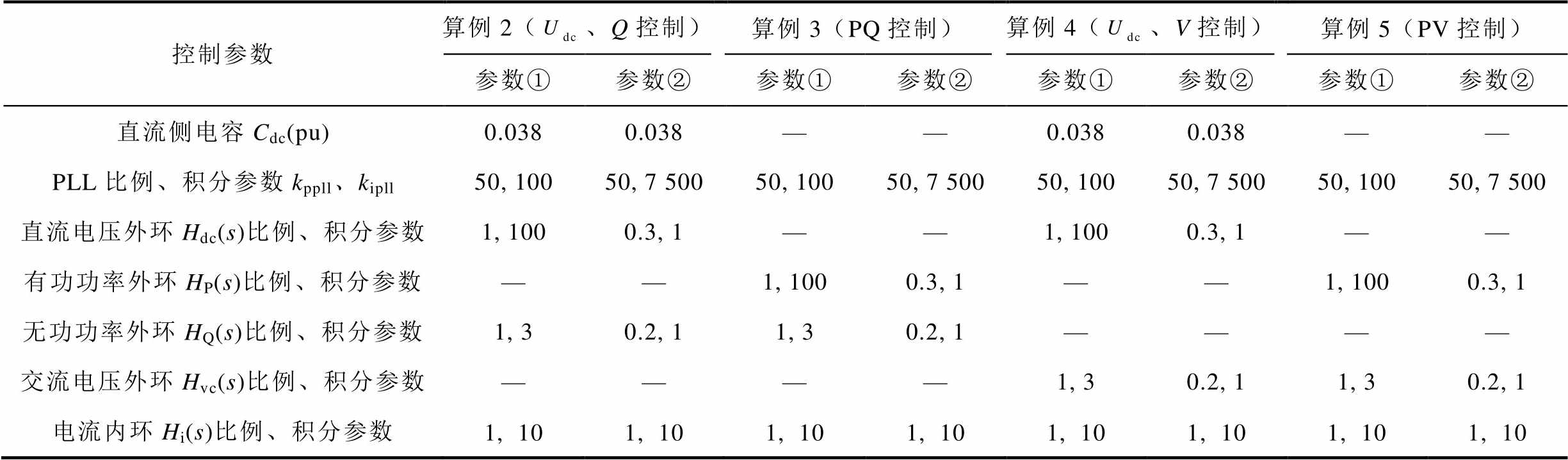
控制参数算例2(、Q控制)算例3(PQ控制)算例4(、V控制)算例5(PV控制) 参数①参数②参数①参数②参数①参数②参数①参数② 直流侧电容Cdc(pu)0.0380.038——0.0380.038—— PLL比例、积分参数kppll、kipll50, 10050, 7 50050, 10050, 7 50050, 10050, 7 50050, 10050, 7 500 直流电压外环Hdc(s)比例、积分参数1, 1000.3, 1——1, 1000.3, 1—— 有功功率外环HP(s)比例、积分参数——1, 1000.3, 1——1, 1000.3, 1 无功功率外环HQ(s)比例、积分参数1, 30.2, 11, 30.2, 1———— 交流电压外环Hvc(s)比例、积分参数————1, 30.2, 11, 30.2, 1 电流内环Hi(s)比例、积分参数1, 101, 101, 101, 101, 101, 101, 101, 10
2)附图1给出了电压外环简化前后的控制框图。如附图1b所示,近似认为电压外环中d轴和q轴前馈系数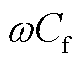 完全抵消了滤波电容的影响,进而在简化后的电压外环动态中忽略了前馈系数
完全抵消了滤波电容的影响,进而在简化后的电压外环动态中忽略了前馈系数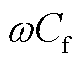 。具体地,简化后的电压外环动态可以表示为
。具体地,简化后的电压外环动态可以表示为
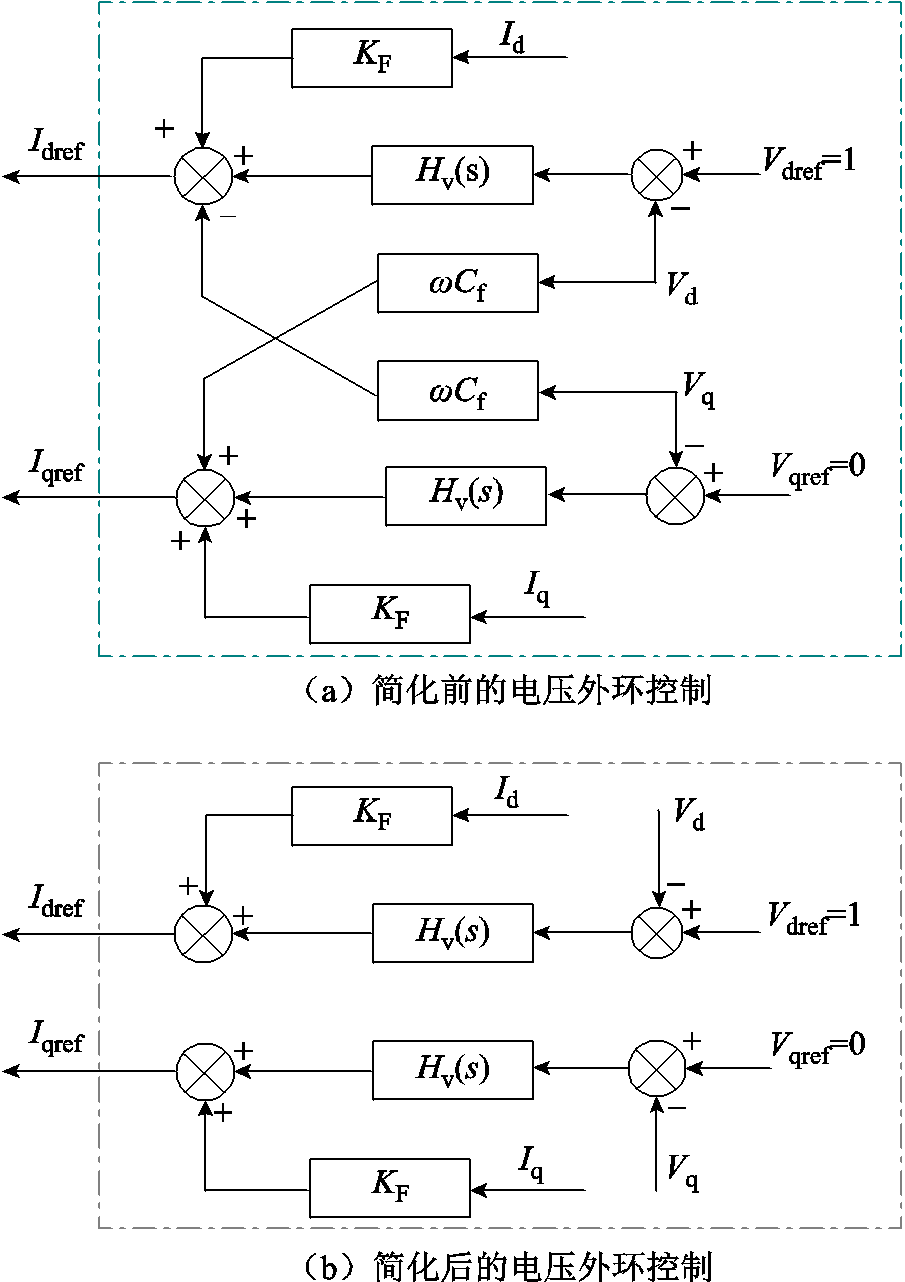
附图1 简化前后的电压外环控制框图
App.Fig.1 Simplified and original voltage outer-loop control block diagram
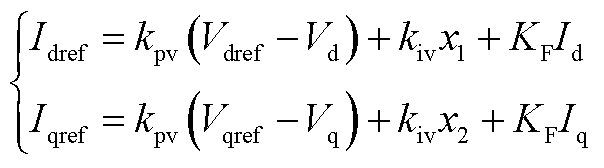 (A2)
(A2)
式中,kpv和kiv分别为交流电压外环PI调节器的传递函数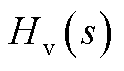 中的比例参数和积分参数;
中的比例参数和积分参数;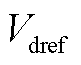 和
和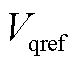 分别为dq坐标系中电压参考值的d轴和q轴分量;Vd和Vq分别为端电压的d轴和q轴分量;
分别为dq坐标系中电压参考值的d轴和q轴分量;Vd和Vq分别为端电压的d轴和q轴分量;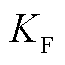 为电流前馈系数;
为电流前馈系数;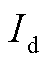 和
和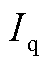 分别为构网型设备电流输出的d轴和q轴分量;
分别为构网型设备电流输出的d轴和q轴分量;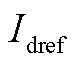 和
和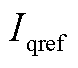 分别为电流参考值的d轴和q轴分量;
分别为电流参考值的d轴和q轴分量;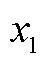 和
和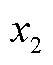 为积分变量,满足以下条件
为积分变量,满足以下条件
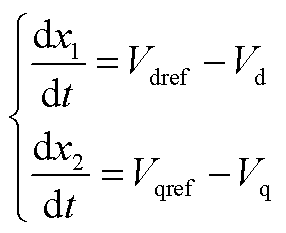 (A3)
(A3)
忽略电流内环后,构网变流器的电流输出等于电流参考值,即
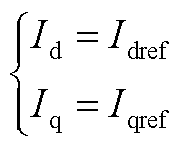 (A4)
(A4)
从dq坐标系到xy坐标系存在如下转换关系
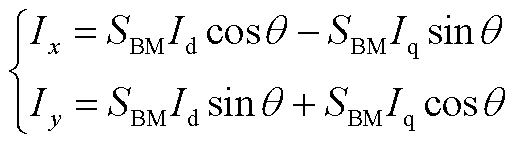 (A5)
(A5)
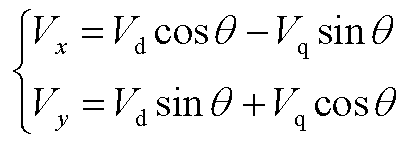 (A6)
(A6)
将式(A1)~式(A6)线性化,得到简化后的构网型设备的导纳模型为
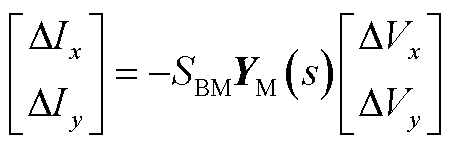 (A7)
(A7)
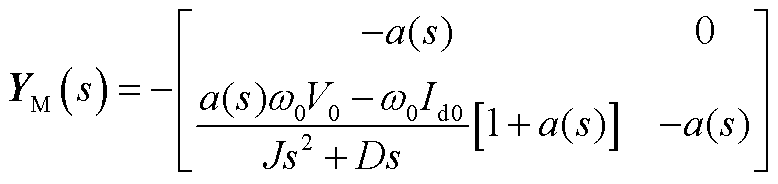 (A8)
(A8)
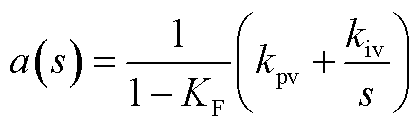 (A9)
(A9)
3. 跟网型设备导纳矩阵的详细推导
式(10)详细推导过程如下。
1)跟网型设备有功外环采用恒直流电压控制及恒有功功率控制两种模式下的动态可分别表示为
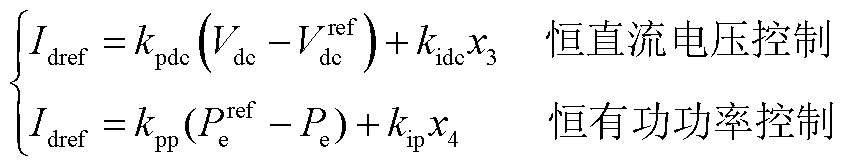 (A10)
(A10)
式中,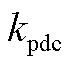 和
和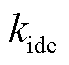 分别为直流电压环PI调节器的传递函数Hdc(s)中的比例参数和积分参数;
分别为直流电压环PI调节器的传递函数Hdc(s)中的比例参数和积分参数;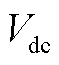 和
和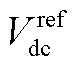 分别为直流母线电压的实际值和参考值;kpp和kip分别为有功功率外环PI调节器的传递函数Hp(s)中的比例参数和积分参数;
分别为直流母线电压的实际值和参考值;kpp和kip分别为有功功率外环PI调节器的传递函数Hp(s)中的比例参数和积分参数;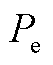 和
和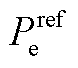 分别为跟网设备有功功率的实际值和参考值;
分别为跟网设备有功功率的实际值和参考值;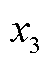 和
和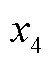 为积分变量,且满足以下条件
为积分变量,且满足以下条件
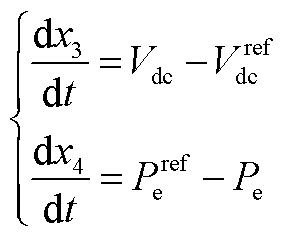 (A11)
(A11)
2)跟网型设备无功环考虑恒无功功率控制和恒交流电压控制两种模式下的动态可分别表示为
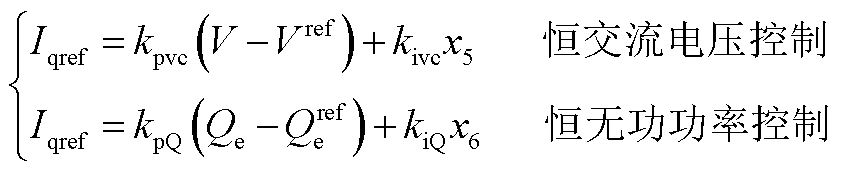 (A12)
(A12)
其中
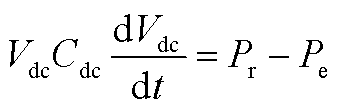 (A13)
(A13)
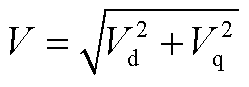 (A14)
(A14)
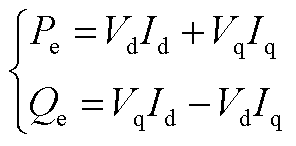 (A15)
(A15)
式中,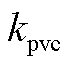 和
和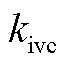 分别为交流电压外环PI调节器的传递函数
分别为交流电压外环PI调节器的传递函数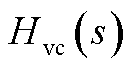 中的比例参数和积分参数;kpQ和kiQ分别为无功功率外环PI调节器的传递函数HQ(s)中的比例参数和积分参数;
中的比例参数和积分参数;kpQ和kiQ分别为无功功率外环PI调节器的传递函数HQ(s)中的比例参数和积分参数;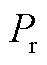 和
和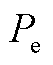 分别为直流母线的实际输入功率(考虑恒定)和输出功率;
分别为直流母线的实际输入功率(考虑恒定)和输出功率;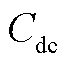 为直流电容;
为直流电容; 和
和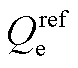 分别为跟网设备无功功率的实际值和参考值;V和
分别为跟网设备无功功率的实际值和参考值;V和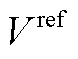 是变流器电压幅值的实际值和参考值;
是变流器电压幅值的实际值和参考值;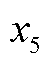 和
和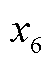 为积分变量,且满
为积分变量,且满
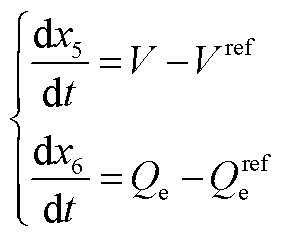 (A16)
(A16)
3)跟网型设备PLL的动态可分别表示为
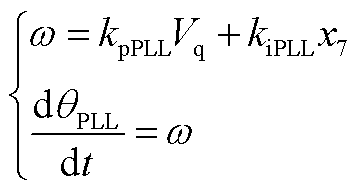 (A17)
(A17)
式中,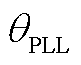 为PLL输出的相角;ω为PLL的角速度;
为PLL输出的相角;ω为PLL的角速度;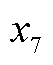 为积分变量,且满足
为积分变量,且满足
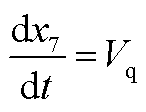 (A18)
(A18)
忽略电流内环后,跟网变流器的电流输出等于电流参考值,即
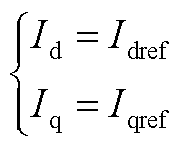 (A19)
(A19)
从dq坐标系到xy坐标系存在如下转换关系
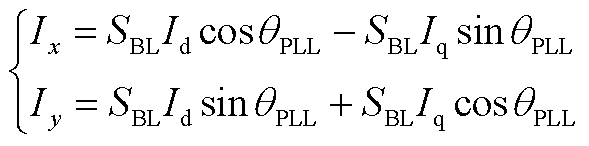 (A20)
(A20)
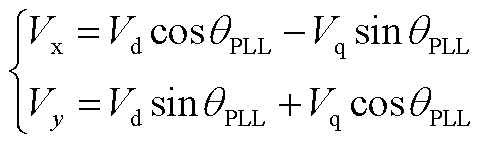 (A21)
(A21)
将式(A10)~式(A21)线性化,得到四种不同控制方式下跟网型变流器的导纳模型
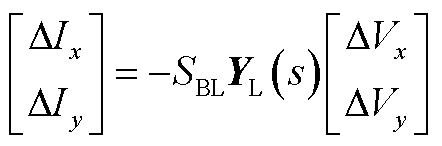 (A22)
(A22)
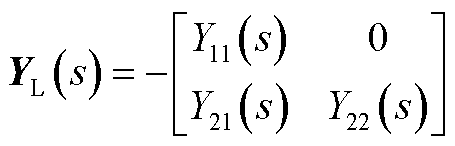 (A23)
(A23)
跟网型设备有功外环采用恒直流电压控制,无功外环采用恒无功功率控制时,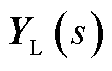 的具体表达式为
的具体表达式为
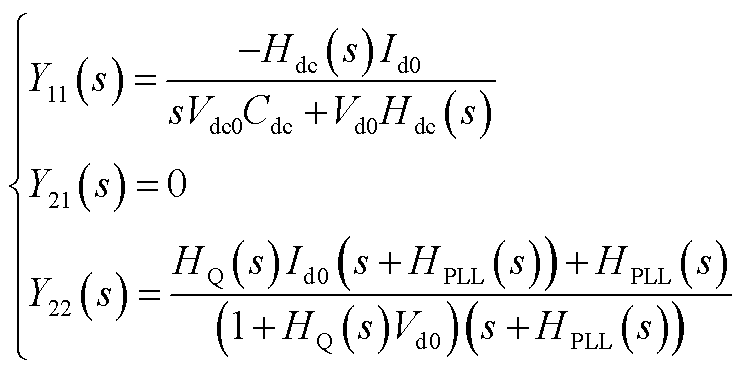 (A24)
(A24)
跟网型设备有功外环采用恒有功功率控制,无功外环采用恒无功功率控制时,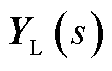 的具体表达式为
的具体表达式为
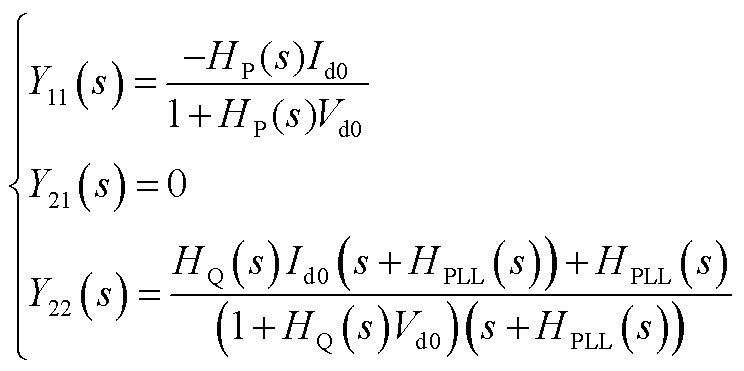 (A25)
(A25)
跟网型设备有功外环采用恒直流电压控制,无功外环采用恒交流电压控制时,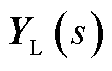 的具体表达式为
的具体表达式为
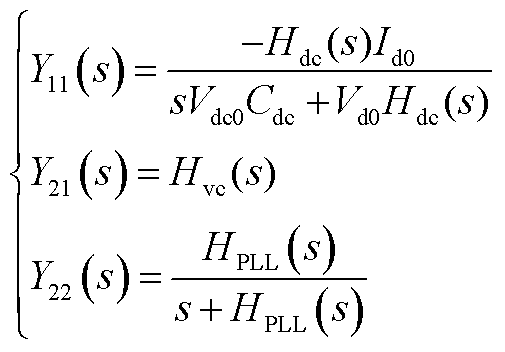 (A26)
(A26)
跟网型设备有功外环采用恒有功功率控制,无功外环采用恒交流电压控制时,YL(s)具体表达式为
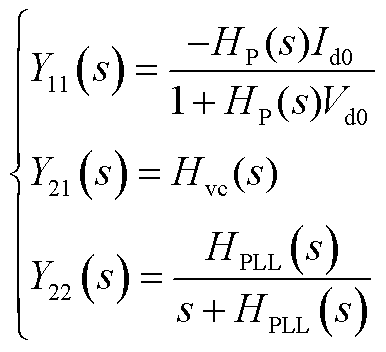 (A27)
(A27)
综合以上分析,式(A24)详细表达式为
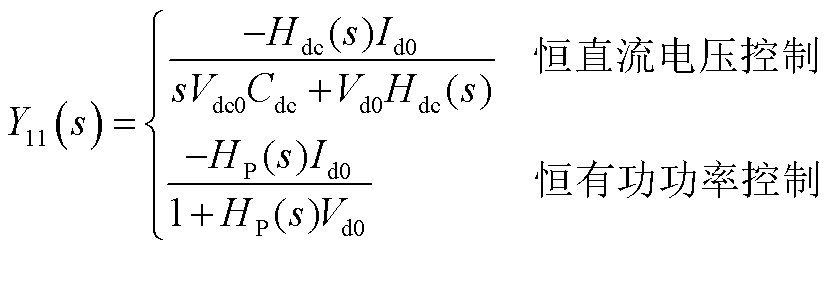 (A28)
(A28)
 (A29)
(A29)
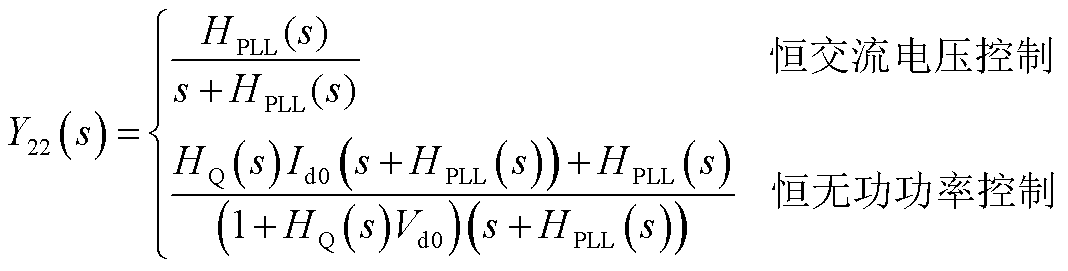 (A30)
(A30)
4. 跟网型设备导纳矩阵奇异值与构网型设备导纳矩阵最大奇异值在低频段下的比值
附图2给出了在不同控制策略下,跟网型设备导纳矩阵奇异值与构网型设备导纳矩阵最大奇异值在低频段下(频率范围为0.1~2.5 Hz)的比值,其中构网型设备的控制参数参考5.1节中的构网型设备1;跟网型设备的控制参数参考附表6算例2~5中的参数②;构网型设备和跟网型设备的容量均为1.0(pu)。从附图2所给奇异值的比值可以看出,在低频段下跟网型设备对原构网型多馈入系统稳定性的影响较小,说明跟网型设备的加入可以理解为对原构网多馈入系统动态的摄动,进一步验证了特征子系统构造的合理性。
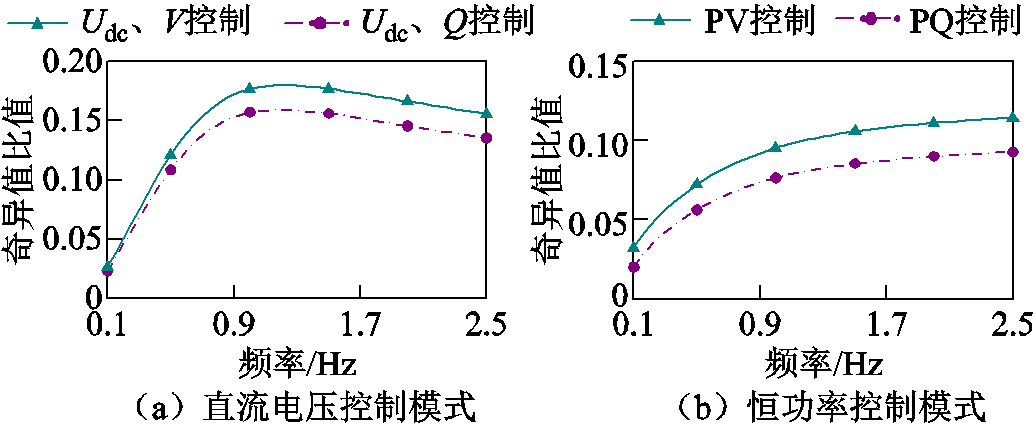
附图2 不同控制策略下,跟网型设备导纳矩阵奇异值与构网型设备导纳矩阵奇异值的比值
App.Fig.2 The ratio of the singular values of the admittance matrix of the GFLD under different control strategies to the singular values of the admittance matrix of the GFMD
5. 加权系数变化对系统CgSCRGFM的影响
设备1不同加权系数下系统的CgSCRGFM见附表7。由附表7可知,构网型设备1的加权系数越大,特征子系统对应的CgSCRGFM越大,说明随着构网型设备1的加权系数增大,设备1对系统稳定性的改善程度增加,系统稳定性逐渐得到改善。此外,也可以理解为随着加权系数增加,设备1与其余设备的交互作用程度增大,对稳定性的影响程度随之增加。
附表7 设备1不同加权系数下系统的CgSCRGFM
App.Tab.7 CgSCRGFM of the system under different weighting coefficients for GFMD1

加权系数p11CgSCRGFM 010.528 0.1813.950 0.2916.074 0.3517.207
参考文献
[1] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[2] 李红, 梁军杨, 王振民, 等. 跟网型变换器的小扰动同步稳定机理分析与致稳控制[J]. 电工技术学报, 2024, 39(12): 3802-3815.
Li Hong, Liang Junyang, Wang Zhenmin, et al. Small signal synchronization stability analysis and improved control strategy for grid following converter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3802-3815.
[3] Ndreko M, Rüberg S, Winter W. Grid forming control scheme for power systems with up to 100% power electronic interfaced generation: a case study on Great Britain test system[J]. IET Renewable Power Generation, 2020, 14(8): 1268-1281.
[4] 朱廷猛, 孙海顺, 秦世耀, 等. 弱电网下双馈风机并网系统的次同步振荡研究[J]. 电网技术, 2021, 45(5): 1641-1648.
Zhu Tingmeng, Sun Haishun, Qin Shiyao, et al. Sub-synchronous oscillation in DFIG system connected to weak grid[J]. Power System Technology, 2021, 45(5): 1641-1648.
[5] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[6] Rosso R, Engelken S, Liserre M. Robust stability investigation of the interactions among grid-forming and grid-following converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 991-1003.
[7] Guo Jian, Chen Yandong, Wang Lei, et al. Impedance analysis and stabilization of virtual synchronous generators with different DC-link voltage controllers under weak grid[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11397-11408.
[8] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1312-1324, 1374.
[9] Tan J, Dong S, Hoke A. Lessons learned from real-world oscillation events[C]//IEEE PES General Meeting, Orlando, FL, USA, 2023: 16-20.
[10] 辛焕海, 李子恒, 董炜, 等. 三相变流器并网系统的广义阻抗及稳定判据[J]. 中国电机工程学报, 2017, 37(5): 1277-1293.
Xin Huanhai, Li Ziheng, Dong Wei, et al. Generalized-impedance and stability criterion for grid-connected converters[J]. Proceedings of the CSEE, 2017, 37(5): 1277-1293.
[11] Liao Yicheng, Wang Xiongfei. Impedance-based stability analysis for interconnected converter systems with open-loop RHP poles[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4388-4397.
[12] Li Yang, Shuai Zhikang, Liu Xuan, et al. Stability analysis and location optimization method for multiconverter power systems based on nodal admittance matrix[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 529-538.
[13] 周瑀涵, 辛焕海, 鞠平. 基于广义短路比的多馈入系统强度量化原理与方法: 回顾、探讨与展望[J]. 中国电机工程学报, 2023, 43(10): 3794-3811.
Zhou Yuhan, Xin Huanhai, Ju Ping. System strength quantification principle and method of multi-infeed systems based on generalized short-circuit ratio: reviews, discussions and outlooks[J]. Proceedings of the CSEE, 2023, 43(10): 3794-3811.
[14] 王子骏, 庄可好, 辛焕海, 等. 虚拟同步直驱风机低频振荡机理分析及阻尼补偿控制[J]. 电力系统自动化, 2024, 48(2): 95-104.
Wang Zijun, Zhuang Kehao, Xin Huanhai, et al. Low-frequency oscillation mechanism analysis and damping compensation control of virtual synchronous direct-driven wind turbine generators[J]. Automation of Electric Power Systems, 2024, 48(2): 95-104.
[15] 王玉坤, 张慕婕, 李壮, 等. 构网型直驱风电机组间控制相互作用研究[J]. 电力自动化设备, 2024, 44(3): 82-90.
Wang Yukun, Zhang Mujie, Li Zhuang, et al. Research on control interaction between grid forming direct-drive wind turbines[J]. Electric Power Automation Equipment, 2024, 44(3): 82-90.
[16] 余光正, 胡越, 刘晨曦, 等. 含跟网/构网型混联多馈入系统协调优化配置方法[J]. 中国电机工程学报, 2025, 45(2): 588-601.
Yu Guangzheng, Hu Yue, Liu Chenxi, et al. Research on the coordinated optimization configuration method for hybrid multi-infeed systems with grid-following or grid-forming[J]. Proceedings of the CSEE, 2025, 45(2): 588-601.
[17] 方正, 黄云辉, 严文博, 等. 构网型与跟网型变流器交互作用对并联系统小干扰稳定性的影响分析[J]. 电力自动化设备, 2025, 45(2): 134-142.
Fang Zheng, Huang Yunhui, Yan Wenbo, et al. Influence analysis of interaction between grid-forming and grid-following converters on small interference stability of parallel system[J]. Electric Power Automation Equipment, 2025, 45(2): 134-142.
[18] 郭小龙, 杨桂兴, 张彦军, 等. 构网型储能与跟网型光伏混联发电系统阻抗建模与小扰动稳定机理分析[J]. 电气工程学报, 2025, 20(1): 299-308.
Guo Xiaolong, Yang Guixing, Zhang Yanjun, et al. Impedance modeling and small-signal stability mechanism analysis of grid-forming energy storage and grid-following PV hybrid power generation system[J]. Journal of Electrical Engineering, 2025, 20(1): 299-308.
[19] 盛李龙, 许津铭, 李威, 等. 弱电网下跟/构网型变流器并联系统的阻抗频率耦合及稳定性分析[J]. 电力系统自动化, 2025, 49(1): 27-37.
Sheng Lilong, Xu Jinming, Li Wei, et al. Impedance frequency coupling and stability analysis of parallel system of grid-following and gridforming converters in weak grid[J]. Automation of Electric Power Systems, 2025, 49(1): 27-37.
[20] Yang Chaoran, Huang Linbin, Xin Huanhai, et al. Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3563-3573.
[21] 辛焕海, 甘德强, 鞠平. 多馈入电力系统广义短路比: 多样化新能源场景[J]. 中国电机工程学报, 2020, 40(17): 5516-5527.
Xin Huanhai, Gan Deqiang, Ju Ping. Generalized short circuit ratio of power systems with multiple power electronic devices: analysis for various renewable power generations[J]. Proceedings of the CSEE, 2020, 40(17): 5516-5527.
[22] 袁辉, 辛焕海, 王冠中, 等. 含SVG的新能源多馈入系统振荡分析和广义短路比计算[J]. 电力系统自动化, 2021, 45(14): 38-46.
Yuan Hui, Xin Huanhai, Wang Guanzhong, et al. Analysis on oscillation of multi-infeed system with renewable energy and static var generator and calculation of its generalized short-circuit ratio[J]. Automation of Electric Power Systems, 2021, 45(14): 38-46.
[23] Gönen T. Modern Power System Analysis[M]. 2nd ed. Oxfordshire: Taylor and Francis, 2013.
[24] 辛焕海, 刘晨曦, 黄林彬, 等. 基于特征子系统的广义短路比导出原理及计算方法[J]. 中国电机工程学报, 2025, 45(7): 2447-2461.
Xin Huanhai, Liu Chenxi, Huang Linbin, et al. Derivation principle and calculation method of generalized short-circuit ratio based on eigen-subsystems[J]. Proceedings of the CSEE, 2025, 45(7): 2447-2461.
[25] Stewart G W. Matrix Perturbation Theory[M]. Salt Lake City: Academic Press, 1990.
Abstract The future power system will present a new hybrid grid-connected configuration with both grid-following devices (GFLDs) and grid-forming devices (GFMDs). Due to the strong stochasticity of renewable power generations, the system may encounter high short-circuit ratio (SCR) scenarios with low penetration of renewable power generations under extreme conditions. This may cause GFMD-induced low-frequency oscillation issues where the oscillation frequency is in the range of [0.1 Hz, 2.5 Hz]. Therefore, it is important to investigate how the interaction among GFMDs influence the low-frequency oscillation stability, and how the connection of GFLDs influence this type of oscillation stability. The existing research commonly investigated the sub-synchronous oscillation issues dominated by GFLDs in weak grids. Only a few works discussed the GFMD-induced low-frequency oscillation issues with the assumption that the GFMDs are homogeneous. However, it is still unknown how the interaction among heterogeneous GFLDs and GFMDs influences this type of low-frequency oscillation issues. Due to this, this paper proposes a novel method to evaluate small-signal low-frequency stability of power systems with GFLDs and GFMDs from the perspective of system strength.
Firstly, to simplify the analysis, this paper constructs simplified dynamic models of GFLDs and GFMDs suitable for low-frequency oscillation analysis. Secondly, based on matrix perturbation theory, equivalent homogeneous systems that approximately reflect the low-frequency dominant mode of the original system are constructed for the multi-GFMDs system considering heterogeneous GFMDs and the connection of GFLDs, where the established homogeneous system retains the network structure characteristics of the original system. Furtherly, the eigen-subsystem are derived, which can reflect the low-frequency dominant mode of the original system. On this basis, from the perspective of system strength, the low-frequency oscillation stability evaluation index of the original complex multi-infeed system is proposed, and the mechanism of the heterogeneous characteristics of grid-forming devices and the interaction between grid-following and grid-forming devices on the low-frequency oscillation of the system is revealed. Finally, the proposed analysis method is validated through case studies on a three-infeed system with two GFMDs and a GFLD and a modified IEEE 39-node system.
The following conclusions can be drawn: (1) The proposed simplified models of GFLD and GFMD are applicable to the low-frequency oscillation stability analysis of hybrid multi-infeed systems, which is verified based on detailed electromagnetic transient models; the constructed eigen-subsystem can approximately reflect the low-frequency stability of the original complex multi-infeed system. (2) The proposed generalized short-circuit ratio (gSCR) index and its critical value effectively reflect system strength and low-frequency stability margin in hybrid renewable energy systems, which simplifies the complexity of the stability analysis. (3) From the perspective of system strength, the connection of GFLDs has no impact on grid strength, but influence the critical value of grid strength. Therefore, the impact of the connection of GFLDs on the low-frequency oscillation stability of the system can be equivalently regarded as changing the maximal SCR requirement of the original multi-grid-forming device grid-connected system, thereby affecting the low-frequency stability of the system. Besides, how the GFLDs influence the maximal gSCR requirement depends on the control structure and control parameters of the GFLDs (the addition of GFLDs may improve or deteriorate the system stability).
Keywords:Grid-following device, grid-forming device, low-frequency oscillation,eigen-subsystems, system strength
詹修瑜 男,2000年生,硕士研究生,研究方向为新能源电力系统稳定分析与控制。
E-mail:22360580@zju.edu.cn
袁 辉 男,1991年生,博士,副教授,研究方向为新能源电力系统稳定分析与控制。
E-mail:Yuan_Hui@zju.edu.cn(通信作者)
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.250039
国家重点研发计划(2023YFB2405900)、国家自然科学基金(52207140)和浙江省自然科学基金(LY23E070003)资助项目。
收稿日期 2025-01-07
改稿日期 2025-04-17
(编辑 赫 蕾)