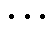 , N)个SVG子模块,vdct.i为t相第i个模块直流侧电压,vn为三相桥臂公共连接点电压。
, N)个SVG子模块,vdct.i为t相第i个模块直流侧电压,vn为三相桥臂公共连接点电压。摘要 近年来,构网控制技术在新能源领域得到了广泛应用,其中构网型静止无功发生器(SVG)被视为同步调相机的理想替代装备。然而,构网型SVG对新能源并网系统稳定性的具体影响机制尚未得到充分研究。该文聚焦构网型SVG在风电场中的应用及其对系统稳定性的影响,开展深入研究。首先,采用多谐波线性化建模方法,建立SVG跟网和构网控制模式下的阻抗模型,重点分析SVG输出阻抗的负阻尼分布特征,并对两种模式下的阻抗特性进行详细的量化分析对比。然后,构建包含SVG的风电场阻抗网络模型,系统地探讨不同模式SVG对风电场稳定性的影响规律。研究结果表明:与跟网型SVG相比,构网型SVG的负阻尼阻抗特征得以显著改善,构网型SVG具备与同步调相机相当的弱电网稳定运行能力。最后,通过RT-Lab硬件在环实验平台,以哈密地区某风电场为例进行多工况实验,实验结果验证了该文分析结果的正确性。
关键词:静止无功发生器(SVG) 同步调相机 构网控制 阻抗模型 稳定性分析 风电场
在“双碳”目标的引领下,我国新能源发电产业快速发展,以高比例风电、光伏和储能为代表的新型电力系统正逐步形成[1-2]。然而,随着新能源并网规模的扩大,由于电力电子装置与电网阻抗的相互作用,易引发宽频振荡问题,这给系统的稳定运行带来了挑战[3-5]。根据现行电网运行规范,为了提高输送容量和电压控制能力,新能源场站通常在并网点按照额定容量的20%~40%配置无功补偿装置,如静止无功发生器(Static Var Generator, SVG)。作为重要控制载体,SVG的接入不仅增强了新能源场站的电压支撑能力,还为系统振荡抑制提供了有力支持[6-7]。
为了分析SVG接入对新能源场站稳定性的影响,学者们开展了大量的研究工作。文献[8]指出大型光伏电站中的SVG对系统稳定性具有重要影响,在分析系统稳定时SVG的影响不可忽略。文献[9]基于阻抗分析法建立SVG的阻抗模型,分析了SVG不同工作模式(定电压和定无功模式)对系统稳定性的影响。文献[10]计及SVG的影响,提出一种针对大规模风电场的序阻抗网络建模与稳定性分析方法。大量研究表明,SVG在新能源场站中的影响不可忽视,且SVG作为新能源场站中的可调配资源在为系统提供附加阻尼方面具有一定的开发潜力。为了充分开发利用SVG的阻尼潜力,学者们提出了各种阻尼塑造方法。按照控制信号和功能可划分为:参数优化[11]、附加阻尼[12-13]、相角补偿控制[14]及虚拟阻抗控制[15]等。其中,文献[15]提出基于SVG的宽频阻抗重塑方法,通过虚拟阻抗的方式推衍出了一种较为通用的阻抗控制方法,极大地拓展了SVG的阻抗塑造潜力。上述研究结果表明,SVG作为一种潜在的阻尼调配资源极具开发潜力。
近年来,随着储能变流器在新能源系统中的大规模应用,构网(Grid-Forming, GFM)技术重新被学术界和工业界重视[16]。大量研究结果表明,构网技术在弱电网应用场景中具有较大潜力,更有利于维持弱电网的稳定性[17-18]。同样地,为了取代新能源系统中的同步调相机,基于SVG的构网型技术也得到学术界和工业界的广泛关注[19]。相较于同步调相机,SVG具有成本低、维护简单以及响应速度快等优势,且在储能和构网控制技术加持下具有自同步、秒级功率支撑及提供足够的暂态支撑(3倍过电流)等性能优势[20-22]。同时,大容量的构网型SVG采用级联H桥结构,具备功率密度高、整体损耗小、寿命长、安装方便等优势,更适合新能源等应用场景,目前工业界已有多个示范工程进行构网型SVG技术的相关验证[23]。文献[24]对比了跟网型和构网型变流器阻抗模型,研究结果表明弱电网条件下构网型变流器相比于跟网型变流器具有更高的稳定裕度。文献[25]研究了基于超级电容的SVG构网控制方法,构网型SVG相比常规SVG具有更高的灵活性,且具备惯量和电压支撑控制能力。文献[26]基于储能型高压直挂SVG,提出了一种基于内电动势下垂+环形限流的自同步电压源控制方法,实现了对电网频率和电压的自主、快速支撑。在实际工程中,2024年10月,具有超级电容的构网型SVG在西藏电网投运成功,为西藏电网的电压支撑和弱/极弱电网运行提供了一种切实可行的技术方案[23]。构网技术的应用有助于进一步挖掘SVG在新型电力系统中的阻尼塑造潜力,为提升新能源并网系统的稳定性提供了新的解决思路。然而,目前关于构网型SVG对新能源场站稳定性影响的研究还处于探索阶段,尤其是构网型SVG的建模及其对新能源场站稳定性的影响规律等都还有待进一步深入研究。
综上所述,现有研究主要集中于储能型变流器的构网控制分析,而工业界对构网型SVG技术的研究仍停留在可行性验证阶段,缺乏从理论层面对其性能进行深入量化和对比分析。本文以哈密某风电场为研究对象,重点探究构网型SVG的阻抗建模及其对风电场并网稳定性的影响规律。与现有研究工作相比,本文的创新点主要体现在以下几个方面:
1)利用多谐波线性化建模方法,建立了完整的基于直流电压同步的构网型SVG序阻抗标准化模型,为并网稳定性分析提供了理论基础。
2)详细对比了构网型SVG与跟网型SVG的阻抗差异,定量分析了构网关键参数对输出阻抗的影响规律,为参数优化设计提供了依据。
3)建立了含构网型SVG的风电场阻抗网络模型,定量评估了跟网/构网型SVG、同步调相机对风电场稳定性的影响差异,明确了构网型SVG对风电场稳定性的提升机制。
构网型控制变流器的外特性呈现电压源特性,因而在弱电网场景下具有较强的稳定性。本节首先简要介绍基于直流电压同步的构网控制方式;然后采用多谐波线性化的方法对该控制下的SVG进行阻抗建模,并定量对比分析跟网型和构网型SVG的阻抗特性。
采用级联H桥模块化多电平变流器(Modular Multilevel Converter, MMC)拓扑的SVG主电路如图1所示。图1中,ust(t=a, b, c)为SVG三相并网点电压,igt为SVG三相并网电流,L为SVG交流侧滤波电感,N为模块数,SM.ti为t相第i(i=1, 2,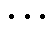 , N)个SVG子模块,vdct.i为t相第i个模块直流侧电压,vn为三相桥臂公共连接点电压。
, N)个SVG子模块,vdct.i为t相第i个模块直流侧电压,vn为三相桥臂公共连接点电压。
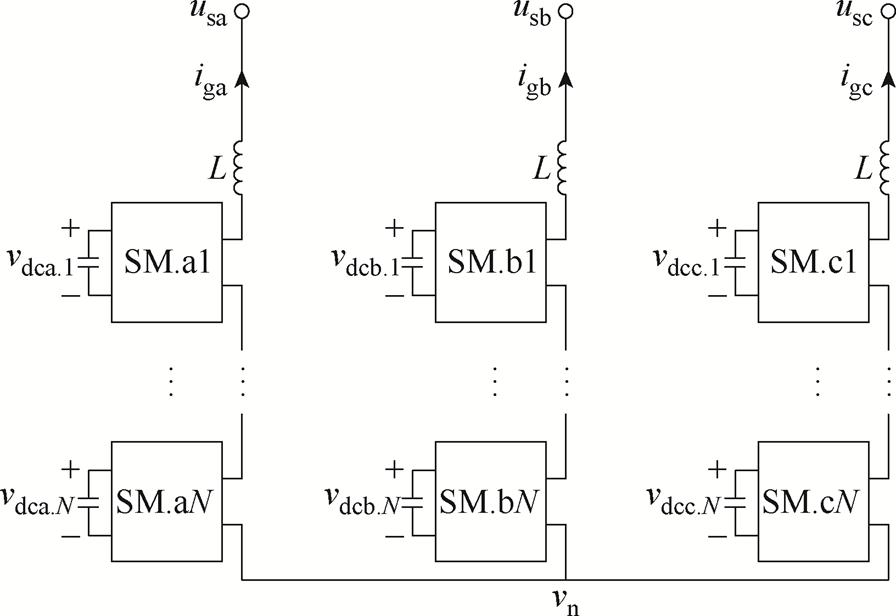
图1 基于直流电压同步的构网型SVG拓扑
Fig.1 Topology of DC voltage synchronization based GFM SVG
基于直流电压同步的构网型SVG控制框图如图2所示,包括直流电压同步、无功电压下垂、虚拟阻抗及相间均压控制。图2中,w1为工频角频率,Vdcref为单模块直流电压参考值,K为直流电压调频系数,Qref和Uoref分别为无功功率参考值和电压幅值参考值,Q和Uo分别为输出无功功率和电压幅值,Kut为电压下垂系数,Kq为无功电压环惯性系数,vdct为t相单模块直流电压平均值,Vdcm为全模块直流电压平均值,Hpv(s)为相间均压电压环PI控制器,Ki为相间均压电流环比例控制器。
文献[25]中提到,两电平SVG直流侧与交流侧满足功率平衡公式为
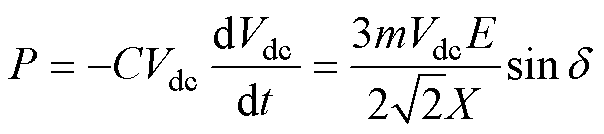 (1)
(1)
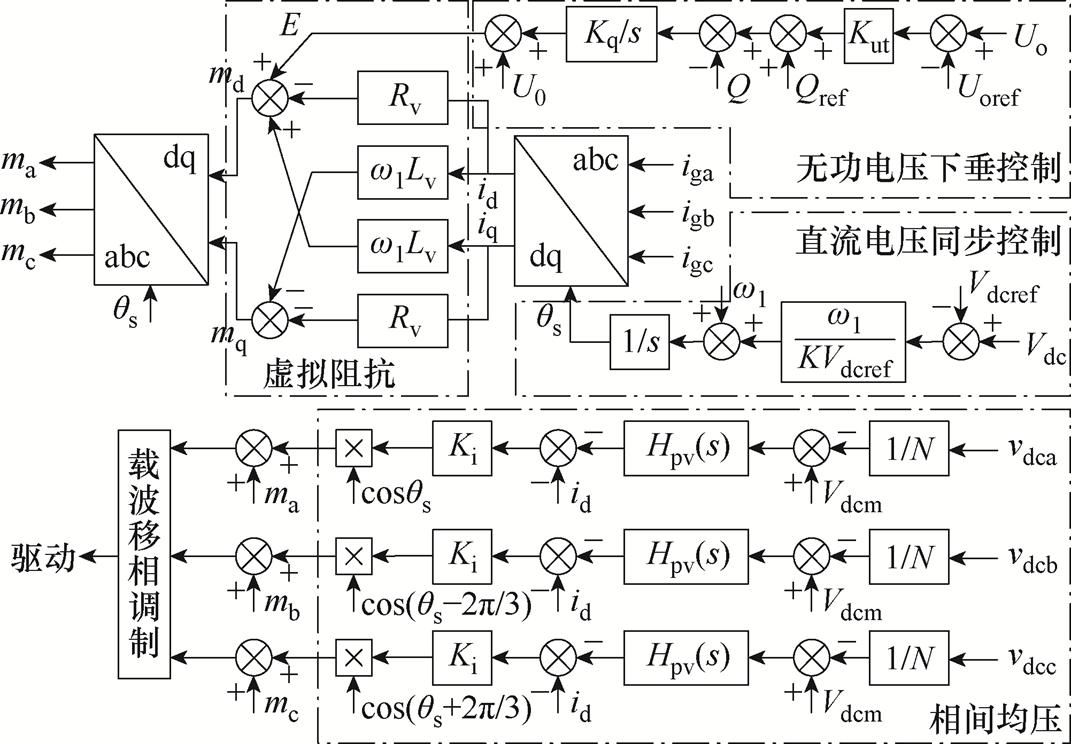
图2 基于直流电压同步的构网型SVG控制框图
Fig.2 Control block diagram of DC voltage synchronization based GFM SVG
式中,C为直流侧电容;Vdc为SVG直流侧电压;m为调制比;E为参考电平;X为输出等效电抗;d为功角。类比同步机功角特性公式,有
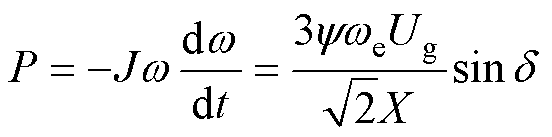 (2)
(2)
式中,J为转动惯量;w为机械角速度;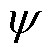 为定子磁链幅值;we为电气角速度;Ug为电网电压幅值。
为定子磁链幅值;we为电气角速度;Ug为电网电压幅值。
SVG可以通过直流电压同步控制将直流侧电容电压Vdc与电网频率建立联系,实现相角同步。该同步方式与跟网型SVG相比,从功能上替代了锁相环及全局均压环并简化了控制结构。无功电压下垂控制通过电压下垂系数Kut对并网点电压幅值进行动态调控,从而控制SVG的无功输出。虚拟阻抗Rv和Lv可以近似等效为在滤波器前串联阻感,对SVG输出限流,并为变换器提供阻尼,实现构网型SVG在多场景下的稳定运行。相间均压控制环路对三相直流侧电压平均值进行均压控制。
根据多谐波线性化频域建模方法,为了获取构网型SVG的阻抗模型,首先需要建立其功率电路频域模型,根据文献[10],SVG主功率电路频域小信号模型为
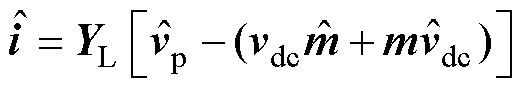 (3)
(3)
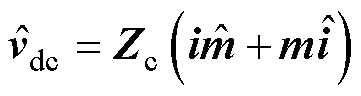 (4)
(4)
式中,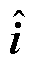 、
、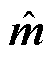 、
、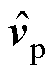 和
和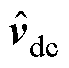 分别为级联H桥SVG的输出电流、调制波信号、并网点电压和桥臂等效电容电压的小信号向量,向量中各元素对应频率为{fp-3f1, fp-2f1, fp-f1, fp, fp+f1, fp+2f1, fp+3f1},其中,fp和f1分别为扰动频率和基频;YL与Zc分别为不同小信号频率下的桥臂电感导纳矩阵与等效模块电容阻抗矩阵,均为7×7阶对角矩阵。
分别为级联H桥SVG的输出电流、调制波信号、并网点电压和桥臂等效电容电压的小信号向量,向量中各元素对应频率为{fp-3f1, fp-2f1, fp-f1, fp, fp+f1, fp+2f1, fp+3f1},其中,fp和f1分别为扰动频率和基频;YL与Zc分别为不同小信号频率下的桥臂电感导纳矩阵与等效模块电容阻抗矩阵,均为7×7阶对角矩阵。
1.1.1 直流电压同步控制
构网型SVG控制相较于跟网型SVG控制,最显著的特点在于同步方式的变化,故其推导相角小信号过程有较大差异。直流电压同步是对全模块直流侧平均电压进行控制,由于交直流侧小信号耦合关系导致全局直流侧电压信号中仅存在零序分量,因此,在推导小信号模型时需要考虑提取零序分量,定义零序分量提取矩阵T0=diag{0, 0, 1/N, 0, 0, 1/N, 0}。结合图2中的控制框图,可以推导出相角小信号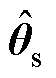 为
为
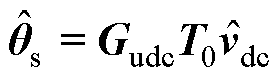 (5)
(5)
其中
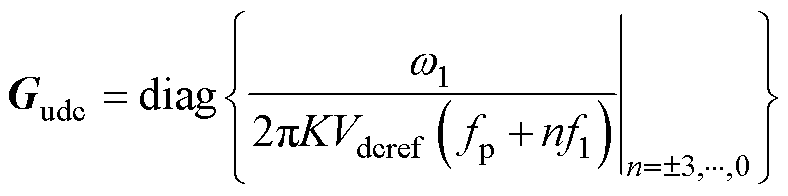
1.1.2 无功电压下垂控制
在对无功电压下垂控制环路进行小信号推导的过程中,需要先对无功及电压幅值小信号进行计算,其中瞬时无功功率及电压dq轴分量小信号模型为
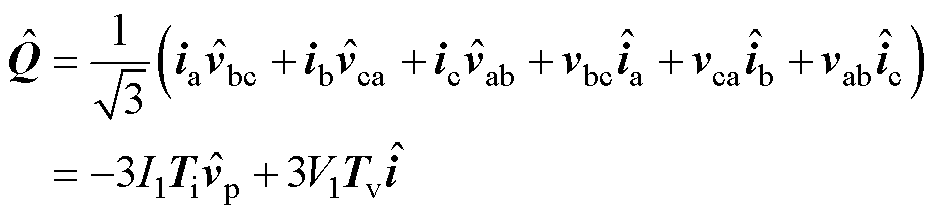 (6)
(6)
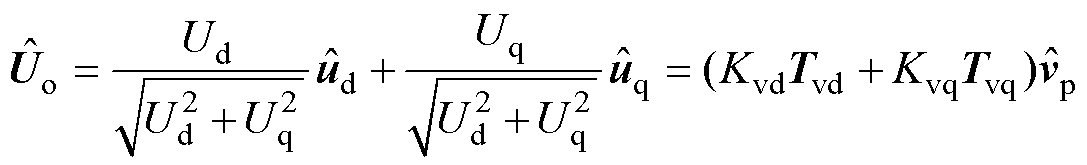 (7)
(7)
式中,V1和I1分别为稳态电压和电流输出幅值;Ti、Tv分别为稳态电流、电压相角提取矩阵;Ud和Uq分别为dq轴电压稳态值;Kvd和Kvq分别为dq轴电压小信号提取系数;Tvd和Tvq分别为dq轴电压小信号传递矩阵。根据控制框图对应关系可以得到参考电平的小信号为
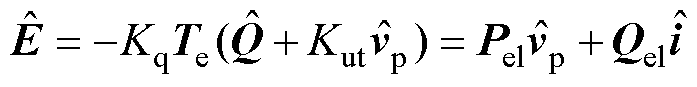 (8)
(8)
其中
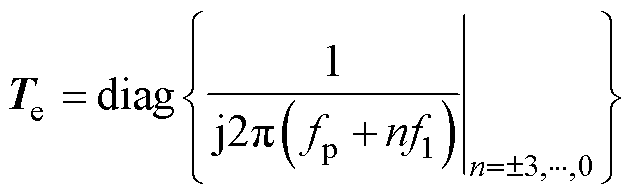
式中,Pel和Qel为对应小信号的传递矩阵。
1.1.3 虚拟阻抗内环控制
虚拟阻抗内环控制结构主要通过dq轴电流信号生成电压信号,继而影响内电动势变化,根据调制信号与电流信号的关系,可以得到虚拟阻抗支路的信号为
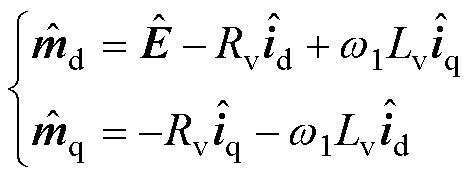 (9)
(9)
进一步考虑相角小信号对式(9)进行dq反变换,即可得到构网控制所引入的调制小信号表达 式为
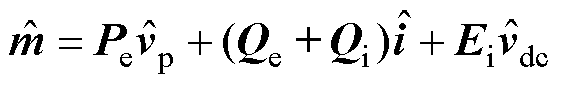 (10)
(10)
式中,Pe和Qe为无功电压下垂控制环路引入的增益矩阵;Qi为不考虑同步角小信号影响下虚拟阻抗引入的增益矩阵;Ei为仅考虑同步角小信号影响下虚拟阻抗引入的增益矩阵。
结合文献[10]中对相间均压控制环路的分析,调制小信号最终表达式为
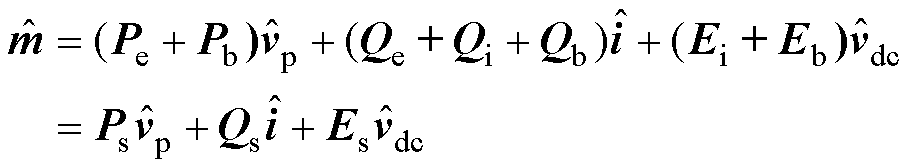 (11)
(11)
式中,Pb、Qb和Eb为相间均压控制环路引入的增益矩阵;Qs、Ps和Es分别为调制小信号与并网电流、并网点电压和模块电容电压小信号的控制增益 矩阵。
联立功率小信号表达式(3)、式(4)和控制小信号表达式(11),可以得到构网型SVG阻抗矩阵表达式为
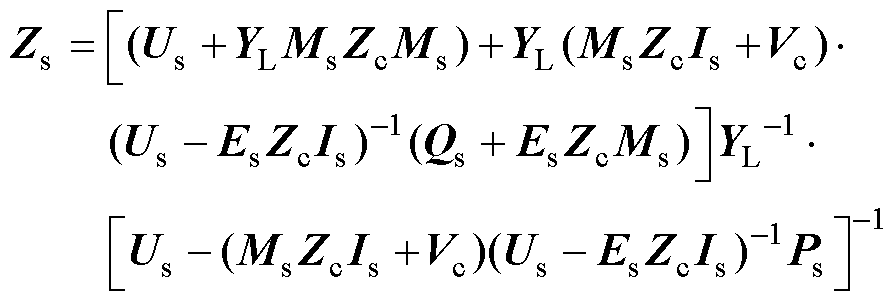 (12)
(12)
式中,Us为单位矩阵;Ms为a相调制信号稳态谐波矩阵;Is为a相并网电流稳态谐波矩阵;Vc为a相模块电容电压总的稳态谐波矩阵;各矩阵皆为7×7阶矩阵。
为了研究构网型SVG在新能源场站中的优势,明确构网型SVG的阻抗特性,本文将对构网型和跟网型SVG的频域阻抗特性进行详细对比。由于跟网型SVG的阻抗模型已有较多文献进行了研究,因此本文不再给出其阻抗建模过程,参照文献[10]所建立的跟网型SVG阻抗模型进行对比分析。构网型和跟网型SVG功率参数和控制参数分别见表1和表2。
表1 级联H桥SVG的功率参数
Tab.1 Power parameters of the cascaded H-bridge SVG

参 数数 值 交流线电压/kV35 模块直流电压/kV12 桥臂子模块数3 子模块电容/mF0.125
表2 不同控制模式下SVG的控制参数
Tab.2 Control parameters of SVG in different control modes
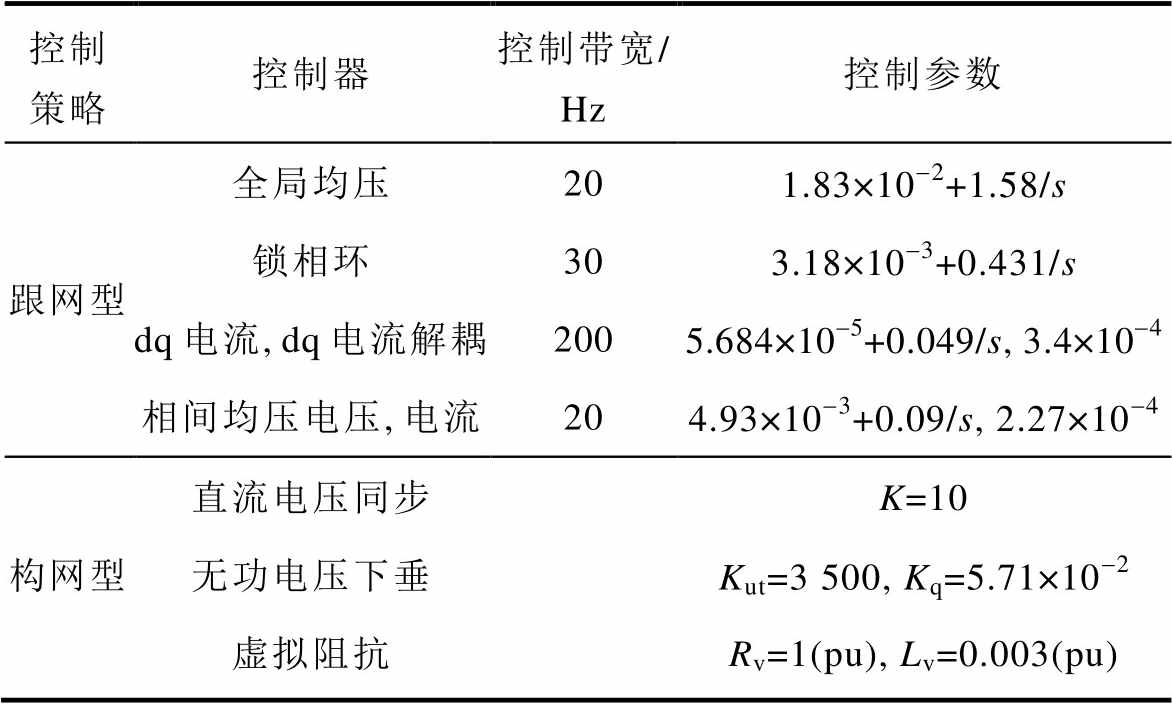
控制策略控制器控制带宽/Hz控制参数 跟网型全局均压201.83×10-2+1.58/s 锁相环303.18×10-3+0.431/s dq电流,dq电流解耦2005.684×10-5+0.049/s, 3.4×10-4 相间均压电压,电流204.93×10-3+0.09/s, 2.27×10-4 构网型直流电压同步K=10 无功电压下垂Kut=3 500, Kq=5.71×10-2 虚拟阻抗Rv=1(pu), Lv=0.003(pu)
根据文献[10]和式(12)所示阻抗模型,采用表1和表2中的参数可以分别得到常规型跟网型SVG阻抗特性曲线ZGFL和构网型SVG阻抗特性曲线ZGFM。这两种控制模式下SVG阻抗特性曲线的对比如图3所示。
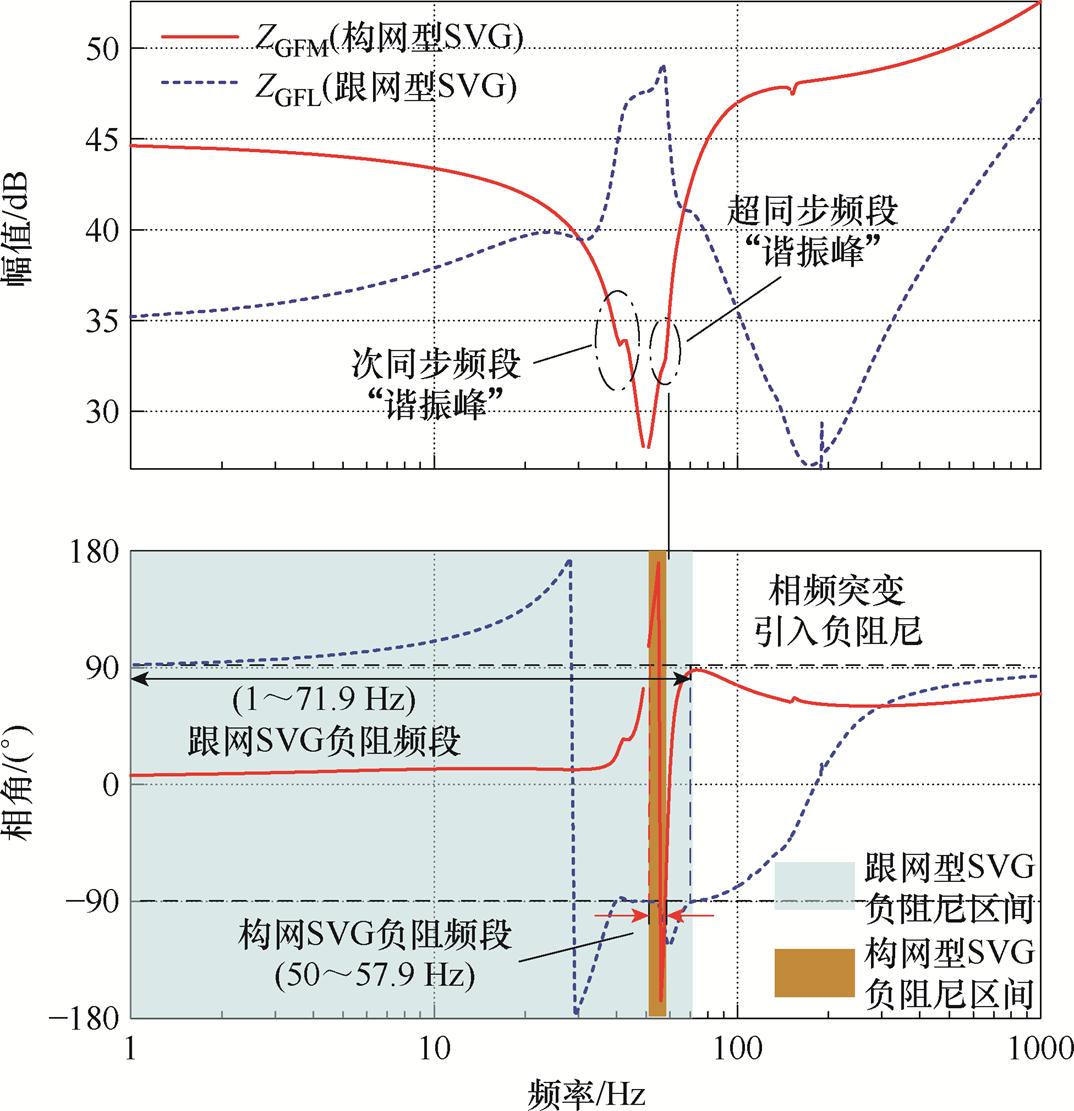
图3 10 MV·A构网型SVG、跟网型SVG阻抗特性曲线对比
Fig.3 Comparison of impedance characteristic curves for 10 MV·A GFM SVG and GFL SVG
由图3可知,在1~10 Hz低频频段内,跟网型SVG幅值低于构网型SVG,主要原因为构网功率控制在此频段范围对阻抗影响较小,而虚拟阻抗起主导作用。虚拟阻抗在中低频对阻抗的影响近似为实际阻感,虚拟阻抗控制环的接入对构网型SVG阻抗幅值会有抬升作用,同时控制虚拟阻感的参数比例,确保了低频频段构网型SVG具有较好的正阻尼特性。
在10~100 Hz频段,跟网型SVG存在较宽范围的负阻尼区间,在该频段内主要受到全局均压环路、锁相环及电流环的共同作用影响且环路耦合严重,这使得跟网型SVG在弱电网条件下存在较大的次/超同步振荡风险[8]。相比之下,构网型SVG在该频段的负阻尼区间明显减小,且具有更低的阻抗幅值,这得益于构网型SVG具有电压源外特性,更有利于维持弱电网条件下的稳定性。但由于功率环节的交互影响,在次同步频段及超同步频段阻抗特性均会出现“谐振峰”,两个谐振峰皆会导致SVG相频特性出现突变,尤其是在超同步频段会引入较窄的负阻尼区间,存在一定的振荡风险。
在100 Hz以上的频段,构网型SVG阻抗曲线会显著高于跟网型SVG,且相角变化较小。跟网型SVG在该频段仍会受到电流环影响,但是随着频率上升超过电流环控制带宽后,跟网型SVG阻抗特性会近似表现为无源器件的特性。而由于虚拟阻感作用范围较宽,构网型SVG在此频段的阻抗特性近似表现为无源器件串联虚拟阻感,使得其幅值抬升,且相频曲线会表现出阻感特性。
综上所述,跟网型SVG存在1~71.9 Hz的负阻尼区间,而构网型SVG的负阻尼频段可以缩减到50~57.9 Hz。采用构网控制可以显著改善单机SVG阻抗的负阻尼特性,降低并网振荡风险。
对于场站级别新能源发电系统的阻抗特性及稳定性分析,可以将复杂的阻抗网络聚合为源-载阻抗互联系统进行分析[10]。参照此方法,本节以哈密地区某实际风电场为例,建立集成SVG的风电场网络聚合阻抗模型,并分析构网型与跟网型SVG接入对风电场稳定性的影响。集成SVG的直驱风电场电路拓扑如图4所示,其主要结构如下:①有三串风电机组共11台4.5 MW直驱风机经620 V/35 kV变压器T3并入35 kV母线,第1串风电机组由3台风机构成,第2、3串风电机组各有4台;②风机间线路长度相同,风机串接入35 kV线路的长度不同,分别为5、2、3 km,线缆阻感分别为0.13 W/km和1.27 mH/km;③35 kV母线下接入10 MV·A SVG装置,35 kV并网母线通过两级变压接入220 kV电网,变压器漏感及线路阻抗不可忽略。
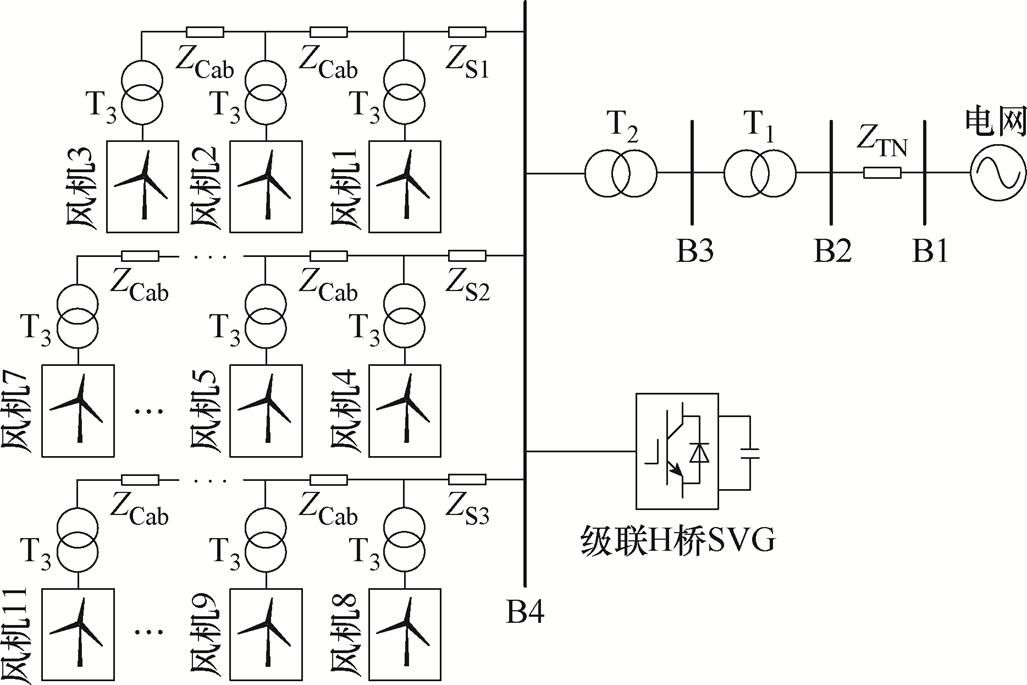
图4 集成SVG的直驱风电场电路拓扑
Fig.4 Circuit topology for direct-drive wind farm with SVG
本文第1节对构网型SVG序阻抗模型进行了推导并对跟网型SVG阻抗模型进行了说明,结合目前相关文献对风机阻抗模型的推导[27],可以建立新能源场站中各功率单元的单机阻抗模型。由于存在频率耦合效应,同时也为了网络计算方便,需要将功率单元、线路及变压器等设备表示成2×2的导纳矩阵形式,SVG及风机单机导纳矩阵分别为
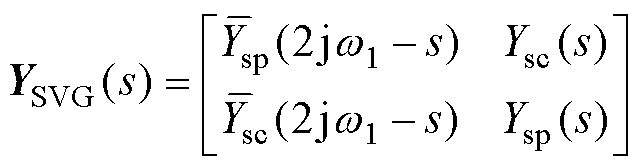 (13)
(13)
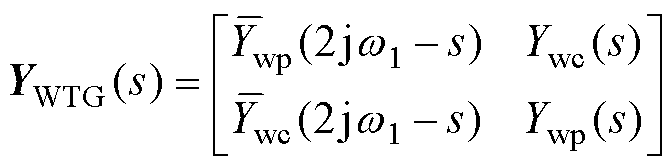 (14)
(14)
式中,Ysp为SVG导纳矩阵中的正序导纳;Ysc为SVG导纳矩阵中的耦合导纳;Ywp为风机导纳矩阵中的正序导纳;Ywc为风机导纳矩阵中的耦合导纳;上划线表示对应变量的共轭。另外,无源网络参数包括线路和变压器的p型阻抗矩阵可参考文献[10]。
进一步地,根据风电场网络间的串并联关系,结合网络阻抗聚合方法,将不含SVG的风电场导纳矩阵记为YW,35 kV电网侧阻抗矩阵记为Zg,则包含SVG的风电场导纳矩阵YWF为
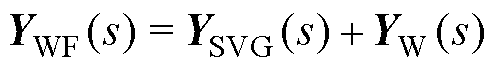 (15)
(15)
由于频率耦合效应的影响,风电场导纳及电网侧阻抗需要表示为2×2矩阵,有
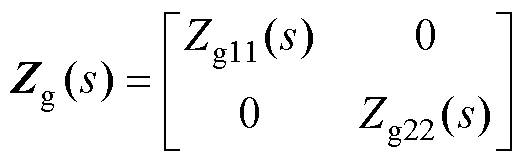 (16)
(16)
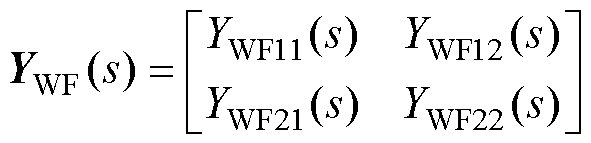 (17)
(17)
聚合后的风电场系统为多输入多输出(Multiple- Input Multiple-Output, MIMO)系统,可以采用广义奈奎斯特判据分析系统的稳定性,其中广义阻抗比矩阵为
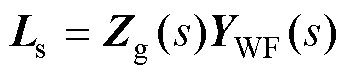 (18)
(18)
通过广义奈奎斯特判据虽然可以准确地分析系统的稳定性,但该方法并不能直观地展示出系统的稳定裕度,也不能提供量化分析结果。为了在判定稳定性过程中获得相位裕度等关键信息,可以进一步将源-载互联MIMO系统等效为单输入单输出(Single-Input Single-Output, SISO)系统,其等效示意图如图5所示。
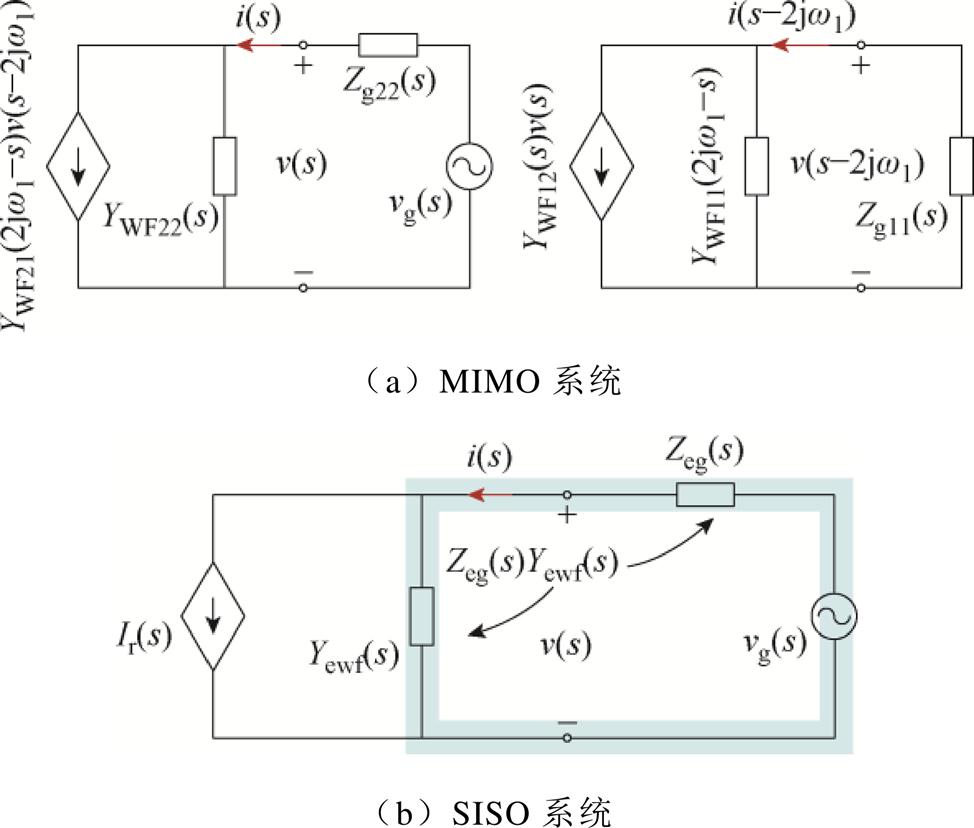
图5 MIMO系统及SISO系统等效示意图
Fig.5 Equivalence diagrams of MIMO system with SISO system
经过上述等效可以得到风电场聚合阻抗Zewf(s)和电网聚合阻抗Zeg(s)表达式为
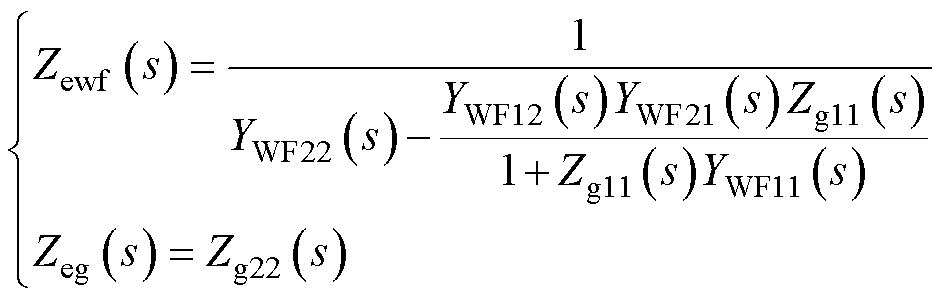 (19)
(19)
此时可以通过等值源-载阻抗比的方式量化风电场并网系统的稳定裕度。假设电网聚合阻抗特性曲线与风电场聚合阻抗存在频率为fx的交点,将该频率处系统的稳定裕度qPM定义为
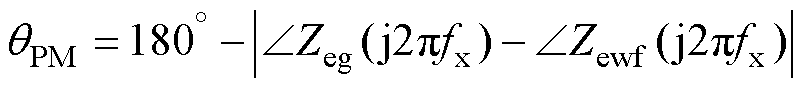 (20)
(20)
根据表3中线路及变压器参数和表4中风机参数,结合前文表2中SVG跟网和构网控制参数,建立接入SVG的风电场站及网侧聚合等效阻抗模型。
表3 风电场站并网系统电气参数
Tab.3 Electrical parameters of wind farm grid-connected systems
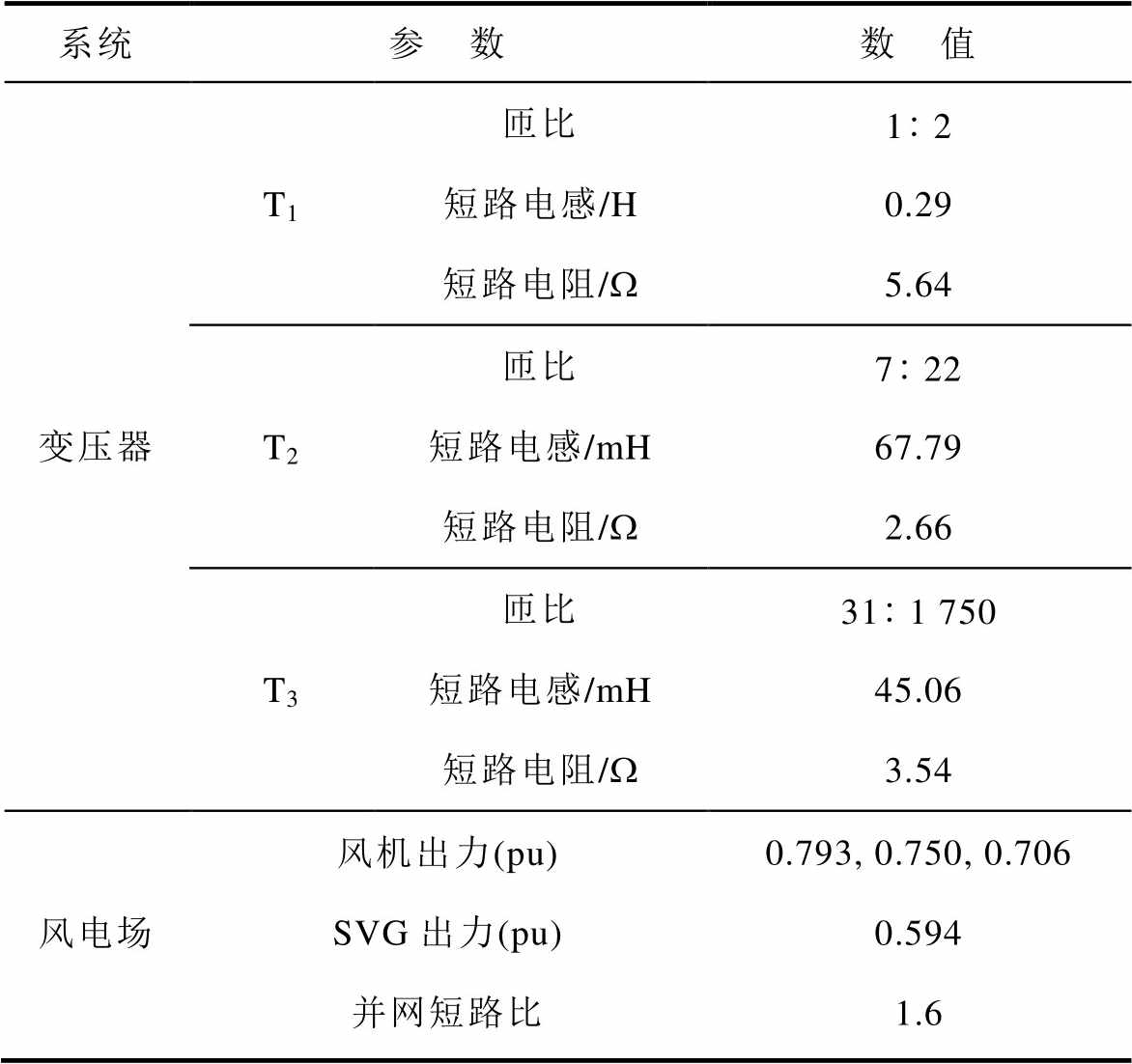
系统参 数数 值 变压器T1匝比12 短路电感/H0.29 短路电阻/W5.64 T2匝比722 短路电感/mH67.79 短路电阻/W2.66 T3匝比311 750 短路电感/mH45.06 短路电阻/W3.54 风电场风机出力(pu)0.793, 0.750, 0.706 SVG出力(pu)0.594 并网短路比1.6
表4 直驱风机功率及控制参数
Tab.4 Direct-drive turbine power and control parameters
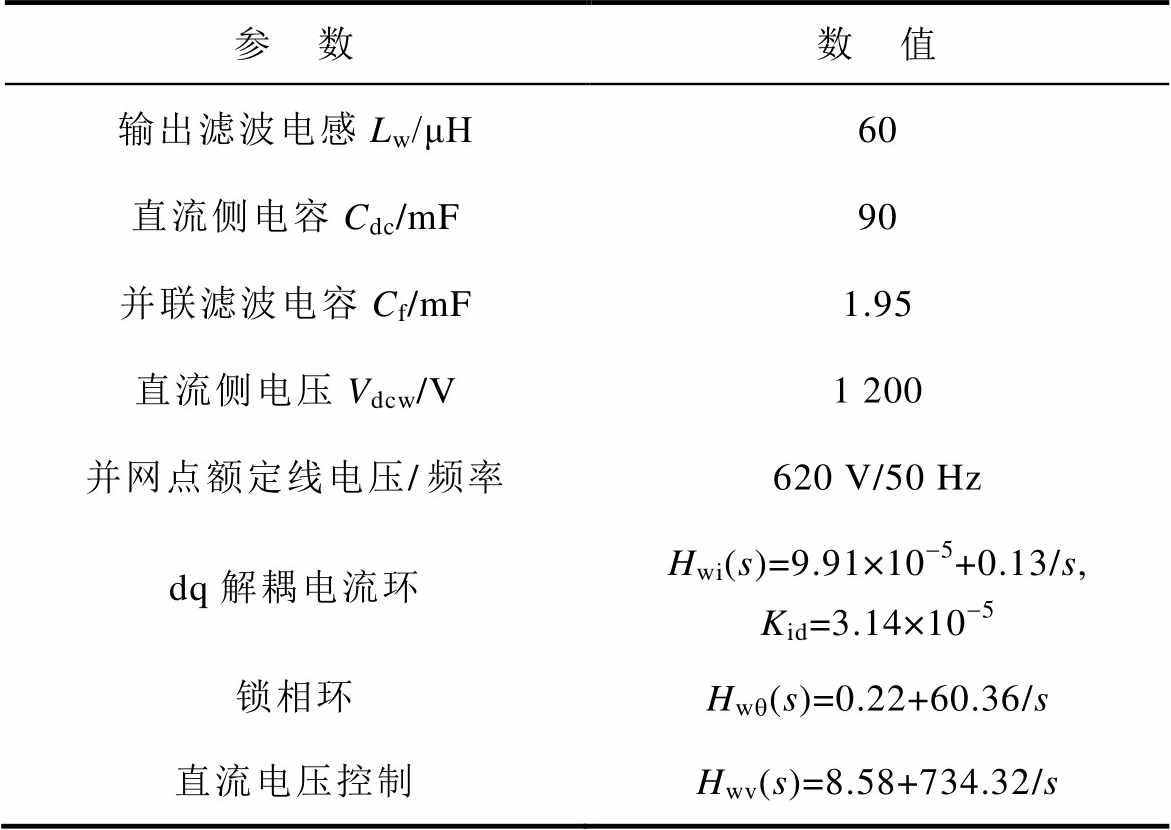
参 数数 值 输出滤波电感Lw/μH60 直流侧电容Cdc/mF90 并联滤波电容Cf/mF1.95 直流侧电压Vdcw/V1 200 并网点额定线电压/频率620 V/50 Hz dq解耦电流环Hwi(s)=9.91×10-5+0.13/s,Kid=3.14×10-5 锁相环Hwq(s)=0.22+60.36/s 直流电压控制Hwv(s)=8.58+734.32/s
对不同控制下SVG接入对风电场稳定性的影响进行分析,并研究相关控制环路对构网型SVG接入新能源场站的影响。根据2.1节建立的SISO系统下等效风电场聚合阻抗模型,对比构网型SVG接入场站聚合阻抗Zewf1、跟网型SVG接入场站聚合阻抗Zewf2和同步调相机接入场站聚合阻抗Zewf3的阻抗特性,如图6所示。
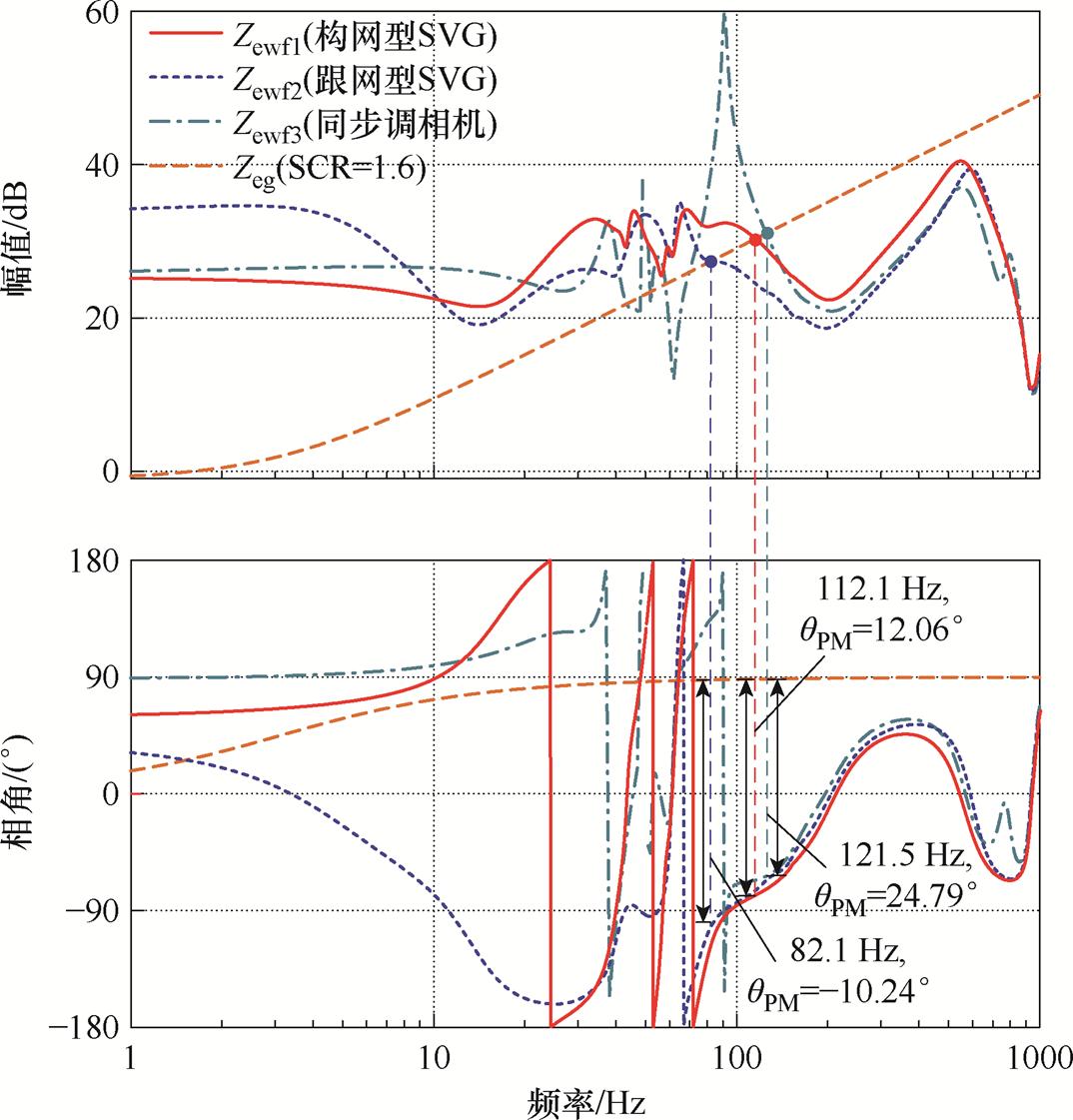
图6 跟网、构网型SVG及同步调相机接入风电场站阻抗特性曲线
Fig.6 Impedance characteristic curves of grid-following, grid-forming SVG and SC integrated into wind farm stations
根据图6中的跟网型与构网型阻抗特性曲线可知,主要影响该工况稳定性的频段为10~120 Hz。接入跟网型SVG的风电场阻抗Zewf2在82.1 Hz处与电网阻抗Zeg交截,此时相位裕度为-10.24°,表征并网系统不稳定。构网型SVG接入的场站聚合阻抗Zewf1抬升了这一区间的阻抗幅值,交点频率后移至112.1 Hz,相位裕度为12.06°,并网系统稳定。同步调相机接入与构网型SVG接入作用效果类似,聚合阻抗与电网阻抗交截于121.5 Hz,相位裕度为24.79°。
对比三者阻抗特性可知,在10~500 Hz频段内,构网型SVG接入下场站聚合阻抗(Zewf1)的幅值高于跟网型SVG接入场景(Zewf2),与电网阻抗交截频率显著后移,从而避免了风电场等效聚合阻抗在负阻尼频段与电网等效阻抗相交。同步调相机接入风电场后,也可提升聚合阻抗(Zewf3)交截频率处的相角。值得注意的是,同步调相机接入的风电场聚合阻抗幅值在基频处跌落明显,与电网阻抗产生了额外交截,可能引发基频处的潜在振荡风险。
对于稳定性而言,考虑构网型SVG接入的风电场阻抗相较跟网型SVG接入变化更加剧烈,但是在一定程度上会缩小风电场聚合阻抗的负阻尼区间,降低振荡风险。上述分析结果表明,构网型SVG在弱电网条件下有利于风电场并网的稳定性。为了量化构网型SVG的阻尼能力和影响规律,有必要对构网型SVG的关键参数进一步展开量化分析。
构网型SVG的关键控制参数主要包括:直流电压调频系数、无功电压环惯性系数及虚拟阻抗等。由于构网控制下各环路难以直观分析出其对场站聚合阻抗及并网稳定性的影响,本节将从直流电压调频系数、无功电压环惯性系数和虚拟阻抗出发,研究构网型SVG接入对直驱风电场阻抗特性及并网稳定性的影响。在分析单一参数变化影响时,构网型SVG其余参数与表1和表2保持一致。
2.3.1 直流电压调频系数
图7a展示了直流电压调频系数变化时,构网型SVG接入下场站聚合阻抗的变化规律。由图7a可知,该系数对聚合阻抗的影响主要集中于基频附近,K值越小,即在越快的调频速度情况下,聚合阻抗幅值越容易剧烈波动。在K=1工况下,风电场聚合阻抗曲线与电网阻抗交互于71.1 Hz和74.2 Hz,且在71.1 Hz处相位裕度为-40.74°,并网系统不稳定。
进一步对直流电压调频系数变化时的风电场聚合阻抗进行遍历分析,图7b给出了直流电压调频系数的稳定设计边界。从图7b中分析可知,当K在0.1~1.3范围内时,直流电压同步控制环与系统主要交互在70~90 Hz频段,聚合阻抗幅值与相角在此频段中会出现大幅度跌落,极易出现系统振荡;当K在5~6.5范围内时,聚合阻抗在基频附近59 Hz处发生幅值跌落,并与电网阻抗交截于负阻尼频段。综上可知,直流电压调频系数取值应避免过小,同时应结合稳定边界条件及下垂动态特性折中考虑,本文选取K=10。
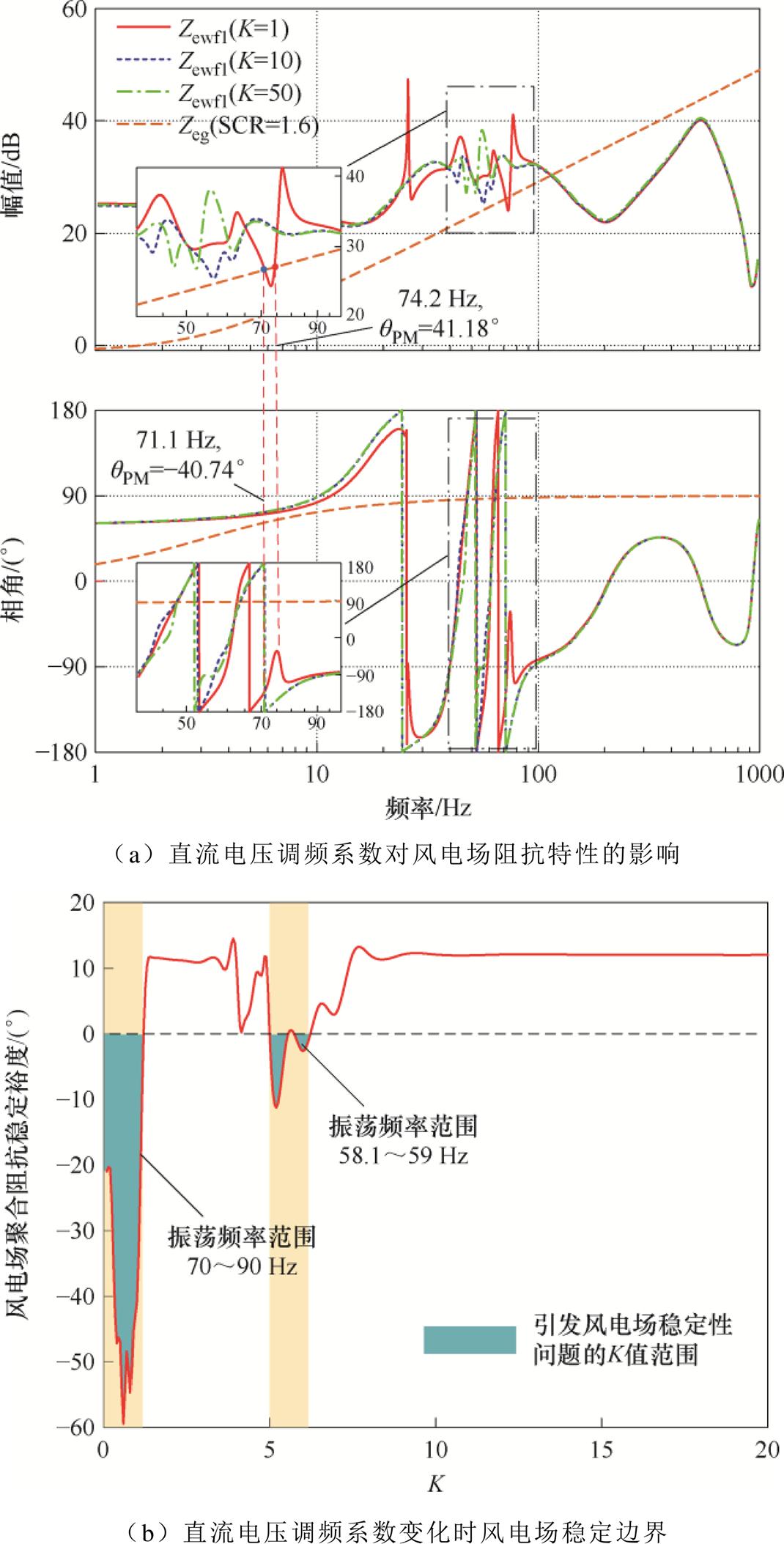
图7 直流电压调频系数对风电场阻抗特性影响及稳定边界
Fig.7 The influence of DC voltage frequency modulation coefficient on wind farm impedance characteristics and stability boundary
2.3.2 无功电压环惯性系数
图8a给出了无功电压环惯性系数变化时,构网型SVG接入下场站聚合阻抗的变化规律,分析可知无功电压环惯性系数Kq主要作用范围为100 Hz以内。惯性系数增大会导致低频相角小幅度跌落;在基频附近,惯性系数的上升会导致阻抗幅值在40 Hz及60 Hz附近下跌,容易出现阻抗相交的现象,并网系统存在潜在失稳风险。图8a中,当Kq= 0.114时,相位裕度为-51.44°,系统发生振荡。
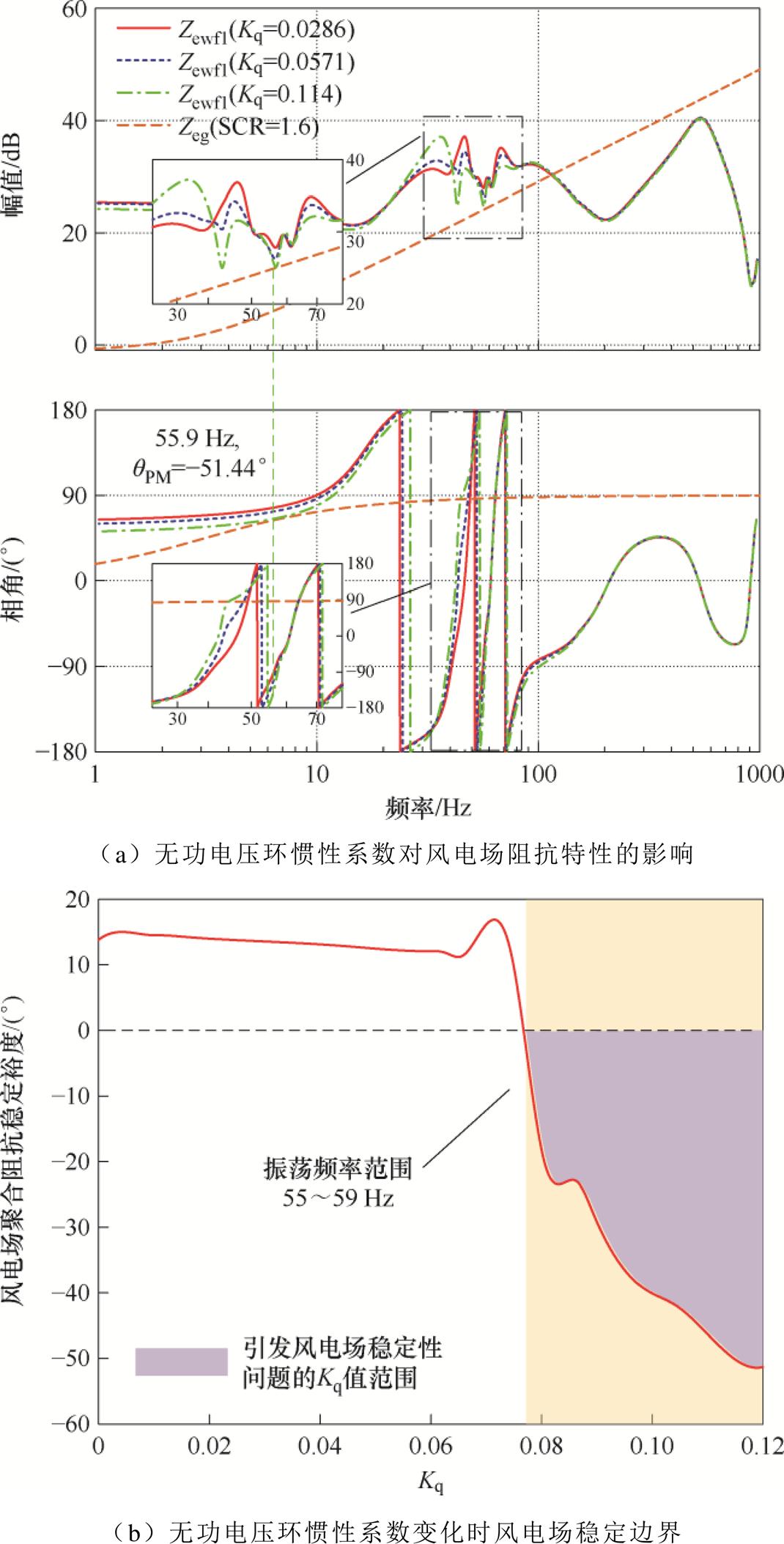
图8 无功电压环惯性系数对风电场阻抗特性影响及稳定边界
Fig.8 The influence of reactive voltage inertia coefficient on wind farm impedance characteristics and stability boundary
图8b给出了无功电压环惯性系数的稳定设计边界。当惯性系数增大,聚合阻抗基频处幅值会显著降低,易与电网阻抗相交,故风电场聚合阻抗稳定裕度逐步降低。当Kq>0.078时,风电场聚合阻抗裕度小于零,导致新能源并网系统振荡失稳。因此,无功电压下垂系数参数优化需要综合无功电压环路动态特性及其稳定边界折中考虑,本文选取Kq=0.057 1。
2.3.3 虚拟阻抗
当虚拟阻抗变化时,等值阻抗变化规律如图9所示。由图9可知,虚拟阻感对Zewf1的影响主要在200 Hz以内。当虚拟电阻较小时,控制环路间的交互作用更强,阻抗谐振峰现象越发明显,因此提升虚拟电阻大小可以显著抑制该现象;但是过大的虚拟电阻会拓宽负阻尼区间,压低基频附近的阻抗幅值,带来新的振荡问题。同时,虚拟电感上升可使聚合阻抗幅值抬升,避免系统出现基频附近频率的振荡问题;但是若虚拟电感过高,在次/超同步频段会出现比较明显的尖峰并发生相角突变。例如,图9中当虚拟电感为0.001(pu)时,基频附近聚合阻抗幅值较小,与电网阻抗相交,但交点频率处qPM>0°,并网系统维持稳定;而当虚拟电感为0.03(pu)时,风电场聚合阻抗尖峰与电网阻抗相交,且交点频率处稳定裕度小于0°,并网系统出现振荡现象。
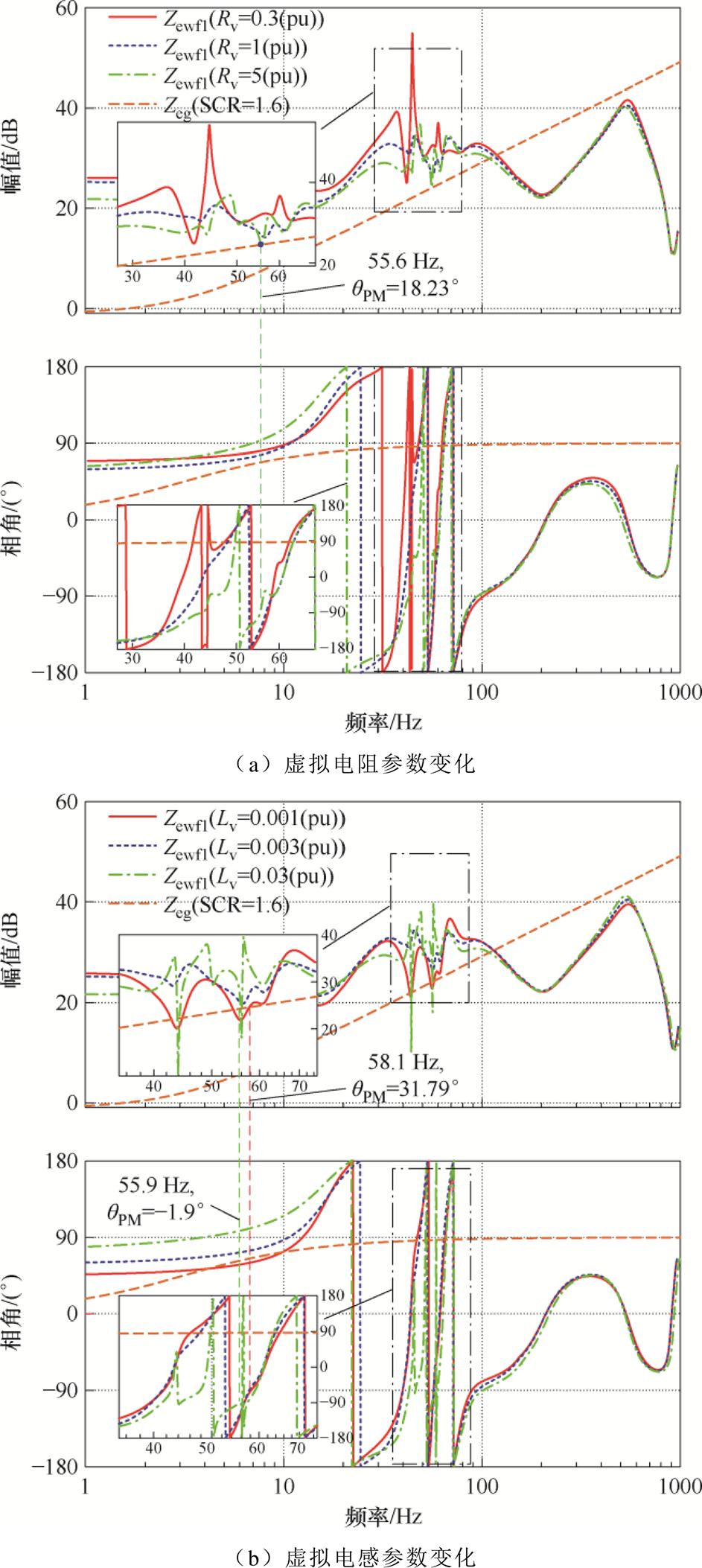
图9 虚拟阻抗对风电场阻抗特性的影响
Fig.9 The impact of virtual impedance on wind farm impedance characteristics
整体而言,由于虚拟阻抗控制环的接入,构网型SVG接入新能源场站相较跟网型SVG接入可以适应更弱的电网。但是随着电网强度进一步下降,除了超同步频段振荡风险,基频附近可能会出现阻抗曲线相交的现象,由此导致新的稳定性风险。并且由于功率控制环路的影响,30~70 Hz范围属于构网控制强交互频段,在该频段内构网型SVG所能提供的阻尼能力十分有限,因此在应用过程中需要特别关注该频段内的阻抗特性。
2.3.4 线路参数
线路参数(即系统短路比(Short Circuit Ratio, SCR))对并网系统的稳定性也有重要影响。图10给出了新能源场站SCR分别为1.29、1.6、1.86时的风电场聚合阻抗模型。随着线路长度增加,系统短路比下降,会导致聚合阻抗的负阻尼频段显著拓宽。同时,由于线路阻抗Zeg幅值上升,更易与风电场聚合阻抗Zewf1在次超同步频段交截,带来振荡风险。图10中,当SCR=1.29时,并网系统在55.8 Hz处的相位裕度为-25.5°,风电场出现振荡现象;而在SCR=1.6和1.86的工况下,风电场聚合阻抗与电网阻抗不会相交,仅在110~120 Hz频段会出现阻抗交截,相位裕度分别为12.06°和26.6°。
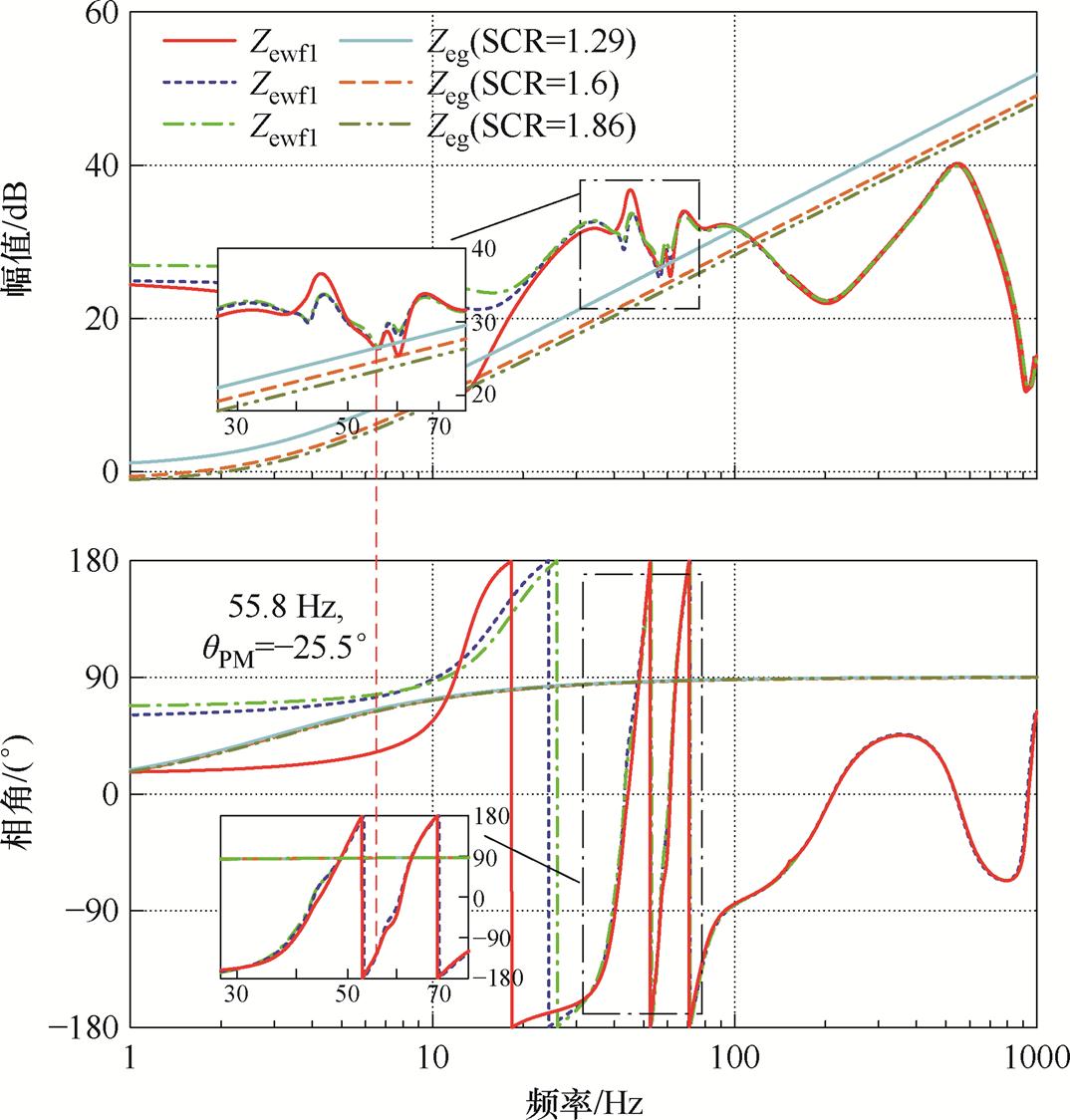
图10 线路参数对风电场阻抗特性影响
Fig.10 The impact of transmission line on wind farm impedance characteristics
结合2.2节分析可知,构网型SVG或同步调相机的接入都能显著地提高风电场的弱电网适应能力。为进一步量化评估不同无功装备接入对系统弱电网适应能力的提升,本文将未接入无功补偿装置时风电场所能适应的最低短路比记作Rb(文中Rb=1.87),并以此作为基准,将含各种无功补偿装置接入后风电场能适应的最低短路比记作Rn,定义短路比提升度指标a为
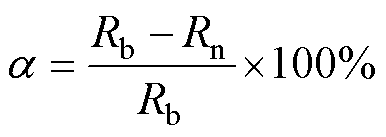 (21)
(21)
跟网型SVG、同步调相机和构网型SVG三种不同的无功补偿装置接入条件下,风电场最低短路比提升效果对比见表5。当风电场接入跟网型SVG时,系统最低短路比为1.78,短路比提升度为4.8%,这说明传统跟网型SVG接入有助于提高风电场的弱电网适应能力,但短路比提升效果并不显著。当采用同步调相机和构网型SVG接入方案时,最低短路比可分别进一步扩展到1.32和1.33,短路比提升度分别显著提高至29.4%和28.9%,两者效果相当。
表5 不同无功补偿设备接入时风电场弱电网适应性提升对比
Tab.5 Comparison of wind farm weak grid adaptability improvement with different reactive power compensation devices
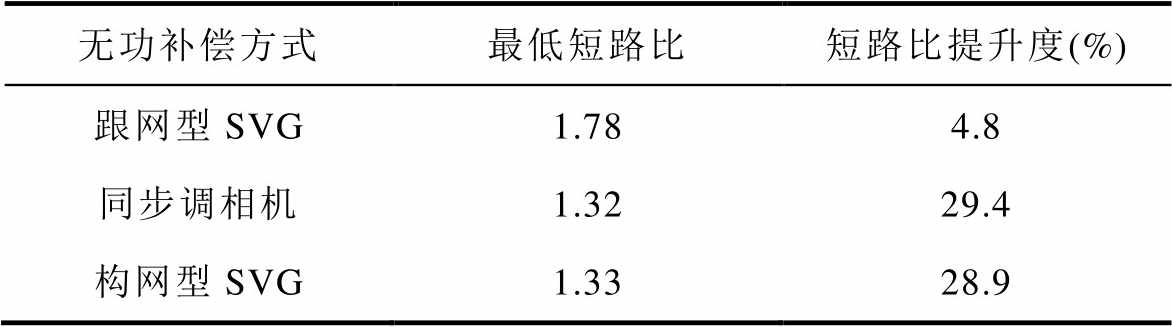
无功补偿方式最低短路比短路比提升度(%) 跟网型SVG1.784.8 同步调相机1.3229.4 构网型SVG1.3328.9
本文基于RT-Lab(OPAL-RT 5600)控制硬件在环实时仿真平台搭建含跟网型和构网型SVG在内的风电场并网系统模型,对SVG不同控制模式下的并网稳定性进行实验验证和分析,实验平台如图11所示。

图11 基于RT-Lab的硬件在环实验平台
Fig.11 RT-Lab based hardware-in-the-loop experiment platform
直驱风电场并网系统中,将风力发电机功率电路及控制电路、级联H桥SVG功率电路、输电线路、变压器及理想220 kV电网的相关模型载入RT- Lab半实物仿真平台中进行运算,SVG由外部控制器提供驱动。SVG控制全部算法通过基于DSP(主控:TMS320F28377,从控:TMS320F28335)+FPGA架构的自研数字控制系统实现。主控首先接收RT- Lab采样信号对SVG进行相关控制;其次将生成的调制信号传递至从控板进行载波移相调制;然后生成驱动通过光纤下发至执行板;最后执行板将驱动传回RT-Lab进行计算。
根据表1和表2给出的构网型SVG参数进行RT-Lab半实物仿真,首先验证构网型SVG控制算法的有效性。在强电网实验条件下,对构网型SVG单机并网模型进行仿真实验,其输出电压电流波形如图12所示。图12中,构网型SVG并网能够稳定运行,且输出电流波形中无明显谐波分量,说明了构网型SVG控制算法的正确性,算法能够确保单机并网系统正常运行。
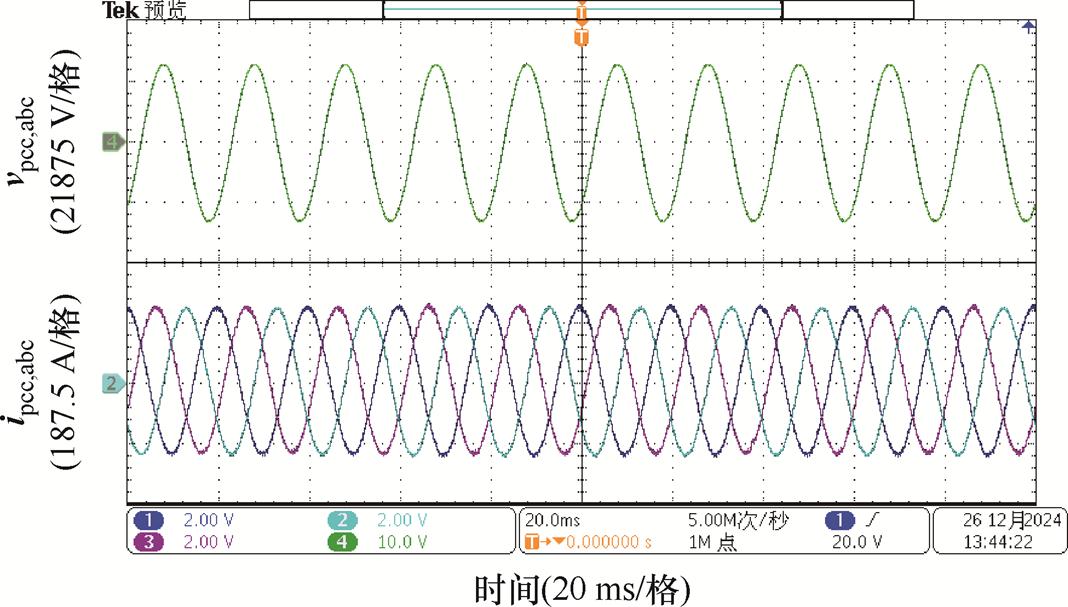
图12 接入强电网单机输出电压电流波形
Fig.12 Output voltage and current waveforms of single SVG accessed to the strong grid
在直流侧接入超级电容,验证基于直流电压同步的SVG具有频率支撑的能力。当源侧频率下跌0.8 Hz时,SVG可以通过直流侧超级电容储能为电网提供有功支撑,频率及有功响应如图13所示。
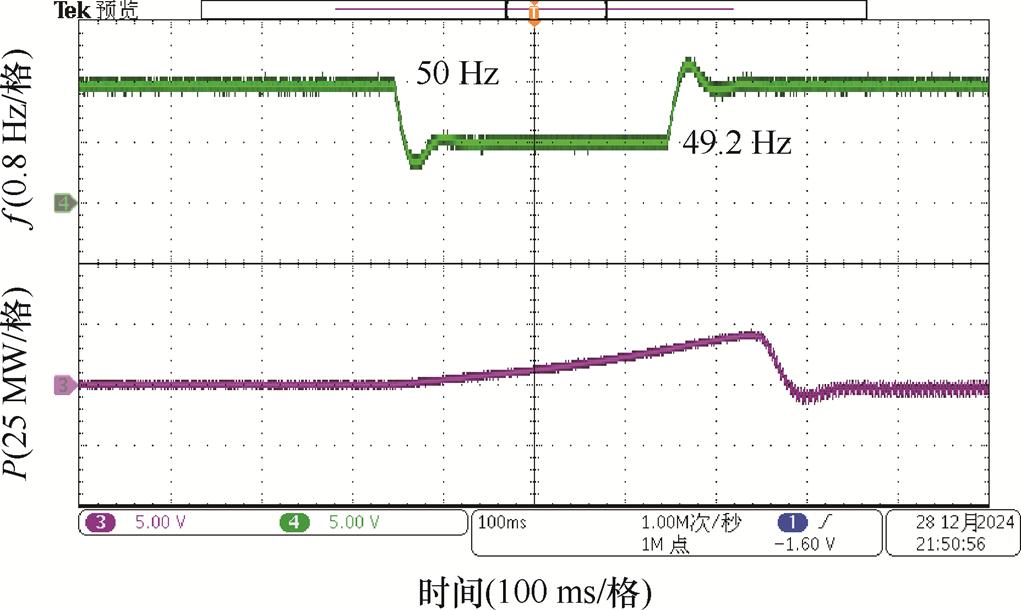
图13 电网频率跌落下有功功率及频率波形
Fig.13 Active power and frequency waveforms under grid frequency dips
图14给出了常规构网型SVG控制对电压支撑能力的验证。当源侧电压幅值跌落20%时,由于无功电压下垂环路作用,可以额外提供无功响应,抬升并网点的电压幅值。
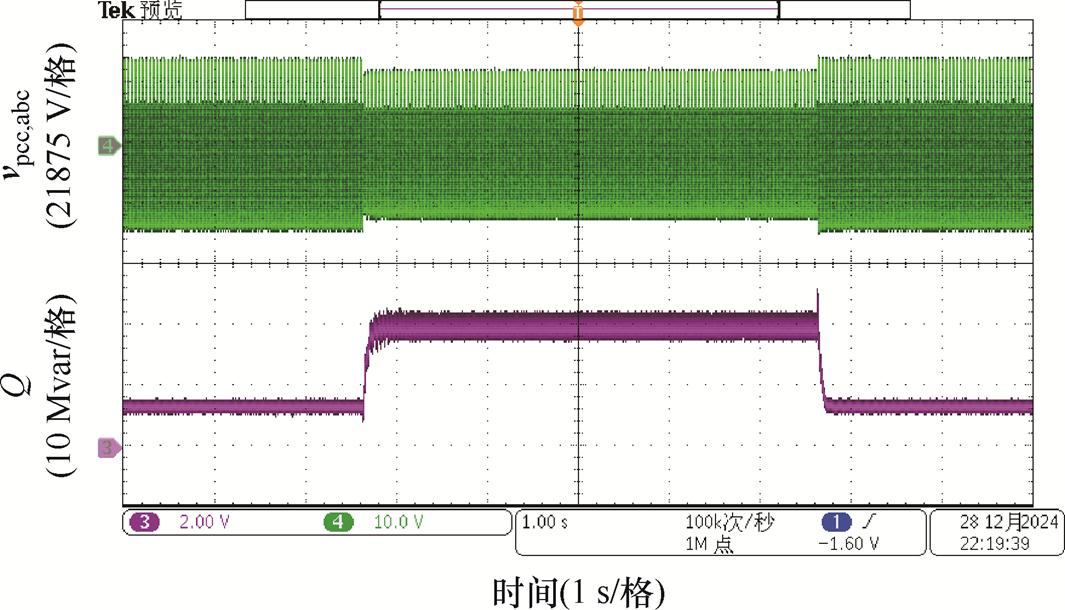
图14 电网电压跌落下无功功率及输出电压波形
Fig.14 Reactive power and output voltage waveforms under grid voltage dips
为验证本文推导的构网型SVG阻抗模型的正确性,基于实验平台对第1节中的直流电压同步构网型SVG阻抗模型进行扫频验证,扫频结果如图15所示。可见,扫频结果与理论阻抗曲线吻合度较高,说明了所推导阻抗数学模型的正确性。
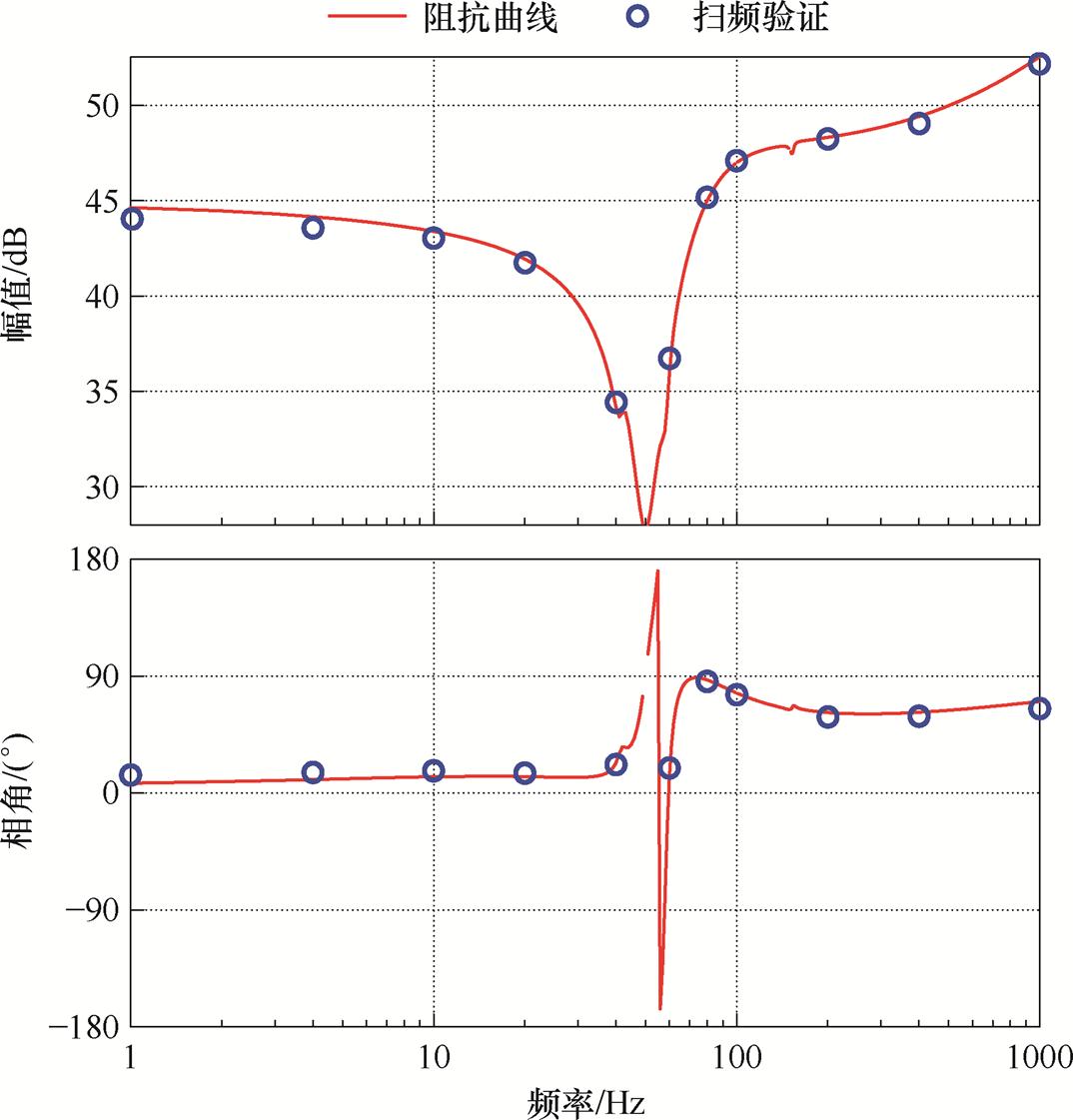
图15 10 MV·A构网型SVG阻抗曲线及扫频验证
Fig.15 Verification of impedance curve and frequency sweep of 10 MV·A GFM SVG
3.2.1 跟网型、构网型SVG接入风电场分析
当风电场接入强电网运行时,无论是跟网型还是构网型SVG接入,风电场均能稳定运行,二者电压电流波形如图16所示。此时跟网型SVG接入与构网型SVG接入的风电场并网电流总谐波畸变率(Total Harmonic Distortion, THD)分别为4.16%和3.66%。
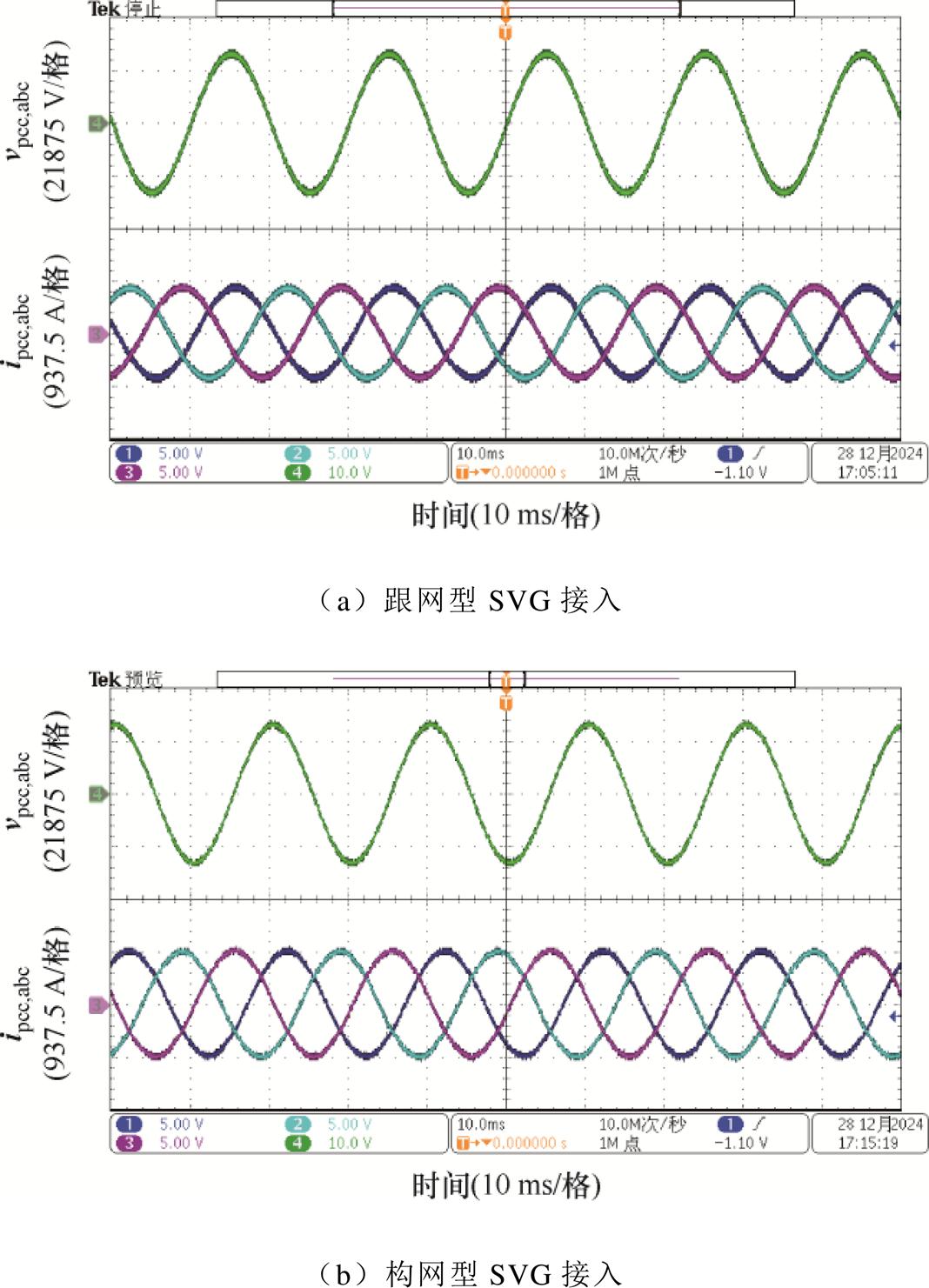
图16 接入强电网下跟网型、构网型SVG接入风电场电压电流波形
Fig.16 Voltage and current waveforms of the wind farm connected to the strong grid under GFL SVG and GFM SVG access
当并网系统短路比为1.6时,再次进行分析。SVG以跟网模式和构网模式运行的并网电压电流波形如图17所示。此时跟网型SVG接入的风电场发生振荡,对振荡处电流进行快速傅里叶变换(Fast Fourier Transform, FFT)分析,此时主要谐波频率为85 Hz,这与前文稳定性分析结果保持一致。而在该工况下,构网型SVG的接入可以抬升超同步频段的风电场聚合阻抗幅值,使得交点频率后移至聚合阻抗正阻尼频段,因此,构网型SVG接入的风电场仍旧可以稳定运行,并网电流谐波含量为4.15%。这也验证了构网型SVG接入风电场站相较跟网型接入条件能够更好地适应弱电网接入场景。

图17 接入弱电网下跟网、构网型SVG接入风电场电压电流波形
Fig.17 Voltage and current waveforms of the wind farm connected to the weak grid under GFL SVG and GFM SVG access
3.2.2 参数影响关系分析
为验证第2.3节构网控制参数分析的正确性,分别对两种构网控制参数所导致的风电场振荡工况(直流电压调频系数K=1,虚拟电感Lv=0.03(pu))进行实验验证。
图18给出了直流电压调频系数K从初始值10变化至1时的风电场输出电压电流波形,图中IH/Il为各次谐波与基波的比例,可知此时风电场发生振荡至发散。对发散处电流波形进行FFT分析可知,发散过程中谐波频率为70 Hz。这是因为过小的直流电压调频系数会导致风电场网络聚合阻抗曲线剧烈波动,并在次/超同步两个频段造成幅值跌落,容易导致风电场聚合阻抗与电网阻抗交截,当交截频率落在负阻尼区间时会产生振荡问题,实验结果与前文阻抗特性分析结论一致。

图18 场站并网电压电流波形及K=1工况下FFT分析
Fig.18 Voltage and current waveforms of grid-connected field station and FFT analysis under K=1 condition
图19给出了虚拟电感Lv从初始值0.003(pu)变化到0.03(pu)时的风电场输出电压电流波形,可知此时风电场输出电压电流振荡并发散。对发散开始处电流波形进行FFT分析可知,主要振荡频率为52.5 Hz和55 Hz,这与2.3节分析交互频率为55.9 Hz的结论相吻合。从而验证了过大的虚拟电感参数会导致风电场聚合阻抗幅值出现尖峰和相角突变,容易引发次/超同步频段振荡。
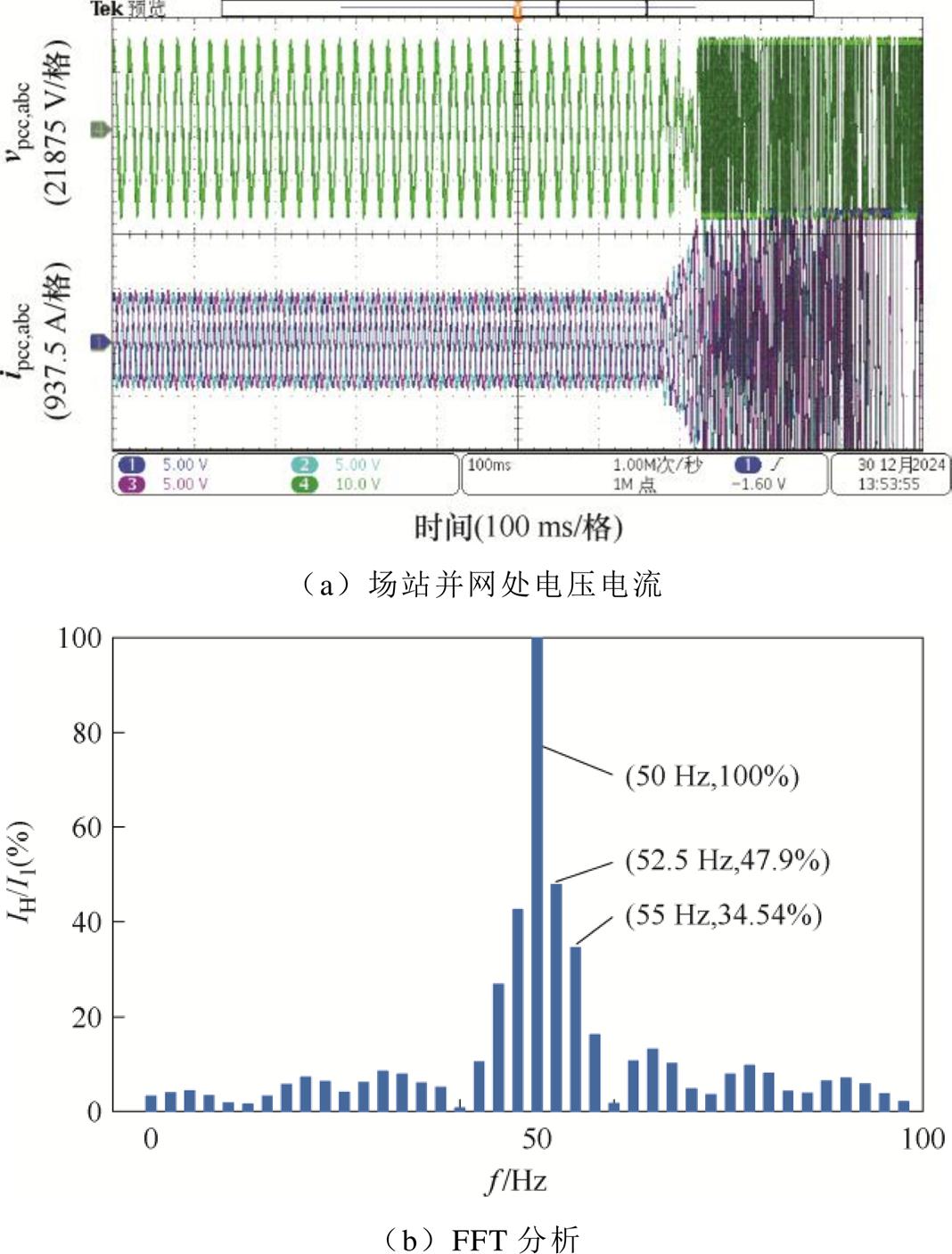
图19 场站并网电压电流波形及Lv=0.03(pu)工况下FFT分析
Fig.19 Voltage and current waveforms of grid-connected field station and FFT analysis under Lv=0.03(pu) condition
本文针对构网型SVG在风电场中的应用进行了深入研究,建立了跟网型和构网型SVG的序阻抗模型,并对两者在风电场稳定性方面的影响进行了详细对比分析,研究结果表明:
1)构网型SVG相比于跟网型SVG,其输出阻抗的负阻尼区间显著缩小,表明构网型SVG能够提供更强的阻尼作用。
2)在风电场接入弱电网条件下,相比于跟网型SVG,构网型SVG接入风电场后容许最低短路比提升度从4.8%提升到28.9%,与同步调相机相当。
3)基于直流电压同步的构网型SVG虽能提供一定的阻尼作用,但在基波频段附近仍存在一定的负阻尼振荡风险,因此在应用过程中需注意可能产生的功率振荡问题。
本文探讨了构网型SVG在风电场站中的应用,相关结论同样适用于光伏、储能等新能源场景,后续工作将围绕构网型SVG全频段的阻抗控制能力、控制边界以及关键影响因素开展分析研究工作,进一步强化构网型SVG的阻尼控制能力。
参考文献
[1] 周孝信, 赵强, 张玉琼. “双碳”目标下我国能源电力系统发展前景[J]. 科学通报, 2024, 69(8): 983-989.
Zhou Xiaoxin, Zhao Qiang, Zhang Yuqiong. Prospect of China’s energy and power system under dual carbon goals[J]. Chinese Science Bulletin, 2024, 69(8): 983-989.
[2] 汤广福, 周静, 庞辉, 等. 能源安全格局下新型电力系统发展战略框架[J]. 中国工程科学, 2023, 25(2): 79-88.
Tang Guangfu, Zhou Jing, Pang Hui, et al. Strategic framework for new electric power system develop- ment under the energy security pattern[J]. Strategic Study of CAE, 2023, 25(2): 79-88.
[3] Zhou Yuhan, Xin Huanhai, Wu Di, et al. Small-signal stability assessment of heterogeneous grid-following converter power systems based on grid strength analysis[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2566-2579.
[4] 王杨, 梁智昊, 王翰文, 等. 基于谐波状态空间的电力系统多类型谐波扰动建模与分析——回顾、探讨与展望[J]. 电力系统自动化, 2025, 49(23): 1-16.
Wang Yang, Liang Zhihao, Wang Hanwen, et al. Modeling and analysis of multi-type harmonic distur- bances in power system based on harmonic state space: review, discussion, and prospect[J]. Automation of Electric Power Systems, 2025, 49(23): 1-16.
[5] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[6] 孙鹏伟, 姚文峰, 黄东启, 等. STATCOM与新型调相机的技术性和经济性比较[J]. 南方电网技术, 2021, 15(1): 82-88.
Sun Pengwei, Yao Wenfeng, Huang Dongqi, et al. Technical and economic comparison between STATCOM and the new generation sychronous condenser[J]. Southern Power System Technology, 2021, 15(1): 82-88.
[7] 张旭, 徐鑫, 董成武, 等. 基于EMD-KPCA-LSTM与SVG控制的双馈风电系统次同步振荡抑制方法[J]. 电气工程学报, 2025, 20(2): 54-67.
Zhang Xu, Xu Xin, Dong Chengwu, et al. Sub- synchronous oscillation suppression method for DFIG wind power systems based on EMD-KPCA-LSTM and SVG damping control[J]. Journal of Electrical Engineering, 2025, 20(2): 54-67.
[8] 张前进, 周林, 李海啸, 等. 考虑SVG补偿装置的大型光伏并网系统振荡分析与抑制[J]. 中国电机工程学报, 2019, 39(9): 2636-2644.
Zhang Qianjin, Zhou Lin, Li Haixiao, et al. Oscillation analysis and suppression of large-scale grid-connected photovoltaic system considering SVG equipment[J]. Proceedings of the CSEE, 2019, 39(9): 2636-2644.
[9] 胡鹏, 艾欣, 肖仕武, 等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报, 2020, 35(17): 3703-3713.
Hu Peng, Ai Xin, Xiao Shiwu, et al. Sequence impedance of static var generator and analysis of influencing factors on subsynchronous oscillation[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3703-3713.
[10] 张旸, 孙龙庭, 陈新, 等. 集成静止无功发生装置的直驱风场序阻抗网络模型与稳定性分析[J]. 中国电机工程学报, 2020, 40(9): 2877-2891.
Zhang Yang, Sun Longting, Chen Xin, et al. Sequence impedance network model and stability analysis for direct-drive wind farm with static var generator[J]. Proceedings of the CSEE, 2020, 40(9): 2877-2891.
[11] Zhang Yang, Yang Yongheng, Chen Xin, et al. Intelligent parameter design-based impedance optimiza-tion of STATCOM to mitigate resonance in wind farms[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3201-3215.
[12] 熊连松, 卓放, 刘小康, 等. 静止同步补偿器抑制电网功率振荡的机理研究[J]. 西安交通大学学报, 2017, 51(12): 112-120.
Xiong Liansong, Zhuo Fang, Liu Xiaokang, et al. Analysis on mechanism of power oscillation mitiga- tion by STATCOM[J]. Journal of Xi’an Jiaotong University, 2017, 51(12): 112-120.
[13] 龚鸿, 江伟, 王渝红, 等. 基于静止同步补偿器与直流调制协调控制的低频振荡抑制方法[J]. 电工技术学报, 2017, 32(6): 67-75.
Gong Hong, Jiang Wei, Wang Yuhong, et al. A survey on damping low frequency oscillation based on coordination strategy of static synchronized com- pensator modulation[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 67-75.
[14] 张东辉, 陈新, 杨舒婷, 等. 含静止无功补偿装置的光伏电站高频谐振分析及抑制策略研究[J]. 中国电机工程学报, 2023, 43(24): 9580-9594.
Zhang Donghui, Chen Xin, Yang Shuting, et al. Analysis of high-frequency resonance and suppres- sion strategy of photovoltaic power plant with static reactive power compensation device[J]. Proceedings of the CSEE, 2023, 43(24): 9580-9594.
[15] Zhang Yang, Wang Yuqing, Zhang Donghui, et al. Broadband impedance shaping control scheme of MMC-based STATCOM for improving the stability of the wind farm[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10278-10292.
[16] 高本锋, 刘培鑫, 孙大卫, 等. 构网/跟网型混合风电场次同步振荡特性与机理分析[J]. 电工技术学报, 2025, 40(6): 1945-1959.
Gao Benfeng, Liu Peixin, Sun Dawei, et al. Analysis of subsynchronous oscillation characteristics and mechanism of grid-forming/grid-following hybrid wind farms[J]. Transactions of China Electrotechnical Society, 2025, 40(6): 1945-1959.
[17] 马富艺龙, 辛焕海, 李知艺, 等. 多馈入系统中变流器多样性对系统强度的影响分析[J]. 电工技术学报, 2025, 40(23): 7590-7607.
Ma Fuyilong, Xin Huanhai, Li Zhiyi, et al. Impact analysis of converter diversity on system strength in multi-infeed power system[J]. Transactions of China Electrotechnical Society, 2025, 40(23): 7590-7607.
[18] 唐宇, 胡光, 刘永江, 等. 基于特征子系统的跟网/构网设备混合外送系统小干扰稳定性分析方法[J]. 电工技术学报, 2025, 40(9): 2766-2779.
Tang Yu, Hu Guang, Liu Yongjiang, et al. Small- signal stability analysis method for hybrid grid- following/grid-forming delivery systems based on eigen-subsystem[J]. Transactions of China Electro- technical Society, 2025, 40(9): 2766-2779.
[19] 刘旭, 张国驹, 裴玮, 等. 构网型变流器的现状与发展趋势[J]. 太阳能学报, 2024, 45(9): 101-111.
Liu Xu, Zhang Guoju, Pei Wei, et al. Current status and development trends of grid type converters[J]. Acta Energiae Solaris Sinica, 2024, 45(9): 101-111.
[20] 尚磊, 唐王倩云, 苏适, 等. 构网型无功补偿抑制新能源送端暂态过电压[J]. 电力工程技术, 2024, 43(2): 83-93.
Shang Lei, Tang Wangqianyun, Su Shi, et al. Suppression of transient overvoltage in renewable energy transmission terminal by grid-forming based reactive power compensation[J]. Electric Power Engineering Technology, 2024, 43(2): 83-93.
[21] 戴朝波, 于弘洋, 赵国亮, 等. STATCOM和同步调相机响应时间的仿真分析和比较[J]. 南方电网技术, 2023, 17(10): 85-93.
Dai Chaobo, Yu Hongyang, Zhao Guoliang, et al. Simulation analysis and comparison of response times of STATCOM and synchronous condensers[J]. Southern Power System Technology, 2023, 17(10): 85-93.
[22] 王若愚, 蔡京陶, 叶键民, 等. STATCOM与新型调相机在交直流受端系统中的暂态特性对比研究[J]. 广东电力, 2021, 34(2): 77-83.
Wang Ruoyu, Cai Jingtao, Ye Jianmin, et al. Comparative study on transient characteristics of STATCOM and new condenser in AC/DC receiving terminal system[J]. Guangdong Electric Power, 2021, 34(2): 77-83.
[23] 南瑞继保. 全国首套电网侧静止同步调相机顺利投运[EB/OL]. (2024-10-29)[2024-12-29]. https://www. in-en.com/article/html/energy-2335357.shtml.
[24] Wu Wenhua, Zhou Leming, Chen Yandong, et al. Sequence-impedance-based stability comparison between VSGs and traditional grid-connected inverters [J]. IEEE Transactions on Power Electronics, 2019, 34(1): 46-52.
[25] Zhang Jiawei, Zhang Chen, Shi Xianqiang, et al. A novel energy-type SVG with grid forming control for grid voltage and inertial support[C]//2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 2023: 821-828.
[26] 张家玮, 张琛, 史先强, 等. 储能型静止无功发生装置及其自同步电压源控制[J]. 高电压技术, 2023, 49(1): 61-71.
Zhang Jiawei, Zhang Chen, Shi Xianqiang, et al. Energy-storage-type static var generator and its autonomous-synchronization voltage source control [J]. High Voltage Engineering, 2023, 49(1): 61-71.
[27] 朱瑛, 何飞, 蔡寿国, 等. 弱电网下直驱风机网侧换流器建模及稳定运行控制策略分析[J]. 电力自动化设备, 2023, 43(9): 71-78.
Zhu Ying, He Fei, Cai Shouguo, et al. Modeling and stable operation control strategy analysis for grid-side converter of direct-drive permanent magnetic synchronous generator in weak grid[J]. Electric Power Automation Equipment, 2023, 43(9): 71-78.
Abstract To enhance grid-connected system voltage support and oscillation suppression capability, new energy power plants are equipped with static var generator (SVG) as a reactive power compensation device. Under the background of widespread deployment of reactive power compensation devices in new energy power stations, grid-forming (GFM) SVG demonstrate superior grid adaptability compared to traditional grid-following (GFL) SVG and synchronous condenser (SC), owing to their self-synchronizing characteristics, second-level dynamic response, and transient support capability. However, current research on the impact of GFM SVG on the stability of new energy power plants is still at an exploratory stage. In particular, the impedance modeling of GFM SVG and the analysis of its influence mechanisms on the stability of new energy power plants still require further in-depth studies. To address the aforementioned issues, this paper establishes the impedance characteristic model of GFM SVG and constructs the aggregated impedance of wind farms after GFM SVG integration. It compares the frequency characteristics between grid-forming and grid-following SVGs, and conducts a quantitative analysis of the influence mechanisms of GFM SVG’s key control parameters on the stability of new energy power plants.
First, a multi-harmonic linearization modeling approach is adopted to derive harmonic small-signal mathematical expressions introduced by the power circuit and control loops of GFM SVG. Based on this, the sequence impedance model of GFM SVG is established. Furthermore, a detailed comparative analysis of impedance characteristics between GFM SVG and GFL SVG is conducted. The analytical results demonstrate that the grid-forming control significantly enhances the amplitude of SVG impedance characteristics in both low-frequency and high-frequency ranges. Additionally, grid-forming control improves the negative damping characteristics in sub/super-synchronous frequency bands of impedance, thereby reducing the risk of grid-connected oscillation.
To quantitatively evaluate the impact of GFM SVG on wind farm stability, this study employs an impedance aggregation method to establish an aggregated impedance model of a wind farm with transmission lines and transformers after GFM SVG integration, using a wind farm in the Hami region as a case study. A comparative analysis is conducted on the aggregated impedance models of wind farms integrated with GFM SVG, GFL SVG, and SCs under three different grid connection scenarios, the stability analysis results demonstrate that: The integration of GFM SVG into wind farms can effectively narrow the negative damping region of the aggregated wind farm impedance while avoiding the introduction of additional impedance crossover points, thereby enhancing the grid-connected stability of new energy power plants. Building on this foundation, the study conducts an in-depth analysis of the impact mechanisms of grid-forming SVG’s key control parameters (including the DC voltage frequency modulation coefficient, reactive voltage inertia coefficient, and virtual impedance) on the aggregated impedance of SVG-integrated wind farms and their grid-connected stability. Furthermore, the stability boundaries for the DC voltage frequency modulation coefficient and reactive voltage inertia coefficient in wind farm grid-connected systems are established quantitatively, proposing systematic parameter optimization methodologies. Finally, the impact of transmission line parameters on grid-connected system stability is analyzed. Short-circuit ratio improvement percentage (a) is defined to quantify the improvement in the adaptability of the weak grid after integrating different reactive power compensation devices into new energy power plants. Compared to GFL SVG, wind farms integrated with GFM SVG exhibit significantly enhanced weak grid adaptability and damping effects comparable to synchronous condensers.
Keywords:Static var generator (SVG), synchronous compensator, grid-forming (GFM) control, impedance model, stability analysis, wind farm
赵力轩 男,2000年生,硕士研究生,研究方向为SVG建模、控制及稳定性分析。
E-mail: zlx0319@nuaa.edu.cn
陈 新 男,1973年生,博士,教授,博士生导师,研究方向为分布式发电和微电网系统的建模、控制与稳定性。
E-mail: chen.xin@nuaa.edu.cn(通信作者)
中图分类号:TM464;TM743
DOI: 10.19595/j.cnki.1000-6753.tces.242392
国家自然科学基金面上项目资助(52277186)。
收稿日期 2024-12-31
改稿日期 2025-03-07
(编辑 李 冰)