图1 GFM系统主电路及控制结构
Fig.1 Main circuit and control structure of GFM system
摘要 构网型变流器(GFM)在高渗透率电网中因弱电网支撑性能而备受关注,其输出阻抗特性成为研究焦点。目前,dq域比例积分(PI)控制和相域准比例谐振(QPR)控制是电流内环控制的主流策略,但关于这两种控制策略的阻抗建模和对比分析尚显不足,特别是相域阻抗建模的研究较少。该文旨在补充此研究内容,深入探索GFM在不同控制域下的阻抗特性。首先,分别构建GFM在PI和QPR控制下的谐波线性化序阻抗模型,揭示两种电流环控制域下阻抗特性的差异。基于所建模型,利用Nyquist判据分析不同电网强度的并网适用性,以及GFM数量对系统稳定的影响。分析结果显示,PI控制相对QPR控制在强电网环境下的适用性较差,而在极弱电网环境下则展现出更好的适用性。同时,两种控制方式在多GFM并网系统中均表现出良好的稳定性。最后,通过Matlab/Simulink与硬件在环仿真验证了理论分析的正确性。
关键词:构网型变流器 序阻抗建模 并网稳定性 内环控制
随着可再生能源的快速发展和电网结构的不断演变,构网型变流器(Grid-Forming Converter, GFM)在高渗透率电网中扮演着日益重要的角色[1-3]。作为新型电力系统的关键组成部分,GFM不仅能够提供必要的电力转换功能,而且能在电网出现故障或扰动时提供有效的电压支撑,显著增强系统的稳定性和可靠性[4-5]。然而,随着GFM在电网中渗透率的不断提高,其输出阻抗特性及对电网稳定性的影响逐渐凸显,成为当前研究的热点和难点问题[6-7]。
目前,GFM电流内环的控制策略主要包括dq域下的比例积分(Proportional-Integral, PI)控制和相域下的准比例谐振(Quasi-Proportional-Resonant, QPR)控制[8],其电流内环控制策略的差异对GFM阻抗特性和并网性能的影响非常大[9-10]。尽管这两种控制策略在实际中都得到了广泛的应用,但关于它们在GFM中的阻抗建模和稳定性分析方面的比较尚显不足。
文献[11-12]通过序阻抗建模对比分析了GFM与传统并网逆变器在弱电网中的不同阻抗特性,揭示了GFM的优势和潜在问题。文献[13]建立了虚拟同步发电机的序阻抗模型,但忽略了电压外环和电流内环的影响。为进一步完善这一模型,文献[14]考虑了电压电流环的影响,并指出在电网强度较大时GFM系统容易出现振荡。文献[15-16]提出一种考虑虚拟阻抗的GFM控制方法,并通过序阻抗建模方法进行了理论验证。然而,这些研究均只考虑了dq域PI控制下的阻抗特性,对于QPR控制下的阻抗建模和稳定性分析则鲜有涉及。文献[17]虽然采用QPR控制的GFM取得了良好的并网效果,但缺乏详细的理论验证和阻抗建模分析。此外,现有研究多针对单机并网场景,缺乏对多GFM并网系统稳定性的量化分析,且对GFM内环控制在强弱电网下的适用性对比尚未形成明确结论。
本文针对上述问题,提出一种基于谐波线性化的GFM序阻抗建模与电流内环控制对比分析框架,主要贡献点如下:
1)揭示了不同电流内环控制域对GFM阻抗特性的影响机制。本文分别构建了dq域PI控制与相域QPR控制的GFM谐波线性化序阻抗模型,通过频域扫频与理论推导,明确了两种控制在低频段(阻容性和感性)与中高频段(阻感性和感性)的阻抗特性差异,为控制策略选择提供了量化依据。
2)提出了电网强度自适应的GFM适用性判据。本文基于Nyquist稳定性判据,发现PI控制在极弱电网(电网强度<2)中因阻抗相位稳定性更优而表现更佳,而QPR控制凭借高频谐波抑制能力在强电网(电网强度>3)中更具优势,为不同电网环境下控制策略的优化配置提供了理论指导。
3)验证了多GFM并网系统的鲁棒稳定性。本文通过阻抗比理论分析与硬件在环实验,证明了两种控制策略在多机并网场景下均能维持稳定,且PI控制的稳定性随GFM并网数量增加而增强的趋势更为显著,为大规模新能源并网提供了理论支撑。
本文通过Matlab/Simulink与硬件在环仿真验证了理论模型的正确性,相关结论可为GFM的优化设计与复杂电网场景下的稳定运行提供重要参考。
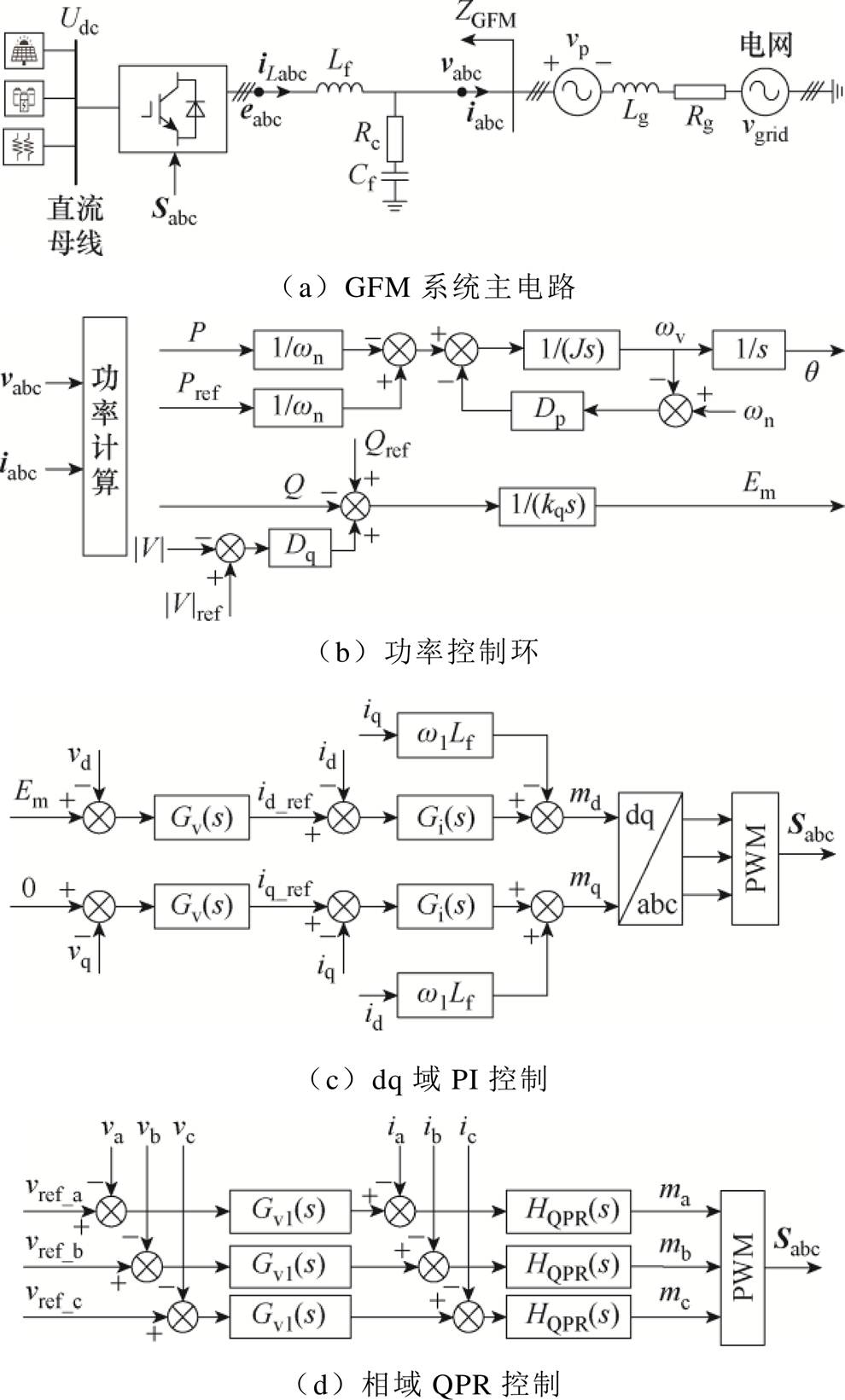
本文所有分析均基于GFM典型拓扑结构:两电平三相桥式变流器拓扑。GFM系统的主电路拓扑结构如图1a所示。图1a中,Udc为直流侧电压;Sabc为控制逆变器的开关信号;eabc为逆变器输出三相内电动势;iLabc为逆变器输出三相电感电流;vabc和iabc分别为逆变器的三相并网电压和并网电流;Lf、Cf、Rc分别为滤波电感、滤波电容、阻尼电阻;vp为谐波注入的扰动电压幅值;Lg、Rg和vgird分别为电网的等效线路电感、电阻和电网电压;ZGFM为GFM的输出阻抗。

图1 GFM系统主电路及控制结构
Fig.1 Main circuit and control structure of GFM system
GFM的功率控制环如图1b所示。图1b中,q为GFM内电动势相位;J和kq分别为虚拟转动惯量和电压系数;wv和wn分别为GFM的输出角频率和电网的额定角频率;Dp和Dq分别为阻尼系数和电压下垂系数;Pref和Qref分别为有功功率和无功功率参考值;P和Q分别为有功功率和无功功率;|V|ref、|V|、Em分别为额定电压、输出电压和内电动势的 幅值。
dq域中的PI控制框图如图1c所示。图1c中,Gv(s)、Gi(s)分别为电压外环控制PI环节、电流内环控制PI环节的传递函数,表达式分别为
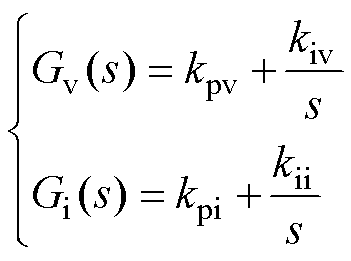 (1)
(1)
式中,kpv、kiv分别为电压外环的比例、积分增益;kpi、kii分别为电流内环的比例、积分增益。
相域中的QPR控制框图如图1d所示。图1d中,Gv1(s)为QPR控制的电压外环控制传递函数,HQPR(s)为QPR的电流内环传递函数,有
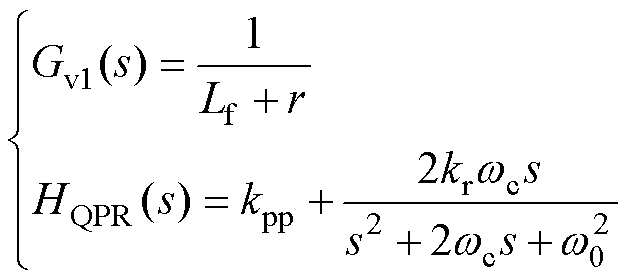 (2)
(2)
式中,r为滤波电感内阻;kpp为比例系数;kr为谐振系数;w0为谐振频率,此处取w0=wn;wc为谐振部分带宽。
根据式(1)和式(2),在电流内环中,通过调整QPR控制HQPR(s)的谐振项等效于PI控制的积分项,同时调整QPR控制与PI控制的比例项,使幅值匹配,此时有HQPR(s)≈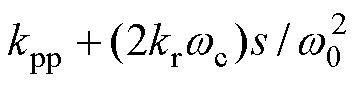 。由此,QPR和PI电流环参数满足等价关系即kpp=kpi,2krwc=kii。该等效关系仅针对电流内环的设计参数调整。
。由此,QPR和PI电流环参数满足等价关系即kpp=kpi,2krwc=kii。该等效关系仅针对电流内环的设计参数调整。
本文研究dq域PI控制与相域QPR控制两种电流内环策略下GFM的阻抗特性。由于主电路拓扑和功率外环控制可独立建模,且与电流内环模型解耦,因此本文分别建立了这两部分的序阻抗模型。其中,2.1节阐述主电路及功率外环控制的建模过程;2.2节与2.3节则在相同主电路和功率外环控制基础上,分别针对采用不同电流内环控制策略的GFM进行建模。
2.1.1 主电路序阻抗模型
根据图1b所示的GFM的控制框图,有功和无功功率控制器的数学模型可分别表示为
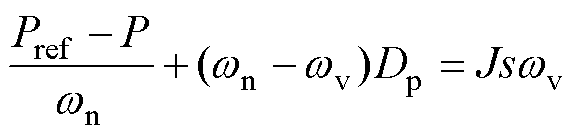 (3)
(3)
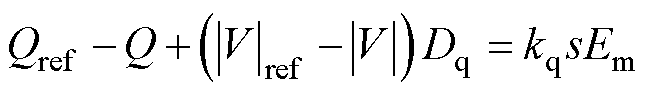 (4)
(4)
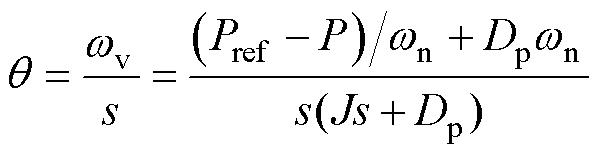 (5)
(5)
根据瞬时功率理论,GFM的瞬时输出有功功率P和无功功率Q可分别表示为
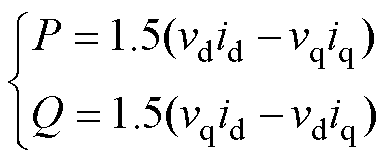 (6)
(6)
式中,vd和id分别为d轴输出电压和电流;vq和iq分别为q轴输出电压和电流。
结合基尔霍夫电流定律和电压定律,可计算得到表征GFM的内电动势eabc、输出端电压vabc和输出电流iabc之间关系的频域主电路核心方程为
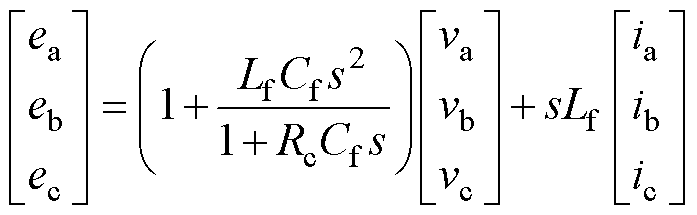 (7)
(7)
GFM采用空间矢量脉宽调制算法,不考虑调制过程以及开关过程,则可将GFM三相调制电压视为桥臂电动势,认为理想调制,即调制比等效为1。
设定时域下网侧注入正序小信号扰动后GFM的a相输出端电压va(t)、电流ia(t)时域表达式分别为
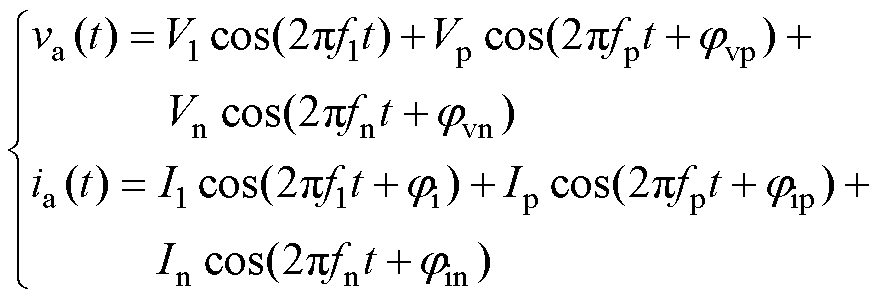 (8)
(8)
式中,V1、Vp、Vn和I1、Ip、In分别为基波、正序、负序扰动电压和电流的幅值;f1为基频;fp、fn分别为正序和负序扰动频率;jvp和jvn分别为正、负序扰动电压的初相位;ji、jip和jin分别为基波及其正负序扰动电流的初相位。
在频域中,a相电压和a相电流可写成
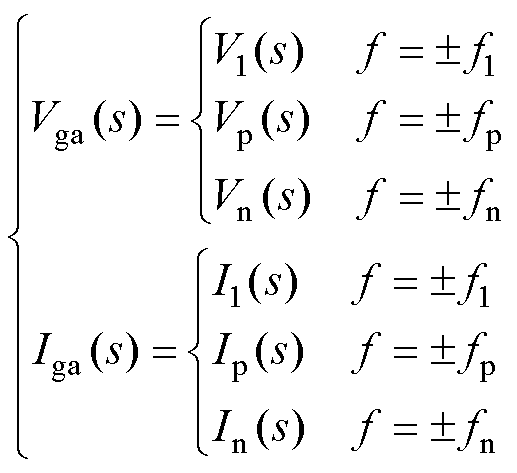 (9)
(9)
其中
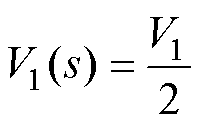
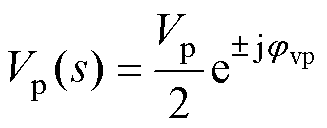
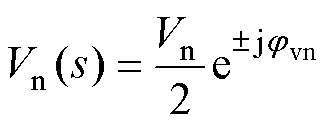
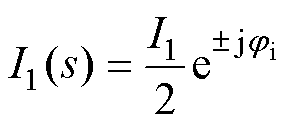
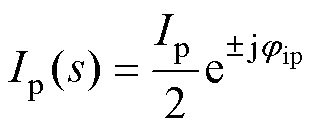
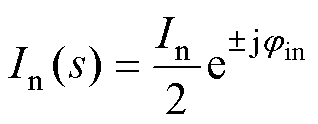
当系统三相对称时,经过基频相位变换模块的dq轴并网电压、并网电流分别为
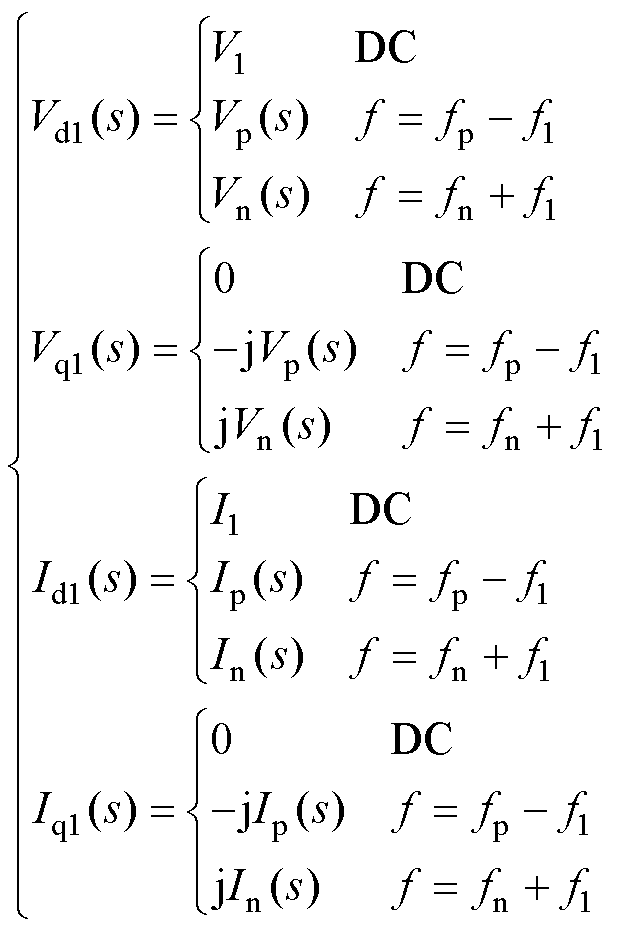 (10)
(10)
2.1.2 功率外环序阻抗模型
将式(10)代入式(6),忽略高阶非线性耦合,利用频域卷积定理,可得GFM的有功功率、无功功率频域表达式分别为
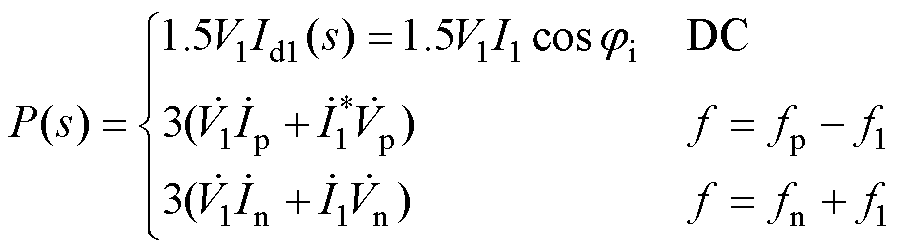 (11)
(11)
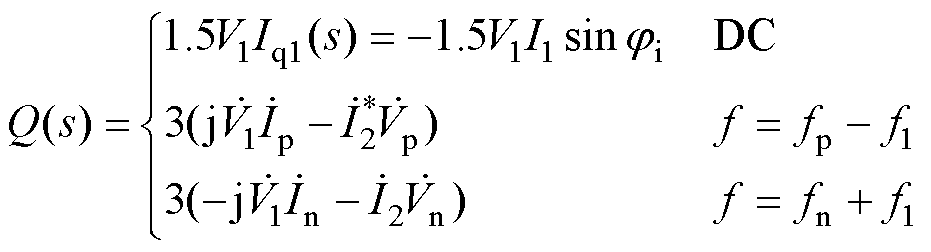 (12)
(12)
其中
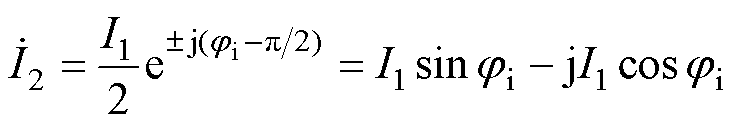
式中,上角标“*”表示复数的共轭;上标“·”表示各量的相量形式。
考虑相位扰动Dq,即q=q1+Dq,将式(11)代入式(5)可以得到GFM输出相位频率的频域表达式为
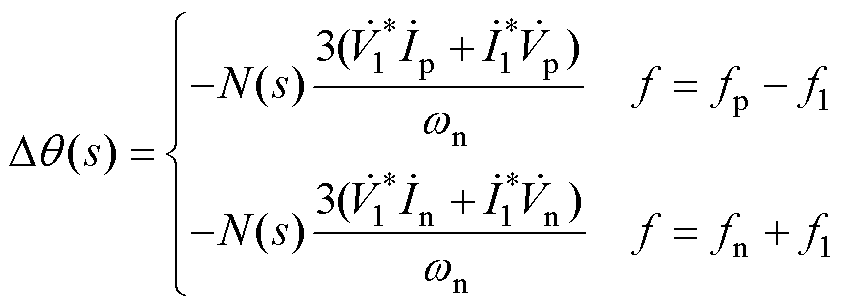 (13)
(13)
式中,q1为基频相位;N(s)=1/(Js2+Dps)。
Dq是相位扰动分量,由于Dq较小,有cosDq≈1,sinDq≈Dq,因此有
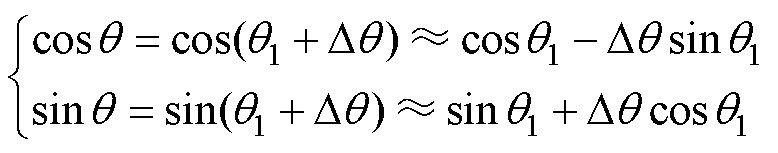 (14)
(14)
将式(5)、式(11)代入式(14),结合频域卷积定理,则cosq的频域表达式为
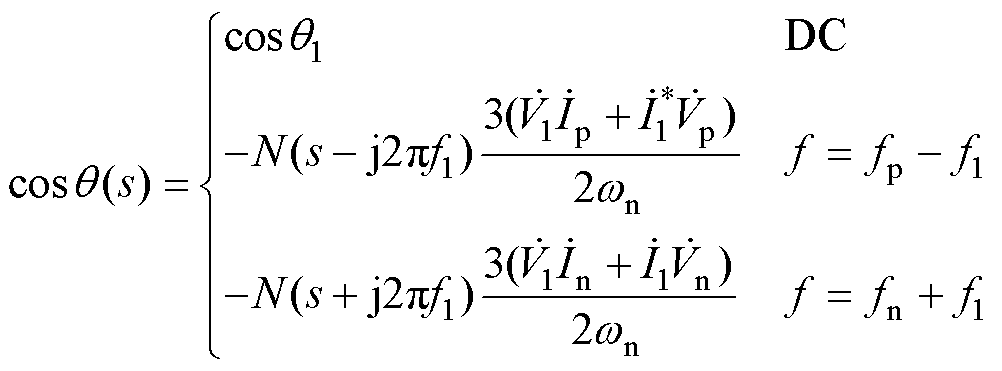 (15)
(15)
本文考虑GFM无功环路对扰动信号的作用,将式(5)变换得到频域表达式后再进行小信号线性化处理,则GFM内电动势幅值Em的各频次分量表达式为
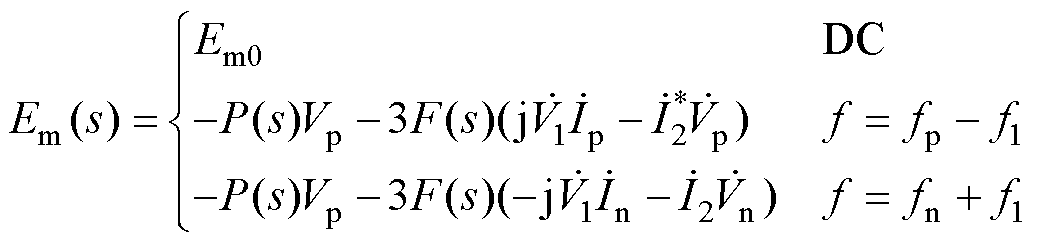 (16)
(16)
式中,Em0为GFM内电动势基频电压;F(s)=1/(kqs),P(s)=Dq/(kqs)。
在讨论dq域PI控制方法时,要考虑的是电压电流双闭环控制系统的建模。这种架构不仅简化了控制逻辑,利用了dq变换的解耦特性,还通过内外环的配合,实现了对逆变器输出电压和电流的精确控制。接下来将详细展开这一建模过程。
2.2.1 电压电流双环建模
根据图1c中电压电流双闭环控制框图的电压外环部分,可知电压外环dq轴参考值频域表达式为
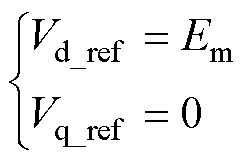 (17)
(17)
并网电压dq轴分量频域表达式为
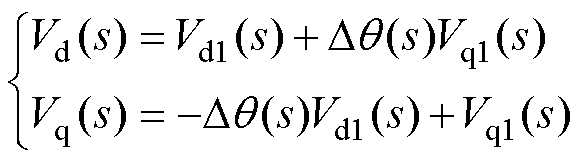 (18)
(18)
将式(8)、式(11)代入式(16)可得
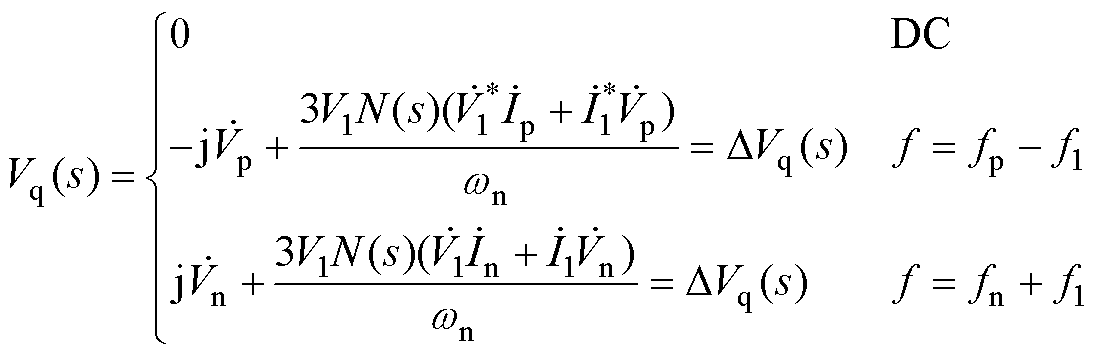 (19)
(19)
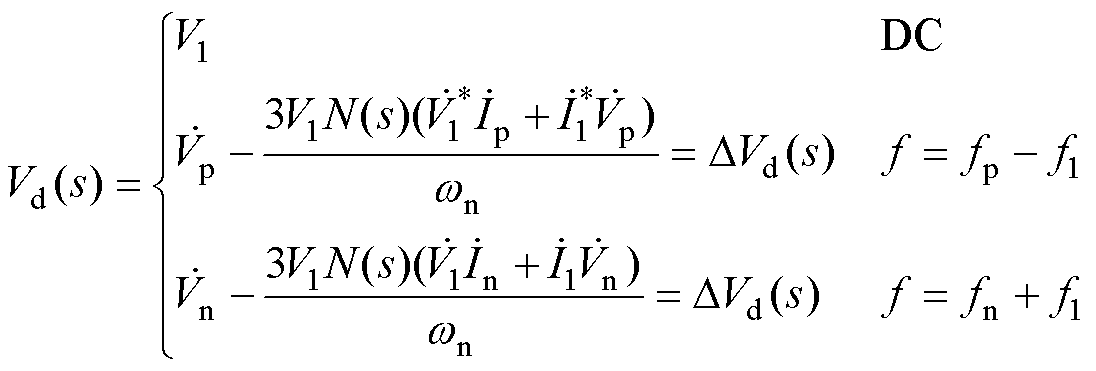 (20)
(20)
同理,可得并网电流dq轴分量Id、Iq分别为
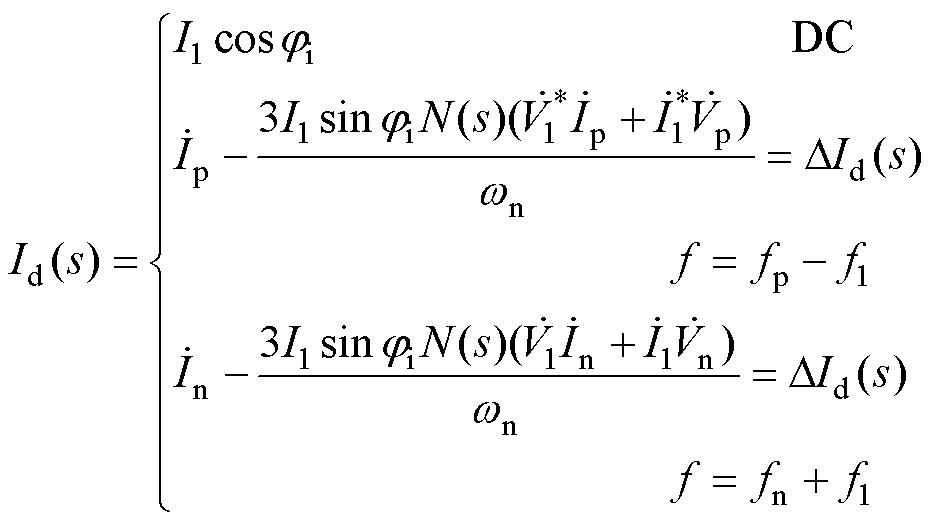 (21)
(21)
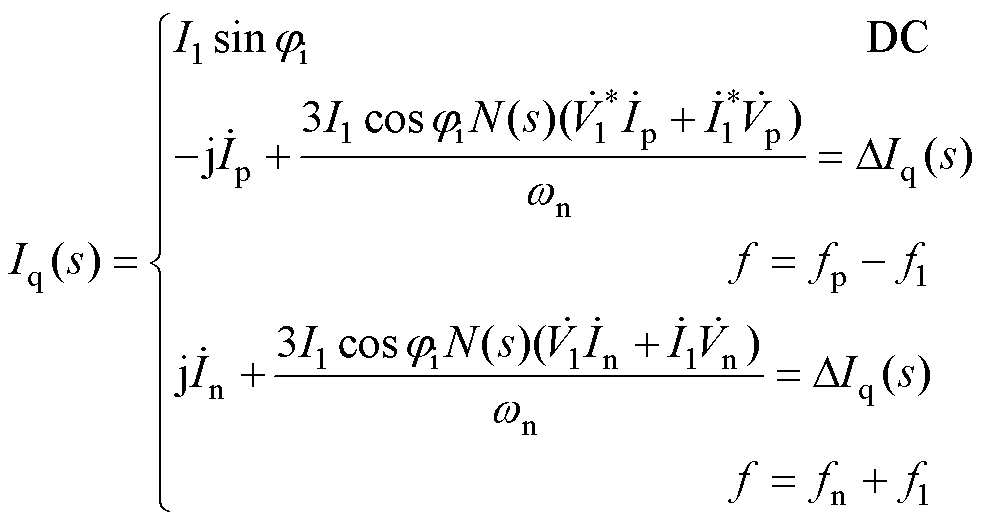 (22)
(22)
并网电压dq轴分量经过电压外环产生电流内环输入参考值Id_ref,考虑dq轴频率偏移,电压外环的频域表达式为
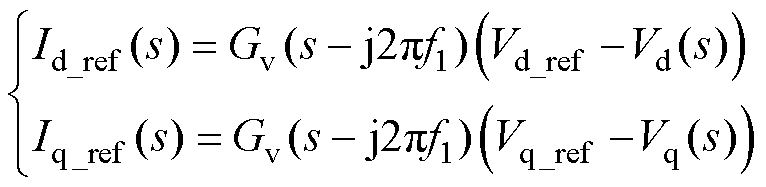 (23)
(23)
式(23)经过小信号线性化处理(Vd_ref和Vq _ref均为常量,DVd_ref、DVq _ref等于0),可得电压外环输入与输出之间的小信号频域表达式为
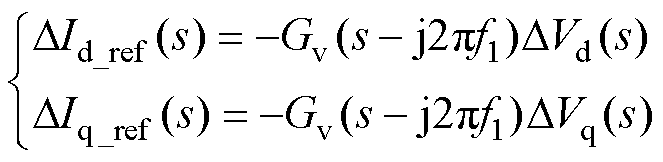 (24)
(24)
并网电压dq轴分量及并网电流dq轴分量通过电压电流双闭环控制环节生成的参考电压Md(s)、Mq(s)为
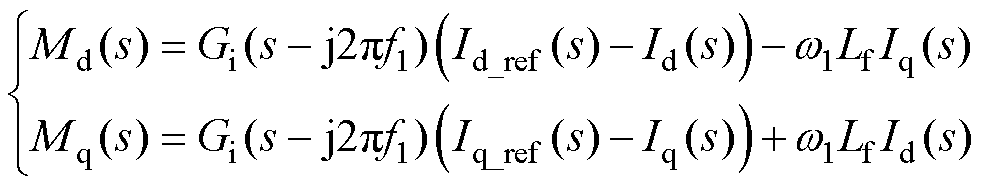 (25)
(25)
式(25)经过小信号线性化处理,可得电流内环输入与输出之间的正序小信号频域表达式为
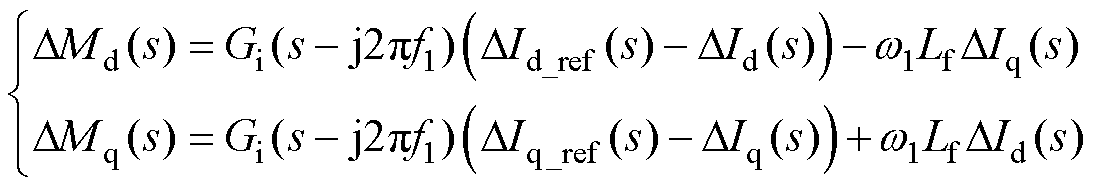 (26)
(26)
2.2.2 dq域PI控制下GFM端口序阻抗模型
将控制系统输出的dq轴参考电压(正序/负序)经过Park反变换后,可获得三相abc坐标系下的参考电压,即逆变器的三相桥臂调制电压Mabc_PI为
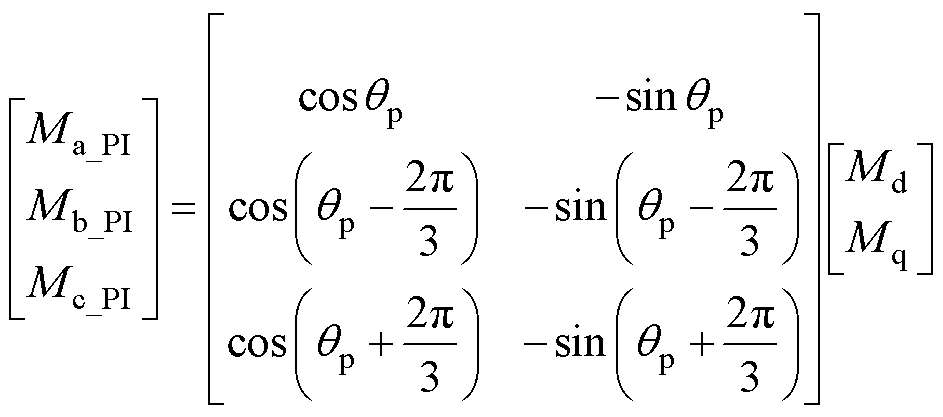 (27)
(27)
式中,qp为Park反变换的旋转角度,且qp=q1。
将Mabc_PI代入GFM的频域主电路核心方程式(7),可计算得到扰动电压关于扰动电流的方程,进一步整理可获得GFM在电流内环采用dq域PI控制下输出端口正负序阻抗模型为
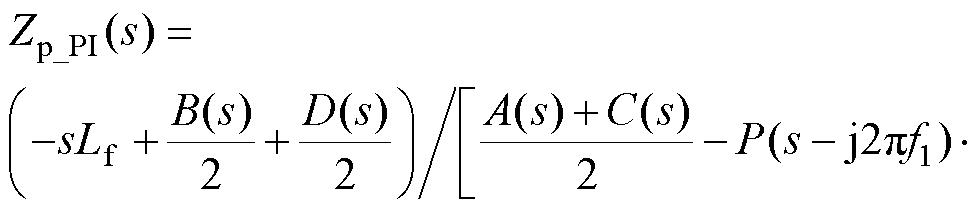
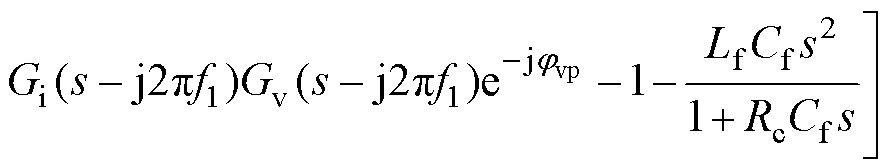 (28)
(28)
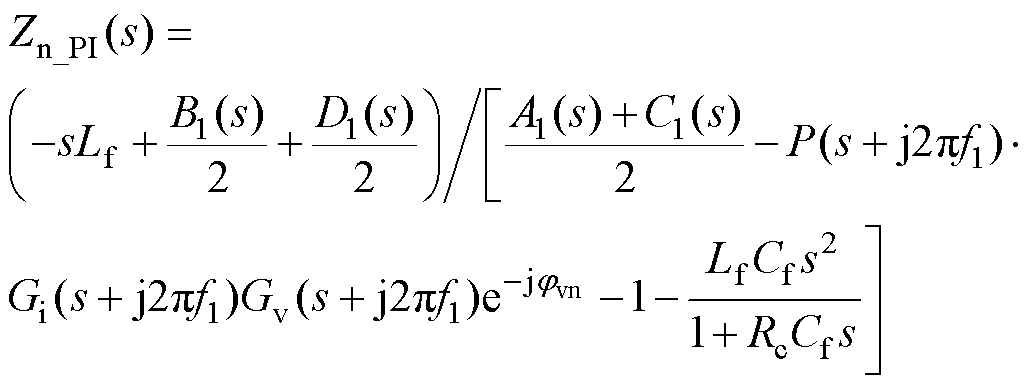 (29)
(29)
式中,A(s)、B(s)、C(s)、D(s)、A1(s)、B1(s)、C1(s)、D1(s)的具体表达式见附录式(A1)~式(A8)。
相域控制下的参考电压Vref_abc等于电压调制波信号eabc_QPR,此时有
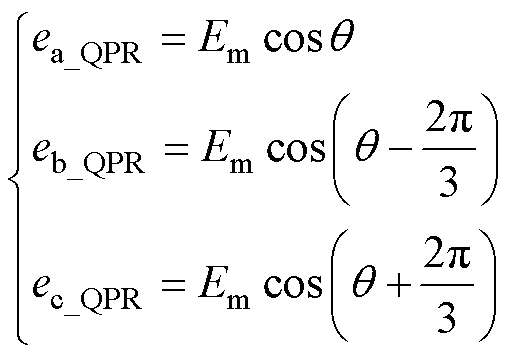 (30)
(30)
由图1c可知,电压电流控制环的表达式为
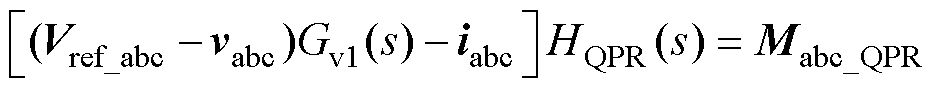 (31)
(31)
式中,Mabc_QPR为相域控制下GFM的三相桥臂调制电压。
根据式(7),以a相为例,a相的频域核心方程为
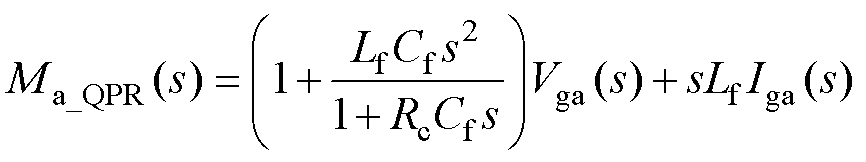 (32)
(32)
考虑正负序的扰动电压,结合式(32),a相调制电压小信号表达式为
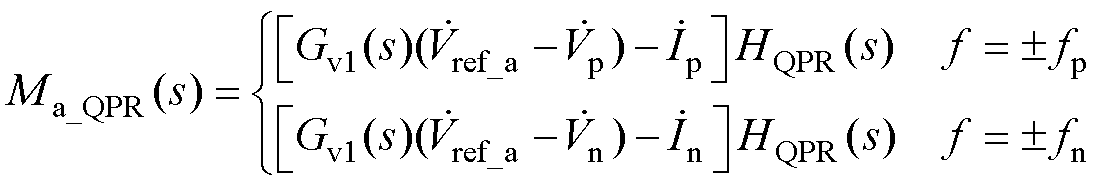 (33)
(33)
联立式(2)、式(30)~式(33),进一步可求解得到静止坐标系下GFM的正负序阻抗解析表达式为
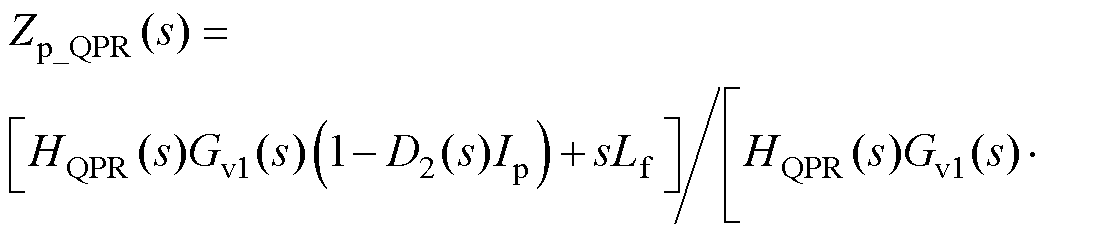
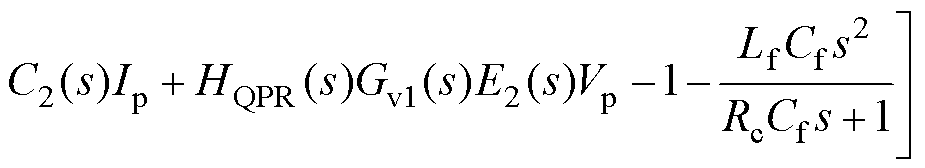 (34)
(34)
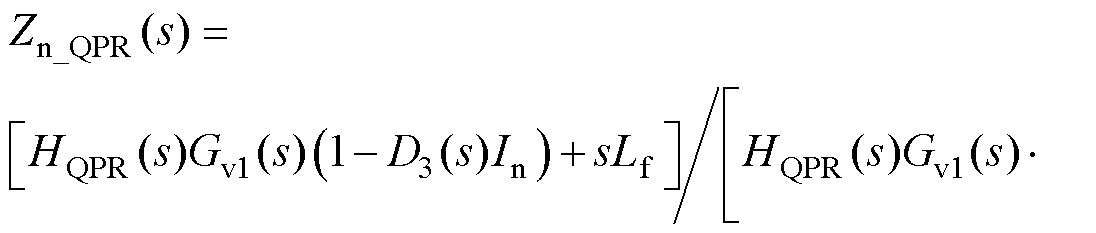
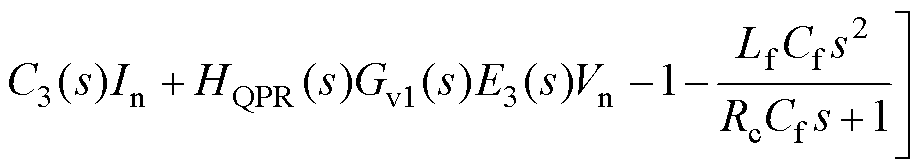 (35)
(35)
式中,C2(s)、D2(s)、E2(s)、C3(s)、D3(s)、E3(s)具体表达式见附录式(A9)~式(A14)。
2.2节和2.3节依次推导了dq域PI控制和相域QPR控制GFM的序阻抗模型,本文研究的不同电流内环控制下的GFM参数见附表1。
为验证所建立序阻抗模型的正确性,在Matlab/ Simulink中建立了阻抗测量模型。dq域PI控制和相域QPR控制的GFM阻抗测量结果如图2所示。图中,实线和虚线分别表示dq域PI控制和相域QPR控制的GFM正负序阻抗理论模型,○和×表示正负序阻抗测量结果。从图2可以看出,GFM输出阻抗测量结果与所建立的序阻抗模型基本吻合,证明了所建立dq域PI控制和相域QPR控制下的GFM序阻抗模型的正确性。
由图2可知,PI控制与QPR控制下的GFM输出阻抗特性差异显著。在低频段(低于基频50 Hz),两种控制策略下的阻抗幅值相近,但PI控制的相位响应为负且波动较大,表现出阻容性特征,意味着其动态响应相对迟缓且稳定性欠佳;相比之下,QPR控制的相位响应更为稳定,阻抗呈感性,表明此频段内QPR控制具有更好的稳定性和更快的响应速度。在50 Hz~1 kHz频段内,PI控制的相位逐渐增大,幅值略有提升,呈现出阻感性特征;而QPR控制的相位则保持稳定,依然呈感性,且幅值显著增加,显示出QPR控制在该频段内具有更强的谐波抑制能力。直至高频段(1~10 kHz),两种控制的阻抗特性趋于一致,均呈现阻容性特征,这表明在此频段内控制策略对阻抗的影响减弱,两种控制的表现相当。两种控制下GFM的具体阻抗特性对比见表1。如表1所示,QPR控制在中低频段提供了更为稳定且高效的阻抗特性,在谐波抑制方面表现更优。而在高频段(1 kHz以上),PI控制与QPR控制的表现则趋于一致。
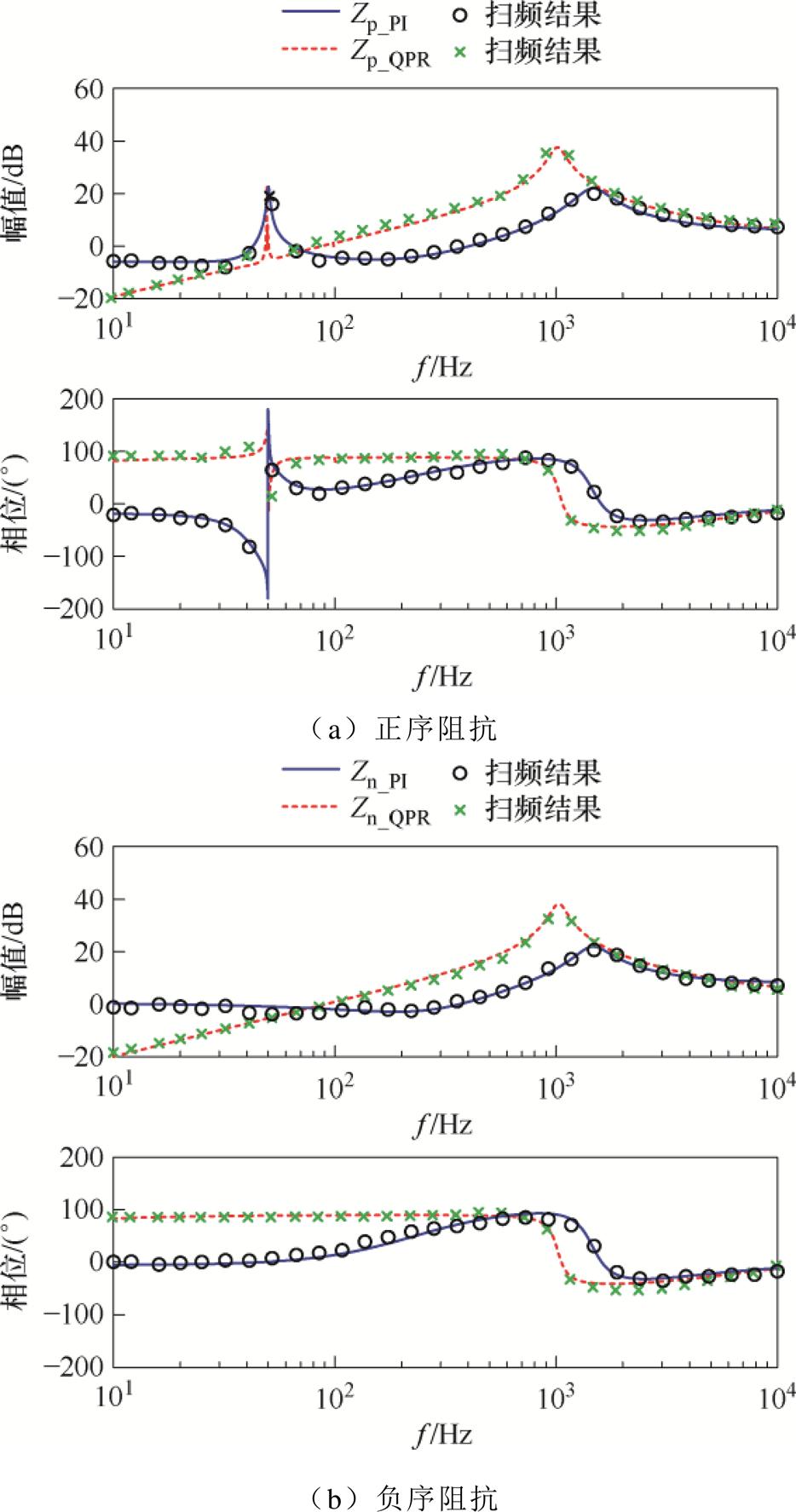
图2 PI和QPR控制下GFM的阻抗扫频模型
Fig.2 Impedance sweep model of GFM controlled by PI and QPR
表1 PI控制和QPR控制下GFM的阻抗特性对比
Tab.1 Comparison of impedance characteristics of GFM under PI control and QPR control
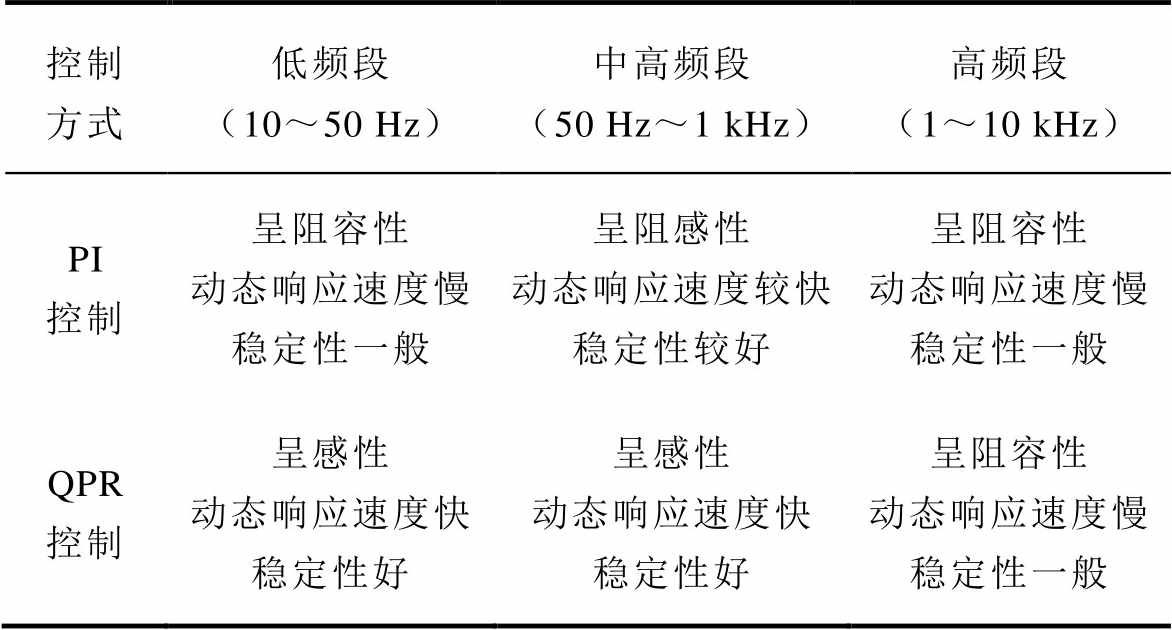
控制方式低频段(10~50 Hz)中高频段(50 Hz~1 kHz)高频段(1~10 kHz) PI控制呈阻容性动态响应速度慢稳定性一般呈阻感性动态响应速度较快稳定性较好呈阻容性动态响应速度慢稳定性一般 QPR控制呈感性动态响应速度快稳定性好呈感性动态响应速度快稳定性好呈阻容性动态响应速度慢稳定性一般
基于2.4节对dq域PI控制及相域QPR控制GFM的阻抗特性分析,本节用Nyquist稳定性判据揭示PI和QPR控制参数对系统稳定性的影响规律,重点分析各参数单独变化时系统稳定裕度的演化 特征。
2.5.1 PI控制参数影响分析
图3展示了PI控制参数对系统频域稳定特性的影响。图3a中,比例增益kpi在0.5~2范围内变化。kpi=0.5时Nyquist曲线失稳,kpi≥1时系统渐近稳定,稳定裕度随kpi的增大先增强后衰减,出现该结果的主要原因在于积分环节相位滞后效应随增益增加而累积,过高的增益会削弱相位裕度,降低高频干扰抑制能力。图3b中,积分系数kii在10~500范围内变化,Nyquist轨迹先趋近后远离临界点(-1, j0),系统始终稳定。当kii超过200后,因积分控制频域补偿机制,积分作用在消除稳态误差与引入动态迟滞间保持平衡,系统稳定性指标趋于稳定。
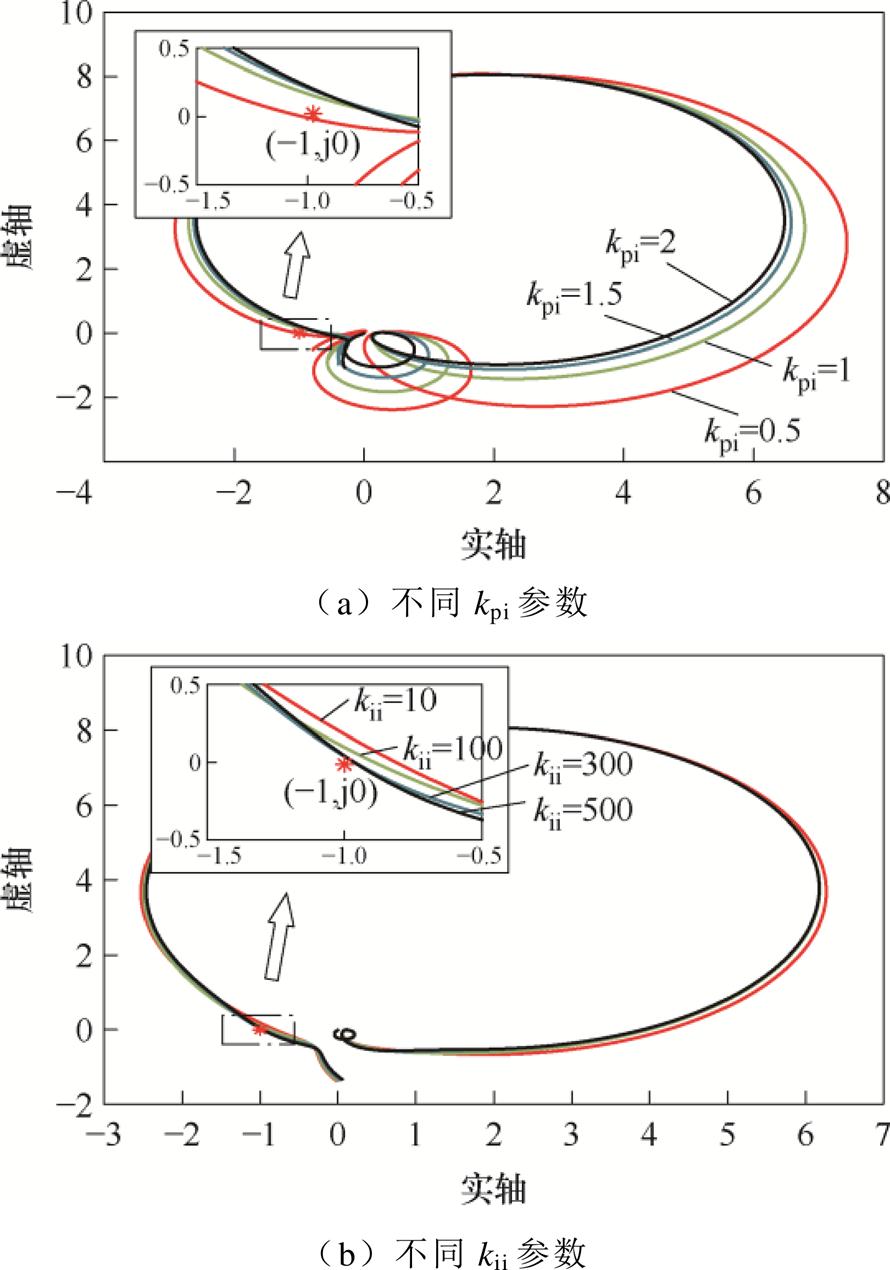
图3 不同PI控制参数下系统的Nyquist图
Fig.3 Nyquist diagram of the system under different PI control parameters
2.5.2 QPR控制参数影响分析
图4揭示了QPR控制参数对系统频域稳定特性的影响机理。图4a展示了比例系数kpp在0.1~0.5区间内的稳定性演变规律:当kpp=0.5时,Nyquist曲线呈现顺时针环绕临界点(-1, j0)的失稳特征;当kpp<0.5时,曲线与负实轴交点始终位于临界点右侧,系统保持渐近稳定。图4b进一步展示了谐振系数kr在1~8范围内的稳定性边界特性。当kr<5时,Nyquist曲线保持与临界点的安全距离;当kr≥5时,曲线在基频处产生显著凹陷并包围临界点,系统失稳。
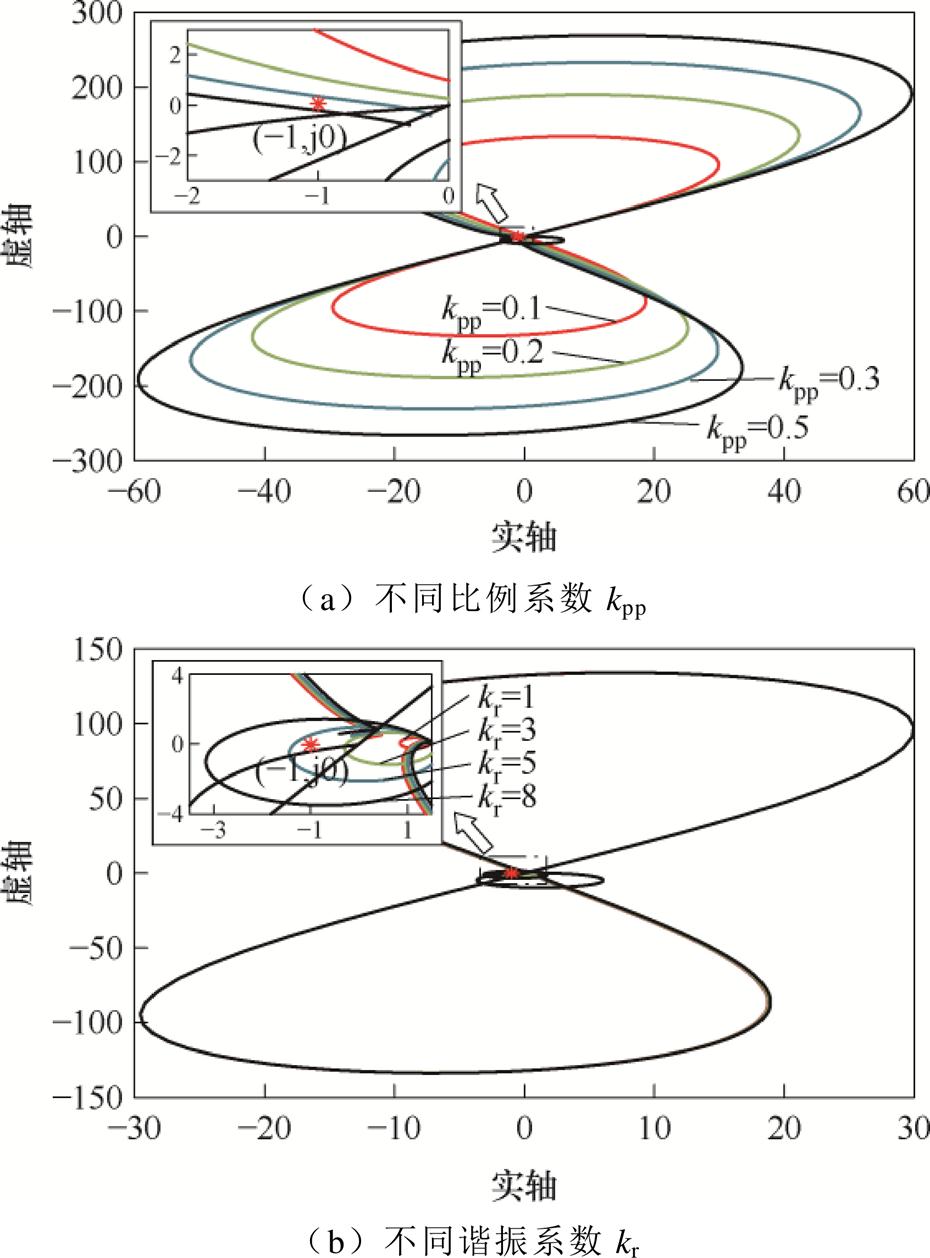
图4 不同QPR控制参数下系统的Nyquist图
Fig.4 Nyquist diagram of the system under different QPR control parameters
本节通过Nyquist稳定性判据,深入分析了PI控制和QPR控制参数对系统稳定性的影响。对于PI控制,比例增益kpi和积分系数kii在不同取值范围内会使系统呈现不同的稳定状态,且稳定裕度随参数变化有特定规律,积分环节的影响存在边际效应,参数调节需平衡稳态精度与动态响应。对于QPR控制,比例系数kpp和谐振系数kr在不同取值区间也会使系统稳定性发生改变,存在失稳边界。这些分析为合理设置控制参数以确保系统稳定性提供了理论依据。
本文考虑电流环控制域差异,建立了不同控制域下GFM并网系统的序阻抗模型,采用Nyquist稳定判据评估系统的稳定性。系统稳定需满足:回比矩阵特征函数的Nyquist曲线绕点(-1, j0)的次数与GFM输出及电网阻抗在右半平面的极点总数一致。因电网阻抗无右半平面极点且GFM独立运行稳定,其输出阻抗亦无此极点,故Nyquist曲线不穿越点(-1, j0),系统稳定[18-19]。理论分析中,电网在公共耦合点(Point of Common Coupling, PCC)通过戴维南等效简化为电网模型。GFM交流并网系统的小信号等效电路如图5所示。图中,VGFM_p(s)、VGFM_n(s)分别为GFM等效的正负序电压源;ZGFM_p(s)、ZGFM_n(s)分别为GFM等效的正负序阻抗;Zg_p(s)、Zg_n(s)分别为电网等效的正负序阻抗;Ig_p(s)、Ig_n(s)分别为GFM的正负序并网电流;Vg_p(s)、Vg_n(s)分别为电网等效的正负序电压源。
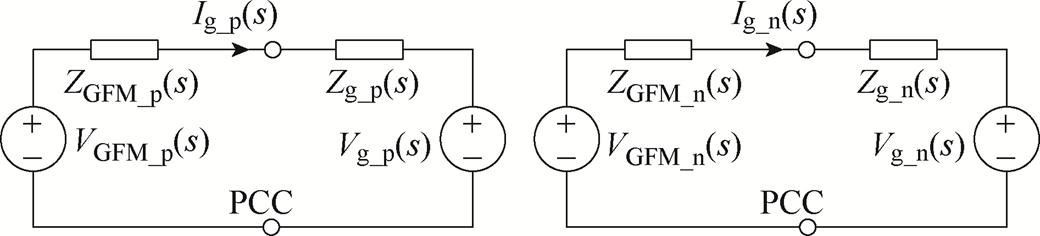
(a)正序 (b)负序
图5 GFM交流并网系统的小信号等效电路
Fig.5 Small signal equivalent circuit of GFM AC grid-connected system
根据图5,对于相位域GFM并网系统,并网点电流Ig(s)的表达式为
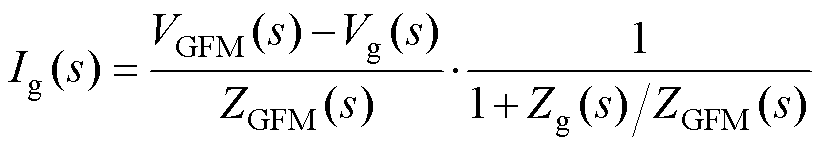 (36)
(36)
可见,系统阻抗比Zg(s)/ZGFM(s)是影响小干扰稳定性的关键,其核心在于并网电流Ig的稳定性,该稳定性取决于阻抗比是否满足Nyquist稳定判据。本文中,将Zg(s)定义为Rg+sLg,其中Rg和Lg分别代表电网的阻性和感性部分。
电网强度可通过短路比(Short Circuit Ratio, SCR)来衡量,其定义为电网短路容量Sshortcut与变流器额定容量SN之比,即
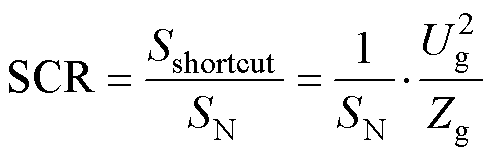 (37)
(37)
由计算可知,当Lg分别为2、5、10、24 mH时,SCR对应为22.9、9.2、4.6、1.9。据此,SCR在2~3之间时电网为弱电网,小于2时为极弱电网,大于3时为强电网。
图6a展示了当电网阻抗不同时,在dq域PI控制下的GFM Nyquist特性。当SCR分别设定为9.2、4.6及1.9时,相应的Nyquist曲线均未穿越单位圆上的临界点(-1, j0),根据Nyquist稳定性判据,此时系统处于稳定状态。然而,当SCR=22.9时,Nyquist曲线包围了临界点(-1, j0),表明系统在此条件下变得不稳定。
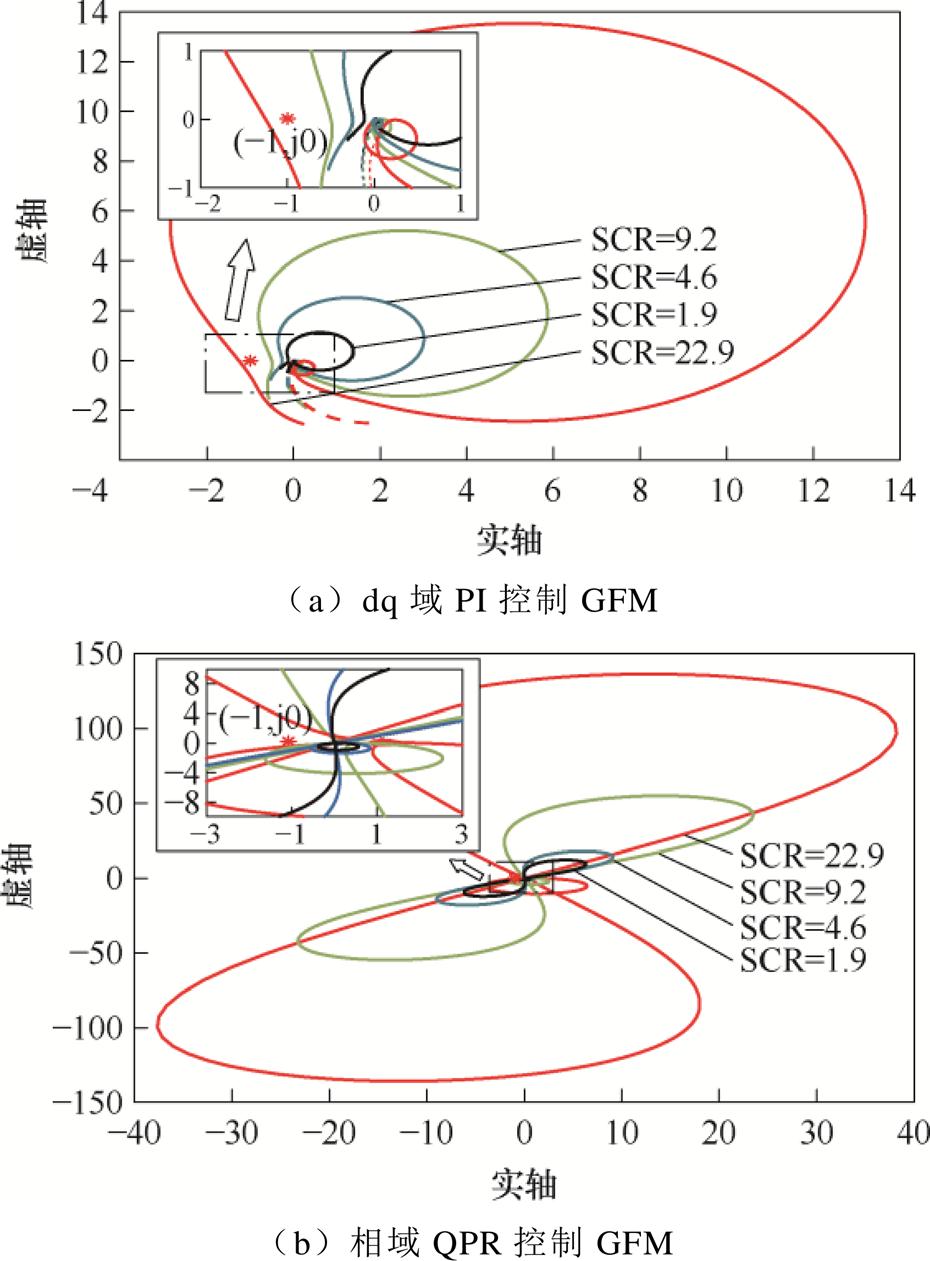
图6 不同电网阻抗下GFM与电网交互的Nyquist图
Fig.6 Nyquist diagram of interaction between GFM and power grid under different grid impedance
相较于dq域PI控制,相域QPR控制展现出不同的电网适用性特征。如图6b所示,在SCR增长至22.9的条件下,相域QPR控制对应的Nyquist曲线并未包围临界点(-1, j0),这表明系统在此环境下依然能够维持稳定状态。而当SCR=1.9时,即电网处于极弱状态时,尽管相域QPR控制的Nyquist曲线同样未包围临界点,但相较于dq域PI控制的Nyquist曲线,它更加接近临界点。由此推断,在极弱电网环境下,dq域PI控制的电网适用性更为优越。
综上所述,在强电网环境中,相域QPR控制相较于dq域PI控制展现出更优的电网适用性;然而,在极弱电网环境下,相域QPR控制的电网适用性则不及dq域PI控制。
图7展示了不同GFM并网数量N下,并网系统阻抗比的Nyquist图。图7a表明,当dq域PI控制的GFM并网数量增加时,Nyquist曲线未包围临界点(-1, j0),并逐渐远离,依据Nyquist稳定性判据,系统保持稳定且稳定性增强。相比之下,图7b显示,当相域QPR控制的GFM在并网数量增多时,Nyquist曲线同样未包围临界点(-1, j0),且远离临界点,表明系统同样保持稳定且稳定性逐渐提升。
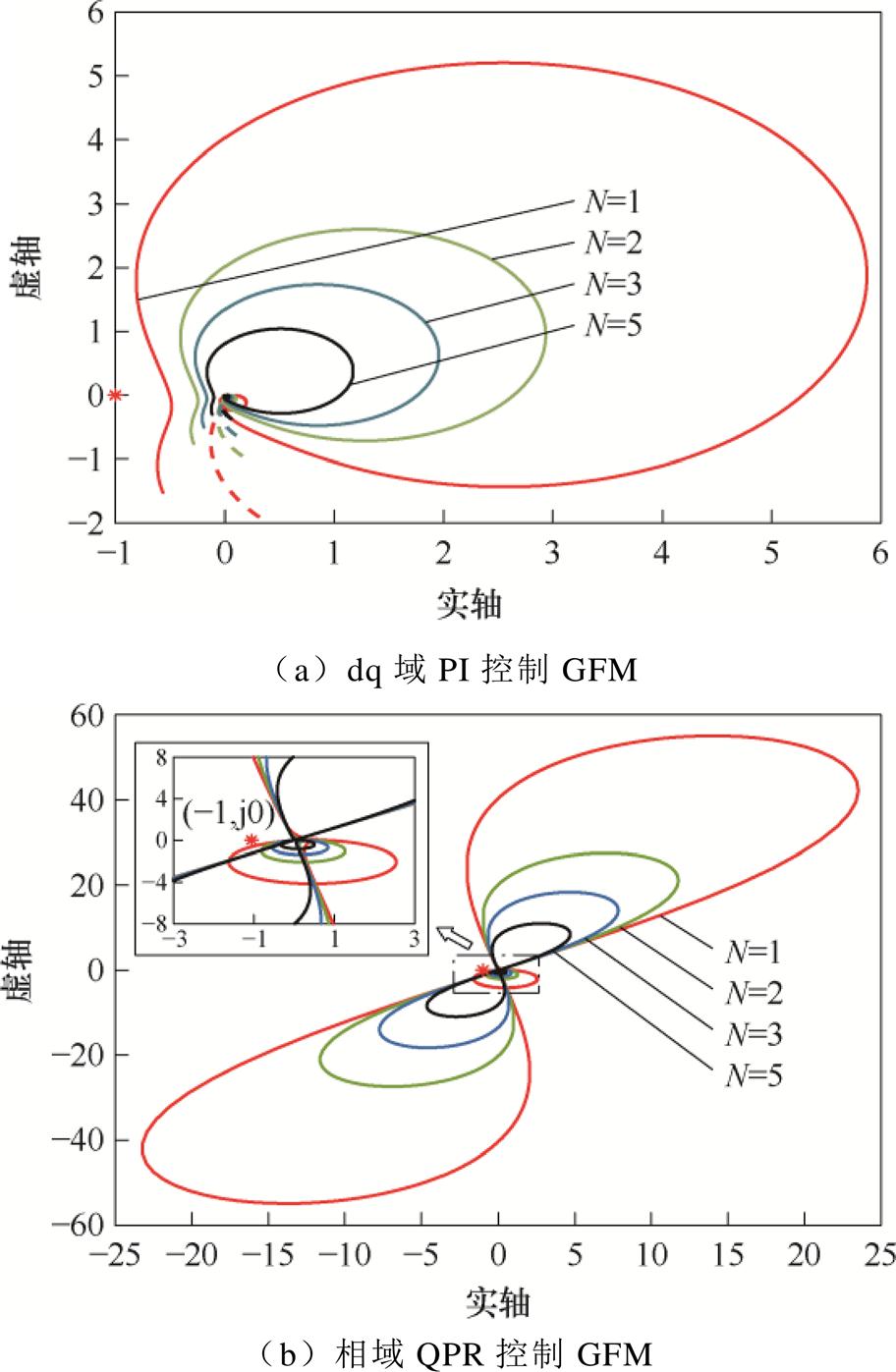
图7 不同GFM并网数量下系统阻抗比的Nyquist图
Fig.7 Nyquist diagram of system impedance ratio under different GFM grid-connected numbers
综上所述,在GFM并网数量增加的情况下,无论是采用dq域PI控制还是相域QPR控制,系统均能保持稳定状态,但dq域PI控制下的系统稳定性随GFM并网数量增加而增强的趋势更为明显。
本文在Matlab/Simulink上分别搭建了电流内环采用dq域PI控制和相域QPR控制的GFM系统仿真模型,仿真具体参数详见附表1。
4.1.1 不同控制域的GFM电网适用性仿真结果
不同电网强度GFM的并网电流如图8所示,从图中可以清楚地看到两种控制策略在不同电网强度条件下的GFM并网电流响应及其总谐波畸变率(Total Harmonic Distortion, THD)。当SCR=22.9时,电网呈现强电网特性。此时,电流内环采用PI控制的GFM并网电流出现了较为明显的振荡,THD高达5.45%;而采用QPR控制的GFM并网电流则表现出良好的稳定性,THD仅为0.74%。仿真结果初步验证了QPR控制在强电网条件下的优越性。
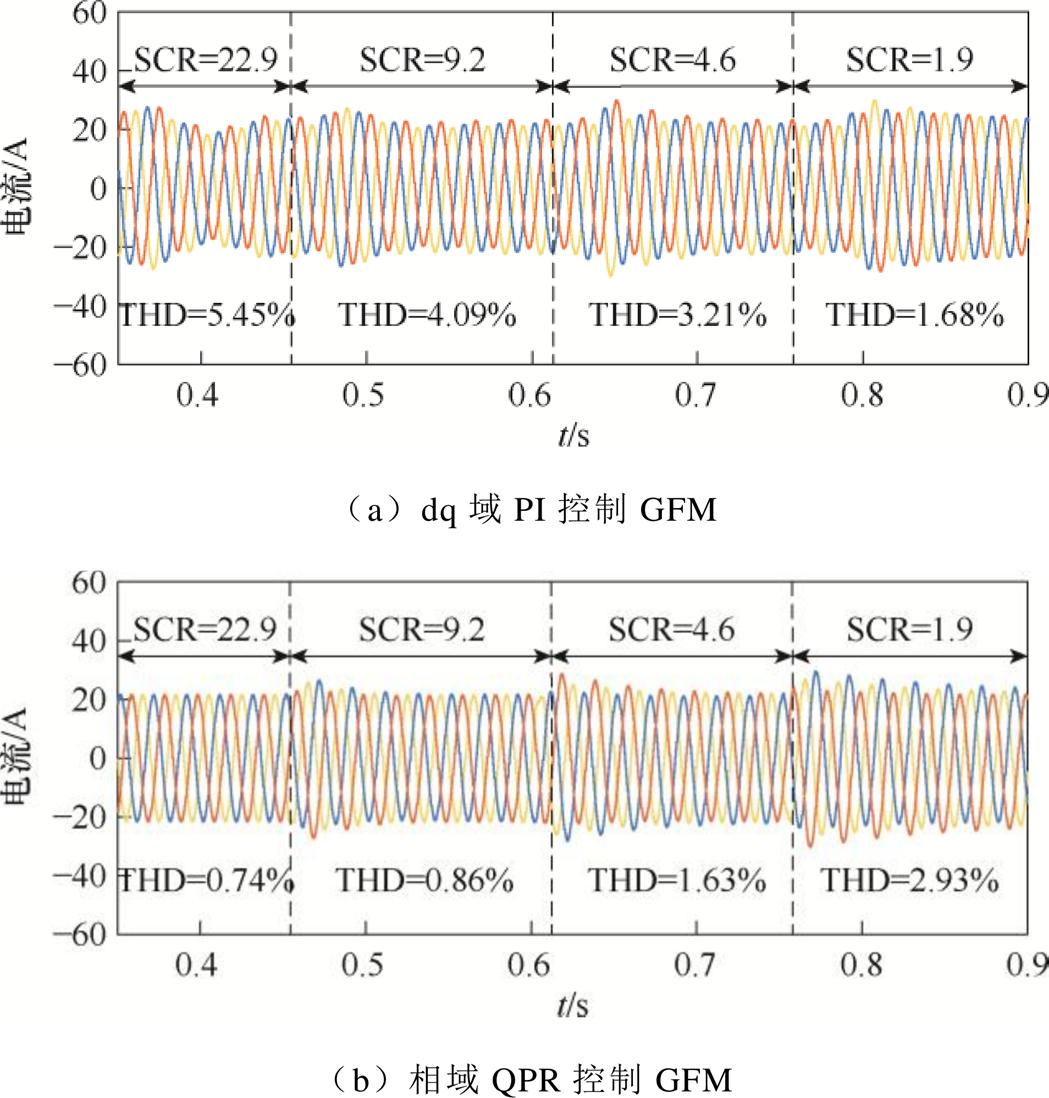
图8 不同电网强度GFM的并网电流
Fig.8 Simulation results of the influence of different power network impedance on system stability
当SCR为9.2和4.6时,电网强度适中。此时,无论GFM是采用PI控制还是QPR控制,并网电流均保持稳定。然而,通过对比THD可知,采用PI控制的GFM并网电流THD分别为4.09%和3.21%,而采用QPR控制的GFM并网电流THD则分别为0.86%和1.63%。仿真结果证实了QPR控制在提高并网电流质量方面的优势。
当SCR为1.9时,电网呈现极弱特性。此时,采用PI控制的GFM并网电流稳定性较好,THD为1.68%;而采用QPR控制的GFM则出现了轻微振荡,THD为2.93%。仿真结果表明,在极弱电网条件下,PI控制的稳定性表现优于QPR控制。
综上所述,随着电网强度的减弱,采用dq域PI控制的GFM并网电流谐波减少,并网稳定性提高。采用相域QPR控制的GFM在强电网条件下表现出优异的并网稳定性,谐波含量低。然而,在极弱电网条件下,其稳定性表现略逊于PI控制。分析结果揭示了QPR控制在不同电网条件下的适用性差异,仿真结果与前文的理论分析一致。
4.1.2 不同GFM并网数量仿真结果
为研究GFM并网数量对系统稳定性的影响,采用两种电流内环控制策略的GFM仿真结果如图9所示,相关仿真均设定SCR为4.6以模拟典型电网场景。
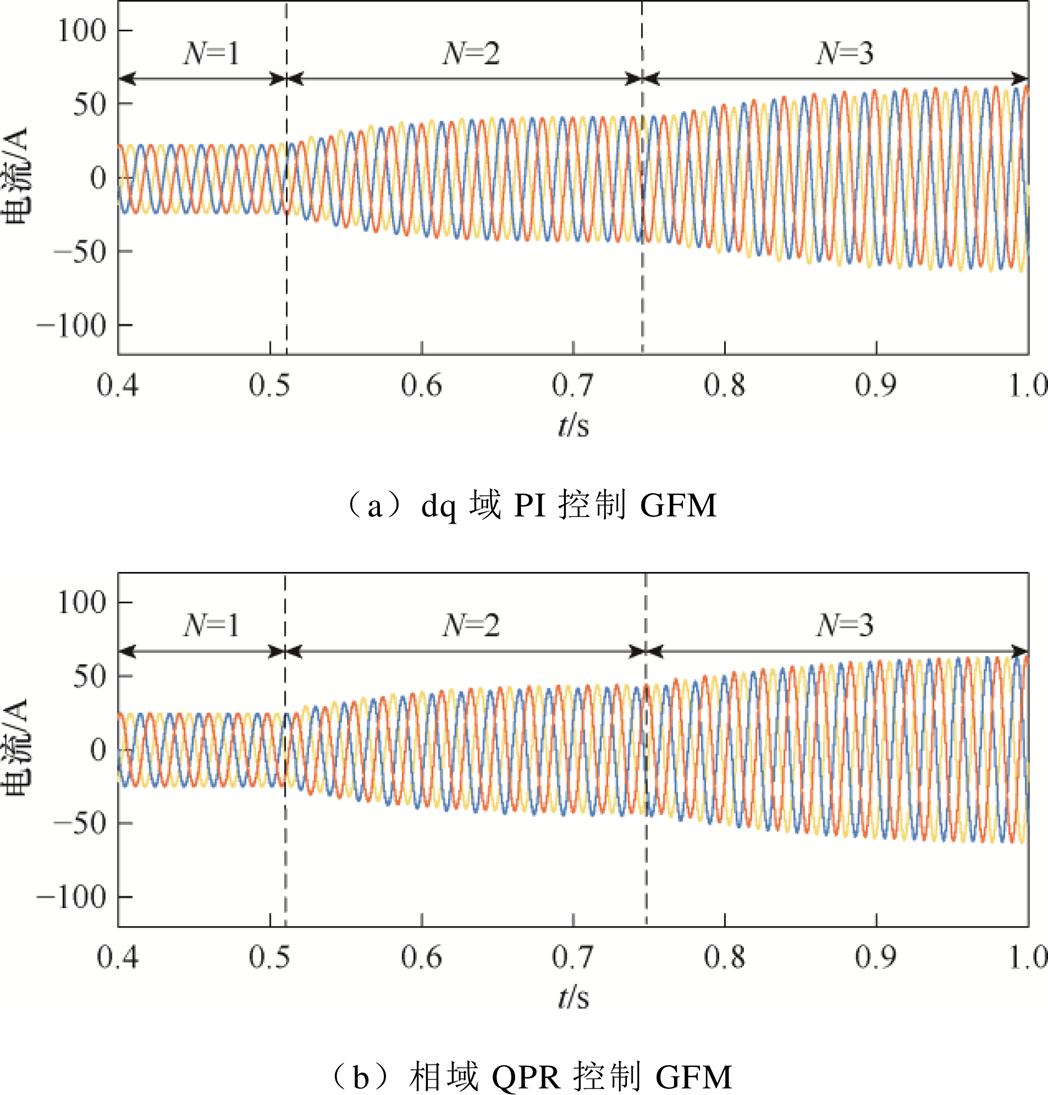
图9 不同GFM数量的并网电流
Fig.9 Grid-connected currents with different numbers of GFM
由图9a可知,在dq域PI控制下,随着GFM并网数量的增加,系统的并网电流波形保持平稳,未出现明显的振荡或谐波失真现象。与dq域PI控制类似,相域QPR控制下的GFM系统在GFM并网数量增加时,同样表现出良好的并网稳定性,其仿真结果如图9b所示,并网电流波形清晰、稳定,未出现明显的波动或异常现象。
综上所述,无论是采用dq域PI控制作为电流内环,还是应用相域QPR控制,当GFM并网数量增加时,系统均展现出优异的并网稳定性。仿真结果验证了两种控制策略在多GFM并网环境下的可行性,且与前文理论分析一致。
为进一步验证上述理论的正确性,本文基于StarSim硬件在环仿真平台搭建了不同电网强度及GFM并网数量在两种控制下的GFM并网系统。硬件在环仿真平台如图10所示。
与Matlab/Simulink仿真验证的方法一致,分别采用不同强度的电网条件,对两种控制方式下的GFM进行适用性差异对比,仿真结果如图11所示。观察图11a可知,当SCR为22.9,即电网强度较大时,采用dq域PI控制的GFM并网电流出现了振荡;相比之下,在SCR为9.2、4.6和1.9的电网条件下,其表现较为稳定。由图11b可知,当SCR同样为22.9时,采用相域QPR控制的GFM未出现振荡;但在SCR为1.9的极弱电网条件下,其电流稳定效果不如图9a中的PI控制。这些分析结果表明,在强电网环境下,相域QPR控制的GFM展现出了卓越的并网稳定性;然而在电网极弱的情况下,其稳定性稍逊于PI控制。仿真分析结果与理论分析一致。

图10 硬件在环仿真平台
Fig.10 Hardware-in-the-loop simulation platform
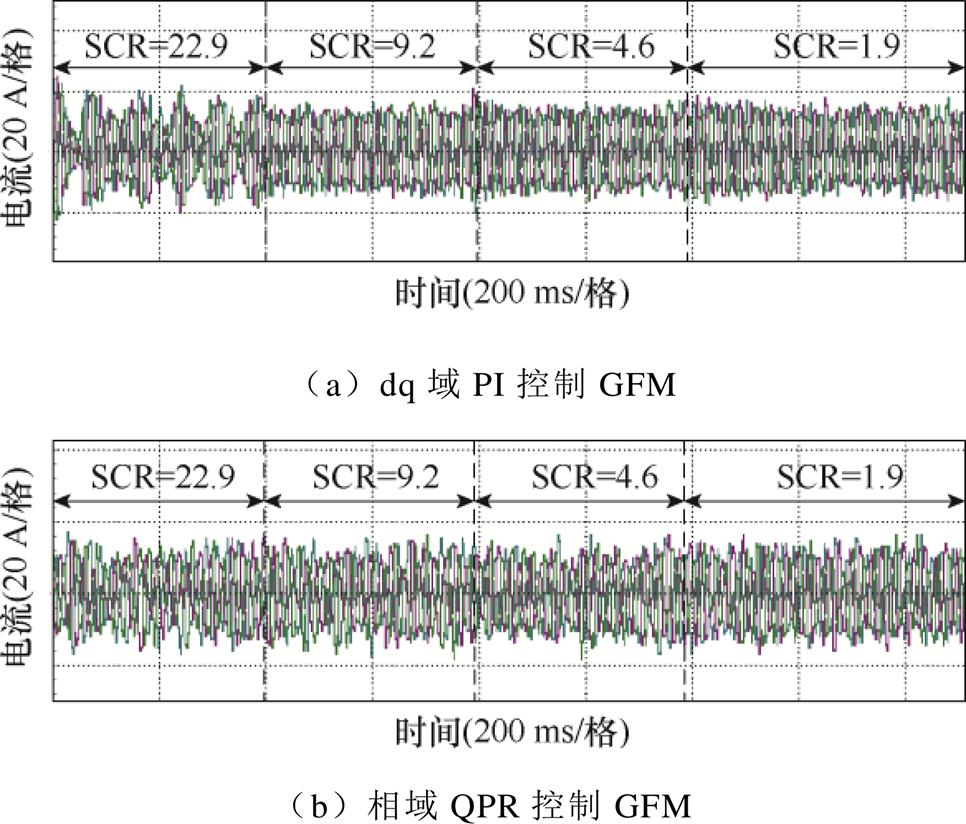
图11 不同电网强度的GFM并网电流在环仿真结果
Fig.11 Simulation results of GFM grid-connected currents with different grid strengths in the loop
考虑GFM并网数量对系统稳定性的影响,两种电流内环控制的GFM仿真结果如图12所示。由图12可知,无论是采用dq域PI控制还是相域QPR控制,当GFM并网数量增加时,GFM系统均展现出优异的并网稳定性。仿真结果与前文理论分析 一致。
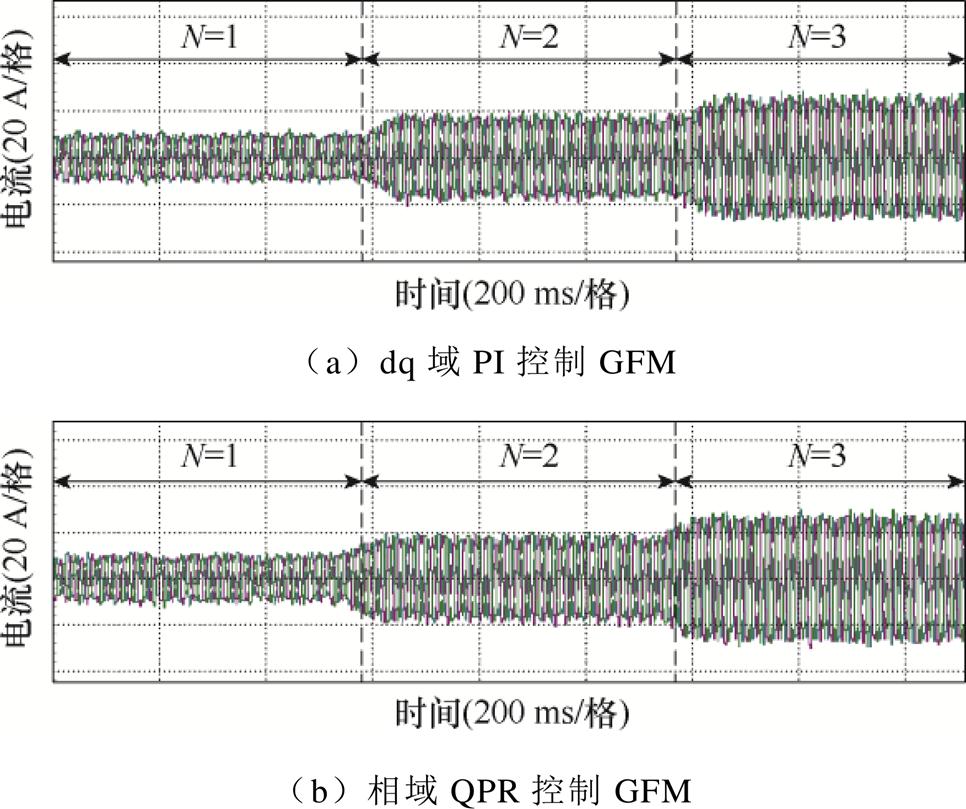
图12 不同GFM数量的并网电流在环仿真结果
Fig.12 Simulation results of grid-connected currents with different GFM numbers in the loop
本文采用谐波线性化序阻抗建模的方法,分别建立了电流内环采用PI控制和QPR控制的GFM系统序阻抗模型,基于序阻抗特性及Nyquist稳定性判据,对两种控制方法下的GFM阻抗特性、强弱电网和多GFM并网场景适用性进行了对比分析,具体结论如下:
1)PI控制和QPR控制GFM阻抗特性差异较大,在中低频段,QPR控制的GFM提供了更为稳定且高效的阻抗特性,表现出良好的谐波抑制能力;在高频段,PI控制和QPR控制的GFM阻抗特性相似。
2)PI控制和QPR控制GFM的电网适应性差异较大,在强电网条件下,相域QPR控制相比于dq域PI控制具有较好的电网适用性;在极弱电网条件下,相域QPR控制的表现略逊于dq域PI控制。
3)无论电流内环是采用dq域PI控制还是相域QPR控制的GFM,在GFM并网数量增加的情况下,系统均可以保持很好的稳定性,证实了两种控制策略在应对多GFM并网场景时的有效性。
以上结论对于指导构网型变流器在实际电网中的稳定运行以及构网型变流器大规模并网运行具有重要意义。
附 录
1. 序阻抗模型中各量表达式
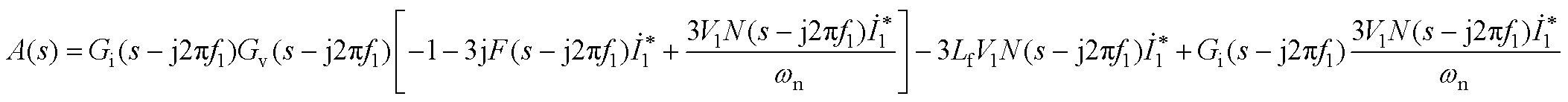 (A1)
(A1)
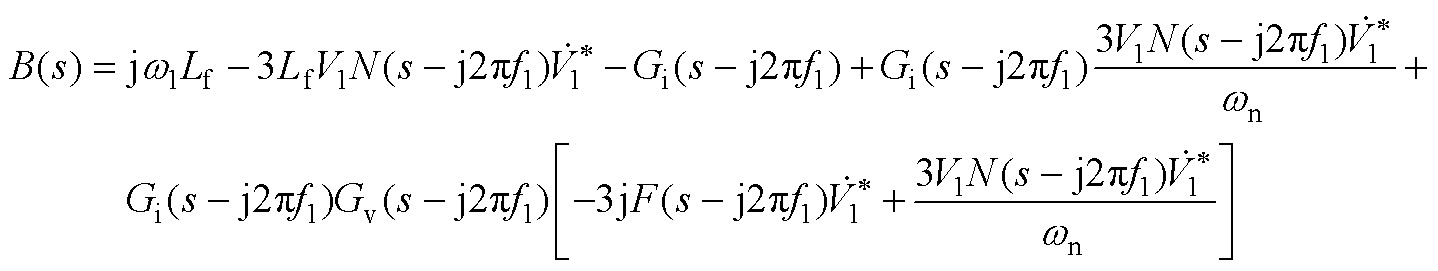 (A2)
(A2)
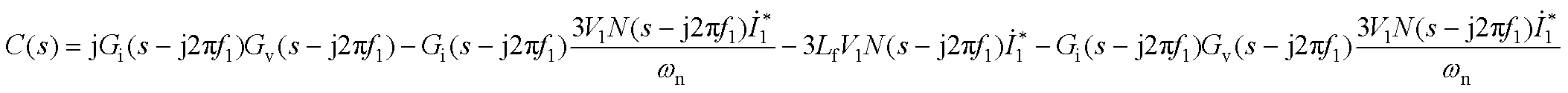 (A3)
(A3)
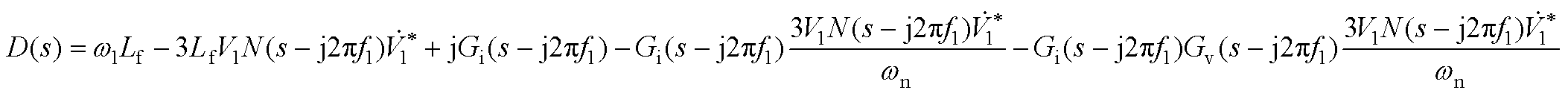 (A4)
(A4)
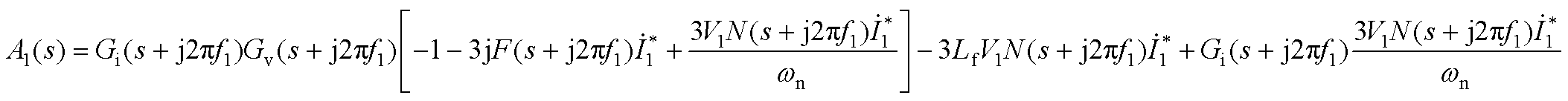 (A5)
(A5)
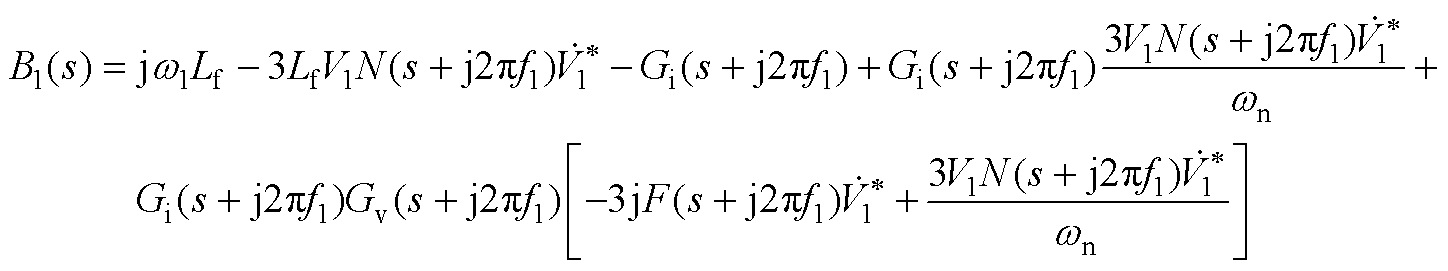 (A6)
(A6)
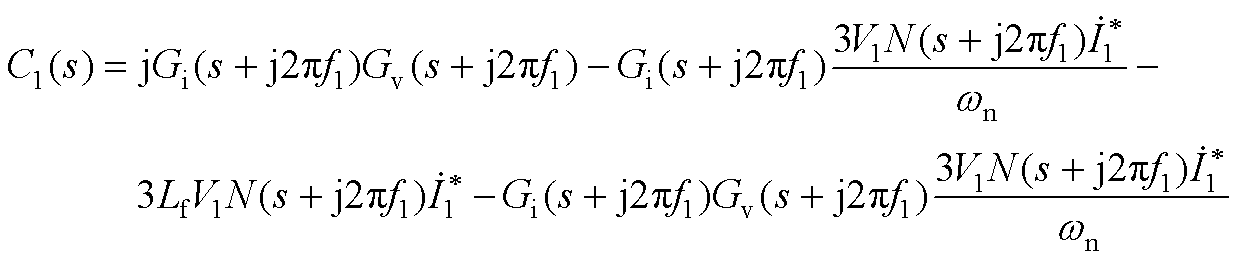 (A7)
(A7)
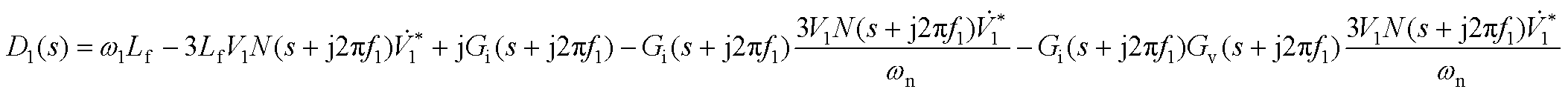 (A8)
(A8)
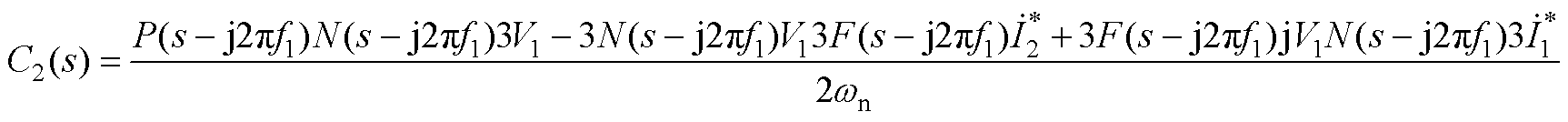 (A9)
(A9)
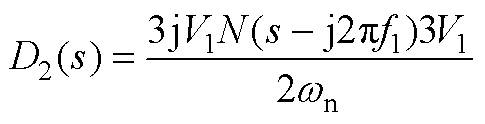 (A10)
(A10)
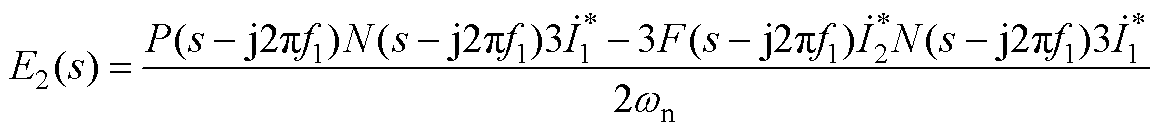 (A11)
(A11)
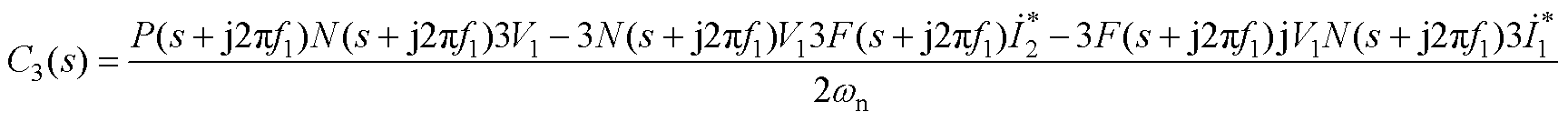 (A12)
(A12)
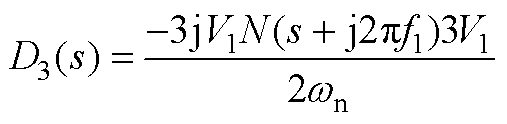 (A13)
(A13)
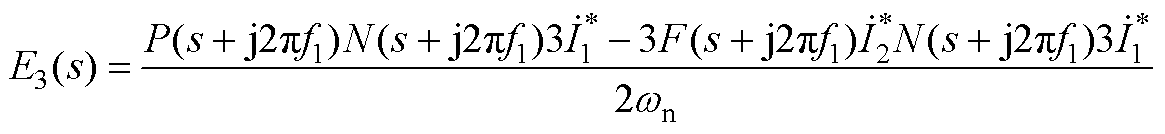 (A14)
(A14)
2. 系统参数
附表1 系统关键仿真参数
App.Tab.1 key simulation parameters of the system
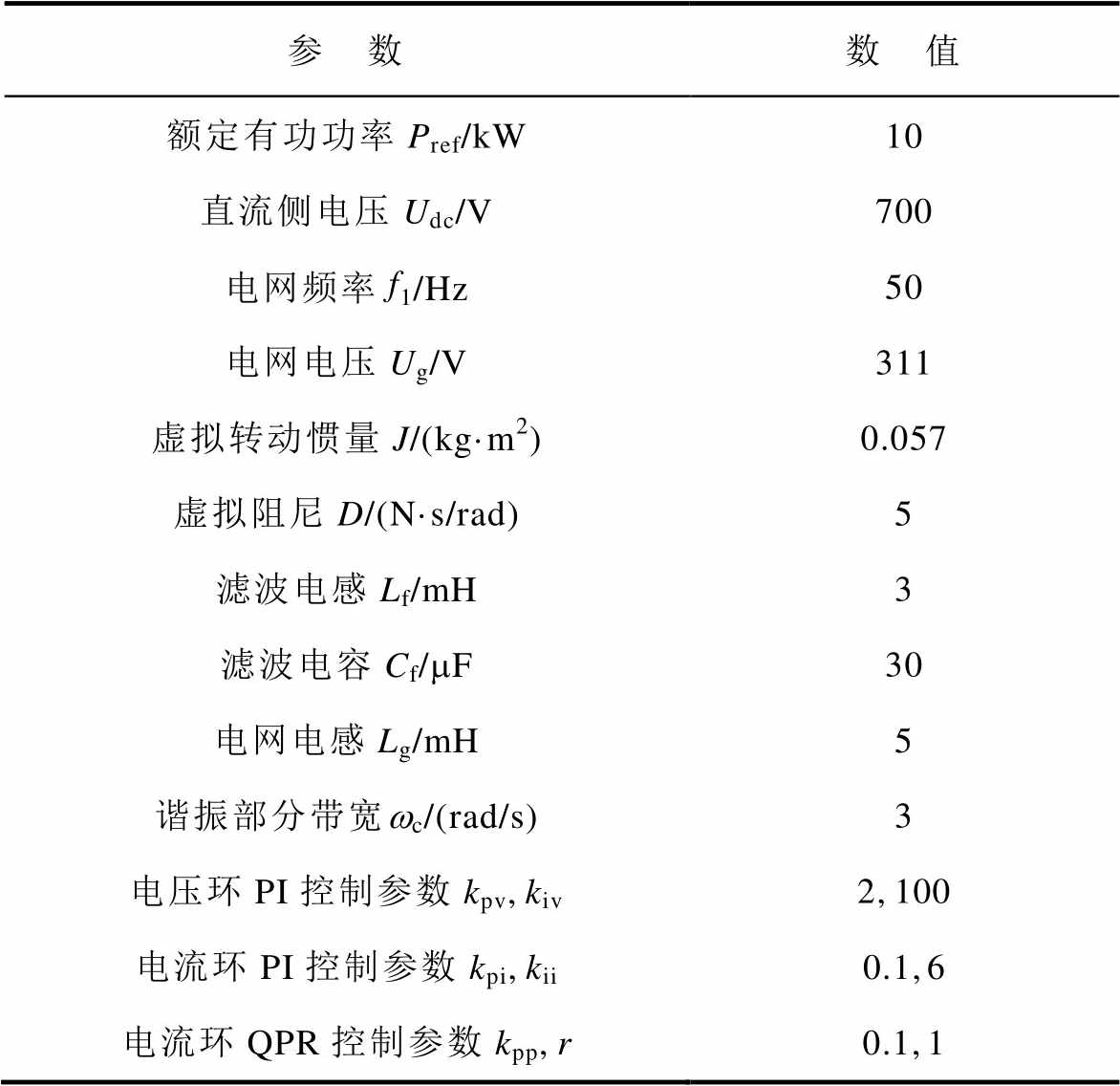
参 数数 值 额定有功功率Pref/kW10 直流侧电压Udc/V700 电网频率f1/Hz50 电网电压Ug/V311 虚拟转动惯量J/(kg·m2)0.057 虚拟阻尼D/(N·s/rad)5 滤波电感Lf/mH3 滤波电容Cf/mF30 电网电感Lg/mH5 谐振部分带宽wc/(rad/s)3 电压环PI控制参数kpv,kiv2,100 电流环PI控制参数kpi,kii0.1,6 电流环QPR控制参数kpp,r0.1,1
参考文献
[1] 张智刚, 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报, 2022, 42(8): 2806-2819.
Zhang Zhigang, Kang Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2819.
[2] 朱冠南, 陈敏, 王鹏程, 等. 低电网阻抗下构网型直挂式储能系统稳定性提升控制[J]. 电工技术学报, 2025, 40(9): 2697-2711.
Zhu Guannan, Chen Min, Wang Pengcheng, et al. Stability enhancement control strategy for grid- forming transformerless energy storage system under low grid impedance conditions[J]. Transactions of China Electrotechnical Society, 2025, 40(9): 2697- 2711.
[3] 谢震, 高翔, 张悬光, 等. 弱电网下功率同步构网型DFIG的阻尼分析及转矩振荡抑制[J]. 电力系统自动化, 2023, 47(11): 29-38.
Xie Zhen, Gao Xiang, Zhang Xuanguang, et al. Damping analysis and torque oscillation suppression of power synchronized grid-forming doubly-fed induction generator in weak grid[J]. Automation of Electric Power Systems, 2023, 47(11): 29-38.
[4] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[5] 熊小玲, 李昕悦, 周琰, 等. 基于陷波器的构网型换流器同步频率谐振抑制策略[J]. 电工技术学报, 2024, 39(12): 3827-3839.
Xiong Xiaoling, Li Xinyue, Zhou Yan, et al. Synchronous frequency resonance suppression of grid-forming converter based on Notch filter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3827-3839.
[6] Ai Cheng, Li Yitong, Zhao Ziwen, et al. An extension of grid-forming: a frequency-following voltage- forming inverter[J]. IEEE Transactions on Power Electronics, 2024, 39(10): 12118-12123.
[7] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[8] Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. Frequency coupling admittance modeling of quasi-PR controlled inverter and its stability comparative analysis under the weak grid[J]. IEEE Access, 2021, 9: 94912-94922.
[9] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[10] 李琳, 张晓楠, 李庚银, 等. 考虑内外环交互作用的VSG并网振荡特性[J]. 电力建设, 2024, 45(4): 66-76.
Li Lin, Zhang Xiaonan, Li Gengyin, et al. Characteris- tics of VSG grid-connected system oscillation considering the interaction between inner and outer loops[J]. Electric Power Construction, 2024, 45(4): 66-76.
[11] Wu Wenhua, Zhou Leming, Chen Yandong, et al. Sequence-impedance-based stability comparison between VSGs and traditional grid-connected inverters [J]. IEEE Transactions on Power Electronics, 2019, 34(1): 46-52.
[12] 雷雨, 李光辉, 王伟胜, 等. 跟网型和构网型新能源并网控制阻抗对比与振荡机理分析[J]. 中国电机工程学报, 2025, 45(1): 150-163.
Lei Yu, Li Guanghui, Wang Weisheng, et al. Comparison of impedance characteristics and oscillation mechanism for grid following and grid forming renewable energy[J]. Proceedings of the CSEE, 2025, 45(1): 150-163.
[13] Shi Kai, Wang Yu, Sun Yuxin, et al. Frequency- coupled impedance modeling of virtual synchronous generators [J]. IEEE Transactions on Power Systems, 2021, 36(4): 3692-3700.
[14] 周于清, 姚伟, 宗启航, 等. 基于运行短路比的新能源场站中跟/构网可切换单元的最优配置方法[J]. 电网技术, 2024, 48(3): 1091-1104.
Zhou Yuqing, Yao Wei, Zong Qihang, et al. Optimal configuration of grid-following/grid-forming switchable units in new energy stations based on operating short-circuit ratio[J]. Power System Technology, 2024, 48(3): 1091-1104.
[15] 杜燕, 朱轲, 杨向真, 等. 考虑频率耦合的VSG虚拟阻抗优化设计[J]. 高电压技术, 2022, 48(12): 5057-5067.
Du Yan, Zhu Ke, Yang Xiangzhen, et al. Optimal design of virtual synchronous generator virtual impedance considering frequency coupling[J]. High Voltage Engineering, 2022, 48(12): 5057-5067.
[16] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance [J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[17] 杨万里, 涂春鸣, 兰征, 等. 基于储能型柔性多状态开关的直流微电网与交流配电网柔性互联策略[J]. 电力自动化设备, 2021, 41(5): 254-260.
Yang Wanli, Tu Chunming, Lan Zheng, et al. Flexible interconnection strategy between DC microgrid and AC distribution grid based on energy storage flexible multi-state switch[J]. Electric Power Automation Equipment, 2021, 41(5): 254-260.
[18] Song Yuanzong, Liu Zhijie, Li Kejun, et al. Accurate identification of frequency-coupling admittance for grid-connected converters under all operating condi- tions[J]. IEEE Transactions on Power Electronics, 2024, 39(12): 15596-15608.
[19] Xie Zhiwei, Wu Wenhua, Chen Yandong, et al. Admittance-based stability comparative analysis of grid-connected inverters with direct power control and closed-loop current control[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8333-8344.
Abstract As an indispensable device in the modern power system, the grid-forming converter (GFM) plays a vital role in the power grid with highly permeability. Especially in the context of the continuous increase in the proportion of renewable energy power generation, its support performance for weak power grids has become a hot topic in the research field. The output impedance characteristics of GFM are not only related to its own operational stability, but also directly affect the dynamic response and stability of the entire power grid. Therefore, it is of great significance to study the output impedance characteristics of GFM to improve the overall performance and reliability of the power system.
In the current internal loop control strategy, the dq domain proportional-integral (PI) control and the phase domain quasi-proportional-resonant (QPR) control are two widely used methods. The dq domain PI control is known for its simplicity and ease of implementation, while the phase domain QPR control excels in harmonic suppression and dynamic response. However, although these two control strategies have achieved good results in practical applications, their impedance modeling and comparative analysis are relatively insufficient. Especially in the modeling of phase domain impedance, where the complexity and nonlinearity of phase-domain control pose additional challenges to related research.
To complement this part of the study, this paper explores in depth the impedance modeling methods of GFM under different control domains. Firstly, we construct the harmonic linearization order impedance model of GFM under PI control and QPR control, respectively. These two models not only consider the fundamental component, but also fully consider the influence of the harmonic component on the impedance characteristics, so as to describe the impedance characteristics of GFM more accurately. By comparing the two models, we find that there are significant differences in the impedance characteristics of GFM under the two control strategies. The impedance characteristics under PI control are relatively stable, but they are easily affected by the strength of the grid and the number of grids. On the other hand, the impedance characteristics under QPR control are more flexible and can better adapt to changes in the grid environment.
Furthermore, we use the established model and combine with the Nyquist criterion to analyze the effects of PI control and QPR control on grid connection stability under different grid strengths and grid connection numbers. The analysis results show that the applicability of PI control is relatively weak in the strong power grid environment, because the stability of the power grid itself is strong and the requirements for converters are relatively low. QPR control can better suppress harmonic interference and improve the steady-state performance of the power grid. However, under extremely weak grid conditions, PI control shows stronger applicability. Because the stability of the power grid is weak at this time, the converter needs to have a stronger support capacity. PI control can achieve better support for the power grid by adjusting the parameters. In addition, we also found that both PI control and QPR control showed good stability in multi-GFM grid-connected systems. This is due to the fact that both control strategies have good current regulation and dynamic response speed.
Finally, we verify the correctness of the above theoretical analysis through simulation experiments. The simulation results show that the GFM under the two control strategies can maintain stable grid-connected operation under different grid conditions. At the same time, we also find that the simulation results are consistent with the theoretical analysis results, which further verifies the effectiveness and accuracy of the impedance model established in this paper. These research results not only provide a useful theoretical reference for the optimal design and stable operation of GFM, but also provide important technical support for the application of grid-based converters in high-permeability power grids.
Keywords:Grid-forming converter, sequential impedance modeling, grid-connected stability, inner loop control
兰 征 男,1985年生,副教授,硕士生导师,研究方向为分布式电源并网技术、微电网控制、柔性电能调控技术等。
E-mail: lanzheng20@foxmail.com
何 东 男,1986年生,副教授,硕士生导师,研究方向为电力电子技术及其在电力系统中的应用。
E-mail: hd861116@163.com(通信作者)
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.242378
国家自然科学基金青年项目(52407206)和湖南省教育厅科学研究重点项目(24A0404)资助。
收稿日期 2024-12-29
改稿日期 2025-04-16
(编辑 李 冰)