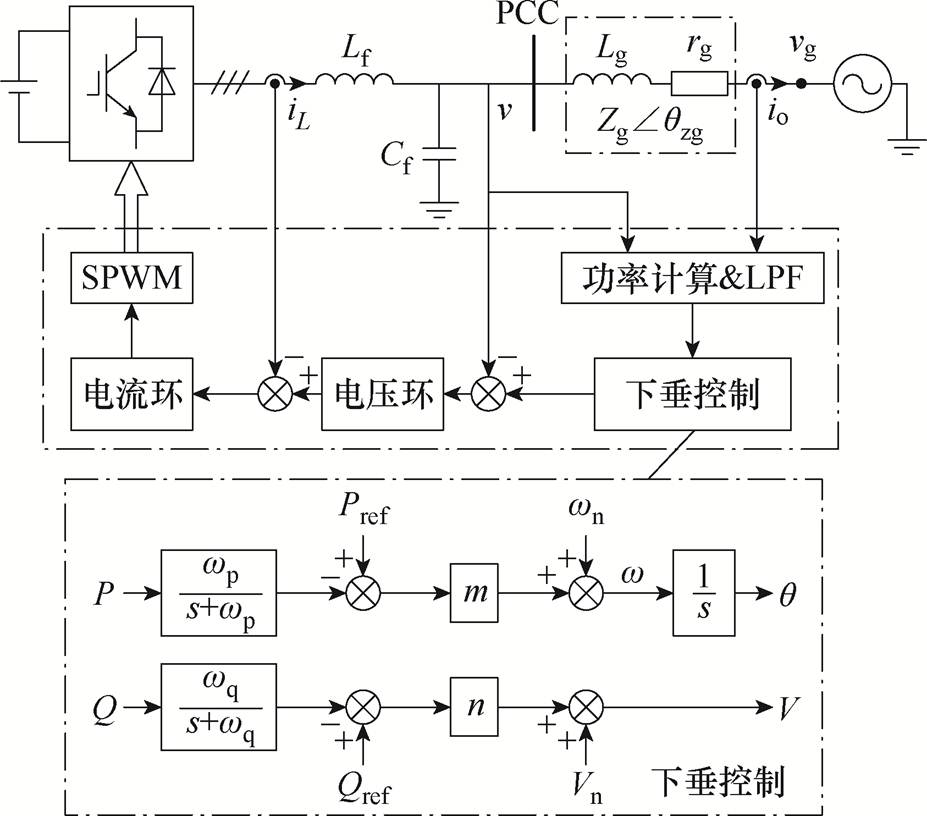
图1 下垂控制拓扑与控制框图
Fig.1 Topology and control block diagram of the droop control
摘要 下垂控制等构网技术是改善新型电力系统稳定性的重要手段,但其固有的功率耦合问题会增大稳态无功偏差、降低系统的稳定裕度,甚至引发振荡失稳。为了解决这一问题,该文采用动态小信号模型分析功率耦合产生的机理,并提出一种基于电压补偿原理的功率解耦策略。通过在电压环分别引入角频率偏差和有功前馈补偿量,减小功率耦合引起的负阻尼及稳态无功偏差。实验结果表明,所提解耦方法在保证系统响应速度的同时,有效地抑制了功率振荡,提升了系统的稳定裕度及稳态无功控制精度,有助于提升下垂控制变换器的动态及稳态性能。
关键词:下垂控制 功率振荡 功率解耦 电压补偿
能源产业的绿色低碳转型促使以同步机为主导的传统电力系统逐渐向新能源占比较高的新型电力系统转变[1]。并网变换器作为新能源与电网进行能量交换的接口,其特性由控制结构决定,并对其入网特性产生深刻影响。根据与电网同步方式的不同,并网变换器的控制结构可以分为跟网型(grid- following)和构网型(grid-forming)两大类[2]。目前,跟网型控制在工程中得到了广泛应用,但跟网型控制采用锁相环与电网保持同步,需要系统内有稳定的电压源,因此在弱电网中的适应性较差。随着电力系统中新能源占比的不断提高,电网强度不断下降,导致跟网型控制的稳定性逐渐下降[3-4]。构网型控制通过控制自身输出功率与电网实现同步[5],主要包括下垂控制[6-8]、虚拟同步机(Virtual Synchro- nous Generator, VSG)控制[9-11]和功率同步控制[12]等。由于构网型控制不依赖交流电网,可以自行构建电压,因此特别适合在新能源占比较高的新型电力系统中应用[13-14]。
但是,构网型控制的有功和无功能够独立控制需要满足传输线路等效阻抗为纯感性及小功角的条件[2]。在分布式新能源接入的中低压电网中,线路电阻不可忽略,功角也会在较大范围内变化,因此,功率耦合问题突出。功率耦合会引入负阻尼,降低系统的稳定裕度[15];还会导致振荡在有功环和无功环之间传递,恶化变换器的动态性能[16-17];严重时可能诱发系统振荡失稳[18]。此外,功率耦合还会增加稳态无功偏差,使变换器在输出有功功率的同时产生不必要的无功功率,降低对电网的功率支撑能力。因此,功率耦合对构网型控制的动态及稳态性能都有负面影响,应当重点关注。
针对功率耦合引起的稳定裕度降低及动态性能变差等问题,文献[19]提出了一种通用的构网控制变换器功率耦合分析模型,为评估不同类型构网控制策略的功率耦合特性提供了定量分析工具。文献[20]指出阻感比R/X和功角q 是影响功率耦合的主要因素,R/X和q 增大都会加重耦合程度。文献[16]指出可以利用虚拟电感(Virtual Inductor, VI)增大变换器与电网间的耦合阻抗,提升稳定裕度。但过大的虚拟电感会使功角增大并可能引发系统失步[21],可以引入虚拟有功和无功功率来模拟主电路电感,削弱有功和无功间的耦合。文献[22]通过构建虚拟稳态同步输出阻抗,并增加电流内环动态解耦补偿,在不满足小功角条件时消除了功率耦合产生的稳态误差及功率振荡。考虑到线路阻抗变化对解耦控制器性能的影响,文献[23]提出了基于扩展观测器的解耦方法,提升了解耦控制器的鲁棒性。但是在无功功率较大时,该方法可能存在较大的误差,因此在运行模式灵活的分布式新能源并网系统中的适应性有待进一步提升。
针对功率耦合引起的稳态无功偏差问题,文献[24]提出了一种虚拟同步电感方法来改善稳态无功控制精度,并且避免了传统虚拟电感方法中电流微分项对稳定性的不利影响。但文献[25]的分析表明稳态功率解耦性能取决于对输出电压的补偿能力,虚拟电感的电压补偿能力存在极限,在R/X较大时无法消除稳态功率耦合。并在此基础上提出了仅q轴虚拟电感解耦策略,提升稳态解耦能力。但该方法需要较大的等效虚拟电感才能实现稳态解耦,减慢了变换器的响应速度。文献[26]提出了一种虚拟电感虚拟电容解耦方法,在实现稳态解耦的同时改善了动态过程中的功率冲击问题。文献[27]提出了一种自适应动态虚拟同步阻抗方法消除功率耦合,但自适应阻抗的阶数较高,需要进一步简化。
因此,当前研究在动态解耦、稳态解耦以及响应速度等方面存在折中。针对上述问题,本文以下垂控制变换器为研究对象,提出了一种基于电压补偿原理的功率解耦策略。首先,通过动态小信号模型分析了功率耦合产生的机理;然后,在电压环引入角频率偏差补偿量,减小功率耦合的负阻尼作用,提升系统动态性能及稳定裕度;之后,在电压环引入有功前馈补偿量,补偿变换器输出电压,减小功率耦合导致的稳态无功偏差;最终,在保证变换器响应速度的同时,提升了系统稳定裕度及稳态无功控制精度,实现了良好的动态及稳态解耦效果。
本文的主要贡献如下:①提出了一种基于电压补偿原理的下垂控制变换器功率解耦方法,可以有效减小功率耦合带来的负阻尼,提升系统稳定性;②所提解耦方法可以在减小稳态无功偏差的同时不会降低有功控制精度;③所提解耦方法不会减慢系统响应速度,确保了较好的动态性能,适合需要频繁功率支撑的分布式新能源发电系统。
下垂控制拓扑和控制框图如图1所示。其中Lf和Cf分别为滤波电感和滤波电容;Lg和rg分别为电网等效电感和电阻;v和vg分别为变换器输出电压和电网电压;iL和io分别为电感电流和并网电流;q为功角。

图1 下垂控制拓扑与控制框图
Fig.1 Topology and control block diagram of the droop control
在下垂控制中,变换器输出电压的相位和幅值参考值分别由有功环和无功环产生,具体表达式为
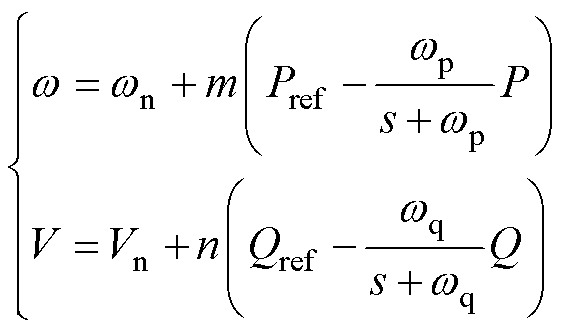 (1)
(1)
式中,Pref和Qref分别为有功及无功功率参考值;P和Q为变换器实际输出的有功及无功功率。为了滤除高频噪声,在功率计算时增加了数字低通滤波器(Low-Pass Filter, LPF),wp和wq分别为有功环和无功环LPF的截止角频率;m和n分别为有功环和无功环下垂系数;wn和w分别为变换器输出电压角频率额定值和实际值;Vn和V分别为输出电压幅值的额定值和实际值。功率环输出的电压参考值输入电压环中,再经电流环对变换器输出电压矢量进行快速控制。
为了分析下垂控制并网系统的小信号稳定性及功率耦合特性,首先根据图1建立dq坐标系下系统的动态小信号模型[12,28],可以得到有功及无功小扰动分量DP、DQ关于功角及变换器电压幅值的小扰动分量Dq、DV的传递函数,即
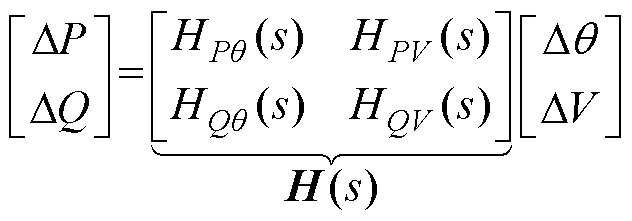 (2)
(2)
式中,H(s)为传递函数矩阵;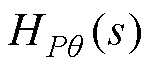 和
和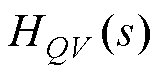 分别为有功-功角及无功-电压传递函数;
分别为有功-功角及无功-电压传递函数; 和
和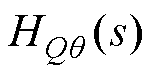 分别为有功-电压及无功-功角耦合项。矩阵各元素的具体表达式见附录式(A1)。
分别为有功-电压及无功-功角耦合项。矩阵各元素的具体表达式见附录式(A1)。
由式(2)可以得到并网系统小信号模型,如图2所示。由于 和
和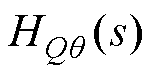 一般不为0,因此DP和DQ同时受到Dq和DV的影响,不能独立控制,有功和无功之间存在耦合。
一般不为0,因此DP和DQ同时受到Dq和DV的影响,不能独立控制,有功和无功之间存在耦合。
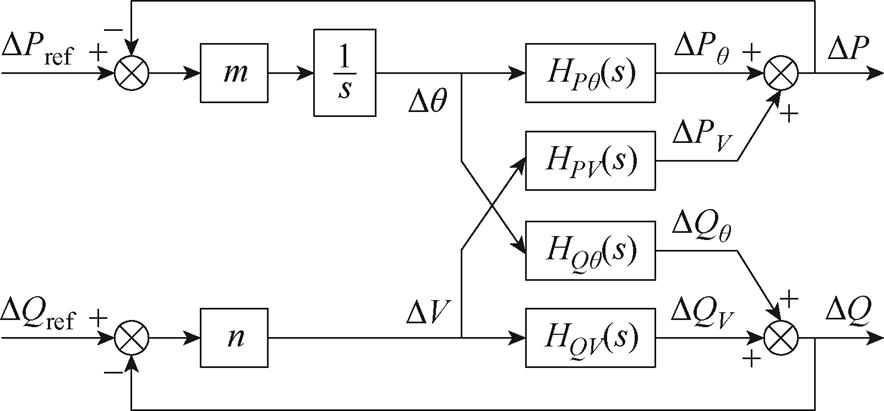
图2 并网系统小信号模型
Fig.2 Small-signal model of the grid-connected system
由图2可知,功率耦合存在时下垂控制系统是典型的多输入多输出(Multi-Input Multi-Output, MIMO)系统。可以将其重构为图3所示的单输入单输出(Single-Input Single-Output, SISO)系统进行稳定性分析[26]。
由图3可知,重构后的SISO系统由前向通路及耦合分量组成。功率耦合存在时,系统有功环开环传递函数GPO_C(s)和无功环开环传递函数GQO_C(s)的表达式为
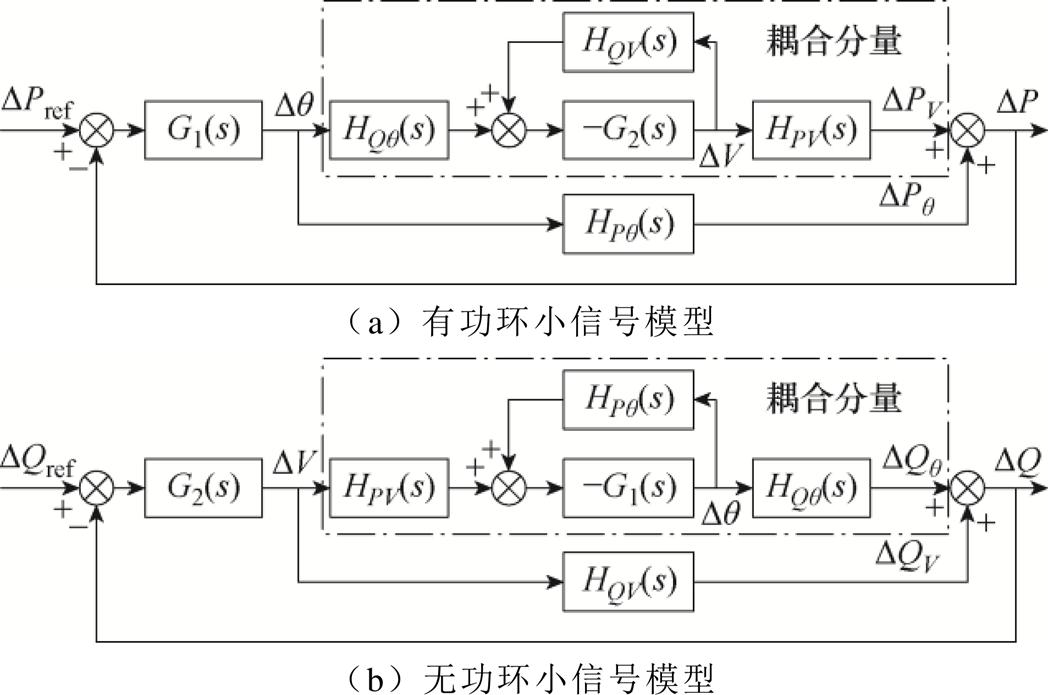
图3 重构的单输入单输出小信号模型
Fig.3 Reconstructed SISO small-signal model
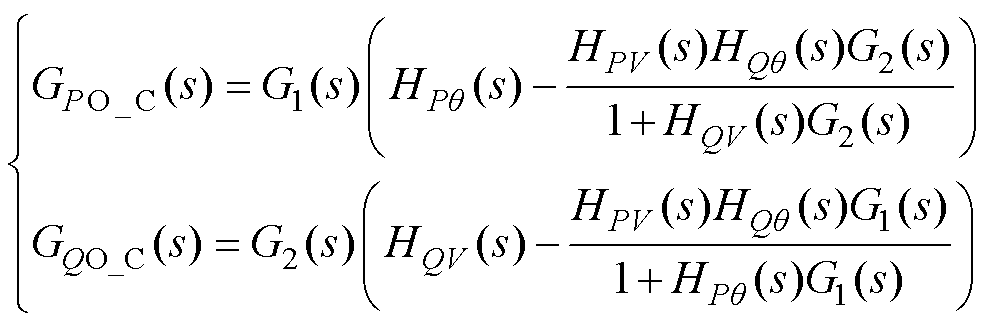 (3)
(3)
式中,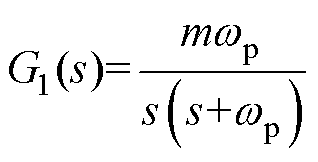 ,
,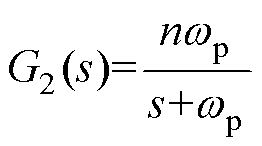 。
。
若图3中的耦合分量不存在,可以得到无耦合时系统的有功环开环传递函数GPO(s)和无功环开环传递函数GQO(s)表达式为
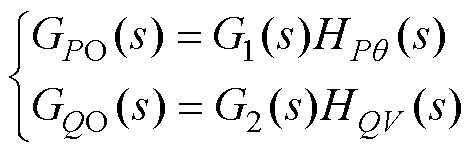 (4)
(4)
根据式(3)和式(4),可以得到R/X=0.3~1.5时并网系统的根轨迹,如图4所示,系统的主要参数见后文(表1)。
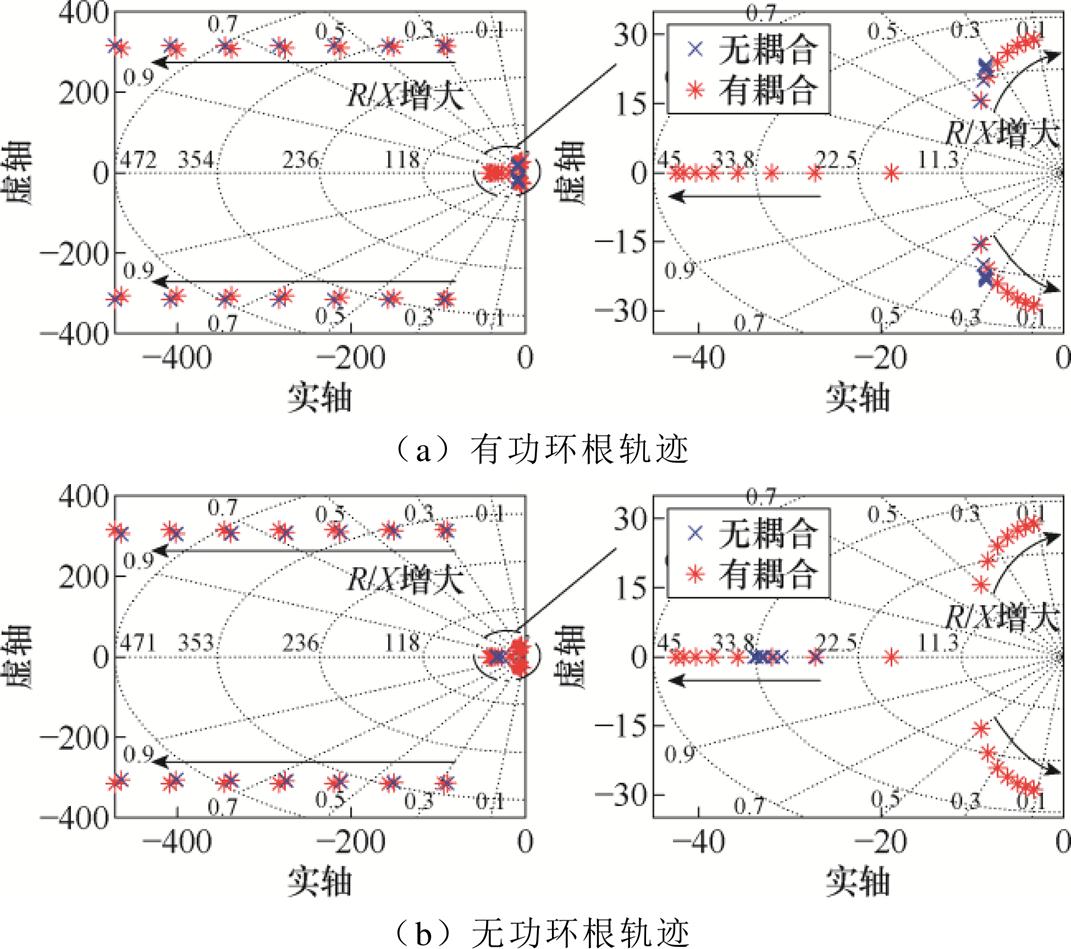
图4 R/X变化时并网系统根轨迹
Fig.4 Root locus of the grid-connected system when R/X varies
由图4a可知,随着R/X增大,两对距离实轴较远的共轭极点逐渐向左移动并远离虚轴,而另一对距离实轴较近的共轭极点成为主导极点并逐渐靠近虚轴,系统稳定裕度逐渐降低。且有耦合时有功环的闭环极点比无耦合时距离虚轴更近,稳定裕度更低。由图4b可知,无耦合时,无功环的主导极点距离虚轴较远且在实轴上;有耦合时,随着R/X增大,距离实轴较近的共轭极点逐渐靠近虚轴。因此,功率耦合会导致系统的稳定裕度下降,且这种负面影响随着R/X的增大而加重。
由图2的下垂控制小信号模型同样可以得到DQ关于DPref的小信号模型,如图5所示。
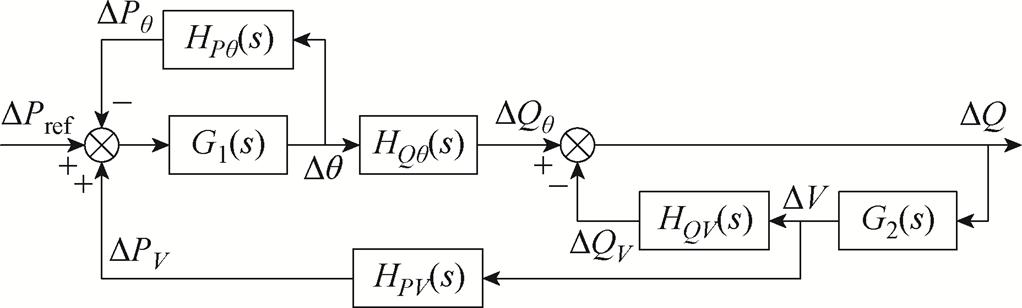
图5 DQ关于DPref的小信号模型
Fig.5 Small-signal model of DPref to DQ
由图5可以得到DQ关于DPref的闭环传递函数GPQ(s)表达式为
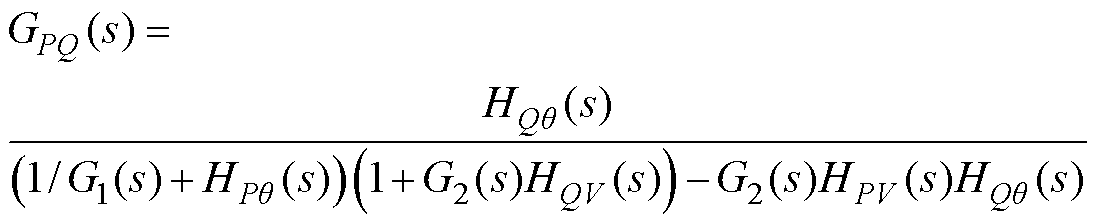 (5)
(5)
进一步地,令s=0,可以得到GPQ(s)的稳态值,并将其定义为稳态功率耦合系数x,用来量化有功变化带来的无功变化量,x的表达式为
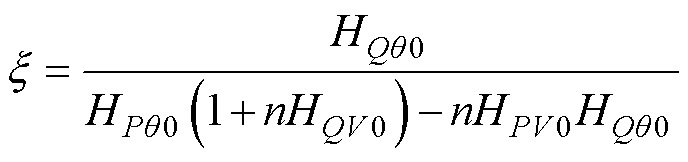 (6)
(6)
式中,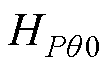 、
、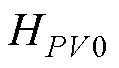 、
、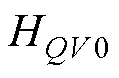 、
、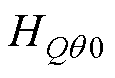 为式H(s)中各元素的稳态值。由式(6)可知,阻感比R/X和功角q都会对稳态功率耦合系数产生影响。
为式H(s)中各元素的稳态值。由式(6)可知,阻感比R/X和功角q都会对稳态功率耦合系数产生影响。
保持Lg不变,改变rg使R/X从0变化到0.8,同时q从0°变化到15°,其他参数见表1,可以得到x随R/X和q变化的曲面如图6所示。
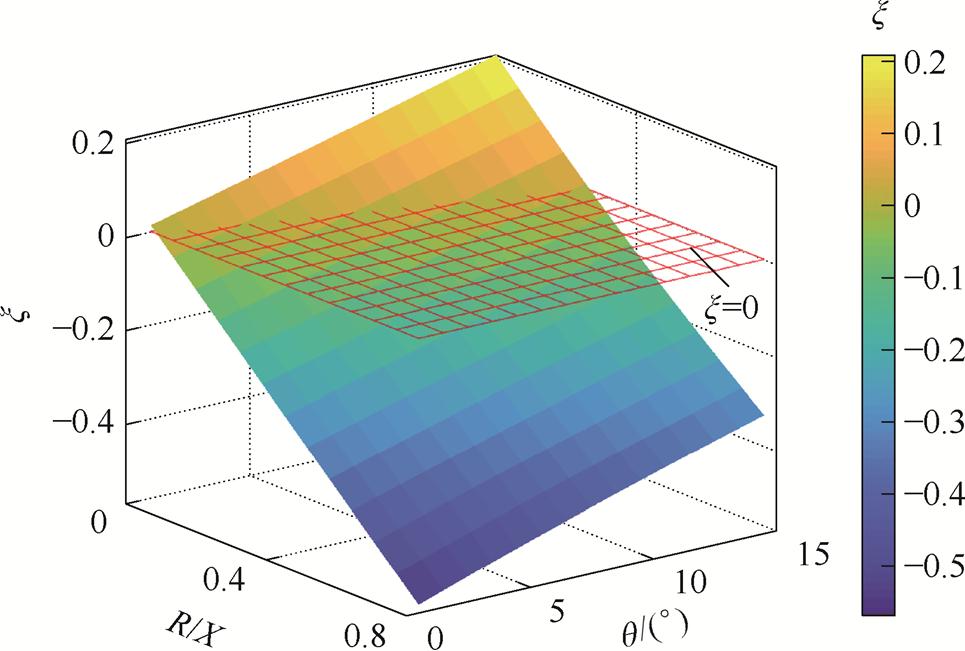
图6 x随R/X和q变化的曲面
Fig.6 Surface of x along with R/X and q
由图6可知,稳态功率耦合系数同时受到R/X和q的影响。在x=0平面以下,x随R/X的增大而单调减小,意味着有功扰动会引起相反方向的无功扰动,且R/X越大,稳态功率耦合程度越严重。当R/X=0.8时,x<-0.5,此时稳态无功控制精度受到严重影响。当R/X较小时,x随q的增大而逐渐增大,意味着有功扰动会引起相同方向的无功扰动,且q越大,稳态功率耦合程度越严重。当R/X较大时,x随q的增大而逐渐向0靠近,可以在一定程度上降低稳态功率的耦合程度。因此,稳态功率耦合程度是R/X和q共同影响的结果,当有功功率变化时,变换器会产生不必要的无功功率,影响无功控制精度,并占用变换器容量。
综上所述,功率耦合会降低系统稳定裕度[19,26],并增大稳态无功偏差[25]。因此,同时考虑动态及稳态解耦控制是十分必要的。
虚拟阻抗是最常用的功率解耦方法之一,等效为在变换器外侧串联阻抗[29],增加了变换器和电网之间的耦合阻抗,可在一定程度上增强系统阻尼,抑制振荡[16],但这同样会降低系统响应速度。
由功率耦合小信号模型可知,可以采用交叉解耦方法消除有功和无功之间的耦合,如图7所示。
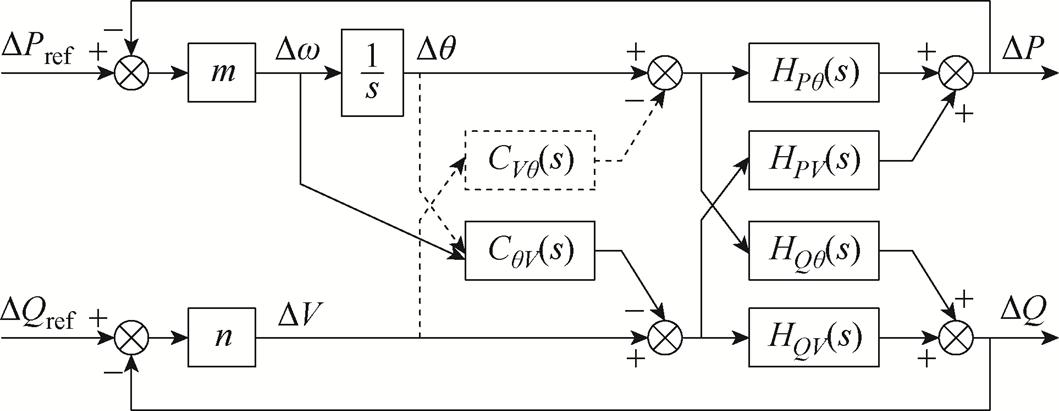
图7 采用动态解耦的小信号模型
Fig.7 Small-signal modelwith dynamic decoupling method
图7中,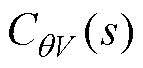 和
和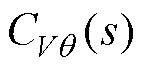 是交叉解耦项,且满足
是交叉解耦项,且满足
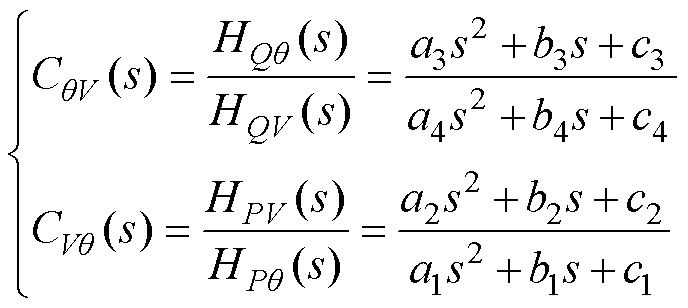 (7)
(7)
理论上,若采用式(7)的解耦控制器,则有功环和无功环被控对象转换为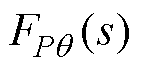 和
和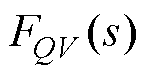 ,且表达式为
,且表达式为
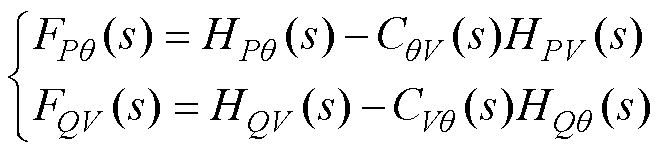 (8)
(8)
此时,功率耦合被消除,有功和无功相互独立。但式(8)中的解耦控制器会给系统引入新的极点和零点,参数设计较为复杂,需要对其进行简化。
为了对解耦控制器进行简化,需要分析功率耦合负阻尼作用的来源。采用幅相分析法[15],从阻尼功率和同步功率两方面入手,分析功率耦合对系统稳定性的影响。以有功环为例,对图2进行重构可以得到有功环的幅相分析模型如图8所示。
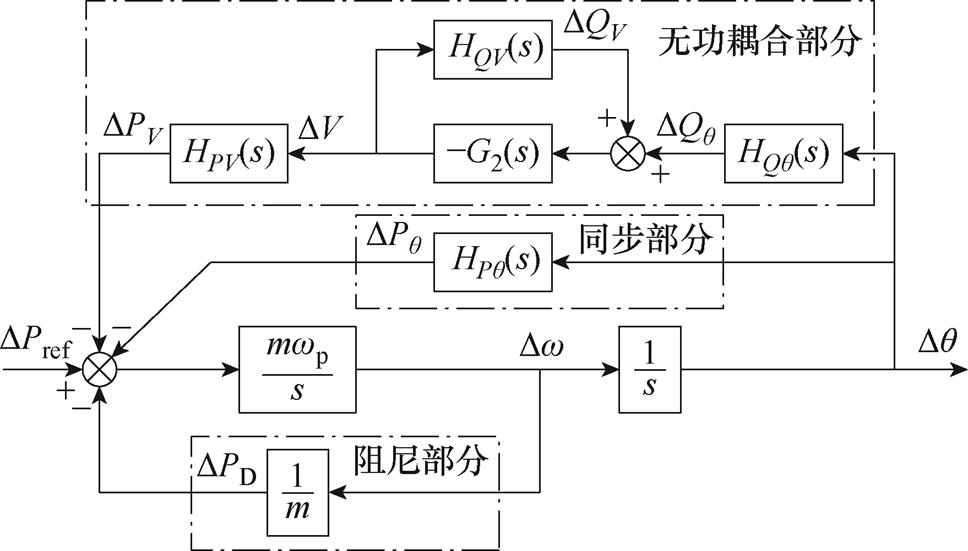
图8 有功环的幅相分析模型
Fig.8 Magnitude-phase model of the active power loop
系统有功环的动态特性可通过合成功率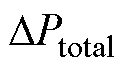 =
= 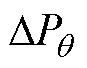 +
+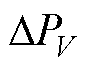 +
+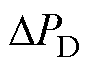 来反映。以Dq的方向为参考零相位,Dw的方向为参考90°相位,
来反映。以Dq的方向为参考零相位,Dw的方向为参考90°相位,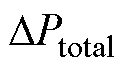 可分解为同步功率和阻尼功率两个维度。同步功率与Dq同向,使系统与电网保持同步;阻尼功率与Dw同向,抑制系统的频率波动。
可分解为同步功率和阻尼功率两个维度。同步功率与Dq同向,使系统与电网保持同步;阻尼功率与Dw同向,抑制系统的频率波动。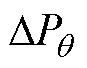 、
、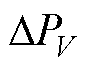 、
、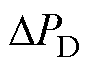 及
及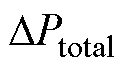 的传递函数
的传递函数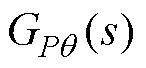 、
、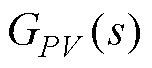 、
、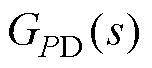 及
及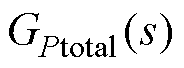 可以表示为
可以表示为
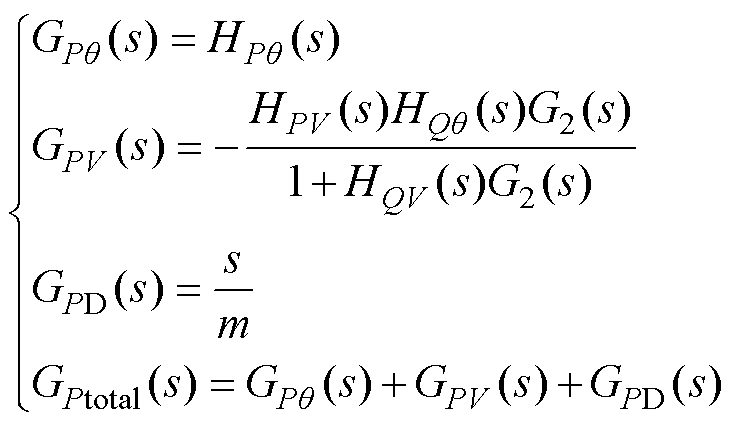 (9)
(9)
由式(9)可以得到不同R/X时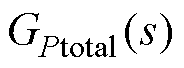 的伯德图及其局部放大图,如图9所示。
的伯德图及其局部放大图,如图9所示。
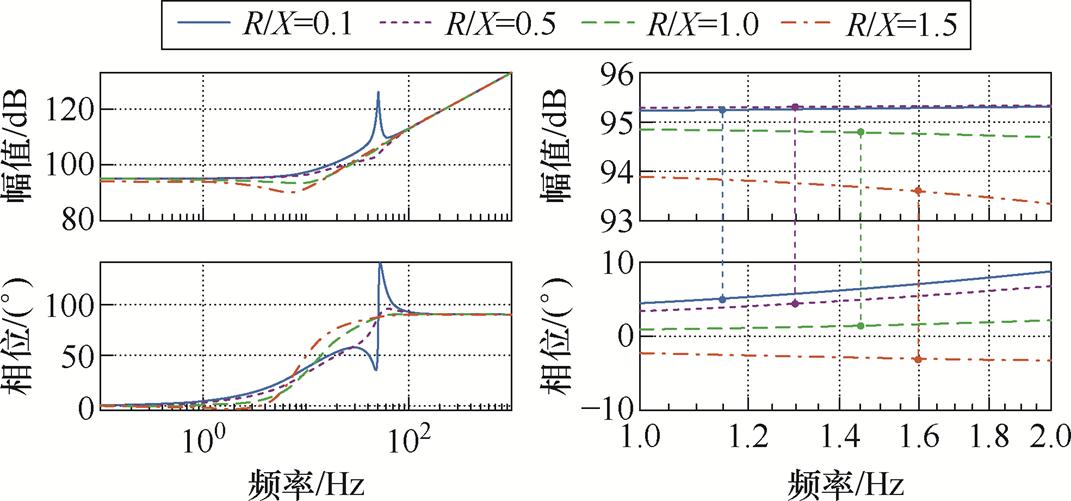
图9 R/X变化时GPtotal(s)的伯德图
Fig.9 Bode plot of GPtotal(s) when R/X varies
由图9可知,随着R/X增大,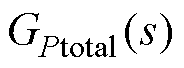 在低频段的幅值几乎不变,但相位逐渐从第一象限移动到第四象限,意味着
在低频段的幅值几乎不变,但相位逐渐从第一象限移动到第四象限,意味着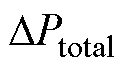 的阻尼分量逐渐从正转变为负,受到扰动时系统存在失稳风险。
的阻尼分量逐渐从正转变为负,受到扰动时系统存在失稳风险。
附录中,附图1给出了无功环幅相分析模型,式(A2)给出了 的表达式,附图2给出了R/X变化时
的表达式,附图2给出了R/X变化时 的伯德图及其局部放大图。由附图2可知,
的伯德图及其局部放大图。由附图2可知, 低频段的幅值及相位受R/X的影响较小,且相位始终在第一象限,说明功率耦合对无功环稳定性的影响较小。因此,功率耦合在有功环产生的负阻尼是系统稳定裕度降低的主要原因。为了简化解耦控制器,可以保留解耦控制器
低频段的幅值及相位受R/X的影响较小,且相位始终在第一象限,说明功率耦合对无功环稳定性的影响较小。因此,功率耦合在有功环产生的负阻尼是系统稳定裕度降低的主要原因。为了简化解耦控制器,可以保留解耦控制器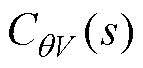 ,并去除
,并去除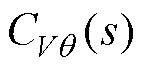 。且由于去除了
。且由于去除了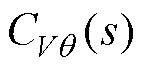 ,即使Q与
,即使Q与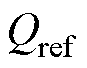 不相等,也不会给有功环引入额外补偿量,因此所提动态解耦方法不会影响有功控制精度。
不相等,也不会给有功环引入额外补偿量,因此所提动态解耦方法不会影响有功控制精度。
但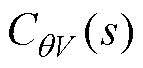 仍然会给系统带来新的零点和极点,需要进一步简化。图10给出了
仍然会给系统带来新的零点和极点,需要进一步简化。图10给出了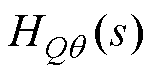 和
和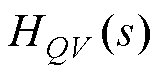 的幅频曲线,由图10可知
的幅频曲线,由图10可知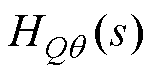 和
和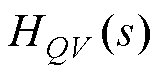 在低频处的增益基本不变,而功率解耦的主要目的是解决功率耦合引起的低频振荡[14],因此可以用
在低频处的增益基本不变,而功率解耦的主要目的是解决功率耦合引起的低频振荡[14],因此可以用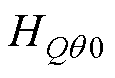 和
和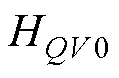 代替
代替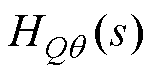 和
和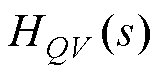 对解耦控制器进行进一步简化。但简化后的解耦控制器需要系统的实时功角信息,而实际运行过程中获取功角较为困难。由于Dw与Dq均能反映有功变化趋势,因此用Dw代替Dq对解耦控制器进行进一步简化。最终,采用动态功率解耦方法的无功环表达式为
对解耦控制器进行进一步简化。但简化后的解耦控制器需要系统的实时功角信息,而实际运行过程中获取功角较为困难。由于Dw与Dq均能反映有功变化趋势,因此用Dw代替Dq对解耦控制器进行进一步简化。最终,采用动态功率解耦方法的无功环表达式为
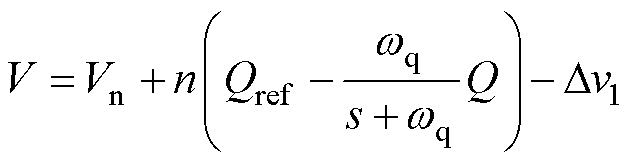 (10)
(10)
式中,Dv1为动态解耦控制器输出的电压补偿量,且满足
 (11)
(11)
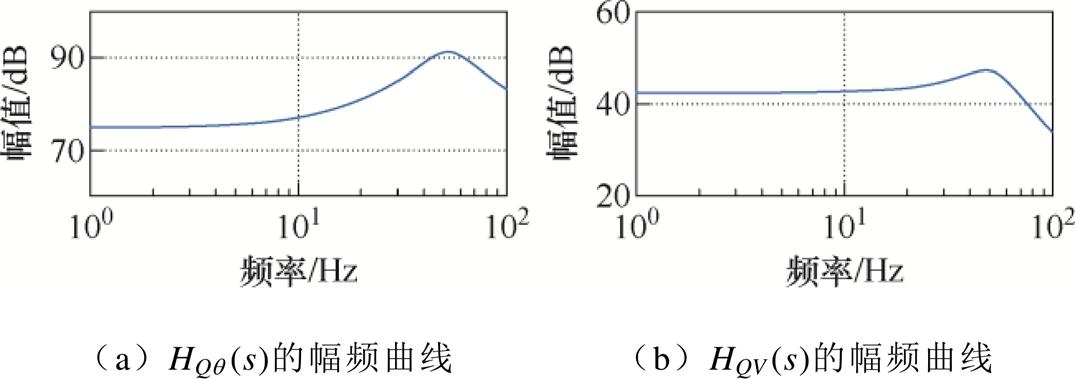
图10 HQq (s)和HQV (s)的幅频曲线
Fig.10 Magnitude plot of HQq(s)and HQV (s)
由式(11)可知,解耦控制器可在动态过程中发挥作用,减小功率耦合的负阻尼。但在稳态时,由于w与wn相同,解耦控制器被旁路,不影响稳态无功功率。因此,动态解耦控制器并不能解决功率耦合带来的无功偏差问题。
VI解耦方法同样可以用来减小阻感比R/X,减轻功率耦合带来的无功偏差问题。但稳态解耦性能取决于对输出电压的补偿能力,而VI解耦的电压补偿能力有限,在R/X较大时不能消除稳态功率耦合[25]。
借鉴电压补偿原理,本文将有功功率前馈到电压环,直接对输出电压进行补偿,提升稳态解耦能力。根据图1所示的并网系统拓扑结构可以得到对应的并网系统相量图,如图11所示。
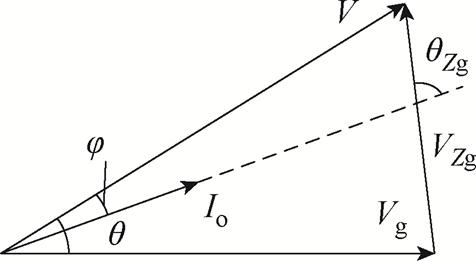
图11 并网系统相量图
Fig.11 Phasor diagram of the grid-connected system
图11中,Vg、Io分别为电网电压、并网电流幅值;j为功率因数角;qZg和VZg分别为线路等效阻抗的阻抗角及其上电压降的幅值。当输出功率等于给定值时,认为消除了稳态功率耦合,达到了理想解耦状态。Videal、qideal、jideal分别为此时的理想输出电压、理想功角及理想功率因数角。由正弦定理可知
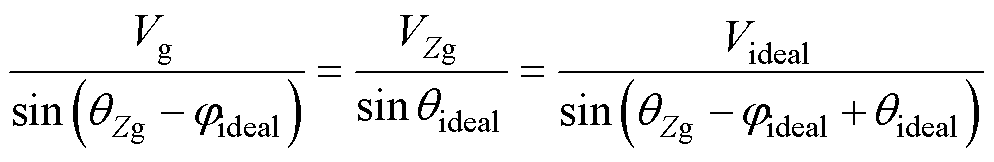 (12)
(12)
式中,jideal=arctan(Qref/Pref)。
由式(12)可以计算得到输出功率等于参考值时,变换器的理想输出电压为
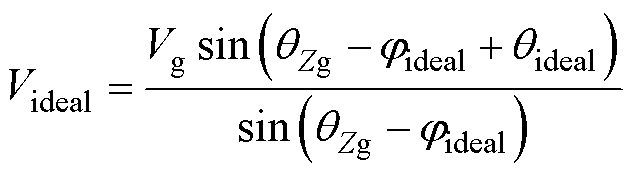 (13)
(13)
根据式(13)绘制了不同P和Q时Videal和V的曲面,如图12所示。由图12可知,功率耦合的存在使输出电压V无法达到理想输出电压Videal,导致变换器无法输出给定无功功率,需要对输出电压进行补偿。
定义理想解耦电压与实际输出电压的差值为Dv2,将Dv2补偿到变换器输出电压参考值上,即可实现按给定值输出功率。Dv2的表达式为
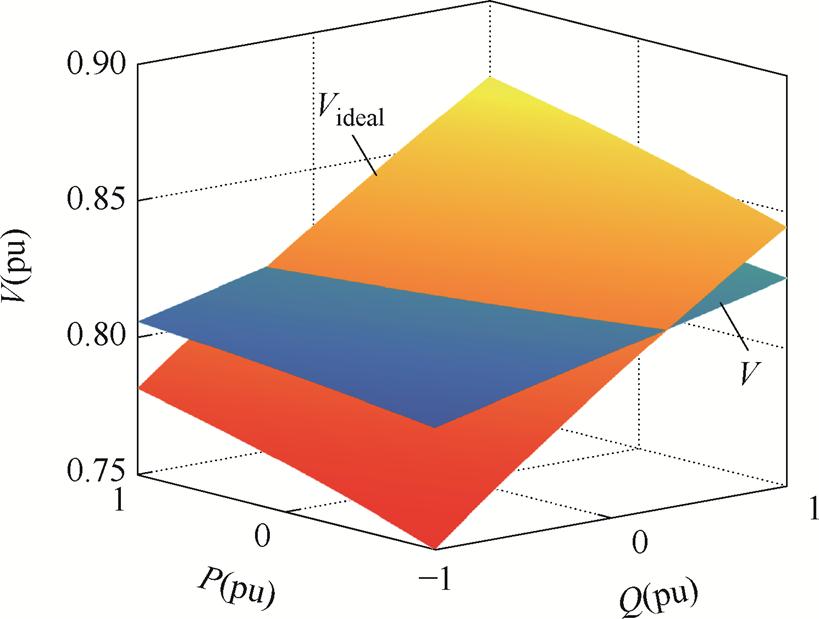
图12 不同P和Q时Videal和V的曲面图
Fig.12 Surfaces of Videal and V for different P and Q
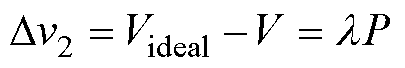 (14)
(14)
采用所提稳态解耦方法后,变换器可以按照给定值输出功率,减小了功率耦合对稳态无功控制精度的负面影响。
根据以上分析,可以得到采用本文所提动态及稳态解耦方法的下垂控制框图,如图13所示。
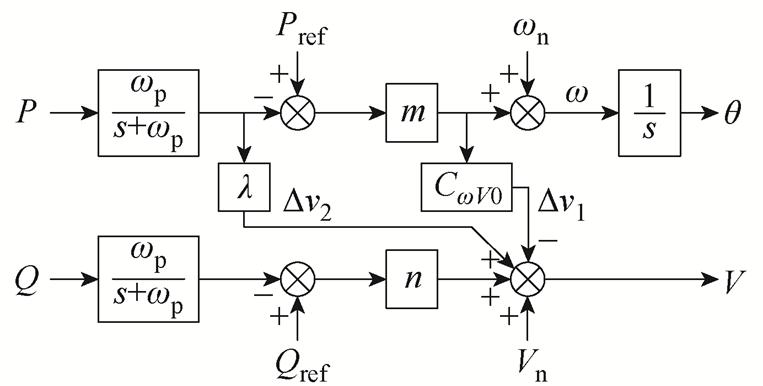
图13 采用所提解耦方法的下垂控制框图
Fig.13 Control block diagram of the droop control with proposed decoupling method
电压补偿系数及采用所提解耦方法后的电压参考值计算流程如图14所示。
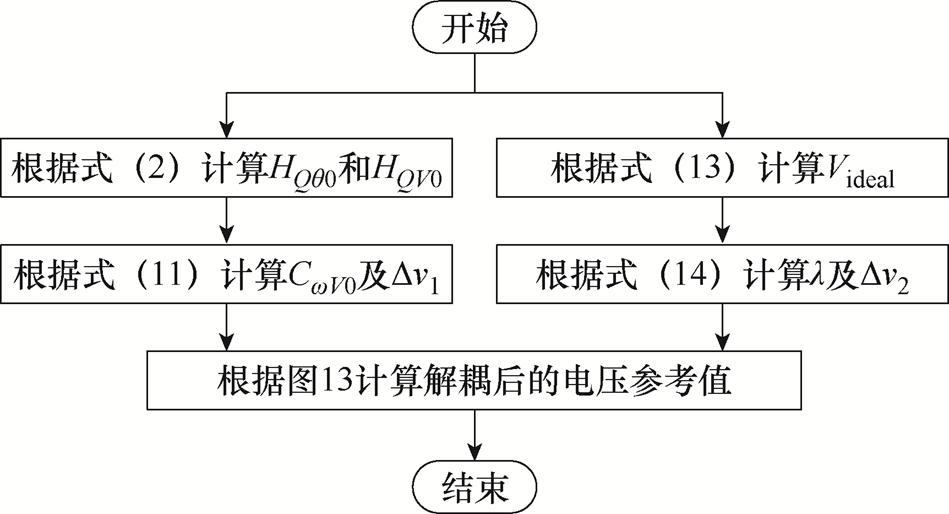
图14 补偿系数计算流程
Fig.14 Flow chart of the calculation process of the compensation coefficient
采用所提解耦方法后,功率耦合引入的负阻尼被补偿项Dv1削弱,系统稳定裕度得到提升。同时,补偿项Dv2减小了功率耦合引起的稳态无功偏差,系统的动态及稳态特性得到了综合提升。
为了验证本文所提功率解耦方法的有效性,搭建了三相变换器并网系统实验平台。采用TMS320F28335 DSP作为主控制器,采用Chroma 62180D作为直流源,采用Chroma 61860模拟电网。利用示波器观察电网电压、变换器输出电压及并网电流,变换器输出功率通过CAN通信上传到上位机中,采样间隔为2 ms。实验平台如图15所示,系统的主要参数见表1。

图15 实验平台
Fig.15 Experimental platform
表1 下垂控制系统主要参数
Tab.1 Main parameters of the droop control system
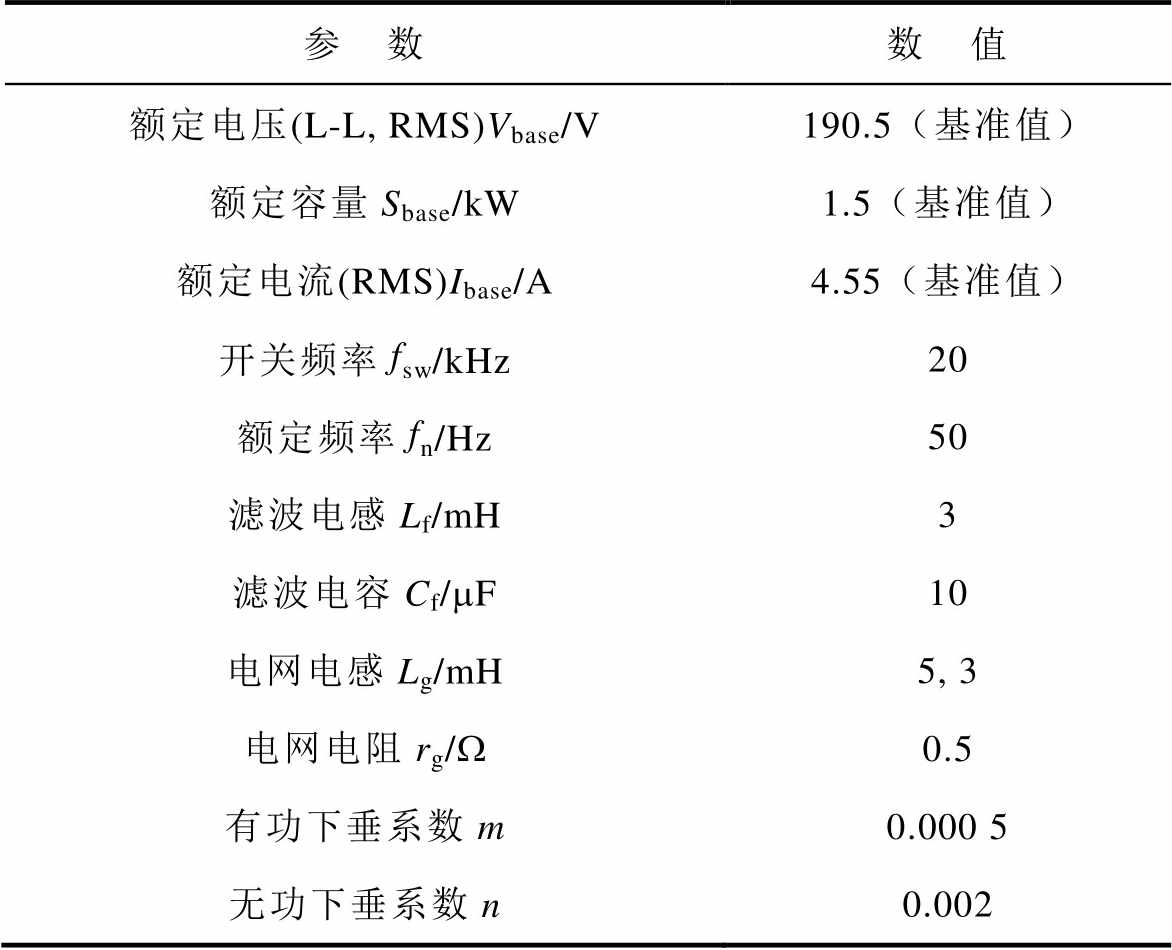
参 数数 值 额定电压(L-L, RMS)Vbase/V190.5(基准值) 额定容量Sbase/kW1.5(基准值) 额定电流(RMS)Ibase/A4.55(基准值) 开关频率fsw/kHz20 额定频率fn/Hz50 滤波电感Lf/mH3 滤波电容Cf/mF10 电网电感Lg/mH5, 3 电网电阻rg/W0.5 有功下垂系数m0.000 5 无功下垂系数n0.002
4.1.1 R/X=0.32时实验结果
首先对功率耦合导致的稳定裕度下降及稳态无功控制偏差问题进行验证。功率参考值的初始设置为Pref =0.5(pu),Qref =0;在t=1.2 s时,Pref阶跃到1(pu),Qref不变,实验结果如图16所示。由图16可知,动态过程中输出有功及无功功率发生了明显的振荡现象。有功最大值为1.22(pu),无功最小值为-0.46(pu),振荡6次之后仍未到达稳态。在稳态无功控制精度方面,有功阶跃前无功为-0.108(pu),有功阶跃后无功为-0.231(pu),均不等于Qref。这表明功率耦合降低了稳态无功控制精度,且随着有功功率的增加,无功与给定值之间的偏差越来越大。使得变换器在输出有功的同时还需要吸收不必要的无功,限制了变换器的有功支撑能力。

图16 R/X=0.32且无解耦控制时实验结果
Fig.16 Experimental results without decoupling control when R/X=0.32
然后,对本文所提的动态解耦方法进行验证,结果如图17所示。采用所提动态解耦方法后,输出功率在动态过程中没有出现振荡,仅存在较小的超调,系统稳定裕度得到了提升。动态过程中有功最大值为1.04(pu),无功最小值为0.28(pu),但动态功率解耦对稳态无功偏差没有作用,有功阶跃前无功为-0.109(pu),有功阶跃后无功为-0.234(pu),与不采用任何解耦方法时基本一致。

图17 R/X=0.32且仅动态解耦控制时实验结果
Fig.17 Experimental results with only dynamic decoupling control when R/X=0.32
之后,对本文所提的稳态解耦方法进行了验证,结果如图18所示。采用所提稳态解耦方法后,有功阶跃前无功为0.001(pu),有功阶跃后无功为-0.003(pu),基本与Qref相等。此外,由于同时采用了动态解耦控制,动态过程中的功率振荡也被有效抑制。

图18 R/X=0.32且动态及稳态解耦控制时实验结果
Fig.18 Experimental results with dynamic and static decoupling control when R/X=0.32
4.1.2 R/X=0.53时实验结果
为了验证所提解耦方法在不同R/X工况下的有效性,改变阻感比R/X进行了实验,功率参考值设定与R/X=0.32时相同,实验结果如图19~图21 所示。
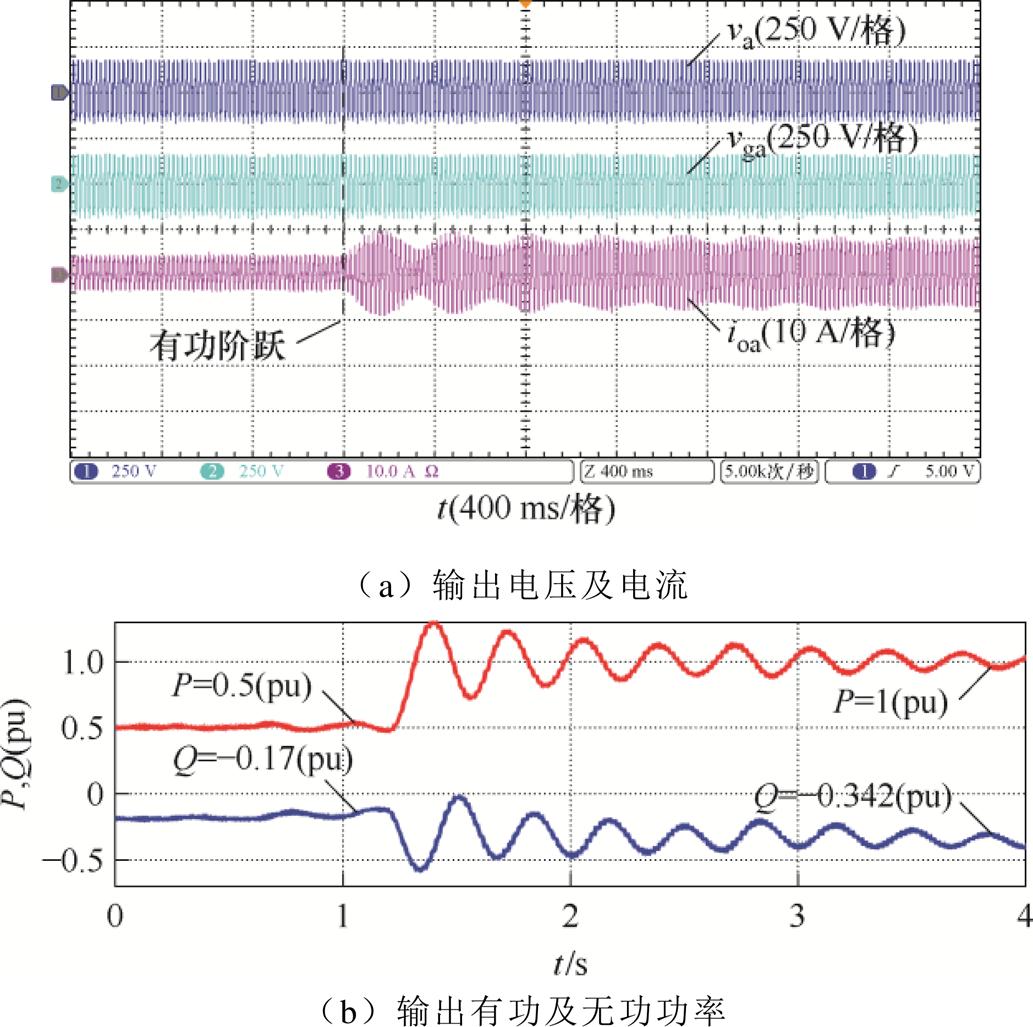
图19 R/X=0.53且无解耦控制时实验结果
Fig.19 Experimental results without decoupling control when R/X=0.53
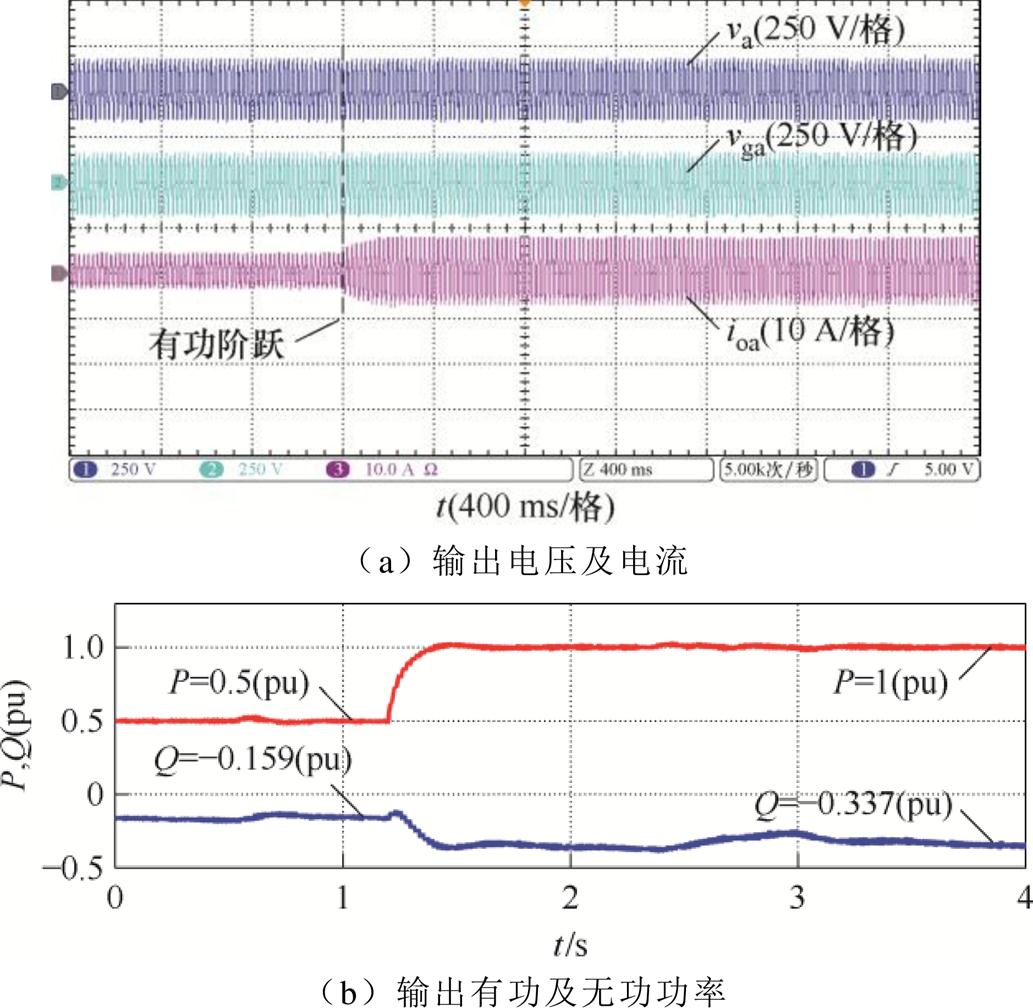
图20 R/X=0.53且仅动态解耦控制时实验结果
Fig.20 Experimental results with only dynamic decoupling control when R/X=0.53

图21 R/X=0.53且动态及稳态解耦控制时实验结果
Fig.21 Experimental results with dynamic and static decoupling control when R/X=0.53
由图19可知,无解耦控制时,动态过程中有功最大值为1.31(pu),无功最小值为-0.59(pu),振荡8次之后仍未到达稳态。
表2对比了不同R/X且无解耦控制时的实验结果。由表2可知,R/X增大时,功率振荡幅度增大,且稳态无功偏差增大。这表明功率耦合程度随R/X的增大而加重,导致系统稳定裕度及稳态无功控制精度进一步降低。
表2 R/X不同且无解耦控制时实验结果对比
Tab.2 Comparison of experimental results without decoupling control when R/X varies (pu)
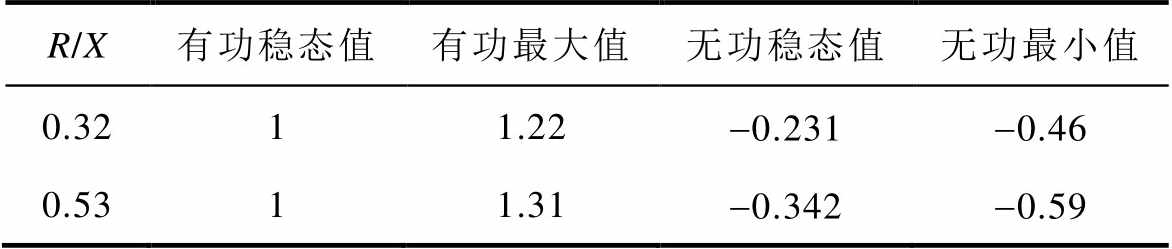
R/X有功稳态值有功最大值无功稳态值无功最小值 0.3211.22-0.231-0.46 0.5311.31-0.342-0.59
由图20可知,采用所提动态解耦方法后,消除了动态过程中的振荡,仅存在较小的功率超调,有功功率最大值为1.03(pu),无功功率最小值为-0.39(pu),但所提动态解耦方法没有补偿稳态无功功率的作用,因此有功阶跃前无功稳态值为-0.159(pu),有功阶跃后无功稳态值为-0.337(pu),均不等于给定值。
由图21可知,采用所提动态及稳态解耦方法后,进一步消除了稳态功率耦合,有功阶跃前无功稳态值为0.008(pu),有功阶跃后无功稳态值为-0.007(pu),基本与给定值保持一致。
为了验证所提解耦方法的有功控制精度,在R/X= 0.32时进行了实验。功率参考值的初始设置为Pref = 0.5(pu),Qref =0;在t=1.2 s时,Qref阶跃到-0.2(pu),Pref不变,实验结果如图22所示。由图22可知,无功阶跃前后的稳态值分别为-0.017(pu)和-0.195(pu),基本与给定值相等。无功阶跃前后有功功率稳态值均为0.5(pu),动态过程中有功最小值为-0.403(pu)因此,所提解耦方法不会影响有功功率的控制精度。
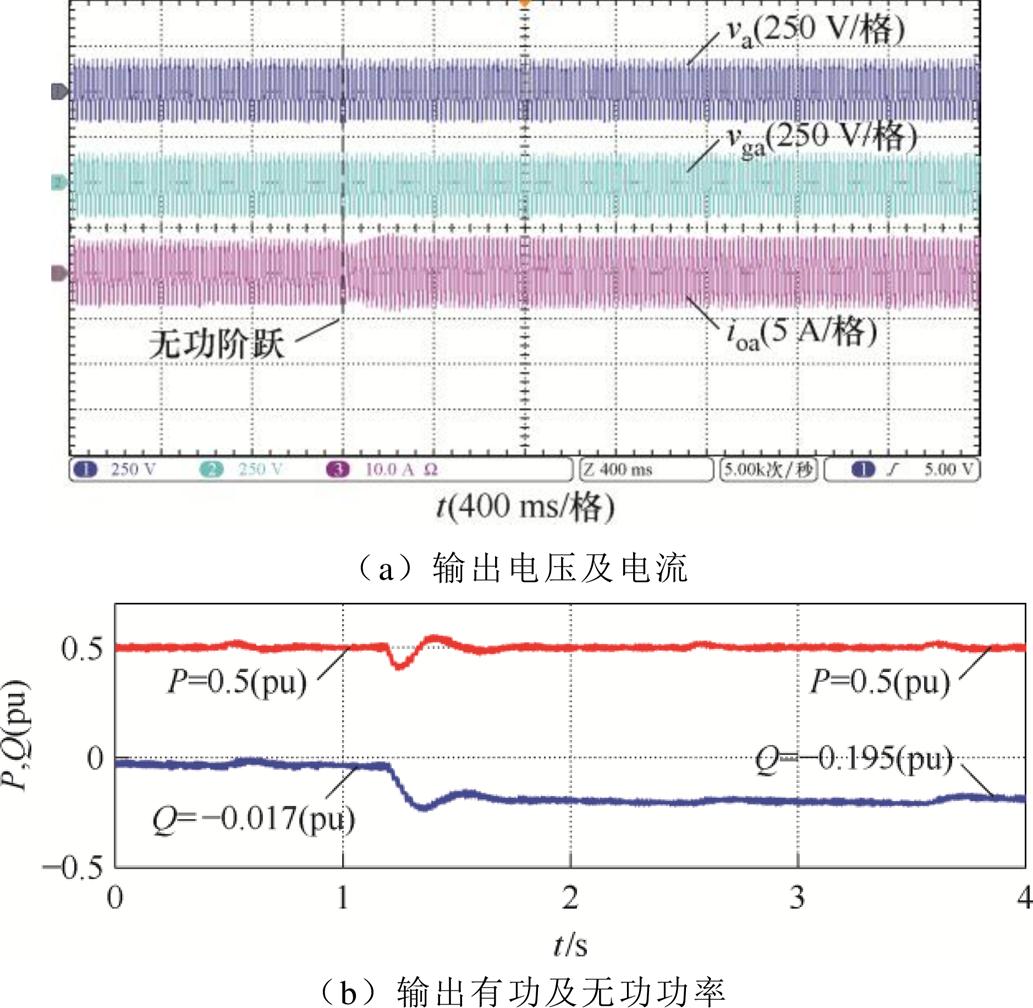
图22 R/X=0.32且Qref改变时实验结果
Fig.22 Experimental results when R/X=0.32 and Qref varies
为了对比不同解耦方法的性能差异,对VI解耦方法也进行了实验验证。由于虚拟电感对电压的补偿效果存在极限,在超过极限值之后即使继续增加虚拟电感也不能改善功率解耦效果[23]。因此实验中虚拟电感选为10 mH,实验结果如图23所示。由实验结果可知,VI解耦方法可以提升系统稳定裕度,消除动态过程中的振荡。但由于其解耦能力有限,稳态无功功率为-0.131(pu),并不能消除无功偏差。
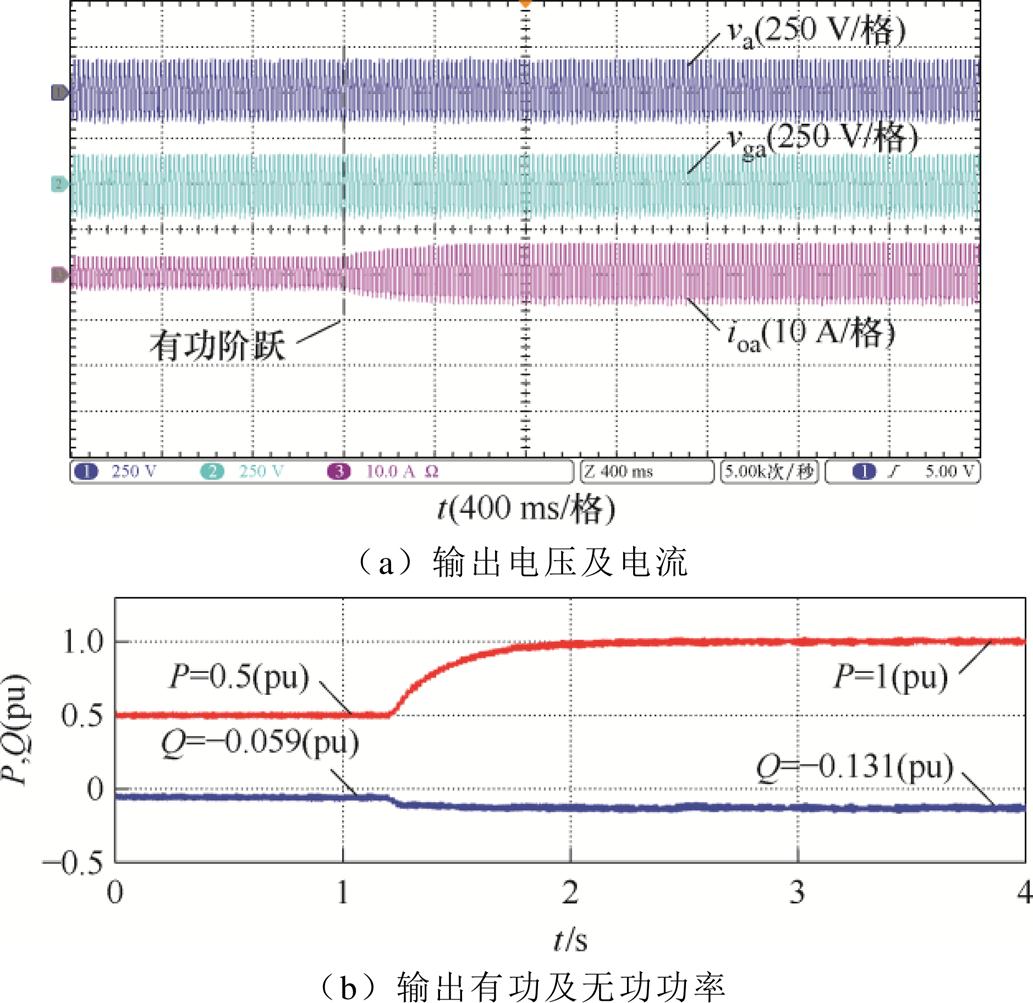
图23 R/X=0.32且采用VI解耦控制时实验结果
Fig.23 Experimental results with VI decoupling control when R/X=0.32
图24对比了R/X=0.32工况下采用VI解耦与所提解耦方法的实验结果。由图24可知,采用所提解耦方法时有功响应时间为120 ms,与不采用任何解耦方法时基本一致。而采用VI解耦方法时有功响应时间为360 ms,这是因为VI解耦方法等效为在变换器和电网间串联电感,降低了动态响应速度。在稳态无功控制性能方向,采用所提解耦方法时稳态无功功率为-0.003(pu),而采用VI解耦方法时稳态无功功率为-0.131(pu),所提解耦方法基本可以消除稳态功率耦合。因此,所提解耦方法可在保证变换器响应速度的同时,抑制动态过程中的振荡,并提升稳态无功控制精度。
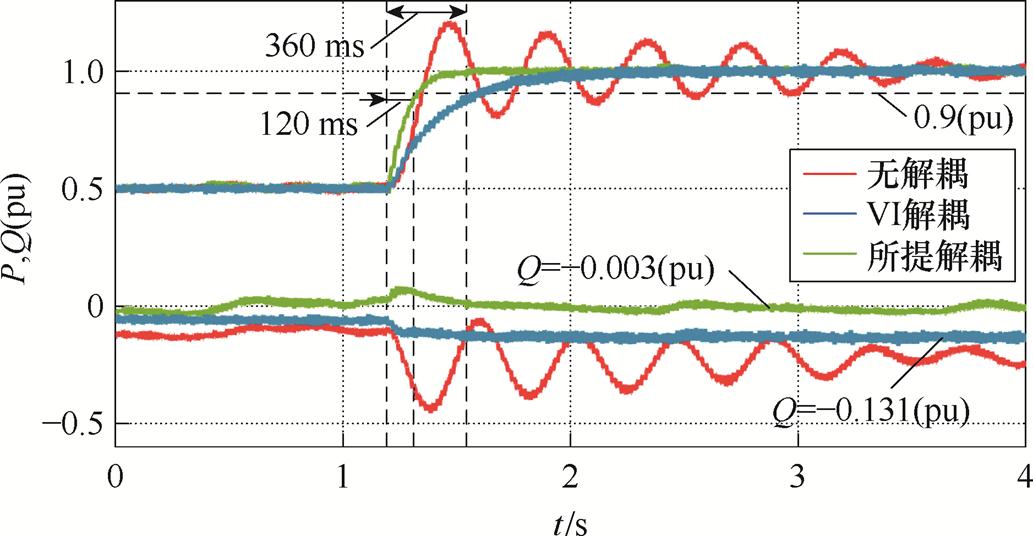
图24 R/X=0.32时采用不同解耦方法的输出功率
Fig.24 Output power using different decoupling methods when R/X=0.32
本文以下垂控制为研究对象,借助动态小信号模型分析了功率耦合的产生机理及其影响。结果表明,功率耦合会降低系统的稳定裕度,增大稳态无功偏差。针对上述问题,提出了一种基于电压补偿原理的功率解耦策略。具体而言,针对功率耦合引发的稳定裕度降低问题,通过在电压环引入角频率偏差补偿量,消除功率耦合的负阻尼效应,提升系统稳定裕度;针对功率耦合导致的稳态无功偏差问题,在电压环中引入有功前馈补偿量,提升稳态解耦能力,减小稳态无功偏差。实验结果表明,所提解耦方法能够在保持系统响应速度的同时,有效抑制功率耦合产生的功率振荡,改善系统的稳定裕度,并且可以提高稳态无功功率的控制精度。所提方法在不同阻感比工况下均表现出良好的效果,且不会影响有功控制精度,有助于提升下垂控制变换器的动稳态性能。
附 录
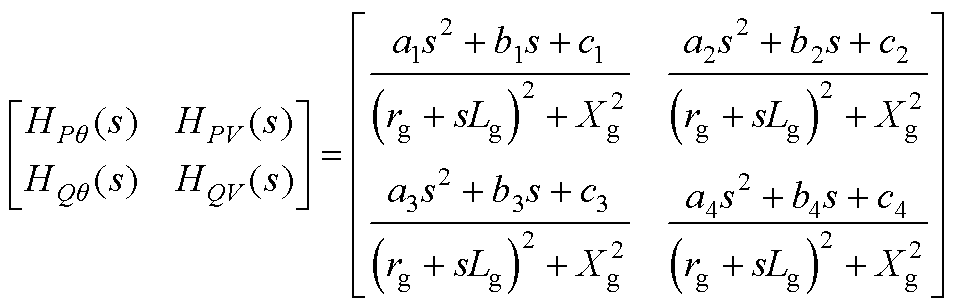 (A1)
(A1)
其中,a1、b1、c1、a2、b2、c2、a3、b3、c3、a4、b4、c4表达式分别为
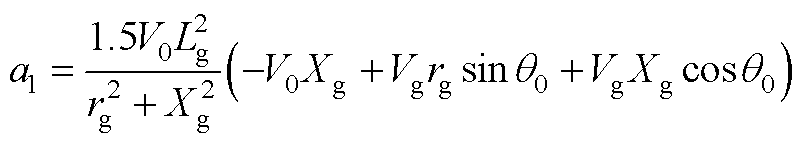
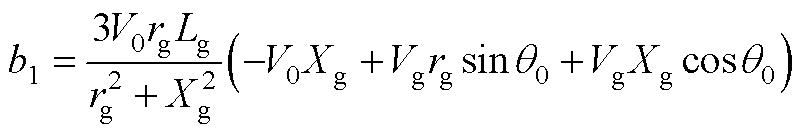
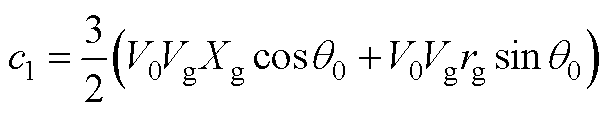
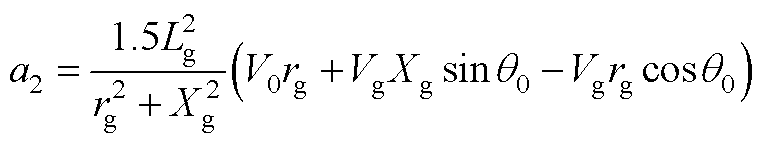
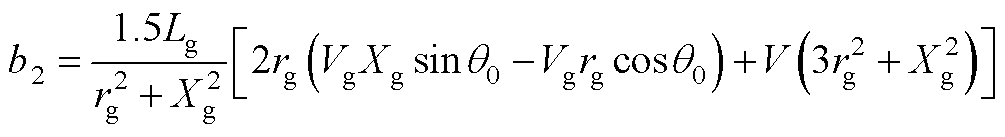
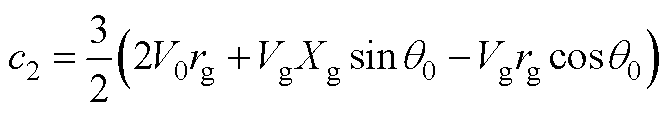
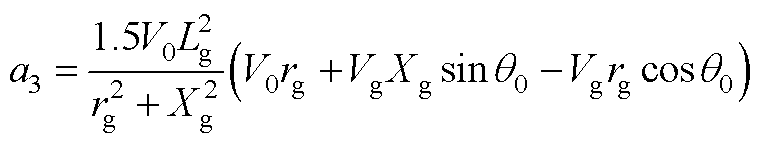
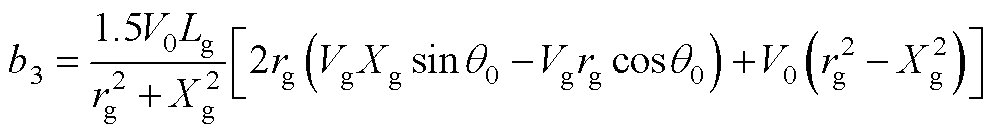
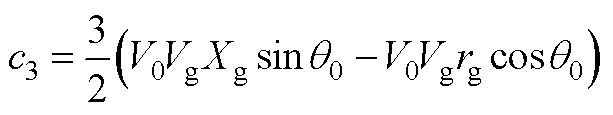
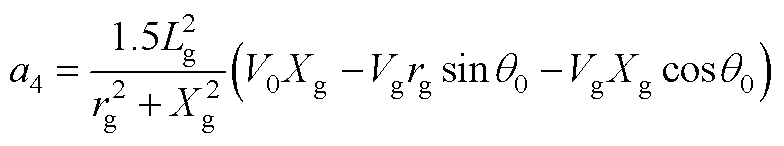
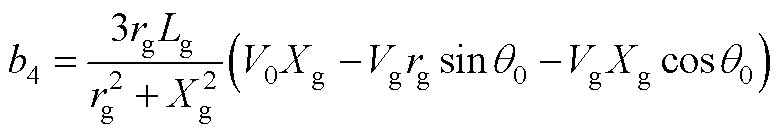
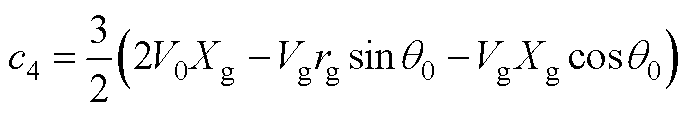
式中,Xg为线路等效电抗,且Xg=wnLg;下标“0”代表各变量的稳态值。
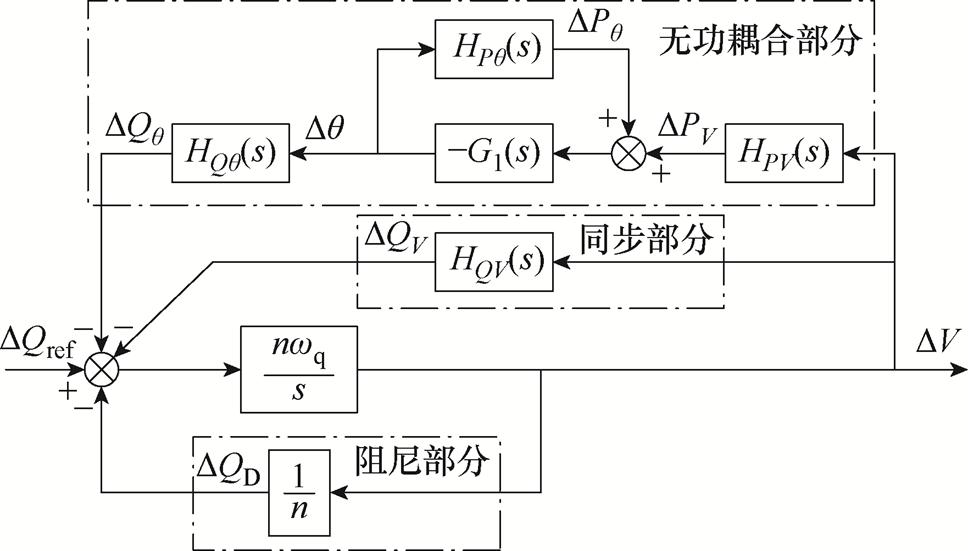
附图1 无功环幅相模型
App.Fig.1 Magnitude-phase model of the reactive power loop
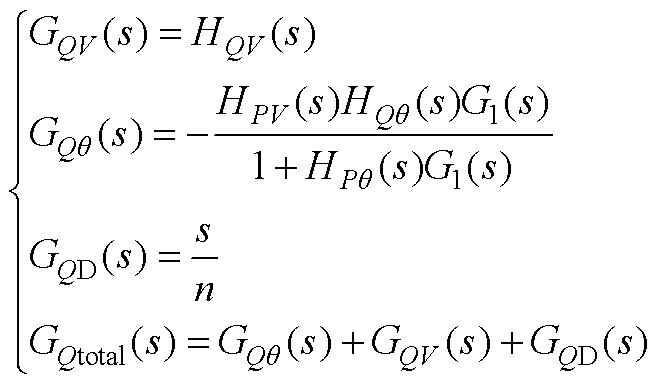 (A2)
(A2)
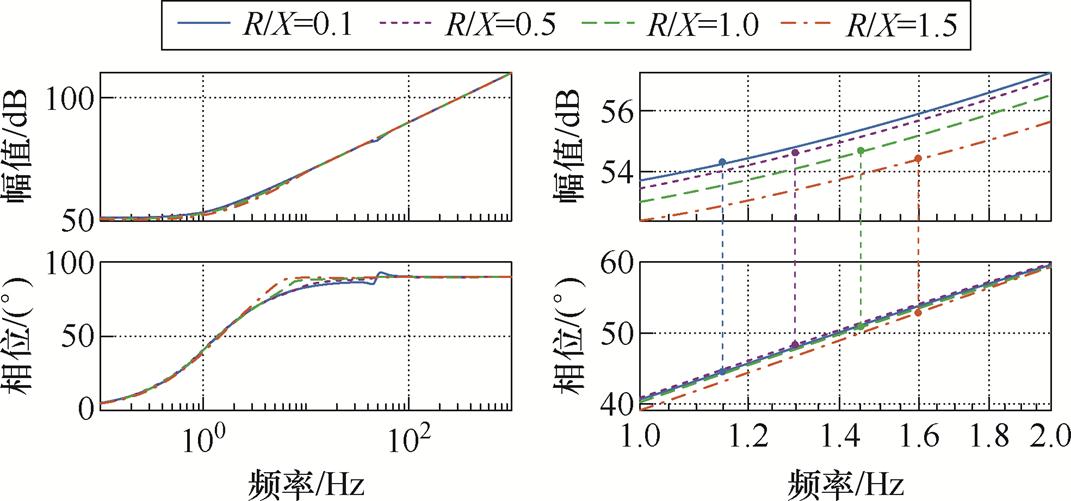
附图2 R/X变化时GQtotal(s)的伯德图
App.Fig.2 Bode plot of GQtotal(s) when R/X varies
参考文献
[1] 舒印彪, 陈国平, 贺静波, 等. 构建以新能源为主体的新型电力系统框架研究[J]. 中国工程科学, 2021, 23(6): 61-69.
Shu Yinbiao, Chen Guoping, He Jingbo, et al. Building a new electric power system based on new energy sources[J]. Strategic Study of CAE, 2021, 23(6): 61-69.
[2] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[3] 胡光, 庄可好, 高晖胜, 等. 低惯量交流系统并网变流器次/超同步振荡分析[J]. 电工技术学报, 2024, 39(8): 2250-2264.
Hu Guang, Zhuang Kehao, Gao Huisheng, et al. Sub/ super synchronous oscillation analysis of grid- connected converter in low inertia AC system[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2250-2264.
[4] 梁军杨, 李红, 宋国杰, 等. 多时间尺度控制下跟网型变换器的同步稳定性分析与改进控制[J]. 电工技术学报, 2024, 39(22): 7182-7196.
Liang Junyang, Li Hong, Song Guojie, et al. Synchro- nization stability analysis and enhanced control of grid-following converters under multi-timescale control [J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7182-7196.
[5] 孙鹏飞, 田震, 查晓明, 等. 功率同步型构网变流器并网系统暂态同步稳定性研究综述[J]. 电力系统自动化, 2025, 49(02): 1-19.
Sun Pengfei, Tian Zhen, Zha Xiaoming, et al. Review on research of transient synchronization stability for grid-connected system based on power-synchronizationgrid-forming converter[J]. Automation of Electric Power Systems, 2025, 49 (2): 1-19.
[6] Gao Mingzhi, Chen Min, Zhao Bin, et al. Design of control system for smooth mode-transfer of grid-tied mode and islanding mode in microgrid[J]. IEEE Trans- actions on Power Electronics, 2020, 35(6): 6419- 6435.
[7] Gao Mingzhi, Chen Min, Wang Chenxi, et al. An accurate power-sharing control method based on circulating-current power phasor model in voltage- source inverter parallel-operation system[J]. IEEE Trans- actions on Power Electronics, 2018, 33(5): 4458- 4476.
[8] Yao Wei, Chen Min, Matas J, et al. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 576-588.
[9] Meng Xin, Liu Jinjun, Liu Zeng. A generalized droop control for grid-supporting inverter based on comparison between traditional droop control and virtual synchronous generator control[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5416-5438.
[10] 李亚楼, 赵飞, 樊雪君. 构网型储能及其应用综述[J]. 发电技术, 2025, 46(2): 386-398.
Li Yalou, Zhao Fei, Fan Xuejun. Review of grid- forming energy storage and its applications[J]. Power Generation Technology, 2025, 46(2): 386-398.
[11] 金楠, 肖晗, 谢欢, 等. NPC三电平虚拟同步机桥臂故障容错模型预测控制[J]. 电源学报, 2024, 22(2): 147-157.
Jin Nan, Xiao Han, Xie Huan, et al. Fault-tolerant model predictive control for bridge arm of NPC three- level virtual synchronous generator[J]. Journal of Power Supply, 2024, 22(2): 147-157.
[12] Zhang Lidong, Harnefors L, Nee H P. Power- synchronization control of grid-connected voltage- source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[13] 伍文华, 周乐明, 陈燕东, 等. 序阻抗视角下虚拟同步发电机与传统并网逆变器的稳定性对比分析[J]. 中国电机工程学报, 2019, 39(5): 1411-1421.
Wu Wenhua, Zhou Leming, Chen Yandong, et al. Stability comparison and analysis between the virtual synchronous generator and the traditional grid- connected inverter in the view of sequence impedance [J]. Proceedings of the CSEE, 2019, 39(5): 1411-1421.
[14] 杜步阳, 邵德军, 朱建行, 等. 电压源型变器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianhang, et al. The interaction between multiple timescales of the grid- tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547-5559.
[15] Li Chang, Yang Yaqian, Mijatovic N, et al. Frequency stability assessment of grid-forming VSG in framework of MPME with feedforward decoupling control strategy [J]. IEEE Transactions on Industrial Electronics, 2022, 69(7): 6903-6913.
[16] Zhao Fangzhou, Zhu Tianhua, Li Zejie, et al. Low- frequency resonances in grid-forming converters: causes and damping control[J]. IEEE Transactions on Power Electronics, 2024, 39(11): 14430-14447.
[17] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual synch- ronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[18] 熊小玲, 李昕悦, 周琰, 等. 基于陷波器的构网型换流器同步频率谐振抑制策略[J]. 电工技术学报, 2024, 39(12): 3827-3839.
Xiong Xiaoling, Li Xinyue, Zhou Yan, et al. Synch- ronous frequency resonance suppression of grid-formingconverter based on Notch filter[J]. Transactions of ChinaElectrotechnical Society, 2024, 39(12): 3827-3839.
[19] Li Mingxuan, Wang Yue, Hu Weihao, et al. Unified modeling and analysis of dynamic power coupling for grid-forming converters[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 2321-2337.
[20] 杜建鹏, 赵晋斌, 曾志伟, 等. 基于虚拟功角功率控制的VSG增强功率解耦策略[J]. 中国电机工程学报, 2024, 44(22): 8808-8819.
Du Jianpeng, Zhao Jinbin, Zeng Zhiwei, et al. Enhanced power decoupling strategy for VSG with power control based on virtual power angle[J]. Proceedings of the CSEE, 2024, 44(22): 8808-8819.
[21] Yang Yaqian, Xu Jiazhu, Li Chang, et al. A new virtual inductance control method for frequency stabilization of grid-forming virtual synchronous generators[J]. IEEE Transactions on Industrial Electro- nics, 2023, 70(1): 441-451.
[22] 李明烜, 王跃, 徐宁一, 等. 松弛小功角约束条件的虚拟同步发电机功率解耦策略[J]. 电力系统自动化, 2018, 42(9): 59-68.
Li Mingxuan, Wang Yue, Xu Ningyi, et al. Power decoupling strategy for virtual synchronous generator relaxing condition of small power angle[J]. Automa- tion of Electric Power Systems, 2018, 42(9): 59-68.
[23] Dong Ningbo, Li Mengfei, Chang Xiaofei, et al. Robust power decoupling based on feedforward decoupling and extended state observers for virtual synchronous generator in weak grid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(1): 576-587.
[24] Li Yun wei, Kao C N. An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid[J]. IEEE Transactions on Power Electronics, 2009, 24(12): 2977-2988.
[25] Wen Tiliang, Zhu Donghai, Zou Xudong, et al. Power coupling mechanism analysis and improved decoup- ling control for virtual synchronous generator[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3028-3041.
[26] Long Bo, Zhu Shihan, Rodriguez J, et al. Enhance- ment of power decoupling for virtual synchronous generator: a virtual inductor and virtual capacitor approach[J]. IEEE Transactions on Industrial Electro- nics, 2023, 70(7): 6830-6843.
[27] 张林, 张海波, 蒋维勇, 等. 基于自适应动态虚拟同步阻抗的虚拟同步机功率解耦策略[J]. 中国电机工程学报, 2024, 44(15): 6010-6023.
Zhang Lin, Zhang Haibo, Jiang Weiyong, et al. Power decoupling strategy for virtual synchronous generator based on adaptive dynamic virtual synchronous impedance [J]. Proceedings of the CSEE, 2024, 44(15): 6010-6023.
[28] 李武华, 王金华, 杨贺雅, 等. 虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J]. 中国电机工程学报, 2017, 37(2): 381-391.
Li Wuhua, Wang Jinhua, Yang Heya, et al. Power dynamic coupling mechanism and resonance suppres- sion of synchronous frequency for virtual synchronous generators[J]. Proceedings of the CSEE, 2017, 37(2): 381-391.
[29] Li Yitong, Gu Yunjie, Zhu Yue, et al. Impedance circuit model of grid-forming inverter: visualizing control algorithms as circuit elements[J]. IEEE Trans- actions on Power Electronics, 2021, 36(3): 3377-3395.
Abstract Grid-forming technologies such as droop control are the key to improving the stability of the modern power system. However, for independent control of active and reactive power, the equivalent impedance of transmission lines must be purely inductive, and the power angle should be small. In low/medium-voltage grids with distributed renewable energy integration, the line resistance cannot be ignored, and the power angle may vary over a more extensive range, leading to significant power coupling issues. Power coupling will increase steady-state reactive power deviation, reduce system stability margin, and even trigger oscillatory instability.
A small-signal model of the grid-connected system with power coupling is first established. Root locus analysis indicates that power coupling reduces the system stability margin, and the larger the R/X ratio, the lower the system stability margin. Further amplitude-phase analysis shows that the negative damping in the active power loop due to power coupling is the primary cause of the reduced system stability margin. The steady-state power coupling coefficient reveals that power coupling increases the steady-state reactive power deviation, and the larger the R/X ratio, the greater the steady-state reactive power deviation.
To address these issues, a power decoupling strategy based on voltage compensation principles is proposed: (1) An angular frequency deviation compensation term is introduced into the voltage loop to reduce the negative damping effect of power coupling and improve the system stability margin. (2) The ideal decoupled voltage when the steady-state reactive power deviation is zero is calculated, and the difference between the actual output voltage and the ideal decoupled voltage is used for active power feedforward compensation, thereby reducing the steady-state reactive power deviation.
Experiments are carried out in a three-phase droop control converter grid-connected system. Under the conditions of R/X=0.32 and 0.53, the proposed decoupling method reduces the minimum reactive power during the dynamic process from -0.46(pu) and -0.59(pu) to 0.001(pu) and 0.008(pu), respectively. The steady-state reactive power deviation also decreases from -0.231(pu) and -0.342(pu) to -0.003(pu) and -0.007(pu), respectively. Furthermore, under the R/X=0.32 condition, the power response time using the proposed decoupling method is 120 ms, which is essentially the same as without the decoupling method. In contrast, with the virtualinductor (VI) decoupling method, the power response time increases to 360 ms, and the steady-state reactive power deviation is -0.131(pu).Therefore, theVI decoupling method not only slows down the response speed but also fails to eliminate steady-state power coupling.
Experimental results show that: (1) The proposed decoupling method can suppress power oscillations during the dynamic process under various R/X conditions and improve the system stability margin. (2) The proposed decoupling method reduces steady-state reactive power deviation, and changes in the reactive power setpoint do not affect active power control accuracy. (3) Compared to the VI decoupling method, the proposed decoupling method does not slow down the converter’s response speed and demonstrates better steady-state decoupling capability, helping to improve the dynamic and steady-state performance of droop-controlled converters in distributed renewable energy generation systems.
Keywords:Droop control, power oscillation, power decoupling, voltage compensation
王鹏程 男,1994年生,博士研究生,研究方向为电力电子化电力系统稳定与控制。
E-mail: pcwang03@zju.edu.cn
陈 敏 男,1979年生,教授,博士生导师,研究方向为电力电子在电力系统中的应用、新能源发电与并网控制技术等。
E-mail: calim@zju.edu.cn(通信作者)
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.250080
国家电网有限公司总部管理科技项目(支撑新型电力系统的构网型SVG技术研究、装备研制与示范应用)(5500-202329500A-3-2-ZN)和台州市-浙江大学科技合作项目(网源友好型电化学储能系统的构网变流技术研究及装备开发)资助。
收稿日期 2025-01-12
改稿日期 2025-03-06
(编辑 郭丽军)