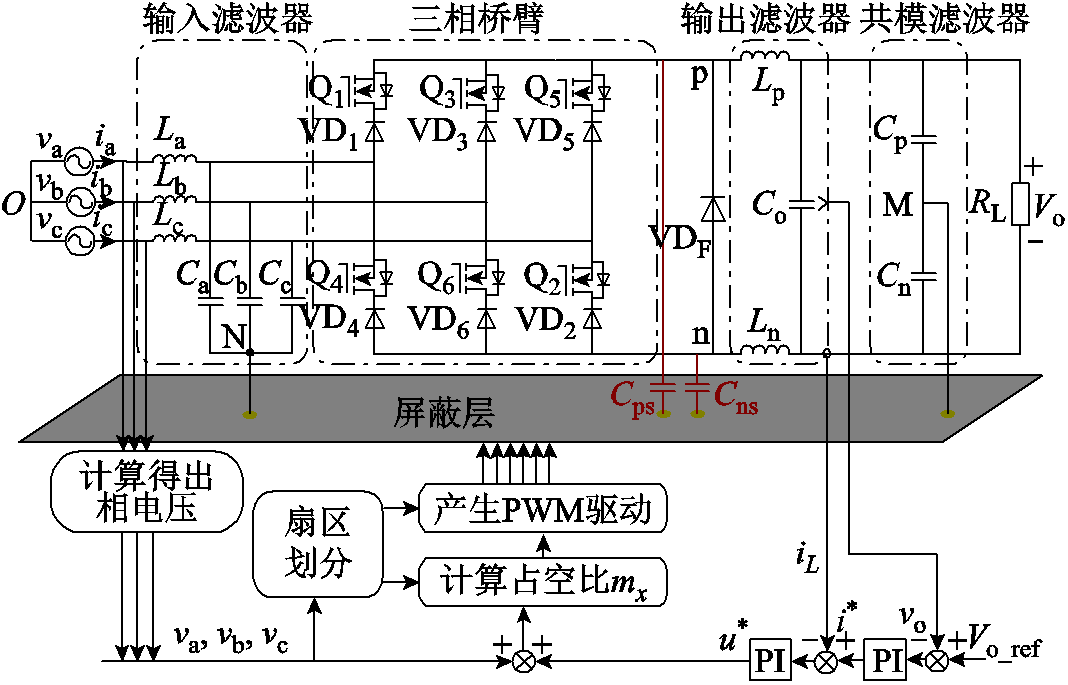
图1 三相Buck整流器拓扑
Fig.1 Topology of three-phase Buck rectifier
摘要 三段式不对称空间矢量脉宽调制（SVPWM）可以有效地抑制三相Buck整流器扇区切换引起的不规则直流链电流纹波，从而降低输入电流总谐波畸变率（THD）。根据矢量作用顺序的不同，可组成多种不对称脉宽调制（PWM）序列，通常认为它们具有等效的矢量合成效果。然而，在相同输入条件、不同的不对称PWM序列的直流链电流纹波特性存在显著差异，进而影响输入电流THD。该文分析了两种不对称PWM调制序列的直流链电流纹波特性，得出对应不同输入电压相序的最优不对称PWM序列。通过相序自适应调制策略，对随机接入的输入电压相序均可实现低直流链电流纹波和低输入电流THD，有效解决了不对称调制的不对称性带来的电流畸变问题。最后设计了一台1 kW的实验样机，验证了理论分析的正确性。
关键词：三相Buck整流器 不对称调制 直流链电流纹波 输入电流畸变 输入相序
三相PWM整流器分为三相Boost整流器和三相Buck整流器两大类，相对于三相Boost整流器，三相Buck整流器具有低启动电流和短路电流抑制能力，因此在多电飞机[1]、动力电池组充电系统[2]及新能源并网发电系统[3]中得到广泛应用。然而，上述应用场景通常对输入电流总谐波畸变率（Total Harmonic Distortion, THD）有严苛的要求[4-7]。为降低三相Buck整流器的输入电流THD，学者们针对调制策略开展了大量研究[8-18]。
三相Buck整流器的开关驱动信号为三值逻辑，因此正弦脉宽调制（Sinusoidal Pulse Width Modulation，SPWM）需要进行二-三值逻辑转换，增加了数字控制的实现难度[11-12]。相对而言，空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）的数字实现方式简单且更加灵活[13]，因此，三相Buck整流器广泛采用SVPWM策略。根据SVPWM策略的脉宽调制（Pulse Width Modulation, PWM）序列是否对称，SVPWM分为对称调制和不对称调制。文献[15-18]针对对称和不对称SVPWM策略，研究了开关损耗、输入侧滤波电容电压纹波、开关管电压应力、扇区切换处电流畸变等特性。
基于传统对称SVPWM策略，文献[15]研究了一种对称调制技术，抑制了输入滤波电容对输入电流的影响。然而与传统对称SVPWM策略相比，存在复杂度大、实现难度高的问题；文献[16]结合两种传统不对称调制技术，通过优化扇区切换时的PWM序列，消除了扇区切换带来的不规则PWM波，降低了输入电流THD；文献[17]通过计算和比较对称调制和不对称调制的输入滤波电容电压纹波的方均根，研究了一种低开关损耗和低输入滤波电容电压纹波的调制技术；文献[18]针对高功率密度三相Buck整流器，提出了一种降低开关管电压应力的三段式不对称调制技术。
文献[16]提出的三段式不对称调制技术存在两种不同的PWM序列，通常认为它们具有等效的矢量合成效果。然而，由于寄生电容的影响，在相同输入电压条件下，这两种不对称PWM序列呈现不同的直流链电流纹波，此外，当输入电压相序发生改变时，其对应的直流链纹波也相应改变，进而显著影响输入电流THD。
为了不同输入电压相序时采用更优的不对称PWM序列，使整流器始终工作在最佳性能，本文对比分析了两种不对称PWM序列的直流链电流纹波特性及其对输入电流THD的影响，提出了不同输入电压相序时的最优不对称PWM序列。根据不同输入电压相序，通过对PWM序列进行移相，即可保证任意输入电压相序时三相Buck整流器均能实现低直流链纹波和低输入电流THD。
三相Buck整流器主要由输入滤波器Lx和Cx（x = a, b, c）、三相六开关桥臂Q1～Q6和VD1～VD6、续流二极管VDF、输出电容Co、滤波电感Ln和Lp组成，如图1所示。为了抑制共模电流对输入电流的影响，提高整流器功率密度，文献[7]提出将共模电容Cp、Cn与输入滤波器电容的中性点N相连，组成共模滤波器，并将它的中线MN设计为屏蔽层，以阻隔主电路与控制电路之间的电气干扰，却导致主电路与屏蔽层之间形成寄生电容Cps和Cns[18]。
图1 三相Buck整流器拓扑
Fig.1 Topology of three-phase Buck rectifier
本文采用十二扇区SVPWM调制，每隔30°划分一个扇区，如图2所示。三相Buck整流器采用的SVPWM调制策略是对空间电流矢量的合成。根据矢量合成方式，控制整流器的开关管进行相应的动作，得到目标参考信号，实现功率因数校正[19-20]。
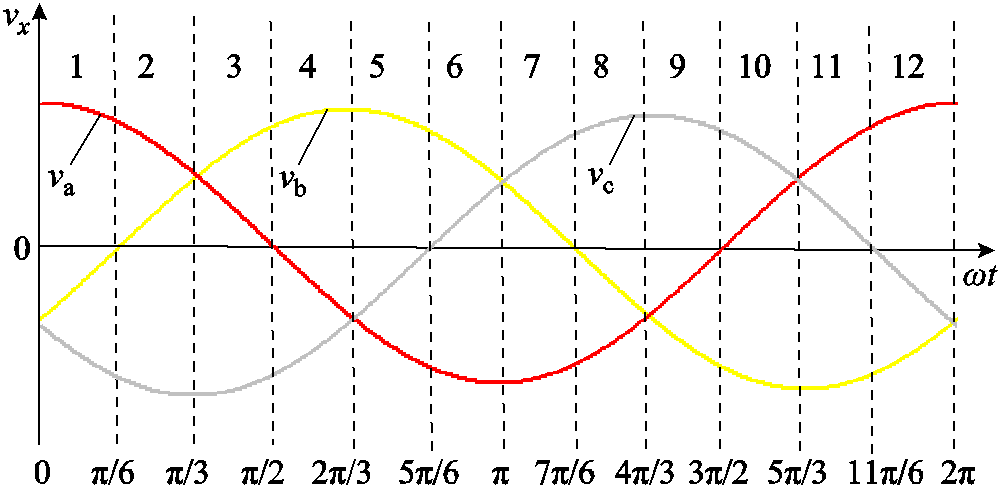
图2 输入电压与十二扇区划分
Fig.2 Input voltage and sector distribution of 12 sectors
为描述三相桥臂开关管的工作状态，定义开关函数Si，开关函数Si的组合为（SaSbSc）。
（1）
三相Buck整流器各桥臂开关管的开关状态与开关函数对应关系见表1。表1中10种开关状态对应三相Buck整流器的10种工作模态，根据工作模态不同，可以定义10个空间电流矢量I1～I10。I1～I6为有效电流矢量，I7～I10为零矢量，其中I7～I9为对应桥臂的上下开关管全部导通，I10（000）为整流桥臂开关管全部关断[21-22]。
表1 开关函数对应的开关状态
Tab.1 Relationship between switching function and switching state
开关状态导通的上管导通的下管Si电流矢量 1Q1Q2101I1 2Q3Q2011I2 3Q3Q4110I3 4Q5Q4101I4 5Q5Q6011I5 6Q1Q6110I6 7Q1Q4100I7 8Q3Q6010I8 9Q5Q2001I9 10均关断均关断000I10
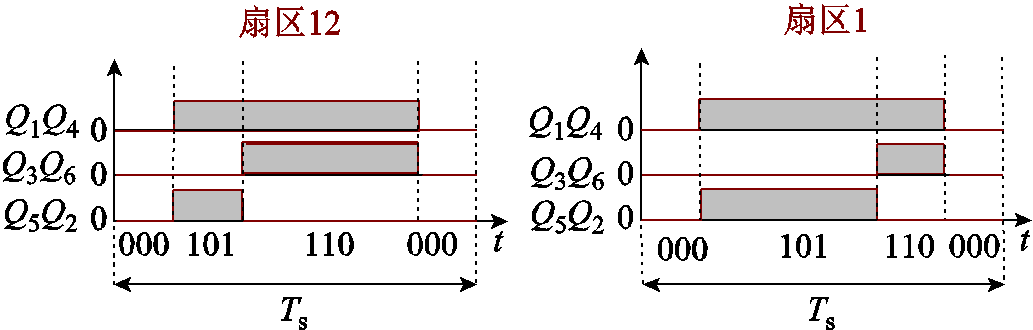
图3 不对称PWM序列1
Fig.3 Asymmetric PWM sequence 1
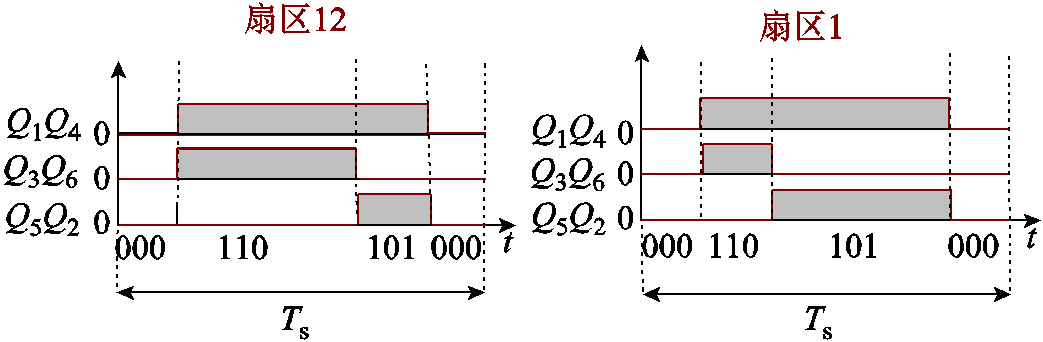
图4 不对称PWM序列2
Fig.4 Asymmetric PWM sequence 2
根据文献[16]，正相序输入时，以扇区12和扇区1为例，定义如图3所示的三段式不对称PWM序列为PWM序列1。在一个开关周期内，PWM序列1的电流矢量作用顺序为000→101→110→000。将电流矢量的作用顺序交换为000→110→101→ 000，可得到第二种不对称PWM序列，定义为不对称PWM序列2，如图4所示，其他扇区的PWM序列可以此类推。
通常认为这两种电流矢量作用顺序具有等效的矢量合成效果，然而，由于寄生电容的影响，矢量作用顺序影响谐波组成。在相同输入条件下，三相Buck整流器的直流链电流纹波特性发生改变，从而导致这两种不对称PWM序列调制三相Buck整流器的输入电流产生明显差异。
图5所示为正相序输入时，扇区12开始阶段PWM序列1和PWM序列2在零矢量（000）作用时三相Buck整流器的几个工作阶段。在每一个工作阶段，路径1为电感续流回路，路径2和路径3为寄生电容的充放电路径。根据Cps、Cns充放电情况，可以分为三个作用阶段。
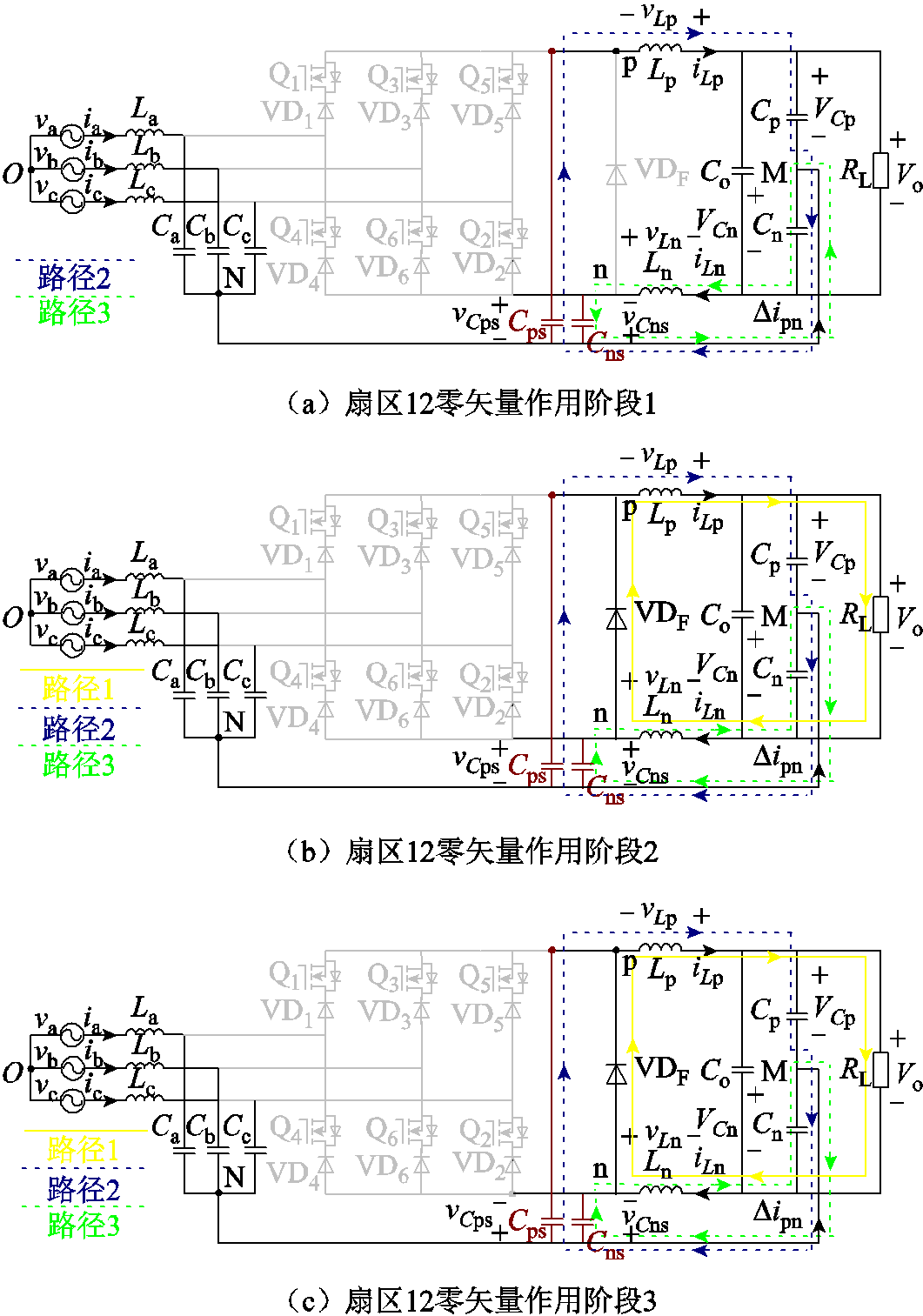
图5 扇区12开始阶段不对称PWM序列1和PWM序列2的零矢量作用时三相Buck整流器工作模态
Fig.5 Equivalent circuit of three-phase buck rectifier at zero vector in the beginning of sector 12 by asymmetric PWM sequence 1 and PWM sequence 2
图6和图7分别给出了采用PWM序列1和PWM序列2时，扇区12的PWM序列、电感电流以及寄生电容Cps和Cns两端电压波形放大图。其中图6和图7的000电流矢量阶段放大图与图5采用不对称PWM序列1和PWM序列2时扇区12的000矢量作用期间所存在的三个阶段相对应。
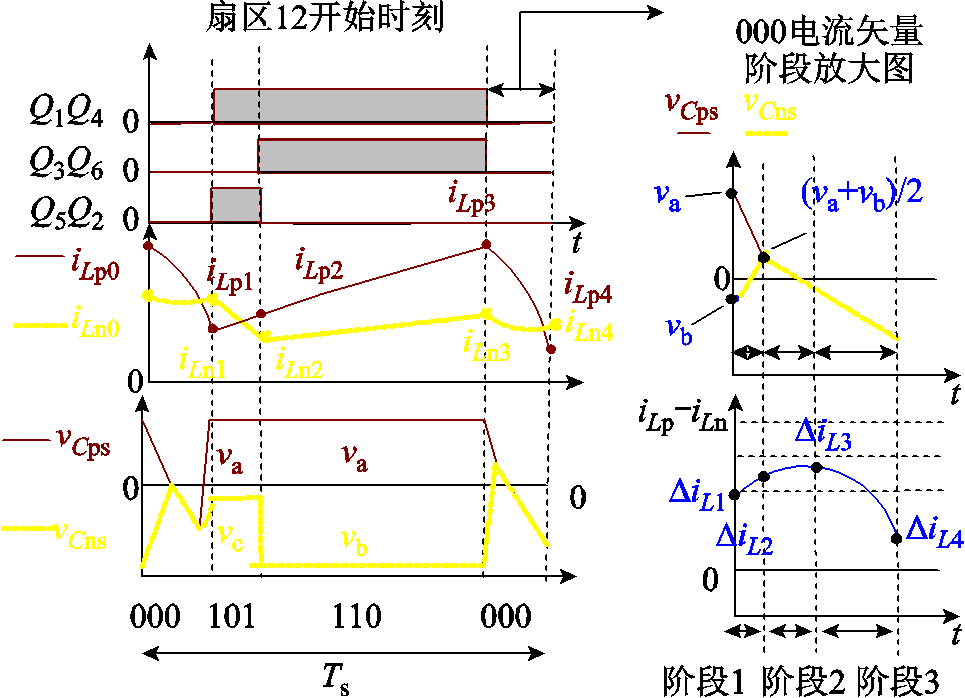
图6 扇区12的不对称PWM序列1关键波形
Fig.6 Current waveforms by asymmetric PWM sequence 1 int sector 12
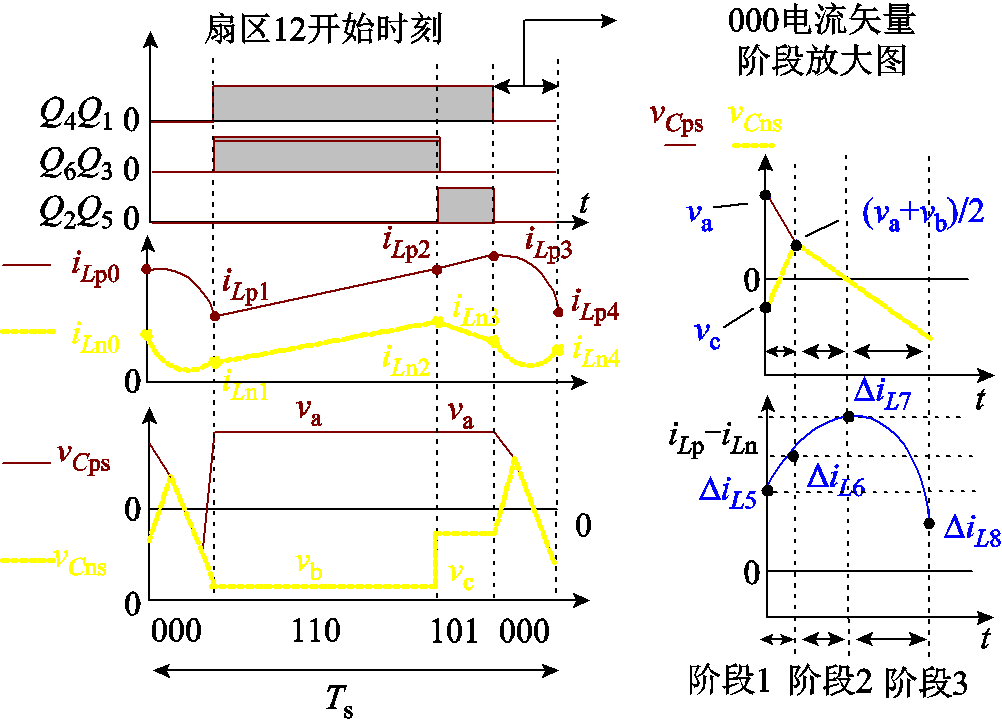
图7 扇区12的不对称PWM序列2的关键波形
Fig.7 Current waveforms by asymmetric PWM sequence 2 in sector 12
图5a描述了PWM序列1和PWM序列2在工作阶段1的两条电路路径。对PWM序列1，工作阶段1开始时刻，vCps = va，-vCns= vb，且vCps≠vCns。电容电压不能突变，此时续流二极管不导通。Cps通过路径2放电，Cns通过路径3放电，因此
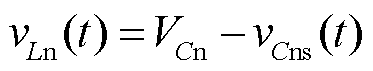（2）
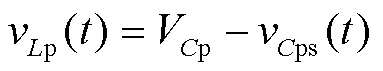（3）
其中，Cp, Cn的电压纹波较小，取VCp = VCn =Vo/2。
由于PWM序列1在扇区12电流矢量作用顺序为101→ 110→ 000，va(t)＞vb(t)，工作阶段1开始时，iLp＞iLn，vCps = va，-vCns = vb。因此在工作阶段1，vLn(t)＞vLp(t)，Ln的放电速率更快，上、下电感电流的差值增加。此时上、下电感电流变化斜率之差为
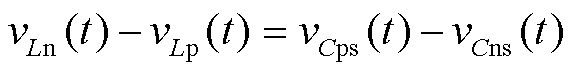（4）
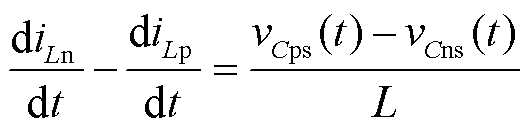（5）
假设L= Lp=Ln, 将vCps、vCns的值代入式（5），可知在工作阶段1，Ln与Lp放电速率的差值为(va+vb)/L。
对PWM序列2，在工作阶段1开始时刻，iLp＞iLn，vCps = va，-vCns = vc且vCps≠vCns，由于电容电压不能突变，此时续流二极管不导通。Cps通过路径2放电，Cns通过路径3放电，此时vLn(t)和vLp(t)为
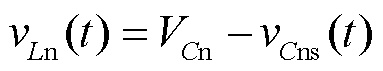（6）
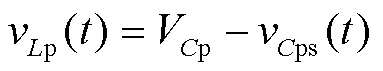（7）
其中，VCn = VCp，因此vLn(t)＞vLp(t)，Ln放电速率较快，上电感电流iLp和下电感电流iLn的差值增加。此时上、下电感电流变化斜率差值为
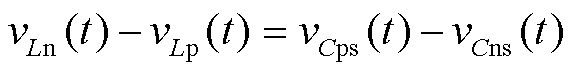（8）
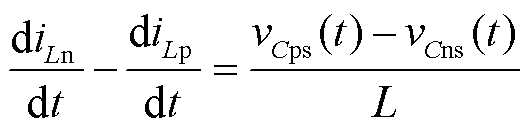（9）
将vCps、vCns的值代入式（9），可知工作阶段1中，Ln放电速率与Lp放电速率的差值为(va+vc)/L。
图5a对应图6和图7的工作阶段1，Cps和Cns放电，当Cns放电至0后，Cps继续放电，Cns充电，直至Cps放电与Cns充电至同一正电压。此阶段，iLp＞iLn，Lp的放电速率小于Ln的放电速率，上、下电感电流差值增大。对PWM序列1，Ln放电速率与Lp放电速率的差值为(va+vb)/L，上、下电感电流差值由ΔiL1增大至ΔiL2；对PWM序列2，Ln放电速率与Lp放电速率的差值为(va+vc)/L，上、下电感电流差值由ΔiL5增大至ΔiL6。当输入电压为正相序时，在扇区12，vc(t)＞vb(t)。因此在工作阶段1，ΔiL6＞ΔiL2，相对于PWM序列1，PWM序列2上、下电感电流差值增大的速率更大，直流链电流纹波更大。
图5b描述了PWM序列1和PWM序列2在工作阶段2的3条电流路径。采用PWM序列1和PWM序列2时，当Cps、Cns充放电至同一正电压时，续流二极管导通。采用PWM序列1时，该正电压为(va+vb)/2；采用PWM序列2时，该正电压为(va+vc)/2。电感电流一部分流经路径2，给Cps提供放电回路，另一部分流经路径3，给Cns提供放电回路。上、下电感与续流二极管构成回路，向负载端提供能量，vLn(t)和vLp(t)为
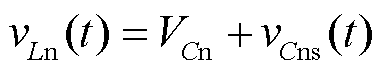（10）
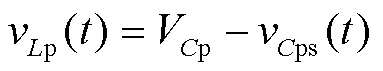（11）
其中，VCn=VCp。
因此vLn(t)＞vLp(t)，Ln放电速率较快，上、下电感电流差值增加，上、下电感电流变化斜率差值为
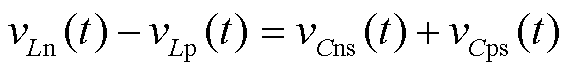（12）
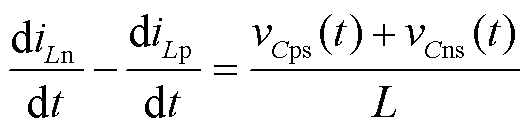（13）
对PWM序列1，在工作阶段2，Ln放电速率与Lp放电速率的差值由(va+vb)/L逐渐减小为0；对PWM序列2时，在工作阶段2，Ln放电速率与Lp放电速率的差值由(va+vc)/L逐渐减小为0。
图5b对应图6和图7的工作阶段2，Cps、Cns从同一正电压放电，iLp＞iLn，Lp的放电速率小于Ln的放电速率，上、下电感电流差值增大。对PWM序列1，Ln放电速率与Lp放电速率的差值由(va+vb)/L，逐渐减小为0，上、下电感电流差值，由ΔiL2增大至ΔiL3；对PWM序列2，Ln放电速率与Lp放电速率的差值由(va+vc)/L，逐渐减小为0，上、下电感电流差值，由ΔiL6增大至ΔiL7。当输入电压为正相序时，在扇区12，vc(t)＞vb(t)，因此在工作阶段2，ΔiL7＞ΔiL3。相对于PWM序列1，PWM序列2上、下电感电流差值增大的速率更大，直流链电流纹波更大。
图5c描述了PWM序列1和PWM序列2在工作阶段3的三条电流路径。当Cps、Cns放电至0时，上、下电感电流通过续流二极管续流，然而由于上、下电感电流不相等，因此通过路径2和路径3分别给Cps和Cns充电，此时vLn(t)和vLp(t)为
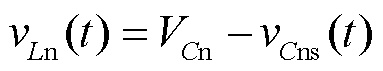（14）
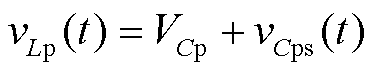（15）
在工作阶段3，Cns和Cps充电，vCns和vCps增大，因此vLn(t)＜vLp(t)，Lp的放电速率大于Ln，上、下电感电流的差值开始减小。
图5c对应图6和图7的工作阶段3，对PWM序列1和PWM序列2，Cps和Cns均充电，iLp＞iLn，Lp的放电速率大于Ln的放电速率, 上、下电感电流的差值减小。PWM序列1的上、下电感电流差值由ΔiL3减小至ΔiL4，PWM序列2的上、下电感电流差值由ΔiL7减小至ΔiL8。
三相正相序输入时，在扇区12，vc(t)＞vb(t)，因此，相对于不对称PWM序列1，不对称PWM序列2的上、下电感电流在阶段1和阶段2中Ln、Lp的放电速率和电感电流差值更大，直流链电感电流纹波更大。且在扇区12开始阶段，va(t)≈vb(t)，此时，对PWM序列1，零矢量仅存在1、3阶段；对PWM序列2，零矢量存在1、2、3阶段。这两种PWM序列在零矢量阶段时，上、下电感电流差值的变化以及寄生电容Cps、Cns的充放电情况见表2。根据表2分析可知，PWM序列2的直流链电流纹波明显增大。
表2 上、下电感电流差值变化及寄生电容充放电情况
Tab.2 The difference in the current of upper and lower inductor and the charging situation of parasitic capacitors
阶段/序列PWM序列1PWM序列2 阶段1Cps放电，Cns先放电后充电，上、下电感电流差值以较小速率增大Cps放电，Cns先放电后充电，上、下电感电流差值以较大速率增大 阶段2Cps、Cns均放电，上、下电感电流差值以较小速率增大Cps、Cns均放电，上、下电感电流差值以较大速率增大 阶段3Cps、Cns均充电，上、下电感电流差值减小Cps、Cns均充电，上、下电感电流差值减小
同理分析其他扇区，可知正相序输入电压时，相较于不对称PWM序列1，不对称PWM序列2的三相Buck整流器的直流链电流及其纹波明显增大。同理可知，输入电压为负相序时，不对称PWM序列2则更具优势。
根据图2，可得三相输入电压为
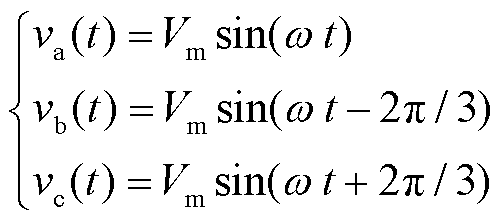（16）
式中，Vm为输入电压的幅值。
三相Buck整流器中，调制信号mx(x = a,b,c)为
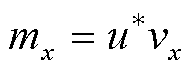（17）
式中，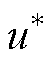
为图1中PI补偿器的控制环路输出。
从图6和图7可知，扇区12的输入电流ia为
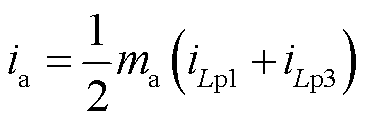（18）
图6和图7中扇区12的电感电流iLp0、iLp1、iLp2和iLp3，可以表示为
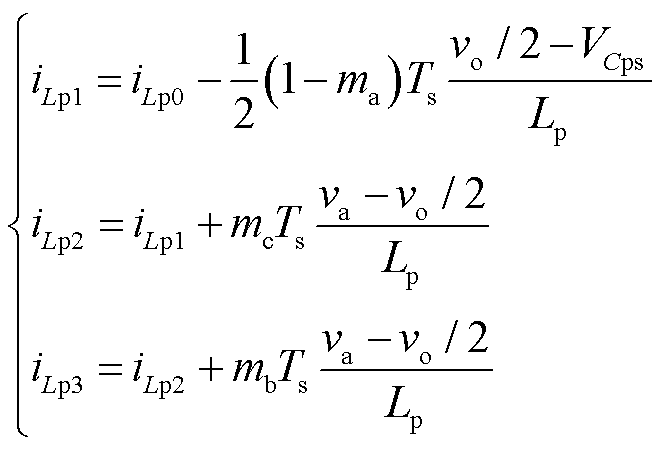（19）
式中，Ts为开关周期；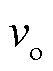
为输出电压。iLp0由输出功率Pout决定，为
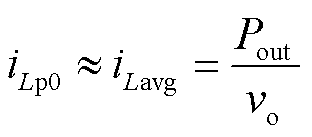（20）
由式（16）～式（20），在扇区12，传统不对称调制三相Buck整流器的A相输入电流为
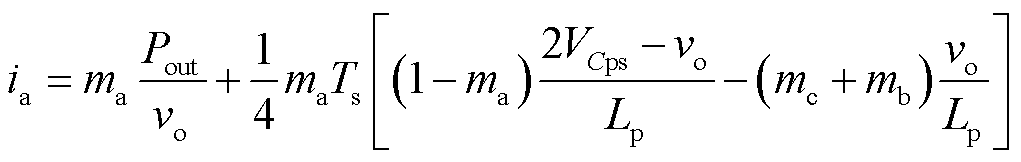（21）
由式（21）可知，在扇区12，ia与VCps成正比。从上述不对称PWM序列1和PWM序列2的直流链纹波特性分析可知，Cps的充放电受PWM序列影响，从而影响输入电流ia。
由2.1节分析可知，PWM序列1在扇区12的零矢量阶段VCps存在三个阶段：va→(va+vb)/2→0→负电压；PWM序列2在扇区12的零矢量阶段VCps存在三个阶段：va →(va+vc)/2 → 0→负电压。输入电压正相序时，在扇区12，vc(t)＞vb(t)。因此，由PWM序列1和PWM序列2的阶段1和阶段2可知，PWM序列2的扇区12的vCps较大，使扇区12的A相电流较大，出现畸变。
正相序输入时，输入电压和输入电流的仿真结果如图8所示，对PWM序列1，三相Buck整流器的输入电流THD为1.6%；对PWM序列2，三相Buck整流器的输入电流THD为3.1%。
当输入电压为正相序输入时，PWM序列1的直流链电流纹波和输入电流THD比PWM序列2更小。然而由于调制策略的不对称性，输入电压相序发生改变后，即由正相序（va相位超前vb相位120°）变为负相序（va相位滞后vb相位120°），两种PWM序列的纹波特性将发生改变，PWM序列2将更具有优势。负相序输入时，输入电流和输入电压的仿真结果如图9所示。对PWM序列1，三相Buck整流器的输入电流THD为3.1%；对PWM序列2，三相Buck整流器的输入电流THD为1.7%。
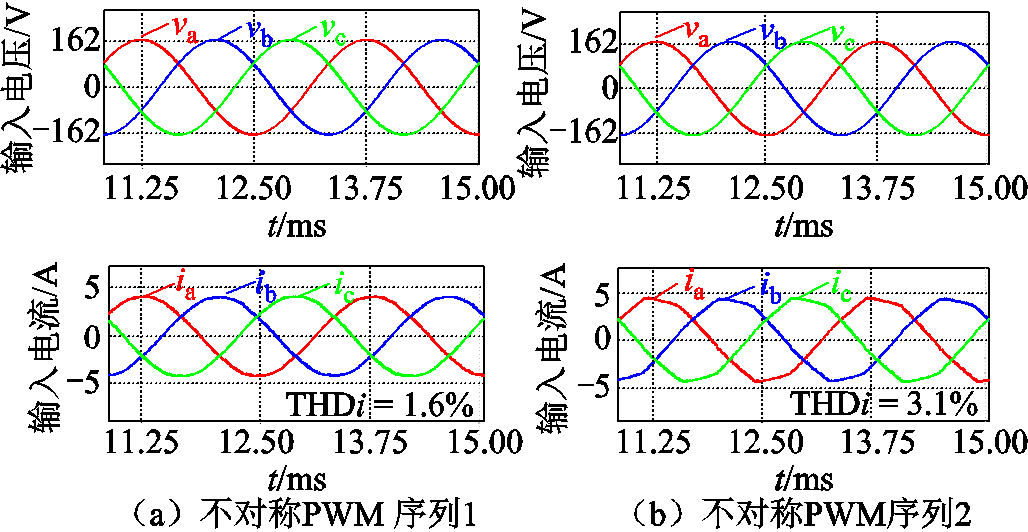
图8 正相序电压输入三相Buck整流器的仿真结果
Fig.8 Simulation result of three-phase buck rectifier at positive phase voltage input
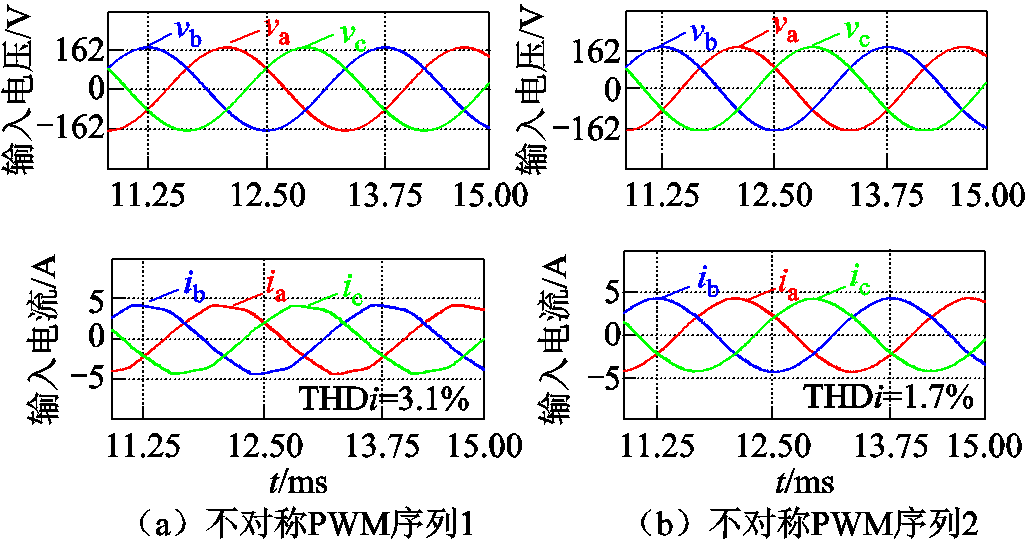
图9 负相序电压输入三相Buck整流器的仿真结果
Fig.9 Simulation result of three-phase buck rectifier at negative phase voltage input
因此，由于不对称调制的不对称性，采用不对称调制技术时，三相Buck整流器的直流链电流及其纹波受输入电压相序影响明显，相序的改变会使得输入电流出现明显畸变。
不对称SVPWM调制可以通过对PWM序列进行移相而直接得到，相比于传统的对称SVPWM更易数字实现。在三相Buck整流器中，占空比Dx（x=a, b, c），可以被表示为
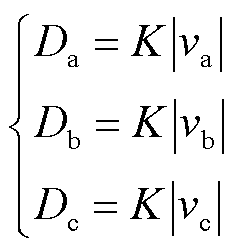（22）
式中，K为控制环路输出，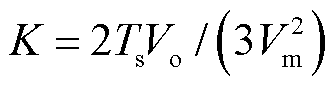
。
由式（22）可见各相桥臂驱动信号占空比与对应输入电压成正比。在扇区判定后，即可确定三相的占空比。在一个扇区中，根据三相输入电压的大小关系，存在Dmax＞Dmid＞Dmin。在确定各相占空比后，通过移相可以非常方便地实现不对称PWM序列。
由上述分析可知，采用不对称调制技术时，三相Buck整流器的直流链电流及其纹波受输入电压相序影响明显，同一PWM序列，输入电压相序改变，输入电流发生明显畸变。针对这一问题，本小节将对移相过程进行优化，实现输入电压相序与PWM序列逻辑的匹配。每相占空比的移相满足关系
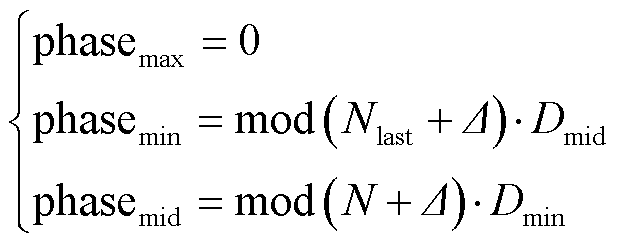（23）
式中，mod(·)为求余函数；N为本扇区的扇区值；Nlast为上一个扇区值；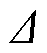
为0-1变量，当扇区判定为正相序时，Δ=1；当扇区判定为负相序时，Δ=0。
三相Buck整流器相序自适应调制策略流程如图10所示。当接通电源后，系统进行初始化和自检。初始化后，会根据扇区是否递增对Δ初始化。然后将环路计算结果代入式（22）和式（23），生成不对称PWM序列。
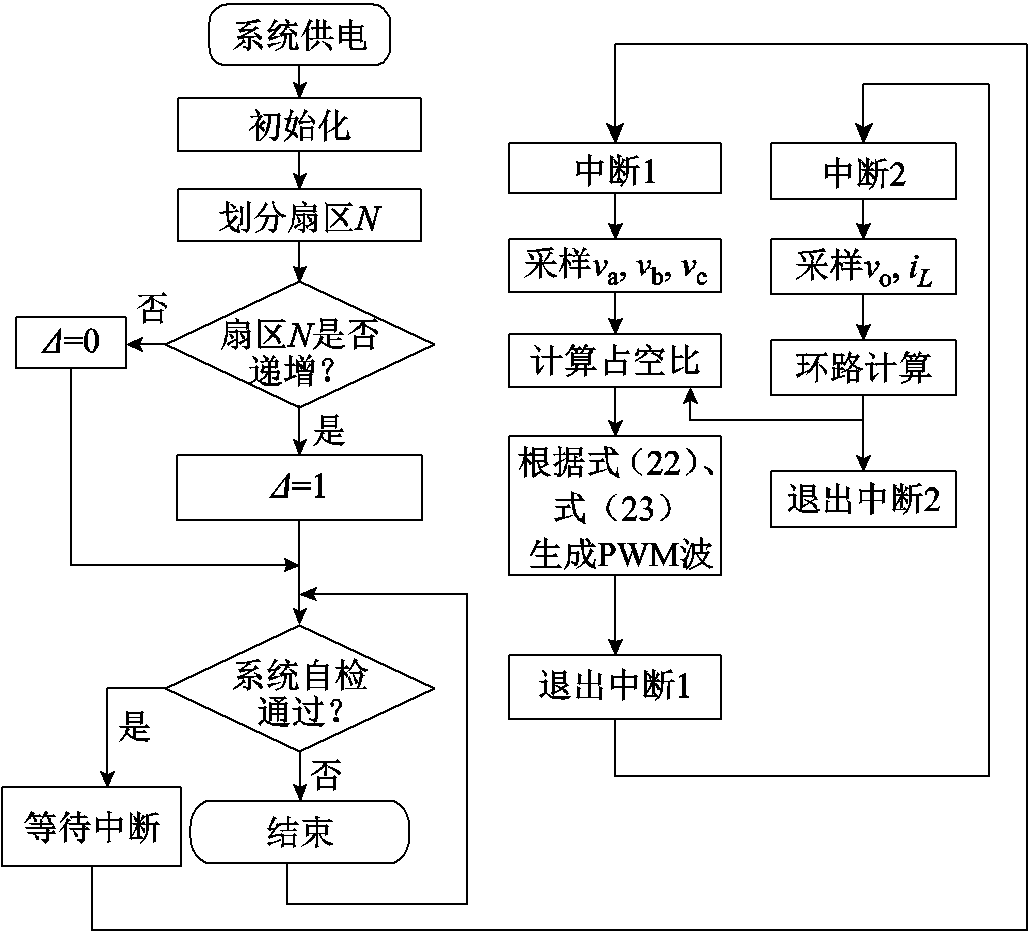
图10 相序自适应调制策略流程
Fig.10 Phase sequence adaptive modulation algorithm
以正相序时扇区12的PWM序列为例，正相序时，Δ = 1代入式（23）得Phasemax=0、Phasemin=0、Phasemid=Dmin，其移相过程如图11所示。由图11可见，输入电压为正相序时，由相序自适应调制策略调制生成的PWM序列为不对称PWM序列1。同理，当输入电压为负相序时，由相序自适应调制算法生成的PWM序列为不对称PWM序列2。
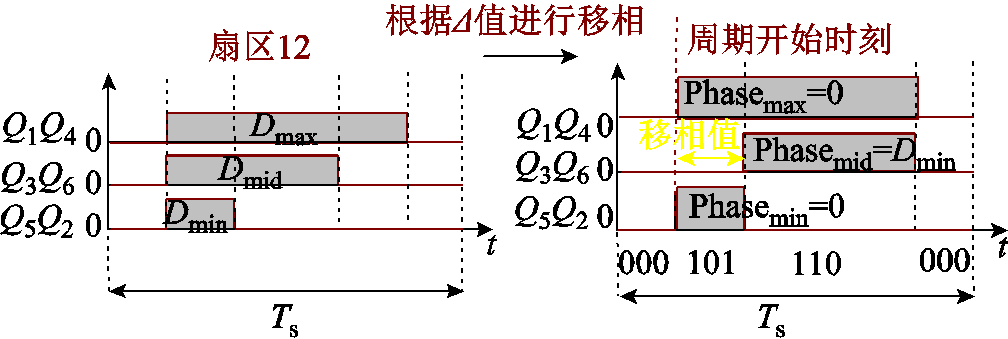
图11 相序自适应调制策略在正相序输入时扇区12的PWM序列的移相
Fig.11 The shift of the phase sequence adaptive modulation in sector 12 for positive phase sequence input
为验证理论分析结果，设计了一台1 kW的三相Buck整流器实验样机，实验样机及平台如图12所示，样机主要电路参数见表3。
图12 三相Buck整流器实验样机及平台
Fig.12 Experimental prototype and platform of three-phase Buck rectifier
表3 主要电路参数
Tab.3 Main circuit parameters
参数数值（型号） 三相输入电压Vac/V115 输入频率f/Hz400 输入滤波电感La,Lb,Lc/µH56 输入滤波电容Ca,Cb,Cc/nF880 开关频率fs/kHz200 输出电压Vo/V200
（续）
参数数值（型号） 输出功率Pout/W1000 输出电感Lp, Ln/µH130 输出电容Co/µF100 共模滤波器Cp, Cn/nF800 屏蔽层电容Cps,Cns/nF5 二极管VD1～VD6, VDFIDD08SG60CXTMA2 MOSFET Q1～Q6IPD60R180P7 微控制单元（MCU）DSPIC33EP64GS505
图13所示为正相序输入和负相序输入时，PWM序列1调制三相Buck整流器的输入电流波形。从图13a可知，输入电压为正相序时，输入电流THD较低，为1.2%；从图13b可知，输入电压为负相序时，输入电流发生明显畸变，THD为3.3%。
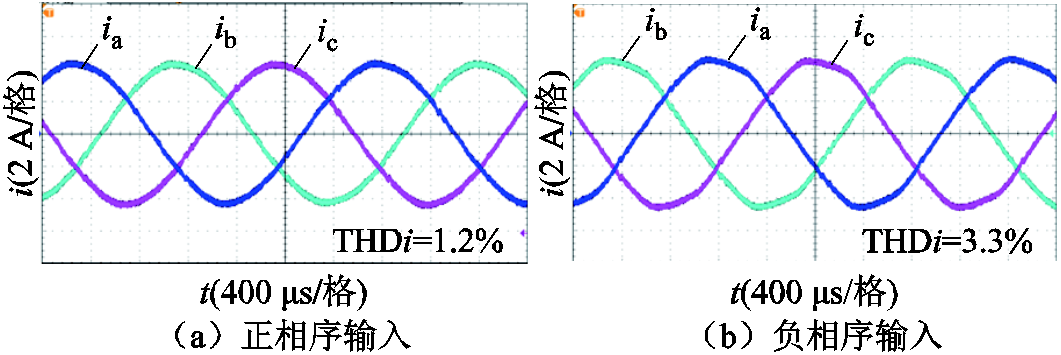
图13 正相序输入和负相序输入时，PWM序列1的三相Buck整流器输入电流实验波形
Fig.13 Experimental results of three-phase Buck rectifier input current by PWM sequence 1 at positive and negative phase sequence of input voltage
图14所示为正相序输入和负相序输入时，PWM序列1的三相Buck整流器输入电流以及电感电流的实验波形。从图14a可知，输入电压为正相序时，直流侧上、下电感电流及其差值较小；从图14b可知，输入电压为负相序时，直流侧上、下电感电流及其差值相对于正相序明显增加。
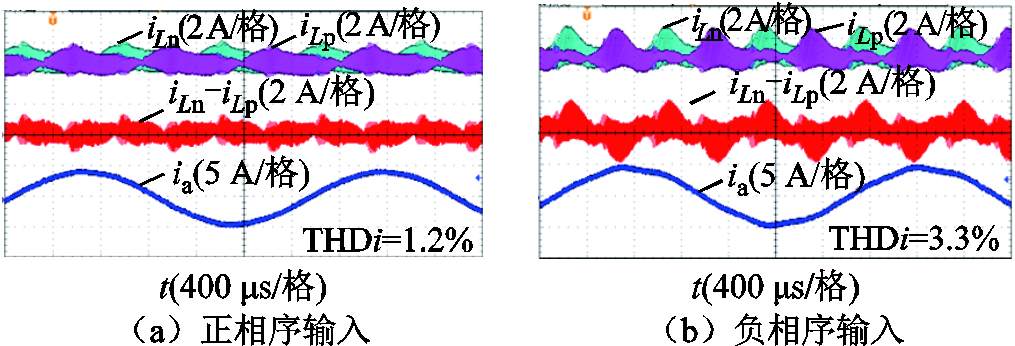
图14 正相序输入和负相序输入时，PWM序列1的三相Buck整流器实验波形
Fig.14 Experimental results of three-phase Buck rectifier by PWM sequence 1 at positive and negative phase sequence of input voltage
采用本文提出的相序自适应调制策略后，正相序和负相序输入时，三相Buck整流器的直流链电流纹波如图15a和图15b所示，输入电流实验波形如图16a和图16b所示。由图15可知，正相序输入和负相序输入时，本文提出的相序自适应调制三相Buck整流器的直流链纹波较小。
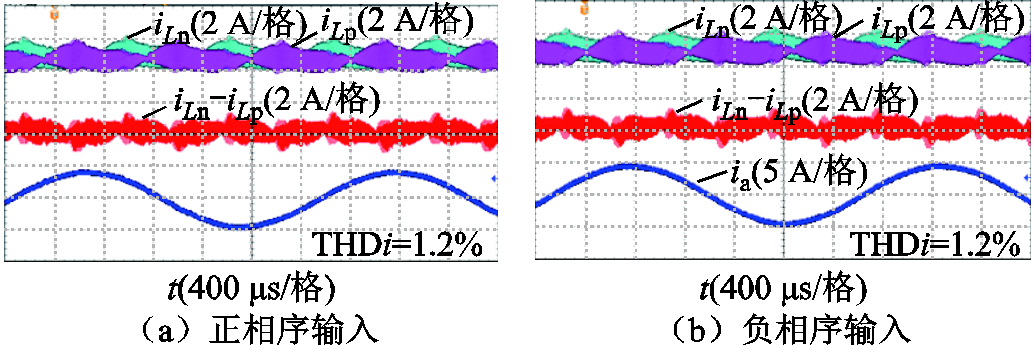
图15 不同输入电压相序时，相序自适应调制三相Buck整流器直流链电流及其纹波实验波形
Fig.15 Experimental results of three-phase Buck rectifier DC chain current and its ripple by phase sequence adaptive modulation at different phase sequence of input voltage
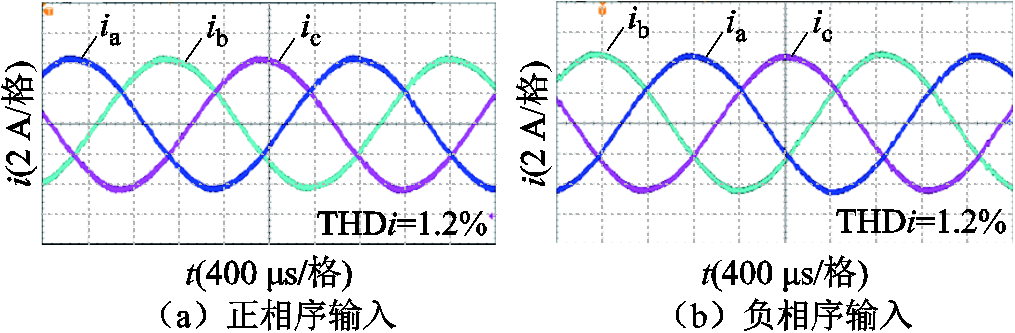
图16 不同输入电压相序时，相序自适应调制三相Buck整流器输入电流实验波形
Fig.16 Experimental results of three-phase Buck rectifier input current by phase sequence adaptive modulation at different phase sequence of input voltage
由图16可知，无论正相序还是负相序输入，输入电流均未发生明显畸变，输入电流THD都较低，为1.2%。
图17为输入电压相序列未知时，采用本文提出的相序自适应调制策略后，三相Buck整流器根据相序判别实现相序自适应调制策略的输入电流以及电感电流动态实验波形。由图17a和图17b可知，阶段1输入电压相序未知，此阶段的PWM序列与输入电压相序不匹配，输入电流出现明显畸变，直流侧上、下电感电流及其差值较大。阶段2系统根据扇区是否递增对输入电压相序进行判断并对Δ赋值，以改变PWM序列实现自适应，阶段2输入电流畸变和电感电流及其差值均减小。
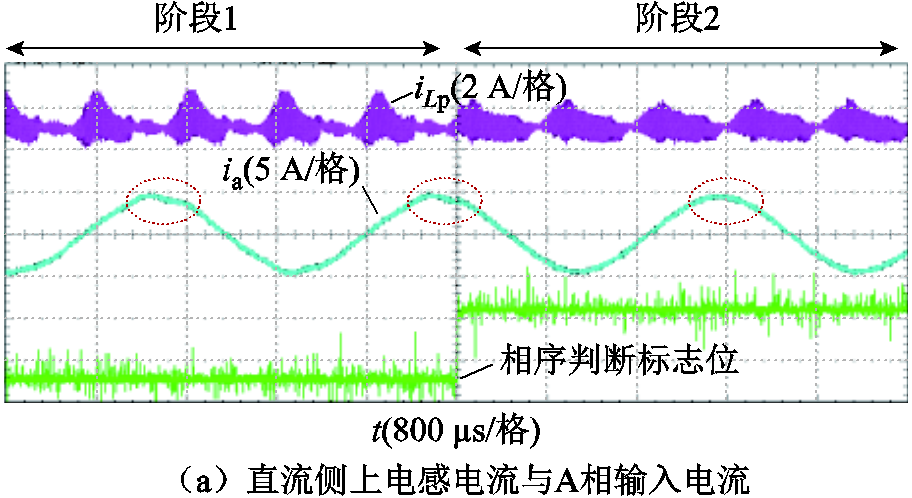
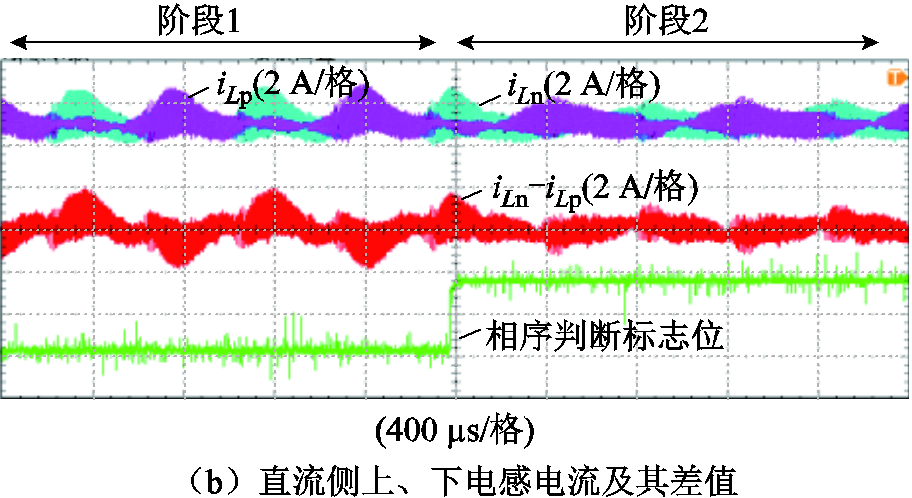
图17 输入电压相序未知时，相序自适应调制三相Buck整流器实验波形
Fig.17 Experimental results of three-phase buck rectifier by phase sequence adaptive modulation at unknown phase sequence of input voltage
实验与仿真波形和理论分析一致，说明整流器有效实现了相序自适应调制，抑制了不对称调制技术的不对称性对直流链电流的影响；在正相序输入和负相序输入时，输入电流均未出现明显畸变。
针对不对称调制的不对称性对三相Buck整流器直流链电流纹波特性的影响，本文分析了两种传统不对称调制的三相Buck整流器直流链纹波特性，解释了不对称调制的不对称性使输入电流发生畸变的原因。最后通过优化PWM序列的移相过程，完成输入电压相序与不对称调制发波逻辑的自适应。实现了三相Buck整流器输入电流在正相序和负相序输入时均不发生畸变，有效解决了不对称调制技术的不对称性带来的直流链电流纹波和输入电流畸变问题。
参考文献
[1] Chen Qiang, Xu Jianping, Zeng Fei, et al. An improved three-phase buck rectifier with low voltage stress on switching devices[J]. IEEE Transactions on Power Electronics, 2020, 36(6): 6168-6174.
[2] 郭强, 刘和平, 彭东林, 等. 一种考虑电池自身特性的电流源型充电系统[J]. 电工技术学报, 2016, 31(16): 16-25.
Guo Qiang, Liu Heping, Peng Donglin, et al. A current-source charging system considering the characteristics of battery[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 16-25.
[3] 曾嵘. 新能源分布式发电系统并网逆变技术研究[D]. 杭州: 浙江大学, 2011.
Zeng Rong. Investigation on the control technique of grid-connected inverter for distributed generation system integrated with renewable energy[D]. Hangzhou: Zhejiang University, 2011.
[4] 何黎鹏, 郭强, 肖蕙蕙, 等. 含负载前馈补偿的电流型PWM整流器改进无差拍控制[J]. 电工技术学报, 2024, 39(2): 501-513.
He Lipeng, Guo Qiang, Xiao Huihui, et al. Improved deadbeat control of current-source PWM rectifiers with load feed-forward compensation[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 501-513.
[5] 谢飞, 许建平, 郭夏, 等. 基于虚拟阻抗的三相Buck整流器输入不平衡控制策略[J]. 电工技术学报, 2024, 39(14): 4456-4466.
Xie Fei, Xu Jianping, Guo Xia, et al. A control strategy based on virtual impedance for three-phase buck rectifier under unbalanced phase-voltages[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4456-4466.
[6] 黄勇军, 李山, 郭强. 电流源型PWM整流器改进预测滑模控制[J]. 电气工程学报, 2024, 19(2): 100-109.
Huang Yongjun, Li Shan, Guo Qiang. Improved mode predictive sliding control of current source PWM rectifier[J]. Journal of Electrical Engineering, 2024, 19(2): 100-109.
[7] Chen Qiang, Xu Jianping, Tao Zhuangyi, et al. Analysis of sector update delay and its effect on digital control three-phase six-switch buck PFC converters with wide AC input frequency[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 931-946.
[8] 段恋鸿, 张代润, 黄钰. 三相三开关降压型PWM整流器的研究[J]. 电气技术, 2017, 18(1): 13-17.
Duan Lianhong, Zhang Dairun, Huang Yu. Research of a three-phase three-switch buck-type PWM rectifier [J]. Electrical Engineering, 2017, 18(1): 13-17.
[9] Guo Xiaoqiang, Yang Yong, Wang Baocheng, et al. Generalized space vector modulation for current source converter in continuous and discontinuous current modes[J]. IEEE Transactions on Industrial Electronics, 2020, 67(11): 9348-9357.
[10] Liu Pengcheng, Wang Zheng, Xu Yang, et al. Improved harmonic profile for high-power PWM current-source converters with modified space-vector modulation schemes[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11234-11244.
[11] 毕洪大, 刘艳辉, 刘金晶, 等. 大功率三电平逆变器SPWM载波调制策略研究[J]. 电气传动自动化, 2021, 43(4): 1-6.
Bi Hongda, Liu Yanhui, Liu Jinjing, et al. Research on SPWM carrier modulation strategy for high power three level inverter[J]. Electric Drive Automation, 2021, 43(4): 1-6.
[12] 邓玉, 李润陆, 徐雄风. SPWM调制法的改进研究[J]. 电工技术, 2018(4): 95-96.
Deng Yu, Li Runlu, Xu Xiongfeng. Research on improved SPWM modulation algorithm[J]. Electric Engineering, 2018(4): 95-96.
[13] 曹海彬, 许建平, 谢飞, 等. 一种低输入电流总谐波畸变率的三相Buck整流器不对称调制策略[J]. 电工技术学报, 2024, 39(8): 2541-2552.
Cao Haibin, Xu Jianping, Xie Fei, et al. An asymmetric modulation strategy for three-phase buck rectifier with low input current total harmonic distortion[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2541-2552.
[14] 王聪, 刘霞, 程红, 等. 一种三相线电压级联单位功率因数整流器负载不均衡特性分析及电压均衡控制策略[J]. 电工技术学报, 2024, 39(2): 525-540.
Wang Cong, Liu Xia, Cheng Hong, et al. Static characteristics and output voltage balance control of a novel line-voltage cascaded three-phase unity power factor rectifier under unbalanced load[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 525-540.
[15] Nussbaumer T, Kolar J W. Improving mains current quality for three-phase three-switch buck-type PWM rectifiers[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 967-973.
[16] Huang Rui, Xu Jianping, Chen Qiang, et al. An optimized asymmetric modulation scheme for three-phase buck rectifier without input current distortion at the sector boundaries[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14040-14044.
[17] Baumann M, Kolar J W. Comparative evaluation of modulation methods for a three-phase/switch buck power factor corrector concerning the input capacitor voltage ripple[C]//2001 IEEE 32nd Annual Power Electronics Specialists Conference, Vancouver, BC, Canada, 2001: 1327-1332.
[18] Cao Haibin, Yang Ping, Guo Xia, et al. An improved asymmetric modulation of current-source rectifier with CM filter for low voltage stress on switching devices[J]. IEEE Transactions on Power Electronics, 2023, 38(7): 7964-7970.
[19] 张强, 吴延飞, 张保顺, 等. 基于三相电流型五电平整流器的空间矢量脉宽调制算法[J]. 电工技术学报, 2020, 35(24): 5134-5141.
Zhang Qiang, Wu Yanfei, Zhang Baoshun, et al. Space vector pulse width modulation strategy based on three-phase five-level current source rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5134-5141.
[20] 郭小强, 杨勇, 王学惠. 电流源变换器直流链电流纹波抑制策略研究[J]. 中国电机工程学报, 2018, 38(20): 6071-6078.
Guo Xiaoqiang, Yang Yong, Wang Xuehui. Research on DC-link current ripple reduction for current source converter[J]. Proceedings of the CSEE, 2018, 38(20): 6071-6078.
[21] 刘高, 陈强, 马红波, 等. 三相Buck整流器级联直流变换器控制策略研究[J]. 电力电子技术, 2019, 53(9): 1-5.
Liu Gao, Chen Qiang, Ma Hongbo, et al. The research on the control strategy of three-phase current rectifier cascaded with buck DC/DC converter[J]. Power Electronics, 2019, 53(9): 1-5.
[22] 汪嘉炜, 许建平, 曹海彬. 适用于三相输入不平衡的电压前馈控制策略[J]. 电力电子技术, 2022, 56(9): 29-32, 49.
Wang Jiawei, Xu Jianping, Cao Haibing. A voltage feedforward control strategy suitable for unbalanced three-phase input[J]. Power Electronics, 2022, 56(9): 29-32, 49.
Abstract The input current total harmonic distortion (THD) of a three-phase buck rectifier is closely related to the modulation strategy. Space vector pulse width modulation (SVPWM) is widely used in three-phase buck rectifiers due to its simple digital implementation and flexible strategy. The three-segment asymmetric SVPWM has two different PWM sequences, which are generally considered to have equivalent vector synthesis effects. However, due to the influence of parasitic capacitances, the order of vector action affects the harmonic composition. Under the same input voltage conditions, these two asymmetric PWM sequences exhibit different DC chain current ripple characteristics. In addition, when the phase sequence of the input voltage changes, the corresponding DC chain current ripple changes accordingly, which leads to significant differences in the input currents of the three-phase buck rectifier. To deal with above issues, this paper proposes a phase sequence adaptive modulation strategy, which suppresses the DC chain current ripple and input current distortion caused by the asymmetry of the modulation technology.
This paper analyzes the operating modes of the two asymmetric PWM sequences in sector 12 when the input voltage is in positive phase sequence, the changes of the difference between the upper and lower inductor currents, the charging and discharging conditions of the parasitic capacitances Cps and Cns, and derives the formula for the input current. The analysis and derivation results show that there are significant differences in the DC chain current ripple characteristics of these two asymmetric PWM sequences and their impacts on the input current. When the input voltage is in positive phase sequence, compared with the asymmetric PWM sequence 1, the DC chain current and its ripple of the three-phase buck rectifier with the asymmetric PWM sequence 2 increase significantly. When the input voltage is in negative phase sequence, the asymmetric PWM sequence 2 has more advantages. For asymmetric modulation technology, the DC chain current and its ripple of the three-phase Buck rectifier are significantly affected by the phase sequence of the input voltage, and the change of phase sequence will cause obvious distortion of the input current.
This paper optimizes the phase shift in the digital implementation process and proposes a phase sequence adaptive modulation strategy to realize the logical matching between the input voltage phase sequence and the PWM sequence. To verify the analysis results, a 1 kW experimental prototype is designed. The experimental results show that when the asymmetric PWM sequence 1 modulation strategy is adopted, the input current THD of the three-phase buck rectifier is low (1.2%) under positive phase sequence input, while the input current is obviously distorted with a THD of 3.3% under negative phase sequence input. With the proposed phase sequence adaptive modulation strategy, both the DC chain current ripple and input current of the three-phase buck rectifier have no obvious distortion under either positive or negative phase sequence input, and the input current THD is low (1.2%) in both cases. In addition, when the input voltage phase sequence is unknown, the system can judge the input voltage phase sequence according to whether the sector is increasing and change the PWM sequence accordingly to achieve adaptation, thus suppressing the DC chain current ripple and input current distortion.
Keywords：Three-phase Buck rectifier, asymmetric modulation, DC chain current ripple, input current distortion, input phase sequence
陈 欣 女，1999年生，硕士，研究方向为电力电子功率变换器。
E-mail：1986490384@qq.com
许建平 男，1963 年生，教授，博士生导师，研究方向为电力电子数字控制技术、开关电源新颖控制技术、再生能源发电技术等。
E-mail：jpxu-swjtu@163.com（通信作者）
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.250310
国家自然科学基金资助项目（52477198）。
收稿日期 2025-02-27
改稿日期 2025-07-21
（编辑 郭丽军）