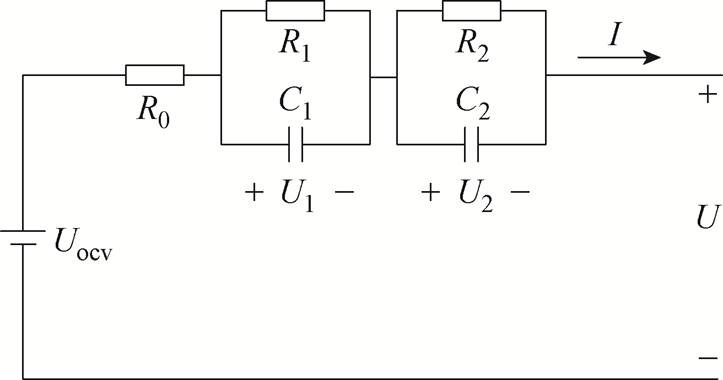
图1 二阶RC等效电路模型
Fig.1 Second order RC equivalent circuit model
摘要 锂电池的剩余电量(SOC)和健康状态(SOH)是优化电池管理、延长电池寿命及提高系统安全性的重要参数。为了提升电池SOC与SOH估计精度,提出一种调节因子改进模糊熵融合加权法(AFFEWF)的锂电池状态联合估计方法。首先以10个并联的18650锂电池为实验样本,进行间歇脉冲恒流放电实验获取OCV-SOC曲线,对比不同阶数拟合曲线的端电压预测效果;其次提出基于调节因子改进模糊熵融合加权法,通过调节因子对数据进行筛选,以端电压残差为依据计算各数据源的权重,从而得到加权后的联合估计结果;然后将调节因子改进模糊熵融合加权法与模糊熵融合加权法(FEWF)、多模型概率融合加权法(MMPWF)进行对比分析,以评估不同融合策略的性能表现;最后通过仿真软件对所提算法进行验证,结果显示,所提调节因子改进模糊熵融合加权法能有效提升锂电池SOC和SOH估计的精确度。
关键词:联合估计 卡尔曼算法 调节因子 模糊熵 融合加权法 锂电池
随着全球能源资源的逐渐枯竭和环境污染的日益加剧,新能源的开发和利用成为全球关注的焦点。其中电池储能技术在新能源领域占据重要地位。锂电池具有高输出电压、高能量密度、长循环寿命等优点[1],被广泛地应用在电动汽车、新型电力系统以及各种电子设备中[2]。准确地估计剩余电量(State of Charge, SOC)和健康状态(State of Health, SOH),有助于精确监控和管理电池状态,可以减少电池的损耗,延长其使用寿命,能够有效预防因电池状态异常引发的过热、短路等安全事故。优化能源分配和使用,确保电池工作在最佳状态,提升整体系统的效率[3-4]。对于电池管理系统(Battery Management System, BMS)而言,一个准确的SOC和SOH估计是很有必要的。
目前SOC的主要估计方法包含开路电压法、安时积分法、物理模型法和数据驱动法[5-6]。开路电压是通过脉冲实验来获得SOC和开路电压(Open Circuit Voltage, OCV)的映射关系,但开路电压需要静置一段时间才能准确获得,不适用于实际的在线实时估计情况[7]。安时积分法是使用电流对应时间的积分来计算当前的SOC值,其缺点在于精确度受到SOC初值、电流测量精度的影响,运行时间越长误差越大,一般无法单独使用[8]。数据驱动法是使用神经网络模型、支持向量机模型等进行估计。这些模型对实验数量依赖性较大,且模型运算量大,难以在实际中应用[9-10]。目前使用最多的是物理模型法,该方法是通过计算电池模型参数,来建立电池状态方程结合滤波算法进行SOC估计,其电池模型大致分为两种,分别是电化学模型和等效电路模型。文献[11-12]中提到了伪二维模型和单粒子模型两种电池的电化学模型,其模型以数学方程对电池内部化学反应和电荷转移过程进行描述,可以精确地反映电池内部变化特性,但缺点是其数学方程通常比较复杂,计算量大,在实际工程应用中不容易实现。等效电路模型是现在主流的研究方向,其模型有Rint模型、Thevenin模型[13]、二阶RC模型[14]、新一代汽车合作伙伴计划(Partnership for a New Generation of Vehicles, PNGV)模型、广义非线性(General Non-Linear, GNL)模型[15]。其中Rint模型精度低,应用性差;PNGV模型与GNL模型两者精度高但结构复杂,计算量大;Thevenin模型和二阶RC模型能够在模型精度与模型复杂度上较为平衡,在目前研究中被广泛使用;而二阶RC模型对比Thevenin模型能更好地模拟电池的动态过程,有着更高的精度。
SOH是BMS中的一个重要参数,其主要表征电池的老化程度。SOH会对SOC估计结果造成影响,不准确的SOC也会对SOH估计造成影响,因此许多学者针对二者的耦合关系进行了联合估计,在一定程度上解决了二者的相互影响[16]。文献[17]中提出基于无迹卡尔曼滤波算法和最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM)结合高斯过程回归(Gaussian Process Regression, GPR)的荷电状态与容量联合估计模型;文献[18]中使用自适应拓展卡尔曼(Adaptive Extended Kalman Filter, AEKF)算法结合麻雀搜索算法(Sparrow Search Algorithm, SSA)优化反向传播神经网络(Back Propagation Neural Network, BPNN)实现联合估计;文献[19]提出近似加权总体最小二乘算法(Fading Memory Approximate Weighted Total Least Squares, FMAWTLS)与基于多时间尺度扩展卡尔曼滤波算法(Multi-scale Extended Kalman Filter, MEKF)的方法来完成联合估计。Pang Hui等[20]使用改进粒子群(Improved Particle Swarm Optimization, IPSO)和粒子滤波(Particle Filter, PF)算法对锂电池的剩余电量和剩余寿命进行了联合估计。上述算法都实现了对联合估计精度的提升,但都存在算法计算复杂、参数敏感等问题,因此有学者提出使用多传感器融合加权法来提升估计精度。Fan Jie等[21]提出了深度神经网络与多传感器的结合实现了SOC和SOH的联合估计;Fu Shiyi等[22]提出了使用贝叶斯概率融合两种容积卡尔曼滤波器来估计SOC值,该方法提高了SOC的估计精度。但这两种方法均采用多个相同算法模型进行加权融合,由于相同算法在估计过程中表现出高度的一致性,导致融合数据缺乏多样性。基于此,本文构建了四种异构卡尔曼滤波的联合估计器,通过差异化估计趋势的动态互补有效抑制单一算法的固有偏差,确保融合数据的多样性。
本文在电池的二阶RC等效电路模型的基础上,提出了基于调节因子改进模糊熵融合加权法(AdjustFactor improved Fuzzy Entropy Weighted Fusion, AFFEWF)的锂电池状态联合估计方法。首先,使用4个不同的卡尔曼联合估计器获取SOC、SOH和端电压残差,不同的卡尔曼滤波算法估计趋势各不相同,有利于进行融合加权;其次,以端电压残差为依据,通过调节因子建立过滤机制用以过滤不良数据,降低不良数据对融合结果的影响,进一步提高融合结果的精度;最后,使用模糊熵融合加权算法计算各模型融合权重,使用美国城市道路循环测试(Urban Dynamometer Driving Schedule, UDDS)动态工况验证,并加入多模型概率融合加权法进行对比。仿真结果表明,该算法提高了SOC与SOH的估计精度。
本文使用二阶RC模型为电池的等效模型,如图1所示。

图1 二阶RC等效电路模型
Fig.1 Second order RC equivalent circuit model
根据基尔霍夫电压定理可得
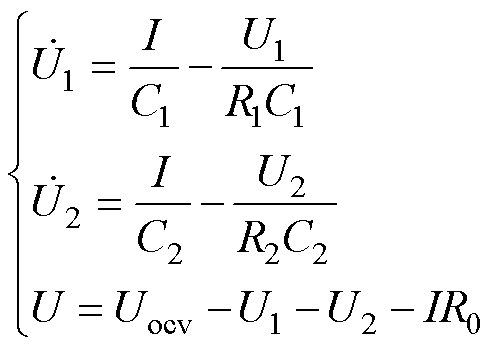 (1)
(1)
式中,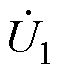 和
和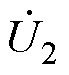 分别为C1和C2上的电压变化率;U1和U2分别为C1和C2上的电压;Uocv为开路电压;
分别为C1和C2上的电压变化率;U1和U2分别为C1和C2上的电压;Uocv为开路电压;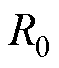 为电池内阻;
为电池内阻;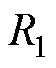 和
和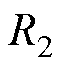 为电池极化内阻;
为电池极化内阻;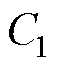 和
和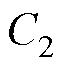 为电池极化电容;U和I分别为电池的端电压和电流。
为电池极化电容;U和I分别为电池的端电压和电流。
本文使用恒流脉冲放电实验来获得开路电压值。但需注意在电池组中,电池的不一致性会造成测量不准确[23],故本文使用的并联电池均采用新电池,保证电池组内的一致性。
实验平台由计算机端、交流隔离变压器、可编程直流电源、可编程电子负载、示波器和并联电池组组成,如图2所示。

图2 锂电池实验平台
Fig.2 Battery experiment platform
设置参数为5%的SOC为一个间隔进行恒流放电,放电电流值为30 A,静置时长为2 h。电池OCV实验端电压如图3所示。
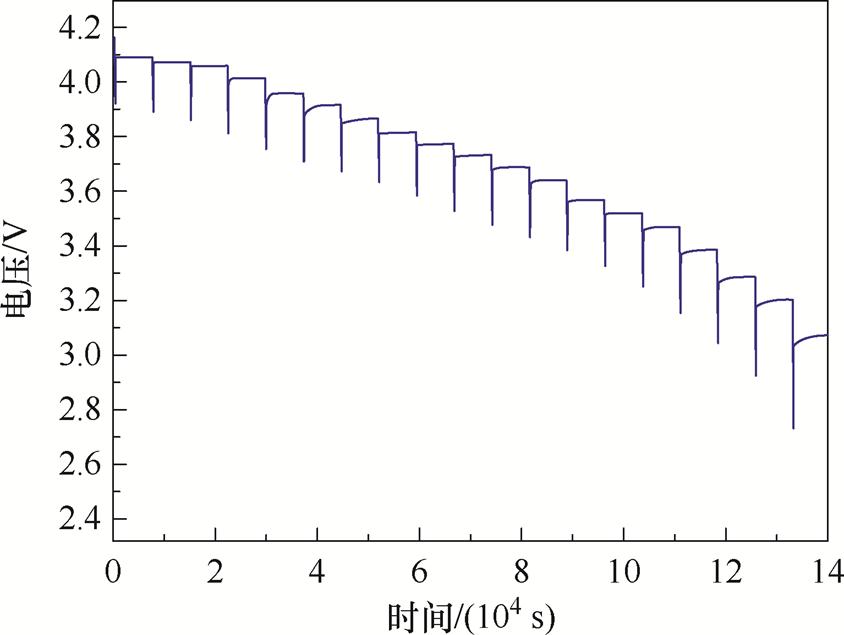
图3 电池OCV实验端电压
Fig.3 Battery OCV experimental end voltage
根据图3可以得到拟合OCV-SOC曲线如图4所示。
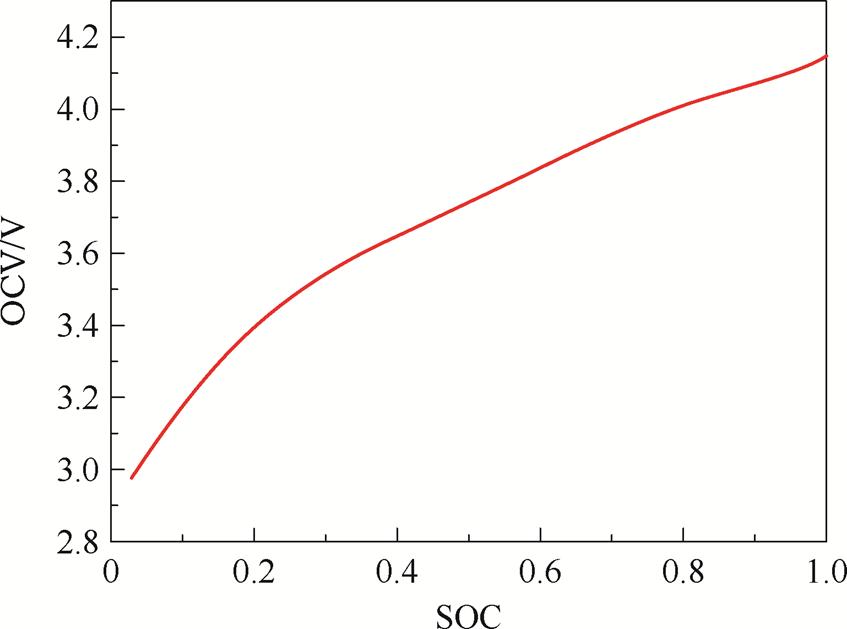
图4 拟合OCV-SOC曲线
Fig.4 Order fitted OCV-SOC curve
通过图3端电压变化曲线可以获得等效电路模型中的电阻电容与端电压、放电电流的关系式。其端电压变化曲线如图5所示。
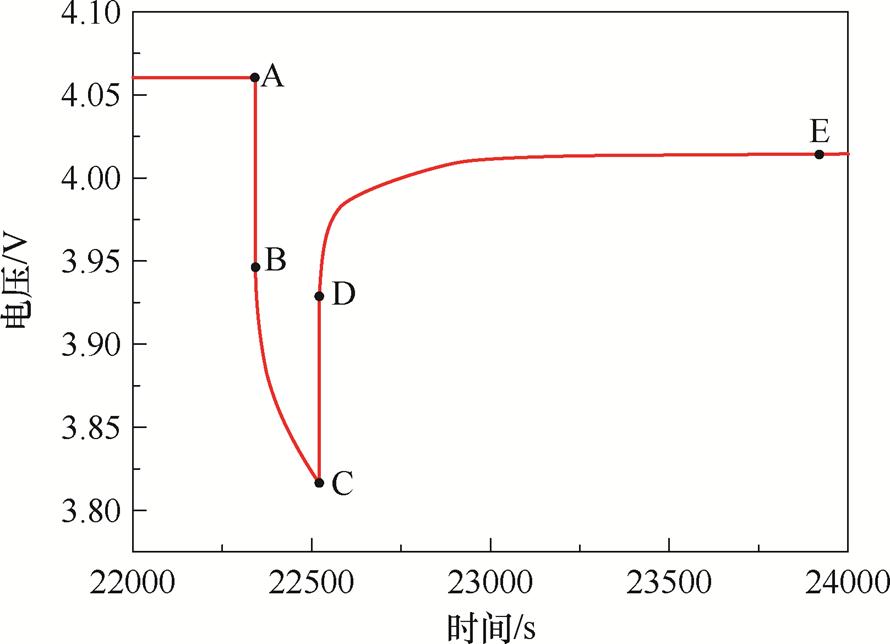
图5 脉冲实验端电压变化曲线
Fig.5 Terminal voltage change curve
由图5所示,造成端电压突变的原因在于电池的欧姆电阻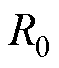 ,由此可得
,由此可得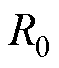 与U、I的关系式为
与U、I的关系式为
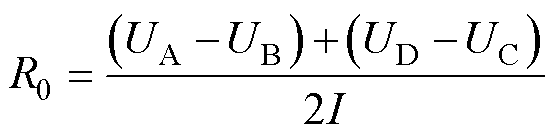 (2)
(2)
由图5所示,电压在DE段缓慢上升。端电压缓慢上升的原因在于极化电容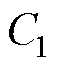 、
、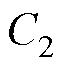 和极化电阻
和极化电阻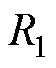 、
、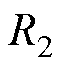 。由此可得
。由此可得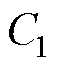 、
、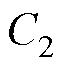 、
、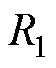 、
、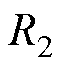 与U、I的关系式为
与U、I的关系式为
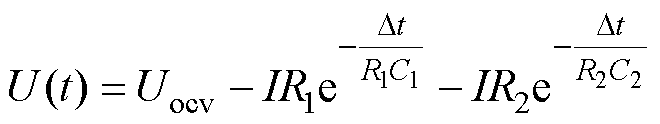 (3)
(3)
式中,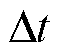 为采样间隔。
为采样间隔。
本文采用卡尔曼联合估计算法,其中一个卡尔曼算法负责估计SOC,称为状态估计器;另一个负责估计SOH和电池的电阻和电容,称为参数估计器。
SOC计算公式为
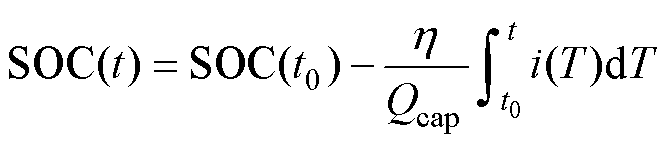 (4)
(4)
式中,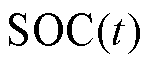 与
与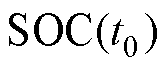 为t时刻和初始时刻
为t时刻和初始时刻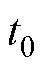 的SOC值;
的SOC值;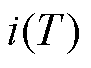 为T时刻瞬时电流值;h为库伦效率;
为T时刻瞬时电流值;h为库伦效率;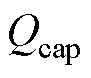 为当前最大容量。
为当前最大容量。
SOH的定义为
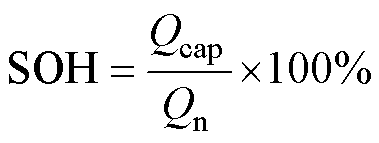 (5)
(5)
式中,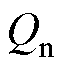 为电池的额定容量。
为电池的额定容量。
对式(1)、式(3)和式(4)进一步进行离散化处理,得
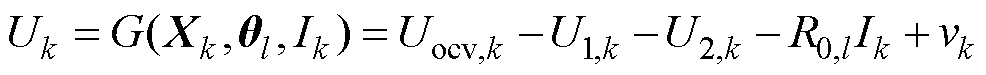 (6)
(6)
式中,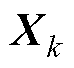 为k时刻的状态变量;
为k时刻的状态变量;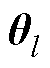 为l时刻的参数变量;R0,l为l时刻的电池内阻;
为l时刻的参数变量;R0,l为l时刻的电池内阻;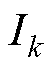 为k时刻的电流值;
为k时刻的电流值;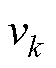 为k时刻的系统观测噪声。
为k时刻的系统观测噪声。
将式(6)改写为
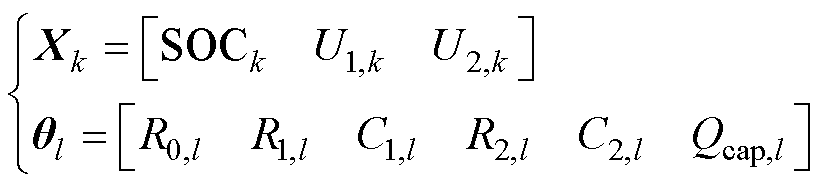 (7)
(7)
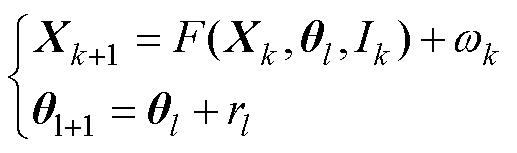 (8)
(8)
式中,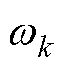 与
与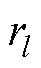 分别为k时刻状态估计器和l时刻参数估计器的系统过程噪声。
分别为k时刻状态估计器和l时刻参数估计器的系统过程噪声。
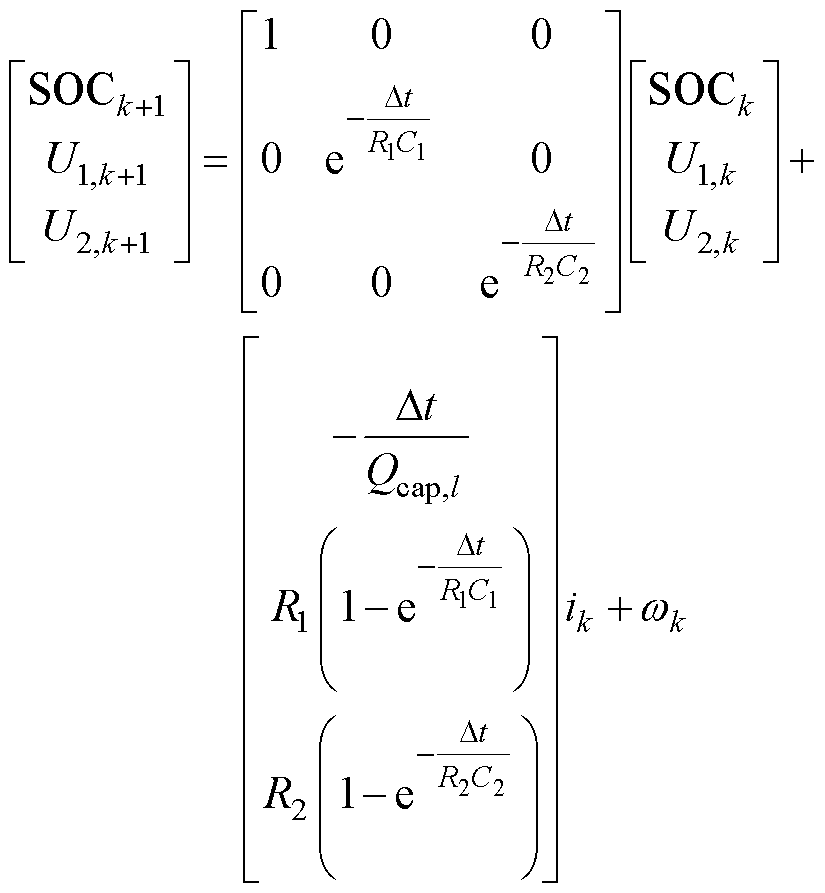 (9)
(9)
式(6)与式(9)为卡尔曼联合估计算法的观测方程与状态方程。
本文将以EKF-UKF算法为例介绍卡尔曼联合估计算法。该算法以EKF为状态估计器,UKF为参数估计器,结合了两种卡尔曼算法,在本文使用的四种卡尔曼联合估计算法中具有代表性。
EKF-UKF算法的具体步骤如下:
1)参数初始化
初始化状态变量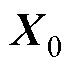 、参数变量
、参数变量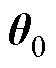 、状态协方差矩阵
、状态协方差矩阵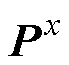 和参数协方差矩阵
和参数协方差矩阵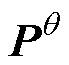 。
。
2)UT变换
对参数协方差矩阵进行Cholesky分解,以便生成Sigma点,其式为
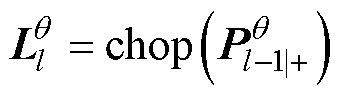 (10)
(10)
式中,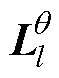 为参数估计器在l时刻的Cholesky分解因子;
为参数估计器在l时刻的Cholesky分解因子;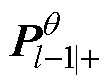 为参数估计器在
为参数估计器在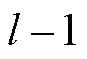 时刻后验估计的方差矩阵。
时刻后验估计的方差矩阵。
对参数变量q进行UT变换生成2n+1个Sigma点,即
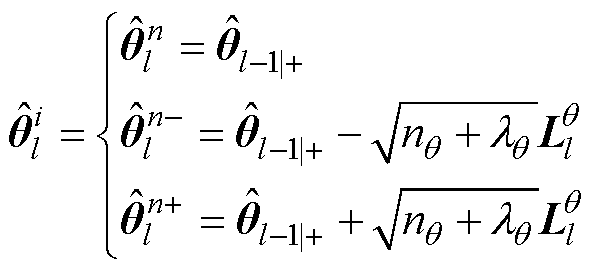 (11)
(11)
式中,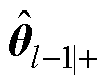 为第l-1时刻后验估计的参数变量的估计值;
为第l-1时刻后验估计的参数变量的估计值;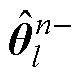 、
、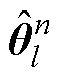 、
、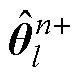 分别为第l时刻参数变量估计值的前n个、第n个、后n个Sigma点;
分别为第l时刻参数变量估计值的前n个、第n个、后n个Sigma点;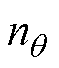 为参数估计变量的维度;
为参数估计变量的维度;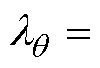
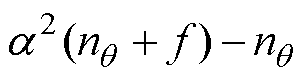 ,其中a为比例因子,一般取值范围是0~1之间,f为Sigma点的自由度。
,其中a为比例因子,一般取值范围是0~1之间,f为Sigma点的自由度。
3)权重计算
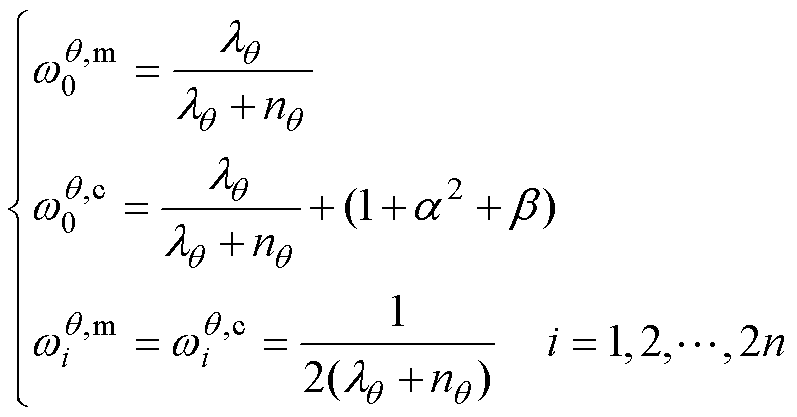 (12)
(12)
式中,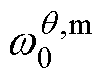 为初始的计算均值的权重值;
为初始的计算均值的权重值;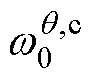 为初始的计算协方差的权重值;
为初始的计算协方差的权重值;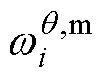 为i时刻的计算均值的权重值;b用于优化Sigma点参数权重,使得Sigma点权重更好地匹配高斯分布的统计特性,对于电池的非线性系统,其值一般取2。
为i时刻的计算均值的权重值;b用于优化Sigma点参数权重,使得Sigma点权重更好地匹配高斯分布的统计特性,对于电池的非线性系统,其值一般取2。
4)先验估计
更新状态变量X、参数变量q、状态协方差矩阵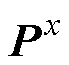 和参数协方差矩阵
和参数协方差矩阵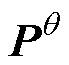 。
。
 (13)
(13)
式中,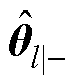 、
、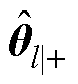 分别为在l时刻参数变量的先验估计、后验估计;
分别为在l时刻参数变量的先验估计、后验估计;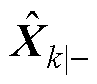 为在k时刻状态变量的先验估计;
为在k时刻状态变量的先验估计;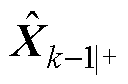 为在k-1时刻状态变量的后验估计;
为在k-1时刻状态变量的后验估计;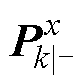 为在k时刻状态协方差矩阵的先验估计;
为在k时刻状态协方差矩阵的先验估计;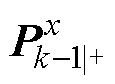 为在k-1时刻状态协方差矩阵的后验估计;
为在k-1时刻状态协方差矩阵的后验估计;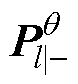 为在l时刻参数协方差矩阵的先验估计;
为在l时刻参数协方差矩阵的先验估计;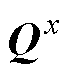 和
和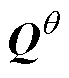 分别为状态估计器和参数估计器的测量噪声协方差矩阵。
分别为状态估计器和参数估计器的测量噪声协方差矩阵。
5)增益计算和量测更新
状态估计器测量更新式为
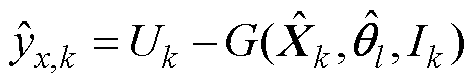 (14)
(14)
式中,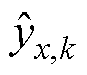 为k时刻状态量测估计值。
为k时刻状态量测估计值。
参数估计器量测更新式为
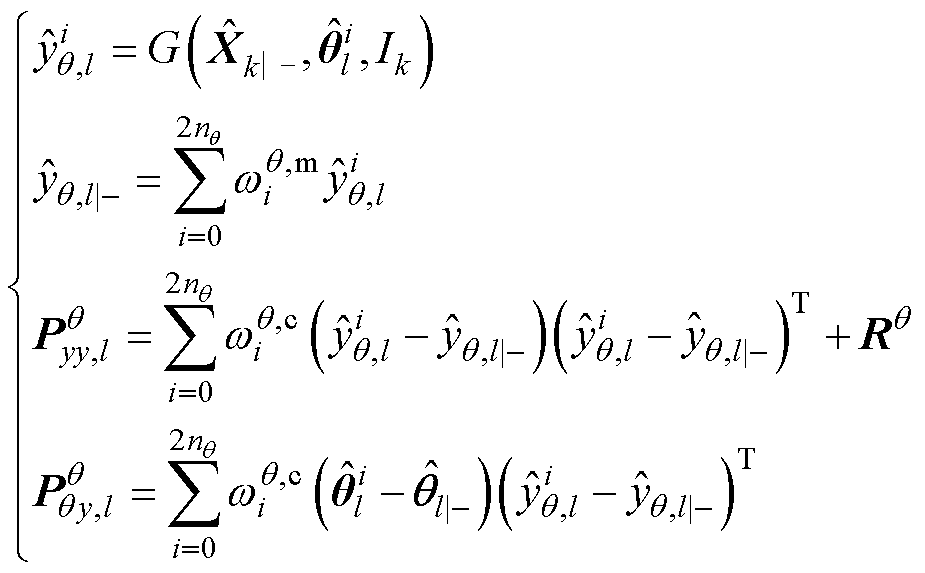 (15)
(15)
式中,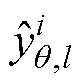 为在l时刻第i个Sigma点的参数量测估计值;
为在l时刻第i个Sigma点的参数量测估计值;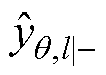 为在l时刻参数量测的先验估计值;
为在l时刻参数量测的先验估计值;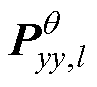 为在l时刻的参数估计器的观测协方差矩阵;
为在l时刻的参数估计器的观测协方差矩阵;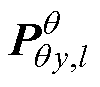 为在l时刻的参数估计器的参数与观测之间的协方差矩阵;
为在l时刻的参数估计器的参数与观测之间的协方差矩阵;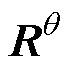 为参数估计器测量噪声;
为参数估计器测量噪声;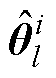 为在l时刻第i个Sigma点的参数变量估计值。
为在l时刻第i个Sigma点的参数变量估计值。
计算状态卡尔曼增益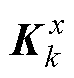 和参数卡尔曼增益
和参数卡尔曼增益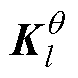 ,其式为
,其式为
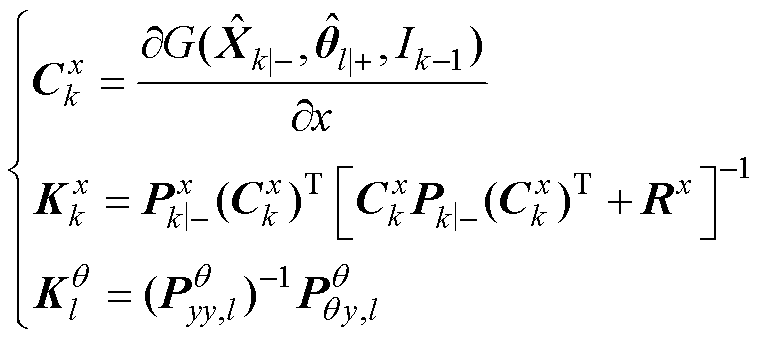 (16)
(16)
式中,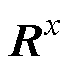 为状态估计器测量噪声。
为状态估计器测量噪声。
6)后验估计
判断状态估计器的取样时间是否满足参数估计器的运行条件,如果满足,则计算参数卡尔曼增益及测量更新;否则,继续运行状态估计器。
参数估计器后验估计式为
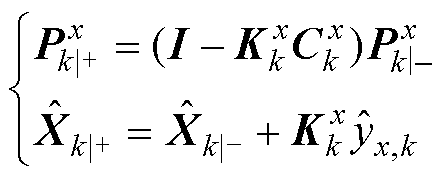 (17)
(17)
式中,I为单位矩阵。
状态估计器后验估计式为
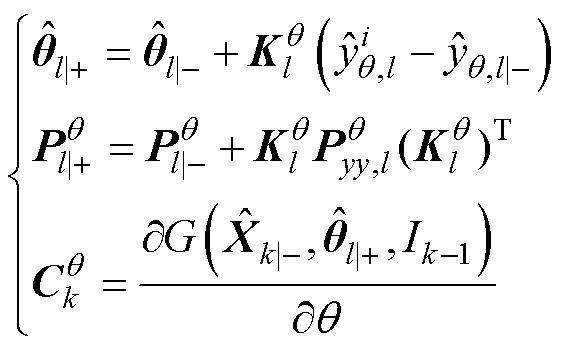 (18)
(18)
等效电路模型的SOC和SOH估计有着很好的精度和抗差能力,但通过单一的优化滤波算法去提高SOC和SOH估计精度较困难[22],因此使用融合加权法来提升联合估计精度。
本文将以多模型概率融合加权法(Multi-Model Probabilities based Weighted Fusion, MMPWF)为例进行对比分析。该算法是基于各个模型中估计精度相关参数,经过相应运算得到对应的权重,在电池等效电路模型中端电压残差就可以对估计模型的精度进行有效评估[24]。故本文使用等效电路模型中端电压残差来构建条件概率密度函数。
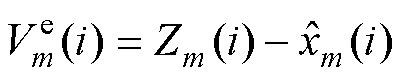 (19)
(19)
式中,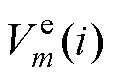 为第m个卡尔曼联合估计模型在i时刻的端电压残差;
为第m个卡尔曼联合估计模型在i时刻的端电压残差;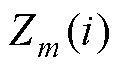 为第m个卡尔曼联合估计模型在i时刻的测量端电压;
为第m个卡尔曼联合估计模型在i时刻的测量端电压;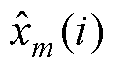 为第m个卡尔曼联合估计模型在i时刻电压的预测值。
为第m个卡尔曼联合估计模型在i时刻电压的预测值。
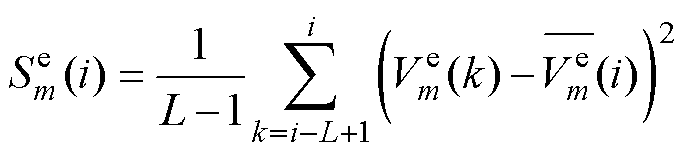 (20)
(20)
式中,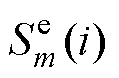 为第m个模型在i时刻的残差协方差;L为开窗长度;
为第m个模型在i时刻的残差协方差;L为开窗长度;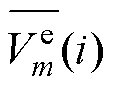 为第m个卡尔曼联合估计模型在以i时刻为末端的窗口内端电压残差的均值。
为第m个卡尔曼联合估计模型在以i时刻为末端的窗口内端电压残差的均值。
计算i时刻第m个卡尔曼联合估计模型的条件概率密度函数,即
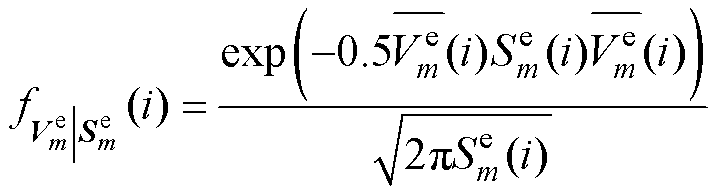 (21)
(21)
计算i时刻第m个卡尔曼联合估计模型的权重值为
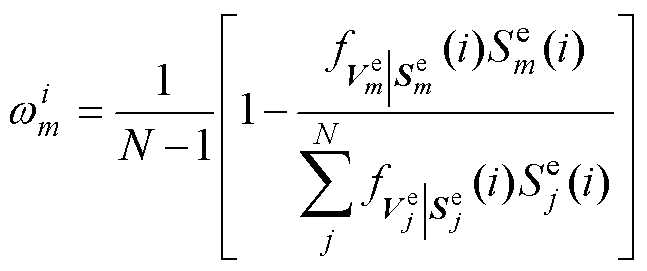 (22)
(22)
式中,N为卡尔曼联合估计模型的总数,本文取N=4。
权重计算后,按照权重将卡尔曼联合估计模型的结果进行融合得出最终的联合估计。
模糊熵融合加权法(Fuzzy Entropy Weighted Fusion, FEWF)是基于Zadeh的模糊熵思想,以模糊熵来表征量测集合的模糊程度[25],使用模糊程度来计算相应权重,其计算式为
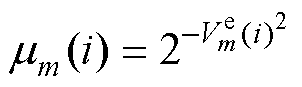 (23)
(23)
式中,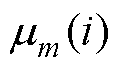 为第m个卡尔曼联合估计模型在i时刻的隶属度函数。
为第m个卡尔曼联合估计模型在i时刻的隶属度函数。
模糊熵的计算公式[24]为
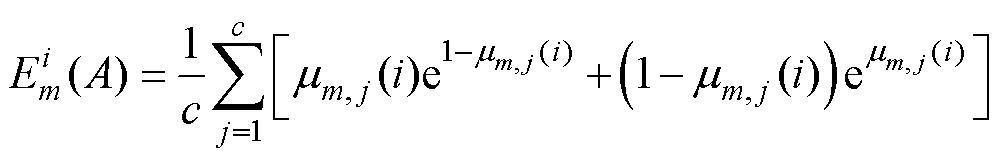 (24)
(24)
式中,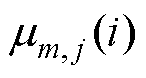 为在i时刻第m个卡尔曼联合估计模型的第j种测量元素的隶属度函数;
为在i时刻第m个卡尔曼联合估计模型的第j种测量元素的隶属度函数;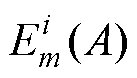 为第m个卡尔曼联合估计模型在i时刻的模糊熵;c为滤波器中测量元素的个数,本文构建隶属度函数只使用了端电压残差,即c=1。
为第m个卡尔曼联合估计模型在i时刻的模糊熵;c为滤波器中测量元素的个数,本文构建隶属度函数只使用了端电压残差,即c=1。
根据模糊熵理论,模糊熵E越大,模糊程度越高,代表该滤波器的可靠性越低。
对模糊熵按式(25)进行处理。
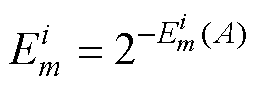 (25)
(25)
权重计算公式为
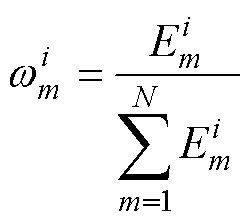 (26)
(26)
FEWF算法基于多个滤波器的结果,通过赋予不同权重来提高预测精度。如果某些滤波器的预测精度不佳,其权重值会减小,但仍可能影响整体预测精度。为此,本文引入调节因子(Adjust Factor)的概念。设置调节因子d,将精度不符合要求的滤波器预测结果摒弃,从而提升预测精度。
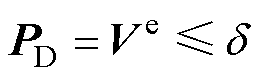 (27)
(27)
式中,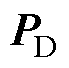 为判断向量,大小为
为判断向量,大小为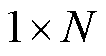 ;当滤波器的端电压残差满足条件时,其值为1,反之为0。
;当滤波器的端电压残差满足条件时,其值为1,反之为0。
权重计算公式变换为
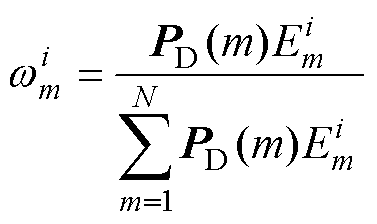 (28)
(28)
在判断出现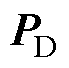 向量为全0向量时,将
向量为全0向量时,将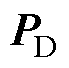 向量取反,使其变为全1向量。
向量取反,使其变为全1向量。
i时刻SOC与SOH值为
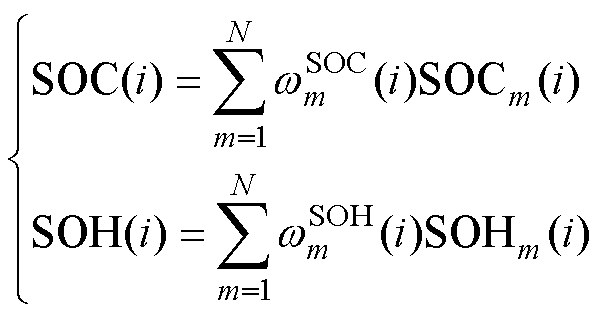 (29)
(29)
式中,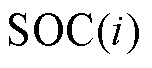 和
和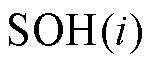 分别为i时刻的SOC和SOH融合估计值;
分别为i时刻的SOC和SOH融合估计值;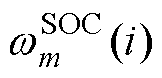 和
和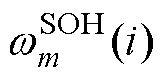 分别为第i时刻第m个滤波器的SOC和SOH的权重;
分别为第i时刻第m个滤波器的SOC和SOH的权重;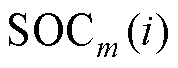 和
和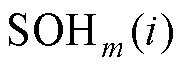 分别为第i时刻第m个滤波器的SOC和SOH的估计值。
分别为第i时刻第m个滤波器的SOC和SOH的估计值。
本文提出的基于调节因子改进模糊熵融合加权法的锂电池状态联合估计方法框架如图6所示。
(1)通过实验获取OCV-SOC曲线和其他工况的端电压电流数据。
(2)建立4个使用不同卡尔曼联合估计算法的电池模型进行联合估计,获取融合所需数据。
(3)以电池模型的端电压残差为依据,使用调节因子过滤不良数据。
(4)计算AFFEWF的权重,根据权重加权求和4个模型的SOC和SOH联合估计结果,从而提升估计精度。

图6 基于AFFEWF融合加权法的锂电池状态联合估计流程
Fig.6 Flow chart of lithium battery state joint estimation based on AFFEWF fusion weighting method
为了验证AFFEWF算法的联合估计性能,本文使用UDDS动态工况对算法参数辨识和联合估计进行验证。工况曲线一个循环时长为1 370 s,模拟了车辆在城市道路行驶过程中加速、减速、匀速和怠速四种情况。测试结果电压电流如图7所示。
本文的参数辨识部分由4个卡尔曼联合估计算法中的参数估计器完成。在UDDS工况下,4个参数估计器的参数估计效果均不相同,其估计效果如图8所示。
图8a所示4个参数估计器对于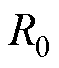 的估计趋势大致相同,在实际情况中锂电池的内阻通常与锂电池的寿命有关,在一次充放电过程中内阻变化较小。故本文中4个参数估计器所估计的内阻大小相近,符合实际情况。
的估计趋势大致相同,在实际情况中锂电池的内阻通常与锂电池的寿命有关,在一次充放电过程中内阻变化较小。故本文中4个参数估计器所估计的内阻大小相近,符合实际情况。
图8b和图8c所示4个参数估计器在对极化电阻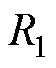 辨识效果相差不大的情况之下,对于极化电容
辨识效果相差不大的情况之下,对于极化电容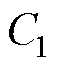 ,EKF参数估计器与UKF参数估计器差别比较大。
,EKF参数估计器与UKF参数估计器差别比较大。
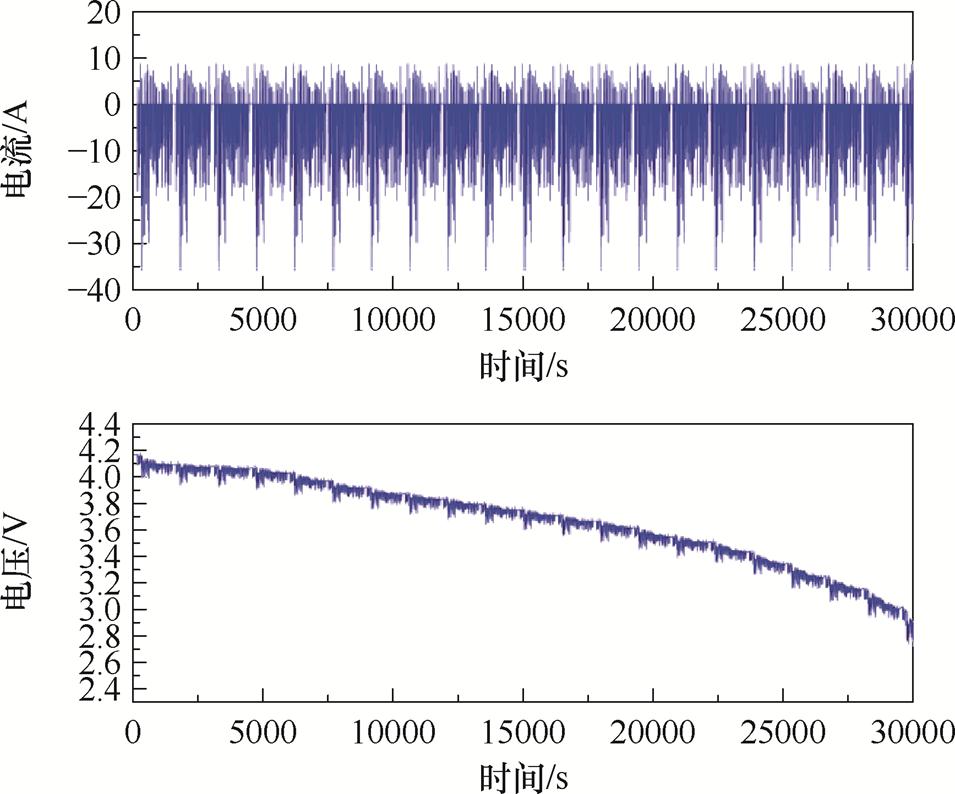
图7 UDDS工况
Fig.7 UDDS condition
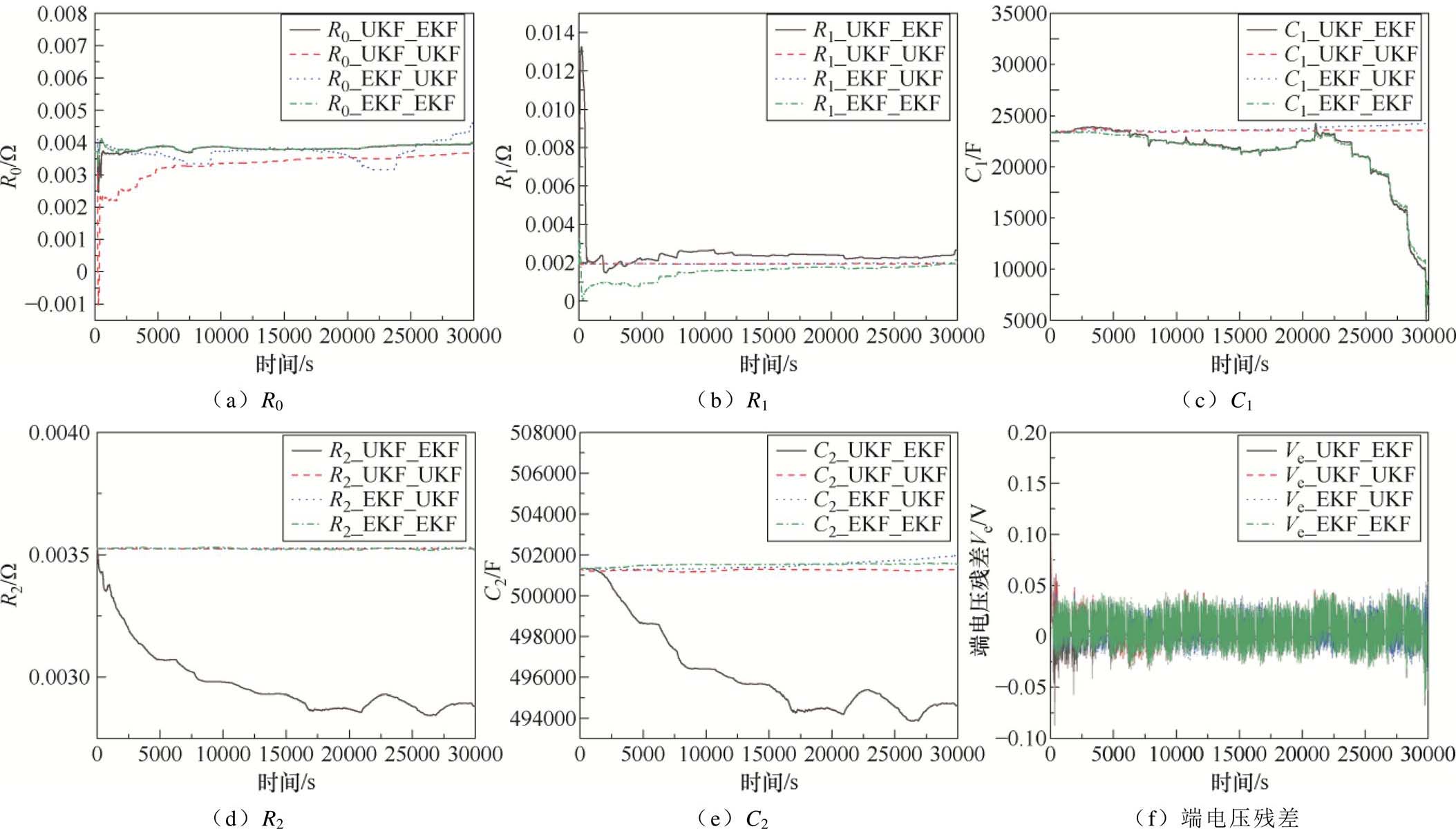
图8 四种卡尔曼联合估计算法参数辨识结果
Fig.8 Parameter identification results of 4 Kalman joint estimation algorithms figure
图8d和图8e中对于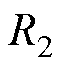 和
和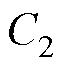 的参数辨识结果由3个参数估计器给出了相差无几的结果,只有UKF-EKF的参数估计器对于
的参数辨识结果由3个参数估计器给出了相差无几的结果,只有UKF-EKF的参数估计器对于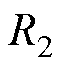 和
和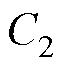 的辨识结果低于其他3个参数估计器。
的辨识结果低于其他3个参数估计器。
如图8f所示,4个参数估计器结果所建立的等效电路模型的端电压残差大致都在0.05 V以下,由此可知,4个等效电路模型的精度均能够满足联合估计的要求。
综上所述,在相同的工况情况下,4个参数估计器均能较好地完成参数估计任务,且所建立的4个等效电路模型在不同时刻的端电压残差不同,适合使用融合加权法进行权重计算。
本文在SOC估计中分别采用了加入调节因子和不加入调节因子的模糊熵融合加权法,用于验证调节因子的效果,其调节因子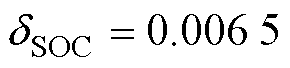 。同时加入多模型概率融合加权法进行估计对比,结果如图9所示。
。同时加入多模型概率融合加权法进行估计对比,结果如图9所示。
为了能够更加直观地对比各个算法的SOC估计的精度,本文将使用最大绝对误差(Maximum Absolute Error, MAX)、平均绝对误差(Mean Absolute Error, MAE)、方均根误差(Root Mean Square Error, RMSE)为估计精度评价标准。SOC估计误差结果见表1。
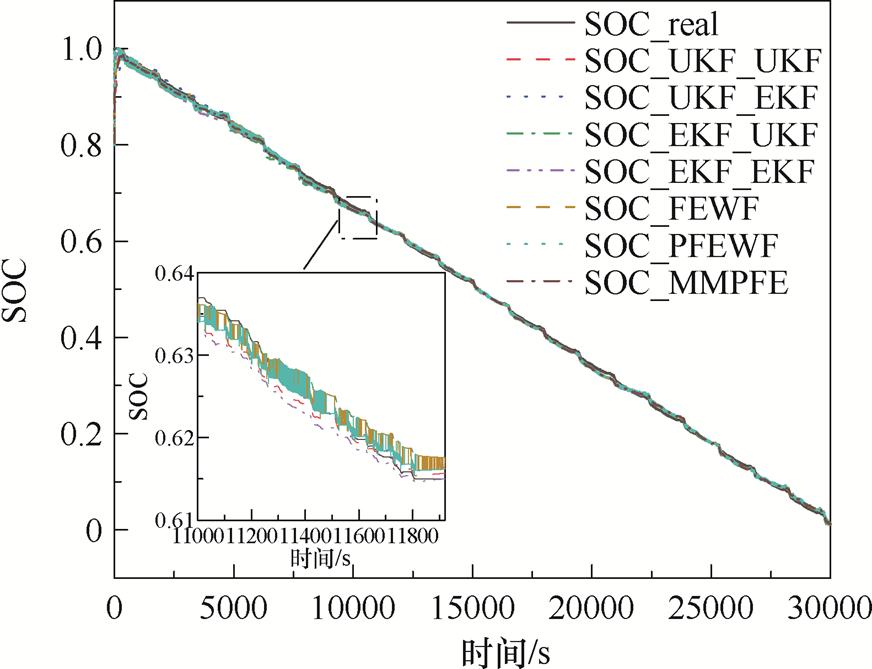
图9 SOC估计值与真实值
Fig.9 SOC estimates and true values
表1 SOC估计误差分析
Tab.1 SOC estimation error analysis
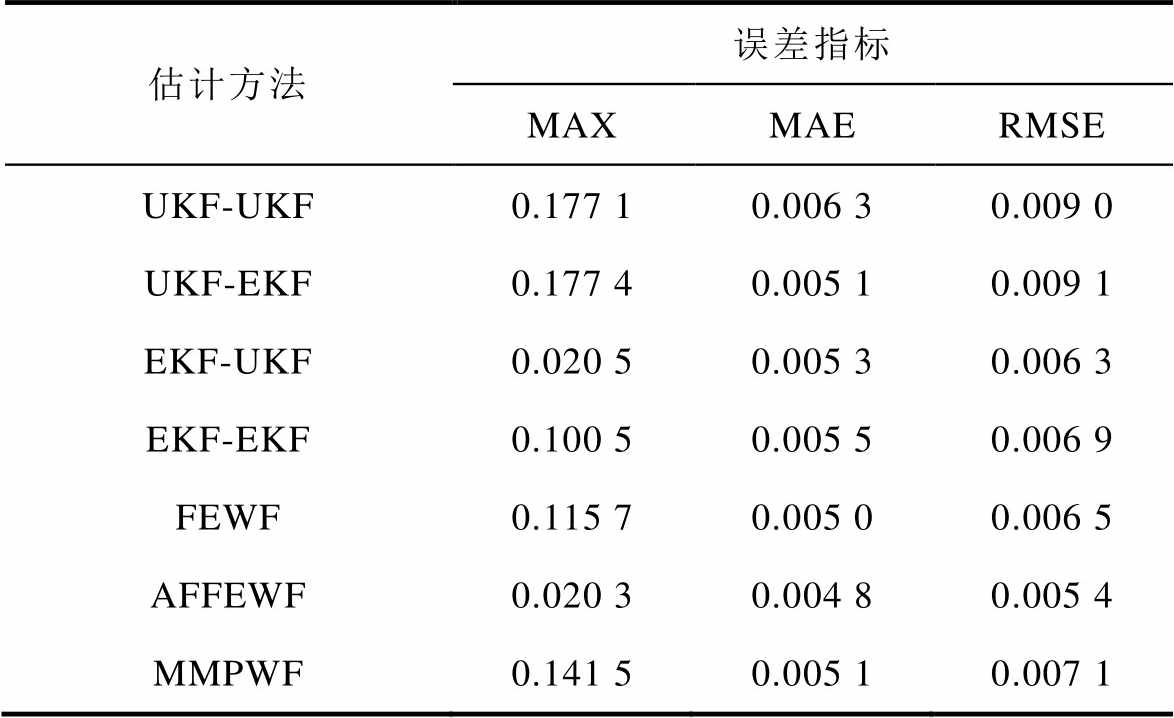
估计方法误差指标 MAXMAERMSE UKF-UKF0.177 10.006 30.009 0 UKF-EKF0.177 40.005 10.009 1 EKF-UKF0.020 50.005 30.006 3 EKF-EKF0.100 50.005 50.006 9 FEWF0.115 70.005 00.006 5 AFFEWF0.020 30.004 80.005 4 MMPWF0.141 50.005 10.007 1
以MAX为依据时,在4个卡尔曼联合估计算法中效果最好的是EKF-UKF算法,其MAX值为0.020 5,AFFEWF算法为0.020 3,约提升了大约1%。FEWF算法和MMPWF算法的MAX值分别为0.115 7和0.141 5,效果仅低于UKF-UKF算法和UKF-EKF算法的0.177 1和0.177 4,不及EKF-UKF算法和EKF-EKF算法的0.020 5和0.100 5;而AFFEWF算法对比FEWF算法和MMPWF算法分别提升了82.45%和85.65%。
以MAE为依据时,单个卡尔曼联合估计算法中效果最好的是UKF-EKF算法,其值为0.005 1;3个融合算法在这个误差度量标准中均取得不错的效果,其中效果最好的AFFEWF值为0.004 8,对比UKF-EKF提升了5.88%。FEWF算法和MMPWF算法在MAE上为0.005 0和0.005 1,AFFEWF算法对比二者分别提升了4%和5.88%。
以RMSE为依据时,表1所呈现的数据情况与MAX相同,卡尔曼联合估计算法中最佳的是EKF-UKF算法,其值为0.006 3。融合算法中FEWF算法与MMPWF算法的效果不佳,二者的值为0.006 5与0.007 1,不如EKF-UKF算法;而AFFEWF算法在RMSE上的值为0.005 4,对比EKF-UKF算法、FEWF算法与MMPWF算法的提升分别为14.29%、16.92%和23.94%。
AFFEWF算法与4个卡尔曼联合估计算法的对比表明,AFFEWF算法能显著提高SOC估计的精度。FEWF算法和MMPWF算法在SOC精度估计上的不足,主要是受到不良数据的影响,导致估计精度下降;而引入调节因子的AFFEWF算法能够有效过滤不良数据,从而提升估计精度。
针对SOH估计,本文采取的对比方法与SOC部分相同,除了4个卡尔曼联合估计算法部分,加入FEWF算法和MMPWF算法来验证调节因子的作用,调节因子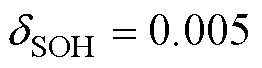 。同样使用MAX、MAE、RMSE 3个误差度量标准为估计精度评价标准。其估计结果如图10所示。
。同样使用MAX、MAE、RMSE 3个误差度量标准为估计精度评价标准。其估计结果如图10所示。
4个卡尔曼联合估计算法对于SOH的估计趋势各不相同,其中EKF-UKF算法和EKF-EKF算法对于SOH的估计整体偏高,而UKF-UKF算法和UKF-EKF算法整体偏低;3个融合算法整体在真实值附近浮动,更加接近于真实值。
对所有算法得到的结果进行MAX、MAE和RMSE计算,其结果见表2。
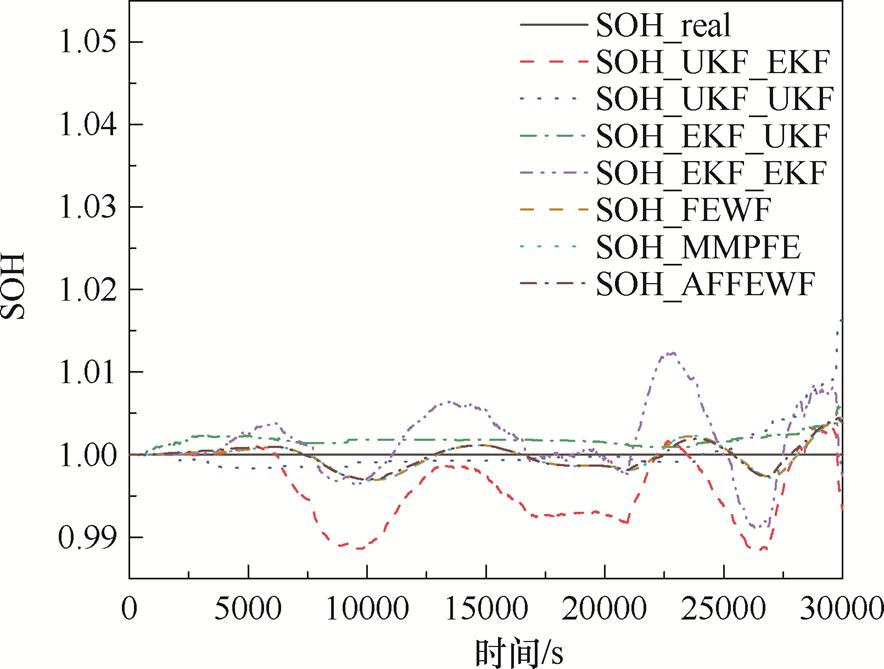
图10 SOH估计值和真实值
Fig.10 SOH estimates and true values
表2 SOH估计误差分析
Tab.2 SOH estimation error analysis
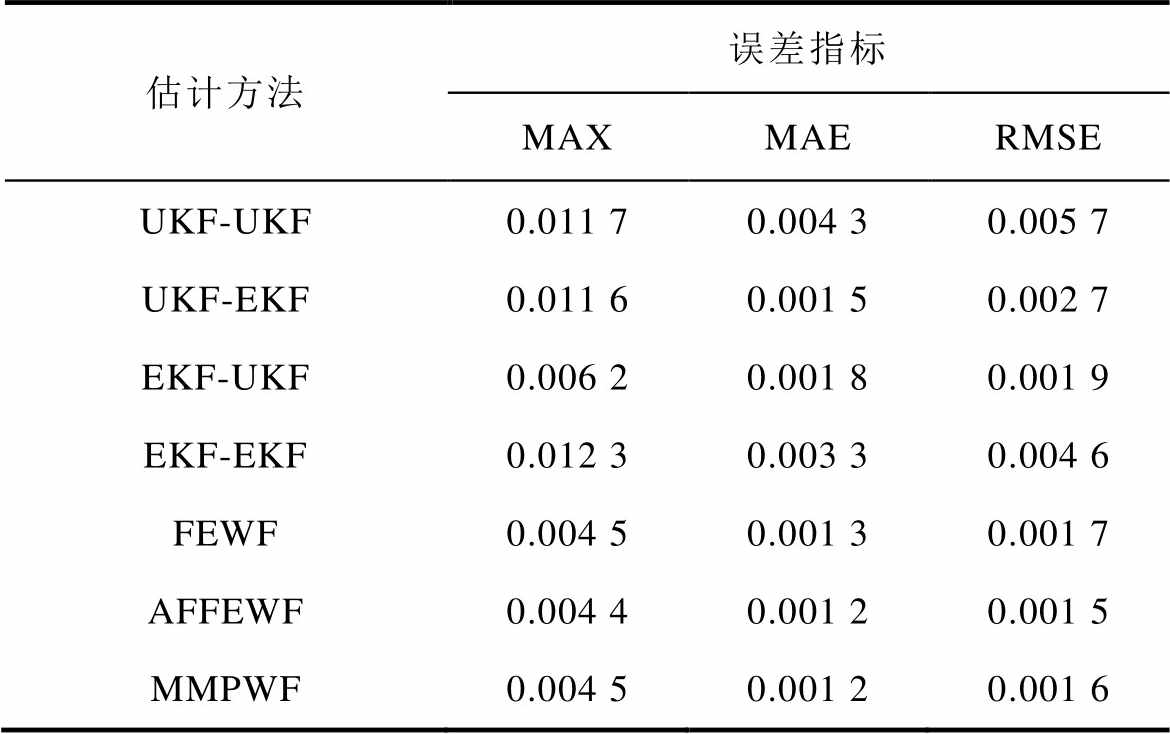
估计方法误差指标 MAXMAERMSE UKF-UKF0.011 70.004 30.005 7 UKF-EKF0.011 60.001 50.002 7 EKF-UKF0.006 20.001 80.001 9 EKF-EKF0.012 30.003 30.004 6 FEWF0.004 50.001 30.001 7 AFFEWF0.004 40.001 20.001 5 MMPWF0.004 50.001 20.001 6
以MAX为误差度量标准,4个卡尔曼联合估计算法MAX值最低的是EKF-UKF算法,其值为0.006 2;而FEWF算法、AFFEWF算法和MMPWF算法分别为0.004 5、0.004 4和0.004 5,相对比各提升了27.42%、29.03%和27.42%。3个算法均有所提升。
在MAE上卡尔曼联合估计算法中最佳的是UKF-EKF算法,其值为0.001 5;3个融合加权法分别为0.001 3、0.001 2和0.001 2;与UKF-EKF算法对比分别提升了13.33%、20%和20%。
在RMSE上误差值最低的卡尔曼联合估计算法是EKF-UKF算法值为0.001 9;融合加权法分别为0.001 7、0.001 5和0.001 6,对比EKF-UKF算法分别提升了10.53%、21.05%和15.79%。
综上所述,可得出SOH在融合估计上与SOC结果不同,3个融合加权算法均取得较好的效果,主要是因为4个卡尔曼联合估计算法对SOH估计的效果较好,且不良数据的减少使得融合加权算法的精度得到了提升。在调节因子的作用下,AFFEWF算法仍然成为3个融合加权算法中效果最好的,对比FEWF算法在MAX、MAE和RMSE上分别提升了2.22%、7.69%和11.76%;对比MMPWF在MAX和RMSE上分别提升了2.22%和6.25%。
AFFEWF算法能够提升SOC和SOH的估计精度,但在算法的运行过程中,需要先使用4个卡尔曼联合估计算法的运行来获取融合的数据和隶属度函数所需的端电压残差,这大大增加了算法的运行时间,故本文对各个算法进行运行时间测试。
本文算法测试设备为联想Rescuer-15ISK,核心显卡为英特尔i5-6300HQ,独立显卡为GeForce GTX 960M,使用系统Windows10;使用的仿真软件为Matlab R2023a。测试运行单次估计所需时间结果见表3。
表3 单次运行时间测试
Tab.3 Single run time test

估计方法运行时间/ms UKF-UKF57.8 UKF-EKF59.7 EKF-UKF17.7 EKF-EKF23.3 AFFEWF80.9
AFFEWF算法在时间上确实有所增加,但对比卡尔曼联合估计算法中用时最长的UKF-UKF算法,仅增加了35.51%;且AFFEWF算法与4个卡尔曼联合估计算法所用时间在数量级上仍处于同一级。对于数据采样时间间隔0.1 s而言,算法运行时间的数量级远远小于采样时间间隔。本文认为AFFEWF算法所增加的运行时间是可以接受的。
本文提出的调节因子改进模糊熵融合加权法的SOC和SOH联合估计方法,能提升SOC和SOH估计的精确度。该方法是加权融合4个卡尔曼联合估计算法估计的SOC和SOH的值,使用测量端电压与估计端电压的残差完成模糊熵公式的权值分配,并使用调节因子减少不良数据的影响,提升算法估计精度。在实验中加入了模糊熵加权融合法和多模型概率融合加权法进行对比验证。实验仿真证明了该方法能够提升SOC与SOH估计的精确度,得出如下结论:
1)使用调节因子改进模糊熵融合加权法对比卡尔曼联合估计算法中整体表现最好的EKF-UKF算法在SOC与SOH估计部分,估计精度得到提升。
2)调节因子改进模糊熵融合加权法使用调节因子来减少不良数据的影响,使得调节因子改进模糊熵融合加权法在SOC和SOH估计部分,相较于模糊熵融合加权法和多模型概率融合加权法,估计精度上得到了一定的提升。
3)对单运行时间的测试,得到调节因子改进模糊熵融合加权法与卡尔曼联合估计算法的运行时间在10-5 s这一数量级,远小于采样时间0.1 s。因此,调节因子改进模糊熵融合加权法所增加的运行时间并不会对整体系统的性能产生显著影响。
参考文献
[1] 李卓昊, 石琼林, 王康丽, 等. 锂离子电池健康状态估计方法研究现状与展望[J]. 电力系统自动化, 2024, 48(20): 109-129.
Li Zhuohao, Shi Qionglin, Wang Kangli, et al. Research status and prospects of state of health estimation methods for lithium-ion batteries[J]. Automation of Electric Power Systems, 2024, 48(20): 109-129.
[2] 李军徽, 宋清龙, 郭琦, 等. 计及可用容量和调频成本的网侧多储能电站双层优化策略[J]. 电力系统自动化, 2025, 49(10): 101-111.
Li Junhui, Song Qinglong, Guo Qi, et al. Bi-level optimization strategy of grid-side multiple energy storage stations considering available capacity and frequency regulation cost[J]. Automation of Electric Power Systems, 2025, 49(10): 101-111.
[3] 王辉, 严欢, 张晓滨, 等. 基于分数阶的锂电池SOC和SOH联合在线估计[J]. 电源学报, 2025, 23(2): 256-265.
Wang Hui, YanHuan, Zhang Xiaobin, et al. Joint online estimation of SOC and SOH for lithium batteries based on fractional order models[J]. Journal of Power Supply, 2025, 23(2): 256-265.
[4] 张宇, 周天宇, 张永康, 等. 一种改进的CNN- Seq2Seq电池荷电与健康状态联合估计方法[J/OL]. 电源学报, 2023: 1-12[2025-06-23]. http://kns.cnki.net/ kcms/detail/12.1420.TM.20231020.1118.002.html.
Zhang Yu, Zhou Tianyu, Zhang Yongkang, et al. Joint estimation of battery SOC and SOH based on CNN- Seq2Seq neural network[J/OL]. Journal of Power Supply, 2023: 1-12[2025-06-23]. http://kns.cnki.net/kcms/detail/12.1420.TM.20231020.1118.002.html.
[5] 潘锦业, 王苗苗, 阚威, 等. 基于Adam优化算法和长短期记忆神经网络的锂离子电池荷电状态估计方法[J]. 电气技术, 2022, 23(4): 25-30, 36.
Pan Jinye, Wang Miaomiao, Kan Wei, et al. State of charge estimation of lithium-ion battery based on Adam optimization algorithm and long short-term memory neural network[J]. Electrical Engineering, 2022, 23(4): 25-30, 36.
[6] 陈治铭, 刘建华, 柯添赐, 等. 基于对抗性的权重注意力机制序列到序列模型的锂离子电池SOC估计方法[J]. 电工技术学报, 2024, 39(19): 6244-6256.
Chen Zhiming, Liu Jianhua, Ke Tianci, et al. SOC prediction of lithium-ion batteries based on sequence- to-sequence model with adversarial weighted attention mechanism[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6244-6256.
[7] 王新栋, 董政, 王书华, 等. 基于改进开路电压模型和自适应平方根无迹卡尔曼滤波的锂离子电池宽温度多工况 SOC 估计[J]. 电工技术学报, 2024, 39(24): 7950-7964.
Wang Xindong, Dong Zheng, Wang Shuhua, et al. State-of-charge estimation for lithium-ion batteries across wide temperature range and multiple working conditions based on improved open-circuit voltage model and adaptive square root unscented Kalman filter algorithm[J]. Transactions of China Electro- technical Society, 2024, 39(24): 7950-7964.
[8] 刘旖琦, 雷万钧, 刘茜, 等. 基于双自适应扩展粒子滤波器的锂离子电池状态联合估计[J]. 电工技术学报, 2024, 39(2): 607-616.
Liu Yiqi, Lei Wanjun, Liu Qian, et al. Joint state estimation of lithium-ion battery based on dual adaptive extended particle filter[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 607-616.
[9] 申江卫, 高承志, 舒星, 等. 基于迁移模型的锂离子电池宽温度全寿命SOC与可用容量联合估计[J]. 电工技术学报, 2023, 38(11): 3052-3063.
Shen Jiangwei, Gao Chengzhi, Shu Xing, et al. Joint estimation of SOC and usable capacity of lithium-ion battery with wide temperature and full life based on migration model[J]. Transactions of China Electro- technical Society, 2023, 38(11): 3052-3063.
[10] 周航, 刘晓龙, 张梦迪, 等. 基于简单循环单元的储能锂离子电池SOC和SOH联合估计方法[J]. 电气工程学报, 2023, 18(3): 332-340.
Zhou Hang, Liu Xiaolong, Zhang Mengdi, et al. Joint SOC and SOH estimation method for energy storage lithium-ion batteries based on simple recurrent unit[J]. Journal of Electrical Engineering, 2023, 18(3): 332- 340.
[11] 高仁璟, 吕治强, 赵帅, 等. 基于电化学模型的锂离子电池健康状态估算[J]. 北京理工大学学报, 2022, 42(8): 791-797.
Gao Renjing, Lü Zhiqiang, Zhao Shuai, et al. Health state estimation of Li-ion batteries based on electrochemical model[J]. Transactions of Beijing Institute of Technology, 2022, 42(8): 791-797.
[12] 刘征宇, 杨昆, 魏自红, 等. 包含液相扩散方程简化的锂离子电池电化学模型[J]. 物理学报, 2019, 68(9): 251-258.
Liu Zhengyu, Yang Kun, Wei Zihong, et al. Electrochemical model of lithium ion battery with simplified liquid phase diffusion equation[J]. Acta Physica Sinica, 2019, 68(9): 251-258.
[13] Ramsey D, German R, Bouscayrol A, et al. Comparison of equivalent circuit battery models for energetic studies on electric vehicles[C]//2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 2020: 1-5.
[14] 周娟, 化毅恒, 刘凯, 等. 一种高精度锂离子电池建模方案研究[J]. 中国电机工程学报, 2019, 39(21): 6394-6403.
Zhou Juan, Hua Yiheng, Liu Kai, et al. Research on a high-precision modeling scheme for lithium-ion battery[J]. Proceedings of the CSEE, 2019, 39(21): 6394-6403.
[15] Guo Feng, Couto L D, Mulder G, et al. A systematic review of electrochemical model-based lithium-ion battery state estimation in battery management systems [J]. Journal of Energy Storage, 2024, 101: 113850.
[16] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J].电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[17] 王萍, 彭香园, 程泽, 等. 基于数据驱动模型融合的锂离子电池多时间尺度状态联合估计方法[J]. 汽车工程, 2022, 44(3): 362-371, 378.
Wang Ping, Peng Xiangyuan, Cheng Ze, et al. A multi-time scale joint state estimation method for lithium-ion batteries based on data-driven model fusion [J]. Automotive Engineering, 2022, 44(3): 362-371, 378.
[18] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
ZhaoJingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[19] 蒋帅, 陈铖, 段砚州, 等. 温度和老化影响下的锂离子电池荷电状态和健康状态联合估计方法研究[J]. 机械工程学报, 2024, 60(18): 266-275.
Jiang Shuai, Chen Cheng, Duan Yanzhou, et al. Joint estimation of state-of-charge and state-of-health for lithium-ion batteries under the influence of temperature and aging[J]. Journal of Mechanical Engineering, 2024, 60(18): 266-275.
[20] Pang Hui, Chen Kaiqiang, Geng Yuanfei, et al. Accurate capacity and remaining useful life predic- tion of lithium-ion batteries based on improved particle swarm optimization and particle filter[J]. Energy, 2024, 293: 130555.
[21] Fan Jie, Zhang Xudong, Zou Yuan, et al. Multiti- mescale feature extraction from multisensor data using deep neural network for battery state-of-charge and state-of-health co-estimation[J]. IEEE Transactions on Transportation Electrification, 2024, 10(3): 5689- 5702.
[22] Fu Shiyi, Liu Wen, Luo Weilin, et al. State of charge estimation of lithium-ion phosphate battery based on weighted multi-innovation cubature Kalman filter[J]. Journal of Energy Storage, 2022, 50: 104175.
[23] Shen Dongxu, Yang Dazhi, Lü Chao, et al. Detection and quantitative diagnosis of micro-short-circuit faults in lithium-ion battery packs considering cell inconsistency[J]. Green Energy and Intelligent Transportation, 2023, 2(5): 100109.
[24] 王春, 唐滔, 张永志. 考虑环境温度影响的超级电容SOC加权融合估计方法[J]. 汽车工程, 2023, 45(4): 627-636.
Wang Chun, Tang Tao, Zhang Yongzhi. A superca- pacitor SOC estimation method based on weighted fusion considering ambient temperature variation[J]. Automotive Engineering, 2023, 45(4): 627-636.
[25] 王冰, 韩冰. 混合型概率犹豫模糊熵和交叉熵测度[J]. 控制与决策, 2023, 38(2): 546-554.
Fang Bing, Han Bing. Hybrid entropy and cross- entropy measures of probabilistic hesitant fuzzy information[J]. Control and Decision, 2023, 38(2): 546-554.
Abstract The state of charge (SOC) and state of health (SOH) of lithium-ion batteries are key parameters that determine the performance, safety, and service life of battery-powered systems. To improve the accuracy of SOC and SOH estimation, this paper presents the regulation factor improved fuzzy entropy fusion weighting (AFFEWF) method. This method integrates multiple Kalman joint estimation algorithms with a regulation factor and a fuzzy entropy-based dynamic weighting mechanism to combine the advantages of various estimation techniques.
Firstly, based on a second-order RC battery model, four distinct Kalman joint estimators are employed to independently calculate SOC, SOH, and terminal voltage residuals. These estimators, which include variants of the extended Kalman filter (EKF) and the unscented Kalman filter (UKF), generate outputs that differ due to variations in algorithm structure and underlying assumptions. Such diversity provides complementary information that is utilized in the fusion process to compensate for the limitations inherent in any single estimator. Secondly, a regulation factor is applied to preprocess the terminal voltage residuals. This factor is used to eliminate data that deviate from expected values due to sensor inaccuracies or environmental disturbances, thereby improving the reliability of the inputs for the subsequent fusion process. Thirdly, a fuzzy entropy fusion weighting algorithm is applied to dynamically assign weights to each estimator’s output. The algorithm quantifies the uncertainty in each estimator’s output using fuzzy entropy. Estimators with lower fuzzy entropy, which indicate more stable outputs, are assigned higher weights during the fusion process. This dynamic weighting mechanism ensures that the final estimation of SOC and SOH predominantly reflects the contributions of models with more stable outputs while reducing the influence of those with greater uncertainty. The formulation of fuzzy entropy in this context is detailed in the paper, providing the rationale for its use as a weighting criterion.Finally, to validate the proposed AFFEWF method, comparative experiments were conducted under urban dynamometer driving schedule (UDDS) conditions, which simulate practical driving scenarios characterized by variable speeds, frequent acceleration and deceleration, and extended idling periods. During these experiments, detailed battery voltage and current data were collected under dynamic load conditions. In addition, the performance of the AFFEWF method was compared with that of a conventional fuzzy entropy weighted fusion method (FEWF) and a multi-model probabilities based weighted fusion method (MMPWF).
Result: (1) Compared with individual Kalman joint estimation algorithms, the AFFEWF method improves the accuracy of both SOC and SOH estimation. (2) The regulation factor effectively mitigates the impact of erroneous data, making the improved fuzzy entropy fusion weighting method superior to both the version without the regulation factor and the multi-model probabilistic fusion weighting method in SOC and SOH estimation. (3) Running time tests show that the fuzzy entropy fusion weighting method, which uses four Kalman joint estimators, operates within the same order of magnitude as the Kalman joint estimation algorithms and is much smaller than the sampling time of 0.1 seconds. This indicates that the computational burden is relatively small and does not significantly affect overall system performance. The computational efficiency of this method ensures its feasibility for real-time applications while maintaining high estimation accuracy.
Keywords:Joint estimation, Kalman algorithm, adjust factor, fuzzy entropy, weighted fusion, lithium batteries
张 程 男,1982年生,副教授,硕士生导师,研究方向为新能源发电、电力系统稳定性分析运行、储能管理等。
E-mail: zhangcheng@fjut.edu.cn(通信作者)
陆万林 男,1998年生,硕士研究生,研究方向为电池能量管理系统。
E-mail: luwanlin@163.com
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.242101
国家自然科学基金(52377088)、福建省财政厅专项(GY-Z220230)和福建省自然科学基金(2023J01951)资助项目。
收稿日期 2024-11-24
改稿日期 2025-02-09
(编辑 郭丽军)