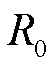 为欧姆内阻。
为欧姆内阻。摘要 针对时变非平稳厚尾噪声影响下锂电池荷电状态(SOC)的高精度估计与动态快速跟踪响应难题,提出了基于广义变遗忘因子最小二乘法(GVFFRLS)参数在线辨识与Gauss-双Gamma混合先验变分H密度抗差容积滤波的锂电池SOC动态估计算法。提出GVFFRLS以动态自适应在线辨识Thevenin等效电路模型参数,并基于Gauss-双Gamma混合分布先验建模的变分容积卡尔曼滤波联合估计电池状态向量与量测随机分布参数;引入L2-1/2分段鲁棒损失函数和状态-量测组合新息,设计H密度损失准则与变分迭代紧结合的抗差方法,强化了滤波的状态预测偏差适应性。基于锂电池不同温度、多种动态工况下的SOC估计仿真实验结果表明,在非平稳厚尾噪声影响下所提算法的参数辨识电压预测精度相比遗忘因子最小二乘法(FFRLS)提升96.32%,SOC估计多指标精度相比多种现有常用滤波估计算法提升了75.05%及以上,大幅增强了SOC快速跟踪收敛性能。
关键词:锂电池SOC估计 容积卡尔曼滤波 变遗忘因子最小二乘法 变分贝叶斯方法 H密度损失准则
在新型储能系统大规模建设的背景下,锂离子电池(Lithium-Ion Battery, LIB)因其具有能量密度高、循环寿命长、自放电率低等优点而作为新型电力系统储能电站的主要电化学储能元件得到广泛应用。截至2023年,全球电化学储能累计装机规模达到45.7 GW,其中锂离子电池储能方式以94.4%的装机占比占据主导地位[1]。电池荷电状态(State of Charge, SOC)用来描述电池中剩余能量百分比,SOC估计是电池管理系统(Battery Management System, BMS)进行能源控制的关键环节。由于锂电池的化学特性不稳定,导致电化学储能事故频繁发生,其大规模应用面临着严峻的安全风险。通过准确估计SOC,可以避免储能电池过度使用、充电,从而延长电池寿命,合理分配能量的使用,优化系统的效能和性能,以提高电池的使用效率和安全性[2-3],同时避免爆炸、燃烧等事故发生,对于新型电化学储能系统运行的安全可靠性优化尤为重要。
1)储能锂电池SOC估计的现存主要困难
在新型储能系统的复杂环境中,锂电池数据量测噪声的主要动态特性表现为分布统计特性未知(Unknown)和产生离群异常值(Ourliers),由此产生的噪声序列一般可用非平稳厚尾分布来描述。这种复杂噪声条件下的SOC高精度估计与快速动态响应是目前电池参数辨识和SOC估计的主要难点之一[4],严重制约着储能锂电池的实际应用。
2)储能锂电池SOC估计算法研究现状与问题
目前新型储能电站内BMS系统应用的锂电池SOC估计的状态估计算法主要有开路电压法、电流积分安时法(Ampere Hour, AH)[5]、基于状态空间模型的非线性滤波方法[6]、基于机器学习算法与深度神经网络的拟合法等[7]。AH方法估计时需要精确的SOC初值,通常难以获得,且电池存在充放电损耗,不同温度工况导致模型偏差下电池容量发生变化时开路电压法、AH法容易受影响造成估计误差累积。得益于人工智能技术的发展,许多学者提出了基于神经网络与深度学习的SOC估计方法[7-10],但实现上述方法需要大量精确的电池先验数据进行训练,而实际复杂耦合噪声条件下获取的复杂工况下的数据难以判断是否准确,且实时计算成本较高,占用空间较大[11]。
卡尔曼滤波(Kalman Filter, KF)基于等效电路状态空间模型和最小均方误差(Minimum Mean Square Error, MMSE)进行状态递推SOC估计,并通过一阶Jacobian近似线性化、UT(unscented transformation)变换或三阶球面-径向准则积分等方法实现非线性系统的状态后验计算,具有易于实现、估计精度高、适用性强等优点。非线性卡尔曼滤波在锂电池的SOC估计问题中得到了大量应用,并取得了良好的效果[12]。但由于现有滤波大多基于噪声分布的高斯先验假设进行计算,因此无法克服复杂环境下量测异常值和等效模型偏差的影响,从而导致估计精度下降甚至跟踪失准。
为了实现锂电池SOC高精度估计与快速跟踪,鲁棒化的非线性滤波算法被提出。文献[12-16]提出了多种改进的无迹卡尔曼滤波(Unscented Kalman Filter, UKF)用于SOC动态估计,但设计的算法多用于增强数值迭代稳定性,缺乏抗差性能和噪声参数估计能力,无法适应复杂的噪声环境;文献[17-18]基于SH(Sage-Husa)方法改进自适应UKF进行SOC估计,能在一定程度上实时修正噪声参数,但SH算法噪声很难同时估计过程与量测噪声,且处理量测异常值能力较弱;文献[19-20]提出了基于最大相关熵准则(Maximum Correntropy Criterion, MCC)的鲁棒SOC估计方法,通过扩展卡尔曼滤波(Extended Kalman Filter, EKF)和容积卡尔曼滤波(Cubature Kalman Filter, CKF)结合不同的广义混合最大熵方法实现非线性估计,具有良好的抵抗量测异常值的性能,但其只是从新息修正的角度处理异常值,没有充分考虑噪声统计量的未知时变特性,无法实时估计未知时变的噪声统计量,且使算法初始响应时间变长,无法实现SOC的快速响应跟踪。文献[21]提出了基于等效模型-EKF数据驱动融合的SOC-SOH联合估计方法。文献[22-23]基于神经网络修正滤波观测值与噪声参数,并结合鲁棒抗差算法提升了SOC估计精度,但其滤波迭代和神经网络预测串行运算成本较高,且现有的抗差损失准则对动态非平稳噪声适应性较差,无异常量测时估计精度低于常规滤波。
针对上述复杂噪声环境下SOC高精度测量与快速响应跟踪估计的问题,本文所做贡献如下:
(1)设计了一种广义变遗忘因子最小二乘法(Gereralized Variational Forgetting Factor Recursive Least Squares, GVFFRLS)用于在线辨识Thevenin等效电路模型参数,并与强跟踪算法结合,提高了电池参数在线辨识的精度与动态适应性。
(2)提出了基于Gauss-双Gamma混合分布先验变分容积卡尔曼滤波的SOC动态估计算法,基于GVFFRLS参数在线辨识与Gauss-双Gamma混合先验变分贝叶斯(Variational Bayes, VB)建模,并利用数值稳定性较强的CKF进行非线性滤波解算,实现了电池状态向量与量测非平稳噪声分布参数的联合估计。
(3)提出新的H密度损失准则,引入L2-1/2分段鲁棒损失函数和状态-量测组合新息,设计了与SOC估计变分迭代过程紧密结合的抗差状态更新方法,增强了算法对异常值噪声、状态模型偏差的适应能力,提高了复杂噪声环境下SOC估计的精度和稳定性。
锂电池等效电路模型能准确地描述电池放电或充电时的动态特性。常用的电池等效电路模型可分为Rint模型、Thevenin等效模型、PNGV等效模型、双极化模型(二阶RC模型)等[24]。其中,Thevenin等效模型利用RC并联描述极化特性,在保持建模精度的同时参数较少,能实现较高计算效率,因此采用Thevenin模型进行锂电池建模。Thevenin等效电路模型如图1所示。图1中,UOC为开路电压;U1为极化电压;UL为回路端电压;IL为回路电流;Rp、Cp分别为极化内阻和极化电容;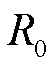 为欧姆内阻。
为欧姆内阻。
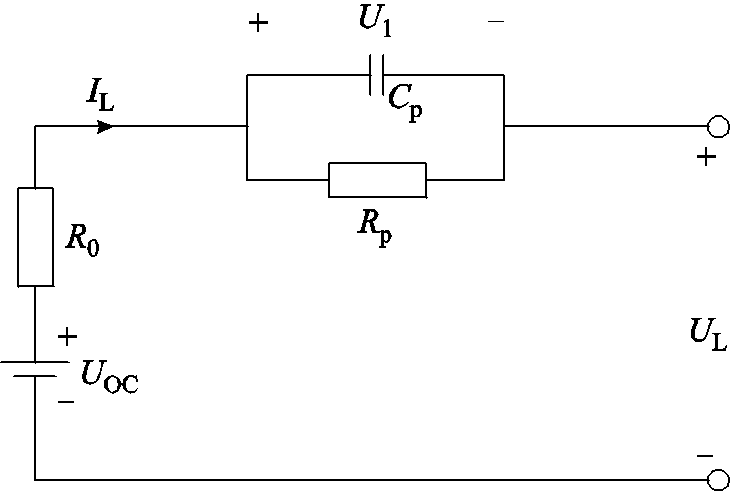
图1 Thevenin等效电路模型
Fig.1 Thevenin equivalent circuit model
根据基尔霍夫定律,电池特性的回路状态空间方程可写为
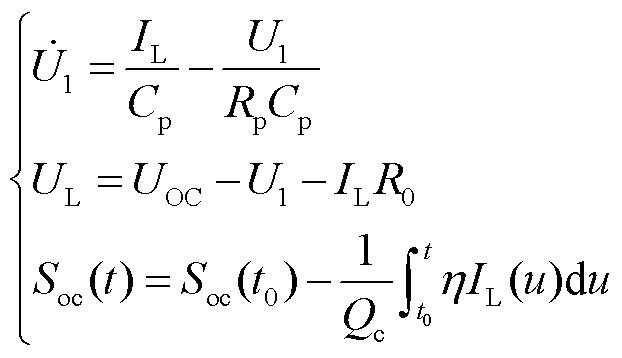 (1)
(1)
式中,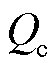 为电池额定容量;
为电池额定容量;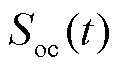 为采样t时刻的SOC值;t0为SOC递推起始时间;
为采样t时刻的SOC值;t0为SOC递推起始时间;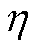 为电池充放效率。根据式(1),利用一阶前向差分法,可以得到Thevenin模型的离散状态空间方程为
为电池充放效率。根据式(1),利用一阶前向差分法,可以得到Thevenin模型的离散状态空间方程为
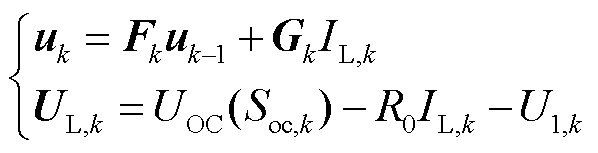 (2)
(2)
式中,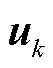 为k点状态向量,
为k点状态向量,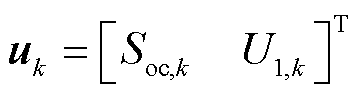 ;
;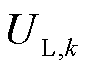 、
、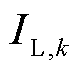 、
、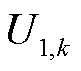 分别为采样k时刻的端电压、电流、极化电压量测值,表示为
分别为采样k时刻的端电压、电流、极化电压量测值,表示为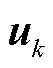 的非线性函数;
的非线性函数;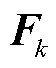 、
、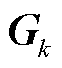 为k点的状态转移矩阵,表示为
为k点的状态转移矩阵,表示为
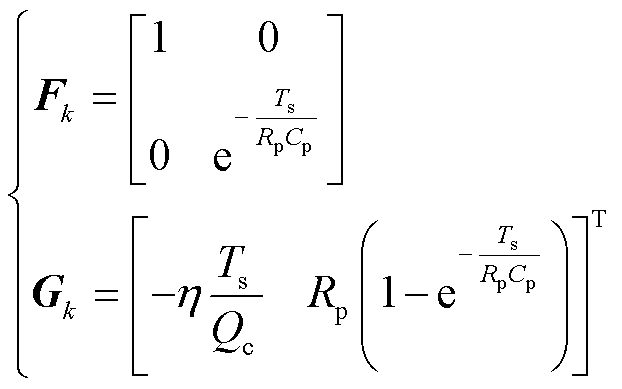 (3)
(3)
式中,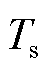 为离散采样间隔;
为离散采样间隔;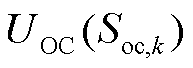 为开路电压(Open Circuit Voltage, OCV)随SOC而变化的函数关系,可根据锂电池充放电特性实验,利用nv阶多项式进行拟合,即
为开路电压(Open Circuit Voltage, OCV)随SOC而变化的函数关系,可根据锂电池充放电特性实验,利用nv阶多项式进行拟合,即
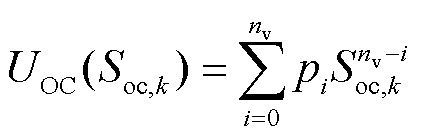 (4)
(4)
式中,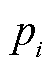 为nv阶多项式第i项系数,可利用充放电电压-时间曲线采样值构造Vandermonde线性方程组,并通过求其最小二乘解获得。
为nv阶多项式第i项系数,可利用充放电电压-时间曲线采样值构造Vandermonde线性方程组,并通过求其最小二乘解获得。
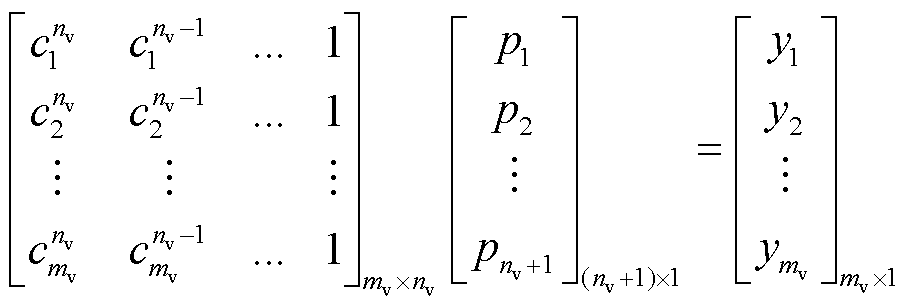 (5)
(5)
式中,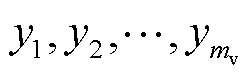 为电池充放电曲线的开路电压采样值;
为电池充放电曲线的开路电压采样值;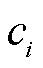 为每个
为每个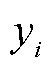 对应的电池SOC值;
对应的电池SOC值;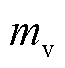 为采样矩阵维数。式(5)可简写为
为采样矩阵维数。式(5)可简写为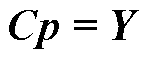 ,利用公式
,利用公式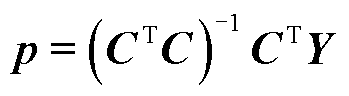 即可进行最小二乘求解,获得SOC-OCV曲线拟合系数。
即可进行最小二乘求解,获得SOC-OCV曲线拟合系数。
由式(2)和式(3),即得到了基于Thevenin等效电路描述锂电池动态特性的离散状态空间模型。进一步地,含过程与量测噪声的锂电池离散模型表示为
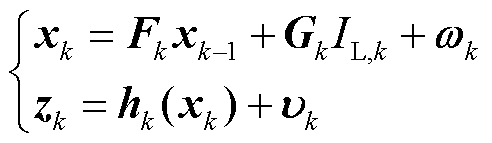 (6)
(6)
式中,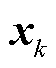 为状态向量,
为状态向量,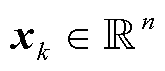 ,n为状态向量维度;
,n为状态向量维度;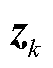 为量测向量,
为量测向量,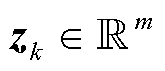 ,m为量测向量维度;非线性量测函数
,m为量测向量维度;非线性量测函数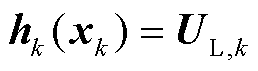 ;
;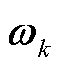 为系统过程噪声,
为系统过程噪声,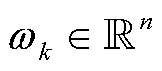 ,服从零均值高斯分布
,服从零均值高斯分布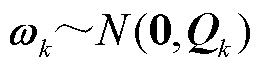 ,表示系统模型与真实状态的随机偏差,其统计特性可表示为
,表示系统模型与真实状态的随机偏差,其统计特性可表示为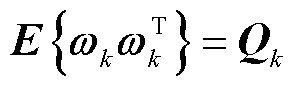 ;
;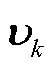 为统计特性未知的时变非平稳量测噪声,
为统计特性未知的时变非平稳量测噪声,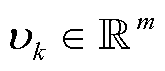 。
。
在1.1节中,由Thevenin电池特性回路状态方程离散化获得了锂电池的状态空间模型,但其并非完整辨识的模型,其中需要确定的参数有内阻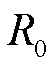 、极化内阻Rp和极化电容Cp,因此需要对上述参数进行实时在线辨识,作为电池SOC估计前置输入。
、极化内阻Rp和极化电容Cp,因此需要对上述参数进行实时在线辨识,作为电池SOC估计前置输入。
将式(1)中的第1、2行进行Laplace变换,并利用变换的微分性质可得
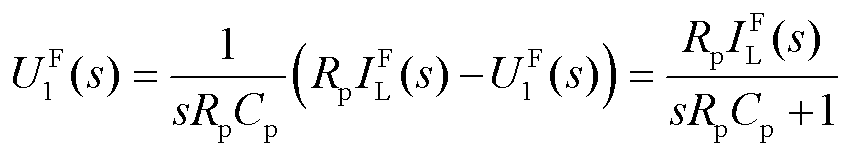 (7)
(7)
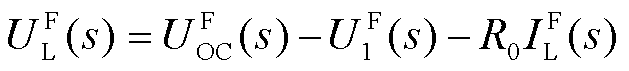 (8)
(8)
式中,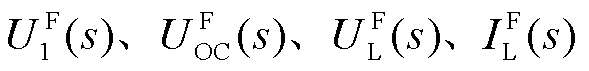 分别为极化电压、开路电压、环端电压、电流的Laplace象函数。根据式(7)和式(8),设变换s域中电压误差传递函数为
分别为极化电压、开路电压、环端电压、电流的Laplace象函数。根据式(7)和式(8),设变换s域中电压误差传递函数为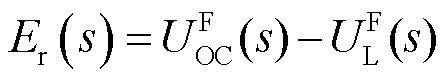 ,可表示为
,可表示为
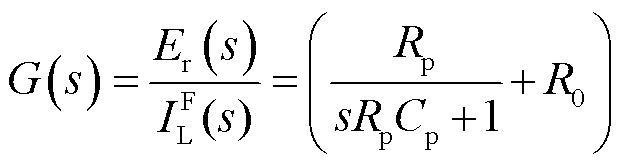 (9)
(9)
利用Tustin变换,将传递函数由s域变换至z域,从而利用后向差分得到离散时间传递函数。将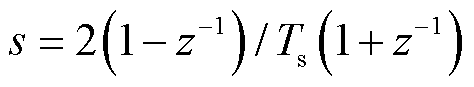 代入式(9),则可得
代入式(9),则可得
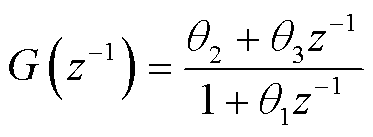 (10)
(10)
通过对计算得到的离散传递函数的识别参数进行反解,可以得到电池模型的各个参数为
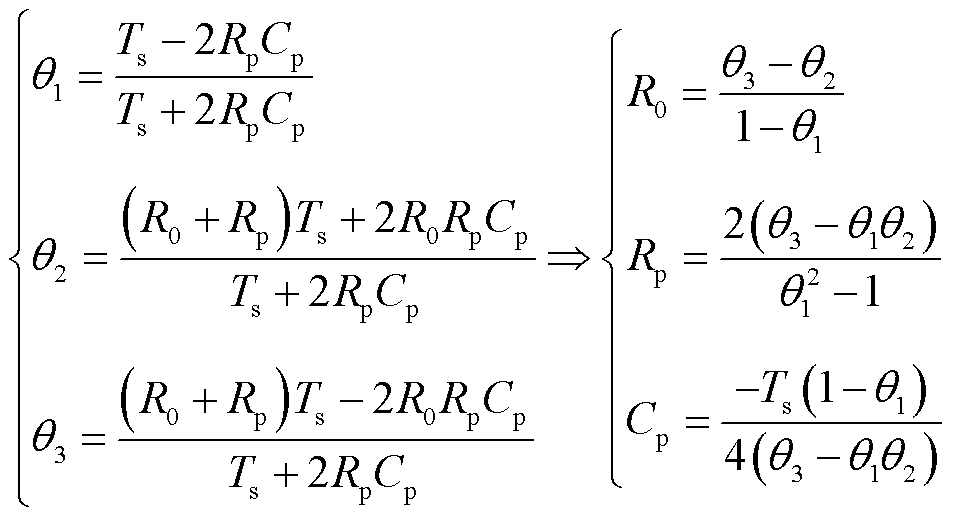 (11)
(11)
利用式(7)和式(8),根据实数位移定理和线性化定理对系统进行离散化,则式(9)可表示为离散形式
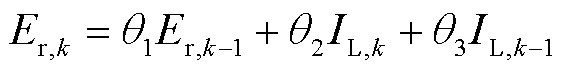 (12)
(12)
式中,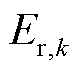 为
为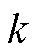 时刻端电压与开路电压的差值。为了进行电池参数的递推在线求解,将式(12)写成向量积的递推表达式为
时刻端电压与开路电压的差值。为了进行电池参数的递推在线求解,将式(12)写成向量积的递推表达式为
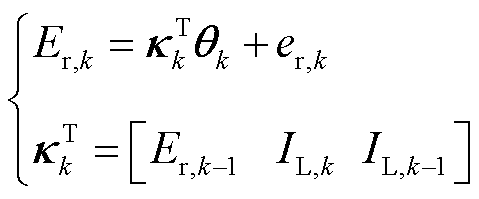 (13)
(13)
式中,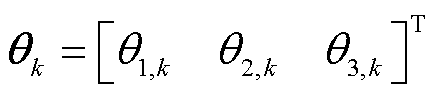 为向量递推中待估计的参数向量;kk为k时刻点的量测向量;
为向量递推中待估计的参数向量;kk为k时刻点的量测向量;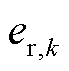 为k时刻点的残差序列。基于模型式(13),即可对锂电池模型参数进行实时递推求解。
为k时刻点的残差序列。基于模型式(13),即可对锂电池模型参数进行实时递推求解。
传统的递推最小二乘法(Recursive Least Squares, RLS)具有计算效率高、易于实现的特点,广泛应用于锂电池的参数辨识。遗忘因子最小二乘法(Forgetting Factor Recursive Least Squares, FFRLS)是对传统最小二乘的扩展,通过在优化目标函数中引入遗忘因子进行递推求解,在当前迭代时间增加创新权值,从而减少传统RLS中旧观测残差数据的影响[25]。然而FFRLS中的定遗忘因子选取不当会较严重地影响其估计性能,造成算法适应性下降;因此需要设计一种新的变遗忘因子自适应RLS方法,从而能够在不同工况下有效分配新旧量测数据的权重,提高电池参数辨识精度和动态工况的适应性。
在最小二乘求解中,经过N次数据采样后,量测向量的残差序列可表示为
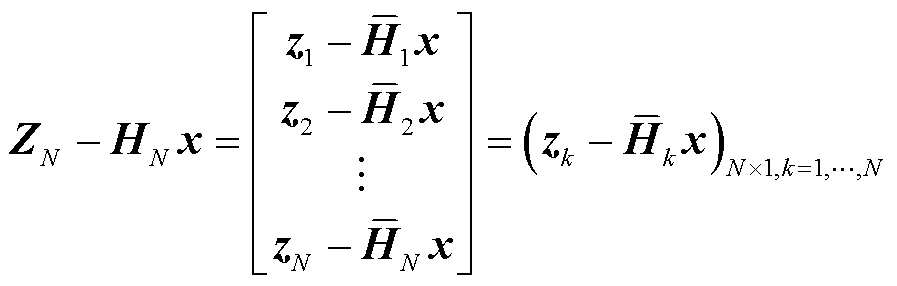 (14)
(14)
式中,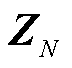 为1~N时刻的量测值集合;N为时间序列的总长度;
为1~N时刻的量测值集合;N为时间序列的总长度;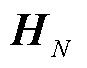 为总体量测矩阵;
为总体量测矩阵;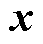 为最小二乘估计向量;
为最小二乘估计向量;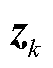 为
为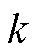 时刻的量测值向量;
时刻的量测值向量;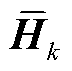 为量测值对应的量测矩阵。
为量测值对应的量测矩阵。
GVFFRLS计算的目的是求解带变遗忘因子加权的递归最小二乘问题。由于FFRLS采用定遗忘因子,算法在不同电池工况下很难保持辨识结果的准确性和数值稳定性。为此,设计改进的GVFFRLS优化目标函数,改写为
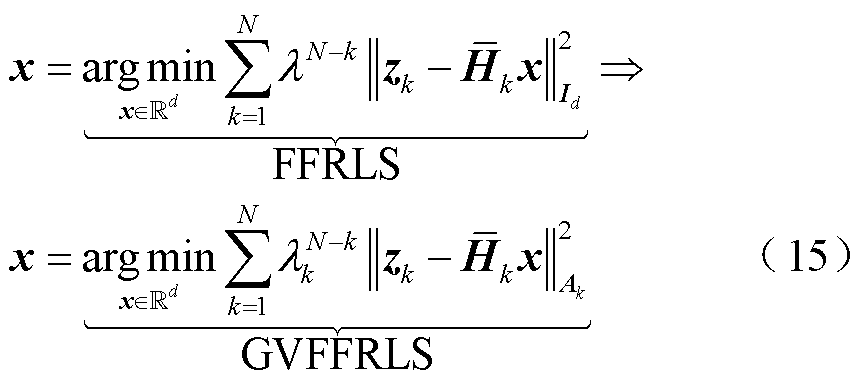
式中,d为待估计向量维数;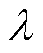 、
、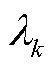 分别为原始定遗忘因子和变遗忘因子;
分别为原始定遗忘因子和变遗忘因子;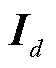 为
为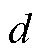 维单位矩阵;
维单位矩阵;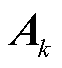 为最小二乘的自适应权矩阵,利用Sage-Husa量测估计方法进行更新,表示为
为最小二乘的自适应权矩阵,利用Sage-Husa量测估计方法进行更新,表示为
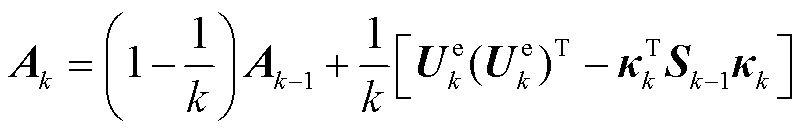 (16)
(16)
式中,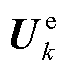 为电压估计残差;
为电压估计残差;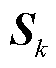 为量测向量
为量测向量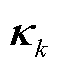 的协方差矩阵。式(15)基于广义高斯核函数设计变遗忘因子,并通过调整核函数系数增强FFRLS算法的适应性。利用矩阵求导方法求解上述优化问题,最后将在线参数辨识解算方法写为递推形式,可得GVFFRLS的递推公式为
的协方差矩阵。式(15)基于广义高斯核函数设计变遗忘因子,并通过调整核函数系数增强FFRLS算法的适应性。利用矩阵求导方法求解上述优化问题,最后将在线参数辨识解算方法写为递推形式,可得GVFFRLS的递推公式为
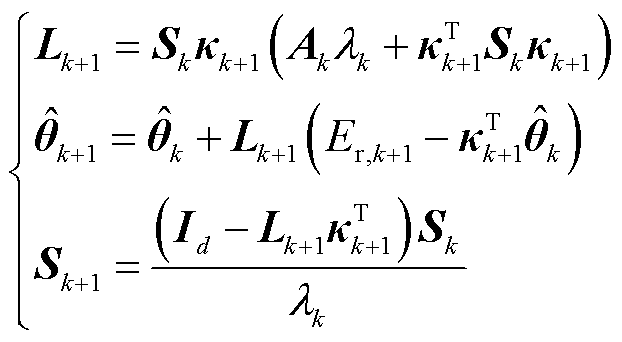 (17)
(17)
其中,自适应权矩阵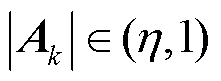 用于增强算法的数值稳定性,变遗忘因子及电压残差表示为
用于增强算法的数值稳定性,变遗忘因子及电压残差表示为
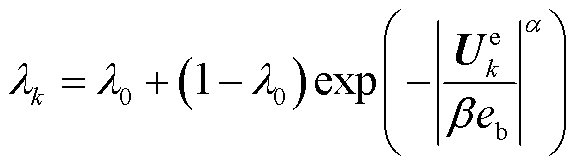 (18)
(18)
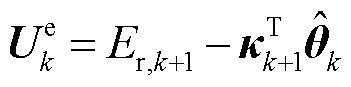 (19)
(19)
式中,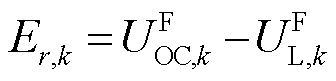 为电压误差,其中,
为电压误差,其中,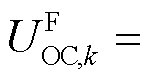
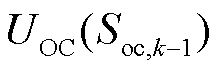 由上一时刻SOC估计值与式(4)中的OCV曲线计算得到;eb为残差比例系数,通常取较小的数;
由上一时刻SOC估计值与式(4)中的OCV曲线计算得到;eb为残差比例系数,通常取较小的数;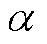 、
、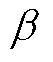 分别为广义高斯核形态参数和核带宽。根据核函数的取值范围,可以得到遗忘因子的取值集合为
分别为广义高斯核形态参数和核带宽。根据核函数的取值范围,可以得到遗忘因子的取值集合为
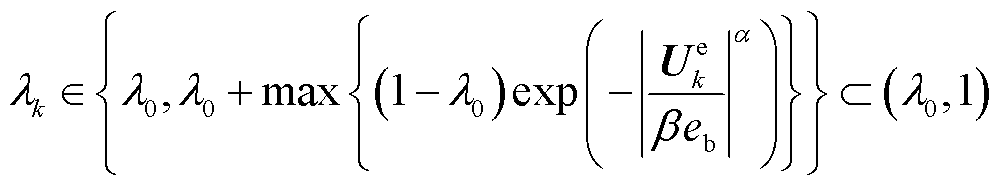 (20)
(20)
根据式(20),遗忘因子上、下确界可写为
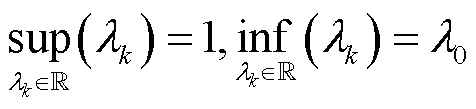 (21)
(21)
通过式(21),自适应因子可放大或缩小为其上界和下界对应的遗忘因子,从而使算法退化为FFRLS或RLS。这保证了算法的迭代稳定性。
基于改进的GVFFRLS进行电池参数在线辨识,并将其嵌入参数实时闭环更新环节,即可完整实现所提的SOC估计算法。图2显示了含GVFFRLS算法在线参数辨识流程的锂电池SOC强跟踪估计整体计算框架。
如图2a所示,与传统RLS离线参数辨识方法不同,GVFFRLS在线参数辨识不需要利用指定工况下的电池测试数据构建最小二乘方程组进行参数-SOC关系拟合,而是根据上一时刻SOC估计值与OCV映射传递端电压误差,并根据参数递推方法进行实时闭环计算,可以增强不同工况下算法对短时间尺度内电池参数动态变化的适应性和灵活性。
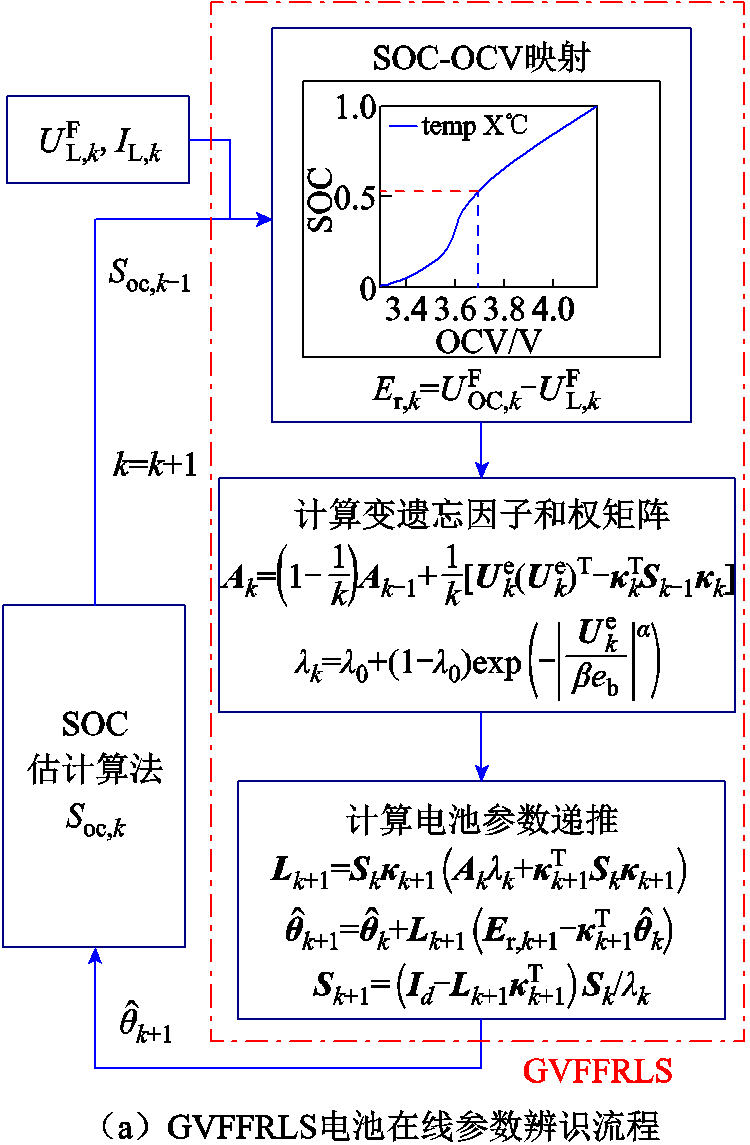
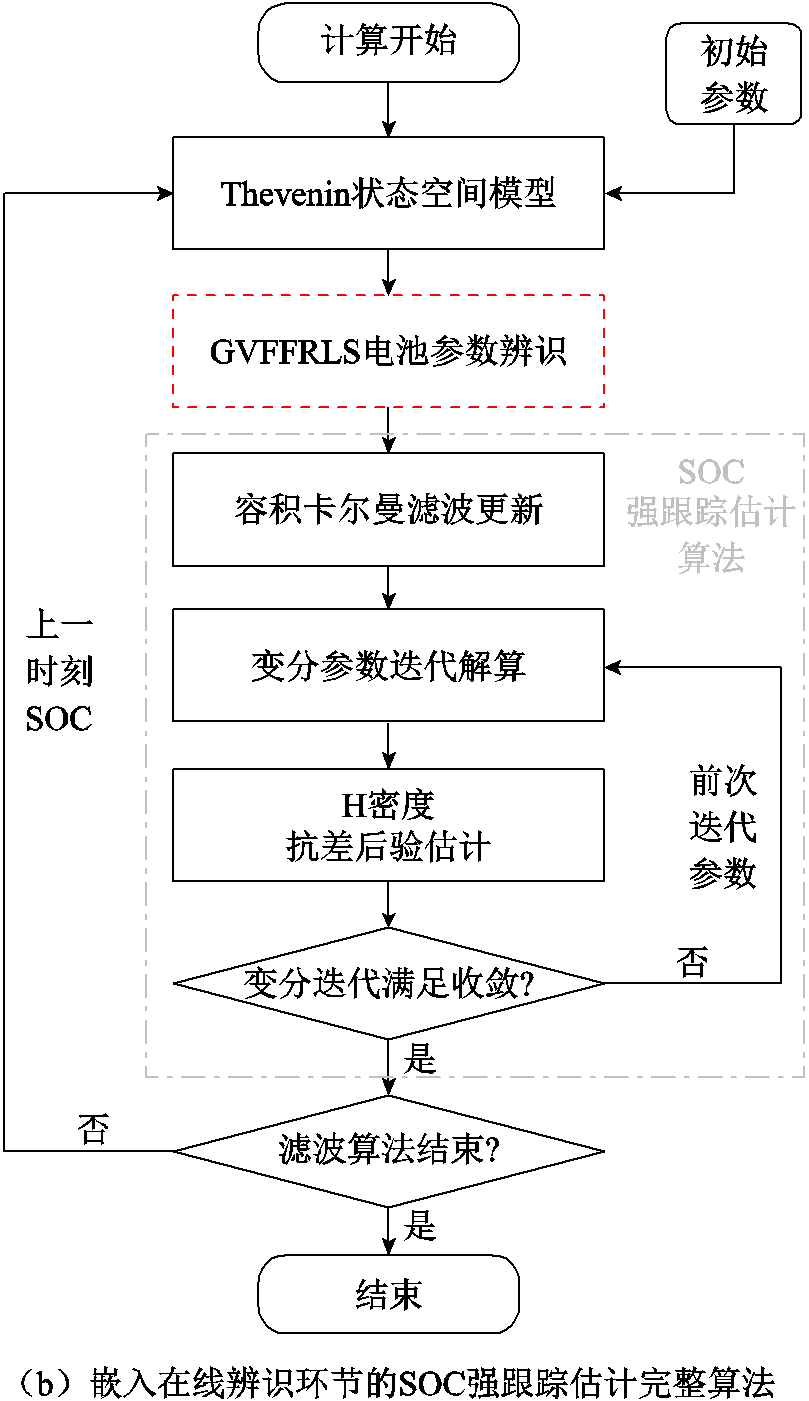
图2 GVFFRLS-SOC强跟踪估计整体计算框架
Fig.2 Total calculation framework of the proposed GVFFRLS-SOC strong tracking estimation algorithm
基于GVFFRLS在线辨识的电池SOC估计整体框架如图2b所示。所提方法将在线参数辨识算法嵌入SOC估计流程中,首先,算法根据当前时刻输入的电池端电压、电流采集数据和前一时刻的SOC估计值,通过OCV曲线映射得到端电压误差,计算变遗忘因子和自适应权矩阵;其次,根据参数递推计算得到后一时刻的参数辨识值,并传递给SOC估计算法,通过容积卡尔曼滤波更新、变分参数迭代解算、H密度抗差后验估计等环节,进行电池SOC的动态跟踪估计;最后,将SOC估计值传递至下一时刻的误差映射与参数辨识环节进行闭环计算,直到完成所有时刻的参数估计。
在电池离散状态空间方程式(6)中,由于量测向量由非线性函数h(x)传递,而卡尔曼滤波仅适用于线性系统,因此需要引入容积滤波方法。
CKF方法相比UKF,在对非线性系统滤波时保持了良好的数值稳定性,其不会随着系统维数的升高而出现频繁发散的情况[21]。CKF在进行容积点采样时利用三阶球面-径向容积准则来计算数值积分,从而以更高精度逼近预测概率分布。
3.1.1 时间更新
根据状态初值先验统计特性,计算状态向量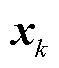 与协方差矩阵
与协方差矩阵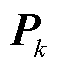 的初始值:
的初始值:
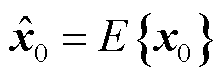 (22)
(22)
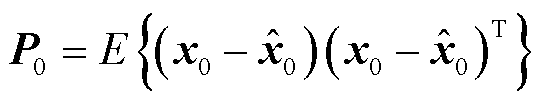 (23)
(23)
式中,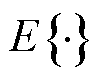 表示计算统计量数学期望。由于式(6)中所构建的Thevenin离散状态空间模型的状态方程是线性的,所以根据常规卡尔曼滤波算法与式(6)中的状态转移矩阵
表示计算统计量数学期望。由于式(6)中所构建的Thevenin离散状态空间模型的状态方程是线性的,所以根据常规卡尔曼滤波算法与式(6)中的状态转移矩阵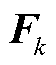 、
、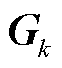 ,即可计算一步预测状态向量
,即可计算一步预测状态向量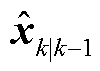 与状态协方差矩阵
与状态协方差矩阵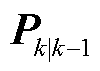 。
。
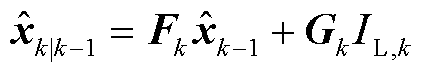 (24)
(24)
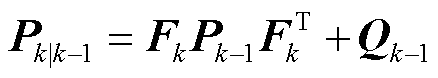 (25)
(25)
3.1.2 量测更新
进行状态容积点重采样,利用时间更新的一步预测参数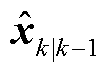 、
、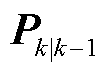 更新状态点集,并通过量测非线性函数
更新状态点集,并通过量测非线性函数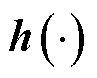 传递重采样容积点。
传递重采样容积点。
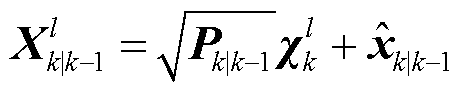 (26)
(26)
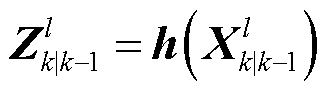 (27)
(27)
式中,容积点基矩阵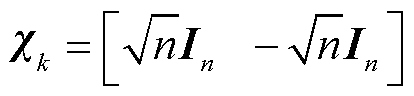 ,
,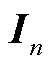 为n阶单位矩阵;
为n阶单位矩阵;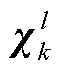 表示取
表示取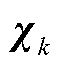 中的第l个基向量。根据状态重采样点集及其量测非线性传递,计算量测一步预测、量测协方差矩阵与交叉协方差矩阵:
中的第l个基向量。根据状态重采样点集及其量测非线性传递,计算量测一步预测、量测协方差矩阵与交叉协方差矩阵:
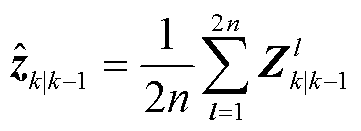 (28)
(28)
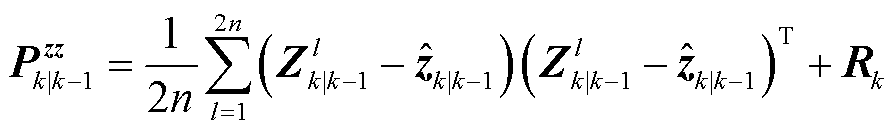 (29)
(29)
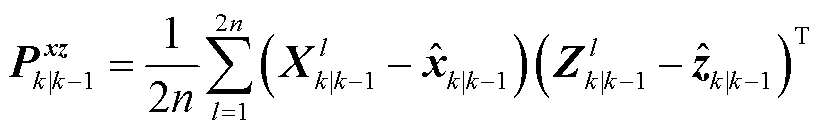 (30)
(30)
式中,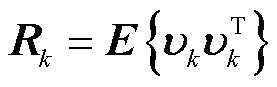 为量测协方差矩阵,当噪声
为量测协方差矩阵,当噪声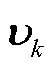 统计量特性未知时,
统计量特性未知时,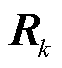 为量测噪声的协方差时变统计参数,需要利用统计估计器进行实时计算。
为量测噪声的协方差时变统计参数,需要利用统计估计器进行实时计算。
根据式(28)~式(30),可进一步计算容积卡尔曼滤波的状态向量与协方差矩阵的后验估计:
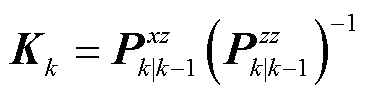 (31)
(31)
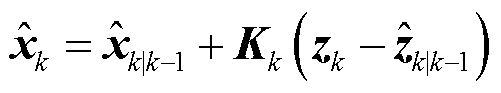 (32)
(32)
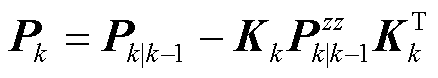 (33)
(33)
式中,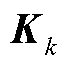 为卡尔曼增益矩阵。通过式(22)~式(33)的计算,即完成了一次量测非线性情况下的容积滤波状态估计。
为卡尔曼增益矩阵。通过式(22)~式(33)的计算,即完成了一次量测非线性情况下的容积滤波状态估计。
3.2.1 变分先验分布层次高斯模型构建
传统容积滤波计算将量测噪声视为平稳高斯分布,需要人为设定量测噪声统计量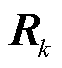 ,当
,当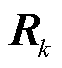 与真实噪声分布参数偏差过大,则会导致滤波后验分布失配,从而使滤波算法发散。为了实现滤波过程中的噪声分布自适应估计,基于层次高斯模型,利用VB方法计算状态与噪声参数的近似联合后验分布。由平均场假设,将条件联合概率密度函数(Probability Density Function, PDF)近似解耦为多个独立分布的乘积,表示为
与真实噪声分布参数偏差过大,则会导致滤波后验分布失配,从而使滤波算法发散。为了实现滤波过程中的噪声分布自适应估计,基于层次高斯模型,利用VB方法计算状态与噪声参数的近似联合后验分布。由平均场假设,将条件联合概率密度函数(Probability Density Function, PDF)近似解耦为多个独立分布的乘积,表示为
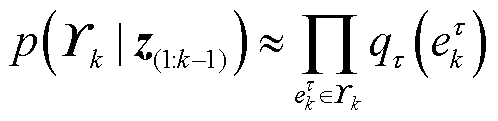 (34)
(34)
式中,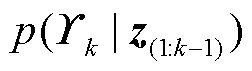 为真实后验分布;
为真实后验分布;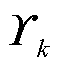 为参数集合;
为参数集合;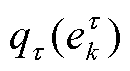 为参数集合
为参数集合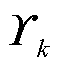 中第
中第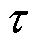 个待估计参数
个待估计参数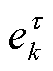 的概率密度似然函数。为了使似然分布尽可能与真实后验分布近似,利用KL散度(Kullback-Leibler Divergence, KLD)对两者在分布空间上的相似性进行衡量,似然密度
的概率密度似然函数。为了使似然分布尽可能与真实后验分布近似,利用KL散度(Kullback-Leibler Divergence, KLD)对两者在分布空间上的相似性进行衡量,似然密度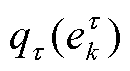 的优化求解目标为[25]
的优化求解目标为[25]
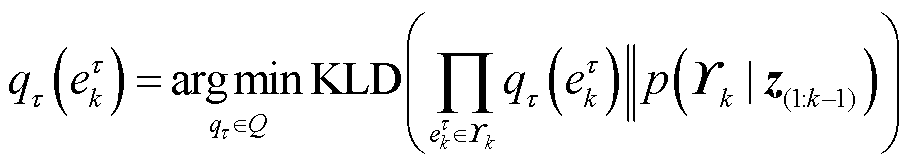 (35)
(35)
其中
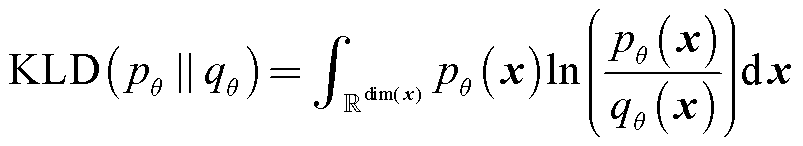
式中,Q为概率分布函数空间,表示满足概率分布PDF定义的所有函数构成的集合;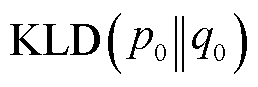 表示两分布
表示两分布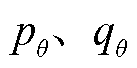 之间的KL散度,其值越小,表示分布空间
之间的KL散度,其值越小,表示分布空间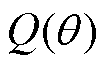 上两者的相似程度越高,从而可以利用似然分布
上两者的相似程度越高,从而可以利用似然分布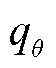 近似真实分布
近似真实分布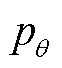 以实现后验估计。在VB方法中,利用变分法,构造欧拉-拉格朗日方程并求解,可得优化问题式(35)的解析解为
以实现后验估计。在VB方法中,利用变分法,构造欧拉-拉格朗日方程并求解,可得优化问题式(35)的解析解为
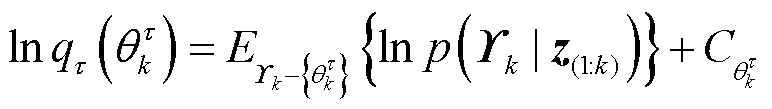 (36)
(36)
式中,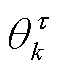 为第
为第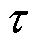 个待估计的解参数;
个待估计的解参数;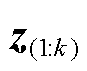 为前k时刻的观测向量集合;
为前k时刻的观测向量集合;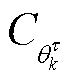 为与
为与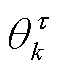 相关的任意常数。利用参数逐级递归求解法可以对式(36)进行数值解算,第i次迭代第
相关的任意常数。利用参数逐级递归求解法可以对式(36)进行数值解算,第i次迭代第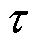 个参数分布表示为
个参数分布表示为
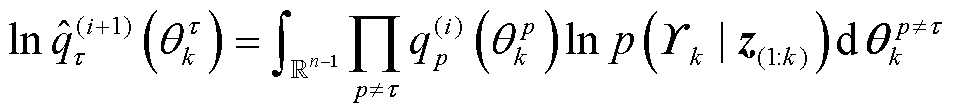 (37)
(37)
式中,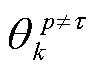 为参数集合
为参数集合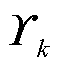 中去掉第
中去掉第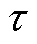 个参数后剩余向量。由于状态空间方程式(6)中过程噪声为高斯噪声,而量测噪声具有非平稳厚尾特性,因此假设状态一步预测、量测似然先验分布分别为高斯分布和Gauss-双Gamma混合分布:
个参数后剩余向量。由于状态空间方程式(6)中过程噪声为高斯噪声,而量测噪声具有非平稳厚尾特性,因此假设状态一步预测、量测似然先验分布分别为高斯分布和Gauss-双Gamma混合分布:
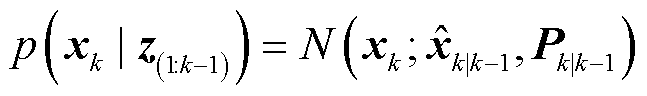 (38)
(38)
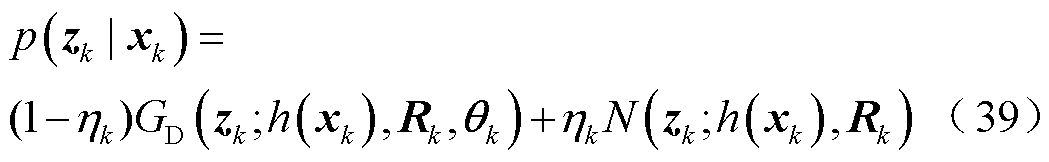
式中,状态一步预测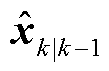 与状态协方差矩阵
与状态协方差矩阵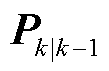 分别由式(24)和式(25)计算;
分别由式(24)和式(25)计算;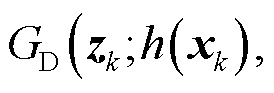
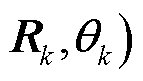 为双重Gamma尺度分布,用于建模非平稳噪声中厚尾时段的噪声分布特性;
为双重Gamma尺度分布,用于建模非平稳噪声中厚尾时段的噪声分布特性;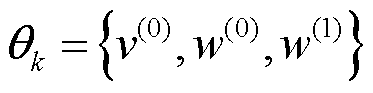 为分布超参数;
为分布超参数;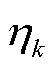 为混合分布比例参数。根据Chapman-Kolmogorov方程与全概率公式,量测似然分布可表示为
为混合分布比例参数。根据Chapman-Kolmogorov方程与全概率公式,量测似然分布可表示为
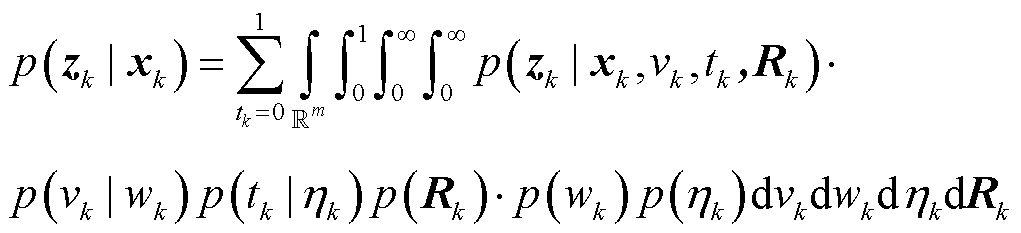 (40)
(40)
式中,量测协方差尺度参数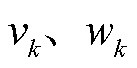 建模为先验Gamma分布;混合分布参数
建模为先验Gamma分布;混合分布参数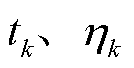 分别建模为0-1分布和Beta分布;量测协方差
分别建模为0-1分布和Beta分布;量测协方差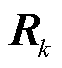 建模为IWishart分布[25]。将各参数的条件尺度先验分布写为层次高斯模型,可得到
建模为IWishart分布[25]。将各参数的条件尺度先验分布写为层次高斯模型,可得到
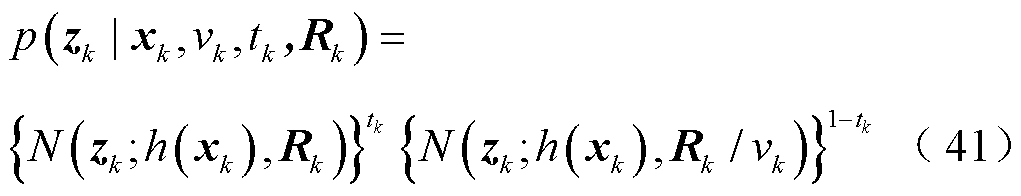
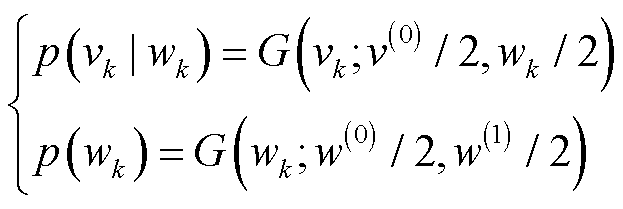 (42)
(42)
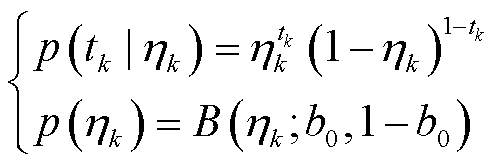 (43)
(43)
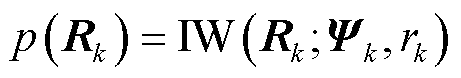 (44)
(44)
式中,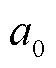 为Beta分布概率参数;
为Beta分布概率参数;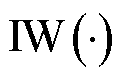 为IWishart分布的PDF;
为IWishart分布的PDF;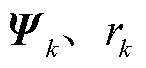 分别为IWishart分布的随机尺度矩阵和自由度参数。
分别为IWishart分布的随机尺度矩阵和自由度参数。
3.2.2 状态与噪声参数变分推断
根据式(41)~式(44)中的层次高斯模型,将其代入先验分布式(35)中,并由条件概率公式可得待估计参数联合分布的概率密度表示为
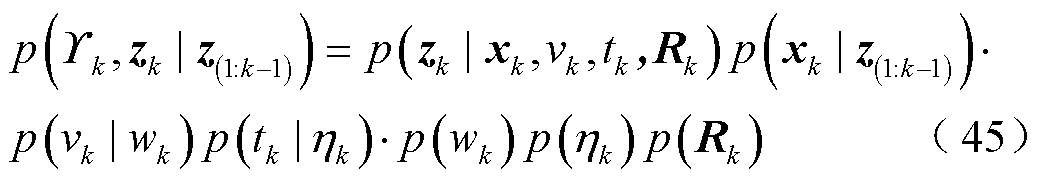
式中,第i次变分迭代时的待估计参数集合表示为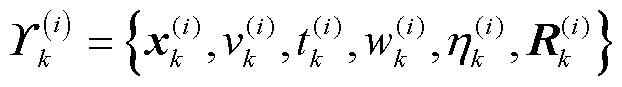 。利用式(37)和式(45)进行变分推断,从而得到各参数的近似后验分布。
。利用式(37)和式(45)进行变分推断,从而得到各参数的近似后验分布。
1)状态向量的后验分布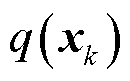
令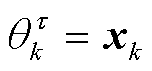 ,根据式(40)和式(45),以及高斯分布的乘积性质,可得状态向量后验估计仍为高斯分布,即
,根据式(40)和式(45),以及高斯分布的乘积性质,可得状态向量后验估计仍为高斯分布,即
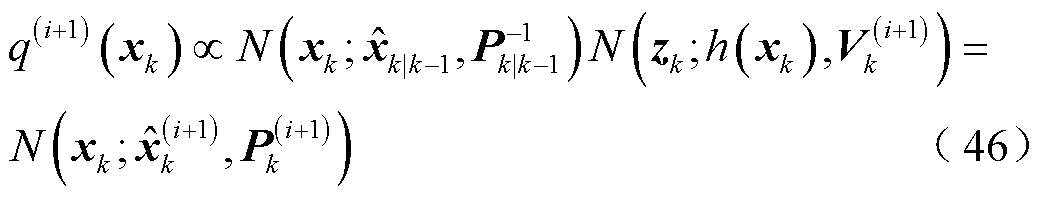
根据式(41)和卡尔曼滤波更新公式,式(46)中量测辅助协方差矩阵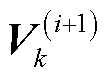 更新为
更新为
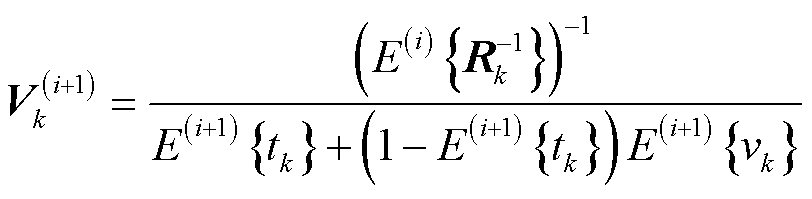 (47)
(47)
式中,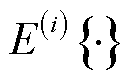 为第i次变分迭代下的期望运算。滤波增益矩阵
为第i次变分迭代下的期望运算。滤波增益矩阵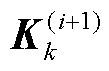 、后验状态向量
、后验状态向量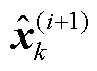 与协方差
与协方差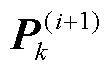 由CKF中式(31)~式(33)计算。
由CKF中式(31)~式(33)计算。
2)尺度参数的后验分布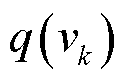
令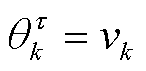 ,根据式(40)和式(45),可得尺度参数
,根据式(40)和式(45),可得尺度参数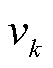 的后验分布匹配为Gamma分布。
的后验分布匹配为Gamma分布。
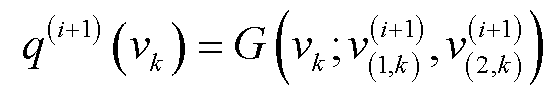 (48)
(48)
其中,自由度参数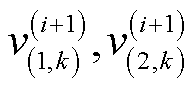 更新为
更新为
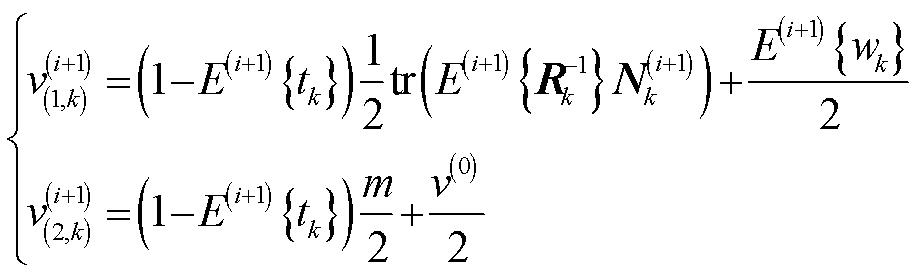 (49)
(49)
式中,tr(A)为矩阵A的迹;E(i+1)为第i+1次变分迭代下的期望运算。
而对于辅助矩阵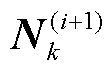 ,由于表示为非线性高斯权重积分,所以其计算无法得到解析表达式。可利用容积卡尔曼滤波中的三阶容积公式进行计算。
,由于表示为非线性高斯权重积分,所以其计算无法得到解析表达式。可利用容积卡尔曼滤波中的三阶容积公式进行计算。
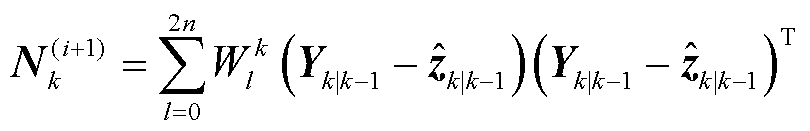 (50)
(50)
参数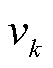 由表1中的Gamma分布期望值进行更新。
由表1中的Gamma分布期望值进行更新。
3)尺度参数的后验分布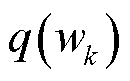
令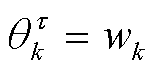 ,根据式(40)和式(45),得到尺度参数
,根据式(40)和式(45),得到尺度参数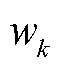 的后验分布同样匹配为Gamma分布,即
的后验分布同样匹配为Gamma分布,即
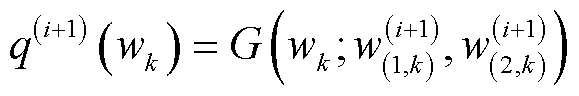 (51)
(51)
式中,自由度参数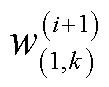 、
、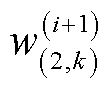 更新为
更新为
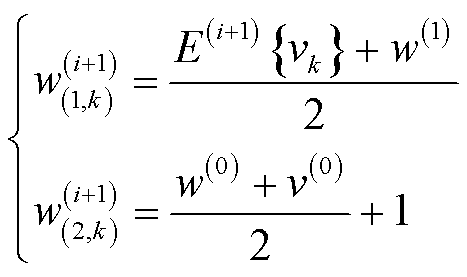 (52)
(52)
表1 不同变分分布迭代参数的后验估计
Tab.1 Posteriori estimation of iterative parameters with different variational distributions

统计量 后验估计 统计量 后验估计
注: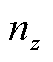 为量测方程的维数。
为量测方程的维数。
参数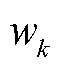 同样更新为Gamma分布的期望值,见表1。
同样更新为Gamma分布的期望值,见表1。
4)0-1参数的后验分布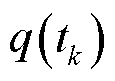
令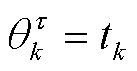 ,根据式(40)和式(45),可得0-1参数
,根据式(40)和式(45),可得0-1参数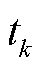 的后验分布匹配仍然为0-1分布。
的后验分布匹配仍然为0-1分布。
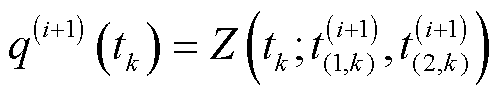 (53)
(53)
其中,概率参数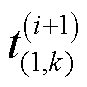 、
、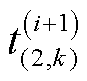 分别表示为
分别表示为
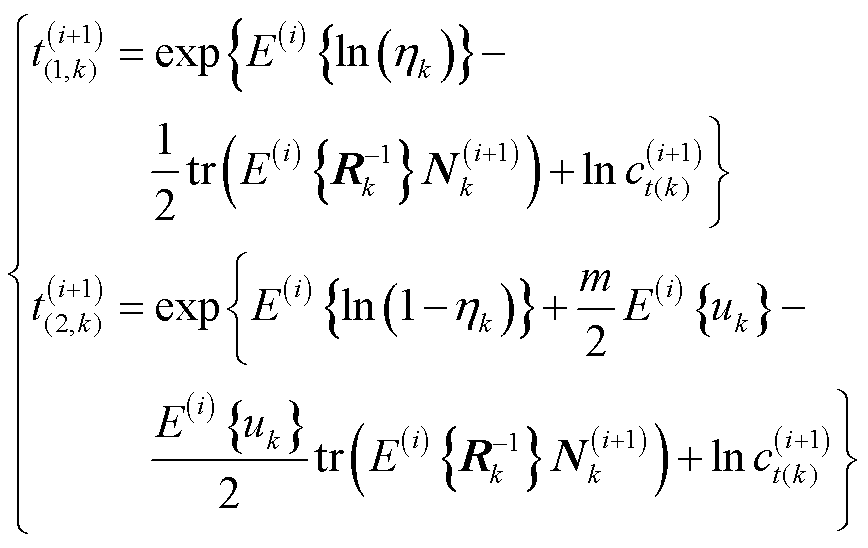 (54)
(54)
参数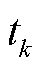 由0-1分布的期望值进行更新,见表1。
由0-1分布的期望值进行更新,见表1。
5)比例参数的后验分布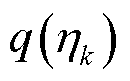
令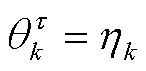 ,根据式(40)和式(45),可得比例参数
,根据式(40)和式(45),可得比例参数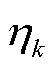 的后验分布匹配为Beta分布。
的后验分布匹配为Beta分布。
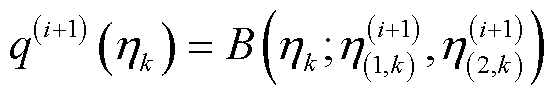 (55)
(55)
式中,概率参数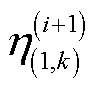 、
、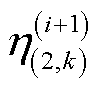 分别表示为
分别表示为
 (56)
(56)
参数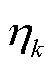 由Beta分布的期望值进行更新,见表1。
由Beta分布的期望值进行更新,见表1。
6)量测协方差参数的后验分布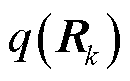
令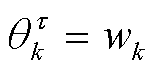 ,根据式(40)和式(45),得到尺度参数
,根据式(40)和式(45),得到尺度参数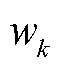 的后验分布同样匹配为Gamma分布。即
的后验分布同样匹配为Gamma分布。即
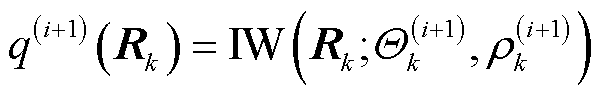 (57)
(57)
其中,随机尺度矩阵与自由度参数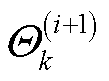 、
、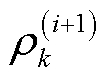 分别表示为
分别表示为
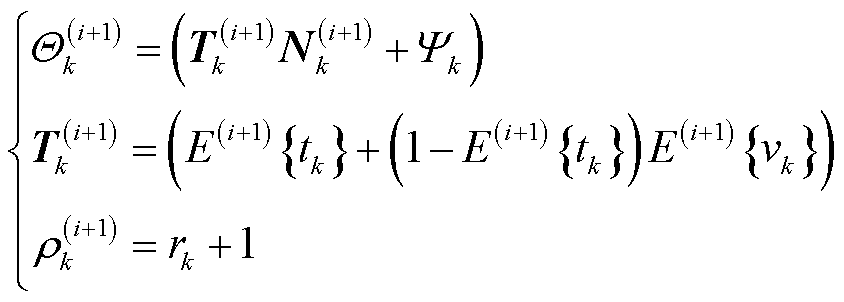 (58)
(58)
而协方差参数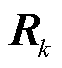 由IWishart分布的期望矩阵进行更新,见表1。
由IWishart分布的期望矩阵进行更新,见表1。
表1给出了参数集合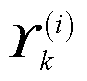 各统计量的变分后验估计。其中
各统计量的变分后验估计。其中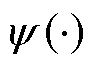 为0阶polyGamma函数,有
为0阶polyGamma函数,有
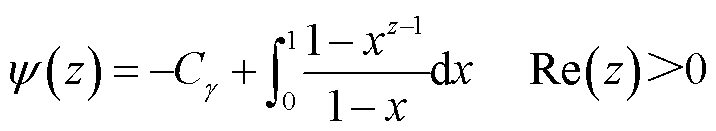 (59)
(59)
3.3.1 鲁棒H密度损失准则设计
现有基于Huber损失等鲁棒化非线性滤波方法中,主要对量测新息向量按残差值分配不同权重,使得质量较低的量测值权重较小,从而抑制量测异常值对状态估计带来的影响[23],没有充分考虑对状态一步预测误差的动态调整,从而在状态模型与真实值发生偏差时不能有效地保持滤波精度;且损失函数中常用的L1范数加权限制异常值的性能有限。因此,提出一种新的L2-1/2型鲁棒H密度损失准则,并与状态估计VB迭代流程紧结合,使得算法能充分利用当前变分迭代的更新值。
考虑如下s阶广义分段损失函数
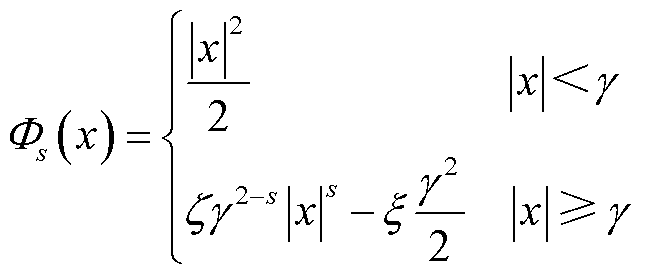 (60)
(60)
式中,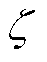 、
、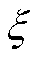 为损失函数系数;s为外窗函数阶数;
为损失函数系数;s为外窗函数阶数; 为H密度窗宽度。为了保持分段函数在边界的平滑可微性与H密度的系数解析性,令s=1/2,设计如下约束以用于解算损失函数系数
为H密度窗宽度。为了保持分段函数在边界的平滑可微性与H密度的系数解析性,令s=1/2,设计如下约束以用于解算损失函数系数
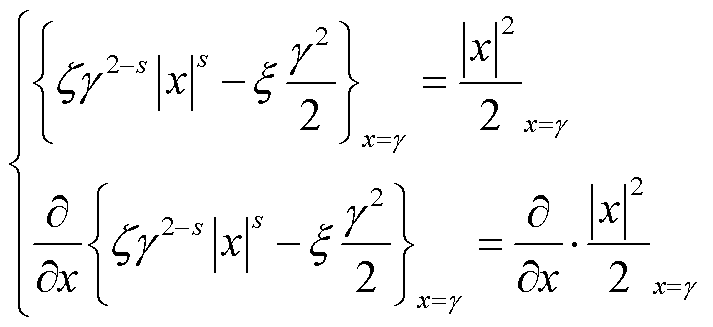 (61)
(61)
根据式(61),可得参数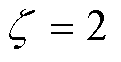 ,
,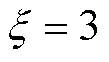 。L2-1/2损失函数调整了分段损失的外窗函数凸性,函数截断内窗
。L2-1/2损失函数调整了分段损失的外窗函数凸性,函数截断内窗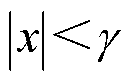 内使用加权L2范数处理,而外窗使用的加权L1/2范数对离群值敏感性比L1范数更小,具有更强的抗异常值能力。在窗口端点处原函数和一阶导函数均连续,满足了平滑可微性。
内使用加权L2范数处理,而外窗使用的加权L1/2范数对离群值敏感性比L1范数更小,具有更强的抗异常值能力。在窗口端点处原函数和一阶导函数均连续,满足了平滑可微性。
为了实现基于H密度的损失函数设计,根据Aleksandr Y. Aravkin的QS函数族概率密度理论[27],可得存在一个均值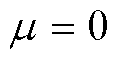 、方差
、方差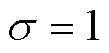 的概率密度
的概率密度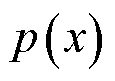 为
为
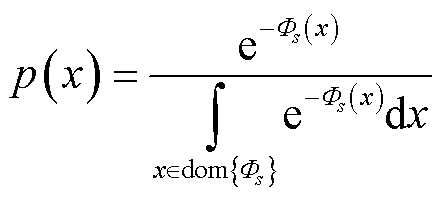 (62)
(62)
其中,归一化常数为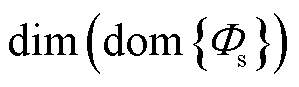 维测度的Lebesgue积分。利用规范化常数表示,将式(60)代入QS概率密度函数式(62)中并取对数,可得H密度函数
维测度的Lebesgue积分。利用规范化常数表示,将式(60)代入QS概率密度函数式(62)中并取对数,可得H密度函数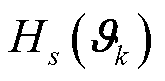 的表达式为
的表达式为
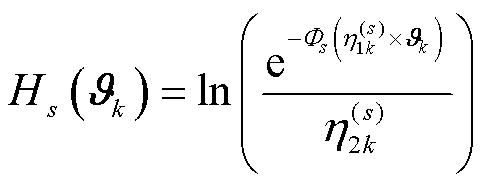 (63)
(63)
进一步,根据Aleksandr Y. Aravkin等的QS概率密度的关键规范化常数计算方法,计算相应损失函数在Lebesgue测度下的负指数二阶矩,可对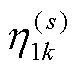 、
、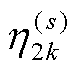 进行解算:
进行解算:
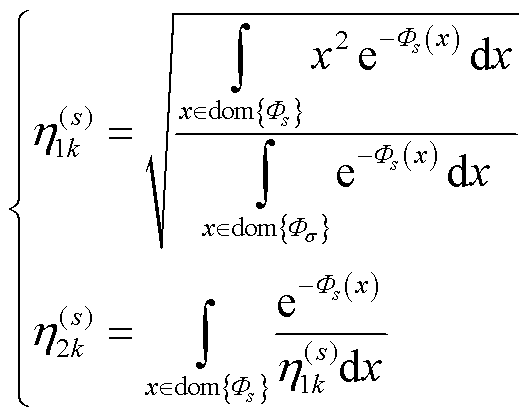 (64)
(64)
计算上述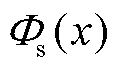 定义域内的Lebesgue积分,可得L2-1/2型H密度损失准则的分段表示形式为
定义域内的Lebesgue积分,可得L2-1/2型H密度损失准则的分段表示形式为
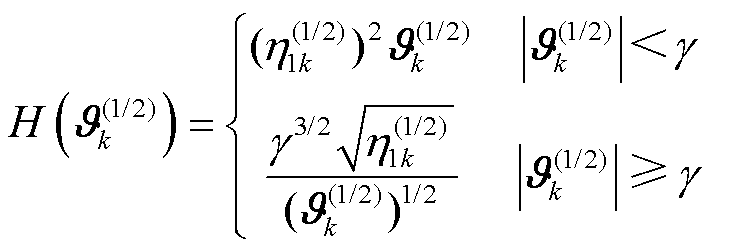 (65)
(65)
其中涉及规范化常数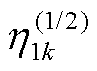 的计算,利用式(64)解得
的计算,利用式(64)解得
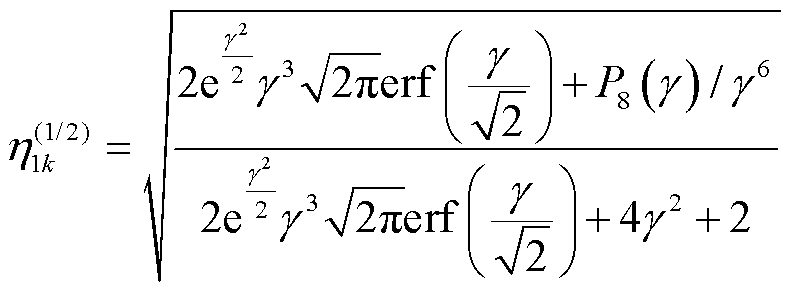 (66)
(66)
式中,多项式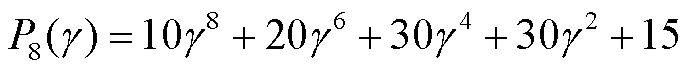 ;
;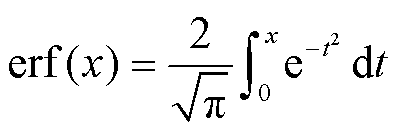 为误差函数。
为误差函数。
3.3.2 基于H密度损失准则的变分紧结合状态后验估计
为了克服传统卡尔曼滤波中MSE准则产生的平方误差对强异常值噪声的敏感性,结合状态-量测新息H密度损失准则,考虑基于VB迭代嵌入型优化目标进行状态向量估计:
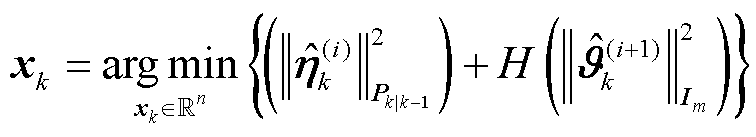 (67)
(67)
式中,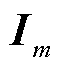 为m阶单位矩阵;状态一步预测误差
为m阶单位矩阵;状态一步预测误差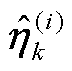 由MSE准则进行优化,而量测-状态线性化新息
由MSE准则进行优化,而量测-状态线性化新息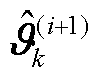 由H密度损失准则优化,滤波时刻为k,当前时刻VB迭代次数为i。
由H密度损失准则优化,滤波时刻为k,当前时刻VB迭代次数为i。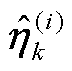 和
和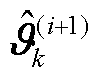 分别表示为
分别表示为
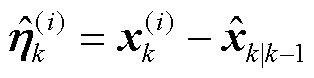 (68)
(68)
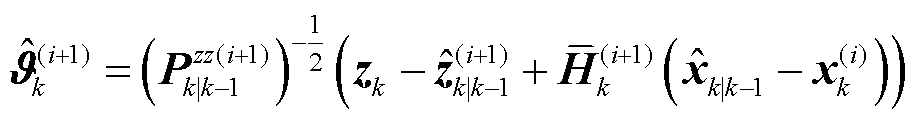 (69)
(69)
式中,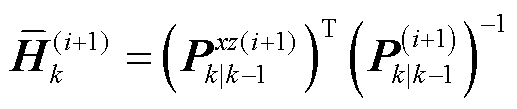 为量测统计线性回归方程
为量测统计线性回归方程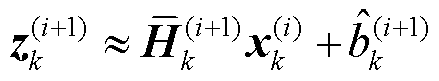 [28]的系数矩阵。利用上述VB迭代嵌入型残差,实现了损失准则(65)与变分推断的计算过程的紧结合,充分考虑了模型不确定性产生的状态偏差,从而加强了后验估计的抗差能力,同时不影响变换新息的迭代形式。
[28]的系数矩阵。利用上述VB迭代嵌入型残差,实现了损失准则(65)与变分推断的计算过程的紧结合,充分考虑了模型不确定性产生的状态偏差,从而加强了后验估计的抗差能力,同时不影响变换新息的迭代形式。
根据式(65)、式(68)和式(69),状态估计的误差最小化目标函数定义为
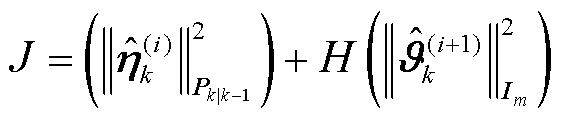 (70)
(70)
为了以递推形式求解优化问题式(67),对式(70)进行关于状态向量的一阶微分运算,得到其向量导数为
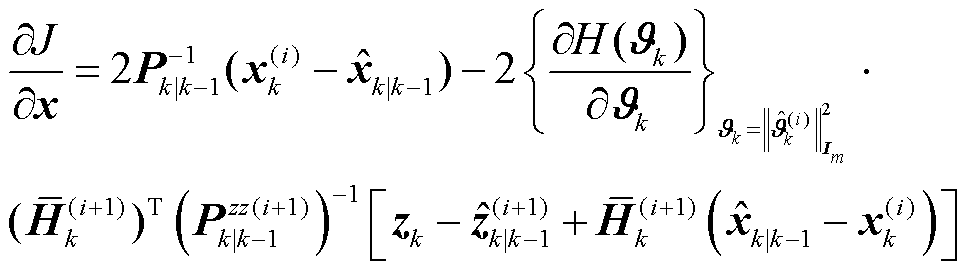 (71)
(71)
其中,H密度关于新息参数的导数可表示为
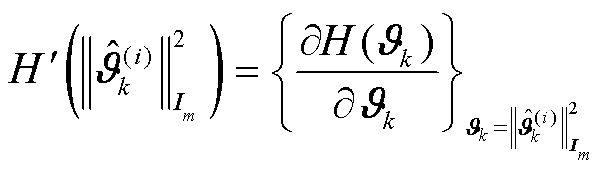 (72)
(72)
令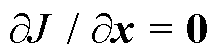 ,根据式(71),可将变分迭代状态向量的递推型后验计算表示为
,根据式(71),可将变分迭代状态向量的递推型后验计算表示为
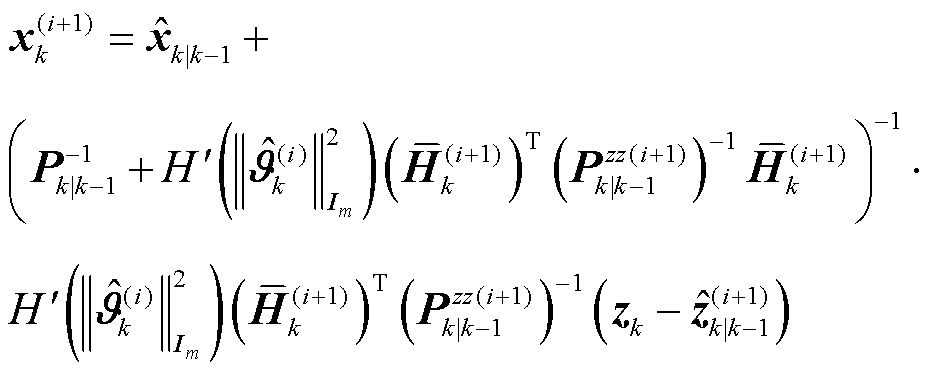 (73)
(73)
化简式(73)写为卡尔曼滤波递推增益形式,可得
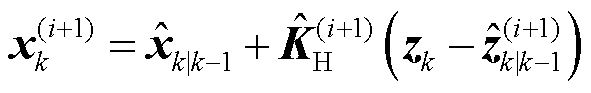 (74)
(74)
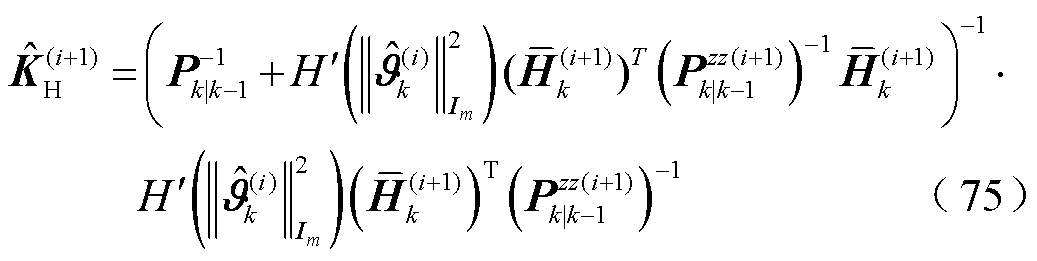
进一步计算当前VB迭代下的状态协方差矩阵。为了增强方差迭代鲁棒性,引入高斯衰减因子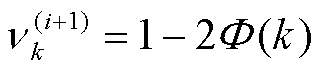 ,可将协方差后验更新为
,可将协方差后验更新为
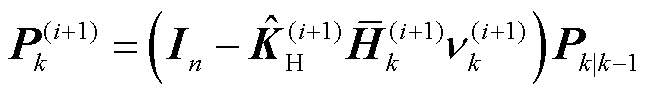 (76)
(76)
式中,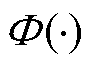 为标准高斯分布函数。利用式(74)~式(76)替换VB迭代计算中状态后验估计式(46),即可得到所提SOC估计算法的完整流程。
为标准高斯分布函数。利用式(74)~式(76)替换VB迭代计算中状态后验估计式(46),即可得到所提SOC估计算法的完整流程。
根据2.1节~3.3节所述参数辨识、SOC估计算法内容,针对图2b中设计的算法框架,得到所提SOC强跟踪估计算法的详细整体计算流程如图3所示。针对任意动态工况,算法初始运行时均由电池SOC-OCV特性曲线与算法初值、输入端电压电流驱动,不需要指定工况内阻/电容参数曲面等其他额外的离线拟合数据辅助计算。计算部分主要由GVFFRLS电池参数在线辨识环节、变分容积滤波环节、H密度抗差后验估计环节三部分组成。其具体执行步骤如下:
(1)根据图2a中的GVFFRLS参数辨识流程进行Thevenin模型的动态参数计算,并传递给状态空间模型进行卡尔曼滤波一步预测。
(2)由式(22)~式(30)计算容积滤波一步预测、容积点采样与量测更新。
(3)由表1中的各期望值计算变分参数推断,其中状态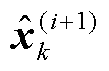 和协方差后验
和协方差后验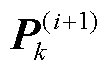 由式(74)~ 式(76)计算。
由式(74)~ 式(76)计算。
(4)根据变分迭代阈值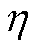 判断VB计算是否收敛,若收敛则将当前变分计算值传递给下一时刻的参数在线辨识环节步骤(1),否则回到步骤(3)继续变分迭代,从而完成SOC估计闭环计算,直到滤波截止时间N为止。
判断VB计算是否收敛,若收敛则将当前变分计算值传递给下一时刻的参数在线辨识环节步骤(1),否则回到步骤(3)继续变分迭代,从而完成SOC估计闭环计算,直到滤波截止时间N为止。
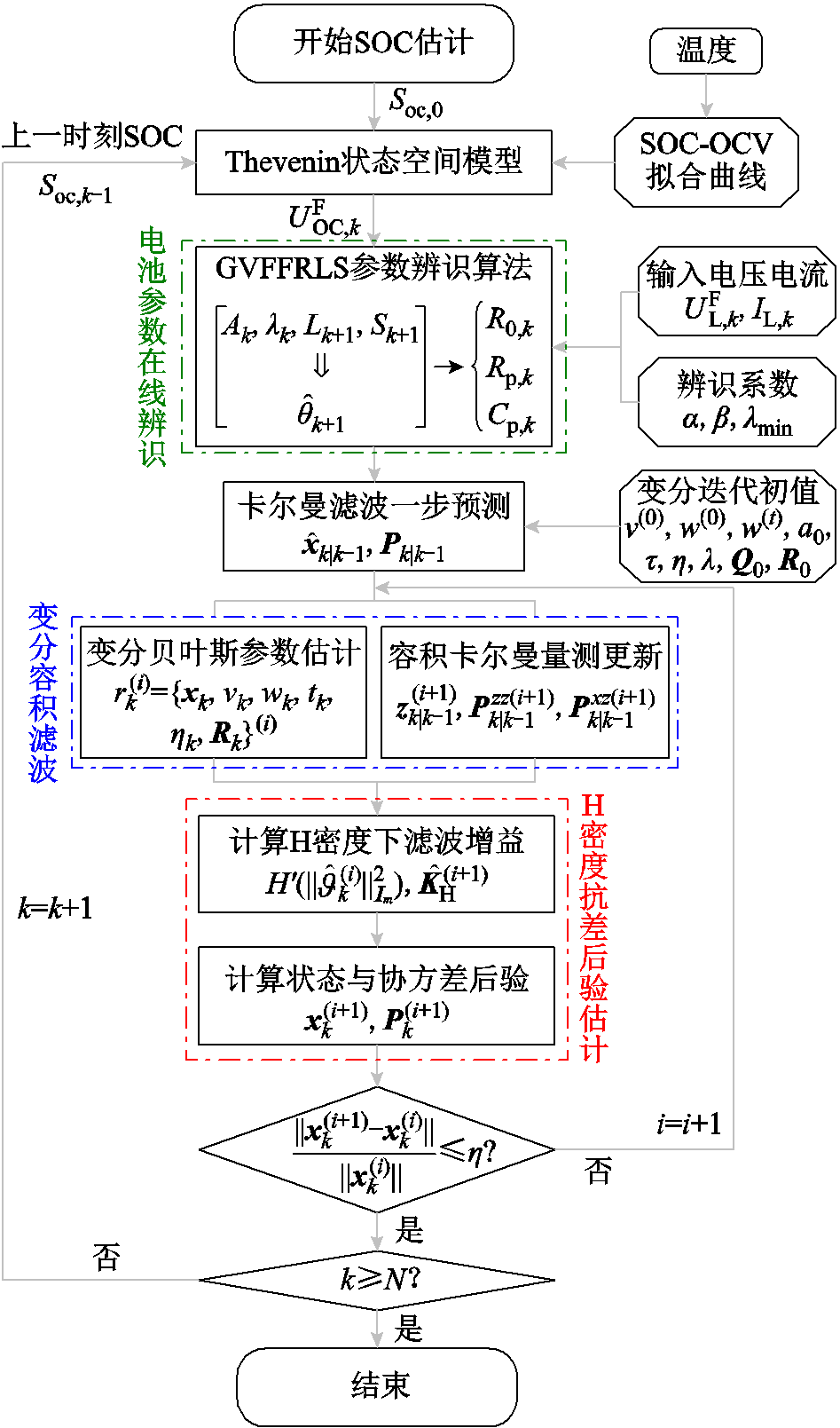
图3 所提SOC强跟踪估计算法总体流程
Fig.3 Calculation flow of the proposed SOC strong tracking estimation algorithm
本节基于MARYLAND大学高级生命周期工程研究中心CALCE电池研究团队开源的INR 18650-20R锂电池测试数据集进行所提算法与现有算法的SOC估计性能对比仿真[29],电池的基本特性参数见表2。
表2 测试锂电池的基本特性参数
Tab.2 Basic characteristic parameters of testing battery

INR 18650-20R Battery 电池参数数值(模型) 额定容量/(mA·h)2 000 电池成分LiNiMnCo/石墨 质量/g45 尺寸/mmd:18.33±0.07 L:64.85±0.15 (充/放电)截止电压/ V4.2/2.5
4.1.1 全温度SOC-OCV映射关系拟合
在电池数据集中,相比低电流放电,增量电流OCV (Incremental Current OCV, ICOCV)测试具有更高的跟踪准确性和更强的鲁棒性[29],其包括若干SOC间隔时段,其测试执行的步骤如下:
(1)将电池完全充电至100%SOC。
(2)以每10%SOC的负脉冲电流放电持续时间进行放电。
(3)利用正脉冲电流,按照相同步骤进行充电。
ICOCV的电压测试数据如图4所示。
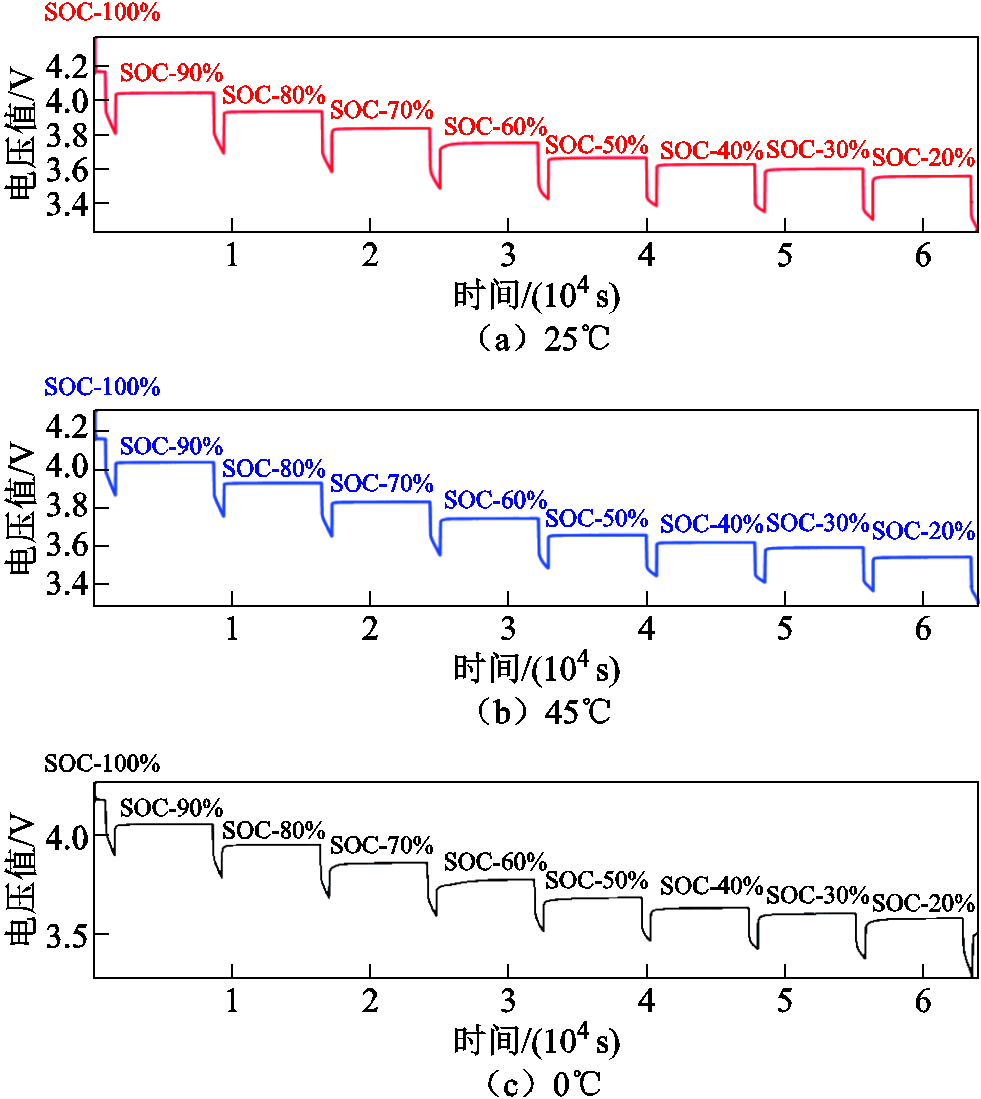
图4 ICOCV实验电压测试数据
Fig.4 Voltage test data of ICOCV experiment
本实验根据第2节的式(4)和式(5),利用增量电流工况下OCV测试数据进行SOC-OCV映射曲线拟合,并通过最小二乘方法对多项式系数进行解算。选用6阶多项式拟合不同温度工况下的OCV曲线,对应温度下的具体多项式系数见表3。
进一步,本实验利用得到的三种温度下的SOC-OCV数据点于温度坐标横向放样,拟合了全温度工况SOC-OCV映射曲面,如图5所示。通过在指定温度断面截取对应的OCV拟合曲线,可实现全温度工况下的SOC动态估计。
表3 三种温度下的6阶多项式SOC-OCV拟合曲线系数
Tab.3 SOC-OCV fitting curve coefficients based on 6th-order polynomials under three temperatures
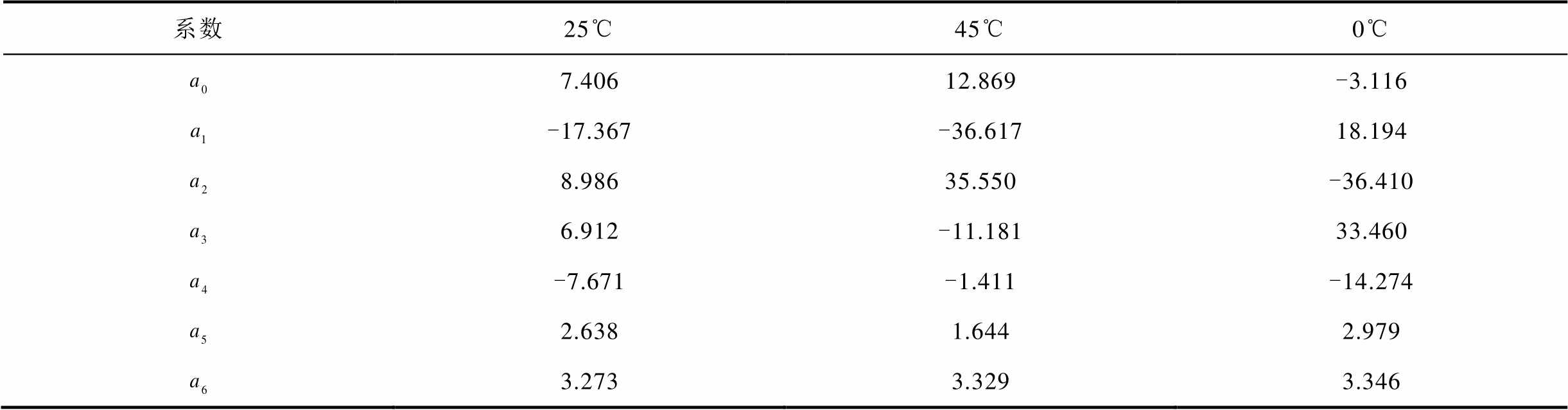
系数25℃45℃0℃ 7.40612.869-3.116 -17.367-36.61718.194 8.98635.550-36.410 6.912-11.18133.460 -7.671-1.411-14.274 2.6381.6442.979 3.2733.3293.346
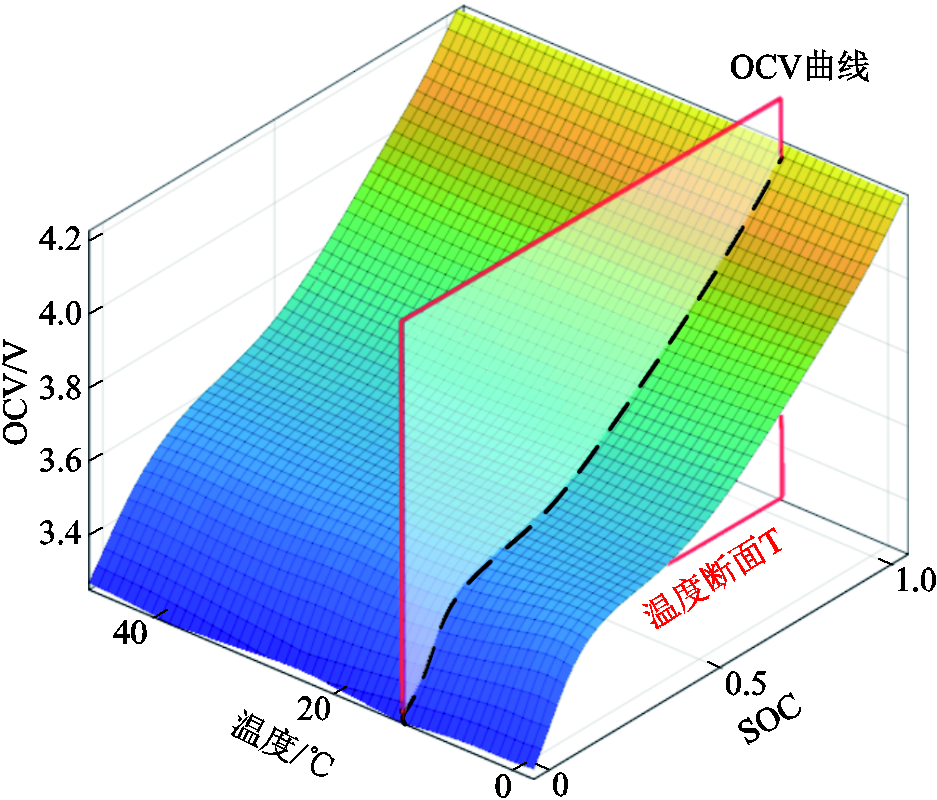
图5 全温度工况下测试电池的SOC-OCV映射拟合曲面
Fig.5 SOC-OCV mapping fitting surface of test battery under working conditions forall temperatures
根据测试数据集提供的输入电压电流数据,本节只针对算法在25℃、45℃、0℃三种温度下的动态工况SOC估计性能进行测试。
4.1.2 噪声工况设定
为了模拟量测噪声中统计参数未知和产生离群异常值两种动态特性,可用一般的非平稳厚尾分布来描述,本节在原模型固有量测误差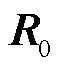 基础上叠加异常值概率混合非高斯分布序列,模拟电池SOC估计中的非平稳厚尾量测噪声环境。在状态空间方程式(6)中,噪声根据如下方法生成。
基础上叠加异常值概率混合非高斯分布序列,模拟电池SOC估计中的非平稳厚尾量测噪声环境。在状态空间方程式(6)中,噪声根据如下方法生成。
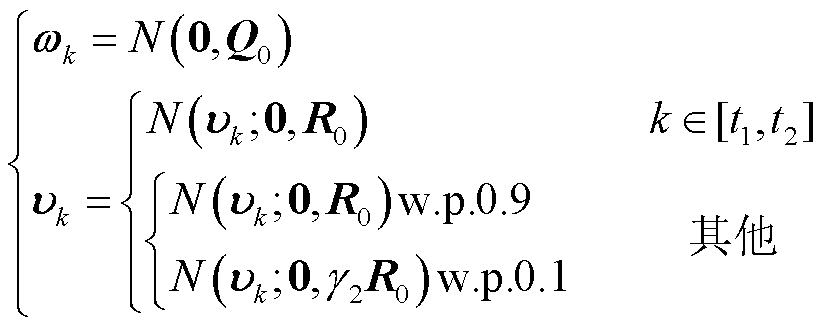 (77)
(77)
式中,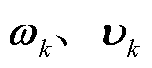 分别为状态与量测噪声,
分别为状态与量测噪声,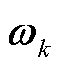 符合零均值高斯分布,
符合零均值高斯分布,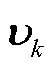 则由非平稳噪声建模,其中高斯时段为普通高斯噪声,而非高斯时段由90%概率的高斯噪声与10%概率的异常值噪声混合而成,时段坐标设为
则由非平稳噪声建模,其中高斯时段为普通高斯噪声,而非高斯时段由90%概率的高斯噪声与10%概率的异常值噪声混合而成,时段坐标设为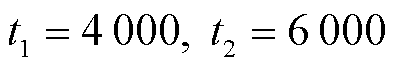 ;量测异常值的偏差倍率设定为
;量测异常值的偏差倍率设定为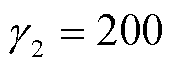 ;w. p. 表示噪声分布切换概率,即量测协方差与标称值出现
;w. p. 表示噪声分布切换概率,即量测协方差与标称值出现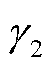 倍偏差的概率为0.1;过程与量测标称协方差设定为
倍偏差的概率为0.1;过程与量测标称协方差设定为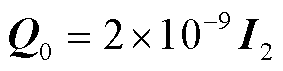 和
和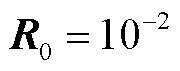 ;初始状态协方差矩阵设置为
;初始状态协方差矩阵设置为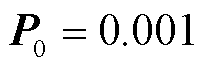 。示例噪声幅值分布如图6所示。
。示例噪声幅值分布如图6所示。
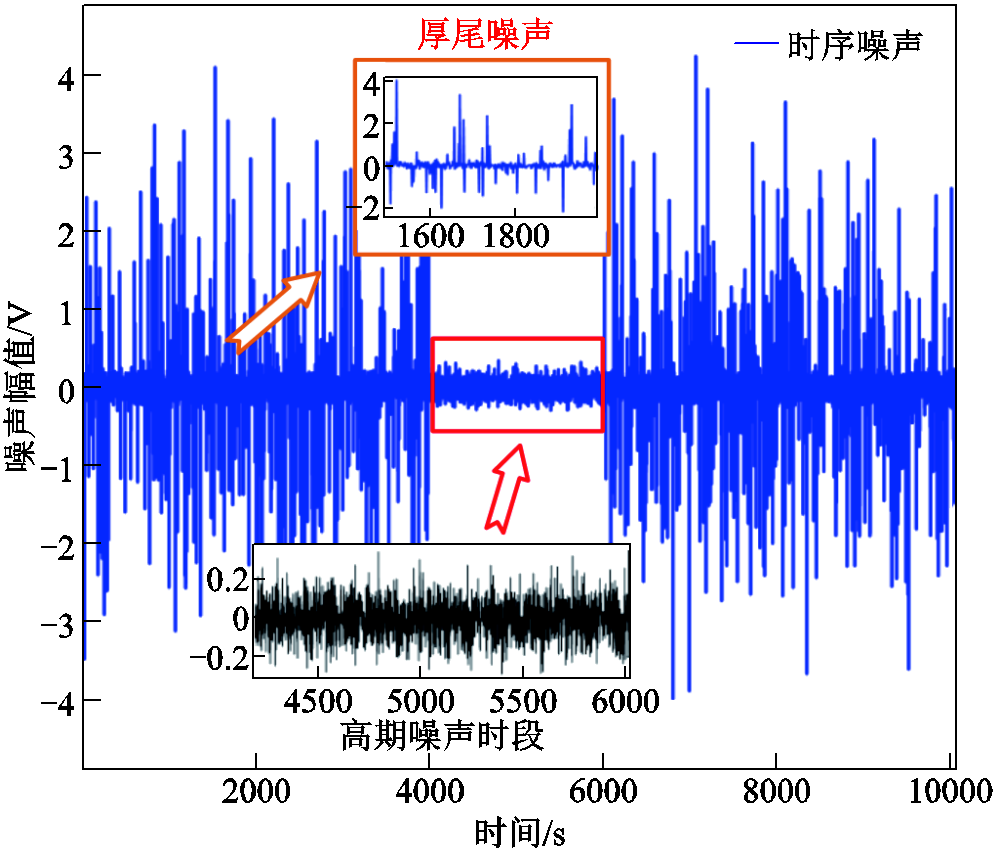
图6 时变非平稳量测噪声的幅值时序分布
Fig.6 Amplitude time distribution of time-varying nonstationary measurement noise
4.1.3 算法初始参数设定
在算法参数设定中,GVFFRLS的广义高斯核参数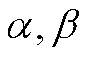 一般可设定在2附近,以在调节峰度时保持高斯核的良好带宽特性;
一般可设定在2附近,以在调节峰度时保持高斯核的良好带宽特性;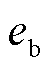 的数量级通常取在10-3~10-4,可有效提升核函数对误差的敏感性;
的数量级通常取在10-3~10-4,可有效提升核函数对误差的敏感性;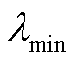 取在0.95~0.99之间,使得变遗忘因子具有较宽适应空间。SOC估计算法中,IWishart分布的初始自由度参数
取在0.95~0.99之间,使得变遗忘因子具有较宽适应空间。SOC估计算法中,IWishart分布的初始自由度参数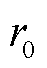 设定合理可增强量测协方差估计对强异常值噪声的适应性;混合分布参数设为1或0表示初始先验为高斯噪声或厚尾噪声,取0~1之间表示初始先验呈混合分布特性,有利于提升先验匹配的准确度。
设定合理可增强量测协方差估计对强异常值噪声的适应性;混合分布参数设为1或0表示初始先验为高斯噪声或厚尾噪声,取0~1之间表示初始先验呈混合分布特性,有利于提升先验匹配的准确度。
所提算法中电池参数在线辨识与SOC估计的初始参数值设定见表4。
4.1.4 辨识与估计精度评价指标
在仿真验证中,电池参数在线辨识的精度评价指标为电压绝对误差的均值MAEv,表示为
表4 算法初始参数设定值
Tab.4 Initial parameter setting of proposed algorithm

参数类型设定值 GVFFRLS参数2, 2, 0.000 1, 0.95 IWishart自由度参数16 量测尺度参数2, 2, 1 混合分布参数0.8 H密度窗宽度1
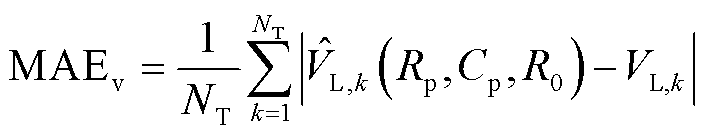 (78)
(78)
式中,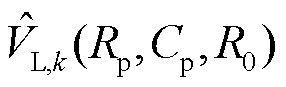 为基于k时刻在线参数辨识所得参数的Thevenin模型端电压预测值;NT为仿真时间;
为基于k时刻在线参数辨识所得参数的Thevenin模型端电压预测值;NT为仿真时间;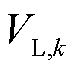 为真实参考端电压。
为真实参考端电压。
而SOC估计的性能评价指标为绝对误差均值MAE、方均根误差RMSE和平均绝对百分比误差MAPE,其定义分别为
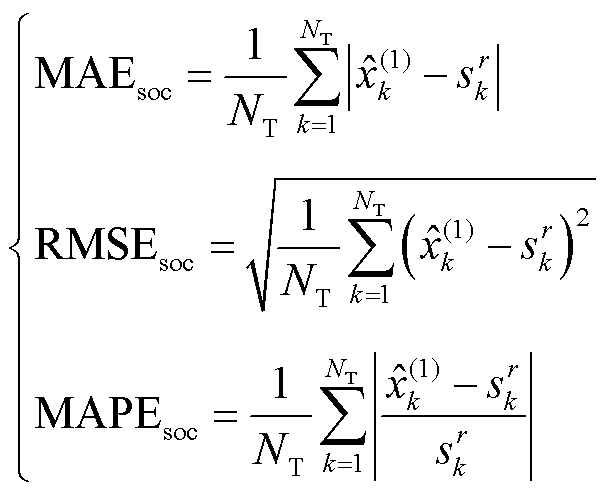 (79)
(79)
式中,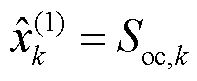 为k时刻状态估计向量中
为k时刻状态估计向量中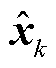 的SOC值元素;
的SOC值元素;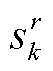 为数据集提供的k时刻真实参考SOC值。
为数据集提供的k时刻真实参考SOC值。
上述指标中,MAEsoc用于衡量SOC估计的整体平均精度;RMSEsoc对估计中的异常值跳变更为敏感,用于评判SOC估计的误差收敛稳定性和初始跟踪性能;MAPEsoc引入了误差与真实值比例,用于衡量SOC估计的相对准确性。
仿真测试基于动态压力测试(Dynamic Stress Test, DST)、联邦城市驾驶计划(Federal Urban Driving Schedule, FUDS)、北京动态压力测试(Beijing Dynamic Stress Test, BJDST)三种动态工况在25℃、45℃、0℃温度下的输入电流、电压进行模型在线参数辨识和SOC估计的联合仿真实验。
实验选用EKF、UKF、Sage-Husa噪声自适应UKF(SHUKF)三种对比算法,联合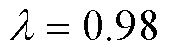 的FFRLS算法(FFRLS-0.98)进行在线参数辨识与SOC估计,并与所提GVFFRLS-强跟踪SOC估计算法进行对比,SHUKF的自适应参数b=0.98。测试中引入已知准确SOC初值的AH积分递推SOC值对状态模型偏差进行直观化表示。AH递推SOC公式为
的FFRLS算法(FFRLS-0.98)进行在线参数辨识与SOC估计,并与所提GVFFRLS-强跟踪SOC估计算法进行对比,SHUKF的自适应参数b=0.98。测试中引入已知准确SOC初值的AH积分递推SOC值对状态模型偏差进行直观化表示。AH递推SOC公式为
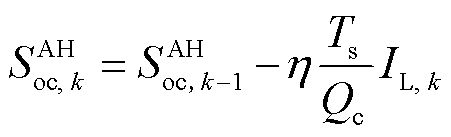 (80)
(80)
由于真实情况下SOC初值难以获取,除AH法外,所有实验中参考真实SOC初值为80%,算法的SOC初值均设为60%,以测试各对比算法在初值未知条件下算法的跟踪与收敛性能。
4.2.1 DST工况下锂电池多温度SOC估计
根据设定测试环境,进行DST动态测试工况下的多温度锂电池在线参数辨识与SOC估计实验。三种测试温度下,端电压预测误差对比如图7所示,SOC估计值与绝对估计误差对比如图8~图10所示。
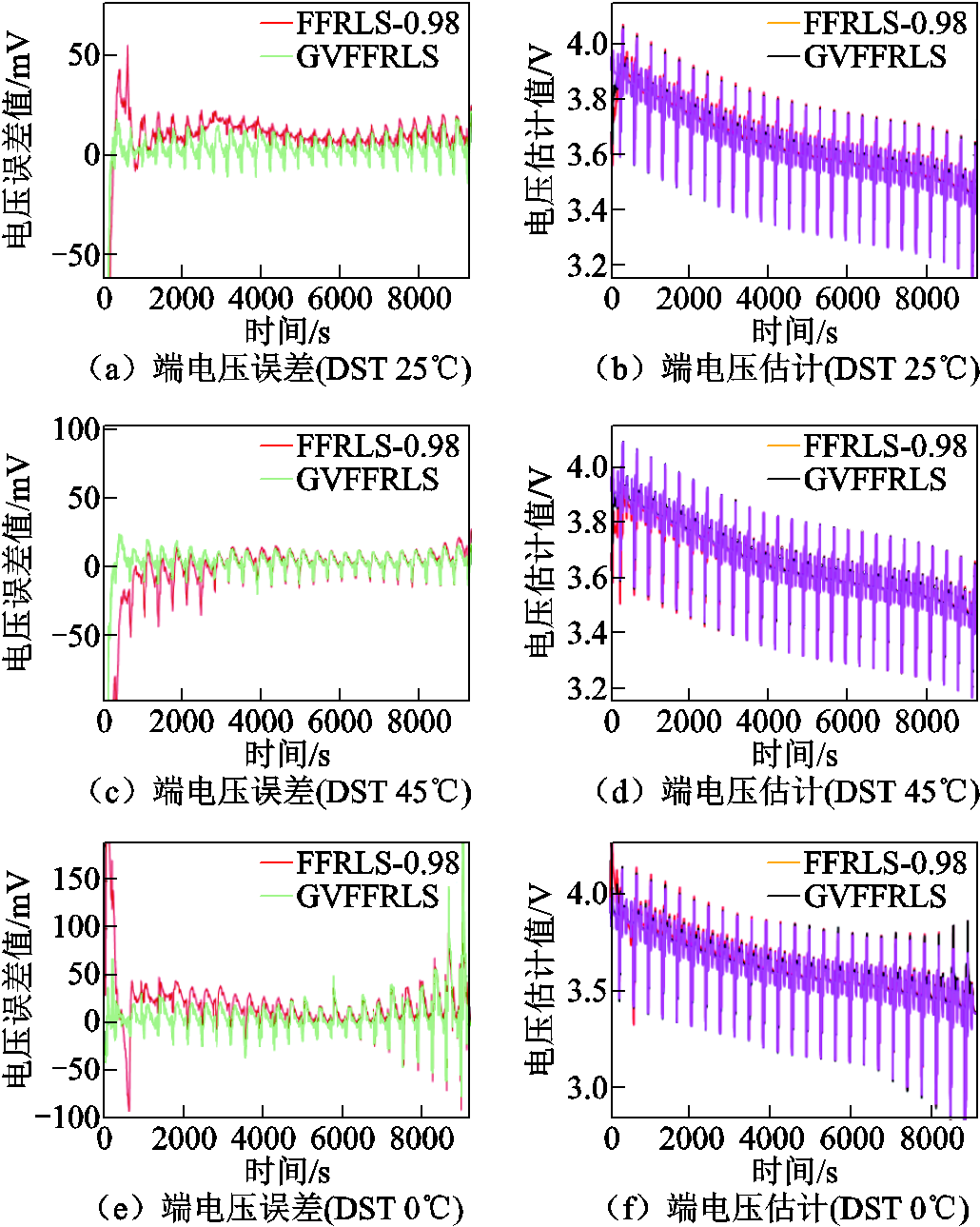
图7 DST工况下基于参数辨识的端电压预测误差对比
Fig.7 Comparison of terminal voltage prediction error based on parameter identification results under DST working condition
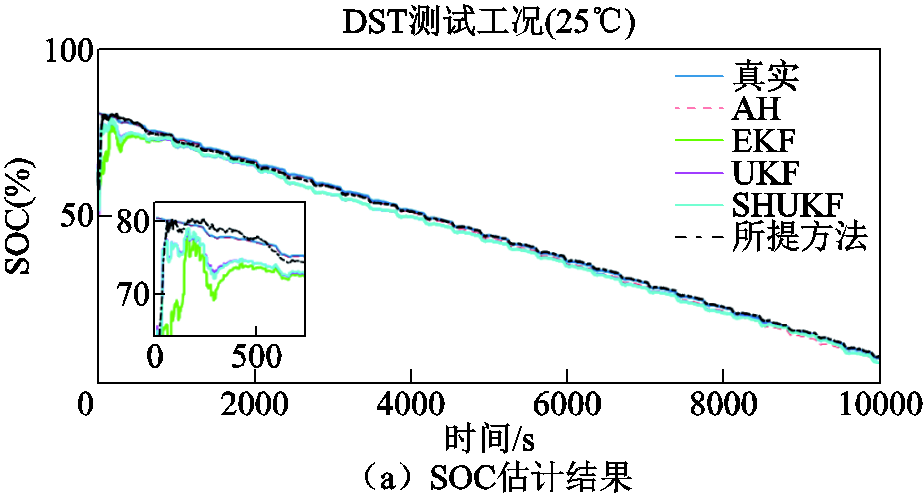
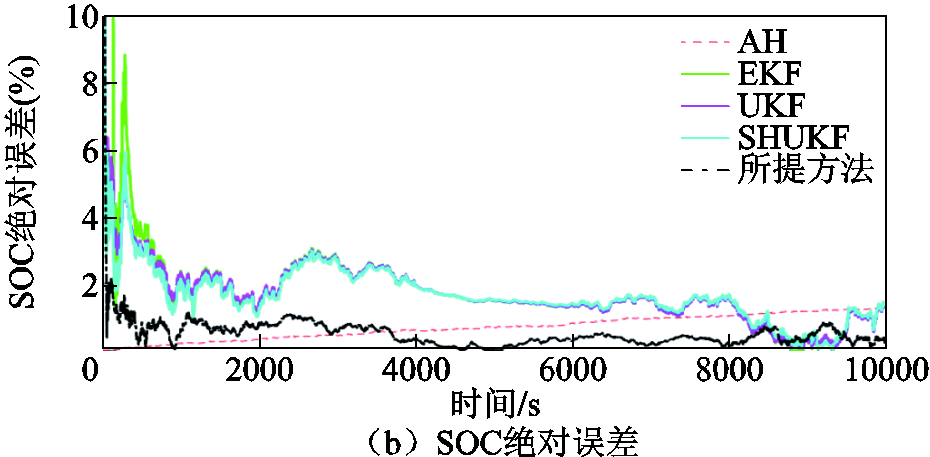
图8 DST工况下SOC估计结果与绝对误差对比(25℃)
Fig.8 Comparison of SOC estimation results and absolute error under DST working condition at 25℃
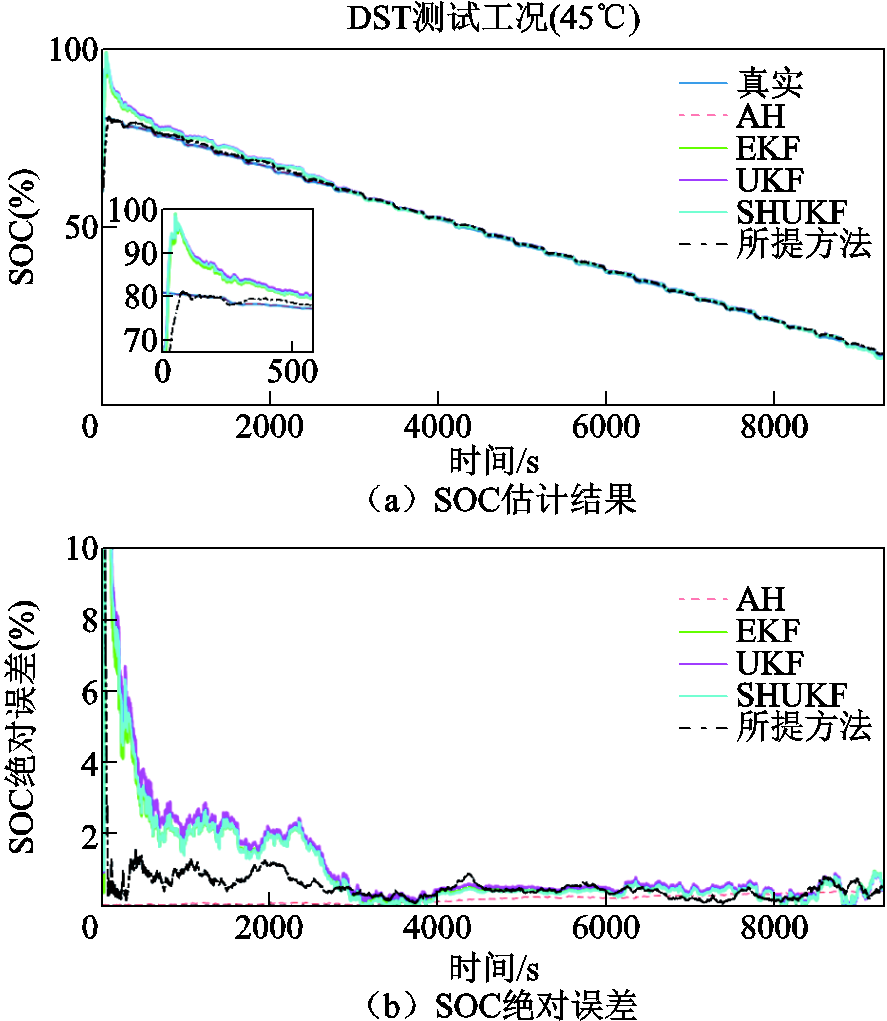
图9 DST工况下SOC估计结果与绝对误差对比(45℃)
Fig.9 Comparison of SOC estimation results and absolute error under DST working condition at 45℃
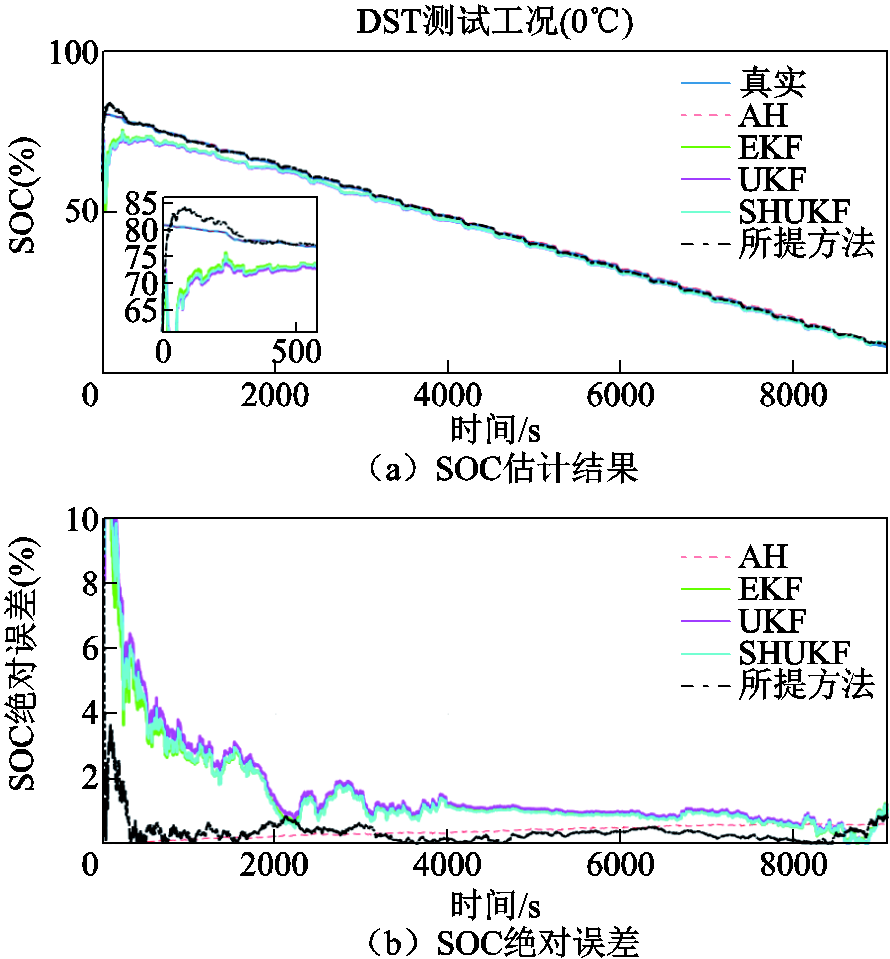
图10 DST工况下SOC估计结果与绝对误差对比(0℃)
Fig.10 Comparison of SOC estimation results and absolute error under DST working condition at 0℃
根据仿真结果,可以看出在0℃、25℃、45℃温度的DST工况下,FFRLS-EKF、UKF、SHUKF三种对比算法的电压误差初始收敛性能与后续持稳性均低于所提算法,FFRLS的端电压预测误差非常不平稳,波动程度较大,而所提GVFFRLS的电压误差始终能保持收敛在0左右;同时,在初始非平稳噪声条件下,高斯先验型非线性滤波EKF、UKF、SHUKF的SOC跟踪性能和估计精度都明显变差,在初始跟踪能力上EKF与UKF相当,弱于SHUKF;且上述三种算法在整体SOC估计性能和数值稳定性上远低于所提算法。
上述实验的参数辨识MAEv误差、SOC估计MAEsoc、RMSEsoc与MAPEsoc误差对比见表5。由表5数据可得,在DST工况下,所提算法三种温度SOC估计的平均MAEsoc精度相比EKF、UKF、SHUKF分别提升了67.24%、68.15%、65.94%;RMSE精度分别提升了57.66%、56.23%、54.41%;MAPE精度分别提升了61.70%、62.73%、61.00%。
表5 DST工况下不同指标的SOC估计精度对比
Tab.5 Comparison of SOC estimation accuracy with different indexes under DST working condition

温度参数辨识模型误差-MAEv/mVSOC估计误差-MAEsoc(%)SOC估计误差-RMSEsoc(%)SOC估计误差-MAPEsoc(%) FFRLS-0.98GVFFRLSEKFUKFSHUKF所提方法EKFUKFSHUKF所提方法EKFUKFSHUKF所提方法 25℃15.3096.8791.8851.7531.720.5472.7112.2212.1581.2164.4734.3174.3591.430 45℃12.9397.5741.0661.1871.0590.5531.9462.1142.0061.1462.5632.7542.5261.415 0℃24.99813.1351.5671.7071.5670.382.6622.7472.6330.7373.4113.6643.3741.156
4.2.2 FUDS工况下锂电池多温度SOC估计
根据设定测试环境,进行FUDS动态测试工况下的多温度锂电池在线参数辨识与SOC估计实验。三种测试温度下,端电压预测误差对比如图11所示,SOC估计值与绝对估计误差对比如图12~图14所示;参数辨识MAEv误差、SOC估计MAEsoc、RMSEsoc与MAPEsoc误差对比见表6。
根据仿真结果图11~图14,可以看出在25℃的FUDS工况下FFRLS-EKF、UKF、SHUKF三种对比算法的电压预测误差持稳性与SOC初始跟踪精度均低于所提算法,而0℃、45℃工况下EKF、UKF、SHUKF产生了跟踪失准问题,导致算法的SOC估计和端电压预测初始状态发散,0℃时无法再跟踪上真实SOC,45℃时经过长时间才以较低精度收敛回真实值附近。相比之下,所提算法的参数辨识电压预测误差和SOC估计误差在初始跟踪状态阶段快速收敛,且从始至终均保持平稳收敛状态。
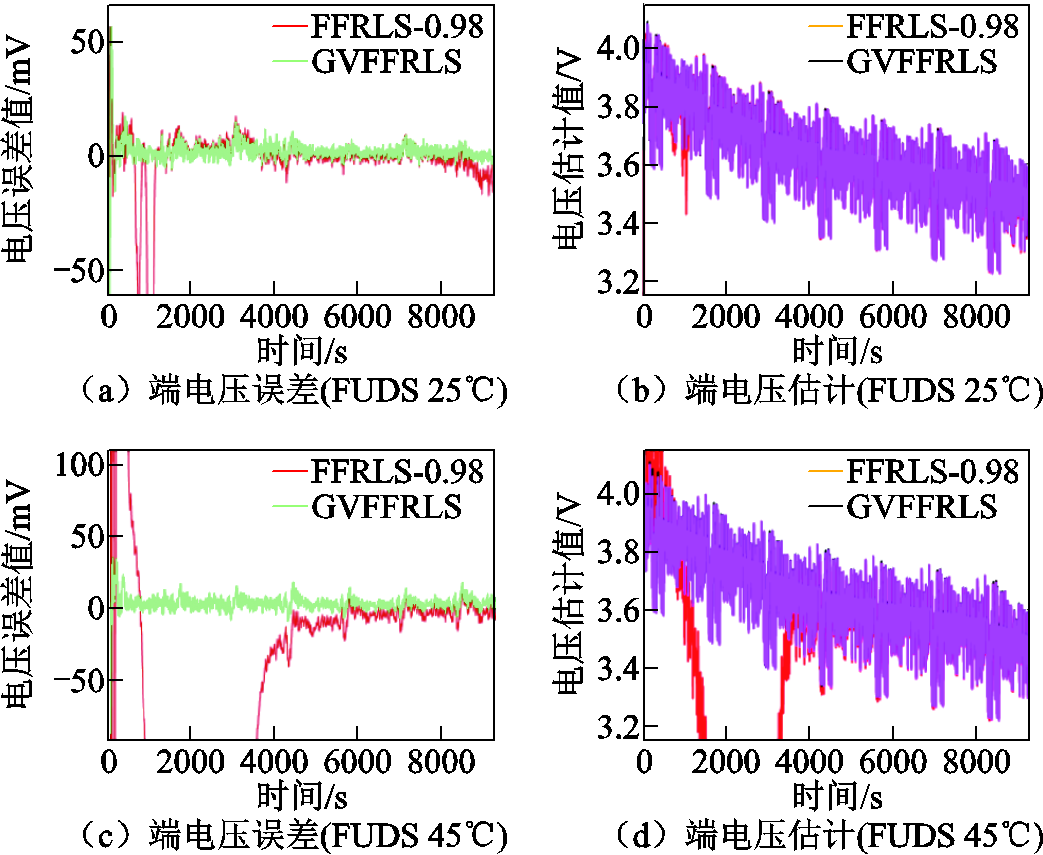
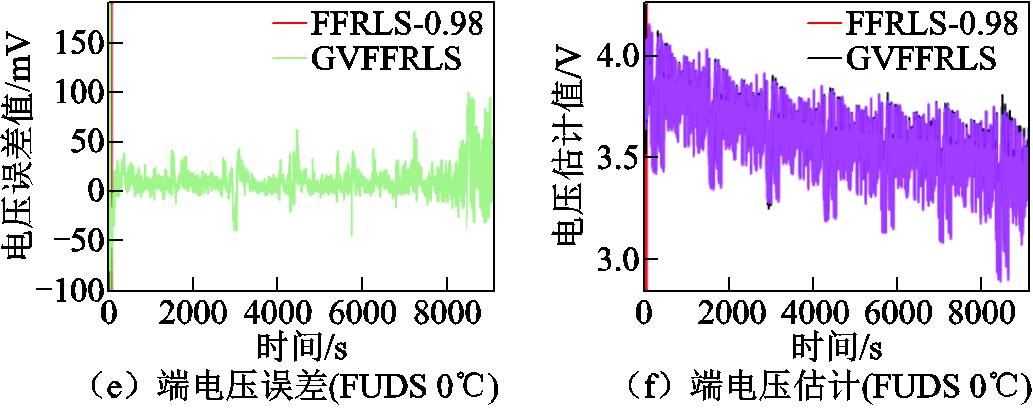
图11 FUDS工况下基于参数辨识的端电压预测误差对比
Fig.11 Comparison of terminal voltage prediction error based on parameter identification results under FUDS working condition
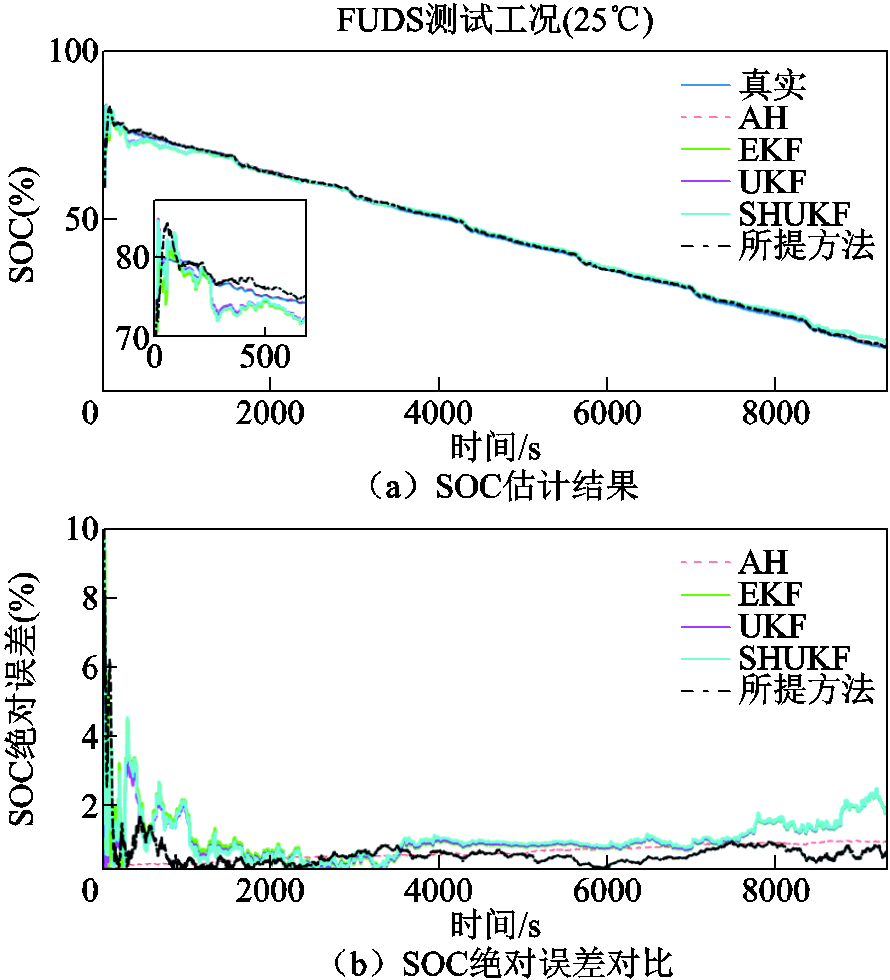
图12 FUDS工况下SOC估计结果与绝对误差对比(25℃)
Fig.12 Comparison of SOC estimation results and absolute error under FUDS working condition at 25℃
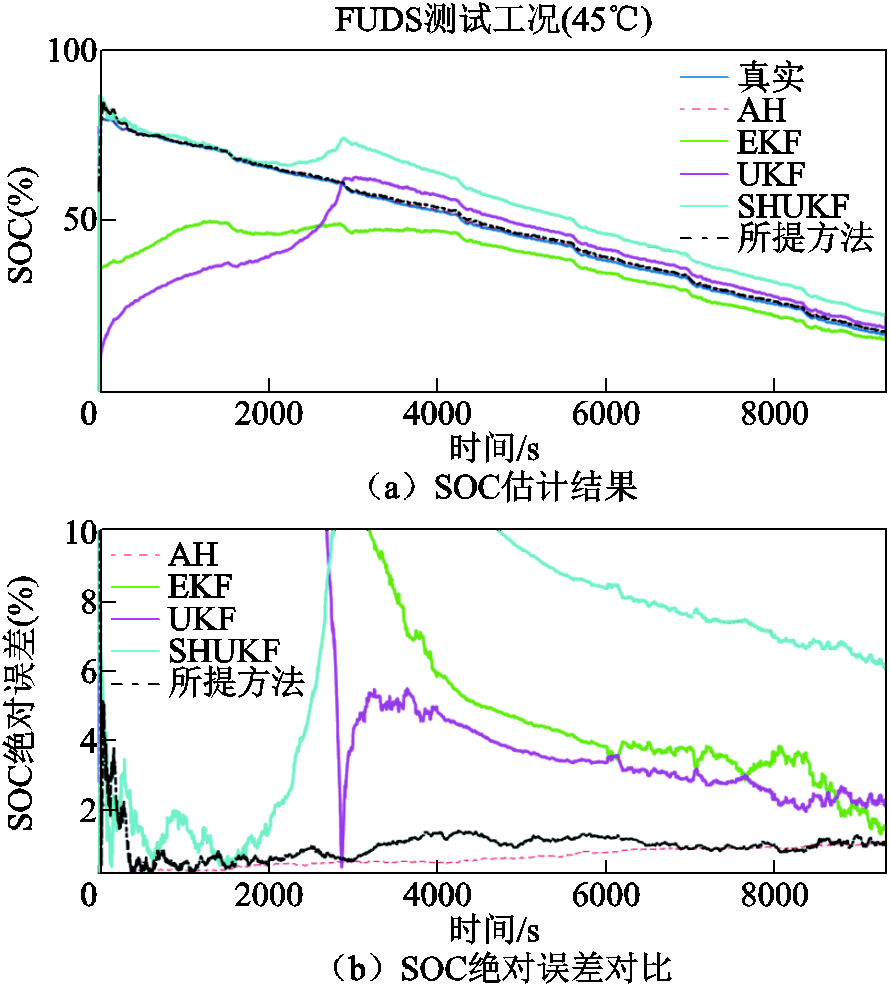
图13 FUDS工况下SOC估计结果与绝对误差对比(45℃)
Fig.13 Comparison of SOC estimation results and absolute error under FUDS working condition at 45℃
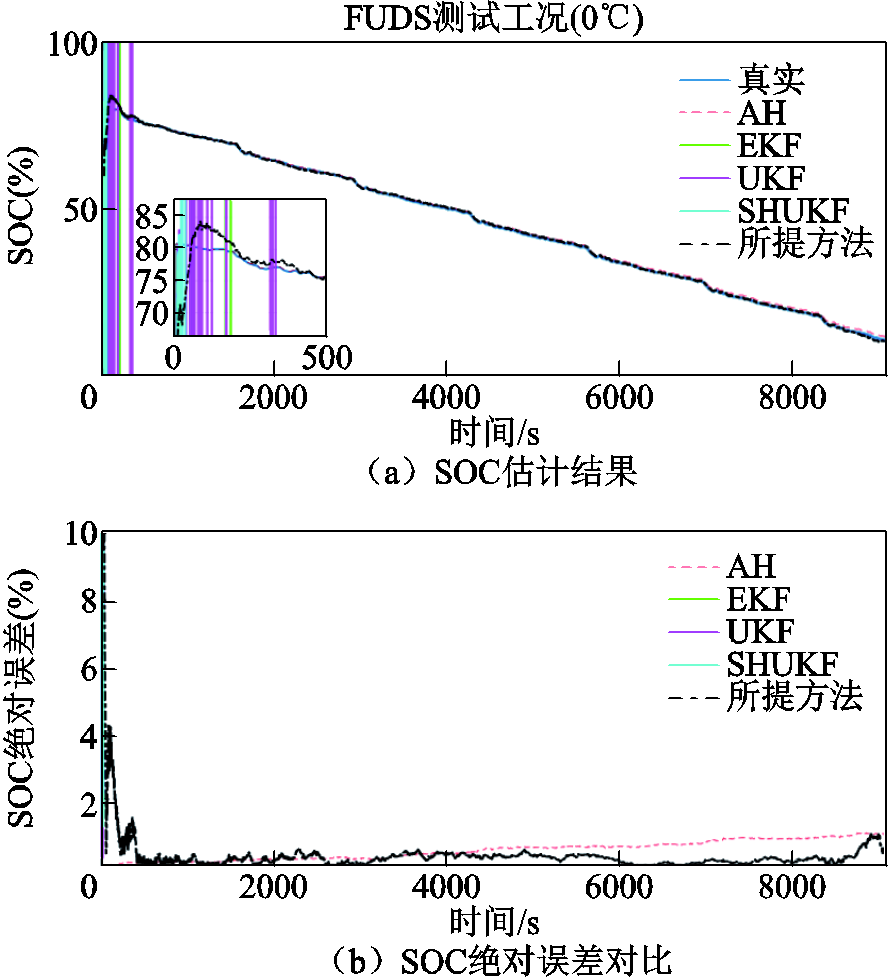
图14 FUDS工况下SOC估计结果与绝对误差对比(0℃)
Fig.14 Comparison of SOC estimation results and absolute error under FUDS working condition at 0℃
表6 FUDS工况下不同指标的SOC估计精度对比
Tab.6 Comparison of SOC estimation accuracy with different indexes under FUDS working condition

温度参数辨识模型误差-MAEv/mVSOC估计误差-MAEsoc(%)SOC估计误差-RMSEsoc(%)SOC估计误差-MAPEsoc(%) FFRLS-0.98GVFFRLSEKFUKFSHUKF所提方法EKFUKFSHUKF所提方法EKFUKFSHUKF所提方法 25℃7.7964.070.8910.8680.90.4321.1861.121.1640.7992.8862.8832.9601.203 45℃1 938.1965.289.41211.416.8360.81414.02719.4997.9251.09916.79520.08421.3172.469 0℃发散14.553发散发散发散0.316发散发散发散0.903发散发散发散0.825
由表6数据可得,在FUDS工况下,除去对比算法发散的45℃测试结果,所提算法SOC估计的平均MAEsoc精度相比EKF、UKF、SHUKF分别提升了87.91%、89.85%、83.89%;RMSE精度分别提升了87.52%、90.79%、79.12%;MAPE精度分别提升了81.34%、84.01%、84.87%。
4.2.3 BJDST工况下锂电池多温度SOC估计
根据设定测试环境,进行BJDST动态测试工况下的多温度锂电池在线参数辨识与SOC估计实验。三种测试温度下,端电压预测误差对比如图15所示,SOC估计值与绝对估计误差对比如图16~图18所示;参数辨识误差MAEv、SOC估计MAEsoc、RMSEsoc与MAPEsoc误差对比见表7。
根据仿真结果图15~图18可以看出,与前两种动态工况下的仿真结果类似,FFRLS-EKF、UKF、SHUKF三种对比算法的电压预测误差持稳性与SOC初始跟踪精度均低于所提算法,相比之下,所提算法的参数辨识电压预测误差和SOC估计误差在初始跟踪状态阶段快速收敛,且始终均保持平稳收敛状态。
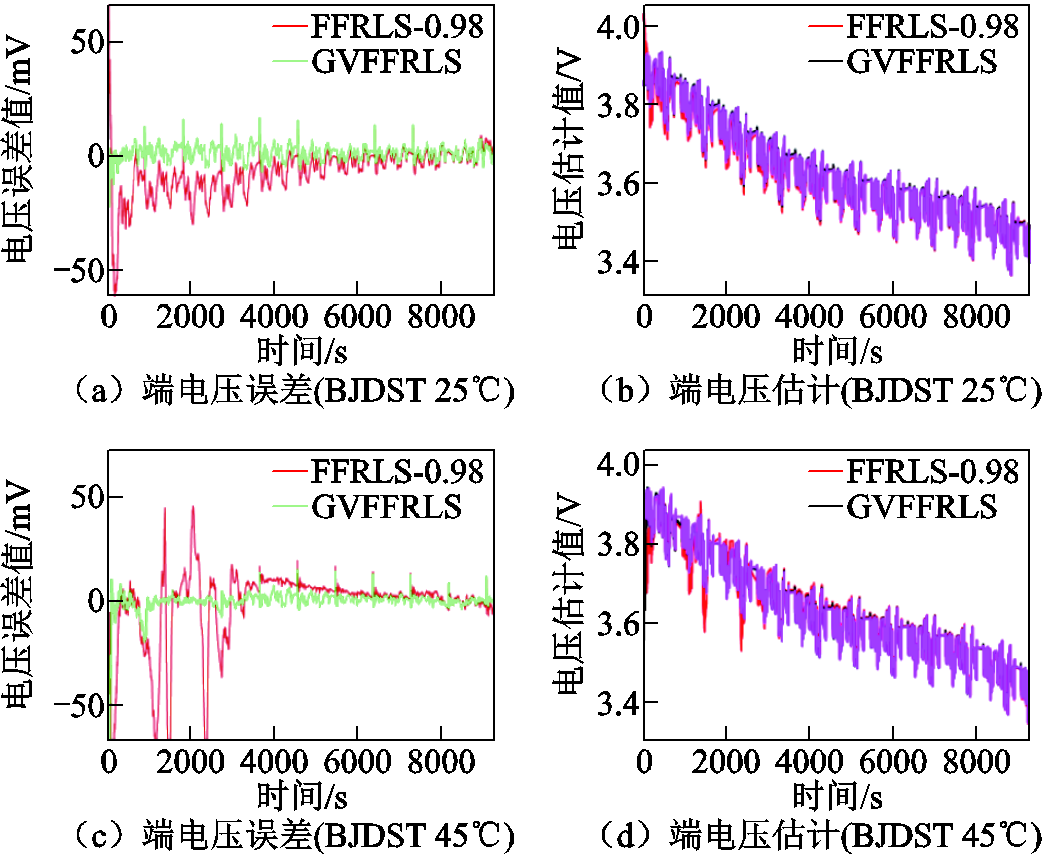
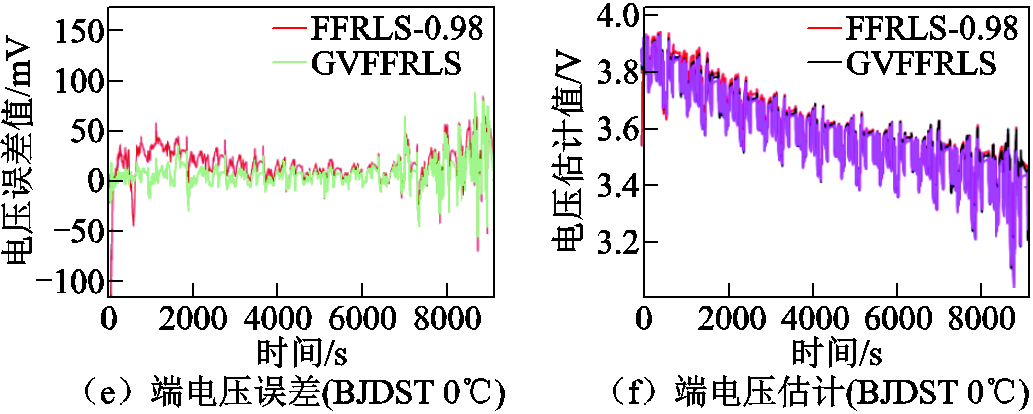
图15 BJDST工况下基于参数辨识的端电压预测误差对比
Fig.15 Comparison of terminal voltage prediction error based on parameter identification results under BJDST working condition
由表7数据可得,在BJDST工况下,所提算法SOC估计的平均MAEsoc精度相比EKF、UKF、SHUKF分别提升了69.93%、68.15%、68.05%;RMSEsoc精度分别提升了59.98%、59.67%、59.73%;MAPEsoc精度分别提升了58.54%、56.58%、56.48%。
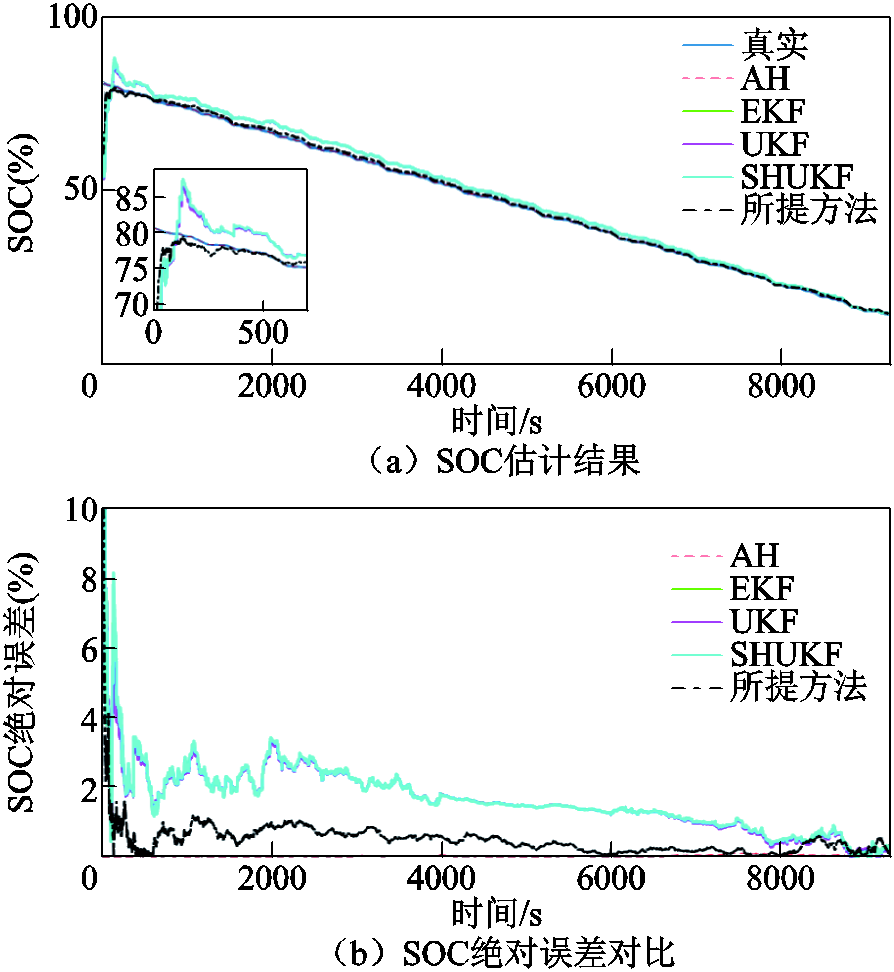
图16 BJDST工况下SOC估计结果与绝对误差对比(25℃)
Fig.16 Comparison of SOC estimation results and absolute error under BJDST working condition at 25℃
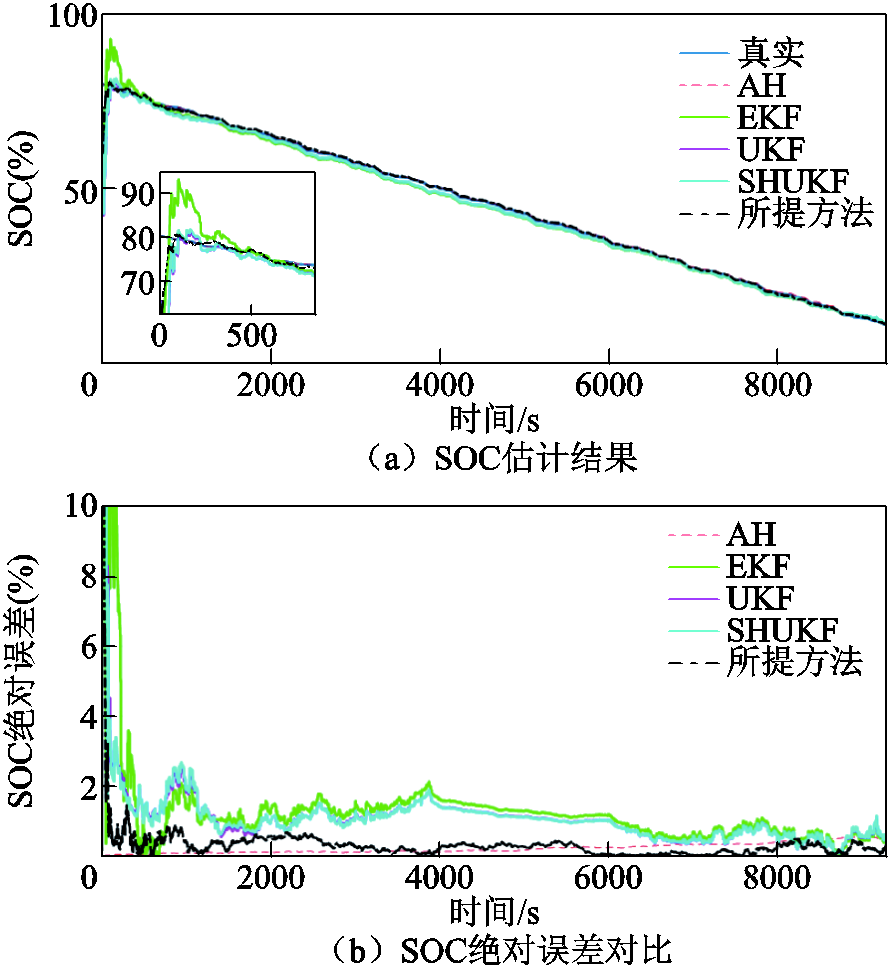
图17 BJDST工况下SOC估计结果与绝对误差对比(45℃)
Fig.17 Comparison of SOC estimation results and absolute error under BJDST working condition at 45℃
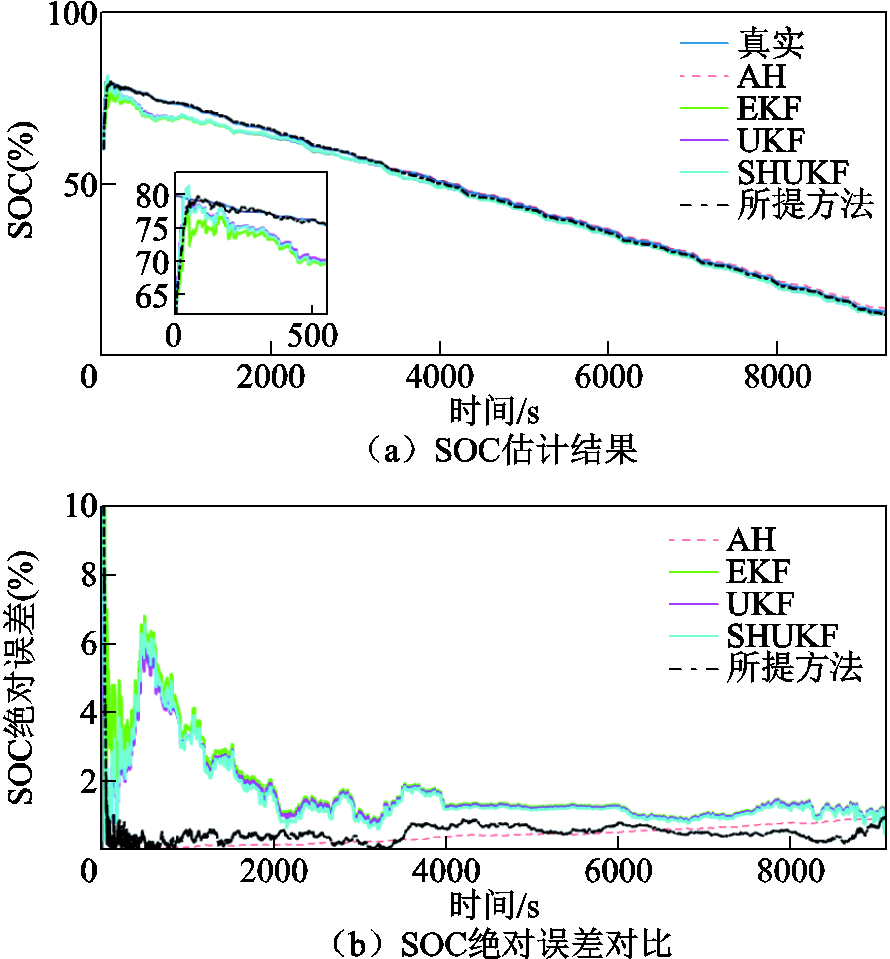
图18 BJDST工况下SOC估计结果与绝对误差对比(0℃)
Fig.18 Comparison of SOC estimation results and absolute error under BJDST working condition at 0℃
表7 BJDST工况下不同指标的SOC估计精度对比
Tab.7 Comparison of SOC estimation accuracy with different indexes under BJDST working condition

温度参数辨识模型误差MAEv/mVSOC估计误差-MAEsoc(%)SOC估计误差-RMSEsoc(%)SOC估计误差-MAPEsoc(%) FFRLS-0.98GVFFRLSEKFUKFSHUKF所提方法EKFUKFSHUKF所提方法EKFUKFSHUKF所提方法 25℃8.553.1641.5691.5681.5930.4932.0782.0772.1060.8313.2143.2123.2831.269 45℃31.098.9691.1861.0751.070.3081.862.052.0210.7632.8422.6032.6140.917 0℃20.50412.1021.6321.4981.4650.5182.0841.8491.8580.8164.0393.8243.7201.999
4.3.1 算法的参数辨识精度与动态性能
根据仿真结果图7、图11和图15,可以看出,FFRLS的初始收敛速度较慢,误差经大幅波动或缓慢变化后才能收敛。在FUDS工况图13和图14中,基于不准确SOC值的FFRLS的参数辨识跟踪失准,甚至无法进行迭代;而所提GVFFRLS算法由于可通过变遗忘因子调整跟踪性能,且具有SH误差自适应能力,在参数辨识开始阶段模型误差就能迅速收敛至0,在算法误差初次过零后误差曲线保持在0附近稳定波动,最大误差值远小于FFRLS的最大估计误差。图19展示了不同非平稳动态测试工况下FFRLS与GVFFRLS方法的参数辨识精度对比。
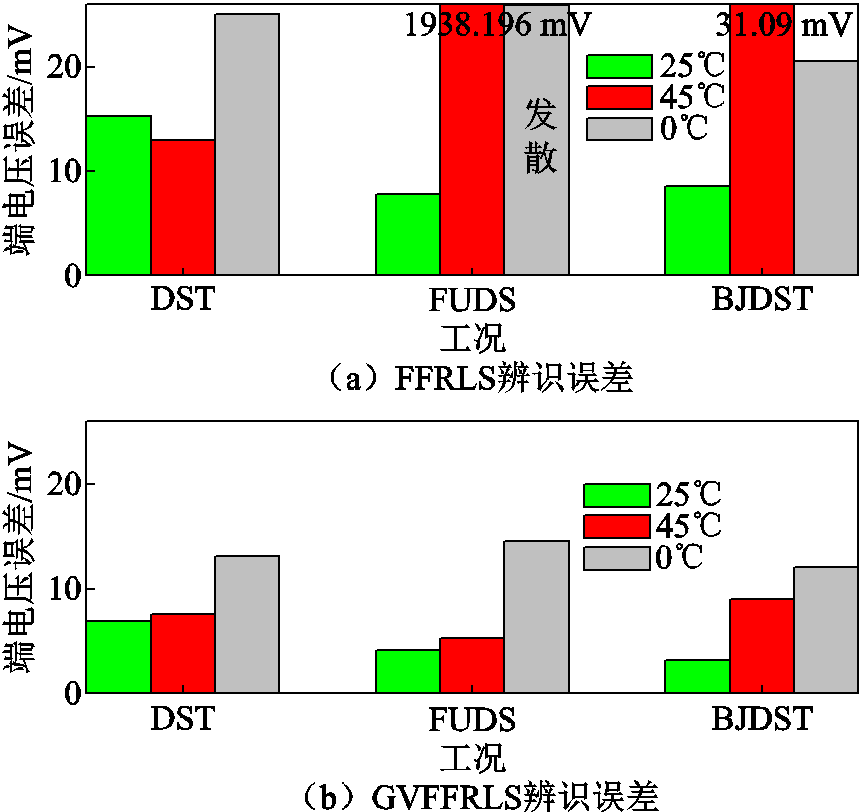
图19 多动态工况下锂电池参数辨识误差对比
Fig.19 Comparison of parameter identification prediction error under multiple dynamic conditions
由图19和表5~表7中的参数辨识精度数据分析,除去对比算法发散的FUDS-0℃实验组,所提GVFFRLS在线辨识在剩余8种测试工况场景下平均绝对估计误差为9.466 mV,而FFRLS的绝对估计误差为257.423 mV,相比之下误差提高了96.32%;若不计跟踪失准的FUDS-45℃实验组,GVFFRLS算法在剩余7种测试工况场景下平均绝对估计误差为7.985 mV,而FFRLS的绝对估计误差为17.312mV,所提算法辨识精度仍提升了53.88%。图20展示了多动态测试工况下所提算法SOC估计的误差平均值对比情况。
4.3.2 算法的SOC估计精度与强跟踪性能
在算法的SOC估计精度方面,根据图20和表5~表7综合对比多工况下的测试结果(不含发散工况FUDS-0℃),EKF估计的平均绝对误差为2.401%,UKF为2.633 25%,两者性能接近;SHUKF具有一定的噪声自适应能力,因此整体估计精度略高于EKF和UKF,平均绝对误差为2.026 25%,但其仍然无法适应具有厚尾特性的噪声,且当噪声分布转换时,其协方差矩阵的递推无法快速响应收敛,造成估计精度降低。而所提方法的平均绝对误差为0.505 625%,相比EKF、UKF、SHUKF分别提升了78.94%、80.80%、75.05%,极大地提高了动态条件下SOC估计精度。
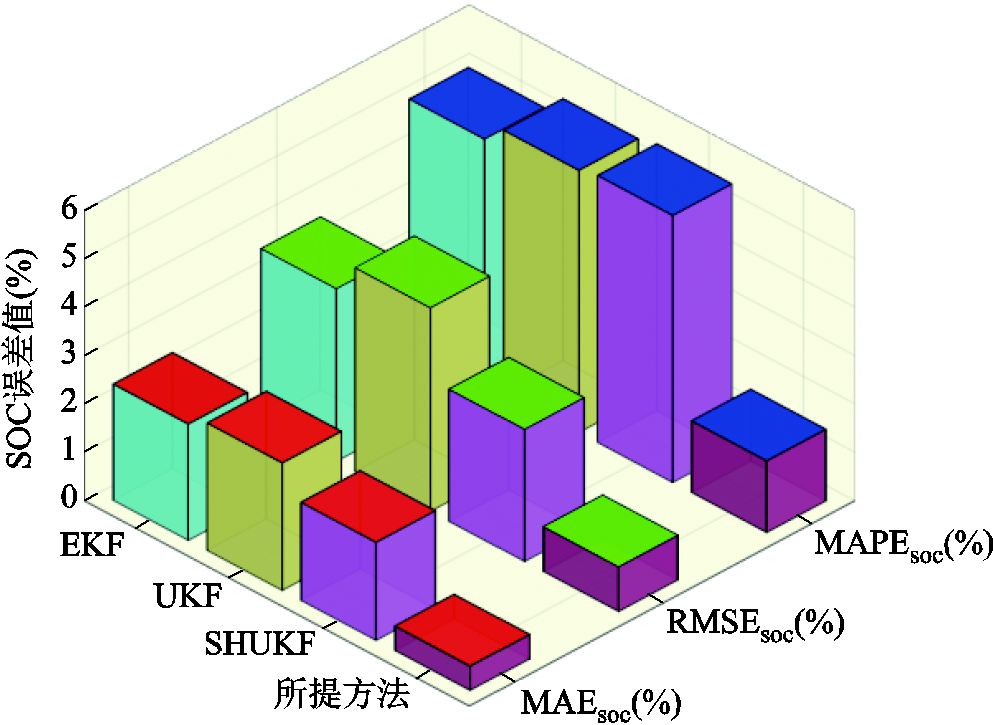
图20 多动态工况的SOC估计误差平均值对比
Fig.20 Comparison of SOC estimation average error under multiple dynamic conditions
在SOC强跟踪性能方面,根据图8~图10、图12~图14、图16~图18可得,所设温度与动态工况下初始SOC值未知,在估计开始一段时间内所有算法都需要对真实SOC值进行跟踪。由于初始跟踪阶段内量测噪声为厚尾噪声,造成高斯先验型非线性滤波EKF、UKF、SHUKF先验分布失配,导致其初始跟踪精度变差,而所提算法具有较强的噪声分布匹配与抗差跟踪性能,这使得其在实验中能以较快收敛速度对真实初始SOC值进行跟踪(如图8~图10,图12~图14,图16~图18中初始跟踪局部放大曲线),并在跟踪收敛后对电池SOC进行持续稳定的高精度估计。
4.3.3 算法的非平稳噪声匹配性能
在所设计测试工况中,T≤4 000 s时间段内量测噪声为厚尾噪声,4 000 s<T≤6 000 s时间段内噪声切换为高斯噪声,T>6 000 s时又变为厚尾噪声。高斯噪声时段内所有算法的噪声参数为设定值不变,由高斯噪声切换至厚尾噪声时,所提算法基于变分迭代进行噪声统计量实时估计,匹配得到真实噪声的近似分布,从而提高了厚尾噪声时段的SOC估计精度和跟踪性能。图21展示了各测试工况在非平稳厚尾噪声影响下,所提算法和对比算法之间的量测噪声真实分布匹配平均性能(不含发散工况FUDS-0℃)。
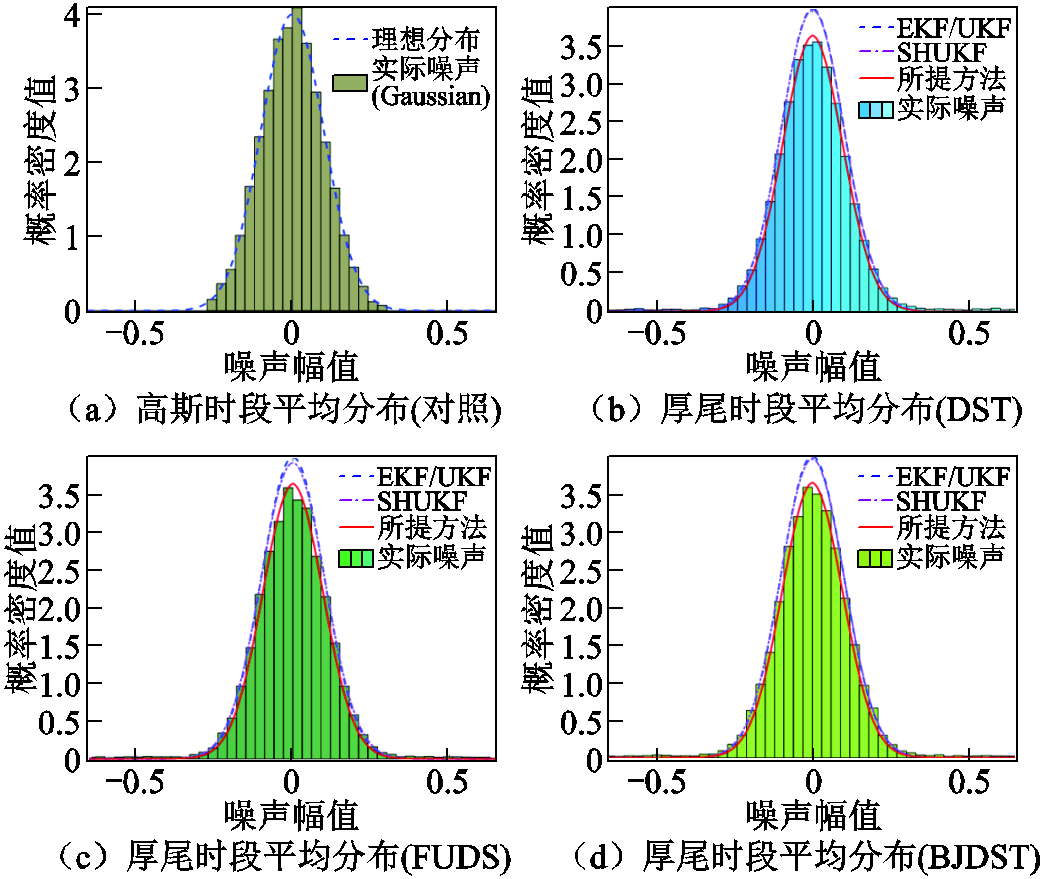
图21 多动态工况的非平稳噪声分布匹配性能对比
Fig.21 Comparison of non-stationary noise distribution matching performance under multiple dynamic conditions
可以看出,厚尾噪声时段中,常规非线性滤波不具有噪声参数迭代性能,无法匹配真实分布;SHUKF的动态噪声估计只基于量测统计误差进行闭环补偿,未考虑噪声分布特性,因此匹配性能差;而所提算法能在非高斯条件下准确匹配真实量测噪声统计分布,从而提高了SOC估计的迭代数值稳定性。
4.3.4 统一参数辨识方法后的SOC估计影响分析
由于参数在线辨识与SOC估计形成闭环系统,SOC估计准确度与在线参数准确度极为相关,为了进一步证明所提强跟踪估计算法的优势抗差性能,基于4.2.2节中的FUDS-25℃工况进行测试,使所提算法不应用GVFFRLS,而是采用参数相同的FFRLS在线辨识方法,分别结合本文第3节中所提SOC估计算法与其他滤波算法,进行仿真实验与分析。
图22展示了统一参数辨识方法为FFRLS后的SOC估计结果对比。由SOC跟踪曲线可以看出,替换参数辨识方法后对SOC跟踪性能并无明显影响,SOC估计MAEsoc为0.67%,端电压预测MAEv为 4.23 mV。分析表明,利用FFRLS结合所提强跟踪算法保持了估计精度,而且相比GVFFRLS-强跟踪SOC估计结合算法精度略有下降,这证明了所提GVFFRLS的辨识精度提升有效性,以及强跟踪SOC估计算法的性能优势。
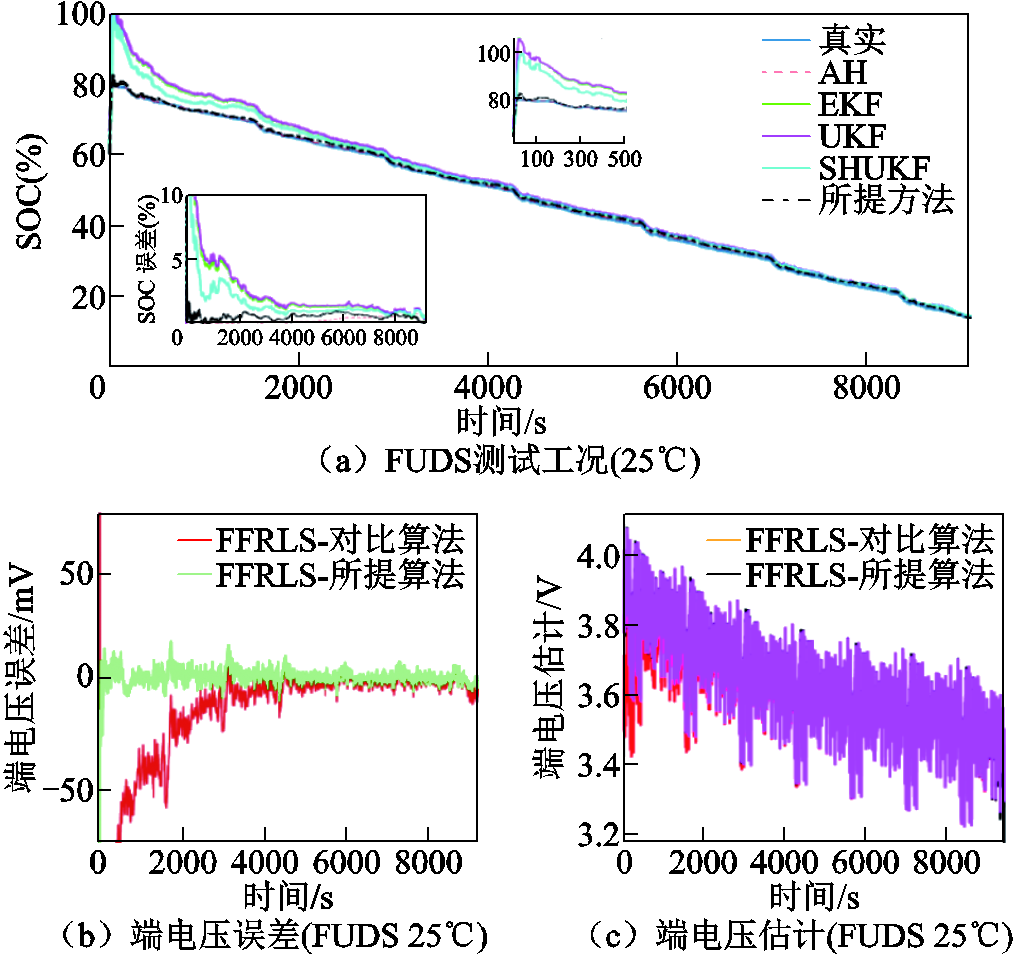
图22 FFRLS-不同滤波算法结合的SOC估计实验
Fig.22 SOC estimation experiment combining FFRLS withdifferent filtering algorithms
4.3.5 状态模型失准偏差下算法的鲁棒性
SOC动态估计中,状态模型失准是由于锂电池在不同温度工况下电池的最大容量发生变化导致电池放电性能受到影响,或者时段内噪声参数失配造成的。在算法中表现为状态空间方程式(1)中额定容量Qc和参数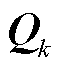 的失准,从而导致模型与真实SOC值发生累积偏差。由图16可以看出,状态模型配准情况下,基于AH法能较准确地估计真实SOC值,而在图8、图14等的状态模型失准情况下,AH递推SOC的误差随着时间推移呈明显的线性增大。在这种偏差之下,其他对比算法无法修正状态模型造成的估计误差,而所提算法由于在变分迭代过程中结合了基于H密度损失准则的鲁棒抗差方法,因此算法在模型发生失准的非平稳噪声条件下仍然能较为准确稳定地跟踪真实参考SOC值,验证了所提算法的SOC跟踪抗差鲁棒性。
的失准,从而导致模型与真实SOC值发生累积偏差。由图16可以看出,状态模型配准情况下,基于AH法能较准确地估计真实SOC值,而在图8、图14等的状态模型失准情况下,AH递推SOC的误差随着时间推移呈明显的线性增大。在这种偏差之下,其他对比算法无法修正状态模型造成的估计误差,而所提算法由于在变分迭代过程中结合了基于H密度损失准则的鲁棒抗差方法,因此算法在模型发生失准的非平稳噪声条件下仍然能较为准确稳定地跟踪真实参考SOC值,验证了所提算法的SOC跟踪抗差鲁棒性。
针对非平稳厚尾量测噪声干扰下的SOC高精度与初始快速响应跟踪估计难题,提出了基于GVFFRLS在线参数辨识与Gauss-双Gamma混合先验变分H密度抗差容积滤波的SOC估计方法。本文验证了如下结论:
1)所提GVFFRLS-强跟踪在线参数辨识方法结合SH自适应权与广义高斯核变遗忘因子,端电压预测MAEv相比FFRLS-KF结合算法(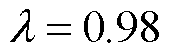 )提升了96.32%,有效地提升了电池参数在线辨识精度与初始误差收敛性能,参数辨识结果能较准确反映不同温度、工况下电池参数的动态特性。
)提升了96.32%,有效地提升了电池参数在线辨识精度与初始误差收敛性能,参数辨识结果能较准确反映不同温度、工况下电池参数的动态特性。
2)所提SOC估计算法采用Gauss-双Gamma混合先验分布噪声建模和变分参数推断,并与基于H密度损失准则的鲁棒状态后验估计紧结合,在非平稳厚尾量测噪声环境下SOC估计平均误差达到0.506%,精度相比EKF、UKF、SHUKF分别提升了78.94%、80.80%、75.05%,极大地提高了动态条件下SOC估计精度;SOC初值跟踪收敛性能、量测异常值噪声分布配准性能均强于现有算法。
3)所提SOC估计算法在不同温度工况下,由于状态模型失准产生累积偏差时,能保持较高的SOC估计精度和稳定性,从而相比基于状态模型预测的常规算法更为精确地逼近真实SOC值。
由于现有数据实测条件有限,所以实验中通过添加随机的符合非平稳厚尾分布的量测噪声以合理模拟真实复杂噪声环境,相比真实运行工况下性能实测的算法验证合理性存在一定不足。后续的研究中将考虑进行复杂噪声环境实测仿真,以实现真实运行工况中非平稳厚尾噪声下的SOC估计。
参考文献
[1] 孟国栋, 李雨珮, 唐佳, 等. 锂离子电池储能电站的热失控状态检测与安全防控技术研究进展[J]. 高电压技术, 2024, 50(7): 3105-3127.
Meng Guodong, Li Yupei, Tang Jia, et al. Research progress of thermal runaway detection and safety control technology for lithium-ion battery energy storage power stations[J]. High Voltage Engineering, 2024, 50(7): 3105-3127.
[2] 程林, 索克兰, 许鹤麟. 新能源侧电池储能系统运行评价: 现状与展望[J]. 电力系统自动化, 2025, 49(15): 1-19.
Cheng Lin, Suo Kelan, Xu Helin. Operation evaluation of battery energy storage systems on renewable energy side: current status and prospects[J]. Automation of Electric Power Systems, 2025, 49(15): 1-19.
[3] Shang Yunlong, Cui Naxin, Duan Bin, et al. Analysis and optimization of star-structured switched- capacitor equalizers for series-connected battery strings[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9631-9646.
[4] Cui Xiangbo, Xu Bowen. State of charge estimation of lithium-ion battery using robust kernel fuzzy model and multi-innovation UKF algorithm under noise[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 11121-11131.
[5] 李斌, 李博睿, 李超, 等. 考虑过充/过放的电化学储能电站建模及故障特性分析[J]. 电力系统自动化, 2024, 48(14): 119-128.
Li Bin, Li Borui, Li Chao, et al. Modeling and fault characteristic analysis of electrochemical energy storage station considering overcharging/overdisch-arging[J]. Automation of Electric Power Systems, 2024, 48(14): 119-128.
[6] Li Xiaoyu, Wang Zhenpo, Zhang Lei. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles[J]. Energy, 2019, 174: 33-44.
[7] 胡明辉, 朱广曜, 刘长贺, 等. 考虑迟滞特性的卡尔曼滤波和门控循环单元神经网络的锂离子电池SOC联合估计[J]. 汽车工程, 2023, 45(9): 1688-1701.
Hu Minghui, Zhu Guangyao, Liu Changhe, et al. Joint estimation of state of charge for lithium-ion battery with Kalman filtering and gated recurrent unit neural networks considering hysteresis characteristics[J]. Automotive Engineering, 2023, 45(9): 1688-1701.
[8] 朱元富, 贺文武, 李建兴, 等. 基于Bi-LSTM/Bi-GRU循环神经网络的锂电池SOC估计[J]. 储能科学与技术, 2021, 10(3): 1163-1176.
Zhu Yuanfu, He Wenwu, Li Jianxing, et al. SOC estimation for Li-ion batteries based on Bi-LSTM and Bi-GRU[J]. Energy Storage Science and Technology, 2021, 10(3): 1163-1176.
[9] How D N T, Hannan M A, Lipu M S H, et al. State-of-charge estimation of Li-ion battery in electric vehicles: a deep neural network approach[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5565-5574.
[10] 陈治铭, 刘建华, 柯添赐, 等. 基于对抗性的权重注意力机制序列到序列模型的锂离子电池SOC估计方法[J]. 电工技术学报, 2024, 39(19): 6244-6256.
Chen Zhiming, Liu Jianhua, Ke Tianci, et al. SOC prediction of lithium-ion batteries based on sequence-to-sequence model with adversarial weighted attention mechanism[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6244-6256.
[11] Zhu Rui, Duan Bin, Zhang Junming, et al. Co-estimation of model parameters and state-of- charge for lithium-ion batteries with recursive restricted total least squares and unscented Kalman filter[J]. Applied Energy, 2020, 277: 115494.
[12] 费亚龙, 谢长君, 汤泽波, 等. 基于平方根无迹卡尔曼滤波的锂电池状态估计[J]. 中国电机工程学报, 2017, 37(15): 4514-4520, 4593.
Fei Yalong, Xie Changjun, Tang Zebo, et al. State-of-charge estimation based on square root unscented Kalman filter algorithm for Li-ion batteries[J]. Proceedings of the CSEE, 2017, 37(15): 4514-4520, 4593.
[13] 范兴明, 吴润玮, 封浩, 等. 基于变窗口自适应无迹卡尔曼滤波的锂离子电池荷电状态预测[J]. 电工技术学报, 2025, 40(6): 1974-1983.
Fan Xingming, Wu Runwei, Feng Hao, et al. Lithium-ion battery state of charge estimation based on variable-window adaptive untraceable Kalman filtering algorithm[J]. Transactions of China Electro- technical Society, 2025, 40(6): 1974-1983.
[14] 王新栋, 董政, 王书华, 等. 基于改进开路电压模型和自适应平方根无迹卡尔曼滤波的锂离子电池宽温度多工况 SOC 估计[J]. 电工技术学报, 2024, 39(24): 7950-7964.
Wang Xindong, Dong Zheng, Wang Shuhua, et al. State-of-charge estimation for lithium-ion batteries across wide temperature range and multiple working conditions based on improved open-circuit voltage model and adaptive square root unscented Kalman filter algorithm[J]. Transactions of China Electro- technical Society, 2024, 39(24): 7950-7964.
[15] Wang Shunli, Stroe D I, Fernandez C, et al. A novel energy management strategy for the ternary lithium batteries based on the dynamic equivalent circuit modeling and differential Kalman filtering under time-varying conditions[J]. Journal of Power Sources, 2020, 450: 227652.
[16] 胡劲, 赵靖英, 姚帅亮, 等. 基于阻容参数滤波优化UKF的锂电池SOC估计[J]. 电源学报, 2025, 23(2): 247-255.
Hu Jin, Zhao Jingying, Yao Shuailiang, et al. SOC estimation of lithium battery based on resistance-capacitance parameters filtering optimization UKF[J]. Journal of Power Supply, 2025, 23(2): 247-255.
[17] Wu Muyao, Wang Li, Wang Yuqing, et al. State of charge estimation of the lithium-ion power battery based on a multi-time-scale improved adaptive unscented Kalman filter[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 9003212.
[18] 董祥祥, 武鹏, 葛传久, 等. 基于自适应无迹卡尔曼滤波的锂电池荷电状态估计[J]. 电工电能新技术, 2021, 40(2): 58-65.
Dong Xiangxiang, Wu Peng, Ge Chuanjiu, et al. State of charge estimation of Li-ion battery based on adaptive unscented Kalman filter[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(2): 58-65.
[19] 巫春玲, 赵玉冰, 耿莉敏, 等. 采用广义混合最大相关熵准则扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 西安交通大学学报, 2025, 59(7): 159-169.
Wu Chunling, Zhao Yubing, Geng Limin, et al. State of charge estimation for lithium-ion batteries using a generalized mixture maximum correlation-entropy criterion-based extended Kalman filter algorithm[J]. Journal of Xi’an Jiaotong University, 2025, 59(7): 159-169.
[20] Ma Wentao, Guo Peng, Wang Xiaofei, et al. Robust state of charge estimation for Li-ion batteries based on cubature Kalman filter with generalized maximum correntropy criterion[J]. Energy, 2022, 260: 125083.
[21] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[22] Liu Xingtao, Li Qiule, Wang Li, et al. Data-driven state of charge estimation for power battery with improved extended Kalman filter[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 1500910.
[23] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[24] 李建林, 彭禹宸, 王茜, 等. 锂离子电池建模研究现状与展望[J]. 发电技术, 2025, 46(5): 857-871.
Li Jianlin, Peng Yuchen, Wang Qian, et al. Research status and prospect of lithium-ion battery modelling[J]. Power Generation Technology, 2025, 46(5): 857-871.
[25] 封居强, 伍龙, 黄凯峰, 等. 基于FFRLS和AEKF的锂离子电池SOC在线估计研究[J]. 储能科学与技术, 2021, 10(1): 242-249.
Feng Juqiang, Wu Long, Huang Kaifeng, et al. Online SOC estimation of a lithium-ion battery based on FFRLS and AEKF[J]. Energy Storage Science and Technology, 2021, 10(1): 242-249.
[26] Huang Yulong, Zhang Yonggang, Shi Peng, et al. Variational adaptive Kalman filter with Gaussian- inverse-wishart mixture distribution[J]. IEEE Transactions on Automatic Control, 2021, 66(4): 1786-1793.
[27] Aleksandr Y Aravkin, James V Burke, Gianluigi Pillonetto. Sparse/robust estimation and Kalman smoothing with nonsmooth log-concave densities: modeling, computation, and theory[J]. The Journal of Machine Learning Research, 2013, 14(1): 2689-2728.
[28] Wang Guoqing, Li Ning, Zhang Yonggang. Maximum correntropy unscented Kalman and information filters for non-Gaussian measurement noise[J]. Journal of the Franklin Institute, 2017, 354(18): 8659-8677.
[29] 范兴明, 封浩, 张鑫. 最小二乘算法优化及其在锂离子电池参数辨识中的应用[J]. 电工技术学报, 2024, 39(5): 1577-1588.
Abstract Under the background of large-scale construction of new power energy storage system, lithium-ion battery (LIBs) has been widely used as the main electrochemical energy storage component of energy storage power station because of its excellent energy characteristics. However, in the complex environment of the new energy storage system, the data measurement noise of lithium batteriesis no longer white Gaussian noise, and its amplitude shows two characteristics: Unknown statistical characteristics of distribution and ourliers. To estimatebattery parameterand state of charge (SOC) with high precision and fast dynamic response under this condition is one of the main difficulties in the research field of lithium-ion battery measurement.
Fan Xingming, Feng Hao, Zhang Xin. Optimization of least squares method and its application in parameter identification of lithium-ion battery model[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1577-1588.
Among the existing SOC estimation algorithms, ampere hour (AH) method and open circuit voltage (OCV) method are affected by the external environment and battery loss, which gravely effected the estimation accuracy. The method based on artificial neural network fitting is difficult to obtain reliable training data set under complex noise conditions, and the operation cost and space occupation are high. Methods based on conventional nonlinear filters are often unable to adapt to SOC estimation in non-Gaussian noise environments and cannot resist state model bias.To solve the problems above, a strong SOC tracking estimation method based on gereralized variable forgetting factor recursive least squares (GVFFRLS) online parameter identification and Gauss-G-Gamma mixed prior variational H-density robust cubature filter is proposed.
Firstly, an online parameter identification method combining Sage-Husa adaptive weighting and generalized Gauss kernel forgetting factor wasproposed to improve the stability and dynamic accuracy of battery online parameter identification.
Then, a hierarchical Gaussian cubature Kalman filter was constructed based on the Gauss-G-Gamma mixed prior distribution noise modeling and variational parameter inference, achieving the adaptive update of variational parameters with the change of real noise distribution. Based on the QS-density function constructed by H-density theory, a new L2-1/2 norm-weighted robust loss function and status-measurement combination innovation was designed. The variational iterative calculation process was closely combined with the robust state posterior estimation constructed by H-density loss criterion, and a strong tracking filtering algorithm for SOC estimation was proposed.
Finally, based on the INR 18650-20R lithium battery test datawith non-stationary thick tail measurement noise under different temperatures and dynamic conditions, the proposed algorithm is simulated and compared with the common SOC estimation filtering algorithm.
The results show that the voltage estimation accuracy is improved by 96.32% compared GVFFRLS with forgetting factor recursive least squares (FFRLS) method, and the average accuracy of SOC estimatedby proposed algorithm under non-stationary thick tail measurement noiseis improved by 78.94%, 80.80% and 75.05% compared with traditional Kalman filters including extended Kalman filter (EKF), unscented Kalman filter(UKF) and Sage-Husa unscented Kalman filter (SHUKF), respectively. The SOC initial value tracking convergence performance and measurement noise distribution registration performance are much stronger than the existing SOC estimation algorithms.
The theoretical derivation process of the proposed algorithm is relatively complex, but the iterative calculation process is simple, and its operational efficiency is similar to that of the existing algorithms. Therefore, this method is easy to be applied to the engineering implementation of battery management system (BMS). This algorithm features adaptability to non-stationary measurement noise and strong adaptive correction performance for SOC state deviation tracking. It can be applied not only in complex noise environments but also in SOC estimation under normal conditions, thereby optimizing and enhancing the performance of the BMS algorithm, improving the utilization efficiency and safety of lithium battery modules. The safety and stability monitoring and maintenance measures for new energy storage power stations have been further enhanced.
Keywords:Battery SOC estimation, cubature Kalman filter,variable forgetting factor recursive least squares,variationalBayes method, H-density loss criterion
施 琳 男,1988年生,博士,研究方向为电力系统调度自动化技术。
E-mail:shilinchina@126.com
王天靖 男,1998年生,硕士,研究方向为电力厂站自动化与鲁棒状态估计技术。
E-mail:wangtianjing@sgepri.sgcc.com.cn(通信作者)
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.250256
国家重点研发计划资助项目(2024YFB2408900)。
收稿日期 2025-02-18
改稿日期 2025-04-15
(编辑 郭丽军)