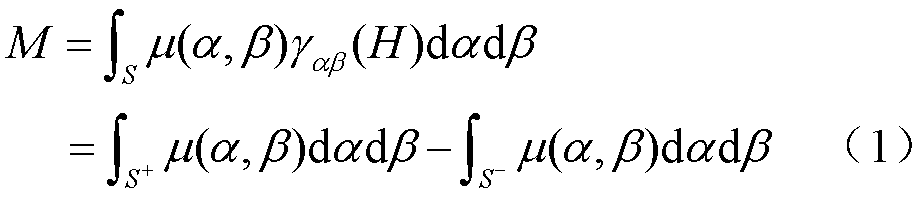
式中，Preisach算子的分布由函数μ(α, β)描述；α和β为判断Preisach算子反转的阈值；H为磁场强度。
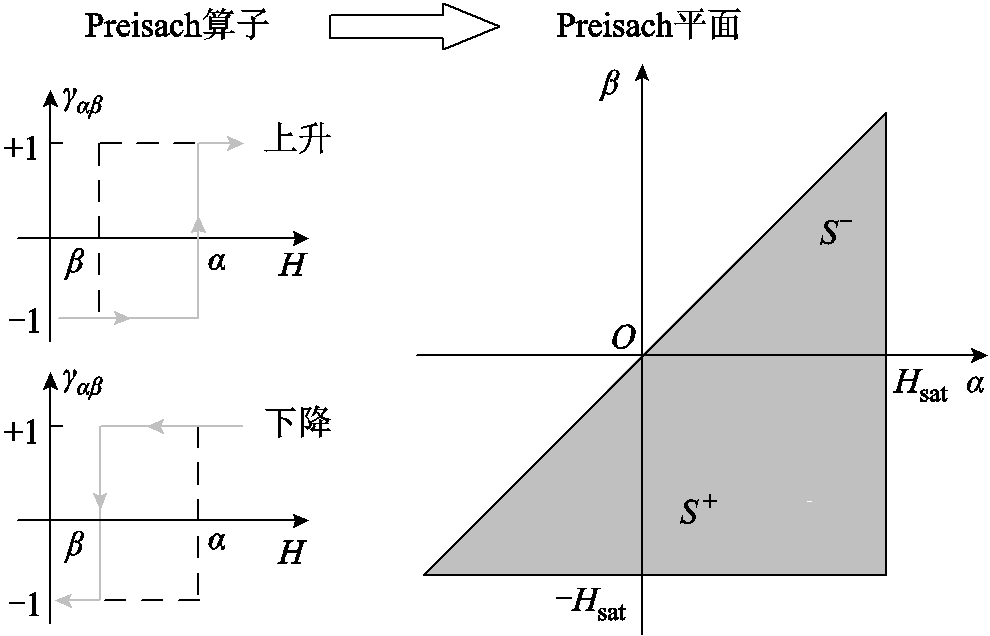
图1 Preisach算子与Preisach平面映射关系示意图
Fig.1 Schematic diagram of the mapping relationship between Preisach operator and Preisach diagram
摘要 随着变压器等电气设备运行工况复杂程度的提高，神经网络磁滞模型已成为预估硅钢等软磁材料磁特性的有效方法之一。为了减少传统神经网络模型对磁特性测量数据样本的依赖性，提高模型对不同磁化方式模拟的适用程度，该文将材料磁化特征融入神经网络模型，提出一种计及Preisach算子状态信息的智能磁滞模型。首先，利用非均匀离散策略构建具有Preisach算子位置信息和状态信息的磁化状态矩阵，并作为反向传播（BP）神经网络的输入；其次，定义一个可以直接反映每个Preisach算子离散点的磁滞特性对整体磁化过程贡献度的有效权重参数，通过提取权重生成具有可视化效果的分布函数，并尝试从图形中寻找材料磁化的某些特征；最后，在测量直流、工频及谐波磁化下硅钢特性的基础上，通过与实测数据对比验证了不同磁化条件下所提模型的计算精度。结果表明，将Preisach算子与神经网络相结合，可以有效地捕捉并反映材料的磁滞特性，同时在减少输入样本的情况下提高模型复杂工况的适用性。
关键词：Preisach算子 神经网络 有效权重参数 分布函数
磁性材料（如硅钢）磁滞特性的准确表征是电气设备铁心损耗计算与铁心结构优化设计的关键[1]，典型代表包括Stoner-Wohlfarth（S-W）模型、Jiles-Atherton（J-A）模型及Preisach模型等[2]。S-W模型基于单轴单畴粒子的磁化能量最小化原理，通过矢量磁滞算子描述磁畴旋转过程[3]。然而，该模型需依赖粒子取向的统计分布表征，在实际应用中分布函数的实验辨识需消耗大量数据资源，导致工程适用性受限[4]。J-A模型构建了含畴壁位移与磁畴旋转耦合效应的微分方程，因具有计算效率高的优势被广泛应用于工程领域[5-6]，目前该模型也在不断被修正以适应复杂工况下的磁滞特性表征需求。
相较而言，Preisach模型通过离散化策略将宏观磁滞现象分解为大量磁滞算子的协同响应，建立了微观磁畴翻转与宏观磁化行为的映射机制[7]。该模型的理论基础源于1935年F. Preisach对磁滞现象的探究[8]，其对巴克豪森阶跃进行了深入观察，指出磁畴翻转过程具有非均匀统计特性，而该模型的核心在于将每个磁畴翻转过程抽象为双稳态Preisach算子。这些算子在外部磁场激励下发生集体切换行为，而系统的整体磁化响应则通过分布函数加权叠加实现。该模型的理论优势体现在：通过分布函数对磁滞算子的动态权重分配，既能反映单畴粒子旋转的微观物理机制，又能复现材料的宏观非线性磁滞特性[1]。
然而，分布函数的辨识过程复杂，有效的辨识方法始终是Preisach模型应用中的难点问题[9]。在传统方法中，一阶反转曲线（First Order Reversal Curve, FORC）与Everett函数的联合解析法被广泛用于辨识Preisach模型的分布函数[10]，该方法需要通过实验测量多条一阶反转曲线。实验过程中存在的噪声干扰与数据采集误差，会在对分布函数进行微分运算时被放大，从而影响模型精度。为此，学者们研究了辨识分布函数的其他方法。例如，有学者提出通过同心磁滞回线实验数据辨识分布函数的方法[11-12]，利用对称磁场循环简化参数辨识过程，并通过拟合来验证模型精度。该方法对分布函数的辨识过程需要进行Everett积分。文献[13]提出了基于同心磁滞回线的均匀离散化方法，建立了矩阵方程来辨识分布函数。同时该文也讨论了由于未考虑不同磁通密度的敏感度差异，导致低磁通密度区计算精度不足的问题。文献[14-15]在均匀离散化方法的基础上，提出了非均匀离散法来改进低磁通密度区的计算精度。该方法的计算精度依赖离散的单元数量，而过高的离散单元数量又会增加求解高阶矩阵的负担，因此需要权衡计算精度和计算效率。
此外，神经网络模型因具有较高的预测效率和预测精度正逐渐成为磁滞行为建模的有效工具[16-17]。尽管神经网络模型在计算精度上表现优异，但因其缺乏内在的物理机制支撑，所以在进行模型训练时需要大量的磁特性实验数据，模拟精度对数据样本量的依赖性较高，这在一定程度上限制了其对复杂工况的模拟应用[18-20]。
近几年学者们提出了融合模型驱动和数据驱动的磁滞模型。文献[21]将Preisach算子与参数法融合，假设分布函数遵循高斯分布，并利用神经网络的深度学习捕捉了非线性磁滞特征。其中，参数法需要预先假设分布函数遵循理想的数学分布（如高斯分布等），再借助优化算法反演特征参数[22-23]。上述方法在利用神经网络辨识模型参数过程中，同样需要大量磁特性测量数据的支撑。
本文提出一种Preisach算子智能磁滞（Preisach Operator Intelligent Hysteresis, POIH）模型，通过非均匀离散化策略对Preisach平面进行网格划分，将构建的磁化状态矩阵作为神经网络的输入，将Preisach传统模型的连续积分运算离散化为神经网络加权和计算。通过反向传播（Back Propagation, BP）算法动态调整网络权重，建立其与Preisach分布函数之间的直接映射关系。该方法由于在神经网络中嵌入了材料的磁化特征，因此仅需要提供一条极限磁滞回环和基本磁化曲线的特性数据给神经网络，弱化了传统神经网络模型对磁特性数据的依赖性，同时也避免了传统Preisach模型复杂的分布函数辨识过程。
Preisach模型描述了由大量独立磁偶极子组成的磁性材料的磁滞特性，其中每个磁偶极子具有独特的矫顽力和状态。在外部磁场作用下，磁偶极子会在特定阈值翻转，形成复杂的磁滞回线。而Preisach算子通过简化的矩形滞后运算符，捕捉了磁偶极子的微观行为。通过对Preisach算子的统计分析，使该模型能够有效地描述材料的宏观磁特性，如磁导率和磁滞行为。
该模型假设每个磁偶极子只能在正向或反向翻转，Preisach算子的磁化状态由γαβ表示，仅取值“+1”或“-1”。Preisach平面根据Preisach算子的磁化状态分为正磁化区域S+（γαβ=1）和负磁化区域S−（γαβ=-1），如图1所示。材料的宏观磁化强度可表示为外部磁场强度下分布函数μ(α, β)与γαβ乘积的积分，即
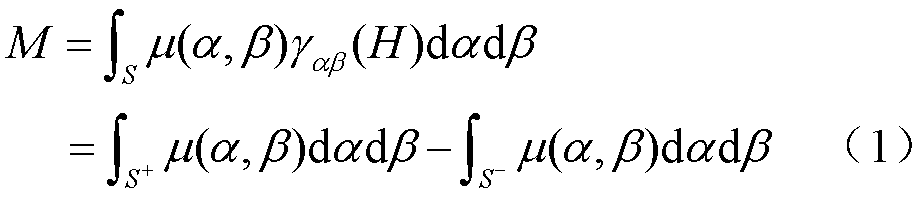
式中，Preisach算子的分布由函数μ(α, β)描述；α和β为判断Preisach算子反转的阈值；H为磁场强度。
图1 Preisach算子与Preisach平面映射关系示意图
Fig.1 Schematic diagram of the mapping relationship between Preisach operator and Preisach diagram
在Preisach模型中，极限磁滞回线代表了材料的饱和状态，并决定了Preisach平面的边界值。图2展示了极限磁滞回线与Preisach平面的对应关系。图2a中实线代表磁滞回线上升支，表示由负饱和状态磁化到正饱和状态；图2d中实线代表磁滞回环下降支，磁化状态与图2a相反。
下面以上升支为例，解释极限磁滞回线与Preisach平面映射关系。当外磁场由负饱和磁化状态（-Hsat）逐渐增大时，会遇到一系列的反转阈值，此时γαβ都将由“–1”变为“+1”。因此，在磁化过程中，S+区域面积持续增大，S −区域面积相应减小，例如位于图2a上升支的P1点，其对应的Preisach平面如图2b所示。当外磁场继续增加到饱和的Hsat
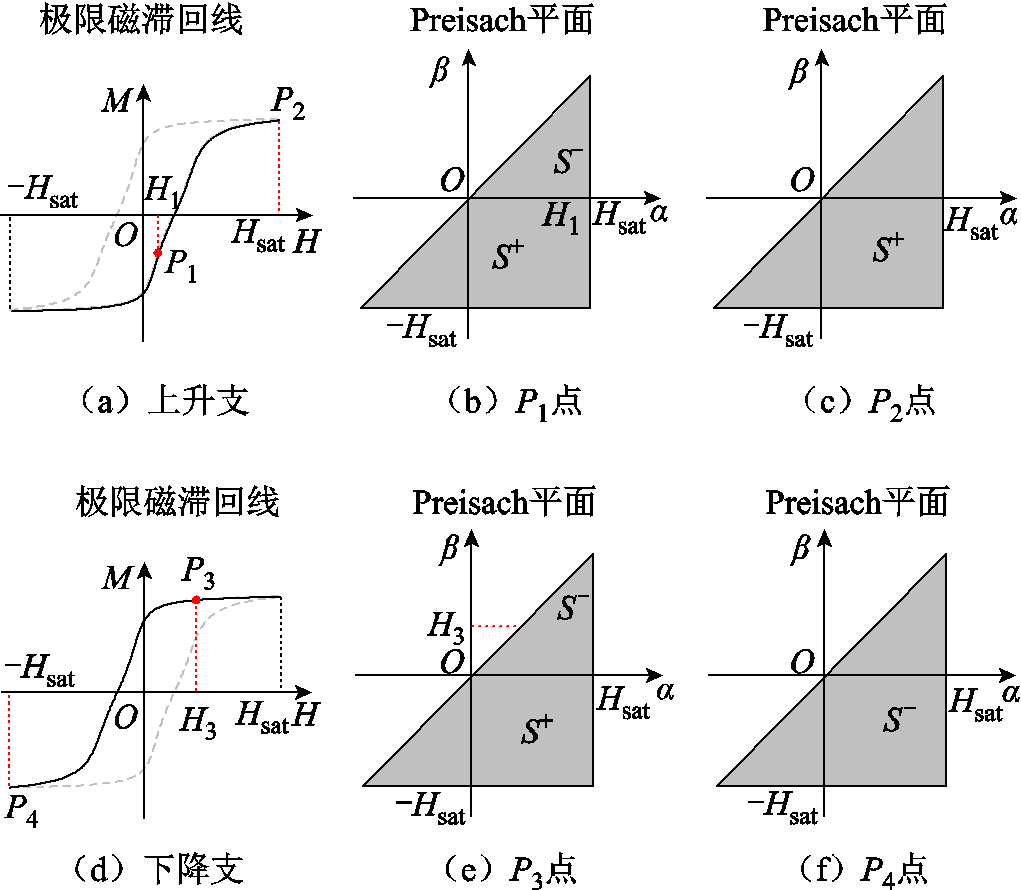
图2 极限磁滞回线与Preisach平面映射关系示意图
Fig.2 Schematic diagram of the mapping relationship between limiting hysteresis loop and Preisach diagram
时，所有γαβ均为“+1”，S+区域面积达到最大，S−区域面积减小为0，对应图2a中P2点，其对应的Preisach平面如图2c所示。下降支磁化过程与上升支相反，如图2d～图2f所示。
通过对Preisach理论的图形化变换，避免了分布函数的直接求解[24]。图3a给出了磁化过程的工作点位于经过n个反转点后的上升支时的Preisach平面面积运算方法，其磁化强度为
（2）
式中，
为对应极限磁滞回线上升支的磁化强度；Hn为第n个反转点的磁场强度；M(Hn)为对应上升支的磁化强度；
为函数T(α,β)，表示为
（3）
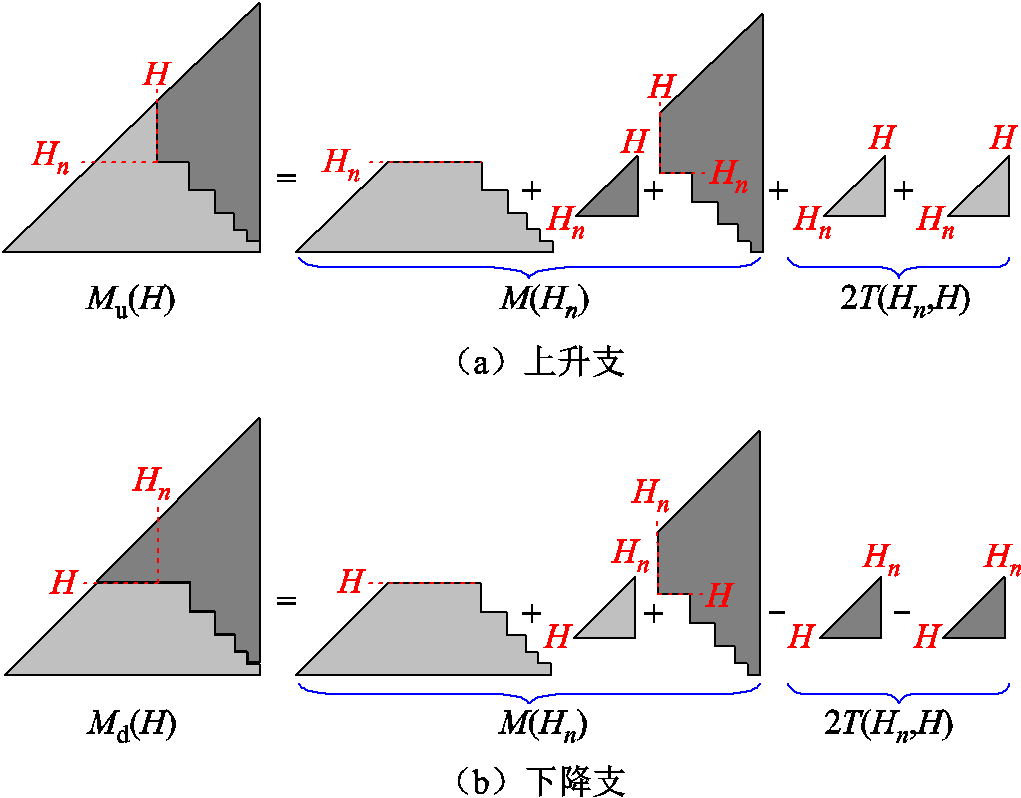
图3 Preisach平面面积运算方法
Fig.3 Preisach diagram area calculation method
其中
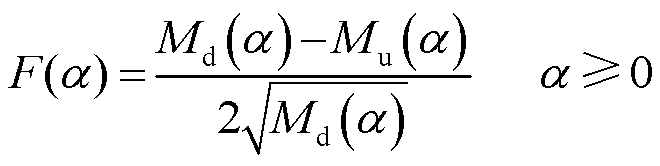（4）
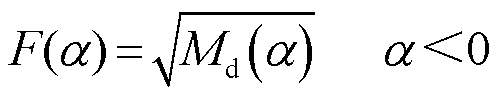（5）
式中，Md为对应极限磁滞回线下降支的磁化强度。
图3b为磁化过程的工作点位于经过n个反转点后的下降支时的Preisach平面面积运算方法，其磁化强度为
（6）
利用极限磁滞回线与Preisach理论的图形化变换，即使不需要分布函数也可求出磁化强度。但该方法存在低磁通密度时误差大的问题[25]。
磁滞回线与Preisach平面的对应关系示意图如图4所示。图4中每条磁滞回线在Preisach平面中都有一个对应的三角单元，其中每个三角单元的边界值就是每条磁滞回线的磁场反转点。
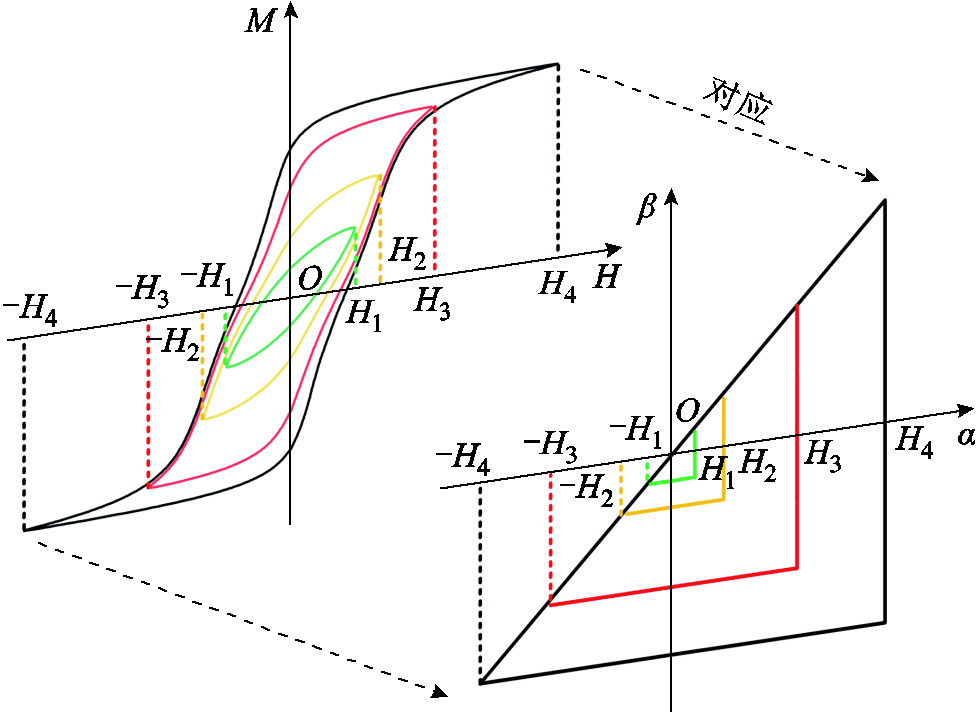
图4 磁滞回线与Preisach平面的对应关系示意图
Fig.4 Schematic diagram of the relationship between the hysteresis loop and the Preisach diagram
基于文献[15]提出的非均匀离散化策略，本文对Preisach平面进行网格划分，实现Preisach算子的离散化，如图5所示。具体而言，通过基本磁化曲线上的2N个磁场强度反转点，将Preisach平面划分为N(2N+1)个非均匀分布的离散网格节点，每个离散点代表一个Preisach算子。离散后的Preisach平面沿着对角线具有对称性。结合图4，在离散点坐标系中，横纵坐标轴的编号对应每条磁滞回线的磁场强度反转点，编号从极限磁滞回线的负饱和磁场强度反转点开始依次增加。其中任意一条磁滞回线的磁场强度反转点均可通过基本磁化曲线得到。
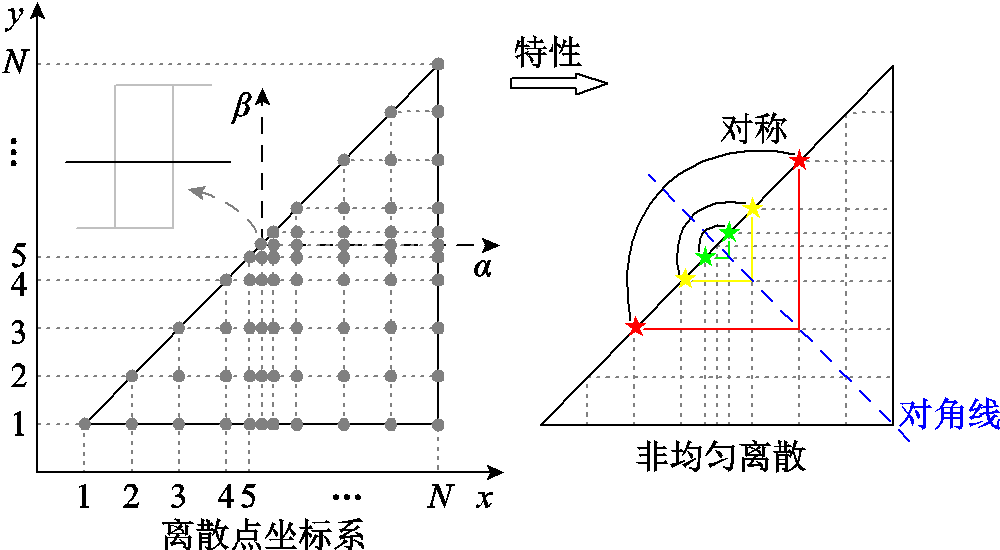
图5 非均匀离散的Preisach平面
Fig.5 Nonuniform discrete Preisach diagram
假设每个离散点的分布函数为常数，于是式（1）的连续积分转换为离散求和，表达式为
（7）
式中，μxy为Preisach分布函数的离散化值；γxy为离散的算子磁化状态。
式（7）将Preisach模型的连续问题转换为有限维优化问题，不仅可以提高计算效率，而且由于分布函数可以反映局部磁畴翻转的贡献，所以更便于微观机理分析[15]。此外，式（7）也为神经网络与Preisach模型的融合提供了数学基础，是本文提出智能磁滞模型的关键。
进一步地，依据算子翻转理论与动态磁化过程，本文将每个离散点当前的磁化状态提取出来（即γxy=1或者γxy=-1），构建了Preisach算子磁化状态矩阵T，即
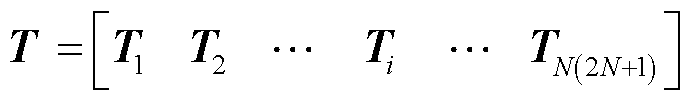（8）
需要注意的是，依据基本磁化曲线，构建的磁化状态矩阵对应的Preisach平面三角单元依次增大。以图4为例，第一个磁化状态矩阵
对应H1的三角单元。每个磁化过程都对应一个矩阵，这些矩阵精确地描述了系统在不同外磁场下的磁滞分布特性，是进一步进行磁滞行为数值求解与模拟的基础。
从2.1节的非均匀化离散过程可以看出，Preisach模型的宏观磁化强度可以表征为微观磁滞算子响应的加权和，这与神经网络的输出结构十分相似，而包含了Preisach算子位置信息和状态信息的磁化状态矩阵T具有BP神经网络模型的输入特征。基于此，本文提出基于BP神经网络的POIH模型，模型结构如图6所示。图6中输入层包含N(2N+1)个节点，对应Preisach算子磁化状态矩阵T；隐藏层包含Mh个神经元；输出层包含一个输出节点，对应宏观磁化强度。可以看出，通过融合离散化的Preisach算子与神经网络，POIH模型不仅具备神经网络模型特征，而且还关联了Preisach模型所建立的微观磁畴翻转与宏观磁化行为映射机制。同时，根据式（7）可以看出，图6中输入层与隐藏层共同构建了Preisach模型的分布函数，因此POIH模型另一个优势在于建立模型的同时也基于神经网络求取了分布函数，不需要像其他智能模型那样事先假设分布函数满足某种数学分布，这样可以避免分布函数的复杂辨识过程。
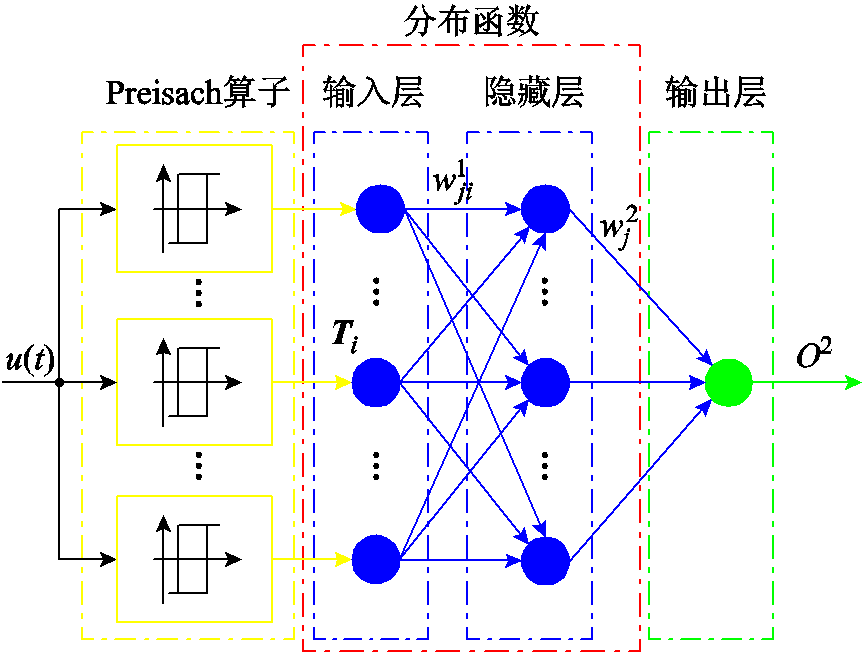
图6 POIH模型结构
Fig.6 POIH model structure
神经网络的训练过程为
（9）
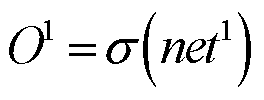（10）
（11）
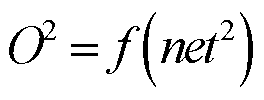（12）
式中，
为隐藏层（第1层）的加权输入；
为输入层到隐藏层的权重；
为隐藏层的偏置；
为隐藏层的输出；σ(·)为输入层到隐藏层的激活函数；
为输出层（第2层）的加权输入；
为隐藏层到输出层的权重；b2为输出层的偏置；
为输出层的输出；f(·)为输出层的激活函数。采用Sigmoid非线性函数作为输入层到隐藏层的激活函数σ，表示为
（13）
POIH模型采用单隐藏层，捕捉输入与输出之间的非线性关系。通过训练数据（Preisach算子磁化状态矩阵和对应的磁感应强度），使用反向传播算法调整网络权重，实现准确的输出预测。
此外，POIH模型求解分布函数时，为每个离散的Preisach算子分配了一个权重，代表不同离散点的磁滞特性对整体磁化过程的贡献。然而，作为输入层到隐藏层的激活函数，Sigmoid非线性函数虽然增强了模型的数学表达能力，但影响了权重与分布函数之间直接映射关系的建立，从而影响权重的物理意义。因此，为了遵循分布函数的物理意义，提升每个Preisach算子权重设置的合理性，POIH模型通过泰勒展开将Sigmoid非线性函数近似为线性函数，定义了有效权重参数
，表达式为
（14）
有效权重参数的作用体现在两个方面：
（1）有效权重参数表征了每个Preisach算子对磁化强度的贡献权重。具体而言，有效权重参数的分布反映了材料中不同阈值的Preisach算子对整体磁化的贡献，有助于理解材料的微观磁化机制。同时，在式（14）中有效权重参数可直接用于构建离散的Preisach分布函数。将克罗内克函数（δ函数）用于离散化修正分布函数，表示在Preisach平面上特定阈值(αi, βi)处的Preisach算子的集中贡献。
（2）有效权重参数可将神经网络与Preisach模型有机结合。有效权重参数综合了输入节点通过网络各层对输出的影响程度，有效权重参数越大则表示该输入节点在决定磁化强度时起着越重要的作用。同时，通过有效权重参数可以将神经网络的学习结果与Preisach模型相结合，实现对磁滞行为的深入理解和分析。
将有效权重参数引入离散分布函数μ(α, β)计算中，将分布函数表达为
（15）
式中，δ函数为克罗内克函数，满足
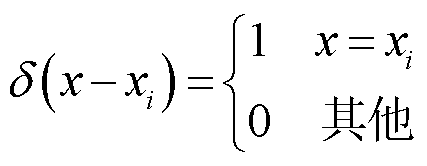（16）
综上所述，POIH模型通过引入离散化修正和近似线性函数假设，定义了能直接反映每个Preisach算子离散点的磁滞特性对整体磁化过程贡献度的有效权重参数；将Preisach算子与神经网络相结合，能够有效捕捉并反映材料的磁滞特性，通过深度学习的能力，揭示数据之间复杂的内在关系，并通过提取权重描述磁滞现象及其分布函数。
图7给出了实验室现有的硅钢磁特性测试装置。该测量系统由功率放大器、隔离放大器、低通滤波器、数据采集系统等构成。所需励磁电压信号经过低通滤波器调理后，进入功率放大器；将信号放大向励磁单元输入励磁信号；测量的磁信号经隔离放大器隔离干扰后进入数据采集卡，转换为数字信号，传输至主控单元。被测硅钢样片为100 mm× 10 mm方片。本文基于该测量系统，测量了低频 3 Hz、工频50 Hz及谐波励磁条件下硅钢片B-H回环，其中3 Hz的特性数据用来近似硅钢的直流磁化特性。图8和图9给出了测得的3 Hz下0.1～1.9 T磁通密度对应的磁滞回线族。
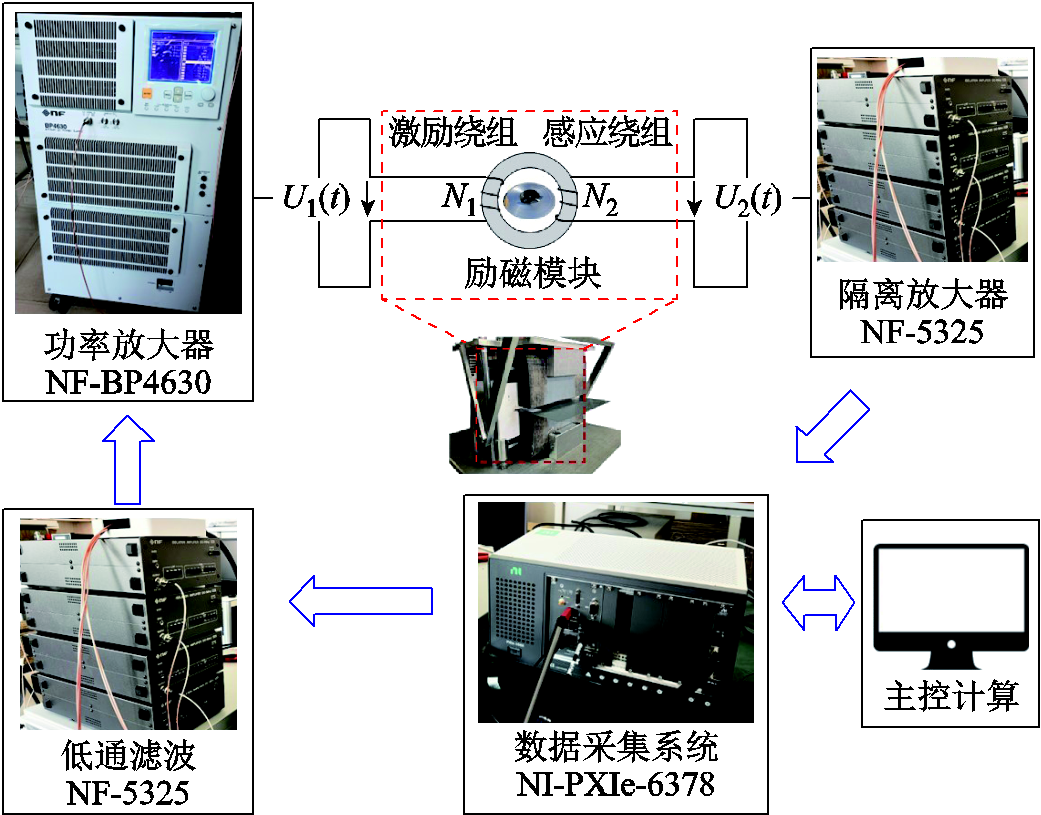
图7 硅钢磁特性测试装置
Fig.7 Experimental device for measuring the magnetic properties of silicon steel
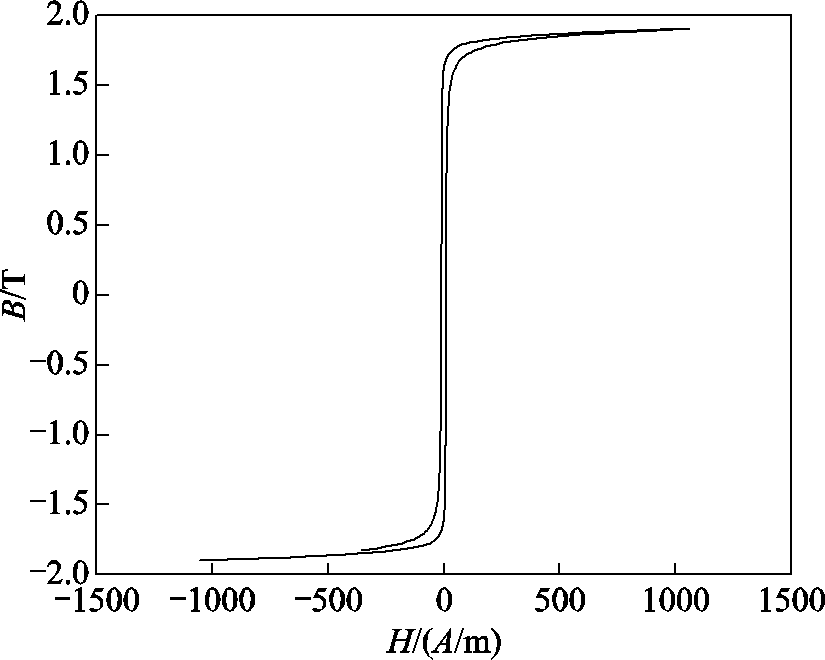
图8 3 Hz下1.9 T磁滞回线
Fig.8 1.9 T hysteresis loop at 3 Hz
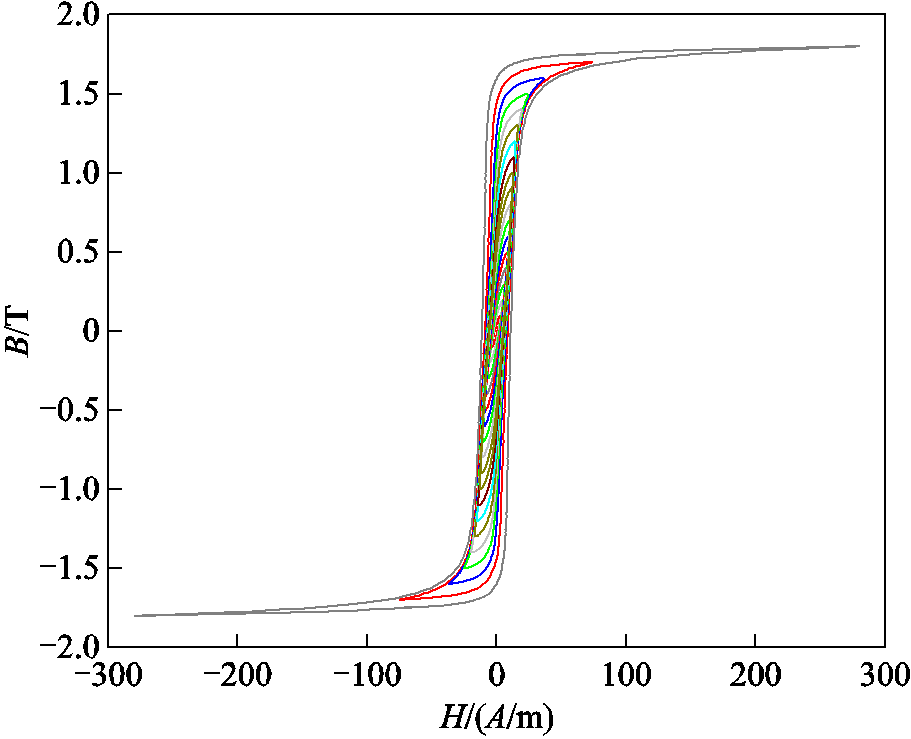
图9 3 Hz下0.1～1.8 T磁滞回线
Fig.9 0.1～1.8 T hysteresis loops at 3 Hz
利用所提出的POIH模型模拟静态磁滞回环时，仅需要输入上述测量的1.9 T的回环数据和一条基本磁化曲线。在模型训练过程中，采用BP算法来动态调整权值，训练参数设定为：训练次数 1 000次，学习率为0.01，目标最小误差为0.000 1。同时，为了讨论增加离散点数量对减小误差的具体影响，本文分别构建了多种N的取值，下面举例分析输入层N=20和80的两种模型，分别命名为POIH-20模型和POIH-80模型。其中，POIH模型由一个输入层、一个包含6个神经元的隐藏层和一个输出层组成。
利用两种POIH模型、极限磁滞回线法Preisach模型[25]及传统神经网络法计算了不同磁感应强度下的静态磁滞回线，并与实验测量结果进行对比，如图10所示。在模拟过程中，POIH模型与极限磁滞回线法Preisach模型的测量数据均仅采用1.9 T回环和基本磁化曲线，其中POIH模型回环离散点数据量为512个，Preisach模型为1 024个；而神经网络法则输入了一族0.1～1.9 T（间隔0.05 T）中30个磁滞回环，共计30×1 024=30 720个数据点。
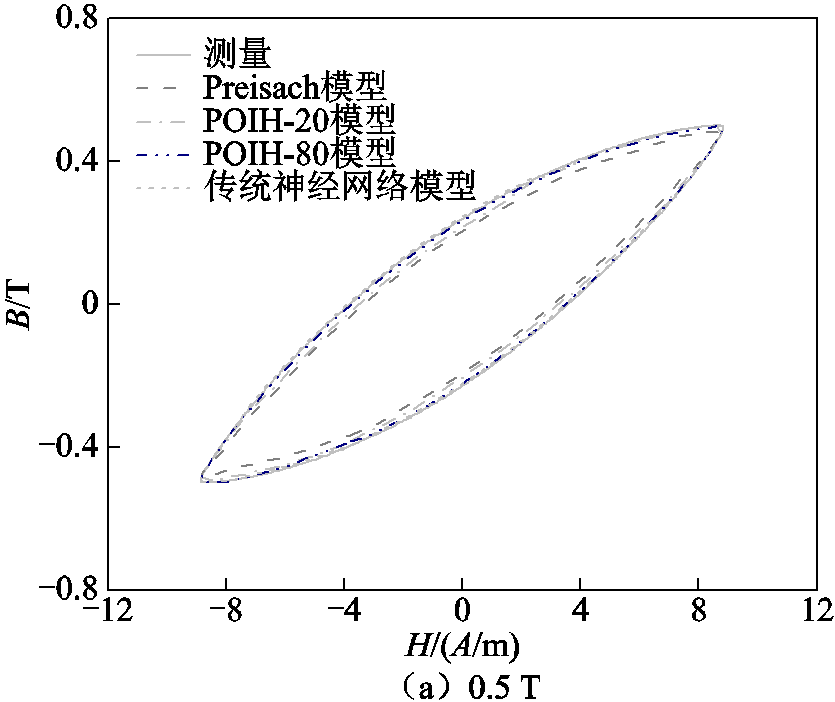
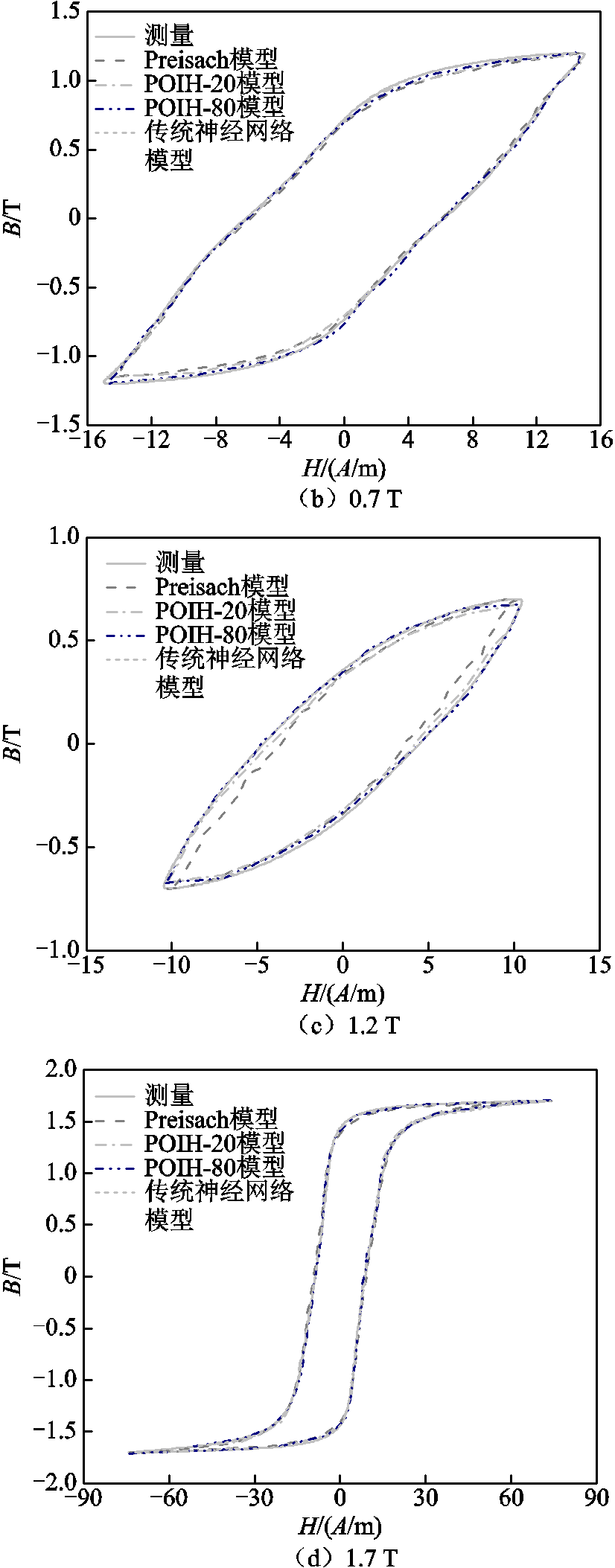
图10 静态磁滞回环对比
Fig.10 Comparison of static hysteresis loops
从图10中可以看出，神经网络模型模拟精度很高，但其数据量要远大于其他模型。而基于极限磁滞回线法Preisach模型在低、中、高磁感应强度时模拟精度都要低于POIH模型。表1也给出了利用上述方法获得的磁滞回线计算得到的静态磁滞损耗。可以看出，POIH模型由于包含了Preisach算子的位置信息和状态信息，因此弱化了传统神经网络对输入数据量的要求，同时也避免了传统Preisach模型求取分布函数的复杂过程。从上面的对比也可以看出，POIH-80模型的精度优于POIH-20模型，能够更精确地捕捉磁化过程中磁畴的翻转行为，显著提高了模型的预测精度。对比多种N取值后，POIH-80模型在计算精度和计算效率方面的综合性能最佳，后续主要用POIH-80模型进行模拟。
表1 磁滞损耗对比
Tab.1 Comparison of hysteresis loss
磁感应强度/T实验测量/(J/m3)传统Preisach模型[25]POIH-20模型POIH-80模型传统神经网络模型 计算/(J/m3)误差(%)计算/(J/m3)误差(%)计算/(J/m3)误差(%)计算/(J/m3)误差(%) 0.55.774.5820.625.1610.575.534.165.745 90.42 0.710.278.6615.689.457.989.943.2110.224 80.44 1.226.4424.547.1925.393.9725.921.9726.3580.31 1.767.8365.812.9866.521.9366.721.6367.612 90.32
分布函数在Preisach模型中具有重要的作用，它不仅是影响磁滞特性的决定性因素，而且是连接单畴粒子旋转微观机制与宏观非线性磁滞特性的桥梁。第2.2节指出，POIH模型在建立的同时也能直接求取分布函数，不需要像其他智能模型那样事先假设分布函数满足某种数学分布，这样可以避免分布函数的复杂辨识过程。本节将重点分析POIH模型计算得到的具有可视化效果的分布函数，并将尝试从图形中寻找材料磁化的某些特征。
图11和图12中分别给出了计算得到的POIH-20模型和POIH-80模型的分布函数μ(α, β)二维和三维可视图。从图形整体来看，计算结果在三角形平面上以α=β的对角线为对称轴呈现对称性。这种对称性是Preisach模型的固有特性，意味着对于具有相同阈值组合的磁化过程，材料的磁畴响应在正负方向上是对称的，图形计算结果与磁性材料的可逆磁化过程相一致。
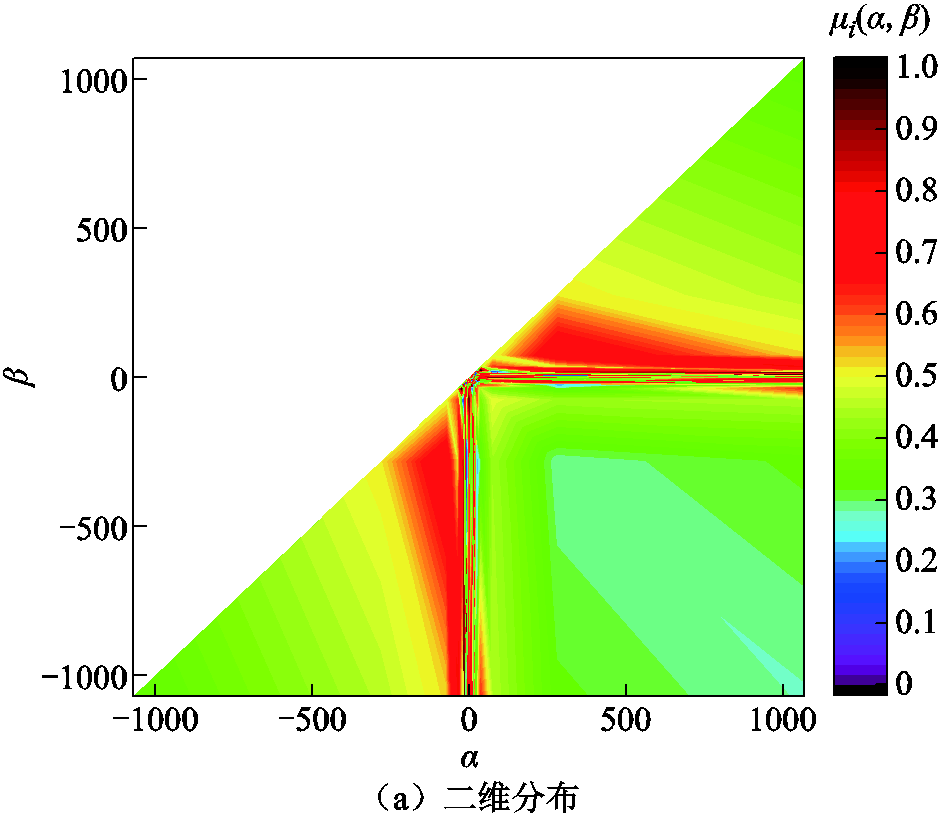
图11 POIH-20模型分布函数
Fig.11 POIH-20 model distribution function
图11和图12中，色标范围从紫色（0）到红色（1.0），反映了不同区域内分布函数值的大小，直观展示了各个Preisach算子在磁化过程中的贡献程度。红色区域对应高的分布函数值，表明这些Preisach算子的磁化翻转响应较强，在这些区域具有较高的磁化倾向。紫色和蓝色区域对应较低的分布函数值，表明这些Preisach算子的磁化翻转响应较弱，在这些区域存在较强的磁畴钉扎效应，使得磁化过程更加困难。黄色和绿色区域对应居中的分布函数值，表明这些Preisach算子的磁化翻转响应中等，在这些区域受到一定的钉扎效应影响。在中心区域，尤其是α和β接近零的位置，分布函数表现出复杂的波动和条纹结构。这些结构并不是由畴壁的运动引起的，而是磁畴翻转过程中微观缺陷对局部响应的影响。虽然Preisach模型不能描述畴壁的连续运动，但这些复杂的波动可能反映了微观结构对翻转过程的局部钉扎作用。同时，在中心区域的色彩交替变化反映了磁滞特性的局部非线性，也说明材料内部存在复杂的微观结构。对比图11和图12可以看出，模型离散点越多，其分布函数反映的磁化信息越多。
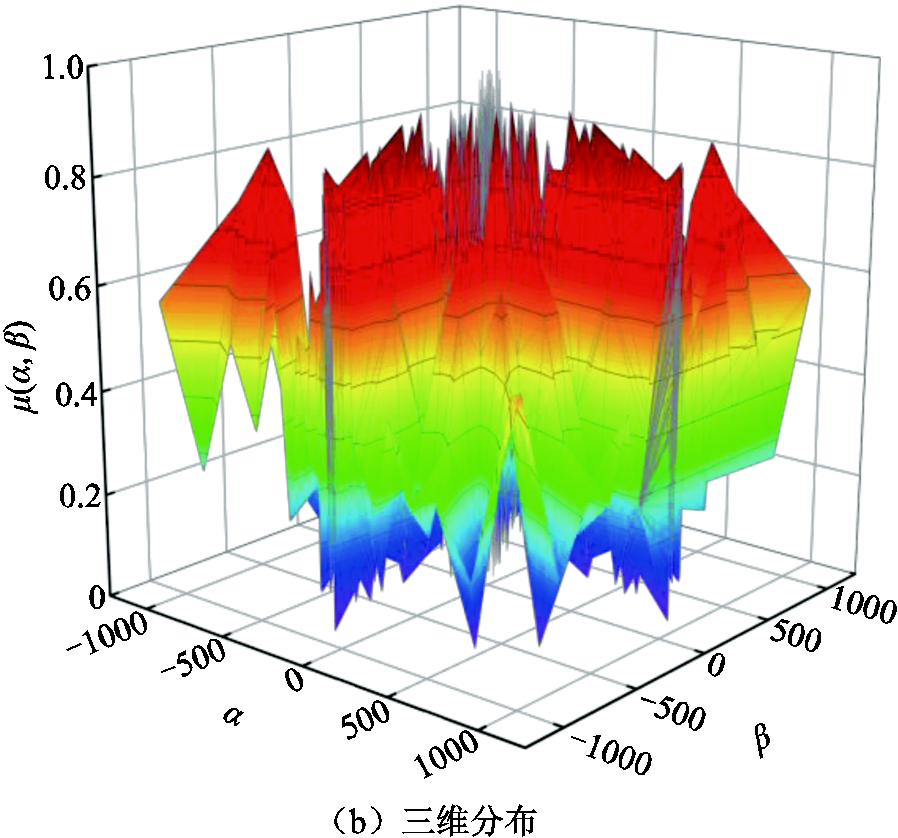
图12 POIH-80模型分布函数
Fig.12 POIH-80 model distribution function
分布函数可视化有助于理解材料磁滞行为，为材料性能优化提供一定参考。文献[26]中利用1 800余次一阶反转曲线实验测量数据，基于构建的Preisach算子得到了分布函数的实验测量图。与文献[26]中依赖实验数据获取的二维分布函数的实验图对比可以看出，POIH模型计算的分布函数与文献给出的分布函数具有几乎相同的变化规律，也进一步体现了本文计算的分布函数的有效性。同时，POIH模型避免了通过大量实验获取分布函数图像的成本。
为了进一步验证POIH模型对动态磁特性的模拟精度，本节在静态磁滞损耗基础上加入涡流和异常损耗影响，其中涡流和异常损耗计算利用梯形等效电路模型实现。
梯形等效电路核心思想在于通过电路模型将动态铁损分解为不同损耗的等效参数组合，实现损耗机制的解耦与等效表征[27-28]。其中，涡流损耗和异常损耗分别由电阻Re和Ra来计算。文献[27-28]给出了求解电路模型中各个等效参数的具体计算方法，此处仅进行简单表述。
涡流损耗Pe和异常损耗Pa分别为
（17）
（18）
式中，T为时间周期；ie为涡流损耗支路的电流；ia为异常损耗支路的电流。
（19）
（20）
式中，Nc为激励线圈匝数；A为硅钢片横截面积；ρm为质量密度；lm为铁心中磁通路径的平均长度；Ce为涡流损耗系数；Ca为异常损耗系数；VL(t)为损耗支路电压。
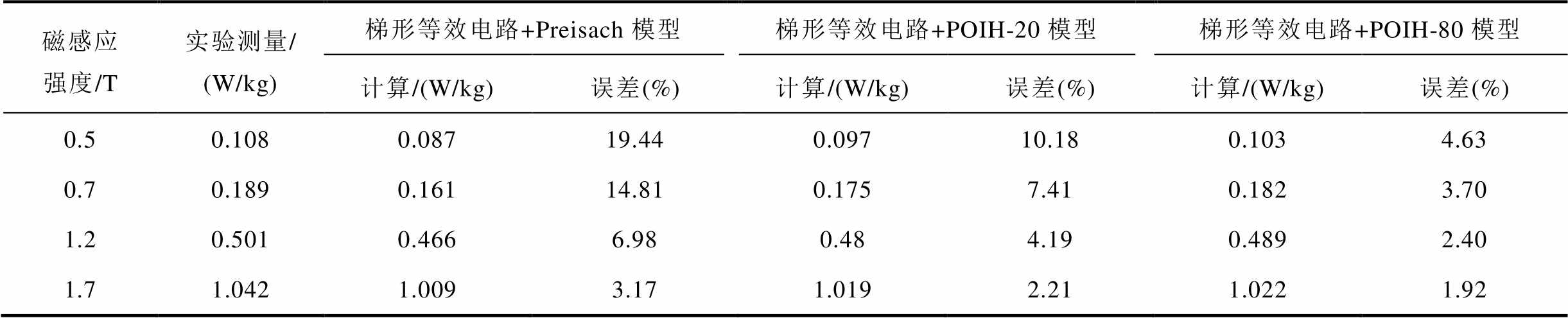
表2给出了结合POIH模型和梯形等效电路模型计算的50 Hz交变磁化动态铁损与实验测量结果的对比，所提模型具有很好的模拟精度。
图13给出了在50 Hz基波叠加谐波激励下磁滞回环的对比结果。可以看出，POIH模型也可以模拟谐波交变激励出现的小局部回环特征，具有良好的复杂磁化模拟精度。
表2 正弦交变磁化下铁损对比
Tab.2 Comparison of iron loss under sinusoidal alternating magnetization
磁感应强度/T实验测量/(W/kg)梯形等效电路+Preisach模型梯形等效电路+POIH-20模型梯形等效电路+POIH-80模型 计算/(W/kg)误差(%)计算/(W/kg)误差(%)计算/(W/kg)误差(%) 0.50.1080.08719.440.09710.180.1034.63 0.70.1890.16114.810.1757.410.1823.70 1.20.5010.4666.980.484.190.4892.40 1.71.0421.0093.171.0192.211.0221.92
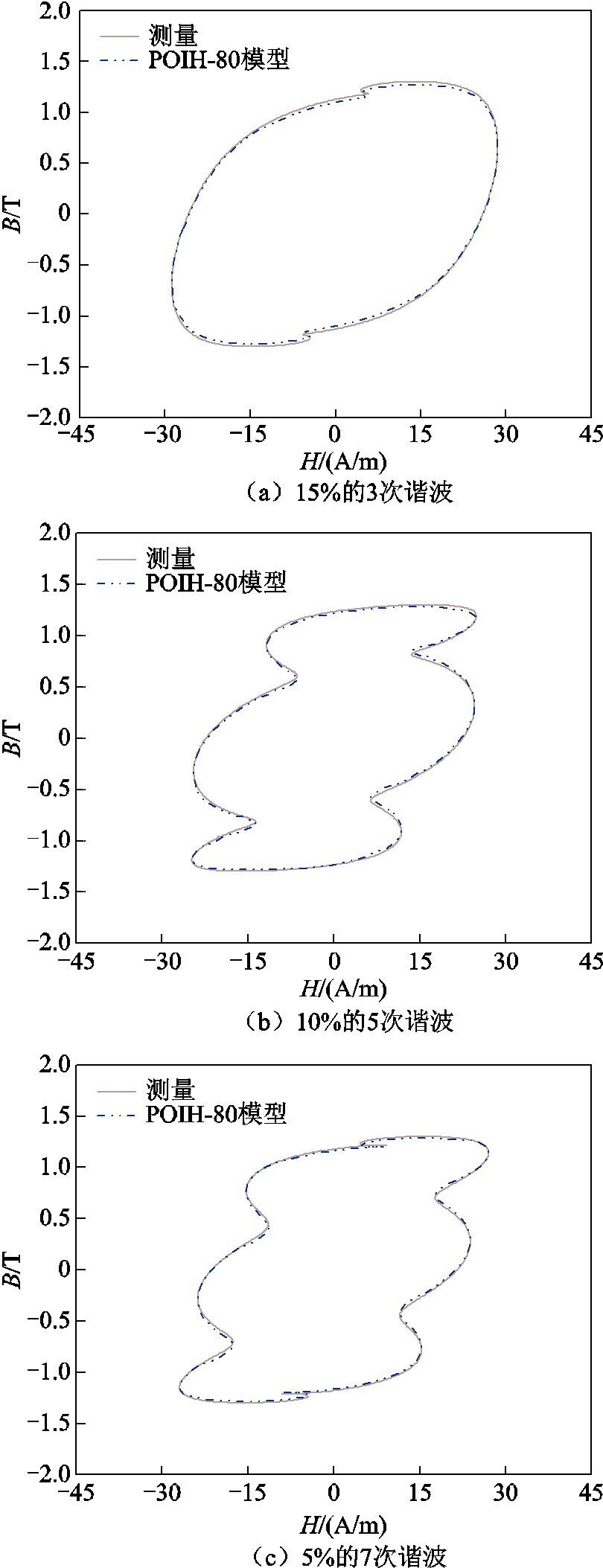
图13 谐波激励下的1.3 T磁滞回线对比
Fig.13 Comparison of 1.3 T hysteresis loops under harmonic excitation
本文提出了一种基于神经网络的POIH模型，通过融合Preisach算子与BP神经网络的非线性拟合能力，为有效解决Preisach模型中分布函数辨识过程复杂、神经网络模型对测量数据量依赖程度高的问题提供了一种新的参考方法，得到以下结论：
1）POIH模型通过非均匀离散化策略对Preisach平面进行网格划分，将构建的磁化状态矩阵作为神经网络的输入，将Preisach模型的积分运算转换为神经网络权重的动态调整。该方法保留了Preisach模型最初对磁化过程的可解释性，借助神经网络实现了分布函数的自适应辨识，避免传统Preisach模型预设理想数学分布函数时，借助优化算法求取待定参数易陷入局部最优的问题。
2）提出通过BP算法动态调整网络权重，定义了具有明确物理意义的有效权重参数，并建立了权重与分布函数之间的直接映射关系，通过提取权重描述了磁滞现象及其分布函数。同时，实现了分布函数的三维可视化，为材料微观磁化过程与宏观磁特性的关联分析提供了参考。
3）与实验对比验证表明，提出的磁滞模型不仅可以模拟直流、正弦交流磁化特性，还可以扩展到谐波磁化情况，展示了模型的泛化性能。
值得指出的是，尽管本文利用数学手段实现了Preisach模型的分布函数从理论示意图具象化为具有材料某些磁化特征的可视图，并对其做了部分磁化特征的解释，使Preisach模型的分布函数与磁化机理关联成为一种可能，但两者的关联关系后续仍需要更深入的探究。
参考文献
[1] 陈彬, 王川源, 刘洋, 等. 基于磁导-电容类比法和解析Preisach模型的铁心动态磁滞建模方法[J]. 电工技术学报, 2024, 39(18): 5576-5587. Chen Bin, Wang Chuanyuan, Liu Yang, et al. Dynamic hysteresis modeling method for iron core based on permeance-capacitance analogy and analytic Preisach model[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5576-5587.
[2] 刘任, 杜莹雪, 李琳, 等. 解析逆Preisach磁滞模型[J]. 电工技术学报, 2023, 38(10): 2567-2576. Liu Ren, Du Yingxue, Li Lin, et al. Analytical inverse Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2567-2576.
[3] Stoner E C, Wohlfarth E P. A mechanism of magnetic hysteresis in heterogeneous alloys[J]. IEEE Transactions on Magnetics, 1991, 27(4): 3475-3518.
[4] ElBidweihy H. Rotational magnetization lag-angle plots using the anisotropic stoner–wohlfarth model[J]. IEEE Transactions on Magnetics, 2017, 53(11): 7300906.
[5] 李永建, 李宗明, 利雅婷, 等. 考虑磁-力耦合效应的混合磁滞模型研究[J]. 电工技术学报, 2024, 39(22): 6941-6951. Li Yongjian, Li Zongming, Li Yating, et al. Study of hybrid hysteresis model considering magnetic-force coupling effect[J]. Transactions of China Electro-technical Society, 2024, 39(22): 6941-6951.
[6] 朱育莹, 李琳. 考虑各向异性和模型参数应力依赖关系的改进Sablik-Jiles-Atherton磁滞模型[J]. 电工技术学报, 2023, 38(17): 4586-4596. Zhu Yuying, Li Lin. An improved Sablik-Jiles-Atherton hysteresis model considering anisotropy and stress dependence of model parameters[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4586-4596.
[7] Alejos O, Della Torre E. Improving numerical simulations of Preisach models for accuracy and speed[J]. IEEE Transactions on Magnetics, 2000, 36(5): 3102-3104.
[8] Preisach F. Über die magnetische nachwirkung[J]. Zeitschrift Für Physik, 1935, 94(5): 277-302.
[9] 刘任, 杜莹雪, 李琳, 等. 解析正Preisach磁滞模型的推导与修正[J]. 中国电机工程学报, 2023, 43(5): 2070-2079. Liu Ren, Du Yingxue, Li Lin, et al. Derivation and modification of analytical forward Preisach hysteresis model[J]. Proceedings of the CSEE, 2023, 43(5): 2070-2079.
[10] De Biasi E. Faster modified protocol for first order reversal curve measurements[J]. Journal of Magnetism and Magnetic Materials, 2017, 439: 259-268.
[11] Szabó Z, Füzi J. Implementation and identification of Preisach type hysteresis models with Everett Function in closed form[J]. Journal of Magnetism and Magnetic Materials, 2016, 406: 251-258.
[12] 赵小军, 仪卓, 武欣怡, 等. 基于同心磁滞回环的Preisach磁滞模型参数辨识及其应用[J/OL]. 西安理工大学学报, 2024: 1-12. (2024-03-30). https://kns. cnki.net/KCMS/detail/detail.aspx?filename=XALD20240327003&dbname=CJFD&dbcode=CJFQ. Zhao Xiaojun, Yi Zhuo, Wu Xinyi, et al. Parameter identification of Preisach hysteresis model based on concentric hysteresis loop and its application[J/OL]. Journal of Xi’an University of Technology, 2024: 1-12. (2024-03-30). https://kns.cnki.net/KCMS/detail/ detail.aspx?filename=XALD20240327003&dbname=CJFD&dbcode=CJFQ.
[13] Bernard Y, Mendes E, Ren Z. Determination of the distribution function of Preisach’s model using centred cycles[J]. COMPEL - the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2000, 19(4): 997-1006.
[14] 李伊玲, 李琳, 刘任, 等. 基于非均匀单元离散法的静态逆Preisach模型分布函数辨识[J]. 中国电机工程学报, 2021, 41(15): 5340-5351. Li Yiling, Li Lin, Liu Ren, et al. The non-uniform element discretization method for identifying distribution function of static inverse Preisach model[J]. Proceedings of the CSEE, 2021, 41(15): 5340-5351.
[15] Peng Daixiao, Sima Wenxia, Yang Ming, et al. An improved centered cycle method for identifying the Preisach distribution function[J]. IEEE Transactions on Magnetics, 2018, 54(11): 7301405.
[16] Zhao Zhigang, Liu Fugui, Ho S L, et al. Modeling magnetic hysteresis under DC-biased magnetization using the neural network[J]. IEEE Transactions on Magnetics, 2009, 45(10): 3958-3961.
[17] Riganti Fulginei F, Salvini A. Neural network approach for modelling hysteretic magnetic materials under distorted excitations[J]. IEEE Transactions on Magnetics, 2012, 48(2): 307-310.
[18] Saliah H H, Lowther D A. The use of neural networks in magnetic hysteresis identification[J]. Physica B: Condensed Matter, 1997, 233(4): 318-323.
[19] Wang Zhen, Zhang Yanli, Ren Ziyan, et al. Modeling of anisotropic magnetostriction under DC bias based on an optimized BP neural network[J]. IEEE Transactions on Magnetics, 2020, 56(3): 7512204.
[20] Wang Yifan, Xu Rui, Zhou Miaolei. Prandtl-ishlinskii modeling for giant magnetostrictive actuator based on internal time-delay recurrent neural network[J]. IEEE Transactions on Magnetics, 2018, 54(11): 7301004.
[21] 马阳阳, 李永建, 孙鹤, 等. 基于深度置信网络算法的面向铁磁材料旋转磁滞损耗的矢量磁滞模型[J]. 电工技术学报, 2023, 38(15): 4063-4075. Ma Yangyang, Li Yongjian, Sun He, et al. Vector hysteresis model for rotational hysteresis loss of ferromagnetic materials based on deep belief network algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4063-4075.
[22] 黄雷, 包广清, 陈俊全. 基于Levenberg-Marquardt算法的改进Preisach模型磁特性模拟与验证[J]. 中国电机工程学报, 2020, 40(18): 6006-6015. Huang Lei, Bao Guangqing, Chen Junquan. Magnetic property simulation and verification with improved Preisach hysteresis model based on Levenberg-Marquardt algorithm[J]. Proceedings of the CSEE, 2020, 40(18): 6006-6015.
[23] 陈龙, 易琼洋, 贲彤, 等. 全局优化算法在Preisach磁滞模型参数辨识问题中的应用与性能对比[J]. 电工技术学报, 2021, 36(12): 2585-2593, 2606. Chen Long, Yi Qiongyang, Ben Tong, et al. Application and performance comparison of global optimization algorithms in the parameter identification problems of the Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2585-2593, 2606.
[24] 段娜娜, 徐伟杰, 李永建, 等. 基于极限磁滞回线法的软磁复合材料磁特性模拟[J]. 电工技术学报, 2018, 33(20): 4739-4745. Duan Nana, Xu Weijie, Li Yongjian, et al. Electromagnetic property modeling of the soft magnetic composite material based on the limiting loop method[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4739-4745.
[25] Hui S Y R, Zhu J. Numerical modelling and simulation of hysteresis effects in magnetic cores using transmission-line modelling and the Preisach theory [J]. IEE Proceedings-Electric Power Applications, 1995, 142(1): 57-62.
[26] Novak M, Eichler J, Kosek M. Difficulty in identification of Preisach hysteresis model weighting function using first order reversal curves method in soft magnetic materials[J]. Applied Mathematics and Computation, 2018, 319: 469-485.
[27] Miyazaki T, Mifune T, Matsuo T, et al. Equivalent circuit modeling of dynamic hysteretic property of silicon steel under pulse width modulation excitation[J]. Journal of Applied Physics, 2015, 117(17): 17D110.
[28] 荆盈, 张艳丽, 王振, 等. 高频激励下软磁复合材料动态磁滞模型及实验验证[J]. 中国电机工程学报, 2025, 45(7): 2845-2855. Jing Ying, Zhang Yanli, Wang Zhen, et al. Dynamic hysteresis model and experimental verification of soft magnetic composites under high frequency excitation [J]. Proceedings of the CSEE, 2025, 45(7): 2845-2855.
Abstract With the increasing complexity of the operating conditions of electrical equipment such as transformers, accurately simulating the magnetic characteristics of soft magnetic materials under various conditions has become particularly important. The neural network hysteresis model has become one of the effective methods for predicting the magnetic properties of soft magnetic materials such as silicon steel. This paper proposes an Preisach operator intelligent hysteresis (POIH) model for predicting the magnetization and loss characteristics. This model embeds the Preisach theory into the neural network framework and can effectively capture and reproduce the hysteresis behavior of materials under different conditions. Meanwhile, the model maintains good adaptability to complex operating conditions while significantly reducing the number of input samples.
In the POIH model, the Preisach diagram is non-uniformly discretized. 2N inversion points are selected to construct N(2N+1) grid nodes, each node corresponding to an Preisach operator and its state. The magnetization state matrix of the Preisach operator is constructed as the input of the back propagation (BP) neural network. In terms of the training strategy, the model only requires one limiting hysteresis loop and one basic magnetization loop to complete the training. To extend the model to dynamic conditions, the POIH model is coupled with the trapezoidal equivalent circuit, achieving the calculation of the iron loss components under sinusoidal and harmonic excitation. To establish the connection between the neural network parameters and physical meanings, the POIH model approximates the Sigmoid nonlinear function by Taylor expansion as a linear function, introduces the effective weight parameter with clear physical meaning, and thereby defines the discrete distribution function.
To verify the performance of the POIH model, the magnetic properties of silicon steel under quasi-static, power frequency and harmonic magnetization were measured. Firstly, the static hysteresis loop prediction values of the POIH model, the limiting magnetic hysteresis loop method Preisach model and the BP neural network model under different magnetic intensities were compared. The comparison results showed that the POIH model had the best comprehensive performance in terms of data volume and prediction accuracy. Secondly, the distribution function characteristics were analyzed to reveal the intrinsic correspondence between them and the material magnetization process. Finally, the dynamic hysteresis loops under power frequency and harmonic magnetization were predicted using the POIH model, and the model showed good accuracy in both cases.
The research results show: (1) The POIH model achieves an equivalent substitution for the integral operation of the Preisach model through the mapping of non-uniformly discretized Preisach diagram and neural network weights, while preserving the physical interpretability and avoiding the problem of easily getting stuck in local optima when traditional models rely on preset distribution functions and optimization algorithms. (2) By dynamically adjusting the weights using the backpropagation algorithm, a direct mapping between network weights and physical distribution functions is established, enabling adaptive identification and three-dimensional visualization of the distribution functions, providing a new means for the study of the correlation between microscopic magnetization mechanisms and macroscopic properties. (3) This model can accurately simulate the characteristics of direct current and sinusoidal alternating current magnetization, simultaneously can be extended to the case of harmonic excitation, demonstrating good generalization ability.
keywords：Preisach operator, neural network, effective weight parameter, distribution function
DOI: 10.19595/j.cnki.1000-6753.tces.251074
中图分类号：TM275
国家自然科学基金面上项目资助（52277015）。
收稿日期 2025-06-18
改稿日期 2025-07-26
荆 盈 女，1994年生，博士研究生，研究方向为工程电磁与磁性材料复杂电磁特性模拟。E-mail：jingying@smail.sut.edu.cn
张艳丽 女，1975年生，教授，博士生导师，研究方向为工程电磁与磁性材料复杂电磁特性模拟。E-mail：zhangyanli_sy@hotmail.com（通信作者）
（编辑 郭丽军）