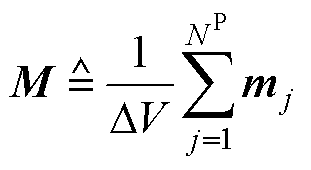（1）
摘要 磁性纳米粒子成像（MPI）的分辨率随着粒径的增大而提高，但在实际应用中，粒径的增大会导致弛豫效应增强，对于正弦激励的MPI，由于激励不断变化，磁粒子的磁化无法达到稳态，会导致分辨率下降。为此，该文提出将激励方式改为脉冲激励，利用脉冲激励等待粒子磁化达到稳态，消除弛豫效应的影响，提高MPI的分辨率。首先，构建基于德拜弛豫的理论磁化模型，建立MPI系统仿真模型，并基于此设计脉冲激励方法，通过模型实现脉冲激励磁场的生成；其次，在激励频率、幅值、粒径等条件相同的情况下利用脉冲和正弦两种不同的激励进行仿真实验，对比两种激励下的粒子磁化信号发现，使用脉冲激励可以使磁粒子的磁化达到稳态，同时测量了不同激励下的信号点扩散函数，结果表明，脉冲激励MPI的点扩散函数的半峰全宽是正弦激励MPI的84%；最后，使用x-space方法进行线源成像，成像结果表明，脉冲激励MPI具有更高的分辨率。因此，采用脉冲激励磁场使磁粒子磁化达到稳态可以消除信号的滞后，有效地提高MPI的分辨率。
关键词：磁性纳米粒子成像（MPI） x-space MPI 磁化稳态 弛豫效应
磁性纳米粒子成像（Magnetic Particle Imaging, MPI）是由B. Gleich和J. Weizenecker在2005年首次发明的医学成像方法，利用磁性纳米粒子的非线性磁化性质进行成像[1]。MPI具备诸多优势，例如，生物相容性佳、安全性高、成像快速且高效、对比度高等[2-3]，因此常用于血管造影、灌注成像和功能性神经成像等。此外，MPI所具有的出色灵敏度为分子靶向成像创造了条件，使其能够应用于炎症斑块检测、干细胞跟踪以及T细胞跟踪等领域[4-6]。
然而，目前MPI的图像分辨率不能满足人体体内成像的临床要求[7]。进行MPI成像，首先需要产生静态磁场梯度场（即选择场）来提供零场区（Field Free Region, FFR）以实现空间编码。目前常用的零场区为零场线（Field Free Line, FFL），在该零场区附近，磁性纳米粒子会被激励并产生信号[8]。然后，通过移动或旋转FFR来收集数据，其中最常用的零场区运动轨迹是李萨如轨迹，该轨迹可由两个正交的正弦磁场合成[9]。最后，通过反投影等算法将收集到的数据重建为磁粒子浓度分布图像[10]。MPI图像的分辨率与FFL的宽度直接相关，FFL的宽度由选择场的梯度所决定[11]。由于现有梯度线圈硬件的局限性，如线圈导线发热限制、机械结构对磁场强度的制约等，提高选择场的梯度需要花费较大的成本，因此，需要采用其他方法来提高MPI的分 辨率。
另一种提高分辨率的方法是增大磁粒子的粒径。根据郎之万理论，在相同梯度条件下，磁粒子的粒径越大，MPI的分辨率越高。但在实际测量中，由于弛豫效应，磁粒子的磁化变化赶不上时刻变化的外加正弦激励磁场，当磁粒子的粒径增大到一定程度后，由于磁粒子磁化达不到稳态，其对图像产生的影响便不再可以忽略。Z. W. Tay等利用频率为25 kHz、幅值为20 mT的正弦磁场激励磁粒子发现，当磁粒子的粒径超过25 nm后，弛豫效应会对成像造成较大的不良影响，即使可以通过降低激励频率或振幅来缓解，也无法完全解决问题，作者称之为“弛豫壁”[12]。此外，通过反卷积方法虽然可以消除部分弛豫效应的影响，但会大大降低信噪比，而且需要关于点扩散函数的先验知识，因此，需要对MPI系统进行改进，使磁粒子磁化达到稳态，消除弛豫效应带来的不良影响。
根据以上背景，本文基于德拜弛豫，通过研究磁粒子的磁化过程，提出一种可以使磁粒子的磁化达到稳态的MPI脉冲磁场激励方法。结合仿真模型，首先通过测量磁粒子的磁化信号验证脉冲激励可以使磁粒子达到磁化稳态；然后测量脉冲、正弦激励下MPI的点扩散函数（Point-Spread Function, PSF）并进行一维成像；最后将二者的PSF与成像效果进行对比，验证当磁粒子达到磁化稳态时可以提高MPI的分辨率。
MPI利用磁性纳米粒子的非线性磁化特性进行空间分布示踪。在外部磁场作用下，磁性纳米粒子被磁化，它们的磁矩会趋于沿外部磁场的磁力线方向对齐。用NP表示小体积DV中的粒子数量，使用磁矩mj表示每个粒子的磁性行为。由于布朗运动的存在，粒子的磁矩方向是随机分布的。在宏观尺度上，磁矩之和为0。所有磁矩之和的密度被称为磁化强度，用M表示，即
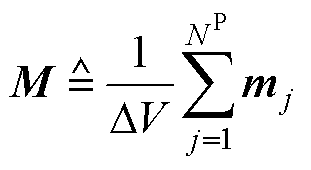（1）
施加外部磁场H后，磁粒子开始与外加磁场对齐，可以观察到沿外加磁场方向的磁化。忽略弛豫效应，磁化强度可以表示为
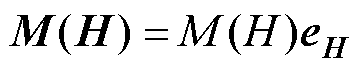（2）
式中，M(H)为磁化强度矢量，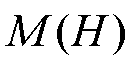
为其大小；eH为磁场强度H的方向。由外部磁场引起的磁性纳米粒子的动力学非常复杂，为将其简化，粒子的磁化由郎之万理论来描述[13]。则M与外加磁场矢量的大小H之间的关系为
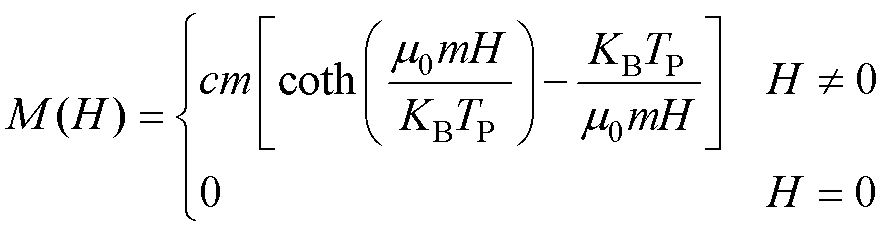（3）
式中，m0为真空中的磁导率；KB为玻耳兹曼常数；TP为粒子温度；c为粒子浓度；m为单个粒子的磁矩模量。当铁元素浓度一定时，粒子的浓度与粒子的体积成反比，因此，表达式中的cm为常数。
式（1）～式（3）都是在绝热假设下推导出的结果，即磁场强度H和磁粒子磁化强度M的方向一致，磁粒子的磁化总能瞬时跟随外加磁场变化。这种情况只有在所施加的磁场是静态的，或磁粒子的弛豫时间常数较小时才近似成立。如果基于此理论进行仿真会导致仿真磁化强度大小与实际测量的磁化强度大小的偏差较大。因此，需要对该理论模型进行修改。
当考虑时变磁场时，粒子磁化矢量会以一定的延迟跟随施加磁场的方向发生变化，磁化强度的变化将比磁场强度的变化稍晚发生。这种延迟可以通过弛豫时间来描述，粒子磁化强度随弛豫时间呈指数下降。关于铁磁流体的经典文献通常将磁性纳米粒子的弛豫建模为一阶德拜过程[14]。
磁粒子同时存在尼尔弛豫和布朗弛豫两种弛豫现象。布朗弛豫描述的是整个磁粒子的机械旋转，而尼尔弛豫描述的是固定磁粒子的磁矩的旋转，两种弛豫的对比如图1所示。
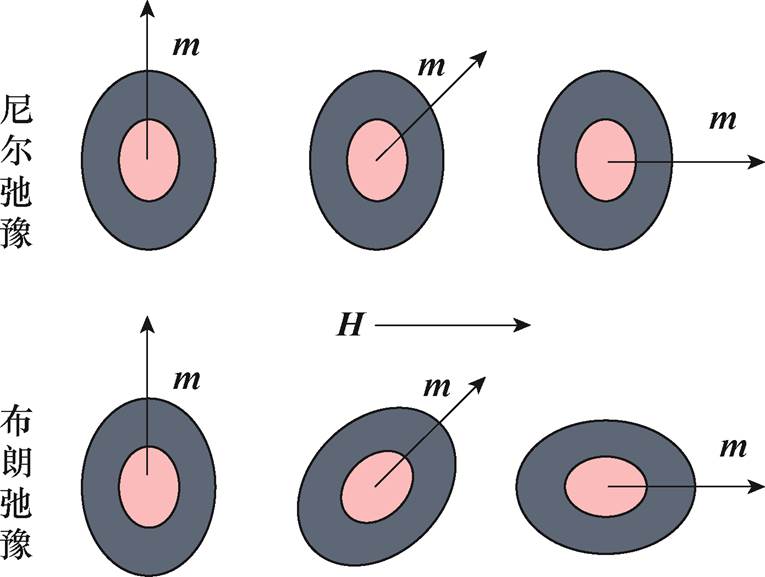
图1 尼尔弛豫和布朗弛豫的对比
Fig.1 Comparison of Neel and Brownian rotation
设磁粒子的布朗弛豫时间为tB，尼尔弛豫时间为tN，则布朗弛豫时间tB为
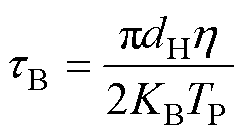（4）
式中，dH为磁粒子的流体动力学直径；h为环境的黏度。尼尔弛豫时间tN[15]为
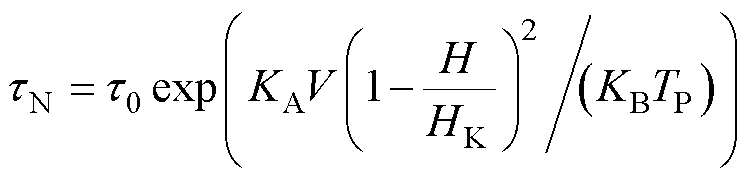（5）
式中，t0为常数，t0≈10-10 s；V为磁粒子核的体积；KA为氧化铁的磁晶各向异性常数，KA≈11 kJ/m3 [16]；HK为各向异性磁场，HK=2KA/MS，MS为磁粒子的饱和磁化强度。
磁粒子总弛豫时间t可以近似为尼尔弛豫时间和布朗弛豫时间的组合，有
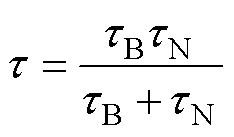（6）
根据式（4）～式（6），t与粒子的粒径以及外加磁场幅值有关，关系如图2所示。基于德拜弛豫效应，磁粒子的磁化强度大小随时间t的变化可描述为
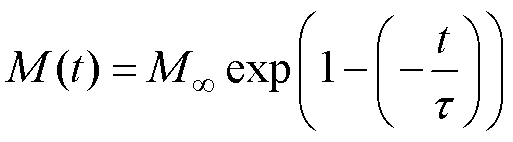（7）
式中，M(t)为t时刻磁粒子的磁化强度大小；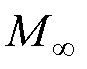
为稳态磁化强度，对于足够大的外加磁场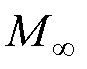，等于磁粒子的饱和磁化强度MS。
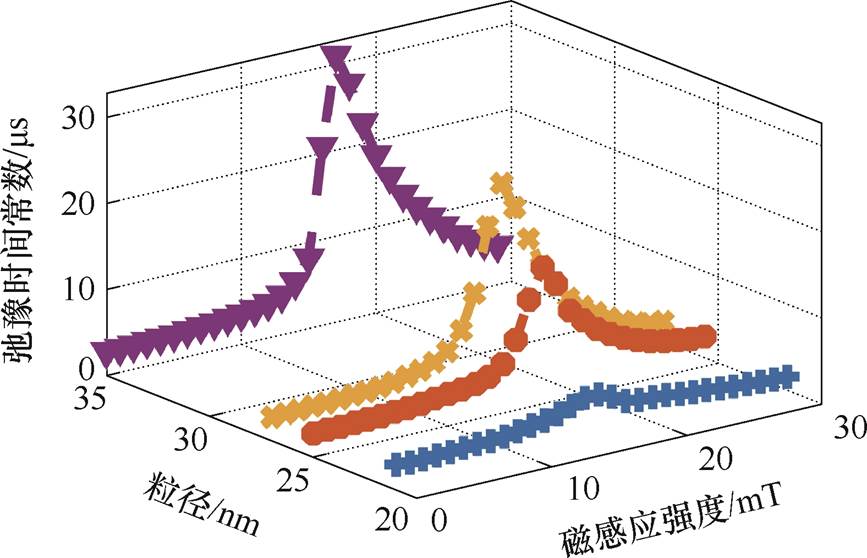
图2 弛豫时间常数与粒径及外加磁场的关系
Fig.2 The relationship between relaxation time constantand particle size and applied magnetic field
由于正弦激励是时刻变化的，对于式（7）描述的磁粒子磁化过程，使用正弦磁场激励磁粒子会使磁粒子的磁化一直处于变化状态，因此需要修改激励。新的激励需要包括一段保持不变的分量，用来等待磁粒子的磁化达到稳态。
开放式MPI系统主要分为单边MPI系统和开放结构MPI系统[17-18]。单边MPI系统的磁体结构仅置于检测对象的一侧，这样的布局使其适合于执行表面的检测任务。开放式结构MPI系统则在检测对象的两侧都配备了磁体结构，四周为开放式的设计，这使得系统能够对检测对象进行更深层次的检测。本文采用开放式结构MPI系统。
对于无弛豫效应的理想磁粒子，研究人员通常通过磁化强度导数的半峰全宽（Full Width at Half Maximum, FWHM）来衡量MPI系统的分辨率大小。对于朗之万函数的导数，磁化强度导数的半峰全宽近似为
≈
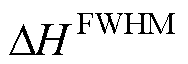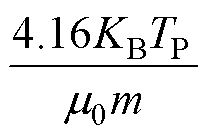（8）
对于实际的磁粒子，郎之万模型并不十分准确，因此无法通过式（8）计算出分辨率。P. W. Goodwill等通过分析和实验发现点扩散函数就是磁性纳米颗粒朗之万函数的导数[19]。因此，本文采用测量法测量磁粒子的信号点扩散函数。为测量磁粒子在不同激励下磁化强度大小随时间变化的M-t曲线以及信号的点扩散函数，建立了如图3所示的脉冲激励MPI系统整体模型。模型内部结构如图4所示。
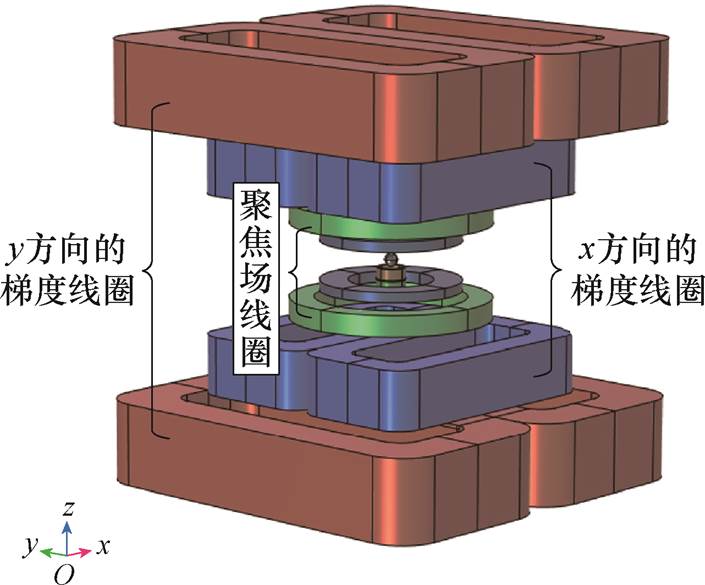
图3 脉冲激励MPI系统整体模型
Fig.3 Pulsed excitation MPI system integrated model
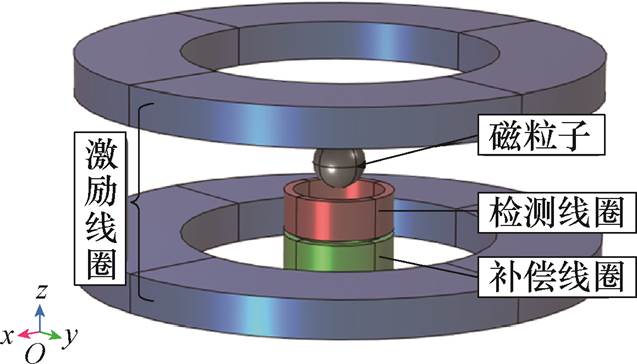
图4 模型内部结构
Fig.4 Model internal structure
模型中放入半径为10 mm的球体模拟磁粒子集群[20]，作为被测物产生信号。利用亥姆霍兹线圈构成激励线圈产生空间上均匀分布的激励磁场，为使线圈产生的均匀磁场范围最优，两线圈间隔距离为线圈直径的1/2[21]。由于感应线圈法具有易于设计、空心结构不占样品空间体积的优点[22]，本文基于此方法，利用检测线圈检测磁粒子的电压信号，同时将补偿线圈和检测线圈反向串联，构成差分线圈，去除变化激励磁场产生的信号。此外，还加入y方向的梯度场线圈、x方向的梯度场线圈（其中x方向和y方向是指梯度线圈产生的FFL延伸的方向）以及聚焦场线圈以实现FFL的旋转、平移和视场（Field of View, FOV）的移动。
本文的梯度线圈采用矩形线圈，矩形线圈的边相当于四条直导线，在与这些导体垂直且距离相等的点上，磁场强度相同，在一定范围内，当线圈平行于某个轴时，它所产生的磁场强度维持恒定[23]。因此，采用矩形线圈可以增强零场线的精度和均匀性[24]。梯度线圈包含x方向的梯度线圈以及y方向的梯度线圈，通过改变x方向梯度线圈和y方向梯度线圈通入电流的比例实现FFL的旋转。此外，对于20 mT的驱动场强度和3 T/m的磁场梯度，FFL在x方向上只能移动27 mm，在y方向上只能移动13 mm。为了扩大成像区域，本文增加了一对聚焦场线圈[25]，在聚焦场线圈和激励线圈的共同作用下移动FFL。MPI系统模型部分线圈参数见表1。
表1 MPI系统模型部分线圈参数
Tab.1 Some coil parameters of the MPI system model
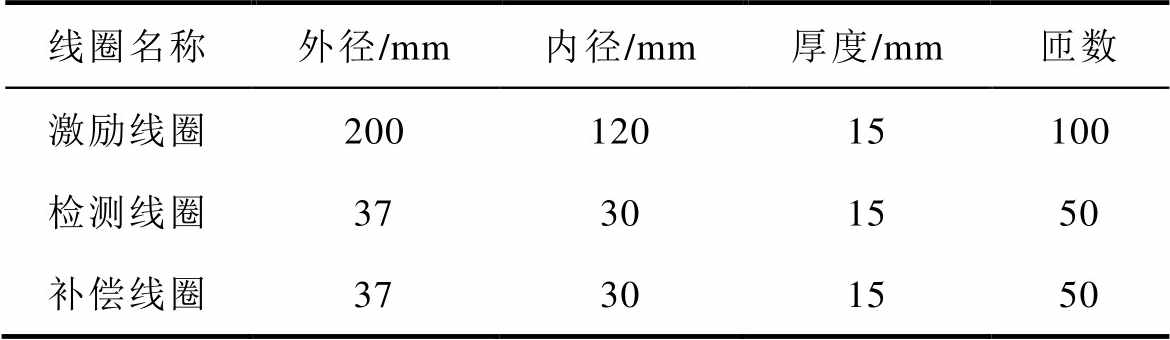
线圈名称外径/mm内径/mm厚度/mm匝数 激励线圈20012015100 检测线圈37301550 补偿线圈37301550
由式（7）可知，当磁粒子突然受到外加磁场的影响时，其磁化过程通常可以描述为一个动态响应，遵循指数增长的规律，经过一段时间的动态响应后，磁化强度大小达到一个不再随时间变化的恒定值，这个值就是稳态磁化强度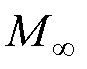。传统MPI采用正弦激励磁场，正弦激励下的磁粒子无法达到磁化稳态状态。对于粒径较小的磁粒子，其弛豫时间常数较小，磁化达不到稳态对成像的影响近似可以忽略；但当磁粒子的粒径增大到一定程度后，这种影响便不再可以忽略。
为使在磁粒子的磁化达到稳态的同时激发粒子产生信号，本文采用了一种复合激励磁场，该磁场需要包含两段关键分量：一段是快速变化的分量，通过迅速改变磁粒子的磁化状态来产生较大的信号；另一段是保持不变的分量，为磁粒子的磁化达到稳态创造必要条件。具体而言，在这个保持不变的磁场分量下，磁粒子有足够长的时间响应磁场的变化，从而达到磁化稳态。这两种分量的结合形成了脉冲激励磁场。广义脉冲信号有多种实现形式，由于方波激励磁场有明确的前后沿，为便于研究粒子磁化过程和激励磁场之间的关系，本文选择方波激励磁场。
实验前需要选择成像参量。为消除激励磁场产生的感应电压的影响，正弦激励的MPI采用电压信号的三次谐波幅值作为成像参量，但脉冲激励是一种宽带激励，无法将信号的三次谐波幅值作为成像参量，因此将激励修改为脉冲磁场后需要选择新的成像参量。脉冲激励磁场下的电压曲线如图5所示，在每个脉冲激励磁场半周期内，粒子产生的电压信号呈现指数衰减趋势。根据相关研究，衰减电压的曲线下面积与连续两个半周期结束时达到的稳态磁化强度之间的差异成正比[26]。因此可以选择衰减电压的曲线下面积作为成像参量，衡量磁化强度大小的变化。设脉冲激励磁场的半周期为T，Mp(x, t)为在脉冲激励磁场作用下磁粒子的磁化强度大小，对于保持时间较长即可以使磁粒子磁化达到稳态的脉冲磁场，Mp(x, t)在时间上的变化趋势与M(t)相同。设零场线FFL的方向为沿x轴，沿x轴的磁粒子分布浓度为c(x)，线圈灵敏度为p(x)，则衰减电压的曲线下面积UAUC的表达式[27]为
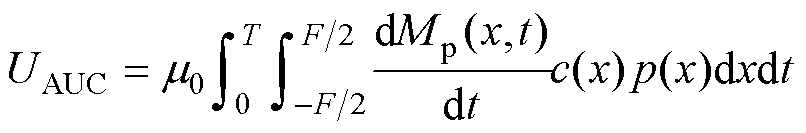（9）
式中，F为视场在x轴方向上的长度。
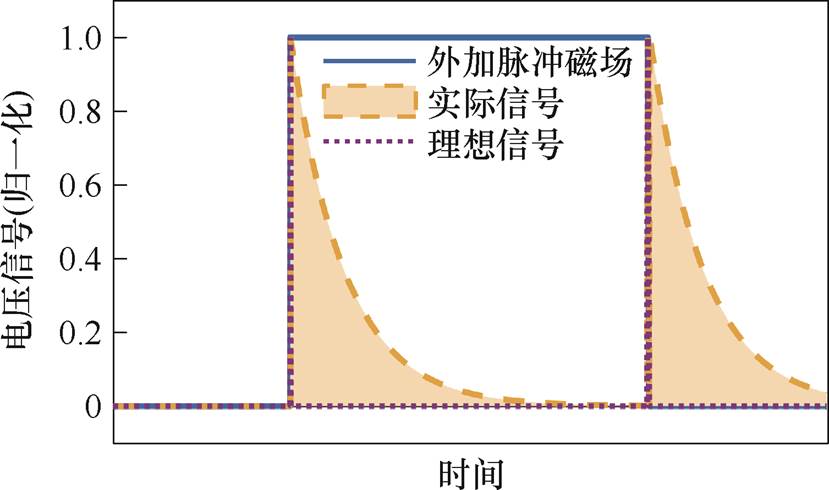
图5 脉冲激励磁场下的电压曲线
Fig.5 The voltage curve under the pulse excitation magnetic field
为了开展后续对比实验，还需要生成脉冲激励磁场。向上述模型中通入幅值为26 A、频率为10 kHz的脉冲电流，激励线圈在z方向上产生均匀时变的脉冲磁场，磁场的幅值为29 mT，通入电流和产生的激励磁场的波形如图6所示。
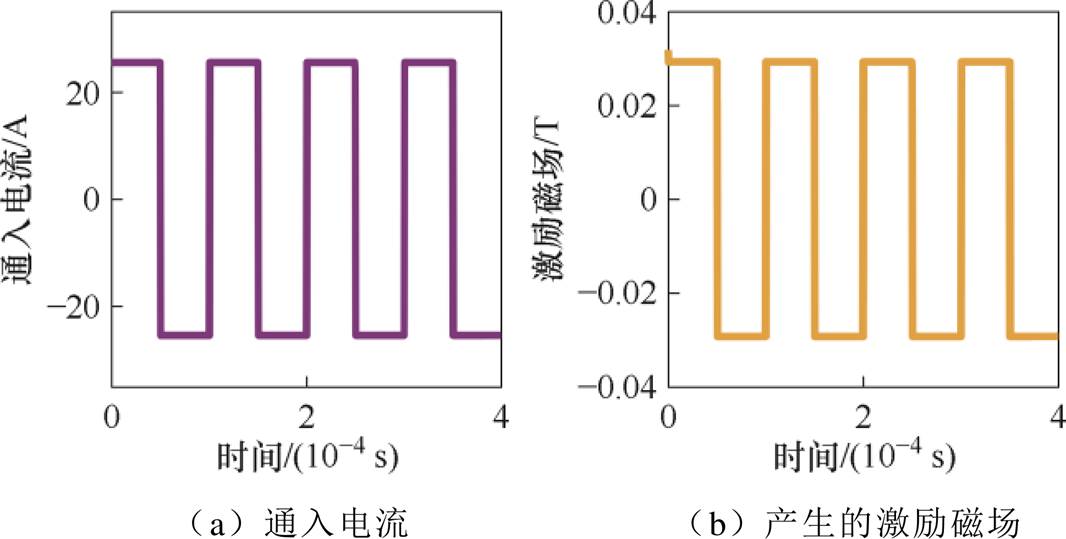
图6 脉冲激励磁场的产生
Fig.6 Generation of the pulsed excitation magnetic field
为研究磁粒子的磁化过程，利用有限元仿真软件COMSOL完成该系统的仿真计算。仿真模型如图3所示，模型各部分的作用如1.2节所示。
在材料的属性设置中添加如图7所示的磁性纳米粒子材料的磁感应强度-磁场强度（B-H）曲线，自定义磁性纳米粒子的非线性磁化特性。此外，还需要自定义磁粒子材料的基本属性，设置磁粒子的电导率为5×10-6 S/m，相对介电常数为20，相对磁导率为1.18，粒径为30 nm，饱和磁化强度MS为7 000 A/m。磁粒子的弛豫时间常数如图2所示，利用1.1节推导的式（7）计算磁化强度大小。
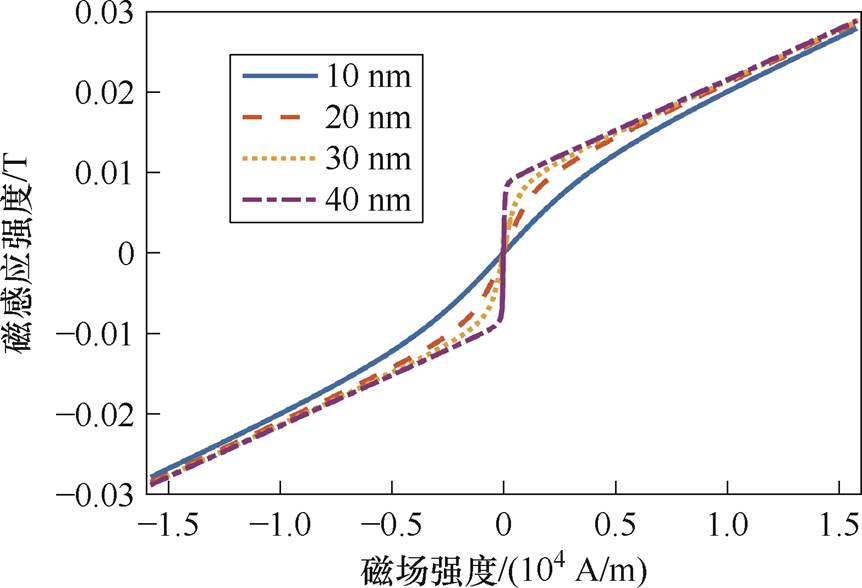
图7 不同粒径磁粒子的B-H曲线
Fig.7 B-H curves of magnetic particles with different particle sizes
将模型先后通入幅值为20 A、频率为10 kHz的脉冲电流和正弦电流，激励线圈在z方向上产生均匀时变的磁场。脉冲、正弦激励磁场的幅值均为23 mT，为磁粒子提供足够大的激励；脉冲磁场的持续时间为50 ms，用来等待磁粒子的磁化达到稳态。
测量系统的磁化强度大小变化，并将结果与无弛豫效应的理想磁粒子的磁化M-t曲线以及归一化外加脉冲磁场放入同一图中进行对比，结果如图8所示。
由对比结果可知，没有弛豫效应的理想磁粒子的磁化强度可以跟随外加磁场瞬时变化。但实际磁粒子的磁化过程会受到弛豫效应的影响，不能立即对外加磁场的变化做出反应，因此需要通过使磁粒子的磁化达到稳态来消除弛豫效应的影响。在正弦磁场激励下，磁粒子的磁化达不到稳态；而脉冲磁场在一段时间内不发生变化，在这段时间内，磁粒子的磁化变化逐渐减慢，直至达到磁化稳态状态。
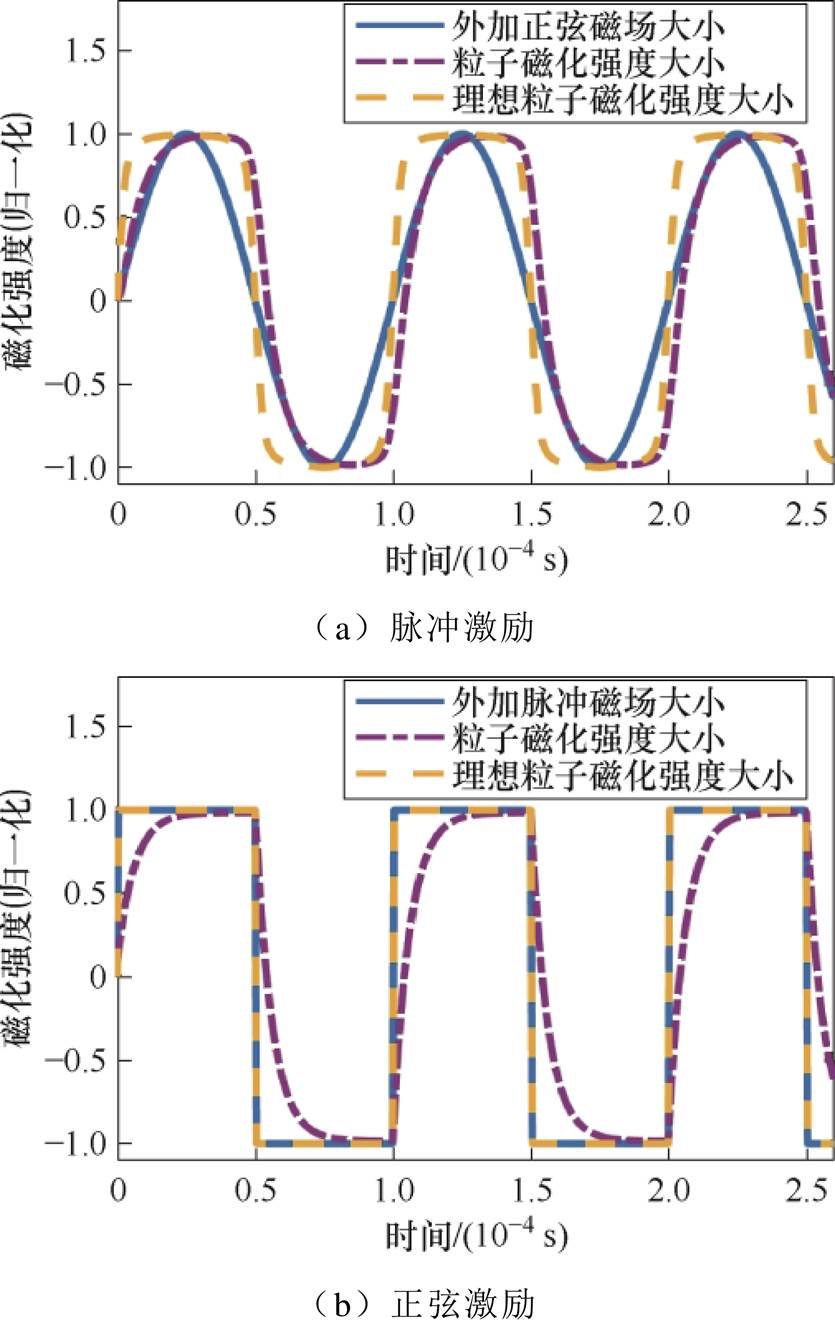
图8 不同激励下磁粒子的M-t曲线
Fig.8 The M-t curves of magnetic particles under different excitations
为进一步研究不同粒径磁粒子对磁化稳态的影响，本文分别选择25、35、46 nm以及上述实验的30 nm粒径的磁粒子，保持其他参数及实验过程不变，测量这些磁粒子在一个激励半周期内的磁化强度大小，结果如图9所示。
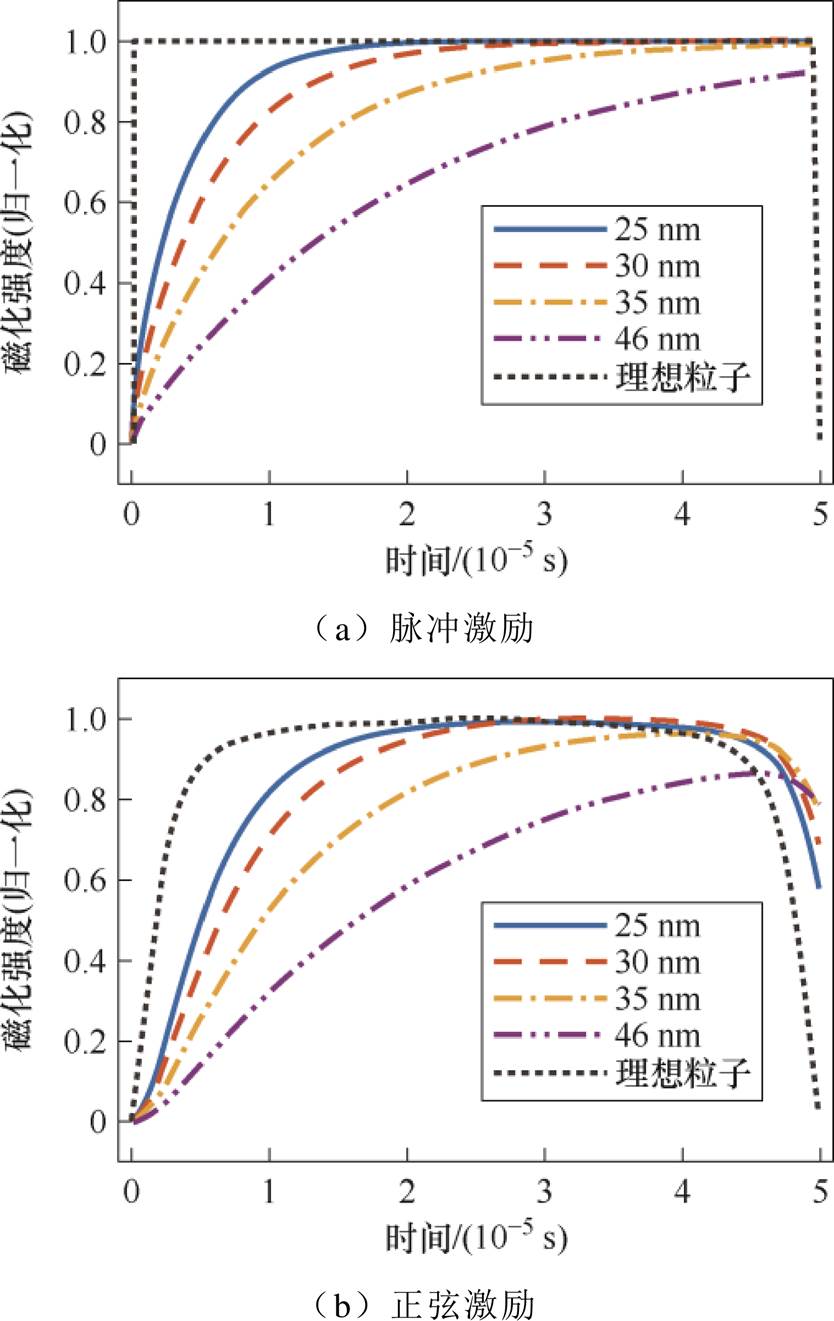
图9 不同粒径磁粒子在脉冲磁场和正弦磁场激励下的M-t曲线
Fig.9 The M-t curves of magnetic particles with different particle sizes under the excitation of pulsed magnetic fields and sinusoidal magnetic fields
实验结果表明，磁粒子粒径越大，其磁化强度大小变化的滞后效应越明显，M-t曲线与理想粒子M-t曲线的差异越大。此外还可以看出，当粒径增大到46 nm时，即便用脉冲磁场激励，粒子在半周期结束时也没有达到磁化稳态状态，这是由于磁粒子的弛豫时间常数较大，而脉冲磁场的保持时间不足以使粒子磁化达到稳态。因此，为使磁粒子的磁化达到稳态，在选择脉冲磁场进行激励的同时，脉冲磁场本身的保持时间需要足够长。
为验证分辨率的提高效果，本文利用脉冲MPI系统分别测量脉冲激励MPI和正弦激励MPI的信号点扩散函数，比较二者的半峰全宽。粒子粒径为25 nm，激励磁场幅值为7 mT，激励频率为10 kHz，并置于相同的磁场梯度下。移动FFL，测量不同采样点下粒子的电压信号，结果如图10所示。
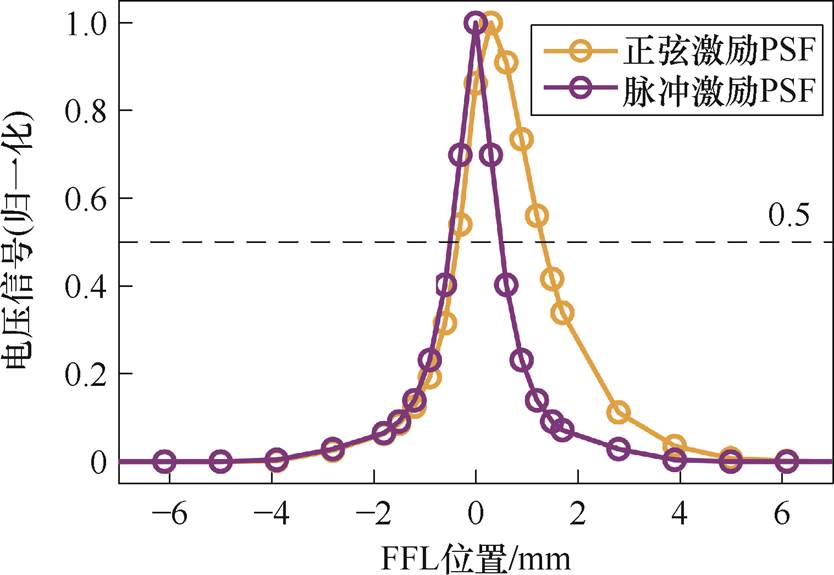
图10 两种激励下PSF的对比
Fig.10 Comparison of PSF under two types of excitation
经计算可得，脉冲激励MPI的PSF半峰全宽约为正弦激励MPI的PSF半峰全宽的84%。分析实验结果可知，在弛豫效应的影响下，正弦激励的磁粒子磁化达不到稳态，使正弦激励MPI信号的产生与消失都滞后于脉冲激励MPI信号，进而导致了正弦激励MPI的PSF的半峰全宽增加，即分辨率降低。此外，正弦激励MPI信号点扩散函数还失去了对称性。这些都会对成像产生不良影响。这说明采用脉冲磁场使磁粒子磁化达到稳态可以消除弛豫效应带来的不良影响，提高重建图像的分辨率。
一维x-space成像公式为
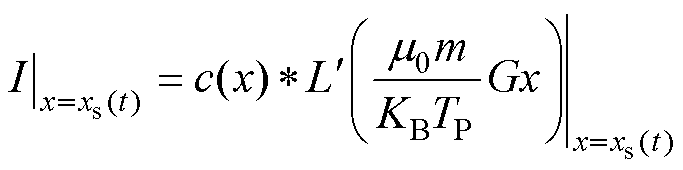（10）
式中，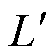
为郎之万函数的导数；G为选择场梯度；设FFL所在位置为x=xs，则图像值I等于磁粒子的分布与郎之万函数导数的卷积，郎之万函数的导数就是3.1节测出的电压信号点扩散函数。
为直观地显示磁粒子达不到磁化稳态对成像的影响，本文进行了一维线源成像实验。首先进行单线源成像，假设磁粒子的分布如图11所示。由式（10）计算像素大小并将结果转换为图片，得到单线源成像结果如图12所示。为了增强视觉效果，更清晰地比较不同激励方法下的成像效果，本文在脉冲激励MPI的成像结果以及正弦激励MPI的成像结果中用黑色的矩形虚线框圈出磁粒子实际分布的位置，并对图像进行了伪彩色映射。
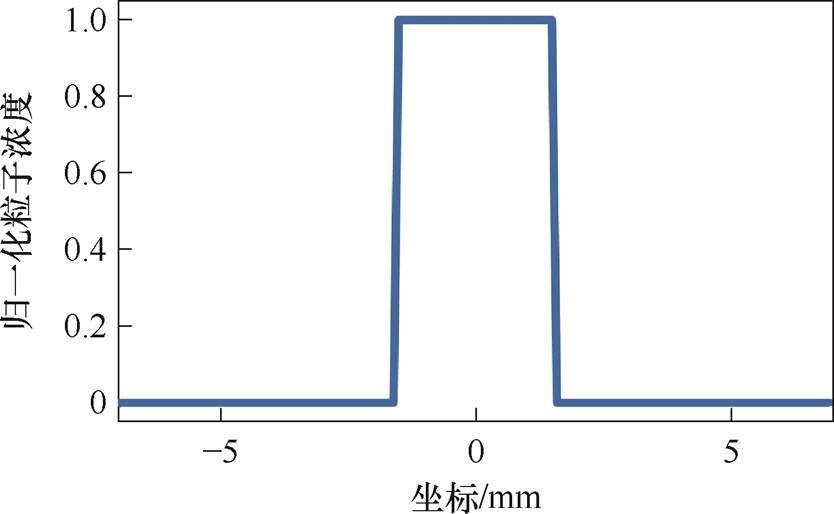
图11 单线源分布
Fig.11 Single-line source distribution
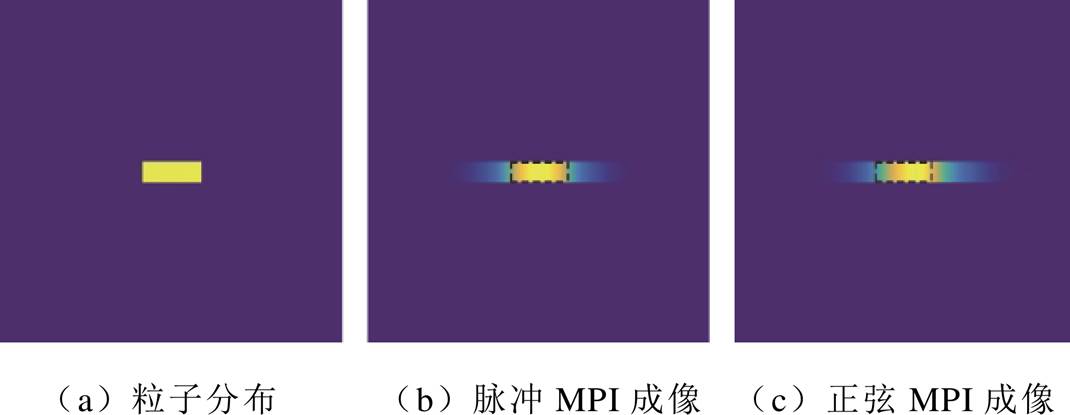
图12 单线源成像结果
Fig.12 Single-line source imaging results
从单线源成像结果中可以看出，脉冲激励MPI的成像结果与正弦激励MPI的成像结果相比表现出较少的伪影。此外，对比实际粒子分布可知，正弦激励MPI的成像结果还出现了偏移。
根据分辨率的定义，MPI系统可以分辨的临近线源的距离越小，分辨率越高。为进一步研究脉冲激励MPI分辨临近线源的能力，本文还设计了双线源成像实验，两个线源间隔1 mm，分布如图13所示，双线源成像结果如图14所示。
由成像结果可得，脉冲激励MPI对相邻线源的分辨能力较强。进一步证明了采用脉冲激励使磁粒子磁化达到稳态可以提高MPI系统的分辨率。
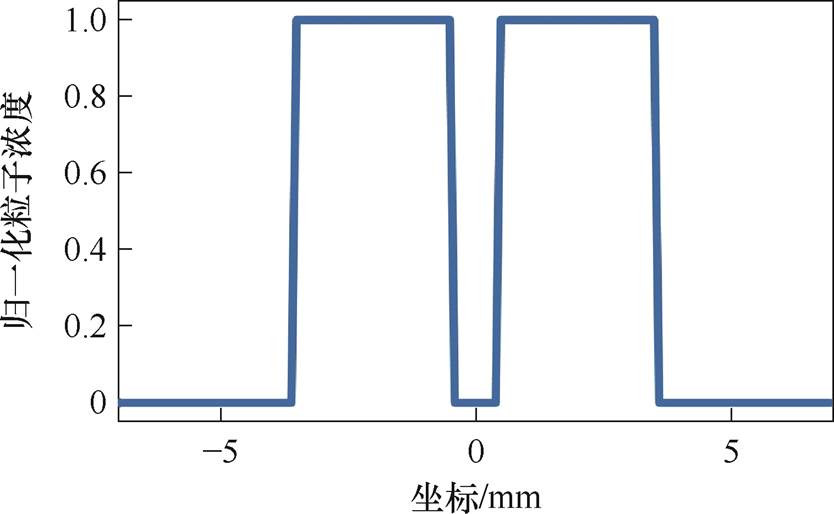
图13 双线源分布
Fig.13 Double-line source distribution
图14 双线源成像结果
Fig.14 Double-line source imaging results
传统MPI采用正弦激励，在正弦激励下，磁粒子的磁化无法达到稳态，进而造成了信号的混叠，降低了MPI的分辨率。针对传统MPI存在的不足，本文提出了脉冲磁场激励方法，将传统MPI的激励修改为脉冲磁场激励，利用脉冲激励不变的分量等待磁粒子磁化达到稳态，消除弛豫效应的影响。并且提出了更符合实际的基于德拜弛豫的磁粒子磁化理论模型，利用该理论模型对脉冲激励MPI系统进行建模，并采用有限元仿真软件COMSOL对系统进行仿真，测量在其他相同条件下不同激励的磁粒子磁化过程以及信号点扩散函数，最后利用信号点扩散函数进行基于x-space方法的成像。理论分析与实验结果均表明，将激励磁场修改为脉冲激励可以使磁粒子的磁化达到稳态，从而消除信号的滞后，提高MPI的分辨率。本文为减少成像伪影、提高MPI分辨率提供了一种新的方法和思路，有助于推动MPI在临床上的应用。
参考文献
[1] Gleich B, Weizenecker J. Tomographic imaging using the nonlinear response of magnetic particles[J]. Nature, 2005, 435(7046): 1214-1217.
[2] 祖婉妮, 柯丽, 杜强, 等. 开放式磁性纳米粒子断层成像线型旋转零磁场设计[J]. 电工技术学报, 2020, 35(19): 4161-4170.
Zu Wanni, Ke Li, Du Qiang, et al. Electronically rotated field-free line generation for open bore magnetic particle tomography imaging[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4161-4170.
[3] Tong Wei, Hui Hui, Shang Wenting, et al. Highly sensitive magnetic particle imaging of vulnerable atherosclerotic plaque with active myeloperoxidase- targeted nanoparticles[J]. Theranostics, 2021, 11(2): 506-521.
[4] Wang Qiyue, Ma Xibo, Liao Hongwei, et al. Artificially engineered cubic iron oxide nanoparticle as a high-performance magnetic particle imaging tracer for stem cell tracking[J]. ACS Nano, 2020, 14(2): 2053-2062.
[5] Sehl O C, Foster P J. The sensitivity of magnetic particle imaging and fluorine-19 magnetic resonance imaging for cell tracking[J]. Scientific Reports, 2021, 11(1): 22198.
[6] Rivera-Rodriguez A, Hoang-Minh L B, Chiu-Lam A, et al. Tracking adoptive T cell immunotherapy using magnetic particle imaging[J]. Nanotheranostics, 2021, 5(4): 431-444.
[7] Pagan J, McDonough C, Vo T, et al. Single-sided magnetic particle imaging device with field-free-line geometry for in vivo imaging applications[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-5.
[8] 刘洋洋, 杜强, 柯丽, 等. 磁性粒子成像线型零磁场设计及性能分析[J]. 电工技术学报, 2020, 35(10): 2088-2097.
Liu Yangyang, Du Qiang, Ke Li, et al. Design and analysis of magnetic field-free line in magnetic particle imaging[J]. Transactions of China Electro- technical Society, 2020, 35(10): 2088-2097.
[9] 张玺, 郑建勇, 梅飞, 等. 基于Lissajous轨迹的电能质量扰动边-云协同高效辨识框架[J]. 电力系统自动化, 2024, 48(22): 210-223.
Zhang Xi, Zheng Jianyong, Mei Fei, et al. Lissajous locus-based efficient identification framework for power quality disturbances based on edge-cloud collaboration[J]. Automation of Electric Power Systems, 2024, 48(22): 210-223.
[10] Konkle J J, Goodwill P W, Carrasco-Zevallos O M, et al. Projection reconstruction magnetic particle imaging[J]. IEEE Transactions on Medical Imaging, 2013, 32(2): 338-347.
[11] 杨丹, 王雨忱, 李天兆, 等. 一种基于线性零磁场的动脉血管扫描成像方法仿真[J]. 电工技术学报, 2024, 39(2): 343-355.
Yang Dan, Wang Yuchen, Li Tianzhao, et al. Simulation of an arterial scanning imaging method based on linear zero magnetic field[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 343- 355.
[12] Tay Z W, Hensley D W, Vreeland E C, et al. The relaxation wall: experimental limits to improving MPI spatial resolution by increasing nanoparticle core size [J]. Biomedical Physics & Engineering Express, 2017, 3(3): 035003.
[13] 武明, 杜强, 柯丽, 等. 磁纳米粒子成像中非线性磁化信号二次谐波检测方法研究[J]. 电子测量与仪器学报, 2022, 36(9): 87-94.
Wu Ming, Du Qiang, Ke Li, et al. Research on second harmonic detection method of nonlinear magnetiza- tion signal in magnetic nanoparticle imaging[J]. Journal of Electronic Measurement and Instrumenta- tion, 2022, 36(9): 87-94.
[14] Muslu Y, Utkur M, Demirel O B, et al. Calibration- free relaxation-based multi-color magnetic particle imaging[J]. IEEE Transactions on Medical Imaging, 2018, 37(8): 1920-1931.
[15] Arami H, Ferguson R M, Khandhar A P, et al. Size- dependent ferrohydrodynamic relaxometry of magnetic particle imaging tracers in different environments[J]. Medical Physics, 2013, 40(7): 071904.
[16] Ferguson R M, Minard K R, Krishnan K M. Optimization of nanoparticle core size for magnetic particle imaging[J]. Journal of Magnetism and Magnetic Materials, 2009, 321(10): 1548-1551.
[17] 姜策, 柯丽, 杜强, 等. 基于圆环磁体阵列的线型零磁场系统研究[J]. 仪器仪表学报, 2021, 42(9): 192-201.
Jiang Ce, Ke Li, Du Qiang, et al. Research on the magnetic field-free line system based on ring magnet array[J]. Chinese Journal of Scientific Instrument, 2021, 42(9): 192-201.
[18] Top C B, Gungor A. Tomographic field free line magnetic particle imaging with an open-sided scanner configuration[J]. IEEE Transactions on Medical Imaging, 2020, 39(12): 4164-4173.
[19] Goodwill P W, Conolly S M. Multidimensional x-space magnetic particle imaging[J]. IEEE Transac- tions on Medical Imaging, 2011, 30(9): 1581-1590.
[20] 闫孝姮, 淡新贤, 陈伟华, 等. 基于改进目标场法梯度线圈的感应式磁声磁粒子浓度成像研究[J]. 电工技术学报, 2024, 39(14): 4305-4316.
Yan Xiaoheng, Dan Xinxian, Chen Weihua, et al. Magneto-acoustic magnetic particle concentration imaging based on improved target field method gradient coil[J]. Transactions of China Electrotech- nical Society, 2024, 39(14): 4305-4316.
[21] 汤云东, 丁宇彬, 金涛. 基于亥姆霍兹线圈装置的磁热疗优化方法[J]. 电工技术学报, 2023, 38(5): 1248-1260.
Tang Yundong, Ding Yubin, Jin Tao. Research on optimization method of magnetic hyperthermia based on Helmholtz coil device[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1248-1260.
[22] 魏文琦, 张绍哲, 谢剑峰, 等. 脉冲强磁场磁感应强度测量技术研究进展[J]. 电工技术学报, 2024, 39(23): 7291-7308.
Wei Wenqi, Zhang Shaozhe, Xie Jianfeng, et al. Progress of magnetic induction intensity measurement techniques in the pulsed high magnetic field[J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7291-7308.
[23] 祖婉妮. 开放结构磁性纳米粒子血管精细成像方法研究[D]. 沈阳: 沈阳工业大学, 2023.
Zu Wanni. Vascular precision imaging methods based on open-structure magnetic particle imaging[D]. Shenyang: Shenyang University of Technology, 2023.
[24] 杨丹, 刘素羽, 张昊, 等. 基于永磁体和线圈复合结构的磁性粒子成像零磁场研究[J]. 电工技术学报, 2025, 40(2): 335-345.
Yang Dan, Liu Suyu, Zhang Hao, et al. Research on magnetic particle imaging zero magnetic field based on permanent magnet and coil composite structure[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 335-345.
[25] Schmale I, Rahmer J, Gleich B, et al. First phantom and in vivo MPI images with an extended field of view[C]//Medical Imaging 2011: Biomedical Applica- tions in Molecular, Structural, and Functional Imaging, Lake Buena Vista, Florida, USA, 2011: 796510.
[26] Tay Z W, Hensley D, Ma Jie, et al. Pulsed excitation in magnetic particle imaging[J]. IEEE Transactions on Medical Imaging, 2019, 38(10): 2389-2399.
[27] Jia Guang, Huang Liyu, Wang Ze, et al. Gradient- based pulsed excitation and relaxation encoding in magnetic particle imaging[J]. IEEE Transactions on Medical Imaging, 2022, 41(12): 3725-3733.
Abstract As an emerging medical imaging technology, magnetic particle imaging (MPI) possesses numerous unique advantages and holds broad application prospects in multiple fields. However, currently, MPI is confronted with a critical problem: its image resolution fails to meet the clinical demands for in-vivo medical human imaging. In theory, increasing the particle size of magnetic nanoparticles can enhance the MPI resolution. Nevertheless, in practical measurements, a larger particle size intensifies the relaxation effect. Due to this relaxation effect, magnetic particles cannot reach the magnetization steady-state under the constantly changing sinusoidal excitation, exerting a non-negligible negative impact on imaging. Therefore, it is necessary to improve the MPI system to enable the magnetization of magnetic particles to reach a steady state and eliminate the influence of the relaxation effect. In view of this, a pulsed magnetic field excitation method is put forward in this paper.
Firstly, to accurately describe the magnetization change process of magnetic particles, the Langevin magnetization theory was combined with the Debye relaxation theory to construct a theoretical magnetization model of magnetic particles. Simultaneously, an open-structure MPI system simulation model is established, which encompasses key components like excitation coils, detection coils, compensation coils, gradient coils, and focus coils. The gradient coil adopts an improved rectangular gradient coil to enhance the accuracy and uniformity of the field free line (FFL).
Secondly, a pulsed excitation method is proposed. The area under the decaying voltage curve is chosen as the imaging parameter for pulsed-excitation MPI. By passing current through the excitation coil in the simulation model, a pulsed magnetic field was generated. This pulsed magnetic field contains quick changing and constant components, capable of exciting magnetic particles to generate signals while enabling magnetic particles to reach the magnetization steady-state.
Subsequently, simulation experiments were carried out using the established simulation model.Under the same conditions of excitation frequency, amplitude, and particle size, the magnetization signals of magnetic particles under pulsed and sinusoidal excitations are compared. The results indicate that pulsed excitation can make the magnetization of magnetic particles reach a steady-state. Meanwhile, the signal point-spread functions under different excitations were also measured. The resolution was evaluated by the full width at half maximum (FWHM) of the signal point-spread function. The experimental results show that the FWHM of the signal point-spread function of pulsed-excitation MPI is 84% of that of sinusoidal-excitation MPI, indicating an improvement in resolution.
Finally, A line-source imaging experiment is carried out using the x-space method to further visually demonstrate the differences in the imaging resolution of MPI under different excitations.The single-line-source imaging results demonstrate that pulsed-excitation MPI has fewer imaging artifacts and no imaging offset occurs. The The double-line-source imaging demonstrates that the pulsed excitation MPI has a stronger resolving ability for two adjacent line sources with an interval of 1 mm.
The results of the simulation experiments and imaging experiments indicate that modifying the sinusoidal excitation magnetic field of traditional MPI to pulsed excitation can enable the magnetization of magnetic particles to reach a steady state, thereby eliminating signal lag and improving the resolution of MPI.
keywords：Magnetic particle imaging (MPI), x-space MPI, magnetization steady state, relaxation effect
DOI: 10.19595/j.cnki.1000-6753.tces.242285
中图分类号：TM153
国家自然科学基金资助项目（52077143）。
收稿日期 2024-12-18
改稿日期 2025-01-21
李美凝 女，1999年生，硕士研究生，研究方向为生物电磁检测与成像。E-mail: limeining1999@163.com
杜 强 男，1975年生，副教授，硕士生导师，研究方向为生物电工技术。E-mail: duqiang@sut.edu.cn（通信作者）
（编辑 李 冰）