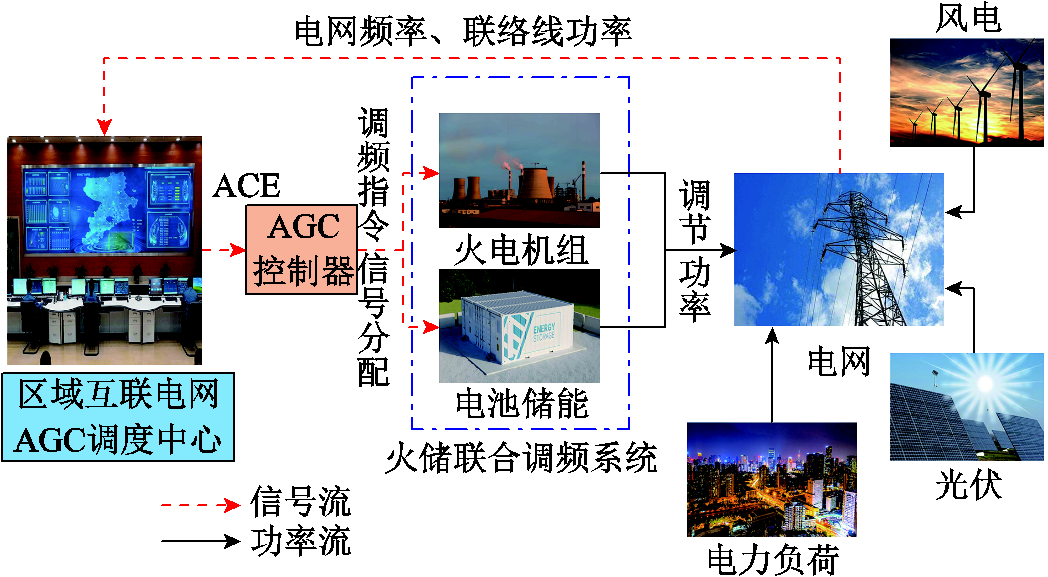
图1 火储联合参与区域电网调频示意图
Fig.1 Schematic diagram of thermal power and energy storage participating in power system frequency regulation
摘要 针对火储联合系统参与电网二次调频,该文提出一种考虑电池储能荷电状态恢复的动态参与因子与自适应模型预测控制策略。首先,基于灵敏度原理获取区域控制偏差模式下储能参与因子与系统频率偏差的对应关系,并根据负荷状态采用模糊控制方法获得动态储能参与因子,由此界定频率调节不同阶段储能与火电机组调频责任大小;其次,通过模型预测控制实时优化储能出力深度,提高频率控制质量;然后,将区域控制偏差信号与储能荷电状态进行分区,综合不同区间特性调节模型预测控制目标函数中荷电状态恢复相关项的权重系数,在改善频率偏差的同时对恢复荷电状态;最后,在Matlab/Simulink中搭建含电池储能和火电机组的双区域互联电网仿真模型,并结合两种典型应用场景对该文所提控制策略的有效性进行验证。结果表明,该文策略在提升调频效果与恢复荷电状态方面具有良好的性能。
关键词:电池储能 二次调频 动态参与因子 自适应模型预测控制 荷电状态
高比例可再生能源并网不仅降低了电力系统的惯性,更给电网带来严重的间歇性与不确定性[1-2],进一步加剧了电源与负载间的功率不平衡,使得频率稳定性无法得到保证。传统发电机组对自动发电控制(Automatic Generation Control, AGC)信号进行跟踪时,依靠现有控制策略无法快速满足调频需求[3],在平滑新能源波动方面表现不佳。
储能因能提高负荷频率控制性能,减小传统发电机组深度动作频次与频繁爬坡带来的磨损,已成为调频领域研究的热点[4-5]。与此同时,充分发挥储能与传统机组各自优势,提升电网调频效果并延长储能电池寿命是促进储能大规模应用的关键问题[6]。电池储能作为一种可双向充放电、响应速度快、调节精度高的新型电力装置,具有较强的频率调节能力[7-9]。火储联合参与区域电网调频示意图如图1所示。

图1 火储联合参与区域电网调频示意图
Fig.1 Schematic diagram of thermal power and energy storage participating in power system frequency regulation
传统的比例积分微分(Proportional Integral Derivative, PID)控制器是二次调频领域应用最广泛的控制手段[10]。然而,日渐复杂的电力系统结构使得PID控制性能受限,导致系统调频效果不佳[11-12]。文献[13]设计了一种利用增强型梯度优化器对分数阶PID进行参数整定的负荷频率控制方案。与传统PID控制相比,分数阶PID具备两个额外的可调参数,从而提高了控制器对系统参数变化的抗扰能力,但改进的PID变体本质上仍具有滞后性,控制器性能表现过于依赖其增益选择,且不适用于处理带约束的多输入输出系统。相较之下,模型预测控制(Model Predict Control, MPC)能够解决含多重约束的AGC问题,是一种超前控制方法。MPC通过预测系统未来的动态行为,在设定的预测时域范围内优化控制目标,具备出色的响应速度和鲁棒性[14-15]。
文献[16]考虑各类调频电源不同的物理约束,提出一种分布式模型预测控制方法用于协调异质储能系统和火电机组出力以优化系统频率偏差,然而没有涉及储能荷电状态(State of Charge, SOC)变化对储能调节功率的影响。因此部分文献在设计储能功率控制策略时将SOC纳入考量范围,避免了过充或过放的现象发生,但仍缺乏对储能SOC恢复控制的研究[17]。文献[18]应用模糊控制方法制定出储能参与二次调频与维持SOC的综合控制策略,并利用传统调频电源剩余容量在系统频率偏差处于较小范围时对储能SOC进行恢复。文献[19]提出一种考虑经济运行成本与SOC一致性的双层AGC调频控制方法,在储能深度充放电和负荷变化较慢的工况下分别对SOC进行粗调和微调管理。以上在储能调频死区或空闲时段提出的SOC恢复方法,某种程度上缓解了由于储能SOC过低或过高导致调频出力不充分的问题,但如果在调频阶段未能适当地恢复SOC,储能仍可能在长时间连续调频过程中失去部分调节能力,对电网频率恢复造成二次冲击[20]。
当前MPC方法多关注储能的频率调节能力,对SOC恢复的研究则较为有限,且未能深入探讨在调频阶段合理恢复SOC,避免储能在长时间调频过程中失去调节能力的问题。MPC目标函数可由多个子目标构成,以最小化系统频率偏差为主目标的同时能够兼顾储能SOC恢复的性能指标,但完全固定的目标函数权重难以适应不同时段频率调节与储能SOC恢复的动态需求,导致调频效果与储能长期可用性之间存在冲突。即当储能需恢复SOC时,若频率调节权重过高,易导致SOC无法及时回到合理水平,影响储能的持续效能;反之,在频率调节紧急情况下,若过度强调SOC恢复,则可能导致频率响应不及时,削弱电网的稳定性。因此需要对以减小区域控制偏差(Area Control Error, ACE)与恢复储能SOC为目标函数的MPC权重系数调节方法进行研究,平衡储能调频与恢复的需求。
在储能参与电网二次调频研究中,文献[21]考虑不同的频率控制要求,提出分布式储能系统频率协调控制策略,但侧重于一次调频储能出力调度研究,通过设置充足的备用功率满足系统二次调频需要,缺乏相应的二次控制策略设计。文献[22]结合ACE和区域控制需求两种分配模式的优点,依据调频容量比例系数对火电机组和储能进行责任分配。文献[23]考虑系统调频需要与储能调频能力,利用Logistic函数对储能输出功率进行约束,构建储能二次调频出力控制规律。上述研究在界定传统机组与储能之间的调频责任时,大多依据调频电源各自的可用容量,但相对固定的比例分配无法充分发挥不同调频电源的优势。
考虑储能容量小响应快和火电机组容量大响应慢的特点,文献[24]通过分析AGC频谱,将高低频分量分别交由储能和火电机组承担,但传统一阶低通滤波器截止频率固定,无法完全平抑多变的调频场景下火电机组的出力波动。针对该滤波算法截止频率固定的缺陷,文献[25]提出一种基于频率偏差变化率的可变滤波时间常数信号分解方法实现抽水蓄能与电池储能的协调配合,但未考虑复合储能与火电机组之间调频指令分配的合理性。且在利用低通滤波器将调频信号分解为高频和低频分量进行后续分配的过程中,信号会不可避免地出现幅值衰减、相位偏移及失真等现象,导致复合储能间调频指令分配的准确性降低。总体上看,鲜有文献能够细致剖析频率偏差与不同调频电源之间动作深度的关系,实时捕捉负荷扰动的动态变化,灵活调整不同机组的调频参与度,从而实现调频责任的自适应分配。
现有研究在进行火储调频责任分配时,忽略了实际电力系统中随机负荷扰动连续变化和无规律高频小信号的特点,致使参与因子的设计缺乏灵活性,无法在复杂负荷波动场景下充分发挥储能与火电机组各自的调频优势。此外,在储能参与长期频率调节过程中,不同时段的系统调频需求与储能SOC恢复之间存在矛盾。基于此,本文提出了一种考虑储能SOC恢复的基于动态参与因子与自适应模型预测控制的电网二次调频策略。主要贡献如下:
1)设计综合考虑灵敏度、频率偏差和负荷波动影响因素的分层判断机制,并提出基于灵敏度计算与双模糊控制确定火储调频参与度的动态参与因子策略。优化火储调频责任分配,发挥储能快速响应和火电机组持续调节能力,从而提升整体调频性能。
2)提出了基于ACE与SOC分区控制,以及自适应MPC的储能调频与恢复控制方法。利用MPC的预测和优化能力增强调频过程的前瞻性和精准性,实现储能充放电决策的优化,并根据实时状态信息灵活调节储能SOC恢复项的权重系数,实现不同运行状态下SOC恢复力度的动态调节,有效缓解了储能调频和恢复SOC的冲突,提升了储能在全工况范围内的双向调频能力。
本文以经典双区互联电网频率响应模型为研究对象,并采用定频率与联络线功率偏差控制(Tie-line Bais Control, TBC)方式,建立如图2所示的火储联合调频等效模型。其中,火电机组参与电网一、二次调频,电池储能仅参与二次调频。
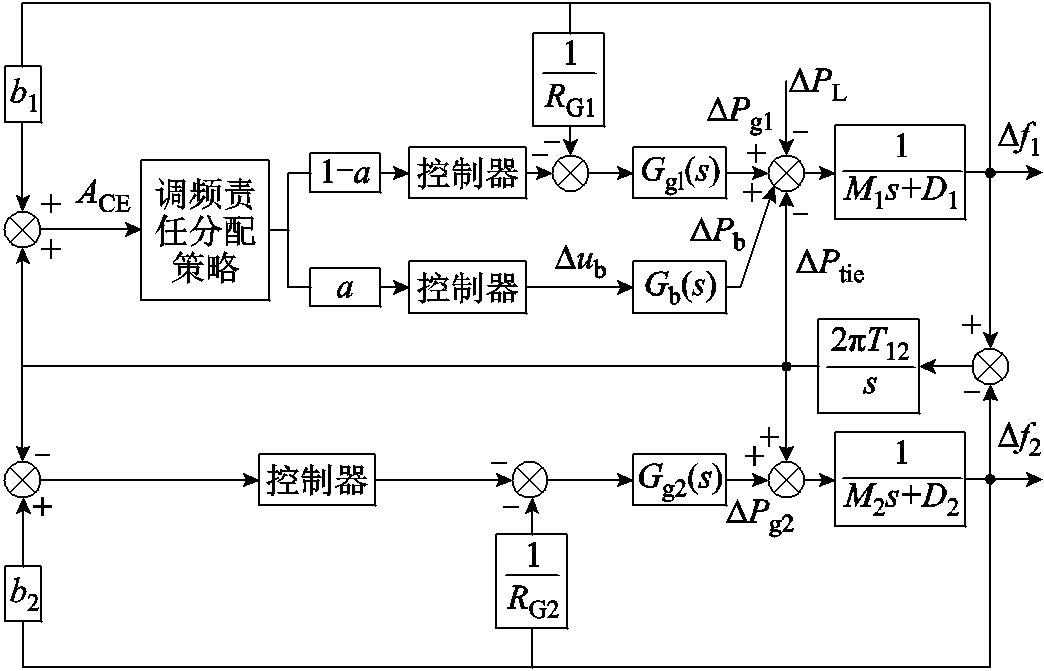
图2 含电池储能的两区域系统调频动态模型
Fig.2 Dynamic modelling of two-area system with battery storage for frequency regulation
图2中,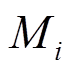 和
和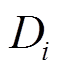 分别为两区域的系统转动惯量和负荷阻尼系数(
分别为两区域的系统转动惯量和负荷阻尼系数(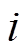 =1, 2,分别代表区域1和区域2,下同),
=1, 2,分别代表区域1和区域2,下同),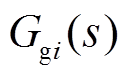 和
和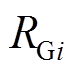 分别为火电机组调频响应模型和一次调频调差系数,
分别为火电机组调频响应模型和一次调频调差系数,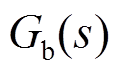 为电池储能频率响应模型,
为电池储能频率响应模型,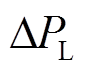 为区域负荷扰动,
为区域负荷扰动,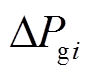 为火电机组出力大小,
为火电机组出力大小,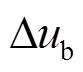 为电池储能出力控制信号,
为电池储能出力控制信号,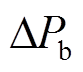 为电池储能出力大小,
为电池储能出力大小,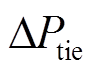 为联络线交换功率偏差,
为联络线交换功率偏差,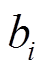 为频率偏差系数,
为频率偏差系数,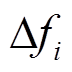 为系统频率偏差,
为系统频率偏差,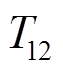 为两区域联络线功率同步系数,
为两区域联络线功率同步系数,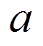 为储能参与因子,
为储能参与因子,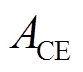 为区域控制偏差信号大小。电网调度中心根据监测到的频率偏差与联络线功率偏差计算区域1的ACE信号为
为区域控制偏差信号大小。电网调度中心根据监测到的频率偏差与联络线功率偏差计算区域1的ACE信号为
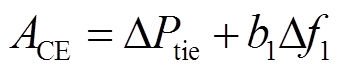 (1)
(1)
ACE信号经控制器处理后按照一定的分配方式下达给调频电源,系统中各调频机组等效模型为火电机组等效传递函数模型和电池储能等效传递函数模型。
1)火电机组等效传递函数模型
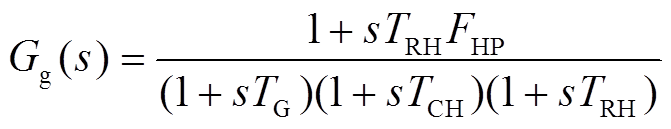 (2)
(2)
式中,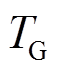 、
、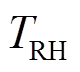 、
、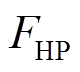 和
和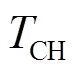 分别为火电机组调速器时间常数、再热器时间常数、再热器增益和汽轮机时间常数。
分别为火电机组调速器时间常数、再热器时间常数、再热器增益和汽轮机时间常数。
2)电池储能等效传递函数模型
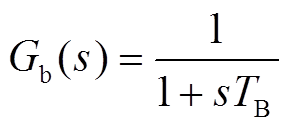 (3)
(3)
式中,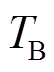 为电池储能出力变量的响应时间常数。
为电池储能出力变量的响应时间常数。
电池储能可用容量与额定容量的比值代表荷电状态(SOC),即
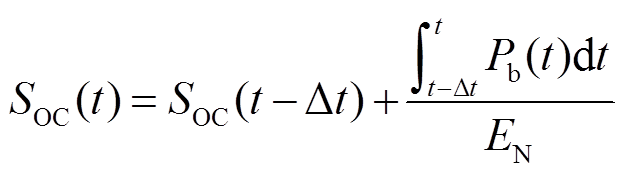 (4)
(4)
式中,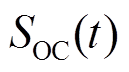 为
为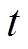 时刻电池储能SOC;
时刻电池储能SOC;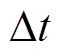 为采样时间间隔;
为采样时间间隔;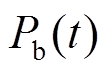 为电池储能在
为电池储能在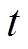 时刻的充、放电功率,以储能放电方向为正;
时刻的充、放电功率,以储能放电方向为正;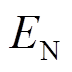 为电池储能额定容量。
为电池储能额定容量。
本节提出了一种基于动态调频责任分配与自适应模型预测控制的储能二次调频策略。为了充分发挥不同阶段储能快速响应与火电机组持续调节的互补优势,首先计算参与因子对频率偏差的灵敏度并结合负荷状态,依托模糊控制器生成动态储能参与因子,灵活分配火储调频责任大小;其次将储能动态调频责任信号作为模型预测控制器的优化目标,滚动求解储能最佳出力控制量,提升系统调频效果;最后在MPC目标函数中引入SOC恢复控制项,通过对ACE信号与储能SOC状态进行分段处理,实现该项权重系数的分区自适应调节,达到平衡调频与SOC恢复的目的,总体策略框架如图3所示。
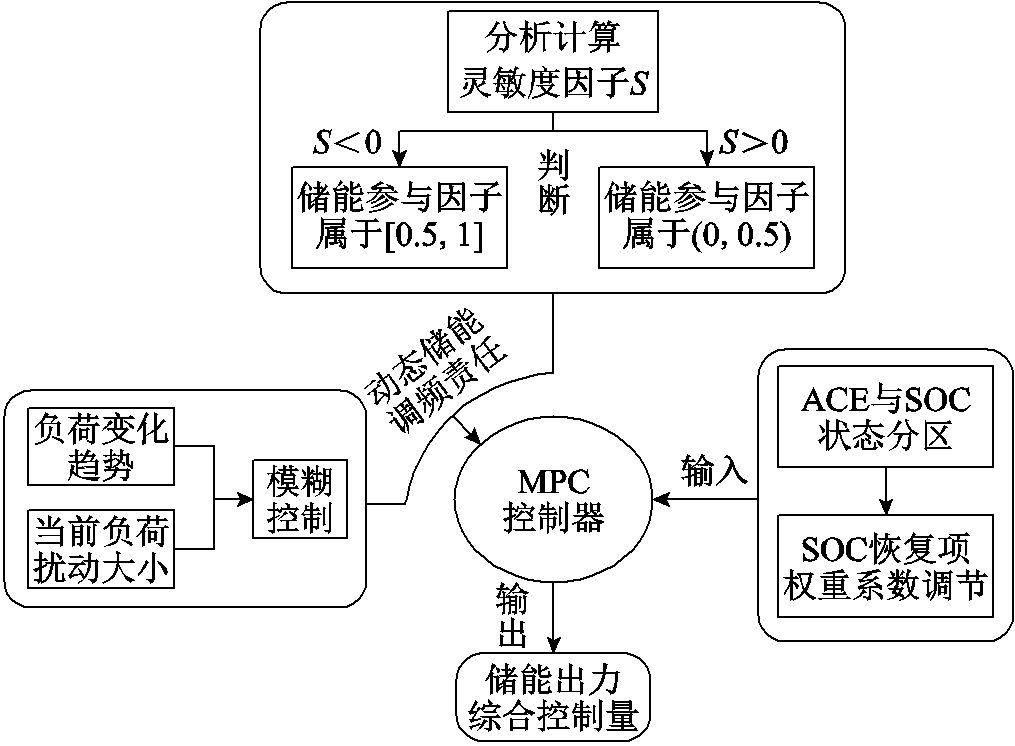
图3 二次调频控制策略架构
Fig.3 Schematic of the secondary frequency regulation control strategy
2.1.1 ACE控制模式下储能参与因子灵敏度分析
本文采用基于ACE信号的分配模式。该方式下二次调频控制回路仅火电机组经过比例积分PI控制器,储能直接响应部分ACE信号以发挥其出力的迅速特性。在复频域中应用灵敏度原理分析储能参与调频的动作深度即参与因子与系统频率偏差之间的关系。灵敏度S定义如下:当自变量z发生1%的变化时,函数y(z)会对应产生S%的改变,且S>0,z与y(z)同向变化;S<0,z与y(z)反向变化[26]。ACE控制模式下含储能的复频域调频模型如图4所示。
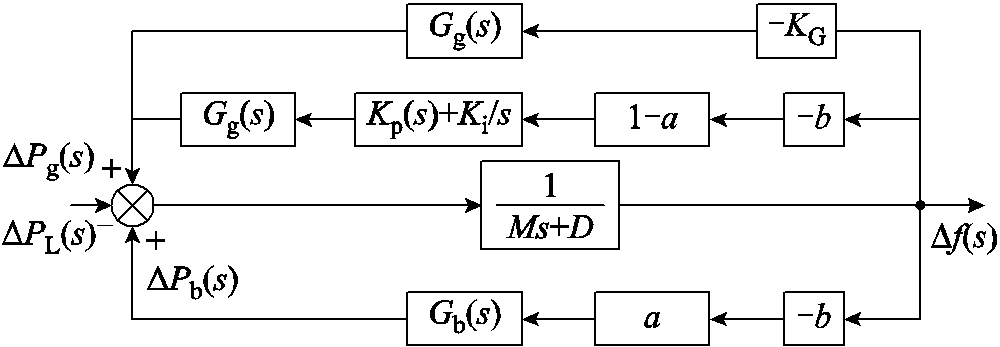
图4 ACE控制模式下区域电力系统频率响应模型
Fig.4 Frequency response modelling of a regional power system under ACE control mode
图4中,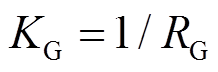 ,
,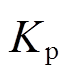 、
、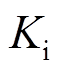 分别为PI控制器比例和积分参数。系统频率偏差、火电机组和电池储能出力变量可分别表示为
分别为PI控制器比例和积分参数。系统频率偏差、火电机组和电池储能出力变量可分别表示为
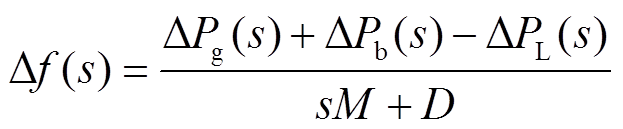 (5)
(5)
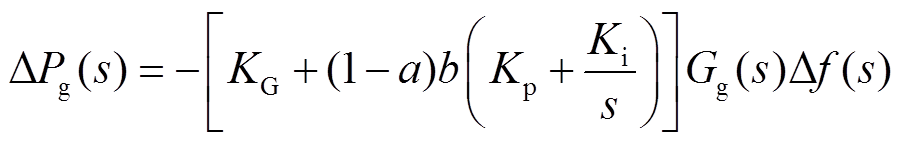 (6)
(6)
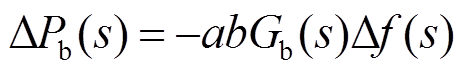 (7)
(7)
将式(6)、式(7)代入式(5),可得
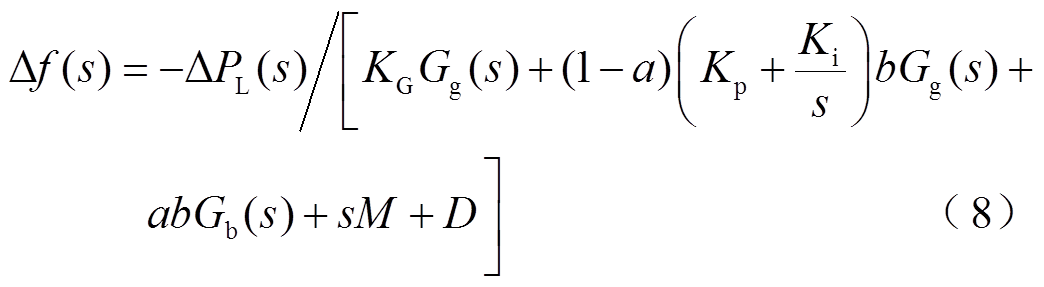
进一步对式(8)求偏导得到储能参与因子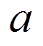 对频率偏差的灵敏度为
对频率偏差的灵敏度为
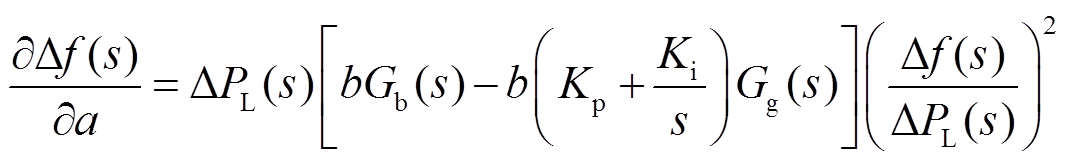 (9)
(9)
由于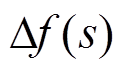 与
与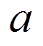 的量纲不一致,可能导致物理意义不明确,因此需对式(9)进行无量纲化处理。通过将
的量纲不一致,可能导致物理意义不明确,因此需对式(9)进行无量纲化处理。通过将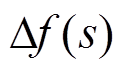 和
和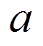 的变化用相对变化量的形式表示,消除量纲差异。灵敏度S无量纲化结果为
的变化用相对变化量的形式表示,消除量纲差异。灵敏度S无量纲化结果为
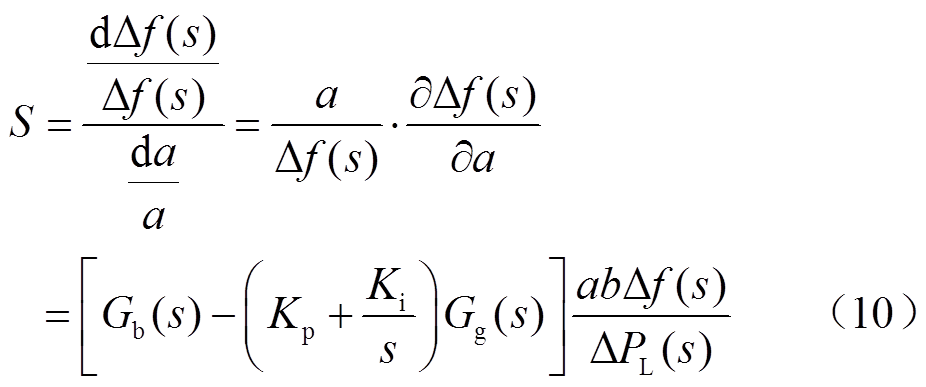
此外,结合阶跃负荷扰动验证分析灵敏度、储能参与因子与系统频率偏差三者的相互联系,其关系曲线如图5所示。可以看出,在扰动初始阶段,灵敏度S<0,随着储能参与因子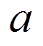 的增大,S变小,系统频率偏差也越小;扰动末期,S>0,此时
的增大,S变小,系统频率偏差也越小;扰动末期,S>0,此时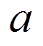 越小,灵敏度S越小,系统频率偏差越小[27]。
越小,灵敏度S越小,系统频率偏差越小[27]。
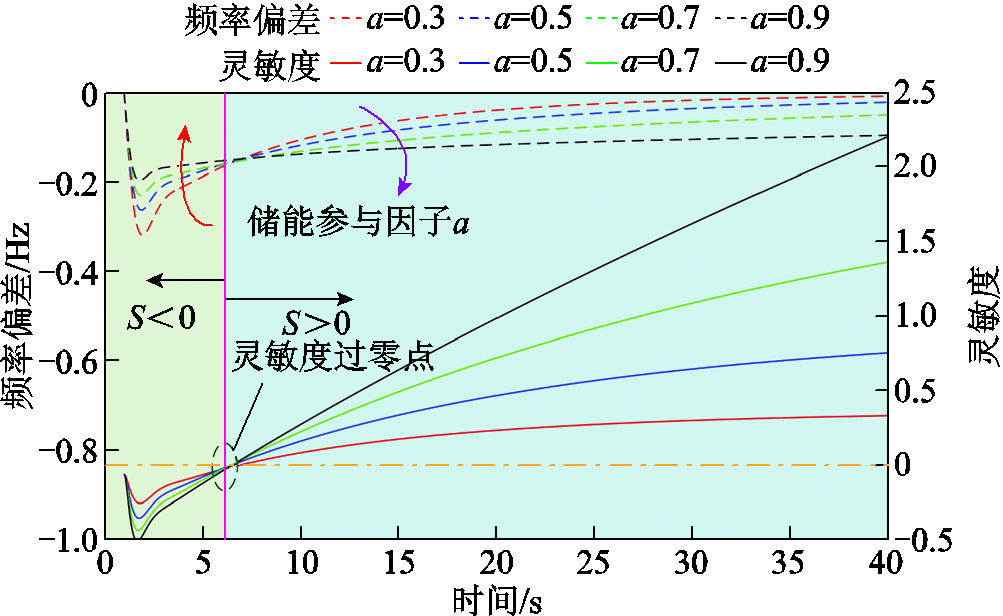
图5 灵敏度、储能参与因子与系统频率偏差关系曲线
Fig.5 Relation curves among sensitivity, energy storage participation factor and system frequency deviation
2.1.2 火储动态调频责任分配策略
参考2.1.1节参与因子灵敏度的规律,本节设计了双层判断机制作为电池储能与火电机组之间调频责任的划分依据。
第一层判断机制:由灵敏度原理分析及图5可知,若灵敏度S<0,储能参与因子越大系统频率偏差越小,故此阶段储能承担较高比例的调频责任更有利于频率偏差调节;若灵敏度S>0,储能参与因子越小系统频率偏差越小,故储能承担较少比例调频责任更有利于频率恢复。因此本文将储能参与因子以0.5作为分界点划分成两部分,包括较大储能参与因子区间(0.5≤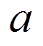 ≤1)和较小储能参与因子区间(0<
≤1)和较小储能参与因子区间(0<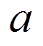 <0.5),通过灵敏度S的正负性确定参与因子的区间范围。需要说明的是,这一分界点的设置并非直接对应储能与火电机组容量或功率比例,而是平衡不同调频阶段储能快速响应特性与火电机组持续稳态调节能力的合理方案。实际选取储能参与因子分界点时,应根据系统整体状态(如火电与储能的容量比、功率范围、负荷扰动强度等因素)灵活调整,以适应不同系统条件和调频需求。
<0.5),通过灵敏度S的正负性确定参与因子的区间范围。需要说明的是,这一分界点的设置并非直接对应储能与火电机组容量或功率比例,而是平衡不同调频阶段储能快速响应特性与火电机组持续稳态调节能力的合理方案。实际选取储能参与因子分界点时,应根据系统整体状态(如火电与储能的容量比、功率范围、负荷扰动强度等因素)灵活调整,以适应不同系统条件和调频需求。
第二层判断机制:参与因子需要根据系统调频需求及电源调频容量等外部条件进行选取,但固定大小的参与因子在面临连续负荷不规则扰动时存在局限性,难以持续应对实际场景频繁变换的调频需要。因此,通过合理预测下一时刻的负荷波动量,提前在预设的参考区间内调整储能参与因子是必要的。具体而言,根据当前时刻实际负荷波动量和负荷波动变化率预测短期内的负荷波动量,再由预测结果于相应区间内对参与因子进行动态调整,以自适应确定储能参与调频的时机和深度。
由于设计的第二层判断机制的模糊性与非线性特点明显,故借助模糊控制器实现不同区间内储能参与因子的动态调节。同时,基于当前时刻负荷扰动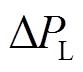 及负荷波动变化率
及负荷波动变化率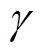 可初步预判下一时刻的负荷发展趋势,有
可初步预判下一时刻的负荷发展趋势,有
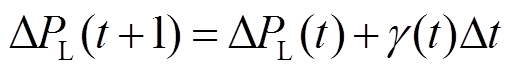 (11)
(11)
设计模糊控制规则为:假设负荷扰动为正。当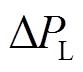 较大,且
较大,且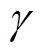 >0时,判断下一时段负荷波动预测量较大,储能需以较大功率参与频率调节,故参与因子设置得较大。当
>0时,判断下一时段负荷波动预测量较大,储能需以较大功率参与频率调节,故参与因子设置得较大。当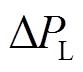 较小,
较小,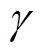 >0,但
>0,但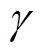 较小时,表明负荷增量小,则判断下一时段负荷波动预测量较小,储能出力相应减少,故参与因子可设置得较小;若
较小时,表明负荷增量小,则判断下一时段负荷波动预测量较小,储能出力相应减少,故参与因子可设置得较小;若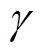 较大,预示负荷增量大,判断负荷波动预测量较大,需要储能提供较大的调节功率,因此将参与因子设置得较大。当
较大,预示负荷增量大,判断负荷波动预测量较大,需要储能提供较大的调节功率,因此将参与因子设置得较大。当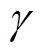 <0时,说明负荷波动量正逐渐变小,即负荷波动预测量较小,储能所需出力减小,将参与因子设置得较小。若系统当前时刻未受到扰动影响,但
<0时,说明负荷波动量正逐渐变小,即负荷波动预测量较小,储能所需出力减小,将参与因子设置得较小。若系统当前时刻未受到扰动影响,但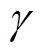 >0,则负荷波动预测量相对较小,储能所需出力小,参与因子设置得较小。当负荷扰动为负时,设计思路与正值相似,此处不再赘述。
>0,则负荷波动预测量相对较小,储能所需出力小,参与因子设置得较小。当负荷扰动为负时,设计思路与正值相似,此处不再赘述。
因此,本文选用双输入单输出的模糊控制器对储能参与因子进行调整。两个输入分别为经过归一化后的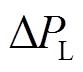 与
与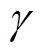 ,采用高斯型隶属度函数实现高频无规律负荷状态更为平滑连续的模糊映射,方便模糊推理;输出为储能参与因子
,采用高斯型隶属度函数实现高频无规律负荷状态更为平滑连续的模糊映射,方便模糊推理;输出为储能参与因子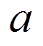 ,其隶属度函数基于离散论域设计,选取若干具有代表性的动态因子取值涵盖不同负荷状态,简化复杂度并提高系统响应速度。
,其隶属度函数基于离散论域设计,选取若干具有代表性的动态因子取值涵盖不同负荷状态,简化复杂度并提高系统响应速度。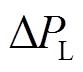 和
和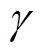 的量化因子分别为
的量化因子分别为
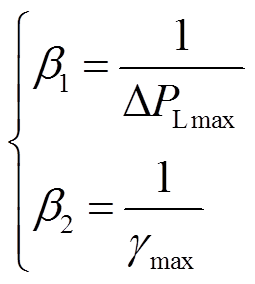 (12)
(12)
式中,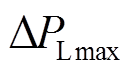 、
、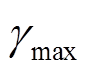 分别为负荷扰动最大值、负荷变化率最大值。
分别为负荷扰动最大值、负荷变化率最大值。
负荷扰动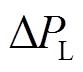 与负荷变化率
与负荷变化率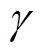 进行归一化后论域为[-1,1],
进行归一化后论域为[-1,1],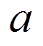 取离散论域{0.1, 0.3, 0.5, 0.7, 0.9}。设置模糊集NB(负大)、NS(负小)、ZO(零)、PS(正小)、PB(正大)描述
取离散论域{0.1, 0.3, 0.5, 0.7, 0.9}。设置模糊集NB(负大)、NS(负小)、ZO(零)、PS(正小)、PB(正大)描述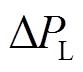 、
、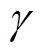 、
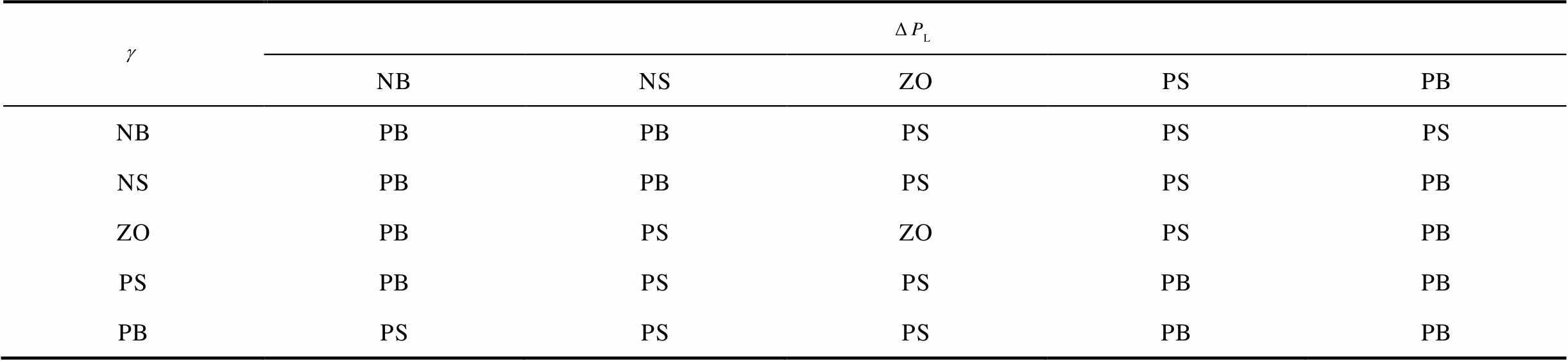
、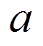 的取值区间。输入、输出量的隶属度函数如附图1~附图3所示,通过图形化方式展示了负荷扰动及其变化率与储能参与因子的模糊集区间,对应了模糊控制器输入模糊化与输出解模糊的逻辑过程,体现了模糊控制器从“负荷状态感知”到“调频责任分配”的设计流程。模糊控制规律如附图4、附图5所示,通过控制面直观反映了不同负荷状态输入组合下储能参与因子的调整策略。模糊控制规则基于灵敏度S的正负性划分区间,对应描述了不同负荷场景下储能参与因子的调整逻辑,储能参与因子控制规则语言见表1和表2。
的取值区间。输入、输出量的隶属度函数如附图1~附图3所示,通过图形化方式展示了负荷扰动及其变化率与储能参与因子的模糊集区间,对应了模糊控制器输入模糊化与输出解模糊的逻辑过程,体现了模糊控制器从“负荷状态感知”到“调频责任分配”的设计流程。模糊控制规律如附图4、附图5所示,通过控制面直观反映了不同负荷状态输入组合下储能参与因子的调整策略。模糊控制规则基于灵敏度S的正负性划分区间,对应描述了不同负荷场景下储能参与因子的调整逻辑,储能参与因子控制规则语言见表1和表2。
表1 S>0储能参与因子控制规则语言
Tab.1 Control rule language for energy storage participation factor with S>0
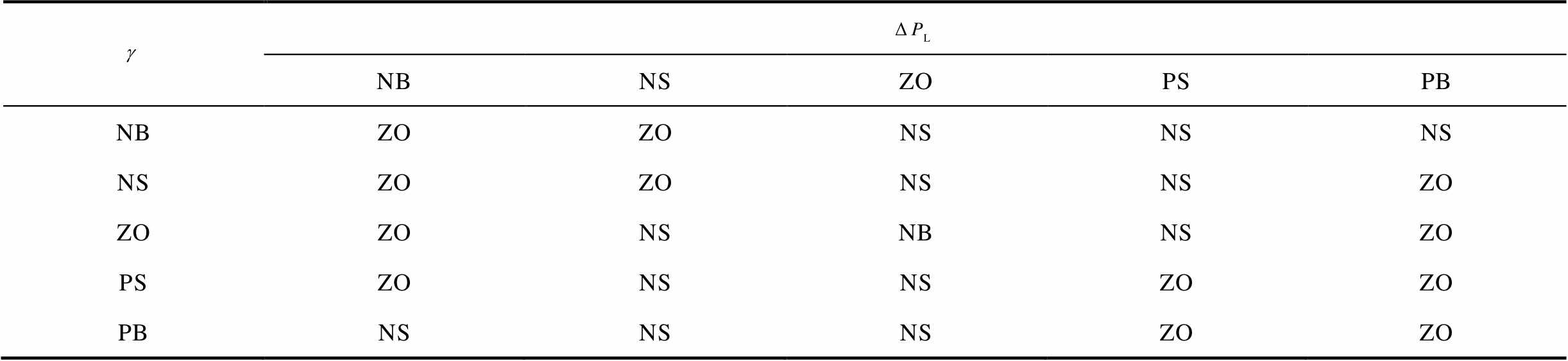
NBNSZOPSPB NBZOZONSNSNS NSZOZONSNSZO ZOZONSNBNSZO PSZONSNSZOZO PBNSNSNSZOZO
表2 S<0储能参与因子控制规则语言
Tab.2 Control rule language for energy storage participation factor with S<0
NBNSZOPSPB NBPBPBPSPSPS NSPBPBPSPSPB ZOPBPSZOPSPB PSPBPSPSPBPB PBPSPSPSPBPB
本节提出的储能参与因子动态调整机制能够捕捉灵敏度和负荷扰动的变化,动态调整储能与常规机组之间的调频责任。但对于储能而言,直接将调频责任信号作为储能输出功率控制指令不具有最优性。鉴于此,2.2节在火储调频责任合理分配基础上将最优区域控制偏差问题建模为对电池储能输出功率的控制问题,以储能动态调频责任为优化目标,应用模型预测控制在多重约束条件下寻找储能出力的最佳控制量,提升系统调频性能。
MPC是一种先进的智能优化控制策略,通过构建描述系统动态行为的物理模型预测系统未来一段时间的输出,并计算当前应采取的控制行动,能够克服控制过程中的非线性与不确定性,鲁棒性良好。
本节以基于动态储能参与因子得到的调频责任为优化目标,利用MPC前瞻性地下达指令信号让储能在调频控制中提前动作,削弱负荷扰动对频率的冲击。含储能的两区域互联电网频率动态响应模型状态空间方程为
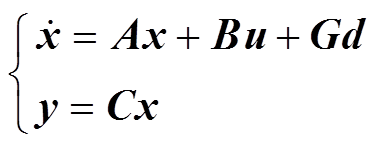 (13)
(13)
式中,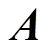 、
、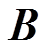 、
、 、
、 分别为系统的状态矩阵、控制矩阵、输入矩阵和输出矩阵;x、u、d、y分别为系统的状态变量、控制变量、输入变量和输出变量。
分别为系统的状态矩阵、控制矩阵、输入矩阵和输出矩阵;x、u、d、y分别为系统的状态变量、控制变量、输入变量和输出变量。
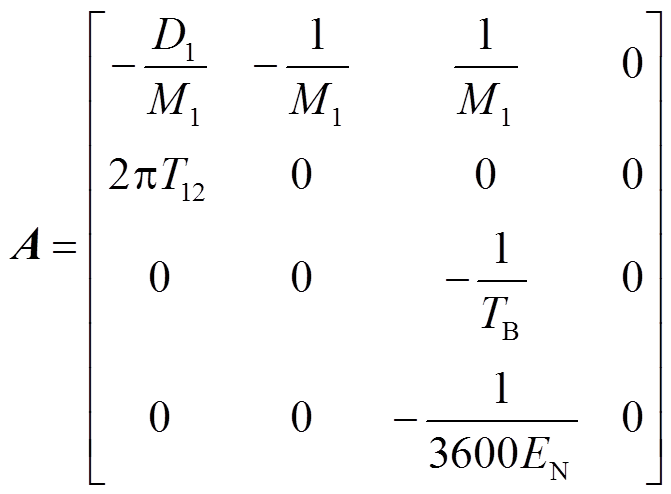 (14)
(14)
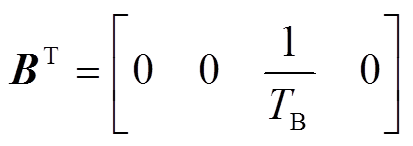 (15)
(15)
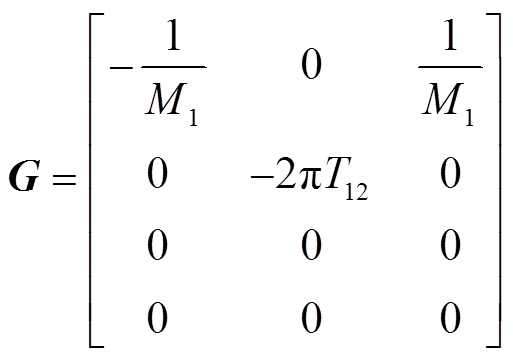 (16)
(16)
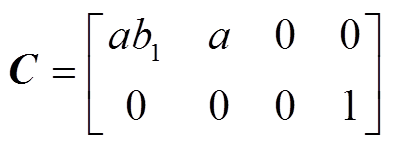 (17)
(17)
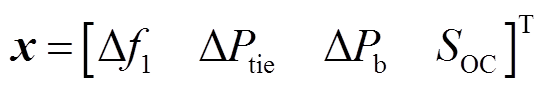 (18)
(18)
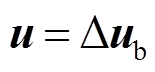 (19)
(19)
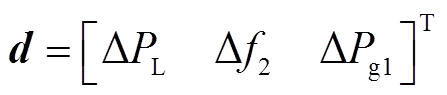 (20)
(20)
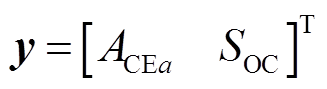 (21)
(21)
式中,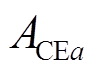 为储能调频责任大小。以
为储能调频责任大小。以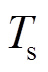 为采样周期将式(13)离散化,转换成的离散时域状态空间模型为
为采样周期将式(13)离散化,转换成的离散时域状态空间模型为
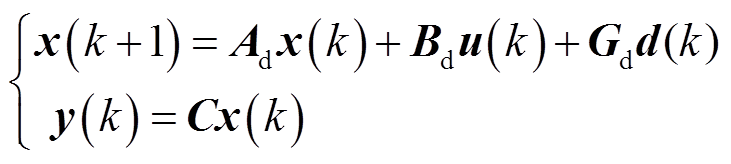 (22)
(22)
式中,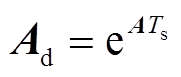 ;
;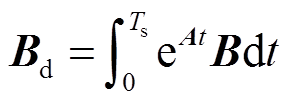 ;
;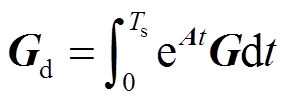 。
。
通常情况下,电力系统AGC旨在调节ACE信号为0。本文基于动态参与因子得到的储能调频责任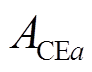 与
与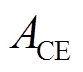 始终保持严格的正比关系,故可将
始终保持严格的正比关系,故可将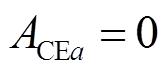 作为MPC控制器的核心优化目标。在
作为MPC控制器的核心优化目标。在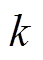 时刻构造二次型性能指标函数为
时刻构造二次型性能指标函数为
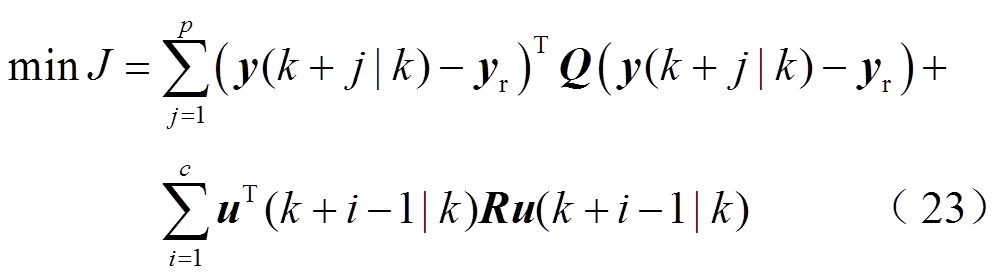
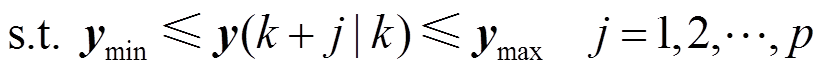 (24)
(24)
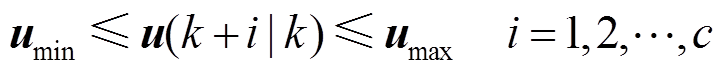 (25)
(25)
式中,Q、R分别为输出权重对角矩阵和控制权重对角矩阵;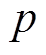 、
、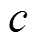 分别为预测时域和控制时域;
分别为预测时域和控制时域;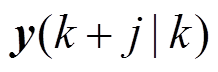 为
为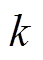 时刻系统输出在未来
时刻系统输出在未来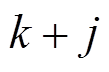 时刻的预测;
时刻的预测;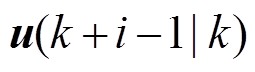 为
为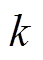 时刻系统控制变量在未来
时刻系统控制变量在未来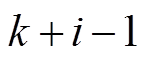 时刻的预测;
时刻的预测;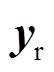 为系统输出参考值,因为控制目标为
为系统输出参考值,因为控制目标为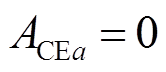 ,故参考值设为0;
,故参考值设为0;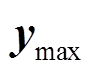 、
、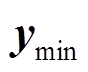 分别为系统输出变量的上、下限,即系统
分别为系统输出变量的上、下限,即系统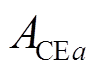 约束与SOC充放电阈值;
约束与SOC充放电阈值;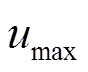 、
、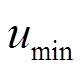 分别为系统控制变量的上、上限,即储能输出功率约束。通过求解目标函数式(23)的有限时域优化问题,可以得到一组最优控制序列
分别为系统控制变量的上、上限,即储能输出功率约束。通过求解目标函数式(23)的有限时域优化问题,可以得到一组最优控制序列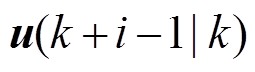 ,仅将控制序列中的第一项作用于电池储能,实现即时的优化调整。到下一采样时刻,重新求解优化问题并重复上述过程,通过滚动优化的方式,确保系统在不同时刻的最优性能。
,仅将控制序列中的第一项作用于电池储能,实现即时的优化调整。到下一采样时刻,重新求解优化问题并重复上述过程,通过滚动优化的方式,确保系统在不同时刻的最优性能。
储能SOC偏低或偏高都将对储能系统可用容量造成限制,影响其双向调频能力。故在适当的时机对储能SOC进行恢复有利于延长储能参与调频的时间[28]。为了储能在后续调频过程中能够提供更充足的充放电空间,本节提出一种基于ACE与SOC分区的自适应模型预测控制方法对SOC进行恢复。
2.3.1 ACE与SOC状态区间分段
实际AGC系统运行时,调频电源以减小区域控制偏差信号作为优先考虑因素。针对不同程度的ACE实施不同的控制策略可以更精细地调节频率偏差,使调频措施更加有效。因此,按照阈值大小将ACE分成不同的区间类型,包括死区、正常调节区、紧急调节区、超紧急调节区。此外,电池储能造价高昂,长时间处于过高或过低的SOC会加速电池老化,降低充放电循环效率。保持SOC在良好的状态,可以延长电池寿命,减少更换频率,是降低调频成本、提升经济性的重要措施。本文将SOC划分为正常充放电区、充电优先区、放电优先区、禁止充放电区。ACE与SOC状态区间划分如图6所示,其中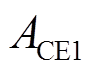 、
、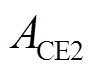 、
、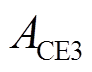 是ACE相邻两个区间的分界值,
是ACE相邻两个区间的分界值,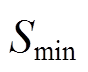 、
、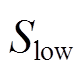 、
、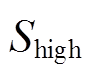 、
、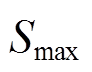 是SOC相邻两个区间的分界值。
是SOC相邻两个区间的分界值。
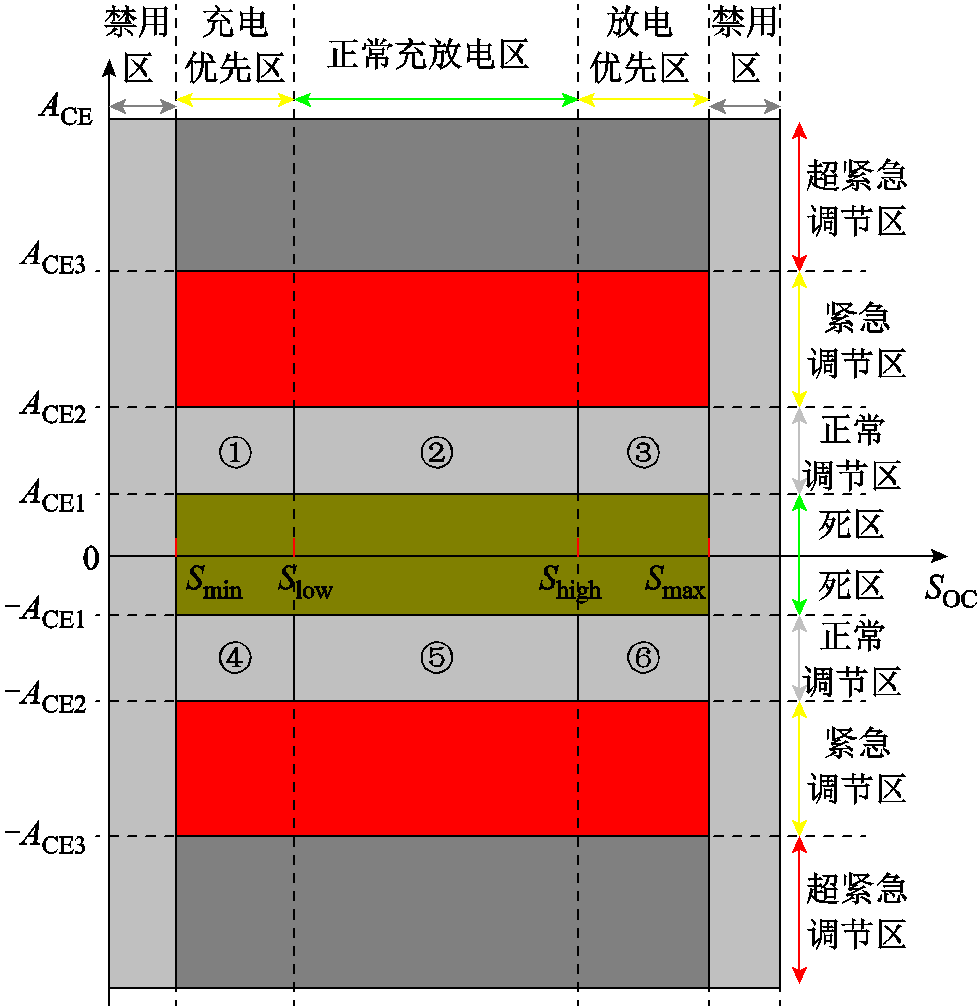
图6 ACE与SOC状态区间划分
Fig.6 ACE and SOC state interval division
根据ACE与SOC所处状态区间,综合考虑各阶段电网调频需求与SOC恢复需求,通过制定考虑SOC恢复的调频控制策略,可实现系统频率调节和储能SOC恢复的双重目标。
2.3.2 考虑储能SOC恢复的自适应MPC策略
本节基于2.2节提出的MPC控制器,在目标函数中添加调节储能SOC恢复的加权项,该项的权重因子用q表示,q的大小代表对SOC恢复的重视程度。因此,新设计的目标函数囊括了调节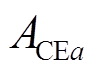 和调节储能SOC恢复量两个子目标。但不同的子目标之间可能存在冲突,故需要分析不同阶段频率调节与SOC恢复的重要程度,通过调整权重寻求目标之间的最佳平衡点。因此本文基于ACE与SOC区间信息提出了考虑储能SOC恢复的MPC权重自适应方法。在不同的区间范围内灵活调整储能SOC恢复项在目标函数中的控制比重实现系统性能的提升。
和调节储能SOC恢复量两个子目标。但不同的子目标之间可能存在冲突,故需要分析不同阶段频率调节与SOC恢复的重要程度,通过调整权重寻求目标之间的最佳平衡点。因此本文基于ACE与SOC区间信息提出了考虑储能SOC恢复的MPC权重自适应方法。在不同的区间范围内灵活调整储能SOC恢复项在目标函数中的控制比重实现系统性能的提升。
根据ACE与SOC分区情况制定控制策略如下:
1)当ACE位于死区范围时,电网频率偏差极小,调频需求可基本忽略。不考虑当前SOC状态,以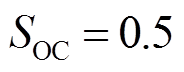 为目标,储能全力进行SOC恢复且不参与调频,此时权重系数q设定为最大取值0.5。
为目标,储能全力进行SOC恢复且不参与调频,此时权重系数q设定为最大取值0.5。
2)当ACE位于正常调节区,储能首要任务是响应电网调频需求,辅以SOC适度恢复,下面以ACE为正时的储能充电调频情况为例进行说明。依据SOC的不同水平,可将正常调节区细分为三个区域进行差异化处理。区域①储能SOC处于充电优先区,进行恢复时的出力方向与调频需求出力方向相同,可设置加权系数q为较大值,取0.3;区域②储能位于正常充放电区,荷电状态相对良好,无需额外恢复措施,设置权重系数q为0;区域③储能位于放电优先区,进行恢复的出力方向与调频需求出力方向相悖,若储能过大进行恢复会影响调频效果,又由于储能双向调节能力并不乐观,权衡下可设置较小的加权系数q为0.1,在保证调频效果的同时,减弱储能继续充电恶化的影响。ACE为负时,区域④、⑤、⑥控制规律与ACE为正时相反。
3)当ACE位于紧急调节区时,恢复电网频率为最高优先级,不考虑荷电状态影响,储能仅参与频率调节,设置权重系数q为0。
4)当ACE位于超紧急调节区时,意味着电网频率已严重偏离正常范围,采用切机或甩负荷的紧急措施直至电网频率恢复稳定。
上述过程中权重系数取值工况如图7所示,且均在模型预测控制器中实现。
本节采用分区设定的方式对MPC目标函数中SOC恢复项的权重因子q进行调整。权重因子的取值依据ACE和SOC的分区结果,分别在不同运行状态下设定离散值0、0.1、0.3、0.5以实现不同调频阶段频率调节与SOC恢复的动态平衡。该策略简化了控制器的复杂度,降低了实时计算量,有效地避免了SOC因过充或过放退出调频过程,提高了系统的整体稳定性和储能寿命。
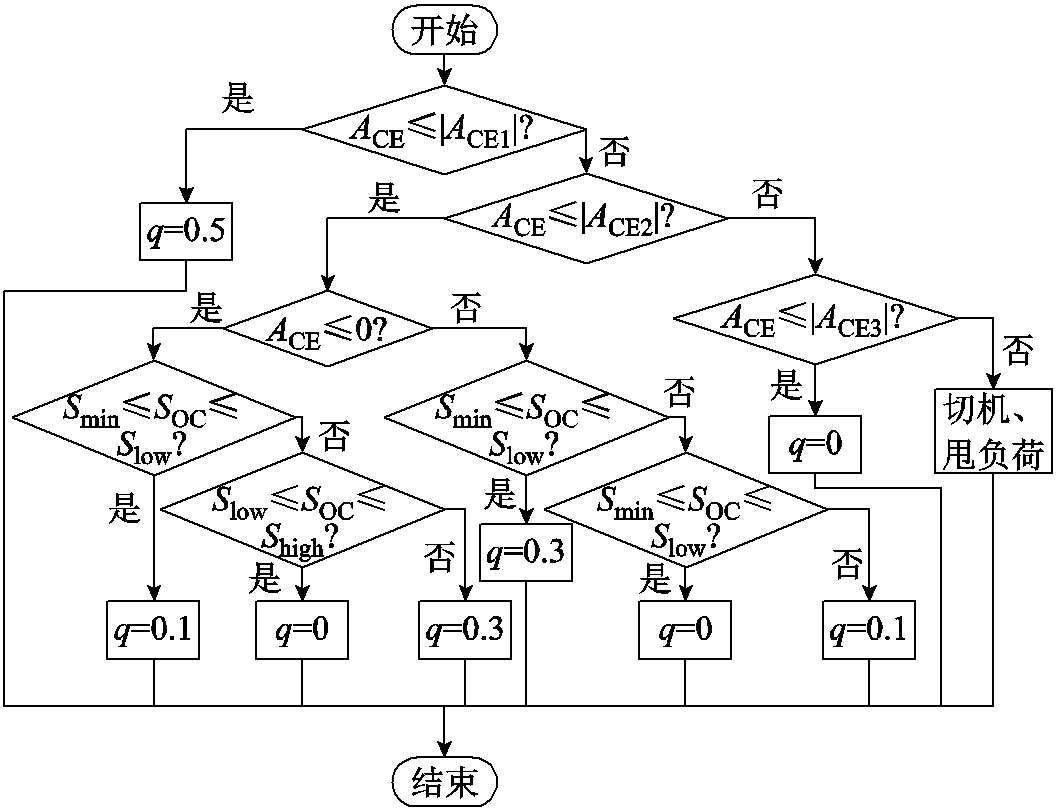
图7 SOC恢复项权重取值工况
Fig.7 SOC recovery term weight value conditions
为了对本文所提方法在调频效果和储能SOC维持方面的性能进行量化评估和比较,针对不同类型的负荷扰动定义如下两方面评价指标。采用包括最大频率偏差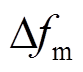 、频率跌落速度
、频率跌落速度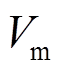 、稳态频率偏差
、稳态频率偏差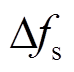 在内可具体反映频率扰动大小和储能调频能力的三种评估标准作为阶跃负荷扰动下的整体评价指标。对于连续负荷扰动,以最大频率偏差
在内可具体反映频率扰动大小和储能调频能力的三种评估标准作为阶跃负荷扰动下的整体评价指标。对于连续负荷扰动,以最大频率偏差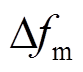 、频率偏差的方均根值
、频率偏差的方均根值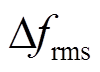 、频率变化量的绝对值积分
、频率变化量的绝对值积分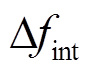 [29]和SOC偏差(偏离0.5的程度)的方均根值
[29]和SOC偏差(偏离0.5的程度)的方均根值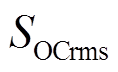 为评价指标。
为评价指标。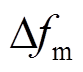 和
和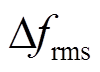 体现系统调频效果,
体现系统调频效果,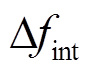 进一步体现频率连续动态变化情况,
进一步体现频率连续动态变化情况,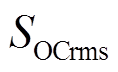 反映储能SOC保持状况。
反映储能SOC保持状况。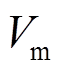 、
、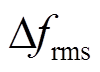 、
、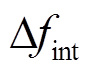 、
、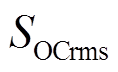 定义为
定义为
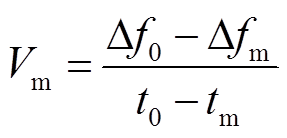 (26)
(26)
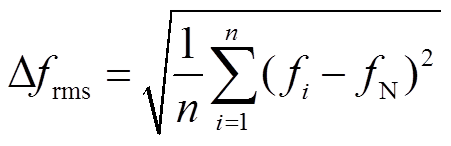 (27)
(27)
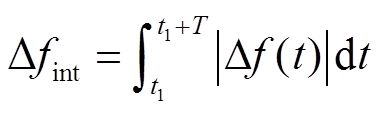 (28)
(28)
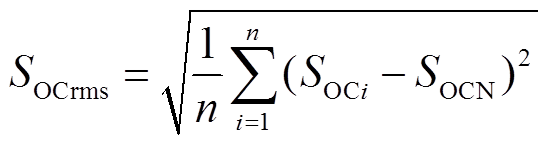 (29)
(29)
式中,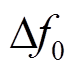 为初始频率偏差;
为初始频率偏差;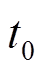 、
、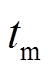 分别为初始频率偏差和最大频率偏差的对应时刻;
分别为初始频率偏差和最大频率偏差的对应时刻;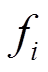 、
、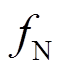 分别为采样点
分别为采样点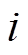 对应的频率和电网额定频率;
对应的频率和电网额定频率;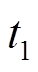 、
、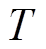 分别为调频起始时刻和二次调频总时长;
分别为调频起始时刻和二次调频总时长;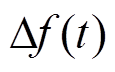 为
为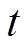 时刻系统频率偏差;
时刻系统频率偏差;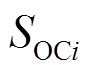 、
、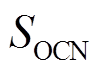 分别为采样点
分别为采样点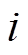 对应的SOC和SOC基准值0.5;
对应的SOC和SOC基准值0.5;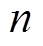 为总的采样点数。
为总的采样点数。
为验证本文提出的控制策略在提升系统性能方面的有效性,以图2所示的双区域互联电网为研究对象,区域1中配置电池储能系统,在Matlab/ Simulink仿真环境下,设计阶跃和连续负荷扰动两类场景下的仿真算例,采用四种不同的控制方法进行对比分析。方法1为火电机组单独调频;方法2为参考文献[27]提出的阶跃极值分配因子法;方法3为模型预测控制策略;方法4为本文所提的动态储能参与因子模型预测控制方法。区域火电机组额定功率为300 MW,储能的额定功率和额定容量分别为8 MW、2 MW·h。以100 MW和50 Hz为基准值进行标幺化。系统相关参数见表3。
表3 系统模型参数
Tab.3 Model parameters of system
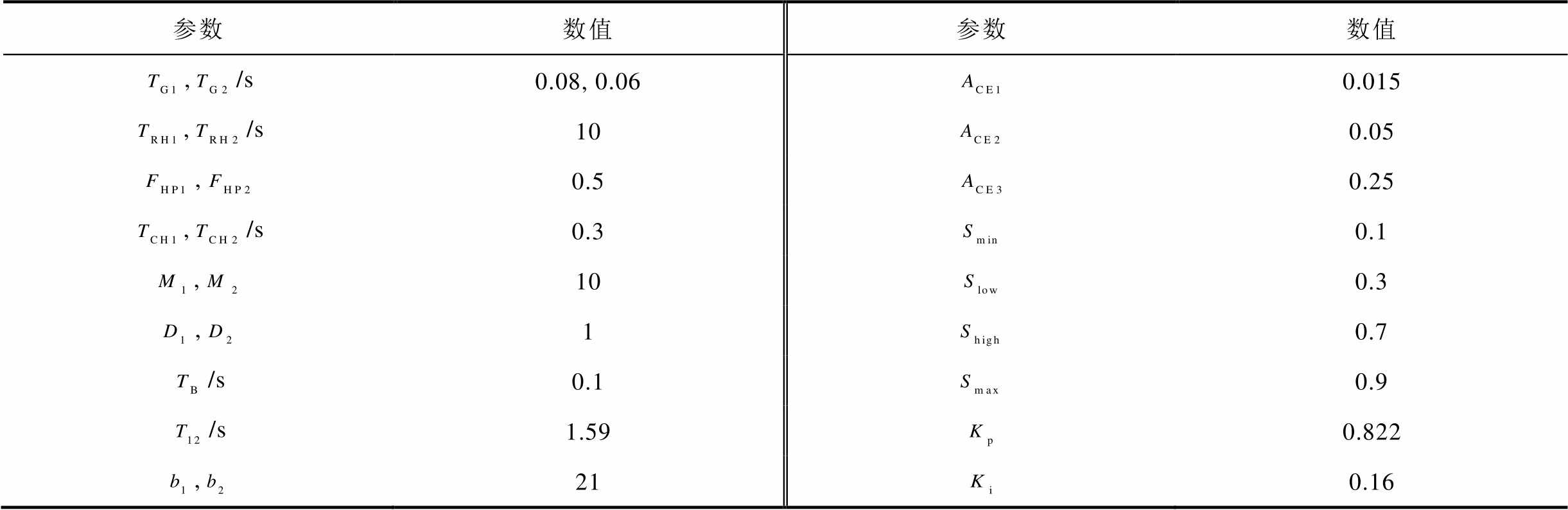
参数数值参数数值 ,/s0.08, 0.060.015 ,/s100.05 ,0.50.25 ,/s0.30.1 ,100.3 ,10.7 /s0.10.9 /s1.590.822 ,210.16
3.2.1 阶跃负荷扰动
1 s时在区域1中加入幅值为0.15(pu)的阶跃负荷扰动,仿真时长80 s,不同控制方法下的系统频率偏差响应曲线如图8所示,调频性能评价指标见表4。
从图8和表4可知,在施加负荷阶跃扰动后,系统频率迅速下降。方法4的频率偏差峰值及频率跌落速率在所有方法中均最小,分别仅为-0.209 7 Hz与0.252 6 Hz/s。方法1没有储能参与调频,频率偏差峰值最大,达到了-0.360 2 Hz,且频率下降速率最快,为0.450 2 Hz/s。当储能加入二次调频后,方法2、3、4的最大频率偏差与频率下降速率较方法1均出现极为显著的提升,表明火储联合调频较火电机组单独调频具备更好的性能。其中方法4调频效果最优,最大频率偏差与频率下降速率比方法2分别降低了13.88%和23.22%;比方法3分别降低了8.07%和32.44%。从稳态性能指标上看,方法4仅次于方法1,且优于其他两种方法。
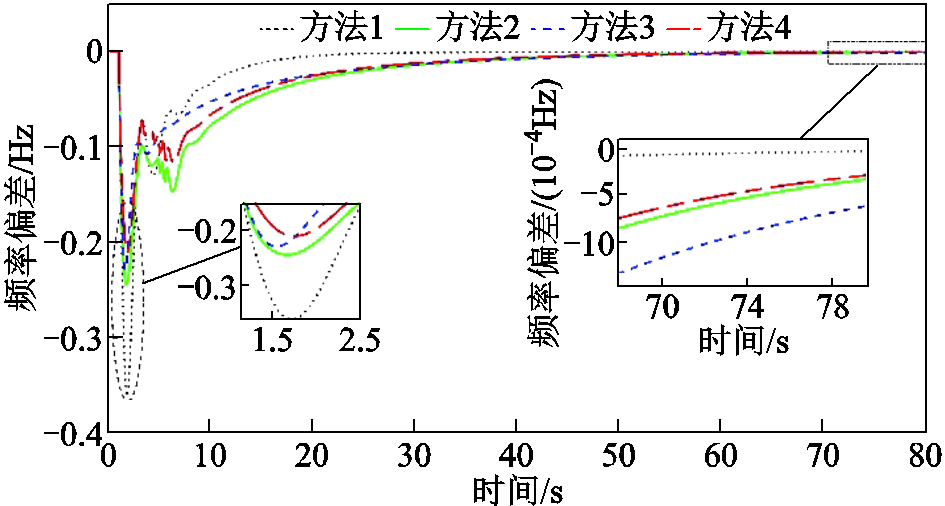
图8 阶跃扰动下区域1频率偏差响应曲线
Fig.8 Frequency deviation response curves of region 1 under step disturbance
表4 阶跃扰动调频性能指标
Tab.4 Performance indexes of frequency regulation under step disturbance

控制策略/Hz/(Hz/s)/(10-4Hz) 方法1-0.360 20.450 20.260 方法2-0.243 50.329 03.22 方法3-0.228 10.373 96.03 方法4-0.209 70.252 62.79
3.2.2 连续负荷扰动
对区域1施加如图9所示的连续负荷扰动,仿真时长设置为1 800 s。
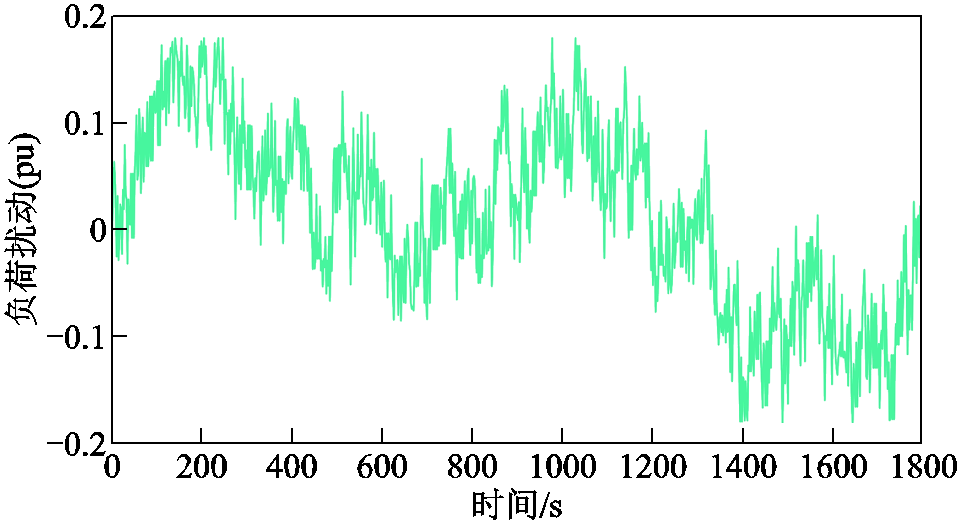
图9 负荷连续扰动
Fig.9 Continuous load disturbance
不同控制策略下的频率变化与储能SOC仿真结果如图10和图11所示,连续扰动调频性能指标见表5。

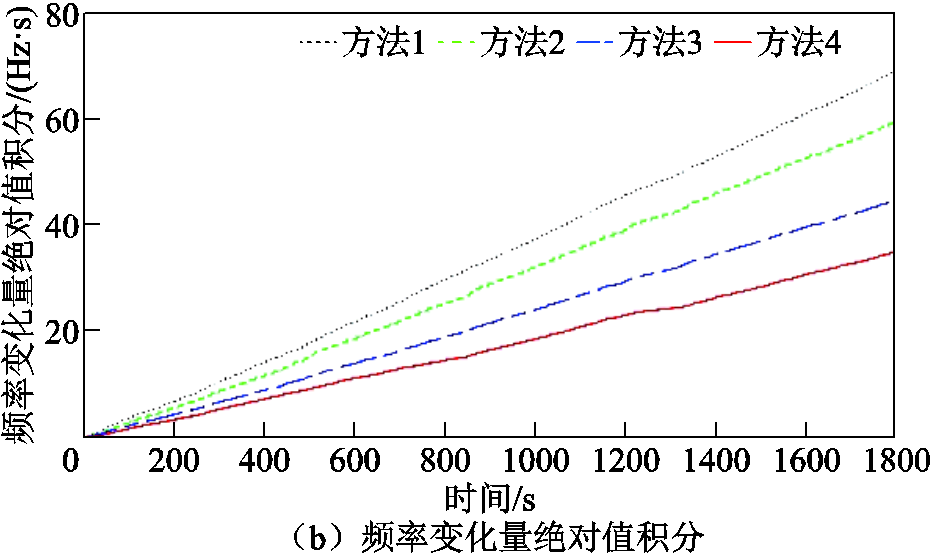
图10 连续扰动下区域1频率曲线
Fig.10 Frequency curves of region 1 under continuous disturbance
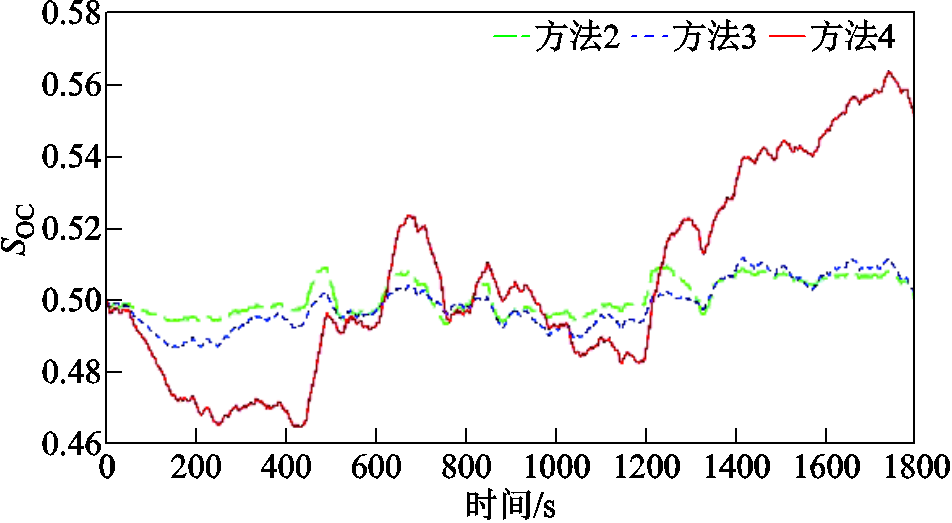
图11 连续扰动下储能SOC曲线
Fig.11 SOC curves of energy storage under continuous disturbance
表5 连续扰动调频性能指标
Tab.5 Performance indexes of frequency regulation under continuous disturbance

控制策略/Hz/Hz/Hz 方法10.135 24.613×10-268.94— 方法20.115 83.964×10-259.384.901×10-3 方法30.091 553.038×10-244.786.677×10-3 方法40.091 112.360×10-235.062.842×10-2
从图10a及表5可知,在负荷连续扰动场景下,方法4的最大频率偏差、频率偏差的方均根值及频率变化量绝对值积分均最小。其最大频率偏差比方法1、方法2、方法3分别降低了32.61%、21.32%、0.48%,频率偏差方均根值分别减小了48.84%、40.46%、22.32%。说明引入储能参与二次调频,并设计合理的控制策略能够有效提升频率调节效果,减小系统频率波动。此外,引入的频率变化幅度积分指标能更加直观地表征频率动态变化情形。由图10b频率变化情况可见,随着调频时间增加,本文方法下的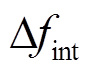 始终小于其他三种对比方法。
始终小于其他三种对比方法。
图11为储能在不同控制方法下的SOC变化曲线,方法4的SOC波动幅度最大,其原因是在相同储能输出功率和SOC限幅等约束条件下,调频时段
对储能出力利用更加充分,即储能承担了更多的二次调频任务,降低了火电机组的动作幅度。所提方法提升了储能在调频过程中贡献的支撑容量,比其他两种方法取得了更为显著的调频效果,进一步缩小了频率偏差。
为了验证提出的MPC自适应分区可调节权重SOC恢复控制方法的实用性,设计了不同的SOC初始状态在连续负荷扰动场景下进行仿真。选取SOC初始值分别为0.12和0.88的场景模拟接近储能充放电阈值状态的情况,在动态参与因子模型预测控制方法的基础上,通过对比分析不考虑SOC恢复策略(策略1)、权重固定的SOC恢复策略(策略2),以及本文所提的分区自适应权重SOC恢复策略(策略3),进而突出本文方法在储能SOC位于不同初值状态的整体性能优势。
3.3.1 储能SOC接近放电阈值情形
SOC初值为0.12时,频率变化与储能SOC仿真结果如图12和图13所示。

图12 SOC初始值为0.12时的频率曲线
Fig.12 Frequency curves for an initial value 0.12 of SOC
由图12和图13可知,当SOC初值设置为0.12时,策略1由于不考虑SOC恢复控制,在129.64 s处储能首次出现放电调频容量不足的情况,达到SOC约束下限从而退出运行,频率出现较大跌落。且整个调频过程中,由图13的局部放大图可以看出,SOC共计7次反复达到约束下限无法正常放电。策略2和策略3均考虑了储能SOC恢复控制,从而避免了SOC因越限退出运行的极端情况。
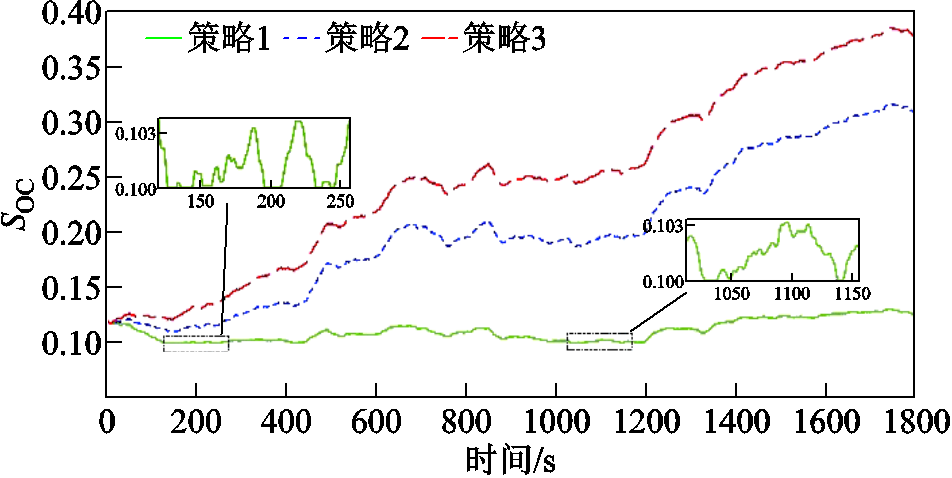
图13 SOC初始值为0.12时的储能SOC曲线
Fig.13 SOC curves of energy storage for an initial SOC value of 0.12
SOC初始值为0.12时的调频性能指标见表6。由定量数据分析可得策略2和策略3的频率偏差方均根值比策略1分别减小了27.30%和28.60%,频率变化量绝对值积分各自降低了24.55%和25.49%,SOC偏差方均根分别减少了21.77%和32.03%。
表6 SOC初始值为0.12时调频性能评价指标
Tab.6 Evaluation indexes for frequency regulation performance with an initial value 0.12 of SOC

控制策略/Hz/Hz/Hz 策略10.119 33.864×10-258.530.389 0 策略20.115 52.809×10-244.160.304 3 策略30.110 32.759×10-243.610.264 4
3.3.2 储能SOC接近充电阈值情形
SOC初值为0.88时,频率变化与储能SOC仿真结果如图14和图15所示。
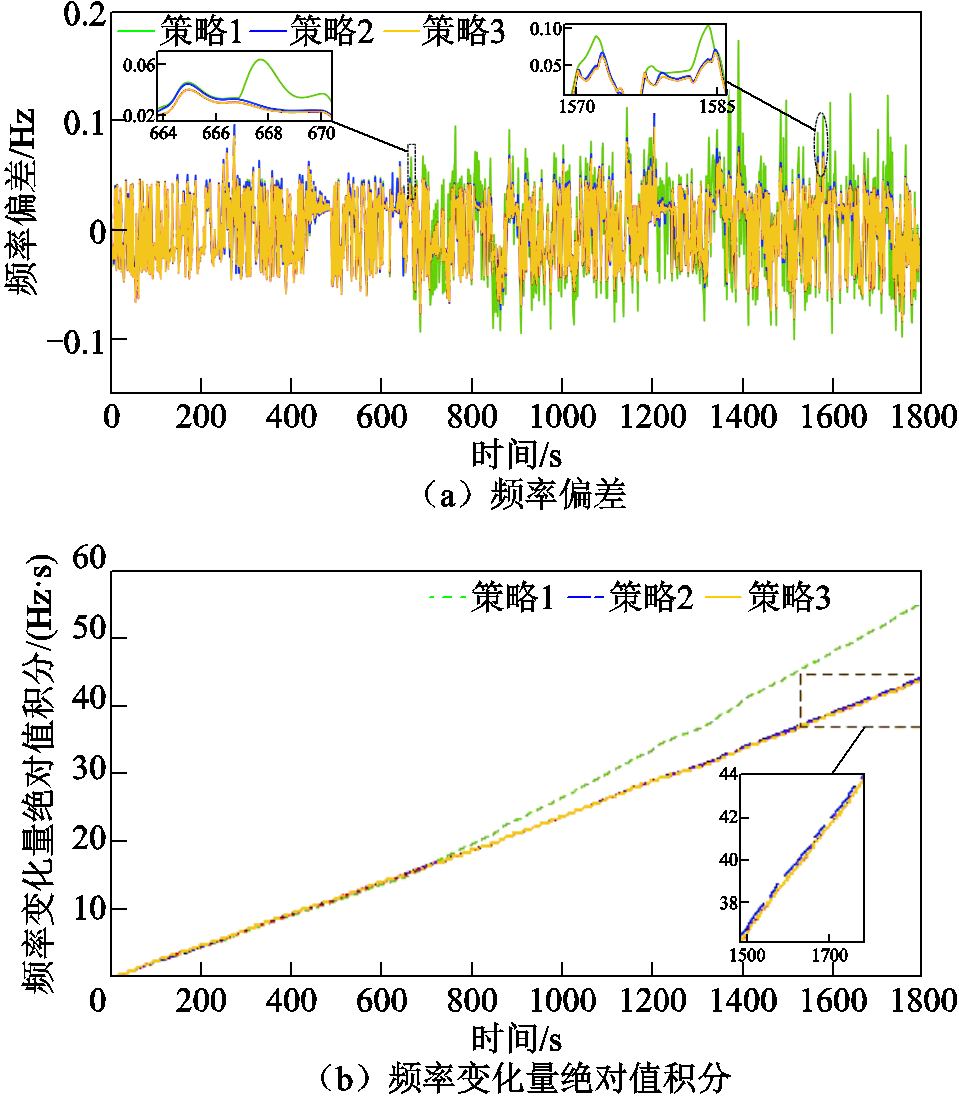
图14 SOC初始值为0.88时的频率曲线
Fig.14 Frequency curves for an initial value 0.88 of SOC
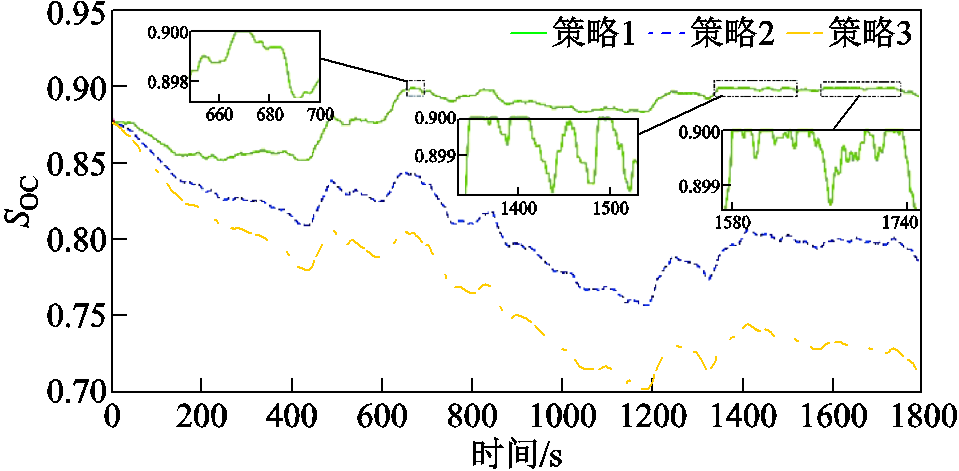
图15 SOC初始值为0.88时的储能SOC响应曲线
Fig.15 SOC curves of energy storage for an initial SOC value of 0.88
由图14和图15可知,当SOC初值设置为0.88时,策略1在666.96 s处首次出现储能充电调频容量不足的情形,达到SOC上限退出二次调频,且接下来在1 300~1 800 s的时段内储能总计16次达到约束上限。相较之下,策略2和策略3则能够在保证频率调节效果的基础上,使SOC向正常充放电区间恢复,避免SOC长时间处于过度充电状态。
SOC初始值为0.88时的调频性能指标见表7。由定量数据分析可得,策略2和策略3的频率偏差方均根值比策略1分别减小了24.24%和25.27%,频率变化量绝对值积分各自降低了19.81%和20.27%,SOC偏差方均根分别减少了19.21%和30.16%。
表7 SOC初始值为0.88时调频性能评价指标
Tab.7 Evaluation indexes for frequency regulation performance with an initial value 0.88 of SOC

控制策略/Hz/Hz/Hz 策略10.177 53.700×10-255.060.384 6 策略20.106 32.803×10-244.150.310 7 策略30.932 12.765×10-243.900.268 6
综上所述,当SOC初值为0.12时,策略3较策略2的频率偏差方均根值、频率变化量绝对值积分和SOC偏差方均根值分别降低1.78%、1.25%和13.11%;当SOC初值为0.88时,三者降幅分别为1.36%、0.57%和13.55%。在优化目标一致的情况下,SOC初始状态不论位于充电优先区或是放电优先区,两种策略的SOC变化趋势都表现出大体相似的方向性,但本文所提的分区自适应权重恢复方法相比固定权重恢复方法能够在保证良好调频效果的同时换取SOC恢复的更大提升,总体性能始终更优。若不考虑SOC恢复,储能将长期处于过度放电或过度充电区间范围,甚至达到运行约束限制退出调频,这对电池寿命极为不利且会降低频率调节质量。而本文方法能够保障储能双向调频能力,降低容量配置需求,有利于长期平稳运行。
在实际应用中,可根据区域调频资源特性调整模糊与分区规则、校准参数阈值,并结合场景扩展与硬件验证等方法缩小仿真与实际场景的差距,从而提升所提动态参与因子与自适应MPC协同优化控制策略的适应性,达到改善系统频率调节效果,维持储能长期稳定运行的目的。
针对电池储能参与两区域互联电网二次调频场景,本文提出一种考虑储能SOC分区恢复控制的动态参与因子自适应模型预测控制策略。根据仿真结果,得到以下结论:
1)本文所提的基于灵敏度分析与模糊控制确定火储调频责任的方法能够区分二次调频不同阶段两种调频电源的参与度,进而基于模型预测控制技术得到储能控制出力,优化频率调节效果。仿真结果表明,在阶跃负荷与连续负荷扰动场景下,本文策略展现出的调频性能指标优于其他三种对比方法,彰显了在提升调频效果方面的优越性能。
2)对储能进行有效的能量管理有助于减缓电池老化过程,延长储能使用寿命,故提出一种基于ACE与SOC分区的自适应模型预测控制储能SOC恢复方法。通过对连续负荷扰动场景下不同SOC初始值状态的仿真验证,表明本文策略能够在保障调频性能的前提下,有效引导SOC回归至理想状态区间,避免SOC因调频容量不足退出调频,导致调频性能下降。良好的SOC能够确保储能在不同工况下始终具备足够的能量储备,提升其可靠性和持续性。
本文围绕电池储能参与电网二次调频控制策略展开研究,但仍存在一些需后续研究解决的问题。如电池储能被等效为一个整体,然而储能电站多由储能单元构成,需进一步考虑内部子单元间功率的协调分配和通信延迟的影响。
附 录
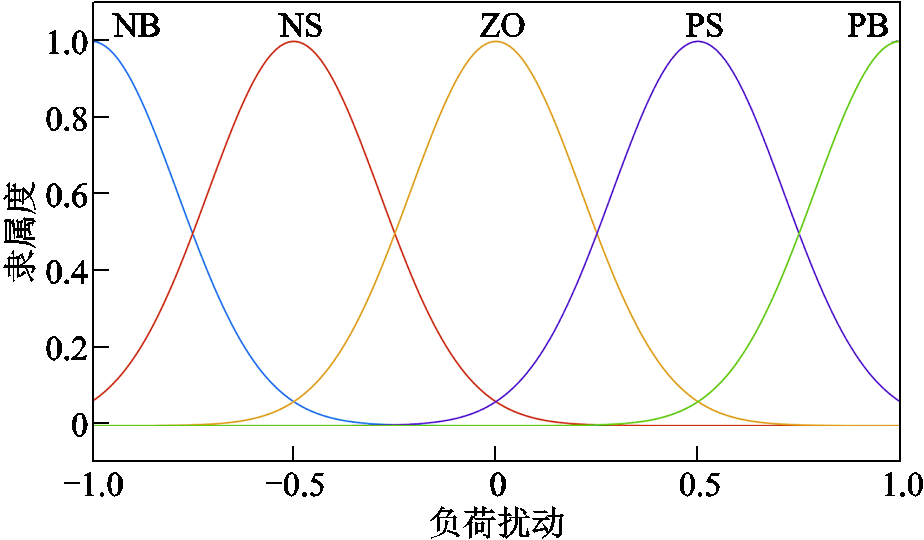
附图1 负荷扰动隶属度函数
App.Fig.1 The membership function of the load disturbance
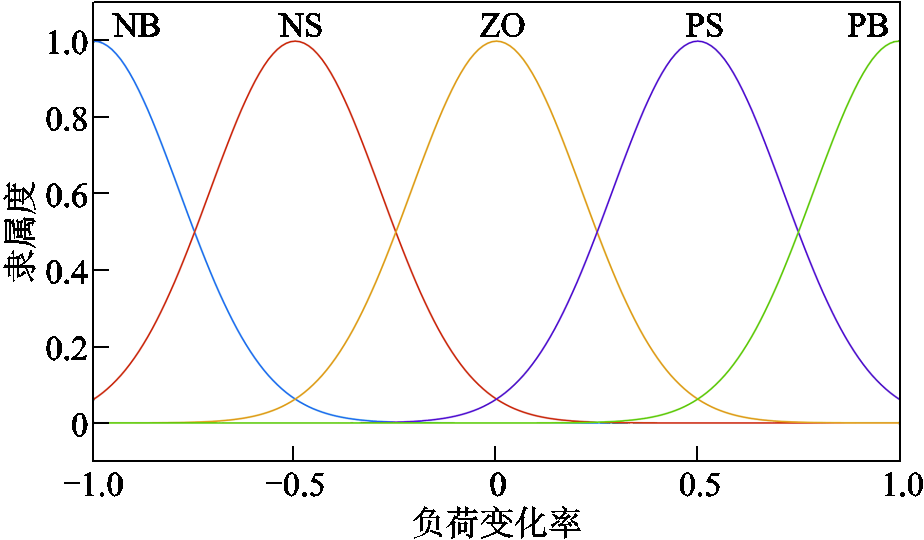
附图2 负荷波动变化率隶属度函数
App.Fig.2 The membership function of the load change rate
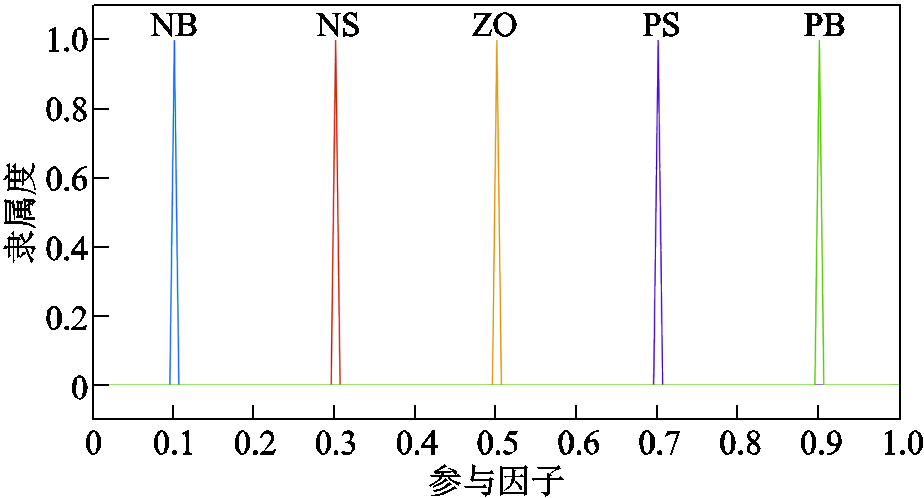
附图3 储能参与因子隶属度函数
App.Fig.3 The membership function of the energy storage participation factor
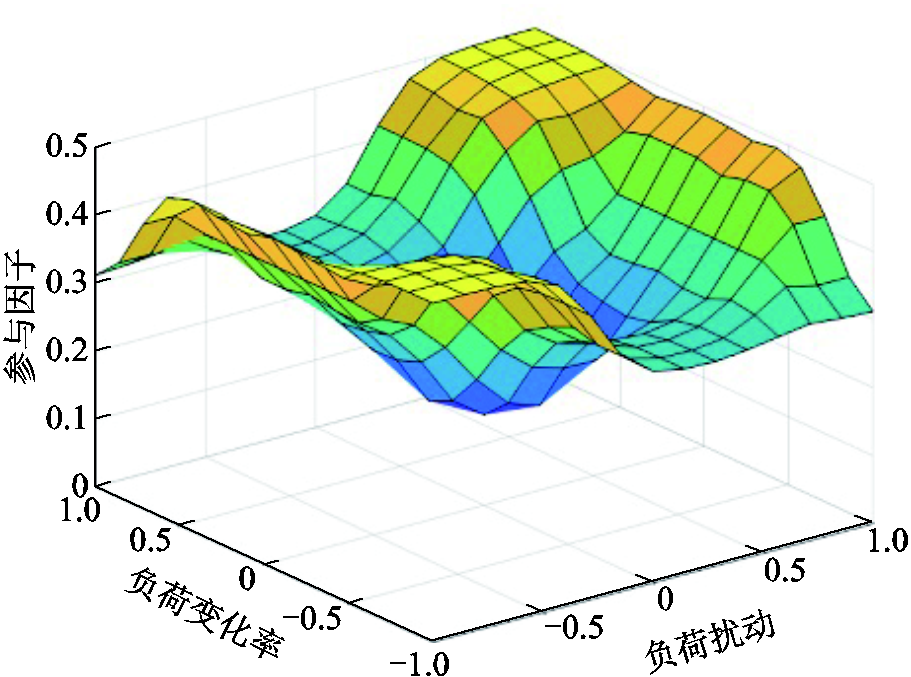
附图4 参与因子位于0~0.5区间内的模糊控制器规律
App.Fig.4 Fuzzy controller laws with participation factor in the interval 0 to 0.5
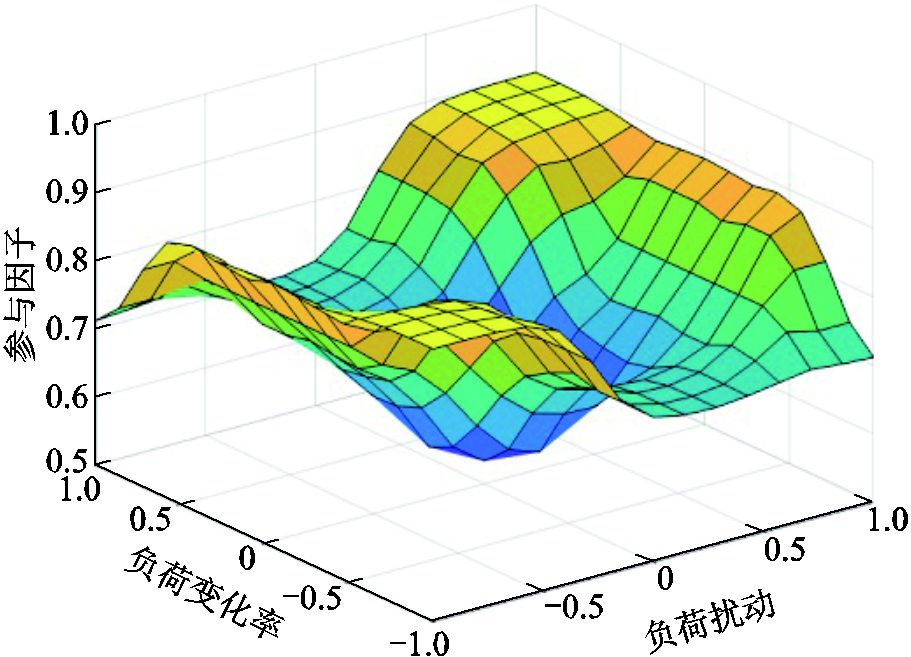
附图5 参与因子位于0.5~1区间内的模糊控制器规律
App.Fig.5 Fuzzy controller laws with participation factor in the interval 0.5 to 1
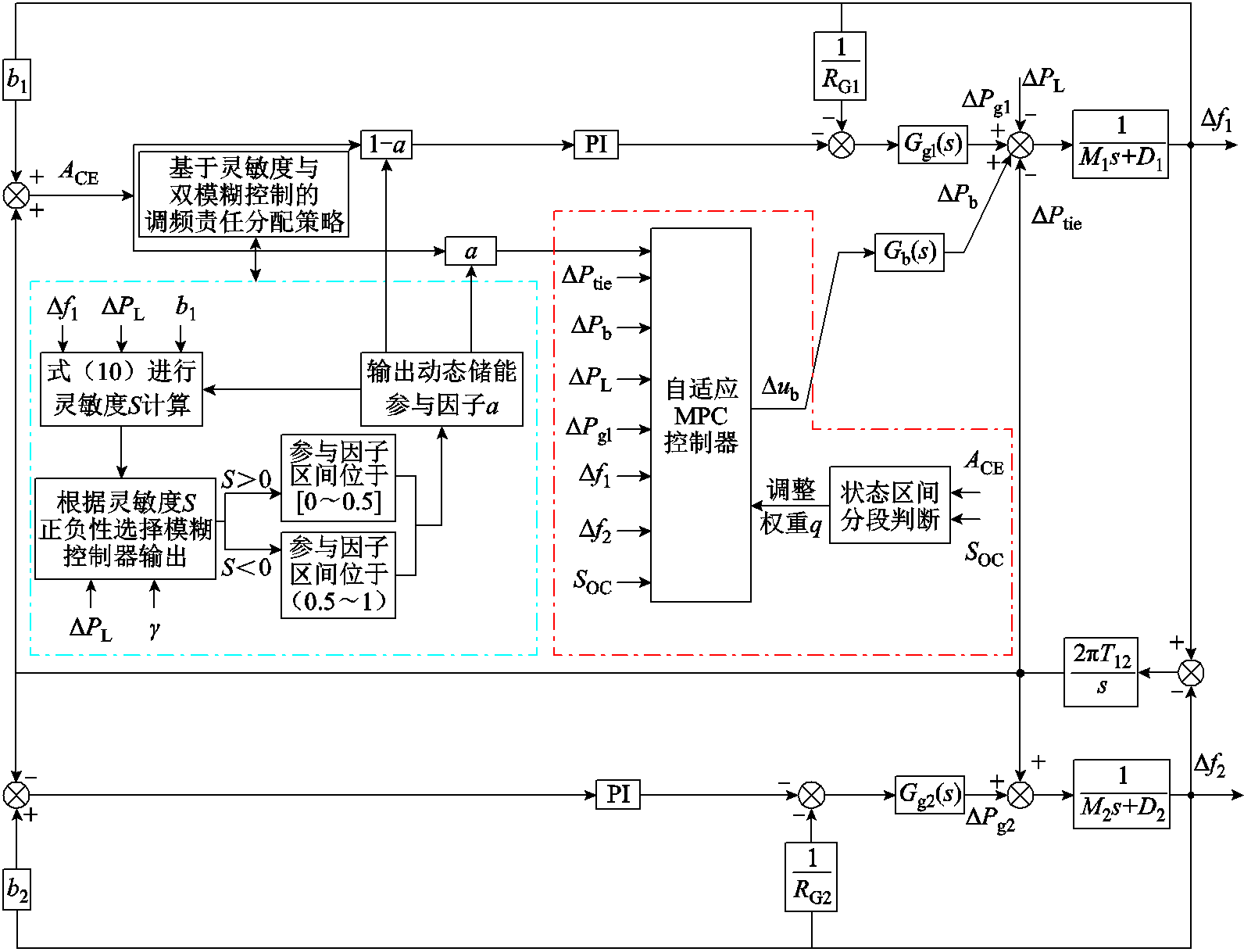
附图6 仿真模型与控制策略架构
App.Fig.6 Simulation model and control strategy architecture diagram
参考文献
[1] 李翠萍, 司文博, 李军徽, 等. 基于集合经验模态分解和多目标遗传算法的火-多储系统调频功率双层优化[J]. 电工技术学报, 2024, 39(7): 2017-2032. Li Cuiping, Si Wengbo, Li Junhui, et al. Two-layer optimization of frequency modulated power of thermal generation and multi-storage system based on ensemble empirical mode decomposition and multi-objective genetic algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2017-2032.
[2] 张怡静, 李智, 时艳强, 等. 基于储能惯量支撑的受端电网频率优化控制方法[J]. 电工技术学报, 2024, 39(11): 3556-3568. Zhang Yijing, Li Zhi, Shi Yanqiang, et al. Optimal frequency control method of receiving power grid based on energy storage inertia support[J]. Transac-tions of China Electrotechnical Society, 2024, 39(11): 3556-3568.
[3] 肖家杰, 李培强, 毛志宇, 等. 基于双层协调控制的电池储能参与电网二次调频策略[J]. 电力自动化设备, 2024, 44(8): 9-17. Xiao Jiajie, Li Peiqiang, Mao Zhiyu, et al. Strategy of battery energy storage participating in power grid secondary frequency regulation based on two-layer coordinated control[J]. Electric Power Automation Equipment, 2024, 44(8): 9-17.
[4] 梁继业, 袁至, 王维庆, 等. 基于电池储能系统的综合自适应一次调频策略[J]. 电工技术学报, 2025, 40(7): 2322-2334. Liang Jiye, Yuan Zhi, Wang Weiqing. Comprehensive adaptive primary frequency control strategy based on battery energy storage system[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2322-2334.
[5] 毛志宇, 李培强, 肖家杰, 等. 面向风功率波动平抑的电池储能双层协调控制策略[J]. 中国电机工程学报, 2024, 44(16): 6494-6507. Mao Zhiyu, Li Peiqiang, Xiao Jiajie, et al. Coordinated two-layer control strategy of battery energy storage for wind power fluctuate mitigation[J]. Proceedings of the CSEE, 2024, 44(16): 6494-6507.
[6] Yang Dejian, Li Jun, Jin Zhaoyang, et al. Sequential frequency regulation strategy for DFIG and battery energy storage system considering artificial deadbands [J]. International Journal of Electrical Power & Energy Systems, 2024, 155: 109503.
[7] 黎静华, 敖国进, 宋诚鑫, 等. 超级电容参与风电调频的动态响应优化策略[J]. 电力系统自动化, 2024, 48(17): 46-55. Li Jinghua, Ao Guojin, Song Chengxin, et al. Optimal dynamic response strategy for supercapacitor parti-cipating in wind power frequency regulation[J]. Automation of Electric Power Systems, 2024, 48(17): 46-55.
[8] Ma Qianli, Wei Wei, Wu Lei, et al. Life-aware operation of battery energy storage in frequency regulation[J]. IEEE Transactions on Sustainable Energy, 2023, 14(3): 1725-1736.
[9] 杨德健, 王鑫, 严干贵, 等. 计及调频死区的柔性风储联合频率控制策略[J]. 电工技术学报, 2023, 38(17): 4646-4656. Yang Dejian, Wang Xin, Yan Gangui, et al. Flexible frequency regulation scheme of DFIG embed battery energy storage system considering deadbands[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4646-4656.
[10] 李志军, 王硕, 张家安, 等. 基于变论域模糊逻辑的互联电力系统负荷频率控制[J]. 电力系统保护与控制, 2021, 49(16): 151-160. Li Zhijun, Wang Shuo, Zhang Jiaan, et al. Variable universe fuzzy logic-based load frequency control in an interconnected power system[J]. Power System Protection and Control, 2021, 49(16): 151-160.
[11] Yin Linfei, Wu Yunzhi. Mode-decomposition memory reinforcement network strategy for smart generation control in multi-area power systems containing renew-able energy[J]. Applied Energy, 2022, 307: 118266.
[12] 王育飞, 程伟, 薛花, 等. 基于串级PI-(1+PD)算法的含飞轮储能互联电网AGC控制器设计[J]. 电力系统保护与控制, 2023, 51(14): 127-138. Wang Yufei, Cheng Wei, Xue Hua, et al. Controller design of an AGC based on a cascade PI-(1+PD) algorithm for an interconnected power grid with flywheel energy storage[J]. Power System Protection and Control, 2023, 51(14): 127-138.
[13] Wang Ping, Chen Xi, Zhang Yunning, et al. Fractional-order load frequency control of an interconnected power system with a hydrogen energy-storage unit[J]. Fractal and Fractional, 2024, 8(3): 126.
[14] 林莉, 林雨露, 谭惠丹, 等. 计及SOC自恢复的混合储能平抑风电功率波动控制[J]. 电工技术学报, 2024, 39(3): 658-671. Lin Li, Lin Yulu, Tan Huidan, et al. Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 658-671.
[15] He Junqiang, Shi Changli, Wei Tongzhen, et al. Stochastic model predictive control of hybrid energy storage for improving AGC performance of thermal generators[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 393-405.
[16] Huang Chongxin, Yang Manting, Ge Hui, et al. DMPC-based load frequency control of multi-area power systems with heterogeneous energy storage system considering SOC consensus[J]. Electric Power Systems Research, 2024, 228: 110064.
[17] Meng Gaojun, Chang Qingqing, Sun Yukun, et al. Energy storage auxiliary frequency modulation control strategy considering ACE and SOC of energy storage[J]. IEEE Access, 2021, 9: 26271-26277.
[18] 崔红芬, 杨波, 蒋叶, 等. 基于模糊控制和SOC自恢复储能参与二次调频控制策略[J]. 电力系统保护与控制, 2019, 47(22): 89-97. Cui Hongfen, Yang Bo, Jiang Ye, et al. Strategy based on fuzzy control and self adaptive modification of SOC involved in secondary frequency regulation with battery energy storage[J]. Power System Protection and Control, 2019, 47(22): 89-97.
[19] Guo Menglei, Zheng Jianyong, Mei Fei, et al. Double-layer AGC frequency regulation control method considering operating economic cost and energy storage SOC consistency[J]. International Journal of Electrical Power & Energy Systems, 2023, 145: 108704.
[20] 严干贵, 王铭岐, 段双明, 等. 考虑荷电状态恢复的储能一次调频控制策略[J]. 电力系统自动化, 2022, 46(21): 52-61. Yan Gangui, Wang Mingqi, Duan Shuangming, et al. Primary frequency regulation control strategy of energy storage considering state of charge recovery[J]. Automation of Electric Power Systems, 2022, 46(21): 52-61.
[21] He Li, Tan Zhuangxi, Li Yong, et al. A coordinated consensus control strategy for distributed battery energy storages considering different frequency control demands[J]. IEEE Transactions on Sustainable Energy, 2024, 15(1): 304-315.
[22] 李欣然, 黄际元, 陈远扬, 等. 基于灵敏度分析的储能电池参与二次调频控制策略[J]. 电工技术学报, 2017, 32(12): 224-233. Li Xinran, Huang Jiyuan, Chen Yuanyang, et al. Battery energy storage control strategy in secondary frequency regulation considering its action moment and depth[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 224-233.
[23] 李若, 李欣然, 谭庄熙, 等. 考虑储能电池参与二次调频的综合控制策略[J]. 电力系统自动化, 2018, 42(8): 74-82. Li Ruo, Li Xinran, Tan Zhuangxi, et al. Integrated control strategy considering energy storage battery participating in secondary frequency regulation[J]. Automation of Electric Power Systems, 2018, 42(8): 74-82.
[24] Cheng Yunzhi, Tabrizi M, Sahni M, et al. Dynamic available AGC based approach for enhancing utility scale energy storage performance[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 1070-1078.
[25] 张仕鹏, 李培强, 张亦君, 等. 基于变滤波时间常数和模糊控制的复合储能二次调频策略[J/OL]. 上海交通大学学报, 2024: 1-26[2024-06-27].https://doi. org/10.16183/j.cnki.jsjtu.2023.516. Zhang Shipeng, Li Peiqiang, Zhang Yijun, et al. Secondary frequency modulation strategy of composite energy storage based on variable filter time constant and fuzzy control[J/OL]. Journal of Shanghai Jiaotong University, 2024: 1-26[2024-06-27]. https://doi.org/ 10.16183/j.cnki.jsjtu.2023.516.
[26] Huang Hao, Li Fangxing. Sensitivity analysis of load-damping characteristic in power system frequency regulation[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1324-1335.
[27] 肖家杰, 李培强, 毛志宇. 基于模糊分配因子的电池储能参与二次调频策略[J]. 电网技术, 2023, 47(9): 3568-3577. Xiao Jiajie, Li Peiqiang, Mao Zhiyu, et al. Battery energy storage participating in secondary frequency regulation based on fuzzy allocation factor[J]. Power System Technology, 2023, 47(9): 3568-3577.
[28] 李军徽, 侯涛, 严干贵, 等. 计及调频成本和荷电状态恢复的多储能系统调频功率双层优化[J]. 中国电机工程学报, 2021, 41(23): 8020-8033. Li Junhui, Hou Tao, Yan Gangui, et al. Two-layer optimization of frequency modulation power in multi-battery energy storage system considering frequency modulation cost and recovery of state of charge[J]. Proceedings of the CSEE, 2021, 41(23): 8020-8033.
[29] 贺悝, 郭罗权, 谭庄熙, 等. 高比例新能源电网中储能调频死区优化设定控制策略[J]. 电力系统保护与控制, 2024, 52(18): 65-75. He Li, Guo Luoquan, Tan Zhuangxi, et al. Improved dead zone setting of a frequency regulation strategy for energy storage with high penetration of RESs[J]. Power System Protection and Control, 2024, 52(18): 65-75.
Abstract Battery energy storage, as an advanced power device with bidirectional charging and discharging capabilities, fast response speed, and high regulation precision, exhibits strong frequency regulation potential. However, existing studies on the participation of energy storage in secondary frequency regulation lack flexibility in designing the frequency regulation responsibility allocation strategy between energy storage and thermal power units. Consequently, they fail to fully leverage the advantages of energy storage and thermal power units under complex load fluctuation scenarios. Moreover, the conventional methods face conflicts between meeting system frequency regulation demands and ensuring the state of charge (SOC) recovery of energy storage. To address this issue, this paper proposes a secondary frequency regulation strategy that integrates dynamic participation factors and adaptive model predictive control (MPC) while considering SOC recovery.
Firstly, based on the sensitivity principle, the relationship between the energy storage participation factor and system frequency deviation under the area control error (ACE) mode is established. A hierarchical decision-making mechanism is then designed, incorporating sensitivity, frequency deviation, and load fluctuations. A fuzzy control approach is employed to dynamically adjust the energy storage participation factor based on the load condition, optimizing the frequency regulation responsibility allocation between energy storage and thermal power units. This approach effectively exploits the rapid response capability of energy storage and the sustained regulation ability of thermal power units. On this basis, since directly using the dynamic frequency regulation responsibility signal as the energy storage power command is suboptimal, it is instead formulated as the optimization objective of an MPC controller. The MPC framework then iteratively computes the optimal power output of energy storage in real time, thereby improving the system's frequency regulation performance. Furthermore, an adaptive MPC-based energy storage regulation and SOC recovery strategy is proposed, incorporating a SOC recovery term into the MPC objective function. By segmenting the ACE signal and SOC state, the weight of this term is adaptively adjusted across different operating regions, effectively mitigating the conflict between frequency regulation and SOC recovery while enhancing the bidirectional frequency regulation capability of energy storage across all operating conditions.
Simulation results demonstrate that under step load disturbances, the proposed method reduces the maximum frequency deviation to -0.209 7 Hz, achieving a 13.88% and 8.07% improvement compared to two conventional energy storage frequency regulation methods. Additionally, the frequency nadir rate is reduced to 0.252 6 Hz/s, with respective improvements of 23.22% and 32.44% compared to two conventional methods. Under continuous load disturbances, the root mean square value of frequency deviation of the proposed method is reduced by 48.84%, 40.46%, and 22.32% compared to three benchmark methods. In the frequency regulation process, the integral of absolute frequency variation of the proposed method remains minimum compared with the three benchmark methods. Moreover, in extreme scenarios where the initial SOC is 0.12 or 0.88, the proposed MPC adaptive partitioning method with adjustable weights for SOC recovery ensures effective frequency regulation while simultaneously achieving significant improvements in SOC recovery. The root mean square value of SOC deviation is reduced to 2.644×10-1 and 2.686×10-1, representing reductions of 32.03% and 30.16% compared to method that disregard SOC recovery, and reductions of 13.11% and 13.55% compared to method that use fixed-weight strategies.
The simulation analysis leads to the following conclusions: The dynamic participation factor and adaptive model predictive control strategy can distinguish the frequency regulation participation of thermal power units and energy storage at different stages of secondary frequency regulation. This approach enhances system frequency regulation performance while guiding the SOC of energy storage back to the ideal operating range, ensuring its long-term stable operation.
keywords:Battery energy storage, secondary frequency regulation, dynamic participation factor, adaptive model predictive control, state of charge
DOI: 10.19595/j.cnki.1000-6753.tces.241924
中图分类号:TM912
福建省科技创新战略联合研究项目资助(2023R0153)。
收稿日期 2024-10-28
改稿日期 2025-02-26
朱振山 男,1989年生,副教授,研究生导师,研究方向为电力系统运行与控制。E-mail:zhenshan198@126.com(通信作者)
翁凯亮 男,1999年生,硕士研究生,研究方向为电力系统稳定控制。E-mail:1477669452@qq.com
(编辑 赫 蕾)