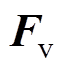为麦克斯韦力
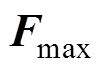和磁致伸缩等效力
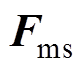的矢量和，即摘要 现有电抗器铁心减振优化措施基于确定性参数，但未能考虑制造公差等因素导致的结构参数的不确定性，使得优化后实际的铁心振动加速度超过原设计值，造成优化方案不可靠。针对上述问题，该文以铁心最大振动加速度为指标，量化了气隙结构参数不确定性对电抗器铁心振动的影响。结果表明，在气隙结构参数存在1 mm不确定性的情况下，采用原始设计参数时，电抗器振动性能满足可靠运行要求的概率为67.67%。基于不确定性的分析结果，建立了适用于电抗器铁心减振的鲁棒优化模型，并通过莫里斯单次单变量筛选法（MOAT）与Sobol灵敏度指标相结合的方法对待优化变量的求解空间进行削减，最终采用二次逼近边界优化算法（BOBYQA）求解得到了电抗器铁心减振设计的鲁棒优化方案。结果表明，该文提出的优化方案显著提高了不确定性扰动下电抗器铁心振动优化方案的鲁棒性，优化后的电抗器铁心最大振动加速度满足可靠运行要求的概率达到97.34%，更适用于工程实际需求。该文可为开展计及不确定性因素的电抗器铁心减振的优化研究及设计提供参考。
关键词：不确定性分析 电抗器铁心 减振 鲁棒优化
电抗器在交流电网中承担着补偿线路无功功率、抑制过电压产生的重要作用，是维持交流电网安全稳定运行的关键设备之一[1]。电抗器铁心由铁磁性材料构成，在磁场作用下产生的电磁力会引起铁心的振动[2]。由于铁心柱气隙引入了麦克斯韦力，导致电抗器铁心的振动强度普遍大于同等容量的变压器[3]。剧烈的振动会引起电抗器内部螺栓松动、悬浮放电和产气异常等一系列故障[4]。振动超标是目前电抗器运行过程中面临的主要难题之一，因此研究电抗器铁心减振技术对于保障电抗器的安全稳定运行有着重要的意义。
近年来，国内外学者在电抗器铁心减振技术领域开展了大量研究。杨帆等结合磁-结构-声多场耦合分析，提出了通过选用磁导率更高的硅钢材料，扩大麦克斯韦力和磁致伸缩力之间的衰减作用，从而降低电抗器铁心振动位移的方法[5]。袁发庭等基于经典J-A模型和二次畴转理论，结合铁心电抗器电磁场-结构力场的耦合关系，提出了一种考虑材料磁致伸缩特性的铁心电抗器振动优化方法[6]。郭佳熠等提出了通过改变电抗器铁心柱上气隙的长度和位置，进而改变铁心受到的电磁力分布，减小电抗器铁心振动的方法[7]。然而，现有研究主要使用确定性的电抗器参数进行振动计算与分析，并制定相应的减振优化策略。但电抗器在制造过程中必然存在一定的随机工程公差，导致设备成品结构参数的不确定性。此外，实际电抗器产品的铁心柱气隙采用气隙垫块叠加构成[8]，长期高强度振动后预紧力的变化会进一步加剧气隙结构参数的不确定性。因此，有必要开展气隙结构参数对振动的不确定性分析，并以此为依据制定不确定性条件下电抗器铁心气隙的减振优化策略。
目前，在电气设备相关领域的不确定性分析方面，于全毅等针对多导体传输线辐射敏感度响应的不确定性问题，提出广义混沌多项式法与Sobol全局灵敏度相结合的分析方法[9]。王洪耀等提出一种基于Sobol阻抗灵敏度分析的中高频谐振抑制策略，定量判别不同控制参数及运行工况下影响模块化多电平换流器阻抗特性的主导因素[10]。何畅等提出了针对多个不确定性变量影响的变压器套管地震易损性及地震失效风险评估方法[11]。上述研究的不确定性分析方法均可作为本文的参考。此外，在电气工程相关领域的不确定性优化方面，不确定性下的优化方法通常有模糊优化[12]、随机优化[13]、鲁棒优化等。其中鲁棒优化以集合的形式表征不确定性变量，面向不确定性变量的“最恶劣”场景进行优化求解，弥补了基于随机优化所得方案对不确定性变量概率分布的高度敏感，更加贴合实际工程的需求[14]。刘一欣等通过对两阶段鲁棒优化模型的求解，得到了微电网在负荷出力波动场景下系统运行成本最小的调度方案[15]。龚夕霞等针对模块化永磁直线同步电机在批量生产中性能易受到制造公差的影响这一问题，提出了一种考虑制造公差的多目标鲁棒优化设计方法[16]。因此，本文选用鲁棒优化方法求解不确定性条件下的优化问题。
本文针对气隙结构参数的不确定性会导致实际电抗器铁心减振优化结果达不到预期值的问题，提出了一种计及气隙结构参数不确定性影响的电抗器铁心减振鲁棒优化方法。首先，在以铁心最大振动加速度为振动指标的前提下，量化气隙结构参数不确定性变化对铁心振动不确定性的影响；其次，建立考虑气隙结构参数不确定性的鲁棒优化模型，采用莫里斯单次单变量（Morrise One at A Time, MOAT）筛选法和Sobol分析对优化模型进行简化，并结合有限元仿真对简化模型进行求解；最后，将本文所提方法与确定性优化方法进行对比，验证其有效性。
并联电抗器作为一种工业制品，其制造过程中会不可避免地存在一定的随机工程公差，导致气隙结构参数的不确定性。因此，有必要从理论和数值两个角度分析这种不确定性对铁心振动的影响。
并联电抗器铁心的振动由铁心受到的电磁力引起，在磁场的作用下，铁心受到的电磁力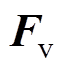为麦克斯韦力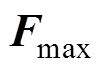和磁致伸缩等效力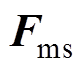的矢量和，即
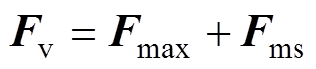（1）
其中，麦克斯韦力Fmax作用在铁心柱上气隙和铁心饼的交界面，计算式为
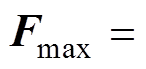
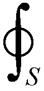TdS （2）
式中，S为包围部分铁心材料的封闭曲面；T为麦克斯韦应力张量，它是一个二阶张量，计算式为
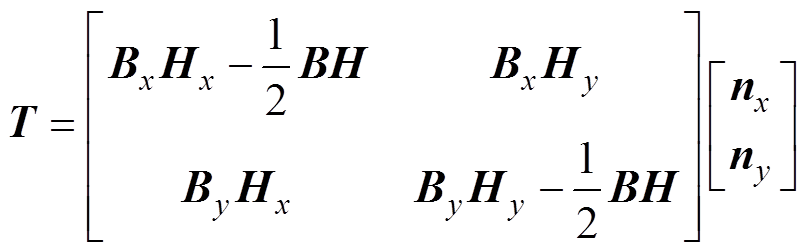（3）
式中，B为电抗器铁心的磁通密度；Bx和By分别为磁通密度在x轴和y轴方向上的分量；H为电抗器铁心的磁场强度；Hx和Hy分别为磁场强度在x轴和y轴方向上的分量；nx和ny分别为单位法向量在x轴和y轴方向的分量。气隙结构参数的不确定性变化会引起铁心内的磁通密度B和磁场强度H发生不确定性变化，由式（2）和式（3）可知，磁通密度和磁场强度变化会导致麦克斯韦应力张量变化，从而引起麦克斯韦力的不确定性变化。
磁致伸缩等效力Fms由铁磁性材料的磁致伸缩应变等效而来，结构力学中线弹性材料的磁致伸缩应力张量与磁致伸缩等效力的关系为
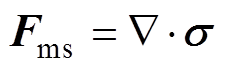（4）
式中，
为梯度算子；s为铁心的磁致伸缩应力张量，计算式为
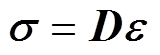（5）
式中，D为弹性张量矩阵；e 为磁致伸缩应变，通常可使用磁致伸缩正交插值法通过铁心中的磁场强度H而求得[17]。弹性张量矩阵D的形式为
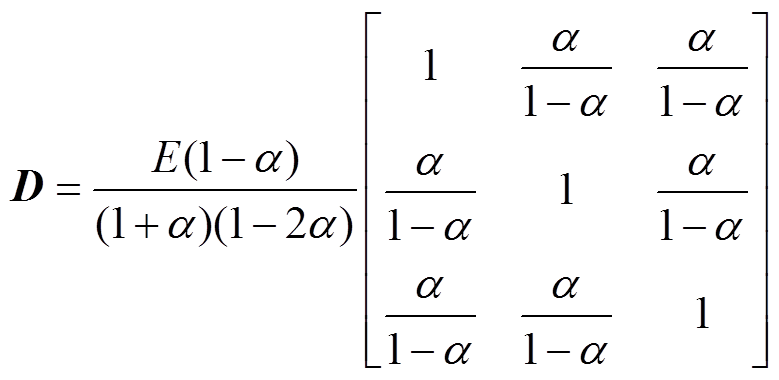（6）
式中，E为铁心的杨氏模量；a为泊松比。
气隙结构参数的不确定性变化会引起铁心内的磁场强度H发生不确定性变化，使得与磁场强度H高度相关的磁致伸缩应变e发生变化。在此基础上，由式（4）和式（5）可知，磁致伸缩应变e变化会导致磁致伸缩应力张量变化，从而引起磁致伸缩等效力的不确定性变化。综上可知，气隙结构参数的不确定性变化导致了麦克斯韦力和磁致伸缩等效力数值的不确定性变化，从而引起由二者共同组成的铁心所受电磁力大小的不确定性变化。
此外，在铁心受到的电磁力分布方面，由于铁心柱上的铁心饼的磁导率和气隙的磁导率相差很大，铁心饼是高磁导率的硅钢材料，而气隙则是低磁导率的大理石材料，磁通在通过气隙与铁心饼的交界面时会产生麦克斯韦应力张量。由于麦克斯韦力作用在铁心饼与气隙的界面处，气隙结构参数的不确定性变化会改变铁心饼与气隙边界的位置，从而改变麦克斯韦力的分布。对于磁致伸缩等效力而言，该力由铁磁性材料磁致伸缩现象等效而来，作用在铁轭和铁心饼上，而气隙结构参数的不确定性变化会改变铁心柱上铁心饼的位置，从而改变磁致伸缩等效力的分布。因此，气隙结构参数的不确定性变化也会改变铁心电磁力的分布。
电抗器铁心的各组件均为线弹性材料，忽略阻尼效应，可以由结构力学中的振动方程求出铁心的振动位移大小，即
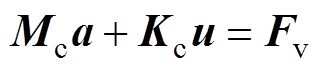（7）
式中，Mc为铁心的质量矩阵；Kc为铁心的刚度矩阵，u为铁心的振动位移；a为铁心的振动加速度。由式（7）可知，气隙结构参数的不确定性变化通过影响铁心所受电磁力的大小和分布，从而改变电抗器铁心振动位点分布和振动数值大小。气隙结构参数的不确定性变化对振动的影响流程如图1所示。
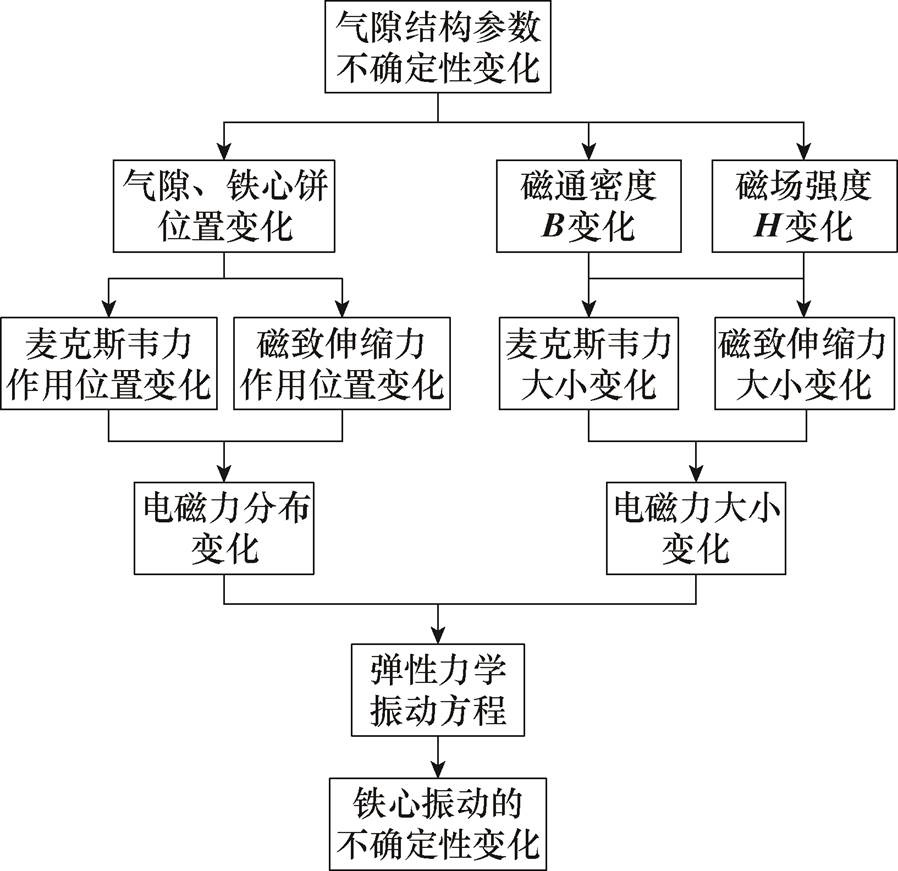
图1 气隙结构参数的不确定性变化对振动影响流程
Fig.1 Flow chart of the impact of uncertain changes in gap structural parameters on vibration
为了量化气隙结构参数的不确定性对电抗器铁心振动的影响，需要开展大量的确定性实验[18]。本文首先通过实验验证确定性情况下搭建的有限元仿真模型的准确性，然后基于搭建的有限元仿真模型定量分析气隙结构参数的不确定性对电抗器铁心振动的影响。
1.2.1 仿真模型验证
为了检验基于铁心振动计算方法（式（1）～式（7））搭建的有限元仿真模型的准确性，本文设计并制造了一台双柱式并联电抗器进行振动测量实验。该电抗器铁心结构如图2所示。电抗器由绕组、铁轭、铁心饼和气隙组成。其中，绕组由铜导线卷制而成；铁心饼、铁轭等由硅钢片叠压而成；气隙则是大理石材质。按照实际电抗器设计制造方法，该电抗器设计为均匀气隙结构，气隙长度为8 mm。将并联电抗器铁心柱上的气隙从上至下、从左至右依次编号为g1、g2、g3、g4、g5、g6、g7、g8、g9、g10。双柱式并联电抗器铁心运行和设计参数见表1。
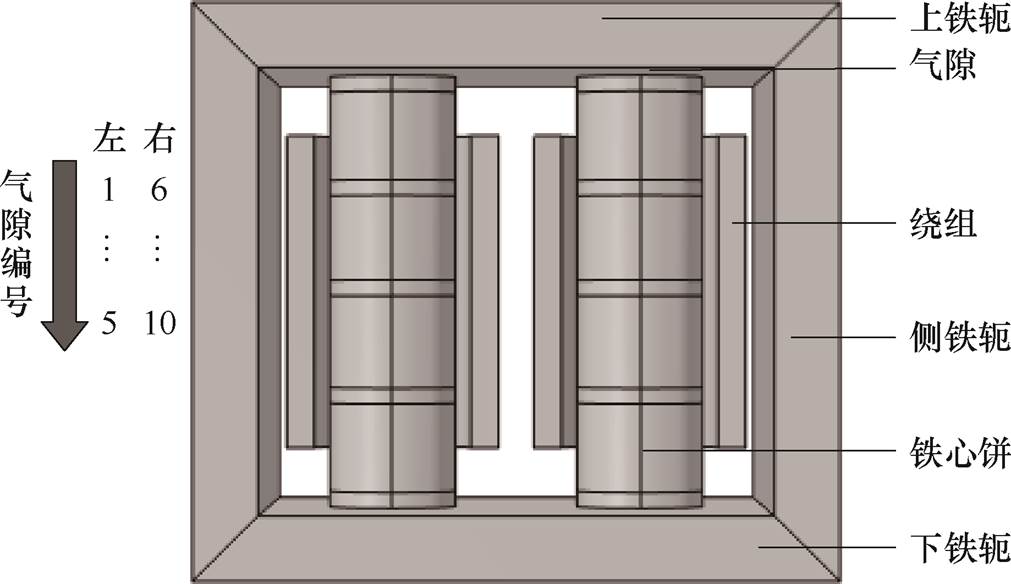
图2 双柱式并联电抗器铁心结构
Fig.2 Double column shunt reactor core structure
表1 双柱式并联电抗器的运行和设计参数
Tab.1 Operation and design parameters of double column shunt reactor
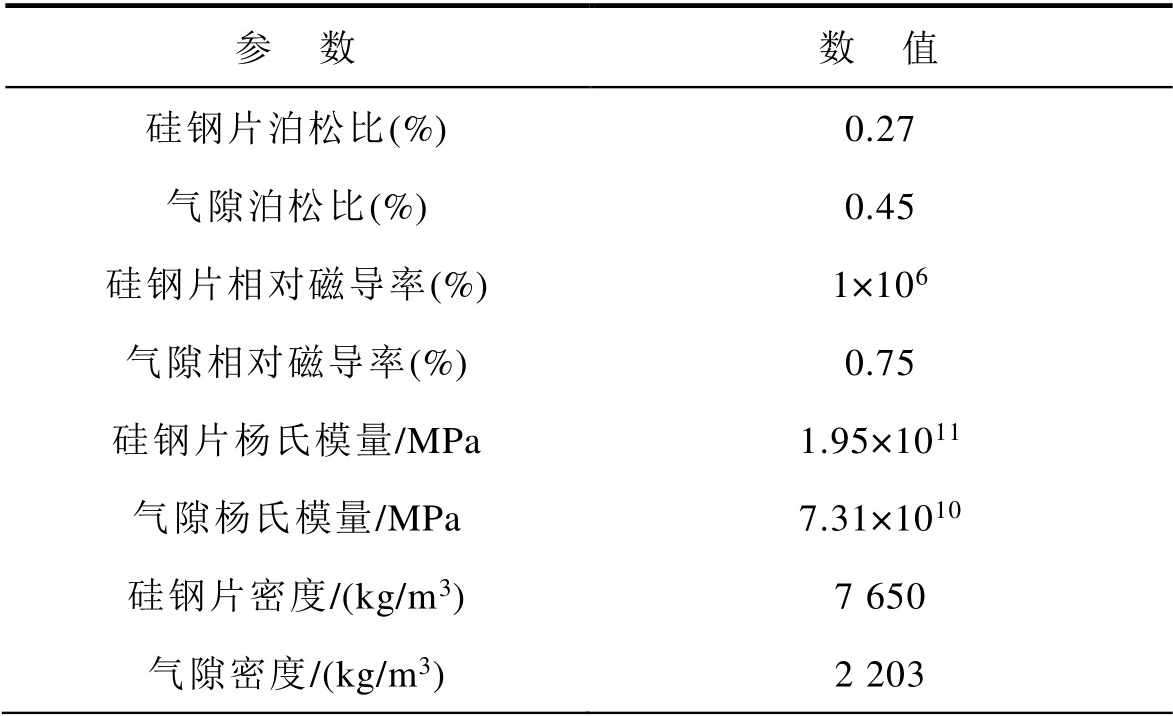
参 数数 值 硅钢片泊松比(%)0.27 气隙泊松比(%)0.45 硅钢片相对磁导率(%)1×106 气隙相对磁导率(%)0.75 硅钢片杨氏模量/MPa1.95×1011 气隙杨氏模量/MPa7.31×1010 硅钢片密度/(kg/m3)7 650 气隙密度/(kg/m3)2 203
（续）
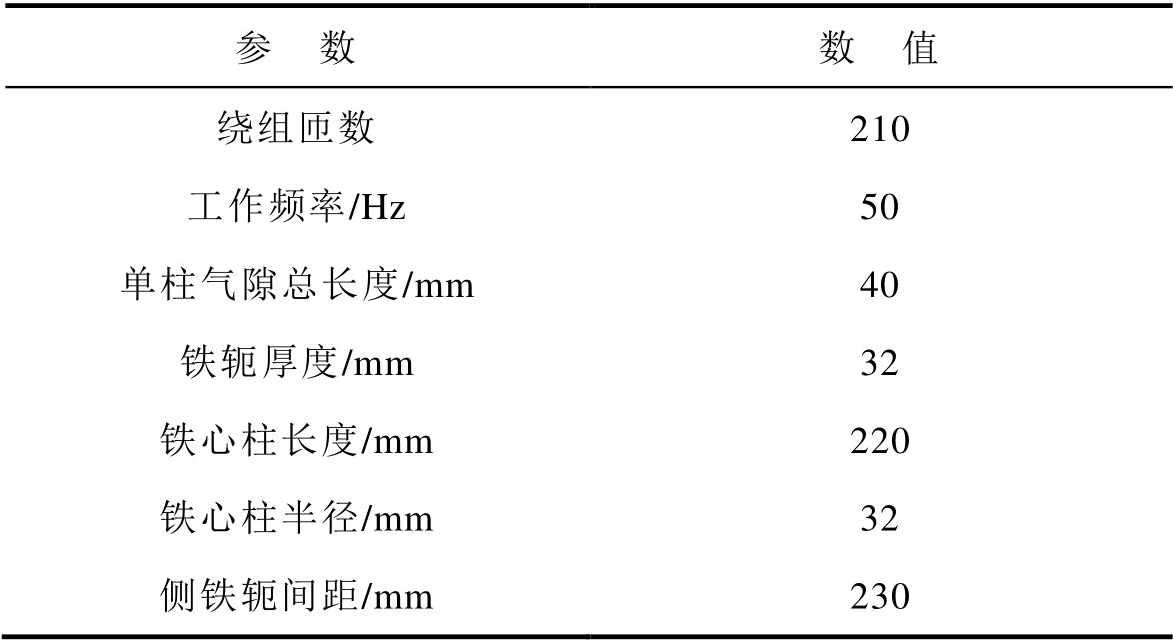
参 数数 值 绕组匝数210 工作频率/Hz50 单柱气隙总长度/mm40 铁轭厚度/mm32 铁心柱长度/mm220 铁心柱半径/mm32 侧铁轭间距/mm230
结合铁心振动计算方法及表1给出的电抗器运行和设计参数，搭建有限元仿真模型模拟电抗铁心振动情况。电抗器铁心的磁通密度和振动加速度分布如图3所示。
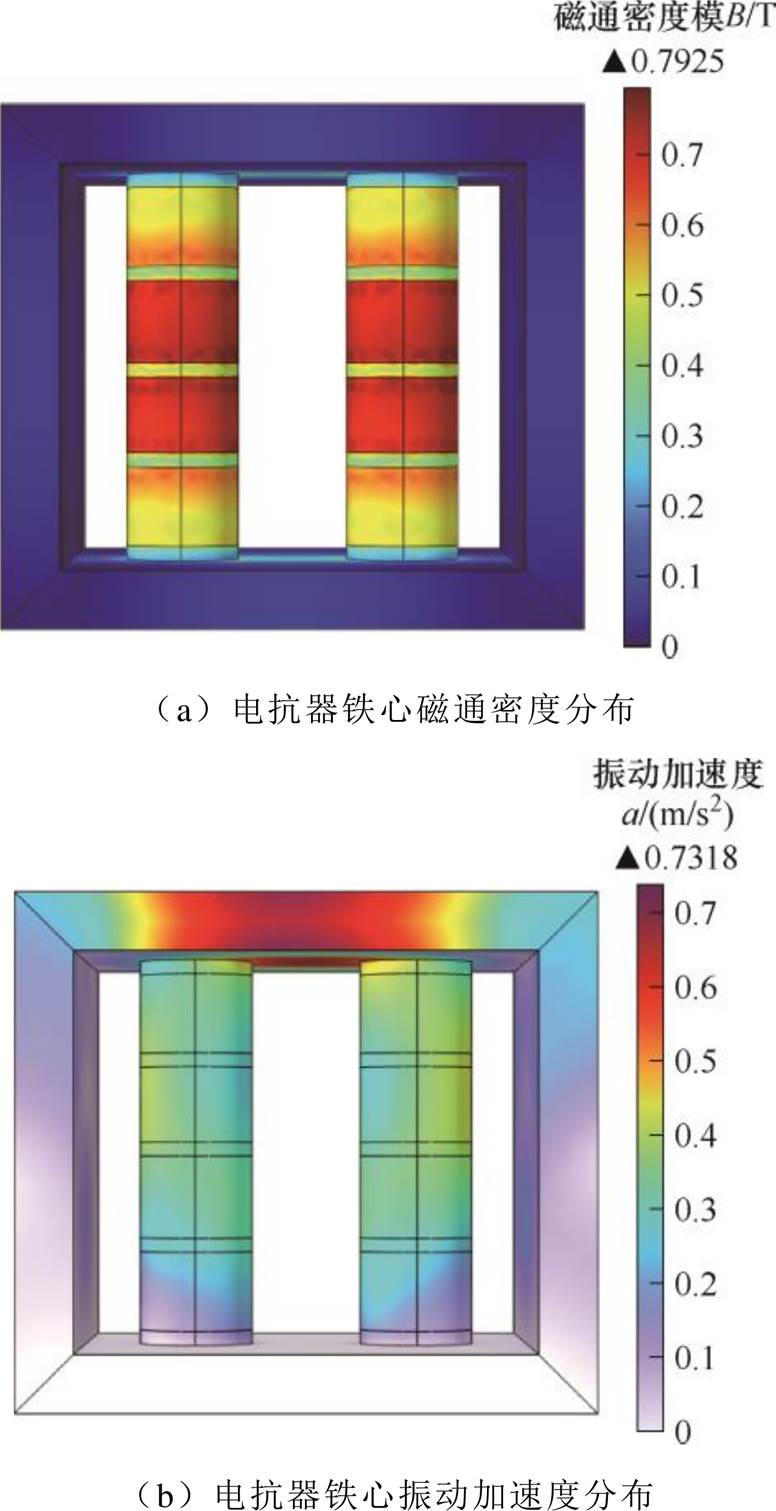
图3 电抗器铁心仿真结果
Fig.3 Simulation results of reactor core
由图3a可知，铁心磁通密度分布上、下对称一致。这是因为铁心内的磁场分布不受铁心下铁轭固定的影响，且所设计的电抗器几何结构对称，故磁场分布也呈对称性。铁心的磁通主要集中在铁心柱和上下轭的中间区域，而侧铁轭和上下轭两侧区域的磁通密度明显较低。这是由于双柱式电抗器铁心内的磁通由两绕组产生的磁通共同构成，在铁心柱和上下轭的中间区域，两绕组产生的磁通方向一致，总磁通密度较大；而在侧铁轭和上下轭的两侧区域，两绕组产生的磁通方向相反，总磁通密度较小。
为验证有限元仿真结果的准确性，对实际电抗器开展实验以测量振动加速度。本文使用的振动加速度传感器型号为SR-TVA2019-A，量程为38.2～112.3 dB，灵敏度为44.16 mV/Pa，基于电容式原理，采用接触式安装方式吸附在测点表面，电压接口为BNC。在电抗器的侧铁轭上选择2个振动测点用于测量振动加速度，左侧测点位置为侧铁轭上g2气隙上表面平行点，右侧测点位置为侧铁轭上g2气隙下表面平行点。振动测量实验平台如图4所示。
图4 振动测量实验平台
Fig.4 Vibration measurement experimental platform
将所选实验测点的振动加速度结果与仿真结果进行对比，并且定义差异率h表征实验与仿真结果之间差异的大小，表达式为
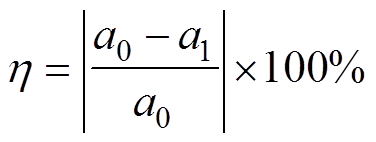（8）
式中，a0和a1分别为实验测得的铁心振动加速度与仿真得到的铁心振动加速度。实验结果与仿真结果对比见表2。
表2 实验结果与仿真结果对比
Tab.2 Comparison between experimental results and simulation results
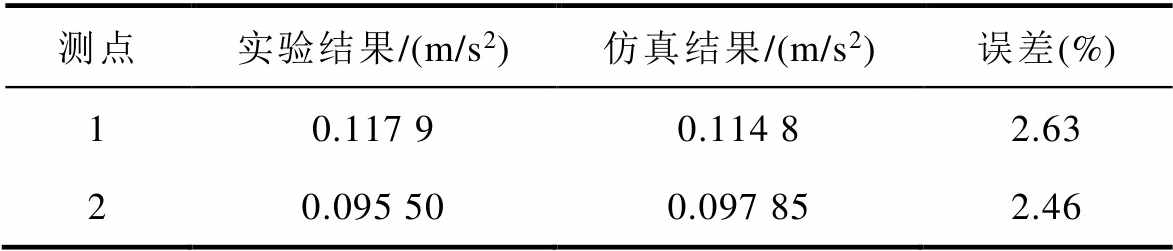
测点实验结果/(m/s2)仿真结果/(m/s2)误差(%) 10.117 90.114 82.63 20.095 500.097 852.46
由表2可见，测点仿真结果与实验结果最大误差为2.63%，说明电抗器仿真模型切合实际模型，本文所提的电抗器铁心振动计算方法准确性良好，可以进一步用于后续研究。
1.2.2 数值定量分析
由1.1节气隙结构参数不确定性下的电抗器铁心振动理论分析可知，由制造公差引起的气隙结构参数的不确定性变化会对铁心的振动加速度产生显著的影响。本文先检验给定制造公差下电抗器铁心加速度的振动分布，假设g1、g2气隙存在-0.12 mm的制造公差，其余结构参数保持原设计值不变，铁心的振动加速度分布如图5所示。
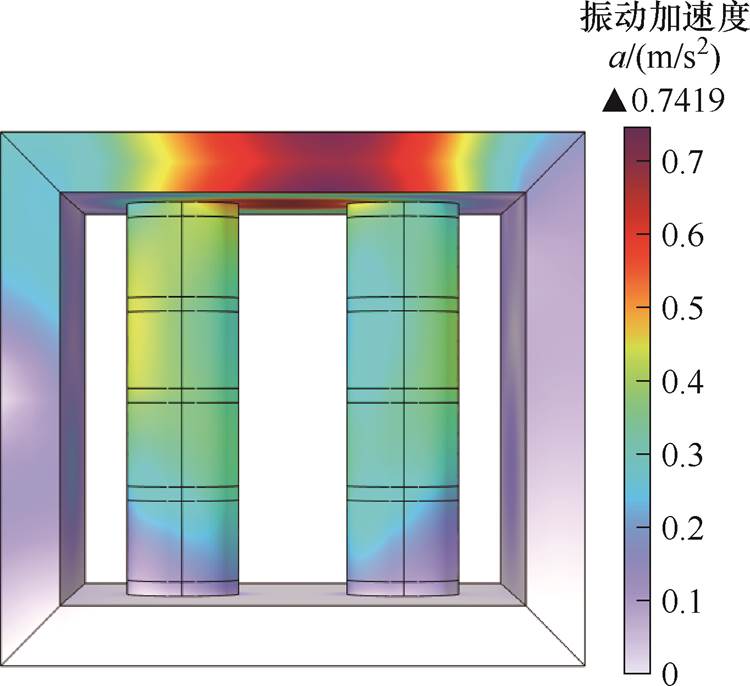
图5 存在公差时的电抗器铁心振动加速度分布
Fig.5 Distribution of vibration acceleration of reactor core with errors
由图3和图5可知，原设计气隙长度下电抗器铁心的最大振动加速度为0.731 8 m/s2，而当铁心柱上的g1、g2气隙存在-0.12 mm的制造公差时，铁心的最大振动加速度为0.741 9 m/s2，明显高于原设计气隙长度下的最大振动加速度，因此气隙结构参数公差的存在会降低电抗器的可靠性。
进一步地，针对气隙结构参数的不确定性对电抗器铁心振动进行定量分析。考虑预紧力的变化更多地反映在电抗器运行工况中的阻尼作用[19]，对气隙结构参数不确定性的影响难以在设计阶段准确预测和量化，因此本文仅考虑制造公差引起的气隙结构参数的不确定性。经与电抗器生产厂家沟通，气隙垫片制造的工程公差允许范围为±1 mm。因此本文假设气隙结构参数的不确定性公差分布符合[-1 mm, 1 mm]内的正态分布函数，保持其余运行和设计参数不变，在[-1 mm, 1 mm]内进行了1 000组各气隙制造公差的随机组合仿真实验。同时，采用核密度估计方法对仿真样本结果进行定量分析。核密度估计提供了一种平滑的概率密度估计曲线，能够更清晰地展示输入不确定性变量时输出结果的分布特征和趋势[20]。当气隙结构参数制造公差符合[-1 mm, 1 mm]的正态分布时，铁心最大振动加速度的核概率密度分布结果如图6所示。
在评估设备或系统的可靠性时，需要设定合适的阈值，以检验系统满足稳定性要求的概率[21]。在不考虑气隙结构参数的不确定性时，本文将电抗器铁心在原设计气隙结构参数下的最大振动加速度0.731 8 m/s2作为可靠阈值。分析图6可知，当气隙结构参数存在±1 mm的不确定性制造公差时，对小于可靠阈值的区域进行积分，最大振动加速度不超过阈值的概率只有67.37%。由此可见，气隙结构参数的不确定性可能会使电抗器振动超出可靠阈值的安全设计范围，从而显著影响电抗器运行的稳定性和可靠性。
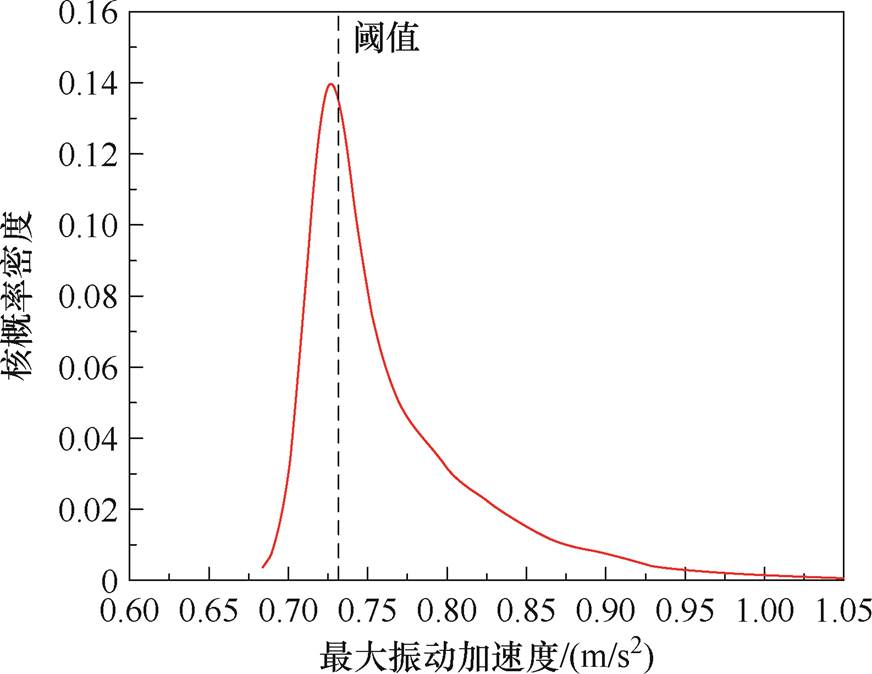
图6 核概率密度分布结果
Fig.6 Kernel density plot
因此，为了提升电抗器铁心在气隙结构参数不确定性条件下的可靠性，需要针对气隙结构参数进行进一步优化设计。
传统的优化方法中假设所有参数是确定性的，相比之下，鲁棒优化考虑了参数的不确定性，尽可能地确保优化方案在参数不确定性朝着“最恶劣”场景发展的情况下，仍然具有良好的性能[22]。以最小化电抗器铁心最大振动加速度amax为目标函数，即
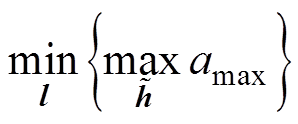（9）
式中，l为待优化变量，即气隙长度；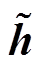
为气隙长度的不确定性变化量。目标函数即为在确保气隙长度存在不确定性的情况下，寻找使得铁心最大加速度最小的气隙长度。经与电抗器生产厂家沟通，本文所设计的电抗器气隙长度可调范围和气隙制造公差分别为
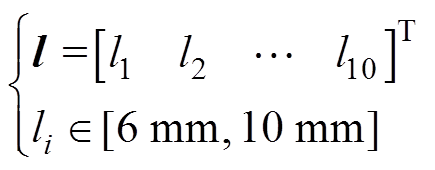（10）
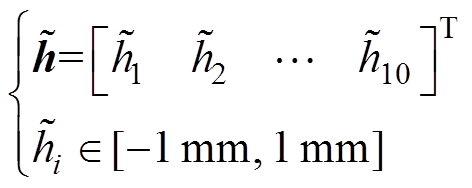（11）
式中，li为第i个气隙的长度，mm；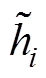
为第i个气隙的气隙长度不确定性变化量，mm。依据国家标准GB/T 1094.6—2011《电力变压器 第6部分：电抗器》对电抗器电感值的要求，额定电压下电抗器的电感偏差应不大于±5%。此外，为避免电抗器铁心产生过高的电磁损耗，保证铁心磁路不发生饱和现象[23]，铁心磁通密度应小于饱和磁通密度。因此，对铁心的电感值L和磁通密度B添加约束为
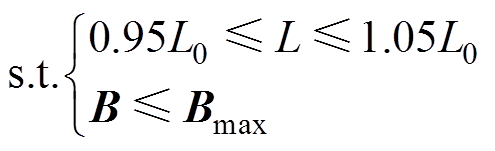（12）
式中，L0为原设计气隙长度的电感值；Bmax为铁心饱和磁通密度。此外，为了满足铁心机械强度的需求，防止出现变形、断裂现象，对铁心的应力s和应变e添加约束，有
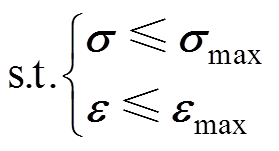（13）
式中，smax为铁心允许的最大应力；emax为铁心允许的最大应变。当不考虑气隙长度的不确定性变化量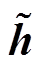时，不确定性鲁棒优化模型降维为确定性优化模型，此时，铁心柱的气隙总长度也应保持不变，即满足约束
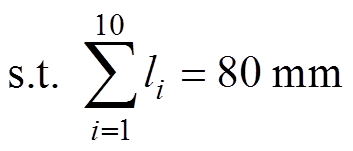（14）
考虑到本文建立的优化模型待优化变量众多，且各气隙结构参数各自对铁心最大振动加速度之间的响应关系尚不明确，直接开展鲁棒优化求解的计算成本庞大。为了同时满足优化求解速度与优化求解精度的需求，本文提出一种对待优化变量的求解空间进行削减的简化方法。
气隙结构参数的变化不仅会单独影响铁心的振动，气隙结构参数之间的交互作用也会对铁心的振动结果产生影响[24]，因此本文使用Sobol灵敏度指标对气隙变量进行筛选。Sobol灵敏度分析能定量评估输入变量的独立影响及各个输入变量之间交互作用对输出响应的贡献度，从而剔除对输出结果影响不明显的变量[25]。Sobol灵敏度分析需要建立代理模型，由于本文研究的气隙变量较多，而代理模型的维度与气隙变量的数量呈指数关系，为降低代理模型的维度，先采用MOAT筛选对气隙变量的数量进行预处理。
2.2.1 MOAT筛选
MOAT筛选是一种有效的变量筛选方法，它通过逐一调整每个输入变量的值，观察输出结果的变化来评估输入变量对模型输出的影响，并按照影响程度的大小对变量排序，为后续的分析和优化提供重要依据[26]。MOAT筛选计算效率高，不需要耗费大量计算资源，对于电抗器这一复杂模型而言，适用于初步筛选对电抗器铁心振动影响较大的气隙结构参数变量，降低代理模型构建的复杂性。
MOAT筛选通过计算每个输入变量的局部效应来量化其对输出结果的具体影响，期望Ei计算式为
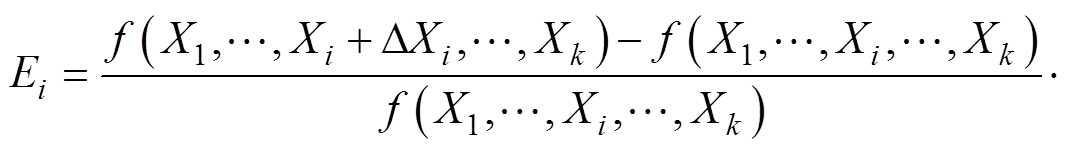
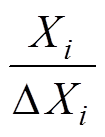（15）
式中，f(·)为模型的输出，本文指电抗器铁心的最大振动加速度；X1,
, Xk为模型的k个输入变量，本文指10个气隙结构参数；DXi为输入变量Xi的扰动幅度，本文指气隙结构参数的不确定性变化量，其分布符合[-1 mm, 1 mm]内的正态分布。通常用平均局部效应的绝对值m反映变量对输出值的平均影响，以衡量变量的整体重要性；用局部效应的标准差d来衡量局部效应的分散程度，反映变量对输出值的非线性影响或相互作用效应，计算式分别为
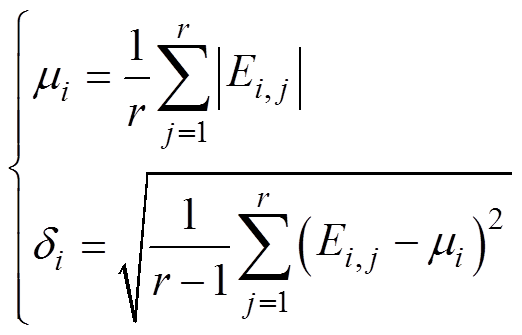（16）
式中，r为对变量Xi的扰动实验次数，结合文献[27]中对多输入变量MOAT筛选样本量的研究，同时为确保筛选结果的可靠性和代表性，本文设置扰动实验次数为4次；Ei, j为第j次扰动实验关于Xi的局部效应。对气隙结构参数进行MOAT筛选的结果如图7所示。
由图7可知，双柱式电抗器两个铁心柱上对称气隙的MOAT指数重合。这是因为两个铁心柱在结构上左右对称、材料参数相同，并且对应的绕组所加电流相同，因此两绕组产生的磁通对称且相同，致使两铁心柱受到的电磁力相同，那么对称气隙变化对铁心振动加速度的影响也相同，所以优化变量可以对称处理，即将g1～g5视作优化变量，g6～g10的优化结果与对称气隙的优化结果一致。
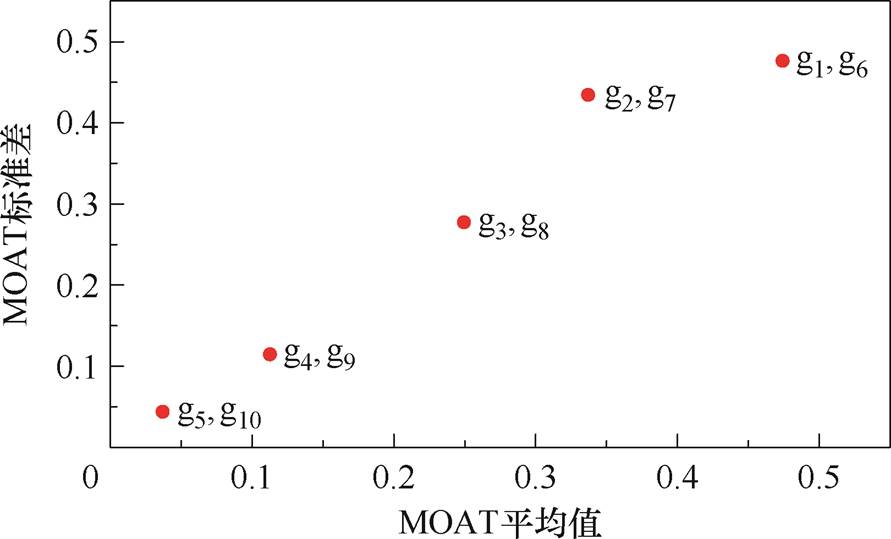
图7 MOAT筛选结果
Fig.7 MOAT screening results
g1、g6气隙的MOAT平均值和标准差最大，而g5、g10气隙的MOAT平均值和标准差最小，这是因为双柱式并联电抗器铁心内的磁通由两绕组产生的磁通共同构成，且电抗器结构对称，导致磁通密度分布上下对称。然而，实际中为了提高电抗器的减振效果，下铁轭会通过定位螺栓与油箱底面紧密固定，由此引入的阻尼作用显著削弱了振动响应。g1、g6气隙位于电抗器铁心柱与上铁轭交界处，受到的阻尼作用小，所以气隙结构参数的改变对振动的影响更大；g5、g10气隙位于电抗器铁心柱与下铁轭交界处，受到的阻尼作用大，所以气隙结构参数的改变对振动的影响很小。
g5、g10气隙的MOAT平均值和标准差均小于0.05，说明该气隙结构参数对铁心振动加速度的影响较小，呈现较低的灵敏度，按照定性分析的结果可以将该不灵敏参数剔除[28]，为Sobol灵敏度定量分析所需的代理模型构建减少输入参数，从而提升计算效率。
2.2.2 Sobol分析
Sobol分析是一种基于方差分解的全局灵敏度分析方法，旨在量化各输入变量及其交互项对模型输出方差的贡献，从而评估每个输入变量的重要程度[29]。当气隙结构参数存在[-1 mm, 1 mm]的不确定性制造公差时，首先基于多项式混沌展开（Polynomial Chaos Expansion, PCE）方法建立可用于计算铁心最大振动加速度的代理模型[30]，基于文献[31]中Sobol灵敏度分析的采样原则，随机抽取10 000组符合正态分布的气隙结构参数制造公差组合，并将其作为输入量计算代理模型的响应值。在此基础上，通过Sobol灵敏度指标分析每个气隙结构参数对铁心最大振动加速度的灵敏度。本文采用主效应指数Si和总效应指数STi作为Sobol灵敏度分析指标，其表达式分别为
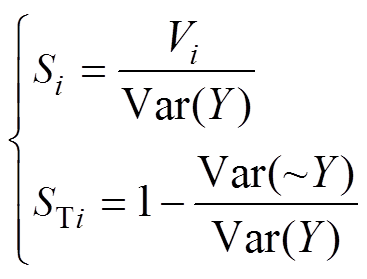（17）
式中，Vi为第i个参数单独作用所引起的输出方差；Y为代理模型输出的响应值；Var(Y)为输出Y的总方差；Var(~Y)为不考虑第i个参数对输出的影响时，输出的剩余方差。
主效应指数Si反映了输入的每个气隙结构参数的不确定性变化对铁心最大振动加速度的独立影响。总效应指数STi反映了输入的每个气隙结构参数的不确定性变化对铁心最大振动加速度的总体影响，包括它单独的贡献和与其他输入变量交互作用时的影响。本文所设计电抗器的气隙结构参数对铁心最大振动加速度的Sobol灵敏度分析结果如图8所示。
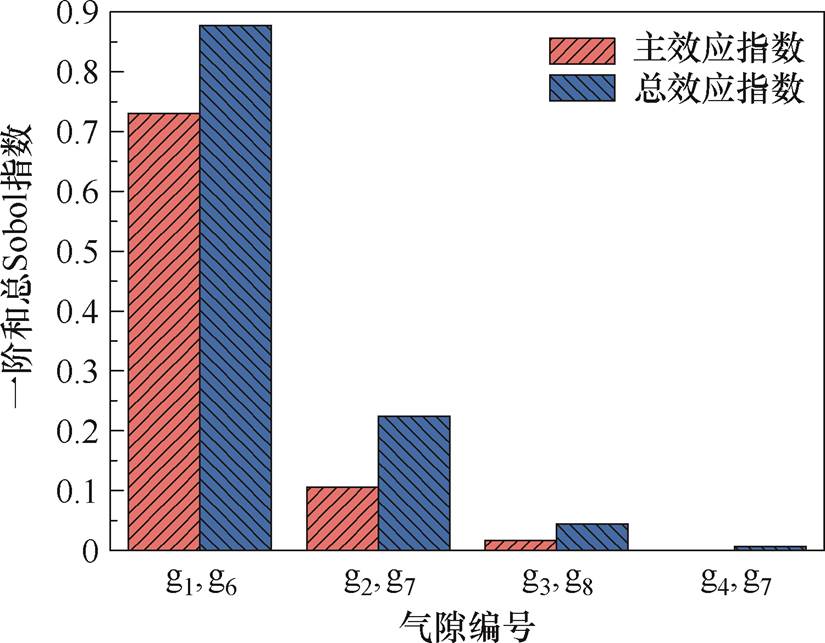
图8 Sobol灵敏度指标分析结果
Fig.8 Sobol sensitivity index results
由图8可知，g1、g6的主效应指数和总效应指数都最大，这是因为该气隙长度的改变不仅直接影响磁通密度，还会导致气隙位置的变化，从而进一步影响磁通密度的分布，引起电磁力分布的显著变化。此外，上铁轭区域的结构阻力较小，电磁力能够更有效地驱动振动响应，因此气隙结构参数的变化对铁心最大振动加速度的影响程度最为显著。
g4、g9的主效应指数和总效应指数都非常小，这是因为下铁轭区域的电抗器受到固定支撑的约束。气隙结构参数的变化会引起电磁力的变化，但支撑结构产生的阻力也会随电磁力的变化而变化，阻力的存在显著削弱了电磁力对振动响应的驱动作用，从而使气隙结构参数变化对铁心最大振动加速度的影响程度较低。根据文献[32]的灵敏度指标阈值选取原则，可以选取综合灵敏度数值不低于0.05的变量作为优化变量。在此基础上，结合2.2.1节中的分析结果，两铁心柱上对称气隙（g1/g6、g2/g7、g3/g8、g4/g9、g5/g10）的参数变化对铁心振动加速度的影响相同，选择g1、g2、g3作为不确定性鲁棒优化的优化变量，其余气隙结构参数则保持原设计值不变。
将降维后的变量与表1给出的参数值代入所构建的电抗器铁心振动不确定性鲁棒优化模型，采用二次逼近边界优化算法（Bound Optimization BY Quadratic Approximation, BOBYQA）与有限元仿真模型联立求解。设置最大迭代次数为1 000次，收敛误差阈值为0.005，收敛判断条件为鲁棒性大于95%。当收敛误差低于0.005且满足收敛条件时，迭代结束，寻得最优鲁棒优化方案；否则，继续下一次迭代过程。具体的鲁棒优化过程如图9所示。
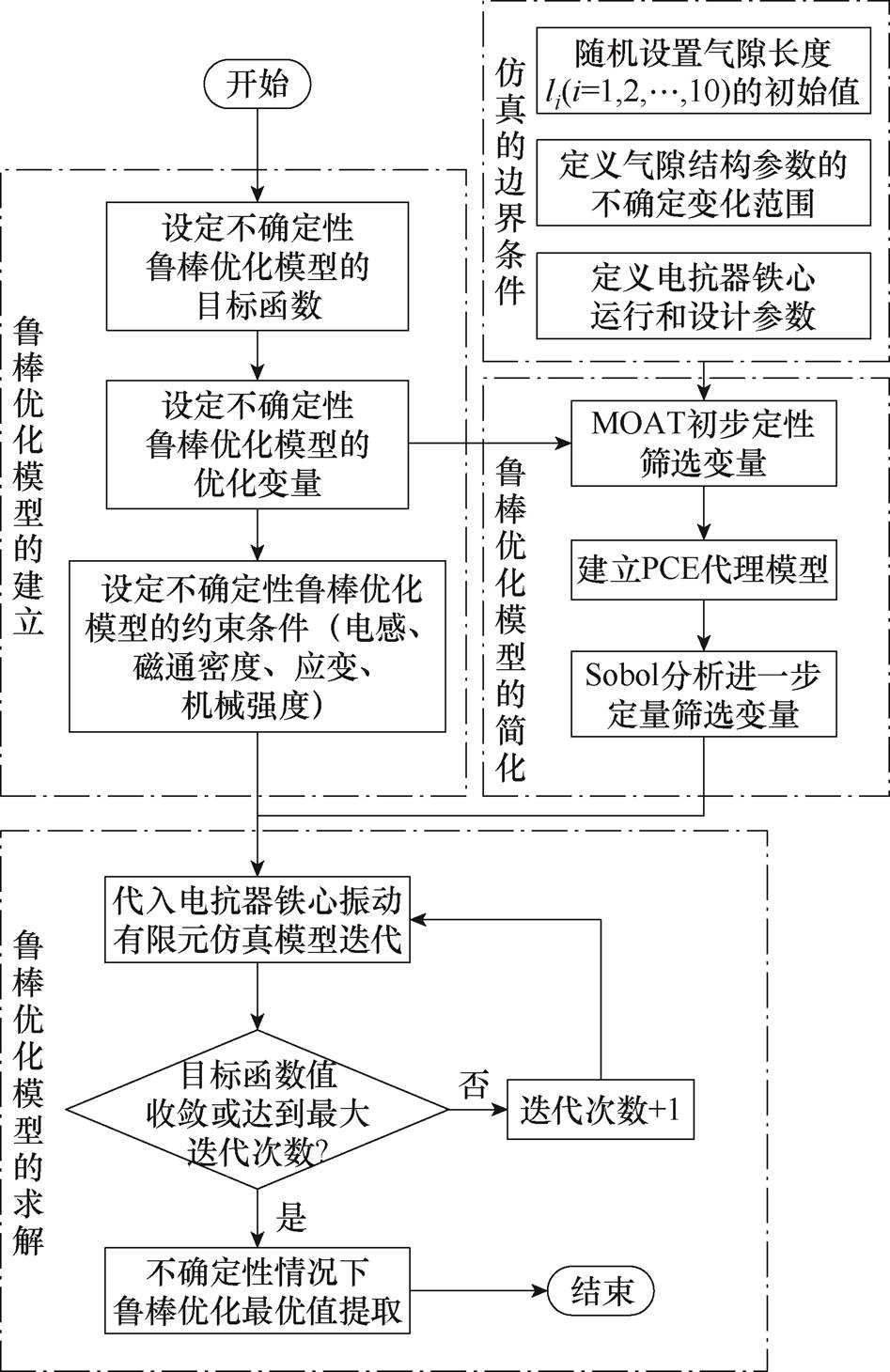
图9 不确定性鲁棒优化过程
Fig.9 Process of robust optimization under uncertainty
对比原设计长度、确定性优化和不确定性鲁棒优化的优化结果，得到气隙结构参数如图10所示，将优化后的气隙结构参数代入电抗器有限元仿真模型，所得铁心最大振动加速度的优化结果见表3。
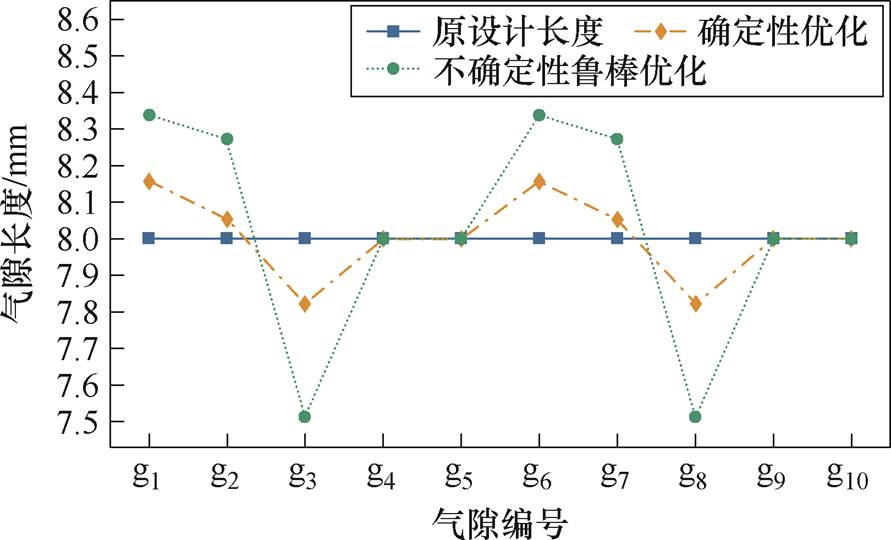
图10 不同优化方案下的气隙结果
Fig.10 Gap results under different optimization schemes
表3 不同优化方案下的振动加速度
Tab.3 Vibration acceleration under different optimization schemes
优化模型最大振动加速度/(m/s2) 原设计长度0.731 8 确定性优化0.707 7 不确定性鲁棒优化0.708 6
由表3可知，确定性优化方法和不确定性鲁棒优化都能一定程度地减小电抗器铁心的最大振动加速度。这是因为气隙结构参数的改变会改变铁心内的磁通密度分布，从而改变麦克斯韦力和磁致伸缩力的大小和作用位置，进而影响铁心受到的电磁力，并由此改变电抗器铁心的振动加速度。确定性优化和不确定性鲁棒优化这两种优化方法都增大了g1气隙的长度，从而减小了g1下方铁心饼的长度，减小了该区域的磁通密度和铁磁性材料的体积。由此减小了电磁力的大小，降低了该区域的振动加速度，同时由于铁心最大振动加速度点位于该区域，进而降低了铁心的最大振动加速度。
虽然在气隙结构参数存在不确定性的情况下，相较于原设计长度，基于确定性优化法的减振效率为3.29%，基于鲁棒优化的减振效率为3.17%，在确定性优化得到的气隙结构参数下的铁心最大振动加速度小于不确定性鲁棒优化的结果，但是基于确定性方法的优化结果忽视了不确定性因素对优化结果鲁棒性的影响。电抗器气隙结构参数的不确定性在工程中普遍存在，实际的气隙结构参数会在确定性优化方案的结果附近波动，从而导致铁心最大振动加速度发生大幅度改变，与预期的优化效果相差甚远。沿用1.2.1节的特例分析，假设铁心柱上的g1、g2气隙仍存在-0.12 mm的制造公差，其余电抗器运行和设计参数保持不变，基于确定性方法和不确定性方法的优化方案在面对上述公差时，电抗器铁心加速度分布分别如图11a和图11b所示。
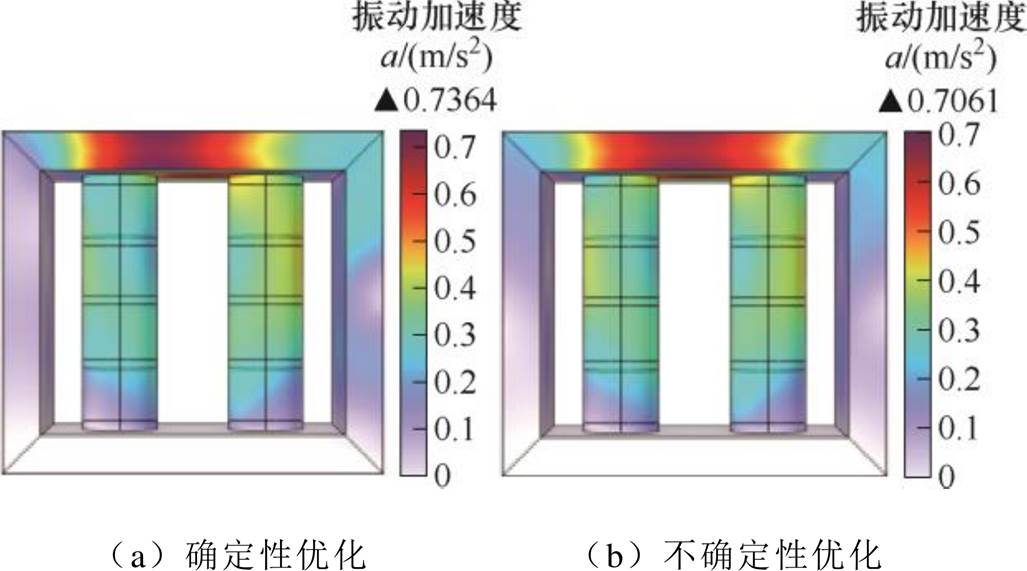
图11 铁心振动加速度分布
Fig.11 Distribution of vibration acceleration of core
由图5和图11可知，当g1、g2气隙存在-0.12 mm的制造公差时，确定性优化方案的铁心最大振动加速度为0.736 4 m/s2，甚至超过了气隙存在相同不确定性公差时基于原设计长度优化方案所得的最大振动加速度；而不确定性优化的铁心最大振动加速度为0.706 1 m/s2，低于气隙存在相同不确定性公差时基于原设计长度优化方案的值。这表明基于确定性优化所得的方案仅在面对气隙结构参数完全符合设计方案的成品设备时呈现较好的减振效果；而对气隙结构参数不确定性的微小扰动减振效果较差。基于不确定性优化的方案则在面对气隙结构参数扰动时，仍能保持一定的减振能力。因此，若不考虑生产过程中无法避免的制造公差影响，仅以气隙结构参数完全符合优化设计值时的铁心最大振动加速度作为选择优化方案的依据，基于确定性优化的设计方案在工程实际中应用时会存在诸多超预期问题。
进一步地，针对气隙结构参数的不确定性对两种优化方案下的铁心振动进行分析。仍设置气隙结构的不确定性公差满足[-1 mm, 1 mm]内的正态分布，保持其余运行和设计参数不变，在不确定性变化范围内分别对两种优化方案进行了1 000组各气隙不确定性公差随机组合的仿真实验。同样使用核密度估计处理样本结果，得到两种优化方案的核概率密度分布结果如图12所示。
仍以原设计气隙结构参数下仿真得到的铁心最大振动加速度为阈值条件，结合核概率密度分布分析，得到原设计长度和两种优化方案在气隙结构参数存在±1 mm的不确定性公差时，满足阈值条件的概率见表4。
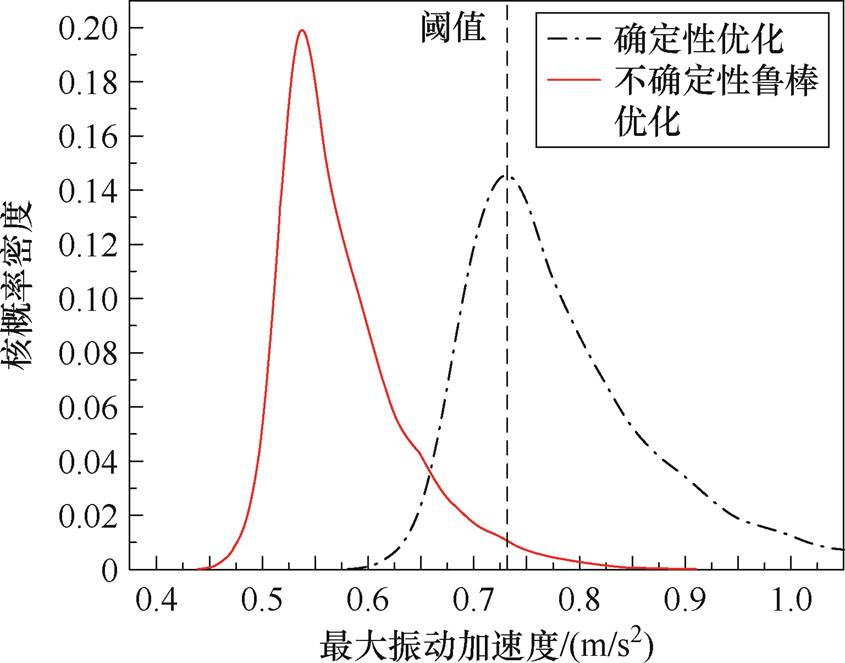
图12 优化核概率密度分布对比
Fig.12 Comparison of optimized kernel density distribution
表4 不同优化方案下的鲁棒性
Tab.4 Robustness under different optimization schemes
优化模型条件概率(%) 原设计长度67.37 确定性优化44.21 不确定性鲁棒优化97.34
由表4可知，确定性优化方法虽然可以减小确定性情况下的铁心最大振动加速度，但也会降低减振效果的鲁棒性。当气隙结构参数存在1 mm的不确定性时，该方法的优化结果满足阈值条件的概率仅有44.21%。而应用不确定性鲁棒优化后的优化结果满足阈值条件的概率为97.34%，与原设计长度方案相比提升了29.97个百分点，与确定性优化方案相比提高了53.13个百分点，显著提高了电抗器面对制造公差导致的气隙结构参数的不确定性分布下减振效果的鲁棒性，更符合电抗器铁心减振优化的工程实际，大幅降低了电抗器振动超标的风险。
本文研究了气隙结构参数不确定性对电抗器铁心振动特性的影响，提出了基于气隙结构参数的不确定性鲁棒优化策略，具体结论如下：
1）气隙结构参数的不确定性对电抗器铁心最大振动加速度有较大影响，会显著降低电抗器结构设计的可靠性。当气隙结构参数存在±1 mm的不确定性时，满足原设计值下铁心最大振动加速度安全阈值的条件概率只有67.37%。
2）提出了一种计及结构参数不确定性的电抗器铁心减振优化设计方案，能够显著提高优化设计结构的鲁棒性，相较于确定性优化方法，不确定性鲁棒优化方法的优化结果将满足电抗器可靠运行的条件概率从44.21%提高到了97.34%，提升效果显著。
参考文献
[1] 贲彤, 方敏, 陈龙, 等. 非晶合金铁心电抗器减振结构的电磁-机械耦合拓扑优化[J]. 电工技术学报, 2023, 38(24): 6553-6564.
Ben Tong, Fang Min, Chen Long, et al. Optimization of magnetic-mechanical coupling topology for vibration damping structures of amorphous alloy core reactor[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6553-6564.
[2] 廖文龙, 杨玥坪, 魏华超, 等. 饱和电抗器用环氧树脂性能提升研究[J]. 绝缘材料, 2024, 57(5): 42-48.
Liao Wenlong, Yang Yueping, Wei Huachao, et al. Study on performance enhancement of epoxy resin for saturated reactor[J]. Insulating Materials, 2024, 57(5): 42-48.
[3] 闫荣格, 程云飞. 动静态力共同作用对电抗器铁心振动影响[J]. 电工技术学报, 2023, 38(4): 1104-1114.
Yan Rongge, Cheng Yunfei. Influence of dynamic and static forces on vibration of reactor core[J]. Trans- actions of China Electrotechnical Society, 2023, 38(4): 1104-1114.
[4] 刘云鹏, 来庭煜, 刘嘉硕, 等. 特高压直流换流阀饱和电抗器振动声纹特性与松动程度声纹检测方法[J]. 电工技术学报, 2023, 38(5): 1375-1389.
Liu Yunpeng, Lai Tingyu, Liu Jiashuo, et al. Vibration voiceprint characteristics and looseness detection method of UHVDC converter valve saturable reactor[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1375-1389.
[5] 杨帆, 张相杰, 王鹏博, 等. 特高压并联电抗器铁芯振动及噪声特征研究[J]. 高电压技术, 2024, 50(2): 725-736.
Yang Fan, Zhang Xiangjie, Wang Pengbo, et al. Study on the vibration and noise characteristics of the iron core in ultra-high voltage shunt reactor[J]. High Voltage Engineering, 2024, 50(2): 725-736.
[6] 袁发庭, 陈步康, 陈炜, 等. 基于电磁-结构力场耦合的铁芯电抗器振动特性分析及优化方法[J]. 高电压技术, 2023, 49(6): 2374-2385.
Yuan Fating, Chen Bukang, Chen Wei, et al. Vibration characteristic analysis and optimization method of iron core reactor based on electromagnetic- structural force field coupling[J]. High Voltage Engineering, 2023, 49(6): 2374-2385.
[7] 郭佳熠, 耿江海, 律方成, 等. 基于气隙结构的特高压并联电抗器铁芯减振技术[J]. 高电压技术, 2021, 47(11): 3892-3901.
Guojia Yi, Geng Jianghai, Lü Fangcheng, et al. Vibration reduction technology of UHV shunt reactor core based on air gap structure[J]. High Voltage Engineering, 2021, 47(11): 3892-3901.
[8] 王革鹏, 金文德, 曾向阳, 等. 特高压并联电抗器铁心振动的分析与控制研究[J]. 电工技术学报, 2022, 37(9): 2190-2198.
Wang Gepeng, Jin Wende, Zeng Xiangyang, et al. Analysis and control research on core vibration of UHV shunt reactor[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2190-2198.
[9] 于全毅, 刘长英, 吴定超, 等. 基于广义混沌多项式法的多导体传输线辐射敏感度分析方法[J]. 电工技术学报, 2020, 35(17): 3591-3600.
Yu Quanyi, Liu Changying, Wu Dingchao, et al. Radiation sensitivity analysis of multiconductor transmission lines based on generalized polynomial chaos method[J]. Transactions of China Electro- technical Society, 2020, 35(17): 3591-3600.
[10] 王洪耀, 张英敏, 廖建权, 等. 基于阻抗灵敏度分析的柔直并网系统中高频谐振抑制策略[J]. 电网技术, 2023, 47(10): 4311-4323.
Wang Hongyao, Zhang Yingmin, Liao Jianquan, et al. Medium-and high-frequency resonance suppression strategy in flexible direct grid connected system based on impedance sensitivity analysis[J]. Power System Technology, 2023, 47(10): 4311-4323.
[11] 何畅, 何紫薇, 江力强, 等. 多重不确定性对特高压变压器瓷套管地震失效风险的影响[J]. 中国电机工程学报, 2022, 42(15): 5763-5775.
He Chang, He Ziwei, Jiang Liqiang, et al. Effects of different sorts of uncertainties on seismic failure risk of ultra-high-voltage porcelain transformer bushing[J]. Proceedings of the CSEE, 2022, 42(15): 5763-5775.
[12] 王岑峰, 王蕾, 孙飞飞, 等. 基于模糊逻辑控制的混合储能辅助风电调频的双层优化配置模型[J]. 高压电器, 2024, 60(10): 54-63.
Wang Cenfeng, Wang Lei, Sun Feifei, et al. Two- layer optimal configuration model of hybrid energy storage assisted wind power frequency regulation based on fuzzy logic control[J]. High Voltage Apparatus, 2024, 60(10): 54-63.
[13] 张伟骏, 李智诚, 陈大玮, 等. 配网侧分布式储能系统的随机优化配置和选址方法[J]. 高压电器, 2023, 59(7): 125-135.
Zhang Weijun, Li Zhicheng, Chen Dawei, et al. Stochastic optimal configuration and site selection method of grid-side distributed energy storage system [J]. High Voltage Apparatus, 2023, 59(7): 125-135.
[14] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485.
Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[15] 刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022, 4307.
Liu Yixin, Guo Li, Wang Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022, 4307.
[16] 龚夕霞, 李焱鑫, 卢琴芬. 模块化永磁直线同步电机考虑制造公差的推力鲁棒性优化[J]. 电工技术学报, 2024, 39(2): 465-474, 513.
Gong Xixia, Li Yanxin, Lu Qinfen. Thrust robustness optimization of modular permanent magnet linear synchronous motor accounting for manufacture tolerance[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 465-474, 513.
[17] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Trans- actions of China Electrotechnical Society, 2018, 33(22): 5273-5281.
[18] Xu Yijun, Netto M, Mili L. Propagating parameter uncertainty in power system nonlinear dynamic simulations using a Koopman operator-based surrogate model[J]. IEEE Transactions on Power Systems, 37(4): 3157-3160.
[19] 闫荣格, 赵路娜, 贲彤, 等. 70基于负超磁致伸缩效应电抗器减振新方法的研究[J]. 振动与冲击, 2018, 37(19): 254-258.
Yan Rongge, Zhao Luna, Ben Tong, et al. A new vibration reduction method for reactors using NGMM[J]. Journal of Vibration and Shock, 2018, 37(19): 254-258.
[20] Hu Bo, Li Yudun, Yang Hejun, et al. Wind speed model based on kernel density estimation and its application in reliability assessment of generating systems[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(2): 220-227.
[21] 杨汾艳, 李海波, 盛超, 等. 多端口级联式电力电子变压器可靠性评估模型及其应用[J]. 电力系统保护与控制, 2019, 47(20): 41-49.
Yang Fenyan, Li Haibo, Sheng Chao, et al. Reliability evaluation model of cascaded multiport power electronic transformer and its application[J]. Power System Protection and Control, 2019, 47(20): 41-49.
[22] 张献, 丁可浩, 赵黎媛, 等. 计及电动汽车混合充电系统接入的综合能源系统鲁棒优化调度[J]. 电工技术学报, 2025, 40(14): 4446-4459.
Zhang Xian, Ding Kehao, Zhao Liyuan, et al. Robust optimal scheduling of integrated energy system considering electric vehicle hybrid charging system[J]. Transactions of China Electrotechnical Society, 2025, 40(14): 4446-4459.
[23] 袁发庭, 吕凯, 刘健犇, 等. 基于电磁-热-结构多物理场耦合的铁心电抗器线圈结构优化方法[J]. 电工技术学报, 2022, 37(24): 6431-6441.
Yuan Fating, Lü Kai, Liu Jianben, et al. Coil structures optimization method of iron core reactor based on electromagnetic-thermal-structure multi- physical field coupling[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6431-6441.
[24] 袁发庭, 曾继皓, 姜岚, 等. 基于多物理场仿真和VIKOR决策的干式铁心电抗器多目标优化[J]. 工程科学与技术, 2023, 55(4): 67-78.
Yuan Fating, Zeng Jihao, Jiang Lan, et al. Multi- objective optimization of the dry core reactor based on multi-physical field simulation and VIKOR decision[J]. Advanced Engineering Sciences, 2023, 55(4): 67-78.
[25] 王长江, 姜涛, 刘福锁, 等. 基于轨迹灵敏度的暂态过电压两阶段优化控制[J]. 电工技术学报, 2021, 36(9): 1888-1900, 1913.
Wang Changjiang, Jiang Tao, Liu Fusuo, et al. Two- stage optimization control of transient overvoltage basedon trajectory sensitivity[J]. Transactions of China Elec- trotechnical Society, 2021, 36(9): 1888-1900, 1913.
[26] Morris M D. Factorial sampling plans for preliminary computational experiments[J]. Technometrics, 1991, 33(2): 161-174.
[27] 陈季凌, 唐进元, 杨铎. 齿面粗糙度参数与接触应力的敏感性分析研究[J]. 西北工业大学学报, 2022, 40(4): 883-891.
Chen Jiling, Tang Jinyuan, Yang Duo. Study on sensitivity analysis of tooth surface roughness parameters and contact stress[J]. Journal of Northwes- tern Polytechnical University, 2022, 40(4): 883-891.
[28] 刘建锋, 陈乐乐, 姚晨曦. 基于SRSM模型的变压器电气参数对绕组变形的敏感性分析[J]. 电力科学与技术学报, 2023, 38(4): 93-103.
Liu Jianfeng, Chen Lele, Yao Chenxi. Sensitivity analysis of transformer electrical parameters to winding deformation based on SRSM method[J]. Journal of Electric Power Science and Technology, 2023, 38(4): 93-103.
[29] Sobol’ I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates [J]. Mathematics and Computers in Simulation, 2001, 55(1/2/3): 271-280.
[30] Blatman G, Sudret B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis[J]. Probabilistic Engineering Mechanics, 2010, 25(2): 183-197.
[31] 李妍, 周洪伟, 沈小伟, 等. 电力变压器绕组电气参数对绕组变形的全局灵敏度分析[J]. 电力系统保护与控制, 2018, 46(7): 31-37.
Li Yan, Zhou Hongwei, Shen Xiaowei, et al. Global sensitivity analysis of winding electrical parameters on power transformer winding deformation[J]. Power System Protection and Control, 2018, 46(7): 31-37.
[32] 刁凯凯, 孙晓东, 杨泽斌. 开关磁阻电机系统级确定性与鲁棒性优化设计方法的对比分析[J]. 中国电机工程学报, 2023, 43(9): 3575-3586.
Diao Kaikai, Sun Xiaodong, Yang Zebin. Compara- tive analysis of system-level deterministic and robust optimization design methods for switched reluctance motors[J]. Proceedings of the CSEE, 2023, 43(9): 3575-3586.
Abstract Reactors are essential equipment for maintaining the safe and stable operation of AC power grids, and excessive vibration is a major challenge in reactor operation. The core is the primary source of vibration in reactors, and core vibration damping technology plays a crucial role in the stability and reliability of reactor operation. Existing methods for vibration reduction optimization of reactor core are typically based on deterministic parameters, without adequately accounting for structural parameter uncertainties introduced by factors such as manufacturing tolerances. This limitation can undermine the reliability of optimization strategies in practical applications and may fail to effectively mitigate core vibrations. To address this challenge, this study uses the maximum vibration acceleration of the core as a key performance indicator, systematically examining the effects of gap structural parameter uncertainties on the vibration characteristics of reactor core, and a robust optimization method is proposed to account for these uncertainties.
Firstly, this paper qualitatively analyzed the impact of gap structural parameter uncertainties on reactor core vibrations from a theoretical perspective. Subsequently, a finite element simulation model was established based on the actual operating and design parameters of the reactor. The kernel density estimation method was used to quantitatively evaluate the probability of reliable operation, ensuring that the vibration acceleration of the reactor core does not exceed the original design value under ±1 mm uncertainty in gap structural parameters. Based on the results of the uncertainty analysis, a robust optimization model for reactor core vibration damping was developed, aiming to minimize the maximum vibration acceleration of the core. The model incorporated multiple constraints, including gap length, inductance, and magnetic flux density, to reflect actual operating conditions. By integrating the Morris one-at-a-time (MOAT) screening method and Sobol global sensitivity indices, the solution space of the optimization variables was reduced, and the model was solved using the bound optimization by quadratic approximation (BOBYQA) algorithm, resulting in a robust optimization scheme for reactor core vibration damping. The results indicate that the proposed optimization scheme significantly improves the robustness of reactor core vibration optimization under uncertain disturbances. The optimized reactor core achieves a 97.34% probability of meeting reliable operation requirements for maximum vibration acceleration, making it more suitable for practical engineering applications. This paper provides a reference for the research and design of reactor core vibration reduction optimization considering uncertainty factors.
The following conclusions are drawn from simulations and experiments: (1) Gap structural parameter uncertainties have a significant impact on the maximum vibration acceleration of reactor core, substantially reducing the reliability of reactor structural designs. Under ±1 mm uncertainty in gap structural parameters, the conditional probability of meeting the safety threshold of the maximum vibration acceleration of the core under the original design value is only 67.37%. (2) This paper proposes a reactor core vibration reduction optimization design scheme that accounts for structural parameter uncertainties, significantly enhancing the robustness of the optimized design. Compared to deterministic optimization methods, the robust optimization approach increases the conditional probability of reliable reactor operation from 44.21% to 97.34%, demonstrating a remarkable improvement.
keywords：Uncertainty analysis, reactor core, vibration reduction, robust optimization
DOI: 10.19595/j.cnki.1000-6753.tces.242255
中图分类号：TM472
河北省教育厅科学研究项目（ZC2025078）和中央高校基本科研业务费专项资金项目（2024MS105）资助。
收稿日期 2024-12-16
改稿日期 2025-01-24
郭佳熠 男，1992年生，博士，讲师，研究方向为高电压与绝缘技术、特高压并联电抗器本体质量提升。E-mail: guojiayi@ncepu.edu.cn
刘雨濛 女，1992年生，博士，讲师，研究方向为电力系统中不确定性建模与优化。E-mail: lym_yomand@163.com（通信作者）
（编辑 李 冰）