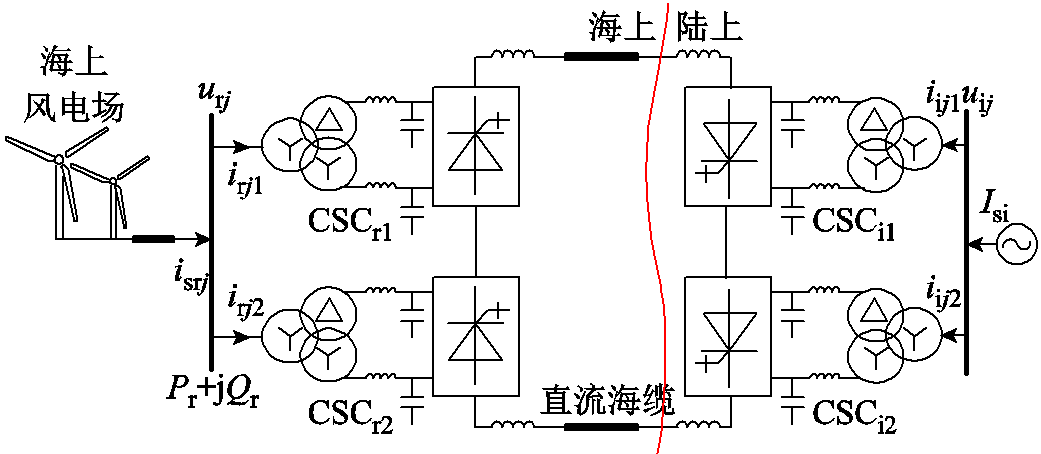
图1 基于EFFM-CSC的海上风电送出系统
Fig.1 Offshore wind power transmission system based on EFFM-CSC
摘要 基频调制电流源换流器（FFM-CSC）是实现海上风电直流送出的新型拓扑。但FFM-CSC的特征谐波含量大，依赖LC滤波器进行补偿，增加了海上平台的体积和重量。同时，其单一控制自由度无法独立控制海上交流母线的电压和频率。改进基频调制CSC（EFFM-CSC）在FFM-CSC基础上，引入补偿角，具备两个控制自由度，其控制海上交流电压的能力亟待发掘。针对CSC送出系统的谐波含量大、LC参数优化和海上电压控制的问题，该文提出一种高低阀移相控制策略的EFFM-CSC用于远海风电直流送出系统。首先，分析普通双12脉动CSC的谐波传递特性，根据移相多重化的思路，提出高低阀触发角移相15°的方法。其次，通过数学推导和谐波传递规律，分析移相EFFM-CSC谐波特性，其不依赖移相15°变压器，即可大幅降低11、13次谐波含量。在此基础上，综合考虑滤波效果、电容电压及体积和重量，提出LC参数优化设计方法，实现LC滤波器轻型化。同时，通过探究海上电压幅值频率与控制量之间的单调规律，设计出海上交流电压控制策略。最后搭建PSCAD仿真模型和物理实验平台，验证了移相EFFM-CSC的工作原理和控制策略的正确性。
关键词：海上风电 电流源换流器 高低阀移相 轻型化
大规模开发海上风电是支撑我国“双碳”战略目标实现的重要措施之一[1-2]。随着海上风电发展走向深远海，高压直流输电是远海风电送出的具有竞争力的输电技术[3-4]。目前世界上的海上风电经直流并网工程，主要采用模块化多电平换流器（Modular Multilevel Converter, MMC）的拓扑[5]。但是，MMC由功率子模块构成，其中储能电容占子模块体积的60%，随着容量的不断提升，海上换流器的体积和重量大的问题尤为突出，造成海上平台建设成本高的难题[6-7]。海上风电经二极管整流器（Diode Rectifier, DR）送出方案，可有效地降低建设成本和开关损耗[8-9]。但是DR不具备控制能力，需要采用构网型风电机组，并且DR不能逆变工作，不具备黑启动能力[10-12]。同时DR需要配置大规模的滤波器组和无功补偿设备[13]，会显著增加海上换流平台的体积和重量。
主动换相型电流源换流器（Current Source Converter, CSC）由逆阻型IGCT构成的12脉动换流器和阀出口LC滤波器组成，兼具LCC和MMC的部分优势，如没有换相失败问题，没有大量储能电容等，具有体积小、重量轻、控制灵活的优点，适用于远海风电送出[14-15]。文献[16-17]提出基于基频调制（Fundamental Frequency Modulation, FFM）的电流源换流器。该方法开关频率低、直流电压波动小，但是仅具有一个控制自由度，无法独立控制海上汇集系统稳定运行。并且，LC滤波器需要补偿FFM-CSC的吸收无功和滤除特征谐波，限制了海上平台的轻型化效果。因此，如何降低CSC的谐波含量，优化滤波器设计方法，以及独立控制海上交流系统的稳定运行，成为海上风电CSC送出系统的核心问题。
对于海上风电CSC送出系统和DR送出系统共性的谐波含量和滤波器优化问题，有相关学者进行了研究。文献[18]提出利用风电机组的滤波器和无功输出能力，对DR进行无功和谐波补偿，但是风电机组输出无功功率有限，且容易造成海上交流电压越限。文献[19]利用移相多重化的思路，提出基于24脉动的海上风电DR-HVDC系统，对其谐波特性进行分析，可大幅度降低谐波电流含量，减少滤波器和无功补偿设备的容量，但是高电压大容量的移相15°变压器的制造难度和成本会制约该方案的实际工程应用[20]。上述技术思路均存在工程可行性的困难，无法适用于海上风电CSC送出系统。
对于海上交流系统独立控制的问题，文献[21]针对基于FFM-CSC的远海风电送出系统，提出一种风电机组和海上CSC的协调控制策略。但该控制方法依赖大规模通信，且需要改造风电机组。同时LC滤波器需要补偿FFM-CSC的吸收无功和滤除特征谐波，存在进一步的轻型化空间。文献[22]提出一种基于海上CSC和陆上CSC协调的海上电压控制策略，该方法虽能实现海上电压幅值和频率的稳定控制，但是会限制陆上CSC的控制灵活度和运行方法，并且海陆换流站之间也需要通信。文献[23]提出改进基频CSC（Enhanced Fundamental Frequency Modulation, EFFM-CSC），具有两个控制自由度，更适用于海上风电送出场景。但是该文仅对调制方法进行了详细讨论，亟待研究分析基于EFFM-CSC的海上风电送出系统及其控制策略。
为进一步提升海上CSC的轻型化效果，并且不依赖通信手段和构网风机，实现海上交流系统的稳定控制，本文提出一种基于高低阀移相EFFM-CSC的海上风电直流送出系统。首先构建系统谐波传递等值模型，分析谐波传递特性和谐波含量；其次，提出LC参数优化方法，提升海上CSC的功率密度；同时，建立海上交流电压幅值和频率数学模型，通过单调性分析，设计海上交流电压控制策略；最后，通过PSCAD仿真模型和物理实验分析，验证移相EFFM-CSC的工作原理和谐波传递特性的正确性以及海上交流电压/频率控制策略的有效性。
本文提出基于EFFM-CSC远海风电直流送出系统如图1所示。海上风电场输出电能汇集至海上平台，经过海上换流站后通过直流海缆输送至陆地，再经过陆上CSC接入岸上电网。海陆换流站均由两个12脉动CSC串联组成，其中CSCr(i)1(2)为单12脉动拓扑，下角标r和i分别代表整流和逆变，下角标1和2分别代表高、低12脉动阀组。海上风电直流送出场景下对称双极接线方式存在设备数量多、接线复杂和工程造价高的缺点[24]，因此，本文所提系统采用的是对称单极接线方式。
图1 基于EFFM-CSC的海上风电送出系统
Fig.1 Offshore wind power transmission system based on EFFM-CSC
图2为整流侧高阀组CSCr1的详细拓扑，由两个6脉动CSC组成。每个6脉动CSC含有6个桥臂，每个桥臂由可承受反压的逆阻型IGCT构成，直流出口串联平波电抗Ldc，交流出口串联LC滤波器，经过换流变压器连接电网。LC滤波器为换相电流提供通路，并对电流谐波进行滤除。
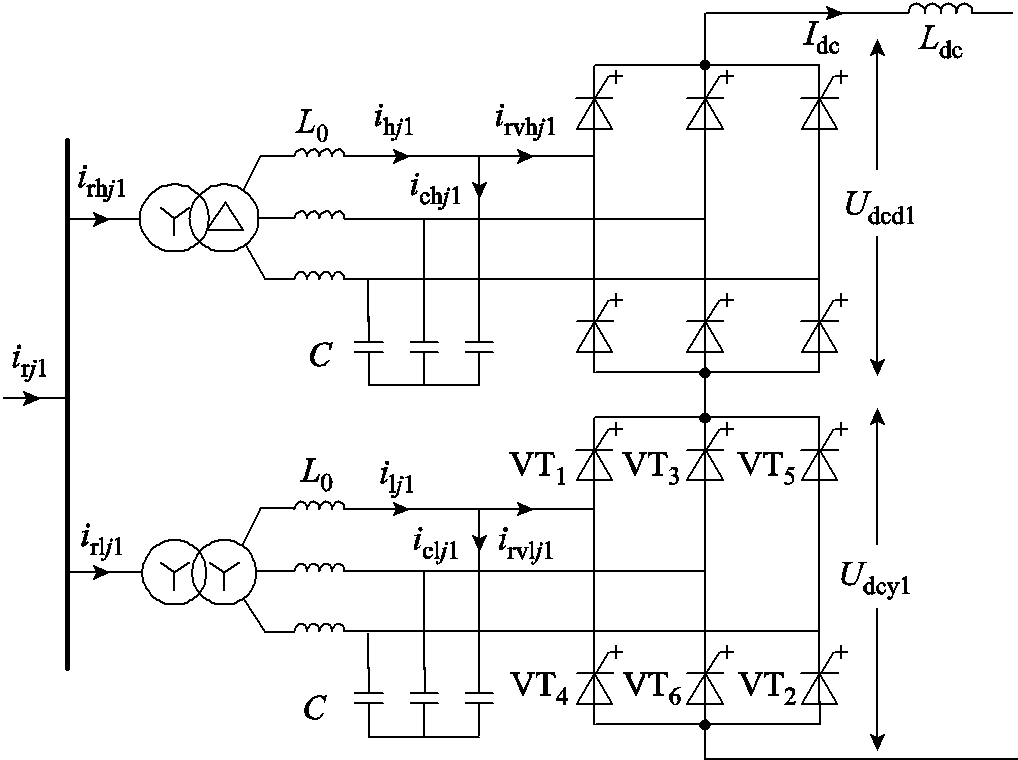
图2 CSCr1的详细拓扑
Fig.2 The detailed topology of CSCr1
对于图1和图2中的电流分量，下角标h和l分别对应星形-三星形（Yd）和星形-星形（Yy）联结变压器所连接的6脉动CSC，j对应相单元（j=a, b, c）。对于高阀组CSCr1，irvhj1和irvlj1分别表示星形-三星形（Yd）和星形-星形（Yy）变压器所连接6脉动CSC阀出口j相电流；irhj1和irlj1分别表示星形-三星形（Yd）和星形-星形（Yy）变压器的一次侧j相电流；irj1和irj2分别表示CSCr1和CSCr2交流侧的j相电流；isrj表示海上CSC换流站的j相电流。
文献[23]提出一种改进基频调制方法，即EFFM，其调制方法示意图如图3所示。图3中，S1_1为正常情况下，基频调制产生的触发信号；S1_2为需要VT1进行主动关断的信号；S1_3为为了维持电流不断续，在基频调制信号后需要补偿的信号；S1为三者叠加后，施加在VT1上的触发信号。t0 = αr+30°时触发VT1开始。当t1 = αr+θr+30°时VT1关断θr电角度时间。为了让电流不发生断续，每个桥臂需保持120°导通时间，因此在t2 = αr+θr+150°时使得VT1导通θr电角度时间。采用EFFM，换流器桥臂按顺序以60°电角度间隔轮流导通，避免直流电流发生断续。与FFM相比，该方法具有触发角αr和补偿角θr两个控制自由度，开关频率为150 Hz，可以实现海上系统独立控制，更加适合海上风电输电场景。
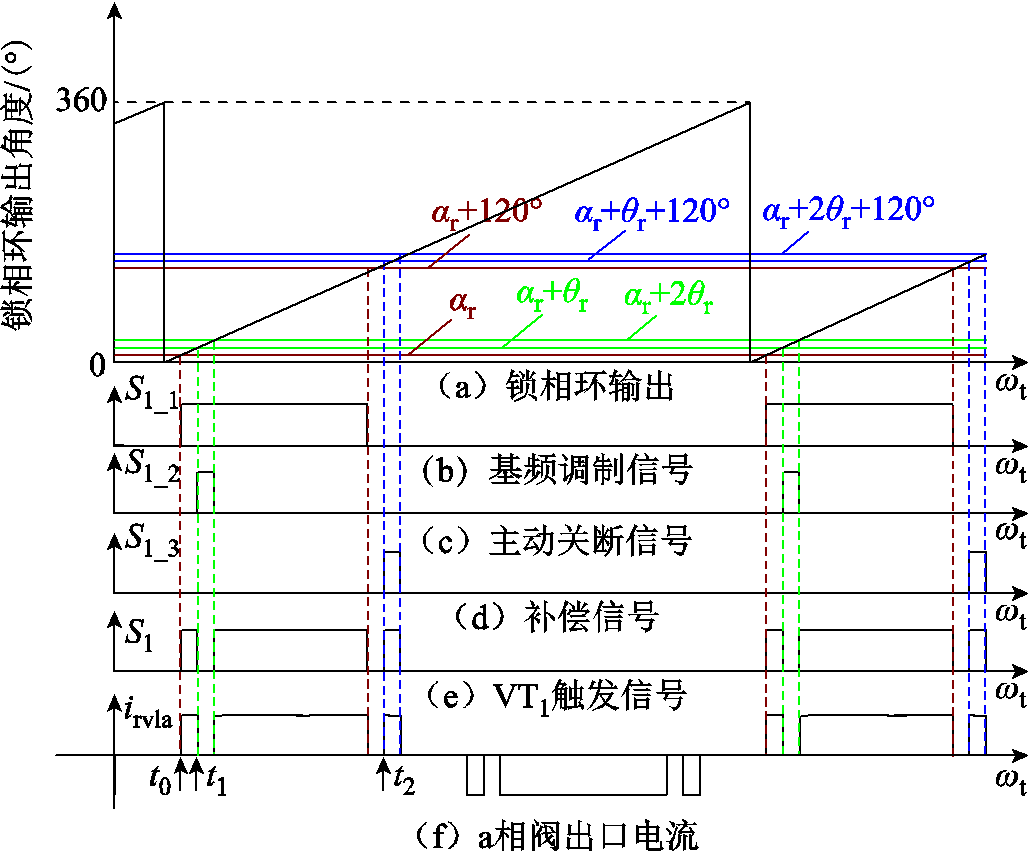
图3 EFFM-CSC调制方法示意图
Fig.3 Schematic diagram of the EFFM-CSC modulation method
6脉动EFFM-CSC的阀出口a相电流irvla如图3f所示，对其进行傅里叶级数展开，可以得到
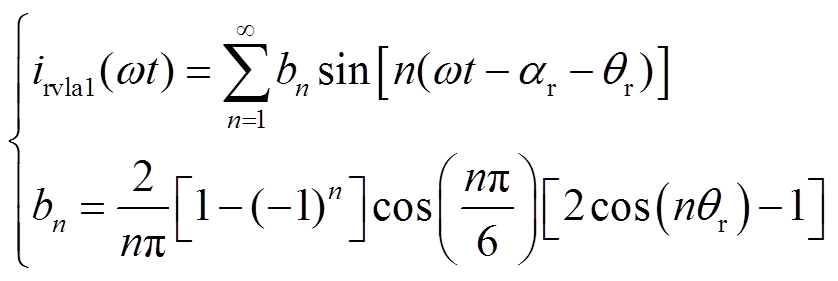（1）
式中，ω为基频分量角速度；n为谐波次数；bn为傅里叶系数。
从式（1）可以看出，对于6脉动EFFM-CSC的阀出口电流，其特征谐波次数为6k±1，与6脉动LCC换流器的特征谐波次数一致。
CSC正常运行时，CSC的交流侧可等效为电流源，其直流侧可等效为电压源。对交流侧的基波通路和特征谐波次数谐波通路进行分析，移相EFFM-CSC的简化等值模型如图4所示。为便于理解分析和谐波计算，简化模型先忽略LC滤波器的滤波效果，视变压器为理想变压器，仅考虑变压器的移相作用，线电压变比为1:1，其中星形-三角形（Yd）变压器的联结组别号为Yd1。同时为直观地展示谐波电流传递通路，图4中绘制了一条交流母线和两个节点，节点Noder1和Noder2分别为高、低阀组的交流出口，母线Bussr为海上CSC换流站的交流母线。
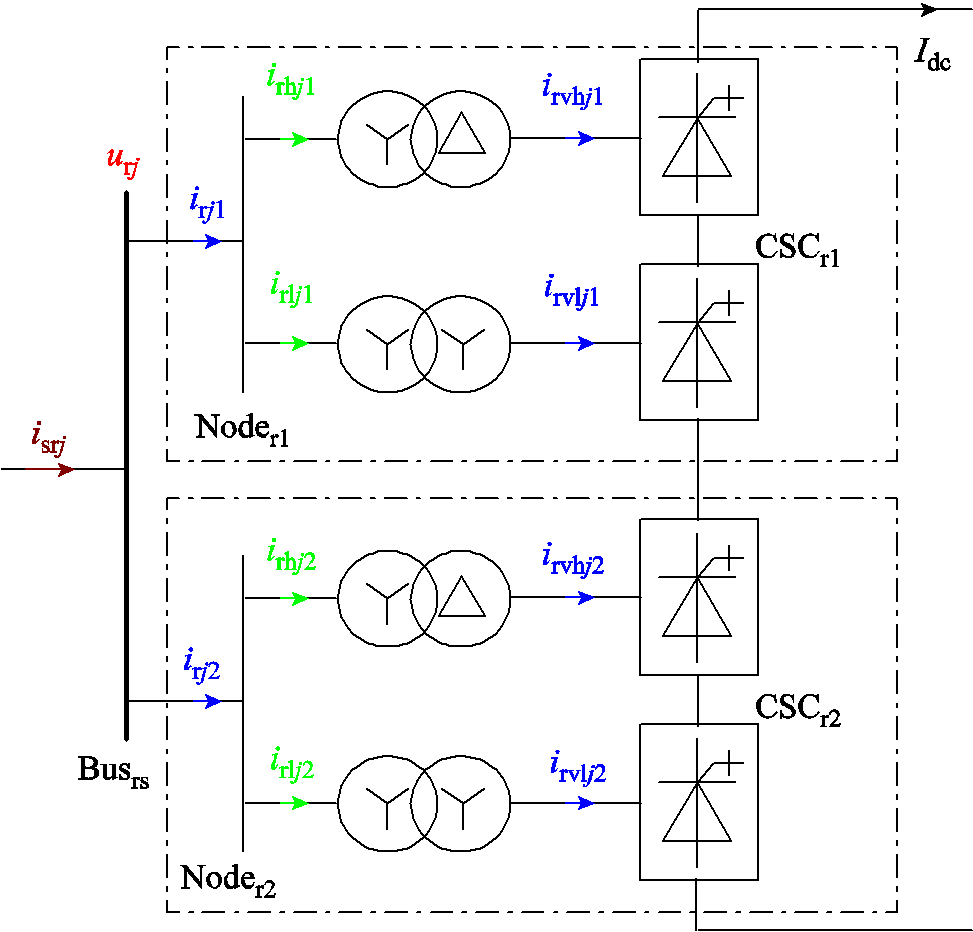
图4 EFFM-CSC谐波传递等值模型
Fig.4 Equivalent model of harmonic of EFFM-CSC
2.2.1 节点Noder1(2)处谐波传递规律
以高阀组CSCr1的交流出口节点Noder1的a相电流为例，分两种情况进行分析。
1）当n = 6(2k-1)±1时，k为自然数，即特征谐波次数为5, 7, 17, 19, …, 其中6(2k-1)+1次谐波电流为正序，6(2k-1)-1次谐波电流为负序。
在一个12脉动CSC中，虽然两个6脉动CSC的触发角和补偿角均相同，但是星形-三角形（Yd）变压器的二次电压滞后星形-星形（Yy）变压器的二次电压，所对应的6脉动CSC的触发信号也滞后星形-星形（Yy）变压器所对应的6脉动CSC的触发信号30°电角度。因此，根据式（1）可以得到，两个6脉动CSC输出的n次谐波电流幅值相等，相位相差n×30°。6脉动CSC阀出口电流经过星形-三角形（Yd）变压器，使得一次电流的正序分量超前于二次侧30°电角度，而一次电流的负序分量滞后于二次侧30°；经过星形-星形（Yy）变压器，无论是正序还是负序电流相量，一次侧与二次侧相位均保持一致。通过以上相位关系可得到
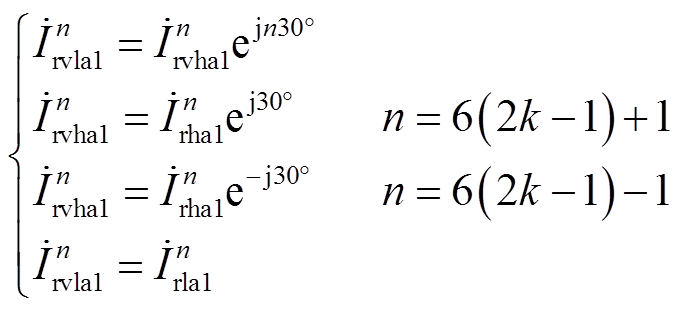（2）
根据式（2），可以得到节点Noder1处的谐波电流相量如图5a所示，图中φ为功率因数角。需要说明的是，为清晰地展现各个谐波电流之间相位关系，图5中仅展示正序电流相量。对于n=6(2k-1)±1次特征谐波电流，无论正序或负序分量，Yd变压器一次侧谐波电流相量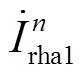
和Yy变压器一次侧谐波电流相量
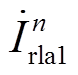均有幅值相等、相位相差180°的规律。因此两者相互抵消，使得CSCr1(2)输出的交流电流不含n= 6(2k-1)±1次特征谐波。
2）当n = 12k±1时，即11, 13, 23, 25, …次特征谐波，其中12k+1次谐波电流为正序，12k-1次谐波电流为负序，其相位关系与式（2）一致。Yd和Yy变压器所对应的6脉动CSC输出谐波电流相位相差n×30°电角度，再经过变压器30°移相，使得谐波电流相量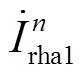和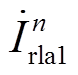呈现幅值和相位均相同的规律，如图5b所示，两者在母线处直接相加。因此经过Yd和Yy变压器后，n=12k±1次特征谐波电流的幅值是单个6脉动的2倍。
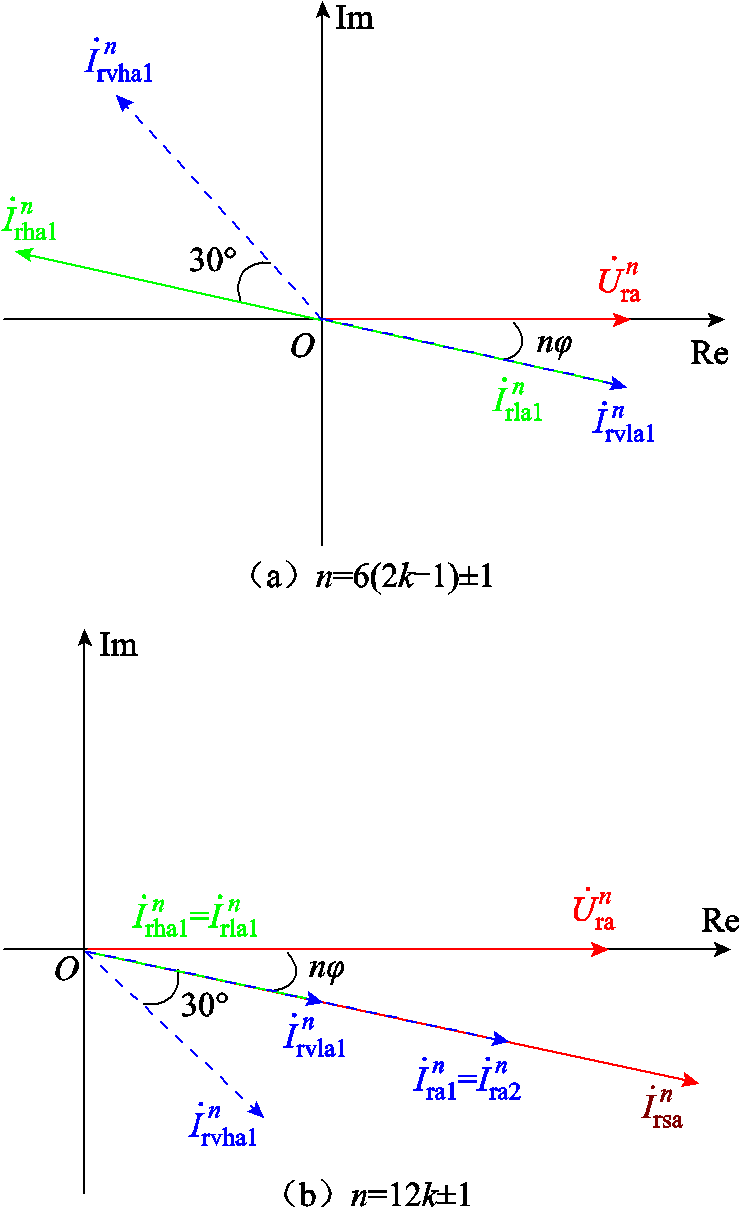
图5 Noder1(2)处6k±1次正序特征谐波相量图
Fig.5 Harmonic phasor diagram of 6k±1 at Noder1(2)
2.2.2 母线Busrs处谐波传递规律
由于高阀组CSCr1和低阀组CSCr2的触发角和补偿角均保持一致，其特征谐波电流相量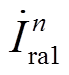
和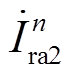
的幅值和相位完全相同。因此母线Busrs处的谐波电流
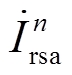次数为12k±1，幅值为
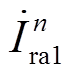的2倍，如图5b所示。
综上所述，双12脉动EFFM-CSC的特征谐波次数为12k±1，同时谐波幅值是单个12脉动的2倍。因此，12k±1次谐波不仅影响海上交流系统的电能质量，还会造成LC滤波器容量的提升，增加海上换流平台的造价。因此亟待研究出一种低谐波含量的海上风电CSC送出系统。
根据2.2.1节的分析可知，经过YY和Y△联结变压器，可以实现12脉动换流器中两个6脉动之间的6(2k-1)±1次（例如5、7次）谐波相互抵消，使得交流侧谐波电流次数为12k±1。如果在上下两个12脉动换流阀之间继续增设移相15°变压器（或移相±7.5°变压器），组成24脉动换流器，可进一步实现11、13次谐波的消除，交流侧最低次谐波电流提高至24k±1次，使得谐波电流次数减少，谐波电流频率提高。因此移相多重化换流电路可以优化滤波器的参数，大幅度降低滤波器的体积重量，实现海上换流平台的轻型化。
但是目前在高压直流输电领域，往往采用12脉动或者双12脉动拓扑，而理论上具有良好谐波特性的24脉动拓扑并未得到推广应用，其原因在于高电压大容量的移相15°变压器制造精度不符合要求，同时绕组接线方式复杂，总体技术经济性较差[22]。
基于2.2.1节的分析和移相多重化思路，针对图1所示单极接线方式的CSC远海风电送出系统，本文提出两个12脉动的高低阀组采用移相控制策略。不同于以往移相15°变压器的方案，本文旨在利用电力电子的灵活控制能力，通过差异化高阀组CSCr1触发角αr1和低阀组CSCr2触发角αr2，使得αr2相对于αr1移相15°电角度，并保持CSCr1的补偿角θr1和CSCr2的补偿角θr2相同，希望能构造出高低阀组输出的交流电流相位偏差，从而降低交流母线处12k±1次电流谐波，优化LC滤波器参数，进一步提升CSC换流器的功率密度。
3.1.1 高低阀移相EFFM-CSC谐波电流计算
图6为高低阀移相EFFM-CSC输出a相电流传递过程示意图。此时，CSCr2的触发角αr2超前于CSCr1的触发角αr1 15°，最终生成高低阀移相EFFM-CSC的交流电流irsa，如图6g所示。对图6g中电流irsa进行傅里叶级数展开为
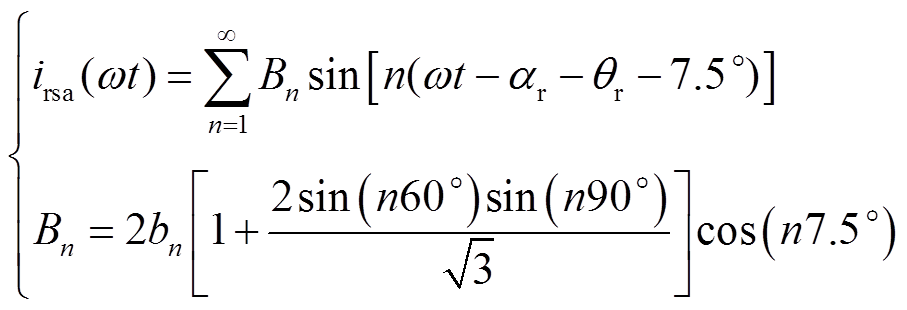（3）
式中，Bn为高低阀移相EFFM-CSC的傅里叶系数。
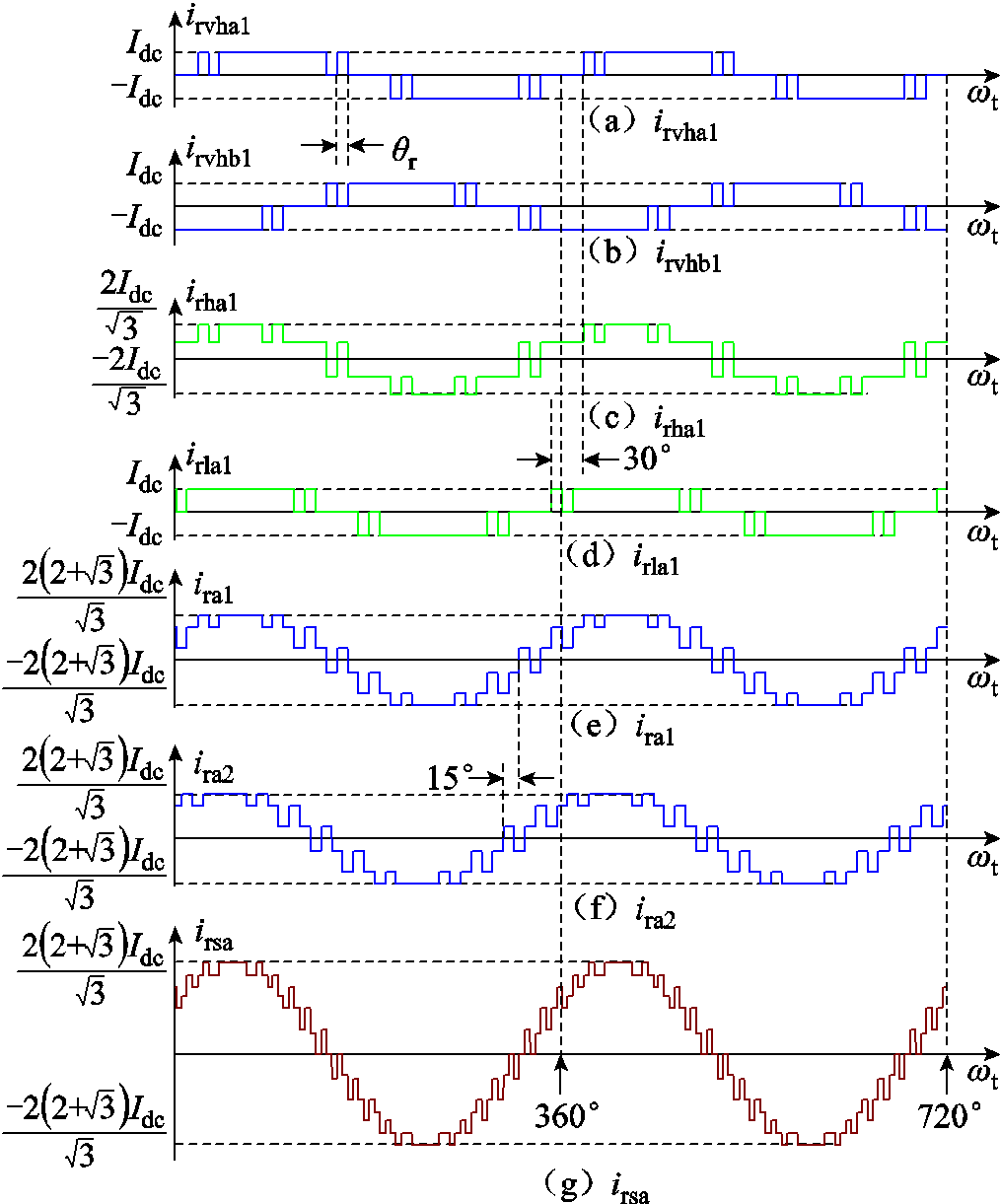
图6 高低阀移相EFFM-CSC谐波传递特性
Fig.6 Diagram of harmonic transmission characteristics of high and low valve phase-shift EFFM-CSC
从式（3）中可以看出，尽管高低阀移相EFFM-CSC的阀出口交流电流的特征谐波次数仍为12k±1，但对于11次和13次谐波，其谐波电流的幅值Bn降为原来双12脉动EFFM-CSC谐波电流4bn的0.13倍。
3.1.2 母线Busrs处谐波传递规律
节点Noder1(2)处n = 6k±1次谐波传递规律与之前一致，对于Busrs处n = 12k±1次谐波传递规律，仍以a相电流为例，分两种情况进行分析。
1）当n=12(2k-1)±1时，k为自然数，即特征谐波次数为11, 13, …，其中12(2k-1)+1次谐波电流为正序，12(2k-1)-1次谐波电流为负序。
将高阀组CSCr1触发角αr1和低阀组CSCr2触发角αr2差异化，使得αr2在αr1基础上移相15°，并保持CSCr1的补偿角θr1和CSCr2的补偿角θr2相同。根据式（1）可以得到，高低阀CSC输出的谐波电流幅值相等，相位相差n×15°，可得到
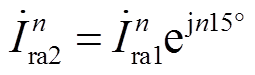（4）
根据式（4），可以得到母线Busrs处的谐波电流相量如图7a所示。由于本文拓扑中并没有增设移相15°变压器，因此电流相量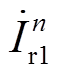
和谐波电流相量
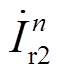幅值相等，对于负序，两者相位差为165°，对于正序，相位差为195°。根据平行四边形法则，就12k±1次谐波电流含量，基于高低阀移相EFFM-CSC是普通双12脉动EFFM-CSC的sin7.5°=0.13倍。虽无法完全滤除12k±1次谐波，但是该方法不需要安装移相15°变压器，仅通过高低阀触发角之间的移相，即可实现87%的滤波效果，为后续的优化LC滤波器和提高海上换流平台的功率密度提供了空间。
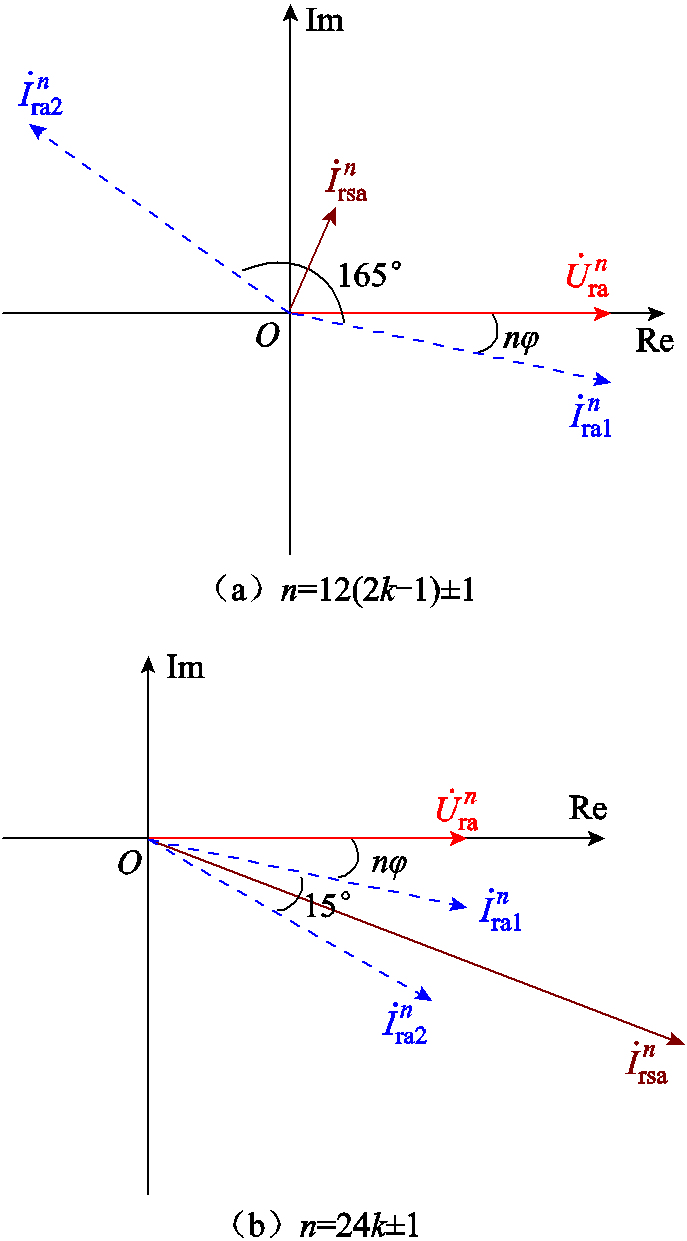
图7 高低阀移相时Busrs处12k±1次特征谐波相量
Fig.7 12k±1th harmonic phasor diagram at Busrs when EFFM-CSC phase shift
2）当n=24k±1时，k为自然数，即特征谐波次数为23, 25, …，其相位关系与式（4）一致。谐波电流相量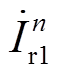和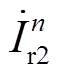
幅值相等，相位差为15°，如图7b所示。根据平行四边形法则，对于24k±1次谐波电流含量，基于高低阀移相EFFM-CSC是普通双12脉动EFFM-CSC的cos7.5°=0.99倍，因此该方法对于24k±1次谐波的影响不明显，但其谐波次数高、幅值小，仅通过LC滤波器即可实现有效滤除。
综上所述，将EFFM-CSC的12脉动、双12脉动和高低阀移相的三种结构的主要谐波次数和幅值进行汇总，结果见表1。可以看出对于11、13次主要谐波电流，高低阀移相EFFM-CSC相比普通双12脉动结构，可实现87%的滤波效果。
表1 不同结构下EFFM-CSC主要谐波次数及幅值
Tab.1 The main harmonic orders and amplitudes of EFFM-CSC under different structures
结构类型主要谐波幅值 12脉动EFFM-CSC11次、13次2b11, 2b13 双12脉动EFFM-CSC11次、13次4b11, 4b13 高低阀移相EFFM-CSC11次、13次0.52b11, 0.52b13
为建立图1中所示的高低阀移相EFFM-CSC的数学模型，本文首先以图2中的Yy变压器对应的12脉动CSC为例进行分析。根据文献[23]，12脉动CSC出口电流为
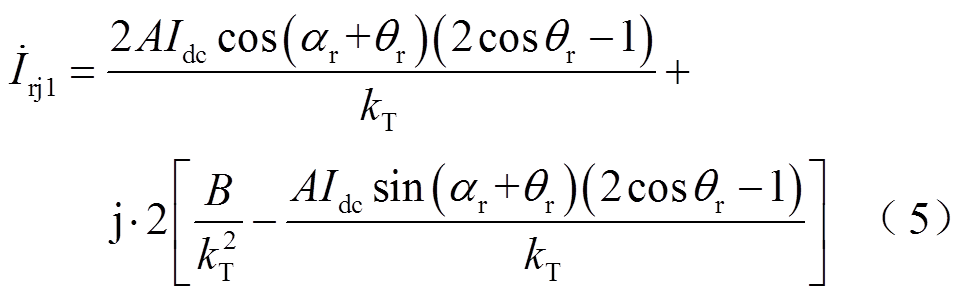
式中，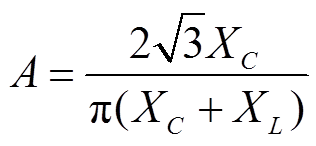
，
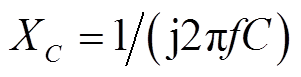，C为滤波电容容值，
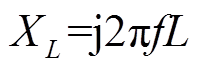，L为滤波电感与换流变压器漏感之和；
，
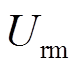为海上交流母线的相电压幅值；kT为换流变压器电压比；Idc为直流电流。
对于海上CSC换流站，将CSCr1的触发角设置为αr，而CSCr2的触发角设置为αr-15°。同时保持CSCr1和CSCr2的补偿角相同，设置为θr，因此，海上侧交流母线处电流Isrj为
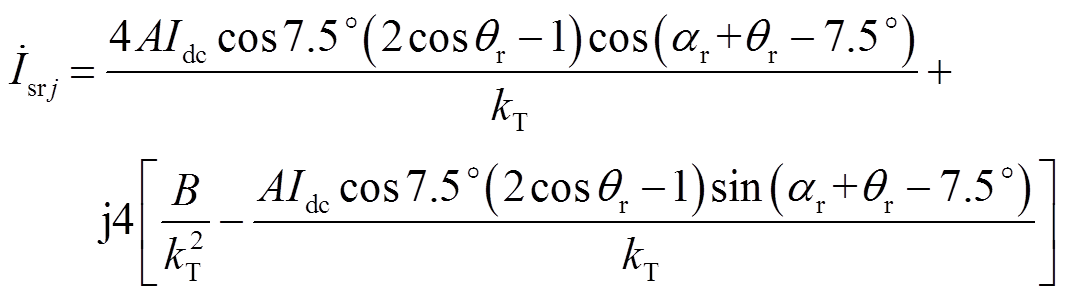（6）
再根据瞬时功率理论，可以得到海上CSC换流站吸收的有功功率Pr和无功功率Qr为
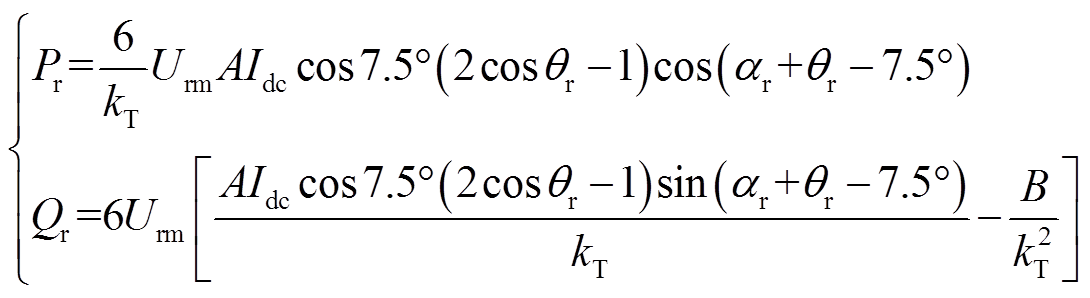（7）
将式（7）变形，可以得到移相EFFM-CSC的直流电压Udcr为
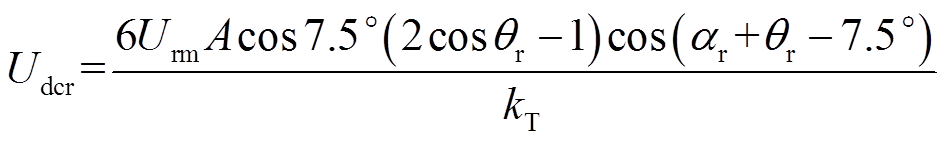（8）
高低阀移相EFFM-CSC不仅可以优化谐波特性，还为LC滤波器参数优化提供空间，且具有两个控制自由度（触发角αr和补偿角θr），可用于实现换流站的有功无功、直流电压电流和海上交流电压频率等电气量的动态调节。
由于移相EFFM-CSC的谐波特性与EFFM-CSC不同，其11次和13次谐波含量显著降低，所需的滤波设备相应减少，因此需要重新设计滤波器。
对于移相EFFM-CSC，需要设计的参数主要为EFFM-CSC换流阀交流侧所连接的滤波电容和滤波电感。为在满足谐波要求的前提下尽可能地减少滤波电容和滤波电感的成本，本文采用多目标规划对参数进行设计。
对于目标函数的选取，本文选取的原则如下。
1）为尽可能降低换流站的建设成本，需要采用体积重量较小的电感和电容。由于电感和电容的体积与其存储的能量成正比例，因此本文采用电感电容储存的能量作为衡量电感电容成本的标准[22]。电容和电感储存的能量之和W为
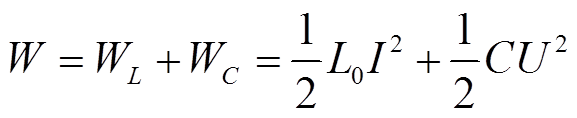（9）
式中，WL为电感储存的能量；WC为电容储存的能量；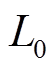
为滤波电感感值；I为流过滤波电感的电流；U为滤波电容两侧的电压。
2）由于CSC每个桥臂上采用的IGCT所承受的电压即为滤波电容两端承受的电压，考虑到IGCT承受的电压越大，所需器件的耐压水平就越高，从而增加换流阀的制造成本。并且由于电容两端的电压随着电容容值的降低而升高，考虑到IGCT的耐压成本，不能让电容降低得太多，因此将电容两端的电压作为IGCT制造成本的衡量标准。
本文将以上两个优化目标的权重设置为1:1，因此构成的目标函数为
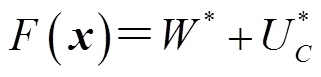（10）
式中，W*为标幺化后的电容电感储能的能量值；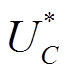
为标幺化后的电容两端的电压值；x为目标函数的自变量矩阵，其包含两个需要设计的参数——滤波电感L和滤波电容C。
在选取目标函数后，还应该设置约束条件。本文考虑的约束条件为LC的参数设计应该满足一定的滤波效果。本文采用交流母线处n次谐波电流幅值与阀出口电流幅值的比值kn来衡量滤波效果，其计算式为
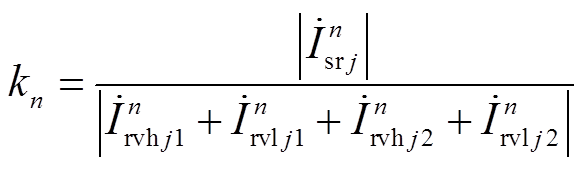（11）
以CSCr1中YY变压器侧阀出口电流为例，由图7b的分析可知，交流母线处电流幅值与其幅值关系为
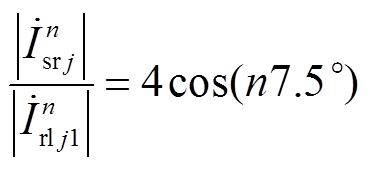（12）
同时由于阀出口电流经过LC滤波器存在如下关系
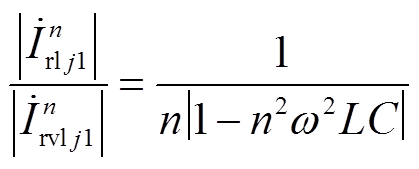（13）
联立式（11）～式（13）即可得到移相EFFM-CSC的谐波特性为
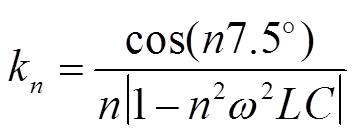（14）
由于考虑到5、7次谐波经过Yy和Yd变压器的作用而相互抵消，因此本文对11次谐波进行约束。根据IEEE 519—2014的规定，11次谐波含有量应小于1%，即k11≤0.01。
由以上分析，得到本文采用的参数设计的数学模型见表2。
表2 参数设计数学模型
Tab.2 Scheme of parameters design
目标函数min F(x) 约束条件
以直流电压为±400 kV、直流电流为2.5 kA的额定工况为例，由表1的数学模型可以解得一个最优解为滤波电感L=8.12 mH，滤波电容C=14.08 μF。滤波电感与滤波电容值的降低，将进一步减小海上CSC的体积和成本。
4.1节中对移相EFFM-CSC进行了参数设计，本节将本文所设计的参数与FFM-CSC及PWM-CSC中的LC滤波器参数进行对比分析，其中PWM-CSC和FFM-CSC的额定运行工况及主要设备参数见文献[21, 25]。
滤波电容与滤波电感的成本与其存储的能量成正比。由于FFM-CSC、PWM-CSC和移相EFFM-CSC的换流变压器电压比不同，在计算储存的能量时需要进行换算，因此将存储的能量换算为单位功率储能峰值进行比较。
本文中移相EFFM-CSC中的滤波电容单位功率储能峰值WPSEFFM_C为
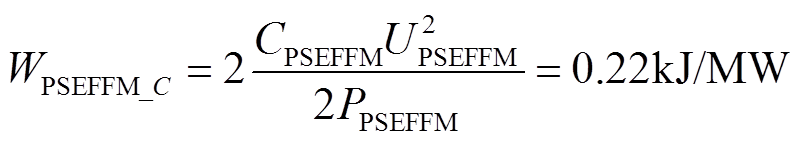（15）
式中，CPSEFFM为移相CSC滤波电容的容值；UPSEFFM为滤波电容两端电压；PPSEFFM为移相CSC的有功功率。
本文移相EFFM-CSC中的滤波电感单位功率储能峰值WPSEFFM_L为
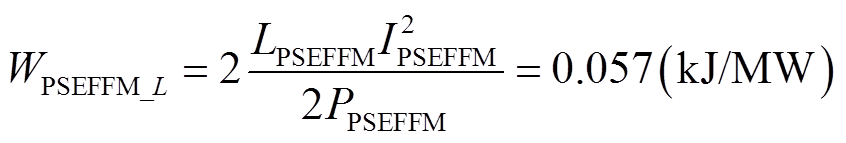（16）
式中，LPSEFFM为移相CSC滤波电感的感值；IPSEFFM为流过移相CSC滤波电感的电流。
同理，可计算得到，FFM-CSC的滤波电感与滤波电容的单位功率储能峰值分别为0.29 kJ/MW和0.32 kJ/MW，而PWM-CSC的储能峰值分别0.09 kJ/ MW和0.94 kJ/MW。图8为不同调制下的CSC的设备成本对比。
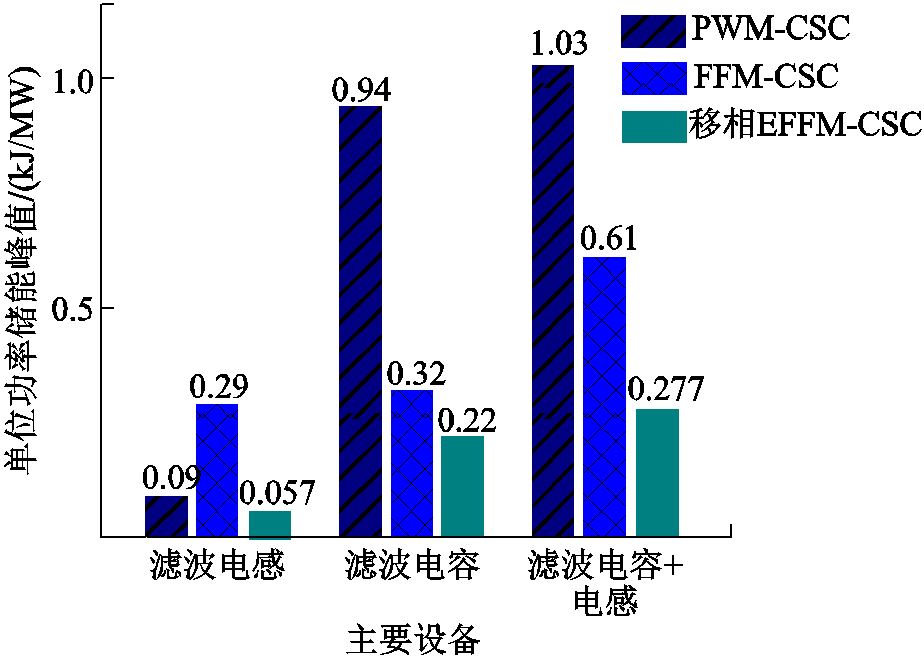
图8 不同调制CSC的设备成本对比
Fig.8 Comparison of equipment costs for different CSC
从图8可以看出，移相EFFM-CSC的滤波电感成本仅为PWM-CSC的63.3%，为FFM-CSC的19.7%，同时移相EFFM-CSC的滤波电容成本仅为PWM-CSC的23.4%，为FFM-CSC的68.8%。从滤波电容与滤波电感的总成本来看，移相EFFM-CSC的成本仅为PWM-CSC的26.9%，为FFM-CSC的45.4%。因此采用移相EFFM-CSC的换流站成本显著降低，体现了本方案的经济性。
对于高低阀移相EFFM-CSC，从式（7）和式（8）可以看出，其具有触发角αr和补偿角θr这两个控制自由度，可以实现海上交流系统的电压幅值和频率的独立控制。由于海上风电场采用最大功率跟踪控制，其输出的有功功率POWF和无功功率QOWF与海上CSC吸收的有功功率Pr和无功功率Qr实时平衡。同时为清晰地展示控制量和被控量之间的对弈关系，构造中间变量
= αr+θr-7.5°，θF = θr，则POWF和QOWF可以表示为
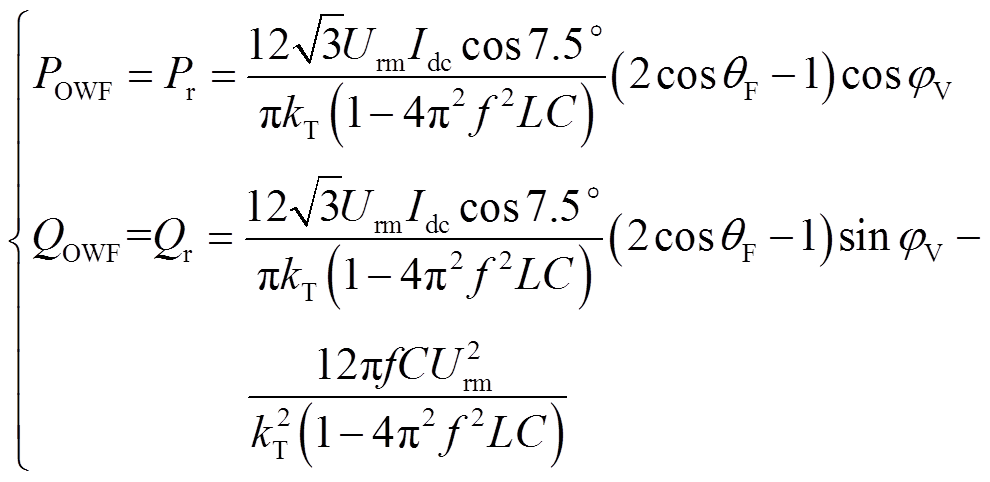（17）
海上CSC作为整流站，φV的运行范围为-90°～90°，θF的运行范围为0°～60°。
为设计海上交流电压幅值Urm和频率f的控制策略，需要讨论海上CSC的两个控制自由度θF和φV与Urm和f的关系。将式（17）进一步转换为
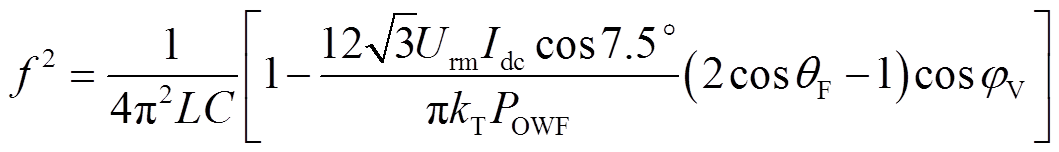（18）
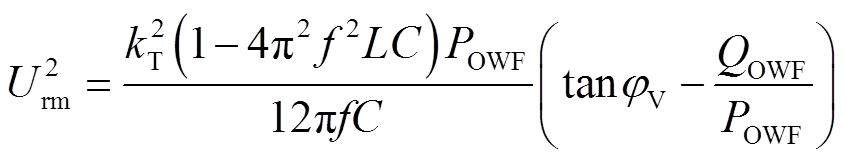（19）
将式（18）、式（19）中的f 2和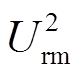
分别对θF和φV求偏导可得
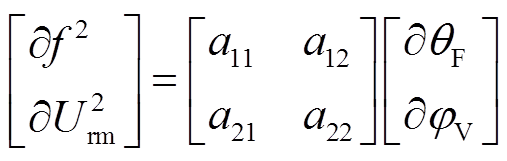（20）
其中
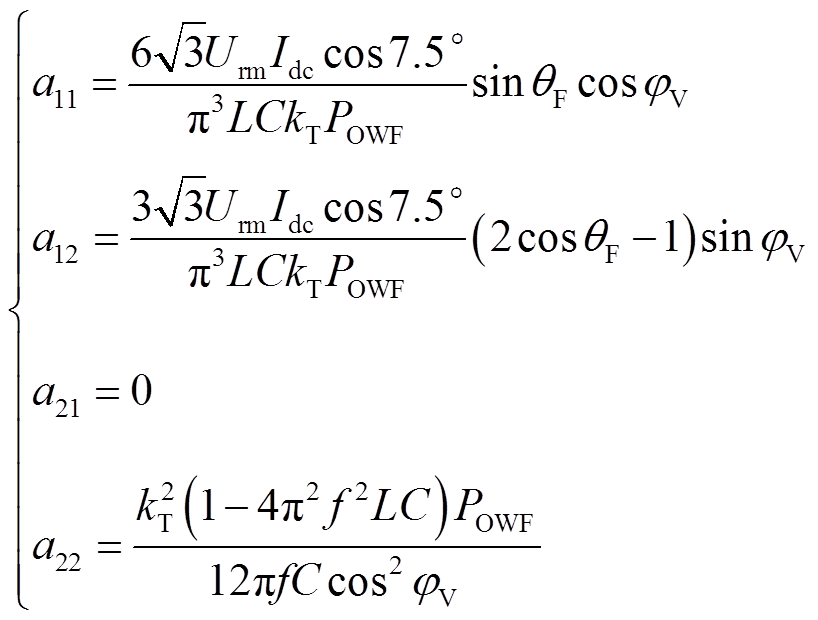
在系统稳态运行工况中，Urm和f均为正值，因此Urm和f关于θF和φV的单调性与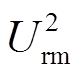和f2关于θF和φV的单调性一致。依据式（20），θF和φV对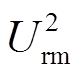和f 2的影响规律如图9所示。从式（20）和图9a可以看出，在运行范围内，a11一直为正，因此f和θF呈现单调递增的关系。对于a12，当φV在 -90°～0°范围时，a12为负数；当φV在0°～90°运行时，a12为正数，因此f和φV的单调性会发生变化。从式（20）和图9b可以看出，在运行范围内，a21恒为零，a22一直为正，因此Urm和φV呈现单调递增的关系。
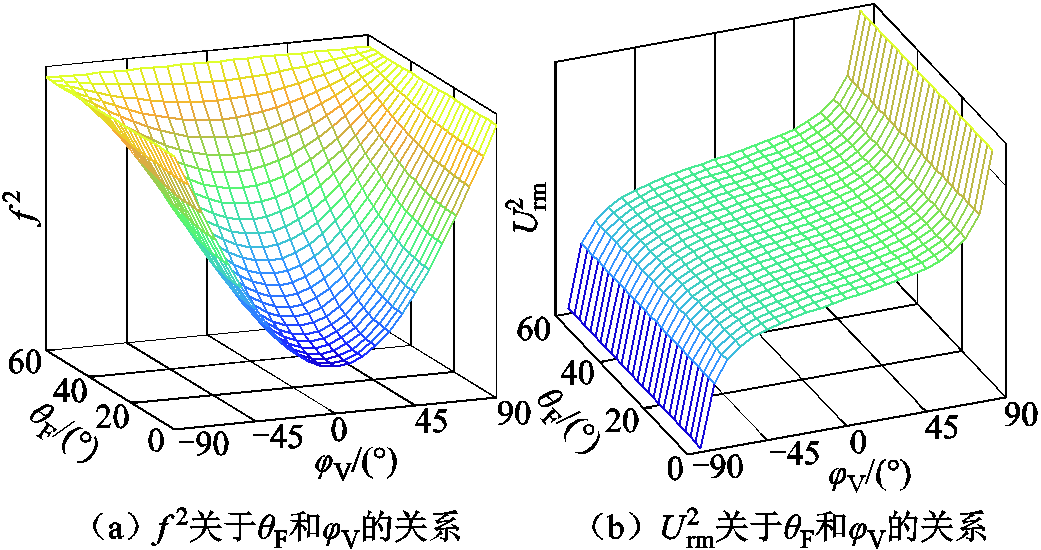
图9 f 2和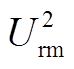
关于θF和φV的关系
Fig.9 Plot of f 2 and 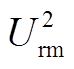with respect to θF and φV
综上所述，在θF和φV的运行范围内，f和θF呈现单调递增的关系，Urm和φV呈现单调递增的关系。因此可以设计海上CSC换流站的稳态控制策略如图10所示，利用θF控制交流电压频率f，利用φV控制交流电压频率幅值Urm。最后，通过中间变量反算即可得到触发角αr和补偿角θr，用于对CSCr1和CSCr2进行调控，维持海上交流电压幅值和频率的稳定运行。
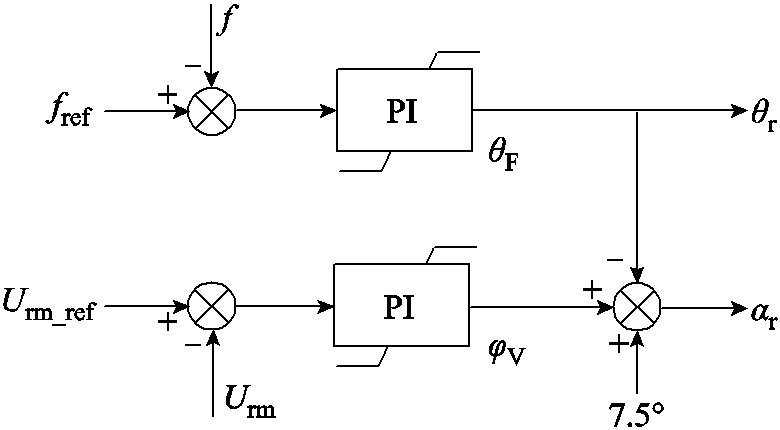
图10 海上CSC控制策略框图
Fig.10 Offshore CSC control strategy block diagram
对于陆上CSC，正常运行时需要控制直流电压和无功功率。同时，当直流功率较小时，低直流电流会发生断续并引发过电压，所以需切换到最小直流电流控制。因此，陆上CSC设计带有电流内环的双环控制。
为设计正常运行时陆上CSC控制策略，首先由整流侧CSC的网侧电流式（6），可以类比推导得到逆变侧CSC的网侧电流Isij，并构建中间变量，Isij在同步旋转坐标系下的dq轴分量isid、isiq分别为
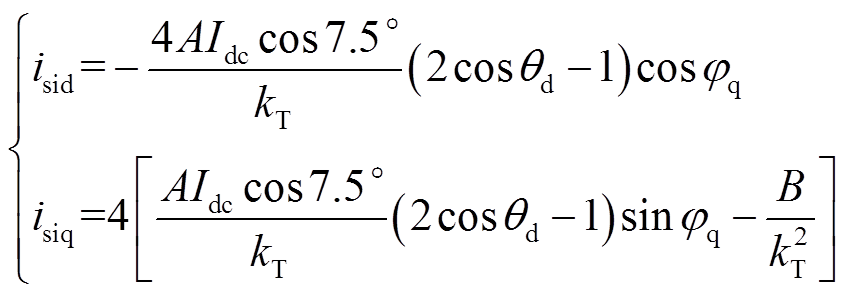（21）
式中，中间变量φq = αi+θi-7.5°，αi为逆变侧CSC的触发角，θi为逆变侧CSC的补偿角；θd = θi。陆上CSC作为逆变站，φq的运行范围为90°～270°，θd的运行范围为0°～60°。
然后将式（21）中的isid和isiq分别对θd和φq求偏导可得
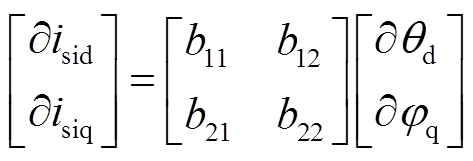（22）
其中
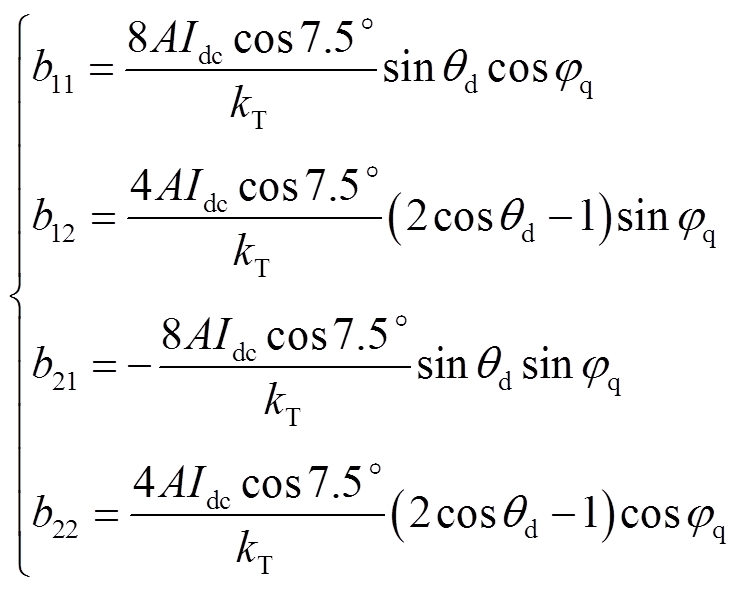
类比5.1节的分析，在运行范围内，b11和b22恒为负数，isid和θd呈现单调递减的关系，isiq和φq呈现单调递减的关系，因此可以设计内环电流控制策略如图11所示，利用θd控制isid，利用θq控制isiq。通过isid实现直流电压Udc_ref的控制，通过isiq实现无功功率Qi_ref的控制。当直流功率较小时，外环切换为最小直流电流控制。
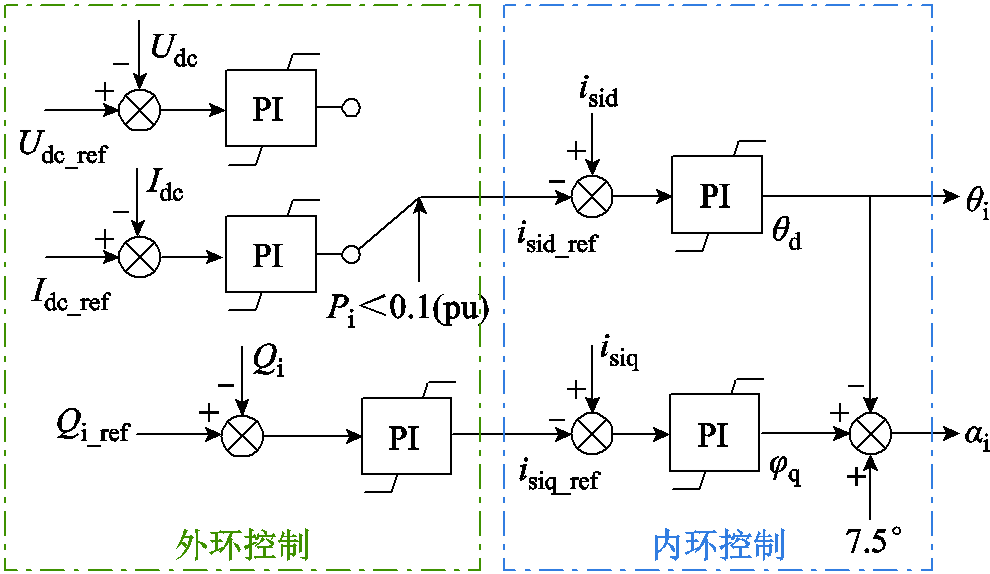
图11 陆上CSC控制策略框图
Fig.11 Block diagram of onshore CSC control strategy
为验证本文提出的采用高低阀移相控制策略的EFFM-CSC海上风电直流输电系统及其海上交流电压控制策略的有效性，在PSCAD/EMTDC中搭建如图1所示的仿真算例。仿真模型的测试参数见表3。
表3 系统参数
Tab.3 System parameters
参数数值 额定直流电压/kV±400 额定直流电流/kA2.5 换流器电压比/(kV/kV)220/155 换流变压器漏抗(pu)0.18 平波电抗器/mH300 滤波电感/mH8.12 滤波电容/μF14.08
为分析验证高低阀移相EFFM-CSC工作原理的正确性，额定工况下系统有功功率为2 000 MW，直流电流为2.5 kA，触发角运行在1.8°，补偿角为14.6°，详细仿真分析如图12所示。
图12a为直流电压波形，其中Udcr1和Udcr2分别为海上CSCr1和CSCr2输出的直流电压。图12b为海上CSCr1和海上CSCr2的滤波电容ab相线电压波形。图12c～图12e分别为海上CSCr1、海上CSCr2输出电流和海上交流母线处a相交流电流。可以看出移相EFFM-CSC可以使得高低阀组交流出口电流相差15°，降低交流母线处的谐波。
对图12c、图12e中交流电流进行快速傅里叶变换（Fast Fourier Transform, FFT）分析，得到谐波频谱如图13所示。图13a为CSCr1阀出口电流irvla1的谐波频谱，可看出6脉动EFFM-CSC的特征谐波为6k±1次。需要说明的是，图13a中5次谐波电流比7次谐波电流小，其原因从式（1）可以看出，影响谐波大小的主要因素是[2cos(nθr-1)]/n。因为额定工况下补偿角θr运行在14.6°，导致5次谐波含量低于7次谐波含量，但补偿角θr并不影响特征谐波次数。图13b为CSCr1交流出口电流ira1的谐波频谱，可以看出经过Yy和Yd变压器以及3.1节所设计的LC滤波器后，5、7次谐波被完全滤除，同时11、13次谐波滤除了一部分，符合2.2节中的理论分析。图13c为海上交流母线处电流irsa的谐波频谱，可以发现11、13次谐波电路被大幅度滤除，电能质量大幅度提升，总谐波电流畸变率为1.4%，因此高低阀移相EFFM-CSC具有良好的交流谐波特性，验证了本文移相理论和参数设计的正确性。
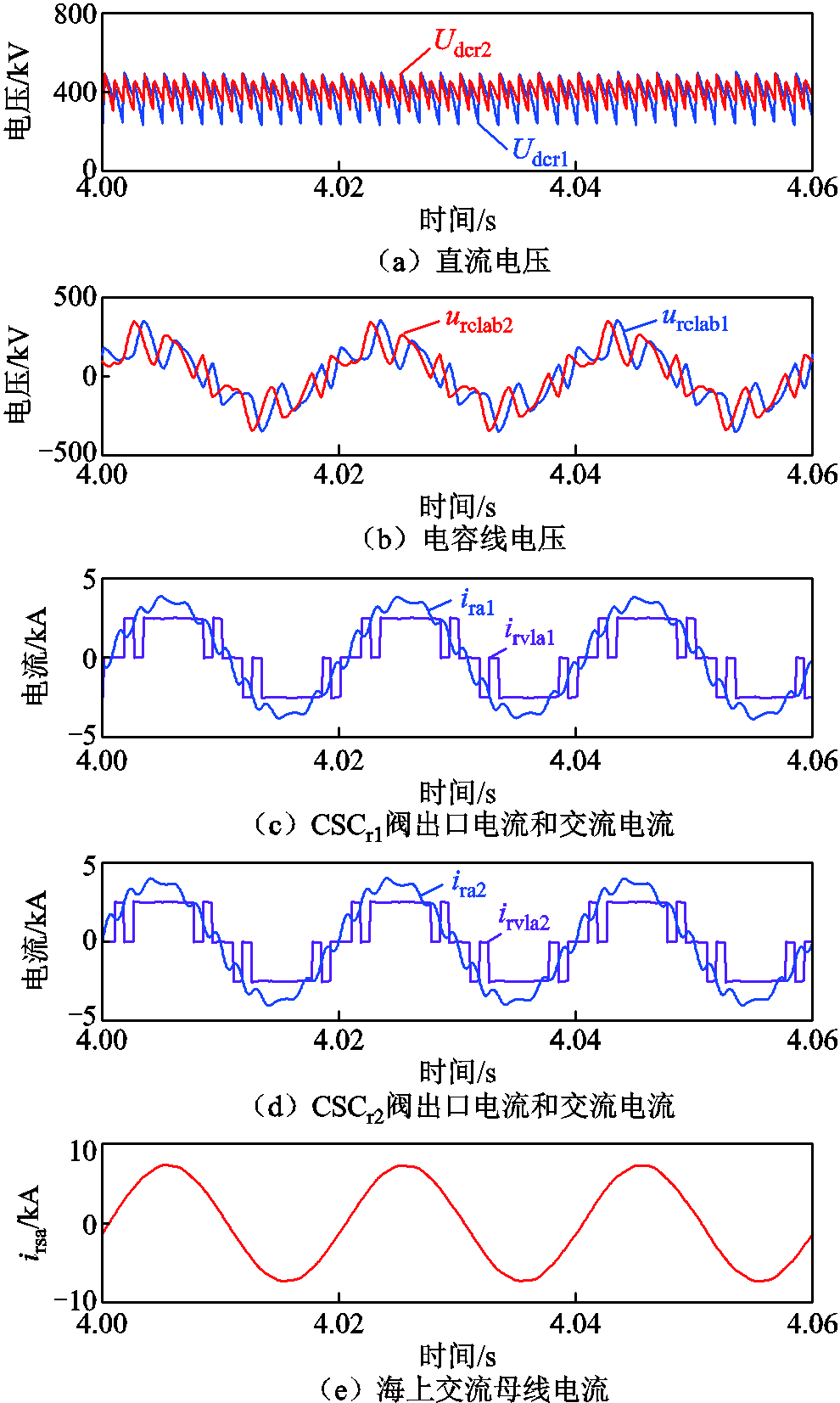
图12 高低阀移相EFFM-CSC稳态波形
Fig.12 High and low valve phase-shifting EFFM-CSC steady-state waveform
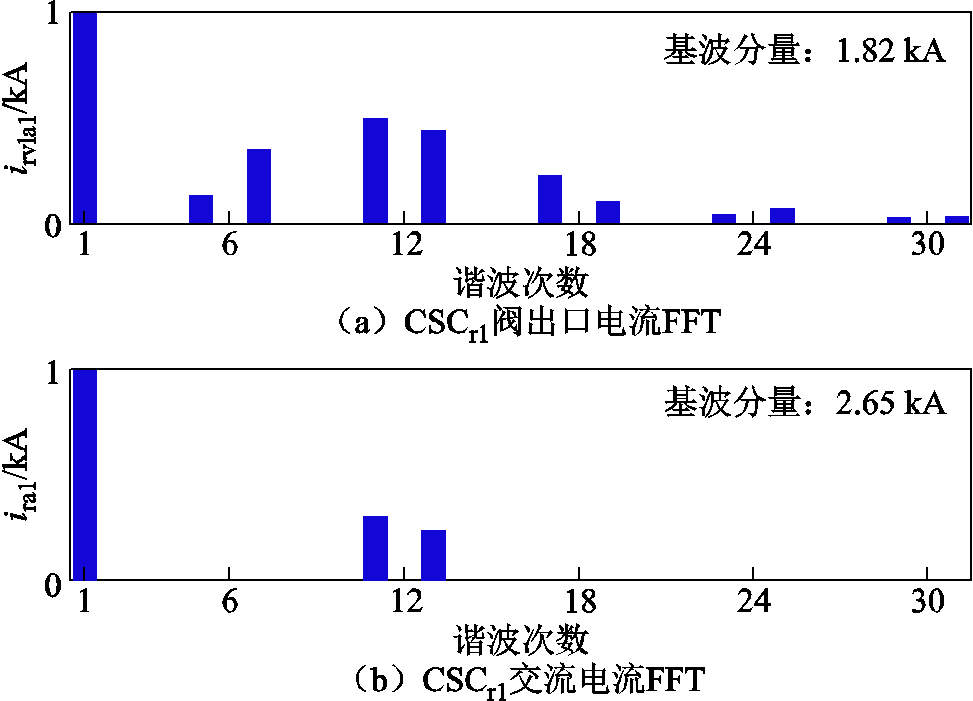
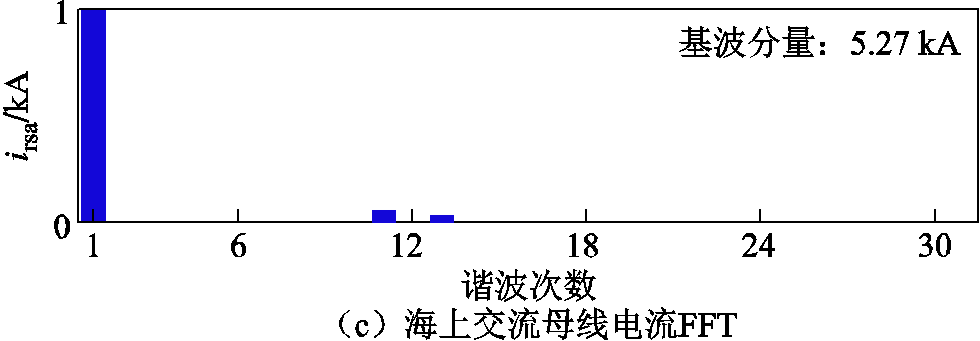
图13 高低阀移相EFFM-CSC谐波频谱
Fig.13 High and low valve phase-shifted EFFM-CSC harmonic spectrum
为分析基于高低阀移相EFFM-CSC海上风电直流输电系统的启动特性，本节针对系统的启动工况特性进行仿真分析，仿真结果如图14所示。
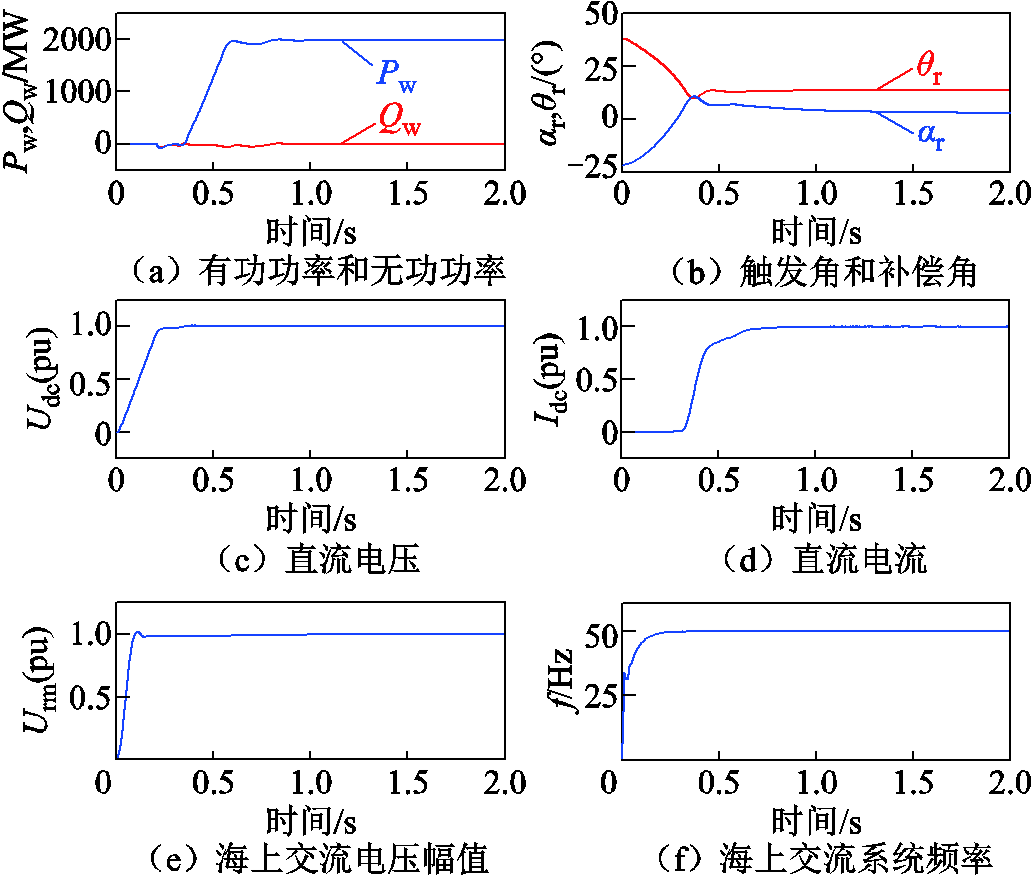
图14 海上风电送出系统启动工况波形
Fig.14 Waveforms of system start-up condition
当t = 0 s时分别解锁两端换流器，逆变侧CSC直流电压控制的指令值按照斜坡上升至额定值，无功功率控制使得逆变侧交流系统处于单位功率因数状态。与此同时，海上CSC控制的海上交流电压幅值和频率控制至稳态值，这样有利于缓解启动过程中出现的过电流和过电压现象。在t = 0.2 s，当基本建立交流电压后，风电场开始黑启动，风电场输出有功功率逐渐增加，CSC-HVDC系统的直流电压和直流电流也随之增长到额定值，系统在t = 1.5 s时达到额定运行状态。
为验证基于CSC的远海风电系统对风电场功率变化的适应性，对风电场的输出功率变化工况进行仿真分析。当t =6 s时，风电场的输出有功功率由1 400 MW增加至2 000 MW；当t = 9 s时，风电场的输出功率由2 000 MW减小至1 800 MW，系统其他控制参数保持不变，得到仿真波形如图15所示。由图15可以看出，当海上风电场输出功率增加时，海上交流电压幅值和频率几乎不受影响，均维持在参考值附近，而触发角αr由6.7°变化为1.8°，补偿角θr由13.5°变化为14.6°，直流电压保持不变，直流电流由0.7(pu)增加至1.0(pu)。当风电场的输出功率下降时，海上交流电压幅值和频率基本不受影响，触发角αr由1.8°变化为2.6°，补偿角θr由14.6°变化为16.1°，直流电压保持不变，直流电流下降至0.9(pu)。综上所述，当风电场功率波动时，海上CSC可以有效地维持交流电压幅值和频率的稳定，有利于直流功率的稳定输送，验证了基于高低阀移相EFFM-CSC的海上交流电压控制策略的正确性。
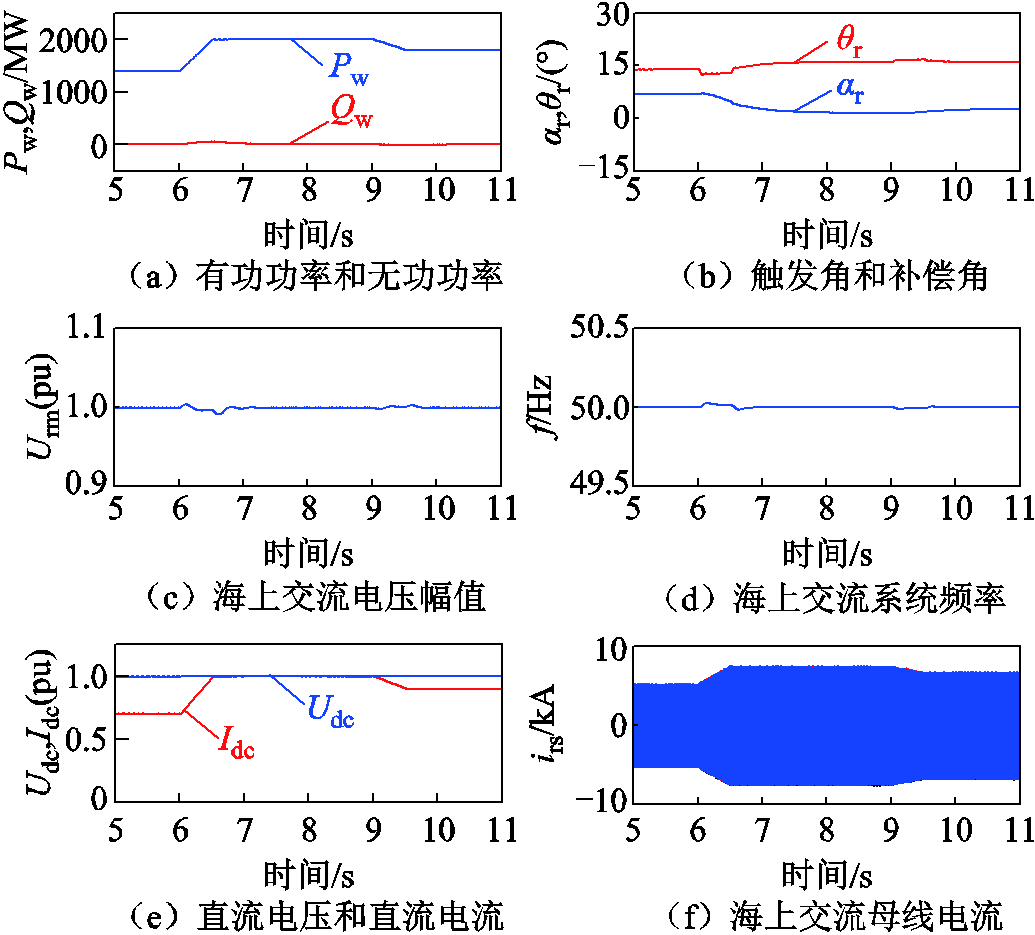
图15 风电场出力波动时送出系统响应特性
Fig.15 Waveforms of the wind farm fluctuates
假设系统在故障发生前一直运行在额定工况下，当t = 12 s时，陆上电网发生三相金属性接地故障，故障持续时间为100 ms。陆上交流系统三相金属性接地故障时的系统响应特性如图16所示。
此时风电场输出有功功率盈余，风机换流器中的直流斩波电路启动，风电场输出的有功功率下降。从仿真波形中可以看出，当t = 12.1 s时，接地故障清除，海上交流系统电压和频率逐渐恢复至正常运行状态，因此基于高低阀移相EFFM-CSC的远海风电送出系统具有良好的故障穿越特性。
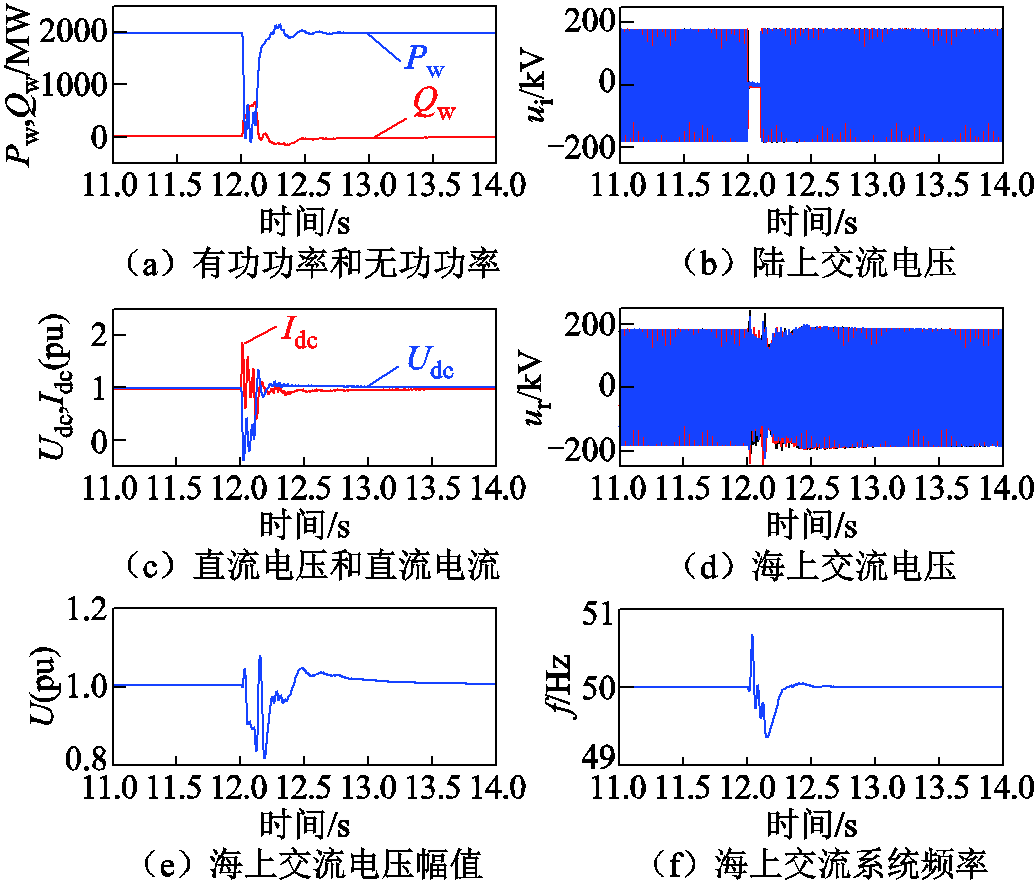
图16 陆上电网三相故障时送出系统响应特性
Fig.16 System characteristics in the event of the three-phase fault in the onshore grid
假设系统在故障发生前一直运行在额定工况下，当t=15 s时，系统发生海上a相短路故障，故障持续时间为100 ms，a相电压跌落至0，其余两相维持不变。故障响应特性如图17所示。
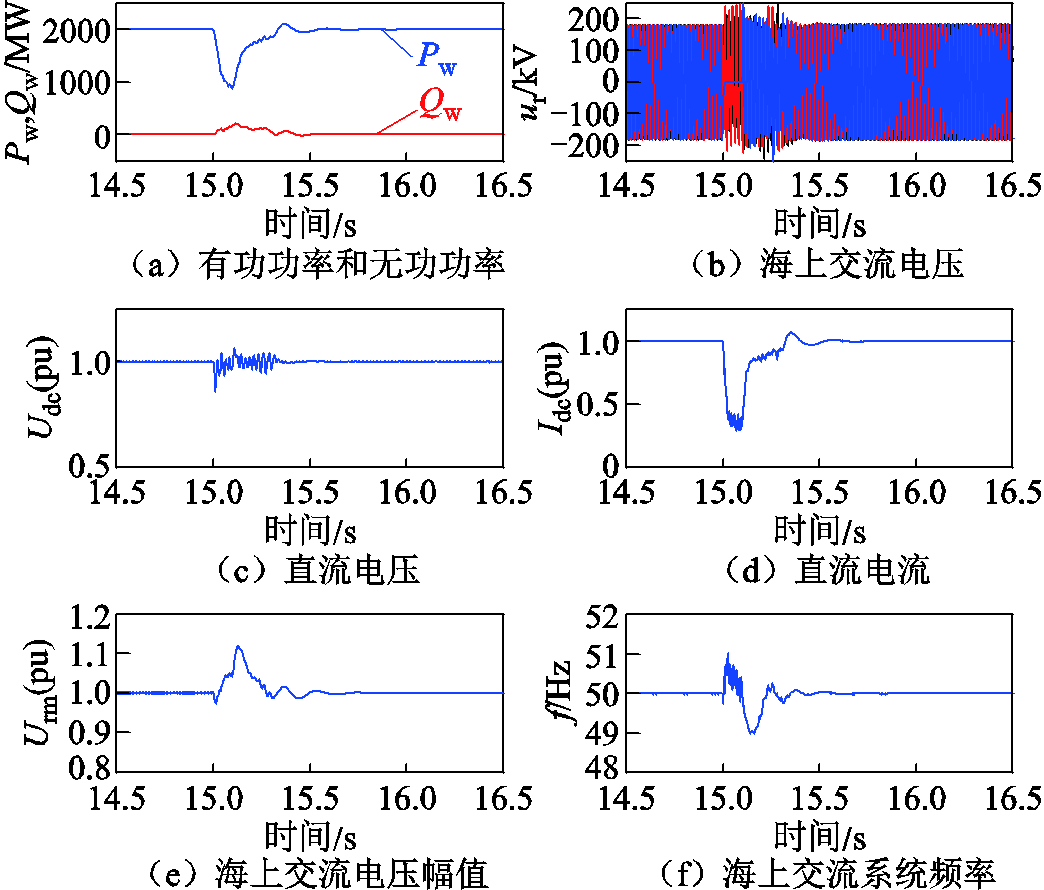
图17 海上a相接地故障工况时系统的运行特性
Fig.17 System characteristics in the event of a-phase fault in the offshore grid
当海上交流系统发生a相短路接地故障时，海上交流电压和交流电流会出现不对称现象，此时直流电流会相应下降，CSC送出有功功率也随之降低，故障期间海上交流电压幅值和频率也发生一定波动。当t=15.1 s时，海上a相短路故障被清除后，交流电压和频率能逐步恢复稳定，风电场输出功率也逐渐稳定。
为更加充分地验证上述理论分析的正确性，在实验室中搭建了小容量的CSC，如图18所示。由于实验条件的限制，将高低阀双12脉动改为由两个6脉动CSC形成高低阀组，均采用Yy变压器联结，其中高阀组采用IGCT器件，低阀组采用IGBT串联二极管器件，实验平台参数见表4。
图18 CSC实验平台
Fig.18 CSC experimental platform
表4 实验平台参数
Tab.4 Parameters of the experimental platform
参数数值（型号） 额定直流电压/V500 额定直流电流/A5 平波电抗器/mH300 滤波电容/μF33 滤波电感/mH40 IGCTCSC5000-33 IGBTFF200R12KT4 DiodeAPT60DQ100BG
在实验中，给定高阀组的触发角αr1为25°，低阀组的触发角αr2为10°，补偿角θr均为10°，实验结果如图19所示。从图19a中看出，直流电流为3 A，滤波前高、低阀组的电流波形irvh1、irvh2的波形与FFM-CSC的理论波形一致。图19b为滤波后的高低阀电流与交流母线电流的FFT分析结果。中高阀的11、13次交流电流谐波幅值分别为30 mA和21 mA，低阀组的11、13次交流电流幅值分别为28 mA和20 mA，母线处的11、13次谐波幅值分别为9.9 mA与5.7 mA。与不采用高低阀移相相比，11、13次谐波电流降低83%，从实验角度验证了高低阀移相EFFM可以大幅度降低11、13次谐波电流。图20a和图20b分别展示了高低阀组直流电压、器件VT1的阀电压和电容线电压的波形，可以看出实验波形与理论分析基本一致。
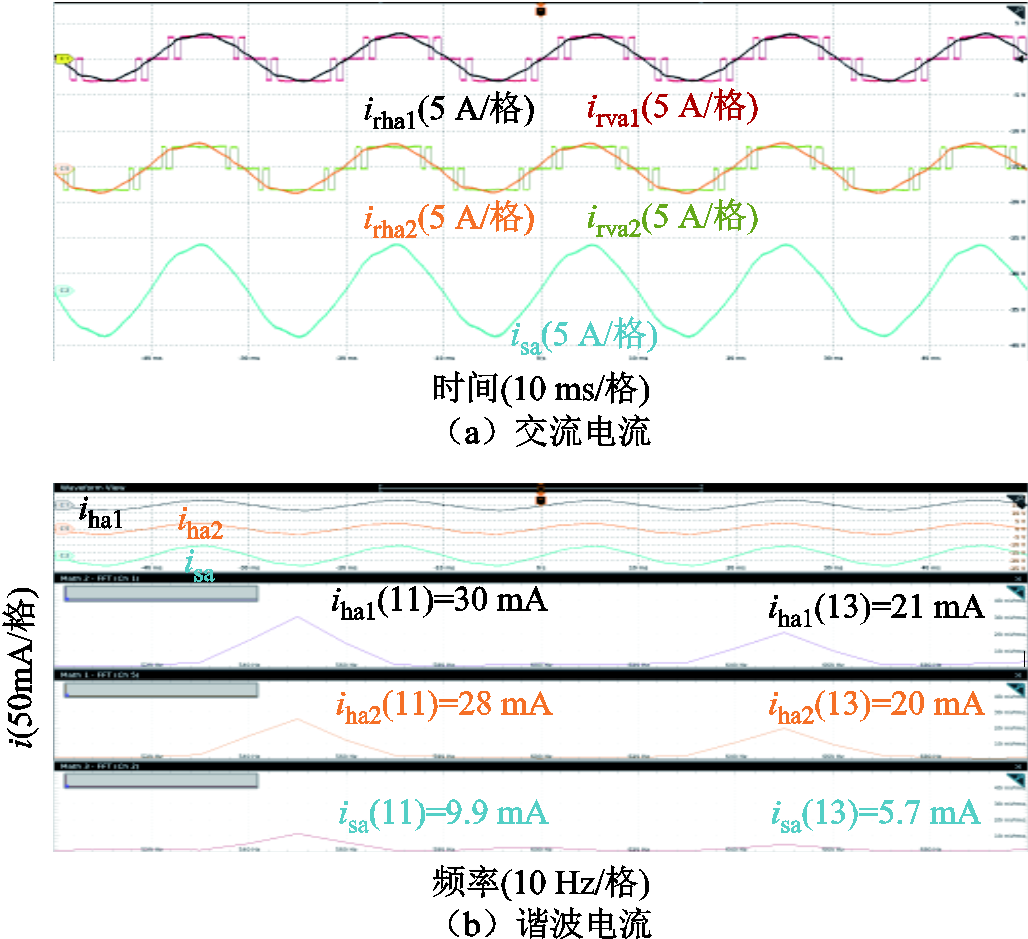
图19 高低阀移相EFFM-CSC交流电流实验波形
Fig.19 High and low valve phase-shifting EFFM-CSC AC current experimental waveforms
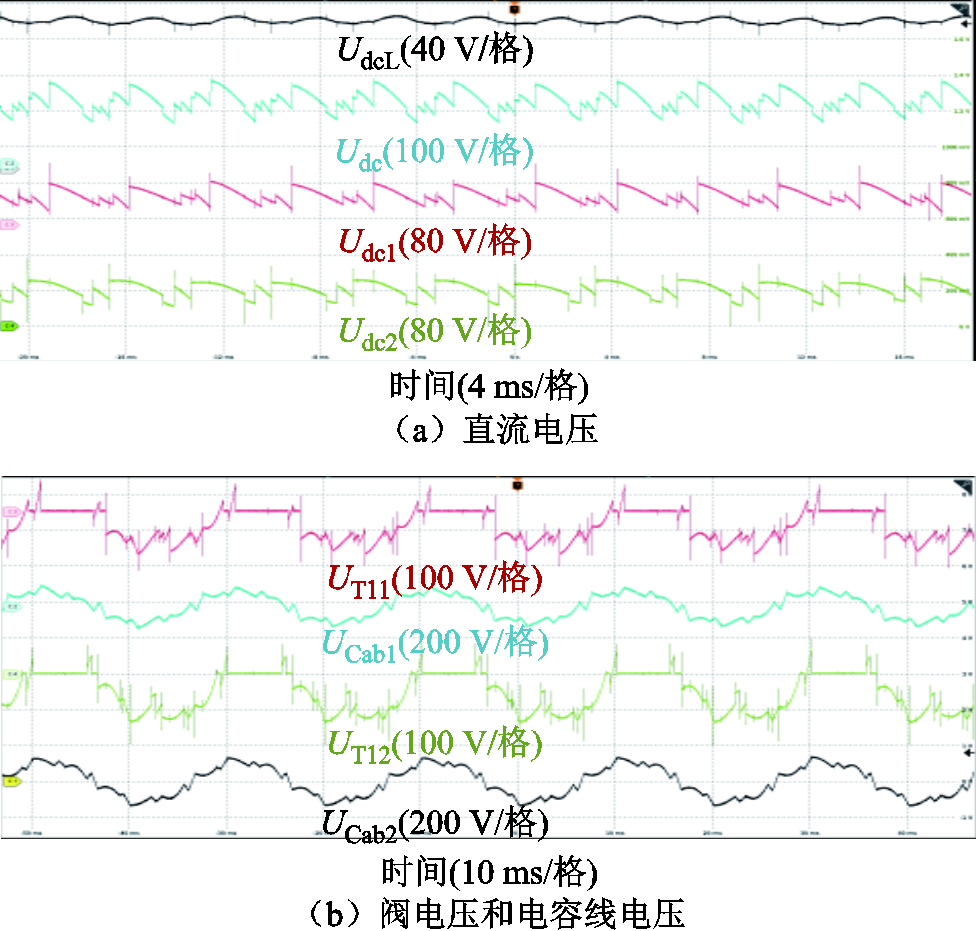
图20 高低阀移相EFFM-CSC电压波形
Fig.20 Valve phase-shifting EFFM-CSC voltage waveforms
针对目前海上风电CSC送出系统存在的谐波含量大、LC参数优化和海上交流电压的无法独立控制的问题，本文提出一种基于高低阀移相EFFM-CSC的远海风电直流送出系统，研究其谐波传递特性、参数优化设计方法和控制策略，主要结论如下：
1）本文建立了EFFM-CSC的谐波等值模型，通过探究普通双12脉动EFFM-CSC谐波传递过程，分析了移相变压器对特征谐波的影响规律。根据移相多重化思路，提出一种利用高低阀组触发角移相15°的控制策略。
2）高低阀移相EFFM-CSC可大幅度降低海上交流母线处11次和13次谐波含量，据此，本文综合考虑滤波效果、电容电压和滤波器的体积和重量，提出基于多目标优化的LC滤波器参数优化设计方法，大大降低了LC滤波器的参数，进一步实现海上平台的轻型化。
3）本文通过构造中间变量，详细地分析了控制目标和控制量之间的单调规律，并据此设计了海上交流电压/频率控制策略。所提策略能实现海上交流系统的电压幅值和频率的稳定运行，有效地适应风电场功率波动和陆上交流故障等工况。
4）基于搭建的高低阀移相EFFM-CSC实验平台验证了理论分析的正确性，证明了所提方法在不增设移相15°变压器的基础上，可大幅降低11、13次谐波电流。
虽然高低阀移相EFFM-CSC具有较高的技术经济性优势，但是仍然存在一些问题有待后续研究：如本文中拓扑结构为对称单极结构，移相策略在对称双极接线方式下的适应性有待研究；需要对比研究高压阀组和低压阀组的器件应力和运行寿命；有待建立送出系统的小信号模型，对其稳定性问题进行详细研究。
参考文献
[1] 申刘飞, 翟雨佳, 吴星徵, 等. 海上超导风电制氢一体化研究进展与发展趋势[J]. 电工技术学报, 2025, 40(11): 3362-3380. Shen Liufei，Zhai Yujia，Wu Xingzheng, et al. Progress and development trend of integrated research on hydrogen production from offshore superconducting wind power[J]. Transactions of China Electrotech-nical Society, 2025, 40(11): 3362-3380
[2] 蔡旭, 杨仁炘, 周剑桥, 等. 海上风电直流送出与并网技术综述[J]. 电力系统自动化, 2021, 45(21): 2-22. Cai Xu, Yang Renxin, Zhou Jianqiao, et al. Review on offshore wind power integration via DC transmission [J]. Automation of Electric Power Systems, 2021, 45(21): 2-22.
[3] 潘俊良, 王明渝. 适用于大型海上风电的谐振型飞跨电容式模块化升压变换器[J]. 电工技术学报, 2024, 39(12): 3746-3760. Pan Junliang, Wang Mingyu. Resonant flying capacitor modular boost converter for large scale offshore wind power[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3746-3760.
[4] 龙潇, 张晋宾, 陈令特. 未来能源技术展望[J]. 发电技术, 2025, 46(4): 651-693. Long Xiao, Zhang Jinbin, Chen Lingte. Prospects for future energy technologies[J]. Power Generation Technology, 2025, 46(4): 651-693.
[5] 郑涛, 章若竹, 吕文轩, 等. 基于故障主动控制的海上风电交流汇集线路时域距离保护[J]. 电工技术学报, 2025, 40(1): 122-138. Zheng Tao, Zhang Ruozhu, Lü Wenxuan, et al. Time-domain distance protection of offshore AC transmission lines based on fault active control considering distributed capacitance’s impact[J]. Tran-sactions of China Electrotechnical Society, 2025, 40(1): 122-138.
[6] 饶宏, 周月宾, 陈煜坤, 等. 高压大容量柔性直流换流阀关键设计和发展趋势[J]. 电源学报, 2024, 22(3): 1-14. Rao Hong, Zhou Yuebin, Chen Yukun, et al. Key design and development trend of high voltage and large capacity flexible DC converter valve[J]. Journal of Power Supply, 2024, 22(3): 1-14.
[7] Li Weixing, Zhu Meng, Chao Pupu, et al. Enhanced FRT and postfault recovery control for MMC-HVDC connected offshore wind farms[J]. IEEE Transactions on Power Systems, 2020, 35(2): 1606-1617.
[8] Yu Lujie, Li Rui, Xu Lie. Distributed PLL-based control of offshore wind turbines connected with diode-rectifier-based HVDC systems[J]. IEEE Tran-sactions on Power Delivery, 2018, 33(3): 1328-1336.
[9] 于浩天, 蔡旭, 杨仁炘, 等. 经DRU-HVDC送出的海上风电场汇集网电气调节特性分析及集群构网控制策略[J]. 中国电机工程学报, 2025, 45(6): 2318-2335. Yu Haotian, Cai Xu, Yang Renxin, et al. Analysis of electrical regulation characteristics of offshore wind farm collection network sent by DRU-HVDC and control strategy of cluster network construction[J]. China Industrial Economics, 2025, 45(6): 2318-2335.
[10] 俞露杰, 付子玉, 朱介北, 等. 远海风电DRU-HVDC送出系统构网控制与启动方法综述[J]. 电力系统自动化, 2023, 47(24): 63-79. Yu Lujie, Fu Ziyu, Zhu Jiebei, et al. Review on grid-forming control and start-up method of diode-rectifier-unit based HVDC transmission system for remote offshore wind farm[J]. Automation of Electric Power Systems, 2023, 47(24): 63-79.
[11] 金砚秋, 张哲任, 吴宏远, 等. 基于构网型风电机组和二极管整流单元的海上风电场黑启动策略[J]. 高电压技术, 2023, 49(9): 3730-3740. Jin Yanqiu, Zhang Zheren, Wu Hongyuan, et al. Black start strategy of offshore wind farm based on grid-forming wind turbines and diode rectifier unit[J]. High Voltage Engineering, 2023, 49(9): 3730-3740.
[12] 陆海洋, 李光辉, 王伟胜, 等. 海上风电经二极管混合直流送出系统的启停策略[J/OL]. 电力系统自动化,1-17[2025-12-09].https://link.cnki.net/urlid/32. 1180.tp.20251119.1615.002. Lu Haiyang, Li Guanghui, Wang Weisheng, et al. Start-stop strategy of diode hybrid DC transmission system for offshore wind power[J]. Automation of Electric Power Systems, 1-17[2025-12-09].https:// link.cnki.net/urlid/32.1180.tp.20251119.1615.002.
[13] Bidadfar A, Saborío-Romano O, Cutululis N A, et al. Control of offshore wind turbines connected to diode-rectifier-based HVDC systems[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 514-523.
[14] 李子欣, 徐飞, 赵成勇, 等. 面向高压直流输电的电流源型主动换相换流器研究综述[J]. 中国电机工程学报, 2021, 41(3): 1053-1069. Li Zixin, Xu Fei, Zhao Chengyong, et al. Research review of current-source type actively commutated converter for high voltage direct current transmission systems[J]. Proceedings of the CSEE, 2021, 41(3): 1053-1069.
[15] Torres-Olguin R E, Garces A, Molinas M, et al. Integration of offshore wind farm using a hybrid HVDC transmission composed by the PWM current-source converter and line-commutated converter[J]. IEEE Transactions on Energy Conversion, 2013, 28(1): 125-134.
[16] Xing Ling, Wei Qiang. Series-connected current-source inverters: fSW = 60 Hz[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 8882-8885.
[17] Zhao Chengyong, Xia Jiahang, Guo Chunyi, et al. An improved control strategy for current source converter-based HVDC using fundamental frequency modulation [J]. International Journal of Electrical Power & Energy Systems, 2021, 133: 107265.
[18] Blasco-Gimenez R, Añó-Villalba S, Aparicio N, et al. Harmonic filter reduction of off-shore wind farms connected with a diode based HVDC link[C]//2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 2012: 1585-1590.
[19] 黄晓明, 许烽, 陆承宇, 等. 海上风电经24脉动二极管整流器送出系统的交流滤波器优化配置[J]. 全球能源互联网, 2024, 7(5): 550-557. Huang Xiaoming, Xu Feng, Lu Chengyu, et al. Optimal configuration of AC filter for 24-pulse diode rectifier unit based offshore wind power integration system[J]. Journal of Global Energy Interconnection, 2024, 7(5): 550-557.
[20] 孙玉伟, 林佶, 汤旭晶, 等. 基于延边三角形接法的24脉波移相变压器设计与电磁特性分析[J]. 船海工程, 2024, 53(4): 48-53. Sun Yuwei, Lin Ji, Tang Xujing, et al. Design and analysis of 24 pulse wave phase shift transformer based on extended edge triangle connection[J]. Ship & Ocean Engineering, 2024, 53(4): 48-53.
[21] 夏嘉航, 王晨欣, 展瑞琦, 等. 基于主动换相型电流源换流器的远海风电并网系统[J]. 中国电机工程学报, 2022, 42(13): 4811-4823. Xia Jiahang, Wang Chenxin, Zhan Ruiqi, et al. Long-distance offshore wind power transmission system based on actively commutated current source converter [J]. Proceedings of the CSEE, 2022, 42(13): 4811-4823.
[22] Xia Jiahang, Guo Xiaojiang, Wang Chenxin, et al. Cooperative control strategy of fundamental frequency modulation-based current source converters for offshore wind farms[J]. IEEE Transactions on Power Delivery, 2022, 37(6): 4805-4815.
[23] 赵成勇, 冯定腾, 熊小玲, 等. 基于改进基频调制电流源换流器的高压直流输电系统[J]. 中国电机工程学报, 2024, 44(19): 7726-7739. Zhao Chengyong, Feng Dingteng, Xiong Xiaoling, et al. Enhanced fundamental frequency modulation based current source converter for HVDC transmission [J]. Proceedings of the CSEE, 2024, 44(19): 7726-7739.
[24] 马向辉, 张梓铭, 吴冇, 等. 2GW海上风电对称单极与对称双极柔直送出方案技术经济性对比[J]. 南方电网技术, 2024, 18(2): 30-38. Ma Xianghui, Zhang Ziming, Wu Mao, et al. Technical and economical comparisons of 2 GW offshore wind power transmission schemes by symmetrical monopole and symmetrical bipolar VSC-HVDC[J]. Southern Power System Technology, 2024, 18(2): 30-38.
[25] 张闻闻, 陈龙龙, 魏晓光, 等. 基于可控关断的电流源型直流输电系统设计及运行方式[J]. 中国电机工程学报, 2022, 42(7): 2532-2542.Zhang Wenwen, Chen Longlong, Wei Xiaoguang, et al. Design and operation mode of based on controllable current source converter HVDC system[J]. Proceedings of the CSEE, 2022, 42(7): 2532-2542.
Abstract With the development of offshore wind power going to the deep and distant sea, HVDC transmission is a competitive transmission technology for offshore wind power delivery. Modular multilevel converter (MMC) is currently the mainstream scheme for offshore wind power DC transmission projects. However, MMC consists of power sub-modules, which causes the problem of high construction costs for offshore platforms. The diode rectifier (DR) scheme, on the other hand, effectively reduces the construction cost. Nevertheless, DR does not have control capability and black start capability. The actively commutated current source converter (CSC) is a new type of topology with the advantages of small size, light weight and flexible control, which is suitable for remote offshore wind power delivery. Currently, CSC adopts fundamental frequency modulation (FFM) method, which uses a lower switching frequency. But there is only one control degree of freedom. Moreover, the reactive power and characteristic harmonics of FFM-CSC need to be compensated, which will limit the corresponding effect of lightning. Therefore, how to reduce the harmonic content of CSC, optimize the filter design method, and realize the stable operation of offshore AC system become the core issues of offshore wind CSC delivery system.
In order to further enhance the lightweight effect of offshore CSC and to realize the stable control of offshore AC system without relying on communication and grid-forming wind turbines. In this paper, an offshore wind power HVDC delivery system based on high-low-valve phase-shifting CSC is proposed and investigated in the following aspects. First, the topology of the offshore wind power transmission system is discussed in detail, and the modulation principle of the enhanced fundamental frequency modulation CSC (EFFM-CSC) is analyzed. Then, the harmonic equivalent model of the EFFM-CSC system is established, and the harmonic characteristics and content are analyzed. It can be found that the 11th and 13th harmonics can be drastically filtered out by shifting the trigger angle by 15° without adding a phase-shifting transformer. Then, this paper constructs a multi-objective optimization LC filter optimization method with the volume weight of the filter and the filter capacitor voltage as the objective function, which can improve the power density of the offshore CSC. Additionally, the mathematical model of offshore AC voltage magnitude and frequency is established, and the control strategy of offshore AC voltage magnitude and frequency is designed through the monotonicity analysis, which is conducive to the stable operation of offshore AC system.
Finally, the working principle and harmonic transfer characteristics of the phase-shifted EFFM-CSC can be verified as well as the effectiveness of the control strategy for the offshore AC system via the analysis of the PSCAD simulation model and physical experiments. From the analysis, the following conclusions can be drawn: (1) This paper proposes a control strategy using the high and low valve group trigger angle shifted by 15°, which can significantly reduce the 11th and 13th harmonic content at the offshore AC bus and achieve 87% of the filtering effect. (2) the optimization method is proposed for the design of the parameters of the LC filter by comprehensively taking into account the filtering effect, capacitance-voltage, and the volume and weight of the filter, which can greatly reduce the parameters of the LC filter, further realizing the lightweight of offshore platforms. (3) this paper analyzes in detail the monotonic law between the control targets and control quantities by constructing the intermediate variables, and designs the offshore AC voltage and frequency control strategy accordingly to realize the stable control of the voltage amplitude and frequency of the offshore AC system. (4) based on the constructed high and low valve phase-shifting EFFM-CSC experimental platform, the correctness of the theoretical analysis is verified, and it is proved that the proposed method can significantly reduce the 11th and 13th harmonic currents.
keywords：Offshore wind power, current source converter, high-low valve phase shift, lightweight
DOI: 10.19595/j.cnki.1000-6753.tces.242280
中图分类号：TM72
国家自然科学基金联合基金资助项目（U23B20119）。
收稿日期 2024-12-18
改稿日期 2025-01-22
冯定腾 男，1999年生，博士研究生，研究方向为高压直流输电和电流源换流器。E-mail：fengdingteng@ncepu.edu.cn
李 明 男，1979年生，博士，教授级高级工程师，研究方向为特高压直流和柔性直流输电成套设计。E-mail：mingli@chinasperi.sgcc.com.cn（通信作者）
（编辑 赫 蕾）