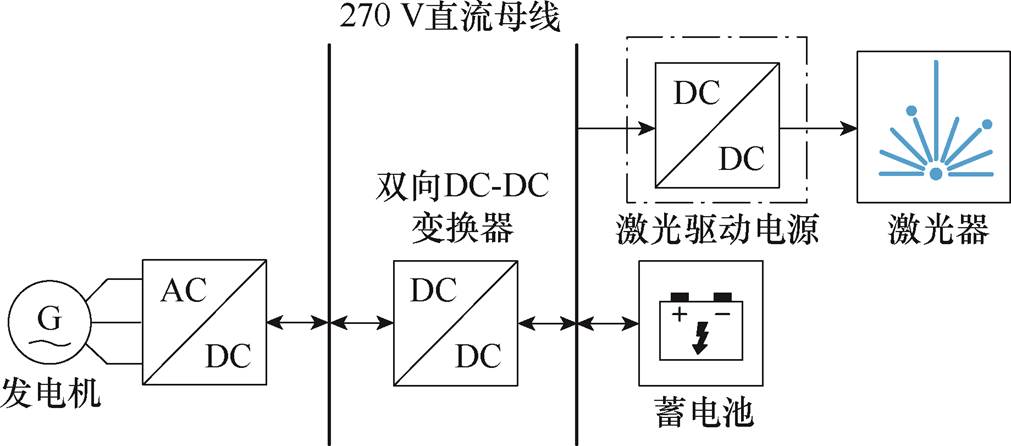
图1 一种机载激光武器供电系统架构
Fig.1 A power supply architecture for airborne laser weapon
摘要 机载激光武器具有定向增益高、攻击迅速、机动灵活等优势，具有重要的军事价值。激光器驱动电源承担着驱动、控制、保护激光器的任务。由于飞机对机载设备的质量、体积的苛刻要求，具有软开关特性的高频开关电源成为其理想选择。该文采用四相交错并联Buck变换器作为激光器驱动电源拓扑，针对现有三角电流模式（TCM）控制策略能量转换过程分析复杂、时序参数求解困难的问题，基于状态平面分析提出最小电流TCM的最优时序参数求解方法，实现变换器全工作范围内软开关。在此基础上，阐明非最优时序参数（开关频率偏低/偏高、死区时间偏大/偏小）对软开关过程的作用机理，为补偿实际电路寄生参数、采样误差等因素的影响提供理论依据。制作了一台200～500 kHz、额定功率4 kW的原理样机，实验结果表明该变换器能够在宽电压、宽负载范围保持软开关运行，且通态损耗达到最低，峰值效率达到97.83%。
关键词：激光器驱动电源 Buck变换器 三角电流模式控制 状态平面
多电飞机、全电飞机将电能作为主要或全部二次能源，驱动机载设备运行[1]，能够有效减轻飞机质量，降低燃油消耗，提高可靠性和可维护性。基于270 V/540 V的高压直流电气系统，具有质量轻、损耗低、可靠性高等优点，已经在国内外多款军用机型中获得应用[2]。
激光武器是一种定向能武器，具有定向增益高、攻击迅速、能量集中、打击距离远等优势，在现代战争中具有重要的战略意义和应用价值。为避免激光武器负载对飞机直流母线电压造成剧烈扰动，一般需配置储能单元对其瞬态功率进行缓冲。图1给出了一种机载激光武器供电系统架构。在进入作战任务之前，由双向DC-DC变换器对储能单元进行充电补能；在进入作战任务后，由储能单元或者由储能联合发电机，为激光武器提供电能[3]。
图1 一种机载激光武器供电系统架构
Fig.1 A power supply architecture for airborne laser weapon
传统的激光器驱动电源多采用线性电源，其输出电流纹波可低至mA级，具有高稳定性与高抗扰能力，但其损耗严重、效率低，难以适用于大功率激光器的驱动。相比而言，具备软开关特性的开关电源，具有运行效率高、功率密度大、开关噪声低的优点[4-5]，是大功率机载激光器驱动电源的理想选择之一。
Buck/Boost变换器具有电路拓扑简单、可靠性高的优点，被广泛应用于各个领域。文献[6]采用交错并联Buck变换器对大功率半导体激光器进行驱动，其工作在硬开关模式，峰值效率为96%。为了实现变换器软开关运行，进一步提升功率密度，文献[7]提出了定频软开关控制方法，通过选取合理的电感值来增加电流纹波，进而实现软开关。但由于定频控制下电感电流的纹波不随负载变化，导致变换器的轻载效率较低。文献[8]提出了一种三角电流模式（Triangular Current Mode, TCM）控制方法，通过控制开关过程中各阶段时间强迫电感电流反向过零，将功率管的输出电容在死区时间内放电至零，能够实现Buck/Boost变换器全范围零电压开关（Zero Voltage Switching, ZVS）。但该控制方法依赖电感电流过零检测电路，而过零检测的精度和延迟会严重影响控制的效果。为解决上述问题，文献[9-10]基于电感电流分段线性简化模型，假设死区时间内电感电流保持不变，通过改变开关频率让反向电感电流的最小值保持恒定，以实现全负载范围ZVS。与文献[8]相比，该方法简化了控制复杂程度，且无需电感电流过零检测。但由于该方法忽略了死区时间内的谐振过程，缺乏对死区时间的精确调节，难以保证变换器的通态损耗达到最低。文献[11-15]通过对变换器状态方程进行解析计算，求解出实现ZVS的最小反向电感电流，进而得出实现ZVS所需的开关频率与死区时间。但这种方法往往需要对电感与电容间的能量传递过程进行复杂的公式推导，难以直观地体现电感和功率管寄生电容的谐振过程。文献[16-17]采用状态平面法，清晰直观地体现了TCM控制策略下电感和功率管寄生电容的谐振过程，但其仅给出了最优状态平面轨迹，并未给出最优时序控制参数的求解方法，同时也缺乏对变换器偏离最优时序控制参数时的软开关特性进行分析。
本文针对大功率激光器驱动应用场景，采用四相交错并联Buck变换器作为驱动电源，提出最小电流TCM控制方法，主要工作有：
1）基于状态平面对Buck变换器的最小电流TCM控制方法进行分析，建立了最优ZVS时序参数计算模型，并通过多项式拟合将最小电流TCM控制在数字控制器中实现，使变换器在保证软开关运行的前提下通态损耗达到最低。
2）基于状态平面分析，阐明非最优时序参数（开关频率偏低/偏高、死区时间偏大/偏小）对软开关过程的作用机理，为如何获得足够的ZVS裕度以克服实际应用中电路寄生参数、采样误差等因素影响，提供理论依据。
高能光纤激光器因其转换效率高、光束质量好、散热性能强等优点，是激光武器的关键部件，其主要包括泵浦源、增益介质、谐振腔等部分。图2为激光武器系统的结构框图。泵浦源是光纤激光器的核心部件，其作用是将电能转换为光能以激发光纤中的掺杂物，使其产生激光。通常采用半导体激光器作为泵浦源。图3为某型976 nm、510 W半导体激光器的功率-电压-电流特性曲线。半导体激光器与普通二极管相似，具有单向导电性，其伏安特性曲线可近似描述为Vo=Vd+rIo，其中，Vd为半导体激光器的开启电压，r为等效串联电阻。由图3可知，在工作过程中半导体激光器的电压范围较窄，因此为保证出光功率的稳定，驱动电源应采用恒流输出形式。
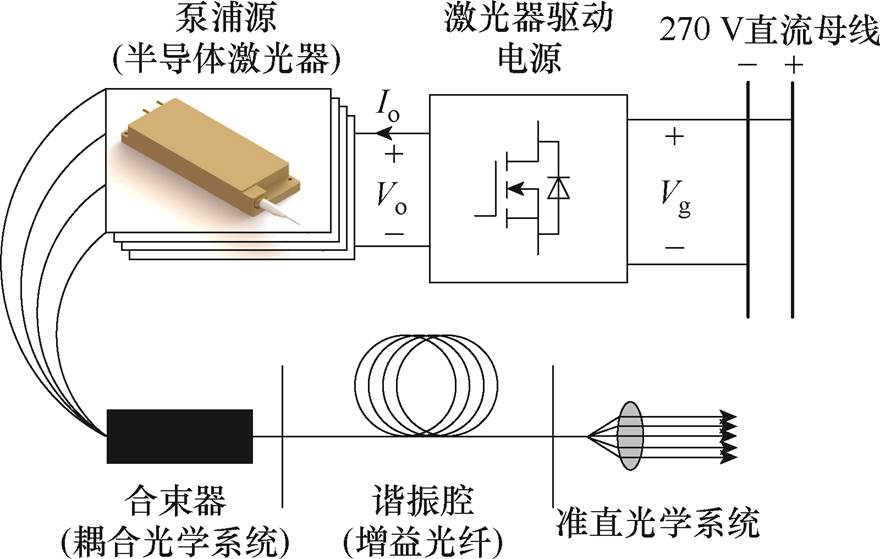
图2 激光武器系统的结构框图
Fig.2 The block diagram of laser weapon systems
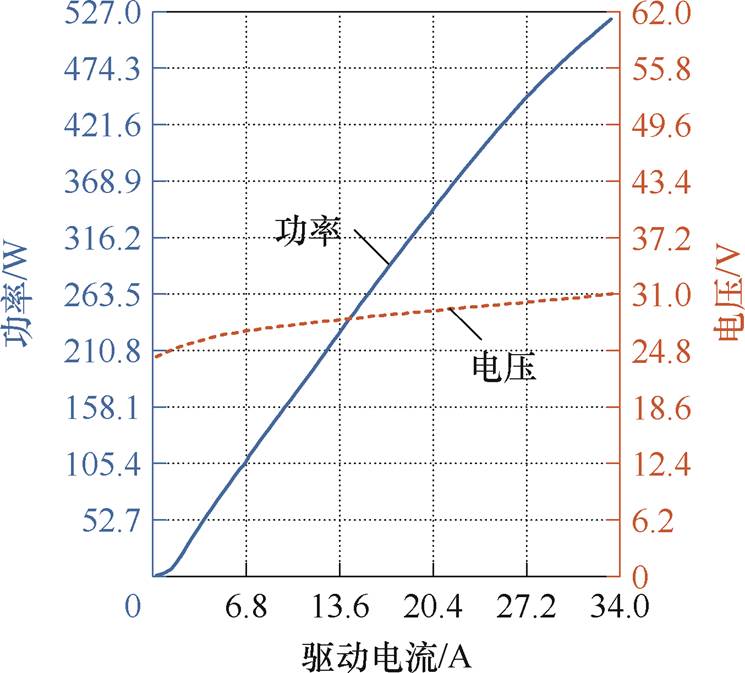
图3 某型976 nm、510 W半导体激光器电特性
Fig.3 Electrical characteristics of a 976 nm, 510 W semiconductor laser
本文所采用的激光器负载由4个976 nm、510 W半导体激光器串联组成。根据图3可得，激光器负载的开启电压为95.8 V，等效串联电阻为0.88 W。激光器工作温度要求在23～27℃以内，因此可认为在工作过程中等效串联电阻r不变。当输出电压大于开启电压Vd时，输出电压与输出电流的关系可表示为Vo=95.8+0.88Io。综上所述，激光器驱动电源的设计指标见表1。
表1 激光器驱动电源设计指标
Tab.1 Specifications ofthe laser driver power supply
指 标数 值 输入电压Vg/V200～300 输出电压Vo/V95.8～124 输出电流Io/A0～34 额定功率Po/kW4
由于在TCM控制下变换器的电感电流具有较大的纹波，在实际应用中常采用多相交错并联的方式来分摊各相的电热应力。同时，多相交错并联结构还能显著降低输出电流的纹波，从而有利于减小输出滤波电容的容量和体积。针对表1给出的输入/输出电压及功率范围，本文采用四相交错并联Buck变换器作为主电路拓扑，如图4所示。变换器的相数综合考虑了功率密度、输出电流纹波、开关器件电热应力的约束[18-19]。图4中，变换器由A、B、C、D四相组成，每相分别由电感Lx和开关器件Sx1和Sx2构成（x=A, B, C, D），Co为输出滤波电容，输出侧激光器负载以二极管VDo和等效串联电阻r表示。
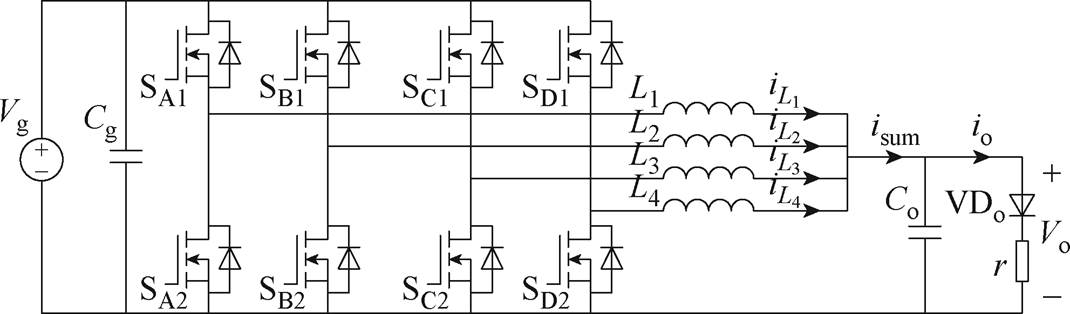
图4 四相交错并联Buck变换器的主电路拓扑
Fig.4 Circuit topology diagram of a four-phase interleaved parallel Buck converter
由于多相交错并联拓扑中各相电路参数一致，因此本节以其中一相为例，对最小电流TCM控制策略进行分析，所得出的结论同样适用于其余各相。
TCM控制通过增大电感电流的纹波，使电感获得足够大的反向电流与MOSFET输出电容在死区时间内进行谐振，从而将MOSFET两端电压降为0来实现ZVS。针对图5a所示的单相同步Buck电路拓扑对TCM控制进行分析。图5b给出了TCM控制下功率管控制信号c1和c2、电感电流、桥臂中点电压的波形。在一个开关周期中，共包含四段时间间隔，分别为上管S1导通时间tS1、下管S2导通时间tS2和两段死区时间td1、td2。
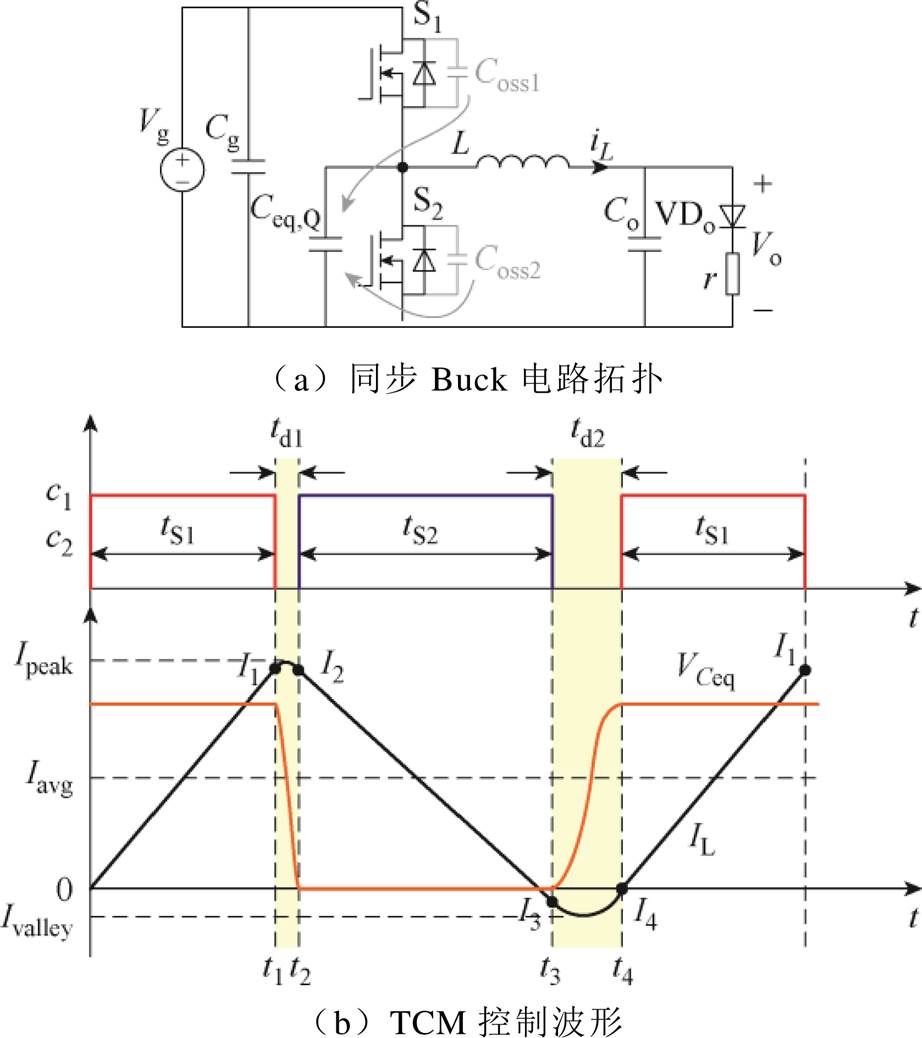
图5 同步Buck电路拓扑及TCM控制波形
Fig.5 Topology and TCM control waveforms ofthe synchronous Buck converter
如图5b所示，当变换器带载工作时，死区时间td1内电感电流通常为较大的正向电流，能够将下管S2的输出电容Coss2完全放电以及上管S1的输出电容Coss1完全充电，使S2零电压开通，该过程称为“自然换流”。但在死区时间td2内，为了使上管S1零电压开通，必须给电感提供足够大的负向电流，才能将上管S1的输出电容Coss1完全放电以及下管S2的输出电容Coss2完全充电，该过程称为“强迫换流”。因此，TCM控制的关键是通过对变换器时序参数（频率和死区时间）进行准确调节，强迫上管S1实现零电压开通[17]。需要说明的是，图5b给出的波形为TCM控制的最优ZVS波形，即当上管开通信号到来时，Coss1和Coss2恰好完成充放电，使变换器实现ZVS的同时，电感电流纹波达到最小，通态损耗最低。定义该控制方式为“最小电流TCM控制”。
由于MOSFET的输出电容Coss与漏源电压vds呈现非线性，因此不宜直接采用传统的线性电路分析方法对Coss的充放电过程进行分析。根据不同的等效原则，可将Coss等效为阻抗等效电容、能量等效电容、电荷等效电容等线性电容[20]。考虑到对软开关过程的分析，其本质是研究死区时间内输出电容电荷量的变化情况，因此应采用电荷等效电容对Coss进行等效[21]。针对一个半桥电路，为方便分析，可将两个MOSFET的输出电容等效为一个并联在桥臂中点与母线负极之间的电荷等效电容Ceq,Q，如图5a所示。当等效电容两端电压vCeq,Q与上管S1两端电压加和恒为输入电压Vg，即vCeq,Q=Vg时，S1漏源极电压降为0 V；当vCeq,Q=0 V时，下管S2漏源极电压为0 V。电荷等效电容Ceq,Q表达式为
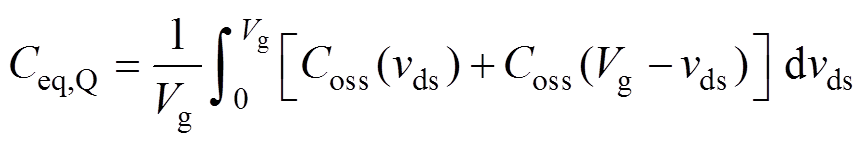（1）
本文所采用的功率开关器件为C3M0065090J。根据式（1）和数据手册所提供的器件输出电容与vds的曲线，可计算出Ceq,Q与Vg关系如图6所示，其中在电压270 V条件下，对应的等效电容约为400 pF。
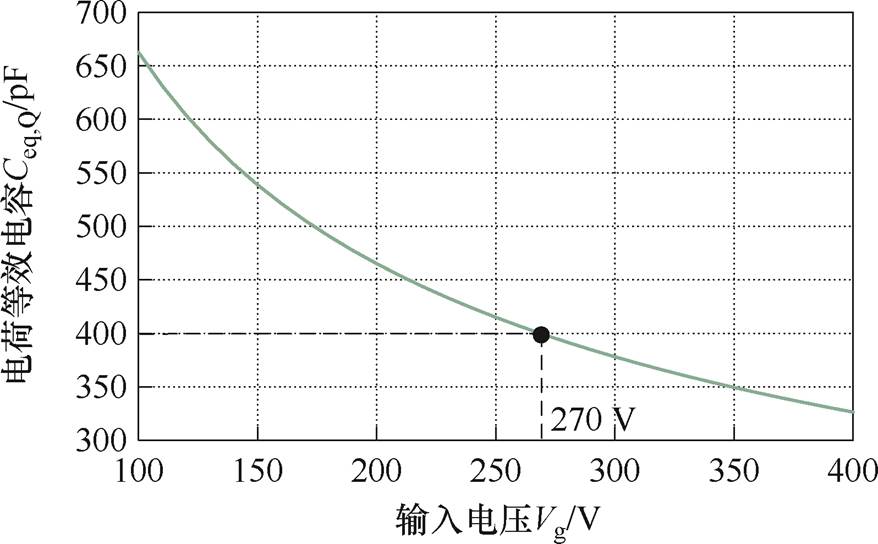
图6 Ceq,Q与输入电压Vg关系曲线
Fig.6 Curve of Ceq,Q versus input voltage Vg
本文将TCM控制下的电感电流和等效电容电压通过状态平面进行描述，给出实现最小电流TCM控制的条件和时序参数计算方法，在实现ZVS的前提下使通态损耗最低。
以死区时间td2内的强迫换流过程为例，对电感L和电荷等效电容Ceq,Q列写状态方程，可得
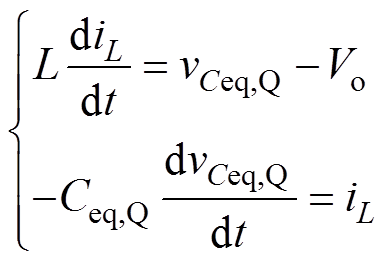（2）
进一步可得
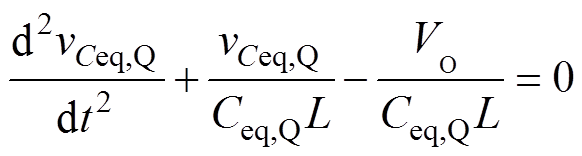（3）
该微分方程的初始条件为死区时间td2起始时刻对应的电压与电流，根据图5b，有
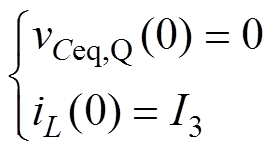（4）
进而可求解出式（4）初始条件下微分方程式（3）的特解为
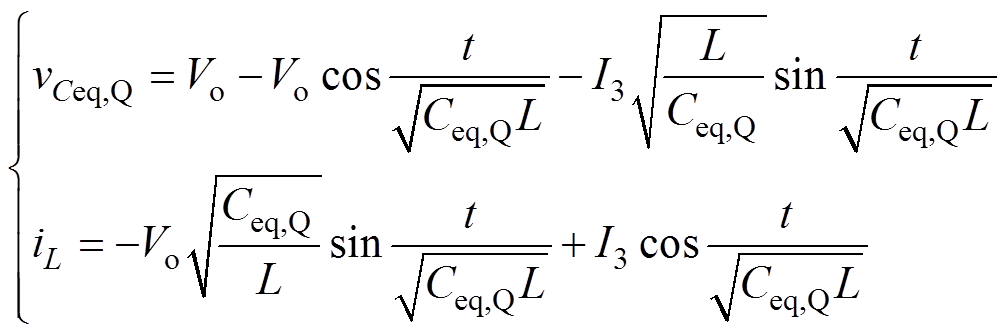（5）
式（5）描述了在死区时间td2内等效电容电压与电感电流的变化规律。
为方便分析，采用表2所示的基值，对式（5）进行归一化处理。归一化后的表达式为
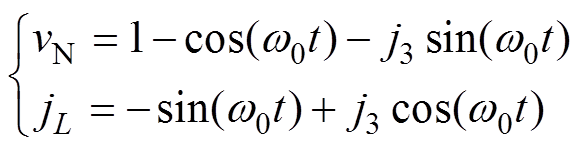（6）
式中，vN为归一化的等效电容电压；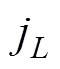
为归一化的电感电流；j3为归一化的初始电感电流I3。从式（6）进一步可得
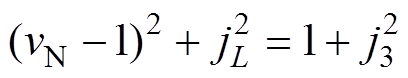（7）
表2 归一化基值
Tab.2 Base values for normalization
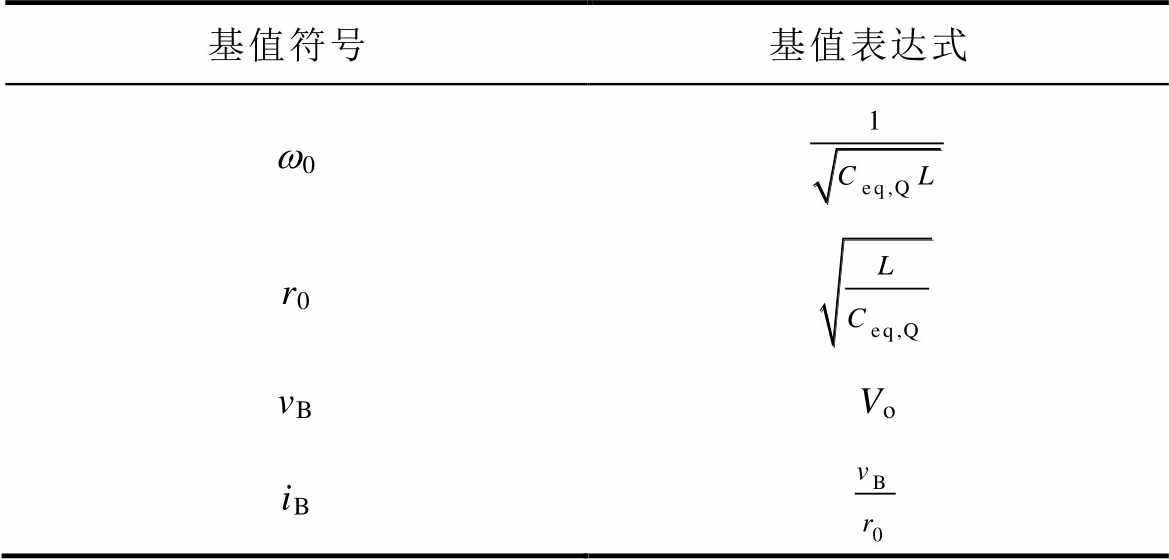
基值符号基值表达式 w0 r0 vBVo iB
取归一化等效电容电压vN为横轴，归一化电感电流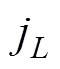为纵轴，则式（7）表明在死区时间td2内，电容电压和电感电流的轨迹为以(1, 0)为圆心、半径为
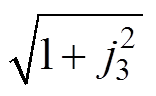的圆。
同理可得，在死区时间td1内，轨迹为以(1, 0)为圆心、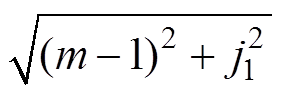
为半径的圆，其中m定义为输入电压与输出电压的比值，即
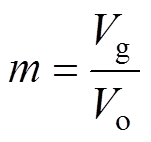（8）
在功率管S1或S2开通期间，即在tS1和tS2内，由图5b可知，等效电容电压保持不变，而电感电流线性变化，因此对应的轨迹为平行于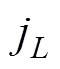轴的直线，其中tS1所对应的轨迹为vN=m，tS2所对应的轨迹为vN=0。
定义最小电流TCM控制所对应的状态平面轨迹为最优ZVS轨迹。针对m＞2、m＜2、m=2三种情况，图7给出了在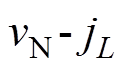
状态平面上的最优ZVS轨迹与对应的归一化强迫换流过程波形。
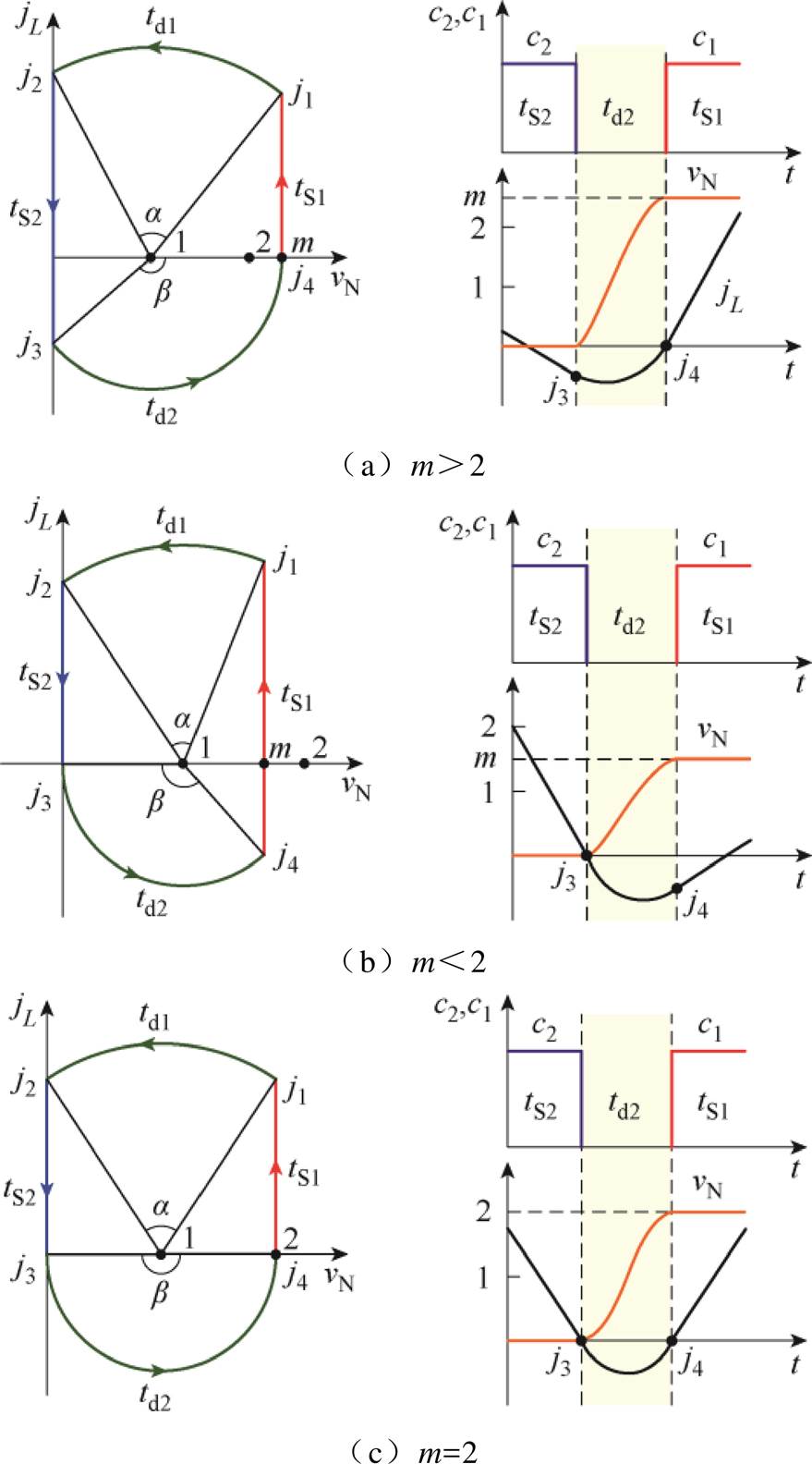
图7 最优ZVS状态平面图与波形
Fig.7 Optimal ZVS state plots and waveforms
图7a为m＞2时的轨迹和波形。可以看出，为了使等效电容在死区时间td2结束时完全充电，需要在下管S2关断时提供足够大的反向电感电流j3。当满足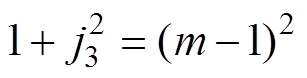
时，td2所对应的圆弧刚好与直线vN=m在点(m, 0)处相切。表明当
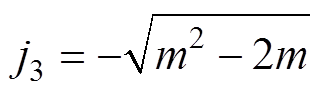时，等效电容在td2结束时恰好充电至输入电压Vg，上管实现零电压开通。从图7a中还可以看出，此时j4=0，电感电流的有效值达到最小。
分析图7b所示的m＜2最优ZVS轨迹可知，当下管S2关断时，若电感电流j3=0，td2所对应的圆弧便会与直线vN=m相交，且交点为(m, j4)。表明j3=0即可将等效电容充电至Vg，且此时电感电流的有效值达到最小。由状态平面可知，与m＞2的情况不同，此时上管S1开通时刻的电感电流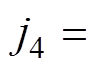
。
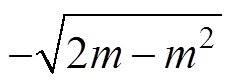图7c为m=2所对应的最优ZVS轨迹及强迫换流波形。由于该情况为m＜2和m＞2两种情形的边界，因此易知此时有j3=0，且j4=0，td2所对应的轨迹为半圆弧。
定义最优ZVS情况下对应的时序参数为最优开关频率与最优死区时间（fsw,opt, td1,opt, td2,opt）。根据上述分析，变换器应在最优ZVS情况下工作，否则将会产生额外的损耗或发生硬开关，降低变换器的效率（具体在第3节中分析）。因此需要对最优ZVS状态平面轨迹进行求解，求出不同工作条件下变换器的最优时序参数。状态平面轨迹中的几何关系、时间间隔、平均电流可表示为
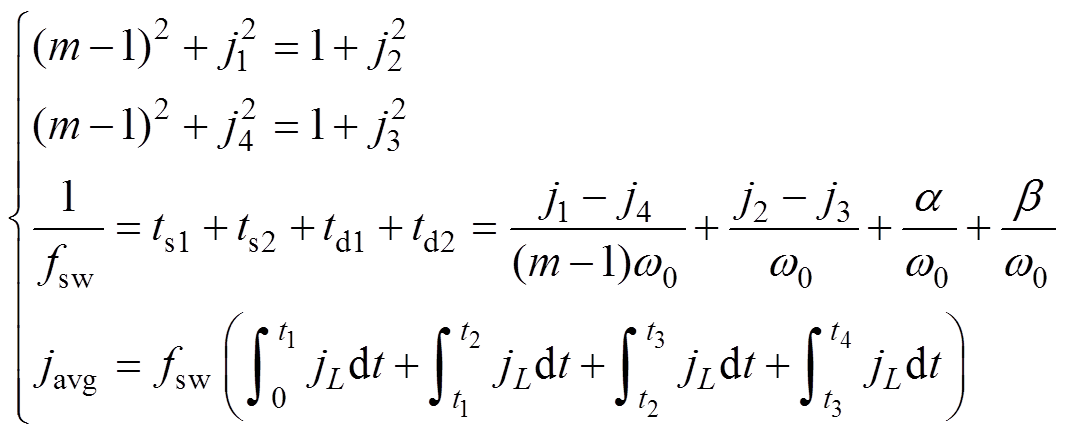（9）
式中，fsw为开关频率；javg为归一化的电感电流平均值，其表达式中各积分的上、下限如图5b所示。式（9）中的前两个等式根据最优ZVS轨迹中的几何关系得出；开关周期表达式中上、下桥臂MOSFET导通时间tS1、tS2由电感的状态方程推导出，而死区时间td1、td2则由ZVS轨迹中圆弧段对应的圆心角a、b来描述。
式（9）中，圆心角a、b以及计算平均电感电流的各段积分为
（10）
式中，a、b的表达式根据状态平面中的几何关系得出；电感电流的分段积分表达式则由图5所示的电流波形积分得到。
由图7状态平面分析可知，为实现最优ZVS，当m＞2时，有j4=0；m＜2时，有j3=0；而m=2时，j3=j4=0。将上述条件代入式（9）和式（10），即可通过数值方法求解出最优时序参数。
针对表1所示的设计指标，利用最优ZVS轨迹求解出TCM控制的最优开关频率fsw,opt和最优死区时间td1,opt、td2,opt，如图8所示。
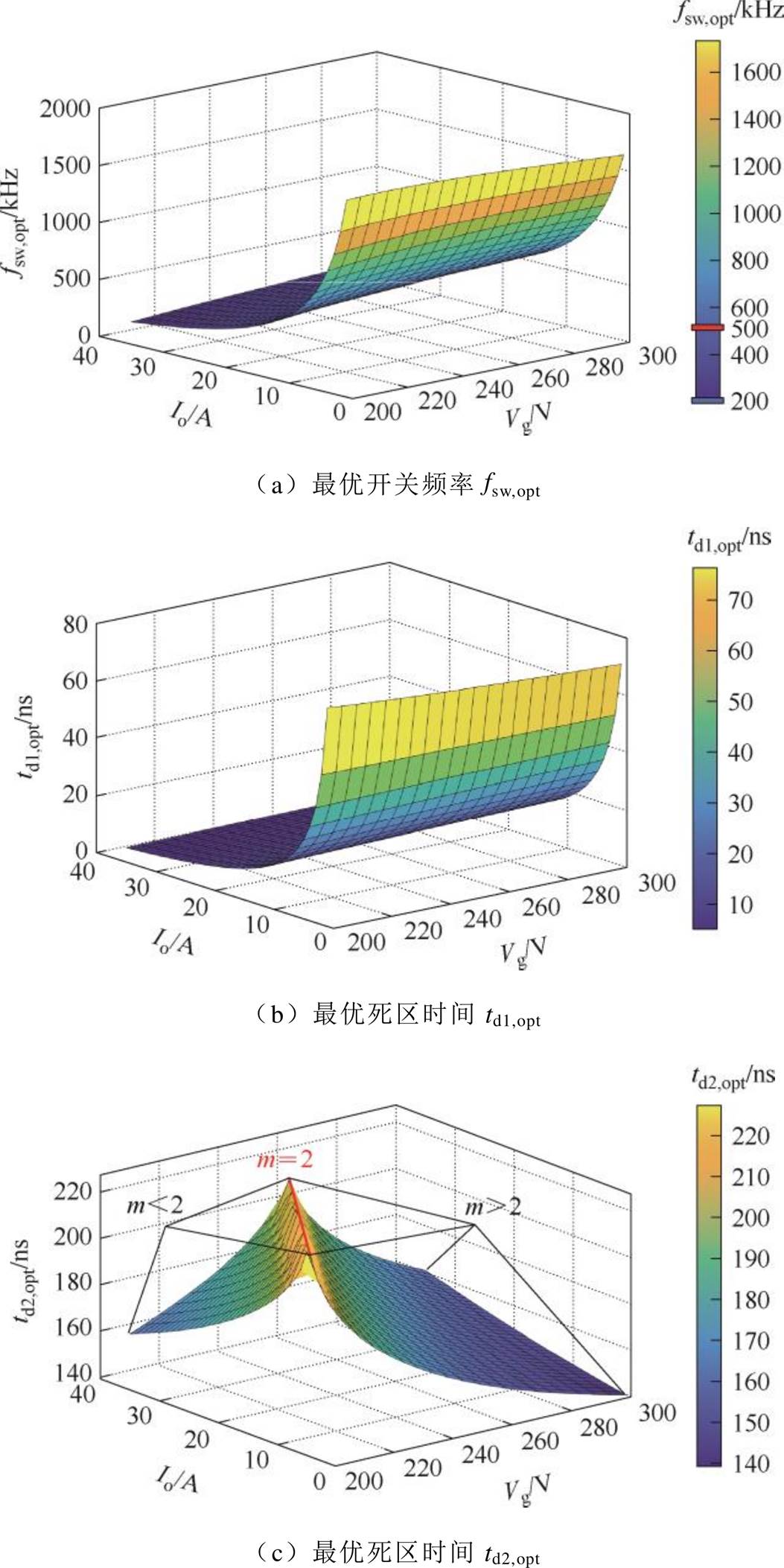
图8 最优时序参数与输入电压、输出电流之间的关系
Fig.8 The optimal timing parameters with respect to input voltages andoutput currents
图8a为开关频率关于输入电压和负载电流的关系，在全工作范围下频率变化范围是204 kHz～1.6 MHz。在实际应用中，考虑磁心的工作频率、驱动电路及开关器件的延迟[22]，需对开关频率进行限制。为此，本文将开关频率限定为500 kHz，在开关频率达到限幅值后，死区时间td2也固定为该工况下500 kHz对应的最优死区时间，不再增长。需要说明的是，由于激光器负载的电压和电流之间存在线性耦合关系（参见第1节），因此时序参数的解仅与输入电压Vg和负载电流Io有关。
为避免桥臂直通，上、下MOSFET驱动信号的最小死区时间应满足
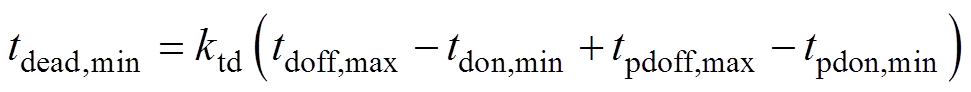（11）
式中，tpdon和tpdoff分别为驱动芯片的开通和关断延迟；tdon与tdoff分别为MOSFET的开通和关断延迟；ktd为确保桥臂不会直通所取的裕度系数，取值为1.5。C3M0065090J关断延迟最大值为90 ns、开通延迟最小值为60 ns；所用驱动芯片NCV57001的关断延迟最大值为15 ns、开通延迟最小值为10 ns。由式（11）可计算出最小死区时间为75 ns。由于图8b中工作范围内的最优死区时间td1均小于最小死区时间td,min，因此将td1固定为75 ns。需要说明的是，td1内首先经过时长为td1,opt的谐振过程，等效电容放电至0 V，剩余时间内电感电流通过下桥臂MOSFET体二极管续流线性下降，与tS2时间内电流下降斜率一致。故固定死区时间td1不会影响死区时间td2内的谐振过程，也不会影响上下桥臂MOSFET的ZVS。
在实际应用中，为了避免在数字控制器中建立复杂的查找表，可对最优开关频率与最优死区时间的解进行多项式拟合[16]，本文所选取的多项式形 式为
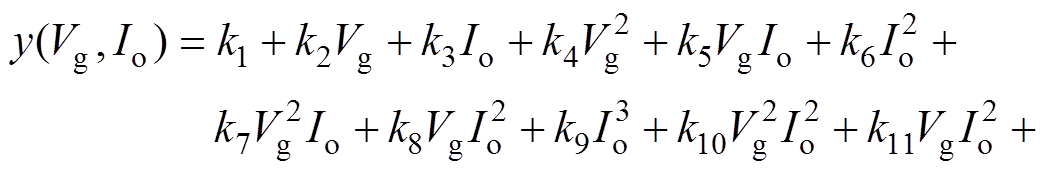
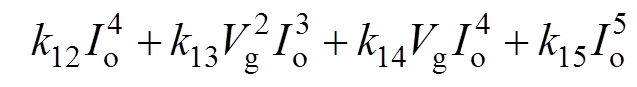（12）
此外，如图8c所示，由于最优死区时间td2,opt的解并非单调变化，因此需要根据m的值进行分段拟合。定义最优开关频率的拟合函数为fsw,opt(Vg, Io)；定义m＞2与m≤2情况下最优死区时间的拟合函数分别为td2,opt1(Vg, Io)和td2,opt2(Vg, Io)。
图9为上述时序参数多项式拟合的残差图，其反映了各时序参数的拟合效果。在限幅值以内，fsw拟合参数的最大残差为3.01 kHz，方均根误差（Root Mean Square Error, RMSE）小于1 kHz；td2的最大残差为12.41 ns，RMSE均小于2 ns，误差均控制在5%以内。各拟合确定系数R-square均接近1，拟合结果能够满足控制精度要求。
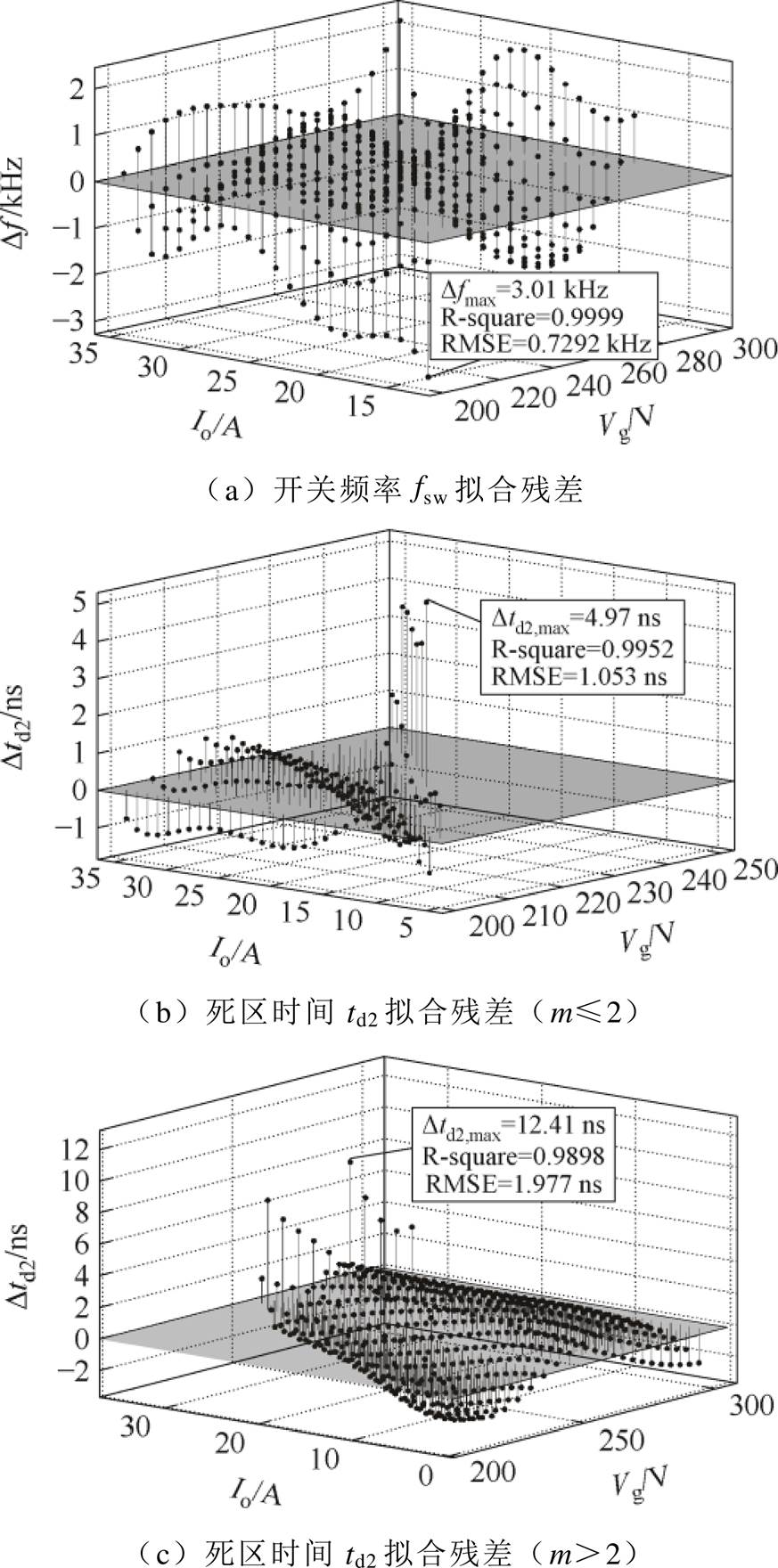
图9 多项式拟合结果残差图
Fig.9 Residual plots of polynomial fitting results
考虑本文所设计的变换器硬件布局对称且驱动芯片、开关器件及电感具有良好的一致性，可认为每相的寄生参数也近似相等。故选取A相电感电流作为被控量，其余各相的控制量与A相相同，以降低系统复杂性。图10为最小电流TCM控制策略在数字控制器中执行的逻辑流程。采用定时器中断服务子程序执行最小电流TCM控制程序，定时器的周期设置为30 ms。
数字控制器首先对输入电压Vg和A相电感电流的平均值IL,avg进行采样与处理，进而得到输出电流Io、输出电压Vo和m。然后，根据m选择相应的时序参数拟合表达式，计算出最优时序参数fsw,opt和td2,opt，并进行限幅处理。同时，参考电流Iref与电感电流平均值IL,avg的差值输入PI补偿器，得到占空比d，对输出电流进行调节。最后，根据所得到的调制变量，更新PWM驱动信号，使变换器在最小电流TCM模式下驱动激光器输出目标功率。
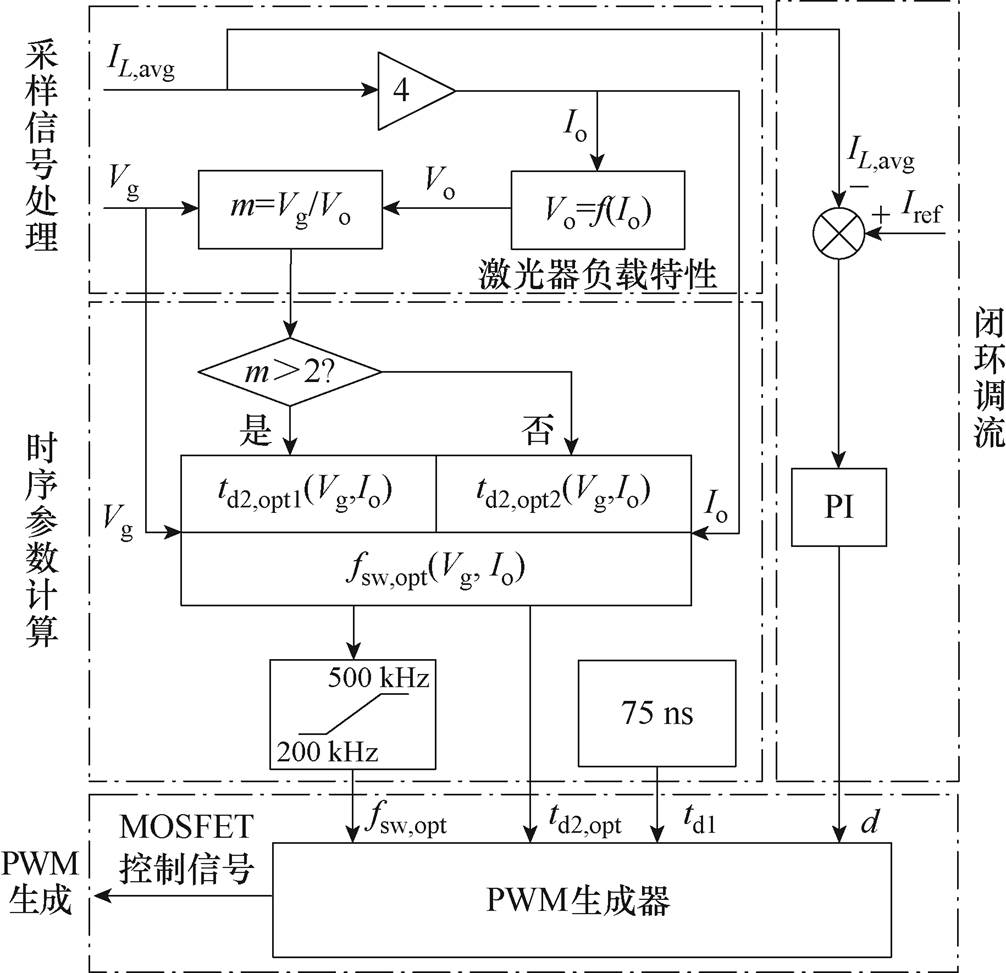
图10 最小电流TCM控制策略逻辑流程
Fig.10 Logical flow chart of the mininum current TCM control
变换器实际工作中，可能会由于电路寄生电阻、电压电流采样误差、等效电容建模不够准确等原因导致计算出的时序参数不能实现最优ZVS，引入额外的MOSFET导通损耗与体二极管导通损耗，甚至会丢失软开关进入硬开关状态，影响变换器效率。下面结合状态平面，对m＞2、m＜2情况下非最优时序参数对软开关特性的影响进行分析。由于m=2的情况同时具备m＞2、m＜2的特点，不作赘述。
当开关频率低于最优开关频率时，变换器将工作在次优ZVS模式下，即功率管仍能实现ZVS，但与最优ZVS相比，通态损耗会更高，其状态平面轨迹如图11a和图11b所示。图11中，实线为次优ZVS轨迹，虚线为最优ZVS轨迹。在电感电流平均值IL,avg不变的前提下，次优ZVS轨迹电流峰、谷值高于最优ZVS轨迹，导致电感电流的有效值增加，产生更大的通态损耗。同时，关断电流的增大也会带来额外的关断损耗。此外，由于电流j3的增大，等效电容充电所需谐振过程的时间也在减小。若死区时间与最优ZVS轨迹保持一致，在等效电容充电完毕后，上管体二极管导通续流，产生体二极管导通损耗。
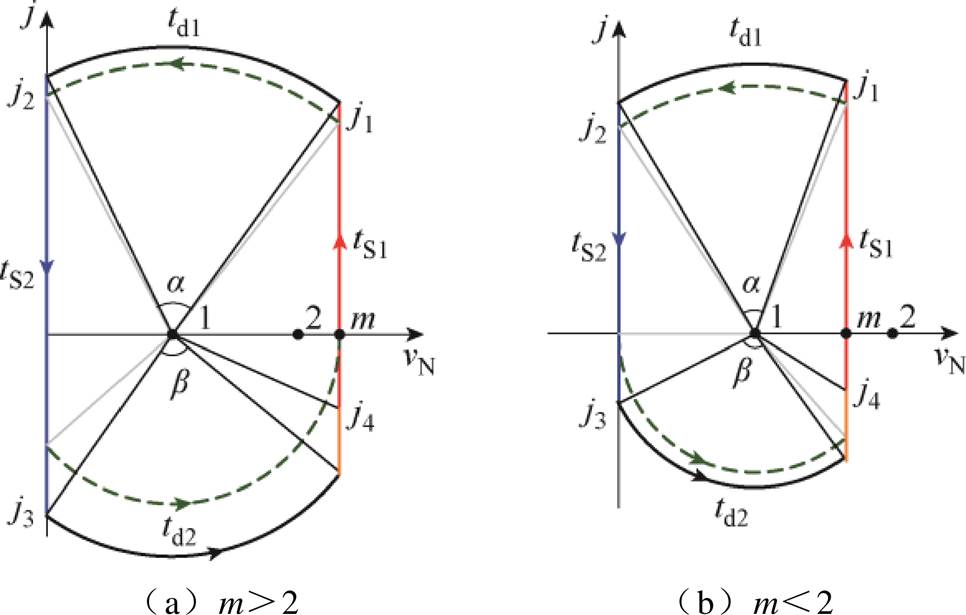
图11 次优ZVS状态平面轨迹
Fig.11 The suboptimal ZVS state planes
当开关频率过高，或者死区时间过长或过短，都将可能导致变换器发生硬开关。
图12a和图12b为开关频率高于最优频率（fsw＞fsw,opt）时的状态平面轨迹。当m＞2时，如图12a所示，在该情况下有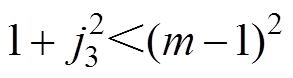
。因此，无论死区时间td2多长，其所对应的圆弧与直线vN=m都没有交点，表明无法将等效电容完全充电，导致变换器发生硬开关；如图12b所示，当m＜2时，过高的开关频率则会导致电流j3变为正电流。在下管S2关断后，其体二极管导通使电感电流下降至0后，再开始电感与等效电容的谐振过程。此时体二极管导通时间增加了实现ZVS所需的死区时间，若不增加td2，则变换器工作在硬开关模式。
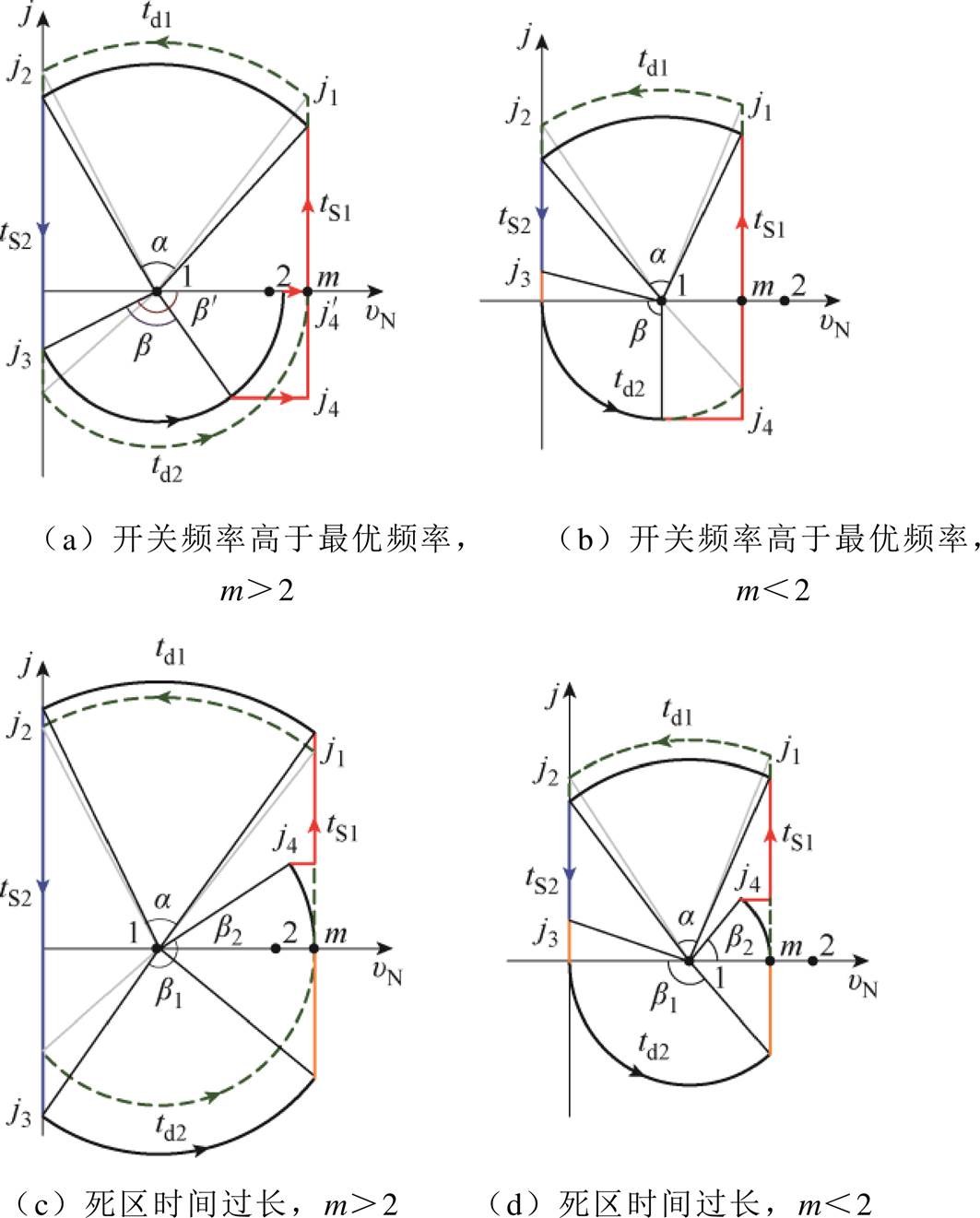
图12 硬开关状态平面图
Fig.12 The state planes with hard-switching
图12c、图12d为死区时间过长时的状态平面轨迹。当m＞2时，如图12c所示，若在图7a最优ZVS轨迹的基础上延长死区时间td2，等效电荷电容两端电压充电至Vg后，又会开始下降，在驱动信号到来时上管S1硬开通。当m＜2时，如图12d所示，死区时间td2过长与图12c相似，驱动信号到来时若电感电流已变为正电流，上管S1硬开通。此外，易知若td2小于最优死区时间td2,opt，则等效电容两端电压没有足够的时间增加至Vg，即S1漏源极电压不能降至0 V，也会导致硬开关。
综上所述，当开关频率低于最优工作频率（fsw＜fsw,opt）时，仍能保证变换器工作在软开关状态，但在一定程度上会加通态损耗；反之，当开关频率高于最优频率（fsw＞fsw,opt），或者死区时间偏离最优死区时间时，均会导致变换器发生硬开通。在实际应用中，为克服电路寄生参数、采样误差、系统延迟等因素对实现ZVS的影响，可通过适当降低开关频率来获得足够的裕度。
本文搭建了一台开关频率为200～500 kHz的四相交错并联Buck变换器原理样机，对所提出的控制方法进行验证。样机的实物图如图13所示，其各指标参数见表1。样机的每相电感L=12 mH，输出滤波电容Co=8 mF。采用STM32G474作为数字控制器，其中基于多项式拟合的最小电流TCM控制算法的执行时间为11.7 ms。在实验中，将电子负载配置为CR-LED模式来模拟激光器负载的特性，其中开启电压和等效串联电阻参数的设置与第1节所述一致。
图13 样机实物图
Fig.13 The picture of prototype
首先，对本文提出的最小电流TCM控制方法进行验证。实验中，变换器的输出电流Io=32 A，输出电压Vo=124 V。输入电压Vg分别设置为270 V、248 V、230 V三个工作点，对应m＞2、m=2、m＜2三种情况。由于变换器每一相的稳态波形基本一致，因此图14以A相波形为例，对最小电流TCM控制的效果进行验证。
图14给出了变换器的稳态测试波形，其中包括A相上、下管栅源电压vgs,S1和vgs,S2，上管漏源电压vds,S1以及电感电流iL。图14a为Vg=270 V（m=2.18）时的实验波形，根据最小电流TCM控制算法，可以得到该工作点对应的时序参数为fsw=302 kHz，td2=179 ns，且下管关断时电感电流的理论值I3=-0.44 A、上管开启时电感电流的理论值I4=0 A。根据实验波形可得，在死区起始时刻，电感电流I3=-0.46 A，与理论计算结果基本一致；在死区时间结束、上管驱动信号vgs,S1置高时，vds,S1刚好降低至0，且此时电感电流I4=0，表明不仅上管实现了ZVS，而且电感电流也达到最低。该实验结果与图7a所示的状态平面轨迹分析结果一致。
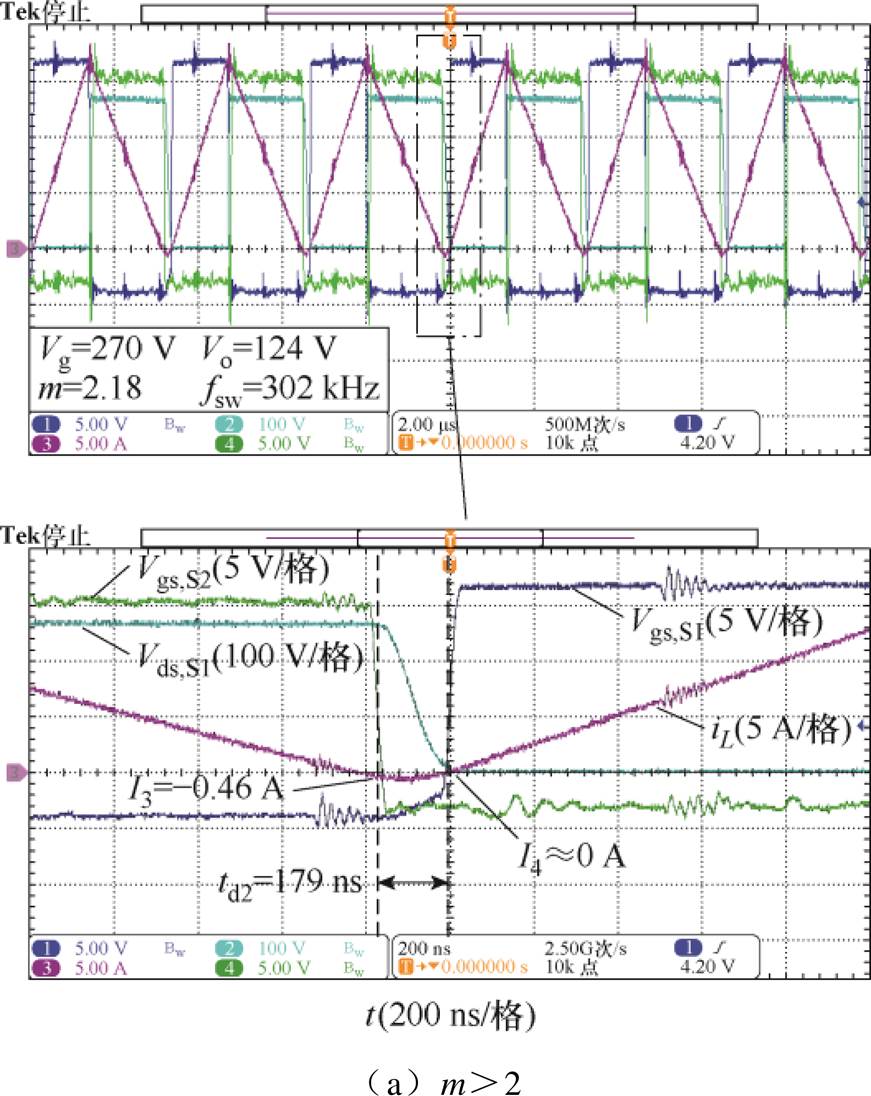
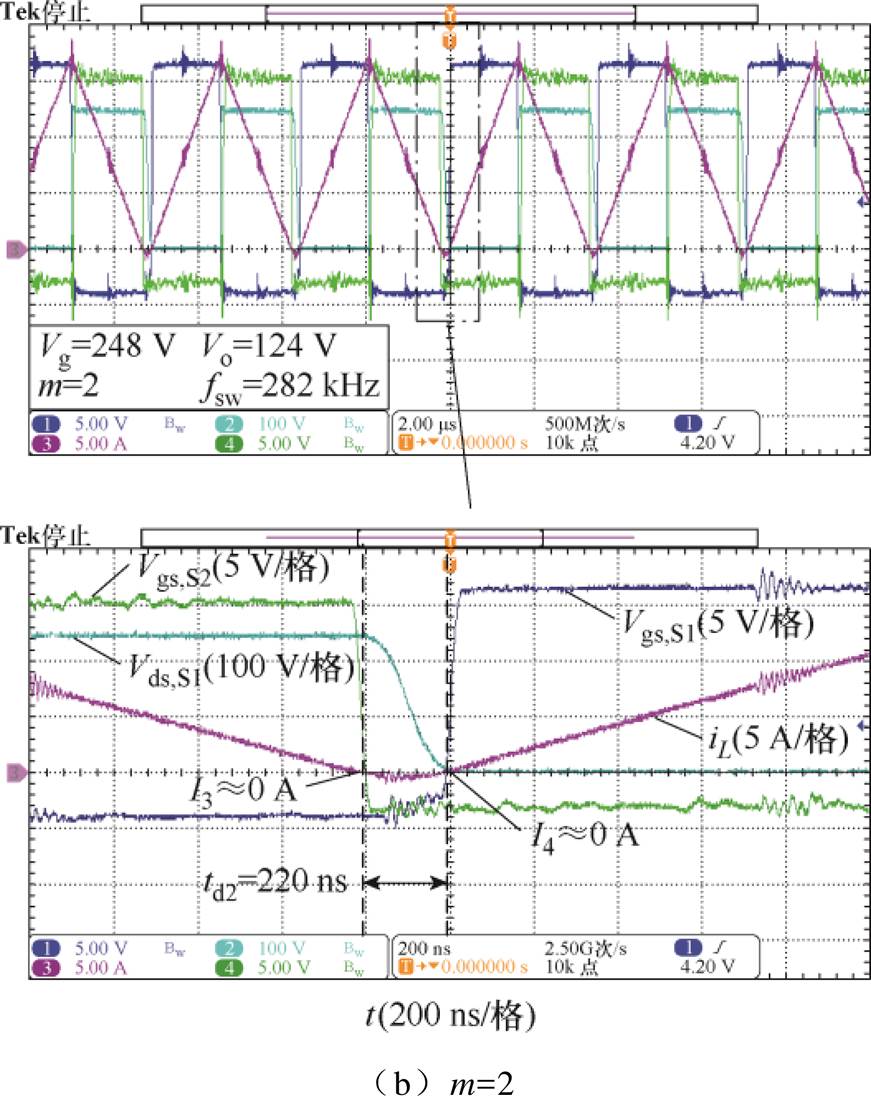
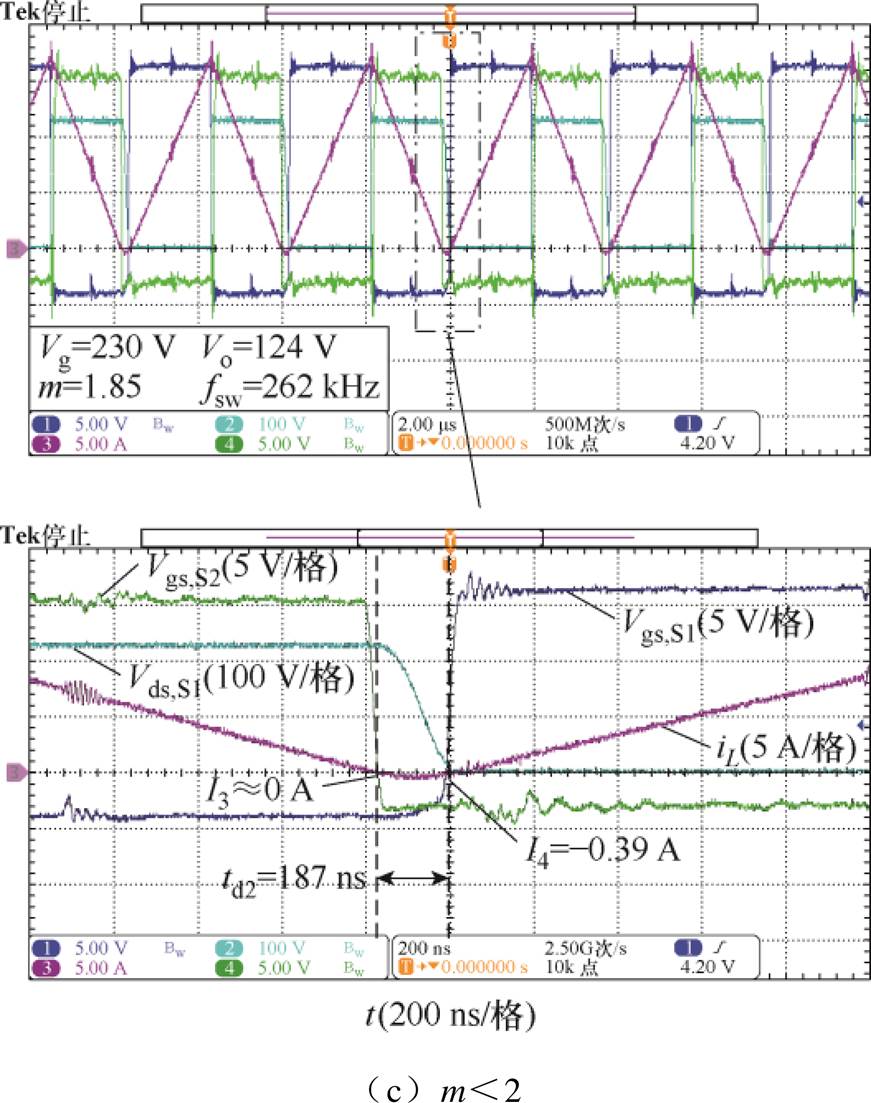
图14 最小电流TCM控制稳态波形
Fig.14 Steady-state waveforms with minimum current TCM control
图14b为Vg=248 V（m=2）时的实验波形，对应最优时序参数fsw,opt=282 kHz，td2,opt=220 ns。实验所得I3、I4均约为0 A，与理论值一致，验证了图7c所示的最优ZVS轨迹；图14c为Vg=230 V（m=1.85）时的实验波形，对应最优时序参数fsw,opt= 262 kHz，td2,opt=187 ns。实验所得I3=0 A、I4=-0.39 A，与理论值I3=0 A、I4=-0.38 A基本一致，验证了图7b所示的最优ZVS轨迹。
该实验结果验证了本文所提出的基于状态平面的最小电流TCM控制方法的正确性，其可以使本文所设计的激光器驱动电源样机在全工作范围内实现软开关，在限幅内能实现最优ZVS，使通态电流有效值达到最小。
图15给出了变换器在Vg=270 V、m=2.18工况下，采用最小电流TCM控制时的四相交错电感电流波形。从实验波形可以看出，各相电感电流的峰值和谷值基本一致，且与图14a所示的电流波形相同，表明变换器各相电感电流具有良好的一致性。
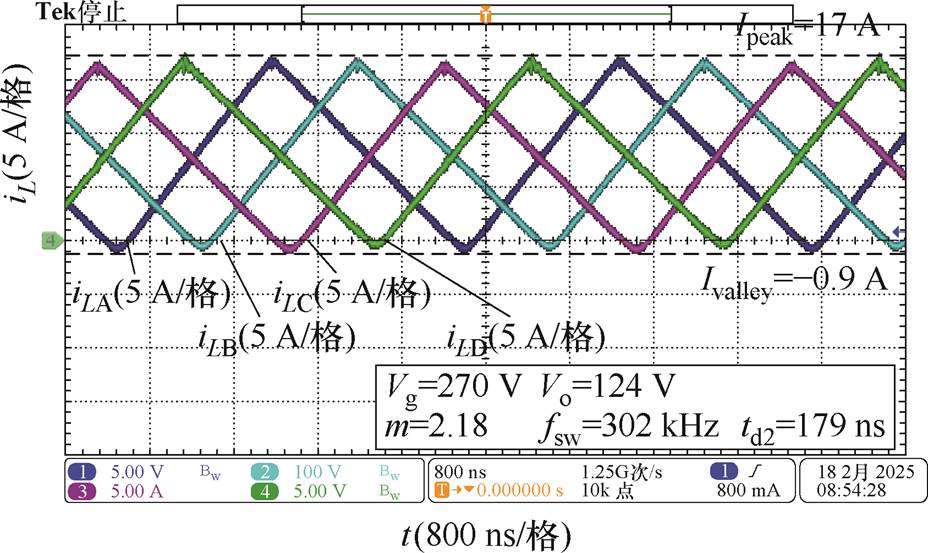
图15 四相交错电感电流波形
Fig.15 Four-phase interleaved inductor current waveforms
以Vg=270 V、Vo=124 V、Io=32 A、m=2.18的工况为例，验证当时序参数偏离最优解时对软开关过程的影响。图16a～图16d分别给出了变换器在上述工况下开关频率过低、开关频率过高、死区时间过长、死区时间过短的稳态波形。
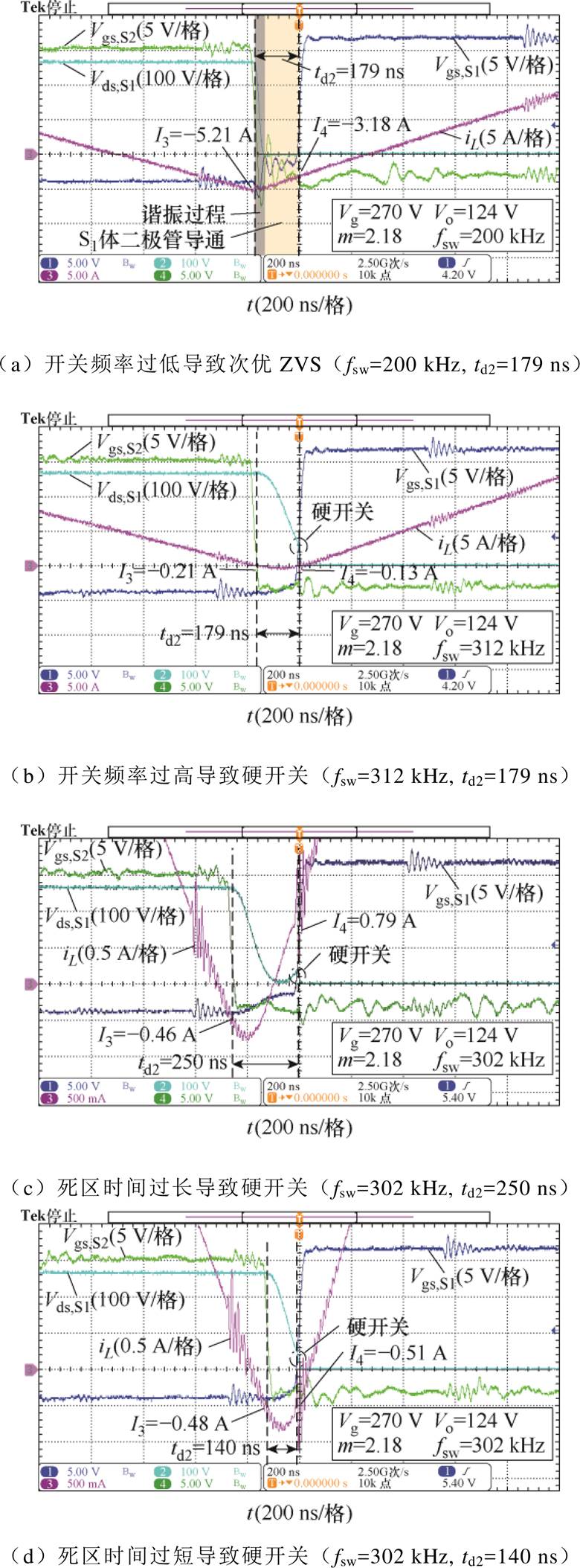
图16 非最优时序参数稳态波形
Fig.16 Steady-state waveforms with non-optimal timing parameters
图16a为变换器在fsw=200 kHz、死区时间td2=179 ns时的实验波形。其较低的开关频率导致I3达到了-5.21 A，远大于最优ZVS所需的反向电流，导致vds,S1在不到80 ns的时间内就降至0，在剩余的死区时间内S1体二极管导通续流，导致引入额外的体二极管导通损耗；同时在输出电流不变的前提下，过大的I3导致电感电流有效值增大，产生额外导通损耗，变换器工作在次优ZVS状况下，与图11a次优状态平面一致。
图16b为变换器在fsw=312 kHz、死区时间td2=179 ns时的实验波形。由于其较高的频率，使I3= -0.21 A，小于最优ZVS所需的反向电流，导致死区时间结束时vds,S1未降到0 V，变换器工作在硬开关模式下，验证了图12a的状态平面分析结果。
图16c为变换器以最优开关频率fsw=302 kHz、过长的死区时间td2=250 ns工作的稳态波形。在谐振过程完成后，电感电流过零变为正电流，导致死区时间内vds,S1先降至0又重新增大，变换器工作在硬开关模式下，验证了图12c的状态平面分析结果。
图16d为变换器以最优开关频率fsw=302 kHz、过短的死区时间td2=140 ns工作时的稳态波形。由波形可见，由于死区时间不足，导致vds,S1未在死区时间内降至0 V，变换器工作在硬开关模式下，与理论分析相符。
上述实验涵盖了所有非最优时序参数条件下的实验波形，验证了非最优时序参数状态平面分析的正确性。可在计算得到的时序参数产生偏差时，为其调整提供有力参考。
图17为变换器在最小电流TCM控制下，对输出电流进行闭环控制得到的动态响应波形，其中输入电压Vg=270 V，输出电流从0 A升至32 A再降至24 A。为了保护半导体激光器，其驱动电源一般要求具有软启动功能，其电流上升时间一般控制在ms级[23]，本样机输出电流从0 A阶跃到32 A的上升时间trise为0.92 ms，从32 A阶跃20 A的下降时间tfall为0.81 ms，满足激光器要求。
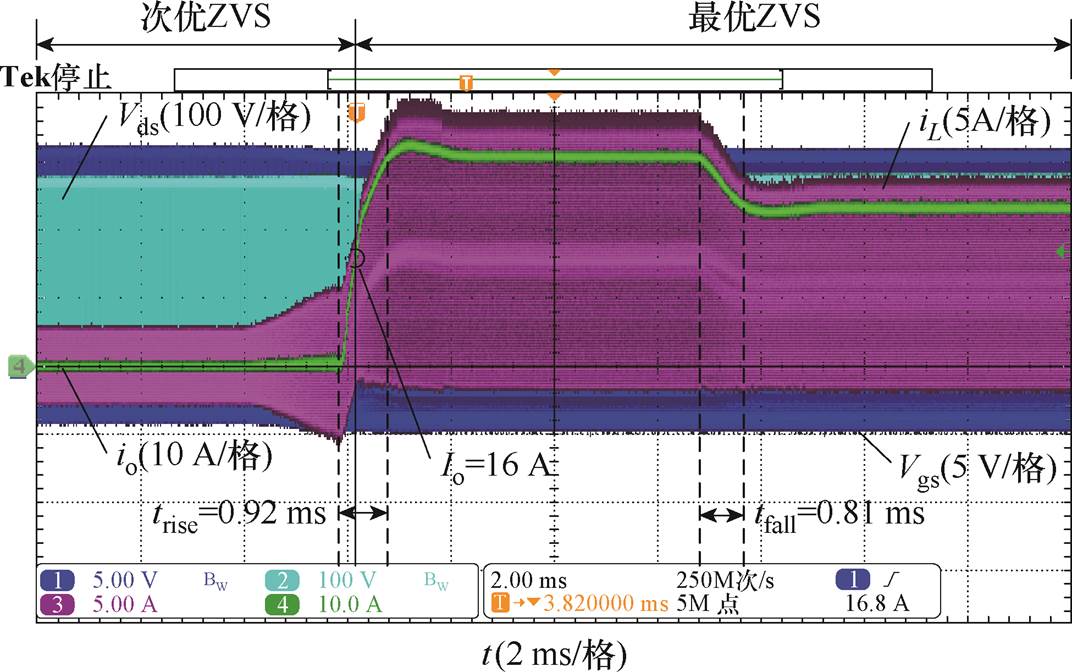
图17 动态过程实验波形
Fig.17 Experimental waveforms of dynamic process
在电流上升到16 A之前，由于其对应的最优开关频率高于500 kHz，故fsw被限制为500 kHz，td2固定在开关频率达到限幅值处所对应的死区时间158 ns，变换器以次优ZVS工作。当电流上升至16 A以上时，变换器根据工作条件计算并采用最优开关频率和死区时间。Io升至32 A时，fsw由500 kHz降至302 kHz，td2由158 ns升至179 ns，以最优ZVS工作；Io降至24 A后，开关频率升至381 kHz，死区时间降至168 ns，以最优ZVS工作。该实验验证了本文所搭建的样机可以在全工作范围实现ZVS的前提下驱动激光器输出目标功率，且具有良好的动态响应。
图18给出了输入电压Vg=270 V时变换器的效率测试曲线，其中实线为采用本文提出的最小电流TCM控制所测得的效率数据，虚线为采用传统定频软开关控制（fsw=200 kHz）所测得的效率数据。
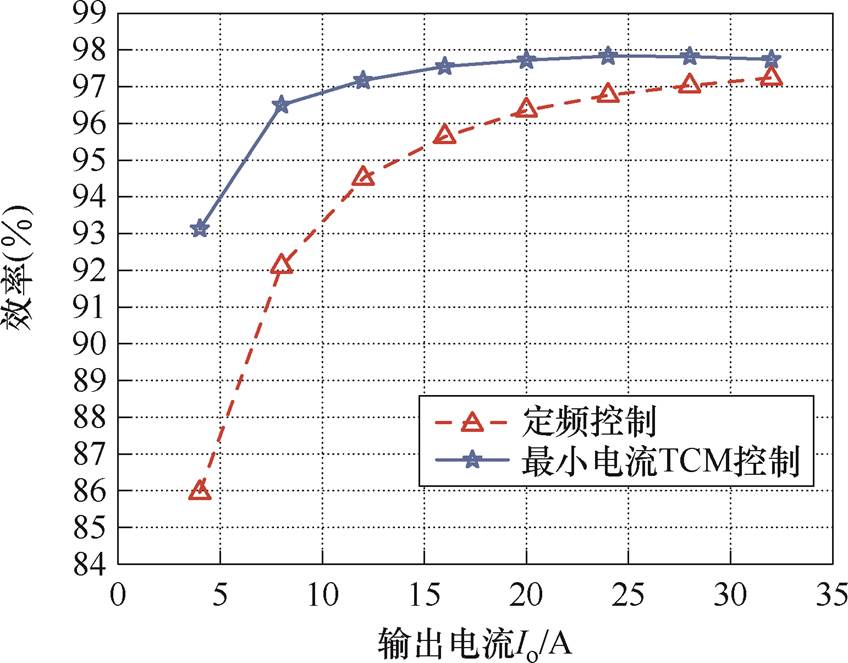
图18 效率测试曲线
Fig.18 Efficiency measurement curves
从实验结果可知，定频软开关控制在满载时的效率为97.23%，且随着负载减轻而明显下降；而在最小电流TCM控制下，变换器的效率获得了明显的提升，在输出电流12～32 A的范围内，变换器的效率始终保持97%以上，峰值效率达到97.83%。实验结果表明，最小电流TCM控制能够使变换器在高频运行的同时，实现更高的运行效率。
针对大功率激光器驱动应用场景，本文采用四相交错并联Buck变换器作为激光器驱动电源。一方面针对传统TCM控制依赖电流过零检测电路、谐振过程分析复杂等问题，提出基于状态平面分析的最小电流TCM控制方法，并给出基于几何分析的最优状态平面求解方法，实现ZVS时序参数的精准计算，在全工作范围内保持较高效率；另一方面针对寄生参数、采样误差、建模不准确会影响最优时序参数的计算准确度问题，绘制并分析非最优时序参数的状态平面，可在时序参数需要调整时给予指导。此外，本文还制作了一台开关频率为200～500 kHz、额定功率为4 kW的四相交错并联Buck变换器样机，其峰值效率达到97.83%，验证了基于状态平面分析的最小电流TCM控制策略的可行性，为多电飞机机载激光器驱动电源提供了一种可靠 方案。
参考文献
[1] 张卓然, 许彦武, 姚一鸣, 等. 多电飞机电力系统及其关键技术[J]. 南京航空航天大学学报, 2022, 54(5): 969-984.
Zhang Zhuoran, Xu Yanwu, Yao Yiming, et al. Electric power system and key technologies of more electric aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2022, 54(5): 969-984.
[2] 李永东, 章玄, 许烈. 多电飞机高压直流供电系统稳定性研究综述[J]. 电源学报, 2017, 15(2): 2-11.
Li Yongdong, Zhang Xuan, Xu Lie. A survey on stability analysis for HVDC power system in MEA[J]. Journal of Power Supply, 2017, 15(2): 2-11.
[3] 宋清超, 陈家伟, 蔡坤城, 等. 多电飞机用燃料电池-蓄电池-超级电容混合供电系统的高可靠动态功率分配技术[J]. 电工技术学报, 2022, 37(2): 445-458.
Song Qingchao, Chen Jiawei, Cai Kuncheng, et al. A highly reliable power allocation technology for the fuel cell-battery-supercapacitor hybrid power supply system of a more electric aircraft[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 445-458.
[4] 王翌琛, 王丰, 卓放, 等. 基于过谐振调频扩展移相控制的CLLC谐振变换器电流优化策略[J]. 电力系统自动化, 2025, 49(3): 178-188.
Wang Yichen, Wang Feng, Zhuo Fang, et al. Current optimization strategy for CLLC resonant converter based on over-resonant frequency modulation and extended phase-shift control[J]. Automation of Elec- tric Power Systems, 2025, 49(3): 178-188.
[5] 黄丫, 田小建, 吴戈, 等. 适用于激光器脉冲驱动系统的低纹波交错并联Boost变换器[J]. 电源学报, 2023, 21(2): 46-54.
Huang Ya, Tian Xiaojian, Wu Ge, et al. Low voltage ripple interleaved parallel Boost converter for pulsed laser driver[J]. Journal of Power Supply, 2023, 21(2): 46-54.
[6] 唐云峰, 谭志远, 刘平, 等. 四模块并联交错大功率激光驱动电源研制[J]. 强激光与粒子束, 2021, 33(7): 71004.
Tang Yunfeng, Tan Zhiyuan, Liu Ping, et al. Design of four-module parallel interleaved high power laser driver[J]. High Power Laser and Particle Beams, 2021, 33(7): 71004.
[7] Zhang Junhong, Lai J S, Kim R Y, et al. High-power density design of a soft-switching high-power bidirec- tional DC-DC converter[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1145-1153.
[8] Marxgut C, Biela J, Kolar J W. Interleaved Triangular Current Mode (TCM) resonant transition, single phase PFC rectifier with high efficiency and high power density[C]//The 2010 International Power Electronics Conference-ECCE ASIA, Sapporo, Japan, 2010: 1725- 1732.
[9] Chen Jianliang, Sha Deshang, Yan Yu, et al. Cascaded high voltage conversion ratio bidirectional nonisolated DC-DC converter with variable switching frequency[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1399-1409.
[10] 赵明, 陈建良, 韩伟健, 等. 基于TCM控制的多相交错并联Buck/Boost软开关变换器的变频范围优化方法[J]. 中国电机工程学报, 2022, 42(22): 8265-8276.
Zhao Ming, Chen Jianliang, Han Weijian, et al. A frequency variation range reduction method for multi- phase parallel interleaved Buck/Boost ZVS converter under TCM control[J]. Proceedings of the CSEE, 2022, 42(22): 8265-8276.
[11] Rodriguez A, Vazquez A, Rogina M R, et al. Synchro- nous Boost converter with high efficiency at light load using QSW-ZVS and SiC MOSFETs[J]. IEEE Trans- actions on Industrial Electronics, 2018, 65(1): 386-393.
[12] Rogina M R, Rodriguez A, Vazquez A, et al. Improving the efficiency of SiC-based synchronous Boost converter under variable switching frequency TCM and different input/output voltage ratios[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7757-7764.
[13] Gutierrez B, Hou Zhengming, Jiao Dong, et al. Practical current derivation method for a highly accurate variable switching frequency ZVS regulation in TCM operated bidirectional Buck/Boost converters [C]//2024 IEEE Applied Power Electronics Conferenceand Exposition (APEC), Long Beach, CA, USA, 2024: 2054-2058.
[14] 孙孝峰, 周杨, 马永正, 等. Buck-Boost双向变换器无过零检测TCM控制研究[J]. 太阳能学报, 2017, 38(7): 1828-1837.
Sun Xiaofeng, Zhou Yang, Ma Yongzheng, et al. Bidirectional Buck/Boost converter TCM control with- outzero-crossing detection[J]. Acta Energiae Solaris Sinica, 2017, 38(7): 1828-1837.
[15] Liu Yuchen, Syu Y L, Dung N A, et al. High- switching-frequency TCM digital control for bidirec- tional-interleaved Buck converters without phase error for battery charging[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2111-2123.
[16] Sankaranarayanan V, Gao Yucheng, Erickson R W, et al. Online efficiency optimization of a closed-loop controlled SiC-based bidirectional Boost converter[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4008-4021.
[17] Sha Deshang, Zhao Yuting, Zhang Debin. ZVS- interleaved synchronous Buck DC-DC converter with a coupled inductor by varying switching frequency and deadtime[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(7): 8190-8198.
[18] 张理, 韩民晓, 范溢文. 多相堆叠交错并联制氢变换器控制策略与特性分析[J]. 电工技术学报, 2023, 38(2): 485-495.
Zhang Li, Han Minxiao, Fan Yiwen. Control strategy and characteristic analysis of multi-phase stacked interleaved Buck converter for hydrogen production[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 485-495.
[19] 徐浩东, 罗嗣勇, 毕闯, 等. 基于SiC MOSFET同步Buck DC-DC变换器的宽频混合EMI滤波器设计[J]. 电工技术学报, 2024, 39(10): 3060-3069.
Xu Haodong, Luo Siyong, Bi Gang, et al. Design of broadband hybrid EMI filter in synchronous Buck DC-DC converter with SiC MOSFETs[J]. Transactionsof China Electrotechnical Society, 2024, 39(10): 3060- 3069.
[20] Costinett D, Maksimovic D, Zane R. Circuit-oriented treatment of nonlinear capacitances in switched-mode power supplies[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 985-995.
[21] 王议锋, 杨绍琪, 马小勇, 等. 基于能量模型的临界导通模式Boost变换器软开关方法[J]. 电工技术学报, 2024, 39(10): 3049-3059.
Wang Yifeng, Yang Shaoqi, Ma Xiaoyong, et al. Soft switching method of boundary conduction mode Boost converter based on energy model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3049- 3059.
[22] 宁继超, 贲洪奇, 王雪松, 等. 带有死区时间补偿及电容电压平衡功能的二极管钳位型三电平逆变器数字调制方法[J]. 电工技术学报, 2024, 39(20): 6444-6461.
Ning Jichao, Ben Hongqi, Wang Xuesong, et al. A digital modulation method for dead-time compensation and capacitor voltage balance in diode clamped three-level inverter[J]. Transactions of China Electro- technical Society, 2024, 39(20): 6444-6461.
[23] 李向君. 大功率光纤激光器恒流驱动电源研究[D]. 南京: 南京理工大学, 2020.
Li Xiangjun. Research on constant current power supply for high power fiber laser[D]. Nanjing: Nanjing University of Science and Technology, 2020.
Abstract Airborne laser weapons offer high directional gain, rapid deployment, and flexibility, making them highly significant for military applications. The laser drive power supply is responsible for driving, controlling, and protecting the laser.Due to the aircraft’s demanding requirements on the weight and volume of airborne equipment, high-frequency switching power supply with soft switching characteristics has become the ideal choice for this application. In this paper, a four-phase interleaved parallel Buck converter is adopted as the topology of the laser drive power supply. A minimum current triangular current mode (TCM) control strategy is proposed based on the state plane analysis, which enables the converter to achieve zero voltage switching (ZVS) across the full operating range. The proposed method does not rely zero crossing detection for inductor current, and hence reduces the sensitivity to switching noise and eliminates the requirement for wide-bandwidth current sensor.
(1) A minimum current TCM control strategy based on state-plane analysis was developed. Firstly, the basic principle of TCM control was explained by taking a single-phase Buck converter as an example. Then, the charge-based equivalent capacitance of a half-bridge was calculated, followed by the analysis of the resonance process between the inductor and the equivalent capacitance during dead time. The resonant process with the ZVS achievement and minimized conduction loss was depicted on the state-plane for different voltage ratios. Based on the state-plane trajectories, a mathematical model was established for numerically calculating the optimal timing parameters which enable the converter operated with ZVS and minimum rms current. For practical application, this work also presents a polynomial fitting method that can be used to calculate the optimal timing parameters online, which facilitates the implementation in a digital controller. The fitting results was evaluated using residual plots which shows good accuracy. Furthermore, a control flow diagram for digital implementation was reported.
(2) The state planes trajectories of non-optimal timing parameters, such as with a lower or a higher switching frequency, with a shorter or a longer dead time were analyzed, to visualize the impact of timing parameter variations on the soft-switching performance. The analysis results provides an effective guideline for providing some margins for the theoretically calculated timing parameters, to compensate the effects due to factors such as circuit parasitic parameters, voltage and current sampling errors, and inaccurate modeling of the equivalent capacitance, etc.
The theoretical analysis and the proposed control method were verified through a 4 kW, 200～500 kHz four phase interleaved parallel Buck converter. The experimental waveform shows that ZVS operation with minimum rms inductor current is achieved for various input/output voltage levels and output power. The experimental results also verified the effects of timing parameter deviation, which are consistent with the theoretical analysis. The experimental waveform also shows the inductor current of each phase has a good consistency, validating the effectiveness of the proposed control scheme. Furthermore, the efficiency measurement results indicated 97.83% peak efficiency and beyond 97% for medium-to-high power level. The dynamic response experimental results also show the rising and falling time during a step response was smaller than 1ms.
keywords：Laser drive power supply, interleaved Buck converter, triangular current mode (TCM) control, state plane
DOI: 10.19595/j.cnki.1000-6753.tces.242192
中图分类号：TM46
国家自然科学基金青年基金项目资助（52407201）。
收稿日期 2024-12-04
改稿日期 2025-02-09
田 雨 男，2001年生，硕士研究生，研究方向为DC-DC变换器的建模与控制。E-mail: tianyu53123@163.com
韩伟健 男，1989年生，讲师，研究方向为高频电力电子变换器的建模与控制。E-mail: weijian.han@hebut.edu.cn（通信作者）
（编辑 郭丽军）