Tab.1 Wind power grid-connected power change standard

风电场装机容量/MWΔP10min/MWΔP1min/MW <30103 30~150Pw.rate/3Pw.rate/10 >1505015
摘要 针对风电场锂离子电池和超级电容混合储能系统(HESS)容量优化配置问题,面向风电场涉网功率平抑和自动发电控制(AGC)功率指令考核与辅助服务的场景,考虑混合储能系统全寿命周期成本,综合风电消纳、峰谷套利、碳交易、功率平抑和AGC功率指令考核与辅助服务等多项收益,提出风电场HESS双层容量优化配置模型,旨在提升风储联合系统的经济效益。上层考虑市场电价和风电出力数据,以储能套利收益最大为目标,基于储能套利最优建立混合储能容量优化模型;下层综合考虑储能全生命周期成本、碳交易规则、风电平抑和AGC功率指令考核与补偿机制,采用预测控制方法构建以风储联合系统效益最大为目标的容量配置模型,并进行上下层迭代求解。针对下层混合储能功率指令分配问题,采用改进希尔伯特黄变换(HHT)确定锂离子电池和超级电容的功率指令。最后,通过算例分析,验证了所提风电场混合储能的容量优化配置方法,能够有效地提升风储联合系统涉网功率平抑与AGC功率指令考核下的经济收益。
关键词:风电功率平抑 AGC功率指令 辅助服务 并网考核 混合储能优化配置
在“双碳”目标和可持续发展战略的推动下,我国以风电为代表的新能源迅猛发展。据国家能源局发布的《2024年全国电力工业统计数据》显示,我国风电装机容量4.921亿kW,占全国发电总装机容量的15.21%,同比增长19.2%[1]。随着风电机组大规模并网,风电引起的功率波动,对电网安全运行产生重要影响。为提升风电场主动参与电网的调控能力,国家能源局在相应省份颁布了“电力并网运行管理实施细则”“电力辅助服务管理实施细则”(以下简称“两个细则”),以激励风电场主动响应电网控制需求,将风电场的经济效益与调控性能挂钩[2-4]。“两个细则”中明确规定了风电场应具备功率波动平抑和响应自动发电控制(Automatic Generation Control, AGC)功率指令的能力,并根据风电场的调控效果进行考核惩罚与补偿奖励。
为应对功率平抑和AGC功率指令考核带来的挑战,若风电场留有备用容量/采用弃风限电的控制策略,则不利于风电消纳,影响售电收益;为保障售电收益,若按照最大风电功率发电,则可能不满足考核要求,受到电量考核,难以获取辅助服务补偿费用。可见,以上措施均难以兼顾风电场综合经济效益。目前,储能技术迅速发展,依靠其响应速度快、调节精度高的特性,风电场通过配置储能以增加灵活调节能力可有助于风电消纳,规避风电平抑和AGC功率指令的考核惩罚,提高风电场AGC辅助服务补偿收益[5]。本文计及风电场涉网功率平抑与AGC考核,研究面向风电场收益提升的储能容量优化配置。
储能设备可分为能量型储能和功率型储能两大类,其中以锂离子电池为代表的能量型储能能量密度大、功率密度小、循环寿命短,不适用于频繁充放电场景[6-7];而以超级电容为代表的功率型储能具有功率密度大、能量密度小、循环寿命长的特征,可满足高频次充放电需求[8-9],两种储能具有明显的互补特性。由于风电功率包含不同频率和振幅的波动分量,混合储能系统(Hybrid Energy Storage System, HESS)兼具能量型和功率型储能的优点,可对应消纳风电中的高低频分量,平抑风电波动[10]。因此,本文针对以锂离子电池-超级电容构成的风电场HESS容量优化配置问题展开研究。
为充分利用HESS对不同频段风功率的消纳能力,风电场HESS容量配置时应考虑不同储能间功率的协调分配[11-12]。文献[13]采用一阶低通滤波算法,通过调节平滑时间常数,进行HESS功率指令分配,但滤波时间常数难以准确控制;文献[14]采用小波包分解获取并网分量,但平抑效果受小波基影响;文献[15]运用希尔伯特变换(Hilbert-Huang Transform, HHT)求解固有模态函数(Intrinsic Mode Function, IMF)的瞬时频率,为分界频率的确定提供依据,但HHT求解IMF分量的瞬时频率可能会存在较大误差。文献[16-17]考虑过度充放电导致的荷电状态(State of Charge, SOC)越限引起响应能力不足的问题,利用模糊控制方法对储能的功率指令进行修正和重新分配,但当针对多应用场景时,控制输入量和控制规则难以合理制定。目前,考虑风电场响应AGC功率指令的HESS容量优化配置研究尚少,部分文献仅围绕储能辅助传统机组响应AGC功率指令开展了储能配置研究。文献[18]基于集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)的超前模糊控制策略,根据HESS当前荷电状态修正HESS系统输出功率;文献[19]则基于EEMD方法构造时空滤波器,以储能辅助传统机组响应AGC功率指令的效益最大为目标优化滤波阶数,减小由模态混叠带来的影响。
此外,以上文献分别针对储能平抑风电波动和响应AGC功率指令的场景进行研究,缺乏考虑两种场景融合下的风电场HESS容量优化配置方案。文献[20]仅针对单储能系统的容量优化配置,考虑了风电平抑和AGC功率指令响应两种场景,但难以兼顾两种场景下考核与补偿机制。综上所述,计及风电场涉网功率平抑与AGC功率指令考核的风电场HESS容量优化配置仍有待进一步研究。
本文面向风电场发电与考核环境下的经济收益提升,针对锂离子电池-超级电容HESS容量优化配置,综合计及风电平抑和AGC功率指令考核与辅助服务收益,提出一种风电场混合储能双层容量优化配置模型,提升风储联合系统的经济效益。上层模型考虑市场电价和风电出力特性,以储能套利收益最大为目标,构建储能最优充放电计划求解模型,确定容量配置方案传递给下层;下层模型计及储能全寿命周期成本、碳交易规则、功率平抑和AGC功率指令考核与补偿机制,为避免SOC越限导致充放电响应能力不足的问题,采用预测控制方法,构建以风储联合系统净效益最大为目标的容量优化配置模型,对容量配置结果进行修正并返回给上层,通过不断迭代求解实现混合储能的最优配置。针对下层模型的功率指令分配问题,采用改进HHT方法分解风电功率和AGC功率指令,求解IMF分量的瞬时频率,以瞬时频率-时间曲线间混叠最少为原则,确定锂离子电池和超级电容的分频频率。针对某100 MW风电场,仿真验证了所提风电场HESS容量优化配置方案的经济性和有效性。
国家能源局在相应省份,如山东省,颁布了“两个细则”[2],旨在要求各类型电源场站参与电网调控,提升电网安全运行水平。针对风电功率波动频繁越限、AGC功率指令响应误差较大的问题,制定了相应的考核机制及辅助服务规则。
为减小风电功率波动,电力并网运行管理实施细则[2]对风电场1 min和10 min功率波动量ΔP1min、ΔP10min的最大限值做出了规定,风电并网功率变化标准见表1,其中Pw.rate为风电场装机容量。
表1 风电并网功率变化标准
Tab.1 Wind power grid-connected power change standard

风电场装机容量/MWΔP10min/MWΔP1min/MW <30103 30~150Pw.rate/3Pw.rate/10 >1505015
风电功率波动越限时,规定的考核电量计算式为
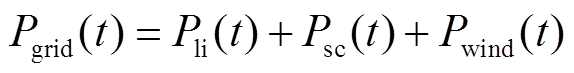 (1)
(1)
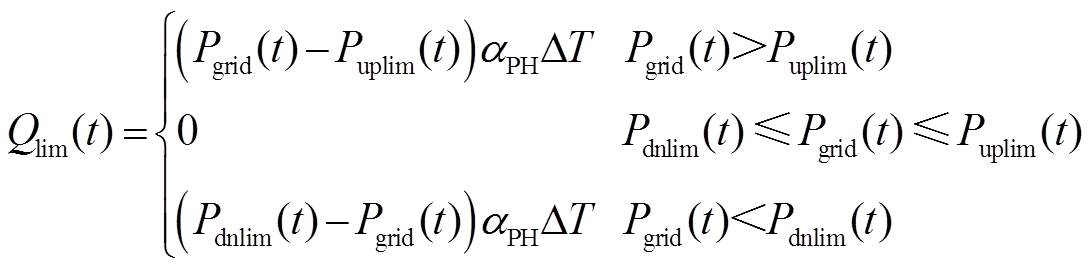 (2)
(2)
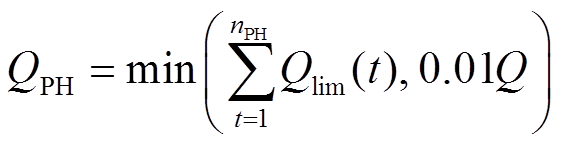 (3)
(3)
式中,Pgrid(t)为t时刻风电场整体并网功率;Pli(t)为锂离子电池的充放电功率;Psc(t)为超级电容的充放电功率;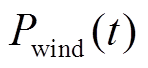 为原始风电功率;Qlim(t)为t时刻受到的功率波动考核电量;Puplim(t)、Pdnlim(t)分别为t时刻风电功率波动的上限和下限;DT为风电功率采样时间步长,本文步长为1 min;aPH为功率波动考核折算系数;QPH为风电功率波动总考核电量;Q为风电场考核时间内的上网电量;nPH为考核时间内的采样次数。当风电功率不发生越限情况时,不进行电量考核。
为原始风电功率;Qlim(t)为t时刻受到的功率波动考核电量;Puplim(t)、Pdnlim(t)分别为t时刻风电功率波动的上限和下限;DT为风电功率采样时间步长,本文步长为1 min;aPH为功率波动考核折算系数;QPH为风电功率波动总考核电量;Q为风电场考核时间内的上网电量;nPH为考核时间内的采样次数。当风电功率不发生越限情况时,不进行电量考核。
1.2.1 AGC功率指令考核机制
AGC功率指令是指由电网调度控制中心min级下发至风电场的有功调控指令,风电场需响应该指令要求,其响应能力通过调节精度来表征,并针对响应不足进行电量考核。调节精度指风储系统实际出力和AGC功率指令之间偏差的绝对值,对精度超过AGC功率指令允许偏差的情况进行考核[3],有
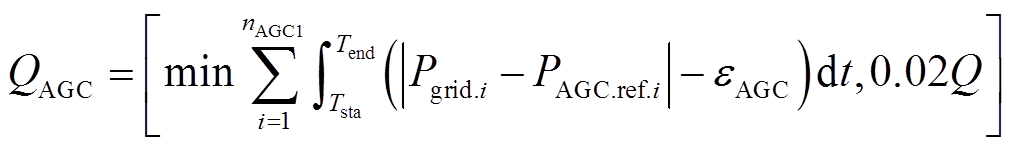 (4)
(4)
式中,QAGC为AGC功率指令调节精度考核电量; PAGC.ref.i为第i次受到考核时的AGC功率指令;eAGC为响应AGC指令的允许误差;Tsta为响应AGC功率指令的开始时刻;Tend为响应AGC功率指令的结束时刻;nAGC1为AGC调节精度úPgrid.i-PAGC.ref.iú>eAGC的考核次数,当AGC功率指令的响应误差满足要求时,不进行电量考核。
1.2.2 AGC功率指令补偿机制
为激励风电场跟踪AGC功率指令,电力辅助服务管理实施细则建立了响应AGC功率指令的补偿机制[4],其补偿收益为
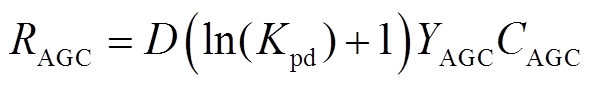 (5)
(5)
式中,RAGC为AGC辅助服务补偿收益;D为总调节深度;YAGC为补偿标准;CAGC为贡献率;Kpd为调节性能综合指标。
1)调节深度D
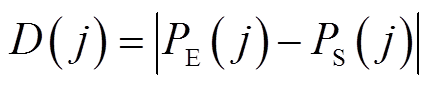 (6)
(6)
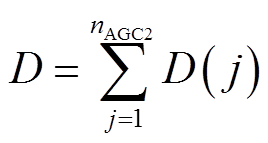 (7)
(7)
式中,D(j)为第j次调节的调节深度;PS( j)为第j次AGC调节开始时的出力;PE(j)为第j次AGC调节结束时的出力;nAGC2为日内响应AGC功率指令的调节次数。
2)调节性能综合指标Kpd
Kpd是衡量AGC功率指令调节效果的指标,由调节速率指标K1、调节精度指标K2及响应时间指标K3构成,表达式为
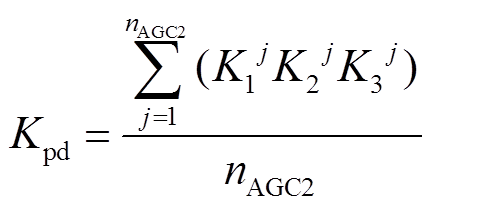 (8)
(8)
式中,K1j为第j次响应AGC功率指令的调节速率指标;K2j为第j次响应AGC功率指令的调节精度指标;K3j为第j次响应AGC功率指令的响应时间评估指标。
3)调节速率评估指标K1
调节速率vi是指风电场响应AGC功率指令的速度,其评估指标K1计算式为
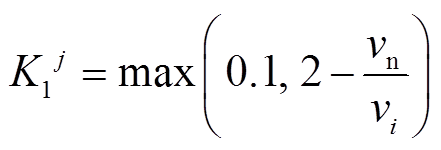 (9)
(9)
式中,vi为第i次响应AGC功率指令的调节速率;vn为标准调节速率。
4)调节精度评估指标K2
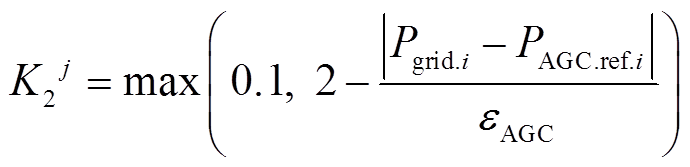 (10)
(10)
5)响应时间评估指标K3
响应时间指从调度控制中心下达AGC指令到风电场开始执行命令的时间间隔,评估指标K3为
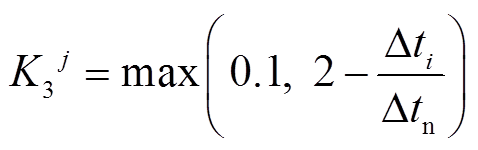 (11)
(11)
式中,Δti为第i次AGC调节的响应时间;Δtn为标准响应时间。
在“两个细则”规定下,风电场面临电量考核风险,若能提升风电场灵活调控性能以响应电网控制需求,则可获取辅助服务补偿。风电场配置储能,可对并网功率进行调节以应对考核并获得补偿,考核与补偿机制作用下的风储联合系统结构框图如图1所示。
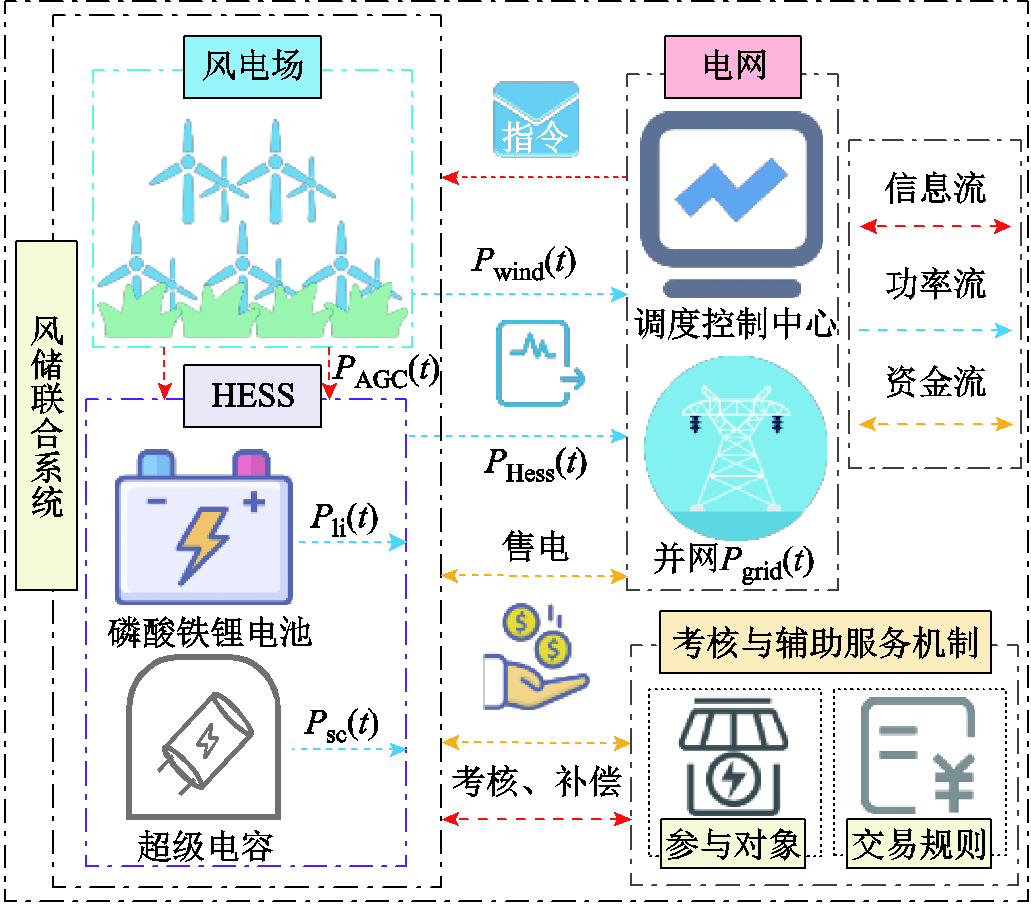
图1 风储联合系统的结构框图
Fig.1 Framework of wind-storage combined system
本文为提升风电消纳,兼顾风电功率平抑和AGC功率指令考核与辅助服务补偿收益,最大化风电功率出力(运行于最大功率跟踪)而不弃风,混合储能系统在保证风电功率平滑并网的基础上,补偿风电场响应AGC功率指令的误差量PAGC,并依靠储能系统较高的响应速率和调节精度,有效地提高风电场响应AGC功率指令的综合性能指标,提升风电场的经济效益。面向风电场平抑功率波动、响应AGC功率指令的应用场景,本文提出一种HESS双层容量优化配置方案,通过两阶段运行模拟的方式迭代优化储能的容量配置,HESS双层容量优化配置框架如图2所示。
受储能充电成本的影响,若混合储能集中于补偿风电场功率平抑需求和AGC功率指令响应误差,可能导致储能的充放电成本增加。因此,为保障储能系统的充放电收益,上层模型基于风电并网的市场电价数据,以电价驱动下峰谷套利收益最大为目标,构建HESS容量优化模型,确定储能容量配置结果传递给下层;下层模型考虑风电功率平抑和AGC功率指令考核与辅助服务补偿机制,构建以风储联合系统收益最大为目标的容量优化配置模型,采用预测控制方法修正储能出力,从而降低储能容量配置需求,将优化更新后的配置结果返回给上层,通过不断迭代求解,确定HESS最优容量配置。针对下层HESS内部功率指令的分配问题,基于改进HHT将风电功率的平抑需求和AGC功率指令的响应误差分别进行分解与重构,给出锂离子电池和超级电容的功率指令。
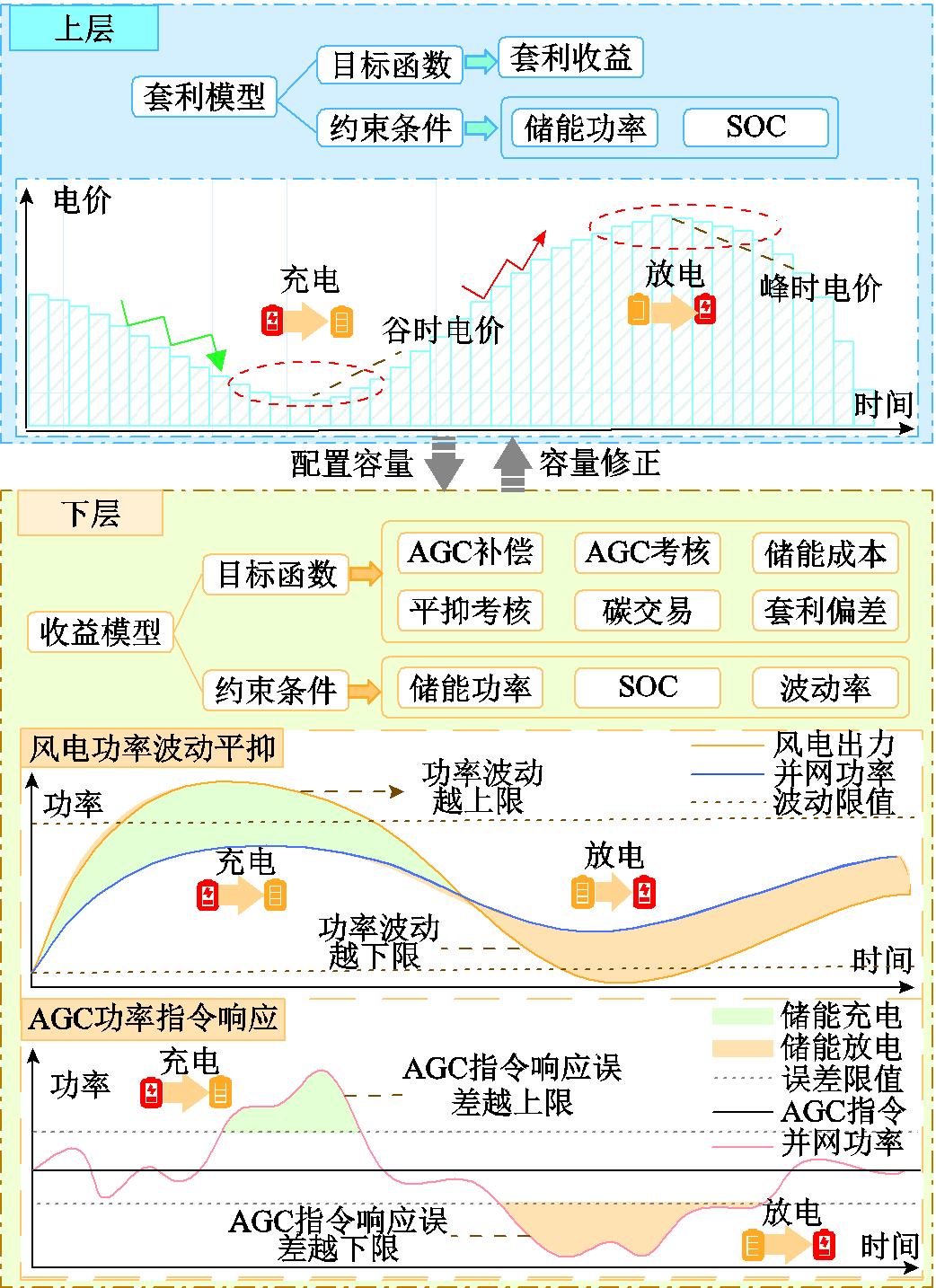
图2 HESS双层容量配置框架
Fig.2 Two-layer capacitor configuration of HESS system
2.2.1 上层目标函数
为降低储能充放电成本,基于市场电价以混合储能系统全寿命周期套利收益最大为目标,构建上层目标函数Jplan为
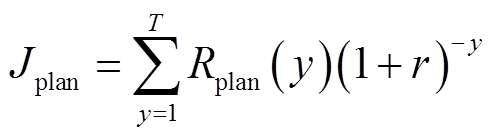 (12)
(12)
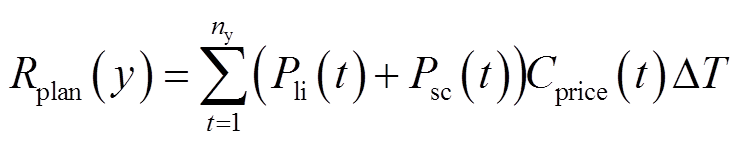 (13)
(13)
式中,Rplan(y)为混合储能系统年套利收益;r为折现率;y为年;Pli(t)为锂离子电池充放电功率;Psc(t)为超级电容充放电功率;Cprice(t)为电价;T为风储系统的运行寿命,本文假设为20年;ny为一年的采样次数,以15 min为步长。
2.2.2 约束条件
1)SOC约束
考虑到储能系统的运行寿命受到充放电深度的影响,因此储能SOC应在合理范围内。本文以放电功率为正,充电功率为负,储能的SOC约束为
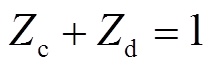 (14)
(14)
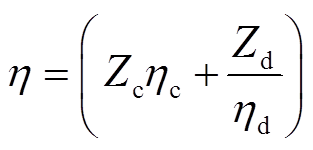 (15)
(15)
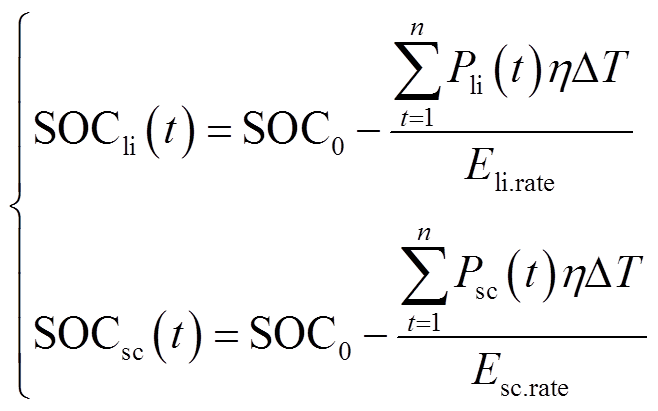 (16)
(16)
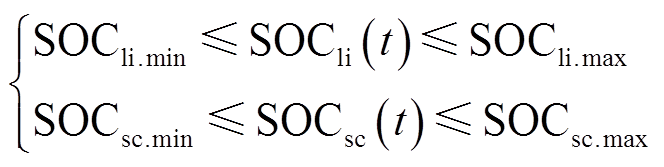 (17)
(17)
式中,Zc与Zd为0-1变量,当储能充电时,Zc=1,Zd=0,当储能放电时,Zd=1,Zc=0;hc为充电效率;hd为放电效率;h为充放电效率;SOC0为储能初始荷电状态;SOCli(t)为锂离子电池t时刻的SOC;SOCli.max和SOCli.min分别为锂离子电池SOC的上、下限;SOCsc(t)为超级电容t时刻的SOC;SOCsc.max和SOCsc.min分为超级电容SOC的上、下限;Eli.rate为锂离子电池的额定容量;Esc.rate为超级电容的额定容量。
2)储能充放电功率约束
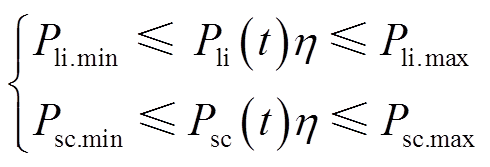 (18)
(18)
式中,Pli.max、Pli.min分别为锂电池充放电功率上、下限;Psc.max、Psc.min分别为超级电容充放电功率上、下限。
2.2.3 下层目标函数
下层模型基于预测控制方法,综合考虑储能全寿命周期成本,计及功率平抑、AGC功率指令考核和辅助服务补偿机制,结合上层套利最优的出力计划,以系统全寿命周期收益最大为目标,目标函数为
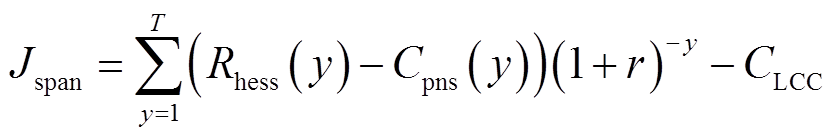 (19)
(19)
式中,Rhess(y)为风储系统第y年的收益;Cpns(y)为风储系统第y年的考核惩罚费用;CLCC为混合储能全寿命周期成本。
1)风储联合系统收益Rhess
风储联合系统收益包括AGC补偿收益RAGC、风电消纳收益Rsale和碳交易收益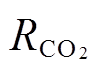 ,有
,有
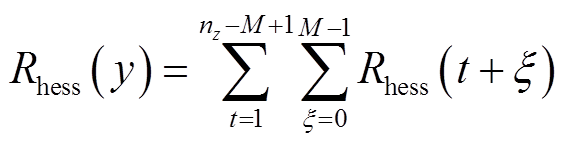 (20)
(20)
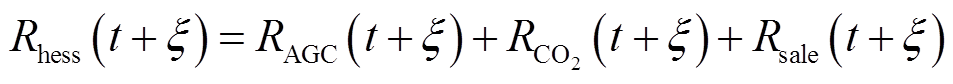 (21)
(21)
式中, x为前瞻步数;M为前瞻时间总长度;nz为一年采样次数,以1 min为步长。
(1)AGC补偿收益RAGC
根据1.2.2节所构建的AGC功率指令辅助服务补偿机制,测算风储系统的补偿收益为
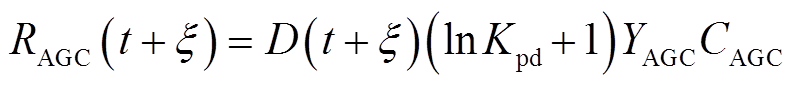 (22)
(22)
(2)风电消纳收益Rsale
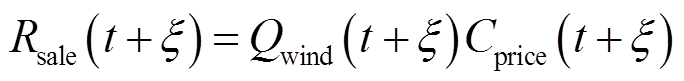 (23)
(23)
式中,Qwind(t+x)为风电消纳量。
(3)碳交易收益
风电作为清洁能源,可以与碳排放较多的企业(如火电厂)进行碳排放配额交易,从而获取碳减排收益,有
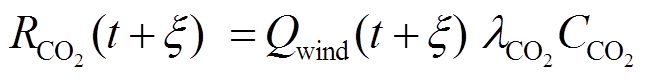 (24)
(24)
式中,λCO2为单位电量碳排放配额;CCO2为碳交易价格。
2)风储系统考核惩罚费用Cpns
风储系统考核惩罚包括AGC考核惩罚、功率平抑考核惩罚和套利计划偏差惩罚,有
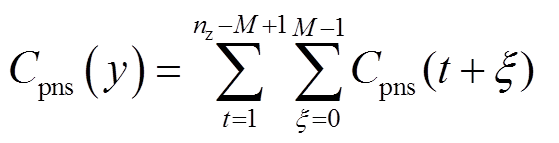 (25)
(25)
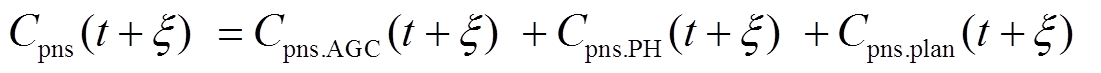 (26)
(26)
式中,Cpns.AGC(t+x)为AGC考核惩罚;Cpns.PH(t+x)为功率平抑考核惩罚;Cpns.plan(t+x)为套利计划偏差惩罚。
(1)AGC考核惩罚Cpns.AGC
根据1.2.1节所构建的AGC功率指令考核机制,测算风储系统的考核惩罚费用,有
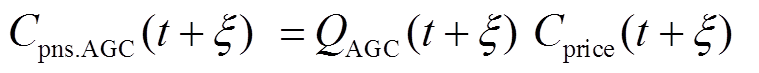 (27)
(27)
(2)功率平抑考核惩罚Cpns.PH
基于1.1节中风电功率平抑考核惩罚机制,针对功率波动越限情况进行考核,考核费用测算式为
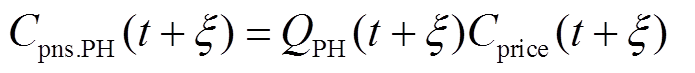 (28)
(28)
(3)套利计划偏差惩罚Cpns.plan
为保障储能系统的充放电收益,将上层套利计划作为惩罚项引导储能出力,有
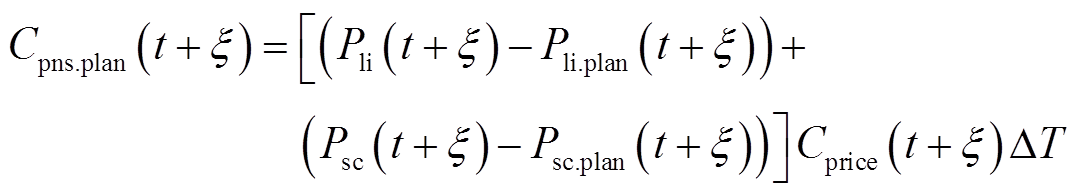 (29)
(29)
2.2.4 约束条件
下层模型同样计及储能SOC和充放电功率约束,如式(17)和式(18),并进一步考虑风电功率波动约束为
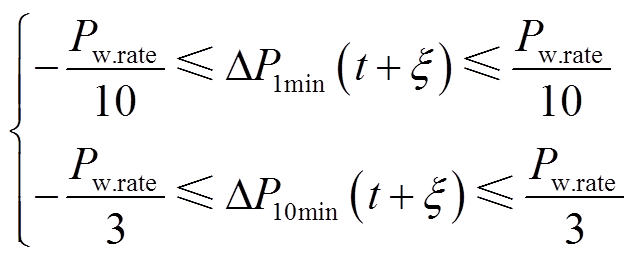 (30)
(30)
2.3.1 HESS运行寿命测算
混合储能的全寿命周期成本CLCC受其循环寿命的影响,超级电容循环使用次数约为几十万次,远大于锂离子电池可用循环次数,因此设定超级电容使用寿命为常数[15,21]。本文主要考虑放电深度(Depth of Discharge, DOD)对锂离子电池循环寿命的影响。根据固定放电深度下电池的最大循环次数,结合文献[22]采用三次多项式表征储能循环寿命,即
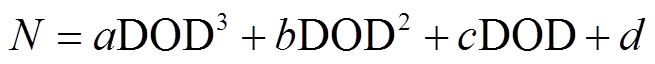 (31)
(31)
式中,N为储能循环寿命;a、b、c、d为曲线拟合系数,分别为0.03、7、−97、10 530。
将不同放电深度DODx对应的充放电循环次数N(DODx)折算到DOD=1情况下的等效循环次数为
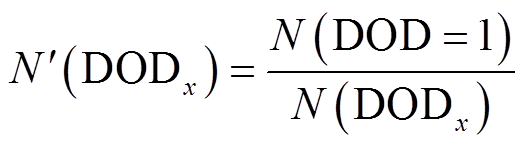 (32)
(32)
式中,N′(DODx)为储能等效循环次数;N(DOD=1)为完全充放电情况下的最大循环次数。
结合式(31)和式(32)测算储能全生命周期T内的等效循次数为
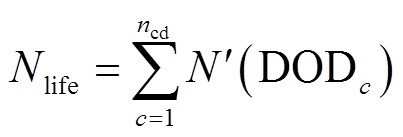 (33)
(33)
式中,Nlife为储能生命周期T内的等效循环次数;ncd为储能充放电循环的总数;DODc为第c个充放电循环对应的放电深度。
根据DOD=1时的循环次数计算储能实际运行寿命Treal,表达式为
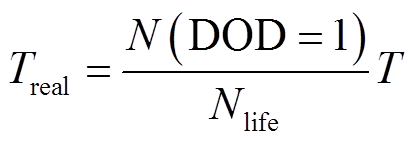 (34)
(34)
2.3.2 基于全寿命周期成本理论的储能成本模型
储能系统全寿命周期成本CLCC包括储能的初始投资成本Cinv、更新置换成本Crep、运行维护成本Com、报废处理成本Cscr和回收残值Cres,构建储能系统全寿命周期的成本模型。
1)全寿命周期总成本CLCC
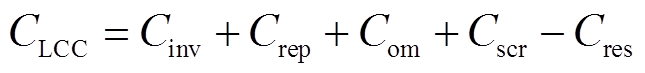 (35)
(35)
2)初始投资成本Cinv
储能设备的初始投资成本由容量投资成本和功率投资成本构成,计算公式为
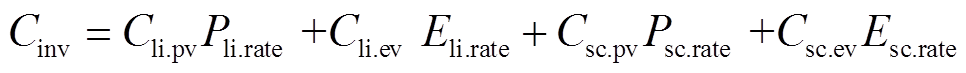 (36)
(36)
式中,Cli.pv、Cli.ev分别为锂离子电池单位功率、单位容量投资成本;Csc.pv、Csc.ev分别为超级电容单位功率、单位容量投资成本;Pli.rate为锂离子电池额定功率;Psc.rate为超级电容额定功率。
3)更新置换成本Crep
更新置换成本是指风储系统运行期间,储能到达寿命年限需更换储能设备产生的成本,即
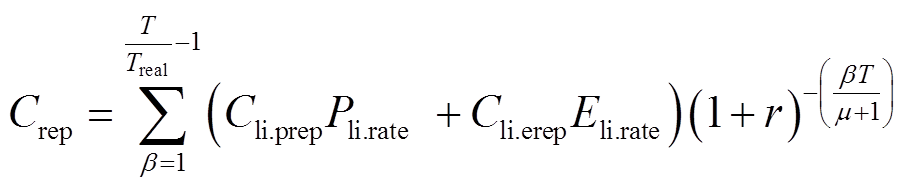 (37)
(37)
式中,Cli.prep、Cli.erep分别为锂离子电池单位功率和单位容量更新成本;m为储能在全寿命周期内的更换次数;b为储能设备更换年限。
4)运行维护成本Com
运行维护成本是指储能系统在使用年限内维持正常运行投入的资金,即
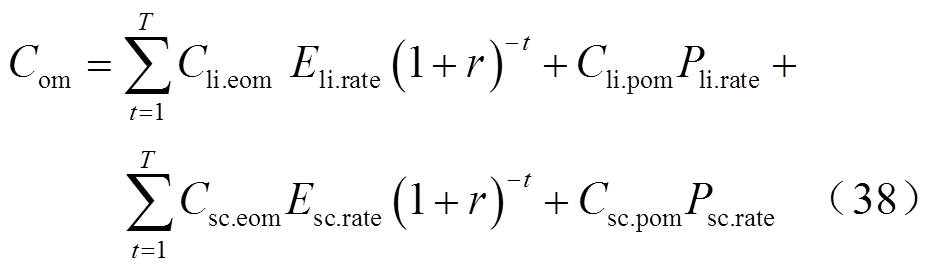
式中,Cli.pom、Cli.eom分别为锂离子电池单位功率、单位容量运维成本;Csc.pom、Csc.eom分别为超级电容单位功率、单位容量运维成本;Pli.rate为电池的额定功率;Psc.rate为超级电容的额定功率。
5)报废处理成本Cscr
报废处理成本是指在储能设备报废后进行无害化处理以及回收的成本,即
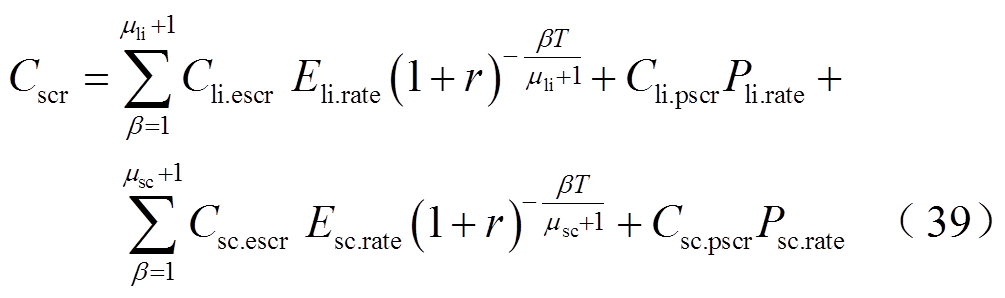
式中,Cli.pscr、Cli.escr分别为锂离子电池单位功率、单位容量报废处理成本;Csc.pscr、Csc.escr分别为超级电容单位功率、单位容量报废处理成本;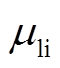 、
、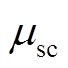 分别为锂离子电池和超级电容在全生命周期内的更换次数。
分别为锂离子电池和超级电容在全生命周期内的更换次数。
6)回收残值Cres
储能到达寿命年限,无法继续使用,但具有一定的回收价值,具体为
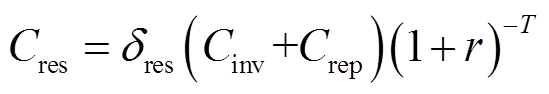 (40)
(40)
式中,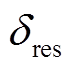 为回收残值率。
为回收残值率。
下层模型在优化求解过程中需响应功率平抑和AGC指令要求,确定混合储能充放电功率Pli和Psc的分配。本文采用改进HHT方法包括改进完全集合经验模态分解(Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, ICEEMDAN)[23]和递归希尔伯特变换[24-25]两部分,可减少传统HHT存在模态混叠现象,降低IMF分量瞬时频率的求解误差,实现对风电平抑的功率需求PPH和AGC功率指令响应误差PAGC的分解与重构,进行混合储能Pli和Psc的具体分配。
2.4.1 改进完全集合经验模态分解
基于ICEEMDAN进行功率分解,其计算式为
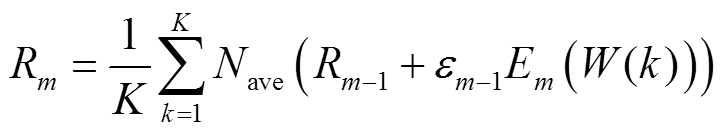 (41)
(41)
 (42)
(42)
式中,Em为由EMD分解产生的m阶模态分量;W(k)为第k组高斯白噪声;Nave为功率信号的局部均值;εm-1为加入高斯白噪声第m个IMF分量Em(W(k))时所乘的系数;K为序列组数;Rm为第m组残差;imfm为第m个模态分量。
针对风电功率的分解结果,根据表1中的并网要求进行重构。当第m1次分解满足并网要求时,将高频分量imf1~imfm1之和作为混合储能功率指令,剩余低频分量与残差作为并网功率,有
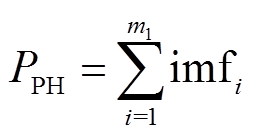 (43)
(43)
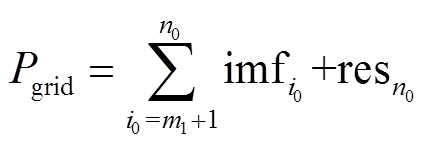 (44)
(44)
式中,PPH为混合储能风电功率平抑指令;Pgrid为并网功率;m1为imf分量分界点;n0为imf分量总数;resn0为残差。
同理,对风电功率平抑需求PPH和风电场响应AGC功率指令的误差量PAGC进行ICEEMAND分解,如式(45)、式(46)所示。针对分解出的imf分量,通过递归希尔伯特变换进行重构。
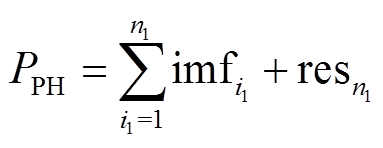 (45)
(45)
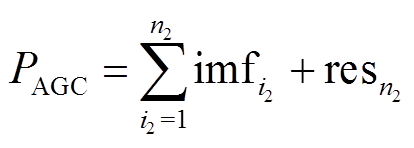 (46)
(46)
式中,n1为风电功率平抑需求量PPH分解的imf分量总数;n2为AGC功率指令的误差量PAGC分解的imf分量总数;PAGC为风电场响应AGC功率指令的误差。
2.4.2 IMF递归希尔伯特变换
由于imfi,0是关于时间的函数,表示为imfi,0(t),设imfi,0(t)经希尔伯特变换的结果为H(imfi,0(t)),有
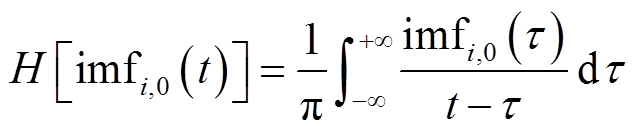 (47)
(47)
基于希尔伯特变换,构建解析信号Zi,0(t)为
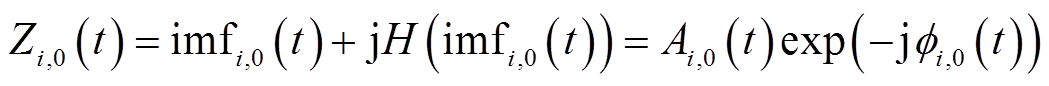 (48)
(48)
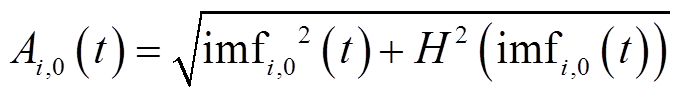 (49)
(49)
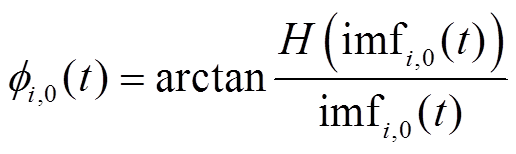 (50)
(50)
式中,Ai,0(t)为imfi,0(t)的幅值;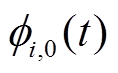 为imfi,0(t)的相位。
为imfi,0(t)的相位。
定义cos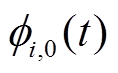 为纯调频函数,以纯调频函数imfi,1(t)=cos
为纯调频函数,以纯调频函数imfi,1(t)=cos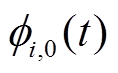 作为新的希尔伯特变换对象,得到新的幅值函数与纯调频信号,不断进行递归计算,递归公式如式(51)所示,直到幅值函数趋于1。最终,计算出imfi,0(t)的瞬时频率如式(52)所示。
作为新的希尔伯特变换对象,得到新的幅值函数与纯调频信号,不断进行递归计算,递归公式如式(51)所示,直到幅值函数趋于1。最终,计算出imfi,0(t)的瞬时频率如式(52)所示。
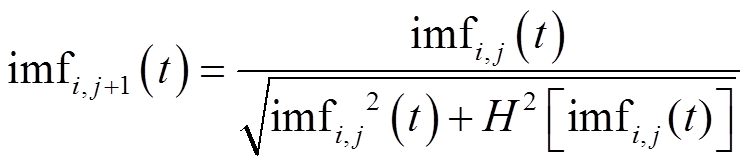 (51)
(51)
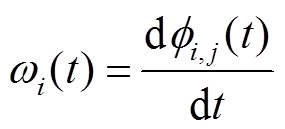 (52)
(52)
式中,ωi(t)为瞬时频率。
针对混合储能的功率和容量配置的求解问题,以下表达式以锂离子电池的额定功率和额定容量进行描述,超级电容额定功率和额定容量的表达形式与锂离子电池储能相似。
2.5.1 额定功率
根据锂离子电池放电为正,充电为负,考虑储能充放电效率,将电池生命周期T内最大放电功率和最小充电功率绝对值的较大者作为额定功率,有
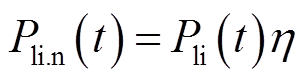 (53)
(53)
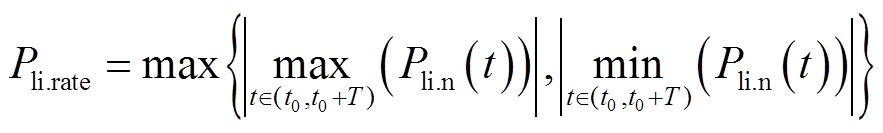 (54)
(54)
式中,Pli.n(t)为考虑充放电效率后电池的充放电功率;t0为初始时刻。
2.5.2 额定容量
锂离子电池额定容量应该满足生命周期内的最大正向能量累积需求和最小负向能量累积需求,考虑SOC的限制,确定的额定容量为
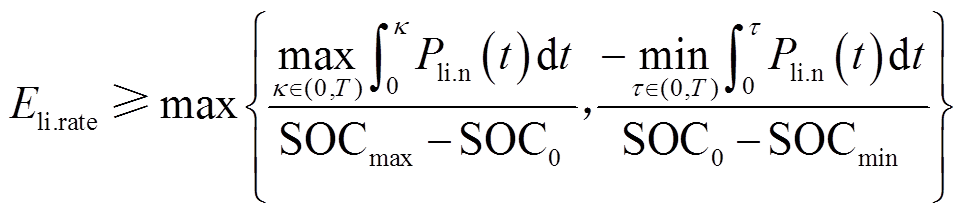 (55)
(55)
式中,k、t为不同的时刻。
初始荷电状态SOC0对锂离子电池额定容量具有直接影响,当SOC0满足式(55)取等号,且满足式(56)时,储能系统的额定容量最小。
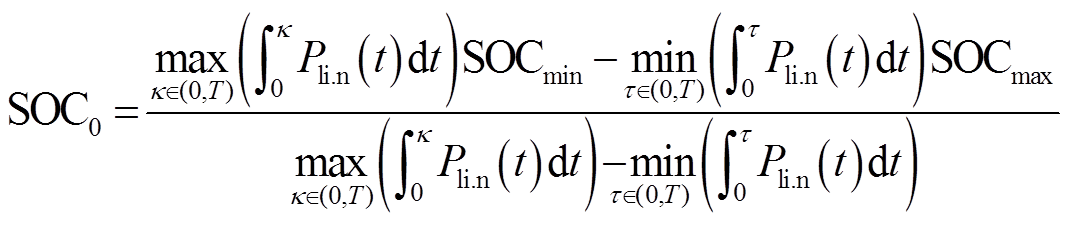 (56)
(56)
结合式(53)~式(56),本文所提风电场HESS容量优化配置求解过程描述为:根据风电功率平抑和AGC功率指令的响应需求,给定HESS的额定功率及容量配置初始值,上层模型基于该初始配置以套利收益最大为目标,确定HESS的额定容量与额定功率传递给下层,下层模型在上层配置结果约束下,以风储系统全寿命周期收益最大为目标,对HESS配置方案进行修正更新并返回上层进行下一次迭代。通过上下层不断迭代求解,获取经济效益最优的HESS容量配置方案。
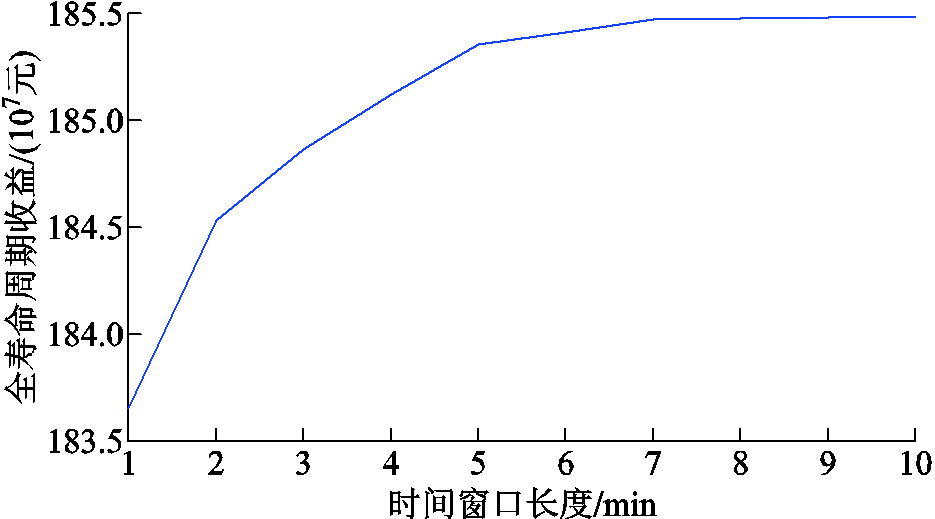
基于某100 MW风电场典型功率数据和AGC功率指令数据,考虑风电功率平抑和AGC功率指令考核与辅助服务,验证本文所提风电场锂离子电池和超级电容混合储能容量优化配置方法的有效性。图3给出了典型日内时间间隔为1 min的原始风电功率数据及其满足平滑并网要求的功率波动范围;图4为时间间隔为1 min的AGC功率指令和原始风电功率数据;用于测算经济效益的相关参数见表2[2-4];混合储能的相关参数见表3[15,21];不同预测控制时间窗口长度M下风储系统的经济效益如附图1所示,当窗口长度M>7时,风储系统全寿命周期收益趋于收敛,且步长较小时可以节省算法运行时间,故选取窗口长度M为7。
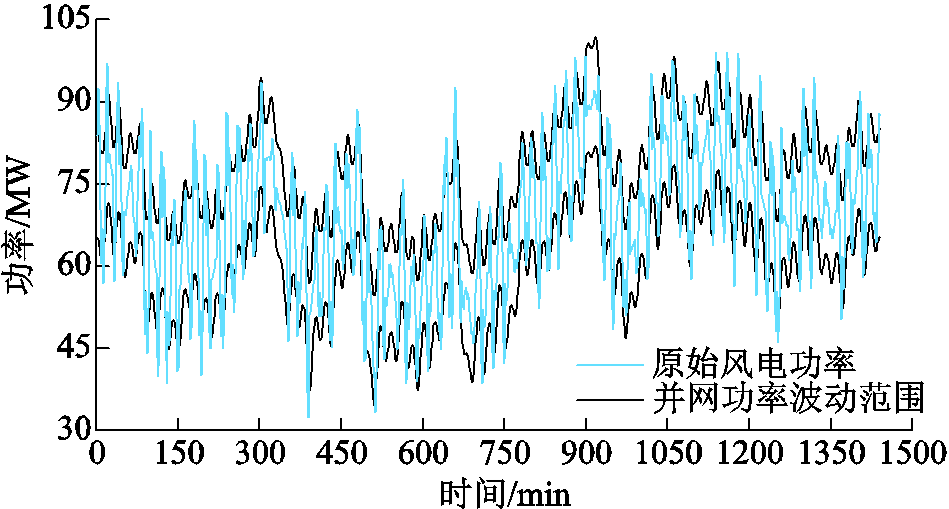
图3 原始风电功率数据和满足并网要求的功率波动范围
Fig.3 Original wind power data and the range of power fluctuations that meet grid connection requirements
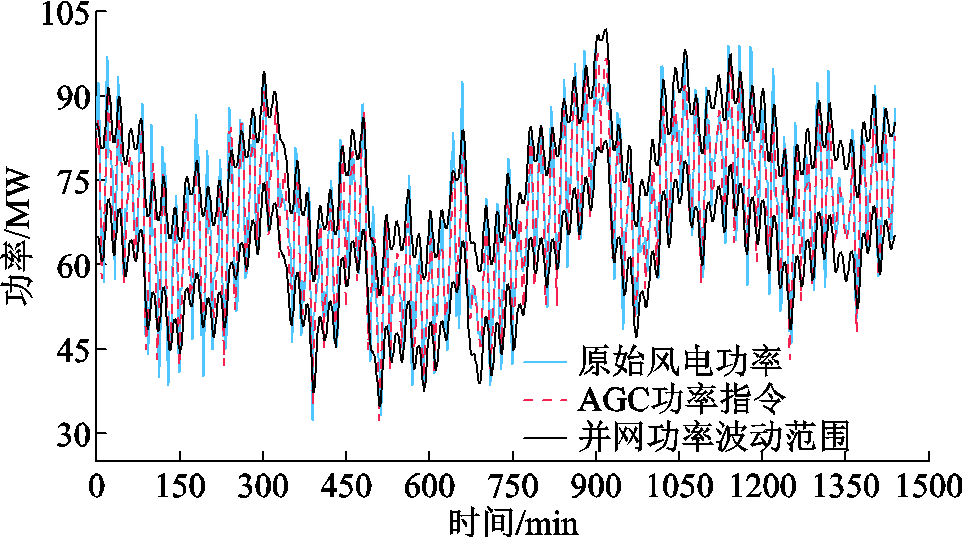
图4 原始风电功率和AGC功率指令
Fig.4 Original wind power and AGC power order
表2 经济效益相关参数
Tab.2 Parameters related to economic benefits

参数数值 AGC响应精度允许偏差/MW1 风电平抑考核系数aPH10 补偿标准YAGC/(元/MW)15 储能贡献率CAGC0.1 单位电量的排放配额/[kg/(MW·h)]997 碳交易价格/(元/t)52 折现率r(%)10
表3 储能相关参数
Tab.3 Energy storage related parameters
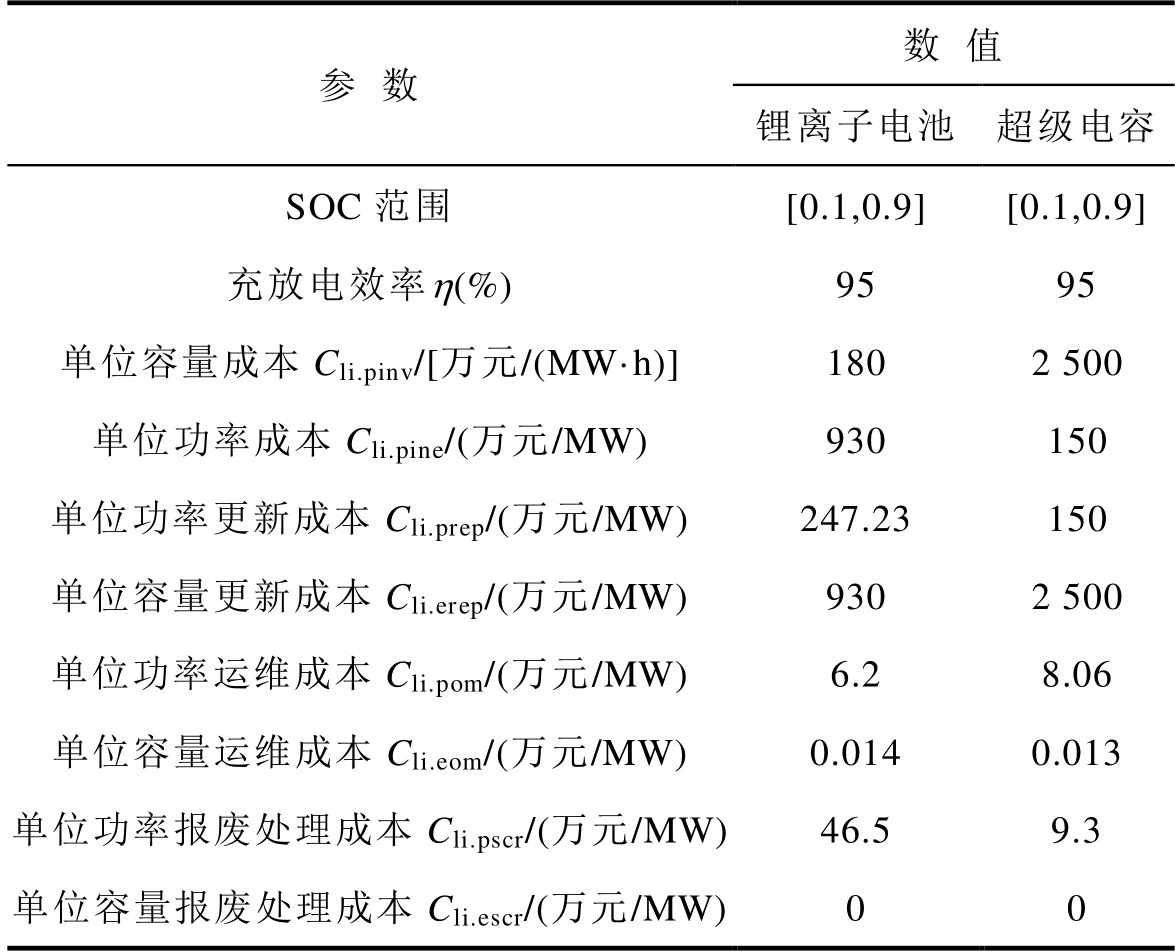
参数数值 锂离子电池超级电容 SOC范围[0.1,0.9][0.1,0.9] 充放电效率h(%)9595 单位容量成本Cli.pinv/[万元/(MW·h)]1802 500 单位功率成本Cli.pine/(万元/MW)930150 单位功率更新成本Cli.prep/(万元/MW)247.23150 单位容量更新成本Cli.erep/(万元/MW)9302 500 单位功率运维成本Cli.pom/(万元/MW)6.28.06 单位容量运维成本Cli.eom/(万元/MW)0.0140.013 单位功率报废处理成本Cli.pscr/(万元/MW)46.59.3 单位容量报废处理成本Cli.escr/(万元/MW)00
本文假设风储系统全寿命周期T为20年[23],HESS双层容量优化模型,上层模型基于市场电价[26],获取峰谷套利阶段HESS最优的容量配置方案传递给下层,下层模型以风储系统收益最大为目标对HESS配置方案进行优化更新并反馈给上层,进行迭代求解。
结合图3和图4,根据风电功率平抑和AGC功率指令的响应需求,本文初始设置的锂离子电池额定功率为5 MW,额定容量为5 MW·h,超级电容额定功率为20 MW,额定容量为5 MW·h,迭代收敛曲线如图5所示。
由图5分析可知,经过3次迭代后风储系统的收益曲线开始趋于收敛,经过不断迭代,最终曲线收敛于185.567千万元。HESS容量配置结果见表4。在本文双层容量优化配置模型下,HESS总装机容量占风电场装机容量的15.270%,满足风电场配置储能的推荐容量占比范围[27]。另外,HESS中的锂离子电池和超级电容的额定容量分别为额定功率的5.625倍和0.107倍,符合能量型和功率型储能的特性。
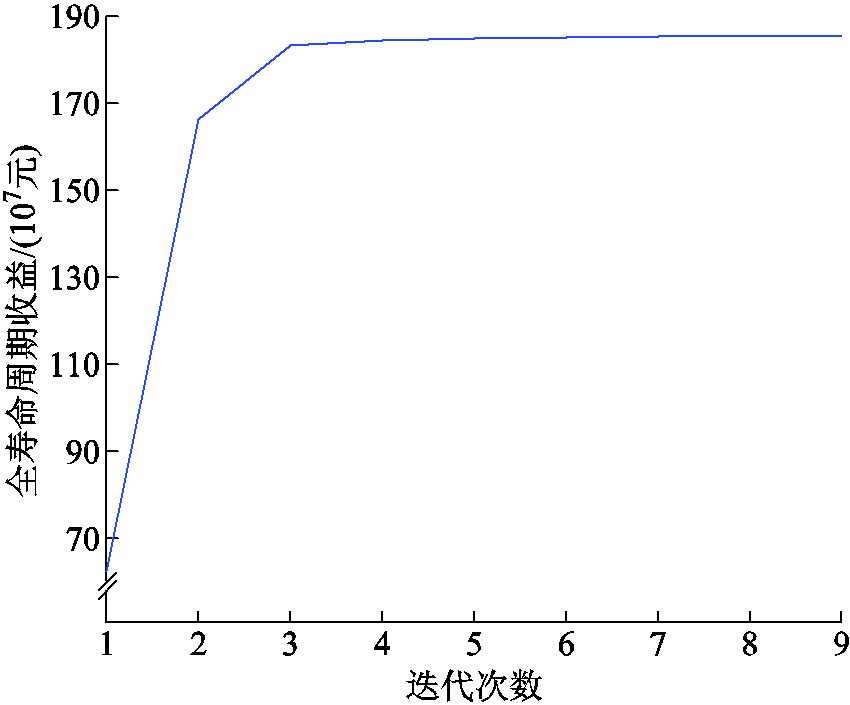
图5 迭代收敛曲线
Fig.5 Iterative convergence process
表4 HESS配置结果
Tab.4 Hybrid energy storage configuration results

储能配置额定容量/(MW·h)额定功率/MW 锂离子电池3.0210.537 超级电容1.58314.733
为进一步说明本文所提面向风电场功率平抑和AGC功率指令考核与辅助服务机制的风电场HESS容量优化配置方案的经济性,进行多个方案之间的对比分析,具体描述如下。
方案一:为本文所提出的计及风电场涉网功率平抑与AGC功率指令响应需求的HESS双层容量优化配置方法。
方案二:为风电场在未配置储能时,仅考虑风电消纳,最大化风电功率出力(运行于最大功率跟踪)而不弃风。
方案三:为风电场在未配置储能时,通过弃风/保留备用的方式进行风电功率平抑和AGC功率指令的响应,其中备用容量与方案一中HESS总装机容量的大小相同(风电场装机容量的15.270%)。
方案四:为风电场仅考虑功率平抑需求的HESS双层容量优化配置方法。
方案五:为风电场仅考虑AGC功率指令响应需求的HESS双层容量优化配置方法。
上述五种方案下的配置结果和收益情况具体见表5,Rpns.AGC为全寿命周期AGC功率指令响应考核费用。
方案二在未配置储能的情况下,风电场始终以最大功率出力,保障了风电场的售电收益Rsale,由于未考虑风电功率平抑和AGC功率指令的响应需求,导致风电场受到3%上网电量的考核惩罚,所获取的AGC功率指令补偿力度RAGC较弱,全寿命周期收益Rspan为176.008千万元,将其视为对比标准。方案一在保障风电消纳的同时,兼顾了风电功率平抑和AGC功率指令的响应需求,实现了风电功率的平滑并网,提高了风电场对AGC功率指令的响应能力,将风电场总考核费用(Cpns.AGC和Cpns.PH)降低84.648%,AGC功率指令辅助服务补偿收益RAGC提升6.642倍,全寿命周期收益Rspan提高5.431%;方案三在风电功率平抑和AGC功率指令响应方面创造的经济价值与方案一接近,但由于过多的弃风,导致全寿命周期收益Rspan降低3.350%;方案四中仅考虑风电场的功率平抑需求,规避了风电平抑的考核惩罚Cpns.PH,但由于风电功率平抑不给予辅助服务补偿费用,且需考虑HESS的配置成本CLCC,使得风储系统全寿命周期的经济效益Rspan与方案二接近;方案五中仅考虑风电场对AGC功率指令的响应需求,几乎规避了AGC功率指令的考核惩罚Cpns.AGC,辅助服务补偿收益RAGC提升7.405倍,全寿命周期收益Rspan提高3.89%。
表5 不同方案下的经济效益
Tab.5 Economic benefits under different scenarios
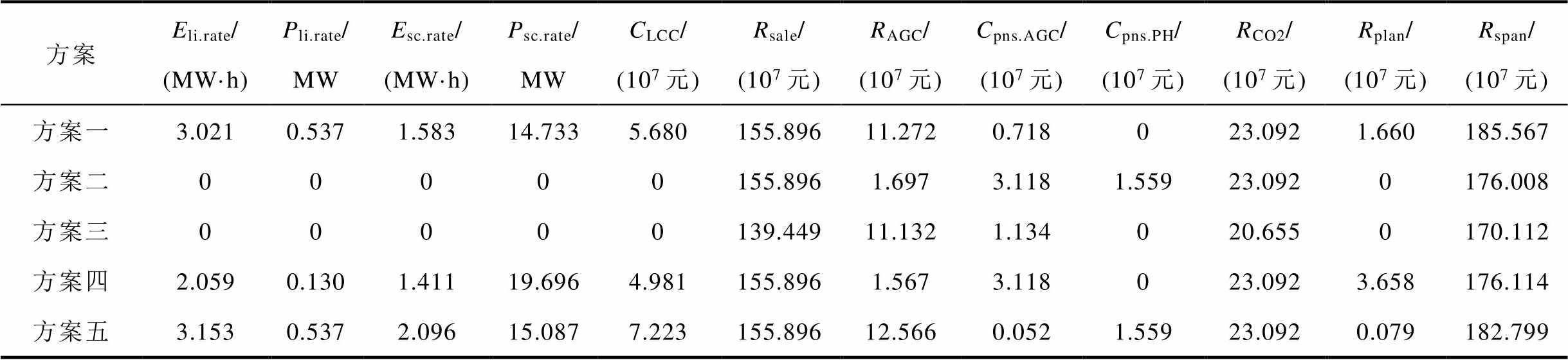
方案Eli.rate/(MW·h)Pli.rate/MWEsc.rate/(MW·h)Psc.rate/MWCLCC/(107元)Rsale/(107元)RAGC/(107元)Cpns.AGC/(107元)Cpns.PH/(107元)RCO2/(107元)Rplan/(107元)Rspan/(107元) 方案一3.0210.5371.58314.7335.680155.89611.2720.718023.0921.660185.567 方案二00000155.8961.6973.1181.55923.0920176.008 方案三00000139.44911.1321.134020.6550170.112 方案四2.0590.1301.41119.6964.981155.8961.5673.118023.0923.658176.114 方案五3.1530.5372.09615.0877.223155.89612.5660.0521.55923.0920.079182.799
对于不同的HESS配置方案,仅考虑平抑需求下HESS的容量需求最小,储能投资成本低。方案一由于考虑AGC功率指令响应需求导致储能系统容量配置结果增大,锂离子电池和超级电容的容量分别增加46.722%和12.190%,引起储能系统总投资成本CLCC上升14.033%,但通过配置更多的储能容量响应AGC功率指令,获得了可观的辅助服务收益RAGC,相比方案四总收益提升5.773%。而方案五脱离了风电波动率的约束,仅考虑AGC功率指令响应需求,需要更大的储能容量支撑,相对方案一HESS的配置成本CLCC增加27.165%,全寿命周期收益Rspan降低1.540%。上述结果表明方案一具有更好的经济效益。
基于上述HESS配置方案,下文对储能系统平抑风电功率波动和响应AGC功率指令的效果进行分析。
采用本文方法获取风电功率的平抑需求PPH,将其分解为8个IMF分量与1个余量,限于篇幅,列出PPH分解的部分IMF分量和余量如图6所示,IMF的瞬时频率-时间曲线如图7所示,分析可知imf7与imf8瞬时频率-时间曲线完全分离,模态混叠最少,因此取j=7作为高低频分量的分界点确定锂离子电池和超级电容的功率指令,储能系统的充放电功率和SOC曲线如附图2和附图3所示,由图分析可知超级电容的功率变化频次大于锂离子电池,可以发挥超级电容循环次数多、充放电速率快的优势,而锂离子电池消纳的是功率数据中的低频分量,充放电功率频次较低,使得超级电容SOC曲线波动频繁,锂离子电池SOC变化平缓,但均在SOC上下限范围内变动。通过HESS充放电对风电功率进行平抑,风电功率的平抑效果如图8所示,为增强图8曲线的分辨率,将其中方案一、方案四和方案五分别拆分成三个图进行描绘,如附图4所示。
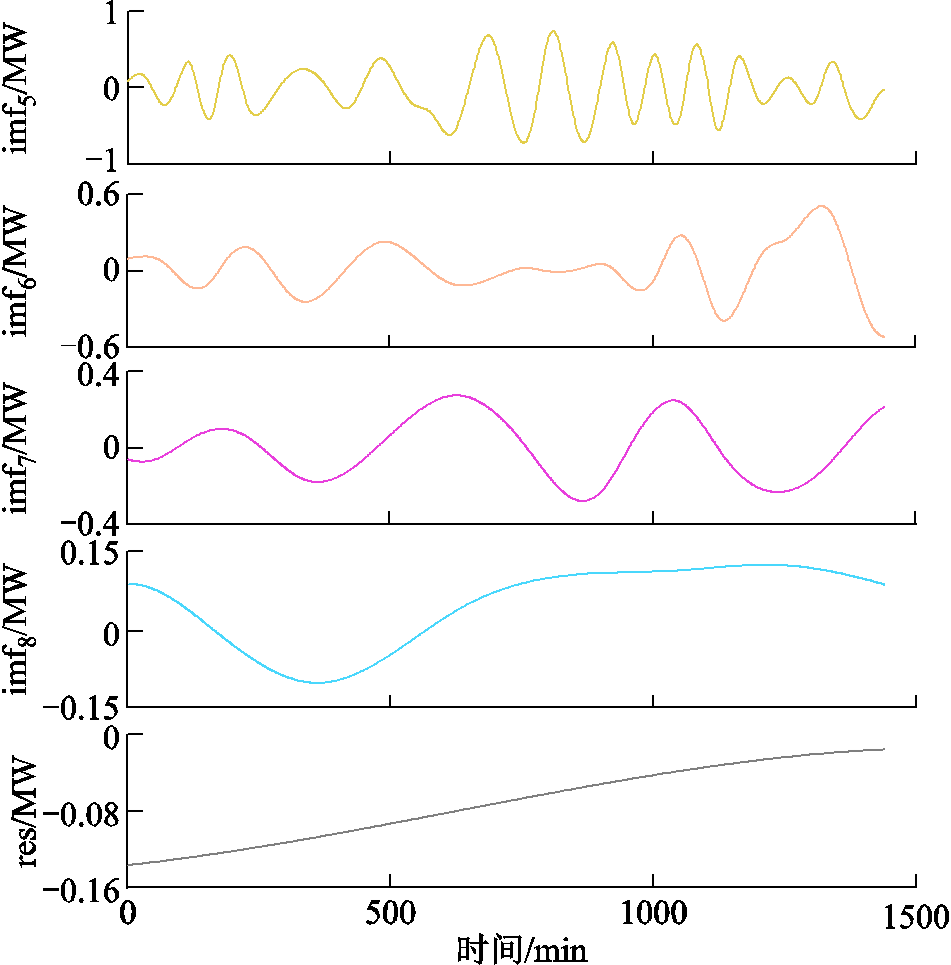
图6 部分IMF分量
Fig.6 Part of the IMF component
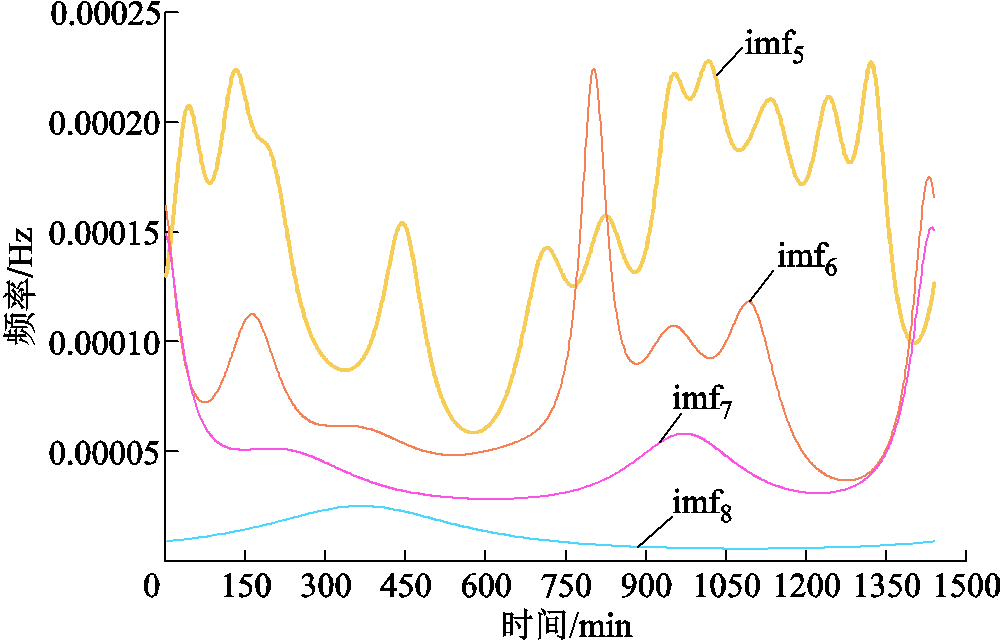
图7 部分IMF瞬时频率-时间曲线
Fig.7 Part of the IMF instantaneous frequency-time curve
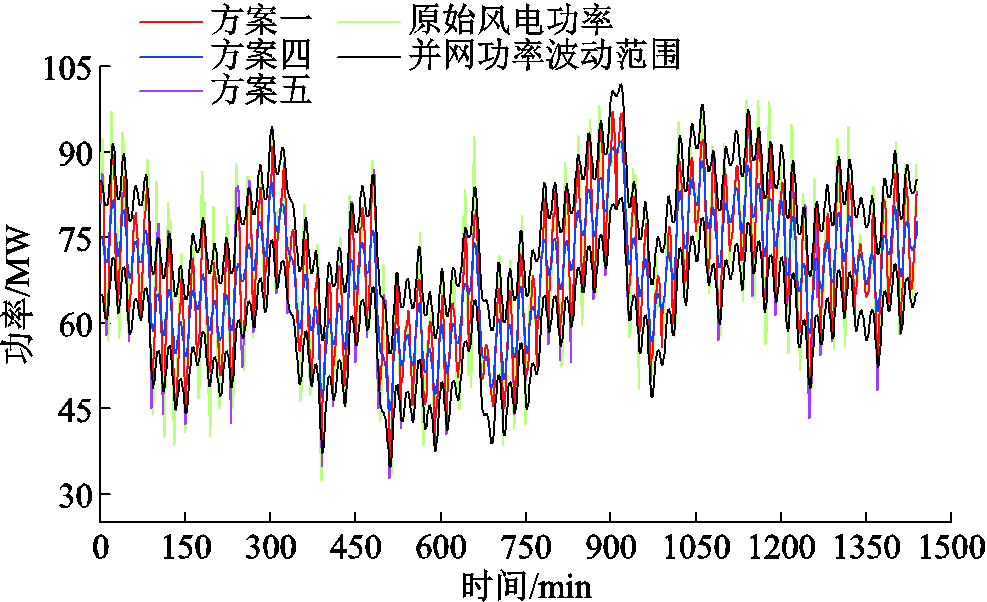
图8 采用混合储能平抑风电功率的效果
Fig.8 Wind power suppression effect with HESS
由图8分析可知,风电场原始出力的功率波动比较大,经HESS平抑之后并网功率波动明显减小,其中方案四和方案一对原始风电功率的平抑效果均能够满足风电平滑并网要求,方案五中并网功率波动较大,超过了功率平抑需满足的波动范围。为了量化分析HESS配置后对风电功率平抑效果的影响,定义波动率与越限率作为评估指标,具体为
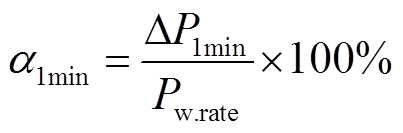 (57)
(57)
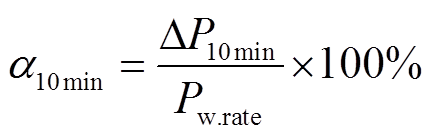 (58)
(58)
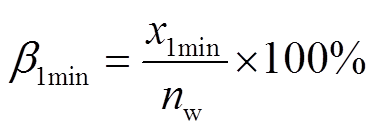 (59)
(59)
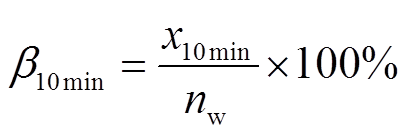 (60)
(60)
式中,α1min为1 min波动率,即1 min功率波动量ΔP1min与风电场装机容量的比值;α10min为10 min波动率,即10 min功率波动量ΔP10min与风电场装机容量的比值;b1min为1 min功率波动的越线率;b10min为10 min功率波动的越限率;x1min为1 min波动率的越限次数;x10min为10 min波动率的越限次数;nw为风电功率采用次数。
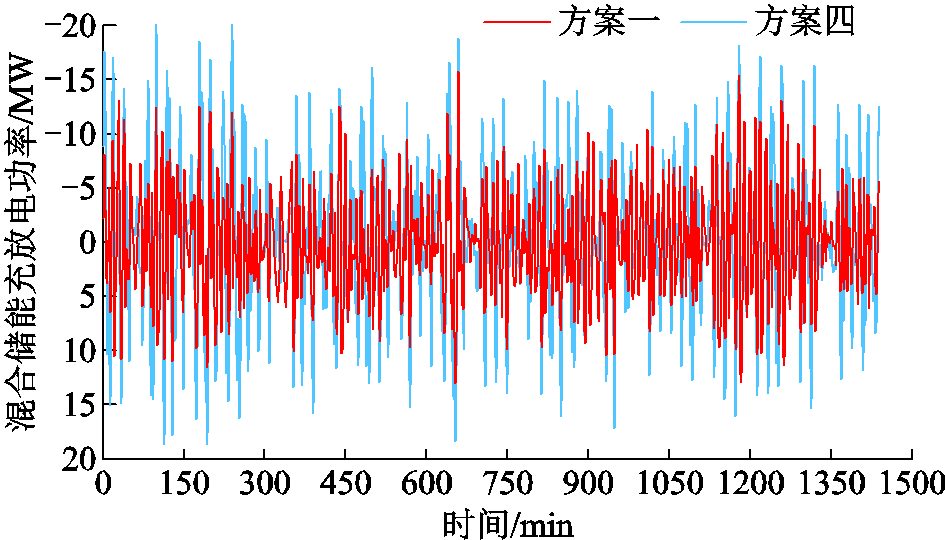
根据我国风电并网标准[3],装机容量为100 MW的风电场,并网功率最大α1min上限为10%,最大α10min上限为33.333%。风电功率平抑效果对比见表6。由表6分析可知,原始风电功率最大α1min为25.671%,最大α10min为42.122%,均不满足并网要求,经HESS平抑之后,风电功率各项波动指标显著下降。其中,方案五对风电功率具有一定的平抑效果,但并网功率未满足风电平滑并网要求。方案四将风电功率最大α1min降低至2.560%,最大α10min降低至17.526%,满足平滑并网要求,但由于波动率下降幅度较大,导致并网功率过度平滑,加重了HESS的负担。方案一在并网功率的波动范围内响应AGC功率指令,使风电功率最大α1min降低至9.758%,最大α10min降低至32.970%。方案一和方案四中HESS的充放电功率如附图5所示,可见方案一中储能系统的充放电功率变化幅度明显小于方案四,相比于方案四,本文在满足风电功率平滑并网的基础上,降低了储能出力,提高了对原始风电功率的跟踪能力,同时规避了风电功率平抑的电量考核惩罚。
表6 风电功率平抑效果对比
Tab.6 Comparison of wind power smoothing effects (%)

方案最大α1min最大α10minβ1minβ10min 原始风电功率25.67142.1223.4713.75 方案一9.75832.97000 方案四2.56017.52600 方案五15.08241.8470.8962.083
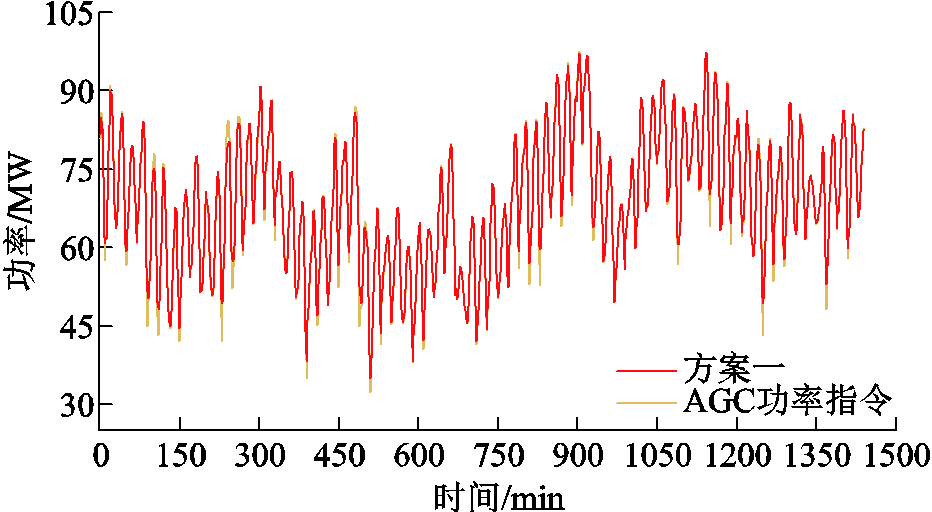
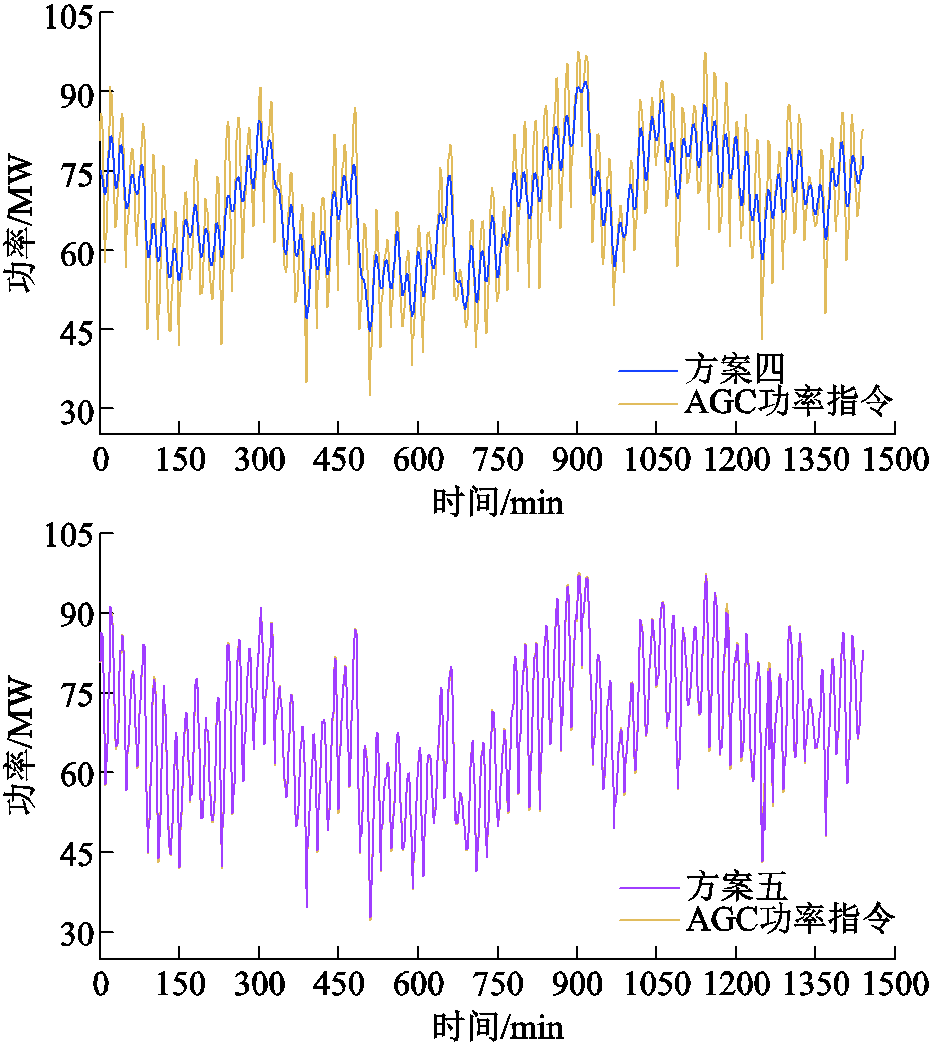
通过配置HESS协助风电场响应AGC功率指令,风储系统响应AGC功率指令的效果如图9所示,为增强图9曲线的分辨率,将图中的方案一、方案四和方案五分别拆分成三个图进行描绘,如附图6所示。
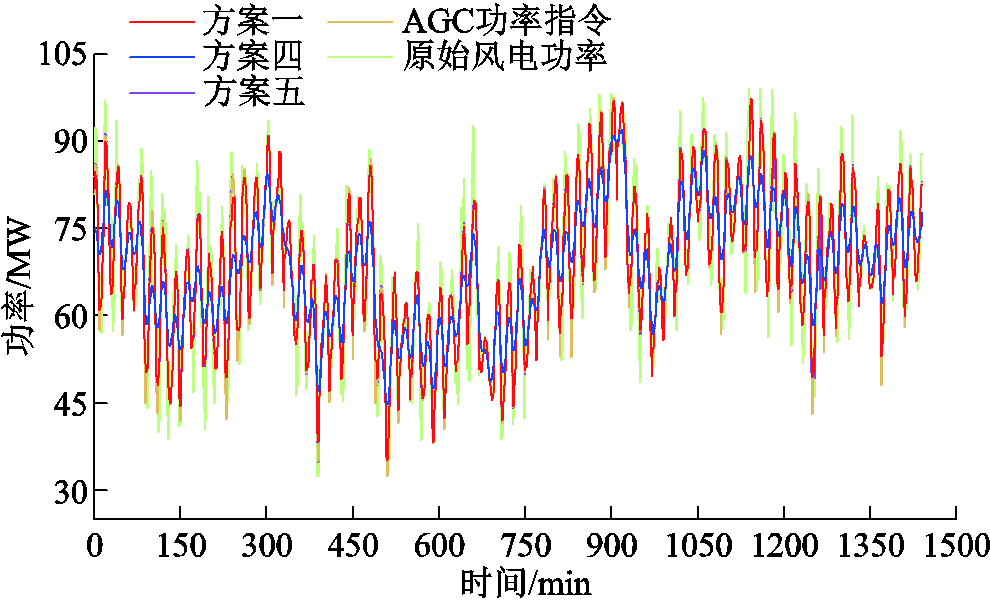
图9 采用混合储能响应AGC功率指令的效果
Fig.9 Effect of responding to AGC power order with HESS
由图9分析可知,原始风电功率与AGC功率指令的偏离程度较大,当风电场配置储能后,方案四因缺乏AGC功率指令引导出力,导致风储系统的并网功率与AGC功率指令的契合程度较低。方案五中风储系统的并网功率几乎与AGC功率指令重合,但由于未考虑功率平抑需求,并网功率波动较大,不满足风电平滑并网要求。方案一在保证风电功率平滑并网的基础上,利用并网功率的波动裕度响应AGC功率指令,显著提升了风电场对AGC功率指令的跟踪能力。
为进一步量化分析风储系统对AGC功率指令的响应效果,引入响应AGC功率指令的评估指标λ,具体为
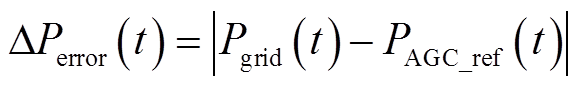 (61)
(61)
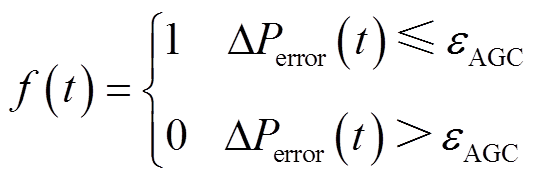 (62)
(62)
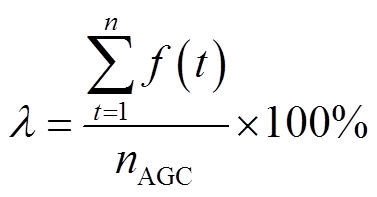 (63)
(63)
式中,PAGC_ref(t)为AGC功率指令;DPerror(t)为风储系统响应AGC功率指令误差的绝对值;f(t)为成功响应AGC功率指令的判断指标,DPerror(t)≤eAGC为成功响应,f(t)=1,否则,f(t)=0;λ为风储系统响应AGC功率指令的合格率,即成功响应指令的次数与采样次数的比值,λ越大说明AGC功率指令响应的效果越好,电量考核惩罚越小;n为成功响应AGC功率指令的次数;nAGC为AGC功率指令的采用次数。
风电场AGC响应指标对比见表7。通过对表7分析可知,风电场在未配置储能时,响应AGC功率指令的合格率λ仅为17.361%,并受到最大考核电量惩罚。风电场在配置储能后,方案四未考虑AGC功率指令的响应需求,合格率λ降低至14.513%。方案五虽对AGC功率指令的响应效果较好,但其响应下的并网功率不满足功率平抑的要求,存在功率平抑考核惩罚。本文在实现风电功率平滑并网的前提下响应AGC功率指令,将合格率λ提升至89.652%,考核电量降低至0.460%,提高了风电场对AGC功率指令的响应能力和经济效益。
表7 风电场AGC响应指标对比
Tab.7 Comparison of AGC response indicators of wind farms (%)

方案λQAGC/Q 原始风电功率17.3612 方案一89.6520.460 方案四14.5132 方案五99.6420.033
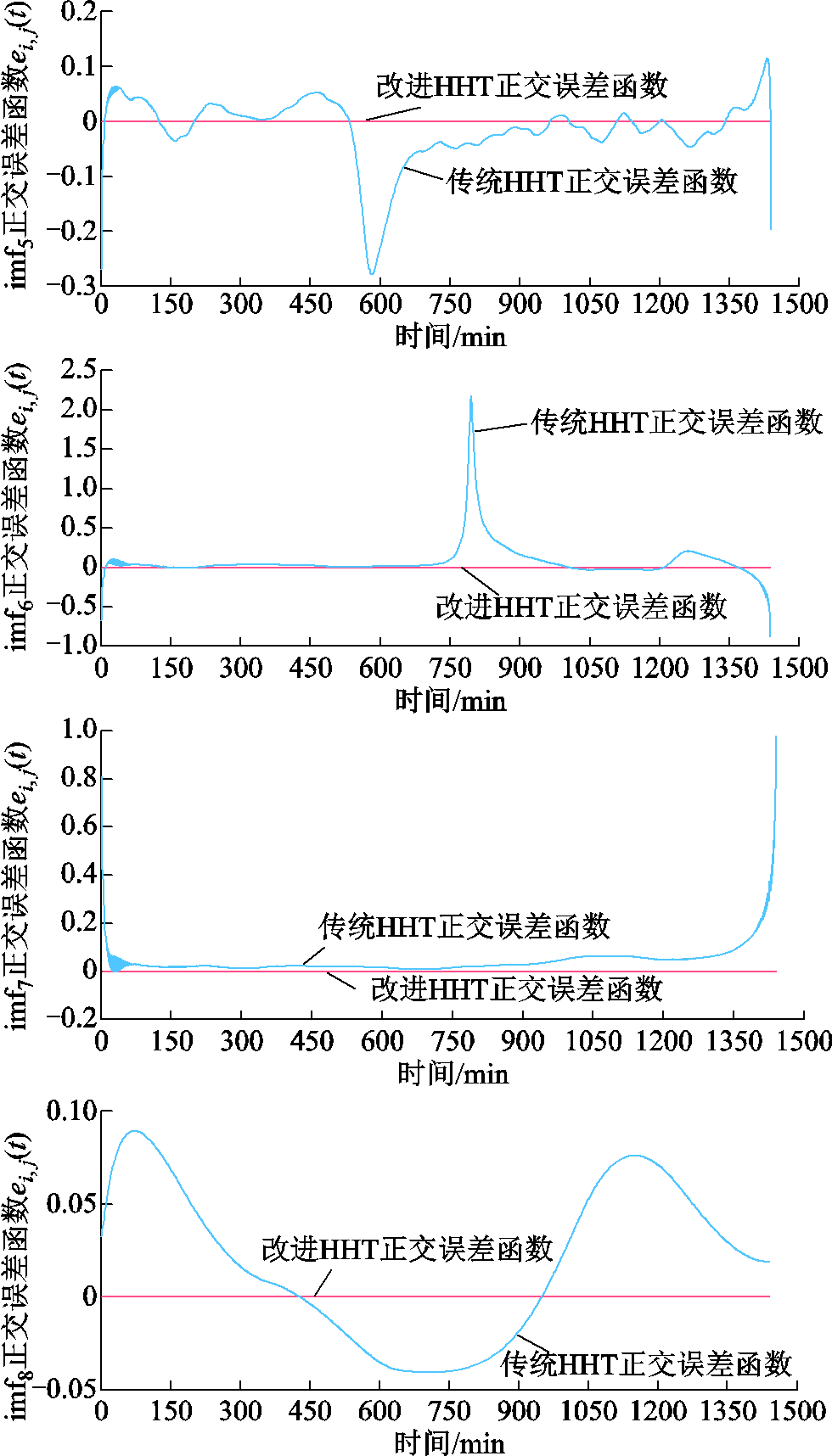
为了量化说明改进HHT对分解精度的提高程度,引入正交误差函数ei,j(t)作为评估指标,如式(64)所示,正交误差函数越小,所求IMF分量的瞬时频率越精确,当纯调频信号cos 的希尔伯特变换结果H(cos
的希尔伯特变换结果H(cos )与其正交信号sin
)与其正交信号sin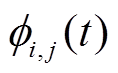 相等时,可以准确求解出IMF分量的瞬时频率,具体结果如附图7所示。
相等时,可以准确求解出IMF分量的瞬时频率,具体结果如附图7所示。
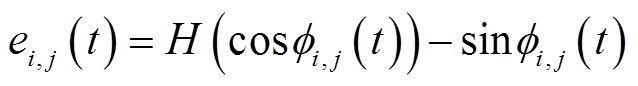 (64)
(64)
式中,sin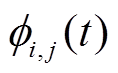 为纯调频信号cos
为纯调频信号cos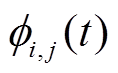 的正交信号。
的正交信号。
由附图7分析可知,传统HHT方法的正交误差函数较大,难以精确求解IMF分量的瞬时频率,改进HHT方法通过递归计算可以将IMF分量的正交误差函数几乎降低至0(误差数量级在1´10-13~1´10-9之间),提高了分解精度。
本文建立了一种计及风电场涉网功率平抑和AGC功率指令辅助服务与考核的锂离子电池-超级电容HESS双层容量优化配置模型,HESS可协助风电场提升并网功率平抑性能和AGC功率指令响应能力,有效地减少考核惩罚并获取相应的辅助服务补偿收益,提高风电场整体经济收益。针对某100 MW风电场,验证了本文所提HESS双层容量优化配置方法的有效性,得到的主要结论如下:
1)本文提出的风电场HESS双层容量优化配置方案,保障了风电发电量收益,满足了“两个细则”中对风电场功率平抑和AGC功率指令跟踪的涉网要求,在储能全寿命周期内风电场收益提高为185.567千万元,收益提升了5.431%,对风电场储能配置以提高综合经济收益具有重要价值。
2)本文HESS配置方案可有效地平抑风电功率波动,最大波动率α1min由25.671%降低至9.758%,α10min由42.122%降低至32.970%,响应了风电功率波动平抑要求,规避了电量考核惩罚。
3)本文HESS配置方案在保证风电功率平滑并网的基础上响应AGC功率指令,将响应AGC功率指令的合格率λ由17.361%提高至89.652%,考核电量QAGC由2%降低至0.460%,AGC功率指令辅助服务补偿收益由1 697万元提升至11 272万元,提高了风电场响应AGC功率指令的经济效益。
附 录
附图1 不同窗口长度下的全寿命周期收益
App.Fig.1 Lifetime benefits under different window lengths
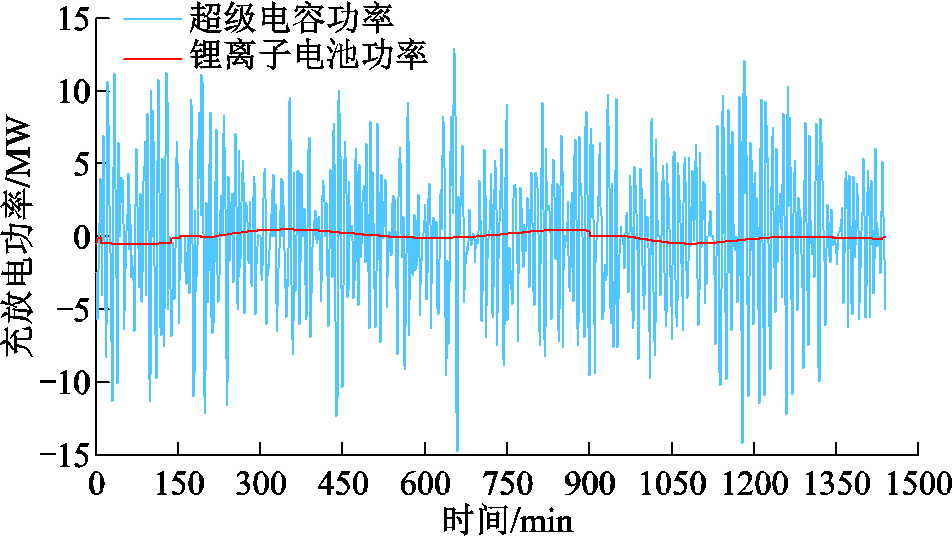
附图2 储能系统出力曲线
App.Fig.2 Energy storage output curves
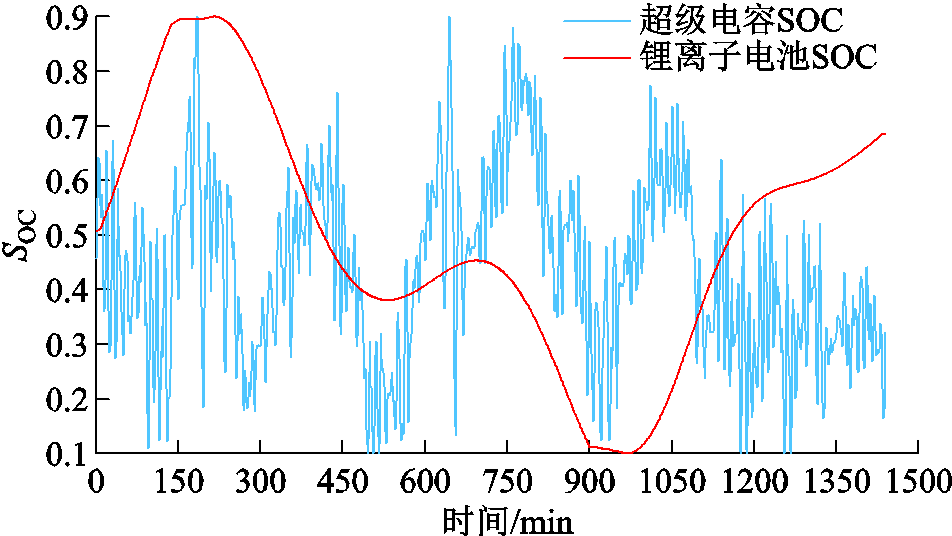
附图3 储能系统SOC曲线
App.Fig.3 Energy storage system SOC curvesfluctuations that meet grid connection requirements
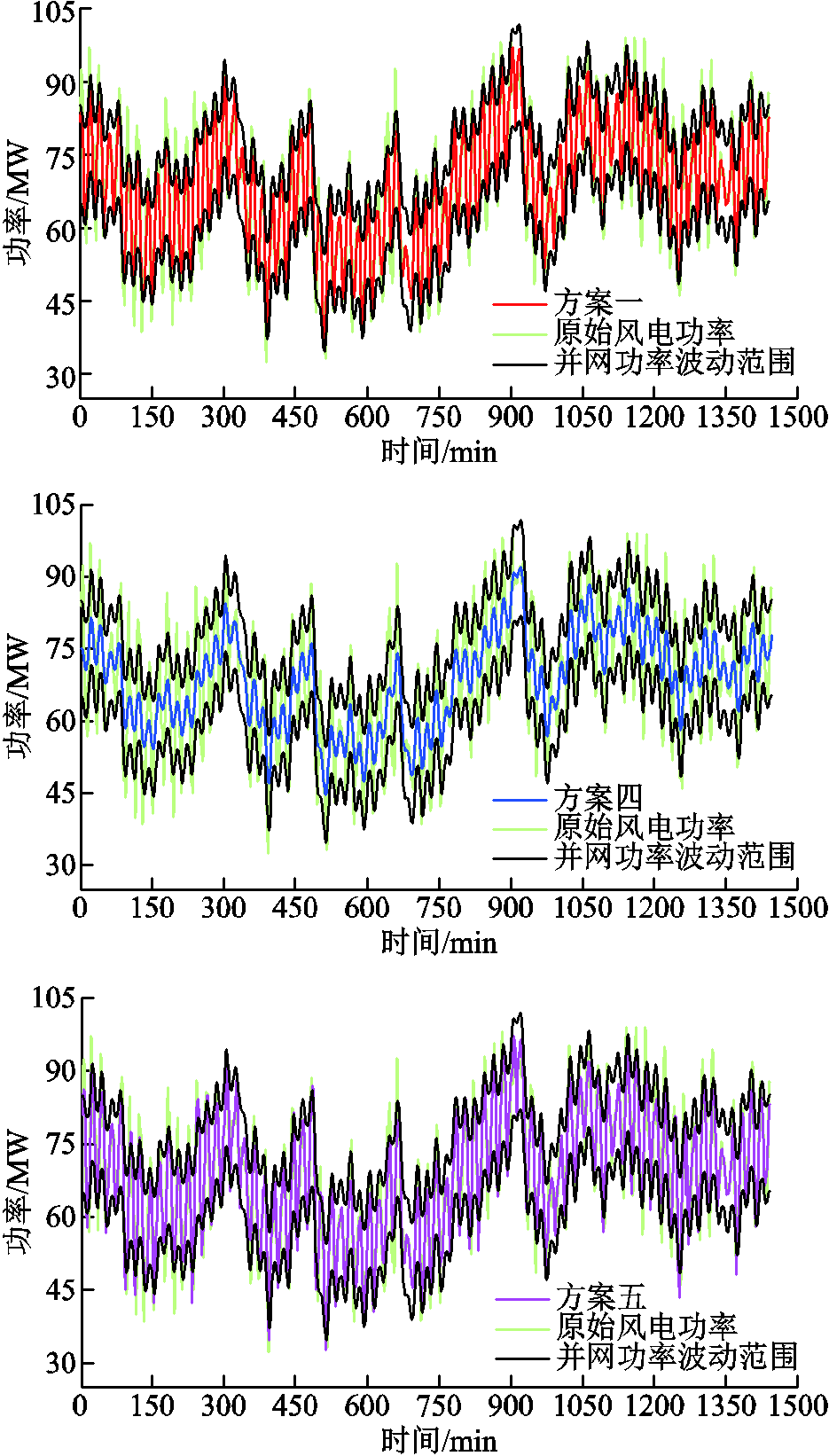
附图4 采用混合储能平抑风电功率的效果
App.Fig.4 Wind power suppression effect with HESS
附图5 方案一与方案四HESS出力曲线
App.Fig.5 Output of HESS in scheme 1 and 4
附图6 采用混合储能响应AGC功率指令的效果
App.Fig.6 Effect of responding to AGC order with HESS
附图7 imf5~imf8分量的正交误差函数
App.Fig.7 Orthogonal error functions of IMF components imf5 to imf8
参考文献
[1] 国家能源局. 国家能源局发布2024年全国电力工业统计数据[EB/OL]. (2024-12-20) [2025-01-24]. https://www.nea.gov.cn.
[2] 国家能源局山东监管办公室. 关于印发《山东省电力并网运行管理实施细则》、《山东省电力辅助服务管理实施细则》的通知[EB/OL]. (2023-07-11) [2024-05-01]. https://sdb.nea.gov.cn/dtyw/tzgg/202309/ t20230919_110474.html.
[3] 国家能源局华北监管局. 华北能源监管局关于征求《华北区域电力并网运行管理实施细则》《华北区域电力辅助服务管理实施细则》(征求意见稿)意见的通知[EB/OL]. (2022-07-01) [2024-05-01]. https:// hbj.nea.gov.cn/xxgk/fdzdgknr/scxxgk/202311/t20231105_195986.html.
[4] 国家能源局山东监管办公室. 山东能源监管办关于《山东电力辅助服务市场运营规则(试行)(2021年修订版)(征求意见稿)》公开征求意见的公告[EB/OL]. (2021-09-03) [2024-05-01]. https://sdb.nea.gov.cn/ dtyw/tzgg/202309/t20230919_110459.html.
[5] 李睿聪, 汪隆君, 尹亮, 等. 兼顾参与调频辅助服务的工商业储能电站充放电策略[J]. 电网技术, 2025, 49(11): 4680-4691. Li Ruicong, Wang Longjun, Yin Liang, et al. Charging and discharging strategy for commercial and industrial energy storage stations with consideration of frequency regulation ancillary services participation[J]. Power System Technology, 2025, 49(11): 4680-4691.
[6] 高飞, 杨凯, 惠东, 等. 储能用磷酸铁锂电池循环寿命的能量分析[J]. 中国电机工程学报, 2013, 33(5): 41-45, 8. Gao Fei, Yang Kai, Hui Dong, et al. Cycle-life energy analysis of LiFePO4 batteries for energy storage[J]. Proceedings of the CSEE, 2013, 33(5): 41-45, 8.
[7] 郭向伟, 王晨, 钱伟, 等. 电池储能系统均衡方法研究综述[J]. 电工技术学报, 2024, 39(13): 4204-4225. Guo Xiangwei, Wang Chen, Qian Wei, et al. A review of equalization methods for battery energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4204-4225.
[8] 田博文, 张志禹, 杨梦飞. 基于多次滑动均值滤波的混合储能功率分配与定容研究[J]. 电工技术学报, 2024, 39(5): 1548-1564. Tian Bowen, Zhang Zhiyu, Yang Mengfei. Research on hybrid energy storage power allocation and capacity determination based on multiple moving average filtering[J]. Transactions of China Electro-technical Society, 2024, 39(5): 1548-1564.
[9] 王力, 胡佳成, 曾祥君, 等. 基于混合储能的交直流混联微电网功率分级协调控制策略[J]. 电工技术学报, 2024, 39(8): 2311-2324. Wang Li, Hu Jiacheng, Zeng Xiangjun, et al. Hierarchical coordinated power control strategy for AC-DC hybrid microgrid with hybrid energy storage[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2311-2324.
[10] 林莉, 林雨露, 谭惠丹, 等. 计及SOC自恢复的混合储能平抑风电功率波动控制[J]. 电工技术学报, 2024, 39(3): 658-671. Lin Li, Lin Yulu, Tan Huidan, et al. Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 658-671.
[11] 高帆, 包道日娜, 赵明智, 等. 多场景规划下混合储能对风光耦合出力波动的平抑方法[J]. 电工技术学报, 2025, 40(9): 2827-2839.Gao Fan, Bao Daorina, Zhao Mingzhi, et al. Smoothing method of wind-solar coupled output fluctuations by hybrid energy storage under multi-scenario planning [J]. Transactions of China Electrotechnical Society, 2025, 40(9): 2827-2839.
[12] 郑熙东, 江修波. 基于小波分解的含备用系统混合储能系统功率分配[J]. 电气技术, 2020, 21(7): 30-34. Zheng Xidong, Jiang Xiubo. Power allocation of hybrid energy storage system with standby system based on wavelet decomposition[J]. Electrical Engineering, 2020, 21(7): 30-34.
[13] 张坤, 毛承雄, 谢俊文, 等. 风电场复合储能系统容量配置的优化设计[J]. 中国电机工程学报, 2012, 32(25): 79-87, 13. Zhang Kun, Mao Chengxiong, Xie Junwen, et al. Optimal design of hybrid energy storage system capacity for wind farms[J]. Proceedings of the CSEE, 2012, 32(25): 79-87, 13.
[14] 李宏仲, 张仪, 孙伟卿. 小波包分解下考虑广义储能的风电功率波动平抑策略[J]. 电网技术, 2020, 44(12): 4495-4504. Li Hongzhong, Zhang Yi, Sun Weiqing. Wind power fluctuation smoothing strategy with generalized energy storage under wavelet packet decomposition[J]. Power System Technology, 2020, 44(12): 4495-4504.
[15] 张晴, 李欣然, 杨明, 等. 净效益最大的平抑风电功率波动的混合储能容量配置方法[J]. 电工技术学报, 2016, 31(14): 40-48. Zhang Qing, Li Xinran, Yang Ming, et al. Capacity determination of hybrid energy storage system for smoothing wind power fluctuations with maximum net benefit[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 40-48.
[16] 毛志宇, 李培强, 郭思源. 基于自适应时间尺度小波包和模糊控制的复合储能控制策略[J]. 电力系统自动化, 2023, 47(9): 158-165. Mao Zhiyu, Li Peiqiang, Guo Siyuan. Control strategy of composite energy storage based on wavelet packet with adaptive time scale and fuzzy control[J]. Automation of Electric Power Systems, 2023, 47(9): 158-165.
[17] 吴杰, 丁明. 采用自适应小波包分解的混合储能平抑风电波动控制策略[J]. 电力系统自动化, 2017, 41(3): 7-12. Wu Jie, Ding Ming. Wind power fluctuation smoothing strategy of hybrid energy storage system using self-adaptive wavelet packet decomposition[J]. Automation of Electric Power Systems, 2017, 41(3): 7-12.
[18] 周丹, 袁至, 李骥, 范玮. 考虑平抑未来时刻风电波动的混合储能系统超前模糊控制策略[J]. 发电技术, 2024, 45(3): 412-422. Zhou Dan, Yuan Zhi, Li Ji, Fan Wei. An advanced fuzzy control strategy for hybrid energy storage systems considering smoothing of wind power fluctuations at future moments[J]. Power Generation Technology, 2024, 45(3): 412-422.
[19] 贾燕冰, 郑晋, 陈浩, 等. 基于集合经验模态分解的火-储联合调度调频储能容量优化配置[J]. 电网技术, 2018, 42(9): 2930-2937. Jia Yanbing, Zheng Jin, Chen Hao, et al. Capacity allocation optimization of energy storage in thermal-storage frequency regulation dispatch system based on EEMD[J]. Power System Technology, 2018, 42(9): 2930-2937.
[20] 刘道兵, 李珏岑, 齐越, 等. 考虑碳效益和运行策略的风电场储能优化配置[J]. 太阳能学报, 2025, 46(2): 664-675. Liu Daobing, Li Juecen, Qi Yue, et al. Wind farm energy storage optimization considering carbon benefit and operation strategy[J]. Acta Energiae Solaris Sinica, 2025, 46(2): 664-675.
[21] 赵靖英, 乔珩埔, 姚帅亮, 等. 考虑储能SOC自恢复的风电波动平抑混合储能容量配置策略[J]. 电工技术学报, 2024, 39(16): 5206-5219. Zhao Jingying, Qiao Hengpu, Yao Shuailiang, et al. Hybrid energy storage system capacity configuration strategy for stabilizing wind power fluctuation considering SOC self-recovery[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5206-5219.
[22] 宾洋, 于静美, 朱英凯, 等. 实时雨流计数法及其在钴酸锂电池健康状态建模中的应用[J]. 中国电机工程学报, 2017, 37(12): 3627-3635, 3692. Bin Yang, Yu Jingmei, Zhu Yingkai, et al. A real-time rain flow algorithm and its application to state of health modeling for LiCoO2 lithium-ion batteries[J]. Proceedings of the CSEE, 2017, 37(12): 3627-3635, 3692.
[23] 洪烽, 贾欣怡, 梁璐, 等. 面向风电场频率支撑的混合储能层次化容量优化配置[J]. 中国电机工程学报, 2024, 44(14): 5596-5607. Hong Feng, Jia Xinyi, Liang Lu, et al. Hierarchical capacity optimization configuration of hybrid energy storage for wind farm frequency support[J]. Proceedings of the CSEE, 2024, 44(14): 5596-5607.
[24] 胡志祥, 任伟新. 基于递归希尔伯特变换的振动信号解调和瞬时频率计算方法[J]. 振动与冲击, 2016, 35(7): 39-43.Hu Zhixiang, Ren Weixin. Vibration signal demodulation and instantaneous frequency estimation based on recursive Hilbert transformation[J]. Journal of Vibration and Shock, 2016, 35(7): 39-43.
[25] 葛乐, 袁晓冬, 王亮, 等. 面向配电网优化运行的混合储能容量配置[J]. 电网技术, 2017, 41(11): 3506-3513. Ge Le, Yuan Xiaodong, Wang Liang, et al. Capacity configuration of hybrid energy storage system for distribution network optimal operation[J]. Power System Technology, 2017, 41(11): 3506-3513.
[26] 山东电力交易平台.山东电力市场运行工作日报 [EB/OL]. https://pmos.sd.sgcc.com.cn/.
[27] 风光储联合发电站设计标准[EB/OL]. http://www. weboos.cn:8083/assets/basicStandard/std_1593915.
Abstract Addressing the issue of optimal capacity configuration for hybrid energy storage systems (HESS) combining lithium-ion batteries and supercapacitors in wind farms, this study focuses on scenarios involving grid-connected power smoothing for wind farms, assessment of automatic generation control (AGC) power instructions, and ancillary services. Considering the life-cycle cost of the HESS, as well as integrating multiple revenue streams such as wind power consumption, peak-shaving and valley-filling arbitrage, carbon trading, power smoothing, and assessment of AGC power instructions along with ancillary services, a bi-level optimal capacity configuration model for the HESS in wind farms is proposed. The aim is to enhance the economic benefits of the combined wind-storage system. The upper layer considers market electricity prices and wind power output data, aiming to maximize the arbitrage revenue from energy storage. Based on optimal energy storage arbitrage, a model for optimizing the capacity of the hybrid energy storage system is established. The lower layer comprehensively considers the full life-cycle cost of energy storage, carbon trading rules, wind power smoothing, and the assessment and compensation mechanism for AGC power instructions. Using predictive control methods, a capacity configuration model is constructed with the objective of maximizing the benefits of the combined wind-storage system. Iterative solutions are then sought between the upper and lower layers. In order to solve the problem of command allocation of lower-level hybrid energy storage power, the improved Hilbert-Huang transform (HHT) is employed to determine the power instructions for lithium-ion batteries and supercapacitors. Finally, through the analysis of examples, the capacity optimization allocation method of HESS in wind farms is verified, which effectively improves the economic benefits of grid-related power stabilization and AGC power command assessment of the combined wind storage system.
The upper-level model considers market electricity prices and wind power output characteristics, aiming to maximize the profit of energy storage arbitrage, and constructs a model to solve the optimal energy storage charge-discharge schedule, determining capacity allocation schemes to be passed to the lower level. The lower-level model takes into account the full lifecycle cost of energy storage, carbon trading rules, power smoothing, AGC power instruction assessment, and compensation mechanisms. To avoid issues such as insufficient charge-discharge response capability due to state of charge (SOC) exceeding limits, a predictive control method is employed to construct a capacity optimization allocation model with the goal of maximizing the net benefits of the wind-energy storage hybrid system. The capacity allocation results are adjusted and returned to the upper level, achieving optimal configuration of mixed energy storage through iterative solving. Regarding the power instruction allocation issue in the lower-level model, an improved HHT method is adopted to decompose wind power instructions and AGC power instructions, determining the instantaneous frequency of IMF components. Based on the principle of minimizing overlap between instantaneous frequency-time curves, the sub-frequency frequencies of lithium-ion batteries and supercapacitors are determined.
For a 100 MW wind farm, simulation was conducted to verify the economic and operational effectiveness of the proposed wind farm HESS capacity optimization allocation scheme. This paper performs a comparative analysis among multiple scenarios considering power smoothing of wind power and the assessment of AGC power instructions along with auxiliary services. The effectiveness of the proposed capacity optimization allocation method for the wind farm's lithium-ion batteries and supercapacitors hybrid energy storage system is validated. Simulation results demonstrate that the proposed wind farm HESS capacity optimization allocation model can effectively reduce wind power fluctuations, accurately respond to AGC power instructions, and enhance the overall economic benefits of the wind farm.
The conclusions of this paper are given as follows: (1) The proposed two-layer capacity optimization scheme for the wind farm HESS ensures the revenue of wind power generation, meets the grid requirements for power smoothing and AGC power instruction tracking as outlined in the "two regulations," and enhances the overall economic benefits of the wind farm. (2) The HESS configuration scheme effectively smooths out fluctuations in wind power, addressing the requirements for mitigating fluctuations in wind power and avoiding penalties in electricity assessments. (3) Building upon ensuring the smooth integration of wind power into the grid, the HESS configuration scheme responds to AGC power instructions, reducing penalties in electricity assessments, acquiring compensation revenue for auxiliary services, and enhancing the economic benefits of wind farms in responding to AGC power instructions.
keywords:Wind power suppression, AGC power order, ancillary services, grid-connected assessment, hybrid energy storage optimization allocation
DOI: 10.19595/j.cnki.1000-6753.tces.242194
中图分类号:TM711
国网江苏省电力有限公司科技项目(J2024162)和吉林省自然科学基金面上项目(20240101108JC)资助。
收稿日期 2024-12-05
改稿日期 2025-02-28
杨 浩 男,1988年生,博士,副教授,研究方向为新能源电力系统安全稳定分析与控制、现代配电网智能化管控与优化和人工智能技术在电力系统中的应用等。E-mail:hao_yang@neepu.edu.cn(通信作者)
宋贞寒 男,2001年生,硕士研究生,研究方向为风电场储能优化配置及运行控制。E-mail:1695201428@qq.com
(编辑 赫 蕾)