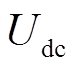为直流电压，uva、iva分别为MMC的A相输出电压、电流，upa、una和ipa、ina分别为上、下桥臂的A相电压和电流，L0、R0分别为桥臂电感和电阻。摘要 双馈风电场接入柔直系统故障响应复杂多变，突出特征为故障电流幅值低、方向不明确的弱馈性，致使基于工频量的交流线路传统保护失灵频发、可靠性骤降。为此，该文提出一种基于虚拟电抗差异特征的交流线路纵联保护方案。首先，建立了考虑低电压穿越（LVRT）控制策略的双馈风机等值模型与融合换流器控制特性的柔直换流站等值模型，用于刻画风电-柔直系统在故障状态下的真实响应；其次，根据系统故障等值网络，构建了不同故障场景下交流线路两端的虚拟电抗，揭示了双端虚拟电抗在区内外故障下存在显著差异，并在此基础上，提出一种基于双端虚拟电抗方差的快速判据；最后，依托RT-LAB半物理实验仿真平台对典型故障场景开展验证，结果表明所提保护方案能准确甄别区内外故障，耐受过渡电阻可达300 Ω，通信需求低，具备较高的灵敏度和适用性。
关键词：双馈风电场 柔性直流输电系统 交流线路保护 纵联保护
随着中西部新能源迅速发展，运行灵活、供电可靠性高的柔性直流输电（Voltage Source Converter based High Voltage Direct Current, VSC-HVDC）系统成为大规模新能源送出场景下广泛应用的手段[1-2]。双馈风电场接入柔直系统呈现出与传统电力系统迥异的故障响应，突出特征为故障电流幅值低、方向不明确的弱馈性[3-4]，且故障行为易受换流器控制策略的影响[5]，导致传统交流线路保护拒动误动风险并存[6]，亟待研究适用于双馈风电场接入柔直系统的交流线路保护。
为应对这一挑战，学者们提出了多种新型保护方案，可归类为时域保护和频域保护[7]。时域方法基于离散采样数据的瞬时值、波形特征和变化率进行故障检测，无需时频变换，原理直观、实现简单；频域方法借助傅里叶变换、小波变换和S变换等时频变换方法，将电气量离散采样数据由时域变换到频域，提取特征频段故障信息，用于构建保护判据。
相较于工频量保护，基于瞬时量分析的时域保护不依赖稳态量或幅值大小，对弱馈问题适应性更强。文献[8]利用Spearman相关系数描述送出线路两端暂态电流波形的差异，提出了基于两端暂态电流相似性的风电场送出线路纵联保护方案，具备较高的灵敏度。文献[9]利用余弦相似度表征线路两侧暂态电流波形的相似程度，算法对频率、幅值和相位差不敏感，鲁棒性更强。上述方法依赖两端波形的高精度传输，通信负担较重，对抗噪性能要求高。文献[10]分别从双馈感应电机（Double Fed Induction Generator, DFIG）换流器控制和撬棒保护的角度分析故障电流的幅频特性，提出一种提高差动保护灵敏度的振幅差动保护方案。文献[11]利用支持向量机辅助数字差动保护实现故障分类。上述方法依赖较高的同步采样精度，且对高阻接地故障的效果有限。文献[12]针对差动保护同步精度要求高的问题，提出了基于Tellegen定理的时间同步和差动保护方法，该方法不受负载和分布电容的影响，具备较高的灵敏度。文献[13]结合最小二乘法和Prony算法进行故障模型辨识。上述方法存在高噪声条件下易失效的问题。文献[14]利用数据延迟构造对称故障下的负序分量，适用于风电场送出线全部故障类型，但仍然存在对称故障下保护动作性能下降的问题。
频域分析方法在提取谐波与暂态特征方面更具优势，尤其适用于电力电子设备大量接入的场景。文献[15]提出一种基于电流行波高低频带Teager能量比值的边界保护，性能优异，但该保护强依赖高压交流线路边界元件对行波的高频折射衰减作用，一旦边界结构改变，会导致保护误判或误动。在暂态过程中，高频分量往往更能反映故障的本质信息[16]。文献[17]提出了一种基于暂态高频阻抗的纵联保护方案，动作速度快，几乎不受换流器控制策略的影响。文献[18]提出了一种新能源场站集电线高频电压突变量纵联保护方案，利用区内外故障两端补偿电压的差异构成保护判据，基本不受逆变器控制策略的影响，抗干扰性强。上述方法采用5 ms保护时间窗，能避开换流器的响应过程，从而在一定程度上规避控制策略对保护性能的影响。然而，光伏场站和双馈风电场的故障响应有所不同，保护方案适用性有待验证。
综合分析说明，时域保护对同步精度、通信能力要求高，频域保护虽更适于复杂场景建模与故障特征提取，但现有保护方案在建模中往往避开交流线路两端柔直换流站控制策略及DFIG的低电压穿越（Low-Voltage Ride-Throngh, LVRT）控制策略对故障响应的影响，从而限制了其在双馈风电场接入柔直输电系统场景中的适用性。
为了解决上述问题，本文提出了一种基于虚拟电抗差异特征的交流线路保护方案。首先，建立了考虑低电压穿越控制策略的DFIG等值模型和融合换流器控制策略的柔直换流站等值模型，用于刻画风电-柔直系统的真实故障响应；其次，根据系统故障等值网络，构建了不同故障场景下交流线路两端的虚拟电抗，揭示了两端虚拟电抗在区内外故障下存在显著差异，在此基础上，提出一种基于双端虚拟电抗方差的快速判据；最后，通过RT-Lab仿真平台对所提保护方案进行验证，结果表明本文保护方案能准确识别区内外故障，具备耐高阻、通信需求低、灵敏度高的特点。
模块化多电平换流器（Modular Multilevel Converter, MMC）的拓扑结构如图1所示。图1中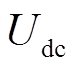，为直流电压，uva、iva分别为MMC的A相输出电压、电流，upa、una和ipa、ina分别为上、下桥臂的A相电压和电流，L0、R0分别为桥臂电感和电阻。
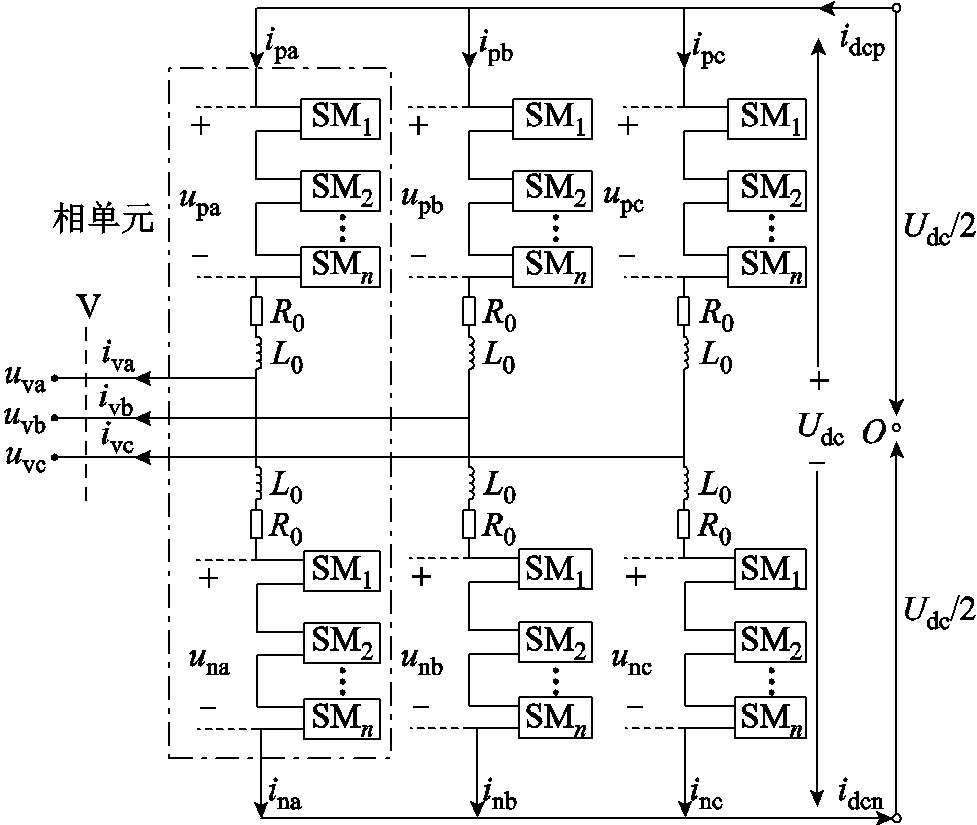
图1 MMC拓扑结构
Fig.1 The topology of the MMC
由图1可得端口电压、电流关系式为
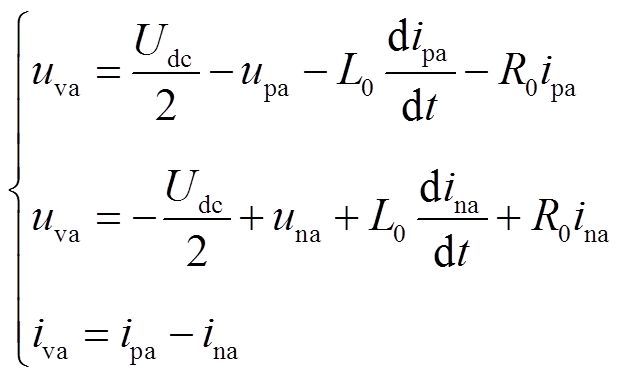（1）
由式（1）可得MMC频域输出电压为
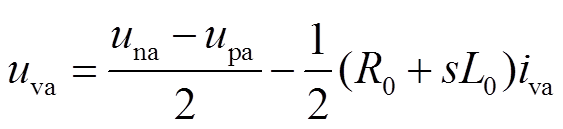（2）
上、下桥臂电压表达式为
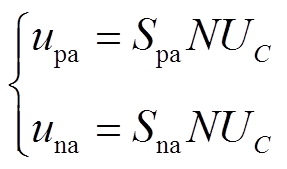（3）
式中，Spa、Sna分别为上、下桥臂的开关函数；N为A相上、下桥臂投入的子模块总数；UC为子模块的电容电压，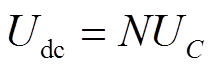
。
根据开关函数的定义，可得
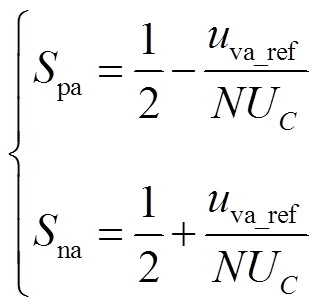（4）
式中，uva_ref为A相电压调制波。
由式（4）可得上、下桥臂电压为
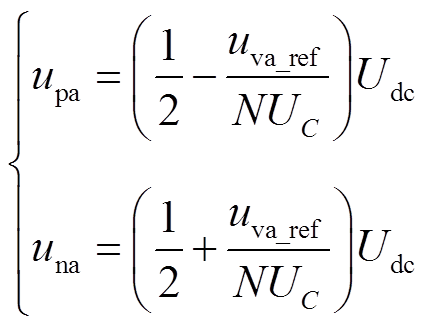（5）
联立式（2）和式（5）可得MMC输出电压为
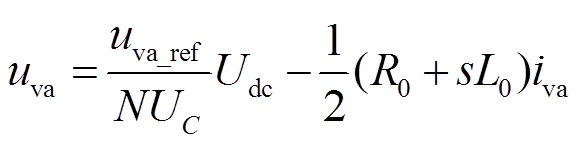（6）
MMC的矢量控制主要由内环电流控制、外环控制和锁相环控制组成，其中内环电流控制器通过调节MMC电压使电流跟踪参考值，控制方程为
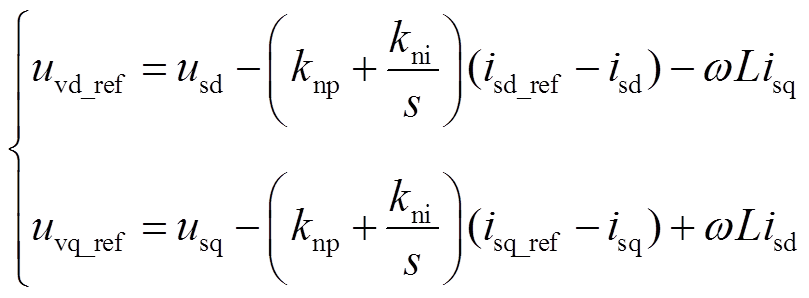（7）
式中，uvd_ref、uvq_ref和isd_ref、isq_ref分别为电压和电流参考值的d、q轴分量；usd、usq和isd、isq分别为dq轴坐标系下换流器交流侧电压和电流的实际值；knp、kni分别为内环控制的比例和积分系数；w为交流系统角频率；L为控制方程等效电感，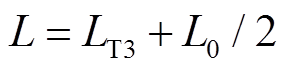
，LT3为换流器端口与交流系统间的电感值。
连接风电场的柔性直流换流站需要控制交流电压和频率，实现稳定追踪交流侧电气量变化的目标，为风电机组提供稳定的电压。外环控制方程为
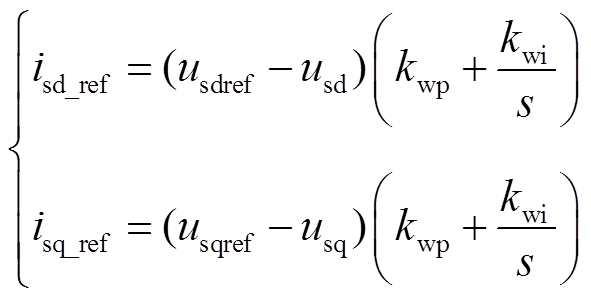（8）
式中，kwp、kwi分别为外环控制的比例和积分系数；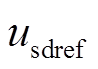
、
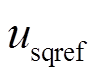分别为d、q坐标系下换流器交流侧电压的指令值。
在推导换流器电流的过程中，还需要建立换流器端口电压方程，有
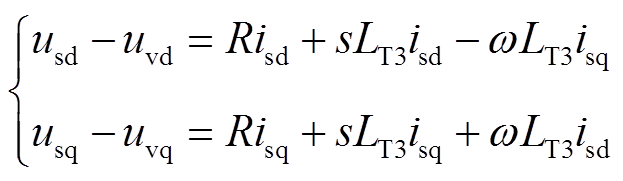（9）
式中，R为换流器端口与交流系统间的等效电阻。
联立式（6）～式（9），可得流经送端换流器的电流关于交流电压和交流电压参考值的表达式为
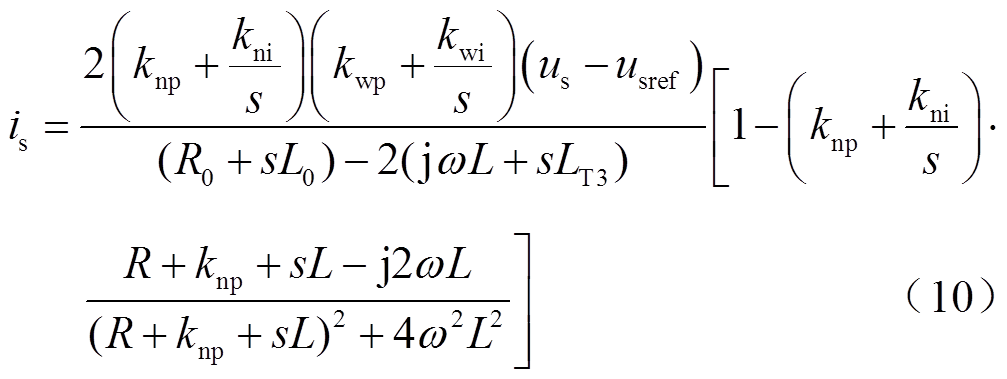
式中，us、usref分别为换流器交流侧电压实际值和参考值。
通过上述分析可以看出，柔性直流系统换流站可以等效为一个导纳和电流源并联的模型[19-20]。
双馈式感应发电机的尺寸小且运行灵活，在风电领域应用广泛。其定子侧直接连接电网，转子侧通过转子侧变换器和网侧变换器与电网连接在一起，定、转子之间存在耦合关系，使得其暂态特性较为复杂。采用三相相变量描述的数学模型具有高阶、非线性、强耦合、多变量的特点，因此需要利用坐标变换对耦合变量进行解耦，可实现对有功、无功的独立控制，确保变速恒频运行。DFIG在同步旋转坐标系下且采用电动机惯例的数学模型为
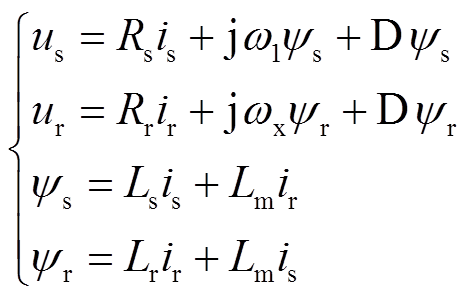（11）
式中，D为微分算子；w为转差角速度，wx=w1-wr，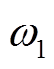
为交流系统同步角频率，
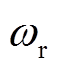为双馈风机转子角频率；Rs、Rr和Ls、Lr分别为定、转子电阻和电感；ψs、ψr分别为定子和转子磁链；
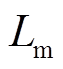为dq坐标系中定、转子同轴等效绕组间的互感。
在变换器控制中，由于故障后电压相位会发生跳变，因此通常采用锁相环技术追踪电网电压，修正相位跳变角度，其控制环节由比例和积分环节构成，控制方程为
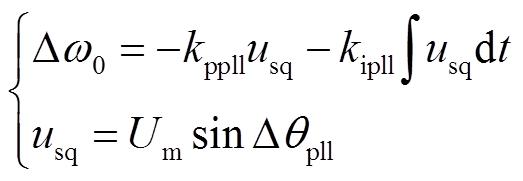（12）
式中，kppll、kipll分别为锁相环比例和积分系数；Δqpll为电压相位跳变角度；Um为并网点电压。
由式（12）可得锁相环输出角频率为
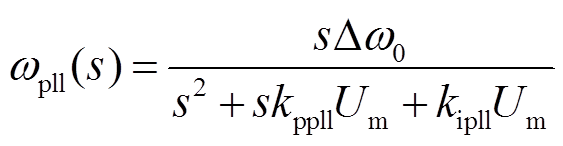（13）
式中，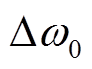
为上个采样周期角频率变化值。
考虑锁相环的影响后，换流器数学模型中的同步角速度w1由we替代，有
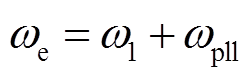（14）
式中，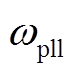
为锁相环的角频率。
根据故障前后定子磁链不会突变的特点，由式（11）可得到定子磁链表达式为
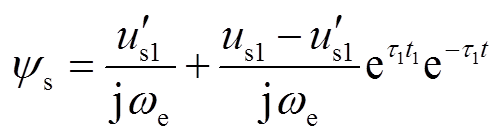（15）
式中，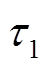
为定子磁链衰减时间常数，
；
、
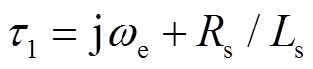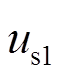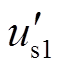分别为DFIG故障前、后的机端电压；t1为故障发生时刻。
将式（15）代入式（11），可得转子电压方程为
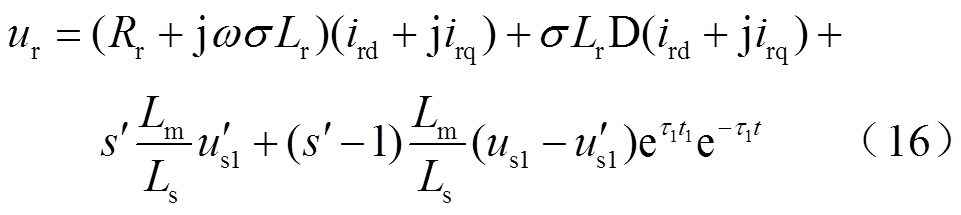
式中，s¢为感应发电机转差率，s¢=(we-wr)/we；s为发电机漏电系数，s=1-L2 m/(LsLr)。
DFIG转子侧变流器控制常采用定子磁链定向的矢量控制方式，内环控制电流，外环控制电压。DFIG的电流内环控制为
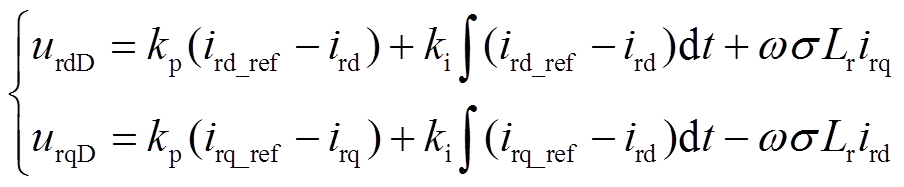（17）
式中，urdD、urqD分别为DFIG坐标系下的转子电压d轴和q轴分量；kp、ki为控制环节系数；ird_ref、irq_ref分别为转子电流参考值的d、q轴分量。
当电力系统的交流线路发生故障，使风电机组接入点电压跌落至20％～90％额定电压时，我国风电并网标准要求风电机组能够实现故障穿越特性，即提供无功电流以使电网电压尽快稳定。此时低电压穿越控制替代风电机组原电压外环控制环节，实现对电流参考值的控制和调节。根据低电压穿越标准，电网故障期间DFIG转子有功和无功电流的指令值ird_ref、irq_ref为
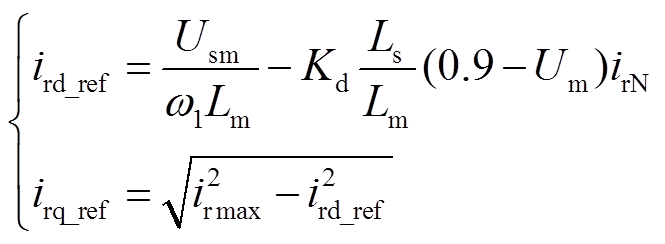（18）
式中，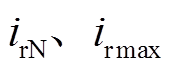
分别为转子额定电流和最大限流电流；
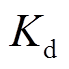为无功电流增益系数，一般取1.5；
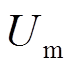为并网点电压。
由于DFIG采用的同步旋转坐标系是以锁相环的输出角度qpll为基准的，而在1.1节中对柔直系统分析时所采用的坐标系是以系统调控输出的相位q0为基准，因此两个坐标系存在相位差Δq=qpll-q0，需要将两个系统统一坐标系，其变换关系为
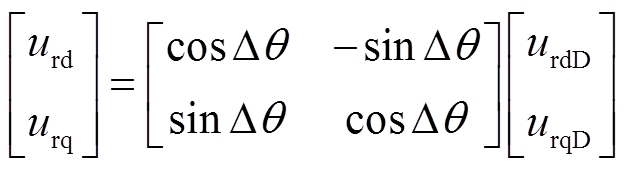（19）
式中，urd、urq分别为转子侧变流器输出电压在统一坐标系下的d、q轴分量。
由式（19）可以看出，当统一坐标系后，d、q轴电压的系数不再对称，不能直接合并为复矢量，因此需要对电压的d、q分量分开求解。将式（16）拆写为转子电压d轴和q轴分量，可得
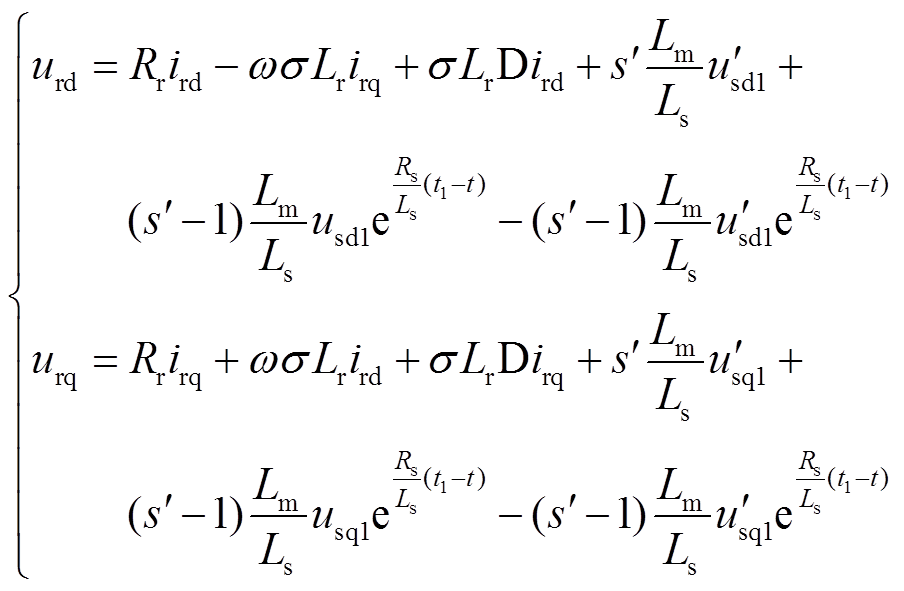（20）
式中，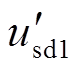
、
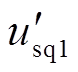分别为故障后风电机组机端电压的d、q轴分量；usd1、usq1分别为故障前风电机组机端电压的d、q轴分量。
联立式（17）、式（19）和式（20）可得到
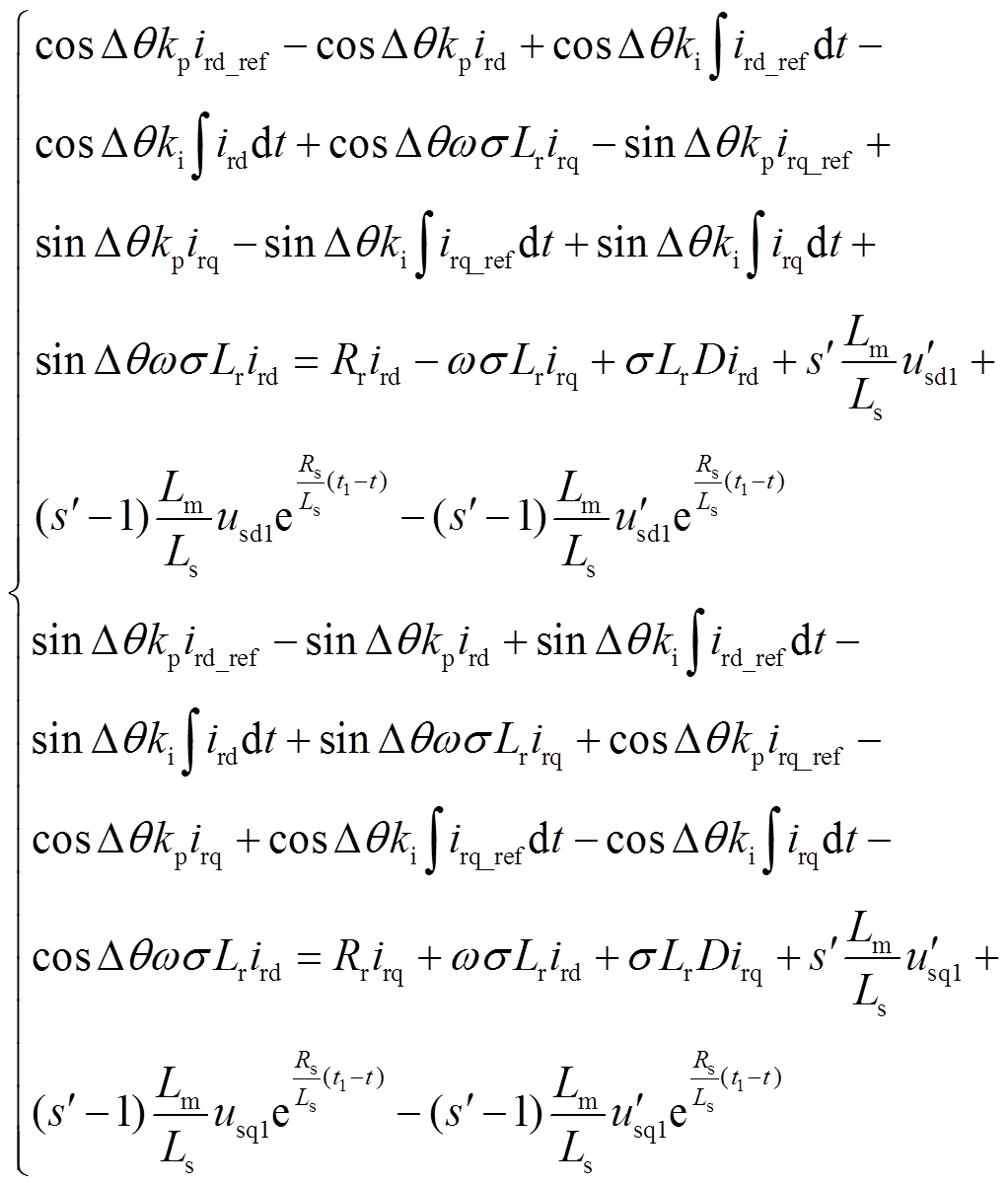（21）
对该方程组求解得到转子电流的d、q轴分量分别为
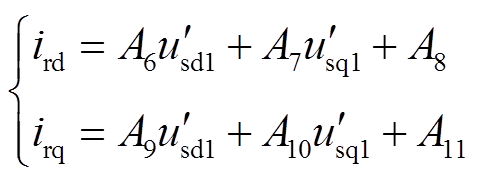（22）
式中，ird_0、irq_0分别为转子电流稳态值的d、q分量；A6～A11的具体表达式见附录式（A1）。
由式（22）可得转子电流为
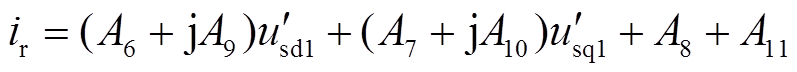（23）
联立式（11）、式（15）和式（23）得到DFIG的定子电流的频域表达式为
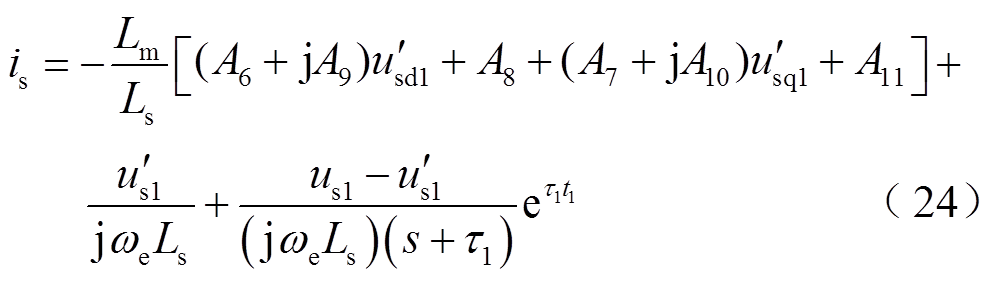
对机端电压前的系数进行分析，发现有
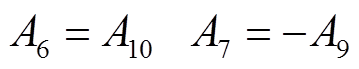（25）
因此可以将定子电压的d、q轴分量合并处理，得到定子电流频域表达式为
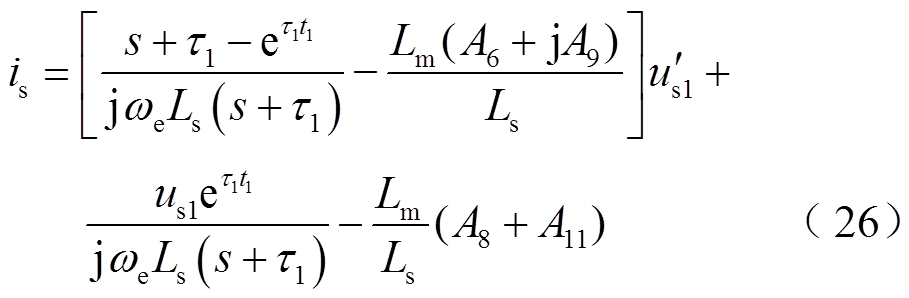
由式（26）可知，每台双馈风电机组可等效为一个时变的受控电流源和导纳并联的模型[21-22]。
风电场经柔直外送线路拓扑如图2所示。图2中，f1为风电场送出线路故障，f2为风电场内部故障，f3为风场区外线路故障，送出线路MN两侧分别连接双馈风电场和柔直换流站。Z1、Z2分别为故障点f1至线路两端的线路阻抗，其值与故障位置相关。
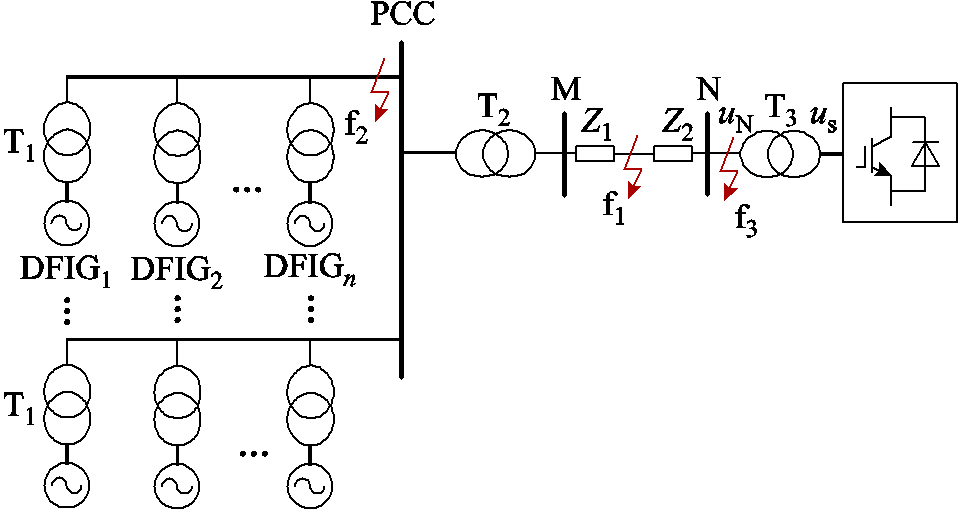
图2 风电场经柔直外送线路拓扑
Fig.2 The topology of the wind farm’s transmission line through a flexible DC system
由式（26）表示的双馈风电机组的短路电流表达式中包含风电机组故障前、后的机端电压及自身控制参数，而在实际风电场中故障后的电机端电压是不能通过测量求得的，因此还需要通过分析系统的网络拓扑，将其表示为风电机组并网点（Point of Common Coupling, PCC）处电压的关系式，才能求出每台风电机组输出的短路电流。由式（26）和式（10）可以看出，双馈风电机组和柔直侧送端换流器的故障模型都可以等效为导纳和电流源并联的模型，因此可以通过提取导纳的不同特征来构建保护判据。
通过式（10）可以看出，柔直侧的等值模型为导纳和一个电流源并联，为方便故障分析时讨论柔直侧的拓扑关系，通过戴维南定理将其等效为电压源和阻抗串联的形式，其表达式为
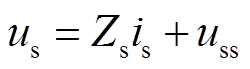（27）
其中
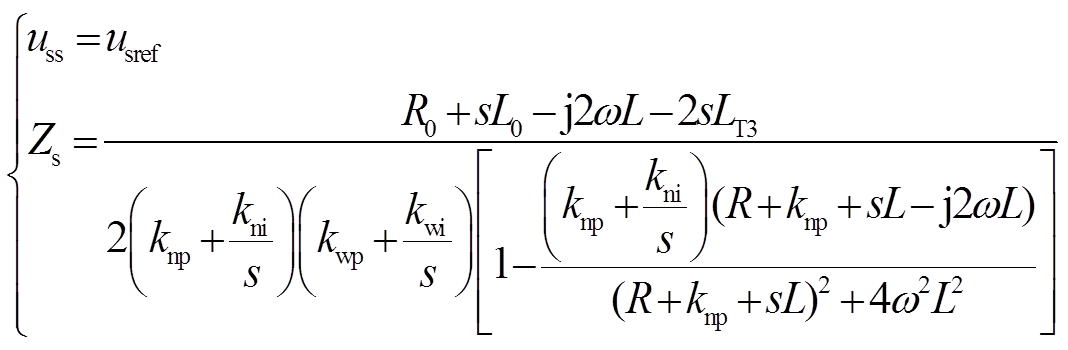
以风电场中1条集电线上接入两台双馈风电机组为例进行分析。当图2中f1处发生故障时，为求解式（26）中故障后风电机组的机端电压，需要得到各风电机组机端电压之间，以及与故障点电压之间的关系式。由于线路电阻相较于变压器阻抗很小，所以忽略该电阻的影响。由图2可得
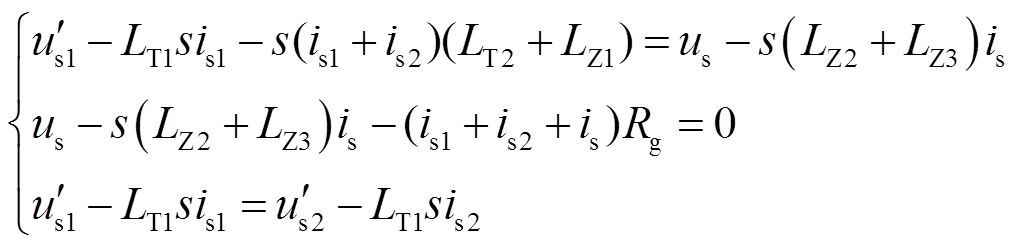（28）
式中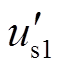，为1号风机故障后的电压；us为送出线路N端电压；is1、is2、is分别为1号、2号风电机组和直流侧输出的电流；LT1、LT2、LZ1、LZ2、LZ3分别为风电场集电线路、送出线路上变压器、送出线路和柔直侧线路的电感，线路电感由故障位置决定。
联立式（10）、式（26）和式（28）可得送出线路N端电压以及1号、2号风电机组的机端电压分别为
（29）
式中，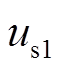
、
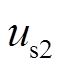分别为1号、2号风电机组故障前的机端电压；Rg为故障点的过渡电阻；D1～D6的具体表达式见附录式（A2）。
此时，风电场侧的风电机组可被等效为一个电压源和阻抗串联的形式，风电场的等值模型为
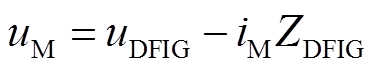（30）
式中，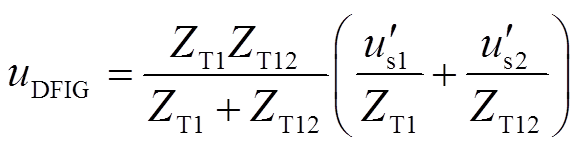
，
、
、
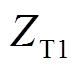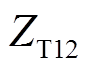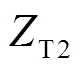分别为1、2号风电机组所在集电线路上的变压器阻抗和并网点至M端之间的变压器阻抗；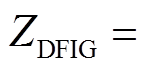
。
根据式（27）和式（30），双馈风电场接入柔直系统送出线路故障的等值网络如图3所示。
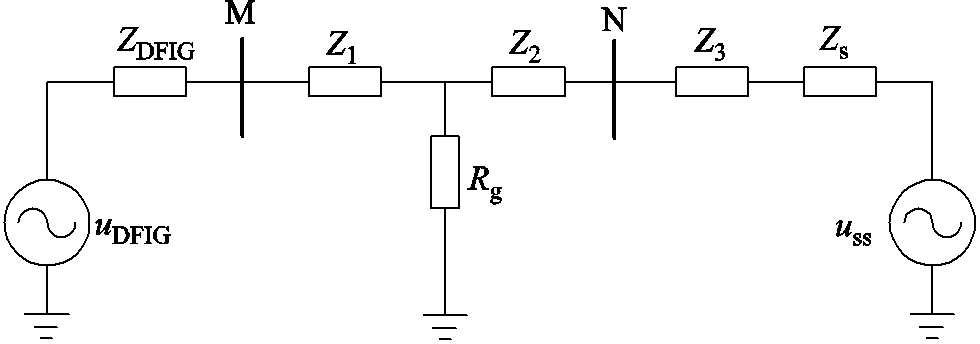
图3 风场经柔直外送系统送出线路故障等值网络
Fig.3 The equivalent network in the event of a failure of the transmission line of the wind field through the flexible DC transmission system
由于集电线路上变压器的电阻远小于电抗值，因此忽略电阻值，式（30）可改写为
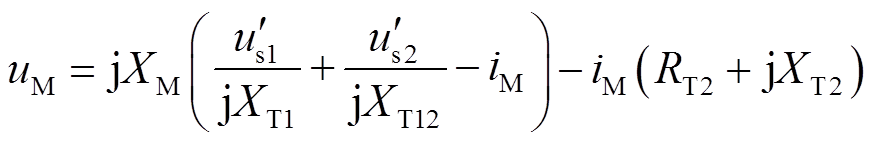（31）
式中，
。
由式（31）可得，当发生区内故障时，M端的等效电抗表达式为
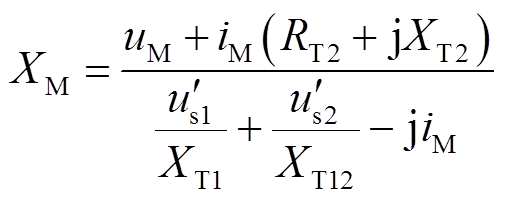（32）
同理，由式（27）可进一步得到
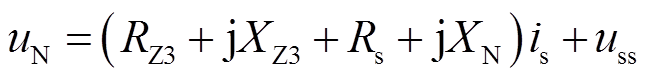（33）
其中
由式（33）可得，发生区内故障时，N端的等效电抗表达式为
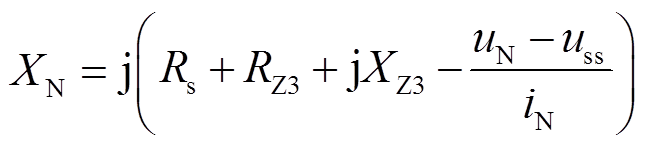（34）
2.2.1 风电场侧故障
当图2中f2处发生故障时，双馈风电机组机端电压、直流侧电压及电流的关系式为
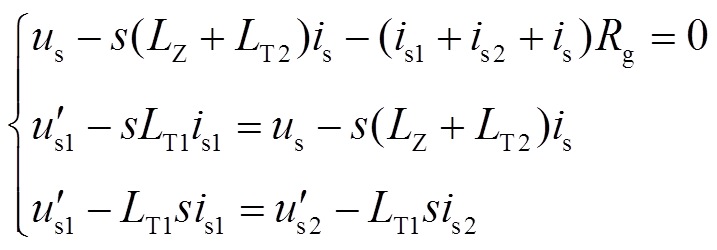（35）
联立式（10）、式（26）和式（35）可得送出线路N端电压、1号和2号风电机组的机端电压分别为
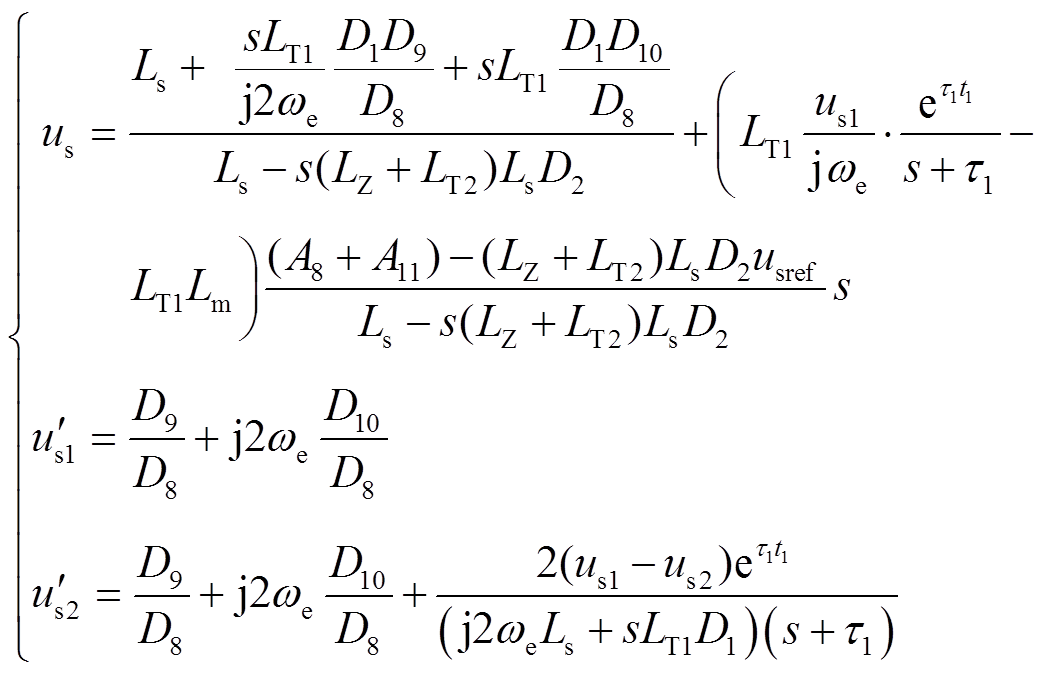（36）
其中
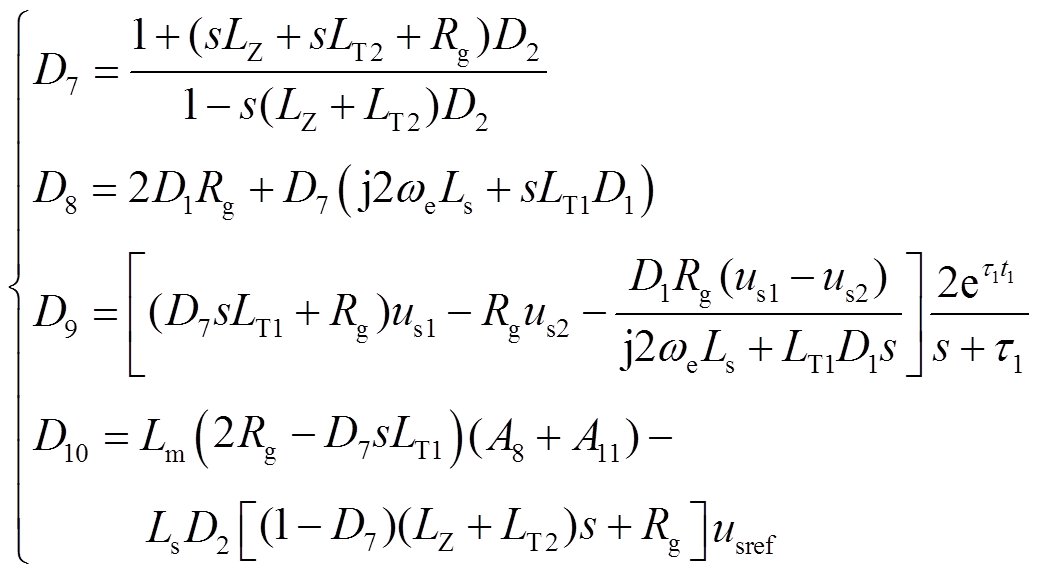
根据式（27）和式（36），双馈风电场接入柔直系统中风电场集电线路故障的等值网络如图4所示。
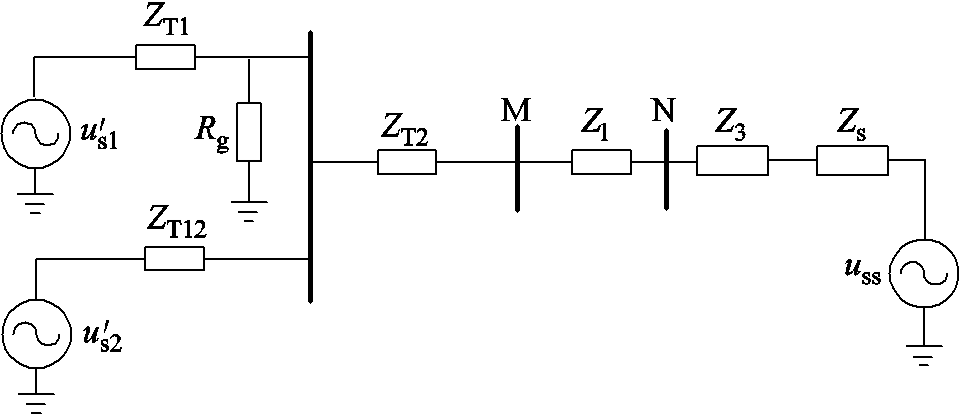
图4 风场经柔直外送系统送出线路故障等值网络
Fig.4 The equivalent network of the wind farm in the event of a failure on the wind farm side of the flexible DC transmission system
由图4可得，当风电场内部集电线路发生故障时，M端等效电抗的表达式为
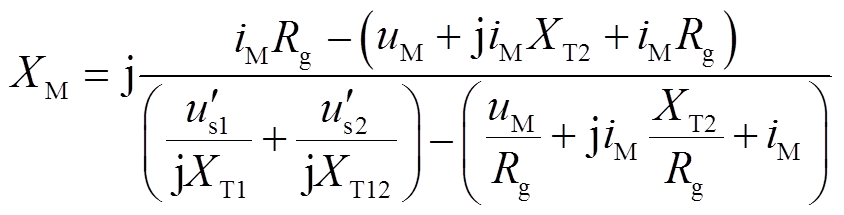（37）
N端等效电抗与式（34）相同，此处不再赘述。
将式（37）与式（32）对比可知，当风电场内部发生故障时，M端的等效电抗与区内故障时M端等效电抗不同，N端等效电抗与区内故障时N端等效电抗相同。
2.2.2 柔直侧故障
当图2中f3处发生故障时，双馈风电机组机端电压、直流侧电压及电流的关系式为
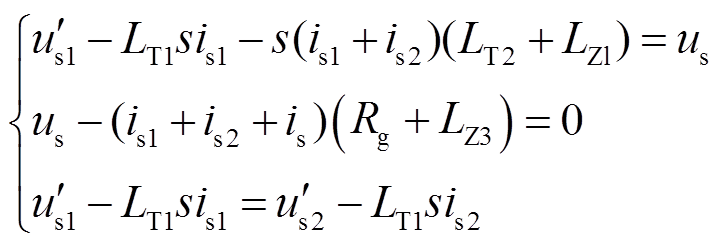（38）
联立式（10）、式（26）和式（38）可得送出线路N端电压、1号、2号风电机组的机端电压分别为
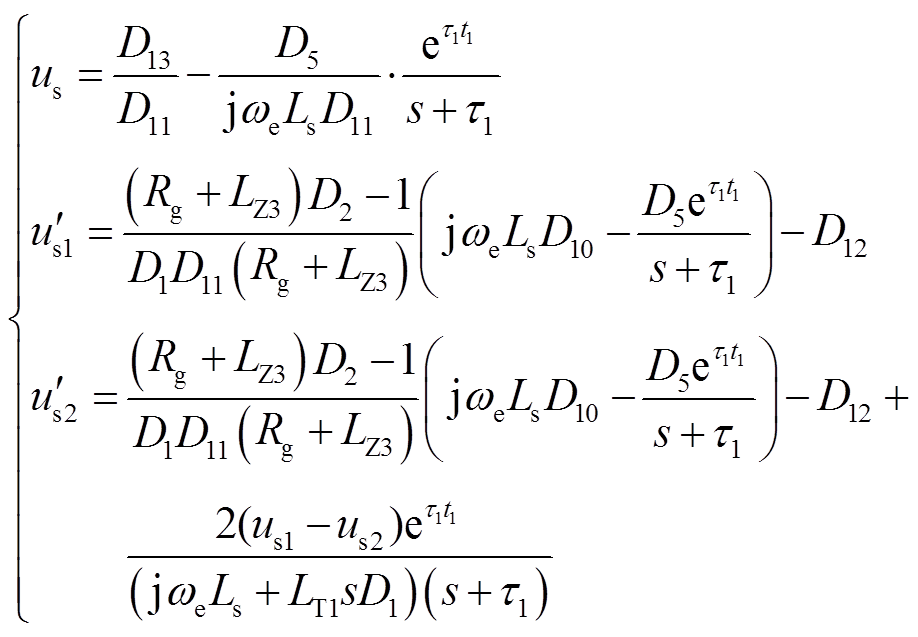（39）
其中
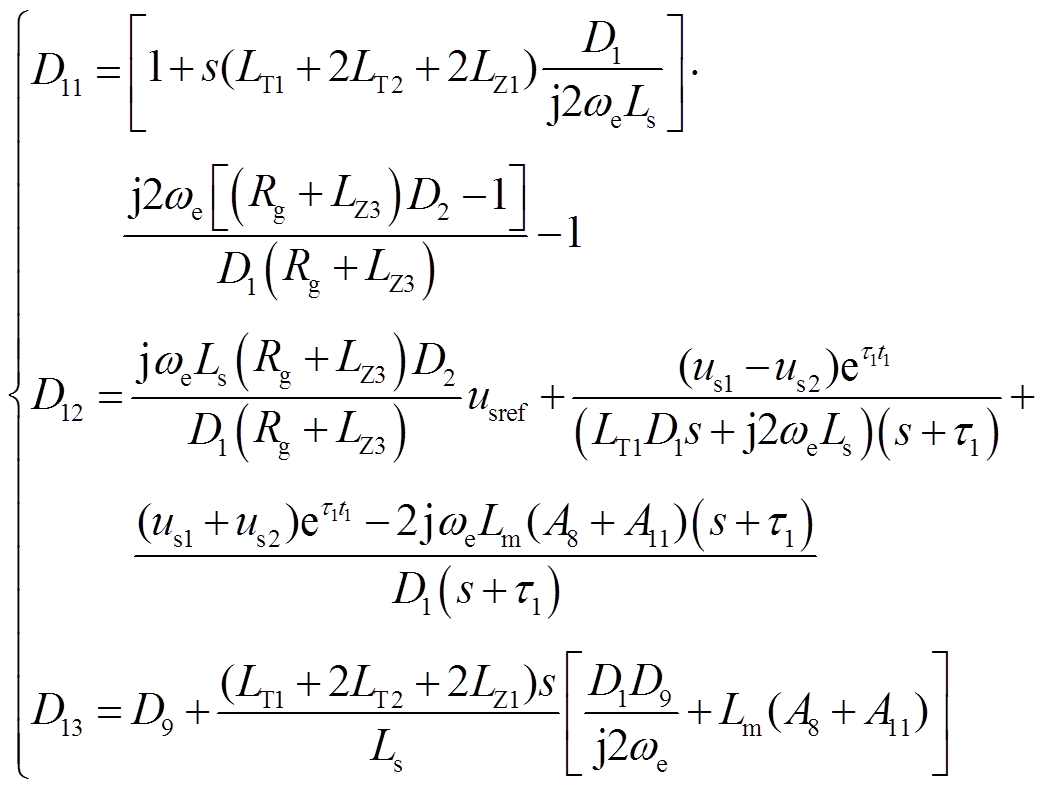
此时，风电场侧的等值模型与区内故障时的模型一致，如式（30）所示。根据式（27）和式（39），双馈风场接入柔直系统中柔直侧发生故障的等值网络如图5所示。
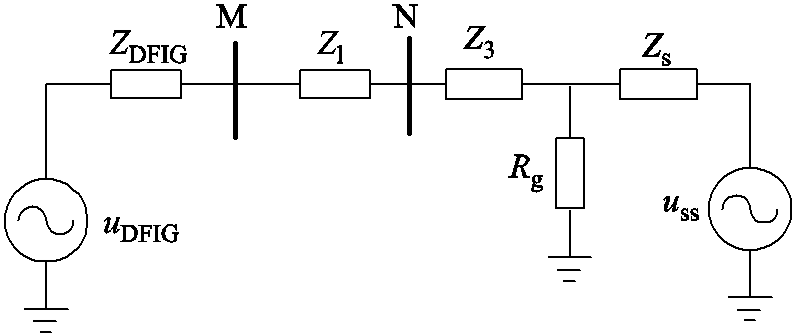
图5 风场经柔直外送系统柔直侧故障等值网络
Fig.5 The equivalent network of the wind field in the event of a failure on the flexible DC side of the flexible DC transmission system
由图5可知，当区外柔直侧发生故障时，M端的等效电抗与式（32）相同，N端等效电抗的表达式为
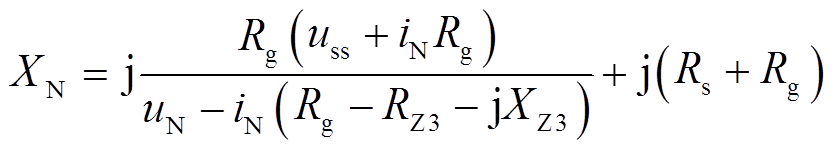（40）
与式（34）对比可知，当柔直侧发生故障时，M端的等效电抗与区内故障时M端等效电抗相同，N端的等效电抗与区内故障时N端等效电抗不同。
根据上述分析可得，当发生区内故障时，M端等效电抗与式（37）不同，N端等效电抗为式（34）；当风电场内部发生故障时，M端等效电抗为式（37），N端等效电抗为式（34）；当柔直侧发生故障时，M端和N端的等效电抗与式（37）和式（34）均不相同。本文利用区内外故障时等效电抗的不同构建交流线路的保护判据。
2.3.1 选频依据与保护判据
根据式（31）和式（33）分别定义M端和N端的虚拟电抗计算值为
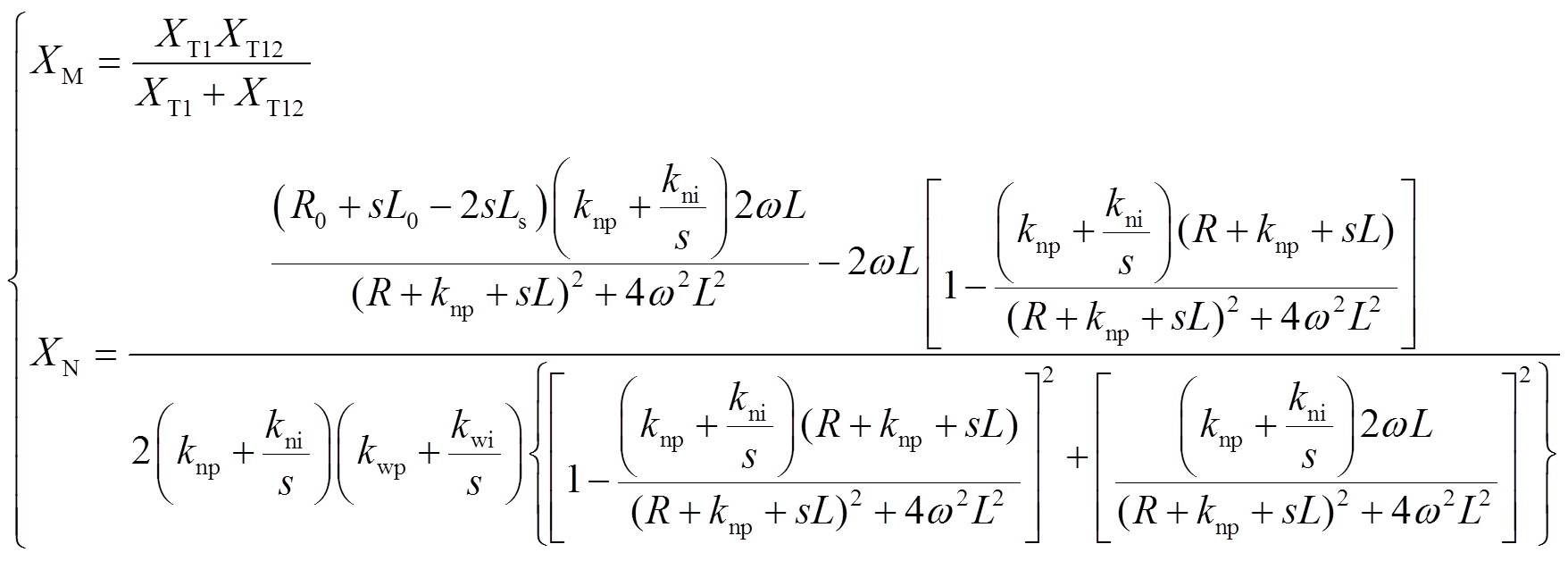（41）
根据式（37）和式（34）分别定义M端和N端的虚拟电抗实际值为
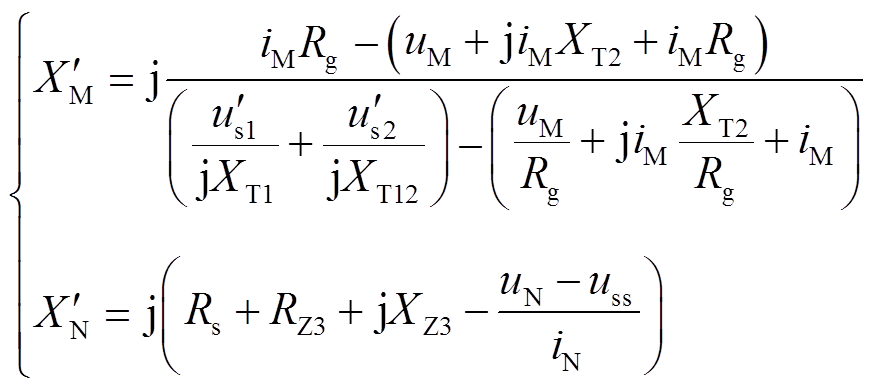（42）
根据分析可知，对于线路MN的保护方案，当发生区内故障时M端虚拟电抗的计算值与实际值差异最大，当柔直侧发生故障时N端虚拟电抗的计算值与实际值差异最大。因此为了使区内和区外故障时保护判据的数值差异最大，将区内故障时M端虚拟电抗与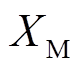
做差，将柔直侧发生故障时N端虚拟电抗与
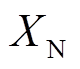做差，选取差值最大时的角频率作为保护装置对电气量提取的频率。
根据以上分析，利用虚拟电抗的方差构造保护判据为
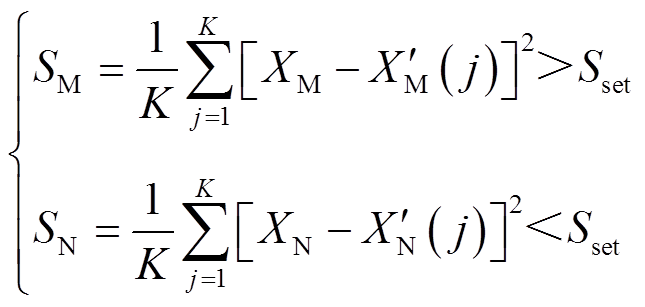（43）
式中，SM、SN分别为M、N端虚拟电抗的方差；K为采样点数；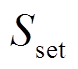
为动作门槛值，考虑测量误差等因素的影响，将门槛值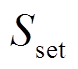取为100。
双端保护识别故障位置的逻辑关系为
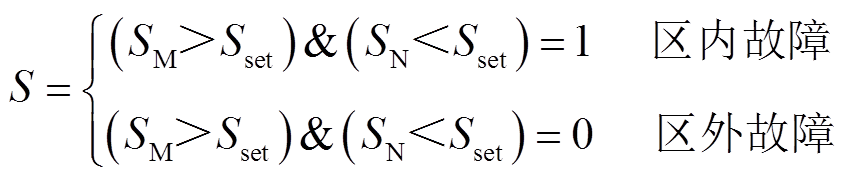（44）
综上所述，提出一种基于虚拟电抗的交流线路保护方案，保护流程如图6所示，其实现的具体步骤如下：
（1）线路MN两端保护装置分别采集各端的实时电压和电流，提取其高频分量。
（2）将电压和电流高频分量代入式（41）和式（42），计算线路两端虚拟电抗的计算值与实际值。
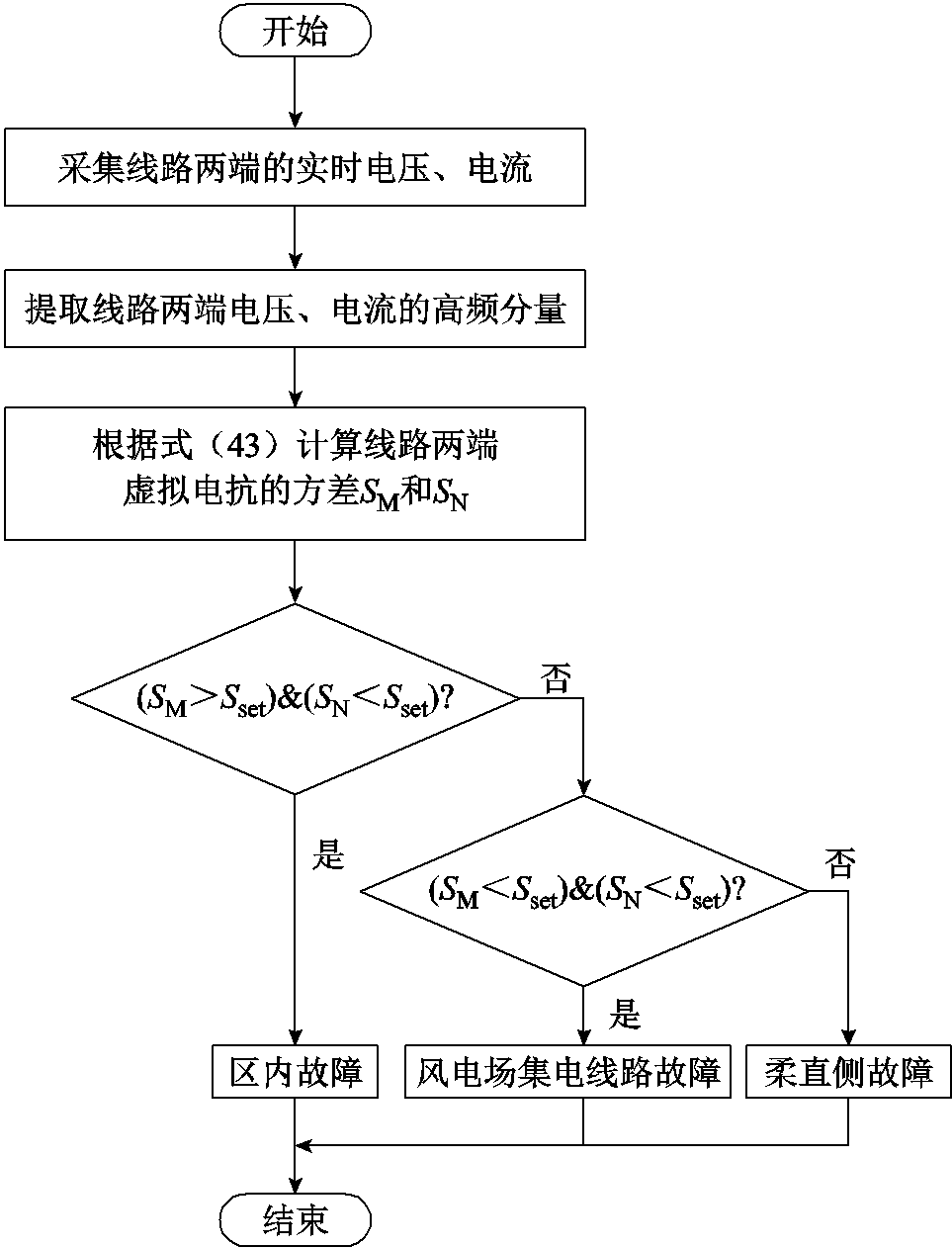
图6 保护方案流程
Fig.6 Protection scheme flow
（3）将MN两端虚拟电抗的计算值与实际值代入式（43）得到虚拟电抗的方差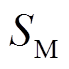
和
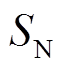，若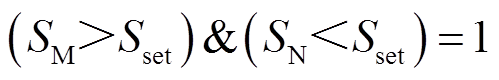
，则故障被识别发生在区内；若
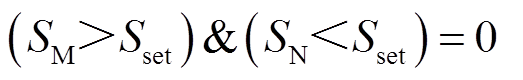，则识别为区外故障，保护被闭锁，线路MN两端的保护装置不动作。
2.3.2 保护阈值整定
由于本文所提保护方案的实质为理论值与实际值的差异，为防止保护不正常动作，需要分析保护动作门槛值，对其阈值进行整定。
当线路MN上发生经高阻接地故障且故障位置在M端保护装置出口时，M端虚拟电抗与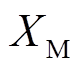差异相对较小，在此故障情况下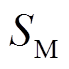有最小值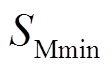
；当MN线路末端发生故障时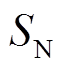，有最大值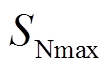
，为保护线路全长需有
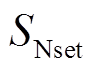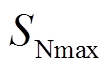＞且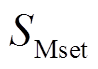
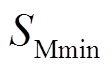＜。当柔直侧出口即N端背侧发生经高阻接地故障时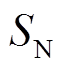，有最小值
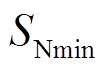，此时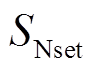为躲过区外故障需小于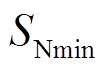。除此之外，还需躲过系统正常运行时的情况，即
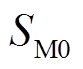和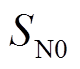
。
根据上述分析，M端和N端保护判据的阈值整定为
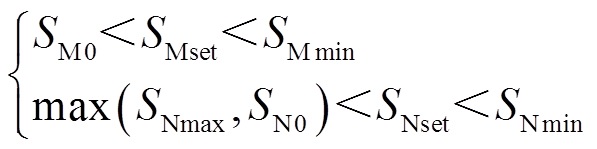（45）
2.3.3 保护启动
当系统正常运行时，被保护线路MN的两侧电压值可被近似认为是定值。故障发生后，线路两端电压会迅速变化，使得电压变化率突变，以此为判据确定是否发生故障，判别式为
（46）
式中，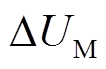
、
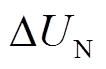分别为前后两个采样点采集到的电压差值；
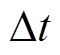为两个采样点间的时间间隔；
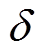为阈值，可根据实际情况进行调整。
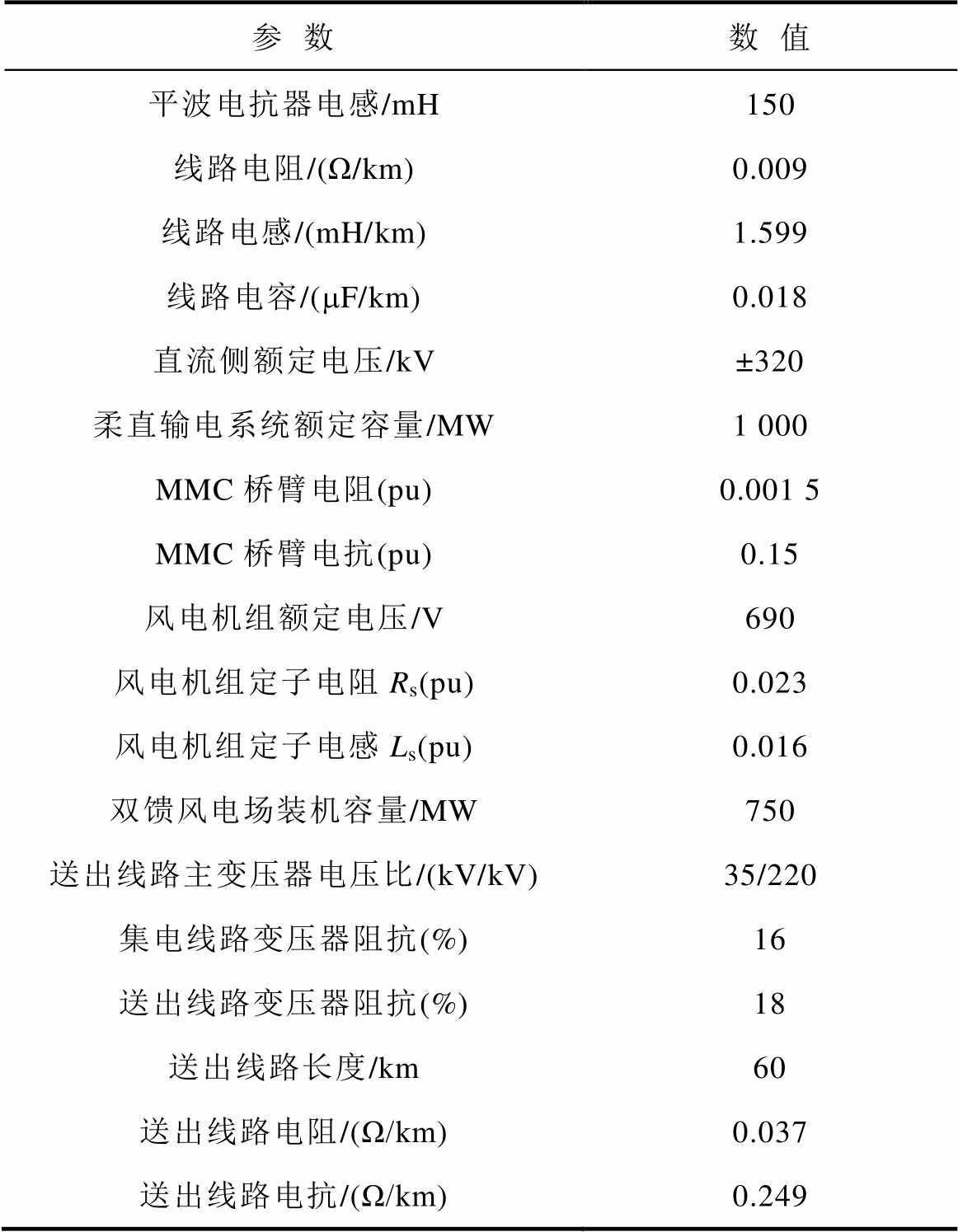
本文通过RT-Lab仿真平台对所提保护方案进行仿真验证，双馈风电场接入柔性直流系统的结构如图2所示，系统的主要参数见表1，RT-Lab仿真平台如图7所示。
表1 双馈风电场接入柔性直流输电系统的主要参数
Tab.1 The main parameters of doubly-fed wind farms connected to flexible DC transmission systems
参数数值 平波电抗器电感/mH150 线路电阻/(Ω/km)0.009 线路电感/(mH/km)1.599 线路电容/(mF/km)0.018 直流侧额定电压/kV±320 柔直输电系统额定容量/MW1 000 MMC桥臂电阻(pu)0.001 5 MMC桥臂电抗(pu)0.15 风电机组额定电压/V690 风电机组定子电阻Rs(pu)0.023 风电机组定子电感Ls(pu)0.016 双馈风电场装机容量/MW750 送出线路主变压器电压比/(kV/kV)35/220 集电线路变压器阻抗(%)16 送出线路变压器阻抗(%)18 送出线路长度/km60 送出线路电阻/(Ω/km)0.037 送出线路电抗/(Ω/km)0.249
结合表1中参数的值，根据选频原则求出所提保护方案对该系统需提取的频率。通过计算，该保护方案选取650 Hz的高频分量，采样率为20 kHz。
图7 RT-LAB仿真平台
Fig.7 RT-LAB simulation platform
M、N两端系统等效电抗是由双馈风电场接入柔直外送系统送出线路故障等值网络推导得到的，两端等效电抗的正确性建立在双馈风电场和柔直侧建模的准确性上。
设置交流线路的中点处在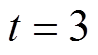
s时发生三相对称短路故障，仿真中采集双馈风电场侧（图8a）和柔直侧（图8b）A相的暂态故障电流，仿真结果与理论推导高度吻合。
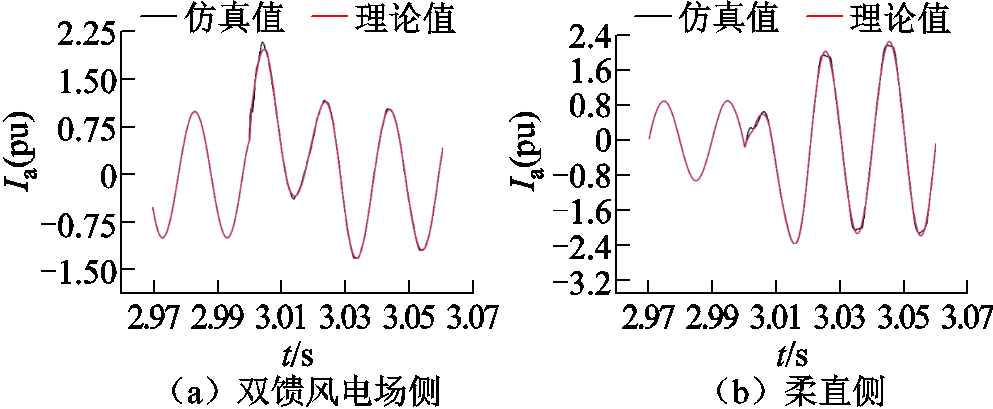
图8 双馈风电场侧和柔直侧故障电流
Fig.8 Fault currents of DFIG-based wind farms and flexible DC side
由图8可以看出，无论是双馈风电场侧还是柔直侧的故障电流，其理论波形和实际波形吻合度较好，表明本文建立的故障暂态模型与实际情况符合度较高，证明了在此基础上推导得到M、N双端系统等效电抗的正确性。
在送出线路MN中点处分别设置三相对称故障、A相接地故障和BC相间故障情况，过渡电阻变化范围为0～300 Ω。A相金属性接地和BC相间故障的电压、电流录波如图9所示，图中粉色实线、蓝色虚线、绿色点画线分别代表A、B、C三相。
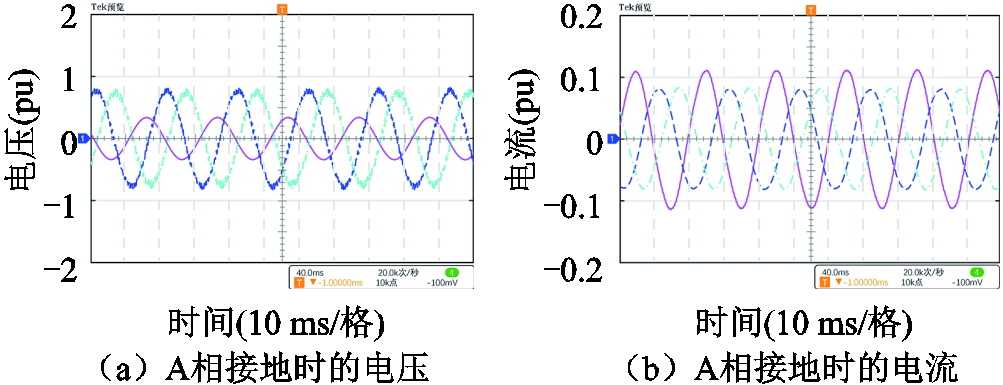
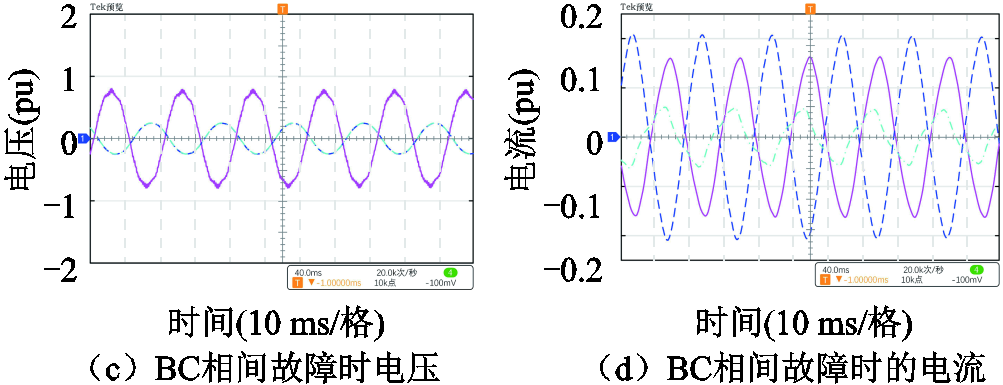
图9 交流线路区内50%位置处发生A相接地、BC相间故障的电压、电流录波
Fig.9 Voltage and current recording diagram when A-phase-to-ground and BC-phase faults occurring at the midpoint (50%) of the AC transmission line
交流线路MN两端保护装置通过计算得到的SM和SN如图10所示。
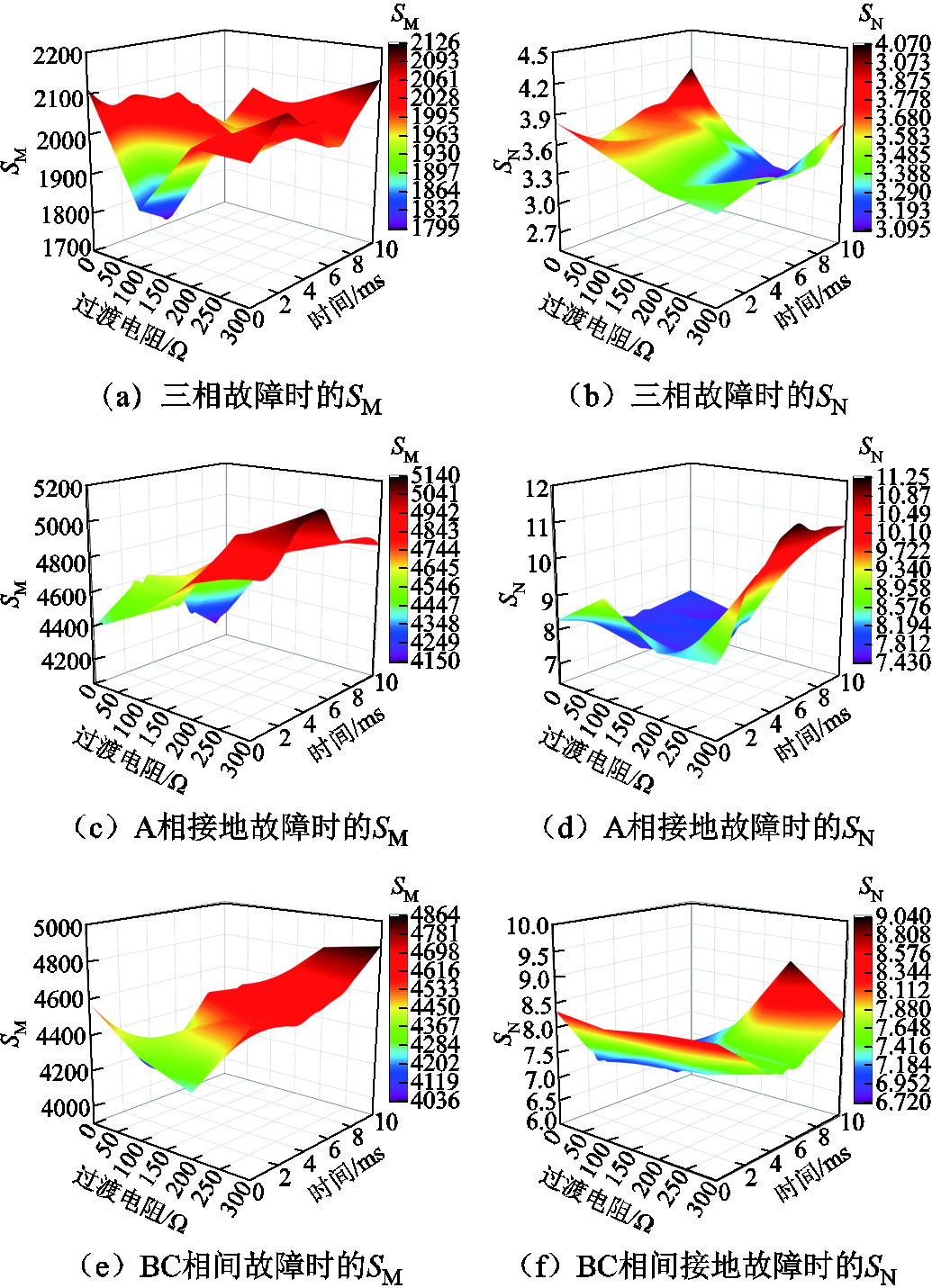
图10 区内经不同过渡电阻故障仿真结果
Fig.10 Simulation results of faults with different transition resistors in the region
由图10可以看出，当送出线路上发生经不同过渡电阻、不同类型的故障时，线路两端保护装置所计算的SM和SN满足SM＞Sset和SN＜Sset的判据。在三相短路的情况下，当过渡电阻为100 Ω，故障后1.724 ms时，SM有最小值1 800.53；当过渡电阻为 0 Ω，故障发生后9.872 ms时，SN有最大值4.028。在A相接地短路的情况下，当过渡电阻为0 Ω，故障后9.061 ms时，SM有最小值4 154.55；当过渡电阻为300 Ω，故障发生后5.617 ms时，SN有最大值11.24。在BC两相相间短路的情况下，当过渡电阻为0 Ω，故障后6.73 ms时，SM有最小值4 037.06；当过渡电阻为200 Ω，故障发生后9.97 ms时，SN有最大值9.023。由于MN两端保护装置所计算的SM和SN均满足式（42），因此均识别故障发生在区内线路上，保护动作。
根据上述分析可知，本文所提保护方法在区内经不同过渡电阻和不同类型故障时都能够准确辨别故障位置，M端保护装置的计算结果远大于动作门槛值，N端保护装置的计算结果远小于动作门槛值，保护能够可靠动作，即使在高阻情况下保护也有很强的灵敏性。
在送出线路MN不同位置处设置三相对称故障，故障位置表示为与M端保护装置距离的百分数，交流线路MN两端保护装置通过计算得到的SM和SN如图11所示。
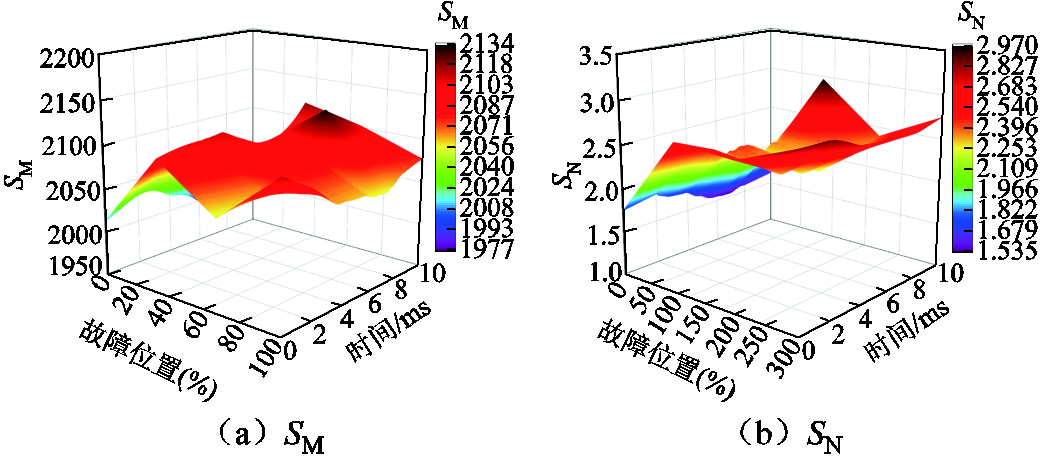
图11 区内不同位置发生故障的仿真结果
Fig.11 Simulation results of failures at different locations in the area
由图11可以看出，当送出线路上不同位置发生故障时，线路两端保护装置所计算的SM和SN满足SM＞Sset和SN＜Sset的判据。在故障位置为23%， t=7.71 ms时，SM有最小值1 977.05；在故障位置为37%，t=10 ms时，SN有最大值2.97。因此当线路MN上任一位置发生故障时，均有SM远大于动作门槛值，SN远小于动作门槛值，两端的保护装置都会将故障识别为区内故障，发送并接收到识别结果后向断路器发出指令，切除故障线路。
在风电场的集电线路上变压器与并网点之间设置三相对称故障，故障位置如图2的f2点，过渡电阻变化范围为0～100 Ω。三相接地故障的电压、电流录波如图12所示，过渡电阻为20 Ω。
交流线路MN两端保护装置计算得到的SM和SN如图13a和图13b所示。
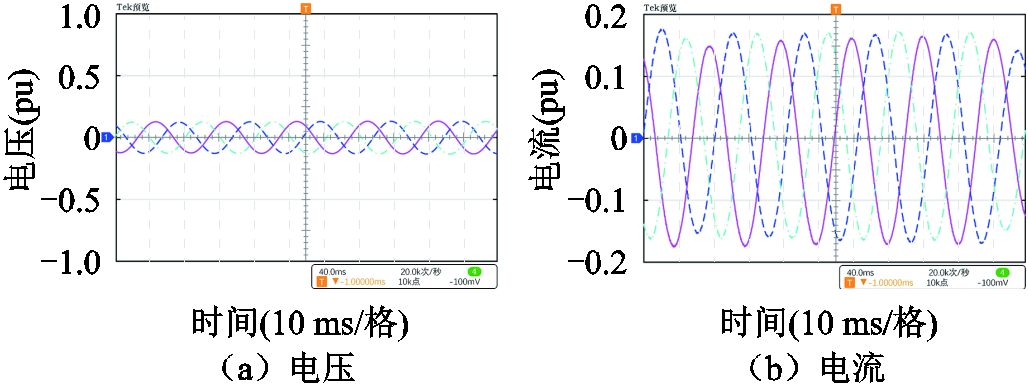
图12 双馈风电场侧发生三相接地故障的电压、电流录波
Fig.12 Voltage and current recording diagrams for a three-phase-to-ground fault at the DFIG wind farm side
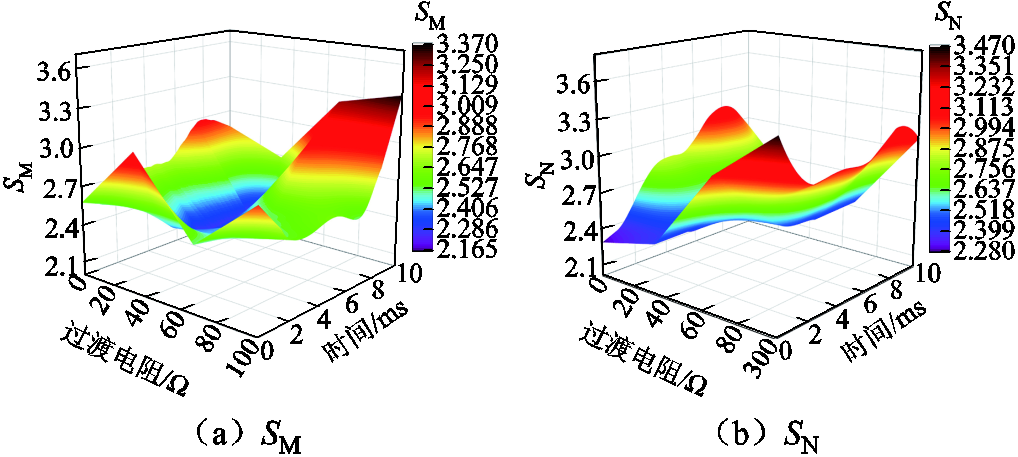
图13 风电场内部经不同过渡电阻发生故障的仿真结果
Fig.13 Simulation results of faults within a wind farm with different transition resistors
由图13可以看出，当风电场集电线路上发生故障时，送出线路上M端保护装置计算的SM＜Sset，不满足区内故障的判别式，N端保护装置计算的SN＜Sset。在过渡电阻为100 Ω，t=9.967 ms时，SM有最大值3.358；在过渡电阻为100 Ω，t=0.066 ms时，SN有最大值3.467。此时N端保护装置认定故障发生在区内，但由于M端判别故障为区外故障，向N端保护装置发送闭锁信号，因此N端保护虽将故障判定为区内故障，但由于收到闭锁信号而不动作，线路MN仍然正常接入电网中。
在柔直侧设置BC两相相间短路故障，故障位置如图2的f3点，过渡电阻变化范围为0～70 Ω。BC相间故障的电压、电流录波如图14所示。
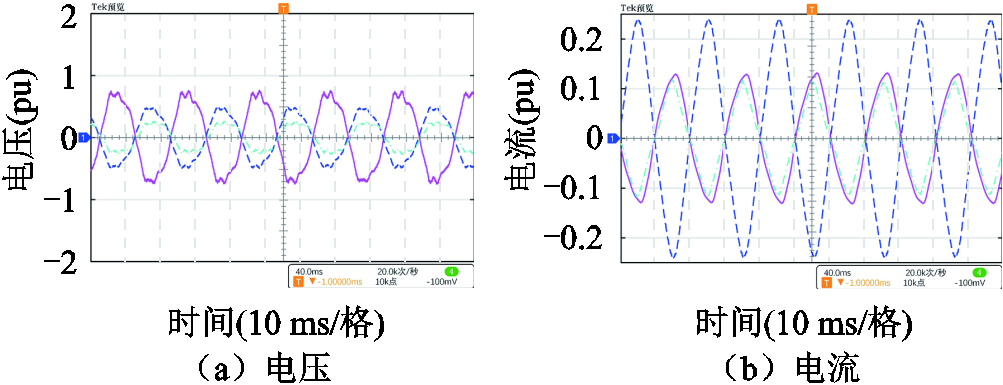
图14 柔直侧发生BC相间故障的电压、电流录波
Fig.14 Voltage and current recording diagrams under BC-phase fault on the VSC-HVDC side
交流线路MN两端保护装置计算得到的SM和SN如图15a和图15b所示。
由图15可以看出，当柔直侧发生故障时，送出线路上M端保护装置计算的SM＞Sset，满足区内故障的判别式，N端保护装置计算的SN＞Sset，不满足区内故障的判别式。在过渡电阻为23 Ω，t=0 ms时，SM有最小值2 548.36；在过渡电阻为0 Ω，t=0 ms时，SN有最小值3 826.33。此时M端和N端保护装置识别故障的过程与风电场集电线路故障时的过程相反，M端保护将故障判定为区内故障，但由于收到N端发送的闭锁信号而不动作。因此当柔直侧发生故障时线路MN两端的保护不动作，线路MN仍然正常接入电网中。
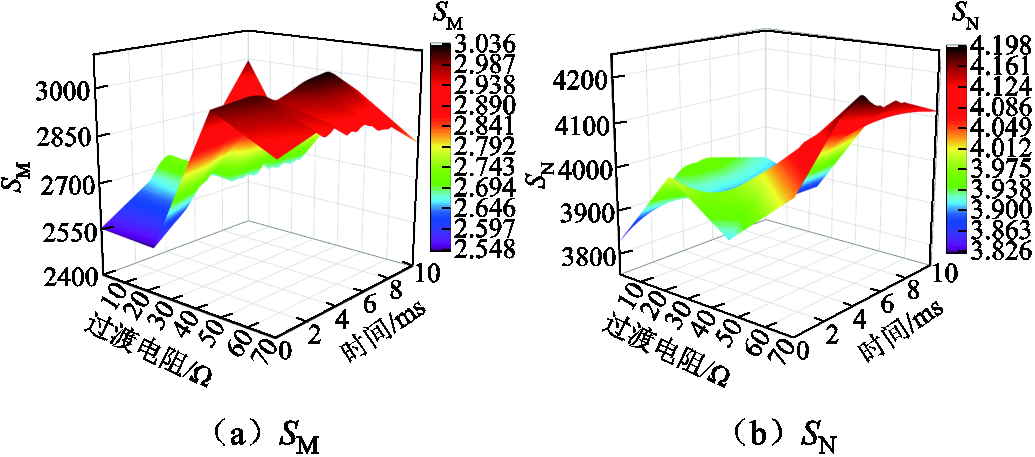
图15 柔直侧经不同过渡电阻发生BC两相相间故障的仿真结果
Fig.15 Simulation results of BC two-phase faults on the flexible DC side through different transition resistors
当区外发生不同类型故障时，保护判据在故障后2 ms的计算结果见表2。
表2 区外发生不同类型故障保护判据计算结果
Tab.2 The result of the calculation of the protection criterion in the event of different types of faults outside the zone
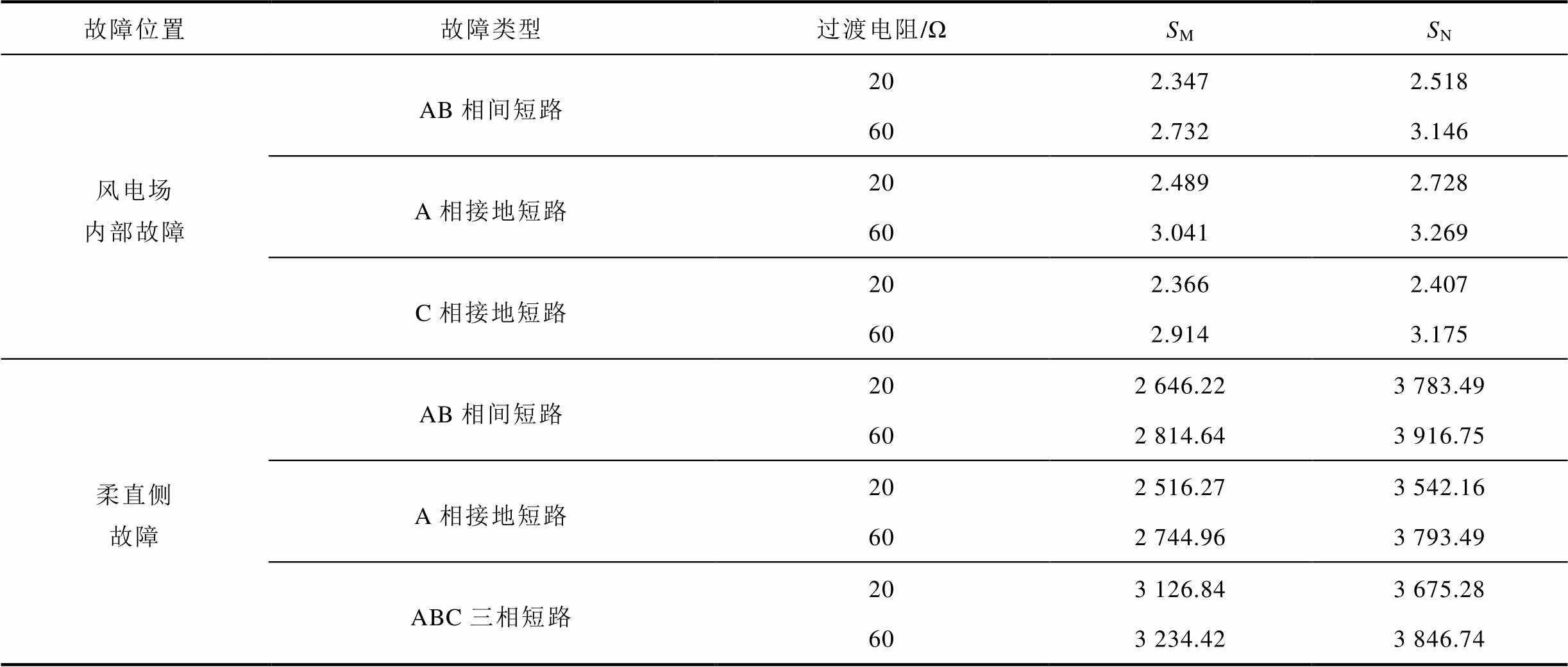
故障位置故障类型过渡电阻/ΩSMSN 风电场内部故障AB相间短路202.3472.518 602.7323.146 A相接地短路202.4892.728 603.0413.269 C相接地短路202.3662.407 602.9143.175 柔直侧故障AB相间短路202 646.223 783.49 602 814.643 916.75 A相接地短路202 516.273 542.16 602 744.963 793.49 ABC三相短路203 126.843 675.28 603 234.423 846.74
由表2可以看出，当风电场内部或柔直侧经不同过渡电阻发生不同类型的故障时，线路MN两端保护交互逻辑信息后判定故障为区外故障，保护可靠不动作。
由于在650 Hz高频下电流互感器传变误差较小[23]，且主保护动作时间在3 ms以内，此时电流互感器铁心并未达到饱和，因此电流互感器传变误差可忽略不计。考虑电压互感器传变时会产生误差，假设电压互感器传变时误差最大可能达到20%，则考虑误差的M与N侧电压表达式为
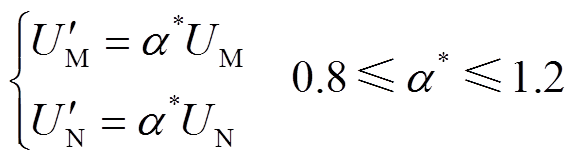（47）
以送出线路MN区内发生三相对称故障为例，分析在传感器存在传变误差下SM和SN取值能否满足保护动作要求。在实际情况下，风电场集电线路变压器阻抗百分数较小，在误差分析时可忽略不计，则由式（43）可得计及传感器误差下关于SM的表达式为
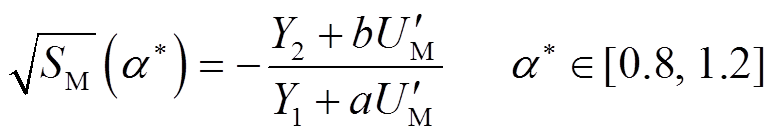（48）
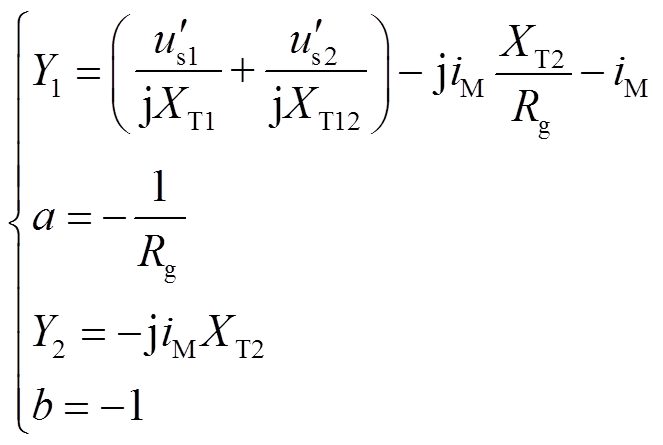（49）
当式（48）中
=1时，为正常传变，即传感器不存在传变误差，对应本文3.1节中第一种仿真实例情况，此时有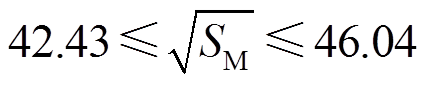
。
当式（48）中≠1时，即传感器存在传变误差，需确定
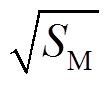的最小值。对式（48）进行求导可知
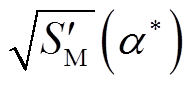＜0恒成立，
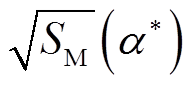为减函数。当=1.2时，有SMmin=1 250.33。但此时仍然远大于100，即所选设定值100仍可明显区分区外故障，满足保护动作要求。
同理对SN而言，经分析可知，当=1.2时，此时有SNmax=5.80，仍然远小于100，所选设定值可以很好地区分送出线路区内外故障，满足动作要求。
综上所述，在考虑传感器的传变误差后，本文所提保护方案仍然能够可靠动作，保护适应性良好。
为验证本文所提保护方案的优越性，将本文方案与现有保护方案进行对比分析。在仿真过程中，考虑不同故障类型和不同过渡电阻情况。交流线路区内50%处发生A相接地、BC相间故障和三相短路时两种保护动作情况见表3。
表3 交流线路区内50%处发生A相接地、BC相间故障和三相短路时两种保护动作情况
Tab.3 Protection actions under A-phase-to-ground fault, BC-phase-to-phase fault, and three-phase fault occurring at the 50% location of the AC transmission line
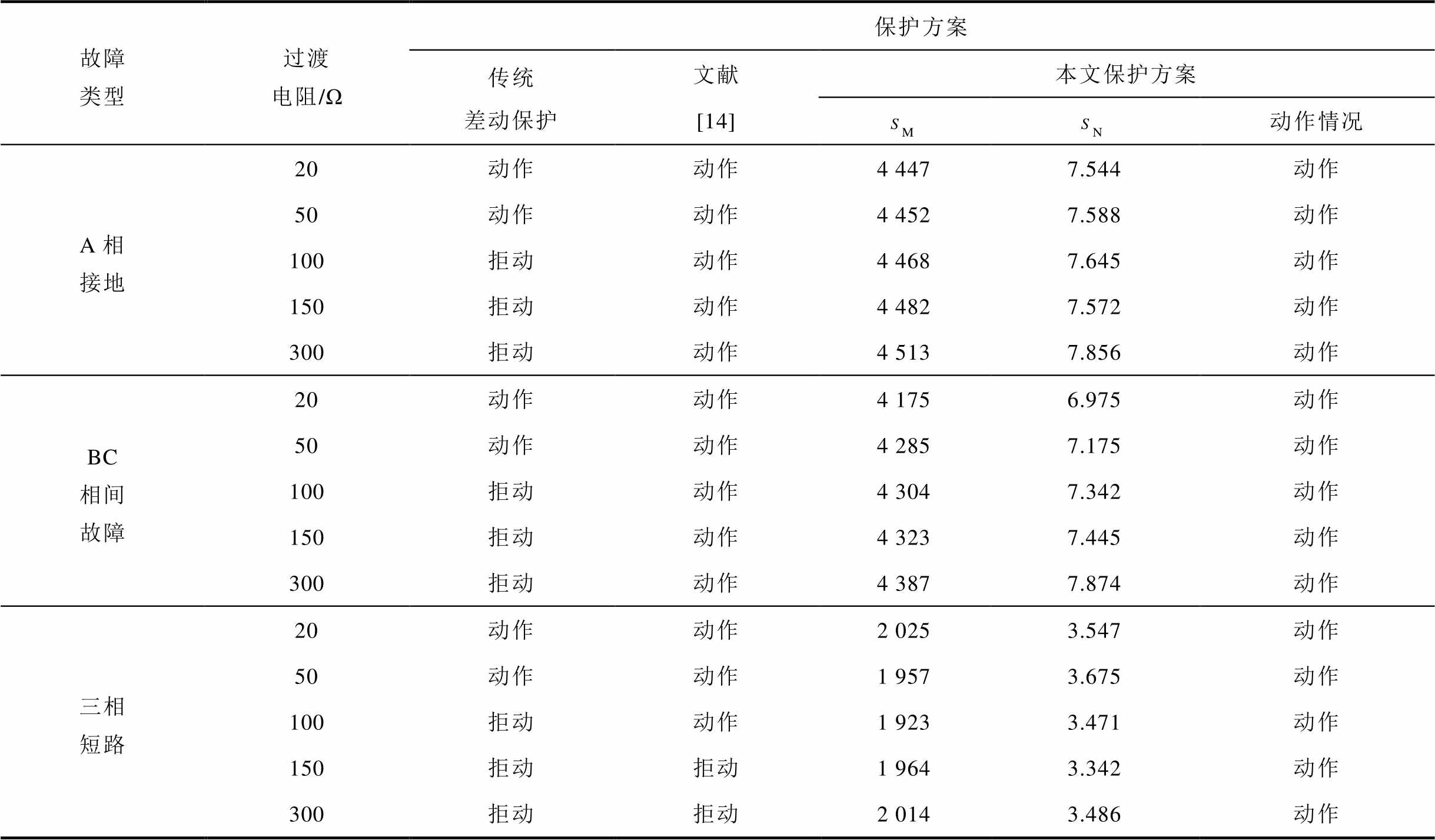
故障类型过渡电阻/Ω保护方案 传统差动保护文献[14]本文保护方案 动作情况 A相接地20动作动作4 4477.544动作 50动作动作4 4527.588动作 100拒动动作4 4687.645动作 150拒动动作4 4827.572动作 300拒动动作4 5137.856动作 BC相间故障20动作动作4 1756.975动作 50动作动作4 2857.175动作 100拒动动作4 3047.342动作 150拒动动作4 3237.445动作 300拒动动作4 3877.874动作 三相短路20动作动作2 0253.547动作 50动作动作1 9573.675动作 100拒动动作1 9233.471动作 150拒动拒动1 9643.342动作 300拒动拒动2 0143.486动作
由表3可知，传统比例式差动保护在过渡电阻较小时能够正确动作，但是受限于依赖两端电流差值的原理，对高阻故障灵敏度低，且换流器的限幅控制会进一步抑制故障电流，削弱保护灵敏度，在双馈风电场接入柔直系统场景下适用性受限。文献[14]基于负序分量构造判据，增强了对高阻故障的耐受能力，但在三相对称故障下利用数据延迟构造的负序分量特征减弱，保护灵敏度降低，当过渡电阻增大至150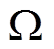
以上时，保护拒动。相比之下，本文所提保护方案在过渡电阻高达300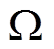时仍能准确识别故障，内部故障时两端判据值相差1个数量级以上，具有较强的高阻耐受能力和灵敏性。
针对双馈风电场接入柔直输电系统故障响应复杂、易受换流器控制策略影响的问题，本文提出了一种基于虚拟电抗差异特征的交流线路纵联保护方案。保护逻辑不再依赖传统幅值和工频，也摆脱了对通信的高需求，增强了保护方案在弱馈条件下的适应能力。该方案具有以下特点：
1）本保护方案建立了考虑低电压穿越控制策略的双馈风电机等值模型和融合换流器控制策略的柔直换流站等值模型。利用区内外故障时线路虚拟电抗的差异特征构造保护判据，在不同故障类型和不同位置发生故障时该保护方案均能准确识别故障，耐受过渡电阻能力可达300。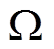
2）本保护方案仅需线路两端保护装置之间传递逻辑量信息，不需要交互实时电气量信息，受同步误差影响较小，对通信装置要求较低。
3）本保护方案通过提取故障特征在频域中显著频点的电气量，使得区内故障时线路两端保护装置计算的判据值相差1个数量级以上，具有较强的容错能力和灵敏性。
附 录
（A1）
（A2）
参考文献
[1] 郑涛, 陈云飞, 马英, 等. 基于复合暂态能量的多端柔性直流电网自适应差动保护[J]. 电工技术学报, 2025, 40(5): 1440-1454. Zheng Tao, Chen Yunfei, Ma Ying, et al. Differential protection for multi terminal flexible DC power grid based on composite transient energy[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1440-1454.
[2] 刘昊霖, 贾科, 毕天姝, 等. 接入新能源大基地汇集系统的柔直换流站低电压穿越方法[J]. 电工技术学报, 2025, 40(3): 759-770. Liu Haolin, Jia Ke, Bi Tianshu, et al. Low voltage ride through methods for flexible DC converter stations connected to the gathering system of new energy base[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 759-770.
[3] 侯冰, 李轶凡, 覃岚莎, 等. 基于故障区域拟合系数的双馈风场送出线路纵联差动保护方案[J]. 电工技术学报, 2025, 40(23): 7694-7706. Hou Bing, Li Yifan, Qin Lansha, et al. Current differential protection for wind farm transmission line based on fault region fitting coefficient[J]. Transactions of China Electrotechnical Society, 2025, 40(23): 7694-7706
[4] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938. Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[5] 郑玉平, 吕鹏飞, 李斌, 等. 新型电力系统继电保护面临的问题与解决思路[J]. 电力系统自动化, 2023, 47(22): 3-15. Zheng Yuping, Lü Pengfei, Li Bin, et al. Problems faced by relay protection in new power system and their solution ideas[J]. Automation of Electric Power Systems, 2023, 47(22): 3-15.
[6] 王增平, 林一峰, 王彤, 等. 电力系统继电保护与安全控制面临的挑战与应对措施[J]. 电力系统保护与控制, 2023, 51(6): 10-20. Wang Zengping, Lin Yifeng, Wang Tong, et al. Challenges and countermeasures to power system relay protection and safety control[J]. Power System Protection and Control, 2023, 51(6): 10-20.
[7] 温志文, 刘昊霖, 贾科, 等. 风电接入海上换流站的交流汇集出线高速保护[J]. 中国电机工程学报, 2024, 44(12): 4775-4788. Wen Zhiwen, Liu Haolin, Jia Ke, et al. High-speed protection of AC collection lines connecting wind power to offshore converter stations[J]. Proceedings of the CSEE, 2024, 44(12): 4775-4788.
[8] Jia Ke, Yang Zhe, Zheng Liming, et al. Spearman correlation-based pilot protection for transmission lineconnected to PMSGs and DFIGs[J]. IEEE Transactions on Industrial Informatics, 2020, 17(7): 4532-4544.
[9] Zheng Liming, Jia Ke, Wu Wenqiang, et al. Cosine similarity based line protection for large scale wind farms part II: the industrial application[J]. IEEE Transactions on Industrial Electronics, 2021, 69(3): 2599-2609.
[10] Li Xu, Lu Yuping. Improved amplitude differential protection scheme based on the frequency spectrum index for distribution networks with DFIG-based wind DGs[J]. IEEE Access, 2020, 8: 64225-64237.
[11] Rezaei N, Uddin M N, Amin I K, et al. A novel hybrid machine learning classifier-based digital differential protection scheme for intertie zone of large-scale centralized DFIG-based wind farms[J]. IEEE Transactions on Industry Applications, 2020, 56(4): 3453-3465.
[12] Liu Shiming, Wang Bo, Zhao Yongsen, et al. Novel differential protection approach of UHV AC transmission lines based on tellegen’s quasi-power theorem[J]. IEEE Transactions on Power Delivery, 2022, 37(2): 1264-1274.
[13] 王春又, 孙士云, 毛肖, 等. 适应于双馈风电场送出线的时域距离纵联方向保护[J]. 电力系统保护与控制, 2021, 49(13): 82-94. Wang Chunyou, Sun Shiyun, Mao Xiao, et al. Longitudinal direction protection of time domain distance applicable to the outgoing line of a double-fed wind farm[J]. Power System Protection and Control, 2021, 49(13): 82-94.
[14] 岳清, 束洪春, 孙士云, 等. 适用于全故障类型的双馈风电场送出线负序电流纵联保护方案[J]. 太阳能学报, 2024, 45(4): 214-225. Yue Qing, Shu Hongchun, Sun Shiyun, et al. Negative sequence current pilot protection scheme for dfig outgoing line with all-fault types[J]. Acta Energiae Solaris Sinica, 2024, 45(4): 214-225.
[15] 吴宇奇, 王楷杰, 黄梓欣, 等. 基于行波频带瞬时能量比值的新能源场站220 kV输电线路单端暂态量全线速动保护方案[J]. 中国电机工程学报, 2025, 45(9): 3420-3436. Wu Yuqi, Wang Kaijie, Huang Zixin, et al. Non-unit transient-based full-line accelerated protection for 220 kV transmission lines of renewable energy power plants based on the instantaneous energy ratio of traveling wave frequency band[J]. Proceedings of the CSEE, 2025, 45(9): 3420-3436.
[16] Jia Ke, Xuan Zhenwen, Feng Tao, et al. Transient high-frequency impedance comparison-based protection for flexible DC distribution systems[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 323-333.
[17] Zheng Xiaodong, Chao Chenxu, Weng Yang, et al. High-frequency fault analysis-based pilot protection scheme for a distribution network with high photovoltaic penetration[J]. IEEE Transactions on Smart Grid, 2022, 14(1): 302-314.
[18] Zhang Yaoyao, Liu Hulin, Ye Hai, et al. High frequency component-based pilot protection for photovoltaic station collection line[C]//2022 4th Inter-national Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 2022: 1979-1983.
[19] 刘岳坤, 汪娟娟, 王泽昊, 等. 定功率控制下柔性直流输电系统交流侧导纳矩阵建模及频率耦合抑制策略研究[J]. 中国电机工程学报, 2023, 43(10): 3718-3731. Liu Yuekun, Wang Juanjuan, Wang Zehao, et al. Research on AC admittance matrix modeling and frequency coupling effect of MMC-HVDC under power control[J]. Proceedings of the CSEE, 2023, 43(10): 3718-3731.
[20] 王祥宇, 辛焕海, 傅闯, 等. 考虑实际工况的新能源经MMC-HVDC送出系统强度评估方法[J]. 电工技术学报, 2025, 40(15): 4708-4721. Wang Xiangyu, Xin Huanhai, Fu Chuang, et al. System voltage support strength evaluation method for renewables MMC-HVDC transmission systemconsidering operating condition[J]. Transactions of China Electrotechnical Society, 2025, 40(15): 4708-4721.
[21] 郑子萱, 宋东徽, 谢琦, 等. 考虑撬棒与直流卸荷协同保护动作特性的双馈风电场通用等值建模方法[J]. 中国电机工程学报, 2024, 44(15): 6023-6035. Zheng Zixuan, Song Donghui, Xie Qi, et al. A general equivalent modeling method for DFIG wind farms considering the coordinated action characteristics of crowbar and chopper protection[J]. Proceedings of the CSEE, 2024, 44(15): 6023-6035.
[22] 于潇寒, 王睿, 邹亮, 等. 基于平衡截断的锁相环完整结构保留双馈风电机组降阶模型构建[J/OL]. 电工技术学报, 2025: 1-15. [2025-04-08]. https://link. cnki.net/doi/10.19595/j.cnki.1000-6753.tces.242362. Yu Xiaohan, Wang Rui, Zou Liang, et al. Construction of reduced order model of doubly-fed wind turbines with the preservation of complete phase-locked loop structure based on balanced truncation[J/OL]. Tran-sactions of China Electrotechnical Society, 2025: 1-15. [2025-04-08]. https://link.cnki. net/doi/10.19595/j. cnki.1000-6753.tces.242362.
[23] 胡应宏, 沈禹辰, 尹光祖, 等. 计及电磁式电流互感器测量环节高频特性的柔性直流输电孤岛空载建模与谐振机理分析[J]. 中国电机工程学报, 2025, 45(18): 7136-7149. Hu Yinghong, Shen Yuchen, Yin Guangzu, et al. Modeling and resonance mechanism analysis of MMC-HVDC under unload condition considering the high frequency characteristics of electromagnetic current transformer measurement link[J]. Proceedings of the CSEE, 2025, 45(18): 7136-7149.
Abstract With the rapid development of renewable energy in central and western China, the flexible DC system has become a widely adopted solution for long-distance, large-scale power delivery. These systems offer high flexibility and reliability. When doubly-fed induction generator (DFIG) based wind farms are integrated into a flexible DC system, the fault response deviates significantly from those of traditional AC systems, especially weak infeed features characterized by low fault current and ambiguous direction. As a result, conventional protection methods based on power-frequency are prone to both maloperation and failure to operate. Therefore, there is an urgent need for a reliable protection scheme suitable for DFIG-based wind farms integrated into a flexible DC system. To address the above issues, this paper proposes a pilot protection scheme based on virtual reactance difference.
Firstly, an equivalent model of the DFIG with low-voltage ride-through (LVRT) control is built. A converter model considering control dynamics is also developed. These models represent the actual response of the DFIG-based wind farms integrated into a flexible DC system during faults. By considering the control strategies of converters and the LVRT behavior of DFIGs at both ends of the AC line during faults, this work improves the accuracy of modeling and enhances the applicability of the proposed scheme in DFIG-based wind farms integrated into a flexible DC system.
Secondly, based on the fault equivalent network, virtual reactance expressions at both ends of the AC line are derived for different fault scenarios. The results reveal distinct differences in virtual reactance between internal and external faults. A high-speed protection criterion is designed using the variance of the virtual reactance at both terminals. The paper also proposes a frequency selection principle for the protection scheme, in which the angular frequency corresponding to the maximum difference in virtual reactance between internal and external faults is selected as the frequency for extracting electrical quantities by the protection device.
Finally, the proposed scheme is tested on the RT-LAB hardware-in-the-loop simulation platform. The results demonstrate that the proposed protection scheme can accurately identify internal and external faults. It also exhibits advantages such as high resistance tolerance, low communication requirements, and high sensitivity.
The conclusions can be drawn as follows: (1) The virtual reactance at both terminals of an AC line shows significant differences under internal and external faults. This distinction forms a solid theoretical foundation for fault discrimination and enhances fault identification reliability. (2) The proposed method uses this feature to build a practical pilot protection scheme. It does not rely on power-frequency quantities or high synchronization accuracy. This improves the adaptability of protection under weak fault current infeed. (3) The method provides a reliable solution for AC line protection in DFIG-based wind farms integrated into flexible DC system.
keywords: DFIG-based wind farms, flexible DC system, AC line protection, pilot protection
DOI: 10.19595/j.cnki.1000-6753.tces.242337
中图分类号：TM77
国家自然科学基金重大集成项目资助（U22B6006）。
收稿日期 2024-12-23
改稿日期 2025-07-14
马 静 男，1981年生，教授，博士生导师，研究方向为电力系统分析、稳定与控制等。E-mail：hdmajing@163.com（通信作者）
吴怡琳 男，2001年生，硕士研究生，研究方向为电力系统控制与保护。E-mail：pauer4558@163.com
（编辑 赫 蕾）