图1 SG和非SG电源二阶并网系统模型拓扑与控制结构
Fig.1 Model topology and control structure of second-order grid-connected systems for SG and CIGs
摘要 同步发电机（SG）和跟网型变流器并网系统在弱电网下会存在稳定性问题，而构网型变流器并网系统在强电网下会存在稳定性问题，但对这三种电源接入电网后强弱电网失稳的特性缺少统一认识。为此，该文对SG和非SG电源并网系统的强弱电网小扰动失稳机理进行比较分析。首先，用特征值分析法对三种电源并网系统的同步环二阶模型和考虑外环（分别对应励磁调节和暂态电势、直流电压控制、端电压控制）的四阶模型的小扰动稳定性进行比较，确定了三种电源并网系统强弱电网失稳现象均与外环控制有关；其次，分别构建三种电源并网系统的类Heffron-Phillips模型，通过以同步环为主导环路、外环控制为附加支路的统一视角进行分析，基于反馈支路传递函数分解法，将三种电源并网系统不同结构的反馈传递函数G(s)分解为统一结构的二阶振荡环节H1(s)和剩余环节H2(s)，统一分析系统强弱电网失稳的附加负阻尼转矩机理；最后，通过Matlab/Simulink仿真和硬件在环实验验证上述理论分析结果的有效性，并对SG和非SG电源接入强弱电网系统小扰动稳定的更加一般化统一认识加以讨论。
关键词：同步发电机 构网型变流器 跟网型变流器 类Heffron-Phillips模型 反馈支路传递函数分解法
当前，电力系统正趋于电力电子化[1]。相较于以同步发电机（Synchronous Generator, SG）为主体的传统电力系统的动态过程由转子的物理运动所主导，以新能源为主体的电力电子化电力系统的动态过程由电力电子变流器的多尺度控制所主导[2]。虽然电力电子装置的灵活控制促进了电力系统结构优化、运行效率提升和智能化发展，但其复杂性也给电力系统的安全稳定运行带来了严峻挑战。2011年美国得克萨斯州风机接入弱电网时产生了次同步振荡[3]。2019年英国发生大面积停电事故，高占比的无惯性电力电子装置是该事故的主要原因[4]。
目前电力系统中的非SG电源，或称变流器接口电源（Converter-Interfaced Generation, CIG）主要包括跟网型变流器（Grid-Following Voltage-Source Converter, GFL-VSC）和构网型变流器（Grid-Forming Voltage-Source Converter, GFM-VSC）。其中GFL-VSC控制结构完善，锁相环（Phase Locked Loop, PLL）技术成熟，已广泛应用于新能源并网[5]。然而当电网较弱时，GFL-VSC对系统稳定性有负面影响[6-10]。文献[6]基于复转矩法，从阻尼的角度揭示GFL-VSC并网系统小扰动同步失稳机理。文献[7]建立GFL-VSC并网系统dq阻抗模型，指出在弱电网下q-q通道阻抗表现的负电阻特性会导致系统失稳。文献[8]从PLL和直流电压控制模态谐振视角解释了弱电网连接的GFL-VSC并网系统的不稳定现象。
GFM-VSC具备主动支撑电网电压与频率控制的能力，近年来取得快速发展[11]。文献[12-13]阐明GFM-VSC在弱电网下具有较好的稳定性。但在强电网下，GFM-VSC可能会存在一些稳定性问题[13-19]。文献[14]通过特征值法分析发现，构网型直驱风电场中匹配控制主导的振荡模态在强电网下呈现负阻尼特性，系统存在次同步振荡的风险。文献[15-16]通过复转矩法进一步揭示了端电压控制会导致系统在强电网下因阻尼转矩不足而失稳。文献[17]基于等效序阻抗模型，揭示了频率耦合效应造成GFM-VSC并入强电网失稳的原因。基于上述单机系统的研究，文献[19]进一步指出GFM-VSC多机系统中线路阻抗不匹配也会引起振荡问题。
因此，GFL-VSC和GFM-VSC虽然都是电压源型变换器，但其控制结构不同，在不同网络强度下也表现出不同的失稳特性[20-23]。文献[20]综述了同步控制时间尺度、多时间尺度交互下并网系统的建模与稳定分析技术，指出这两种电源并网系统会因多时间尺度控制环节间的交互作用导致系统小扰动失稳。文献[21]指出，GFM-VSC表现为受控电压源，存在强电网失稳现象，而GFL-VSC表现为受控电流源，存在弱电网失稳现象，两种电源并网系统的强弱电网失稳现象具有对偶性。实际上，SG通常被认为是电压源，工程经验普遍显示在远距离重负荷下，SG并网系统会出现低频振荡[24-27]，存在弱电网失稳现象。因此，有必要在更合理、更统一的视角下分析三种电源并网系统强弱电网小扰动失稳的本质原因。
本文首先对SG和非SG电源并网系统的同步环二阶模型进行建模，发现系统均不会发生强弱电网失稳现象；其次对考虑外环的四阶并网系统的小扰动稳定性进行分析，发现随着线路电抗的改变，系统存在强电网或弱电网失稳现象，进一步通过构建类Heffron-Phillips模型，以统一的视角分析三种电源并网系统稳定性；然后基于提出的反馈支路传递函数分解法，采用统一结构的二阶振荡环节H1(s)分析稳定性；最后通过Matlab/Simulink仿真和硬件在环实验验证了上述理论的正确性，并对SG和非SG电源接入强弱电网系统小扰动稳定的更加一般化统一认识加以讨论。
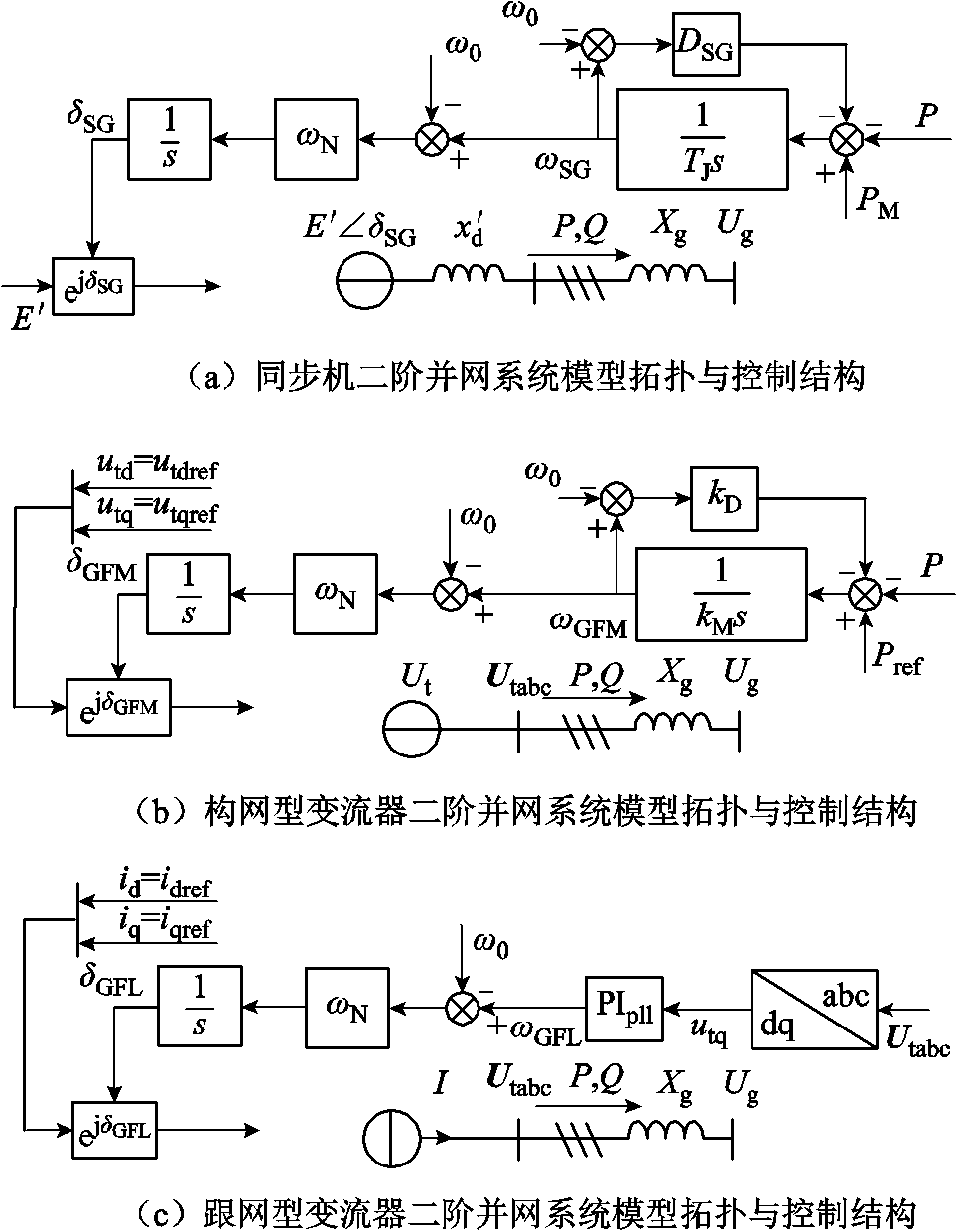
典型的SG、GFM-VSC和GFL-VSC二阶并网系统模型拓扑与控制框图分别如图1a、图1b、图1c所示。SG的转子摇摆方程生成功角，暂态电动势幅值恒定，对外表现为电压源特性；GFM-VSC由虚拟同步控制环节生成电压相位，端电压的dq分量幅值给定，对外表现为电压源特性；GFL-VSC的PLL跟踪电压相位，并网侧电流的dq分量幅值给定，对外表现为电流源特性。详细的变量符号注释见附表1，其中下标“d”和“q”分别代表dq旋转坐标系下的分量，下标“ref”表示参考值，下标“pll”表示锁相控制的变量，下标“SG”“GFM”和“GFL”分别表示SG、GFM-VSC和GFL-VSC的变量，“PI”表示比例积分控制器。
图1 SG和非SG电源二阶并网系统模型拓扑与控制结构
Fig.1 Model topology and control structure of second-order grid-connected systems for SG and CIGs
电网强度用短路比（Short Circuit Ratio, SCR）度量，有
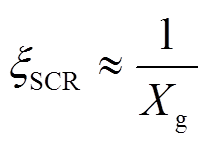（1）
式中，ξSCR为短路比；Xg为线路电抗。通常ξSCR越大则电网强度越强。强弱电网划分目前并没有严格的统一界限，工程上一般认为界限是ξSCR=3(pu)[16]，当Xg＜0.33(pu)时交流电网为强电网，Xg≥0.33(pu)时为弱电网。
SG二阶并网系统模型的微分方程为转子摇摆方程，表达式为
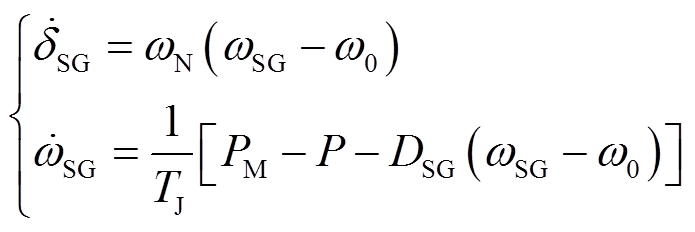（2）
式中，δSG和ωSG分别为功角和输出角频率；DSG和TJ分别为阻尼系数和惯性时间常数；PM为机械输入功率；P为输出功率，具体表达式见附录第2节。
通过状态空间建模，可得到SG二阶并网系统的状态矩阵，具体的微分代数方程和状态矩阵见附录第2节。受静态工作点存在条件及本文功率、电压稳态值约束，在Xg＜1(pu)（ξSCR＞1(pu)）时，系统有静态工作点。而本文Xg取值范围均在有静态工作点的前提下，系统因失去静态工作点而失稳的情况不在本文的研究范围内。系统特征根随Xg变化的轨迹如图2a所示，可以看出：系统有一对共轭特征根，随着Xg的增大，特征根的实部不变，虚部逐渐减小，即系统振荡频率逐渐降低。系统特征根始终在左半平面，因此SG二阶并网系统始终小信号稳定。
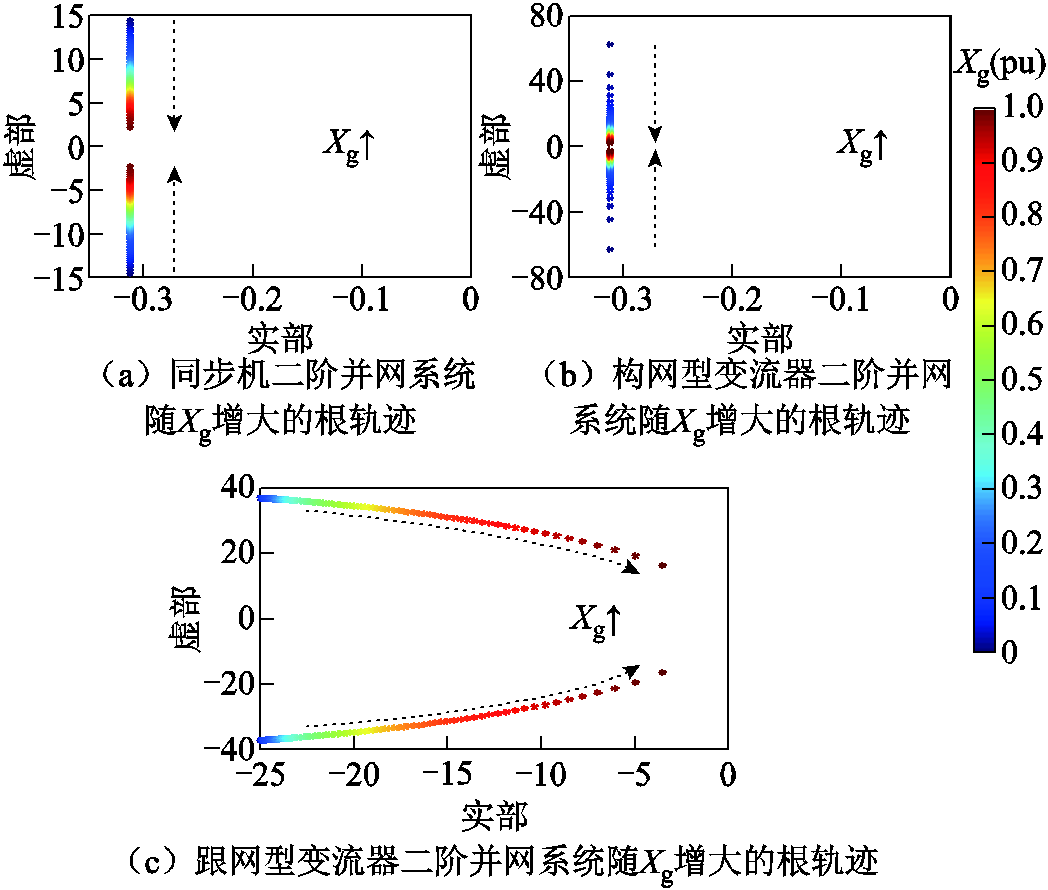
图2 SG和非SG电源二阶并网系统随Xg增大的根轨迹
Fig.2 Root locus of second-order grid-connected systems for SG and CIGs as Xg increases
GFM-VSC二阶并网系统模型的微分方程为虚拟同步环方程，其表达式为
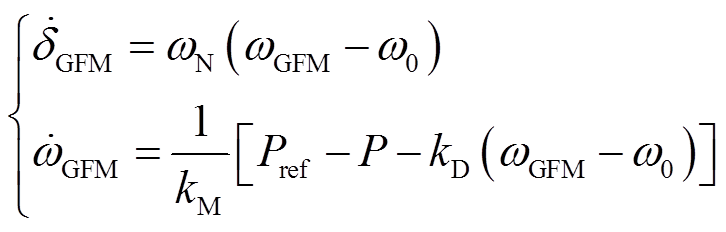（3）
式中，δGFM和ωGFM分别为虚拟同步环输出相位和角频率；kD和kM分别为阻尼系数和惯性系数；Pref为有功功率参考值。
通过状态空间建模，可得到GFM-VSC二阶并网系统的状态矩阵，具体表达式见附录第2节。系统特征根随Xg变化的轨迹如图2b所示，可以看出：系统有一对共轭特征根，随着Xg增大，特征根的实部不变，虚部逐渐减小，系统振荡频率也逐渐降低。系统特征根始终在左半平面，因此GFM-VSC二阶并网系统始终小信号稳定。此外，SG和GFM-VSC二阶并网系统随Xg变化的根轨迹规律相同，但在相同Xg参数下，GFM-VSC并网系统的系统振荡频率更大。
GFL-VSC二阶并网系统模型的微分方程为锁相同步环方程，其表达式为
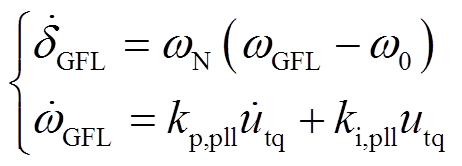（4）
式中，δGFL和ωGFL分别为PLL输出相位和角频率；kp,pll和ki,pll分别为锁相控制的比例系数和积分系数；utq为端电压q轴分量。
通过状态空间建模，可得到GFL-VSC二阶并网系统的状态矩阵，具体表达式见附录第2节。系统特征根随Xg变化的轨迹如图2c所示。可以看出：系统有一对共轭特征根，随着Xg增大，特征根的实部向右半平面移动，虚部逐渐减小，系统振荡频率也逐渐降低。系统特征根始终在左半平面，因此GFL-VSC二阶并网系统始终小信号稳定。
SG四阶并网系统拓扑与控制结构如图3所示。为维持机端电压基本不变，引入比例式自动励磁调节器。励磁调节器将发电机机端电压UG与参考电压UGref之差作为调节信号，经放大后作用于励磁系统，通过调整励磁电压从而使机端电压基本维持不变。当不考虑附加励磁控制时，励磁调节装置表达式为
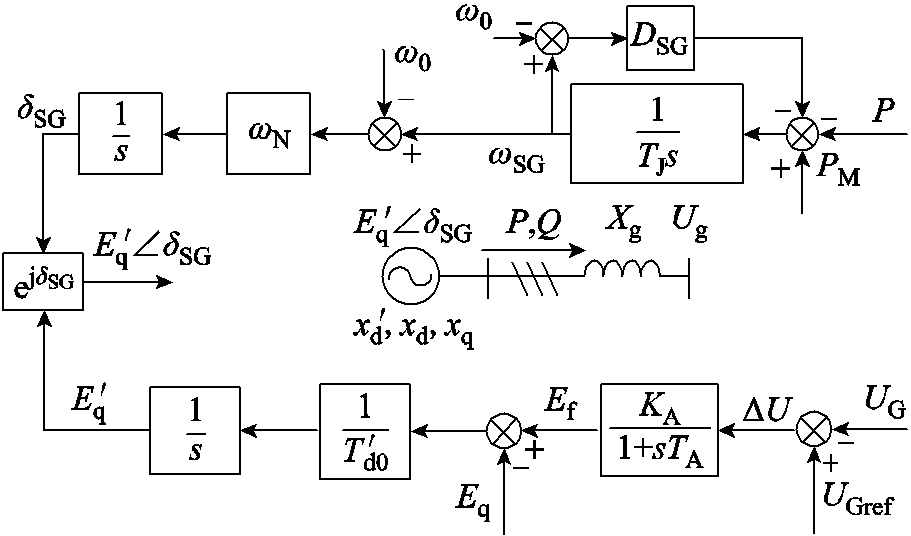
图3 SG并网系统拓扑与控制结构
Fig.3 Topology and control structure of the grid-connected system for SG
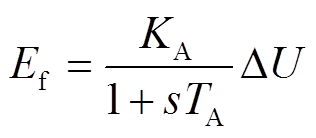（5）
式中，∆U为输入电压的偏差量，∆U =UGref-UG；KA为调节器放大倍数；TA为时间常数；Ef为励磁电压。
同时，为衡量励磁调节器的调节效果，考虑发电机电动势的变化方程为
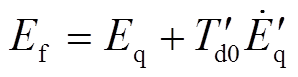（6）
式中，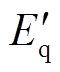
为q轴暂态电动势；Eq为空载电动势；
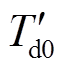为暂态时间常数。
通过状态空间建模，得到SG四阶并网系统的状态矩阵，具体表达式见附录第2节。系统特征根随Xg变化的轨迹如图4所示，可以看出：当Xg较小时，系统所有特征根均位于左半平面，系统小信号稳定。随着Xg增大到0.78(pu)，离虚轴最近的一对共轭特征根向右穿越虚轴，系统小信号不稳定。所以，SG四阶并网系统发生弱电网失稳。
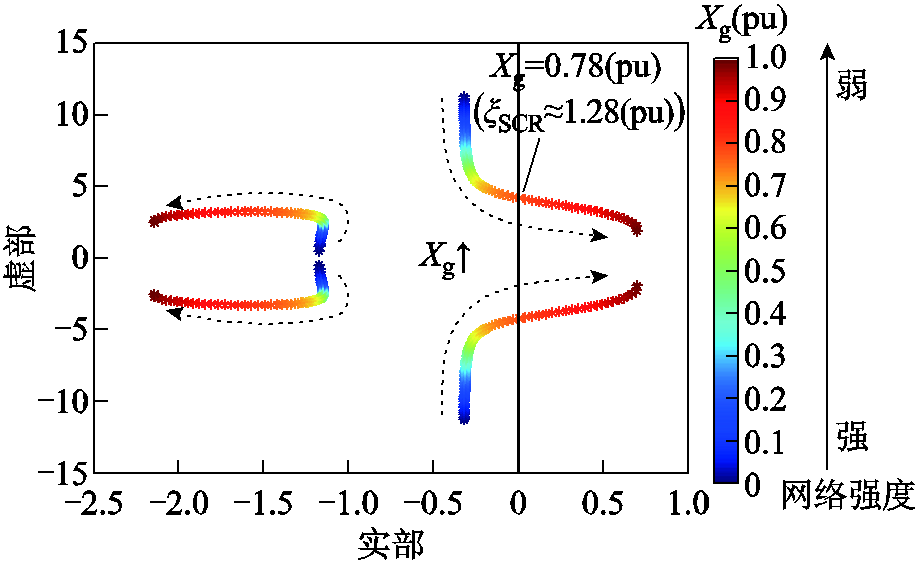
图4 SG四阶并网系统随Xg增大的根轨迹
Fig.4 Root locus of fourth-order grid-connected system for SG as Xg increases
GFM-VSC并网系统拓扑与控制结构如图5所示。假设直流侧的输入功率Pin保持不变；电流环足够快，从而忽略电流环动态，电流dq分量将始终等于其参考值，即id =idref ，iq =iqref ；电感用相量描述且变流器采用平均模型。其中下标“tvc”表示端电压控制的变量，下标“acc”表示交流电流控制的变量。
虚拟同步环节生成端电压相位，为矢量控制提供dq坐标系。d轴外环控制生成d轴电流指令值idref ，实现维持d轴电压utd恒定的功能；q轴外环控制生成q轴电流指令值iqref ，实现维持q轴电压utq恒定的功能。端电压控制的微分代数方程分别为
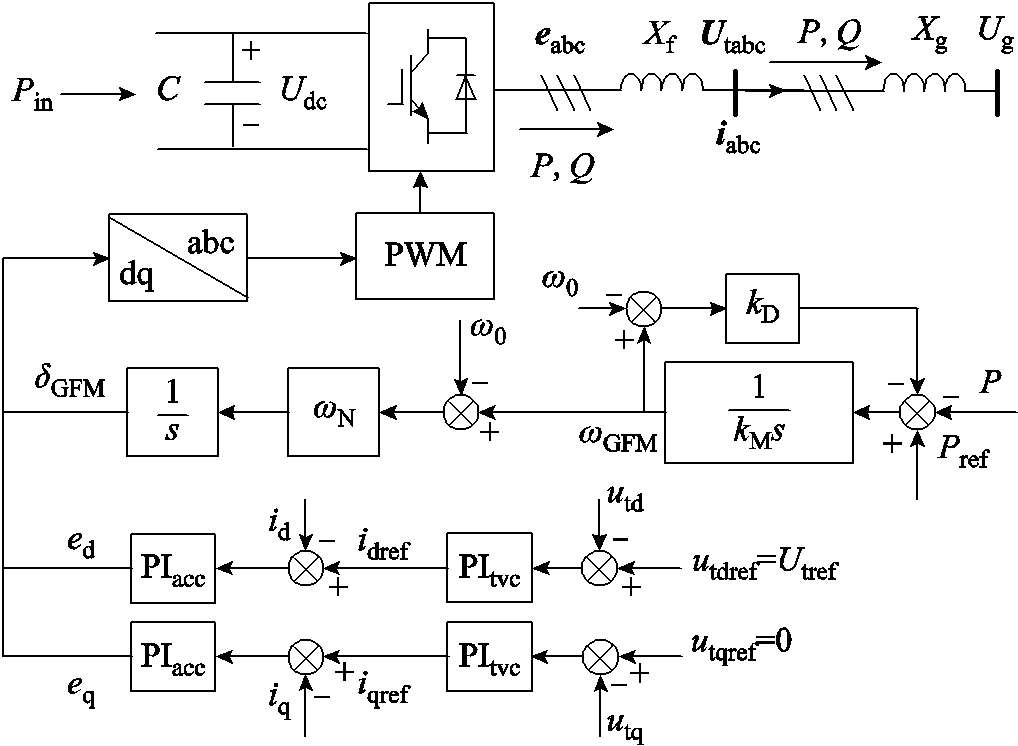
图5 GFM-VSC并网系统拓扑与控制结构
Fig.5 Topology and control structure of the grid-connected system for GFM-VSC
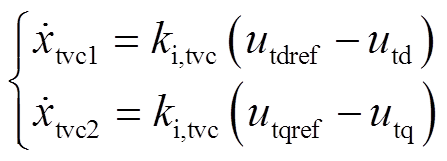（7）
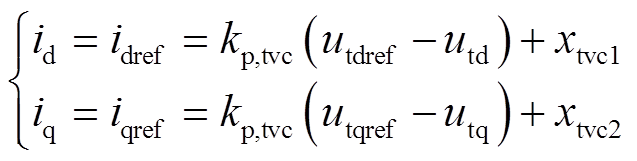（8）
式中，xtvc1和xtvc2分别为d、q轴端电压控制的状态变量；kp,tvc和ki,tvc分别为端电压控制的比例系数和积分系数。
通过状态空间建模，得到GFM-VSC四阶并网系统的状态矩阵，具体表达式见附录第2节。系统特征根随Xg变化的轨迹如图6所示，可以看出：当Xg比较小时，始终有一对共轭特征根位于右半平面，系统小信号不稳定。随着Xg增大到0.29(pu)，这对共轭特征根向左穿越虚轴，系统小信号稳定。与图4相比，失稳方向与趋势发生了逆转。所以，GFM-VSC四阶并网系统发生强电网失稳。
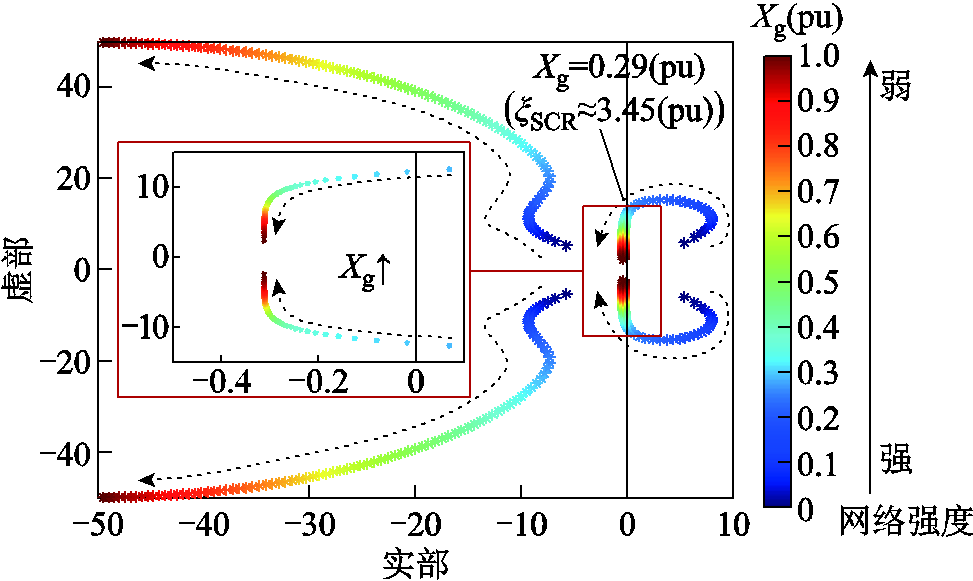
图6 GFM-VSC四阶并网系统随Xg增大的根轨迹
Fig.6 Root locus of fourth-order grid-connected system for GFM-VSC as Xg increase
GFL-VSC并网系统拓扑与控制结构如图7所示。同样假设Pin不变；电流dq分量始终等于其参考值，即id =idref ，iq =iqref ；忽略端电压环动态，端电压幅值将始终等于其参考值，即Ut =Utref ；电感用相量描述且变流器采用平均模型。其中下标“dvc”表示直流电压控制的量。
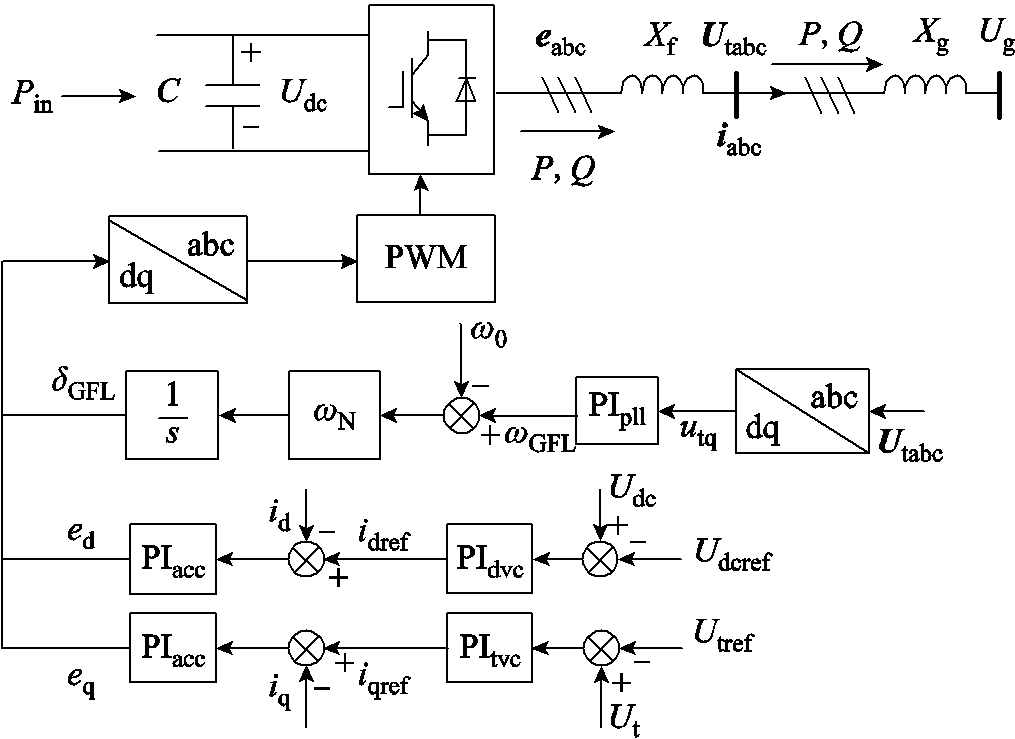
图7 GFL-VSC并网系统拓扑与控制结构
Fig.7 Topology and control structure of the grid-connected system for GFL-VSC
PLL跟踪端电压相位，为矢量控制提供dq坐标系。d轴外环控制生成d轴电流指令值idref ，实现维持直流电容电压Udc恒定的功能。直流电压控制和直流电容动态的微分代数方程分别为
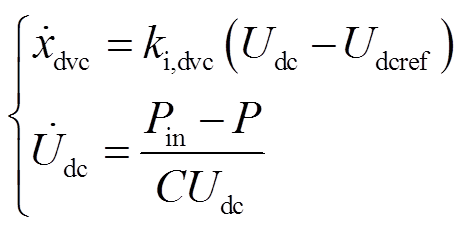（9）
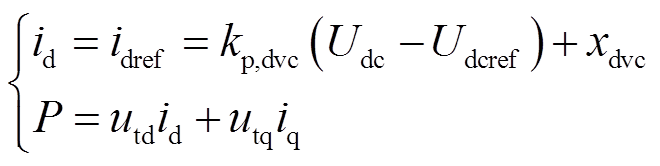（10）
式中，xdvc为直流电压控制的状态变量；kp,dvc和ki,dvc分别为直流电压控制的比例系数和积分系数。
通过状态空间建模，得到GFL-VSC四阶并网系统的状态矩阵，具体表达式见附录第2节。系统特征根随Xg变化的轨迹如图8所示，可以看出：当Xg比较小时，系统所有特征根均位于左半平面，系统小信号稳定。随着Xg增大到0.88(pu)，离虚轴最近的一对共轭特征根向右穿越虚轴，系统小信号不稳定。所以，GFL-VSC四阶并网系统发生弱电网失稳。
表1总结了SG和非SG电源并网系统强弱电网失稳现象。首先，三种电源的同步二阶并网系统均不发生失稳，即网络强弱对系统稳定性表现为中性。在同步二阶模型基础上，分别考虑含自动励磁调节器、端电压控制和直流电压控制的四阶并网系统模型，它们的小信号稳定性均随网络强度发生改变。SG和GFL-VSC并网系统表现为弱电网失稳，GFM-VSC并网系统表现为强电网失稳。所以，三种电源并网系统出现不同强弱电网失稳现象是由于不同的外环控制所造成的。
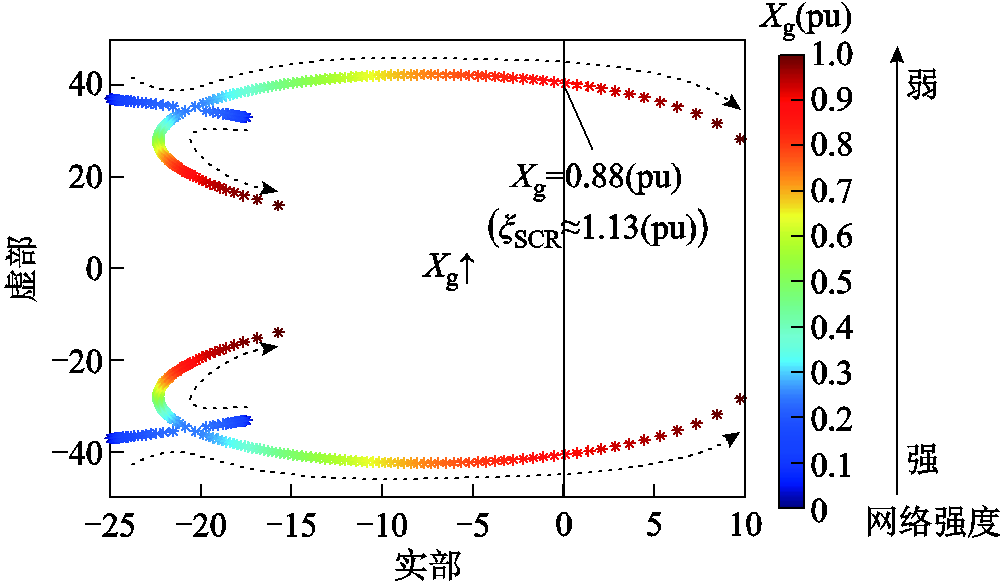
图8 GFL-VSC四阶并网系统随Xg增大的根轨迹
Fig.8 Root locus of fourth-order grid-connected system for GFL-VSC as Xg increase
表1 SG和非SG电源并网系统强弱电网失稳现象比较总结
Tab.1 Comparison of stiff or weak grid-tied instability for SG and CIGs
电源类型模型失稳现象 SG二阶不失稳 四阶弱电网失稳 GFM-VSC二阶不失稳 四阶强电网失稳 GFL-VSC二阶不失稳 四阶弱电网失稳
在Matlab/Simulink中分别搭建了SG、GFM-VSC和GFL-VSC三种电源的同步二阶和四阶并网系统，具体参数取值详见附录第3节。
固定Xg=0.75(pu)（ξSCR≈1.33(pu)），在t=0.2 s时施加扰动使Xg增大0.05(pu)，得到SG二阶并网系统和四阶并网系统的输出功率PSG的时域波形，如图9a所示。结果表明：SG二阶并网系统波形振荡收敛，而四阶并网系统波形振荡发散。
固定Xg=0.32(pu)（ξSCR≈3.125(pu)），在t=0.2 s时施加扰动使Xg减小0.05(pu)，得到GFM-VSC二阶并网系统和四阶并网系统的输出功率PGFM的时域波形，如图9b所示。结果表明：GFM-VSC二阶并网系统波形振荡收敛，而四阶并网系统波形振荡发散。
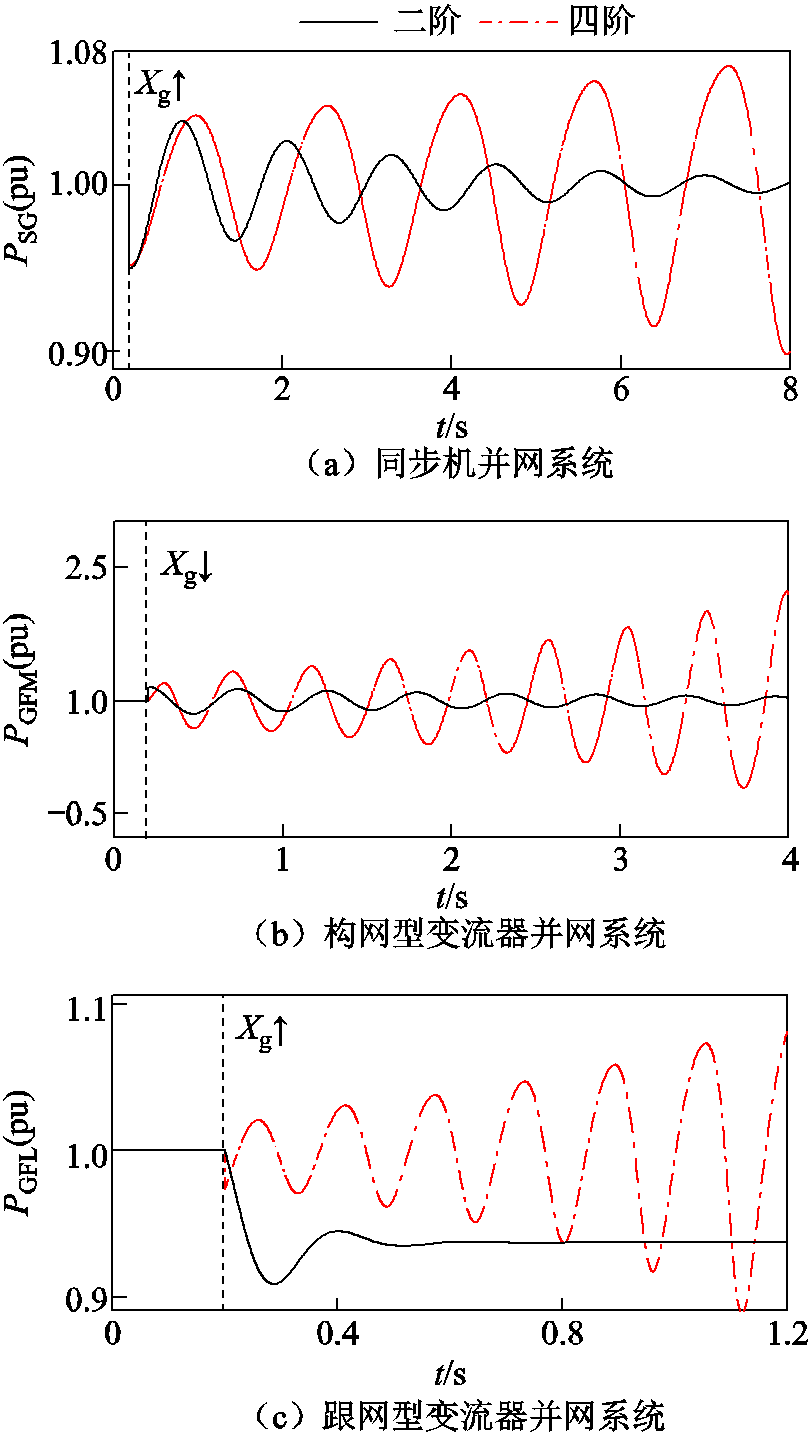
图9 SG和非SG电源并网系统强弱电网时域仿真
Fig.9 Time domain simulation of grid-connected systems for SG and CIG in stiff or weak grids
固定Xg=0.85(pu)（ξSCR≈1.18(pu)），在t=0.2 s时施加扰动使Xg增大0.05(pu)，得到GFL-VSC二阶并网系统和四阶并网系统的输出功率PGFL的时域波形，如图9c所示。结果表明：GFL-VSC二阶并网系统波形振荡收敛，而四阶并网系统波形振荡发散。
可见Matlab/Simulink中时域仿真结果与前文理论分析均保持一致。
为进一步分析SG和非SG电源并网系统强弱电网失稳机理，可以类似于SG的Heffron-Philips模型，分析得到三种电源并网系统的同步转矩和阻尼转矩。这样外环控制的作用可以等效成附加的同步转矩和阻尼转矩，进而分析附加控制对同步环节的作用[24-27]。
分别对三种电源四阶并网系统的微分代数方程线性化，将线性化模型以框图的形式表示，再进行流程图化简，最终得到的类Heffron-Philips统一模型如图10所示，其中D、K、M分别为同步环路的等效阻尼、等效同步系数和等效惯量，G(s)为除同步环外附加控制环节反馈的传递函数。
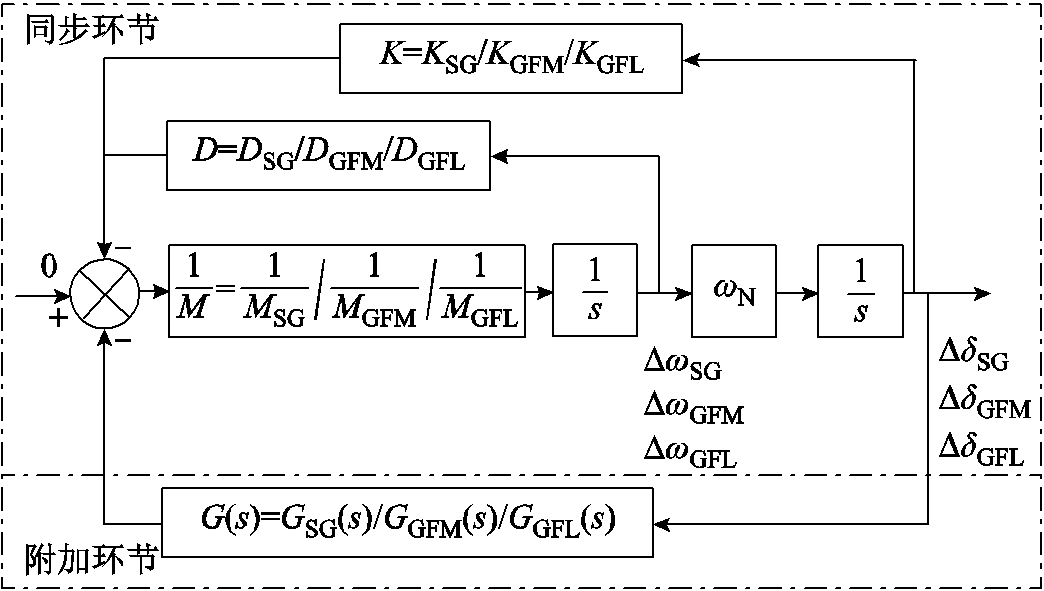
图10 类Heffron-Philips统一模型
Fig.10 Unified Heffron-Philips-like model
此时，系统的固有阻尼转矩系数Dint和固有同步转矩系数Ｋint计算公式为
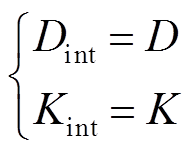（11）
将s=jωs代入附加反馈传递函数G(s)，可分析附加控制的等效作用。等效附加阻尼转矩系数Dadd和等效附加同步转矩系数Kadd的求解公式为
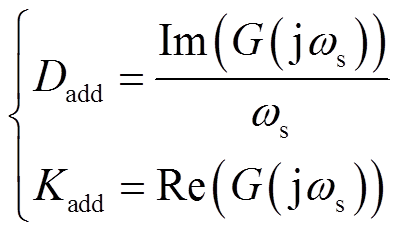（12）
式中，ωs为系统虚轴附近主导模态的虚部。
所以系统总阻尼转矩系数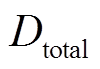
和总同步转矩系数
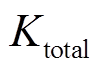可定义为
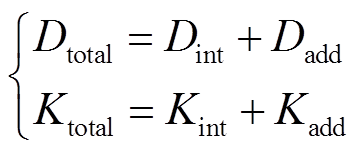（13）
当且仅当
＞0且
＞0时，系统才稳定；若＜0且＞0，系统振荡失稳。
由以上分析可知，在强弱电网下，系统可能发生振荡失稳，所以重点观察的指标为，同时因为
恒为正，所以着重分析
。若等效附加阻尼转矩系数为负，则可能导致为负，不利于系统稳定性，且这种风险随着的绝对值增大而逐渐升高。从定义可看出，也可认为是传递函数G(jωs)的ω轴（纵轴）投影。所以G(jωs)相位越接近-90°，幅值越大，系统越容易失稳。
由此可得，若G(s)在系统振荡角频率ωs处的传递函数G(jωs)满足以下两个条件之一：①幅值很大；②相位接近-90°，就可能使得外环附加控制反馈的传递函数G(s)有很大的等效负阻尼系数，此时系统失稳风险也很高。
如图10将SG四阶并网系统模型整理成以二阶同步环为主导环路、自动励磁调节器控制为附加支路的类Heffron-Philips统一模型结构，其中DSG、KSG、MSG为只与同步环和网络参数有关的系数，GSG(s)只与附加励磁调节器控制和网络参数有关。
对于SG，图10中各个系数分别为
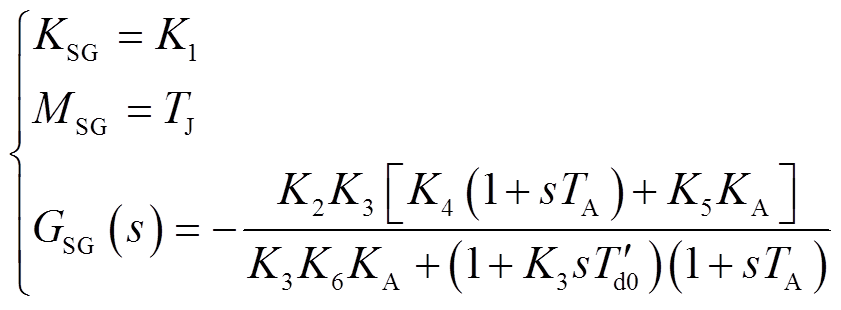（14）
式中，K1～K6表达式见附录第2节，也可见文献[25]。
对于SG二阶并网系统，只考虑Heffron-Philips模型的上半部分。当Xg变化时，因为DSG、KSG恒为正，系统不会发生小扰动失稳。而考虑四阶并网系统时，虽然DSG恒为正，但自动励磁调节器控制反馈的传递函数GSG(s)在弱电网时有很大的等效负阻尼系数，抵消DSG的作用，导致系统总阻尼不足，发生小扰动失稳。
图11所示为随着Xg以0.01(pu)间隔增大时，传递函数GSG(jωs)的变化情况。可见随着Xg增大，GSG(jωs)幅值逐渐增大，相位逆时针旋转逐渐接近-90°，在弱电网下同时满足条件①和②，即SG并网系统存在着弱电网失稳风险。
进一步将传递函数GSG(s)分解成二阶振荡环节H1SG(s)和剩余环节H2SG(s)两部分，即
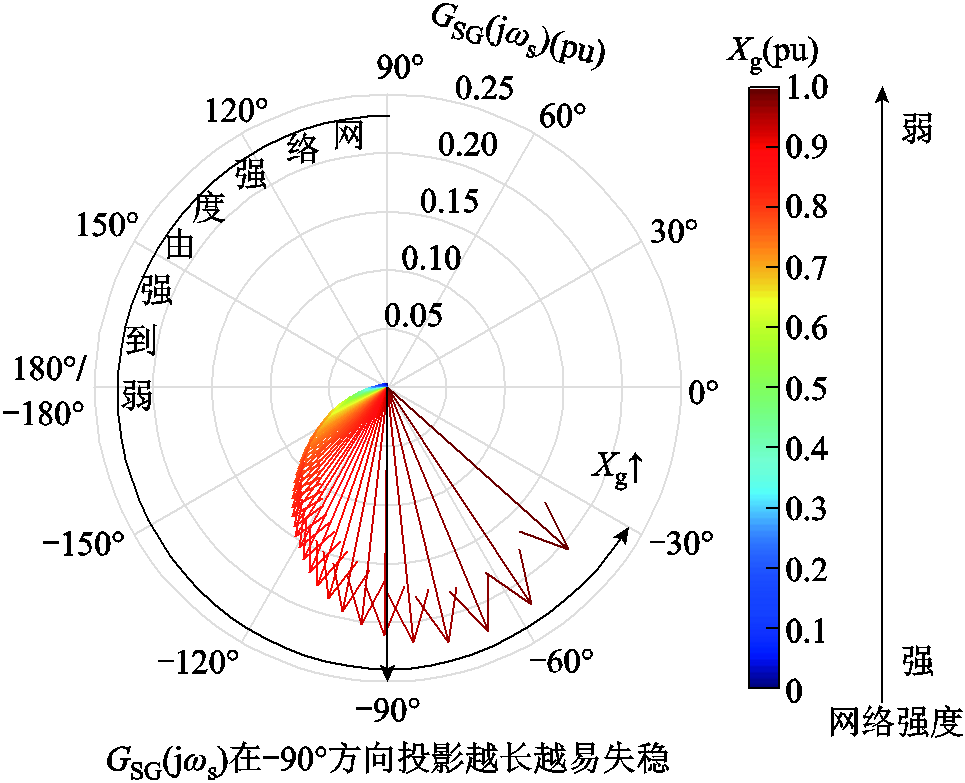
图11 GSG(jωs)随Xg变化
Fig.11 Variation of GSG(jωs) with Xg’s change
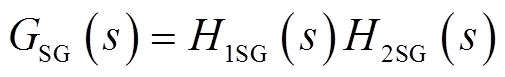（15）
其中，二阶振荡环节传递函数H1SG(s)的表达式为
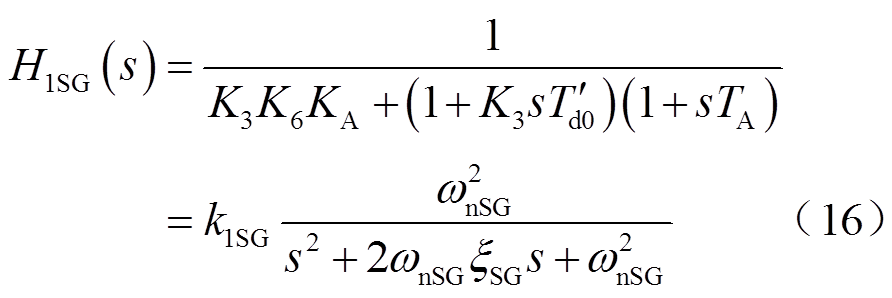
式中，k1SG为比例系数；ωnSG为系统自然振荡角频率；ξSG为系统的阻尼比。
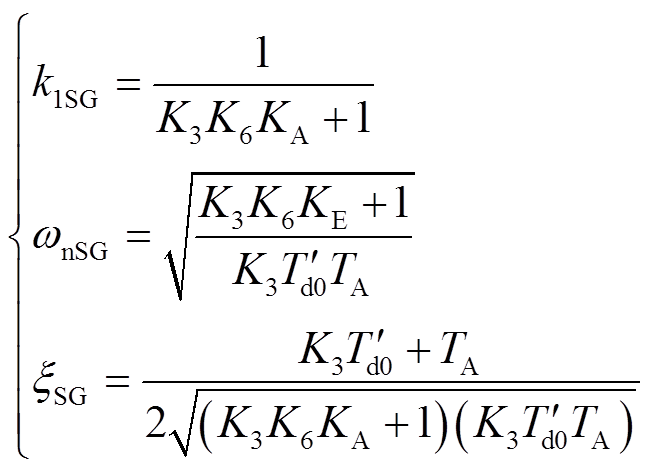（17）
H1SG(s)随Xg以0.1(pu)间隔增大时的Bode图如图12a所示，其中fs=ωs/(2π)为系统振荡频率，fn=ωn/(2π)为二阶振荡环节H1(s)的自然振荡频率。为了三种电源比较形式的统一性，在分析中略去不同下标而采取统一的表达形式。可以看出，随着Xg增大，fn逐渐增大，fs和fn逐渐靠近，在弱电网时两个频率点相对距离最近。进一步分析fs处的传递函数H1SG(jωs)，当Xg以0.01(pu)间隔增大时，H1SG(jωs)的变化如图12b所示。随着Xg增大，H1SG(jωs)幅值逐渐增大，相位逆时针旋转逐渐接近-90°，在弱电网下呈现幅值大、相位接近-90°的特性。
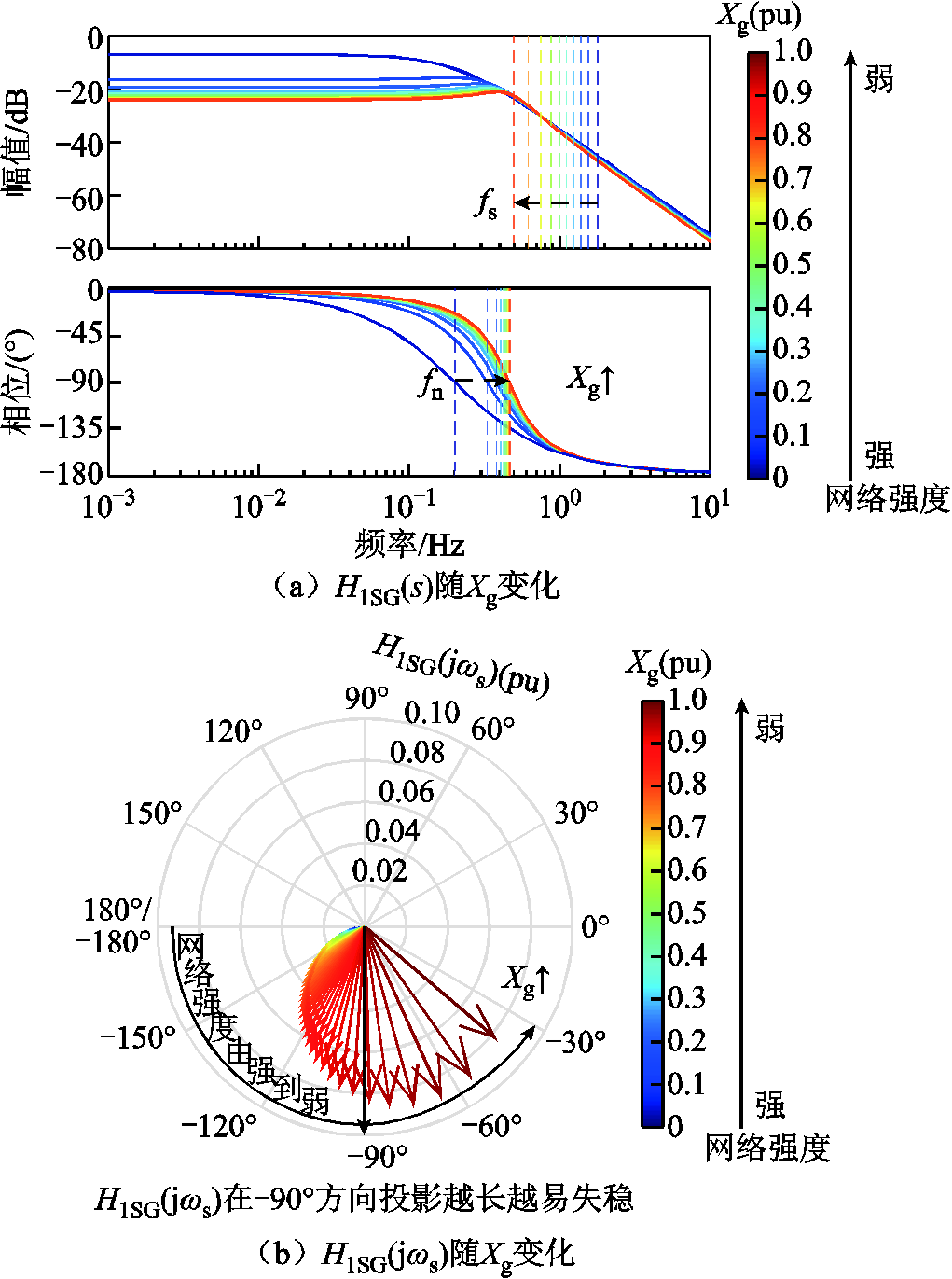
图12 H1SG(s)和H1SG(jωs)随Xg变化
Fig.12 Variation of H1SG(s) and H1SG(jωs) with Xg’s change
剩余环节传递函数H2SG(s)的表达式为
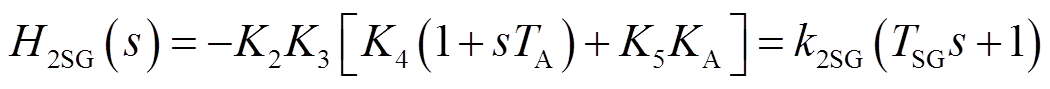（18）
式中，k2SG为比例系数；TSG为时间常数。
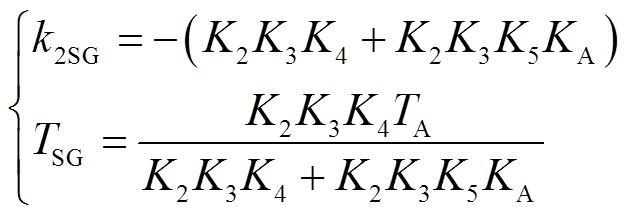（19）
将剩余环节传递函数H2SG(jωs)的幅值和相位特性看成对于二阶振荡环节传递函数H1SG(jωs)幅值和相位的附加作用，有
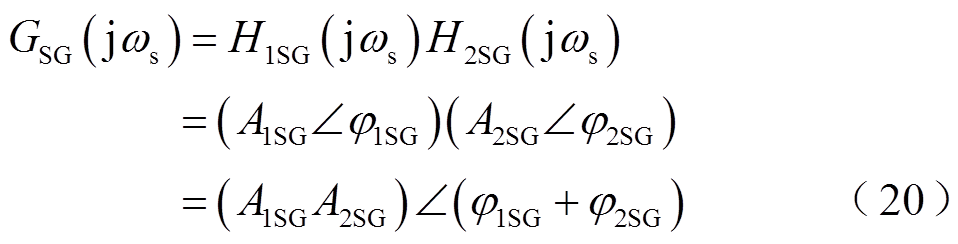
式中，ASG为传递函数的幅值；φSG为传递函数的相位；下标“1”和“2”分别代表二阶振荡环节和剩余环节传递函数。
H2SG(jωs)幅值随Xg的变化如图13a所示。强电网时，H2SG(jωs)对H1SG(jωs)幅值的放大倍数小；弱电网时，H2SG(jωs)对H1SG(jωs)幅值的放大倍数大。所以H2SG(jωs)保留H1SG(jωs)幅值强电网小、弱电网大的特点，并进一步加剧强弱电网时幅值的差距。H2SG(jωs)相位随Xg的变化如图13b所示，除强电网外的Xg参数范围内，相位都接近于0°，即H2SG(jωs) 对H1SG(jωs)相位的作用很小。所以H2SG(jωs)基本保留H1SG(jωs)相位随Xg变化时的特点。
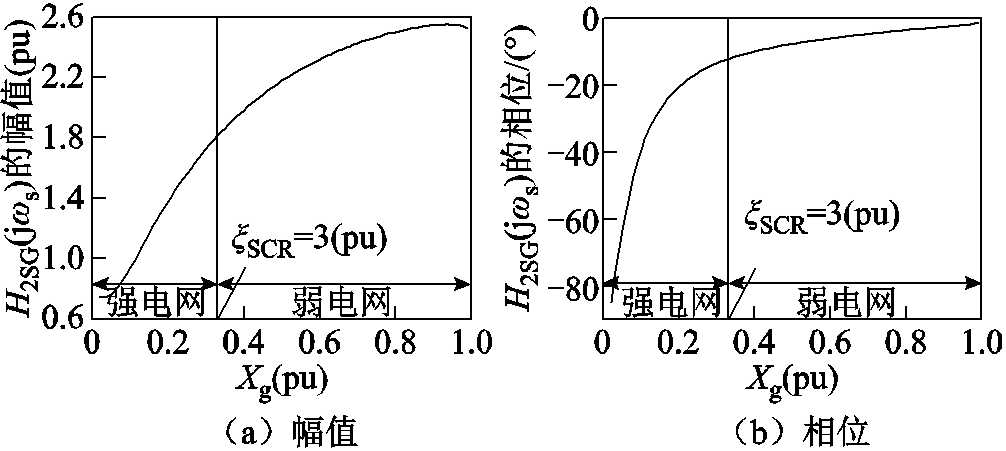
图13 H2SG(jωs)幅值和相位随Xg变化
Fig.13 Magnitude and phase variation of H2SG(jωs) with Xg’s change
总的来看，在满足GSG(jωs)幅值很大且相位接近-90°的Xg参数条件下，可使GSG(s)有很大的等效负阻尼系数，此时系统失稳风险也最高。通过反馈支路传递函数分离可得：在s=jωs时，剩余环节传递函数H2SG(s)基本保留振荡环节H1SG(s)的幅值和相位信息，所以失稳时从H1SG(s)可以判断系统处于强电网还是弱电网。又因为fn处H1SG(jωn)相位为-90°[28]，所以fs和fn距离越近，fs处H1SG(jωs)相位越接近-90°；fs和fn距离越远，fs处H1SG(jωs)相位越接近0°或-180°。基于此，可由fs和fn的相对距离分析H1SG(jωs)的相位。
弱电网时SG的fs和fn距离最近，H1SG(jωs)的相位接近-90°，此时H1SG(jωs)幅值也很大。综合H1SG(jωs)的幅值和相位特性可得：SG并网系统在弱电网时附加负阻尼系数最大，失稳风险最高。
同理，将GFM-VSC四阶并网系统模型整理成以二阶虚拟同步环为主导环路，二阶端电压控制为附加支路的类Heffron-Philips模型结构，其中DGFM、KGFM、MGFM为只与虚拟同步环和网络参数有关的系数，GGFM(s)只与端电压控制和网络参数有关。
对于GFM-VSC，各个系数分别为
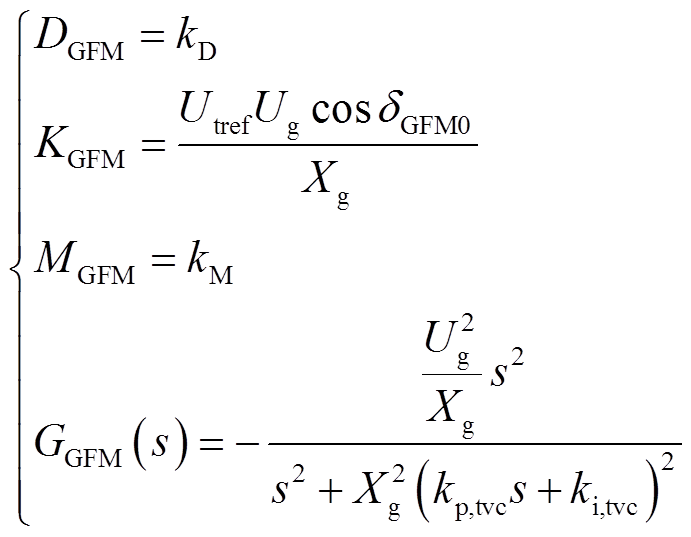（21）
对于GFM-VSC二阶并网系统，当Xg变化时，因为DGFM、KGFM恒为正，系统不会发生小扰动失稳。而考虑GFM-VSC四阶并网系统时，虽然DGFM恒为正，但端电压控制反馈的传递函数GGFM(s)在强电网时有很大的等效负阻尼系数，会抵消DGFM的作用，导致系统总阻尼不足，发生小扰动失稳。
当Xg以0.01(pu)间隔增大时，传递函数GGFM(jωs)的变化如图14所示。随着Xg增大，传递函数GGFM(jωs)幅值逐渐减小，相位逆时针旋转迅速接近-90°后远离，在强电网时同时满足条件①和②，即GFM-VSC并网系统存在强电网失稳风险。
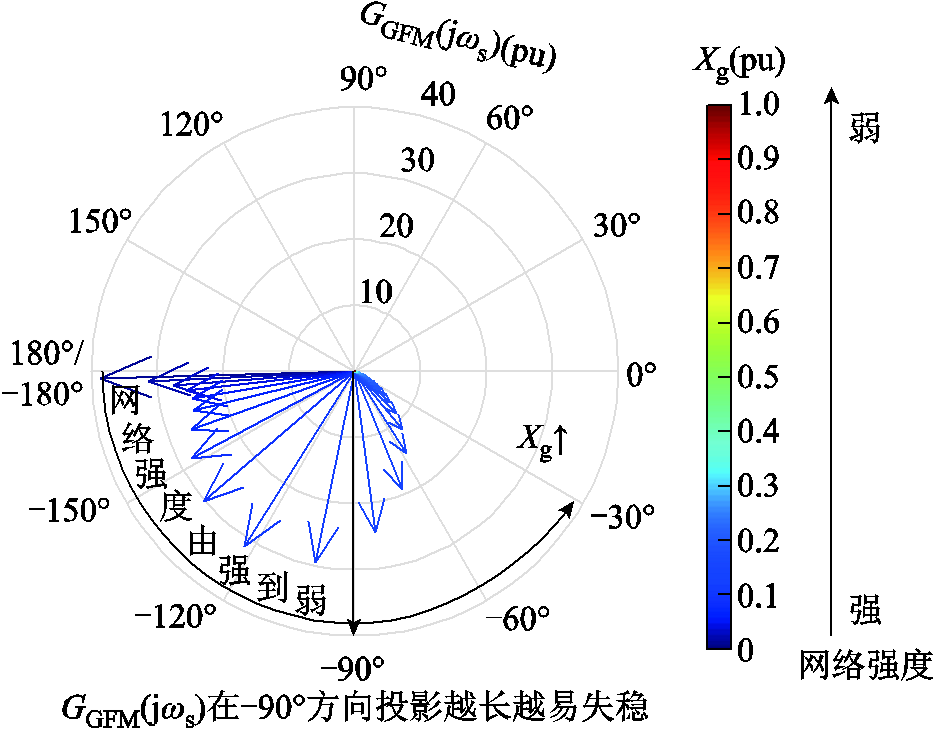
图14 GGFM(jωs)随Xg变化
Fig.14 Variation of GGFM(jωs) with Xg’s change
同理，将GGFM(s)进一步分解成二阶振荡环节H1GFM(s)和剩余环节H2GFM(s)两部分，有
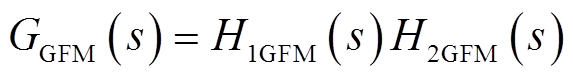（22）
二阶振荡环节传递函数H1GFM(s)为
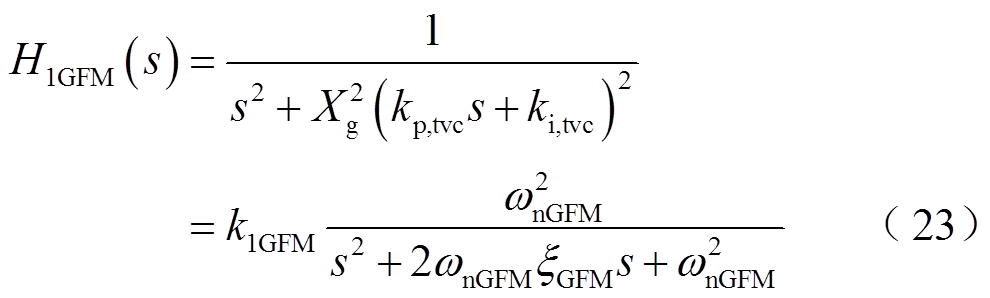
其中
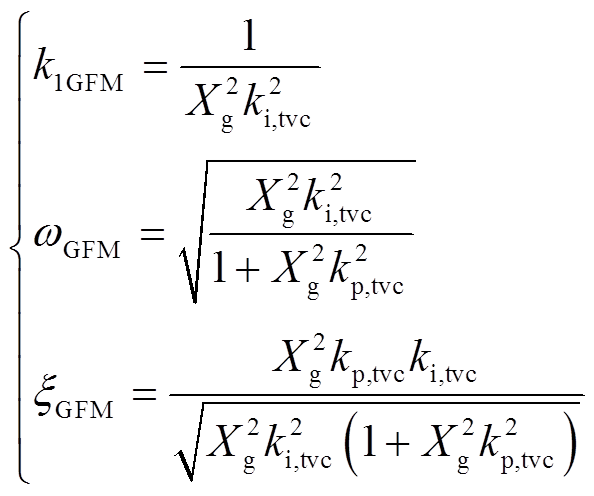（24）
H1GFM(s)随Xg以0.1(pu)间隔增大时的Bode图如图15a所示。可见随着Xg增大，fn逐渐增大，fs和fn迅速靠近后远离，在强电网时两个频率点相对距离最近。进一步分析fs处的H1GFM(jωs)，随着Xg以0.01(pu)间隔增大，H1GFM(jωs)的变化如图15b所示。随着Xg增大，H1GFM(jωs)幅值逐渐减小，相位逆时针旋转迅速接近-90°后远离，在强电网下呈现幅值大、相位接近-90°的特性。
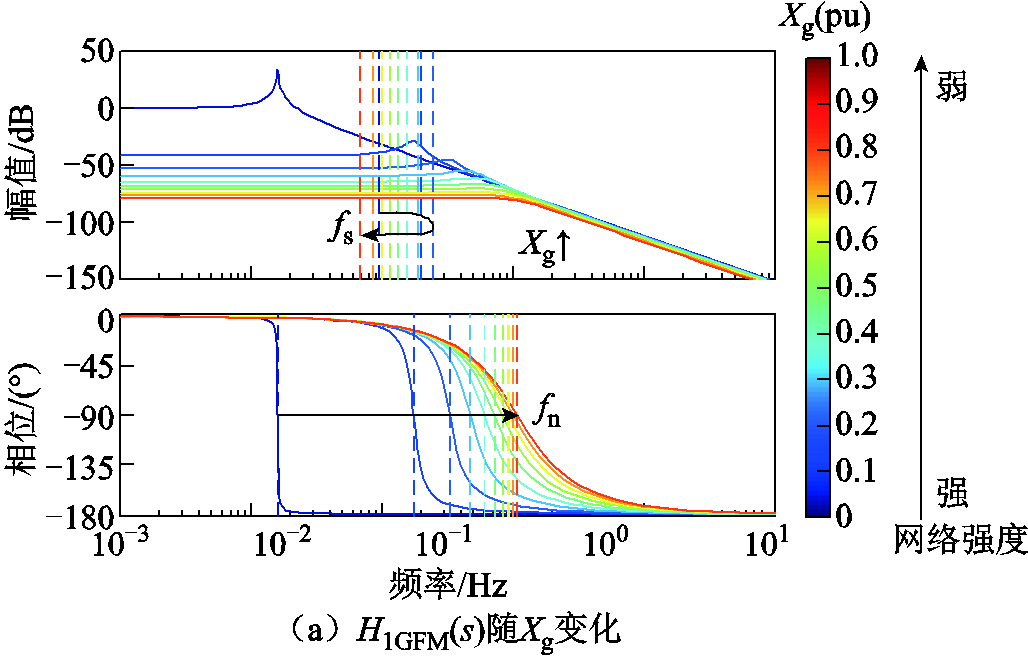
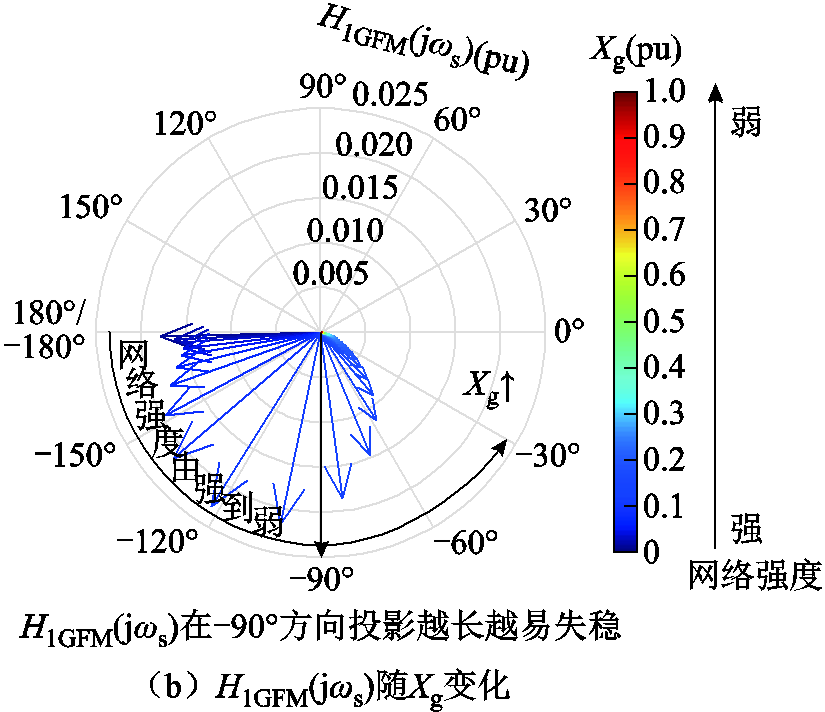
图15 H1GFM(s)和H1GFM(jωs)随Xg变化
Fig.15 Variation of H1GFM(s) and H1GFM(jωs) with Xg’s change
剩余环节传递函数H2GFM(s)为
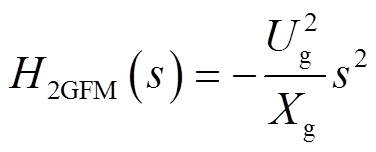（25）
H2GFM(jωs)幅值随Xg的变化如图16a所示。强电网时，H2GFM(jωs)对H1GFM(jωs)幅值的放大倍数大；弱电网时，H2GFM(jωs)对H1GFM(jωs)幅值的放大倍数小。所以H2GFM(jωs)保留H1GFM(jωs)幅值强电网大、弱电网小的特点，并进一步加剧强弱电网时幅值的差距。H2GFM(jωs)相位随Xg的变化如图16b所示，相位恒为0，即H2GFM(jωs)对H1GFM(jωs)相位的作用为0。所以H2GFM(jωs)完全保留H1GFM(jωs)相位随Xg变化时的特点。
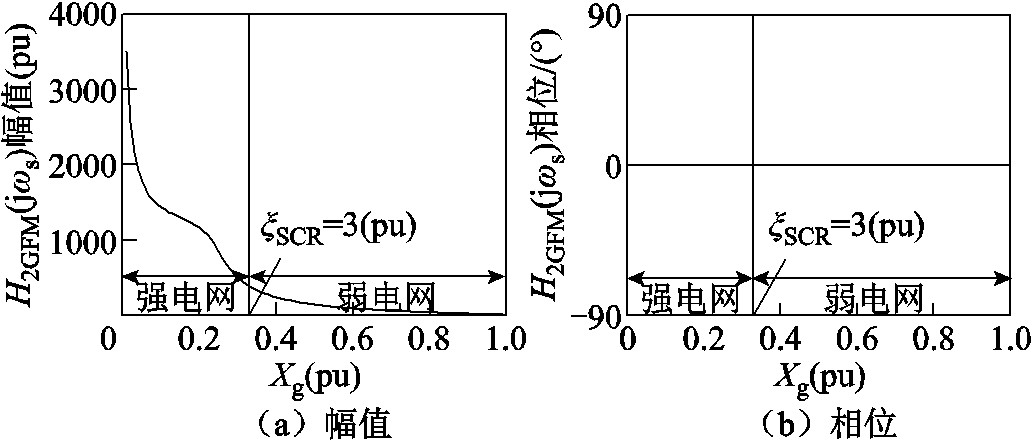
图16 H2GFM(jωs)幅值和相位随Xg变化
Fig.16 Magnitude and phase variation diagrams of H2GFM(jωs) with Xg’s change
同理，找寻满足GGFM(jωs)幅值很大且相位接近-90°的Xg参数条件，分析系统失稳机理。通过反馈支路传递函数分离和以上分析可得：在s=jωs时，失稳时可从H1GFM(s)判断系统处于强电网还是弱电网。
强电网时GFM-VSC的fs和fn距离最近，H1GFM(jωs)的相位接近-90°，此时H1GFM(jωs)幅值也很大。综合H1GFM(jωs)的幅值和相位特性可得：GFM-VSC并网系统在强电网时附加负阻尼系数最大，失稳风险最高。
同理，将GFL-VSC四阶并网系统模型整理成以二阶锁相同步环为主导环路、二阶直流电压控制为附加支路的类Heffron-Philips模型结构，其中DGFL、KGFL为只与锁相同步环和网络参数有关的系数。因为PLL不存在天然的二阶Heffron-Philips模型，而是经框图变换得到，所以GGFL(s)与直流电压控制、锁相同步环和网络参数都有关。
对于GFL-VSC，各个系数分别为
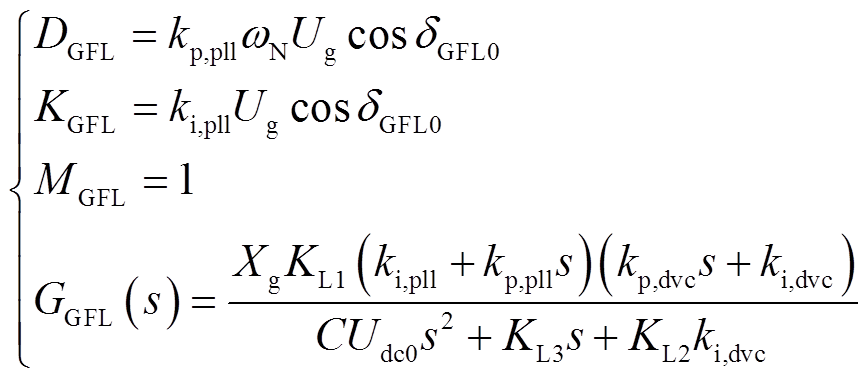（26）
式中，KL1～KL3表达式见附录第2节。
对于GFL-VSC二阶并网系统，在Xg变化时，因为DGFL、KGFL恒为正，系统不会发生小扰动失稳。而考虑GFL-VSC四阶并网系统时，DGFL虽恒为正，但直流电压控制反馈的传递函数GGFL(s)在弱电网时有很大的等效负阻尼系数，会抵消DGFL的作用，导致系统总阻尼不足，发生小扰动失稳。
当Xg以0.01(pu)间隔增大时，传递函数GGFL(jωs)的变化如图17所示。随着Xg增大，GGFL(jωs)幅值逐渐增大，相位顺时针旋转逐渐接近-90°，在弱电网时同时满足条件①和②，这说明GFL-VSC并网系统存在弱电网失稳风险。
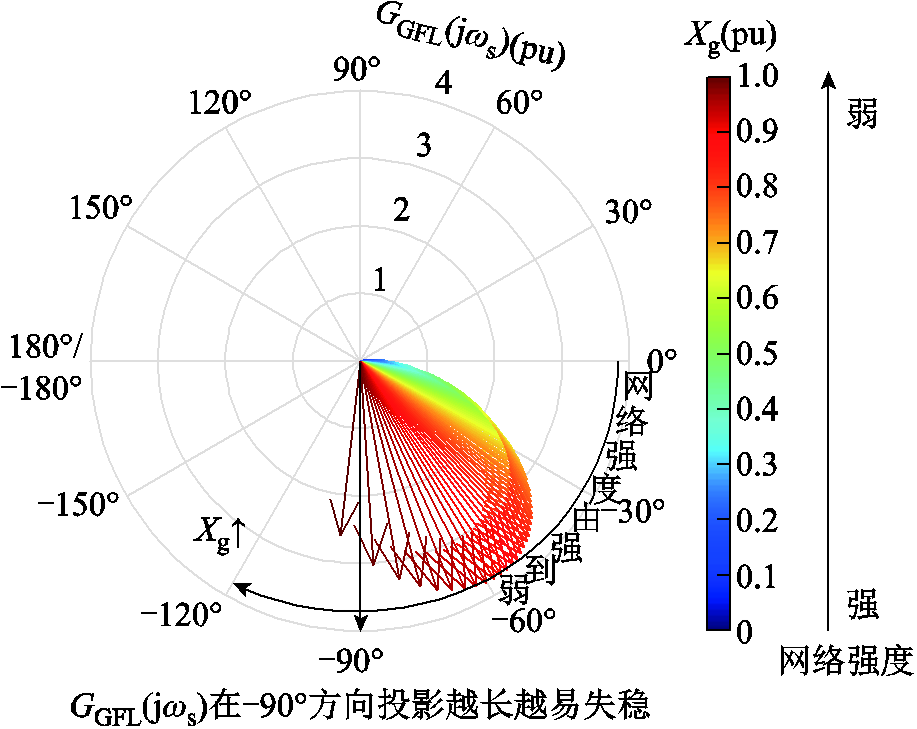
图17 GGFL(jωs)随Xg变化
Fig.17 Variation of GGFL(jωs) with Xg’s change
将GGFL(s)进一步分解成二阶振荡环节传递函数H1GFL(s)和剩余环节传递函数H2GFL(s)两部分，有
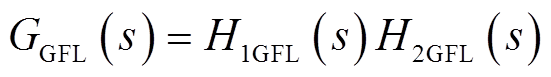（27）
二阶振荡环节传递函数H1GFL(s)为
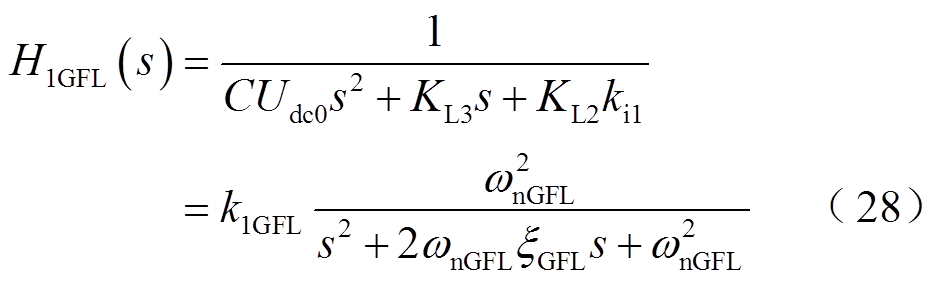
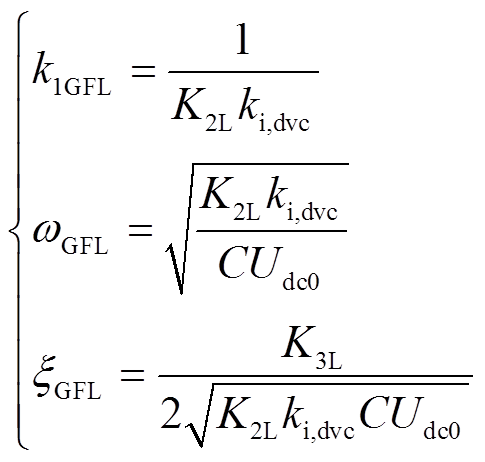（29）
H1GFL(s)随Xg以0.1(pu)间隔增大时的Bode图如图18a所示。随着Xg增大，fn逐渐减小，fs和fn靠近后逐渐远离，在弱电网时两个频率点相对距离最远。进一步分析fs处的H1GFL(jωs)，当Xg以0.01(pu)间隔增大时，传递函数H1GFL(jωs)的变化如图18b所示。随着Xg增大，H1GFL(jωs)幅值逐渐增大，相位顺时针旋转接近-180°，在弱电网下呈现幅值大、相位接近-180°的特性。这里H1GFL(jωs)分析相位-180°而不是-90°的原因后文会进一步解释。
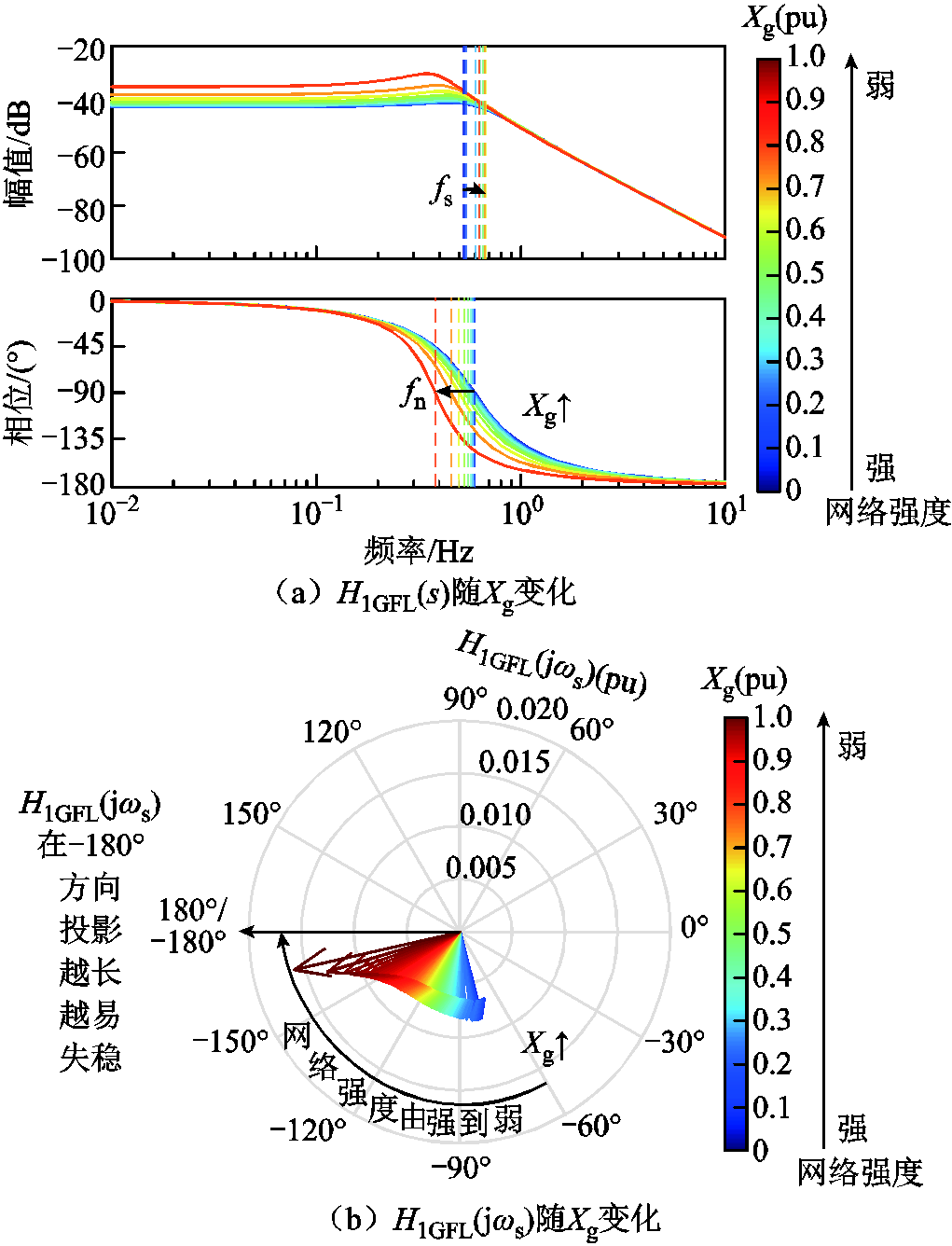
图18 H1GFL(s)和H1GFL(jωs)随Xg变化
Fig.18 Variation of H1GFL(s) and H1GFL(jωs) with Xg’s change
剩余环节传递函数H2GFL(s)的表达式为
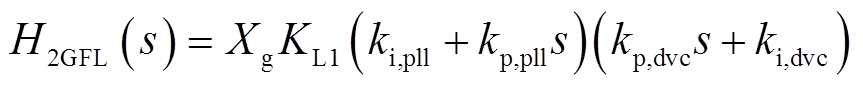（30）
H2GFL(jωs)幅值随Xg的变化如图19a所示。强电网时，H2GFL(jωs)对H1GFL(jωs)幅值的放大倍数小；弱电网时，H2GFL(jωs)对H1GFL(jωs)幅值的放大倍数大。所以H2GFL(jωs)保留H1GFL(jωs)幅值强电网小、弱电网大的特点，并进一步加剧强弱电网时幅值的差距。H2GFL(jωs)相位随Xg的变化如图19b所示，相位在90°左右，即H2GFL(jωs)对H1GFL(jωs)相位有超前约90°的作用。所以H2GFL(jωs)保留H1GFL(jωs)相位随Xg增大时顺时针变化趋势，但会使H1GFL(jωs)相位整体超前约90°。
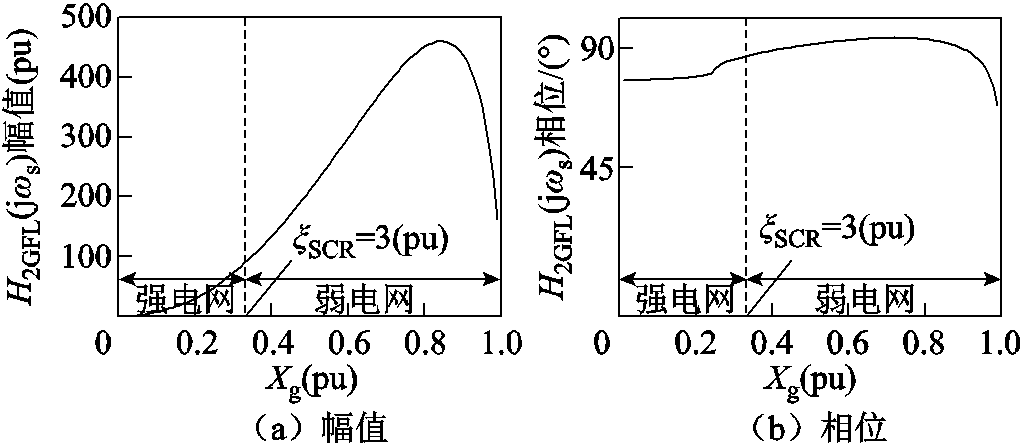
图19 H2GFL(jωs)幅值和相位随Xg变化
Fig.19 Magnitude and phase variation diagrams of H2GFL(jωs) with Xg’s change
同理，找寻满足GGFL(jωs)幅值很大且相位接近-90°的Xg参数条件，分析系统失稳机理。通过反馈支路传递函数分离和前文分析可得：在s=jωs时，失稳时系统处于强电网还是弱电网也可以从H1GFL(s)判断。需要注意的是，因为H2GFL(jωs)使得相位超前约90°，所以需要找H1GFL(jωs)相位-180°的Xg参数条件而不再是-90°。
弱电网时GFL-VSC的fs和fn距离最远，H1GFL(jωs)的相位接近-180°，此时H1GFL(jωs)幅值也很大。综合H1GFL(jωs)的幅值和相位特性可得：GFL-VSC并网系统在弱电网时附加负阻尼系数最大，失稳风险最高。
通过反馈支路传递函数分解法，将不同形式的反馈传递函数G(s)都简化成统一结构的二阶振荡环节H1(s)。这样，用于分析不同电源并网系统稳定性的传递函数没有结构性差异，只有系数差别，提高了三种电源并网系统稳定性比较的统一性。
表2总结了利用反馈支路传递函数分解法的三种电源并网系统强弱电网失稳机理。随着Xg增大，SG的fn缓慢增大，fn逐渐靠近fs，弱电网时fn和fs距离最近，H1SG(jωs)接近-90°；随着Xg增大，GFM-VSC的fn迅速增大，fn快速靠近fs并逐渐远离，强电网时fn和fs距离最近，H1GFM(jωs)接近-90°；随着Xg增大，GFL-VSC的fn逐渐减小，fn靠近fs后逐渐远离，弱电网时fn和fs距离最远，H1GFL(jωs)接近-180°，加上H2GFL(jωs)超前约90°的影响以及幅值的特点，最终三种电源并网系统呈现不同的强弱电网失稳趋势。
表2 SG和非SG电源并网系统强弱电网失稳机理比较
Tab.2 Comparison of stiff or weak grid-tied instability mechanism for SG and CIGs
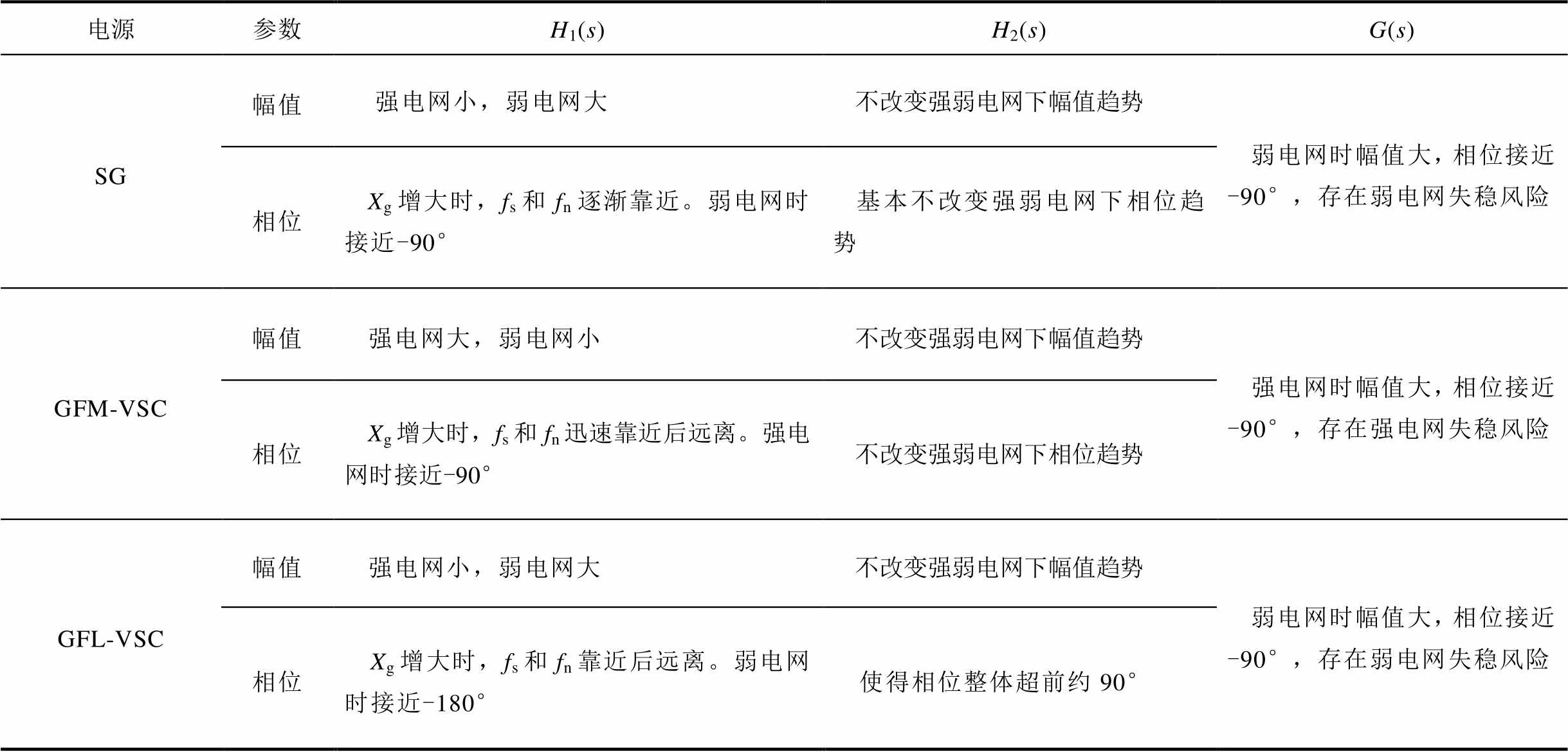
电源参数H1(s)H2(s)G(s) SG幅值强电网小，弱电网大不改变强弱电网下幅值趋势弱电网时幅值大，相位接近-90°，存在弱电网失稳风险 相位Xg增大时，fs和fn逐渐靠近。弱电网时接近-90°基本不改变强弱电网下相位趋势 GFM-VSC幅值强电网大，弱电网小不改变强弱电网下幅值趋势强电网时幅值大，相位接近-90°，存在强电网失稳风险 相位Xg增大时，fs和fn迅速靠近后远离。强电网时接近-90°不改变强弱电网下相位趋势 GFL-VSC幅值强电网小，弱电网大不改变强弱电网下幅值趋势弱电网时幅值大，相位接近-90°，存在弱电网失稳风险 相位Xg增大时，fs和fn靠近后远离。弱电网时接近-180°使得相位整体超前约90°
为验证上述结论的有效性，在SpaceR平台上进行硬件在环实验，实验平台示意图如图20所示。模型的具体参数取值详见附录第3节，分别设计了三组实验。
图20 实验平台示意图
Fig.20 Experimental platform diagram
实验一：固定Xg=0.75(pu)（ξSCR≈1.33(pu)），在t =2 s时施加扰动使Xg增大0.05(pu)，得到SG并网系统的输出功率PSG和A相端电压Uta的实验波形，如图21a所示。结果表明：SG并网系统在弱电网下存在失稳现象。
图21 SG和非SG电源并网系统强弱电网实验波形
Fig.21 Experimental waveforms of the grid-connected systems for SG and CIG in stiff or weak grids
实验二：固定Xg=0.32(pu)（ξSCR≈3.12(pu)），在t=2 s时施加扰动使Xg减小0.05(pu)，得到GFM-VSC并网系统输出功率PGFM和A相端电压Uta的实验波形，如图21b所示。结果表明：GFM-VSC并网系统在强电网下存在失稳现象。
实验三：固定Xg=0.85(pu)（ξSCR≈1.17(pu)），在t =2 s时施加扰动使Xg增大0.05(pu)，得到GFL-VSC并网系统输出功率PGFL和A相端电压Uta的实验波形，如图21c所示。结果表明：GFL-VSC并网系统在弱电网下存在失稳现象。
可见实验结果与前文理论分析均保持一致。
本文在统一视角下研究了SG和非SG三种类型电源并网系统的小扰动稳定性，针对不同的强弱电网失稳现象，采用反馈支路传递函数分解法进行分析，并揭示其由负阻尼导致的失稳机理。详细结论如下：
1）构建三种电源并网系统的类Heffron-Philips统一模型，研究得到不同的强弱电网失稳现象是由不同外环控制参与造成的。虽然SG和GFM-VSC并网系统同步环节模型相同，但因外环控制结构差异，分别在弱电网和强电网下具有较大幅值的负阻尼系数，最终表现为SG并网系统弱电网失稳，而GFM-VSC并网系统强电网失稳。由于GFM-VSC控制形式多样，文中所得到的强电网失稳结论是基于图5所示构网型控制结构。
2）提出用于失稳机理分析的反馈支路传递函数分解法。基于这种方法，能够消除不同电源并网系统用于稳定性分析的传递函数的结构性差异，提高三种电源并网系统稳定性比较的统一性。
3）由于在H1(s)自然振荡频率fn处，H1(jωn)的相位为-90°，而H1(s)系数的区别会导致系统振荡频率fs和fn相对距离变化趋势不同，最终失稳时的网络强度也有所区别。可以得到：弱电网时SG的fn靠近fs，存在失稳风险；强电网时GFM-VSC的fn靠近fs，存在失稳风险；弱电网时GFL-VSC的fn远离fs，加上剩余环节相位影响，存在失稳风险。
上述结论为理解SG和非SG电源的失稳行为提供了理论支撑，但仍有问题需要进一步探讨：
1）本文采用的反馈支路传递函数分解法本质上是基于传统SG的Heffron-Philips模型，通过阻尼转矩法分析小信号稳定性。将四阶模型通过框图化简转换成以二阶同步环为主导环路、二阶外环控制为反馈支路的类Heffron-Philips模型，二阶外环控制的作用可等效为向系统提供了附加的阻尼及同步转矩。进而通过观察发现，三种电源的二阶外环控制反馈支路传递函数表达式都有一部分为统一的二阶振荡环节形式，所以将反馈支路传递函数分解成二阶振荡环节和剩余环节，便于统一分析。
2）在有静态工作点的参数条件下，针对GFL-VSC二阶并网系统，当不考虑线路频率动态时，系统不会发生弱电网失稳；考虑线路频率动态后，系统可能会发生弱电网失稳。这一理论分析过程可见附录第4节。目前基于PLL二阶的稳定性分析大多集中于后者，本文为与SG和GFM-VSC并网系统模型保持统一，均未考虑线路频率动态。另一方面，本文并未考虑电流动态和电流控制环的影响，通过参与因子分析以及仿真验证都可说明当电流环带宽比较大时，电流动态对系统稳定性影响不大。
3）在四阶模型中，GFM-VSC在强电网下失稳，而同步发电机在弱电网下失稳，研究结果显示其来源于不同的端电压控制。从物理方面理解，GFM-VSC内环动作较快，一般认为其端电压幅值恒定，对外表现为电压源，且正好处于并网点处[29]，对该处电压矢量的控制与无穷大母线电压源的存在在无穷强电网条件下会发生冲突，故而造成强电网失稳。而对于同步发电机一般认为其内电动势幅值恒定，对外表现虽然同样为电压源，但是位于内电动势处，其与无穷大母线电压源不存在冲突，即使在强电网下也不失稳[13]。
4）在本文的比较研究中，对于GFM-VSC四阶模型并未考虑直流电压动态和其所对应的功率不平衡效应，即认为在理想情况下有超级电容或储能的存在。如果进一步考虑真实的新能源应用场景（即考虑直流电容动态），研究可发现其同样会出现弱电网失稳[30]，由此在不同网络条件下可出现强电网和弱电网失稳。可见，考虑转子或直流电压上的不平衡功率动态后，三种电源并网系统均可能出现弱电网失稳。弱电网失稳应该是任何交流并网装备（包括同步发电机、GFL-VSC和GFM-VSC电源）的通用特征，即通常与网络交互越弱，系统越容易失稳。额外增加的反常效应是GFM-VSC因其端电压控制和同步环的交互作用导致强电网失稳。这应该是SG和非SG电源接入强弱电网系统小扰动稳定的更加一般化统一认识。
附 录
1. 参数定义
附表1 本文参数
App.Tab.1 Parametres of the paper
参数含义 PMSG机械输入功率 ωSGSG输出角频率 δSGSG功角 E′SG暂态电动势
（续）
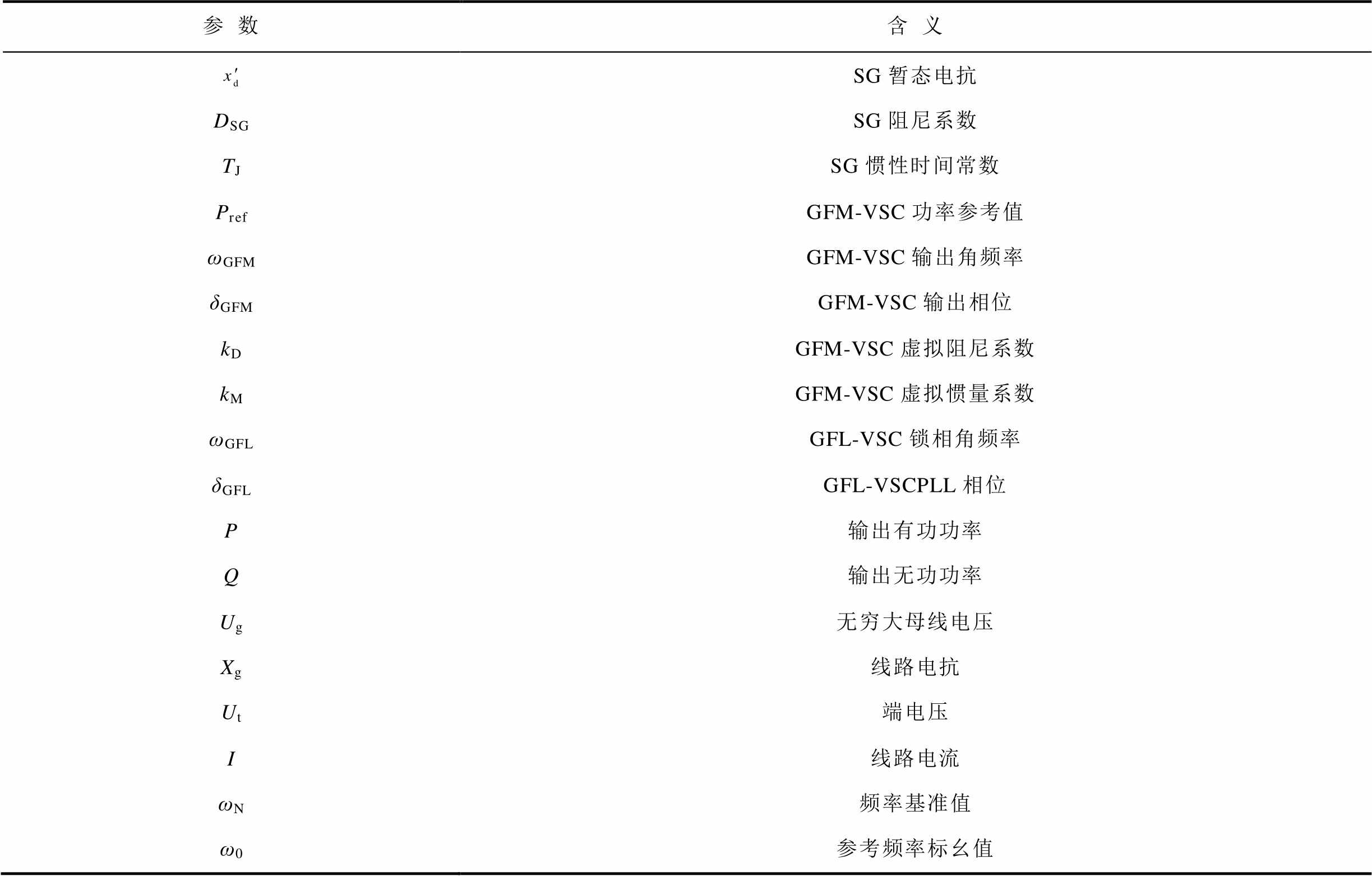
参数含义 SG暂态电抗 DSGSG阻尼系数 TJSG惯性时间常数 PrefGFM-VSC功率参考值 ωGFMGFM-VSC输出角频率 δGFMGFM-VSC输出相位 kDGFM-VSC虚拟阻尼系数 kMGFM-VSC虚拟惯量系数 ωGFLGFL-VSC锁相角频率 δGFLGFL-VSCPLL相位 P输出有功功率 Q输出无功功率 Ug无穷大母线电压 Xg线路电抗 Ut端电压 I线路电流 ωN频率基准值 ω0参考频率标幺值
2. 同步机和非同步机电源二阶与四阶并网系统微分代数方程和状态矩阵
1）SG二阶并网系统微分代数方程和状态矩阵
SG二阶并网系统微分方程为
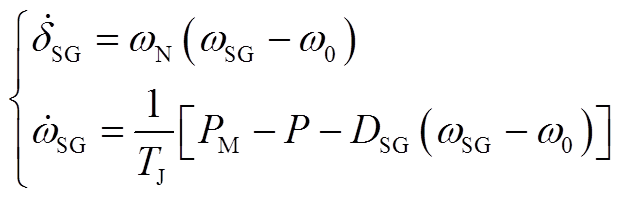（A1）
代数方程为
（A2）
状态矩阵为
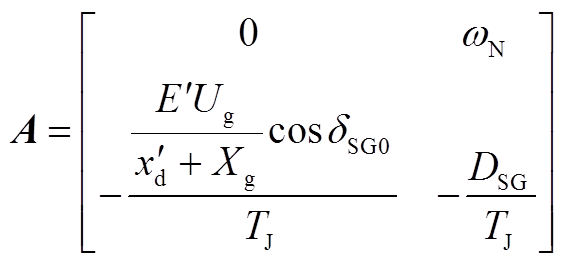（A3）
2）GFM-VSC二阶并网系统微分代数方程和状态矩阵
GFM-VSC二阶并网系统微分方程为
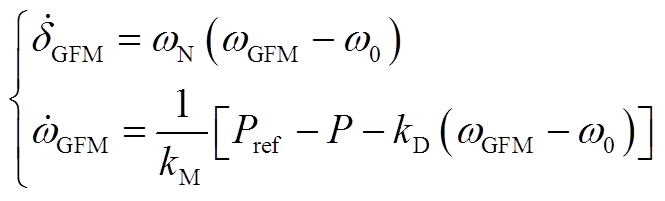（A4）
代数方程为
（A5）
状态矩阵为
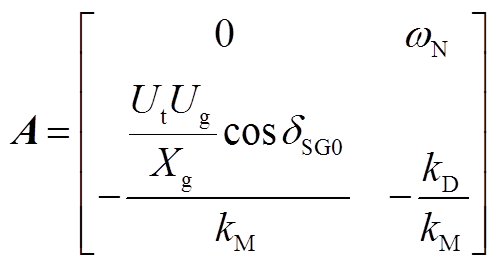（A6）
3）GFL-VSC二阶并网系统微分代数方程和状态矩阵
GFL-VSC二阶并网系统微分方程为
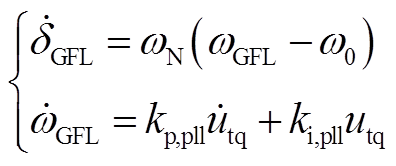（A7）
代数方程为
（A8）
状态矩阵为
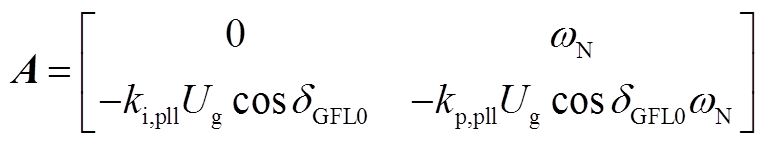（A9）
4）SG四阶并网系统微分代数方程和状态矩阵
SG四阶并网系统微分方程为
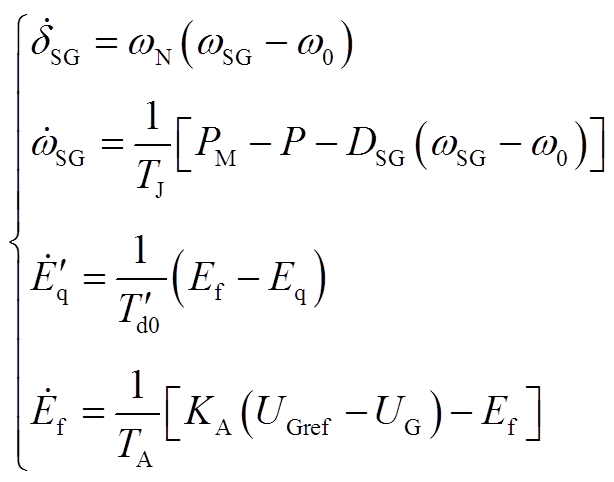（A10）
代数方程为
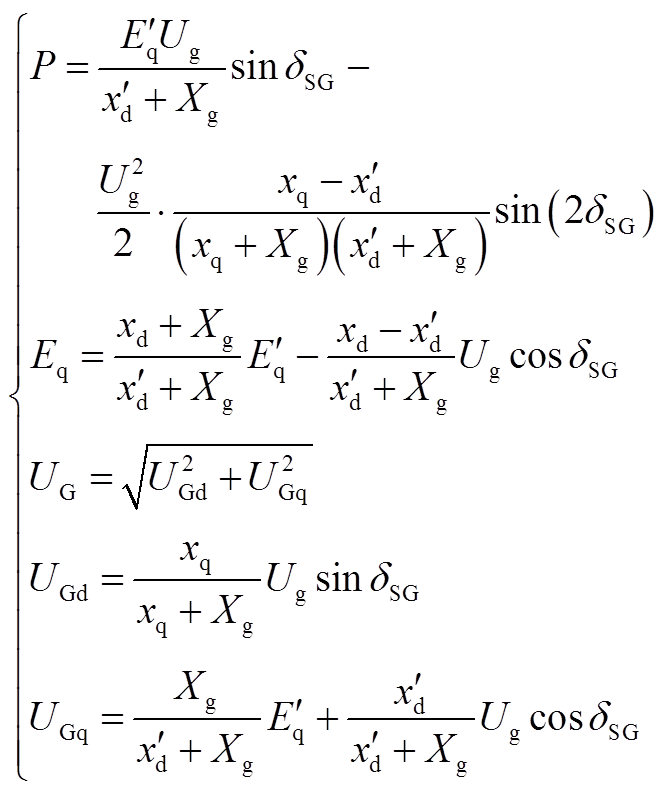（A11）
状态矩阵为
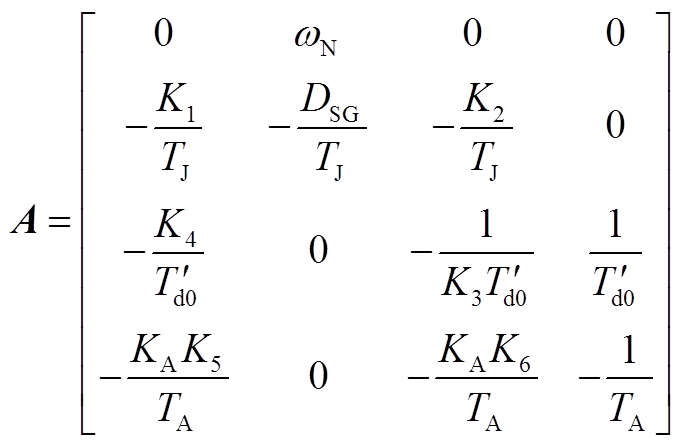（A12）
式中，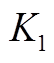
～
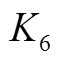分别为
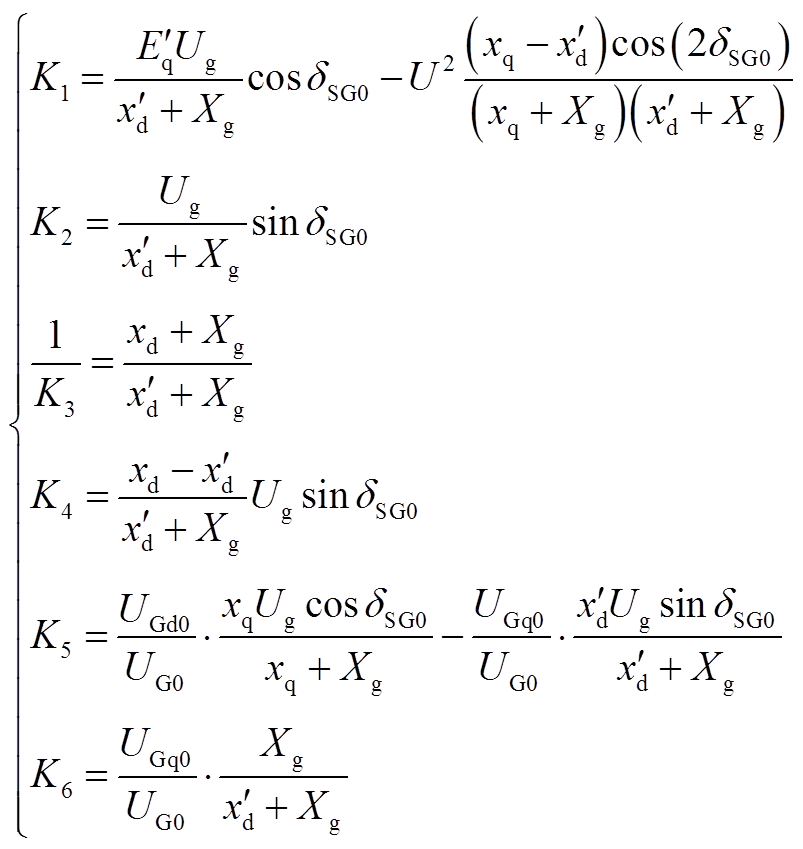（A13）
5）GFM-VSC四阶并网系统微分代数方程和状态矩阵
GFM-VSC四阶并网系统微分方程为
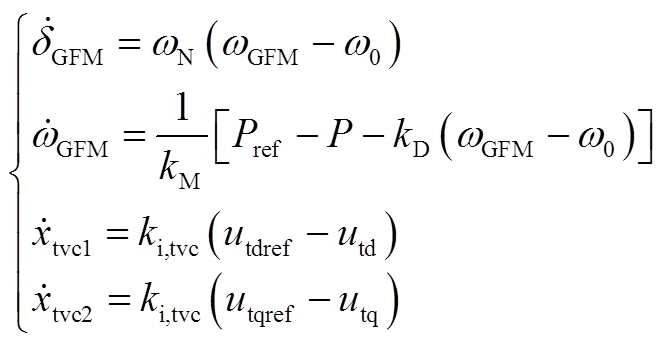（A14）
代数方程为
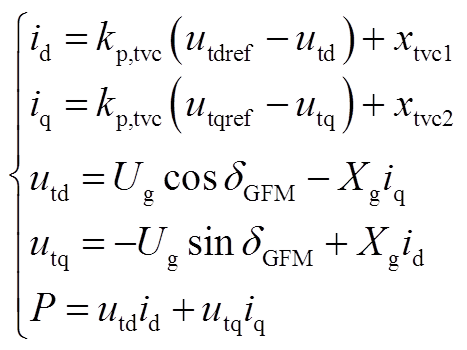（A15）
状态矩阵为
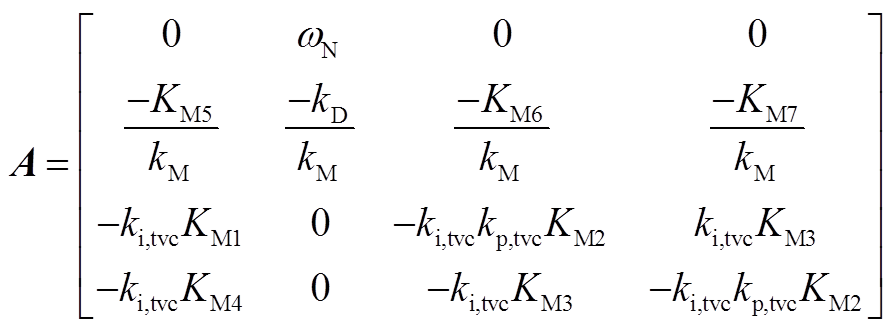（A16）
式中，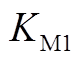
～
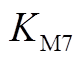分别为
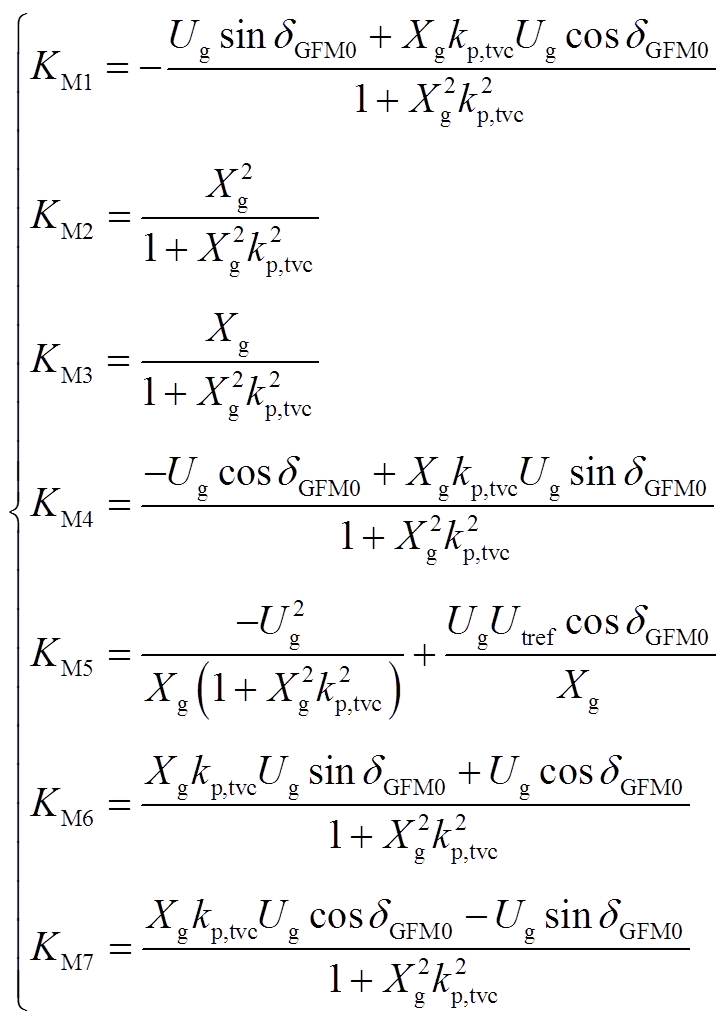（A17）
6）GFL-VSC四阶并网系统微分代数方程和状态矩阵
GFL-VSC四阶并网系统微分方程为
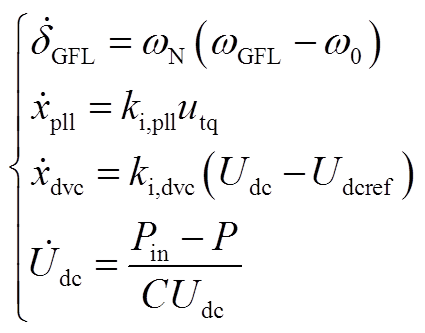（A18）
代数方程为
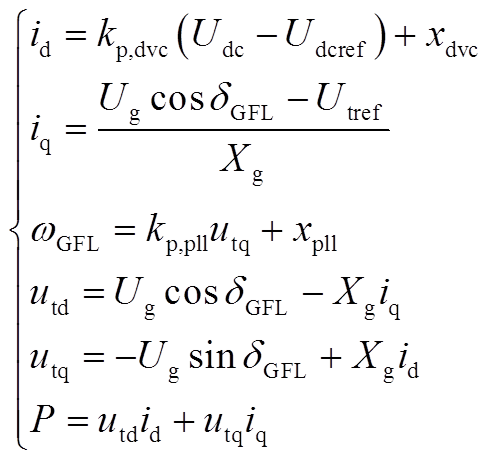（A19）
状态矩阵为
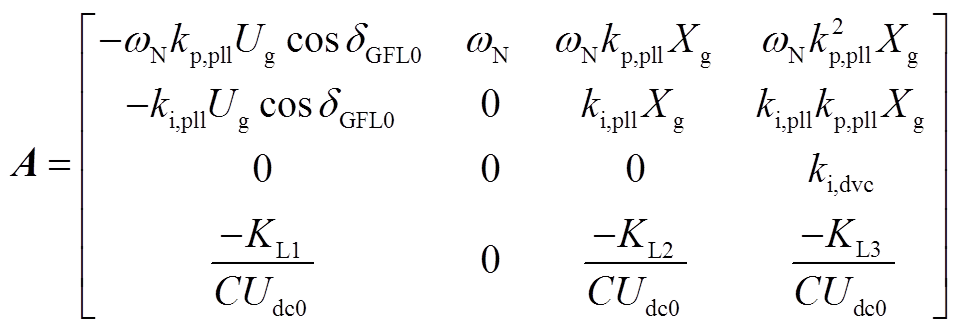（A20）
式中，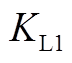
～
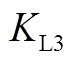分别为
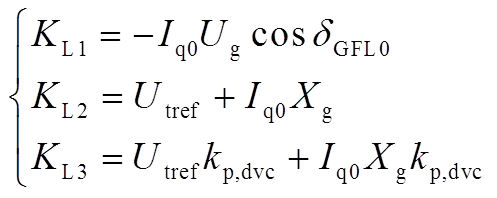（A21）
3. SG、GFM-VSC和GFL-VSC单机无穷大系统模型参数
系统参数：Sbase=2 MW，Ubase=690 V，fbase=50 Hz，Udcbase=1 400 V，Ug=1(pu)，ω0=1(pu)，Pref=1(pu)，Xf =0.05(pu)。
SG控制器参数：DSG=5，TJ=8，E′=1.2(pu)，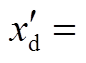
0.2(pu)，xd=0.3(pu)，xq=0.3(pu)，KA=20，TA=0.5，
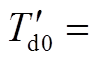4(pu)。
GFM-VSC控制器参数：kD=5，kM=8，kp,tvc=1，ki,tvc=100，Utref =1(pu)。
GFL-VSC控制器参数：kp,pll=50/(100π)，ki,pll=2 000/ (100π)，kp,dvc=3.5，ki,dvc=140，Udcref =1(pu)。
4.考虑/不考虑线路频率动态的跟网型变流器二阶并网系统的小扰动稳定性讨论
在有静态工作点的参数条件下，针对GFL-VSC二阶并网系统，不考虑线路频率动态时，系统不会发生弱电网失稳；考虑线路频率动态后，系统可能会发生弱电网失稳。理论分析如下：
1）不考虑线路频率动态时的GFL-VSC二阶并网系统
微分代数方程见附录第2节，计算可求得系统特征根为
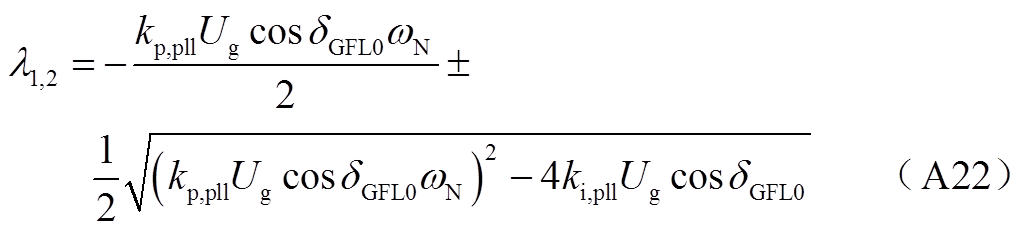
若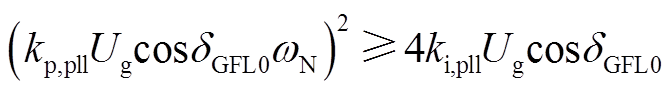
，则特征根为两个实根，其中数值较大的实根λmax为
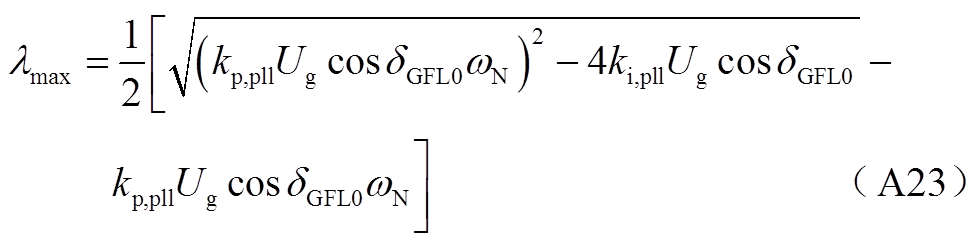
计算可知，λmax恒小于0，所以不存在右半平面实根。
若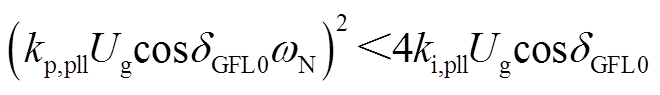
，则特征根为一对共轭特征根，共轭根实部
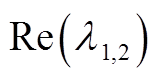为
（A24）
计算可知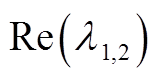，恒小于0，所以不存在右半平面实根。
综上所述，针对GFL-VSC二阶并网系统，不考虑线路频率动态时，系统特征根恒在系统左半平面，系统不会发生弱电网小扰动失稳。
2）考虑线路频率动态时的GFL-VSC二阶并网系统
微分方程同情况1，代数方程为
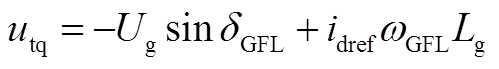（A25）
式中，Lg为电感标幺值，在数值上同电抗标幺值Xg。
计算可得状态矩阵为
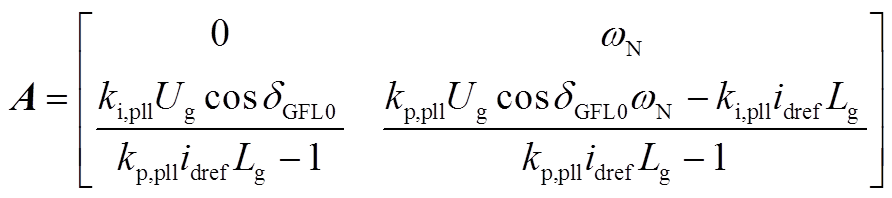（A26）
可求得系统特征根为
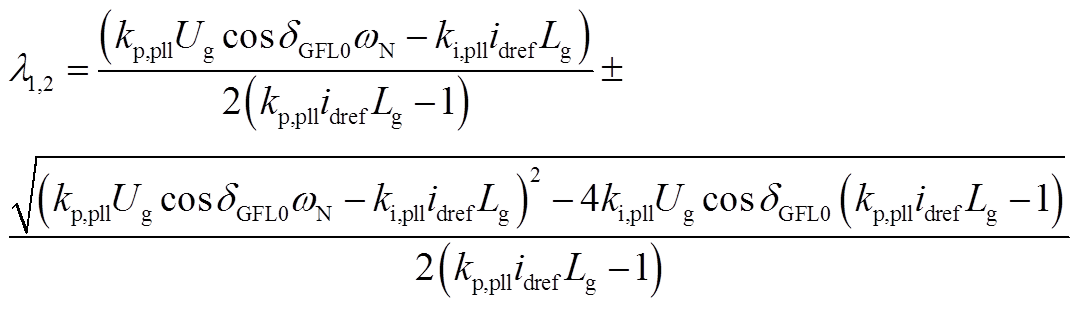（A27）
一般参数条件下，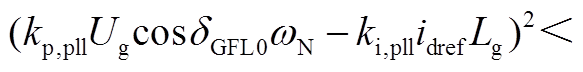
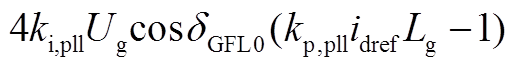，特征根为一对共轭根，共轭根的实部Re(λ1,2)为
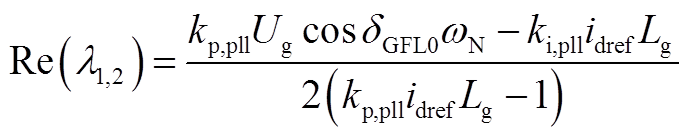（A28）
当满足
和
时，共轭根实部小于0。在弱电网时，可能无法满足
，共轭根实部大于0，存在右半平面特征根，系统发生失稳。
所以针对GFL-VSC二阶并网系统，考虑线路频率动态后，弱电网时系统特征根可能在右半平面，系统发生弱电网小扰动失稳。
参考文献
[1] 国家能源局关于印发2023年度全国可再生能源电力发展监测评价结果的通知[EB/OL]. 国家能源局, [2024-10-10]. https://zfxxgk.nea.gov.cn/2024-10/10/ c_13107871 15 .htm.
[2] 袁小明, 程时杰, 胡家兵. 电力电子化电力系统多尺度电压功角动态稳定问题[J]. 中国电机工程学报, 2016, 36(19): 5145-5154, 5395. Yuan Xiaoming, Cheng Shijie, Hu Jiabing. Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems[J]. Proceedings of the CSEE, 2016, 36(19): 5145-5154, 5395.
[3] Huang S H, Schmall J, Conto J, et al. Voltage control challenges on weak grids with high penetration of wind generation: ERCOT experience[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 2012: 1-7.
[4] 孙华东, 许涛, 郭强, 等. 英国“8·9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192. Sun Huadong, Xu Tao, Guo Qiang, et al. Analysis on blackout in Great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[5] 刘林, 王大龙, 綦晓, 等. 基于双锁相环的海上风场综合惯量调频策略研究[J]. 发电技术, 2024, 45(2): 282-290． Liu Lin, Wang Dalong, Qi Xiao, et al. Study on double phase-locked loop on the synthetic inertia control of offshore wind farm frequency regulation[J]. Power Generation Technology, 2024, 45(2): 282-290.
[6] 李红, 梁军杨, 王振民, 等. 跟网型变换器的小扰动同步稳定机理分析与致稳控制[J]. 电工技术学报, 2024, 39(12): 3802-3815. Li Hong, Liang Junyang, Wang Zhenmin, et al. Small signal synchronization stability analysis and improved control strategy for grid following converter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3802-3815.
[7] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[8] Wang Dong, Liang Liang, Shi Lei, et al. Analysis of modal resonance between PLL and DC-link voltage control in weak-grid tied VSCs[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1127-1138.
[9] Dong Dong, Wen Bo, Boroyevich D, et al. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 310-321.
[10] 梁军杨, 李红, 宋国杰, 等. 多时间尺度控制下跟网型变换器的同步稳定性分析与改进控制[J]. 电工技术学报, 2024, 39(22): 7182-7196. Liang Junyang, Li Hong, Song Guojie, et al. Synchronization stability analysis and enhanced control of grid-following converters under multi-timescale control[J]. Transactions of China Electrote-chnical Society, 2024, 39(22): 7182-7196.
[11] 吴峰, 鲍颜红, 郑建勇, 等. 改善暂态稳定性的多构网型变换器频率同步协同控制[J]. 电力系统自动化, 2025, 49(22): 55-67. Wu Feng Bao Yanhong Zheng Jianyong, et al. Cooperative frequency synchronization control of multiple grid-forming converters for improvement of transient stability[J]. Automation of Electric Power Systems, 2025, 49(22): 55-67.
[12] 刘朋印, 谢小荣, 李原, 等. 构网型控制改善跟网型变流器次/超同步振荡稳定性的机理和特性分析[J]. 电网技术, 2024, 48(3): 990-997. Liu Pengyin, Xie Xiaorong, Li Yuan, et al. Mechanism and characteristics of grid-forming control for improving sub/super synchronous oscillation stability of grid-following-based grid-connected converter[J]. Power System Technology, 2024, 48(3): 990-997.
[13] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359. Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[14] 高本锋, 邓鹏程, 孙大卫, 等. 基于匹配控制的构网型直驱风电场次同步振荡机理与特性研究[J]. 电工技术学报, 2024, 39(9): 2755-2770. Gao Benfeng, Deng Pengcheng, Sun Dawei, et al. Mechanism and characteristics of subsynchronous oscillation of grid-forming direct-drive wind farm based on matching control[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2755-2770.
[15] Hong Zhenkun, Xu Hongsheng, Hou Zhuoqi, et al. Origin of anomalous instability of grid-forming converters tied to stiff grid[J]. IET Renewable Power Generation, 2023, 17(10): 2563-2574.
[16] 洪镇堃, 占萌. 构网型变流器并网系统在强弱电网下的分岔分析[J]. 电力自动化设备, 2023, 43(9): 27-32, 54. Hong Zhenkun, Zhan Meng. Bifurcation analysis of grid-forming converter system connected with stiff or weak AC grids[J]. Electric Power Automation Equipment, 2023, 43(9): 27-32, 54.
[17] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146. Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance [J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[18] 姚兴, 占萌, 刘琦. 构网型变流器并网系统中功率同步环与端电压环相互作用分析[J]. 电力系统自动化, 2025, 49(16): 175-186. Yao Xing, Zhan Meng, Liu Qi. Analysis on interaction between power synchronization loop and terminal voltage loop in gridconnected system of grid-forming converter[J]. Automation of Electric Power Systems, 2025, 49(16): 175-186
[19] 黄萌, 凌扬坚, 耿华, 等. 功率同步控制的构网型变流器多机交互分析与稳定控制研究综述[J]. 高电压技术, 2023, 49(11): 4571-4583. Huang Meng, Ling Yangjian, Geng Hua, et al. An overview on multi-VSCs interaction analysis and stability controls of grid-forming converters with power synchronization control[J]. High Voltage Engineering, 2023, 49(11): 4571-4583.
[20] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994. Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[21] Li Yitong, Gu Yunjie, Green T C. Revisiting grid-forming and grid-following inverters: a duality theory[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4541-4554.
[22] 屈子森. 高比例新能源电力系统电压源型变流器同步稳定性分析与控制技术[D]. 杭州: 浙江大学, 2021. Qu Zisen. Synchronizing stability analysis and control technology of voltage source converters in power system with high penetration renewables[D]. Hang-zhou: Zhejiang University, 2021.
[23] 李明, 常永康, 毛永涛, 等. 高渗透率新能源发电并网变流器跟网/构网型稳定控制技术综述与展望[J]. 高电压技术, 2024, 50(11): 4773-4788. Li Ming, Chang Yongkang, Mao Yongtao, et al. Review and prospect of stability control techniques for grid-following/grid-forming converters in high-penetration renewable energy generation[J]. High Voltage Engineering, 2024, 50(11): 4773-4788.
[24] Demello F P, Concordia C. Concepts of synchronous machine stability as affected by excitation control[J]. IEEE Transactions on Power Apparatus and Systems, 1969, PAS-88(4): 316-329.
[25] 刘取. 电力系统稳定性及发电机励磁控制[M]. 北京: 中国电力出版社, 2007.
[26] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[27] 闵勇, 陈磊, 姜齐荣. 电力系统稳定分析[M]. 北京: 清华大学出版社, 2016.
[28] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 1979.
[29] Yang Ziqian, Zhan Meng, Liu Dan, et al. Small-signal synchronous stability of a new-generation power system with 100% renewable energy[J]. IEEE Transactions on Power Systems, 2023, 38(5): 4269-4280.
[30] Guo Jian, Chen Yandong, Wang Lei, et al. Impedance analysis and stabilization of virtual synchronous generators with different DC-link voltage controllers under weak grid[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11397-11408.
Abstract The grid-connected systems of synchronous generators (SG) and grid-following converters may experience stability issues under weak grid conditions, while the grid-forming converter systems may face stability issues under stiff grid conditions. Nevertheless, a unified understanding of the instability characteristics of these three types of power sources under varying grid strengths is still lacking. To address this, this paper conducts a comparative analysis of the instability mechanisms under stiff or weak grid conditions for the SG and converter-interfaced generations. Firstly, the small-signal stability of the second-order synchronization loop model and the fourth-order model considering the outer loop for the three types of grid-connected systems was compared using eigenvalue analysis. It is determined that the instability issues under stiff or weak grid conditions for all three power source grid-connected systems are produced by the outer loop control. Next, the Heffron-Phillips-like models were constructed. Analysis is conducted from a unified perspective where the synchronization loop is the dominant loop and the outer loop control is treated as an additional branch. Based on the feedback branch transfer function decomposition method, the feedback transfer functions G(s) with different structures were decomposed into a unified second-order oscillation component H1(s) and a left component H2(s). A unified analysis of the instability mechanisms under stiff or weak grid conditions is conducted. The conclusions of this paper are as follows:
(1) A unified Heffron-Philips-like model was developed for three types of power source grid-connected systems. The study reveals that the different instability phenomena in the weak or stiff grids are due to the involvement of outer loop control. Although the SG and grid-forming converter systems have the same synchronization loop, they exhibit significantly large negative damping coefficients under weak and stiff grid conditions, respectively, due to their differences in the outer loop control structure. This ultimately leads to instability under different grid strengths.
(2) A feedback branch transfer function decomposition method was proposed for the analysis of instability mechanisms. Based on this method, the structural differences in the transfer functions used for stability analysis in different grid-connected systems can be eliminated, enhancing the uniformity of stability comparisons and analyses.
(3) Since the phase of H1(jωn) at the natural oscillation frequency fn is -90°, the differences in the coefficients of H1(s) among the three types of power sources lead to different trends in the relative distance between the system oscillation frequency fs and fn. Consequently, the grid strengths at the instability also differ. It can be deduced that: in weak grids, the fn of the SG is close to fs, leading to instability; in strong grids, the fn of the GFM-VSC is close to fs, resulting in instability; and in weak grids, the fn of the GFL-VSC is far from fs, with the additional influence of the phase from the additional transfer function causing instability.
keywords：Synchronous generator, grid-forming voltage-source converter (GFM-VSC), grid-following voltage-source converter(GFL-VSC), Heffron-Phillips-like model, feedback branch transfer function decomposition method
DOI: 0.19595/j.cnki.1000-6753.tces.242348
中图分类号：TM712
国家自然科学基金资助项目（U22B6008）。
收稿日期 2024-12-26
改稿日期 2025-06-12
刘 琦 女，2001年生，硕士研究生，研究方向为构网型变流器并网系统稳定性。E-mail：liuqi67@hust.edu.cn
占 萌 男，1974年生，教授，博士生导师，研究方向为电力电子化电力系统动态、新能源并网稳定。E-mail：zhanmeng@hust.edu.cn（通信作者）
（编辑 赫 蕾）