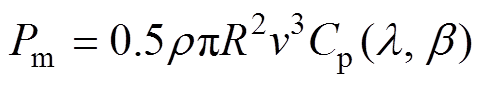 (1)
(1)
摘要 通过变桨减载预留备用容量是变速风电机组参与调频的一种重要技术方案,但参数设置不当时风电机组可能出现振荡甚至不稳定。该文首先通过变桨减载调频风电机组模型,对不合理风机参数下风电机组发生振荡的场景进行仿真。然后在该场景下分析变桨减载调频风电机组的稳定性,对机组动态方程进行线性化,基于阻尼转矩法分析了风电机组电磁功率、机械功率各部分的阻尼转矩及不同因素的影响,重点分析桨距角控制产生的阻尼转矩,得到参数不当时桨距角控制产生的负阻尼转矩是导致风电机组不稳定的主要原因。最后推导了具有解析表达式的参数稳定条件,当控制参数满足所提约束条件时,可以保证调频风电机组的稳定性。仿真结果验证了所提方法的有效性。
关键词:风电机组 变桨减载调频 稳定性 桨距角控制器 阻尼转矩 参数稳定条件
高比例新能源接入电网导致系统频率安全问题凸显,因此风电、光伏等新能源参与电网调频已经成为一种现实需求[1]。调频需要能量储备,风电机组可通过调节转子转速或桨距角减载运行,预留一部分功率备用,在系统发生频率跌落时增发有功功率参与一次调频[2-3]。因为桨距角控制的调节能力较强,调节范围较大[3],所以变桨减载是一种重要的技术方案。但变桨减载风机在采用不同的桨距角控制参数时,风电机组稳定性不同甚至可能引起失稳[4],其机理有待进一步研究。
有关于风机接入对于系统稳定性的影响,相关学者进行了大量机理性研究。文献[5]对含双馈感应发电机(Doubly-Fed Induction Generator, DFIG)系统进行小扰动建模,利用特征值分析了不同电网强度对系统振荡的影响规律,得出了锁相环是导致DFIG系统在弱电网下振荡的主导因素这一结论。文献[6]建立了DFIG系统的全维状态空间模型,使用状态空间分析法对DFIG并网的次同步振荡问题进行了研究。文献[7]中构建了精细化的DFIG线性化模型,并基于转矩分析法分析了电网频率控制对于风机的传统系统阻尼的影响。文献[8]针对构网型风机接入二极管整流单元型高压直流送出系统,分析了换流器关键控制参数对暂态稳定性的影响。文献[9]针对风火打捆经串补外送系统,对各元件进行“模块化”建模,通过将火电机组复频域模型推广至双馈风机,提出一种适用于含双馈风电场系统的分散消元式复转矩系数法,利用该方法从阻尼特性角度阐释系统引起多模态次同步谐振的机理,并分析主导振荡因素对次同步谐振的影响。上述研究均表明,风机的接入对于系统稳定性会产生深刻影响,但是已有机理研究大多是针对采用最大功率点跟踪(Maximum Power Poing Tracking, MPPT)模式的风机,缺少对风机变桨调频场景下的稳定性研究。
而关于变桨风机,由于桨距角PI控制器一般采用固定参数,且有较大迟延,无法很好地适应非线性和时变性严重的风电系统[4]。现有针对变桨风机的研究多集中于以修改控制参数或控制方法等方式改善其稳定性,却未能从理论层面给出影响稳定性的环节[10-17]。文献[10-11]通过优化变桨PI控制参数,保证了功率的稳定输出。文献[12]考虑引入功率信号调节桨距角,抑制电网低频振荡,提高系统稳定性。文献[13, 15]利用模糊自适应整定PID控制方法提升了风力发电系统中变桨距控制的效果。文献[14]以永磁直驱机组为研究对象,围绕永磁直驱机组的能量捕捉、传递、转化过程,结合机组风能捕捉系数与桨距角、叶尖速比之间的关系,从机理角度进行定量分析,构建了典型机组的能量传递模型。文献[16]提出了风电平滑功率控制方法,在保证平滑控制效果的同时,能有效降低变桨动作频率和幅度,并减小变桨伺服机构的疲劳和叶片载荷。文献[17]采用人工蜂群算法进一步对自抗扰变桨控制器的参数进行优化,简化了控制器参数的整定过程,转速响应速度有所提高。文献[4]基于风电调频控制建立线性化方程用于系统特征结构分析,通过仿真讨论变桨响应时间对PI参数的影响,却缺乏机理层面的分析和推导。文献[18]基于DFIG详细模型,计算风电系统特征值以调节控制参数,但由于模型过于复杂,无法定量给出具体环节的影响和其解析表达。
已有研究发现桨距角控制器参数设置不当时,风电机组可能出现振荡甚至不稳定,并通过仿真进行分析,但只能定性讨论其规律,对风机变桨时各个环节对稳定性的影响缺乏机理层面的分析和推导,无法给出解析解以分析验证。因为风速大部分时间位于风机的MPPT区,所以本文研究重点放在了风机的MPPT区间。本文基于简化变桨调频风电机组模型进行理论分析和解析推导,对其中的非线性部分进行线性化,并利用阻尼转矩法分析各环节的阻尼转矩、影响因素,给出了其解析表达式,定量分析得到了风机不稳定的主要原因。这对其他文献中的结论从理论上给出了验证,并可以定量给出其影响。本文进一步推导得到解析的参数稳定条件。在具体参数整定时还需要考虑许多其他的约束和不同的目标,从而整定出不同的参数。整定参数时考虑该约束可有效避免系统不稳定。
风机变桨减载调频模型包括风机转子运动方程、风机空气动力学模型、风机桨距角控制模型、功率控制模型以及风机调频控制模型。风机输出功率通过电力电子装置控制,非常快速、灵活。在相对较慢的机电暂态过程中,可忽略风力发电系统的电磁暂态过程及其对应的控制器等快动态部分,因此,风电机组电气部分简化为一个受控功率源,可以迅速输出指令功率,这也是风电调频模型中一种常用的做法[19]。
风机输入机械功率公式为
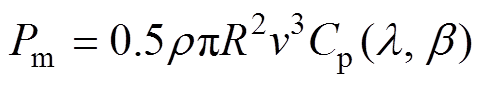 (1)
(1)
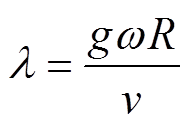 (2)
(2)
式中,Cp为风能利用系数;r为空气密度;v为风速;R为风轮叶片半径;l为叶尖速比;b为桨距角;w为风机发电机转速;g为齿轮箱传动比。
风能利用系数的具体函数形式与风机有关,常用以下函数来拟合[20]。
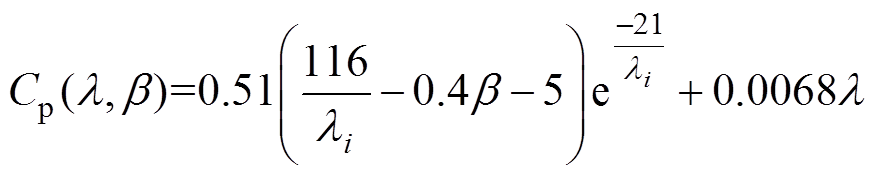 (3)
(3)
其中
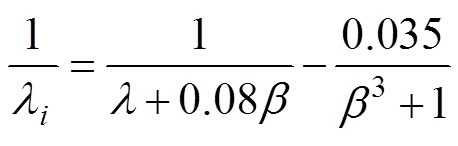 (4)
(4)
风电机组处于稳定运行模式时变桨减载运行,风电机组减载率d%的定义为
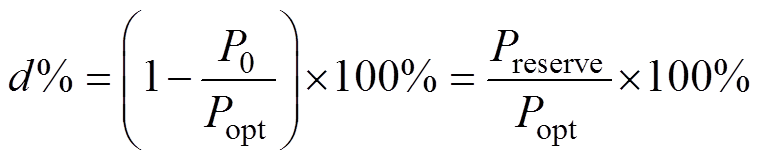 (5)
(5)
式中,P0为风电机组的有功功率初始值;Popt为当前风速下可获得的最大有功功率;Preserve为风电机组的备用功率。
变桨控制器的动态特性一般用一阶惯性环节表示,桨距角控制器模型如图1所示,最终通过对转速的PI控制实现转速基本不变,释放预留的功率到电磁功率中达到调频的效果。控制方程[19]为
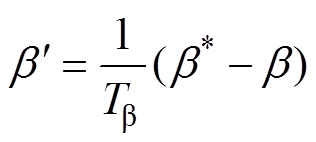 (6)
(6)
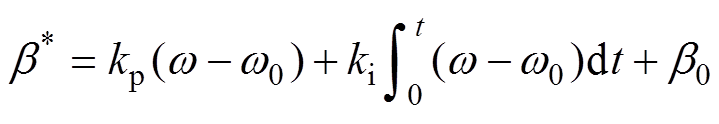 (7)
(7)
式中,kp、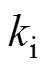 分别为PI控制器中比例和积分参数;w0为转速初值;Tb为桨距角控制器中的时间常数;
分别为PI控制器中比例和积分参数;w0为转速初值;Tb为桨距角控制器中的时间常数;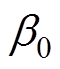 为风电机组功率初值所对应的桨距角初值;
为风电机组功率初值所对应的桨距角初值;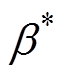 为PI控制的桨距角参考值;b为实际桨距角。
为PI控制的桨距角参考值;b为实际桨距角。
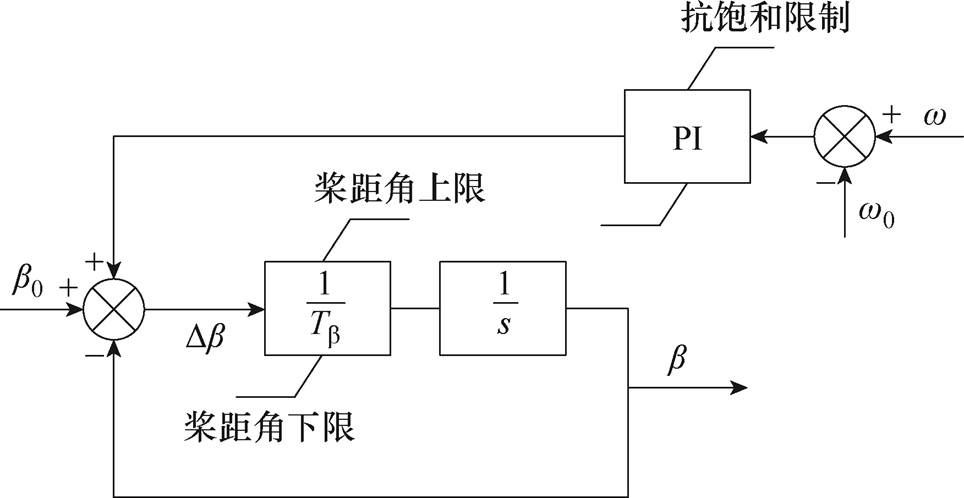
图1 桨距角控制器模型
Fig.1 Pitch angle controller model
风机电功率控制策略如下。风机常规的MPPT控制是使其与风机转速三次方成正比[21]。
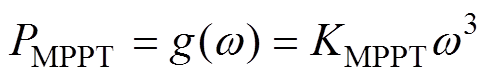 (8)
(8)
变桨减载情况下需要修正比例系数。在桨距角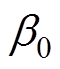 的情况下得到减载运行下的类MPPT控制系数kde,kde跟随工况改变而改变。小扰动研究的短时间尺度内近似认为风速不变,因此可以将kde视为定值。实现正常运行时的功率控制,得到减载运行功率Pde,即
的情况下得到减载运行下的类MPPT控制系数kde,kde跟随工况改变而改变。小扰动研究的短时间尺度内近似认为风速不变,因此可以将kde视为定值。实现正常运行时的功率控制,得到减载运行功率Pde,即
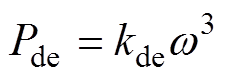 (9)
(9)
风机参与调频并采用最经典的频率下垂控制策略,风机的调频功率为
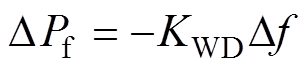 (10)
(10)
式中,KWD为频率下垂系数。
根据风机基准功率的不同,有两种控制策略。一种是变基准功率策略,将风机调频功率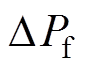 叠加到风机功率运行控制的变基准功率信号Pde上,得到参与调频时风机输出电功率信号PWe为
叠加到风机功率运行控制的变基准功率信号Pde上,得到参与调频时风机输出电功率信号PWe为
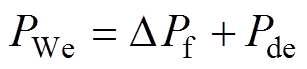 (11)
(11)
另一种是定基准功率控制策略,将调频功率叠加到固定的基准功率上(一般为调频前机组输出功率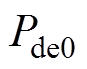 ),风机输出功率为
),风机输出功率为
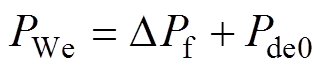 (12)
(12)
系统频率变化时,风机改变电磁功率后导致转速变化,转速服从式(13)的转子运动方程,即
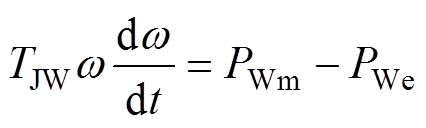 (13)
(13)
式中,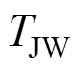 为风机转子惯量时间常数;
为风机转子惯量时间常数;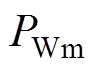 为风机输入机械功率。
为风机输入机械功率。
如果电力系统遭遇功率缺额将导致系统频率下降,风机转速将会降低,根据图1,为了维持转速,桨距角开始减小,从而释放出备用容量。
综上所述,本文建立的风机减载调频模型如图2所示,包含风能捕获、正常的MPPT功率控制和调频功率控制、风机转子运动方程以及桨距角控制等环节,上述环节是影响风电调频动态过程的关键环节。
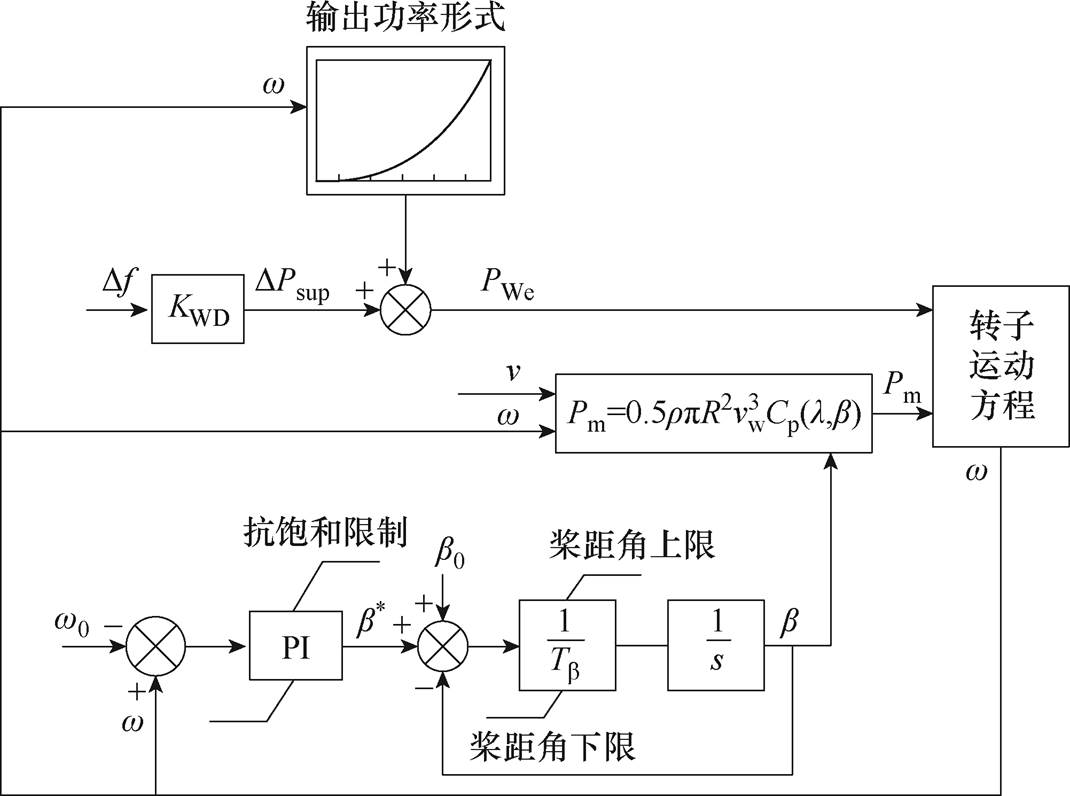
图2 变桨减载调频风电机组模型
Fig.2 Model of deloaded wind turbine generator participating in frequency regulation with pitch angle reserve
此外,因为本文研究的振荡频率较低(图3中振荡的频率为0.14 Hz左右),远低于风电机组轴系多质量块之间扭振的频率,因此风机模型中采用单质量块。
本文重点关注风电机组小扰动稳定性,由于随机风对于风机而言就是一个外部扰动,在稳定性分析中可作为外部扰动量,因此下文仿真中都为定风速场景。风电机组参数TJW=2 s, Tb=2 s[22]。风机风速为8.501 0 m/s,该风速下风机理论最大功率为0.56(pu),根据目前电网一次调频要求,本文减载率定为6%[23],风机初始桨距角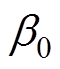 =1.115 4°,初始转速0.977 6(pu),减载后运行功率
=1.115 4°,初始转速0.977 6(pu),减载后运行功率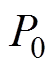 =0.526 4(pu),风机减载预留的功率备用为0.033 6(pu)。
=0.526 4(pu),风机减载预留的功率备用为0.033 6(pu)。
为了说明参数设置不当时会出现小扰动不稳定情况,本文设置kp=30、ki=100,在图2的功率信号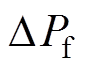 处施加微小功率扰动(0.000 01(pu)),得到风机转速、功率、桨距角曲线如图3所示。图3证明了在控制参数不合理时,风电机组发生小扰动不稳定为发散的振荡,此时该平衡点为不稳定平衡点。
处施加微小功率扰动(0.000 01(pu)),得到风机转速、功率、桨距角曲线如图3所示。图3证明了在控制参数不合理时,风电机组发生小扰动不稳定为发散的振荡,此时该平衡点为不稳定平衡点。
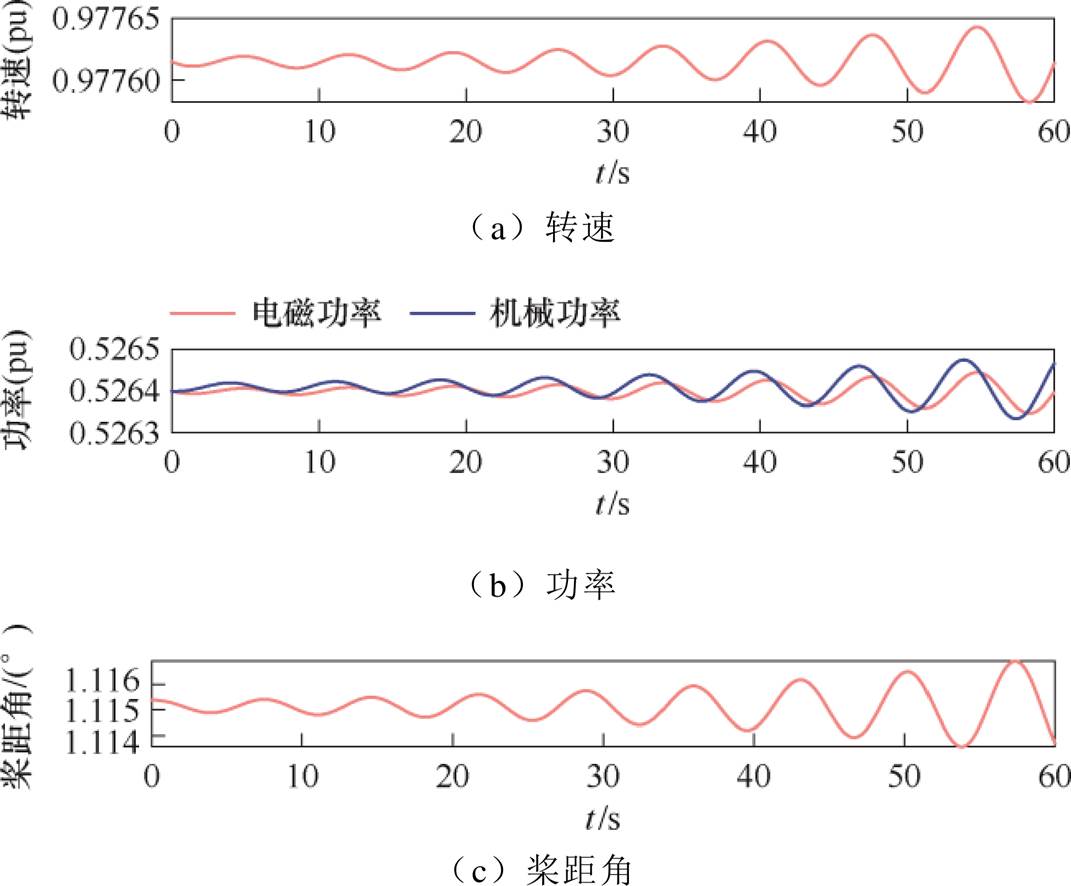
图3 风机转速、调频功率、桨距角曲线
Fig.3 Wind turbine rotor speed, frequency regulation power, pitch angle curves
根据第1节仿真可知,不合理控制参数下风电机组会出现小扰动不稳定,本节重点对变桨减载调频的风电机组进行稳定性分析。文中的风机模型考虑了输出功率控制环节与输入机械功率环节,具体包括变桨控制、转速控制、电磁功率控制。
由式(7)可得桨距角控制器频域方程为
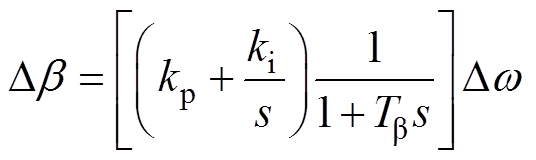 (14)
(14)
式中,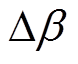 为桨距角偏差;
为桨距角偏差;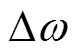 为机组转速偏差。
为机组转速偏差。
式(13)转子运动方程可线性化为
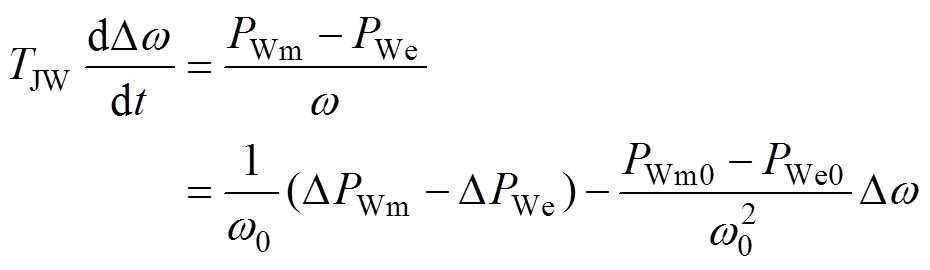 (15)
(15)
由于稳态时机械功率等于电磁功率,即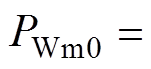
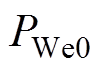 ,式(15)转换为频域方程为
,式(15)转换为频域方程为
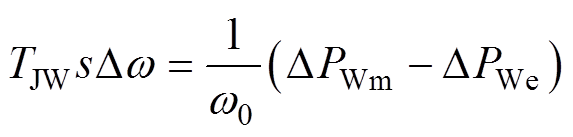 (16)
(16)
风机机械功率有较强非线性(见式(1)),结合式(3)可知,风机机械功率与w和b相关。在小扰动稳定问题的时间尺度上,可以认为桨距角和转速对风机机械功率的影响是相互独立的,可线性化表示为
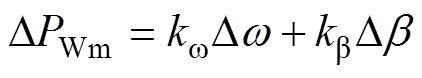 (17)
(17)
式中,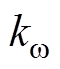 为机械功率-转速灵敏度;
为机械功率-转速灵敏度;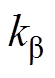 为机械功率-
为机械功率-
桨距角灵敏度。
将调频功率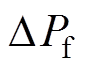 视为外部功率扰动
视为外部功率扰动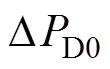 ,变基准功率策略下,转速变化导致的电磁功率变化可以表示为
,变基准功率策略下,转速变化导致的电磁功率变化可以表示为
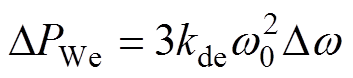 (18)
(18)
综合式(14)、式(16)~式(18),可以得到变基准功率策略下风电机组外部功率扰动量和转子转速偏差的框图如图4所示。图4中,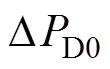 为外部功率扰动。其闭环传递函数为
为外部功率扰动。其闭环传递函数为
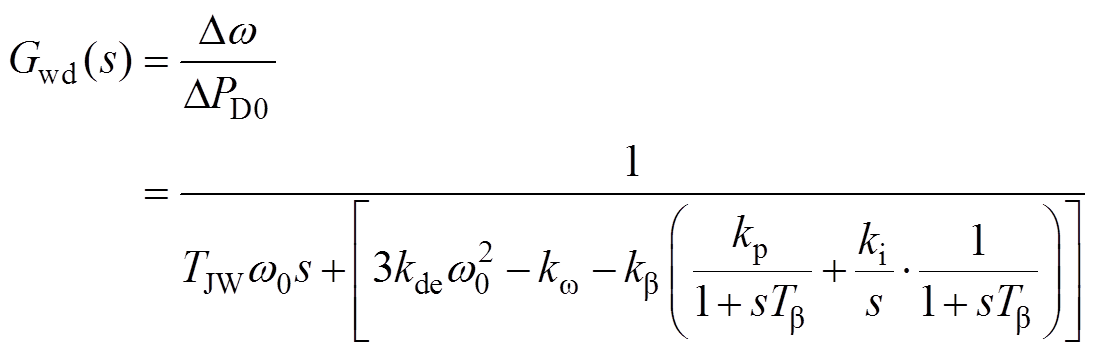 (19)
(19)
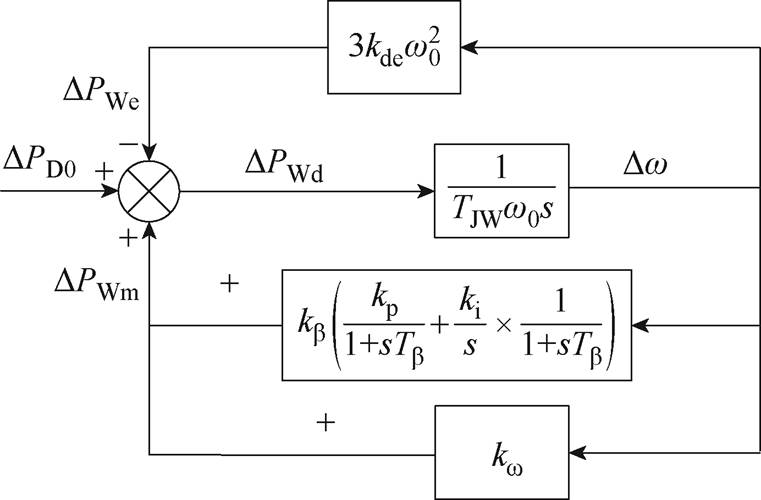
图4 变桨减载调频风电机组模型
Fig.4 Linearized model of deloaded wind turbine generator participating in frequency regulation with pitch angle reserve
计算式(19)得到传递函数的极点为-1.319 7和0.036 92±j0.881 7。其中有一对正实部的极点,可知风机此时确实小扰动不稳定,和前面时域仿真的结果一致,也验证了线性化模型的正确性。
由于本文推导得到风机小扰动模型(见图4)和同步机小扰动模型具有相通之处,因此本节利用阻尼转矩法[23]分析风电机组阻尼特性与稳定性,掌握风机不稳定的机理,并为解析推导参数稳定条件提供基础。
根据阻尼转矩法的基本思想,图4中各反馈支路形成的功率偏差中,和转速Dw同相位的部分即为阻尼转矩。DPWm中和Dw同相位的部分为负阻尼转矩,DPWe中和Dw同相位的部分为正阻尼转矩。具体做法为假设根据反馈支路,功率偏差和转速偏差之间的传递函数为DP=G(s)Dw,将s=jwd代入可得
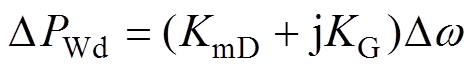 (20)
(20)
式中,wd为振荡角频率;KmD为阻尼转矩系数;KG为同步转矩系数。
根据图4,风电机组总阻尼系数表达式为
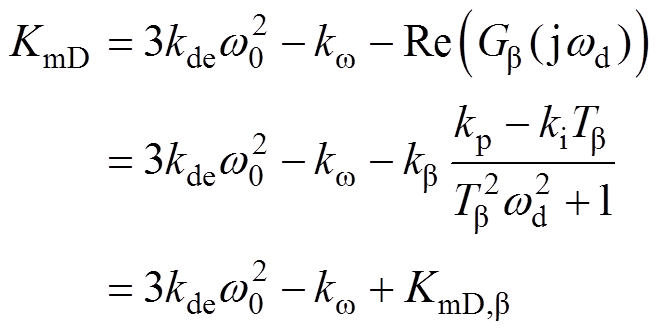 (21)
(21)
式中,电功率反馈支路对应阻尼为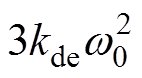 ,机械功率反馈支路对应阻尼为
,机械功率反馈支路对应阻尼为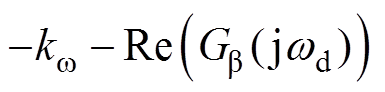 ,传递函数
,传递函数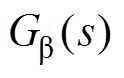 为图4中桨距角控制环节对应的反馈支路,表示为
为图4中桨距角控制环节对应的反馈支路,表示为
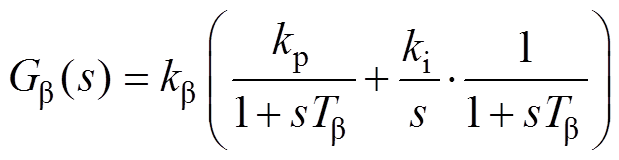 (22)
(22)
从总阻尼表达式(21)中可以得出:
(1)电磁功率阻尼:功率策略是风电机组阻尼转矩系数的重要组成部分。选取变基准功率策略,此项为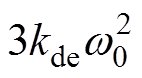 ,恒为正,在上面的算例中,该阻尼转矩大小为1.615 4。当功率策略为定功率策略时,则为0。因此,变基准功率策略更有利于风机的稳定性。(2)机械功率阻尼包含两个部分:机械功率-转速系数-kw和
,恒为正,在上面的算例中,该阻尼转矩大小为1.615 4。当功率策略为定功率策略时,则为0。因此,变基准功率策略更有利于风机的稳定性。(2)机械功率阻尼包含两个部分:机械功率-转速系数-kw和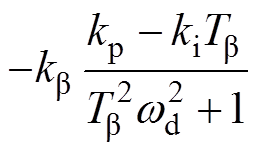 ,同样是风电机组阻尼转矩系数的组成部分。
,同样是风电机组阻尼转矩系数的组成部分。
根据图5转速-机械功率曲线可知,在最大机械功率点Pmax左边曲线斜率即kw为正,右边为负,即运行点在曲线左半支时该阻尼转矩为负,右半支为正。但是,本文的控制策略为变桨减载调频,在类MPPT控制下转速一般为Pmax对应转速大小,该系数-kw比较小,在1.2节算例中,该阻尼转矩系数为-0.157 0。
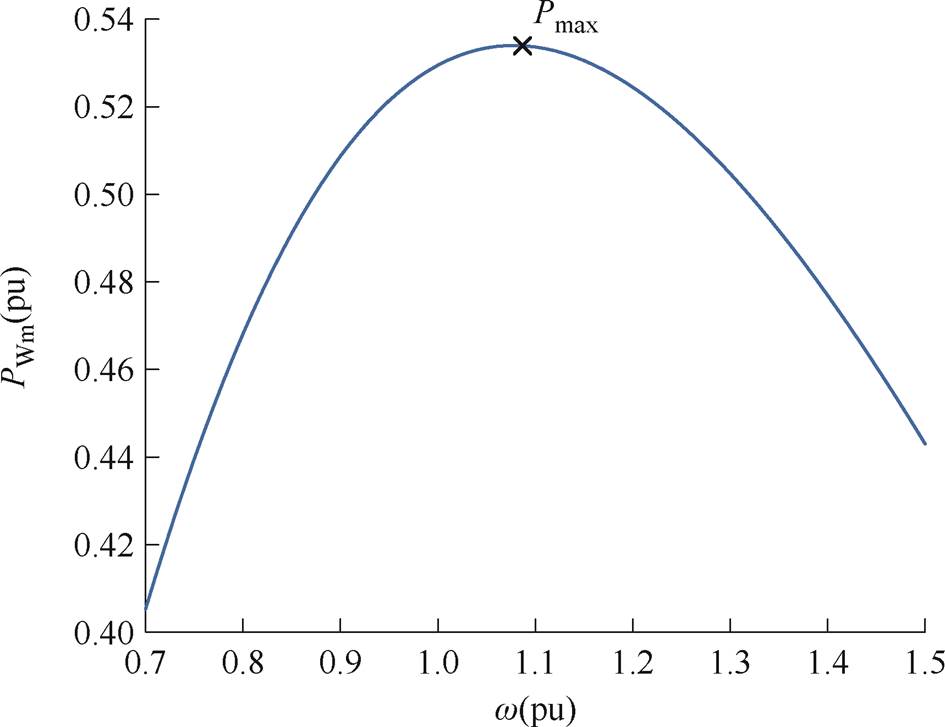
图5 转速-机械功率曲线
Fig.5 Rotor speed-mechanical power curve
机械功率阻尼的第二部分为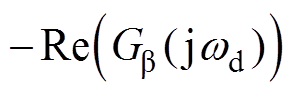 ,由桨距角控制产生,具体表示为
,由桨距角控制产生,具体表示为
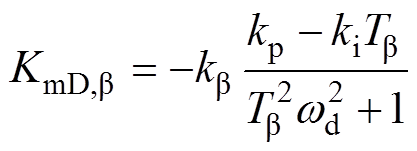 (23)
(23)
在1.2节算例中,该阻尼转矩系数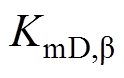 为-1.662 4。
为-1.662 4。
三部分阻尼转矩系数相加得到总阻尼转矩系数为-0.204 1,总阻尼转矩为负,系统不稳定,和前面时域仿真以及极点分析的结果一致。同时,分析各反馈支路阻尼转矩可以得到:桨距角控制产生的负阻尼转矩是导致风电机组不稳定的主要原因。
下面重点分析桨距角控制产生的阻尼转矩。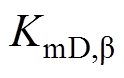 主要受
主要受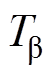 、
、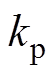 、
、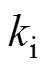 三个参数影响。
三个参数影响。
(1)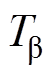 越大,
越大,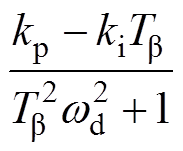 会越小,由于
会越小,由于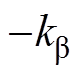 为正数,所以
为正数,所以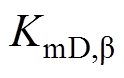 会越小,因此桨距角动作的延时越大,风电机组越容易不稳定。
会越小,因此桨距角动作的延时越大,风电机组越容易不稳定。
(2)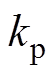 越大或
越大或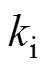 越小,则
越小,则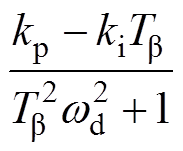 会越大,
会越大,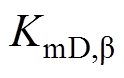 越大,因此,增大比例系数或减小积分系数
越大,因此,增大比例系数或减小积分系数
有利于风电机组的稳定性。
上述结论和文献[4]中的结论是一致的,但文献[4]中是通过仿真分析归纳的结论,本文则通过解析推导进行了机理上的说明。以上分析和下文给出的稳定条件并未针对容量大小加以要求,所以对于不同容量大小的机组都是适用的。
根据第2.2节中阻尼转矩分析可得使风机稳定的桨距角控制器参数条件,由此可避免参数设置不合理。除了相关参数外,由上文可知,变基准功率策略和定基准功率策略也对风电机组稳定性有较大影响。
而在调频过程中,相比变基准功率策略,定基准功率策略可以提升系统频率稳定性,但是定基准功率策略对转速保护是不利的。以频率下降场景一次调频为例,由于风机惯性和延迟,电磁功率无法迅速跟踪风机机械功率,导致风机转速下降。定基准功率策略下电磁功率PWe不随转速变化保持稳定值;变基准功率策略下的电磁功率PWe会跟随转速下降,从而减少了转速超调。因此,定基准功率策略会更容易触及风机转速下限进而退出调频,对电网频率而言,也会更容易出现二次跌落。除此之外,定基准功率策略会涉及控制切换,如从MPPT控制切换到定基准功率上,会导致振荡等问题。两种策略各有利弊,一般可以认为定基准功率对调频更为有利,变基准功率对风机转速保护更为有利。
通过上文分析,不论哪种策略,为了保证风机稳定,总的阻尼转矩应大于0,由此得到了风机稳定条件如下:
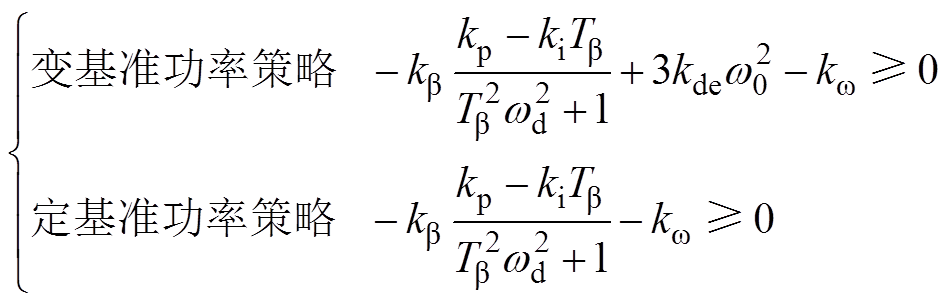 (24)
(24)
进一步变形得到桨距角控制器参数的稳定条件为
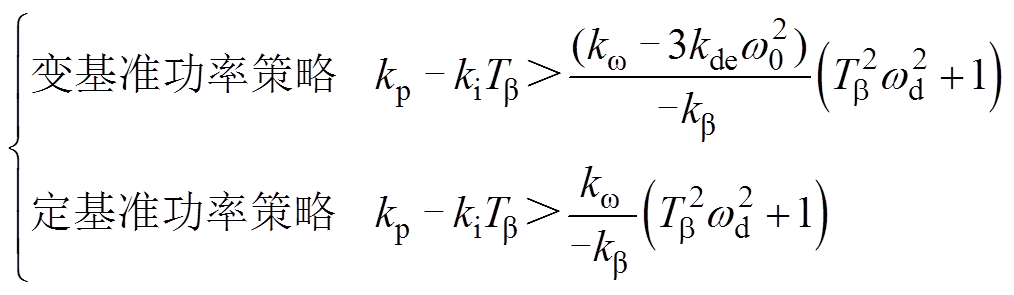 (25)
(25)
式中,振荡角频率wd是一个未知的变量,需要事先估计wd的范围,然后取保守解,保证该范围内上述稳定条件都得到满足。以变基准功率策略为例,根据式(24)的表达式和各项的正负,wd应取下限wlow,此时有
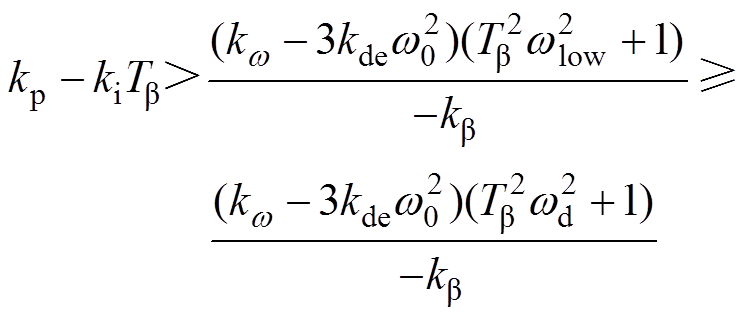 (26)
(26)
机组可以保证稳定性。
本节在RTLab实时仿真平台上利用双馈风机的电磁暂态模型进行仿真验证,详细模型如图6所示。实时仿真平台RTLab设备和环境见附录第1节。
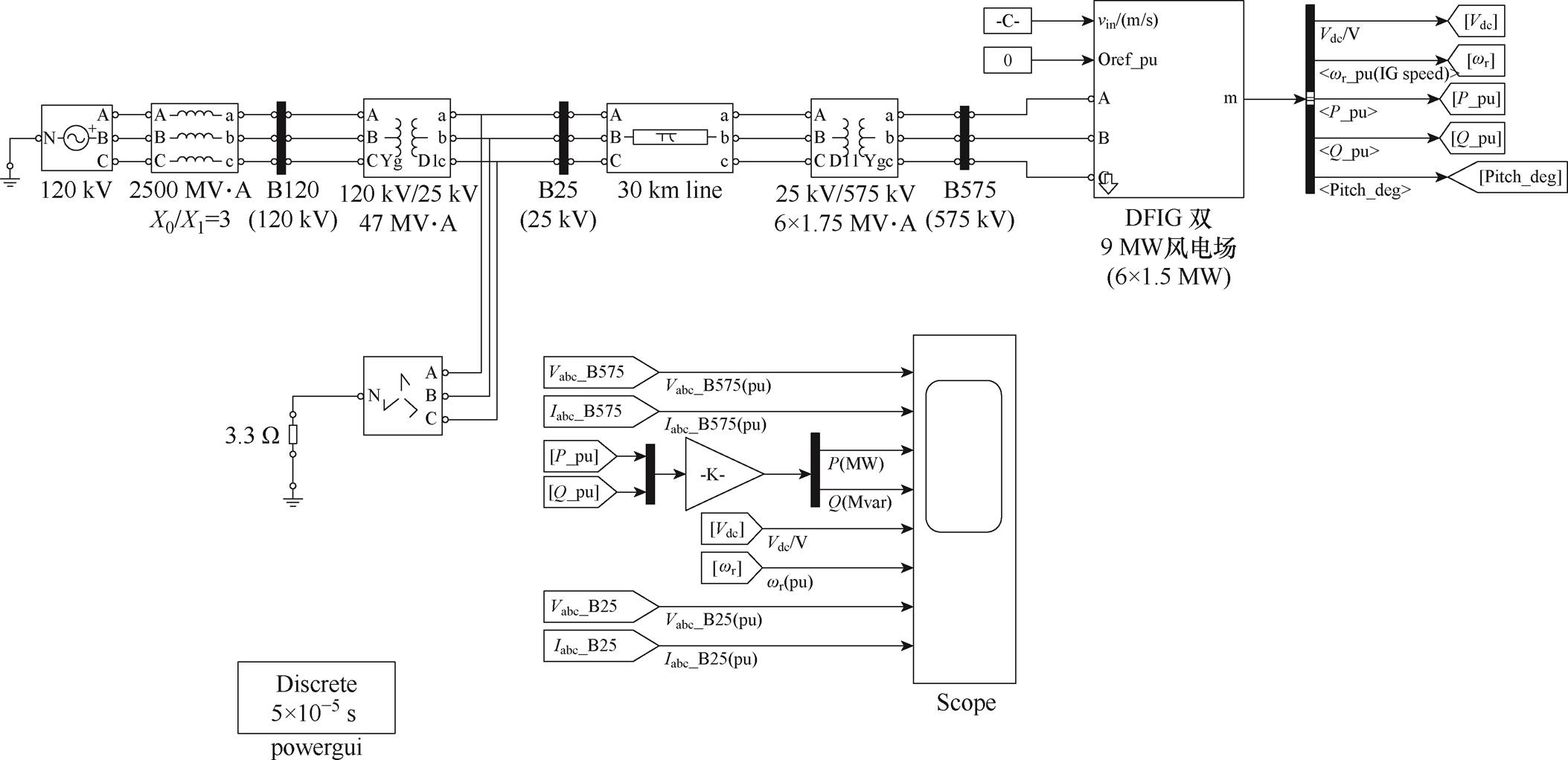
图6 双馈风机电磁暂态详细模型
Fig.6 Detailed model of DFIG
风电机组在不同工况下进行分析。风机风速为8.501 0 m/s时相关仿真参数已于第1.2节处给出。风速7.501 0 m/s下,风机理论最大功率为0.385(pu),减载率为6%,减载后运行功率P0=0.361 9(pu),风机减载预留的功率备用为0.023 1(pu),初始转速为0.862 5(pu),桨距角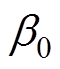 =1.115 4°。
=1.115 4°。
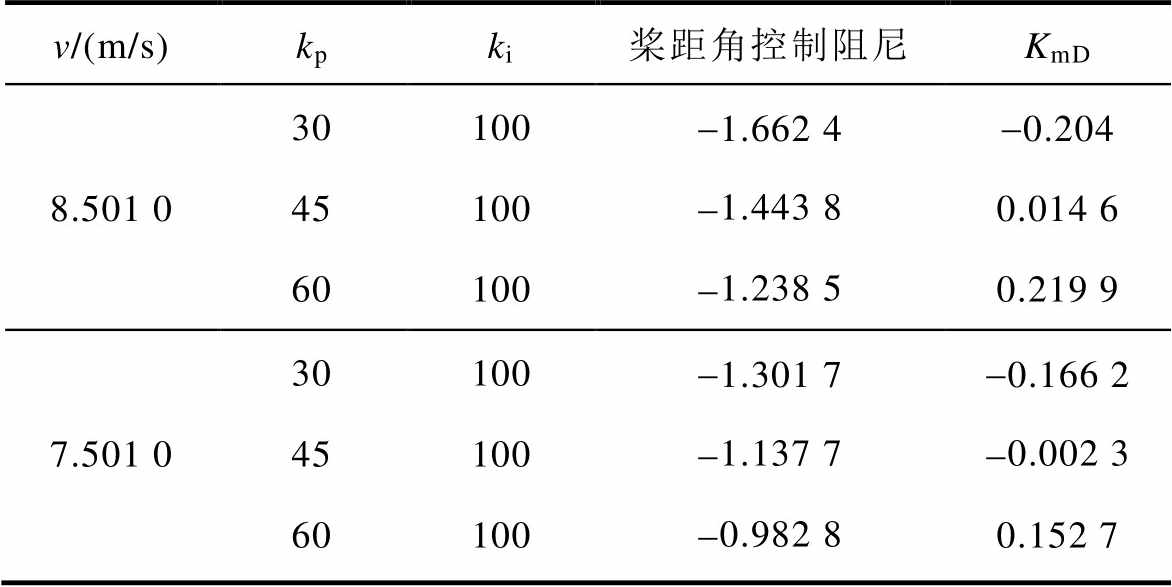
本节为了验证阻尼转矩法的有效性,通过改变kp、ki参数使得阻尼转矩系数分别为负、接近零、正。参数设置和阻尼转矩系数见表1。
表1 不同参数下的阻尼转矩系数
Tab.1 Damping torque coefficient under different parameters
v/(m/s)kpki桨距角控制阻尼KmD 8.501 030100-1.662 4-0.204 45100-1.443 80.014 6 60100-1.238 50.219 9 7.501 030100-1.301 7-0.166 2 45100-1.137 7-0.002 3 60100-0.982 80.152 7
按照表1参数设置,风电机组在小扰动下的功率仿真结果如图7和图8所示。转速、桨距角结果见附图3和附图4。图7和图8中绿线为阻尼转矩系数为负时的仿真结果,表明该平衡点为不稳定平衡点,此时kp=30,ki=100;蓝线为阻尼转矩系数接近零时的仿真结果,表明该平衡点为不稳定平衡点,此时kp=45,ki=100;红线为阻尼转矩系数为正时的仿真结果,表明该平衡点为稳定平衡点,此时kp=60,ki=100。其中,功率曲线中虚线为电磁功率,实线为机械功率。图7、图8中仿真结果显示与阻尼转矩法分析结果一致。
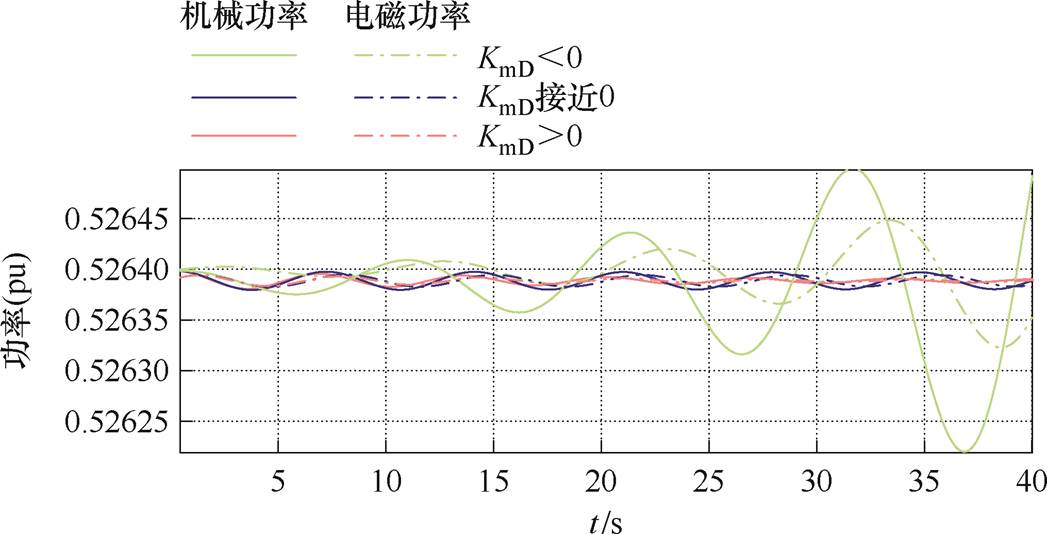
图7 8.501 0 m/s风电机组阻尼转矩法验证仿真结果
Fig.7 Simulation verification of damping torque method for wind turbine at 8.501 0 m/s wind speed
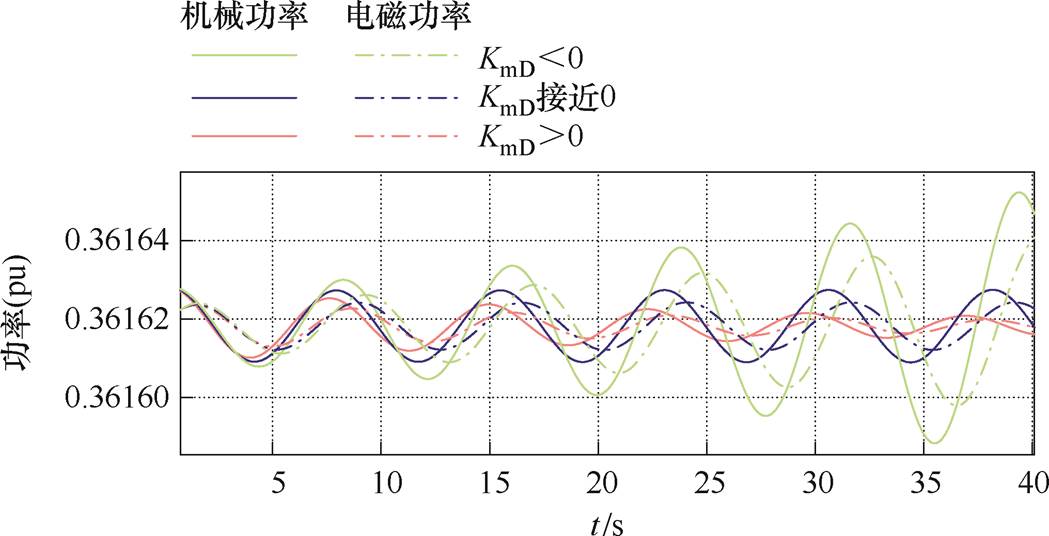
图8 7.501 0 m/s风电机组阻尼转矩法验证仿真结果
Fig.8 Simulation verification of damping torque method for wind turbine at 7.501 0 m/s wind speed
在验证阻尼转矩法有效性的基础上,验证定基准功率策略和变基准功率策略关于稳定性的结论。在风速分别8.501 0 m/s、7.501 0 m/s工况下,采用参数kp=60,ki=100,分别在定基准功率策略和变基准功率策略两种场景中测试。
小扰动下定基准功率策略和变基准功率策略对比的功率仿真结果如图9、图10所示。转速、桨距角结果见附图5和附图6。蓝色为定基准功率策略曲线,红色为变基准功率策略曲线。功率曲线中,实线为机械功率曲线,虚线为电磁功率曲线。结果显示,采用变基准功率策略更有利于风机的稳定性,和前面理论分析结果一致。
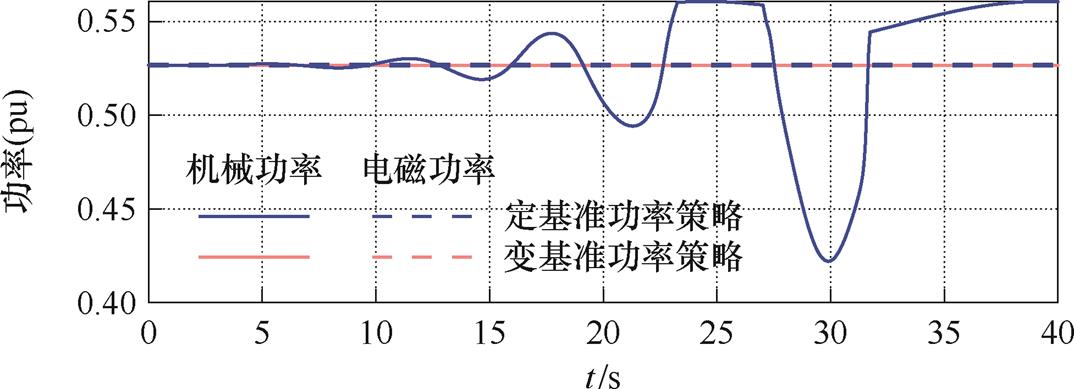
图9 8.501 0 m/s风电机组功率策略对比验证
Fig.9 Comparison of power strategies for wind turbine at 8.501 0 m/s wind speed
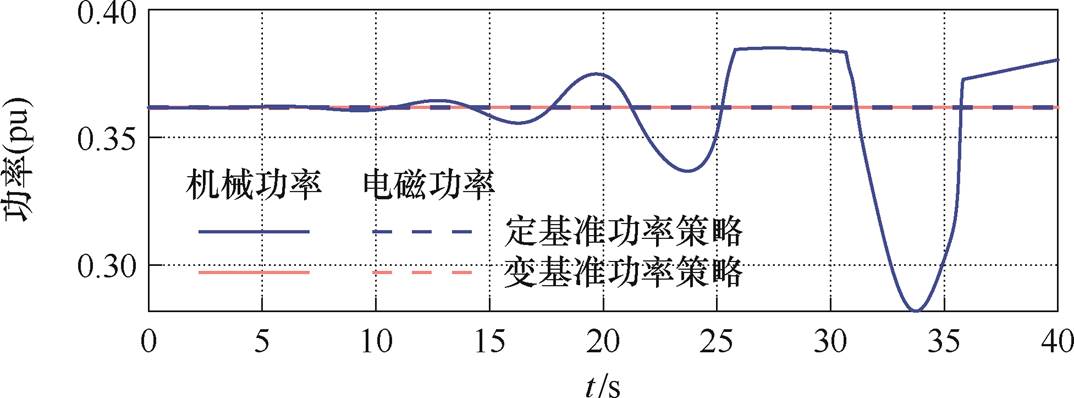
图10 7.501 0 m/s风电机组功率策略对比验证
Fig.10 Comparison of power strategies for wind turbine at 7.501 0 m/s wind speed
本节为了验证桨距角控制器参数稳定条件的有效性,在变基准功率策略下,不同工况下固定桨距角控制器的参数ki,设置三组不同的桨距角时间常数,采用本文提出的参数稳定条件计算对应kp的临界值。参数设置和计算结果见表2。
表2 风机参数
Tab.2 Wind turbine parameters
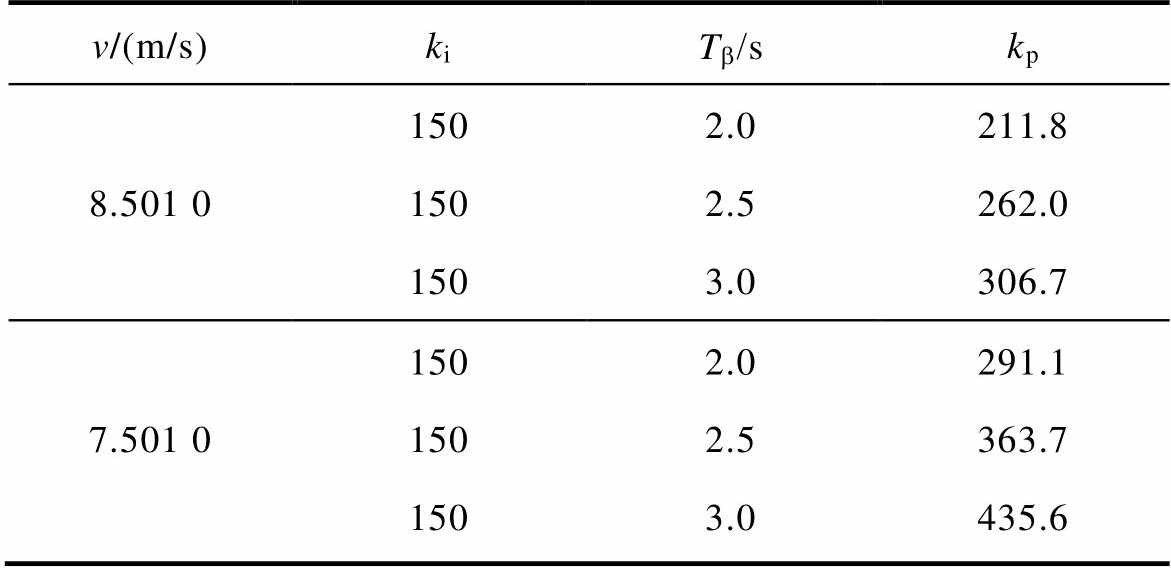
v/(m/s)kiTb/skp 8.501 01502.0211.8 1502.5262.0 1503.0306.7 7.501 01502.0291.1 1502.5363.7 1503.0435.6
按照表2参数设置与同样设置下只有kp不合理时对比,风电机组在小扰动下的仿真结果如图11、12所示。转速、桨距角仿真结果如附图7和附图8所示。图11和图12中功率曲线中红线为按照表2参数设置仿真结果,蓝线为kp不合理仿真结果,虚线为电磁功率,实线为机械功率。仿真结果表明在所设参数下,平衡点为稳定平衡点,机组都是稳定的,所提出的参数稳定条件有效。
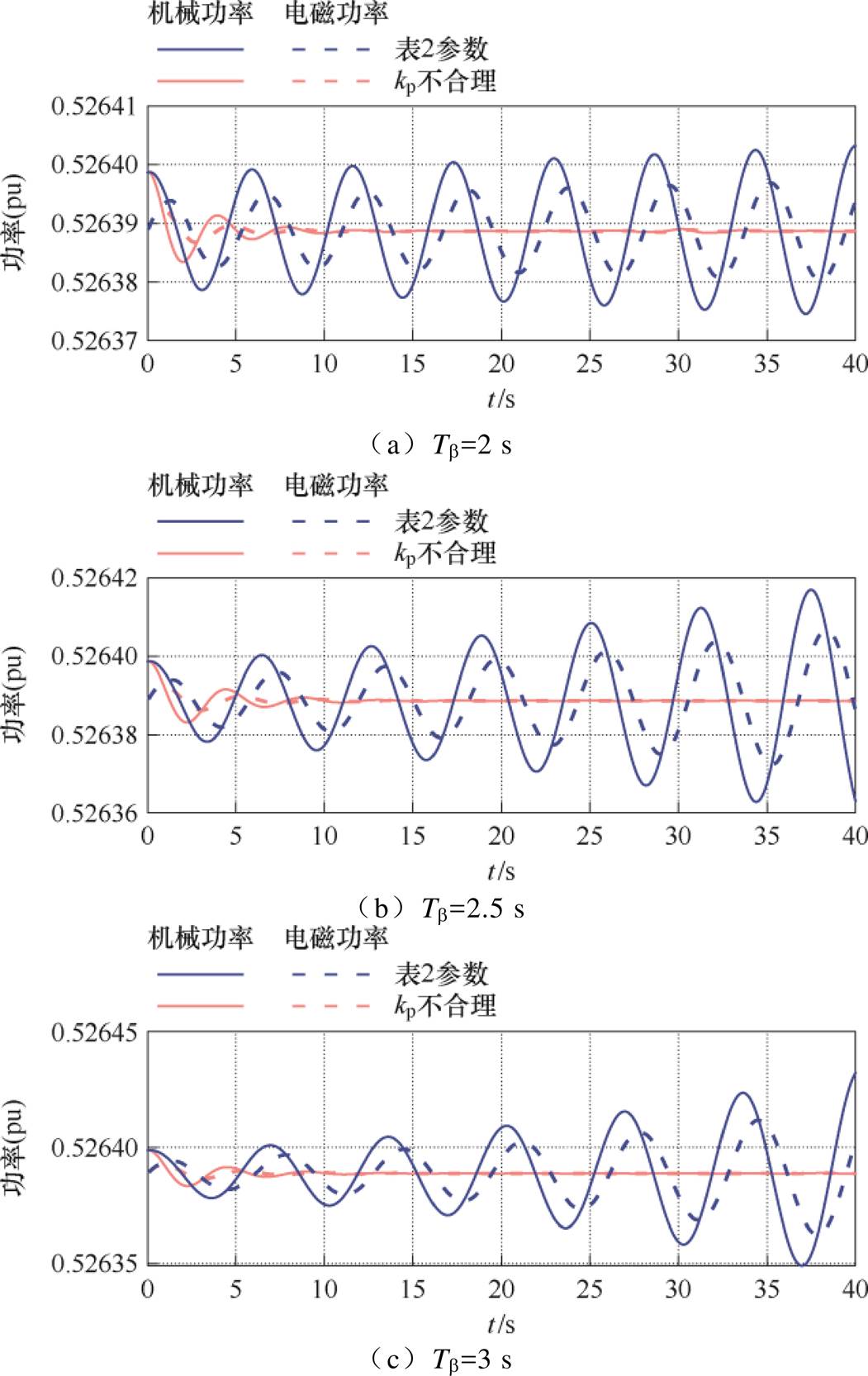
图11 8.501 0 m/s风电机组参数稳定条件验证
Fig.11 Verification of parameter stability conditions for wind turbine at 8.501 0 m/s wind speed
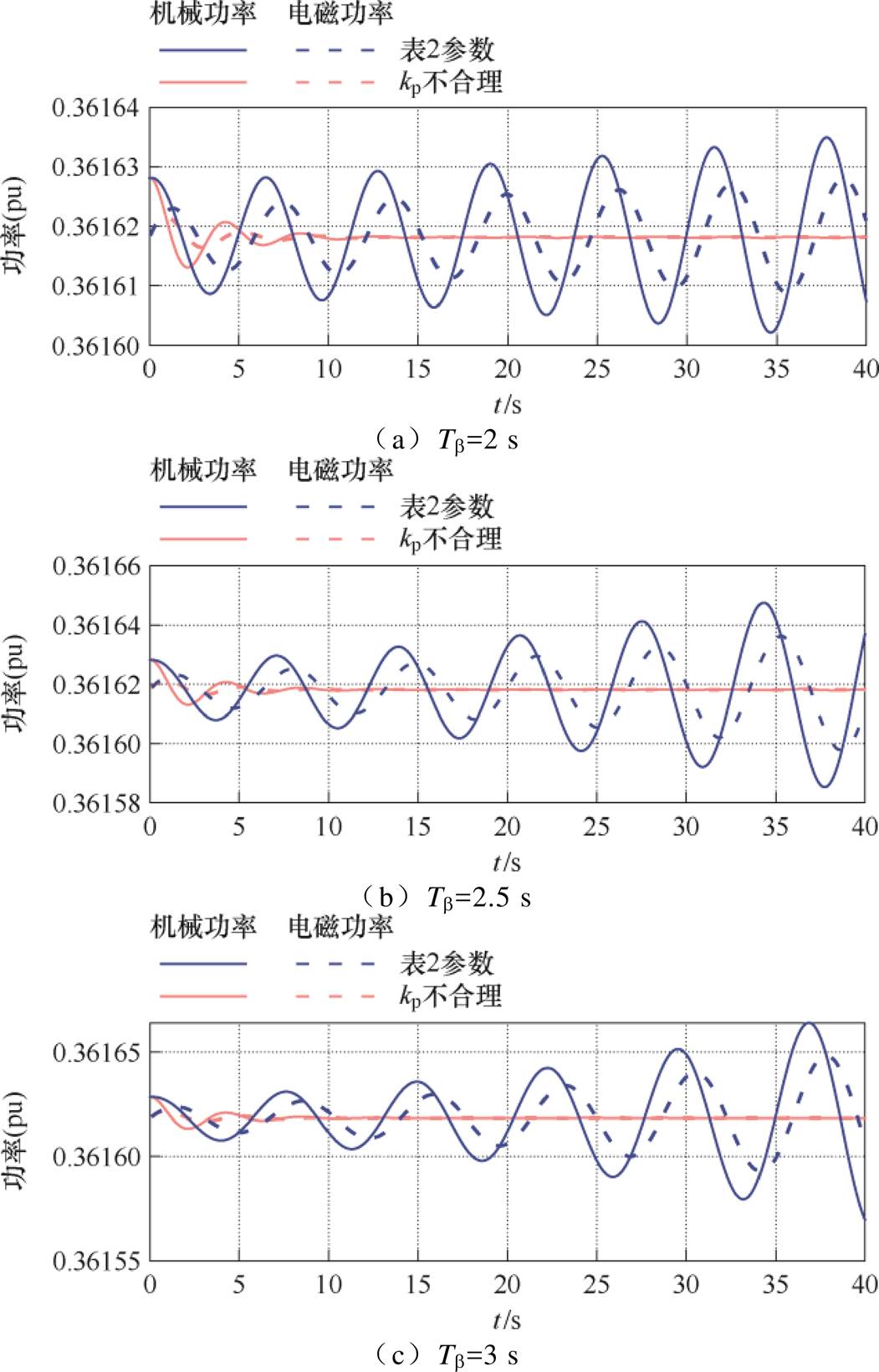
图12 7.501 0 m/s风电机组参数稳定条件验证
Fig.12 Verification of parameter stability conditions for wind turbine at 7.501 0 m/s wind speed
对于采用变桨减载调频的风电机组,若参数设置不当,可能会发生振荡失稳。针对该问题,通过建立简化的变桨减载调频风电机组模型,并对模型非线性方程进行线性化,然后基于阻尼转矩法分析了风电机组电磁功率、机械功率各部分的阻尼转矩,发现采用变基准功率策略时,电磁功率阻尼转矩为正,更有利于风机的稳定性,而机械功率阻尼主要受桨距角控制产生的阻尼转矩KmD,b影响,参数不当时由桨距角控制产生的负阻尼转矩是导致风电机组不稳定的主要原因。而KmD,b受Tb、kp、ki三个参数影响,桨距角动作的延时Tb 越大,风电系统越容易不稳定,增大比例系数kp或减小积分系数ki,则有利于风电系统的稳定性。
进一步地,推导得到了解析的风机控制参数稳定条件,当控制参数满足所提约束条件时,可以保证调频风电机组的稳定性。并且在RTLab半实物仿真平台上的详细模型上的仿真结果验证了所得结论。
论文工作厘清了变桨减载调频风电机组的稳定机理,并为风机桨距角控制器参数优化的相关研究提供了指导。后续将采用实际的风机控制器进行硬件在环仿真进行测试。
附 录
1. 实时仿真平台RTLab设备和环境

附图1 RT-LAB实时仿真平台设备
App.Fig.1 RT-LAB real-time simulation platform equipment
附图2 RT-Lab实时仿真平台操作界面
App.Fig.2 RT-Lab real-time simulation platform interface
2. 仿真算例结果
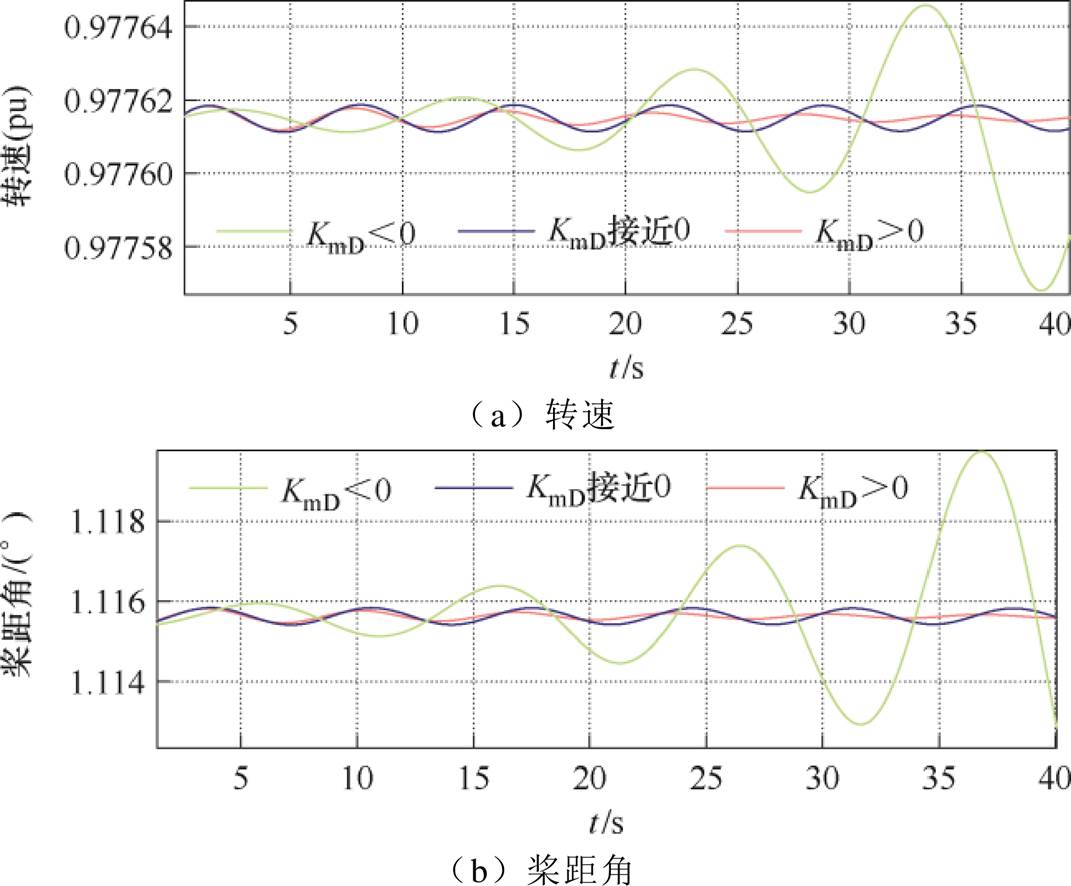
附图3 8.501 0 m/s风电机组阻尼转矩法验证其他仿真结果
App.Fig.3 Other simulation results of damping torque method for wind turbine at 8.501 0 m/s wind speed
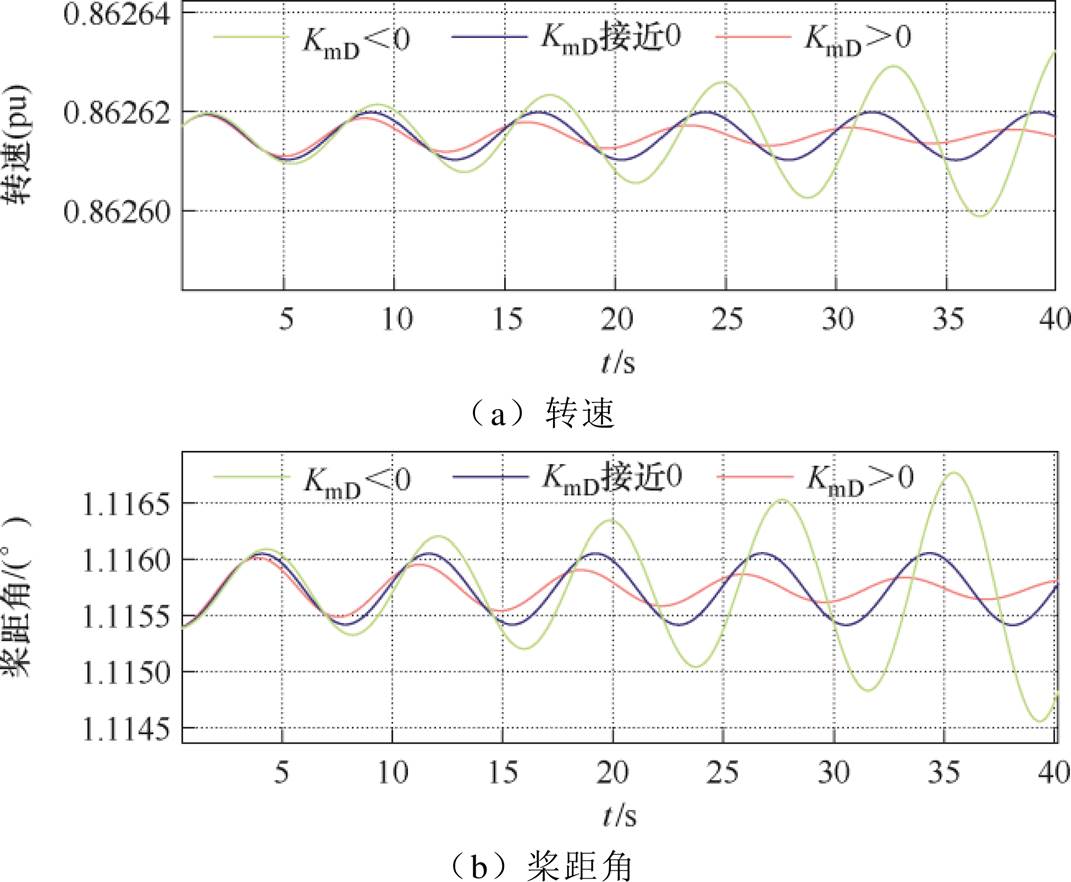
附图4 7.501 0 m/s风电机组阻尼转矩法验证其他仿真结果
App.Fig.4 Other simulation results of damping torque method for wind turbine at 7.501 0 m/s wind speed
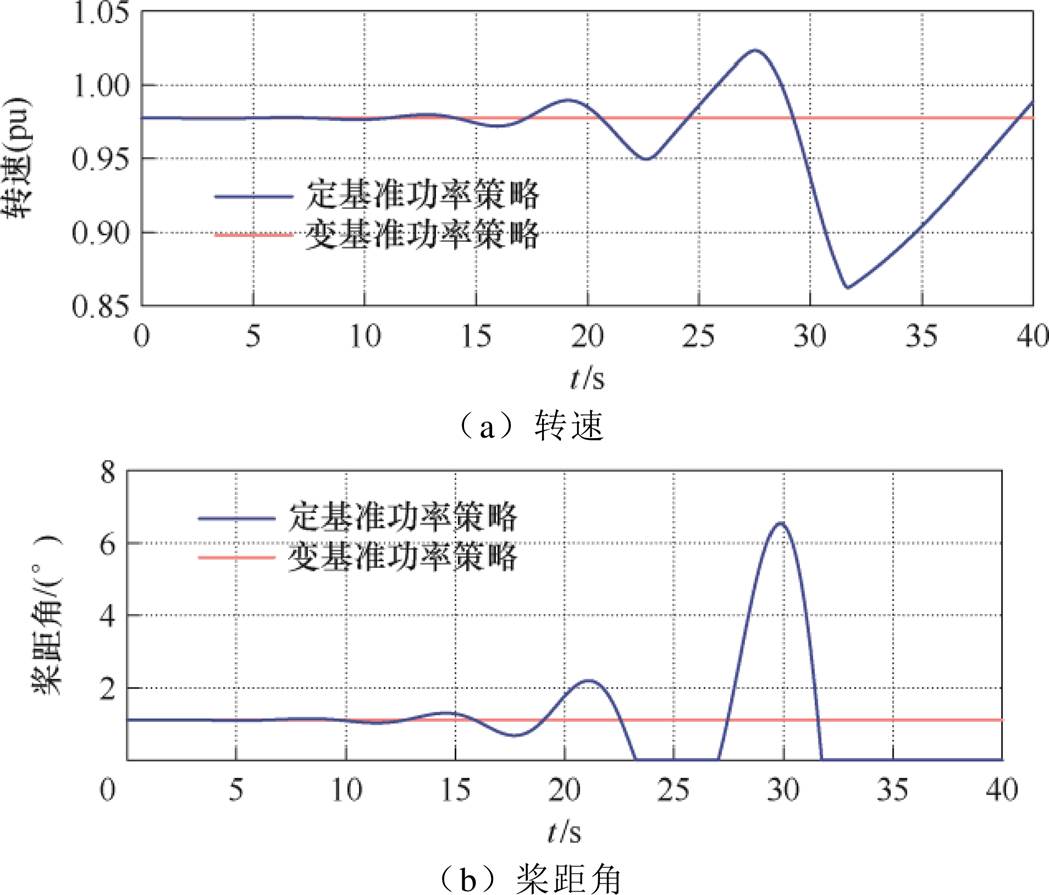
附图5 8.501 0 m/s风电机组功率策略其他对比结果
App.Fig.5 other Comparison results of power strategies for wind turbine at 8.501 0 m/s wind speed
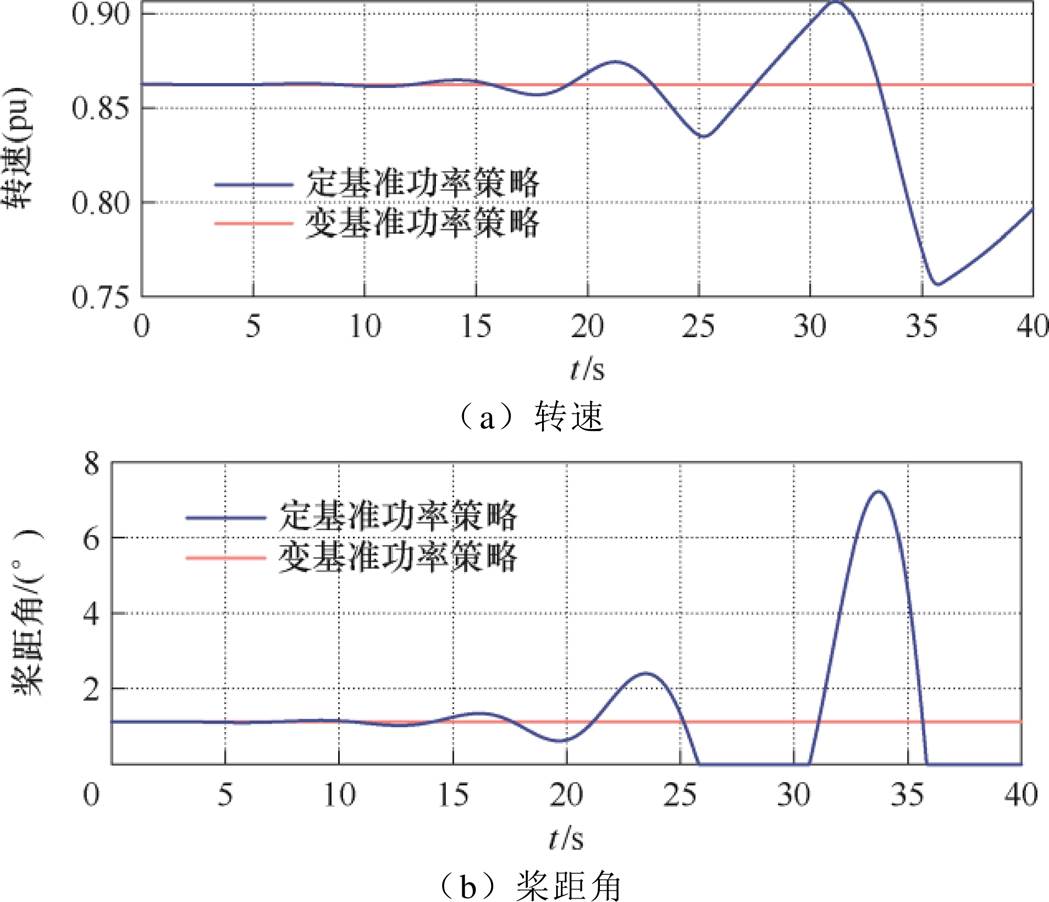
附图6 8.501 0 m/s风电机组功率策略其他对比结果
App.Fig.6 other Comparison results of power strategies for wind turbine at 8.501 0 m/s wind speed

附图7 8.501 0 m/s风速稳定约束验证仿真结果
App.Fig.7 Simulation results for wind speed stability constraint verification 8.501 0 m/s
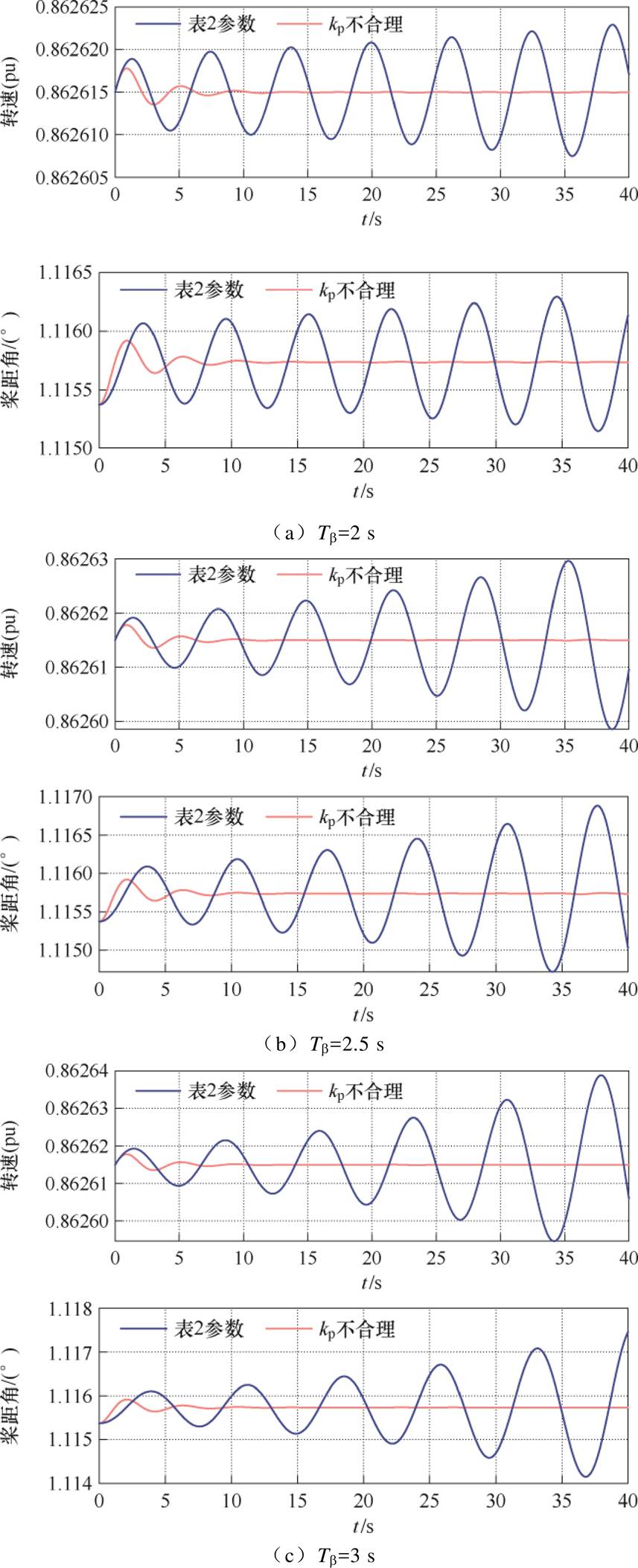
附图8 7.501 0 m/s风速稳定约束验证仿真结果
App.Fig.8 Simulation results for wind speed stability constraint verification 7.501 0 m/s
参考文献
[1] 胡正阳, 高丙团, 张磊, 等. 风电机组双向支撑能力分析与自适应惯量控制策略[J]. 电工技术学报, 2023, 38(19): 5224-5240.
Hu Zhengyang, Gao Bingtuan, Zhang Lei, et al. Bidirectional support capability analysis and adaptive inertial control strategy of wind turbine[J]. Trans- actions of China Electrotechnical Society, 2023, 38(19): 5224-5240.
[2] 颜湘武, 宋子君, 崔森, 等. 基于变功率点跟踪和超级电容器储能协调控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2020, 35(3): 530-541.
Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency regulation strategy of doubly-fed wind turbine based on variable power point tracking and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 530-541.
[3] 黄晟, 凌吉莉, 魏娟, 等. 大规模风电机群服役质量调控方法研究综述[J]. 电工技术学报, 2025, 40(10): 3274-3300.
Huang Sheng, Ling Jili, Wei Juan, et al A review of regulation method of service quality of large-Scale wind farm[J]. Transactions of China Electrotechnical Society, 2025, 40(10): 3274-3300.
[4] 李生虎, 朱国伟. 基于特征结构分析的风电机组调频控制桨距角参数选择[J]. 太阳能学报, 2017, 38(3): 662-668.
LiShenghu, Zhu Guowei. Selection of pitch angle parametersfor wind turbine frequency control based on feature structure analysis[J]. Journal of Solar Energy, 2017, 38(3): 662-668.
[5] 刘巨, 姚伟, 文劲宇. 考虑PLL和接入电网强度影响的双馈风机小干扰稳定性分析与控制[J]. 中国电机工程学报, 2017, 37(11): 3162-3173, 3371.
Liu Ju, Yao Wei, Wen Jinyu. Small signal stability analysis and control of double-fed induction generator considering influence of PLL and power grid strength[J]. Proceedings of the CSEE, 2017, 37(11): 3162-3173, 3371.
[6] 朱廷猛, 孙海顺, 秦世耀, 等. 弱电网下双馈风机并网系统的次同步振荡研究[J]. 电网技术, 2021, 45(5): 1641-1648.
Zhu Tingmeng, Sun Haishun, Qin Shiyao, et al. Sub- synchronous oscillation in DFIG system connected to weak grid[J]. Power System Technology, 2021, 45(5): 1641-1648.
[7] Sun Li, Liu Kai, Hu Jiabing, et al. Analysis and mitigation of electromechanical oscillations for DFIG wind turbines involved in fast frequency response[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4547-4556.
[8] 俞露杰, 付子玉, 朱介北, 等. 经二极管整流并网的构网型风机大扰动建模与稳定性分析[J]. 电力系统自动化, 2025, 49(2): 84-95.
Yu Lujie, Fu Ziyu, Zhu Jiebei, etcLarge disturbance modeling and stability analysis of grid connected wind turbine via diode rectification[J]. Power System Automation, 2025, 49(2): 84-95.
[9] 马燕峰, 程有深, 赵书强, 等. 双馈风电场并网引起火电机组多模态次同步谐振机理分析[J]. 电工技术学报, 2025, 40(5): 1395-1410.
Ma Yanfeng, Cheng Youshen, ZhaoShuqiang, et al. Mechanism analysis of multi-mode SSR of thermal power unit caused by doubly fed wind farm integration[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1395-1410.
[10] 王乐, 蔺红. 减载风电机组协调控制策略及PI参数优化[J]. 控制工程, 2021, 28(4): 744-750.
Wang Le, Lin Hong. Coordinated control strategy and PI parameter optimization of load shedding wind turbine[J]. Control Engineering of China, 2021, 28(4): 744-750.
[11] 张兴, 郑立纹, 王峰. 参与电网调频的风电机组线性变参数变桨控制策略[J]. 中国设备工程, 2022(5): 142-143.
Zhang Xing, Zheng Liwei, Wang Feng. Linear variable parameter pitch control strategy for wind turbines participating in grid frequency regulation[J]. China Equipment Engineering, 2022(5): 142-143.
[12] 田中伟. 感应风力发电机利用PSS的桨距控制及参数整定[D]. 长沙: 湖南大学, 2014.
Tian Zhongwei. Research on the pitch control using pss and the setting of pssparameters based on induction wind generator[D]. Changsha: Hunan University, 2014.
[13] 李飞飞. 基于双模糊PID控制策略的风力发电机组变桨系统研究[J]. 模糊系统与数学, 2019, 33(3): 29-34.
Li Feifei. Pitch system of the wind turbines based on the double fuzzy PID control strategy[J]. Fuzzy Systems and Mathematics, 2019, 33(3): 29-34.
[14] 柴海棣, 赵晓艳, 史波. 基于能量传递模型的永磁直驱变桨变速风电机组功率特性测试方法[J]. 发电技术, 2019, 40(4): 396-402.
Chai Haidi, Zhao Xiaoyan, Shi Bo. Power perfor- mance characteristics measurement method of PMSG- based wind turbines with energy transmitted model[J]. Power Generation Technology, 2019, 40(4): 396-402.
[15] 李少林, 王伟胜, 张兴, 等. 基于频率响应区间划分的风电机组虚拟惯量模糊自适应控制[J]. 电网技术, 2021, 45(5): 1658-1665.
Li Shaolin, Wang Weisheng, Zhang Xing, et al. Fuzzy adaptive virtual inertia control strategy of wind turbines based on system frequency response interval division[J]. Power System Technology, 2021, 45(5): 1658-1665.
[16] 汤雪松, 殷明慧, 李冬运, 等. 变速与变桨协调的风电机组平滑功率控制[J]. 电力系统自动化, 2019, 43(2): 112-120.
Tang Xuesong, Yin Minghui, Li Dongyun, et al. Power smoothing control of wind turbine generator via coordinated rotor speed and pitch angle regula- tion[J]. Automation of Electric Power Systems, 2019, 43(2): 112-120.
[17] 任丽娜, 吕明月, 王振臣. 改进蜂群算法在风机变桨距控制中的应用[J]. 机械设计与制造, 2015(3): 43-46.
Ren Lina, Lü Mingyue, Wang Zhenchen. Improved bee colony algorithm on the wind turbine pitch control [J]. Machinery Design & Manufacture, 2015(3): 43-46.
[18] 李生虎, 蒋以天, 于新钰, 等. 考虑DFIG桨距角参数优化的小干扰稳定约束最优潮流模型[J]. 电力自动化设备, 2019, 39(11): 20-26.
Li Shenghu, Jiang Yitian, Yu Xinyu, et al. Small- signal stability constrained optimal power flow model considering optimization of DFIG pitch angle[J]. Electric Power Automation Equipment, 2019, 39(11): 20-26.
[19] 朱凌志, 董存, 陈宁, 等. 新能源发电建模与并网仿真技术[M]. 北京: 中国水利水电出版社, 2018.
[20] Zertek A, Verbic G, Pantos M. Optimized control approach of frequency control contribution of variable speed wind turbines[J]. IET Renewable Power Generation, 2012, 6: 17-23.
[21] 张正阳, 殷明慧, 李阳, 等. 考虑机组稳定约束的风机一次调频控制策略[J]. 中国电机工程学报, 2023, 43(4): 1471-1481.
Zhang Zhengyang, Yin Minghui, Li Yang, et al. Wind turbine primary frequency regulation control strategy considering unit stability constraints[J]. Chinese Journal of Electrical Engineering, 2023, 43(4): 1471-1481.
[22] Li Yuju. Advanced control strategies for renewable energy integration for system support[D]. Hong Kong, China: The Hong Kong Polytechnic University, 2017.
[23] 国家市场监督管理总局, 国家标准化管理委员会. 并网电源一次调频技术规定及试验导则: GB/T 40595—2021[S]. 北京: 中国标准出版社, 2021.
Abstract Reserve capacity through variable pitch deloading is an important technical solution for variable speed wind turbines to participate in frequency regulation. However, improper parameter settings may cause wind turbines to oscillate or even become unstable. The stability of the variable pitch deloading frequency regulation wind turbine was analyzed in this scenario. So the parameter stability conditions with analytical expressions were derived, and when the control parameters meet the proposed constraints, the stability of the frequency regulation wind turbine can be guaranteed.
Firstly, This article establishes a frequency regulation model for wind turbines and simulates the scenario of wind turbine oscillation under unreasonable wind turbine parameters. Then, the stability of the variable pitch deloading frequency regulation wind turbine was analyzed in this scenario, and the dynamic equation of the unit was linearized. Based on the damping torque method, the damping torque of each part of the electromagnetic power and mechanical power of the wind turbine, as well as the influence of different factors, were analyzed. The damping torque generated by pitch angle control was emphasized, and the negative damping torque generated by pitch angle control when the parameters were inappropriate was the main reason for the instability of the wind power system.
This article validates the electromagnetic transient model of a doubly-fed induction generator (DFIG) on the RT-Lab real-time simulation platform. The wind turbine was simulated and verified at 8.501 0 m/s and 7.501 0 m/s, respectively. To verify the effectiveness of the damping torque method, the parameters of the pitch angle controller were changed to make the damping torque coefficients negative, close to zero, and positive, respectively. The simulation results are consistent with the analysis results of the damping torque method. On the basis of verifying the effectiveness of the damping torque method, verify the stability conclusions of the reference power strategy and the variable reference power strategy mentioned in the paper. Under wind speeds of 8.501 0 m/s and 7.501 0 m/s, tests were conducted in scenarios with both fixed reference power strategy and variable reference power strategy. The results showed that using the variable reference power strategy is more conducive to the stability of the wind turbine, consistent with the previous theoretical analysis. In addition, to verify the effectiveness of the stability conditions of the pitch angle controller parameters, under the variable reference power strategy, the parameters of the pitch angle controller were fixed under different operating conditions, and three different sets of pitch angle time constants were set. The corresponding critical values were calculated using the parameter stability conditions proposed. The results indicate that under the set parameters, the equilibrium point is a stable equilibrium point, and the units are stable. The proposed parameter stability conditions are effective.
The following conclusions can be drawn from the simulation analysis: (1) It is found that adopting a variable baseline power strategy would be more beneficial for the stability of the wind turbine. (2) Mechanical power damping is affected by the damping generated by pitch angle control, and is influenced by three parameters of the pitch angle controller. Among them, the larger the delay of pitch angle action, the more likely the wind power system is to be unstable; Increasing the proportional coefficient or decreasing the integral coefficient is beneficial for the stability of the wind power system. (3) Furthermore, analytical stability conditions for wind turbine control parameters isderived. When the control parameters meet the proposed constraints, the stability of the frequency regulation wind turbine can be guaranteed.
keywords:Wind turbine generator, frequency regulation with pitch angle reserve, stability, pitch angle controller, damping torque, stability condition of parameters
DOI: 10.19595/j.cnki.1000-6753.tces.242210
中图分类号:TM614
国家自然科学基金项目(U2066602)和内蒙古电力(集团)有限责任公司科技项目(内电科创〔2024〕5号)资助。
收稿日期 2024-12-08
改稿日期 2025-02-06
奥博宇 男,1997年生,博士研究生,主要研究方向为电力系统频率控制。E-mail: aby20@mails.tsinghua.edu.cn
陈 磊 男,1982年生,博士,研究员,主要研究方向为电力系统动态分析与控制。E-mail: chenlei08@tsinghua.edu.cn(通信作者)
(编辑 郭丽军)