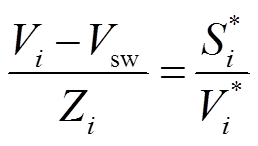 (1)
(1)摘要 电力系统的电压-无功安全域对于监测节点电压状态和避免发电机无功出力越限具有重要意义。因此,该文提出一种基于非线性网络分解的节点电压-无功可视化安全域方法,能够实时可视化监测各个节点的电压水平及发电机的无功状态,并预测潜在越限事件发生的风险。首先,通过建立两节点虚拟通道对电力系统进行解耦,并引入表征节点电压-无功状态的复数型指标;其次,运用物理性全纯嵌入法(HEM)求解随着系统负荷状态变化时的节点电压-无功状态指标轨迹(SIT);然后,分别推导节点电压和发电机无功出力的安全域边界解析表达式,并将其与节点电压-无功状态指标轨迹在同一复平面内可视化;最后,在不同规模节点系统中验证了所提电力系统节点电压-无功可视化安全域的有效性。
关键词:静态安全域 电压安全域 无功安全域 可视化 两节点虚拟通道 全纯嵌入法
随着社会经济的发展、电力能源需求的不断增加,电力负荷越来越接近重载状态,使得系统电压越来越接近电压稳定边界。同时,高比例新能源接入电力系统,新型电力系统规模不断扩大,间歇性与随机性较强的新能源发电容易引起局部电压越限[1-3]。除此之外,伴随着新能源大量接入电力系统,电容器和静态无功补偿器等无功补偿装置也大量接入电网,其接入电网时瞬态冲击大,容易造成无功功率越限,从而增加暂态过电压,继而引发电压越限,使电力系统面临更加严重的过电压风险[4-5]。因此,对于调度员来说,实时监控电力系统中各节点的电压和无功功率状态,提前预测它们可能发生的越限事件,对于电力系统,特别是高比例新能源接入的新型电力系统的安全运行有着重要的指导意义[6]。
传统的做法是,系统调度员基于逐点法,在电力系统某一运行工况下考虑某一种或某几种预想事故,不断地进行大量重复的潮流计算来检查各个节点电压和发电机无功出力状态,然而该方法在应用中面临着较重的计算负担[7]。对此,学者们提出了静态安全域法以刻画符合安全性需求的电网运行区域,从而根据当前运行点与安全域边界的关系来定性或定量地评估电网运行状态[9-10]。文献[11]推导了各个节点的有功和无功注入功率的限制值,即如果注入功率在相应限制范围内,则系统运行在满足安全约束的安全域内;文献[12]基于直流潮流模型推导了电力系统的最大静态安全域;文献[13]运用仿射变换性质直接推导了电网的无功静态安全域;文献[14]提出了一种可扩展的优化框架,用于估计静态安全域的凸内近似。然而,现有静态安全域法在推导安全域边界时往往存在假设前提,例如采用直流潮流模型代替交流潮流模型等。此外,在推导静态安全域边界的解析表达式时,许多研究运用分段线性拟合法来近似逼近非线性高维边界,这会影响实际应用的结果精度[15]。对此,文献[16]基于“全纯嵌入+解析延拓”理论离线推导出电压稳定性边界,虽然该方法降低了在线计算的时间成本,但它只能判断电压稳定性的总体状态,无法独立地监督各个节点电压和发电机无功出力的具体状态,也难以预测相应的节点电压-无功越限事件[17-18]。
总的来说,现有研究的不足之处有以下两点:①对于传统逐点法,仅能定性地判断电网当前运行工况是否安全,无法提供量化的安全裕度信息,且难以满足在线应用的需求;②对于现有静态安全域法,虽然能够从整体上指示系统的运行状态和安全裕度,但难以独立监测各节点具体的电压-无功状态及其裕度,且存在求解精度不足的问题。
针对上述问题,本文提出了一种基于非线性网络分解的节点电压-无功可视化安全域方法,能够实时可视化地监测各个节点电压和发电机无功出力状态,并预测相应的越限事件。首先,基于非线性网络分解方法,引入表征节点电压和发电机无功出力状态的复数型指标;其次,运用物理性全纯嵌入法(Holomorphic Embedding Method, HEM)求解随着系统负荷状态变化时的节点电压-无功状态指标轨迹(Status Index Trajectory, SIT);然后,推导节点电压和发电机无功出力的安全域边界解析表达式,并将安全域可视化;最后,分别在不同规模节点系统中验证了所提可视化节点电压-无功安全域的可行性与有效性。
本文提出的节点电压-无功可视化安全域方法建立在文献[19]中提出的非线性网络分解理论基础之上,保留非线性关系不改变,将多节点系统分解为多个虚拟两节点等效通道,然后构造系统电压崩溃的统一抛物线边界。如文献[20]所指出,有且只有两节点系统电路具有潮流解析解,本文所使用的非线性网络分解正是在多节点系统中每个节点(包括PQ节点与PV节点)与系统平衡节点之间加入虚拟阻抗,并建立两节点间虚拟通道,从而将原系统虚拟为多个虚拟两节点等效通道。
下面进行简单介绍:在某节点i与平衡节点之间构建虚拟通道,由欧姆定律推导潮流方程可得
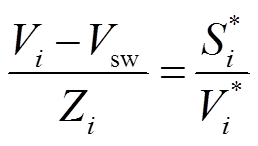 (1)
(1)
式中,*表示共轭;Vi和Vsw分别为节点i和平衡节点电压;Zi为节点i与平衡节点间的虚拟等效阻抗;Si为节点i处注入复功率。
由两节点系统推广至多节点系统,对于由m个PQ节点(集合为M)、p个PV节点(集合为P)和一个平衡节点组成的多节点系统,可以在每个节点与平衡节点之间加入虚拟等效阻抗Zi,从而分解为多个虚拟通道。多节点系统分解所得虚拟两节点等效通道示意图如图1所示,每个PQ或PV节点均通过虚拟等效阻抗Zi与平衡节点相连。
对于每个虚拟通道i,均引入对应的表征节点电压-无功状态的复数型指标σi[19],每个状态指标σi中都集成了各个虚拟两节点等效通道的非线性关系,包括Zi、Vsw和Si,有
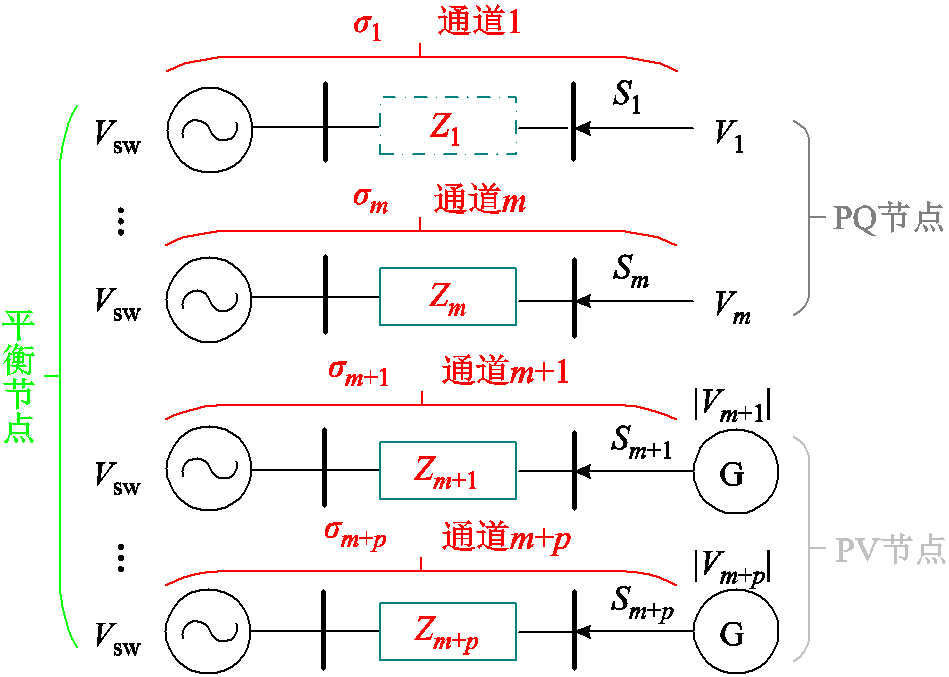
图1 多节点系统分解所得虚拟两节点等效通道示意图
Fig.1 Schematic diagram of a virtual two-bus equivalent channel obtained by decomposing a multi-bus system
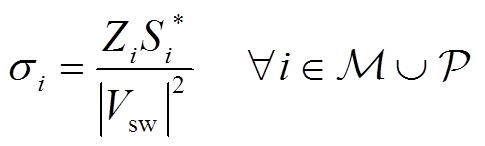 (2)
(2)
将式(2)代入两节点虚拟通道i的潮流方程式(1)中,可得
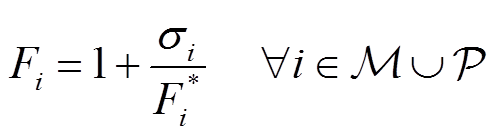 (3)
(3)
式中,Fi为节点i的归一化电压,Fi=Vi/Vsw。
将式(3)实部虚部拆分之后,其本质是一个二次方程。因此,可由二次方程求根公式获得某节点i的解析解为
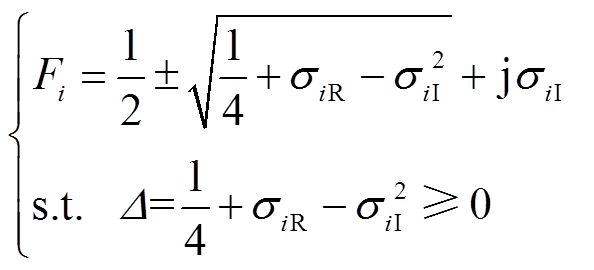 (4)
(4)
式中,σiR和σiI分别为状态指标σi的实部和虚部;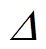 为二次方程判别式。
为二次方程判别式。
由式(4)可知,其中非负被开方数Δ>0是节点电压可行解存在的必要条件,同时原方程在等效节点状态复平面(后文简称为“σ复平面”)中形成抛物线。易知,Δ>0恰好表示σ复平面上抛物线的内部区域存在节点电压可行解,因此式(4)所得出抛物线为系统电压崩溃边界,抛物线外部为系统电压发生崩溃。电压崩溃统一抛物线边界和复数型指标示意图如图2所示。因此,只要求解出多节点系统中所有通道的状态指标σi,然后将σi和系统电压崩溃统一边界绘制在同一σ复平面内,即可快速判断节点电压是否存在可行解。
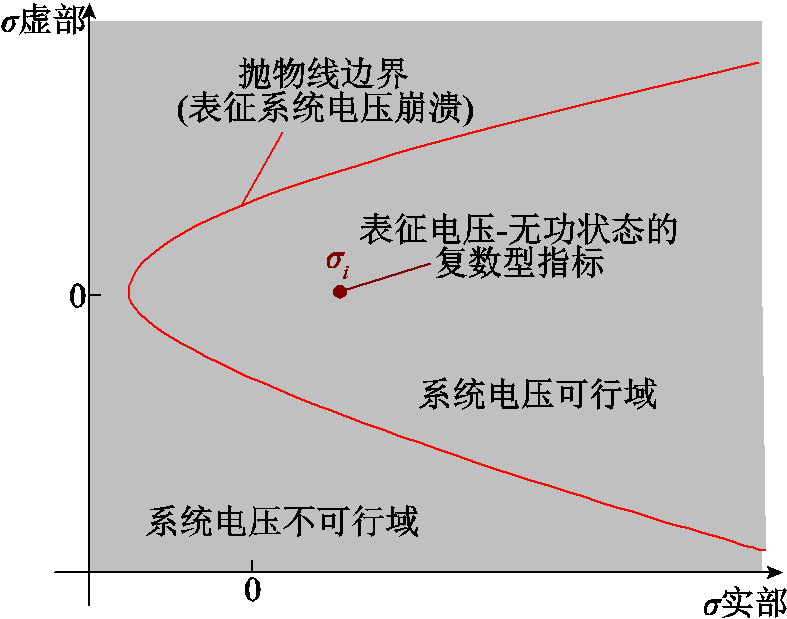
图2 电压崩溃统一抛物线边界和复数型指标示意图
Fig.2 Parabolic voltage collapse boundary and the equivalent bus status index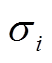
值得注意的是:①图2中的状态指标σi仅对当前运行工况有效,在运行工况发生改变时,需要重新求解σi[17];②图2中的抛物线边界只能指示系统整体电压崩溃(即当σi越过式(4)中Δ=0至外部区域时意味着触发系统电压崩溃),而不能单独表征各个节点电压和发电机节点无功出力的安全性[16]。
为了克服上述不足,本文在第2节推导了状态指标σi随系统负荷状态变化时的节点电压-无功状态指标轨迹表达式,在3.1节和3.2节分别推导了节点电压安全域(Voltage Safety Region, VoSR)和发电机节点无功安全域(Var Safety Region, VaSR),并将其可视化,从而直观有效地对节点电压和发电机无功出力可能的越限进行预测。
为了使状态指标能够表示当系统中负荷发生变化时的节点电压-无功状态,本节基于HEM,推导了表征节点电压-无功状态的复数型指标σi随系统负荷状态变化的轨迹表达式,所得节点电压-无功SIT能够跟踪系统工况变化,避免了系统运行条件变化后的大量重复计算。
首先简单介绍全纯嵌入的基础理论。全纯函数数学定义为:对于一个复函数x(s),其中复变量s=p+jq,若该复函数x(p+jq)在某复数域内连续可微,且满足柯西-黎曼方程式(5),则称x(s)是复可微的,且在该复数域内全纯[21]。
![]() (5)
(5)
若x(s)为全纯函数,则可在其收敛域C内表示为幂级数形式,有
当待求方程g(x)=0难以直接求解时,将所构建的全纯函数x(s)代入方程中,得到复合函数g(x)=g[x(s)]=0。此时,只要求得其中幂级数的各项系数x[n],即可得到所需要的显式表达式。
全纯嵌入法就是将电力系统领域与全纯函数相结合,从而求解电力系统中某些较为复杂的非线性方程组[22],例如潮流方程组[23]等。潮流方程本质上是表示功率平衡方程的非线性方程组g(x)=0,其难以直接进行求解,可将方程组中表示系统电压的未知变量x表示为全纯函数x(s),并将其嵌入方程组中。接着,对全纯函数x(s)进行展开,由于等式两边各阶幂级数系数相等,可以得到各阶幂级数的递推式,将原函数x(s)进行显式化,最终求解x(s),即可得到非线性方程g(x)=0的解[24]。
全纯嵌入法的核心在于合理构造嵌入函数x(s),通过引入复变量s将原非线性方程组转化为关于s的解析函数,进而求得目标变量x。目前,全纯嵌入法已在电力系统多个领域得到广泛应用,涵盖不确定性潮流分析[25]、交直流混联系统潮流分析[26]、潮流收敛性提升[27]、综合能源系统[28]以及电压稳定性评估[29]等。鉴于此,本文采用全纯嵌入法求解节点电压-无功SIT问题。
对于某N节点电力系统,其包括平衡节点、PQ节点和PV节点,三种节点在直角坐标系下的交流潮流方程为
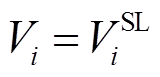 (7)
(7)
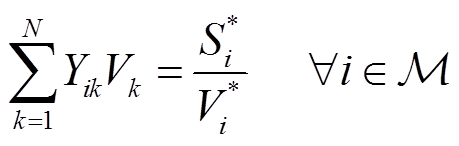 (8)
(8)
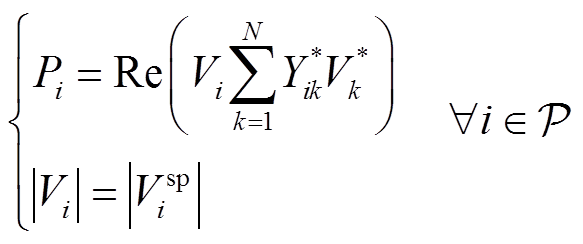 (9)
(9)
式中,Re表示取实部;Yik为节点导纳矩阵中的[i, k]元素;Vi为节点i电压;Vk为节点i的相邻节点k电压;ViSL为平衡节点电压;|Visp|为PV节点的固定电压幅值;Si*为节点i处的复功率;Pi为PV节点i的有功功率。
为了表征系统在不同负荷下的工况,本文采用物理性全纯嵌入法,即嵌入因子s在不同值时均有对应的实际电网运行状态[30]。具体而言,s=0时表示全网无负荷和无发电的“死网”状态,s=1时表示电网的当前运行状态,s=1.3时表示全网负荷功率增大为基础负荷的1.3倍,s=0.8时表示全网负荷功率减小为基础负荷的0.8倍。对式(7)~式(9)嵌入全纯因子s代表不同负荷状态时的交流潮流方程。假设系统负荷状态统一由嵌入因子s进行调整,可得到式(10)~式(12)的物理性全纯嵌入方程[31]。
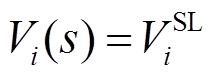 (10)
(10)
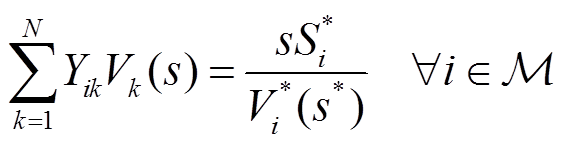 (11)
(11)
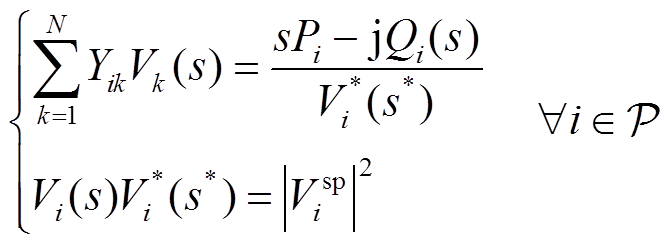 (12)
(12)
式中,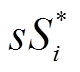 为PQ节点的负荷状态变化;PV节点的发电机无功出力由Qi(s)调整以维持其电压幅值不变;sPi为PV节点的发电机有功出力。
为PQ节点的负荷状态变化;PV节点的发电机无功出力由Qi(s)调整以维持其电压幅值不变;sPi为PV节点的发电机有功出力。
观察式(10)~式(12),物理性全纯嵌入方程在s为不同值时均能回归到式(7)~式(9),且有对应的实际运行状态。
同理,将物理性全纯因子s嵌入式(3),得到
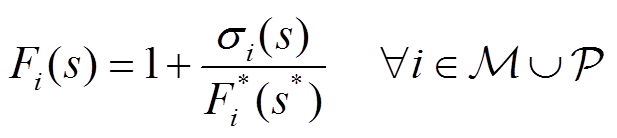 (13)
(13)
σi(s)=σi[0]+σi[1]s+…+σi[n]sn是幂级数形式的全纯函数,式(13)在s为不同值时均能回归到式(3)。因此,由式(13)所得状态指标σi(s)可以表示系统不同负荷状态时的节点电压-无功SIT。
求解节点电压-无功SIT时只需联立式(10)~式(13),将全纯函数V(s)、Qi(s)、σi(s)写为幂级数形式,比较方程两边对应阶的s的系数,即可求得高阶项未知系数和低阶项已知系数的递归矩阵方程,从而递归地计算σi(s)的系数。节点电压-无功SIT σi(s)的具体求解过程见附录第1节。当系统网络拓扑结构发生变化时,需要根据拓扑发生的变化将式(11)、式(12)中的原导纳矩阵元素Yik修正为Yik-m,进行全纯嵌入,更新并求解新的σi(s)。附录第2节分析了计算σi(s)过程相关的数学复杂性和计算量。
式(10)~式(12)对交流潮流方程进行嵌入时,用s统一表示全网负荷状态变化,这是其中一种嵌入方法,具有一定局限性。本文用这种嵌入形式来推导所构建的VoSR、VaSR,以简化二者推导过程。针对上述不足,文献[32-33]给出了两种考虑其他运行方式时的嵌入形式。例如文献[32]考虑不同节点或负荷独立变化的情形,在交流潮流方程中嵌入多个s,每个s单独调整不同区域或节点的负荷功率状态,使其更加符合电网的实际运行情况;对于负荷状态多变,不严格按预期方向增长,而是存在增长方向误差的场景,可采用多段全纯嵌入法[33]。
在考虑新能源或储能接入时,节点类型将发生变化,部分节点表现出下垂控制特性。在此情况下,需要重新构建全纯嵌入潮流方程,具体形式见附录第1节。值得注意的是,该方程也可采用类似传统潮流方程的方法,并与式(13)结合,且不会影响后续安全域可视化的推导过程。
根据第2节的物理性全纯嵌入法,本节推导了VoSR、VaSR的解析表达式,并将其与节点电压-无功SIT在同一σ复平面内可视化,以便调度员可以直观地监控系统各节点的电压-无功状态,并预测其相应的越限事件,做出相应的应对措施。
首先,设置平衡节点电压相位为0°,并将式(13)重新整理可得
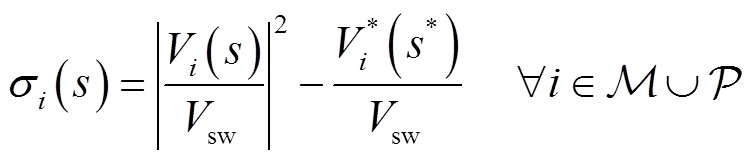 (14)
(14)
接着将式(14)的实部、虚部拆分为
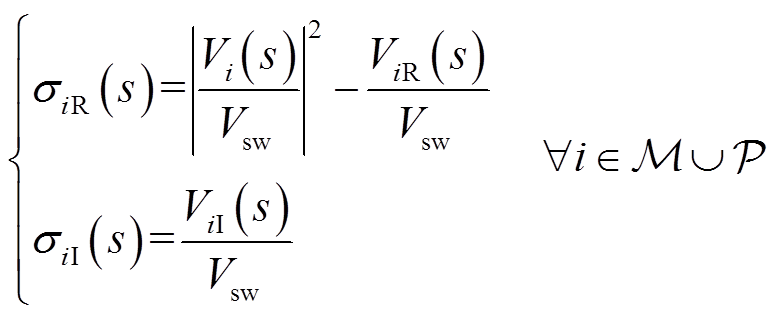 (15)
(15)
显然,式(15)实际上构成了σ复平面内圆心为(|Vi(s)/Vsw|2, 0)、半径为|Vi(s)/Vsw|的圆。同时,将圆方程式(16)代入式(4)所表示的抛物线方程中,易得二者为相切关系,即圆内切于抛物线。
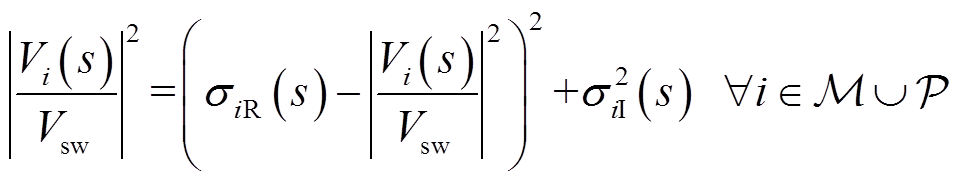 (16)
(16)
根据式(16),调度员可以灵活地为不同的节点预设不同的电压范围。例如,假设节点i电压在ViL和ViH之间浮动。分别将ViL和ViH代入式(16)中,并将所得结果与统一抛物线边界可视化在同一σ复平面内即可得到图3。其中,虚线(蓝色)抛物线表示电压崩溃统一抛物线边界,绿色和红色的两个圆分别表示ViL和ViH所形成的VoSR,由上述三个边界所围成的黄色区域即为节点i的VoSR。由此,通过绘制σi(s)的轨迹,调度员可以直观地监测电压状态。
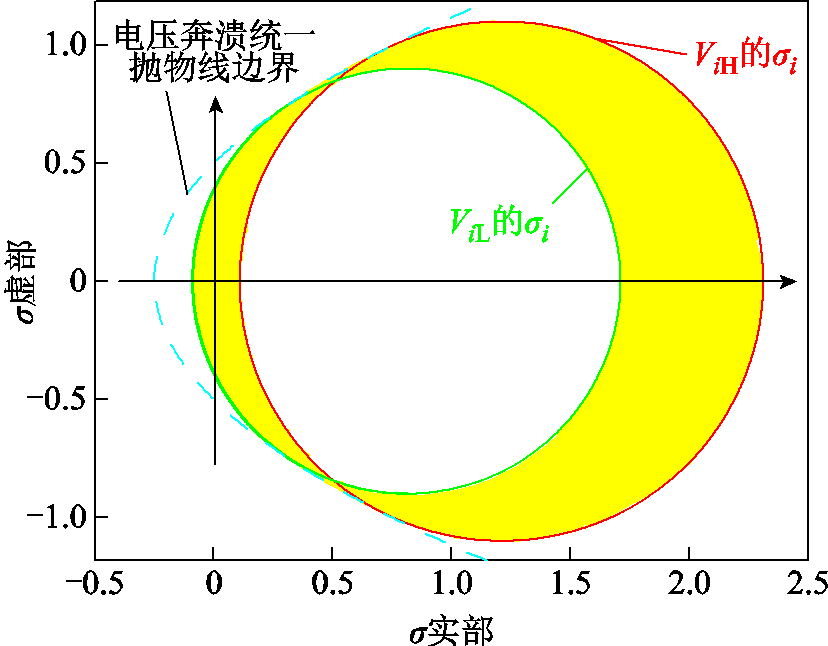
图3 节点VoSR及安全域边界的可视化示意图
Fig.3 Visualization of voltage safety region and boundaries
下面详细介绍节点VoSR的形成过程。可视化VoSR的形成过程示意图如图4所示,由式(16),可将节点i电压Vi(s)=VX映射为σ复平面内由节点电压-无功SIT σi(s)形成的圆,每个圆代表一个电压值。需要强调的是,只有恰好在圆上的σ点才表示Vi(s)=VX,圆内或圆外的σ既不一定表示Vi(s)<VX也不一定代表Vi(s)>VX。
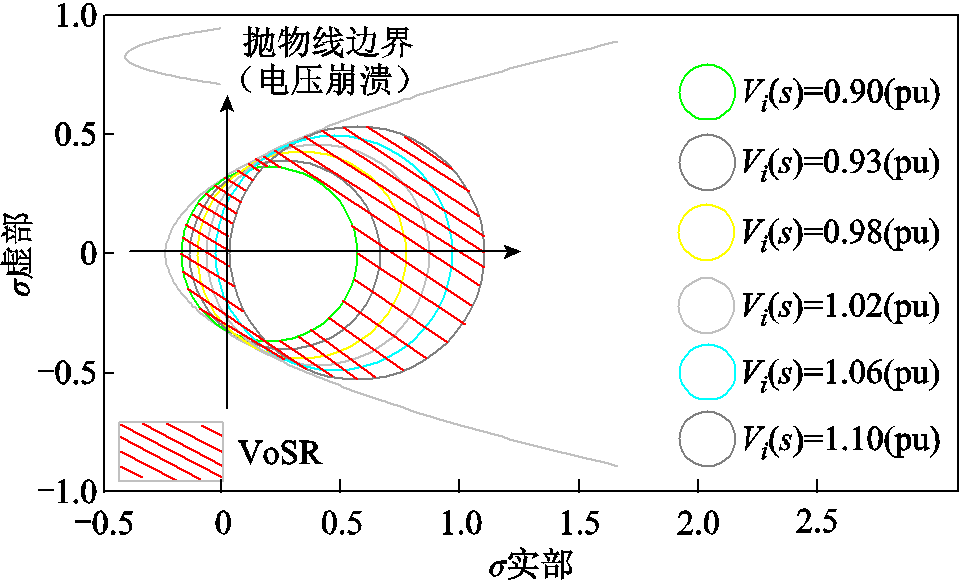
图4 可视化VoSR的形成过程示意图
Fig.4 The formation process of visualized voltage safety region
假设节点i电压Vi(s)在[0.90(pu), 1.10(pu)]之间浮动,如图4中展示的6个圆分别表示区间内的不同电压值,这6个圆上的σ点代表对应的电压值。因此,该区间内电压值可映射出无数个圆,这些圆上无数个σ点可形成一个如图4中的红色条纹所示区域,即表征电压位于该区间内的可视化VoSR。由此,可将数值型的电压上下限映射为σ复平面内的可视化节点VoSR,需要注意的是,VoSR适用于电压节点。
发电机无功出力越限不仅会损坏发电设备,还会影响系统电压的安全性。因此,有必要监测发电机节点的无功出力状态并预测其可能的越限事件。3.1节得到了电压节点的VoSR,本节将对适用于发电机节点的VaSR进行推导。
首先,将物理性全纯因子s嵌入式(2)得
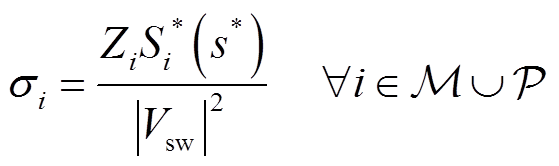 (17)
(17)
式中,Si*(s*)为发电机节点i处的复功率,Si*(s*)= sPi-jQi(s);Zi(s)为虚拟两节点等效通道i的虚拟等效阻抗,Zi(s)=Ri(s)+jXi(s)。
接着,将式(17)拆分为实部和虚部,并消去|Vsw|2得
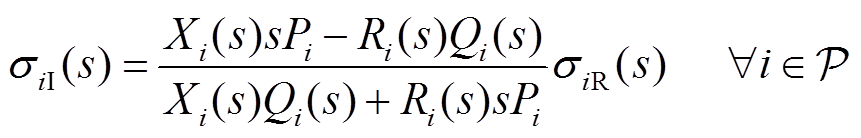 (18)
(18)
观察式(18)可知,发电机无功出力SIT σi(s)的实部和虚部实际上在σ复平面内形成一条直线,此直线过原点且斜率与s有关。
对于输电网而言,一般有电抗远大于电阻(即X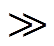 R),可将R近似为0。因此,将式(18)中的Ri(s)设为0,消去Xi(s),可简化为
R),可将R近似为0。因此,将式(18)中的Ri(s)设为0,消去Xi(s),可简化为
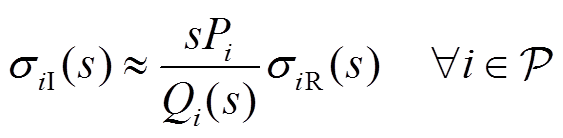 (19)
(19)
由式(19),系统调度员能够灵活设置不同的发电机无功出力范围。假设节点i处的发电机无功出力满足QiL≤Qi≤QiH,分别将QiL和QiH代入式(18),与电压节点过程类似,可得σ复平面内的两条过原点的直线,且斜率分别为sPi/QiL和sPi/QiH,如图5所示。其中,蓝色抛物线表示电压崩溃边界,发电机无功出力下限QiL和上限QiH分别由绿色直线和红色直线表示。那么,由上述三个边界所围成的黄色区域即为发电机节点i的VaSR。与VoSR类似,通过绘制σi(s)的轨迹,调度员可直观地监测发电机无功出力状态。
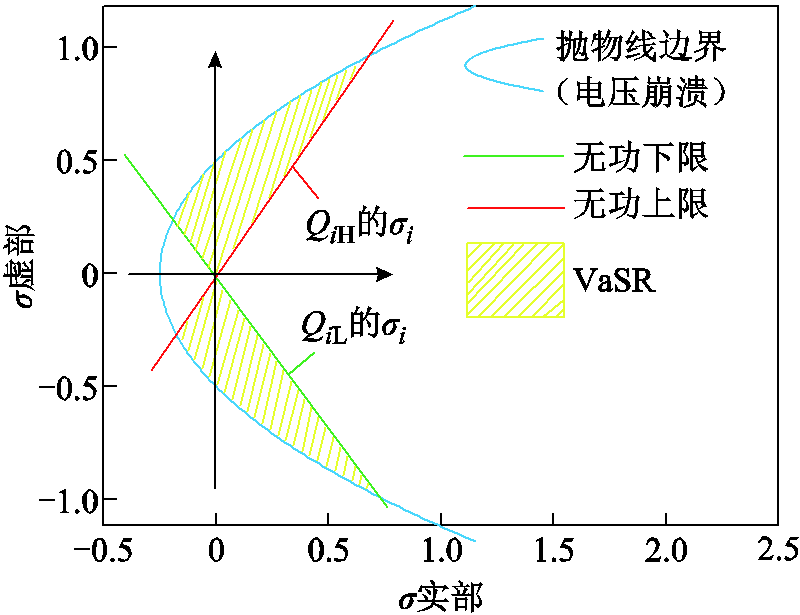
图5 发电机VaSR及安全域边界的示意图
Fig.5 Visualization of Var safety region and boundaries
对于配电网而言,式(18)中的电阻参数R会显著影响发电机VaSR,因此不可被忽略。系统调度员应该严格按照式(18)来可视化发电机VaSR,可视化过程与图4类似。
对于实际电力系统中某些参数的临界运行范围显著大于其实际运行变化范围的情况[34],本文提出的可视化方法仍具有适用性。所提出的节点电压-无功安全域方法允许系统调度员根据实际需求预设多个节点电压-无功安全域边界,在临界运行范围大于实际运行工况的情况下,所设置的多个安全域边界可以增强调度的灵活性和适应性。下面通过一个例子对本方法在上述情况的适用性进行说明。
以发电机VaSR为例,假设某发电机i的无功出力Qi的理论临界范围为−30 Mvar<Qi<50 Mvar,而其实际运行变化范围仅为[−20 Mvar, 30 Mvar]。
在此情况下,调度员可以根据实际工况需求,预设多组无功出力范围边界,例如图6所示的[-20 Mvar, 20 Mvar],[−30 Mvar, 30 Mvar]和[−50 Mvar, 50 Mvar]多条直线。通过调整无功出力边界范围与实际运行状态的贴合度,可以在特定场景下更准确地构建节点电压-无功可视化安全域,从而为电力系统的调度与运行提供更可靠的安全性评估依据。
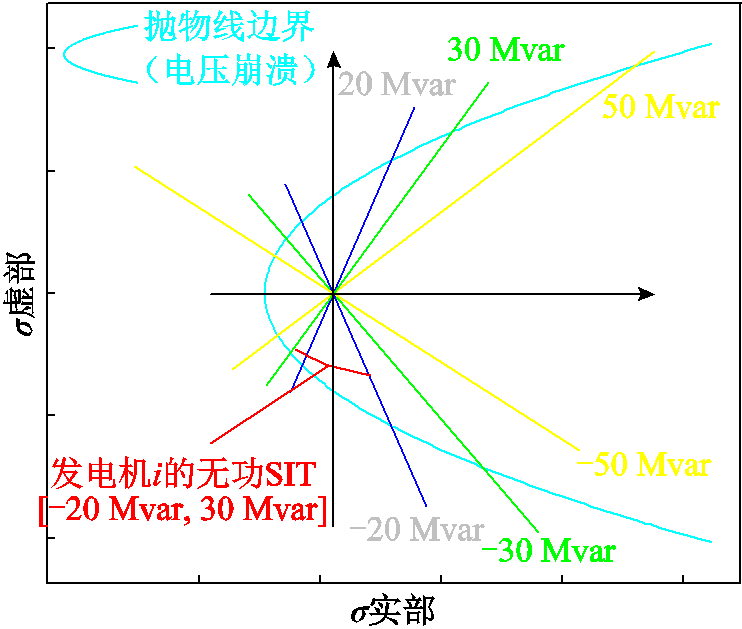
图6 多个预设的发电机无功出力范围和某发电机i的无功SIT可视化示意图
Fig.6 Illustration of multiple preset Var boundaries and a possible trajectory of generator Var index
本文所提方法能够将各节点电压VoSR与各发电机无功出力VaSR独立地可视化在同一等效节点状态复平面内。同时,结合3.1节和3.2节推导的节点电压-无功SIT σi(s),可以在等效节点状态复平面内可视化地监测各节点电压与发电机无功出力状态,及时预测相关节点可能发生的越限事件,从而及时采取相应的应对措施,提高电力系统运行的安全性。本文所提节点电压-无功安全域方法的整体框架如图7所示。
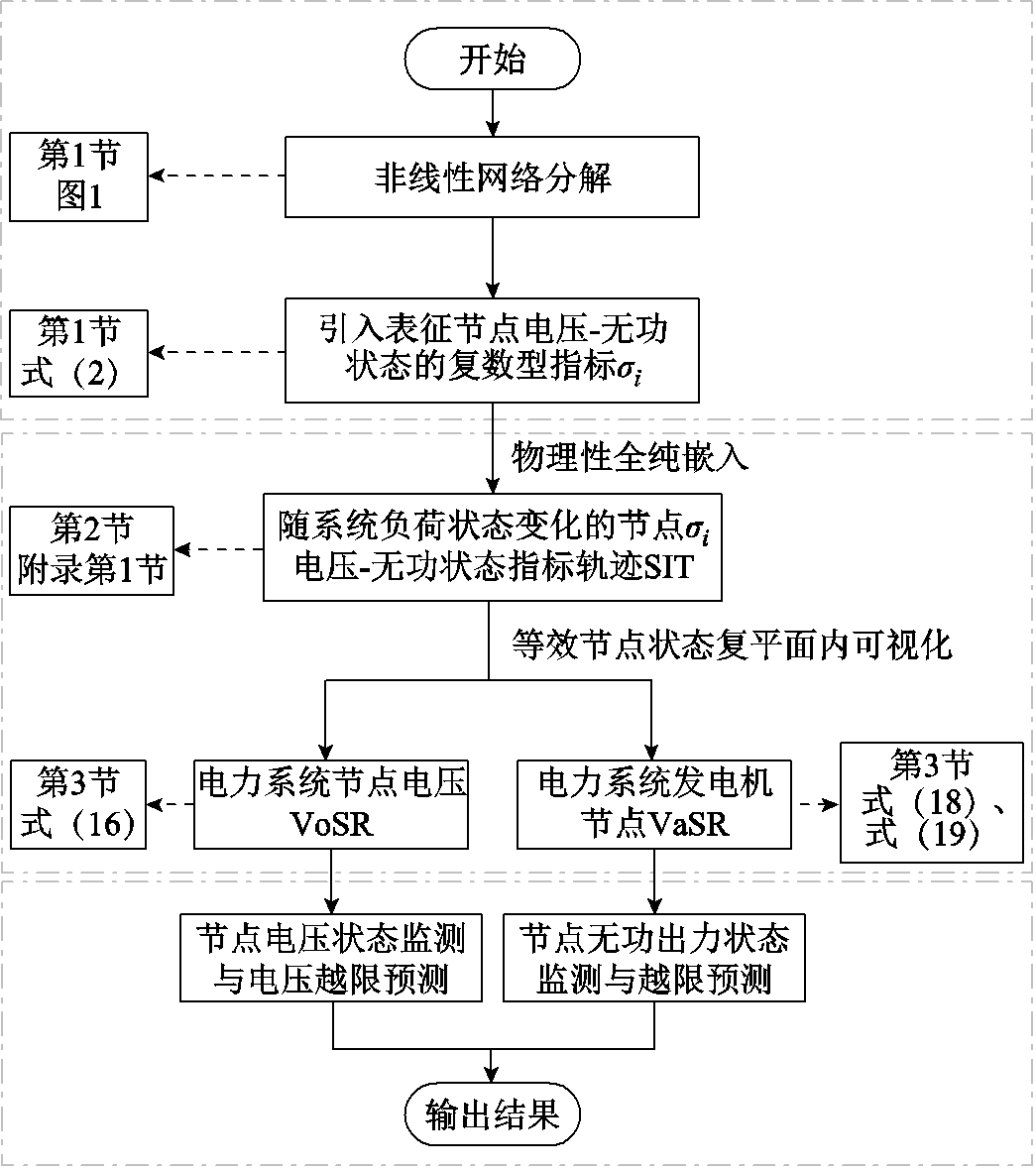
图7 本文所提节点电压-无功安全域方法整体框架
Fig.7 The overall framework of the proposed method
最终,采用节点电压-无功安全域方法所构建并可视化的节点电压VoSR由表征系统电压崩溃统一抛物线边界与两个σi(s)形成的圆轨迹围成,发电机节点VaSR由表征系统电压崩溃统一抛物线边界与两条σi(s)形成的直线轨迹围成。
本节在IEEE 9节点、IEEE 14节点、IEEE 39节点系统中对上述所提基于非线性网络分解的节点电压-无功可视化安全域方法进行有效性验证。潮流计算使用MATPOWER 4.1编程实现,并将潮流计算结果与牛顿-拉夫逊(Newton-Raphson, NR)法进行对比分析。
为了便于说明,对IEEE 9节点系统中所有节点预设统一的电压上、下限,即电压下限VL=0.90(pu)和电压上限VH=1.10(pu),且系统负荷从基准工况s=1.00(pu)开始不断增长。根据本文所提方法,得到VoSR和各节点电压-无功SIT σi(s)如图8所示。
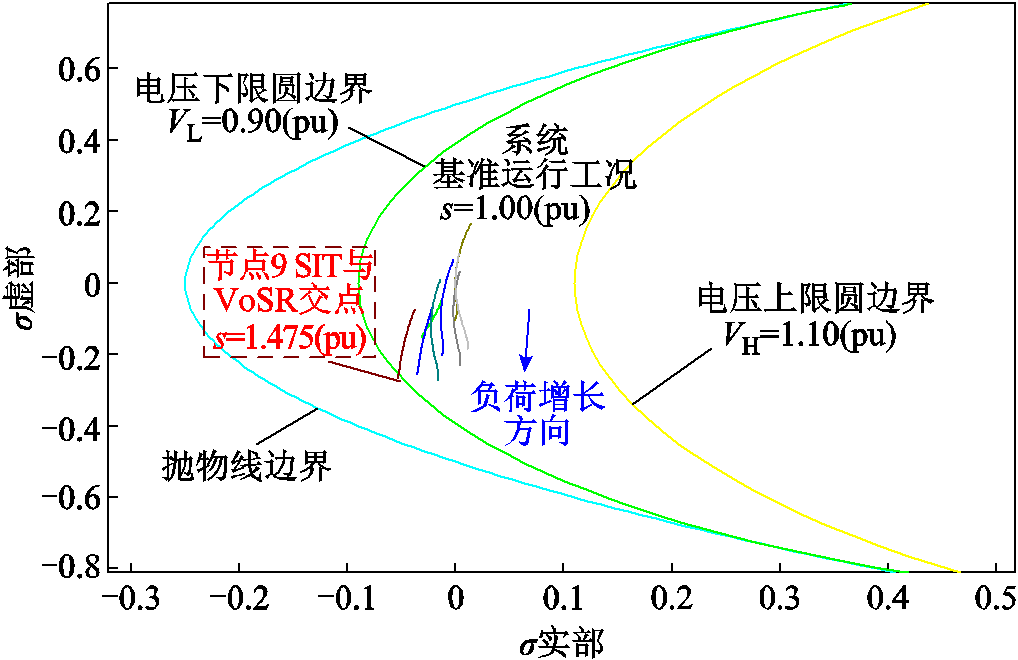
图8 IEEE 9节点系统电压VoSR以及节点电压-无功SIT的可视化结果
Fig.8 Visualization results of IEEE 9 bus system SIT, VoSR and boundaries when system load increases from s = 1.00(pu) to s=1.475(pu)
观察图8可知,节点9电压SIT σ9(s)在系统负荷增长至s=1.475(pu)时首先触及了由电压下限VL=0.90(pu)形成的绿色圆边界。这意味着当系统负荷增长至基准工况的1.475倍时,节点9电压将低于下限0.90(pu)。因此,系统调度员能够可视化地监督并预测各个节点的电压状态。
为了验证所提电力系统节点电压-无功可视化安全域的有效性,与IEEE 9节点系统类似,在IEEE 39节点系统中预设电压下限VL=0.90(pu)和电压上限VH=1.10(pu),系统负荷仍从基准工况s=1.00(pu)开始不断增长。其可视化结果如图9所示。
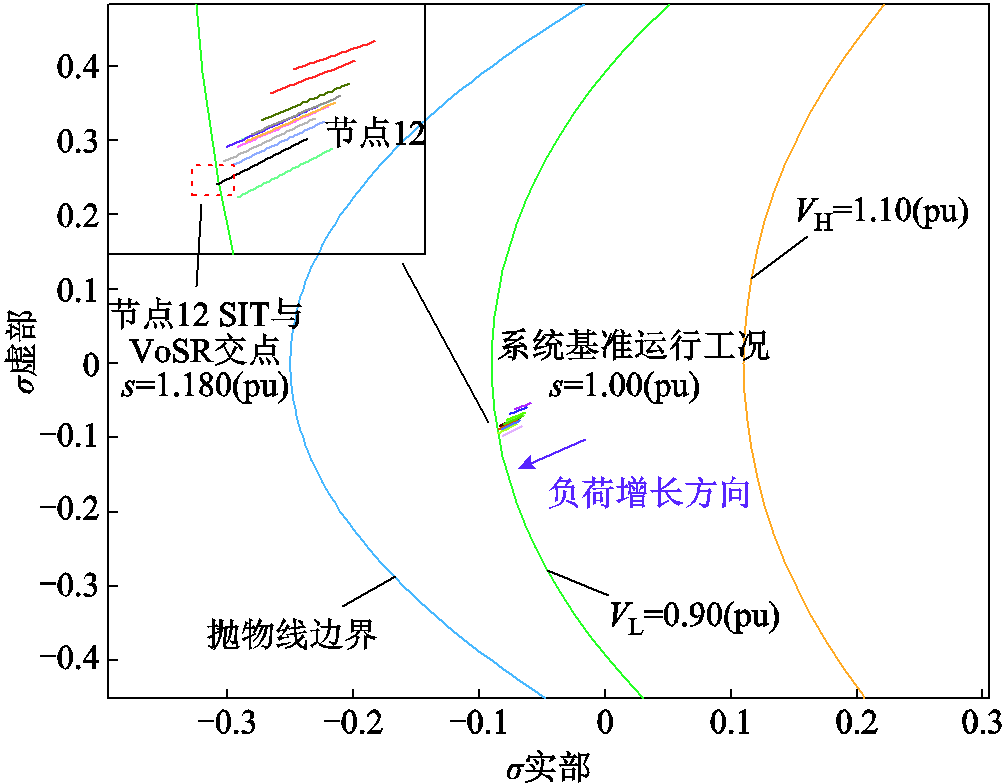
图9 IEEE 39节点系统电压VoSR以及节点电压-无功SIT的可视化结果
Fig.9 Visualization results of IEEE 39 bus system SIT, VoSR and boundaries when system load increases from s=1.00(pu) to s=1.180(pu)
由图9可知,节点12电压SIT σ12(s)在系统负荷增长至s=1.180(pu)时首先触及了由电压下限VL=0.90(pu)形成的绿色圆边界,即当系统负荷增长至基准工况1.18倍时,其电压将低于下限0.90(pu)。
以IEEE 9节点系统中发电机3为例,预设其无功出力上、下限分别为Q3H=300 Mvar和Q3L= −300 Mvar,且系统负荷从0.5倍基准工况s= 0.50(pu)开始不断增长。根据本文所提方法,得到可视化发电机VaSR和各节点电压-无功SIT σi(s)如图10所示。
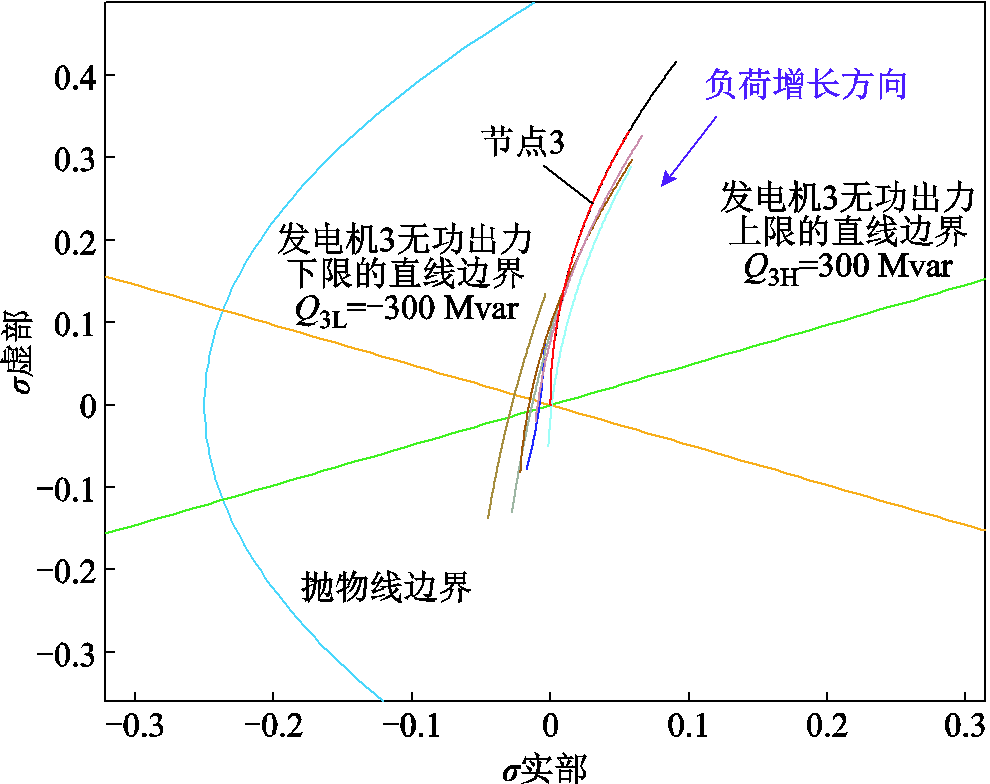
图10 IEEE 9节点系统发电机VaSR以及节点电压-无功SIT的可视化结果
Fig.10 Visualization results of IEEE 9 bus system SIT, VaSR and boundaries when system load increases from s=0.50(pu) to s=1.715(pu)
观察图10中红色轨迹可知,当系统负荷从0.5倍基准工况s=0.50(pu)不断增长至s=1.715(pu)时,发电机3的无功出力SIT σ3(s)不断趋近直线边界,直至触及无功出力直线边界。这意味着当系统负荷增长至基准工况的1.715倍时,发电机3的无功出力发生越限。
为了验证所提电力系统节点电压-无功可视化安全域的有效性,与IEEE 9节点系统类似,在IEEE 14节点系统中预设其无功出力上、下限分别为Q2H=50 Mvar和Q2L=−40 Mvar,且系统负荷从1.0倍基准工况s=1.00(pu)开始不断减小。根据本文所提方法,得到可视化发电机VaSR和各节点电压-无功SIT σi(s)如图11所示。
当系统负荷从基准工况s=1.00(pu)不断减小至s=0.70(pu)时,发电机2的无功出力SIT σ2(s)不断趋近直线边界,但并未触及。这意味着当系统负荷减小至基准工况的0.70倍时,发电机2的无功出力不会越限。此外,由于任何发电机的无功越限均会导致SIT轨迹的不连续,而图11中所有的节点电压-无功SIT均是连续变化的,可知上述判断是可靠的。
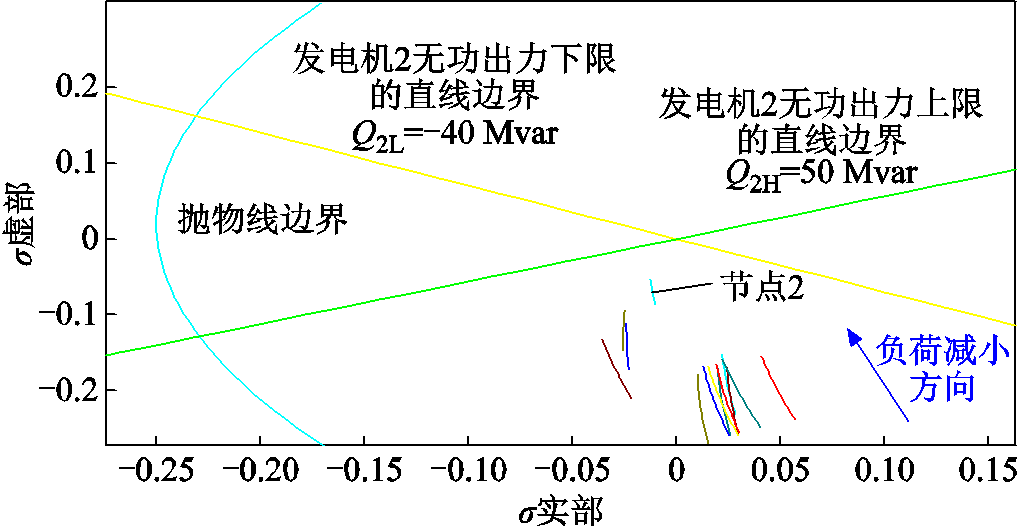
图11 IEEE 14节点系统发电机VaSR以及节点电压-无功SIT的可视化结果
Fig.11 Visualization results of IEEE 14 bus system SIT, VaSR and boundaries when system load decreases from s=1.00(pu) to s=0.700(pu)
综上所述,针对不同规模的电力系统,系统调度员能够根据电压VoSR、发电机VaSR及节点电压-无功SIT的可视化,较为准确地监督并预测系统节点与发电机的状态。
为验证本文所提算法的计算效率,针对多个测试系统进行了仿真测试,并与NR法进行了对比分析,后者作为参考基准。本节中计算收敛精度设置为1×10−6(pu),最大递归次数设置为30次。
图12展示了在9节点、14节点、39节点、57节点和118节点系统中,两种方法的计算时间对比结果。可以看出,采用HEM在时间性能上优于NR法。
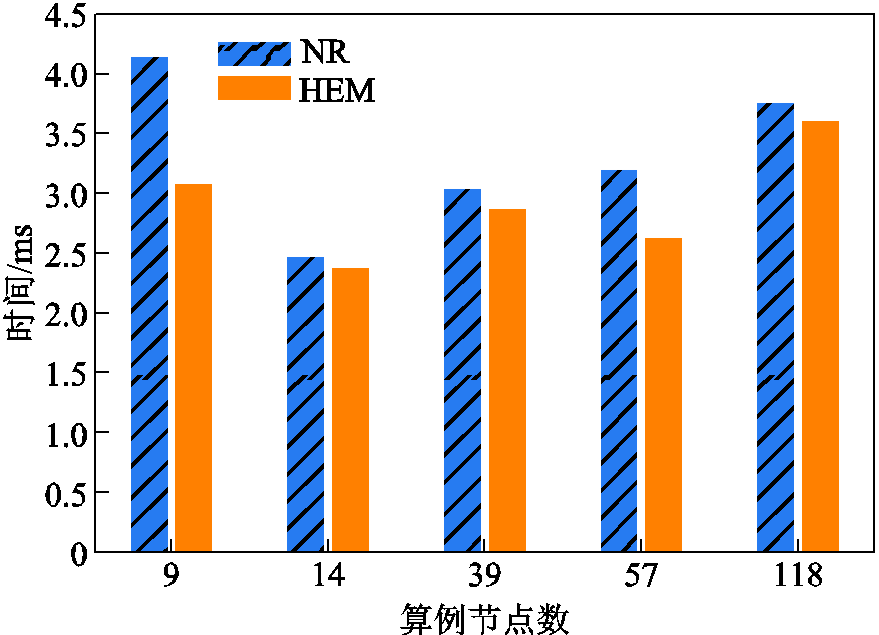
图12 多个不同规模算例NR法与HEM计算耗时对比
Fig.12 Comparison of computation time between NR and HEM for multiple different scale cases
本文针对电力系统节点电压与无功安全域的问题,提出了基于非线性网络分解的节点电压安全域和发电机节点无功安全域,并将二者可视化,从而直观方便地监测各节点的状态。首先,在第1节介绍的非线性网络分解的基础上,引入表示节点电压-无功状态的状态指标σi;其次,采用物理性全纯嵌入法获得随系统负荷状态变化的节点电压-无功状态指标轨迹;然后,推导了各节点电压安全区域、发电机节点无功安全域,并将其与节点电压-无功状态指标轨迹绘制在同一σ复平面内;最后,分别在不同规模节点系统中验证了所提方法的可行性、准确性与有效性。本文所得的主要结论如下:
1)本文在保留系统非线性关系的前提下将多节点系统分解为多个虚拟两节点等效通道,在集成了系统中各个节点的非线性关系的同时为每个节点引入表征节点电压-无功状态的状态指标σi;然后运用物理性全纯嵌入法计算系统工况发生改变时的节点电压-无功状态指标轨迹,以表征在系统不同运行环境下的节点电压和发电机无功出力状态,避免了大量重复的潮流计算,从而节省了计算空间与时间。
2)本文推导了节点电压安全域和发电机无功出力安全域边界的准确表达式,并将所得节点电压安全域VoSR、发电机无功出力安全域VaSR及节点电压-无功状态指标轨迹SIT可视化在同一复平面,可以更加直观可视化地监测节点电压和发电机无功出力状态,并预测它们相应的越限事件,有效地解决了传统静态安全域法在应用中常常面临的直流潮流模型简化或通过分段近似来逼近安全域边界,导致其无法精确反映系统的真实运行特性,从而影响安全域的准确性与可靠性的问题。
3)在IEEE 9节点、IEEE 14节点、IEEE 39系统中进行算例分析,测试了所提方法的有效性、准确性与计算效率,即所提方法能够可视化地独立监督各个节点电压和发电机无功出力状态,准确预测并定位未来运行环境中的电压-无功越限事件。
附 录
1. 节点电压-无功状态指标轨迹σi(s)
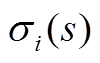 通过将式(13)和全纯嵌入功率流方程相结合进行求解。本文以式(10)~式(12)为例,其中PQ节点的负荷状态变化由sSi*表示,PV节点的发电机无功出力由
通过将式(13)和全纯嵌入功率流方程相结合进行求解。本文以式(10)~式(12)为例,其中PQ节点的负荷状态变化由sSi*表示,PV节点的发电机无功出力由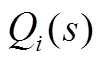 调整以维持其电压幅值不变,PV节点的发电机有功出力由sPi表示。
调整以维持其电压幅值不变,PV节点的发电机有功出力由sPi表示。
为了便于计算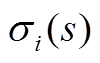 ,在此引入一个新变量Mi,满足式(A1)。
,在此引入一个新变量Mi,满足式(A1)。
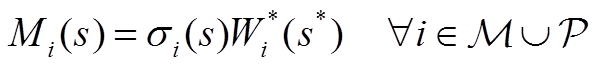 (A1)
(A1)
式中,Wi为节点电压Vi的倒数。
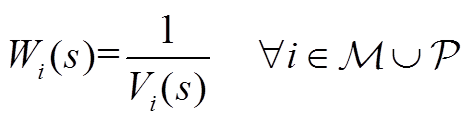 (A2)
(A2)
由于引入了一个新变量Mi,需增加一个方程以保证方程组的可解性。建立Wi和Mi之间的关系为
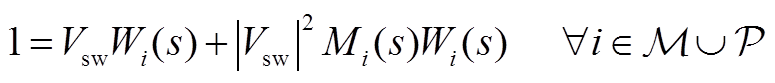 (A3)
(A3)
将式(13)代入式(10)~式(12),并结合式(A1)和式(A2),可得
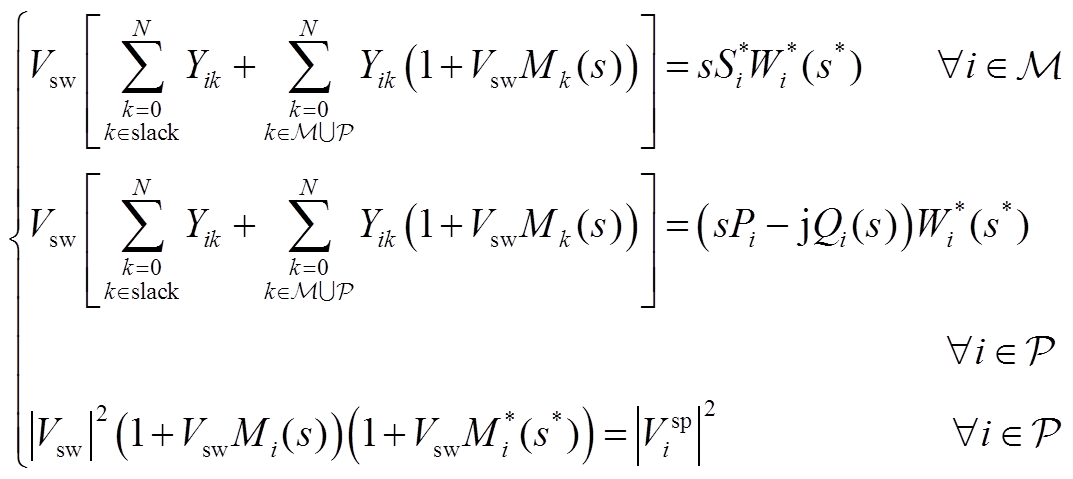 (A4)
(A4)
式中,slack为平衡节点集合;Wi(s)、Mi(s)和Qi(s)均为幂级数形式的全纯函数,有
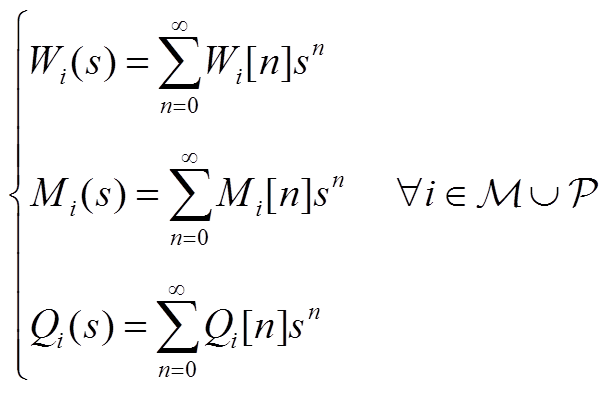 (A5)
(A5)
为了求解Wi(s)、Mi(s)和Qi(s)的所有系数(即Wi[n]、Mi[n]和Qi[n]),将式(A3)和式(A4)中的所有幂级数展开,则各同阶项的系数应对应相等,以此构建出所有幂级数系数前后项之间的递归关系矩阵方程,如式(A6)所示。
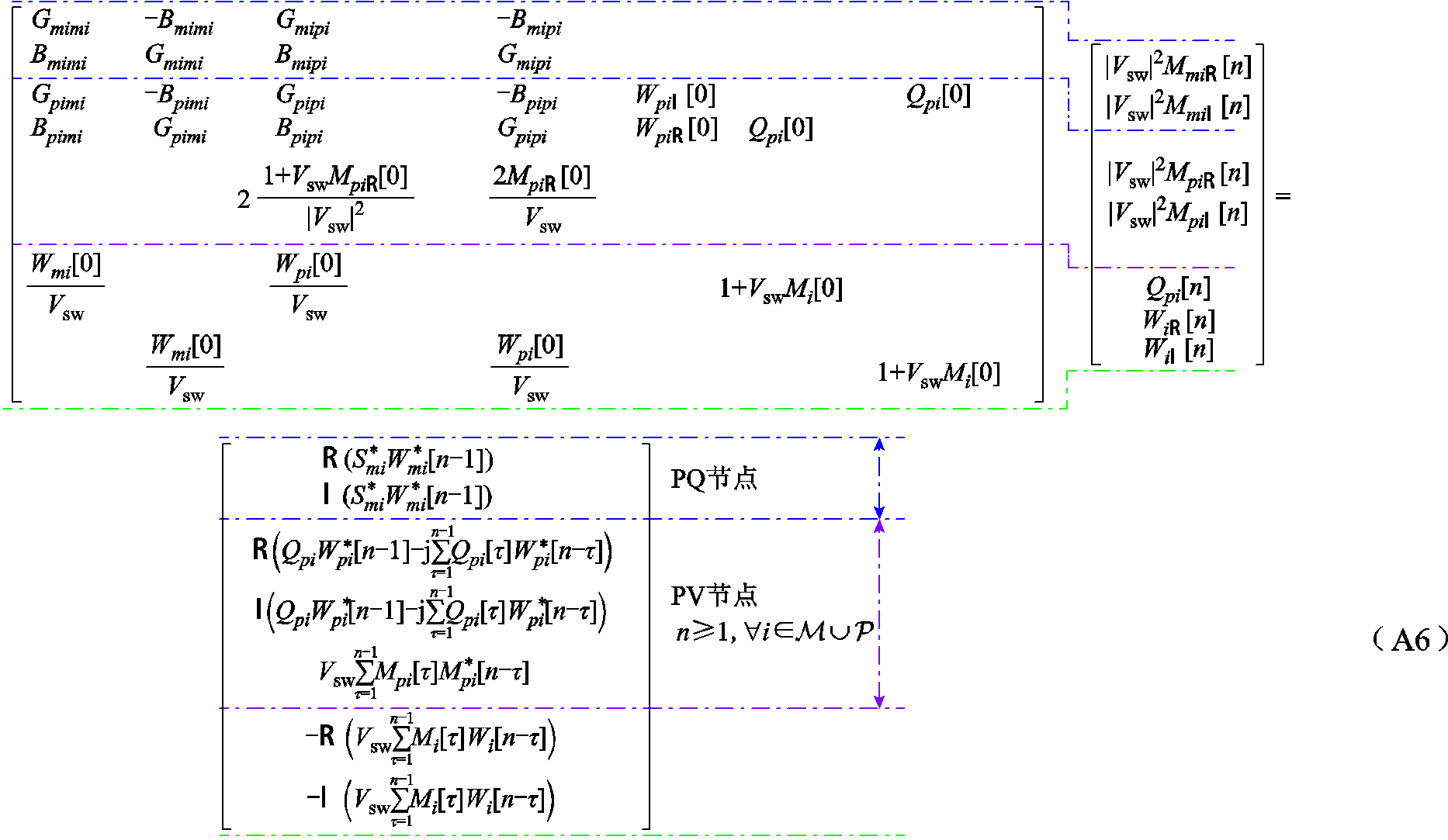
由式(A6)可知,只要将s=0代入式(A4)求得未知量Wi(s)、Mi(s)和Qi(s)的初始解Wi[0]、Mi[0]和Qi[0],则未知量的后续系数可通过式(A6)进行递归求解。
类似地,也可得到σi(s)和Wi(s)及Mi(s)之间的系数关系为
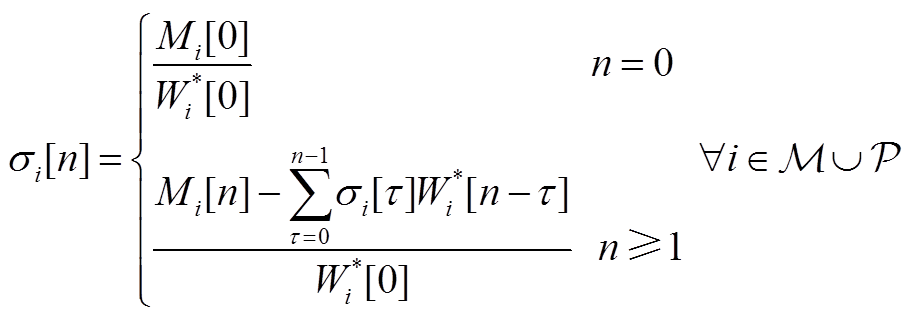 (A7)
(A7)
因此,节点电压-无功状态指标轨迹σi(s)的解析表达式为
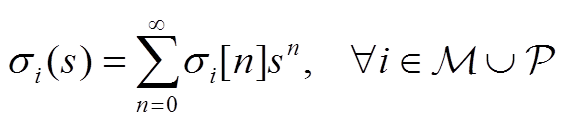 (A8)
(A8)
在考虑新能源或储能接入时,节点类型将发生变化,例如某些节点的有功与频率、无功与电压呈现出下垂控制特性,如式(A9)所示。
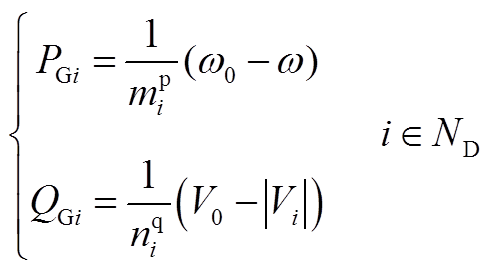 (A9)
(A9)
式中,PGi和QGi为下垂节点i的输出功率;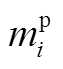 和
和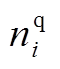 分别为P-f和Q-V下垂曲线的斜率;V0为下垂母线初始节点电压,假定所有下垂母线V0保持恒定;
分别为P-f和Q-V下垂曲线的斜率;V0为下垂母线初始节点电压,假定所有下垂母线V0保持恒定;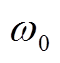 为系统空载角频率;ND为下垂节点集合。
为系统空载角频率;ND为下垂节点集合。
含下垂控制电力系统中通常不含平衡节点,其待求状态变量除了节点电压外还有系统角频率。在此情况下,需要重新构建全纯嵌入潮流方程。采用物理性全纯嵌入法对两种节点在直角坐标系下的交流潮流方程嵌入可得
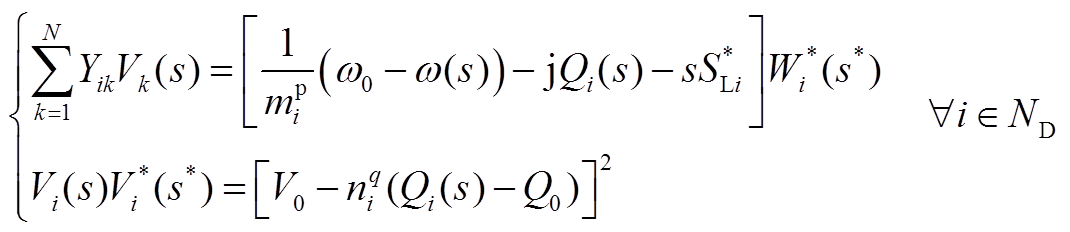 (A10)
(A10)
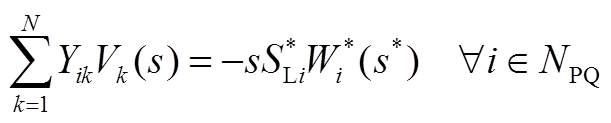 (A11)
(A11)
式中,Fi=Vi/V0;SGi为节点i的输出功率,SGi=PGi+QGi;Si为节点i的功率,Si=SGi−SLi;Q0通常取0;NPQ为PQ节点集合。
接着,采用将幂级数展开的方式,利用同阶幂级数项相等的原则,完成递归关系式的推导,即可完成潮流求解。
求解节点电压-无功SIT时,将式(13)与潮流方程联立,比较方程两边对应阶的s的系数,即可求得高阶项未知系数和低阶项已知系数的递归矩阵方程,从而递归地计算σi(s)的系数,求解过程与前述过程相同。
2. 计算复杂度
联立式(10)~式(12),方程组两侧同阶s的系数对应相等,然后将所有复数型系数拆分为实部和虚部,并令实部等于实部、虚部等于虚部,可得式(A12)所示的递归关系矩阵方程。
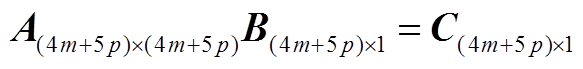 (A12)
(A12)
式中,A为(4m+5p)×(4m+5p)维的固定常数方阵;B为(4m+5p)×1维的向量,表示当前阶未知量;C为(4m+5p)×1维的向量,表示之前阶已知量。
以第h阶为例:
1)式(A12)中矩阵相乘AB的计算复杂度为O((4m+5p)2)。
2)式(A12)中的C包含2m+5p个离散卷积,如果使用快速傅里叶变换算法,那么离散卷积的计算复杂度为(2m+5p) O(hlog2h)。
因此,如果一直计算至第H阶,那么总体计算复杂度为
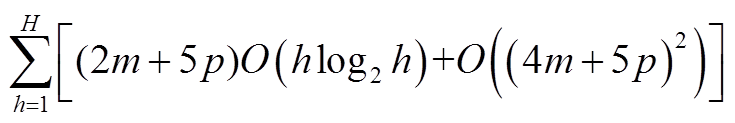 (A13)
(A13)
根据文献[35]中的计算复杂度算法分析可知,联立式(10)~式(13)求解节点电压-无功SIT σi(s)的计算复杂度为O((2m+5p)Hlog2H)。
参考文献
[1] 崔庆雪, 李霞林, 葛磊蛟, 等. 计及时滞的含风电配电网节点电压安全分析[J]. 电工技术学报, 2023, 38(5): 1299-1311. Cui Qingxue, Li Xialin, Ge Leijiao, et al. Analysis on node voltage security of distribution network with wind power considering time delay[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1299-1311.
[2] 朱泽安, 周修宁, 王旭, 等. 基于稳暂态联合仿真模拟的区域多可再生能源系统评估决策[J]. 电工技术学报, 2020, 35(13): 2780-2791. Zhu Zean, Zhou Xiuning, Wang Xu, et al. Evaluation and decision-making of regional multi-renewable energy system based on steady-transient integrated simulation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2780-2791.
[3] 张兆毅, 胡浩, 王子江, 等. 基于非线性仿射的风电场电压实时计算和优化方法[J]. 电工技术学报, 2024, 39(13): 3975-3989. Zhang Zhaoyi, Hu Hao, Wang Zijiang, et al. Real-time voltage calculation and optimization method for wind farms based on nonlinear affine transformation[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3975-3989.
[4] Su Xiangjing, Fang Liying, Yang Jiajia, et al. Spatial-temporal coordinated volt/Var control for active distribution systems[J]. IEEE Transactions on Power Systems, 2024, 39(6): 7077-7088.
[5] Han Yang, Li Hong, Shen Pan, et al. Review of active and reactive power sharing strategies in hierarchical controlled microgrids[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2427-2451.
[6] 陈刚, 刘万彬, 杨悦荣, 等. 考虑新能源不确定波动的交直流混联电网静态电压稳定裕度区间计算[J]. 电网技术, 2023, 47(3): 1127-1137. Chen Gang, Liu Wanbin, Yang Yuerong, et al. Calculation of static voltage stability margin interval for AC/DC hybrid power system considering the uncertainty of renewable energy[J]. Power System Technology, 2023, 47(3): 1127-1137.
[7] Chiang H D, Flueck A J, Shah K S, et al. CPFLOW: a practical tool for tracing power system steady-state stationary behavior due to load and generation variations[J]. IEEE Transactions on Power Systems, 1995, 10(2): 623-634.
[8] Yu Yixin, Liu Yanli, Qin Chao, et al. Theory and method of power system integrated security region irrelevant to operation states: an introduction[J]. Engineering, 2020, 6(7): 754-777.
[9] 李雪, 职梦磊, 姜涛, 等. 电力系统电压稳定域边界的全纯嵌入搜索方法[J]. 电力系统自动化, 2025, 49(10): 123-134. Li Xue, Zhi Menglei, Jiang Tao, et al. Holomorphic embedding search method for voltage stability region boundary of power systems[J]. Automation of Electric Power Systems, 2025, 49(10): 123-134.
[10] 张天策, 李庚银, 王剑晓, 等. 基于可行域投影理论的新能源电力系统协同运行方法[J]. 电工技术学报, 2024, 39(9): 2784-2796. Zhang Tiance, Li Gengyin, Wang Jianxiao, et al. Collaborative operation method for renewable energy power systems based on feasible region projection theory[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2784-2796.
[11] Wu F, Kumagai S. Steady-state security regions of power systems[J]. IEEE Transactions on Circuits and Systems, 1982, 29(11): 703-711.
[12] Liu C C. A new method for the construction of maximal steady-state security regions of power systems[J]. IEEE Transactions on Power Systems, 1986, 1(4): 19-26.
[13] 黄纯华, 余贻鑫, 葛少云. 电力系统无功静态安全域[J]. 天津大学学报, 1987, 20(3): 77-86. Huang Chunhua , Yu Yixin, Ge Shaoyun. Reactive power steady state security region[J]. Journal of Tianjin University, 1987, 20(3): 77-86.
[14] Nguyen H D, Dvijotham K, Turitsyn K. Constructing convex inner approximations of steady-state security regions[J]. IEEE Transactions on Power Systems, 2019, 34(1): 257-267.
[15] 陈中, 朱政光, 严俊. 基于安全距离灵敏度的交直流混联系统安全校正策略[J]. 电力自动化设备, 2019, 39(9): 144-150, 165. Chen Zhong, Zhu Zhengguang, Yan Jun. Security correction strategy of AC/DC hybrid system based on security distance sensitivity[J]. Electric Power Auto-mation Equipment, 2019, 39(9): 144-150, 165.
[16] Lai Qiupin, Liu Chengxi, Sun Kai. Analytical static voltage stability boundary based on holomorphic embedding[J]. International Journal of Electrical Power & Energy Systems, 2022, 134: 107386.
[17] Trias A. Sigma algebraic approximants as a diagnostic tool in power networks: US, 9563722[P]. 2017-02-07.
[18] Trias A. HELM: the Holomorphic Embedding loadflow Method. Foundations and implementations [J]. Foundations and Trends® in Electric Energy Systems, 2018, 3(3/4): 140-370.
[19] 刘承锡, 赖秋频, 姚良忠, 等. 基于全纯嵌入法的电力系统解耦模型: 薄弱节点辨识[J]. 中国电机工程学报, 2022, 42(5): 1736-1748. Liu Chengxi, Lai Qiupin, Yao Liangzhong, et al. Power system decoupling model based on holomorphic embedding method: weak bus identification[J]. Proceedings of the CSEE, 2022, 42(5): 1736-1748.
[20] Cutsem T, Vournas C. Voltage Stability of Electric Power Systems[M]. Cham: Springer US, 1998.
[21] Range R M. Holomorphic Functions and Integral Representations in Several Complex Variables[M]. Cham: Springer New York, 1986.
[22] 李雪, 李博, 姜涛, 等. 主动配电网潮流的全纯嵌入计算方法[J]. 中国电机工程学报, 2024, 44(11): 4210-4227. Li Xue, Li Bo, Jiang Tao, et al. A holomorphic embedding power flow algorithm for active distribution network[J]. Proceedings of the CSEE, 2024, 44(11): 4210-4227.
[23] 刘承锡, 徐慎凯, 赖秋频. 基于全纯嵌入法的非迭代电力系统最优潮流计算[J]. 电工技术学报, 2023, 38(11): 2870-2882. Liu Chengxi, Xu Shenkai, Lai Qiupin. Non-iterative optimal power flow calculation for power systems based on holomorphic embedding method[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2870-2882.
[24] 李雪, 高翔, 姜涛, 等. 电力系统全纯嵌入潮流的并行计算[J]. 电工技术学报, 2024, 39(18): 5839-5854. Li Xue, Gao Xiang, Jiang Tao, et al. Parallel computation of holomorphic embedding power flow for power systems[J]. Transactions of China Electro-technical Society, 2024, 39(18): 5839-5854.
[25] 李雪, 赵书康, 姜涛, 等. 基于稀疏多项式混沌展开的交直流系统全纯嵌入概率潮流计算[J]. 电力系统自动化, 2025, 49(17): 165-175. Li Xue, Zhao Shukang, Jiang Tao, et al. Holomorphic embedding probabilistic power flow calculation for AC/DC systems based on sparse polynomial chaos expansion[J]. Automation of Electric Power Systems, 2025, 49(17): 165-175.
[26] 姜涛, 张勇, 李雪, 等. 电力系统交直流潮流的全纯嵌入计算[J]. 电工技术学报, 2021, 36(21): 4429-4443, 4481. Jiang Tao, Zhang Yong, Li Xue, et al. Holomorphic embedding calculation of AC/DC power flow for power systems[J]. Transactions of China Electro-technical Society, 2021, 36(21): 4429-4443, 4481.
[27] 张逸, 蓝天, 李传栋, 等. 基于功率重启动的全纯嵌入潮流算法[J]. 电工技术学报, 2025, 40(21): 7046-7061. Zhang Yi, Lan Tian, Li Chuandong, et al. Holomorphic embedding power flow algorithm based on power restart[J]. Transactions of China Electrotechnical Society, 2025, 40(21): 7046-7061.
[28] 李宏仲, 滕佳伦. 基于全纯嵌入的电热综合能源系统动态能流计算方法[J]. 电工技术学报, 2025, 40(4): 1254-1267. Li Hongzhong, Teng Jialun. Dynamic energy flow calculation method for electricity-heat integrated energy systems based on holomorphic embedding[J]. Transactions of China Electrotechnical Society, 2025, 40(04): 1254-1267.
[29] 都念纯, 唐飞, 廖清芬, 等. 基于全纯嵌入法的电力系统静态电压稳定性研究[J]. 智慧电力, 2021, 49(9): 8-15, 69. Du Nianchun, Tang Fei, Liao Qingfen, et al. Static voltage stability based on holomorphic embedding method[J]. Smart Power, 2021, 49(9): 8-15, 69.
[30] Liu Chengxi, Wang Bin, Hu Fengkai, et al. Online voltage stability assessment for load areas based on theholomorphic embedding method[J]. IEEE Transactions on Power Systems, 2018, 33(4): 3720- 3734.
[31] Lai Qiupin, Liu Chengxi, Sun Kai. Vulnerability assessment for voltage stability based on solvability regions of decoupled power flow equations[J]. Applied Energy, 2021, 304: 117738.
[32] Liu Chengxi, Wang Bin, Xu Xin, et al. A multidimensional holomorphic embedding method to solve AC power flows[J]. IEEE Access, 2017, 5: 25270- 25285.
[33] Wang Bin, Liu Chengxi, Sun Kai. Multi-stage holomorphic embedding method for calculating the power-voltage curve[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1127-1129.
[34] 国家能源局. 电力系统无功补偿及调压设计技术导则: DL/T 5554—2019[S]. 北京: 中国计划出版社, 2019.
[35] Alsac O, Stott B. Optimal load flow with steady-state security[J]. IEEE Transactions on Power Apparatus and Systems, 1974, PAS-93(3): 745-751.
Abstract With the rapid economic development and growing electric power demand, power systems tend to be operated under heavier loads and closer to their stability limits. Consequently, it is critical for system operators to monitor the voltage and reactive power (volt/var) status in real-time at each bus and promptly detect violations to initiate remedial control actions proactively. Traditional methods, requiring extensive repeated power flow calculations to assess volt/var status against safety regions at each bus, impose an excessive computational burden unsuitable for online applications. Furthermore, conventional power flow analysis only evaluates the current operating point and cannot directly anticipate violations without supplementary sensitivity analysis. To address these limitations, this paper proposes a novel method for defining volt/var safety regions and their visualization based on nonlinear network decomposition. The objective is to provide a computationally efficient framework for assessing bus voltage conditions and generator reactive power outputs, eliminating the need for repeated power flow solutions. This method facilitates the rapid identification of buses at risk of volt or var violations and supports proactive voltage stability assessment under foreseeable operating conditions.
The proposed method begins by constructing a set of virtual two-bus channels through nonlinear network decomposition, effectively transforming the original multi-bus system. Each bus is modeled as a virtual equivalent channel, enabling localized analysis of volt-var characteristics. A complex-valued index is introduced to describe the coupled volt/var status. To trace the status under varying load conditions, the holomorphic embedding method (HEM) is employed to derive the status index trajectory (SIT), capturing the complex-plane trajectory of each bus’s Volt and Var status.
Leveraging the analytical properties of HEM, closed-form expressions for safety region boundaries are derived. Specifically, the voltage safety region (VoSR) and its boundary are characterized as a circular region in the complex plane, while the reactive power safety region (VaSR) is represented by a linear boundary. These boundaries are visualized concurrently with the SIT, providing a comprehensive and intuitive depiction of the margin information.
The effectiveness of the proposed method is validated on multi-bus test systems of varying scales. Simulation results demonstrate that visualizing the VoSR and VaSR enables early detection of weak buses and potential reactive power limit violations. Compared to traditional dispatching procedures—requiring operators to perform repeated power flow calculations for each operating status—the proposed method significantly reduces computational burden and enhances online applicability. It enables continuous, real-time assessment of the system’s voltage stability margins and supports more informed decision-making for system operation and control.
Overall, this research introduces a physical-HEM-based, analytical, and computationally efficient method for visualizing voltage safety regions and reactive power safety regions in power systems. The method's ability to predict and prevent voltage violations and reactive power exceedances enhances the reliability and stability of modern renewable-integrated power systems. This work provides fundamental insights into volt/var coupling behavior and contributes an operationally practical tool for real-time system monitoring and voltage stability management.
keywords:Static safety region, voltage safety region, var safety region, visualization, virtual two-bus channel, holomorphic embedding method
DOI: 10.19595/j.cnki.1000-6753.tces.242199
中图分类号:TM744
收稿日期 2024-12-08
改稿日期 2025-07-24
刘承锡 男,1985年生,教授,博士生导师,研究方向为电力系统仿真计算、电力系统稳定与控制、高比例新能源电力系统不确定性和随机性问题等。E-mail:liuchengxi@whu.edu.cn
罗永建 男,1995年生,博士,研究方向为电力系统电压稳定分析,潮流计算。E-mail:yongjianluo@whu.edu.cn(通信作者)
(编辑 赫 蕾)