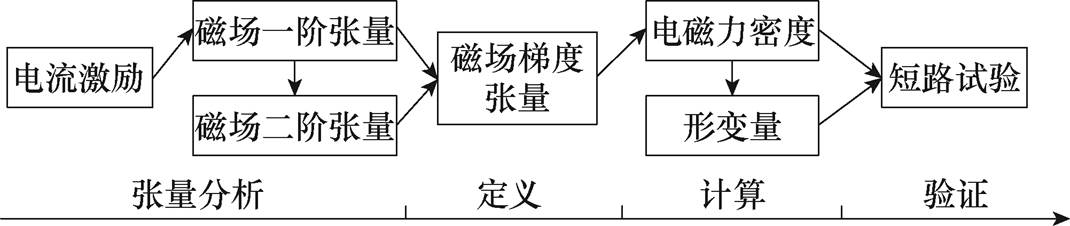
图1 求解流程
Fig.1 Solution process
摘要 该文提出一种基于磁场梯度张量的电磁力计算方法，用于分析变压器绕组中的电磁力和形变。首先，分析绕组中磁场一阶张量和二阶张量的分布特征，探讨张量分布与电磁力之间的内在关系和相互作用机制。然后，基于该关系，定义一个新的张量G，命名为磁场梯度应力张量，通过其进一步计算了三维坐标上每个方向的电磁力密度。最后，搭建一个配备磁场、应力和应变传感器的35 kV单相油浸式缩比变压器试验平台，通过短路试验结果与3D模型的计算对比，验证了该方法的有效性。研究表明，通过磁场梯度法计算得到的电磁力和形变结果与试验结果的最大误差分别为2.4%和2.7%，满足工程实际需求。该方法简化了电磁力的计算过程，同时保持了较高的精度，可为绕组磁-热-力耦合形变分析奠定良好基础，提高变压器在短路条件下的稳定性和安全性。
关键词：变压器 磁场梯度 电磁力 短路故障 形变分析
在能源系统中，变压器作为电力传输的枢纽发挥着至关重要的作用。由电流引起的磁场和力的变化与变压器的运行稳定性密切相关。据统计，由于短路故障引起的巨大电磁力，导致绕组形变后发生严重事故的占比超过所有变压器损坏事故的30%[1-3]。因此，对绕组承受的电磁力进行准确的评估和分析，特别是短路故障情况下的电磁力计算，对确保变压器的稳定运行尤为重要[4]。
变压器短路故障中，绕组中瞬时冲击电流的峰值可以达到其额定电流的数十倍，而电磁力的大小与电流的二次方成正比，由此短路故障产生的电磁力将百倍于其额定运行时承受的电磁力[5]。如此强大的冲击力将会瞬间击穿绕组，使其出现弯曲、移位和倾倒等故障[6]，甚至引发起火、爆炸等更加严重的后果。同时，由于短路力对变压器的损伤较大，通过短路试验的方式对其稳定性进行分析的成本过高。因此，当前的研究普遍采用关键部件的材料特性分析[7-8]、状态评估和预测[9-11]以及仿真计算[12-14]等方法对短路力进行探究。
对短路力的研究主要集中于两个方面：一是变压器的磁特性研究，如磁场的强度和位置；二是电磁力作用的大小和方向以及形变程度。在磁场研究方面，文献[15]通过数字电路模型，分析了短路电流和重合闸电流对变压器漏磁场的影响以及其数值分布。文献[16]通过磁特性研究分离变量解析计算方法，求取了变压器故障绕组漏磁场分布的解析公式。文献[17]采用时域分析的方式，计算了正弦激励下非线性各向异性的叠片铁心中的三维漏磁场。文献[18]推导了变压器绕组在空间中的磁通密度公式，随后分析了变压器正常运行时的轴向漏磁分布对称性规律。文献[19]采用棱边有限元法，对变压器的磁场进行了分析，并确定了损耗分布。
在对电磁力特性的研究中，文献[20]比较了基于虚功原理（Principle of Virtual Work, WPV）的节点力与应用于不同表面的麦克斯韦张量，结果表明，WPV能更准确地分析局部磁压力。文献[21]对110 kV真型变压器进行了多次短路试验，研究了绕组在累积效应下的轴向电磁力及振动特性。文献[22]通过三维有限元模型和实验测量，分析了不同的绕组交叉换位结构对变压器漏磁场和电磁力的影响规律。文献[23-25]通过细化的绕组轴向结构的质量-弹簧-阻尼等效模型，提出了绕组短路振动特性及承受能力的评估方法。文献[26]建立了绕组形变对应振动的数学模型，研究了绕组形变后的振动变化规律。文献[27]将绕组等效为具有不同弹性系数的弹簧系统建立了动稳定特性分析模型，并结合压力试验，分析了绕组受到的冲击力及静压力特性。文献[28]介绍了通过虚位移进行受力分析的方法，但其研究对象为开关磁阻电机，并未涉及变压器相关内容的计算。
综上所述，大多数关于绕组短路力计算的研究使用麦克斯韦应力法、虚位移法和经验公式等方法。这些方法的准确性在很大程度上依赖积分路径的选择，且计算量较大，导致它们无法描述电磁力的动态变化或解决局部应力问题。本研究首先深入分析了变压器绕组中磁场一阶张量和二阶张量的内在原理；然后，基于工程实际和磁场能量分布，定义了磁场梯度张量G，并分析了其梯度与电磁力和绕组形变之间的关系；最后，搭建了一个35 kV缩比变压器3D模型和试验平台，通过仿真分析和短路试验验证了所提方法的有效性。
磁场的高阶张量通常可以反映磁场的某些特性。如，磁通密度的大小可描述磁场在空间中的强度，而二阶张量则代表了磁场在空间中的分布特性和变化率。通过各自方向上的磁通密度与二阶张量的计算，可以直接得到绕组中的电磁力分布状态。
本文计算方法的求解流程如图1所示。首先，根据厂家提供的变压器真实材料参数、工况和边界条件，求解得到绕组中的磁通密度；然后，计算磁通密度的一阶张量及二阶张量，观察其在三维空间中的分布情况，并通过定义的磁场梯度应力张量，对其电磁力密度和形变量进行计算；最后，通过仿真分析和短路试验平台，对数值计算结果进行验证。
图1 求解流程
Fig.1 Solution process
变压器中待求解区域的受力分析如图2a和图2b所示，由此可见，变压器的内绕组与外绕组所受的轴向力方向相同，辐向力方向相反。其中，V1表示涡流区，主要存在于铁心中，V2表示非涡流区；在边界SH上给定磁场的切向分量，在边界SB上给定磁场的法向分量。
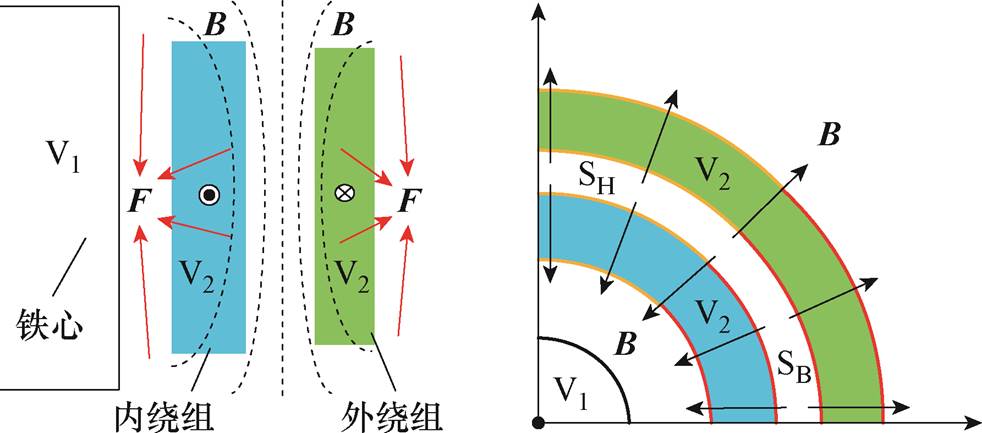
（a）主视图 （b）俯视图
图2 电磁力方向
Fig.2 Direction of electromagnetic force
将求解范围进一步细化后，绕组中每个节点上均包含三个方向的磁通密度，其中，Bx、By为辐向磁通密度，产生轴向力Fz；Bz为轴向磁通密度，产生辐向力Fx和Fy，如图3所示。
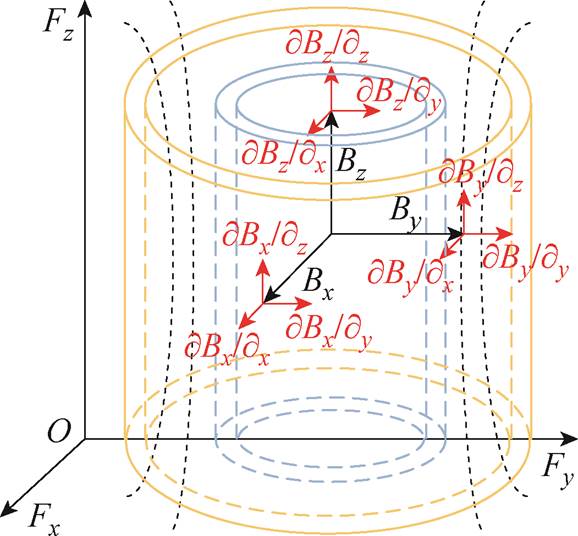
图3 节点受力分析
Fig.3 Node force analysis
首先采用A、j-A方法建立了一个涡流场数学模型。当电流流入绕组时，涡流区和非涡流区符合库伦规范的磁场控制方程如下。
涡流区：
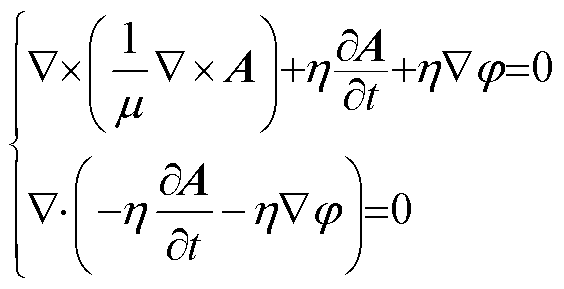（1）
非涡流区：
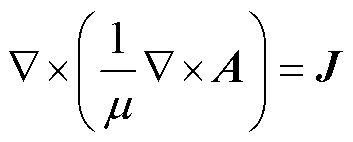（2）
式中，m为磁导率；h为电导率；A为矢量磁位；j为标量电位；J为电流密度。
边界条件：
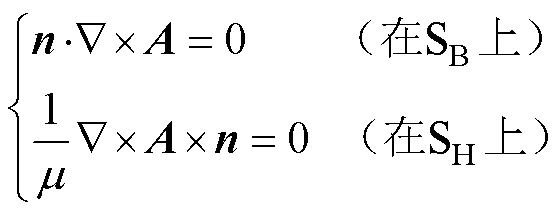（3）
式中，n为界面上的法向量。
矢量磁位A通常采用Nédélec第一类边元函数进行插值。对于每一个四面体单元e，磁矢势可表示为
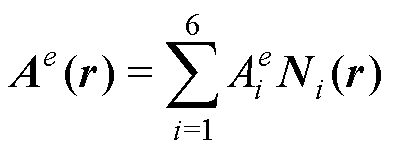（4）
式中，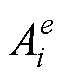
为单元e第i条棱边上的磁矢势环量；
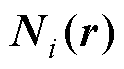为与该棱边关联的矢量形函数；r(x, y, z)为空
间位置向量。则单元中任意一点的磁通密度矢量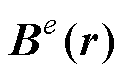
为
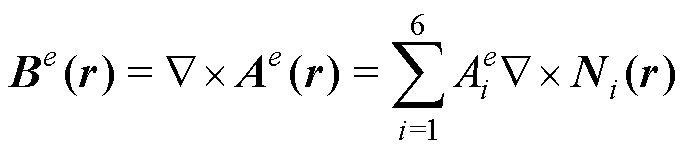（5）
由于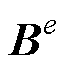
在每个单元内为常量矢量场，难以直接获得其空间梯度。为实现对磁场空间变化的高精度建模，本文通过二阶多项式拟合方法，对多个单元磁通密度数据进行加权最小二乘拟合，构造出连续可导磁场函数。由此得到磁通密度矢量B(Bx, By, Bz)，其本质上为一阶张量，用以表征磁场在三维空间中的方向与强度分布。
工程实际中，通过对多台受损变压器的拆解分析发现，绕组损坏的位置通常并非磁场强度最大的地方，而是磁场变化率（即磁场梯度）最大的地方。根据能量守恒原理，磁场梯度较大的位置，其能量和能量密度的变化率同样较大。
受到这一现象的启发，并通过多次数值仿真计算，本文提出了一种基于磁场能量密度的梯度计算电磁力密度的新方法，命名为磁场梯度法，同时定义了一个新的张量——磁场梯度应力张量G。具体分析如下。
在各向同性且均匀的介质中，磁场的能量密度可表示[29]为
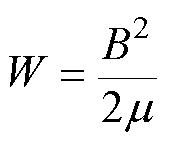（6）
其梯度形式表示为
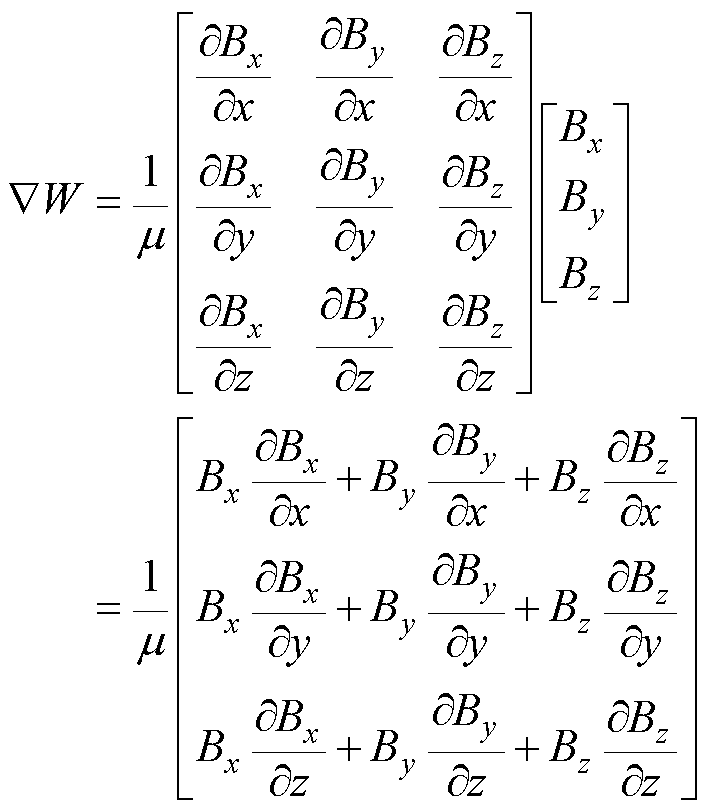（7）
将磁场能量密度梯度中磁阻率与包含磁场梯度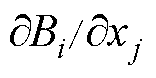
的二阶张量的乘积，定义为一个新的二阶张量，即磁场梯度应力张量G，即
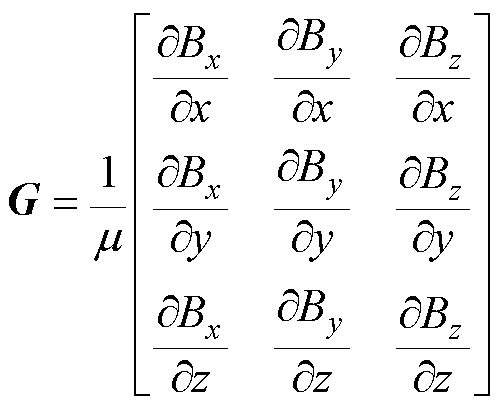（8）
由此可见，张量G的每一行Gi都反映了磁场本身的变化率和方向性。为了与传统电磁力计算方法在物理意义上相吻合，需要进一步加入能够代表强度的磁场分量值。
在笛卡尔坐标系中，磁场的正负通常表示其方向，为了消除方向性的影响，对磁场分量取绝对值。随后，将磁场绝对值矩阵与张量G相乘，可得到单位体积上的电磁力密度f，表示为
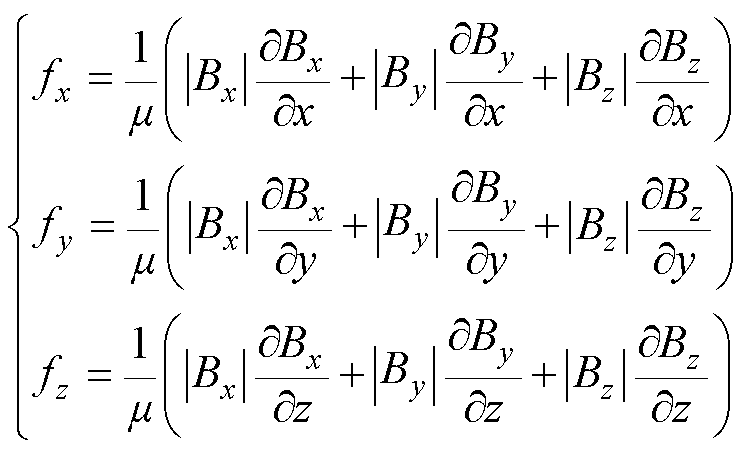（9）
与传统方法相比，磁场梯度法可减少对复杂几何结构上边界选取与积分路径选择的依赖，而是直接计算域内的电磁力密度分布，通过体积分得到总电磁力。其积分过程简洁、路径简洁，尤其适用于复杂结构绕组中的局部应力集中的问题分析。此外，将电磁力通过张量矩阵形式进行表达，将更方便后续与热应力同时进行磁-热-力耦合分析。
求得电磁力后，根据大变形理论和应变-位移关系，可以得到力的平衡方程为
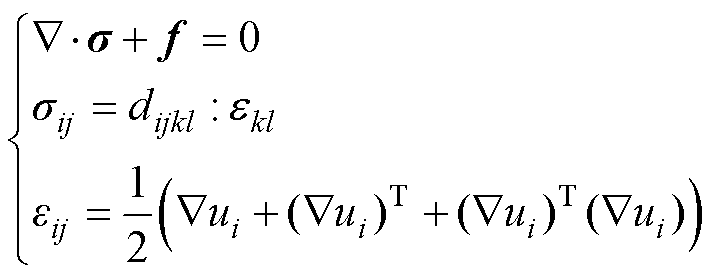（10）
式中，s为应力张量；sij为应力张量分量；dijkl为四阶弹性张量；ekl为应变张量；ui为位移分量。
本文的研究对象为一台35 kV（800/35-10.5）单相油浸式缩比变压器。图4所示为该变压器的3D模型，其短路阻抗为19.5%。模型包含铁心、支架、绕组、绝缘纸板、撑条和油箱等关键组件。油箱的尺寸为1.6 m（x）× 0.7 m（y）× 1.1 m（z）。高压绕组的高度为460 mm，辐向尺寸为123 mm；低压绕组的高度为480 mm，辐向尺寸为74 mm。油箱壁厚为10 mm。油箱顶部有四个油流出口，底部有四个油流入口。结构按照铁心→低压绕组→高压绕组的顺序排列。其余主要参数汇总见表1。
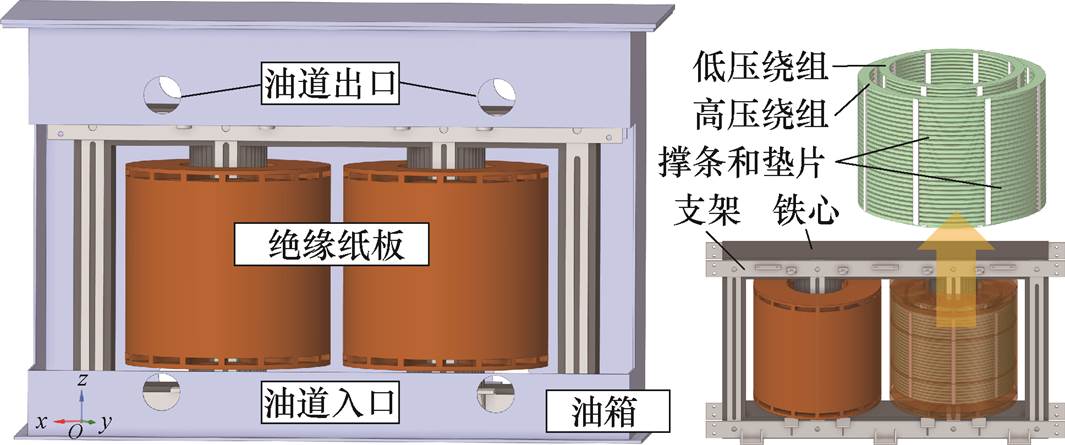
图4 变压器结构
Fig.4 Transformer structure
表1 变压器主要参数
Tab.1 Main parameters of the transformer
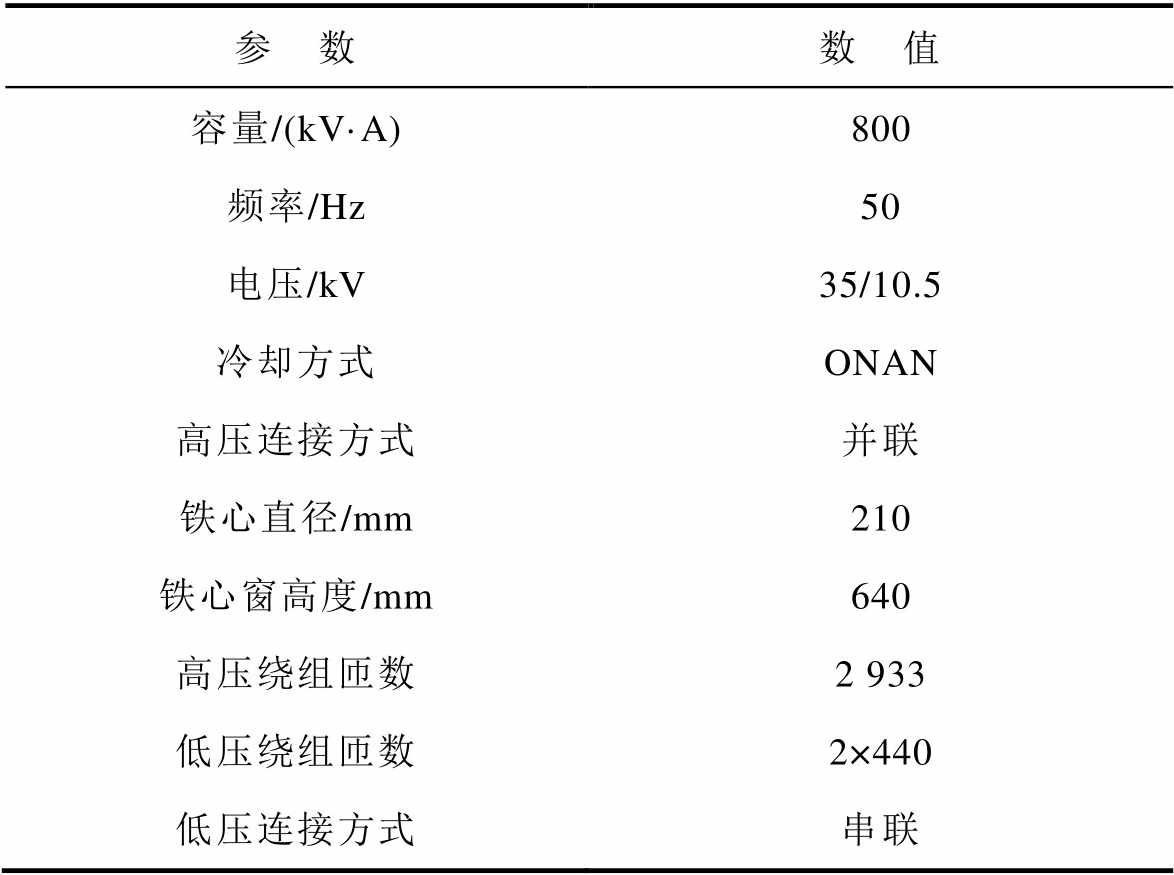
参 数数 值 容量/(kV·A)800 频率/Hz50 电压/kV35/10.5 冷却方式ONAN 高压连接方式并联 铁心直径/mm210 铁心窗高度/mm640 高压绕组匝数2 933 低压绕组匝数2×440 低压连接方式串联
变压器模型采用多区域分解方法进行四面体网格剖分，并对绕组区域进行扫掠和局部加密。网格优化过程测试了节点数约为1 300万、1 700万、2 000万和4 000万的网格剖分计算结果，并验证了不同网格数量之间的结果差异如图5a所示。最终，从时效性的角度出发，采用网格节点数为17 130 871，平均网格质量约为0.88。较低质量的网格主要位于油箱和结构件等位置，这些区域对绕组形变的计算影响较小，如图5b所示，可以满足计算需求。
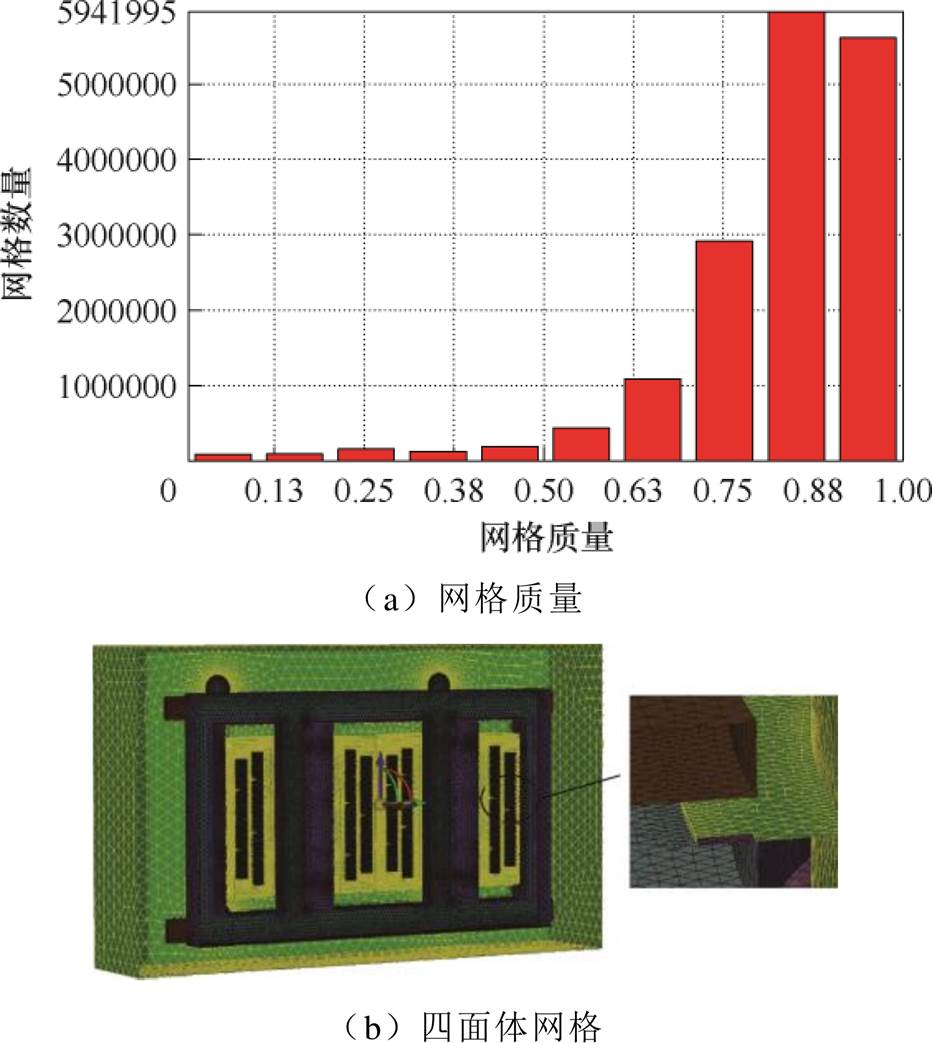
图5 多区域网格分解
Fig.5 Multi-region mesh decomposition
在结构力仿真中，首先设置整体的地球重力作用，环境温度为20℃；其次，在撑条两端施加对应的预紧力；最后，导入磁场载荷并计算应力及形变。
绕组中漏磁通的大小取决于电流值。据统计，在所有的短路故障中，单相短路发生的占比最大，其中，低压绕组短路的故障电流最大，所以本文针对低压侧绕组单相短路工况进行分析。根据当前电力系统中装备的断路器工作时间及变压器19.5%的短路阻抗设定短路电流的大小和持续时间，如图6所示。其中0～20 ms为额定电流，20～85 ms为短路电流，随后断路器切断线路。
为了最大程度地分析绕组的形变特性，本文选取短路电流最大时刻，即25 ms时进行分析。通过有限元仿真分析得到的单相短路状态下绕组中的磁场分布如图7所示。漏磁通主要分布在两绕组之间的主通道位置，最大值约为611 mT，出现在铁心窗内的绕组中部位置，并向两端逐渐减小。由此可见，绕组中部承受的辐向力会大于端部承受的轴向力。同时，低压绕组外侧的漏磁通大于内侧，而高压绕组与之相反。由此说明，高压绕组的辐向力主要为从内向外的拉应力，而低压绕组的辐向力主要为由外向内的压应力。
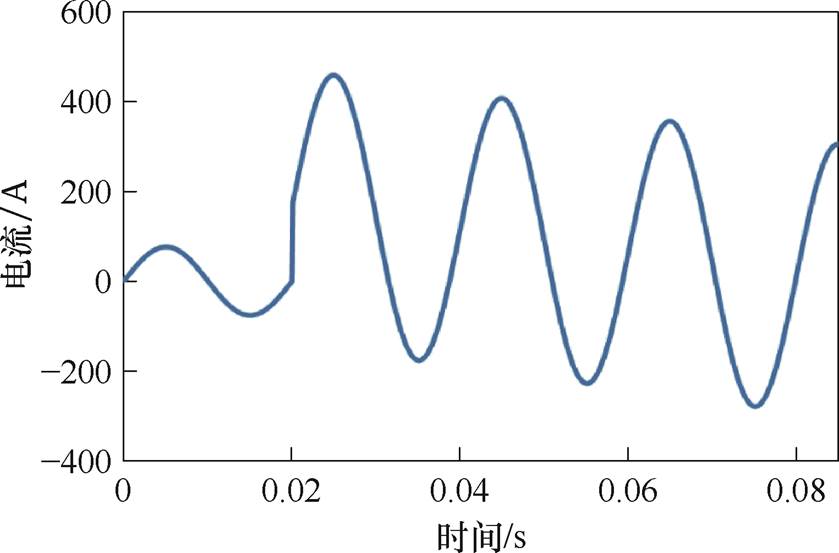
图6 低压绕组短路电流波形
Fig.6 Low voltage winding short-circuit current waveform
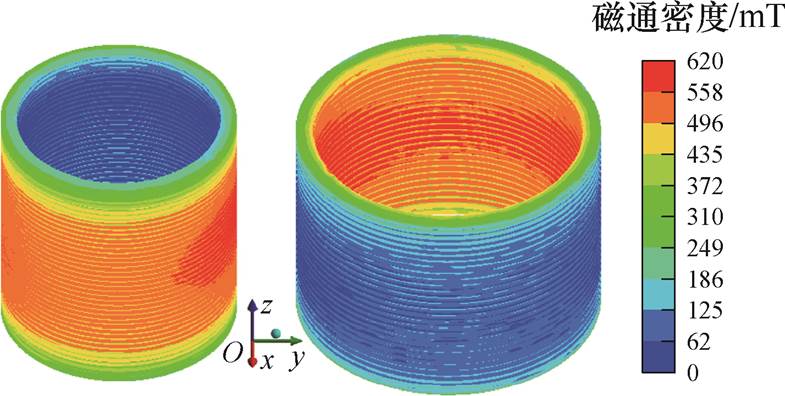
图7 磁场分布
Fig.7 Magnetic field distribution
通过上述结果可以看出，高压绕组中的磁场分量梯度更加明显，且由于受力方向的原因，通常来说外绕组的形变量大于内绕组，有利于进一步探究磁场与电磁力的本质关系。所以接下来，本文将重点针对高压绕组进行分析。提取出磁通密度数据后，使用Python和Matlab编写程序对其二阶张量和电磁力密度进行计算。
图8所示为高压绕组磁通密度的矢量分布结果。可以看出，其辐向磁场Bx和By主要集中在绕组端部，大小相等方向相反，最大值约为297 mT。而轴向磁场Bz则主要集中在绕组的内侧和外侧，且内侧的磁通密度远大于外侧，约为613 mT。这说明，绕组中的磁场在经过端部拐点时的发散情况较为明显。
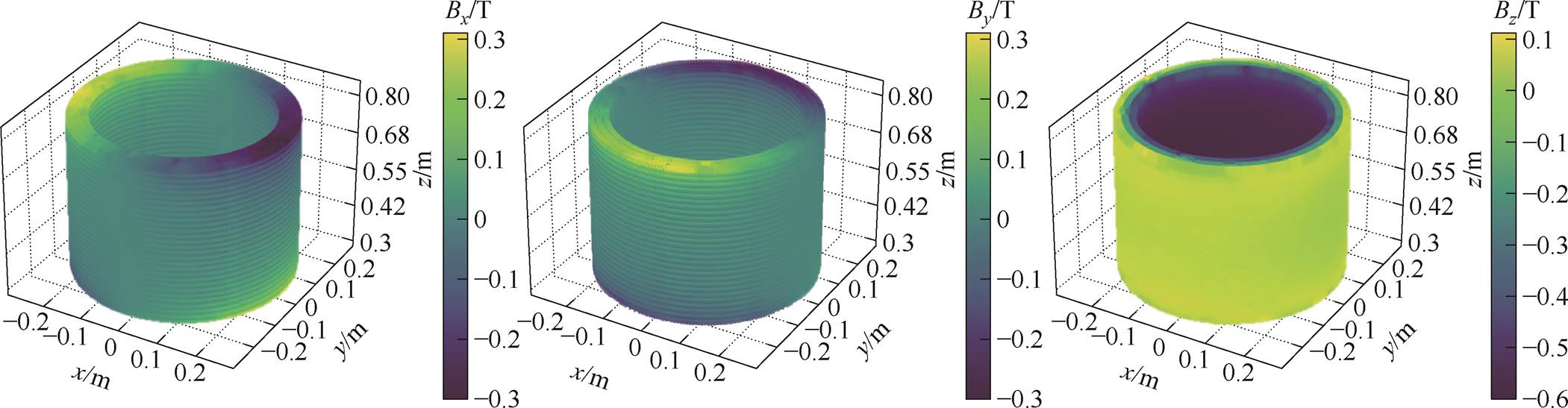
图8 磁场矢量分布
Fig.8 Magnetic field vector distribution
若将磁场分量取绝对值，去掉方向性的影响，可以直接看出高压绕组中磁场的数值分布。如图9所示，可以清晰地对应到不同位置电磁力的强度。
下面将进一步观察高压绕组中磁场的二阶张量分布情况，去除畸变点后的结果如图10所示。可以看出，轴向磁场的幅向分量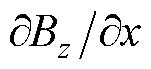
、
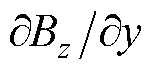范围在-35～35 T/m之间。而辐向磁场的轴向分量
、
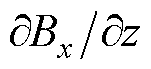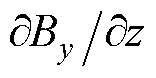的范围均在-17.5～17.5 T/m之间，其数值代表了磁场的变化率。其余分量没有实际意义且数值接近于零，可以忽略不计。
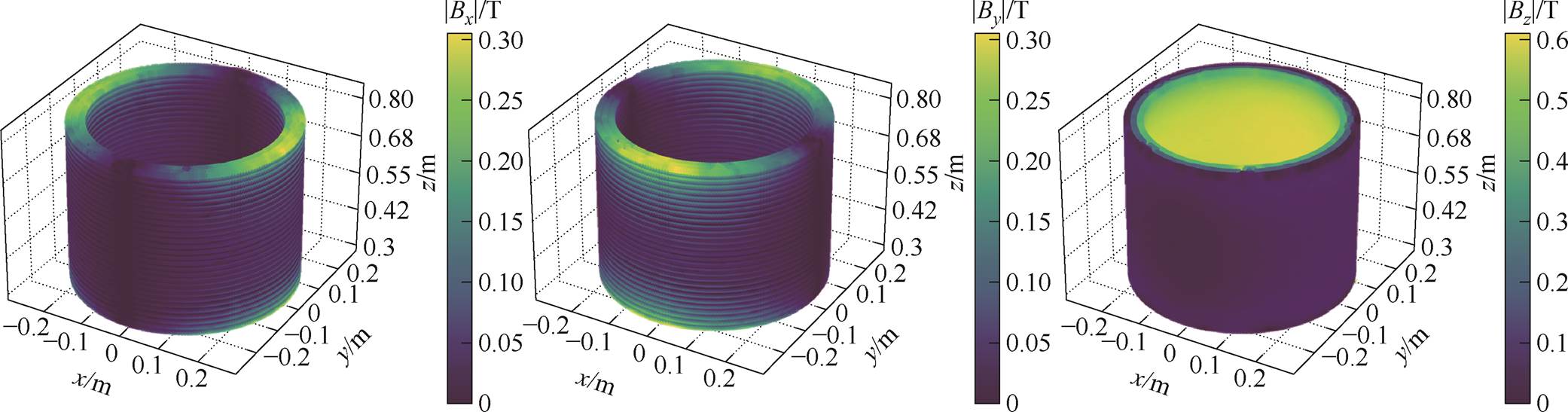
图9 磁场数值分布
Fig.9 Magnetic field scalar distribution
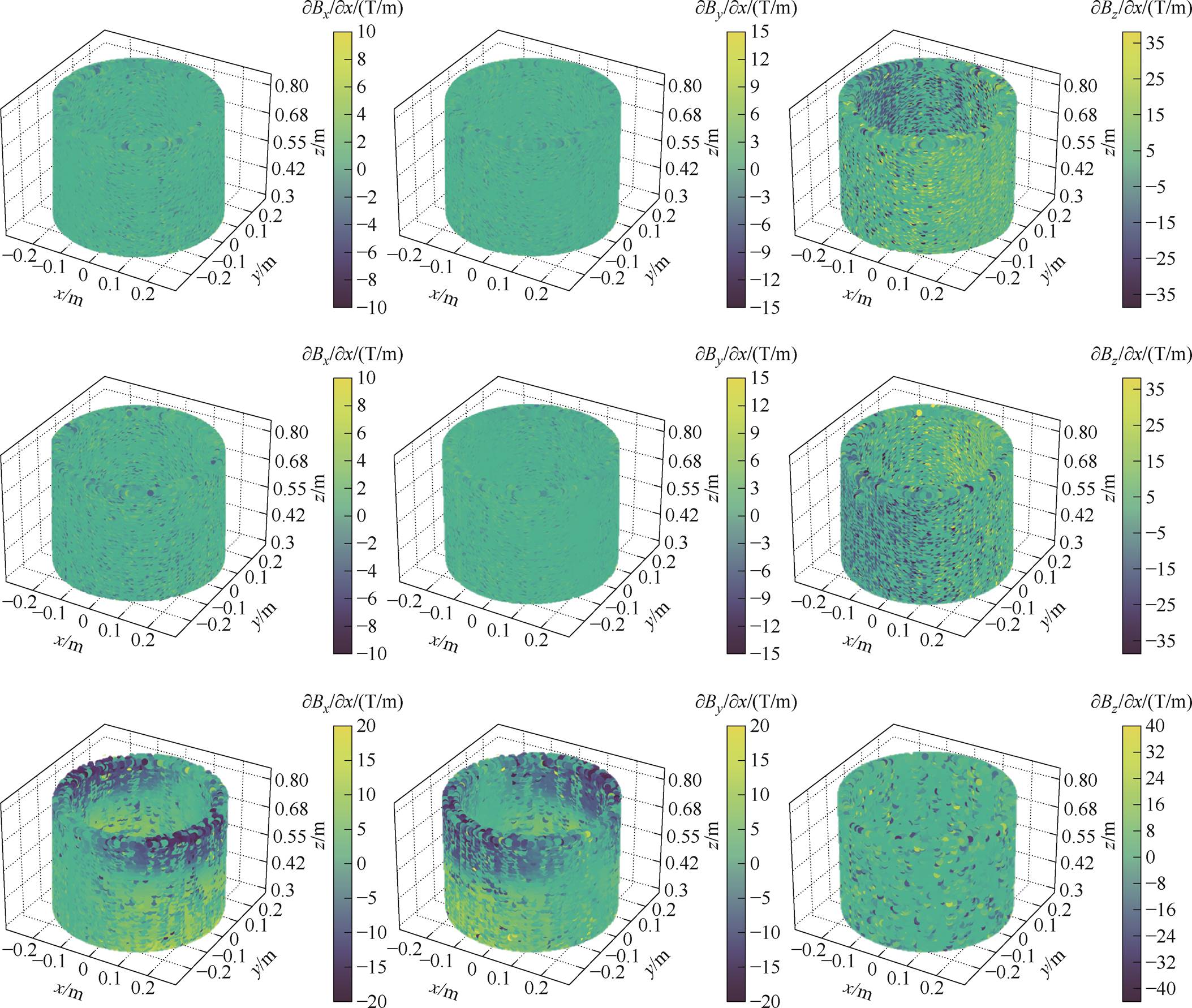
图10 二阶张量分布
Fig.10 Second-order tensor distribution
图11所示为高压绕组中的电磁力密度分布情况，其中数值为正表示其方向指向坐标轴正方向，反之为负方向。由此可见，绕组受到由内向外的辐向力和由两端向中间压缩的轴向力，其辐向力密度最大值约为1.7×107 N/m3，远大于轴向力密度（约为7.99×106 N/m3），与上述通过磁场分布对绕组受力情况的初步判断结果一致。
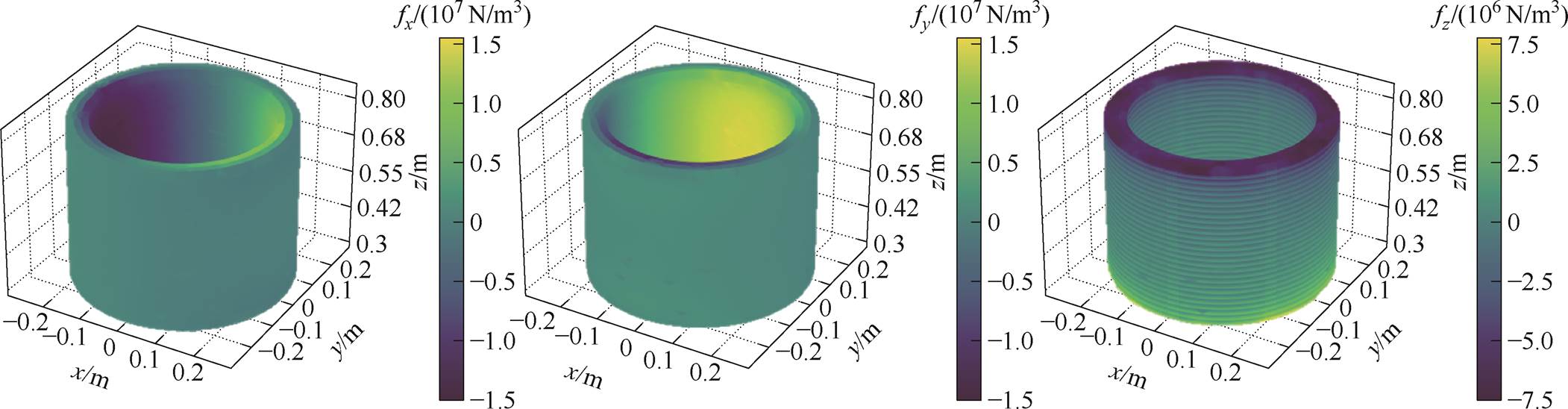
图11 电磁力密度分布
Fig.11 Electromagnetic force distribution
同时，通过对比电磁力密度与磁场二阶张量可以发现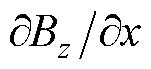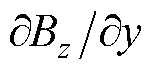，、与辐向力密度fx和fy的分布情况几乎一致，将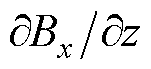和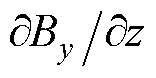合并后与轴向力密度fz的分布同样高度一致。这说明可以通过磁场的二阶张量来确定电磁力方向。
图12所示为使用有限元计算得到在短路电流峰值时绕组形变的仿真结果。具体表现为高压绕组辐向向外膨胀，而低压绕组辐向向内压缩，轴向形变均为两端向内压缩。最大形变部分集中在绕组相邻的位置，与磁场的分布情况相同，验证了上述分析的准确性。绕组的最大综合形变量约为0.983 mm，位于高压绕组的端部。
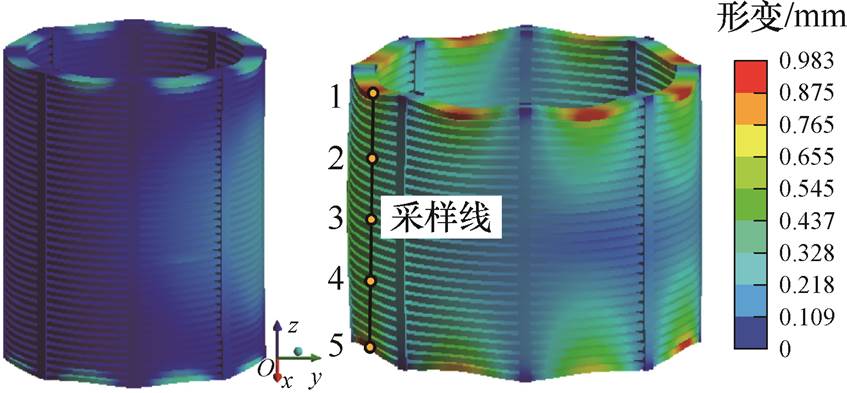
图12 绕组短路形变
Fig.12 Winding short-circuit deformation
沿高压绕组形变量最大的位置画一条轴向采样线，并等距选取5个采样点，对数值计算结果进行进一步验证。沿采样线分别使用有限元软件和本文提出的磁场梯度法计算了绕组轴向和辐向的磁场、电磁力密度以及形变。结果比较如图13～图15所示。
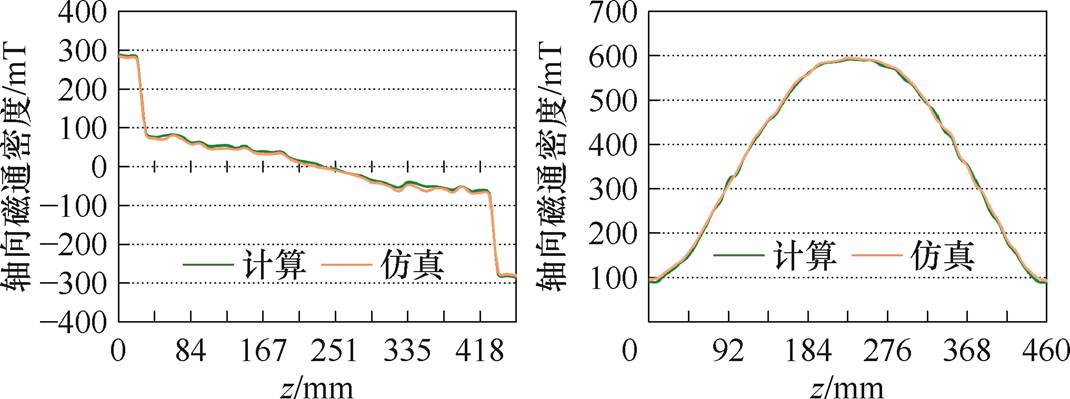
图13 磁场分布曲线
Fig.13 Magnetic distribution curves
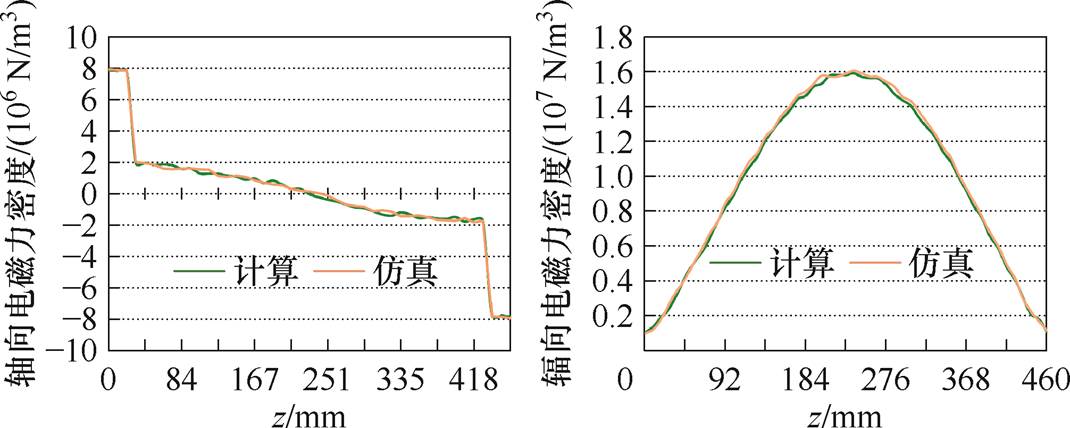
图14 电磁力密度分布曲线
Fig.14 Electromagnetic force density distribution curves
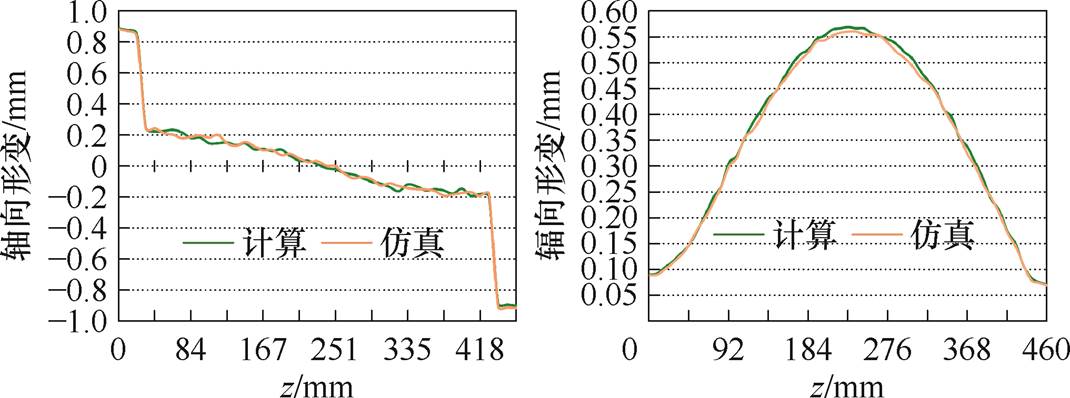
图15 形变量分布曲线
Fig.15 Deformation distribution curves
根据仿真计算结果，绕组轴向力密度最大值位于上端部，约为7.86×106 N/m3，对应的最大形变量约为0.902 mm；最大辐向力密度和形变量分别为1.58×107 N/m3和0.553 mm，位于绕组中部位置。
5个采样点的详细对比数据见表2。由此可知，高压绕组在短路电流的峰值时刻，其辐向力和辐向形变的最大误差约为1.8%和3.5%；轴向力和轴向形变的最大误差约为1.4%和2.3%。结果满足工程实际要求，验证了本文所提方法的准确性和有效性。
表2 电磁力与形变量对比
Tab.2 Comparison of electromagnetic force and deformation
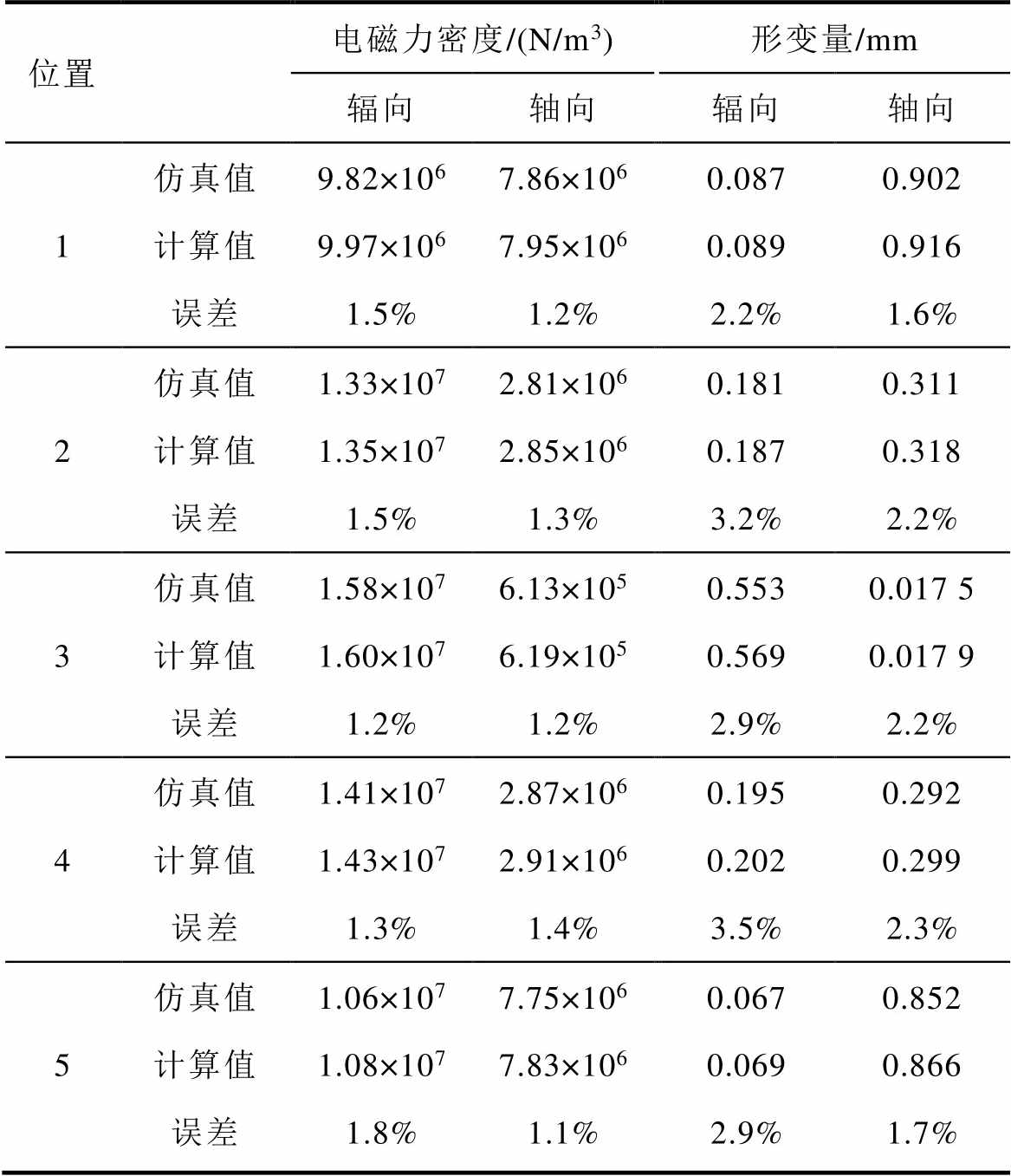
位置电磁力密度/(N/m3)形变量/mm 辐向轴向辐向轴向 1仿真值9.82×1067.86×1060.0870.902 计算值9.97×1067.95×1060.0890.916 误差1.5%1.2%2.2%1.6% 2仿真值1.33×1072.81×1060.1810.311 计算值1.35×1072.85×1060.1870.318 误差1.5%1.3%3.2%2.2% 3仿真值1.58×1076.13×1050.5530.017 5 计算值1.60×1076.19×1050.5690.017 9 误差1.2%1.2%2.9%2.2% 4仿真值1.41×1072.87×1060.1950.292 计算值1.43×1072.91×1060.2020.299 误差1.3%1.4%3.5%2.3% 5仿真值1.06×1077.75×1060.0670.852 计算值1.08×1077.83×1060.0690.866 误差1.8%1.1%2.9%1.7%
在满足计算精度的同时，使用磁场梯度法的计算效率相比于有限元仿真也有大幅度的提升，计算效率对比见表3。计算时间由9.8 h缩短至5.5 h，提升约43.9%，占用内存由292 GB减小至135 GB，提升约53.8%，进一步说明了磁场梯度法的优越性。
表3 计算效率对比
Tab.3 Comparison of computational efficiency
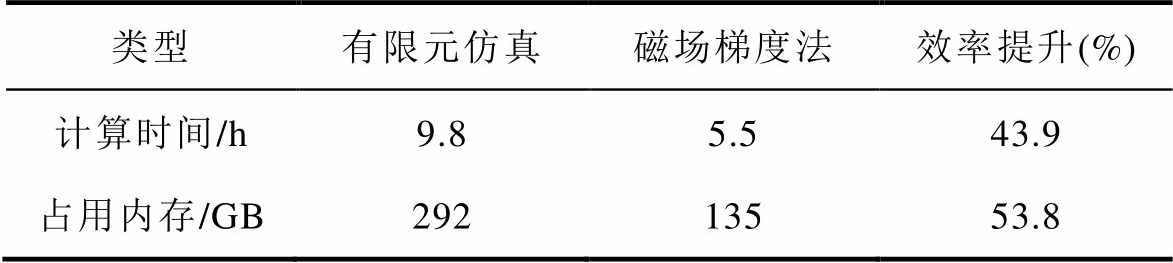
类型有限元仿真磁场梯度法效率提升(%) 计算时间/h9.85.543.9 占用内存/GB29213553.8
通过上述对比分析，对方法做了初步验证。下面将搭建35 kV单相油浸式缩比变压器试验平台，并通过短路冲击试验做进一步验证。
图16所示为平台的基本结构和传感器布置方案。本次试验共使用8个霍尔磁场传感器、8个光纤光栅应力传感器和8个位移传感器，分别布置在绕组的顶部和中部，沿圆周呈90°分布。其中，磁场传感器放置在高、低压绕组中间的主通道位置，应力和应变传感器放置在高压绕组线饼中间，并将放置位置编号为1～8。传感器通过内部光纤连接变压器顶部的法兰盘，再通过外部光纤连接至高精度解调仪进行数据分析。
图16 传感器布置
Fig.16 Sensor arrangement
试验平台采用与在运±800 kV系统变压器相同的铁心、绕组、绝缘纸板和变压器油等材料，并采用文献[30]中的比例公式进行设计，以确保相似的电气特性。试验平台现场接线如图17所示。
图17 试验现场接线
Fig.17 Test site wiring
为了避免热应力的影响，试验在变压器冷机时进行。将变压器低压侧短接，高压侧接入短路电流，持续0.1 s，试验现场环境温度为18℃。同时，根据文献[31]中的相关标准要求，通过绕组结构参数，将电磁力密度换算为电磁力，并在结果中以MPa作为辐向力的单位，以kN作为轴向力的单位。试验结果与计算结果的对比如图18所示。
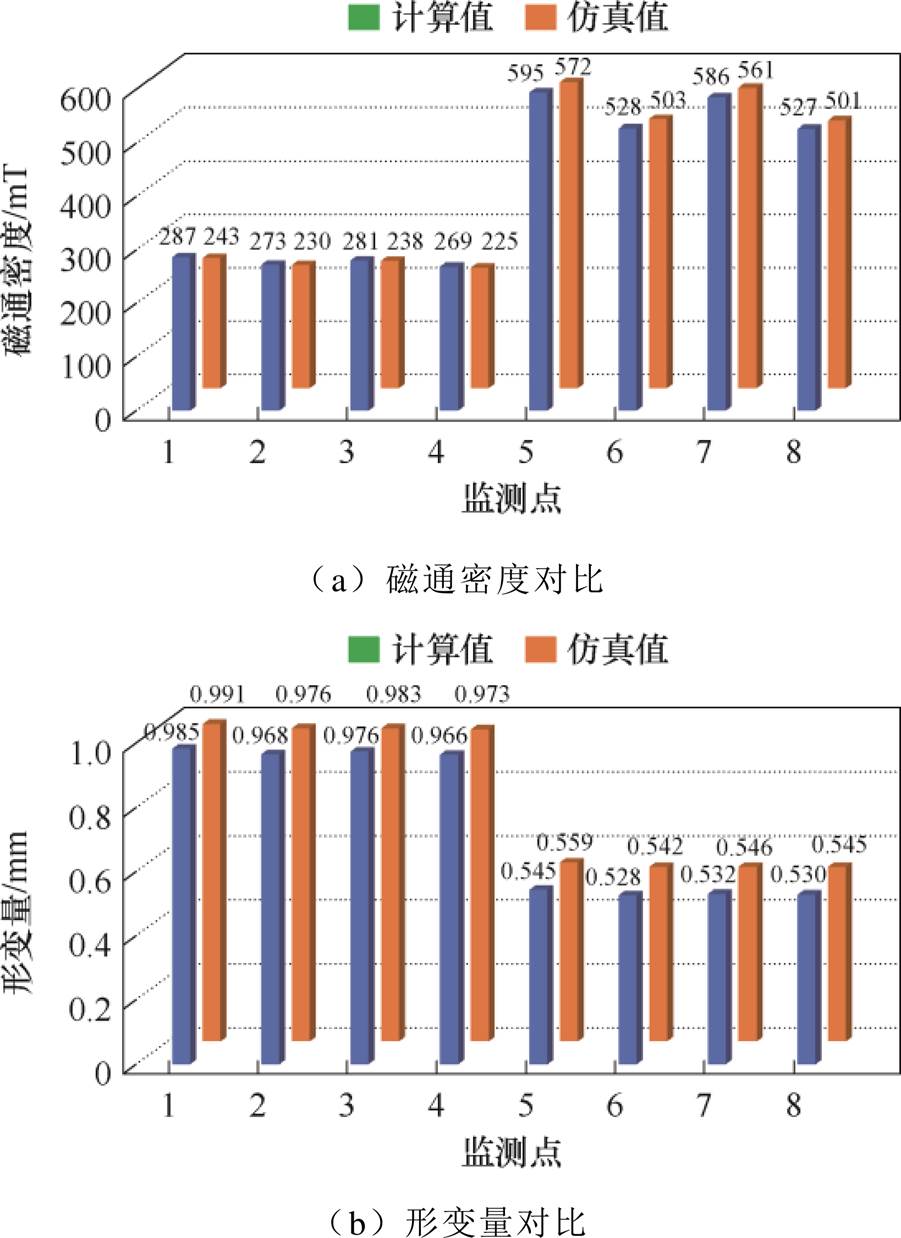
图18 试验结果对比
Fig.18 Comparison of test results
如图18a和图18b所示分别为磁场强度和形变的试验结果与采用磁场梯度应力张量得到的计算结果对比。其中，磁场的最大误差约为16.8%，平均误差约为8.8%。这是由于磁场传感器的安装位置距离绕组本体稍远，导致误差较大。进一步分析可以看出，磁场误差较大的位置集中在绕组顶部，最大误差出现在点4，而绕组中部的位置误差相对较小，最大误差出现在点8，约为4.9%，这是由于顶部磁场相比于中部更加发散，传感器更加难以捕捉。尽管磁场测量结果存在较大的误差，但是绕组形变量的最大误差仅约为2.7%，可以看出，本文所提计算方法具有较强的有效性。
表4比较了通过虚功法、洛伦兹力法[32]、麦克斯韦应力张量法[33]、磁场梯度法和短路测试获得的绕组电磁力，并给出了基于试验结果的误差对比。结果表明，通过虚功法计算得到的电磁力结果与试验结果最为接近，其中轴向力误差约为1.5%，辐向力误差约为2%。本文提出的磁场梯度法虽不及虚功法，但其误差同样较小且优于洛伦兹力法和麦克斯韦应力张量法，其中，轴向力误差约为2.1%，辐向力误差约为2.4%。这可能是因为该方法在准确捕捉磁场分布的空间不均匀性方面具有更好的能力，使其更敏感于局部应力集中的位置，尤其是在绕组两端和中部等磁场梯度变化显著的区域。
表4 结果与误差对比
Tab.4 Comparison of results and errors
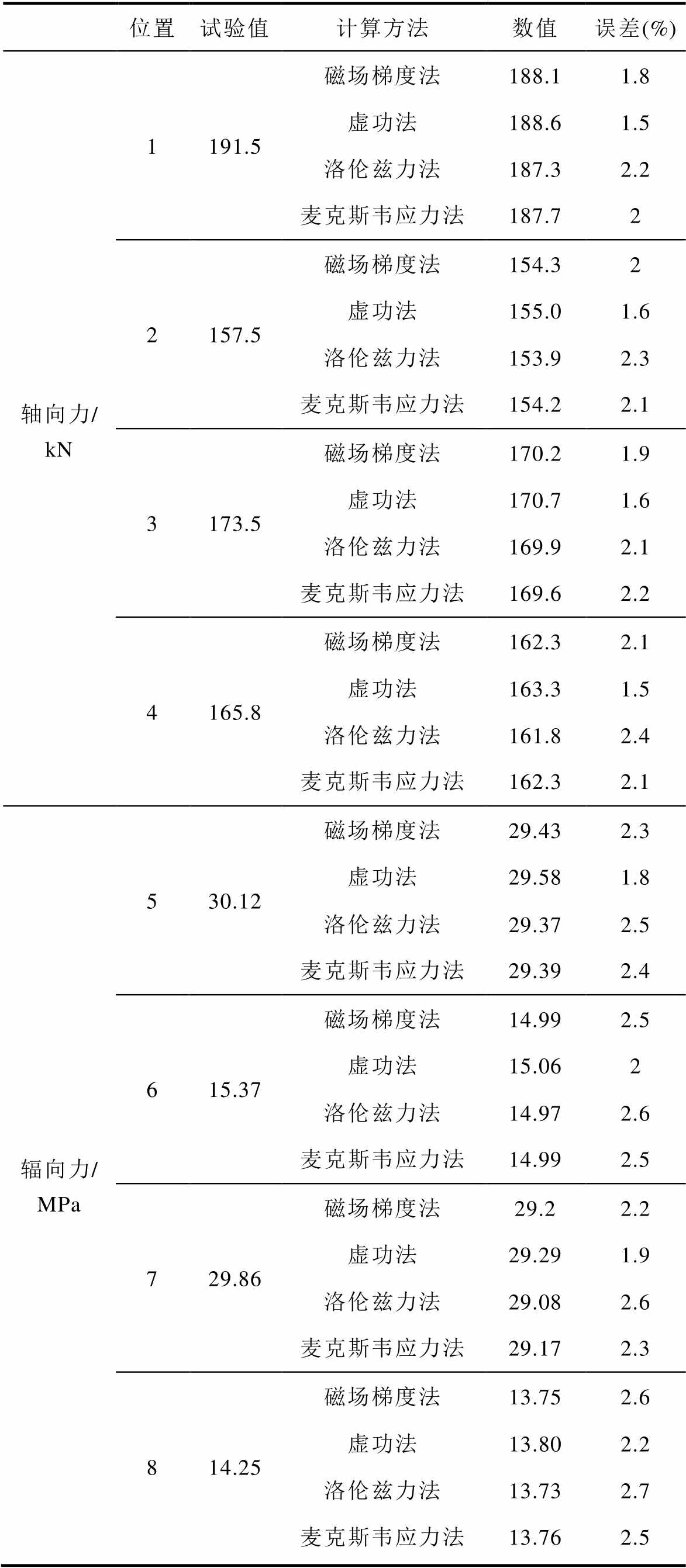
位置试验值计算方法数值误差(%) 轴向力/kN1191.5磁场梯度法188.11.8 虚功法188.61.5 洛伦兹力法187.32.2 麦克斯韦应力法187.72 2157.5磁场梯度法154.32 虚功法155.01.6 洛伦兹力法153.92.3 麦克斯韦应力法154.22.1 3173.5磁场梯度法170.21.9 虚功法170.71.6 洛伦兹力法169.92.1 麦克斯韦应力法169.62.2 4165.8磁场梯度法162.32.1 虚功法163.31.5 洛伦兹力法161.82.4 麦克斯韦应力法162.32.1 辐向力/MPa530.12磁场梯度法29.432.3 虚功法29.581.8 洛伦兹力法29.372.5 麦克斯韦应力法29.392.4 615.37磁场梯度法14.992.5 虚功法15.062 洛伦兹力法14.972.6 麦克斯韦应力法14.992.5 729.86磁场梯度法29.22.2 虚功法29.291.9 洛伦兹力法29.082.6 麦克斯韦应力法29.172.3 814.25磁场梯度法13.752.6 虚功法13.802.2 洛伦兹力法13.732.7 麦克斯韦应力法13.762.5
本文提出了一种通过磁场梯度张量计算变压器绕组中电磁力的方法，并进一步通过电磁力计算出绕组的形变量。首先，详细研究了绕组中磁场的一阶张量与二阶张量分布情况，并分析了磁场张量的本质规律和含义。其次，定义了磁场梯度应力张量G，通过其计算了沿坐标轴三个方向的电磁力密度。最后，通过完整的仿真分析和短路试验对所提方法进行了验证。结果表明，磁场梯度法计算得到的电磁力和形变量与试验结果的误差约为2.4%和2.7%，满足工程实际需求，且能够大幅提高计算时间、节省计算资源，验证了方法的有效性。
参考文献
[1] 中国电力科学研究院有限公司. 变压器短路线圈损坏故障案例[R]. 北京: 国家电网有限公司, 2018.
[2] Rommel D P, Di Maio D, Tinga T. Transformer hot spot temperature prediction based on basic operator information[J]. International Journal of Electrical Power & Energy Systems, 2021, 124: 106340.
[3] 闫晨光, 张芃, 徐雅, 等. 换流变压器有载分接开关级间短路故障差动保护动作特性[J]. 电工技术学报, 2023, 38(21): 5878-5888, 5912.
Yan Chenguang, Zhang Fan, Xu Ya, et al. Differential protection performance for converter transformer intertap short-circuit faults in on-load tap changers[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5878-5888, 5912.
[4] Zheng Tao, Liu Xiaoxiao, Guo Xingchao. Analysis of fault-induced inrush current of converter transformer in LCC HVDC system considering DC control and protection[J]. International Journal of Electrical Power & Energy Systems, 2021, 125: 106536.
[5] 靳铭凯, 郭鹏鸿, 陈维江, 等. 磁场-结构场双向耦合作用对变压器绕组轴向振动过程的影响[J]. 高电压技术, 2023, 49(8): 3296-3304.
Jin Mingkai, Guo Penghong, Chen Weijiang, et al. Two- way magnetic-structural coupling effect on vibration process of power transformer windings[J]. High Voltage Engineering, 2023, 49(8): 3296-3304.
[6] 刘云鹏, 周旭东, 王博闻, 等. 油浸变压器端部垫块脱落故障准稳态模式研究[J]. 高电压技术, 2022, 48(10): 3859-3870.
Liu Yunpeng, Zhou Xudong, Wang Bowen, et al. Research on quasi-steady-state pattern of end block shedding in oil immersed transformer[J]. High Voltage Engineering, 2022, 48(10): 3859-3870.
[7] 汪佐宪, 张书琦, 徐征宇, 等. 多因素条件下变压器自粘换位导线抗弯能力试验及评估[J]. 高电压技术, 2022, 48(9): 3660-3669.
Wang Zuoxian, Zhang Shuqi, Xu Zhengyu, et al. research and evaluation of bending resistance of epoxy continuously transposed conductors in trans- formers under multi-factor conditions[J]. High Voltage Engineering, 2022, 48(9): 3660-3669.
[8] Barros R M R, da Costa E G, Araujo J F, et al. Contribution of inrush current to mechanical failure of power transformers windings[J]. High Voltage, 2019, 4(4): 300-307.
[9] 杜厚贤, 刘昊, 雷龙武, 等. 基于振动信号多特征值的电力变压器故障检测研究[J]. 电工技术学报, 2023, 38(1): 83-94.
Du Houxian, Liu Hao, Lei Longwu, et al. Power transformer fault detection based on multi- eigenvalues of vibration signal[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 83-94.
[10] Shan Yi, Ai Mengmeng, Liu Wenhui. Research on simulation calculation on short-circuit electrodynamics force of power transformer winding[J]. International Journal of Applied Electromagnetics and Mechanics, 2021, 65(3): 451-465.
[11] 欧强, 罗隆福, 李勇, 等. 一种电力变压器短路累积机械损伤评价方法[J]. 电工技术学报, 2024, 39(8): 2578-2590.
Ou Qiang, Luo Longfu, Li Yong, et al. An evaluation method for short-circuit cumulative mechanical damage of power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2578-2590.
[12] Li Zhongxiang, Tan Yanghong, Li Yong, et al. Radial stability evaluation and cumulative test of transformer windings under short-circuit condition[J]. Electric Power Systems Research, 2023, 217: 109112.
[13] Li Yi, Xu Qiuyuan, Lu Yanfeng. Electromagnetic force analysis of a power transformer under the short- circuit condition[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 0603803.
[14] Wang Shuhong, Zhang Haijun, Wang Song, et al. Cumulative deformation analysis for transformer winding under short-circuit fault using magnetic- structural coupling model[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 0606605.
[15] 王谦, 任志刚, 滕景竹, 等. 基于变压器磁—路—力数字模型的永久性短路故障下重合闸配置研究[J/OL]. 高压电器, 2024: 1-8[2025-07-25]. http://kns.cnki. net/kcms/detail/61.1127.TM.20241011.1509.004.html.
Wang Qian, Ren Zhigang, Teng Jingzhu, et al. Transformer magnetic field-circuit-force digital model during reclosing and configuration study[J/OL]. High Voltage Apparatus, 2024: 1-8[2025-07-25]. http://kns.cnki.net/kcms/detail/61.1127.TM.20241011.1509.004.html.
[16] 邓祥力, 朱宏业, 严康, 等. 基于光纤漏磁场测量的变压器磁平衡保护研究[J]. 电工技术学报, 2024, 39(3): 628-642.
Deng Xiangli, Zhu Hongye, Yan Kang, et al. Magnetic balance protection of transformers based on optical fiber leakage magnetic field Measurement[J]. Transactions of China Electrotechnical Society, 2024, 39(03):628-642.
[17] 朱占新, 谢德馨, 张艳丽. 大型电力变压器三维漏磁场与结构件损耗的时域分析[J]. 中国电机工程学报, 2012, 32(9): 156-160, 22.
Zhu Zhanxin, Xie Dexin, Zhang Yanli. Time domain analysis of 3D leakage magnetic fields and structural part losses of large power transformers[J]. Proceedings of the CSEE, 2012, 32(9): 156-160, 22.
[18] 郑玉平, 龚心怡, 潘书燕, 等. 变压器匝间短路故障工况下的漏磁特性分析[J]. 电力系统自动化, 2022, 46(15): 121-127.
Zheng Yuping, Gong Xinyi, Pan Shuyan, et al. Analysis on leakage flux characteristics of turn-to- turn short-circuit fault for power transformer[J]. Automation of Electric Power Systems, 2022, 46(15): 121-127.
[19] 邓永清, 阮江军, 董旭柱, 等. 基于自适应网格控制的10 kV油浸式变压器多物理场仿真计算[J]. 高电压技术, 2022, 48(8): 2924-2933.
Deng Yongqing, Ruan Jiangjun, Dong Xuzhu, et al. Simulation of multi-physical field of 10 kV oil- immersed transformer based on adaptive grid control[J]. High Voltage Engineering, 2022, 48(8): 2924-2933.
[20] Pile R, Devillers E, Le Besnerais J. Comparison of main magnetic force computation methods for noise and vibration assessment in electrical machines[J]. IEEE Transactions on Magnetics, 2018, 54(7): 8104013.
[21] 律方成, 汪鑫宇, 王平, 等. 基于振动偏离及加权熵的多次短路冲击下变压器绕组机械形变辨识[J]. 电工技术学报, 2023, 38(11): 3022-3032.
Lü Fangcheng, Wang Xinyu, Wang Ping, et al. Mechanical deformation identification of transformer winding under multiple short-circuit impacts based on vibration deviation and weighted entropy[J]. Trans- actions of China Electrotechnical Society, 2023, 38(11): 3022-3032.
[22] 陈彬, 梁旭, 肖乔莎, 等. 绕组布置方式对高频变压器漏磁场和电磁力的影响分析[J]. 高压电器, 2022, 58(2): 95-102.
Chen Bin, Liang Xu, Xiao Qiaosha, et al. analysis on influence of winding layout on leakage magnetic field and electromagnetic force of high⁃frequency trans- former[J]. High Voltage Apparatus, 2022, 58(2): 95-102.
[23] Gao Shuguo, Sun Lu, Tian Yuan, et al. Research on the distribution characteristics of transformer axial vibration under short-circuit conditions considering damping parameters[J]. Applied Sciences, 2022, 12(17): 8443.
[24] 师愉航, 汲胜昌, 张凡, 等. 变压器绕组多倍频振动机理及特性[J]. 高电压技术, 2021, 47(7): 2536- 2544.
Shi Yuhang, Ji Shengchang, Zhang Fan, et al. Multi- frequency vibration mechanism and characteristics of transformer windings[J]. High Voltage Engineering, 2021, 47(7): 2536-2544.
[25] 张凡, 李秀广, 朱筱瑜, 等. 计及热老化程度的变压器绕组内线圈短路承受能力评估方法[J]. 中国电机工程学报, 2022, 42(10): 3836-3846.
Zhang Fan, Li Xiuguang, Zhu Xiaoyu, et al. Assessment of the withstand ability to short circuit of inner windings in power transformers considering the degree of thermal aging[J]. Proceedings ofthe CSEE, 2022, 42(10):3836-3846.
[26] 曹辰, 徐博文, 李辉. 基于振动与电抗信息的变压器绕组形变状态综合监测方法[J]. 高电压技术, 2022, 48(4): 1518-1530.
Cao Chen, Xu Bowen, Li Hui. Composite monitoring method for the state of transformer winding deforma- tion based on vibration and reactance information[J]. High Voltage Engineering, 2022, 48(4): 1518-1530.
[27] 李金忠, 张书琦, 程涣超, 等. 特高压换流变压器绕组动稳定能力分析[J]. 中国电机工程学报, 2023, 43(8): 3237-3248.
Li Jinzhong, Zhang Shuqi, Cheng Huanchao, et al. Dynamic stability analysis of UHV converter trans- former winding[J]. Proceedings of the CSEE, 2023, 43(8): 3237-3248.
[28] 阎秀恪. 开关磁阻电机性能的场—路—运动耦合分析[D]. 沈阳: 沈阳工业大学, 2005.
Yan Xiuke. Field-circuit-motion coupled analysis for switched reluctance motor[D]. Shenyang: Shenyang University of Technology, 2005.
[29] 王赞基, 唐起超, 刘秀成. 电力变压器内部短路故障对短路电抗的影响[J]. 中国电机工程学报, 2006, 26(21): 15-21.
Wang Zanji, Tang Qichao, Liu Xiucheng. Effects of internal short circuit faults on short circuit reactance of power transformer[J]. Proceedings of the CSEE, 2006, 26(21): 15-21.
[30] Linan R, Ponce D, Betancourt E, et al. Optimized models for overload monitoring of power transfor- mers in real time moisture migration model[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(6): 1977-1983.
[31] 国家质量监督检验检疫总局, 国家标准化管理委员会. 电力变压器 第5部分: 承受短路的能力: GB 1094.5—2008[S]. 北京: 中国标准出版社, 2008.
[32] Huei-Huang Lee. Finite Element Simulations with ANSYS Workbench 2019[M]. Kansas: SDC Publica- tions, 2019.
[33] Najafi A, Iskender I. Electromagnetic force investiga- tion on distribution transformer under unbalanced faults based on time stepping finite element methods[J]. International Journal of Electrical Power & Energy Systems, 2016, 76: 147-155.
Abstract To address the challenges of high modeling complexity and insufficient computational efficiency in conventional methods for calculating electromagnetic forces in transformer windings under three-dimensional multiphysics coupling, this study proposes a novel analytical approach based on magnetic field gradient tensor theory. Through systematic analysis of multiple transformer short-circuit failure cases, it was identified that critical deformation zones in windings consistently occur at locations with maximal magnetic field gradient variations rather than at peak magnetic flux density regions. This observation highlights the intrinsic correlation between magnetic energy density gradients and mechanical strain localization. Building on this principle, a magnetic gradient stress tensor G is formulated to characterize electromagnetic-mechanical energy conversion, and the 3D electromagnetic force density distribution can be directly calculated using G. This framework establishes a mathematical equivalence between magnetic field gradients and force densities, circumventing the need for intricate current density reconstruction in traditional methods by leveraging second-order differential properties of magnetic gradient tensors, thereby transforming volumetric integrals into tensor differential operations.
For validation, a 3D model of a 35 kV oil-immersed transformer was developed using magneto-mechanical fully coupled governing equations. Detailed simulations of magnetic fields, deformations, and electromagnetic forces under single-phase short-circuit conditions were performed via Ansys software suite, with preliminary results confirming theoretical predictions. A dedicated experimental platform was constructed, integrating eight Hall-effect magnetic sensors, eight fiber Bragg grating (FBG) stress sensors, and eight FBG strain sensors to synchronously capture magnetic fields, mechanical stresses, and deformations. Standard short-circuit tests demonstrated strong agreement between theoretical and experimental data: axial force exhibited a bimodal distribution along the circumferential direction, with a calculated peak of 188.1 kN showing a 1.8% deviation from the measured 191.5 kN, while the average error in radial forces remained at 2.4%. Cross-validation against conventional methods revealed an 43.9% reduction in computational time (from 9.8 h to 5.5 h) and a 53.8% decrease in memory consumption (from 292 GB to 135 GB) without compromising accuracy.
This work establishes a direct theoretical linkage between electromagnetic and structural fields through tensor differential analysis, offering a new paradigm for multiphysics coupling studies in power equipment. The proposed algorithm has been validated via an in-house developed transformer short-circuit withstand design platform and further verified in simulations of critical devices such as ±800 kV converter transformers. These advancements significantly enhance the timeliness and reliability of short-circuit force predictions, providing a robust theoretical foundation for optimizing the mechanical stability and operational safety of large-scale power transformers under fault conditions.
keywords：Transformer, magnetic field gradient, electromagnetic force, short-circuit fault, deformation analysis
DOI: 10.19595/j.cnki.1000-6753.tces.242272
中图分类号：TM41
国家重点研发计划资助项目（2021YFB2401700）。
收稿日期 2024-12-17
改稿日期 2025-02-04
杨 帆 男，1980年生，教授，博士生导师，研究方向为变电设备多物理场分析及数字孪生应用等。E-mail: yangfan@cqu.edu.cn
高三策 男，1995年生，博士研究生，研究方向为变压器多物理耦合计算及状态监测等。E-mail: gaosc@cqu.edu.cn（通信作者）
（编辑 郭丽军）