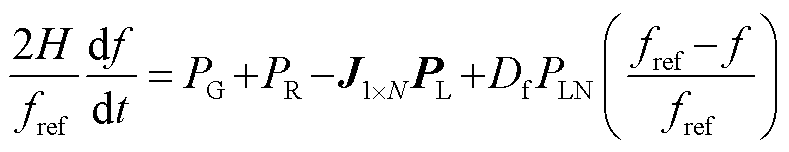（1）
摘要 构建以新能源为主体的新型电力系统是实现“双碳”目标的重要举措，而新能源的大规模并网使得电力系统亟须更多调频资源来保证频率安全。电压敏感型负荷是需求侧重要的调频资源，其消耗的有功功率与电压密切相关。为此，该文提出一种针对电压敏感型负荷的控制策略，通过控制无功设备来调节负荷节点电压，从而改变其有功功率，以参与频率响应。该策略分为两层：上层基于集中式模型预测控制设计，根据频率测量值计算负荷有功功率参考值，并将其提供给下层；下层基于分散式模型预测控制设计，由多个本地鲁棒控制器构成，每个本地控制器根据上层提供的负荷有功功率参考值计算其对应无功设备输出的无功功率。下层本地控制器之间互不通信，使用基于管道的鲁棒方法补偿通信缺失。仿真结果验证了所提策略的有效性。
关键词：模型预测控制 分层控制 电压敏感型负荷 频率响应 电压控制
在“双碳”目标的推动下，我国电网正向以新能源为主体的新型电力系统加速转型[1-3]。然而，新能源固有的间歇性和低惯量特征给电网的频率安全带来了挑战[4-6]。同时，随着新能源占比的逐年提高，电网中以传统火电机组为主导的发电侧调频资源逐渐减少，而新能源发电的不确定性导致其自身调频能力相对有限[7]。因此，仅依靠发电侧的资源已难以完全满足新型电力系统对调频的要求，需求侧的资源也能为频率支撑提供重要的助力。
电压敏感型负荷是需求侧关键的调频资源，此类负荷普遍存在于民用和工业领域，例如电热负荷、电解铝负荷、照明负荷等[8-10]，其消耗的有功功率与其所在节点的电压幅值密切相关。在此背景下，研究电压敏感型负荷参与电网频率的响应具有重要意义[10]。具体而言，通过控制电网中能够快速响应的无功补偿设备，例如静止同步补偿器（Static Synchronous Compensator, STATCOM）等[11]，可以迅速改变此类负荷所在的节点电压，从而控制其消耗的有功功率，实现调频的目的。
目前，国内外已有部分研究工作聚焦于通过调节电压敏感型负荷的节点电压来参与电网调频。文献[10, 12-13]应用PI控制，分别通过功率变流器的电压控制、同步发电机的励磁控制，实现对负荷节点电压的调控。文献[14-15]利用下垂控制策略，分别调节分布式电源的无功功率和智能变压器的电压设定值，以此来调节负荷的节点电压。文献[8]提出了一种基于输出调节理论的状态反馈控制策略，通过调节发电机的励磁电压改变负荷节点电压。文献[16]提出一种基于严格Lyapunov能量函数的非线性自适应控制策略，通过改变静止无功补偿器的无功输出进而控制负荷节点电压。文献[17]提出一种基于非线性模型预测控制的策略，通过调节分布式电源的机端电压设定值来控制负荷节点电压。
然而，现有研究在控制策略的设计中，或未考虑电压敏感型负荷的模型，或仅采用其静态模型，忽略了负荷动态响应的过程，难以充分利用此类负荷的调频能力。此外，现有相关研究普遍未考虑节点电压的动态模型，这在调频控制过程中可能会导致电压越限现象发生，危害电网的安全稳定运行。为弥补以上不足，调频控制策略需同时考虑电压敏感型负荷和节点电压的动态模型，且能够处理节点电压的约束条件，其实质是一个基于模型且含约束的控制问题。模型预测控制（Model Predictive Control, MPC）以模型为基础构建控制问题，且能够显式地处理约束条件，为解决此类问题提供了一种有效的理论框架[18]。
MPC通过实时求解基于模型的控制问题生成控制指令，其控制效果受到计算代价和通信网络负担的影响。然而，控制电压敏感型负荷涉及对节点电压的调节，电网中节点众多，导致计算代价较高。分层MPC将总控制问题分解成若干个相关的子控制问题，有效降低了计算代价，为克服上述困难提供了可行方案[19]。同时，电网中许多节点之间距离较远，导致通信网络负担较大。分散式MPC将原系统划分为多个子系统，每个子系统由一个本地控制器独立控制，子系统之间无需通信，显著减轻了通信负担，为解决这一问题提供了有效的途径[20]。
基于以上考虑，本文提出一种考虑电压敏感型负荷动态模型的分层调频控制策略，该策略分为两层：上层控制策略基于集中式MPC策略设计，计算频率事件发生时电网中各个电压敏感型负荷的有功功率参考值，并将参考值提供给下层；下层控制策略基于分散式MPC策略设计，由多个互不通信的本地鲁棒MPC控制器共同构成，每个无功设备被一个本地控制器独立控制，并采用基于管道的鲁棒方法对通信缺失进行补偿，实现次优控制，从而显著减轻了通信负担。根据上层提供的负荷有功参考值，下层本地控制器计算对应无功设备的无功功率输出，以此改变负荷所在的节点电压，使得负荷消耗的有功功率达到上层所确定的参考值。下层策略的控制问题构建中，包含了电压敏感型负荷和节点电压的动态模型，考虑了负荷功率和节点电压的动态响应过程，在不违反电压约束的前提下，实现了有效的负荷有功功率控制。
在交流电网中，当发电侧与负荷侧的有功功率不匹配时，电网频率会偏移其额定值。摆动方程描绘了扰动发生时电网中有功不平衡量和频率变化率的动态关系。在含高比例新能源的电力系统中，根据摆动方程可得到频率的动态模型[18]为
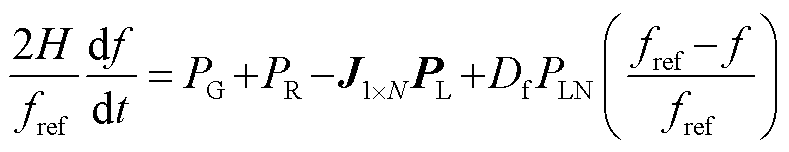（1）
式中，f为电网实际频率；fref为电网额定频率；H为系统惯性时间常数；PG为所有传统火电机组有功功率总和；PR为所有新能源发电场有功功率总和；J为全1向量；N为电网中节点的个数；PL = [PL,1PL,2… PL,N]T为各个节点处负荷消耗的有功功率，若节点i处不存在负荷，则PL,i = 0；Df为阻尼系数；PLN为额定频率下的系统负载。
若要精准控制电压敏感型负荷参与频率响应，需要对负荷的动态响应过程进行建模。电压敏感型负荷的动态模型将消耗的有功功率表示为电压幅值和时间的函数，其中被广泛使用的是指数型负荷动态模型，该模型[21-22]为
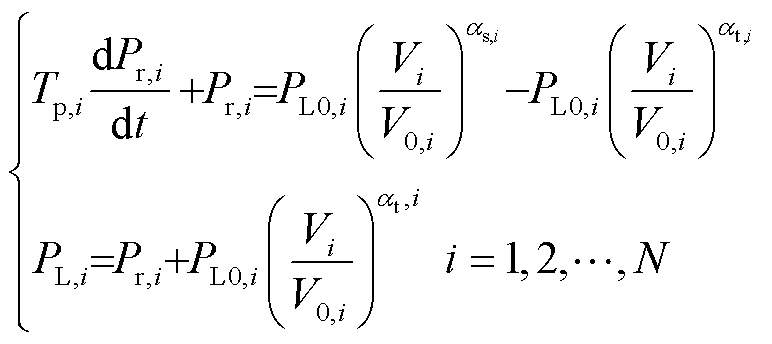（2）
式中，Vi为节点i处的电压幅值；Tp,i为节点i处负荷的功率恢复时间常数；Pr,i为该处负荷的有功功率恢复值；PL0,i和V0,i分别为该处负荷初始有功功率和电压幅值；at,i和as,i分别为该处负荷的暂态和稳态功率-电压敏感系数。
在含有高比例新能源的电网中，为了维持电压稳定性，通常会在某些节点配置能够快速响应的无功设备，例如STATCOM[23]。本文在调频过程中需要控制无功设备的无功功率，调节负荷节点电压以改变其有功消耗。因此，需要对电网节点电压幅值进行动态建模，其模型[18]为
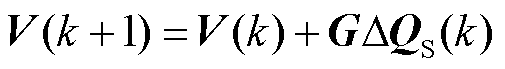（3）
式中，V(k) = [V1(k) V2(k)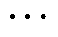 
VN(k)]T为电网中所有节点在k时刻的电压幅值；QS(k) = [QS,1(k) QS,2(k) 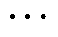QS,NS(k)]T为各个无功设备输出的无功功率，NS为电网中无功设备的个数；DQS(k) = QS(k) – QS(k–1)为无功功率改变量；G为节点电压相对于无功设备输出的无功功率的灵敏度矩阵。
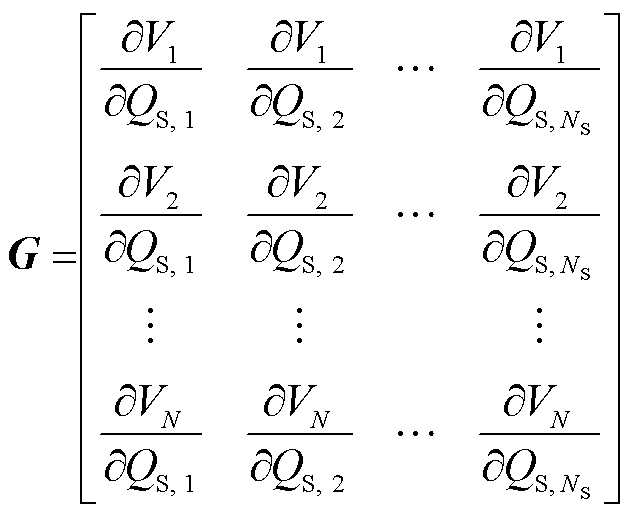（4）
计算G的常用方法是通过牛顿-拉夫逊潮流计算法中实时更新的雅可比矩阵求得电压灵敏度系数[18]。
本文旨在建立含高比例新能源的电力系统中电压敏感型负荷参与电网调频的控制策略。当电网发生频率事件时，本文所提出的策略控制电网中多个无功设备输出的无功功率，对电压敏感型负荷所在节点的电压幅值进行调节，以此改变负荷所消耗的有功功率，为电网提供频率支撑。该控制策略涉及对节点电压的调节，电网中节点众多，导致计算代价较高，分层MPC可以有效降低计算代价[19]。鉴于此，本文设计了如图1所示的双层MPC策略。
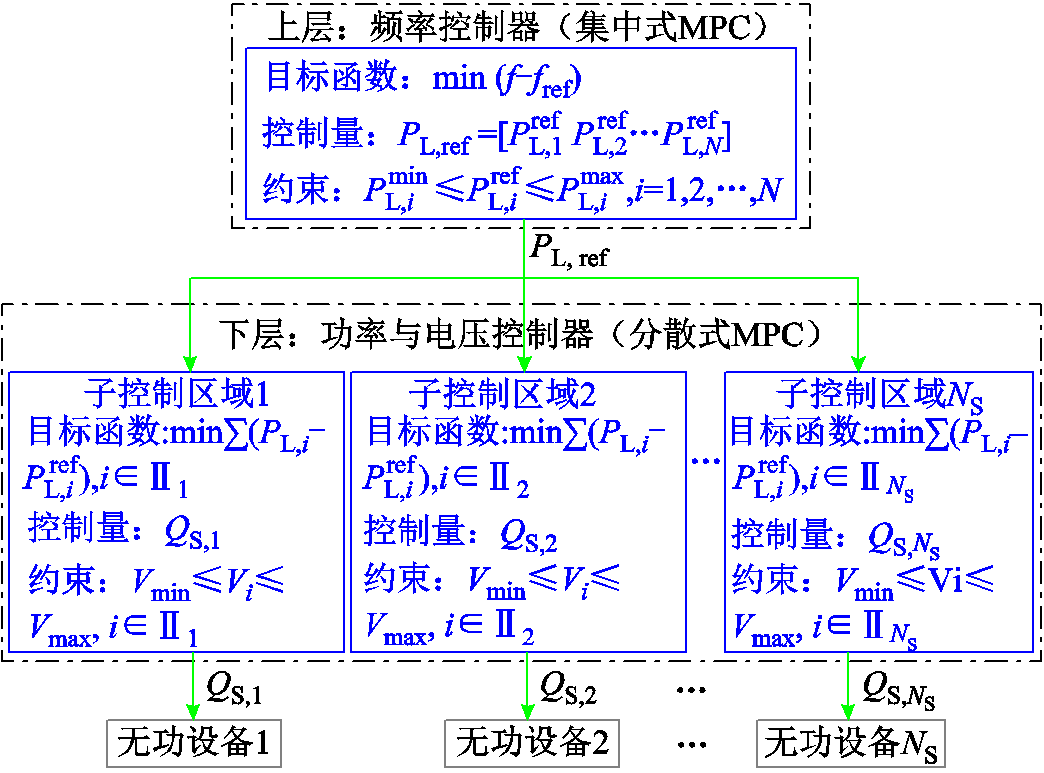
图1 电压敏感型负荷参与调频的分层控制策略结构
Fig.1 Structure of the hierarchical control strategy for voltage-dependent loads participating in frequency regulation
上层控制策略根据电网频率的实时测量值，计算出各个电压敏感型负荷的有功功率参考值，以达到动态平抑频率偏移的目的，将计算得到的有功功率参考值输送给下层控制策略。本文的频率模型式（1）中考虑全网统一频率，因此上层基于集中式MPC设计。
下层控制策略根据上层确定的负荷有功功率参考值控制电网中无功设备的无功功率，调节各负荷所在节点的电压幅值，使其消耗的有功功率与参考值相匹配，控制过程中不违反电网节点电压约束。电网中许多节点之间距离较远，通信负担较大。因此，为了减轻通信负担，下层基于分散式MPC设计，由多个互不通信的本地鲁棒MPC控制器构成。具体而言，以节点的电压灵敏度为基准，根据每个无功设备所在位置将电网分成多个子控制区域，子控制区域j内的无功设备j受控于一个本地鲁棒MPC控制器j。
下层的本地鲁棒MPC控制器j由一个管道（Tube）-MPC控制器j和一个辅助的鲁棒状态反馈控制器j组成，两者均仅依赖子控制区域j内的本地状态测量值。Tube-MPC控制器j根据本地的名义预测模型j计算得到无功设备j的次优无功功率输出，将所有非本地区域的控制输入视为有界扰动，并采用基于Tube的鲁棒方法对通信缺失进行补偿。同时，辅助鲁棒状态反馈控制器j将系统真实状态量与名义状态量之间的误差尽可能降低到接近0，从而提高了Tube-MPC控制器对非本地控制输入干扰的鲁棒性[20]。通过这种方式，下层控制策略以完全分散的方式实现，即下层本地鲁棒控制器之间无需进行通信，显著减轻了通信负担。
根据上下层通信负担的差异，此分层控制策略可以采用多时间尺度的方式实施。上层控制策略需要实时测量所有负荷消耗的有功功率、所有发电厂输出的有功功率以及电网频率，通信范围涉及整个电网，为了减轻通信负担，可以将上层的控制周期设为较大的数值；下层控制策略仅需要实时测量子控制区域内部的节点电压和负荷功率，通信负担相对较小，为了提高控制精度，可以将下层的控制周期设为较小的数值。
值得注意的是，无功设备能参与调频的前提是具备足够快的响应速度，以STATCOM为代表的快速响应无功补偿设备已经在电网中得到越来越广泛的应用[23]。以修改后含高比例风电的IEEE 39节点系统为例，假设系统中有三台STATCOM，以节点的电压灵敏度为基准，系统被分为三个子控制区域，所提出的分层MPC策略的控制框图如图2所示。
为了验证电压敏感型负荷的调频能力，本文中新能源发电场本身不参与调频。当电网出现频率事件时，上层集中式MPC策略的目标是计算得出电网中各个电压敏感型负荷的有功功率参考值。在MPC框架下，为了预测被控量的未来变化，需要确定其离散时间预测模型。上层控制策略的被控量是电网频率，因此根据系统频率动态模型式（1），采用零阶保持离散化方法，将模型式（1）离散化，可以得到采样时刻k的电网频率离散时间预测模型为
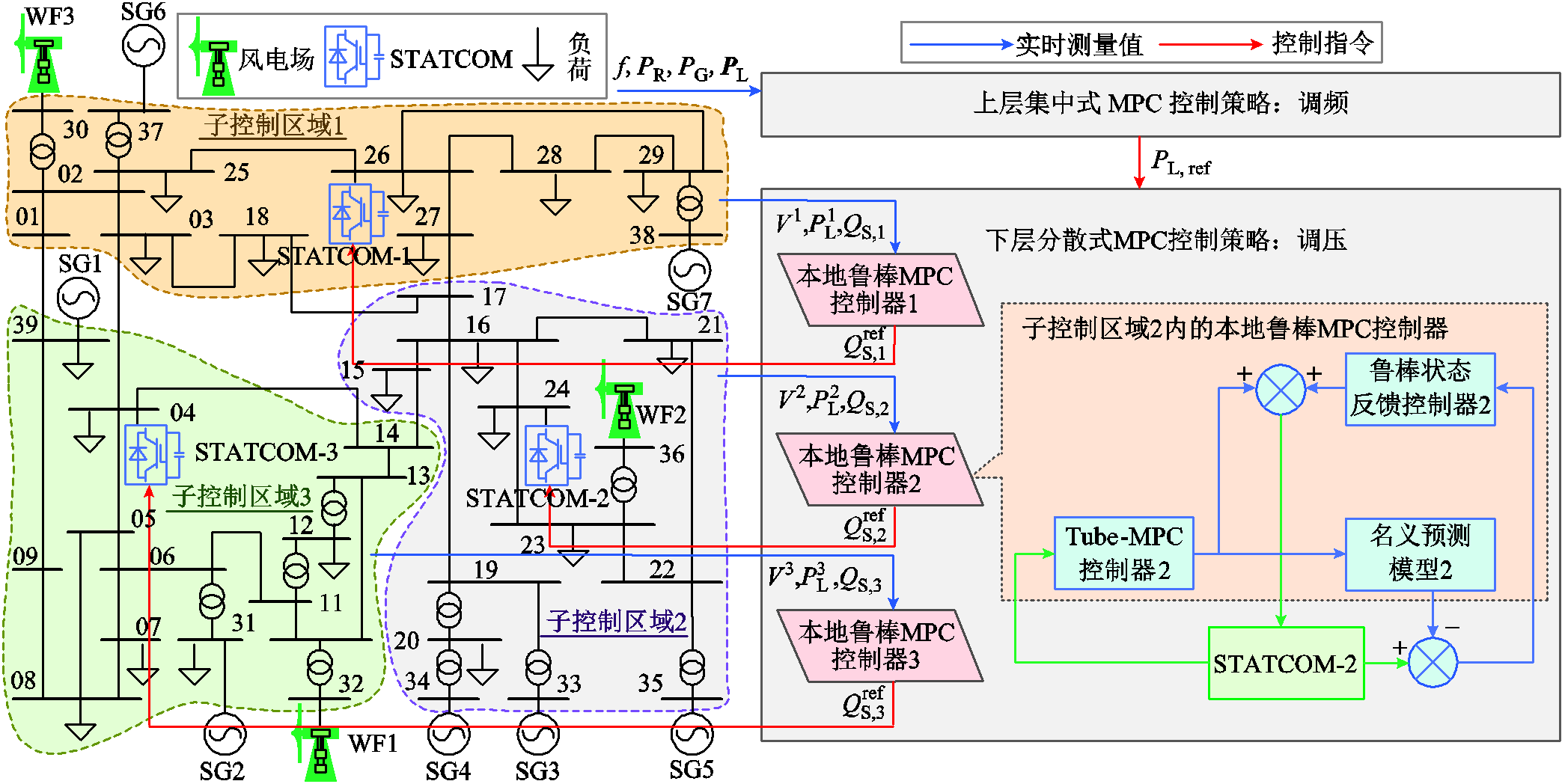
图2 电压敏感型负荷参与调频的分层控制策略框图
Fig.2 Block diagram of the proposed two-layer control strategy
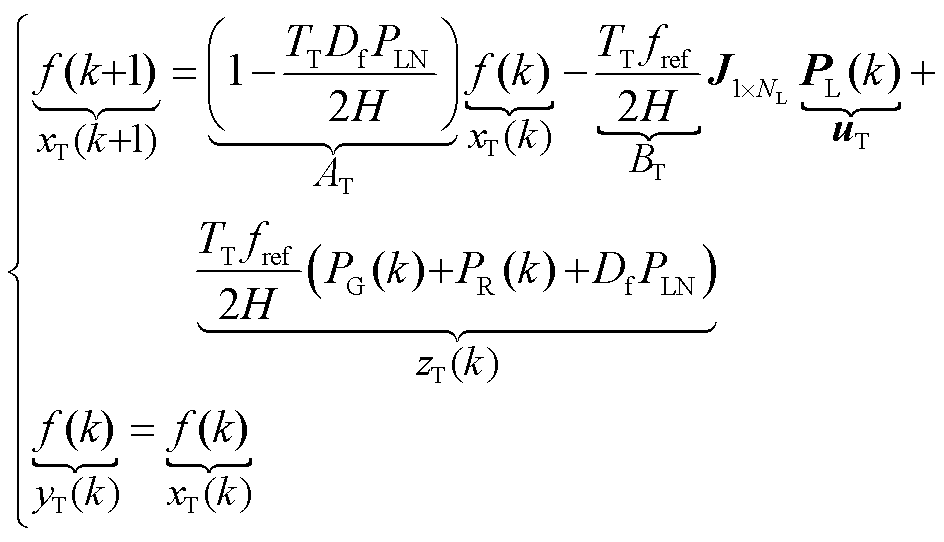（5）
式中，TT为上层控制策略的采样周期；xT为上层的状态变量；uT= [uT,1 uT,2 … uT,N]T为上层的控制输入；yT为上层的控制输出。该模型可作为上层集中式MPC策略的预测模型。
为了计算最优控制指令/动作，需要确定代价函数。当电网发生频率事件时，上层控制策略的主要目标是通过控制负荷的有功功率参考值，尽可能平抑电网频率的波动，同时最小化控制代价。据此，可以将上层MPC策略的代价函数写为
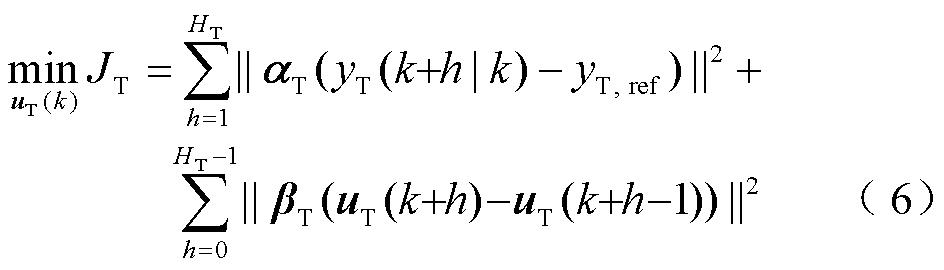
式中，(k+h|k)为根据k时刻的信息预测所得的k+h时刻的变量值；HT为上层控制策略的预测时域和控制时域；aT和bT分别为上述两个惩罚项之间的加权向量。
在最小化代价函数式（6）的同时，必须满足负荷的有功功率约束，节点i处的负荷有功功率PL,i需要遵守如下约束：
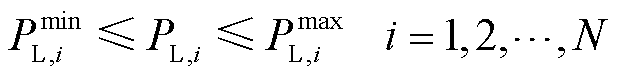（7）
式中，
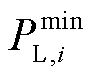和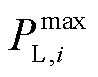
分别为负荷消耗有功功率的最小允许值和最大允许值。
预测模型式（5）、目标函数式（6）和约束条件式（7）共同构成上层MPC的优化问题。在k时刻求解该问题得到的解是k时刻的最优控制输入序列，取该序列的第一组元素为当前k时刻各个负荷的最优有功功率参考值，将该参考值传递给下层控制策略。在下一时刻时，即k+1时刻，应用新得到的数据重复此计算过程[18]。
下层控制策略基于分散式MPC设计，其目标是根据上层确定的负荷有功功率参考值，控制电网无功设备的无功功率输出，调节电压敏感型负荷的节点电压，使负荷消耗的有功功率达到参考值。根据电网中每个无功设备的所在位置，以电压灵敏度为基准，将电网分成多个子控制区域，一个无功设备对应一个子控制区域。子控制区域j内的无功设备j受控于一个本地鲁棒MPC控制器j，不同子控制区域之间的本地控制器以分散式的控制架构互相协同，且互不通信，共同组成下层分散式MPC策略[20]。本地鲁棒MPC控制器j由一个Tube-MPC控制器j和一个辅助的鲁棒状态反馈控制器j组成，分别在下面两小节介绍。
2.3.1 Tube-MPC控制器
在Tube-MPC框架下，为了预测被控量的未来变化，需要确定被控量的离散时间预测模型。下层控制策略的被控量是电网中各个电压敏感型负荷的有功功率和电网节点电压，因此需要根据负荷功率模型式（2）和节点电压模型式（3）建立相应的离散时间预测模型。
鉴于下层控制以完全分散的形式实现，不同子控制区域之间不存在通信，因此需要将节点电压模型式（3）分解为多个电压子模型，每个子模型对应一个特定的子控制区域。对于每个子控制区域，其相关的子模型受到本地控制输入和相互连接的其他子控制区域的控制输入的影响。子控制区域j的电压子模型可以写为
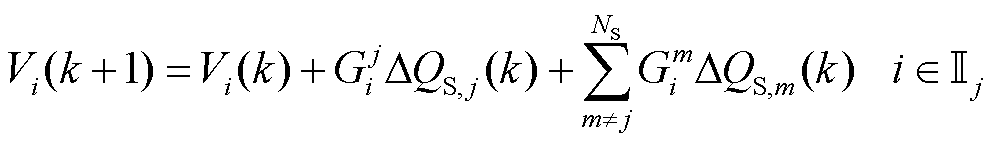（8）
式中，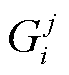
为无功设备j针对节点i的电压灵敏度；Ij为子控制区域j内的节点集合，等式右侧最后一项代表非本地控制输入的影响。根据Tube-MPC的原理，将该项视为子控制区域j的局部有界扰动，可以表示为
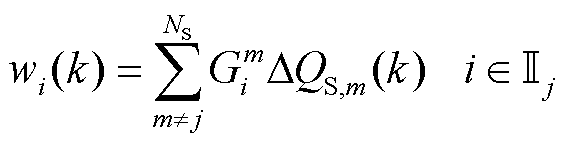（9）
将式（9）代入式（8），可以得到子控制区域j的电压子模型为
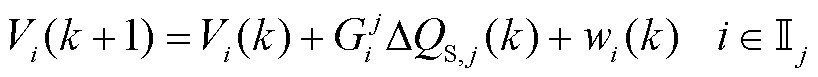（10）
将忽略式（10）中扰动项后的模型定义为子控制区域j的电压名义模型，该模型[21]可以写为
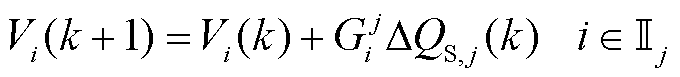（11）
电压名义模型式（11）忽略了扰动量式（9），仅受到本地控制量的影响，可以用作Tube-MPC中的名义预测模型。然而，由于扰动量式（9）被完全忽略，基于此模型的控制器不具有鲁棒性，且不能保证满足约束。鉴于此，本文引入一个辅助的鲁棒状态反馈控制器对此进行补偿，2.3.2小节将对该控制器进行介绍。
电压敏感型负荷的功率模型式（2）是含有幂指数项的非线性模型，应用泰勒展开对其进行线性化得到[22]
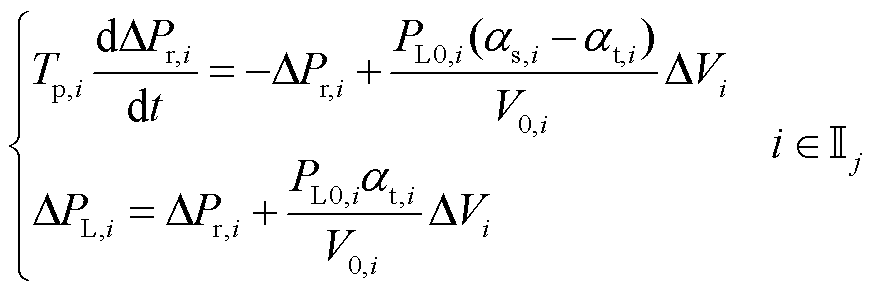（12）
式中，DPL,i = PL,i – PL0,i，DVi = Vi – V0,i。基于式（12），对节点i处的负荷有功功率PL,i进行求导，可以得到
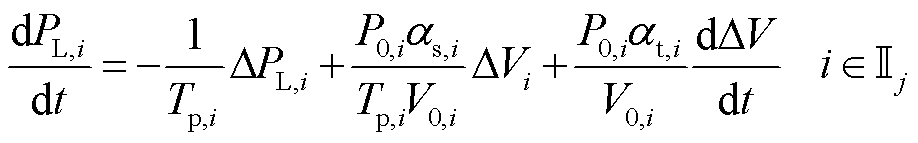（13）
采用零阶保持离散化方法将模型式（13）离散化，并结合式（11），可以得到采样时刻k的负荷动态方程为
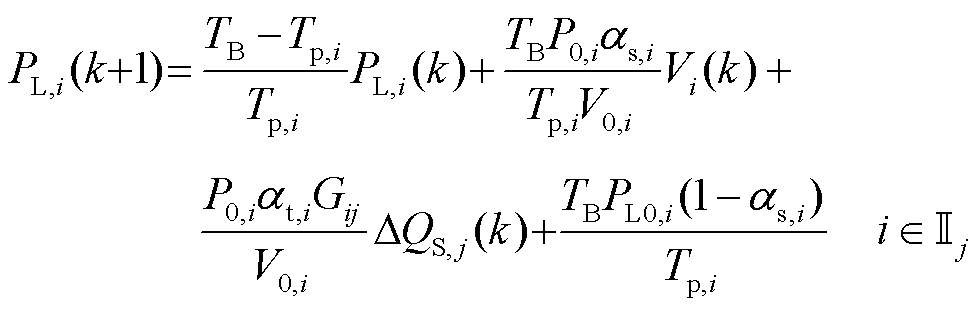（14）
式中，TB为下层控制策略的采样周期。式（11）和式（14）共同组成Tube-MPC的名义预测模型。假设子控制区域j内含有节点d(1)、d(2)、…、d(n)，根据式（11）和式（14），子控制区域j的名义状态空间模型可以写为
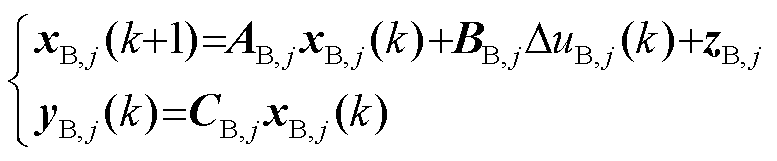（15）
其中
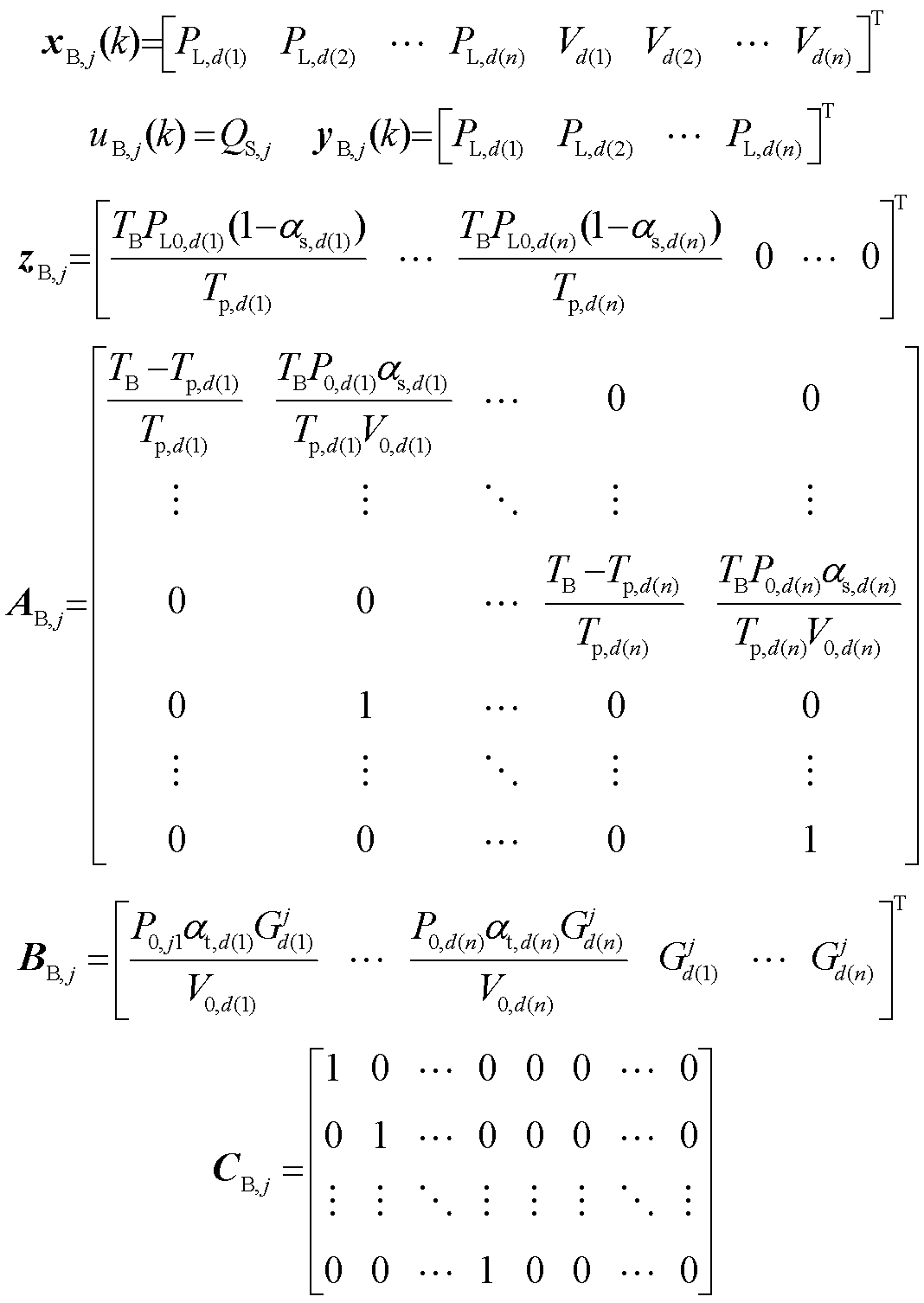
式中，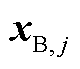
为子控制区域j的状态变量；uB, j为控制输入；
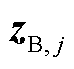为扰动量；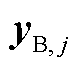
为控制输出。式（15）可作为子控制区域j内Tube-MPC控制器的名义预测模型。
为了计算控制输入，需要确定Tube-MPC控制器的代价函数。下层控制策略的主要目标是根据上层确定的负荷有功功率参考值，控制电网的无功设备输出相应的无功功率，对电压敏感型负荷的节点电压进行调节，使得负荷消耗的有功功率达到参考值，同时最小化控制代价。据此，可以将Tube-MPC控制器的代价函数写为
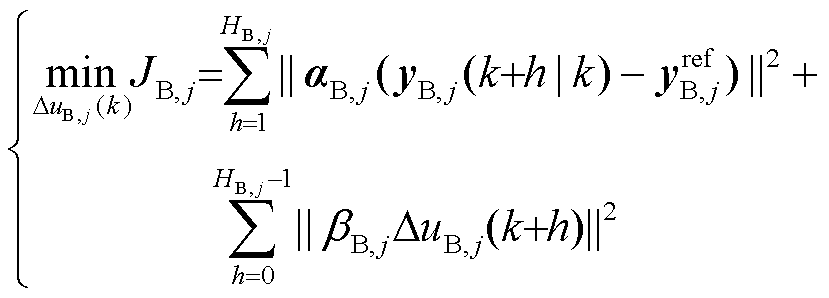（16）
式中，HB为Tube-MPC的预测时域和控制时域；aB和bB分别为上述两个惩罚项之间的加权向量。
在最小化代价函数（16）的同时，不能违反区域j内各个节点电压提前设定的约束，即区域j内的所有节点电压Vi需要遵守如下约束：
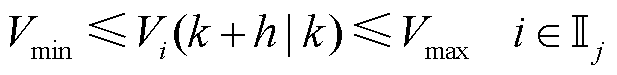（17）
式中，Vmax和Vmin分别为节点电压幅值的最大允许值和最小允许值。通过对每个节点电压施加约束，可以保证扰动量式（9）的有界性。
其次，在控制过程中，必须满足无功设备输出的无功功率约束限制，区域j内无功设备j的无功功率QS, j需要遵守如下约束：
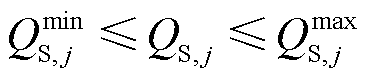（18）
式中，
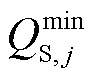和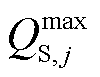
分别为无功设备输出无功功率的最小允许值和最大允许值。
名义预测模型式（15）、目标函数式（16）和约束条件式（17）、式（18）共同构成子控制区域j内Tube-MPC的优化问题。由于式（15）中的电压名义预测模型（11）忽略了扰动项，因此约束式（17）、式（18）应该被缩紧，即式（17）、式（18）应写为
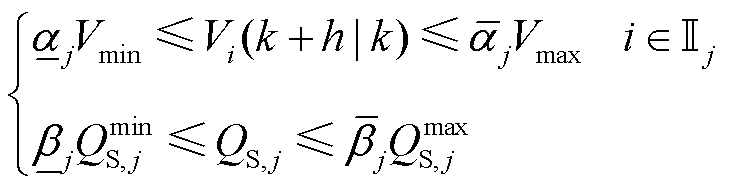（19）
式中，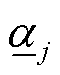
、
、
、
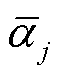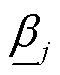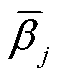为Tube-MPC缩放因子，其取值基于优化鲁棒控制不变性理论来确定[20,24]。
在子控制区域j内Tube-MPC的优化问题中，目标函数式（16）是二次函数，名义预测模型式（15）和约束条件式（19）均为线性，故此优化问题是一个标准的二次规划问题。求解该问题可以得到一个次优控制输入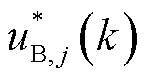
，该次优输入是下层本地鲁棒MPC控制律的一部分，另一部分由一个辅助的鲁棒状态反馈控制器构成，2.3.2小节将对该控制器进行介绍。
2.3.2 辅助的鲁棒状态反馈控制器
从式（8）中可以看到，子控制区域j内的电压模型由其本地状态变量、本地控制输入及非本地控制干扰组成。然而，在Tube-MPC的电压名义模型式（11）中，没有考虑非本地控制干扰的影响，即扰动量式（9）被完全忽略。因此，名义预测模型和实际模型之间的差异可能会导致Tube-MPC的实时控制效果受到影响。针对此问题，文献[25]提出了一种辅助的鲁棒状态反馈控制器，旨在提高Tube-MPC的鲁棒性。
辅助的鲁棒状态反馈控制器j的控制律为
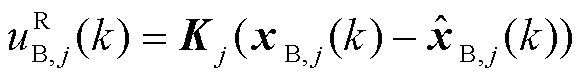（20）
式中，Kj为子控制区域j的反馈增益；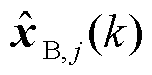
为子控制区域j的名义状态量，其值通过名义预测模型式（15）计算得到；
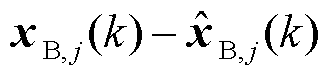为子控制区域j的真实值与名义值之间的误差。
文献[26]提出了一种离线计算矩阵Kj的方法，将Kj设计为与矩阵Qj≥0和Rj≥0相关的线性二次控制增益，有
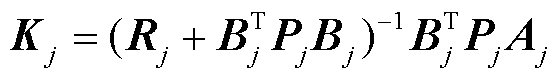（21）
Pj为代数Riccati方程式（22）的解。
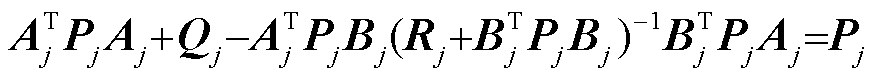（22）
根据式（21）和式（22）求得Kj后，针对子控制区域j中无功设备j的总控制律为
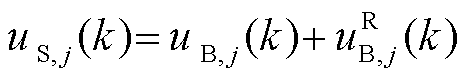（23）
式中，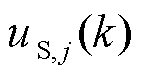
为应用于无功设备j的最终控制动作；
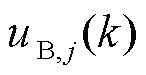由Tube-MPC控制器j给出；
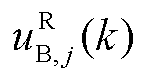由辅助的鲁棒状态反馈控制器j给出。式（23）中的总控制律如图3所示。
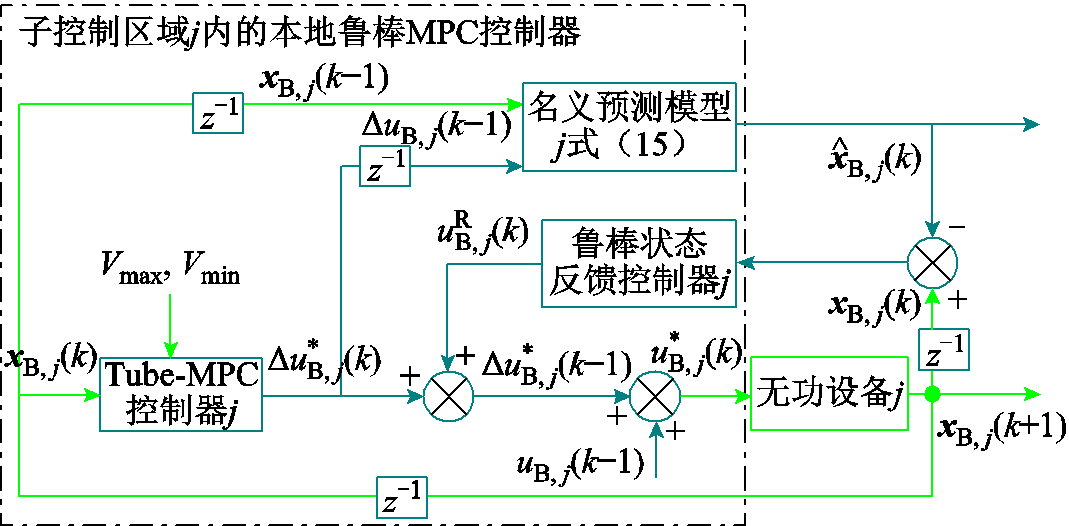
图3 本地鲁棒MPC控制器j的总控制律（含Tube-MPC控制器j和辅助鲁棒状态反馈控制器j）
Fig.3 Block diagram of overall control law in local robust MPC-j, consisting of a tube-MPC-j and an ancillary robust state-feedback controller-j
2.3.3 分散式MPC协同机制
在本文提出的下层分散式MPC策略中，不同区域的本地鲁棒MPC控制器互相之间不存在通信，各个无功设备之间的相互影响被视为作用于子控制区域的有界干扰量。在每一个本地鲁棒MPC控制器中，Tube-MPC基于名义预测模型和本地状态量对本地无功设备进行控制，而其他无功设备的动作会使得名义模型的预测结果和真实系统动态有误差，该误差以两种方式被补偿。①这种误差以Tube-MPC中管道的形式被加以限制，即通过引入缩放因子，使Tube-MPC的约束条件式（19）是原始约束条件式（17）、式（18）的缩紧形式；②引入辅助的鲁棒状态反馈控制器，将系统真实状态量与名义状态量之间的误差尽可能降低到接近0，从而提高Tube-MPC控制器对非本地控制输入干扰的鲁棒性，使得分散式MPC最终输出近似最优的控制指令。换言之，此分散式MPC策略隐式地考虑了多个无功设备的耦合动态，从而满足了闭环鲁棒稳定性和鲁棒约束，因此是一种隐式协同控制策略。
在集中式MPC和分布式MPC中，不同的本地MPC之间均存在一定程度的通信。分散式MPC策略的本地鲁棒MPC控制器没有用到其他子控制区域的信息，因此与集中式MPC和分布式MPC相比，分散式MPC通常会导致控制性能下降。然而，分散式MPC中不同的本地MPC之间不需要任何通信，因此可实现无通信控制。
当风电场发生出力变化甚至故障脱网时，根据潮流计算得到的电压灵敏度结果和名义状态空间模型将受到影响，从而导致子控制区域划分结果和反馈增益Kj取值的变化。因此，为了实现更好的控制效果，需要周期性地根据电网的最新状态重新划分子控制区域并更新反馈增益Kj的值。
为验证所提出的分层调频控制策略的有效性，本文以修改后含高比例新能源的IEEE 39节点系统为例，在Matlab/Simulink环境下搭建如图4所示的仿真模型。IEEE 39节点系统原本含有10台容量为1 000 MV·A的传统同步机组，本文将原位于30节点、32节点和36节点所在的同步机组替换为同等容量的大型风电场，即WF1、WF2和WF3。由于风速差异，三个风电场的实际运行功率分别为430、650、730 MW，三个风电场均运行于单位功率因数。系统总负荷为6 498 MW，其中电压敏感型负荷占比为40%[27]。因篇幅限制，不便将所有电压敏感型负荷的参数设置列出，以节点4所在的电压敏感型负荷为例，该负荷的额定消耗有功功率为500 MW，功率恢复时间常数取值为0.36 s，暂态和稳态功率-电压敏感系数的取值分别为2.2和1.7[22, 28]。系统频率的初始值和参考值均为50 Hz，节点电压的最大允许值和最小允许值分别为1.05(pu)和0.95(pu)。
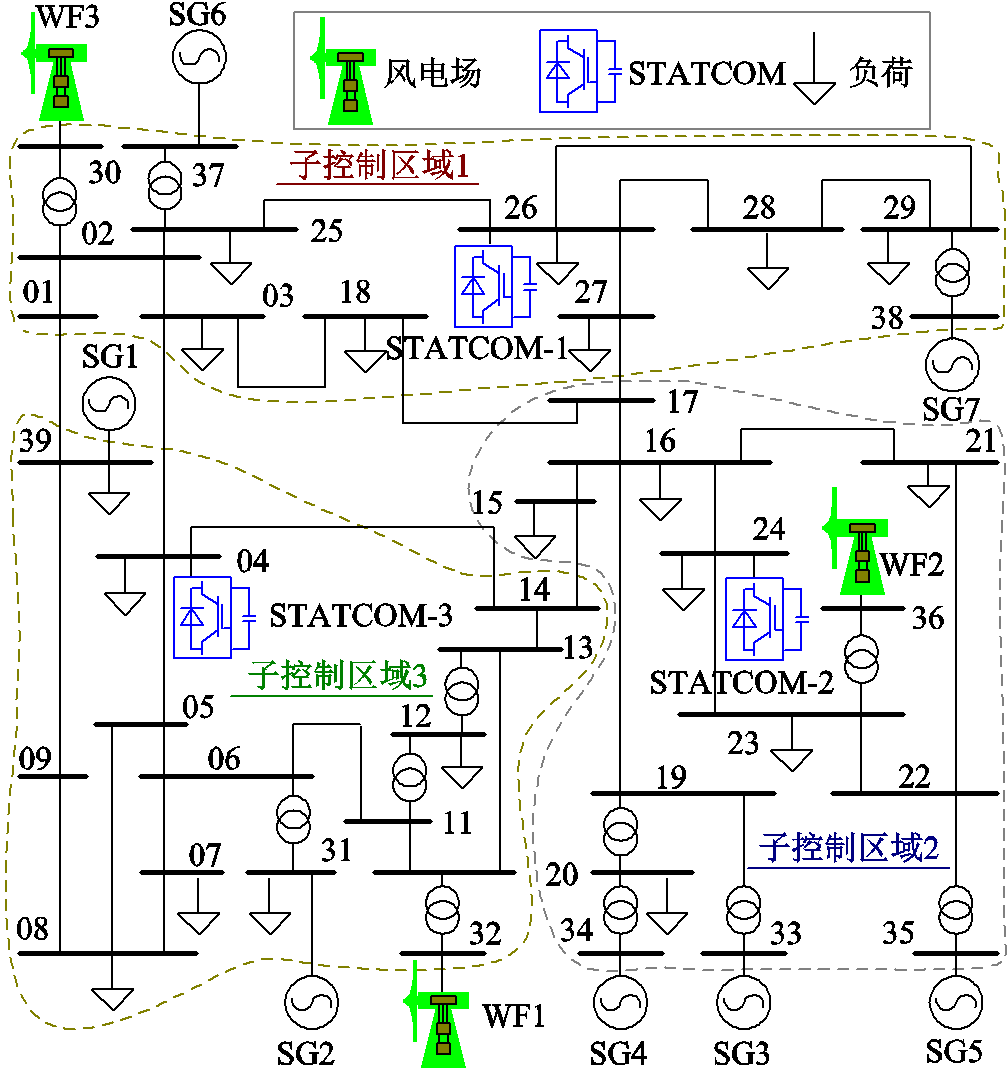
图4 仿真算例中的修改版IEEE 39节点系统
Fig.4 Diagram of the modified IEEE 39-bus system used in the simulations
系统中所安装的无功设备为STATCOM，在电压敏感型负荷较为密集的三个节点附近各配置一台额定功率为400 Mvar的STATCOM，即在节点4、节点24和节点26处。电压灵敏度系数∂Vi/∂QS, j代表无功设备j的无功功率改变对节点i处的电压幅值的影响程度，系数越大，说明影响程度越显著。因此，本文根据电网中每个无功设备的所在位置，以电压灵敏度的大小为基准，将电网分成多个子控制区域，每个无功设备对应一个特定的子控制区域，并负责调节该区域内的节点电压。具体而言，仿真算例中配置了三台STATCOM，因为∂V26/∂QS,1＞∂V26/∂QS,2且∂V26/∂QS,1＞∂V26/∂QS,3，故节点26被划分为STATCOM-1所在的子控制区域，其余节点以相同原则划分至对应的STATCOM子控制区域。
在选取集中式MPC控制周期时，需要综合考虑控制周期的可行性和控制效果两方面因素。
1）应确保所选控制周期的可行性，即所选控制周期的时长需大于控制系统的控制时延。控制系统中的控制时延主要包括控制器的计算时间和通信时延。本文的仿真算例在Matlab R2024a环境中运行，运行平台为搭载Intel (R) Core (TM) i7-12700处理器（主频2.10 GHz）、32 GB内存的计算机，操作系统为Windows 11。在该平台上，所提出的集中式MPC控制器每个控制周期的计算时间通常小于30 ms。尽管上层集中式MPC控制策略依赖全系统范围的通信，实时通信负担较重，但其在现代电力系统中广域测量系统的广泛应用，使得实时获取并传输电网频率等全系统范围的测量信号成为可能，从而为集中式频率控制的实现提供了基础[29]。鉴于广域测量系统的通信时延一般小于200 ms，而集中式MPC控制器每个控制周期的计算时间通常小于30 ms，因此，本文选取250 ms作为集中式MPC控制器的控制周期[30-31]。
2）应确保所选控制周期能够实现预期的调频控制效果。现有文献中已多次采用相近于本文设置的控制周期，并在集中式调频控制中展现了显著的控制效果，如文献[32-33]。此外，本文仿真算例的结果也进一步验证了所选取控制周期能够实现满意的调频控制效果。同时，下层控制策略的通信负担和计算代价相对较小，且STATCOM的响应时间通常小于10 ms，故仿真中下层分散式MPC的控制周期设为50 ms[34]。
本节评估所提出的分层MPC策略在应对频率事件时的控制性能，该策略通过控制STATCOM的无功功率改变电压敏感型负荷所消耗的有功功率，进而参加频率响应。因此，本文选取的对比方法为文献[14]中的频率/无功功率下垂控制策略，该下垂控制策略通过频率测量值与额定值的偏差来计算STATCOM的无功功率，其控制框图如图5所示，图5中R为下垂系数，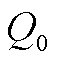
为STATCOM输出无功功率的初始值。
图5 频率/无功功率下垂控制框图
Fig.5 Frequency/reactive power droop control diagram
在第5 s时，节点8处522 MW的负荷由于故障而断开，使电网产生大量有功盈余，引发了高频事件。图6展示了不同控制策略下电网的频率动态特性。从图6中可以看到，此时若电压敏感型负荷不参与电网频率响应，即STATCOM不动作，负荷断开会导致电网频率最高上升到50.29 Hz，频率最终稳定在50.19 Hz；若采用常规下垂控制令STATCOM控制电压敏感型负荷参与频率响应，则电网频率在故障发生时最高上升到50.22 Hz，频率最终稳定在50.16 Hz。
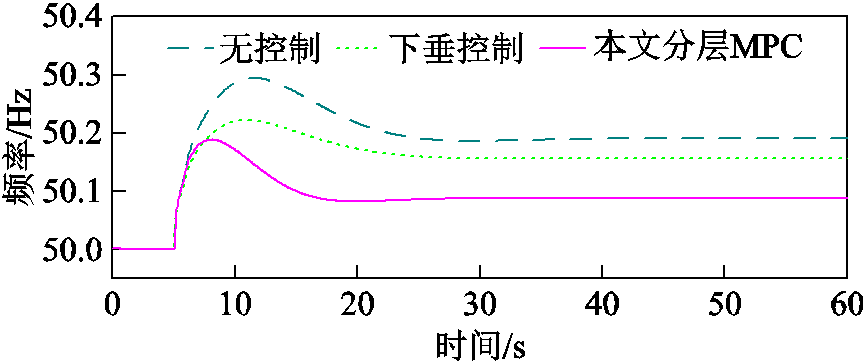
图6 负荷断开后电网的频率动态特性
Fig.6 Grid frequency dynamics after the load disconnection
相比之下，若采用本文所提针对电压敏感型负荷的分层MPC策略，电网频率在负荷断开时最高上升到50.18 Hz，频率最终稳定在50.08 Hz。根据以上分析可以得知，与传统的下垂控制相比，本文所提电压敏感型负荷分层MPC策略降低了频率的峰值和稳态值，显著改善了频率动态。
图7～图9说明了频率控制性能改善的原因，这几张图分别展示了高频事件期间STATCOM的无功功率、电网节点电压幅值，以及三个代表性节点的电压敏感型负荷消耗有功功率的动态。可以看到，当负荷断开导致高频事件发生后，本文所提的分层MPC策略使得电网中STATCOM的无功功率输出增加，以此控制整个电网的节点电压幅值水平升高，使电网中电压敏感型负荷的有功功率消耗变多，平抑产生的有功盈余，进而实现了减轻高频事件严重性的目的。
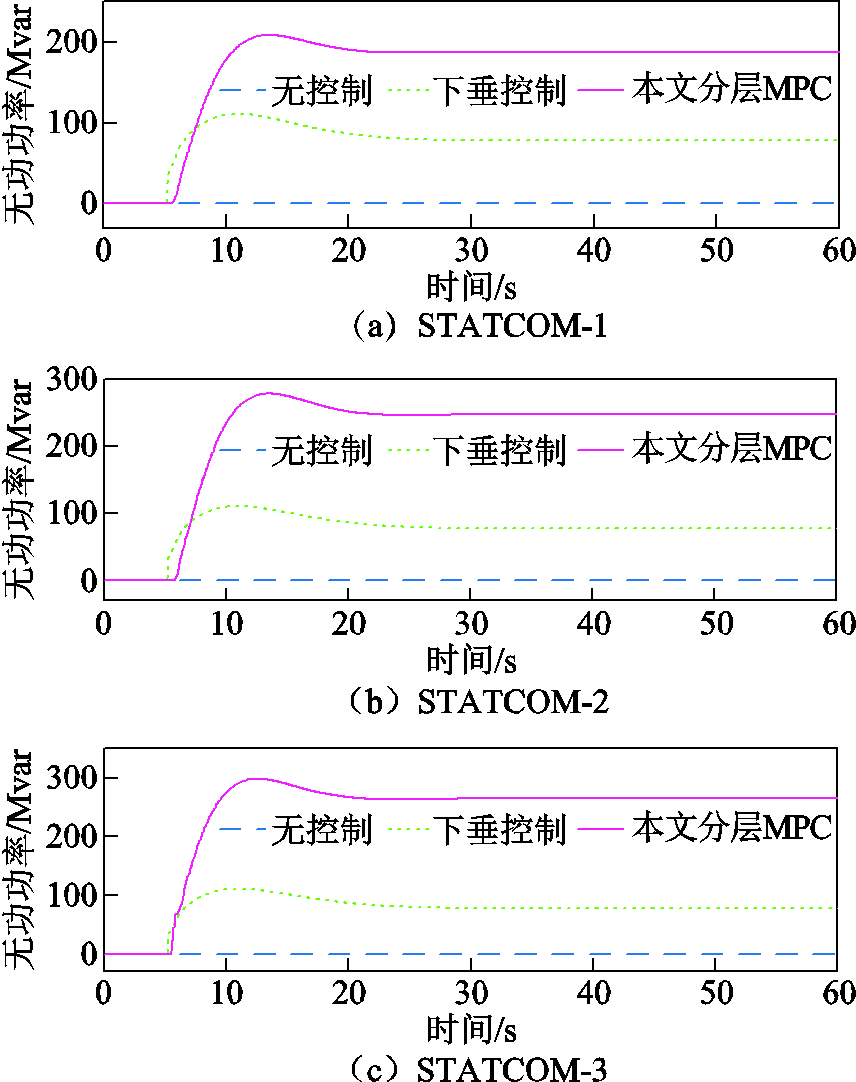
图7 负荷断开后无功功率输出
Fig.7 Reactive power outputs after the load disconnection
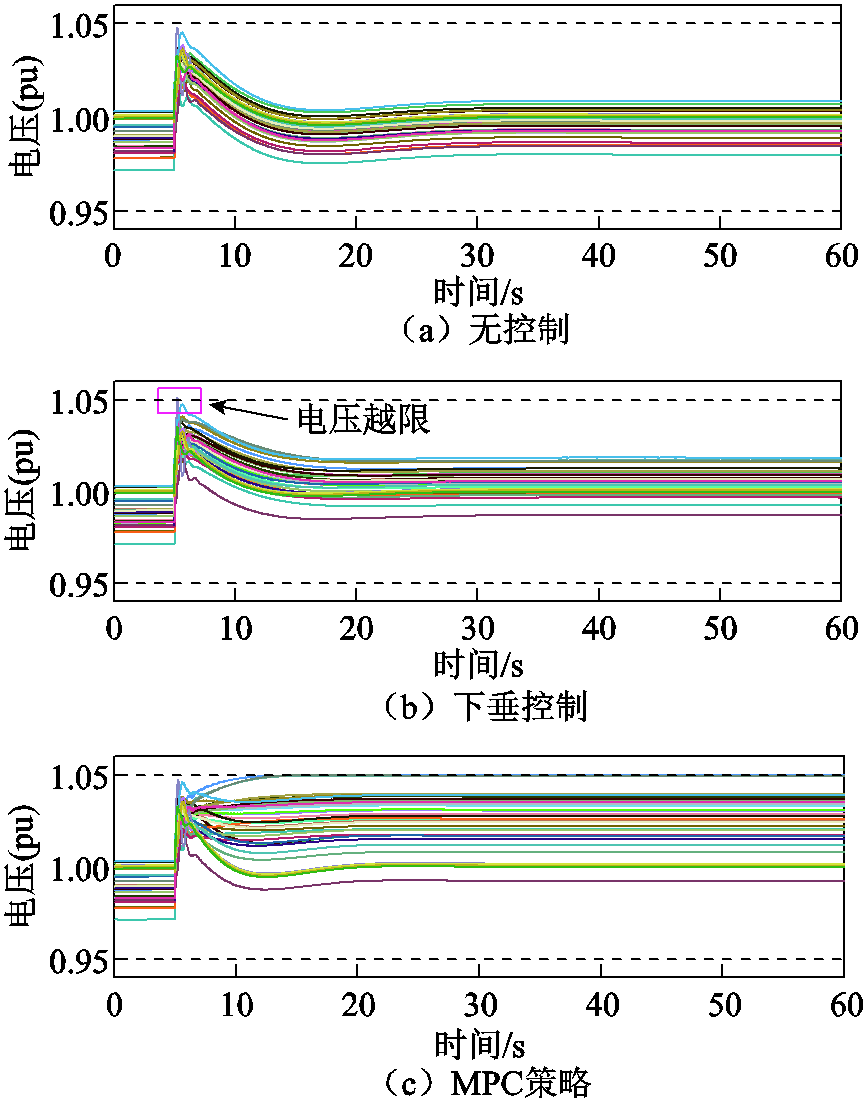
图8 负荷断开后系统节点电压动态
Fig.8 Bus voltage dynamics after the load disconnection
图7展示了在发生高频事件时，不同控制策略下三台STATCOM的无功功率输出变化。可以看出，一旦发生高频事件，三台STATCOM的无功功率输出均迅速上升，从而提高电网整体的节点电压幅值水平。与下垂控制相比，所提出的分层MPC策略可以根据电网实际电压水平动态决定其无功输出。
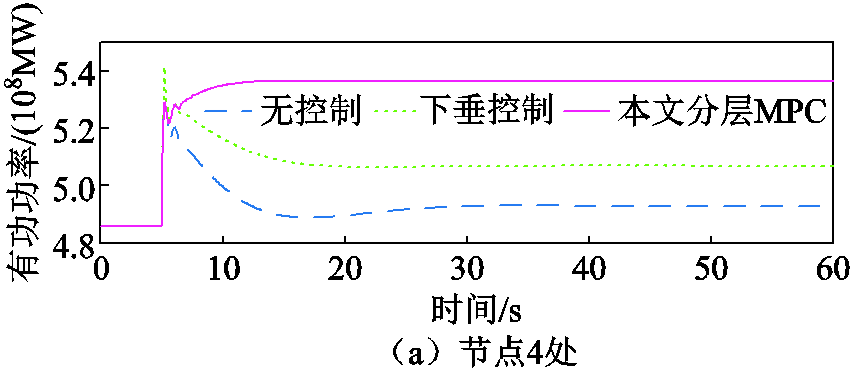
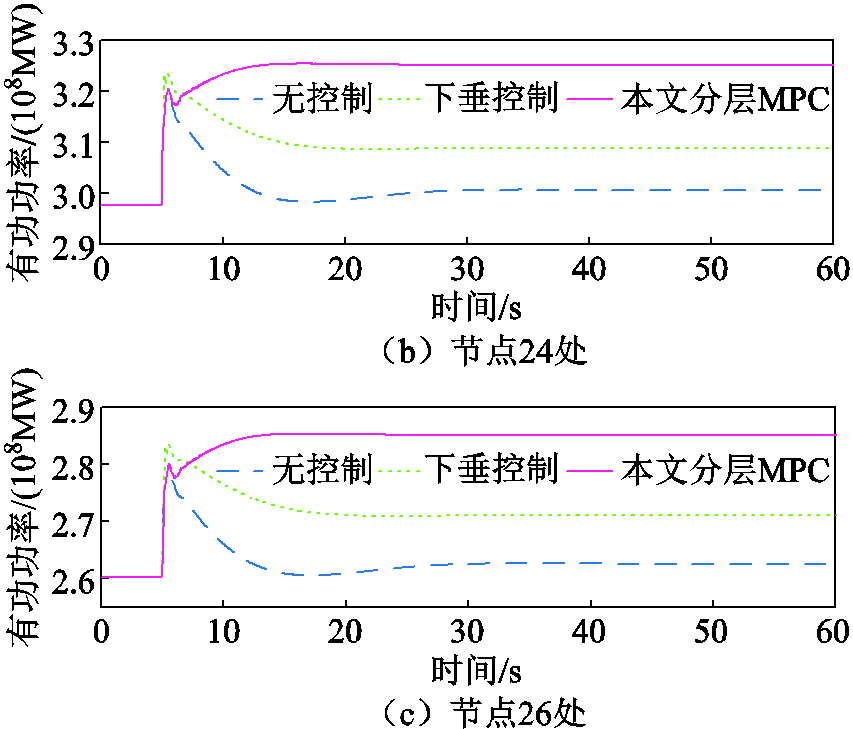
图9 负荷断开后各节点处电压敏感型负荷消耗的有功功率动态
Fig.9 Active power consumption of the voltage- dependent loads after the load disconnection
图8展示了在发生高频事件时，不同控制策略下电网所有节点电压幅值的变化。在第5 s时，节点8处的522 MW负荷断开后产生大量有功功率盈余，引发了电网高频事件，同时也使得系统节点电压升高，如图8a所示。发生高频事件后，分层MPC策略会控制STATCOM输出无功功率，使电网的各个节点电压幅值均上升，进而使电压敏感型负荷的有功功率消耗增加。与下垂控制相比，所提出的分层MPC策略可以在节点电压约束的限制内，使得电压幅值上升到最高水平，实现电压敏感型负荷的最大化利用。同时，分层MPC策略可以避免节点电压超出所设定的限值，即所有节点电压均被限制在1.05(pu)以内，如图8c所示；而下垂控制则导致节点电压出现了短暂的越限现象，如图8b所示。
由于篇幅限制，不便于展示电网中所有电压敏感型负荷的有功功率消耗，因此本文选取节点4、节点24、节点26的电压敏感型负荷作为代表，将三者消耗的有功功率变化在图9中进行展示。可以看到，一旦发生高频事件，随着电网的各个节点电压幅值被STATCOM调节而增加，电压敏感型负荷的有功功率消耗也随之增加，平抑产生的有功盈余，进而实现减轻高频事件严重性的目的。
图10a展示了负荷断开后节点4、节点24和节点26处电压敏感型负荷有功功率参考值和实际值，其中参考值即为集中式MPC的下发功率曲线；图10b展示了负荷断开后STATCOM-1、STATCOM-2和STATCOM-3无功功率参考值和实际值，其中参考值即为分散式MPC的下发功率曲线。从图10中可以观察到，两组功率参考值和对应的功率实际值几乎一致，表明集中式MPC和分散式MPC下发功率曲线均实现了有效的跟踪控制。
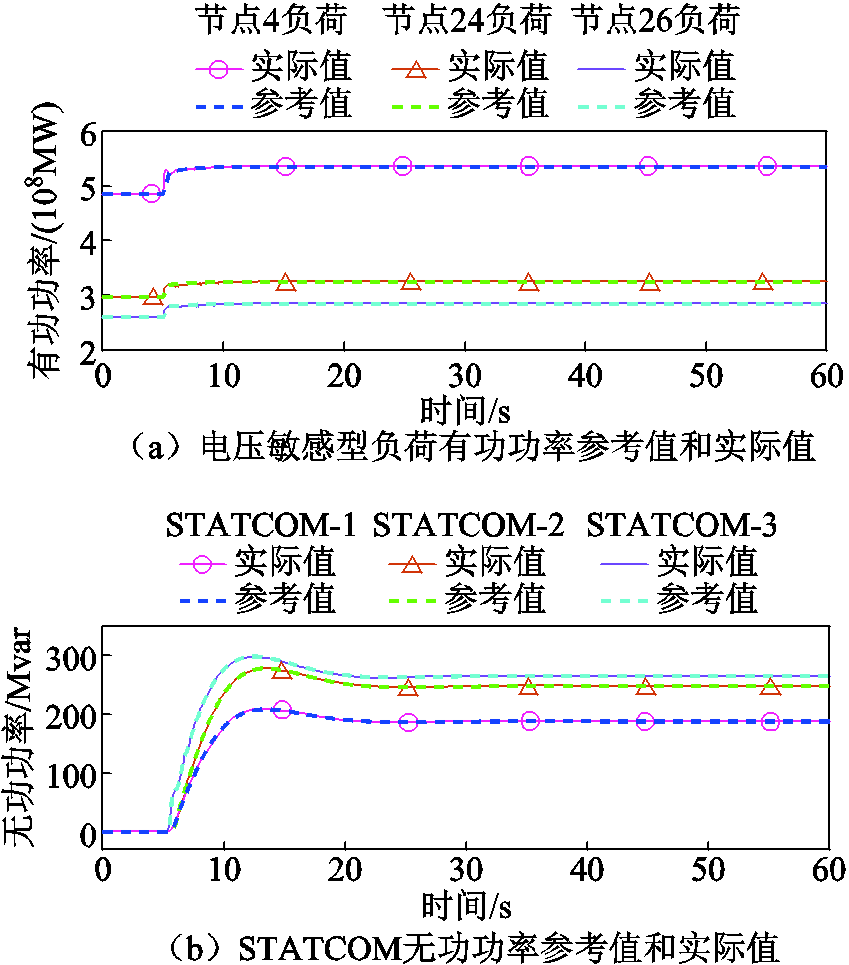
图10 负荷断开后有功功率、无功功率参考值和实际值
Fig.10 The references and actual values of active power and reactive power after the load disconnection
为了评估系统控制时延对所提出策略的影响，本文在仿真中对比分析了控制时延分别超出控制周期0、50、100、200 ms时的调频控制效果。图11展示了在第5 s负荷断开引发高频事件后，不同控制时延下所提出MPC策略的电网频率动态。可以看到，随着控制时延的增大，STATCOM参与频率响应的速度减慢，响应时间相应延后，进而导致频率峰值略微升高，表明频率响应的暂态性能有所下降。此外，控制时延的变化对频率的稳态值无显著影响。因此，所提出的MPC策略对控制时延具有一定的鲁棒性，能够在存在一定控制时延的条件下维持良好的控制性能。
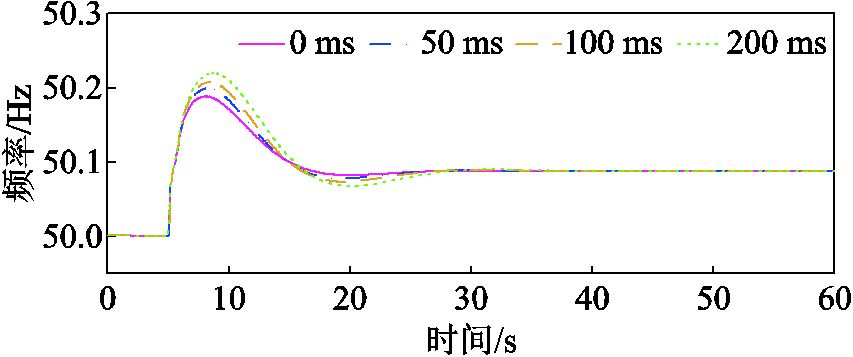
图11 负荷断开后不同控制时延下的电网频率动态
Fig.11 Grid frequency dynamics after the load disconnection under different delays
本小节测试了当三个风电场功率因数均为0.95且风电场WF3由于风速改变导致输出功率发生突变后的电网调频控制效果。在第5 s时，由于风速的改变，风电场WF3的输出功率由730 MW骤降至430 MW，导致电网出现大量有功缺额，并引发低频事件，图12～图15展示了相应的仿真结果。图12呈现了不同控制策略下电力系统的频率动态。由图12可见，当电压敏感型负荷未参与电网频率响应，即STATCOM不动作时，风场功率骤降会导致电网频率最低降至49.83 Hz，最终稳定于49.88 Hz；若采用常规下垂控制，令STATCOM控制电压敏感型负荷参与频率响应，则电网频率最低下降至49.87 Hz，最终稳定于49.91 Hz。
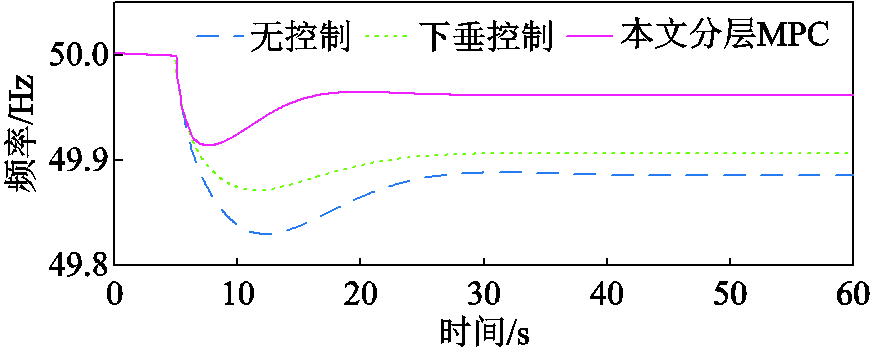
图12 风电场WF3输出功率骤降后的电网频率动态
Fig.12 Grid frequency dynamics after the power output change of WF3
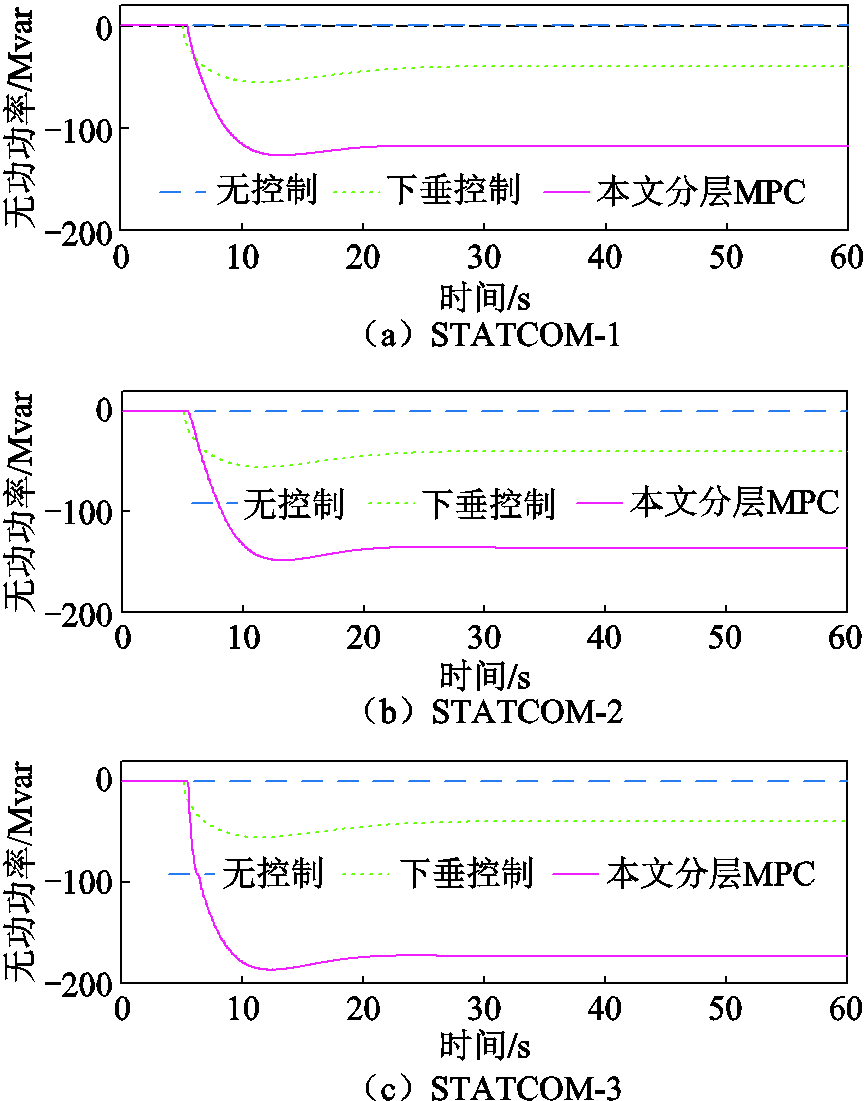
图13 风电场输出功率骤降后无功功率输出
Fig.13 Reactive power outputs after the power output change of WF3
相比之下，采用本文提出的针对电压敏感型负荷的分层MPC策略时，电网频率在风电场功率骤降的情况下最低下降至49.92 Hz，最终稳定在49.96 Hz。上述分析表明，与传统的下垂控制相比，本文所提电压敏感型负荷分层MPC策略有效地提升了频率的最低点和稳态值，显著改善了频率动态。
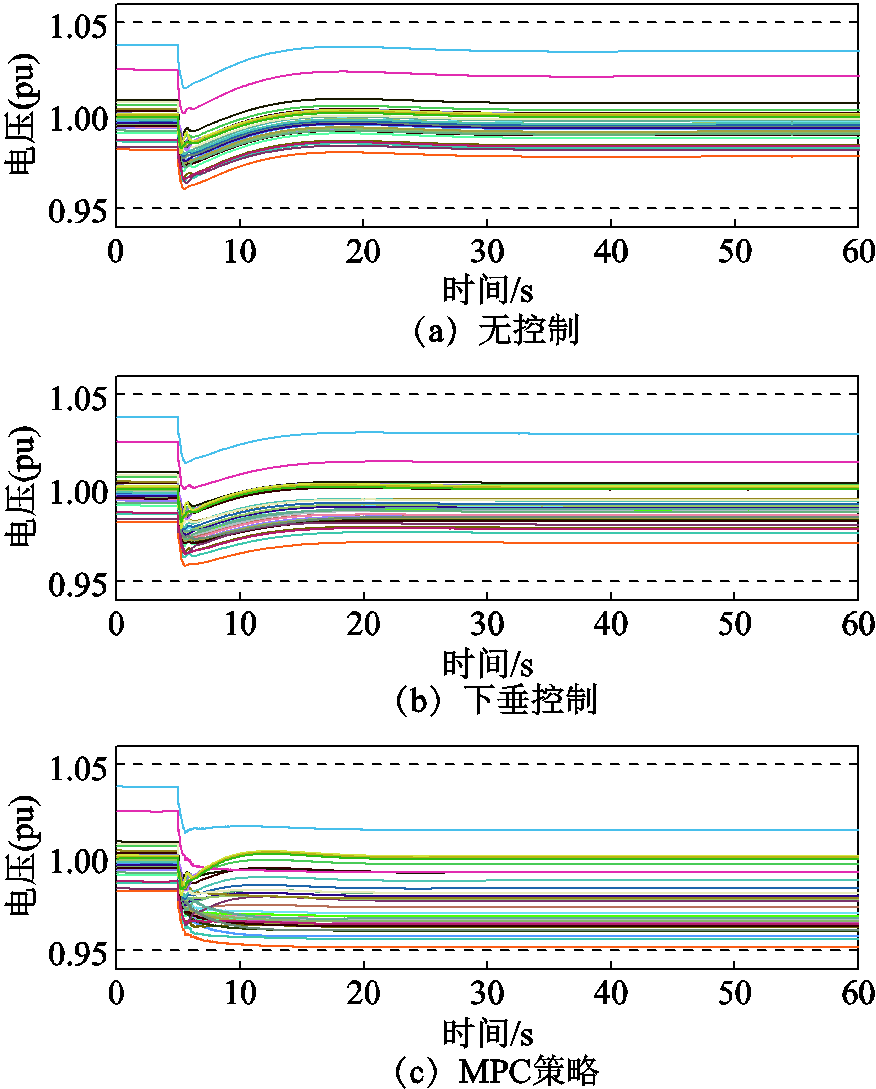
图14 风电场输出功率骤降后系统节点电压动态
Fig.14 Bus voltage dynamics after the power output change of WF3
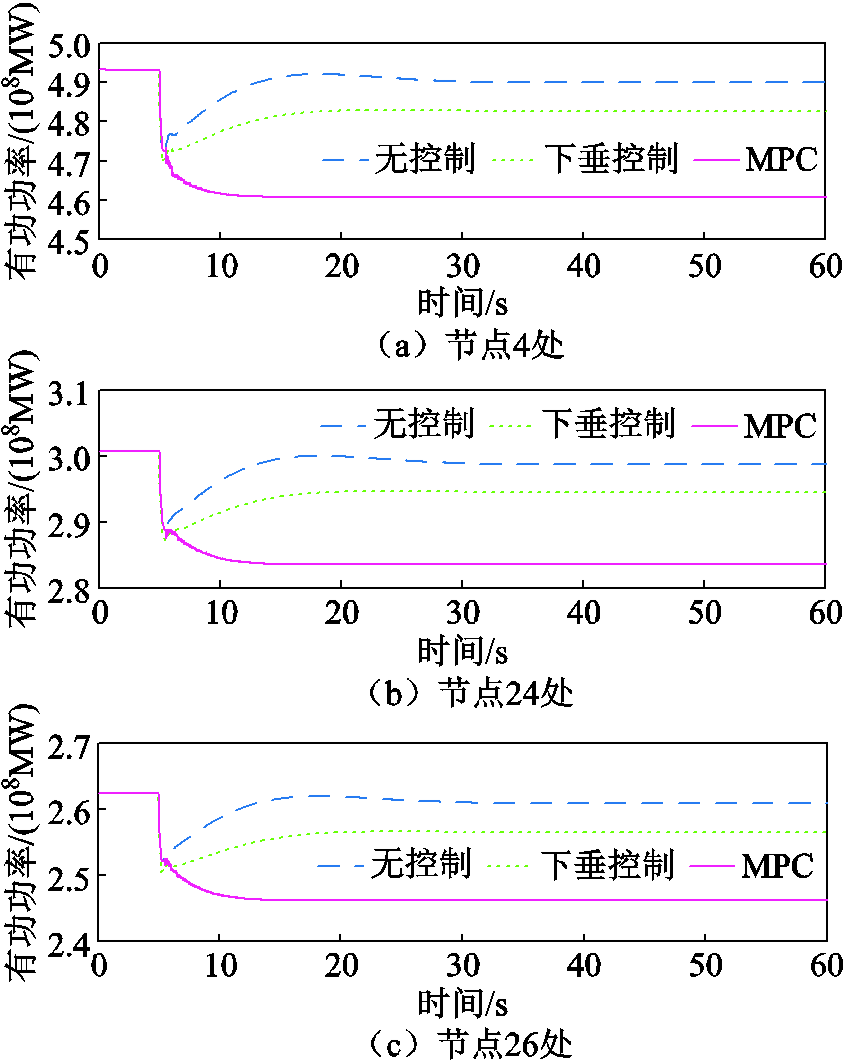
图15 风电场输出功率骤降后电压敏感型负荷消耗的有功功率动态
Fig.15 Active power consumption of the voltage- dependent loads after the power output change of WF3
图13～图15揭示了频率控制性能改善的原因，分别展示了低频事件期间STATCOM的无功功率、电网节点电压幅值，以及三个代表性节点的电压敏感型负荷消耗有功功率的动态。可以观察到，当风电场输出功率骤降引发低频事件后，本文所提的分层MPC策略使得电网中STATCOM的无功功率输出减少，以此控制整个电网的节点电压幅值水平降低，使电网中电压敏感型负荷的有功功率消耗变少，从而减少有功缺额，最终降低了低频事件可能带来的严重后果。
图13展示了在发生低频事件时，不同控制策略下三台STATCOM的无功功率输出变化。结果表明，在低频事件发生后，三台STATCOM的无功功率输出均迅速下降，从而降低电网整体的节点电压幅值水平。相比传统下垂控制，本文所提分层MPC策略可以根据电网实际电压水平动态决定其无功输出。
图14展示了风电场输出功率骤降后，不同控制策略下电网所有节点电压幅值的变化。在第5 s时，风电场WF3的输出功率骤降引发了低频事件，同时也使得系统节点电压降低，如图14a所示。发生低频事件后，分层MPC策略会控制STATCOM输出无功功率，使电网的各个节点电压幅值均降低，从而减少电压敏感型负荷的有功功率消耗。相比传统下垂控制，所提出的分层MPC策略在满足节点电压约束的前提下，将电压幅值动态调整至最低允许水平，实现电压敏感型负荷的最大化利用。同时，分层MPC策略可以避免节点电压超出所设定的限制，即所有节点电压均被限制在0.95(pu)以内，如图14c所示。
由于篇幅限制，不便于将电网中所有电压敏感型负荷的有功功率消耗均在文中展示，因此本文选取节点4、节点24、节点26的电压敏感型负荷作为代表，将三者消耗的有功功率变化在图15中进行展示。结果显示，在低频事件发生后，随着STATCOM调节导致电网各节点电压幅值降低，电压敏感型负荷的有功功率消耗也相应减少，从而有效地减少了有功缺额，最终缓解了低频事件的严重性。由于三个风电场的功率因数均调整为0.95，相较于单位功率因数的情形，系统整体的电压水平有所提高。因此，在节点电压的允许范围内，负荷所消耗的功率具备更大的下降潜力，这表明风电场功率因数的调整会影响电压敏感型负荷的调频能力。
本文提出了一种控制电压敏感型负荷参与电网频率响应的分层MPC策略。该策略分为两层：上层基于集中式MPC，计算频率事件发生后负荷的有功功率参考值，并将其传递给下层；下层基于分散式MPC，由多个本地鲁棒MPC控制器组成，根据上层提供的负荷有功功率参考值，控制无功设备输出相应的无功功率，以此改变电压敏感型负荷的节点电压，进而调节负荷消耗的有功功率达到上层的参考值，使得负荷向电网提供频率支撑。通过仿真算例验证，可以得到以下结论：
1）当发生频率事件后，本文所提的分层MPC策略使得无功设备的无功功率输出迅速增加，控制整个电网的电压幅值升高，使电网中电压敏感型负荷的有功功率消耗变多，平抑了产生的有功盈余，有效减轻了频率事件的严重性。
2）该分层MPC策略考虑了电压敏感型负荷、电网频率和节点电压的动态模型，可以根据具体情况动态地调整无功设备的调节幅度，以实现对频率的有效控制，传统下垂控制策略则无法实现这一点，因此其控制效果要差于分层MPC策略。
3）在频率响应过程中，即使在无功设备之间缺乏通信的情况下，分层MPC策略仍能有效地将电网节点电压限制在约束范围内。相比之下，传统下垂控制策略下的节点电压则出现了电压越限的现象。
本文方法存在以下局限性：首先，本文所提出的方法在控制电压敏感型负荷参与频率响应的过程中，仅针对一次调频提供支撑，没有考虑其惯量支撑的能力；其次，该方法未涵盖风电场故障脱网等突发情况对频率响应的影响。因此，将在后续研究中重点关注电压敏感型负荷的惯量支撑及风电场故障脱网等突发情况对频率响应的影响。
参考文献
[1] 李兆伟, 方勇杰, 吴雪莲, 等. 频率紧急控制中动作时延和措施量对低惯量系统控制有效性的影响[J]. 电工技术学报, 2024, 39(17): 5394-5405. Li Zhaowei, Fang Yongjie, Wu Xuelian, et al. Influence of action delay and amount on the control effectiveness of low inertia systems in frequency emergency control[J]. Transactions of China Electro-technical Society, 2024, 39(17): 5394-5405.
[2] 谢开, 刘敦楠, 李竹, 等. 适应新型电力系统的多维协同电力市场体系[J]. 电力系统自动化, 2024, 48(4): 2-12. Xie Kai, Liu Dunnan, Li Zhu, et al. Multi-dimensional collaborative electricity market system for new power system[J]. Automation of Electric Power Systems, 2024, 48(4): 2-12.
[3] 高倩, 杨知方, 李文沅. 电力系统混合整数线性规划问题的运筹决策关键技术综述与展望[J]. 电工技术学报, 2024, 39(11): 3291-3307. Gao Qian, Yang Zhifang, Li Wenyuan. Prospect on operations research for mixed-integer linear programming problems in power systems[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3291-3307.
[4] 白国岩, 李春宝, 孟繁丞, 等. 多端柔性直流输电系统的自适应下垂控制策略研究[J]. 电气技术, 2022, 23(5): 1-8. Bai Guoyan, Li Chunbao, Meng Fancheng, et al. Research on an adaptive droop control strategy applied in voltage source converter based multi-terminal high voltage direct current transmission system[J]. Electrical Engineering, 2022, 23(5): 1-8.
[5] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994. Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[6] 刘林, 王大龙, 綦晓, 等. 基于双锁相环的海上风场综合惯量调频策略研究[J]. 发电技术, 2024, 45(2): 282-290. Liu Lin, Wang Dalong, Qi Xiao, et al．Study on double phase-locked loop on the synthetic inertia control of offshore wind farm frequency regulation[J]. Power Generation Technology, 2024, 45(2): 282-290.
[7] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677. Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[8] 崔挺. 带电压型负荷的孤立电力系统电压和频率控制策略研究[D]. 武汉: 武汉大学, 2015. Cui Ting. Research on voltage and frequency control strategy of isolated power system with voltage load[D]. Wuhan: Wuhan University, 2015.
[9] Price W W, Chiang H D, Clark H K, et al. Load representation for dynamic performance analysis (of power systems)[J]. IEEE Transactions on Power Systems, 8(2): 472-482.
[10] Langwasser M, De Carne G, Liserre M, et al. Primary frequency regulation using HVDC terminals controlling voltage dependent loads[J]. IEEE Transactions on Power Delivery, 2020, 36(2): 710-720.
[11] 颜湘武, 郭燕, 彭维锋, 等. 基于旋转移相变压器的电压源型无功补偿器及其控制策略[J]. 电工技术学报, 2023, 38(16): 4448-4464. Yan Xiangwu, Guo Yan, Peng Weifeng, et al. Voltage source var compensator based on rotary phase shifting transformer and its control strategy[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4448-4464.
[12] Farrokhabadi M, Cañizares C A, Bhattacharya K. Frequency control in isolated/islanded microgrids through voltage regulation[J]. IEEE Transactions on Smart Grid, 2015, 8(3): 1185-1194.
[13] Alghamdi B, Cañizares C. Frequency and voltage coordinated control of a grid of AC/DC microgrids[J]. Applied Energy, 2022, 310: 118427.
[14] Zhong Weilin, Tzounas G, Milano F. Improving the power system dynamic response through a combined voltage-frequency control of distributed energy resources[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4375-4384.
[15] De Carne G, Buticchi G, Liserre M, et al. Real-time primary frequency regulation using load power control by smart transformers[C]//2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2020: 1.
[16] Wan Yong, Murad M A A, Liu Muyang, et al. Voltage frequency control using SVC devices coupled with voltage dependent loads[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1589-1597.
[17] Alghamdi B, Cañizares C A. Frequency regulation in isolated microgrids through optimal droop gain and voltage control[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 988-998.
[18] Zhang Yuanhang, Kou Peng, Zhang Zhihao, et al. Coordinated frequency and voltage optimal control of wind farm with nonlinear power constraints[J]. IEEE Systems Journal, 2023, 17(3): 4934-4945.
[19] Aksland C T, Tannous P J, Wagenmaker M J, et al. Hierarchical predictive control of an unmanned aerial vehicle integrated power, propulsion, and thermal management system[J]. IEEE Transactions on Control Systems Technology, 2023, 31(3): 1280-1295.
[20] Kou Peng, Liang Deliang, Gao Rong, et al. Decentralized model predictive control of hybrid distribution transformers for voltage regulation in active distribution networks[J]. IEEE Transactions on Sustainable Energy, 2019, 11(4): 2189-2200.
[21] Rouhani A, Abur A. Real-time dynamic parameter estimation for an exponential dynamic load model[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1530-1536.
[22] Choi B K, Chiang H D, Li Yinhong, et al. Measurement-based dynamic load models: derivation, comparison, and validation[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1276-1283.
[23] Liu Junwei, Xu Yan, Qiu Jing, et al. Non-network solution coordinated voltage stability enhancement with STATCOM and UVLS for wind-penetrated power system[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1559-1568.
[24] Baldivieso Monasterios P R, Trodden P. Low-complexity distributed predictive automatic generationcontrol with guaranteed properties[J]. IEEE Transactions on Smart Grid, 2017, 8(6): 3045-3054.
[25] Mayne D Q, Seron M M, Raković S V. Robust model predictive control of constrained linear systems with bounded disturbances[J]. Automatica, 2005, 41(2): 219-224.
[26] Riverso S, Farina M, Ferrari-Trecate G. Plug-and-play decentralized model predictive control for linear systems[J]. IEEE Transactions on Automatic Control, 2013, 58(10): 2608-2614.
[27] Brooks J, Barooah P. Coordination of loads for ancillary services with Fourier domain consumer QoS constraints[J]. IEEE Transactions on Smart Grid, 2019, 10(6): 6148-6155.
[28] Chávarro-Barrera L, Pérez-Londoño S, Mora-Flórez J. An adaptive approach for dynamic load modeling in microgrids[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 2834-2843.
[29] 孙凯祺, 邱伟, 李可军, 等. 面向快速频率响应系统的网络攻击防御控制策略[J]. 中国电机工程学报, 2021, 41(16): 5476-5486. Sun Kaiqi, Qiu Wei, Li Kejun, et al. Cyber attack defense control for fast frequency response system[J]. Proceedings of the CSEE, 2021, 41(16): 5476-5486.
[30] Xue Nan, Chakrabortty A. Parallel identification of power system dynamic models under scheduling constraints[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4584-4594.
[31] Neyestanaki M K, Ranjbar A M. An adaptive PMU-based wide area backup protection scheme for power transmission lines[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1550-1559.
[32] Stanojev O, Markovic U, Aristidou P, et al. MPC-based fast frequency control of voltage source converters in low-inertia power systems[J]. IEEE Transactions on Power Systems, 2022, 37(4): 3209-3220.
[33] Zhang Yifu, Cortés J. Distributed bilayered control for transient frequency safety and system stability in power grids[J]. IEEE Transactions on Control of Network Systems, 2020, 7(3): 1476-1488.
[34] 李春华, 张永康, 王永源, 等. 南方电网±200 Mvar静止同步补偿器人工短路试验及分析[J]. 电力系统自动化, 2013, 37(4): 125-129. Li Chunhua, Zhang Yongkang, Wang Yongyuan, et al. Artificial short circuit test and analysis of ±200 Mvar STATCOM in China Southern Power Grid[J]. Automation of Electric Power Systems, 2013, 37(4): 125-129.
Abstract Driven by the national goal of “double carbon”, China's power system is accelerating the transition to a new kind of power system with high renewable energy penetration. However, the inherent intermittency and low inertia characteristics of renewable energy bring challenges to the frequency stability of the power grid. In this context, modern power systems require additional frequency regulation resources to ensure grid stability. Voltage-dependent loads are important frequency regulation resources, whose active power consumption is strongly correlated with bus voltage. For this reason, this paper proposes a control strategy for voltage-dependent loads. The proposed strategy regulates multiple reactive power devices, controlling the bus voltage of the load to change its active power consumption and contributing to frequency response.
Firstly, the proposed strategy has two layers. The upper layer, employing centralized model predictive control (MPC), calculates the active power references of loads and delivers the references into the lower layer. The lower layer employs decentralized MPC to calculate the reactive power of reactive power devices based on the active power references of the loads from the upper layer. Secondly, the control problem formulation of the lower layer includes the dynamic models of voltage-dependent loads and bus voltages, thus realizing effective load active power control without violating voltage constraints. Thirdly, the lower decentralized MPC strategy consists of multiple local controllers that do not communicate with each other, and the interactions between controllers are regarded as disturbances. A tube-based robust method is used to compensate for the communication deficiencies and achieve suboptimal control, thus significantly reducing the communication burden.
Simulation results on the modified IEEE 39-bus system show that, when a 522 MW load is suddenly disconnected, the grid frequency rises to 50.29 Hz at the highest level without the load support and is stabilized at 50.19 Hz in the end. If the conventional droop control is employed to regulate the voltage-dependent loads to participate in the frequency response, then the grid frequency rises to 50.22 Hz and eventually stabilizes at 50.16 Hz. In contrast, if the proposed hierarchical MPC strategy is adopted for voltage-dependent loads, the grid frequency rises to 50.18 Hz and is finally stabilized at 50.08 Hz. Based on the above analysis, it can be learned that, compared with the traditional droop control, the hierarchical MPC strategy for voltage-dependent loads reduces the peak and steady-state values of the frequency and significantly improves the frequency dynamics.
We can draw the following conclusions from the simulation results: (1) When an over-frequency event occurs, the proposed hierarchical MPC strategy makes the reactive power outputs of reactive devices increase rapidly. In this way, the voltage amplitude of the entire grid rises, and thus the active power consumption of voltage-dependent loads increases, effectively mitigating the severity of the over-frequency event. (2) To realize effective frequency control, the proposed hierarchical MPC strategy takes into account the dynamic model of voltage-dependent loads, grid frequency and bus voltage, and can dynamically adjust the outputs of reactive power devices according to the specific situation. (3) During the frequency response, the hierarchical MPC strategy can still effectively limit the bus voltages within the constraints even in the absence of communication between reactive power devices. In contrast, the bus voltages under the conventional droop control strategy suffer from voltage violations.
keywords：Model predictive control, hierarchical control, voltage-dependent load, frequency response, voltage control
DOI: 10.19595/j.cnki.1000-6753.tces.242243
中图分类号：TM73
国家自然科学基金资助项目（52077165）。
收稿日期 2024-12-23
改稿日期 2025-02-04
张远航 男，1998年生，博士研究生，研究方向为电力系统调频调压、预测控制、新能源发电。E-mail：zhangyh1998@stu.xjtu.edu.cn
寇 鹏 男，1983年生，博士，教授，博士生导师，研究方向为可再生能源并网、电力系统预测与控制等。E-mail：koupeng@mail.xjtu.edu.cn（通信作者）
（编辑 赫 蕾）