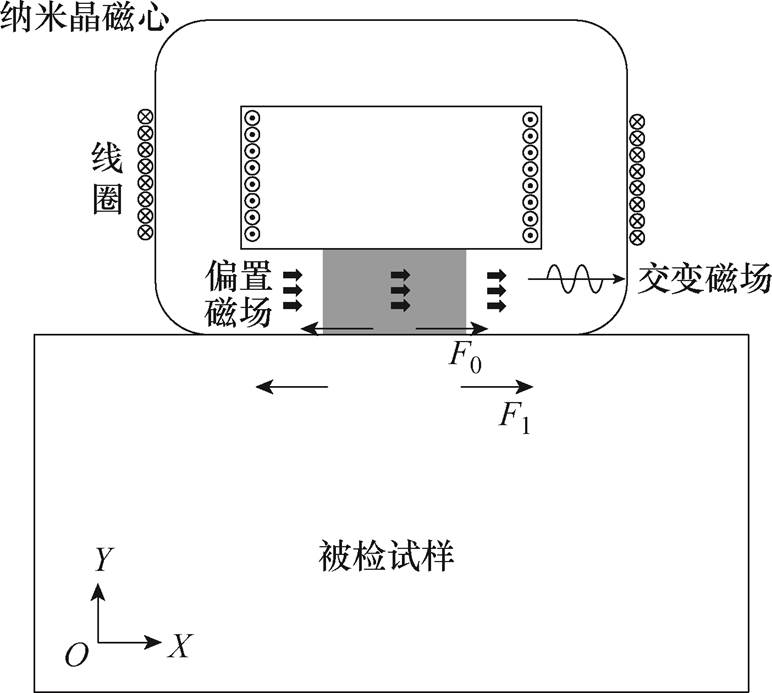
图1 GMPT的换能机理
Fig.1 Conversion mechanism of GMPT
摘要 该文提出了一种无永磁体超磁致伸缩贴片换能器及其检测电路。首先,建立了无永磁体超磁致伸缩贴片换能器的有限元模型,分析了电压参数、线圈几何参数、贴片尺寸等因素对接收幅值的影响;然后,设计并搭建了无永磁体超磁致伸缩贴片换能器检测系统,并通过实验对仿真规律进行了验证。结果表明:所提换能器与直流电压具有非线性响应关系,而与交变电压具有线性响应关系,可以调节电压幅值来改变Terfenol-D贴片的工作点,从而提高直达波幅值。直达波幅值随线圈匝数的增加而减小,随线圈导线直径的增大而增强。Terfenol-D贴片厚度与纳米晶磁心气隙高度接近时可以接收到最佳的直达波信号。考虑到直达波的信号幅值,无永磁体磁致伸缩贴片换能器最佳参数为:线圈匝数为21,线圈导线直径为0.55 mm,磁致伸缩贴片厚度为4 mm、长度为12 mm。
关键词:磁致伸缩贴片换能器 Terfenol-D 纳米晶磁心 优化设计
磁致伸缩贴片换能器(Magnetostrictive Patch Transducer, MPT)是一种基于磁致伸缩效应设计的装置,该效应反映了铁磁材料中机械场与磁场之间的相互作用。磁致伸缩贴片换能器一般由永磁体、线圈和磁致伸缩贴片组成,贴片采用高铁磁性材料,如镍或铁钴合金,制成薄片并将其粘附或固定在被测结构表面[1]。这种贴片显著提升了超声波的激发效率,不仅能够用于非铁磁性和非金属材料的超声检测,还大大提高了换能效率。磁致伸缩贴片换能器的应用包括管材或棒材[2]、管道[3-4]和旋转轴[5-6]等结构的健康监测。
国内外学者围绕磁致伸缩贴片换能器的优化设计进行了广泛的研究。S. H. Cho等[7]以铝板为对象,使用圆形镍贴片和八字形线圈,探讨了磁场与超声导波的相互作用,以及它们的方向依赖性和贴片尺寸的影响。J. S. Lee等[8]使用平面螺线管阵列线圈替代S. H. Cho等早期研究中的八字形线圈来实现更高分辨率的波转换,并成功地在铝板中激励出高能量的SH0模态。J. K. Lee等[9]在之前研究的基础上提出了一种轴对称磁致伸缩贴片换能器,通过在永磁体外部安装多个轴对称线圈来产生全向Lamb波,并表明当波长等于贴片直径的2/3时,产生效率最高。H. M. Seung等[10]提出了一种全向剪切水平(Shear-Horizontal, SH)磁致伸缩贴片换能器,通过模拟和实验验证了其全向性,并研究了该换能器频率特性与贴片尺寸的关系。J. H. Oh等[11]开发了一种有限元分析方法用于预测磁致伸缩贴片换能器的波辐射模式,并进行了时谐分析以提高数值计算效率,解释了特定辐射方向的形成原因。A. Zitoun等[12]探讨了静态磁场和交变磁场的变化对贴片振动的影响,同时发现适当的频率和磁场组合能够产生更高的超声波信号。B. Yoo等[13]使用超磁致伸缩材料Fe-Ga合金设计并制作了超磁致伸缩贴片换能器(Giant Magnetostrictive Patch Transducer, GMPT)应用于超声导波检测,并提出了利用圆形和十字形GMPT来控制并改善GMPT的方向灵敏度。
然而,上述研究大多依赖永磁体产生偏置磁场,导致传统永磁体式磁致伸缩贴片换能器容易吸附铁磁性颗粒。此外,永磁体的磁场强度恒定且会在长期使用下发生磁性衰退,降低换能效率和回波信号幅值。针对这些问题,D. Rueter[14-15]和K. Rieger[16]等提出了仅线圈式电磁超声换能器(Electromagnetic Acoustic Transducer, EMAT)的配置方案,在不依赖永磁体的条件下,对单个螺旋线圈通以高频、高幅值的射频电流和类DC电流,在铝、不锈钢等金属材料中实现了超声波的激励与接收。
本文利用Terfenol-D[17]这种超磁致伸缩材料的特性,以铝合金为检测对象,提出一种无永磁体超磁致伸缩贴片换能器。首先,分析GMPT的换能机理并设计检测电路;然后,建立GMPT的有限元模型,研究电压参数、线圈参数、贴片尺寸等因素对接收信号幅值的影响规律;最后,制作无永磁体GMPT,搭建检测实验平台,对仿真规律进行实验验证。
磁致伸缩效应是指当铁磁性材料受到外磁场作用时,自身的磁畴发生旋转,导致长度或体积发生变化[18-20]。利用此效应在线圈中通入含有高频、高幅值的射频电流来产生交变磁场,可以使磁致伸缩贴片产生高频振动从而激励出超声波。为了避免倍频效应使系统的高次谐波成分增加,可以在线圈中通入类直流成分的电流来产生偏置磁场,从而消除倍频效应[21]。
纳米晶合金材料[22-23],特别是铁基纳米晶材料,具有高饱和磁感应强度、高磁导率和低损耗等优势,其晶粒尺寸接近nm尺度,远小于传统晶粒铁心材料,在高频条件下磁滞损耗和涡流损耗比较低。其矫顽力只有1.2 A/m,意味着在外加磁场撤除后,材料内部的磁畴几乎能自发回位,在通电/断电循环后不会保留显著剩余磁性。因此,选择纳米晶合金材料制作磁心以减小磁场的损耗并降低磁心的发热。
无永磁体GMPT的换能机理如图1所示。将磁致伸缩贴片用环氧树脂耦合到铝合金试样上,带气隙的回形纳米晶磁心用于聚集磁场,电路导通时线圈会产生水平方向的偏置磁场和交变磁场,磁致伸缩贴片在磁致伸缩效应下发生磁致伸缩应变并加载到铝合金试样上,激励出的超声波主要是沿着厚度方向的横波。

图1 GMPT的换能机理
Fig.1 Conversion mechanism of GMPT
铁磁性材料的磁弹性本构方程为
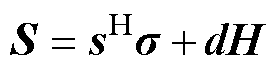 (1)
(1)
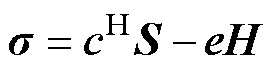 (2)
(2)
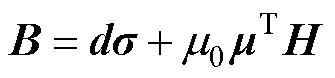 (3)
(3)
式中,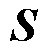 为应变矩阵;
为应变矩阵;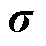 为应力矩阵;
为应力矩阵;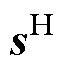 为柔性系数矩阵;
为柔性系数矩阵;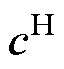 为刚度系数矩阵;
为刚度系数矩阵;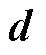 为压磁矩阵;
为压磁矩阵;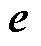 为逆压磁矩阵;
为逆压磁矩阵; 为磁场强度矩阵;
为磁场强度矩阵;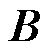 为磁通密度矩阵;
为磁通密度矩阵;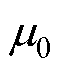 为真空磁导率;
为真空磁导率;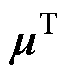 为相对磁导率矩阵。式(1)和式(2)表示磁致伸缩效应,即施加磁场会引起应变;式(3)表示逆磁致伸缩效应,即施加应变时,磁场会产生变化。
为相对磁导率矩阵。式(1)和式(2)表示磁致伸缩效应,即施加磁场会引起应变;式(3)表示逆磁致伸缩效应,即施加应变时,磁场会产生变化。
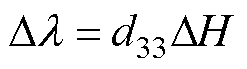 (4)
(4)
式中,Dl为在交变场下的峰值应变变化量;DH为交变磁场的峰值;d33为磁致伸缩应变曲线l-H的斜率,即d33=dl/dH,一般以其最大值作为材料的动态磁致伸缩系数。磁场强度H与磁致伸缩应变l的关系如图2所示。图2中,Hb为偏置磁场,交变磁场为[-DH, +DH],表示幅值为DH的交变磁场在偏置磁场的中心附近正负对称交变。可以发现,要想获得比较大的Dl,材料的饱和磁致伸缩应变ls要高,应变曲线要陡,d33值要大。因此,选择Terfenol-D这种超磁致伸缩材料来设计换能器。
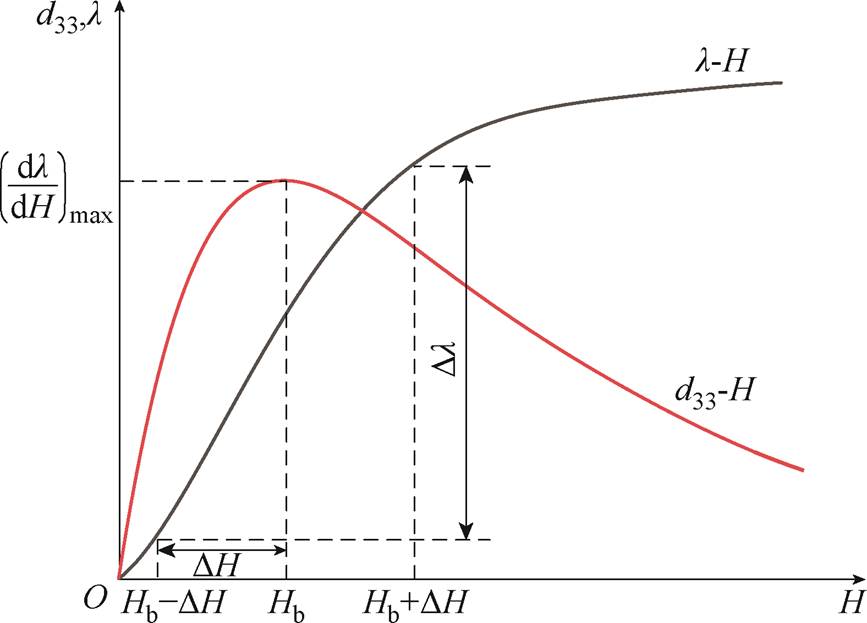
图2 磁致伸缩应变曲线及d33-H曲线[24]
Fig.2 Magnetostrictive strain curve and d33-H curve[24]
无永磁体GMPT检测电路如图3所示。其中,IGBT与MOSFET的驱动芯片为2EDF7275F,IGBT型号为IXGK320N60B3,MOSFET型号为NTHL020N120SC1。R1、R2、R3、R4为限流电阻,R5为康铜丝采样电阻。C1为容值为470 mF的电解电容,C2为容值为300 nF的高压薄膜电容,二极管VD1和VD2的型号为P600U。方波信号由外部的FPGA模块产生,IGBT和MOSFET的脉冲宽度分别为300 ms和0.5 ms,工作周期为0.5 s。由于磁场总作用时间的占空比仅为0.06%,在低占空比下,尽管瞬时电流较大,但平均功耗极低,远低于传统持续通电电磁铁的能耗水平。同时,非工作状态下无剩余磁场,因此可显著减少对铁磁性颗粒的持续吸附。在方波脉冲信号到达前,+30 V与+300 V电源会给电容C1和C2充电;脉冲信号到达时,IGBT先导通,电容C1放电,当线圈中类直流成分达到最大时,再导通MOSFET释放出高频、高幅值的射频电流。IGBT导通时间较长,会在线圈中形成相对平滑的类直流成分,用于提供偏置磁场,MOSFET释放的高频、高幅值的射频电流用于提供交变磁场。
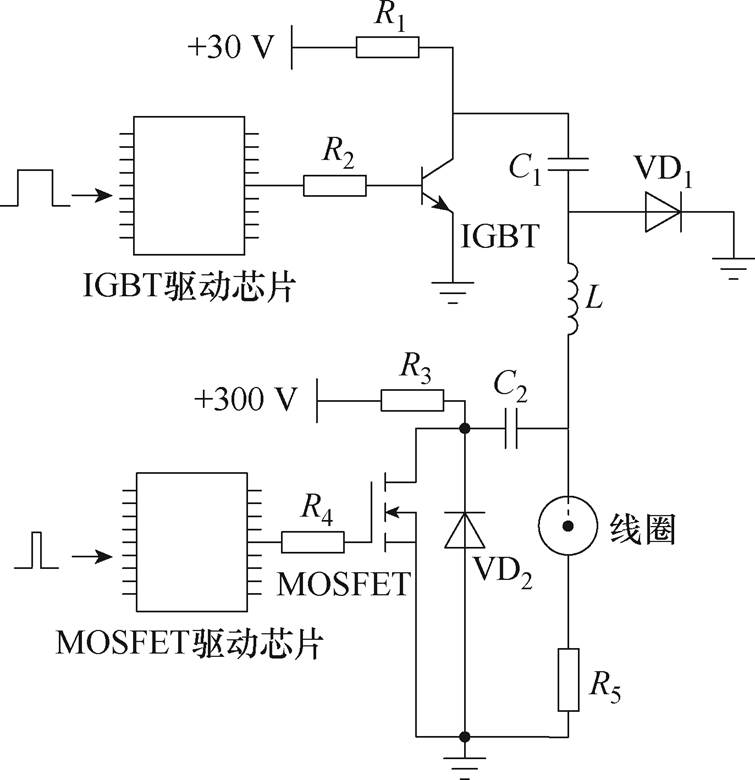
图3 GMPT检测电路
Fig.3 GMPT detection circuit
采用有限元仿真软件COMSOL建立无永磁体磁致伸缩贴片的二维有限元模型,其网格划分如图4所示。Terfenol-D贴片和多匝线圈采用映射网格,纳米晶磁心和铝合金试样采用自由三角形网格,Terfenol-D贴片和多匝线圈的最大网格单元分别为0.1 mm、0.2 mm,纳米晶磁心和铝合金试样的最大网格单元选择普通物理极细化程度的单元大小,空气域选择普通物理常规程度的单元大小。该有限元模型包括26 400个域单元和1 262个边界单元,当设置计算时间步长为0.01 ms时,计算结果收敛。无永磁体GMPT模型设计参数见表1;纳米晶磁心的磁性能参数见表2;Terfenol-D的材料参数见表3。
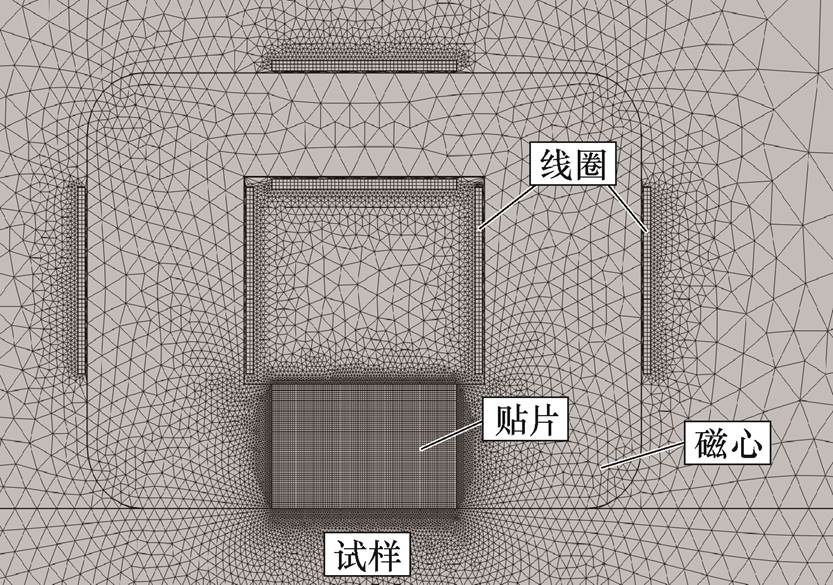
图4 有限元模型网格划分
Fig.4 Meshing grids of finite element model
表1 有限元模型参数
Tab.1 Finite element model parameters
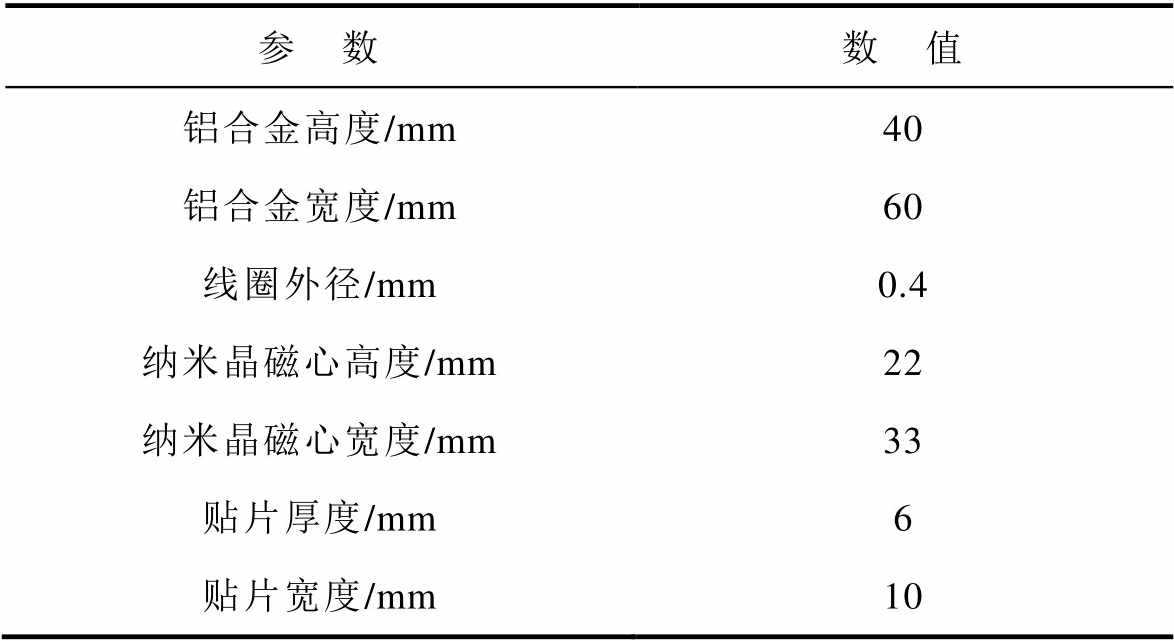
参 数数 值 铝合金高度/mm40 铝合金宽度/mm60 线圈外径/mm0.4 纳米晶磁心高度/mm22 纳米晶磁心宽度/mm33 贴片厚度/mm6 贴片宽度/mm10
表2 纳米晶材料参数
Tab.2 Parameters of nanocrystalline materials
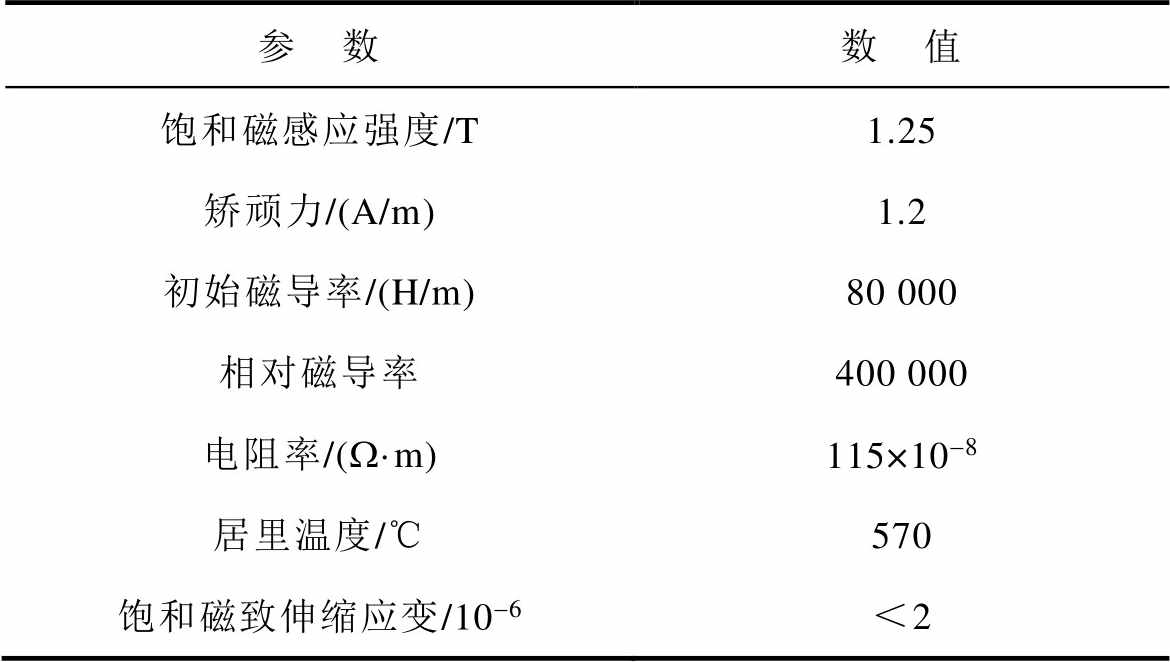
参 数数 值 饱和磁感应强度/T1.25 矫顽力/(A/m)1.2 初始磁导率/(H/m)80 000 相对磁导率400 000 电阻率/(W·m)115×10-8 居里温度/℃570 饱和磁致伸缩应变/10-6<2
表3 磁致伸缩材料参数
Tab.3 Parameters of magnetostrictive materials
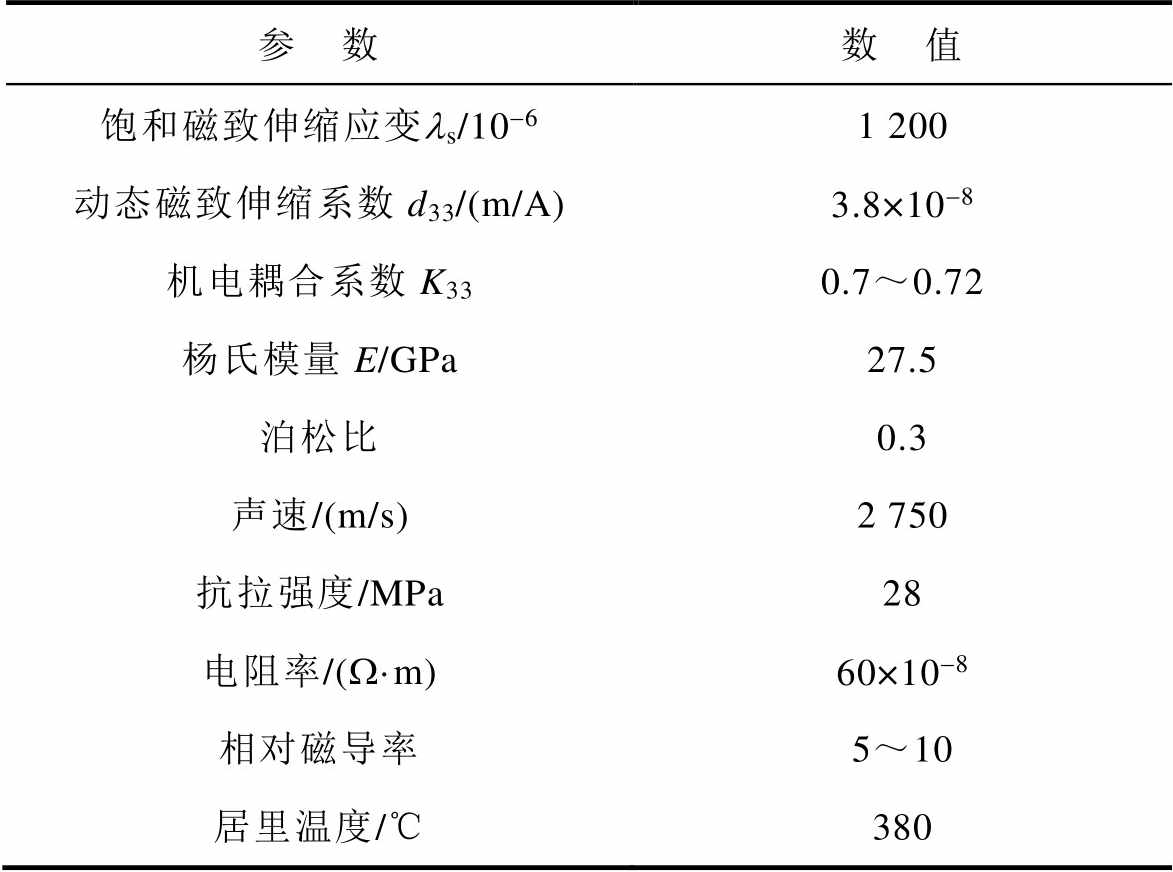
参 数数 值 饱和磁致伸缩应变ls/10-61 200 动态磁致伸缩系数d33/(m/A)3.8×10-8 机电耦合系数K330.7~0.72 杨氏模量E/GPa27.5 泊松比0.3 声速/(m/s)2 750 抗拉强度/MPa28 电阻率/(W·m)60×10-8 相对磁导率5~10 居里温度/℃380
无永磁体GMPT激发的超声波在铝合金试样中传播的声场快照如图5所示。由图5可知,该配置的无永磁体GMPT激励的超声波以横波为主。
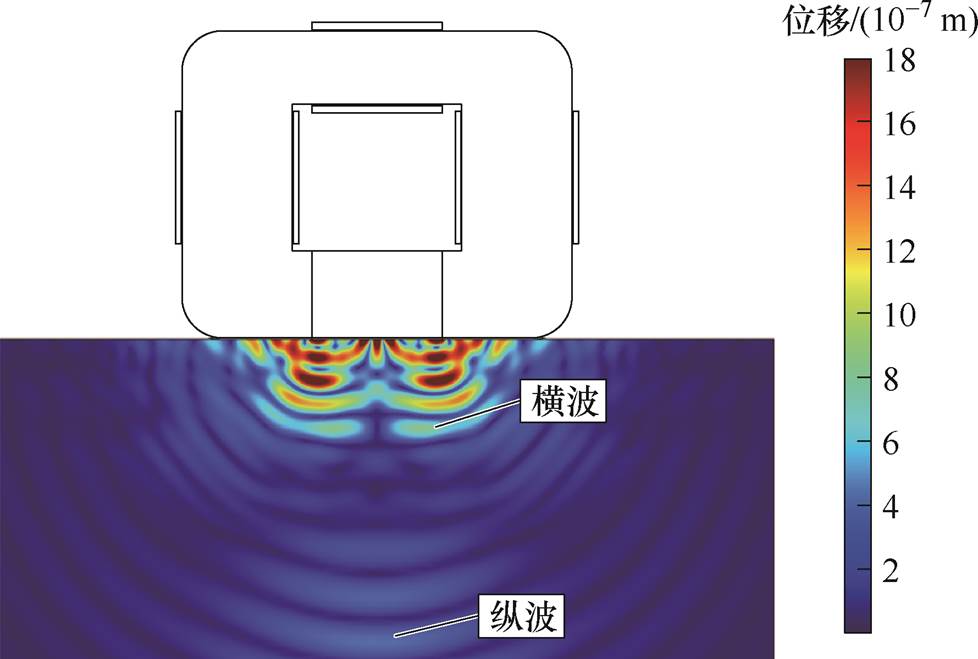
图5 超声波传播的声场快照
Fig.5 Snapshot of the acoustic field of ultrasonic propagation
在线圈中提供交变磁场和偏置磁场的电压表达式分别为
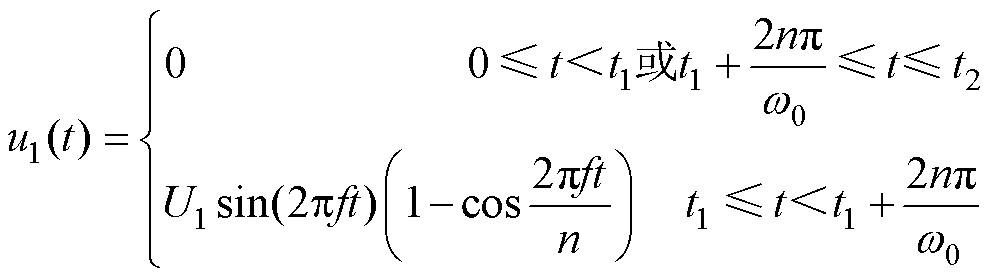 (5)
(5)
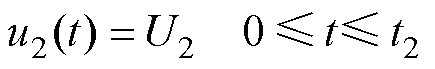 (6)
(6)
式中,u1为提供高频交变磁场的交变电压,在t1= 50 ms时开启,持续时间5 ms;f为交变电压频率,f= 1 MHz;w0=2pf;n为正弦脉冲串的周期数,n=5;u2为提供偏置磁场的直流电压,持续时间t2=300 ms;U1和U2为直流电压源。下面将通过控制U1和U2来分析直流电压与交变电压对激励的超声波位移信号的影响。
2.2.1 直流电压
U1保持200 V不变,改变直流电压U2为18~28 V,步长为2 V,计算得到的X分量和Y分量位移回波如图6所示。提取X、Y分量位移回波中纵波和横波的峰值进行归一化,结果如图7所示。随着直流电压的增加,横波和纵波的幅值均出现先增加后减小的趋势。横波和纵波最大幅值对应的直流电压分别为24 V和26 V,说明此时偏置磁场的磁场强度Hb在工作点d33的最大处,Terfenol-D贴片在交变磁场驱动下的磁能达到最高,进而转化为磁弹性能,使磁致伸缩贴片的应变达到峰值。因此,要尽可能地选择合适的直流电压,以提高磁致伸缩贴片换能器的换能效率。
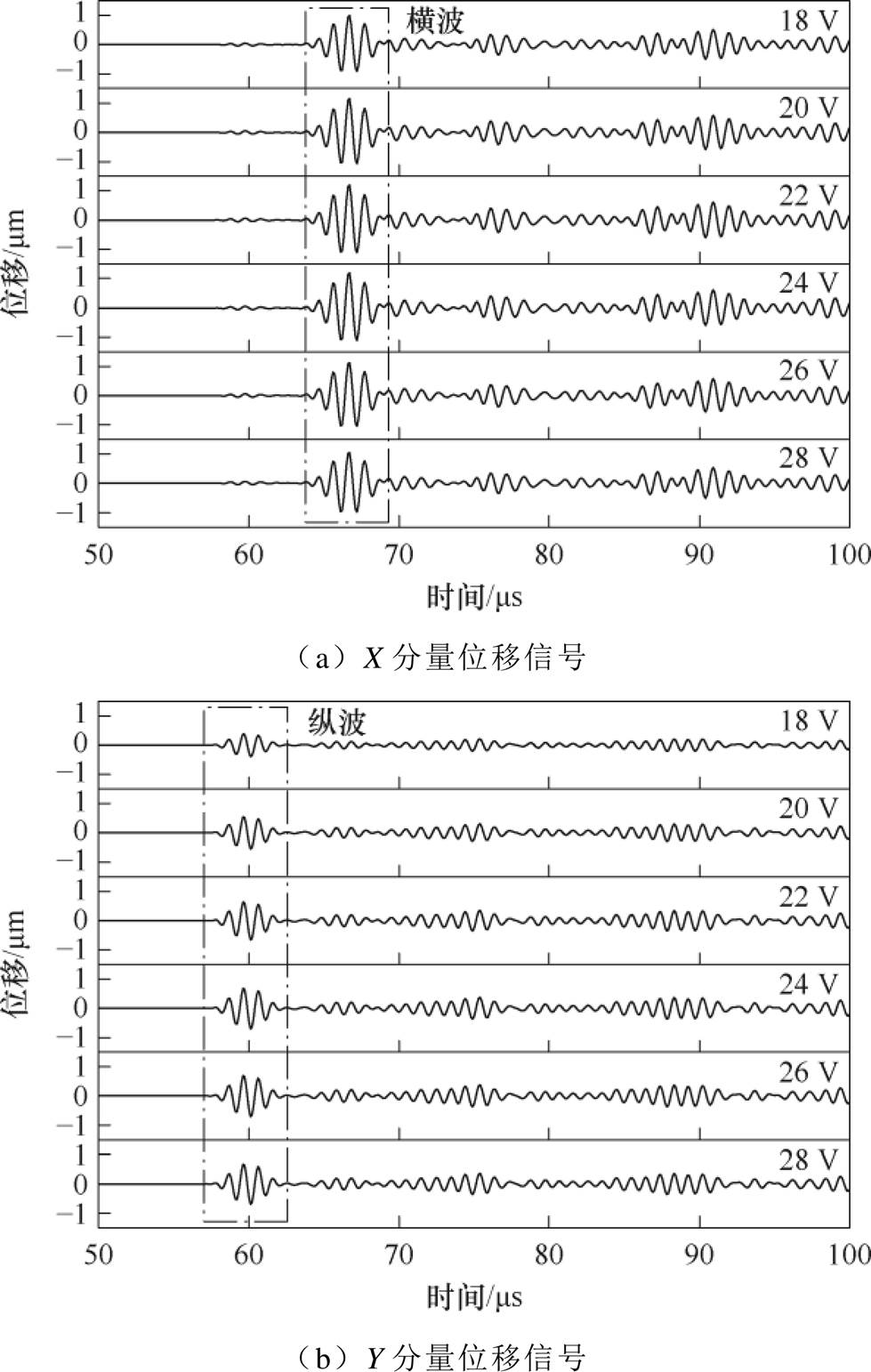
图6 不同直流电压的超声波位移信号
Fig.6 Ultrasonic displacement signals of different DC voltages
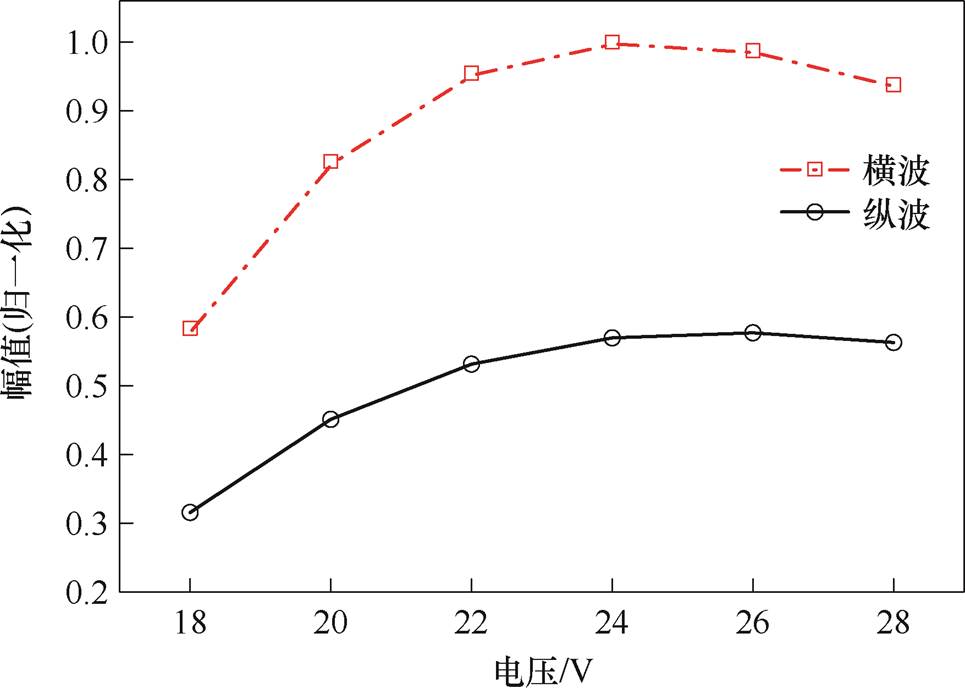
图7 直流电压对体波幅值的影响
Fig.7 Influence of DC voltage on bulk wave amplitude
2.2.2 交变电压
为了探究交变电压对给定直流电压下位移信号幅值的影响,在50~250 V范围内以50 V为步长改变U1,得到U1分别为50、100、150、200、250 V时的X分量和Y分量位移回波如图8所示。提取X、Y分量位移回波中纵波和横波的峰值的归一化结果如图9所示。随着脉冲电压的增加,横波和纵波的幅值均出现逐渐增加的趋势,并且满足线性关系。给磁致伸缩贴片施加一个位于d33处的偏置磁场,交变电压经过激励电路产生高频的交变磁场,交变电压幅值越高,作用在磁致伸缩贴片上的DH越强,所产生的磁致伸缩应变Dl就越大。
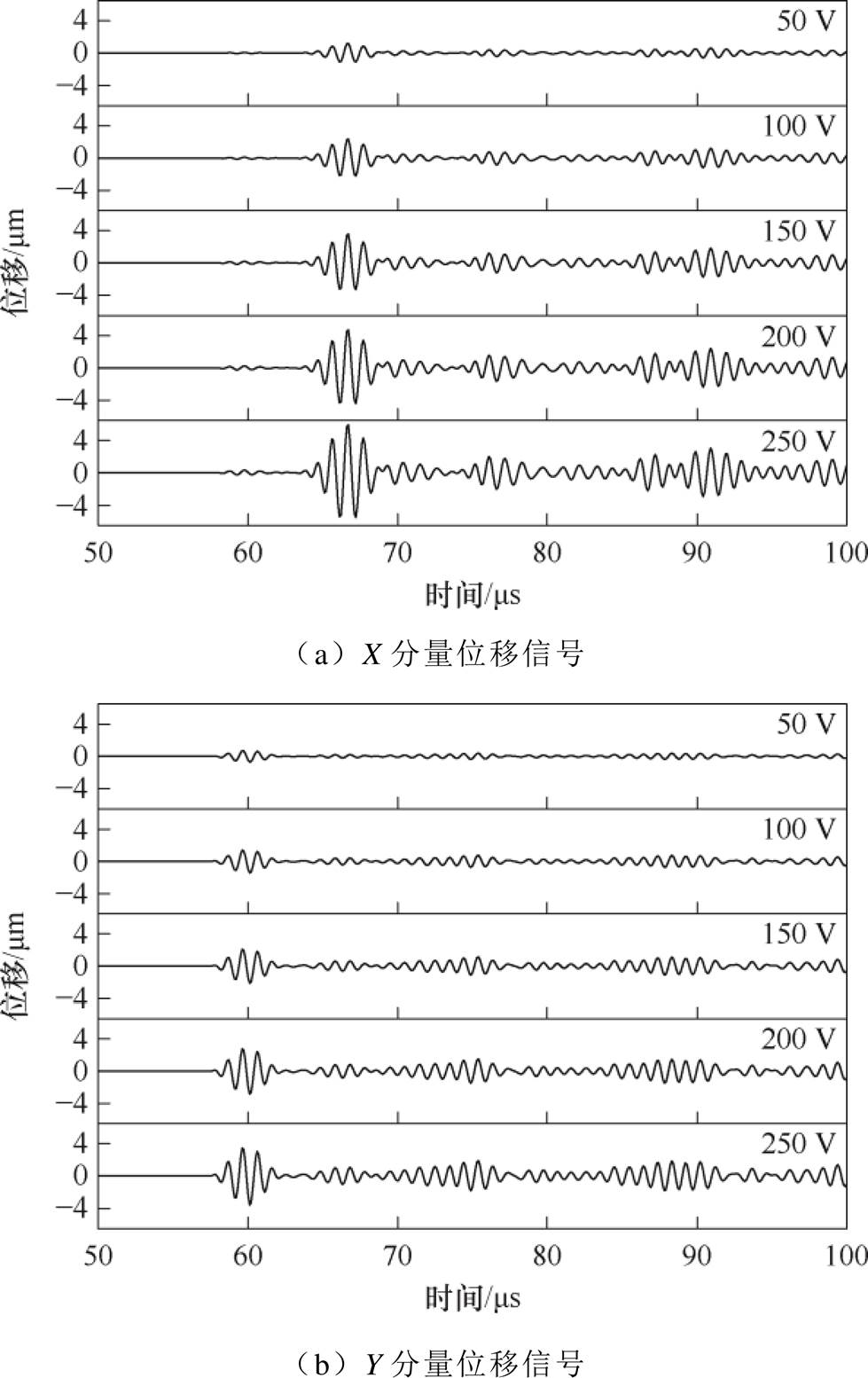
图8 不同交变电压的超声波位移信号
Fig.8 Ultrasonic displacement signals of different alternating voltages
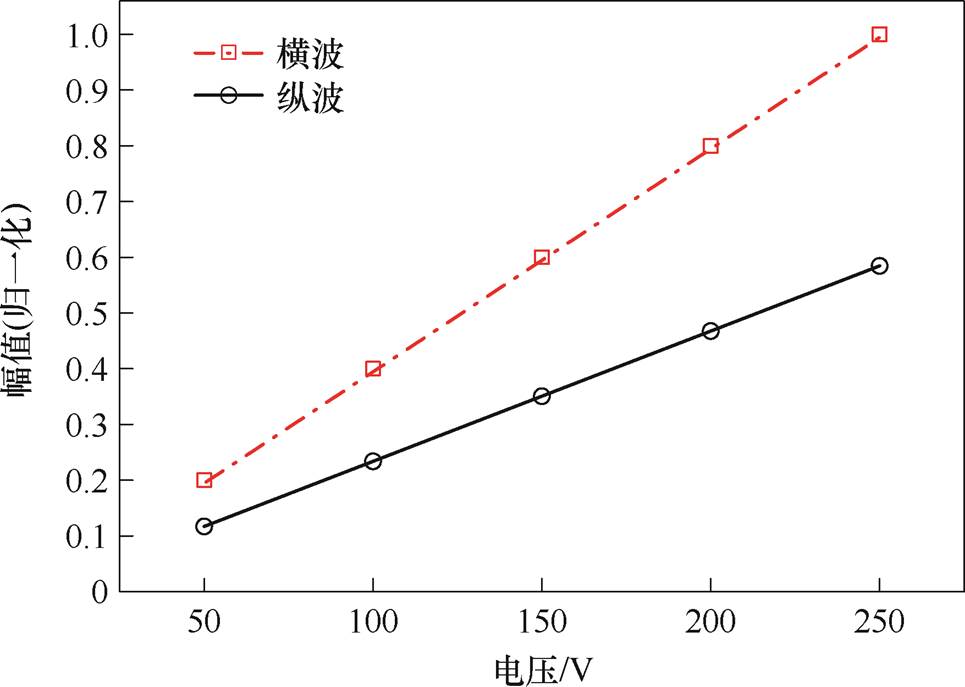
图9 交变电压对体波幅值的影响
Fig.9 Influence of alternating voltage on bulk wave amplitude
2.3.1 线圈匝数
为了研究线圈参数对信号幅值的影响,将线圈导线直径保持在0.4 mm不变,设置线圈匝数为21~57匝,步长为9匝,计算得到的X分量和Y分量位移回波如图10所示。图11为提取X、Y分量位移回波中纵波和横波的峰值的归一化结果。由图10和图11可知,横波与纵波的信号幅值均随线圈匝数的增加而减小,并且减小的趋势逐渐减小。当线圈导线直径不变时,增大线圈匝数,电路系统内部感抗增加,激励电路通入的电流减小,偏置磁场和交变磁场的磁场强度相应减小,从而磁致伸缩贴片的应变Dl减小。因此,设计磁致伸缩贴片换能器时要尽可能地选择匝数少的线圈,以提高磁致伸缩贴片换能器的换能效率。
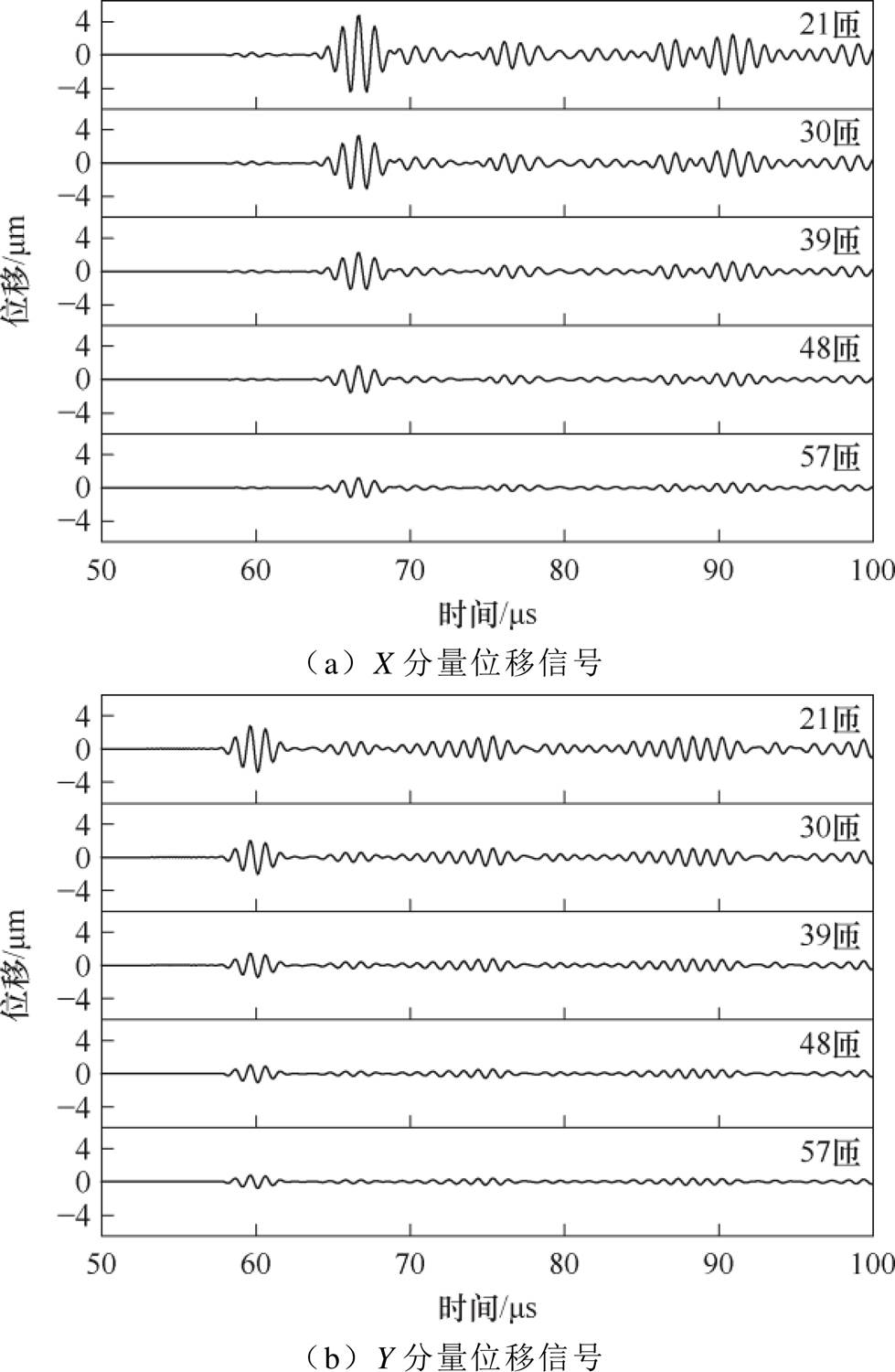
图10 不同线圈匝数的超声波位移信号
Fig.10 Ultrasonic displacement signal of different coil turns
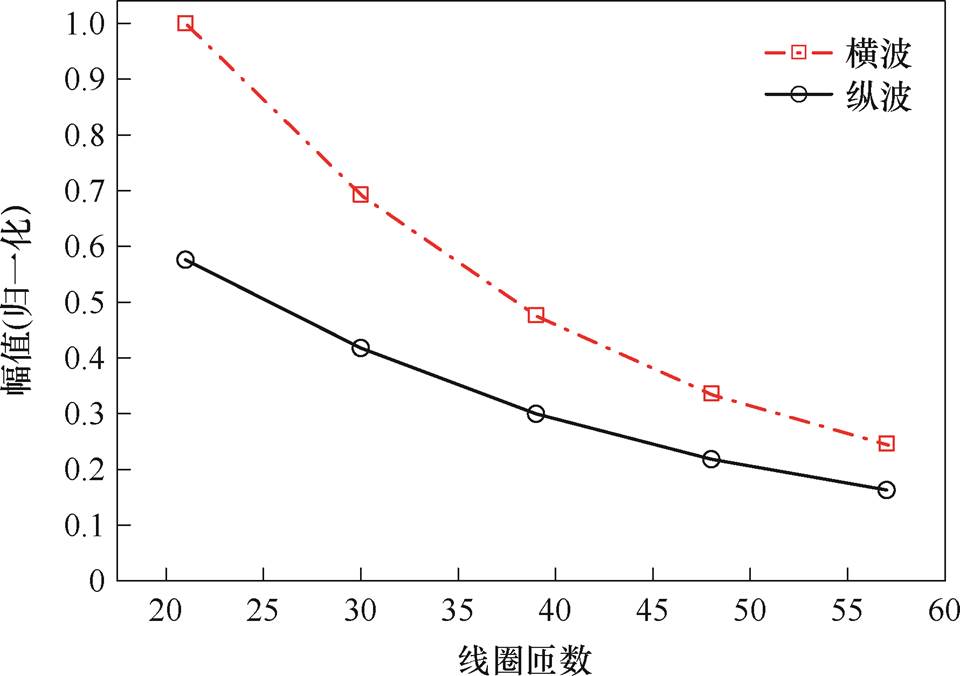
图11 线圈匝数对体波幅值的影响
Fig.11 Influence of coil turns on bulk wave amplitude
2.3.2 线圈导线直径
为了探究线圈导线直径对给定线圈匝数下信号幅值的影响,在0.26~0.48 mm范围内改变导线直径,得到导线直径分别为0.26、0.30、0.35、0.40、0.48 mm时的X分量和Y分量位移回波如图12所示,图13为提取X、Y分量位移回波中纵波和横波的峰值的归一化结果。可见,横波和纵波的幅值随着导线直径的增加而增加,并且增加的幅度逐渐减小。这是因为当线径增大时,导线的横截面积增大,电阻降低,减少了电流通过时的能量损耗,导致信号幅值增大。然而,在1 MHz的高频下,趋肤效应使电流集中在导线表面流动,增大线径只能在一定程度上降低电阻。随着线径继续增加,电阻降低的效果逐渐减小,信号幅值的增加幅度也变小。因此,在不影响换能器体积的前提下,应尽可能地选择线径较大的导线。
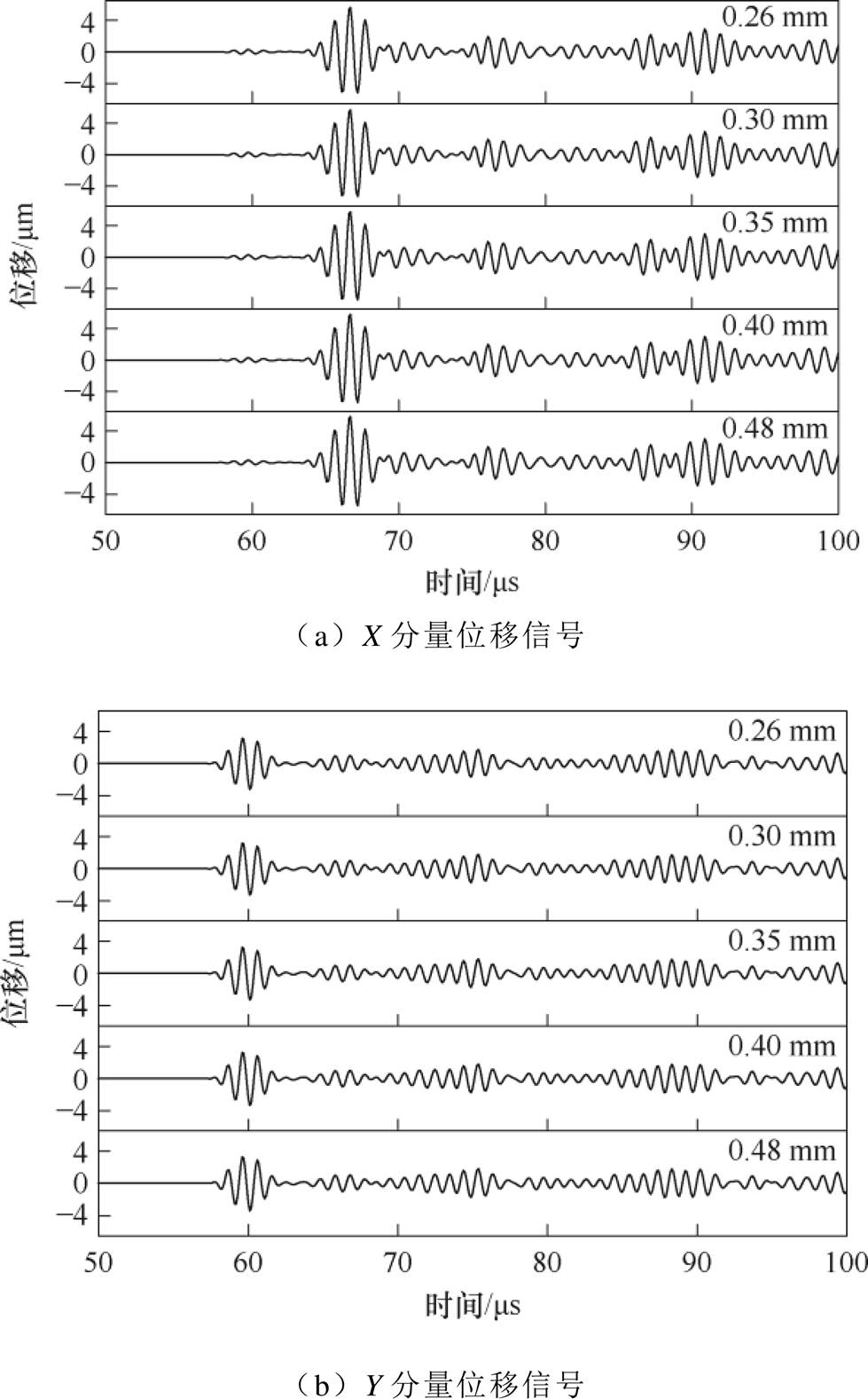
图12 不同导线直径的超声波位移信号
Fig.12 Ultrasonic displacement signals of different conductor diameters
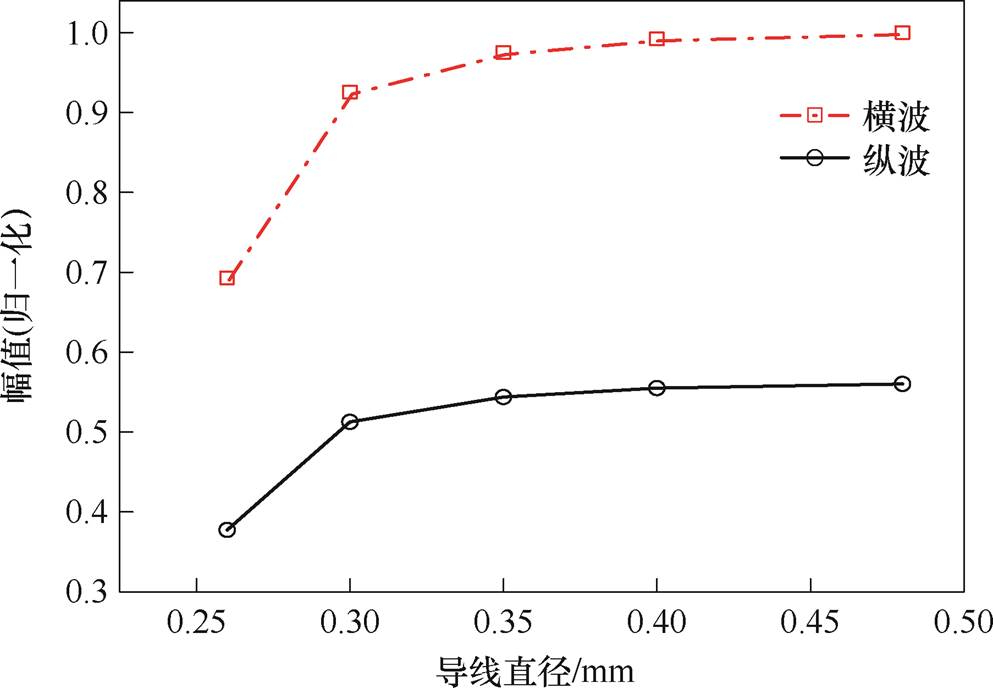
图13 线圈导线直径对体波幅值的影响
Fig.13 Influence of conductor diameter on bulk wave amplitude
2.4.1 贴片厚度
为了研究贴片厚度对体波幅值的影响,将贴片长度设置为10 mm,并在1~8 mm范围内改变贴片厚度,步长为1 mm,位移回波中纵波和横波的峰值归一化结果如图14所示。由图14可知,随着贴片厚度的增加,横波幅值先增加后减小,在6 mm厚度时达到最大;纵波幅值则整体呈逐渐减小的趋势。出现这种情况的原因是,当贴片厚度小于磁心气隙高度时,磁场基本可以均匀地穿透整个贴片,使得Terfenol-D产生较大的磁致伸缩应变。随着贴片厚度的增加,磁致伸缩效应继续增强,横波幅值继续增大,然而随着厚度增加直至高于磁心高度时,穿过贴片的偏置磁场均匀性会受到影响,并且材料的机械阻抗和能量耗散增大,阻碍了振动的传递效率,导致纵波信号幅值逐渐减小。因此,贴片厚度为6 mm时与磁心气隙高度达到最佳匹配,过薄或过厚的贴片都会使信号幅值减小。
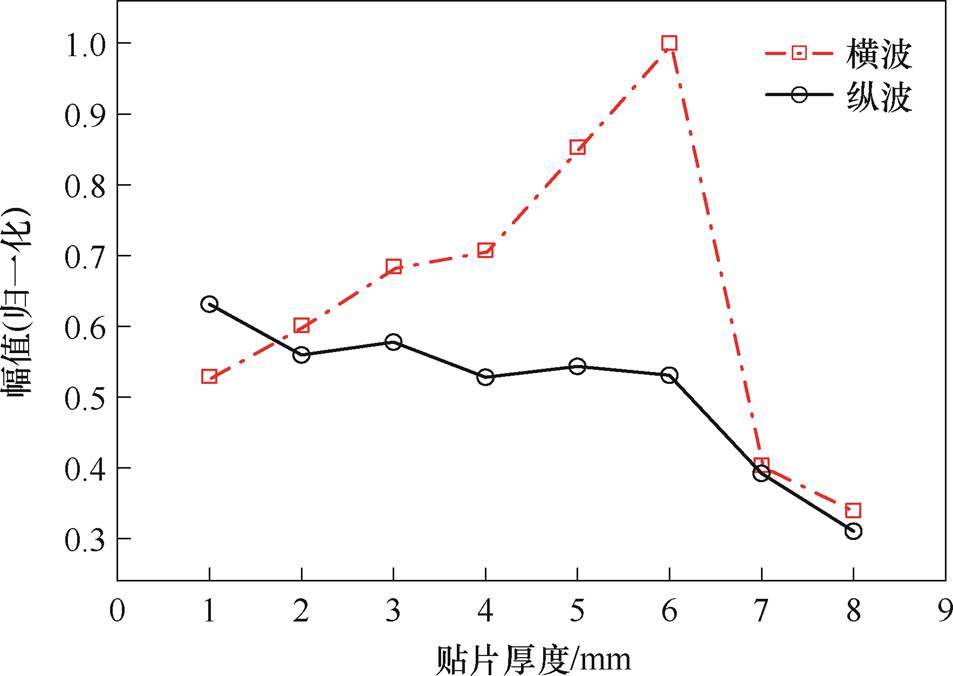
图14 贴片厚度对体波幅值的影响
Fig.14 Influence of patch thickness on bulk wave amplitude
2.4.2 贴片长度
为了探究贴片长度对给定贴片厚度下信号幅值的影响,在10~14 mm范围内改变贴片长度,步长为2 mm。位移回波中纵波和横波的峰值的归一化结果如图15所示。随着贴片长度的增加,横波和纵波幅值都出现了逐渐减小的趋势。信号幅值减小主要有以下两个原因:第一个原因是磁致伸缩贴片受磁场的驱动会在靠近两端产生较强的振动,而中间部分受到的磁场要小于两端,振动幅值减弱。随着贴片长度增加,这种不均匀分布的效应更加明显,因此横波的幅值下降更快。纵波虽然也是由磁致伸缩效应引发的,但由于其主要依赖整体结构的垂直振动,且振动传递路径受水平长度变化的影响较小,因此纵波幅值的减小幅度较缓慢。第二个原因是当贴片的水平长度增加时,振动需要在更长的距离上传播。由于材料内部的阻尼效应和能量损耗,信号会在传递过程中逐渐衰减。因此,随着贴片长度的增加,横波和纵波的信号幅值都逐渐减小。
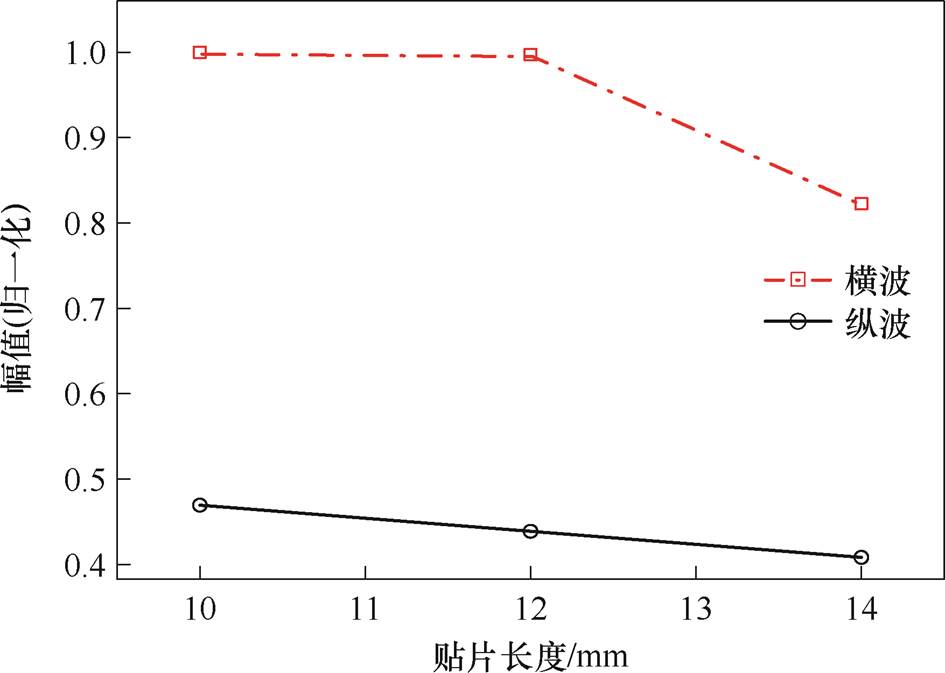
图15 贴片长度对体波幅值的影响
Fig.15 Influence of patch length on bulk wave amplitude
为了验证有限元计算的准确性,搭建无永磁体GMPT实验系统如图16所示。FPGA模块产生控制无永磁体GMPT激励电路的方波信号,多路直流稳压电源用于调节直流高压电源的Vadj端来控制输出电压,直流高压与低压经激励电路后产生1 MHz的高频交变电流和低压类直流通入线圈。磁致伸缩贴片至铝合金试样表面产生的超声波信号被压电探头拾取后进入前置放大器,放大器增益为30 dB,放大的信号由数据采集卡接收并传入计算机,最后使用LabVIEW软件显示和存储超声回波信号。图16中圆柱形铝合金试样直径为100 mm,高度为80 mm;Terfenol-D贴片长度为10 mm,宽度为6 mm,高度为4 mm;纳米晶磁心开气隙的高度为6 mm,气隙宽度为10 mm。

图16 GMPT实验系统
Fig.16 Coil-only GMPT experimental system
根据安培定律,通电线圈产生的磁场强度H与通入线圈的电流I成正比,实验中通过调节直流低压电源的输出电压来影响Terfenol-D贴片的工作状态。为了确定无永磁体GMPT的最佳工作点,固定直流高压为200 V不变,铝合金试样的底波信号分别用直径为10 mm的1 MHz横波压电探头和纵波压电探头接收。图17为直流电压在18~28 V时的横、纵波压电探头接收信号。图18为提取纵波和横波峰值的归一化处理对比结果。随着直流电压的增加,横波和纵波的幅值先增大后减小,18 V时接收到的横波和纵波的峰值分别为556 mV、71 mV,而横波在24 V时达到了1 270 mV,信号幅值提升了128%;纵波在26 V时达到了244 mV,信号幅值提升了244%,说明横波和纵波的振动模式对磁场的响应不同,不同的振动模式对应的磁致伸缩应变分布和应力状态不同,因此它们的最佳工作点也不同。实验结果表明,直流电压提供的偏置磁场对磁致伸缩贴片的工作点起到了关键的调节作用,合适的偏置磁场能够最大化磁致伸缩效应,而过强或过弱的磁场则会使振动幅值下降,反映了磁致伸缩效应的非线性特性。
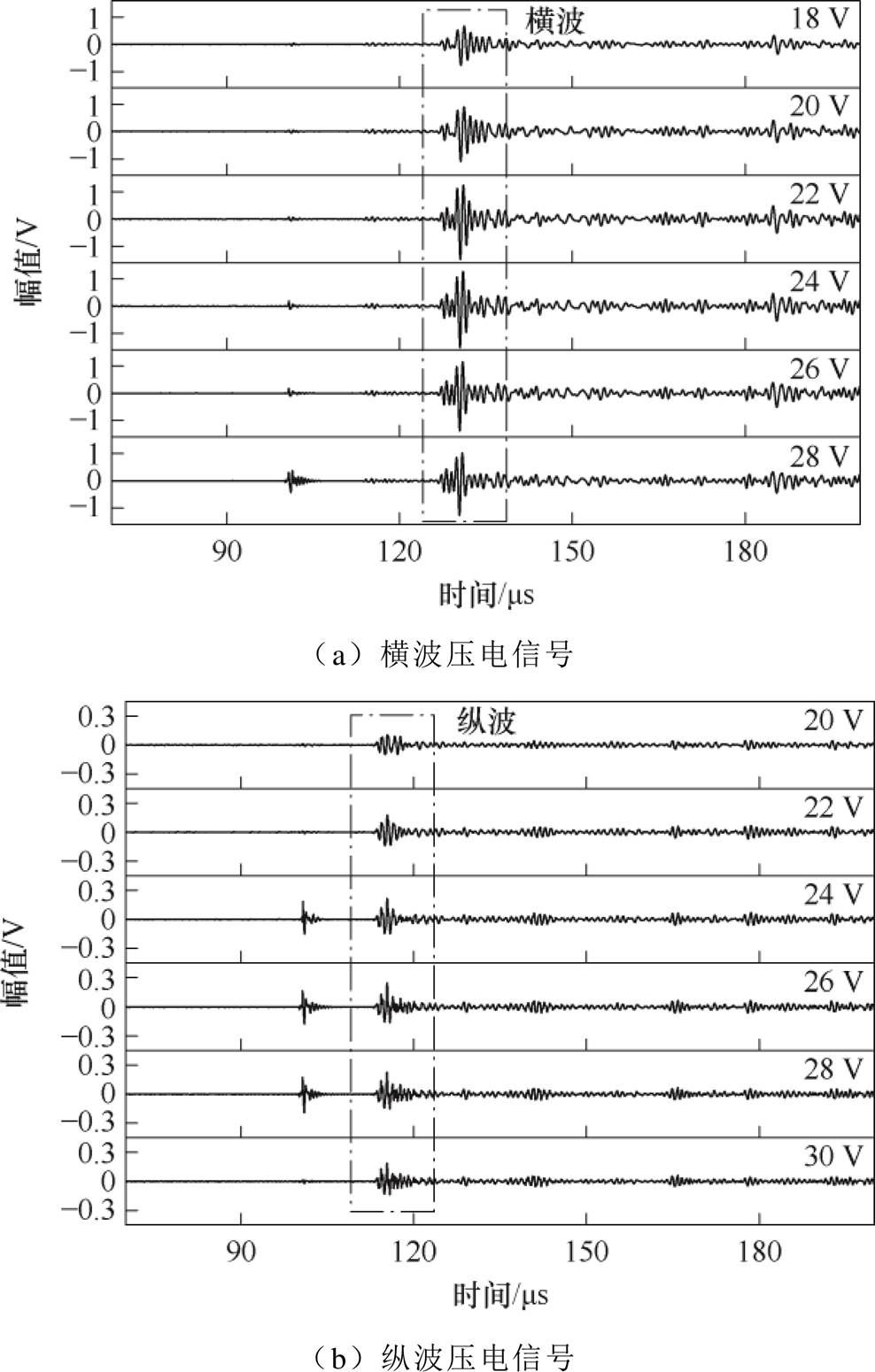
图17 不同直流电压激励下的体波信号
Fig.17 Bulk wave signals under different DC voltage excitation
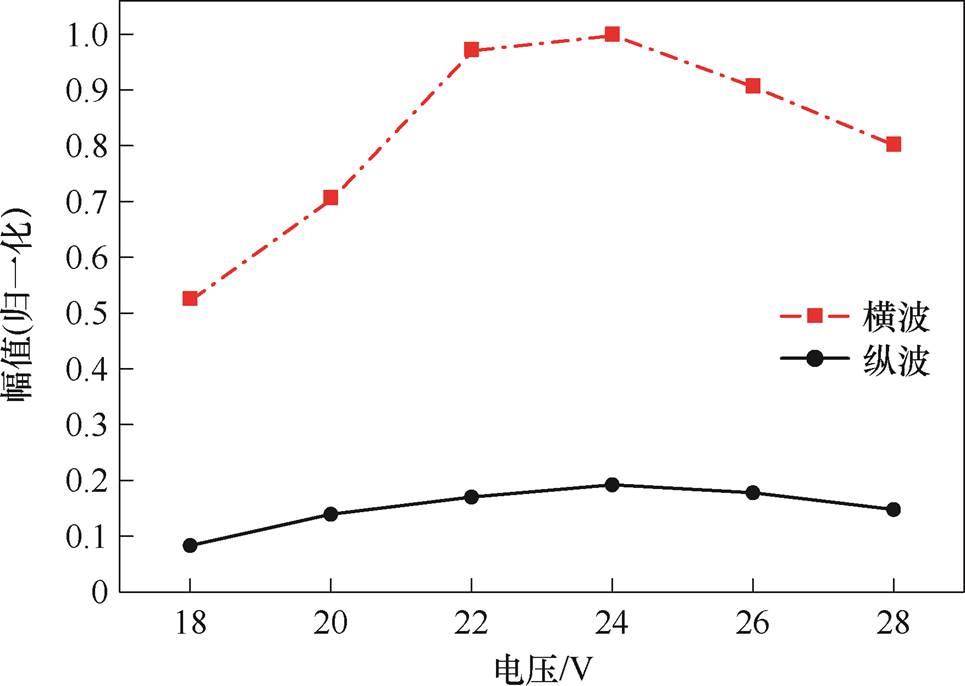
图18 直流电压对体波幅值影响的实验结果
Fig.18 Experimental results on the influence of DC voltage on bulk wave amplitude
3.1节通过实验确定了Terfenol-D贴片的最佳工作点,本节选取横波最佳工作点处的直流电压来探究交变电压对信号幅值的影响。将高压直流电源的输出电压设置在50~250 V范围内,步长为50 V,得到不同交变电压下的横波与纵波的波形如图19所示。图20为提取纵波和横波峰值的归一化结果。可见实验结果与仿真规律基本一致,随着交变电压的增加,横波与纵波的信号幅值逐渐增加,且与仿真中的线性关系相吻合。这一结果验证了仿真模型的准确性,证明了交变电压对磁致伸缩贴片振动幅值的线性增强效应3002xc dcxx l n 47-548====
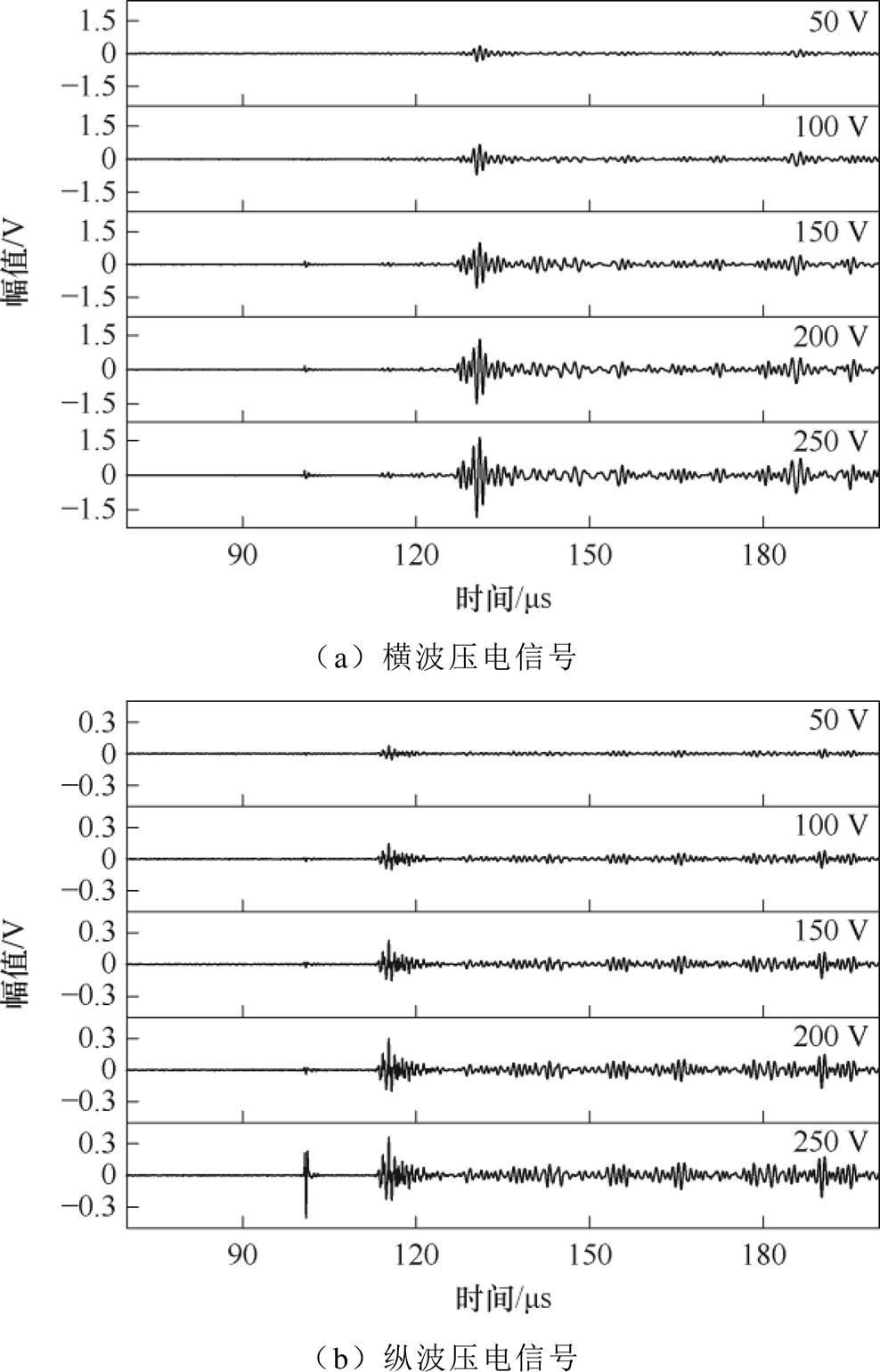
图19 不同交变电压激励下的体波信号
Fig.19 Bulk wave signals under different alternating voltage excitation
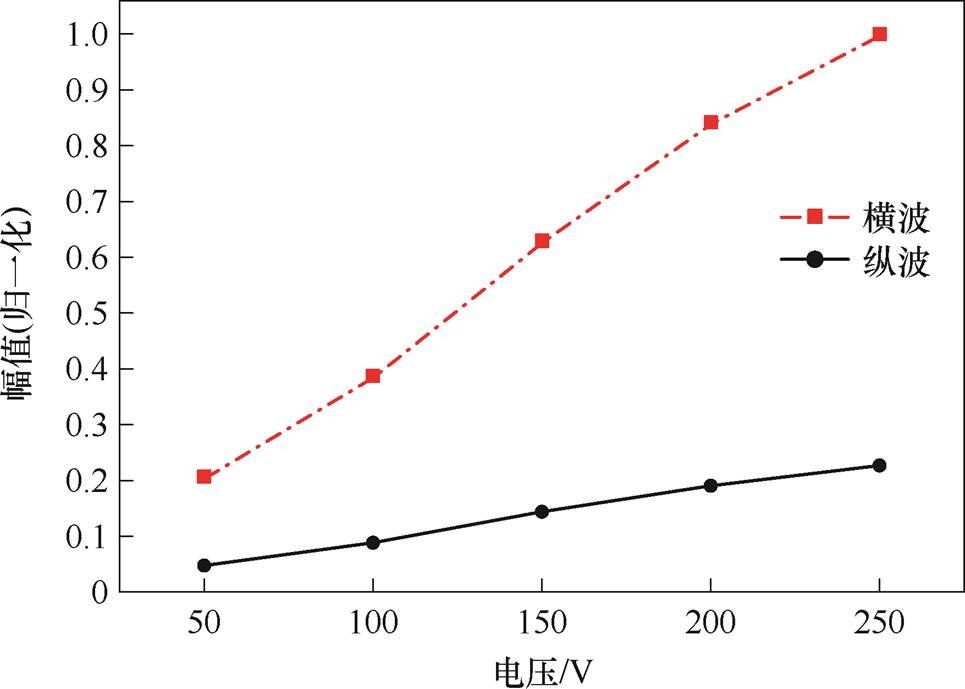
图20 交变电压对体波幅值影响的实验结果
Fig.20 Experimental results on the influence of alternating voltage on bulk wave amplitude
考虑到纳米晶磁心的实际长度,将缠绕匝数设置为21、30、39、48、57匝来验证线圈匝数对信号幅值的影响,图21为不同线圈匝数下的检测信号,图22为横、纵波的峰值归一化后的结果。随着线圈匝数的增加,信号幅值开始明显减小,当匝数继续增加时,信号幅值下降的趋势缓慢减弱。
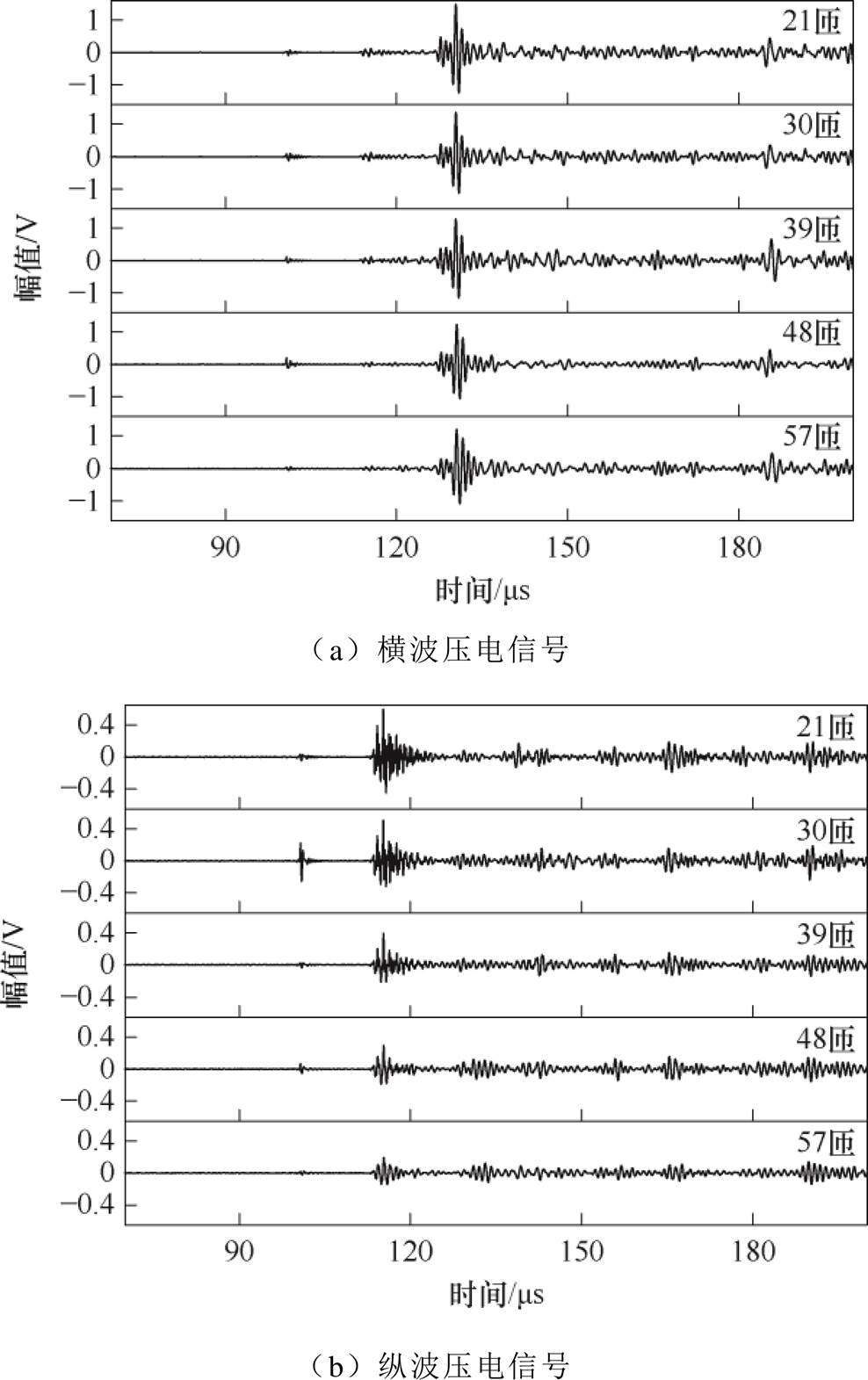
图21 不同线圈匝数下的体波信号
Fig.21 Bulk wave signals under different coil turns
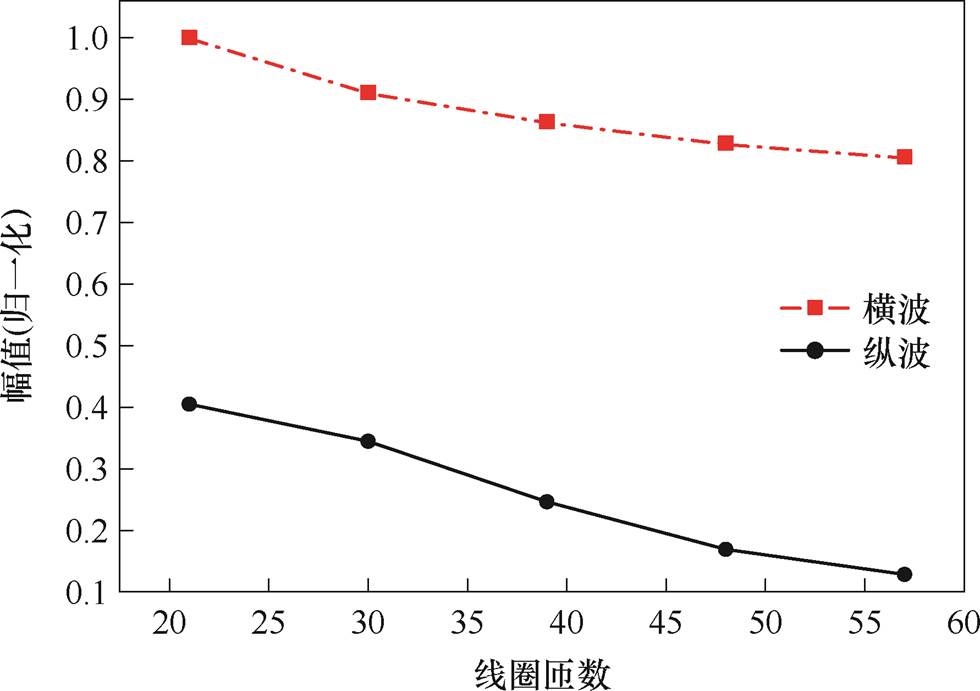
图22 线圈匝数对体波幅值影响的实验结果
Fig.22 Experimental results on the influence of coil turns on bulk wave amplitude
在1 MHz的高频下,由于趋肤效应的影响,电流趋于集中在导线表层流动,导致导线有效导电面积减小、能量损耗增加。相比于常用的漆包线,多股丝包线由于其绞合结构和较大的表面积,能够有效地减弱趋肤效应,不仅可提升导线的电流承载能力,而且有效地抑制了导通瞬间的局部温升。常用多股丝包线的线径规格有0.21、0.30、0.35、0.40、0.48 mm等,为了验证线圈导线直径对信号幅值的影响,采用多股丝包线制作线圈,并在0.26~0.48 mm范围内改变导线直径,得到导线直径分别为0.26、0.30、0.35、0.40、0.48 mm时的检测信号如图23所示。图24为横、纵波信号峰值归一化的结果。随着导线直径的增大,无永磁体GMPT的换能效率显著增加。
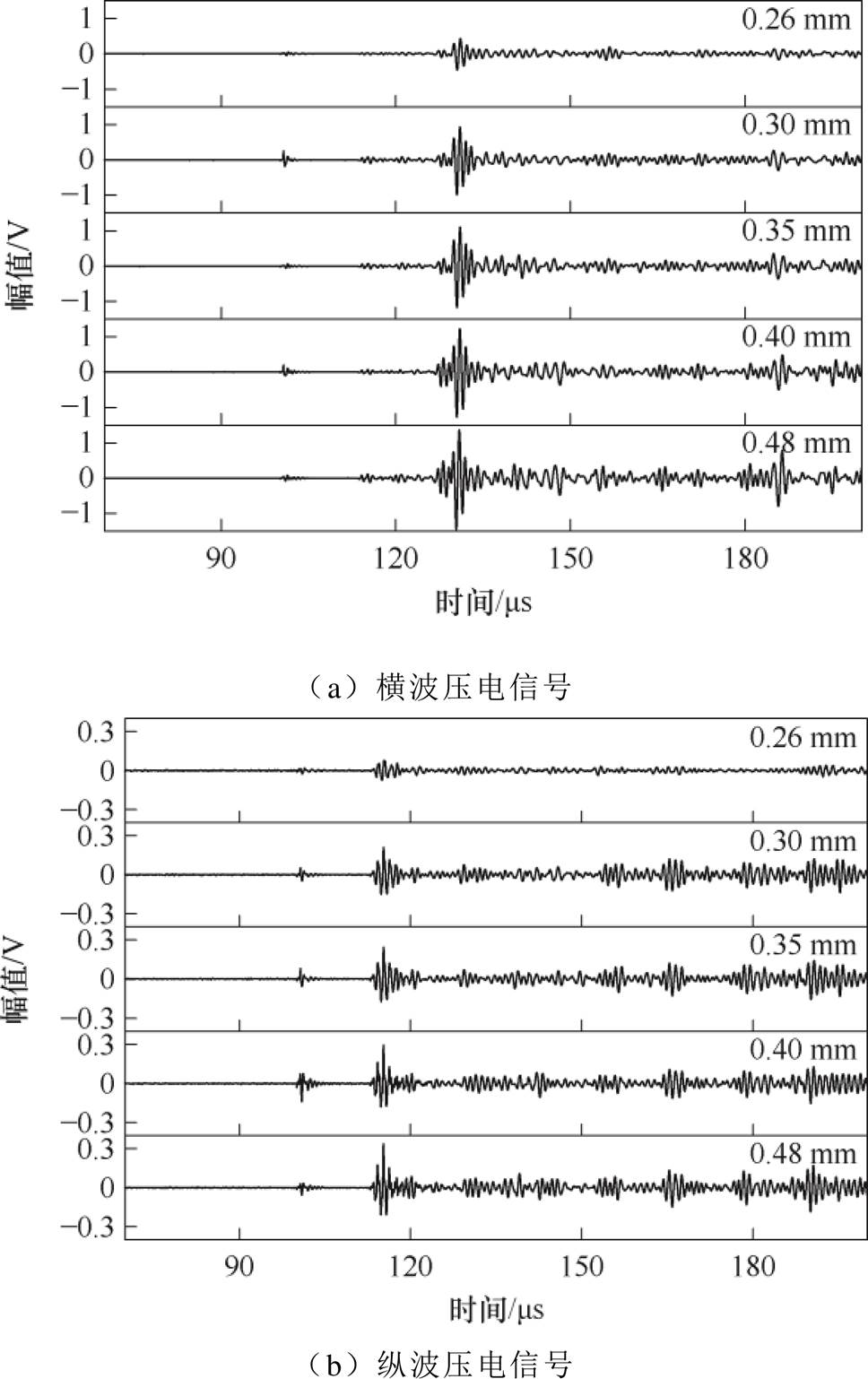
图23 不同导线直径下的体波信号
Fig.23 Bulk wave signals under different conductor diameters
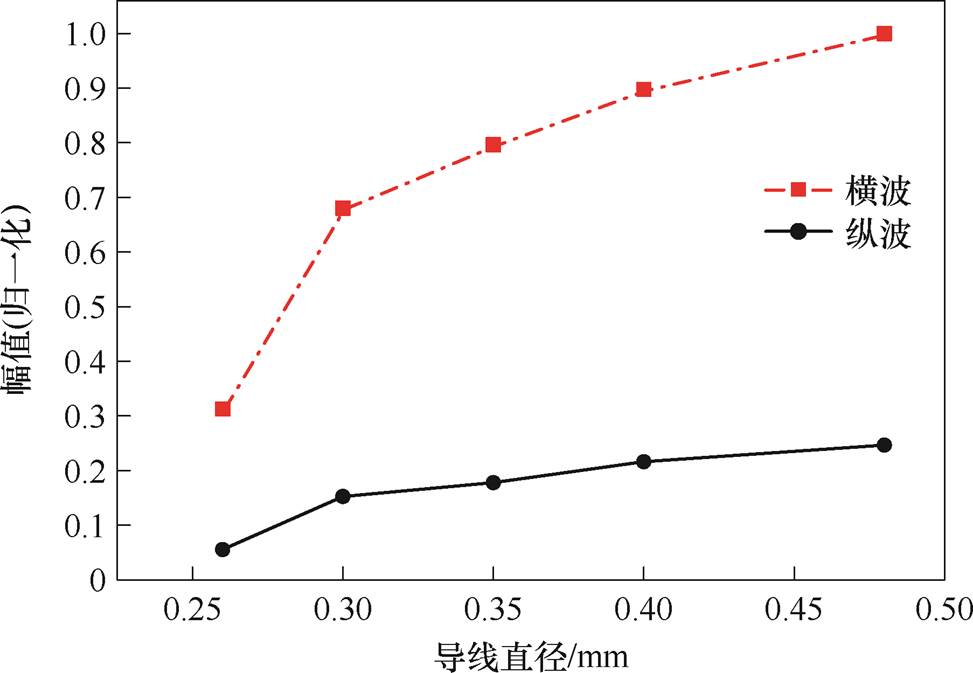
图24 导线直径对体波幅值影响的实验结果
Fig.24 Experimental results on the influence of conductor diameter on bulk wave amplitude
常规结构中多采用镍等金属材料,其具备良好的延展性,便于加工成较薄的贴片。而本文使用的Terfenol-D材料是一种金属间化合物(成分为Tb0.3Dy0.7Fe2),具有显著的脆性。当其厚度小于1 mm时,容易在加工过程中断裂。因此,出于材料特性与制造可行性的考虑,本文采用了更厚的贴片设计。为研究磁致伸缩贴片厚度对信号幅值的影响,对不同厚度(2、4、6、8 mm)的磁致伸缩贴片进行实验,测试其信号幅值随厚度变化的情况,得到横、纵波信号峰值归一化的结果如图25所示。随着厚度增加,信号幅值先增后减,并在4 mm时达到最大值。相比之下,2 mm贴片信号幅值较低,说明厚度过薄时磁致伸缩效应不足;而6 mm和8 mm贴片的信号幅值有所减小,表明过厚的贴片会使磁场穿透的均匀性受到影响,内部应力分布不均匀,导致信号幅值下降。仿真结果与实验结果趋势一致,但仿真中信号幅值最大值出现在6 mm而非4 mm厚度。仿真与实验的差异可能源于仿真过程中,材料的均匀性和边界条件常被理想化处理,此外,实验中纳米晶磁心和贴片的加工误差也可能会对结果产生一定影响。尽管如此,实验和仿真均表明贴片厚度对信号幅值有显著影响,优化贴片厚度能够提高换能器的换能效率。
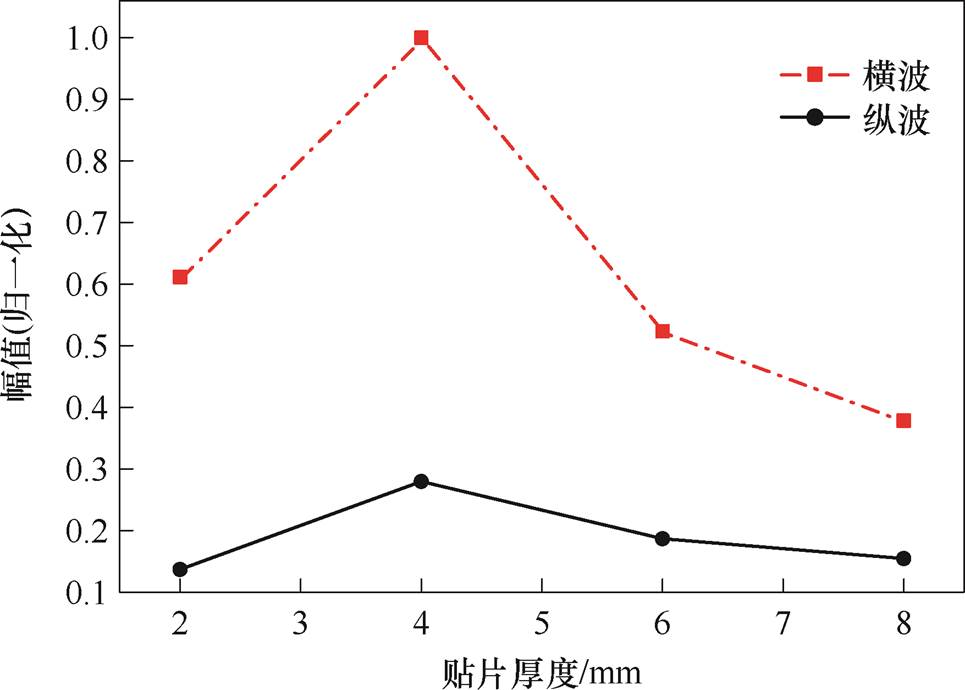
图25 贴片厚度对体波幅值影响的实验结果
Fig.25 Experimental results on the influence of patch thickness on bulk wave amplitude
为研究磁致伸缩贴片长度对信号幅值的影响,对贴片长度分别为10、12、14 mm的情况进行了实验,得到横、纵波信号峰值归一化的结果如图26所示。随贴片长度的增加,信号幅值先增大后减小,12 mm时信号幅值达到最大值,而在10 mm和14 mm时信号幅值较小。同时,纵波的幅值变化较为平缓,幅值的变化幅度明显小于横波。对于纵波而言,由于其主要依赖垂直振动,水平长度对其影响较小,因此纵波幅值变化相对平稳。实验结果与仿真结果有所不同,仿真中信号幅值随着长度增加逐渐减小,而实验中则表现为先增后减的趋势。导致这种差异的原因是仿真过程对材料属性和边界条件进行了理想化处理,而实际实验中,贴片的振动模式和能量损耗更加复杂,从而使得信号幅值在贴片长度为12 mm时最大。
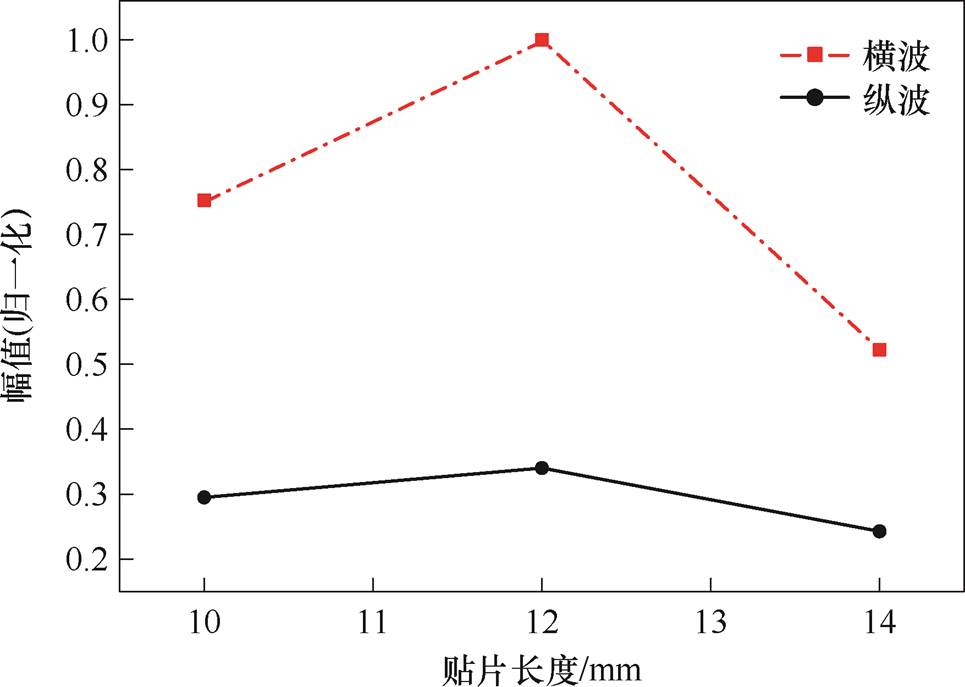
图26 贴片长度对体波幅值影响的实验结果
Fig.26 Experimental results on the influence of patch length on bulk wave amplitude
1)激励电压对磁致伸缩贴片的振动幅值有显著影响。随着直流电压的增加,横波和纵波的幅值均表现出先增加后减小的趋势;随着交流电压的增加,信号幅值线性增加。因此,调节直流电压的大小使贴片在最佳工作点附近,并控制交变磁场大小在DH以内,可以最大程度地激发超声波,提高换能器的换能效率。
2)信号幅值与线圈的几何参数有关。当线圈匝数从27匝增加到57匝时,横波与纵波信号幅值逐渐减小,并且减小趋势不断减弱;而当导线直径从0.15 mm增大到0.55 mm时,横波与纵波的信号幅值逐渐增大。这些规律表明,线圈的几何参数对信号幅值具有显著影响,为优化系统设计提供了重要的参考依据。
3)Terfenol-D贴片厚度和长度对信号幅值起到重要作用。过薄的贴片不能有效地利用线圈产生的磁场,过厚则会增加其机械阻抗,提高能量耗散。随着贴片长度的增加,贴片中的偏置磁场将很难保持均匀分布。设计换能器时,贴片厚度应与纳米晶磁心气隙高度接近,贴片长度则要考虑磁场分布的均匀性。
4)本文解决了永磁体式磁致伸缩贴片换能器易吸附铁磁性杂质、温度变化或长期使用会导致永磁体磁场强度衰减等问题,将其应用于温度变化显著的场景(如发电设备)进行在线监测,具有重要的工程应用价值,也对超磁致伸缩贴片换能器的性能提高和广泛应用具有指导作用。
参考文献
[1] Ribichini R, Cegla F, Nagy P B, et al. Study and comparison of different EMAT configurations for SH wave inspection[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(12): 2571-2581.
[2] Kwun H, Kim S Y, Choi M S, et al. Torsional guided- wave attenuation in coal-tar-enamel-coated, buried piping [J]. NDT & E International, 2004, 37(8): 663-665.
[3] Kwun H, Kim S Y, Light G M. Improving guided wave testing of pipelines with mechanical attach- ments[J]. Materials Evaluation, 2010, 68(8): 927-932.
[4] Kim H W, Lee H J, Kim Y Y. Health monitoring of axially-cracked pipes by using helically propagating shear-horizontal waves[J]. NDT & E International, 2012, 46: 115-121.
[5] Cho S H, Han S W, Park C I, et al. Noncontact torsional wave transduction in a rotating shaft using oblique magnetostrictive strips[J]. Journal of Applied Physics, 2006, 100(10): 104903.
[6] Kim Y Y, Park C I, Cho S H, et al. Torsional wave experiments with a new magnetostrictive transducer configuration[J]. The Journal of the Acoustical Society of America, 2005, 117(6): 3459-3468.
[7] Cho S H, Lee J S, Kim Y Y. Guided wave transduction experiment using a circular magnetostrictive patch and a figure-of-eight coil in nonferromagnetic plates[J]. Applied Physics Letters, 2006, 88(22): 224101.
[8] Lee J S, Kim Y Y, Cho S H. Beam-focused shear-horizontal wave generation in a plate by a circular magnetostrictive patch transducer employing a planar solenoid array[J]. Smart Materials and Structures, 2009, 18(1): 015009.
[9] Lee J K, Kim H W, Kim Y Y. Omnidirectional Lamb waves by axisymmetrically-configured magneto-strictivepatch transducer[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2013, 60(9): 1928-1934.
[10] Seung H M, Kim H W, Kim Y Y. Development of an omni-directional shear-horizontal wave magneto- strictive patch transducer for plates[J]. Ultrasonics, 2013, 53(7): 1304-1308.
[11] Oh J H, Sun K H, Kim Y Y. Time-harmonic finite element analysis of guided waves generated by magnetostrictive patch transducers[J]. Smart Materials and Structures, 2013, 22(8): 085007.
[12] Zitoun A, Dixon S, Kazilas M, et al. The effect of changes in magnetic field and frequency on the vibration of a thin magnetostrictive patch as a tool for generating guided ultrasonic waves[J]. Sensors, 2022, 22(3): 766.
[13] Yoo B, Na S M, Flatau A B, et al. Directional magnetostrictive patch transducer based on Galfenol’s anisotropic magnetostriction feature[J]. Smart Materials and Structures, 2014, 23(9): 095035.
[14] Rueter D, Morgenstern T. Ultrasound generation with high power and coil only EMAT concepts[J]. Ultrasonics, 2014, 54(8): 2141-2150.
[15] Rueter D. Experimental demonstration and circuitry for a very compact coil-only pulse echo EMAT[J]. Sensors, 2017, 17(4): 926.
[16] Rieger K, Erni D, Rueter D. A compact and powerful EMAT design for contactless detection of inhomogenei- ties inside the liquid volume of metallic tanks[J]. tm- Technisches Messen, 2020, 87(5): 349-359.
[17] Li Pengyang, Liu Qiang, Zhou Xuan, et al. Effect of Terfenol-D rod structure on vibration performance of giant magnetostrictive ultrasonic transducer[J]. Journal of Vibration and Control, 2021, 27(5/6): 573-581.
[18] 宁倩, 李桥, 高兵, 等. 电-磁-机-声多场边界下的超磁致伸缩Ⅳ型弯张换能器设计方法[J]. 电工技术学报, 2023, 38(12): 3112-3121.
Ning Qian, Li Qiao, Gao Bing, et al. Design of giant magnetostrictive class Ⅳ flextensional transducer under electrical-magnetic-mechanical-acoustic multi- field boundaries[J]. Transactions of China Electrotech- nical Society, 2023, 38(12): 3112-3121.
[19] 赵能桐, 杨鑫, 陈钰凯, 等. 考虑超磁致伸缩材料非均匀性的大功率电声换能器阻抗特性[J]. 电工技术学报, 2021, 36(10): 1999-2006.
Zhao Nengtong, Yang Xin, Chen Yukai, et al. The impedance characteristics of high power electro- acoustic transducer considering the inhomogeneity of giant magnetostrictive material[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 1999-2006.
[20] 黄文美, 房昱同, 刘雨欣, 等. 计及偏置磁场变化的磁致伸缩逆效应能量平均磁滞模型[J]. 电工技术学报, 2025, 40(9): 2840-2851.
Huang Wenmei, Fang Yutong, Liu Yuxin, et al. Magnetostrictive inverse effect energy-averaged hys- teresis model accounting for bias field variations[J]. Transactions of China Electrotechnical Society, 2025, 40(9): 2840-2851.
[21] 高兵, 吴泽伟, 赵能桐, 等. 基于AFSA-eCS混合算法的超磁致伸缩换能器输出特性分析[J]. 电工技术学报, 2025, 40(2): 346-357.
Gao Bing, Wu Zewei, Zhao Nengtong, et al. Analysis of output characteristics of giant magnetostrictive transducers based on AFSA-eCS hybrid algorithm[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 346-357.
[22] 王怡凡, 邹亮, 张黎, 等. 矩形波激励对纳米晶合金高频磁化过程的微观影响机理[J]. 电工技术学报, 2024, 39(11): 3259-3269.
Wang Yifan, Zou Liang, Zhang Li, et al. Effect of rectangular wave excitation with different duty ratio on magnetization process of nanocrystalline alloys[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3259-3269.
[23] 代岭均, 邹亮, 郭凯航, 等. 纳米晶合金晶粒尺寸与体积分数对高频磁损耗特性影响分析[J]. 电工技术学报, 2023, 38(18): 4853-4863.
Dai Lingjun, Zou Liang, Guo Kaihang, et al. Analysis of grain size and volume fraction of nanocrystalline alloy on high frequency magnetic loss characteristics [J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4853-4863.
[24] 周寿增, 高学绪. 磁致伸缩材料[M]. 北京: 冶金工业出版社, 2017.
Abstract The magnetostrictive patch transducer is an ultrasonic transducer based on the magnetostrictive effect, capable of generating and detecting ultrasonic waves in both ferromagnetic and non-ferromagnetic materials. The conventional permanent magnet type magnetostrictive patch transducer has problems such as easy adsorption of ferromagnetic particles, non-adjustable magnetic field strength and magnetic degradation after long-term use, which leads to a decrease in the magnetostrictive excitation efficiency. To solve these problems, this study proposes a permanent magnet-free giant magnetostrictive patch transducer and its detection circuit.
Firstly, we designed the detection circuit for permanent magnet-free giant magnetostrictive ultrasonic transducer. The circuit dynamically adjusted the on-time sequence of the IGBT and MOSFET elements to generate strong, prolonged current (pulse widths greater than 200 ms) and a short 1 MHz pulse current in the coil, resulting in the formation of a composite field of bias and high-frequency alternating magnetic fields in the coil. Under the combined action of these superimposed magnetic fields, the patch generated magnetostrictive stress. The stress coupled through the patch-specimen interface and ultimately excited ultrasonic wave propagation to the specimen’s bottom. Secondly, a finite element model for the permanent magnet-free giant magnetostrictive patch transducer was established based on the linear constitutive equations of the magnetostrictive effect. This model successfully excited bulk waves dominated by shear wave components within the aluminum alloy specimen. To enhance transduction efficiency, the effects of voltage parameters, coil geometric parameters, and patch dimensions on received signal amplitude were analyzed. Finally, a permanent magnet-free giant magnetostrictive patch transducer testing system was designed and constructed, and the effects of key parameters such as voltage amplitude, coil geometry and patch dimensions on the received signal amplitude were experimentally verified.
The experimental results showed that the proposed ultrasonic transducer had a non-linear response with DC voltage and a linear response with alternating voltage. When the DC voltage increased from 18 V to 24 V, shear wave amplitude increased by 228%. With a further increase to 26 V, longitudinal wave amplitude rose by 344%,while the shear wave exhibited a declining trend. It is shown that adjusting the voltage parameter can optimise the operating state of the Terfenol-D patch to improve the direct wave amplitude. The direct wave amplitude decreased with the increase in the number of turns of the coil and increased with the increase in the diameter of the coil wire. The optimum signal amplitude for the transducer was obtained when the thickness of the Terfenol-D patch was close to the height of the nano-core air gap.
The following conclusions can be drawn from the analysis: (1) There exists an optimal operating point for the permanent magnet-free giant magnetostrictive patch transducer, where the peak response amplitude can be excited when the excitation voltages (DC voltage and alternating voltage) are in the optimal interval. (2) Reducing the number of coil turns and increasing the wire diameter improves transducer efficiency. The optimal thickness of the Terfenol-D patch should match the air gap height of the nanocrystalline magnetic core to balance magnetic field utilization and mechanical impedance, while the patch length must satisfy uniform bias magnetic field distribution requirements.
keywords:Magnetostrictive patch transducer, Terfenol-D, nanocrystalline cores, optimization design
DOI: 10.19595/j.cnki.1000-6753.tces.242298
中图分类号:TB552
国家实验室技术基础研究类项目(S2024-5-005)、“慧眼行动”成果转化应用项目(62502010311)和南昌航空大学研究生创新专项资金项目(YC2023-064)资助。
收稿日期 2024-12-19
改稿日期 2025-05-26
吴振建 男,2001年生,硕士研究生,研究方向为电磁超声无损检测技术。E-mail: 1935210160@qq.com
卢 超 男,1971年生,教授,博士生导师,研究方向为声学检测技术及检测信号处理等。E-mail: luchaoniat@163.com(通信作者)
(编辑 李 冰)