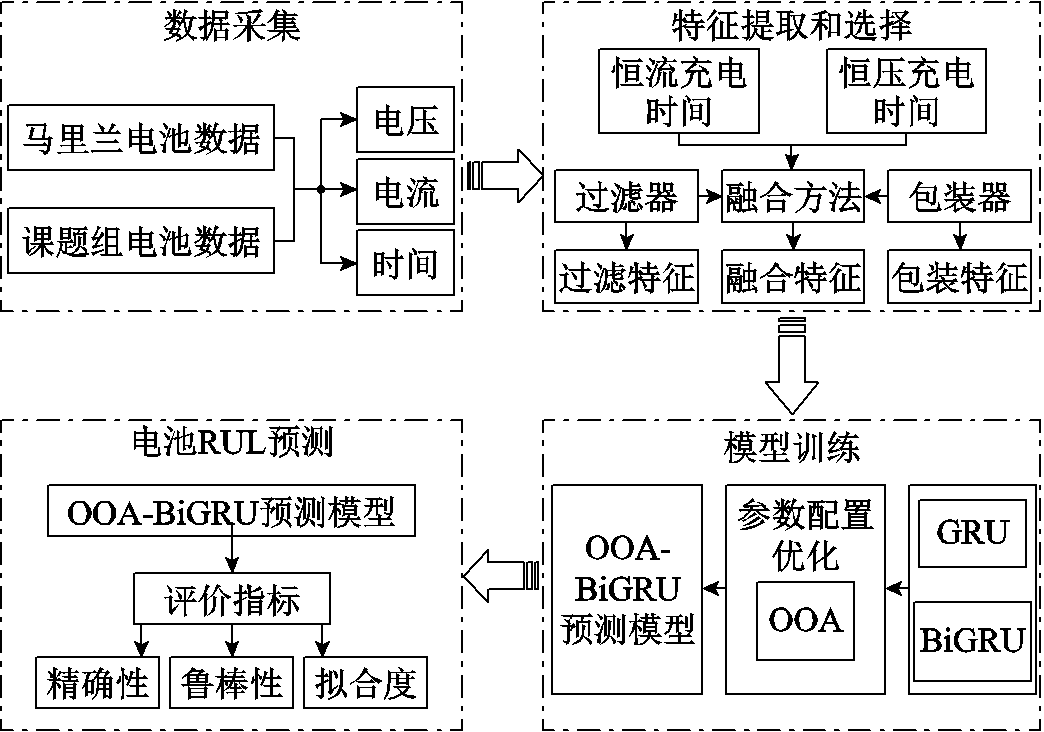
图1 基于融合特征和OOA-BiGRU模型的RUL预测流程
Fig.1 RUL prediction process based on fusion feature and OOA-BiGRU model
摘要 随着新能源汽车产业的持续发展,锂离子电池被大量用作车载动力电池。电池管理系统(BMS)负责监测、评估、维护和优化锂离子电池的性能和寿命,其中剩余使用寿命(RUL)预测是BMS中的重要组成部分。该文提出一种基于融合特征和鱼鹰优化算法(OOA)优化双向门控循环单元(BiGRU)网络的锂离子电池RUL预测方法。针对电池容量难以直接测量的问题,采集电池老化过程中简单易测量的电流、电压和时间数据,从中提取能反映电池老化趋势的健康因子。提出一种结合过滤器与包装器的融合特征筛选策略,降低模型的复杂度,防止模型过拟合。搭建BiGRU网络,深入地研究序列整体结构和动态特性,整合多维度特征,适应不同时间尺度的依赖关系。采用OOA对BiGRU模型内部的超参数进行有效的优化,提高了模型的预测精度,同时实现了参数的自配置。将所提方法与传统网络模型在不同电池数据上进行比对,验证所提OOA-BiGRU模型的可靠性。另外,将提出的融合特征预测与全部特征预测和过滤特征预测的效果进行比较,证明融合特征可更好地表示电池的老化程度,提高模型预测的准确度。
关键词:锂离子电池 剩余使用寿命 双向门控循环单元 健康因子 融合特征
锂离子电池因其具有能量密度高[1]、自然放电率低[2]、使用寿命长、绿色清洁等优势,被广泛用作新能源汽车的动力电池[3-4]。然而,锂离子电池在使用的过程中随着环境温度的变化和循环充放电次数的累积,其容量会不断衰退,内阻持续增加,进而带来膨胀、漏液或热失控等安全风险[5]。电池剩余使用寿命(Remaining Useful Life, RUL)预测是电池管理系统(Battery Management System, BMS)的重要组成部分,其通过先进的算法和模型来预测电池在当前使用条件下可以继续安全有效工作的时间,对提高能效、优化维护和更换计划,以及确保电池系统的安全运行至关重要[6-8]。通过准确地预测RUL,BMS能够提示用户及时对电池进行维护检查或更换,从而避免潜在的安全事故发生,确保电池和设备的长期稳定运行。
近年来,许多研究者为设计一个精度高、复杂度低且鲁棒性强的锂离子电池RUL预测模型展开了广泛的研究,目前已有的研究方法主要分为基于机理模型的预测方法和基于数据驱动的预测方法。
基于机理模型的RUL 预测方法通过深入分析和理解电池内部的结构变化和失效机理,以及电池在不同工作条件下的行为和外在特性的变化,构建反映电池老化状态的数学模型。文献[9-11]采用基于经验模型的方法,通过识别和利用能够准确反映电池性能衰减趋势的状态变量,构建状态变量与电池充放电循环次数之间的关系表达式来实现RUL预测。此类方法的模型泛化能力受限于数据集的范围和多样性,无法有效预测未经训练的新条件下的电池性能。文献[12-14]采用基于电化学模型的方法,通过深入分析电池内部的电化学反应机制,搭建电化学模型来实现RUL预测。此类方法虽然能够通过对电池老化机制深入的理解实现RUL的预测,但准确描述电池内部的多种电化学反应和物理过程的复杂性使得模型的建立和参数估计变得困难且耗时。文献[15-17]采用基于等效电路的方法,使用电阻、电容和电感等电路元件来模拟电池的电化学反应,通过电路元件的组合来近似电池在充放电过程中内阻的变化、电荷的存储以及电流的传导路径。但电池的物理和化学属性随着使用时间变化而改变,为此,需要定期更新等效电路模型的电阻、电容等参数。
基于数据驱动的方法不直接依赖对电池内部物理或化学机理的深入了解,而是通过先进的算法从电池的使用数据中学习和识别电池衰退的模式与趋势来预测电池RUL,有效地解决了基于机理模型方法泛用性低的问题。文献[18-20]采用模型滤波算法,通过结合数学模型和统计滤波技术来处理不确定性和噪声的RUL预测方法,但这种方法的性能在很大程度上依赖所使用的电池模型的准确性。文献[21-23]采用人工智能算法,通过机器学习和深度学习技术有效地处理大规模数据集,学习电池的复杂老化模式,提供准确的RUL预测。此类算法通常包含多个可调参数,这些参数的选择对预测性能有显著影响。文献[24-26]采用随机过程的方法,通过统计学算法对电池老化过程中的随机性进行建模和分析,以此来预测电池的未来性能和寿命,但此类方法预测结果本身具有不确定性,进行长期预测时可能会积累较大的不确定性,使其在预测电池RUL时准确度持续降低。
现有基于数据驱动的方法大多通过电池历史容量预测未来容量的方式实现RUL预测,而在实际应用中容量数据难以直接获取,限制了此类方法的使用。如何提取简单易测的老化特征成为基于数据驱动方法面临的问题。同时,提取出的多维度特征给网络的序列信息捕捉能力带来了考验。此外,网络搭建过程中的关键超参数对模型的预测效果起到决定性影响。人工调节参数效率低且难以达到最优搭配,实现网络超参数的自配置成为RUL预测亟须解决的另一难题。
鉴于此,本文提出了一种基于融合特征和鱼鹰优化算法(Osprey Optimisation Algorithm, OOA)优化双向门控循环单元(Bidirectional Gated Recurrent Unit, BiGRU)网络的锂离子电池RUL预测方法,流程如图1所示。首先,从电池使用过程中直接可测的电流、电压和时间数据中提取能够反映电池老化趋势的健康因子(Health Factor, HF),解决电池容量数据难以直接获取的问题。经异常点删除和滤波处理后,采用过滤器与包装器结合的融合特征筛选策略从HF中筛选出网络模型的输入特征,去除相关性低的HF以及冗余HF,提高模型预测效率。其次,采用BiGRU网络深入地理解序列整体结构和动态特性,整合多维度特征,适应不同时间尺度的依赖关系。此外,利用OOA实现BiGRU网络内部超参数的自配置,提高运行效率和预测精度。

图1 基于融合特征和OOA-BiGRU模型的RUL预测流程
Fig.1 RUL prediction process based on fusion feature and OOA-BiGRU model
本文所提的RUL指的是电池使用过程中以充放电循环次数为单位的剩余循环寿命,表示电池容量降低到规定失效阈值(70%~80%)之前的剩余可用充放电循环次数。RUL的公式定义为
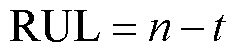 (1)
(1)
式中,n为电池可用的充放电循环次数;t为当前的充放电循环次数。
为了能够准确地获取反映电池状态的性能参数,本研究借用山东大学电动汽车动力电池研究课题组实验室配备的先进电池测试设备,构建了如图2所示的锂离子电池测试平台。该平台主要由Arbin BT-5HC动力电池测试仪、温控箱、测试电池以及上位机组成。使用Arbin测试仪进行电池的充放电循环测试,测试电池为18650LiFePO4电池,电池型号为M09和M10,额定容量为1.55 A×h。温控箱负责平衡锂离子电池的内部和表面温度,上位机用于编程和存储电压、电流、表面温度、环境温度等实验数据[27]。LiFePO4电池首先以2.5 A的恒定电流进行充电,直至电压升至4.2 V时切换为恒压充电,当电流小于0.05 A或恒压充电时长满1 h后停止充电,电池静置1 h。接下来以2.5 A的恒定电流对电池进行放电,直至电压下降至3 V时结束放电,电池静置1 h。如此进行循环的充放电试验,直至电池寿命终止。

图2 课题组自有电池老化测试平台
Fig.2 The group's own battery aging test platform
此外,选用马里兰大学电池公开数据集进行RUL预测方法研究。马里兰大学电池数据由高级生命周期工程中心(CALCE)Arbin BT2000电池试验系统对电池进行连续充放电试验获得,充放电过程在25℃的室温下进行。由LiCoO2正极材料制成的标称容量为1.1 A×h和1.35 A×h的CS2型电池和CX2型电池,在恒流-恒压(Constant Current-Constant Voltage, CC-CV)充电协议下独立充电。首先,电池以0.5 C的固定电流速率充电,直到电压达到4.2 V;然后将这些电池维持在4.2 V的恒定电压下,直到电流降至50 mA以下;随后进行放电过程,CS2_33和CX2_37电池均以1C的恒流速率放电直至电压降至2.7 V。不同型号电池详细属性参数见表1。
表1 不同型号电池属性参数
Tab.1 Parameters of battery properties for different models
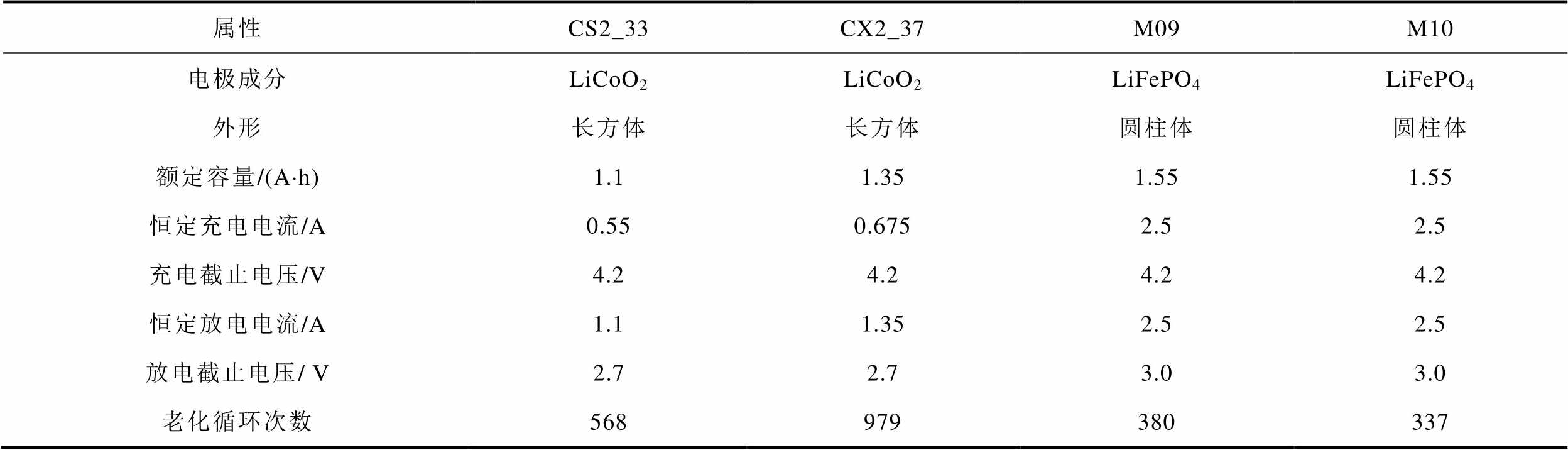
属性CS2_33CX2_37M09M10 电极成分LiCoO2LiCoO2LiFePO4LiFePO4 外形长方体长方体圆柱体圆柱体 额定容量/(A×h)1.11.351.551.55 恒定充电电流/A0.55 0.6752.52.5 充电截止电压/V4.2 4.24.24.2 恒定放电电流/A1.1 1.352.52.5 放电截止电压/ V2.72.73.03.0 老化循环次数568979380337
在锂离子电池的存储与运行过程中,电池内部会因老化而经历一系列的物理和化学变化,这些变化导致欧姆内阻的增加及电池容量的损失,最终使得电池的充电电压曲线发生变化。BMS可以直接测量出电池使用时的电流、电压和时间数据,从这些变量中能够提取出基于电压的HF[28]。直接提取出的HF中包含异常点和噪声,在特征筛选之前对HF进行异常点删除和噪声过滤。之后,采用基于过滤器(Filter)和包装器(Wrapper)相结合的融合特征筛选策略选出用于模型训练的输入特征。过滤器采用皮尔逊相关性分析,分析每个HF与电池的老化状态之间的相关程度,过滤相关性低的HF。包装器采用序列前向搜索方法,去除过滤后的冗余HF,降低模型复杂度,提高预测效率。
Savitzky-Golay滤波(SG滤波)是一种用于数据平滑处理的数字滤波方法,其原理为将电池老化过程中提取出的HF数据点的子集拟合为一个多项式上,然后利用这个多项式的评估结果来平滑HF数据,从而去除噪声并保留反映电池老化趋势的重要特征。整个滤波过程分为选择窗口大小、计算滤波器系数、滑动窗口以及输出平滑后HF数据几个步骤。
首先,选择一个合适的窗口大小W。窗口大小是SG滤波中的一个重要参数,决定了拟合多项式的阶数以及每个窗口中要使用的数据点数量。窗口大小通常选择为奇数,以确保窗口中心位于原始数据点之间。
其次,需要计算SG滤波器的系数矩阵C。该系数矩阵的计算取决于所选择的窗口大小和多项式拟合的阶数,可通过对多项式拟合和最小二乘法求解得到。多项式拟合通过将每个窗口内的数据点作为多项式函数的一部分,拟合此多项式来实现平滑数据的效果,拟合函数可以表示为
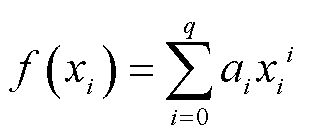 (2)
(2)
式中,q为多项式的阶数,决定了拟合多项式的复杂度;ai为合多项式的系数,需要通过最小二乘法求解;xi为窗口内的自变量数据点。对于每个数据点(xi, yi),xi为对应的自变量值,yi为原始信号值。
残差ei为拟合函数f(xi)对应的预测值与实际值之间的差异,即
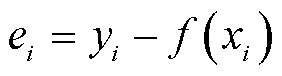 (3)
(3)
然后,采用最小二乘法,通过对损失函数求导并令导数为零,可以得到系数的解析解。构建一个设计矩阵X,其中包含了每个数据点的自变量值,通过以下公式求解系数向量a:
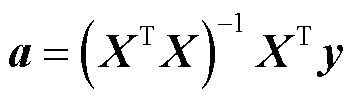 (4)
(4)
式中,X为设计矩阵,其中每一列代表数据点的不同幂次(包括常数项);y代表原始信号数据值构成的列向量;a代表待求解的系数向量。求解得到系数向量a组成了SG滤波器的系数矩阵C,利用该系数矩阵实现对窗口内的数据进行加权平均。
接着,将窗口在原始信号数据上滑动,对窗口内的所有数据进行SG滤波。在每个窗口中,取窗口内的数据点mi,通过滤波器系数矩阵C进行滤波,滤波后的结果si即为该窗口内平滑后的数据点。滤波过程的公式为
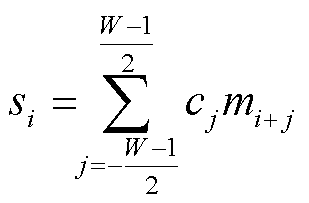 (5)
(5)
式中,W表示窗口大小;cj表示SG滤波器的系数;i为当前数据点的索引;j为相对位置;mi+j表示窗口内的数据点; si表示平滑后的数据点。
由此得到整个信号经过SG滤波器处理后的平滑数据,该数据可用于后续的特征提取分析和应用。
皮尔逊相关性分析是一种用于衡量两个连续变量之间线性关系的统计方法。根据计算求出的皮尔逊相关系数能够有效地判断X和Y的相关程度,这里X代表电池老化过程中提取出的HF,Y代表电池的老化状态。
首先,计算X和Y之间的样本协方差,即两个变量偏差的乘积的均值。协方差表示了两个变量的变化趋势是否一致,计算公式为
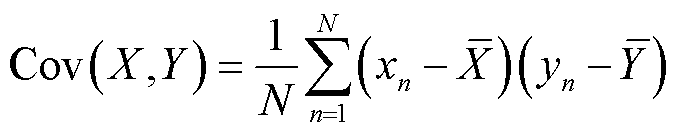 (6)
(6)
式中,N为样本数量;xn和yn分别为电池第n次循环下X和Y的对应值; 和
和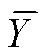 分别为X和Y的样本均值。
分别为X和Y的样本均值。
其次,分别计算X和Y的样本标准差,即每个变量偏差的平方和的均值的平方根。标准差表示了每个变量的变化程度,计算公式为
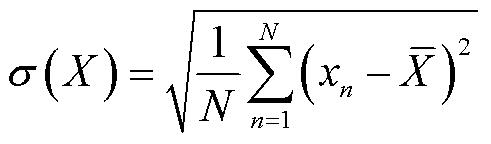 (7)
(7)
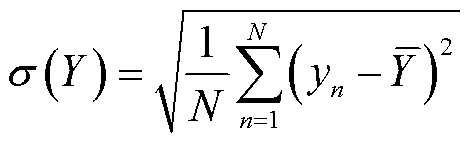 (8)
(8)
最后,将协方差除以两个变量的标准差的乘积,得到皮尔逊相关系数r。相关系数r表示两个变量之间的线性关系程度,其取值范围为-1~1之间。计算公式为
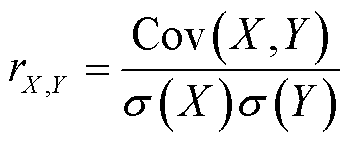 (9)
(9)
通过计算相关系数r的值,可以判断HF和电池老化状态之间的相关性强弱及方向。其中,当rX,Y=1时,表示X和Y之间存在完全的正相关关系;当rX,Y=-1时,表示X和Y之间存在完全的负相关关系;当rX,Y=0时,表示X和Y之间不存在线性相关关系。
序列前向搜索(Sequential Forward Selection, SFS)是一种基于包装器的特征选择方法,其主要目的是通过迭代地选择特征来增加模型的预测性能,同时减少特征的数量以简化模型和降低过拟合的风险。SFS从一个空集开始,逐步探索特征空间。在每一次迭代中,都考虑添加一个新的特征到已经选定的特征集合中,从而逐步扩展这个集合。此类方法依赖对候选特征集合的连续评估,以确定能实现最佳效果的特征子集。
在本文研究中,利用SFS对提取出的HF进行筛选,以组合成一个用于RUL预测的特征集。具体而言,HF被视为潜在的特征,并逐步构建最佳特征集。在SFS中,初始状态是一个空特征集,每一步操作都表示将一个新的HF添加到当前特征集中。通过逐步评估每个可能的HF的贡献,寻找能够最大化预测性能的特征组合。最终目标是找到一个特征集,使基于该特征集的RUL预测模型能够达到最佳性能。该方法不仅提高了模型的预测精度,还有效地减少了特征冗余,提升了模型的泛化能力。
门控循环单元(Gated Recurrent Unit, GRU)网络是长短期记忆(Long Short Term Memory, LSTM)网络的变体,二者均可解决循环神经网络(Recurrent Neural Network, RNN)由于不同时间步的数据之间的长期依赖关系而导致的梯度消失和梯度爆炸问题。但从结构复杂性来看,LSTM包含输入门、遗忘门和输出门三个门结构,并且有一个专门用来携带跨越长时间步信息的单元状态,这使得LSTM能够捕捉电池老化特征中不同时间步的数据的长期依赖关系,同时提高了网络的计算成本。相比于LSTM,GRU只有更新门和重置门两个门结构,这种简化结构使得GRU在计算上更为高效。GRU因其参数相对较少,相比LSTM,在参数调整和训练速度上有优势,该优势在数据量较少的情况下更为明显[29]。此外,GRU虽然结构更为简单,但在很多预测任务中的表现与LSTM相近,尤其在锂离子电池RUL预测此类序列长度较短的领域[30]。综合来看,GRU比LSTM更适用于新能源汽车BMS中RUL的在线预测。为了提高预测模型在处理多维度特征输入时捕捉电池老化信息的能力,将仅基于历史信息预测的GRU网络改进为能同时处理序列前向和后向信息的BiGRU网络,可更加深入地理解序列整体结构和动态特性,更好地整合多维度特征,适应不同时间尺度对应老化信息的依赖关系。同时,采用OOA对BiGRU模型内部的超参数进行有效的优化,提高模型的预测精度,实现参数的自配置。
GRU的单元结构如图3所示,其中 和tanh都是非线性函数。
和tanh都是非线性函数。
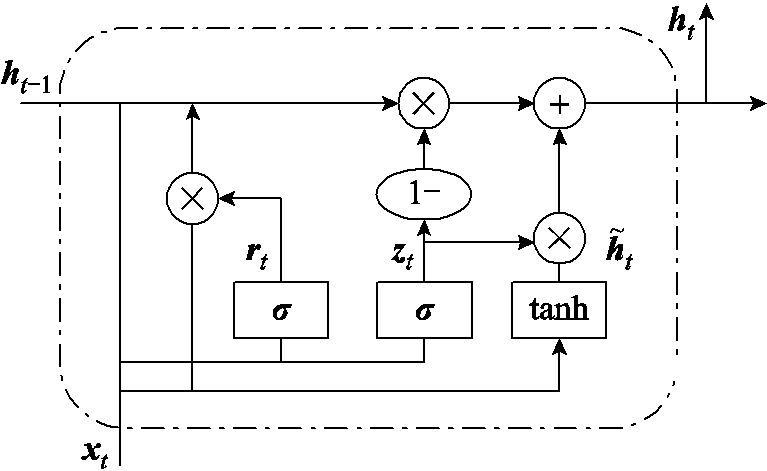
图3 GRU单元结构
Fig.3 Unit structure of GRU
更新门决定了在当前隐藏状态的计算中,应该保留多少旧的信息以及添加多少新的信息。具体来说,更新门控制了上一个时间步的隐藏状态对当前时间步隐藏状态的影响程度。更新门zt公式表示为
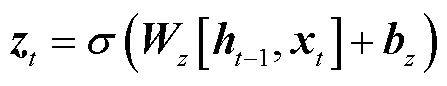 (10)
(10)
式中,σ(×)为Sigmoid激活函数;Wz为更新门的权重矩阵;bz为偏置项;ht-1为前一个时间步的隐藏状态;xt为当前时间步的输入。
重置门决定了应该忘记多少之前的信息,其允许模型抛弃与当前任务不相关的一些旧信息,或者在必要时完全重写隐藏状态。这对于模型处理变化的数据环境非常重要。重置门rt公式表示为
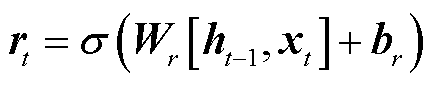 (11)
(11)
式中,Wr为重置门的权重矩阵,其余部分与更新门相同。
在更新门和重置门的作用下,GRU最终计算新的隐藏状态ht,这个隐藏状态是基于历史信息和当前输入的综合输出。隐藏状态的更新公式包括重置门对前一个隐藏状态的调节作用,使得网络可以决定在计算新的候选隐藏状态时忽略多少之前的信息,其具体表达式为
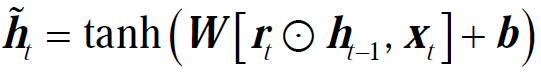 (12)
(12)
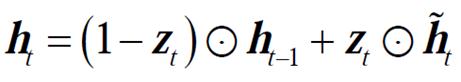 (13)
(13)
式中,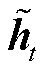 为在当前时间步计算出的候选隐藏状态;W和b为相关的权重和偏置;
为在当前时间步计算出的候选隐藏状态;W和b为相关的权重和偏置; 表示元素乘法。
表示元素乘法。
通过这种结构,GRU能够有效地控制信息流,允许网络在必要时保留长期信息,以及在面对新情况时迅速适应,从而优化性能并解决梯度相关问题。这使得GRU在处理电池RUL预测任务中,特别是在部分电池的老化特征存在复杂时间依赖性数据的任务中,有着出色的表现。
BiGRU网络是一种特殊的RNN,是对传统的单向GRU网络模型的改进升级。BiGRU结合了两个独立的GRU层,允许网络同时从正向和反向处理序列数据。这种双向结构能够捕捉到可能被单向GRU网络忽略的电池老化特征中存在的长短期关联信息,使得BiGRU在分析多维度特征这种复杂时间序列时表现出更强的特征捕捉能力[31]。BiGRU的网络结构如图4所示。
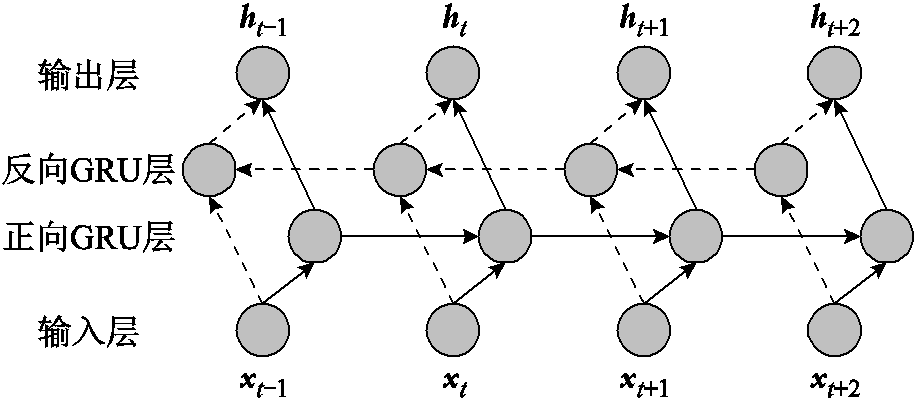
图4 BiGRU网络结构
Fig.4 Network structure of BiGRU
BiGRU的最终输出结果由正向GRU层和反向GRU层共同决定,通过同时学习两个方向上的依赖关系,进一步增强模型对长期依赖信息的捕捉能力[32]。BiGRU的正向隐藏状态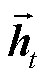 和反向隐藏状态
和反向隐藏状态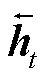 分别表示为
分别表示为
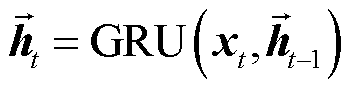 (14)
(14)
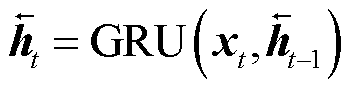 (15)
(15)
式中,GRU表示GRU单元;xt为输入序列中的第t个元素。最终的隐藏状态ht可表示为
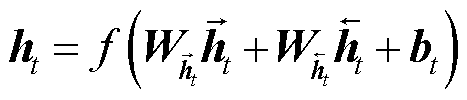 (16)
(16)
式中,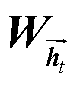 和
和 分别为t时刻前向和后向GRU层状态对应的权重矩阵;bt为t时刻隐藏层状态的偏置。
分别为t时刻前向和后向GRU层状态对应的权重矩阵;bt为t时刻隐藏层状态的偏置。
OOA是一种新颖的元启发式算法,该算法模拟了鱼鹰捕食的过程,将求解优化问题的过程比喻为鱼鹰捕食的策略。其中,鱼鹰搜索猎物的过程视为在给定范围内实现BiGRU网络内部超参数寻优的过程,最终捕食到的猎物视为适用于此类型号电池RUL预测的最优解。鱼鹰在捕食时通常会采取一系列复杂的行为,如观察、搜索、选择目标和捕获,这些行为都是通过鱼鹰对环境的感知和适应来完成的。此算法主要由三个阶段组成:初始化、探索和捕捞。
在初始化阶段,首先需要定义鱼鹰优化算法的搜索空间,并在此基础上随机初始化每个鱼鹰的位置为
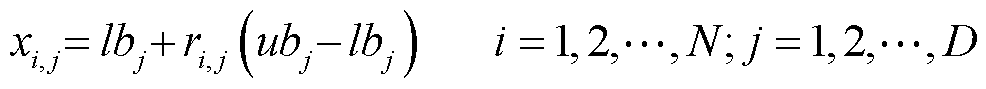 (17)
(17)
式中,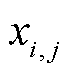 为第i个鱼鹰在第j个维度上的位置;lbj与ubj分别为搜索空间在第j个维度上的下界和上界;ri,j为位于区间[0, 1]内的随机数;N为鱼鹰种群的个体数。
为第i个鱼鹰在第j个维度上的位置;lbj与ubj分别为搜索空间在第j个维度上的下界和上界;ri,j为位于区间[0, 1]内的随机数;N为鱼鹰种群的个体数。
此初始化确保所有鱼鹰均分布在给定的搜索空间内。每个鱼鹰均对应RUL预测过程中BiGRU网络参数优化问题的一个候选解,其适应度选择均方根误差进行评估。
在探索阶段,鱼鹰通过探测水下鱼群的位置来获取更优的搜索方向,该阶段分为全局探测和局部追踪两个部分。全局探测部分公式为
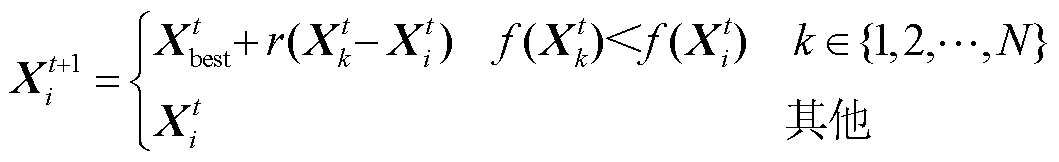 (18)
(18)
式中,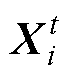 为第i个鱼鹰在t次迭代的位置,
为第i个鱼鹰在t次迭代的位置,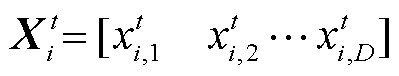 ;
;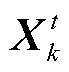 为从种群中随机选取的第k个鱼鹰的位置;
为从种群中随机选取的第k个鱼鹰的位置;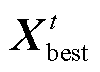 表示当前种群中适应度最优的鱼鹰位置;r表示位于区间(0, 1)内的随机数;
表示当前种群中适应度最优的鱼鹰位置;r表示位于区间(0, 1)内的随机数;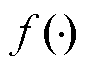 为适应度函数。在探测到鱼群后,鱼鹰会进一步靠近目标以增强局部搜索能力,其位置更新公式为
为适应度函数。在探测到鱼群后,鱼鹰会进一步靠近目标以增强局部搜索能力,其位置更新公式为
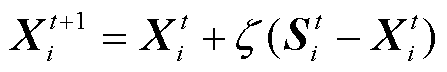 (19)
(19)
式中,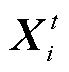 为鱼鹰i在第t次迭代时的位置;
为鱼鹰i在第t次迭代时的位置;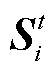 为鱼鹰i在当前阶段选中的局部目标位置;z为随机选取的步长因子,用于控制追踪速度,
为鱼鹰i在当前阶段选中的局部目标位置;z为随机选取的步长因子,用于控制追踪速度,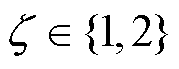 。
。
在捕捞阶段,鱼鹰将捕获的猎物带到相对安全的位置,此时算法会缩小搜索范围,以增强局部搜索能力和加速收敛。更新公式可以定义为
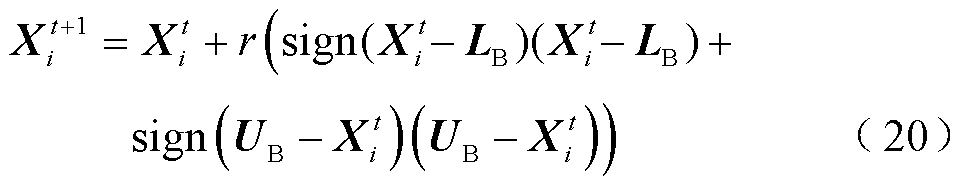
式中,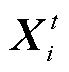 为鱼鹰i在第t次迭代时的位置;
为鱼鹰i在第t次迭代时的位置;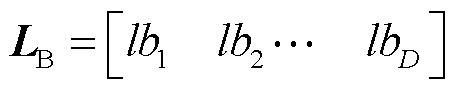 表示每个维度的下界构成的向量;
表示每个维度的下界构成的向量;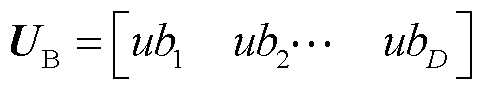 表示每个维度的上界构成的向量;r为(0, 1)内的随机数;sign(x)为符号函数,如果x≥0则为1,否则为-1,它用于判断当前维度是否接近边界,并决定鱼鹰是否需要向内收缩。
表示每个维度的上界构成的向量;r为(0, 1)内的随机数;sign(x)为符号函数,如果x≥0则为1,否则为-1,它用于判断当前维度是否接近边界,并决定鱼鹰是否需要向内收缩。
如果更新后得到的新位置超出了预定的搜索空间,则需要对其进行边界修正。
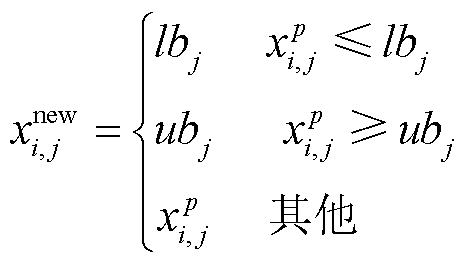 (21)
(21)
式中,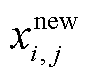 为修正后的位于搜索空间内的位置;
为修正后的位于搜索空间内的位置;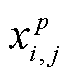 为经上述任一更新(探测、追踪或捕捞)后计算得到的候选位置。
为经上述任一更新(探测、追踪或捕捞)后计算得到的候选位置。
从马里兰大学电池数据集和课题组自有电池数据集的全周期老化数据中提取出每轮循环的恒流充电时间(Constant Current Charging Time, CCCT)和恒压充电时间(Constant Voltage Charging Time, CVCT),不同电池的CCCT曲线和CVCT曲线如图5~图8所示。根据图中曲线变化趋势可以判断,CCCT随着电池老化过程中容量的衰减而递减,而CVCT随着电池老化过程中容量的衰减而递增。此现象代表CCCT和CVCT与电池的老化程度存在关联,因此将二者作为RUL预测的HF。
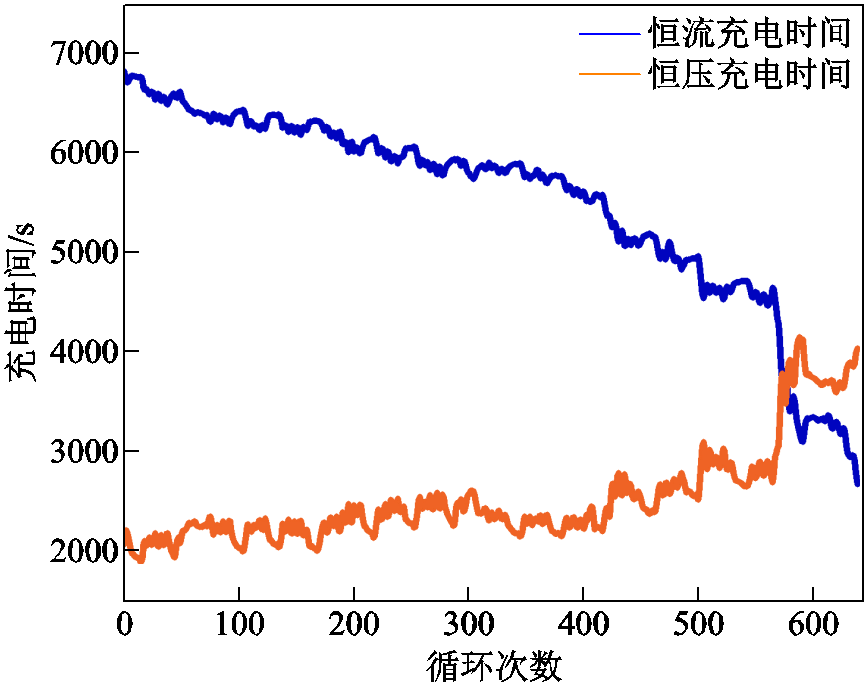
图5 CS2_33的CCCT曲线和CVCT曲线
Fig.5 CCCT curve and CVCT curve for CS2_33
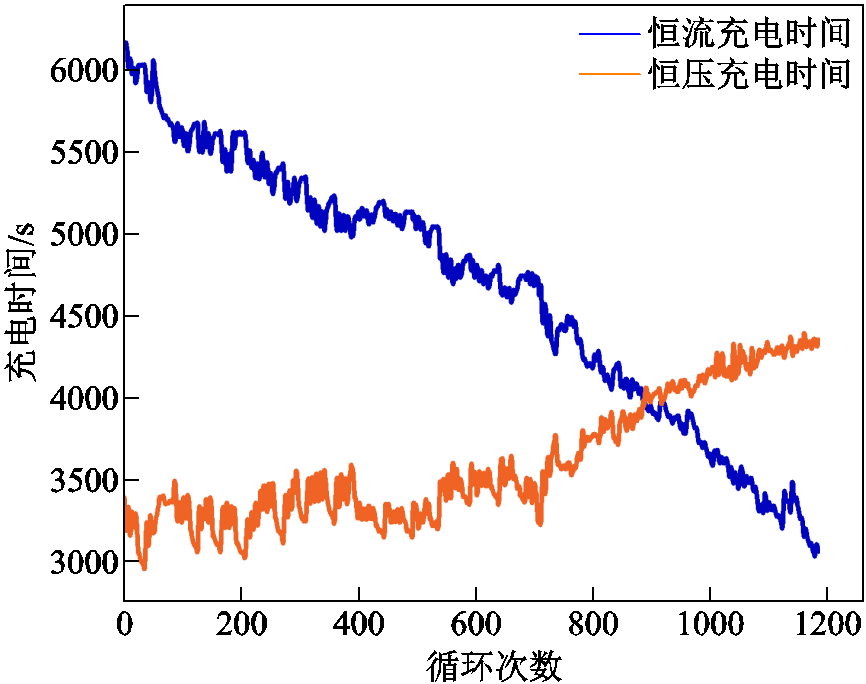
图6 CX2_37的CCCT曲线和CVCT曲线
Fig.6 CCCT curve and CVCT curve for CX2_37
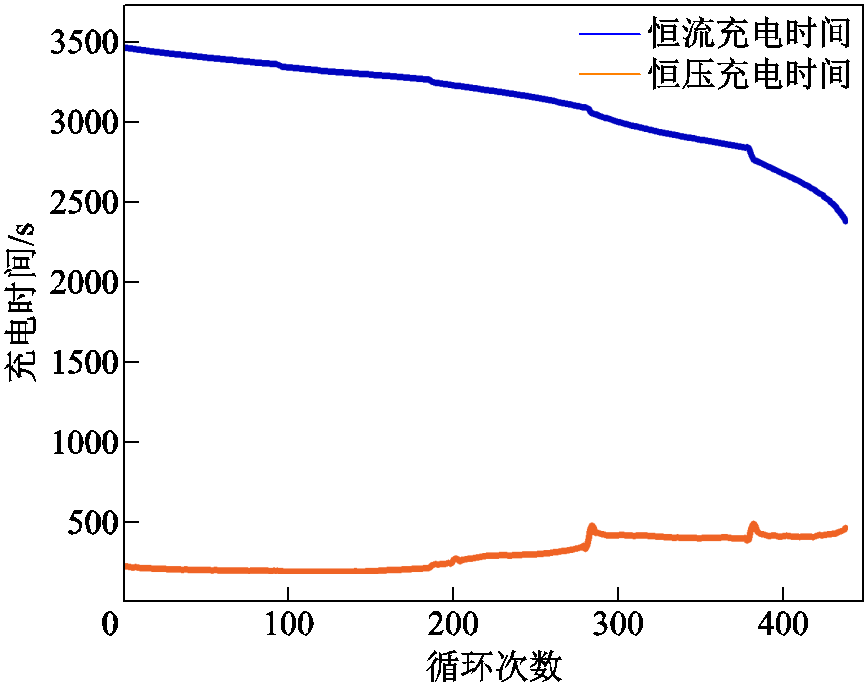
图7 M09的CCCT曲线和CVCT曲线
Fig.7 CCCT curve and CVCT curve for M09
以CS2_33电池为例,CCCT曲线中具体每个循环的充电电压随时间的变化曲线如图9所示,进一步提取不同范围的等时间电压增量以及等电压上升时间,以此作为能够反映电池老化程度的不同HF。另外曲线中斜率最低点对应的时间及位置等信息也包含潜在的老化规律,这些信息也属于HF提取的考虑范围。最终,共选取出了12个HF(F1~F12)组成锂离子电池RUL预测的特征,具体见表2。
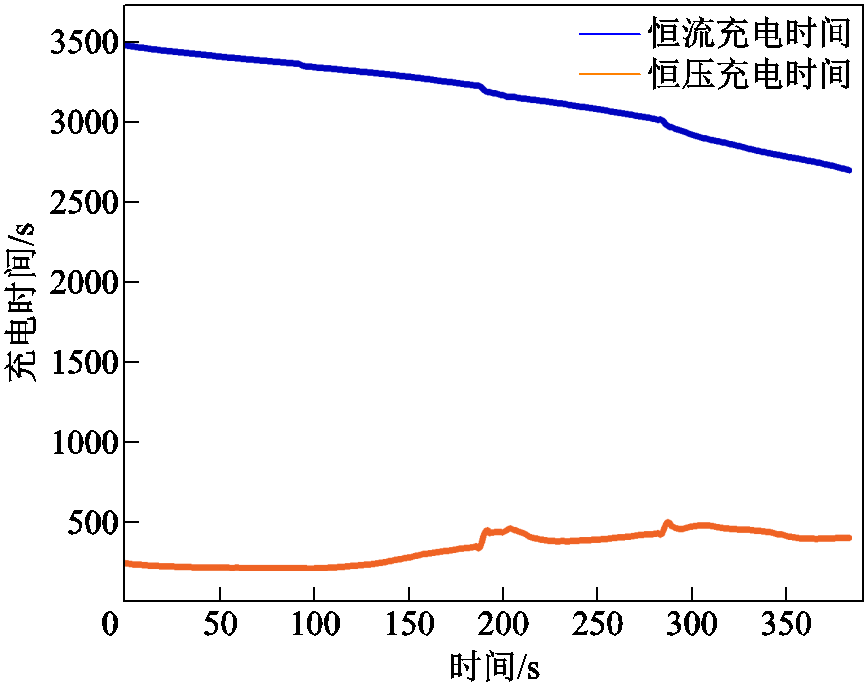
图8 M10的CCCT曲线和CVCT曲线
Fig.8 CCCT curve and CVCT curve for M10
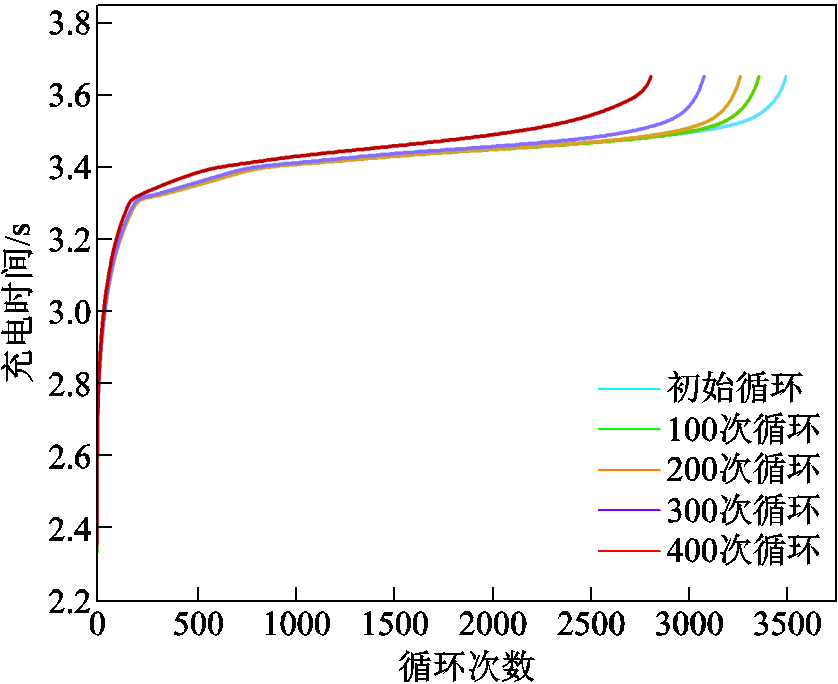
图9 每个循环的充电电压随时间的变化曲线
Fig.9 Charging voltage versus time curve for each cycle
表2 不同电池选取出的HF
Tab.2 Selected HF from different batteries
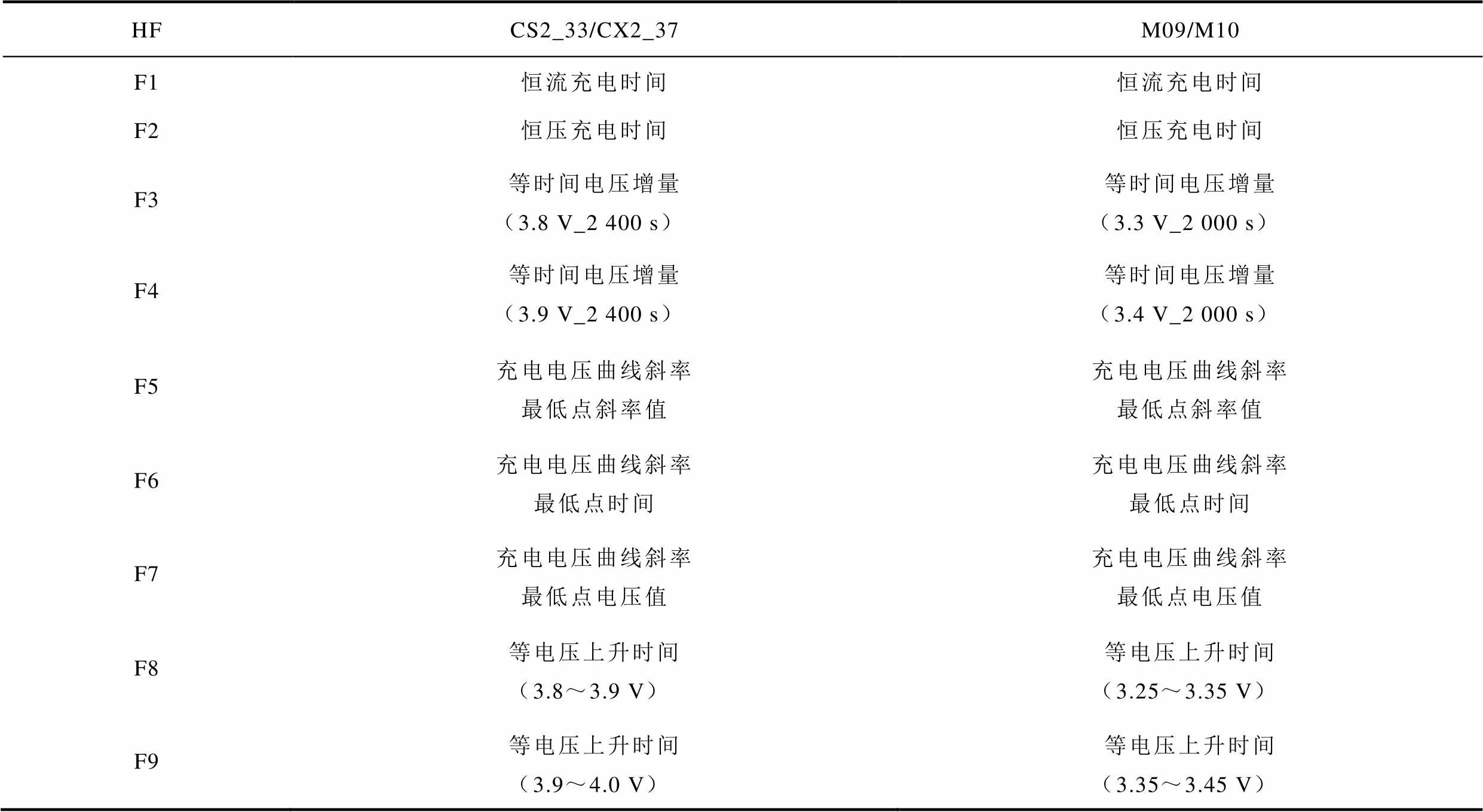
HFCS2_33/CX2_37M09/M10 F1恒流充电时间恒流充电时间 F2恒压充电时间恒压充电时间 F3等时间电压增量(3.8 V_2 400 s)等时间电压增量(3.3 V_2 000 s) F4等时间电压增量(3.9 V_2 400 s)等时间电压增量(3.4 V_2 000 s) F5充电电压曲线斜率最低点斜率值充电电压曲线斜率最低点斜率值 F6充电电压曲线斜率最低点时间充电电压曲线斜率最低点时间 F7充电电压曲线斜率最低点电压值充电电压曲线斜率最低点电压值 F8等电压上升时间(3.8~3.9 V)等电压上升时间(3.25~3.35 V) F9等电压上升时间(3.9~4.0 V)等电压上升时间(3.35~3.45 V)
(续)

电池CS2_33/CX2_37M09/M10 F10等电压上升时间(3.8~4.0 V)等电压上升时间(3.25~3.45 V) F11等电压上升时间(3.9~4.1 V)等电压上升时间(3.35~3.55 V) F12等电压上升时间(3.8~4.1 V)等电压上升时间(3.25~3.55 V)
从电池电流、电压和时间数据中直接提取的HF存在异常值和噪声,需要对其进行删除和过滤处理。首先,将提取出的每个HF分割成多个子集。然后根据3 原则,将偏离均值超过三个标准差的数据点标记为异常点,删除该异常点对应循环次数的全部HF。之后,采用Savitzky-Golay滤波器,通过调整滑动窗口长度和多项式阶数来适应不同HF的特点,对异常值处理后的HF进行平滑处理,以减少数据的噪声和波动,使其更加平滑且易于分析。
原则,将偏离均值超过三个标准差的数据点标记为异常点,删除该异常点对应循环次数的全部HF。之后,采用Savitzky-Golay滤波器,通过调整滑动窗口长度和多项式阶数来适应不同HF的特点,对异常值处理后的HF进行平滑处理,以减少数据的噪声和波动,使其更加平滑且易于分析。
对HF进行异常点删除及平滑滤波工作后,不同电池的等时间电压增量和等电压上升时间曲线如图10~图17所示。
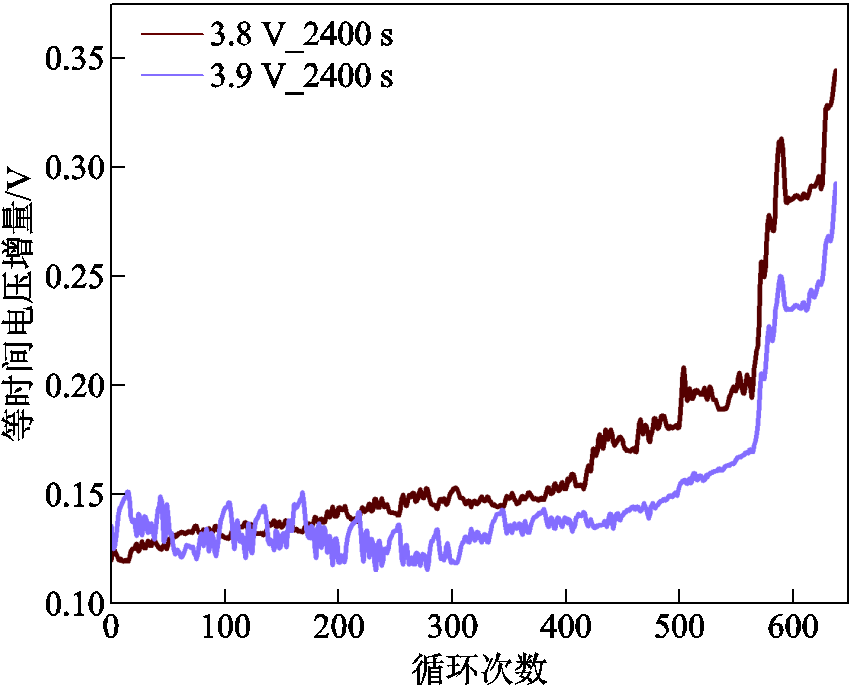
图10 CS2_33的等时间电压增量
Fig.10 Equal time voltage increments for CS2_33
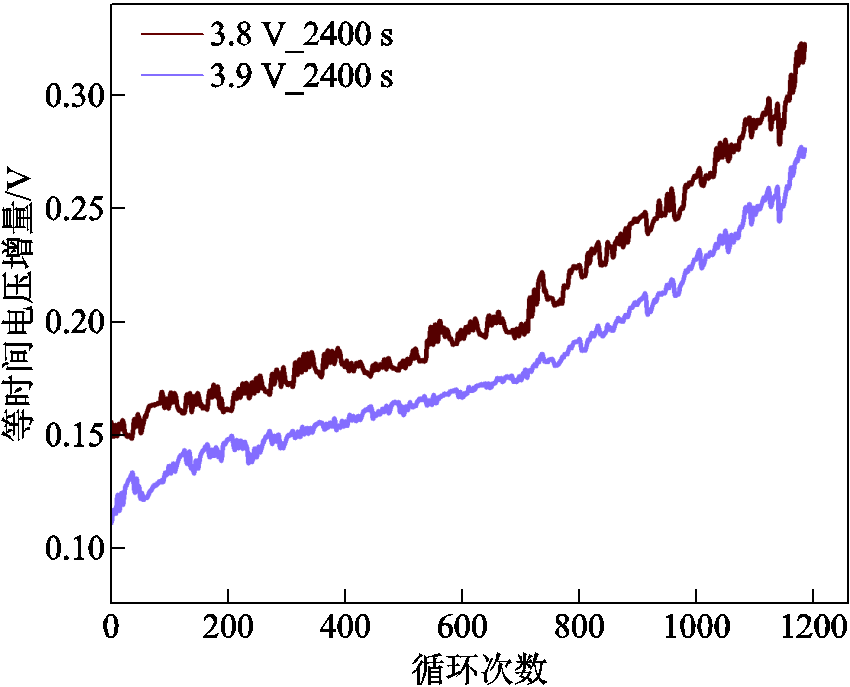
图11 CX2_37的等时间电压增量
Fig.11 Equal time voltage increments for CX2_37
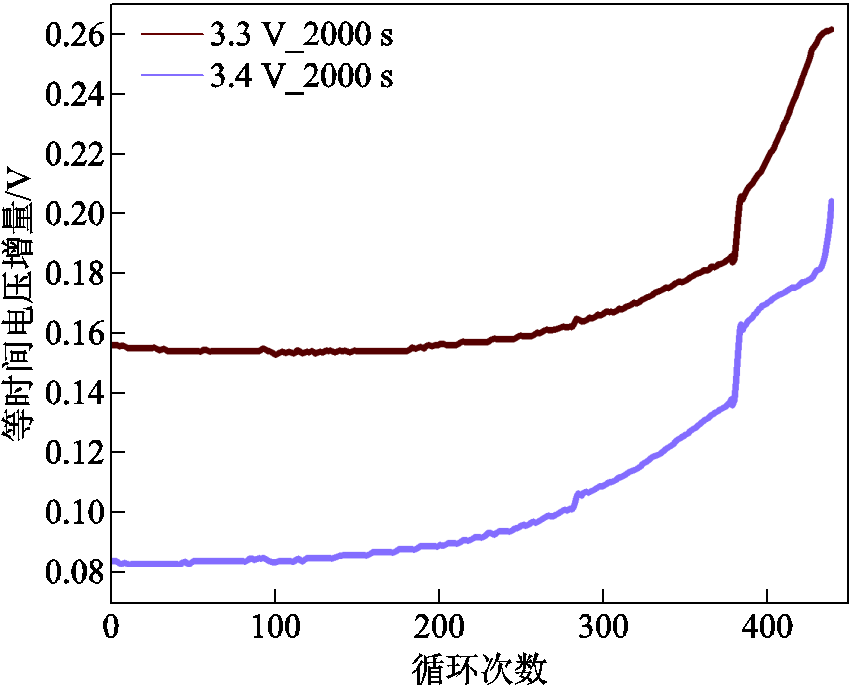
图12 M09的等时间电压增量
Fig.12 Equal time voltage increments for M09
从图10~图13可以观察到,所有电池的等时间电压增量会随着循环次数的增加而递增。图中紫色曲线对应的电压计算起点的设定值比红色曲线的电压计算起点高了0.1 V。而结果反映出,紫色曲线在相同时间内测量出的电压增长值整体低于红色曲线,这代表随着电压测量起点的增高,对应的等时间电压增量会相应地降低。从图中还可以观察到,不同电池的等时间电压增量的上升趋势有所不同。其中CS2_33电池和M09电池的等时间电压增量在充放电循环的后期出现骤然上升的情况,而CX2_37电池和M10电池的等时间电压增量的增长速度整体较为平缓。CS2_33电池和CX2_37电池对应的等时间电压增量相较于M09和M10电池有着频繁的抖动,在预测的过程中会更加考验模型的非线性捕捉能力。
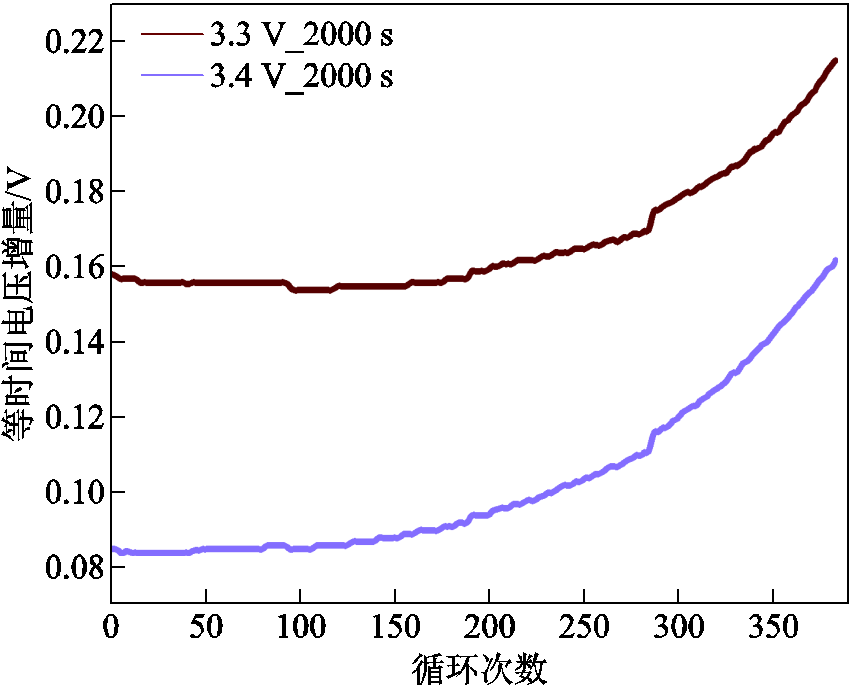
图13 M10的等时间电压增量
Fig. 13 Equal time voltage increments for M10
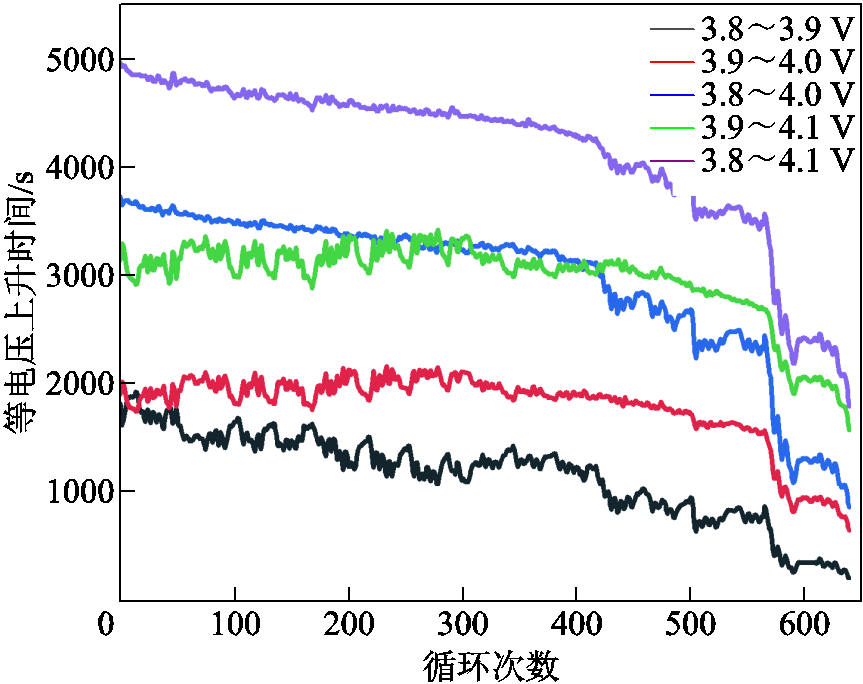
图14 CS2_33的等电压上升时间曲线
Fig.14 Equal voltage rise time curves for CS2_33
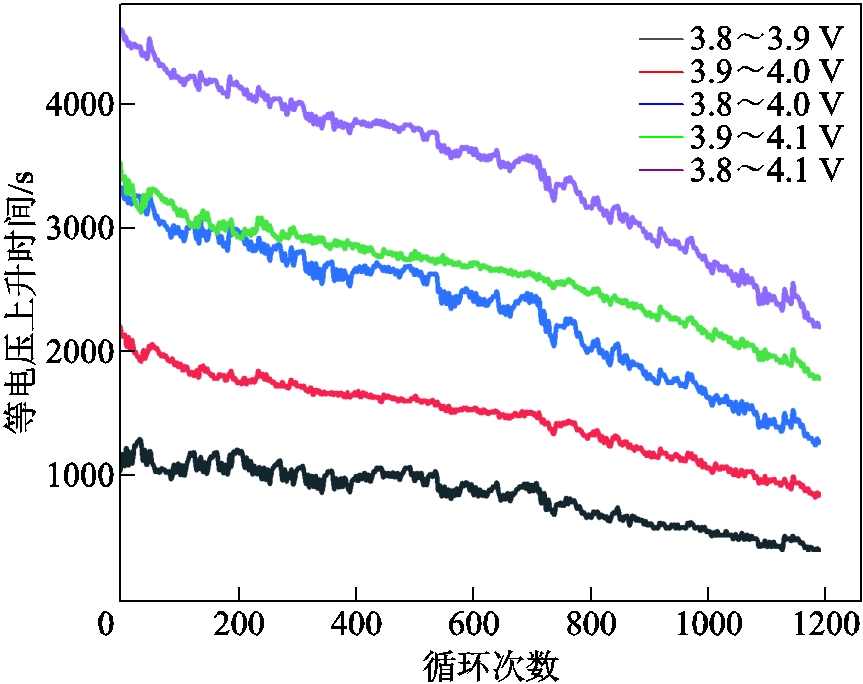
图15 CX2_37的等电压上升时间曲线
Fig.15 Equal voltage rise time curves for CX2_37
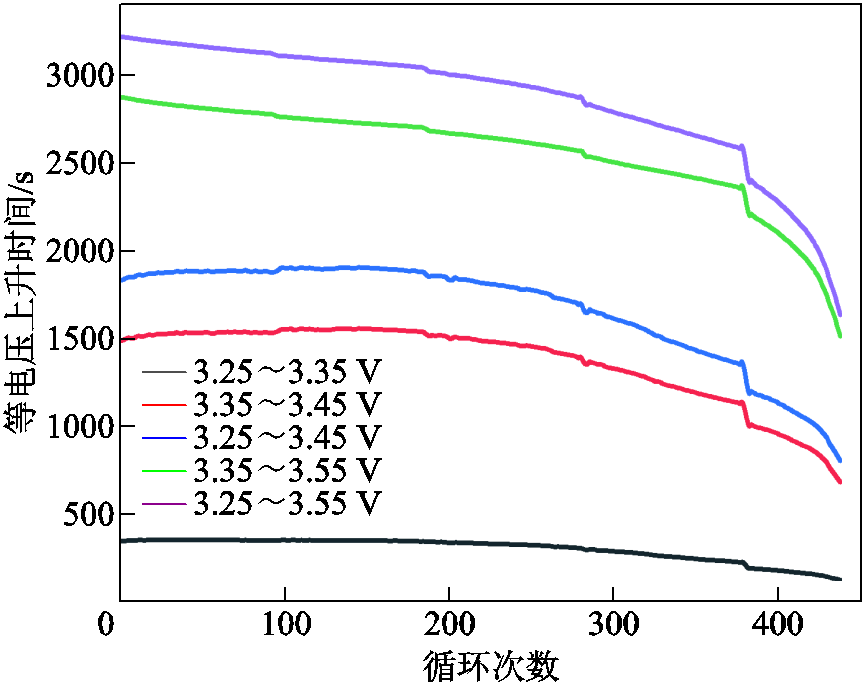
图16 M09的等电压上升时间曲线
Fig.16 Equal voltage rise time curves for M09
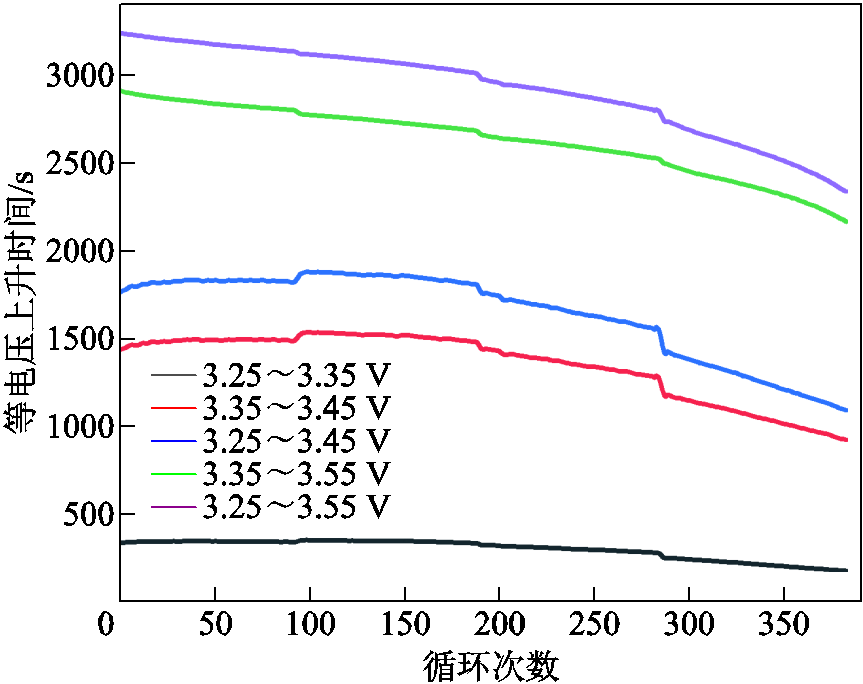
图17 M10的等电压上升时间曲线
Fig.17 Equal voltage rise time curves for M10
不同电池的等电压上升时间曲线如图14~图17所示。由图可知,等电压上升时间会随着电池的老化而递减,且CS2_33电池和M09电池的等电压上升时间的下降程度随着循环次数的增加而加快。
提取出的12个HF可整体作为实现电池RUL预测的特征,这些特征由于包含复杂的老化信息,极大地考验了网络模型对多输入信息的捕捉能力。因此可将全部HF组成的特征用于后文的网络模型验证过程,验证BiGRU对多维度特征拥有更好的整合能力。
已提取的HF组合中存在部分HF与电池老化状态相关性较低的问题,这些相关性低的HF会使模型难以从数据中捕捉到电池RUL的有效信息,从而降低预测的准确性。同时,相关性低的HF增加了模型的计算成本,导致训练时间增加,以及模型复杂度提高。因此,采用基于过滤器方法的皮尔逊相关性分析对提取的所有HF进行关联度评估,计算出不同HF与电池老化状态之间的关联程度。根据皮尔逊相关系数的高低,选择出相关性最高的四个HF作为初步筛选后的特征,同时过滤掉其余HF。经计算,针对马里兰大学CS2_33和CX2_37电池、课题组自有M09和M10电池,所提取HF的皮尔逊相关系数见表3。
表3 不同HF与电池老化状态的皮尔逊相关系数
Tab.3 Pearson's correlation coefficients between different HFs and battery aging states
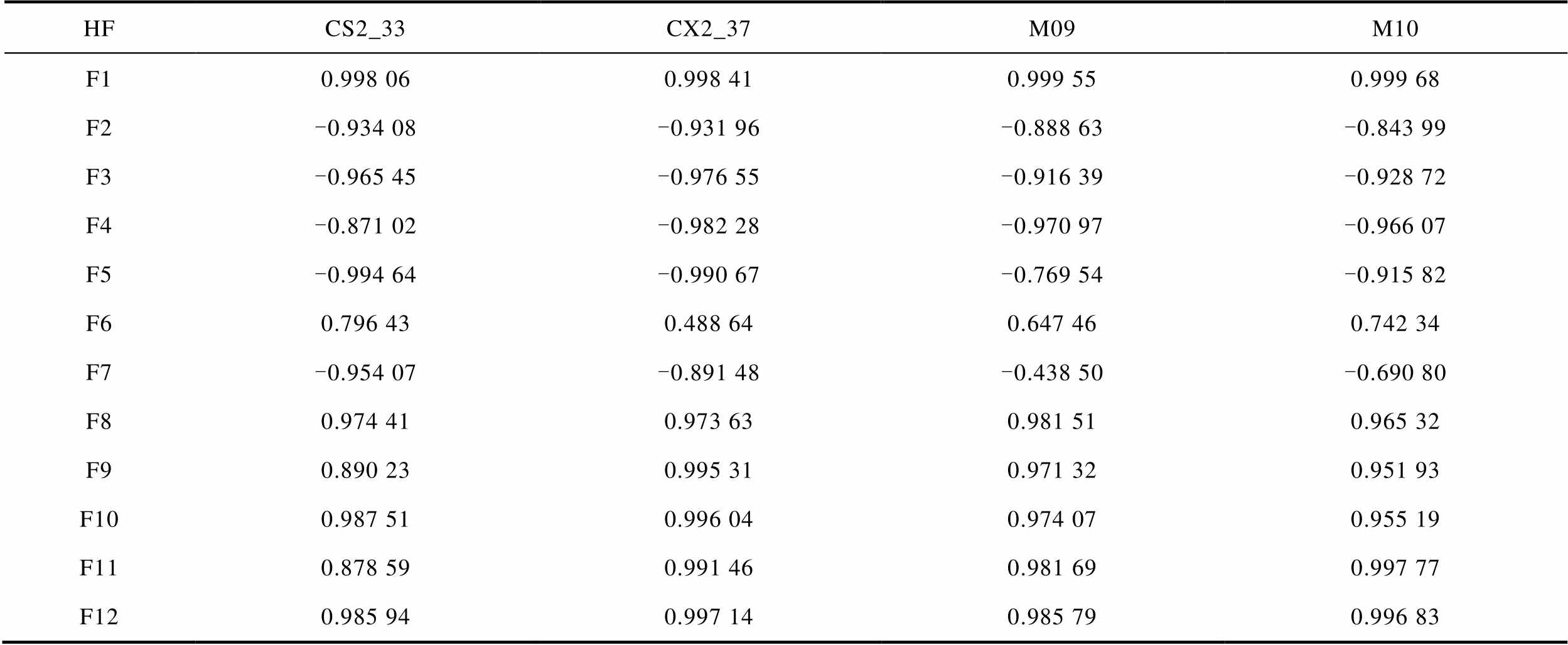
HFCS2_33CX2_37M09M10 F10.998 060.998 410.999 550.999 68 F2-0.934 08-0.931 96-0.888 63-0.843 99 F3-0.965 45-0.976 55-0.916 39-0.928 72 F4-0.871 02-0.982 28-0.970 97-0.966 07 F5-0.994 64-0.990 67-0.769 54-0.915 82 F60.796 430.488 640.647 460.742 34 F7-0.954 07-0.891 48-0.438 50-0.690 80 F80.974 410.973 630.981 510.965 32 F90.890 230.995 310.971 320.951 93 F100.987 510.996 040.974 070.955 19 F110.878 590.991 460.981 690.997 77 F120.985 940.997 140.985 790.996 83
从表3中可以看出,F1、F3、F8、F10和F12这五个HF与电池老化状态之间的整体相关性较高,对应四组电池的相关性评分均维持在0.9以上。而代表充电电压曲线斜率最低点时间的F6相关程度不够理想,在CX2_37电池中最低仅为0.488 64。经过皮尔逊相关性分析的筛选,CS2_33电池选用F1、F5、F10、F12作为过滤后的输入特征;CX2_37电池选用F1、F9、F10和F12作为过滤后的输入特征;M09电池选用F1、F8、F11和F12作为过滤后的输入特征;M10电池选用F1、F4、F11和F12作为过滤后的输入特征。
高度相关或相似的HF会增加特征内部的冗余性,这种情况会对模型的预测效果产生负面影响。当模型使用过多相关的HF进行训练时,容易导致过拟合。这是由于模型会过度关注训练数据中的冗余噪声或细微差异,而忽略了真正重要的老化模式和变化趋势。冗余HF会使模型变得更加复杂且难以解释,同时冗余HF的存在意味着模型需要处理更多的HF,而这些HF可能并没有实质性地提升预测性能,从而增加了模型的运行成本。采用序列前向搜索方法(SFS)可以探索不同HF组合的特征空间,从单HF开始进行空间搜索,逐步添加至多HF子集。然后,根据模型的预测性能进行评估,找到最适合RUL预测的特征组合,在提高模型性能的同时减少了特征空间的维度。以模型预测的方均根误差为评估标准,当SFS子集模型相较于使用过滤特征模型的方均根误差降低了40%时,SFS达到终止条件。经过皮尔逊相关性分析的过滤以及SFS的去冗余,最终通过融合特征筛选方法选择出的用于电池RUL预测的融合特征见表4。
表4 不同电池RUL预测的融合特征
Tab.4 Fusion feature of RUL prediction for different batteries

HFCS2_33CX2_37M09M10 F1×√√× F2×××× F3×××× F4×××√ F5√××× F6×××× F7×××× F8××√× F9×√×× F10√××× F11××√√ F12√√××
表4结果显示,CS2_33电池从HF中最终选用F5、F10和F12作为实现RUL预测的融合特征,CX2_37电池选用F1、F9和F10作为融合特征,M09电池选用F1、F8和F11作为融合特征,M10电池选用F4和F11作为融合特征。
本研究基于Tensorflow框架的python语言实现,利用统一计算设备架构(Compute Unified Device Architecture, CUDA)加速,实验硬件平台设置:CPU为AMD Ryzen 7 5800H 3.2 GHz,内存RAM为 16 GB,GPU为Nvidia GeFore RTX 3060 6G。
输入的电池数据共划分为两部分:前50%为训练数据,用于训练OOA-BiGRU网络预测模型;后50%为测试数据,用于验证预测的准确性与鲁棒性。BiGRU网络采用双层结构,引入dropout算法,将方均根误差作为网络的损失函数,采用Adam优化器,学习率调整为0.001。在训练开始前及训练结束后分别对数据进行归一化及反归一化操作。设计OOA对BiGRU内部第一层神经元数量d1、第二层神经元数量d2、批次大小batch_size以及迭代次数epochs组成的超参数进行优化搜索,搜索下限为[10,3,100,100],搜索上限为[80,64,800,800]。
为了全方位评判模型预测性能的优劣,共选取了四个评价指标,分别为方均根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)以及决定系数(R2)。它们对应的计算公式分别为
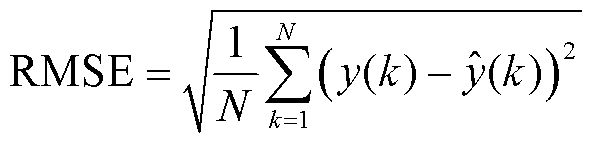 (22)
(22)
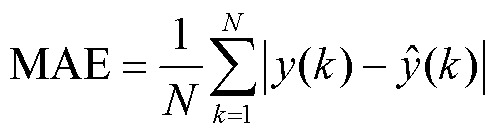 (23)
(23)
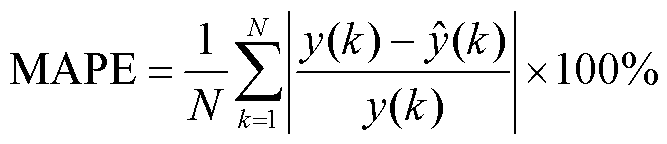 (24)
(24)
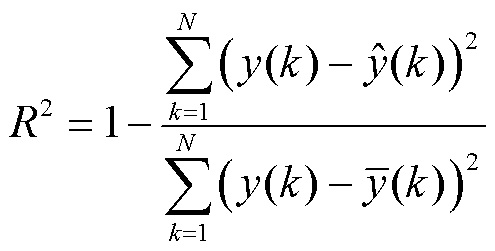 (25)
(25)
式中,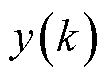 和
和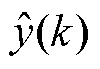 分别为第k个循环的实际值和预测值;
分别为第k个循环的实际值和预测值;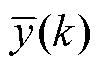 为实际的平均值;N为测试集的样本数量。
为实际的平均值;N为测试集的样本数量。
RMSE用于衡量预测值和真实值之间的差距,更容易观测到预测过程中产生的误差,RMSE值越小代表模型的稳定性越高。MAE提供了预测误差的平均水平,是一个直观的衡量误差大小的度量。与RMSE相比,MAE对异常值的反应相对不敏感,更能反映实际的预测误差。MAPE是一个表现预测准确度的相对指标,代表模型预测结果的误差占真实数据的比例。R2是衡量模型整体拟合度的一个重要指标,能够反映模型预测的准确性和可靠性。R2越接近于1代表模型预测的拟合程度越好。
多维特征相比于单维特征在能够提供更多老化信息的同时,对模型的信息捕捉能力要求也大大提高。从电池老化数据中提取的12个HF组成能够实现电池RUL预测的全部特征,将其直接作为输入特征会提高模型预测的复杂度,从而更能考验模型对多维信息的捕捉能力。利用RMSE、MAE、MAPE和R2四个评价指标来评估BiGRU模型与其他模型在全部特征上的预测效果,实验结果见表5。
表5 BiGRU模型与其他模型基于全部特征的预测效果对比
Tab.5 Comparison of predictive effectiveness of BiGRU model with other models based on all features
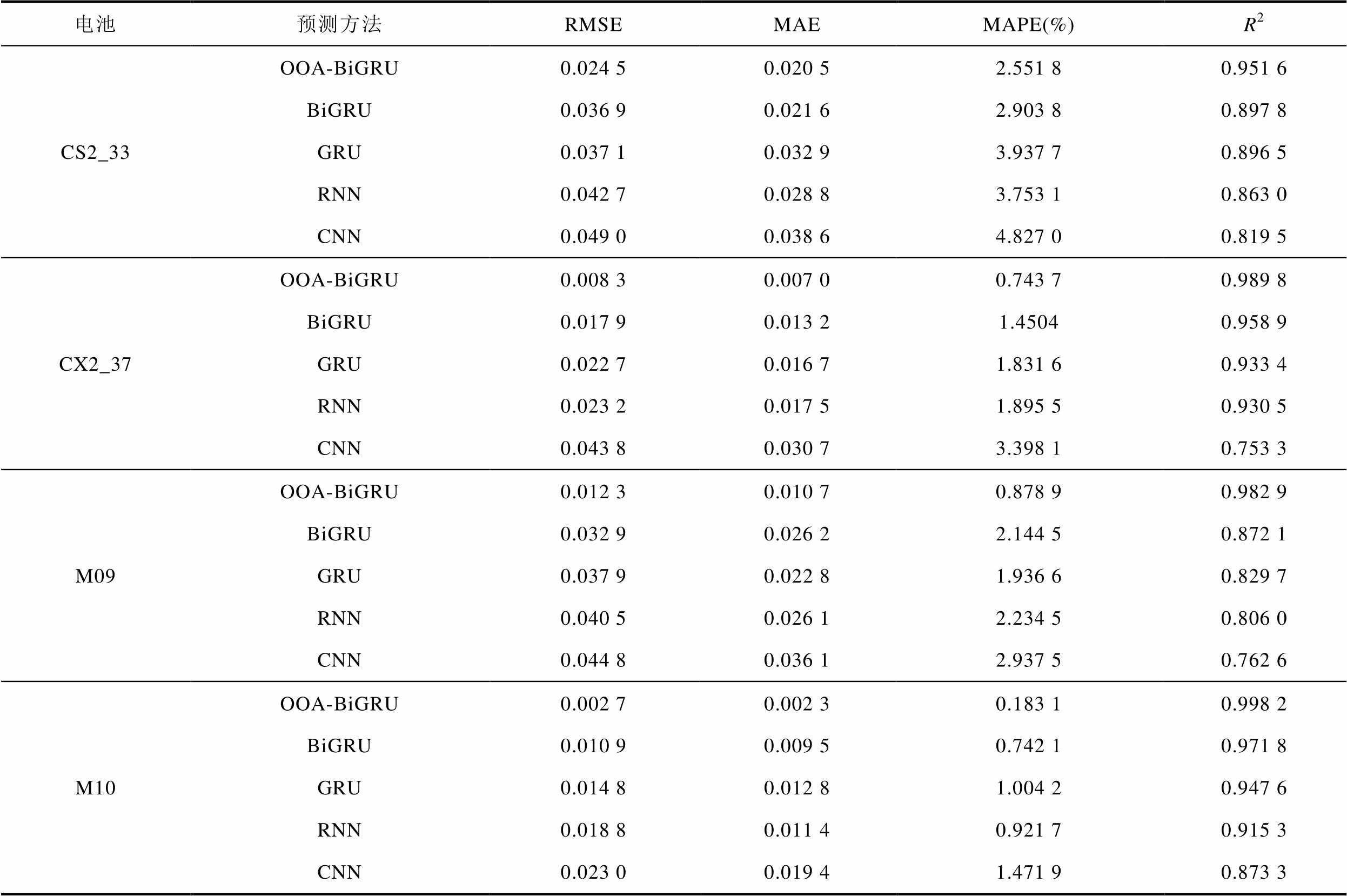
电池预测方法RMSEMAEMAPE(%)R2 CS2_33OOA-BiGRU0.024 50.020 52.551 80.951 6 BiGRU0.036 90.021 62.903 80.897 8 GRU0.037 10.032 93.937 70.896 5 RNN0.042 70.028 83.753 10.863 0 CNN0.049 00.038 64.827 00.819 5 CX2_37OOA-BiGRU0.008 30.007 00.743 70.989 8 BiGRU0.017 90.013 21.45040.958 9 GRU0.022 70.016 71.831 60.933 4 RNN0.023 20.017 51.895 50.930 5 CNN0.043 80.030 73.398 10.753 3 M09OOA-BiGRU0.012 30.010 70.878 90.982 9 BiGRU0.032 90.026 22.144 50.872 1 GRU0.037 90.022 81.936 60.829 7 RNN0.040 50.026 12.234 50.806 0 CNN0.044 80.036 12.937 50.762 6 M10OOA-BiGRU0.002 70.002 30.183 10.998 2 BiGRU0.010 90.009 50.742 10.971 8 GRU0.014 80.012 81.004 20.947 6 RNN0.018 80.011 40.921 70.915 3 CNN0.023 00.019 41.471 90.873 3
从表5中可以看出,CNN在所有电池上的预测结果均不够理想。除M10电池外,CNN在其余电池上预测的RMSE均高于0.04。这表示CNN主要用于处理静态网格结构的数据,而对于时间序列数据的建模能力相对较弱。对比CX2_37和M10电池,RNN的容量预测效果比CNN更好。其中,在CX2_37中RNN的RMSE和MAE比CNN低了0.020 6和0.013 2,而在M10中RNN的MAPE比CNN低了0.55个百分点。此外,RNN在其他两节电池的评价指标上相比于CNN也略微领先,体现出RNN更适合处理序列数据中的时序信息。对比GRU和RNN的预测效果,GRU在所有电池的RMSE和R2评价指标上均要优于RNN。此结果验证了GRU相比RNN更具有预测的稳定性,这得益于GRU独特的门控机制能够有效缓解RNN的梯度消失和梯度爆炸问题。
BiGRU在GRU的基础上增加了双向结构,在处理多特征输入预测方面的能力要优于传统的GRU。数据结果显示,BiGRU在四个电池的RMSE上相比于GRU平均降低了15.3%,同时在MAE和MAPE上分别按比例平均降低了16.5%和15.6%。这表明BiGRU相比单向的GRU具有更好的信息获取能力、特征表示能力和序列建模能力,在处理噪声和干扰方面更具有鲁棒性。综合来看,BiGRU在基于全部特征的预测上表现出最好的预测效果,因此选用BiGRU模型进行特征筛选并对其参数配置进行优化,最大程度地提高模型的预测精度。
经过计算可以得出,CS2_33电池中OOA-BiGRU相较于BiGRU在RMSE、MAE和MAPE评价指标上分别按比例降低了33.6%、5.1%和12.1%。在CX2_37中三个指标分别降低了53.6%、47.0%和48.7%。而在M09和M10中三个指标得到了进一步的降低,在M09中降低了62.6%、59.2%和59.0%,在M10中降低了75.2%、75.8%和75.3%。针对所有电池,经过OOA参数优化的BiGRU模型在预测性能上均得到了不同程度的提高,意味着OOA有效地提升了模型预测的准确性和稳定性。另外,通过R2数据可以观察到OOA的应用能够提高BiGRU模型进行电池老化预测的拟合度,且至少提升了2.7%。而在M09电池上,拟合度的提升幅度达到了12.7%。拟合度的提高意味着OOA-BiGRU模型能够更有效地捕捉输入特征与目标变量之间的关系,能更好地描述数据之间的复杂关系。这有助于揭示输入特征和目标变量之间的内在联系,同时模型的泛化能力也随之提高。
采用OOA-BiGRU模型对电池RUL进行预测,分别对基于全部特征预测、基于过滤特征(Filtered Feature, FIF)预测以及基于融合特征(Fusion Feature, FUF)预测的锂离子电池RUL预测效果进行比较,对比结果见表6。
基于不同特征预测方法在马里兰数据集上的预测结果及误差箱线图如图18~图21所示。从图18和图20可以看出,基于FIF的模型预测结果相较于基于全部特征预测更加贴合实际曲线,反映出经过过滤器筛选后的FIF在一定程度上提高了模型预测的准确性。局部放大图显示,基于所提FUF的预测实现了三种特征中的最好预测效果,其在寿命终止(End of Life, EOL)处相比其他两种特征预测结果更接近真实值,说明基于FUF的方法能实现更精准的RUL预测。
表6 OOA-BiGRU模型在不同特征上的老化预测结果
Tab.6 Comparison of predictive effectiveness of OOA-BiGRU model with other models based on all features
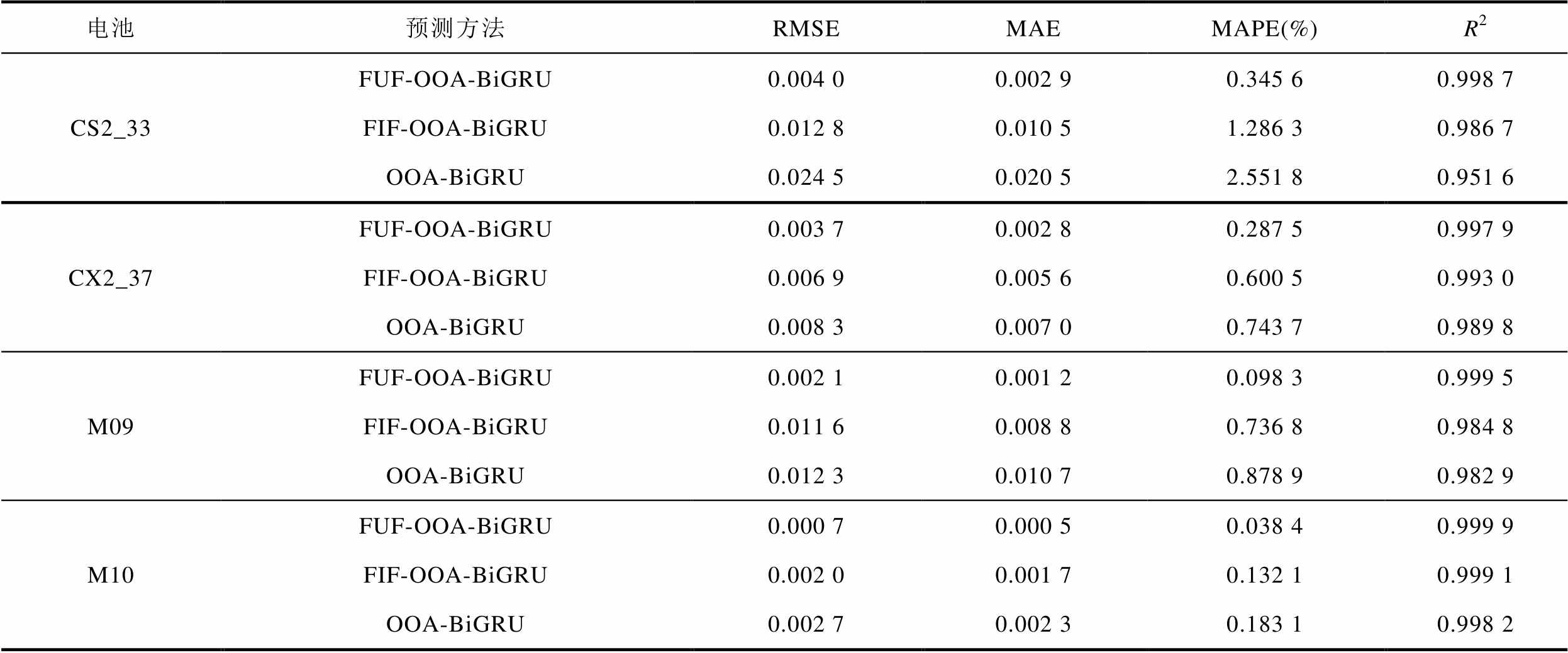
电池预测方法RMSEMAEMAPE(%)R2 CS2_33FUF-OOA-BiGRU0.004 00.002 90.345 60.998 7 FIF-OOA-BiGRU0.012 80.010 51.286 30.986 7 OOA-BiGRU0.024 50.020 52.551 80.951 6 CX2_37FUF-OOA-BiGRU0.003 70.002 80.287 50.997 9 FIF-OOA-BiGRU0.006 90.005 60.600 50.993 0 OOA-BiGRU0.008 30.007 00.743 70.989 8 M09FUF-OOA-BiGRU0.002 10.001 20.098 30.999 5 FIF-OOA-BiGRU0.011 60.008 80.736 80.984 8 OOA-BiGRU0.012 30.010 70.878 90.982 9 M10FUF-OOA-BiGRU0.000 70.000 50.038 40.999 9 FIF-OOA-BiGRU0.002 00.001 70.132 10.999 1 OOA-BiGRU0.002 70.002 30.183 10.998 2
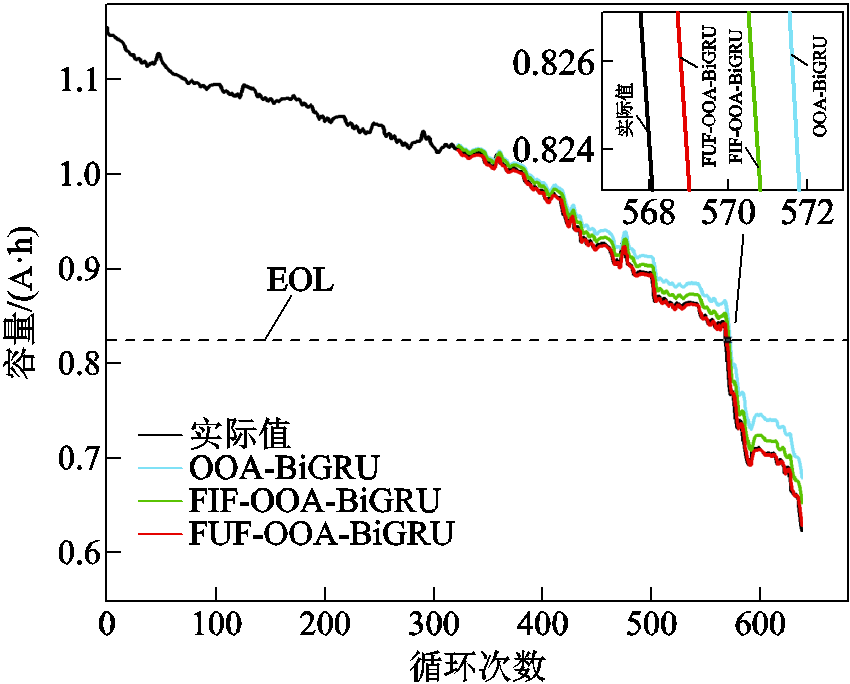
图18 CS2_33RUL预测结果
Fig.18 RUL prediction result for CS2_33
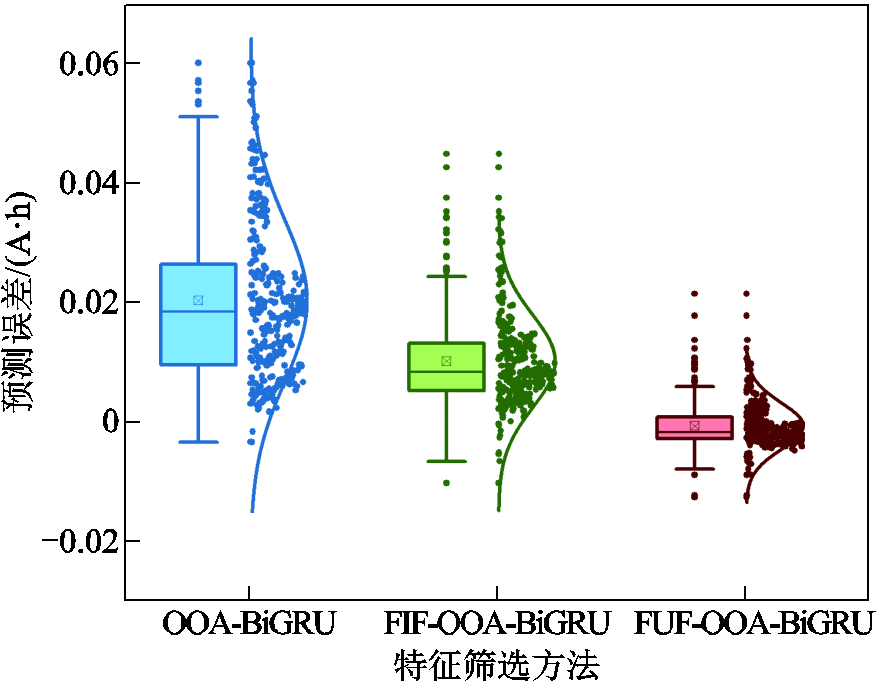
图19 CS2_33 RUL预测误差箱线图
Fig.19 Boxplot of RUL prediction error for CS2_33
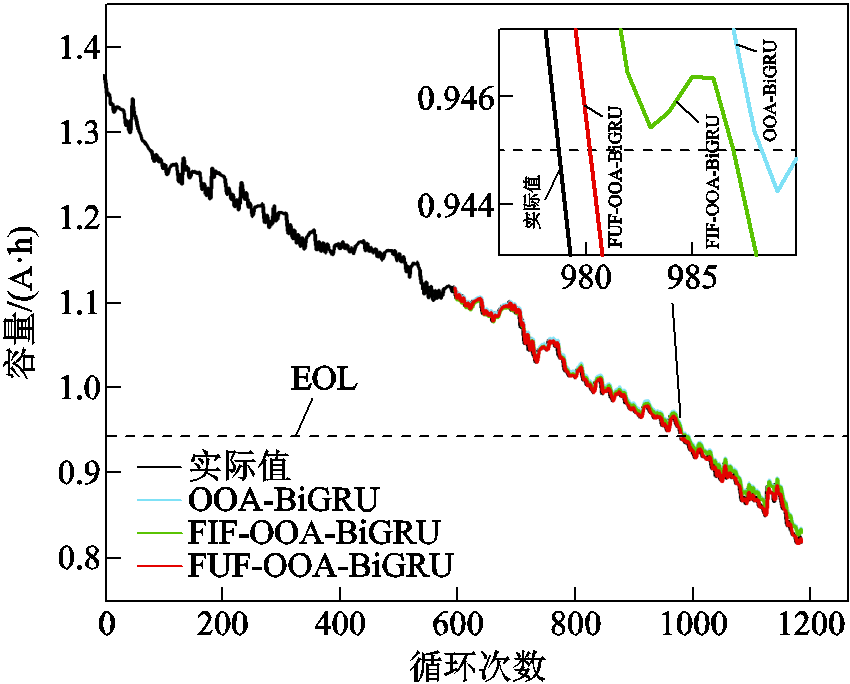
图20 CX2_37 RUL预测结果
Fig.20 RUL prediction result for CX2_37
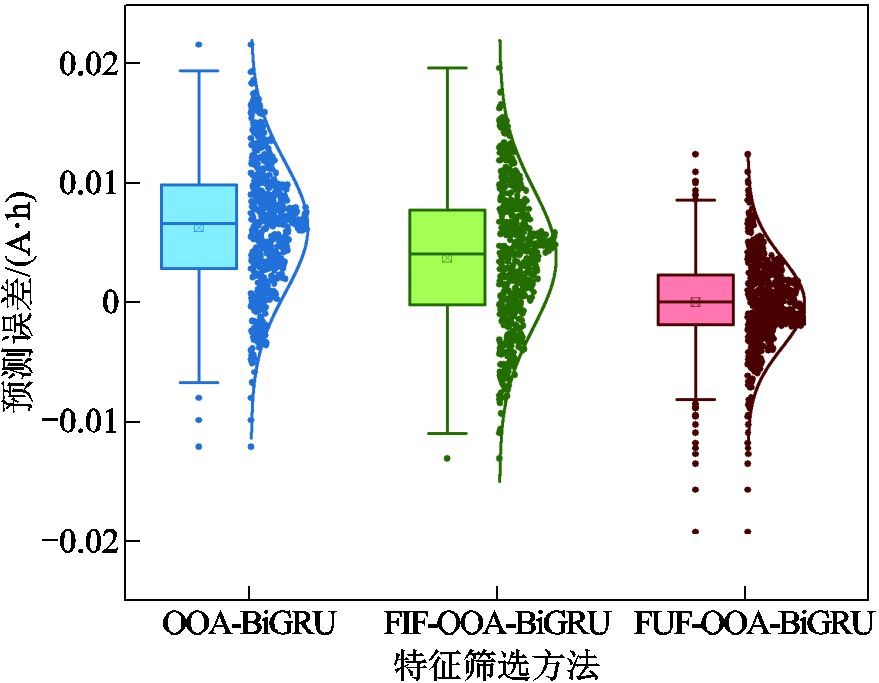
图21 CX2_37RUL预测误差箱线图
Fig.21 Boxplot of RUL prediction error for CX2_37
图19和图21分别为CS2_33和CX2_37电池RUL预测的误差箱线图。箱线图的上下两条横线分别代表误差的最大值和最小值。箱体的下边缘表示为误差的第一四分位数(Q1),即误差大小排在25%处的误差点位置。箱体的上边缘表示为误差的第三四分位数(Q3),对应75%处的误差点位置。箱体内的横线表示误差大小的中位数(Q2)。箱体表示从第一四分位数到第三四分位数的范围,这个区域称为四分位距(Interquartile Range, IQR),是衡量数据集中度和离散度的重要指标。箱体中心的小方点位置代表对应预测误差大小的平均值。从箱体到数据最小值和最大值的线(不包括异常值)称为胡须,代表数据的变异范围。而胡须范围之外的点被称为异常值,异常值被定义为小于Q1-1.5IQR或大于Q3+ 1.5IQR的值。从CS2_33和CX2_37的预测误差箱线图中可以看出,FUF-OOA-BiGRU的误差范围要明显小于另外两种预测方法,且整体误差箱体接近于零线。箱线图右侧直观地画出了三种方法在预测过程中每个循环的误差大小以及整个生命周期内的误差正态分布曲线。从正态分布图中也能看出,基于全部特征下以及FIF的模型预测误差较为离散,而基于FUF的OOA-BiGRU模型预测产生的误差点除个别点浮动外基本聚集在0附近,展示出了所提方法具有较高的稳定性和预测精度。
课题组自有电池数据的RUL预测结果如图22~图25所示。从老化趋势预测图中可以看出,相较于OOA-BiGRU,FIF-OOA-BiGRU在模型预测准确度上得到了提高,而FUF-OOA-BiGRU进一步提升了FIF-OOA-BiGRU的预测性能,以此说明FUF比FIF和全部特征更能反映电池的老化状态。从EOL处的局部放大图也能观察到,采用FUF预测相较于其他两个特征的对应曲线更加接近于原始真实值,代表其最终预测出的RUL精度也要高于另外两种方法,这得益于FUF方法提取特征的适应性和灵活性。对于不同的数据集或预测任务,FUF能够通过融合筛选过程找到最优的特征组合。FUF有效地避免了噪声和冗余特征的干扰,从而提高了整体的预测精度和稳定程度。由箱线图23可以观察出,基于FUF方法的箱体长度远低于其他方法,意味着该方法有着更高的预测精度和高度的一致性。高一致性意味着误差数据点较少地偏离中心区域,从而使该方法的预测结果更加可靠。另外能够观察出,FUF- OOA-BiGRU的平均值和中位线都接近于0,而其他方法都更接近于0.1,这种差距反映出其他两种模型的预测能力要低于所提方法。由箱线图25中能够看到,基于FIF和FUF的两种RUL预测方法在各个循环的预测误差的分布相较于基于全部特征预测都更加集中,这说明经过噪声特征的过滤,模型的鲁棒性得到了有效的提升。FIF和FUF的箱线图对比表明:FUF的箱体位置比FIF更趋近于0;FIF的预测误差整体高于零值,误差值位置在零值上下浮动。这表明二者在预测稳定性相近的情况下,FUF预测有着更高的预测准确性,这得益于在FUF方法中对FIF内的冗余项做到了有效剔除,从而提高了模型的预测精度。
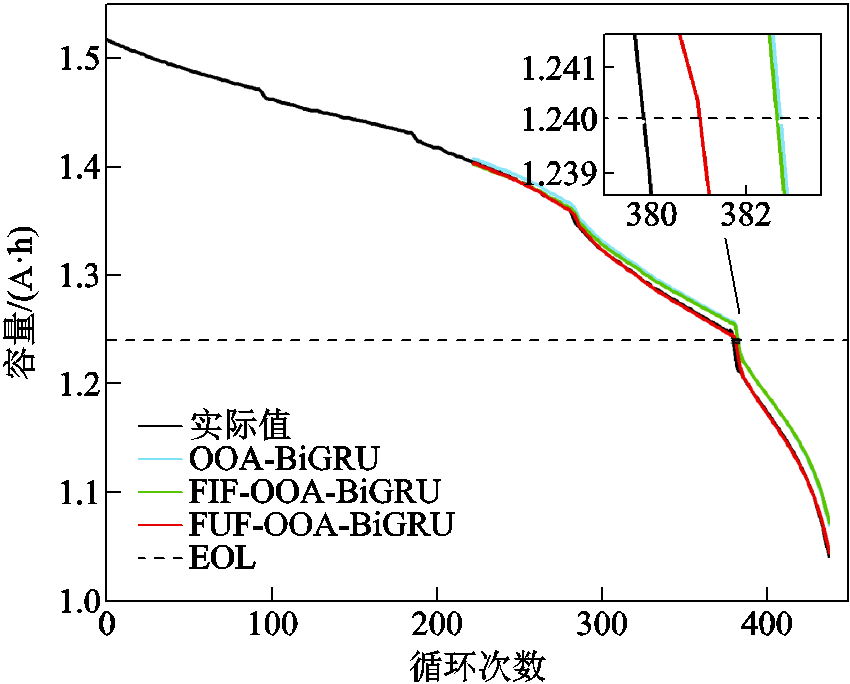
图22 M09 RUL预测结果
Fig.22 RUL prediction result for M09
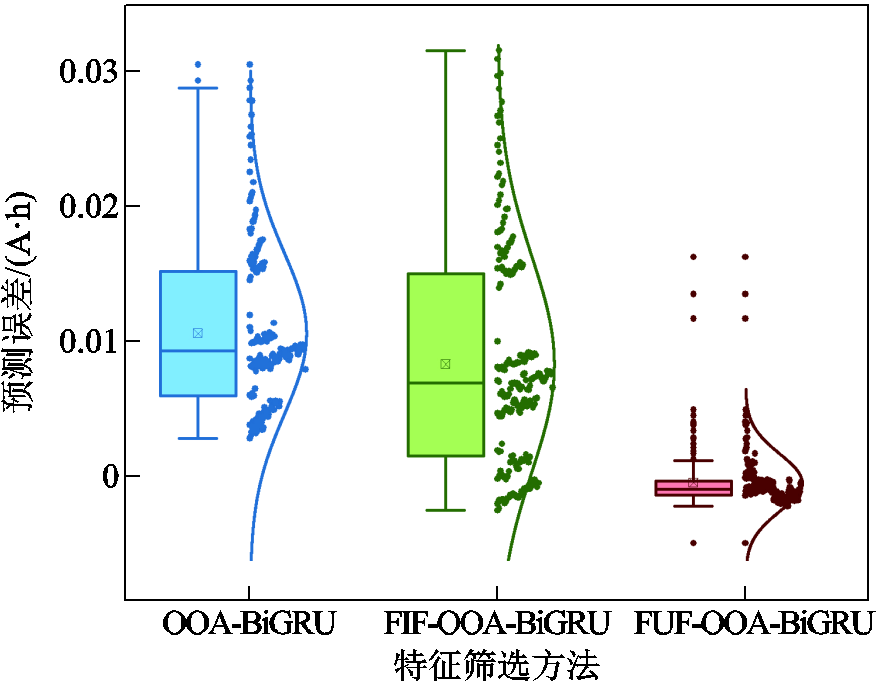
图23 M09 RUL预测误差箱线图
Fig.23 Boxplot of RUL prediction error for M09
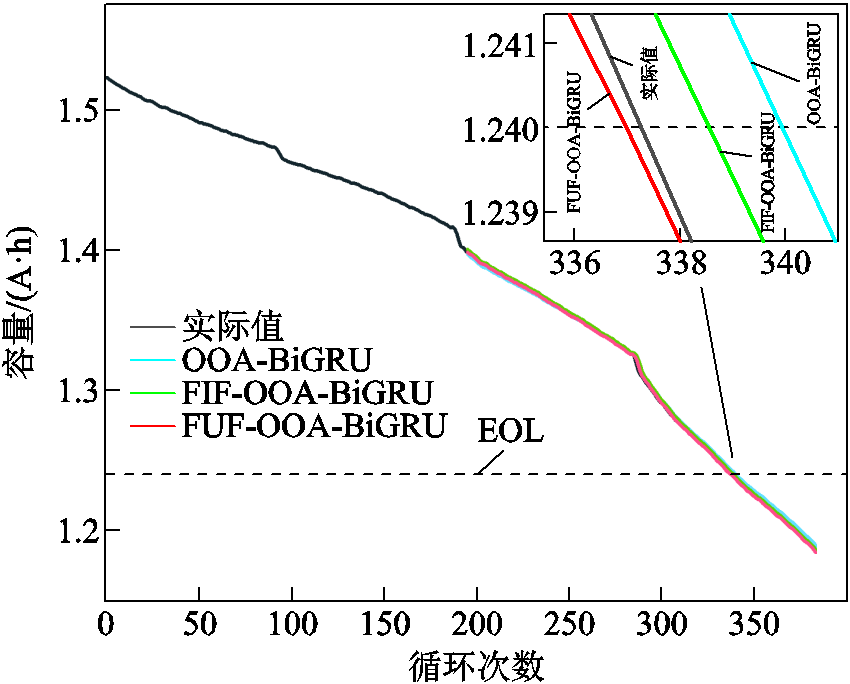
图24 M10 RUL预测结果
Fig.24 RUL prediction result for M10
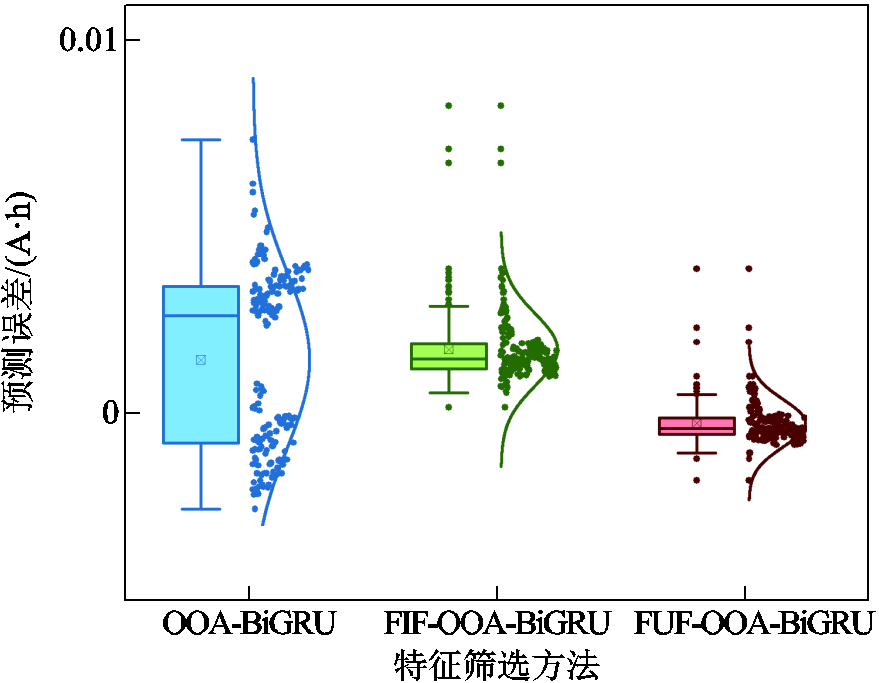
图25 M10 RUL预测误差箱线图
Fig.25 Boxplot of RUL prediction error for M10
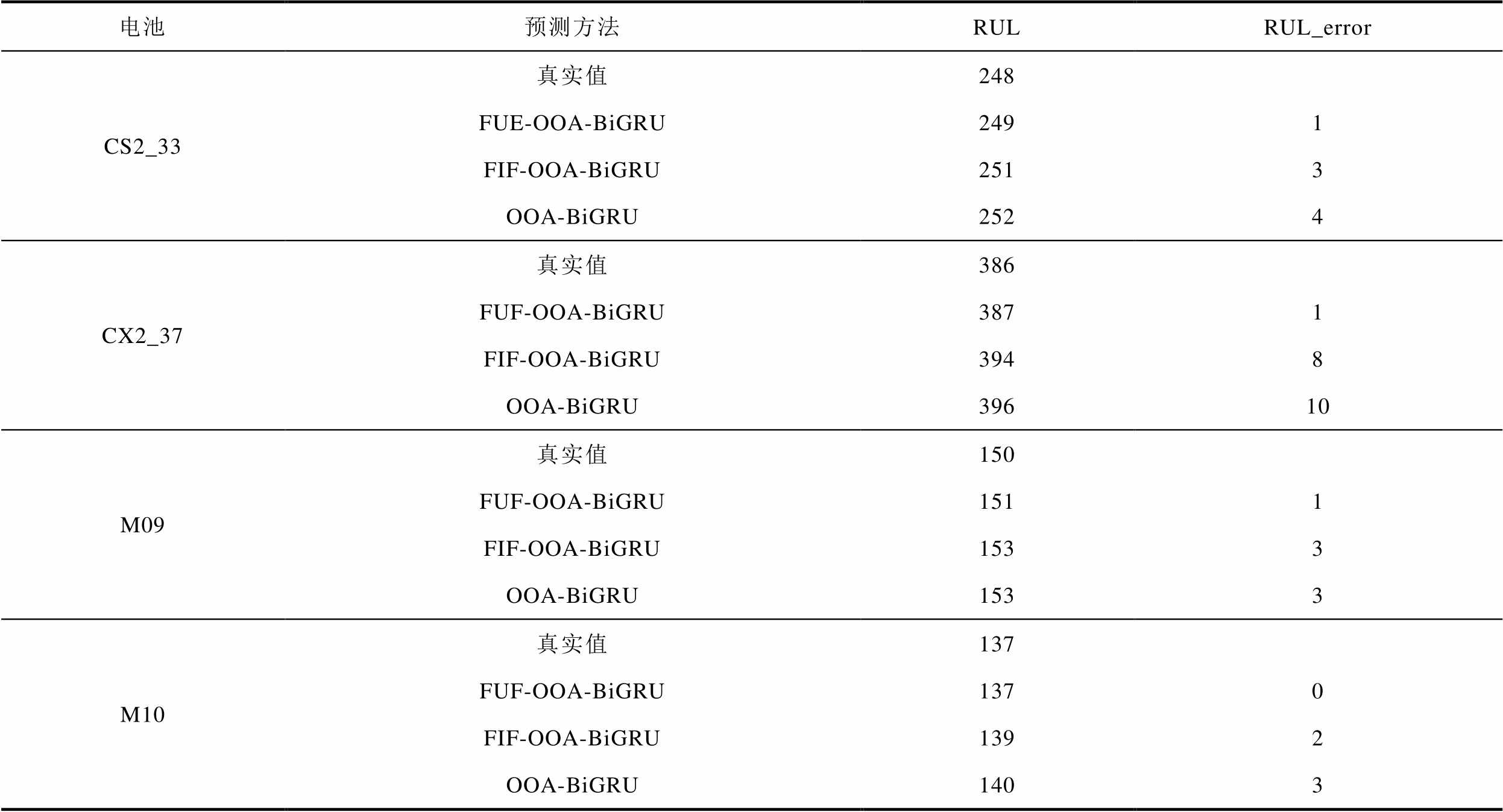
OOA-BiGRU模型在不同特征的RUL预测结果与误差数据见表7。可以观察到,表中所有模型均实现了较为精准的RUL预测。但所提方法相较于FIF-OOA-BiGRU和基于全部特征的OOA-BiGRU在CS2_33、CX2_37和M09电池的RUL预测精度上实现了进一步的提高;在M10电池中,FUF-OOA-BiGRU模型实现了RUL的零误差预测。实际数据证明,基于FUF-OOA-BiGRU的模型满足了高精度RUL预测的要求,且保障了预测方法的普适性。
表7 OOA-BiGRU模型在不同特征上的RUL预测结果及误差
Tab.7 RUL prediction results and errors of OOA-BiGRU model on different features
电池预测方法RULRUL_error CS2_33真实值248 FUE-OOA-BiGRU2491 FIF-OOA-BiGRU2513 OOA-BiGRU2524 CX2_37真实值386 FUF-OOA-BiGRU3871 FIF-OOA-BiGRU3948 OOA-BiGRU39610 M09真实值150 FUF-OOA-BiGRU1511 FIF-OOA-BiGRU1533 OOA-BiGRU1533 M10真实值137 FUF-OOA-BiGRU1370 FIF-OOA-BiGRU1392 OOA-BiGRU1403
本文提出了一种基于融合特征和OOA-BiGRU的锂离子电池RUL预测方法,从HF提取、特征筛选和模型预测三个方面对现有研究方法的不足进行改进。
从电流、电压和时间三个简单易测的参数中提取能够反映电池老化状态的HF,提高数据采集的效率,解决电池容量难以在线直接测量且测量成本高的问题。考虑到提取出的HF并非都能对RUL的预测精度及可靠性起到正向作用,采用基于过滤器和包装器相融合的方法对HF进行筛选,选择出最终用于RUL预测的融合特征。将GRU模型升级为能同时处理过去和未来信息的BiGRU模型,增强了模型对电池性能随时间变化的长期依赖关系的捕获能力。采用OOA算法对BiGRU模型进行优化,降低了人工调试网络的时间成本以及提高了模型的预测精度,实现了超参数的自配置。
本文的研究成果在马里兰大学电池数据以及课题组自有电池数据上得到了验证。将所提的预测模型与其他常用的预测模型做对比,验证了BiGRU模型在处理多特征输入预测方面的精确性和可靠性。同时对比了融合特征与其他特征对RUL预测结果的影响,验证提取出的融合特征提取方法进一步提高了RUL预测的准确性,同时确保了研究方法的鲁棒性。本研究方法对硬件配置要求低且可以在线实现,适用于新能源汽车电池管理系统中的RUL预测模块,具有现实意义。
参考文献
[1] 邹才能, 陈艳鹏, 熊波, 等. 碳中和目标下中国新能源使命[J]. 中国科学院院刊, 2023, 38(1): 48-58.
Zou Caineng, Chen Yanpeng, Xiong Bo, et al. Mission of new energy under carbon neutrality goal in China [J]. Bulletin of Chinese Academy of Sciences, 2023, 38(1): 48-58.
[2] 方斯顿, 刘龙真, 孔赖强, 等. 基于双向长短期记忆网络含间接健康指标的锂电池SOH估计[J]. 电力系统自动化, 2024,48(4): 160-168.
Fang Sidun, Liu Longzhen, Kong Laiqiang, et al. State-of-health estimation for lithium-ion batteries incorporating indirect health indicators based on bi-directional long short-term memory networks[J]. Automation of Electric Power Systems, 2024, 48(4): 160-168.
[3] 王晓姬, 王道涵, 王柄东, 等. 电动汽车驱动/充电一体化系统及其控制策略综述[J]. 电工技术学报, 2023, 38(22): 5940-5958.
Wang Xiaoji, Wang Daohan, Wang Bingdong, et al. A review of drive-charging integrated systems and control strategies for electric vehicles[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5940-5958.
[4] 李弈, 张金龙, 漆汉宏, 等. 基于变分深度嵌入-带有梯度惩罚的生成对抗网络的锂离子电池老化特性建模[J]. 电工技术学报, 2024, 39(13): 4226-4239.
Li Yi, Zhang Jinlong, Qi Hanhong, et al. Ageing performance modeling of Li-ion batteries based on variational deep embedding-Wasserstein GAN with gradient penalty[J]. Transactions of China Electro-technical Society, 2024, 39(13): 4226-4239.
[5] 于淼, 朱昱豪, 顾鑫, 等. 基于膨胀应力的锂离子电池剩余使用寿命预测[J]. 电气工程学报, 2024, 19(1): 49-56.
Yu Miao, Zhu Yuhao, Gu Xin, et al. Remaining useful life prediction of lithium-ion batteries based on expansion stress[J]. Journal of Electrical Engineering, 2024, 19(1): 49-56.
[6] 赵珈卉, 田立亭, 程林. 锂离子电池状态估计与剩余寿命预测方法综述[J]. 发电技术, 2023, 44(1): 1-17.
Zhao Jiahui, Tian Liting, Chen Lin. Review on state estimation and remaining useful life prediction methods forlithium-ion battery[J]. Power Generation Technology, 2023, 44(1): 1-17.
[7] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342.
Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium-ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
[8] 余佩雯, 郁亚娟, 常泽宇, 等. 相关向量机预测锂离子电池剩余有效寿命[J]. 电气技术, 2023, 24(2): 1-5.
Yu Peiwen, Yu Yajuan, Chang Zeyu, et al. Remain useful life prediction of lithium-ion battery based on relevance vector machine[J]. Electrical Engineering, 2023, 24(2): 1-5.
[9] Nájera J, Arribas J R, de Castro R M, et al. Semi-empirical ageing model for LFP and NMC Li-ion battery chemistries[J]. Journal of Energy Storage, 2023, 72: 108016.
[10] Hoekstra F S J, Donkers M C F, Bergveld H J. Rapid empirical battery electromotive-force and overpotentialmodelling using input-output linear parameter-varyingmethods[J]. Journal of Energy Storage, 2023, 65: 107185.
[11] Montaru M, Fiette S, Koné J L, et al. Calendar ageing model of Li-ion battery combining physics-based and empirical approaches[J]. Journal of Energy Storage, 2022, 51: 104544.
[12] Zhang Wei, Ma Fenfen, Guo Sibei, et al. A model cathode for mechanistic study of organosulfide electrochemistry in Li-organosulfide batteries[J]. Journal of Energy Chemistry, 2022, 66: 440-447.
[13] Khodadadi Sadabadi K, Jin Xin, Rizzoni G. Prediction of remaining useful life for a composite electrode lithium ion battery cell using an electrochemical model to estimate the state of health[J]. Journal of Power Sources, 2021, 481: 228861.
[14] Hosseininasab S, Lin Changwei, Pischinger S, et al. State-of-health estimation of lithium-ion batteries for electrified vehicles using a reduced-order electro-chemical model[J]. Journal of Energy Storage, 2022, 52: 104684.
[15] Torregrosa A J, Broatch A, Olmeda P, et al. A generalized equivalent circuit model for lithium-iron phosphate batteries[J]. Energy, 2023, 284: 129316.
[16] Koseoglou M, Tsioumas E, Panagiotidis I, et al. A lithium-ion battery equivalent circuit model based on a hybrid parametrization approach[J]. Journal of Energy Storage, 2023, 73: 109051.
[17] Li Guishu, Xie Song, Guo Wenqi, et al. Equivalent circuit modeling and state-of-charge estimation of lithium titanate battery under low ambient pressure[J]. Journal of Energy Storage, 2024, 77: 109993.
[18] Lü Hang, Liao Youping, Zhao Changlu, et al. State of charge estimation of lithium-titanate battery based on multi-model extended Kalman filter considering temperature and current rate[J]. Journal of Energy Storage, 2024, 77: 109890.
[19] El-Dalahmeh M, Al-Greer M, El-Dalahmeh M, et al. Physics-based model informed smooth particle filter for remaining useful life prediction of lithium-ion battery[J]. Measurement, 2023, 214: 112838.
[20] Duan Bin, Zhang Qi, Geng Fei, et al. Remaining useful life prediction of lithium-ion battery based on extended Kalman particle filter[J]. International Journal of Energy Research, 2020, 44(3): 1724-1734.
[21] WangJiaolong, Zhang Fode, Zhang Jianchuan, et al. A flexible RUL prediction method based on poly-cell LSTM with applications to lithium battery data[J]. Reliability Engineering & System Safety, 2023, 231: 108976.
[22] 李英顺, 阚宏达, 郭占男, 等. 基于数据预处理和VMD-LSTM-GPR的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024,39(10): 3244-3258.
Li Yingshun, Kan Hongda, Guo Zhannan, et al. Prediction of remaining useful life of lithium-ion battery based on data preprocessing and VMD-LSTM-GPR[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3244-3258.
[23] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024,39(1): 289-302.
Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
[24] Zhang Senju, Kang Rui, Lin Yanhui. Remaining useful life prediction for degradation with recovery phenomenon based on uncertain process[J]. Reliability Engineering & System Safety, 2021, 208: 107440.
[25] Streb M, Ohrelius M, Siddiqui A, et al. Diagnosis and prognosis of battery degradation through reevaluation and Gaussian process regression of electrochemical model parameters[J]. Journal of Power Sources, 2023, 588: 233686.
[26] Xu Xiaodong, Tang Shengjin, Yu Chuanqiang, et al. Remaining useful life prediction of lithium-ion batteries based on Wiener process under time-varying temperature condition[J]. Reliability Engineering & System Safety, 2021, 214: 107675.
[27] Zhou Zhongkai, Duan Bin, Kang Yongzhe, et al. Health feature extraction and efficient sorting of second-life lithium-ion batteries[J]. IEEE Transactions on Energy Conversion, 2024, 39(2): 1373-1382.
[28] Peng Simin, Sun Yunxiang, Liu Dandan, et al. State of health estimation of lithium-ion batteries based on multi-health features extraction and improved long short-term memory neural network[J]. Energy, 2023, 282: 128956.
[29] Li Lei, Li Yuanjiang, Mao Runze, et al. Remaining useful life prediction for lithium-ion batteries with a hybrid model based on TCN-GRU-DNN and dual attention mechanism[J]. IEEE Transactions on Transportation Electrification, 2023, 9(3): 4726-4740.
[30] Guo Fei, Wu Xiongwei, Liu Lili, et al. Prediction of remaining useful life and state of health of lithium batteries based on time series feature and Savitzky-Golay filter combined with gated recurrent unit neural network[J]. Energy, 2023, 270: 126880.
[31] Zhang Jiusi, Huang Congsheng, Chow M Y, et al. A data-model interactive remaining useful life predictionapproach of lithium-ion batteries based on PF-BiGRU-TSAM[J]. IEEE Transactions on Industrial Informatics, 2024, 20(2): 1144-1154.
[32] Mazzi Y, Ben Sassi H, Errahimi F. Lithium-ion battery state of health estimation using a hybrid model based on a convolutional neural network and bidirectional gated recurrent unit[J]. Engineering Applications of Artificial Intelligence, 2024, 127: 107199.
Abstract With the continuous development of the new energy vehicle industry, lithium-ion batteries are used in large quantities as on-board power batteries. The battery management system (BMS) is responsible for monitoring, evaluating, maintaining, and optimizing the performance and life of Li-ion batteries, and the prediction of c is an important part of the BMS. Accurate prediction of a battery's RUL helps identify batteries that are nearing the end of their life to prevent potential safety risks such as overheating, combustion, or explosion, and allows O&M personnel to schedule battery maintenance and replacements based on the battery’s actual state of health, rather than on a pre-determined schedule, thereby reducing unnecessary O&M costs. However, lithium-ion batteries exhibit nonlinear aging trends due to their complex internal chemical reactions during use, and the aging process of batteries usually exhibits multi-stage degradation, which increases the difficulty of RUL prediction. In view of this, this paper proposes a RUL prediction method for lithium-ion batteries based on public battery data from the University of Maryland and lithium iron phosphate battery data collected by the group's own laboratory, and the main research contributions are as follows:
Aiming at the problem that battery capacity is difficult to be measured directly, and the poor ability of traditional network models to capture multi-feature input information, a method is proposed to optimize the bidirectional gated recurrent unit (BiGRU) network based on the fusion feature and the osprey optimization algorithm (OOA) for RUL prediction of lithium-ion batteries. Simple and easy-to-measure current, voltage and time data during battery aging are collected, from which the health factors that can reflect the aging trend of the battery are extracted. The Savitzky-Golay filtering method is selected to reduce the influence of noise on the prediction accuracy. A fusion feature screening strategy combining filter and wrapper is proposed to reduce the complexity of the model and prevent model overfitting. Considering the insufficient ability of the traditional model to capture battery aging information when dealing with multi-feature inputs, the GRU network, which predicts only based on historical information, is upgraded to the BiGRU network, which is capable of handling both forward and backward information of the sequences. The BiGRU network is able to understand the overall structure and dynamic properties of the sequences in a more in-depth manner, better integrate the multi-dimensional features, and adapt to dependencies in different time scales. OOA is used to effectively optimize the hyper parameters inside the BiGRU model, which improves the prediction accuracy of the model and also realizes the automatic configuration of the parameters. Different types of battery data are used to compare the proposed method with traditional network models to verify the reliability of the proposed OOA-BiGRU model. In addition, the effect of the proposed fusion feature prediction is compared with all feature prediction and filtered feature prediction, which proves that the fusion feature better represents the aging degree of the battery and improves the accuracy of the model prediction.
The research results of this paper provide a new method and idea for RUL prediction of lithium-ion power batteries, which can be applied to the BMS system of new energy vehicles and is of practical significance.
Keywords:Lithium-ion batteries, remaining useful life (RUL), bidirectional gated recurrent unit (BiGRU), health factor (HF), fusion feature
中图分类号:TM912.9
DOI: 10.19595/j.cnki.1000-6753.tces.241243
烟台市科技创新发展计划基础研究类项目(2023JCYJ043)、山东省自然科学基金项目(ZR2021ME236)和山东省高校青年创新团队科技支撑计划(2020KJN005)资助。
收稿日期 2024-07-12
改稿日期 2024-11-17
孙 静 女,1979年生,副教授,硕士生导师,研究方向为锂离子电池管理技术。
E-mail:sunjing@sdu.edu.cn(通信作者)
翟千淳 男,1999年生,硕士研究生,研究方向为锂离子电池健康状态估计与剩余使用寿命预测。
E-mail:1030033160@qq.com
(编辑 郭丽军)