图1 本文技术路线
Fig.1 Technical roadmap of this study
摘要 准确地预测电池荷电状态(SOC)对于提高电池的利用效率及安全性能具有重要意义。传统电池SOC预测方法高度依赖机理模型和统计模型,存在异常值敏感、实践精度受限等问题。该文提出一种卷积神经网络-长短时记忆神经网络-注意力机制(CNN-LSTM-AM)模型,通过电池可测变量预测SOC变化趋势。该模型首先利用一维卷积神经网络(CNN)提取可测变量的空间特征;然后将其送至长短时记忆(LSTM)进行时间序列分析;最后引入注意力机制(AM)筛选关键特征,并降低特征数据冗余程度。此外,CNN-LSTM-AM模型在训练过程中采用雾凇优化算法(RIME)进行超参数寻优,有效地提高训练效率、降低训练成本。在磷酸铁锂公开数据集上开展实践测评,结果表明,基于CNN-LSTM-AM模型的电池SOC预测性能良好,优于传统时间序列预测方法,其方均根误差为0.64%、平均绝对误差为0.52%(25℃)。此外,该模型适用于动态工况下的电池状态预测,具有较高的预测精度和鲁棒性。
关键词:储能锂离子电池 荷电状态 长短时记忆 注意力机制 雾凇优化算法
随着风能、太阳能等可再生能源的快速发展,锂离子电池在储能领域得到广泛应用。为了确保锂离子电池安全稳定运行,对于电池荷电状态(State of Charge, SOC)的监测至关重要,有助于预防过充、过放等事故发生[1]。然而,由于电池内部反应机理复杂,直接测量SOC十分困难,这给电池SOC的准确估计带来挑战[2-3]。因此,开展储能锂离子电池SOC测量研究具有重要理论和实际意义[4-6]。
SOC预测方法大致可归纳为三种类型,即机理方法、直接法和数据驱动方法。其中,机理方法是利用先验专家知识预估电池运行状态,建立的模型包括等效电路模型和电化学模型。S. J. Navas等[7]应用二阶RC等效电路模型预测锂离子电池SOC,平均相对误差为0.15%。王静荣等[8]基于电化学模型建立一种锂离子电池SOC估计方法,适用于不同温度条件,具有较强的泛化能力。然而,机理方法在实践应用过程中存在一定弊端,如高度依赖专家知识、容易受运行环境因素干扰。直接法主要通过分析电池的放电曲线和充电曲线预测电池SOC,常见的方法有库仑计数法和开路电压(Open Circuit Voltage, OCV)法。黄聪生[9]建立一种库仑计数故障诊断算法,通过测量电池负载电流和端电压获悉SOC变化趋势。然而,由于电池初始SOC不确定,库仑计数法的预计精度偏低。相比之下,开路电压法性能更为稳定,无需电池先验信息即可准确预测SOC。A. Gismero等[10]提出了一种基于开路电压法的电池SOC预测方法,具有计算复杂度低、可靠性强等优势。但不足之处在于开路电压法仅能离线测量,难以在线估计电池SOC。
目前,大量研究工作致力于数据驱动方法估计电池状态,通过离线学习电池历史数据建立在线预测模型。常见的数据驱动方法包括粒子群算法[11]、支持向量机[12]和反向传播神经网络等。E. D. Bobobee等[13]基于粒子群算法建立了一种具备温度补偿功能的SOC估计模型,实现锂离子电池状态的在线诊断。针对不同温度条件下电池的检测问题,反向传播神经网络建立了电池可测变量(如电压、电流和温度)和电池SOC的端到端映射,预测精度得到明显提升。值得注意的是,锂离子电池SOC是一个连续变化过程,即当前状态与过去充放电状态存在联系,然而传统预测模型关注的是当前时刻的电池信息,而忽略了历史信息的影响。
针对这种情况,基于时间序列的电池SOC预测方法相继被提出,如循环神经网络(Recurrent Neural Network, RNN)。V. Prakash等[14]提出一种基于RNN的电池SOC预测方法,并用于分析电池充放电动态特性。然而,传统RNN在训练过程中易遭遇梯度消失等问题,造成SOC预测性能较差。李宁等[15]提出了一种门控循环单元以解决模型训练问题,有效地提高了锂离子电池SOC估计方法的可靠性。在此基础上,一种基于长短时记忆(Long Short-Term Memory, LSTM)网络的模型被提出,可有效解决电池SOC预测方法学习长期依赖的问题。刘素贞等[16]对锂电池充放电的超声信号进行特征提取,并结合LSTM网络实现SOC的精确估计。为了进一步减轻计算负担,赵芬等[17]利用卷积神经网络(Convolutional Neural Network, CNN)提取电池可测变量的深层特征,然后输入RNN以实现SOC的精确估计。
虽然基于时间序列的SOC预测方法可以捕获数据连续变化关系,但面对高维数据输入仍难以筛选出关键输入特征。鉴于此,本文首先提出一种CNN-LSTM-AM模型,并应用于电池SOC预测任务,有效捕获重要输入特征、提高预测精度;然后,设计一种雾凇优化算法(Rime optimization algorithm, RIME),可以自动搜索CNN-LSTM-AM模型最优解,有效降低超参数寻优的时间成本;最后,研究不同环境温度和初始SOC数值对CNN-LSTM-AM预测精度的影响,并将其与传统预测模型进行性能比较,以验证其强鲁棒性和高泛化能力。
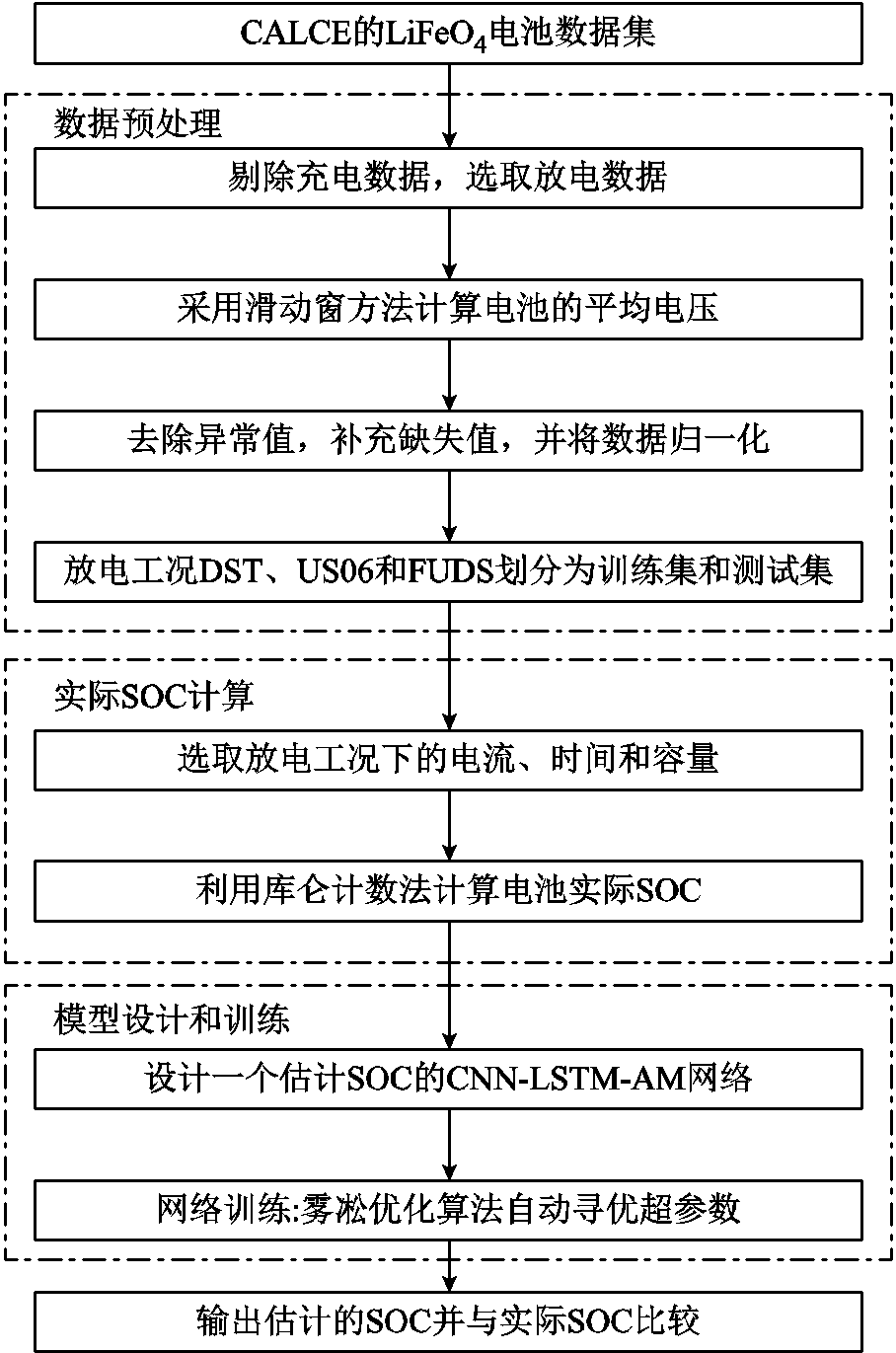
基于电池可测变量数据,本文提出一种CNN-LSTM-AM模型,并利用雾凇优化算法对其超参数寻优,最终实现电池SOC预测。具体技术路线如图1所示。
首先,对可测变量数据进行预处理,并将其划分为训练数据集和测试数据集;其次,将训练数据集输入CNN-LSTM-AM模型中,输出预测的SOC。通过迭代训练,不断更新模型参数。在测试阶段,首先加载已训练模型,然后利用测试集检验SOC预测性能,以验证模型的精确性和泛化性。电池SOC预测模型的结构具体分为三部分:①数据库的选取和划分、数据预处理;②所提出的CNN-LSTM-AM模型结构;③以训练集更新模型参数和寻优超参数,以测试集验证模型的准确性和鲁棒性。

图1 本文技术路线
Fig.1 Technical roadmap of this study
本文建立的CNN-LSTM-AM模型的结构框架如图2所示。电池可测变量数据包括电池的电流、电压、温度和平均电压,通过输入层输入。其中,平均电压可以有效地反映OCV的趋势变化[18],该变化与电池SOC紧密相关。平均电压的引入使输入数据具有缓慢时变信息,有助于神经网络学习输入数据快速波动时的电池内部特性,并减小输出SOC波动。具体来说,本文采用滑动平均滤波技术,将当前时刻之前的一个窗口时间内的电压平均作为该时刻对应的滑动窗口平均电压,计算过程表示为
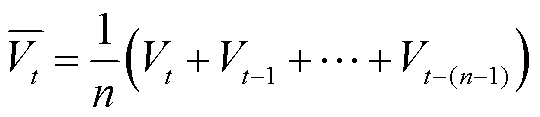 (1)
(1)
式中,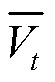 为t时刻对应的窗口平均电压;
为t时刻对应的窗口平均电压;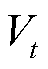 为t时刻的电压;n为滑动窗口的大小。
为t时刻的电压;n为滑动窗口的大小。
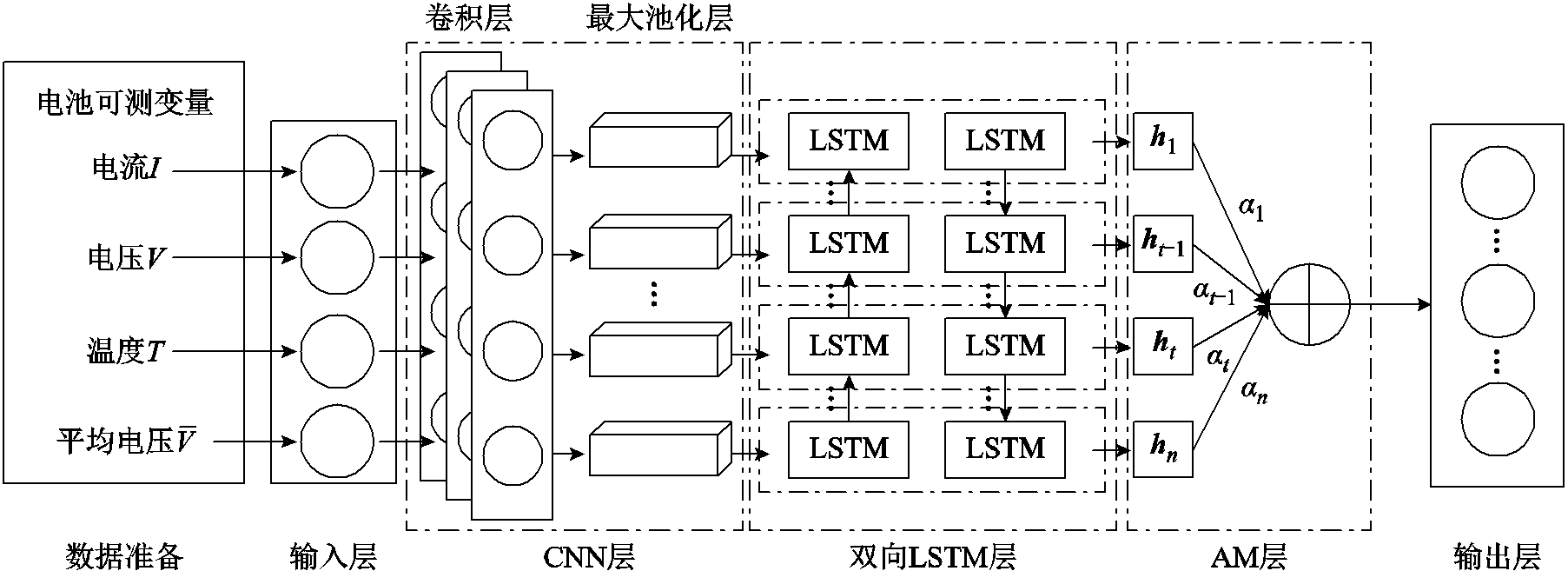
图2 CNN-LSTM-AM模型框架
Fig.2 CNN-LSTM-AM framework
CNN-LSTM-AM模型的超参数设置见表1。理论上,时间步长越大,网络跟踪效果越好。然而,考虑到计算能力限制,本文设置步长为30时效果较好。滑动窗尺寸至关重要,直接关系平均电压的时变程度,经过多次实验后选定为30。模型其他超参数设置由雾凇优化算法进一步确定。
表1 CNN-LSTM-AM模型的超参数设置
Tab.1 Hyperparameter settings for CNN-LSTM-AM model
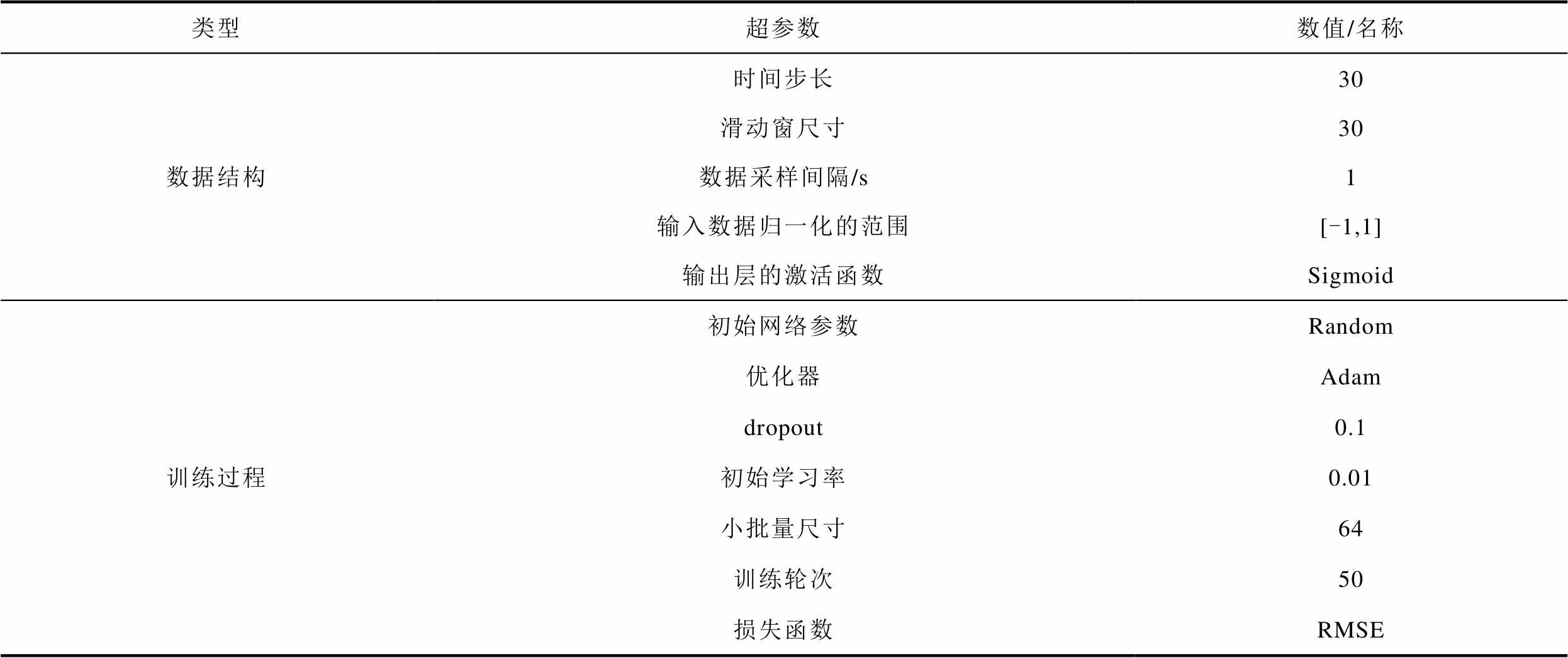
类型超参数数值/名称 数据结构时间步长30 滑动窗尺寸30 数据采样间隔/s1 输入数据归一化的范围[-1,1] 输出层的激活函数Sigmoid 训练过程初始网络参数Random 优化器Adam dropout0.1 初始学习率0.01 小批量尺寸64 训练轮次50 损失函数RMSE
卷积神经网络能够处理一维数据,称为一维卷积神经网络(1D-CNN)[19-20]。由于电压、平均电压、电流和温度等电池数据均是时间序列数据,因此可利用1D-CNN进行特征提取。CNN模型结构如图3所示。
CNN模型通常包括输入层、卷积层、池化层、全连接层和输出层五部分。本文使用的CNN网络增加dropout层进一步减少过拟合的影响。CNN特征提取的计算公式为
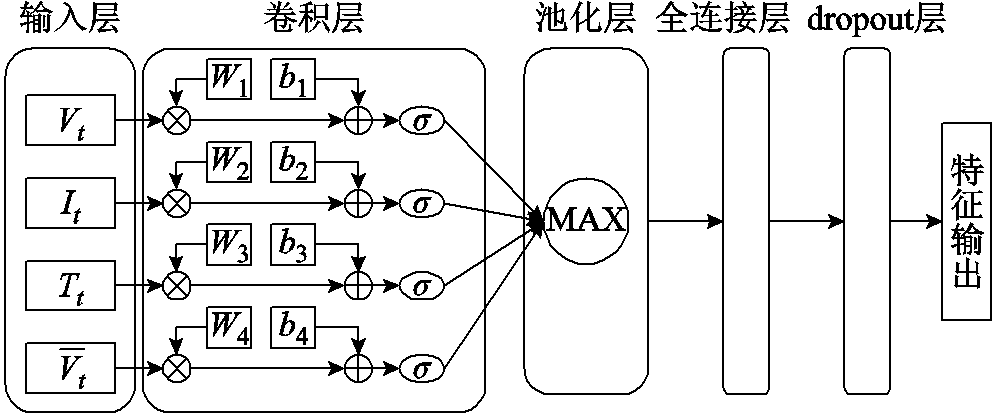
图3 CNN模型结构
Fig.3 CNN model structure
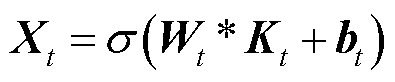 (2)
(2)
式中,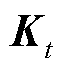 为图2中输入层t时刻的序列数据;
为图2中输入层t时刻的序列数据;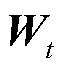 和
和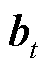 分别为权重矩阵和偏置量,需要通过训练得到最优参数;
分别为权重矩阵和偏置量,需要通过训练得到最优参数;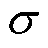 为激活函数;
为激活函数; 表示离散卷积;
表示离散卷积;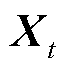 为输出序列。
为输出序列。
RNN在训练过程中,易遭遇梯度消失或梯度爆炸等问题,缺乏解决数据长期依赖性的能力[21]。相较而言,LSTM通过使用隐藏记忆细胞替代普通的隐藏节点,可有效避免此缺点[22]。LSTM网络结构如图4所示。
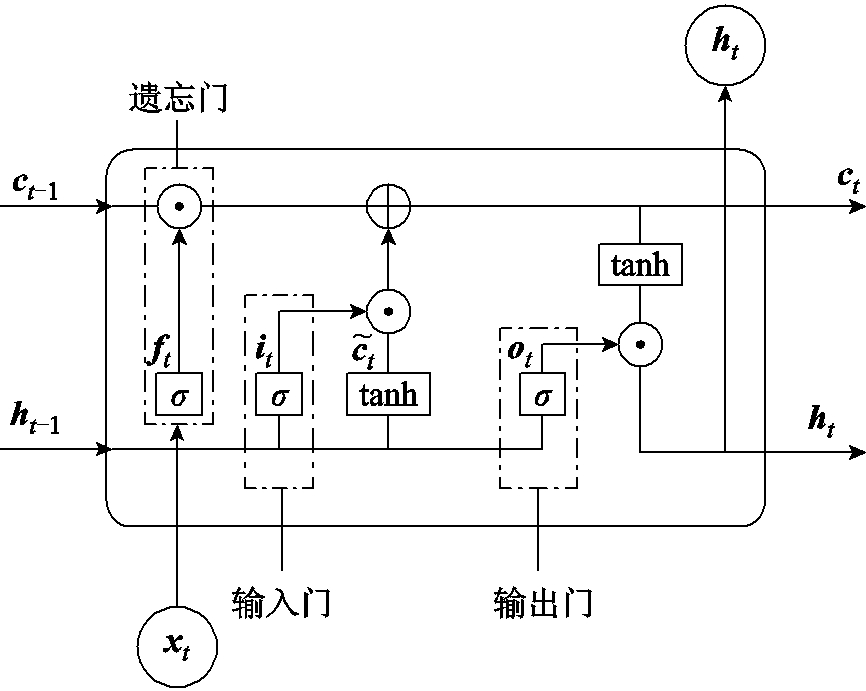
图4 LSTM网络结构
Fig.4 Structure diagram of LSTM network
LSTM包含输入门、遗忘门和输出门。其中,输入门i用来控制当前时刻记忆细胞的输入信息,遗忘门f用来控制上一个时刻记忆细胞中存储的历史信息,输出门o用来控制当前时刻记忆细胞的输出信息。LSTM计算公式为
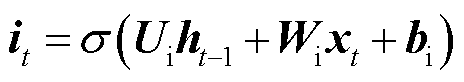 (3)
(3)
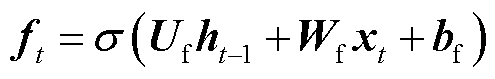 (4)
(4)
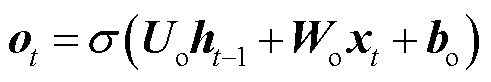 (5)
(5)
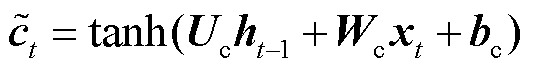 (6)
(6)
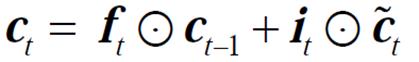 (7)
(7)
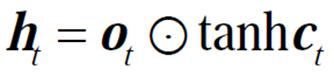 (8)
(8)
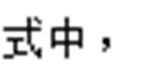
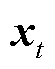 为当前t时刻的输入;
为当前t时刻的输入;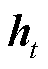 为当前t时刻细胞的状态值;
为当前t时刻细胞的状态值;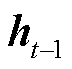 为上一个时刻细胞的状态值;
为上一个时刻细胞的状态值;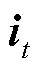 、
、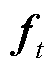 和
和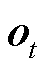 分别为输入门、遗忘门和输出门的激活向量;
分别为输入门、遗忘门和输出门的激活向量;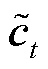 为候选存储记忆细胞的状态;
为候选存储记忆细胞的状态;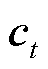 为记忆细胞的内部状态;U和W为权重矩阵;b为偏置量;
为记忆细胞的内部状态;U和W为权重矩阵;b为偏置量; 表示矩阵的点乘。
表示矩阵的点乘。
双向LSTM模块[23]将两个时序相反的LSTM单元连接起来,以获取输入序列的双向数据信息,并将此信息反馈至输出层。双向LSTM的基本结构如图5所示,其隐藏层的数据变换过程为
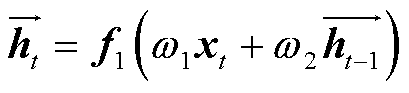 (9)
(9)
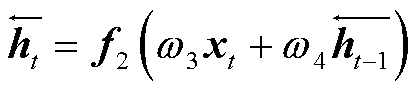 (10)
(10)
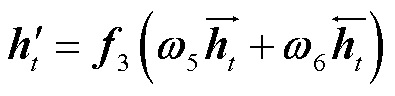 (11)
(11)
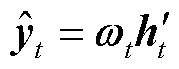 (12)
(12)
式中,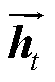 和
和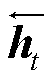 分别为LSTM单元的向前值和向后值;
分别为LSTM单元的向前值和向后值;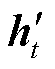 为隐藏层值;
为隐藏层值;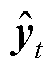 为输出值;f和
为输出值;f和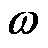 分别为激活向量和权重矩阵。
分别为激活向量和权重矩阵。
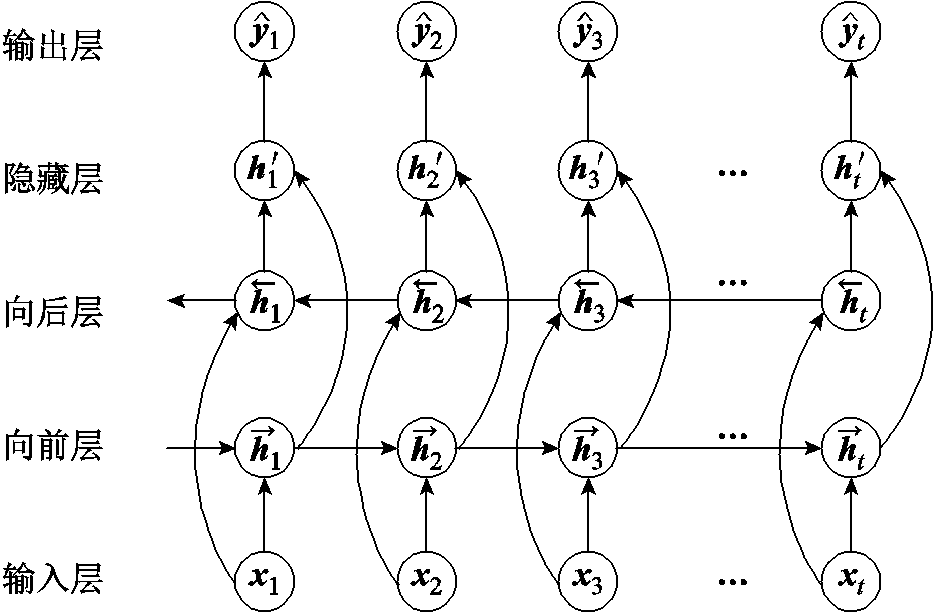
图5 双向LSTM的基本结构
Fig.5 Basic structure of a bidirectional LSTM
注意力机制(Attention Mechanism, AM)通过筛选不相关信息和放大相关信息来增强关键信息的重要性,最终提高模型的准确性和泛化性。注意力机制通过采用概率分布来充分关注关键信息,补偿LSTM网络由于序列过长而导致的信息损失。注意力机制结构如图6所示。
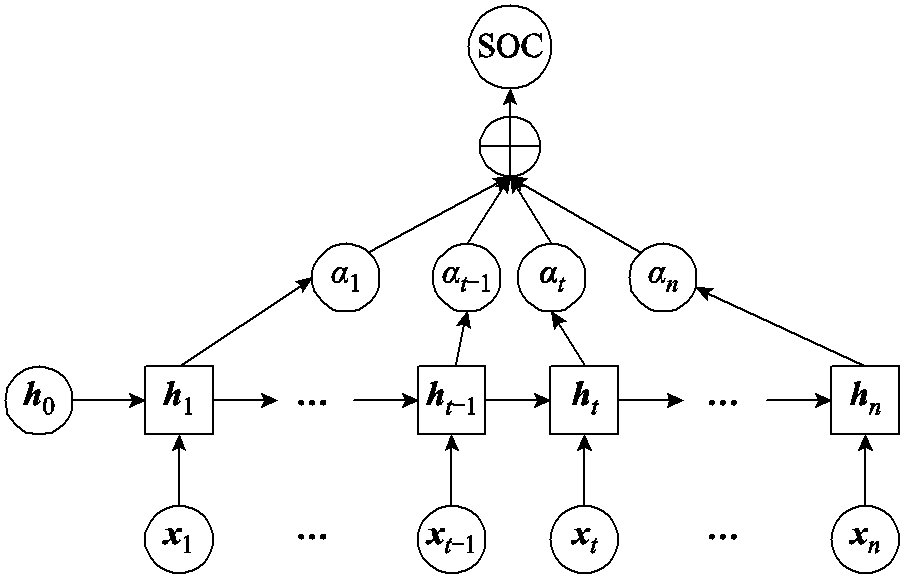
图6 注意力机制结构
Fig.6 Attention mechanism structure
图6中,x为LSTM网络的输入序列,h为LSTM隐藏层的输出序列,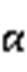 为输出到LSTM隐藏层的注意力机制的概率分布,通过注意力机制优化的LSTM输出电池SOC。注意力的权重计算过程为
为输出到LSTM隐藏层的注意力机制的概率分布,通过注意力机制优化的LSTM输出电池SOC。注意力的权重计算过程为
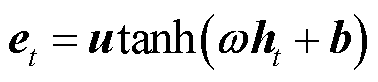 (13)
(13)
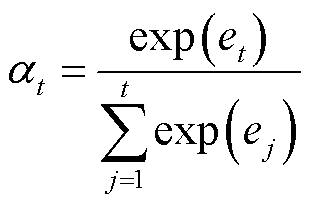 (14)
(14)
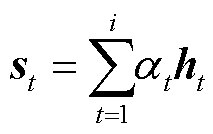 (15)
(15)
式中,u和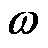 为权重系数;
为权重系数;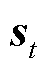 为t时刻注意力层的输出;注意力分数函数
为t时刻注意力层的输出;注意力分数函数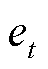 表示在t时刻LSTM网络输出向量和SOC之间的相关性。
表示在t时刻LSTM网络输出向量和SOC之间的相关性。
雾凇优化算法是一种基于自然现象的元启发式算法,其灵感来源于自然界中雾凇的生长行为[24]。RIME主要由三部分组成:①模拟雾凇中软雾凇粒子的运动,并提出一种软雾凇搜索策略,用于探索该算法;②模拟硬雾凇代理之间的交叉行为,提出一种硬雾凇穿刺机制,用于开发该算法;③增强算法的贪婪机制,提出正贪婪选择机制。RIME整体流程如图7所示。
RIME数学模型及计算公式为
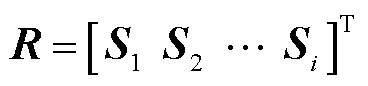 (16)
(16)
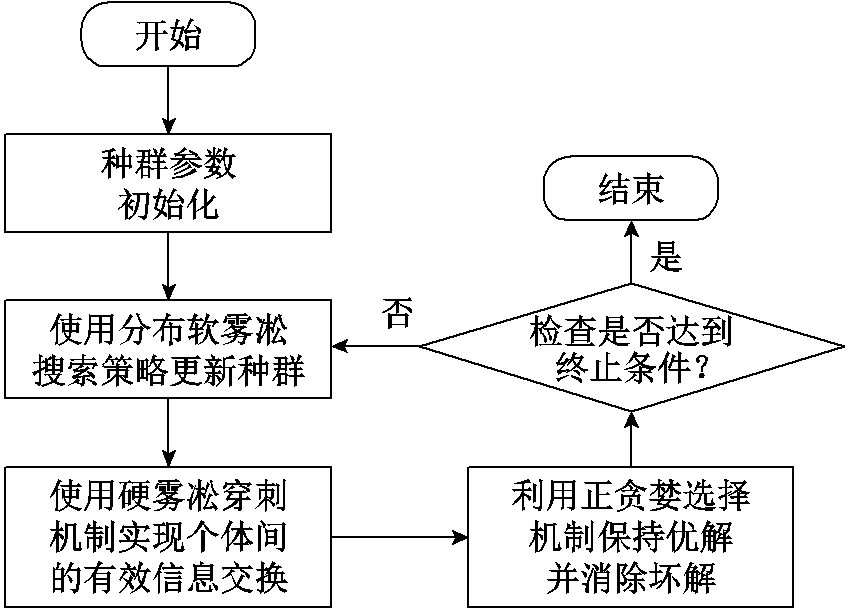
图7 RIME整体流程
Fig.7 RIME overall flow chart
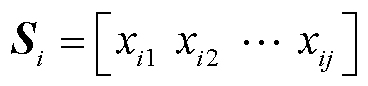 (17)
(17)
式中,R为雾凇集群初始化的状态;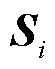 为霜剂;
为霜剂;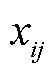 为每一个雾凇粒子的位置。式(16)和式(17)表示雾凇集群初始化的过程。
为每一个雾凇粒子的位置。式(16)和式(17)表示雾凇集群初始化的过程。
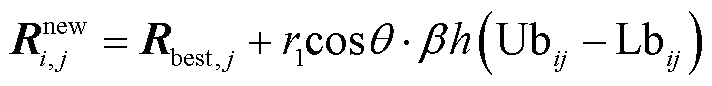 (18)
(18)
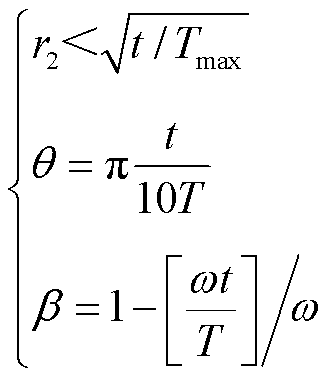 (19)
(19)
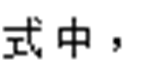
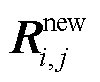 为更新粒子的位置;
为更新粒子的位置; 为集群R最佳霜剂的第j个粒子;
为集群R最佳霜剂的第j个粒子;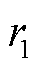 为(-1,1)范围内的随机数,并且控制粒子运动方向
为(-1,1)范围内的随机数,并且控制粒子运动方向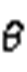 随迭代次数的增加而变化;h为粘附度,是(0,1)范围内的随机数,用于控制两个雾凇粒子的中心距离;
随迭代次数的增加而变化;h为粘附度,是(0,1)范围内的随机数,用于控制两个雾凇粒子的中心距离;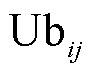 和
和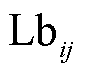 分别为粒子逃逸空间的上限和下限;t为当前迭代次数;Tmax为最大迭代次数;
分别为粒子逃逸空间的上限和下限;t为当前迭代次数;Tmax为最大迭代次数;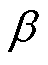 为阶跃函数;
为阶跃函数;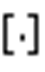 表示四舍五入;
表示四舍五入;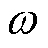 为控制阶跃函数的段数,默认为5;
为控制阶跃函数的段数,默认为5;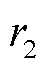 为(0,1)范围内的随机数。式(18)和式(19)为软雾凇搜索过程。
为(0,1)范围内的随机数。式(18)和式(19)为软雾凇搜索过程。
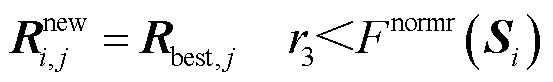 (20)
(20)
式中,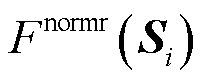 为当前智能体适应度的归一化值;
为当前智能体适应度的归一化值;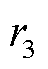 为(-1,1)范围内的随机数。
为(-1,1)范围内的随机数。
RIME算法的主要优势包括:①软雾凇搜索策略使RIME算法具有独特的逐步勘探开发方法;②硬雾凇穿刺机制使RIME算法能够快速锁定全局近似最优解,实现高效率和高精度;③正贪婪选择机制使RIME算法能够主动改变智能体的位置,显著降低算法的性能损失。学习率区间为0.001~0.1,卷积核大小设置范围为2~5,隐藏神经元数量为50~60。雾凇算法优化超参数的结果见表2。
表2 雾凇算法优化超参数的结果
Tab.2 Results of optimizing hyperparameters using the RIME algorithm
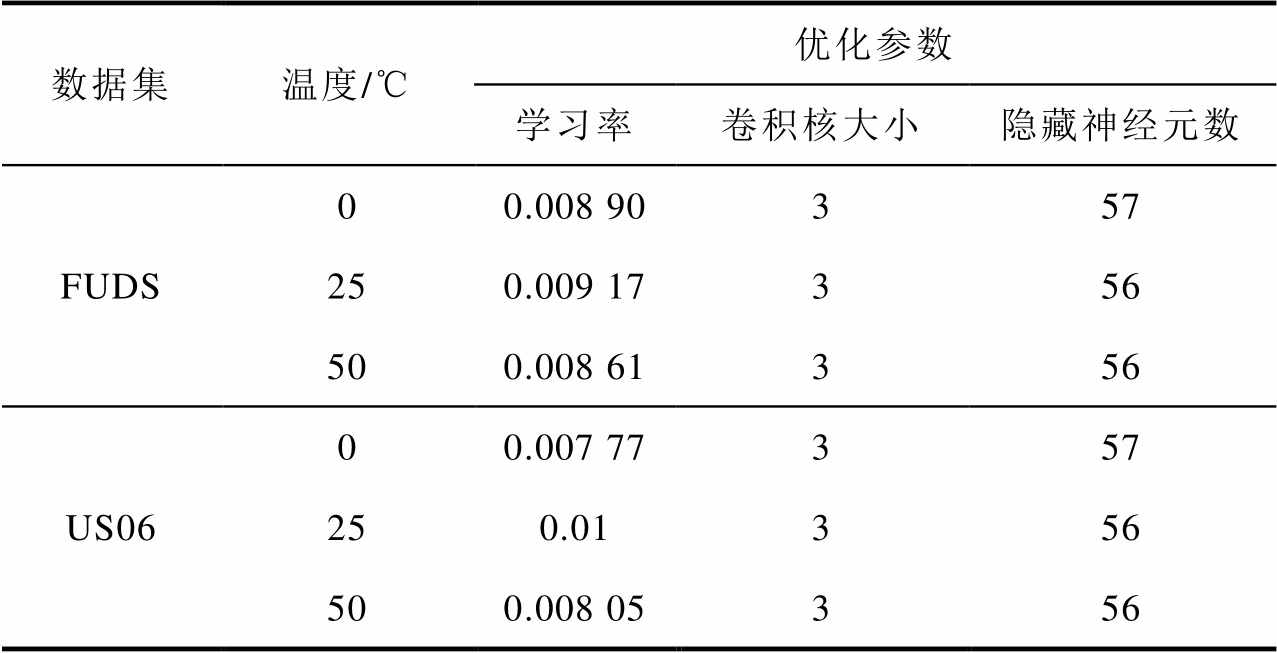
数据集温度/℃优化参数 学习率卷积核大小隐藏神经元数 FUDS00.008 90357 250.009 17356 500.008 61356 US0600.007 77357 250.01356 500.008 05356
储能电池在实际运行过程中面临复杂的运行条件,因此本文拟采用不同工况条件进行测试,包括动态压力测试(Dynamic Stress Test, DST)、美国联邦城市运行工况(Federal Urban Driving Schedule, FUDS)和US06驾驶时间表对锂离子电池运行条件仿真。考虑到神经网络需要大量数据进行学习,因此将DST工况下收集的数据作为训练集。为了验证SOC估计方法的泛化能力,训练集应与测试集不同,以评价SOC估计在未知数据上的性能。因此,将FUDS和US06工况下收集的数据作为未知测试数据集,用于测试所提方法的SOC估计性能。
电池储能系统最常用的锂电池是磷酸铁锂电池(LiFeO4)和三元锂电池,因此实验使用马里兰大学高级生命周期工程中心(CALCE)的LiFeO4公共数据集[25]。考虑到低温条件下电池动态工况不稳定,同时低温会影响电池使用寿命,将增加SOC估计难度,特别是对于LiFeO4电池来说。鉴于此,本文采用的DST、US06和FUDS的数据集均为0℃及以上,即0、10、20、25、30、40、50℃,采样时间为1 s。其中,DST、US06和FUDS数据集在25℃下的电流、电压、温度和平均电压曲线如图8所示。
2.2.1 SOC的定义
SOC定义为
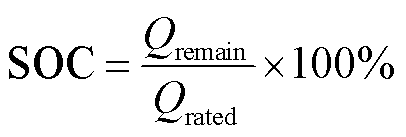 (21)
(21)
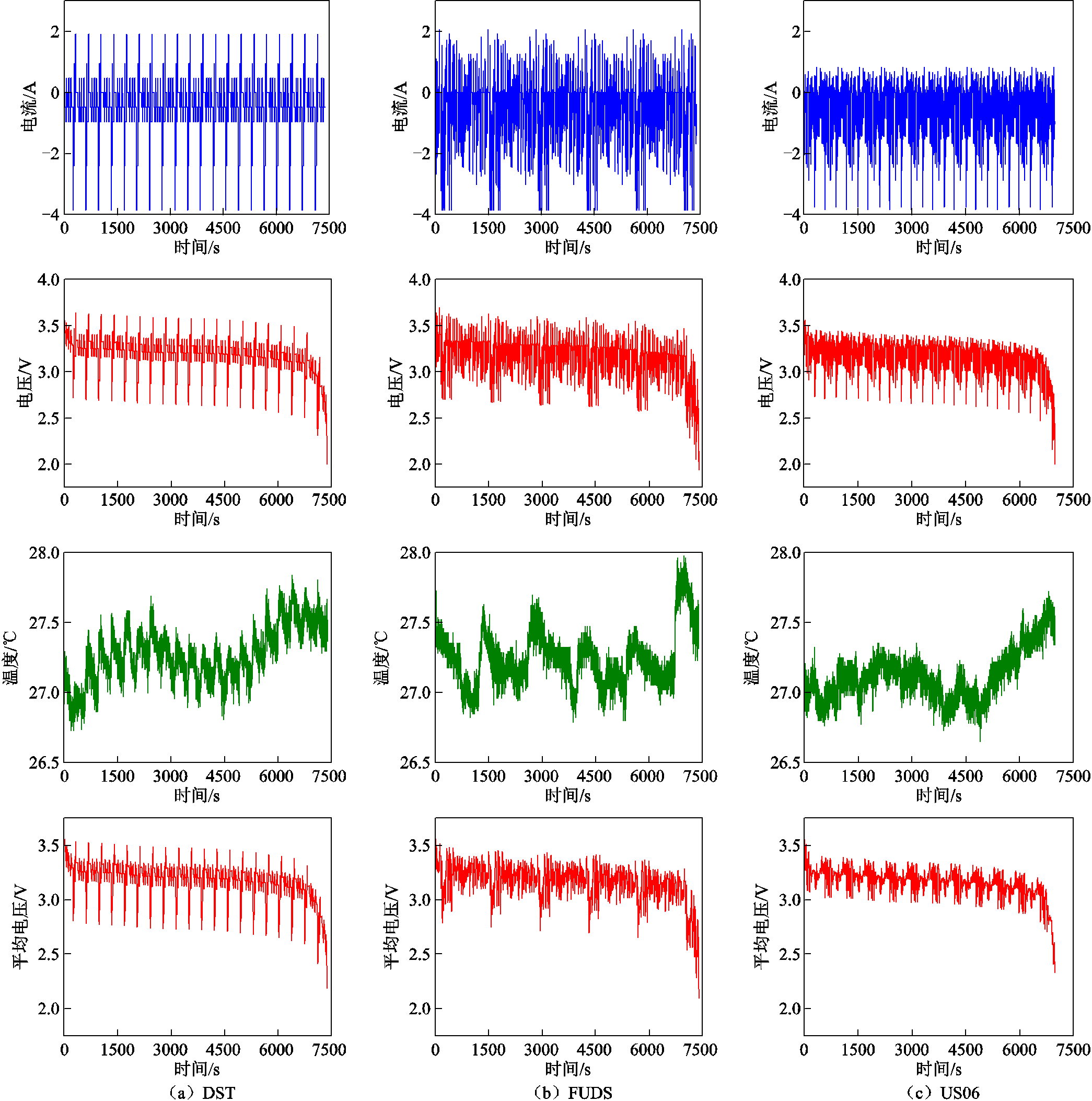
图8 25℃下DST、FUDS和US06的电流、电压、温度和平均电压
Fig.8 Current ,voltage, temperature and average voltage of DST,FUDS and US06 at 25℃
式中, 为电池当前剩余容量;
为电池当前剩余容量; 为电池最大可用容量。
为电池最大可用容量。
2.2.2 数据归一化及性能评估指标
为了提高网络的鲁棒性,可测变量(电流、电压、温度和平均电压)需要归一化。本文采用最大最小归一化原则预处理电池数据,具体公式为
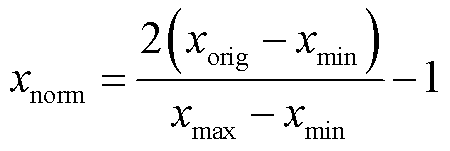 (22)
(22)
式中,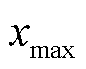 和
和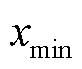 分别为数据库所测变量的最大值和最小值;
分别为数据库所测变量的最大值和最小值;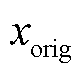 为原始数据;
为原始数据;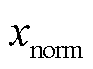 为归一化后的数据。此外,本文使用方均根误差(Root Mean Square Error, RMSE)和平均绝对误差(Mean Absolute Error, MAE)评估所提方法的SOC估计性能,定义为
为归一化后的数据。此外,本文使用方均根误差(Root Mean Square Error, RMSE)和平均绝对误差(Mean Absolute Error, MAE)评估所提方法的SOC估计性能,定义为
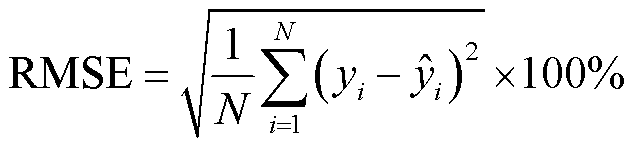 (23)
(23)
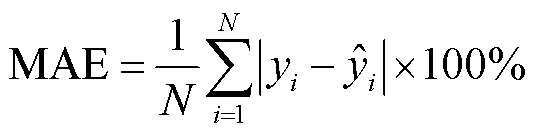 (24)
(24)
式中,N为样本总数;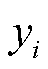 为库仑计数法得出的SOC真实值;
为库仑计数法得出的SOC真实值;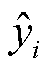 为SOC估计方法中的估计值。RMSE和MAE越接近于0,表示预测性能越好。
为SOC估计方法中的估计值。RMSE和MAE越接近于0,表示预测性能越好。
本节重点探讨了CNN-LSTM-AM模型估计SOC的性能。根据表1中超参数设置,在0~50℃温度范围内使用DST数据集对CNN-LSTM-AM进行训练。值得注意的是,CNN-LSTM-AM模型采用DST全温度数据进行训练。为了全面评估模型的训练效果,本文引入FUDS数据集和US06数据集作为验证集。此外,使用相同的数据集对CNN-LSTM进行训练,通过比较CNN-LSTM和CNN-LSTM-AM的估计误差,可以验证添加注意力机制以提高SOC的估计性能。
利用与训练集不同的未知数据集FUDS和US06验证训练后的CNN-LSTM和CNN-LSTM-AM在不同温度下的SOC估计性能。使用FUDS和US06数据集在0、25、50℃下两个神经网络的SOC估计结果和对应的估计误差如图9~图12所示,可以看出,两种神经网络都可以捕获在不同温度下未知数据集SOC的下降趋势。基于不同模型的电池SOC预测性能比较见表3,真实的SOC由库仑计数法计算得到。通过比较图9~图12可以看出,与CNN-LSTM相比,CNN-LSTM-AM输出的SOC与真实SOC更加吻合。如表3所示,CNN-LSTM-AM估计SOC的RMSE均低于2%,MAE均低于1.5%。这表明注意力机制的加入可以提高网络的估计性能。
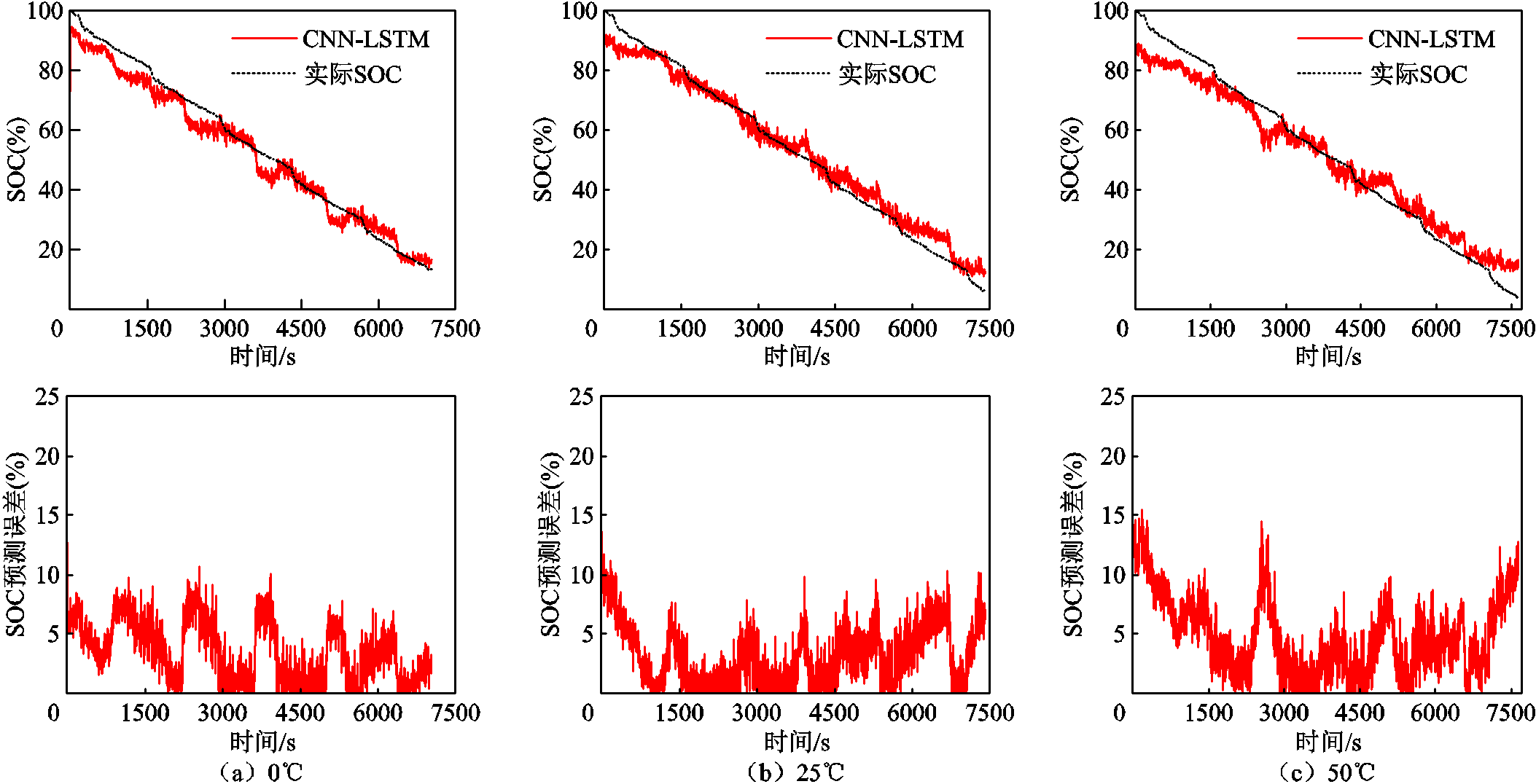
图9 FUDS的CNN-LSTM在不同温度条件下SOC预测结果
Fig.9 SOC prediction results of the CNN-LSTM for FUDS under different temperature conditions
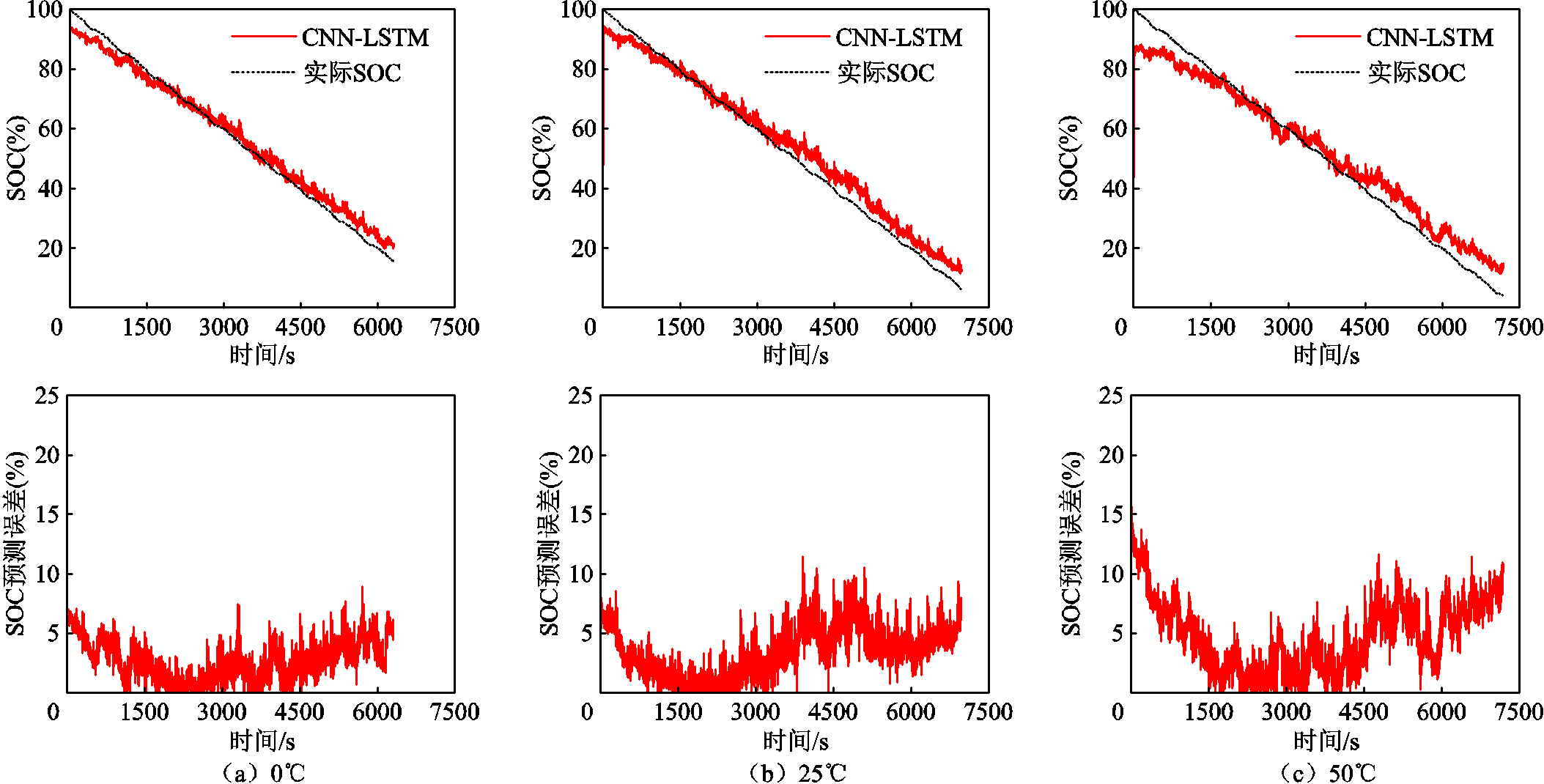
图10 US06的CNN-LSTM在不同温度条件下SOC预测结果
Fig.10 SOC prediction results of the CNN-LSTM for US06 under different temperature conditions
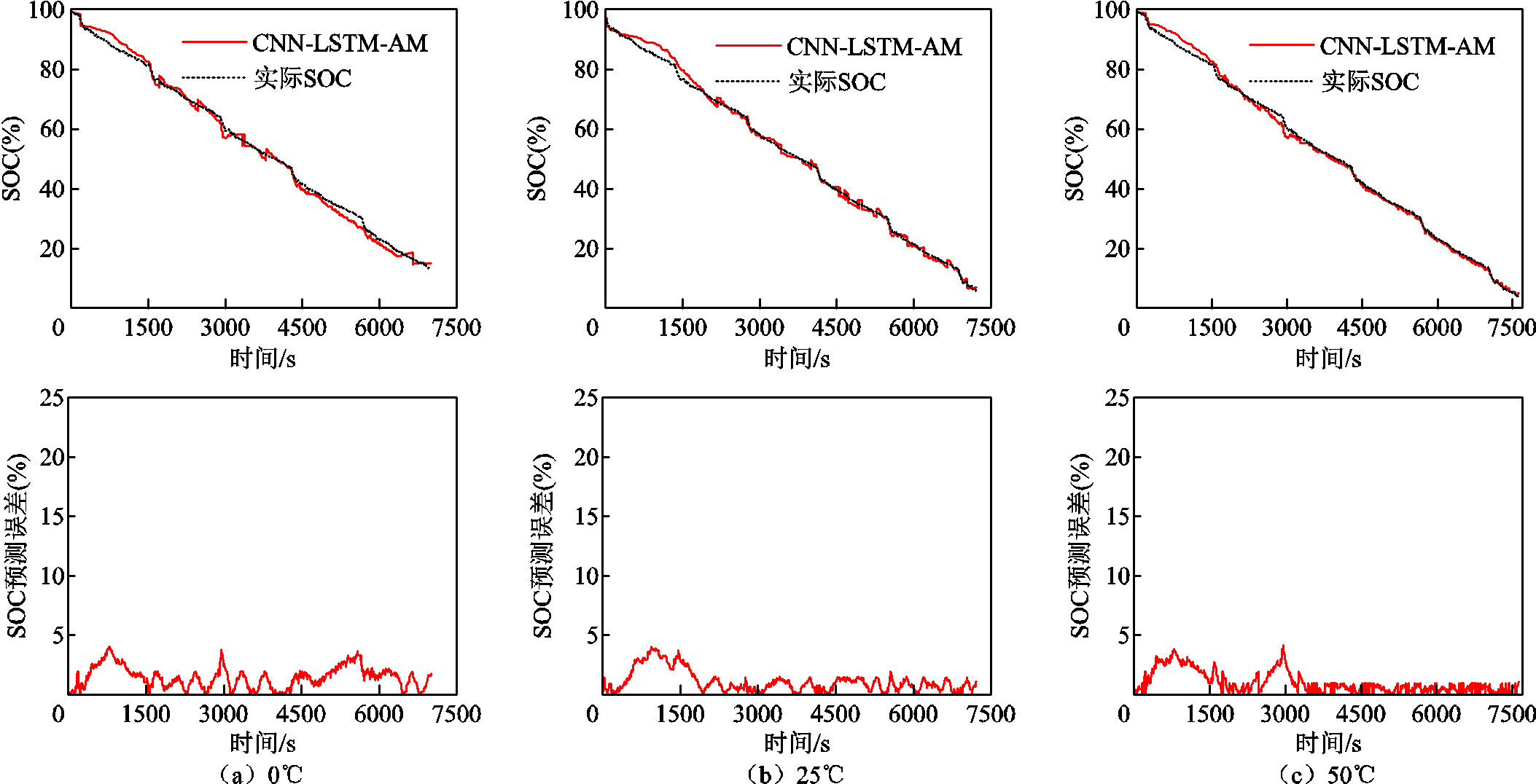
图11 FUDS的CNN-LSTM-AM在不同温度条件下SOC预测结果
Fig.11 SOC prediction results of the CNN-LSTM-AM for FUDS under different temperature conditions
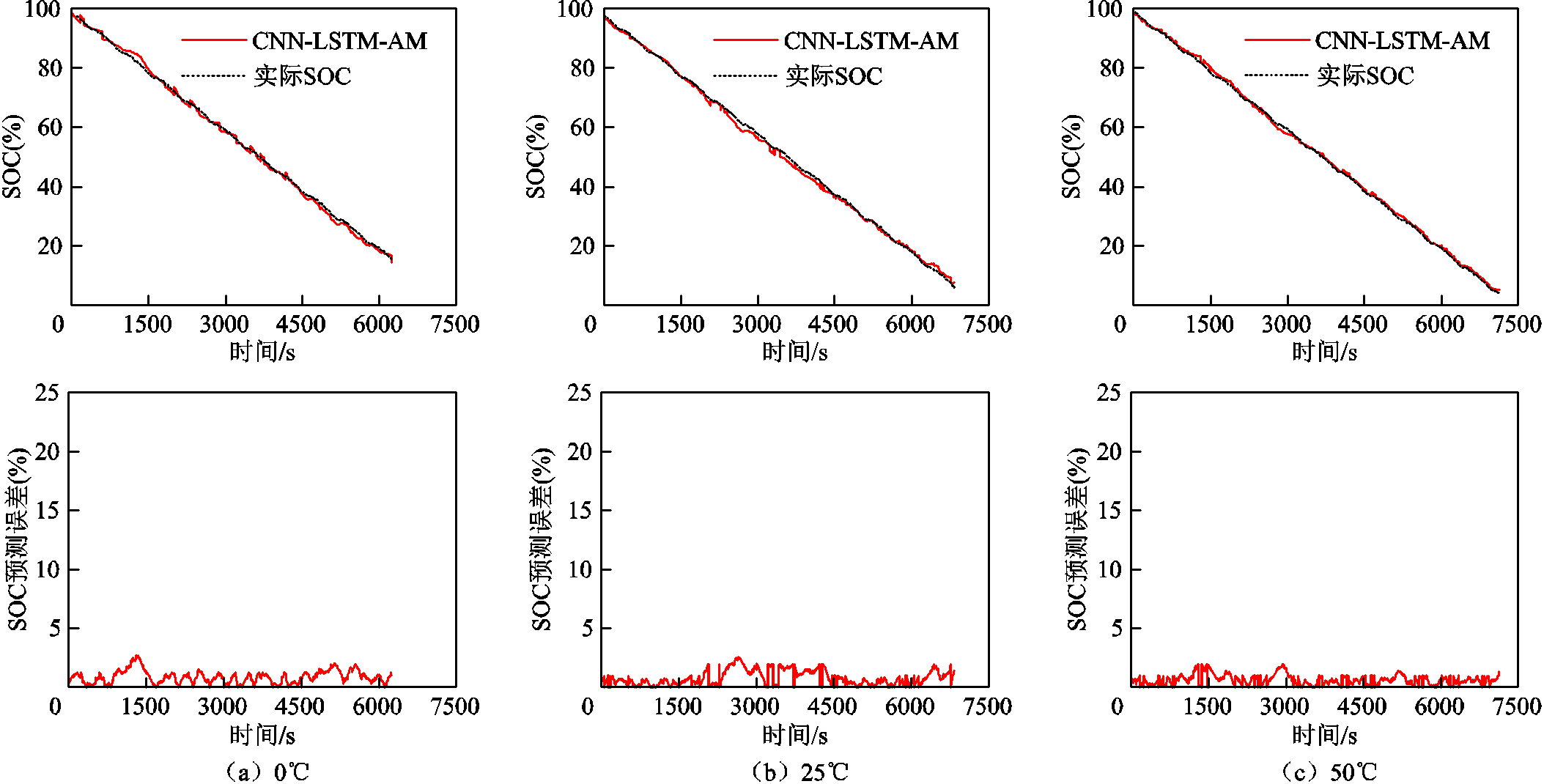
图12 US06的CNN-LSTM-AM在不同温度条件下SOC预测结果
Fig.12 SOC prediction results of the CNN-LSTM-AM for US06 under different temperature conditions
综上所述,CNN-LSTM-AM模型在训练阶段采用了全温度范围的DST数据,在验证阶段则使用两种动态工况(即FUDS、US06)以及三种温度条件(即0、25、50℃)下的数据。高精度的SOC预测结果证实,CNN-LSTM-AM模型具有良好的泛化能力,能够适应不同的动态工况和温度变化。
通过在CNN-LSTM网络中加入注意力机制,可降低电池SOC估计误差。然而,模型预测精度RMSE和MAE变化较小,网络超参数调整过于冗杂。因此,本文采用雾凇优化算法自动寻优超参数以提高SOC估计的精度和稳定性。图13和图14分别是FUDS和US06数据集下使用雾凇优化算法后SOC的估计结果,所有温度下SOC估计结果汇总于表3。通过对比图11、图12和图13、图14可以看出,采用雾凇优化算法不仅可以减少超参数寻优的时间,而且可以进一步降低SOC估计的误差,其中RMSE均低于1%,MAE均低于0.8%。
表3 基于不同模型的电池SOC预测性能比较
Tab.3 Comparison of battery SOC prediction performance based on different models
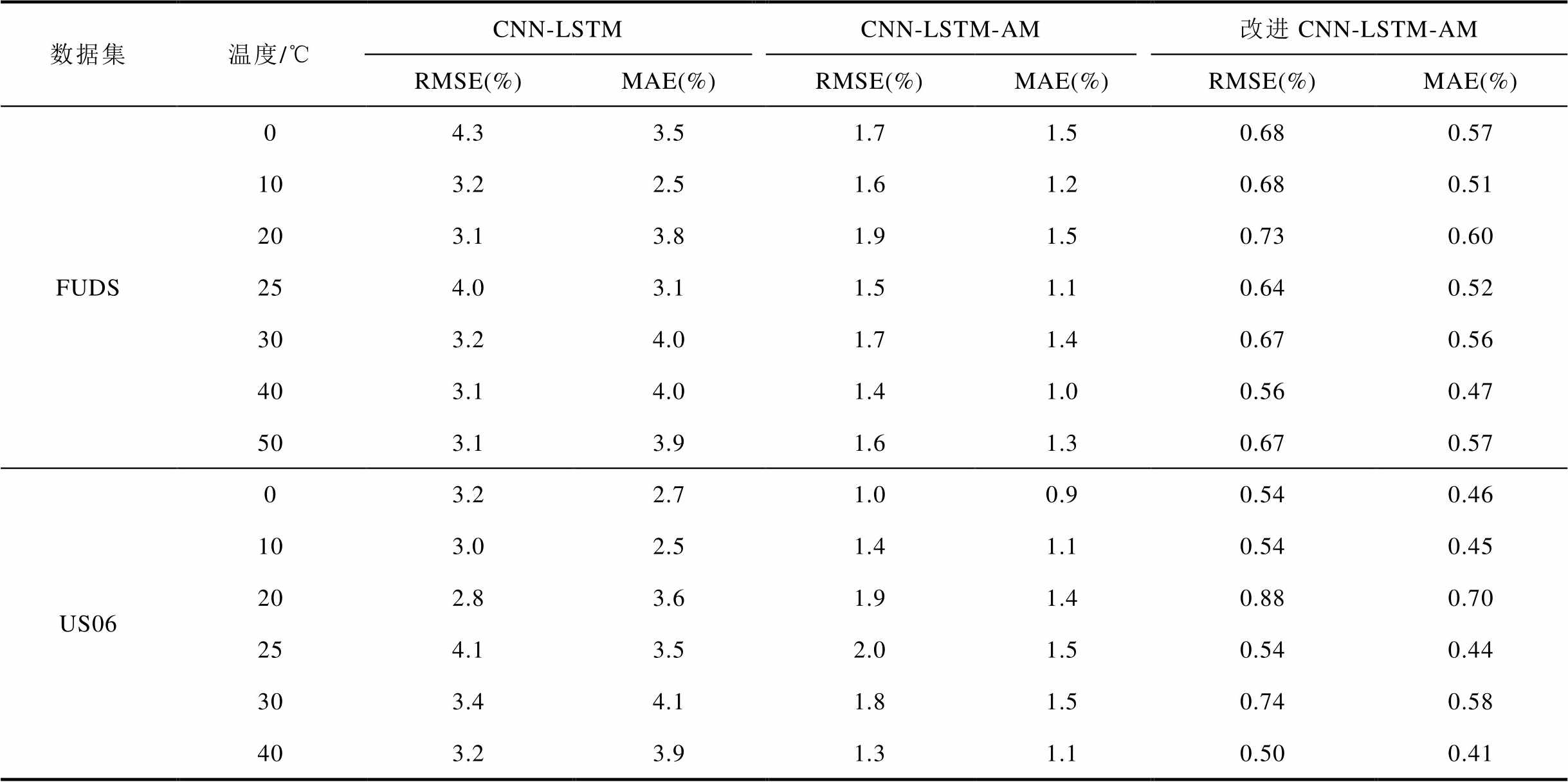
数据集温度/℃CNN-LSTMCNN-LSTM-AM改进CNN-LSTM-AM RMSE(%)MAE(%)RMSE(%)MAE(%)RMSE(%)MAE(%) FUDS04.33.51.71.50.680.57 103.22.51.61.20.680.51 203.13.81.91.50.730.60 254.03.11.51.10.640.52 303.24.01.71.40.670.56 403.14.01.41.00.560.47 503.13.91.61.30.670.57 US0603.22.71.00.90.540.46 103.02.51.41.10.540.45 202.83.61.91.40.880.70 254.13.52.01.50.540.44 303.44.11.81.50.740.58 403.23.91.31.10.500.41
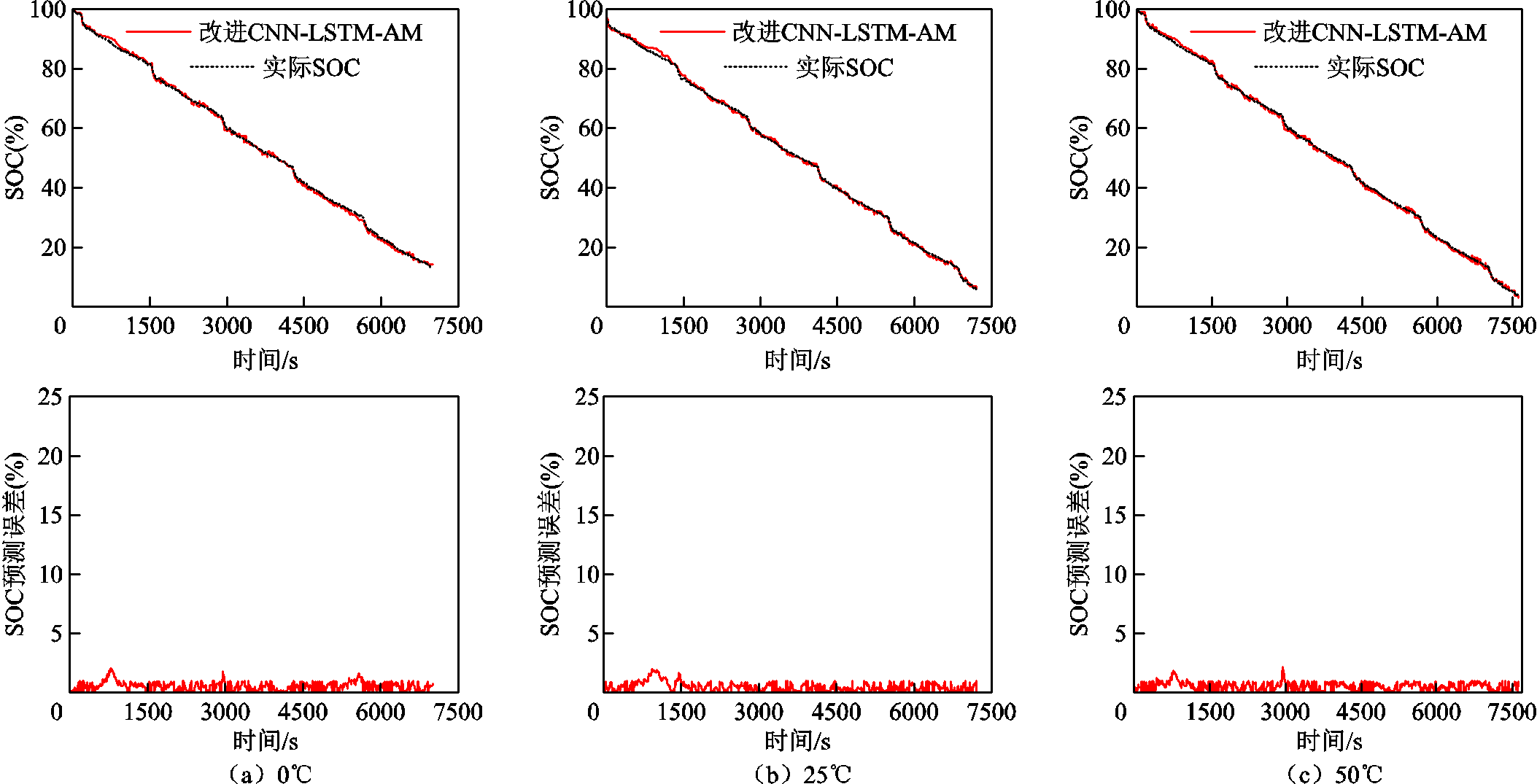
图13 FUDS的改进CNN-LSTM-AM在不同温度条件下SOC预测结果
Fig.13 SOC prediction results of the improved CNN-LSTM-AM for FUDS under different temperature conditions
在实际操作中,初始SOC并不确定,因此网络对于未知初始状态具有鲁棒性就显得非常必要。通过去除25℃的FUDS数据集中SOC大于80%的数据,生成初始SOC为80%的测试集。将25℃的DST数据集作为训练集训练网络,不同初始SOC下预测结果和误差如图15和图16所示。
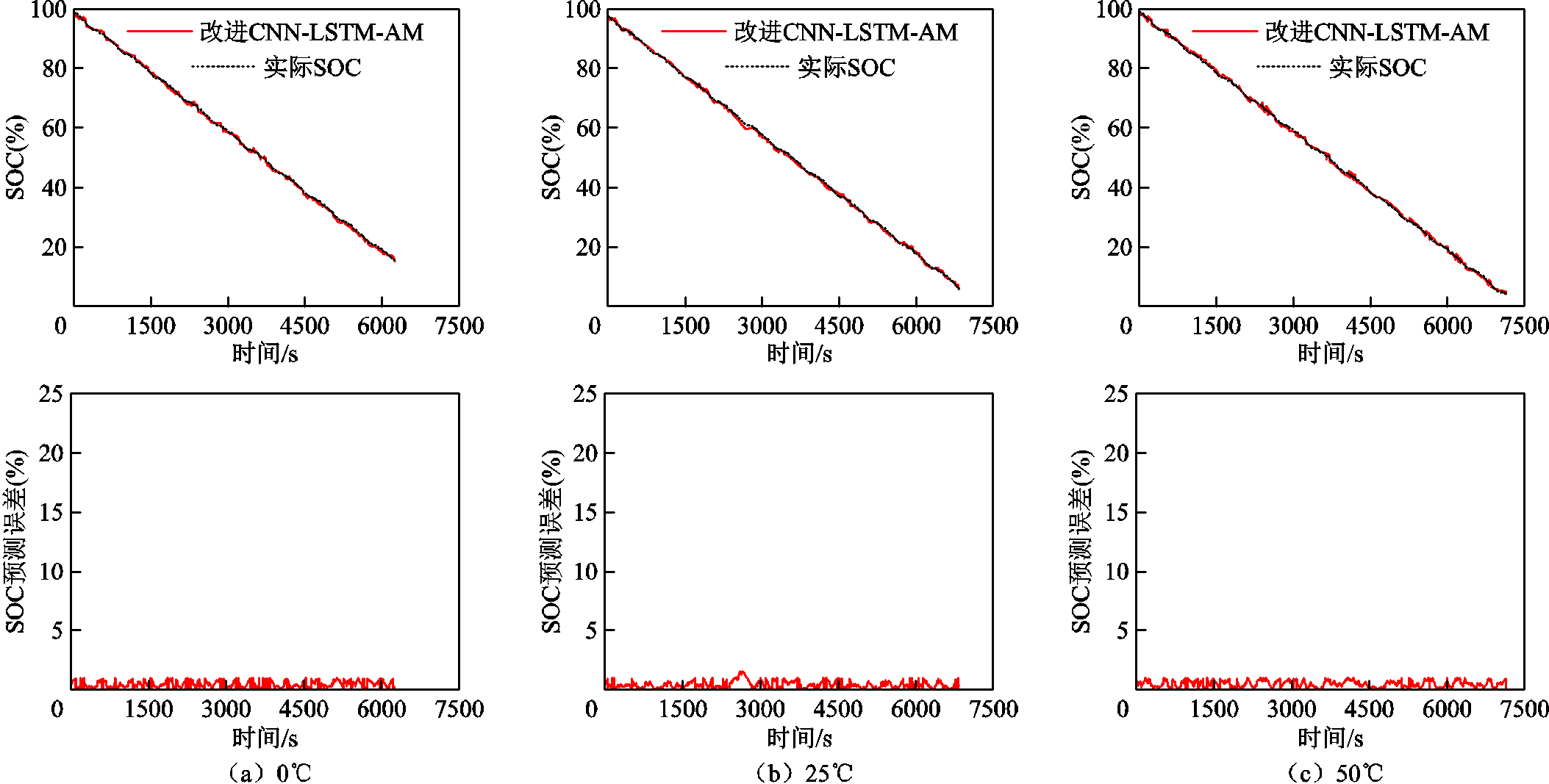
图14 FUDS的改进CNN-LSTM-AM在不同温度条件下SOC预测结果
Fig.14 SOC prediction results of the improved CNN-LSTM-AM for US06 under different temperature conditions
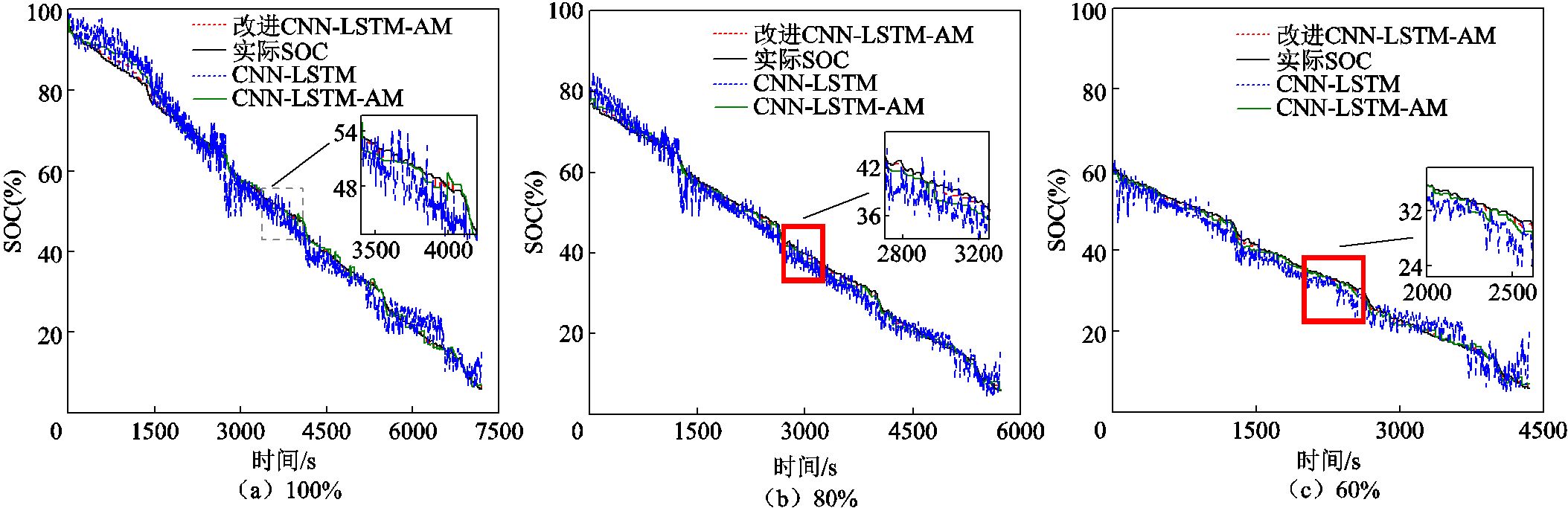
图15 不同初始SOC条件下模型预测结果
Fig.15 Model prediction results under different initial SOC conditions
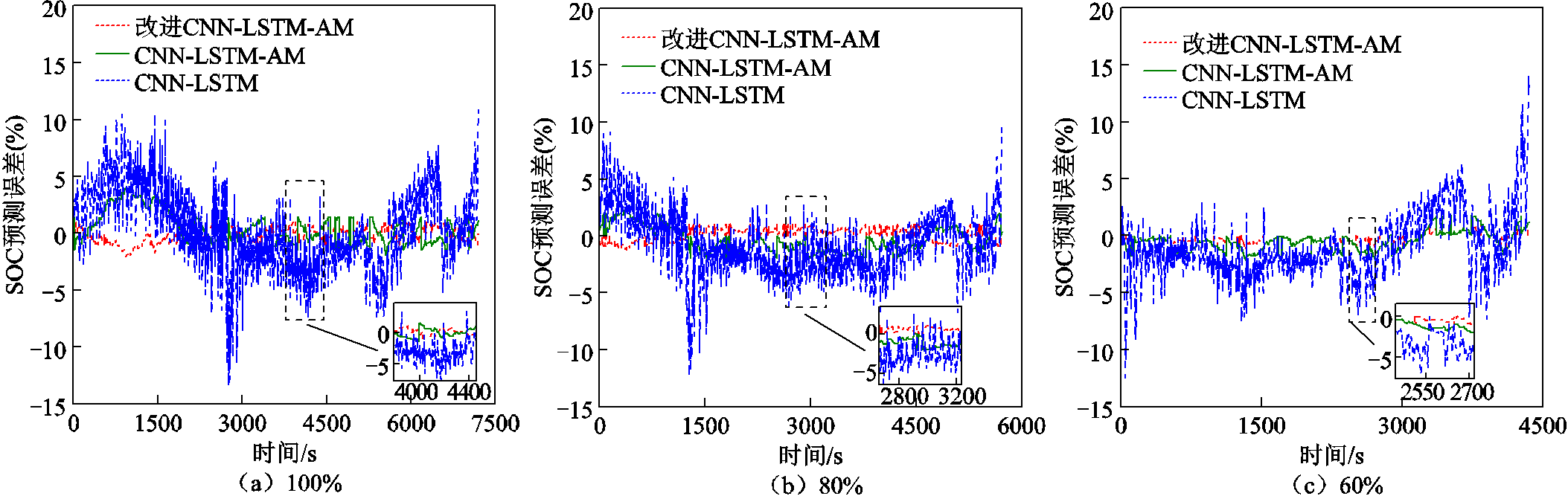
图16 不同初始SOC条件下模型预测误差
Fig.16 Model prediction errors under different initial SOC conditions
当SOC从80%开始时,如图15b和图15c所示,CNN-LSTM网络跟踪SOC的效果较差,其中RMSE和MAE均大于2%。而添加了注意力机制后,SOC跟踪效果得到了显著提升,其中RMSE和MAE均在1.5%以内。改进CNN-LSTM-AM模型在初始SOC未知的情况下,能够快速跟踪实际SOC,并且所设计网络的鲁棒性和稳定性较好(RMSE=0.6%,MAE=0.5%)。三种网络在不同初始状态下的SOC预测结果见表4。表4中,初始SOC从100%到20%依次递减,可以看出本文所提出网络的RMSE和MAE结果均小于CNN-LSTM、CNN-LSTM-AM。
表4 不同初始状态下SOC预测性能比较
Tab.4 Comparison of SOC prediction performance under different initial states
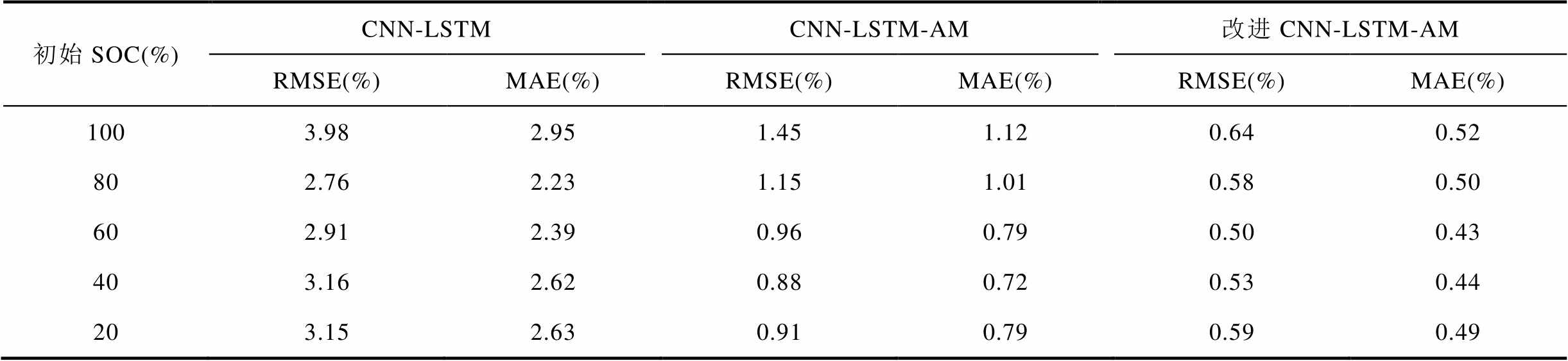
初始SOC(%)CNN-LSTMCNN-LSTM-AM改进CNN-LSTM-AM RMSE(%)MAE(%)RMSE(%)MAE(%)RMSE(%)MAE(%) 1003.982.951.451.120.640.52 802.762.231.151.010.580.50 602.912.390.960.790.500.43 403.162.620.880.720.530.44 203.152.630.910.790.590.49
为了综合比较不同SOC预测方法的性能,将本文所提出的CNN-LSTM-AM模型与其他实验结果进行对比。为了确保对比的有效性,本文选取的实验数据集均来自CALCE,不同温度条件下SOC预测性能比较见表5。其中,AT-CNN-LSTM方法[26]的训练集为DST-US06,测试集为FUDS,输入数据为电压、电流、温度和电压变化率;具有扩展输入和受约束输出的LSTM(Extended Input-LSTM-Constrained Output, EI-LSTM-CO)方法[18]的训练集为DST,测试集为US06和FUDS,输入数据为电压、电流、温度和平均电压。为了方便比较,表5仅列出FUDS对比的情况。从表5可以看出,本文所提出的方法相较于AT-CNN-LSTM,RMSE明显更低;同时考虑到所提出方法使用的训练集数据量更少,也能看出所设计网络的优势。与EI-LSTM-CO对比,可以发现两者误差较为接近;并且EI-LSTM-CO对所预测的SOC进行了一定的后处理,也能侧面反映所提出方法的优越性。
表5 不同温度条件下SOC预测性能比较
Tab.5 Comparison of SOC prediction performance under different temperature conditions
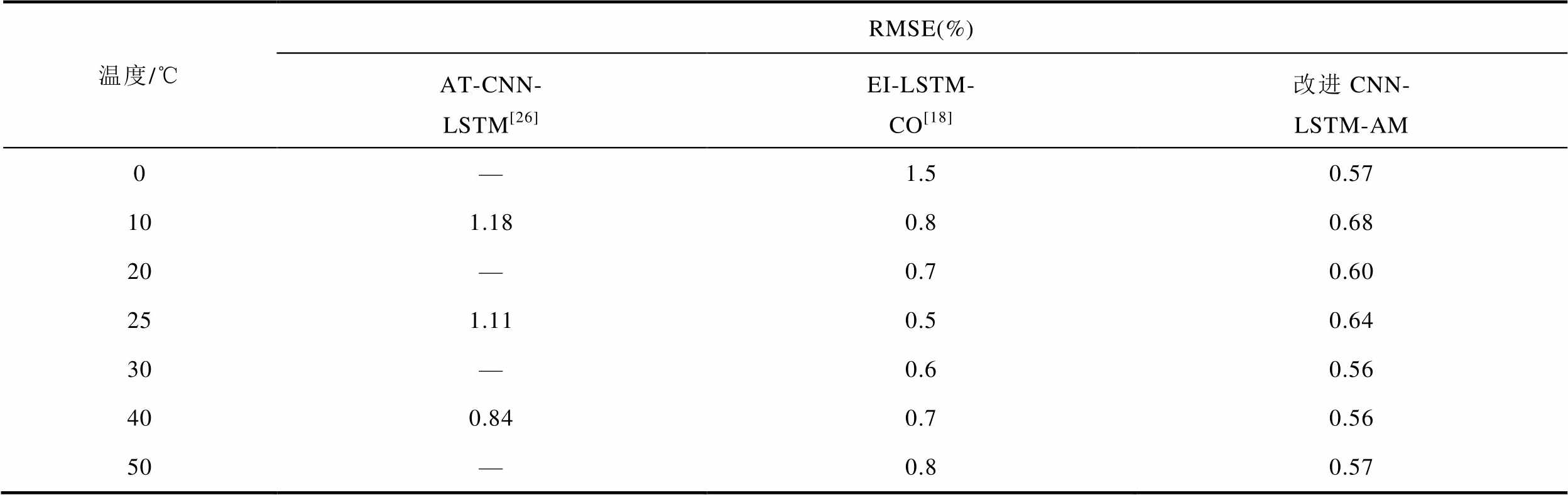
温度/℃RMSE(%) AT-CNN-LSTM[26]EI-LSTM-CO[18]改进CNN-LSTM-AM 0—1.50.57 101.180.80.68 20—0.70.60 251.110.50.64 30—0.60.56 400.840.70.56 50—0.80.57
储能锂离子电池SOC的精确预测对于电池运行管理至关重要,关系到电池的性能、寿命及安全性。本文提出了一种基于CNN-LSTM-AM模型的电池SOC预测方法,并将其应用于LiFeO4数据集进行实践验证。实验结果表明,注意力机制可以有效地提高预测模型训练性能,所采用的雾凇优化算法有助于减少模型超参数,从而得到更高的预测精度。在不同温度条件下测试CNN-LSTM-AM模型性能,所得RMSE和MAE均小于1%,足以证实模型预测SOC的可行性。此外,即便是在初始SOC不确定的情况下,所提出的CNN-LSTM-AM模型仍能准确地跟踪SOC趋势变化,整体预测精度达到RMSE<1.5%和MAE<1.5%,展现出较强的鲁棒性和泛化能力。
参考文献
[1] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[2] 刘旖琦, 雷万钧, 刘茜, 等. 基于双自适应扩展粒子滤波器的锂离子电池状态联合估计[J]. 电工技术学报, 2024, 39(2): 607-616.
Liu Yiqi, Lei Wanjun, Liu Qian, et al. Joint state estimation of lithium-ion battery based on dual adaptive extended particle filter[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 607-616.
[3] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[4] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[5] 李卓昊, 石琼林, 王康丽, 等. 锂离子电池健康状态估计方法研究现状与展望[J]. 电力系统自动化, 2024, 48(20): 109-129.
Li Zhuohao, Shi Qionglin, Wang Kangli, et al. Research status and prospects of state of health estimation methods for lithium-ion batteries[J]. Automation of Electric Power Systems, 2024, 48(20): 109-129.
[6] 方斯顿, 刘龙真, 孔赖强, 等. 基于双向长短期记忆网络含间接健康指标的锂电池SOH估计[J]. 电力系统自动化, 2024, 48(4): 160-168.
Fang Sidun, Liu Longzhen, Kong Laiqiang, et al. State-of-health estimation for lithium-ion batteries incorporating indirect health indicators based on bi-directional long short-term memory networks[J]. Automation of Electric Power Systems, 2024, 48(4): 160-168.
[7] Navas S J, Cabello González G M, Pino F J, et al. Modelling Li-ion batteries using equivalent circuits for renewable energy applications[J]. Energy Reports, 2023, 9(12): 4456-4465.
[8] Wang Jingrong, Meng Jinhao, Peng Qiao, et al. An electrochemical-thermal coupling model for lithium-ion battery state-of-charge estimation with improve dual particle filter framework[J]. Journal of Energy Storage, 2024, 87(5): 111473.
[9] 黄聪生. 一种用于准确库仑计数充电状态估计的锂离子电池故障诊断方法[J]. 电气工程学报, 2023, 19(1): 433-442.
Huang Congsheng. A lithium-ion batteries fault diagnosis method for accurate coulomb counting state-of-charge estimation[J]. Journal of Electrical Engineering & Technology, 2023, 19(1): 433-442.
[10] Gismero A, Schaltz E, Stroe D I. Recursive state of charge and state of health estimation method for lithium-ion batteries based on coulomb counting and open circuit voltage[J]. Energies, 2020, 13(7): 1811.
[11] Salkind A J, Fennie C, Singh P, et al. Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology[J]. Journal of Power Sources, 1999, 80(1/2): 293-300.
[12] Zheng Yuejiu, Lu Languang, Han Xuebing, et al. LiFePO4 battery pack capacity estimation for electric vehicles based on charging cell voltage curve transformation[J]. Journal of Power Sources, 2013, 226(3): 33-41.
[13] Bobobee E D, Wang Shunli, Takyi-Aninakwa P, et al. Improved particle swarm optimization–long short-term memory model with temperature compensation ability for the accurate state of charge estimation of lithium-ion batteries[J]. Journal of Energy Storage, 2024, 84(4): 110871.
[14] Prakash V, VigneswaranT. State of charge estimation of lithium batteries in electric vehicles using IndRNN[J]. IETE Journal of Research, 2023, 69(5): 2886-2896.
[15] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.
Li Ning, He Fuxing, Ma Wentao, et al. State-of-charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decomposition[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4528-4536.
[16] 刘素贞, 陈云龙, 张闯, 等. 融合多维超声时频域特征的锂离子电池荷电状态估计[J]. 电工技术学报, 2023, 38(17): 4539-4550, 4563.
Liu Suzhen, Chen Yunlong, Zhang Chuang, et al. State of charge estimation of lithium-ion batteries fused with multi dimensional ultrasonic time-frequency domain features[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4539-4550, 4563.
[17] Zhao Fen, Li Yinguo, Wang Xinheng, et al. Lithium-ion batteries state of charge prediction of electric vehicles using RNNs-CNNs neural networks[J]. IEEE Access, 2020, 8(5): 98168-98180.
[18] Chen Junxiong, Zhang Yu, Wu Ji, et al. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output[J]. Energy, 2023, 262(1): 125375.
[19] Le Cun Y, Boser B, Denker J S, et al. Backpropagation applied to handwritten zip code recognition[J]. Neural Computation, 1989, 1(4): 541-551.
[20] 顾久祥, 王振华, 马连阳, 等. 卷积神经网络的最新进展[J]. 模式识别, 2018, 77(3): 354-377.
Gu Jiuxiang, Wang Zhenhua, Ma lianyang, et al. Recent advances in convolutional neural networks[J]. Pattern Recognition, 2018, 77(3): 354-377.
[21] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1735.
[22] Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166.
[23] Lu Wenjie, Li Jiazheng, Wang Jingyang, et al. A CNN-BiLSTM-AM method for stock price prediction[J]. Neural Computing and Applications, 2021, 33(10): 4741-4753.
[24] 苏杭, 赵东, 刘磊, 等. RIME:一种基于物理的优化[J]. 神经计算, 2023, 532(5): 183-214.
Su Hang, Zhao Dong, Liu Lei, et al. RIME:A physics based optimization[J]. Neurocomputing, 2023, 532(5): 183-214.
[25] 刑银娇, 何伟, Pecht Michael, 等. 不同环境温度下基于开路电压的锂离子电池电荷状态估计[J]. 应用能源, 2014, 113(1): 106-115.
Xing Yinjiao, He Wei, Michael P, et al. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures[J]. Applied Energy, 2014, 113(1): 106-115.
[26] 张帅涛, 蒋品群, 宋树祥, 等. 基于注意力机制和CNN-LSTM融合模型的锂电池SOC预测[J]. 电源学报, 2022, 21(2): 1-15.
Zhang Shuaitao, Jiang Pinqun, Song Shuxiang, et al. SOC prediction for lithium battery based on fusion model of attention mechanism and CNN-LSTM[J]. Journal of Power Supply, 2022, 21(2): 1-15.
Prediction of State of Charge for Energy Storage Lithium-Ion Batteries Based on CNN-LSTM-AM Model
Abstract Accurate prediction of the battery state of charge (SOC) is of great significance to improve the utilization efficiency and safety performance of the battery, and the monitoring of the battery state of charge is very important to help prevent overcharge and overdischarge accidents. The traditional SOC prediction methods are highly dependent on the mechanism model and statistical model, and have problems such as sensitive outliers and limited practical accuracy. In this study, a CNN-LSTM-AM (convolutional neural network - long short term memory neural network - attention mechanism) model is proposed to predict SOC variation trend through battery measurable variables.
The model first uses a one-dimensional convolutional neural network to extract spatial features of measurable variables, including battery current, voltage, temperature and average voltage, and then sends them to bidirectional long and short time memory for time series analysis. Finally, the attention mechanism is introduced to screen key features, reduce the redundancy of feature data, and improve the accuracy and generalization of the model. In addition, CNN-LSTM-AM model adopts rime optimization algorithm to optimize the hyperparameters in the training process, which effectively improves the training efficiency and reduces the training cost.
The actual evaluation on CALCE (Center for Advanced Life Cycle Engineering) data set of lithium iron phosphate shows that the attention mechanism can effectively improve the training performance of the prediction model, and the rime optimization algorithm adopted can help reduce the model hyperparameters, so as to obtain higher prediction accuracy. The performance of CNN-LSTM-AM model was tested under different temperature conditions, and both RMSE and MAE were less than 1%, which was sufficient to confirm the feasibility of the model to predict SOC. In addition, even if the initial SOC is uncertain, the proposed CNN-LSTM-AM model can still accurately track SOC trend changes, and the overall prediction accuracy reaches RMSE<1.5% and MAE<1.5%. The RMSE and MAE results of the network proposed in this study are smaller than those of CNN-LSTM and CNN-LSTM-AM. It shows strong robustness and generalization ability. Finally, in order to comprehensively compare the performance of different SOC prediction methods, the CNN-LSTM-AM model proposed in this study is compared with other experimental results. It can be seen that the method proposed in this study has significantly lower RMSE compared with AT-CNN-LSTM. At the same time, considering that the proposed method uses less training set data, we can also see the advantages of the designed network. Compared with EI-LSTM-CO(extended input-LSTM-constrained output), it can be found that the error is close. In addition, EI-LSTM-CO performs some post-processing on the predicted SOC, which can also reflect the superiority of the proposed method.
The following conclusions are drawn from the simulation analysis: (1) A CNN-LSTM-AM model is proposed and applied to the SOC prediction task of battery, which can effectively capture important input features and improve the prediction accuracy. (2) Design a rime optimization algorithm, which can automatically search the optimal solution of CNN-LSTM-AM model, effectively reduce the time cost of hyperparameter optimization. (3) The influence of different ambient temperatures and initial SOC values on the prediction accuracy of CNN-LSTM-AM was studied, and the performance of CNN-LSTM-AM was compared with that of traditional prediction models to verify its strong robustness and high generalization ability.
Keywords:Energy storage battery, state of charge, long and short-term memory, attention module, RIME
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.240706
国家重点研发计划(2023YFB4102904)和低碳智能燃煤发电与超净排放全国重点实验室开放课题(D2022FK080)资助项目。
收稿日期2024-05-06
改稿日期 2024-10-08
杜 伟 男,1998年生,硕士研究生,研究方向为储能电池的状态估计。
E-mail:220210465@seu.edu.cn
许传龙 男,1978年生,教授,博士生导师,研究方向为智能传感与检测、能源动力测试、能源系统工程。
E-mail:chuanlongxu@seu.edu.cn(通信作者)
(编辑 赫 蕾)