
图1 交通流数据的时空异质性
Fig.1 The spatial and temporal heterogeneity of traffic flow data
摘要 随着电动汽车(EV)数量的急剧增长和渗透率的不断提高,为大规模电动汽车进行充电引导成为缓解局部有限的充电资源与旺盛的充电需求间矛盾的重要措施,为此该文提出一种基于动态交通推演的电动汽车充电快速引导策略。首先,建立基于时空自监督学习(ST-SSL)的动态交通信息预测模型,分别设计面向交通数据空间异质性与时间异质性的自监督学习(SSL)模块,实现多时段交通流量信息的精准预测;其次,设计城市路网多时刻动态阻抗建模方法,建立兼顾用户多需求场景、多导航目标的充电导航策略,提出基于动态Dijkstra算法的求解方法,并基于全域充电导航结果对城市充电站服务范围进行动态评估,从而实现电动汽车充电快速引导;最后,以洛杉矶某区域实际路网为例,验证了预测模型的准确性与充电引导策略的有效性,能够有效感知动态交通信息,快速实现城市充电站服务范围划分与电动汽车充电引导,同时有效地降低充电导航计算资源消耗。
关键词:电动汽车 交通系统 交通流量预测 充电导航 服务范围
随着电动汽车(Electric Vehicle, EV)渗透率的不断提高[1],大规模EV无序接入电网,将带来负荷增长[2-3]、电能质量下降[4-5]、电网运行控制难度增加[6]等负面影响,对引导EV进行有序充电提出越来越高的要求。由于EV用户行为、EV类型和充电站选址等多重因素,在用电高峰期容易出现EV堆积在某些特定充电站的现象,给EV出行和电网安全带来负面影响[7]。因此,为大规模EV进行充电引导,能够有效减少电池容量限制给电动汽车用户带来的里程焦虑,同时有助于缓解局部有限的充电资源与旺盛的充电需求间的矛盾[8]。
由于城市内的交通信息随时间动态更新,交通流预测成为建立电动汽车充电引导策略的重要前提。现有研究多采用基于传统机器学习和基于深度学习的方法进行交通流量预测。传统机器学习方法主要分为三类:基于特征的方法[9-10]、高斯过程方法[11-12]和状态空间法。上述方法具有一定的规模化数据处理能力,然而,其性能较为有限[13-14],在处理动态的复杂数据时往往表现不佳。在基于深度学习的方法方面,文献[15]提出了一种新的端对端深度学习模型ST-3DNet,通过量化交通数据空间相关性实现交通流量预测。文献[16]研究了部分缺失数据和恢复数据对交通信息预测的影响,并基于GraphSAGE(Graph Sample and Aggregated)模型对路网内空间异质的交通流量进行预测。然而,上述研究更多是从挖掘交通数据空间相关性角度展开,对时间相关性的考虑较为薄弱。文献[17]基于提出的M-B-LSTM模型处理交通流数据在时间尺度上的随机性,减少网络学习过程中分布不平衡和过拟合问题对预测结果的影响。文献[18]提出了一种用于交通信息预测的周期性神经元折叠深度神经网络,有效地解决了对大规模序列数据时间依赖性建模难的问题。同样,上述方法更多是从时间相关性角度进行建模,难以兼顾空间相关性。近年来,不少研究采用自注意力机制与图卷积神经网络结合的方式,统筹考虑时间相关性与空间相关性对交通信息预测的影响[19-20],并取得了较好的预测效果。然而,现有的预测模型大多直接对所有区域的交通流量进行预测,未考虑空间异质性的影响。同时,现有模型在所有预测时段共享网络参数,无法捕捉交通信息随时间变化的时间异质性。
在充电导航方面,文献[21]基于出行链和蒙特卡洛法建立EV用户出行模型,实现用户出行需求与充电需求的动态交互。文献[22]提出了电动汽车、交通网与充电站间的信息流动框架,建立了路段传输模型实现城市路网充电导航。文献[23]建立了融合电网信息和交通信息的充电导航框架,并提出了智能交通系统实时播报充电站可用容量信息。电动汽车作为交通工具,在实际导航场景中更多受用户意愿与交通流量信息的影响,但上述模型均未考虑实时及未来交通状况与充电导航决策间的关系,难以实现长时间尺度下的最优路径规划。文献[24]提出了“时间-流量”动态路阻模型,兼顾道路通行时间与充电站车辆数,建立充电导航模型。然而,该模型对动态路阻的建模较为粗糙,通过不断采集交通数据建立动态路阻,难以有效反映未来一段时间交通数据的变化对导航策略的影响。同时,上述模型均未针对用户不同出行需求设计多样化充电导航方案,忽视了用户目标对充电导航结果的影响。
当存在大规模充电引导需求时,计算耗时将成为评价引导策略优劣程度的重要指标。传统充电引导策略多采用对EV个体单独充电导航方式,在EV规模较大时,难以快速给出引导方案。通过对充电站服务范围进行研究,将路网节点与充电站进行配对,可以实现电动汽车充电快速引导。现有的充电站服务范围研究多采用结合空间基尼系数等指标的修正引力模型,并以规则化圆形对充电站服务范围进行表征[25]。该方法对于服务范围的划分较为粗糙,由于交通节点在地理上分布并不均匀,同时交通信息也随着时间动态更新,充电站的服务范围必然是不规则的。综上所述,基于预测的交通信息进行动态交通建模,并通过充电导航逆向推导充电站服务范围,最后进行导航策略的分配,将成为解决大规模充电引导高耗时难题的一种新思路。
基于上述研究存在的问题,本文考虑未来交通信息变化对导航策略的影响,兼顾方案多样性与计算时效性,提出一种基于动态交通推演的电动汽车充电快速引导策略。本文主要创新点如下:①建立基于时空自监督学习(Spatio-Temporal Self-Supervised Learning, ST-SSL)的动态交通信息预测模型,设计了考虑未来交通信息变化的城市路网多时刻动态阻抗建模方法;②提出兼顾用户多需求场景、多导航目标的充电导航策略,进一步提出了改进的动态Dijkstra算法实现最优充电站与导航路径的求解规划;③提出一种基于全域充电导航结果的城市充电站服务范围评估方法,并应用于充电导航策略的快速分配。最后,通过算例证明预测模型的准确性与充电引导策略的有效性,能够有效感知动态交通信息,快速实现城市区域充电站服务范围划分与电动汽车充电引导,同时有效降低充电导航计算资源消耗。
动态交通信息预测是实现充电站范围划分的基础,通过对交通流信息的准确预测,为构建区域动态交通阻抗提供数据支撑,以实现区域最优充电路径的规划。
交通流信息具有空间异质性与时间异质性,交通流数据的时空异质性如图1所示。图1a中的A、B为城市中两个具有不同功能的区域,由图1b可观察到A、B区域交通流量呈现不同的数据分布形状,即A与B区域的交通流量存在空间异质性。时间异质性方面,如图1c所示,同一区域在工作日和节假日的夜间交通模型也存在显著差异。

图1 交通流数据的时空异质性
Fig.1 The spatial and temporal heterogeneity of traffic flow data
为充分挖掘空间异质性与时间异质性,引入ST-SSL[26]模型实现交通流信息预测。
首先,对城市网与交通网进行建模分析。将城市区域划分为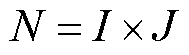 个互不相交的地理网格,每个网格视为一个空间区域
个互不相交的地理网格,每个网格视为一个空间区域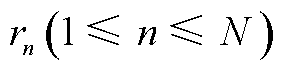 ,仅包含一条道路,以
,仅包含一条道路,以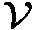
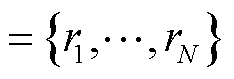 来表示城市中的空间区域集合。其次,将交通流图定义为
来表示城市中的空间区域集合。其次,将交通流图定义为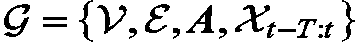 ,其中
,其中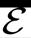 为连接两个空间区域的边的集合,
为连接两个空间区域的边的集合,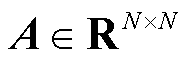 为交通流的邻接矩阵,
为交通流的邻接矩阵,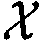
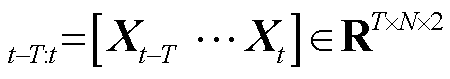 表示所有道路在T时间尺度上的两个方向的交通流量,在t时刻的交通流量表示为
表示所有道路在T时间尺度上的两个方向的交通流量,在t时刻的交通流量表示为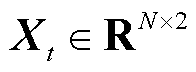 。
。
基于ST-SSL的交通流预测架构如图2所示,由时空编码器模块、自适应图增广模块、面向空间异质性建模的SSL模块与面向时间异质性建模的SSL模块四部分组成。在实际预测时,输入交通流图 ,即可得到下一时刻的交通流量
,即可得到下一时刻的交通流量 。
。
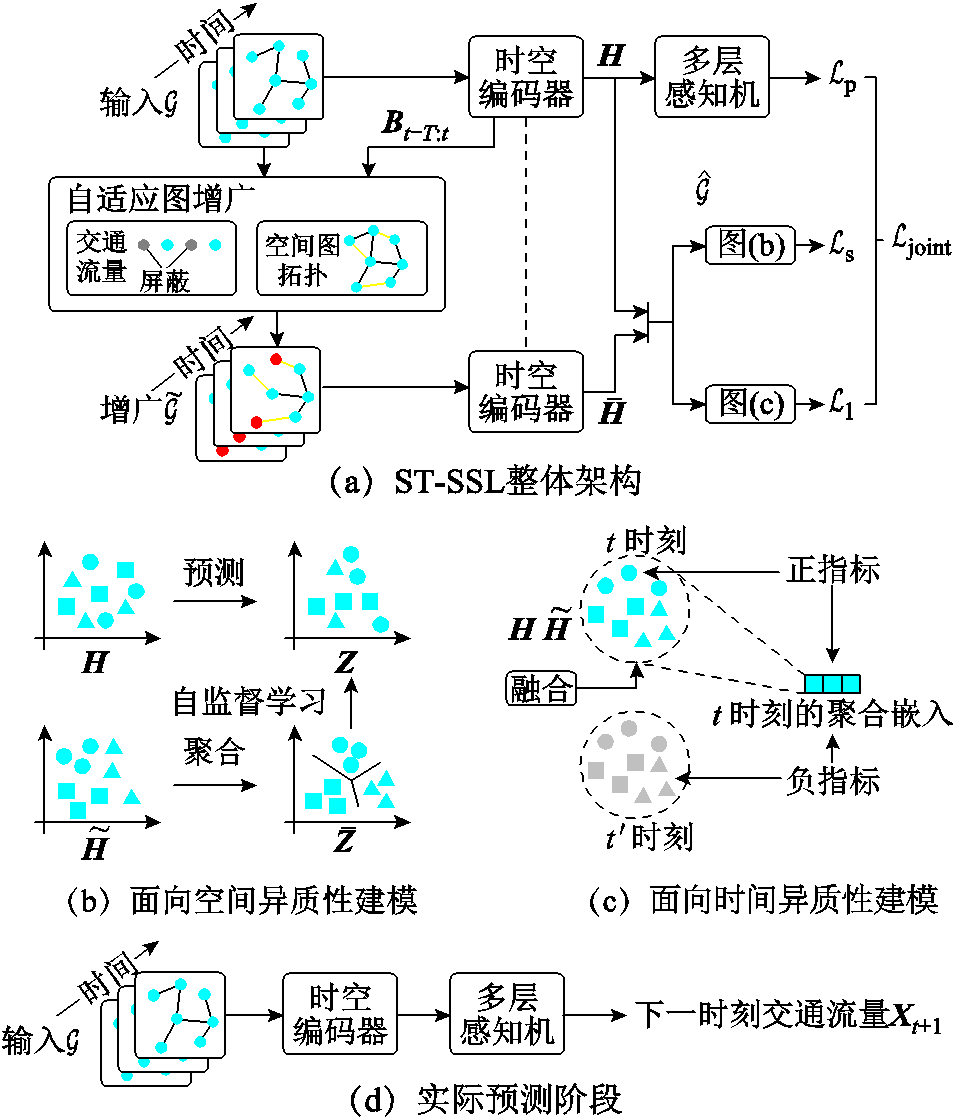
图2 基于ST-SSL的交通流预测架构
Fig.2 The traffic flow prediction architecture bused on ST-SSL
时空编码器分别采用时间卷积(Temporal Convolution, TC)与空间卷积(Spatial Convolution, SC)对不同时刻交通流序列的时间相关性和空间区域之间的地理相关性进行建模。
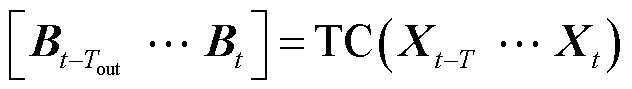 (1)
(1)
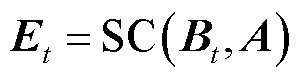 (2)
(2)
式中,Bt为t时刻的区域嵌入的时间感知模块矩阵,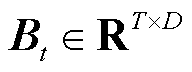 ,D为嵌入维度;
,D为嵌入维度;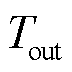 为卷积运算后输出嵌入序列长度;TC为时间卷积模块;SC为空间卷积模块;Et为经过这两个模块后的输出矩阵。
为卷积运算后输出嵌入序列长度;TC为时间卷积模块;SC为空间卷积模块;Et为经过这两个模块后的输出矩阵。
对所有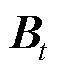 进行式(2)所示运算后,得到输出序列
进行式(2)所示运算后,得到输出序列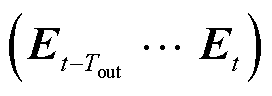 ,可作为下一层TC的输入序列。每个时空编码器模块由多个结构为
,可作为下一层TC的输入序列。每个时空编码器模块由多个结构为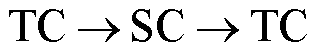 的子模块堆叠而成,通过堆叠多个子模块,在多次卷积后获得时间维度为
的子模块堆叠而成,通过堆叠多个子模块,在多次卷积后获得时间维度为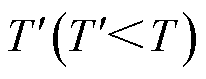 的嵌入矩阵
的嵌入矩阵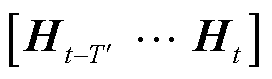 ,直到时间维度降为1,得到时空编码器最终的区域嵌入矩阵
,直到时间维度降为1,得到时空编码器最终的区域嵌入矩阵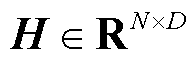 。
。
首先,定义区域依赖系数描述不同区域间在时间维度上的依赖性,表示为
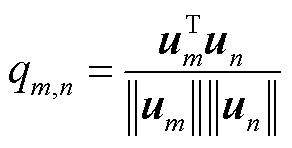 (3)
(3)
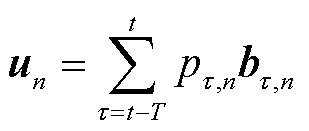 (4)
(4)
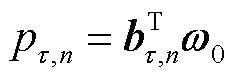 (5)
(5)
式中,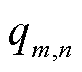 为两个区域
为两个区域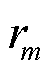 和
和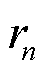 之间的依赖系数,值越大,说明在时间维度上的依赖性越高,异质性越低;
之间的依赖系数,值越大,说明在时间维度上的依赖性越高,异质性越低;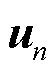 为基于聚合权重
为基于聚合权重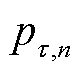 进行时间区域
进行时间区域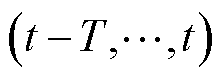 的聚合;聚合权重
的聚合;聚合权重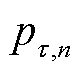 反映了
反映了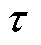 时刻交通模式
时刻交通模式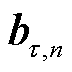 和整体交通变化模式
和整体交通变化模式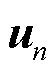 在时间上的相关性;
在时间上的相关性;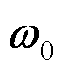 为用于变换的可学习参数向量;
为用于变换的可学习参数向量;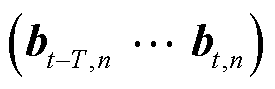 为经过TC层得到的嵌入矩阵
为经过TC层得到的嵌入矩阵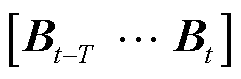 的第n行。
的第n行。
其次,分别设计面向交通流量的数据增广子模块和面向空间图拓扑的结构增广子模块来实现自适应图增广。
1)数据增广子模块:基于伯努利分布得到不同区域的屏蔽概率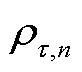 ,
,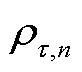 越大,说明
越大,说明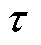 时刻
时刻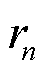 区域的交通流量
区域的交通流量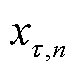 越可能被屏蔽,即由于其与整体交通模式的相关性较低,更容易被视为噪声扰动,
越可能被屏蔽,即由于其与整体交通模式的相关性较低,更容易被视为噪声扰动,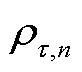 的表达式为
的表达式为
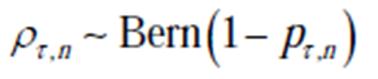 (6)
(6)
式中, 为伯努利分布。增广后的交通流量数据表示为
为伯努利分布。增广后的交通流量数据表示为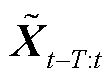 。
。
2)结构增广子模块:对于两个相邻的空间区域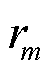 和
和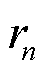 ,若两者在交通模式上不是高度相关,即依赖参数
,若两者在交通模式上不是高度相关,即依赖参数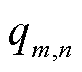 较小,则两者间的连边
较小,则两者间的连边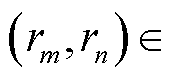
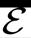 将被屏蔽,以消除交通模式相关性较低的区域之间的连接,屏蔽概率为
将被屏蔽,以消除交通模式相关性较低的区域之间的连接,屏蔽概率为
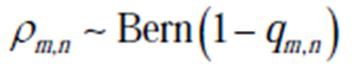 (7)
(7)
对于两个不相邻的空间区域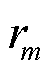 和
和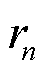 ,若两者在交通模式上高度相关,即依赖参数
,若两者在交通模式上高度相关,即依赖参数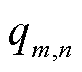 较大,则在两者间添加连边,以捕获远距离区域相关性,屏蔽概率为
较大,则在两者间添加连边,以捕获远距离区域相关性,屏蔽概率为
 (8)
(8)
基于上述两种增广子模块,得到增广后的交通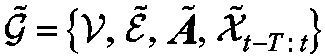 流量图 。
流量图 。
为了使区域嵌入矩阵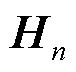 能够有效地保留空间异质性,设计面向空间异质性建模的SSL模块,反映不同城市区域功能的潜在空间关系,例如住宅区、购物中心、交通枢纽等。
能够有效地保留空间异质性,设计面向空间异质性建模的SSL模块,反映不同城市区域功能的潜在空间关系,例如住宅区、购物中心、交通枢纽等。
将聚类的K个簇的嵌入矩阵表示为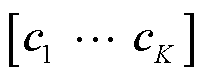 ,聚类过程可以表示为
,聚类过程可以表示为
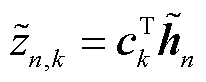 (9)
(9)
式中,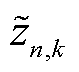 为区域
为区域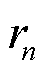 和第k个簇的嵌入矩阵之间的相关性得分;
和第k个簇的嵌入矩阵之间的相关性得分;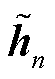 为增广后的交通数据
为增广后的交通数据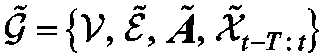 通过时空编码器模块输出的区域嵌入矩阵
通过时空编码器模块输出的区域嵌入矩阵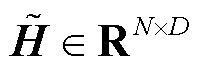 的第n行,
的第n行,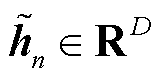 。区域
。区域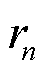 的聚类分配为
的聚类分配为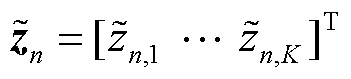 。
。
定义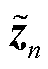 的预测分配分数
的预测分配分数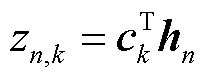 ,则SSL任务的优化函数定义为
,则SSL任务的优化函数定义为
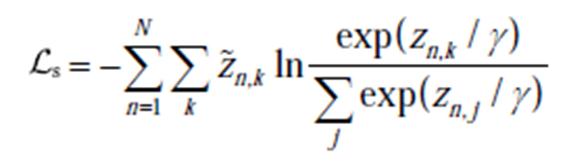 (10)
(10)
式中,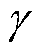 为控制输出平滑度的参数。
为控制输出平滑度的参数。
设计面向时间异质性建模的SSL模块,首先,融合基于原始区域嵌入矩阵 和增广区域嵌入矩阵
和增广区域嵌入矩阵 得到时间感知区域嵌入矩阵为
得到时间感知区域嵌入矩阵为
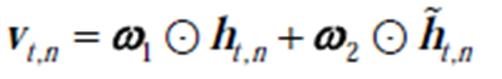 (11)
(11)
式中, 表示对应元素的乘积;
表示对应元素的乘积;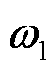 与
与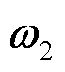 为可学习的参数。通过聚合所有区域的嵌入矩阵,生成t时刻的所有区域嵌入表征为
为可学习的参数。通过聚合所有区域的嵌入矩阵,生成t时刻的所有区域嵌入表征为
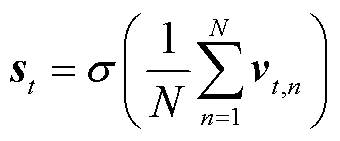 (12)
(12)
式中,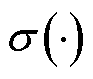 为激活函数。
为激活函数。
为了得到不同时刻之间的表征区分能力,将来自同一时刻的区域和空间嵌入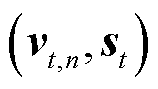 作为正指标,而将来自不同时刻的嵌入作为负指标。其中,正指标有助于捕捉特定时刻的空间交通相关性,负指标有助于捕捉不同时刻的时间异质性。将SSL模型通过式(13)损失函数进行优化。
作为正指标,而将来自不同时刻的嵌入作为负指标。其中,正指标有助于捕捉特定时刻的空间交通相关性,负指标有助于捕捉不同时刻的时间异质性。将SSL模型通过式(13)损失函数进行优化。
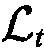
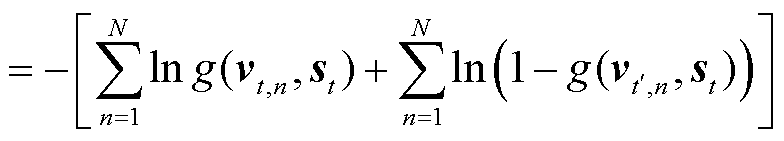 (13)
(13)
式中,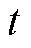 和
和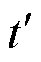 为两个不同的时刻;
为两个不同的时刻;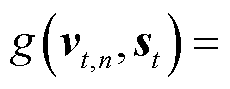
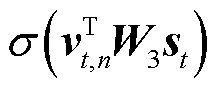 ,
,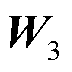 为可学习的参数矩阵,
为可学习的参数矩阵,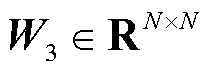 。
。
本节首先提出城市路网环境下动态阻抗计算方法;其次,基于动态阻抗,以单辆EV为研究对象,建立考虑用户多目标、多场景的充电导航策略;最后,通过计算每个节点对应的最优充电站,评估城市充电站服务范围,从而实现电动汽车充电快速引导。
城市路网环境下,道路交通信息随时间变化显著,不同路段的行驶时间具有较大的随机性。本文在文献[22]建立的行程时间模型基础上,提出动态交通阻抗计算方法,以及充电站内动态充电时间阻抗和动态排队时间阻抗计算方法,为充电导航提供支撑。
2.1.1 动态交通阻抗
对每一段路径,其耗时可以用交通流模型求得,以节点i到节点j的路径为例进行分析。依据交通流量、密度和速度三者之间的关系,自由流速度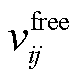 表示为
表示为
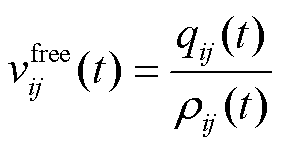 (14)
(14)
式中,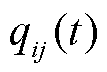 为路径交通流量;
为路径交通流量;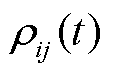 为路径车流密度。已知最大通行能力
为路径车流密度。已知最大通行能力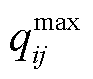 ,临界密度
,临界密度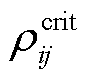 可表示为
可表示为
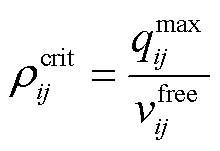 (15)
(15)
假设路段自由流部分的车辆在路径中均匀分布,结合ST-SSL模型预测结果,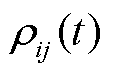 可表示为
可表示为
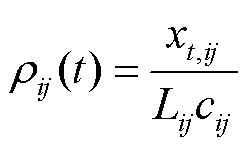 (16)
(16)
式中,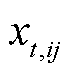 为t时刻路径车辆数;
为t时刻路径车辆数;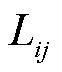 为路径长度;
为路径长度;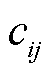 为单位距离能容纳的车辆数。
为单位距离能容纳的车辆数。
已知车流密度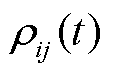 、自由流速度
、自由流速度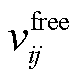 和最小行车速度
和最小行车速度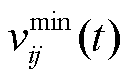 ,行驶速度
,行驶速度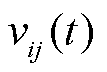 可表示为
可表示为
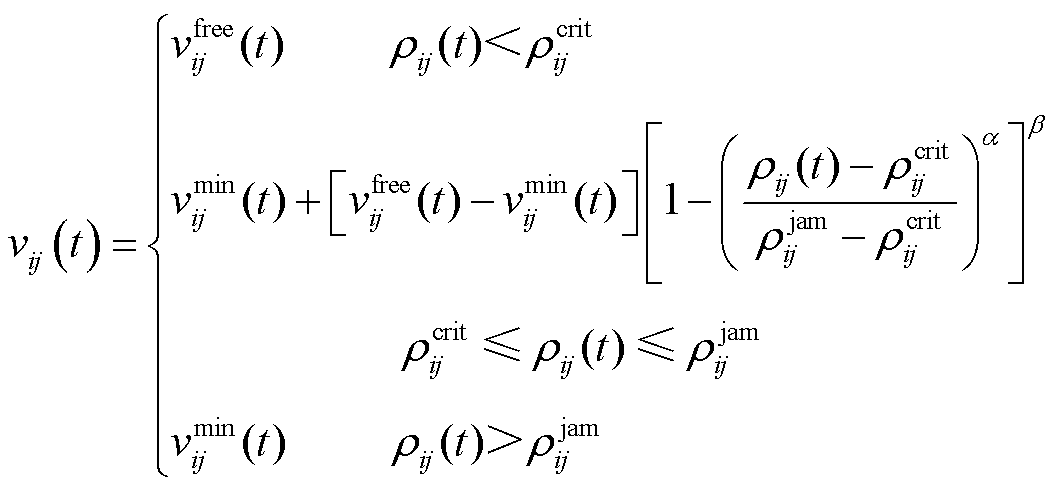 (17)
(17)
式中,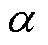 和
和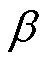 为模型参数。通过路径所用时间可表示为
为模型参数。通过路径所用时间可表示为
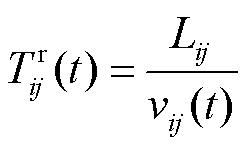 (18)
(18)
考虑交通流预测时间间隔,式(18)可表示为
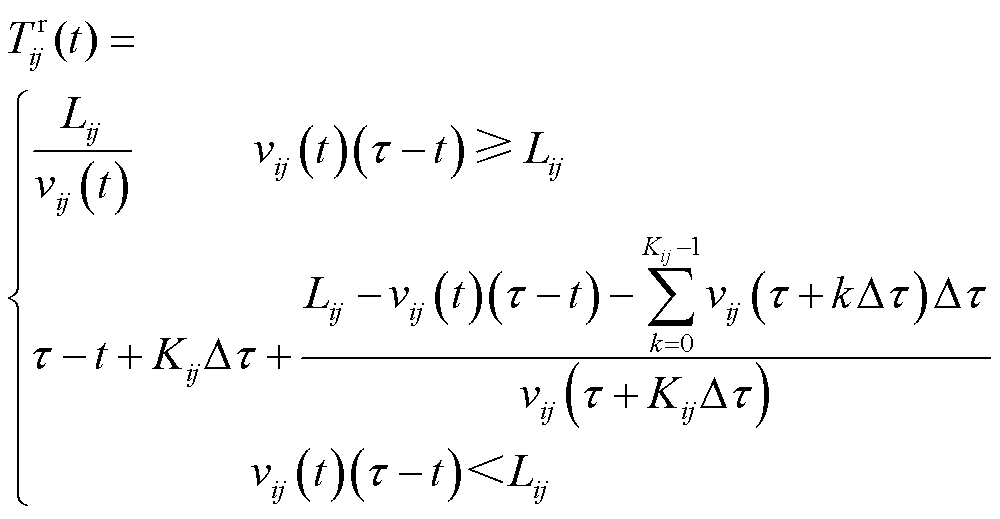 (19)
(19)
式中,k为累加的索引;Dt为预测的时间间隔;t为下一次交通流模型预测的时间;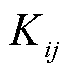 为同时满足式(20)的自然数。
为同时满足式(20)的自然数。
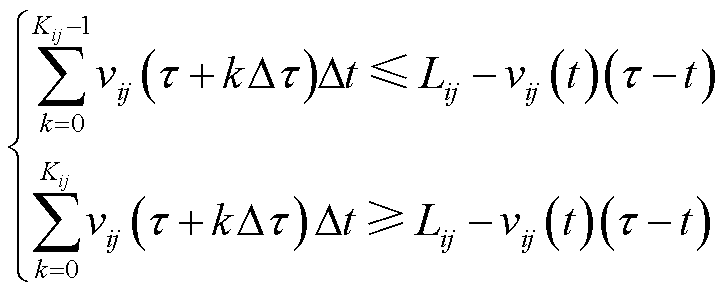 (20)
(20)
因此,可得到路径平均通过速度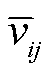 为
为
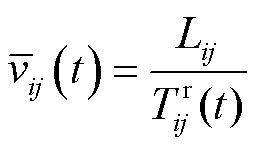 (21)
(21)
2.1.2 动态充电时间阻抗
不同的环境温度会对EV充放电效率产生影响,通过对文献[27]得到的t时刻温度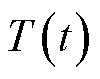 和放电效率
和放电效率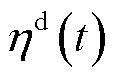 曲线进行拟合,得到关系式为
曲线进行拟合,得到关系式为
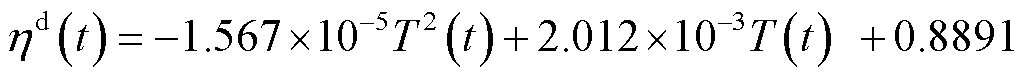 (22)
(22)
在不同的交通情况下,EV的能耗也会有所区别。文献[28]给出的城区各级道路行驶速度区间见表1。
表1 不同道路等级和拥堵程度下的行驶速度区间
Tab.1 Driving speed range with different road classes and congestion levels(单位:km/h)

城市道路极度拥堵中度拥堵轻度拥堵基本畅通极度畅通 快速道[0,25)[25,35)[35,50)[50,65)[65,∞) 主干道[0,15)[15,25)[25,35)[35,45)[45,∞) 次干道[0,10)[10,15)[15,25)[25,35)[35,∞) 支干道[0,10)[10,15)[15,25)[25,35)[35,∞)
参考文献[29]提出的单位能耗与行驶速度之间的关系,得到不同道路等级的单位里程耗电量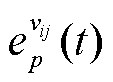 为
为
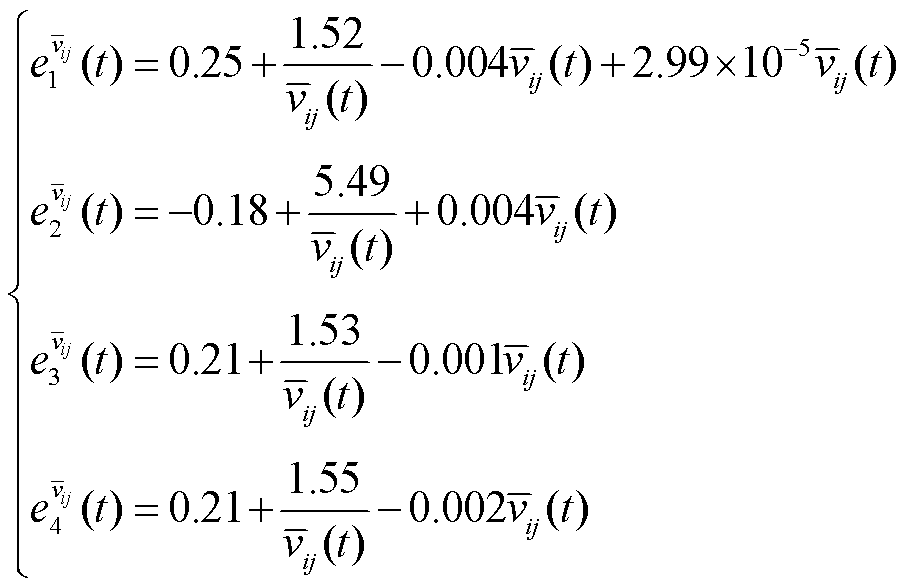 (23)
(23)
式中, ,分别表示快速道、主干道、次干道、支干道。
,分别表示快速道、主干道、次干道、支干道。
基于上述分析,得到EV从节点s到达充电站b时的剩余电量为
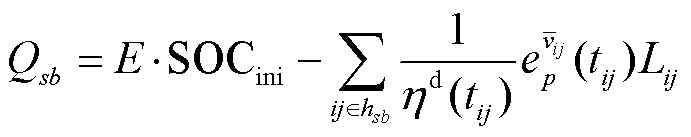 (24)
(24)
式中,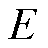 为EV的电池容量;
为EV的电池容量;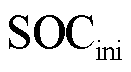 为初始荷电状态;
为初始荷电状态;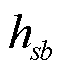 为从节点s到充电站b某一可行路线;
为从节点s到充电站b某一可行路线;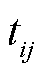 为沿路线
为沿路线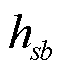 进入路径ij的时间。可以求得充电所需的时间
进入路径ij的时间。可以求得充电所需的时间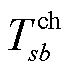 为
为
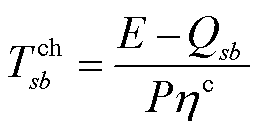 (25)
(25)
式中,P为电动汽车的额定充电功率;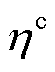 为EV的充电效率,是一个定值。
为EV的充电效率,是一个定值。
2.1.3 动态排队时间阻抗
充电站b内每个充电桩的等待时间为前序正在等待车辆的充电时间之和,在理想状态下,最新到达充电站的EV排队时间为所有充电桩等待时间的最小值,其表达式为
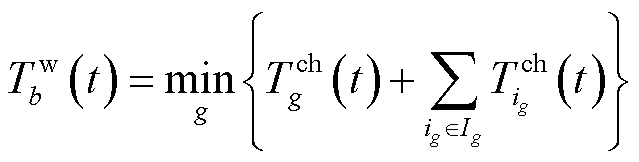 (26)
(26)
式中,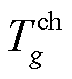 为正在第g个充电桩充电的EV剩余充电时间;
为正在第g个充电桩充电的EV剩余充电时间;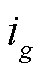 为即将在第g个充电桩上充电的EV;
为即将在第g个充电桩上充电的EV;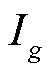 为正在第g个充电桩排队等待充电的EV集合。
为正在第g个充电桩排队等待充电的EV集合。
对于进行充电导航的目标EV,在到达充电站最优路线上,往往存在以相同充电站为目的地且行驶时间更短的潜在车辆。在进行排队时间阻抗的计算时,需要考虑潜在车辆的排队时间和充电时间对目标EV的影响,式(26)更新为
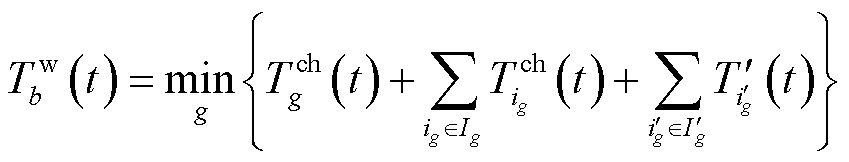 (27)
(27)
式中,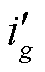 为即将在第g个充电桩上充电的潜在车辆;
为即将在第g个充电桩上充电的潜在车辆;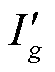 为潜在EV集合;
为潜在EV集合;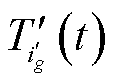 为潜在车辆对排队时间的增量。
为潜在车辆对排队时间的增量。
考虑到即使潜在车辆选择了本文推荐的最优方案,但在行驶途中仍有概率选择其他充电站,而潜在车辆越靠近充电站,其毁约的概率就越低,定义式(28)对潜在车辆带来的排队时间增量进行刻画。
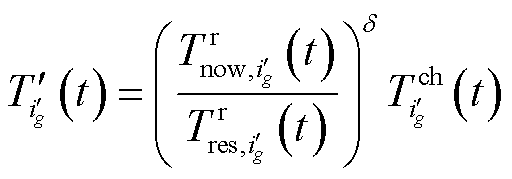 (28)
(28)
式中,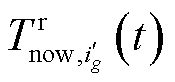 为该潜在车辆在推荐路线中当前一段所花的时间;
为该潜在车辆在推荐路线中当前一段所花的时间;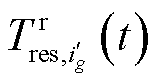 为沿推荐路线到达充电站的剩余时间;d 为模型参数,
为沿推荐路线到达充电站的剩余时间;d 为模型参数,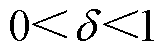 。
。
充电导航是实现区域EV负荷有序分配的重要手段。针对不同用户存在不同的充电导航目标与需求场景,分别设计定制化充电导航方案,提升用户响应率。
2.2.1 多导航目标设计
在不同情况下,不同EV用户选择充电导航的目标有所不同。例如在电量相对充裕时,对于成本敏感型用户,倾向于选择成本最小的导航,而时间敏感型用户,则倾向于选择时间最短的导航;而在电量较低时,用户可能选择耗电最小的导航,以满足充电需求。基于上述分析,本节设计了三种决策目标选择,分别为以最小成本、最短耗时和最少耗电为目标。
1)最小成本为目标
对目标节点到所有充电站的最小成本代价进行比较,选择其中成本代价最小的充电站。本文定义成本并非单指充电成本,而是充电成本与时间成本之和,其中充电成本为主要影响因素,时间成本保证导航结果的合理性。以目标节点s为例,表达式为
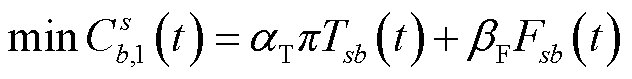 (29)
(29)
式中,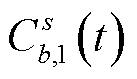 为从节点s到充电站b的成本代价;
为从节点s到充电站b的成本代价;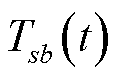 为从节点s到充电站b充电完成所消耗的所有时间;
为从节点s到充电站b充电完成所消耗的所有时间;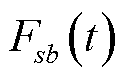 为从节点s达到充电站b后的充电费用;
为从节点s达到充电站b后的充电费用;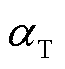 与
与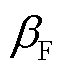 为权重系数;π为单位时间社会底薪。
为权重系数;π为单位时间社会底薪。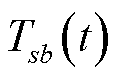 和
和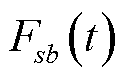 的具体表达式为
的具体表达式为
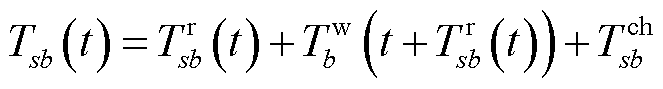 (30)
(30)
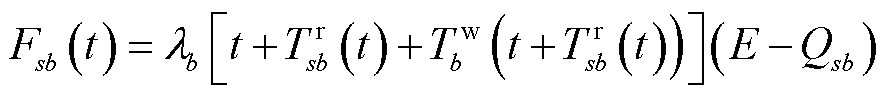 (31)
(31)
式中,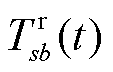 为节点s到达充电站b沿某一可行路线所消耗的时间;
为节点s到达充电站b沿某一可行路线所消耗的时间;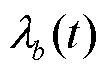 为充电站b在t时刻的充电价格,在合理范围内通过调整
为充电站b在t时刻的充电价格,在合理范围内通过调整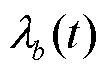 可影响对EV的吸引程度,由于本文未涉及充电站定价问题,设置
可影响对EV的吸引程度,由于本文未涉及充电站定价问题,设置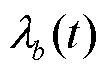 为分时电价。
为分时电价。
2)最短耗时为目标
对目标节点到所有充电站的最小时间代价进行比较,选择其中花费时间代价最小的充电站。以目标节点s为例,表达式为
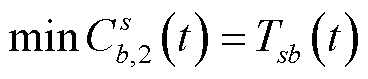 (32)
(32)
式中,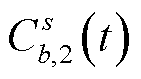 为从节点s到充电站b的时间代价。
为从节点s到充电站b的时间代价。
3)最少耗电为目标
对目标节点到所有充电站的最少耗电代价进行比较,选择其中花费耗电代价最小的充电站。以目标节点s为例,表达式为
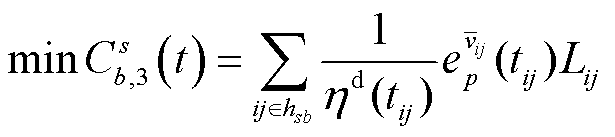 (33)
(33)
式中,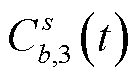 为从节点s到充电站b的耗电代价。
为从节点s到充电站b的耗电代价。
2.2.2 多需求场景设计
不同EV用户选择充电导航的场景也有所不同,多需求场景如图3所示,设计两种典型场景,制定不同的充电导航策略。
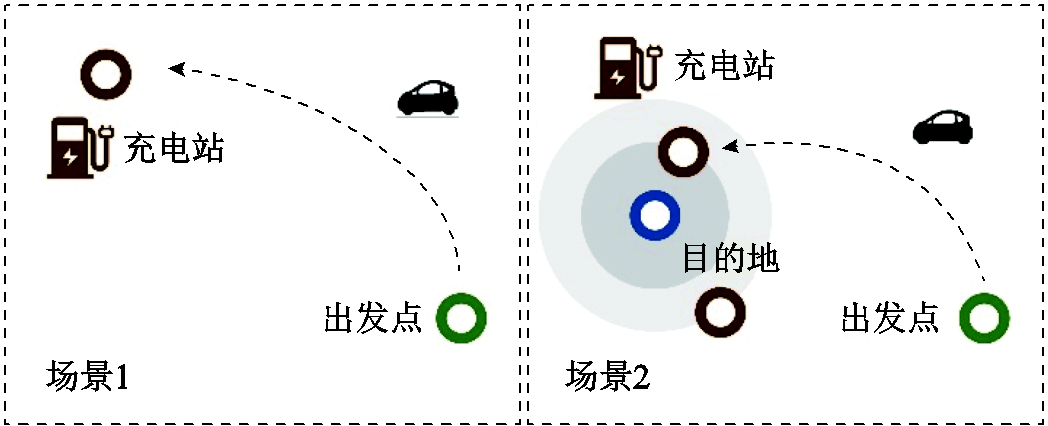
图3 多需求场景
Fig.3 Multiple demand scenarios
1)场景1
在场景1中,EV直接以充电站为目的地,导航某一目标下的最优路径。此场景下充电导航目标函数表达式为
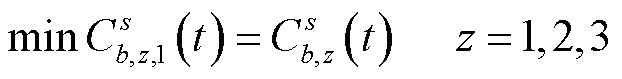 (34)
(34)
式中,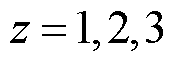 分别表示用户选择以最小成本、最短耗时和最少耗电为目标。
分别表示用户选择以最小成本、最短耗时和最少耗电为目标。
2)场景2
在场景2中,EV选择目的地,并希望在离目的地较近的充电站进行充电。此场景下充电站与目的地距离为影响充电站选择的重要标准,将充电站与目的地距离作为惩罚项,构建充电导航目标函数,表达式为
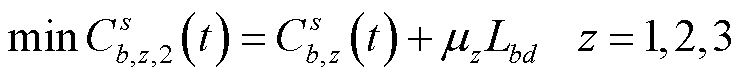 (35)
(35)
式中,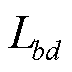 为充电站b到目的地d的距离;
为充电站b到目的地d的距离;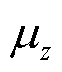 为权重系数,对于不同目标z,需要根据
为权重系数,对于不同目标z,需要根据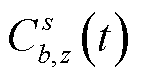 的量级合理设置
的量级合理设置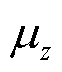 ,以提高
,以提高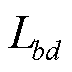 在式(35)中的占比,突出充电站与目的地距离对充电导航结果的影响。
在式(35)中的占比,突出充电站与目的地距离对充电导航结果的影响。
2.3.1 充电站服务范围定义
对于二维空间中的某个设施,会对其周围一定范围内的用户产生吸引力,当用户存在需求时,将选择对应的设施满足自身需求[25]。定义充电站服务范围由城市中特定道路节点组成,位于这些道路节点上的EV用户将会选择对应充电站进行充电。充电站服务范围示意图如图4所示,对于两个充电站的情况,充电站A和B同时对EV产生吸引力,两种颜色分别表示两个充电站的服务范围,当处于A服务范围的EV在需要充电引导时,将会直接选择充电站A进行充电。

图4 充电站服务范围示意图
Fig.4 Charging station service area diagram
2.3.2 基于动态Dijkstra的求解方法
由式(29)~式(35)可知,不同场景、目标下的充电导航动态阻抗可分解为路网阻抗和充电站相关阻抗的加权和,表达式为
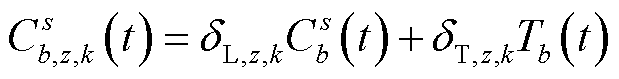 (36)
(36)
式中,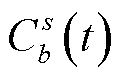 为节点s到充电站b的路网阻抗,影响节点s到充电站b最优路径的选择;
为节点s到充电站b的路网阻抗,影响节点s到充电站b最优路径的选择;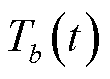 为充电站b相关阻抗,包括充电站b内时间阻抗和充电站b与目的地d的距离路阻,与路径选择无关,影响充电站的选择;
为充电站b相关阻抗,包括充电站b内时间阻抗和充电站b与目的地d的距离路阻,与路径选择无关,影响充电站的选择;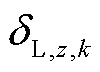 与
与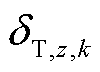 分别为k场景、z目标下路网阻抗和充电站相关阻抗的权重。
分别为k场景、z目标下路网阻抗和充电站相关阻抗的权重。
基于上述分析,首先建立求解模型,实现最优路径的求解。与传统计算最短路径实现充电导航的方式不同,本文以路网节点为对象,在同一时刻内一次性求解每个节点到其他节点的最优路径。
为实现上述目标,采用动态Dijkstra算法对充电导航问题进行求解。相较于其他路径规划算法,Dijkstra采用贪心策略对每一个有向图节点到目标节点的最短路径进行计算,计算复杂度较大。然而,Dijkstra的贪心策略在本文所提模型中能够发挥出较大的优势,减少了区域路网计算次数,反而缩短了计算时间。考虑动态路阻的动态Dijkstra算法计算步骤如下。
设每个t时刻节点参数为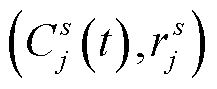 ,其中
,其中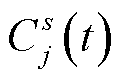 存放从起点s到j点的最小路网阻抗,
存放从起点s到j点的最小路网阻抗,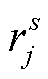 为从起点s到节点j的最优路径中j的前一节点编号。求解从起点到j点的最优路径的过程如下:
为从起点s到节点j的最优路径中j的前一节点编号。求解从起点到j点的最优路径的过程如下:
1)初始化,设初始点为s。
(1)从s到s的最小路阻为0,即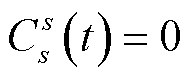 ,
,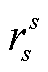 为空。
为空。
(2)设从s到其他任意节点i的路阻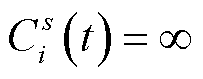 ,
,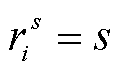 。
。
(3)计算s的标号,令所有己标记节点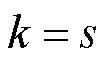 ,其他节点全部设为未标记。
,其他节点全部设为未标记。
2)对所有与k相邻的未标记节点。
(1)检验从已标记节点k到与其相邻的未标记节点j的距离,令
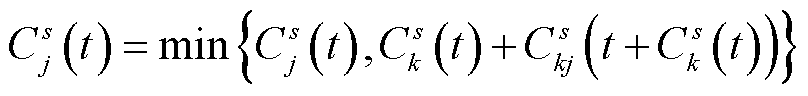 (37)
(37)
式中,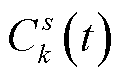 为从s到k的最小路阻;
为从s到k的最小路阻;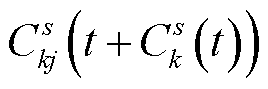 为两相邻节点k和j之间直接的路阻。
为两相邻节点k和j之间直接的路阻。
(2)检验同一级路径选择,令
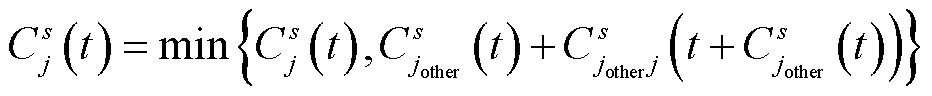 (38)
(38)
式中, 为与j相连的k相邻的节点。
为与j相连的k相邻的节点。
3)确定并标记每个与k相邻的未标记节点。
(1)确定每个j的最小路阻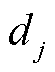 对应的前一节点
对应的前一节点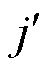 ,令
,令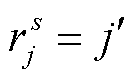 。
。
(2)标记点j。
4)若所有节点均己被标记,则每个节点的最优路径求解完成,否则令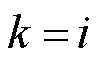 ,重复步骤2)直至所有点完成标记。
,重复步骤2)直至所有点完成标记。
通过上述步骤,即可得到t时刻节点s到每个节点的最小路网阻抗与最优路径矩阵为
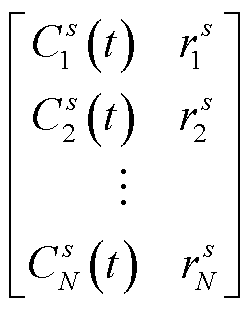 (39)
(39)
式中,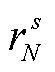 从节点s到节点N的最优路径中N的前一节点编号。
从节点s到节点N的最优路径中N的前一节点编号。
得到最小路网阻抗后,即可计算得到节点s在k场景下以z为目标选择的最优充电站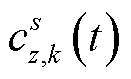 ,表达式为
,表达式为
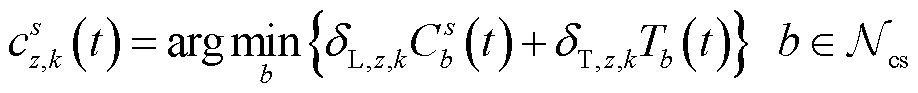 (40)
(40)
式中,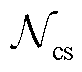 为所有充电站节点的集合。
为所有充电站节点的集合。
将不同场景、不同目标下各节点与对应的最优充电站节点进行绑定,从而实现城市内充电站服务范围的评估,不同场景目标下充电站服务范围划分如图5所示,由于各场景各目标下动态阻抗的计算方法不同,服务范围的评估结果也会存在差异。t时刻充电站b的服务范围表达式为
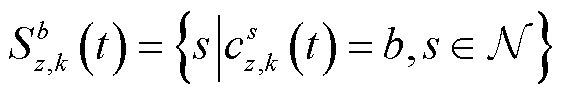 (41)
(41)
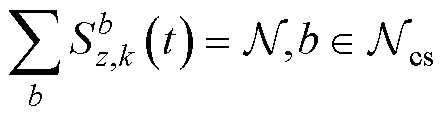 (42)
(42)
式中,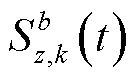 为所有归输于充电站b的节点集合;
为所有归输于充电站b的节点集合;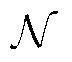 为所有路网节点的集合。对于节点s处的用户,可通过查询式(41)与式(39)得到的节点集合实现充电站和最优路径的快速引导。
为所有路网节点的集合。对于节点s处的用户,可通过查询式(41)与式(39)得到的节点集合实现充电站和最优路径的快速引导。

图5 不同场景目标下充电站服务范围划分
Fig.5 Charging station service area division under different scenarios and targets
充电站的服务能力的评估是充电站建设规划的一个重要环节。考虑城市内所有节点历史充电需求量和不同场景目标历史响应率,即可通过用户数对充电站的服务能力进行量化,表达式为
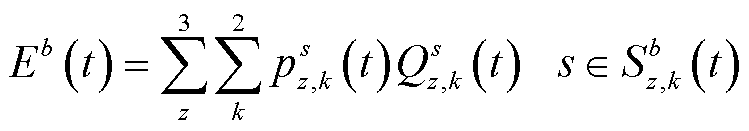 (43)
(43)
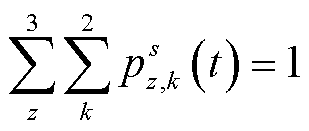 (44)
(44)
式中,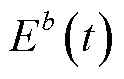 为t时刻充电站b的服务能力;
为t时刻充电站b的服务能力;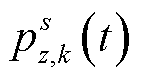 为由历史数据得到的t时刻用户选择k场景z目标的概率;
为由历史数据得到的t时刻用户选择k场景z目标的概率;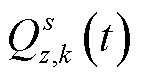 为由历史数据得到的t时刻s节点需要充电的用户数。
为由历史数据得到的t时刻s节点需要充电的用户数。
本文所提基于动态交通推演的电动汽车充电快速引导方法整体计算流程如图6所示。由于计算每隔5 min进行一次,每次计算流程相同,故仅展示了t时刻的充电引导策略计算方法。同时,由于动态Dijkstra算法已在2.3.2节进行了详细介绍,图6更倾向于对充电引导策略整体计算流程进行描述,故只是将动态Dijkstra作为了其中的一个环节。

图6 电动汽车充电快速引导方法流程
Fig.6 Flow chart of the fast guidance method for electric vehicle charging
与传统实时导航不同,本文采用“规划-分配”的模式进行充电导航。其中,规划指每隔一定时间进行一次全局交通流预测与最优路径规划,分配指根据用户节点与意愿进行实时的导航策略分配。例如,在实际运行中,设置模型预测间隔与最优路径规划间隔均为5 min,对5 min内有导航需求的用户,均通过最优路径矩阵进行路径分配,对于已经推荐了最优路径的EV,除非用户主动选择更新策略,否则后续不再推荐新的方案。在交通数据采集间隔允许的前提下,可根据实际情况将规划间隔从5 min缩至更短。
本节将分别从预测模型效果和交通仿真结果两方面,验证本文所提模型的有效性与先进性。
为验证本文所提电动汽车充电引导策略的有效性,参考文献[24]路网模型设置方式,选择美国洛杉矶城市路网环境进行实例分析,地图数据来自于开源平台OpenStreetMap[30],并采用开源地理信息系统QGIS对数据进行处理。洛杉矶某区域路网拓扑结构如图7所示,所选区域面积包含32个道路节点和53条主要公路,根据各节点周围建筑功能将节点划分为:商业区、工作区和居住区,仿真参数设置见附表1。
采用加州高速路网PeMS交通数据[31]对ST-SSL模型进行性能验证,采集从2022年1月1日—2023年12月31日两年共210 240组样本数据,其中交通流量由传感器5 min测量一次。设置ST-SSL模型参数嵌入维度D=64,时空编码器的时间和空间卷积核大小为3,优化器为Adam,训练批次大小为32,基于pytorch框架搭建模型。

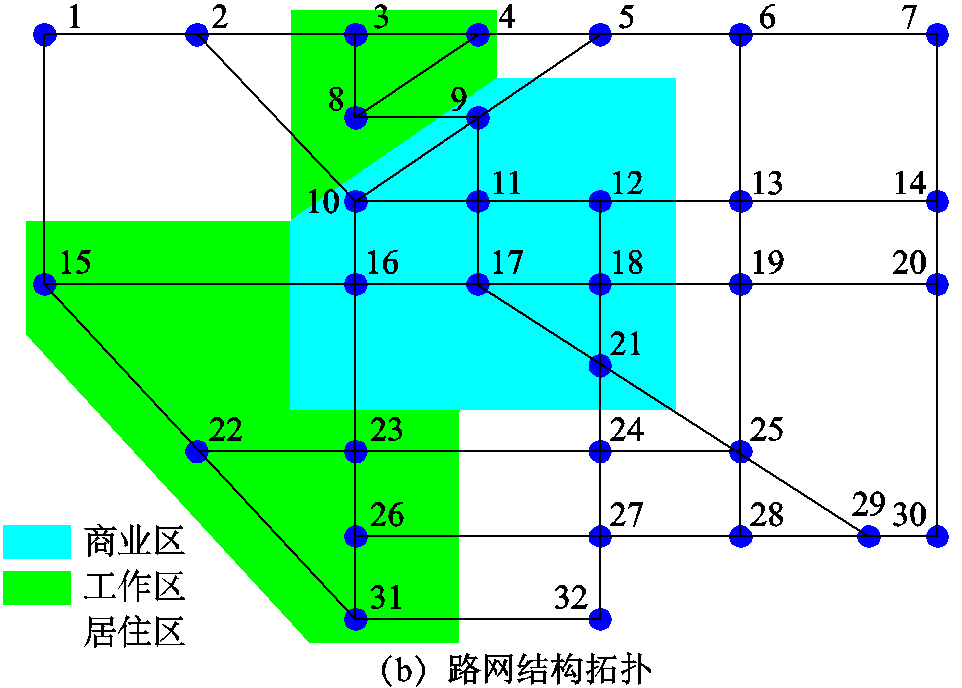
图7 洛杉矶某区域路网拓扑结构
Fig.7 Topological structure of a regional road in Los Angeles
图8a和图8b展示了ST-SSL模型对2023年12月1日路段6的交通流量预测结果,定义从节点3到节点8方向车道为正向车道。由图8可知,ST-SSL模型的预测结果与实际车辆具有高度重合性,能够较好地拟合交通流量数据,实现高精度的交通流量预测。

图8 ST-SSL预测结果
Fig.8 Prediction results of ST-SSL
为进一步展示ST-SSL模型预测效果,本文采用以下指标表征预测精度。
1)平均绝对误差(Mean Average Error, MAE),即各次测量值的绝对偏差绝对值的平均值,表达式为
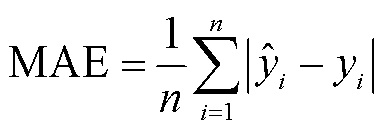 (45)
(45)
式中,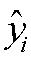 和
和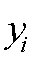 分别为预测值和实际值。
分别为预测值和实际值。
2)平均绝对百分比误差(Mean Average Percentage Error, MAPE),为常用于衡量预测准确性的统计指标,如时间序列的预测,表达式为
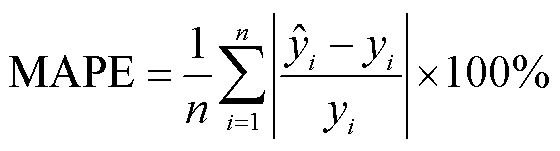 (46)
(46)
分别采用ARIMA[32]、ST-ResNet[33]、AGCRN[34]和STFGNN[35]模型与ST-SSL模型在同一组测试集上进行预测,并比较MAE和MAPE指标。不同模型预测误差如图9所示,ARIMA模型和STFGNN模型整体拟合效果相对较差,且存在较多异常点。ST-ResNet模型和AGCRN模型效果较为接近,在波峰与波谷的预测值与实际值的偏差较大,预测准确度在波峰和波谷下降较为明显。而ST-SSL模型在波峰与波谷的预测值与实际值的偏差较小,拟合度较高,且在预测过程中异常点较少。从指标上看,不同模型在MAE与MAPE上的比较见表2,ST-SSL模型的MAE和MAPE相较于其他模型提升明显,指标平均降低了29.3%和16.5%。
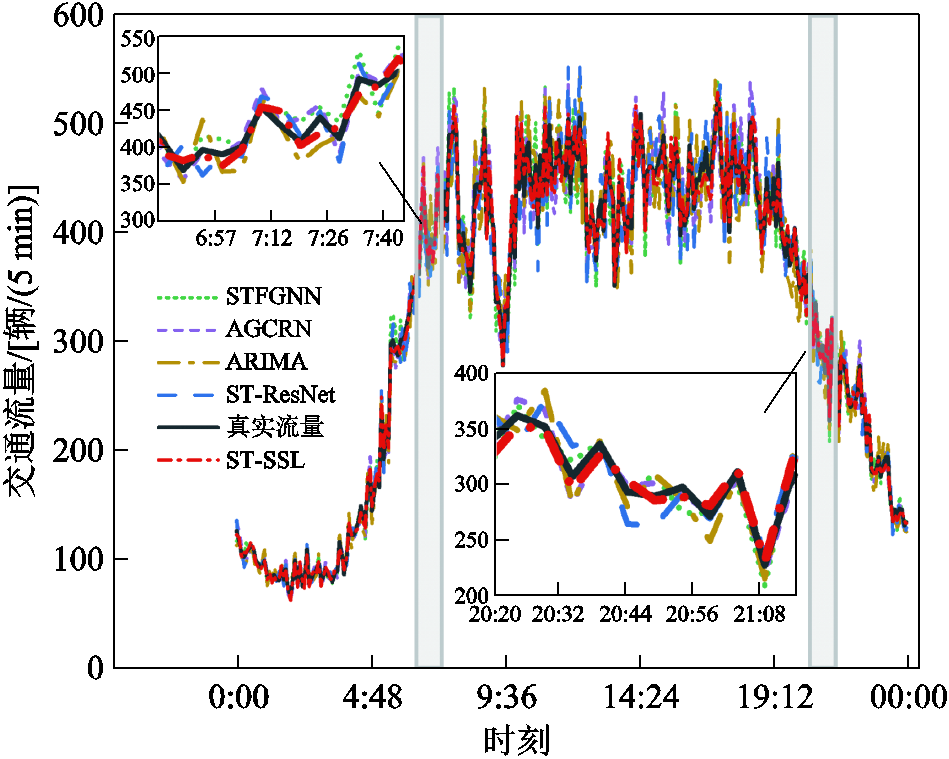
图9 不同模型预测误差
Fig.9 Prediction error of different models
表2 不同模型在MAE与MAPE上的比较
Tab.2 Model comparison in terms of MAE and MAPE
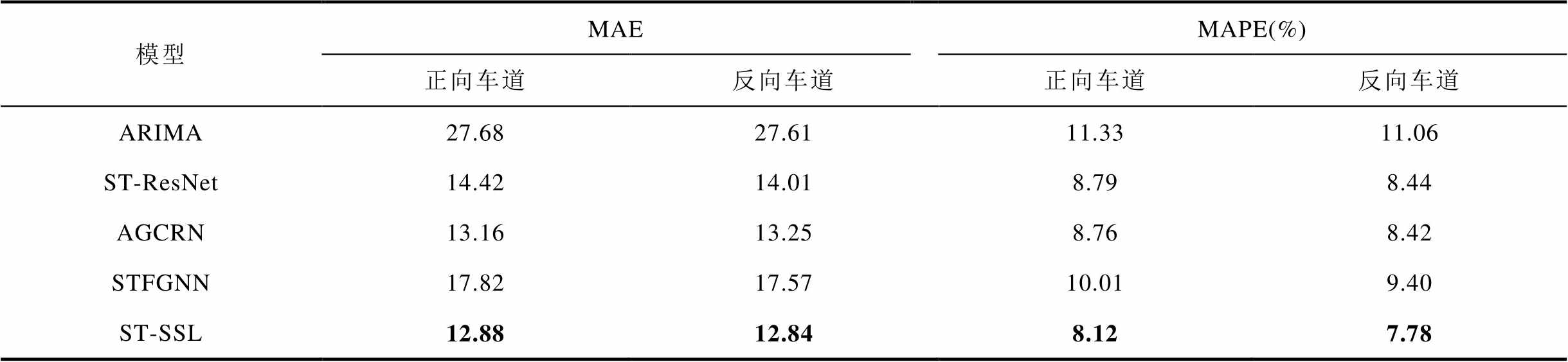
模型MAEMAPE(%) 正向车道反向车道正向车道反向车道 ARIMA27.6827.6111.3311.06 ST-ResNet14.4214.018.798.44 AGCRN13.1613.258.768.42 STFGNN17.8217.5710.019.40 ST-SSL12.8812.848.127.78
基于ST-SSL对交通流量的预测结果,得到评估时段内城市区域交通流量分布,8:00、12:00、 18:00和22:00的交通流量分布情况如图10所示。

图10 不同时刻交通流量分布
Fig.10 Traffic flow distribution at different times
由图10可知,交通流量在空间上分布不均匀,节点9-11、节点16-17区域为城市中心交通枢纽,在多个时段均出现交通流量过大导致的堵塞。而节点1区域附近存在较多旅游资源,节点15区域靠近洛杉矶机场,交通流量相对较大。节点7、节点14与节点29区域处于城市边缘,故交通流量相对较小。在时间分布方面,同样存在不均匀性。在8:00与18:00上下班高峰,整个城市区域交通堵塞现象较为明显,而12:00与22:00,交通流量则主要分布在城市中心区域。
3.3.1 单辆电动汽车充电导航结果分析
在交通流量预测结果的基础上验证充电导航策略的有效性。其中,充电电价根据美国2023年12月商用电价[36]进行折算,社会底薪根据美国平均时薪(月薪)[37]进行折算,环境温度采用洛杉矶真实数据[38],设置所有EV充电功率为7 kW,电池容量为50 kW·h,SOCini=0.3。设置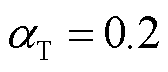 ,
,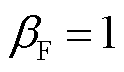 ,
,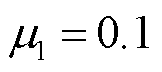 ,
,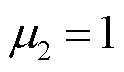 ,
,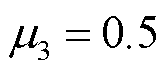 。对场景1,设置充电站分布于节点5、10、13、25、26,选择单辆EV进行分析,出发节点为21,出发时间为8:00。对场景2,充电站分布与场景1相同,为分析不同目的地对充电站选择的影响,设置EV1出发节点为21,目的地为节点10与节点11中间处,设置EV2出发节点为6,目的地为节点5与节点6中间处,出发时间均为8:00。图11a和图11b分别给出了不同场景、目标下EV的充电导航路径,具体路径分析结果见表3,表中场景2各列已折算目的地间距影响。需要注意的是,图11仅展示了拓扑结构,实际的地理距离需要对照图7a与附表1。
。对场景1,设置充电站分布于节点5、10、13、25、26,选择单辆EV进行分析,出发节点为21,出发时间为8:00。对场景2,充电站分布与场景1相同,为分析不同目的地对充电站选择的影响,设置EV1出发节点为21,目的地为节点10与节点11中间处,设置EV2出发节点为6,目的地为节点5与节点6中间处,出发时间均为8:00。图11a和图11b分别给出了不同场景、目标下EV的充电导航路径,具体路径分析结果见表3,表中场景2各列已折算目的地间距影响。需要注意的是,图11仅展示了拓扑结构,实际的地理距离需要对照图7a与附表1。

图11 不同场景目标下充电导航路径
Fig.11 Charging navigation path under different scenarios and targets
表3 不同场景目标下充电导航路径
Tab.3 Charging navigation path under different scenarios and targets

场景目标规划路径成本代价时间代价耗电代价 1最小成本21→256.0625.91.63 最短耗时21→18→19→136.3519.23.59 最少耗电21→17→11→106.0831.51.54 2(EV 1)最小成本21→18→12→11→106.2527.12.61 最短耗时21→18→12→11→106.2527.12.61 最少耗电21→17→11→106.2633.32.42 2(EV 2)最小成本6→137.4225.88.71 最短耗时6→137.4225.88.71 最少耗电6→57.5141.38.4
由图11和表3可知,在场景1下,EV直接以充电站为目标进行导航,受不同路径交通状况的影响,分别以最小成本、最短耗时和最少耗电为目标得到的推荐路径和充电站存在差异。在场景2中,目的地与充电站间的距离是路径选择的强相关因素;对EV1,由于节点10充电站与目的地距离最短,在三种目标下,该充电站均为最优选择,不同目标仅对最优路径产生影响。然而,这并不代表目的地附近充电站一定为最优选择。对EV2,虽然节点5充电站与目的地距离最短,但节点13充电站与出发地距离更近,同时节点13与目的地间距未超出节点5与目的地间距过多,综合考虑交通堵塞的影响,在以最小成本和最短耗时为目标时,反而选择与目的地较远的节点13充电站。说明在场景2下目的地距离并不会成为决定充电站选择的唯一因素,交通状况等因素对充电导航的影响仍然无法忽略。
记录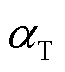 取值从0.01到0.5过程中不同充电站成本代价变化情况,以验证不同
取值从0.01到0.5过程中不同充电站成本代价变化情况,以验证不同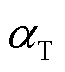 和
和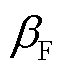 设置对充电站选择的影响,结果如图12所示,其中EV设置与图11中场景1下EV和场景2下EV2相同。虽然
设置对充电站选择的影响,结果如图12所示,其中EV设置与图11中场景1下EV和场景2下EV2相同。虽然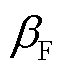 保持不变,但通过改变
保持不变,但通过改变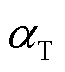 取值依旧可以反映两者间相对大小变化对结果的影响。可以看到,在场景1下,当
取值依旧可以反映两者间相对大小变化对结果的影响。可以看到,在场景1下,当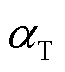 较小时,充电成本为主导因素,最小成本目标下充电站选择结果与最少耗电目标相同,随着
较小时,充电成本为主导因素,最小成本目标下充电站选择结果与最少耗电目标相同,随着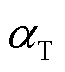 增大,时间成本占比逐渐增加。在场景2下,目的地距离为重要影响因素,改变成本权重对决策结果影响不大。
增大,时间成本占比逐渐增加。在场景2下,目的地距离为重要影响因素,改变成本权重对决策结果影响不大。
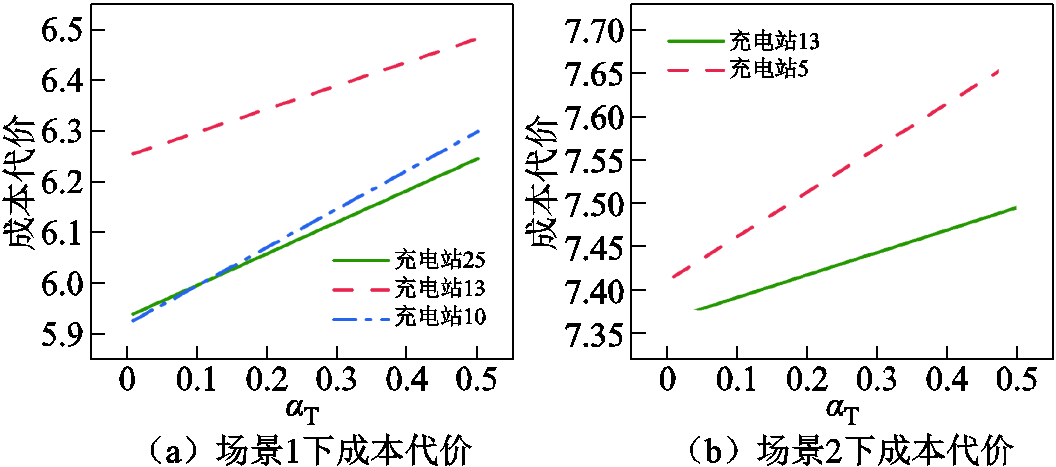
图12 不同成本权重下充电站选择
Fig.12 Charging station selection under different cost weights
为比较本文提出的动态充电导航方法与传统静态方法的优劣,以场景1最短耗时为目标进行最优路径规划,EV设置与图11a相同。在预计耗时与实际耗时误差和计算时间上对两种方法进行比较,此处静态方法指未考虑动态交通流的传统Dijkstra路径规划方法,结果见表4。
表4 不同充电导航方法比较
Tab.4 Comparison of different charging navigation methods

方法规划路径预计耗时/min实际耗时/min计算时间/s 静态充电导航21→18→12→11→1020.1225.410.186 动态充电导航21→18→19→1319.2119.090.385
本文所提动态方法在视野上包含了路径规划需要的所有时段,有效地避免了决策短视。由于接入了交通流滚动预测,在进行路径规划时考虑到了未来交通状况,能够有效地避开未来可能发生交通堵塞的路段,预计耗时与实际耗时误差较小。而静态方法只关注当前时刻的交通状况,规划路径容易受交通状况变化影响,预计耗时与实际耗时差距较大,在最短耗时目标下,规划方案耗时大于动态方法。但在计算时间上,静态方法具有优势,这是因为动态方法存在较多迭代环节。然而,本文对于大规模EV的充电引导并不采用每辆车单独规划的方法,而是基于充电站服务范围进行充电引导。
3.3.2 电动汽车充电快速引导效果分析
由混合Logit模型[39]得到不同节点EV选择各场景各目标充电导航的概率。由于本节算例的主要目的是展示EV的不同选择对充电站服务范围边界产生的影响,而非精准刻画EV对于不同场景目标的选择概率,故对于EV选择概率的设置较为简单。本文采用python中statsmodels库的mixedlm函数实现混合Logit模型,得到各场景各目标的选择概率如图13所示。根据城市交通流量状况,引入一定规模的有充电导航需求的EV,具体引入规则见附表2。
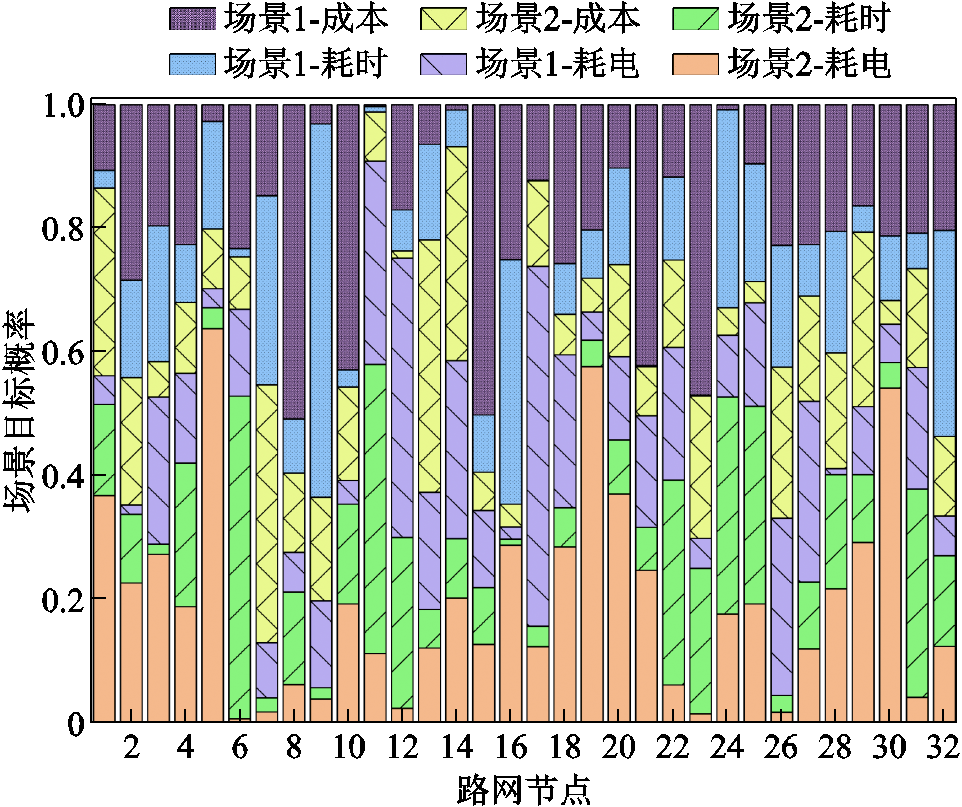
图13 不同场景目标选择概率
Fig.13 Selection probability of different scenarios and targets
设置充电站位置为节点5、10、13、25、26,分别对上午、傍晚和夜间三个时间段的充电站服务范围评估划分,其中上午时间选择10:00,傍晚时间选择17:00,夜间选择21:00,评估结果如图14a~图14c所示,17:00时刻相邻区域不同需求EV充电站选择差异见表5。
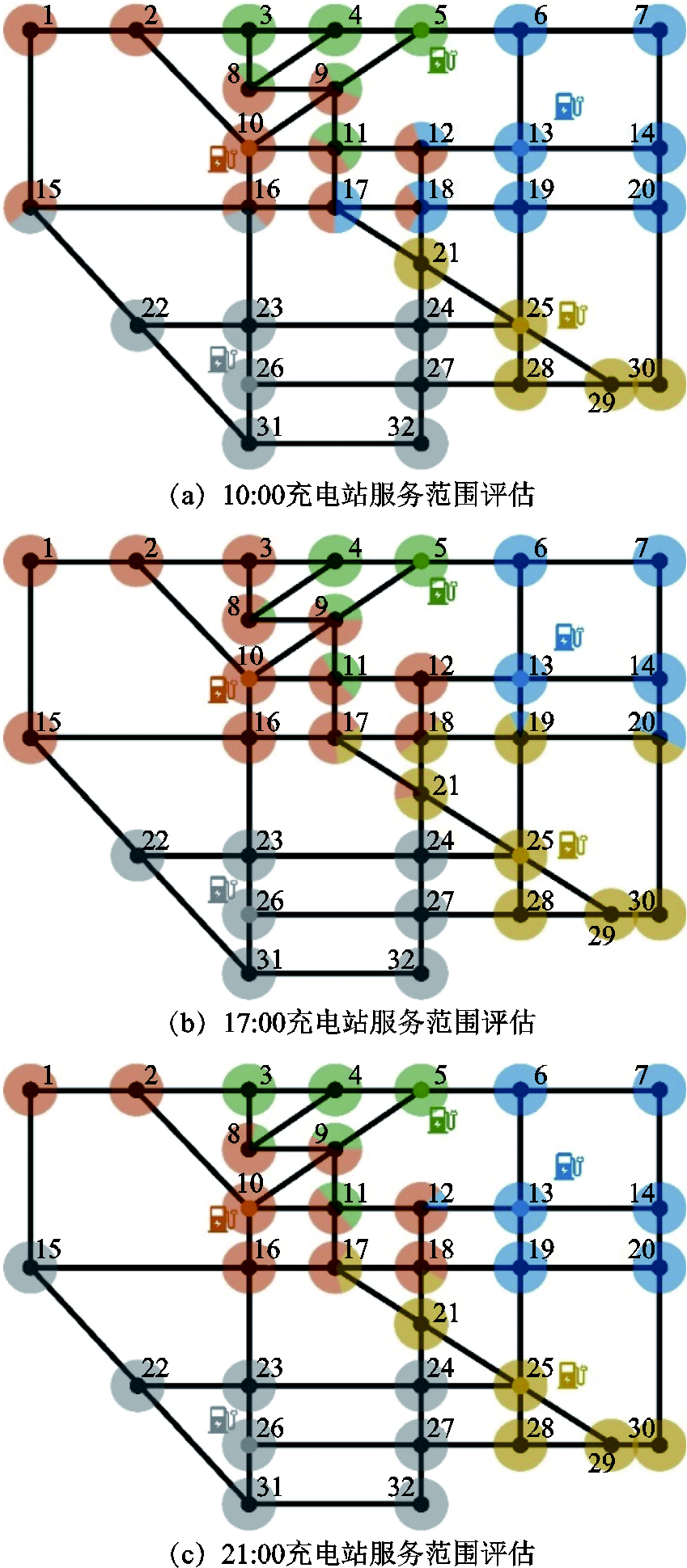
图14 不同时刻充电站服务范围评估结果
Fig.14 Evaluation results of charging station service scope at different times
表5 17:00时刻不同节点不同需求EV充电站选择
Tab.5 EV charging station selection for different nodes with different requirements at 17:00
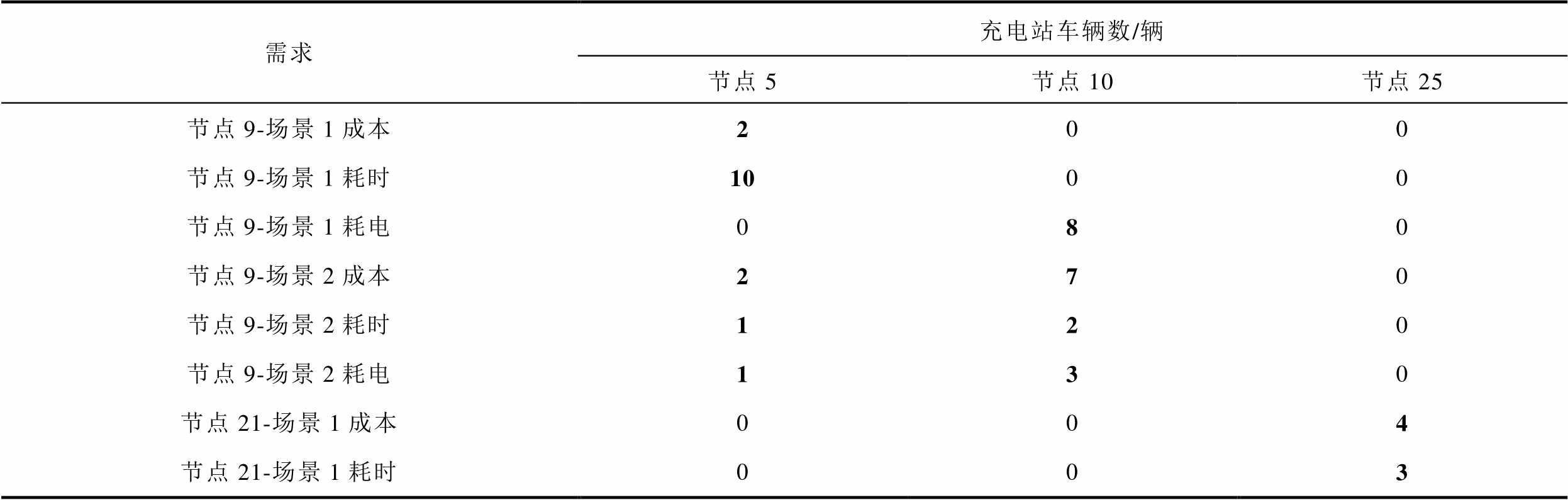
需求充电站车辆数/辆 节点5节点10节点25 节点9-场景1成本200 节点9-场景1耗时1000 节点9-场景1耗电080 节点9-场景2成本270 节点9-场景2耗时120 节点9-场景2耗电130 节点21-场景1成本004 节点21-场景1耗时003
(续)

需求充电站车辆数/辆 节点5节点10节点25 节点21-场景2成本011 节点21-场景2耗时012 节点21-场景2耗电045
在同一时刻,部分节点被同时划分给多个充电站,这是由于EV在不同场景目标下,得到了不同最优充电站推荐,因此,各充电站服务范围在边缘处存在明显的混合现象,如图14b节点9,5/9的节点面积划分给节点10处充电站,即说明节点9处有5/9的EV推荐前往节点10充电。由表5可知,对于场景1,在特定目标下,节点匹配的充电站是固定的;而对于场景2,受不同EV选择目的地的影响,分配结果不固定。在不同时刻,充电站服务范围评估结果存在较大差异,尤其是位于各充电站服务范围边缘的节点,如节点8-9、11-12、15-20,各充电站在该处的影响能力呈现出较强的时间敏感性,这是由于不同时刻交通情况变化较大,伴随着交通阻抗随时间变化显著,而位于这些节点的用户在特定场景和目标下前往多个充电站的代价接近,其细微的差别受交通流量的影响明显,因此时间成为决定该时刻节点归属的重要指标。而对于一些稳定的节点,如节点1-2、6-7、31-32、28-30等,由于在较小代价范围内只存在一个充电站,故交通流量的影响较为有限,这些节点的归属几乎不随时间发生变化。
为验证本文所提电动汽车充电引导策略在计算效率方面的优势,比较了不同方法的计算耗时。方法①为1 000辆车采用Dijkstra算法计算导航路径总耗时;方法②为1 000辆车采用动态交通推演与动态Dijkstra算法计算导航路径总耗时;方法③为按图6流程计算耗时;方法④为基于充电站服务范围对1 000辆车进行策略分配。不同充电引导策略计算耗时见表6,本文所提方法在全局规划阶段耗时较长,考虑每5 min进行一次规划,在实际运行中,可以灵活调整规划开始时间以规避耗时较长的影响。在实时策略分配方面具有极大优势,仅需0.492 s即可实现1 000辆车的充电引导,大大减少计算消耗资源,实现s级的充电导航任务。
表6 不同充电引导策略计算耗时
Tab.6 Calculation of different charging guidance strategies consumes time

方法计算时间/s ①分别对1 000辆车进行静态充电导航193.892 ②分别对1 000辆车进行动态充电导航379.104 ③求解全局最优矩阵与充电站服务范围7.386 ④基于充电站服务范围对1000辆车进行充电引导0.492
本文考虑未来交通信息变化对导航策略的影响,兼顾方案多样性与计算时效性,提出一种基于动态交通推演的电动汽车充电快速引导策略。最后,以洛杉矶某区域实际路网为例,通过仿真对比验证所提策略的有效性,结果表明:
1)基于ST-SSL模型对动态交通信息进行预测,能够充分挖掘交通流信息的空间异质性与时间异质性,提升预测效果,为构建动态交通阻抗提供有效的数据基础。
2)所提基于动态阻抗的多场景多目标充电导航策略能够有效感知交通信息并兼顾用户多样化需求,有效降低不同用户充电导航代价,合理引导电动汽车负荷分布。
3)所提动态Dijkstra算法可以根据未来交通信息推荐最优路径,既可以作为导航算法规划行驶路径,也可以根据用户需求进行定制化最优充电站推荐。
4)基于全域充电导航结果进行充电站服务范围划分,能够有效评估充电站影响范围,为充电站建设规划提供重要参考。基于划分结果对各节点电动汽车进行充电导航策略的快速分配,有效地降低了充电导航计算资源消耗。
尽管本文交通流数据和路网数据采用真实测量方法得到,但在用户信息和充电站信息的设置上依旧基于仿真方法得到,在今后的工作中将采用实测数据对模型进行完善与效果验证。
附录 仿真系统参数
附表1 道路参数
App.Tab.1 Parameters of roads
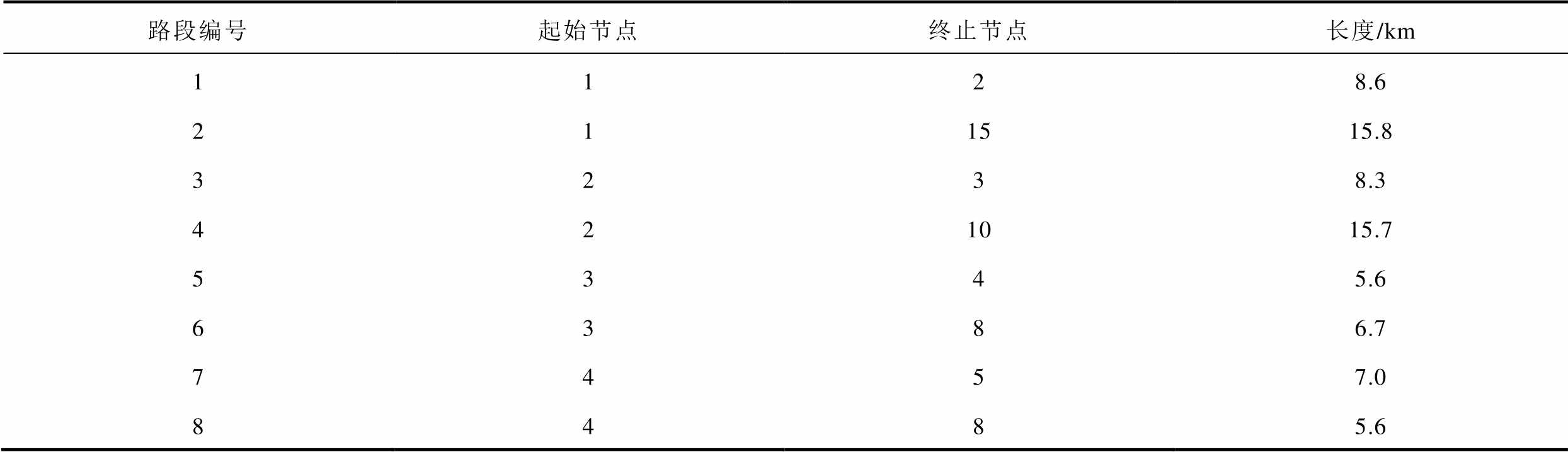
路段编号起始节点终止节点长度/km 1128.6 211515.8 3238.3 421015.7 5345.6 6386.7 7457.0 8485.6
(续)

路段编号起始节点终止节点长度/km 95618.4 105911.6 116712.32 126138.8 137146.3 14893.3 159102.9 169113.0 1710113.5 1810163.5 1911124.7 2011172.8 21121315.5 2212183.0 23131418.0 2413194.4 2514208.1 26151614.8 27152213.2 2816175.4 29162312.1 3017184.7 3117214.5 32181913.2 3318212.2 34192018.7 35192512.3 36203018.2 37212412.0 38212511.4 3922238.3 40223113.0 4123249.7 4223266.3 4324259.9 4424274.1 4525287.2 46252914.3 4726278.4 4826311.8 4927288.2 5027325.7 51282911.7 5229309.6 5331328.4
附表2 不同时段引入电动汽车车辆数量
App.Tab.2 Quantity of electric vehicles introduced during different time periods

时段每隔5 min引入车辆数/辆引入总车辆数/辆 7:00—9:003608 640 9:00—12:001204 320 12:00—14:001603 840 14:00—17:001204 320 17:00—19:003608 640 19:00—23:001205 760 其余时段403 840
参考文献
[1] 房宇轩, 胡俊杰, 马文帅. 计及用户意愿的电动汽车聚合商主从博弈优化调度策略[J]. 电工技术学报, 2024, 39(16): 5091-5103.
Fang Yuxuan, Hu Junjie, Ma Wenshuai. Optimal dispatch strategy for electric vehicle aggregators based on Stackelberg game theory considering user intention[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5091-5103.
[2] 兰威, 陈飞雄. 计及阻塞管理的虚拟电厂与配电网协同运行策略[J]. 电气技术, 2022, 23(6): 30-41.
Lan Wei, Chen Feixiong. Cooperative operation strategy of distribution network and virtual power plants considering congestion management[J]. Electrical Engineering, 2022, 23(6): 30-41.
[3] 胡俊杰, 陆家悦, 马文帅, 等. 面向电网调峰的电动汽车聚合商多层级实时控制策略[J]. 电力系统自动化, 2024, 48(22): 84-95.
Hu Junjie, Lu Jiayue, Ma Wenshuai, et al. Multi-layered real-time control strategy for electric vehicle aggregators aimed at grid peak shaving[J]. Automation of Electric Power Systems, 2024, 48(22): 84-95.
[4] 范培潇, 杨军, 温裕鑫, 等. 基于可进化模型预测控制的含电动汽车多微电网智能发电控制策略[J]. 电工技术学报, 2024, 39(3): 699-713.
Fan Peixiao, Yang Jun, Wen Yuxin, et al. A multi microgrid intelligent generation control strategy with electric vehicles based on evolutionary model predictive control[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 699-713.
[5] 范培潇, 杨军, 温裕鑫, 等. 考虑电动汽车与微电网参与的配电网双层协调控制策略[J]. 电力系统自动化, 2024, 48(19): 60-68.
Fan Peixiao, Yang Jun, Wen Yuxin, et al. Bi-layer coordinated control strategy of distribution network considering participation of electric vehicles and microgrid[J]. Automation of Electric Power Systems, 2024, 48(19): 60-68.
[6] 吴巨爱, 薛禹胜, 谢东亮, 等. 电动汽车参与电量市场与备用市场的联合风险调度[J]. 电工技术学报, 2023, 38(23): 6407-6418.
Wu Juai, Xue Yusheng, Xie Dongliang, et al. The joint risk dispatch of electric vehicle in day-ahead electricity energy market and reserve market[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6407-6418.
[7] 程瑜, 邰宇峰, 丁肇豪, 等. 基于网络流的共享电动汽车优化调度[J]. 电工技术学报, 2022, 37(增刊1): 145-152.
Cheng Yu, Tai Yufeng, Ding Zhaohao, et al. Optimal scheduling of sharing electric vehicles based on network flow[J]. Transactions of China Electro-technical Society, 2022, 37(S1): 145-152.
[8] 贾龙, 胡泽春, 宋永华, 等. 储能和电动汽车充电站与配电网的联合规划研究[J]. 中国电机工程学报, 2017, 37(1): 73-84.
Jia Long, Hu Zechun, Song Yonghua, et al. Joint planning of distribution networks with distributed energy storage systems and electric vehicle charging stations[J]. Proceedings of the CSEE, 2017, 37(1): 73-84.
[9] Li Wengen, Cao Jiannong, Guan Jihong, et al. A general framework for unmet demand prediction in on-demand transport services[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(8): 2820-2830.
[10] Tang Liyang, Zhao Yang, Cabrera J, et al. Forecasting short-term passenger flow: an empirical study on Shenzhen metro[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(10): 3613-3622.
[11] Diao Zulong, Zhang Dafang, Wang Xin, et al. A hybrid model for short-term traffic volume prediction in massive transportation systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(3): 935-946.
[12] Lin Lu, Li Jianxin, Chen Feng, et al. Road traffic speed prediction: a probabilistic model fusing multi-source data[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(7): 1310-1323.
[13] Duan Peibo, Mao Guoqiang, Liang Weifa, et al. A unified spatio-temporal model for short-term traffic flow prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(9): 3212-3223.
[14] Shin J, Sunwoo M. Vehicle speed prediction using a Markov chain with speed constraints[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(9): 3201-3211.
[15] Guo Shengnan, Lin Youfang, Li Shijie, et al. Deep spatial–temporal 3D convolutional neural networks for traffic data forecasting[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(10): 3913-3926.
[16] Liu Jielun, Ong G P, Chen Xiqun. GraphSAGE-based traffic speed forecasting for segment network with sparse data[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(3): 1755-1766.
[17] Qu Zhaowei, Li Haitao, Li Zhihui, et al. Short-term traffic flow forecasting method with M-B-LSTM hybrid network[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(1): 225-235.
[18] Wang Tiange, Zhang Zijun, Tsui K L. PFFN: periodic feature-folding deep neural network for traffic condition forecasting[J]. IEEE Internet of Things Journal, 2024, 11(2): 3108-3120.
[19] Guo Shengnan, Lin Youfang, Feng Ning, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 922-929.
[20] Zhao Yiji, Lin Youfang, Wen Haomin, et al. Spatial-temporal position-aware graph convolution networks for traffic flow forecasting[J]. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(8): 8650-8666.
[21] 刘洪, 张旭, 刘畅, 等. 考虑充电设施充裕性的电动私家车出行与充电需求时序交互分析[J]. 中国电机工程学报, 2018, 38(18): 5469-5478.
Liu Hong, Zhang Xu, Liu Chang, et al. Timing interactive analysis of electric private vehicle traveling and charging demand considering the sufficiency of charging facilities[J]. Proceedings of the CSEE, 2018, 38(18): 5469-5478.
[22] 刘洪, 阎峻, 葛少云, 等. 考虑多车交互影响的电动汽车与快充站动态响应[J]. 中国电机工程学报, 2020, 40(20): 6455-6468.
Liu Hong, Yan Jun, Ge Shaoyun, et al. Dynamic response of electric vehicle and fast charging stations considering multi-vehicle interaction[J]. Proceedings of the CSEE, 2020, 40(20): 6455-6468.
[23] Guo Qinglai, Xin Shujun, Sun Hongbin, et al. Rapid-charging navigation of electric vehicles based on real-time power systems and traffic data[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1969-1979.
[24] 邢强, 陈中, 冷钊莹, 等. 基于实时交通信息的电动汽车路径规划和充电导航策略[J]. 中国电机工程学报, 2020, 40(2): 534-550.
Xing Qiang, Chen Zhong, Leng Zhaoying, et al. Route planning and charging navigation strategy for electric vehicles based on real-time traffic information[J]. Proceedings of the CSEE, 2020, 40(2): 534-550.
[25] 吴佳龙, 蔡晔, 唐夏菲, 等. 基于Isard法的充电站服务范围划分与实时定价策略[J]. 电力建设, 2023, 44(10): 72-83.
Wu Jialong, Cai Ye, Tang Xiafei, et al. Isard method based charging station service range division and real-time pricing strategy[J]. Electric Power Construction, 2023, 44(10): 72-83.
[26] Ji Jiahao, Wang Jingyuan, Huang Chao, et al. Spatio-temporal self-supervised learning for traffic flow prediction[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2023, 37(4): 4356-4364.
[27] 沈祖英, 肖雷雷, 单丰武, 等. 环境温度对NCM动力电池系统充放电性能的实验研究[C]//2020中国汽车工程学会年会, 上海, 2020: 8.
[28] 中华人民共和国住房和城乡建设部. 城市道路工程设计规范: CJJ 37—2012[S]. 北京: 中国建筑工业出版社, 2012.
[29] 宋媛媛. 基于行驶工况的纯电动汽车能耗建模及续驶里程估算研究[D]. 北京: 北京交通大学, 2014.
Song Yuanyuan. Research on energy consumption modeling and driving range estimation of pure electric vehicles based on driving conditions[D]. Beijing: Beijing Jiaotong University, 2014.
[30] 洛杉矶标准地图数据[EB/OL].(2024-07-06)[2024-07-06]. https://www.openstreetmap.org/export#map= 11/33.9898/-118.0488.
[31] PeMS Data [EB/OL].(2024-04-20)[2024-04-20]. https: //pems.dot.ca.gov/.
[32] Kumar S V, Vanajakshi L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data[J]. European Transport Research Review, 2015, 7(3): 21.
[33] Zhang Junbo, Zheng Yu, Qi Dekang. Deep spatio-temporal residual networks for citywide crowd flows prediction[C]//Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, California USA, 2017: 1655-1661.
[34] Bai Lei, Yao Lina, Li Can, et al. Adaptive graph convolutional recurrent network for traffic forecasting [EB/OL]. 2020:2007.02842.https://arxiv.org/abs/ 2007. 02842v2.
[35] Li Mengzhang, Zhu Zhanxing. Spatial-temporal fusion graph neural networks for traffic flow forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(5): 4189-4196.
[36] 美国电价, 12月2023[EB/OL]. (2024-03-24)[2024-07-06]. https://zh.globalpetrolprices.com/USA/electricity_prices/.
[37] 美国平均时薪(月薪)[EB/OL]. (2024-07-06)[2024-07-06]. https://zh.tradingeconomics.com/united-states/ average-hourly-earnings.
[38] 洛杉矶地区气象数据[EB/OL]. (2024-08-24)[2024-08-24]. https://www.ncdc.noaa.gov/cdo-web/datasets/ LCD/stations/WBAN:93134/detail.
[39] 栾鑫, 邓卫, 程琳, 等. 特大城市居民出行方式选择行为的混合Logit模型[J]. 吉林大学学报(工学版), 2018, 48(4): 1029-1036.
Luan Xin, Deng Wei, Cheng Lin, et al. Mixed Logit model for understanding travel mode choice behavior of megalopolitan residents[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(4): 1029-1036.
Fast Guidance Strategy for Electric Vehicle Charging Based on Dynamic Traffic Inference
Abstract Electric vehicles (EV) have the characteristics of both traffic and mobile load, and their charging behavior will have an interactive impact on the power grid. With the rapid increase in the number of electric vehicle and the continuous improvement of their penetration rate, charging guidance for large-scale EVs has become an important measure to alleviate the contradiction between local limited charging resources and strong charging demand. Therefore, considering the influence of future traffic information changes on navigation strategy, this paper proposes a fast guidance strategy for electric vehicle charging based on dynamic traffic inference.
First of all, a dynamic traffic information prediction model based on spatio-temporal self-supervised learning (ST-SSL) is established. A self-supervised learning (SSL) module for spatial and temporal heterogeneity of traffic data is designed to achieve accurate prediction of multi-period traffic flow information. Secondly, a multi-time dynamic impedance modeling method for urban road network considering future traffic information changes is designed, a charging navigation strategy considering multi-demand scenarios and multi-navigation objectives of users is established, and a solution method based on dynamic Dijkstra algorithm is proposed to realize the selection of the optimal charging station and the planning of the optimal navigation path. Based on the global charging navigation results, the service range of urban charging stations is dynamically evaluated, to achieve rapid charging guidance for electric vehicles. Finally, taking the actual road network of a certain area in Los Angeles as an example, the accuracy of the prediction model and the effectiveness of the guidance strategy are proved, which can effectively perceive the dynamic traffic information and quickly realize the service range division of urban charging stations and the charging guidance for electric vehicles.
In this paper, a fast guidance strategy for electric vehicle charging based on dynamic traffic inference is proposed, based on the case simulation results, the main conclusions can be obtained as follows. (1) The model based on ST-SSL can make full use of the spatial and temporal heterogeneity of traffic data, improve the prediction effect of traffic flow information, and provide an effective data basis for the construction of dynamic traffic impedance. (2) The proposed multi-scenario and multi-objective charging navigation strategy based on dynamic impedance can effectively perceive traffic information and take into account the diversified needs of users, effectively reduce the cost of charging navigation for different users, and reasonably guide the load distribution of electric vehicles. (3) The proposed dynamic Dijkstra algorithm can recommend the optimal path according to the future traffic information, which can be used as a navigation algorithm to plan the driving path, and can also recommend the customized optimal charging station according to the needs of users. (4) The division of charging station service range based on the global charging navigation results can effectively evaluate the service range of charging station, and provide an important reference for the construction planning of charging station. Based on the evaluation results, the charging navigation strategy is quickly assigned to each node, which effectively reduces the computing resource consumption of charging navigation.
Keywords:Electric vehicle, traffic system, traffic flow prediction, charging navigation, service coverage
中图分类号:TM761
DOI: 10.19595/j.cnki.1000-6753.tces.240722
国家自然科学基金(52177080)和国家重点研发计划(2021YFB1600203)资助项目。
收稿日期2024-05-07
改稿日期2024-10-29
胡俊杰 男,1986年生,教授,博士生导师,研究方向为新能源电力系统与微网,电动汽车与电网互动等。
E-mail:junjiehu@ncepu.edu.cn
张 宽 男,1994年生,讲师,硕士生导师,研究方向为新能源电力系统及综合能源微网等。
E-mail:kuanzhang@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)