图1 交直流混联系统结构框图
Fig.1 Structural diagram of AC/DC hybrid system
摘要 对于交直流混联系统，常规阻抗模型难以同时涵盖交直流网络各装备的导纳/阻抗（电流/电压源型）特性，无法准确地表征交直流网络的复杂耦合关系。为此该文构建了交直流混联系统的统一导阻网络模型，提出基于混联系统导阻模型的稳定性评估及振荡溯源方法。首先，该文根据装备不同端口特性提出混联系统划分方法，将交直流混联系统划分为单一和复合导阻网络，标准化系统装备的模型形式，降低了网络模型维数；其次，依据系统网络的连接关系，建立包含混联系统完整振荡信息以及同时覆盖装备阻抗/导纳特性的统一导阻网络模型，推导涵盖混联系统各交直流端口交互关系的统一导阻网络稳定判据，并结合导阻网络的拓展性分析将判据推广至一般交直流混联系统，进一步基于导阻网络模型给出面向混联系统的振荡溯源方法；最后，针对交直流混联系统应用实例，对该文所提导阻网络模型及其稳定性分析方法进行评估验证。
关键词：交直流混联 导阻 稳定性分析 振荡溯源
为加快构建以新能源为主体的新型电力系统，满足新能源发电单元和负荷中心迅猛增长的需要，近年来以柔性直流输电技术为代表的多端交直流混联电力系统因其呈现多电源、多落点、大容量以及跨区域灵活输电的特点，成为大规模消纳新能源的有效方案[1-2]。但面临高比例电力电子化的多端混联系统，“源-网-荷”中各电力电子装备在交直流网络间的交互作用复杂、宽频稳定性问题突出[3-5]，如欧洲北海风电-柔直输电系统发生中高频谐波振荡[6]、张北四端柔直工程换流变压器起动时发生3.2 kHz的高频振荡[7]、厦门柔直工程出现25.2 Hz的次同步振荡[8]等。
为探究混联系统的宽频振荡问题，近年来基于阻抗模型的分析方法受到学术界和工业界的广泛关注[9-12]。文献[13-14]以连接换流站交流端口为视角，将输电系统划分为源-载子系统的形式，并通过奈氏判据分析系统交流侧稳定性。同样为了分析直流断面稳定性，文献[15-17]建立了直流侧阻抗模型，并以直流端口为断面评估混联系统直流侧稳定性。文献[18]以系统间各交-直断面为切入点，分别针对不同交-直断面聚合断面两侧装备的阻抗，依次评估混联系统各交-直断面的稳定性。但需要注意的是，现有绝大多数研究仅聚焦于系统单一交流或直流侧稳定性问题，难以同时兼顾多端条件下的交-直混合断面的稳定性问题。此外，对交直流阻抗的简单聚合难以准确地表征交直流网络的复杂耦合关系，且面临右半平面极点求解复杂的问题。
为了能够同时兼顾交直流侧的稳定性信息，简化混联系统稳定性分析过程，有学者将现有单一阻抗模型进行了延拓。例如文献[19-20]提出一种能够同时刻画换流站交直流端口小信号动态的三端口导纳模型，实现了交直流网络端口的统一分析，在一定程度上避免了换流站交直流端口阻抗折合带来的问题，但难以实现交直流混联系统层面的振荡机理分析与稳定性判定。文献[21]将系统拆解为无源网络和连接换流站两部分，结合三端口导纳模型，提出了并网换流站互联系统的稳定判据。但该方法在分析时将实际系统中的新能源场站等效为三相交流源，忽略了新能源外送系统导纳模型带来的影响，若面对网络中连接换流站的装备阻抗特性不同时，文中所述方法难以实现新能源导纳模型与交直流网络中阻抗模型的统一，将面临失效风险。现有方法在分析系统稳定性时，一般只针对网络中各有源装备阻抗特性均一致的情形，因此，若分析对象涉及多种电力电子装备和交直流网络相结合，那么如何建立同时涵盖系统各装备导纳/阻抗特性的统一模型，如何有效分析系统运行过程中的不稳定模态，形成针对交直流混联系统的系统化稳定性分析方法，这些都是目前迫切需要解决的关键科学问题。
针对上述问题，本文在文献[22]所提导阻（immittance）概念的基础上，拓展应用到交直流混联系统，标准化混联系统各子模块的导纳/阻抗形式，同时以模块交直流端口特性为视角，将系统划分为包含不同阻抗特性的单一和复合导阻网络，构建系统统一导阻网络模型，进而提出一种涵盖交直流端口完整振荡信息，判稳过程清晰简洁且适用于一般交直流系统的统一导阻网络稳定性分析方法，并基于导阻网络模型提出一种振荡溯源策略。最后，为阐述清晰，本文针对张北四端柔直工程，结合硬件在环实验平台对研究工作展开分析论证。
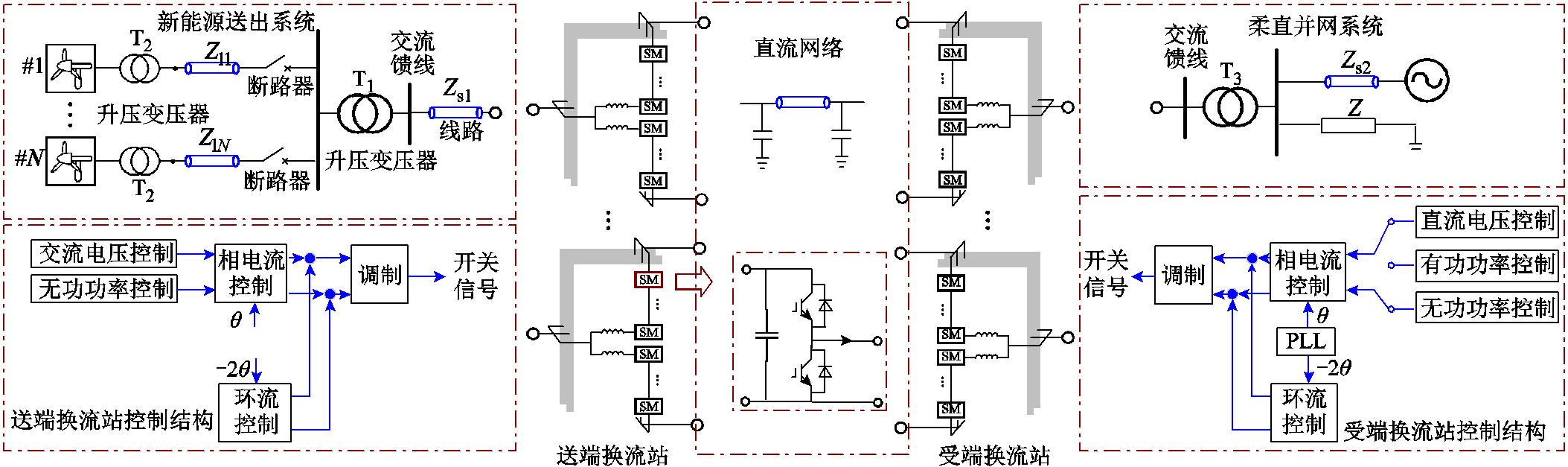
以风电场经柔直送出系统为例的典型交直流混联系统结构如图1所示。
图1 交直流混联系统结构框图
Fig.1 Structural diagram of AC/DC hybrid system
混联系统中，直驱风机机组经数级升压变压器构成系统的功率发生端，由送端换流站通过直流网络将功率传输至受端换流站，再经过交流传输网络将能量馈入负载电网。其中，负责调控混联系统直流电压的并网（受端）换流站控制部分由直流电压控制、无功功率控制、交流电流内环控制、二倍频环流抑制和锁相环构成。新能源侧送端换流站控制部分由交流电压控制、无功功率控制、交流电流内环控制和二倍频环流抑制构成。为不失一般性，本文所述换流站基于目前广泛应用的模块化多电平换流器（Modular Multilevel Converter, MMC）结构展开研究分析。
结合上述混联系统网络拓扑，本节提出一种交直流混联系统的网络划分及建模方法。首先，将混联系统拆解为不同的网络子模块，并标准化各子模块阻抗/导纳形式。其次，为进一步聚合各装备网络模型,基于各子模块交直流混合导纳/阻抗模型端口特性，将系统网络划分为两类：具备单一交流或直流端口特性的单一导阻（Mono-Imp-Adm, MIA）网络，以及同时复合交直流端口特性的复合导阻（Hybrid-Imp-Adm, HIA）网络。
因混联系统装备数量众多，各装备模块连接复杂，为便于分析，将混联系统拆分为新能源网络、交流负载网络、直流网络、送端换流站系统和受端换流站系统五个系统网络子模块。网络模型划分示意图如图2所示，为方便区分，下标w/g分别代表送端/受端换流站交-直端口信号。
同时，混联系统覆盖了交直流网络，为保证系统网络同时涵盖交直流侧的稳定性信息，根据各网络模块的端口连接特性将混联系统划分为单一和复合网络。其中，新能源网络、交流负载网络、直流网络仅连接系统交流端口或直流端口，所覆盖系统模块仅具有单一交流或直流端口阻抗特性，共同构成单一网络，如图中黑色点画线框所示；送端/受端换流站系统跨接于交流-直流网络之间，同时复合直流和交流的端口阻抗特性，共同构成复合网络，如图中红色点画线框所示。
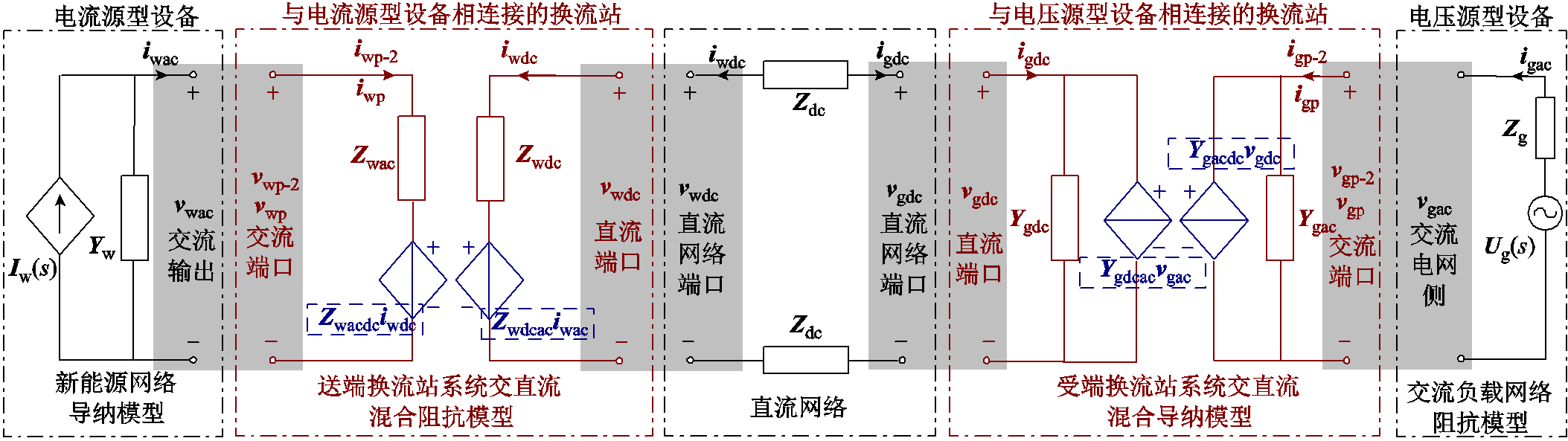
图2 混联系统模型划分示意图
Fig.2 Model division diagram of hybrid system
模型中Zwac和Ygac分别为送端换流站交流端口自阻抗、受端换流站交流端口自导纳，Zwdc和Ygdc分别为送端换流站直流端口自阻抗、受端换流站直流端口自导纳，Zwdcac、Zwacdc和Ygdcac、Ygacdc分别为送端/受端换流站交直流耦合阻抗/导纳，Zdc表示直流网络矩阵。vwac和iwac分别由vwp-2、vwp和iwp-2、iwp共同构成，分别代表送端换流站交流端口处不同频率的电压和电流信号向量，vgac与igac同理，分别由vgp-2、vgp和igp-2、igp共同构成，分别代表受端换流站交流端口处不同频率的电压和电流信号向量。vwdc、iwdc和vgdc、igdc分别为送端/受端换流站直流端口电压/电流信号向量。
将跟网型新能源场站等效为电流源（Iw(s)）并联新能源变流器导纳（Yw）的形式，交流电网系统等效为电压源（Ug(s)）串联交流传输线路等效阻抗（Zg）的形式。同时，为后续便于将系统网络模型等效为相应的传递函数，避免求解右半平面极点的问题，对送端/受端换流站分别建立其交直流混合阻抗/导纳网络模型。可知，当系统中新能源场站和交流电网系统满足自稳性时，新能源变流器等效导纳矩阵和交流传输线路等效阻抗矩阵中无右半平面极点。若所有换流站均可稳定运行，柔直换流站混合阻抗/导纳矩阵同样不存在右半平面极点。
结合上述分析，提出交直流混联系统的一般性建模标准，将电流源型设备等效为电流源并联导纳的形式，电压源型设备等效为电压源串联阻抗的形式，即电流/电压源型设备模型分别对应导纳/阻抗特性。针对与电流源型设备相连接的换流站建立交直流混合阻抗模型，对与电压源型设备连接的换流站建立混合导纳模型，模型包含交直流端口约束关系，兼顾了交直流侧稳定性信息。按照上述系统模块划分及建模原则可以避免之后运算过程中求解右半平面极点的问题，简化了分析过程。同时，各子模块相互独立，方便后续系统网络模型的扩展。
针对上述系统网络，可知送端换流站交流侧连接电流源型新能源风电单元（导纳特性），而受端换流站连接电压源型电网负载（阻抗特性），在分析此类复杂系统时，若应用单一阻抗或导纳模型描述，则无法全面涵盖系统各装备的不同阻抗特性，实现系统级稳定性评估。为此，依照图2所示模型，基于本文所提系统网络划分方法及网络模块的交直流混合阻抗/导纳模型，构建混联系统单一和复合导阻网络模型，再结合单一/复合导阻网络模型的交互关系共同构成系统统一导阻网络模型。其中，单一导阻网络模型中同时包含新能源场站的交流导纳特性、负载侧的交流阻抗特性和直流网络的直流端口特性，复合导阻网络模型中同时包含送端/受端换流站交流-直流端口的阻抗/导纳特性。
统一导阻网络模型涵盖了混联系统交直流各端口处的频率特征，将系统网络由单一直流或交流网络拓展至交直流网络；同时，将导纳特性的新能源网络与阻抗特性的负载网络统一，解决了因阻抗特性不同而导致不同网络设备难以统一分析的难题，实现了不同阻抗特性装备模型的统一覆盖。
本节针对单一和复合导阻网络进行建模分析，并结合系统交直流网络端口处的交互关系，建立能够描述混联系统稳定特性的统一导阻网络模型。
2.1.1 单一导阻网络建模
单一导阻网络建模包括新能源发电单元与交直流网络建模。其中，新能源发电单元的具体建模工作已经相对完善[23]，在此不做过多说明。因新能源网络不含直流端口，故其交直流混合模型中与直流元素有关的部分均置零，定义新能源网络交直流混合模型为
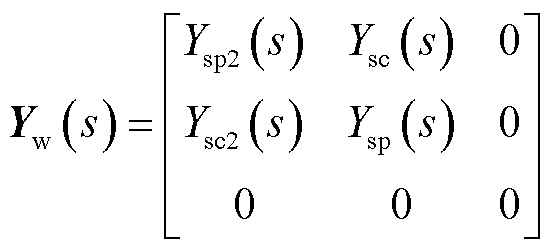（1）
同理，结合图2中各网络子模块的标准化形式，定义交流负载网络交直流混合模型为
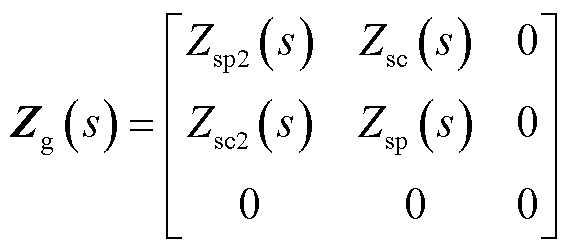（2）
式中，Ysp2(s)、Zsp2(s)分别为模型耦合频率导纳、阻抗；Ysp(s)、Zsp(s)分别为模型扰动频率导纳、阻抗；Ysc(s)、Zsc(s)和Ysc2(s)、Zsc2(s)分别为模型转移频率导纳、阻抗。
对于直流网络的建模，依照具体直流网络拓扑，本节结合节点电压方程给出直流网络矩阵的具体描述。
为与电流源型设备阻抗特性相统一，直流网络中以新能源侧送端换流站直流端口为节点的直流量可描述为
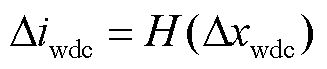（3）
同样地，为与电压源型设备阻抗特性统一，直流网络中以并网侧受端换流站直流端口为节点的直流量可描述为
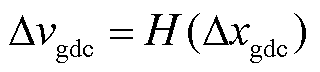（4）
式中，Δ代表小信号量；Δiwdc和Δvgdc分别为送端换流站直流端口电流小信号量和受端换流站直流端口电压小信号量；Δxwdc和Δxgdc分别为直流网络中与Δiwdc和Δvgdc有关的直流网络端口节点电压电流小信号量。
定义电流方向以流向换流站为正方向，对任意直流网络，结合节点电压方程和式（3）、式（4）中直流网络矩阵描述方法，得到不同拓扑下直流网络统一矩阵形式，即
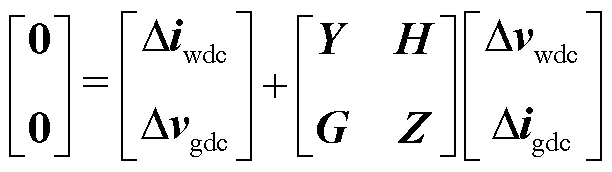（5）
式中，Δiwdc、Δvwdc、Δigdc、Δvgdc分别为送端/受端换流站直流端口电流电压小信号向量组，Δiwdc= [Δiwdc1 … Δiwdcm]T,Δigdc=[Δigdc1 … Δigdcn]T，下标m、n分别为送端、受端换流站的数量；Δvwdc与Δvgdc为类似向量组；Y、H、G、Z为直流网络拓扑中连接换流站直流端口处电压和电流小信号向量的矩阵描述，此时定义直流网络矩阵为
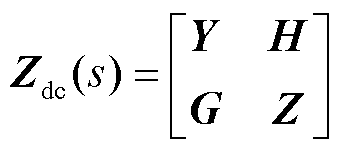（6）
2.1.2 复合导阻网络建模
复合导阻网络建模包括各连接换流站建模。以电网侧受端换流站为例，柔直换流站跨接于混联系统的交流网络和直流网络，需同时考虑扰动信号在换流站交直流端口的响应。交直流网络小信号频率映射关系如图3所示。
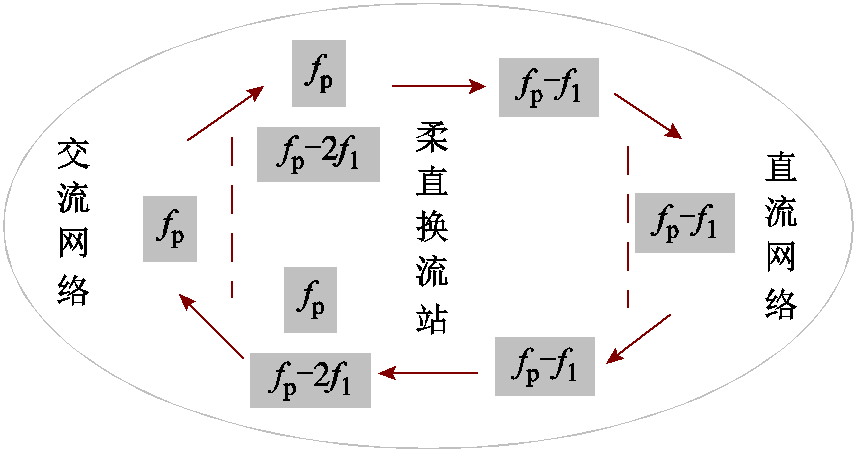
图3 交直流网络小信号频率映射关系
Fig.3 Frequency mapping relationship of small signals in AC/DC networks
如图3所示，若换流站交流侧存在频率为fp的电压扰动，在考虑交流频率耦合的情况下，换流站交流端口会产生频率为fp-2f1和fp的小信号响应，其中f1为基频。同时，由于abc/dq变换的影响，频率为fp的扰动还会在换流站直流端口处引起频率为fp-f1的小信号响应。同理，直流网络小信号响应也会通过直流端口传入换流站交流端口，进而影响系统交流网络。
为此，在对受端换流站的导纳矩阵进行建模时，需要在原有仅考虑单一交流端口处扰动频率和耦合频率的二端口网络矩阵基础上，进一步扩展为增加交直流约束关系的三端口网络矩阵，即
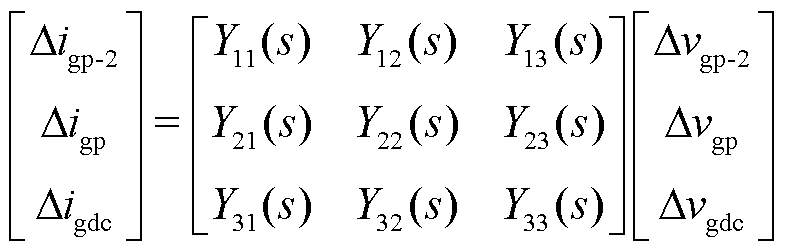（7）
式中，Δigp-2、Δigp、Δvgp-2、Δvgp分别为并网换流站交流端口频率为fp-2f1和fp的电流小信号和电压小信号；增加的Δigdc和Δvgdc分别对应柔直换流站直流端口处直流电流、电压小信号；Y11(s)和Y22(s)分别为交流端口频率为fp-2f1和fp的交流自导纳；Y33(s)为直流端口处的直流自导纳；Y12(s)和Y21(s)为交流端口不同频率处的耦合导纳；Y13(s)和Y31(s)反映交流端口频率为fp-2f1的交流信号与直流端口直流信号的约束关系；Y23(s)和Y32(s)反映交流端口频率为fp的交流信号与直流端口直流信号的约束关系。
上述换流站交直流混合模型在保证没有丢失换流站交流端口信息的情况下，加入直流端口和交流端口处物理量的约束关系，使换流站的外特性导纳矩阵更加完备。基于此对受端换流站进行交直流混合导纳建模，若受端换流站交流侧存在扰动频率为fp的三相电压小信号，此时换流站交直流端口处电压小信号为
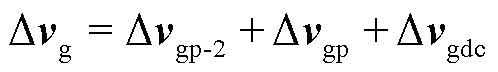（8）
式中，Δvg为受端换流站交直流端口电压小信号。将电压小信号按频率为fp+xf1的形式展开为7×1的列向量，其中x=-3,-2,-1,0,1,2,3。定义桥臂电流小信号Δiu、桥臂调制小信号Δmu、桥臂等效电容电压小信号Δvu、换流站交流侧电压小信号Δvs均为7×1的谐波向量。
根据MMC换流站功率拓扑可得其功率方程为
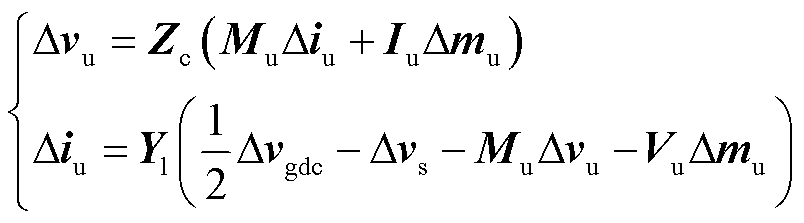（9）
式中，Zc与Yl分别为不同小信号频率所对应的MMC等效电容阻抗与桥臂电感7×7导纳矩阵；Mu、Iu和Vu分别为上桥臂调制信号、桥臂电流和等效电容电压7×7稳态信号矩阵。结合图1中控制部分可得锁相环影响为
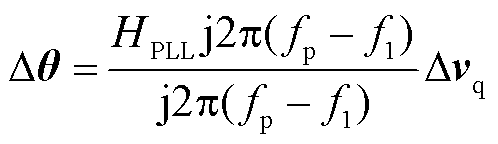（10）
环流抑制与电流内环控制结构类似，此处以电流环内环影响为例，有
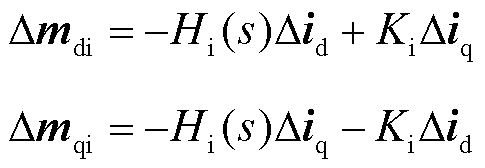（11）
直流电压外环影响为
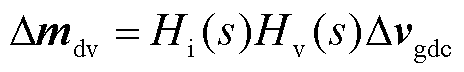（12）
式中，Δθ、Δid、Δiq、Δvq分别为锁相角、d轴电流、q轴电流、q轴电压小信号向量；Δmdi、Δmqi分别为电流环对调制小信号d轴分量和q轴分量的影响；Δmdv为电压环对调制小信号的影响；Hi(s)、Hv(s)、HPLL分别为电流环、电压环及锁相环控制器；Ki为电流环控制器解耦系数。联立式（10）～式（12），得到dq坐标轴下的调制信号Δmd和Δmq，对其进行反变换得
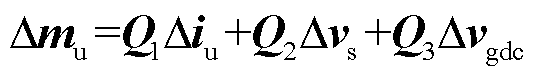（13）
将上述控制小信号方程代入功率方程得到
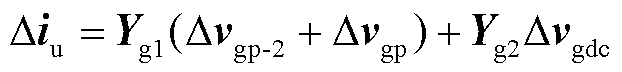（14）
其中
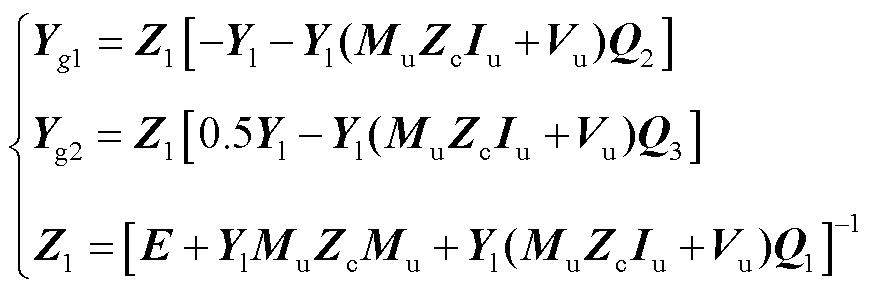（15）
式中，Q1为与电流内环和环流抑制有关的控制矩阵；Q2为与锁相环控制有关的矩阵；Q3为与电压外环有关的控制矩阵。Q1、Q2、Q3均为7×7矩阵；E为7×7单位矩阵。
根据换流站拓扑结构可得，换流站交流端口交流电流小信号量为Δiu中交流小信号分量的两倍，换流站直流端口直流电流小信号量为Δiu中直流小信号分量的三倍，结合7×7导纳矩阵Yg1和Yg2，依照矩阵频率对应关系得到电网侧受端换流站的交直流混合导纳矩阵为
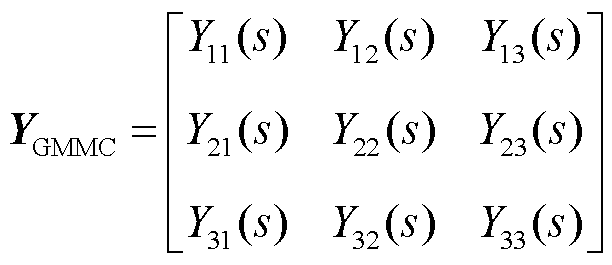（16）
与受端并网换流站交直流混合建模思路相似，结合图1中具体控制可以得到
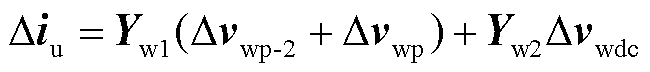（17）
其中
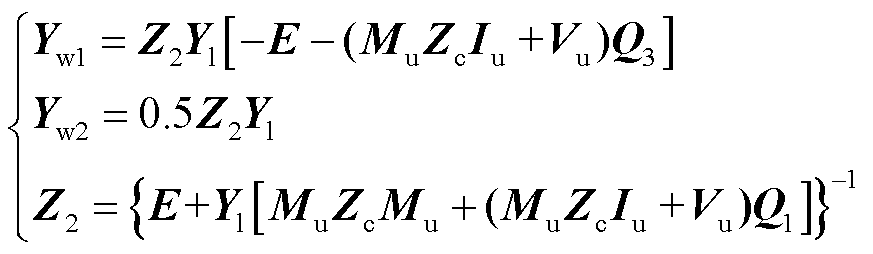（18）
同样结合矩阵中频率对应关系可以得到送端换流站的交直流混合导纳矩阵YWMMC，则交直流混合阻抗矩阵ZWMMC满足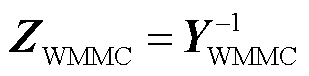
。
为直观地解释系统统一导阻网络模型的物理意义，结合上述系统网络划分原则和建模分析，归纳获取系统统一导阻网络模型如图4所示。
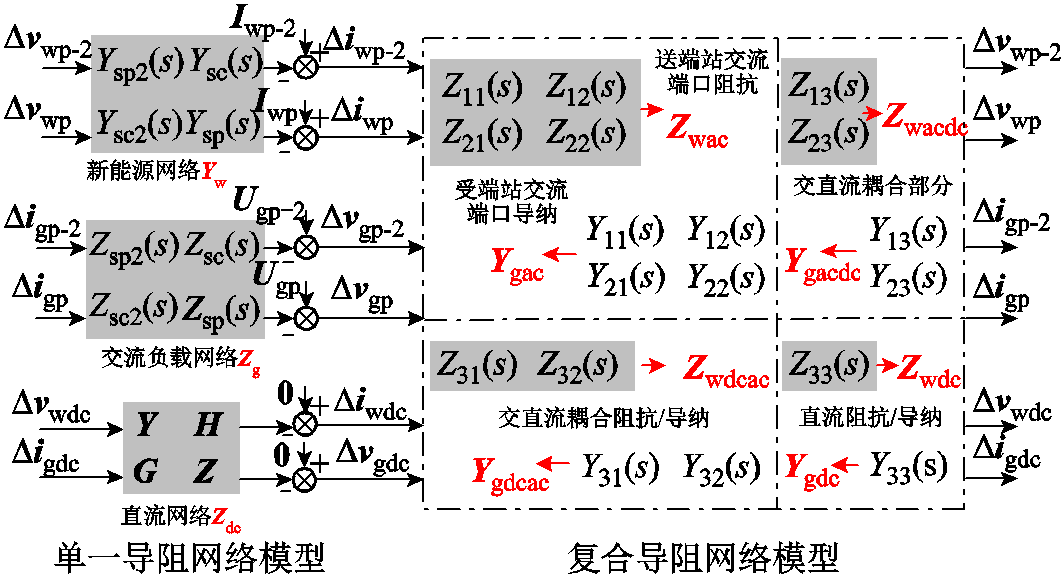
图4 混联系统的统一导阻网络模型
Fig.4 Modeling of unified immittance network for hybrid system
图4展现了单一和复合导阻网络模型之间的数学关系。在单一导阻网络中，混联系统交流端口电压电流信号经新能源网络模型和交流负载网络模型与复合导阻网络交互，系统直流端口电压电流信号经直流网络矩阵与复合导阻网络交互；复合导阻网络中，混联系统交直流端口电压电流信号经连接换流站交直流混合模型与单一导阻网络交互。结合图4中所示统一导阻网络模型给出单一导阻网络矩阵GMIA和复合导阻网络矩阵GHIA分别为
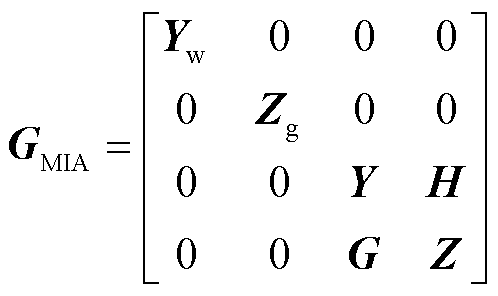（19）
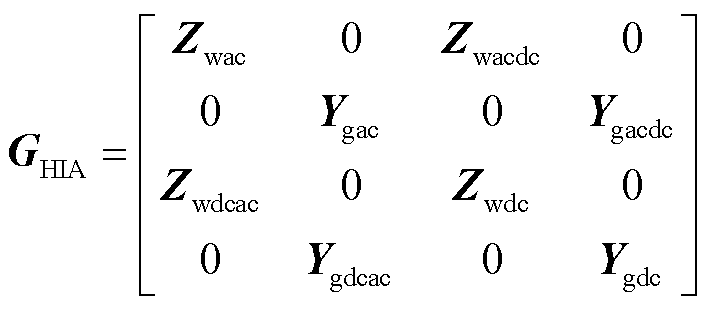（20）
导阻网络清晰地刻画了混联系统网络中电压电流小信号的传播路径，展现了各交直流端口间的映射关系，在面对复杂交直流系统时，能够实现系统模型的简化。
随着日益增长的负荷需求和新增新能源场站的需要，能源输送/负载侧电力网络和装备的扩建不可避免。为使统一导阻网络的适用范围进一步拓展至一般交直流混联系统，本小节提出一种基于换流站节点分类的系统网络拓展办法，以新能源/电网负载为例说明电流/电压源型设备的拓展。
能源输送侧系统的拓建主要包括送端换流站和新能源场站的拓建。在拓建送端网络的过程中，增加的节点有些连接换流站，有些仅为新能源场站间的连接点。本小节基于增加节点是否连接换流站将其归类到Y、N两个点集，其中连接换流站的节点定义为Y点集，未连接换流站的节点定义为N点集。新能源侧增设节点扩展方式如图5所示。
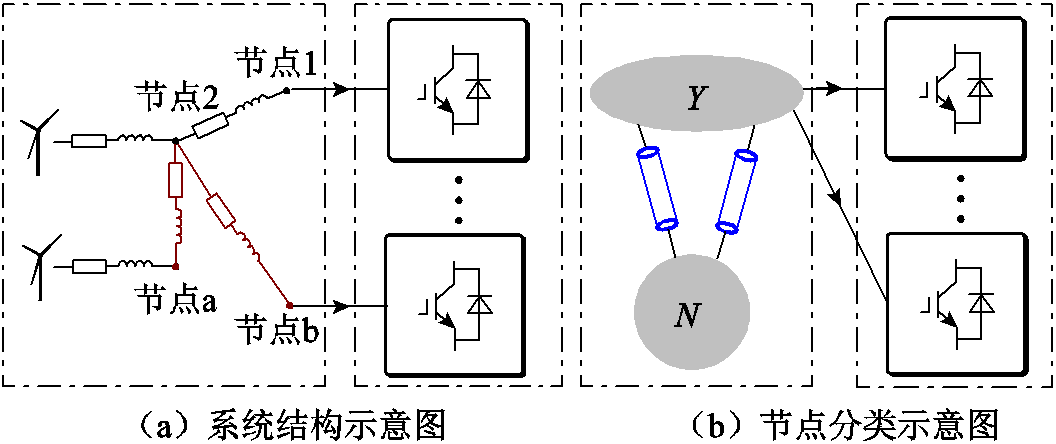
图5 新能源侧增设节点扩展方式
Fig.5 Expansion method for adding nodes on the new energy side
结合电网络理论，对于N集合中的节点，其节点电压方程可写为
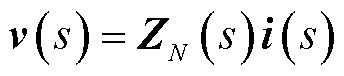（21）
式中，v(s)、i(s)分别为节点电压、电流向量；ZN(s)为节点电压电流向量对应的节点阻抗矩阵。此时复合导阻网络矩阵中Zwac项拓展为Zwac1，导阻矩阵中其余部分用相应零矩阵拓展矩阵的整体维数。拓展后的矩阵为
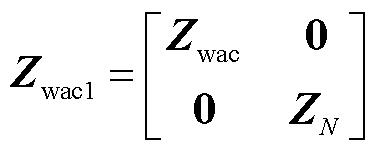（22）
对于Y集合中的节点，因其连接换流站，故Y中节点数目的增加表征送端换流站数目增加。此时复合导阻网络矩阵中Zwac项拓展为Zwac2，其中定义向量Zwac(exp)=diag(Zwac(1)… Zwac(Δm)),Δm为增加换流站的数量，拓展后的矩阵为
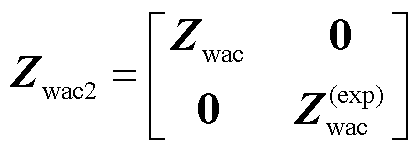（23）
相应地，随着新能源变流器数目的增加，单一导阻网络矩阵也会相应变化，如式（24）所示，导阻矩阵中Yw项拓展为
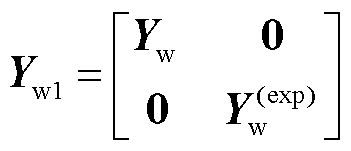（24）
式中，Yw(exp)=[Yw(1)… Yw(i)]；i为增加的新能源变流器的数量。但网络中增加的节点数一般大于系统增加的变流器数量，故将单一导阻网络矩阵中相应部分通过补零拓展，使其矩阵维数与复合导阻网络矩阵相对应。负载侧及受端站系统拓建主要包括受端换流站和负荷的拓建，同理，其拓展方式与能源输送侧系统拓展类似，在此不过多赘述。
将跟网型新能源网络推广为一般性的电流源型设备网络，负载网络推广为一般性的电压源型设备网络，送端/受端换流站推广为与电流/电压源型设备相连接的换流站，结合图4及上述分析给出如图6所示的一般化单一/复合导阻网络模型。
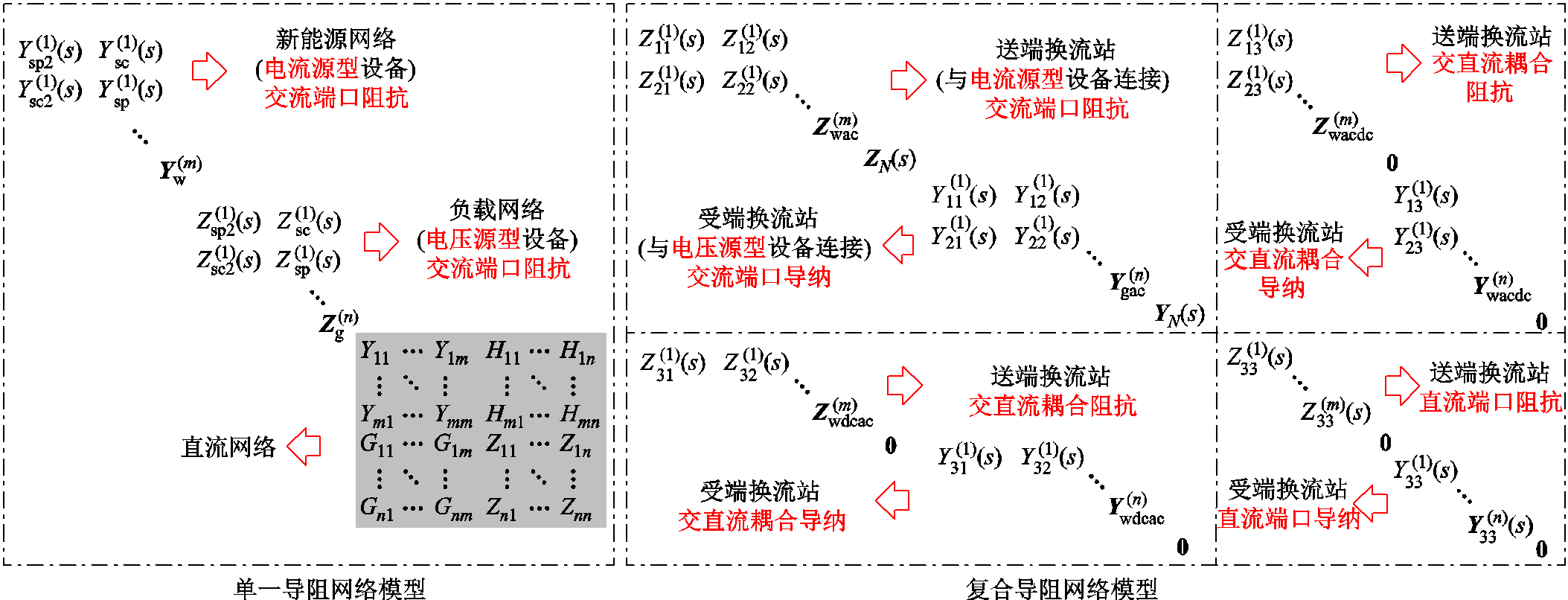
图6 复杂交直流混联系统统一导阻网络模型的一般性扩展
Fig.6 General extension of unified immittance network model for complex AC/DC hybrid systems
现有阻抗建模方法无法全面涵盖交直流混联系统中不同阻抗特性的系统装备，导阻模型将单一阻抗特性的矩阵网络拓展至同时包含导纳和阻抗特性的系统矩阵网络。相较于仅聚合单一阻抗特性或单一导纳特性的矩阵模型，统一导阻网络覆盖了不同阻抗特性的交直流系统，实现了导纳特性新能源单元与阻抗特性负载网络的相互统一，使得在面对同时包含电流/电压源特性装备（导纳/阻抗特性设备）的交直流系统时，能够准确建立其网络数学模型，实现不同阻抗特性装备模型的统一建模分析。同时，统一导阻网络基于系统模块化建模标准建立系统各装备模块交直流混合模型，网络涵盖系统各交直流端口稳定性信息，准确地表征了交直流端口的约束关系，将系统网络矩阵从单一交流或直流系统拓展至交直流系统，进一步结合上述导阻网络的推衍变化过程，通过系统模块化的拓展方式使得导阻网络可以适用于不同拓扑的分析对象，将统一导阻网络推广应用至一般交直流混联系统。此外，相较于现有基于有源节点的网络划分方法，依照端口特性将不同装备和部件划分至单一和复合网络，使得网络矩阵维度下降为原来的一半，降低了计算难度和矩阵的复杂度，使得统一导阻网络在应用到大规模混联系统时更具优势。
为清晰刻画混联系统是否存在谐振风险，首先基于导阻网络将传统电力系统s域节点导纳矩阵判稳方法拓展；然后结合交直流网络小信号映射关系提出一种适用于交直流混联系统的统一导阻稳定判据；最后基于统一导阻网络给出系统振荡定位方法。
对任意电力网络均可通过其节点导纳矩阵求取特征值来判断系统稳定性。对系统中节点i注入电流扰动Δii时，在节点k上产生电压响应Δvk，其s域下节点电压方程为
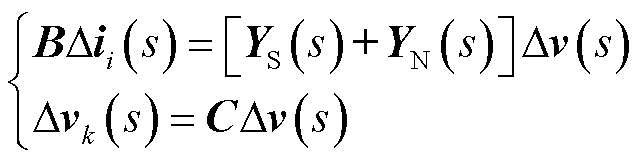（25）
式中，B和C分别为一维列向量和行向量，B向量第i个元素为1，C向量第k个元素为1，其余元素为0；YS(s)和YN(s)分别为连接注入节点有源设备和无源网络的等效导纳。结合系统网络拓扑，基于本文所提导阻网络，依照节点电压方程，对系统中节点i注入扰动ΔFi时，在节点k上产生响应ΔYk，其s域下交直流端口节点电压电流方程为
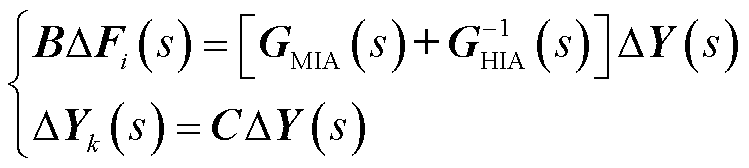（26）
据此可以得到
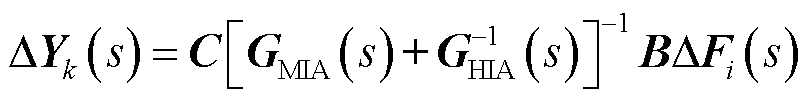（27）
根据相应数学关系可知
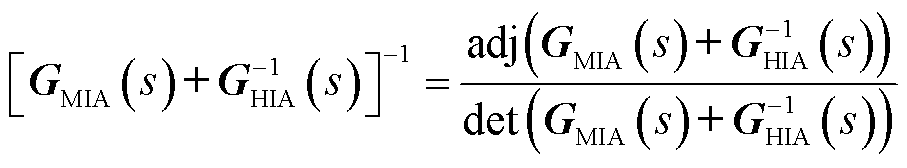
因此，det(GMIA+GHIA-1)的零点为节点导阻矩阵闭环特征根，通过计算其零点求取系统导阻矩阵特征根，从而判断混联系统是否稳定。需要注意的是，由于混联系统节点数量多，网络交织复杂，闭环系统的节点导阻矩阵阶数较高，求取特征根的过程较为复杂。此外，在计算系统特征根之前需先判断系统导阻矩阵右半平面极点，这些都会增加系统判稳复杂度。为此，下文将结合导阻网络及交直流端口约束关系对判据进一步改进。
结合图4并基于统一导阻网络中交直流网络端口处的交互关系得到如图7所示的混联系统等效传递函数。
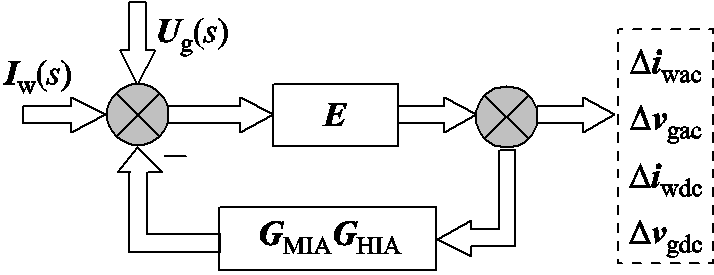
图7 统一导阻网络的等效传递函数
Fig.7 Equivalent transfer function of unifiedimmittance network
结合图7统一导阻网络的等效传递函数模型可以得到
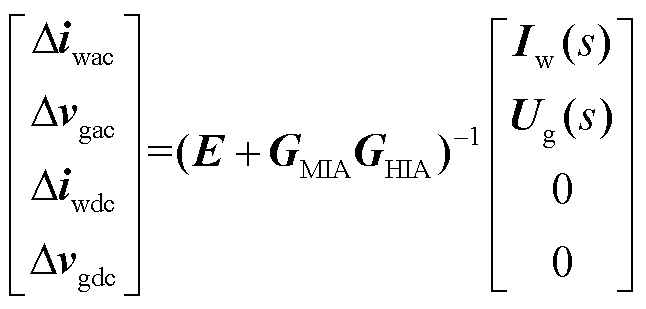（28）
式中，E为单位矩阵。由此可看出，(E+GHIAGMIA)-1可表征混联系统交直流端口物理量的动态特性，对其进行进一步数学变换可得
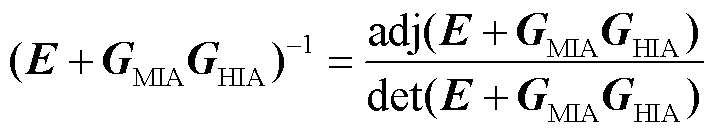（29）
可知det(E+GHIAGMIA)是否存在右半平面极点是判断混联系统是否失稳的关键，结合上述分析推导出刻画混联系统是否失稳的等效开环传递函数为
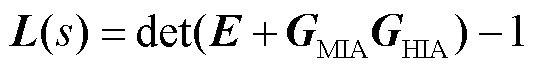（30）
基于上述分析，系统稳定性取决于L(s)的奈氏曲线是否包裹(-1,0j)点[24]。需要说明的是，上述基于统一导阻网络模型的稳定判据按照1.2节中网络模块化的建模原则，即对电流/电压源型设备建立其交直流混合导纳/阻抗模型，若系统各网络模块满足自稳性时，混联系统中单一和复合导阻网络均满足自稳性，此时应用式（30）所述稳定判据可以避免求解系统模型右半平面极点的问题，有效降低系统判稳的复杂度。
此外，结合上述导阻网络判据中矩阵的推衍变化过程，将统一导阻网络判据推广应用至一般交直流混联系统。若系统网络相应地减少某些装备，或仅分析系统局部稳定性问题时，只需将导阻网络中相应部分置零即可，故面临分析单一交流或直流系统时，统一导阻网络判据同样适用。
将det(E+GMIAGHIA)进行等价数学变换可得
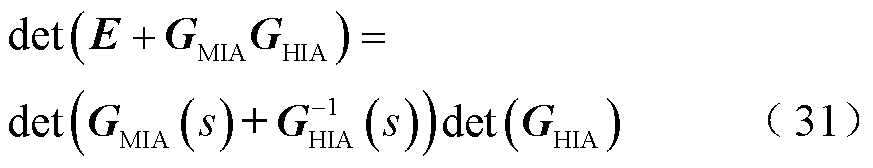
基于前文分析，判据中GMIA和GHIA均不存在右半平面极点，det(GHIA)的零点为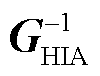
极点，故det(E+GMIAGHIA)的零点即可表征系统的特征根，证明两种判据等价。相较于对混联系统网络整体进行推衍得出的稳定判据，统一导阻网络判据通过将系统划分为单一和复合网络，将闭环系统特征值矩阵转换为导阻网络相乘的传递函数形式。对比式（27）和式（28），其降低了分析矩阵的复杂度，且无需求解导阻矩阵右半平面极点，相应地降低了判稳复杂度。
综上所述，给出交直流混联系统稳定性评估流程如图8所示。
结合上述评估流程得到的程序化交直流混联系统稳定性评估方法，针对具体系统网络计算得出其稳态工作点。结合本文提到的统一导阻稳定判据能有效分析混联系统不稳定模态，实现系统级评估。
为有效抑制系统振荡，对系统振荡源进行定位分析至关重要，结合系统谐振模态分析方法，本文提出一种基于统一导阻网络模型的混联系统振荡参与因子评估方法。结合式（28）可以得到
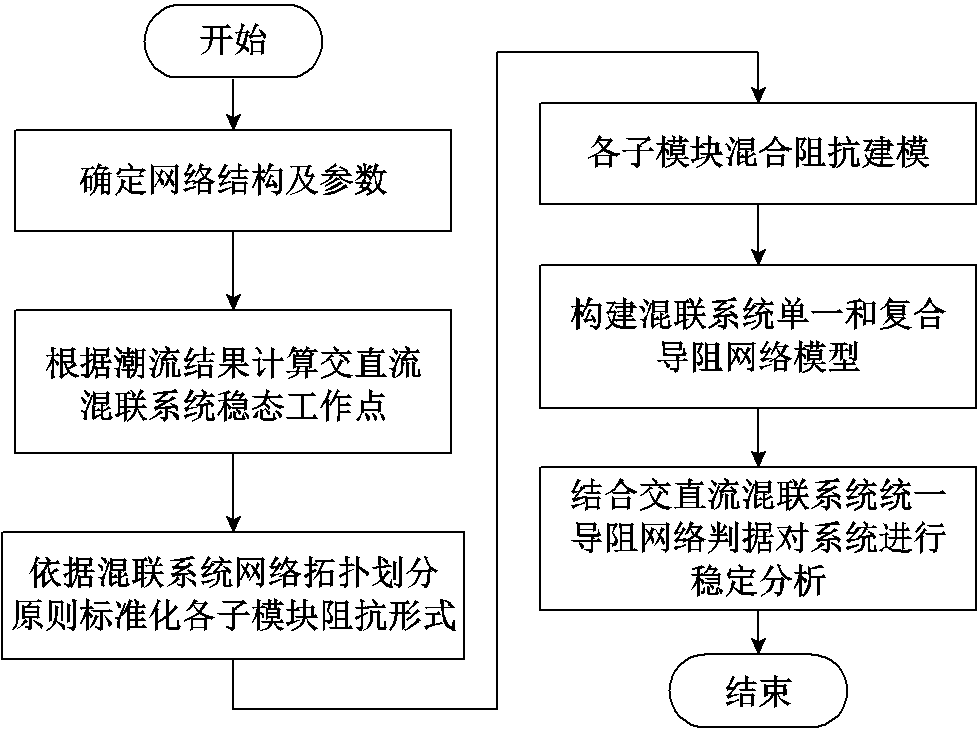
图8 交直流混联系统稳定性评估流程
Fig.8 Stability evaluation flow chart of AC/DC hybrid system
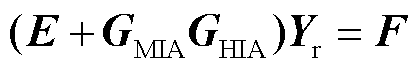（32）
式中，F为式（28）右侧列向量即节点电压电流激励；式（28）左侧列向量为节点电压电流相应的响应，用字母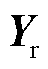
表示。可知，(E+GMIAGHIA)为一个可逆矩阵[25]，则可对角化为(E+GMIAGHIA)=LΛT，L和T分别为矩阵对角化后的左右特征向量，Λ为特征值矩阵，其中L-1=T。令U=TYr,J=TF,可以得到
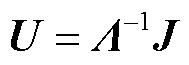（33）
式中，U为模态响应；J为模态激励。可以得到
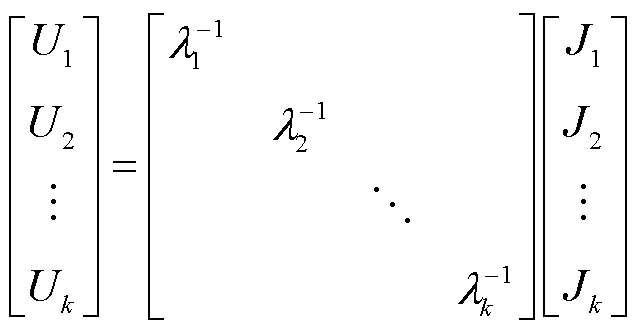（34）
式中，k为系统节点数量。此时各网络节点间相互解耦，谐振对应某个特定模态。若λx=0，其中x为模态号，则很小的模态激励Jx会产生很大的模态响应Ux，故在模态域中可以容易地识别出谐振的“位置”。左右特征向量分别反映系统谐波谐振的可观测性和可激励性，故系统各节点对谐振模态可定义为
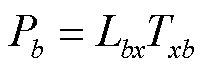（35）
式中，b为系统节点位置；Lbx为左特征向量矩阵的第b行x列元素；Txb为右特征向量矩阵的第x行b列元素。定义基于统一导阻网络模型的系统振荡模式参与因子为
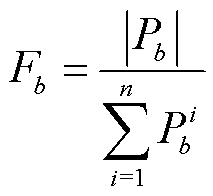（36）
至此，针对拓展至一般性交直流混联系统的统一导阻网络模型开展振荡模态分析，实现混联系统的振荡参与因子评估与振荡溯源分析，在降低振荡参与因子计算复杂度的同时，能够实现对系统振荡源的精准定位。
本节结合RT-Lab硬件在环实验平台（如图9所示），以张北四端柔直工程为应用实例（如图10所示）[26]，验证交直流混联系统统一导阻网络模型的正确性；然后以张北柔直工程康保站交流-直流端口作为验证节点，基于统一导阻网络判据开展稳定性分析。其中，主要功率参数、风机及相应换流站的控制参数在图10中给出。需要说明的是，按照带宽和裕度指标合理设计的控制器参数，使得所述参数配置的系统网络装备满足自稳性前提。
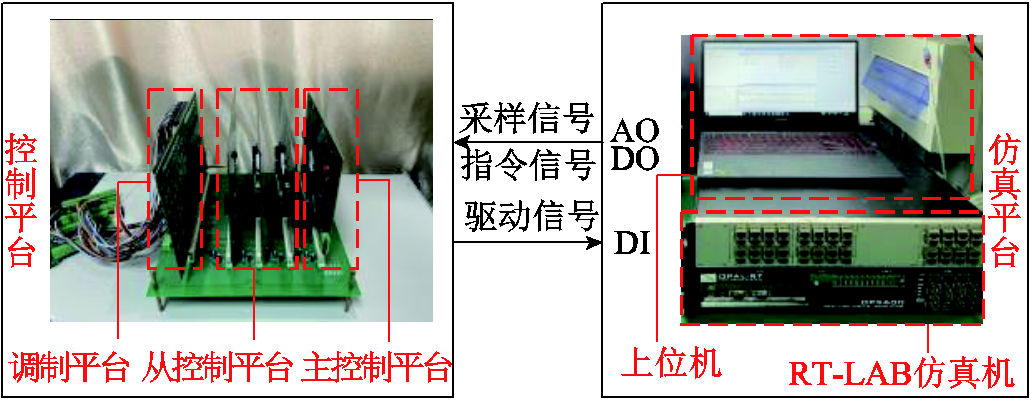
图9 RT-Lab硬件在环实验平台
Fig.9 A RT-Lab simulator-based HIL experimental platform
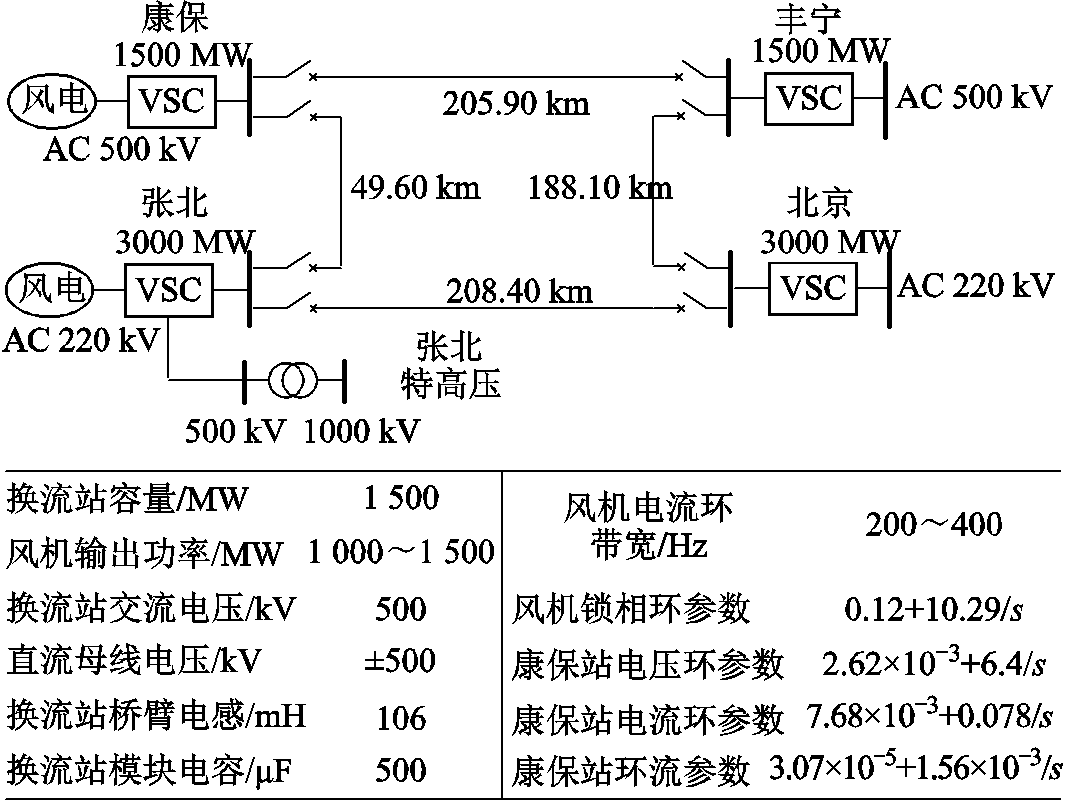
图10 张北四端柔直工程结构框图及主要参数
Fig.10 Structural block diagram and main parameters of Zhangbei four-terminal HVDC project
实时仿真平台由OP5600仿真机与仿真主机共同组成，负责海上聚合风电模型和康保、丰宁侧换流站功率电路的实时运行。其中，RT-Lab仿真机与仿真主机通过RJ45接口进行数据的实时传输。实际控制平台基于DSP和FPGA芯片，分为主控、从控和调制部分，主要负责接收仿真平台下发的相关信息，实时完成MMC换流站的全部控制功能。控制平台中DSP型号为TI公司的TMS320F28377D，FPGA芯片则采用Intel公司Cyclone系列的EP3C25Q240C8。
为不失一般性，以康保送端换流站为例，选择代表换流站交流端口阻抗特性和直流端口阻抗特性的Z22(s)和Z33(s)两个元素进行验证，如图11所示。
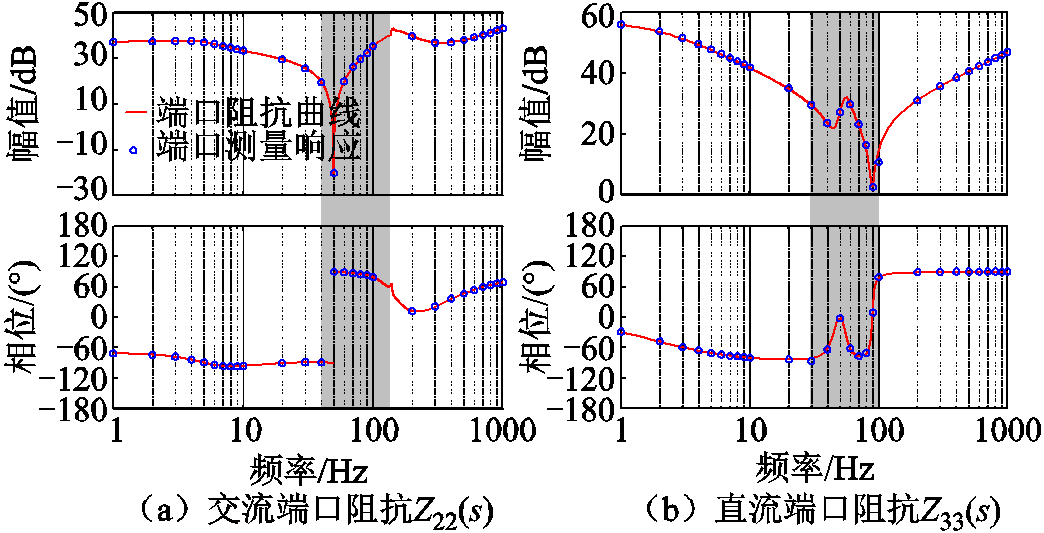
图11 康保送端换流站阻抗模型验证
Fig.11 Impedance model verification of the Kangbao transmission converter station
可以看到理论模型与测量结果在较宽的频带范围内保持一致，验证了所述混合阻抗模型的正确性。
柔直工程振荡问题可分为两类：一类为新能源场站与柔直换流站系统间交互或换流站系统与交流负荷交互产生的振荡问题；另一类为柔直换流站系统间交互引发的振荡问题。对第一类振荡问题，振荡由连接于交流网络两端系统交互引起，能量通过交流网络传输，故将其归类为交流振荡问题；第二类振荡问题涉及多站交互引发振荡，而换流站间能量通过直流网络传输，故可归类为直流振荡。选取工况一、二分别针对交流、直流振荡现象进行分析验证。
4.2.1 工况一：新能源出力改变系统的稳定性分析
实际系统中，随着风电机组出力的增大，混联系统可能会产生不稳定问题，工况一针对风电场输出功率由1 000 MW增大到1 500 MW时，基于统一导阻网络模型对交直流混联系统稳定性问题进行分析，并与传统阻抗分析方法进行对比论证。其中，系统直流网络中直流电抗器取值为75 mH。应用图9所示硬件在环实验平台得到换流站的交流端口三相电压和电流时域波形如图12所示，可以看到电流波形存在明显振荡现象。其中，由于实时仿真平台的模数转换电平限制，相关测量信号需经过必要缩放调理，本文中所有实验波形刻度均以考虑调理放大倍数后的实际数值单位标注。
图12 换流站交流端口电压和电流波形
Fig.12 Voltage and current waveforms of AC port of converter station
对图12中振荡电流波形进行傅里叶分析，得到结果如图13所示。可以看到交流电流中存在频率为27.5 Hz和72.5 Hz的谐波分量。
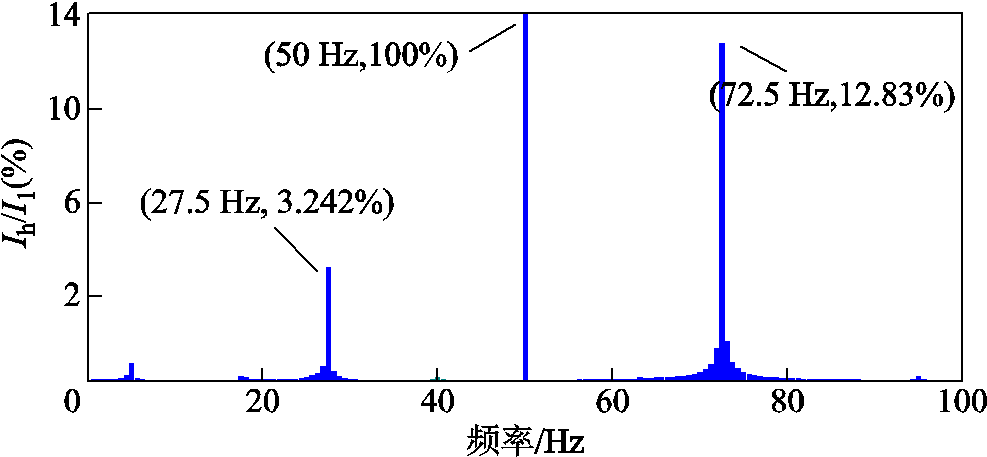
图13 交流电流波形傅里叶分析
Fig.13 Fourier analysis of AC current waveform
对于案例中提及的张北四端柔直工程，若要分析系统整体稳定性，需涉及新能源场站导纳特性模型与受端站负载侧阻抗特性模型的统一。因目前基于阻抗模型的稳定性分析方法，面对网络中连接送/受端换流站的装备阻抗特性不同时，无法同时涵盖装备的阻抗和导纳特性。为整体分析系统稳定性，需将新能源场站相应简化，因而无法反映新能源功率变化对混联系统带来的影响，故只能分析新能源与送端站所构成的局部系统稳定性，此时送端站直流端口的影响则被相应地弱化，同样换流站交直流端口处的耦合影响也被相应弱化，可能会出现稳定性误判的问题。
图14给出两种阻抗稳定分析方法的奈氏曲线结果，分别采取传统阻抗分析方法（无法实现不同阻抗特性的统一故只能局部判断）和本文所提统一导阻稳定性分析方法进行对比论证。传统阻抗网络矩阵无法实现不同阻抗特性的统一分析，只能实现局部阻抗网络稳定性分析，弱化了换流站中的交直流约束关系，由相应判据得到的奈氏曲线（图中以紫色标注）所示，传统阻抗网络判据的奈氏曲线并未包裹(−1,0j)点，理论分析结果判定系统稳定，但实际交直流系统发生振荡，故对于多站交直流互联系统的振荡问题，应用传统阻抗分析方法不能准确地反映系统的谐振风险；采用本文所提的统一导阻网络矩阵，解决了因装备阻抗特性不统一导致的系统整体判稳难的问题，且在对系统整体进行稳定性分析时，覆盖了系统各交直流的约束关系，可以得到统一导阻网络判据的特征根轨迹曲线（图中以蓝色标注），其特征根轨迹包裹了(−1,0j)点，同时曲线与单位圆的交点为27.6 Hz和72.4 Hz，与图12和图13所示实验结果保持一致，验证了本文所提出的统一导阻稳定判据的正确性。
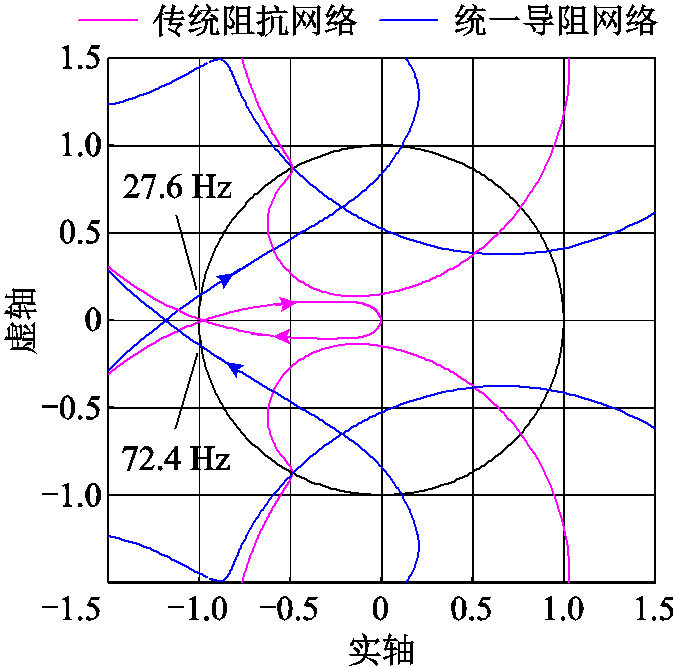
图14 交流端口稳定性分析
Fig.14 AC port stability analysis
同时，针对工况一的不稳定模态进行分析，通过数值求解得到系统不稳定模态为：s=1.877+ 456.385j，s=1.877+171.996j，结合3.3节分析得到各换流站交直流端口的振荡参与因子见表1。
表1 换流站节点振荡模式参与因子
Tab.1 Converter station node oscillation mode participation table
换流站交流扰动项参与因子交流扰动项参与因子直流端口 参与因子 康保站6.734 091.768 50.676 0 并网站0.019 40.084 00.718 2
可以看到，此时系统的振荡中，康保换流站参与度最高，也与上述理论分析一致，验证了基于导阻网络模型的振荡定位方法的可行性，同时为系统振荡抑制提供参考。
4.2.2 工况二：不同直流网络参数下系统的稳定性分析
对于交直流混联网络，新能源场站和交流电网/负载经不同换流站通过直流网络连接，各电力电子装备在不同直流网络的交互作用下同样可能会导致系统出现稳定性问题。为验证第二类振荡问题，工况二针对不同直流网络参数，对系统稳定性进行分析。
图15为直流电抗值分别取75 mH和100 mH时，直流端口电压电流时域波形。对图15b中振荡电流波形进行傅里叶分析，得到结果如图16所示，可以看到直流电流中存在频率为56.88 Hz的谐波分量。
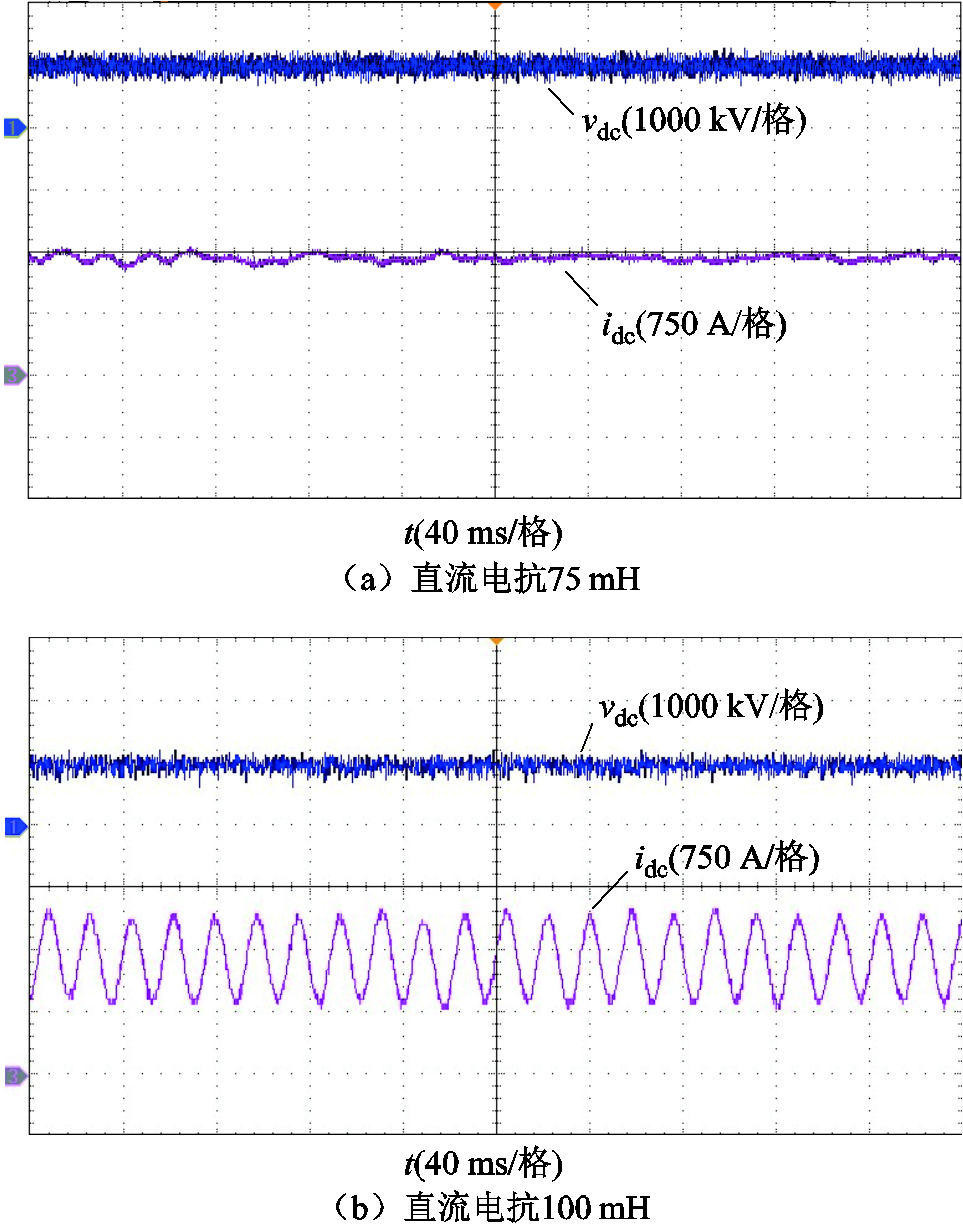
图15 换流站直流端口电压电流波形
Fig.15 Voltage and current waveforms of DC port of converter station
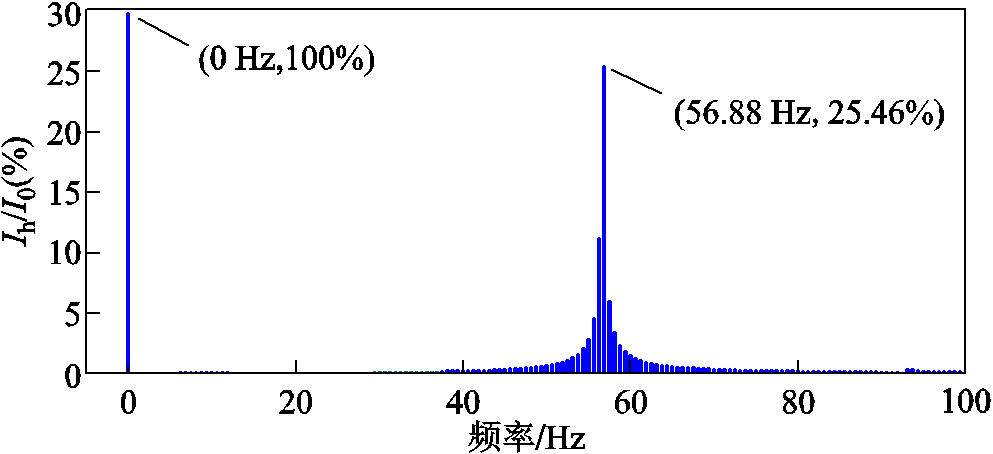
图16 直流电流波形傅里叶分析
Fig.16 Fourier analysis of DC current waveform
结合统一导阻网络判据得到两种直流网络参数下的根轨迹曲线如图17所示。
可以看出，直流电抗值为75 mH时，所得根轨迹曲线未包裹(−1,0j)点，理论分析结果判定系统稳定；直流电抗值为100 mH时，特征根轨迹包裹了(−1,0j)点，理论分析结果判定系统振荡，同时曲线与单位圆的交点为56.6 Hz，即直流侧理论振荡频率为56.6 Hz。可得理论分析结果与上述实验结果基本相符。
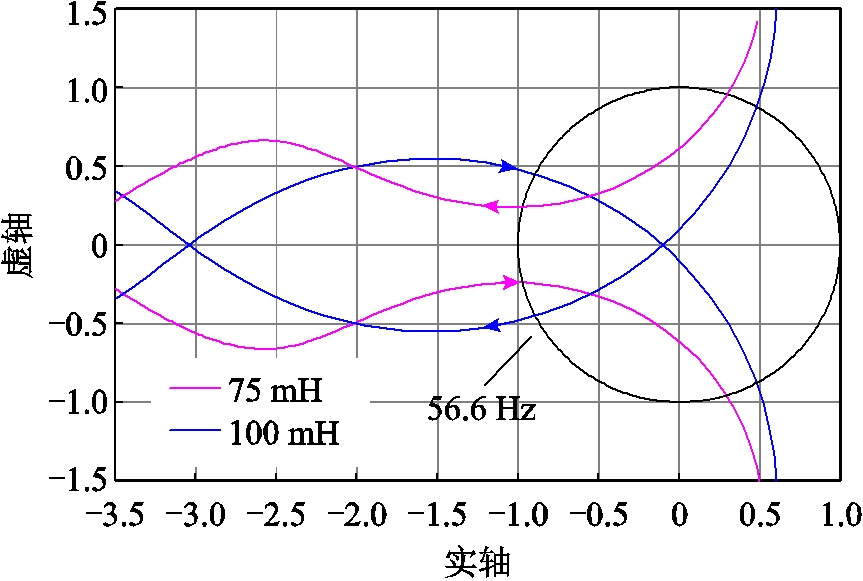
图17 直流端口稳定性分析
Fig.17 DC port stability analysis
针对工况二中直流电抗取100 mH时的不稳定模态进行分析，通过数值求解获取系统不稳定模态为：s=1.793+669.731j，进而得到各换流站交直流端口的振荡参与因子见表2。可知，系统此时的振荡中，康保换流站参与度最高，与选取的验证换流站一致。
表2 换流站节点振荡模式参与因子
Tab.2 Converter station node oscillation mode participation table
换流站交流扰动项参与度交流扰动项参与度直流端口 参与度 康保站55.716 60.158 632.516 8 并网站0.113 82.807 58.686 7
上述分析印证了本文所提统一导阻网络模型的稳定性分析方法不仅能反映交流端口稳定性问题，同样可以准确地反映系统直流稳定性问题，从而验证了本文所述统一导阻网络矩阵全面覆盖了混联系统各类交直流端口处稳定性信息，实现了系统交直流侧的统一分析，保证了稳定性分析的全面性。同时对系统振荡的溯源分析再次验证了基于导阻网络的振荡定位方法的可行性。
针对上述混联系统稳定性分析与振荡定位结果，本节结合混联系统中交直流端口的阻抗特性实现系统振荡抑制，并通过硬件在环实验进行分析验证。
4.3.1 系统工况一振荡问题抑制
4.2.1节工况一稳定性结果表明，康保站振荡参与度最高，由于换流站电压外环对100 Hz以下频段的交直流端口阻抗影响较大，因此本文重点针对康保换流站的电压环参数进行优化配置，以实现工况一振荡的有效抑制。可知，换流站端口稳定性取决于交互系统的阻抗幅值曲线在交点频率处的相位裕度是否大于0，即是否满足
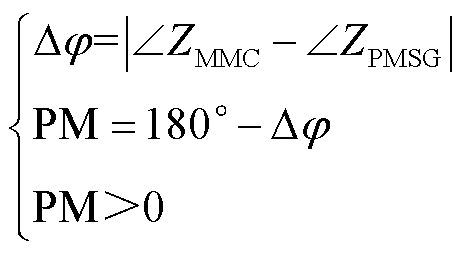（37）
式中，Δφ为交互系统阻抗曲线相位差的绝对值；PM为相位裕度。
针对工况一中的振荡问题，重新配置换流站电压外环控制器参数为1.048×10-2+6.448/s，可得如图18所示的换流站交流端口阻抗曲线。其中，蓝色点画线为新能源侧交流阻抗，紫色虚线、绿色实线分别代表优化前后换流站交流端口阻抗（计及其他换流站和交直流网络参数影响）。可以看到，在交接频率处换流站交流端口阻抗的相位裕度由-2.75°抬升至7.25°，结合图19所示的统一导阻网络曲线可以看到，曲线由原本包裹(−1,0j)点变为不包裹(−1,0j)点，理论分析系统稳定。
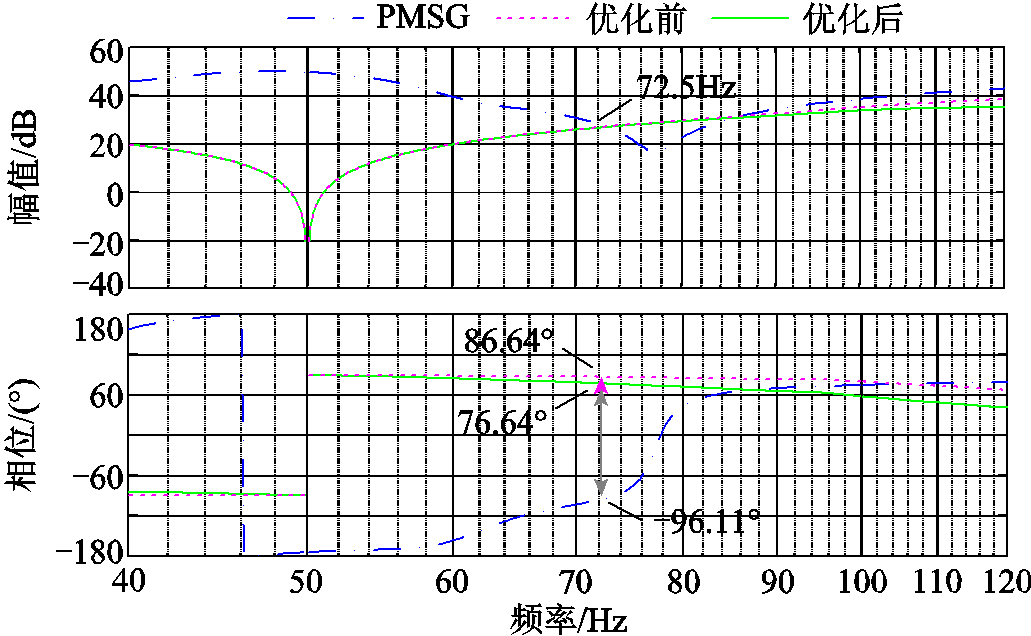
图18 换流站交流端口阻抗特性优化前后对比
Fig.18 Comparison of impedance characteristic of AC port of converter station before and after optimization
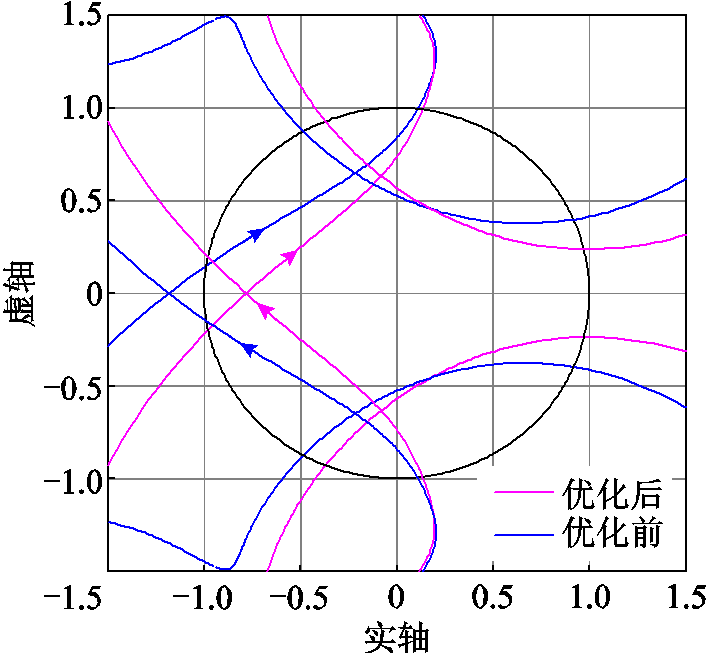
图19 工况一优化前后根轨迹曲线对比
Fig.19 Comparison of root locus curves before and after optimization inworking condition 1
图20给出系统换流站控制参数优化前后的交流端口三相电压电流时域波形。可以看到系统切换控制参数后，换流站交流端口由原本的振荡模态逐步趋于稳定，系统振荡得以抑制。
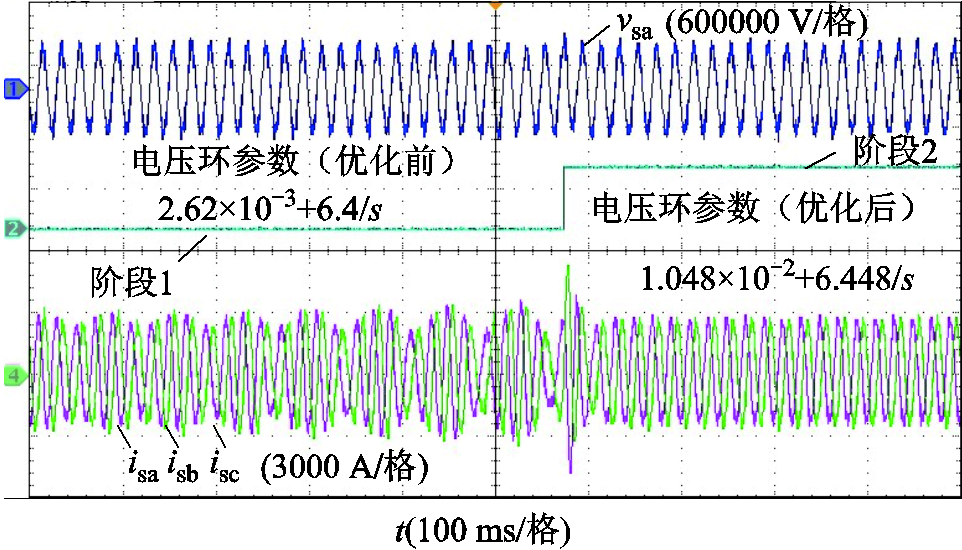
图20 工况一优化前后换流站交流端口电压电流波形
Fig.20 Voltage and current waveforms of AC port of converter station before and after optimization inworking condition 1
4.3.2 系统工况二振荡问题抑制
针对工况二中系统振荡问题，优化康保站电压外环参数为4.366×10-3+6.448/s。可得优化前后换流站直流端口阻抗曲线交互变化如图21所示。其中，蓝色点画线为计及直流网络参数和其他换流站影响的直流系统等效阻抗，紫色虚线、绿色实线分别代表参数优化前后考虑新能源场站影响的送端换流站直流端口阻抗曲线。可以看到，在交接频率处换流站直流端口阻抗的相位裕度由原本的-6.97°抬升至10.32°。
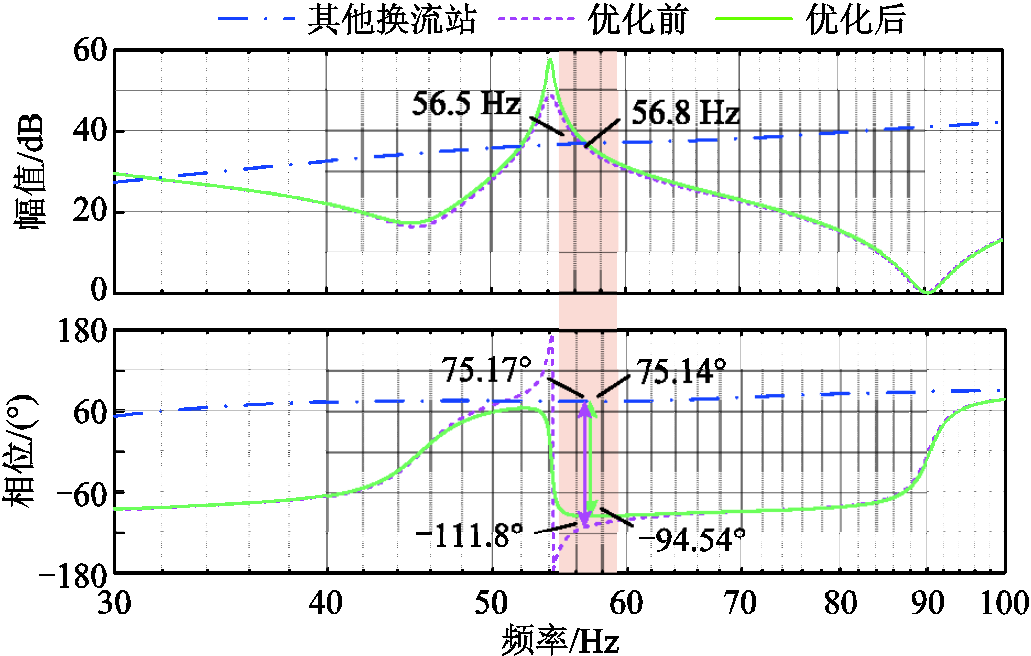
图21 换流站直流端口阻抗特性优化前后对比
Fig.21 Comparison of impedance characteristic of DC port of converter station before and after optimization
结合图22所示统一导阻网络曲线，可以看到曲线同样由包裹(−1,0j)点变为不包裹(−1,0j)点。图23给出系统换流站控制参数优化前后直流母线电压电流时域波形。同样可以看到，系统切换控制参数后，换流站直流端口由原本的振荡模态逐步趋于稳定，系统振荡得以抑制。
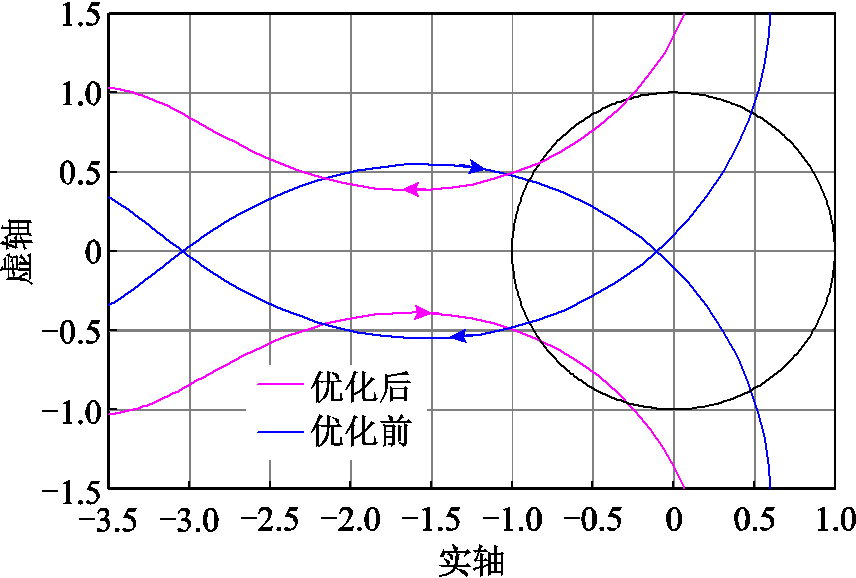
图22 工况二优化前后根轨迹曲线对比
Fig.22 Comparison of root locus curves before and after optimization inworking condition 2
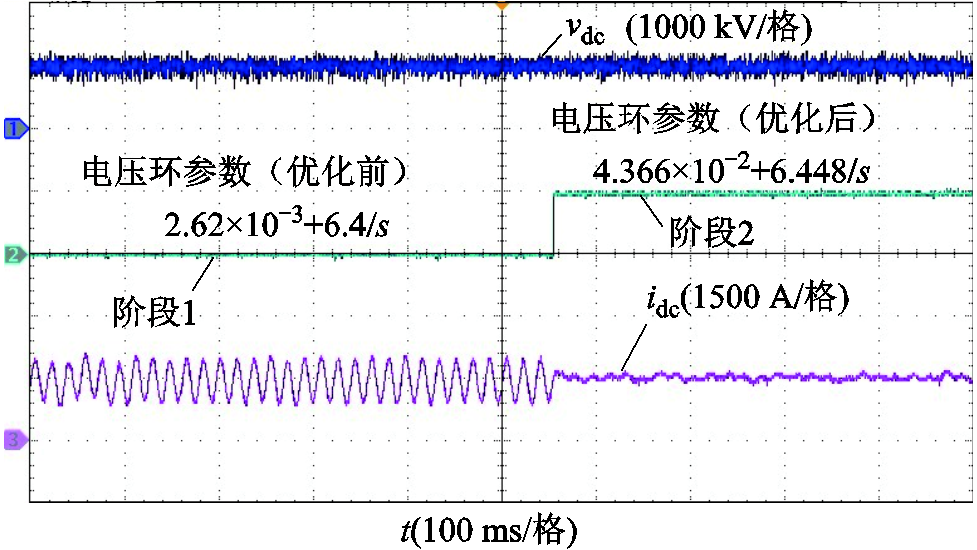
图23 工况二优化前后换流站直流端口电压电流波形
Fig.23 Voltage and current waveforms of DC portof converter station before and after optimization inworking condition 2
综上所述，针对上述基于换流站交直流端口处的稳定性分析，并结合相应硬件在环实验，得到的实验时域波形分析与基于统一阻抗网络模型的分析结果相互印证，验证了本文所提统一导阻网络模型和统一导阻网络判据在分析交直流混联系统时的正确性。
本文基于统一导阻网络模型，提出一种面向交直流混联系统的稳定性分析及振荡溯源方法，结合全文分析，得到如下结论：
1）基于电压/电流源型设备特性，标准化系统各网络模块的阻抗/导纳形式，避免系统稳定分析过程中右半平面极点的求解问题，所提建模方法具有一般性。
2）从交直流端口视角出发，将混联系统划分为包含不同阻抗/导纳特性的单一和复合导阻网络，建立具有一般性的交直流混联系统统一导阻网络模型，所述导阻网络模型统一了不同阻抗特性的装备，清晰直观地展现各网络模块间的交互关系，涵盖系统完整稳定性信息，并结合网络拓展方法使得导阻模型具有较高的拓展性和灵活性。
3）相较于现有基于阻抗法的稳定判据，统一导阻网络判据将适用范围推广至一般交直流混联系统，判据全面覆盖交直流系统稳定性问题，保证对混联系统交直流侧谐振风险评估的准确性，并且降低了矩阵阶数，避免了求解右半平面极点问题，简化了分析过程。同时基于导阻网络模型提出相应的振荡定位方法，并通过相应工程案例验证交直流混联系统稳定性分析与振荡抑制的可行性。
参考文献
[1] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12.
Xu Dianguo, Liu Yuchao, Wu Jian. Review on control strategies of multi-terminal direct current transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 1-12.
[2] Ansari J A, Liu Chongru, Khan S A. MMC based MTDC grids: a detailed review on issues and challenges for operation, control and protection schemes[J]. IEEE Access, 2020, 8: 168154-168165.
[3] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.
Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[4] 马宁宁, 谢小荣, 贺静波, 等. 高比例新能源和电力电子设备电力系统的宽频振荡研究综述[J]. 中国电机工程学报, 2020, 40(15): 4719-4731.
Ma Ningning, Xie Xiaorong, He Jingbo, et al. Review of wide-band oscillation in renewable and power electronics highly integrated power systems[J]. Proceedings of the CSEE, 2020, 40(15): 4719-4731.
[5] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianxing, et al. The interaction between multiple timescales of the grid-tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547-5559.
[6] Buchhagen C, Rauscher C, Menze A, et al. BorWin1- First Experiences with harmonic interactions in converter dominated grids[C]//International ETG Congress 2015; Die Energiewende - Blueprints for the new energy age, Bonn, Germany, 2015: 1-7.
[7] 胡应宏, 李雨, 李阳, 等. 面向柔直换流站高频谐振问题的换流变压器建模与参数辨识[J]. 电工技术学报, 2024, 39(22): 7154-7166.
Hu Yinghong, Li Yu, Li Yang, et al. Modeling and parameter identification of converter transformer for high-frequency resonance problem of flexible DC converter station[J]. Transactions of China Electro-technical Society, 2024, 39(22): 7154-7166.
[8] 李云丰, 汤广福, 贺之渊, 等. MMC型直流输电系统阻尼控制策略研究[J]. 中国电机工程学报, 2016, 36(20): 5492-5503.
Li Yunfeng, Tang Guangfu, He Zhiyuan, et al. Damping control strategy research for MMC based HVDC system[J]. Proceedings of the CSEE, 2016, 36(20): 5492-5503.
[9] Sun Jian. Frequency-domain stability criteria for converter-based power systems[J]. IEEE Open Journal of Power Electronics, 2022, 3: 222-254.
[10] 吴翔宇, 张晓红, 尚子轩, 等. 基于频域阻抗网络建模分析的交直流微电网振荡问题研究[J]. 电工技术学报, 2024, 39(8): 2294-2310.
Wu Xiangyu, Zhang Xiaohong, Shang Zixuan, et al. Research on the oscillation problem of AC-DC microgrids based on frequency domain impedance network modeling and analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2294-2310.
[11] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid [J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[12] 刘欣, 郭志博, 贾焦心, 等. 基于单输入单输出等效序阻抗的微网VSG并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报,2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Microgrid VSG grid-connection stability analysis and virtual impedance design based on single-input single-output equivalent sequence impedance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[13] 吕敬, 董鹏, 施刚, 等. 大型双馈风电场经MMC-HVDC并网的次同步振荡及其抑制[J]. 中国电机工程学报, 2015, 35(19): 4852-4860.
Lü Jing, Dong Peng, Shi Gang, et al. Subsynchronous oscillation and its mitigation of MMC-based HVDC with large doubly-fed induction generator-based wind farm integration[J]. Proceedings of the CSEE, 2015, 35(19): 4852-4860.
[14] 郭贤珊, 刘泽洪, 李云丰, 等. 柔性直流输电系统高频振荡特性分析及抑制策略研究[J]. 中国电机工程学报, 2020, 40(1): 19-29.
Guo Xianshan, Liu Zehong, Li Yunfeng, et al. Characteristic analysis of high-frequency resonance of flexible high voltage direct current and research on its damping control strategy[J]. Proceedings of the CSEE, 2020, 40(1): 19-29.
[15] Liu Jianing, Tao Xin, Yu Miao, et al. Impedance modeling and analysis of three-phase voltage-source converters viewing from DC side[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 3906-3916.
[16] 李国庆, 孙银锋, 吴学光. 柔性直流输电稳定性分析及控制参数整定[J]. 电工技术学报, 2017, 32(6): 231-239.
Li Guoqing, Sun Yinfeng, Wu Xueguang. VSC-HVDC stability analysis and control parameter setting[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 231-239.
[17] Ji Ke, Tang Guangfu, Yang Jie, et al. Harmonic stability analysis of MMC-based DC system using DC impedance model[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1152-1163.
[18] Li Yang, Shuai Zhikang, Fang Junbin, et al. Small-signal stability analysis method for hybrid AC–DC systems with multiple DC buses[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2021, 11(1): 17-27.
[19] 吴天昊, 谢小荣, 姜齐荣, 等. 考虑频率耦合及交直流端口耦合效应的并网变流器三端口导纳模型[J]. 中国电机工程学报, 2022, 42(1): 248-259.
Wu Tianhao, Xie Xiaorong, Jiang Qirong, et al. Three-port admittance modeling of grid-connected converters considering frequency-coupling and AC/DC coupling effects[J]. Proceedings of the CSEE, 2022, 42(1): 248-259.
[20] Zhang Haitao, Mehrabankhomartash M, Saeedifard M, et al. Stability analysis of a grid-tied interlinking converter system with the hybrid AC/DC admittance model and determinant-based GNC[J]. IEEE Transactions on Power Delivery, 2022, 37(2): 798-812.
[21] Zhang Haitao, Wang Xiuli, Mehrabankhomartash M, et al. Harmonic stability assessment of multiterminal DC (MTDC) systems based on the hybrid AC/DC admittance model and determinant-based GNC[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1653-1665.
[22] Sun Jian. Two-port characterization and transfer immittances of AC-DC converters–part II: applications [J]. IEEE Open Journal of Power Electronics, 2021, 2: 483-510.
[23] 李光辉, 王伟胜, 张兴, 等. 考虑机侧模型的直驱风电机组序阻抗建模及分析[J]. 中国电机工程学报, 2019, 39(21): 6200-6211.
Li Guanghui, Wang Weisheng, Zhang Xing, et al. Sequence impedance modeling and analysis of permanent magnet synchronous generator considering machine side model[J]. Proceedings of the CSEE, 2019, 39(21): 6200-6211.
[24] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[25] 张东辉, 陈新, 张旸, 等. 基于有源节点序阻抗模型的风电场稳定性分析及其振荡参与风险评估方法[J]. 中国电机工程学报, 2023, 43(10): 3832-3843.
Zhang Donghui, Chen Xin, Zhang Yang, et al. Stability analysis and resonance participation risk assessment of wind farm based on active node sequence impedance model[J]. Proceedings of the CSEE, 2023, 43(10): 3832-3843.
[26] 汤广福, 王高勇, 贺之渊, 等. 张北500kV直流电网关键技术与设备研究[J]. 高电压技术, 2018, 44(7): 2097-2106.
Tang Guangfu, Wang Gaoyong, He Zhiyuan, et al. Research on key technology and equipment for Zhangbei 500 kV DC grid[J]. High Voltage Engineering, 2018, 44(7): 2097-2106.
Modeling and Stability Analysis of Unified Immittance Network for AC/DC Hybrid System
Abstract AC/DC hybrid system has become an effective solution for large-scale new energy consumption because of its characteristics of multiple power sources, multiple drop points, large capacity and cross-regional flexible transmission. However, the wide-frequency oscillation problem of AC/DC hybrid power system with high proportion of power electronics is prominent, which threatens the safe and stable operation of the system. At present, the stability analysis of hybrid system is mainly faced with the problem of how to take into account the AC and DC sections of the hybrid system at the same time and how to cover the system equipment with different impedance characteristics, so as to realize the unified analysis of the AC/DC hybrid network with multiple power electronic equipment. To address the above issues, this paper establishes a unified immittance network model for system-level stability assessment of hybrid systems.
First, based on the voltage/current source type device characteristics of the network devices, the impedance/ admittance forms of each network module of the system are standardized to avoid the problem of solving for the right half-plane poles in the process of system stability analysis. Secondly, from the perspective of the AC and DC ports of the system equipment, the AC/DC hybrid system can be divided into mono immittance subsystem and hybrid immittance subsystem.Finally, based on the interaction relationship between system immittance networks, a unified immittance network model containing complete oscillation information of the hybrid system is established.Under the premise of covering the stability information at each AC and DC port of the hybrid system, the unified immittance network model reduces the dimension of the system network model, at the same time expands the system network matrix from a single AC or DC system to an AC/DC system. Furthermore, combined with the derivation and change process of the immittance network, and through the modularization of the system expansion, this paper makes the immittance network applicable to the analysis of objects with different topologies,and extends the unified immittance network to general AC/DC hybrid systems.In addition,in contrast to the matrix model that merely aggregates a single impedance feature or a single admittance feature, the unified immittance network encompasses the AC/DC systems with various impedance characteristics, accomplishing the mutual unification of the new energy unit with admittance properties and the load network with impedance properties. This facilitates the precise establishment of the network mathematical model when confronted with the AC/DC system that concurrently incorporates equipment with current/voltage source characteristics, and realizes the unified coverage of equipment models with dissimilar impedance characteristics.
Based on the immittance network model, a unified immittance network stability criterion covering the interaction relationship of each AC/DC port of the hybrid system is derived. Combined with the expansion analysis of the immittance network, the criterion is extended to the general AC/DC hybrid system. The stability criterion comprehensively covers the stability problems of the AC/DC system, and avoids solving the problem of poles in the right half-plane, simplifying the analysis process. Furthermore, an oscillation traceability method for the hybrid system is given based on the immittance network model. Finally, based on the application examples of the AC/DC hybrid system, the immittance network model and its stability analysis method proposed in this paper are evaluated and verified.
Keywords：AC/DC hybrid, immittance, stability analysis, oscillation traceability
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.240723
国家自然科学基金资助项目（52277186）。
收稿日期2024-05-07
改稿日期2024-07-24
滕志远 男，2000年生，博士研究生，研究方向为MMC柔性直流输电系统建模、控制及稳定性分析等。
E-mail：tzy2203902@nuaa.edu.cn
陈 新 男，1973年生，博士，教授，博士生导师，研究方向为分布式发电和微电网系统的建模、控制与稳定性等。
E-mail：chen.xin@nuaa.edu.cn（通信作者）
（编辑 赫 蕾）