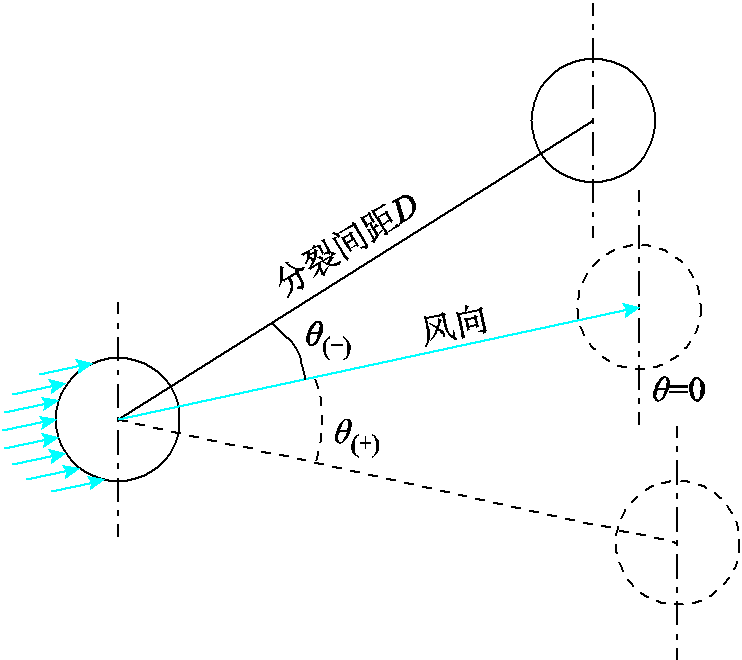
图1 遮蔽角θ示意图
Fig.1 Schematic of shadowing angle θ
摘要 冬季架空输电线路覆冰会对电力系统安全稳定运行构成重大威胁。对于分裂导线而言,由于上风侧子导线对下风侧子导线的遮蔽效应的影响,导致其覆冰特性将出现较大差异,而现有研究缺乏对分裂子导线间覆冰遮蔽效应的定量研究。针对上述问题,该文首先通过数值仿真方法对分裂导线覆冰特性进行研究。采用欧拉模型求解分裂导线覆冰过程中的气-液两相流场分布特性,基于控制体思想及水滴冻结质量平衡与热力学平衡方程,获取了不同覆冰环境下分裂导线的覆冰质量与形貌。然后通过遮蔽角与遮蔽系数的定义分析了分裂子导线间的覆冰遮蔽效应及其影响因素。结果表明:分裂导线上、下风侧子导线覆冰强度之差与子导线间遮蔽效应的强度呈正相关,遮蔽角绝对值和分裂间距的增加会导致遮蔽效应减弱乃至消失;液滴中值体积直径的增加将加剧遮蔽效应;在5~20 m/s的风速范围内,遮蔽效应先增强后减弱,风速为15 m/s时遮蔽效应最强烈。最后,基于遮蔽效应分析,提出了针对不同分裂形式分裂导线的覆冰量快速计算方法,并通过分裂导线自然环境覆冰观测试验对快速计算方法的准确性进行了验证。研究结果可为架空输电线路的防覆冰设计与运维提供理论指导。
关键词:架空输电线路 覆冰 分裂导线 数值模拟 自然覆冰试验
由于暴露在复杂自然环境中,冬季架空输电线路的覆冰现象不可避免。2024年初,我国南方地区大规模寒潮再度来袭,造成大范围冰冻。湖南、湖北等省份主、配电网覆冰灾害频发,严重覆冰导致多处线路出现断线断股、金具损坏、风振舞动与闪络跳闸事故,严重威胁人民群众正常生产生活[1-2]。数十年来,国内外学者对输电线路覆冰进行了大量研究,累积了较为丰富的理论成果与实践经验[3-4]。但由于覆冰的复杂性和随机性,频繁极端天气导致的输电线路覆冰事故依然难以杜绝,电网覆冰灾害机理及其防御方法是仍未解决的科学与工程问题。
传输导线作为架空输电线路的主体,其空间跨度大,结构较为薄弱,最易受覆冰侵害,其覆冰机理是输电线路覆冰灾害研究关注的重点。早在1984年,L. Makkonen [5]就采用数值模拟的方法建立了导线覆冰增长模型,利用碰撞、捕获和冻结系数表征覆冰增长过程,该模型被视为导线覆冰数值计算的开端。在此基础上,郭昊、梁曦东、郝艳捧等[6-8]基于实际覆冰工况分别对导线覆冰模型进行了改进,分析了自然环境、电场等因素对导线覆冰的影响,获得了导线覆冰质量、覆冰形状等参数的变化规律,并通过试验进行了验证。杨国林等[9]针对导线覆冰过程中出现的扭转现象,基于自然环境覆冰观测数据提出了单导线覆冰扭转模型,并通过试验验证了模型的准确性。刘国特等[10]聚焦导线覆冰湿增长过程,建立了考虑导线表面水膜运动的改进Messinger覆冰模型,并利用该模型对导线局部表面传热系数和液态水局部冻结系数进行了计算。
对于分裂导线而言,由于上风侧子导线对下风侧子导线遮蔽效应的影响,下风侧子导线的气-液两相流场及液滴收集特性发生变化,进一步导致其覆冰特性存在差异。R. Veerakumar等[11]在冰风洞中对2分裂钢芯铝绞线的覆冰过程进行了试验研究,结果表明覆冰主要发生在上风侧子导线,但该研究并未定量分析子导线覆冰参数的差异。何青等[12]通过数值模拟以及冰风洞试验发现下风侧子导线的覆冰强度受分裂间距的影响较大,但忽略了来流角度的影响。吴海涛、毕聪来等[13-14]通过数值计算与自然环境观测对比研究了分裂导线与扩径导线的覆冰特性,重点分析了导线直径和液滴参数对分裂导线覆冰的影响。蔡萌琦等[15]以4分裂导线为研究对象,分析了新月形覆冰对分裂导线受力与扭转的影响,并通过风洞试验进行了验证,但是其覆冰形状只是基于现有数据的简单模拟,并未进行详细的覆冰参数计算。Mou Zheyue等[16]基于气象数据集和Extra-trees算法评估了4分裂导线的覆冰情况,并进一步研究了分裂导线覆冰形貌对气动特性的影响。巢亚锋[17]基于数值计算对2、4、6分裂导线的过冷却液滴碰撞特性进行了研究,重点分析了分裂间距、导线直径对导线表面局部碰撞率的影响,但未进一步对覆冰参数进行分析。
综上所述,虽然众多学者已对分裂导线的覆冰特性进行了数值模拟及试验研究,但是缺乏对子导线之间的遮蔽效应影响覆冰特性的定量研究,导致分裂导线覆冰特性参数的计算出现偏差,影响后续导线覆冰气动特性以及防除冰方法的研究。
针对上述问题,本文首先通过数值仿真方法对分裂导线覆冰质量及覆冰形状等参数进行研究,重点分析了子导线间的覆冰遮蔽效应及其影响因素;然后提出了一种分裂导线覆冰质量快速计算方法;最后基于分裂导线自然环境覆冰观测试验,验证了本文数值计算方法的准确性。本文研究结论可为易覆冰地区架空输电线路分裂导线的设计及运维提供理论指导。
架空输电线路常见的分裂形式有2分裂、3分裂、4分裂、6分裂、8分裂。分析其遮蔽效应可知,多分裂导线覆冰均可拆分为多组单导线及2分裂的组合。因此为便于分析,先以2分裂导线为例对分裂导线覆冰特性及遮蔽效应进行研究。
在实际过程中,分裂导线的布置角度和来流角度都会影响分裂导线的气-液两相流场分布及其遮蔽效应与覆冰特性。为了统一描述分裂导线布置角度和来流角度的影响,定义来流风向与两子导线圆心连线的夹角θ为遮蔽角,风向在中心连线上方时θ为正,在下方为负。遮蔽角θ示意图如图1所示。

图1 遮蔽角θ示意图
Fig.1 Schematic of shadowing angle θ
本文研究对象为LGJ-400/35导线,直径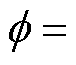 26.82 mm,初始分裂间距D = 400 mm。为保证计算流场的充分发展,数值计算域来流区长度取导线直径的25倍,尾流区长度取导线直径的30倍。为了方便改变来流方向,将左边界和上边界均设置为速度入口;右边界和下边界均设置为压力出口。
26.82 mm,初始分裂间距D = 400 mm。为保证计算流场的充分发展,数值计算域来流区长度取导线直径的25倍,尾流区长度取导线直径的30倍。为了方便改变来流方向,将左边界和上边界均设置为速度入口;右边界和下边界均设置为压力出口。
数值计算域整体网格尺寸为10 mm。为了保证导线附近流场计算精度,对导线附近区域进行加密与边界层划分处理。导线附近2倍直径区域内网格尺寸为2 mm,以y+值为1校核确定导线边界层首层厚度为0.02 mm,然后按照扩散比1.2生成5层边界层网格。网格独立性研究表明,该网格尺寸对空气与液滴流动的影响可以忽略不计,满足计算要求。本文数值计算模型与网格划分如图2所示。

图2 模型及网格划分
Fig.2 Model and meshing
导线附近的流场可以视为黏性不可压缩流动,其流场特性由连续性方程、动量方程以及能量方程描述[18-19],表示为
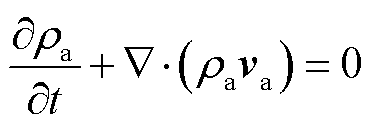 (1)
(1)
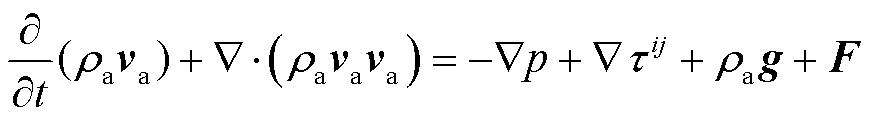 (2)
(2)
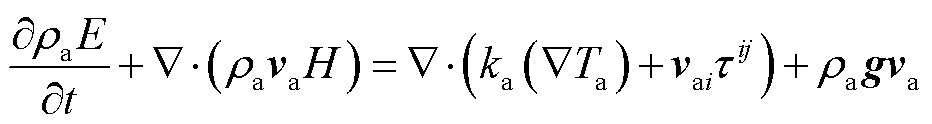 (3)
(3)
式中,ρa为空气密度;t为时间;va为空气流速;τij为黏性应力张量;p为压强;g为重力加速度;F为外部体积力;E为流体能量;H为流体总焓值;ka为流体的热导率;Ta为流体温度。
采用欧拉-欧拉两相流模型求解过冷液滴与导线表面碰撞的过程,在该模型中,液滴相被视为连续相。假设液滴为球形,变形和相变忽略不计,液滴的特性可由连续性方程和动量方程[20]描述为
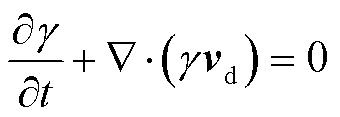 (4)
(4)
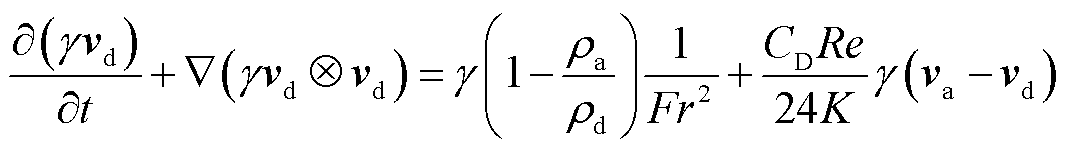 (5)
(5)
式中,γ为液滴的体积分数;vd为液滴速度;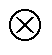 为张量积运算符;ρd为液滴密度;CD为空气对液滴的阻力系数;Re为液滴的雷诺数;K为液滴惯性系数;Fr为局部弗劳德数。
为张量积运算符;ρd为液滴密度;CD为空气对液滴的阻力系数;Re为液滴的雷诺数;K为液滴惯性系数;Fr为局部弗劳德数。
本文基于有限体积法,采用SST k-ω湍流模型对分裂导线气-液两相流动控制方程进行求解,分别获取其分布特性,然后基于气-液两相体积密度的计算,获取导线表面的液滴局部碰撞率。
过冷液滴与导线表面碰撞后形成覆冰,该过程由质量守恒方程式(6)和能量守恒方程式(7)共同决定[21]。
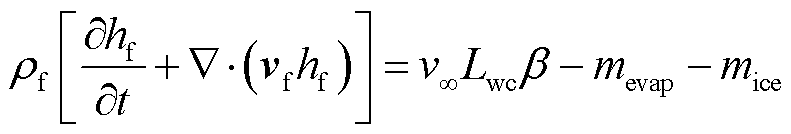 (6)
(6)
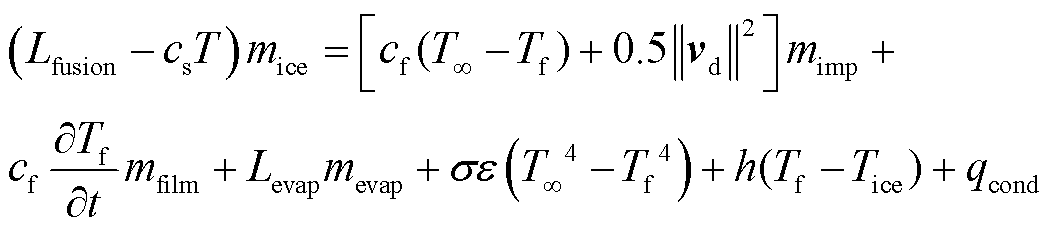 (7)
(7)
式中,ρf为水膜密度;hf为水膜高度;vf和v∞分别为水膜速度和远场气流速度;Lwc为空气中液态水含量;β为碰撞效率;mevap和mice分别为蒸发和结冰过程中的质量转移;Lfusion和Levap分别为冰的融化潜热和蒸发潜热;T、T∞、Tf和Tice分别为冻结温度、远场气流温度、环境温度和冰面温度;mimp和mfilm分别为水滴和水膜撞击的质量转移;cs和cf分别为冰和水的平均热容;σ为斯忒藩-玻耳兹曼常量;发射率ε=0.95;h为表面传热系数;qcond为传导热通量。
求解式(6)和式(7)获取导线表面的覆冰质量。通过Bain-Gayet覆冰密度模型[22]式(8)计算得到导线表面覆冰密度ρice(单位为g/cm3)之后,基于法向生长准则和网格迭代技术,可以得到导线表面覆冰形貌。
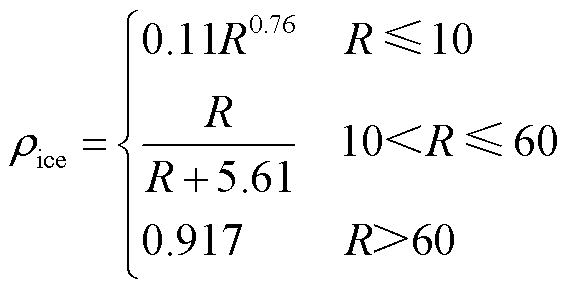 (8)
(8)
其中
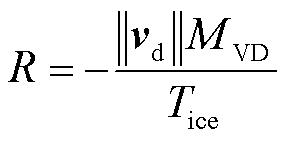
式中,R为Macklin冰密度参数[23];MVD为液滴中值体积直径。
以θ= -2°为例对2分裂导线覆冰特性进行分析,计算覆冰时长t =60 min,其余环境参数均选取常见覆冰环境参数,相关参数取值见表1。表中,V为远场来流速度,即风速。
表1 覆冰仿真环境参数
Tab.1 Parameters of icing simulation

参数数值参数数值 Tf/℃-5V/(m/s)10 Lwc/(g/m3)0.6θ/(°)-2 MVD/μm20t/min60
1.6.1 空气相分布
导线绕流时的气流速度分布云图如图3a所示。由图3a可知,气流速度在上风侧子导线的迎风面边缘位置相较于初始速度有一定的增加,最大值达到了12.73 m/s,而在驻点处由于阻滞作用导致气流速度明显下降;在上风侧子导线后方则形成了大面积的低速尾流区,导致下风侧子导线来流速度降低。
1.6.2 液滴相分布
导线绕流时周围液态水含量分布云图如图3b所示。由图3b可知,由于导线的阻滞作用,液滴向上风侧子导线两侧运动累积,导致局部液态水含量升高,最大值达到了0.76 g/m3。但在上风侧子导线的后方区域将会形成大面积的低液水含量区域,这将影响下风侧导线表面的液滴碰撞率分布,导致覆冰形貌发生偏移。

图3 气流速度及液态水含量分布
Fig.3 Distributions of airflow velocity and Lwc
1.6.3 碰撞率分布
θ = 0°和θ = -2°两种情况下导线表面局部液滴碰撞率分布如图4所示。上风侧子导线碰撞率在导线截面迎风驻点位置达到最大值,然后向两侧不断降低。由于遮蔽效应的影响,下风侧子导线的碰撞率要明显小于上风侧子导线,但两者之差随着θ绝对值的增大而减小。
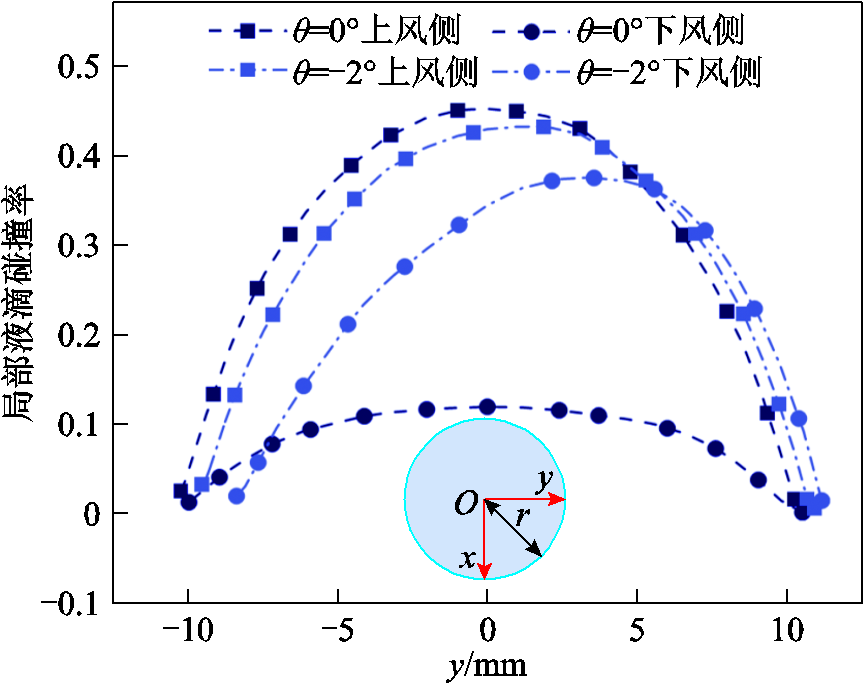
图4 导线表面局部液滴碰撞率分布
Fig.4 Distributions of local collision efficiency
1.6.4 冰形及覆冰质量
两子导线覆冰冰形及覆冰强度(单位长度导线覆冰质量)随时间的变化情况分别如图5和图6所示。由图可知:①覆冰大部分出现在上风侧子导线,冰形呈新月状且导线上下两侧的覆冰边界随着时间的增加逐渐向中心推移;②两子导线的覆冰强度随着时间推移而增加,且上风侧子导线的增加速度比下风侧子导线快。
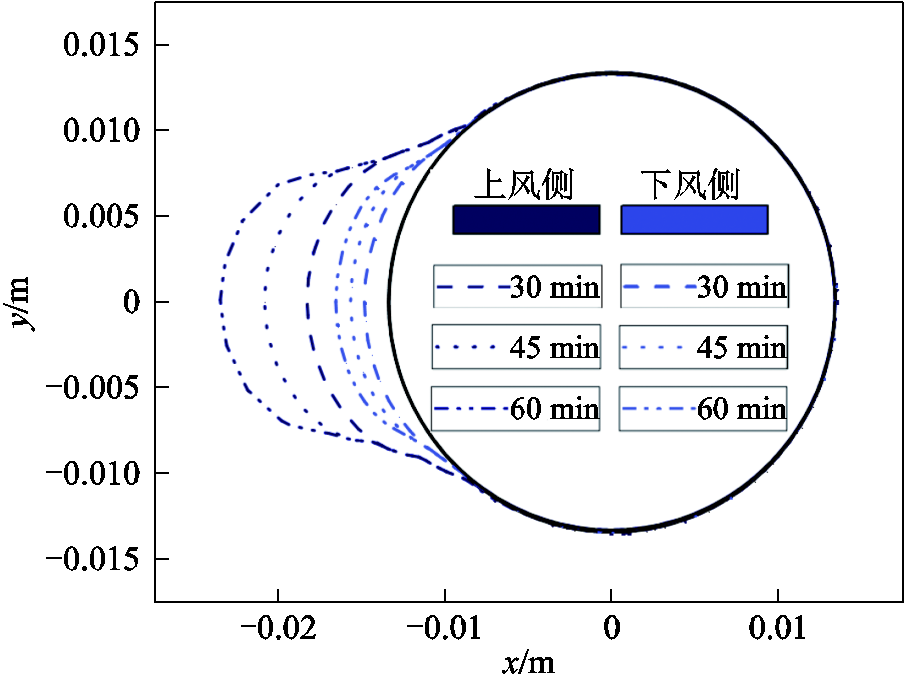
图5 覆冰冰形
Fig.5 Icing shape
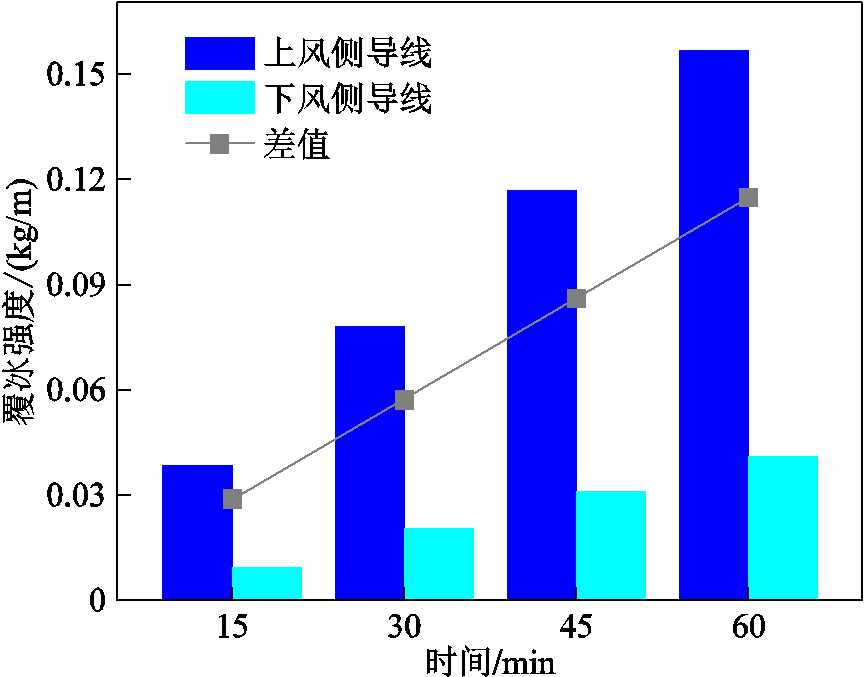
图6 覆冰强度
Fig.6 Icing intensity
上风侧子导线对下风侧子导线的遮蔽影响了下风侧子导线周围的流场-液滴两相分布,进而导致覆冰强度出现差异。为了量化这种遮蔽效应,定义遮蔽系数k为
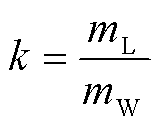 (9)
(9)
式中,mL为下风侧子导线的覆冰强度;mW为上风侧子导线的覆冰强度。
改变θ从0°~-6°变化,其他参数保持表1中数值不变,得到2分裂导线不同遮蔽角下覆冰冰形如图7所示。由图7可知,对于上风侧子导线,随着θ绝对值的增大,冰形沿导线表面向上方移动,但冰厚基本保持不变;对于下风侧子导线,冰厚也会随着θ绝对值的增大而增加。
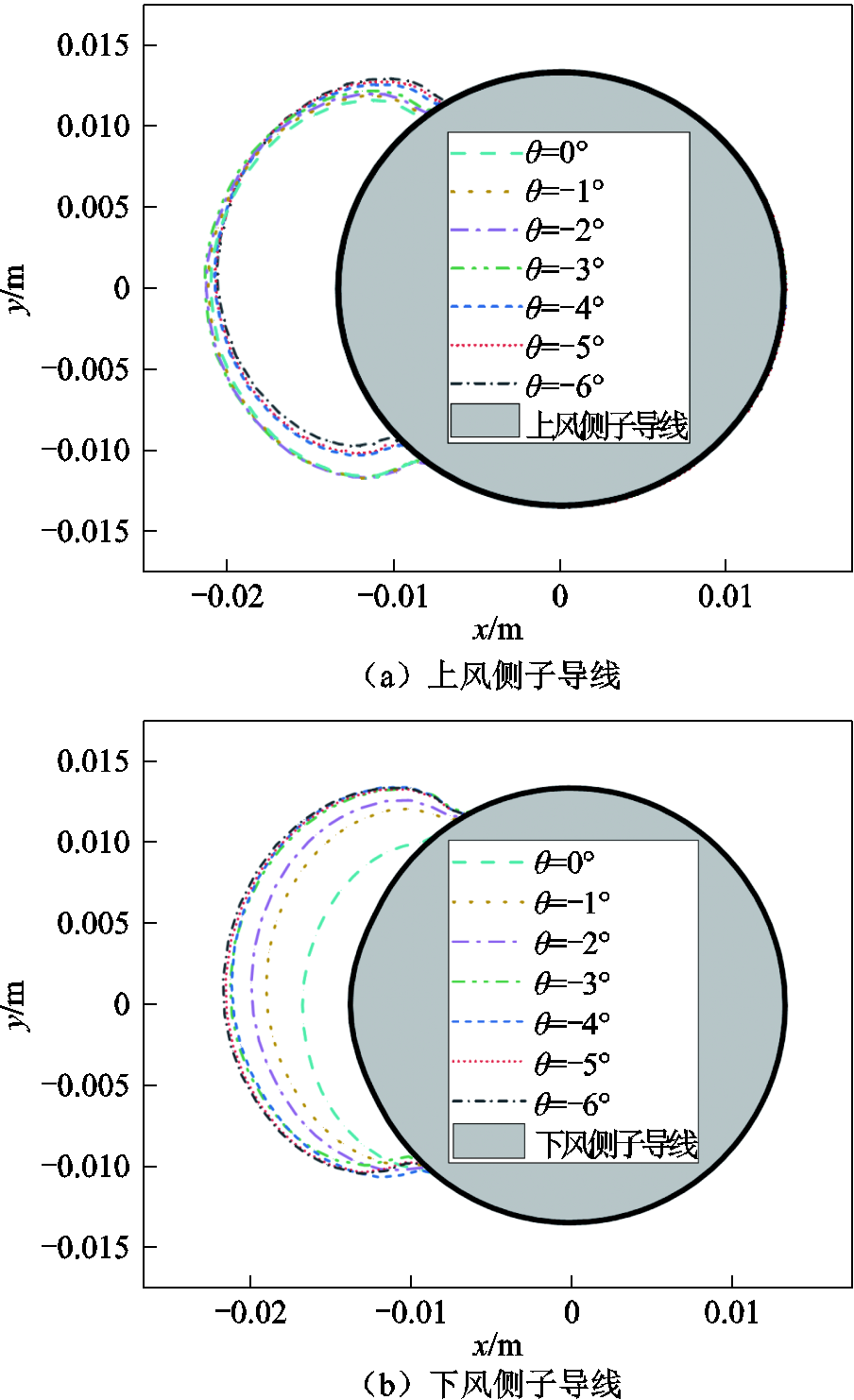
图7 不同遮蔽角θ覆冰冰形
Fig.7 Icing shape under different shadowing angle θ
遮蔽角θ对遮蔽系数k的影响如图8所示。由图8可知,随着θ绝对值的增加,遮蔽系数k迅速增大并最终趋向于1。结合图7冰形变化可知,θ绝对值的增大使得上风侧子导线尾流区域逐渐偏离下风侧子导线,遮蔽效应减弱,下风侧子导线上的冰厚增加。当θ绝对值到达一定值时,下风侧子导线将完全不受上风侧子导线影响,本文将此特定值定义为临界遮蔽角θk。θk主要受到导线直径与分裂间距的影响,在实际情况下一般不超过10°。
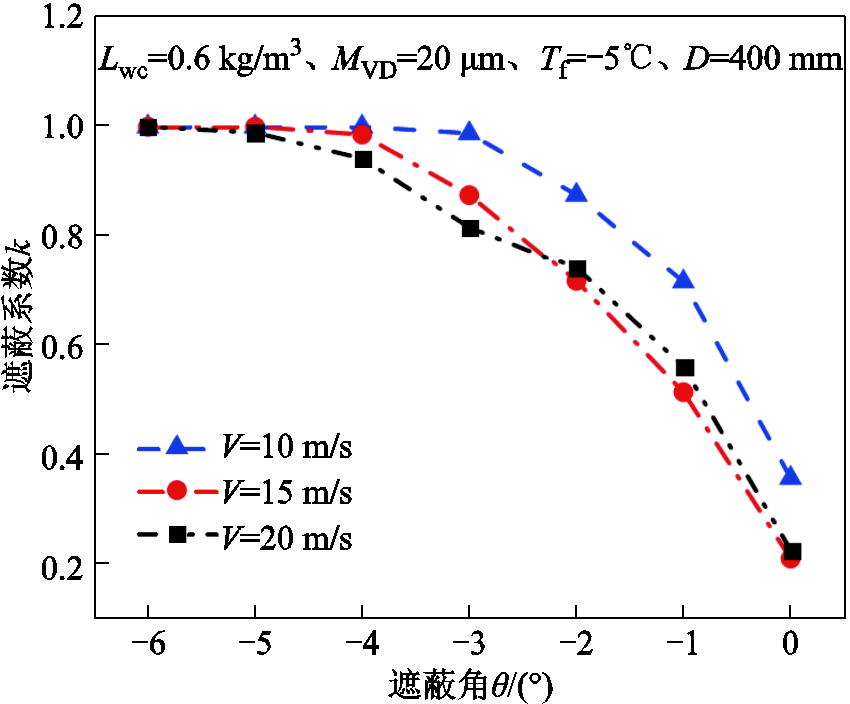
图8 遮蔽角θ对遮蔽系数k的影响
Fig.8 Influence of shadowing angle θ on shadowing coefficient k
分裂间距D对遮蔽系数k的影响如图9所示。遮蔽系数k随着分裂间距D的增大而增大,这是因为较大的分裂间距使得上风侧子导线尾流区域的气-液两相流场有充足的空间恢复均匀分布,下风侧子导线受尾流的影响减弱。当分裂间距足够大时,遮蔽效应将会完全消失,此时k=1。
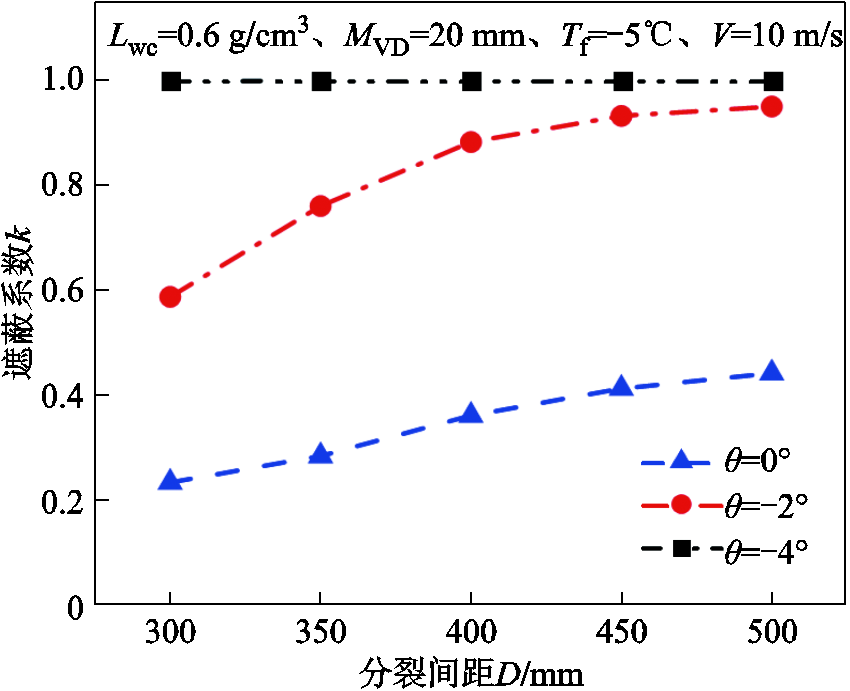
图9 分裂间距D对遮蔽系数k的影响
Fig.9 Influence of bundled spacing D on shadowing coefficient k
液滴中值体积直径MVD对遮蔽系数k的影响如图10所示。由图10可知,当MVD从10 μm增加到40 μm时,不同风速下的遮蔽系数k均出现明显下降,最大降幅达到了47.53%。这是由于MVD的增加对应着液滴质量的增加,导致其惯性增加,更难跟随空气绕流至下风侧子导线。因此在较大的MVD条件下,分裂导线的遮蔽系数k更小,遮蔽效应更强。
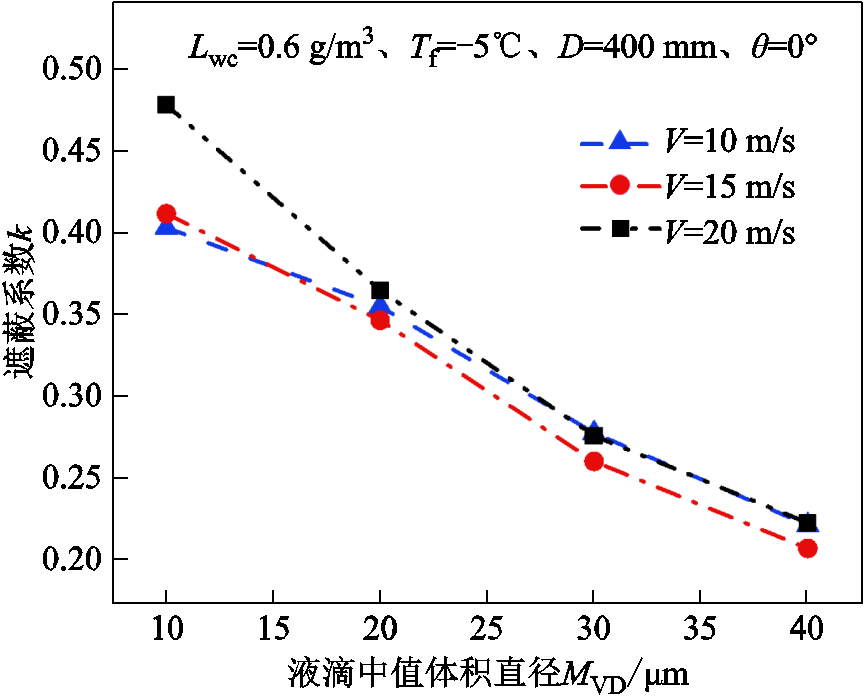
图10 MVD对遮蔽系数k的影响
Fig.10 Influence of MVD on shadowing ecoefficiency k
图11为遮蔽系数k随来流风速V的变化曲线。由图11可知,随着来流风速的增大,遮蔽系数k先减后增,最小值出现在风速V=15 m/s处。这可能是由于风速较小时,提高风速可以增加单位时间内到达导线表面的过冷液滴质量,进而使得覆冰强度增加;而风速过大将会使得液滴难以粘附在导线表面,导致覆冰强度减小甚至完全消失。在风速较小时,两子导线覆冰强度都处于上升状态,但上风侧子导线处的风速增加得更快,单位时间内覆冰强度上升更多,因此遮蔽系数k下降;当风速上升至一定值时,上风侧子导线覆冰强度开始下降,而下风侧子导线周围风速较小,覆冰强度仍处于上升状态,故k上升。
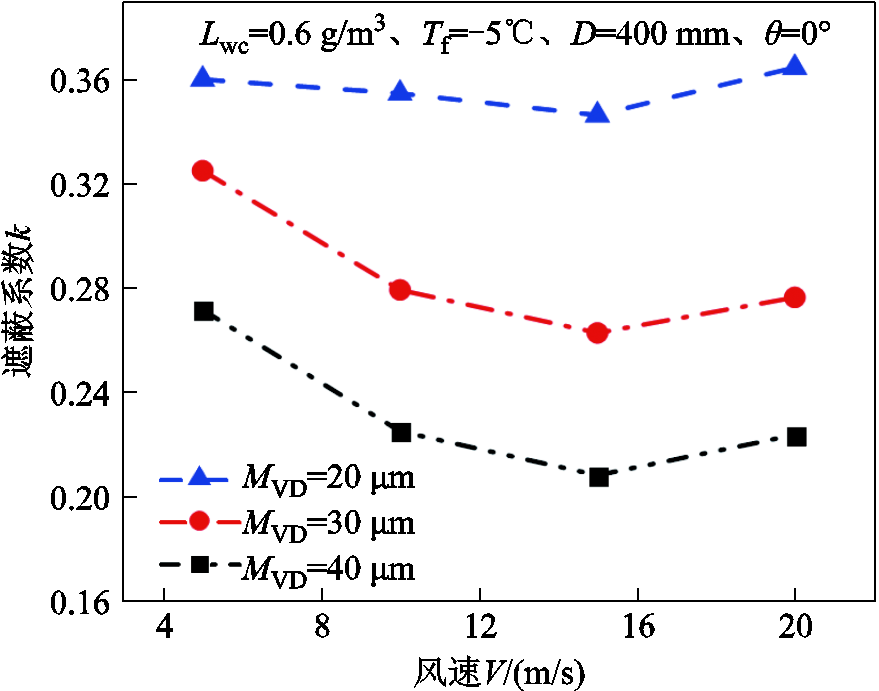
图11 风速V对遮蔽系数k的影响
Fig.11 Influence of wind speed V on shadowing coefficient k
综上所述,遮蔽角θ、分裂间距D、液滴中值体积直径MVD以及来流风速V均会对遮蔽系数k产生影响。此外,研究还发现环境温度Tf和空气中液态水含量Lwc对遮蔽效应的影响并不显著。
基于对分裂导线遮蔽效应的分析及叠加原理,本文提出了一种分裂导线覆冰量快速计算方法:将分裂导线的整体覆冰量M拆分为无遮蔽子导线(单导线)覆冰量m0与遮蔽系数k的线性组合,因此只需计算单导线的覆冰强度及相应条件下的遮蔽系数,即可通过简单的计算获取不同分裂导线的覆冰量。考虑几何对称性,遮蔽角θ的取值范围为[0°, 90°]。本节基于遮蔽特性分析,推导不同分裂形式分裂导线的覆冰强度快速计算公式。
3.1.1 2分裂导线
2分裂导线遮蔽效应示意图如图12a所示,当遮蔽角θ小于临界遮蔽角θk时,下风侧子导线受到遮蔽效应影响,遮蔽系数k取子导线分裂间距情况下的值。推导得到2分裂导线覆冰强度快速计算公式为
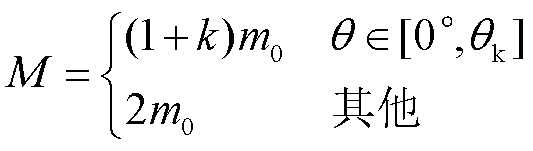 (10)
(10)
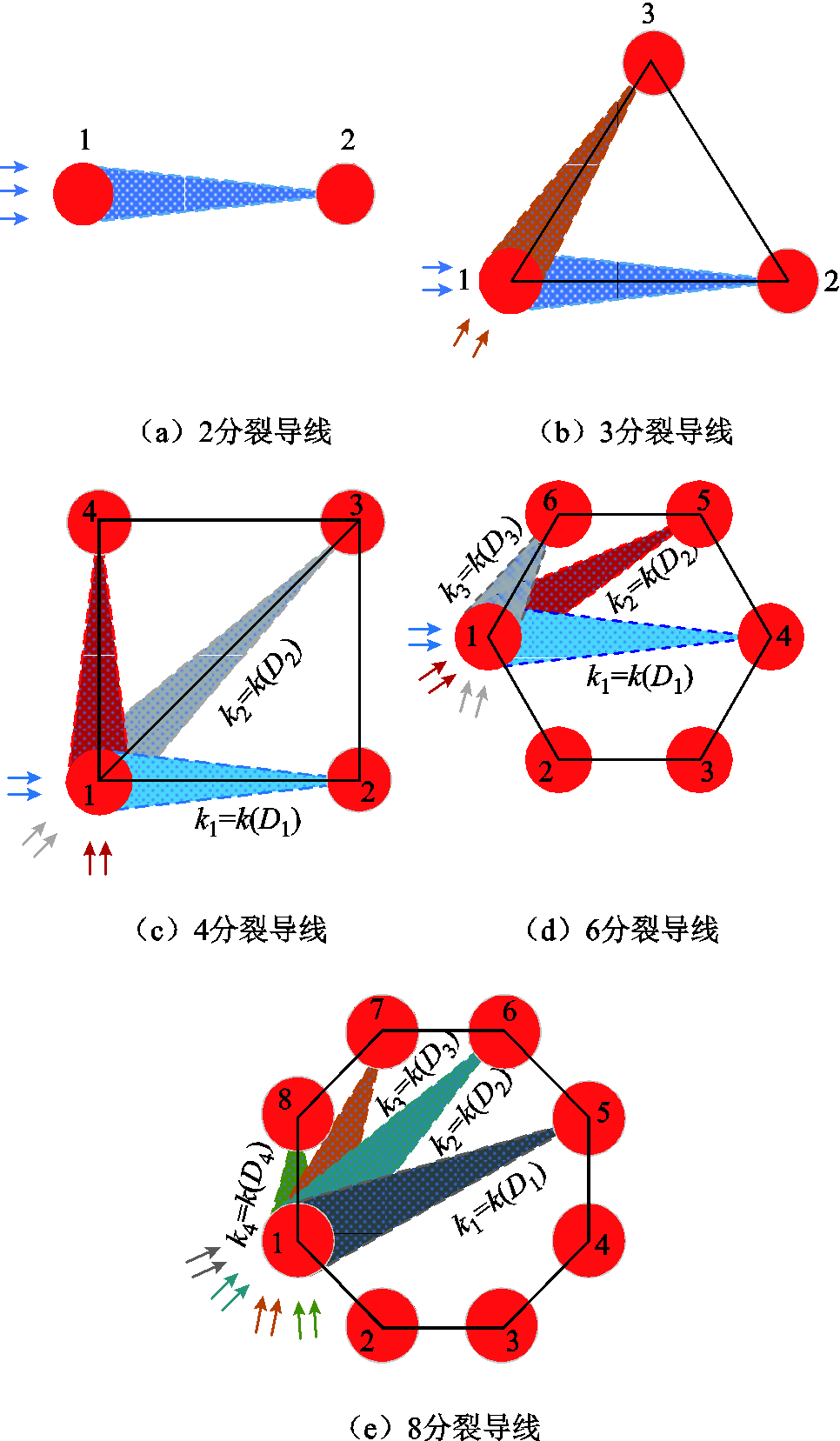
图12 分裂导线遮蔽效应示意图
Fig.12 Schematic of shadowing effect on various bundled conductors
3.1.2 3分裂导线
3分裂导线通常呈正三角形排列,如图12b所示。分析不同遮蔽角时的遮蔽情况可知:当θ∈[0°, θk]时,子导线1对于子导线2存在遮蔽效应,子导线3独立;当θ∈[60°-θk, 60°+θk]时,子导线1对于子导线3存在遮蔽效应,子导线2独立。两种情况下的k取值均为分裂间距下的取值,将其合并得到3分裂导线覆冰强度快速计算公式为
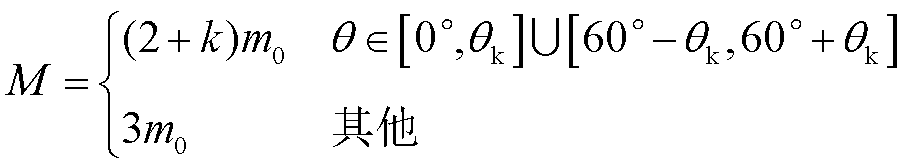 (11)
(11)
3.1.3 4分裂导线
4分裂导线呈正方形排列,如图12c所示。在多数情况下4分裂导线可以看作两组2分裂导线,但在遮蔽角θ=45°时,1号子导线会对3号子导线造成影响,而2、4号子导线独立。分析可得4分裂导线覆冰强度计算公式为
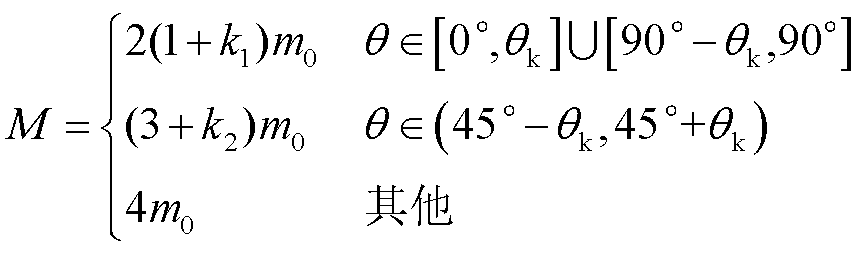 (12)
(12)
其中
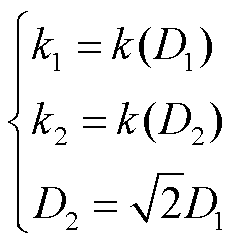
式中,D1为子导线1-2及子导线1-4间的分裂间距;k1为分裂间距D1下遮蔽系数k的取值;D2为子导线1-3间的分裂间距;k2为分裂间距D2下遮蔽系数k的取值。
3.1.4 6分裂导线
6分裂导线呈正六边形排列,情况相对复杂。以1号子导线为例,图12d为指定遮蔽角范围内1号子导线对其他子导线的遮蔽效应示意图。图中,k3=k(D3)、k2=k(D2)、k1=k(D1)分别为子导线1-6、子导线1-5及子导线1-4间的分裂间距下遮蔽系数k的取值。D2、D1与分裂间距D3的关系为D2 =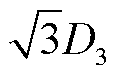 ,D1 = 2D3。分析所有子导线遮蔽情况即可得到6分裂导线覆冰强度计算公式为
,D1 = 2D3。分析所有子导线遮蔽情况即可得到6分裂导线覆冰强度计算公式为
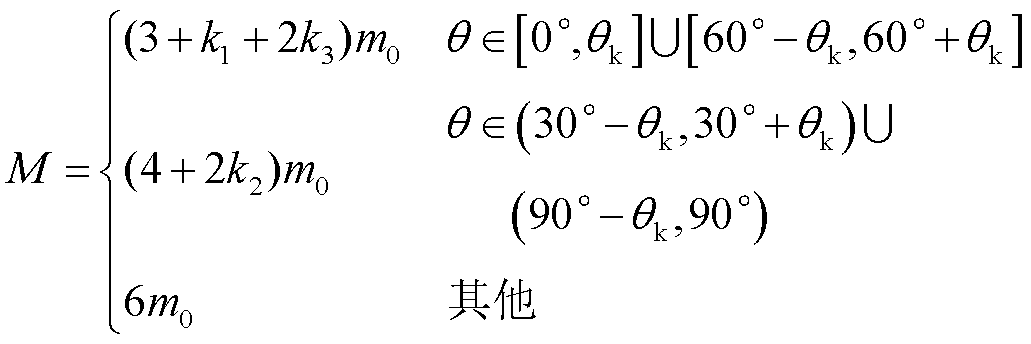 (13)
(13)
3.1.5 8分裂导线
8分裂导线遮蔽效应示意图如图12e所示。8分裂导线中各子导线之间有4个不同的间距,对应着4个不同的k值,其中k4=k(D4)、k3=k(D3)、k2=k(D2)、k1=k(D1)分别为遮蔽系数k在子导线1-8、子导线 1-7、子导线1-6和子导线1-5分裂间距D4、D3、D2、D1下的取值。D3、D2、D1与分裂间距D4之间的关系分别为D3 = 2cos(22.5°)D4、D2 = (1+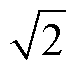 )D4、D1 = D4/sin(22.5°),推导得到8分裂导线的覆冰强度计算公式为
)D4、D1 = D4/sin(22.5°),推导得到8分裂导线的覆冰强度计算公式为
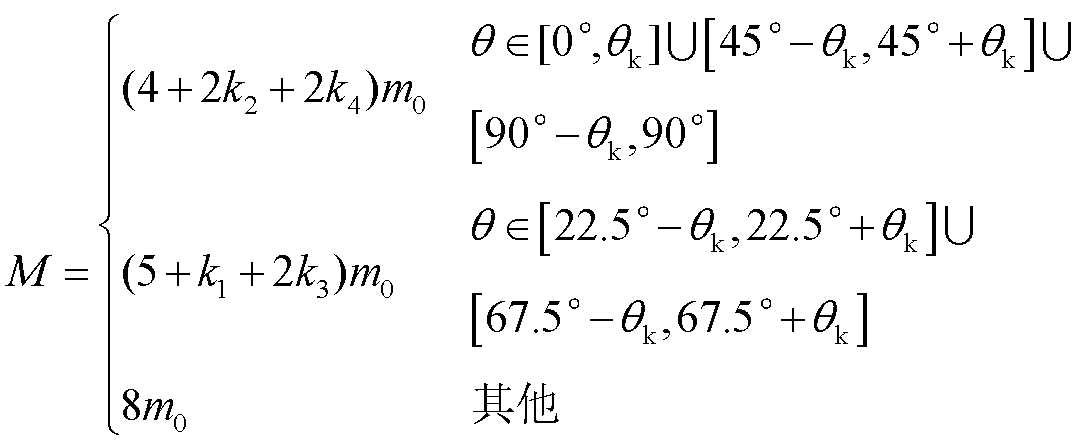 (14)
(14)
根据表1中的覆冰环境参数,利用快速计算方法得到不同类型分裂导线单根子导线的覆冰强度及总覆冰强度随遮蔽角θ变化曲线如图13所示。由图13可知:①在特定的遮蔽角范围内,某些下风侧子导线由于受上风侧子导线遮蔽效应的影响,其覆冰强度存在V形减小波动,即出现极小值;②覆冰强度的波动极值与极值出现的具体角度因分裂导线的分裂形式不同而不同,且同一分裂导线不同角度出现的极小值也存在差异,这是由于几何关系与遮蔽角的变化导致发生遮蔽的子导线对象发生改变;③不同分裂形式的分裂导线总覆冰强度为各子导线覆冰强度之和,其极小值变化等于各子导线极小值的叠加。
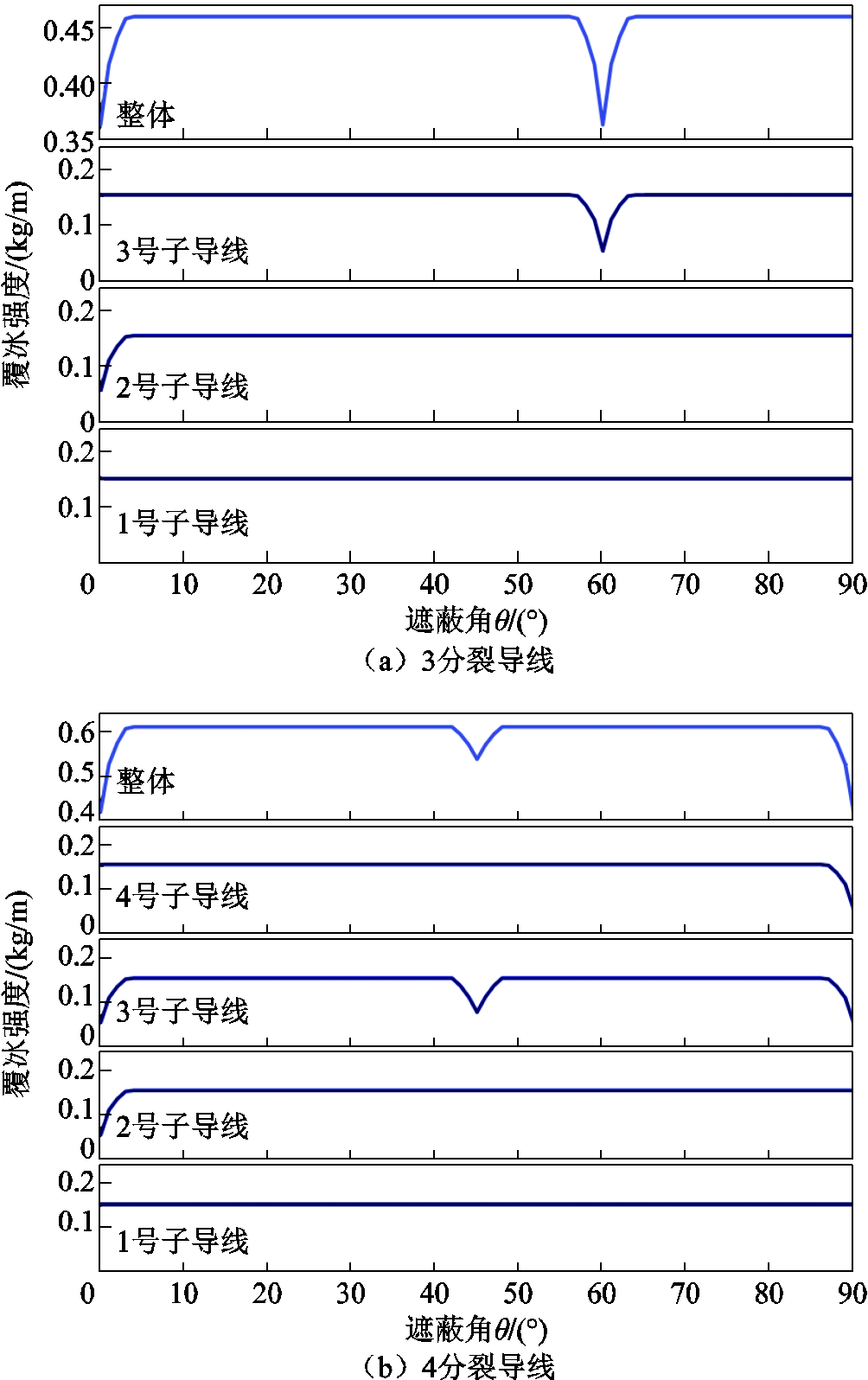
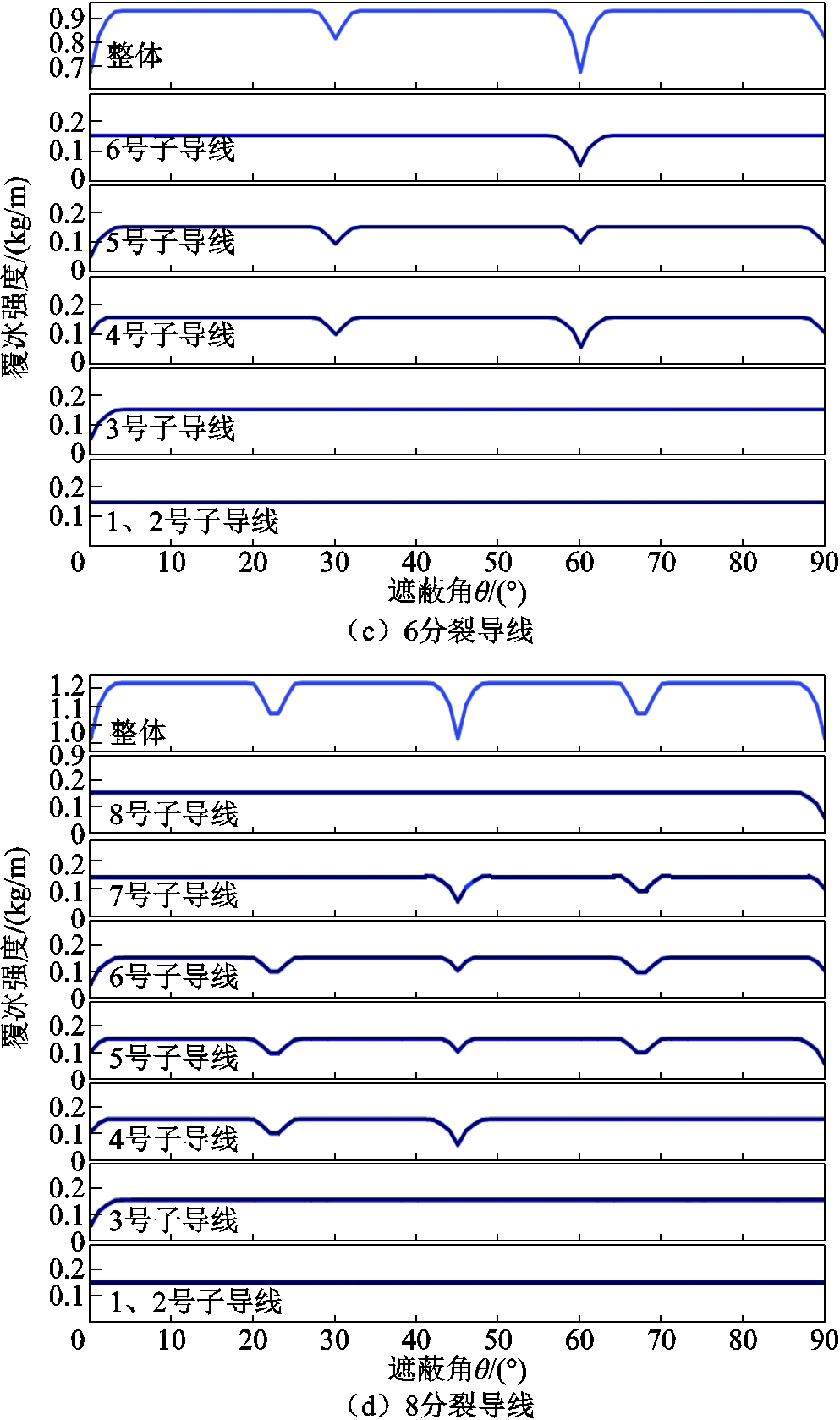
图13 不同分裂导线覆冰强度快速计算值
Fig.13 Rapid calculation results on difference bundled conductors
为了进一步研究分裂导线的覆冰特性并验证本文数值计算结果和快速计算方法的准确性,在雪峰山能源装备安全国家野外科学观测研究站进行了4×LGJ-400/35分裂导线覆冰观测试验。该站海拔为1 400 m,冬季气候寒冷湿润,且配备完善的气象及液滴参数测量装置,可对温度、风速、风向、液滴参数等数据进行实时记录,是自然覆冰观测的理想场所。
将4根LGJ-400/35导线安装在两个门型架上,分裂间距为400 mm,导线长度为100 m。为了防止导线在覆冰过程中发生扭转并确保分裂间距一致,每30 m安装一个间隔棒。对子导线进行编号,以方便记录并分析其覆冰数据。自然覆冰观测试验布置图如图14所示。

图14 自然覆冰观测试验布置图
Fig.14 Natural icing observation test layout
根据气象数据及覆冰装置监测,在一个覆冰初期开始对分裂导线覆冰特性进行观测[24]。在15、30、45、60 min时对分裂导线覆冰特性进行测量并记录。观测试验期间的环境参数范围为:Tf=-2~-2.2 ℃,MVD = 25.3~25.6 μm,LWC=0.6~0.62 g/m3,V = 9.8~10.2 m/s。风向仪测得该覆冰时段内导线附近来流风向为5°,利用水平仪测出4分裂导线布置的偏转角度为3°,即遮蔽角θ = 2°。
4.2.1 覆冰冰形及厚度分析
分裂导线表面覆冰形貌采用截断法测量,即在覆冰导线上切割出冰层截面,采用游标卡尺测量对应位置的覆冰厚度,并结合截面照片绘制覆冰形貌。测量点从导线驻点位置开始向两侧延展分布,相邻两点间夹角为15°,共取5个测量点,并在覆冰试验开始前使用记号笔在洁净导线上划线作好标记。由于①、②号子导线与③、④号子导线覆冰特性相同,因此文中只给出了③、④号子导线的覆冰冰形测量结果,分别如图15a和15b所示。为了方便对比,仿真计算结果也在图中给出。
将仿真值与试验值之差除以试验值并转换成百分数即可得到仿真与试验结果的百分比差异,见表2。由表2可知,试验结果与模拟结果的差异在1.66%~-6.36%之间,证明了本文分裂导线覆冰数值计算具有较好的精度。值得注意的是,导线驻点附近区域差异相对较小,两侧差异较大。这可能是由于导线周围的气流运动,导致水膜从导线驻点向两侧移动并发生冻结。
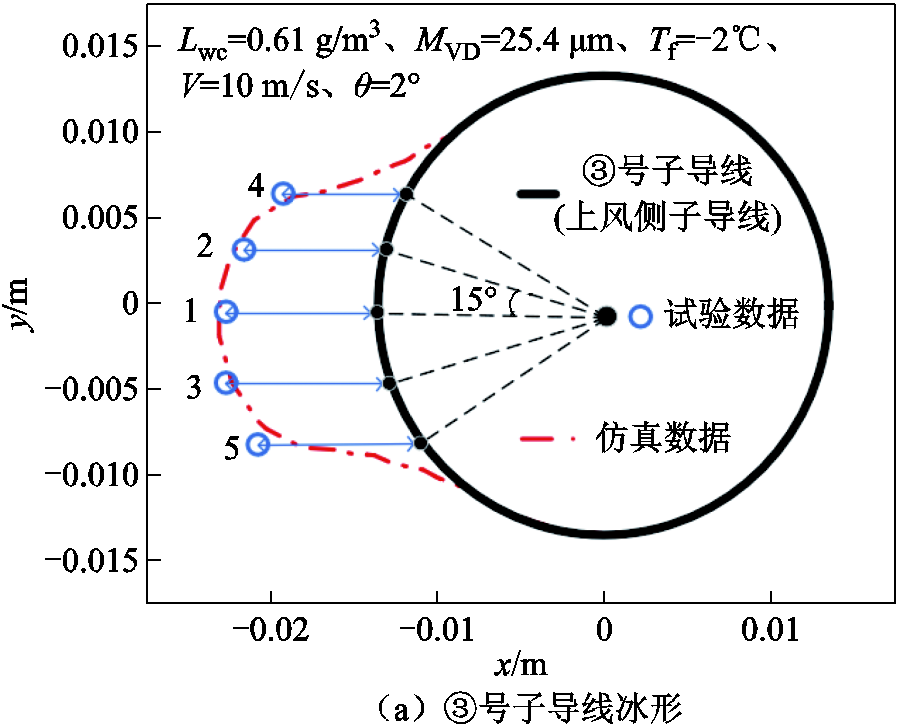
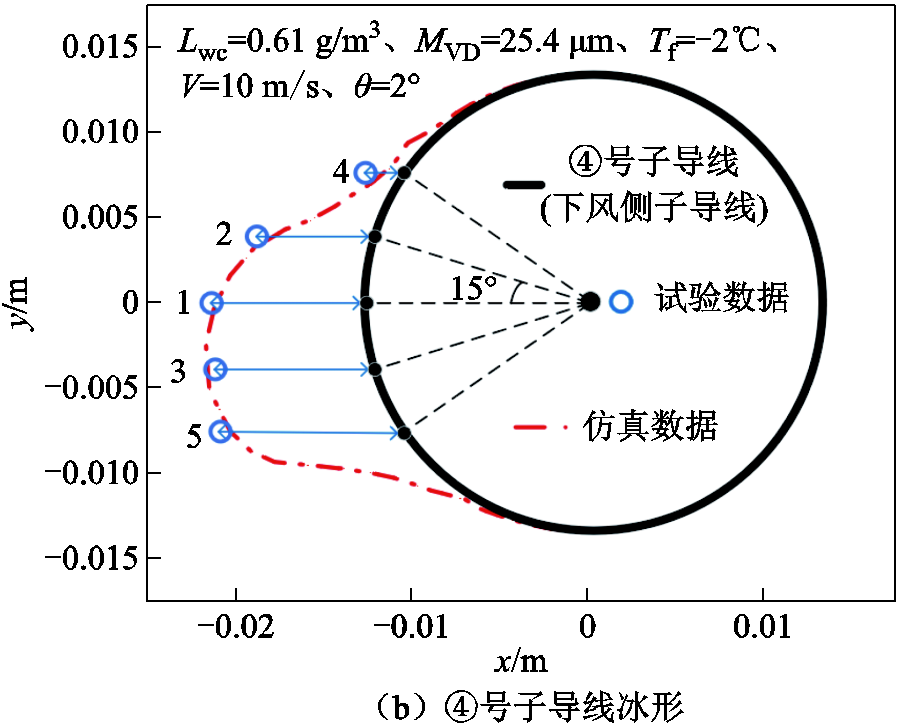
图15 冰形截取示意图
Fig.15 Ice shape truncation schematic
表2 观测点覆冰厚度及差异
Tab.2 Ice thicknesses and differences at test points
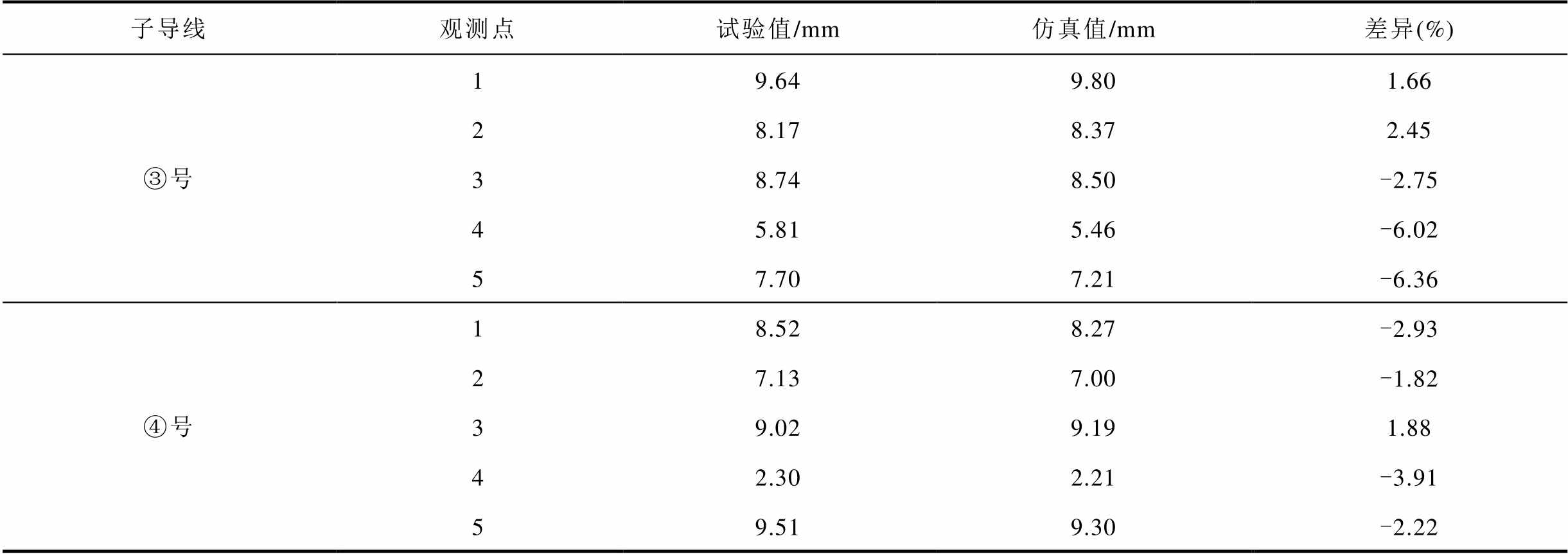
子导线观测点试验值/mm仿真值/mm差异(%) ③号19.649.801.66 28.178.372.45 38.748.50-2.75 45.815.46-6.02 57.707.21-6.36 ④号18.528.27-2.93 27.137.00-1.82 39.029.191.88 42.302.21-3.91 59.519.30-2.22
4.2.2 覆冰强度及遮蔽系数分析
观测试验中各子导线的覆冰强度如图16所示,同时还给出了在观测试验过程中覆冰参数平均值(Tf=-2℃,MVD= 25.4 μm,LWC= 0.61 g/m³,V = 10 m/s,θ = 2°)下各导线覆冰快速计算方法所得结果。由图16可知:计算结果均小于观测结果,且差异在覆冰初始阶段非常显著,达到-19.77%;但差异在后期相对较小,在-4.01%~-8.46%的范围内。这可能是由于观测试验中导线表面存在绞纹并不光滑,有利于过冷液滴粘附,导致前期覆冰强度较大。而随着覆冰时间的增加,绞纹被冰层所覆盖其影响逐渐消失,因此差异随着时间的推移逐渐下降到稳定值。
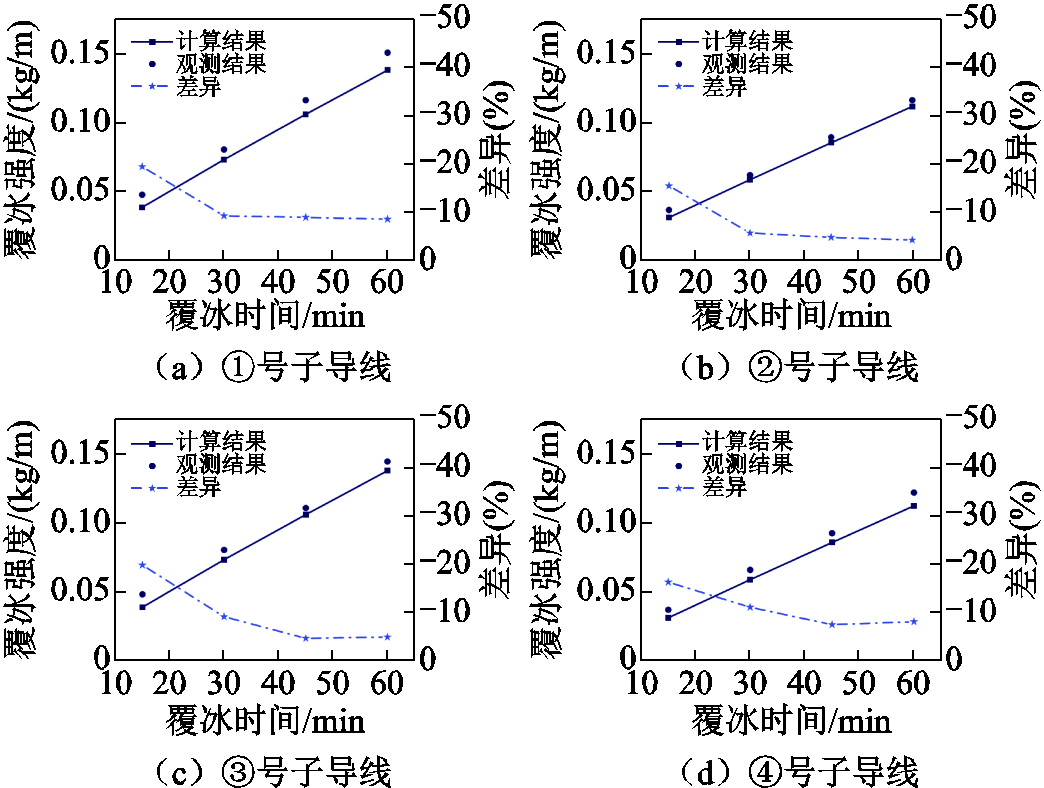
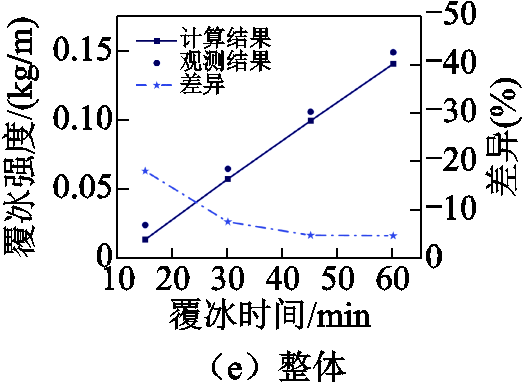
图16 计算及观测试验覆冰强度
Fig.16 Icing intensity of calculation and test
①-②号及③-④号子导线之间的遮蔽系数k随覆冰时间的变化如图17所示。由图17可知,①-②号子导线k的试验结果与计算结果之间的差异在4.05%~5.00%之间;③-④号子导线k的差异位于4.12%~5.33%,较好地验证了本文提出的快速计算方法的准确性。
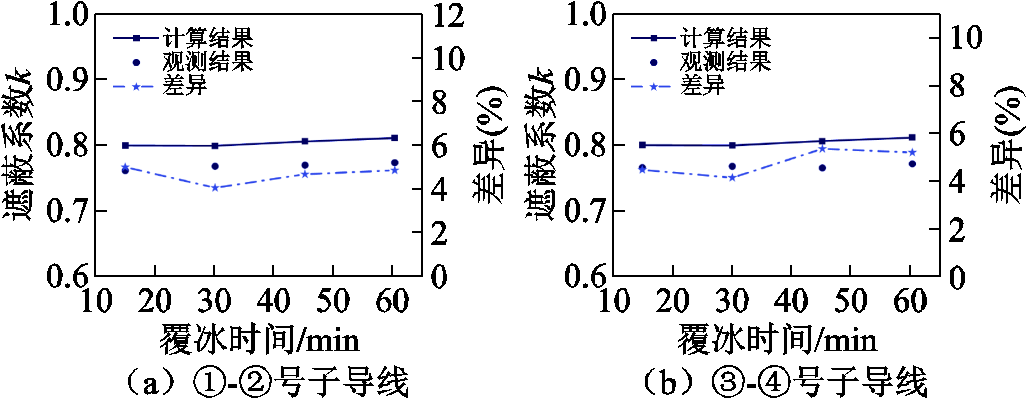
图17 计算及观测试验遮蔽系数k
Fig.17 Shadowing coefficient k of calculation and test
本文通过理论分析、数值计算以及自然环境覆冰试验研究了分裂导线的覆冰特性及子导线遮蔽效应的影响,并以此为基础提出了一种分裂导线覆冰量快速计算方法,主要结论如下:
1)上风侧子导线的覆冰特性不受下风侧子导线影响,但下风侧子导线的覆冰特性受上风侧子导线遮蔽效应的影响较大:下风侧子导线的覆冰强度小于上风侧子导线,且覆冰冰形向来流侧偏移更为严重。
2)子导线覆冰量的遮蔽效应受遮蔽角、分裂间距、液滴直径、风速的影响。其中,遮蔽效应随遮蔽角θ的绝对值以及分裂间距D的增加而减弱,随MVD的增加而增强,且在一定范围内(5~20 m/s)随风速的增加先增强后减弱,出现极大值。
3)基于叠加原理和遮蔽效应定量分析,提出了一种考虑遮蔽角的分裂导线整体覆冰量快速计算方法,利用遮蔽系数的变化规律将分裂导线分解为无遮蔽导线(单导线)覆冰强度与遮蔽系数的线性组合,简化了分裂导线覆冰量的计算。
4)由分裂导线自然覆冰观测试验结果得到,采用快速计算方法得到的覆冰强度结果与观测数据的差异在-4.01%~-19.77%之间,子导线的覆冰厚度差异在1.66%~-6.36%之间,遮蔽系数k的差异在4.05%~5.33%之间,证明本文提出的分裂导线覆冰量快速计算方法具有良好的准确性。需要指出的是,本文提出的快速计算方法主要适用于分裂导线覆冰的前中期,而对于长时间重覆冰的情况需要进一步研究。
参考文献
[1] 曾伟, 蒋兴良, 杨国林, 等. 基于记忆合金双程形状记忆效应的导线雾凇防冰方法及现场试验[J]. 电工技术学报, 2024, 39(7): 2174-2183.
Zeng Wei, Jiang Xingliang, Yang Guolin, et al. Research on anti-icing method for fog freezing and field test of wires based on two-way shape memory effect of memory alloy[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2174-2183.
[2] Li Bo, Bai Jie, He Jinhang, et al. A review on superhydrophobic surface with anti-icing properties in overhead transmission lines[J]. Coatings, 2023, 13(2): 301.
[3] 杨国林, 蒋兴良, 王茂政, 等. 输电线路单导线覆冰形状对直流大电流融冰时间的影响[J]. 电工技术学报, 2024, 39(9): 2916-2924.
Yang Guolin, Jiang Xingliang, Wang Maozheng, et al. The impact of ice accumulation shape on the DC high current ice-melting time for a single conductor on power transmission line[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2916-2924.
[4] Zhu He, Tang Wenpeng, Zhang Renqi, et al. Dynamic response analysis of asynchronous deicing of quad bundle conductor spacer system during DC ice melting[J]. IEEE Access, 2022, 10: 118072-118081.
[5] Makkonen L. Modeling of ice accretion on wires[J]. Journal of Climate and Applied Meteorology, 1984, 23(6): 929-939.
[6] 郭昊, 刘沛清, 屈秋林, 等. 输电线雾凇覆冰的工程估算方法[J]. 高电压技术, 2011, 37(4): 1041-1049.
Guo Hao, Liu Peiqing, Qu Qiulin, et al. Estimation engineering method of rime accretion process on transmission lines[J]. High Voltage Engineering, 2011, 37(4): 1041-1049.
[7] 梁曦东, 李雨佳, 张轶博, 等. 输电导线的覆冰时变仿真模型[J]. 高电压技术, 2014, 40(2): 336-343.
Liang Xidong, Li Yujia, Zhang Yibo, et al. Time-dependent simulation model of ice accretion on transmission line[J]. High Voltage Engineering, 2014, 40(2): 336-343.
[8] 郝艳捧, 魏发生, 王斌, 等. 特殊地形下输电线路等值覆冰厚度计算模型有效性分析和改进研究[J]. 电网技术, 2022, 46(7): 2786-2793.
Hao Yanpeng, Wei Fasheng, Wang Bin, et al. Research on validity analysis and improvement of calculation model of equivalent icing thickness of transmission lines under special terrain[J]. Power System Technology, 2022, 46(7): 2786-2793.
[9] 杨国林, 蒋兴良, 廖乙, 等. 输电线路单导线自由扭转覆冰动态仿真研究[J]. 电工技术学报, 2024, 39(13): 4079-4089.
Yang Guolin, Jiang Xingliang, Liao Yi, et al. Simulation study of the free torsional icing on single conductors of transmission lines[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4079-4089.
[10] 刘国特, 郝艳捧, 阳林, 等. 基于改进Messinger覆冰模型导线防冰临界电流计算及其影响因素分析[J]. 电工技术学报, 2016, 31(18): 176-183.
Liu Guote, Hao Yanpeng, Yang Lin, et al. Caculation and influencing factors analysis of conductor anti-icing critical current based on improved messinger icing model[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 176-183.
[11] Veerakumar R, Hu Haiyang, Tian Linchuan, et al. An experimental study of rime ice accretion on bundled conductors[J]. Experimental Thermal and Fluid Science, 2023, 147: 110962.
[12] 何青, 李军辉, 张暕, 等. 分裂导线覆冰的数值分析与实验研究[J]. 中南大学学报(自然科学版), 2019, 50(6): 1485-1491.
He Qing, Li Junhui, Zhang Jian, et al. Numerical analysis and experiment of icing condition of bundled conductors[J]. Journal of Central South University (Science and Technology), 2019, 50(6): 1485-1491.
[13] 吴海涛, 韩兴波, 蒋兴良, 等. 基于水滴碰冻效率的扩径导线防冰特性分析[J]. 电工技术学报, 2023, 38(11): 3033-3040, 3051.
Wu Haitao, Han Xingbo, Jiang Xingliang, et al. Analysis of anti-icing characteristics of expanded diameter conductor based on water droplet collision and freezing efficiency[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3033-3040, 3051.
[14] 毕聪来, 蒋兴良, 韩兴波, 等. 采用扩径导线替代分裂导线的防冰方法[J]. 电工技术学报, 2020, 35(11): 2469-2477.
Bi Conglai, Jiang Xingliang, Han Xingbo, et al. Anti-icing method of using expanded diameter conductor to replace bundle conductor[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2469-2477.
[15] 蔡萌琦, 周林抒, 严波, 等. 覆冰四分裂导线动态气动系数风洞试验[J]. 实验力学, 2020, 35(2): 267-275.
Cai Mengqi, Zhou Linshu, Yan Bo, et al. Wind tunnel tests on dynamic aerodynamic coefficients of iced quad bundle conductors[J]. Journal of Experimental Mechanics, 2020, 35(2): 267-275.
[16] Mou Zheyue, Yan Bo, Yang Hanxu, et al. Prediction model for aerodynamic coefficients of iced quad bundle conductors based on machine learning method [J]. Royal Society Open Science, 2021, 8(10): 210568.
[17] 巢亚锋. 分裂导线和多串并联绝缘子覆冰模型与影响因素的研究[D]. 重庆: 重庆大学, 2011.
Chao Yafeng. Study on the model and impact factors of boundled conductors and parallel composite insulator strings icing[D]. Chongqing: Chongqing University, 2011.
[18] Huang Yafei, Jiang Xingliang, Virk M S. Ice accretion study of FXBW4-220 transmission line composite insulators and anti-icing geometry optimization[J]. Electric Power Systems Research, 2021, 194: 107089.
[19] Han Xingbo, Wang Jie, Xing Bin, et al. Collision characteristics of water droplets in icing process of insulators[J]. Electric Power Systems Research, 2022, 212: 108663.
[20] 黄亚飞, 蒋兴良, 杨国林, 等. 不同配置形式倒T型布置绝缘子串直流冰闪特性研究[J]. 电工技术学报, 2021, 36(24): 5294-5303.
Huang Yafei, Jiang Xingliang, Yang Guolin, et al. DC flashover characteristics of the iced-covered inverted T-type insulator strings with different configuration [J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5294-5303.
[21] Han Xingbo, Jian Xingliang, Dong Shaojiang, et al. Analysis of the growth conditions of icicles during insulator icing[J]. Electric Power Systems Research, 2021, 201: 107512.
[22] Fu Ping, Farzaneh M, Bouchard G. Two-dimensional modelling of the ice accretion process on transmission line wires and conductors[J]. Cold Regions Science and Technology, 2006, 46(2): 132-146.
[23] Macklin W C. The density and structure of ice formed by accretion[J]. Quarterly Journal of the Royal Meteorological Society, 1962, 88(375): 30-50.
[24] 蒋兴良, 周文轩, 董莉娜, 等. 基于旋转圆柱三电极阵列的覆冰测量方法[J]. 电工技术学报, 2024, 39(5): 1524-1535.
Jiang Xingliang, Zhou Wenxuan, Dong Lina, et al. Research on icing measurement method based on rotating cylindrical three-electrode array[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1524-1535.
Icing Characteristics and Rapid Calculating Method of Bundled Conductor of Transmission Line Based on Shadowing Effect Analysis
Abstract For bundled conductors, the shadowing effect of upwind sub-conductor will affect the airflow and droplets distributions of downwind one, resulting in the difference in icing characteristics. Traditional icing calculation process generally ignored these differences and, hence, only giving an identical icing mass result of each sub-conductor. This affects the study of the aerodynamic characteristics and deicing methods of icing bundled conductor. Although some scholars have pointed out that the shadowing effect between sub-conductors will influence the icing process, there is no quantitative study. Therefore, this paper further explores the shadowing effect and relevant influencing factors of bundled conductors through numerical simulation and test research. Furthermore, based on the analysis of the shadowing effect and the superposition principle, a rapid calculation method of ice mass accreted on the bundled conductor is proposed.
Firstly, the distributions of airflow and droplets around bundled conductor are solved by Eulerian-Eulerian two-phase flow model. Secondly, combined with the mass and thermodynamic balance equations, the icing mass and shape accreted on bundled conductor under various icing environments are obtained. Then a new parameter called shadowing coefficient is defined to investigate the shadowing effect and influencing factors as well. The results show that: Shadowing effect is weakened with increasing absolute value of shadowing angle and bundled-spacing, but intensified with the increase of median volume diameter (MVD) of droplets; Meanwhile, the shadowing effect experiences a growth and then drops down along with the increase of wind speed, and reach to the max at 15 m/s range 5~20 m/s.
Based on the superposition principle and shadowing effect analysis, a rapid calculating method for ice mass on bundled conductor is proposed. Where iced bundled conductor is regarded as a linear combination of non-shadowed sub-conductor (single conductor) icing intensity and shadowing coefficient, so the icing intensity of various types of bundled conductor can be obtained only requiring the icing intensity of single conductor and the shadowing coefficient in the corresponding environment. Then the rapid icing calculation formulars of 3,4,6,8-bundled conductor under various shadowing angle is given by geometry analysis, respectively, which simplifies the calculation of the icing mass on bundled conductor.
Finaly, a 4-bundled conductor nature icing test was carried out at the Xuefeng Mountain Energy Equipment Safety National Observation and Research Station to validate the accuracy of the numerical simulation and rapid calculation method. Results show that under the environment parameters of ambit temperature Tf = -2℃, MVD = 25.4 μm, liquid water content Lwc = 0.61 g/m3, wind speed V = 10 m/s and shadowing angle θ = 2°, the difference in icing intensity between rapid calculation and test results was within -4.01% to -19.77%, the icing thickness differences of sub-conductors were between 1.66% to -6.36% and the differences in shadowing coefficient were between 4.05% to 5.33%, which well verifies the accuracy of the rapid calculation method proposed in this paper.
Keywords:Transmission line, icing, bundled conductor, numerical simulation, nature icing test
中图分类号:TM85
DOI: 10.19595/j.cnki.1000-6753.tces.240609
国家自然科学基金项目(U23B20121, 52177015, 52307158)和湖南省教育厅科研项目(22C0157)资助。
收稿日期2024-04-22
改稿日期2024-05-28
黄亚飞 男,1994年生,博士,讲师,研究方向为电网防灾减灾、电力设备覆冰灾害防御。
E-mail:huang_yafei@foxmail.com
杨 鑫 男,1983年生,教授,博士生导师,研究方向为低温高压绝缘技术、过电压及其防治技术、多场耦合的相关计算等。
E-mail:yan_19830713@163.com(通信作者)
(编辑 李 冰)