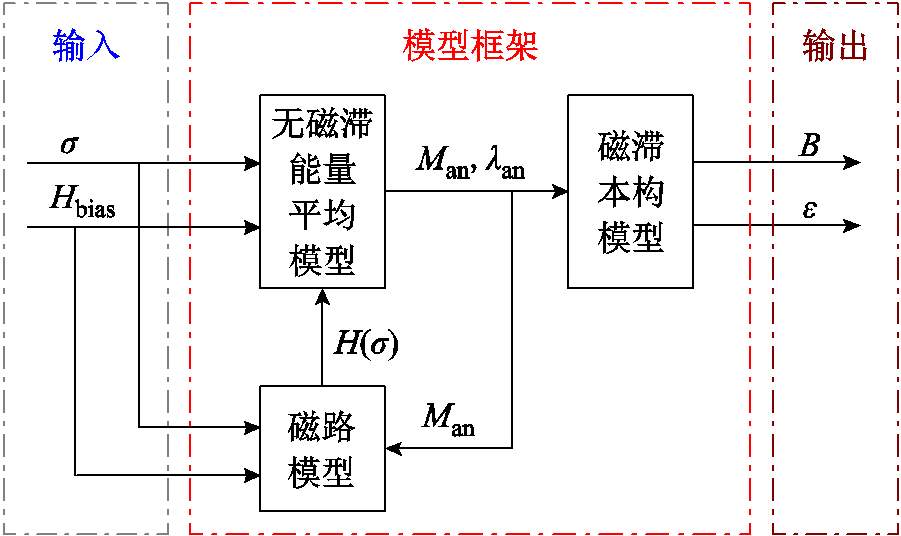
图1 模型关系框图
Fig.1 Model relationship block diagram
摘要 磁致伸缩器件的输出特性通常表现出对偏置条件很强的依赖性,现有的磁致伸缩本构模型难以直接表征偏置磁场动态变化时材料的磁化过程,为了指导磁致伸缩材料在应力激励下的应用,建立能够反映偏置磁场变化的磁致伸缩逆效应磁滞模型具有重要意义。该文首先基于自由能理论引入材料钉扎系数,得到应力依赖的不可逆磁滞分量Mirr和λirr,建立考虑磁滞行为的磁致伸缩材料逆效应本构模型;其次基于磁路等效理论引入偏置磁场与磁阻的非线性相关项,将模型拓展为计及偏置磁场变化的能量平均磁滞模型;最后基于实验数据,采用引入非线性自适应步长因子的改进布谷鸟灰狼算法提取模型参数。模型计算结果与实验数据对比表明,所建模型能够准确描述磁致伸缩材料在恒定以及非恒定偏置磁场条件下的磁通密度-应力响应和应变-应力响应,为磁致伸缩逆效应在力磁传感与能量收集等领域的应用提供理论指导。
关键词:磁致伸缩逆效应 偏置磁场 能量平均磁滞模型 磁路模型 参数辨识
磁致伸缩材料表现为磁能与机械能之间的耦合,具有响应速度快、能量密度大等特点[1-2],是一种新型智能材料。当受到机械应力时材料表现出的磁化强度变化即磁致伸缩逆效应行为,已经广泛应用于能量收集[3-4]、传感[5-6]和阻尼减震[7]等领域,基于磁致伸缩逆效应设计的器件受到了越来越多的关注。
磁致伸缩器件的输出特性通常表现出很强的对偏置条件的依赖性,而由恒定电流提供的偏置磁场会随应力激励下材料磁导率的改变而发生非线性变化(表现为非恒定偏置磁场),这对材料磁化过程的准确表征和偏置点的合理设计造成一定影响。目前磁致伸缩逆效应的模型主要集中在恒定偏置磁场下的材料表征,然而只考虑磁场恒定建立的模型难以准确反映器件实际工作环境下的输出特性,因此建立计及偏置磁场动态变化的磁致伸缩逆效应磁滞模型有着重要的研究意义。
对于磁致伸缩材料磁滞部分的建模研究,J-A模型基于模拟畴壁位移来描述整个磁化过程,通过将磁化分量分为可逆分量和不可逆分量来反映材料的磁滞行为,物理意义直接,但对于不同工况下的参数需要重新确定[8]。文献[9]在J-A磁滞模型的基础上,引入压应力相关项修正了模型参数,得到改进的计及预应力加载的磁滞模型,但该模型无法描述磁致伸缩材料应力循环加载下的磁化过程。文献[10]基于S-W模型的基本思想,通过最小化单个磁畴自由能显示计算了应力激励下的局部磁化响应,提出能够描述Terfenol-D磁致伸缩材料非线性磁滞行为的离散能量模型,但计算磁滞模型需要确定的参数较多。文献[11]从能量角度出发建立了热力学模型,并引入应力、场和方向相关的滞回因子来描述磁致伸缩材料的磁滞行为,较好地预测了铁镓合金的逆效应特性,但只局限于恒定偏置磁场条件进行的研究。
文献[12]对铁镓合金进行了不同偏置条件下的磁致伸缩逆效应实验,并基于Armstrong模型进行建模,在不考虑磁滞的前提下预测了材料在恒定电流偏置下的非线性磁化过程。文献[13]基于能量模型对铁镓合金进行应力激励下的模型验证,较好地预测了铁镓合金在非恒定偏置磁场下的无磁滞磁化过程。文献[14]基于有限元模型和亥姆霍兹自由能对能量收集器输出特性进行模拟,较为准确地预测了装置在应力激励下的输出特性,但所建模型同样没有考虑材料的磁滞特征。因此,本文旨在建立考虑磁滞的能量平均模型,并结合磁路理论来描述偏置磁场变化下的磁致伸缩材料逆效应行为。
本文首先基于自由能理论推导得到无磁滞磁化强度的表达式,并借鉴J-A模型对正效应磁滞现象的建模思想,引入不可逆分量Mirr、λirr与应力的一阶微分方程,得到能够表征磁致伸缩材料逆效应的磁滞模型;其次基于磁路等效理论,将应力对磁场强度的影响通过磁阻的变化来反映,建立了计及偏置磁场变化的能量平均磁滞模型;然后针对磁滞模型参数辨识困难的问题,提出改进的布谷鸟-灰狼(Cuckoo Search-Grey Wolf Optimizer, CS-GWO)混合算法进行模型的参数提取;最后分两步进行模型验证:首先通过恒定偏置磁场下的实验数据验证本文磁滞部分建模的合理性,然后基于恒定电流偏置下的实验数据验证本文模型模拟非恒定偏置磁场条件下的磁致伸缩逆效应的有效性。
磁致伸缩器件通常处于磁场和机械场多物理场耦合作用的环境,宏观表现为磁通密度和应变的改变。因此,磁致伸缩材料的本构模型通常以磁场和机械应力为输入,磁通密度和应变为输出。本节建立的模型关系框图如图1所示,模型具体包括无磁滞能量平均模型、磁滞本构模型和计及偏置磁场变化的等效磁路模型。

图1 模型关系框图
Fig.1 Model relationship block diagram
磁致伸缩材料的磁化过程是磁畴磁矩旋转和畴壁移动的体现,整个过程涉及多个能量的变化。本节基于Armstrong理论[15],通过分析自由能组成建立了描述磁致伸缩材料磁化过程的无磁滞能量平均模型。
用磁畴的单位磁化矢量m表示磁畴的磁矩方向,[α1 α2 α3]表示对应θ、φ方向磁化矢量的方向余弦,极坐标中磁畴的单位磁化矢量可以表示为
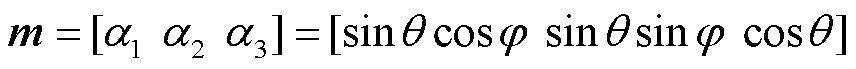 (1)
(1)
磁晶各向异性能为
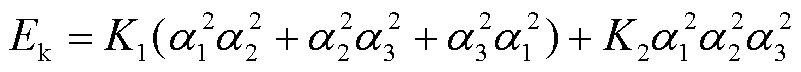 (2)
(2)
式中,K1和K2为各向异性常数。
磁弹性能为
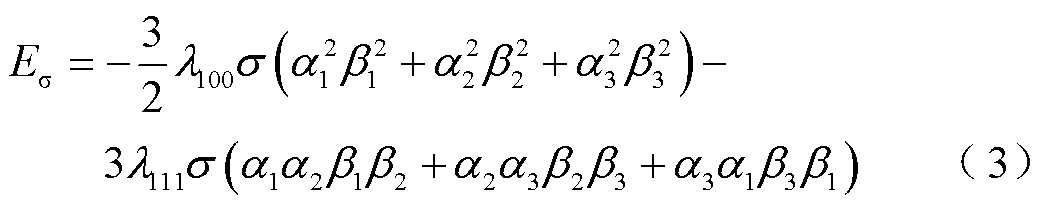
式中,λ100和λ111为[100]和[111]取向上的磁致伸缩常数;[β1 β2 β3]为应力σ对应的方向余弦;σ为σ的模值。
磁场能为
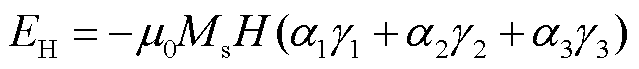 (4)
(4)
式中,μ0为真空磁导率;Ms为饱和磁化强度,[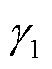

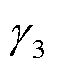 ]为磁场强度H对应的方向余弦。
]为磁场强度H对应的方向余弦。
在外施激励应力σ和磁场H下,磁畴的总自由能可以表示为
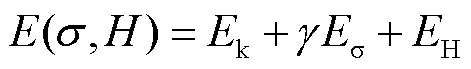 (5)
(5)
式中,γ为引入的矫正系数,用于缩放磁弹性能以准确捕捉应力对磁机械耦合行为的影响。
磁晶在任意方向的磁化概率可由含自由能的Boltzmann 函数表示为[15]
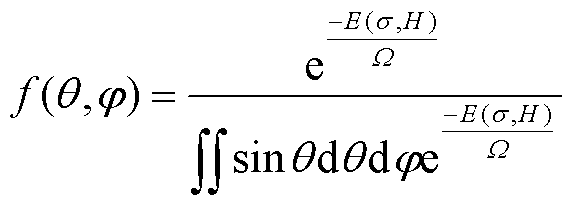 (6)
(6)
式中,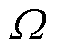 为能量分布参数。
为能量分布参数。
磁晶沿着x轴方向的无磁滞磁化强度为
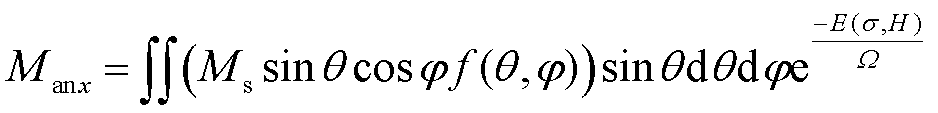 (7)
(7)
沿着y轴和z轴方向的无磁滞磁化强度Many和Manz由Mssinθsinφ和Mscosθ用相似的思路计算,则任意方向的无磁滞磁化强度可以由其方向余弦[β1R β2R β3R]表示为
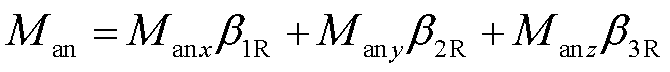 (8)
(8)
无磁滞磁致伸缩量为
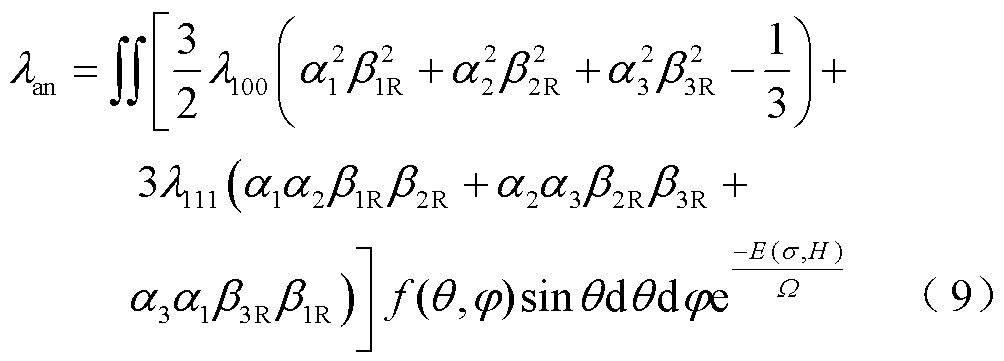
在1.1节的假设中认为整个磁化过程是可逆的,得到的是无磁滞磁化强度。但实际的铁磁材料中往往存在晶体结构的错位和非磁性夹杂物,磁畴壁的移动需要考虑钉扎效应的影响。在本节中,类比J-A模型的思想,引入应力激励下的不可逆分量来表示磁化过程的磁滞现象,建立描述磁致伸缩材料逆效应的本构磁滞模型。
J-A模型是一种通过描述畴壁在钉扎效应下移动的磁滞模型。磁化强度M由畴壁弯曲引起的可逆磁化分量Mrev和畴壁取代引起的不可逆磁化分量Mirr构成,c为可逆磁化系数,并通过不可逆磁化强度Mirr和有效场He的微分方程来描述激励H和响应M的磁滞现象[16],各物理量之间的关系式为
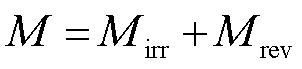 (10)
(10)
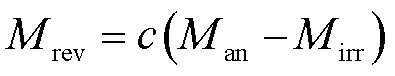 (11)
(11)
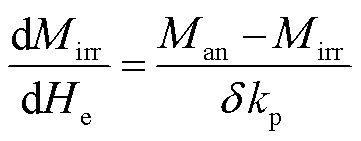 (12)
(12)
式中,kp为钉扎系数,用于量化应力激励下材料中钉扎位点的密度;δ为方向系数,当dσ/dt≥0时,δ=1,当dσ/dt<0时,δ=-1。
为了描述磁致伸缩材料动态应力输入下的磁滞行为,类比式(12)得到应力依赖的不可逆磁化强度Mirr的表达式为
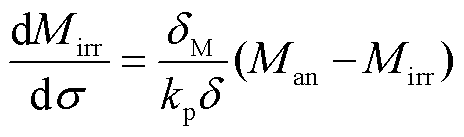 (13)
(13)
式中,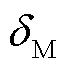 为防止出现非物理解而引入的方向系数,表示为
为防止出现非物理解而引入的方向系数,表示为
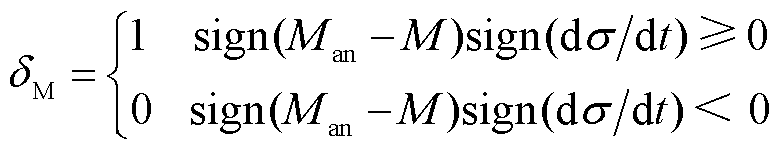 (14)
(14)
结合式(10)、式(11)、式(13),最终得到描述磁滞的应力激励下的磁化强度-应力微分表达式为
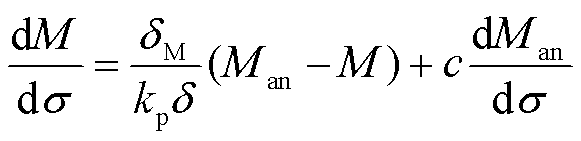 (15)
(15)
钉扎位置的能量损失同样会引起材料磁致伸缩的磁滞现象。定义体积分数为υ,一定磁畴体积变化下磁化强度的变化量dM=Msdυ,磁致伸缩变化量dλ=λsdυ(λs为饱和磁致伸缩量),得到以应力σ为输入变量的考虑磁滞的磁致伸缩-应力微分表达式为
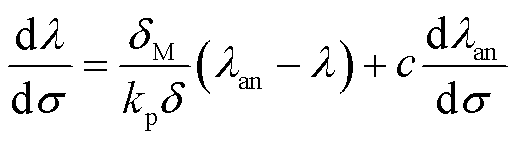 (16)
(16)
磁致伸缩材料的磁通密度B和总应变ε为
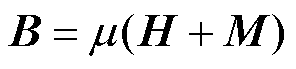 (17)
(17)
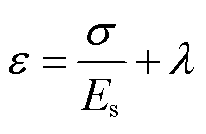 (18)
(18)
式中,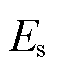 为弹性模量;
为弹性模量;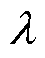 为磁致伸缩量。
为磁致伸缩量。
至此,考虑磁滞的磁致伸缩逆效应本构模型得以建立,可以用于给定应力驱动和偏置磁场下的磁致伸缩逆效应的模拟。
在实际器件应用环境下,难以具备恒定偏置磁场控制条件,偏置磁场通常由恒定电流下的激励线圈提供。当磁致伸缩材料受到外部机械应力驱动时,其内部磁化状态和磁导率会发生变化,恒定电流提供给材料的偏置磁场会成为因磁导率改变而改变的非恒定偏置磁场。为了描述这一动态变化的非线性关系,本节对测试装置的磁路结构进行等效建模,标量磁路如图2所示。
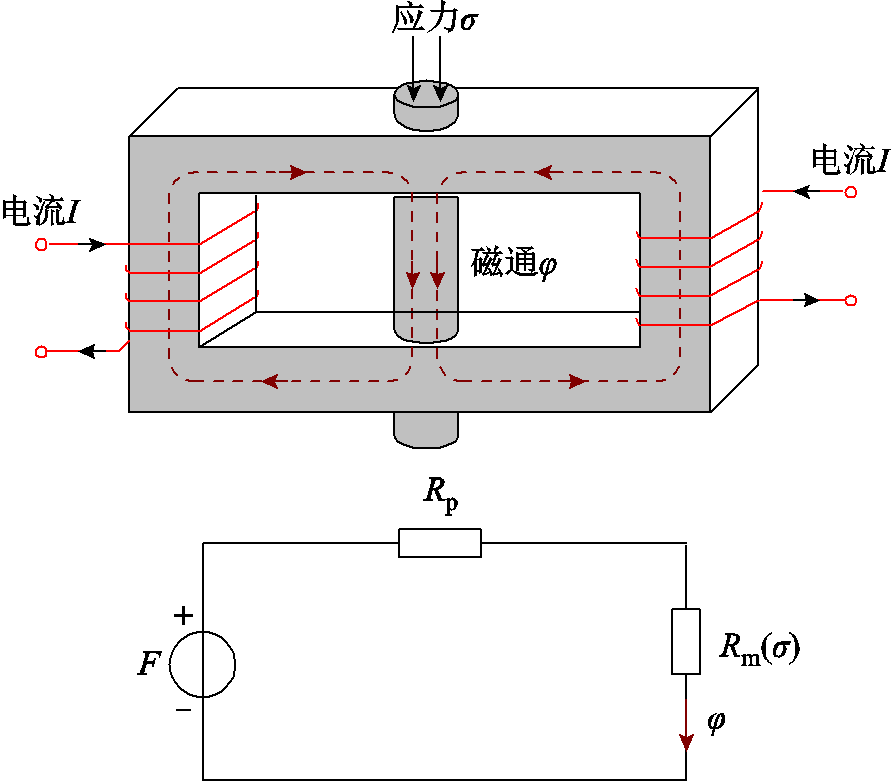
图2 实际磁路模型与等效磁路模型
Fig.2 Actual magnetic circuit model and equivalent magnetic circuit model
当N匝线圈通入电流I时,激励线圈产生的磁动势F在闭合磁路中产生磁通φ。若将磁路和磁致伸缩材料的磁阻分别记为Rp和Rm(σ),则磁通φ可以表示为
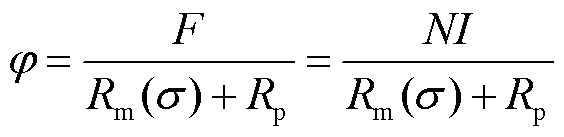 (19)
(19)
材料磁动势Fm可以由磁通与磁阻的乘积表示为
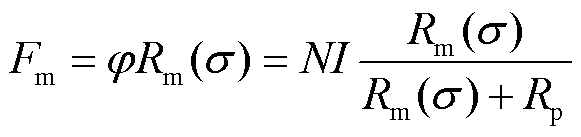 (20)
(20)
磁致伸缩材料动态应力下的偏置磁场H(σ)可以由磁阻Rm(σ)表示为
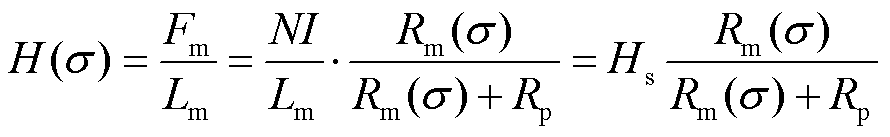 (21)
(21)
式中,Lm为磁致伸缩棒材的有效磁路长度;Hs=NI/Lm为由测试装置结构和输入条件确定的参数,表示不同电流下不考虑磁阻Rp时的理想磁场强度。各磁阻在模型的迭代中不需要准确计算实际值,利用实验已知的零应力下的初始偏置磁场通过式(21)计算Rm(0)与Rp的比值,再归一化总磁阻Rm(0)+Rp,确定模型迭代过程中Rm(0)和Rp的值。
由磁阻的定义式R=L/(µA)(L为磁路长度,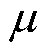 为材料磁导率,A为磁阻的横截面积)可知,磁阻与磁导率成反比,则磁阻可以表示为
为材料磁导率,A为磁阻的横截面积)可知,磁阻与磁导率成反比,则磁阻可以表示为
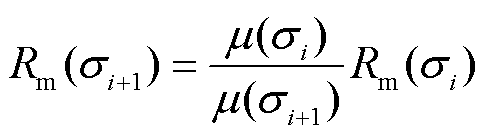 (22)
(22)
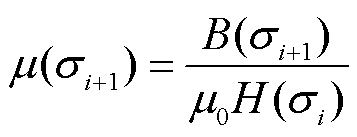 (23)
(23)
式中,σi为第i次迭代计算的应力值;磁导率由磁通密度B=μ(H+Man)决定,这样每次应力变化下的磁阻都可以通过上一次迭代过程的模型数据计算得到,应力激励下材料磁特性的改变引起磁阻的非线性实时变化,最终影响偏置磁场的大小。
至此,建立起计及偏置磁场动态变化的磁致伸缩逆效应能量平均磁滞模型。无磁滞能量平均模型中,已知外施激励应力σ和磁场H(0),通过计算磁畴的总自由能得到无磁滞磁化强度Man和无磁滞磁致伸缩λan;磁路模型考虑了磁致伸缩材料和磁路的相互作用,推导得到偏置磁场与磁阻的非线性相关式(21),在每次的迭代过程中,将随应力非线性变化的偏置磁场输入无磁滞能量平均模型,得到偏置磁场变化下的无磁滞磁化强度Man和无磁滞磁致伸缩λan;由于能量平均模型假设磁化过程可逆,没有考虑材料在磁化过程的磁滞现象,因此引入磁滞本构模型来反映材料在应力激励下的磁滞。
针对磁滞模型参数极值点多导致的参数辨识困难问题,提出改进的混合算法提取模型参数,来验证不同偏置磁场下的模型对磁致伸缩逆效应的模拟效果。灰狼算法(GWO)高效的狼群信息反馈机制[17]在复杂问题的求解精度和收敛速度上有良好的表现,然而头狼的位置在很大程度上影响个体行为,导致算法全局寻优能力不足。本文通过结合布谷鸟算法(CS)的Levy飞行策略提高算法整体的全局搜索能力[18-19]。为使算法前期能以较大步长增加探索范围,后期又能够稳定在较小步长保证解区域的寻优精度,通过引入非线性自适应步长因子α(t)建立改进的布谷鸟灰狼混合算法(CS-GWO),以提高参数提取的准确性和迭代速度,并对算法的有效性进行验证。
能量平均磁滞模型的未知参数有Ms、λ100、γ、K1、Ω、kp、c、Es、Hs,定义XH=[Ms λ100 γ K1 Ω kp c]为恒定偏置磁场下的待辨识参数,XI=[Ms λ100 γ K1 Ω kp c Hs] 为非恒定偏置磁场下的待辨识参数,杨氏模量Es可以由应变-应力实验数据线性区的斜率直接获得,本文Es取值为59 GPa。
若偏置条件为恒定偏置磁场,以磁通密度实测值BH(i)与模型计算值BM(i)的方均根误差f1(XH)为目标函数,利用恒定偏置磁场下的B-σ实验数据提取参数XH的值,N表示测量数据点的数量。
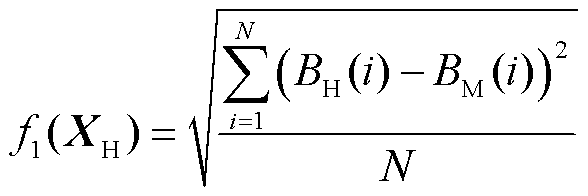 (24)
(24)
若偏置条件为非恒定偏置磁场,以f2(XI)为目标函数,BI(i)表示恒定电流偏置下的实测磁通密度,利用恒定电流偏置下的B-σ实验曲线来提取参数XI的值。
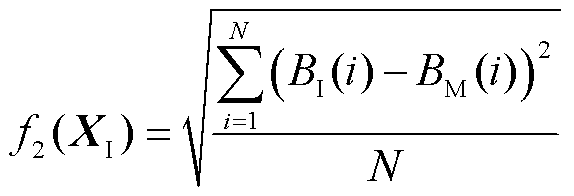 (25)
(25)
CS-GWO算法提取实测磁滞曲线的各个参数流程如图3所示,参数具体识别的步骤如下:
(1)初始化种群,并通过能量平均磁滞模型输出结果计算初始适应度值。
(2)执行CS算法生成新解:对当前解X(t)以Levy飞行策略生成新解X(t+1),并计算新适应度值,解的更新满足关系
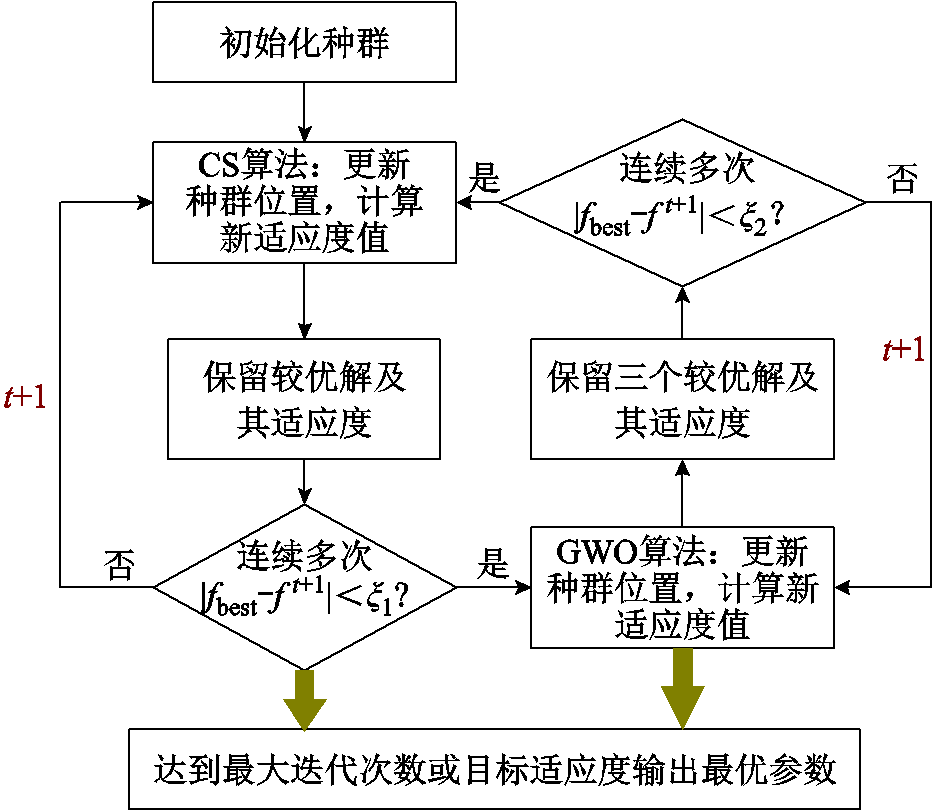
图3 参数辨识流程
Fig.3 Parameter identification flow chart
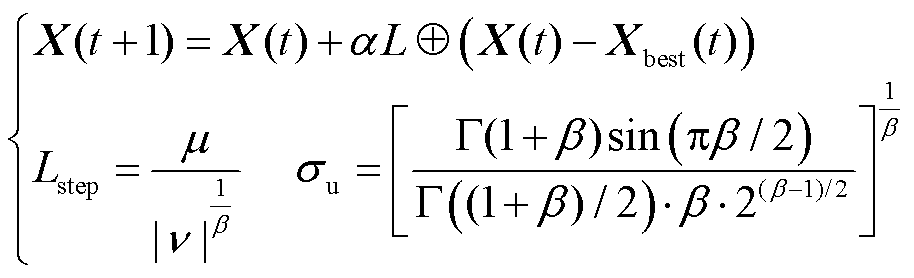 (26)
(26)
式中,t为迭代次数;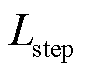 为步长;⊕表示点对点的乘法;Xbest(t)为当前方案的最优解;μ和
为步长;⊕表示点对点的乘法;Xbest(t)为当前方案的最优解;μ和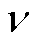 符合正态分布;
符合正态分布;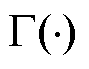 为伽马函数;β取1.5,μ~N(0,
为伽马函数;β取1.5,μ~N(0,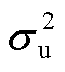 ),
),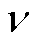 ~N(0,1),步长因子α通常取值为0.01,本文改进为关于迭代次数t的非线性函数,取值范围为[0.5, 0.001],即
~N(0,1),步长因子α通常取值为0.01,本文改进为关于迭代次数t的非线性函数,取值范围为[0.5, 0.001],即
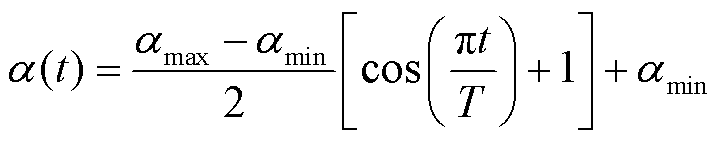 (27)
(27)
式中,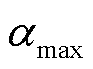 和
和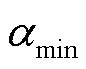 分别为
分别为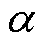 的最大值和最小值;T为总迭代次数。
的最大值和最小值;T为总迭代次数。
(3)比较适应度值,保留最优解。当连续多次满足| fbest- f t+1|<ξ1(fbest、f t+1分别为Xbest的适应度值、第t +1次迭代的适应度值)时,表明布谷鸟算法虽然找到最优解区域,但可能并未找到区域中的最优解,此时切换为GWO算法进入步骤(4);否则更新迭代次数并返回步骤(2)。
(4)通过GWO算法生成新解:
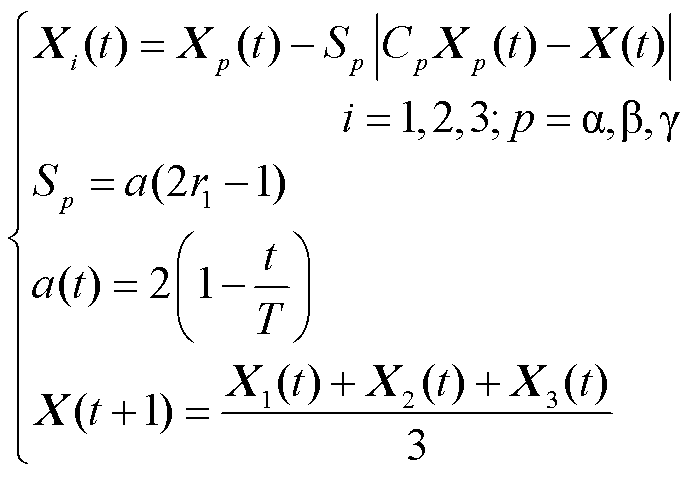 (28)
(28)
式中,S为搜索步长;a为线性收敛系数;Cp= 2r2;r1、r2为0~1之间的随机数;Xp(t)表示Xα、Xβ、Xγ精英狼的位置;X1、X2、X3表示灰狼个体在受三只精英狼各自影响下的位置,加权平均得到灰狼个体最终的更新位置X(t+1)。
(5)计算新的适应度值,保留最优解、次优解、较次优解。当连续多次满足| fbest- f t+1|<ξ2时,表明灰狼算法找到最优解,但可能陷入局部最优,此时切换为CS算法进入步骤(2);否则更新迭代次数,返回步骤(4)。
(6)若迭代次数达到最大或精度满足要求,则输出此时的最优辨识模型参数。
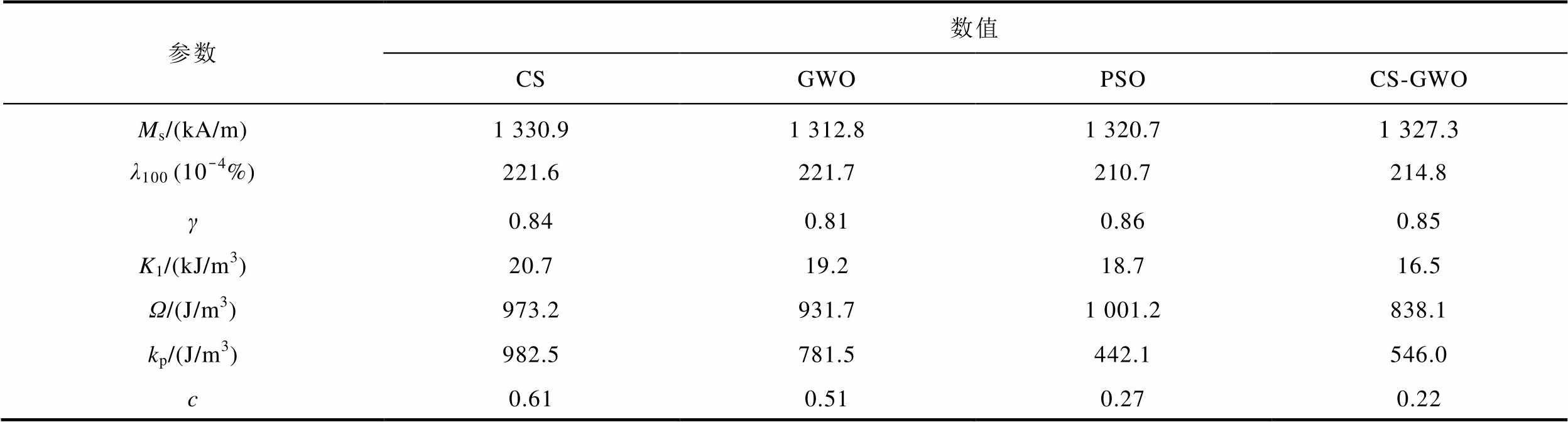
选取恒定偏置磁场条件下偏置磁场为66.9 Oe、89.1 Oe(1 Oe=100 mT)的两组实验为数据集,验证CS-GWO算法对能量平均磁滞模型参数辨识的有效性,设置最大迭代次数为100,基本参数XH的辨识结果见表1。为了更全面地验证算法的合理性,用CS、GWO和PSO算法作为对照实验进行参数辨识,参数辨识结果见表1,基于参数辨识结果的计算数据与实验数据得到恒定偏置磁场下不同算法的B-σ拟合曲线效果图如图4所示。
表1 四种参数的辨识结果
Tab.1 Recognition results for four parameters
参数数值 CSGWOPSOCS-GWO Ms/(kA/m)1 330.91 312.81 320.71 327.3 λ100 (10-4%)221.6221.7210.7214.8 γ0.840.810.860.85 K1/(kJ/m3)20.719.218.716.5 Ω/(J/m3)973.2931.71 001.2838.1 kp/(J/m3)982.5781.5442.1546.0 c0.610.510.270.22
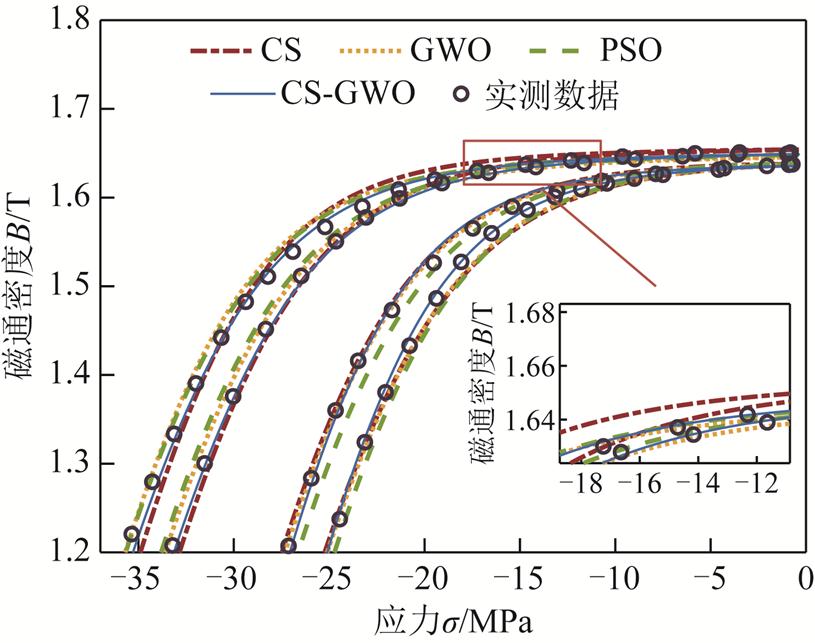
图4 恒定偏置磁场下不同算法的B-σ拟合曲线
Fig.4 Different algorithms on B-σ fitting curves under constant magnetic field condition
用e%表示模型模拟结果与实验数据的误差,有
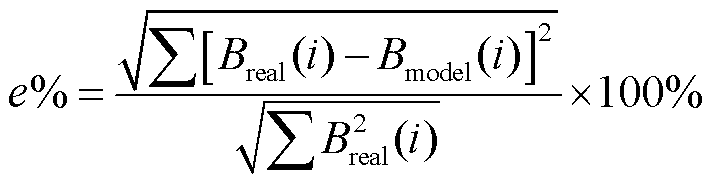 (29)
(29)
式中,Breal为实测数据;Bmodel为模型计算结果。图4中CS-GWO混合算法对参数的辨识精度最高,模拟结果与实验数据的误差仅为2.13%。
适应度值随迭代次数的变化如图5所示,表2展示了不同算法的性能指标。由表2和图5可知,CS-GWO算法精度最高且收敛速度最快,仅迭代25次就能精确有效地辨识出能量平均磁滞模型的全局最优参数。
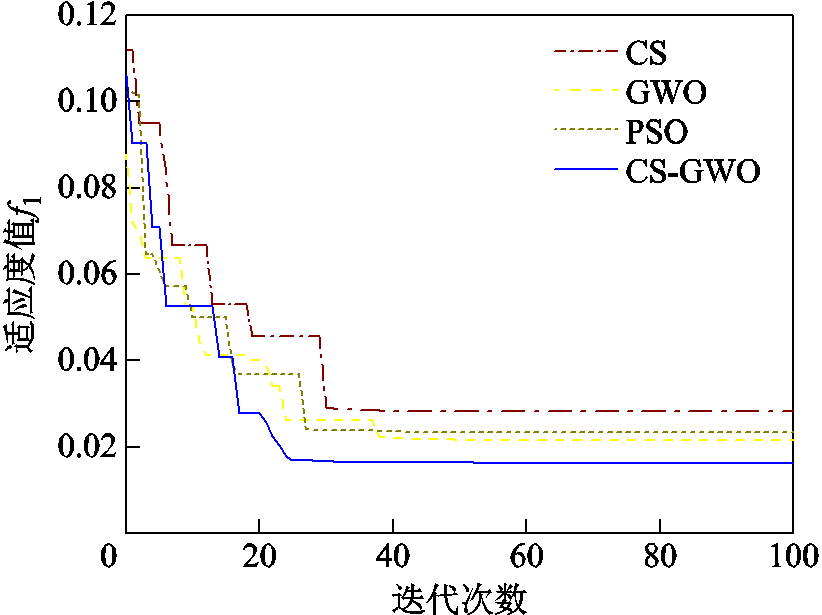
图5 各算法适应度值随迭代次数的变化
Fig.5 Plot of adaptation value of each algorithm with the number of iterations
表2 四种算法性能对比
Tab.2 Performance comparison of four algorithms

参数数值 CSGWOPSOCS-GWO 迭代次数30382725 收敛时间/s411.7319.5362.1308.5 误差(%)6.144.034.292.13
文献[12]给出了利用MTS应力加载装置对[100]取向的Fe81Ga19合金棒材应力驱动下的测量实验,棒材长度为25.4 mm,直径为6.35 mm,偏置磁场由装置两侧的直流线圈通过磁路提供,实验装置如图6a所示。实验中对Fe81Ga19合金棒材施加频率为0.01 Hz、峰-峰值为115 MPa的正弦应力。实验中恒定电流由直流电流源直接提供。恒定偏置磁场通过反馈控制系统(PID控制器)调节电流来实现,具体的磁场反馈控制系统如图6b所示。
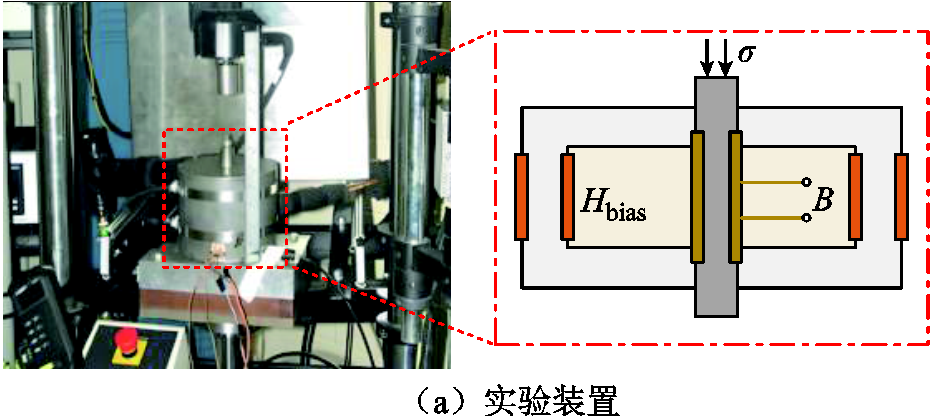
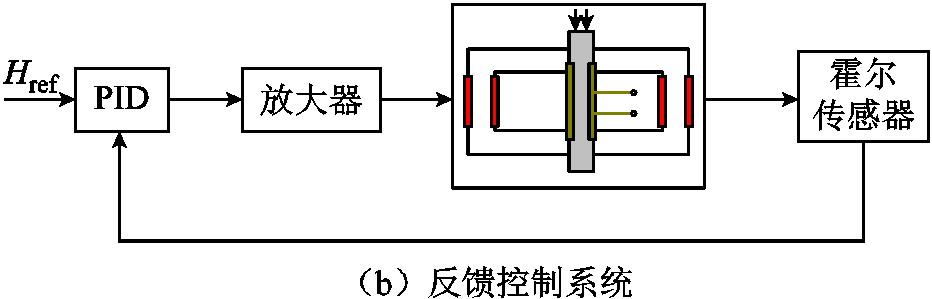
图6 实验装置和偏置磁场反馈控制系统
Fig.6 Experimental setup and biased magnetic field feedback control system
图7和图8分别展示了恒定磁场和恒定电流偏置下,Fe81Ga19合金棒材的偏置磁场Hbias、磁通密度B、应变ε与应力σ的实验数据。恒定磁场下的偏置磁场Hbias分别为 22.3、44.6、66.9、89.1、111、167、223、446 Oe,恒定电流偏置下各个电流产生的零应力时刻初始偏置磁场Hbias(0)仍与22.3~446 Oe保持一致,随着偏置磁场逐渐增大,实测数据用蓝色过渡到红色的实线表示。
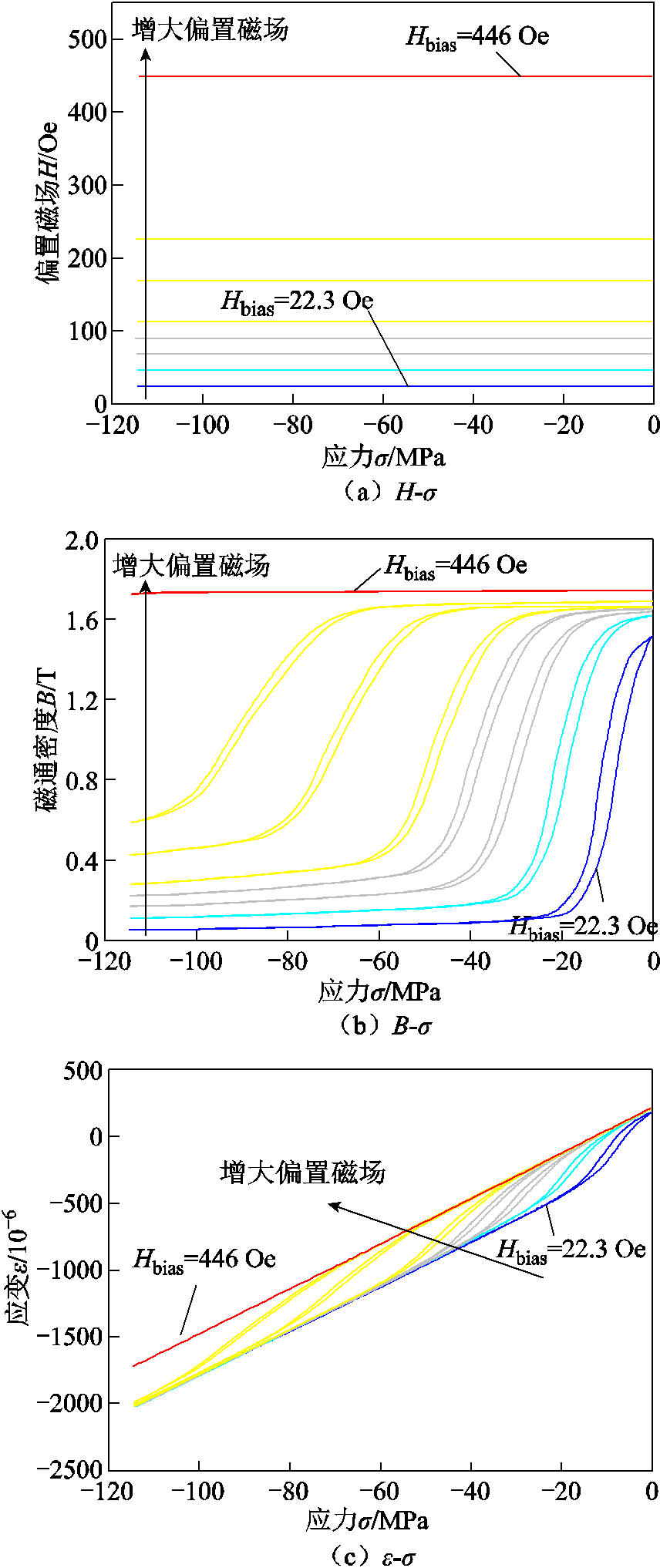
图7 不同恒定偏置磁场下Fe81Ga19合金的H-σ、B-σ、ε-σ实验曲线
Fig.7 Experimental H-σ,B-σ, and ε-σ curves of Fe81Ga19 alloys under different constant bias magnetic fields
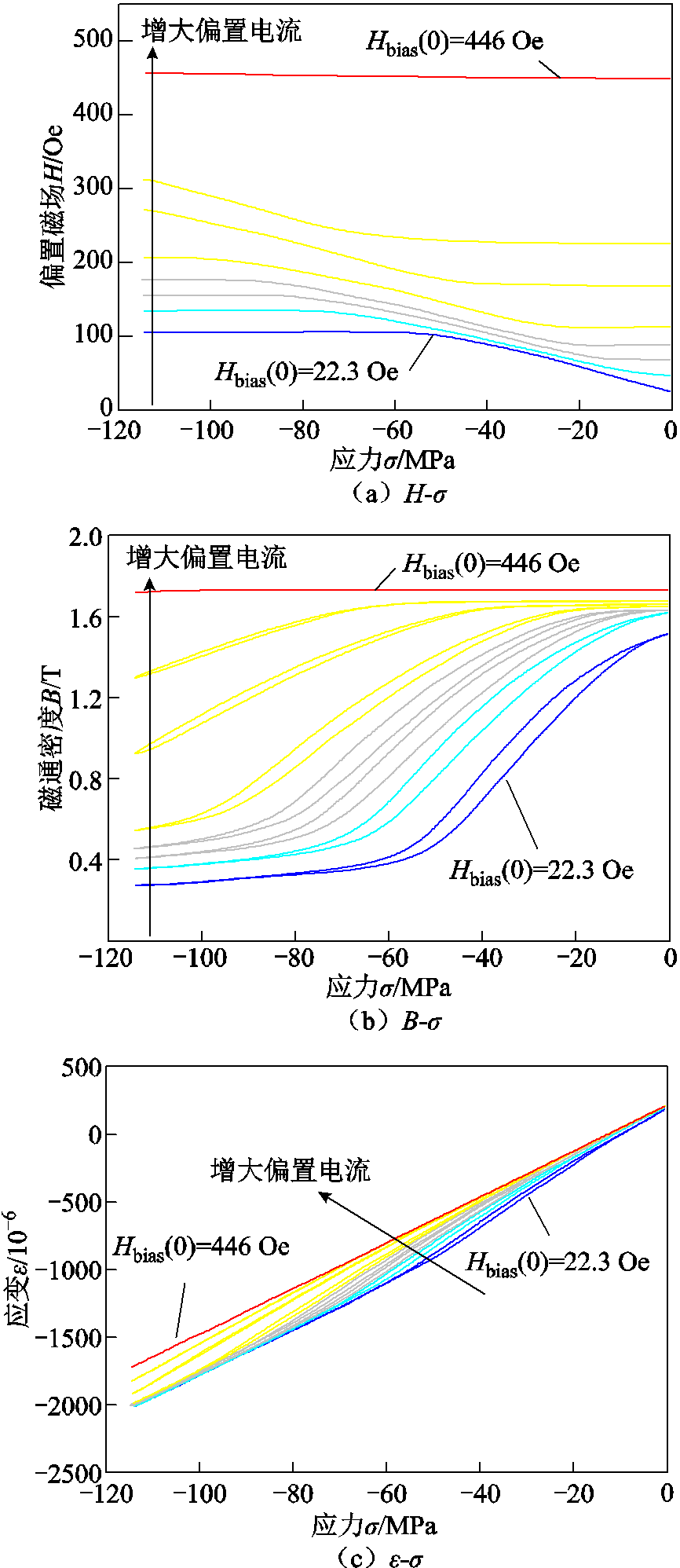
图8 不同恒定电流偏置下Fe81Ga19合金的H-σ、B-σ、ε-σ实验曲线
Fig.8 Experimental H-σ, B-σ, and ε-σ curves of Fe81Ga19 alloys at different constant current biases
模型计算不考虑磁路模型和本构模型的耦合时,可以用于表征恒定偏置磁场条件下磁致伸缩材料的逆效应行为。本节利用恒定偏置磁场下的实验数据对前半部分建立的本构磁滞模型进行验证。
利用表1中CS-GWO算法辨识所得的7个基本参数XH=[Ms λ100 γ K1 Ω kp c]对22.3、44.6、66.9、89.1、111、167、223、446 Oe偏置下的B-σ磁滞回线进行模拟,预测结果与实验数据的对比如图9a所示,模型模拟结果与实验的平均误差为3.85%。图9b表示传统本构模型的计算结果,平均误差为6.79%,由此可见,忽略磁滞现象会导致材料输出特性的模拟与预测产生较大偏差。
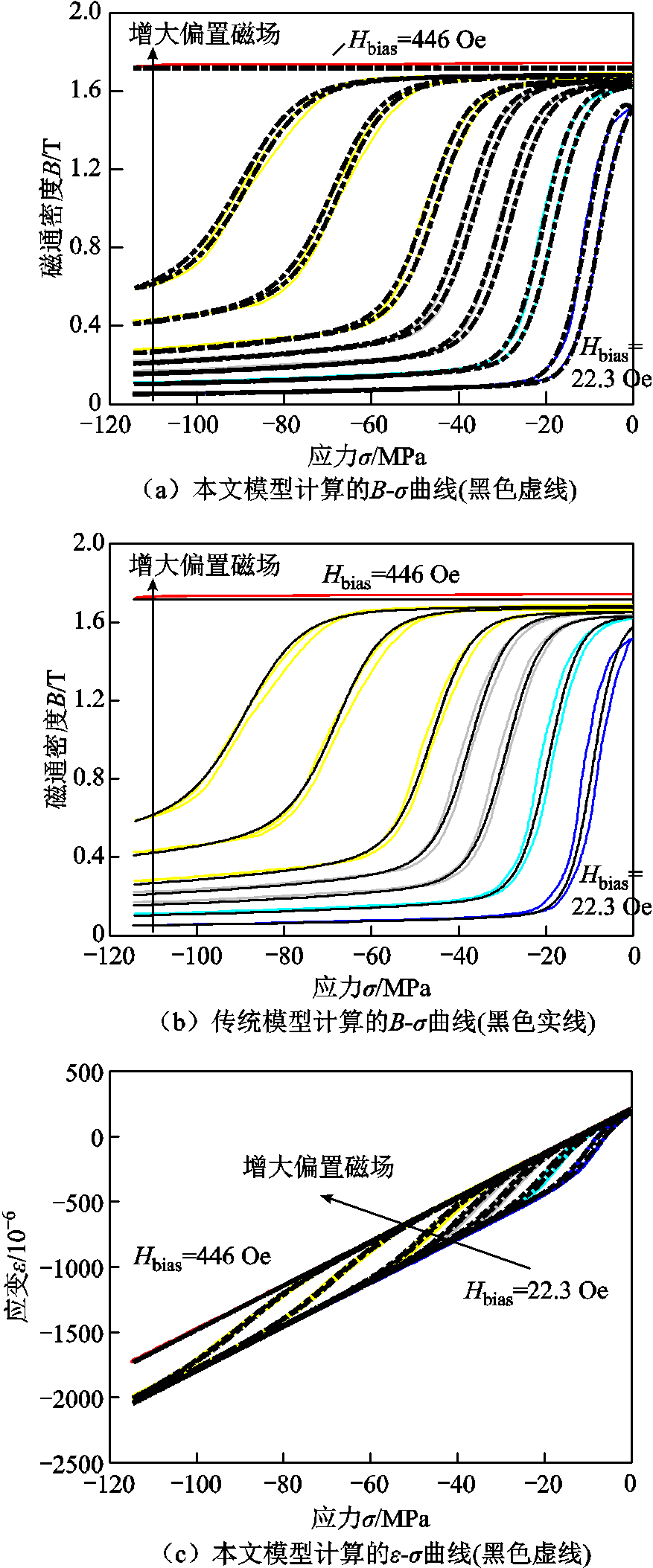
图9 不同偏置磁场的模型预测结果(黑色线)与实验数据(彩色实线)对比
Fig.9 Model predictions (black line) versus experimental data (colored solid line) for different bias magnetic fields
由图9a可知,随着压应力的增大,磁矩逐渐从平行于轴向转到垂直于轴向,宏观表现出材料磁通密度的下降,下降最快的区域即线性区表现出材料
最大的传感灵敏度,此时材料的输出特性最优。从曲线趋势可以看出,随着偏置磁场的增大,线性区位置向更大的应力区域转移,这是因为需要更大的应力能来平衡磁场能;不同的偏置磁场下均存在一个拐点,这是由于此时绝大部分磁畴已经偏转到垂直于轴向的方向,压应力的增大或者减小几乎不再导致磁畴旋转。整体来看,拐点处所对应的压应力大小随着偏置磁场强度的增加而增加,这是由于随着偏置磁场强度的增加,需要更大的应力才能将全部磁畴偏转到垂直于轴向方向。同时,较高的磁场限制了钉扎位置的断裂等不可逆磁化的过程,B-σ曲线的磁滞现象也逐渐减弱。
模型模拟的不同偏置磁场下Fe81Ga19合金棒材在动态应力下的应变-应力响应如图9c所示。对比模拟结果与实测数据,模型计算结果的平均误差为2.93%。在非线性区域,随着应力的增大,应变随着磁致伸缩量的减少而明显减少,这是因为偏置磁场引起的磁矩旋转逐渐被压应力抵消。整体来讲,随着偏置磁场的增加,应变相对于应力的响应强烈程度先增加再减小。这表明Fe81Ga19材料的刚度(应力和应变的比例关系)随着偏置磁场的上升先增加再减小。在较低的偏置磁场下,磁通密度随压应力的增加而显著下降。但在高偏置磁场下,材料的磁致伸缩达到饱和,几乎不受应力影响,Fe81Ga19合金棒材的应变-应力曲线近似为线性。
综合分析图9的模型计算结果,基于CS-GWO算法的能量平均磁滞模型对不同偏置磁场下的实验曲线模拟效果均较好,可以准确反映材料磁化过程中磁滞现象较强以及较弱的区域,有效地模拟了Fe81Ga19合金棒材在恒定偏置磁场下的非线性逆效应磁化过程及其磁滞行为。
将磁路模型与本构磁滞模型耦合可以表征偏置磁场变化下磁致伸缩逆效应的磁化过程。本节利用恒定电流偏置下的实验数据,对本文计及偏置磁场变化的能量平均磁滞模型进行验证。对图8a不同电流偏置下的H-σ实验数据进行8个参数XI=[Ms λ100 γ K1 Ω kp c Hs]的提取,各参数辨识结果见表3和表4,各偏置电流用对应线圈电流产生的初始偏置磁场22.3、44.6、66.9、89.1、111、167、223、446 Oe表示。
利用辨识所得参数XI,对非恒定磁场条件下Fe81Ga19合金的磁通密度B和偏置磁场Hbias进行计算,模拟结果如图10a、图10b所示。
图10a展示了H-σ曲线模型计算与实验数据的对比结果,平均误差为4.74%,这表明本文构建的磁路模型可以很好地反映偏置磁场随应力的非线性增加趋势。对比图7a所示恒定磁场条件下的H-σ曲线,偏置磁场呈现较大的非线性变化。整体来看,偏置磁场会随着应力的增大而增大,这是材料磁化状态的变化即磁导率的减小导致的,这一现象也与实验数据相符。以22.3 Oe初始偏置磁场为例,偏置磁场随着应力数值增大最大增加至120.9 Oe,变化幅度达到5倍。整体来看,在初始偏置磁场强度为22.3~223 Oe时,随着偏置电流的增大,偏置磁场因应力增加而非线性增大的现象逐渐加剧。当初始偏置磁场为446 Oe时,偏置磁场几乎不变,这是由于材料的磁化状态达到饱和,磁导率基本不受应力影响。而在高应力区域,模型计算的偏置磁场强度与实验数据出现一定的偏差,这可能是实验测试装置在高应力加载下磁路结构的轻微形变,以及磁致伸缩测试样品与磁路之间的非线性相互作用导致。
表3 不同偏置电流下的基本参数值
Tab.3 Basic parameter values at different bias currents

参数数值 Ms/(kA/m)1 309.1 λ100(%)218.2´10-4 γ0.82 K1/(kJ/m3)22.1 Ω/(J/m3)985.7 kp/(J/m3)1 085.6 c0.24
表4 不同偏置电流下Hs的参数值
Tab.4 Parameter values of Hs for different bias currents

初始偏置磁场Hbias(0)/Oe参数Hs/(kA/m)初始偏置磁场Hbias(0)/Oe参数Hs/(kA/m) 22.312.0111121.91 44.615.0616732.01 66.917.0322342.89 89.118.5944653.49
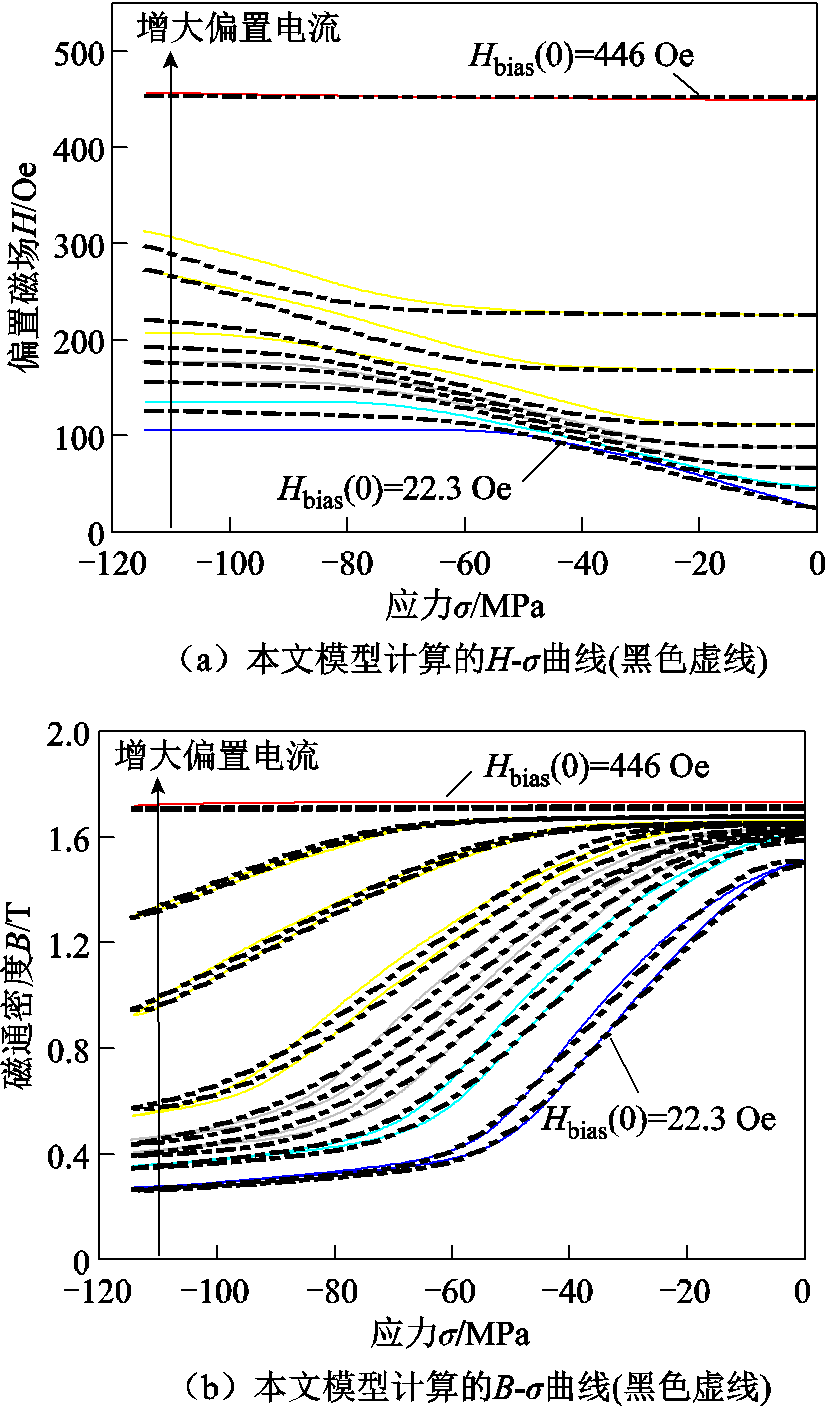
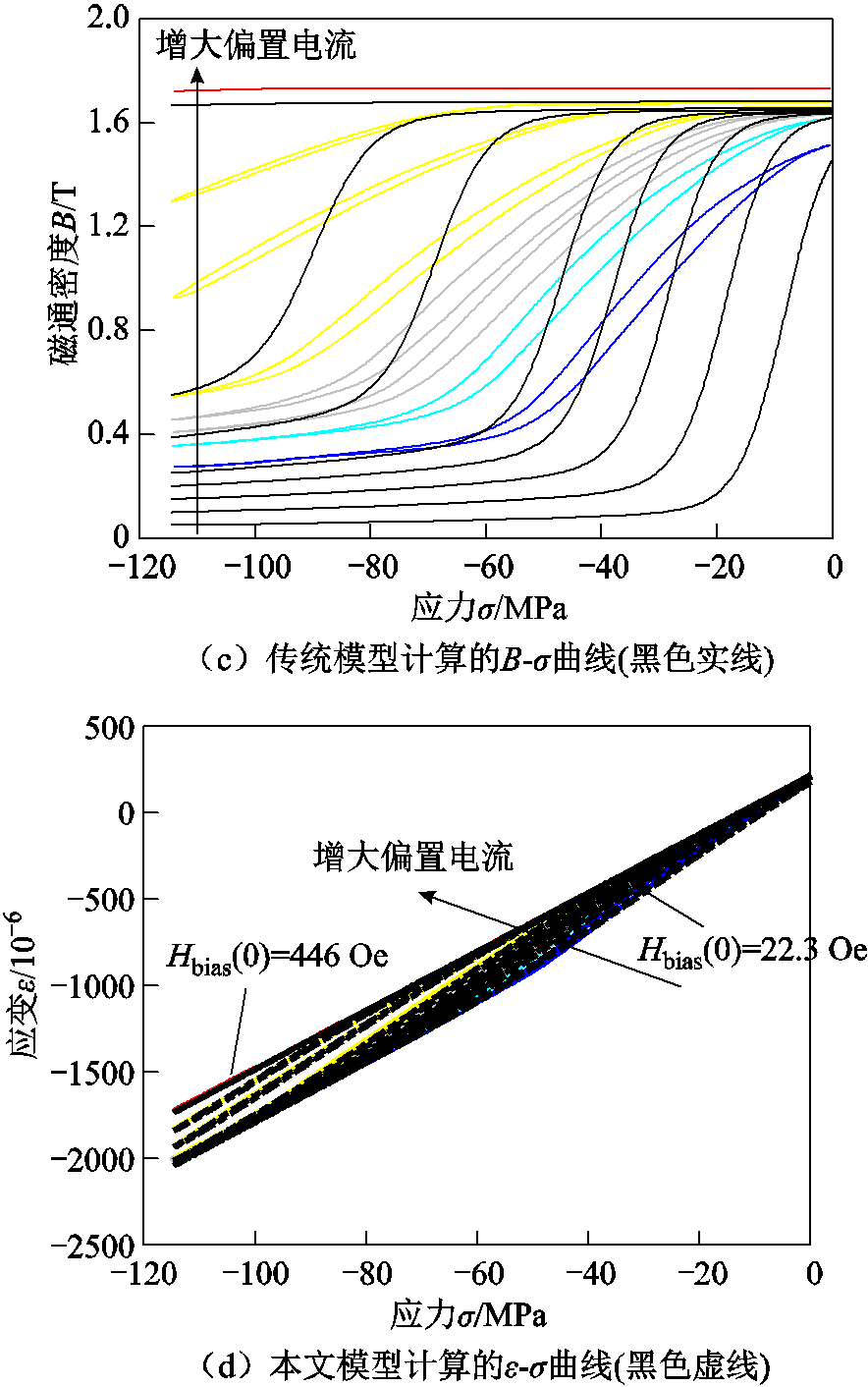
图10 不同偏置电流的模型预测结果(黑色线)与实验数据(彩色实线)对比图
Fig.10 Model predictions (black line) versus experimental data (colored solid line) for different bias currents
图10b所示的B-σ曲线模型预测结果与实验数据的平均误差为4.31%,表明本文建立的模型可以准确地反映Fe81Ga19合金棒材非恒定偏置磁场条件下的磁化过程。图10c为传统本构模型的模拟结果,可以直观看出,没有磁路模型反映非线性变化的偏置磁场,会导致模型预测磁致伸缩器件输出特性时产生很大的误差。整体来看,非恒定偏置磁场下磁滞回环的斜率比恒偏置磁场下的更小,使得实际应用中设备的机-磁转换能力减弱。这是由于没有磁场控制,压应力的增加会降低材料的磁导率(即增大材料的磁阻),导致磁场增加,进而阻碍磁矩的旋转。由式(21)可知,磁路中材料偏置磁场的大小是由磁阻Rm(σ)和磁路磁阻Rp共同影响的,磁路磁阻Rp越小,材料磁阻Rm(σ)的变化对偏置磁场的影响就越小。因此,实际装置中可以考虑通过减小磁路磁阻来减弱偏置磁场变化对输出特性的影响。
图10d所示为不同偏置电流下的Fe81Ga19合金棒材的应变-应力响应,模拟结果与实验的平均误差为3.97%。对比恒磁场的应变-应力响应,恒定电流条件下的曲线在非线性区的斜率更平缓,这同样是因为磁场随应力的增大而增大造成的。
输出特性的准确模拟还可以支撑材料偏置点的合理选择与器件谐振频率的调整。用压磁系数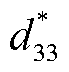 反映磁致伸缩材料受到机械应力驱动时的磁通密度变化程度,材料工作于最佳偏置条件即最大压磁系数时,传感器和能量收集器对外表现出最优输出特性,其定义式为
反映磁致伸缩材料受到机械应力驱动时的磁通密度变化程度,材料工作于最佳偏置条件即最大压磁系数时,传感器和能量收集器对外表现出最优输出特性,其定义式为
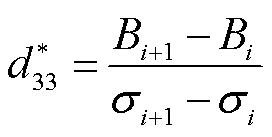 (30)
(30)
定义非恒定偏定偏置磁场下的压磁系数为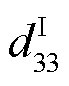 ,取磁滞回环上下两部分压磁系数的平均值作为B-σ环的压磁系数,不同电流偏置下压磁系数随应力的变化曲线如图11所示。随着偏置磁场的增加,峰值压磁系数逐渐下降,并且转移向应力更大的区域,当外加压应力与各向异性能和磁场能平衡时,压磁系数达到峰值,此时磁致伸缩材料的能量转换效率达到最大。非恒定磁场条件下,在22.3 Oe偏置磁场和-34.9 MPa压应力偏置点处有最大峰值压磁系数24.4 T/GPa。
,取磁滞回环上下两部分压磁系数的平均值作为B-σ环的压磁系数,不同电流偏置下压磁系数随应力的变化曲线如图11所示。随着偏置磁场的增加,峰值压磁系数逐渐下降,并且转移向应力更大的区域,当外加压应力与各向异性能和磁场能平衡时,压磁系数达到峰值,此时磁致伸缩材料的能量转换效率达到最大。非恒定磁场条件下,在22.3 Oe偏置磁场和-34.9 MPa压应力偏置点处有最大峰值压磁系数24.4 T/GPa。
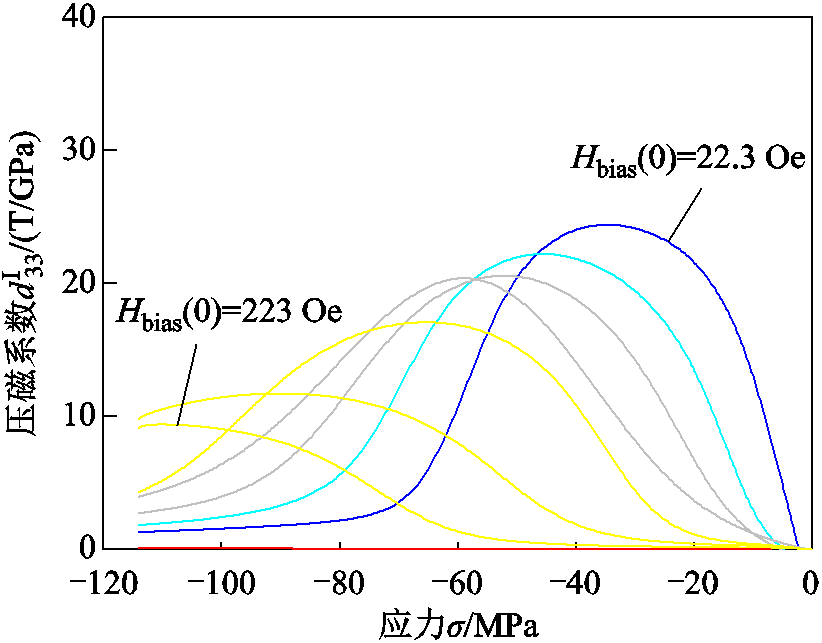
图11 不同偏置电流下B-σ曲线的压磁系数
Fig.11 Piezomagnetic coefficients of B-σ curves at different bias currents
用杨氏模量E来反映材料应力驱动下的形变程度,这一参数可以用于磁致伸缩器件的变刚度设计和谐振频率调整,定义为
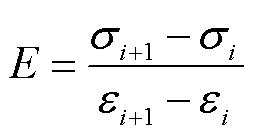 (31)
(31)
定义非恒定偏置磁场条件下的杨氏模量为EI,计算过程与压磁系数的思路一致,不同电流偏置下杨氏模量随应力的变化曲线如图12所示。总体来看,随着偏置磁场增加,材料的ΔE效应逐渐减弱,在22.3 Oe初始偏置磁场和-37 MPa压应力下,杨氏模量从59 GPa减小到了45 GPa,此时ΔE效应最明显。
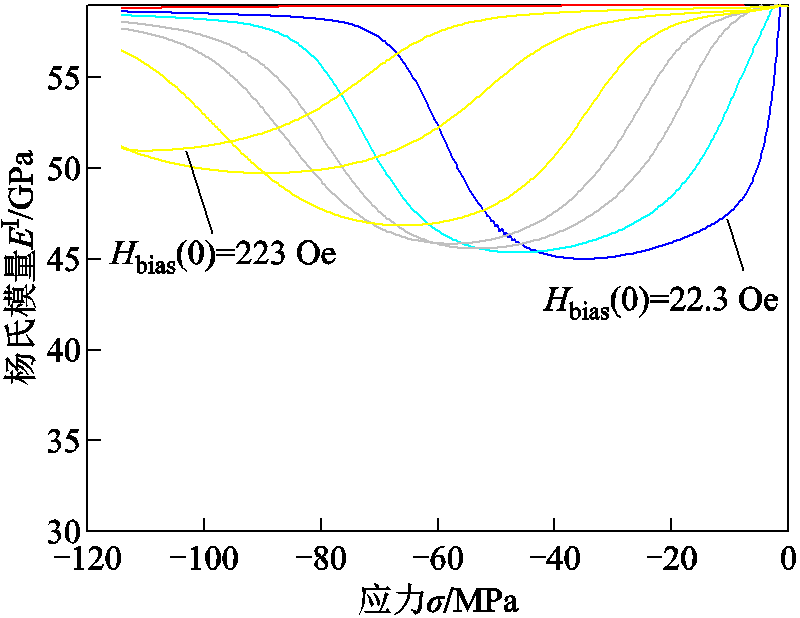
图12 不同偏置电流下ε-σ曲线的杨氏模量
Fig.12 Young's modulus of ε-σ curves at different bias currents
1)通过类比J-A模型的磁滞建模思想引入应力依赖的不可逆磁滞分量,基于自由能理论建立了应力驱动下磁致伸缩逆效应的本构磁滞模型,并基于Fe81Ga19合金棒材在22.3~446 Oe偏置磁场下的实验数据,验证了模型对材料磁滞行为及非线性磁化的模拟效果。针对装置中偏置磁场随应力变化的情况,构建偏置磁场与磁阻的应力相关项,将模型拓展为能反映偏置磁场与应力非线性关系的磁致伸缩逆效应模型,并基于实验数据,验证了将磁路模型耦合到磁滞本构模型模拟实际装置传感响应的可行性。模型模拟结果表明,偏置磁场随应力的增大呈非线性增大的趋势,这一现象也导致了恒定电流偏置比恒磁场偏置条件下的传感响应更浅。
2)所建模型除了预测装置的传感响应,也可以用于追踪材料的最佳偏置条件以及预测材料ΔE效应的变化趋势,为基于磁致伸缩材料逆效应的传感器、能量收集器等器件的性能调控和变刚度设计提供理论指导。
3)本研究主要考虑了偏置点(预应力、偏置磁场)对材料输出特性的影响,以及装置磁路结构对材料偏置磁场的非线性影响。未来可进一步考虑温度、应力、频率等因素的影响对模型进行优化改进,以便适应磁致伸缩逆效应器件在更复杂工况环境下的模型应用。
参考文献
[1] 舒亮, 李传, 吴桂初, 等. Fe-Ga合金磁致伸缩力传感器磁化模型建立与特性分析[J]. 农业机械学报, 2015, 46(5): 344-349.
Shu Liang, Li Chuan, Wu Guichu, et al. Magnetization model of Fe-Ga magnetostrictive force sensor and its characteristics[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 344-349.
[2] Ueno T, Saito C, Imaizumi N, et al. Miniature spherical motor using iron-gallium alloy (Galfenol)[J]. Sensors and Actuators A: Physical, 2009, 154(1): 92-96.
[3] Deng Zhangxian, Dapino M J. Review of magnetostrictive vibration energy harvesters[J]. Smart Material Structures, 2017, 26(10): 103001.
[4] 黄文美, 刘泽群, 郭万里, 等. 磁致伸缩振动能量收集器的全耦合非线性等效电路模型[J]. 电工技术学报, 2023, 38(15): 4076-4086.
Huang Wenmei, Liu Zequn, Guo Wanli, et al. Fully coupled nonlinear equivalent circuit model for magnetostrictive vibration energy harvester[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4076-4086.
[5] 翁玲, 罗旭, 齐芳芳, 等. 用于纹理识别与重建的铁镓合金触须传感器阵列[J]. 电工技术学报, 2024, 39(4): 966-975.
Weng Ling, Luo Xu, Qi Fangfang, et al. Galfenol whisker sensor array for texture recognition and reconstruction[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 966-975.
[6] Liu Yang, Weng Ling, Li Zhuolin, et al. Cross-shaped Fe-Ga alloy three-dimensional force tactile sensor and friction recognition[J]. Sensors and Actuators A: Physical, 2024, 368: 115141.
[7] Deng Zhangxian, Zhang Qian, Dapino M J. Dynamic model for magnetostrictive systems with applications to damper design[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(4): 1823-1831.
[8] 郑加驹, 王洪礼, 曹淑瑛. 超磁致伸缩驱动器频率相关的动态磁滞模型[J]. 机械工程学报, 2008, 44(7): 38-44.
Zheng Jiaju, Wang Hongli, Cao Shuying. Frequent-dependent dynamic hysteresis model of giant magnetostrictive actuator[J]. Chinese Journal of Mechanical Engineering, 2008, 44(7): 38-44.
[9] 黄文美, 陶铮, 郭萍萍, 等. 变压应力条件下铁镓合金棒材高频磁特性测试与模型构建[J]. 电工技术学报, 2023, 38(14): 3769-3778.
Huang Wenmei, Tao Zheng, Guo Pingping, et al. Analysis and modeling of high frequency magnetic properties of rod gallium iron alloy under variable compressive stress[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3769-3778.
[10] Deng Zhangxian. Explicit and efficient discrete energy-averaged model for Terfenol-D[J]. Journal of Applied Physics, 2017, 122(4): 043901.
[11] Evans P G, Dapino M J. Measurement and modeling of magnetic hysteresis under field and stress application in iron–gallium alloys[J]. Journal of Magnetism and Magnetic Materials, 2013, 330: 37-48.
[12] Atulasima J, Flatau A B, Cullen J R. Energy-based quasi-static modeling of the actuation and sensing behavior of single-crystal iron-gallium alloys[J]. 2008, 103(1): 014901.
[13] Weng Ling, Walker T, Deng Zhangxian, et al. Major and minor stress-magnetization loops in textured polycrystalline Fe81.6Ga18.4 Galfenol[J]. Journal of Applied Physics, 2013, 113(2): 24508-24508-9.
[14] Ahmed U, Jeronen J, Zucca M, et al. Finite element analysis of magnetostrictive energy harvesting concept device utilizing thermodynamic magneto-mechanical model[J]. Journal of Magnetism and Magnetic Materials, 2019, 486: 165275.
[15] Armstrong W D. An incremental theory of magneto-elastic hysteresis in pseudo-cubic Ferro-magnetostrictive alloys[J]. Journal of Magnetism and Magnetic Materials, 2003, 263(1/2): 208-218.
[16] Ma Yilin, Wang Enlong, Yang Huan, et al. Reconsideration of nonphysical solution in Jiles-Atherton model for real-time hysteresis estimation[J]. IEEE Transactions on Magnetics, 2022, 58(6): 7300509.
[17] 刘帼巾, 刘达明, 缪建华, 等. 基于变分模态分解和改进灰狼算法优化深度置信网络的自动转换开关故障识别[J]. 电工技术学报, 2024, 39(4): 1221-1233.
Liu Guojin, Liu Daming, Miao Jianhua, et al. Fault identification of automatic transfer switching equipment based on VMD-WPE and IGWO optimized DBN[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1221-1233.
[18] Yang Qiangda, Huang Huan, Zhang Jie, et al. A collaborative cuckoo search algorithm with modified operation mode[J]. Engineering Applications of Artificial Intelligence, 2023, 121: 106006.
[19] 陈杰, 刘昌咏, 邓文明, 等. 四开关三电平半桥LLC变换器的控制策略与效率优化[J]. 电工技术学报, 2024, 39(24): 7833-7845.
Chen Jie, Liu Changyong, Deng Wenming, et al. Control improvement and efficiency optimization of four switch three-level half-bridge LLC converter[J]. Transactions of China Electrotechnical Society, 2024, 39(24): 7833-7845.
Abstract The output characteristics of magnetostrictive devices usually show a strong bias condition dependence. The bias magnetic field provided by constant current will change nonlinearly with the change of the material permeability under stress excitation (manifested as non-constant bias magnetic field). This change affects the accurate characterization of material magnetization process and the rational design of bias points. At present, the inverse effect models of magnetostriction mainly focus on material characterization under constant bias magnetic field. Models that solely consider a constant magnetic field fail to accurately reflect the output characteristics of devices in their actual operating environments. Establishing a hysteresis model that accounts for the inverse magnetostrictive effect with dynamic variations in the bias magnetic field holds significant research importance.
The models established in this paper include the average model of non-hysteresis energy, the hysteresis constitutive model and the equivalent magnetic circuit model taking into account the variation of the bias magnetic field. Firstly, based on the free energy theory, the expression of the non-hysteretic magnetization is derived, and the average model of the non-hysteretic energy is established. Secondly, using the modeling idea of J-A model for positive hysteresis phenomenon, the first order differential equations of irreversible component Mirr, λirr and stress are introduced. The hysteresis constitutive model which can characterize the inverse effect of magnetostrictive materials is obtained. Based on the equivalent theory of magnetic circuit, the influence of stress on magnetic field strength is reflected by the change of magnetoresistance. Finally, an energy average hysteresis model is established which can account for the change of bias magnetic field. Hysteresis models often have difficulty in parameter identification. An improved cuckoo search-grey wolf optimizer (CS-GWO) hybrid algorithm is proposed by introducing nonlinear adaptive step factor α(t). Comparing the optimization results of the traditional optimization algorithms of CS, GWO, and PSO, the CS-GWO algorithm has the highest accuracy and the fastest convergence speed, and can accurately and efficiently identify the globally optimal parameters of the energy-averaged hysteresis model. Model validation is performed in two steps. First, the basic parameters of the model were extracted based on the experiments of Fe81Ga19 alloy bar under -115~0 MPa compressive stress and 22.3~446 Oe constant bias magnetic field. The error between the B-σ curve simulated by the model and the existing experimental data is only 3.85%, which is better than the error calculated by the traditional model of 6.79%. The error of ε-σ curve simulated by the model is 2.93%. Then, based on the experimental data of Fe81Ga19 alloy bar under constant current bias, the parameter Hs is further extracted. The errors of the simulated H-σ curve, B-σ curve and ε-σ curve with experimental data are 4.74%, 4.31% and 3.97%, respectively. The simulation results can accurately describe the tendency of the bias field to increase nonlinearly with the increase of stress, which also leads to a shallower sensing response under constant current bias than under constant field bias.
The proposed model, in addition to predicting the sensing response of the device, can also be used to track the optimal bias conditions of the material as well as to predict the trend of the ΔE effect of the material. The model can provide theoretical guidance for the performance tuning and variable stiffness design of devices such as sensors and energy harvesters based on the inverse effect of magnetostrictive materials.
Keywords:Magnetostritive inverse effect, bias magnetic field, energy-averaged hysteresis model, magnetic circuit model, parameters identification
中图分类号:TM274
DOI:10.19595/j.cnki.1000-6753.tces.240680
国家自然科学基金资助项目(51777053, 52077052)。
收稿日期2024-04-29
改稿日期2024-11-16
黄文美 女,1969年生,博士,教授,研究方向为磁性材料与器件、电机电器及其控制。
E-mail:huzwm@hebut.edu.cn(通信作者)
房昱同 男,1999年生,硕士研究生,研究方向为磁性材料与器件、电机电器及其控制。
E-mail:1085564729@qq.com
(编辑 郭丽军)