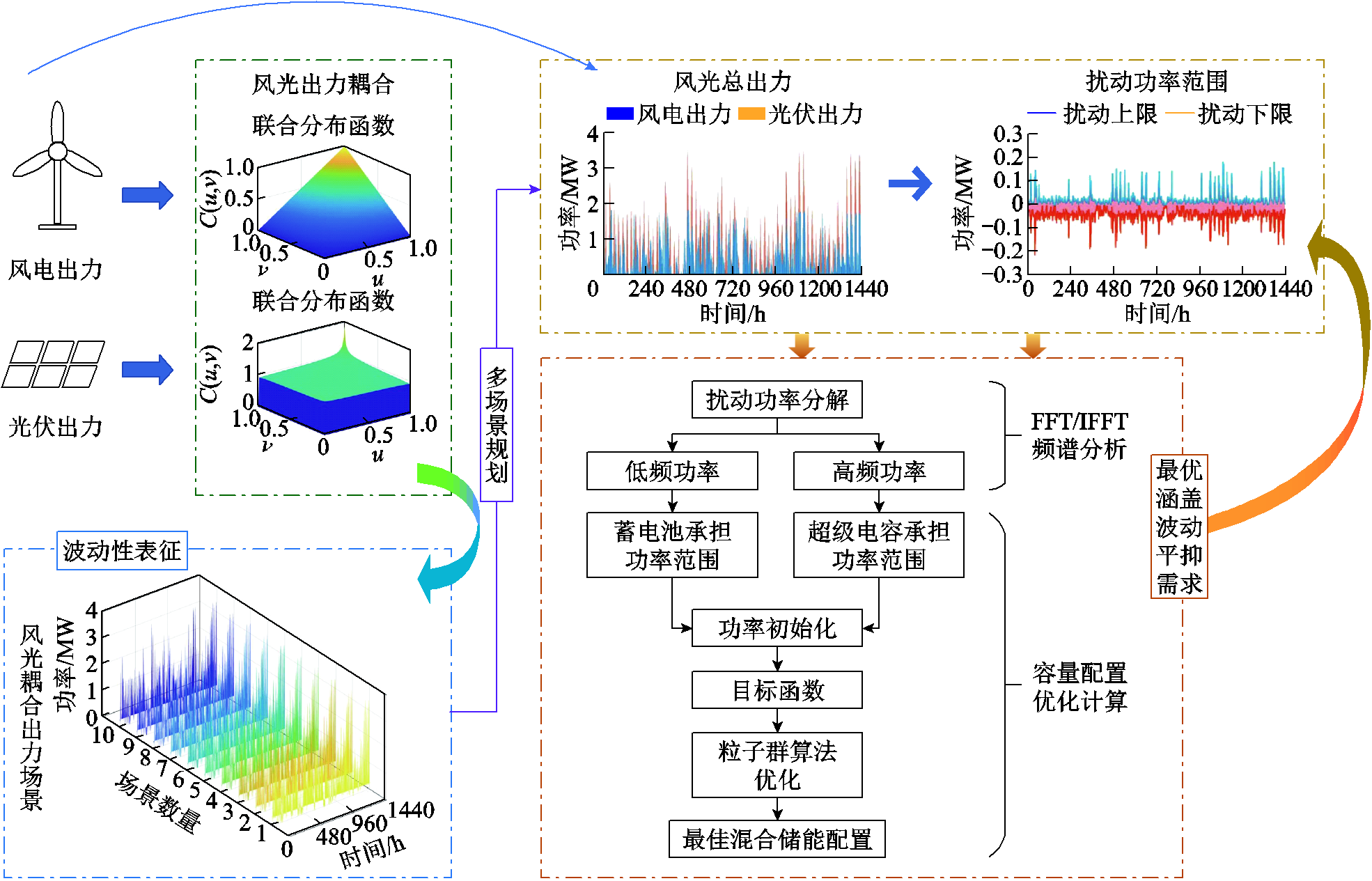
图1 混合储能对电源侧波动的平抑策略框架
Fig.1 Framework of hybrid energy storage smoothing strategies for power source-side fluctuations
摘要 为了解决分布式风光互补系统在耦合出力时对波动性刻画的不准确,以及混合储能系统对电源侧波动的容纳特性不明显的问题,提出一种考虑多场景规划下混合储能平抑风光耦合出力波动的方法。首先,基于Copula理论生成风光耦合出力的场景,以此刻画电源侧耦合出力的波动情况,并将场景功率与风光总功率的差值作为产生波动的扰动功率;其次,通过扰动功率确定混合储能的目标功率,采用快速傅里叶变换及其逆变换对多场景下的扰动功率进行频谱分析,以确定各储能单元的承担功率;最后,以混合储能的运行周期成本最小为目标函数建立优化模型,采用罚函数改进的粒子群算法进行求解计算。算例结果表明,基于多场景规划的混合储能容量配置能够对电源侧的扰动功率进行有效的调频,其调频能力会随着扰动功率变化的复杂程度的加剧而增强,同时扩大对风光耦合出力的波动容纳程度,提升风光互补系统的安全应用效益。
关键词:风光耦合 场景生成 频谱分析 混合储能配置 波动容纳
在“双碳”目标指引下,发展结合风电和光伏出力特点的分布式风光互补系统已然成为构建新型能源体系的重要方式之一[1-2]。然而自然资源的间歇性和随机性使得风光互补系统存在较大的弃风、弃光问题,同时与之配合应用的储能系统也存在经济成本和利用效益不平衡的问题[3-4]。因此,如何实现分布式系统的高效应用成为能源转型过程中重要的研究课题。
分布式风光互补系统的主要特征是具有出力波动性,因此相关的研究主要体现在风光出力的波动性描述,以及储能系统对波动的平抑策略两方面。
风光出力的波动性可通过出力的随机变化进行刻画,即利用出力的时变特性进行概率分布拟合,进而建立不确定性出力的多元场景[5]。文献[6]采用随机规划和鲁棒优化结合的方法来表征风光出力的不确定性,但在选择概率分布函数时只能依据现有数据进行拟合估计,容易产生较大误差。文献[7]利用累积分布的逆变换生成风光出力的随机变量,通过随机抽样模拟生成出力场景集来反映出力的波动性,但并未考虑场景数量对出力波动性的影响。文献[8]以Weibull分布和Beta分布来描述风电出力特性和光伏出力特性,并采用多场景分析法模拟风光出力的随机性,但多场景的线性组合使得计算量过于庞大。文献[9]以相关系数为指标,对不同类型组合的风光耦合出力进行随机性表征,但风光耦合的关系仅停留在表层的线性组合上,缺乏对深层耦合关系的刻画。
在利用储能系统对波动进行平抑时,则多采用功率型和能量型储能相结合,通过对目标波动功率进行分解以确定混合储能中各储能单元承担的功率,进而达到平抑的效果[10-11]。文献[12]采用VMD-ST-QF算法对光伏输出与负荷之间的净功率进行分频处理,利用混合储能实现了对高频模态分量和低频模态分量的平抑,但净功率包含负载所需的缺失功率,不能完全体现其波动特征。文献[13]提出一种低频相关性与混合储能高频平抑的风光出力并网平抑方法,但仅以独立场景做分析,并未考虑场景集的整体平抑效果。文献[14]以并网需求功率作为混合储能的目标功率,采用多次滑动均值滤波(Multiple Moving Average Filtering, MMAF)算法获得混合储能的总功率指令,但没有考虑蓄电池与超级电容各自的运行状态。文献[15]以负荷需求与可再生能源出力的不平衡功率作为混合储能的目标功率,利用离散傅里叶变换法对一个周期内的不平衡功率进行频谱分析,但分界频率是通过经验方法获得的,不具有普适性。
上述文献虽然对相关问题进行了研究,但对分布式的风光互补系统来讲,风光出力的波动性分析和储能系统的平抑策略仍存在一定问题:①通过不确定性场景描述风光耦合出力的波动性时,多将风电和光伏刻画为线性的耦合关系;②混合储能的承担功率多从负荷端或并网功率的需求出发,弱化了混合储能在电源侧对风光出力波动的容纳特性。
针对现有研究存在的上述问题,本文从电源侧出发,采用构建多元联合分布的方式刻画风、光出力之间的非线性耦合关系,以优化电源侧混合储能容量配置、提高电源端出力波动的容纳特性为目的,提出一种考虑多场景规划的混合储能平抑风光耦合出力波动的方法。首先,基于历史数据采用核密度估计(Kernel Density Estimation, KDE)和Copula理论建立风电和光伏的联合分布函数,通过随机抽样生成不同场景数量的场景集,以此来表征不同条件下风光耦合出力的波动变化;其次,利用快速傅里叶变换(Fast Fourier Transform, FFT)及其逆变换(Inverse Fast Fourier Transform, IFFT)对多场景下产生波动的扰动功率进行频谱分析,确定蓄电池和超级电容用于平抑波动的承担功率;最后,建立运行周期内混合储能成本最小的容量配置模型,采用罚函数改进的粒子群算法(Particle Swarm Algorithm, PSO)进行求解,通过算例进行验证。
在研究风光出力的波动性问题时,需要确定产生波动的那部分扰动功率,通过储能系统对其进行平滑处理或者直接消纳。扰动功率主要来源于电源侧和负荷侧[16],电源侧是由风速和辐照强度的随机性引起,同时也包含风电和光伏的设备特性的影响;负荷侧是由输出功率与负载或并网的需求功率不匹配产生的差额功率所引起。为研究混合储能对电源侧波动的容纳特性,本文从电源侧确定扰动功率,并通过混合储能进行平抑。电源侧出力波动的平抑策略框架如图1所示。
在电源侧,可通过确定风电出力和光伏出力的边际分布,进而确定风光耦合的联合分布。由于联合分布能够表征风电和光伏的相关关系,故由联合分布进行随机抽样得到的出力场景具有一致的相关性,因而生成的场景可以表征复杂条件下功率的扰动变化。进一步可以确定混合储能的目标功率为场景功率与出力功率的差值,其可以表示为

图1 混合储能对电源侧波动的平抑策略框架
Fig.1 Framework of hybrid energy storage smoothing strategies for power source-side fluctuations
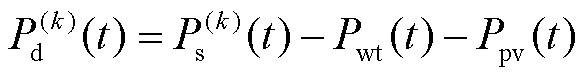 (1)
(1)
式中,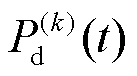 为第
为第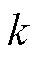 个场景下
个场景下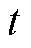 时刻风光耦合的扰动功率,即混合储能的目标功率;
时刻风光耦合的扰动功率,即混合储能的目标功率;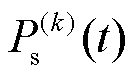 为第
为第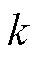 个场景下
个场景下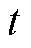 时刻风光耦合的出力功率;
时刻风光耦合的出力功率;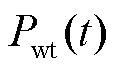 为
为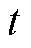 时刻风电出力;
时刻风电出力;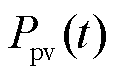 为
为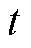 时刻光伏出力。
时刻光伏出力。
由于生成的风光耦合出力场景是一个集合,因此得到的扰动功率也是集合,通过该集合可以确定各时刻混合储能承担的总目标功率范围 为
为
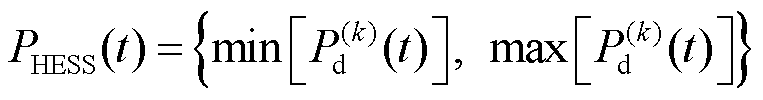 (2)
(2)
确定了总目标功率的范围后,进一步需要分析在总目标功率范围内蓄电池与超级电容各自的容量配置,并确保蓄电池与超级电容的功率特性最优的涵盖所有的扰动功率场景。
在描述风电出力和光伏出力的分布特征时,常常采用概率分布的方法进行刻画。过往的研究近似地将描述风速的Weibull分布和描述辐照强度的Beta分布用于描述风、光出力的不确定性[17]。但Weibull分布和Beta分布作为含参的函数模型,参数的值会影响模型刻画的准确度,同时风电出力和光伏出力的理论计算公式也反映出影响出力的因素并非仅仅是风速和辐照强度[18]。因此相较于参数法,采用非参数的KDE法能够更准确地刻画风、光出力的分布特点。
KDE的结果取决于核函数和带宽,对于任意样本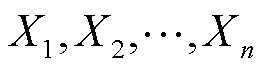 在任意一点
在任意一点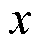 处的密度函数
处的密度函数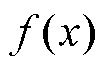 的KDE结果可以表示为
的KDE结果可以表示为
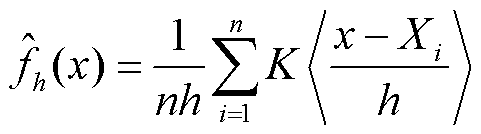 (3)
(3)
式中,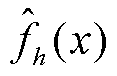 为KDE估计的密度函数;
为KDE估计的密度函数;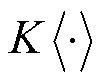 为核函数;
为核函数;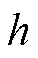 为带宽;n为样本数量。
为带宽;n为样本数量。
对于离散型变量,带宽可以通过样本的拟合概率密度与经验概率密度的均方差进行计算,即
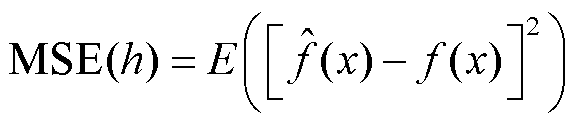 (4)
(4)
式中,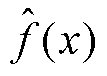 为经验概率密度;
为经验概率密度;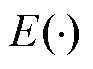 为期望函数。
为期望函数。
式(4)是在已知样本拟合概率密度的基础上进行带宽的计算,而拟合概率密度又需要通过参数法确定。若采用高斯核函数进行核密度估计,则带宽就可以通过样本的标准差来计算[19],对应的高斯核函数及带宽分别为
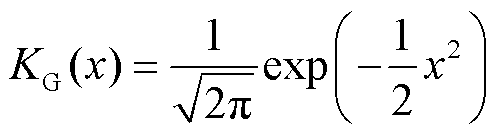 (5)
(5)
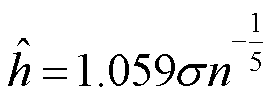 (6)
(6)
式中,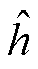 为高斯核函数对应的带宽;
为高斯核函数对应的带宽;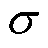 为样本标准差。
为样本标准差。
为对比参数法和非参数法对样本的拟合程度,此处以锡林郭勒某地1 440 h的风电出力和光伏出力数据为例,对数据样本进行标准化和清洗。采用Weibull分布、Beta分布和KDE分别对风电出力和光伏出力进行分布拟合,得到不同电源对应分布的概率密度拟合结果如图2所示。从图2中可以看出,参数法的结果偏向于对某一区域内的出力数据样本进行整体性描述,而KDE的结果偏向于对数据样本的细节进行刻画,能够更好地反映直方图的凹凸趋势。本文主要针对风电出力和光伏出力进行耦合建模的研究,故能反映较多数据样本细节的KDE结果更为适用。
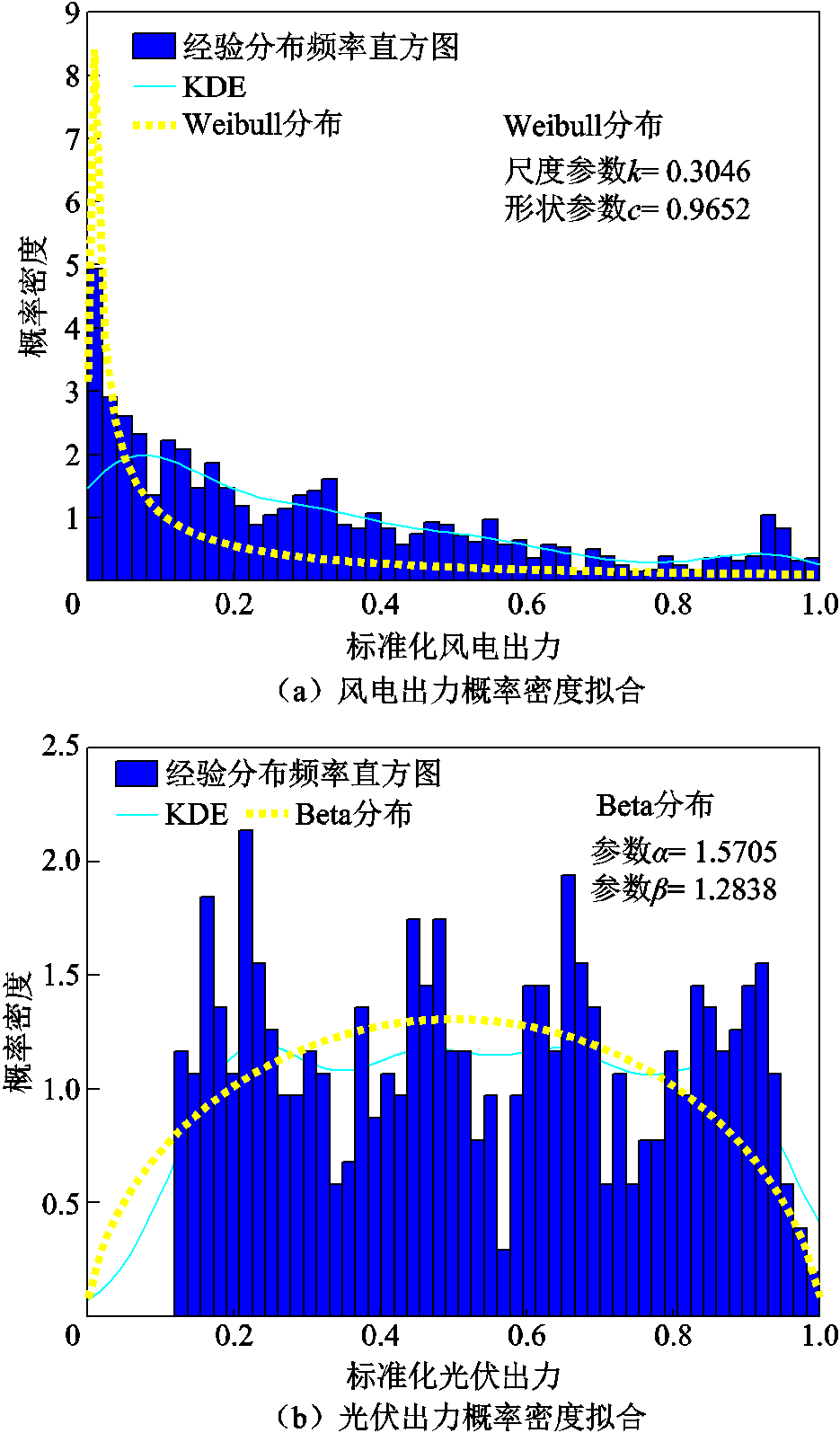
图2 风光出力的概率密度拟合结果
Fig.2 Probability density fitting results for wind and photovoltaic outputs
Copula理论最早是由A. Sklar在1959年所提出[20],其主要原理是通过一个Copula函数将多个不同变量的概率分布进行联结,以构建变量之间的相关关系,即建立不同变量的联合分布函数。为选择合适的Copula函数建立风电出力和光伏出力的联合分布函数,本文引入经验Copula函数作为描述风电出力与光伏出力耦合的实际分布,采用瓦瑟斯坦距离作为验证拟合Copula模型的指标。相比于欧氏距离,瓦瑟斯坦距离能够有效地避免离散变量在计算中梯度下降过快的影响。对于二维变量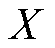 和
和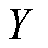 ,经验Copula函数可以表示为
,经验Copula函数可以表示为
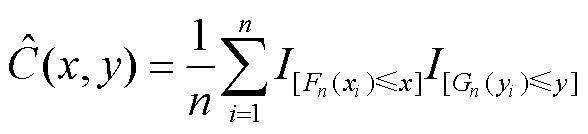 (7)
(7)
式中,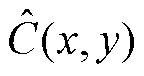 为经验Copula函数;
为经验Copula函数;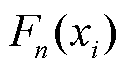 、
、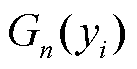 分别为变量
分别为变量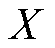 和
和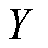 的经验分布;
的经验分布;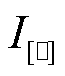 为示性函数,若满足
为示性函数,若满足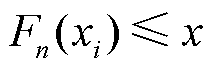 ,则
,则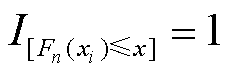 ,否则
,否则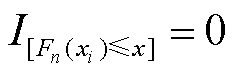 。
。
瓦瑟斯坦距离可以表示为
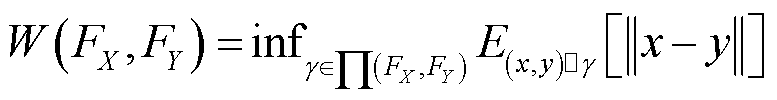 (8)
(8)
式中,inf为下界;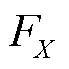 、
、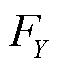 分别为变量
分别为变量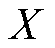 、
、 的概率分布;
的概率分布; 为
为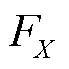 与
与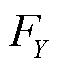 所有可能的联合分布;
所有可能的联合分布;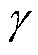 为
为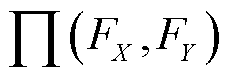 中的一个特异性分布;
中的一个特异性分布;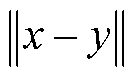 为
为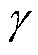 的随机样本
的随机样本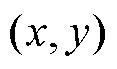 之间的距离;
之间的距离;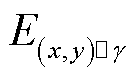 为路径
为路径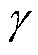 下
下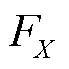 和
和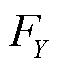 的最小平均距离。
的最小平均距离。
对五种常见的Copula函数采用极大似然估计法估计参数,计算其与经验Copula的瓦瑟斯坦距离结果见表1。结果显示采用Gumbel-Copula函数计算得到的瓦瑟斯坦距离最小,因此更适合作为风光出力联合分布的联结函数。
表1 不同Copula函数的拟合验证结果
Tab.1 Validation results of fitting different Copula functions

Copula函数参数值/自由度瓦瑟斯坦距离 Gaussian-Copula-0.062 50.109 4 t-Copula-0.160 7/2.587 50.119 7 Gumbel-Copula1.012 50.103 5 Clayton-Copula1.450 9×10-60.104 8 Frank-Copula-0.838 10.115 9
采用Gumbel-Copula函数联结风电出力和光伏出力的联合分布可表示为
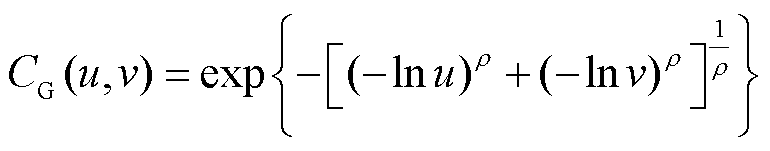 (9)
(9)
式中,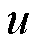 为风电出力的KDE;
为风电出力的KDE;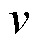 为光伏出力的KDE;
为光伏出力的KDE;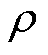 为参数。
为参数。
本文采用马尔科夫链-蒙特卡洛法对风光耦合出力的联合分布函数进行随机抽样[21]。以式(9)的联合分布函数作为目标概率,具体步骤如下。
1)确定数据样本的分布函数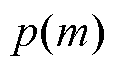 作为抽样的目标概率,构造转移矩阵Q满足
作为抽样的目标概率,构造转移矩阵Q满足
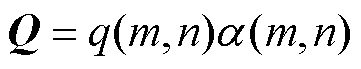 (10)
(10)
式中,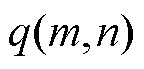 为从状态
为从状态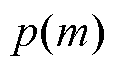 转移到状态
转移到状态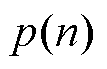 的结果;
的结果;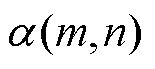 为接受率,表示从状态
为接受率,表示从状态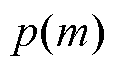 转移到状态
转移到状态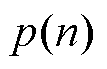 的过程中以
的过程中以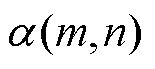 的概率接受转变,或者以
的概率接受转变,或者以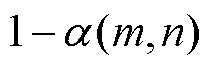 的概率拒绝转变。
的概率拒绝转变。
2)确定目标概率和接受率的细致平衡条件
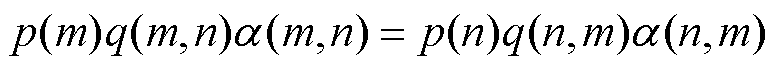 (11)
(11)
3)采用两边放大思想,对式(11)进行处理得到
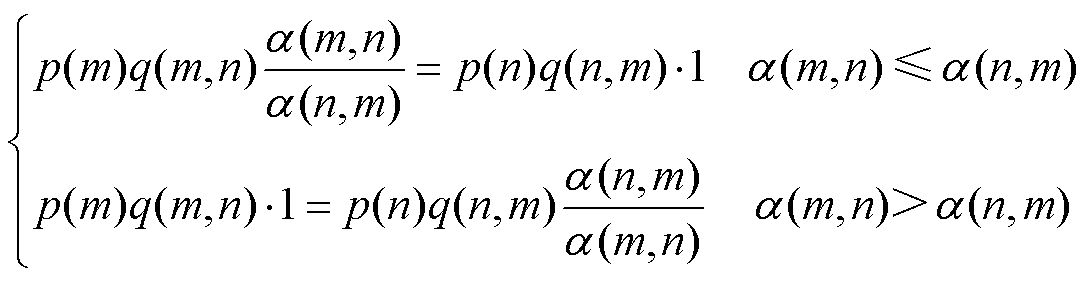 (12)
(12)
4)由此可以综合确定放大后的接受率为
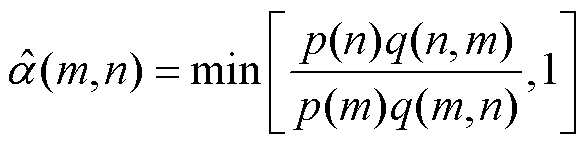 (13)
(13)
5)确定接受率后,即可通过生成随机数判断其与接受率的大小,进而得到符合目标概率的随机分布,进一步采用式(4)计算带宽,通过KDE的逆变换得到出力场景。
将功率信号从时域变换到频域可以直观地提取信号的特征,合理地分配蓄电池和超级电容承担的功率。本文采用FFT及IFFT对式(1)得到的扰动功率信号进行时频转换。由于傅里叶变换具有对称性,因此在进行频谱分析时只需要确定前半部分的分界频率即可。对于采样点数量为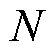 的时域信号
的时域信号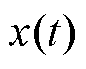 ,其FFT变换为
,其FFT变换为
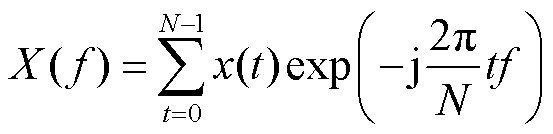 (14)
(14)
式中,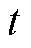 为时间序列;
为时间序列;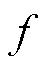 为对应时序的频率序列。
为对应时序的频率序列。
IFFT变换为
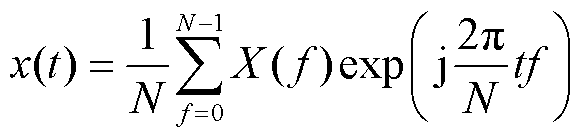 (15)
(15)
在第1节中已阐明风光耦合出力的多场景具有一致的相关性,因此分别对扰动功率场景和风光总出力进行FFT变换得到频域下的功率信号,进而确定蓄电池与超级电容的分界频率。二维随机信号之间的互相关函数可以表示为
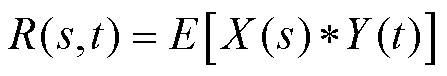 (16)
(16)
式中,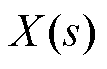 为随机信号在时刻
为随机信号在时刻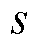 的取值;
的取值;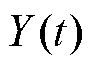 为随机信号在时刻
为随机信号在时刻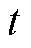 的取值;*表示卷积运算;
的取值;*表示卷积运算;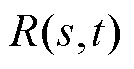 为随机信号的互相关函数,其表示
为随机信号的互相关函数,其表示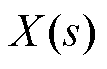 和
和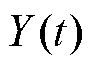 在不同时刻
在不同时刻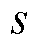 和
和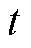 的取值之间的相关程度。
的取值之间的相关程度。
由式(16)可以得到每个扰动功率场景与风光总出力的互相关系数,选择场景集中互相关系数最大时对应的最大采样点作为分界点,其对应的频率值即为蓄电池与超级电容的分界频率。后续通过IFFT即可得到蓄电池与超级电容的功率场景,进而确定响应扰动功率的混合储能功率的变化范围。
根据蓄电池和超级电容的工作原理,建立对应的功率、容量和荷电量模型。
1)功率模型
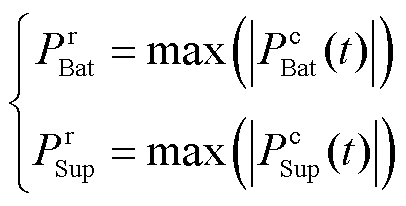 (17)
(17)
式中,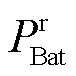 、
、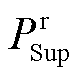 分别为蓄电池和超级电容的额定功率;
分别为蓄电池和超级电容的额定功率;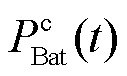 、
、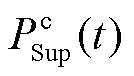 分别为蓄电池和超级电容t时刻的实际功率。
分别为蓄电池和超级电容t时刻的实际功率。
2)容量模型
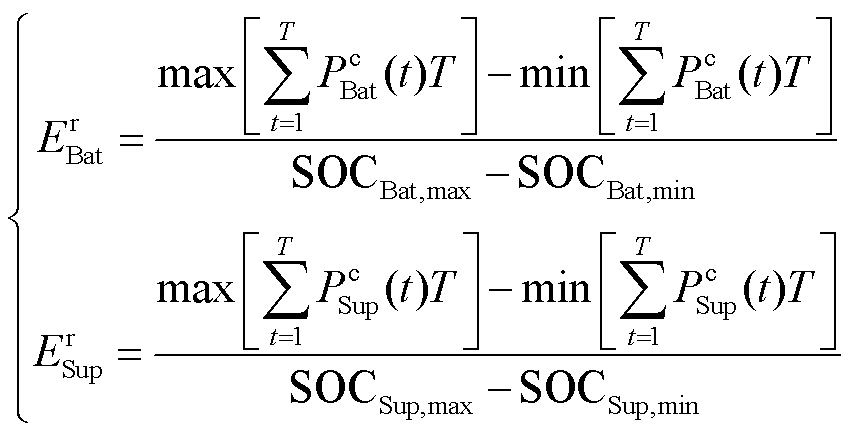 (18)
(18)
式中,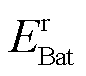 、
、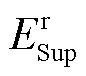 分别为蓄电池和超级电容的额定容量;
分别为蓄电池和超级电容的额定容量;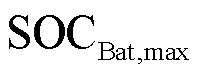 、
、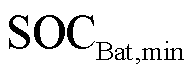 分别为蓄电池荷电量上、下限;
分别为蓄电池荷电量上、下限;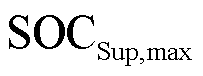 、
、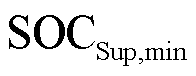 分别为超级电容荷电量上、下限;
分别为超级电容荷电量上、下限;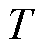 为采样周期。
为采样周期。
3)荷电量模型
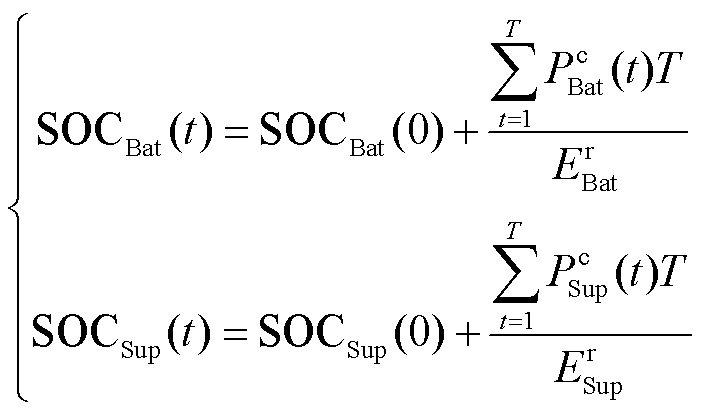 (19)
(19)
式中,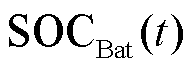 、
、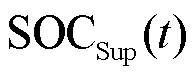 分别为蓄电池和超级电容t时刻的荷电量;
分别为蓄电池和超级电容t时刻的荷电量;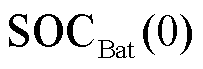 、
、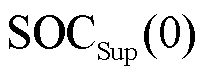 分别为蓄电池和超级电容初始荷电量,本文均选取0.5。
分别为蓄电池和超级电容初始荷电量,本文均选取0.5。
本文以混合储能在运行过程中的全生命周期成本最小为目标函数,包括初始建设成本、运行维护成本及回收处理成本三部分,所建目标函数为
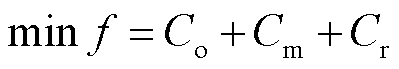 (20)
(20)
式中,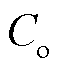 为初始建设成本;
为初始建设成本;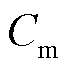 为运行维护成本;
为运行维护成本;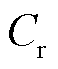 为回收处理成本。
为回收处理成本。
1)初始建设成本
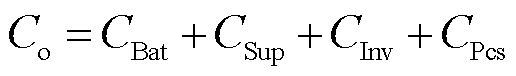 (21)
(21)
式中,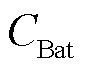 为蓄电池成本;
为蓄电池成本;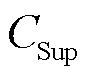 为超级电容成本;
为超级电容成本;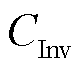 为设备建设成本;
为设备建设成本;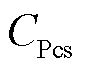 为辅助设备成本。
为辅助设备成本。
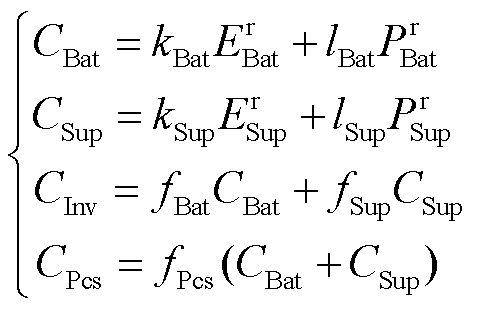 (22)
(22)
式中,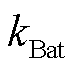 、
、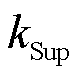 分别为蓄电池和超级电容的单位容量成本;
分别为蓄电池和超级电容的单位容量成本;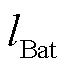 、
、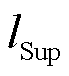 分别为蓄电池和超级电容的单位功率成本;
分别为蓄电池和超级电容的单位功率成本;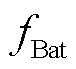 、
、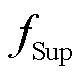 分别为蓄电池和超级电容的建设成本系数;
分别为蓄电池和超级电容的建设成本系数;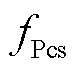 为辅助设备成本系数。
为辅助设备成本系数。
2)运行维护成本
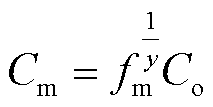 (23)
(23)
式中,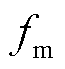 为运行维护成本系数;
为运行维护成本系数;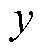 为寿命周期,本文设计寿命周期为10年。
为寿命周期,本文设计寿命周期为10年。
3)回收处理成本
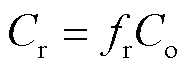 (24)
(24)
式中,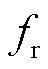 为回收处理成本系数。
为回收处理成本系数。
根据混合储能模型建立功率约束、容量约束和荷电量约束。
1)功率约束
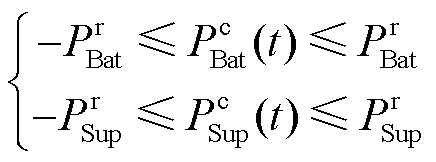 (25)
(25)
2)容量约束
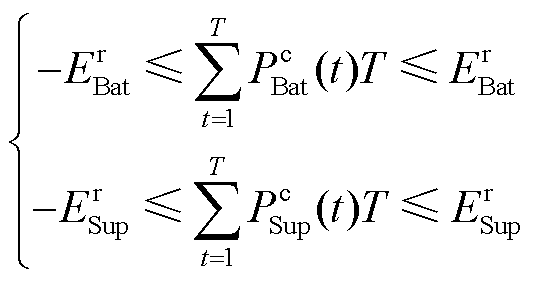 (26)
(26)
3)荷电量约束
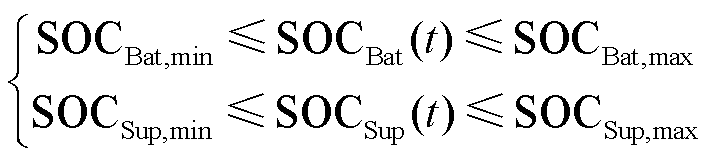 (27)
(27)
PSO在处理非线性、高维度问题时具有良好的寻优速度和收敛效果,因此本文采用PSO作为基础优化算法。传统的PSO在处理约束条件时,通过生成在约束条件范围内的可行解作为初始粒子进行优化。由于本文已经确定了混合储能承担的总目标功率范围,可以生成随机可行解作为初始粒子,因此对于PSO中的约束条件采用罚函数法处理[22],即对目标函数添加一罚函数项,将约束问题转换为无约束问题进行优化计算。基于罚函数法的目标函数可以表示为
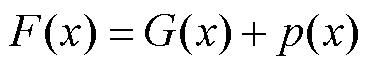 (28)
(28)
式中,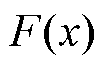 为施加惩罚项的目标函数;
为施加惩罚项的目标函数;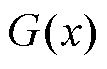 为目标函数;
为目标函数;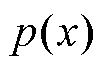 为罚函数。
为罚函数。
罚函数采用动态惩罚函数,可表示为
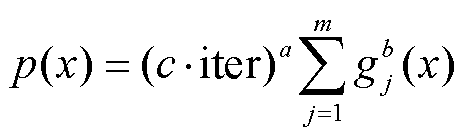 (29)
(29)
式中,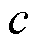 为惩罚因子,本文取0.5;
为惩罚因子,本文取0.5; 为当前迭代次数;
为当前迭代次数;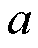 和
和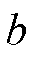 为参数,通常情况下
为参数,通常情况下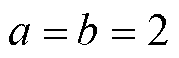 ;
;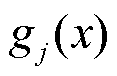 为第
为第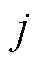 个约束条件上的约束违反程度,
个约束条件上的约束违反程度,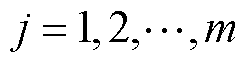 。
。
本文采用线性递减策略对粒子速度更新时的权值进行计算,有
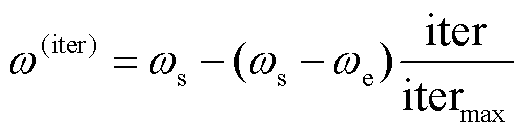 (30)
(30)
式中,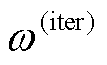 为当前迭代次数下的权值;
为当前迭代次数下的权值;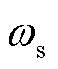 为迭代开始权值;
为迭代开始权值;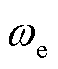 为迭代结束权值;
为迭代结束权值;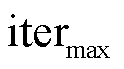 为最大迭代次数。
为最大迭代次数。
本文以锡林郭勒某风电场和某光伏电站1 440 h的出力数据为例进行分析,风电与光伏的装机容量均为2 MW。混合储能相关参数见表2,粒子群算法相关参数见表3。
表2 混合储能参数
Tab.2 Hybrid energy storage parameters
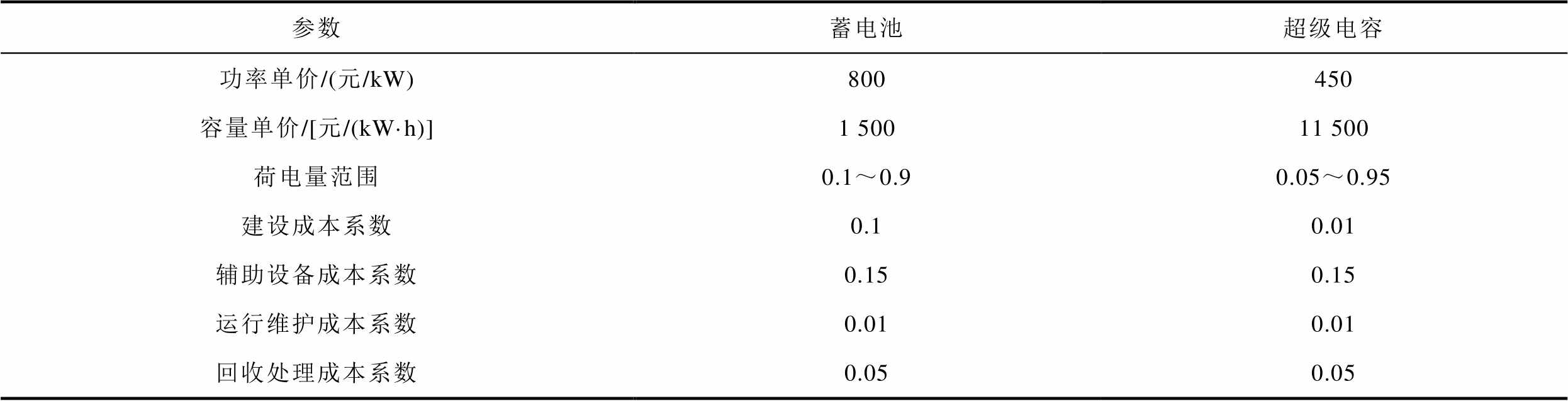
参数蓄电池超级电容 功率单价/(元/kW)800450 容量单价/[元/(kW·h)]1 50011 500 荷电量范围0.1~0.90.05~0.95 建设成本系数0.10.01 辅助设备成本系数0.150.15 运行维护成本系数0.010.01 回收处理成本系数0.050.05
表3 粒子群算法参数
Tab.3 Particle swarm optimization parameters

参数数值 粒子个数200 迭代次数100 自我学习因子2 群体学习因子2 迭代初始权值0.9 迭代结束权值0.4 速度范围[-0.01,0.01]
根据场景生成方法以10个场景数量为差额,设置数量从10~100共10个场景集。由于风光耦合出力的多场景具有一致的相关性,因此场景的数量对于分界频率没有影响。通过FFT和式(16)分别计算不同数量场景下蓄电池与超级电容的分界频率均为1.880 8×10-4 Hz。
图3为不同数量场景下扰动功率与混合储能功率的频谱。由图中可以看出,不同数量的场景集中峰值数均为两个,峰值所对应的频率点分别为2.893 6×10-5 Hz和5.787 0×10-5 Hz,这表明各出力场景集的功率频率特性较为一致,符合分界频率下蓄电池承担的低频部分。各场景集的不同之处在于峰值所对应的幅值不同,其中10个场景下的幅值最小为0.025 0,80个场景的幅值最大为0.045 2,并且随着场景数量的增加,整体幅值也在增加,这反映出场景数量越多,蓄电池承担低频功率的特性也就越强。同时,在低频部分混合储能功率对应的幅值要小于扰动功率的幅值,在高频部分则是大于扰动功率的幅值,并且不同频率的幅值变化相对稳定。由此可见以1.880 8×10-4 Hz作为蓄电池和超级电容的分界频率能够较好地应对不同场景下扰动功率的频谱变化。
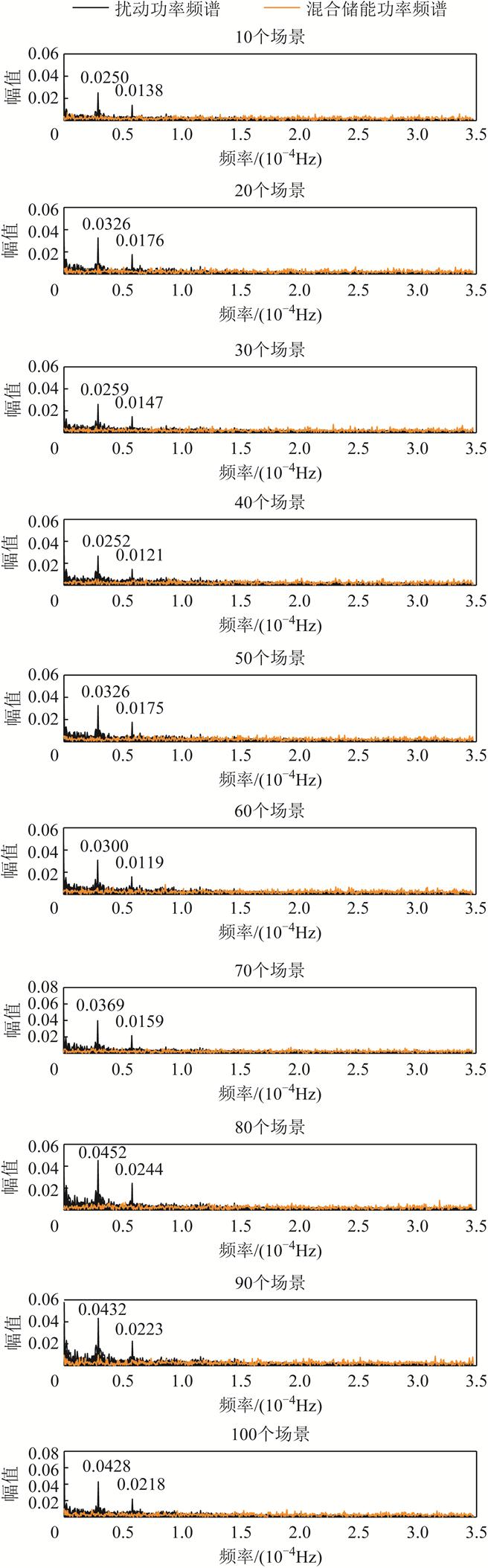
图3 不同数量场景下扰动功率和混合储能的频谱图
Fig.3 Spectrogram of disturbed power and hybrid energy storage in different quantity scenarios
图4为不同数量场景下扰动功率与混合储能功率的频率偏差。由图4中可知,随着场景数量的增加,扰动功率的频率波动也增大,而配置混合储能进行调频后能够有效地降低扰动功率的频率波动,并且波动的幅度更小。同时,随着场景数量的增加,混合储能的调频特性就越明显,对于频率幅度变化较大的时刻,混合储能也具有较好的调频特性。
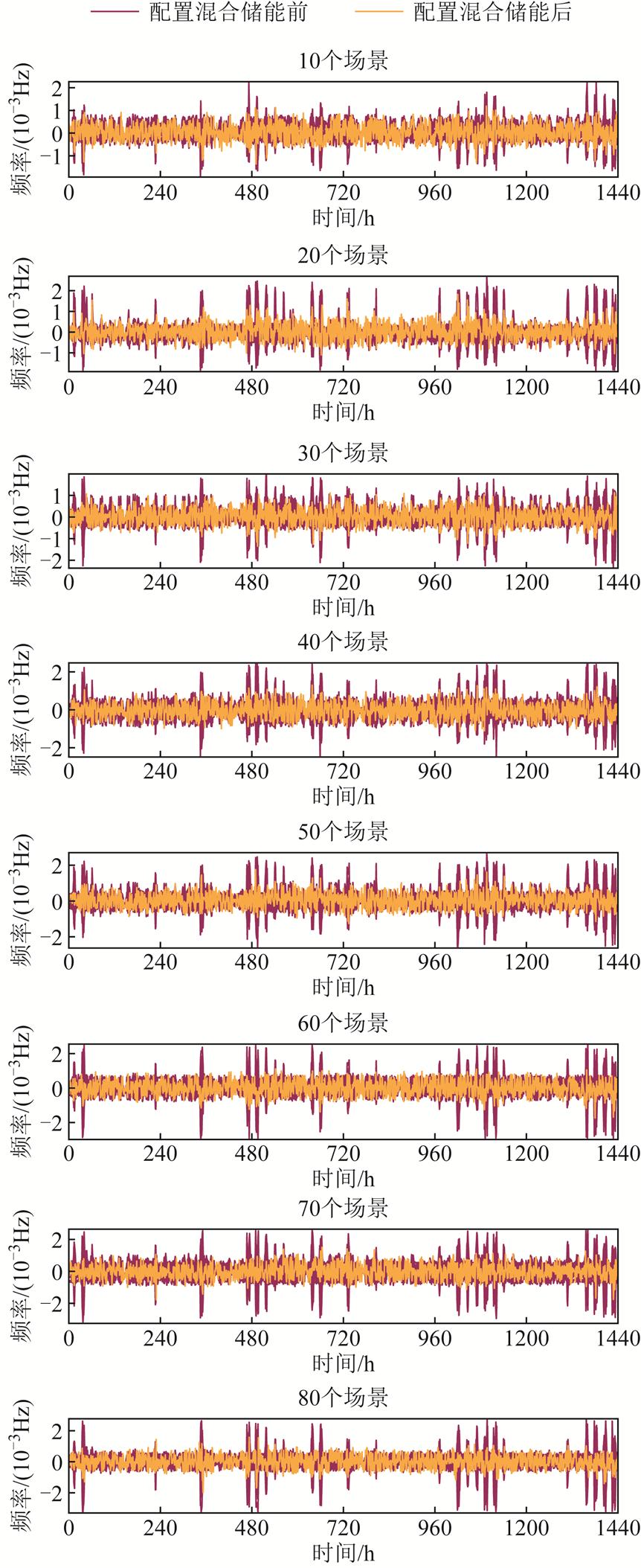
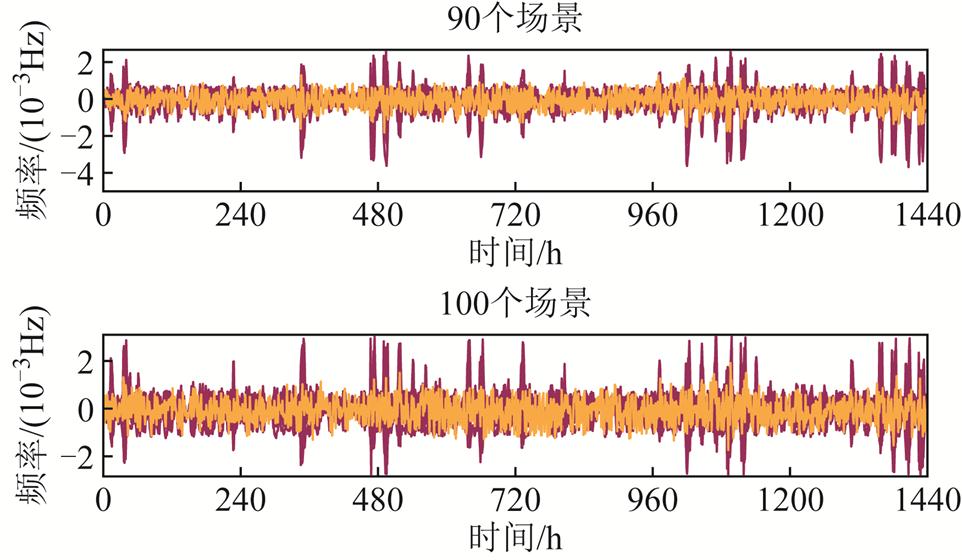
图4 不同数量场景下配储前后的频率偏差
Fig.4 Frequency deviation before and after configuration of energy storage in different quantity scenarios
为进一步比较不同数量场景集下扰动功率和混合储能功率在频率上的差距,验证配置混合储能后能够降低扰动频率的有效性,基于图4所示配置混合储能前后的结果,采用功率频率偏差的方均根误差(Root Mean Squared Error, RMSE)作为混合储能调频的评价指标[23],其表达式为
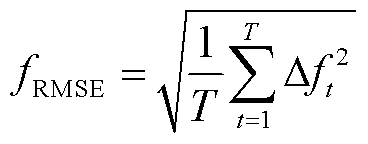 (31)
(31)
式中,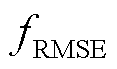 为频率评价指标,其值越小,表明功率频率波动越小,调频效果也就越好;
为频率评价指标,其值越小,表明功率频率波动越小,调频效果也就越好;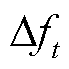 为t时刻的功率频率偏差。
为t时刻的功率频率偏差。
配置储能前后功率频率偏差的RMSE结果见表4。相比于配置储能前,配置储能后10个场景下频率偏差的RMSE下降率最小为60.0%,100个场景下频率偏差的RMSE下降率最大为83.5%,且随着场景数量的增加,下降率也在逐渐增大,这表明场景数量越多,混合储能调节频率的作用也就越强。而场景频率偏差的平均RMSE集中在3.00×10-4附近,表明不同数量的场景集中单个场景的频率偏差并不大,验证了本文采用场景生成方法的有效性。
表4 配储前后功率频率偏差的RMSE
Tab.4 RMSE of power frequency deviation before and after energy storage configuration
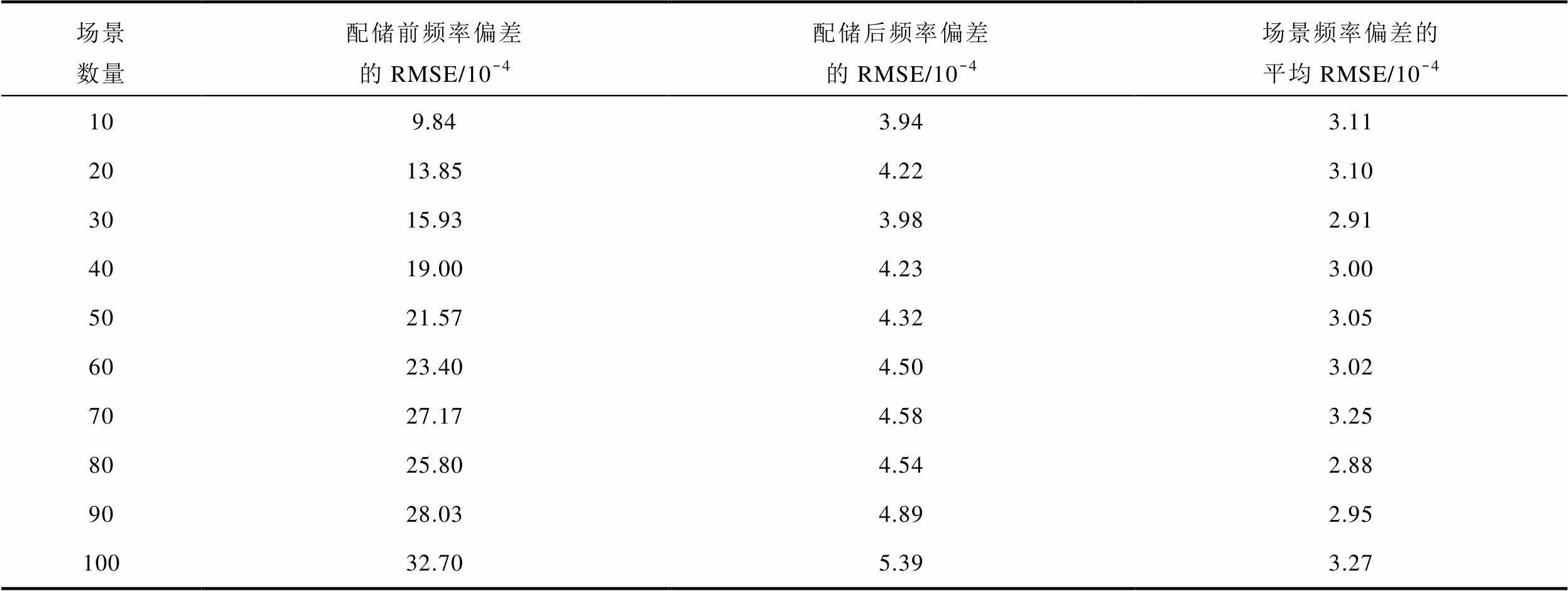
场景数量配储前频率偏差的RMSE/10-4配储后频率偏差的RMSE/10-4场景频率偏差的平均RMSE/10-4 109.843.943.11 2013.854.223.10 3015.933.982.91 4019.004.233.00 5021.574.323.05 6023.404.503.02 7027.174.583.25 8025.804.542.88 9028.034.892.95 10032.705.393.27
基于第3节中的方法进行混合储能的优化配置,其结果见表5。从表5中可以看出,场景数量的增加会对蓄电池和超级电容的容量配置产生较大的影响,蓄电池的额定功率和额定容量最大增幅分别为77.1%和54.9%,超级电容的额定功率和额定容量最大增幅分别为40.0%和42.4%。此外,超级电容的额定功率基本大于蓄电池的额定功率,而超级电容额定容量则小于蓄电池的额定容量,这反映出蓄电池更多用来平抑功率波动的功率特性,而超级电容更多用于调整功率频率的功率特性。
表5 不同数量场景下混合储能容量配置结果
Tab.5 Hybrid energy storage capacity allocation results in different quantity scenarios
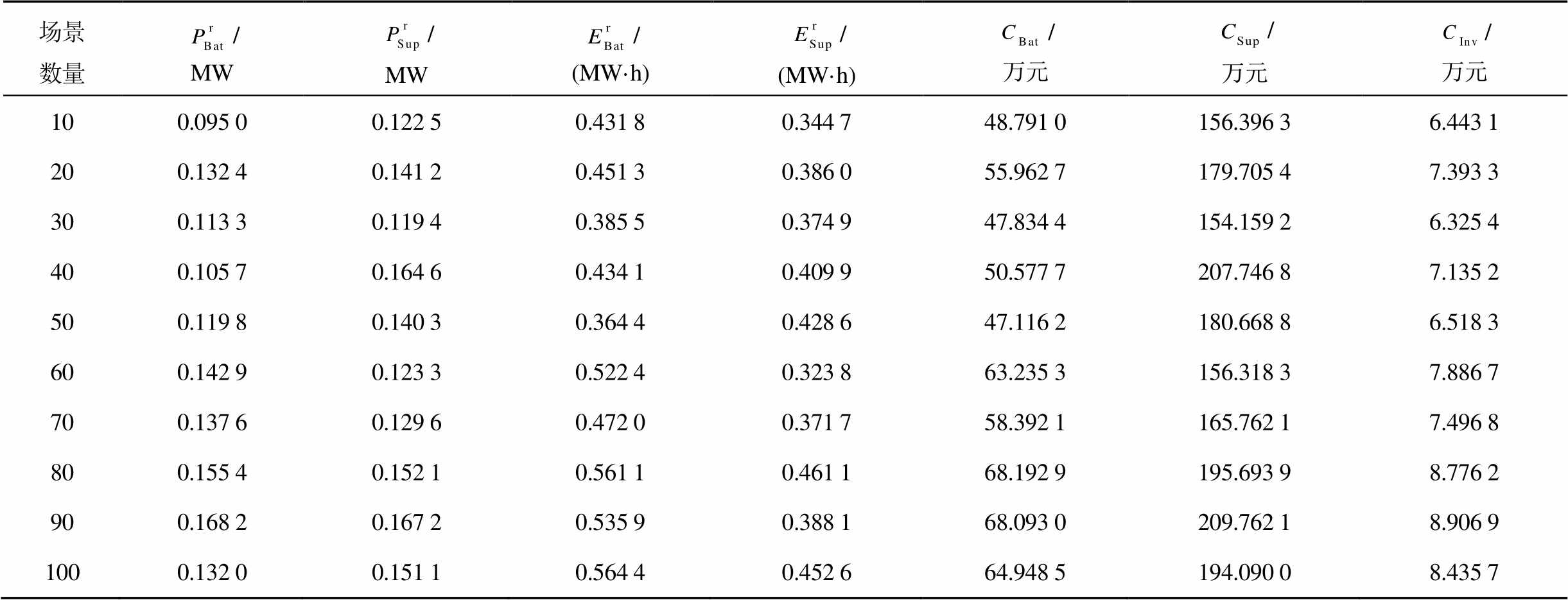
场景数量/MW/MW/(MW·h)/(MW·h)/万元/万元/万元 100.095 00.122 50.431 80.344 748.791 0156.396 36.443 1 200.132 40.141 20.451 30.386 055.962 7179.705 47.393 3 300.113 30.119 40.385 50.374 947.834 4154.159 26.325 4 400.105 70.164 60.434 10.409 950.577 7207.746 87.135 2 500.119 80.140 30.364 40.428 647.116 2180.668 86.518 3 600.142 90.123 30.522 40.323 863.235 3156.318 37.886 7 700.137 60.129 60.472 00.371 758.392 1165.762 17.496 8 800.155 40.152 10.561 10.461 168.192 9195.693 98.776 2 900.168 20.167 20.535 90.388 168.093 0209.762 18.906 9 1000.132 00.151 10.564 40.452 664.948 5194.090 08.435 7
进一步对比两种储能方式之间额定功率和额定容量的变化量如图5所示。可见场景数量的增加对于两种储能方式之间在额定功率上的变化影响较小,在额定容量上则变化较大,这也反映在超级电容的设备成本随着场景的增加而有明显的增大。通过混合储能的配置结果可以在节约成本的基础上选择最佳的混合储能配置方式。
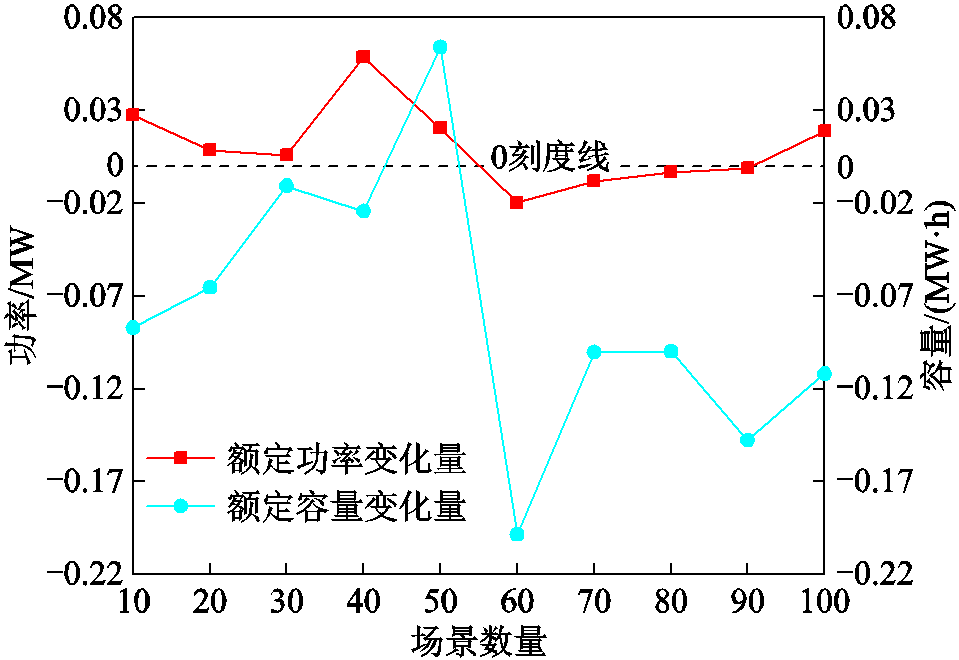
图5 蓄电池和超级电容之间的参数变化量
Fig.5 Amount of parameter variation between battery and super-capacitor
因为没有考虑负荷的变化,所以得到的混合储能容量优化配置结果需要反映在风光耦合的出力上。图6为10个场景集中混合储能出力构成的出力场景结合风光总出力曲线。从图中可以看出,配置储能后风光的耦合出力就具有了一定的可波动范围,且每一个时刻都具备容纳扰动功率增加及减少的上限与下限,即在该上、下限内任意的出力波动都可以通过混合储能进行平抑。同时,在0刻度线以下也具有混合储能的功率部分,这表明当风光耦合出力接近或为0时,混合储能具有仍能进行充电的功率特性,可减缓功率突变对系统产生的影响。
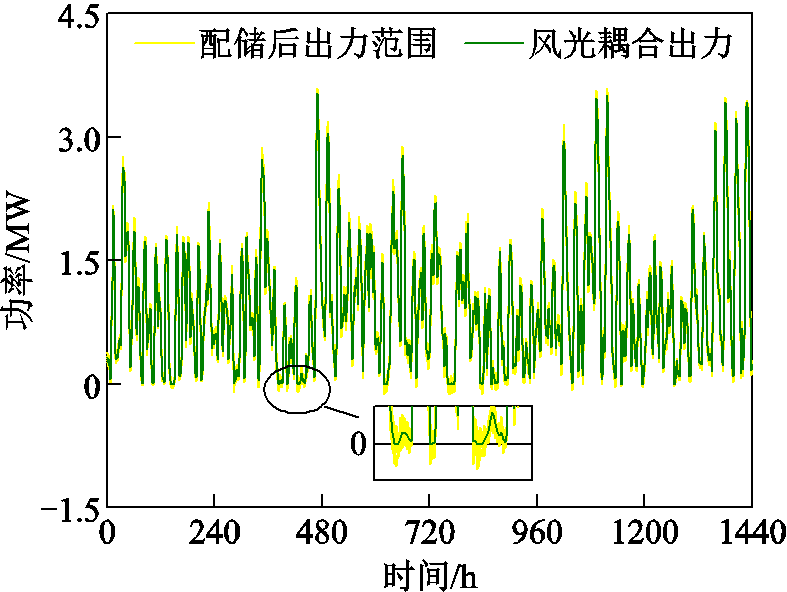
图6 配储前后风光耦合出力曲线
Fig.6 Wind-solar coupled output curves before and after energy storage configuration
为分析配置储能前后对风光耦合出力的影响,进一步计算配置储能前后出力的波动率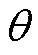 ,其可表示为在时间间隔
,其可表示为在时间间隔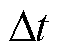 内最大输出功率
内最大输出功率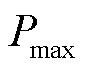 和最小输出功率
和最小输出功率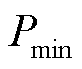 之差与额定功率
之差与额定功率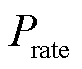 的比值,即
的比值,即
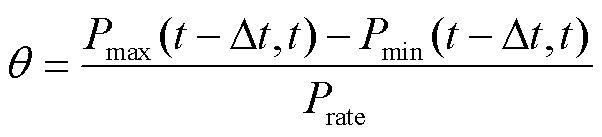 (32)
(32)
根据中长期时间范围划分,通过式(32)分别计算时间间隔为1、10、60、240 h,配储前后的出力波动率,结果见表6。从表6中可以明显看出,当时间间隔为1 h时,配储后的波动率小于配储前;当时间间隔大于1 h时,配储后的波动率大于配储前。由于数据样本的采样间隔为1 h,由此可见,混合储能对在相邻时刻的功率波动有较好的平抑作用。而在区间内的功率波动,配置储能后则能够有效地扩大风光耦合出力的波动区间,即从电源侧来讲,配置储能后对于风光耦合出力的波动有更大的包容能力。此外,时间间隔为10、60、240 h的波动容纳范围分别提升了12.9%、7.4%和6%,可见随着时间间隔的增加,波动容纳范围的提升幅度逐渐减小,这表明在一定的时间区间内,风光耦合出力的波动性越小,混合储能能够容纳波动的能力就越强;反之,混合储能能够容纳波动的能力就越差。尽管如此,混合储能仍然能够稳定地提供一定的裕度来容纳风光耦合出力的波动性。
表6 不同时间区间的系统出力波动率
Tab.6 Volatility of system output in different time intervals

配置储能情况 配储前0.045 50.298 70.589 10.764 4 配储后0.037 30.337 20.632 90.810 1
基于分布式风光互补系统在电源侧的出力波动性及其影响下混合储能的平抑策略,本文提出一种考虑多场景规划的混合储能平抑风光耦合出力波动的方法,使得混合储能在平抑电源侧波动的基础上,提升了对电源侧波动的容纳特性。得到主要结论如下:
1)采用场景规划得到的扰动功率场景与风光总出力具有一致的相关性,因此蓄电池与超级电容的分界频率并不会随着场景的数量而改变,这使得混合储能在不脱离实际出力的前提下可以有效地对具有随机性的扰动功率进行调频,达到最优涵盖所有场景的平抑需求。
2)多场景规划下配置储能前后频率偏差的RMSE下降率随10个场景下的60.0%增加至100个场景下的83.5%,而单个场景的频率偏差并不大,这表明场景规划下混合储能能够有效地调节风光耦合出力时的扰动功率频率,且扰动功率的频率变化越复杂,混合储能的调频能力也就越发明显。
3)混合储能的配置结果反映出超级电容的额定功率基本大于蓄电池的额定功率,而超级电容额定容量则小于蓄电池的额定容量,结合两种储能的功率特性,本文所提方法能够较好地发挥混合储能的运行特点,同时考虑经济成本可以更好地选择混合储能的配置方式。
4)经过配置混合储能后风光耦合出力的波动范围最大可提升12.9%,同时在风光耦合出力接近或为0时仍具有一定的调节能力,且无论风光耦合出力的波动性如何变化,混合储能均能够保证有一定的裕度对其进行容纳,较好地提升了风光互补系统的安全性。
通过本文所提方法,能够有效地提升风光互补系统对电源侧出力波动的包容能力,降低储能系统的波动平抑成本,提高系统的安全应用效益。
参考文献
[1] 黎博, 陈民铀, 钟海旺, 等. 高比例可再生能源新型电力系统长期规划综述[J]. 中国电机工程学报, 2023, 43(2): 555-581.
Li Bo, Chen Minyou, Zhong Haiwang, et al. A review of long-term planning of new power systems with large share of renewable energy[J]. Proceedings of the CSEE, 2023, 43(2): 555-581.
[2] 肖先勇, 郑子萱. “双碳”目标下新能源为主体的新型电力系统: 贡献、关键技术与挑战[J]. 工程科学与技术, 2022, 54(1): 47-59.
Xiao Xianyong, Zheng Zixuan. New power systems dominated by renewable energy towards the goal of emission peak & carbon neutrality: contribution, key techniques, and challenges[J]. Advanced Engineering Sciences, 2022, 54(1): 47-59.
[3] 张智刚, 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报, 2022, 42(8): 2806-2819.
Zhang Zhigang, Kang Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2819.
[4] 张宇涵, 杜贵平, 雷雁雄, 等. 直流微网混合储能系统控制策略现状及展望[J]. 电力系统保护与控制, 2021, 49(3): 177-187.
Zhang Yuhan, Du Guiping, Lei Yanxiong, et al. Current status and prospects of control strategy for a DC micro grid hybrid energy storage system[J]. Power System Protection and Control, 2021, 49(3): 177-187.
[5] 申建建, 王月, 程春田, 等. 水风光多能互补发电调度问题研究现状及展望[J]. 中国电机工程学报, 2022, 42(11): 3871-3885.
Shen Jianjian, Wang Yue, Cheng Chuntian, et al. Research status and prospect of generation scheduling for hydropower-wind-solar energy complementary system[J]. Proceedings of the CSEE, 2022, 42(11): 3871-3885.
[6] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485.
Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[7] 吕海鹏, 希望·阿不都瓦依提, 孟令鹏. 计及源-荷预测不确定性的微电网双级随机优化调度[J]. 电力自动化设备, 2022, 42(9): 70-78.
Lü Haipeng, Xiwang Abuduwayiti, Meng Lingpeng. Two-level stochastic optimal scheduling of microgrid considering uncertainty of source-load prediction[J]. Electric Power Automation Equipment, 2022, 42(9): 70-78.
[8] 程杉, 张芮嘉, 钟仕凌, 等. 计及需求响应柔性调节的可再生能源优化配置[J]. 电力系统及其自动化学报, 2023, 35(2): 94-102.
Cheng Shan, Zhang Ruijia, Zhong Shiling, et al. Optimal allocation of distributed renewable generations considering flexible regulation of demand-side response[J]. Proceedings of the CSU-EPSA, 2023, 35(2): 94-102.
[9] 陈泽西, 孙玉树, 张妍, 等. 考虑风光互补的储能优化配置研究[J]. 电工技术学报, 2021, 36(增刊1): 145-153.
Chen Zexi, Sun Yushu, Zhang Yan, et al. Research on energy storage optimal allocation considering complementarity of wind power and PV[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 145-153.
[10] Hajiaghasi S, Salemnia A, Hamzeh M. Hybrid energy storage system for microgrids applications: a review[J]. Journal of Energy Storage, 2019, 21: 543-570.
[11] 李建林, 郭斌琪, 牛萌, 等. 风光储系统储能容量优化配置策略[J]. 电工技术学报, 2018, 33(6): 1189-1196.
Li Jianlin, Guo Binqi, Niu Meng, et al. Optimal configuration strategy of energy storage capacity in wind/PV/storage hybrid system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1189-1196.
[12] Tang Rongchuan, Xu Qingshan, Fang Jicheng, et al. Optimal configuration strategy of hybrid energy storage system on industrial load side based on frequency division algorithm[J]. Journal of Energy Storage, 2022, 50: 104645.
[13] 张宇华, 李青松, 王丛, 等. 区域风光低频相关性互补与高频混合储能平抑的并网方法研究[J]. 中国电机工程学报, 2023, 43(4): 1492-1504.
Zhang Yuhua, Li Qingsong, Wang Cong, et al. Grid-connected method of regional wind-solar low-frequency correlation complementation and high-frequency hybrid energy storage stabilization[J]. Proceedings of the CSEE, 2023, 43(4): 1492-1504.
[14] 田博文, 张志禹, 杨梦飞. 基于多次滑动均值滤波的混合储能功率分配与定容研究[J]. 电工技术学报, 2024, 39(5): 1548-1564.
Tian Bowen, Zhang Zhiyu, Yang Mengfei. Research on hybrid energy storage power allocation and capacity determination based on multiple moving average filtering[J]. Transactions of China Electro-technical Society, 2024, 39(5): 1548-1564.
[15] 汪凯琳, 许仪勋, 潘瑞媛, 等. 考虑风光可靠性的微电网混合储能优化配置[J]. 电测与仪表, 2023, 60(5): 39-44, 50.
Wang Kailin, Xu Yixun, Pan Ruiyuan, et al. Optimal configuration of hybrid energy storage systems in micro-grid considering wind-solar reliability[J]. Electrical Measurement & Instrumentation, 2023, 60(5): 39-44, 50.
[16] 孟旭瑶, 付立军, 赖心怡, 等. 计及源荷互补特性的“源网荷储一体化项目”优化配置[J]. 电力自动化设备, 2024, 44(7): 123-131.
Meng Xuyao, Fu Lijun, Lai Xinyi, et al. Optimal configuration of “source-network-load-storage integrated project” considering source-load complementarity characteristics[J]. Electric Power Automation Equipment, 2024, 44(7): 123-131.
[17] 汪惟源, 窦飞, 程锦闽, 等. 一种风光联合出力概率模型建模方法[J]. 电力系统保护与控制, 2020, 48(10): 22-29.
Wang Weiyuan, Dou Fei, Cheng Jinmin, et al. A modeling method for a wind and photovoltaic joint power probability model[J]. Power System Protection and Control, 2020, 48(10): 22-29.
[18] Karimi H, Jadid S. A strategy-based coalition formation model for hybrid wind/PV/FC/MT/ DG/battery multi-microgrid systems considering demand response programs[J]. International Journal of Electrical Power & Energy Systems, 2022, 136: 107642.
[19] Wahbah M, Mohandes B, EL-Fouly T H M, et al. Unbiased cross-validation kernel density estimation for wind and PV probabilistic modelling[J]. Energy Conversion and Management, 2022, 266: 115811.
[20] Nelsen R B. An Introduction to Copulas[M]. New York: Springer, 2006.
[21] Sreekumar S, Khan N U, Rana A S, et al. Aggregated net-load forecasting using Markov-Chain Monte-Carlo regression and C-vine copula[J]. Applied Energy, 2022, 328: 120171.
[22] 贾彦, 李文雄, 赵萌, 等. 罚函数改进粒子群算法的风光储系统优化配置[J]. 太阳能学报, 2019, 40(7): 2071-2077.
Jia Yan, Li Wenxiong, Zhao Meng, et al. Optimal configeration for solar-wind-battery hybrid power system based on penalty function improved particle swarm optimization[J]. Acta Energiae Solaris Sinica, 2019, 40(7): 2071-2077.
[23] 李军徽, 侯涛, 穆钢, 等. 基于权重因子和荷电状态恢复的储能系统参与一次调频策略[J]. 电力系统自动化, 2020, 44(19): 63-72.
Li Junhui, Hou Tao, Mu Gang, et al. Primary frequency regulation strategy with energy storage system based on weight factors and state of charge recovery[J]. Automation of Electric Power Systems, 2020, 44(19): 63-72.
Smoothing Characteristic of Wind-Solar Coupled Output Fluctuations by Hybrid Energy Storage under Multi-Scenario Planning
Abstract The purpose of the wind-solar complementary system (WSCS) is to couple wind power and photovoltaic (PV) in a complementary way to strengthen the ability to generate power continuously in the medium and long term. However, due to the uncertainty of natural resources, the power output of WSCS is still unstable. In recent years, hybrid energy storage systems (HESS) have been used to match the WSCS to reduce the volatility of system output, but there are still some problems leading to the system's economic cost making it difficult to control. For example, the coupling relationship between wind and solar is linear, and the premise of the fluctuation smoothing strategy is to meet the power demand of load-side or grid-connected. In order to solve the mentioned problems, this paper proposes a method that HESS smooths fluctuations of wind-solar coupling power considering multi-scenario planning. By constructing a nonlinear coupling relationship between wind and solar and optimizing the capacity allocation of power source-side hybrid energy storage, the system accommodation characteristics for power fluctuations are improved.
Firstly, the marginal distributions of the two power sources are constructed using KDE based on the historical data of wind power and PV, and the joint distribution is obtained by preferably using the Gumbel-Copula functions. The multi-scenario set obtained by random sampling of the joint distribution is able to reflect the intensity of the fluctuation changes. Secondly, the FFT and its IFFT are used to analyze the spectral analysis of the unstable power in scenarios set to determine the power borne by each energy storage unit. In this part, since the multi-scenario ensemble originates from a joint distribution, the correlation of each scenario in the ensemble is consistent, which means the cut-off frequency that distinguishes battery and super-capacitor does not change with the change of scenario. Finally, an optimization model is established with the objective function of minimum the cycle operating cost of HESS, and the capacity configuration of the HESS is calculated using an improved PSO. The result of capacity configuration provides room to accommodate fluctuations in power source-side output, which reduces the instability of the system.
The results of the simulation example show that the increase in frequency deviation before the HESS configuration is much larger than that after the HESS configuration. The change rate of RMSE for calculating the frequency deviation before and after the configuration of HESS ranges from 60.0% to 83.5%, the change rate gradually increases with the increase of the number of scenarios in the ensemble. This suggests that the role of HESS in regulating frequency increases as the number of scenarios increases. Meanwhile, with the increase in the number of scenarios in the set, the maximum growth in the rated power and rated capacity of the batteries is 77.1% and 54.9%, respectively. And that of the super-capacitors is 40.0% and 42.4%. However, this makes the increase in equipment cost of the super-capacitor more prominent. Further, the configuration of HESS makes the power fluctuation of the system at adjacent moments smoother. The fluctuation accommodation range of the power source-side within the time intervals of 10 h, 60 h, and 240 h is enhanced by 12.9%, 7.4%, and 6%, respectively. The amplification of the fluctuation accommodation range decreases with the longer of the time intervals. Nevertheless, the HESS still has rechargeable power characteristics when the power source-side output is zero.
From the simulation results, the following conclusions can be drawn: (1) Different numbers of scenarios in the set have consistent correlation, so the dividing frequency of the battery and the super-capacitor does not change with the number of scenarios, which makes the HESS can be effective for the fluctuating power to modulate frequency. (2) The more complex the frequency variations of the fluctuating power at the wind-solar coupling output, the more pronounced the capability of HESS modulating frequency. (3) The results of the HESS configuration reflect that super-capacitors and batteries have greater advantages in the rated power and rated capacity, respectively. (4) Even if the wind-solar coupling output is close to 0 or 0 after the configuration of HESS, the system is still able to ensure that there is a certain margin to counteract the fluctuating impact of sudden power changes.
Keywords:Wind-solar coupled, scenario generation, frequency analysis, hybrid energy storage configuration, fluctuating accommodations
中图分类号:TM61
DOI: 10.19595/j.cnki.1000-6753.tces.241679
锡林郭勒盟科技计划资助项目(202201)。
收稿日期2024-09-26
改稿日期2024-11-23
高 帆 男,1997年生,硕士研究生,研究方向为新能源发电、储能技术的应用及优化等。
E-mail:gfan158@163.com
包道日娜 女,1976年生,教授,硕士生导师,研究方向为智能微电网、风光储系统一体化、全钒液流电池等。
E-mail:bdrn125@163.com(通信作者)
(编辑 赫 蕾)