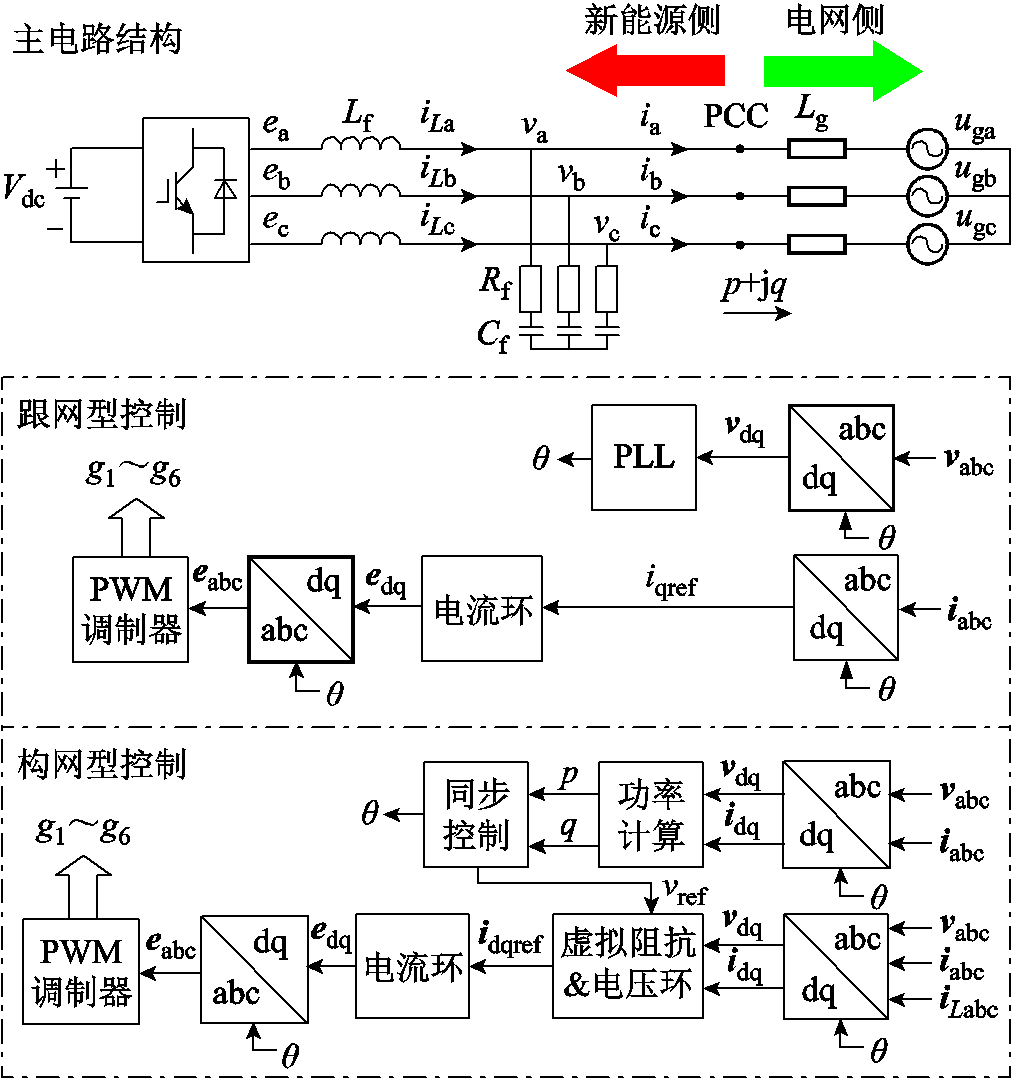
图1 新能源变流器并网系统拓扑及GFL/GFM控制结构
Fig.1 The topology of renewable energy converter grid-integration system and GFL/GFM control structure
摘要 目前新能源发电主要采用跟网型(GFL)控制同步并网,接入弱电网系统后易引发宽频振荡等小干扰稳定问题,且对电网支撑能力不足。构网型(GFM)技术通过功率同步控制自主构建电网电压,如何合理规划新能源并网系统GFM型单元的接入容量和位置,提高系统稳定特性,成为工程应用重点关注的问题。该文面向新能源集群/场站并网系统,研究计及小干扰稳定约束的GFM型单元配置问题。首先,根据新能源变流器单机并网系统小信号模型构建系统功率-电压闭环传递反馈模型,并验证前者和电流-电压闭环传递反馈模型在分析系统稳定特性时的一致性;其次,将单机并网系统模型和分析方法拓展至多机系统中,构建系统小干扰稳定与稳定支撑量化评估指标以及GFM型单元选点配置指标,提出系统GFM型单元配置求解方法;最后,基于实际新能源集群并网系统搭建分析算例,并通过时域仿真验证所提方法的有效性。
关键词:新能源并网系统 构网型单元配置 宽频振荡 小干扰稳定 稳定支撑能力
集中开发、远距离输送是我国新能源开发利用的重要形式,新能源发电基地通常远离交流系统主网架,缺少常规同步电源支撑。目前新能源发电主要采用跟网型(Grid-Following, GFL)控制,通过锁相控制实现同步并网,接入弱电网系统后易引发宽频振荡问题[1-2]。并且,当系统受到扰动时,GFL型新能源发电对电网的支撑能力不足,新能源发电基地逐渐呈现低抗扰和低支撑特性,安全稳定问题日益突出[3]。
近年的研究表明,构网型(Grid-Forming, GFM)控制通过功率同步控制自主构建并网点电压,当系统受到扰动时,GFM型新能源发电能够主动支撑电网电压和频率,提升系统稳定运行能力[4-5]。2024年8月,国家发展改革委联合国家能源局和国家数据局发布的《加快构建新型电力系统行动方案(2024—2027年)》中指出,要根据电力系统运行需要,选择典型场景应用构网型控制技术,提升系统安全稳定运行水平[6]。在我国新能源大规模、持续、快速发展态势下,开展以新能源集群/场站为主体的GFM型技术改造和升级,是新能源发展新阶段的重要工程课题。通过技术改造和升级,一方面可提升弱电网下新能源发电的支撑和稳定运行能力,另一方面能为后续新能源规模持续增长提供稳定裕度空间。
由于采用GFM型控制的新能源发电通常需预留部分出力以实现充足的支撑能力,因此,在现有技术和经济条件约束下,如何合理规划新能源并网系统内GFM型单元的容量和布点位置,在保证新能源的支撑和稳定能力的同时,尽量减少GFM型单元配置容量,成为现阶段新能源开发和运行亟须解决的问题。
针对上述问题,业界已开展了相关研究。在GFM型单元接入系统的建模与稳定性分析方面,文献[7-9]基于单机或两机系统探究了GFM型单元对系统稳定性的影响与提升作用;文献[10]基于直驱风电场并网系统聚合模型,研究了GFM型风电机组比例对系统稳定运行的影响。在GFM型单元在系统中的优化配置方面,文献[11]建立了新能源场站及网络元件的聚合阻抗模型,并分析了全功率域下GFM型变流器小干扰稳定问题;文献[12]基于系统广义短路比方法,将GFM型变流器建模为恒定内阻抗的电压源,在系统阻抗矩阵中将其描述为对地电纳支路,研究了GFM型变流器选址定容对系统小干扰稳定的影响;文献[13]在文献[12]的基础上,基于模态解耦思想,通过分析在低/次同步频段多个单馈入同构系统的稳定性,从而逼近GFL/GFM型新能源混联系统在对应频段的小干扰稳定性结果;文献[14]将系统广义短路比和GFM/GFL型变流器的容量比例相联系,分析了不同接入场景以及不同控制GFM型单元接入系统后对系统强度提升的影响;文献[15]考虑源荷多时间尺度波动性,建立了GFM型储能电站定容选址的调度模型,提升系统惯量与储能电池循环寿命;文献[16]建立了100%新能源场景下“源储荷”一体化系统中储能配置优化问题,并分析了GFM型场站在系统中占比对储能配置的影响。
综上所述,在新能源并网系统建模方面,现有研究大多基于两机系统或串并联汇集线路聚合等值模型,对系统内部节点接入的设备特性给系统稳定特性造成的影响考虑不足。另外,由于实际系统存在多类异构设备,可能向系统引入不同的振荡模态,将其等效为同构设备的方法适用性不足。在GFM型单元配置方面,现有研究采用的简化方法未能充分考虑GFM型单元的全频段动态特性对系统小干扰稳定性的影响,且鲜有文献考虑小干扰稳定和稳定支撑能力等系统稳定特性对GFM型单元配置的影响。因此,在计及新能源发电异构设备及网络特性情况下,如何配置新能源并网系统中的GFM型单元,以提升系统稳定运行特性,仍需深入探究。
本文以新能源集群并网系统为研究对象,研究并提出计及小干扰稳定约束的新能源并网系统GFM型单元配置方法。首先对新能源变流器单机并网系统建模,根据系统功率-电压传递反馈关系分析并验证系统的稳定特性;然后将单机并网系统分析拓展至多机系统中,基于系统阻抗网络电路模型,构建系统小干扰稳定和稳定支撑量化评估指标以及GFM型单元选点配置指标,提出系统GFM型单元配置求解方法;最后根据实际工程搭建典型新能源集群并网系统仿真模型,从集群和场站两个层面对新能源并网系统进行GFM型单元接入容量和布点的配置,分析汇集结构、电网强度和GFL型控制等因素对GFM型单元配置的影响,并通过时域仿真验证所提方法的有效性。
本文采用的新能源并网变流器电路拓扑及控制结构如图1所示。GFL型控制包括锁相环和电流环等控制环节。GFM型控制包括同步控制环和级联电压电流内环等控制环节。同步控制环采用虚拟同步控制策略,其中有功控制通过模拟同步发电机的运动方程生成相位角与电网保持同步,无功控制模拟同步发电机的励磁调节特性,级联电压电流内环实现端口电压和输出电流控制。另外,控制环节通常加入虚拟阻抗,以提升变流器的动态特性和稳定性。

图1 新能源变流器并网系统拓扑及GFL/GFM控制结构
Fig.1 The topology of renewable energy converter grid-integration system and GFL/GFM control structure
根据图1主电路拓扑,假设电网侧线路为纯感性阻抗,建立并网系统电网侧电路方程为
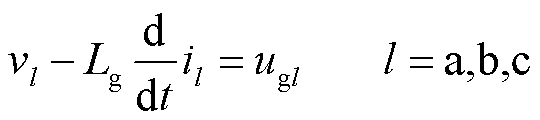 (1)
(1)
式中,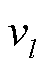 与
与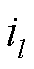 分别为三相并网点电压与电流;
分别为三相并网点电压与电流;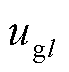 为三相理想电网电压;
为三相理想电网电压;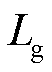 为电网线路电感。将式(1)转换至dq同步旋转坐标系下,设定电流流向电网为正方向,得到电网侧电路方程和p、q功率方程为
为电网线路电感。将式(1)转换至dq同步旋转坐标系下,设定电流流向电网为正方向,得到电网侧电路方程和p、q功率方程为
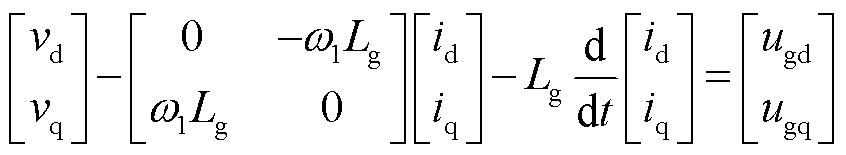 (2)
(2)
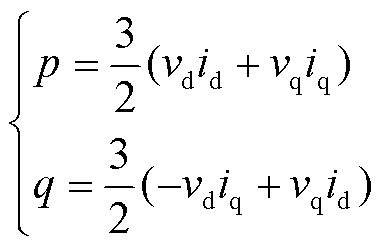 (3)
(3)
式中,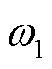 为额定角速度;p和q分别为系统中有功功率和无功功率;id, iq、vd, vq和ugd, ugq分别为并网点电流、电压和理想电网电压的d、q轴分量。线性化式(2)和式(3)并经拉氏变换到频域下有
为额定角速度;p和q分别为系统中有功功率和无功功率;id, iq、vd, vq和ugd, ugq分别为并网点电流、电压和理想电网电压的d、q轴分量。线性化式(2)和式(3)并经拉氏变换到频域下有
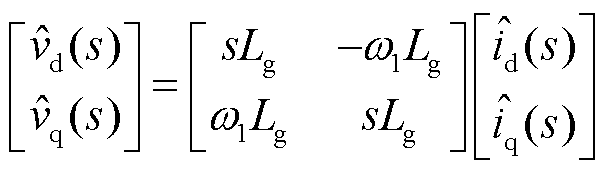 (4)
(4)
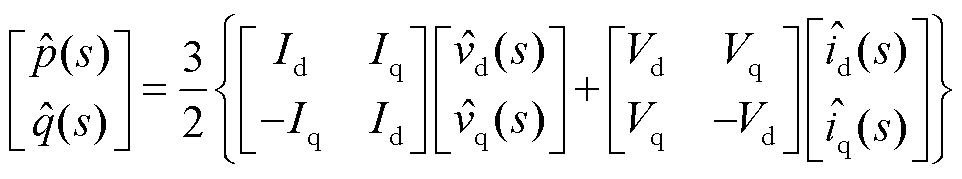 (5)
(5)
式中, 表示小信号量;
表示小信号量;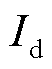 、
、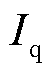 分别为并网点电流d、q轴稳态分量;
分别为并网点电流d、q轴稳态分量;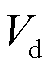 、
、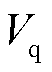 为并网点电压d、q轴稳态分量。式(4)中的传递函数矩阵即为电网侧阻抗矩阵
为并网点电压d、q轴稳态分量。式(4)中的传递函数矩阵即为电网侧阻抗矩阵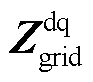 ,将式(4)左乘矩阵
,将式(4)左乘矩阵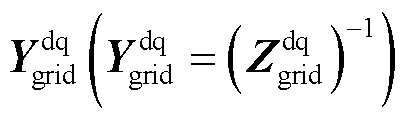 后联立式(5),可得
后联立式(5),可得
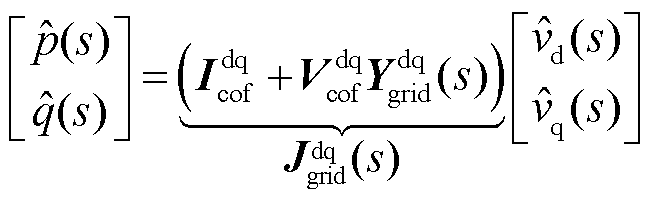 (6)
(6)
式中,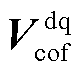 、
、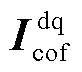 分别为同步旋转坐标系下并网点电压与电流的稳态分量系数矩阵;
分别为同步旋转坐标系下并网点电压与电流的稳态分量系数矩阵;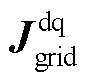 为dq同步旋转坐标系下电网侧的功率-电压雅克比传递函数矩阵。类似地,列写新能源侧在并网点处的电压电流关系,获得变流器小信号导纳矩阵
为dq同步旋转坐标系下电网侧的功率-电压雅克比传递函数矩阵。类似地,列写新能源侧在并网点处的电压电流关系,获得变流器小信号导纳矩阵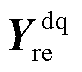 ,并联立式(5)可得
,并联立式(5)可得
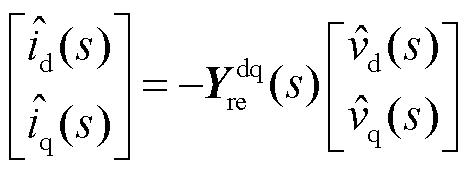 (7)
(7)
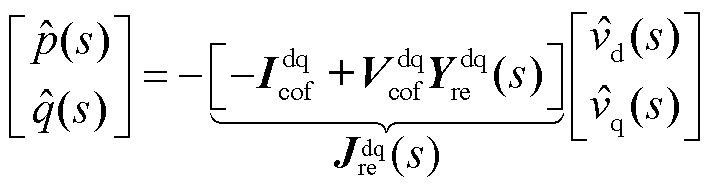 (8)
(8)
式中,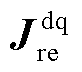 为dq同步旋转坐标系下新能源侧的功率-电压雅克比传递函数矩阵。
为dq同步旋转坐标系下新能源侧的功率-电压雅克比传递函数矩阵。
根据式(6)与式(8),可建立以并网点电压与功率小信号分量作为输入输出的系统传递反馈关系,并获得系统闭环传递函数矩阵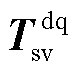 。
。
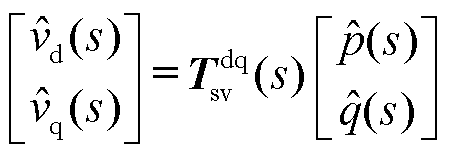 (9)
(9)
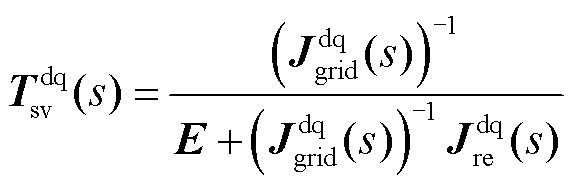 (10)
(10)
式中,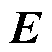 为单位矩阵。
为单位矩阵。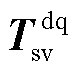 描述了新能源变流器与电网之间的交互作用,即变流器的输出功率扰动引起并网点电压波动,电压波动反作用于变流器,形成对功率扰动的反馈。传递函数矩阵
描述了新能源变流器与电网之间的交互作用,即变流器的输出功率扰动引起并网点电压波动,电压波动反作用于变流器,形成对功率扰动的反馈。传递函数矩阵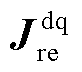 与
与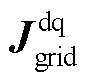 由新能源变流器、电网的阻抗/导纳以及系统稳态运行点组成,即上述因素共同决定了系统的动态和稳态特性。同时,无论新能源采用GFL型或GFM型控制,上述模型结构不变,只是传递函数矩阵中新能源侧的阻抗/导纳矩阵发生变化。
由新能源变流器、电网的阻抗/导纳以及系统稳态运行点组成,即上述因素共同决定了系统的动态和稳态特性。同时,无论新能源采用GFL型或GFM型控制,上述模型结构不变,只是传递函数矩阵中新能源侧的阻抗/导纳矩阵发生变化。
由于静止坐标系下的序阻抗模型与同步旋转坐标系下的dq阻抗模型之间可以相互等价转换[17],并且序阻抗建模方法物理含义清晰且信号易测量,方法适用性广,近年来得到了广泛的研究与应用[18-20]。因此本文后续推导和分析都基于静止坐标系下的序阻抗模型。将式(9)转换至静止坐标系下有
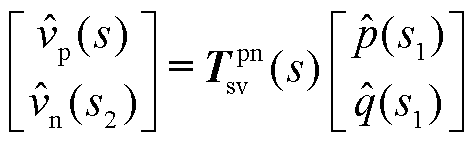 (11)
(11)
其中
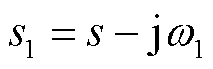
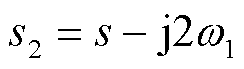
式中,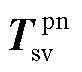 为静止坐标系下功率-电压系统闭环传递函数矩阵,具体可表示为
为静止坐标系下功率-电压系统闭环传递函数矩阵,具体可表示为
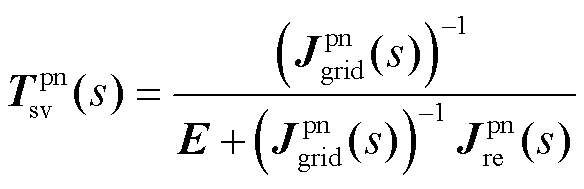 (12)
(12)
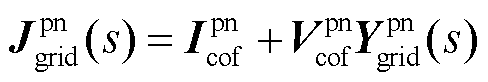 (13)
(13)
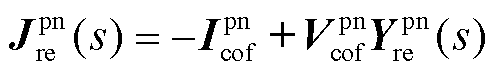 (14)
(14)
式中,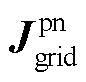 与
与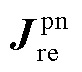 分别为静止坐标系下电网侧与新能源侧的功率-电压雅克比传递函数矩阵;
分别为静止坐标系下电网侧与新能源侧的功率-电压雅克比传递函数矩阵;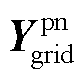 和
和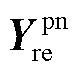 分别为静止坐标系下电网侧导纳矩阵和新能源侧导纳矩阵;
分别为静止坐标系下电网侧导纳矩阵和新能源侧导纳矩阵;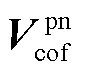 和
和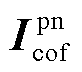 分别为静止坐标系下并网点电压与电流的稳态分量系数矩阵,表示为
分别为静止坐标系下并网点电压与电流的稳态分量系数矩阵,表示为
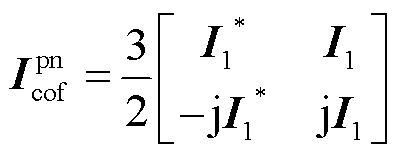 (15)
(15)
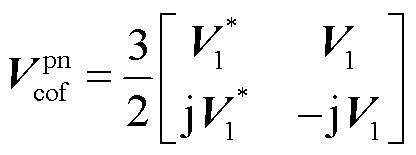 (16)
(16)
式中,*表示共轭运算;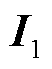 与
与 分别为新能源并网系统在并网点处电流与电压的稳态基频分量。
分别为新能源并网系统在并网点处电流与电压的稳态基频分量。
由1.1节可知,由于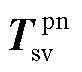 包含了新能源并网系统源-网之间的完整反馈动态过程,因此根据新能源并网系统稳定特性分析的目标不同,可基于统一的闭环传递反馈关系,通过不同角度分析系统小干扰稳定性和稳定支撑能力。
包含了新能源并网系统源-网之间的完整反馈动态过程,因此根据新能源并网系统稳定特性分析的目标不同,可基于统一的闭环传递反馈关系,通过不同角度分析系统小干扰稳定性和稳定支撑能力。
对于系统的小干扰稳定性,可基于系统的闭环特征方程,通过特征值分析法进行分析[21-23]。系统闭环特征方程可表示为
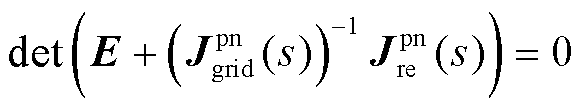 (17)
(17)
式中, 表示求解矩阵行列式。因为
表示求解矩阵行列式。因为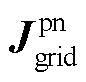 是由电网侧线路等无源器件组成的矩阵,故可将式(17)中矩阵左乘
是由电网侧线路等无源器件组成的矩阵,故可将式(17)中矩阵左乘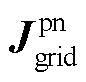 ,得到
,得到
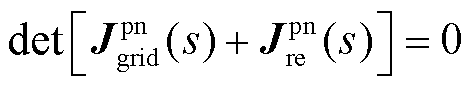 (18)
(18)
进一步地,将式(13)和(14)代入式(18)中,可得
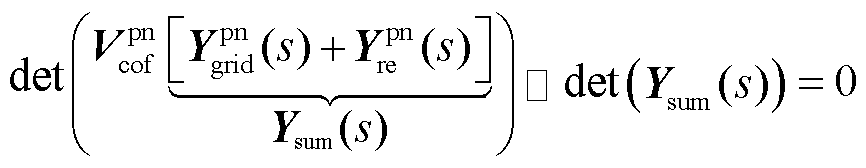 (19)
(19)
式中,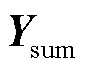 为新能源侧与电网侧频域导纳矩阵之和。可以发现,在特定运行点下,
为新能源侧与电网侧频域导纳矩阵之和。可以发现,在特定运行点下,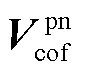 为常系数矩阵,不影响稳定性判断结果,因此,由新能源变流器频域导纳与电网频域导纳组成的
为常系数矩阵,不影响稳定性判断结果,因此,由新能源变流器频域导纳与电网频域导纳组成的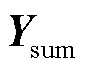 可以用来判断系统的小干扰稳定性。
可以用来判断系统的小干扰稳定性。
对于系统的小干扰稳定支撑能力,可理解为当稳定系统受到输入干扰时,系统输出对当前稳定状态的维持效果。在鲁棒控制理论中,可基于系统的灵敏度函数衡量[24]。因此,对于通过功率-电压闭环反馈模型描述的新能源并网系统,分析在稳定运行点时,受到功率扰动输入后系统电压输出的抗扰特性,进而评估系统的小干扰稳定支撑能力。建立新能源并网系统的灵敏度函数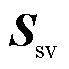 为
为
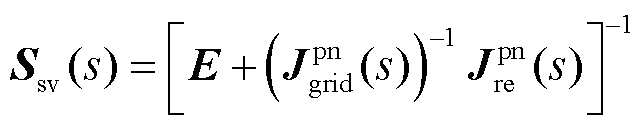 (20)
(20)
灵敏度函数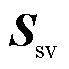 增益越小,说明系统电压输出对功率扰动输入的抗扰能力越强,或者系统对当前稳定状态的保持能力越好。灵敏度函数增益可通过范数表示为
增益越小,说明系统电压输出对功率扰动输入的抗扰能力越强,或者系统对当前稳定状态的保持能力越好。灵敏度函数增益可通过范数表示为
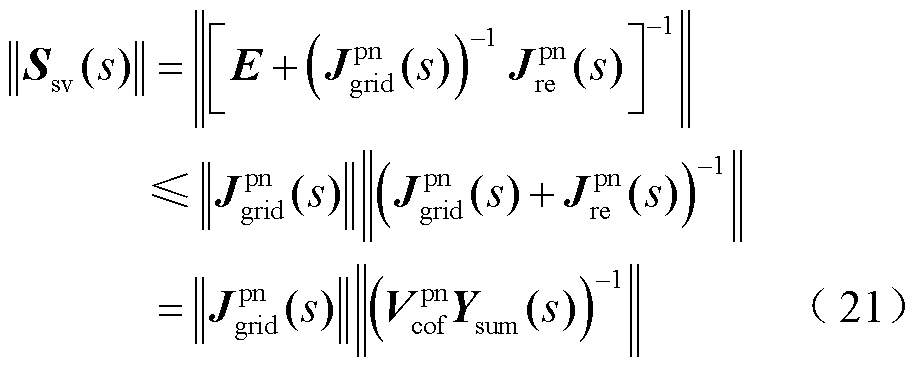
在宽频范围内,灵敏度函数增益可表示为
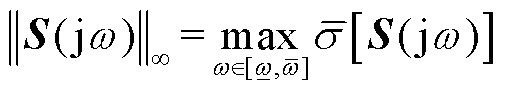 (22)
(22)
式中,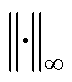 为求解矩阵无穷范数;
为求解矩阵无穷范数;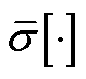 为求矩阵最大奇异值;
为求矩阵最大奇异值;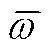 和
和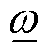 分别为系统待观测角频率的上、下限。可以发现,当电网和系统运行点不变时,
分别为系统待观测角频率的上、下限。可以发现,当电网和系统运行点不变时,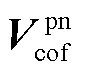 为常系数矩阵,
为常系数矩阵,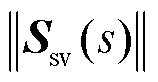 变化与
变化与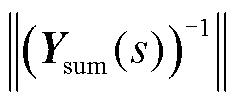 有关。因此,由新能源变流器频域导纳与电网频域导纳组成的
有关。因此,由新能源变流器频域导纳与电网频域导纳组成的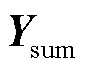 可以用来判断系统的小干扰稳定支撑特性。
可以用来判断系统的小干扰稳定支撑特性。
上述新能源并网系统闭环传递反馈模型中的功率信号输入-电压信号输出也可以替换为电流信号输入-电压信号输出,并得到相应的系统闭环传递函数矩阵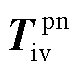 为
为
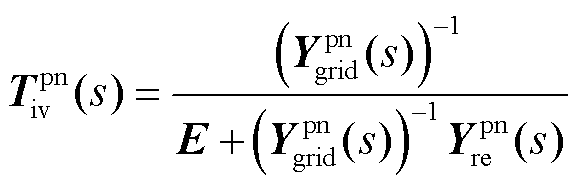 (23)
(23)
该系统的闭环特征方程可表示为
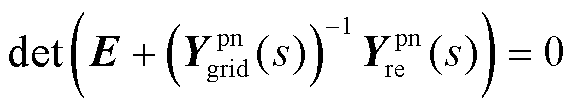 (24)
(24)
因为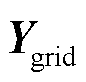 是由电网侧线路等无源器件组成的矩阵,故可将式(17)中矩阵左乘
是由电网侧线路等无源器件组成的矩阵,故可将式(17)中矩阵左乘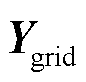 后写为
后写为
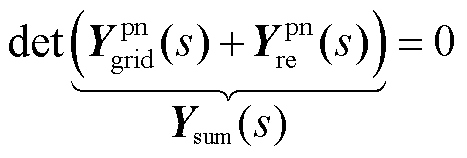 (25)
(25)
由式(25)可知,新能源变流器频域导纳与电网频域导纳组成的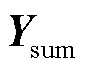 可以用来判断系统的小干扰稳定性。
可以用来判断系统的小干扰稳定性。
该系统灵敏度函数的主增益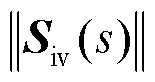 可表示为
可表示为
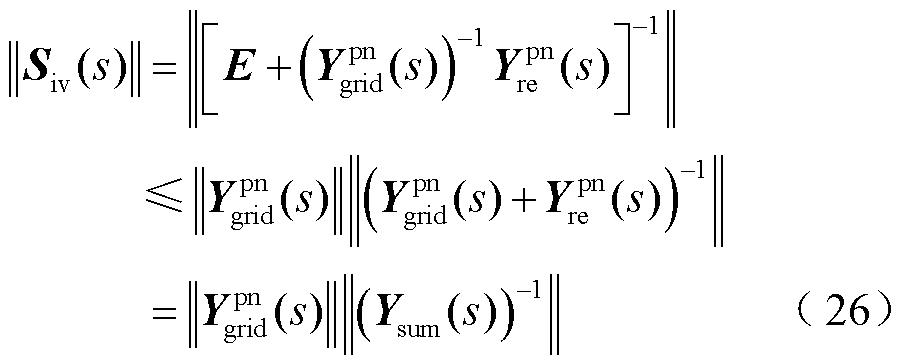
由式(26)可知,当电网侧不变时,系统灵敏度函数的主增益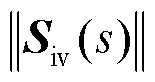 与
与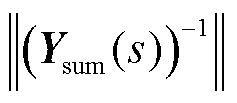 有关。因此,由新能源变流器频域导纳与电网频域导纳组成的
有关。因此,由新能源变流器频域导纳与电网频域导纳组成的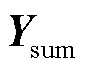 可以用来判断系统的小干扰稳定支撑特性。
可以用来判断系统的小干扰稳定支撑特性。
不同输入信号下系统闭环传递反馈关系示意图如图2所示。新能源并网系统的两种闭环传递反馈模型本质上是从不同输入角度描述同一个系统,而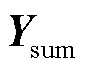 包含了系统新能源侧变流器和电网侧线路的动态特性,故可以准确反映系统中功率、电流等不同的输入信号扰动对输出电压响应之间的反馈关系。因此,通过
包含了系统新能源侧变流器和电网侧线路的动态特性,故可以准确反映系统中功率、电流等不同的输入信号扰动对输出电压响应之间的反馈关系。因此,通过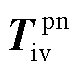 或
或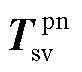 分析系统小干扰稳定能力与稳定支撑能力的效果是一致的。与
分析系统小干扰稳定能力与稳定支撑能力的效果是一致的。与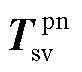 不同的是,
不同的是,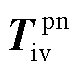 的传递反馈通道为新能源侧和电网侧的阻抗/导纳矩阵。
的传递反馈通道为新能源侧和电网侧的阻抗/导纳矩阵。
图2 不同输入信号下系统传递反馈关系示意图
Fig.2 Schematic diagram of feedback relationship of system under different input signals
搭建如图1所示的新能源变流器单机并网系统模型,分析验证系统的小干扰稳定性。设定新能源变流器接入短路比(Short Circuit Ratio, SCR)为1.3的弱电网,运行在单位功率因数下,变流器相关参数详见附表1。系统稳定特性结果见表1。由表1可知,当变流器的有功功率增至0.76(pu)时,根据式(19)计算系统特征值,GFL型变流器并网系统的特征值实部临近于0,系统接近失稳,而GFM型变流器并网系统的特征值实部远小于0,系统稳定。根据式(22)计算系统灵敏度函数增益,GFL型变流器并网系统灵敏度函数增益远大于GFM型变流器并网系统,说明前者稳定支撑特性不如后者。
表1 新能源并网系统稳定特性分析结果
Tab.1 Stability characterization results of renewable energy grid-integration system

参数GFL型变流器GFM型变流器 有功出力(pu)0.76 特征值实部-0.034-69.65 特征频率/Hz10.5/89.550 灵敏度函数增益21517
最后通过时域仿真对分析结果进行验证。系统小干扰稳定性仿真结果如图3所示。增加变流器有功出力,观测并网点电流波形时域仿真波形。当变流器有功出力为0.76(pu)时,GFL型变流器并网点电流发生如图3a所示振荡。对电流信号进行快速傅里叶变换(Fast Fourier Transform, FFT)分析,结果显示电流信号中存在10.5 Hz/89.5 Hz的谐波分量,表示系统存在宽频振荡风险。GFM型变流器并网点电流波形如图3b所示,波形平稳无明显谐波分量,系统可以稳定运行。系统小干扰稳定支撑特性仿真结果如图4所示。在仿真第5 s时刻分别向系统中注入0.1(pu)的基频功率扰动,观测并网点电压幅值相位时域仿真波形。从图4中发现,当系统受到相同幅度的功率扰动时,GFL型变流器的并网点电压幅值和相位波动远大于GFM型变流器。

图3 GFL/GFM型变流器仿真波形分析
Fig.3 Simulation waveforms analysis of GFL/GFM converter
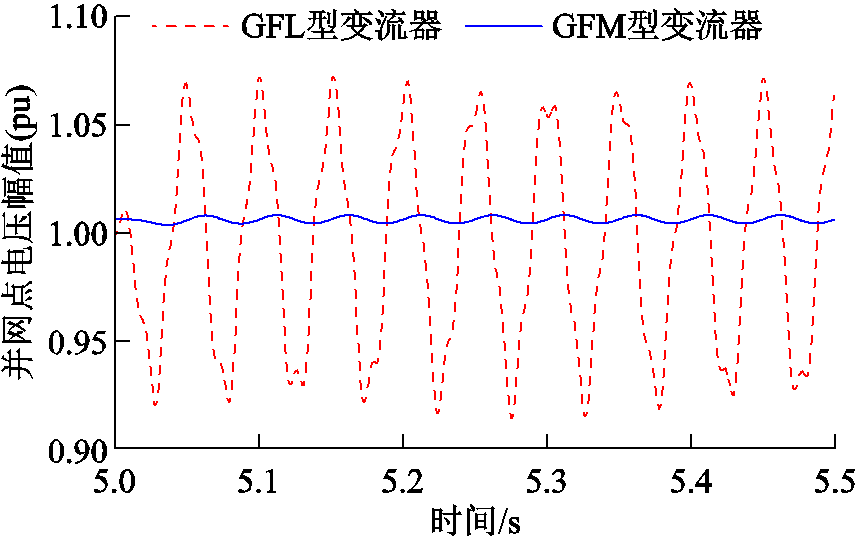
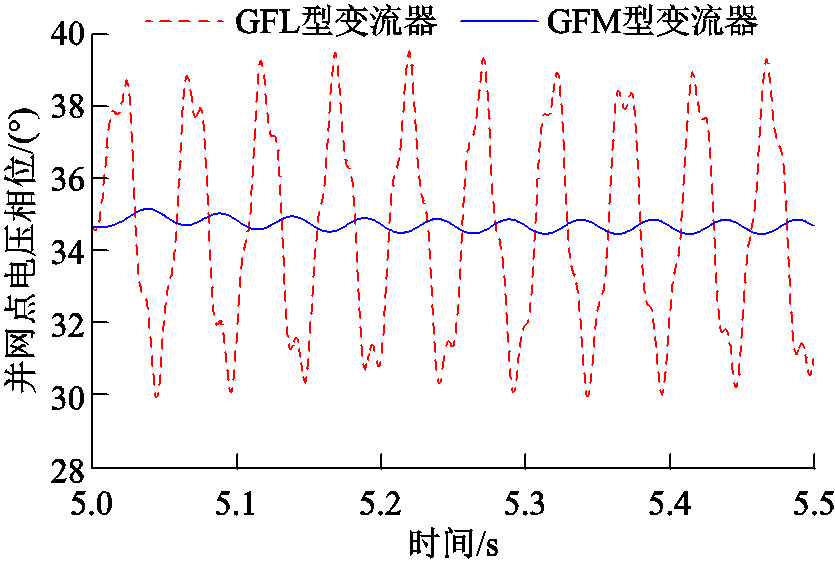
图4 GFL/GFM型变流器并网点电压幅值/相位波形
Fig.4 Simulation waveforms diagram of voltage amplitude/phase at the PCC of GFL/GFM converter
前文中新能源变流器单机并网系统闭环传递反馈关系可进一步拓展至新能源集群并网系统等多机系统中。在此基础上,本节设定多机新能源并网系统GFM型单元接入容量和布点配置问题。该问题的求解目标为系统中配置GFM型单元的总容量最小,约束条件为系统有充足的稳定裕度和稳定支撑能力。求解上述问题有两个关键点:一是满足GFM型单元接入系统的稳定性要求,即准确刻画系统小干扰稳定性约束,以及新能源对电网的稳定支撑特性,量化评估GFM型单元对系统的稳定运行提升能力;二是保证GFM型单元接入系统的经济性要求,即在满足稳定性要求的基础上,在新能源并网系统内寻找最优节点配置GFM型单元。
两个关键点侧重方向不同,前者重点考虑新能源并网系统外部整体特性的评估,后者着重关注新能源并网系统内部节点特性的变化。因此,本文基于新能源并网系统阻抗网络电路模型,当评估系统支撑能力和稳定送出能力时,采用计及网络拓扑的系统聚合阻抗模型;当指导GFM型单元在系统中的布点配置时,采用基于多变量反馈的系统节点阻抗模型。
以典型新能源发电场站为例构建典型新能源并网系统。每个新能源变流器单元经过箱式升压变压器并联接入中压馈线,多条馈线统一接入汇集母线,最后通过主变压器并入电网。构建新能源并网系统阻抗网络电路模型如图5所示。
阻抗网络模型共有n+1个节点,包含n个系统网络节点和并网点0号节点。以正序电路模型为例,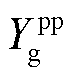 为正序电网导纳,
为正序电网导纳,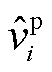 为系统内节点i的正序电压小信号分量,
为系统内节点i的正序电压小信号分量,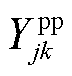 为系统中节点j、k间的正序线路导纳。考虑频率耦合效应的新能源并网变流器可表示为变流器正序导纳
为系统中节点j、k间的正序线路导纳。考虑频率耦合效应的新能源并网变流器可表示为变流器正序导纳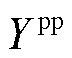 并联一个受控电流源
并联一个受控电流源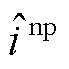 。计及网络拓扑的阻抗建模方法和系统阻抗网络电路模型同样适用于新能源集群等其他具有任意网络拓扑的新能源并网系统的分析。
。计及网络拓扑的阻抗建模方法和系统阻抗网络电路模型同样适用于新能源集群等其他具有任意网络拓扑的新能源并网系统的分析。
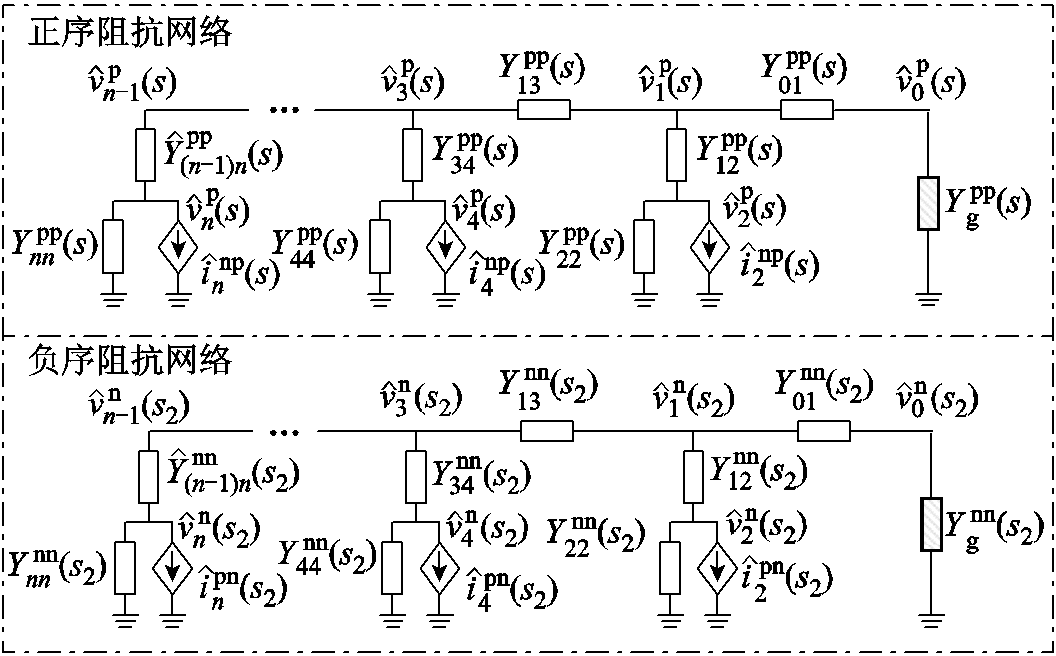
图5 新能源并网系统阻抗网络电路模型
Fig.5 Impedance network circuit model of renewable energy grid-integration system
根据阻抗网络电路模型,可按照各节点电压电流小信号分量关系,将正负序电压电流小信号分量、网络节点导纳矩阵和变流器导纳矩阵按照系统节点顺序组合,得到描述新能源并网系统内各节点的闭环传递反馈关系如图6所示。由图6可得
 (27)
(27)
式中, 和
和 分别为系统节点阻抗网络的电压和电流小信号分量,具体可表示为
分别为系统节点阻抗网络的电压和电流小信号分量,具体可表示为
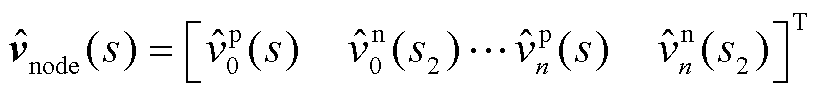 (28)
(28)
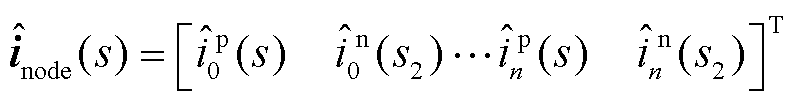 (29)
(29)
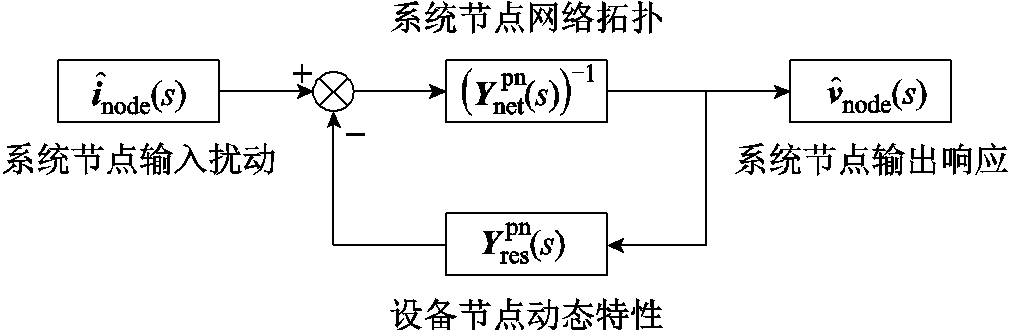
图6 新能源并网系统节点传递反馈关系示意图
Fig.6 Schematic diagram of feedback relationship between nodes in renewable energy grid-integration system
系统节点闭环传递函数矩阵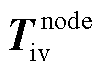 具体可表示为
具体可表示为
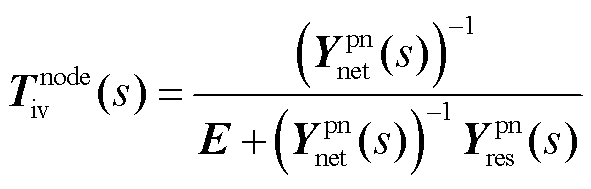 (30)
(30)
式中,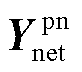 为
为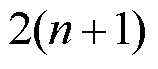 维网络元件导纳矩阵;
维网络元件导纳矩阵;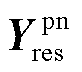 为
为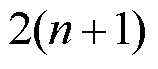 维变流器导纳矩阵,矩阵元素详见附录。
维变流器导纳矩阵,矩阵元素详见附录。
对比图2和图6可发现,从新能源单机并网系统拓展至多机并网系统后,主要变化在于电网侧从单节点线路导纳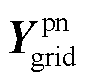 拓展为多节点导纳网络
拓展为多节点导纳网络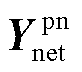 ,新能源侧从单个新能源变流器接入并网点的导纳矩阵
,新能源侧从单个新能源变流器接入并网点的导纳矩阵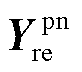 拓展为多个新能源变流器接入多个网络节点的导纳矩阵
拓展为多个新能源变流器接入多个网络节点的导纳矩阵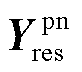 ,输入输出信号从并网点电流电压单变量拓展为网络节点电流电压多变量。然而,新能源侧与电网侧之间的传递反馈关系不变,因此,第1节中有关单机系统的稳定特性分析方法可拓展适用于多机系统中。
,输入输出信号从并网点电流电压单变量拓展为网络节点电流电压多变量。然而,新能源侧与电网侧之间的传递反馈关系不变,因此,第1节中有关单机系统的稳定特性分析方法可拓展适用于多机系统中。
根据阻抗网络电路模型,将新能源侧内部节点等值聚合在并网点处,以便分析系统在并网点处的稳定特性以及新能源与电网之间的交互作用。新能源侧在并网点处电压电流小信号关系可表示为
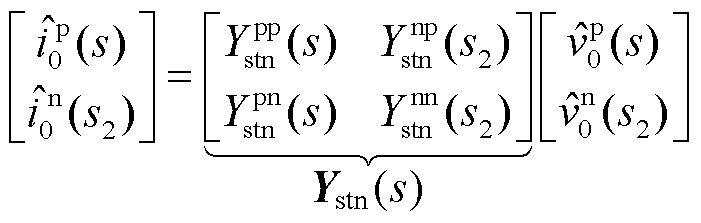 (31)
(31)
式中,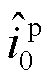 和
和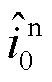 分别为并网点正、负序电流小信号分量;Ystn为新能源侧在并网点处的二阶等值导纳矩阵。Ystn为新能源侧的全阶频域模型,计及了阻抗网络及内部各新能源发电单元的频率耦合效应对系统并网点电压与电流小信号分量的影响,矩阵中各元素详细表达式可参考文献[25]。
分别为并网点正、负序电流小信号分量;Ystn为新能源侧在并网点处的二阶等值导纳矩阵。Ystn为新能源侧的全阶频域模型,计及了阻抗网络及内部各新能源发电单元的频率耦合效应对系统并网点电压与电流小信号分量的影响,矩阵中各元素详细表达式可参考文献[25]。
2.2.1 系统小干扰稳定裕度指标
将Ystn转换至等效正序导纳模型,可表示为
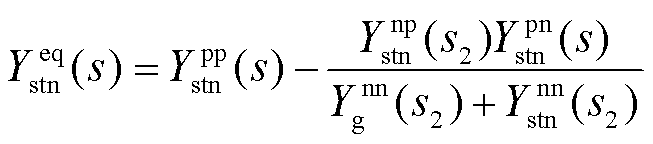 (32)
(32)
通过求解新能源侧正序阻抗与电网正序阻抗比值的Nyquist曲线,并通过系统稳定裕度函数G,依托Nyquist稳定性判据评估系统稳定性[26]。
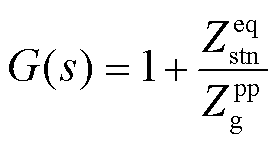 (33)
(33)
式中,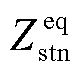 为新能源侧等效正序阻抗;
为新能源侧等效正序阻抗;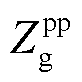 为电网正序阻抗。G包含完整的系统动态特性,可作为新能源并网系统的宽频振荡风险约束条件。
为电网正序阻抗。G包含完整的系统动态特性,可作为新能源并网系统的宽频振荡风险约束条件。
根据系统稳定裕度函数定义新能源并网系统小干扰稳定指标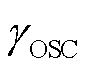 以评估系统稳定程度,即
以评估系统稳定程度,即
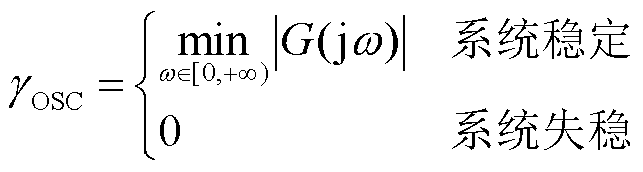 (34)
(34)
式中,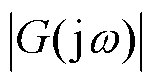 为系统稳定裕度函数的模。当系统稳定时,γOSC等于
为系统稳定裕度函数的模。当系统稳定时,γOSC等于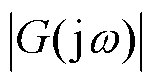
 最小值;当系统失稳时,规定γOSC=0。设定系统小干扰稳定指标的限值
最小值;当系统失稳时,规定γOSC=0。设定系统小干扰稳定指标的限值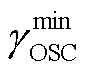 ,对于不同电网结构和运行方式下系统的稳定要求,可以适当调整限值大小。
,对于不同电网结构和运行方式下系统的稳定要求,可以适当调整限值大小。
2.2.2 系统小干扰稳定支撑指标
当系统中发生功率扰动时,GFM型单元首先要控制系统内并网点等关键节点电压的波动程度。系统灵敏度函数主增益可表示为
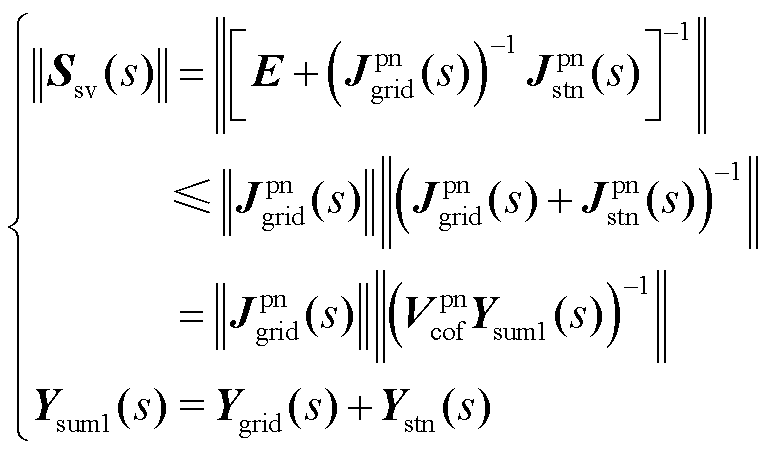 (35)
(35)
根据1.2节可知,当电网和系统运行点不变时,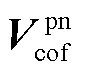 为常系数矩阵,
为常系数矩阵,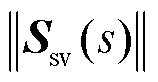 变化与
变化与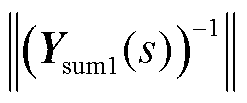 有关。假设新能源并网系统中原有GFM型单元容量比例为
有关。假设新能源并网系统中原有GFM型单元容量比例为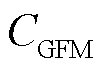 %,当系统中GFM型单元容量比例变化
%,当系统中GFM型单元容量比例变化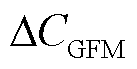 %时,对应系统等值导纳矩阵和变化
%时,对应系统等值导纳矩阵和变化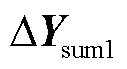 ,进而引起系统灵敏度函数增益变化。
,进而引起系统灵敏度函数增益变化。
因此,定义GFM型单元接入对系统小干扰稳定支撑能力的增益变化率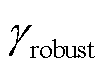 为
为
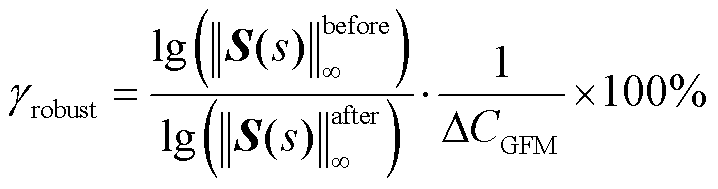 (36)
(36)
式中,lg表示以10为底对数运算,通过对数等效变换修正数据波动对结果带来的影响;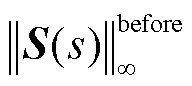 和
和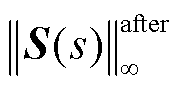 分别为系统初始和最终的灵敏度函数增益;
分别为系统初始和最终的灵敏度函数增益;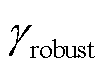 反映了系统灵敏度函数增益变化随系统中GFM型单元容量比例变化的增长关系,
反映了系统灵敏度函数增益变化随系统中GFM型单元容量比例变化的增长关系,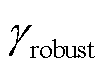 越大,说明当前接入系统中GFM型单元容量比例平均变化对系统并网点的小干扰稳定支撑的增益越显著。当系统中GFM型单元的容量达到一定比例时,继续向系统中配置更多容量的GFM型单元可能使得
越大,说明当前接入系统中GFM型单元容量比例平均变化对系统并网点的小干扰稳定支撑的增益越显著。当系统中GFM型单元的容量达到一定比例时,继续向系统中配置更多容量的GFM型单元可能使得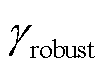 减小,意味着系统灵敏度函数增益的提升效果减弱,对系统小干扰稳定支撑能力的增益效果下降,导致设备冗余配置。
减小,意味着系统灵敏度函数增益的提升效果减弱,对系统小干扰稳定支撑能力的增益效果下降,导致设备冗余配置。
设定系统稳定支撑增益变化率的限值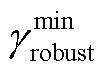 。根据实际工程案例需要适当调整限值大小,量化评估新能源并网系统中GFM型单元接入后对系统支撑能力增益的提升效果。
。根据实际工程案例需要适当调整限值大小,量化评估新能源并网系统中GFM型单元接入后对系统支撑能力增益的提升效果。
基于新能源并网系统节点阻抗模型,采用频域模态参与因子定位系统内各节点阻抗特性变化对系统稳定性的影响。根据图6推导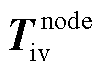 闭环特征方程为
闭环特征方程为
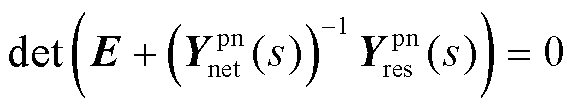 (37)
(37)
因为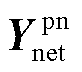 是由系统网络线路等无源器件组成的矩阵,故可将式(37)中矩阵左乘
是由系统网络线路等无源器件组成的矩阵,故可将式(37)中矩阵左乘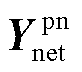 ,写为
,写为
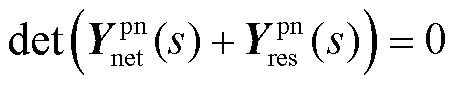 (38)
(38)
通过矩阵舒尔变换,将式(38)转换为求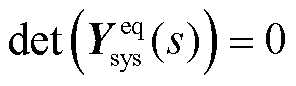 的解,
的解,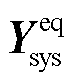 具体元素详见附录。当系统失稳时,对应
具体元素详见附录。当系统失稳时,对应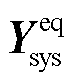 至少存在一个特征值
至少存在一个特征值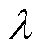 =0。对
=0。对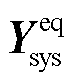 进行特征值分解,可得
进行特征值分解,可得
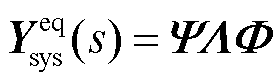 (39)
(39)
式中,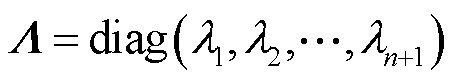 为特征值对角矩阵;
为特征值对角矩阵;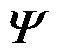 和
和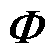 分别为
分别为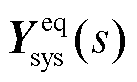 的左和右特征向量矩阵。定义在
的左和右特征向量矩阵。定义在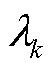 代表的主导振荡模态k下,系统内变流器接入节点
代表的主导振荡模态k下,系统内变流器接入节点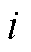 的参与因子
的参与因子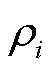 为
为
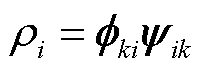 (40)
(40)
式中,左特征向量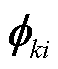 反映节点
反映节点 注入电流对主导振荡模态k的作用;右特征向量
注入电流对主导振荡模态k的作用;右特征向量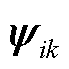 为对应系统模态的权重。
为对应系统模态的权重。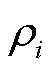 越大,表明节点
越大,表明节点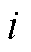 对系统失稳的影响程度越大,是系统网络中的薄弱节点。因此,根据新能源并网系统节点阻抗模型特征方程计算系统在该运行点的主导振荡模态,计算该振荡模态下系统的节点参与因子
对系统失稳的影响程度越大,是系统网络中的薄弱节点。因此,根据新能源并网系统节点阻抗模型特征方程计算系统在该运行点的主导振荡模态,计算该振荡模态下系统的节点参与因子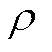 ,作为指导GFM型单元选点配置指标,并选取最大参与因子所在节点替换配置GFM型单元。对于包含不同类型异构设备的新能源并网系统,可能存在不同频率的多个振荡模态,应优先选取在复平面中位置最靠近右半平面的特征值,将其代表的振荡模态作为主导振荡模态,优先根据该振荡模态节点参与因子配置GFM型单元。
,作为指导GFM型单元选点配置指标,并选取最大参与因子所在节点替换配置GFM型单元。对于包含不同类型异构设备的新能源并网系统,可能存在不同频率的多个振荡模态,应优先选取在复平面中位置最靠近右半平面的特征值,将其代表的振荡模态作为主导振荡模态,优先根据该振荡模态节点参与因子配置GFM型单元。
结合前述提出的系统稳定特性量化评估指标以及GFM型单元选点配置指标,本文提出一种新能源并网系统GFM型单元配置求解方法,流程如图7所示,具体步骤如下。
(1)输入系统数据。系统数据主要包括新能源并网系统的运行点参数、新能源并网系统网络拓扑参数和新能源发电单元的控制参数。
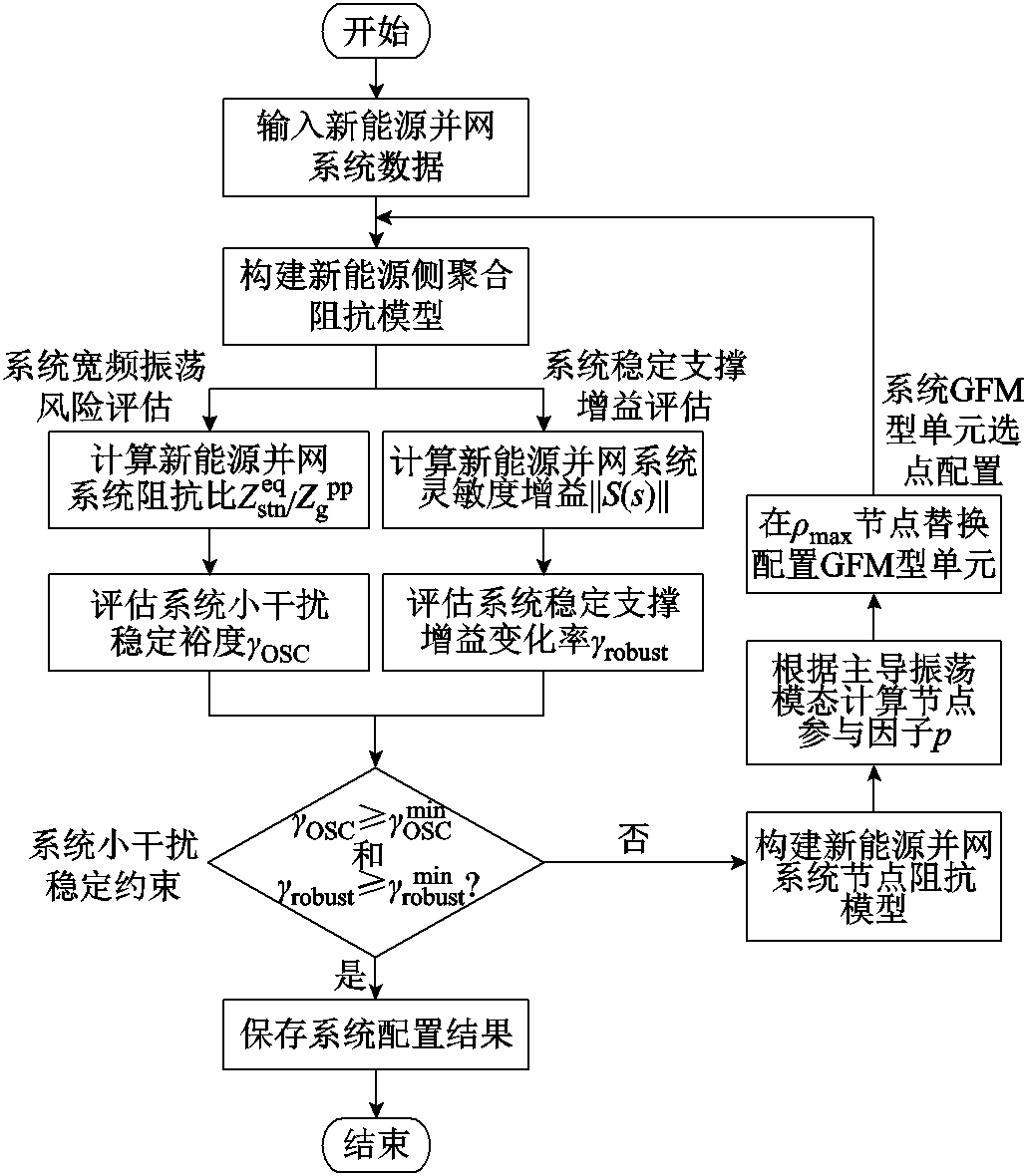
图7 新能源并网系统GFM型单元配置方法流程
Fig.7 Flow chart of the configuration method for GFM units of renewable energy grid-integration system
(2)评估系统稳定特性。构建新能源侧聚合阻抗模型,在特定运行点分别计算系统阻抗比和系统灵敏度增益,评估系统的宽频振荡风险以及稳定支撑增益变化率;若不满足系统小干扰稳定约束,则进行系统GFM型单元选点配置。
(3)系统GFM型单元选点配置。构建新能源并网系统的节点阻抗模型,计算模型特征方程与节点参与因子,选取参与因子最大节点配置GFM型单元。
(4)配置结果检验。新能源并网系统GFM型配置完毕后,重复运行步骤(2)和步骤(3)迭代检验新能源并网系统GFM型单元配置结果,直至系统满足系统稳定特性要求,系统配置求解结束。
本节基于典型新能源集群并网系统构建算例,从实际工程规划角度,从两个层面分别对新能源集群和集群内各场站进行GFM型单元(以并网变流器为例)的容量和布点配置。在新能源集群并网系统层面,优先配置集群内各场站GFM型单元的接入容量,提升集群并网运行的小干扰稳定能力。在新能源场站并网系统层面,确定GFM型单元在场站内的布点配置,进一步减小场站的小干扰失稳风险,同时评估场站对并网汇集点的稳定支撑能力。另外,基于场站算例分析了系统汇集结构、电网强度和GFL型单元控制参数等因素对GFM型单元配置的影响。最后通过时域仿真验证所提方法的有效性。考虑所构建算例系统的稳定运行能力和动态特性,参照阻抗稳定性分析相关标准[27],设定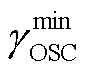 = 0.2,
= 0.2,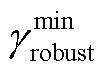 =25%。
=25%。
建立如图8所示的典型新能源集群并网系统仿真模型,集群由8个额定容量为99 MW的GFL型新能源发电场站构成。在实际工程中,集群内部可能存在多个新能源发电设备供应商,不同新能源发电单元采用的GFL型控制策略及参数会存在差异,影响系统并网动态特性。因此,根据控制参数的差异,新能源发电场站又分为A、B两种类型,其中B型场站的动态特性相对较差。集群中各新能源场站分别通过35 kV和220 kV两级升压变压器和不同距离汇集线路接入220 kV主电网,系统具体参数详见附表1和附表2。
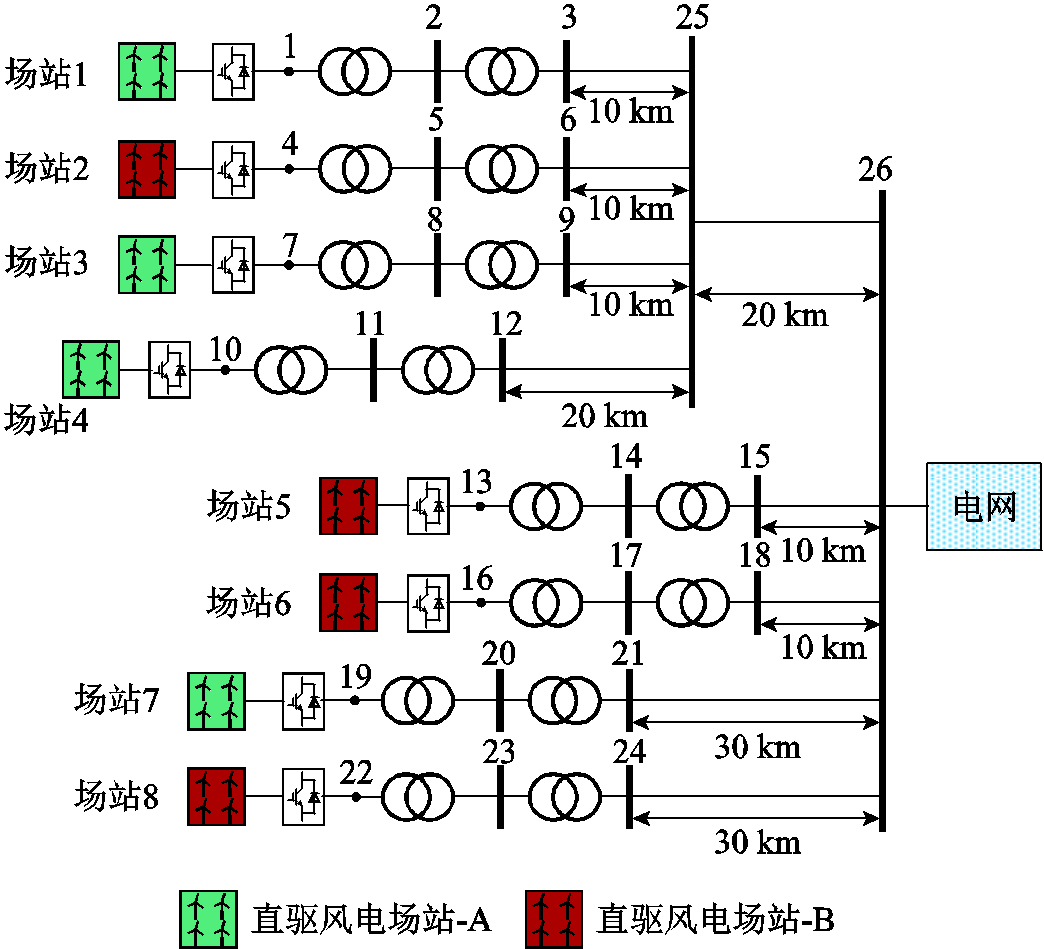
图8 新能源集群并网系统网络拓扑示意图
Fig.8 Network topology diagram of renewable energy cluster grid-integration system
设定新能源集群接入SCR=2.5的弱电网,在新能源集群并网系统场景下,考虑集群内所有机组运行工况的组合会导致计算维数灾,因此设定集群内各场站内部所有机组类型和控制参数相同,且出力一致,集群内场站采用单机容量等值模型进行模拟。
GFM型单元配置最终结果如图9所示。由图9可知,新能源集群共替换配置84 MW的GFM型单元,约占系统总容量的10.6%。根据图9可知:①场站2配置GFM型单元的比例在集群中最高,GFM型单元容量占比约为场站2总容量的15%。这是由于场站2为B型场站,其并网动态特性相较于场站4到并网点之间的长距离汇集线路,对集群并网系统稳定性的影响更大,并且场站2经2条汇流母线并网,易受母线功率和电压扰动影响,引发小干扰稳定性问题。②对比场站3与场站4之间的配置结果可发现,场站距离汇流母线和并网点的距离越远,其对系统稳定性的影响越大,相应需要配置更多GFM型单元。③对比场站2与场站1、3、4之间,以及场站7与场站8之间的配置结果可发现,由于B型场站相比A型场站的动态特性较差,因此需要对其配置更高容量比例的GFM型单元。
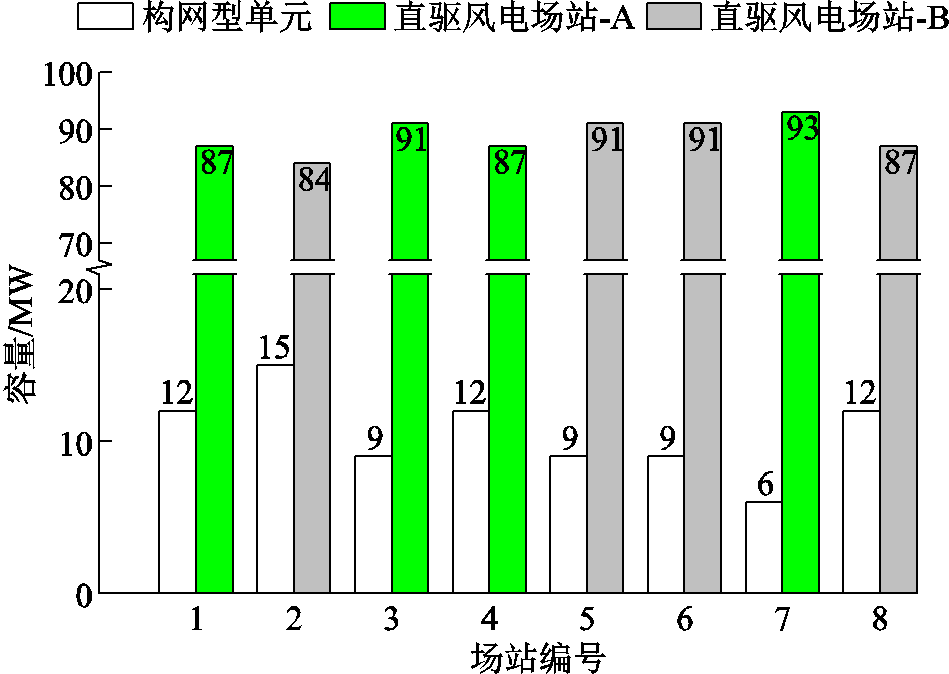
图9 新能源集群GFM型单元配置结果
Fig.9 Capacity configuration results of GFM units in renewable energy cluster
新能源集群并网系统配置结束后,在新能源场站并网系统层面,继续对集群内场站进行GFM型单元布点配置。以集群内场站1为例,建立典型新能源场站并网系统仿真模型如图10所示。
场站内包含3条35 kV馈线,每条馈线接入11台额定容量为3 MW的GFL型单元,馈线1、馈线2和馈线3的新能源发电单元接入间距分别为5 km、3 km和1 km,代表由新能源发电单元接入间距不同引起的系统汇集结构变化。
设定场站近似接入等效SCR为1.5的电网,已知场站内需要配置4台共计12 MW的GFM型单元。新能源场站对GFM型单元布点分配求解结果见表2。首先在馈线1和馈线2线路末端配置1台GFM型单元后,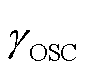 >0,系统虽然恢复稳定,但仍小于
>0,系统虽然恢复稳定,但仍小于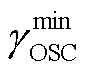 ,不满足稳定裕度要求。当系统中配置4台GFM型单元后,系统恢复额定运行能力,
,不满足稳定裕度要求。当系统中配置4台GFM型单元后,系统恢复额定运行能力,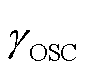 =0.33,满足配置要求。另外由表2可知,每向系统中替换接入一台GFM型单元,系统的灵敏度增益也逐渐降低,证明系统的支撑能力在不断提升,最终
=0.33,满足配置要求。另外由表2可知,每向系统中替换接入一台GFM型单元,系统的灵敏度增益也逐渐降低,证明系统的支撑能力在不断提升,最终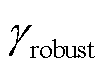 =28.42%,满足配置要求。
=28.42%,满足配置要求。
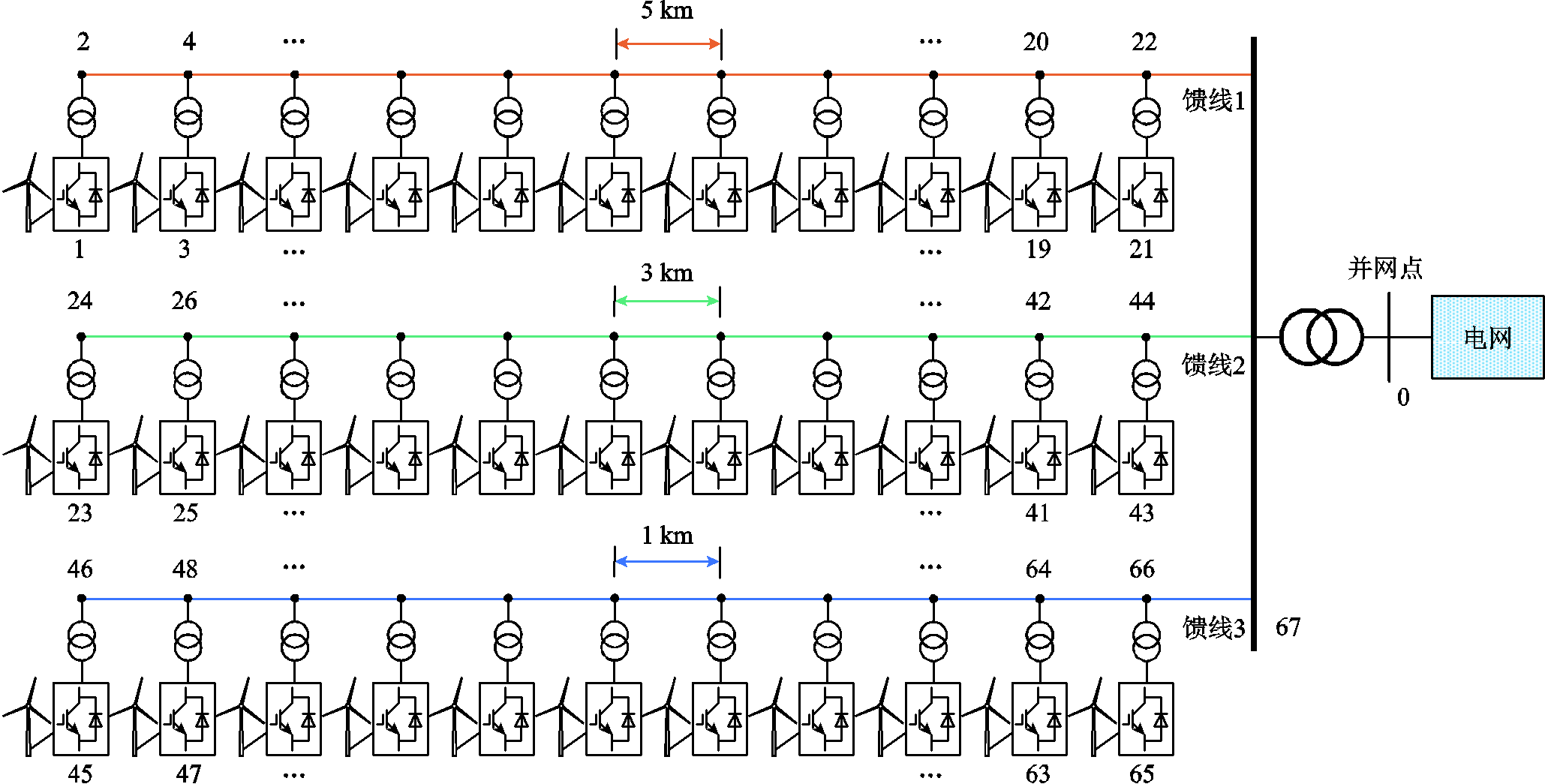
图10 新能源场站并网系统网络拓扑示意图
Fig.10 Network topology diagram of renewable energy station grid-integration system
表2 新能源场站GFM型单元配置求解结果
Tab.2 Results for the configuration of GFM units in renewable energy station
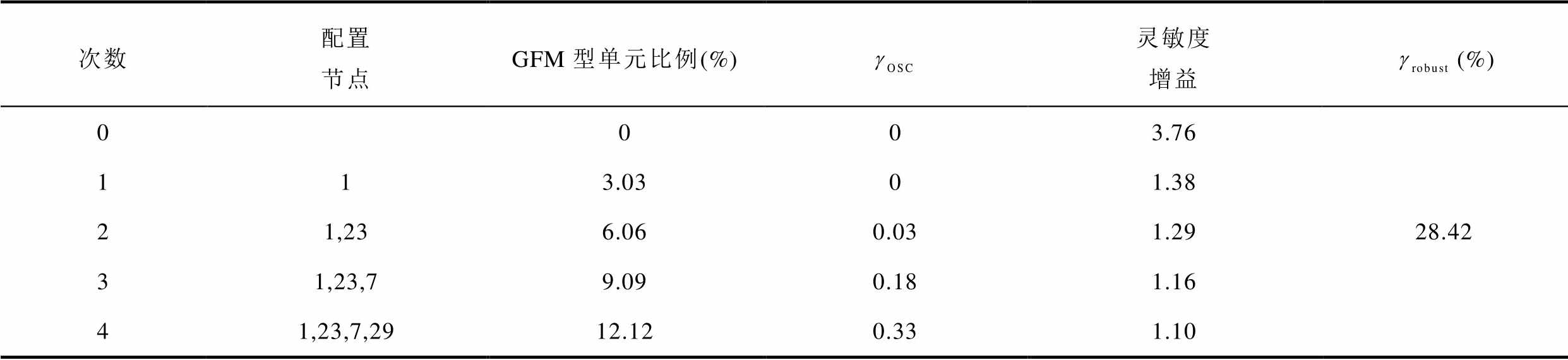
次数配置节点GFM型单元比例(%)灵敏度增益(%) 0003.7628.42 113.0301.38 21,236.060.031.29 31,23,79.090.181.16 41,23,7,2912.120.331.10
新能源场站并网系统稳定性分析如图11所示。配置前,当系统到达临界稳定出力点附近时,图11a中系统Nyquist曲线刚刚包围(-1, j0)点,图11b中场站并网系统阻抗曲线与电网阻抗曲线交截于 118 Hz,并且在交截频率处系统相位裕度不足,存在小干扰失稳风险。配置后,系统Nyquist曲线不再包围(-1, j0)点,系统聚合阻抗曲线与电网阻抗交截频率处相位裕度约为25°,系统恢复额定出力运行。
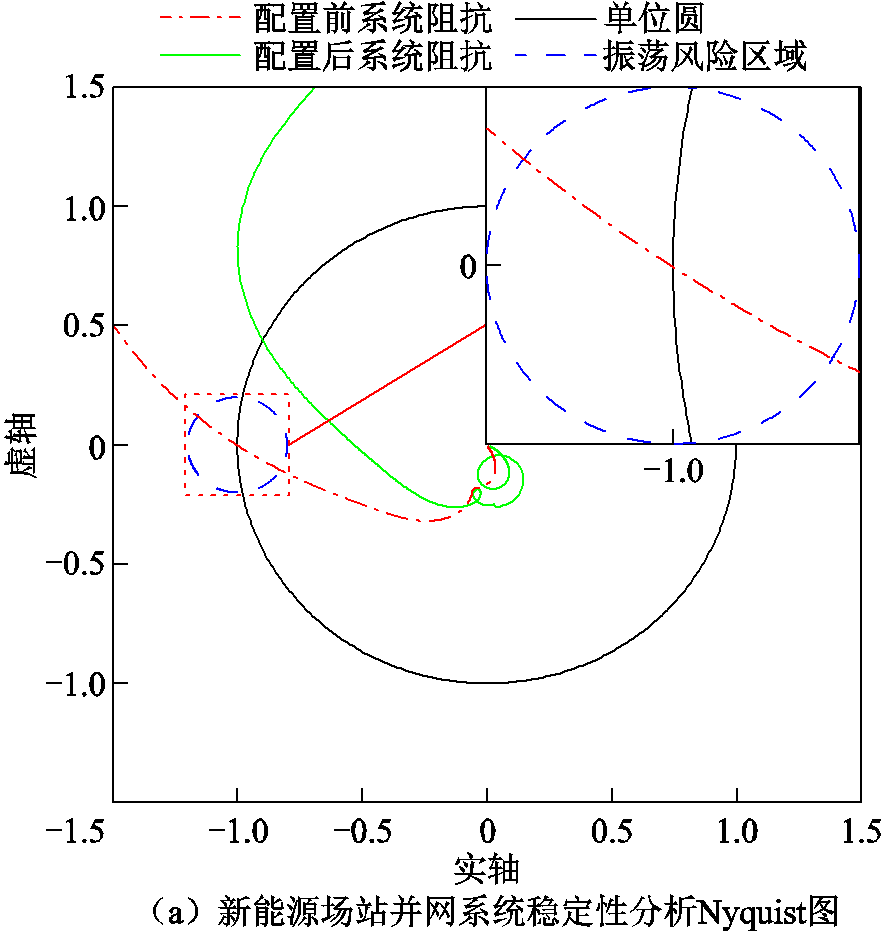
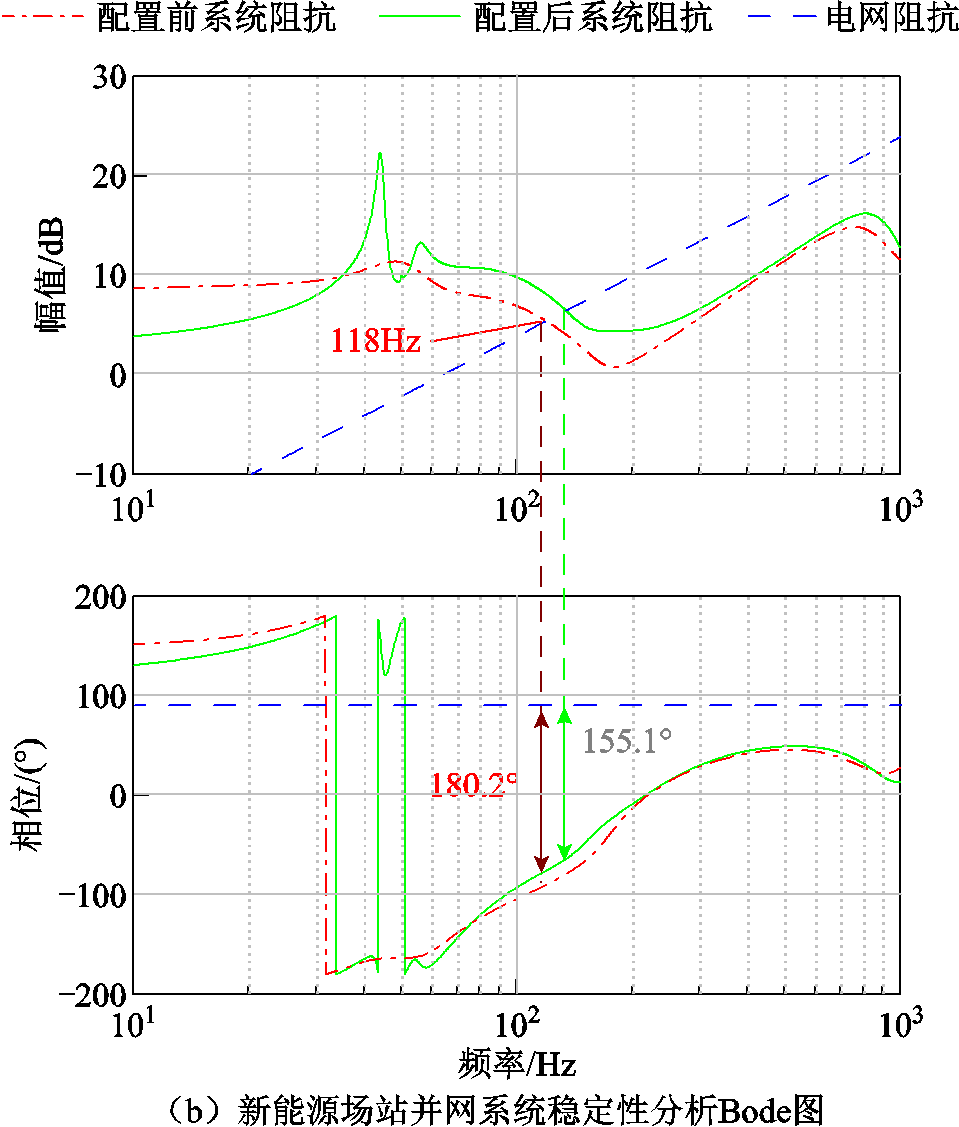
图11 新能源场站并网系统稳定性分析
Fig.11 Stability analysis of renewable energy station grid-integration system
新能源场站GFM型单元配置节点参与因子迭代过程如图12所示。由图12可知,场站内对系统稳定性影响较大的节点经过迭代配置后,节点参与因子值逐渐下降。开始配置前,馈线1中节点1和7参与因子高于馈线2中节点23和29的参与因子,由于馈线1的接入间距大于馈线2,对系统稳定性影响相对更大,因此首先配置馈线1末端节点。之后,节点对系统稳定影响的比例随配置变化而改变,馈线1节点参与因子下降,馈线2节点参与因子整体上升,随之配置馈线2末端节点。之后馈线1和馈线2交替配置节点7和29,两条馈线的整体参与因子下降,对系统的稳定特性风险影响减小,满足系统小干扰稳定和稳定支撑能力要求,新能源场站GFM型单元布点配置结束。
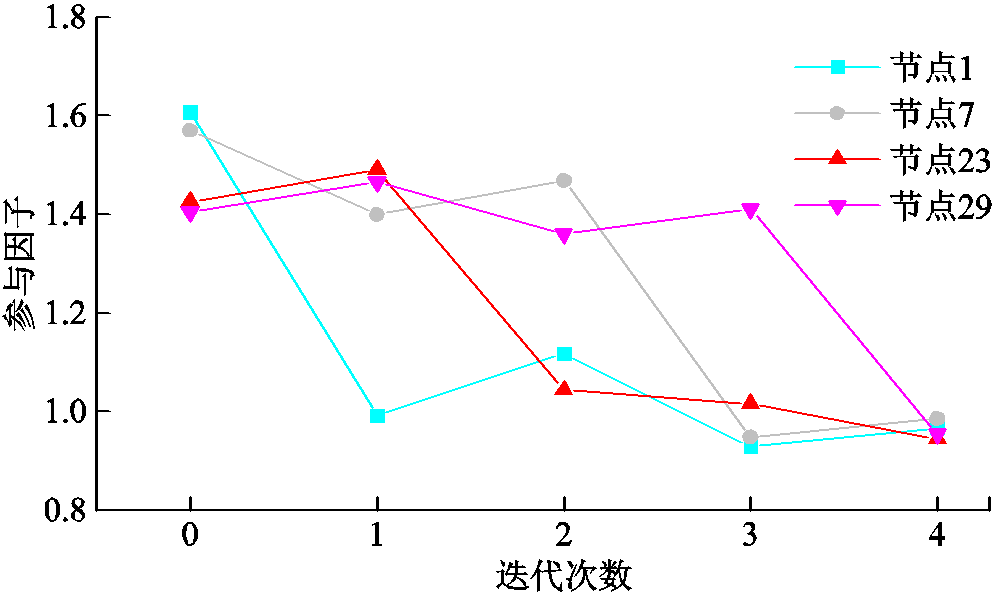
图12 新能源场站被优化节点参与因子迭代过程
Fig.12 The iterative process of participating factors for optimized nodes in renewable energy station
基于上述新能源场站并网系统模型,进一步探究汇集结构、电网强度和GFL单元控制参数等因素对GFM型单元配置和系统稳定特性的影响。
新能源场站节点参与因子热力图如图13所示。从图13中可知,虽然各馈线上的单元汇集距离存在差异,但都遵循节点参与因子大小与其到并网点的距离成反比的规律,即每条馈线的末端节点参与因子最大,馈线的首端节点参与因子最小。
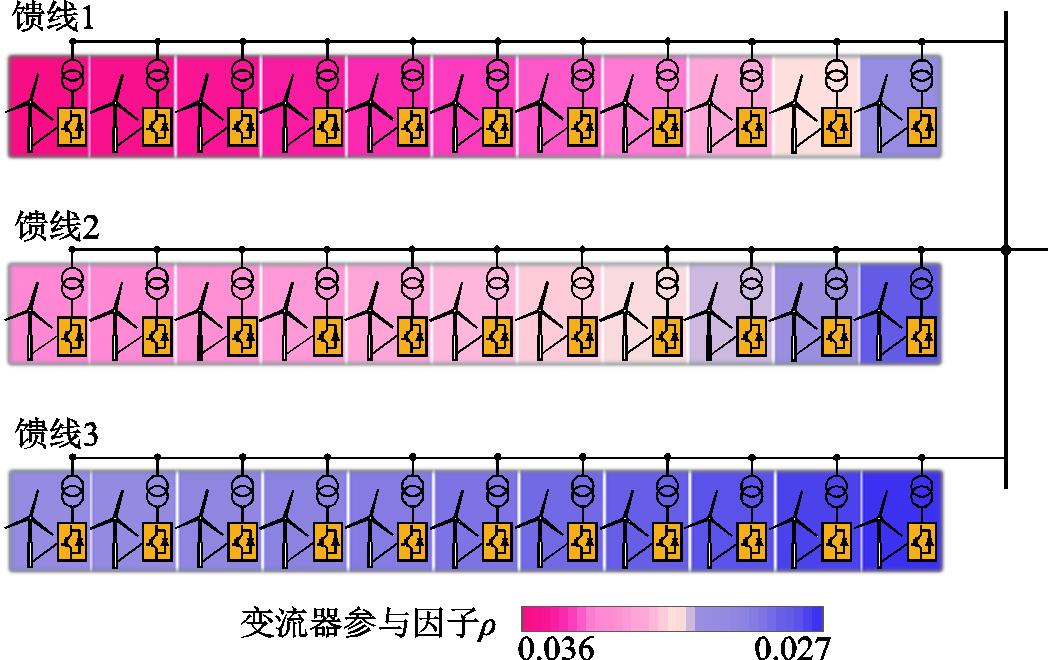
图13 新能源场站节点参与因子热力图
Fig.13 Heat map of participation factors for renewable energy station nodes
设定新能源场站分别接入SCR为1.5、1.7、1.9和2.1的弱电网场景。新能源场站GFM型单元配置结果见表3。
表3 不同电网强度下系统GFM型单元配置结果
Tab.3 Configuration results of GFM units in system under different SCR
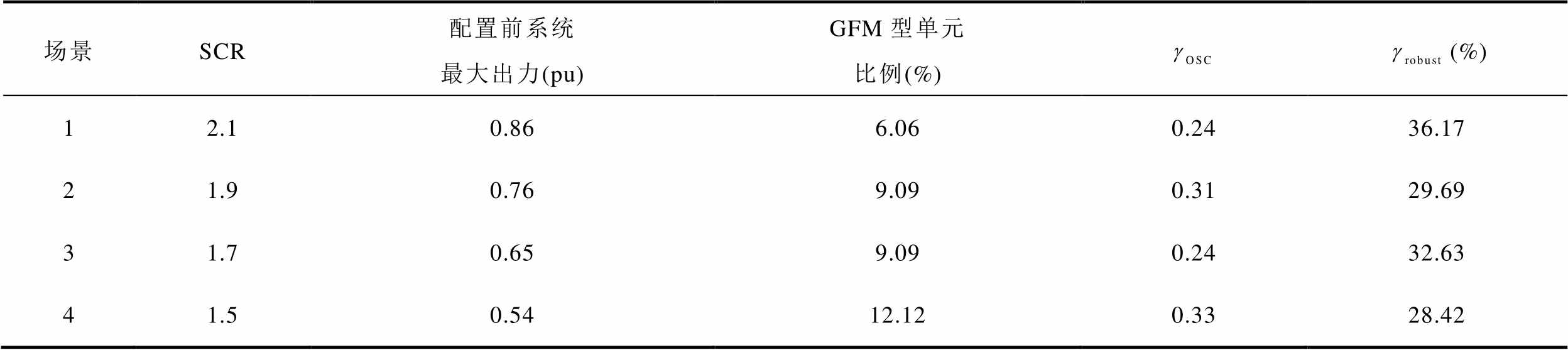
场景SCR配置前系统最大出力(pu)GFM型单元比例(%)(%) 12.10.866.060.2436.17 21.90.769.090.3129.69 31.70.659.090.2432.63 41.50.5412.120.3328.42
由表3可知,随着电网强度逐渐降低,系统临界稳定最大出力逐渐变小。当各场景配置不同容量比例的GFM型单元后,能够明显提升新能源场站在一定弱电网强度范围下的稳定运行能力。配置后,各场景下系统的临界稳定最大出力依次提升了85.2%、53.8%、31.6%和16.3%,系统稳定特性指标均满足要求,最终全部具备在额定工况稳定运行的能力。同时,配置后系统稳定裕度相对给定值具有部分余量,保证了新能源场站在电网强度发生小范围波动时,仍能够维持稳定运行。另外,当GFM型单元容量占比不变时(场景2和3),SCR越小,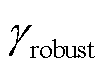 越高,说明弱电网特性越明显时,接入相同容量的GFM型单元对系统的稳定支撑能力的提升作用越显著。
越高,说明弱电网特性越明显时,接入相同容量的GFM型单元对系统的稳定支撑能力的提升作用越显著。
下面分析当新能源场站内存在采用不同GFL型控制参数的新能源发电单元时,新能源侧接入弱电网对GFM型单元优化配置的影响。设定新能源场站接入SCR=2.1的弱电网,新能源场站中安装的GFL型单元控制参数含A、B两种类型,其主要差别在于锁相环的控制参数不同。根据GFL-B型单元在场站中的占比,分为0%、33%、67%和100%等四个场景。配置前,场景1~4中新能源并网系统的临界稳定运行点分别为0.86(pu)、0.62(pu)、0.51(pu)和0.4(pu),均无法在额定工作点稳定运行。
根据节点参与因子计算结果分别对各场景进行GFM型单元优化配置,不同GFL型控制参数混合比例下系统GFM型单元配置结果见表4。由表4可知,GFL-B型单元在场站中的混合比例越高,系统相应需要配置的GFM型单元比例越大。配置后,各场景下系统都可在额定工作点稳定运行,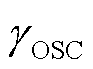 满足稳定裕度要求。然而在场景3和4中,为优先保证系统稳定裕度,系统出现了支撑增长率不足的问题,降低
满足稳定裕度要求。然而在场景3和4中,为优先保证系统稳定裕度,系统出现了支撑增长率不足的问题,降低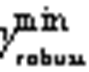 至15%后满足配置要求。
至15%后满足配置要求。
表4 不同GFL型控制参数混合比例下系统GFM型单元配置结果
Tab.4 Scenario table for mixing proportions of units with different grid-following parameters

场景GFL-B型单元接入位置GFL-B型参数占比(%)GFM型单元比例(%)(%) 1不接入06.060.2436.17 2馈线1339.090.2227.19 3馈线1,36715.150.3018.01 4全部接入10018.180.2815.00
各场景下新能源场站侧的三维Bode图如图14所示。由图14a看出,GFL-B型单元在场站中的混合比例越高,新能源场站阻抗曲线的中低频段幅值下陷越明显,更易与弱电网下的阻抗曲线相交,交截处相位裕度明显不足,如图中红色虚线圈所示。这是因为GFL-B型锁相环的控制参数设计不佳,导致设备阻抗特性相比GFL-A型单元,其负阻尼区域更大,接入系统后恶化了场站整体的中低频段阻抗特性。配置后,由图14b看出,GFM型单元的接入大幅改善了测试场景下大部分新能源场站中低频段的阻抗幅值曲线下陷和相位裕度不足问题,如图中绿色点画线圈所示,系统负阻尼区域部分大幅减小,能够显著降低新能源场站接入弱电网后系统发生宽频振荡失稳的风险。
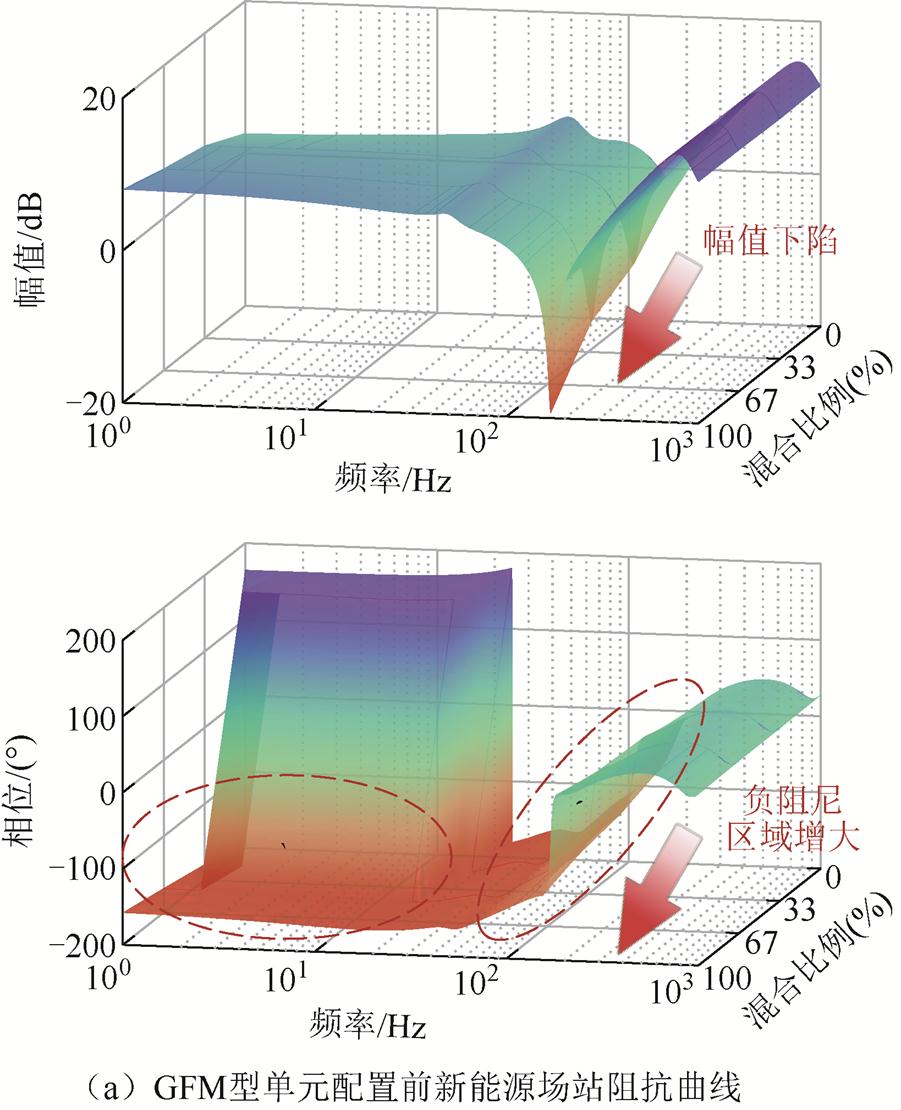
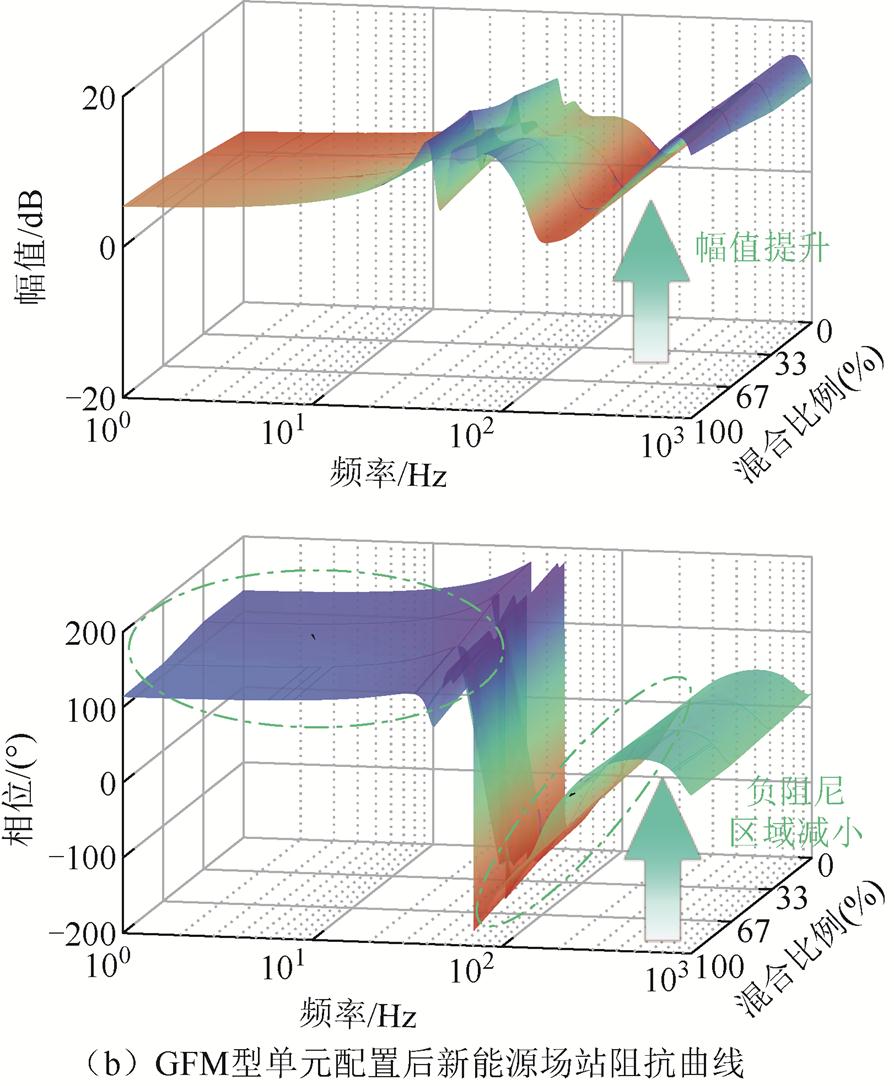
图14 不同混合比例场景下新能源场站三维Bode图
Fig.14 3D Bode diagram of renewable energy station for different proportions of heterogeneous GFL control parameters scenarios
当GFL-B型单元混合比例较高时(场景3和4),场站整体的阻抗特性较差,改进后的场站仍有极小部分区域存在负阻尼特性,这也说明了单纯依赖接入GFM单元的配置方法,并不能完全改善所有场景下新能源场站的全频段阻抗特性,并且会造成GFM型单元的过多配置,影响整体配置的经济性。因此,未来仍需要结合GFL/GFM型控制参数优化或额外的控制策略等手段对不同场景进行针对性优化,以保证GFM型单元配置和经济性之间的平衡。
通过时域仿真对上述算例进行验证。首先验证新能源集群并网系统小干扰稳定能力,新能源集群并网点电流仿真波形如图15所示。配置前,新能源集群出现小干扰失稳风险,此时并网点电流发生如图15a所示振荡。提取电流信号进行FFT分析,结果显示电流信号中存在26 Hz/126 Hz谐波分量。根据主导振荡模态计算节点参与因子,针对谐波分量优化新能源集群中各场站的GFM型单元容量,最终系统恢复稳定运行能力,此时系统并网点电流波形如图15b所示,波形平稳无谐波分量。
下面验证新能源场站并网系统小干扰稳定能力,新能源场站并网系统并网点电流波形如图16所示。配置前,系统临界稳定最大出力为0.54(pu),并网点电流发生如图16a所示振荡。提取电流信号进行FFT分析,结果显示电流信号中存在18 Hz/118 Hz的谐波分量,表示系统存在小信号失稳风险。配置后,系统恢复额定运行能力,此时场站并网电流波形如图16b所示,波形平稳无谐波分量。
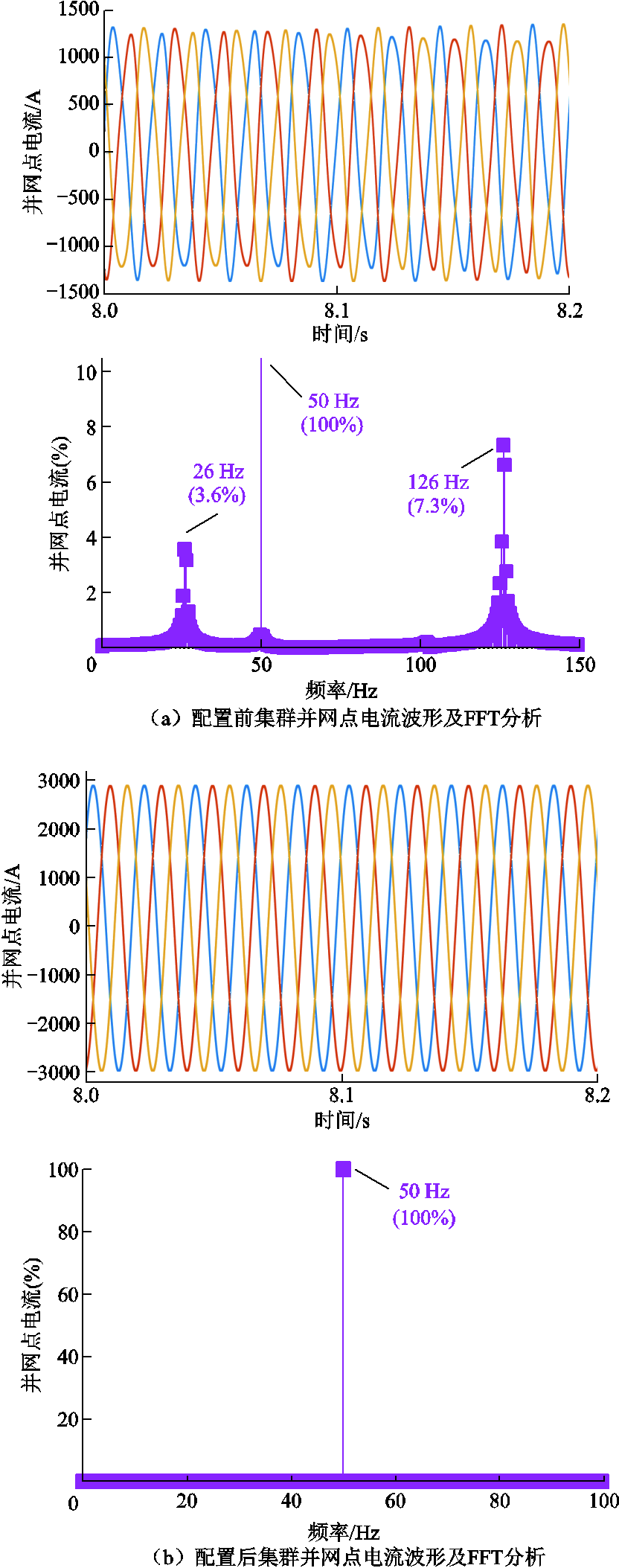
图15 新能源集群并网点电流波形及FFT分析
Fig.15 Current simulation waveforms and FFT analysis at the PCC of renewable energy cluster
下面验证新能源场站并网系统稳定支撑能力,当系统达到稳定运行状态后,在第5 s时向系统中

图16 新能源场站并网点电流波形及FFT分析
Fig.16 Current simulation waveforms and FFT analysis at the PCC of the renewable energy station
注入0.1(pu)的基频功率扰动。分别测试场站中接入0台、2台和4台GFM型单元后,系统发生功率扰动时场站并网点电压瞬时值。场站并网点电压幅值相位仿真波形如图17所示。由图17可知,在系统受到相同幅度的功率扰动时,随着场站内GFM型单元比例的提升,并网点电压幅值和相位产生的波动依次减小。另外,当场站GFM型单元从0台提升至2台时,并网点电压幅值和相位波动的幅度减小约0.018(pu),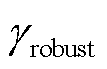 提升约48.09%。GFM型单元从2台继续提升至4台,波动幅度减小约0.011(pu),在此基础上
提升约48.09%。GFM型单元从2台继续提升至4台,波动幅度减小约0.011(pu),在此基础上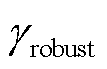 只提升约19.35%。这说明初始增加少部分GFM型单元对系统稳定支撑能力改善非常明显,继续向系统中增加GFM型单元,系统稳定支撑能力增长率反而随GFM型单元比例提升而减小。
只提升约19.35%。这说明初始增加少部分GFM型单元对系统稳定支撑能力改善非常明显,继续向系统中增加GFM型单元,系统稳定支撑能力增长率反而随GFM型单元比例提升而减小。
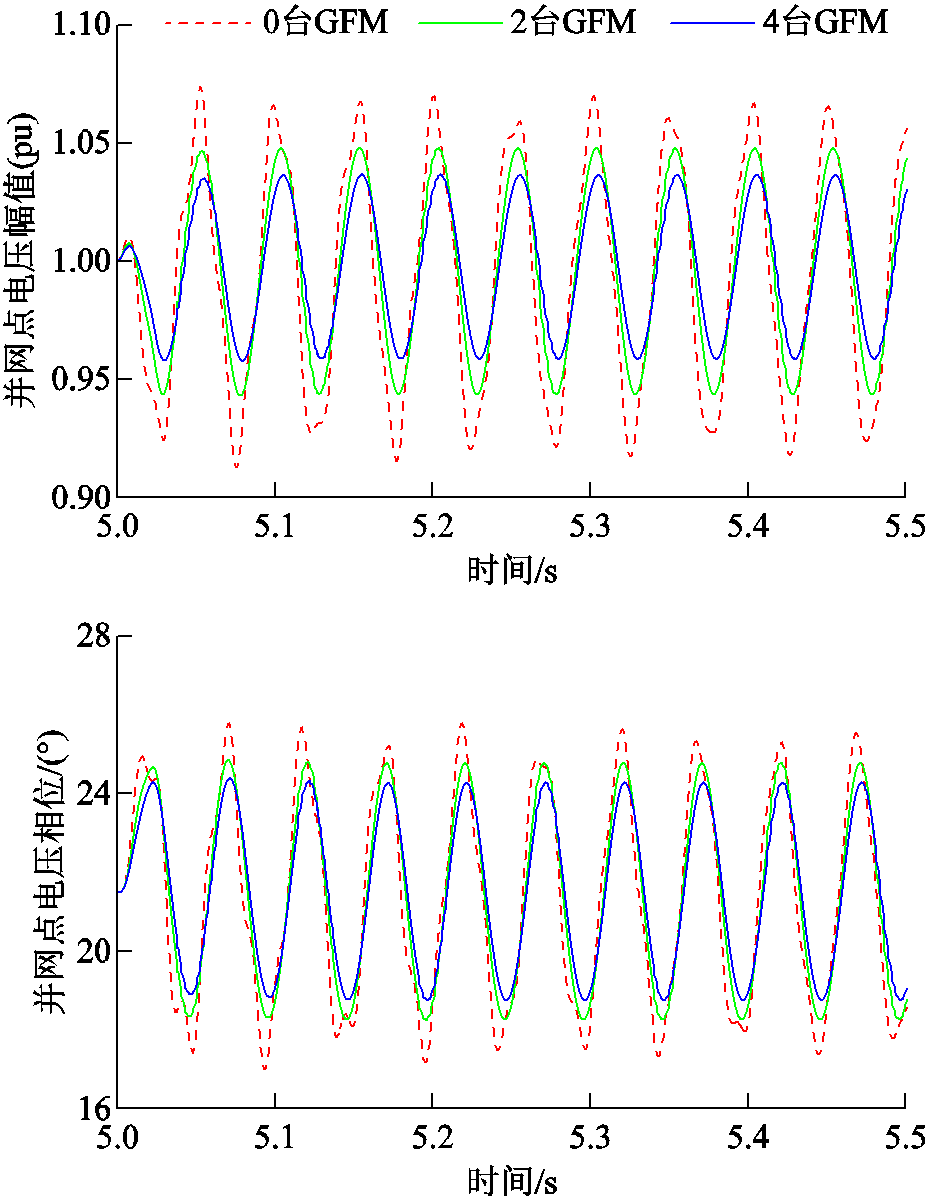
图17 不同比例GFM型单元接入系统后并网点电压幅值/相位波形
Fig.17 Simulation waveforms of voltage amplitude/phase at the PCC with different ratios of GFM units in the system
本文面向新能源集群/场站并网系统,基于系统功率-电压闭环传递反馈模型与阻抗网络电路模型,构建了系统小干扰稳定裕度和稳定支撑能力量化评估指标,并提出了新能源并网系统GFM型单元配置方法。主要结论如下:
1)系统功率-电压闭环传递反馈模型与电流-电压闭环传递反馈模型,本质上是从不同输入角度对同一系统的动态特性描述,两者分析小干扰稳定与稳定支撑能力等系统稳定特性的效果是一致的。
2)本文提出的系统GFM型单元配置方法,考虑了系统新能源侧多机接入和电网侧网络拓扑的完整动态特征,能有效分析和评估新能源多机并网系统的稳定特性。
3)在系统小干扰稳定约束下,合理配置GFM型单元的容量和布点位置,可保证新能源并网系统在宽频带范围内具有充足的小干扰稳定裕度和稳定支撑能力,同时减少GFM型单元配置容量,降低系统经济性成本。
GFM型单元接入可能给系统带来新的控制动态特性,引起次/超同步振荡以外的其他稳定性问题,后续可深入研究以探明GFM型单元接入新能源并网系统带来的优势与适用场景,并进一步探究交直流复杂电网场景下GFM型单元的配置方法。
附 录
1. 系统仿真参数
附表1 新能源发电单元控制参数
App.Tab.1 Control parameters of renewable energy generation units
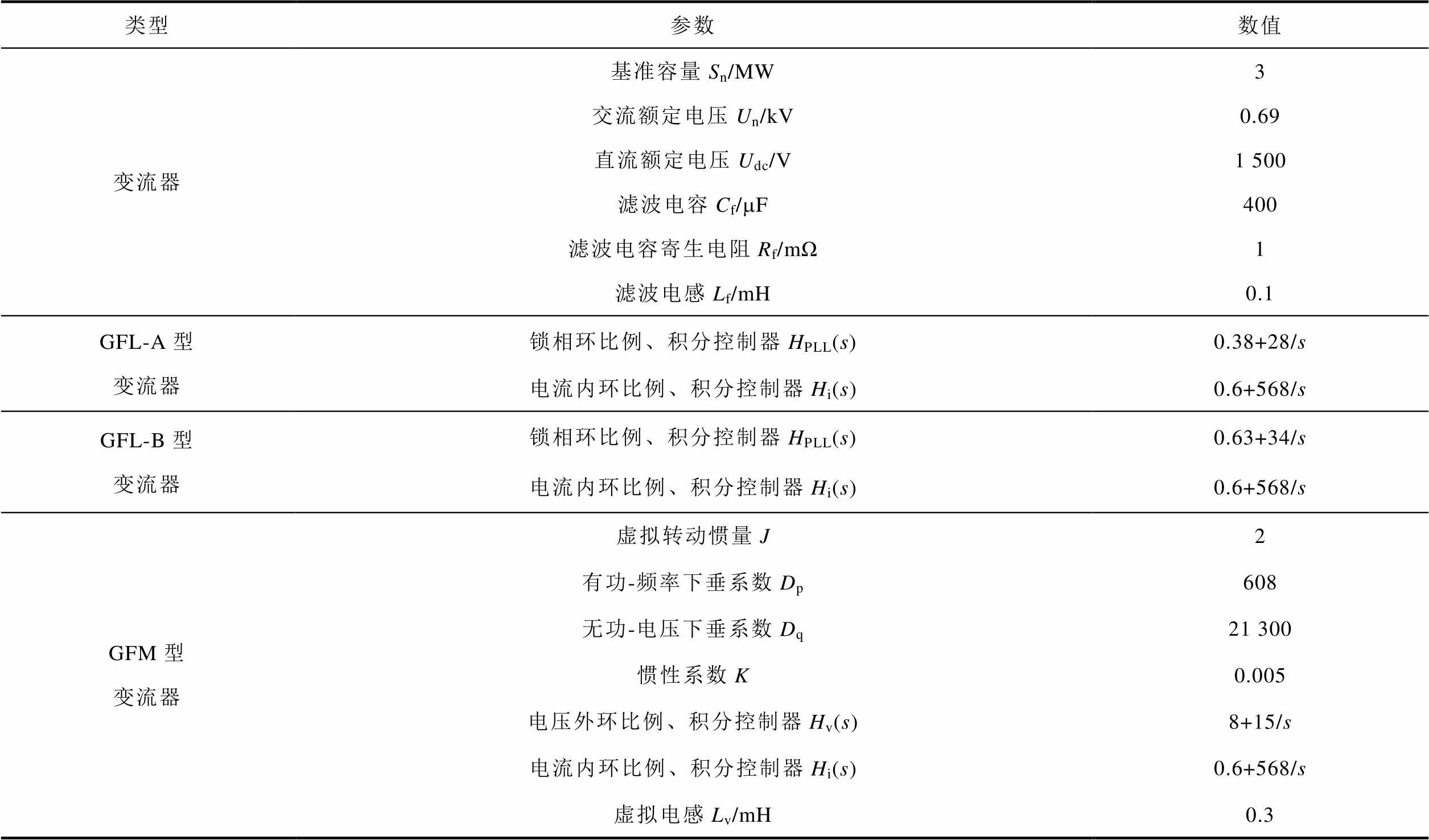
类型参数数值 变流器基准容量Sn/MW3 交流额定电压Un/kV0.69 直流额定电压Udc/V1 500 滤波电容Cf/mF400 滤波电容寄生电阻Rf/mΩ1 滤波电感Lf/mH0.1 GFL-A型变流器锁相环比例、积分控制器HPLL(s)0.38+28/s 电流内环比例、积分控制器Hi(s)0.6+568/s GFL-B型变流器锁相环比例、积分控制器HPLL(s)0.63+34/s 电流内环比例、积分控制器Hi(s)0.6+568/s GFM型变流器虚拟转动惯量J2 有功-频率下垂系数Dp608 无功-电压下垂系数Dq21 300 惯性系数K0.005 电压外环比例、积分控制器Hv(s)8+15/s 电流内环比例、积分控制器Hi(s)0.6+568/s 虚拟电感Lv/mH0.3
附表2 仿真系统主要参数
App.Tab.2 Main parameters of simulation system

设备参数数值 汇集线路线路电阻Rline/(Ω/km)0.03 线路电感Lline/(mH/km)0.97
(续)

设备参数数值 220 kV变压器基准容量Sn/(MV×A)100 高压侧额定电压Uhigh/kV220 低压侧额定电压Ulow/kV35 短路电压百分比Uk(%)10 35 kV变压器基准容量Sn/(MV×A)3 高压侧额定电压Uhigh/ kV35 低压侧额定电压Ulow/kV0.69 短路电压百分比Uk(%)6.5
2. 矩阵元素说明
1) ,
, 矩阵元素说明
矩阵元素说明
文中矩阵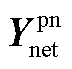 、
、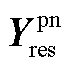 中的元素可表示为
中的元素可表示为
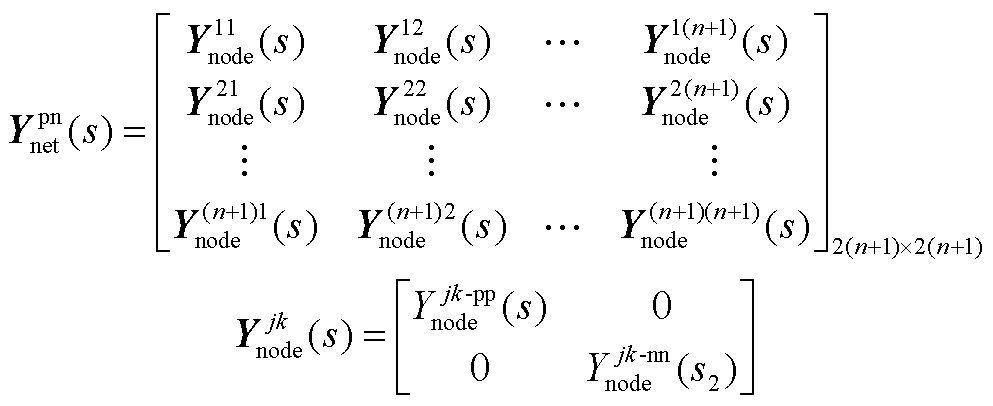
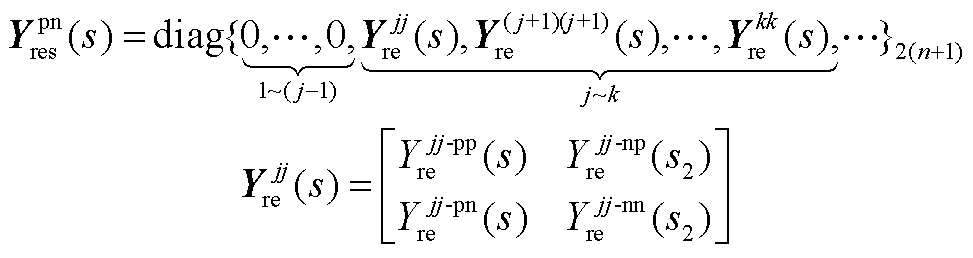
2) 矩阵元素说明
矩阵元素说明
文中 具体可表示为
具体可表示为
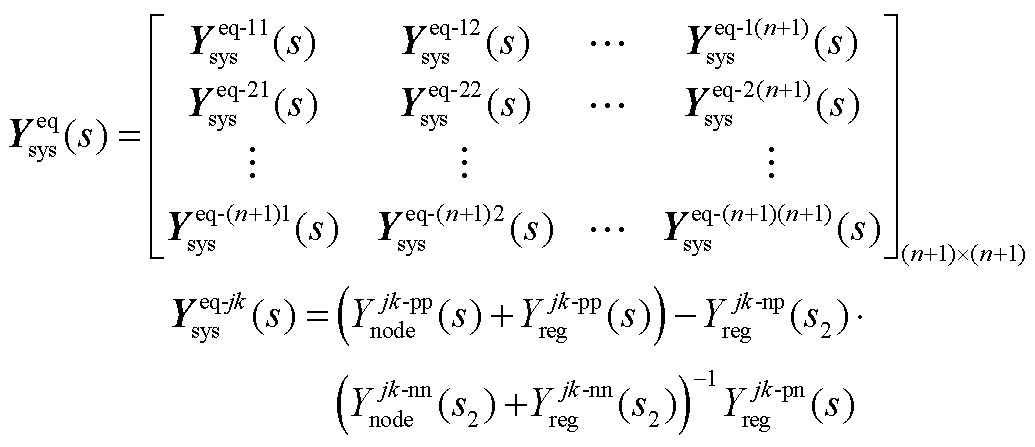
参考文献
[1] 王伟胜, 李光辉, 何国庆, 等. 新能源并网系统宽频振荡分析与抑制[M]. 北京: 中国电力出版社, 2022.
[2] 李红, 梁军杨, 王振民, 等. 跟网型变换器的小扰动同步稳定机理分析与致稳控制[J]. 电工技术学报, 2024, 39(12): 3802-3815.
Li Hong, Liang Junyang, Wang Zhenmin, et al. Small signal synchronization stability analysis and improved control strategy for grid following converter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3802-3815.
[3] 李亚楼, 赵飞, 樊雪君. 构网型储能及其应用综述[J]. 发电技术, 2025, 46(2): 386-398.
Li Yalou, Zhao Fei, Fan Xuejun. A review of grid-forming energy storage and its applications[J]. Power Generation Technology, 2025, 46(2): 386-398.
[4] 刘朋印, 谢小荣, 李原, 等. 构网型控制改善跟网型变流器次/超同步振荡稳定性的机理和特性分析[J]. 电网技术, 2024, 48(3): 990-997.
Liu Pengyin, Xie Xiaorong, Li Yuan, et al. Mechanism and characteristics of grid-forming control for improving sub/super synchronous oscillation stability of grid-following-based grid-connected converter[J]. Power System Technology, 2024, 48(3): 990-997.
[5] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[6] 国家发展改革委, 国家能源局, 国家数据局. 《加快构建新型电力系统行动方案(2024—2027年)》[R]. 2024.
National Development and Reform Commission, National Energy Administration, National Data Administration Action. Plan for Accelerating the Construction of a New Electricity System (2024-2027)[R]. 2024.
[7] 吴家杰, 陈新, 张东辉, 等. 构网型储能变换器在新能源接入场景下并网稳定性分析及提升策略[J]. 中国电机工程学报, 2024, 44(23): 9341-9354.
Wu Jiajie, Chen Xin, Zhang Donghui, et al. Grid-connected stability analysis and improvement strategy for grid-forming energy storage system in new energy access scene[J]. Proceedings of the CSEE, 2024, 44(23): 9341-9354.
[8] 雷雨, 李光辉, 王伟胜, 等. 跟网型和构网型新能源并网控制阻抗对比与振荡机理分析[J]. 中国电机工程学报, 2025, 45(1): 150-163.
Lei Yu, Li Guanghui, Wang Weisheng, et al. Comparison of impedance characteristics and oscillation mechanism for grid following and grid forming renewable energy[J]. Proceedings of the CSEE, 2025, 45(1): 150-163.
[9] 刘威, 谢小荣, 王衡, 等. 基于频率耦合阻抗模型的并网变流器全工况小信号稳定性分析[J]. 中国电机工程学报, 2020, 40(22): 7212-7221.
Liu Wei, Xie Xiaorong, Wang Heng, et al. Frequency-coupled impedance model-based small-signal stability analysis of grid-tied converters under all operating conditions[J]. Proceedings of the CSEE, 2020, 40(22): 7212-7221.
[10] 王奕宁, 向往, 张浩博, 等. 构网型直驱风力发电机组比例优化配置分析[J]. 电网技术, 2025, 49(2): 490-500.
Wang Yining, Longing, Zhang Haobo, et al. Analysis of optimal proportion configuration of grid forming direct drive wind turbine[J]. Power System Technology, 2025, 49(2): 490-500.
[11] 刘朋印, 刘辉, 吴林林, 等. 满足全运行域振荡约束的跟网-构网组合控制及优化配置[J]. 电力系统自动化, 2024, 48(12): 139-146.
Liu Pengyin, Liu Hui, Wu Linlin, et al. Grid-following and grid-forming combined control and optimal configuration to satisfy oscillation constraints across whole operating region[J]. Automation of Electric Power Systems, 2024, 48(12): 139-146.
[12] 吴琛, 刘晨曦, 黄伟, 等. 提升新能源电力系统稳定性的构网型变流器选址定容方法[J]. 电力系统自动化, 2023, 47(12): 130-136.
Wu Chen, Liu Chenxi, Huang Wei, et al. Siting and sizing method of grid-forming converters for improving stability of power system with renewable energy[J]. Automation of Electric Power Systems, 2023, 47(12): 130-136.
[13] 余光正, 胡越, 刘晨曦, 等. 含跟网/构网型混联多馈入系统协调优化配置方法[J]. 中国电机工程学报, 2025, 45(2): 588-601.
Yu Guangzheng, Hu Yue, Liu Chenxi, et al. Research on the coordinated optimization configuration method for hybrid multi-infeed systems with grid-following or grid-forming[J]. Proceedings of the CSEE, 2025, 45(2): 588-601.
[14] Xin Huanhai, Liu Chenxi, Chen Xia, et al. How many grid-forming converters do we need? A perspective from small signal stability and power grid strength[J]. IEEE Transactions on Power Systems, 2025, 40(1): 623-635.
[15] 杨天鑫, 黄云辉, 何珍玉, 等. 基于多时间尺度调节的构网型储能电站定容选址优化配置[J]. 电力系统自动化, 2024, 48(23): 54-64.
Yang Tianxin, Huang Yunhui, He Zhenyu, et al. Optimal configuration of siting and sizing for grid-forming battery energy storage station based on multi-timescale regulation[J]. Automation of Electric Power Systems, 2024, 48(23): 54-64.
[16] 赵冬梅, 宋晨铭, 冯向阳, 等. 100%新能源场景下考虑频率稳定约束的源网荷储一体化系统储能优化配置[J]. 电工技术学报, 2025, 40(7): 2146-2161.
Zhao Dongmei, Song Chenming, Feng Xiangyang, et al. the optimal configuration of energy storage in the source-grid-load-storage integrated system considering frequency stability constraints in 100% new energy scenarios[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2146-2161.
[17] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[18] 年珩, 徐韵扬, 陈亮, 等. 并网逆变器频率耦合特性建模及系统稳定性分析[J]. 中国电机工程学报, 2019, 39(5): 1421-1432.
Nian Heng, Xu Yunyang, Chen Liang, et al. Frequency coupling characteristic modeling of grid-connected inverter and system stability analysis[J]. Proceedings of the CSEE, 2019, 39(5): 1421-1432.
[19] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance [J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[20] 刘其辉, 逄思敏, 吴林林, 等. 大规模风电汇集系统电压不平衡机理、因素及影响规律[J]. 电工技术学报, 2022, 37(21): 5435-5450.
Liu Qihui, Pang Simin, Wu Linlin, et al. The mechanism, factors and influence rules of voltage imbalance in wind power integration areas[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5435-5450.
[21] 辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027.
Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[22] Liu Huakun, Xie Xiaorong, Zhang Chuanyu, et al. Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model[J]. IEEE Transactions on Power Systems, 2017, 32(1): 474-483.
[23] He Guoqing, Wang Weisheng, Wang Haijiao. Coordination control method for preventing sub/super synchronous oscillations of multi-wind farm systems [J]. CSEE Journal of Power and Energy Systems, 2023, 9(5): 1655-1665.
[24] Skogestad S, Postlethwaite I, Multivariable Feedback Control: Analysis and Design[M]. New York, USA: Wiley, 2007.
[25] 汪海蛟, 何国庆, 刘纯, 等. 计及频率耦合和汇集网络的风电场序阻抗模型等值方法[J]. 电力系统自动化, 2019, 43(15): 87-92.
Wang Haijiao, He Guoqing, Liu Chun, et al. Equivalent method for sequence impedance model of wind farms considering frequency coupling and collecting network[J]. Automation of Electric Power Systems, 2019, 43(15): 87-92.
[26] 宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(一): 机理模型与稳定判据适用性[J]. 中国电机工程学报, 2022, 42(12): 4405-4419.
Gong Zexu, Yaermaimaiti Ailixier, Xin Huanhai, et al. Small signal stability analysis of equipment in renewable energy power system (part Ⅰ): mechanism model and adaptation of stability criterion[J]. Proceedings of the CSEE, 2022, 42(12): 4405-4419.
[27] 国家能源局. 风电场阻抗特性评估技术规范: NB/T 10651—2021[S]. 北京: 中国电力出版社, 2021.
Configuration Method for Grid-Forming Units of Renewable Energy Grid-Integration System Considering Small Signal Stability Constraints
Abstract At present, renewable energy generation mainly use grid-following (GFL) control, which is prone to cause small signal stability problems such as broadband oscillation when connecting to the weak grid system. What’s more, the GFL units have insufficient support capacity for the grid. Grid-forming (GFM) technology construct the grid voltage independently through power synchronization control.When the system is disturbed, GFM units can actively support the grid voltage and frequency to improve the stable operation of the system. Under the situation of rapid development of renewable energy, it’s important to carry out GFM technological transformation and upgrading with renewable energy clusters/stations as the main body. How to reasonably plan the access capacity and location of GFM units of renewable energy grid-integration systemand improve the system stability characteristics, has become a key concern for engineering applications. The paper studies the configuration problem of the GFM unitsin renewable energy grid-integration system, with the focus on the small signal stability constraints.
Firstly, the singlerenewable energy converter grid-integration system was established. Based on the small signal model of the renewable energy converter grid-integration system, a closed-loop power-voltage feedback model was constructed, and the consistency between the former and the current-voltage closed-loop feedback model was verified in analyzing the stability characteristics of the system. Secondly, based on the impedance network circuit model, the system stability characteristic analysis method was extended to the multi-machine system. What’s more, the GFM units access capacity and distribution configuration problem of the multi-machine system was set. The objective of the problem is to minimize the total capacity of GFM units in the system, the constraints are that the system has sufficient small signal stability margin and stability support capability. Finally, the small signal stability margin index, the small signal stability support gain growth rate index, the GFM units access point selection index and the configuration method for GFM units of the system were proposed respectively. An analytical example was constructed based on the real renewable energy cluster grid-integration system, and the effectiveness of the proposed method was verified by time-domain simulation.
The conclusions are as follows: (1) Under the constraint of system small signal stability, the reasonable configuration of the capacity and location of GFM units can ensure that the whole system has sufficient small signal stability margin and stability support capability. Furthermore, reducing the capacity of the GFM units configuration can minimize the economic cost of the system. (2) The proposed configuration methodcan enhance the system's stable operation capability, particularly within a specific range of weak grid strength. It appears that when the capacity proportion of GFM units is constant, the weaker the grid characteristics, the more GFM units needs to be accessed. (3) The higher the percentage of GFL units with poor dynamic characteristics in the system, the larger the proportion of GFM units needs to be accessed. Optimization of system control parameters or control strategies, and explore the configuration method of GFM units in complex system scenarios will be the future research direction.
Keywords:Renewable energy grid-integration system, grid-forming (GFM) units configuration, broadband oscillation, small signal stability, stable support capability
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.242035
国家电网公司总部科技项目资助(4000-202317083A-1-1-ZN)。
收稿日期2024-11-13
改稿日期2025-01-02
孙培博 男,1997年生,博士研究生,研究方向为电力系统及其自动化。
E-mail:pbsun@foxmail.com
王伟胜 男,1968年生,教授级高级工程师,博士生导师,研究方向为新能源发电并网运行技术。
E-mail:wangws@epri.sgcc.com.cn(通信作者)
(编辑 郭丽军)