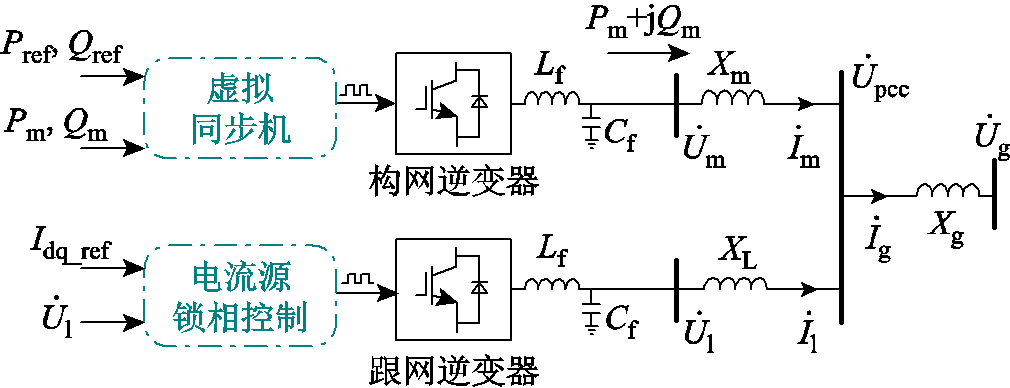
图1 跟/构网混联系统结构
Fig.1 Structure of GFL/GFM hybrid system
摘要 随着新能源发电渗透率的逐步提高,逆变器并网系统呈现出大容量汇集、远距离集中外送的特性。跟/构网逆变器混联并网可以充分利用二者各自优势,确保新能源外送系统的稳定运行及高效消纳。混联系统的有效暂态稳定评估对其运行具有重要的指导意义,但混联系统阶数高、非线性强,难以使用已有解析方法进行暂态同步稳定评估。为解决这一问题,该文首先建立了包含锁相环及虚拟同步机的跟/构网混联系统四阶非线性模型;然后,提出一种基于轮换计算的跟/构网逆变器混联系统暂态稳定性求解方法,其在功角域中进行能量计算及角速度求解,并映射回时间域,在各时刻下建立跟网控制和构网控制功角的对应关系,将大扰动下混联系统复杂交互运动形态分离,形成跟/构网系统的并行对称运动形态,实现了混联系统跟/构网系统相关变量的同步计算求解,其兼具能量法的动力学机理明晰、离散迭代法高计算精度的优势;最后,在仿真及实验中构建算例验证了所提方法的有效性。
关键词:跟/构网逆变器混联系统 暂态同步稳定性 四阶非线性系统 功角域 时间域
随着以“风、光、储”为主体的“双高”新型电力系统逐渐形成,以逆变器为并网接口的电源比例将不断增加,使得电力系统的稳定性表现出多控制环路主导的宽频带特性[1-2]。尤其是在新能源富集区域,如“三北”地区,新能源送出基地往往展现出大规模、长距离及缺乏常规同步机支撑的特点。传统跟网控制虽然能够通过锁相环(Phase-Locked Loop, PLL)锁定电网电压,实现稳态下有功/无功解耦控制,然而,基于电流注入的锁相跟随模式降低了系统惯量水平,在弱网下可能呈现振荡失稳,这进一步给系统的稳定性带来了新的不确定性及挑战[3]。构网控制通过自身建立电压、模拟同步发电机摇摆特性,以功率主导同步的方式接入电网,有效地提升惯量水平并增强逆变器电压支撑能力[4-5],在弱网下有着更强的适用性。综合以上控制方式的优点,可对现有跟网场站进行构网化改造,即利用场站中配备的储能容量,将其设置为构网运行模式,同时新能源电源仍跟网运行并与构网储能形成控制优势互补,跟/构网混联系统应运而生[6]。跟/构网混联系统能够实现弱网下鲁棒运行及功率灵活控制,是保障新能源高效稳定消纳的有效手段。但混联系统控制环节多样、影响因素复杂,其稳定性分析难度进一步提升[7]。
已有相关研究揭示了混联系统的运行稳定性与跟/构网控制布局和参数设置高度相关[6,8]。文献[9]基于建立的混联系统阻抗模型,研究了不同逆变器运行方式对于系统阻尼的影响规律。文献[10]在光伏/火电打捆送出的背景下,说明跟网机组占比过高会削弱系统阻尼水平,并表明构网机组可代替同步机提升电网支撑能力。文献[11-12]从布局角度,通过合理配置构网机组占比、优化构网机组接入位置,提升混联系统的电网强度。文献[13]分析了逆变器与同步机混联系统的有功互动机理,引入虚拟电抗或重新分配功率,从而提升系统稳定水平。然而,这些研究主要揭示了系统在平衡点周围的小信号稳定性。在新能源并网系统规模化送出的情景下,不稳定现象常常发生在持续的深度故障中[14],这导致混联系统更多地偏离了稳态工作点,系统非线性特征增强,上述研究在大扰动层面可能不适用。
暂态稳定性分析围绕微分方程组的求解进行,能够直接反映系统的非线性特性。对于混联系统,其中的跟网机组和构网机组可以被看作二阶系统,文献[15]利用李雅普诺夫直接法和拉萨尔不变集原理,对跟/构网逆变器分别进行了稳定域的刻画。然而,李雅普诺夫能量函数角度下的渐近稳定依赖于正阻尼的存在,跟网系统的微分方程难以满足该条件。等面积法则亦基于物理能量进行稳定性计算,文献[16-17]利用等面积法则分析了构网系统的同步稳定性,并通过设计反馈支路提升暂态稳定水平,但其未精确刻画阻尼能量,相关分析难以作为有效的稳定性评估手段。文献[18]通过改进的等面积法则,利用迭代的手段消除了能量函数对于阻尼参数的估计缺失问题,能够精确地刻画二阶系统的稳定域范围。文献[19]将风火打捆系统建模为包含电流源风机的二阶模型,从而使用等面积法则研究系统的暂态稳定性。但在混联系统中,跟/构网逆变器是两个平行的二阶系统,这使得暂态分析的对象提升至四阶。在现有的高阶暂态分析方法中,文献[20]将分析对象提升为包含功率外环的三阶系统;文献[21]则引入奇异摄动方法考虑电流内环的动态,但这些方法的共性是将系统划分为快/慢子系统,不适用于混联系统中跟/构网并行的动态分析。综合而言,现有面向混联四阶系统的暂态分析方法中,或采用下垂控制进行低阶系统的暂态分析[22-23],或建立微分方程组并利用时域微分仿真方法进行求解[24]。这两种方法存在牺牲求解精度或减慢求解速度的问题,尚未有方法能够在两者间做出平衡。
针对这一问题,本文结合能量法中明晰的动力学机理和离散迭代法中高计算精度的优势,将跟/构网系统视作两个并行运动的非线性系统,并建立功角-时间域中离散的对应关系,同步进行两个二阶系统的并行计算,最终形成离散域下基于轮换计算的跟/构网逆变器混联系统暂态稳定性求解方法。所提方法在仿真及实验算例下,准确刻画相轨迹并评估了系统的暂态稳定情况,有效地计算了系统极限切除时间(Critical Clearing Time, CCT),保证了暂态分析的计算精度与速度,是一种兼具明确机理及高效计算的四阶混联系统暂态求解方法。
本文研究的跟/构网逆变器混联系统指的是在新能源发电场站内,既配置有跟网控制的发电单元,也以一定比例配置构网控制的发电单元的情景。这些发电单元通过单元变压器及不同长度的汇集线路,连接至场站的公共耦合点(Point of Common Coupling, PCC),经升压变压器进入该新能源场站的送出线路并进入大电网,其对应的的系统结构如图1所示。由于本文研究的范畴为机电暂态,故所有网络电抗以线性模型建模。混联系统中,逆变器出口LC滤波参数为Lf、Cf,跟/构网逆变器分别经过其单元变压器及线路电抗Xl/Xm汇集至PCC,PCC经过升压变压器及送出线路电抗Xg连接到无穷大电网Ug;跟/构网逆变器出口电压电流分别为Ul/Um与Il/Im,构网逆变器参考有功、无功功率分别为Pref、Qref,其输出功率为Pm+jQm,PCC及无穷大母线电压分别为Upcc和Ug,Ig为PCC送出电流。所有电气量正方向均如图1所示。

图1 跟/构网混联系统结构
Fig.1 Structure of GFL/GFM hybrid system
混联系统中,跟网逆变器采用电流源型锁相控制,锁相控制的输入量为逆变器端口电压,其目标是控制输出电流的幅值和相位;构网逆变器采用基于虚拟同步机(Virtual Synchronous Generator, VSG)的电压源控制,控制器由输出功率与参考功率间的不平衡驱动,并控制逆变器的输出电压进行构网。
对于暂态建模与分析,为聚焦主要矛盾,同时保证方法的有效判断和简明展示,本文提出以下假设与简化:
1)构网逆变器参与无功下垂控制。为避免过电流问题,跟网逆变器在暂态下电流指令锁定[23-24],同时单位功率因数并网,在跟网逆变器保证有功输出的前提下,考察其最弱同步稳定性能[25]。
2)因电流环的时间尺度远小于本文研究的暂态同步尺度[26],故忽略电流环路动态,认为逆变器的输出电流与其参考值相等。
3)因本文聚焦新能源高压外送场景,故忽略了网络中的电阻损耗[27]。
需要说明的是,对于以上假设1)与假设3),如果考虑跟网无功下垂控制和网络电阻,会增加模型多项式的复杂度,但不改变其阶数[25, 28],本文方法仍保留适用性,由于篇幅限制不再展开讨论。
本节将首先对混联系统的关键电气量进行推导,获得逆变器控制环路输出、输入间关系;继而,将电气关系代入控制结构中,形成基于四阶微分方程的暂态系统;最后,将四阶的非线性系统视作动力学模型,表征混联系统的暂态特性。
对于图1所示的混联系统,其对应的电压方程为
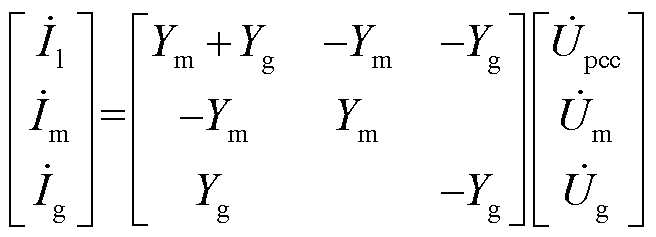 (1)
(1)
式中,Ym、Yg分别为Xm、Xg对应线路的导纳。
由式(1)可得PCC的电压相量为
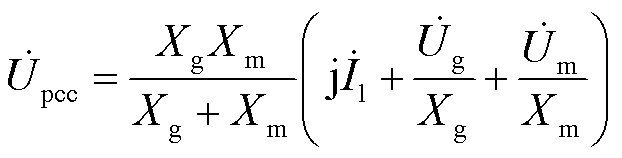 (2)
(2)
作为跟网控制的输入量,跟网逆变器的端口电压为
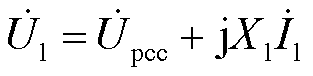 (3)
(3)
对于构网逆变器,由式(1)可求得其输出电流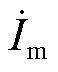 为
为
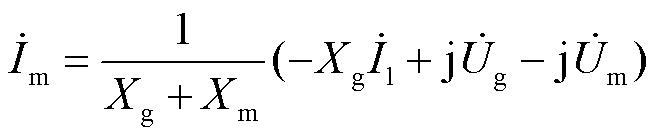 (4)
(4)
从而可进一步计算其输出有功功率、无功功率分别为
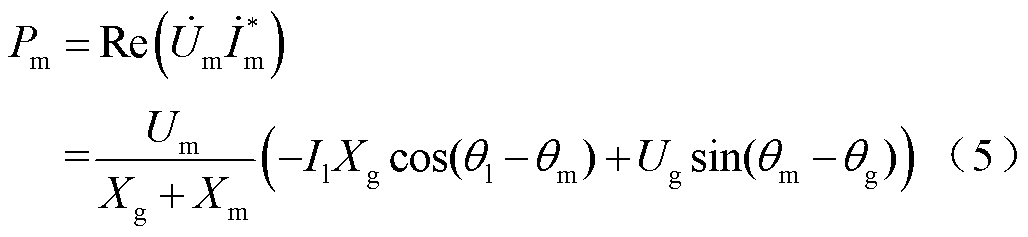
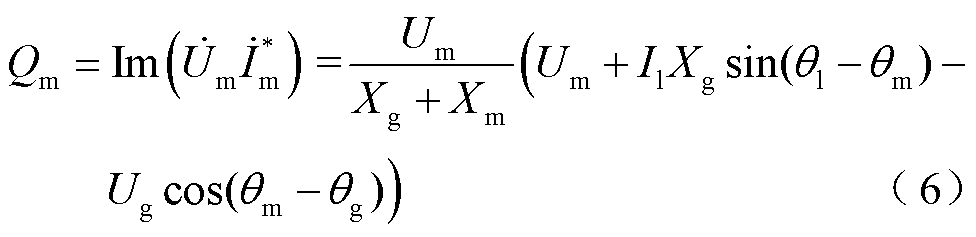
式中,ql、qm和qg分别为Il、Um和Ug在静止坐标系中的相位;上标“*”表示共轭。暂态过程中各相量的角度关系如图2所示。
跟网型控制结构如图3所示,其主要包含作为同步环节的PLL和控制输出电流Ild、Ilq幅值的电流环。当Ilq=0时,有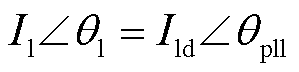 。
。
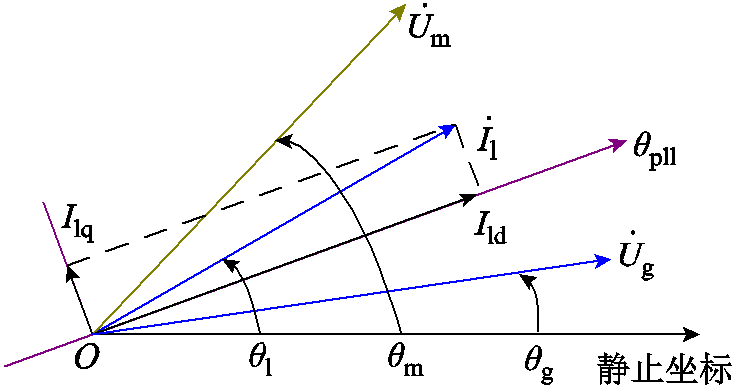
图2 暂态过程中各相量的角度关系
Fig.2 Angular relationship of the phasors in transient processes
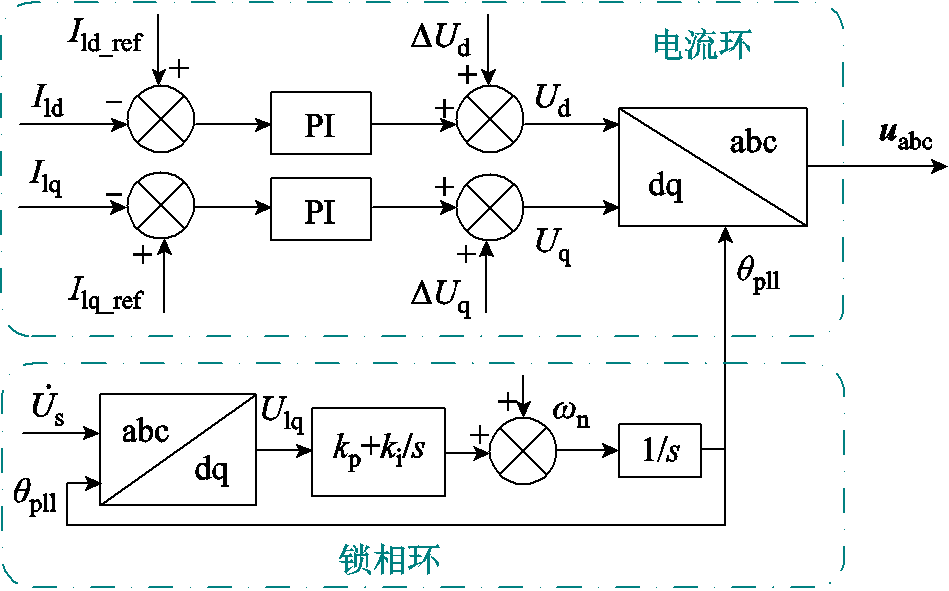
图3 跟网型控制结构
Fig.3 Structure of GFL control
首先,PLL借助其输出相位qpll,通过park变换获得电压相量的q轴分量Ulq,即
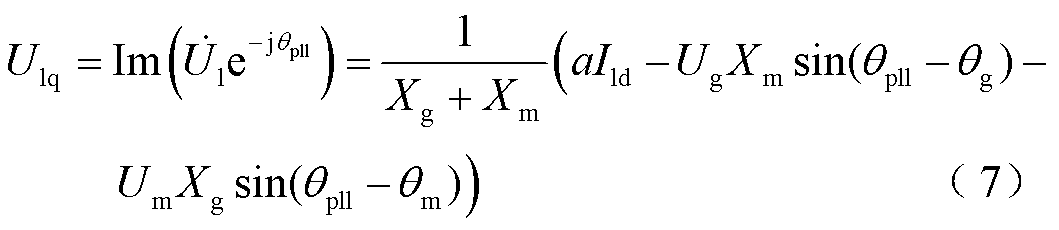
其中
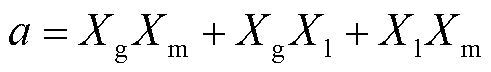 (8)
(8)
进一步地,PLL利用PI控制器锁定变流器端口电压频率偏差,并经过积分控制器计算PLL输出相位qpll为
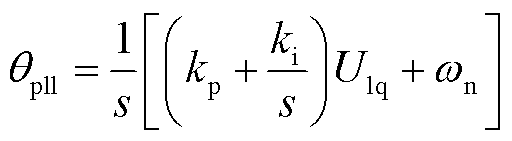 (9)
(9)
式中,kp、ki和wn分别为PI控制器的比例、积分系数和系统的额定角速度。将式(7)代入式(9)的微分方程,得到
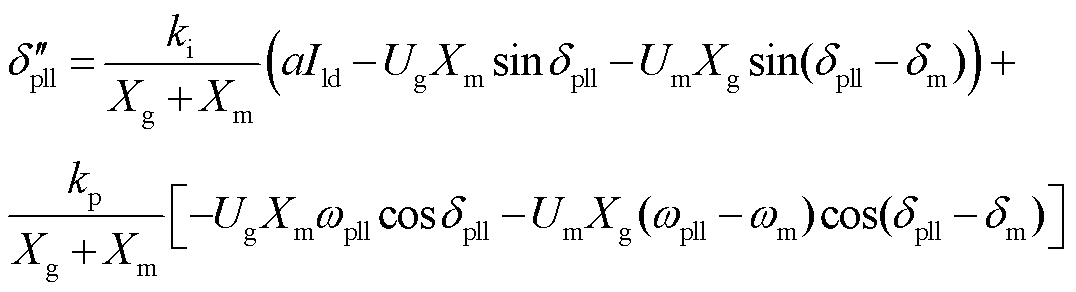 (10)
(10)
式中,dpll、dm分别为跟网控制和构网控制的功角,有
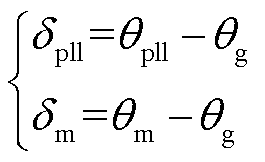 (11)
(11)
式中,wpll和wm分别为dpll、dm的角速度,有
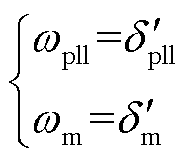 (12)
(12)
构网型控制结构如图4所示。
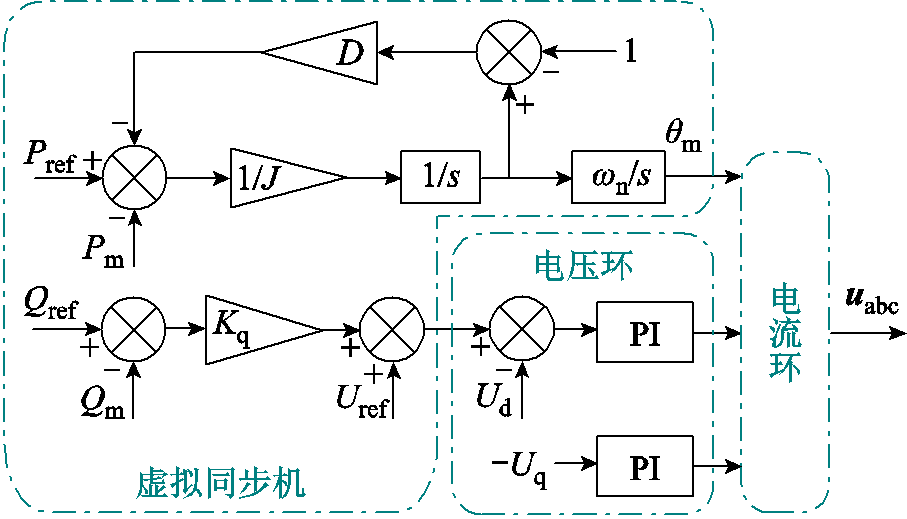
图4 构网型控制结构
Fig.4 Structure of GFM control
本文模型中双环构网控制包括VSG、电压环和电流环,其中电流环的结构与跟网控制相同,其相位由VSG的有功环路给定,其方程为
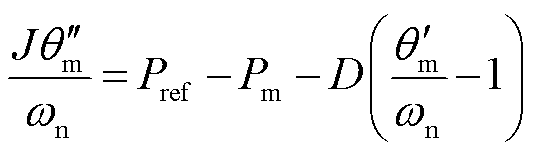 (13)
(13)
式中,J、D分别为VSG控制的虚拟阻尼和惯量,结合式(5)、式(11)、式(12),可进一步整理为
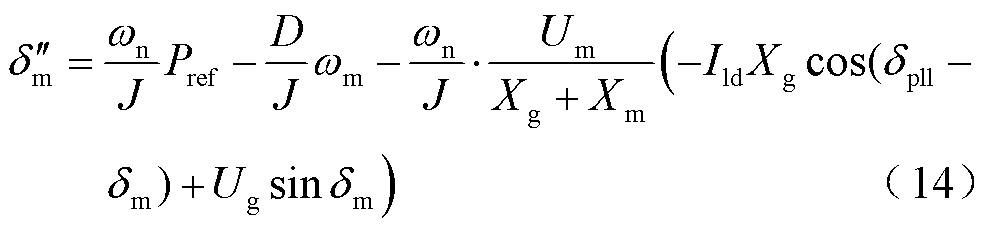
电压环路将VSG中无功下垂控制的输出电压作为d轴电压,其q轴电压参考值为0。无功下垂控制是一个代数环节,它的代数方程为
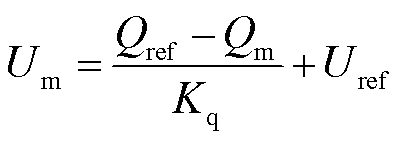 (15)
(15)
式中,Kq为无功下垂系数;Uref为参考电压。结合式(6),解析Um的解为
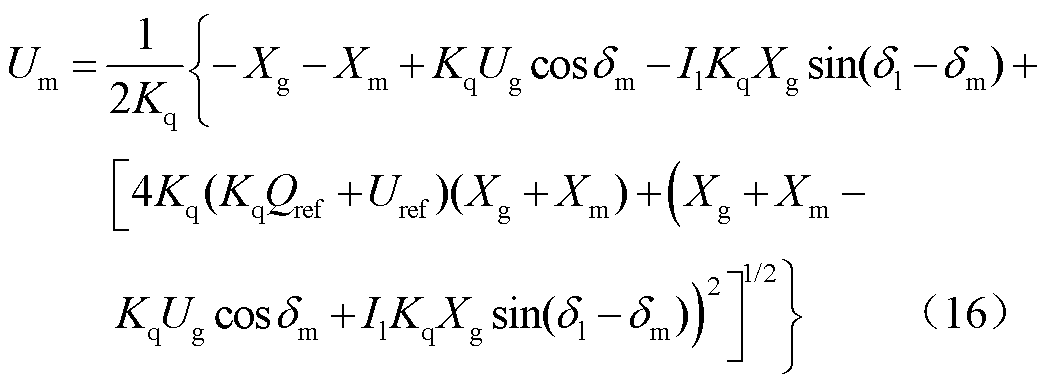
推导PLL与VSG的微分方程后,混联系统的四阶模型已经被明晰,其为式(10)、式(14)和式(16)的联立,对应暂态模型如图5所示。其中,状态变量为dpll、wpll、dm和wm,系数b=1/(Xm+Xg)。
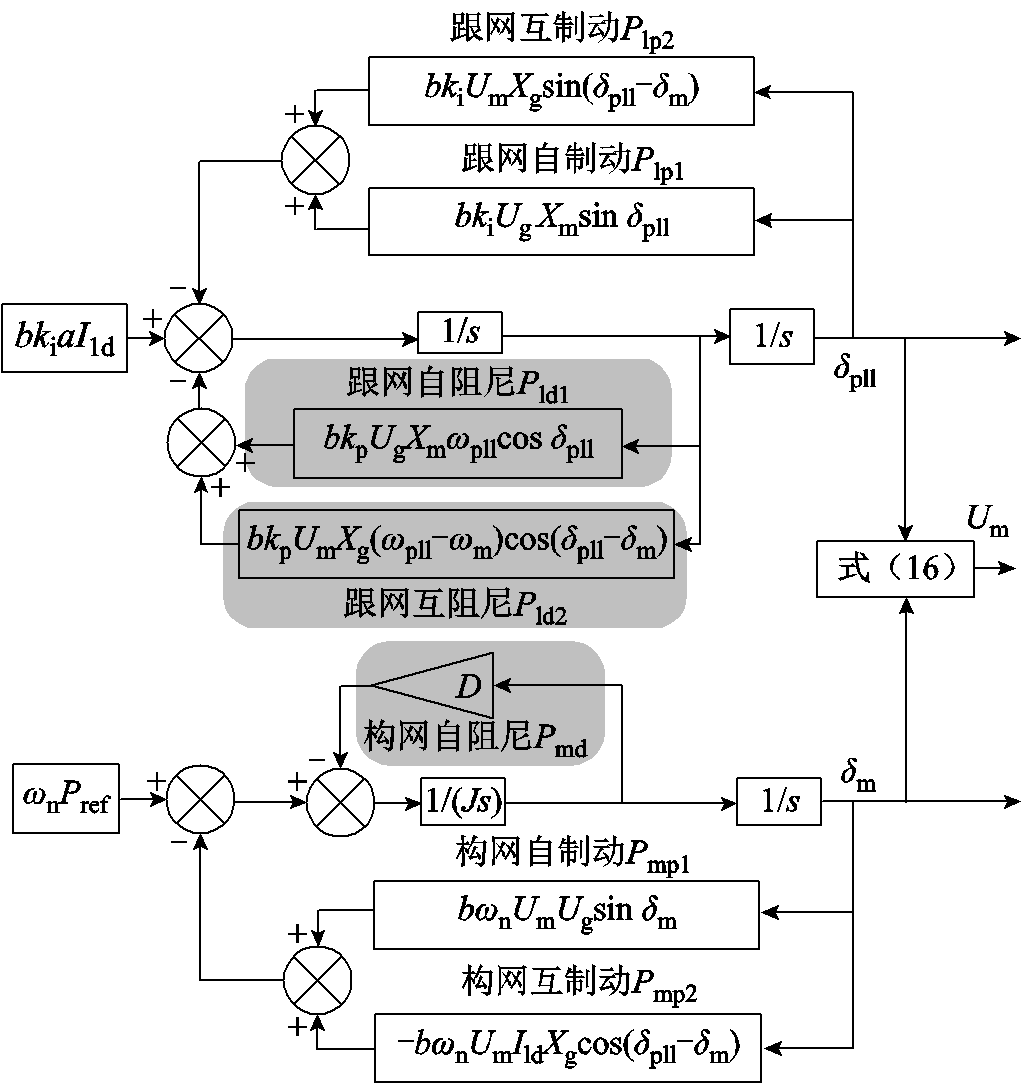
图5 混联系统的四阶暂态模型
Fig.5 Fourth-order transient model of hybrid system
由图5可以看出,暂态过程中,PLL与VSG的动态是两个并行的二阶非线性系统。其中系统的负反馈环节有两种类型:一种反馈功率是关于速度量w和位置量d的函数,这部分功率说明系统在每次到达某一位置状态时,运动的速度是不同的,这类反馈功率被定义为与速度相关的阻尼功率;另一种反馈功率仅与位置量d相关,这种以位置定义的功率被定义为系统自身的制动功率。此外,在上述两种功率中,仅包含本系统的状态变量的功率项被定义为自功率,其余功率被定义为互功率。由以上功率划分形成的等效物理模型如图6所示。
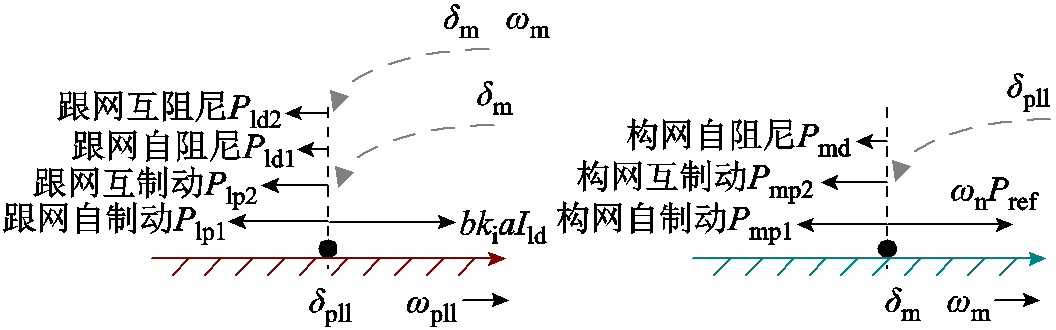
图6 混联系统的等效物理模型
Fig.6 Equivalent physical model for hybrid system
图6中灰色虚线代表互功率的传导路径,可见,跟/构网二阶系统通过互功率的传递路径相互影响。由于控制结构的特性,构网系统仅存在自阻尼功率,它的功率交互路径更加清晰。在制动功率和阻尼功率为正的情况下,阻尼/制动功率均为系统的减速贡献能量,使系统动能水平降低并趋近稳定。
由第1节的分析,混联系统的暂态计算是一个复杂的结构对称四阶非线性系统求解问题,本文将提出一种离散轮换计算方法对其进行求解。在确定算法结构和具体实施步骤前,需对非线性运动的初值进行确定。
由图4可知,构网控制的二阶VSG中包括两个积分器,由于积分器的输出不会突变,所以dm和wm的初值维持故障前数值,即
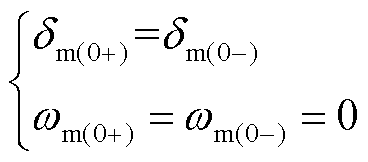 (17)
(17)
式中,下角标代表离散计算的节点序号,0-为故障前时刻,0+为故障发生时刻。在故障前的稳态中,dm保持恒定,wm=0。
由式(16),无功环路输出量Um完全与故障后时刻的功角相关,鉴于积分器输出的dpll同样不会突变,以无穷大母线电压跌落故障为例,Um(0+)为
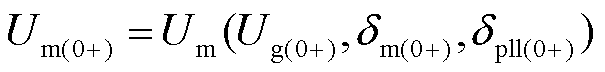 (18)
(18)
即故障时刻的Um为Ug、dm和dpll的代数函数。
如图3所示,当暂态电压突变时,跟网控制锁相环PI的比例部分会使输出量wpll突变,因积分部分不会突变,速度增量即Ulq突变通过kp呈现,故dpll和wpll初值为
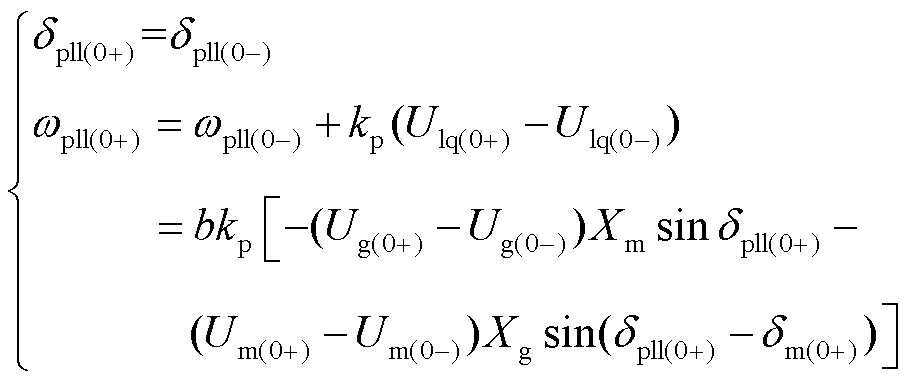 (19)
(19)
二阶系统的求解依赖暂态能量的计算,混联系统包括两个并行且相互影响的二阶系统。将能量法应用于两个系统并行计算的难点是,任一单独的能量计算是在功角域内进行的,但两者的并行计算需要保证在两个功角域中建立不同时刻下的对应关系,其后才可在单独的功角域分别计算能量变化。
在极短的功角位移中,为了求解运动,可利用微积分的基本思想将其运动线性化,即认为这一段中的运动速度不变,来计算其运动时间和该段运动中的能量累计。
第一摆中混联系统暂态计算结构如图7所示,利用这一思想,本文将在功角区间线性化的基础上,试图建立一种并行的暂态同步计算方法。
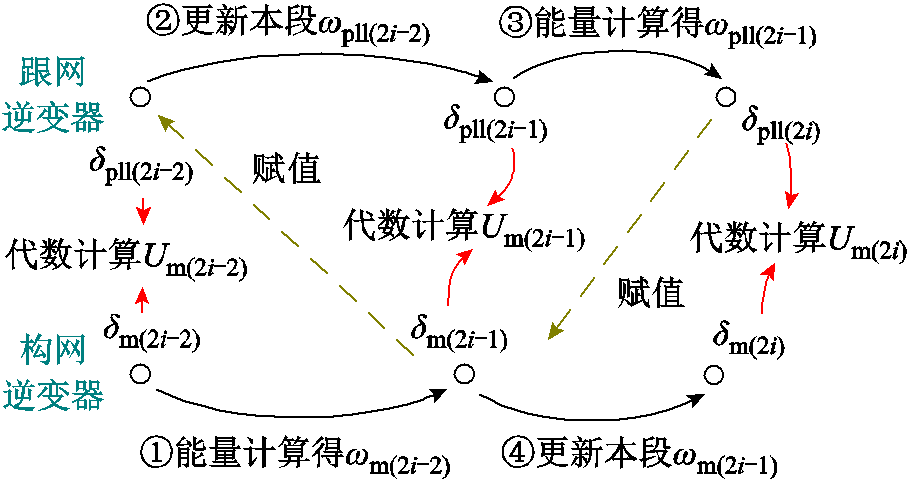
图7 第一摆中混联系统暂态计算结构
Fig.7 The structure of transient calculations for hybrid systems in the first swing
在故障发生的零时刻,利用2.1节提出的求解方法获得初值。首先在固定的位移dstep中,利用能量函数对1时刻构网逆变器的速度进行求解,并在求解后,将0~1时刻的wm、dm和区间用时Dt向跟网计算进行赋值。在该段线性化区间中,跟网二阶系统被认为先以wpll(0+)进行运动,功角的位移dgap为Dt与wpll(0+)的乘积,故可使用能量法在dpll(0+)~dpll(0+)+dgap中进行求解,并获得新的速度wpll(1),这完成了对于该段速度的计算和更新。在1节点,Um(1)可通过dm和dpll进行代数计算。在第②步中,计算的对偶可以保证单一运动系统计算可能存在的误差累积被消除,故首先计算在dstep位移中跟网二阶系统的能量变化,进而对构网系统进行赋值,继而计算其暂态能量。
从计算量的角度来说,以上计算的步数是单一二阶系统进行离散暂态计算步数与二阶系统数量的乘积,这有效地避免了维数灾的问题;从机理的角度来说,不同于高阶非线性方程的数值求解方法,二阶系统的并行计算可以基于能量清晰直观地进行分析,这些能量的来源可以被简洁地划分为自/互阻尼或自/互功率,使得研究人员从机理出发,分析出失稳是由于交互产生还是自身稳定产生;从误差的角度来说,图7中对偶的计算过程①/②和③/④,使得二阶运动方程的线性化中可能存在的误差被通过反方向的计算进一步抵消或弱化,进而使计算中不存在静差或误差发散。此外,Um的动态被独立于能量计算进行代数求解,这是由于感性系统中,Um关于无功输出敏感,变化较小,将Um的代数变化纳入能量解析将加大解析式的复杂度,不利于算法的工程实施。以下将推导算法的具体计算公式,并列明可能发生的多摆暂态过程处理方法。
对式(14)两侧乘dm关于时间的导数,并对时间做不定积分,有
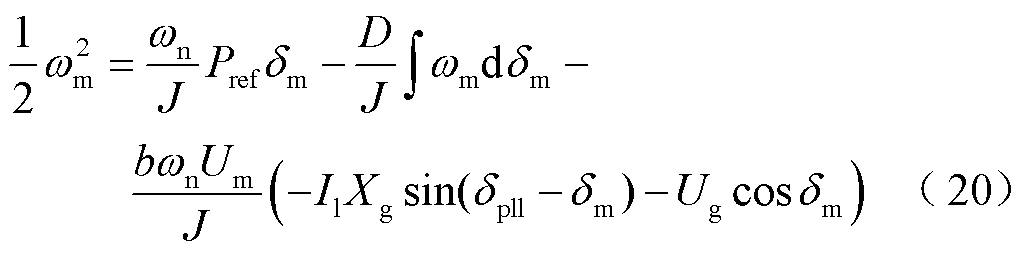
式中,等号左边为速度的二次方项,可以被定义为构网系统的等效动能Ekm。基于运动的微分,在2i-2~2i-1步中,计算构网系统在固定步长dstep区间中动能变化为
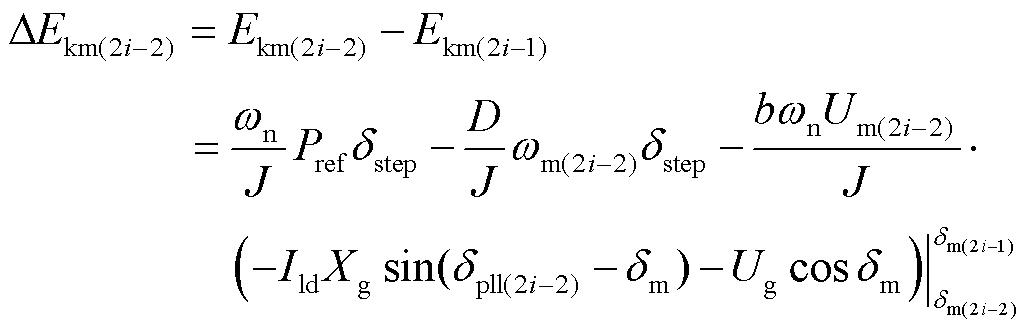 (21)
(21)
其中
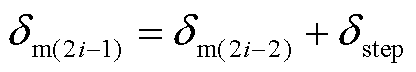 (22)
(22)
在运动微分下,该段运动的阻尼功率积分项可以借用wm(2i-2)解析获得。该段的动能变化完全可以解析求解。
节点2i-1时刻,构网系统的动能及运动速度为
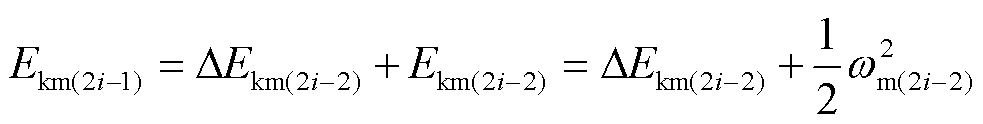 (23)
(23)
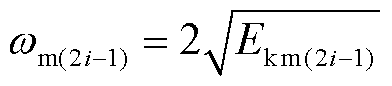 (24)
(24)
基于运动的线性化,该段运动所需的时间Dt为
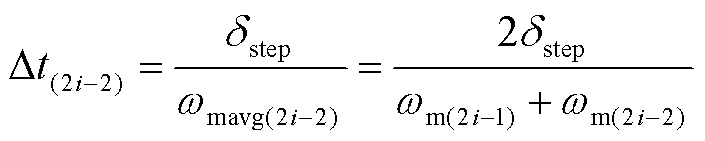 (25)
(25)
式中,wmavg(2i-2)为构网系统在2i-1~2i-2区间的平均速度。
轮换至跟网逆变器计算,在时间区间Dt内,构网逆变器的功角区间为
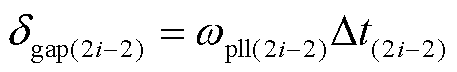 (26)
(26)
即可确定在故障发生同一Dt后,跟网逆变器的功角位置dpll(2i-1)为
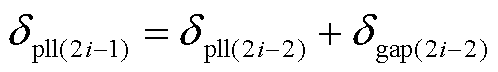 (27)
(27)
此时,确定了在2i-1时刻下dm与dpll的位置,进而能够对wpll开展进一步的更新。
对式(10)两侧乘dpll关于时间的导数,并对时间不定积分,得到
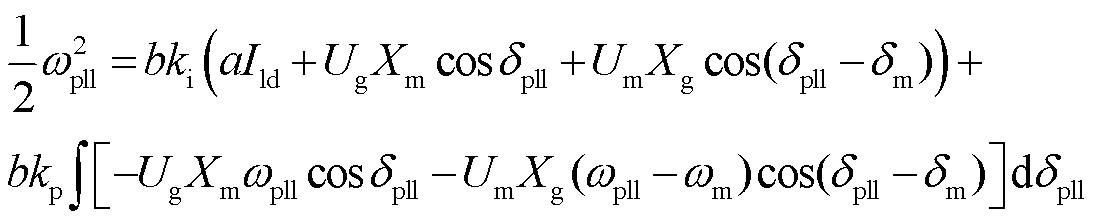 (28)
(28)
同样地,将等号左边定义为跟网系统的等效动能Ekpll,在dpll(2i-2)~dpll(2i-1)的区间内,跟网系统的动能变化为
 (29)
(29)
进一步地,计算节点在2i-1时刻跟网系统动能及速度分别为
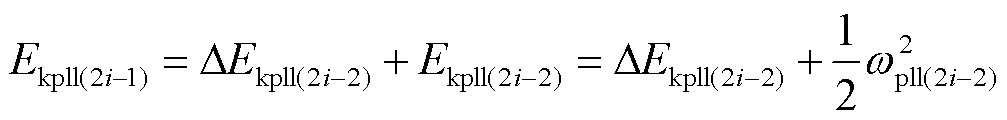 (30)
(30)
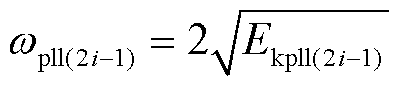 (31)
(31)
进而,2i-1时刻,Um的值可以被更新为
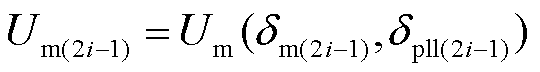 (32)
(32)
至此,2i-1时刻,各状态变量dpll、wpll、dm、wm和关键变量Um都已解得。在2i-1~2i的区间中,暂态计算轮换为跟网系统以固定步长dstep进行能量计算,并获得这一时刻的功角-时间域关系,进而更新构网系统在2i时刻的速度。这一阶段的能量计算函数与式(21)及式(29)相同,相关线性化类比计算可得,不再正文赘述。
在功角-时间域轮换的暂态计算中,可能会出现Ekx(n)<0的情况(x代表m或pll),这说明x系统在n-1时刻已经到达了上一摆的终点,且不会到达这一时刻的dx(n),而是在n时刻进入下一摆。对于两摆之间的轮换过程,本文做以下赋值和处理:
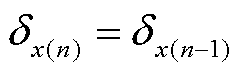 (33)
(33)
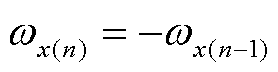 (34)
(34)
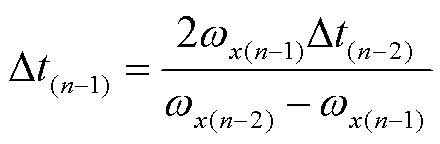 (35)
(35)
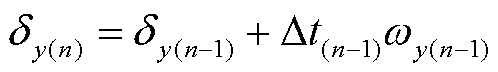 (36)
(36)
式中,下角标x代表某一两摆交替中的系统,y代表另一单向运动系统。式(33)~式(36)代表在n时刻前,x系统到达了前一摆的止点,并在n时刻再次回到dx(n-1)。在这个过程中,系统减速并反向运动,故n时刻的wx(n)为wx(n-1)的相反数。式(35)代表系统以上一时刻的加速度进行wx(n)到wx(n-1)的运动,从而计算该段时间内的Dt,完成了这一步中功角域与时域的对应。在运动时间已知后可以计算出dy(n),利用上文所述的跟网或构网能量计算获得wy(n),并代数计算Um(n)。至此,n时刻的初值dpll(n)、wpll(n)、dm(n)、wm(n)和Um(n)已经确定,在下一阶段的暂态计算中,为保证运动的计算精度,在速度较慢的轮换系统x进行第一步固定步长的暂态计算,并通过功角-时间映射轮换至y系统进一步更新其运动速度wy(n+1),下一步轮换至y系统进行固定步长暂态计算,在x系统中校正暂态速度 wx(n+2),这一过程与图7类似,不再重复画出。当x与y系统的暂态速度绝对值小于阈值wth时,判断系统暂态稳定。最终,形成离散域下基于轮换计算的暂态稳定性求解方法如图8所示,其中,由于首摆中构网系统的初速度为0,将其定义为x,并定义跟网系统为y系统,利用其速度初值计算dgap。
值得说明的是,电力系统中存在对不同CCT的暂态校核,本文方法依然适用。当方法用于校核CCT时,整体算法为图8中算法的两步串联,即第一步中,使用算法进行计算,但其将结束判断语句修改为故障时间或功角是否大于CCT,当判断为真时,记录结束值,并调整系统中电压或阻抗参数为恢复状态,重新计算故障恢复后暂态过程初值,再次完成图8中全流程计算从而判断系统稳定性。
本节在Matlab/Simulink中建立图1系统的时域仿真模型,并与所提方法进行对比,在不同暂态稳定条件下观察分析系统的暂态行为。然后从暂态故障恢复角度,通过对比所提方法计算的CCT与仿真得出的CCT,验证方法的准确性。
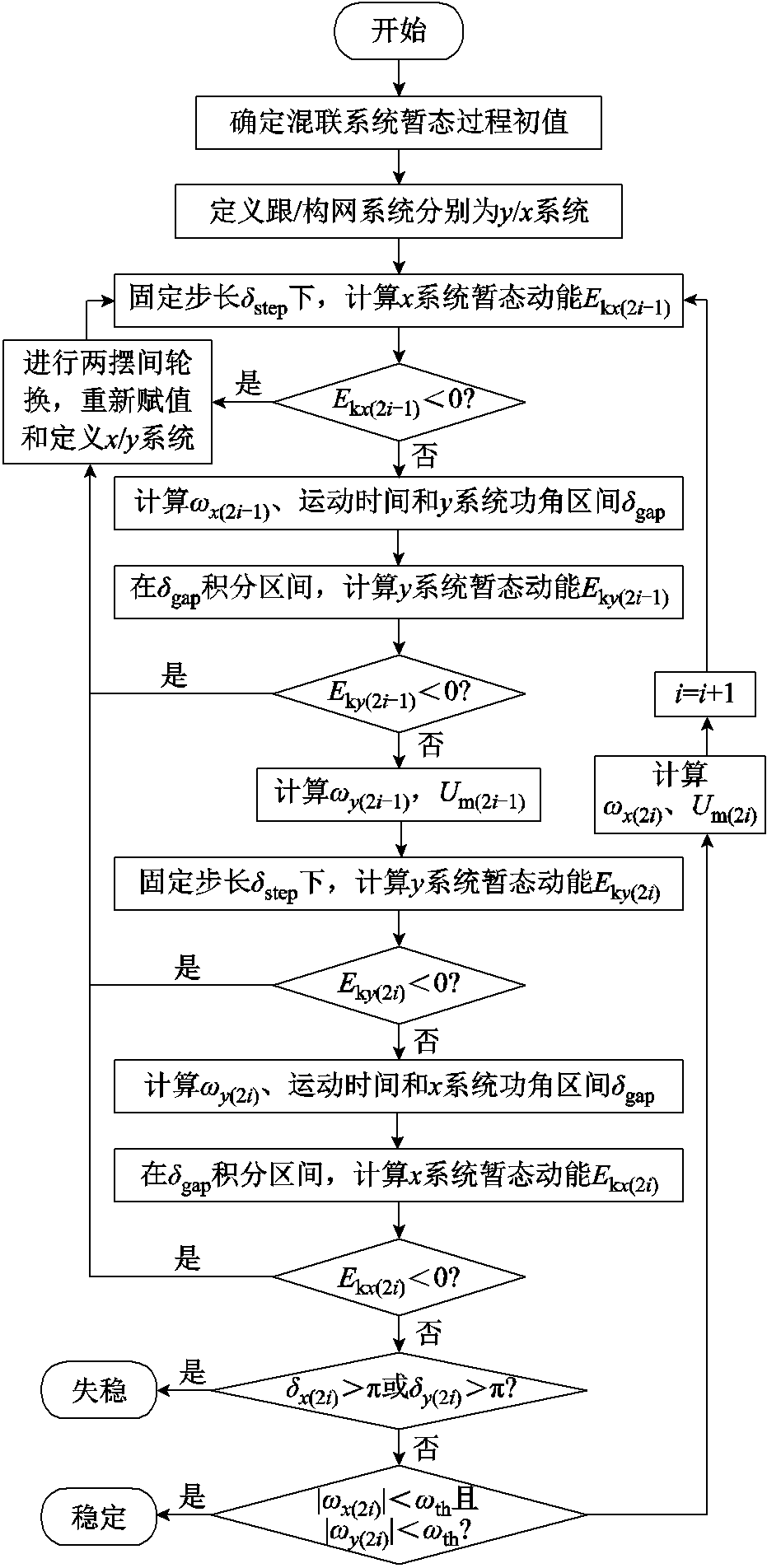
图8 基于轮换计算的暂态稳定性求解方法
Fig.8 Transient stability solver based on alternating calculation
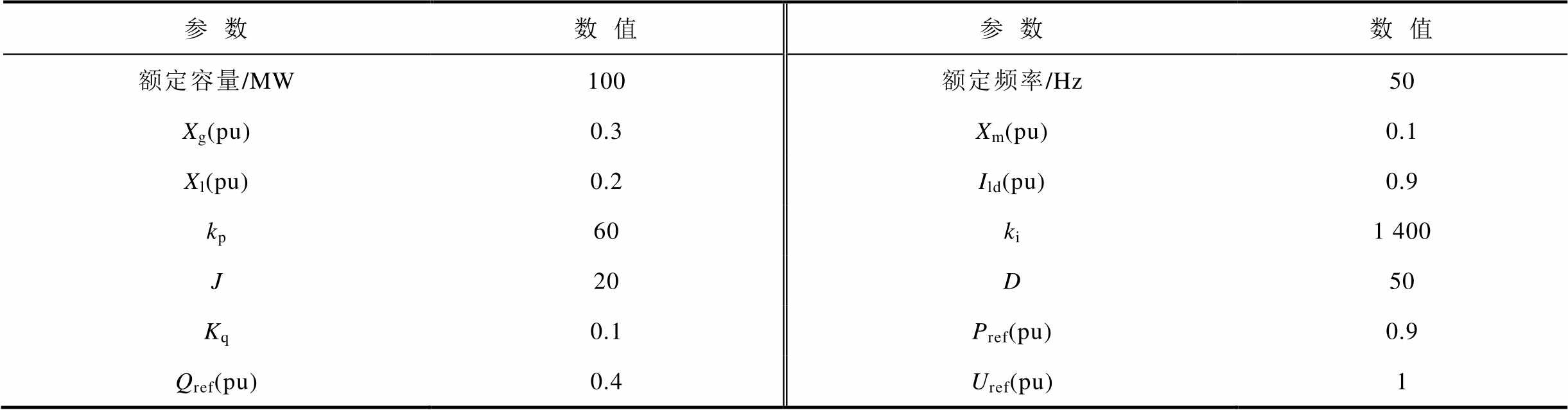
为验证方法的有效性,建立与图1相同结构的测试系统,系统中各参数见表1。
表1 测试系统参数
Tab.1 Parameters of benchmark system
参数数值参数数值 额定容量/MW100额定频率/Hz50 Xg(pu)0.3Xm(pu)0.1 Xl(pu)0.2Ild(pu)0.9 kp60ki1 400 J20D50 Kq0.1Pref(pu)0.9 Qref(pu)0.4Uref(pu)1
为了验证所提方法能够准确地估计混联系统暂态过程中的轨迹,在1 s时引入两个不同程度的持续电压跌落,其跌落深度分别为0.3(pu)和0.31(pu),即跌落后的母线电压分别为0.7(pu)和0.69(pu)。图9和图10分别展示了0.3(pu)及0.31(pu)电压跌落下的暂态相轨迹,以及时域下各变流器出口电压、功率波形。
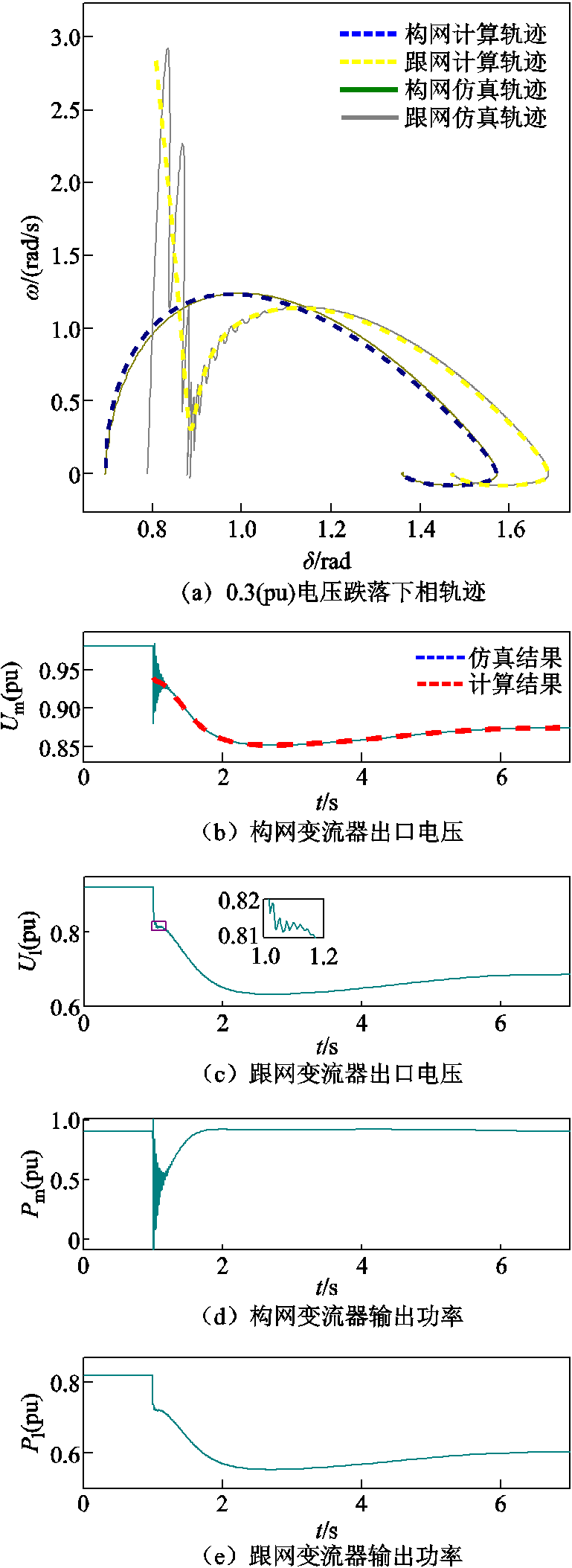
图9 0.3(pu)电压跌落下各系统相轨迹及电压、功率波形
Fig.9 Phase trajectories and voltage/power waveforms of system under 0.3(pu) voltage dips
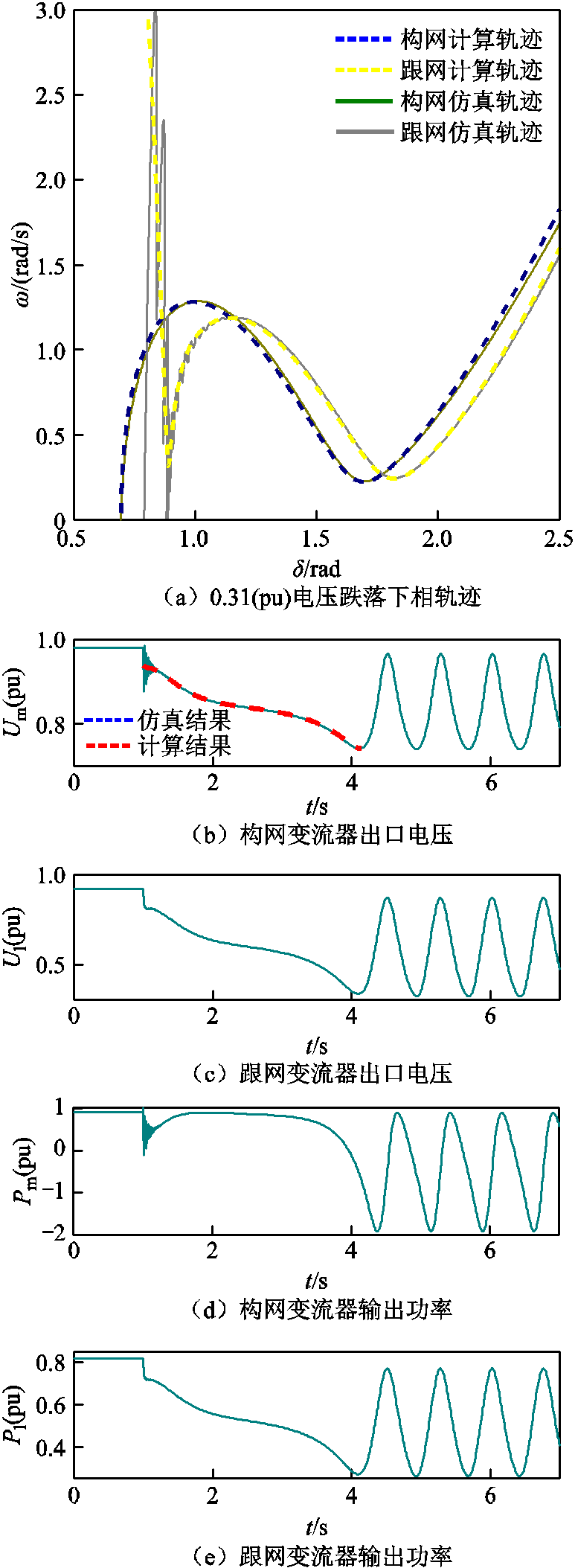
图10 0.31(pu)电压跌落下各系统相轨迹及电压、功率波形
Fig.10 Phase trajectories and voltage/power waveforms of system under 0.31(pu) voltage dips
由图9a可以看出,本文所提方法获得的跟/构网计算相轨迹,能够较好地拟合实际系统的相轨迹,并且在暂态的全过程中,没有出现持续误差,这首先证明了该方法的有效性。由于跟网系统存在比例环节,故其在故障时刻发生了速度的跳变,在较大速度的驱动下,跟网系统的阻尼功率水平较高,同时,其制动功率随着功角快速增大也进一步提升,形成了先减速后加速的相轨迹。构网系统的速度在故障时不发生突变。此外,由于其阻尼仅由自身阻尼系数决定,且两系统在暂态过程中的功角相对位置并未展现出明显差异,故其互制动功率因素相对恒定,更多地展现出单机的暂态轨迹特性。
如图9b所示,计算方法获得的暂态过程构网变流器出口电压与仿真结果拟合度较高,构网变流器的下垂特性被准确地在本方法中充分考虑到。图9c的跟网变流器电压波形中,在0.2 s时间尺度的电磁暂态中,展现了一定的输出抖动,端口电压的抖动会通过PLL的比例环节对跟网系统的速度造成干扰,这解释了图9a中跟网变流器在纵轴上出现的较大跳跃,但电磁暂态持续时间较短,且其速度抖动中点与实际四阶模型重合,不构成对暂态能量计算结果的影响。图9d、图9e反映了跟/构网变流器的有功输出水平,可以看出,构网变流器通过不平衡功率驱动,最终恢复参考功率水平;跟网变流器则在暂态过程中展现出了恒流的输出水平,其有功功率输出随着端口电压近似成正比降低,并受功角摆动的影响。
图10a展现的是临界不稳定下的相轨迹曲线,同样地,所提方法能够与实际相轨迹高度重合,并显示系统最终趋于失稳。当跟/构网系统功角分别达到1.85 rad/1.65 rad时,其制动及阻尼功率无法将其进一步减速,随着驱动功率超过制动及阻尼功率,系统不断加速,功角增大,导致暂态失稳。
图10b展现了时间域下计算方法估计的构网变流器端口电压,约4.2 s时,由于跟网系统功角超过了稳定阈值p,方法停止计算并输出系统不稳定的判断,故计算方法的波形在图中仅覆盖部分时间。图10c~图10e展现了暂态失稳后电压及功率的失步过程,可看出,当4.2 s功角超过p时,系统加速失步,故相关稳定性提升手段应在该点前进行投入。
在以上的两个算例验证中,相关的计算用时被记录在表2中。对比的时域四阶方程解法是基于图5所搭建的数值仿真模型进行,时域仿真方法采用平均值模型进行。以上两种方法停止计算的条件与所提方法相同,即速度小于阈值判断稳定,功角大于阈值判断失稳。相关步长与计算时间见表2。结合仿真结果可看出,所提方法在设置步长下,不仅获得了与时域仿真高度一致的相轨迹波形,其计算时间也较已有数值方法至少提升了一个数量级。这是由于时域求解的龙格库塔方法是通过在时间轴上刻画计算步长,进一步求解偏微分并推导泰勒级数进行四阶微分方程增量计算。而本文方法有效地利用了并行二阶系统物理含义,计算时间尺度通过步长除以运动速度定义,在保证功角精度的同时自适应地确定时间步长。所以,本文方法在精度相当的前提下,能够进行变步长计算,实现计算效率的提升,具有较强的工程实践价值。其亦可通过接口并入大电网暂态分析,降低大规模系统的暂态稳定计算时间。
表2 暂态求解时间对比
Tab.2 Comparison of transient computation time

暂态场景求解方法求解步长求解时长/ms 场景1(稳定)本文方法1×10-4 rad5.58 时域四阶方程1×10-4 s274 时域仿真(加速)1×10-4 s448 场景2(失稳)本文方法1×10-4 rad11.59 时域四阶方程1×10-4 s217 时域仿真(加速)1×10-4 s283
注:以上数据的计算环境为: AMD R7 7840Hs@3.8 GHz,32 GB RAM,Matlab/Simulink R2020a。
为展现方法在故障-恢复的全过程中能够有效估计CCT的值,在系统各参数同表1条件下,本部分设置了两个深度电压跌落并切除的算例,算例的电压跌落为0.7(pu),即电网电压降至0.3(pu),故障持续时间分别为409 ms与414 ms。两算例下跟/构网系统计算相轨迹及仿真相轨迹如图11所示。由图11可以看出,在深度故障下,跟网系统同样展现出了速度跳动,但所提方法计算的相轨迹与仿真相轨迹展现了高度重合,计算方法对短时深度故障的暂态行为能够准确估计。对于CCT的估计,在该场景下可以实现5 ms的分辨率。
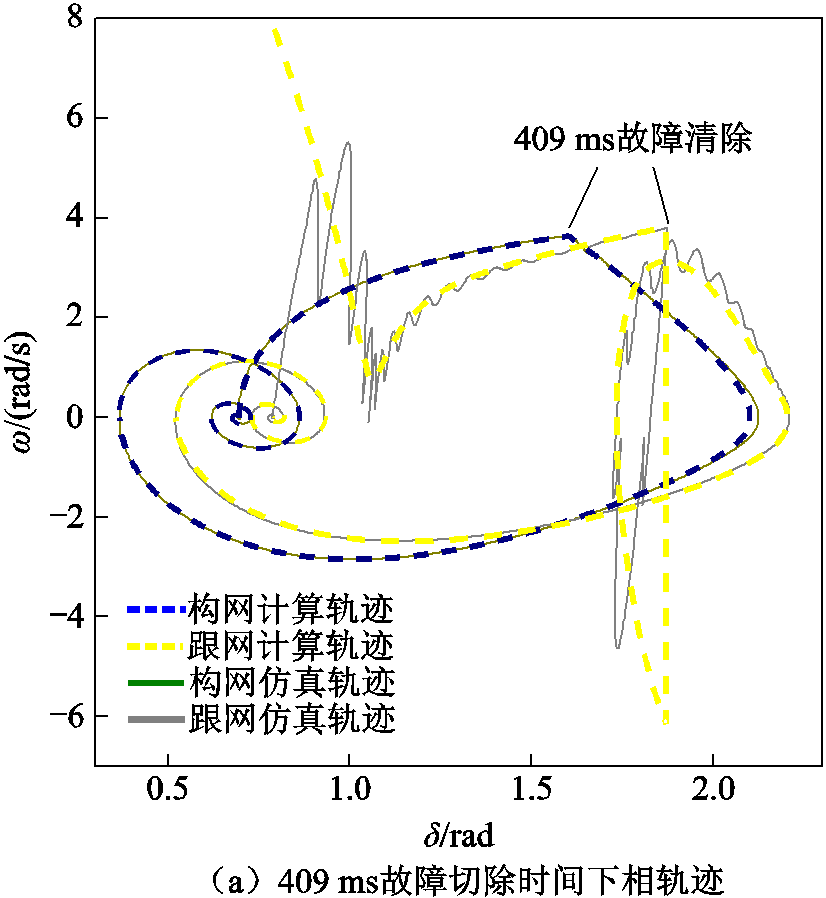
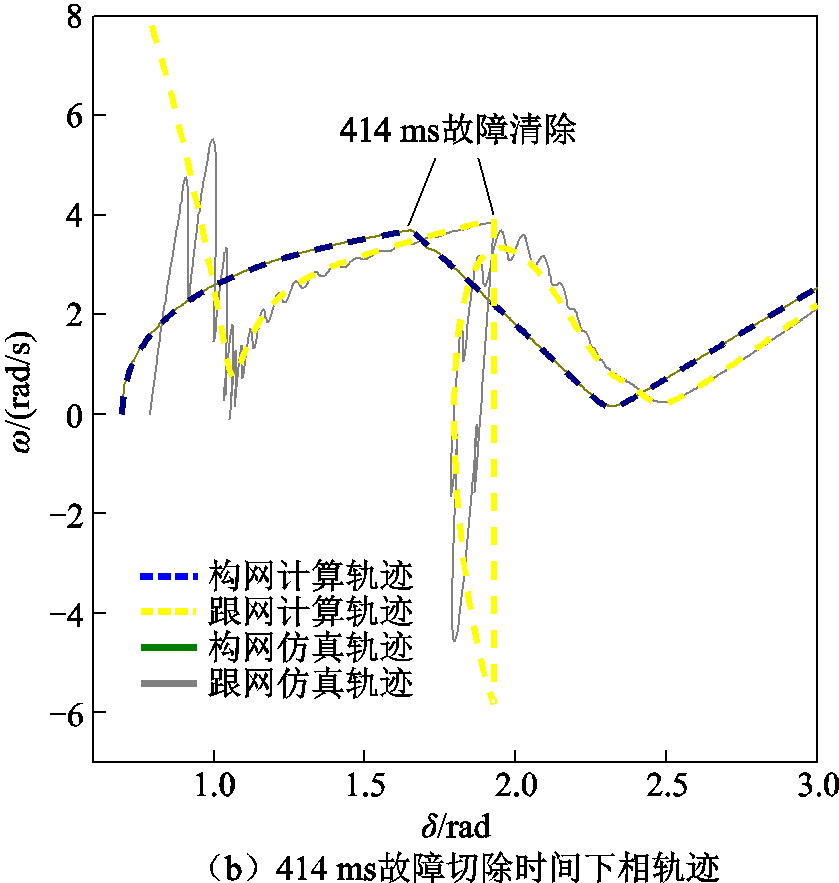
图11 0.7(pu)电压跌落至电压恢复过程中系统相轨迹
Fig.11 System phase trajectory during 0.7(pu) voltage dips to voltage recovery
对于图11a,在故障清除的瞬间,跟网系统电压恢复使得其速度再一次发生突变为负,即此时跟网系统的功角进行反向运动。构网系统由于其转速不发生突变,其功角在惯性的作用下进一步增大,但其制动功率此时恢复到较高水平,速度不断下降。在恢复时刻的跟/构网系统的速度符号相反,说明此时两者转变为异调机组,即两者功角反向运动,这在传统的惯量中心法中无法估计到,而本文方法可以准确刻画,其具有先进性。随着构网机组功角不断加大,跟网机组进一步被加速至功角正向运动,此时两机组变为同调机群,并趋于稳定。
图11b中,在故障切除后,两机组同样先进入异调运动,后统一至同调状态,但由于故障时间较长,两者均积攒了更多的加速能量。在跟/构网机组功角分别为2.5 rad/2.3 rad时,其速度趋近于0,但此时驱动功率仍大于阻尼/减速功率,系统再一次加速,并趋于失稳。
为验证本文所提算法的工程有效性,搭建图12所示的硬件在环测试平台。电路和逆变器的全阶物理模型建立在SpaceR平台内,跟/构网逆变器各由一台快速控制原型控制。实验环节中的系统拓扑及参数与仿真验证部分保持一致。
图13a、图13b分别对应系统电压Ug跌落0.3(pu)、0.31(pu)下跟/构网逆变器的功角及角速度情况。图13a中,系统为临界稳定状态,在跌落发生约1.5 s后,随着系统减速到达新的稳定点,wpll、wm趋近于0。图13b中,由于系统扰动过大,减速能量呈现不足,最终角速度无法减速至0,从而越过不稳定平衡点,系统失稳。在以上两实验状态下,故障波形展现了0时刻wpll的跳变及故障后400 ms内wpll先减速后加速的特征,与图9及图10中的相轨迹高度统一,说明了所提计算方法获得相轨迹的准确性。此外,由于实验中的电路模型为全阶,故所提方法的有效判断也说明了网络电抗的线性化不影响同步稳定求解。

图12 SpaceR硬件在环测试平台
Fig.12 Test platform based on SpaceR HiL setup

图13 不同永久跌落下跟/构网系统功角及角速度波形
Fig.13 Waveforms of GFL/GFM system under different permanent drops
设定瞬时电压跌落深度为0.7(pu),图14a、图14b分别对应在CCT为409 ms与414 ms下的暂态功角及角速度波形。图14a中,由于故障持续时间处于稳定切除时间内,系统在电压恢复后经历功角摆动最终回归初始稳定点。图14b中的切除时间较长,在故障加速能量的进一步累积下,wpll、wm无法在电压恢复后减速至0,使系统越过稳定平衡点并进一步失稳。在以上两实验中,故障切除后的瞬间wpll跳变为负值,在约100 ms后增大至0,并进一步变为正值,表现了故障切除后跟/构网机组先异调后同调的运行过程,与图11中计算相轨迹中的故障切除后跳变一致。

图14 不同CCT下跟/构网系统功角及角速度波形
Fig.14 Waveforms of GFL/GFM system with different CCT
跟/构网混联系统具有阶数高、非线性强的特点,已有方法难以对其暂态稳定性进行评估并求解。针对这一问题,本文建立了混联系统的四阶非线性暂态模型,其中包括PLL、VSG及其无功环路动态。针对混联系统中存在的PLL及VSG暂态并行计算,本文从能量变化角度入手,设计了在离散域下的轮换计算结构,并建立了从功角域到时间域的映射,最终形成基于离散轮换计算的暂态求解方法,相关理论分析和算例验证表明:
1)本文所提基于功角-时间域的离散计算方法能够准确地刻画跟/构网混联系统在暂态过程中的功角、角速度及构网逆变器电压变化,有效地判断暂态过程中系统稳定情况,其求解时间较已有数值方法至少提升一个数量级。
2)所提方法同样适用于对CCT的计算,在本文算例中,CCT估计值的分辨率在5 ms以内。针对故障恢复过程中跟/构网机组异调运行情况,该方法也能实现准确刻画。
3)本文方法具有物理机理明确、算力需求较低的优点,有望作为大型仿真的下级子系统加快仿真速度,如何设计此类上下级迭代仿真的接口是未来的工作方向之一。
参考文献
[1] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[2] 马宁宁, 谢小荣, 贺静波, 等. 高比例新能源和电力电子设备电力系统的宽频振荡研究综述[J]. 中国电机工程学报, 2020, 40(15): 4720-4732.
Ma Ningning, Xie Xiaorong, He Jingbo, et al. Review of wide-band oscillation in renewable and power electronics highly integrated power systems[J]. Pro-ceedings of the CSEE, 2020, 40(15): 4720-4732.
[3] 雷雨, 李光辉, 王伟胜, 等. 跟网型和构网型新能源并网控制阻抗对比与振荡机理分析[J]. 中国电机工程学报, 2025, 45(1): 150-163.
Lei Yu, Li Guanghui, Wang Weisheng, et al. Comparison of impedance characteristics and oscillation mechanism for grid following and grid forming renewable energy[J]. Proceedings of the CSEE, 2025, 45(1): 150-163.
[4] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[5] 郭小龙, 杨桂兴, 张彦军, 等. 构网型储能变流器并网系统SISO环路增益建模与重塑控制[J]. 电气技术, 2023, 24(2): 24-31, 51.
Guo Xiaolong, Yang Guixing, Zhang Yanjun, et al. Modeling and reshaping control of single input and single output loop gain of the grid-forming energy storage converter grid-connected system[J]. Electrical Engineering, 2023, 24(2): 24-31, 51.
[6] 张兴, 战祥对, 吴孟泽, 等. 高渗透率新能源发电并网变流器跟网/构网混合模式控制综述[J]. 电力系统自动化, 2024, 48(21): 1-15.
Zhang Xing, Zhan Xiangdui, Wu Mengze, et al. Review on grid-following/grid-forming hybrid mode control for grid-connected converter in high penetration rate of renewable energy generation[J]. Automation of Electric Power Systems, 2024, 48(21): 1-15.
[7] 杨铭, 曹武, 赵剑锋, 等. 受控电压/电流源型变流器混合多机暂态电压支撑策略[J]. 电工技术学报, 2023, 38(19): 5207-5223, 5240.
Yang Ming, Cao Wu, Zhao Jianfeng, et al. Transient voltage support strategy for hybrid multi-converter of controlled voltage/current source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5207-5223, 5240.
[8] 贾焦心, 沈钟毓, 秦本双, 等. 构网型和跟网型电力电子装备混联系统惯量响应的匹配问题综述[J]. 电力自动化设备, 2024, 44(6): 77-89.
Jia Jiaoxin, Shen Zhongyu, Qin Benshuang, et al. Review on inertia response matching problem of hybrid power systems with grid-forming and grid-following power electronic devices[J]. Electric Power Automation Equipment, 2024, 44(6): 77-89.
[9] 郭小龙, 杨桂兴, 张彦军, 等. 构网型储能与跟网型光伏混联发电系统阻抗建模与小扰动稳定机理分析[J]. 电气工程学报, 2025, 20(1): 299-308.
Guo Xiaolong, Yang Guixing, Zhang Yanjun, et al. Impedance modeling and small-signal stability mechanism analysis of grid-forming energy storage and grid-following PV hybrid power generation system[J]. Journal of Electrical Engineering, 2025, 20(1): 299-308.
[10] 张加卿, 郭春义. 跟网-构网光伏与火电打捆经传统直流外送系统次同步扭振机理研究[J/OL]. 中国电机工程学报, 2024: 1-15[2024-09-30]. https://link. cnki.net/urlid/ 11.2107.TM.20240801.1521.007.
Zhang Jiaqqing, Guo Chunyi. Research on sub-synchronous torsional vibration mechanism for grid-following and gridforming photovoltaic and thermal power bundling system via LCC-HVDC transmission [J/OL]. Proceedings of the CSEE, 2024: 1-15[2024-09-30].https://link.cnki.net/urlid/11.2107.TM.20240801. 1521.007.
[11] 余光正, 胡越, 刘晨曦, 等. 含跟网/构网型混联多馈入系统协调优化配置方法研究[J]. 中国电机工程学报, 2025, 45(2): 588-601.
Yu Guangzheng, Hu Yue, Liu Chenxi, et al. Research on the coordinated optimization configuration method for hybrid multi-infeed systems with grid-following or grid-forming[J]. Proceedings of the CSEE, 2025, 45(2): 588-601.
[12] Yang Chaoran, Huang Linbin, Xin Huanhai, et al. Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems[J]. IEEE Transactions on Power Systems, 2020, 36(4): 3563-3573.
[13] 赵郅毅, 许寅, 吴翔宇, 等. 含异构微源的混合型孤岛微电网暂态有功响应分析与控制策略[J]. 电工技术学报, 2024, 39(19): 6072-6084.
Zhao Zhiyi, Xu Yin, Wu Xiangyu, et al. Transient active power response analysis and control strategy of hybrid island microgrid containing heterogeneous microsources[J]. Transactions of China Electro-technical Society, 2024, 39(19): 6072-6084.
[14] 徐式蕴, 王一鸣, 孙华东, 等. 国外新能源脱网事故对中国电网安全稳定运行的启示[J]. 电力系统自动化, 2024, 48(13): 1-8.
Xu Shiyun, Wang Yiming, Sun Huadong, et al. Insights from renewable energy outage accidents abroad for secure and stable operation of power grids in China[J]. Automation of Electric Power Systems, 2024, 48(13): 1-8.
[15] Fu Xikun, Sun Jianjun, Huang Meng, et al. Large-signal stability of grid-forming and grid-following controls in voltage source converter: a comparative study[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7832-7840.
[16] Luo Cong, Chen Yandong, Xu Yuancan, et al. Two-stage transient control for VSG considering fault current limitation and transient angle stability[J]. IEEE Transactions on Industrial Electronics, 2023, 71(7): 7169-7179.
[17] Luo Cong, Chen Yandong, Liao Shuhan, et al. Design-oriented analysis and transient control for VSG with current saturation unit[J]. IEEE Transactions on Power Electronics, 2025, 40(1): 2472-2483.
[18] Li Xilin, Tian Zhen, Zha Xiaoming, et al. An iterative equal area criterion for transient stability analysis of grid-tied converter systems with varying damping[J]. IEEE Transactions on Power Systems, 2024, 39(1): 1771-1784.
[19] 张锋, 陈武晖, 康佳乐, 等. 双馈风电场故障穿越控制策略对风火打捆系统暂态稳定性影响及提升控制策略研究[J]. 电工技术学报, 2025, 40(3): 717-729.
Zhang Feng, Chen Wuhui, Kang Jiale, et al. Research on the effect of fault ride-through control strategy of doubly fed wind farms on transient stability of wind-fire bundling system and enhancement control strategy[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 717-729.
[20] Li Ruibo, Yan Xiangwu, Wang Yanbo, et al. Improved transient modeling and stability analysis for grid-following wind turbine: third-order sequence mapping EAC[J]. IEEE Transactions on Power Delivery, 2024, 39(4): 2015-2027.
[21] 张梓钦, 朱东海, 马玉梅, 等. 弱电网故障下新能源并网变换器的奇异摄动模型与暂态稳定性分析[J]. 中国电机工程学报, 2023, 43(2): 454-465.
Zhang Ziqin, Zhu Donghai, Ma Yumei, et al. Singular perturbation model and transient stability analysis of grid-connected converter under weak grid faults[J]. Proceedings of the CSEE, 2023, 43(2): 454-465.
[22] Tian Zhen, Li Xilin, Zha Xiaoming, et al. Transient synchronization stability of an islanded AC microgrid considering interactions between grid-forming and grid-following converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(4): 4463-4476.
[23] 李锡林, 查晓明, 田震, 等. 频率突变影响下基于Lyapunov法的孤岛微电网暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31, 55.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Lyapunov based transient stability analysis of islanded microgrid under the influence of frequency abrupt change[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31, 55.
[24] 黄森, 姚骏, 钟勤敏, 等. 含跟网和构网型新能源发电单元的混联电力系统暂态同步稳定分析[J]. 中国电机工程学报, 2024, 44(21): 8378-8392.
Huang Sen, Yao Jun, Zhong Qinmin, et al. Transient synchronous stability analysis of series-parallel power system with grid-following and grid-structured new energy generating units[J]. Proceedings of the CSEE, 2024, 44(21): 8378-8392.
[25] Hu Qi, Fu Lijun, Ma Fan, et al. Impact of LVRT control on transient synchronizing stability of PLL-based wind turbine converter connected to high impedance AC grid[J]. IEEE Transactions on Power Systems, 2023, 38(6): 5445-5458.
[26] 唐王倩云, 张睿, 胡家兵. 用于系统暂态行为分析的双馈风机转子转速控制时间尺度暂态模型[J]. 中国电机工程学报, 2021, 41(9): 3037-3046.
Tang Wangqianyun, Zhang Rui, Hu Jiabing. Modelling of DFIG-based WT for power system transient responses analysis in rotor speed control timescale[J]. Proceedings of the CSEE, 2021, 41(9): 3037-3046.
[27] 梁帅, 姚良忠, 徐箭, 等. 基于电力电子变换器虚拟同步构网控制的电力系统暂态稳定极限提升方法[J]. 中国电机工程学报, 2025, 45(8): 2911-2925.
Liang Shuai, Yao Liangzhong, Xu Jian, et al. Power system transient stability limit enhancement method based on virtual synchronous grid-forming control of power electronic converters[J]. Proceedings of the CSEE, 2025, 45(8): 2911-2925.
[28] 颜湘武, 蔡光, 李锐博, 等. 计及功角偏差和阻尼效应的构网型双馈风机暂态稳定性分析[J]. 中国电机工程学报, 2025, 45(7): 2616-2633.
Yan Xiangwu, Cai Guang, Li Ruibo, et al. Transient stability analysis of grid forming-doubly fed induction generator with power angle deviation and damping effect[J]. Proceedings of the CSEE, 2025, 45(7): 2616-2633.
Transient Stability Solver for Grid-Following/Forming-Converter Hybrid System Based on Alternating Calculation in Discrete Domain
Abstract As modern power system toward high renewable energy integration with wind, solar, and storage sources, the increasing share of inverter-based resources leads to stability challenges dominated by multi-loop control with wide-band frequency characteristics. In systems with high penetration of renewable energy, converter-based systems have presented new features, such as large-scale integration and long-distance transmission, causing system faults to exhibit large-signal transient characteristics. The hybrid connection of grid-following (GFL) and grid-forming (GFM) converters has emerged as a potential solution to enhance the stability and efficiency of new energy transmission. However, the high order and strong nonlinearity of these hybrid systems pose challenges to the assessment of their transient stability. Therefore, this study is dedicated to designing an effective method for evaluating the transient stability of GFL/GFM converter hybrid systems.
The research methodology starts with the construction of a detailed fourth-order nonlinear model of the hybrid system, integrating phase-locked loops and virtual synchronous generators, which serves as the basis for the proposed transient stability solution method based on alternating calculation. Further, by calculating the mutation portion at the failure moment, the method derives the computed initial values for each system of the transient process. The essence of the rotation calculations lies in performing energy calculations and resolving the angular velocities in the power angle domain, subsequently mapping them back to the time domain. In the method implementation, energy calculations are first performed for a certain converter system, the dynamics of this system is used to further estimate the motion of the other system in this step, and the order of calculations for the two systems is exchanged to perform the alternating calculations. In this process, the correspondence between the power angles of GFL and GFM control is established, which enables the complex interactive motion patterns of the hybrid system under severe disturbances to be evaluated. During the alternating computation process, for the GFL/GFM system, the equivalent kinetic energy change over the step is computed by integrating the relevant equations that take into account the damped power and kinematic properties, avoiding the uncertainty associated with neglecting damping. During the continuous iterative computation process, the computed values are exchanged and updated between the two systems to ensure accurate transient behavior of the system. Eventually, the computation is stopped after the judgment condition of stability is satisfied.
The experimental and simulation results confirm the feasibility and effectiveness of the proposed method. It accurately depicts the variations in power angles, angular velocities, and GFM converter voltages during the transient processes of the hybrid system. The computational time of this method is significantly reduced compared to existing numerical methods, with at least an order of magnitude improvement. Additionally, the method is applicable to calculating the critical clearing time (CCT), achieving a resolution within 5 ms in the presented examples. It can also accurately characterize the out-of-sync operation of GFL and GFM converters during the fault recovery process.
In conclusion, this study provides a practical solution for evaluating the transient stability of hybrid converter systems. The developed method based on alternating calculation in the discrete domain exhibits clear physical mechanisms and relatively low computational requirements. It has the potential to be incorporated as a subsystem in large-scale simulations to accelerate the simulation speed.
Keywords:Grid-following/forming-converter hybrid system, transient synchronization stability, fourth-order nonlinear system, power angle domain, time domain
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.241955
国家自然科学基金(52207102)和北京市自然科学基金(3212037)资助项目。
收稿日期 2024-11-01
改稿日期 2025-01-03
李锐博 男,1997年生,博士研究生,研究方向为并网新能源发电建模、控制和稳定性分析。
E-mail:rb_li@ncepu.edu.cn
颜湘武 男,1965年生,教授,博士生导师,研究方向为新能源电力系统分析与控制、现代电力变换、新型储能与节能技术等。
E-mail:xiangwuy@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)