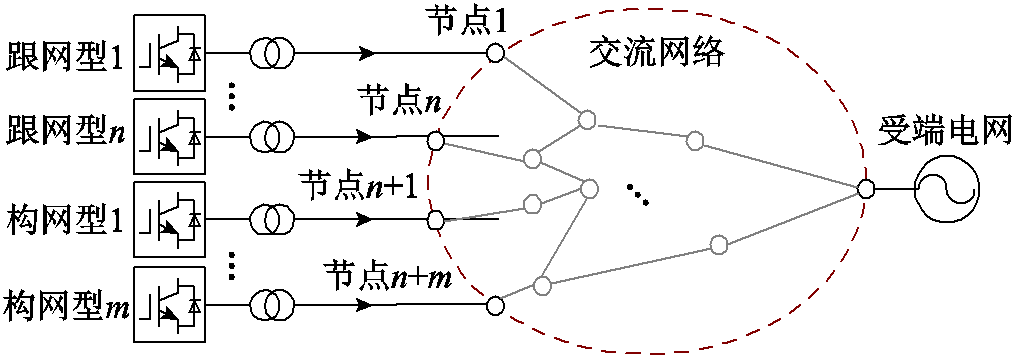
图1 混合外送系统示意图
Fig.1 Diagram of GFL/GFM hybrid delivery system
摘要 新能源外送系统中已呈现跟网与构网设备混合并网的发展趋势。外送系统动态阶数高，跟网/构网等异构设备集群间、设备集群与网络间动态交互复杂，给小干扰稳定性的机理分析与量化计算带来了挑战。该文提出了面向跟网/构网设备混合外送系统小干扰稳定性分析的特征子系统计算方法，通过将复杂高维系统等效为跟网/构网两机互联的特征子系统，降低了外送系统动态阶数，保留了上述动态交互过程，实现了外送系统小干扰稳定性的高效准确分析。首先，构建含跟网/构网设备的新能源外送系统全阶模型，基于矩阵块对角化原理，得到了模式等效的特征子系统；然后，面向一般化场景，采用节点分裂方法解决跟网/构网设备数量不平衡问题，提出基于特征子系统的外送系统小干扰稳定性分析方法；最后，基于时域仿真验证了该文方法在跟网/构网设备混合外送系统小干扰稳定性分析中的有效性和所得结论的正确性。
关键词：新能源外送系统 跟网和构网设备 特征子系统 小干扰稳定性 模式等效
随着“双碳”目标的稳步推进，我国电力系统逐渐向高比例新能源新型电力系统转型[1]。为保障新型电力系统的稳定运行，大规模并网的新能源发电设备迫切需要电网支撑服务[2]。与目前应用广泛的跟网（Grid-Following, GFL）控制策略相比，构网（Grid-Forming, GFM）控制策略使电力电子设备具备响应外部电网变化并提供必要支撑的能力[3]。新能源外送系统中呈现跟网与构网设备混合并网的发展趋势，形成了含跟网和构网两类电力电子设备的混合外送系统[4]。混合外送系统动态阶数高，跟网/构网等异构设备集群间、设备集群与交流网络间动态交互复杂，给小干扰稳定性（后文简称为稳定性）的机理分析与量化计算带来了挑战。
系统稳定性分析方法主要有时域仿真法、数据驱动的人工智能法及基于模型的理论分析法几类[5-17]。基于仿真或人工智能方法得到的稳定性分析结果准确，但结论仅适用于特定的工况[5]。基于模型的理论分析法可以建立系统稳定性和其主要影响因素的解析关系，可进行灵敏度分析，并得到一般性的结论。其中，状态空间法在传统同步机主导的电力系统中的稳定性分析中有广泛的应用，为传统电力系统中多机间交互和区域间振荡的内在机理提供了深刻认识和理解[6]。此外，对于含新能源设备的稳定性分析，状态空间法也在含两类设备系统的分析中得到了一些指导性的结论[7-8]。然而，状态空间法在多机的混合外送系统中可能不再适用，一方面状态空间法依赖详细的设备模型信息，而电力电子设备的控制算法和硬件设计通常为厂商的知识产权，不做公开[9]，难以准确建模并实际应用；另一方面电力电子设备模型复杂，状态变量繁多，高阶的全系统状态空间矩阵需要消耗大量的计算资源[8]，计算效率不高。阻抗分析法可以作为状态空间法的替代方案进行稳定性分析[10]。针对电力系统的多时间尺度振荡问题，学者们提出了多种形式的传递函数矩阵，将系统整体的稳定性从不同“侧面”进行观察和表述[11-15]，且具体模型可以直接通过端口测量[16]，无需获取设备内部参数信息。
但传统的阻抗分析方法主要聚焦于单机并网系统，且在多机系统的分析中仍需直接求解高阶传递函数矩阵，存在计算量过大的问题。对此，文献[17]针对多跟网设备馈入系统，提出了模态解耦的方法，将多机并网系统的稳定性分析简化为等效单机系统并网的稳定性分析，并进一步将同构场景推广到了参数弱异构的场景[18]。文献[19]对构网设备进行了详细的建模，并证明在一定假设的情况下，可以将构网设备等效为接入节点经过等值阻抗连接理想电压源。文献[20-21]通过摄动将包含两类异构设备的系统简化为两类设备加权的特征子系统，但这种方法适用于处理两类设备容量差别较大的弱异构场景。文献[22]基于特征子空间摄动理论，指出文献[17-21]本质上是通过特征子空间的方法导出与多机并网系统模式等效的低阶特征子系统，给出了处理此类含高阶动态的多机并网系统的一般方法。然而针对含跟网/构网设备的强异构系统，单机并网形式的特征子系统不再能完全反映原系统的稳定性。如何选取并得到合适的特征子系统，实现混合外送系统降阶并进行稳定性分析值得进一步探索。
为此，本文构建了与原系统稳定性等效的跟网/构网两机互联的特征子系统，提出了混合外送系统小干扰稳定性分析的一般性方法。首先，对混合外送系统进行了动态建模；其次，对于两类设备数量一致的系统，推导了与原系统模式等效的跟网/构网两机互联的特征子系统，实现了子系统降阶与解耦；然后，面向一般场景，提出了解决两类设备数量不平衡问题的节点分裂的方法，以及基于特征子系统的混合外送系统通用稳定性分析方法；最后，采用时域仿真验证了本文所提出的方法在混合外送系统小干扰稳定分析中的有效性。
本节分别构建了交流电网和设备的动态模型，形成了混合外送系统的全阶模型，明确了本文的关注场景与关键问题。
考虑n台跟网设备和m台构网设备组成的混合外送系统，其示意图如图1所示。节点1～n为跟网设备接入节点，节点n+1～n+m为构网设备接入节点，节点n+m+1为受端交流电网接入节点。红色虚线将该系统划分为两部分，虚线内为交流网络侧，虚线外为设备侧。其中，受端交流电网可视作理想电压源，分析需计及受端电网强度影响时，可将受端电网进行戴维南等效，等值阻抗划分进交流网络侧即可[23]。下面通过分别建立这两部分的动态模型形成系统的全阶模型。
图1 混合外送系统示意图
Fig.1 Diagram of GFL/GFM hybrid delivery system
首先，建立系统中交流网络的动态模型。全局xy坐标系下，以电流流入网络节点为正方向，交流网络侧的动态模型可以表示[24]为
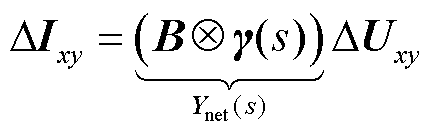（1）
其中
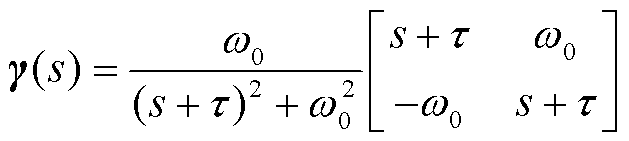
式中，Δ表示变量的微增量；Uxy=[Ux1 Uy1 Ux2 Uy2 … Ux(n+m) Uy(n+m)]T，Uxi、Uyi分别为节点i的电压x轴和y轴分量；Ixy=[Ix1 Iy1 Ix2 Iy2 … Ix(n+m) Iy(n+m)]T，Ixi、Iyi分别为注入节点i的电流x轴和y轴分量（i=1～n为跟网型设备节点，i=n+1～n+m为构网型设备节点）；Ynet(s)为交流网络的导纳传递函数矩阵；B为经过Kron变换消去内部无源节点后的节点导纳矩阵；⊗表示Kronecker积；s为拉普拉斯算子；ω0=2πf0为工频f0角速度；τ为线路电阻R与电感L的比值，τ = R/L。
其次，建立系统中设备侧的动态模型。全局xy坐标系下，设备侧的动态模型可以表示为
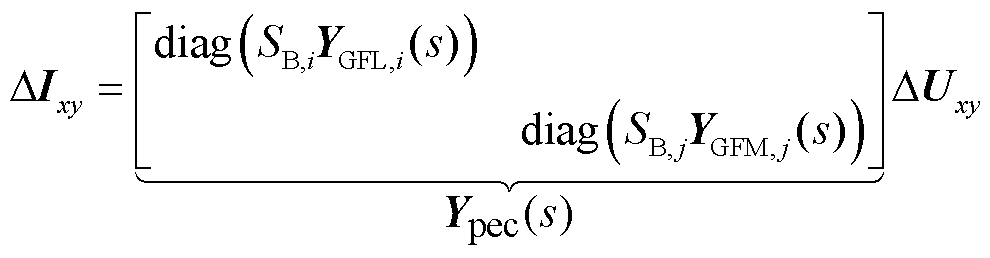（2）
式中，Ypec(s)为设备侧的导纳传递函数；diag(·)为对角矩阵；YGFL,i(s)为第i台跟网型设备以自身容量标幺后的导纳传递函数矩阵[11]；SB,i为第i台跟网型设备经系统基准容量标幺后的自身额定容量；YGFM, j(s)为第j台构网型设备以自身容量标幺后的导纳传递函数矩阵[19]；SB,j为第j台构网型设备经系统基准容量标幺后的自身额定容量。结合式（1）中网络侧和式（2）中设备侧的动态，混合外送系统全阶模型为
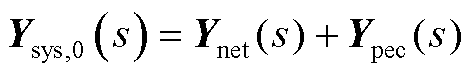（3）
将式（3）中各设备额定容量折算到网络侧，Ysys,0(s)可进一步写为
（4）
其中
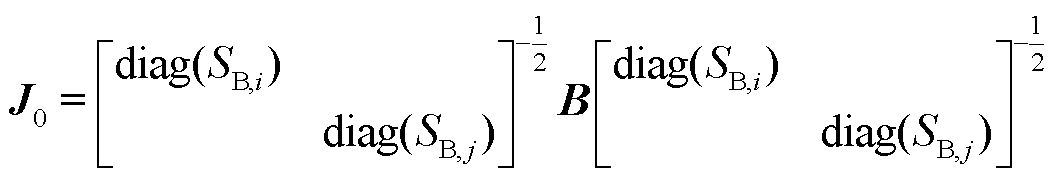（5）
式中，J0为考虑了设备容量加权后得到的等效节点导纳矩阵。后续分析将基于式（4）所建立的系统全阶模型展开。
求解系统闭环特征方程det(Ysys,0(s))=0（det(·)表示求矩阵的行列式），可根据闭环特征根实部是否全部小于0判断系统的稳定性。对于式（4）描述的混合外送系统的闭环特征方程，直接求解其特征根计算效率较低，面对大规模新能源外送系统时更是会存在难以求解的“维数灾”问题。因此需要构建与原高阶系统模式等效的降阶特征子系统，通过分析特征子系统的模式特征，等效判定原高阶系统的稳定性，提升混合外送系统稳定性分析的效率。
对于仅含跟网设备的多馈入系统，式（4）建立的系统全阶模型[22]可写为
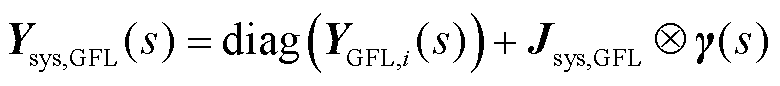（6）
式中，Ysys,GFL(s)为仅含跟网设备的多馈入系统的全阶模型；Jsys,GFL为该系统考虑设备容量加权后得到的等效节点导纳矩阵。
文献[22]指出，可通过高阶系统的特征子空间解耦得到与原系统模式等效的低阶特征子系统。
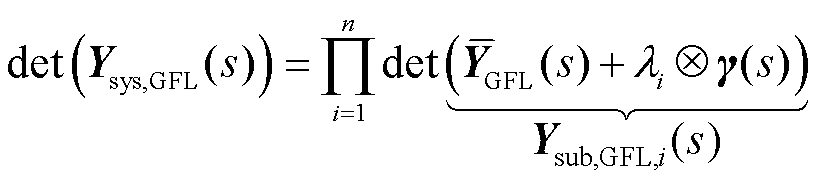（7）
式中，λi为Jsys,GFL的第i个特征值；Ysub,GFL,i(s)为通过特征子空间解耦得到的第i个跟网设备单机并网形式的特征子系统；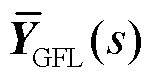
为特征子系统设备侧的导纳传递函数矩阵。当
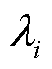大于临界短路比SCR0时，第i个跟网设备单机并网形式的特征子系统稳定，当且仅当所有特征子系统稳定时，原多馈入系统稳定。
然而，对于式（4）所示混合外送系统，跟网设备与构网设备的动态截然不同，异构设备侧动态特性难以通过线性近似将其处理为等效的同构设备，单机并网形式的特征子系统无法反映原系统的稳定性。从物理认知直观地解释：将混合外送系统等效为单机并网形式的特征子系统，忽略了跟网和构网设备之间的相互作用，因此单机并网形式的特征子系统不能完全表示混合外送系统的动力学。单机并网形式的特征子系统不再适合这种强异构的混合外送系统。
为了解决这个问题，本文提出了跟网/构网两机互联的特征子系统。这种形式的特征子系统保留了原系统的相互作用动力学和振荡模式，允许通过对特征子系统的分析来追溯原系统的稳定性特性。
针对图1中包含跟网构网和设备的混合外送系统，本文聚焦其正常运行状态下系统整体的小干扰稳定性，拟研究问题可以归纳为以下两点：①如何得到混合外送系统的特征子系统；②如何基于特征子系统判断原系统的稳定性。
为了更直观地阐述和论证本文所研究的问题，做出以下合理假设：①交流网络感性占优，各线路的阻感比一致[12]；②跟网设备的动态特性相似，构网设备的动态特性相似，且两类设备各自间的电压相位差较小[18]。对于一般化的网络和同类设备异构的情况，可参考文献[18]对本文方法进行拓展，本文不再赘述。
本节以跟网/构网设备数量一致的场景为例，构建与混合外送系统模式等效的跟网/构网两机互联的特征子系统，提出基于特征子系统的稳定性判据。
对于两类设备数量一致的混合外送系统（m=n），可改变混合外送系统全阶模型即式（4）的排列方式，改写为跟网设备和构网设备一一对应的形式，得到如式（8）所示的全阶模型。
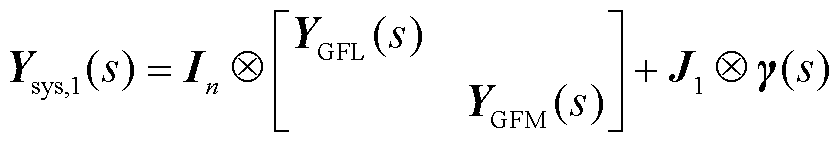（8）
式中，Ysys,1(s)为两类设备数量一致的混合外送系统的全阶模型；In为n维的单位矩阵；J1为该系统考虑设备容量加权后得到的等效节点导纳矩阵。
存在正交矩阵P∈Rn×n使得式（8）中J1相似变换[24-25]为
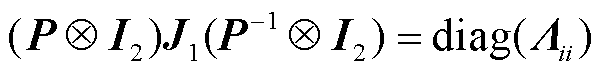（9）
式中，Λii为对角线上第i个2×2的矩阵块，Λii∈R2×2（1≤i≤n）。那么，根据特征子空间的定义[22]，P
I4和P-1I4为Ysys,1(s)的特征子空间。
原高阶系统可以通过特征子空间解耦为n个跟网/构网两机互联的特征子系统。
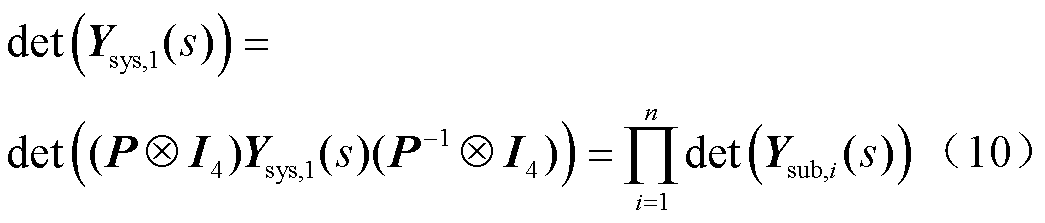
式中，Ysub,i(s)为通过特征子空间解耦得到的第i个特征子系统，具体表达式为
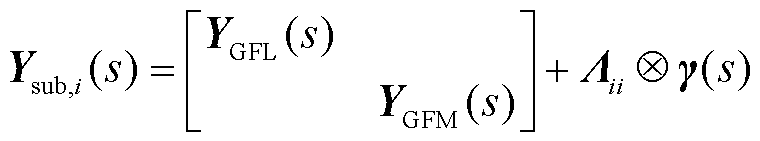（11）
式（10）通过特征子空间推导出了与原高阶系统稳定性等效的低阶跟网/构网两机互联的特征子系统，实现了对复杂高阶系统的降阶分析。事实上，式（9）是矩阵特征值分解理论的进一步拓展，处理对象从矩阵对角化拓展至矩阵块对角化，在降阶的同时保持了跟网设备和构网设备的动态。对于一般的对称正定矩阵J1，即节点导纳矩阵（或经容量加权后的等效节点导纳矩阵），有式（9）成立或近似成立。值得一提的是，由于J1为数值矩阵，可通过数值计算的方法快速求解P，详细证明和特征子空间的快速求解方法详见附录第1节。
与原高阶复杂系统相比，跟网/构网两机互联的特征子系统模型阶数较低且形式清晰，降低了稳定性分析的计算量，便于分析关键参数对系统稳定性的影响，且可以进一步形成具体的电路模型。根据电路原理，图2给出了第i个特征子系统模型对应的小信号电路模型，保留了设备间、设备和网络间的动态交互，不仅从数学上实现了解耦，且能在电路视角下表示出该特征子系统所对应的物理系统。
式（11）中第i个特征子系统中网络侧节点阻抗矩阵Λii与图2中各线路的阻抗满足式（12）中的关系。
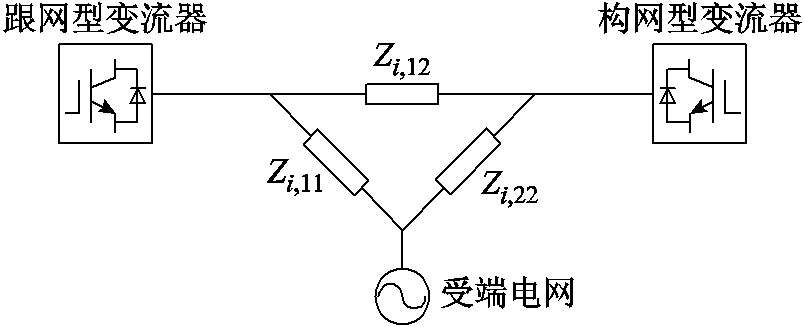
图2 第i个特征子系统的等效电路模型
Fig.2 Small signal circuit model of the i-th eigen-subsystem
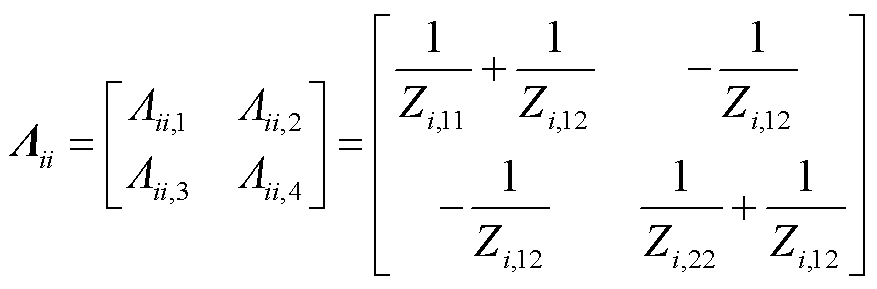（12）
混合外送系统闭环特征方程即式（10）解耦得到的n个特征子系统网络阻抗构成的集合Ω1为
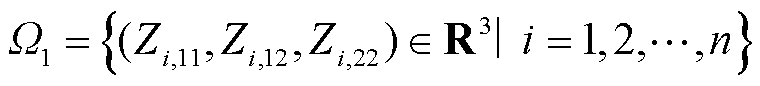（13）
对于两类设备各自同构的混合外送系统，且将各设备的容量归算至网络侧后，解耦后得到的n个特征子系统的区别在于线路阻抗不同，即给定设备模型后，系统的稳定性由解耦后的三个线路阻抗决定。给定网络阻抗Z11、Z12和Z22后，可得特征子系统的稳定性判断结果，由此可以得到一个仅与这三个网络阻抗Z11、Z12和Z22相关的，特征子系统的三维稳定运行稳定域Ω，如式（14）所示，具体的三维稳定域示意图详见第4节。
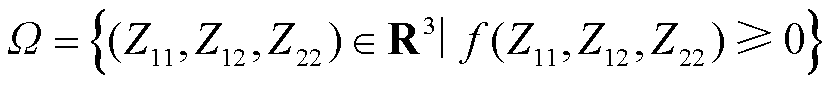（14）
式中，Ω为给定设备模型后得到的两机互联的特征子系统的稳定运行域；f(Z11,Z12,Z22)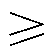
0表示两机系统稳定，有多种形式的判据与分析方法[26-28]，本文不再赘述。跟网/构网设备数量一致的混合外送系统稳定判据为
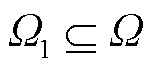（15）
若式（15）成立，则混合外送系统稳定；反之，混合外送系统失稳。
考虑到实际系统中常存在跟网/构网设备数量不平衡问题，本节提出了节点分裂方法用于系统解耦的预处理，使之满足式（10）的适用条件，并提出了面向一般化混合外送系统的稳定性分析方法。
对于某个设备接入的节点，根据该节点与其连接的节点间线路串并联关系，可将该节点分裂成若干个子节点，并且与原系统模式等效。图3给出了节点分裂的示意图。为说明清晰，考虑系统中含有n台跟网设备和1台构网设备，其中右侧节点为待分裂的构网设备节点。根据图3的变换，可将该节点分裂为m个构网设备接入节点。图3中，Yi表示分裂节点与其他设备节点之间的互导纳；Ix+jIy为从对应节点注入电网的电流。
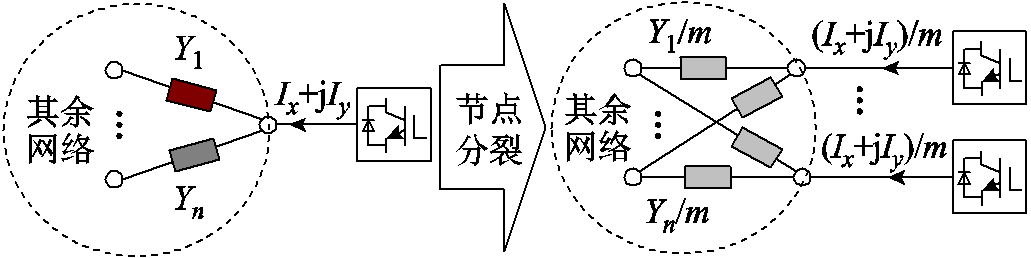
图3 节点分裂示意图
Fig.3 Schematic diagram of node splitting
根据上述方法得到模式的等效系统（设备容量已折算到网络侧），节点分裂后网络侧模型主要包含下面几个特征：
1）未分裂节点自导纳和未分裂节点间的互导纳与分裂前一致。
2）分裂出的m个节点与未分裂节点间的互导纳为分裂前待分裂节点与未分裂节点间的互导纳的1/m。
3）分裂出的m个节点间的互导纳为0，分裂出的m个节点自导纳与分裂前待分裂节点自导纳的1/n。
4）(n+1)×(n+1)维的节点导纳矩阵经节点分裂后，变为(n+m)×(n+m)维的节点导纳矩阵。
对于设备侧的模型特征，分裂前设备动态为
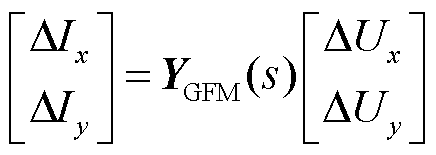（16）
经节点分裂为m台设备后，单台设备的动态为
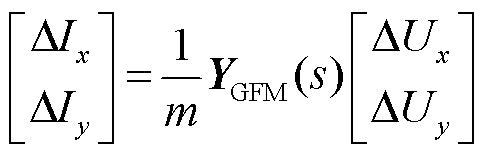（17）
分裂后的每一台构网设备的参数、特性均一致，仅输出的电流（功率）变为分裂前的1/m，即分裂出的m台设备的额定容量为分裂前的1/m。
通过上述方法，可以将数量少的设备对应的接入节点进行分裂，得到两类设备数量一致的等效系统，从而可以通过第2节中的方法得到跟网/构网两级互联的特征子系统。值得一提的是，由于式（4）即混合外送系统的闭环特征方程中的J0包含了各设备容量的加权，为保持其数值特性良好，节点分裂应从数量少的设备类型中最大容量的设备接入节点开始操作。
节点分裂前后系统的稳态潮流及电路视角下的电压电流动态与原系统一致，但其与原系统的小干扰稳定性角度的联系需要进一步阐述说明。为叙述方便，仍采用图3所示系统。
节点分裂前系统的闭环特征方程可以表示为
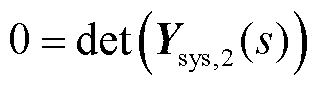（18）
节点分裂后系统的闭环特征方程为
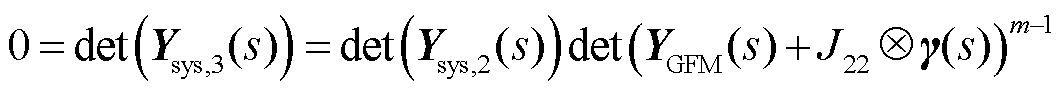（19）
式中，J22∈R1×1，为分裂前待分裂节点的自导纳。式（19）的详细推导过程见附录第2节。比较式（18）和式（19），节点分裂时，新增了m-1个节点，体现在系统闭环传递函数中为额外引入了m-1个相同的构网单机并网形式的振荡模态，与分裂前系统间无耦合作用，有自然解耦关系，且并网线路阻抗为分裂节点自导纳的倒数。根据此特性，在后续特征子系统的导出中可直接剔除节点分裂时引入的系统。事实上，在快速计算时，可忽略节点分裂额外引入的振荡模态，设备节点分裂引入的闭环特征方程的特征根与原系统中该设备引入的特征根基本重合，因此可近似认为节点分裂后系统与原系统稳定性等效，考虑引入的特征根得到的分析结果是保守的。
综合上述分析，对于含n个跟网设备、m个构网设备（m＜n）即式（4）所示一般的混合外送系统，经节点分裂扩充至数量一致的等效系统后，经特征子空间解耦会得到与等效系统模式等效的n个跟网/构网两机互联的特征子系统。进一步地，考虑等效系统额外引入的n-m个构网设备单机并网形式的振荡模态与原系统满足自然解耦关系，即n个跟网/构网两机互联的特征子系统中有n-m个特征子系统（令其为第m+1～n个特征子系统）的网络侧节点导纳矩阵即Λii（m+1≤i≤n）的副对角元素为0，即可进一步解耦为n-m个跟网设备单机并网形式的振荡模态，以及n-m个构网单机并网形式的振荡模态，即节点分裂时额外引入的振荡模态且并网线路阻抗值为分裂节点的自导纳的倒数，应当剔除。剩下的n-m个跟网设备单机并网形式的特征子系统和m个跟网/构网两机互联的特征子系统共同反映了原系统的稳定性，即式（4）可以被解耦为
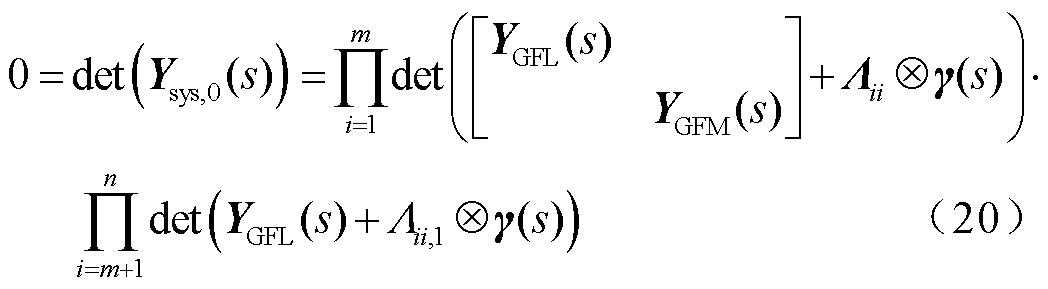
对于含单构网设备和多跟网设备的系统，通过所提分析方法得到的结论与文献[8]中的特殊拓扑下的解耦结论一致，这也验证了本文方法的正确性。
结合第2节和3.1节，提出基于特征子系统的一般化混合外送系统稳定性分析方法，其具体流程如图4所示。
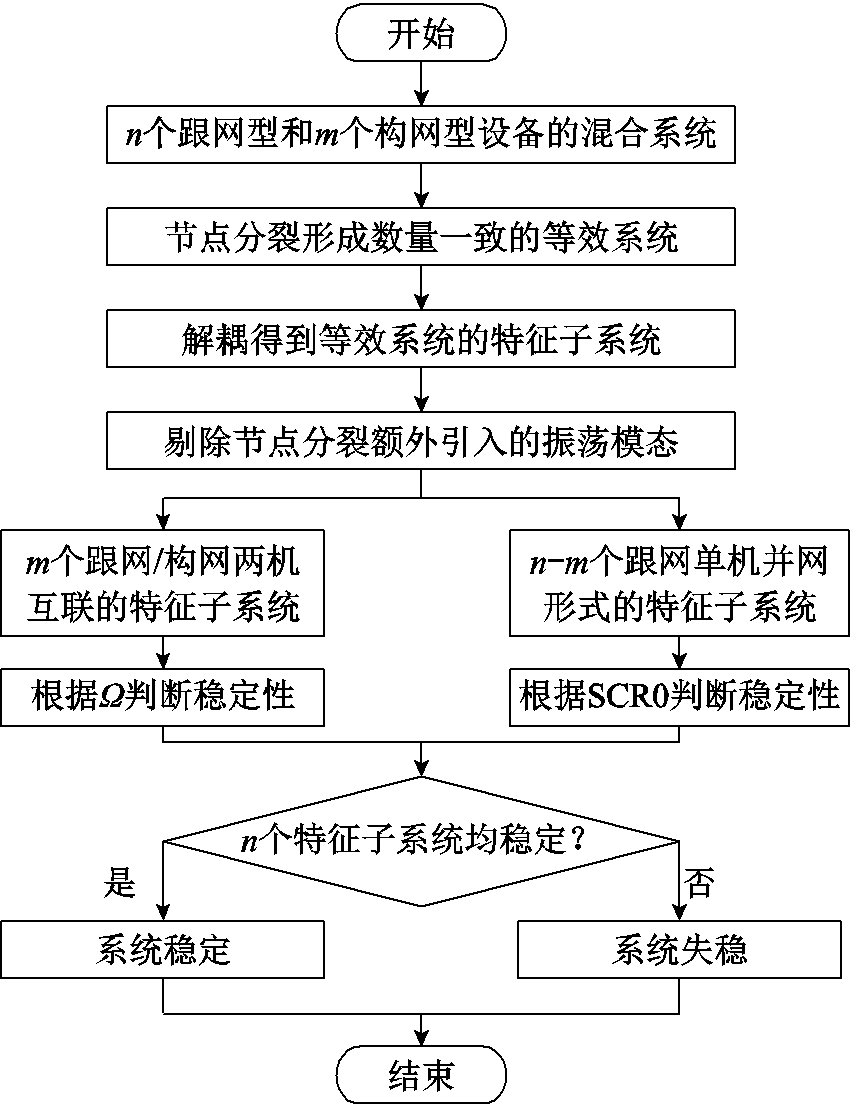
图4 混合外送系统稳定性分析流程
Fig.4 Flow chart of stability analysis for GFL/GFM hybrid delivery system
对于一般的含n台跟网设备、m台构网设备（n≥m，弱构网设备更多亦可照此流程进行分析）的混合外送系统，可通过特征子空间的方法导出n-m个跟网单机并网形式的特征子系统和m个跟网/构网两机互联的特征子系统，这n个特征子系统与原系统模式等效，可判断原系统的稳定性并反映原系统的振荡模式。当n个特征子系统均稳定时，原系统稳定。若特征子系统失稳定；原系统不稳定，出现和特征子系统一样的稳定问题。对于含有更多类设备，如含跟网、构网和同步机的系统亦可按此方法导出跟网、构网、同步机三机互联的特征子系统进行简化分析，区别仅在于如何选择和求取该系统的特征子空间进而导出特征子系统。
本节首先基于IEEE 3机9节点系统从频域和时域分别验证了上述理论分析的正确性；然后基于中国西北某新能源基地外送系统，进一步验证了所提方法在实际大系统中的适用性。实际电网中小干扰同步稳定问题频发，算例主要设置了小干扰同步失稳的情形，对于其他小干扰稳定问题亦可采用本文所提方法进行分析，受限于文章篇幅，不再赘述。
本节在Matlab/Simulink中搭建了如图5所示的3机9节点系统的电磁暂态模型验证所提理论分析方法有效性。其中，节点2接入构网设备，节点1和节点3接入跟网设备，设备关键控制参数、设备容量和交流网络线路参数见附表1和附表2。
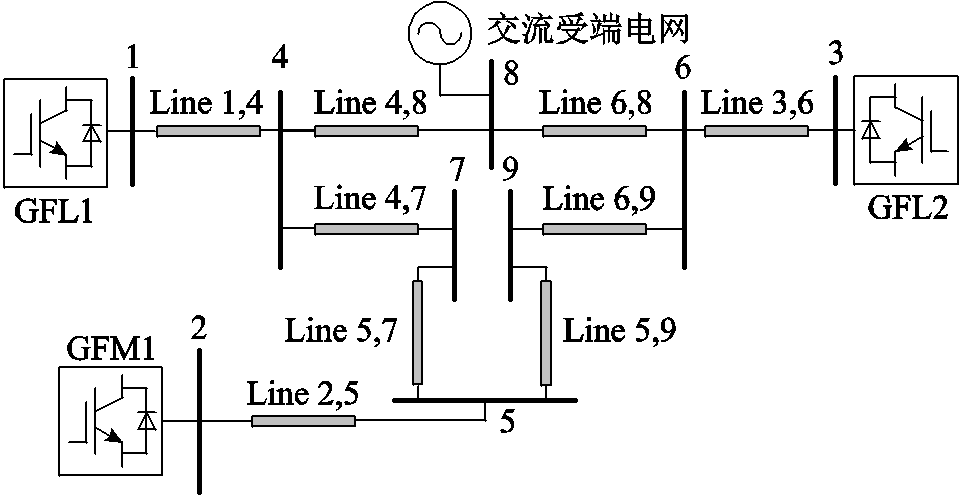
图5 3机9节点系统拓扑
Fig.5 Topology of 3-devices 9-bus system
首先验证节点分裂理论构造的数量一致的等效系统与原系统模式等效。其中原系统的特征值通过Matlab/Simulink中搭建模型的状态空间方程计算得到，特征子系统的特征值通过Matlab中的.m文件编程计算得到。原3机系统、节点分裂后形成的两类设备数量一致的4机系统，以及解耦得到的特征子系统的主导特征根对比如图6所示。可以看出，节点分裂后的4机系统的主导特征根与节点分裂前的主导特征根基本一致，仅新增了一对构网主导模态的特征根，且与原构网主导模态的特征根基本重合。这证明节点分裂得到的等效系统与原系统近似模式等效，且与理论分析中得到的分裂额外引入的振荡模态完全重合，说明可以快速剔除这一额外引入的模态。值得一提的是，在考虑节点分裂引入的构网单机并网模态进行稳定性分析时，会得到偏保守的结果，且该模态与原模态偏差较小，所得结果不会过于保守，在简化分析时可直接计算。
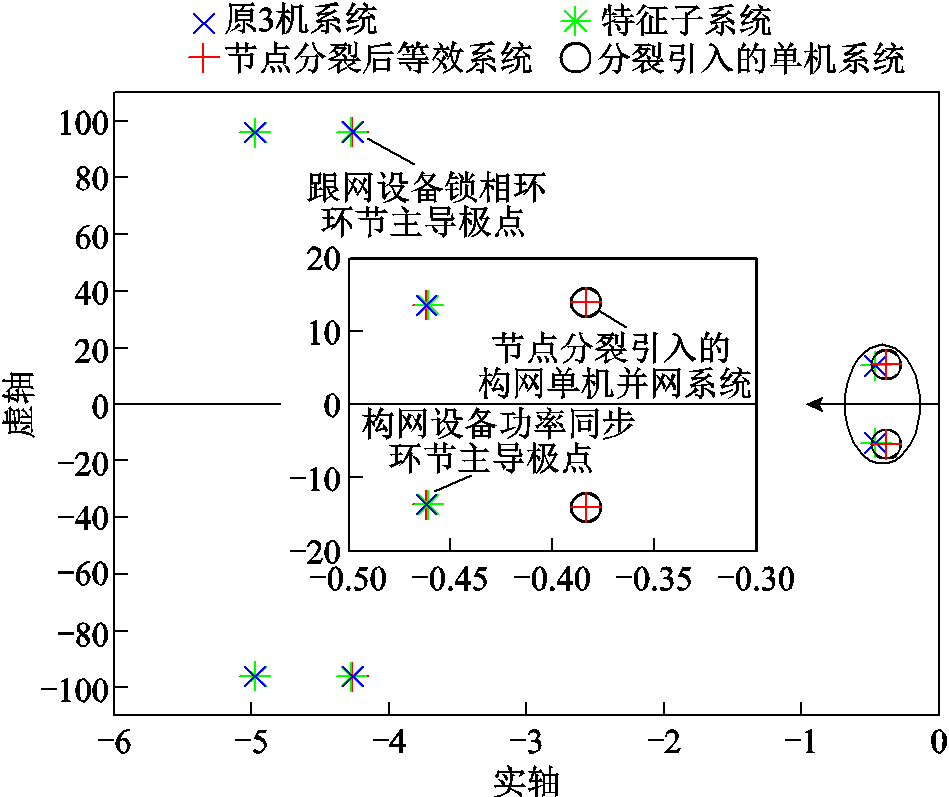
图6 3机系统解耦前后主导特征根对比
Fig.6 Comparison of dominant eigenvalues before and after decoupling in a 3-devices 9-bus system
然后验证特征子系统与原系统稳定性模式等效。根据图4流程得到的各特征子系统的线路参数见表1。特征子系统b中互联阻抗Z12极大，即可视为两个单机并网系统，且构网单机并网系统所连线路阻抗即为解耦前该节点自导纳的倒数，该系统即为节点分裂引入的振荡模态，应当剔除。1个3机混合外送系统，可解耦得到1个跟网/构网两机互联的特征子系统和1个跟网单机并网形式的特征子系统。由图6可知，在剔除节点分裂引入的构网单机并网形式的振荡模态后，2个特征子系统与原系统的主导特征根几乎完全重合，这说明本文所提的特征子系统与原系统模式等效。
表1 3机系统的特征子系统
Tab.1 Eigen-subsystem of a three-devices system
特征子系统Z11(pu)Z22(pu)Z12(pu) a0.2730.9671.687 b0.1850.6181 176.424
为了比较传统特征值分析方法与本文所提基于特征子系统的分析方法的计算效率，设置系统规模分别包含3、4、6、8和10台变流器设备。在3机系统中采用图5所示拓扑，其余系统保持构网设备和跟网设备数量一致。在相同计算机环境下进行编程计算，分别采用传统特征值分析方法（直接求解系统特征值）与本文方法（构建特征子系统后求解特征值），每种规模的系统进行10次计算，每次随机生成节点导纳矩阵。结果表明：在3机系统中，本文方法计算耗时为传统方法的40%；在10机系统中，计算耗时进一步降低至传统方法的12%。含不同设备数量的混合外送系统的平均计算耗时对比如图7所示。随着设备数量的增加，传统方法的计算耗时呈指数增长，而本文方法的计算耗时与设备数量呈线性关系。相较于传统方法，本文方法在确保分析准确性的基础上显著提升了计算效率，尤其在设备数量较多的混合外送系统中具有显著优势。
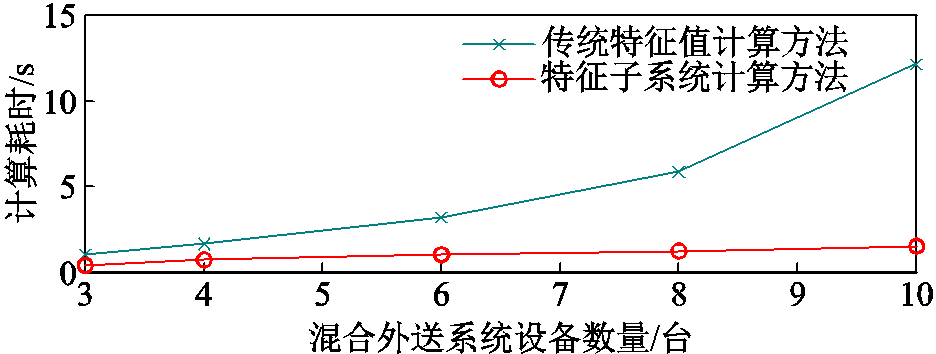
图7 计算耗时比较
Fig.7 Comparison of calculation time-consuming
进一步从时域角度验证所提理论的准确性。首先遍历解耦得到的跟网/构网两机互联的特征子系统的阻抗参数，通过数值计算判断各参数点处系统的稳定性，进而给出了如图8所示的两机互联特征子系统三维稳定运行域。此外，稳定域的获得还可以通过状态方程、阻抗分析法和人工智能等方法，本文不做展开分析。
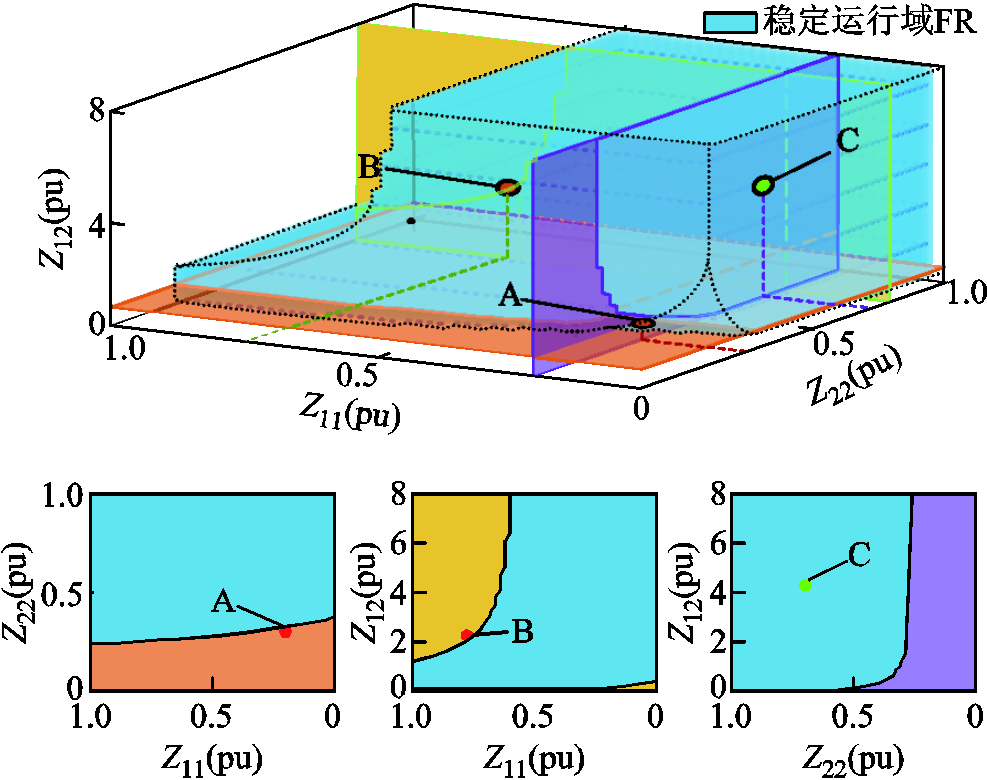
图8 跟网/构网两机互联的特征子系统稳定域
Fig.8 Stability region of the eigen-subsystem for two interconnected grid-following/grid-forming devices
图8中，联络阻抗Z12较大时，跟网设备与构网设备交互较弱，两机系统可以近似为两个单机并网系统。此时，跟网设备在高连接阻抗即弱网下容易失稳，构网设备在低连接阻抗即强网下容易失稳。伴随联络阻抗Z12的减小，两类设备的交互加强，能够提升系统的稳定性，即能够增强跟网设备在弱网中的表现和构网设备在强网中的表现，这与文献[3,26]中的结论一致。当联络阻抗Z12与跟网节点处Z11均较小时，即图8中稳定域右下角出现缺块，此时跟网设备对构网设备在强网下稳定性能的提升弱于Z11与Z12线路阻抗较小对构网设备稳定性能的恶化，构网设备出现低频振荡问题。所提的跟网/构网两机互联的特征子系统能够有效反映设备间、设备和网络间的动态。
通过改变线路参数，分别设置A、B、C三个算例，其解耦得到的特征子系统判稳结果如图8所示，其中算例A落于构网主导失稳区域，算例B落于跟网主导失稳区域，算例C稳定。解耦得到的特征子系统具体线路信息和判稳结果见表2。
表2 3机系统稳定性分析结果
Tab.2 Stability analysis results of the 3-devices 9-bus system
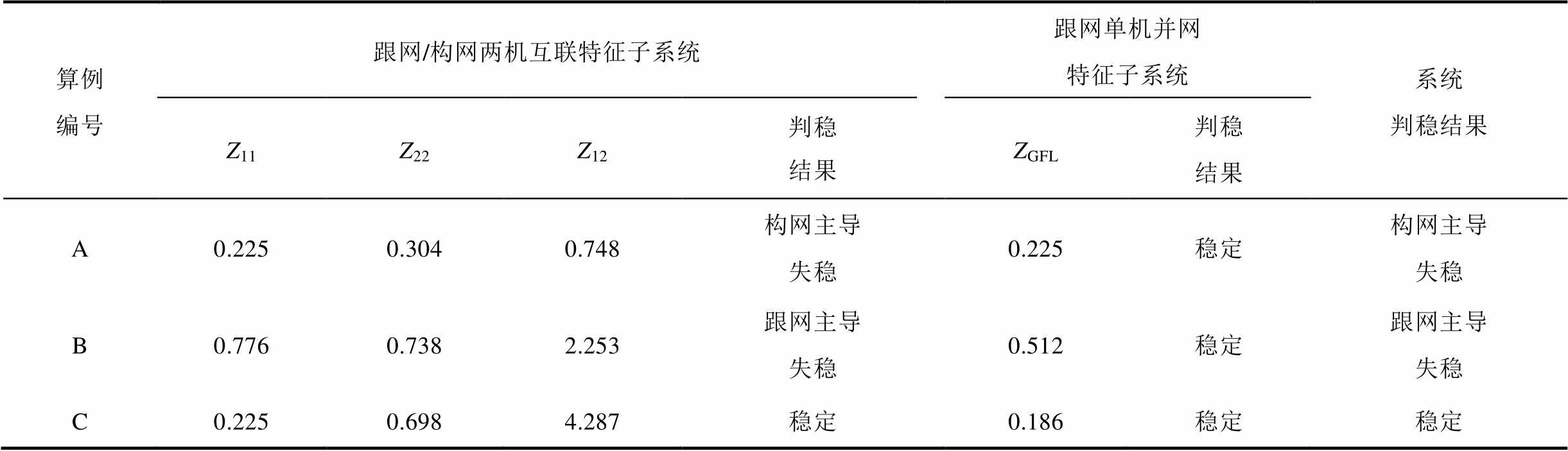
算例编号跟网/构网两机互联特征子系统跟网单机并网特征子系统系统判稳结果 Z11Z22Z12判稳结果ZGFL判稳结果 A0.2250.3040.748构网主导失稳0.225稳定构网主导失稳 B0.7760.7382.253跟网主导失稳0.512稳定跟网主导失稳 C0.2250.6984.287稳定0.186稳定稳定
在Matlab/Simulink中搭建图5的3机9节点系统的电磁暂态仿真模型，验证基于特征子系统的混合外送系统的稳定性分析方法的正确性。对于附表2中原系统不同线路参数的情况，图9给出了对应的时域仿真波形。在系统运行于平衡点的情况下，0.5 s时在无穷大并网点施加了微小的端电压骤升并快速切除。可以看出，在A、B和C三个算例中，时域波形分别振荡发散、振荡发散和振荡收敛。其中算例A出现低频振荡问题，其振荡频率为2.98 Hz，此时解耦得到的特征子系统主导特征根为0.715 3±j19.068 6，振荡频率为3.03 Hz。算例B出现次/超同步振荡，其振荡频率为13.69 Hz，此时特征子系统主导特征根为1.470 6±j87.271 3，振荡频率为13.88 Hz。算例C振荡收敛，此时解耦得到的特征子系统特征根实部均小于零。原系统的稳定性与解耦得到的特征子系统模式等效，且原3机系统与解耦得到的最弱特征子系统振荡频率基本一致，说明原3机系统和解耦得到的特征子系统最弱振荡模式相同，验证了本文所述方法的有效性。
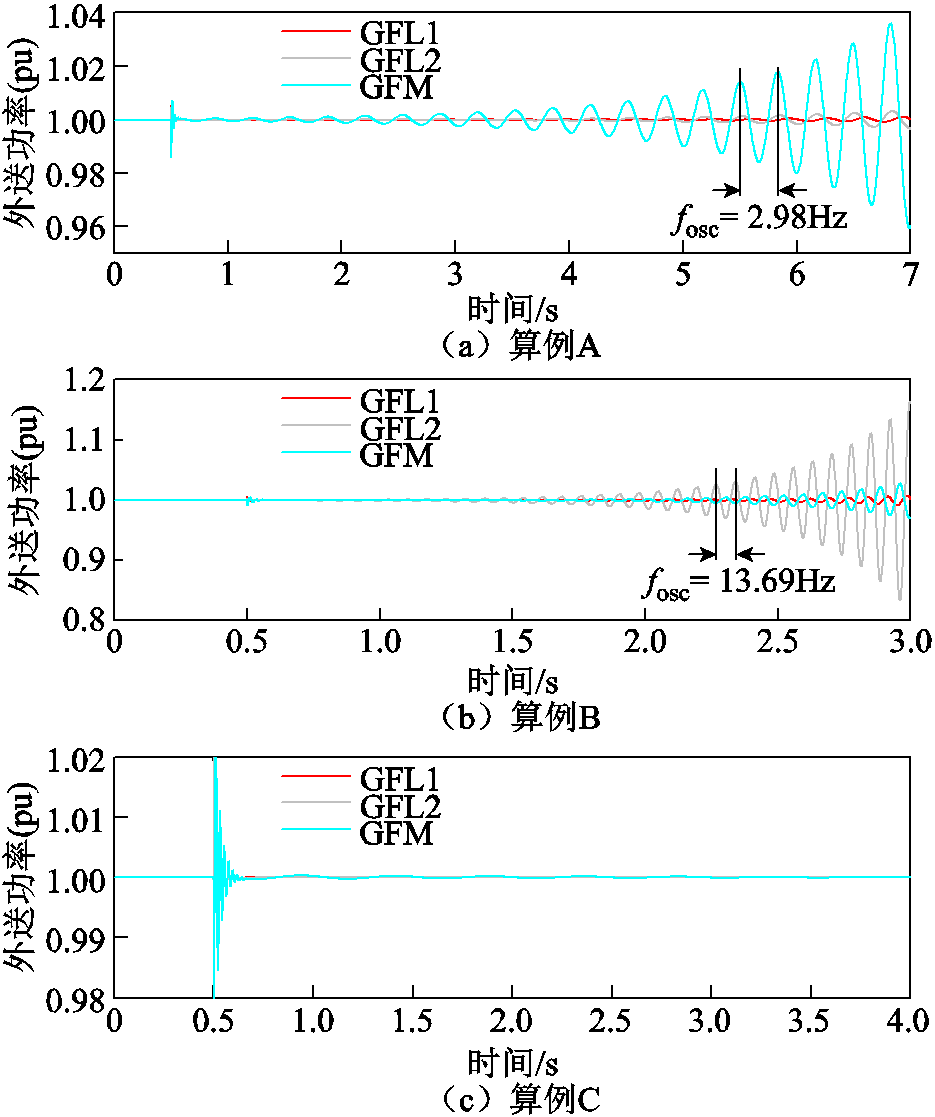
图9 3机系统时域仿真波形
Fig.9 Time domain simulation waveforms of the 3-devices 9-bus system
为验证本文所述方法在实际大系统中的有效性，本节在CloudPSS平台搭建了西北某新能源场站的电磁暂态仿真模型，系统拓扑如图10所示。其中，节点1～54为新能源设备接入节点，由36台跟网设备和18台构网设备组成，节点55～92为无源中间节点，节点93为新能源基地并网节点。设备控制参数与3机9节点系统一致，见附表1，网络参数见附表3。
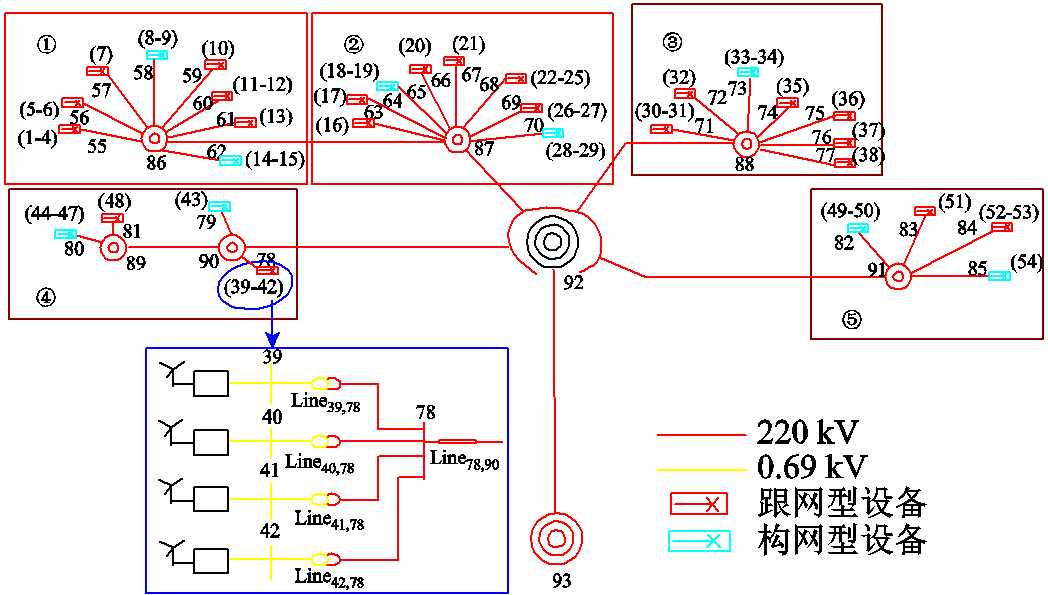
图10 某实际新能源场站拓扑
Fig.10 Topology of a practical renewable energy plant
具体地，各设备参数保持不变，将送出基地馈入电网的关键线路Line92,93阻抗参数X92,93分别设置为2.227×10-3(pu)、1.598×10-3(pu)和1.093×10-3(pu)。可以采用本文所述方法分别进行解耦，并根据各特征子系统的阻抗是否落入稳定域，从而判断原系统的稳定性。对于X92,93=2.227×10-3(pu)，其最弱特征子系统阻抗集为Z={0.873, 0.552, 2.187}(pu)，落入跟网设备失稳的区域，为跟网设备主导的失稳，其主导特征根为0.803 3±j86.956 6，振荡频率为13.84 Hz；对于X92,93=1.598×10-3(pu)，其阻抗集均落于稳定域FR内，原系统稳定，其所有特征根实部均小于0；对于X92,93=1.093×10-3(pu)，其最弱特征子系统阻抗集为Z={0.235 4, 0.384 6, 0.588 7}(pu)，落入构网设备失稳的区域，为构网设备主导的失稳，其主导特征值为0.241 6± j17.436 8，振荡频率为2.78 Hz。进一步地，在CloudPSS平台中设置算例扰动，在仿真时间T = 0.5 s时，在无穷大母线处施加了5%的端电压骤升并快速切除。图11分别给出了三个算例的部分跟网/构网设备外送功率的时域曲线和外送线路（Line92,93）的三相电流的时域仿真曲线。可以看出，算例A出现振荡频率为13.26 Hz的次/超同步发散振荡，为跟网主导的次超同步振荡；算例B出现振荡频率为2.82 Hz的低频发散振荡，为构网主导的振荡；算例C振荡收敛。基于时域仿真的同步稳定评估结果与本文所述方法解耦得到的特征子系统评估结果一致，这进一步验证了本文所述方法的正确性和在实际大系统中的适用性。关键线路Line92,93阻抗大小的物理意义为受端电网强度，即受端电网与混合外送系统的支撑能力，阻抗越大，电气距离越远，支撑能力越弱。从该算例可以看出，受端电网强度较低时，跟网型变流器主导的稳定问题比较突出；受端电网强度较大时，构网型变流器主导的稳定问题比较突出。
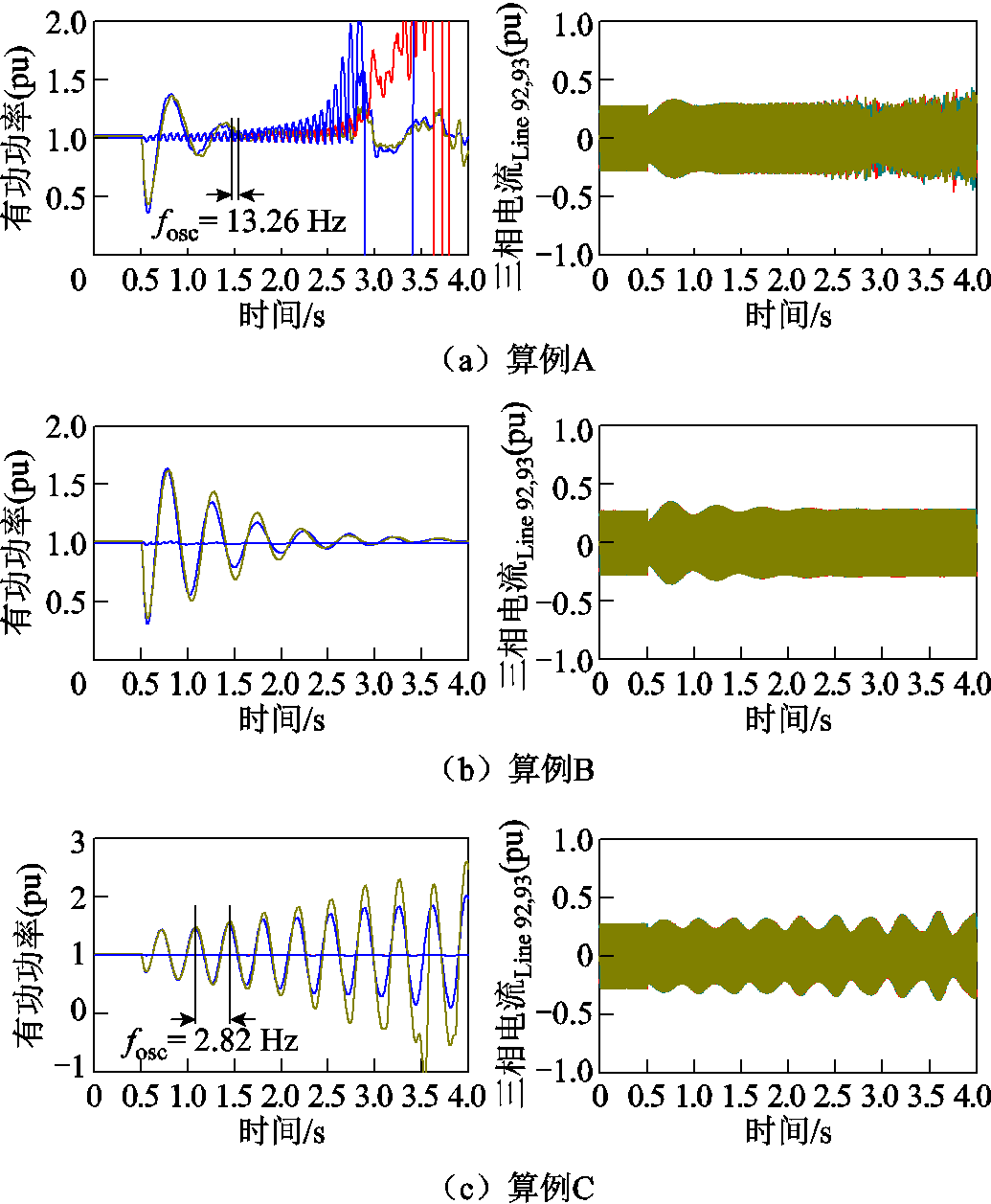
图11 设备外送功率时域波形与外送线路（Line92,93）三相电流幅值时域波形
Fig.11 Time-domain waveform of devices active power and three-phase current amplitude of delivery lines (Line92,93)
本文构建了含跟网/构网设备混合外送系统的特征子系统，可将高阶系统降阶为低阶的特征子系统进行稳定性分析，并构建了特征子系统的稳定运行域，给出了具有一定普适性的混合外送系统稳定性分析方法。主要结论如下：
1）混合外送系统与各特征子系统模式等效，根据各特征子系统可以追溯原系统的稳定特性。
2）对于一般的含n个跟网设备和m个构网设备的混合外送系统，通过节点分裂构造模式等效的系统并降阶解耦，可以得到m个跟网/构网两机互联的特征子系统和n-m个跟网单机并网形式的特征子系统（n＞m，反之亦然）。
3）设备参数给定时，可确定反映设备侧特性的稳定运行域Ω。混合外送系统解耦得到的特征子系统网络侧信息构成网络阻抗集Ω1，根据Ω1是否属于Ω可快速判断原系统的稳定性。
目前主要针对跟网/构网两机互联的特征子系统分析了小干扰同步稳定性。如何综合分析不同环节交互下的系统稳定性问题和量化混合外送系统的稳定裕度是未来的工作之一。
附 录
1. 特征子空间数值计算方法
可通过数值计算的方法构造与原系统特征子空间近似的正交矩阵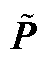
∈Rn×n[24]，使得
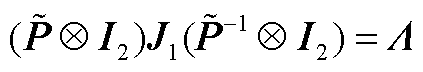（A1）
其中
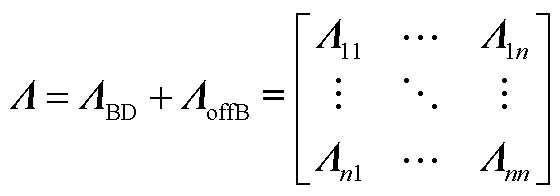
式中，
BD为Λ对角线上的矩阵块组成的块对角矩阵，BD=diag(Λii)（1≤i≤n）；ΛoffB为Λ去除对角线上矩阵块后的矩阵。满足式（A2）时，Λ为块对角严格占优矩阵[25]。
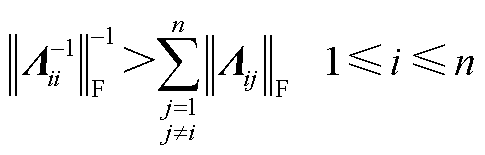（A2）
式中，||·||F表示求矩阵的F范数。文献[26]将Gershgorin圆盘定理进一步拓展至分块矩阵中，Λ为块对角严格占优矩阵时，可将ΛoffB视作对矩阵ΛBD的微小摄动，有式（A3）成立。
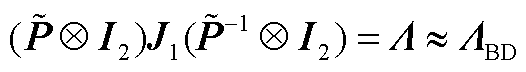（A3）
构造近似特征子空间的问题可以表示为式（A4）所示的优化问题。
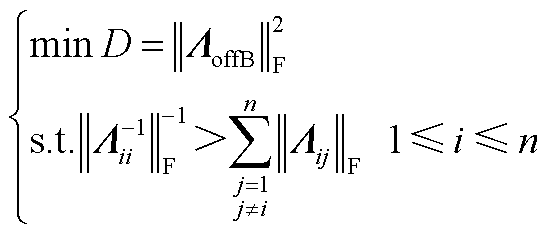（A4）
式中，D为代价函数，该代价函数可表征特征子空间的近似程度，越接近0，所构造的特征子空间与真实系统的特征子空间近似程度越高。
针对（A4）所示优化问题，本文给出了一种基于Givens旋转的求解方法，求解矩阵P将式（A5）所示的矩阵尽可能块对角化。
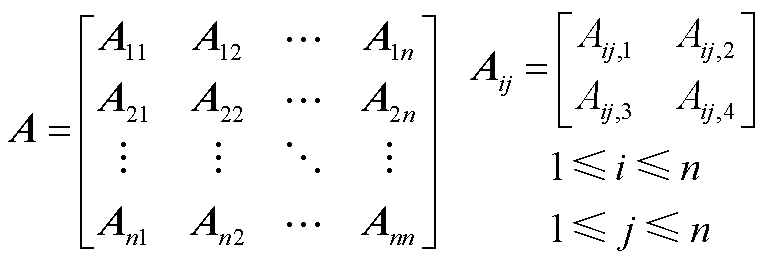（A5）
式中，A∈R2n×2n，满足A=AT；Aij∈R2×2（1≤i≤n，1≤j≤n），为2×2的矩阵块。每步选取F范数最大的矩阵块Apq，记录其所在行列，即第p行、第q列，得到变换矩阵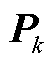
为
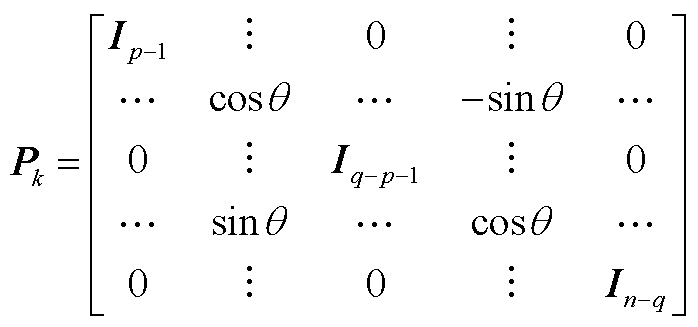（A6）
式中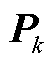，为第k次迭代时得到的变换矩阵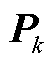，∈Rn×n，满足式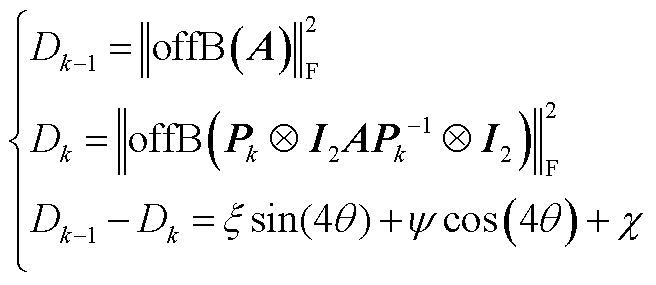（A7）。
（A7）
其中
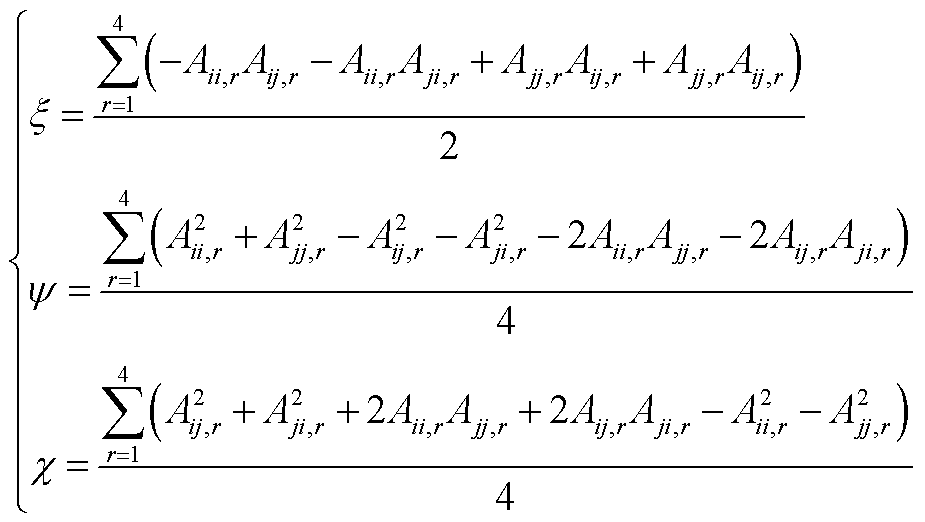（A8）
式中，offB(A)表示将矩阵A对角线上的2×2的矩阵块Aii(i=1,2,…,n)置零；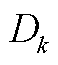
表示第k次迭代后矩阵块对角化的程度，当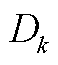=0时矩阵完全块对角化。分析式（A7）可知，适当选择θ可使
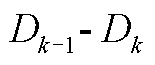的值最大化，即在每一步中选取最合适的θ最大化块对角的程度，此时迭代得到新的矩阵P为
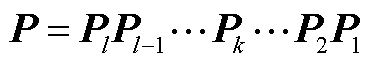（A9）
式中，P即为满足式（A3）的矩阵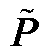A
A。
2. 节点分裂模式等效证明
分裂前系统的闭环传递函数为
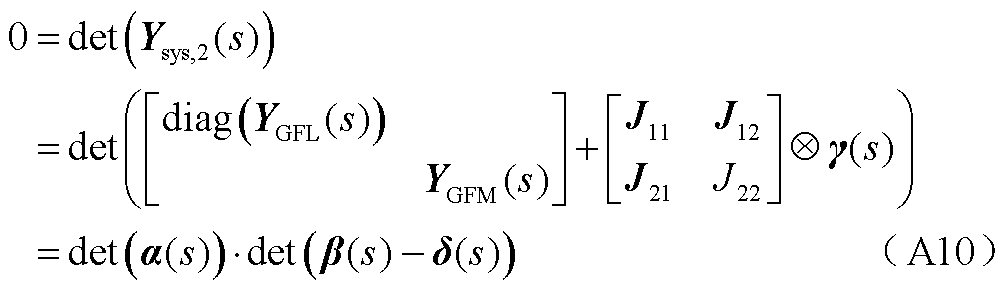
其中
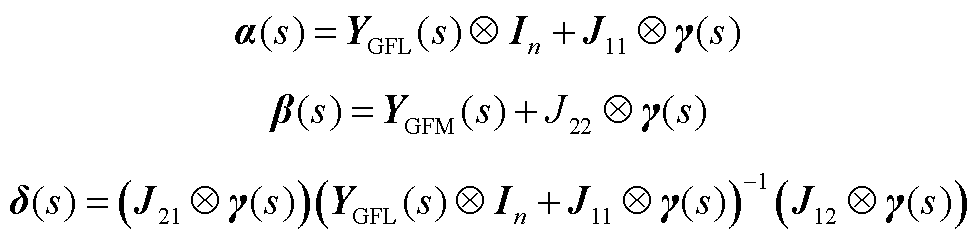
节点分裂后的系统闭环传递函数为
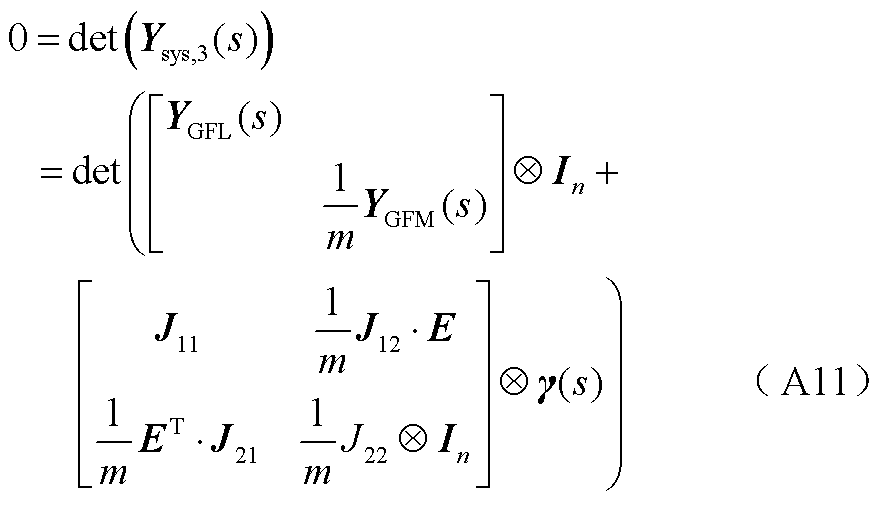
式中，E=[1 1 … 1]∈R1×n对式（A11）进行舒尔补，有
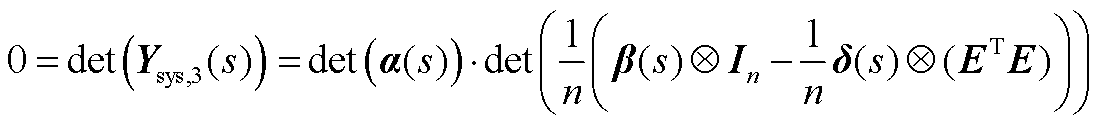（A12）
构造矩阵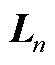
和
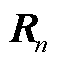
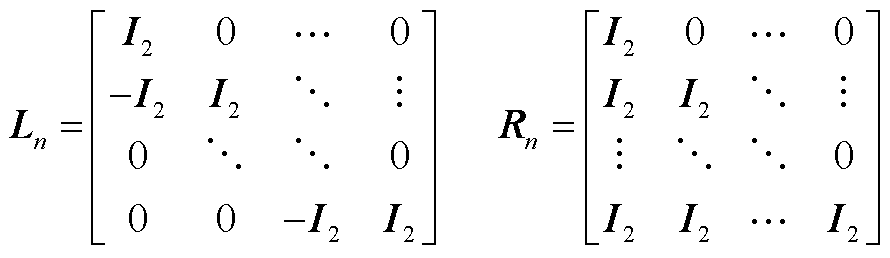（A13）
式中，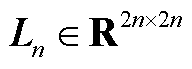
，
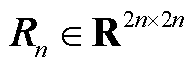，且det(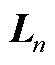)=1，det(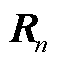)=1，有式（A14）成立。
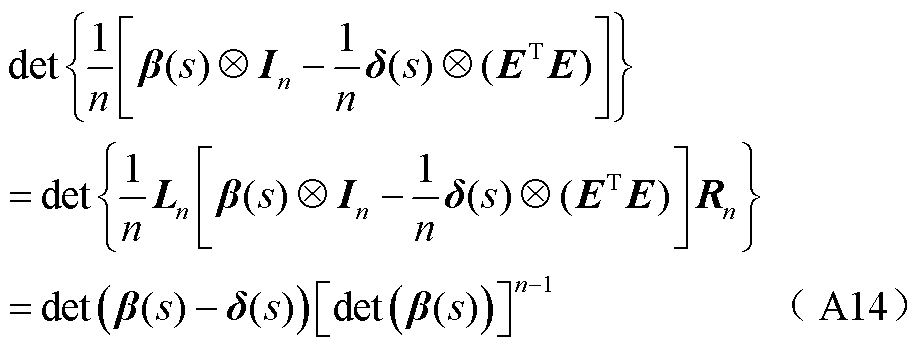
联立式（A12）和式（A14）可得
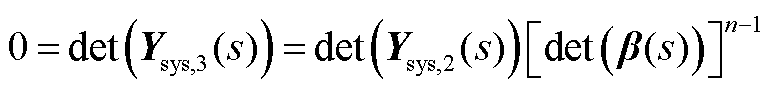（A15）
比较式（A10）和式（A15）可以看出，节点分裂前后仅增加了[det(β(s))]n-1这n-1个构网单机并网系统的并网模态。该单机并网系统并网线路导纳为分裂前该节点的自导纳，会使稳定性分析结果相对保守，但该模态与原系统中构网主导模态比较接近，带来的误差较小，且可以在后续数值解耦中快速剔除节点分裂引入的模态。
3. 仿真系统参数
附表1 变流器控制参数
App.Tab.1 Control parameters of converters
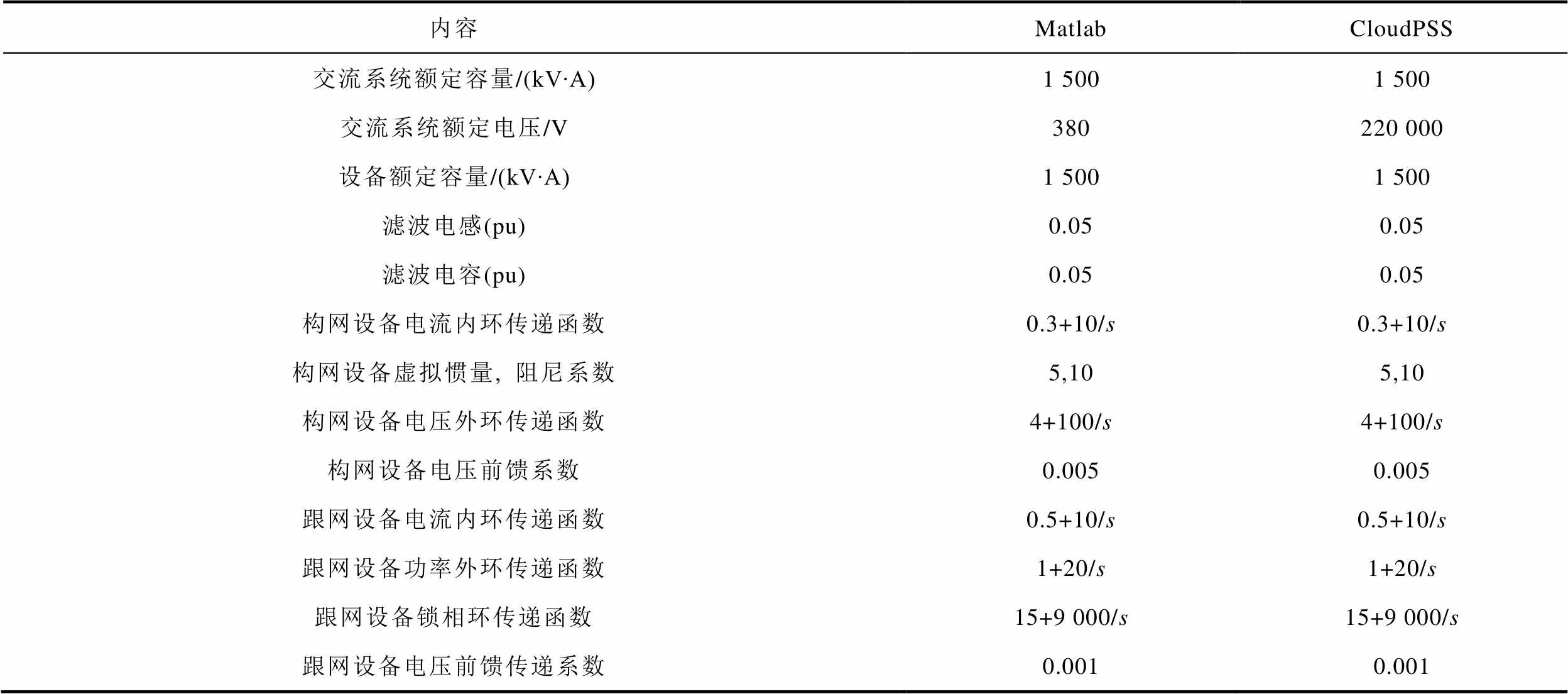
内容MatlabCloudPSS 交流系统额定容量/(kV∙A)1 5001 500 交流系统额定电压/V380220 000 设备额定容量/(kV∙A)1 5001 500 滤波电感(pu)0.050.05 滤波电容(pu)0.050.05 构网设备电流内环传递函数0.3+10/s0.3+10/s 构网设备虚拟惯量, 阻尼系数5,105,10 构网设备电压外环传递函数4+100/s4+100/s 构网设备电压前馈系数0.0050.005 跟网设备电流内环传递函数0.5+10/s0.5+10/s 跟网设备功率外环传递函数1+20/s1+20/s 跟网设备锁相环传递函数15+9 000/s15+9 000/s 跟网设备电压前馈传递系数0.0010.001
附表2 3机9节点系统电网参数
App.Tab.2 Parameters of the network in 3-devices 9-bus system（10-3pu）
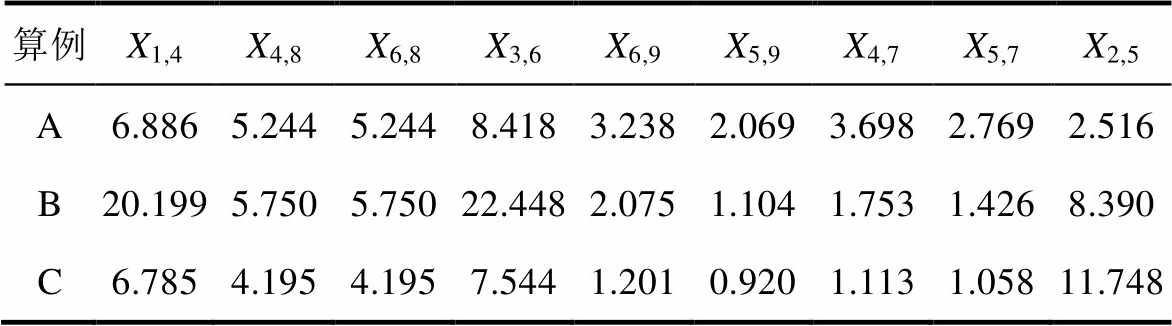
算例X1,4X4,8X6,8X3,6X6,9X5,9X4,7X5,7X2,5 A6.8865.2445.2448.4183.2382.0693.6982.7692.516 B20.1995.7505.75022.4482.0751.1041.7531.4268.390 C6.7854.1954.1957.5441.2010.9201.1131.05811.748
附表3 某实际新能源基地仿真模型电网参数
App.Tab.3 Parameters of the network in a practical renewable energy plant（10-3pu）
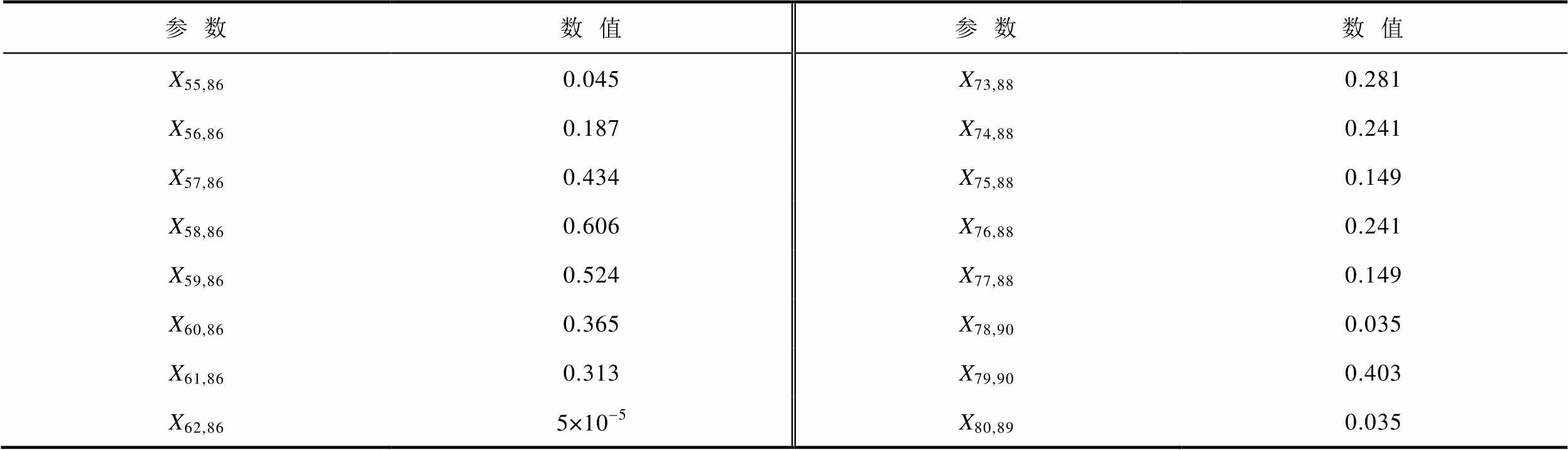
参数数值参数数值 X55,860.045X73,880.281 X56,860.187X74,880.241 X57,860.434X75,880.149 X58,860.606X76,880.241 X59,860.524X77,880.149 X60,860.365X78,900.035 X61,860.313X79,900.403 X62,865×10-5X80,890.035
（续）
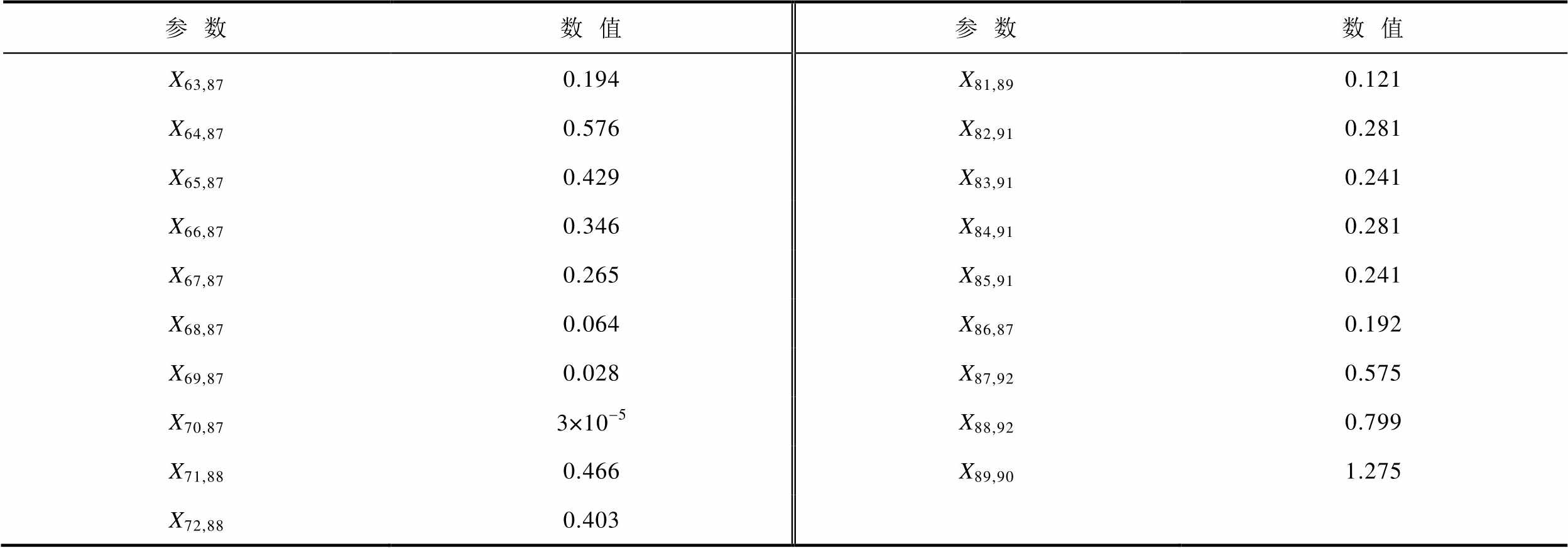
参数数值参数数值 X63,870.194X81,890.121 X64,870.576X82,910.281 X65,870.429X83,910.241 X66,870.346X84,910.281 X67,870.265X85,910.241 X68,870.064X86,870.192 X69,870.028X87,920.575 X70,873×10-5X88,920.799 X71,880.466X89,901.275 X72,880.403
参考文献
[1] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[2] 陈国平, 李明节, 许涛, 等. 关于新能源发展的技术瓶颈研究[J]. 中国电机工程学报, 2017, 37(1): 20-27.
Chen Guoping, Li Mingjie, Xu Tao, et al. Study on technical bottleneck of new energy development[J]. Proceedings of the CSEE, 2017, 37(1): 20-27.
[3] Rosso R, Wang Xiongfei, Liserre M, et al. Grid-forming converters: control approaches, grid-synchro-nization, and future trends: a review[J]. IEEE Open Journal of Industry Applications, 2021, 2: 93-109.
[4] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[5] 陈剑, 杜文娟, 王海风. 采用深度迁移学习定位含直驱风机次同步振荡源机组的方法[J]. 电工技术学报, 2021, 36(1): 179-190.
Chen Jian, Du Wenjuan, Wang Haifeng. A method of locating the power system subsynchronous oscillation source unit with grid-connected PMSG using deep transfer learning[J]. Transactions of China Electro-technical Society, 2021, 36(1): 179-190.
[6] Kundur. Power System Stability and Control[M]. Columbus, OH: McGraw-Hill, 1994.
[7] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[8] 邵冰冰, 赵书强, 高本锋. 基于相似变换理论的直驱风电场经柔直并网系统次同步振荡简化模型[J]. 中国电机工程学报, 2020, 40(15): 4780-4791.
Shao Bingbing, Zhao Shuqiang, Gao Benfeng. Simplified model for studying the sub-synchronous oscillation of direct-drive wind farms via VSC-HVDC system based on similar transformation theory[J]. Proceedings of the CSEE, 2020, 40(15): 4780-4791.
[9] 金宇清, 鞠平, 刘伟航, 等. 基于量测信号扰动的DFIG变流器控制参数辨识方法[J]. 电力系统自动化, 2016, 40(8): 36-42.
Jin Yuqing, Ju Ping, Liu Weihang, et al. Parameter identification method for converter controller of DFIG based on measurement signal disturbance[J]. Automation of Electric Power Systems, 2016, 40(8): 36-42.
[10] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[11] 辛焕海, 李子恒, 董炜, 等. 三相变流器并网系统的广义阻抗及稳定判据[J]. 中国电机工程学报, 2017, 37(5): 1277-1293.
Xin Huanhai, Li Ziheng, Dong Wei, et al. Generalized-impedance and stability criterion for grid-connected converters[J]. Proceedings of the CSEE, 2017, 37(5): 1277-1293.
[12] 张冲, 王伟胜, 何国庆, 等. 基于序阻抗的直驱风电场次同步振荡分析与锁相环参数优化设计[J]. 中国电机工程学报, 2017, 37(23): 6757-6767, 7067.
Zhang Chong, Wang Weisheng, He Guoqing, et al. Analysis of sub-synchronous oscillation of full-converter wind farm based on sequence impedance and an optimized design method for PLL parameters [J]. Proceedings of the CSEE, 2017, 37(23): 6757-6767, 7067.
[13] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
[14] 宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(一): 机理模型与稳定判据适用性[J]. 中国电机工程学报, 2022, 42(12): 4405-4419.
Gong Zexu, Yaermaimaiti Ailixier, Xin Huanhai, et al. Small signal stability analysis of equipment in renewable energy power system (partⅠ): mechanism model and adaptation of stability criterion[J]. Proceedings of the CSEE, 2022, 42(12): 4405-4419.
[15] Huang Linbin, Xin Huanhai, Li Zhiyi, et al. Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 501-516.
[16] 谢志为, 陈燕东, 伍文华, 等. 双模式扰动下新能源发电装备的宽频带序阻抗在线精确测量方法[J]. 中国电机工程学报, 2020, 40(9): 2903-2914.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A wide-bandwidth sequence-impedance online precise measurement method for renewable energy generation equipment with dual-mode disturbance[J]. Proceedings of the CSEE, 2020, 40(9): 2903-2914.
[17] 辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027.
Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[18] 辛焕海, 甘德强, 鞠平. 多馈入电力系统广义短路比: 多样化新能源场景[J]. 中国电机工程学报, 2020, 40(17): 5516-5527.
Xin Huanhai, Gan Deqiang, Ju Ping. Generalized short circuit ratio of power systems with multiple power electronic devices: analysis for various renewable power generations[J]. Proceedings of the CSEE, 2020, 40(17): 5516-5527.
[19] Yang Chaoran, Huang Linbin, Xin Huanhai, et al. Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3563-3573.
[20] 胡光, 庄可好, 高晖胜, 等. 低惯量交流系统并网变流器次/超同步振荡分析[J]. 电工技术学报, 2024, 39(8): 2250-2264.
Hu Guang, Zhuang Kehao, Gao Huisheng, et al. Sub/super synchronous oscillation analysis of grid-connected converter in low inertia AC system[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2250-2264.
[21] 袁辉, 辛焕海, 王冠中, 等. 含SVG的新能源多馈入系统振荡分析和广义短路比计算[J]. 电力系统自动化, 2021, 45(14): 38-46.
Yuan Hui, Xin Huanhai, Wang Guanzhong, et al. Analysis on oscillation of multi-infeed system with renewable energy and static var generator and calculation of its generalized short-circuit ratio[J]. Automation of Electric Power Systems, 2021, 45(14): 38-46.
[22] 辛焕海, 刘晨曦, 黄林彬, 等. 基于特征子系统的广义短路比导出原理及计算方法[J]. 中国电机工程学报, 2025, 45(7): 2447-2461.
Xin Huanhai, Liu Chenxi, Huang Linbin, et al. Derivation principle and calculation method of generalized short circuit ratio based on characteristic subsystem[J]. Proceedings of the CSEE, 2025, 45(7): 2447-2461.
[23] 张伯明, 陈寿孙, 严正. 高等电力网络分析[M]. 2版. 北京: 清华大学出版社, 2007.
[24] Shim S, Kwak J S, Heath R W, et al. Block diagonalization for multi-user MIMO with other-cell interference[J]. IEEE Transactions on Wireless Communications, 2008, 7(7): 2671-2681.
[25] Salas H N. Gershgorin’s theorem for matrices of operators[J]. Linear Algebra and Its Applications, 1999, 291(1/2/3): 15-36.
[26] 胡宇飞, 田震, 查晓明, 等. 构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J]. 电力系统自动化, 2022, 46(24): 121-131.
Hu Yufei, Tian Zhen, Zha Xiaoming, et al. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid-following converters[J]. Automation of Electric Power Systems, 2022, 46(24): 121-131.
[27] Zou Zhixiang, Tang Jian, Wang Xiongfei, et al. Modeling and control of a two-bus system with grid-forming and grid-following converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 7133-7149.
[28] 刘朋印, 谢小荣, 李原, 等. 构网型控制改善跟网型变流器次/超同步振荡稳定性的机理和特性分析[J]. 电网技术, 2024, 48(3): 990-997.
Liu Pengyin, Xie Xiaorong, Li Yuan, et al. Mechanism and characteristics of grid-forming control for improving sub/super synchronous oscillation stability of grid-following-based grid-connected converter[J]. Power System Technology, 2024, 48(3): 990-997.
Small-Signal Stability Analysis Method for Hybrid Grid-Following/Grid-Forming Delivery Systems Based on Eigen-Subsystem
Abstract The global consensus has emerged to replace traditional fossil fuel-based power generation with renewable energy sources such as photovoltaic and wind power, leading to the formation of renewable energy delivery systems (REDSs). Within these systems, a trend towards the integration of grid-following (GFL) and grid-forming (GFM) devices has emerged. The REDS incorporating GFL and GFM devices exhibit high dynamic order, with complex dynamic interactions between heterogeneous equipment clusters and between equipment clusters and the network, posing challenges for the mechanism analysis and quantitative computation of small-signal stability. This paper proposes an eigen-subsystem computation method for the small-signal stability analysis of REDSs. It defines the double-infeed eigen-subsystem (DIES), which includes a GFL device and a GFM device. By equivalently reducing the complex, high-dimensional REDS to several low-dimensional DIES, the method preserves the dynamic interactions both between devices and between devices and the network. This approach enables efficient and accurate small-signal stability analysis of REDSs.
Firstly, for a REDS incorporating GFL and GFM devices, a full-order small-signal model of the system is constructed. The general approach for deriving the eigen-subsystem is briefly outlined, which involves reducing the complex high-dimensional system to several simple low-dimensional eigen-subsystems through decoupling. Subsequently, for a REDS with an equal number of n GFL devices and n GFM devices, based on the full-order model of the system, a matrix block diagonalization method is proposed on top of the matrix diagonalization method. A fast algorithm based on the Givens method is presented to solve for P⊗I4 (P∈Rn×n), thus decoupling the REDS into n DIESs. Stability criteria for the DIES are also provided. When the device parameters are given, the stability operating region Ω of the DIES can be determined. The DIES remains stable if its network impedance falls within Ω. Thirdly, for more generalized scenarios, a node-splitting method is introduced to increase the number of less abundant devices, addressing the imbalance in the number of GFL and GFM devices. An eigen-subsystem-based method for small-signal stability analysis of REDSs is proposed. The REDS is stable if the set of network impedances Ω1, formed by all decoupled DIESs, lies within the stability region Ω. Otherwise, the REDS becomes unstable and exhibits the same stability issues as the unstable DIES. Finally, time-domain simulations are conducted, and a 3-machines 9-nodes system as well as a 54-machines system are used to validate the effectiveness and correctness of the proposed method in the small-signal stability analysis of REDSs incorporating GFL and GFM devices. Experimental comparisons show that, compared to traditional eigenvalue analysis methods, the proposed method significantly improves computational efficiency.
The following conclusions can be drawn: (1) The REDS is mode-equivalent to its DIESs, and the stability characteristics of the original system can be traced back through DIESs. (2) For general REDS with n GFL devices and m GFM devices, the system can be decoupled and reduced in order by constructing a mode-equivalent system through node-splitting. This results in m DIESs, and (n-m) eigen-subsystems of single GFL devices (where n＞m, or vice versa). (3)When the device parameters are given, the stability operating region Ω of the device-side characteristics can be determined. The network-side information of the eigen-subsystems obtained from the decoupling of the REDS forms a set of network impedances Ω1. By checking whether Ω1 belongs to Ω, the stability of the original system can be quickly assessed. Currently, small-signal synchrony stability has primarily been analyzed for the DIES. A future challenge is how to comprehensively analyze system stability under interactions among different components and quantify the stability margin of hybrid delivery systems.
Keywords：Renewable energy delivery systems, grid-following and grid-forming devices, eigen-subsystem, small-signal stability, mode equivalence
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241755
国家重点研发计划重点专项资助项目（2023YFB2405900）。
收稿日期2024-10-09
改稿日期2024-12-17
唐 宇 男，2001年生，硕士研究生，研究方向为新能源并网稳定分析。
E-mail：3190105624@zju.edu.cn
辛焕海 男，1981年生，教授，博士生导师，研究方向为交直流系统稳定分析与控制、新能源并网稳定分析与控制。
E-mail：xinhh@zju.edu.cn（通信作者）
（编辑 赫 蕾）