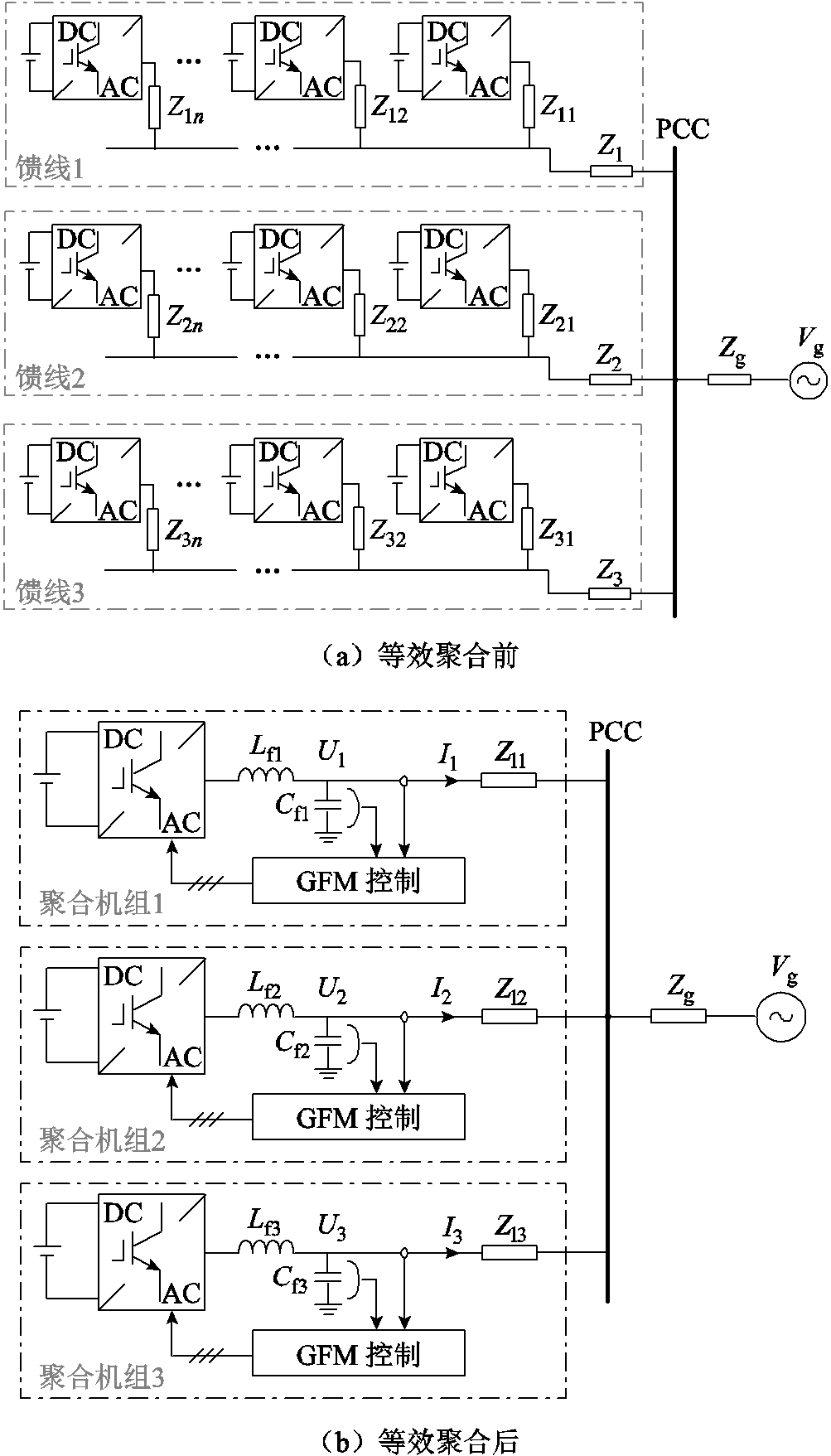
图1 构网型变流器多机并联系统等效拓扑
Fig.1 Equivalent topology of multiple grid-forming converters system
摘要 以构网型变流器为接口的新能源在具有频率和电压支撑能力的同时，面临严峻的暂态同步失稳风险。现有研究多专注于构网型变流器单机系统，无法推广应用至存在复杂交互的多机并联系统，缺少多机系统稳定域的定量估计。为此，该文首先建立了机组外交互与有功无功内耦合的构网型变流器多机并联系统大信号等值模型；其次，基于该模型，构造了计及电压动态、阻尼耗散以及机组暂态交互的李雅普诺夫函数集，该函数集不依赖运动路径与响应时间，能直观且准确地刻画多机并联系统最大稳定域，并通过故障清除点位置预判暂态同步稳定性；然后，通过比较稳定域大小，量化了控制参数和电网参数对构网型多机系统暂态同步稳定边界的影响，探究了阻尼耗散、电压动态及机组间交互对暂态稳定裕度的影响；最后，搭建硬件在环实验平台验证了所估计最大稳定域与分析的准确性。
关键词：构网型变流器 暂态同步 稳定域 多机并联系统
大力发展风电、太阳能等新能源，加快能源供给侧、消费侧的清洁化、低碳化转型，是缓解能源危机、应对全球环境及气候问题的有效途径[1]。在我国，当前已投运的风/光新能源主要以跟网型变流器为并网接口，不具备传统同步发电机的惯量和阻尼特性[2]。为提升新能源支撑能力，构网型变流器（Grid-Forming Inverter, GFMI）成为可行的技术手段[3]。其基本思路是通过改进控制和电路结构模拟同步发电机惯性和阻尼特性，使得新能源具备接近同步发电机的电网构建与主动支撑能力。
在具备同步发电机优点的同时，构网型变流器受到大扰动时也会发生类似的暂态同步失稳问题，而电力电子变流器在控制上存在的多尺度、强耦合、非线性等特征使得构网型变流器的暂态行为更加复杂，严重威胁新能源的安全可靠消纳[4-6]。近年来，构网型变流器暂态同步失稳问题受到国内外研究人员的广泛关注。
暂态故障下，系统运行点远远偏移初始工作点，基于线性化近似处理的传统小信号模型无法准确地描述大扰动下系统的暂态特性[7]。为此，文献[7]构建了计及非线性环节的单台构网型变流器大信号模型，探究了大扰动后稳态工作平衡点的存在性对构网型变流器暂态同步稳定性的影响。随后，通过类比同步发电机，文献[8-11]采用等面积法、李雅普诺夫直接法定性或定量地分析构网型变流器暂态稳定性。基于数值解析方法，文献[12-14]利用相轨迹刻画构网型变流器暂态特性，并探究系统参数对暂态稳定性的影响。然而，上述研究都是以单台构网型变流器为研究对象，无机组间暂态交互作用，难以准确评估多机并联系统的暂态稳定性。
由于机组之间非线性暂态交互作用的存在，多机系统的等值建模和分析比单机系统更加复杂[15]。迄今为止，关于多机系统暂态同步稳定性的研究报道有限，多集中于跟网型多机系统。文献[16]建立了跟网型变流器并联系统暂态等值模型，探究平衡点的存在性，提出跟网型多机系统暂态稳定性评估方法。在此基础上，文献[17]利用相轨迹定性分析控制参数对跟网型多机系统暂态稳定性的影响规律。文献[18]忽略跟网型变流器阻尼耗散能量，构造跟网型多机系统的李雅普诺夫能量函数，定量估计临界故障清除时间。文献[19]计及阻尼耗散能量，利用数值迭代法刻画跟网型并联系统的安全稳定域。由于构网型变流器与跟网型变流器在控制结构与同步机制上的不同，上述研究无法推广应用于构网型多机系统。
针对构网型多机系统的暂态稳定性，文献[20]构建了两台构网型变流器并联系统的统一摇摆方程。基于该方程，文献[21]建立了双机频率和功角差的三阶暂态同步模型，分析双机出力差异对于暂态稳定的影响。然而，文献[20-21]中的整个系统不与外部电网相连，在分析时将其中一台构网型变流器等效为电网，本质上还是单机系统。在多机并网场景下，文献[22]计及变流器与电网的交互，通过功角曲线定性分析构网型变流器并联系统的交互效应和暂态特性。定量分析方面，文献[23]直接应用为同步发电机设计的李雅普诺夫函数估计构网型多机并联系统的临界清除时间，却忽略了构网型变流器阻尼耗散的影响。文献[24]在同步发电机李雅普诺夫函数的基础上进一步考虑了阻尼耗散，但该函数依赖运动路径与响应时间，无法直观地刻画多机系统稳定域，无法进行定量分析与计算。更为重要的是，与同步发电机相比，构网型变流器有功环与无功环是密切耦合的，无功环电压动态对暂态稳定性有重要影响。然而，文献[20-24]忽略了无功环电压动态，这给暂态稳定性分析带来了较大的保守性。
综上所述，构网型变流器多机并联系统暂态同步稳定性研究尚不充分，缺少稳定域直观且准确的定量估计。为此，本文首先建立了机组间外交互与有功无功内耦合的构网型并联系统大信号等值模型；其次，基于该模型，构建了计及电压动态、阻尼耗散、机组间暂态交互的李雅普诺夫函数集，该函数集不依赖运动路径与响应时间，可精确估计故障清除后多机并联系统稳定域；然后，利用稳定域大小探究了控制参数、电网参数及关键环节对构网型多机并联系统暂态同步稳定性的影响规律；最后，通过硬件在环实验验证了所估计最大稳定域与分析的准确性。
以构网型变流器为接口的新能源集群具有频率和电压支撑能力，其典型拓扑结构如图1a所示。由于前级变流器直流电压控制的存在，构网型变流器直流侧视作恒定。构网型变流器通过不同的分支集电线连接到馈线，而不同的馈线通过输电线共同连接至公共耦合点（Point of Common Coupling, PCC）。对于新能源集群而言，机组数量多、模型阶数高，难以直接对其进行暂态建模、求解与分析。因此，通常利用等值聚合法对系统进行一定程度的简化[25]。
图1 构网型变流器多机并联系统等效拓扑
Fig.1 Equivalent topology of multiple grid-forming converters system
假设同一馈线中的构网型变流器由同一制造商生产，具有类似的输出特性，则同一馈线中的构网型变流器可以通过聚合转换为一台等效的变流器。有关构网型变流器等值聚合建模方法和聚合参数计算的详细介绍可参见文献[26]，由于篇幅限制，此处不做详细介绍。等效聚合后的构网型变流器并联系统等效拓扑如图1b所示。图中，Ui、Ii和Ug分别为构网型变流器i的输出电压、输出电流和电网电压；Lfi和Cfi为滤波环节；Zli为等效聚合后输电线路阻抗。
构网型控制利用功率同步环节实现与电网的同步，其结构如图2所示。以电网电压Vg作为参考向量，构网型变流器输出与电网之间的功角和角频率差定义为δi和ω∆i，表示为
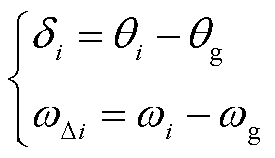（1）
式中，qi、ωi分别为GFMIi的相位和角频率；qg、ωg分别为电网的相位和角频率。
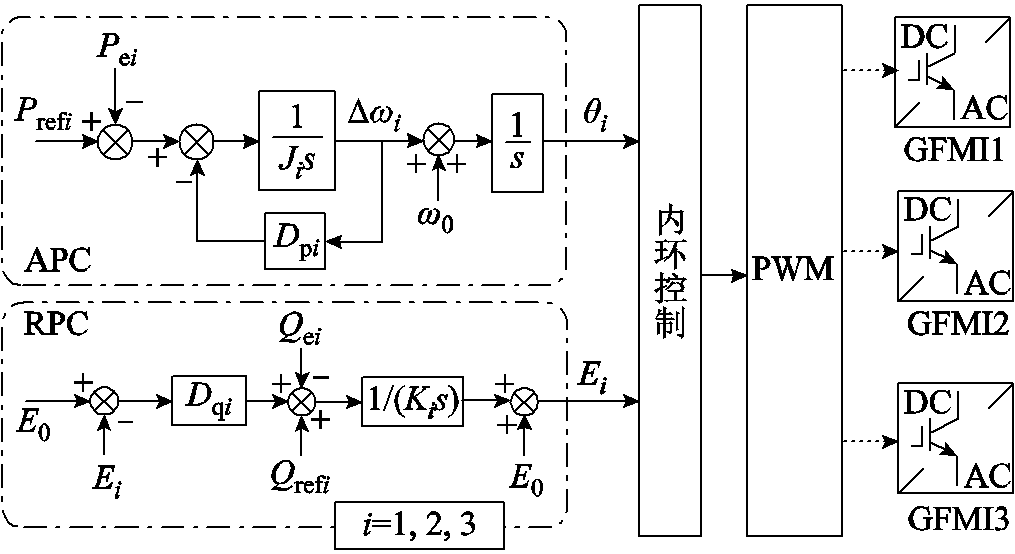
图2 构网控制策略结构
Fig.2 Structure of grid-forming control
由图2可知，有功环（Active Power Control, APC）模拟同步发电机摇摆特性，无功环（Reactive Power Control, RPC）调节构网型变流器电压输出，其动态方程为
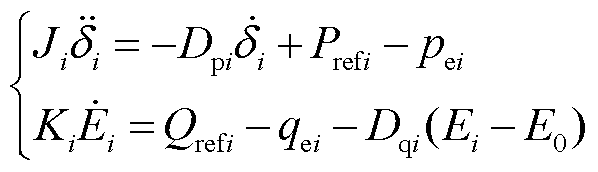（2）
式中，Ji和Dpi分别为GFMIi的惯量和阻尼系数，i=1, 2, 3；Dqi为无功下垂系数；Ki为积分系数；Prefi、Qrefi分别为参考有功、无功功率；pei、qei分别为实际有功、无功输出功率；Ei为GFMIi的输出电压；E0为额定电压幅值。
在实际工程应用中，变流器内环控制的带宽远高于功率环。因此，在研究构网型变流器暂态同步过程中，内环控制对系统暂态同步稳定性的影响可以忽略不计[8-13]，构网型变流器可以被视为受控电压源，表示为Ei∠δi。考虑到高压输电线路电阻远小于线路电抗，忽略线路电阻，近似认为输电线路为纯感性。因此，构网型变流器并联系统进一步简化等效为图3a。
暂态故障下，构网型变流器之间存在强交互作用，其对并联系统暂态行为及暂态稳定性存在不可忽略的影响。为了准确地刻画系统的暂态特性，本节建立计及机组间暂态交互作用的大信号等效模型。
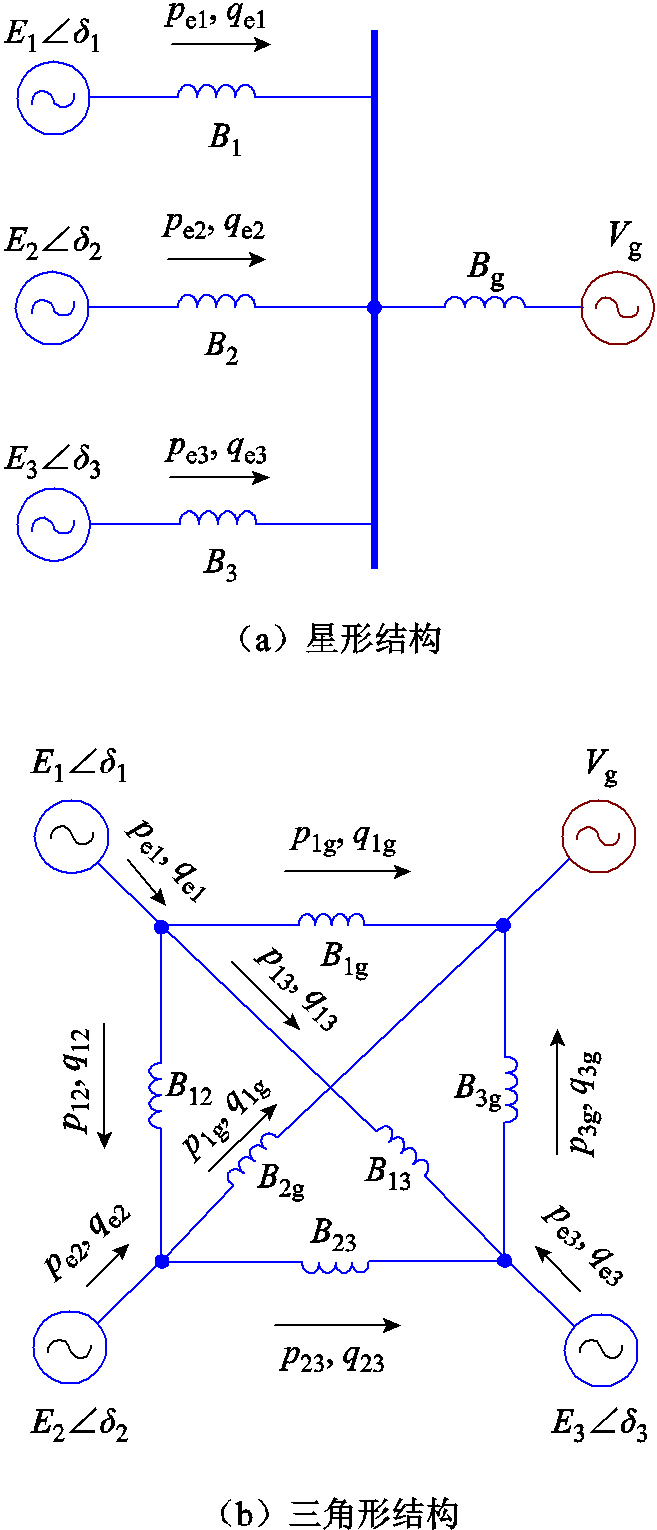
图3 构网型变流器并联系统等效电路
Fig.3 Equivalent circuit of multiple grid-forming converter
图3a中，B1、B2、B3、Bg为线路导纳。B1=1/ (wnL1)，B2=1/(wnL2)，B3=1/(wnL3)，Bg=1/(wnLg)，wn为额定角频率。为了便于传输功率计算，将星形联结的并联系统转换为三角形联结，如图3b所示。图中，B12、B13、B23分别表示GFMI1、GFMI2、GFMI3之间的等效线路导纳，Big是GFMIi与电网之间的等效导纳。根据星形-三角形转换关系，有
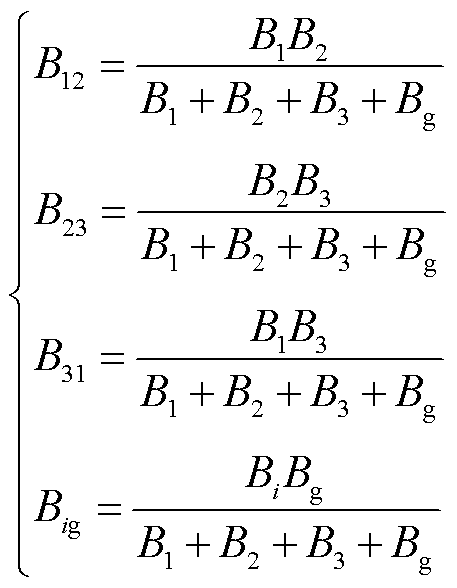（3）
基于功率传输定理，GFMI1、GFMI2、GFMI3之间的等效传输功率p12、q12、p13、q13、p23、q23为
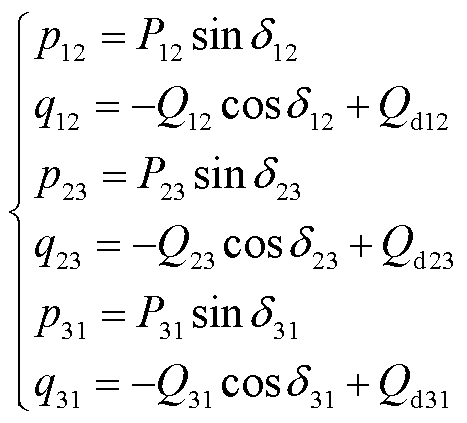（4）
式中，Qd12=1.5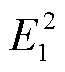
B12，Qd23=1.5
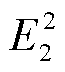B23，Qd31= 1.5
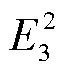B31，P12=Q12=1.5E1E2B12，P23=Q23=1.5E2E3B23，P31=Q31= 1.5E3E1B31，
。
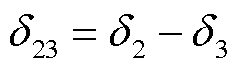GFMIi与电网之间的等效传输功率pig、qig可以表示为
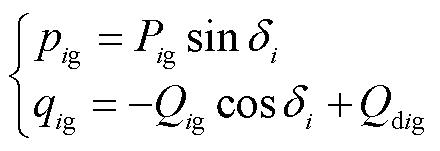（5）
式中，Qdig=1.5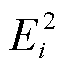
Bg；Qig=1.5EiEgBig；
；
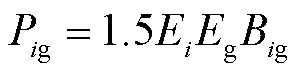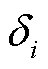为第i台变流器的功角。
进一步地，根据图3b，GFMI1、GFMI2和GFMI3的总输出功率pe1、qe1、pe2、qe2、pe3、qe3可以推导为
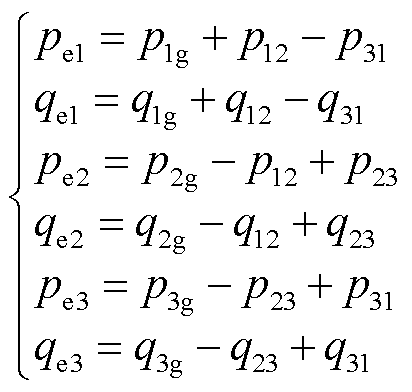（6）
结合式（1）～式（6），可以得到计及机组间暂态交互的构网型变流器并联系统大信号等效模型，如图4所示。由此可见，构网型变流器之间存在成对的交互作用，构网型变流器内部有功无功耦合，呈现外交互内耦合特性。为验证模型的准确性，大扰动下仿真模型与等效模型暂态特性对比如图5所示。可以明显看出，大信号等效模型能够准确地反映系统的动态特性，证明了所建模型的准确性。
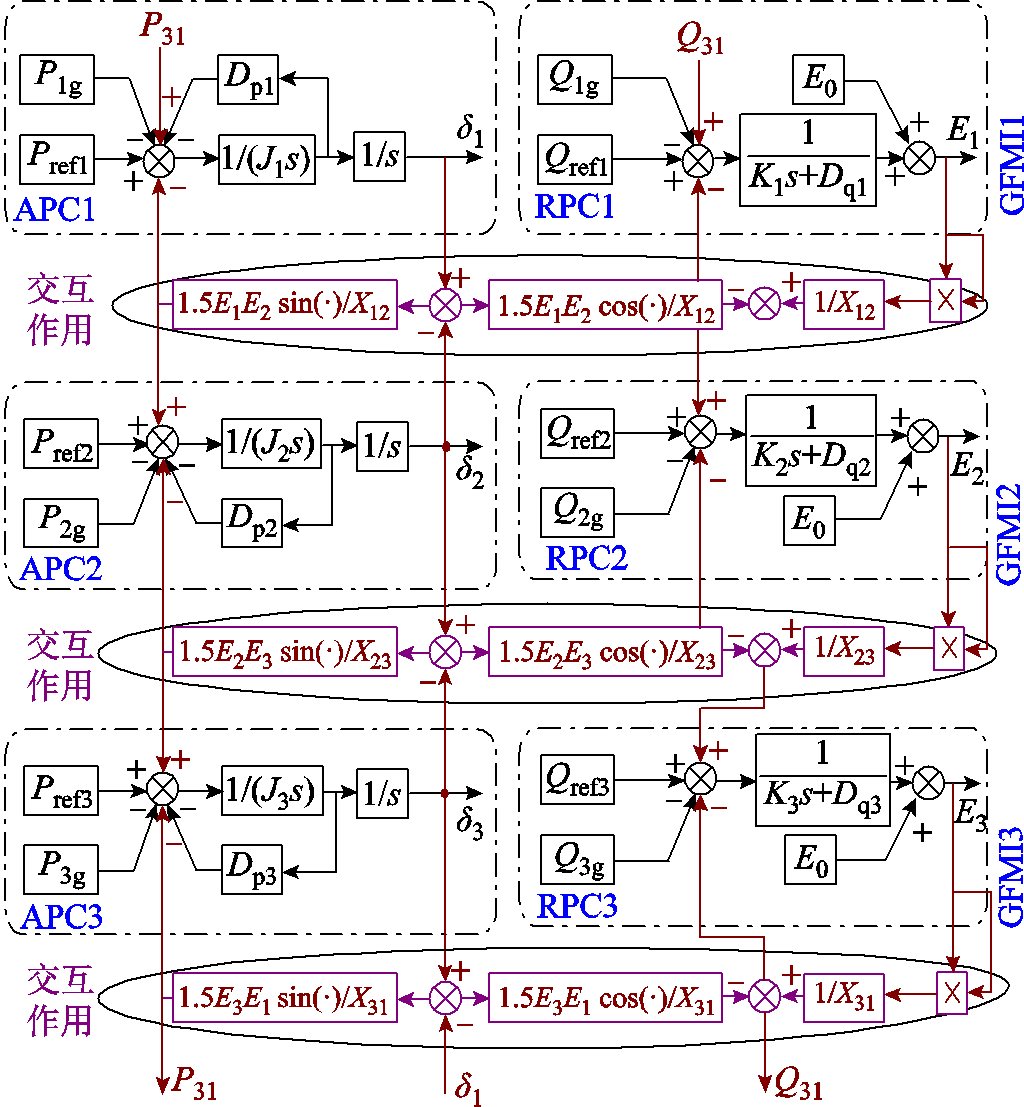
图4 构网型变流器多机并联系统大信号等效模型
Fig.4 Large-signal equivalent model of multiple grid-forming converter system
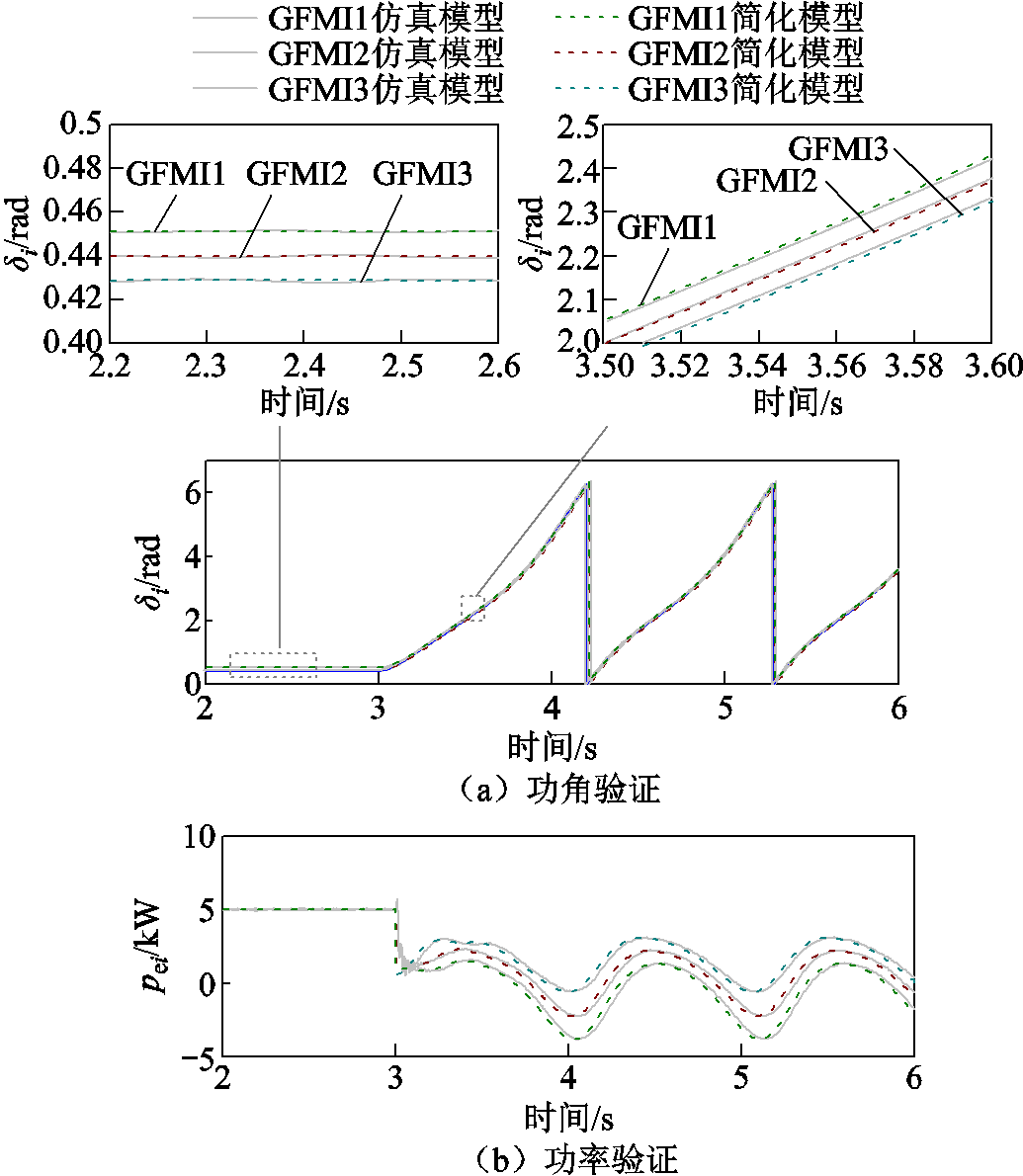
图5 构网型多机系统大信号等效模型验证
Fig.5 Verification of large-signal equivalent model under large disturbance
根据并联系统大信号等效模型，机组间交互作用与有功无功耦合下的电压动态对并联系统暂态稳定性具有重要影响。为此，本文构建了计及电压动态、阻尼耗散及机组间暂态交互的李雅普诺夫函数集，开展多机并联系统暂态同步稳定域的定量估计。
基于构网型多机并联系统等效模型，GFMI1的暂态同步方程可以表示为
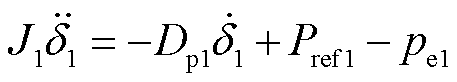（7）
将式（7）两边同时乘以wD1得到
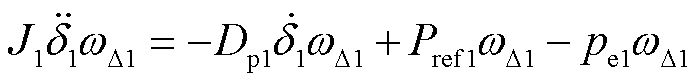（8）
式中，wD1为δ1的导数。利用首次积分法，将式（8）对时间进行积分，得到GFMI1的能量守恒方程为
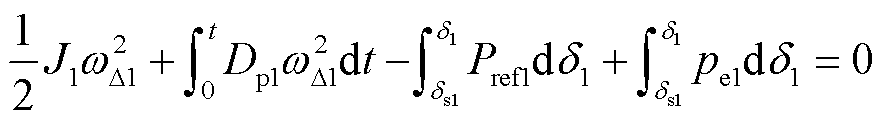（9）
式中，dsi为GFMIi的稳定平衡点。
同理，GFMI2和GFMI3的能量守恒方程可表示为
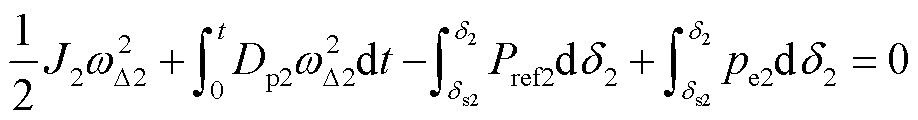（10）
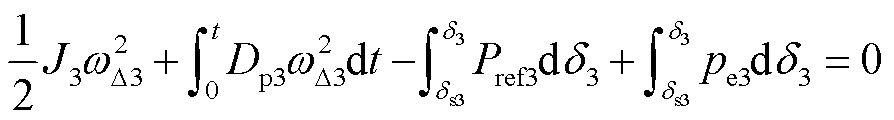（11）
式（9）～式（11）中，pe1、pe2和pe3是同时关于δ1、δ2和δ3的函数，使得其左侧最后一项无法直接积分求解。为此，将式（9）、式（10）、式（11）相加，得到构网型多机并联系统总的能量守恒方程为
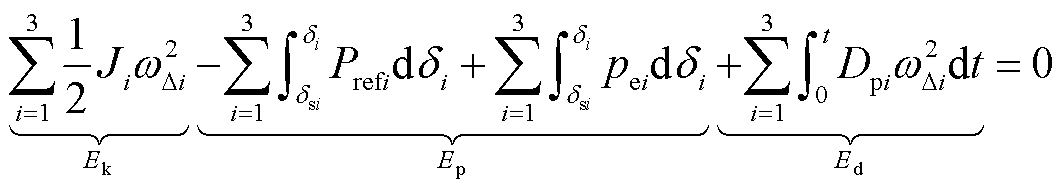（12）
式中，Ek、Ep、Ed分别为多机系统的动能、势能和阻尼耗散能量。显然，势能Ep和阻尼耗散能量Ed依赖于系统运动路径与响应时间，无法直接求解。因此，本文构建李雅普诺夫函数的关键在于如何处理势能Ep和阻尼耗散能量Ed，将其转换为不依赖运动路径与响应时间的可计算量，从而实现稳定域定的量估计。接下来给出具体介绍。
对于势能Ep，有
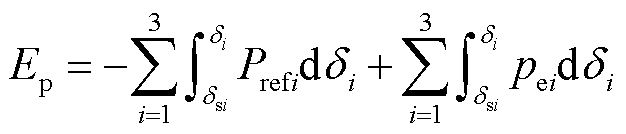（13）
若计及无功环电压动态，pei是同时关于di、ω∆i和Ei的函数。为此，将式（6）代入式势能Ep表达式（13）的第二项中，有
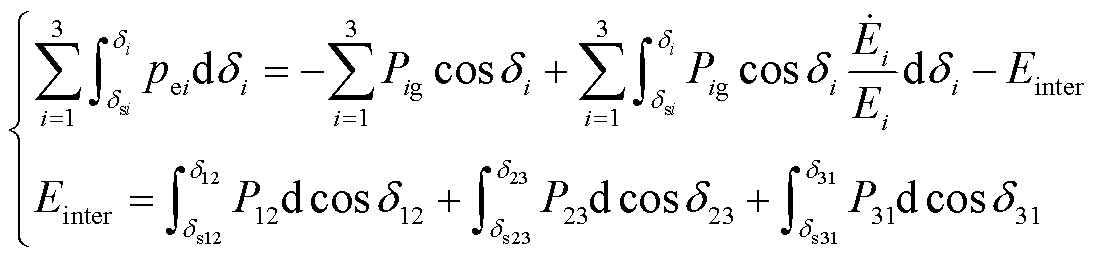（14）
式中，Einter为机组间暂态交互作用能量，是势能Ep的一部分；P12、P13和P23包含变量Ei，根据积分变换，Einter进一步转换为
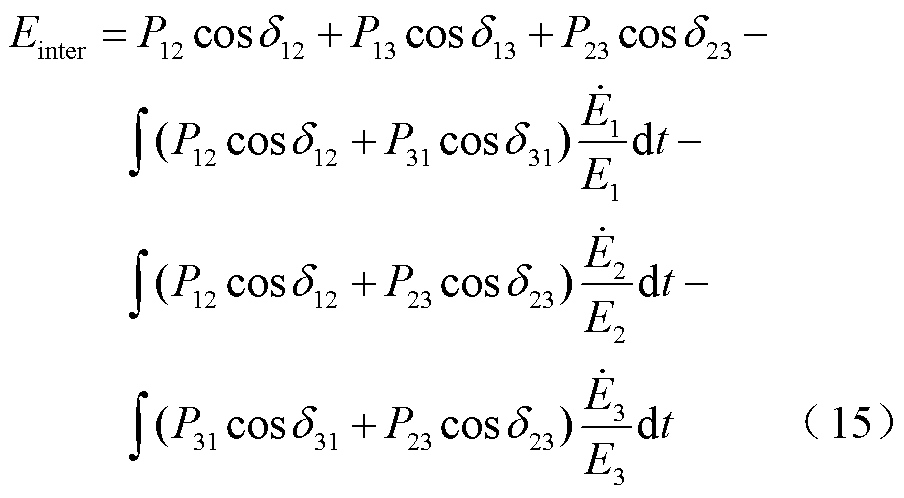
将式（15）代入式（14）得到
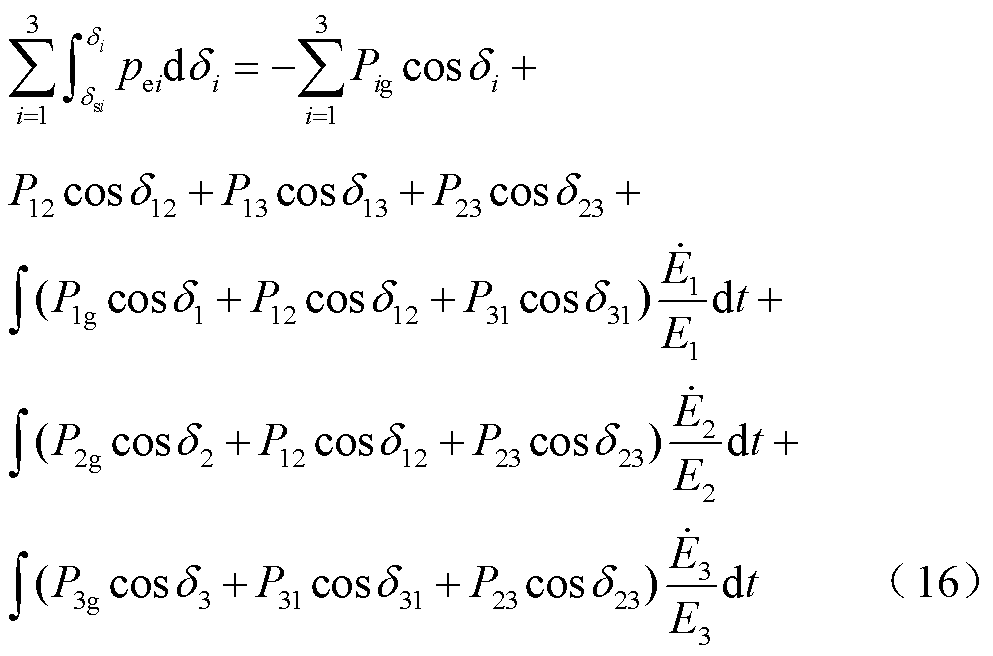
根据式（4），有P1g=Q1g，P12=Q12，P13=Q13，P23=Q23，则式（16）右侧第二项可进一步转换为
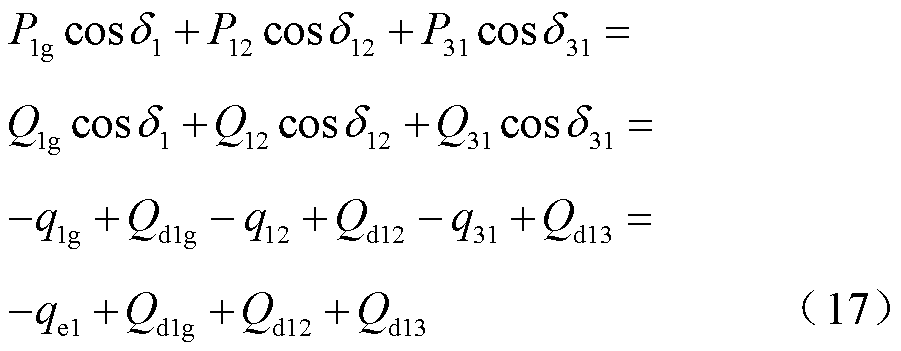
同理，式（16）等式右侧第三项和第四项转换为
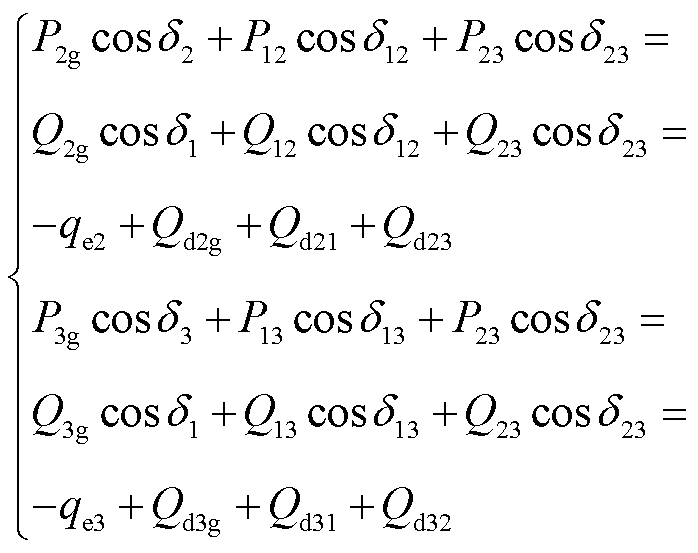（18）
式（17）和式（18）中，qei项可用式（2）进行替换，基于积分变换，式（14）进一步推导为
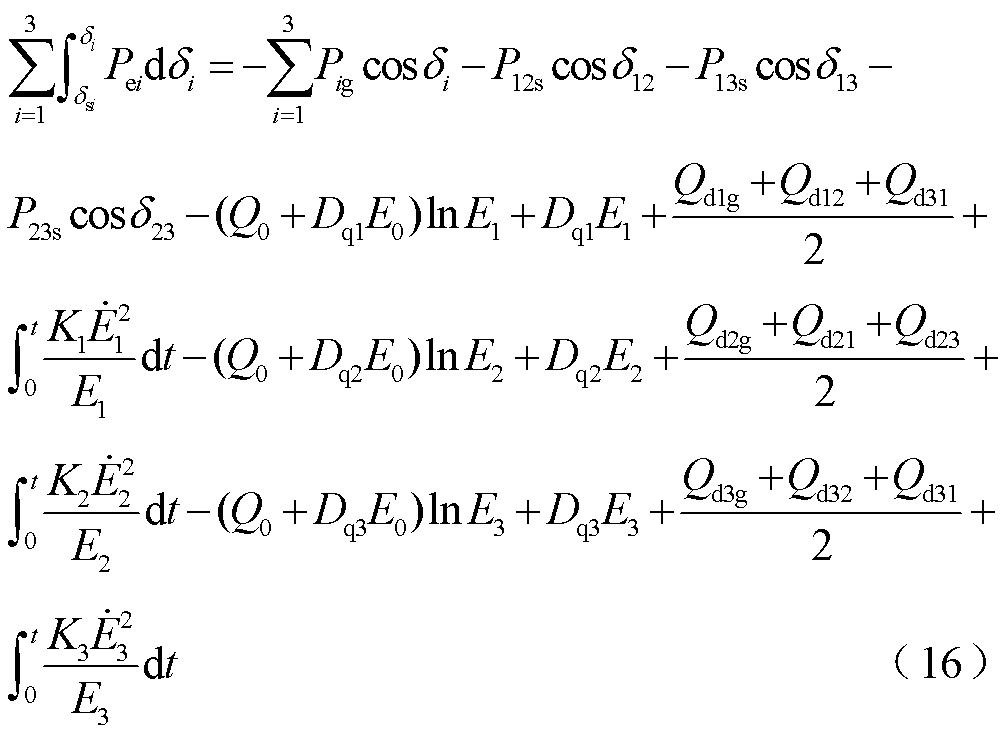
将式（19）代入式（13），势能Ep可表示为
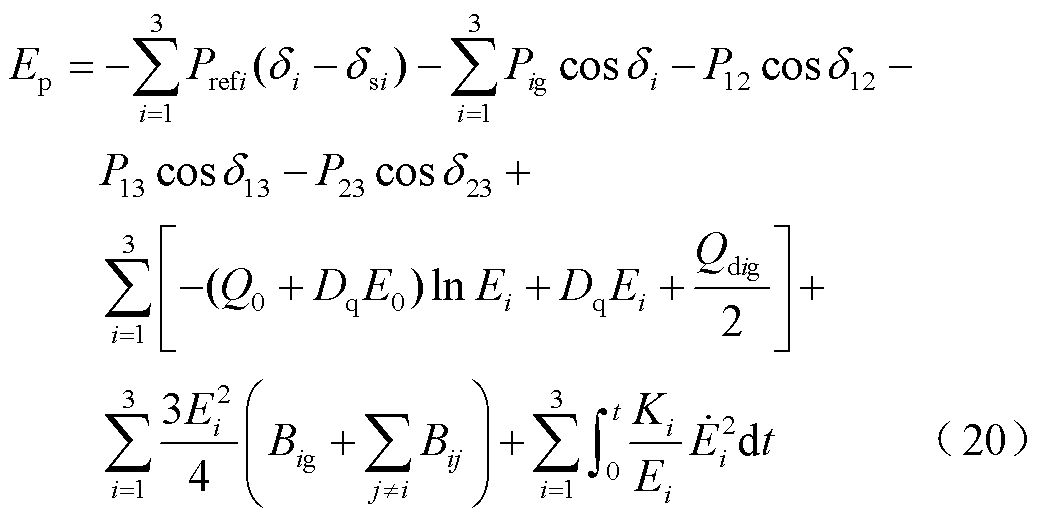
式（20）中存在与路径、响应时间相关的电压积分项。若不考虑阻尼耗散，引入附加积分项消除电压积分项，计及无功环电压动态的李雅普诺夫函数构造为
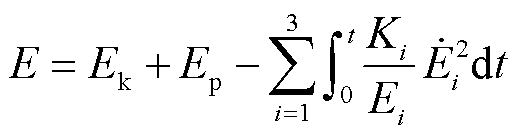（21）
此时，李雅普诺夫函数E与路径、响应时间无关，但未考虑阻尼耗散能量Ed对暂态稳定性的影响，忽略阻尼导致估计的稳定域趋向保守。为了降低稳定域的保守性，应该将阻尼耗散能量Ed纳入李雅普诺夫函数中。
对于阻尼耗散能量Ed，有
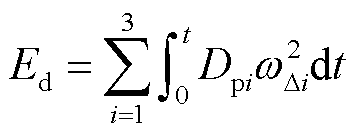（22）
式中，w∆i为di的导数，同样是Δdi的导数，Δdi=di-dsi。式（22）进一步转换为
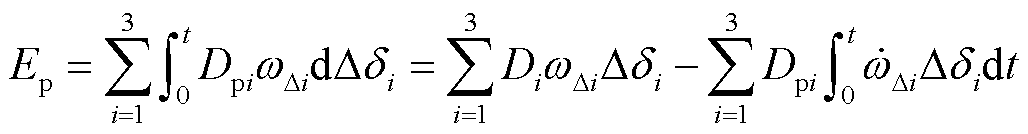（23）
将式（2）代入式（23）第二项，得到
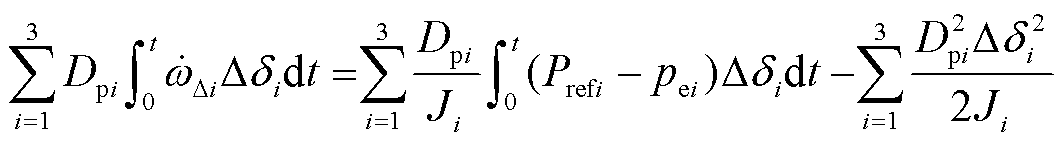（24）
阻尼耗散能量Ed进一步转换为
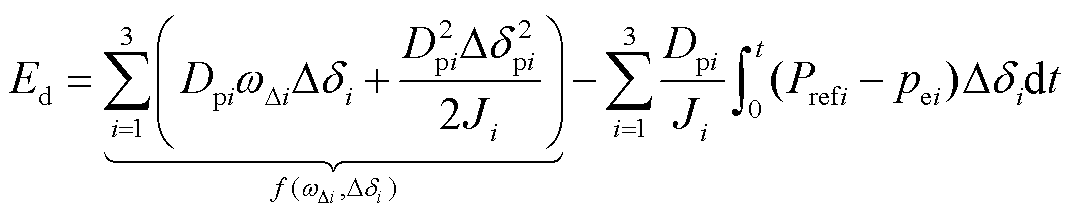（25）
由于式（25）中存在积分项，引入可变参数l，对阻尼耗散能量Ed进行缩放[27]，有
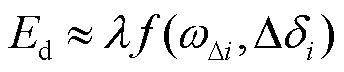（26）
此时，构造考虑阻尼耗散的李雅普诺夫函数集为
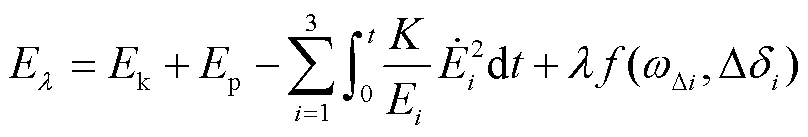（27）
在李雅普诺夫函数集El中，有多个状态变量，即δi、w∆i和Ei，状态变量向量表示为x=[δi w∆i Ei]。显然，李雅普诺夫函数集Eλ随可变参数λ变化，是多个函数的集合，但与运动路径和响应时间无关。接下来论证李雅普诺夫函数集Eλ的可行性。
在李雅普诺夫直接法中，正定和半负定条件是李雅普诺夫函数构造的依据。但由于李雅普诺夫直接法严苛性的正定条件，拉萨尔不变性定理成为稳定域估计的常用方法[28]，其基本定义如下。
拉萨尔不变性定理：对于一阶偏导连续的函数V(x)，假设有界区域W∈{V(x)＜l, l＞0}满足dV(x)/dt≤0；集合R是区域W内满足dV(x)/dt=0的点的集合；集合M是集合R中最大的不变集。如图6所示，任何起始于区域W的初始点x0，随时间t→∞会收敛于不变集M。如果不变集M只有平衡点，在稳定域内的点都将收敛于平衡点。
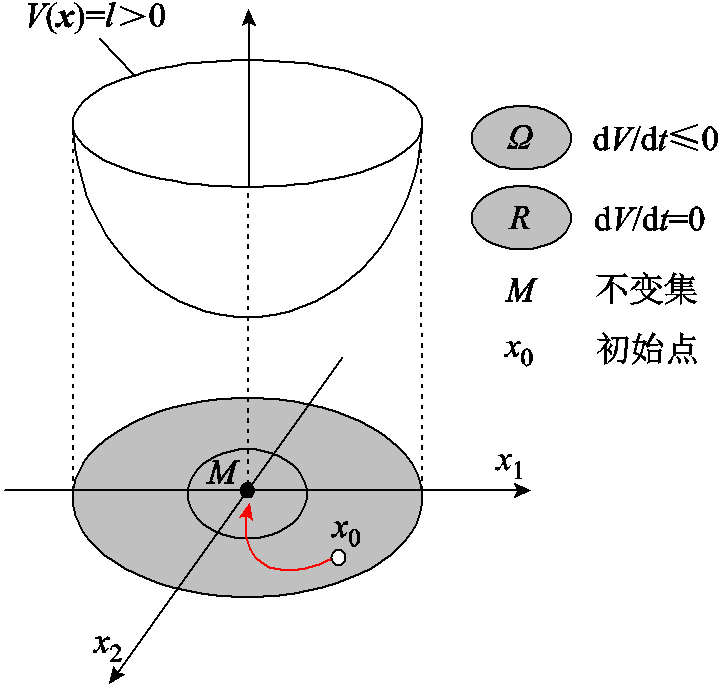
图6 拉萨尔不变性定理
Fig.6 Lassalle invariance theorem
基于上述定理，应用拉萨尔不变性定理估计稳定域的前提条件是：区域W 内，连续函数V(x)有上界；区域W内，连续函数V(x)的导数半负定；③区域W内，存在平衡点。
满足上述条件时，区域W即为稳定域。拉萨尔理论实际上是在正阻尼区域内找到封闭等势面作为稳定域的估计，而稳定域内部的初始点将会收敛稳定于平衡点。针对本文所构建的李雅普诺夫函数集El，拉萨尔不变性定理前提条件可表示为
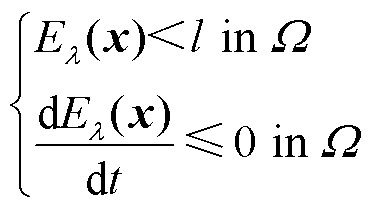（28）
为验证李雅普诺夫函数集Eλ满足拉萨尔不变性定理前提条件，将式（12）与式（25）代入式（27），有
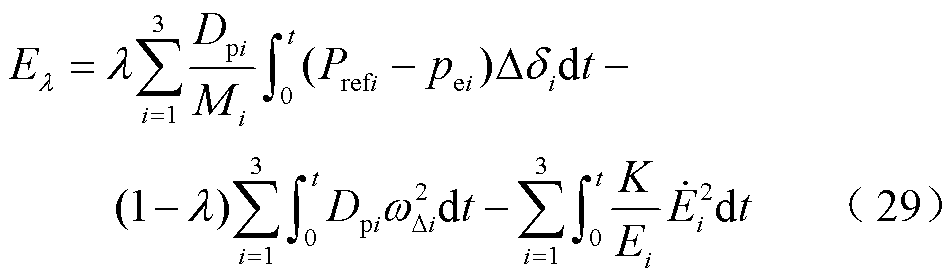
进一步求导得到
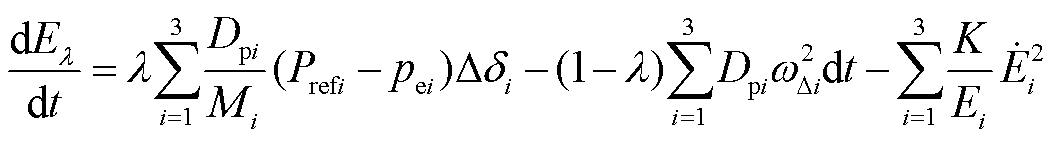（30）
若李雅普诺夫函数集Eλ满足拉萨尔不变性定理半负定条件，则
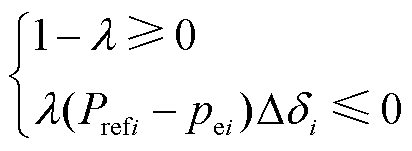（31）
在平衡点附近，(Prefi-pei)Δdi≤0始终成立，证明见附录。因此，当λ∈[0,1]时，李雅普诺夫函数集Eλ的导数满足半负定要求。若能找到合适的最大上界l，使得Eλ(x)≤l，Eλ(x)便满足拉萨尔不变性定理半负定与有界性要求，有界区域W即为最大稳定域。
在拉萨尔不变性定理中，关键步骤是找到最大的上界l，又称为临界能量Ecr。过大的临界能量导致稳定域边界不闭合，过小的临界能量导致稳定域保守性增大。依据不稳定平衡点法[29]，不稳定平衡点的能量Eλ(xu)可当作临界能量。这是因为当Ecr＞Eλ(xu)时，等势能曲面不再闭合，无封闭稳定域。对于不稳定平衡点xu，系统状态不再随时间变化，满足式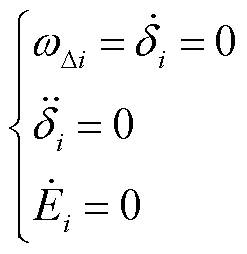（32）。
（32）
将式（32）代入式（2），可求得不稳定平衡点xu。此时，最大稳定域可表示为
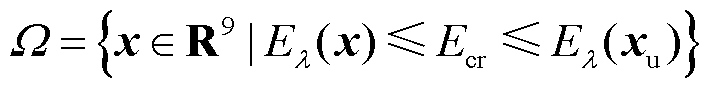（33）
式（33）的求解可通过Matlab中fimplicit3指令实现，曲面包围区域即为稳定域。对于多机并联系统，系统存在多个不稳定平衡点xui。取所有不稳定平衡点能量的最小值为临界能量，即
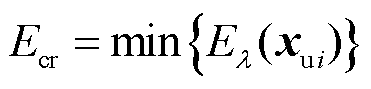（34）
在构造的能量函数式（27）中，有9个状态变量d1、d2、d3、w∆1、w∆2、w∆3、E1、E2、E3，稳定域为九维的空间区域，无法直观展示。为了准确地刻画稳定域以及故障清除点与稳定域的位置关系，可将w∆i固定为w∆i(0+)，Ei固定为Ei(0+)，进而将九维稳定域降为在d1-d2-d3空间内的三维稳定域。w∆i(0+)、Ei(0+)为故障清除时刻GFMIi的角频率差和输出电压，可通过广域同步测量装置或传感设备获取[30]。
构网型多机并联系统稳定域估计流程如图7所示。基于所估计稳定域，可实现故障清除后系统暂态同步稳定性判定。若故障清除点在稳定域内，意味着系统能量小于临界能量，能量耗散衰减，系统可回到平衡点，判定为暂态稳定；若故障清除点在稳定域外，意味着系统总能量超出临界能量，能量无法耗散衰减，系统不能回到平衡点，判定为暂态失稳。
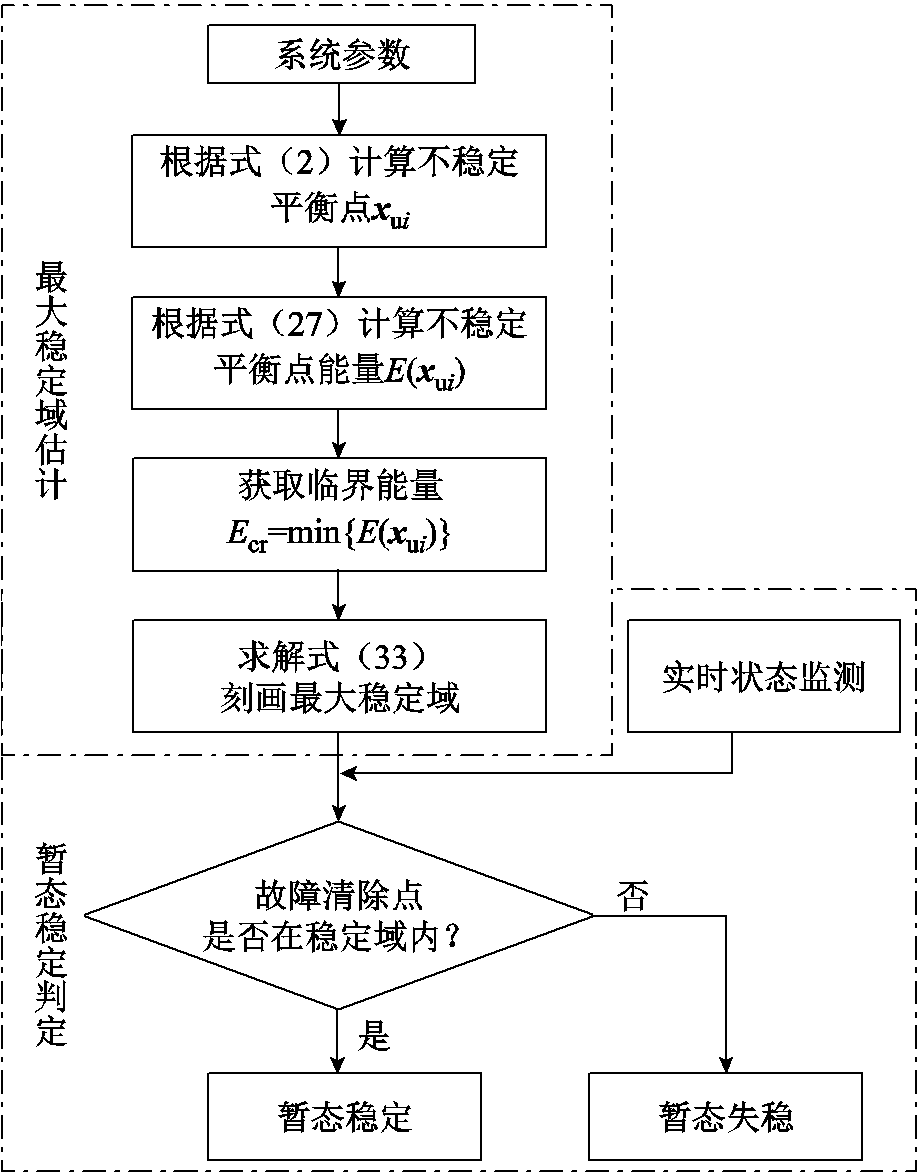
图7 稳定域估计与稳定性判定流程
Fig.7 Flow chart of stability region estimation and stability prediction
在李雅普诺夫函数集中，参数λ可取[0,1]之间任意值。依据上述稳定域估计方法，可绘制不同参数λ下多机系统三维稳定域。系统参数见表1。随着λ的增大，稳定域不断增大。稳定域的并集为李雅普诺夫函数集估计的稳定域，故可取λ=1时的稳定域作为多机并联系统最大稳定域估计。
表1 构网型变流器多机并联系统参数
Tab.1 System parameters of multi-paralleled GFMIs system
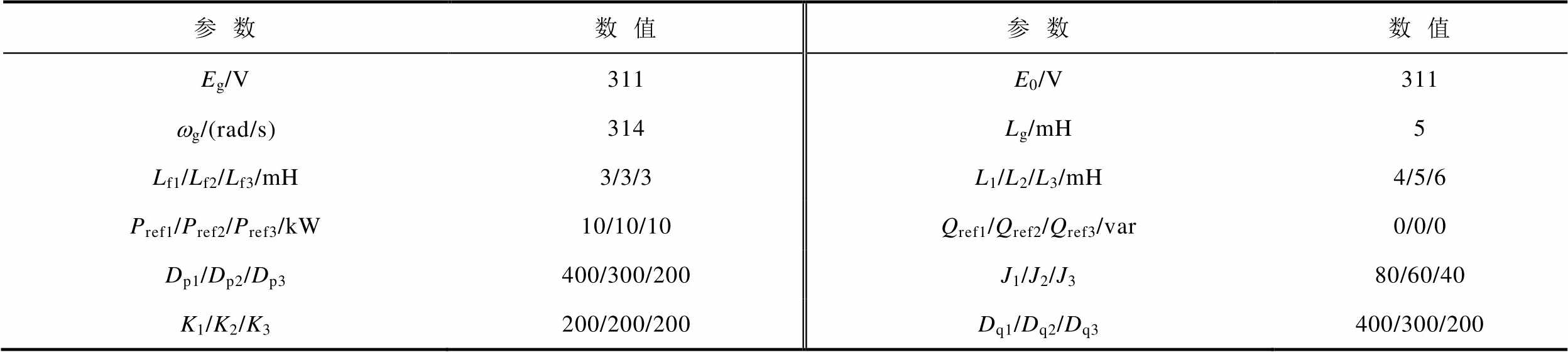
参数数值参数数值 Eg/V311E0/V311 wg/(rad/s)314Lg/mH5 Lf1/Lf2/Lf3/mH3/3/3L1/L2/L3/mH4/5/6 Pref1/Pref2/Pref3/kW10/10/10Qref1/Qref2/Qref3/var0/0/0 Dp1/Dp2/Dp3400/300/200J1/J2/J380/60/40 K1/K2/K3200/200/200Dq1/Dq2/Dq3400/300/200
为了验证所估计的最大稳定域边界准确性，设置电压跌落深度为0.5(pu)，绘制不同故障持续时间（Fault Duration, FD）的状态轨迹，如图8所示。图中xf1和xf2分别表示FD=0.10 s和0.11 s时的故障清除点。结果显示，xf1在稳定域内，其状态轨迹收敛至平衡点xs。当故障持续时间增加到0.11 s时，故障清除点xf2位于稳定域外。此时，状态轨迹发散，系统暂态失稳。因此，所提李雅普诺夫函数集能够准确地估计最大吸引区域，并通过故障清除点的位置预判多机并联系统暂态稳定性。
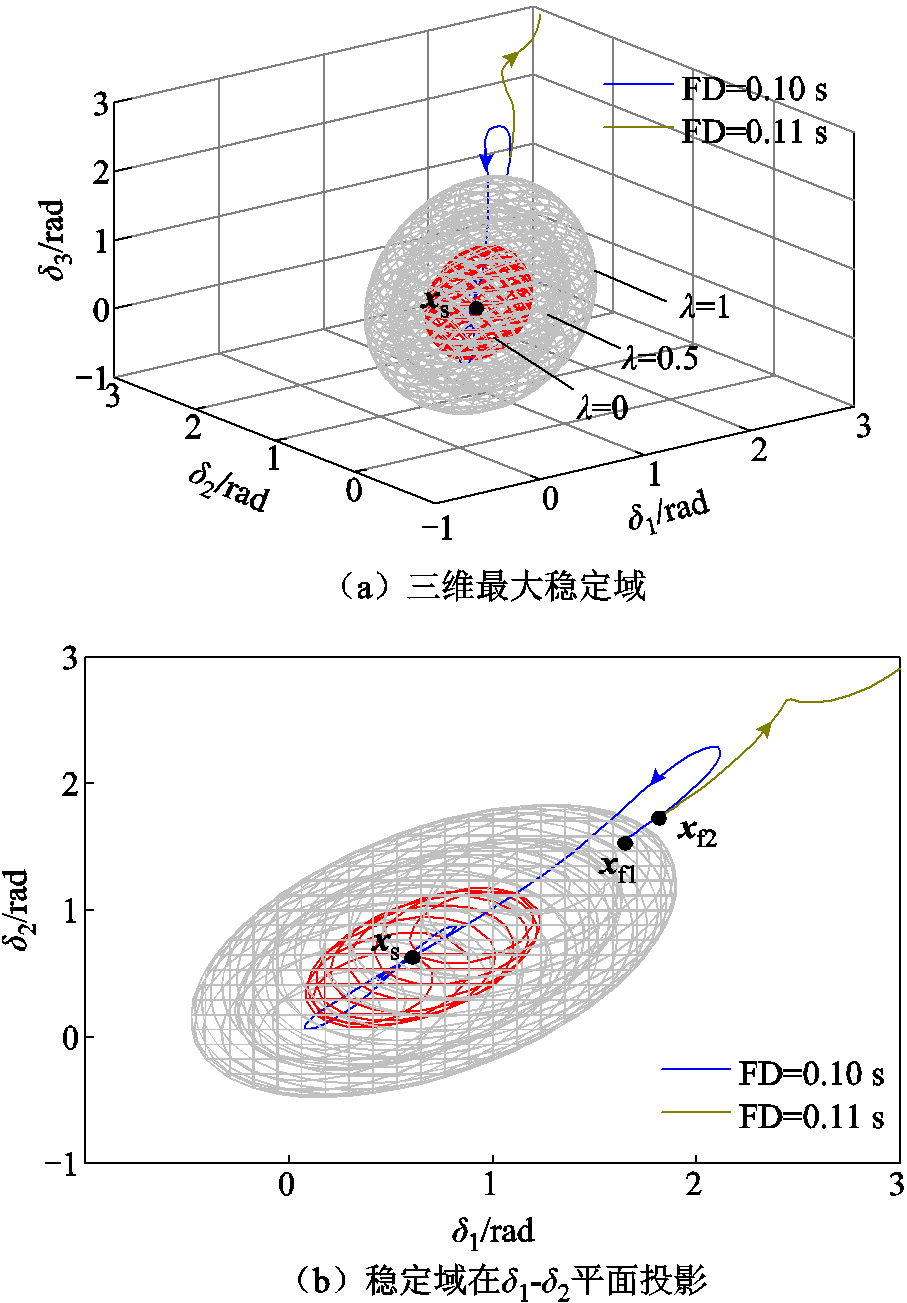
图8 最大稳定域边界验证
Fig.8 Verification of maximum stability region
三维稳定域可以直观地反映构网型多机并联系统暂态同步稳定性，故本节利用所建的李雅普诺夫函数集分析控制参数、电网参数、关键环节对稳定域的影响，结果见表2。具体分析如下。
表2 构网型多机并联系统暂态同步稳定性影响规律
Tab.2 Influencing law of transient stability of multi-paralleled GFMIs system
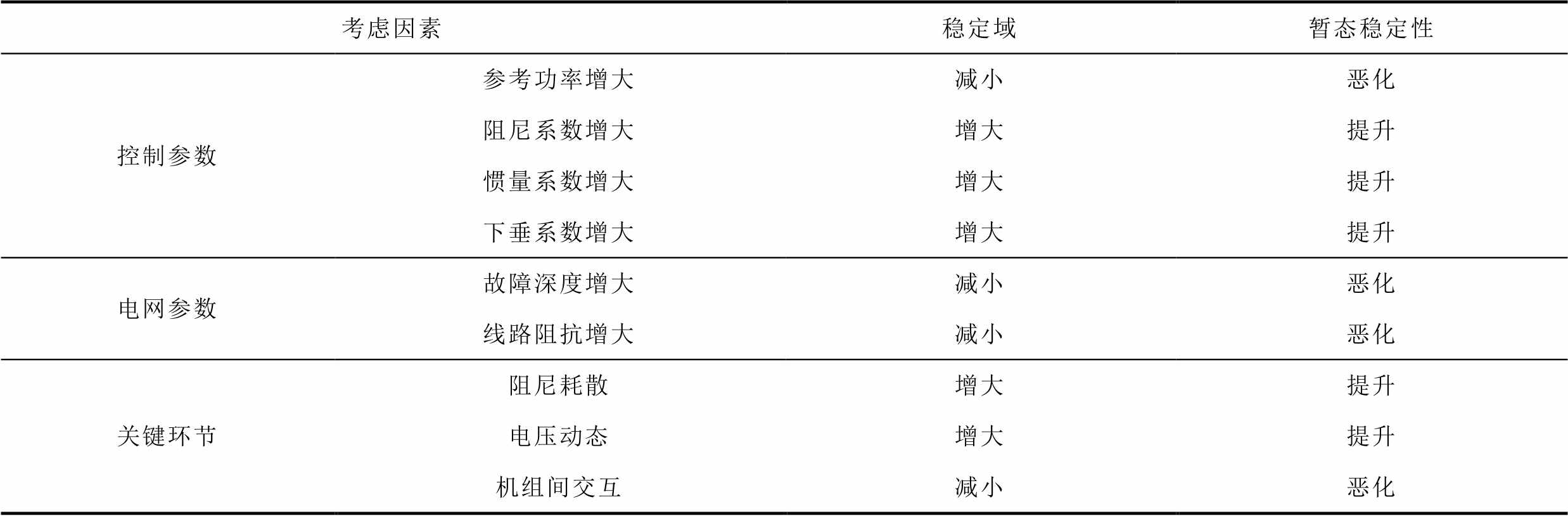
考虑因素稳定域暂态稳定性 控制参数参考功率增大减小恶化 阻尼系数增大增大提升 惯量系数增大增大提升 下垂系数增大增大提升 电网参数故障深度增大减小恶化 线路阻抗增大减小恶化 关键环节阻尼耗散增大提升 电压动态增大提升 机组间交互减小恶化
当参考功率Prefi增大时，系统的加速面积也随之增大，最大减速面积减小，最终导致暂态同步稳定性恶化。因此，构网型变流器并联系统暂态稳定域会随着有功功率参考值Prefi的增大而减小，如图9a所示。
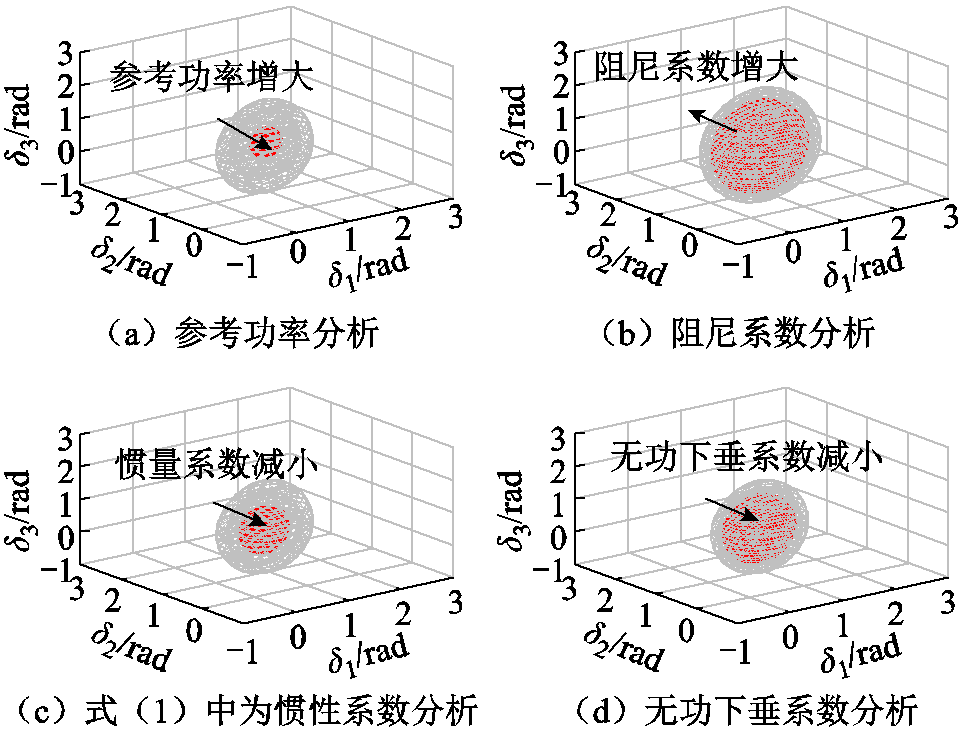
图9 控制参数对稳定域影响
Fig.9 Effect of control parameters on stability region
不同阻尼系数Dpi条件下，并联系统暂态稳定域变化趋势如图9b所示。因为系统的减速面积随Dpi增大而增加，正阻尼加快系统暂态能量消耗，所以构网型变流器并联系统的暂态稳定域也随之增大。
在不同虚拟转动惯量系数Ji下的暂态稳定域变化趋势如图9c所示。随着惯量系数Ji的减小，稳定域减小，不利于暂态同步稳定性稳定。
不同无功下垂系数Dq下的系统暂态稳定域如图9d所示。结果表明，减小Dq不利于系统的稳定。这是因为Dq的减小会使构网型变流器的输出电压Ei进一步降低，功率传输能力减弱，故系统暂态稳定域也随之减小。
电网参数对稳定域的影响如图10所示，电网故障电压跌落深度Vsag的增加会使系统稳定域减小。这是因为随着故障跌落深度增加，电网电压降低，构网型变流器输出有功功率也随之降低，导致构网型变流器直流侧与交流侧的功率存在缺额，系统暂态同步稳定性变差，稳定域减小。
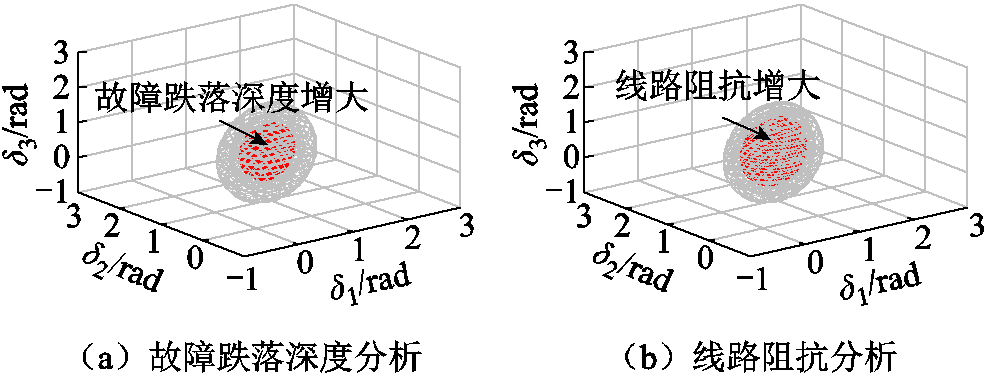
图10 电网参数对稳定域影响
Fig.10 Effect of power grid parameters on stability region
不同线路电感Lg条件下的稳定域变化如图10b所示。Lg增大，构网型变流器功率传输能力受限，系统加速面积变大，减速面积变小，从而恶化系统暂态同步稳定性，稳定域减小。
为刻画多机并联系统的暂态同步稳定性，本文构建了计及阻尼耗散、无功环电压动态、机组间暂态交互作用的李雅普诺夫函数集。本节探究阻尼耗散、电压动态、暂态交互等关键环节对构网型变流器并联系统暂态稳定性的影响。
阻尼耗散对稳定域的影响如图11所示。图11中橘色三维区域为忽略阻尼耗散时稳定域，灰色区域为真实吸引域。图中xf1和xf2分别为FD=0.10 s、FD=0.11 s时的故障清除点。可见，xf1在灰色区域内，但在橘色区域之外。这意味着不考虑阻尼耗散的稳定域预判系统是暂态失稳的，而其状态轨迹却最终收敛至稳态平衡点xs。因此，忽略阻尼耗散的稳定域造成暂态同步稳定性误判。计及阻尼耗散时，多机并联系统稳定域增大，阻尼耗散可提升系统暂态同步稳定性。这是因为阻尼做功产生“等效热能”，加快暂态过程中系统能量耗散和衰减，间接性地增大系统临界能量，从而使得稳定域增大、暂态同步稳定性提升。
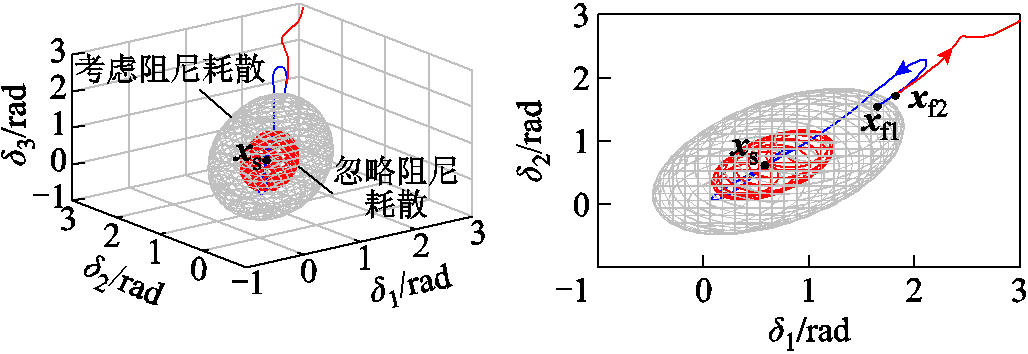
图11 阻尼耗散对稳定域影响
Fig.11 Effect of damping dissipation on stability region
电压动态对稳定域的影响如图12所示。图12中橘色三维区域为忽略电压动态的稳定域，浅灰色区域为考虑电压动态的真实吸引域。图中，xf1在灰色区域内，但在橘色区域之外。意味着不考虑电压动态的稳定域预判系统发生暂态失稳，但状态轨迹却收敛至稳态平衡点xs。因此，忽略电压动态的稳定域造成暂态同步稳定性误判。由图12可知，计及无功环电压动态，稳定域增大。在本文，是否考虑电压动态特指能量函数构造过程中是否将电压参量Ei视为独立变量。若将电压参量Ei视为独立变量，能量函数特性与积分型无功环控制的构网型变流器相同；若将电压参量Ei视为非独立变量，能量函数特性与比例型无功环相同（暂态过程可直接求得电压解析表达[8]）。因此，考虑电压动态特性等效于在比例型无功环基础上引入了电压“惯性”环节，可抑制暂态过程中构网型变流器输出电压的快速跌落，提升功率传输能力。因此，计及无功环电压动态，稳定域增大，系统暂态稳定性提升。
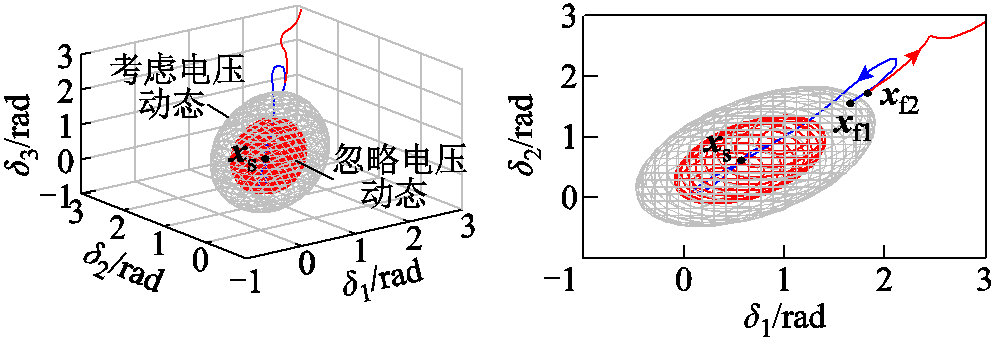
图12 电压动态对稳定域影响
Fig.12 Effect of dynamic of voltage on stability region
机组交互对稳定域的影响如图13所示。图13中浅灰色三维区域为忽略机组交互作用时的稳定域，而橘色区域为真实吸引域。图中，xf2在灰色区域内，但在橘色区域之外。意味着不考虑机组交互作用的稳定域预判系统发生暂态稳定，但状态轨迹却发散不收敛。因此，忽略机组间暂态交互作用造成暂态同步稳定性误判。此外，由图13可知，计及机组间暂态交互作用时，稳定域减小，暂态交互作用不利于多机并联系统暂态稳定性。这是因为机组间交互作用降低机组功率传输能力，暂态失稳风险增大。
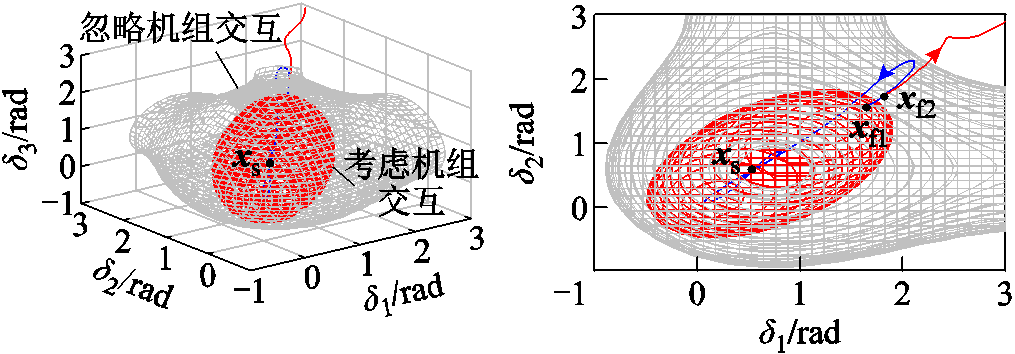
图13 机组交互对稳定域影响
Fig.13 Effect of transient interaction on stability region
综上所述，阻尼耗散、无功环电压动态以及机组间暂态交互作用对构网型变流器多机系统的暂态稳定性有着不可忽略的影响。为准确地刻画构网型变流器多机并联系统稳定域，本文提出计及阻尼耗散、无功环电压动态以及机组间暂态交互作用的李雅普诺夫函数集。与传统李雅普诺夫函数相比，本文李雅普诺夫函数集具有相对更高的准确性，可降低暂态稳定性预判的保守性。
为了验证所估计稳定域的准确性，基于硬件在环平台搭建如图1b所示的构网型变流器多机并联系统。主电路在RT-Lab OP5607实时仿真器中搭建，控制算法在DSP28335平台实现，步长为10 ms。具体实验平台如图14所示。
图14 构网型变流器并联系统硬件在环实验平台
Fig.14 Hardware-in-the-loop experiment platform of multi-paralleled GFMIs system
图15a为0.5(pu)电压骤降深度下，当故障清除时间为0.10 s时，构网型变流器多机并联系统的实验结果，系统参数见表1。此时，多机并联系统的功角未发散，暂态同步稳定性得以保持。然而，当故障持续时间增加到0.11 s时，如图15b所示，三台构网型变流器功角发散，与电网失去同步运行，发生暂态同步失稳。
实验结果与图8中的最大稳定域估计结果一致：故障持续时间为0.10 s时，故障清除点位于稳定区域内，保持暂态同步稳定性；而故障持续时间0.11 s时，故障清除点位于稳定区域外，发生同步失稳。因此，本文构造的李雅普诺夫函数集可准确估计最大稳定域，基于故障清除点是否在稳定域内预判多机并联系统故障清除后的暂态稳定性，进而指导继电保护装置动作。
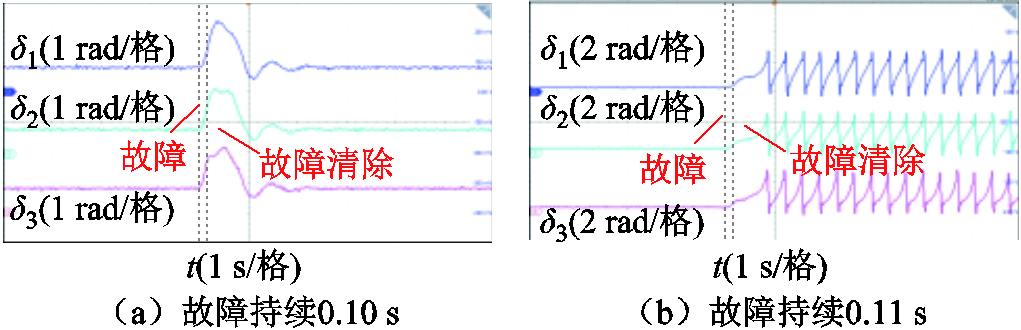
图15 最大稳定域验证
Fig.15 Verification of maximum stability region
为充分验证控制参数与电网参数对构网型变流器并联系统暂态同步稳定性的影响，基于RT-Lab平台设计七组不同工况实验，故障清除时间均为0.10 s，具体参数见表3，实验结果如图16所示。
表3 实验工况与相关参数
Tab.3 Experimental conditions and related parameters
工况参数结果 1FD=0.10 s, 其他参数见表1稳定 2FD=0.10 s, 参考功率Prefi增大，其他参数见表1失稳 3FD=0.10 s, 阻尼系数Dpi减小，其他参数见表1失稳 4FD=0.10 s, 惯量系数Jpi减小，其他参数见表1失稳 5FD=0.10 s, 无功下垂系数Dqi减小，其他参数见表1失稳 6FD=0.10 s, 故障深度Vsag增大，其他参数见表1失稳 7FD=0.10 s, 线路阻抗Lg增大，其他参数见表1失稳
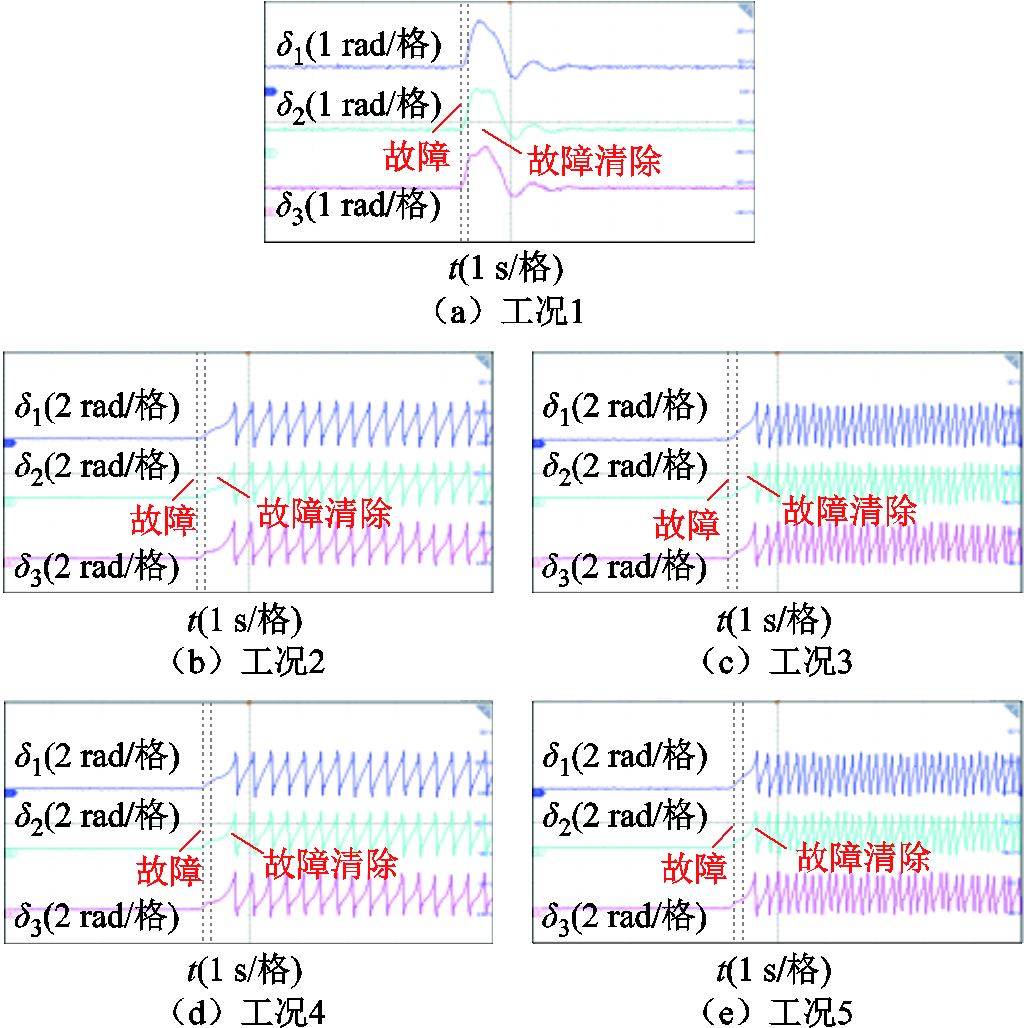
图16 参数对多机系统暂态同步稳定性影响验证
Fig.16 Verification of the parameters’ influence on transient stability
结果表明，当参考功率Prefi增大、阻尼系统Dpi减小、惯量系数Ji减小、无功下垂系数Dqi减小、故障跌落深度Vsag增大、线路阻抗Lg增大时，构网型变流器并联系统从工况1的稳定变为失稳，暂态稳定性恶化。该结果与图9、图10参数分析相一致，验证了基于稳定域定量探究多机系统暂态同步稳定性的可行性与准确性。
基于稳定域分析，系统阻尼加快暂态过程中的能量耗散和衰减，提升暂态同步稳定性。为验证稳定域分析的准确性，在图16工况1基础上，进一步减小系统阻尼系数，实验结果如图17a所示。由此可见，减小系统阻尼后，构网型变流器并联系统发生暂态同步失稳，与稳定域分析结果一致。
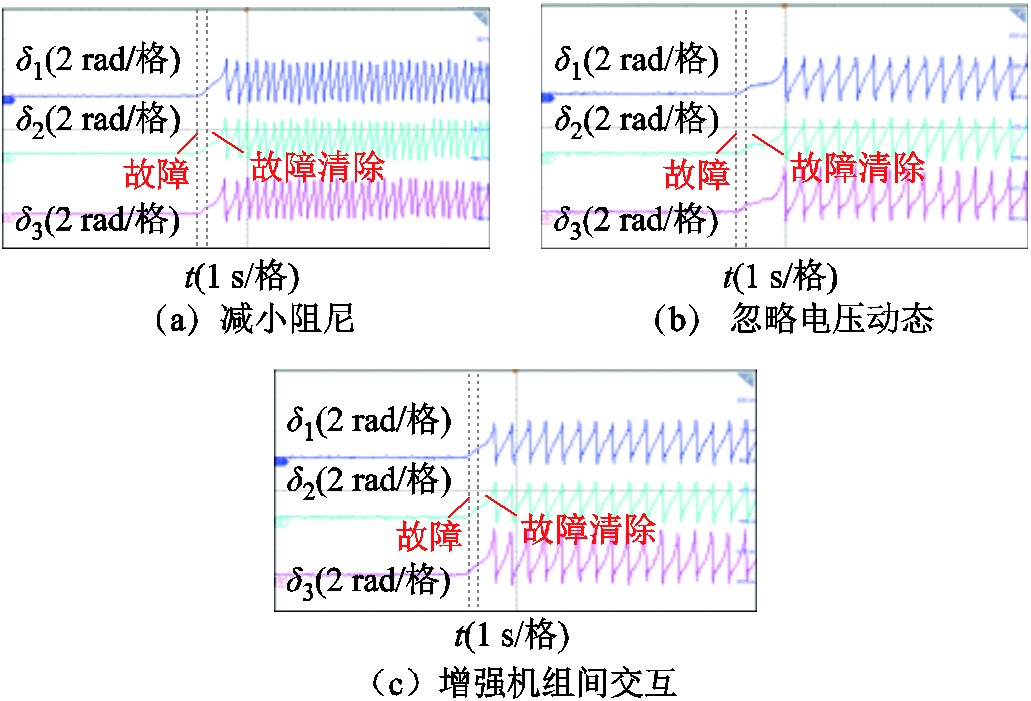
图17 关键环节对多机系统暂态同步稳定性影响验证
Fig.17 Verification of the key component’s influence on transient stability
基于稳定域分析，考虑电压动态特性等效于在比例型无功环基础上引入了电压“惯性”环节，系统暂态同步稳定性提升。为验证稳定域分析的准确性，在图16工况1基础上，将积分型无功环改为比例型无功环，间接性验证无功环电压动态影响，实验结果如图17b所示。由此可见，采用比例型无功环后，构网型变流器并联系统发生暂态同步失稳，忽略无功环电压动态特性系统稳定性恶化，与稳定域分析结果一致。
基于稳定域分析，机组间暂态交互造成系统稳定域减小、暂态同步稳定性恶化。根据式（4），机组间暂态交互作用与机组间等效阻抗成反比。因此，本实验通过增大机组1与机组2之间等效导纳B12间接验证交互作用对并联系统暂态稳定性影响，其结果如图17c所示。由此可见，减小机组间等效阻抗后，机组间交互作用增强，并联系统发生暂态同步失稳，验证稳定域分析的准确性。
针对构网型变流器多机并联系统暂态同步稳定性问题，本文建立了机组外交互与有功无功内耦合的构网型变流器多机并联系统大信号等效模型，构造了李雅普诺夫函数集定量估计多机系统最大稳定域。所得到的研究结论如下：
1）由于复杂交互作用的存在，构网型多机系统的等效模型和暂态特性比单机系统更复杂，电压动态、阻尼耗散及机组间交互对多机系统的暂态同步稳定性存在重要影响。
2）计及电压动态、阻尼耗散及机组暂态交互的李雅普诺夫函数集可以准确地估计多机并联系统最大稳定域，并通过故障清除点位置预判暂态同步稳定性。若故障清除点在稳定域内，则暂态同步稳定；若故障清除点在稳定域外，则暂态同步失稳。
3）通过比较稳定域大小可知，参考功率、故障深度及线路阻抗的增大会使稳定域减小，而阻尼系数、惯量系数及无功下垂系数的增大造成稳定域增大。电压动态与阻尼耗散可提升系统稳定裕度，而机组间暂态交互降低稳定裕度。
附 录
李雅普诺夫函数集Eλ满足拉萨尔不变性定理半负定条件，则
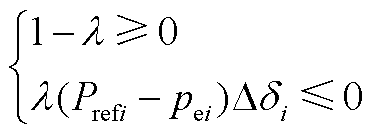（A1）
根据式（6），pei-di曲线如附图1所示，为近似正弦曲线。图中，dsi为稳定平衡点，dui为不稳定平衡点。由附图1可知，当di＜dsi时，pei＜Prefi，(Prefi-pei)∆di＜0；当 di＞dsi时，pei＞Prefi，(Prefi-pei)∆di＜0。因此，在平衡点dsi附近，始终有(Prefi-pei)∆di≤0。
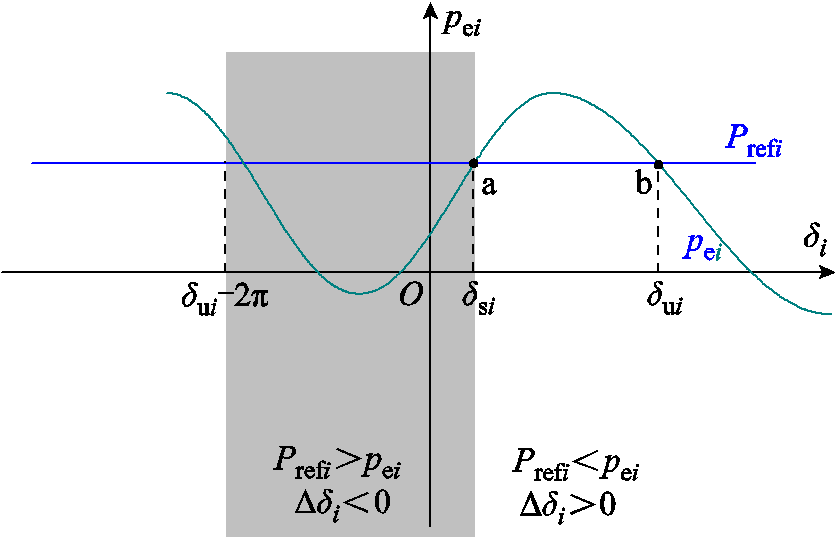
附图1 pei-di曲线
App.Fig.1 pei-dicurve
参考文献
[1] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters [J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[2] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics [J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[3] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[4] 熊小玲, 李昕悦, 周琰, 等. 基于陷波器的构网型换流器同步频率谐振抑制策略[J]. 电工技术学报, 2024, 39(12): 3827-3839.
Xiong Xiaoling, Li Xinyue, Zhou Yan, et al. Synchronous frequency resonance suppression of grid-forming converter based on Notch filter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3827-3839.
[5] Luo Cong, Chen Yandong, Xu Yuancan, et al. Two-stage transient control for VSG considering fault current limitation and transient angle stability[J]. IEEE Transactions on Industrial Electronics, 2024, 71(7): 7169-7179.
[6] 李锡林, 查晓明, 田震, 等. 频率突变影响下基于Lyapunov法的孤岛微电网暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31, 55.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Lyapunov based transient stability analysis of islanded microgrid under the influence of frequency abrupt change[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31, 55.
[7] Xiong Xiaoling, Wu Chao, Blaabjerg F. Effects of virtual resistance on transient stability of virtual synchronous generators under grid voltage sag[J]. IEEE Transactions on Industrial Electronics, 2022, 69(5): 4754-4764.
[8] Pan Donghua, Wang Xiongfei, Liu Fangcheng, et al. Transient stability of voltage-source converters with grid-forming control: a design-oriented study[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1019-1033.
[9] 李明飞, 吴在军, 全相军, 等. 计及阻尼特性的构网型并网逆变器暂态同步稳定性分析[J]. 电力系统自动化, 2023, 47(15): 198-207.
Li Mingfei, Wu Zaijun, Quan Xiangjun, et al. Transient synchronization stability analysis of grid-forming grid-connected inverter considering damping characteristics[J]. Automation of Electric Power Systems, 2023, 47(15): 198-207.
[10] 张静怡, 田震, 李锡林, 等. 考虑阻尼影响的虚拟同步发电机暂态同步稳定性量化分析[J]. 电力系统自动化, 2025, 49(7): 13-24.
Zhang Jingyi, Tian Zhen, Li Xilin, et al. Quantitative analysis of transient synchronous stability of virtual synchronous generator considering damping effect[J]. Automation of Electric Power Systems, 2025, 49(7): 13-24.
[11] Shuai Zhikang, Shen Chao, Liu Xuan, et al. Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4648-4661.
[12] Fu Xikun, Sun Jianjun, Huang Meng, et al. Large-signal stability of grid-forming and grid-following controls in voltage source converter: a comparative study[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7832-7840.
[13] Ge Pingjuan, Tu Chunming, Xiao Fan, et al. Design-oriented analysis and transient stability enhancement control for a virtual synchronous generator[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2675-2684.
[14] 魏凤廷, 张海涛, 王秀丽, 等. 计及电压动态特性的虚拟同步机暂态稳定性分析[J]. 电网技术, 2024, 48(7): 2910-2918.
Wei Fengting, Zhang Haitao, Wang Xiuli, et al. Transient stability analysis of virtual synchronous generator considering voltage dynamic characteristics[J]. Power System Technology, 2024, 48(7): 2910-2918.
[15] 黄萌, 凌扬坚, 耿华, 等. 功率同步控制的构网型变流器多机交互分析与稳定控制研究综述[J]. 高电压技术, 2023, 49(11): 4571-4583.
Huang Meng, Ling Yangjian, Geng Hua, et al. An overview on multi-VSCs interaction analysis and stability controls of grid-forming converters with powersynchronization control[J]. High Voltage Engineering, 2023, 49(11): 4571-4583.
[16] He Xiuqiang, Geng Hua. PLL synchronization stability of grid-connected multiconverter systems[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 830-842.
[17] 王继磊, 张兴. 多逆变器并联系统暂态稳定性分析及其暂态电流注入策略[J]. 高电压技术, 2025 51(1): 390-400.
Wang Jilei, Zhang Xing. Transient stability analysis and transient current injection strategy of multi-inverter parallel system[J]. High Voltage Engineering, 2025 51(1): 390-400
[18] Pal D, Panigrahi B K. Reduced-order modeling and transient synchronization stability analysis of multiple heterogeneous grid-tied inverters[J]. IEEE Transactions on Power Delivery, 2023, 38(2): 1074-1085.
[19] Li Xilin, Tian Zhen, Zha Xiaoming, et al. Nonlinear modeling and stability analysis of grid-tied paralleled-converters systems based on the proposed dual-iterative equal area criterion[J]. IEEE Transactions on Power Electronics, 2023, 38(6): 7746-7759.
[20] He Xiuqiang, Pan Sisi, Geng Hua. Transient stability of hybrid power systems dominated by different types of grid-forming devices[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 868-879.
[21] 邹赵悦, 吴超, 王勇, 等. 基于等效同步功率的孤岛并联构网变流器系统暂态稳定性分析[J]. 电力系统自动化, 2024, 48(2): 140-150.
Zou Zhaoyue, Wu Chao, Wang Yong, et al. Transient stability analysis of islanded system with parallel grid-forming converters based on equivalent synchronous power[J]. Automation of Electric Power Systems, 2024, 48(2): 140-150.
[22] Wang Jilei, Zhang Xing, Li Ming. Transient stability analysis and improvement of multiparalleled virtual synchronous generators grid-connected system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2024, 12(4): 4094-4105.
[23] Li Yujun, Lu Yiyuan, Yang Jialun, et al. Synchronization stability of multiple VSGs embedded power system with controller limits[J]. IEEE Trans-actions on Power Systems, 2025, 40(1): 834-849.
[24] Chen Lei, Tang Jingguang, Qiao Xuefeng, et al. Investigation on transient stability enhancement of multi-VSG system incorporating resistive SFCLs based on deep reinforcement learning[J]. IEEE Transactions on Industry Applications, 2024, 60(1): 1780-1793.
[25] 易相彤, 沈超, 彭也伦, 等. 基于同调等值的多变流器系统聚合降阶建模[J]. 中国电机工程学报, 2022, 42(15): 5664-5675.
Yi Xiangtong, Shen Chao, Peng Yelun, et al. Aggregation reduced-order modeling of multi-converter systems based on coherency equivalence method[J]. Proceedings of the CSEE, 2022, 42(15): 5664-5675.
[26] 李承昱, 许建中, 赵成勇, 等. 基于虚拟同步发电机控制的VSC类同调等值方法[J]. 电工技术学报, 2016, 31(13): 111-119.
Li Chengyu, Xu Jianzhong, Zhao Chengyong, et al. Coherency equivalence method for voltage source converter based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 111-119.
[27] Moon Y H, Choi B K, Roh T H. Estimating the domain of attraction for power systems via a group of damping-reflected energy functions[J]. Automatica, 2000, 36(3): 419-425.
[28] 付熙坤, 黄萌, 凌扬坚, 等. 功率耦合和电流限幅影响下构网型变流器的暂态同步稳定分析[J]. 中国电机工程学报, 2024, 44(7): 2815-2825.
Fu Xikun, Huang Meng, Ling Yangjian, et al. Transient synchronization stability analysis of grid-forming converter influenced by power-coupling and current-limiting[J]. Proceedings of the CSEE, 2024, 44(7): 2815-2825.
[29] Yorino N, Popov E, Zoka Y, et al. An application of critical trajectory method to BCU problem for transient stability studies[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4237-4244.
[30] Wang Huaiyuan, Ouyang Yucheng. Adaptive data recovery model for PMU data based on SDAE in transient stability assessment[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 2519611.
Transient Model and Stability Region Estimation for Multiple Paralleled Grid-Forming Inverter System
Abstract In China, the current renewable energy resources mainly use grid-following converters as grid-connected interfaces, which cannot provide inertia and damping support for power systems. In order to enhance the support capacity of renewable energy resources, grid-forming inverters are emerging as a promising solution as they can emulate the dynamic property of synchronous generator and provide support. However, the grid-forming inverter faces significant risks of transient synchronous instability. Current research primarily focuses on single grid-forming inverter systems, which cannot be applied to multi-machine systems due to complex interactions between converters. Quantitative transient analysis and the method of stability region estimation for multiple paralleled grid-forming inverter systems are absent.
To fill this gap, taking transient interaction and power coupling into consideration, the large-signal equivalent model of multiple grid-forming inverters system is established. Based on this model, a set of Lyapunov functions is constructed, which accounts for damping dissipation, reactive power loop dynamics, and transient interactions, enabling intuitively and accurately plotting the stability region for multi-machine system. Then, by comparing the sizes of the stability regions, the impact of control parameters and grid parameters on the stability boundaries of grid-forming multi-machine systems is quantified. Furthermore, the influence of damping dissipation, reactive power loop dynamics, and transient interactions on the transient stability margin is explored. Finally, hardware-in-the-loop experiments validate the accuracy of the estimated maximum stability region.
The following conclusions can be drawn from the analysis in this paper: (1) Due to the complex interaction, the equivalence model and transient characteristics of multi-machine system are more complex than those of single-machine system. (2) The Lyapunov function set, which takes into account voltage dynamics, damping dissipation and transient interaction, can accurately estimate the maximum stability region of multiple grid-forming inverter systems, and predict the transient synchronization stability via the location of the fault clearing point. (3) By comparing the size of the stability region, the increase of reference power, fault depth, and line impedance will reduce the stability region, and the increase of damping coefficient, inertia, and reactive droop coefficient will enlarge the stability region. The voltage dynamics and damping dissipation can increase the stability margin of the system, and the transient interaction between units can reduce the stability margin.
Keywords:Grid-forming inverter, transient synchronous stability, stability region, multi-machine system
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.242179
国家电网有限公司科技项目资助（4000-202332455A-3-2-ZN）。
收稿日期2024-12-04
改稿日期2025-01-15
罗 聪 男，1997年生，博士研究生，研究方向为新能源并网系统建模、分析与控制。
E-mail：congluo@hnu.edu.cn
陈燕东 男，1979年生，教授，博士生导师，研究方向为新能源发电系统建模与控制、微电网技术、特种电源技术。
E-mail：yandong_chen@hnu.edu.cn（通信作者）
（编辑 赫 蕾）