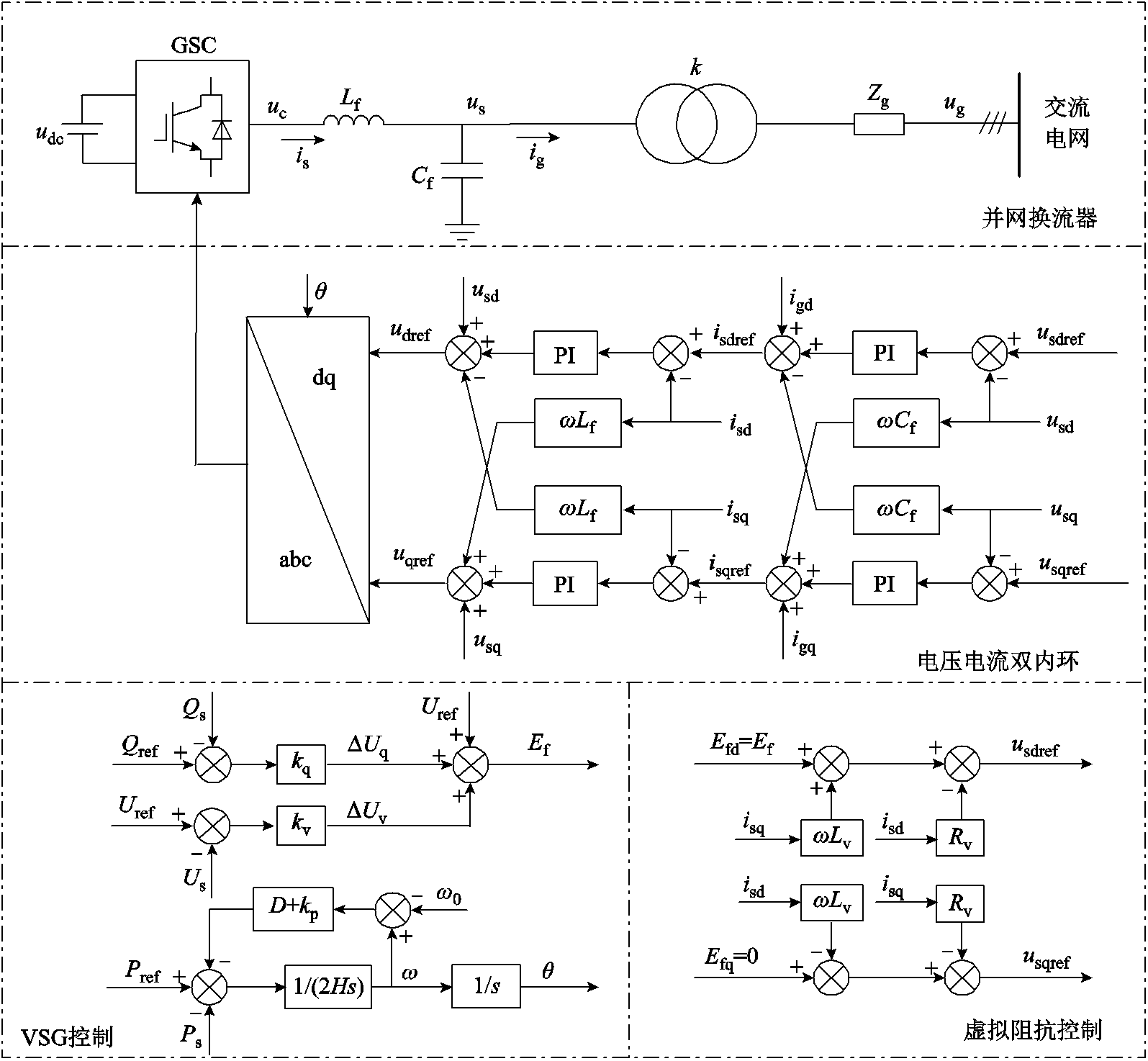
图1 基于VSG控制的并网变流器拓扑结构
Fig.1 Topology of grid-connected converter based on VSG control
摘要 虚拟同步机（VSG）控制因其主动支撑特性而受到广泛关注，但其电压支撑能力的影响因素尚不明确，兼顾电压支撑能力与短路电流限制的VSG控制策略需要进一步研究。针对上述问题，首先，基于变流器电压源特性分析稳态时各控制环节等效阻抗，并建立系统等效电路模型；其次，基于等效电路推导机端电压表达式，并进行影响因素分析；然后，兼顾限流要求与电压支撑能力，提出虚拟阻抗与电压补偿系数自适应控制策略；最后，通过Matlab/Simulink仿真平台进行验证，结果表明，通过减小虚拟阻抗、无功电压下垂系数或增大电压补偿系数，能够提高VSG电压支撑能力。该文所提出的虚拟阻抗与电压补偿系数自适应控制，能够在短路电流不越限的情况下最大限度地实现电压支撑。
关键词：虚拟同步机 等效阻抗 电压支撑 自适应
随着新能源渗透率逐年增加[1]，具有“双高”特性的新型电力系统无功电压问题突出[2]，系统故障时，如何有效地实现电压支撑已成为当前研究的热点。传统基于跟网型（Grid-Following, GFL）控制的变流器由于其固有的无功调压能力有限，在接入大量分布式能源后，往往导致系统的整体电压支撑能力下降[3]。相比之下，构网型（Grid-Forming, GFM）变流器通过模拟同步发电机的行为，具备显著的电压源特性与主动支撑能力。因此，亟须深入研究构网型变流器的电压支撑特性，以应对新型电力系统中不断增长的无功电压挑战。
构网型控制策略包括下垂控制、匹配控制和虚拟同步机（Virtual Synchronous Generator, VSG）控制等[4]。其中，下垂控制通过功率下垂曲线实现调压调频，响应速度快，但不具备阻尼惯量；匹配控制将直流电容特性与同步机特性类比，通过吸收释放直流电容能量实现调频，通过无功电压下垂特性实现调压；VSG控制通过模拟同步发电机运行特性实现调压调频，具备主动支撑系统频率和电压的功能，而且可以有效地提高新能源机组的惯量水平[5]，是目前常见的构网型控制策略[6-8]。
现阶段，有一些文献针对VSG主动支撑功能展开了研究。文献[9]分析了惯量响应与一次调频的功能及物理意义，明确了二者在频率响应过程中的功能定位；文献[10]提出一种基于VSG的自适应惯性频率控制策略，提高了频率动态响应能力；文献[11]分析VSG控制惯量支撑机理，并通过等效惯性常数量化VSG惯量支撑能力；文献[12]计及转子稳定性整定有功频率下垂系数，提出变下垂系数的VSG控制策略，提升了系统的频率稳定性。当前关于VSG主动支撑功能的研究主要针对频率支撑和惯量支撑的相关机理及控制策略改进，对于VSG电压支撑的研究相对较少。
对于单机系统稳态电压支撑的研究主要在无功控制策略[13]。文献[14]在故障期间闭锁无功调节器，提高无功输出能力；文献[15]基于同步机三阶模型改善无功电压控制，提高了机组无功电压支撑能力；文献[16]对VSG控制的功率环进行改进，根据功角整定电压参考值，改善了故障期间无功功率的特性；文献[17]采用无功优先控制，通过注入动态无功电流为系统提供电压支撑。基于电力电子变流器的新型电力系统灵活性高、可控性强，通过控制变流器输出无功功率可以实现电压支撑。但关于VSG电压支撑的研究集中于控制策略改进，并未考虑控制参数对VSG电压支撑能力的影响。
VSG控制提升系统电压支撑的关键在于改变了变流器外特性。传统跟网型控制的外特性表现为受控电流源，故障时电压支撑能力差，容易发生机组脱网事故，不利于系统的安全稳定运行[18]。基于VSG控制的构网型变流器外特性表现为受控电压源[19]，能够主动支撑系统电压，但由于故障时内电势几乎恒定，将产生很大的短路电流[20]。
构网型变流器的限流策略可分为两类：①改变变流器外特性，故障期间将构网型控制切换为基于锁相环同步的跟网型控制[21-23]或通过限流器使电流环达到饱和[24-25]，均使变流器外特性由电压源特性变为电流源特性；②基于虚拟阻抗限流，此类方法不改变变流器外特性，通过增大系统等效阻抗实现限流[26-28]。当前在短路电流抑制方面进行了诸多有意义的研究，但短路电流与电压支撑是相互影响的，兼顾短路电流与电压支撑能力的控制策略鲜有文献说明。
针对上述问题，本文将VSG控制系统中各控制环节转换为等效阻抗，基于等效阻抗展开对VSG电压支撑问题的研究。首先，介绍基于VSG控制的构网型变流器系统拓扑结构；其次，建立VSG控制并网变流器系统等效电路，并推导内电势与机端电压之间的等效阻抗；然后，基于等效阻抗分析VSG电压支撑影响因素，并兼顾短路电流限制提出改进的VSG控制策略；最后，基于Matlab/Simulink仿真平台验证本文理论分析的正确性，以及所提控制策略的有效性。
变流器功率外环控制采用VSG控制生成虚拟电压幅值和相位[29]；虚拟电压经过虚拟阻抗后生成内环控制的参考电压，虚拟阻抗用来模拟同步发电机的定子电阻和同步电抗；变流器内环采用电压电流双环控制，经过电压电流双环控制生成电压参考值。本文中的变流器采用平均值模型，故参考电压无需经过脉冲宽度调制，可直接作为驱动电压控制变流器。基于VSG控制的并网变流器拓扑结构如图1所示。图1中，udc为直流电压，Lf、Cf分别为滤波器电感、电容，Zg为线路等值阻抗，uc为变流器端电压，us为机端电压，is为变流器端电流，ig为机端电流，ug为电网电压。
图1 基于VSG控制的并网变流器拓扑结构
Fig.1 Topology of grid-connected converter based on VSG control
VSG控制通过模拟同步发电机外特性，使变流器具备调压调频功能，系统具备阻尼和惯量支撑，并且能够实现阻尼惯量可调[30]。功率外环控制环节是VSG控制的核心，包括有功频率控制和无功电压控制两部分。
根据同步发电机的转子运动方程与一次调频特性构建有功频率控制，有
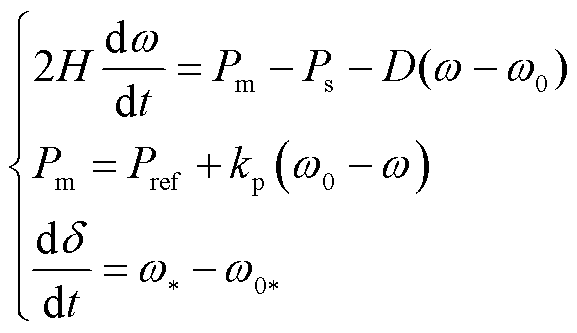（1）
式中，下标“*”表示有名值，其余均为标幺值；H为惯性时间常数；ω为系统角速度；Pm为机械功率；ω0为同步角速度；Pref为有功功率参考值；Ps为变流器机端输出有功功率；kp为有功频率下垂系数；D为阻尼系数；δ为发电机功角。
为简化控制结构，将式（1）中不平衡功率方程与一次调频特性方程合并，得到有功频率控制表达式为
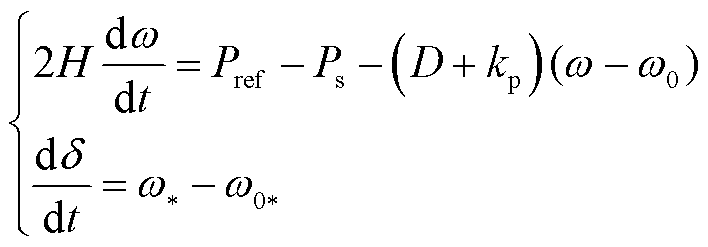（2）
无功电压控制由无功功率调节、机端电压调节、空载电动势三部分构成，其数学表达式为
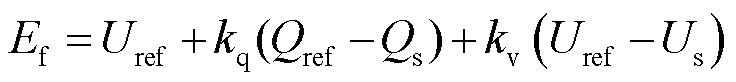（3）
式中，Ef为虚拟电压幅值；Uref为电压参考值；kq为无功电压下垂系数；kv为电压补偿系数，当kv=0时，式（3）为无功电压下垂控制；Qref为无功功率参考值；Qs为变流器机端输出无功功率。
基于VSG控制的构网型变流器通过有功频率控制和无功电压控制实现调频调压，其外特性表现为一个串联内阻、幅值相位可控的受控电压源，如图2所示。图2中，Zc为构网型变流器串联等效阻抗，IGFM为构网型控制输出电流。
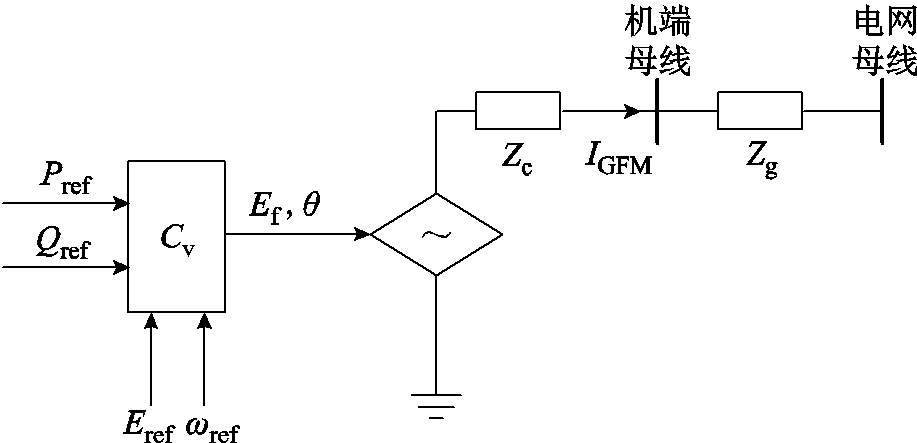
图2 构网型变流器等效外特性
Fig.2 Equivalent external characteristic of grid-forming converter
当发生三相短路故障时，构网型变流器等效电路如图3所示。此时，虚拟同步机的短路电流可根据式（4）求得[31]。
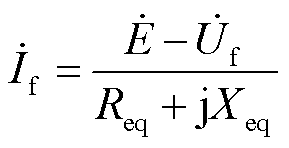（4）
式中，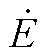
为虚拟同步机内电势矢量；
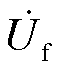为故障点电压矢量；Req和Xeq分别为内电势与故障点之间的等效电阻和等效电抗。
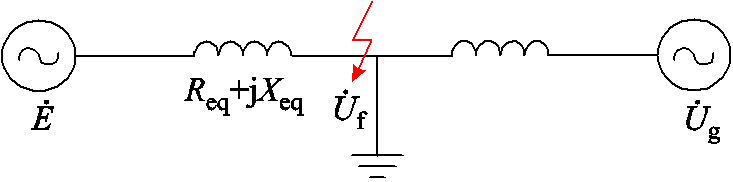
图3 故障时构网型变流器等效电路
Fig.3 Equivalent circuit of grid-forming converter under grid faults
根据构网型变流器的电压源特性，虚拟同步机的内电势几乎保持不变，当电网故障情况一定时，故障电流与等效阻抗成反比。内电势与故障点之间的等效阻抗比较小，当电网故障时，会产生很大的故障电流，且故障越严重、电压跌落程度越大，故障电流越大。
针对故障期间构网型变流器存在短路电流越限的问题，常采用虚拟阻抗控制实现限流。虚拟阻抗控制是通过在无功电压控制与电压环之间串入虚拟阻抗实现的。稳态情况下，电压环参考值满足
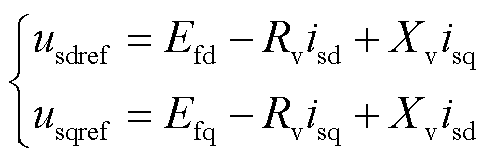（5）
式中，usdref、usqref分别为电压环d、q轴电压参考值；Efd、Efq分别为虚拟电压d、q轴分量；isd、isq分别为变流器输出电流d、q轴分量；Rv为虚拟电阻；Xv为虚拟电抗。
基于虚拟阻抗限流不改变原有的VSG控制的结构，只是增加虚拟阻抗控制中虚拟电阻或者虚拟电感值，降低电压环电压参考值，增大内电势与故障点之间的等效阻抗，从而减小故障期间的短路电流。
基于VSG控制的变流器可以等效为串联内阻、幅值相位可控的受控电压源，构建系统等效电路，将系统各控制环节采用等效阻抗替代，基于等效阻抗分析系统各控制环节输出外电压。
基于变流器电压源特性构建系统等效电路时，认为系统内各控制环节已达到稳态。参数设计时为使系统呈感性，虚拟电阻和线路电阻远小于虚拟电抗和线路电抗，后续分析中可忽略不计。根据图2基于VSG控制的并网变流器拓扑结构可知，内电势与电网之间的等效阻抗可分为以下五部分：无功电压控制环节等效阻抗Xq、虚拟阻抗Xv、电压电流双内环控制环节等效阻抗Xd、滤波电抗Xf及线路阻抗Xg（包括变压器阻抗和传输线路阻抗）。
基于VSG控制系统等效电路如图4所示。图4中滤波电抗与线路阻抗属于物理阻抗，由系统参数决定。根据1.2节分析，虚拟阻抗为串联内阻的一部分，本节将详细分析无功电压控制环节和电压电流双内环控制环节等效阻抗。
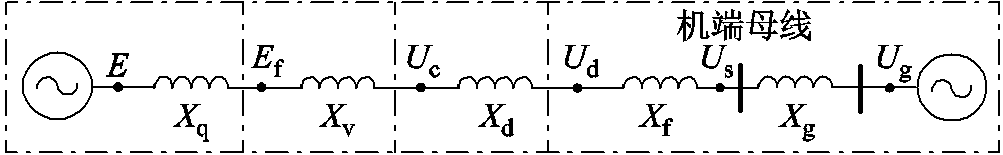
图4 基于VSG控制系统等效电路
Fig.4 Equivalent circuit of VSG control system
通过VSG功率传输公式求解无功电压控制环节的等效阻抗。以经过无功电压下垂控制后的电势Ef为参考点，VSG输出无功功率满足式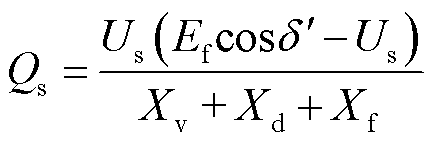（6）。
（6）
式中，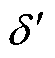
为虚拟电压Ef与并网点电压Ug之间的功角。
当虚拟电压Ef与并网点电压Ug之间的功角很小时，可认为cosδ′=1，此时式（6）可化简为
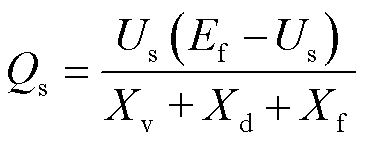（7）
根据图1中无功电压环控制结构，当kv=0时，无功电压控制环节为无功电压下垂控制，虚拟电压幅值可表示为
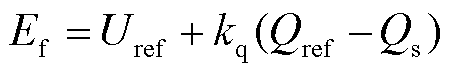（8）
将式（8）代入式（7），可得
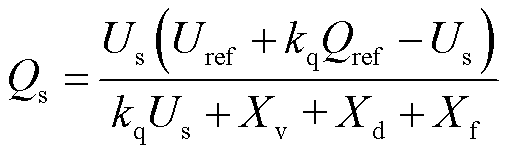（9）
将电压参考值Uref定义为变流器内电势E，由于无功参考值Qref =0，所以式（9）可改写为
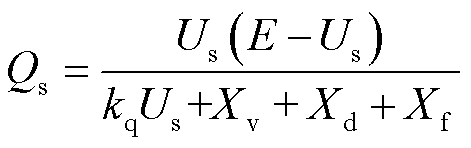（10）
式（10）与式（7）具有相似的形式，故式（10）的分母为内电势与并网点之间的等效阻抗，无功电压下垂控制的等效阻抗可表示为
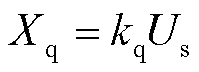（11）
当kv≠0时，无功电压控制环节与无功电压下垂控制相比，参考电压由Uref变为Uref+ΔUv，相当于在无功电压下垂控制中附加电压补偿。将式（3）代入式（7），可求得附加电压补偿后的无功功率为
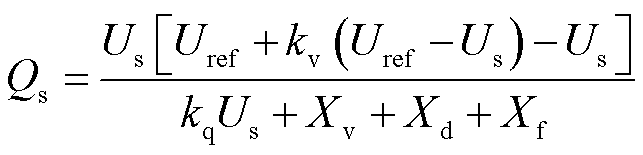（12）
此时，附加电压补偿后系统内电势为
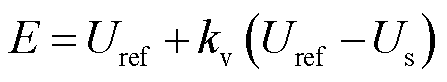（13）
无功电压控制环节的等效阻抗仍满足式（11），即Xq=kqUs。
电压电流双内环等效阻抗可根据其控制结构与电路方程进行求解。根据基尔霍夫电流定律，图1中流经滤波电容上的三相电流满足
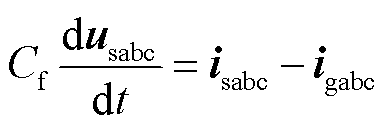（14）
式中，usabc为机端三相电压；isabc为变流器输出三相电流；igabc为机端三相电流。
对式（14）进行Park变换，可得到dq坐标系下的电流方程为
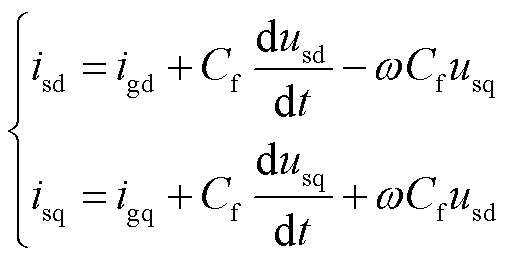（15）
对式（15）进行拉氏变换得到
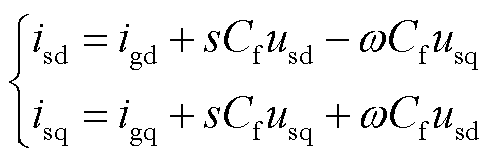（16）
采用PI调节器进行电压环控制结构设计时，电压环的控制方程可表示为
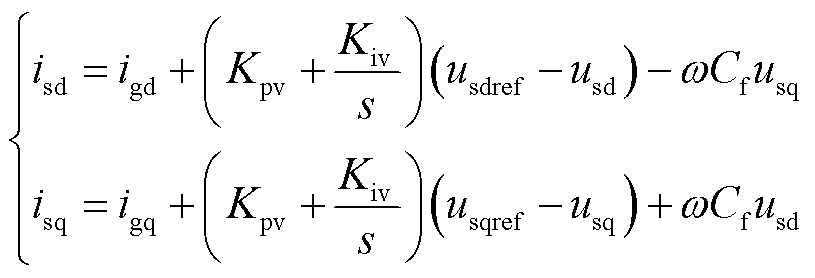（17）
式中，Kpv、Kiv分别为电压环比例、积分系数。
由于电流环响应速度远高于电压环，所以在进行电压环设计时，可将电流环等效为单位增益，即isdref=isd，isqref=isq。根据电压环电路方程式（16）与电压环控制方程式（17）可以得到电压环的解耦控制结构如图5a所示。电压环控制结构中的前馈项和dq轴交叉耦合项与电路方程中的前馈项和dq轴交叉耦合项相互抵消[32]，抵消后的电压环的解耦控制结构如图5b所示。
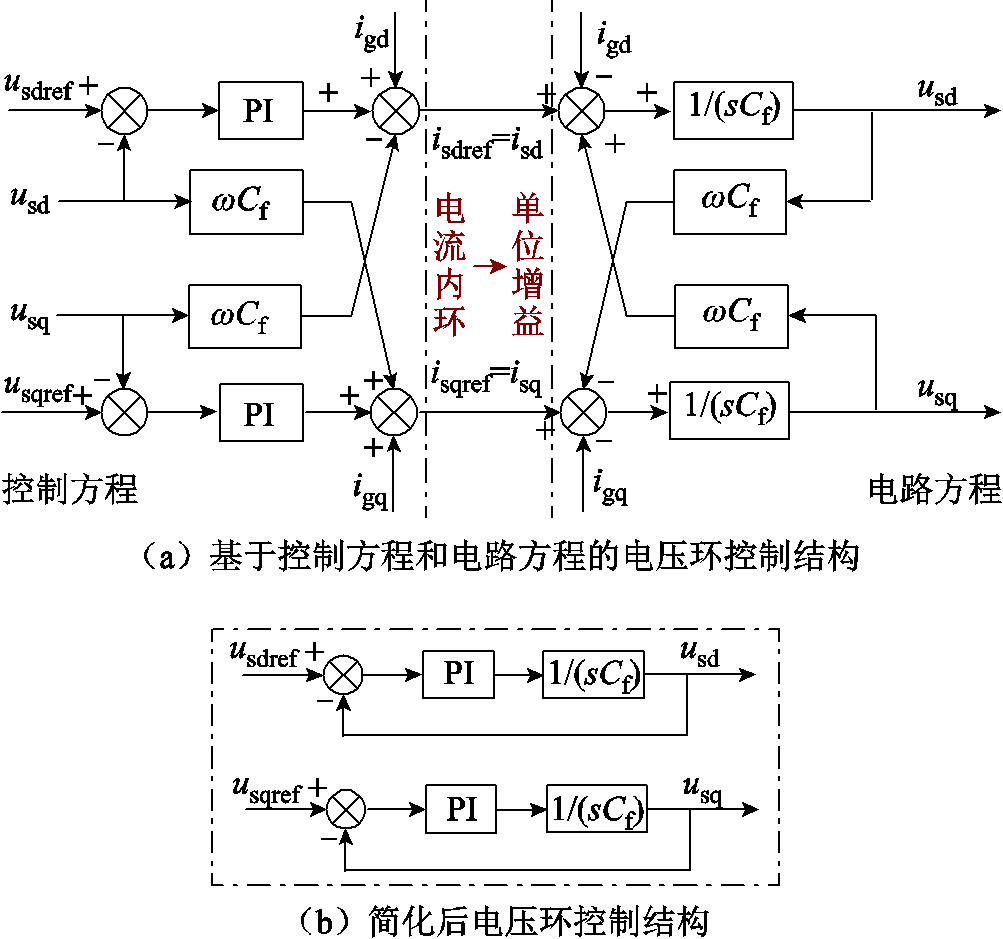
图5 电压环的解耦控制结构
Fig.5 Decoupled control structure of voltage loop
根据图1基于VSG控制的并网变流器拓扑结构，电压环参考值是经过虚拟阻抗后的电压，即图4中的Uc，滤波电容电压实际值是经过滤波阻抗后的电压，等于机端电压Us。图5b所示滤波电容电压实际值与给定值构成负反馈，通过对电压环PI参数进行合理设计，可以实现滤波电容电压实际值跟随给定值，即Uc=Us，所以图4中电压电流双环控制等效阻抗Xd与滤波电抗Xf相互抵消。
综上所述，内电势与电网之间的等效阻抗可视为只有无功电压下垂环节等效阻抗Xq、虚拟阻抗Xv和线路阻抗Xg三部分，系统的等效电路如图6所示。根据系统等效电路，可以量化机端电压与内电势和系统阻抗之间的关系，表征系统各环节输出电压。
图6 简化后基于VSG控制系统等效电路
Fig.6 Simplified equivalent circuit of VSG control system
根据第2节分析可求得系统各控制环节等效阻抗。本节根据系统等效阻抗推导机端电压表达式，基于等效阻抗模型分析虚拟阻抗、无功电压下垂系数与电压补偿系数对机端电压的影响。
根据第2节分析可知，VSG控制生成的虚拟电压与机端电压之间的等效阻抗为虚拟阻抗Xv。VSG输出无功功率可表示为
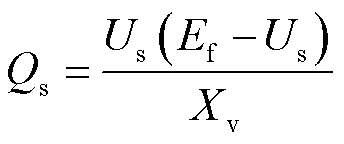（18）
将式（8）代入式（18），可得
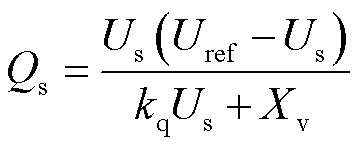（19）
当电网电压跌落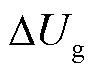
时，可根据串联分压原理计算机端电压，有
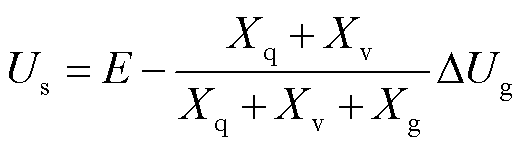（20）
将式（11）代入式（20），可得
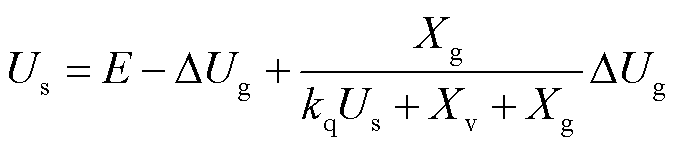（21）
对式（21）进行求导，可得
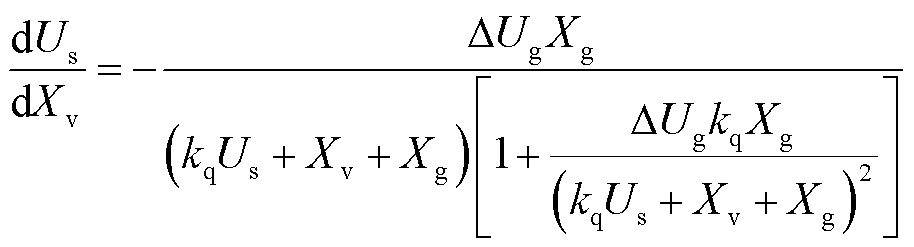（22）
根据式（22）可知，机端电压关于虚拟阻抗的导数小于0，当其他控制参数和线路参数不变、电压跌落程度一定时，减小虚拟阻抗可以增大机端电压，提高电压的支撑能力。
无功电压下垂系数对机端电压的影响仍可根据机端电压表达式进行分析，对式（21）进行求导，可得
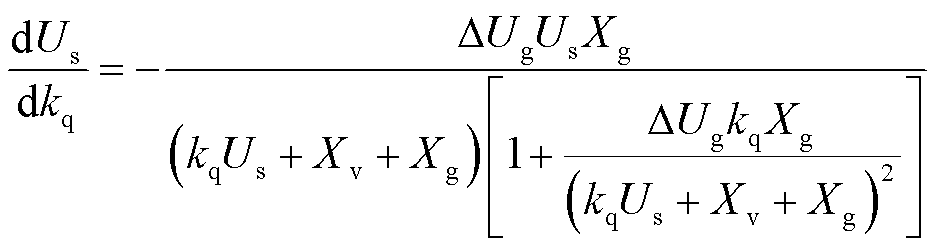（23）
根据式（23）可知，机端电压关于无功电压下垂系数的导数小于0，当其他控制参数和线路参数不变、电压跌落程度一定时，减小无功电压下垂系数可以增大机端电压，提高电压的支撑能力。
当电网电压跌落0.25(pu)时，根据式（21）绘制机端电压与虚拟阻抗、下垂系数三维曲线，如图7所示。当电网电压幅值跌落时，机端电压与虚拟阻抗和无功电压下垂系数有关，且随着虚拟阻抗与无功电压下垂系数的增大而减小。
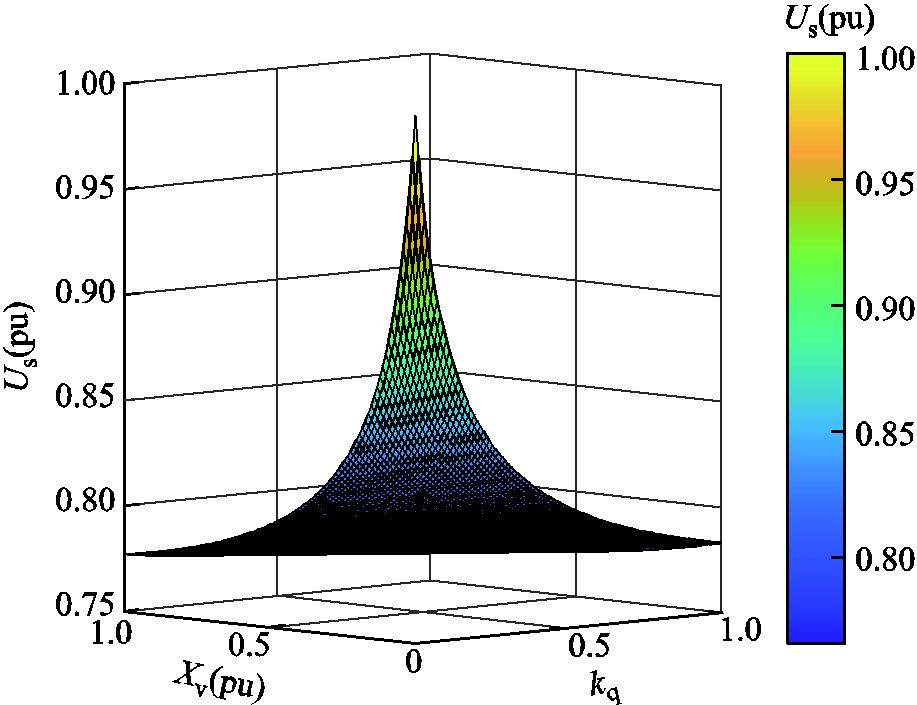
图7 机端电压与虚拟阻抗、下垂系数三维曲线
Fig.7 Three dimensional curves of terminal voltage, virtual impedance and sag coefficient
根据式（12）可得附加电压补偿后的无功功率，式（12）中kv(Uref -Us)＞0，与式（19）相比增加了VSG输出无功功率，从而提高了故障期间的电压支撑能力。附加电压补偿前后VSG输出无功功率表达式分母不变，即内电势与电网电压之间的等效阻抗未变，分子增大相当于增大内电势，由式（13）可知内电势由E=Uref变为E=Uref+kv(Uref-Us)。
将式（13）代入式（20），可求得电网电压跌落时附加电压补偿后的机端电压为
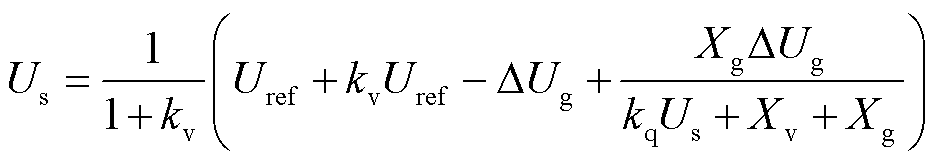（24）
对式（24）进行化简，得到
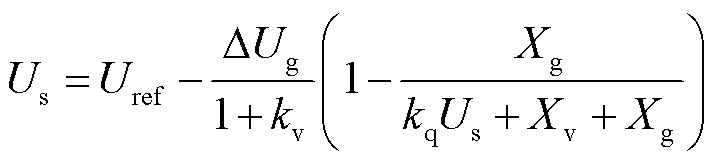（25）
对式（25）进行求导，可得
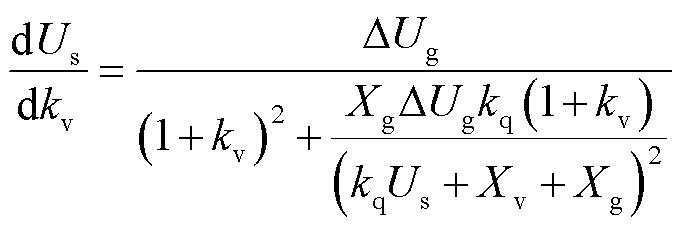（26）
根据式（26）可知，机端电压关于无功电压下垂系数的导数大于0，当其他控制参数和线路参数不变、电压跌落程度一定时，增大电压补偿系数可以增大机端电压，提高电压的支撑能力。当电压补偿系数kv=0时，式（21）与式（25）相等。
当电网电压跌落0.25(pu)时，根据式（25）绘制机端电压与电压补偿系数曲线，如图8所示。当电网电压幅值跌落时，机端电压与电压补偿系数有关，且随着电压补偿系数的增大而增大。
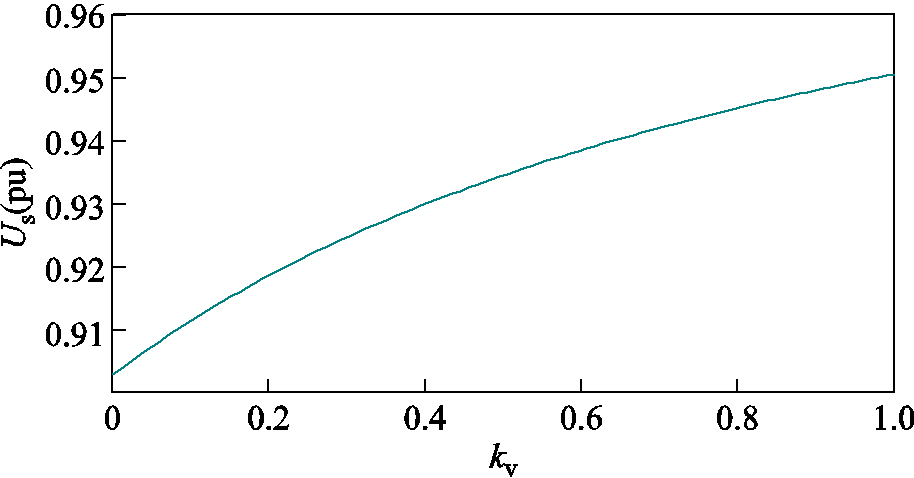
图8 机端电压与电压补偿系数曲线
Fig.8 Terminal voltage voltage compensation coefficient curve
分析表明，减小无功电压下垂系数、减小虚拟阻抗、在无功环附加电压补偿控制均可以提高电压支撑能力，为优化VSG在不同运行条件下的性能表现提供理论依据。
本节分析第3节中电压支撑的影响因素对短路电流的影响，综合考虑电压支撑能力和短路电流限制的要求，对VSG控制策略进行改进。
由第3节分析可知，减小虚拟阻抗与下垂系数，或附加电压补偿控制均可以提高机端电压支撑能力。其中减小虚拟阻抗和下垂系数会降低变流器内阻，在无功环附加电压补偿控制可以实现对内电势的控制，即实现受控电压源的幅值可控，当kv＞0时，附加电压补偿控制相当于增大构网变流器内电势。
根据1.2节分析可知，系统短路电流与等效阻抗和内电势密切相关。当传输线路中点发生三相接地短路故障时，忽略系统等效电阻，故障电流为
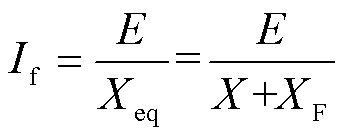（27）
式中，X为变流器内阻；XF为机端母线与故障点间的阻抗。其中，变流器内阻为无功电压控制等效阻抗与虚拟阻抗，将式（13）代入式（27），故障电流可表示为
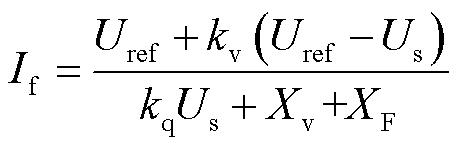（28）
根据式（28）可知，减小虚拟阻抗、减小下垂系数、附加电压补偿控制在提高电压支撑能力的同时，也给系统带来了过电流风险。
虚拟阻抗和下垂系数与故障电流呈负相关，与机端电压呈正相关；电压补偿系数与故障电流呈正相关，与机端电压呈正相关。考虑短路电流限制，附加电压补偿控制需要增大等效阻抗限制短路电流，且电压补偿系数取值变化时，需要提供不同的等效阻抗以满足短路电流限制。
GB/T 3898.1—2020定义无功调压系数kqv为无功功率变化量与电压变化量的比值[33]，如式（29）所示，取值范围为12.5～33.3。
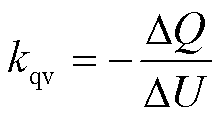（29）
本文中无功电压下垂系数kq为电压变化量与无功功率变化量的比值，如式（30）所示。kq与kqv互为倒数，所以kq应取0.03～0.08。
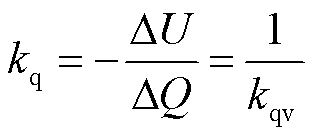（30）
参照国标要求，kq可变范围较小，当故障情况确定时，XF一定，故等效阻抗的变化主要依赖于虚拟阻抗，可根据当前电压补偿系数调整虚拟阻抗，以满足系统限流要求。
增大电压补偿系数在提高电压支撑能力的同时对系统限流能力提出了更高的要求，需要重新计算与之匹配的虚拟阻抗以达到限流要求，不匹配的虚拟阻抗会导致系统电流超过最大短路电流限制。因此，本文提出虚拟阻抗与电压补偿系数自适应控制策略，虚拟阻抗根据计算结果自适应配置，从而实现在不同电压补偿系数下，短路电流始终满足限流要求。
系统具有良好的电压支撑能力关键在于能够充分利用短路电流，发出及时且适量的无功功率。兼顾电压支撑能力与短路电流限制，在设计虚拟阻抗时要满足两个条件：①确保故障电流始终不大于最大短路电流，防止电流越限；②故障期间充分利用短路电流，以达到最佳电压支撑效果。
综合上述条件，可根据当前内电势与最大短路电流求得满足要求的虚拟阻抗，虚拟阻抗表达式为
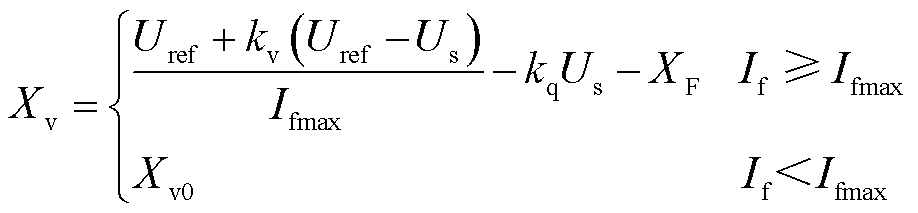（31）
式中，Ifmax为最大短路电流，取Ifmax=3IN。此时，在故障期间短路电流被限制在3倍额定电流，短路电流既不越限又能得到充分利用。
当电网电压跌落程度较小时，故障电流不会超过变流器允许的最大电流，此时为保证VSG的电压支撑能力，虚拟阻抗值可以保持初始设定值；当电网电压跌落程度较大或系统发生短路故障时，检测到故障电流超过变流器允许的最大电流，此时为防止电力电子器件因过电流而损坏，根据式（31）求得当前电压补偿系数下，故障电流为变流器允许上限值（3IN）时所需要的虚拟阻抗值。基于式（31）对图1所示的VSG控制结构进行改进，得到虚拟阻抗与电压补偿系数自适应控制结构如图9所示。
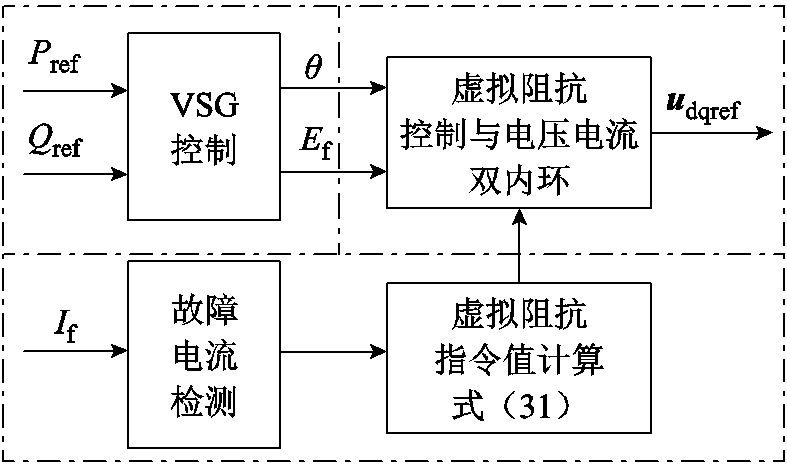
图9 虚拟阻抗与电压补偿系数自适应控制结构
Fig.9 Virtual impedance and voltage compensation coefficient adaptive control structure
在Matlab/Simulink中搭建基于VSG控制并网变流器的电磁暂态仿真模型，相关参数见表1。
设置电网电压在t=2 s时跌落至0.75(pu)，t=4 s时恢复至1(pu)，仿真结果如图10所示。当电网电压幅值下降时，虚拟阻抗控制环输出的外电压与机端测量电压近似相等，证明电压电流双环控制的等效阻抗与滤波电路等效阻抗相互抵消的结论是正确的。此外，根据表1中的参数进行仿真，图6中各环节阻抗比满足Xq:Xv:Xg=1:1:3，图10中各点电压降落按照等效阻抗比例下降，ΔEf:ΔUs(ΔUc):ΔUg= 1:1:3，证明控制环节等效阻抗、虚拟阻抗与物理阻抗在稳态时是可以等效的，基于VSG控制变流器各环节等效阻抗分析VSG输出功率与机端电压支撑效果是合理的。
表1 系统基本参数
Tab.1 Basic system parameters
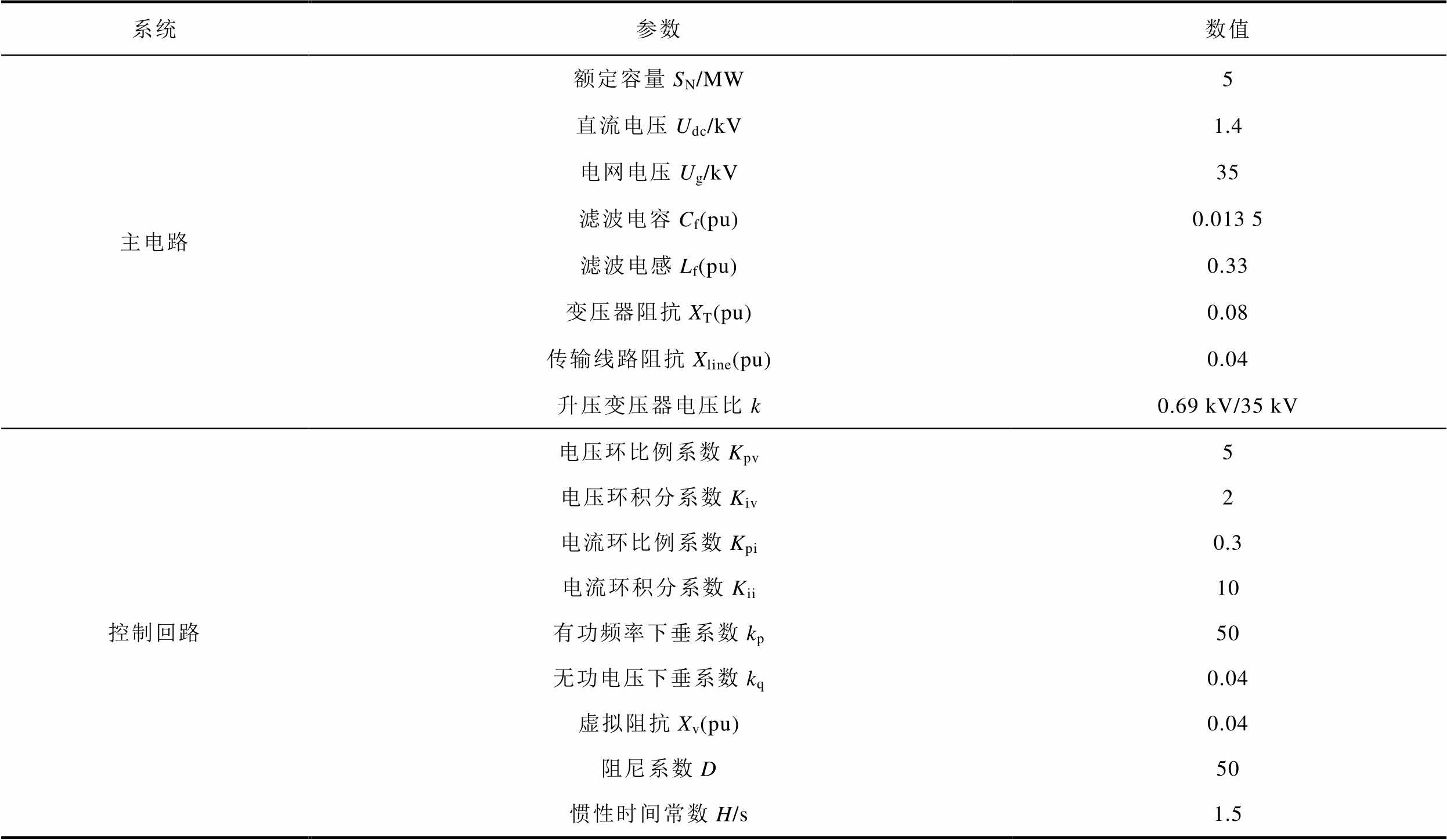
系统参数数值 主电路额定容量SN/MW5 直流电压Udc/kV1.4 电网电压Ug/kV35 滤波电容Cf(pu)0.013 5 滤波电感Lf(pu)0.33 变压器阻抗XT(pu)0.08 传输线路阻抗Xline(pu)0.04 升压变压器电压比k0.69 kV/35 kV 控制回路电压环比例系数Kpv5 电压环积分系数Kiv2 电流环比例系数Kpi0.3 电流环积分系数Kii10 有功频率下垂系数kp50 无功电压下垂系数kq0.04 虚拟阻抗Xv(pu)0.04 阻尼系数D50 惯性时间常数H/s1.5
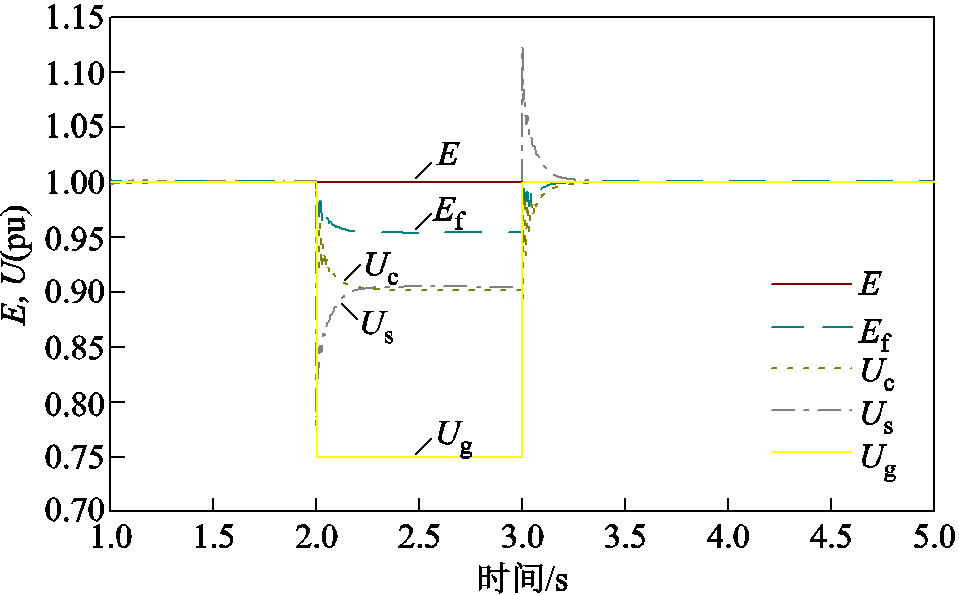
图10 电网电压跌落系统各点电压波形
Fig.10 Voltage waveforms of each point of the grid voltage drop system
系统控制参数一定，有无电压电流双内环的系统电压波形如图11所示。基于第2节分析，电压电流双内环控制的等效阻抗与滤波电抗抵消，无电压电流双内环控制，图4中电压电流双内环控制等效阻抗Xd=0，此时滤波电抗不能被抵消，机端电压表达式为
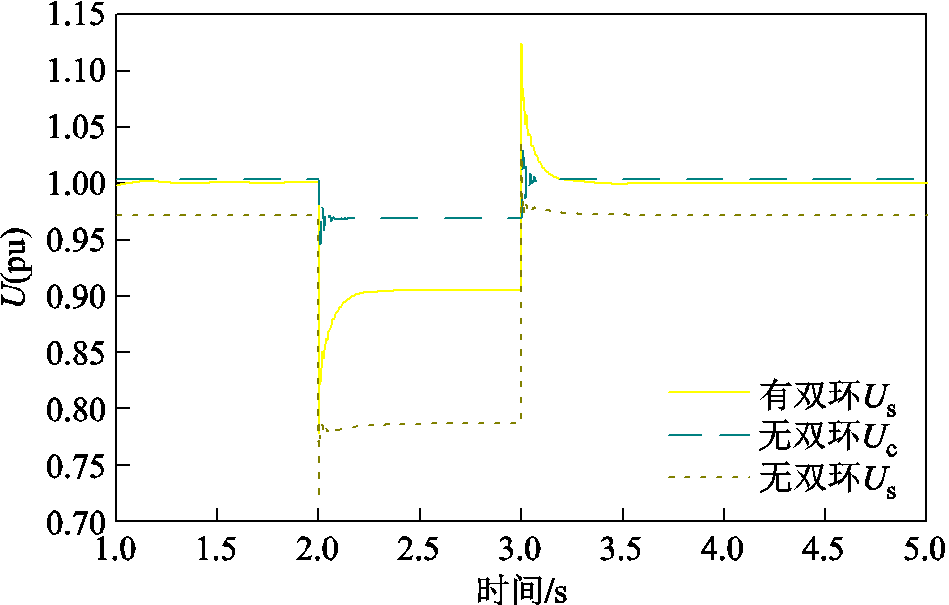
图11 有无双内环时虚拟阻抗控制输出外电压与机端电压波形
Fig.11 Waveforms of external voltage and terminal voltage under virtual impedance control with and without dual inner loops
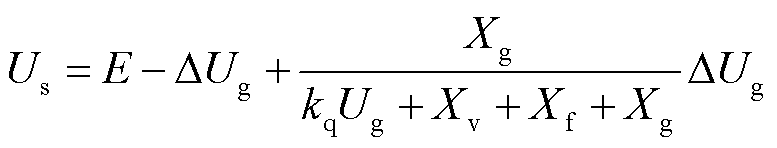（32）
式（32）与式（21）相比，第三项分母增大，机端电压降低。此外，基于VSG构网型变流器控制的电压为经过虚拟阻抗后的电压Uc，电压环控制使得机端电压Us=Uc，无内环控制使得Us≠Uc，所以稳态时机端电压不为1(pu)，如图11所示。
5.2.1 虚拟阻抗
设置电网电压在t=2 s时跌落至0.75(pu)，t=4 s时恢复至1(pu)，虚拟阻抗分别取0.1(pu)、0.2(pu)、0.3(pu)时，机端电压波形如图12所示。当电网电压跌落程度一定，系统其他参数不变时，随着虚拟阻抗值增大，故障期间机端电压值降低，电压支撑能力减弱，与3.1节理论分析一致。
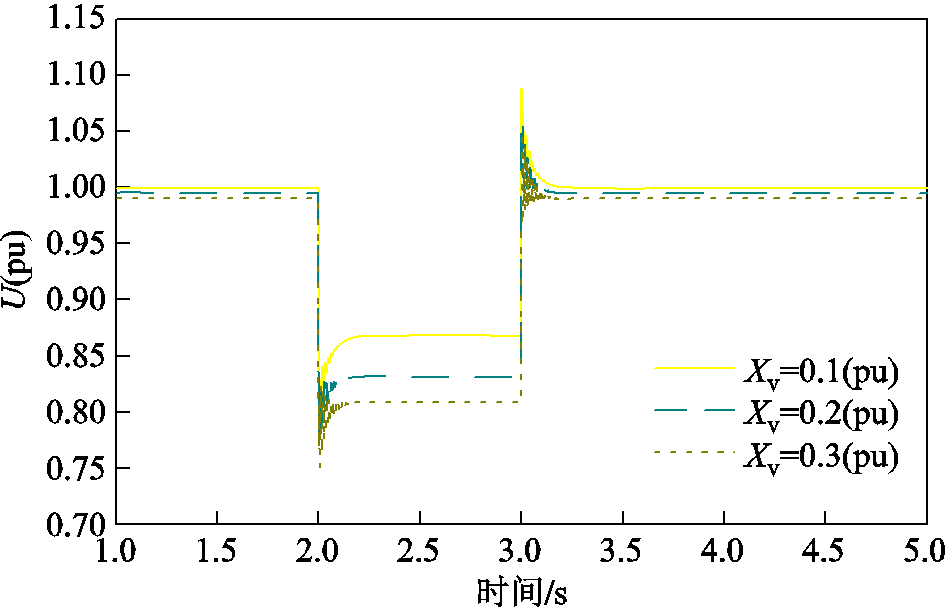
图12 不同虚拟阻抗下机端电压波形
Fig.12 Terminal voltage waveforms at different virtual impedance
5.2.2 无功电压下垂系数
无功电压环无功电压下垂系数分别取0.04、0.06、0.08时，机端电压波形如图13所示。当电网电压跌落程度一定时，无功下垂系数增大，机端电压跌落越严重，电压支撑效果越差，与3.2节理论分析一致。
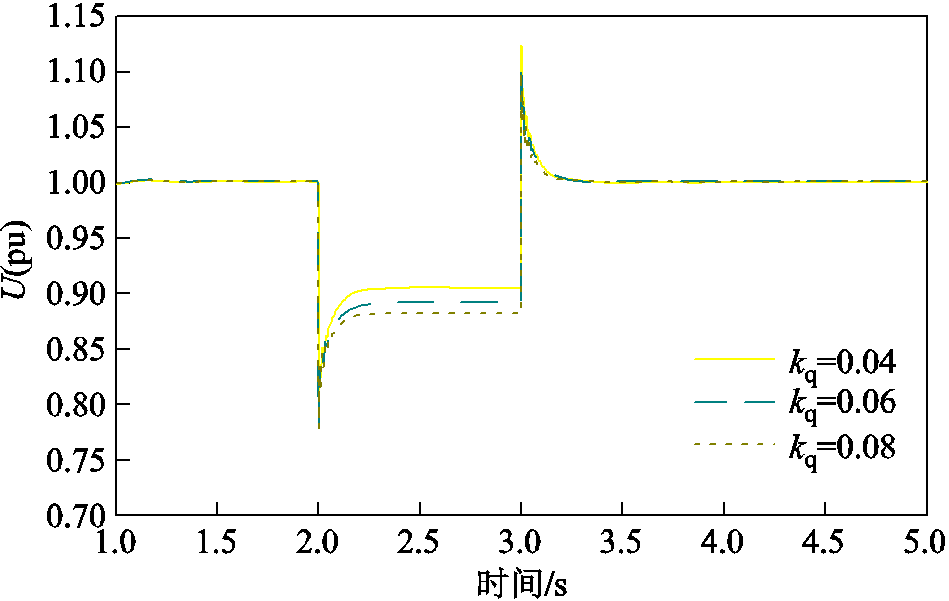
图13 不同下垂系数下机端电压波形
Fig.13 Terminal voltage waveforms at different droop coefficients
5.2.3 电压补偿系数
当电压补偿系数分别取0、0.25、0.5、0.75时，机端电压波形如图14所示。当电网电压跌落程度一定时，通过在无功电压环附加电压补偿环节可以提高故障期间电压支撑能力，且随着电压补偿系数的增大，故障期间机端电压幅值逐渐增大，但电压支撑效果逐渐减弱，与3.3节理论分析一致。
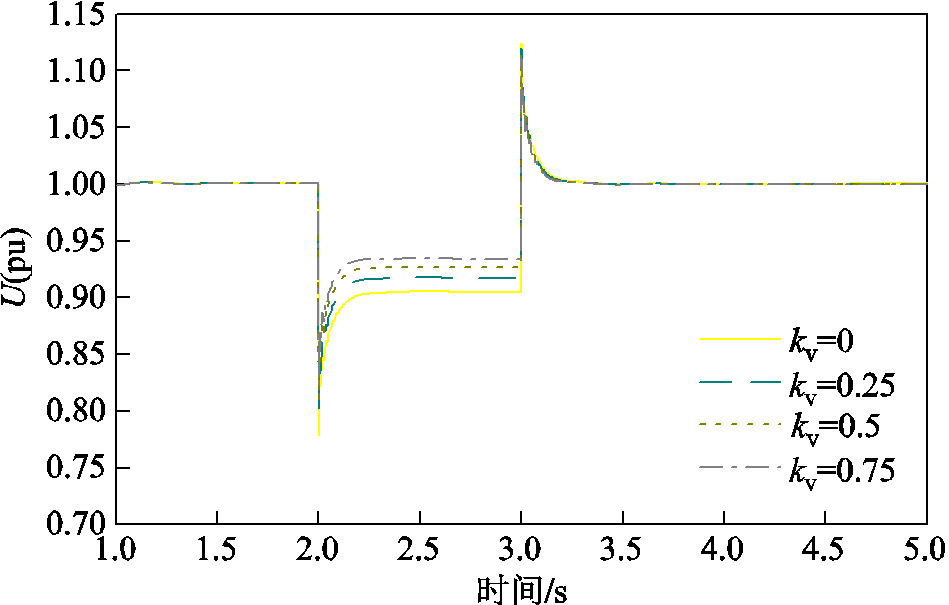
图14 不同电压补偿系数下机端电压波形
Fig.14 Terminal voltage waveforms with different voltage compensation coefficients
当电网电压跌落幅值变化时，附加电压控制可以根据电压跌落程度对机端电压进行不同程度的补偿，电压跌落幅值越大，电压补偿程度越大，电压支撑效果越好。电压跌落程度不同时附加电压补偿控制对机端电压支撑效果如图15所示。
5.3.1 常规VSG控制
设置t=2 s时在传输线路中点发生三相短路故障，0.5 s后故障切除，无功下垂系数kq分别取0.04、0.06、0.08时，常规VSG控制下机端电压电流波形如图16所示。由于无功电压下垂系数可变范围很小，考虑短路电流限制，kq对机端电压的影响很小，但随着kq增大会带来暂态电流冲击风险。故后续分析在短路电流限制下虚拟阻抗与电压补偿系数之间的关系时，kq取0.04恒定不变。
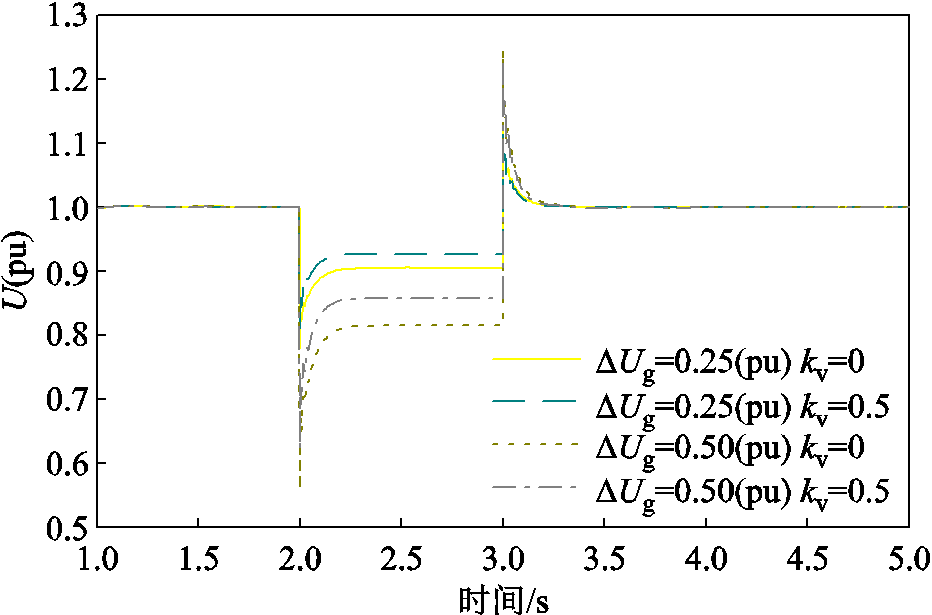
图15 不同电压跌落程度下附加电压控制补偿对机端电压影响
Fig.15 Terminal voltage waveforms with different voltage compensation coefficients
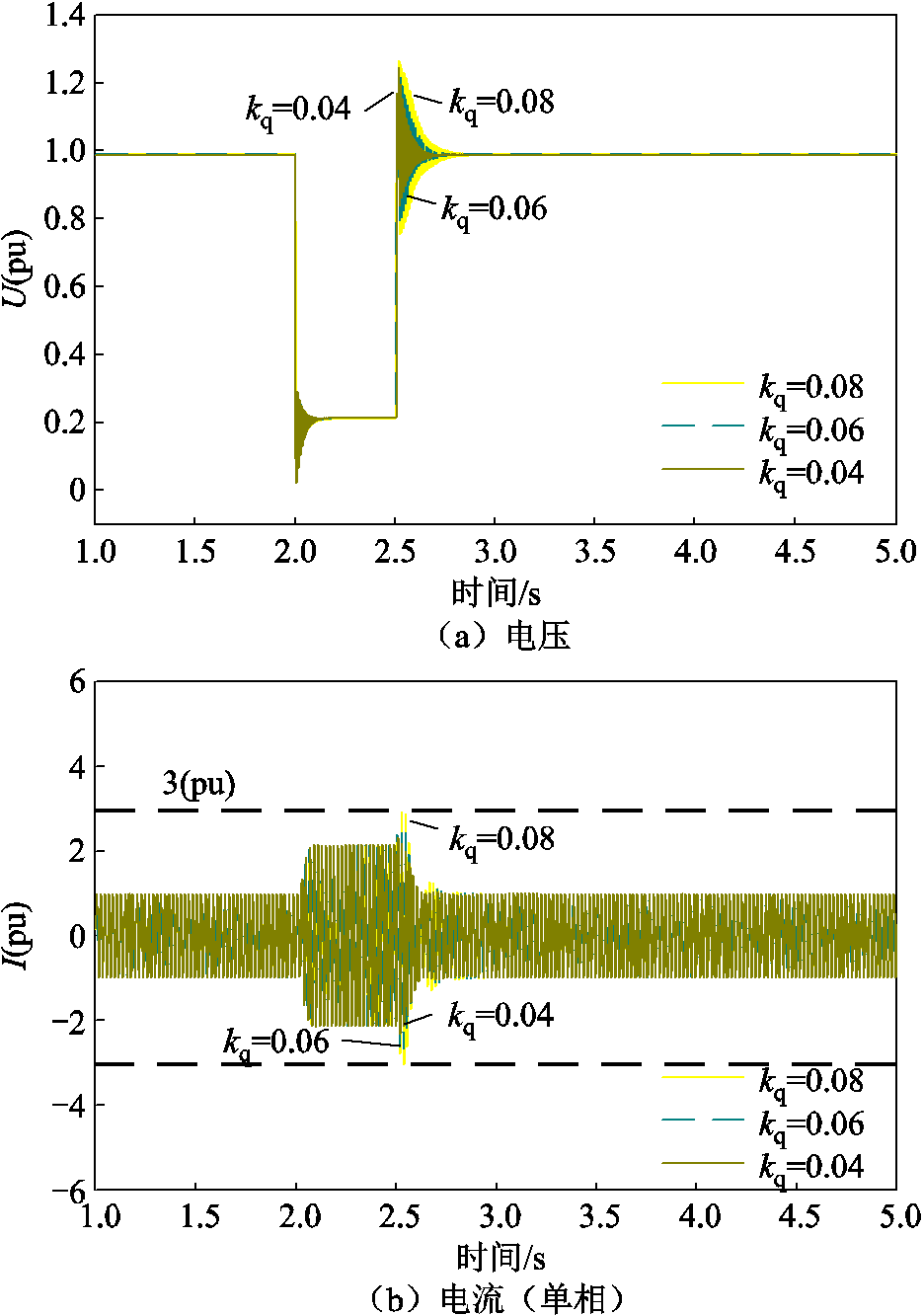
图16 三相短路故障下不同下垂系数对机端电压电流的影响
Fig.16 The influence of different droop coefficients on terminal voltage and current under three-phase short-circuit fault
三相短路故障下虚拟阻抗与电压补偿系数对机端电压电流影响如图17所示。由图17a可以看出，常规VSG控制下减小虚拟阻抗或附加电压补偿控制故障期间机端电压有所提升。由图17b可以看出，当电压补偿系数为0.5时，虚拟阻抗Xv=0.36(pu)下的电流限制在3倍额定电流以内，但当电压补偿系数减小时，短路电流不能被充分利用。
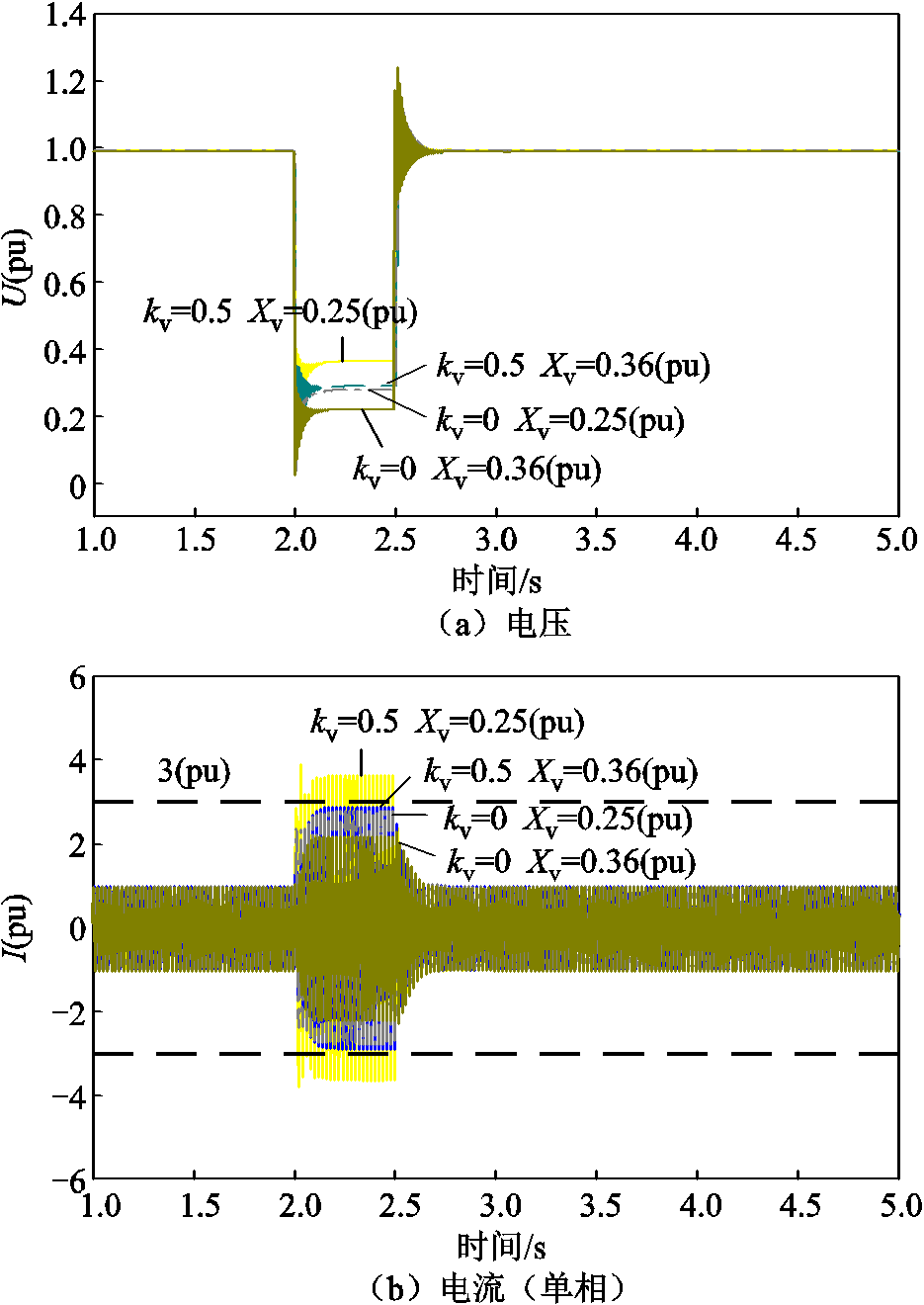
图17 三相短路故障下采用常规VSG控制的机端电压电流波形
Fig.17 Conventional VSG control controls the terminal voltage and current waveforms under three-phase short-circuit fault
考虑到短路电流限制，通过合理地配置参数，无附加电压补偿控制、采用低虚拟阻抗限流与附加电压补偿控制、采用高虚拟阻抗限流，在短路故障期间对机端电压支撑可以达到同等效果。但电压补偿系数变化时，需要根据当前电压补偿系数值重新计算虚拟阻抗并手动修改，虚拟阻抗设置不合理会使短路电流不能被充分利用或存在电流越限风险。
5.3.2 虚拟阻抗与电压补偿系数自适应控制
为使短路电流在不超过限制的前提下得到充分利用，提高电压支撑能力，采用4.2节提出的虚拟阻抗与电压补偿系数自适应控制，三相短路故障下机端电压电流和虚拟阻抗波形如图18所示。采用虚拟阻抗与电压补偿系数自适应控制，虚拟阻抗可以跟随电压补偿系数变化而变化，且能够实现在故障期间短路电流始终为系统允许的最大短路电流，在满足短路电流限制下达到最优的电压支撑效果。
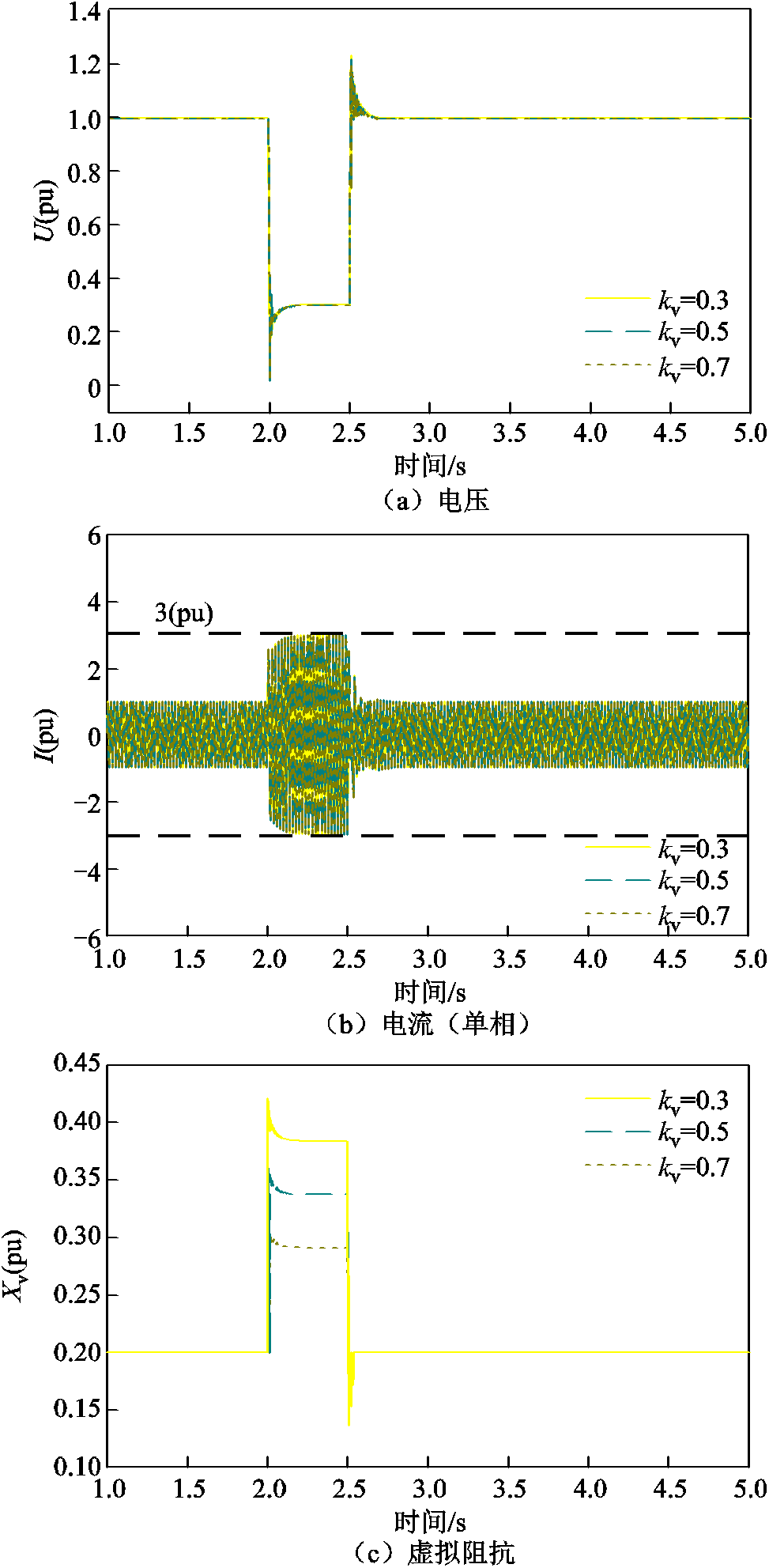
图18 三相短路故障下采用虚拟阻抗与电压补偿系数自适应控制的机端电压电流及虚拟阻抗波形
Fig.18 The virtual impedance and voltage compensation coefficient adaptively control the terminal voltage and current and virtual impedance waveforms under three-phase short-circuit fault
在考虑短路电流限制下进行多组仿真测试，结果见表2。根据表2中数据，kv＞0、kv=0或kv＜0均可以实现虚拟阻抗自适应控制，电压支撑效果达到最佳。
表2 不同kv仿真结果
Tab.2 Different kv simulation results
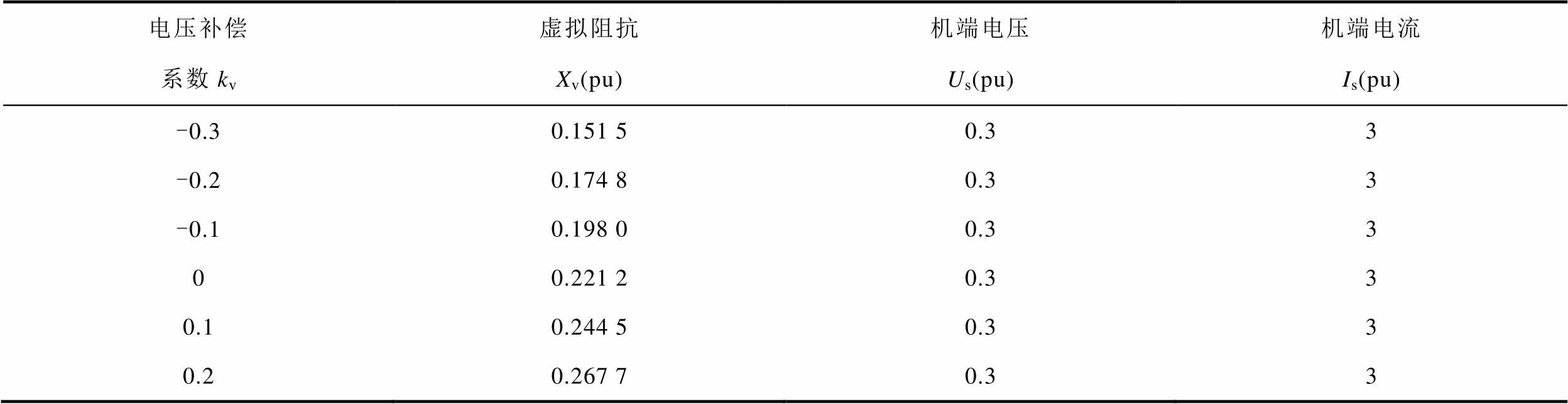
电压补偿系数kv虚拟阻抗Xv(pu)机端电压Us(pu)机端电流Is(pu) -0.30.151 50.33 -0.20.174 80.33 -0.10.198 00.33 00.221 20.33 0.10.244 50.33 0.20.267 70.33
本文基于VSG控制的构网型变流器电压源特性，给出了直观表现VSG电压支撑的研究方法，并依据此方法分析了VSG电压支撑的影响因素。在此基础上，综合考虑电压支撑能力与限流要求提出了改进的VSG控制策略。本文主要研究结论如下：
1）提出基于等效阻抗分析VSG电压支撑的研究方法。基于构网型变流器的电压源特性，通过推导各控制环节的等效阻抗，量化机端电压与内电势和系统阻抗之间的关系。
2）VSG电压支撑能力与虚拟阻抗、无功电压下垂系数、电压补偿系数有关。减小无功电压下垂系数、减小虚拟阻抗、在无功环附加电压补偿控制均可以提高电压支撑能力。
3）VSG电压支撑能力与短路电流限制是相互影响的。本文提出的虚拟阻抗与电压补偿系数自适应控制，可以充分利用短路电流，在短路电流不超过限制的前提下，最大限度地提升VSG的电压支撑能力。
参考文献
[1] 张智刚, 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报, 2022, 42(8): 2806-2819.
Zhang Zhigang, Kang Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2819.
[2] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics [J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[3] 高洁, 王彤, 赵伟, 等. 提升电力系统安全稳定水平的风电光伏场站主动支撑技术发展及展望综述[J]. 新型电力系统, 2024(2): 201-222.
Gao Jie, Wang Tong, Zhao Wei, et al. Review on the development and prospect of active support technologies for wind power and photovoltaic stations to improve the security and stability level of power system[J]. New Type Power Systems, 2024(2): 201-222.
[4] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3595.
Xu Jieyi, Liu Wei, Liu Shu, et al. Current state and development trends of power system converter grid-forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3595.
[5] 张宸宇, 杨赟, 袁晓冬, 等. 考虑阻尼和惯性的虚拟同步机建模方法研究[J]. 电力工程技术, 2018, 37(5): 45-49.
Zhang Chenyu, Yang Yun, Yuan Xiaodong, et al. Modeling method of virtual synchronous machine considering damping and inertia[J]. Electric Power Engineering Technology, 2018, 37(5): 45-49.
[6] 潘子迅, 杨晓峰, 赵锐, 等. 不平衡电网下虚拟同步机的多模式协调策略[J]. 电工技术学报, 2023, 38(16): 4274-4285.
Pan Zixun, Yang Xiaofeng, Zhao Rui, et al. Multi-mode coordination control of virtual synchronous generator under unbalanced power grid[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4274-4285.
[7] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance [J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[8] 胡石阳, 刘国荣.基于虚拟同步机的新能源并网智能控制研究[J]. 电气技术, 2022, 23(10): 10-17.
Hu Shiyang, Liu Guorong. Research on intelligent control of new energy grid connection based on virtual synchronous[J]. Electrical Engineering, 2022, 23(10): 10-17.
[9] 秦晓辉, 苏丽宁, 迟永宁, 等. 大电网中虚拟同步发电机惯量支撑与一次调频功能定位辨析[J]. 电力系统自动化, 2018, 42(9): 36-43.
Qin Xiaohui, Su Lining, Chi Yongning, et al. Functional orientation discrimination of inertia support and primary frequency regulation of virtual synchronous generator in large power grid[J]. Automation of Electric Power Systems, 2018, 42(9): 36-43.
[10] 李美依, 黄文焘, 邰能灵, 等. 频率扰动下虚拟同步电机控制型分布式电源自适应惯性控制策略[J]. 电网技术, 2020, 44(4): 1525-1533.
Li Meiyi, Huang Wentao, Tai Nengling, et al. Adaptive inertial control strategy for inverter interfaced distributed generator based on virtual synchronous generator under frequency disturbances[J]. Power System Technology, 2020, 44(4): 1525-1533.
[11] 韩平平, 陈鹏飞, 丁明, 等. VSG控制下直驱风机惯量支撑能力定量分析[J]. 电网技术, 2025, 49(2): 501-510.
Han Pingping, Chen Pengfei, Ding Ming, et al. Quantitative analysis of inertia support capacity of direct drive fan under VSG control[J]. Power Grid Technology, 2025, 49(2): 501-510.
[12] 闻章, 姚良忠, 程帆, 等. 考虑转子稳定性约束的直驱风机虚拟同步发电机构网频率支撑控制[J/OL].电网技术, 2024: 1-10[2024-10-20]. https://doi.org/ 10.13335/j.1000-3673.pst.2024.0116.
Wen Zhang, Yao Liangzhong, Cheng Fan, et al. Network frequency support control of virtual synchronous generator for direct drive fan considering rotor stability constraints[J/OL]. Power Grid Technology,2024: 1-10[2024-10-20]. https://doi.org/10.13335/j. 1000-3673.pst.2024.0116.
[13] 王渝红, 宋雨妍, 廖建权, 等. 风电电压主动支撑技术现状与发展趋势[J]. 电网技术, 2023, 47(8): 3193-3205.
Wang Yuhong, Song Yuyan, Liao Jianquan, et al. Review and development trends of DFIG-based wind power voltage active support technology[J]. Power System Technology, 2023, 47(8): 3193-3205.
[14] 尚磊, 胡家兵, 袁小明, 等. 电网对称故障下虚拟同步发电机建模与改进控制[J]. 中国电机工程学报, 2017, 37(2): 403-412.
Shang Lei, Hu Jiabing, Yuan Xiaoming, et al. Modeling and improved control of virtual synchronous generators under symmetrical faults of grid[J]. Proceedings of the CSEE, 2017, 37(2): 403-412.
[15] 王雪梅, 王艺博, 刘雨桐, 等. 基于虚拟电抗的主动支撑型新能源机组低电压穿越控制方法[J]. 电网技术, 2022, 46(11): 4435-4444.
Wang Xuemei, Wang Yibo, Liu Yutong, et al. Low voltage ride-through control of actively-supported new energy unit based on virtual reactance[J]. Power System Technology, 2022, 46(11): 4435-4444.
[16] 张余余, 赵晋斌, 李芬, 等. 基于功角动态补偿的VSG故障穿越方法研究[J]. 电网技术, 2021, 45(9): 3667-3673.
Zhang Yuyu, Zhao Jinbin, Li Fen, et al. VSG fault crossing method based on dynamic compensation of power angle[J]. Power System Technology, 2021, 45(9): 3667-3673.
[17] 符杨, 陈禹瑾, 季亮, 等. 考虑功率解耦的构网型逆变器的低电压穿越控制策略[J]. 电力系统保护与控制, 2024, 52(15): 1-13.
Fu Yang, Chen Yujin, Ji Liang, et al. Low voltage ride-through control strategy of a grid-forming inverter considering power decoupling[J]. Power System Protection and Control, 2024, 52(15): 1-13.
[18] 张兴, 战祥对, 吴孟泽, 等. 高渗透率新能源发电并网变流器跟网/构网混合模式控制综述[J]. 电力系统自动化, 2024, 48(21): 1-15.
Zhang Xing, Zhan Xiangdui, Wu Mengze, et al. Review on grid-following/grid-forming hybrid mode control for grid-connected converter in high penetration rate of renewable energy generation[J]. Automation of Electric Power Systems, 2024, 48(21): 1-15.
[19] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[20] 杨铭, 曹武, 赵剑锋, 等. 受控电压/电流源型变流器混合多机暂态电压支撑策略[J]. 电工技术学报, 2023, 38(19): 5207-5223, 5240.
Yang Ming, Cao Wu, Zhao Jianfeng, et al. Transient voltage support strategy for hybrid multi-converter of controlled voltage/current source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5207-5223, 5240.
[21] Shuai Zhikang, Huang Wen, Shen Chao, et al. Characteristics and restraining method of fast transient inrush fault currents in synchronverters[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7487-7497.
[22] Lin Xinchun, Zheng Yun, Liang Zhigang, et al. The suppression of voltage overshoot and oscillation during the fast recovery process from load short-circuit fault for three-phase stand-alone inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 858-871.
[23] Oureilidis K O, Demoulias C S. A fault clearing method in converter-dominated microgrids with conventional protection means[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4628-4640.
[24] 姜卫同, 胡鹏飞, 尹瑞, 等. 基于虚拟同步机的变流器暂态稳定分析及混合同步控制策略[J]. 电力系统自动化, 2021, 45(22): 124-133.
Jiang Weitong, Hu Pengfei, Yin Rui, et al. Transient stability analysis and hybrid synchronization control strategy of converter based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2021, 45(22): 124-133.
[25] Paquette A D, Divan D M. Virtual impedance current limiting for inverters in microgrids with synchronous generators[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1630-1638.
[26] Liu Chang, Cai Xu, Li Rui, et al. Optimal short-circuit current control of the grid-forming converter during grid fault condition[J]. IET Renewable Power Generation, 2021, 15(10): 2185-2194.
[27] Zhang Yu, Zhang Chen, Yang Renxin, et al. Current-constrained power-angle characterization method for transient stability analysis of grid-forming voltage source converters[J]. IEEE Transactions on Energy Conversion, 2023, 38(2): 1338-1349.
[28] 彭放, 高厚磊, 郭一飞, 等. 构网逆变电源故障穿越控制策略及其对保护影响的研究综述[J]. 电网技术, 2024, 48(9): 3673-3685.
Peng Fang, Gao Houlei, Guo Yifei, et al. A review of fault ride-through control strategies for grid-connected inverters and their impact on protection[J]. Power System Technology, 2024, 48(9): 3673-3685.
[29] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters [J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[30] 温春雪, 黄耀智, 胡长斌, 等. 虚拟同步发电机接口变换器并联运行虚拟阻抗自适应控制[J]. 电工技术学报, 2020, 35(增刊2): 494-502.
Wen Chunxue, Huang Yaozhi, Hu Changbin, et al. Adaptive control of virtual impedance in parallel operation of virtual synchronous generator interface converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 494-502.
[31] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14): 3676-3687.
Ge Pingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter considering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3676-3687.
[32] 刘辉, 于思奇, 孙大卫, 等. 构网型变流器控制技术及原理综述[J]. 中国电机工程学报, 2025, 45(1): 277-297.
Liu Hui, Yu Siqi, Sun Dawei, et al. Review on control technology and principle of grid-type converter[J]. Proceedings of the CSEE, 2025, 45(1): 277-297.
[33] 国家市场监督管理总局, 国家标准化管理委员会. 虚拟同步机第1部分：总则: GB/T 38983.1—2020 [S]. 北京: 中国标准出版社, 2020.
Research on the Analysis of Virtual Synchronous Generator Voltage Support Influence Factors and Improvement Control Strategies Based on Equivalent Impedance
Abstract Under the impetus of "dual carbon" targets, new energy sources are increasingly integrated into the power grid through power electronic converters, leading to a gradual decline in the proportion of synchronous machines. To enhance the stability of "highly renewable and highly flexible" systems, the flexible controllability of converters can be leveraged by employing grid-forming control to provide reliable voltage and frequency support to the system. Virtual synchronous generator (VSG) control emulates the operating characteristics of synchronous generators to achieve voltage and frequency regulation, providing active frequency and voltage support capabilities while effectively increasing the inertia level of new energy units. VSG control has garnered significant attention due to its active support features; however, the factors influencing its voltage support capability are not yet fully understood, necessitating further research on VSG control strategies that balance voltage support with short-circuit current limitations.
To address these issues, this paper first analyzes the equivalent impedance of each control stage of grid-forming converters based on VSG control during steady-state operation and establishes an equivalent circuit model of the system. Secondly, based on the system's equivalent circuit, the expression for terminal voltage is derived, quantifying the relationship between terminal voltage, internal electromotive force, and system impedance, and analyzing the factors affecting the voltage support capability of VSG. Subsequently, improvements to VSG control are made considering both current limitation requirements and voltage support capability, proposing adaptive control strategies for virtual impedance and voltage compensation coefficients. Finally, the accuracy of the theoretical analysis and the effectiveness of the proposed strategy are verified using the Matlab/Simulink electromagnetic simulation platform.
The analysis results show that reducing virtual impedance, reactive power voltage droop coefficient, or increasing the voltage compensation coefficient can enhance the voltage support capability of VSG. However, decreasing virtual impedance and reactive power voltage droop coefficient reduces the system's equivalent impedance, while increasing the voltage compensation coefficient increases the system's internal electromotive force, thus imposing higher demands on the system's current-limiting capacity. By adopting the proposed adaptive control strategy for virtual impedance and voltage compensation coefficients, virtual impedance can be self-adaptively configured according to the system state, ensuring voltage support capability under the premise of meeting current-limiting requirements.
Through theoretical analysis and simulation experiments, the following conclusions can be drawn: (1) When the grid-forming converter system based on VSG control enters a steady state, its various control stages can be represented by equivalent impedance, which characterizes the relationship between terminal voltage, internal electromotive force, and system impedance. (2) The voltage support capability of VSG is related to virtual impedance, reactive power voltage droop coefficient, and voltage compensation coefficient. Reducing the reactive power voltage droop coefficient, decreasing virtual impedance, and adding voltage compensation control to the reactive power loop can all improve voltage support capability. (3) Voltage support capability and short-circuit current limitation of VSG interact. Through adaptive control of virtual impedance and voltage compensation coefficients, short-circuit currents can be fully utilized, maximizing the voltage support capability of VSG without exceeding the short-circuit current limit.
Keywords：Virtual synchronous generator, equivalent impedance, voltage support, adaptive
中图分类号：TM341
DOI: 10.19595/j.cnki.1000-6753.tces.241876
国网冀北电力有限公司科技项目资助（520101240005）。
收稿日期2024-10-21
改稿日期2025-01-21
刘思佳 女，2000年生，硕士，研究方向为新能源电力系统分析与控制。
E-mail：1264993435@qq.com
高本锋 男，1981年生，副教授，研究方向为高压直流输电和电力系统次同步振荡。
E-mail：gaobenfeng@126.com（通信作者）
（编辑 赫 蕾）