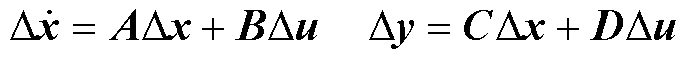 (1)
(1)
摘要 随着构网型逆变器(GFM)在电力系统中的渗透率不断提高,电力系统的动态特性发生了重大变化。基于阻抗模型的模态分析(MAI)方法通过阻抗参与因子评估电源与电网的交互作用。然而,由于MAI使用阻抗端口模型,将GFM视为一个整体,难以揭示GFM内部不同控制回路之间的复杂动力学耦合机制。该文提出一种扩展阻抗模态分析(EMAI)方法,首先将GFM动态等效分解为功率频率同步控制主导的同步动态和电压控制主导的电磁动态;其次,分别计算两类动态的等效阻抗参与因子和参与比,确定系统的主导动态;然后,提出显式参数参与因子,用于进一步识别主导动态控制回路的关键参数,为提升系统的稳定性奠定基础;最后,通过对改造的14和68母线系统进行仿真,验证所提方法的有效性。EMAI方法使得基于阻抗模型分析GFM内部各控制环节的动力学特性成为可能,无需建立全系统状态空间模型即可有效识别影响系统稳定性的关键控制回路,具有广泛的应用价值。
关键词:构网型逆变器 扩展阻抗模态分析 阻抗分解 参与因子
构网型逆变器(Grid-Forming Inverter, GFM)具备频率调节和电压控制的能力,使其可以像同步发电机一样对电网提供稳定支撑,受到工业界和学术界的广泛关注[1-2]。然而,构网型逆变器的动态特性与同步发电机不同,主要受控制策略的影响,与电网交互可能引发振荡等失稳问题。同时,GFM内部不同时间尺度控制器之间的交互耦合使稳定性分析变得更加复杂[3]。因此,亟须开发新的分析框架,便于详细分析GFM内部各控制环节的动力学特性,来解决不断变化的复杂稳定性问题[4-6]。
基于状态空间模型的模态分析(Modal Analysis based on the State-Space model, MASS)是确定影响系统关键因素的重要方法。MASS使用参与因子(Participation Factor, PF)量化每个状态变量对特定模式的贡献[7]。然而,新型电力系统中电气元件数量呈爆炸式增长,全系统状态空间建模的难度急剧增长[8]。此外,状态空间建模需要详细的系统结构拓扑和各电气元件完整的控制参数,逆变器通常只有描述电压电流端口特性的阻抗模型,具有灰盒或黑盒特性。因此,利用MASS分析含GFM的新型电力系统稳定性有待进一步研究[9]。
阻抗分析法是研究电力系统振荡稳定性的另一种常用方法,有学者提出利用阻抗模型识别振荡关键因素的方法。文献[10]引入谐振模式分析技术,确定参与度最高的母线。特征值灵敏度被用于确定影响某些特定振荡模式的网络关键元件[11-12]。为了分析系统中影响振荡的回路或母线,有学者提出由频域矩阵定义的回路/节点参与因子[13]。此外,文献[14]提出了特征值轨迹并用于评估控制器参数如何影响系统稳定性。文献[15]指出,在分析谐振模式时,不仅要考虑特征值的幅频响应,其品质因数也是影响模态分析的重要指标。然而,虽然这些研究可以确定影响系统稳定性最大的电源或母线,但却无法提供改善稳定性的建议。
为了探究系统所有电气元件之间的交互特性,全系统动态矩阵通过闭环反馈公式构建了整个系统的动态模型[16]。在此基础上,基于阻抗模型的模态分析(Modal Analysis based on Impedance model, MAI)方法利用阻抗参与因子在设备层面评估不同逆变器对振荡模式的贡献[17-18]。此外,相应的参数参与因子还能提供改善系统阻尼的建议。然而,与MASS不同的是,MAI将逆变器视为一个整体元器件,这限制了其在控制回路或状态变量层面找出系统主导动态的能力。
深入研究GFM内部影响系统稳定性的根本原因,对有针对性地提升系统稳定性具有重要意义。一种电气和机械端口双向映射的方法为分析不同原因造成的稳定性问题提供了新的视角[19]。此外,扩展阻抗模型通过引入不同端口输入和输出变量实现了GFM内部动态的分离,但是在实际应用中不同端口阻抗信息获取困难,导致该方法存在一定的局限性[20]。将不同的控制回路分解为等效电路元件,为逆变器的内部动态稳定性分析提供了可能[21-22]。然而,如何在阻抗模型中分解得到GFM内部动态的等效阻抗仍有待探索。
为了解耦分析GFM内部动态对稳定性的影响,并找出影响复杂电力系统稳定性的根本原因,本文提出了扩展阻抗模态分析(Extended Modal Analysis based on Impedance model, EMAI)方法。本文的主要贡献如下:
1)提出了基于矩阵求逆引理的GFM阻抗分解方法,将GFM的动态分为由功率频率同步环(Power Frequency synchronization Loop, PFL)主导的同步动态(Synchronous Dynamics, SD)和由电压控制环(Voltage Control Loop, VCL)主导的电磁动态(Electromagnetic Dynamics, ED)。详细的动态分类有助于深入探讨不同时间尺度控制器之间复杂的交互特性。
2)提出了表征GFM内部动态的等效阻抗参与因子和参与比(Participation Ratio, PR)指标,评估SD和ED对不同失稳模式的贡献,从而实现对稳定性关键影响因素的溯源追踪。为了精准定位相应控制回路中的关键控制参数,本文进一步提出显式参数参与因子,并将其作为优化控制参数和增强系统阻尼的指标。
电力系统状态空间模型在平衡点处线性化之后可以表示为
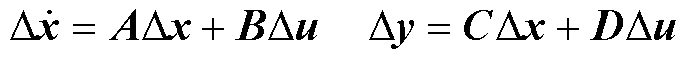 (1)
(1)
式中, 、
、 和
和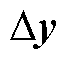 分别为状态向量、输入向量和输出向量;A、B、C和D分别为状态矩阵、输入矩阵、输出矩阵和前馈矩阵。
分别为状态向量、输入向量和输出向量;A、B、C和D分别为状态矩阵、输入矩阵、输出矩阵和前馈矩阵。
通过坐标变换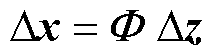 ,对状态矩阵A进行对角化可得对角状态矩阵
,对状态矩阵A进行对角化可得对角状态矩阵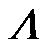 为
为
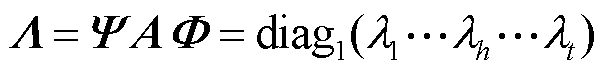 (2)
(2)
式中,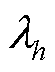 为矩阵A第h个特征值;
为矩阵A第h个特征值;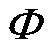 为右特征矩阵,
为右特征矩阵,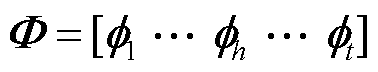 ;
; 为左特征矩阵,
为左特征矩阵,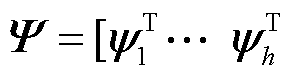
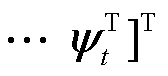 ,其中
,其中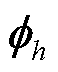 和
和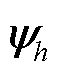 分别为
分别为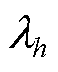 的右特征向量和左特征向量,并满足
的右特征向量和左特征向量,并满足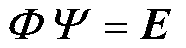 ,E为单位矩阵;diag1( )表示由标量生成对角矩阵;t为系统状态变量的维数。
,E为单位矩阵;diag1( )表示由标量生成对角矩阵;t为系统状态变量的维数。
特征值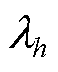 对矩阵A的第k行和第j列元素akj的灵敏度[7]为
对矩阵A的第k行和第j列元素akj的灵敏度[7]为
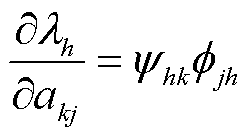 (3)
(3)
式中,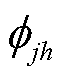 和
和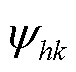 分别为右特征向量
分别为右特征向量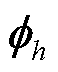 的第j个元素和左特征向量
的第j个元素和左特征向量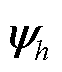 的第k个元素。
的第k个元素。
系统参与矩阵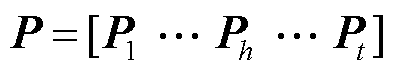 ,其中
,其中
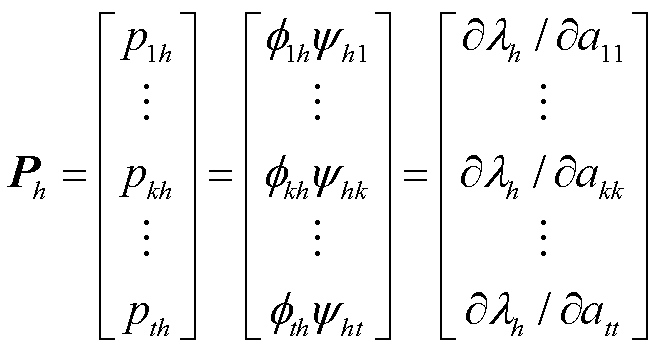 (4)
(4)
式中,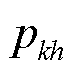 为第h个模式中第k个状态变量的相对参与程度,等于
为第h个模式中第k个状态变量的相对参与程度,等于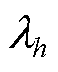 对矩阵A的第k个对角元素akk的灵敏度。
对矩阵A的第k个对角元素akk的灵敏度。
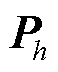 被用于定位影响系统动态的关键状态变量。然而,MASS需要系统完整的控制细节,这在很大程度上受限于逆变器和网络模型的黑盒和灰盒特性。此外,MASS在大规模电力系统中具有维数灾和可扩展性弱的问题,进一步削弱了实用性。
被用于定位影响系统动态的关键状态变量。然而,MASS需要系统完整的控制细节,这在很大程度上受限于逆变器和网络模型的黑盒和灰盒特性。此外,MASS在大规模电力系统中具有维数灾和可扩展性弱的问题,进一步削弱了实用性。
考虑图1所示的全系统小信号阻抗模型,系统母线总数为n,o和p均为母线编号(o, p=1,2,…,n)。后文用DQ坐标系和dq坐标系分别代表系统的全局坐标系和单个逆变器自身同步控制环的摇摆坐标系[16]。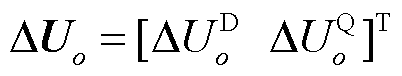 、
、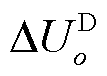 和
和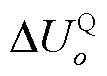 分别为DQ坐标系中母线o的电压、D轴电压和Q轴电压。
分别为DQ坐标系中母线o的电压、D轴电压和Q轴电压。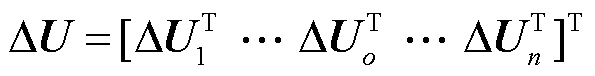 为所有母线的电压。
为所有母线的电压。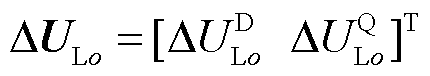 、
、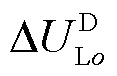 和
和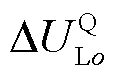 分别为逆变器o所连线路的虚拟电压、D轴电压和Q轴电压。
分别为逆变器o所连线路的虚拟电压、D轴电压和Q轴电压。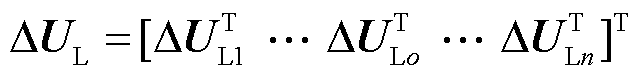 为所有逆变器所连线路的虚拟电压。
为所有逆变器所连线路的虚拟电压。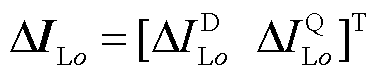 、
、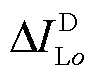 和
和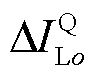 分别为逆变器o所连线路的电流、D轴电流和Q轴电流。
分别为逆变器o所连线路的电流、D轴电流和Q轴电流。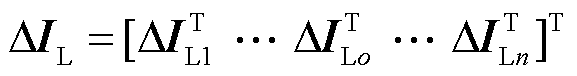 为所有逆变器所连线路的电流。ZN为网络的节点阻抗矩阵。所有电源阻抗模型在连接之前需要将各自坐标系对齐到全局坐标系。其中全局DQ坐标系中母线m所连电源m的导纳和阻抗分别为
为所有逆变器所连线路的电流。ZN为网络的节点阻抗矩阵。所有电源阻抗模型在连接之前需要将各自坐标系对齐到全局坐标系。其中全局DQ坐标系中母线m所连电源m的导纳和阻抗分别为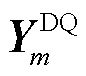 和
和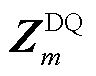 ,有
,有
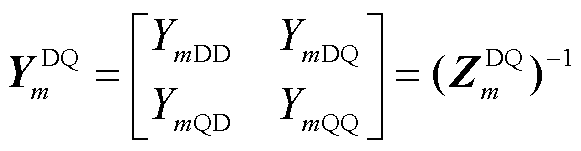 (5)
(5)
式中,YmDD、YmDQ、YmQD和YmQQ为系统全局DQ坐标系中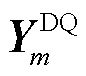 的四个分量;
的四个分量;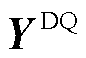 =diag2
=diag2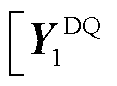 …
…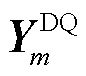 …
…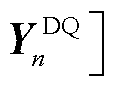 为所有母线的电源导纳矩阵,diag2[·]为由二阶方阵生成对角矩阵。
为所有母线的电源导纳矩阵,diag2[·]为由二阶方阵生成对角矩阵。
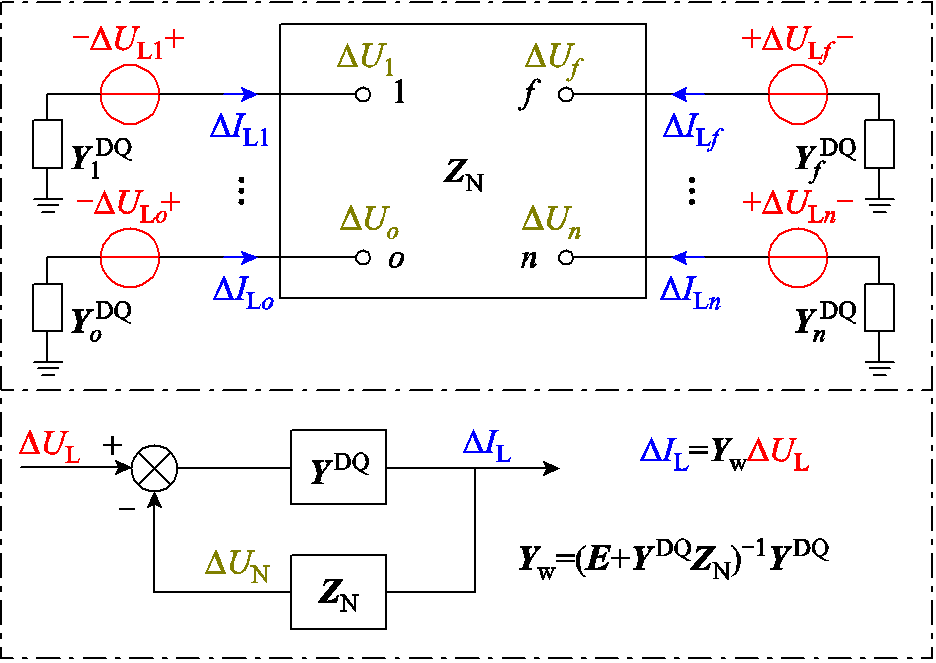
图1 全系统小信号阻抗模型
Fig.1 Whole system small signal impedance model
根据图1所示闭环反馈关系,全系统动态导纳矩阵Yw为
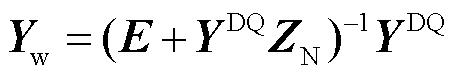 (6)
(6)
定义评估电源m对系统第h个特征值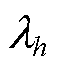 的整体阻抗参与因子为PFm[17],有
的整体阻抗参与因子为PFm[17],有
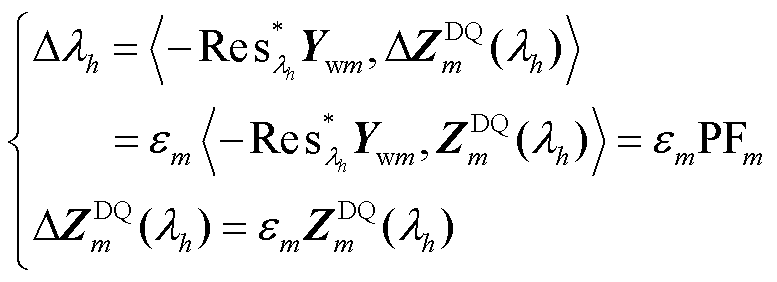 (7)
(7)
式中,Ywm为矩阵Yw第2m-1~2m行和第2m-1~2m列中四个元素对应的分块矩阵,Ywm表示电源m所在回路的导纳;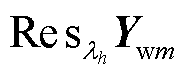 表示对全系统动态矩阵元素Ywm在特征值
表示对全系统动态矩阵元素Ywm在特征值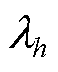 处取留数;*表示对矩阵取共轭转置;
处取留数;*表示对矩阵取共轭转置;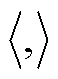 表示Frobenius内积;
表示Frobenius内积;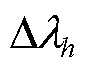 和
和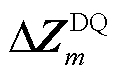 分别为
分别为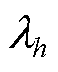 和
和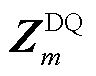 的扰动量;
的扰动量;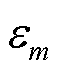 为归一化
为归一化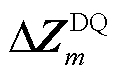 扰动程度的标量。
扰动程度的标量。
值得注意的是,对于电源m,系统其余部分在电源m端口的戴维南等效阻抗记为Zgm。根据图1电路关系,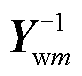 =(
=(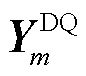 )-1+Zgm成立。因此计算式(7)所需的Ywm和
)-1+Zgm成立。因此计算式(7)所需的Ywm和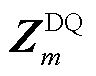 都可以直接通过测量拟合计算得到,这表明MAI的计算只需要系统对应端口的阻抗/导纳部分信息,即在大规模系统中计算复杂度降低为单机系统的计算复杂度,具有较强的可扩展性。此外,一种特征系统实现算法(Eigensystem Realization Algorithm, ERA)开辟了一条利用时域数据直接提取
都可以直接通过测量拟合计算得到,这表明MAI的计算只需要系统对应端口的阻抗/导纳部分信息,即在大规模系统中计算复杂度降低为单机系统的计算复杂度,具有较强的可扩展性。此外,一种特征系统实现算法(Eigensystem Realization Algorithm, ERA)开辟了一条利用时域数据直接提取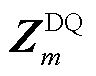 和Zgm信息的途径[23],从而进一步实现MAI的计算。电源内部不同控制环路的相互作用整体效果体现在变流器阻抗模型中,而电源经过电网的相互作用效果体现在式(7)中的PFm,因此MAI是设备层面的模态分析方法。然而,不同于状态变量层面的模态分析方法MASS,MAI无法确定影响动态的电源主导控制环路。
和Zgm信息的途径[23],从而进一步实现MAI的计算。电源内部不同控制环路的相互作用整体效果体现在变流器阻抗模型中,而电源经过电网的相互作用效果体现在式(7)中的PFm,因此MAI是设备层面的模态分析方法。然而,不同于状态变量层面的模态分析方法MASS,MAI无法确定影响动态的电源主导控制环路。
构网型逆变器结构如图2所示。图中,R、L和C分别为LC滤波电路的电阻、电感和电容,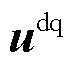 和
和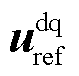 分别为电容电压及其参考值,
分别为电容电压及其参考值,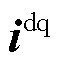 和
和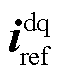 分别为电感电流及其参考值。值得注意的是,因为网络元件一般采用负载惯例,阻抗建模时GFM需与网络元件的电压电流关系保持一致。P和Pref分别为有功功率及参考值。同步环采用带低通滤波器的下垂控制。电压控制采用电压电流双闭环控制。
分别为电感电流及其参考值。值得注意的是,因为网络元件一般采用负载惯例,阻抗建模时GFM需与网络元件的电压电流关系保持一致。P和Pref分别为有功功率及参考值。同步环采用带低通滤波器的下垂控制。电压控制采用电压电流双闭环控制。
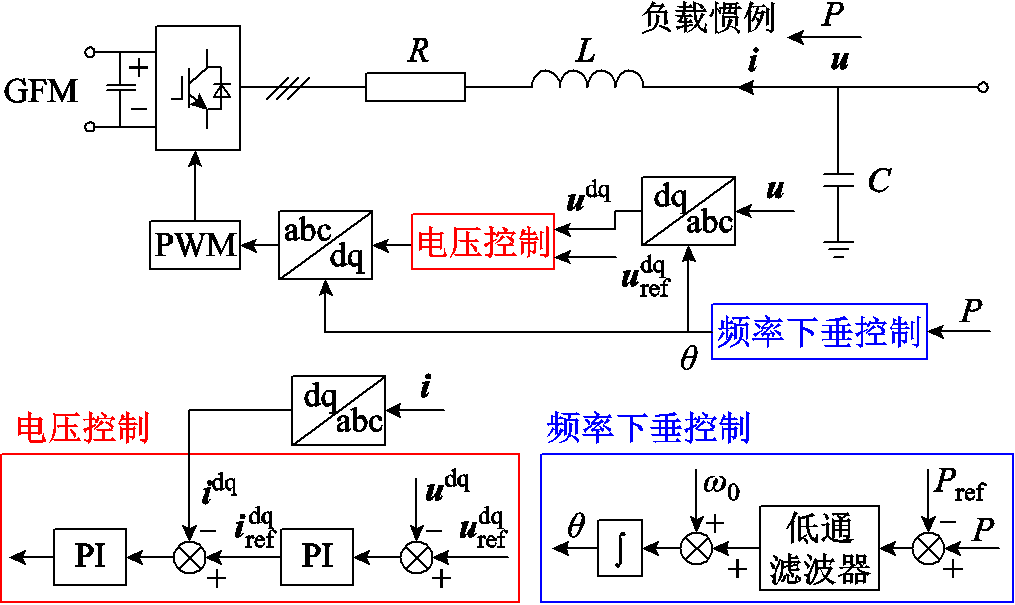
图2 构网型逆变器结构
Fig.2 GFM structure
GFMm表示接在母线m上的GFM。所有电源阻抗必须对齐到系统的全局DQ坐标系[16]。坐标系变换如图3所示。在图3中,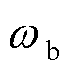 为系统参考电源的角速度,
为系统参考电源的角速度,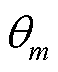 、
、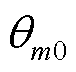 和
和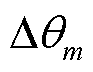 分别为GFMm相对于参考电源的角度、稳态角度和角度偏差。当坐标变换的频率参考信号为恒定值或PFL断开时,即不考虑PFL的同步动态(SD)时,
分别为GFMm相对于参考电源的角度、稳态角度和角度偏差。当坐标变换的频率参考信号为恒定值或PFL断开时,即不考虑PFL的同步动态(SD)时,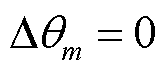 ,这意味着摇摆坐标系和稳态坐标系重合。此时逆变器动态中只存在且只需考虑电磁动态(ED)。文献[21]指出电压环的所有控制参数均可以等效为在不同位置与滤波电路串联或并联的阻抗,关于逆变器电磁动态的等效阻抗
,这意味着摇摆坐标系和稳态坐标系重合。此时逆变器动态中只存在且只需考虑电磁动态(ED)。文献[21]指出电压环的所有控制参数均可以等效为在不同位置与滤波电路串联或并联的阻抗,关于逆变器电磁动态的等效阻抗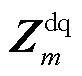 已经得到了充分讨论。本节将重点讨论考虑GFM内部ED和SD交互作用的阻抗分解。
已经得到了充分讨论。本节将重点讨论考虑GFM内部ED和SD交互作用的阻抗分解。
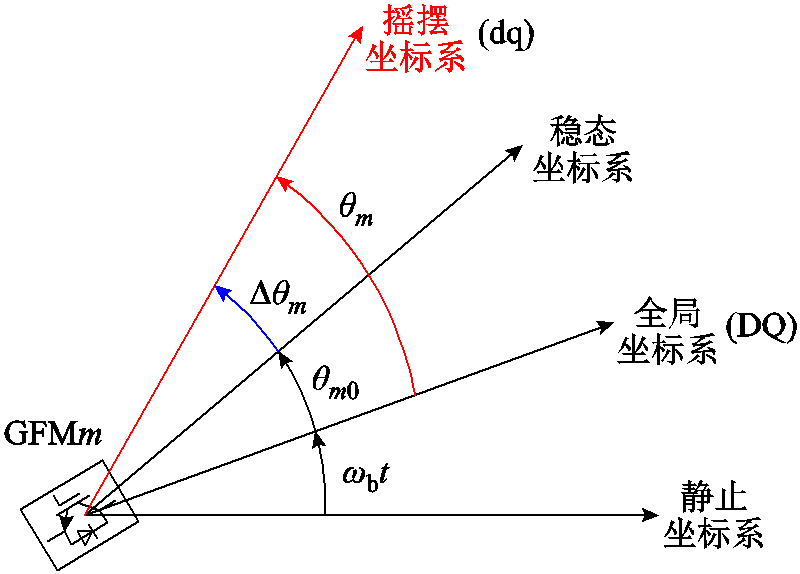
图3 坐标系变换
Fig.3 Coordinate system transformation
PFL的小信号传递函数为
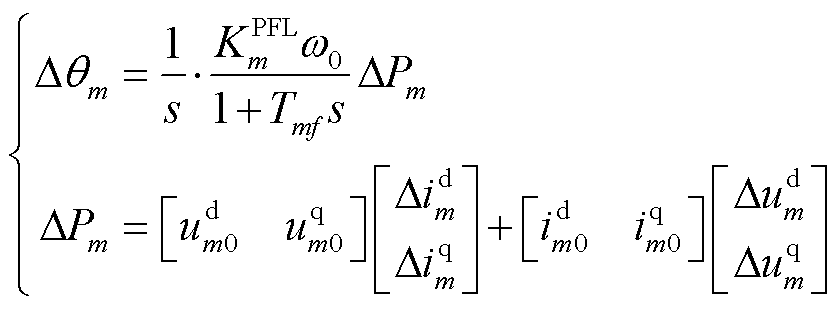 (8)
(8)
式中,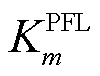 为下垂增益;
为下垂增益;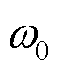 为系统额定角频率;Tmf为PFL低通滤波时间常数,Tmf=1/(2πfmf),fmf为PFL低通滤波带宽;
为系统额定角频率;Tmf为PFL低通滤波时间常数,Tmf=1/(2πfmf),fmf为PFL低通滤波带宽;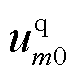 和
和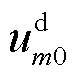 分别为稳态时公共连接点的q轴和d轴电压;
分别为稳态时公共连接点的q轴和d轴电压;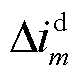 、
、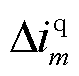 分别为dq坐标系中的d轴电流增量和q轴电流增量;
分别为dq坐标系中的d轴电流增量和q轴电流增量;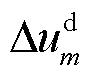 和
和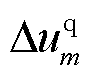 分别为dq坐标系中的d轴电压和q轴电压;
分别为dq坐标系中的d轴电压和q轴电压;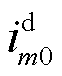 和
和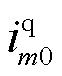 分别为平衡点上公共连接点的d轴电流和q轴电流。
分别为平衡点上公共连接点的d轴电流和q轴电流。
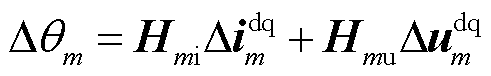 (9)
(9)
其中
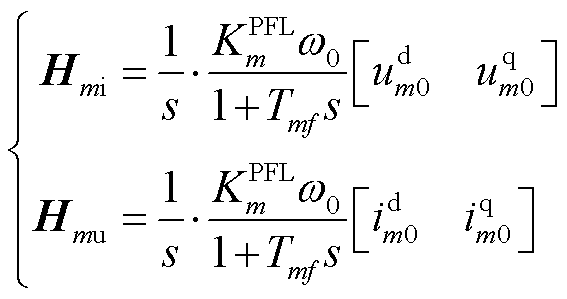
式中,Hmi为电流到角度的传递函数;Hmu为电压到角度的传递函数。
由图3可知,通过坐标变换可将GFMm的电压变量从摇摆坐标系变换到全局坐标系,之后在平衡状态下对其进行线性化可得
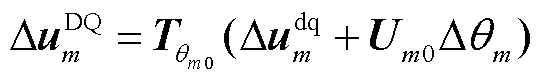 (10)
(10)
其中
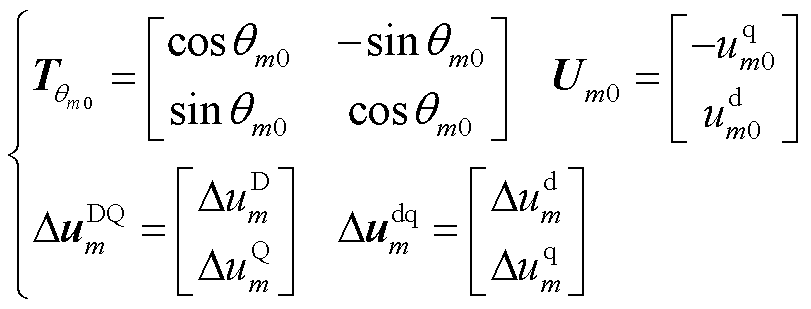
式中,Um0为稳态时公共连接点的电压;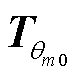 为由初始潮流分析确定的坐标变换矩阵;
为由初始潮流分析确定的坐标变换矩阵;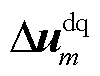 为摇摆坐标系的电压向量;
为摇摆坐标系的电压向量;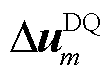 、
、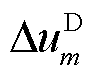 和
和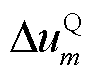 分别为全局坐标系的电压向量、D轴和Q轴电压。
分别为全局坐标系的电压向量、D轴和Q轴电压。
电流的关系与式(10)类似。考虑到全局坐标系中PFL引入的额外动态,全局坐标系GFM整体阻抗为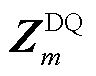 ,摇摆坐标系和全局坐标系阻抗关系如图4所示。
,摇摆坐标系和全局坐标系阻抗关系如图4所示。
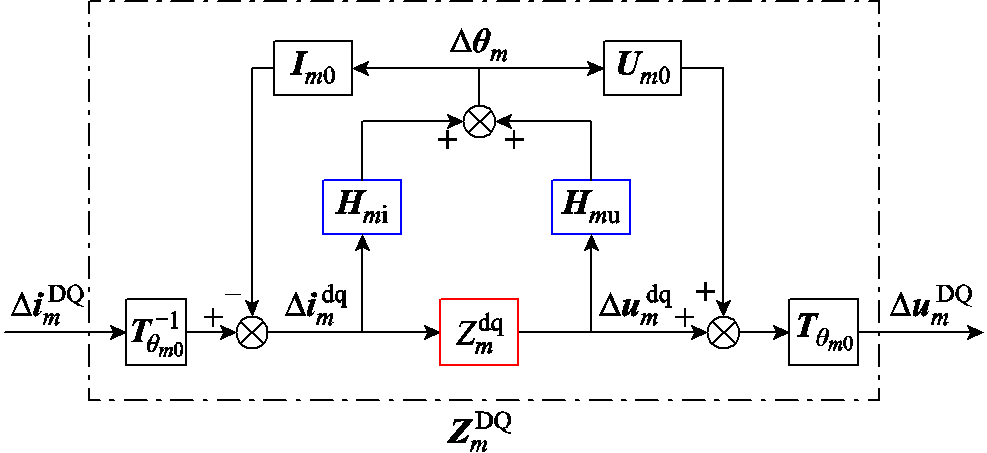
图4 摇摆坐标系和全局坐标系阻抗关系
Fig.4 Impedance relationship between swing frame and global frame
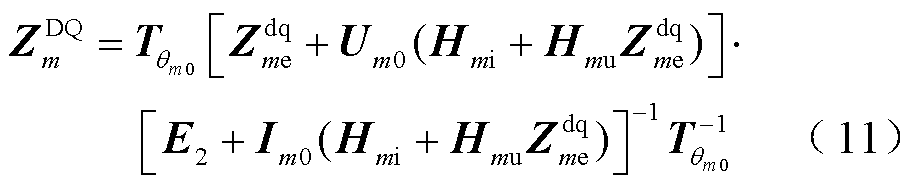
式中,E2为二阶单位矩阵;Im0为平衡点上的公共连接点外送电流,Im0=[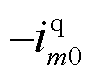
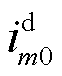 ]T;
]T;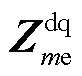 为图4中表征ED的等效阻抗
为图4中表征ED的等效阻抗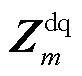 。
。
由于GFM与同步机类似的同步机制,GFM会存在低频振荡模式。此外,GFM的同步环、电压环和强电网的交互作用可能会诱发次同步振荡[24]。这两种振荡的频率都较小,一般情况下都低于电压环带宽。在电压环带宽内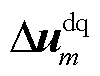 =0,因此式(8)可改写为[21,24]
=0,因此式(8)可改写为[21,24]
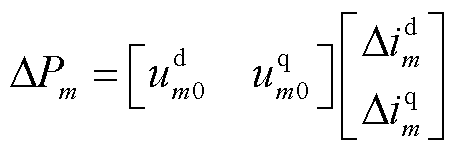 (12)
(12)
一般地,GFM电压环PI控制器的积分控制器等效为并联在dq坐标系电容上的电感[21]。由于电感在0 Hz时阻抗为0,以及并联元件的总阻抗小于任意并联元件的阻抗,会使得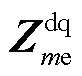 在较低频段内幅值极小。
在较低频段内幅值极小。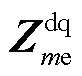 的4个元素只有2个是独立的[21],图5给出了一组不同电压环控制器参数下
的4个元素只有2个是独立的[21],图5给出了一组不同电压环控制器参数下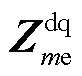 伯德图的dd和qd项。电压环PI控制参数见附表2,其余参数与附表1中GFM3相同,其中交叉解耦、虚拟和前馈控制均设置为0。图5中
伯德图的dd和qd项。电压环PI控制参数见附表2,其余参数与附表1中GFM3相同,其中交叉解耦、虚拟和前馈控制均设置为0。图5中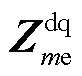 在次同步频段内阻抗幅值极小。在额定工况下,GFMm的输出电压、有功功率和无功功率分别为:Um=1(pu)、Pm=1(pu)、Qm=0(pu)。因此结合伯德图可以得出
在次同步频段内阻抗幅值极小。在额定工况下,GFMm的输出电压、有功功率和无功功率分别为:Um=1(pu)、Pm=1(pu)、Qm=0(pu)。因此结合伯德图可以得出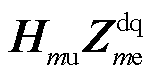 远小于
远小于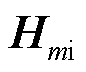 的结论。值得注意的是,当GFM存在电流限幅时,该结论不成立。
的结论。值得注意的是,当GFM存在电流限幅时,该结论不成立。
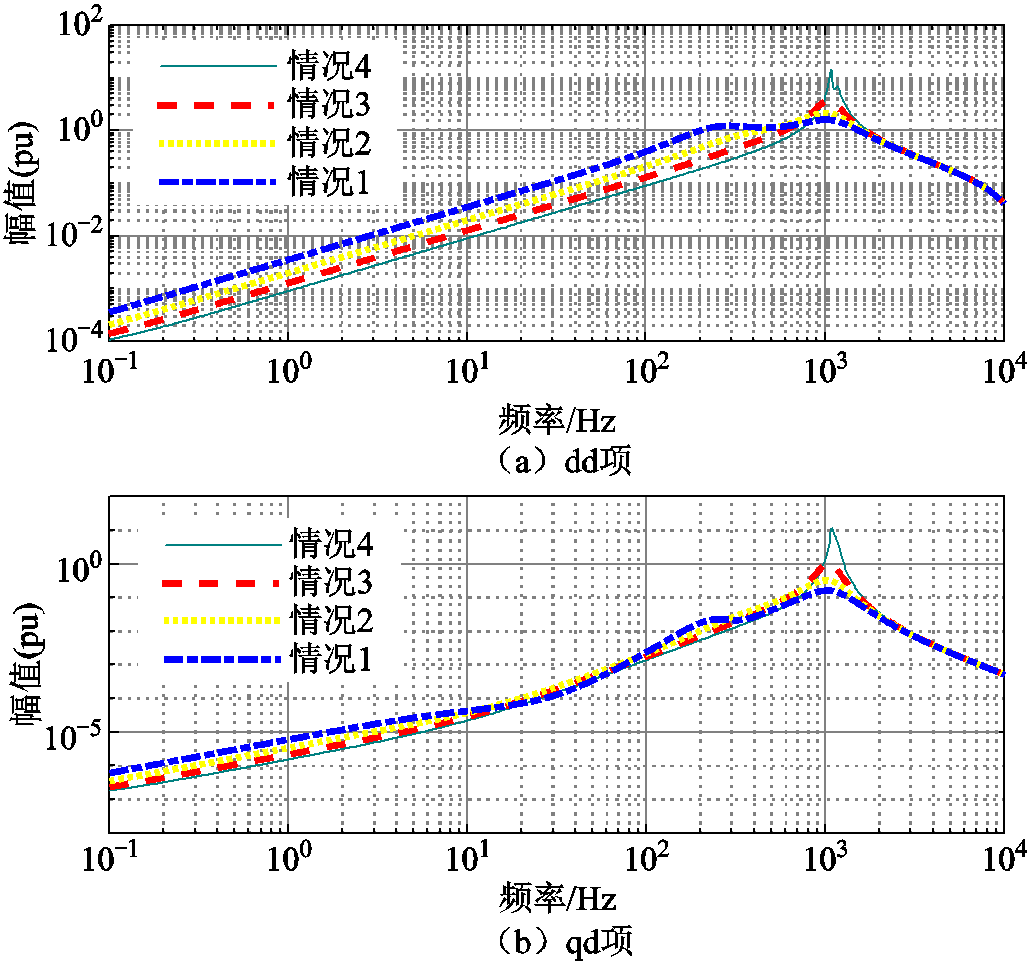
图5 阻抗伯德图
Fig.5 Impedance Bode diagram
因此式(11)可改写为
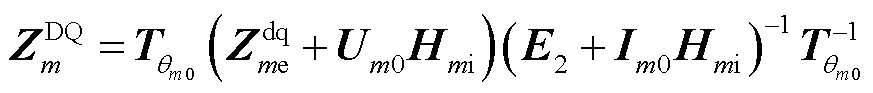 (13)
(13)
此外,额定工况下,附图1还给出情况4的GFM在简化前后的阻抗对比。DQ坐标系的4项在简化前后均几乎重合,进一步说明了推导的合理性。
由于Im0和Hmi分别是阶数为2×1和1×2的矩阵,因此(E2+Im0Hmi)-1可写成(E2+Im0×1×Hmi)-1,这可以用式(14)的矩阵求逆引理将其化简为式(15)。
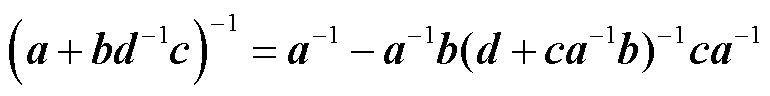 (14)
(14)
式中,a、b、c和d为任意矩阵,它们在维度上是符合矩阵乘法规则的相容矩阵。
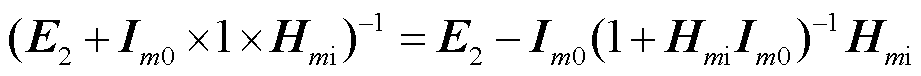 (15)
(15)
将式(15)代入式(13),注意到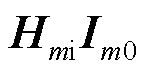 是标量,将
是标量,将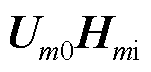 写为
写为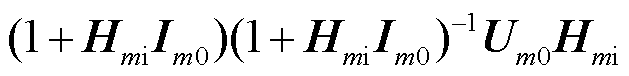 便于合并化简,最后式(13)被分解为三个部分。
便于合并化简,最后式(13)被分解为三个部分。
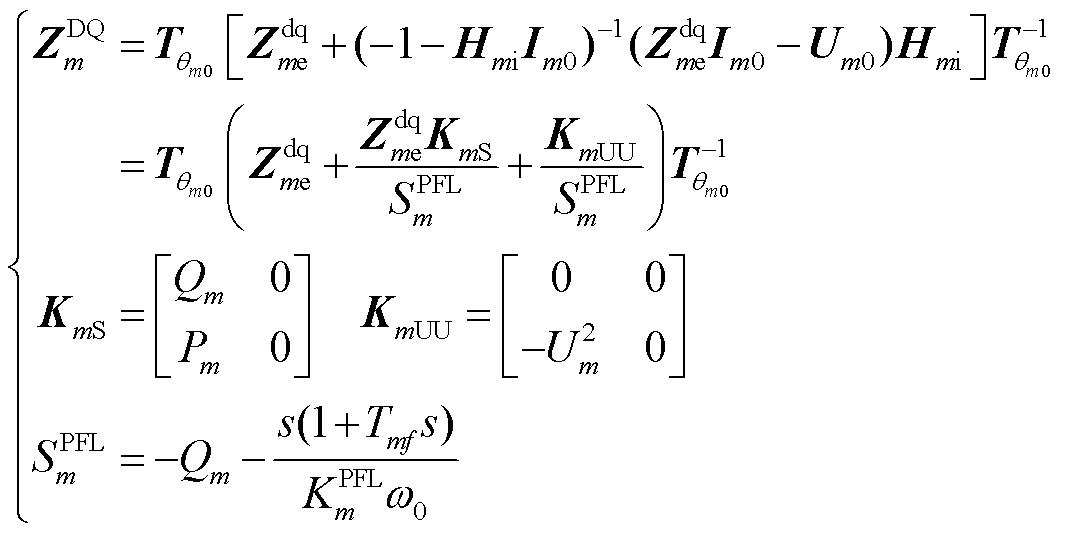 (16)
(16)
式中,KmS和KmUU分别为与稳态功率和电压相关的系数矩阵;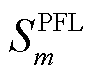 为PFL参数引起的等效功率;Um、Pm和Qm分别为在公共连接点测得的电压、有功功率和无功功率。
为PFL参数引起的等效功率;Um、Pm和Qm分别为在公共连接点测得的电压、有功功率和无功功率。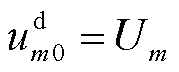 ,
,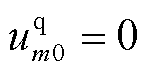 ,
,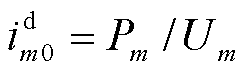 ,
,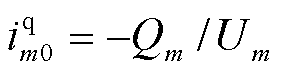 。
。
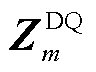 第一部分和第三部分分别只与VCL和PFL有关,而第二部分则受到VCL和PFL耦合效应的影响。因此,
第一部分和第三部分分别只与VCL和PFL有关,而第二部分则受到VCL和PFL耦合效应的影响。因此,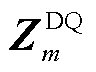 的分解可简写为
的分解可简写为
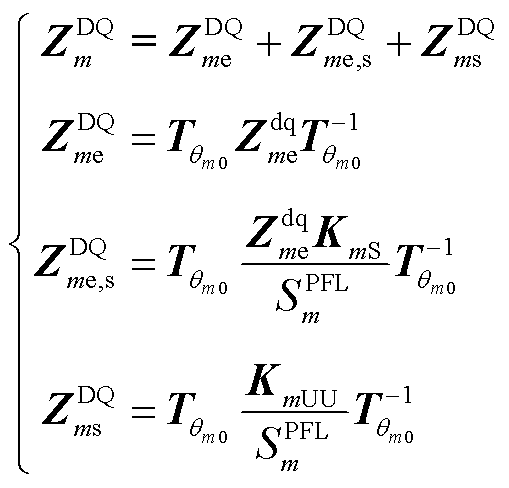 (17)
(17)
可以通过测量拟合计算出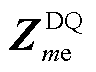 、
、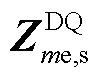 和
和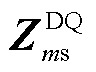 。断开PFL控制环路,即将PFL的频率参考信号设置为恒定值或下垂增益
。断开PFL控制环路,即将PFL的频率参考信号设置为恒定值或下垂增益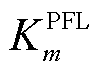 设为零。此时
设为零。此时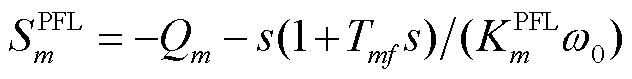 为无穷大,因此
为无穷大,因此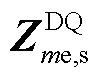 和
和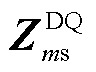 的所有项都为0,就可以将
的所有项都为0,就可以将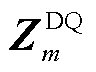 分离为
分离为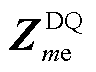 和
和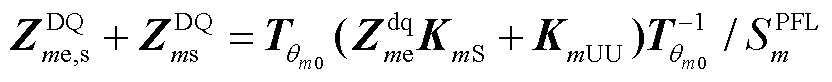 。在
。在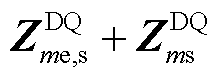 中,只有
中,只有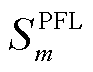 未知。
未知。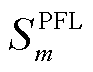 是关于
是关于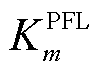 和
和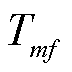 的函数,且
的函数,且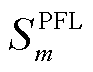 是标量,因此这相当于已知
是标量,因此这相当于已知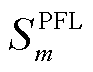 的频谱,求解关于
的频谱,求解关于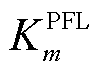 和
和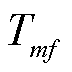 的二元方程。可以通过最小二乘法求解
的二元方程。可以通过最小二乘法求解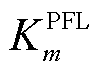 和
和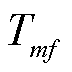 。因此,
。因此,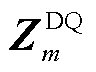 的三个部分均可通过数据驱动的方法结合测量进行拟合计算,具有较强的实用性。
的三个部分均可通过数据驱动的方法结合测量进行拟合计算,具有较强的实用性。
与式(7)中MAI的GFMm元件整体参与因子PFm不同,本节将分别推导出表征GFMm内部ED和SD的等效阻抗参与因子。由于MAI方法已经从元件整体动态评估扩展到逆变器内部动态评估,故将所提方法称为扩展阻抗模态分析(EMAI)。
对式(17)做微分运算,计算过程如图6所示。
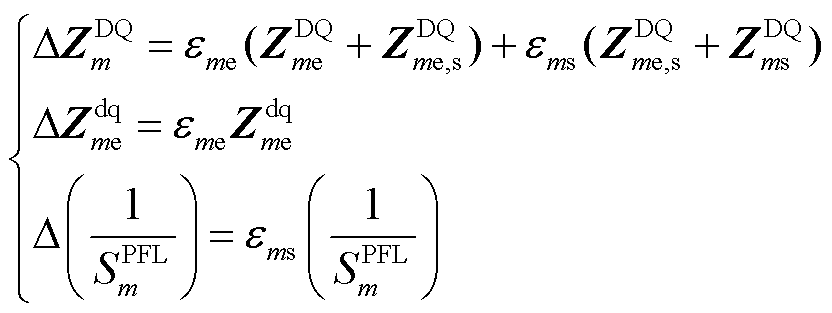 (18)
(18)
式中,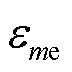 和
和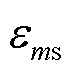 分别为
分别为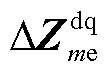 和
和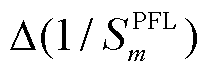 的扰动系数。
的扰动系数。
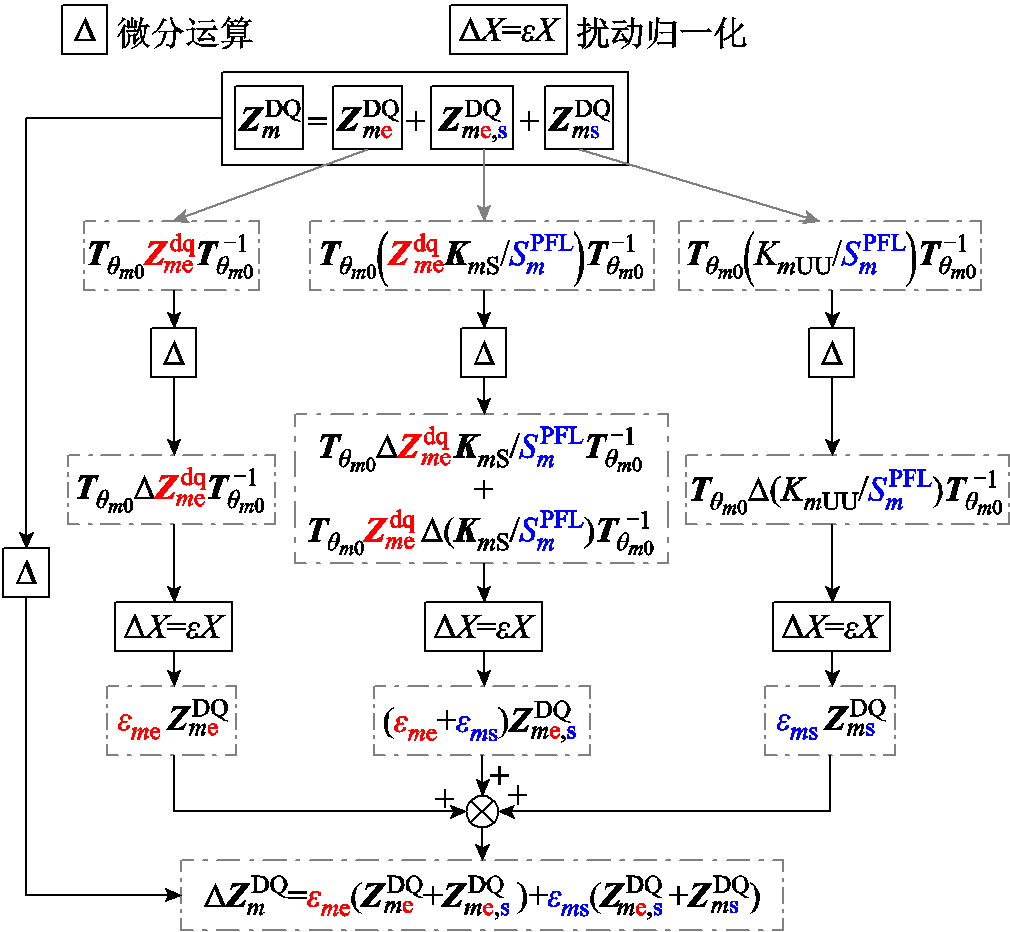
图6 阻抗微分运算
Fig.6 Impedance differential operation
联立式(7)和式(18)得到式(19),即可计算出ED和SD的参与情况,分别用PFme1和PFms1表示。
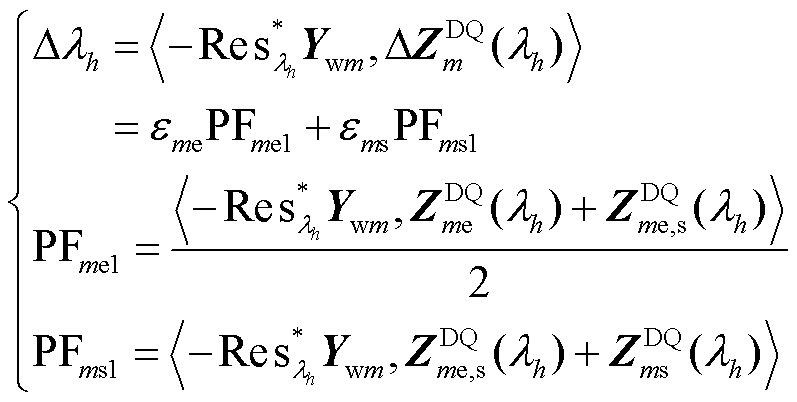 (19)
(19)
式中,下标1表示使用EMAI计算的结果;PFme1和PFms1分别为ED和SD的等效阻抗参数因子。值得注意的是,PFme1受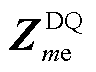 和
和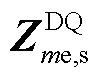 的共同影响,而PFms1则是
的共同影响,而PFms1则是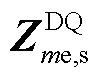 和
和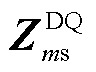 的相互作用的结果。由于电压控制本质上是交流电压电流双闭环,1/2是EMAI方法阻抗参与的换算系数。
的相互作用的结果。由于电压控制本质上是交流电压电流双闭环,1/2是EMAI方法阻抗参与的换算系数。
ED和SD的参与也可以使用MASS方法从状态变量参与因子中进行评估。
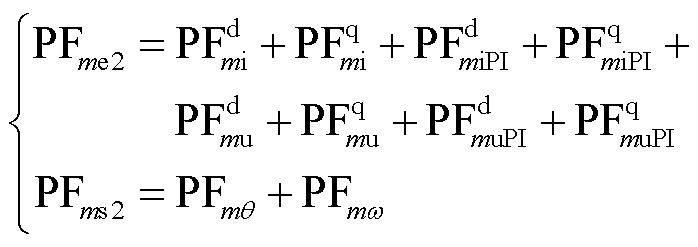 (20)
(20)
式中,下标2表示使用MASS方法计算得出的结果;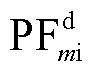 、
、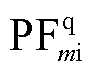 和
和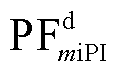 、
、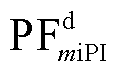 分别为dq坐标系电感电流的参与因子和电流控制环中PI控制器积分器的参与因子;
分别为dq坐标系电感电流的参与因子和电流控制环中PI控制器积分器的参与因子;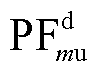 、
、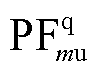 和
和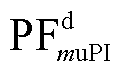 、
、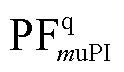 分别为dq坐标系电容电压的PF和VCL中PI控制器积分器的参与因子;
分别为dq坐标系电容电压的PF和VCL中PI控制器积分器的参与因子;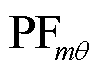 和
和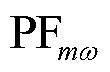 分别为PFL的角度变量和滤波器状态变量的参与因子。它们可通过式(4)计算得到。
分别为PFL的角度变量和滤波器状态变量的参与因子。它们可通过式(4)计算得到。
为了评估MAI、EMAI和MASS计算出的参与因子,定义参与比(Participation Ratio,PR)对不同方法得到的参与因子进行归一化,表示为
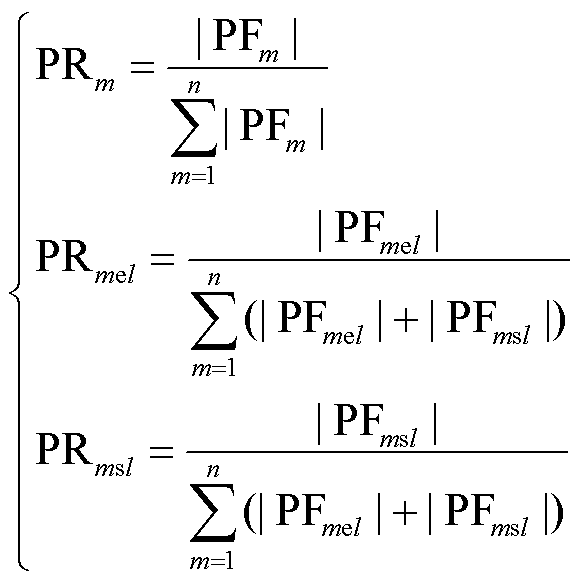 (21)
(21)
式中,|·|表示取绝对值;下标l=1或2分别为根据EMAI和MASS方法计算的参与因子或参与比。
参数参与因子为特征值对特定参数的灵敏度(偏导数),因此根据参数参与因子可以估计特定参数变化导致的特征值变化。参数参与因子实部为正/ 负则减小/增加该参数数值,有利于阻尼提升。为了使得特定参数更加灵敏地改善系统阻尼,需要挑选不同控制环路中实部绝对值更大的参数参与因子。在文献[17]中,参数参与因子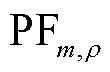 定义为
定义为
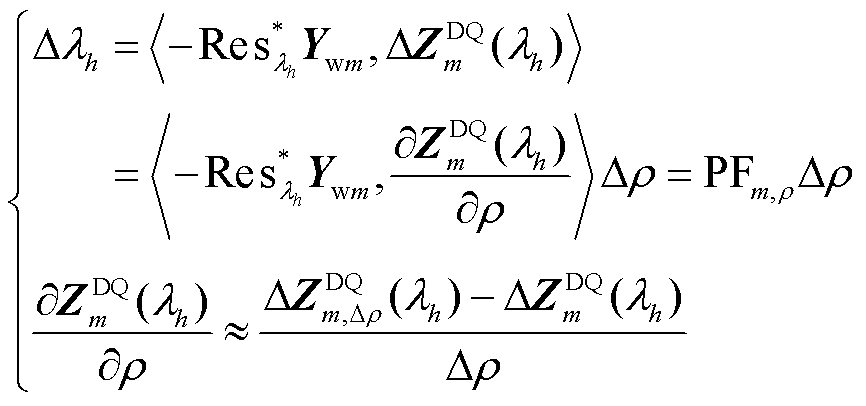 (22)
(22)
但等效阻抗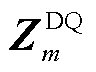 对特定参数
对特定参数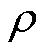 的灵敏度
的灵敏度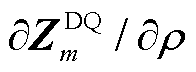 很难通过解析的方式获得。文献[17]使用数值差分来替代偏导数计算,但数值差分要求参数增量足够小,可能会导致不可预期的误差。本节根据式(7)阻抗分解的结果推导不同控制环路参数参与因子的显式表达式。
很难通过解析的方式获得。文献[17]使用数值差分来替代偏导数计算,但数值差分要求参数增量足够小,可能会导致不可预期的误差。本节根据式(7)阻抗分解的结果推导不同控制环路参数参与因子的显式表达式。
基于式(17)和式(18)的阻抗分解和阻抗微分方法,本文推导了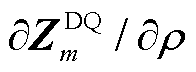 的显式表达式。首先考虑VCL中PI控制器的比例增益
的显式表达式。首先考虑VCL中PI控制器的比例增益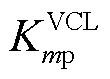 和积分增益
和积分增益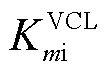 。由图6可知,
。由图6可知,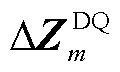 可写为
可写为
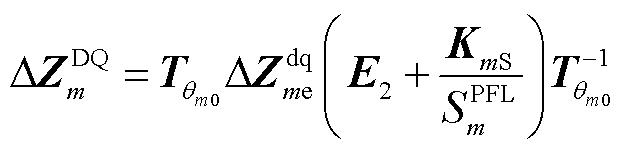 (23)
(23)
VCL中所有控制均可等效为与滤波电路串联或并联的阻抗[21]。以PI控制器为例,考虑将交叉解耦、虚拟和前馈控制均设置为0。由于VCL的PI控制器可等效为与滤波电容并联的导纳[21],可将阻抗微分转换为导纳微分,即
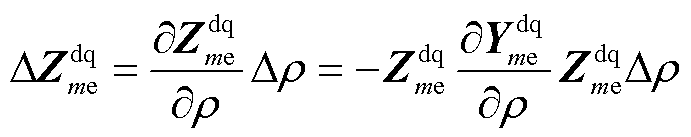 (24)
(24)
VCL中PI控制器的比例增益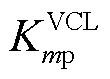 和积分增益
和积分增益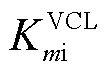 的参数灵敏度为
的参数灵敏度为
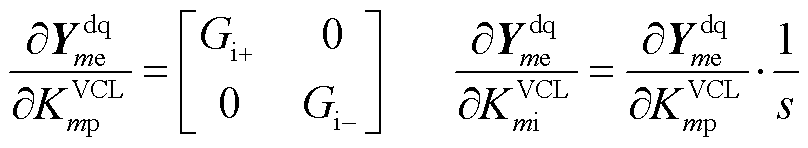 (25)
(25)
式中,Gi+和Gi-分别为正序和负序电路的电流环增益[21]。
考虑PFL的控制参数时,参数灵敏度只与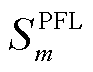 相关。
相关。
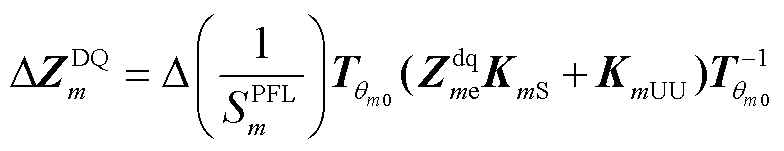 (26)
(26)
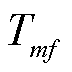 和
和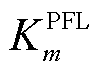 的阻抗灵敏度为
的阻抗灵敏度为
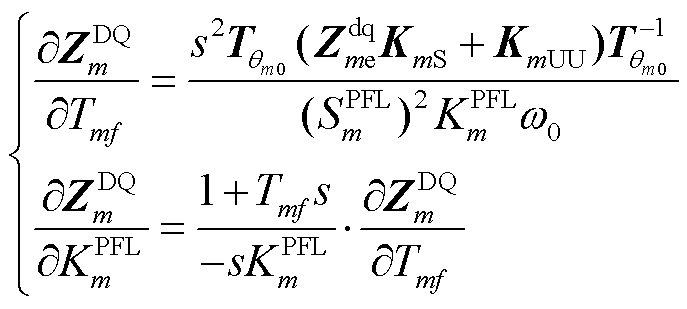 (27)
(27)
PFL和VCL的参数参与因子可通过联立式(22)~式(27)计算获得。
本节通过两个不同规模的系统来探讨所提EMAI方法的性能。改造的IEEE 14母线系统用于验证EMAI能够充分捕获不同情况下GFM内的主导动态。改造的IEEE 68母线系统用于验证EMAI在大规模电力系统中的适用性,以及所提出的参数参与因子在指导系统阻尼改善控制中的有效性。这两个系统中GFM的参数见附表1和附表3。仿真所有GFM的控制结构与图2一致。所有仿真模型和数据均使用开源软件包Simplus Grid Tool生成[24]。
改造IEEE 14母线系统如图7所示。母线1被设置为无穷大母线。母线2、3、6和8连接GFM。所有GFM的参数见附表1。系统极点分布如图8所示。模式1、2、3和4是四个处于不同频率的模式,分别是2π(-1.23+j12.33)、2π(-3.90+j4.55)、2π(-10.62+ j36.97)和2π(-2.64+j42.95)。14母线系统的基准频率为50 Hz。
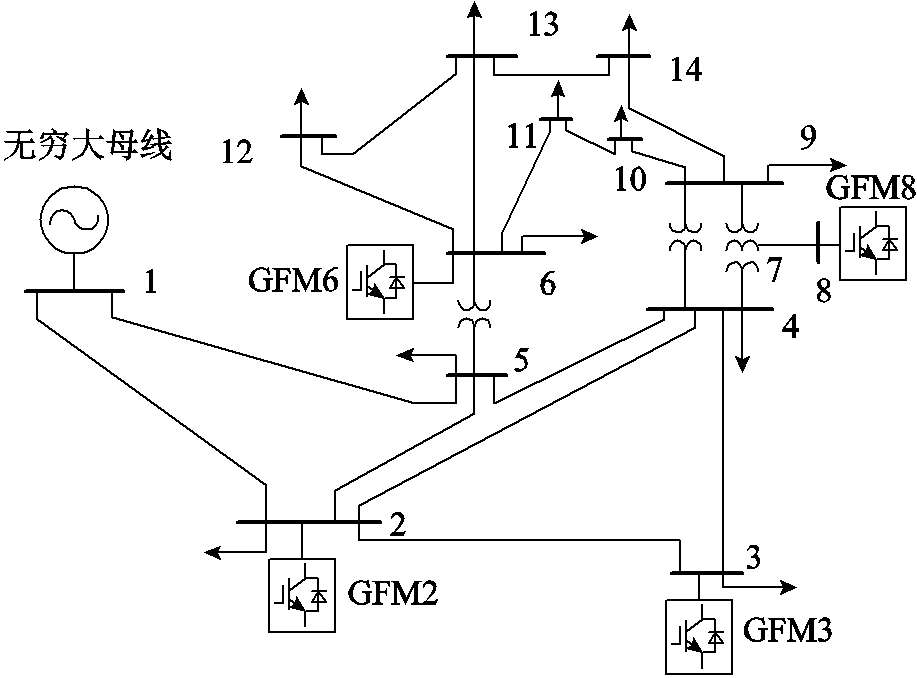
图7 改造IEEE 14母线系统
Fig.7 Modified IEEE 14 bus system
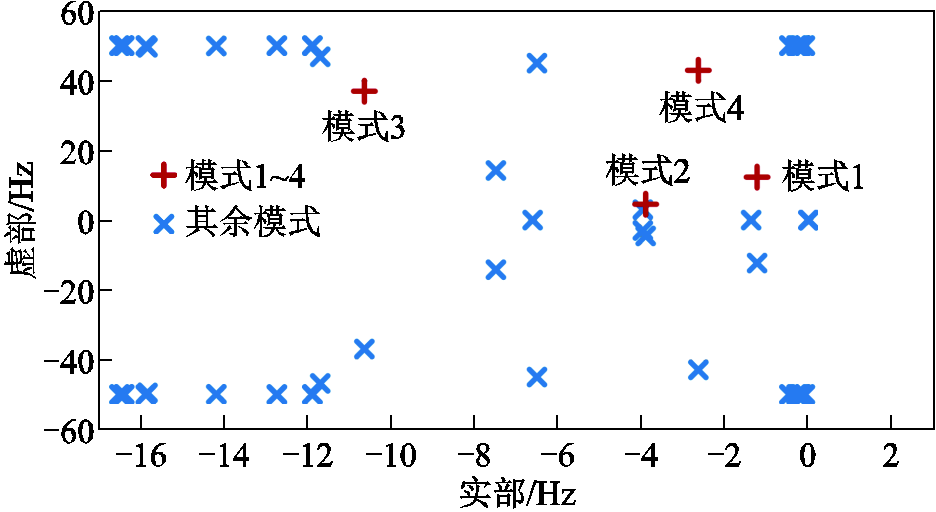
图8 改造IEEE 14母线系统极点分布
Fig.8 Modified IEEE 14 bus system pole distribution
不同方法的PR计算结果如图9所示。例如,对于模式1,GFM2的ED参与程度在所有GFM中最高,故后文及图中简称为GFM2主导ED。图9中不同模式几乎相同高度的柱状图表明,三种方法对所有GFM参与的总体评估效果相同。显然,MAI可以对GFM的参与情况进行整体评估,但它无法捕获单个GFM的主导动态。相比之下,本文所提EMAI不仅能识别各GFM与电网的交互作用,还能量化GFM内部动态之间复杂的耦合交互。EMAI方法和MASS方法的结果高度相似,进一步验证了EMAI方法的有效性。模式1中EMAI对GFM的整体评估结果比MAI更接近MASS的评估结果,这说明了EMAI方法对电源整体参与评估效果也更准确。此外,图9还表明随着振荡模式的频率下降,每个GFM中主导动态逐渐由ED向SD转变,与一般的认知一致。

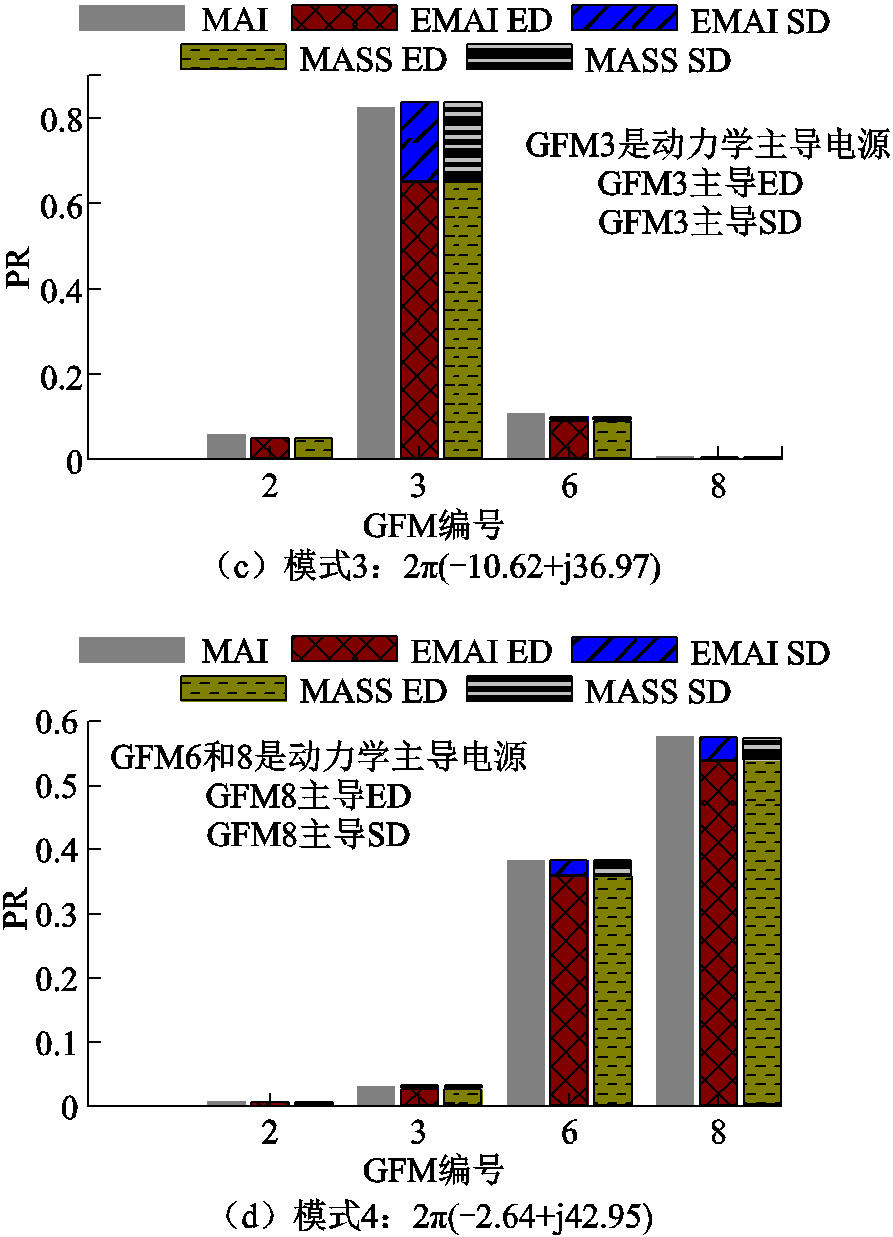
图9 改造IEEE 14母线系统GFM参与评估
Fig.9 Modified IEEE 14 bus system GFM participation assessment
模式1在这四个模式中阻尼最弱,因此模式1更容易被激发。从图7中可以看出,GFM2相比于GFM3离无穷大母线的电气距离更近。由于GFM的强电网不稳定性,GFM2对模式1的参与程度预计比GFM3更高,所以无穷大母线发生扰动,预计会对GFM2造成更大的影响。然而图9a表明,GFM3对模式1的整体参与程度比GFM2更高,其中GFM3的SD占比很高,这是GFM3中PFL较大的下垂系数导致的。GFM2离无穷大母线的电气距离更近,体现为GFM2的ED占比比GFM3更高。0.1 s时将无穷大母线的电压设置为幅值为0.05(pu)且频率与模式1相同的强迫振荡,GFM2和GFM3的振荡波形如图10所示,其中振荡频率与模式1相同,均为12.33 Hz。GFM2的d轴和q轴电压波形振荡幅值分别为0.07(pu)和0.05(pu)(平稳的振荡阶段),GFM3的d轴和q轴电压波形振荡幅值分别为0.016(pu)和0.012(pu)。GFM2的电压波形振荡幅值高于GFM3,这表明GFM2主导了ED。GFM2和GFM3的频率振荡幅值分别为0.008(pu)和0.03(pu),GFM3的频率振荡幅值更大,这表明GFM3主导了SD。仿真与图9a的结论保持一致,因此EMAI方法可以精确捕获不同GFM内部动态的主导情况,说明了所提EMAI方法的有效性。
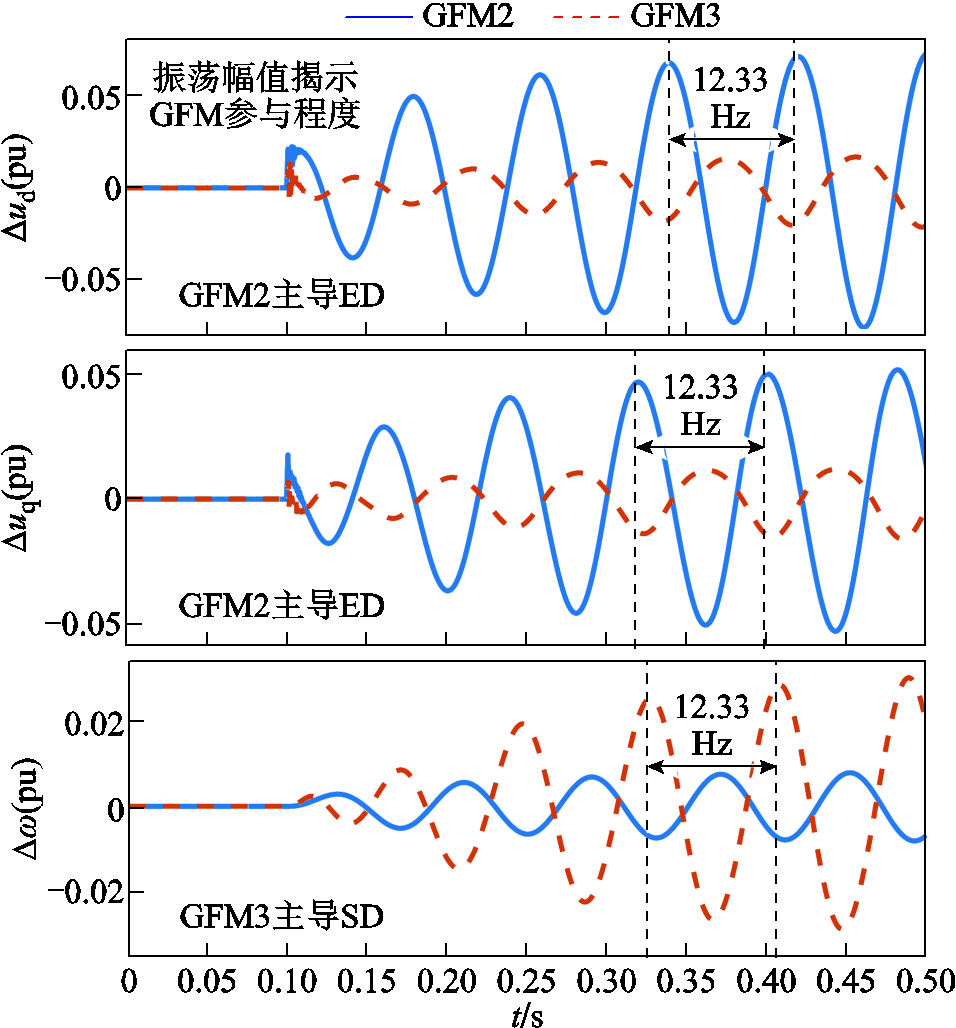
图10 GFM2和GFM3振荡波形
Fig.10 GFM2 and GFM3 oscillation waveforms
本文提出了EMAI,用EMAI对GFM的阻抗进行了严格的分解,并确定了表征其内部动态的阻抗参与因子。EMAI结合了MAI和MASS各自的优点,有效地解决了MAI评估GFM内部动态方面的局限性。表1总结了MASS、MAI和EMAI三种不同模态分析方法的比较结果。
表1 不同模态分析方法的对比
Tab.1 Comparison of different modal analysis methods

方法MASSMAIEMAI 适用于灰盒或黑盒系统—++ 计算仅需系统部分信息—++ 确定主导电源+++ 确定主导电源的关键动态+—+
改造的IEEE 68母线系统如图11所示,其中母线1和16被设置为无穷大母线,母线2~15连接同步机,其余GFM被分散连接到不同母线上,所有GFM的参数均相同,见附表3。IEEE 68母线系统的基准频率为60 Hz。四个模式的三种方法的参与评估结果如图12所示。PR的条形图表明三种方法的总体参与结果几乎相同,并且EMAI方法和MASS方法对GFM内部动态的参与评估结果也高度一致,这充分说明了所提方法在大规模电力系统中的适用性。同时随着所选模式振荡频率的减小,所有GFM的主导动态逐渐由ED转变为SD。
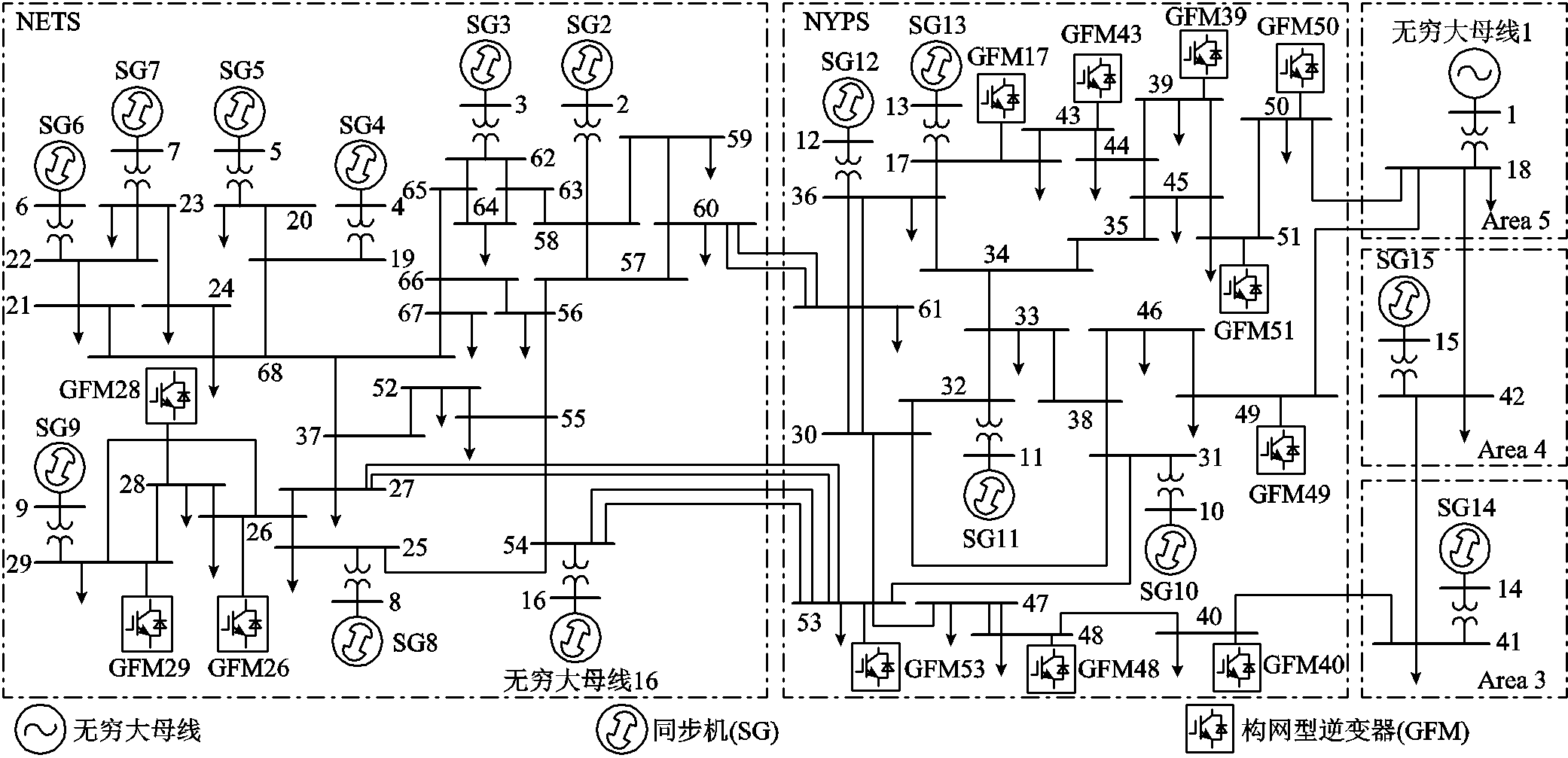
图11 改造IEEE 68母线系统
Fig.11 Modified IEEE 68 bus system
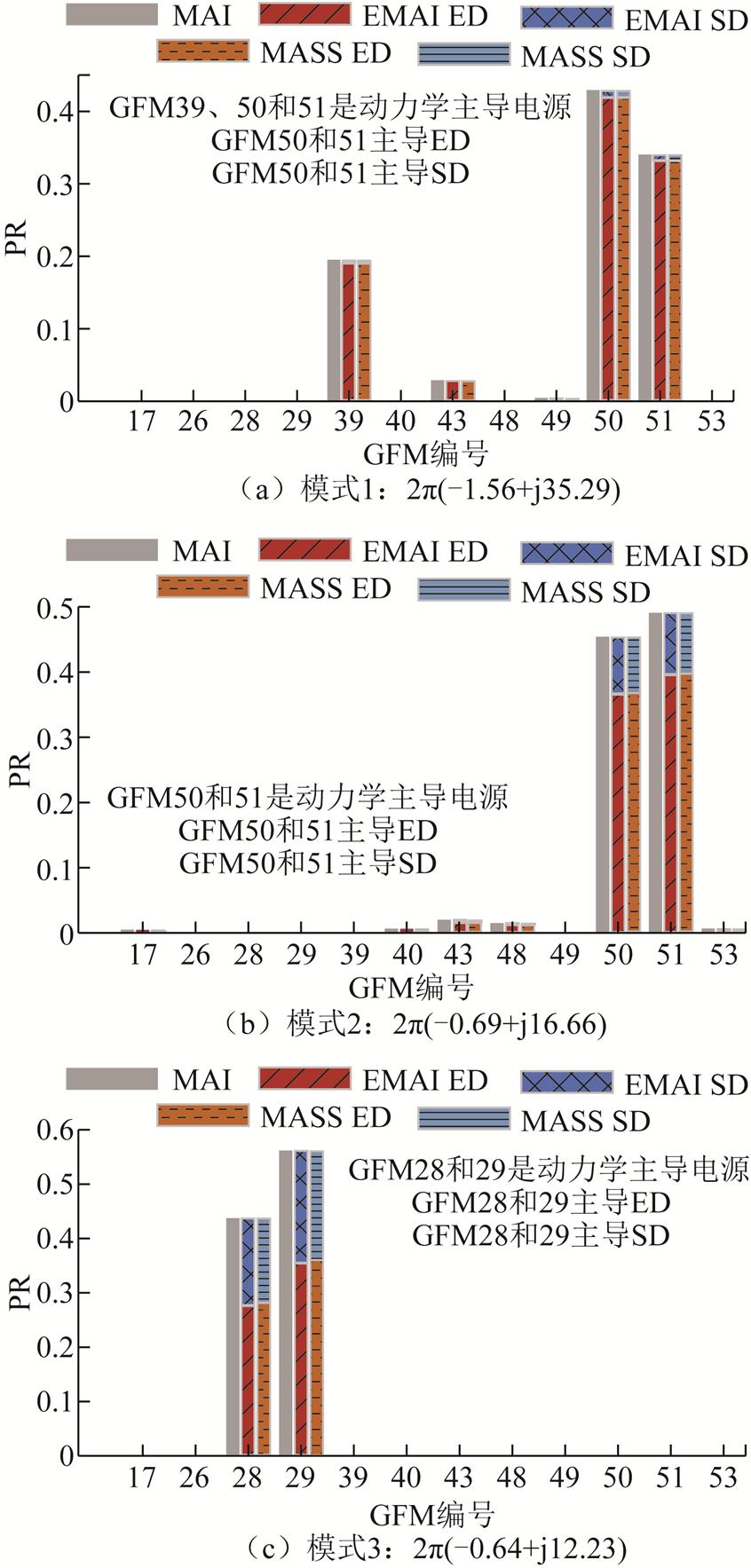
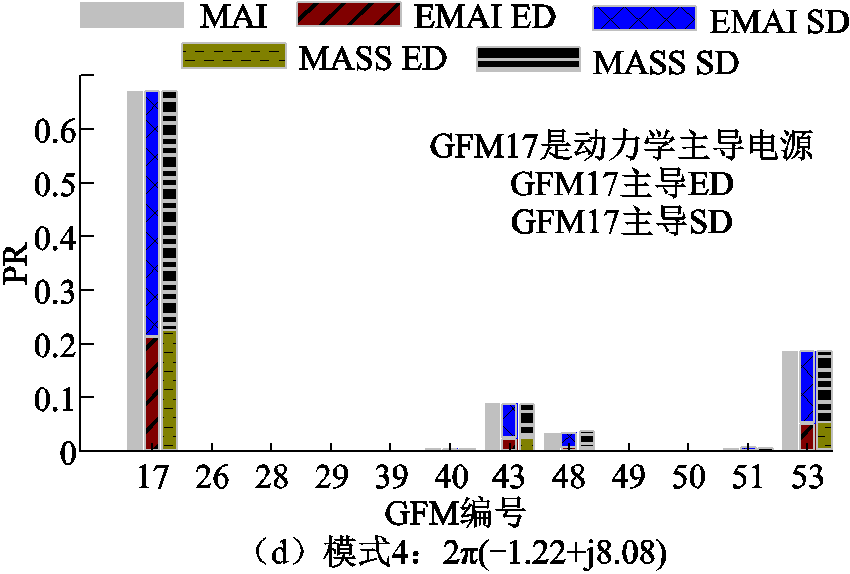
图12 改造IEEE 68母线系统GFM参与评估
Fig.12 Modified IEEE 68 bus system GFM participation assessment
图12b中模式2:2π(-0.69+j16.66)的参与评估结果中GFM50和GFM51显示很高,因此考虑对GFM50和GFM51进行控制参数调整以优化该模式阻尼,改善系统稳定性。GFM50和GFM51的参数参与因子见表2。
表2 IEEE68母线系统模式2的参数参与因子
Tab.2 IEEE 68 bus system mode 2 parameter PF
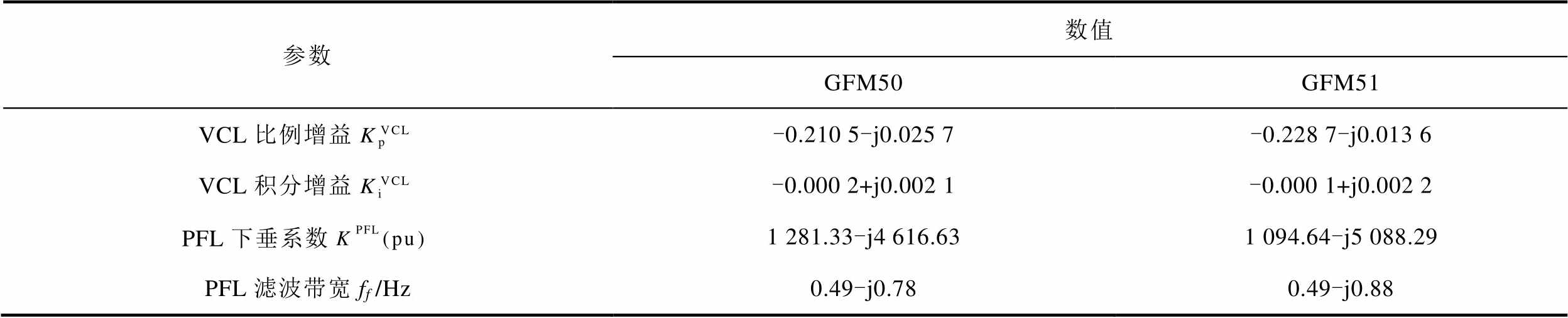
参数数值 GFM50GFM51 VCL比例增益-0.210 5-j0.025 7-0.228 7-j0.013 6 VCL积分增益-0.000 2+j0.002 1-0.000 1+j0.002 2 PFL下垂系数1 281.33-j4 616.631 094.64-j5 088.29 PFL滤波带宽ff /Hz0.49-j0.780.49-j0.88
由参数参与因子的实部可知,在VCL中提高PI控制器的比例增益,以及在PFL中减小下垂系数是不同控制环中改善系统稳定性的较好方式。图13给出了将GFM50和GFM51的下垂增益由0.001减小为0.000 5的极点分布,模式2阻尼的增大说明了所提参数参与因子在指导改善系统稳定性方面的有效性。
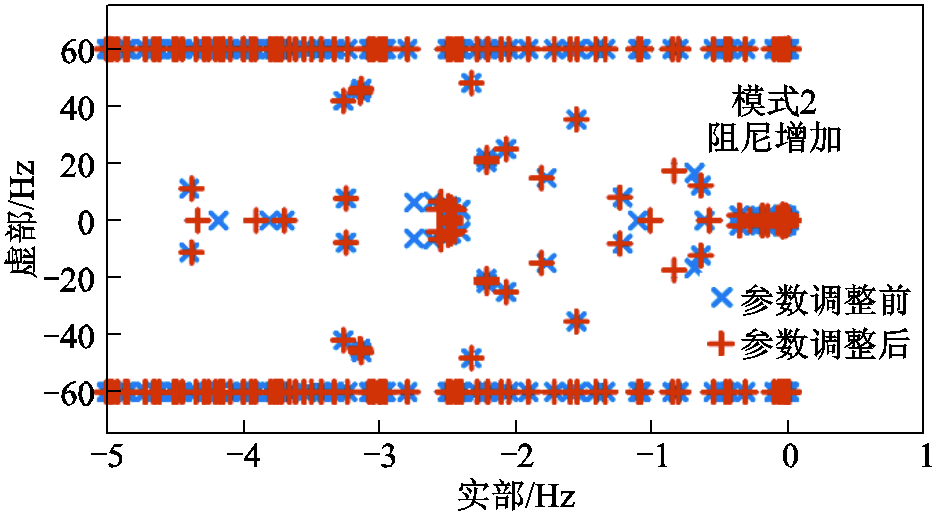
图13 参数调整前后极点分布
Fig.13 Pole distribution before and after parameter tuning
MASS需要完整的系统信息,且不适用于黑箱或灰箱模型。MAI可对逆变器进行整体动态评估,但无法深入洞察逆变器的内部动态。本文所提出的EMAI结合了MASS和MAI的优点,实现了对GFM内部动态的统一度量。GFM的交流电压环和电气地理位置引起的动态交互体现为GFM的电磁动态,GFM的功率频率同步环引起的动态交互体现为GFM的同步动态。EMAI有助于厘清影响系统稳定性的根本原因,并且EMAI的计算只需要系统局部的阻抗/导纳模型,这意味着EMAI应用于大规模电力系统时具有很强的可扩展性。未来的工作重点是将这种方法扩展到不同控制结构的逆变器。
附 录
附表1 IEEE 14母线系统逆变器参数
App.Tab.1 IEEE 14 bus system inverter parameters
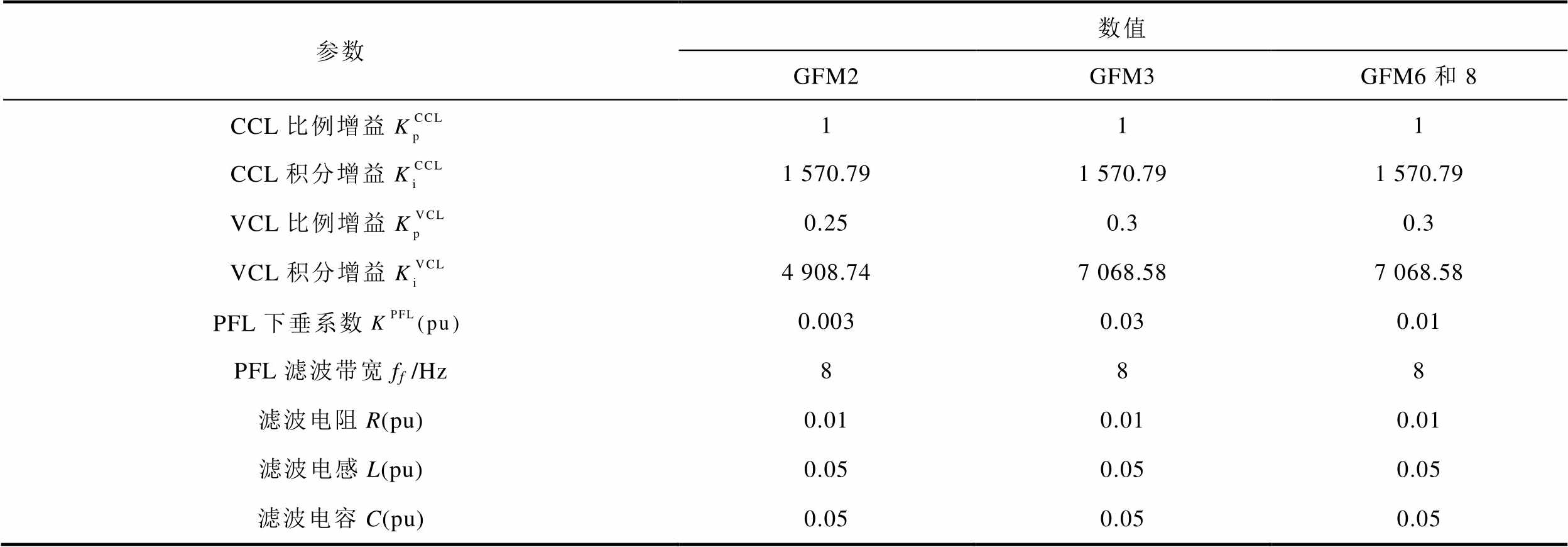
参数数值 GFM2GFM3GFM6和8 CCL比例增益111 CCL积分增益1 570.791 570.791 570.79 VCL比例增益0.250.30.3 VCL积分增益4 908.747 068.587 068.58 PFL下垂系数0.0030.030.01 PFL滤波带宽ff /Hz888 滤波电阻R(pu)0.010.010.01 滤波电感L(pu)0.050.050.05 滤波电容C(pu)0.050.050.05
附表2 情况1~4的PI控制参数
App.Tab.2 Case 1~4 PI control parameters

参数数值 情况1情况2情况3情况4 VCL比例增益0.150.20.250.3 VCL积分增益1 767.153 141.594 908.747 068.58
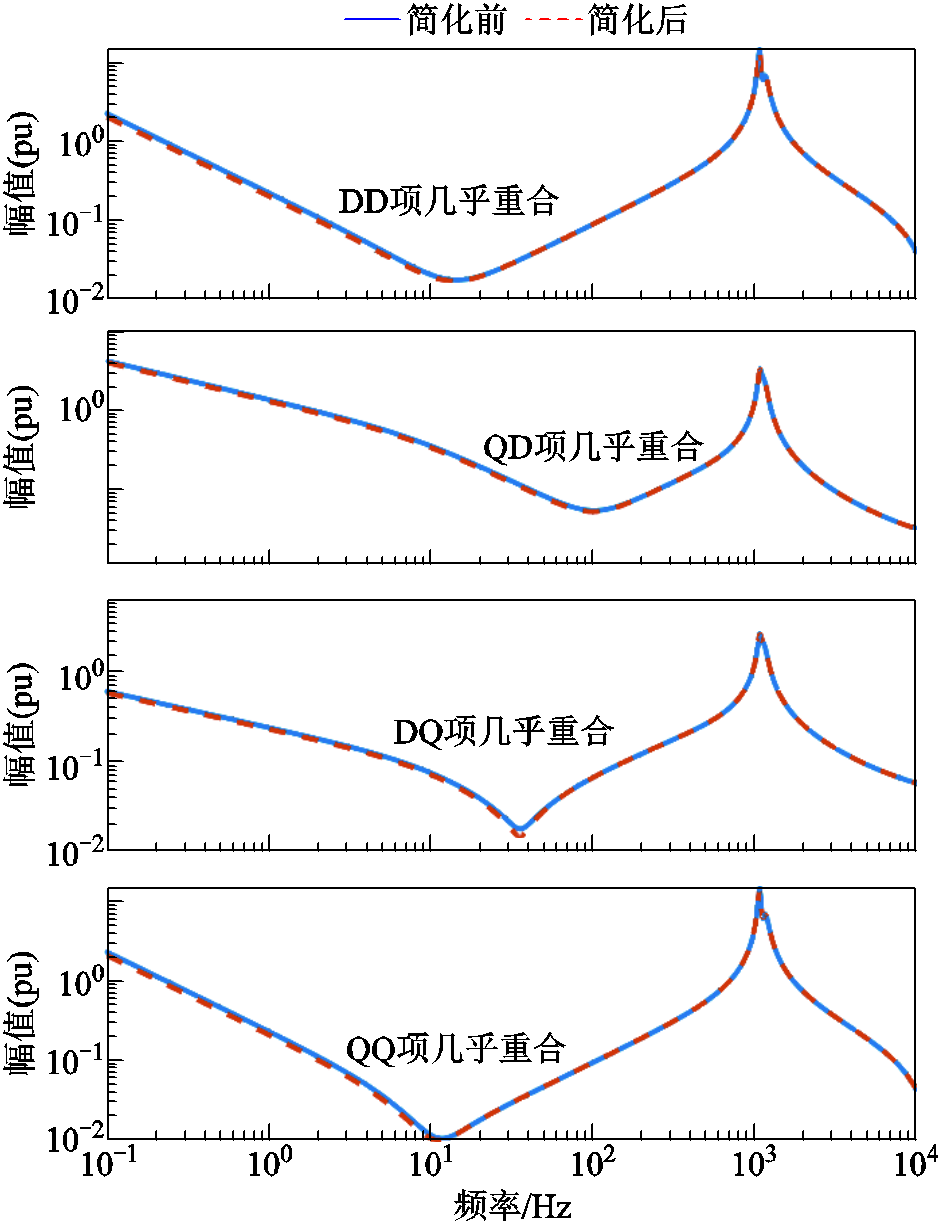
附图1 GFM简化前后的阻抗对比
App.Fig.1 Impedance comparison before and after GFM simplification
附表3 IEEE 68母线系统逆变器参数
App.Tab.3 IEEE 68 bus system inverter parameters

参数数值(所有GFM) CCL比例增益0.83 CCL积分增益1 308.99 VCL比例增益0.46 VCL积分增益19 798.58 PFL下垂系数0.001 PFL滤波带宽ff /Hz5 滤波电阻R(pu)0.01 滤波电感L(pu)0.05 滤波电容C(pu)0.05
参考文献
[1] Blaabjerg F, Yang Yongheng, Kim K A, et al. Power electronics technology for large-scale renewable energy generation[J]. Proceedings of the IEEE, 2023, 111(4): 335-355.
[2] Kim J K, Kang J, Shim J W, et al. Dynamic performance modeling and analysis of power grids with high levels of stochastic and power electronic interfaced resources[J]. Proceedings of the IEEE, 2023, 111(7): 854-872.
[3] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[4] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528-3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528-3541.
[5] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes' participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[6] Hatziargyriou N, Milanovic J, Rahmann C, et al. Definition and classification of power system stability–revisited & extended[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3271-3281.
[7] Kundur P. Power System Stability and Control[M]. New York: McGraw-Hill, Inc, 1994.
[8] Kouki M, Marinescu B, Xavier F. Exhaustive modal analysis of large-scale interconnected power systems with high power electronics penetration[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2759-2768.
[9] Cao Wenchao, Ma Yiwei, Yang Liu, et al. D–Q impedance based stability analysis and parameter design of three-phase inverter-based AC power systems [J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 6017-6028.
[10] Xu W, Huang Zhenyu, Cui Yu, et al. Harmonic resonance mode analysis[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1182-1190.
[11] Huang Zhenyu, Cui Yu, Xu W. Application of modal sensitivity for power system harmonic resonance analysis[J]. IEEE Transactions on Power Systems, 2007, 22(1): 222-231.
[12] Cui Yu, Wang Xiaoyu. Modal frequency sensitivity for power system harmonic resonance analysis[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 1010-1017.
[13] Zhan Ying, Xie Xiaorong, Liu Huakun, et al. Frequency-domain modal analysis of the oscillatory stability of power systems with high-penetration renewables[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1534-1543.
[14] Li Yang, Shuai Zhikang, Liu Xuan, et al. Stability analysis and location optimization method for multiconverter power systems based on nodal admittance matrix[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 529-538.
[15] Chou S F, Wang Xiongfei, Blaabjerg F. Frequency-domain modal analysis for power-electronic-based power systems[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 4910-4914.
[16] Gu Yunjie, Li Yitong, Zhu Yue, et al. Impedance-based whole-system modeling for a composite grid via embedding of frame dynamics[J]. IEEE Transactions on Power Systems, 2021, 36(1): 336-345.
[17] Zhu Yue, Gu Yunjie, Li Yitong, et al. Participation analysis in impedance models: the grey-box approach for power system stability[J]. IEEE Transactions on Power Systems, 2022, 37(1): 343-353.
[18] Zhu Yue, Gu Yunjie, Li Yitong, et al. Impedance-based root-cause analysis: comparative study of impedance models and calculation of eigenvalue sensitivity[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1642-1654.
[19] Li Yitong, Gu Yunjie, Green T C. Mapping of dynamics between mechanical and electrical ports in SG-IBR composite grids[J]. IEEE Transactions on Power Systems, 2022, 37(5): 3423-3433.
[20] Hu Guang, Xiao Yi, Xin Huanhai, et al. An extended impedance model for power electronics converters retaining explicit synchronization dynamics[J]. IEEE Transactions on Power Electronics, 2025, 40(1): 2355-2370.
[21] Li Yitong, Gu Yunjie, Zhu Yue, et al. Impedance circuit model of grid-forming inverter: visualizing control algorithms as circuit elements[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3377-3395.
[22] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[23] Fan Lingling, Miao Zhixin. Time-domain measurement-based DQ-frame admittance model identification for inverter-based resources[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2211-2221.
[24] Li Yitong, Gu Yunjie, Green T C. Revisiting grid-forming and grid-following inverters: a duality theory [J]. IEEE Transactions on Power Systems, 2022, 37(6): 4541-4554.
Abstract The dynamic characteristic of grid-forming inverter (GFM) is mainly affected by the control strategy, and the interaction with the power grid may cause instability such as oscillation. At the same time, the interactive coupling between different time-scale controllers in GFM makes the stability analysis more complicated. Modal analysis based on the state-space model (MASS) uses the participation factor (PF) to quantify the contribution of each state variable to a particular pattern. However, the number of electrical components in new power systems is increasing explosively, and the difficulty of state-space modeling of the whole system is increasing rapidly. In addition, state-space modeling requires detailed system structure topology and complete control parameters of each electrical component, and inverters usually only have impedance models that describe the characteristics of voltage and current ports, with gray box or black box characteristics.
In order to explore the interaction characteristics among all electrical components of the system, the dynamic model of the whole system is constructed by the closed-loop feedback formula of the whole system dynamic matrix. Based on this foundation, the modal analysis based on impedance model (MAI) can evaluate the contribution of each power device to oscillation modes at the device level. However, MAI treats inverters as single, holistic components, which limits its ability to identify dominant system dynamics at the control loop or state variable level. Decomposing different control loops into equivalent circuit components enables the stability analysis of internal inverter dynamics. However, the decomposition of synchronization control loops remains to be explored. This paper proposes an extended modal analysis based on impedance model (EMAI) method to address the current challenges faced by MAI.
First, a decomposition method for the GFM impedance model based on the matrix inversion lemma was proposed, dividing GFM dynamics into synchronous dynamics (SD), dominated by the power frequency synchronization loop (PFL), and electromagnetic dynamics (ED), governed by the voltage control loop (VCL). The detailed categorization of dynamics facilitates an in-depth exploration of the complex coupling mechanisms among controllers operating on different time scales. Subsequently, overall impedance participation factors and participation ratios (PR) were introduced to characterize different internal dynamics of GFM, enabling the evaluation of SD and ED contributions at the control loop level. These metrics help identify the dominant system dynamics and trace the root causes of system instability. Finally, an explicit parameter PF was introduced to precisely locate the critical control parameters of identified loops, serving as a metric for optimizing control parameters and enhancing system damping.
The analysis yields the following conclusion: as the frequency of oscillation modes decreases, the dominant dynamics within each GFM gradually shift from ED to SD. MAI can provide an overall assessment of GFM participation but fails to capture the dominant dynamics of individual GFMs. EMAI not only identifies interactions between various GFMs and the grid but also evaluates the contributions of ED and SD within GFM through overall impedance participation factors, thereby pinpointing the primary causes affecting system dynamics to specific control loops. Moreover, the results of EMAI and MASS in assessing the participation levels of different GFM dynamics are highly consistent, validating the effectiveness of the EMAI method. Furthermore, the explicit parameter PF provides effective recommendations for improving system damping and enhancing stability. EMAI offers nuanced insights into system stability analysis, enabling the rapid identification of the root causes of system instability.
Keywords:Grid-forming inverter (GFM), extended impedance modal analysis, impedance decomposition, participation factor
中图分类号:TM614
DOI:10.19595/j.cnki.1000-6753.tces.242266
国家自然科学基金资助项目(52307095)。
收稿日期2024-12-17
改稿日期 2025-01-07
郑 乐 男,1989年生,副教授,研究方向为人工智能及其在电力系统稳定与控制的应用。
E-mail:zhengl20@ncepu.edu.cn(通信作者)
郑佳杰 男,2001年生,硕士研究生,研究方向为电力系统稳定与控制。
E-mail:zjj978626117@163.com
(编辑 赫 蕾)