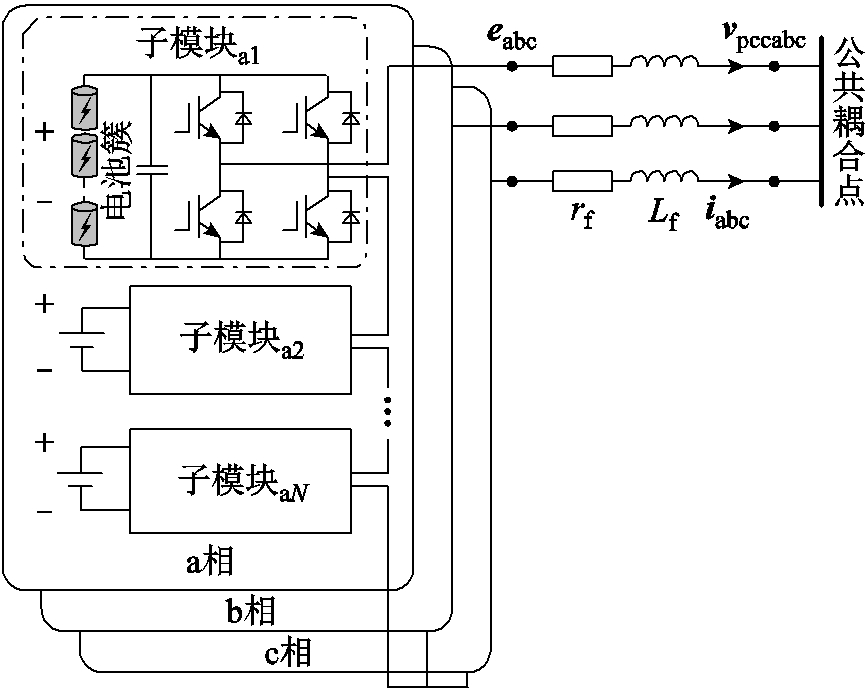
图1 基于级联H桥的直挂式储能系统拓扑
Fig.1 Topology of the cascaded H-bridge transformerless energy storage system
摘要 构网型储能技术是提升新型电力系统稳定性的重要手段,而直挂式储能系统凭借其高效率、模块化和无需变压器等优势,成为实现大容量构网型储能的优选方案。然而,由于直挂式储能系统直接接入中高压电网,与电网之间的电气距离更近,导致其面临更低的电网阻抗。电网阻抗的减小会降低构网型系统的稳定裕度,构网型控制的稳定性面临严峻挑战。为解决这一问题,该文提出了基于阻抗增强的稳定性提升控制策略。通过等效内电压控制将滤波电感复用为耦合阻抗,从而在物理层面增强了耦合阻抗,将低电网阻抗下的不稳定系统转变为稳定系统;针对阻尼不足而引发的功率振荡问题,通过自适应虚拟阻抗等效增强耦合阻抗,提高系统阻尼比,并提供可靠的限流功能。等效内电压控制与虚拟阻抗协同作用,有效地提升了低电网阻抗下的构网型直挂式储能系统的稳定性。零电网阻抗下的实验结果验证了策略的有效性。
关键词:直挂式储能 构网 稳定性 虚拟阻抗 虚拟同步机
随着以新能源为主体的新型电力系统的加速构建,以电池储能为代表的新型储能技术因其快速响应和灵活布局等优势,已成为保障新能源高效开发和电力系统稳定运行的重要支撑[1]。截至2024年6月底,我国新型储能累计装机容量已达到48.18 GW,预计到2030年将增至313.9 GW[2]。在各类储能技术中,基于级联H桥结构的直挂式电池储能系统由于无需变压器即可接入中高压电网,且具有大容量、高效率和模块化等优势,已成为大容量储能并网的优选方案[3-4]。
储能变流器作为电池与电网之间功率交换的核心接口,其控制方式对系统整体性能与稳定性起着决定性作用。从同步机制的角度来看,储能变流器的并网控制策略主要分为跟网型和构网型两类[5]。跟网型控制采用锁相环与电网电压保持同步,通过控制电流来调节输出功率[6]。然而,跟网型本质上是电流源,难以为电网提供电压支撑。研究表明,跟网型控制在低频段存在负阻抗效应,在弱电网下容易出现稳定性问题[7]。相比之下,构网型控制通过功率控制与电网同步,自主构建交流侧电压的幅值和频率,作为电压源为电网提供电压和频率的支撑[8-9]。此外,虚拟同步机(Virtual Synchronous Generator, VSG)通过模拟同步发电机的摇摆方程,可以为电网提供惯量和阻尼[10]。凭借上述优势,构网型储能技术已成为提升新型电力系统稳定性的重要手段,各国已制定多项政策与技术标准,以推动构网型储能技术的发展和应用[11]。
与跟网型系统不同,构网型系统作为电压源,在弱电网条件下具有较高的稳定性,但在强电网条件下却易出现同步失稳问题[12]。根据 IEEE 标准 1204—1997,通常采用短路比(Short Circuit Ratio, SCR)来衡量电网的强度[13]。短路比与电网阻抗呈反比关系,阻抗较低的电网被定义为强电网[14]。目前,关于构网型系统稳定性的研究主要集中于弱电网条件,但由强电网引发的失稳问题暂未得到有效解决[15-16]。其物理机制为:构网变流器作为电压源运行,若电网阻抗较低,构网电压与电网电压之间的微小偏差可能引发显著的电流冲击,最终导致失稳。现有研究通过小信号模型分析指出,强电网下VSG系统的虚轴附近存在一对共轭极点,是导致同步失稳的根本原因[17]。
为提升系统稳定性,一种方法是调整控制回路参数,例如增大惯性系数或减小阻尼系数[18]。然而,该方法的有效性依赖电网阻抗,当电网阻抗低于一定阈值时,系统极点可能进入右半平面,导致失稳[19]。另一种稳定性提升方法是虚拟阻抗技术,通过引入虚拟电阻或虚拟电感对系统耦合阻抗进行补偿,提高系统稳定性与谐波抑制能力[20-21]。然而,虚拟阻抗的补偿能力有限,过大的虚拟阻抗可能引发新的振荡问题[22]。此外,虚拟阻抗是通过控制算法等效增加源侧等效内阻抗,难以从物理层面替代真实阻抗的隔离作用[23],系统在低电网阻抗下仍然面临稳定性问题。
此外,上述研究多针对低压系统展开,而直挂式储能系统因直接接入中高压电网,与电网间的电气距离更近、电网阻抗更低,其构网型控制稳定性会面临更严峻的挑战。然而,目前针对直挂式储能系统的构网型控制技术尚缺乏系统性研究,其在低电网阻抗条件下的稳定性风险仍未得到有效解决。
为解决上述问题,本文以构网型直挂式储能系统为研究对象,提出了一种基于阻抗增强的稳定性提升控制策略。首先,通过小信号模型分析了电网阻抗对系统稳定性的影响机制,表明电网阻抗的降低会降低系统稳定裕度,甚至可能引发次同步振荡问题;其次,针对该问题,提出了一种等效内电压控制策略,通过复用滤波电感从物理层面增强耦合阻抗,使低电网阻抗下的不稳定系统转变为稳定系统;然后,在此基础上,通过自适应虚拟阻抗策略等效增加耦合阻抗,提升系统阻尼比,从而抑制功率振荡;最后,基于级联H桥直挂式储能系统实验平台,在零电网阻抗的极端工况下进行实验,结果表明,所提控制策略能够有效地提升系统稳定性。
基于级联H桥的直挂式电池储能系统拓扑如图1所示。其中,每个子模块具有相同的电路结构,包括电池簇、电容和H桥。各相由N个子模块串联后,通过电感滤波器Lf连接到公共耦合点(Point of Common Coupling, PCC)。图1中,rf为Lf的等效电阻,eabc为在滤波器之前由变流器开关产生的内电压,vpccabc为PCC电压,iabc为注入电网的输出电流。本文中,下标“dq”和“abc”分别表示对应坐标系下的变量。

图1 基于级联H桥的直挂式储能系统拓扑
Fig.1 Topology of the cascaded H-bridge transformerless energy storage system
图2为基于虚拟同步机控制的直挂式储能并网系统等效电路与控制框图。公共耦合点至电网间的电网电感和电阻分别以Lg和rg表示,vg为电网电压。
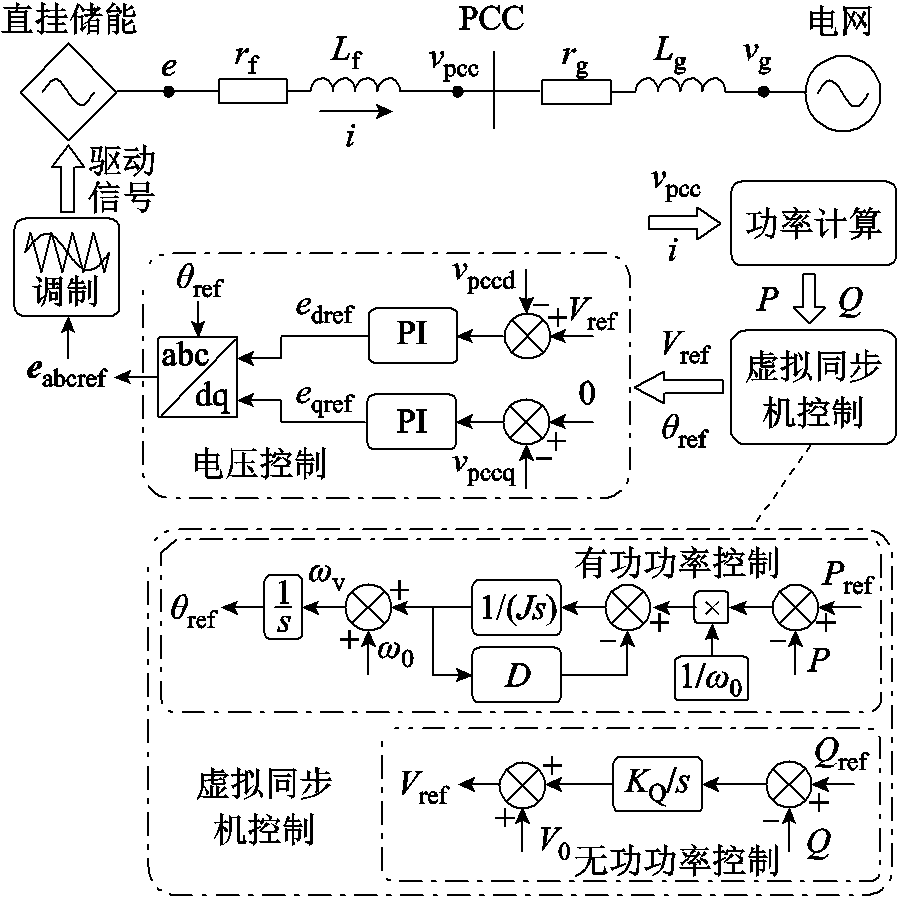
图2 基于虚拟同步机的直挂式储能系统等效电路与控制框图
Fig.2 Equivalent circuit and control block diagram of the transformerless energy storage system based on the VSG
虚拟同步机控制包含有功功率控制与无功功率控制两部分,分别根据输出有功功率和无功功率产生电压参考相位θref和参考电压Vref,其过程可描述为[10]
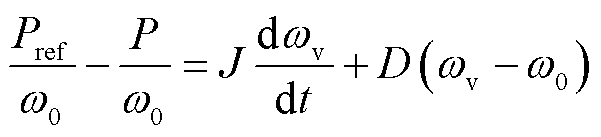 (1)
(1)
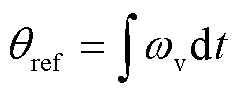 (2)
(2)
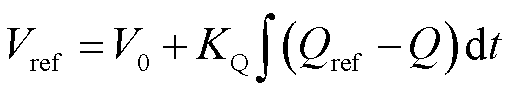 (3)
(3)
式中,ωv为虚拟同步机输出的转子角频率;P和Q分别为输出有功功率和无功功率;J和D分别为虚拟同步机惯量系数和阻尼系数;KQ为无功功率控制系数;ω0和V0分别为电网电压的额定角频率和幅值。
构网型系统最简单的电压控制方法是将功率同步控制生成的参考电压直接作为调制信号。但由于缺少反馈机制,这种方法难以应对外部扰动。为提高抗扰性,常通过比例积分控制器对电压矢量进行闭环控制,从而实现对输出电压的精准调节[24]。电压控制调节vpcc跟踪θref和Vref,产生调制信号参考eref。而后,再通过多电平调制策略产生驱动信号,最终驱动直挂式储能系统运行。
电网阻抗是影响构网型储能系统并网性能与稳定性的关键因素[7]。从公共耦合点向电网看去,电网阻抗的主要构成包括传输线路阻抗、变压器阻抗以及电网内部阻抗。图3给出了低压储能系统和直挂式储能系统的典型并网结构示意图。需要说明的是,Zf1和Zf2分别为低压和直挂式储能系统自身的滤波器阻抗,不属于电网阻抗。假设220 kV电网为无穷大电网,忽略其内部阻抗。传输线路和变压器的典型阻抗参数见表1。
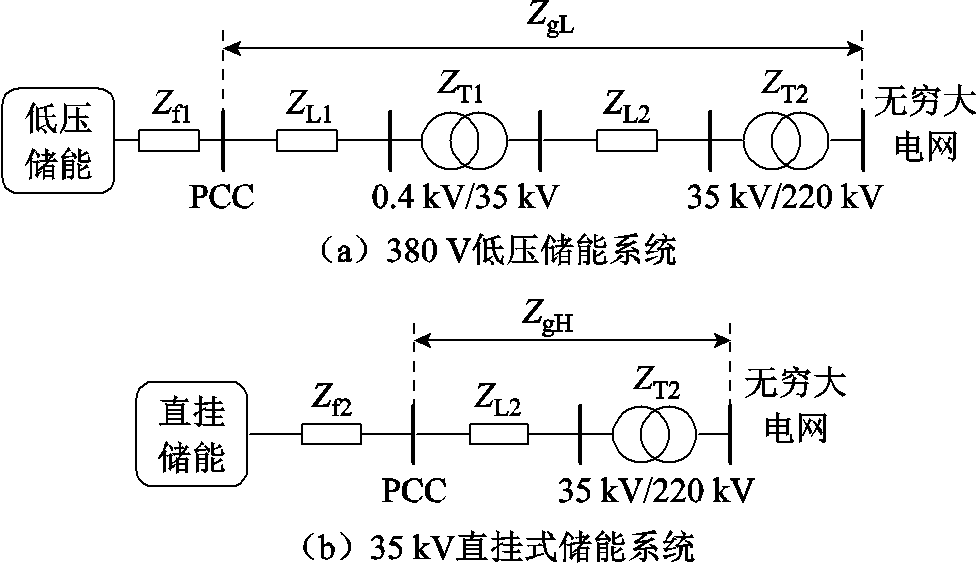
图3 两种储能系统并网结构示意图
Fig.3 Grid-connected structure of two energy storage systems
表1 传输线路和变压器的典型阻抗参数[23, 25]
Tab.1 Typical impedance parameters of transmission lines and transformers[23, 25]

参数数值阻感比 0.4 kV线路阻抗ZL10.647 Ω/km7.70 35 kV线路阻抗ZL20.249 Ω/km0.85 0.4 kV/35 kV变压器阻抗ZT1(pu)0.065— 35 kV/220 kV变压器阻抗ZT2(pu)0.12—
相较于低压储能系统,直挂式储能系统的接入方式显著缩短了与无穷大电网之间的电气距离。低压储能系统通过低压传输线路(ZL1)和0.4 kV/35 kV低压变压器(ZT1)接入35 kV电网,再经过高压传输线路(ZL2)和35 kV/220 kV变压器(ZT2)逐级接入无穷大电网。对于低压储能系统,其电网阻抗ZgL可表示为
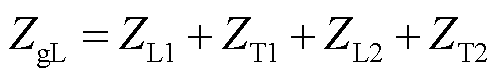 (4)
(4)
相比之下,直挂式储能系统直接接入35 kV电网,仅通过高压传输线路和35 kV/220 kV变压器接入无穷大电网。由于省略了低压传输线路和低压变压器,对于直挂式储能系统的电网阻抗ZgH为
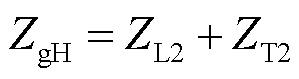 (5)
(5)
显然,直挂式储能系统的电网阻抗明显低于低压储能系统,即ZgH<ZgL。从短路比的角度来看,单馈入系统的短路比定义[14]为
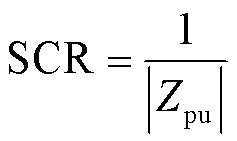 (6)
(6)
式中,Zpu为电网阻抗的标幺值。由式(6)可知,更低的电网阻抗意味着更高的短路比或更强的电网。
对于构网型设备而言,其作为电压源运行,必须依赖物理阻抗来隔离自身与电网之间的耦合。采用图2所示的构网型控制时,由于控制的电压是PCC电压,构网电压和电网电压间的耦合阻抗等于电网阻抗。当电网阻抗较低时,PCC电压与电网电压之间的微小偏差会导致大幅度的电流冲击和功率波动,这种动态失配可能进一步引发同步失稳。另一方面,中高压传输线路的阻感比显著低于低压传输线路,电网阻抗中电阻成分占比降低,可能影响构网型系统的稳定性。
综上所述,直挂式储能系统由于直接接入中高压电网,与大电网的电气距离更近,其应用场景通常表现出电网阻抗更低的特征,可能影响构网型系统的运行稳定性。针对该问题,需开展电网阻抗对构网型系统稳定性的影响性分析。
为分析电网阻抗对构网型直挂式储能系统稳定性的影响,建立了系统的小信号模型。基于基尔霍夫电压定律,对图2所示的系统进行建模,系统的动态行为可通过小信号模型描述为
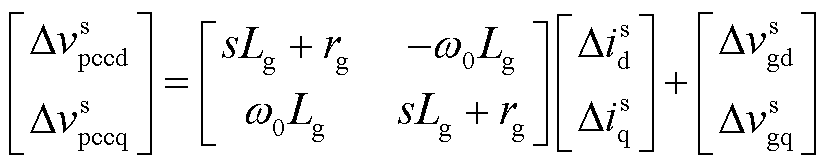 (7)
(7)
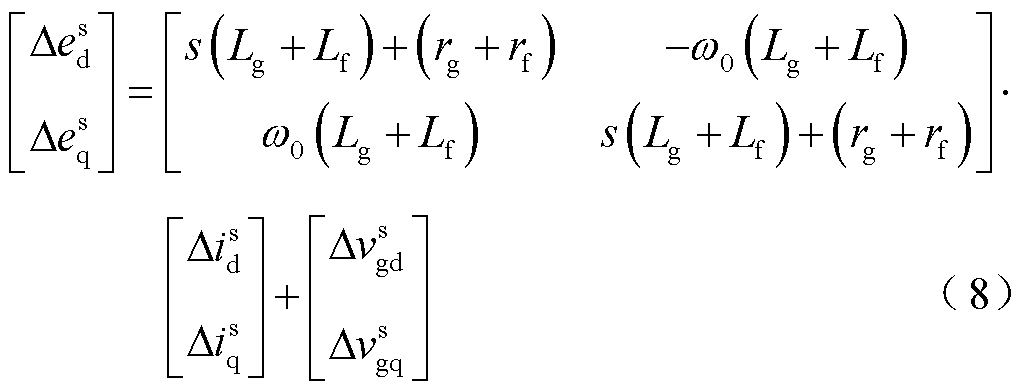
式中,上标“s”表示由电网电压定义的系统dq坐标系下的变量。虚拟同步机控制引入了变流器并网系统中的两个dq坐标系[26]——系统dq坐标系和控制器dq坐标系。系统和控制器dq坐标系如图4所示,其中,上标“c”表示控制器dq坐标系下的变量。
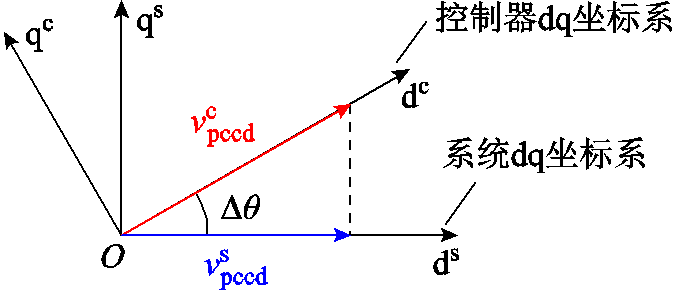
图4 系统和控制器dq坐标系
Fig.4 The dq coordinate system of the system and the controller
系统dq坐标系以电网电压为基准定义,而控制器dq坐标系由虚拟同步机控制产生的θref决定,其位置通过有功功率控制和电压控制来确定。在稳态运行时,这两个坐标系保持一致。
当电网电压受到小信号扰动时,系统dq坐标系的位置会随之变化。然而,由于虚拟同步机控制固有的动态特性(包括惯性和阻尼),控制器dq坐标系无法实时跟随系统dq坐标系的变化,这将导致两个坐标系之间出现角度偏差Δθ。Δθ由虚拟同步机控制决定,其小信号模型可以表示为
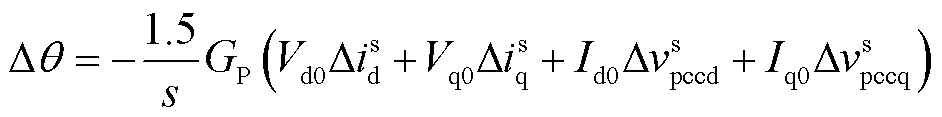 (9)
(9)
式中,大写变量和下标“0”表示对应变量在小信号扰动发生前的稳态值;GP为虚拟同步机控制的传递函数,其表达式为
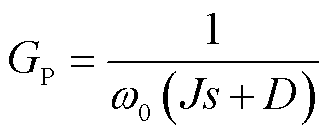 (10)
(10)
在控制器dq坐标系下,图2所示电压控制的小信号模型可以描述为
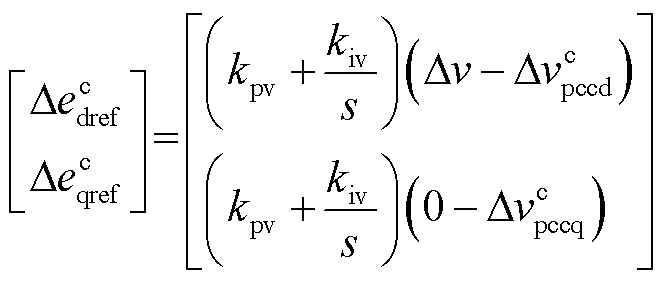 (11)
(11)
式中,Δv为电压参考上的小信号扰动;kpv、kiv分别为电压PI控制器的比例和积分系数。系统dq坐标系下的矢量通过矩阵TΔθ变换到控制器dq坐标系下,其表达式为
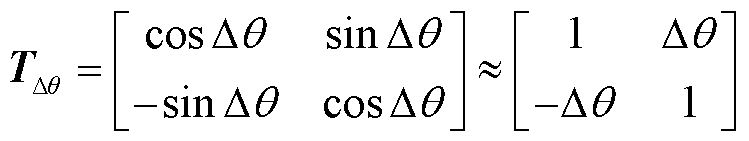 (12)
(12)
两坐标系间PCC电压、内电压和输出电流的变换关系为
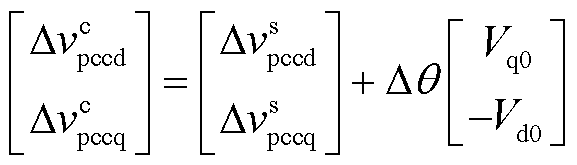 (13)
(13)
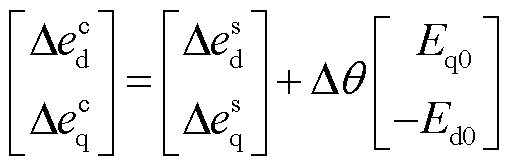 (14)
(14)
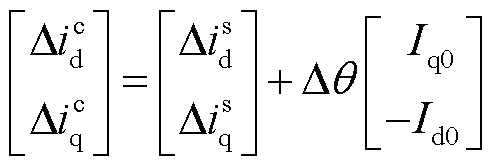 (15)
(15)
将式(12)分别代入式(13)~式(15),整理得到控制器dq坐标系下的变量表达式为
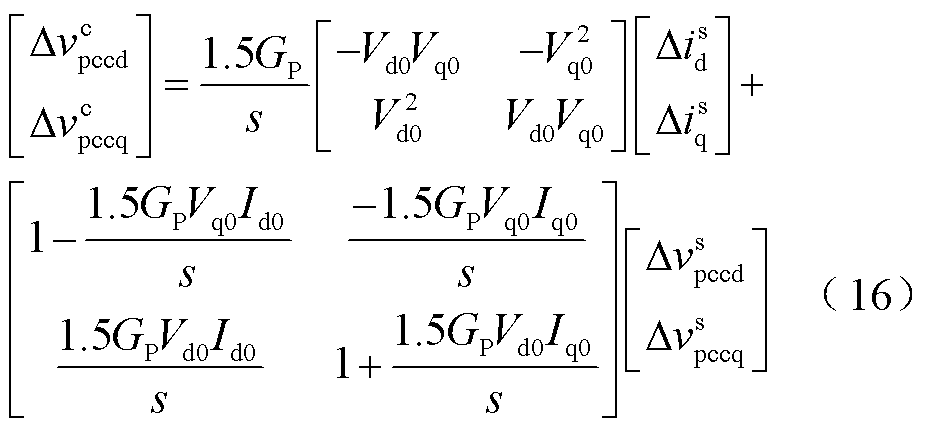
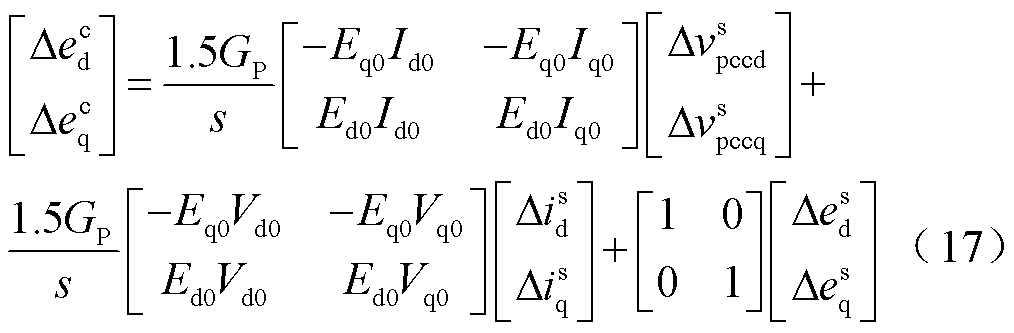
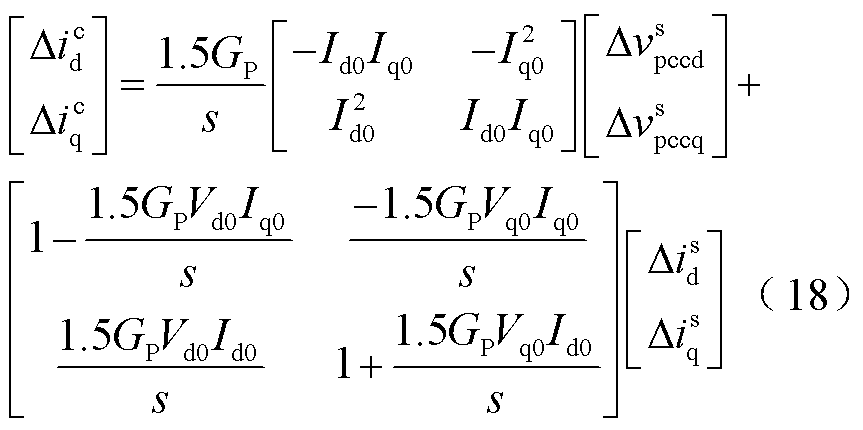
最后,联立式(7)、式(8)、式(11)、式(16)~式(18),得到基于虚拟同步机控制的构网型直挂式储能系统的全阶小信号模型。
构网型变换器常表现为两种典型的低频振荡,分别为同步振荡(约ω0)和次同步振荡(低于ω0)[15, 27]。这两种振荡的产生机制较为复杂,受到多方面因素的影响。总体来看,同步振荡主要由构网功率控制模型中的固有极点引发,可以通过优化整定功率控制参数抑制[20, 28]。另外,当构网变换器接入强电网时,功率控制和电压控制间的相互作用容易引发次同步振荡[27, 29]。
考虑到2.1节中全阶小信号模型较为复杂,难以直接观察到具体的不稳定机制。首先以虚拟同步机的简化模型为例进行分析。在功角较小时,sinΔθ≈Δθ,ΔP可以近似计算为
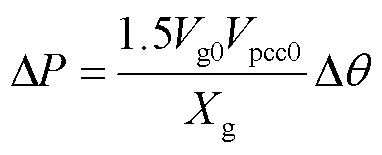 (19)
(19)
式中,Xg为电网电抗;Δθ由虚拟同步机控制产生。由于电压控制的带宽通常远高于虚拟同步机控制,系统的开环传递函数可以简化描述[27]为
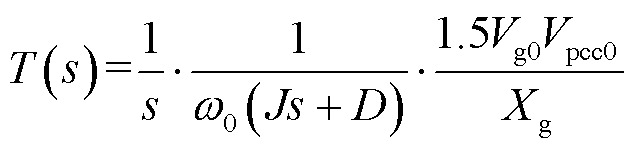 (20)
(20)
则系统的闭环传递函数为
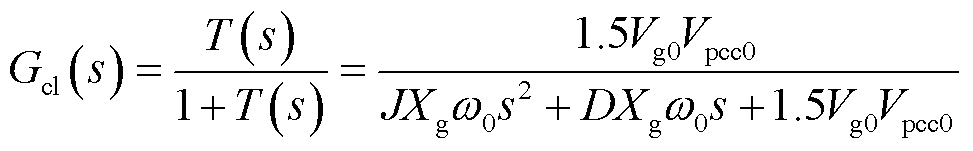 (21)
(21)
根据式(21),可以求得系统的阻尼比为
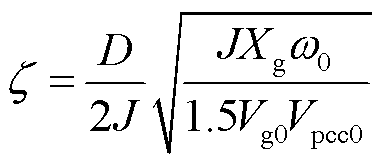 (22)
(22)
从式(22)可以看出,电网阻抗的降低会削减系统的阻尼比,从而降低系统的稳定裕度。为定量分析电网阻抗对构网型系统稳定性的影响,以及强电网下的系统振荡模式,基于2.1节建立的系统全阶小信号模型,利用Matlab求解系统闭环极点。分别针对电网电感降低和电网电阻降低的情况,探讨不同阻抗条件对系统稳定性的影响。
首先,分析电网电感大小对系统稳定性的影响。在电网电阻一定的情况下(rg=0.04(pu)),电网电感从0.18(pu)逐渐减小至0,系统的闭环极点分布如图5所示。随着电网电感的降低,主导极点逐渐向右移动。当电网电感值低于临界点(约0.1(pu))时,极点穿越虚轴进入右半平面,系统转变为不稳定状态。
电网电感降低时的不稳定主导极点见表2。结果表明频率主要集中在6~14 Hz,具有典型的次同步振荡特征。不同电网电感下的构网变换器并网过程的仿真波形(rg=0.04(pu))如图6所示。当电网电感为0.3(pu)时,系统能够保持稳定;但当电网电感减小为0.1(pu)时,有功功率出现了约11.9 Hz的次同步振荡,振荡频率与模型结果接近。因此,过低的电网电感会导致系统稳定裕度降低,甚至导致主导极点进入右半平面,引发次同步振荡问题。
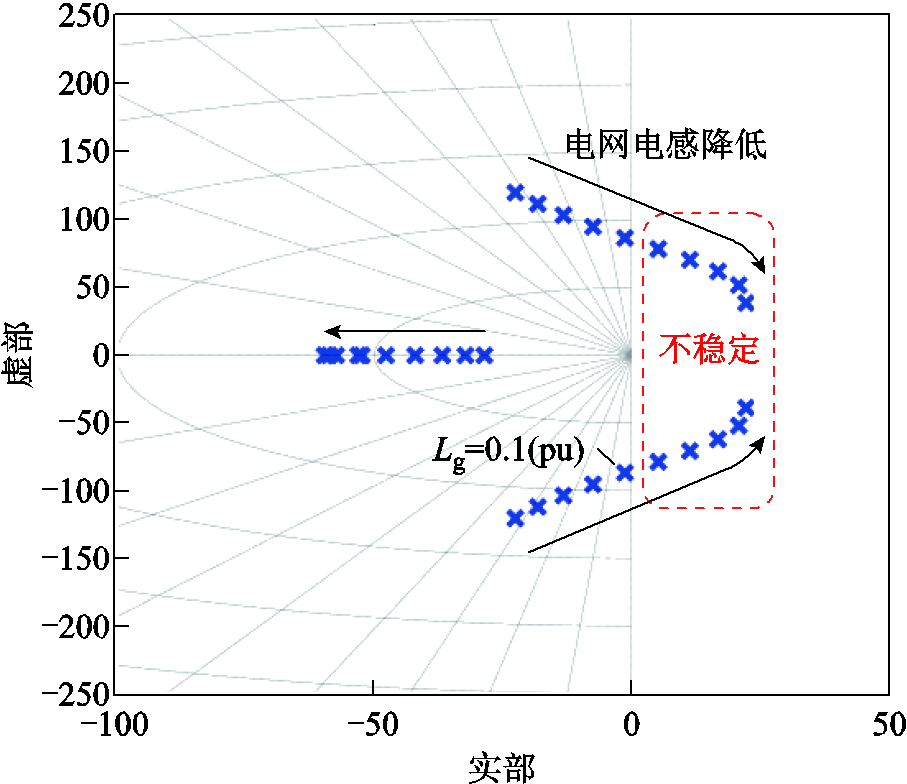
图5 电网电感降低时的系统极点分布
Fig.5 System pole distribution when the grid inductance decreases
表2 电网电感降低时的主导极点
Tab.2 Dominant poles when the grid inductance decreases
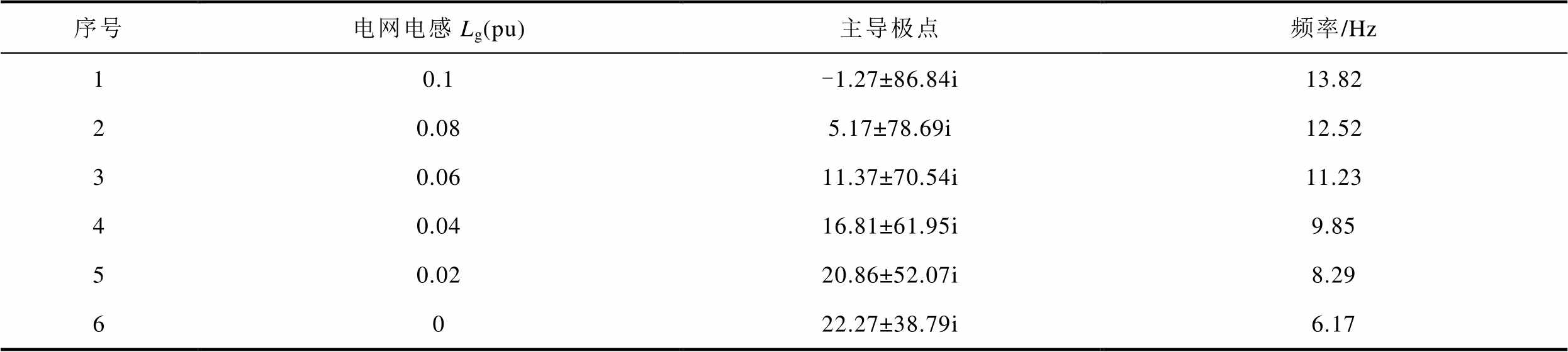
序号电网电感Lg(pu)主导极点频率/Hz 10.1-1.27±86.84i13.82 20.085.17±78.69i12.52 30.0611.37±70.54i11.23 40.0416.81±61.95i9.85 50.0220.86±52.07i8.29 6022.27±38.79i6.17
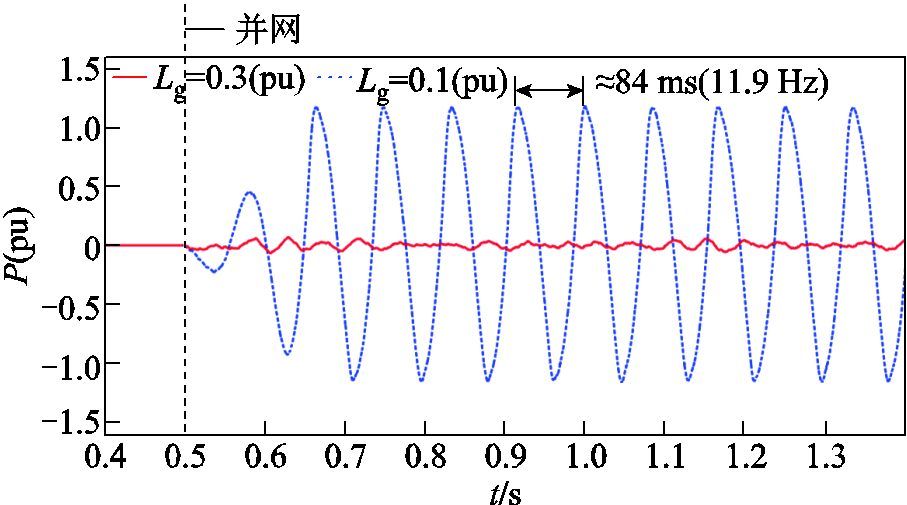
图6 不同电网电感下的并网过程仿真波形
Fig.6 Simulation waveforms of grid-connected process under different grid inductances
进一步研究了电网电阻变化对系统稳定性的影响。图7展示了在电网电感一定的情况下(Lg= 0.2(pu)),电网电阻从0.18(pu)逐步减小至0时系统的闭环极点分布。随着电网电阻的降低,主导极点逐渐向更低阻尼比的方向移动,并逐步靠近虚轴。在电网电阻接近0的情况下,主导极点几乎完全逼近虚轴,系统处于临界稳定状态,系统的稳定裕度显著降低。
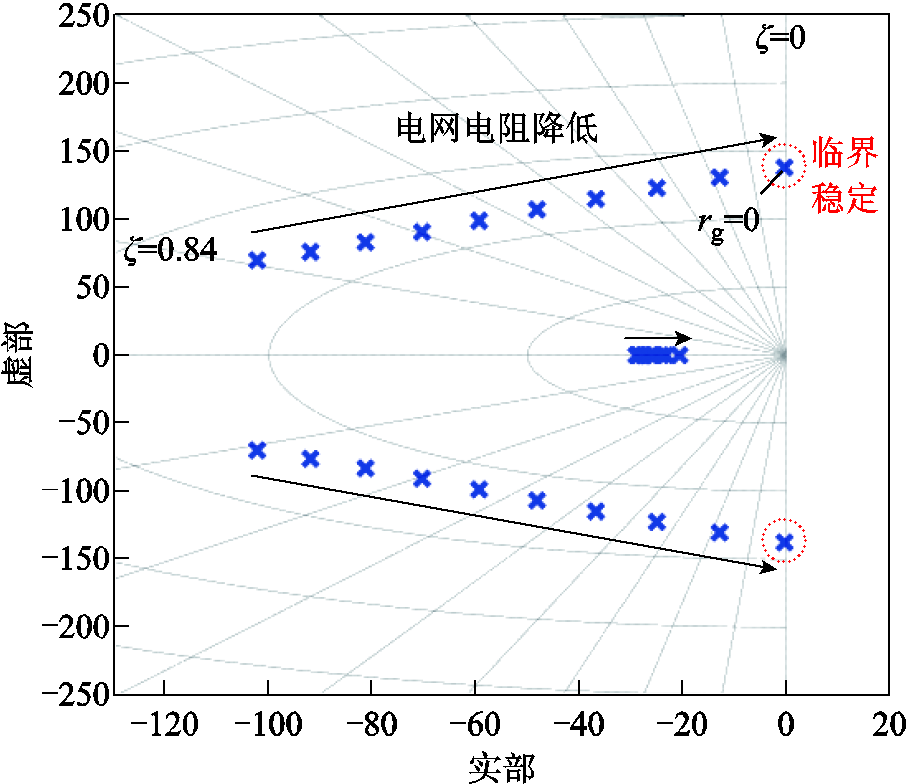
图7 电网电阻降低时的系统极点分布
Fig.7 System pole distribution when the grid resistance decreases
电网电阻降低时的主导极点见表3。结果显示随着电网电阻的降低,系统的阻尼比显著下降。图8展示了不同电网电阻下的构网变换器有功功率阶跃过程的仿真波形(Lg=0.2(pu))。当电网电阻为0.1(pu)时,系统能够完成稳定的阶跃响应;而当电网电阻减小为0(pu)时,阶跃过程中有功功率逐渐发散,并出现约24.4 Hz的次同步振荡,系统失稳。上述分析表明,电网电阻较低时,会显著削弱系统的阻尼比,增加系统失稳风险。
表3 电网电阻降低时的主导极点
Tab.3 Dominant poles when the grid resistance decreases
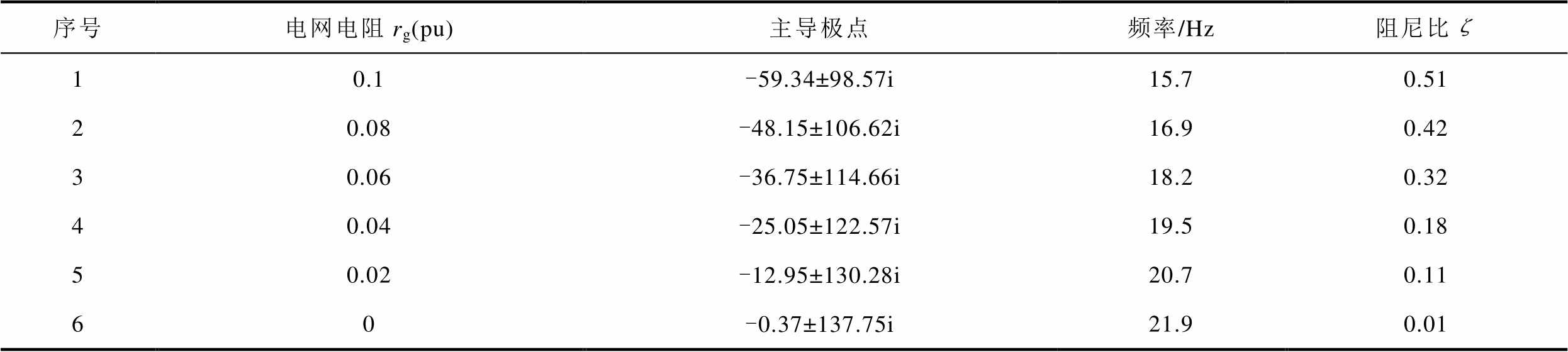
序号电网电阻rg(pu)主导极点频率/Hz阻尼比ζ 10.1-59.34±98.57i15.70.51 20.08-48.15±106.62i16.90.42 30.06-36.75±114.66i18.20.32 40.04-25.05±122.57i19.50.18 50.02-12.95±130.28i20.70.11 60-0.37±137.75i21.90.01
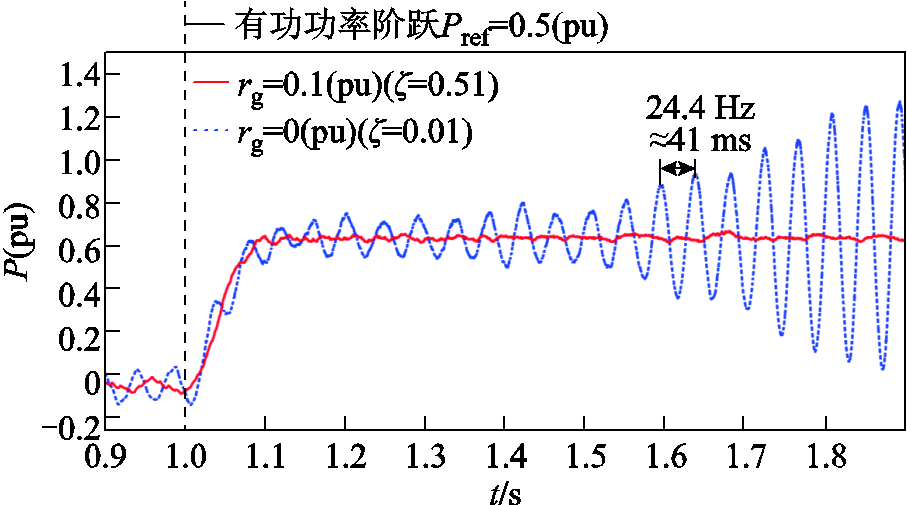
图8 不同电网电阻下的有功功率阶跃仿真波形
Fig.8 Simulation waveforms of active power step response under different grid resistances
通过上述分析可知,电网阻抗的减小会降低构网型系统的稳定裕度,可能引发次同步振荡问题。其中,过低的电网电感会导致系统极点移至右半平面,而过低的电网电阻会对系统阻尼比产生负面影响。中高压场景下的低电网阻抗特性,严重威胁了构网型直挂储能系统的稳定性。为解决这一问题,亟须开展稳定性提升控制策略研究。
针对构网型直挂式储能系统在低电网阻抗场景下稳定性不足的问题,本文提出一种基于等效内电压控制与虚拟阻抗的阻抗增强策略。
图2所示的传统构网型控制中,PCC电压作为受控电压源,构网系统与电网间的耦合阻抗等于电网阻抗。然而,在低电网阻抗条件下,PCC电压的小幅波动可能导致显著的电流冲击和功率振荡,严重影响系统的稳定性。针对上述问题,若将受控电压从PCC前移至变流器侧的内电压,通过将滤波器阻抗纳入系统与电网之间的耦合阻抗,可以实现物理阻抗的增强。在图2控制结构的基础上,通过替换电压环的反馈变量为内电压e,理论上可实现物理阻抗的增强。然而,变流器内电压通过高频开关直接调制生成,直接测量内电压需要高精度的采样硬件与算法,增加了系统的成本与复杂性。
由于内电压由调制电压参考值决定,其值可以通过调制电压参考值近似估算。为避免直接测量变流器内电压,采用上一控制周期的调制电压参考值对内电压进行估测,控制结构如图9所示,得到的等效内电压edq,EQ为
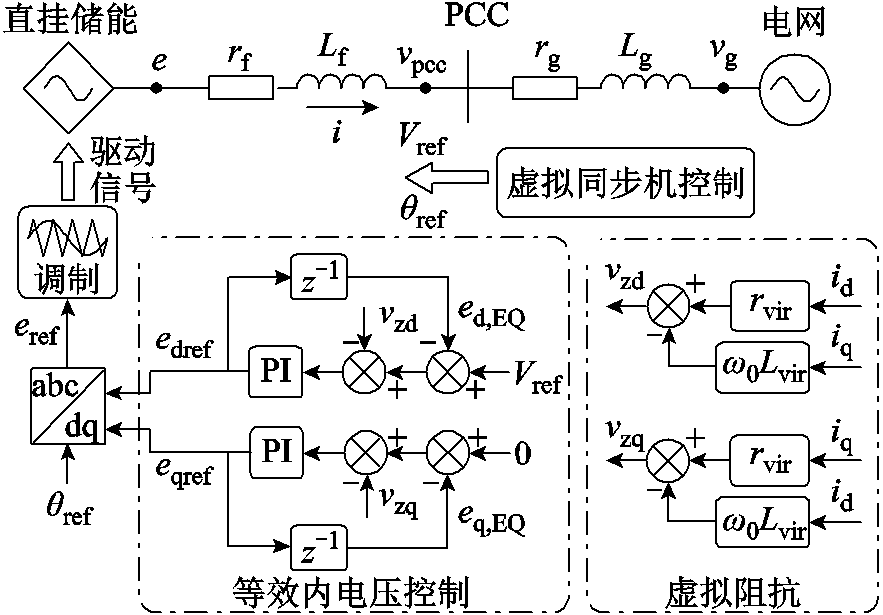
图9 基于等效内电压控制与虚拟阻抗的阻抗增强策略
Fig.9 Impedance enhancement strategy based on the equivalent internal voltage control and the virtual impedance
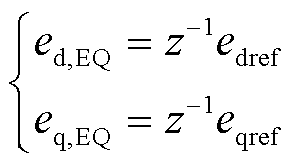 (23)
(23)
式中,z-1为数字控制器一个控制周期的延时。通过这种方式,无需额外增加硬件即可实现对内电压的控制,从而在物理层面增大耦合阻抗。
此外,考虑到变换器自身滤波器阻抗通常较小(一般≤0.1(pu)),系统在低电网电阻条件下,仍可能因阻尼比导致失稳。为进一步提升系统的稳定性,在等效内电压控制的基础上引入虚拟阻抗Zvir,表示为
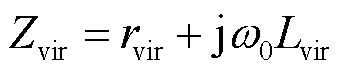 (24)
(24)
式中,rvir为虚拟电阻;Lvir为虚拟电感。通过在电压参考值中引入Zvir的电压压降,可以模拟更高耦合阻抗下的电压输出特性,该压降可表示为
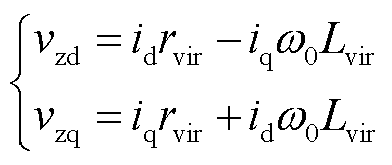 (25)
(25)
式中,vzd和vzq分别为Zvir在d轴和q轴上的电压压降。基于等效内电压控制和虚拟阻抗的阻抗增强策略,其调制电压参考edqref计算公式为
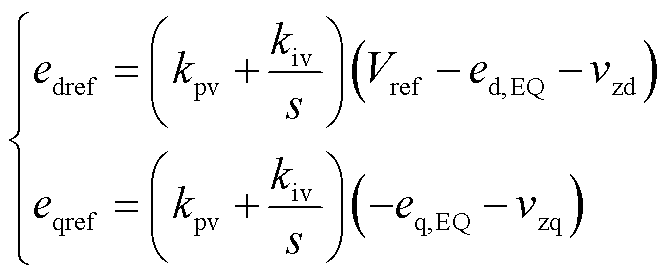 (26)
(26)
所采用的虚拟阻抗策略分为静态虚拟阻抗和限流虚拟阻抗两部分,共同构成自适应虚拟阻抗,如图10所示。
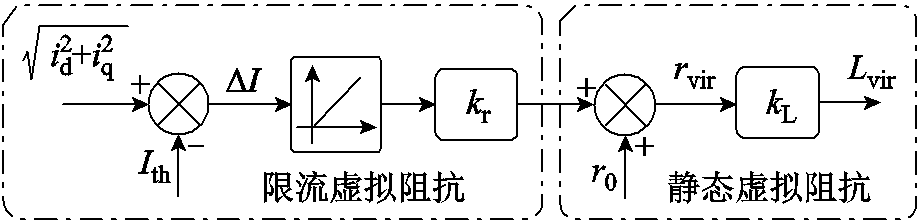
图10 自适应虚拟阻抗策略
Fig.10 Adaptive virtual impedance strategy
虚拟电阻和虚拟电感的计算公式分别为
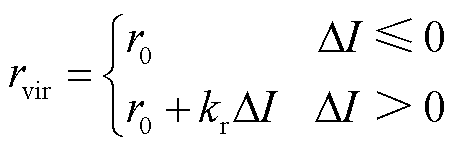 (27)
(27)
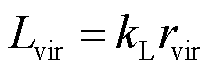 (28)
(28)
式中,kr和kL分别为虚拟电阻和虚拟电感比例系数;r0为静态虚拟电阻;ΔI为过电流幅值,其表达式为
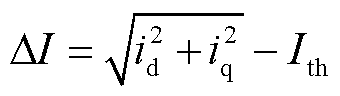 (29)
(29)
式中,Ith为虚拟阻抗限流阈值,其设定值一般会留出一定的裕度。例如,当系统最大电流值为1.2(pu)时,为确保可靠的限流,Ith可设计为1.1(pu)。
当系统正常运行时,静态虚拟阻抗生效,其作用在于增加系统阻尼比,减缓电压和电流的变化率,改善系统动态性能。当系统电流超过限流阈值时,自适应策略中的限流虚拟阻抗被激活,其将根据过电流情况动态增加虚拟阻抗,从而在极端工况下抑制过电流,避免变流器过电流或保护性脱网。
根据3.1节所提阻抗增强策略,建立系统小信号模型[30],如图11所示。图中,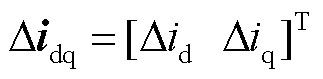 。Gv为电压环的比例积分控制器,Gd1为调制和采样的等效小惯性环节,Gd2为获取edq,EQ的延时,Gvir为虚拟阻抗的传递函数,Gf为滤波阻抗的传递函数,各环节的表达式分别为
。Gv为电压环的比例积分控制器,Gd1为调制和采样的等效小惯性环节,Gd2为获取edq,EQ的延时,Gvir为虚拟阻抗的传递函数,Gf为滤波阻抗的传递函数,各环节的表达式分别为
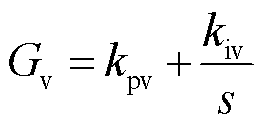 (30)
(30)
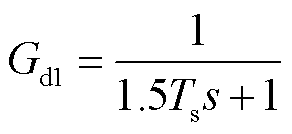 (31)
(31)
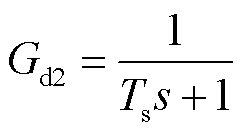 (32)
(32)
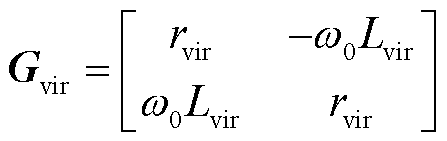 (33)
(33)
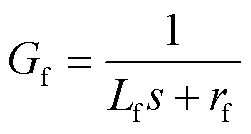 (34)
(34)
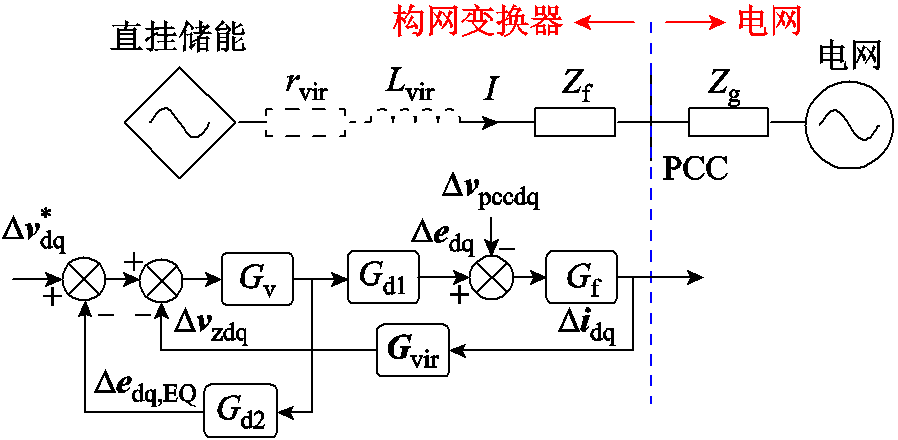
图11 采用所提阻抗增强控制的系统小信号模型
Fig.11 Small-signal model of the system with the proposed impedance enhancement control
根据图11的小信号模型,可以求解构网变换器的系统方程,即
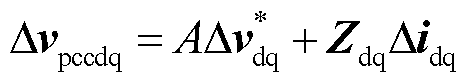 (35)
(35)
其中
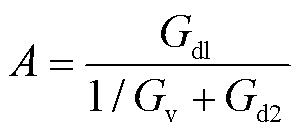 (36)
(36)
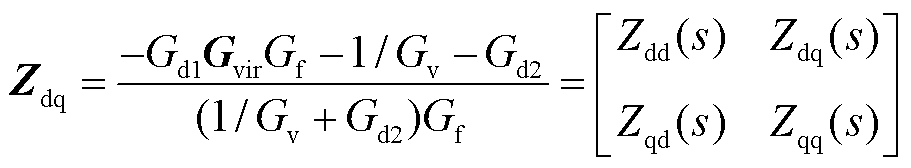 (37)
(37)
式中,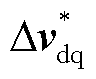 为dq电压参考值的小信号扰动;Zdq为构网变换器的等效阻抗,形式为2×2的矩阵。
为dq电压参考值的小信号扰动;Zdq为构网变换器的等效阻抗,形式为2×2的矩阵。
由于系统三相对称,矩阵对角元素相同,选取Zdd(s)和Zdq(s)进行分析[31]。根据Zdd(s)和Zdq(s)的传递函数绘制系统等效阻抗伯德图,如图12所示。由图12可知,在低频范围内(0~10 Hz),虚拟阻抗对Zdd(s)的增益提升约为+15 dB,与物理阻抗效果接近;而对Zdq(s)低频范围内增益提升较小(+5 dB),低于实际阻抗(+15 dB)。在高频范围内(大于 100 Hz),虚拟阻抗几乎不会改变Zdd(s)和Zdq(s)幅频特性,对系统高频范围内的阻抗影响可忽略。上述分析表明,虚拟阻抗无法完全代替实际阻抗的效果。
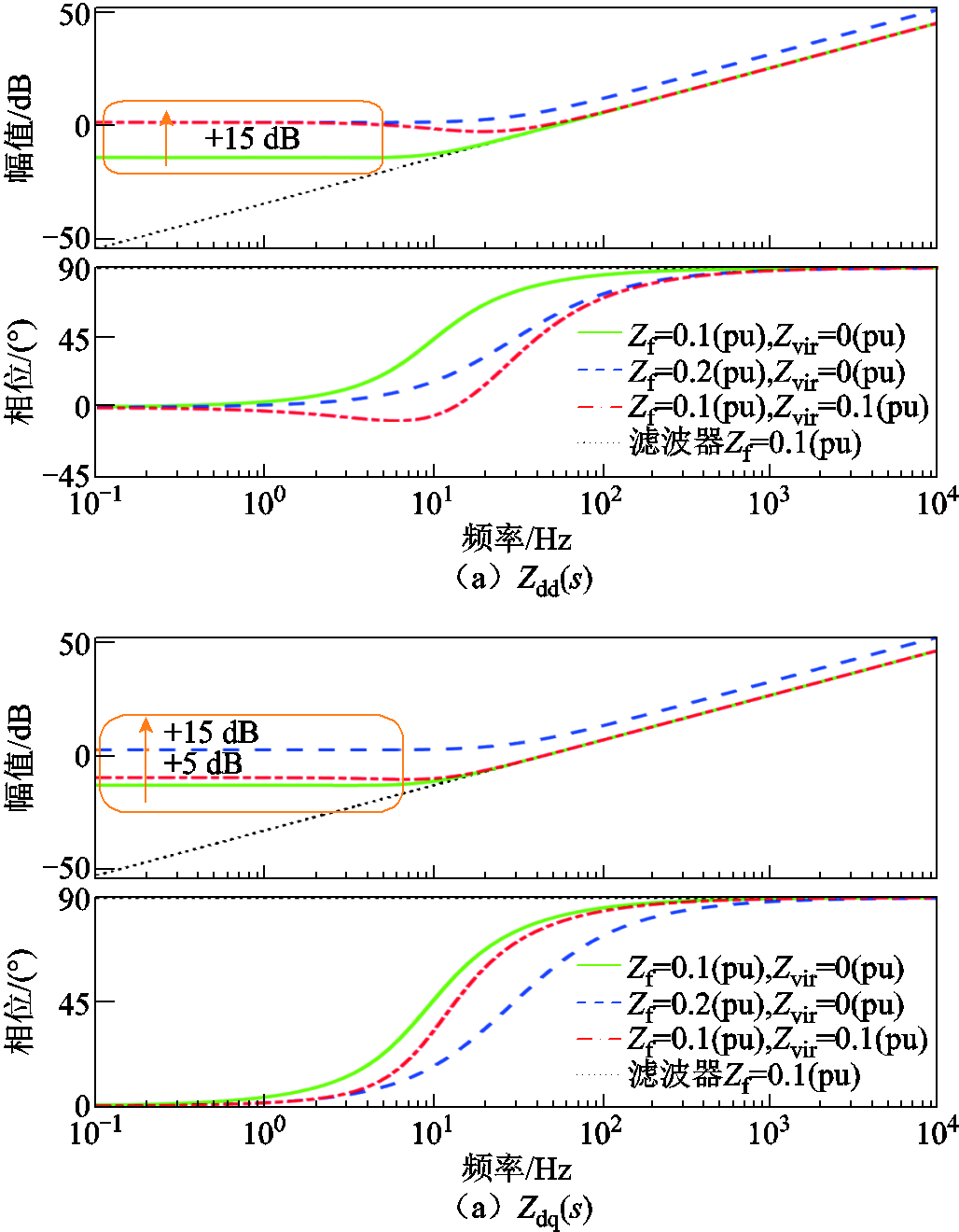
图12 增加实际或虚拟阻抗时的系统等效阻抗伯德图
Fig.12 Bode plot of system equivalent impedance with increased physical or virtual impedance
为确保系统的稳定性与动态性能,需要开展虚拟阻抗参数的优化设计。基于2.1节的小信号模型,并结合式(25)~式(28),对不同静态虚拟电阻下系统的极点分布特性进行了分析,结果如图13所示。从图13可以看出,增大虚拟电阻r0可以使系统主导极点逐渐远离虚轴。另外,当kL=0时,r0从0增加到0.2(pu),阻尼比ζ从0.34提高至0.92,表明系统的阻尼特性得到了增强。
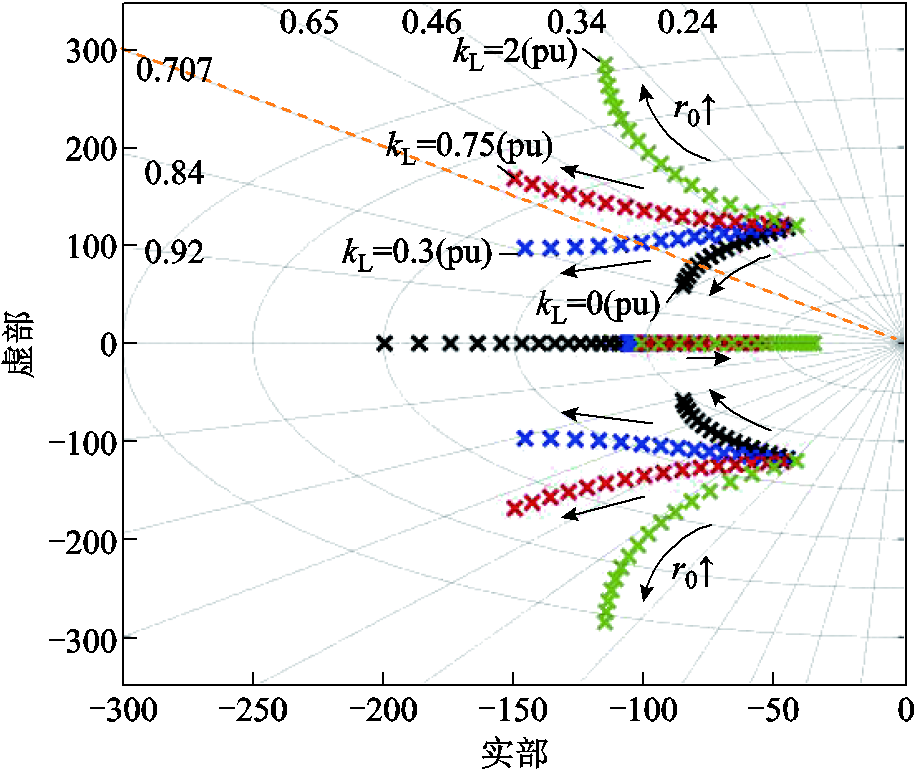
图13 低电网阻抗下采用不同策略时的系统极点分布
Fig.13 System pole distribution with different strategies under low grid impedance
同时,图13中还展示了不同kL值(分别为2(pu)、0.75(pu)、0.3(pu)和0(pu))的极点轨迹。结果表明,随着r0增大,当kL=2(pu)时,极点轨迹向更低阻尼比的方向移动,系统的阻尼特性减弱,可能导致动态特性的恶化;当kL=0(pu)时,极点轨迹向更高阻尼比的方向移动,但极点左移幅度较小,稳定裕度提升效果有限;当kL=0.3(pu)或0.75(pu)时,极点轨迹距离虚轴较远,可提供更大的稳定裕度,同时极点轨迹更接近最佳阻尼比ζ=0.707,能够在保证系统稳定性的同时提供更优的动态性能。综合考虑系统稳定裕度和阻尼特性,本文r0设计范围为0.1(pu)~0.15(pu),kL设计范围为0.3(pu)~0.75(pu),具体取值可根据实际需求进一步优化调节。
以图14所示直挂式储能系统的并网结构为例,说明采用不同策略时的系统耦合阻抗特性。在传统控制方法下,由于构网电压为PCC电压,耦合阻抗仅包含电网阻抗Zg。采用所提等效内电压控制后,受控电压由PCC电压转变为变流器侧的内电压。在这种情况下,构网电压与电网电压间的耦合阻抗将在物理层面增加滤波器阻抗Zf。
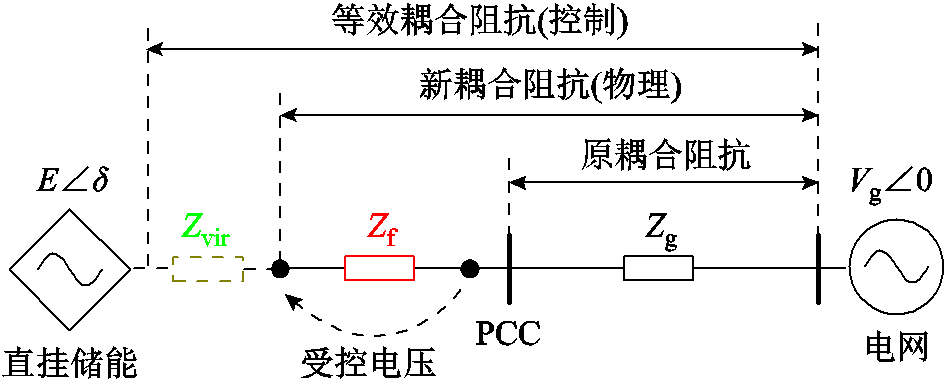
图14 采用不同策略时的系统耦合阻抗特性
Fig.14 System coupling impedance characteristics under different strategies
图15展示了在低电网阻抗条件下,采用传统控制方法、等效内电压控制策略及加入虚拟阻抗策略的系统极点分布。采用传统方法时,主导极点位于右半平面,系统处于不稳定状态。相比之下,采用等效内电压控制后,由于在物理层面增强了耦合阻抗,主导极点移动至左半平面,系统由不稳定转变为稳定。然而,此时仍具有较低的阻尼比(ζ=0.34),系统的动态过程可能存在明显的振荡特征。而当引入虚拟阻抗后,主导极点向更高阻尼比(ζ=0.707)的方向移动,并且进一步远离虚轴,在提高稳定裕度的同时增强了系统的阻尼,可有效改善系统的稳定性和动态性能。
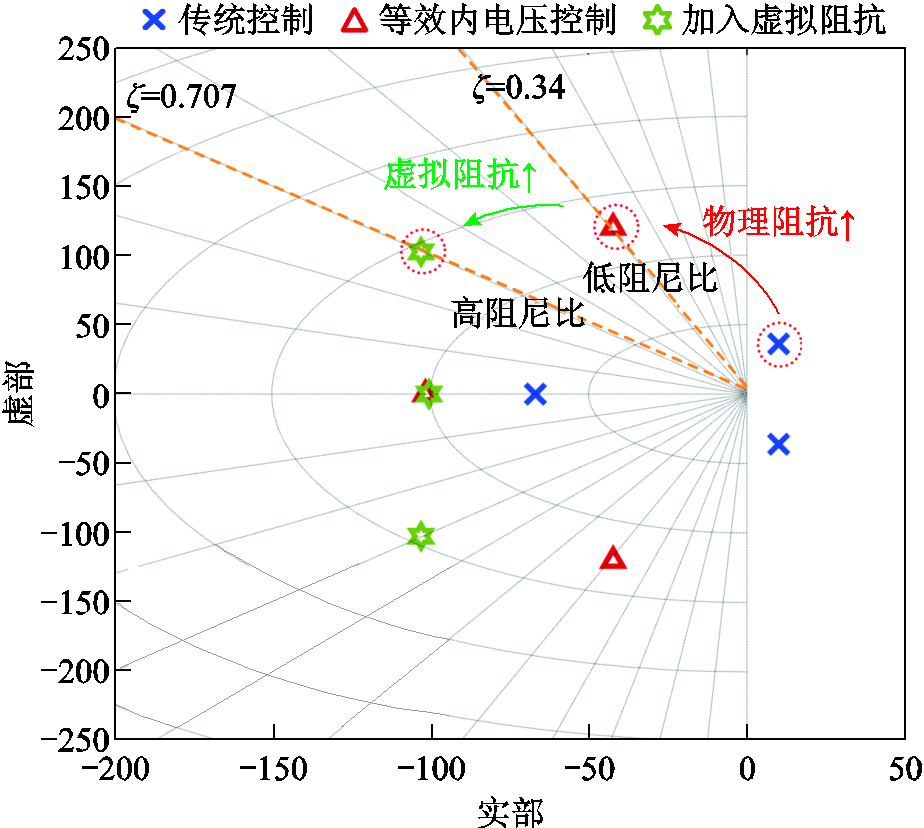
图15 低电网阻抗下采用不同策略时的系统极点分布
Fig.15 System pole distribution with different strategies under low grid impedance
图16展示了当采用所提阻抗增强策略控制时,系统在连续有功功率阶跃下的仿真波形。图中,Emag为内电压的幅值,Emag,EQ为通过等效内电压计算得到的调制电压幅度,ε为两者间的幅值误差。由于内电压含有高频分量,为更清晰地表征动态变化过程,测量过程中将Emag和Emag,EQ分别通过相同的100 Hz低通滤波器。由图16可见,在功率阶跃过程中,Emag,EQ与Emag的动态行为几乎保持一致,两者幅值误差小于0.5%。该误差通过功率控制式(2)和式(3)中的积分作用得到有效修正,从而避免了功率的静态误差。仿真中,系统实现了稳定的动态响应,能够准确跟踪参考值,验证了所提策略的可行性。
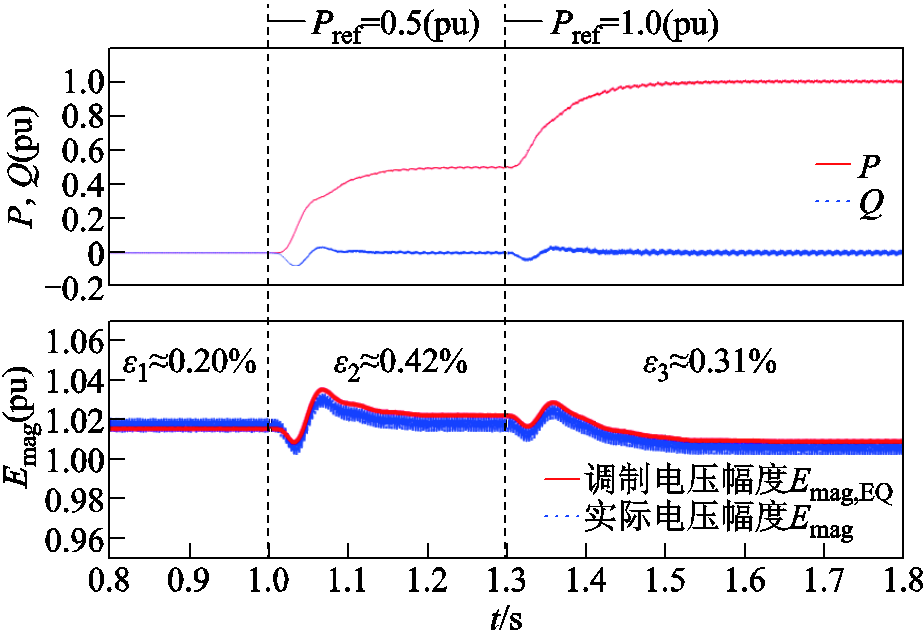
图16 采用所提策略的有功功率阶跃仿真波形
Fig.16 Simulation waveforms of active power step response with the proposed strategy
综上所述,所提阻抗增强策略通过在物理层面引入滤波阻抗Zf,控制层面叠加虚拟阻抗Zvir,使系统的等效耦合阻抗由单一的电网阻抗Zg增强为三者的共同作用。等效内电压控制和虚拟阻抗协同作用,可有效提升低电网阻抗条件下构网型直挂式储能系统的稳定性。
为了验证所提策略的有效性,在图17所示的三相七电平级联H桥直挂式储能系统实验平台进行了实验测试。直挂式储能系统的控制和数据采集由TMS320F28335 DSP和Cyclone IV EP4CE15 FPGA完成。电网电压和不同的扰动由Chroma 61860电网模拟器模拟。实验中使用的系统主要参数见表4。

图17 级联H桥直挂式储能系统实验平台
Fig.17 Experimental platform of the cascaded H-bridge transformerless energy storage system
表4 实验系统主要参数
Tab.4 Main parameters of the experimental system

参数数值 电网参数电网电压/V113.14 电网频率/Hz50 电网阻抗/Ω≈0 储能系统参数额定功率/(kV·A)1.5 相模块数N3 模块直流电压/V50 滤波电感Lf(pu)0.074
(续)

参数数值 控制参数J(pu)0.001 6 D(pu)1.02 电压PI控制器(pu)kpv=0.2kiv=100 自适应虚拟阻抗(pu)Ith=1.1kr=0.3
为模拟低电网阻抗场景,直挂式储能系统滤波电感Lf通过导线直接连接至电网,而未额外配置电网电感,电网阻抗近似为0。在这种情况下,储能系统电压和电网电压之间的微小差异可能会导致较大的电流冲击。因此,零电网阻抗对构网型控制来说是一个极具挑战性的实验条件,是对所提控制策略更为充分的验证。
首先开展系统稳定性方面的验证。作为对比,采用图2所示传统控制策略进行预同步和并网操作,实验结果如图18所示。实验过程中,系统发生了严重的同步失稳,导致电流越限并触发了系统过电流保护。这是因为,系统缺乏足够的耦合阻抗,PCC电压的微小波动会放大为显著的电流冲击和功率振荡,严重影响系统的稳定性。因此,传统控制策略在零电网阻抗工况下难以维持正常运行。
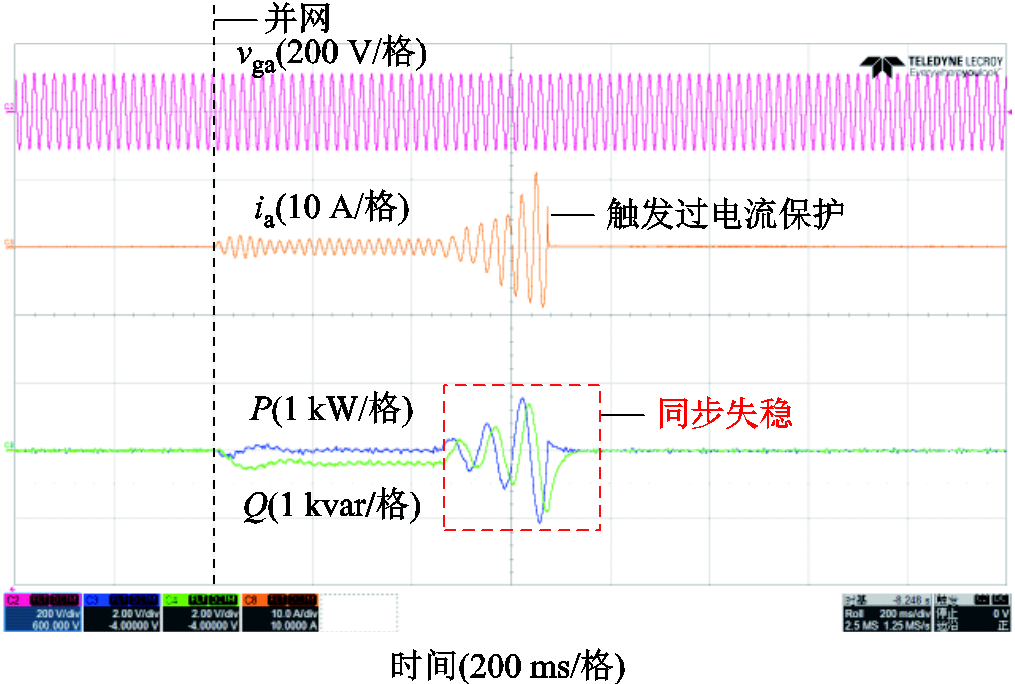
图18 采用传统控制策略时系统并网的实验波形
Fig.18 Experimental waveforms during grid connection using traditional control strategy
其次,应用本文所提的阻抗增强策略,同时配置较小的静态虚拟电阻r0=0.03(pu),并施加有功功率阶跃Pref=1 kW,相应的动态响应结果如图19所示。结果表明,应用阻抗增强策略后,系统在零电网阻抗条件下能够稳定运行。相较于传统策略,系统由不稳定变为稳定,验证了所提策略对提升系统稳定性的有效性。
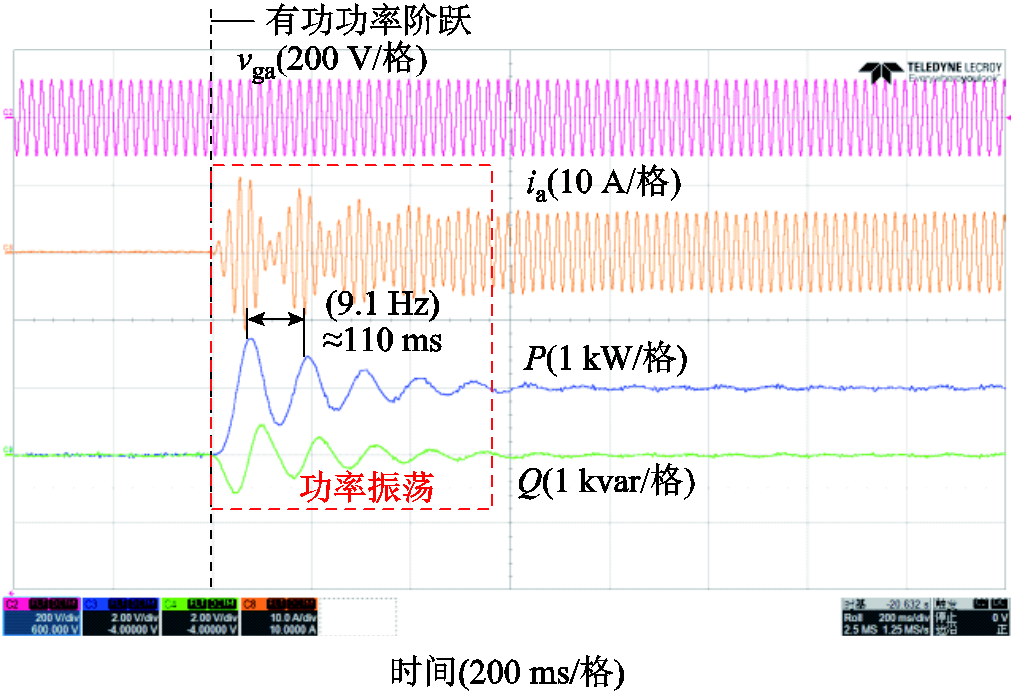
图19 采用阻抗增强策略时系统有功功率阶跃的实验波形(r0=0.03(pu))
Fig.19 Experimental waveforms of active power step response with the impedance enhancement strategy(r0= 0.03(pu))
然而可以观察到,在图19所示的实验过程中出现了较明显的振荡现象。尽管此时将滤波电感(Lf= 0.074(pu))作为耦合电感,并使用了较小的静态虚拟电阻r0=0.03(pu),但整体耦合阻抗仍较低,系统处于低阻尼比的状态,出现了约9.1 Hz的次同步振荡现象。为了抑制振荡,将静态虚拟电阻r0提升至0.1(pu),并施加相同的有功功率阶跃。实验结果如图20a所示。实验结果表明,阶跃响应过程中的振荡被消除,系统实现了平滑稳定的动态响应。此外,还进行了充放电切换的测试,功率参考值从1 kW阶跃至-1 kW,对应实验结果如图20b所示。结果显示,系统在充放电切换过程中同样完成了平滑稳定的动态调节。上述实验验证了所提策略在提升系统稳定性方面的有效性,同时说明虚拟阻抗可以有效地抑制系统的功率振荡。
然后,为验证改进策略下直挂式储能系统的构网能力,分别在电网频率故障和电网电压故障的暂态故障条件下进行实验。实验首先模拟了电网频率跌落的场景,电网频率以−5 Hz/s的频率变化率从50 Hz下降到49.5 Hz,相应实验结果如图21a所示。在频率跌落期间,储能系统主动增加了约0.67(pu)的有功功率,以支撑电网频率。然后,模拟电网频率以+5 Hz/s的频率变化率从50 Hz上升至50.5 Hz,实验结果如图21b所示。储能系统在频率上升期间主动降低了约0.67(pu)的有功功率。上述结果表明,在频率故障期间,系统有主动频率支撑能力和良好的动态响应能力,验证了所提策略在电网频率故障场景中的构网特性。
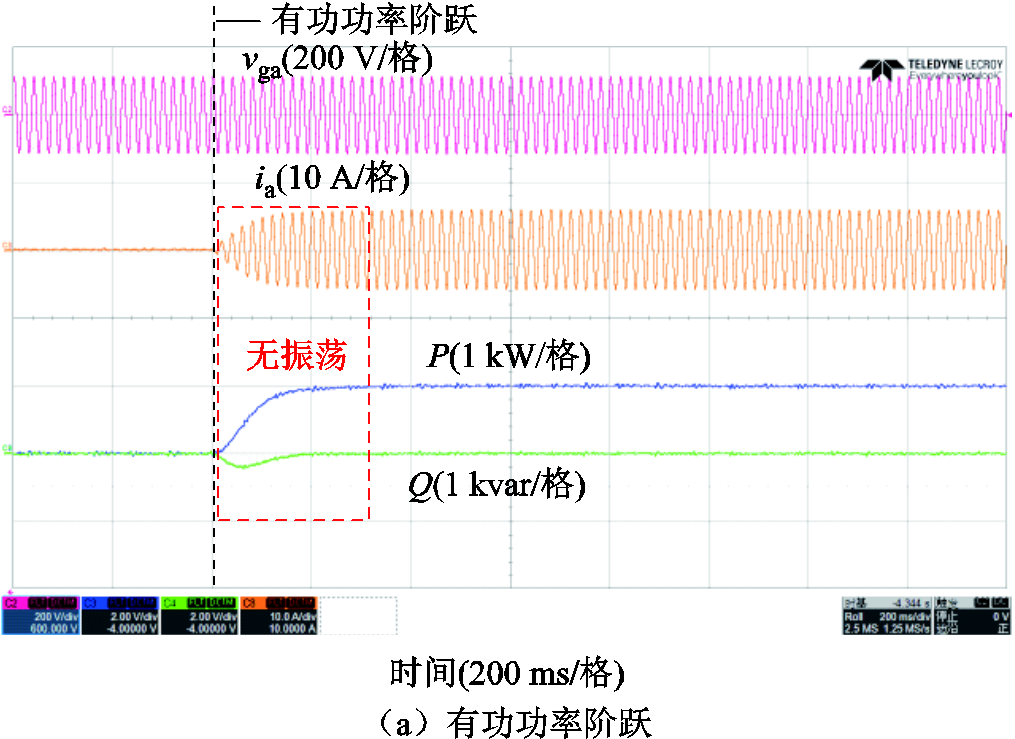
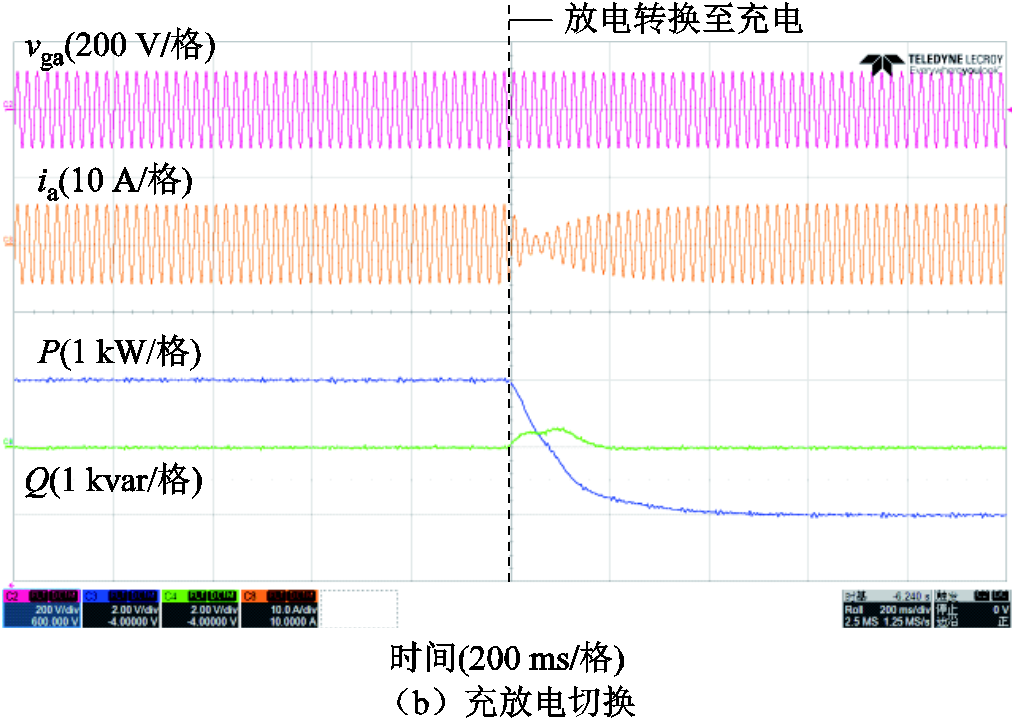
图20 采用阻抗增强策略时系统有功功率阶跃的实验波形(r0 = 0.1(pu))
Fig.20 Experimental waveforms of active power step response with the impedance enhancement strategy(r0 = 0.1(pu))

图21 电网频率故障时的实验波形
Fig.21 Experimental waveforms under grid frequency fault conditions
此外,在电压跌落至0.5(pu)的三相对称电压故障下进行了实验,结果如图22所示。在电压故障发生时,直挂式储能系统快速提供了约0.5(pu)的无功功率,以支撑电网电压。同时,在故障期间,限流虚拟阻抗被激活,有效地在故障期间将输出电流限制在1.2(pu)以内,确保了系统的安全。上述实验验证了所提策略在电网电压故障下的构网能力,并且验证了限流功能的有效性。
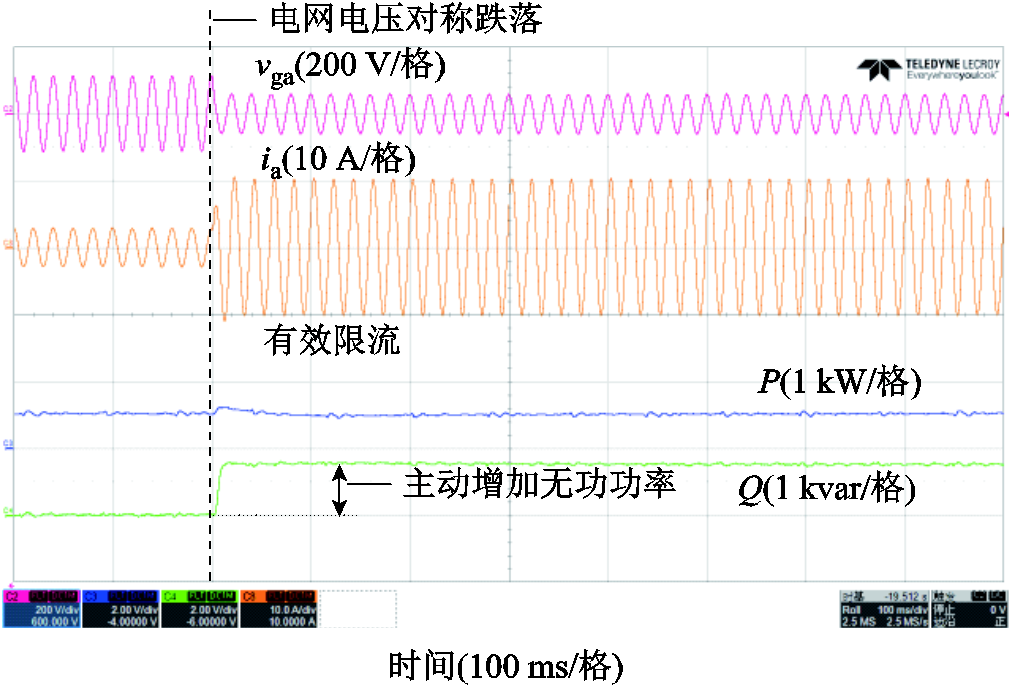
图22 电网电压对称跌落故障时的实验波形
Fig.22 Experimental waveforms under grid voltage symmetrical sag fault conditions
本文基于小信号模型分析了电网阻抗对构网型直挂式储能系统稳定性的影响,电网阻抗的降低会降低系统稳定裕度,甚至可能引发次同步振荡问题。为解决该问题,提出了一种基于等效内电压控制与虚拟阻抗的阻抗增强策略,分别从物理层面和控制层面共同增强系统的耦合阻抗,从而提升系统的稳定性。此外,所提策略无需额外硬件,仅需对现有控制方案进行简单修改即可实现。在零电网阻抗的极端强电网条件下开展了实验验证,结果表明,所提策略显著提升了构网型直挂式储能系统的稳定性,并能够提供有效的构网支撑和限流功能。
参考文献
[1] 李建林, 马会萌, 惠东. 储能技术融合分布式可再生能源的现状及发展趋势[J]. 电工技术学报, 2016, 31(14): 1-10, 20.
Li Jianlin, Ma Huimeng, Hui Dong. Present development condition and trends of energy storage technology in the integration of distributed renewable energy[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 1-10, 20.
[2] 中关村储能产业技术联盟.中国新型储能累计装机突破50GW,中标价首次跌破0.5元/Wh[EB/OL]. [2024-11-14]. http://www.esresearch.com.cn/report/ info/detail/?id=5862.
[3] 蔡旭, 李睿, 刘畅, 等. 高压直挂储能功率变换技术与世界首例应用[J]. 中国电机工程学报, 2020, 40(1): 200-211, 387.
Cai Xu, Li Rui, Liu Chang, et al. Transformerless high-voltage power conversion system for battery energy storage system and the first demonstration application in world[J]. Proceedings of the CSEE, 2020, 40(1): 200-211, 387.
[4] 刘畅, 吴胜兵, 吴西奇, 等. 35 kV高压直挂大容量电池储能系统[J]. 高电压技术, 2024, 50(2): 881-892.
Liu Chang, Wu Shengbing, Wu Xiqi, et al. High-voltage large-capacity battery energy storage system connecting to 35 kV grid without transformer[J]. High Voltage Engineering, 2024, 50(2): 881-892.
[5] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[6] 梁军杨, 李红, 宋国杰, 等. 多时间尺度控制下跟网型变换器的同步稳定性分析与改进控制[J]. 电工技术学报, 2024, 39(22): 7182-7196.
Liang Junyang, Li Hong, Song Guojie, et al. Synchronization stability analysis and enhanced control of grid-following converters under multi-timescale control[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7182-7196.
[7] 汪春江, 孙建军, 宫金武, 等. 并网逆变器与电网阻抗交互失稳机理及阻尼策略[J]. 电工技术学报, 2020, 35(增刊2): 503-511.
Wang Chunjiang, Sun Jianjun, Gong Jinwu, et al. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 503-511.
[8] Yao Wei, Chen Min, Matas J, et al. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 576-588.
[9] Gao Mingzhi, Chen Min, Zhao Bin, et al. Design of control system for smooth mode-transfer of grid-tied mode and islanding mode in microgrid[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6419-6435.
[10] 屈子森. 高比例新能源电力系统电压源型变流器同步稳定性分析与控制技术[D]. 杭州: 浙江大学, 2021.
Qu Zisen. Synchronizing stability analysis and control technology of voltage source converters in power system with high-penetration renewables[D]. Hangzhou: Zhejiang University, 2021.
[11] 周京华, 李津. 构网型储能变流器国内外技术标准对比与分析[J/OL]. 电力系统自动化, 2024: 1-22 [2024-11-14]. http://kns.cnki.net/KCMS/detail/detail. aspx?filename=DLXT20240926004&dbname=CJFD&dbcode=CJFQ.
Zhou Jinghua, Li Jin. Comparison and analysis of domestic and foreign technical standards of reticulated energy storage converter[J/OL]. Automation of Electric Power Systems, 2024: 1-22[2024-11-14]. http://kns. cnki.net/KCMS/detail/detail.aspx?filename=DLXT20240926004&dbname=CJFD&dbcode=CJFQ.
[12] Gao Xian, Zhou Dao, Anvari-Moghaddam A, et al. Stability analysis of grid-following and grid-forming converters based on state-space modelling[J]. IEEE Transactions on Industry Applications, 2024, 60(3): 4910-4920.
[13] IEEE. Guide for Planning DC Links Terminating at AC Locations Having Low Short-Circuit Capacities: IEEE Std 1204—1997[S]. IEEE, 1997.
[14] 于琳, 孙华东, 赵兵, 等. 新能源并网系统短路比指标分析及临界短路比计算方法[J]. 中国电机工程学报, 2022, 42(3): 919-929.
Yu Lin, Sun Huadong, Zhao Bing, et al. Short circuit ratio index analysis and critical short circuit ratio calculation of renewable energy grid-connected system[J]. Proceedings of the CSEE, 2022, 42(3): 919-929.
[15] 胡光, 庄可好, 高晖胜, 等. 低惯量交流系统并网变流器次/超同步振荡分析[J]. 电工技术学报, 2024, 39(8): 2250-2264.
Hu Guang, Zhuang Kehao, Gao Huisheng, et al. Sub/super synchronous oscillation analysis of grid-connected converter in low inertia AC system[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2250-2264.
[16] Gao Mingzhi, Chen Min, Wang Chenxi, et al. An accurate power-sharing control method based on circulating-current power phasor model in voltage-source inverter parallel-operation system[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4458-4476.
[17] Li Xin, Hu Yaowei, Shao Yuting, et al. Mechanism analysis and suppression strategies of power oscillation for virtual synchronous generator[C]// IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 2017: 4955-4960.
[18] 严文博, 黄云辉, 方正, 等. 低阻抗下构网型变流器稳定性机理分析[J]. 高电压技术, 2025, 51(3): 1444-1453.
Yan Wenbo, Huang Yunhui, Fang Zheng, et al. Stability mechanism analysis of reticulated converter under low impedance[J]. High Voltage Engineering,2025, 51(3): 1444-1453.
[19] Du Wei, Chen Zhe, Schneider K P, et al. A comparative study of two widely used grid-forming droop controls on microgrid small-signal stability[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 8(2): 963-975.
[20] Zhang Lidong, Harnefors L, Nee H P. Power-synchronization control of grid-connected voltage-source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[21] 温春雪, 黄耀智, 胡长斌, 等. 虚拟同步发电机接口变换器并联运行虚拟阻抗自适应控制[J]. 电工技术学报, 2020, 35(增刊2): 494-502.
Wen Chunxue, Huang Yaozhi, Hu Changbin, et al. Virtual impedance adaptive control for parallel operation of virtual synchronous generator interface converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 494-502.
[22] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[23] 范宸珲, 秦晓辉, 齐磊, 等. 构网型下垂控制中虚拟阻抗的作用、改进及研究前景分析[J]. 电网技术, 2024, 48(6): 2237-2250.
Fan Chenhui, Qin Xiaohui, Qi Lei, et al. Analysis of the role, improvement, and research prospects of virtual impedance in grid-forming droop control[J]. Power System Technology, 2024, 48(6): 2237-2250.
[24] Liu Teng, Wang Xiongfei. Unified voltage control for grid-forming inverters[J]. IEEE Transactions on Industrial Electronics, 2024, 71(3): 2578-2589.
[25] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电力变压器第5部分:承受短路的能力: GB/T1094.5—2008[S]. 北京: 中国标准出版社, 2009.
[26] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[27] Zhao Fangzhou, Zhu Tianhua, Li Zejie, et al. Low-frequency resonances in grid-forming converters: causes and damping control[J]. IEEE Transactions on Power Electronics, 2024, 39(11): 14430-14447.
[28] Huang Linbin, Yang Chaoran, Song Meiyan, et al. An adaptive inertia control to improve stability of virtual synchronous machines under various power grid strength[C]//2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 2019: 1-5.
[29] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianhang, et al. The interaction between multiple timescales of the grid-tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547-5559.
[30] Huang Liang, Wu Chao, Zhou Dao, et al. A simplified SISO small-signal model for analyzing instability mechanism of grid-forming inverter under stronger grid[C]//2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), Cartagena, Colombia, 2021: 1-6.
[31] 曾志杰. 并网逆变器DQ阻抗模型的建立方法研究[D]. 南京: 东南大学, 2021.
Zeng Zhijie. Research on DQ impedance modelling method of grid-tied inverters[D]. Nanjing: Southeast University, 2021.
Abstract Grid-forming energy storage technology serves as a critical solution for enhancing power system stability. Transformerless energy storage systems, characterized by high efficiency, modularity, and direct medium/high-voltage grid integration, have emerged as the preferred choice for large-scale grid-connected energy storage. However, the reduced electrical distance between transformerless systems and the grid results in significantly lower grid impedance, posing severe challenges to the stability of grid-forming control. The underlying mechanism lies in the voltage-source operation of grid-forming converters: under low grid impedance conditions, minor voltage deviations between the converter and grid can trigger substantial current surges, ultimately leading to instability. To address these challenges, this study establishes a full order small signal model to analyze the impact of low grid impedance on stability and proposes impedance enhancement strategies.
The research begins by developing a dynamic model that integrates virtual synchronous generator (VSG) control, voltage-loop regulation, and grid interactions. Pole trajectory analysis reveals two critical instability mechanisms: 1) Excessively low grid inductance shifts system poles to the right-half plane, inducing instability; 2) Insufficient grid resistance reduces damping ratios, exacerbating oscillatory behavior. These combined effects diminish system stability margins and may provoke subsynchronous oscillations. To mitigate these issues, a dual-layer impedance enhancement strategy is proposed: (1) Physical impedance reconstruction: The equivalent internal voltage control strategy repurposes filter inductance as coupling impedance by relocating the controlled voltage from the point of common coupling (PCC) to the converter side. This hardware-free modification enhances physical coupling impedance without requiring additional components. (2) Adaptive virtual impedance: A composite virtual impedance module combines static impedance for damping optimization and a dynamic current-limiting component. The static virtual impedance elevates damping ratios near to 0.707, while the current-limiting module dynamically adjusts impedance parameters based on real-time overcurrent thresholds, ensuring fault current suppression.
In the analysis of impedance enhancement effect, it is shown that equivalent internal voltage control causes the dominant pole of the system under strong power grid to shift to the left into the stable region, while the introduction of adaptive virtual impedance further enhances damping characteristics and improves dynamic response performance. The proposed impedance enhancement strategy enhances the system stability by introducing filtering impedance at the physical level and superimposing virtual impedance at the control level, thereby increasing the equivalent coupling impedance of the system from a single grid impedance to the combined effect of the three.
Experimental validation on a cascaded H-bridge transformerless energy storage platform under zero grid impedance conditions confirms the strategy's effectiveness. The proposed method eliminates oscillatory instability observed in conventional approaches, achieving smooth active power step responses without overshoot. During grid frequency fluctuations (±0.5 Hz), the system provides 0.67(pu) active power support, demonstrating effective grid-forming capabilities. Under symmetrical voltage sags (0.5(pu)), it delivers 0.5(pu) reactive power while constraining currents within 1.2(pu) safety thresholds, validating robust fault ride-through performance. Experimental and theoretical analyses confirm: (1) The proposed impedance enhancement architecture synergizes physical-layer reconstruction with control-layer virtual compensation, demonstrating superior stability improvement over conventional methods through coordinated impedance augmentation. (2) A pole trajectory analysis-based parameter optimization framework achieves concurrent enhancement of stability and dynamic performance, with virtual impedance implementation optimizing damping ratios to eliminate oscillatory instabilities. This work validates the effectiveness of the proposed strategy in extreme low-impedance scenarios, providing technical support for grid-forming transformerless energy storage applications in power grids.
Keywords:Transformerless energy storage, grid-forming, stability, virtual impedance, virtual synchronous generator
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.242382
国家电网有限公司总部管理科技项目(5500-202329500A-3-2-ZN)和台州市-浙江大学科技合作项目资助。
收稿日期 2024-12-30
改稿日期2025-03-05
朱冠南 男,1997年生,博士研究生,研究方向为直挂式储能系统及构网型控制技术。
E-mail:12010036@zju.edu.cn
陈 敏 男,1979年生,教授,博士生导师,研究方向为电力电子在电力系统中的应用、新能源发电与并网控制技术等。
E-mail:calim@zju.edu.cn(通信作者)
(编辑 赫 蕾)