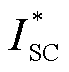控制储能充放电，关于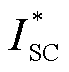的给定方式将在第3节给出。摘要 风机最大功率跟踪运行模式，以及自身有限的旋转动能，导致构网型直驱风机暂态支撑能力受到制约。而构网型直驱风储一体机由于接入储能，拥有额外能量来源，其暂态支撑性能得到大幅提升，但风储一体机在暂态支撑过程中对旋转动能和储能的调用机制尚不明晰，仍需进一步探究。该文建立了虚拟同步构网型直驱风机及风储一体机动态模型：首先通过分析构网型直驱风机在频率、电压跌落工况下的暂态响应特性，归纳总结了风力机动态特性对构网型直驱风机支撑能力及暂态稳定性的约束；其次考虑风储一体机内部能量流动特性，对虚拟同步控制的暂态响应功率进行分解，提出基于暂态响应功率分解的储能驱动控制策略，实现了转子动能和储能的灵活调用，将储能纳入虚拟同步构网控制主动支撑体系中；最后形成基于风储一体化的构网型直驱风电机组暂态支撑能力提升策略。经过多种工况的仿真验证，该策略能够提升风储一体机暂态支撑能力，为风电发挥主动支撑功能提供技术指导。
关键词：构网型直驱风机 风储一体机 虚拟同步控制 超级电容 暂态支撑
“十四五”期间我国风电装机将持续快速增长，风电高比例接入后会给电网频率电压稳定带来一系列问题，新型电力系统需要风电承担保障供电的主体责任[1]。现有研究表明，包括构网型风电机组在内的构网型设备具有良好的频率/电压主动暂、稳态支撑能力，并且在弱电网场景下具有更好的暂、稳态适应能力[2-3]。基于这些优势，构网型风电机组有望在未来低惯量、弱电压支撑的电网中发挥更大的作用，保障新型电力系统稳定运行[4]。
由理想直流源供能的构网型设备能够提供完整的暂态响应支撑，然而构网型直驱风机的直流侧能量由风力机提供，其运行特性会给构网型风机的暂态性能带来以下约束：
1）对构网型风机频率支撑能力的约束
目前在风电并网中应用的构网型控制策略大多具备惯量响应或一次调频功能[5]。当利用风机旋转动能进行调频时，最大功率跟踪运行（Maximum Power Point Tracking, MPPT）曲线会抵消一部分惯量和一次调频环节响应，导致旋转动能无法充分释放，制约了构网型风机的调频能力[6]。另外，当结束调频后风机需要能量以恢复转速，又由此引发转速恢复过程中的功率二次跌落问题，与频率支撑目标相悖[7]。此外，构网型风电机组频繁地提供频率支撑，对风机机械结构的载荷具有一定程度的影响，从而可能影响风机寿命[8]。
2）对构网型风机暂态稳定性的约束
构网型风机在模拟同步机运行特性的同时，也存在暂态稳定问题[9]。由等面积法和暂态能量函数法等分析方法可知，故障发生后设备输出功率与参考功率之间的失衡若不加以控制，将导致机端功角不断加速使得构网型风机暂态失稳[10]。
除了功角失稳，构网型风机的暂态失稳还会体现在风机系统内部[11]，不同控制模式的直驱风机表现如下[12]：机侧控制功率、网侧控制直流母线电压时，直流母线电容处累积暂态失衡能量，导致直流母线过电压[13]；反之暂态失衡能量转换为旋转动能，导致风机过速[14]。相比理想构网型设备，除了功角的暂态同步稳定，构网型风机还需要考虑风机转子和直流母线电压的暂态稳定。
针对以上问题，在风机侧配置储能构成风储一体机的技术路线，实现构网型变流器控制与储能充放电控制的直接耦合，是一种有效的解决方案[15]。目前储能的接入方式多为在直流侧或交流侧并联储能[16-17]，其中跟网型控制驱动的储能对电网频率的支撑采用响应频率采集信号的被动模式[18]，构网型控制驱动的储能大多接入在风机交流侧[19]，未能将储能纳入构网型控制体系中。因此，在构网型控制的背景下，风储一体机在主动支撑过程中对转子动能和储能的暂态能量共同调用机制尚不明晰，仍需进一步探究。
本文选用以超级电容器为代表的功率型储能，与构网型直驱风机组成构网型直驱风储一体机，并构建构网型直驱风机及构网型直驱风储一体机动态模型。首先，通过分析构网型直驱风机在频率、电压跌落下的暂态响应，归纳总结风力机动态对构网型直驱风机频率支撑能力和暂态稳定性的约束；其次，结合风储一体机在暂态支撑过程中的能量流动特性，将虚拟同步控制暂态响应功率分解为惯量响应功率信号和阻尼响应功率信号以驱动储能，形成基于风储一体化的构网型直驱风电机组暂态支撑能力提升策略，实现转子动能和储能的灵活分配和调用，将转子动能和储能纳入虚拟同步构网控制主动支撑体系中，提升构网型直驱风储一体机频率支撑能力和暂态稳定性；最后，通过仿真验证其可靠性。
本文所研究的构网型直驱风储一体机系统结构及控制如图1所示。其由风力机、永磁同步发电机（Permanent Magnet Synchronous Motor, PMSG）、机侧变流器（Machine-Side Converter, MSC）、网侧变流器（Grid-Side Converter, GSC）、储能电池（本文采用超级电容储能）、双向DC-DC变换器、直流母线等环节构成，并经过网侧变流器滤波阻抗Rf+jXf、变压器阻抗（电抗为jXT）及线路阻抗RL+jXL接入电网，为方便后续分析计算，将变压器和线路阻抗等效为并网阻抗Rg+jXg。
网侧变流器采用图1b所示虚拟同步机（Virtual Synchronous Generator, VSG）控制。机侧变流器采用图1c所示的直流母线电压控制，稳定直流母线电压UDC。储能DC-DC变换器采用图1d所示的电流环控制，通过改变参考电流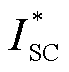控制储能充放电，关于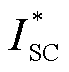的给定方式将在第3节给出。
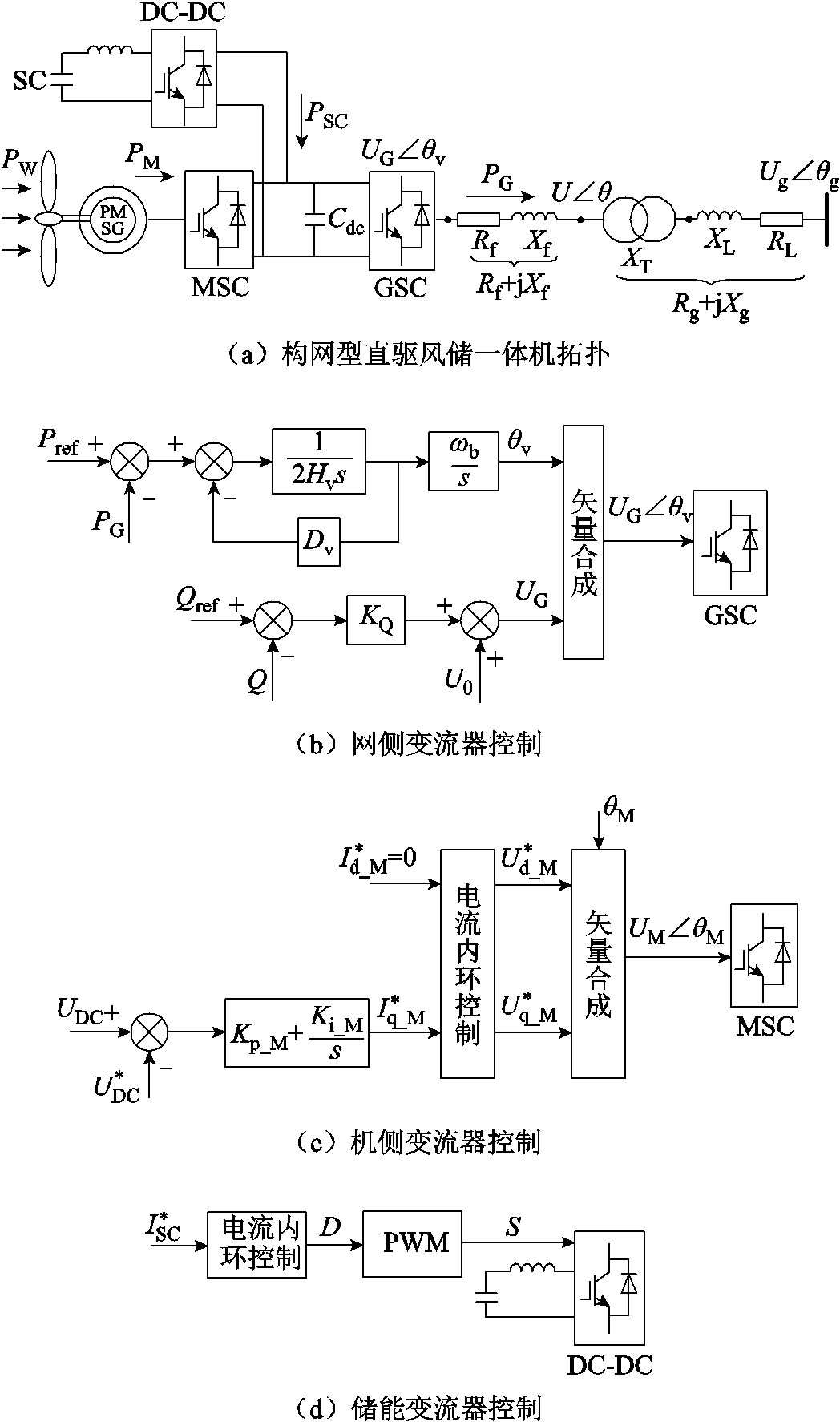
图1 构网型直驱风储一体机系统结构及控制
Fig.1 Structure and control of grid-forming PMSG-based wind-storage generator
为了进一步研究风储一体机的动态响应特性，需要对其进行动态建模，其中关于风力机和机侧动态环节的建模已有诸多文献阐述[20-21]，具体建模过程详见附录第1节，在此不再赘述，仅给出关键变量的说明：PW为风力机捕获风功率，ωg为发电机转速，PM为机侧变流器端口功率。其余动态环节建模过程如下。
1）网侧动态模型
本文网侧变流器采用虚拟同步型构网控制，通过摇摆方程以及无功-电压下垂方程生成网侧变流器端口电压的相位和幅值，有
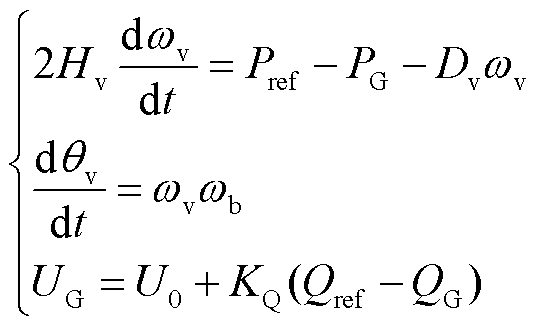（1）
式中，Hv为虚拟惯量系数；ωv为虚拟同步转速；Pref为有功功率参考值；PG为网侧变流器端口功率；Dv为虚拟阻尼系数；θv为虚拟同步相位；ωb为基准同步转速；UG为网侧端口电压；U0为电压初值；KQ为虚拟励磁系数；Qref为无功功率参考值；QG为网侧端口无功功率。
根据电网电压幅值Ug和相位θg可获得端口功角δv，并计算网侧变流器端口功率PG，有
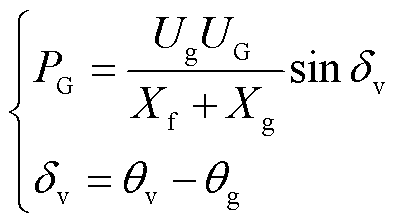（2）
为使风机运行在MPPT下，需要将式（1）中有功参考值设置为
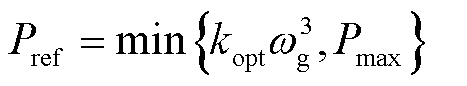（3）
式中，kopt为MPPT功率曲线系数；Pmax为风机最大功率。
最大功率跟踪控制直接决定了网侧变流器功率PG的大小，机侧变流器功率PM在机侧直流母线电压控制的影响下与PG保持平衡，因此在最大功率跟踪模式下，Pref可以间接控制PM的大小，使其满足式（3），进而实现风机的最大功率运行。
2）超级电容及DC-DC变换动态模型
为简化计算，将超级电容及其DC-DC变化环节等效为如图2所示电路拓扑。
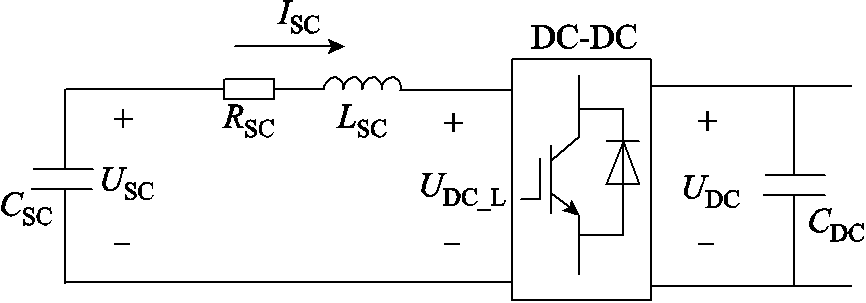
图2 超级电容和DC-DC变换器等效电路
Fig.2 Equivalent circuit of supercapacitor and DC-DC converter
结合图1d所示，通过电流环生成的占空比D，可以调节DC-DC变换器储能侧端口电压UDC_L，即
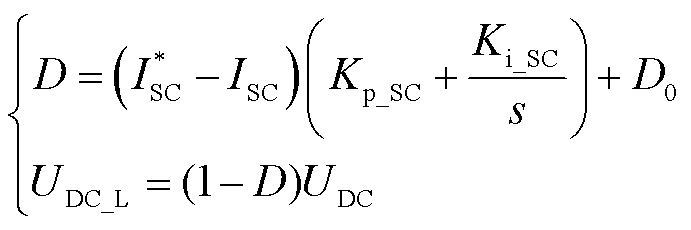（4）
式中，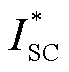
为超级电容输出电流参考值；ISC为超级电容输出电流；D0为初始占空比；Kp_SC为电流环比例系数；Ki_SC为电流环积分系数。
超级电容输出电流ISC及电压USC可表示为
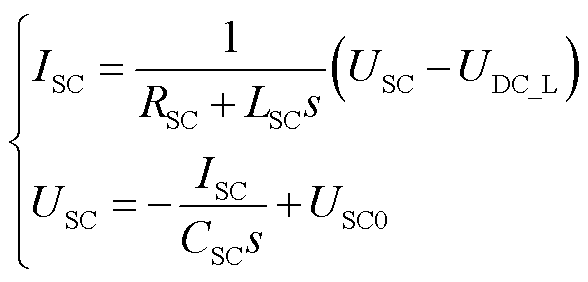（5）
式中，RSC、LSC分别为等效电路电阻及电感；USC0为超级电容初始电压；CSC为超级电容的等效电容。
储能充放电功率PSC为
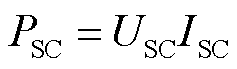（6）
将以上环节与附录第1节中所述环节组合后得到图3所示构网型直驱风机与构网型直驱风储一体机动态响应模型，模型参数及超级电容容量配置方法见附录第2节。
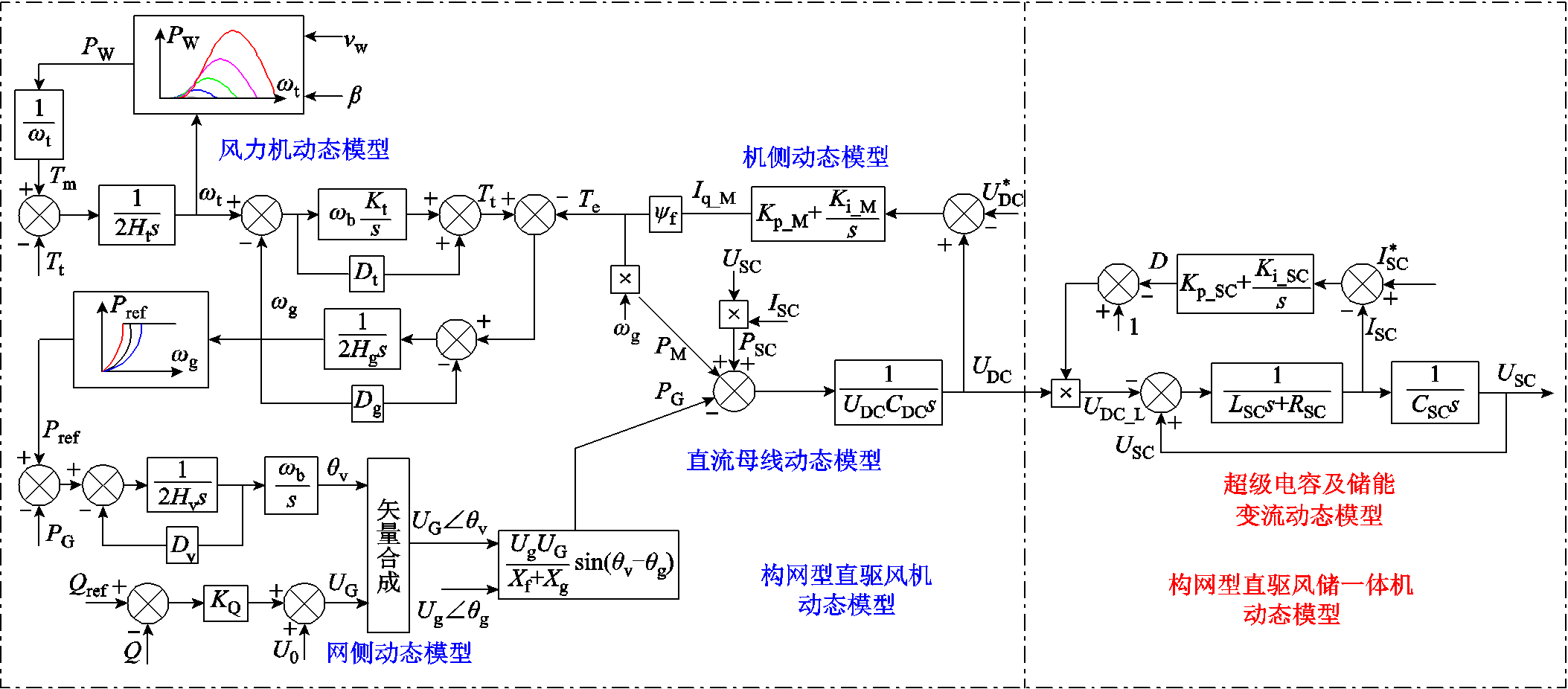
图3 构网型直驱风机与构网型直驱风储一体机动态响应模型
Fig.3 Dynamic response model of grid-forming PMSG and grid-forming PMSG-based Wind-storage generator
本节基于构网型直驱风机动态模型，通过对比电网频率、电压跌落等工况下的暂态响应特性，展现风力机动态对构网型直驱风机的约束。
由于转子动能储备有限，并且虚拟同步控制环节中的Pref变化同样会影响风机的暂态响应特性。因此在风速为10 m/s的场景下设置以下运行模式：模式1——MPPT模式，Pref随转速ωg变化；模式2 ——Pref恒定，对应10 m/s的最优功率；模式3——故障时Pref恒定，结束后回归MPPT模式。
设置电网频率在5 s时跌落0.2 Hz，并在10 s后恢复，得到图4所示频率跌落响应波形。将图4a中的转速作为x轴，功率作为y轴，即可得到图4b所示PG-ωg相平面轨迹。
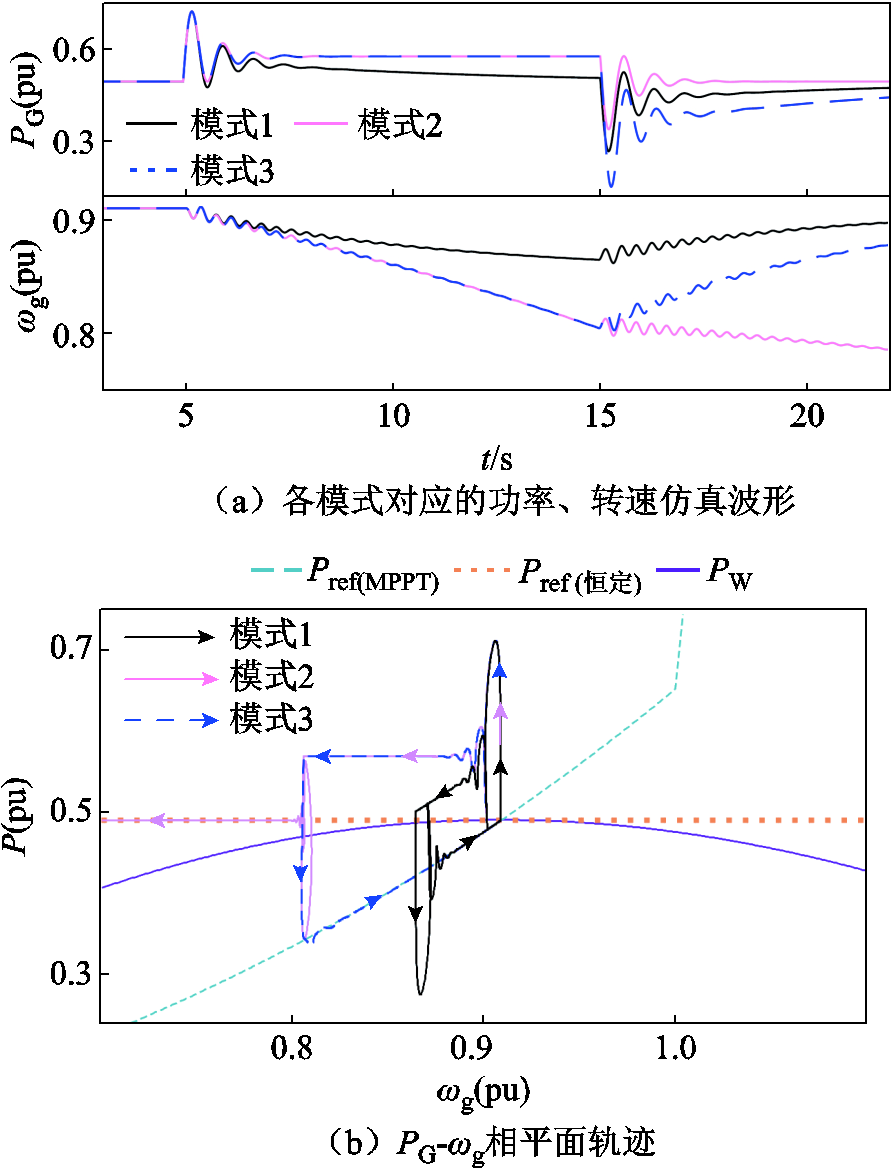
图4 频率跌落响应波形
Fig.4 Frequency drops response waveforms
图4b中除了风机PG-ωg运动轨迹外，还展现了风力机风捕获功率PW和功率跟踪曲线Pref，可以看出二者皆随转速变化而变化。
风机在模式1下提供频率支撑时PG＞PW，旋转动能得到释放的同时，伴随着转速下降，导致支撑期间的Pref和PG一同降低，使转速下降幅度有限，旋转动能无法得到充分释放。
相比之下，模式2和模式3在频率跌落期间Pref恒定，转速下降幅度更大，旋转动能获得充分释放，风机能够提供稳定的功率支撑。
故障结束后，如图4b所示PG-ωg轨迹，模式2继续运行在恒功率模式，PG依旧大于PW，转速进一步下降，不利于风机安全运行；而模式3切换回MPPT模式，PG会快速下降，然后沿着功率跟踪曲线上升，以恢复转速，在这个过程中会伴随明显的功率缺口，即风机功率的“二次跌落”。由此可见，构网型风机频率支撑能力受到了风力机运行特性的制约。
由于机侧与网侧之间的耦合，导致风力机的动态平衡也会影响构网型直驱风机的暂态稳定，下面将通过图5所示虚拟功-角特性曲线与风力机功率-转速特性曲线解释风力机动态对暂态稳定的影响。
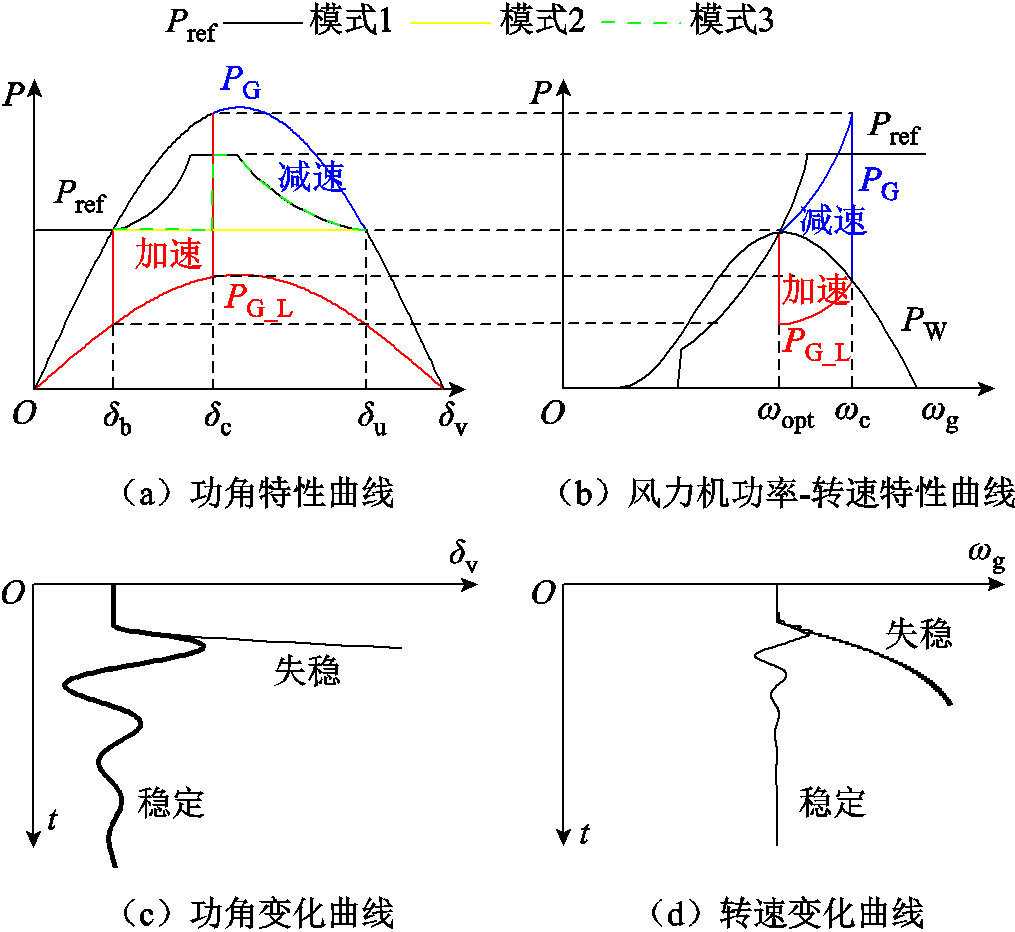
图5 虚拟功-角特性曲线和风功率-转速曲线
Fig.5 Virtual power-angle curves and wind power-rotor speed curves
电压跌落时，PG跌落为PG_L，Pref与PG_L之间形成功角加速区，δv加速[9]；故障结束后，Pref与PG之间形成功角减速区，δv减速；若功角减速区面积小于功角加速区，则会出现首摆失稳。另外值得一提的是，虚拟阻尼Dv在δv运动过程中始终提供制动功率，因此首摆失稳后，仍有可能在之后的数个摇摆周期后重新恢复暂态稳定[22]。
与之相似，电压跌落时，PW与PG_L之间形成转速加速区，ωg加速；故障结束后，PW与PG之间形成转速减速区，ωg减速。
如图5所示，若采用MPPT模式，故障期间风机转速的加速带动参考功率的增加，最终导致加速区面积增大，减速区面积减小，使风机暂态稳定性恶化。
设置Ug在t =5 s时跌落至0.2(pu)，持续tf后故障结束，电压恢复，设置持续时间tf分别为0.3、3、5 s三组工况，得到如图6所示暂态响应波形。
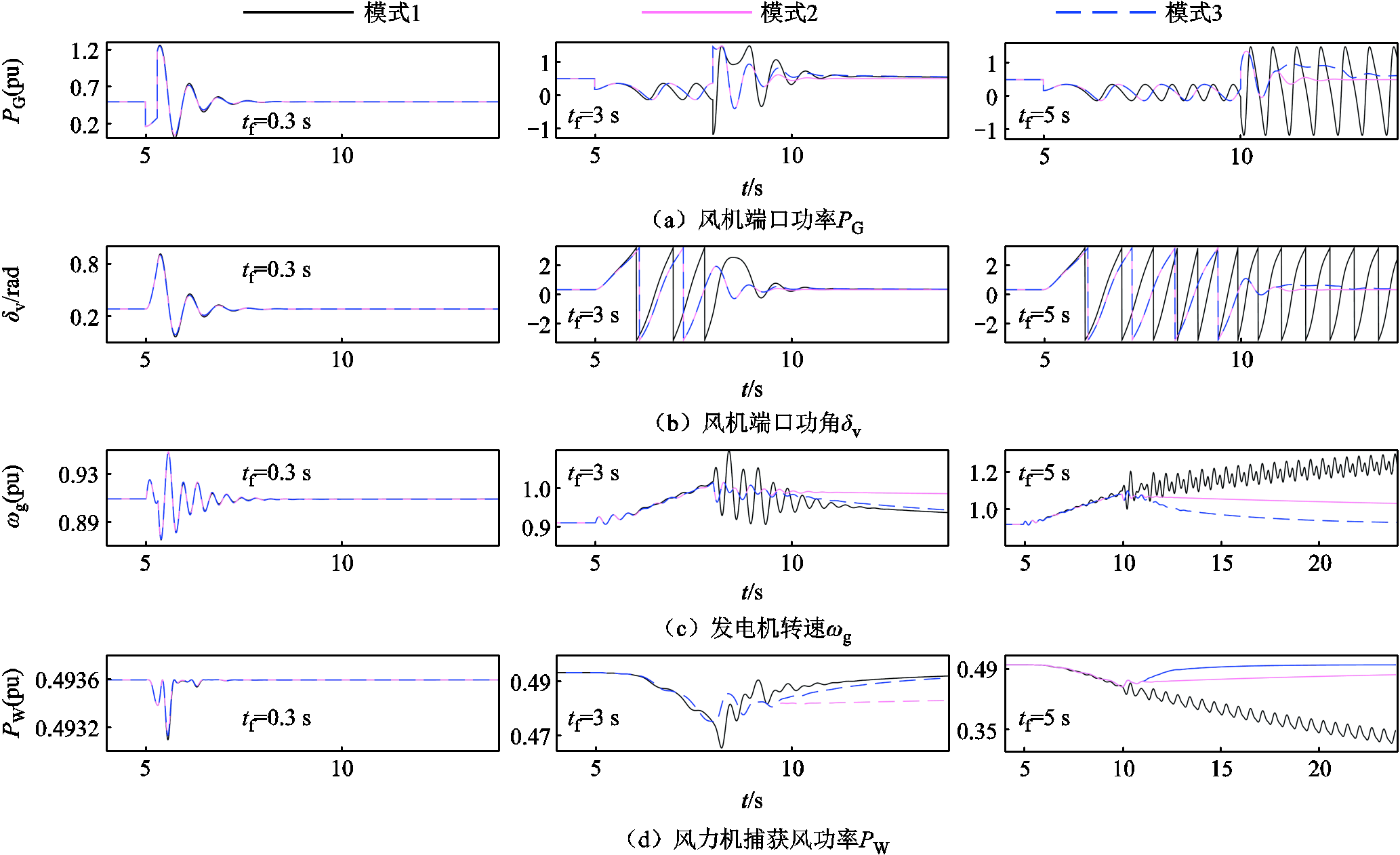
图6 不同故障持续时间下的暂态响应波形
Fig.6 Transient response waveforms under different fault duration
下面分别对各tf对应的仿真结果进行分析。
1）故障持续时间tf=0.3 s
PG在故障期间短暂跌落，故障结束后经过大幅暂态波动后恢复至稳态。模式1、2、3对应的δv皆未失稳；这个过程中PG的暂态波动传递到PMSG，进而引发风机的轴系扭振[23]，导致ωg出现小幅振荡；由于ωg的振幅较小，对MPPT模式Pref以及PW的影响甚微。
2）故障持续时间tf=3 s
模式1、2、3在故障期间失稳，δv越过数个周期，并伴随着PG振荡在较低水平。由于此刻PG＜PW，导致ωg上升，PW小幅下降。故障结束后，在PG和Dv的制动下，风机恢复暂态稳定。
由于ωg上升幅度较大，对MPPT模式Pref的影响难以忽略，模式1与模式2、3的暂态响应特性开始出现较为明显的差异：
（1）结合图5可知，模式1加速面积大于模式2、3，导致模式1的δv增速快于模式2、3。
（2）故障结束时模式1的δv与模式2、3不同，导致故障结束后模式1的PG形态也不同于模式2、3，结合图5可知，模式1减速面积小于模式2、3，因此需要PG在高水平维持更长的时间对δv进行减速。
（3）故障结束后模式1的PG暂态波动较大，引发了更为明显的ωg振荡。
3）故障持续时间tf=5 s
故障期间模式1的ωg快速上升，导致Pref大幅增加，大大压缩了减速面积，仅靠PG和Dv难以对δv制动，风机彻底暂态失稳，PW也随之大幅下降，最终ωg维持在较高转速持续振荡。
模式2、3对应的暂态特性变化趋势相比tf =3 s时没有明显区别，但由于模式2的Pref恒定，故障结束后缺乏对风机转速的制动功率，因此需要更长的时间使转速恢复至稳态。
为更加直观地展现不同故障时间对构网型直驱风机的影响，在附录第3节中，根据风机功角-功率相平面轨迹展开进一步分析。
由2.2节分析可知，参考功率与风机功率的失衡是导致构网型风机失衡的主要原因。因此为提升构网型风机故障穿越功角稳定性，可在虚拟同步环节附加控制以保持PG和δv的稳定，通常包括降低故障期间有功功率参考值[24]、增加故障期间阻尼大小[25]等方式，本质都是降低虚拟同步控制环节的失衡功率。本文以图7所示的故障穿越功角稳定控制策略为代表进行后续分析。
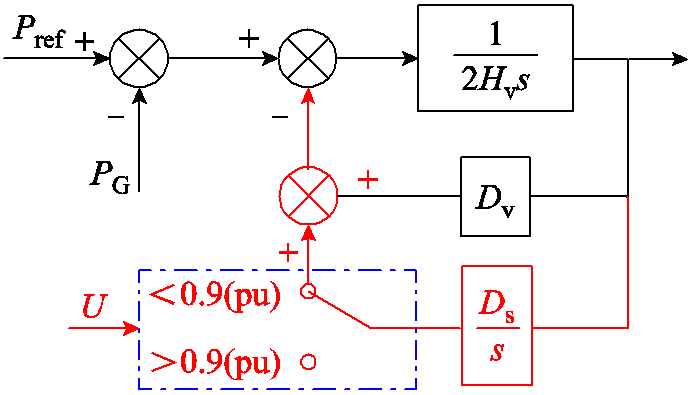
图7 故障穿越功角稳定控制策略
Fig.7 Fault-through control strategy of power angle
图7所示控制中，当电压跌落到设定范围内时，投入积分阻尼环节Ds/s进一步提高阻尼功率，保证δv稳定。投入所提控制策略后，模式1、2、3在2.2节电压跌落工况（tf=5 s）下的暂态响应波形如图8所示。
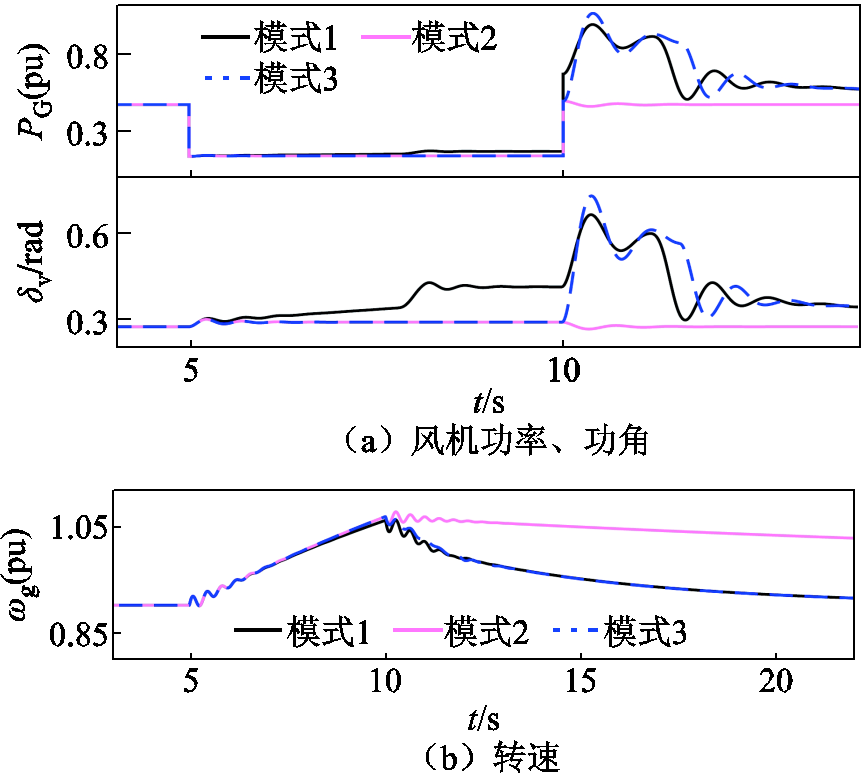
图8 故障穿越控制下风机暂态响应波形
Fig.8 Transient response waveforms under fault-through control strategy of power angle
故障期间，模式1、2、3的功角都遏制在较低水平，PG也相对平滑稳定，ωg逐渐增加，由于风机保持暂态稳定，并未发生δv明显摇摆加速过程。故障结束后模式1、3和模式2之间的暂态差异可结合图9所示各模式对应的风机功率-转速关系曲线进行分析。
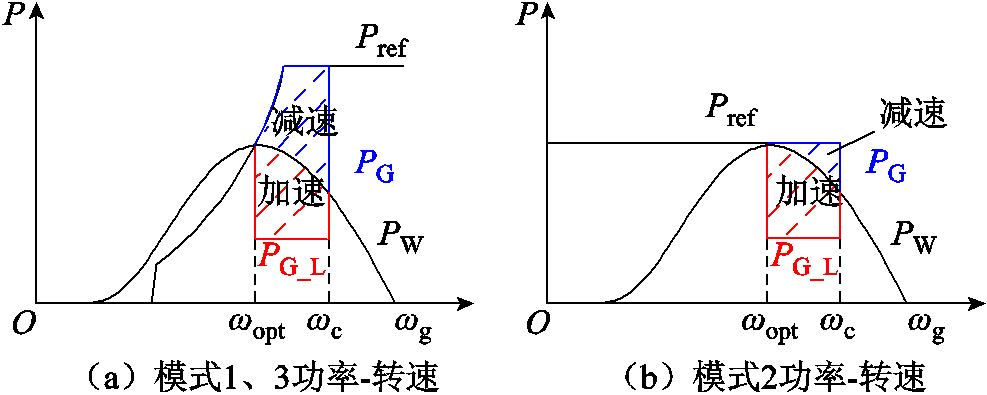
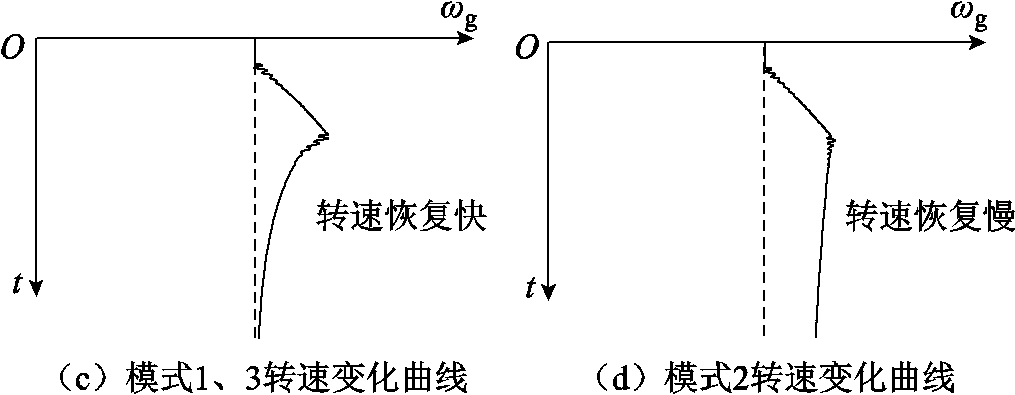
图9 各模式对应的风机功率-转速关系曲线
Fig.9 Wind power-rotor speed curve of each mode
故障结束后，模式1、3都处于MPPT功率跟踪状态，此时转速较快，Pref处于高位，PG随Pref升高，PG与PW之间形成减速区，并对ωg进行减速，在这个过程中PG也沿着功率跟踪曲线降低。
图9中模式1、3和模式2对应的故障期间转速加速面积近似相同，由于模式2的Pref与ωg解耦且恒定，故障结束后的转速减速区面积小于模式1和3，导致模式2的转速恢复速度较慢。
对于风机而言，无论是否投用故障穿越控制，较长时间的电压跌落故障、风力机功率和端口功率的不平衡都会导致风机转速上升，转换为部分旋转动能。但是为了保障风机的发电效率，转速最终还是会恢复至最优转速，使这部分能量无法保留，造成弃风。
通过以上分析，剖析了风力机动态给构网型直驱风机在主动支撑能力和暂态稳定性带来的影响，并通过表1归纳总结了构网型直驱风机所受制约。
表1 构网型直驱风机所受制约
Tab.1 Limitations of grid-forming PMSG without storage
参考功率模式频率跌落工况电压跌落工况 电压严重跌落（短时间）电压严重跌落（长时间）投入故障穿越控制策略 MPPT参考功率随转速变化的特性导致无法充分地利用风机旋转动能，削弱了虚拟同步控制的频率支撑能力机侧功率跟随端口功率产生暂态波动，进而引发轴系扭振故障期间端口功率的跌落导致转速大幅上升，同时也降低了风能捕获效率，使风力机功率下降MPPT模式不利于构网型风机的暂态稳定，相比其他模式更容易暂态失稳提升了风机故障穿越的暂态稳定性，但降低端口功率输出水平，无法避免风机转速上升，造成能量浪费 恒功率支撑能力表现最符合虚拟同步控制目标，但不利于风机转速的恢复转速恢复较慢 故障期间恒功率，结束后MPPT频率跌落结束后，为了恢复风机转速，功率“二次跌落”现象较为明显—
本节将基于配置超级电容储能的构网型直驱风储一体机，根据构网型直驱风储一体机能量流动特性及虚拟同步控制的暂态响应特性，提出基于暂态响应功率分解的储能驱动控制策略。
直驱风储一体机的能量流动示意图如图10所示。风力机风轮捕获风能后经转动轴、永磁同步发电机、机侧变流器馈入直流母线，储能能量也可经过DC-DC变换器馈入直流母线，最终通过网侧变流器馈入电网。
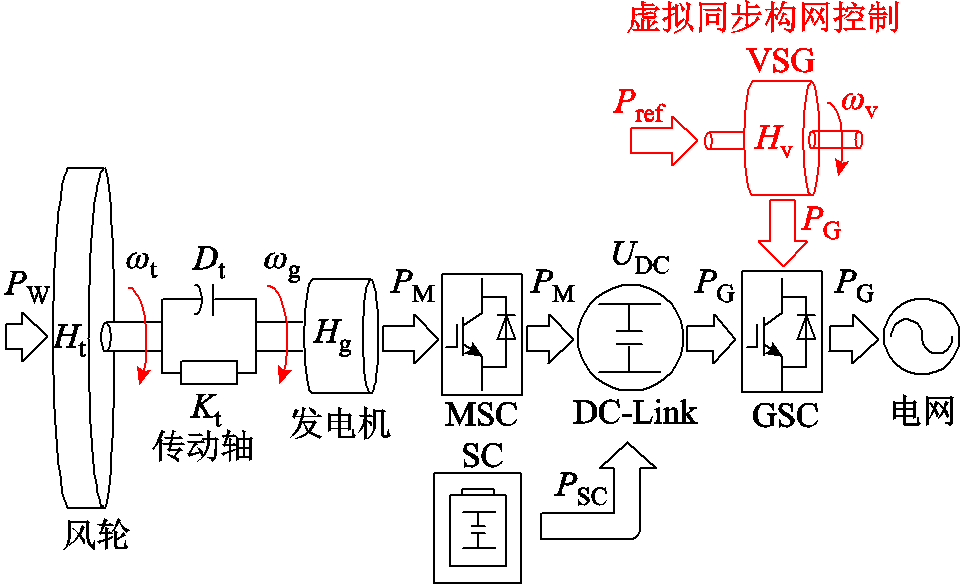
图10 构网型直驱风储一体机能量流动示意图
Fig.10 Diagram of energy flow of of grid-forming PMSG-based wind-storage generator
当电网发生扰动时，作为与电网连接的唯一端口，风机向电网提供多少暂态响应能量，由网侧变流器虚拟同步控制的暂态响应特性主导，而网侧变流器的首要能量来源于直流母线电容。机侧变流器通过定直流电压控制，将风力机捕获能量馈入直流母线以保持电压稳定。当机侧变流器功率大于风力机捕获功率时，风机降低转速释放自身旋转动能，提供额外支撑能量。
而当储能也向直流母线馈入能量时，由于风机整体对外输出功率由网侧控制主导，因此对旋转动能的需求也相应减少，单独控制储能能同时实现风机主动支撑时对旋转动能和储能的调用。因此，如何将储能控制与虚拟同步控制耦合，是将储能纳入构网主动支撑体系的关键。
构网型风机的虚拟同步控制对2.1节频率跌落工况的暂态响应特性如图11所示。
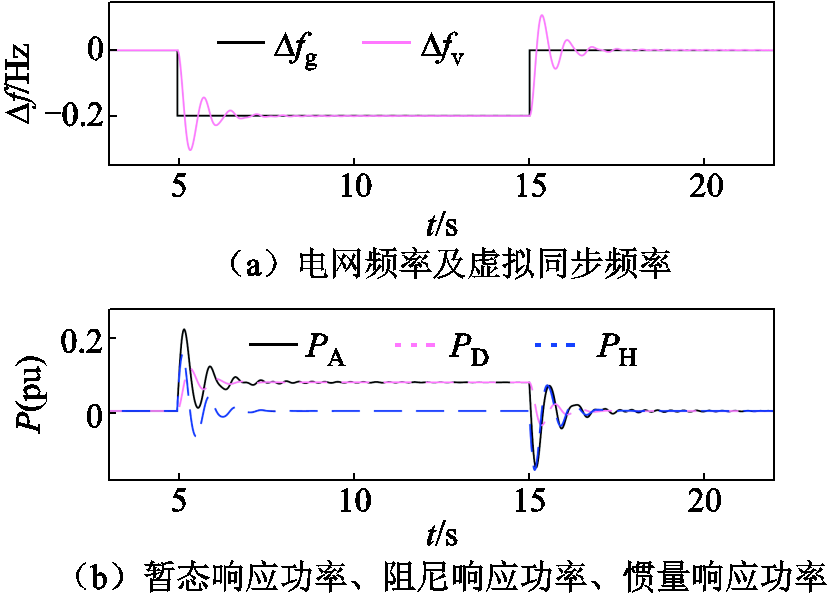
图11 虚拟同步控制对电网频率跌落的响应特性
Fig.11 Response of VSG to frequency drop
由图11a可知，虚拟同步控制环路自同步生成的虚拟同步频率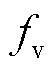
能够反映电网频率的变化。由图11b中能够看出，虚拟同步控制对频率跌落响应的暂态响应功率PA能够分解为惯量响应功率PH和阻尼响应功率PD，PH对频率瞬态变化进行响应，存在于频率变化初期，PD对频率偏差进行响应，存在于整个频率跌落过程。
无论是频率信号还是频率微分信号都天然地存在于图12所示的虚拟同步控制环路中，无需额外测量环节，并且PH和PD信息能够从控制环路中获取，这也是虚拟同步构网控制优势所在。
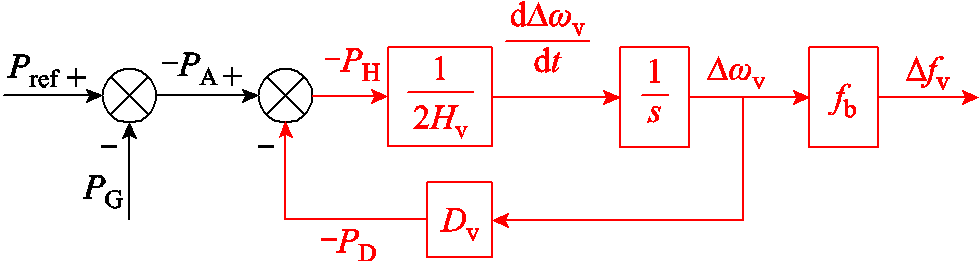
图12 虚拟同步控制环路
Fig.12 VSG control loop
图12中各功率的关系为
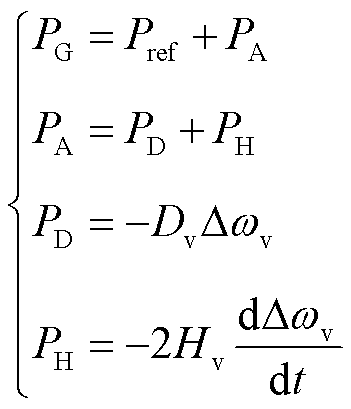（7）
另外，在2.2节电压跌落工况下PA同样能够分解为PH和PD，功率及∆ωv暂态响应如图13所示。图13中展示了tf=0.3 s和tf=5 s时虚拟同步控制的暂态响应。如图13a所示，故障持续时间较短时，∆ωv存在时间较短，相比之下，整个暂态过程中其微分变化d∆ωv/dt更加明显，因此PA以PH为主。如图13b所示，当故障持续时间较长时，∆ωv在故障期间持续存在，因此在故障持续期间PA以PD为主，PH在0附近来回振荡。由此可以看出，PH主要存在于故障开始和结束阶段，PD主要存在于故障持续阶段。
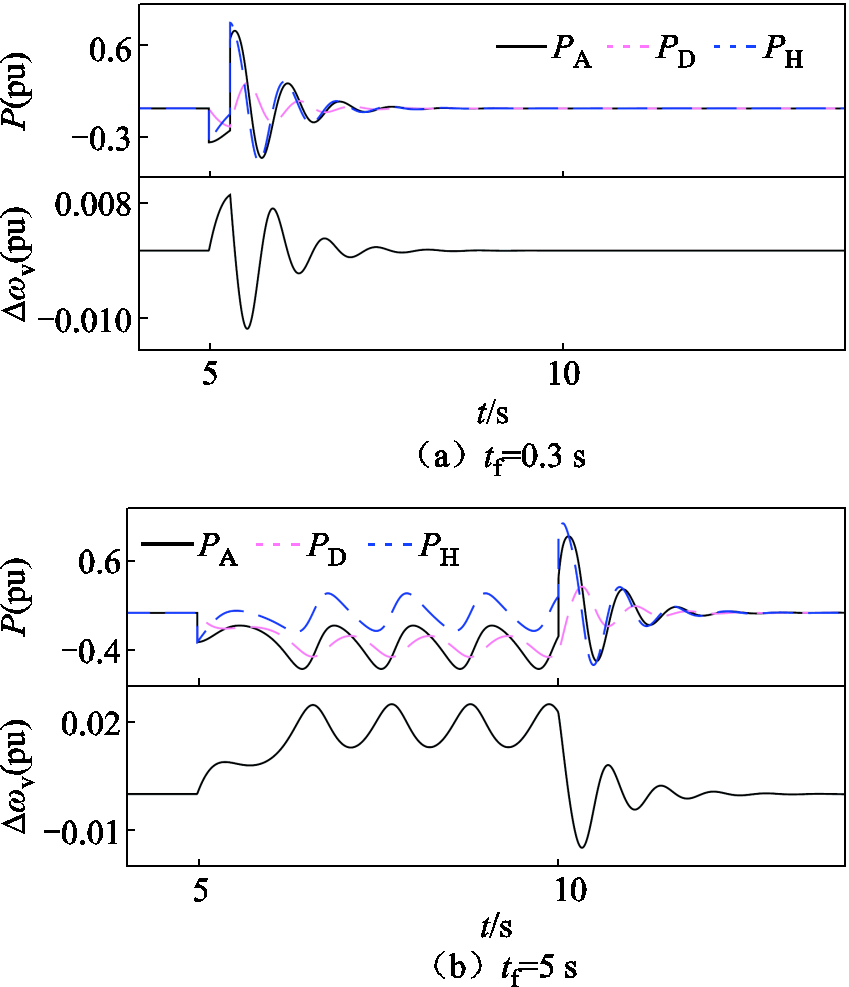
图13 虚拟同步控制对电网电压跌落的响应特性
Fig.13 Response of VSG to voltage drop
将虚拟同步控制环节暂态响应功率PA分解为PH和PD后，传递给储能变流控制环节，能够形成如图14所示的储能驱动策略。
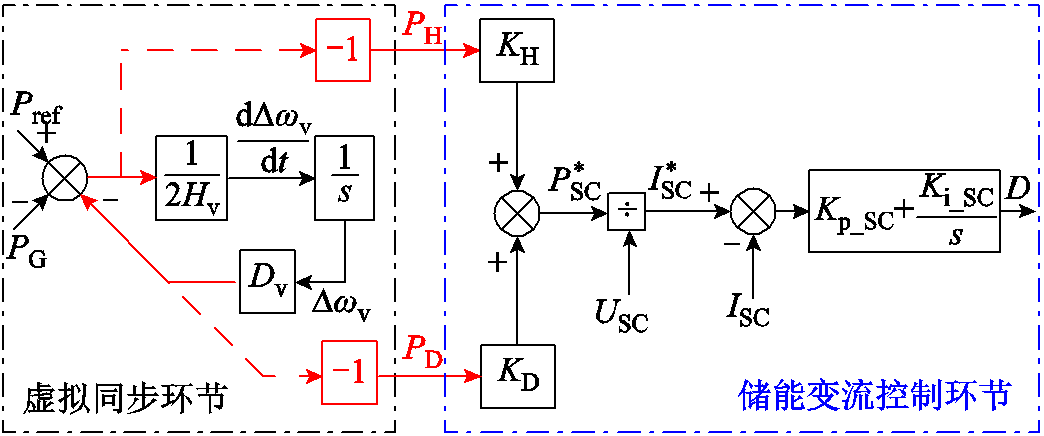
图14 基于暂态响应功率分解储能驱动策略
Fig.14 Energy storage drive strategy based on transient response power decomposition
图14中参考电流可表示为
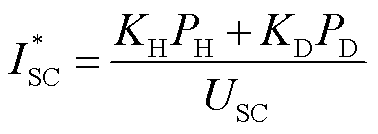（8）
式中，KH为储能对PH的参与系数；KD为储能对PD的参与系数。通过调节KH、KD的大小决定储能对PH和PD的响应程度。
为验证所提策略的有效性，分别在频率、电压跌落工况下进行仿真验证。
为简化论证过程，本节选用模式3参考功率设定模式进行仿真验证，工况设置与2.1节相同，设置不同的KH和KD，得到机侧响应功率∆PM、储能响应功率∆PSC的仿真结果如图15所示。
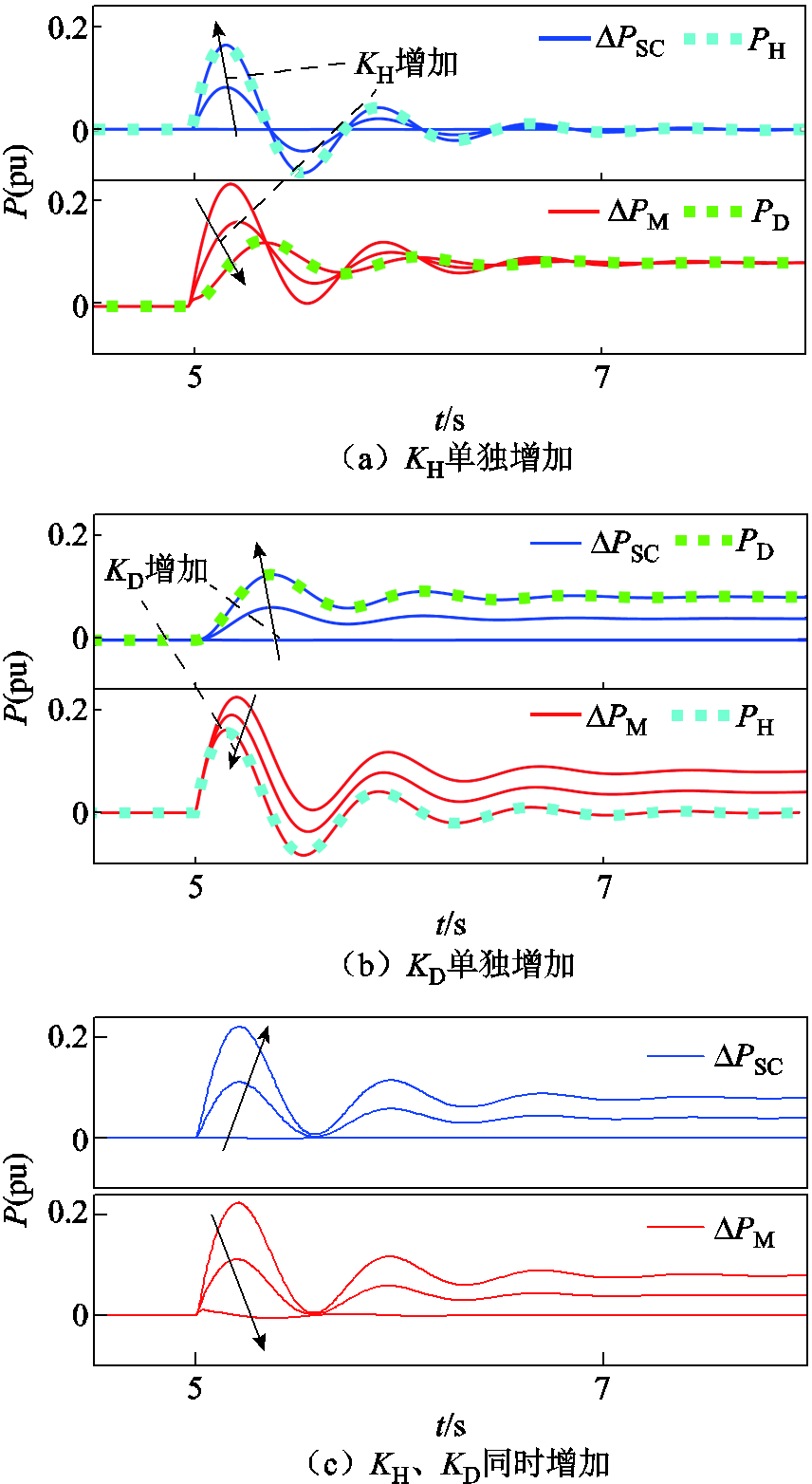
图15 ∆PM、∆PSC响应功率
Fig.15 Response power of ∆PM and ∆PSC
首先在图15a中单独增加KH（KH=0、0.5、1.0），可以看出，增加KH提高了∆PSC对PH的响应程度，同时也压缩了∆PM对PH的响应。当KH=1时，∆PM只剩下对PD的响应，能量调用策略将对PH和PD的响应任务分别分配给了储能和转子动能。图15b中，增加KD（KD=0、0.5、1.0）提高了∆PSC对PD的响应程度，压缩了∆PM对PD的响应。图15c证明了在虚拟同步控制下储能的参与会减少对机侧功率的响应需求。
随着储能出力占比的提升，对转子动能的需求也逐渐减少，风机转速ωg、超级电容电压USC、风机端口功率PG的变化如图16所示。可以看出，随着储能参与度的提升，USC下降幅度增加，ωg下降幅度减少，因此在结束频率支撑后，恢复转速所需能量减少，PG的二次跌落得到了显著改善。
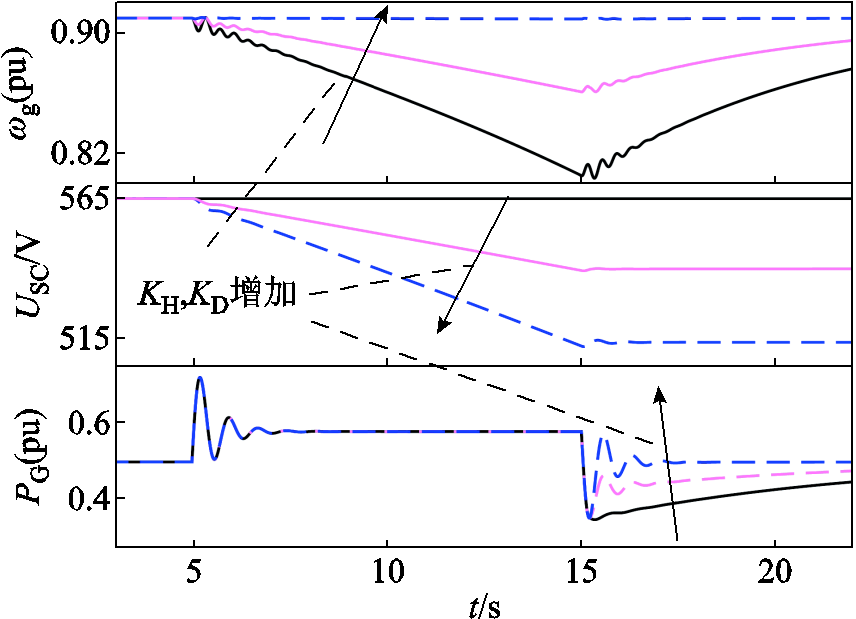
图16 储能出力增加时的ωg、USC、PG
Fig.16 ωg，USC，PG when storage output increases
若采用模式1中的MPPT模式，随着储能参与度的提升，ωg和USC的变化与图16相似，而PG的变化则如图17所示，由于避免了ωg下降对Pref的影响，提高了风机支撑过程的功率。
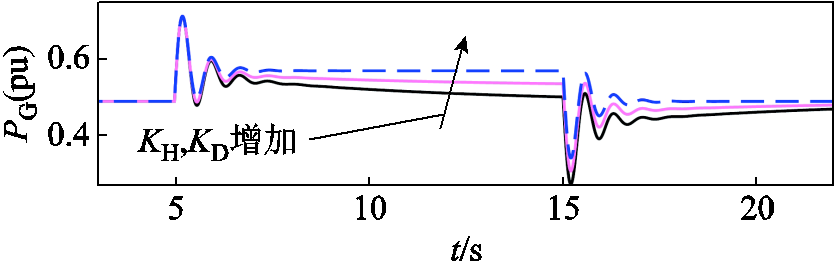
图17 储能出力增加时的PG（模式1）
Fig.17 PG when storage output increases (case1)
以上仿真验证表明，本文所提能量调用策略可以将虚拟同步环节的暂态响应功率灵活分配给转子动能和储能来响应，储能出力占比越高，构网型风机的频率支撑能力越强。
为简化论证过程，本节选用2.2节中暂态稳定性最差的模式1进行仿真验证，电压跌落故障设置与2.2节相同，设置不同的KH和KD，分别在tf =0.3 s、tf=5 s的工况下进行仿真验证；另外结合2.3节所提故障穿越控制策略，在tf =0.3 s、tf =5 s的工况下进行仿真验证。
4.2.1 故障持续时间tf=0.3 s
图18中对比了单独增加KH（KH=0、0.5、1.0）的仿真结果，结合图16分析可知，低电压故障持续时间较短时，端口响应功率∆PG以PH为主，随着KH的增加，∆PSC增加，并压缩了∆PM，∆PM暂态波动受到一定程度的抑制。
随着∆PM暂态波动受到抑制，ωg的暂态振荡程度逐渐减小，轴系扭振得到了一定的缓解，取而代之的是USC的暂态波动，与此同时直流母线电压UDC的暂态波动也得到了轻微抑制。
由图13a可知，当低电压故障持续时间较短时，PD占比较低，因此如图19所示，单独增加KD（KD=0、0.5、1.0）的效果并不显著。
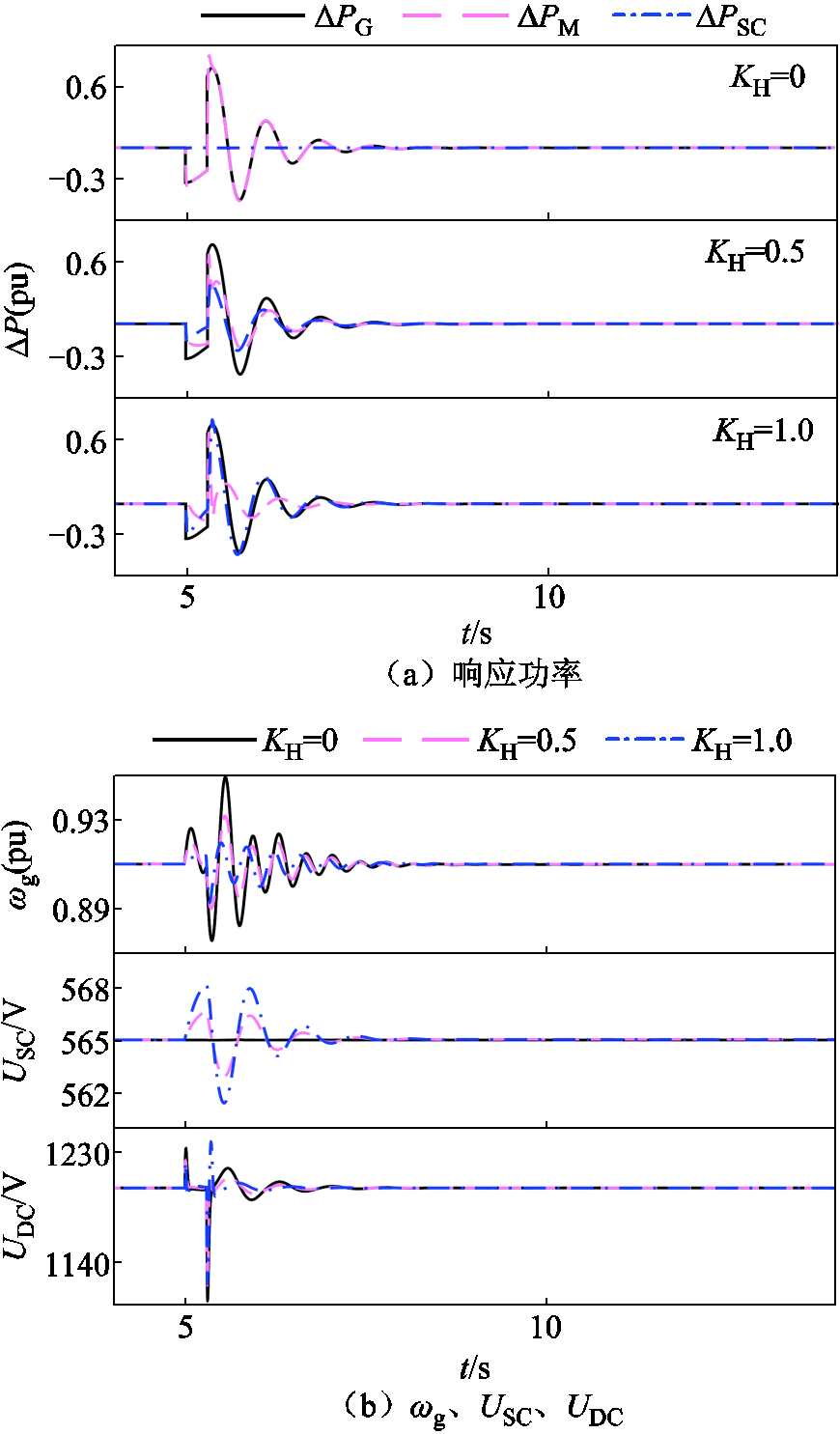
图18 短时间故障仿真结果（KH单独增加）
Fig.18 Short-time fault simulation result (KH added separately)
图19b中，提高储能对阻尼响应功率的占比，仅增加了超级电容电压在故障穿越前后的暂态波动程度，对ωg、UDC暂态波动的抑制作用尚浅。
4.2.2 故障持续时间tf=5 s
图20中对比了单独增加KH（KH=0、0.5、1.0）的仿真结果，结合图13b可知，低电压故障持续时间较长，当风机首摆失稳进入暂态失稳状态时，PD居高不下。因此，由∆PSC承担PH之后，仍有大量PD需要∆PM承担，此刻ωg如图20b所示，仍不可避免地上升，导致加速面积增加，减速面积减小，恶化了暂态稳定性，风机在故障持续期间和结束后始终处于失稳状态。
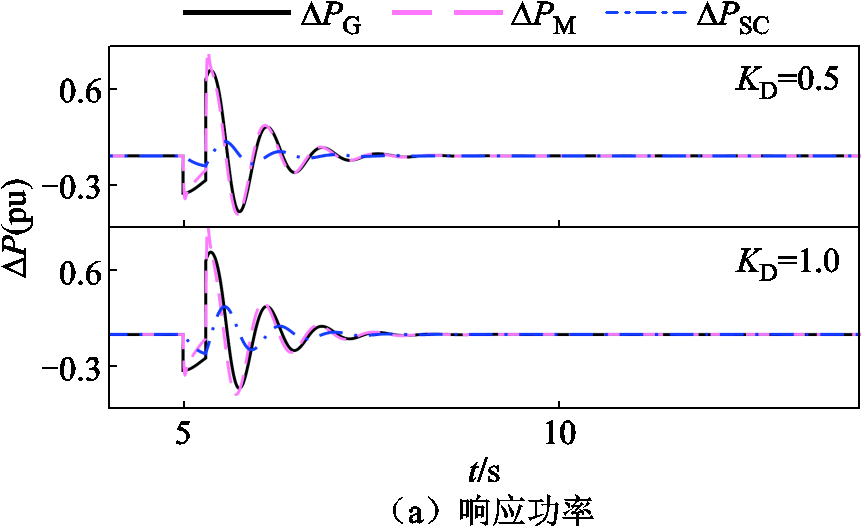
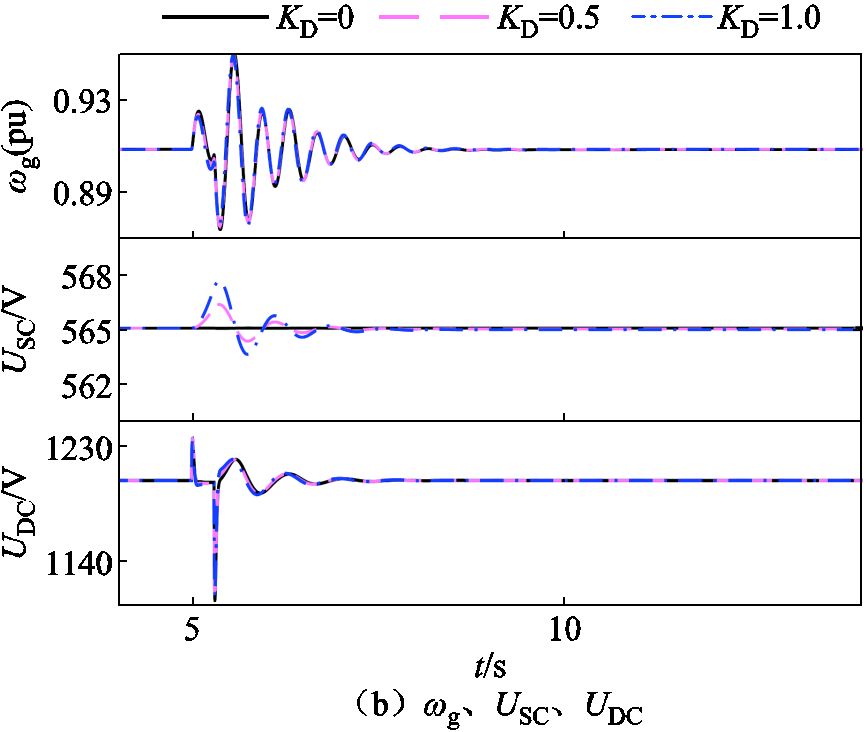
图19 短时间故障仿真结果（KD单独增加）
Fig.19 Short-time fault simulation results(KD added separately)
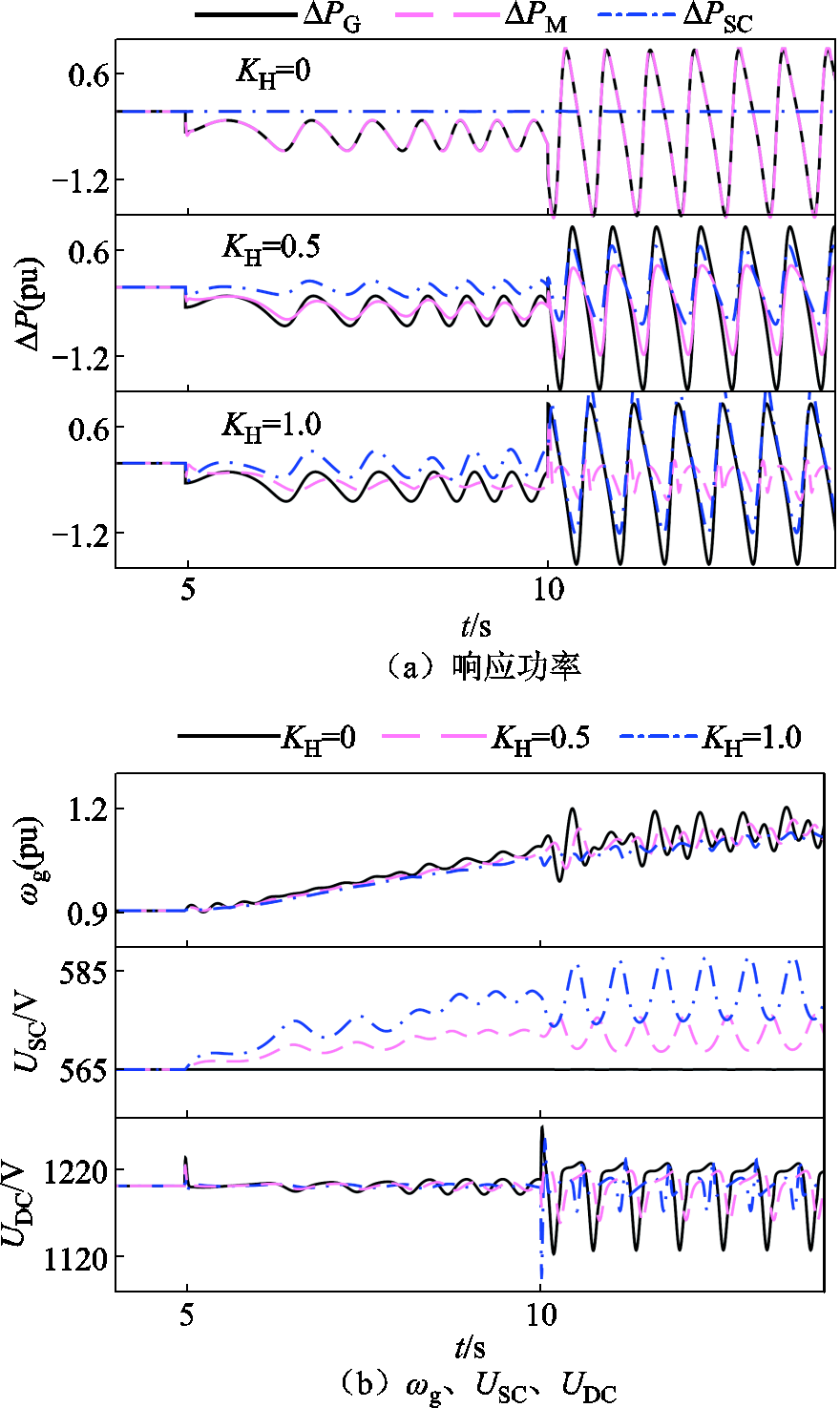
图20 长时间故障仿真结果（KH单独增加）
Fig.20 Long-time fault simulation results (KH added separately)
在这个过程中，虽然风机处于失稳状态，但是提高∆PSC对PH的响应，对ωg、UDC暂态波动的抑制效果依然明显，取而代之的是USC暂态波动。从图20b中ωg、USC的上升可以看出，暂态失稳的情况下构网型风机在故障前后产生了大量冗余能量，而单纯提高∆PSC对PH的响应，不能完全消耗产生的冗余能量。
因此，在图21中可以看出，增加KD（KD=0、0.5、1.0），提高∆PSC对PD的响应，极大程度地抑制了故障期间ωg的上升，冗余能量大部分转换为储能能量，使USC大幅上升。由于ωg的上升得到抑制，避免了加速面积的增加以及减速面积的减小，故障结束后风机恢复暂态稳定。
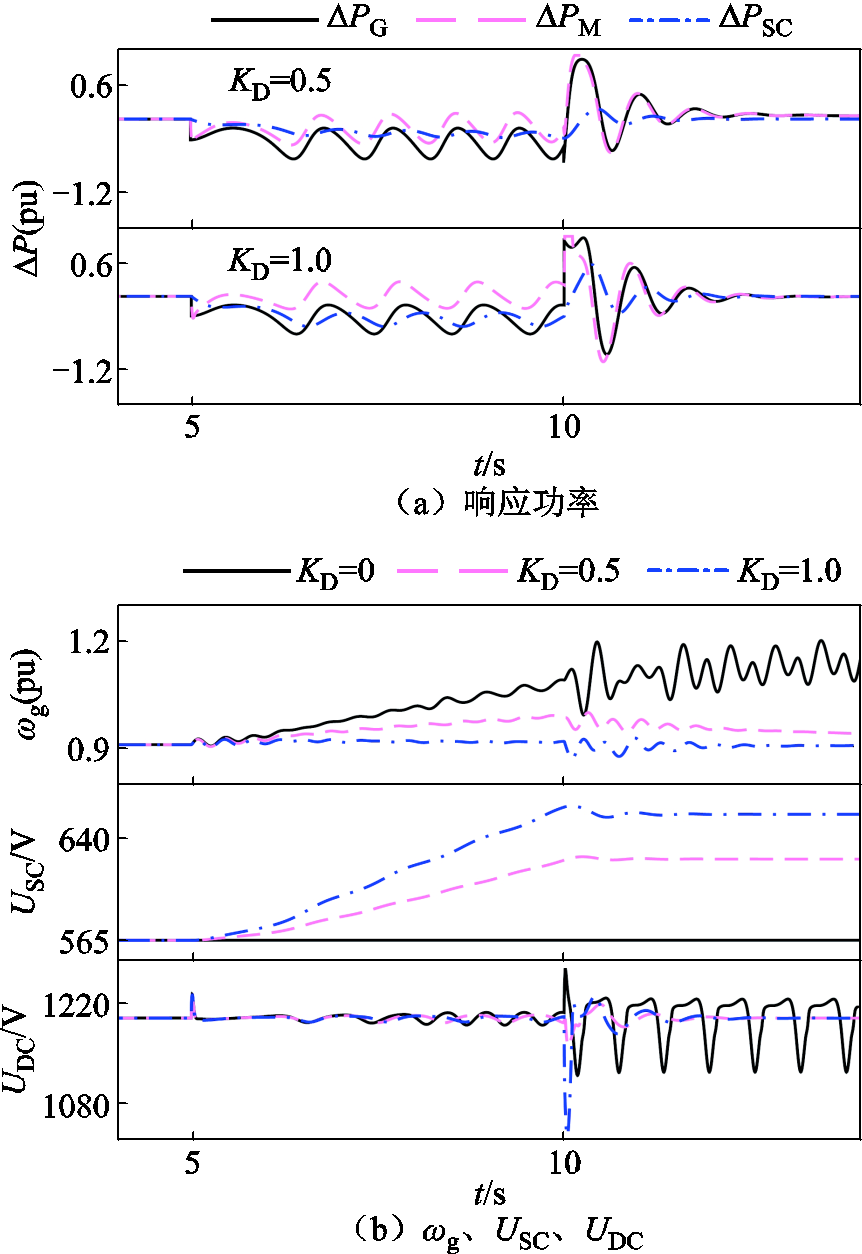
图21 长时间故障仿真结果（KD单独增加）
Fig.21 Long-time fault simulation results (KD added separately)
在图21中，由于PH变为由∆PM承担，导致故障发生时和故障结束时ωg、UDC暂态波动依旧存在。在KD=1.0的基础上，增加KH（KH=0、0.5、1.0）后，ωg、UDC暂态波动可以得到有效抑制，效果如图22所示。
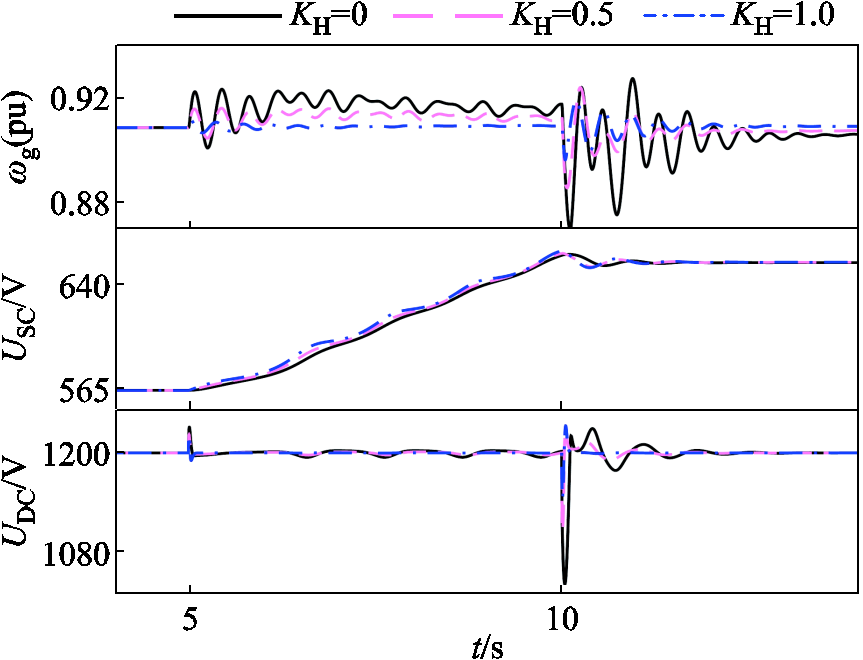
图22 增加KH对暂态波动的抑制效果
Fig.22 The effect of increasing KH on the suppression of transient fluctuations
以上仿真验证表明，提高∆PSC对PH的响应度（增加KH），可以有效地抑制ωg、UDC的暂态波动；提高∆PSC对PD的响应度（增加KD），可以有效地吸收故障穿越产生的冗余能量，提高构网型风机的暂态稳定性。
4.2.3 故障持续时间tf=5 s，并投入故障穿越功角稳定控制策略
增加KH、KD（KH,D=0、0.5、1.0），得到图23所示仿真结果。
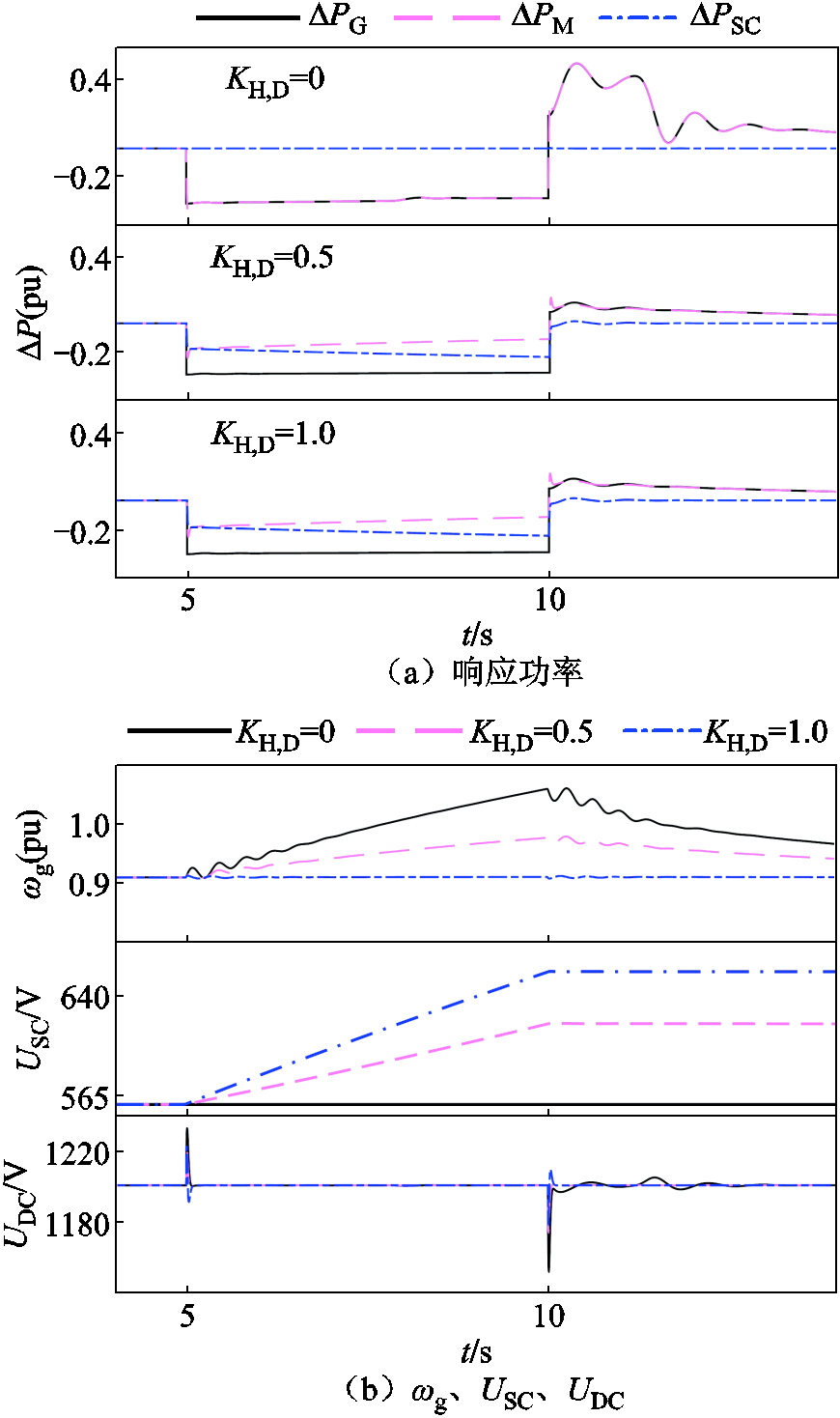
图23 故障穿越功角稳定控制仿真结果（增加KH、KD）
Fig.23 Simulation results of power angle stability control for fault through(KH and KD added)
可以看出，随着∆PSC的提高，冗余能量向储能转换的比例随之提升，降低了弃风浪费。另外，在储能承担大部分冗余能量后，扼制了ωg上升，故障结束后不再需要提高PG对转子进行制动，降低了UDC的欠电压冲击幅度。此外，相比图21a、图23a，∆PSC的暂态波动幅度也相对较小，在相同KH、KD的参数下，仅需要更低的∆PSC参与暂态响应。储能的参与进一步完善了故障穿越功角稳定控制策略的效果，而故障穿越功角稳定控制策略的投入也降低了对储能功率容量的需求，二者相辅相成。
构网型直驱风储一体机在本文所提暂态能量调用控制策略下，获得的性能提升表现见表2。
表2 所获性能提升表现
Tab.2 improvement performance
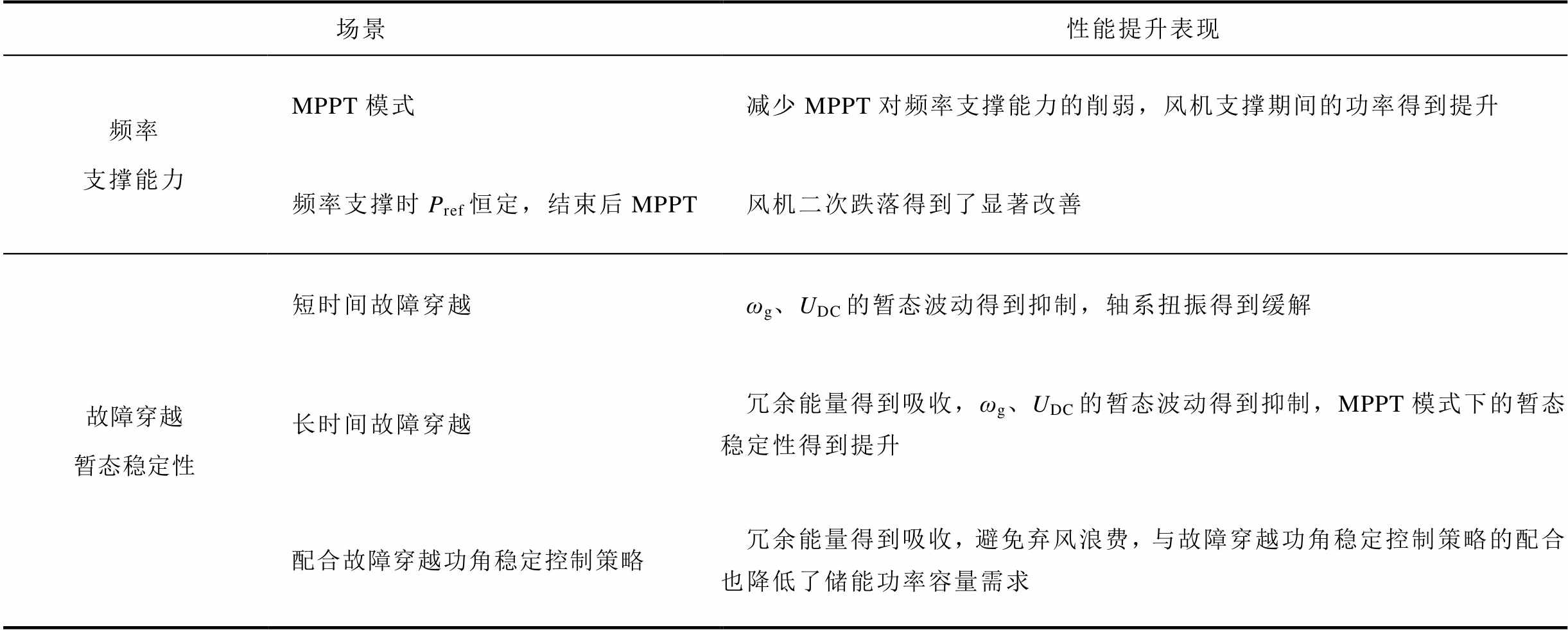
场景性能提升表现 频率支撑能力MPPT模式减少MPPT对频率支撑能力的削弱，风机支撑期间的功率得到提升 频率支撑时Pref恒定，结束后MPPT风机二次跌落得到了显著改善 故障穿越暂态稳定性短时间故障穿越ωg、UDC的暂态波动得到抑制，轴系扭振得到缓解 长时间故障穿越冗余能量得到吸收，ωg、UDC的暂态波动得到抑制，MPPT模式下的暂态稳定性得到提升 配合故障穿越功角稳定控制策略冗余能量得到吸收，避免弃风浪费，与故障穿越功角稳定控制策略的配合也降低了储能功率容量需求
本文通过建立动态模型在各种工况下归纳总结了构网型直驱风机暂态能力所受到的制约，并提出了基于超级电容储能接入直流母线形成构网型直驱风储一体机的暂态支撑能力提升方法。通过将虚拟同步控制暂态响应功率分解为惯量、阻尼响应功率，提出基于暂态响应功率分解的储能驱动控制，实现了对构网型直驱风储一体机暂态支撑过程中对转子动能和储能的调用，提升了构网型风机的频率支撑能力和故障穿越稳定性。通过一系列理论分析和仿真验证，构网型直驱风储一体机采用本文所提暂态能量调用策略后，整机性能得到以下提升：
1）频率支撑能力得到提升，减少了MPPT模式和转速恢复“二次跌落”对风机频率支撑能力的约束。
2）故障穿越能力得到提升，其中，增加KH可以有效地抑制ωr、UDC暂态波动，增加KD可以有效地吸收故障穿越产生的冗余能量，提高构网型风机暂态稳定性。
3）结合故障穿越功角稳定控制策略，将故障期间冗余能量转换为储能能量，避免风机发电效率降低，减少能量浪费，与此同时，故障穿越功角稳定控制策略也能够降低储能容量的需求。
在后续研究中，将考虑变桨控制和电流限幅，进一步优化风储一体机储能驱动控制策略。
附 录
1.剩余环节的建模过程
1）风力机动态模型
根据空气动力学原理，风力机输出功率为
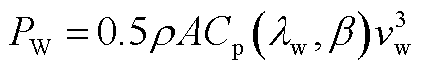（A1）
式中，ρ为空气密度；A为风机的桨叶迎风扫掠面积；Cp为风机的风能利用系数，可表示为叶尖速比λw和桨距角β的函数；vw为风速。
根据经验公式，Cp可以写为
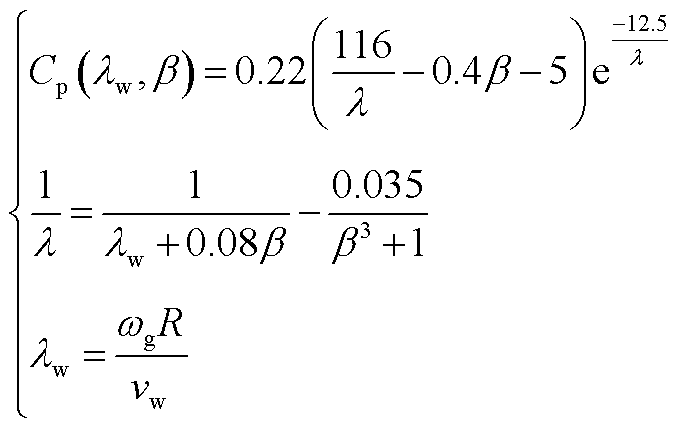（A2）
本文传动链采用二质量块模型，其转子运动方程可表示为
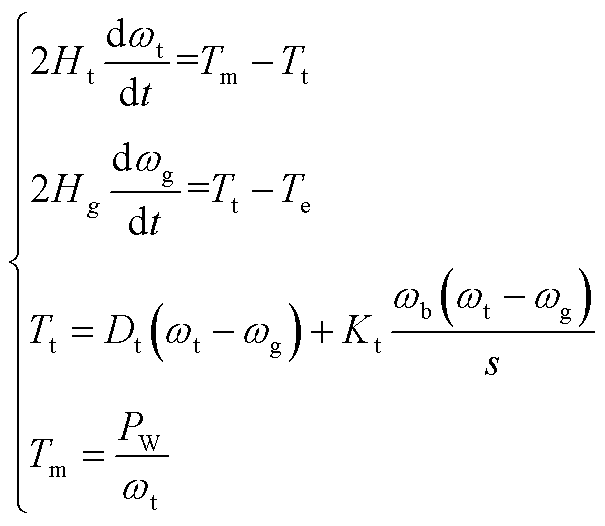（A3）
式中，ωt、Tm分别为风力机转速和风力机输入转矩；Ht为风力机惯性时间常数；Hg为发电机惯性时间常数；Kt为轴系刚度系数；Dt为轴系阻尼系数；Tt为轴系转矩；Te为发电机电磁转矩。
2）机侧动态模型
本文机侧变流器采用零d轴控制，该控制下PMSG的电磁转矩以及机侧有功功率为
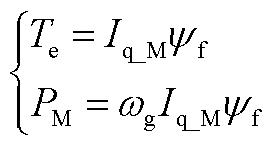（A4）
式中，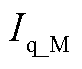
为机侧变流器的q轴电流；
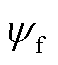为永磁体磁链。
随后忽略电流内环动态，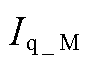
=
，
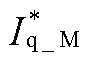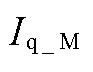可表示为
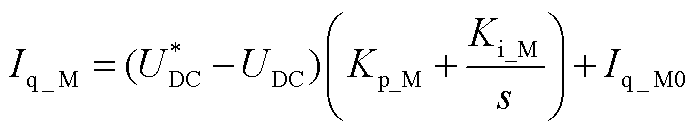（A5）
式中，Kp_M和Ki_M分别机侧直流电压环的比例和积分系数；Iq_M0为机侧q轴电流初始值。
3）直流母线电压动态模型
直流母线存在三个端口，直流母线电压为
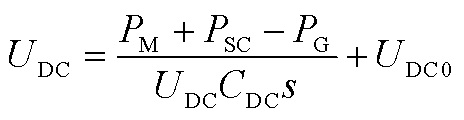（A6）
式中，CDC为直流母线电容；UDC0为直流母线初始电压。
2. 构网型直驱风储一体机模型参数及储能容量配置方法
附表1 构网型直驱风储一体机模型参数
App.Tab.1 Simulation parameters of grid-forming PMSG-based Wind-storage generator
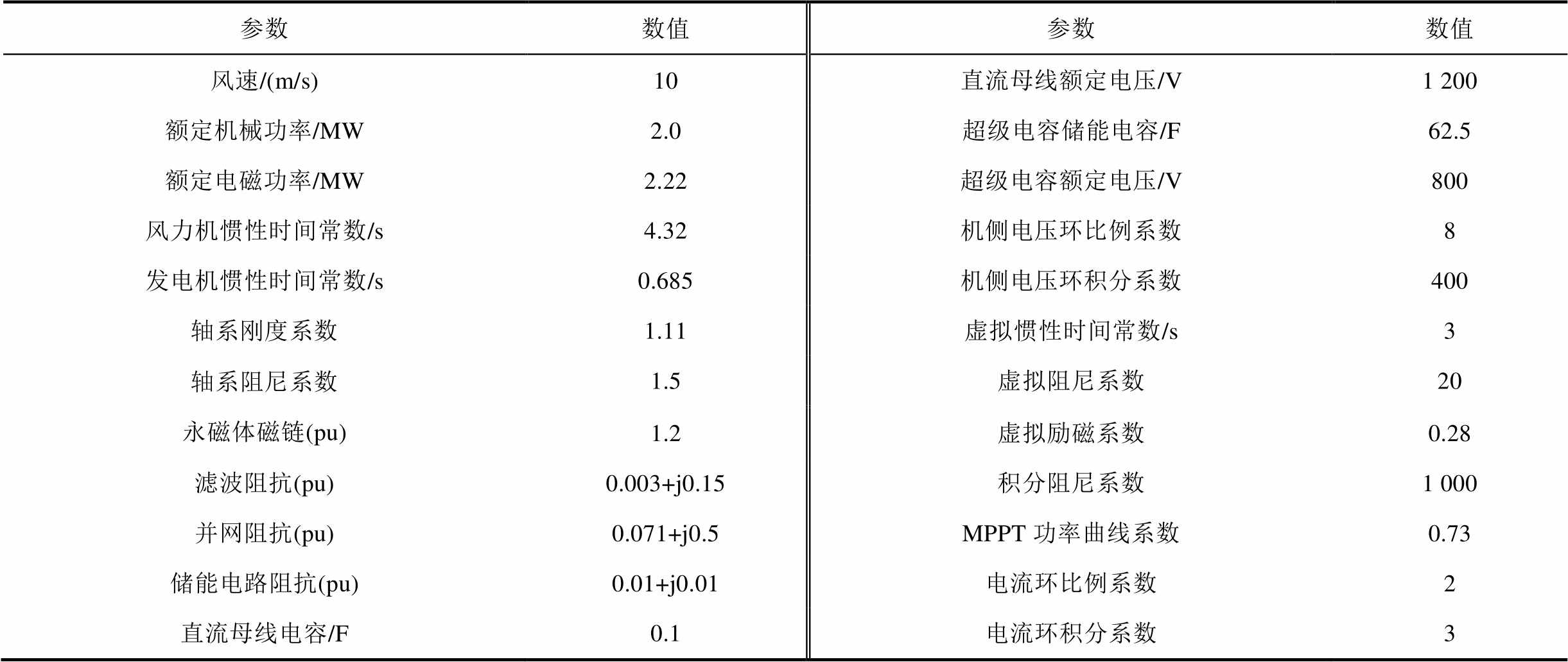
参数数值参数数值 风速/(m/s)10直流母线额定电压/V1 200 额定机械功率/MW2.0超级电容储能电容/F62.5 额定电磁功率/MW2.22超级电容额定电压/V800 风力机惯性时间常数/s4.32机侧电压环比例系数8 发电机惯性时间常数/s0.685机侧电压环积分系数400 轴系刚度系数1.11虚拟惯性时间常数/s3 轴系阻尼系数永磁体磁链(pu)1.5虚拟阻尼系数20 1.2虚拟励磁系数0.28 滤波阻抗(pu)0.003+j0.15积分阻尼系数1 000 并网阻抗(pu)0.071+j0.5MPPT功率曲线系数0.73 储能电路阻抗(pu)0.01+j0.01电流环比例系数2 直流母线电容/F0.1电流环积分系数3
根据标准Q/GDW11826—2018《风电机组虚拟同步发电机技术要求和试验方法》，虚拟同步发电机若能调节有功输出参与电网一次调频，当频率下降时，其有功出力可增加量的最大值至少为10%的装机容量[26]。而标准GB/T 40595—2021《并网电源一次调频技术规定及试验导则》中则规定了储能应能够提供额定功率20%的有功支撑[27]。文献[28]中对1.5 MW双馈风机配置了150 kW×30 s的超级电容，本文综合考虑，对2 MW直驱风机配置了400 kW× 40 s的超级电容，电容储能计算公式为
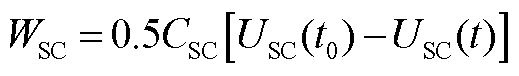（A7）
超级电容从满电状态（荷电状态SOC=100%，USC=800 V）按额定功率放电，直至SOC达到20%下限值（USC=357.77 V），需要超级电容能够释放WSC=400 kW× 40 s的电量，根据式（A7），可以得到超级电容的电容值为62.5 F。
3. 基于相平面的暂态稳定分析
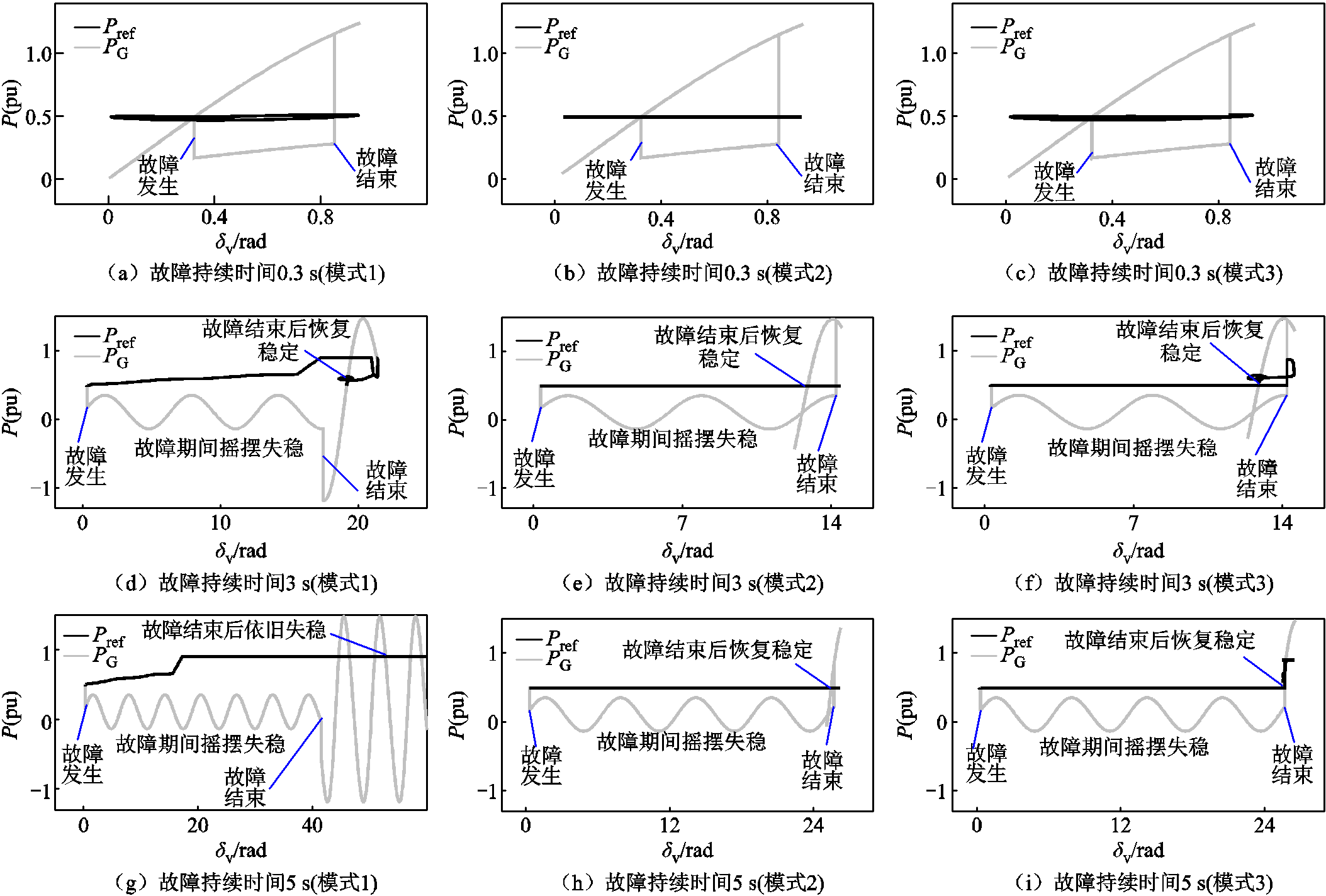
正文图6中展现了不同故障清除时间下MPPT对构网型风机暂态稳定程度的影响，在图6相同的仿真工况下，将构网型风机功角作为x轴，功率作为y轴，得到如附图1所示的功角-功率相平面轨迹。
可以看出，附图1本质是对图5的拓展，展示了不同故障持续时间下，构网型风机功率随功角的变化。在附图1中可以看到构网型风机采用MPPT（模式1）参考功率模式在不同故障持续时间下暂态响应的不同。对比附图1a、附图1b、附图1c可知，当故障时间持续时间为0.3 s时，MPPT模式的参考功率变化较小，与其他模式的功角-功率轨迹相近；对比附图1d、附图1e、附图1f可知，当故障持续时间为3 s时，MPPT模式的参考功率开始明显上升，在故障期间比其他模式的摇摆周期多一个周期；对比附图1g、附图1h、附图1i可知，当故障持续时间为5 s时，MPPT模式的参考功率上升至限幅并在故障期间持续饱和，且在故障清除后，风机依旧持续摇摆失稳。
综上所述，MPPT模式对构网型风机暂态稳定的恶化主要体现在较长故障持续时间的工况下，若故障持续时间较短，则影响较小。
附图1 功角-功率相平面轨迹
App.Fig.1 Phase trajectories of power angle andpower
参考文献
[1] 全球能源互联网发展合作组织. 中国“十四五”电力发展规划研究[R]. 北京: 全球能源互联网发展合作组织, 2015.
[2] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters [J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[3] 郭小龙, 杨桂兴, 张彦军, 等. 构网型储能变流器并网系统SISO环路增益建模与重塑控制[J]. 电气技术, 2023, 24(2): 24-31, 51.
Guo Xiaolong, Yang Guixing, Zhang Yanjun, et al. Modeling and reshaping control of single input and single output loop gain of the grid-forming energy storage converter grid-connected system[J]. Electrical Engineering, 2023, 24(2): 24-31, 51.
[4] 蔡旭, 秦垚, 王晗, 等. 风电机组的自同步电压源控制研究综述[J]. 高电压技术, 2023, 49(6): 2478-2490.
Cai Xu, Qin Yao, Wang Han, et al. Review of self-synchronous voltage source control for wind turbine generator[J]. High Voltage Engineering, 2023, 49(6): 2478-2490.
[5] 秦世耀, 齐琛, 李少林, 等. 电压源型构网风电机组研究现状及展望[J]. 中国电机工程学报, 2023, 43(4): 1314-1334.
Qin Shiyao, Qi Chen, Li Shaolin, et al. Review of the voltage-source grid forming wind turbine[J]. Proceedings of the CSEE, 2023, 43(4): 1314-1334.
[6] Xi Jiangbei, Geng Hua, Zou Xin. Decoupling scheme for virtual synchronous generator controlled wind farms participating in inertial response[J]. Journal of Modern Power Systems and Clean Energy, 2021, 9(2): 347-355.
[7] 王鑫, 杨德健. 基于变系数PI控制的双馈风电机组自适应转速恢复策略[J]. 电工技术学报, 2023, 38(15): 4120-4129.
Wang Xin, Yang Dejian. Adaptive speed recovery strategy of doubly-fed induction generator based on variable PI control coefficient[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4120-4129.
[8] 杨德健, 王鑫, 严干贵, 等. 计及调频死区的柔性风储联合频率控制策略[J]. 电工技术学报, 2023, 38(17): 4646-4656.
Yang Dejian, Wang Xin, Yan Gangui, et al. Flexible frequency regulation scheme of DFIG embed battery energy storage system considering deadbands[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4646-4656.
[9] 张锋, 陈武晖, 康佳乐, 等. 双馈风电场故障穿越控制策略对风火打捆系统暂态稳定性影响及提升控制策略研究[J]. 电工技术学报, 2025, 40(3): 717-729.
Zhang Feng, Chen Wuhui, Kang Jiale, et al. Research on the effect of fault ride-through control strategy of doubly fed wind farms on transient stability of wind-fire bundling system and enhancement control strategy [J]. Transactions of China Electrotechnical Society, 2025, 40(3): 717-729.
[10] 颜湘武, 蔡光, 李锐博, 等. 计及功角偏差和阻尼效应的构网型双馈风机暂态稳定性分析[J]. 中国电机工程学报, 2025, 45(7): 2616-2633.
Yan Xiangwu, Cai Guang, Li Ruibo, et al. Transient stability analysis of grid forming-doubly fed induction generator with power angle deviation and damping effect[J]. Proceedings of the CSEE, 2025, 45(7): 2616-2633.
[11] Yu Jianfeng, Ouyang Jinxin, Zhang Aogui, et al. Modeling of dynamic control error and emergency frequency control for direct-drive PMSG-based wind turbine under grid fault[J]. IEEE Transactions on Sustainable Energy, 2024, 15(3): 1690-1702.
[12] 饶仪明, 吕敬, 戴金水, 等. 不同控制策略下直驱风电机组的机网耦合特性及稳定性分析[J]. 电力系统自动化, 2024, 48(4): 150-159.
Rao Yiming, Lü Jing, Dai Jinshui, et al. Analysis of generator-grid coupling characteristics and stability for direct-drive wind turbines with different control strategies[J]. Automation of Electric Power Systems, 2024, 48(4): 150-159.
[13] 张宇, 蔡旭, 张琛, 等. 并网变换器的暂态同步稳定性研究综述[J]. 中国电机工程学报, 2021, 41(5): 1687-1701.
Zhang Yu, Cai Xu, Zhang Chen, et al. Transient synchronization stability analysis of voltage source converters: a review[J]. Proceedings of the CSEE, 2021, 41(5): 1687-1701.
[14] 王子骏, 庄可好, 辛焕海, 等. 自同步型直驱风电机组暂态稳定分析[J]. 浙江大学学报(工学版), 2024, 58(4): 867-878.
Wang Zijun, Zhuang Kehao, Xin Huanhai, et al. Transient stability analysis of direct-driven wind turbines based on self-synchronous control[J]. Journal of Zhejiang University (Engineering Science), 2024, 58(4): 867-878.
[15] 张祥宇, 朱永健, 付媛. 基于系统惯量需求的风储协同快速频率响应技术[J]. 中国电机工程学报, 2023, 43(14): 5415-5429.
Zhang Xiangyu, Zhu Yongjian, Fu Yuan. Wind-storage cooperative fast frequency response technology based on system inertia demand[J]. Proceedings of the CSEE, 2023, 43(14): 5415-5429.
[16] 颜湘武, 孙雪薇, 崔森, 等. 基于转子动能与超级电容器储能的双馈风电机组惯量和一次调频改进控制策略[J]. 电工技术学报, 2021, 36(增刊1): 179-190.
Yan Xiangwu, Sun Xuewei, Cui Sen, et al. Improved control strategy for inertia and primary frequency regulation of doubly fed induction generator based on rotor kinetic energy and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 179-190.
[17] 唐飞, 亓君锋, 谢家锐, 等. 避免频率二次跌落的风储联合调频控制策略[J]. 中国电机工程学报, 2024, 44(10): 3824-3836.
Tang Fei, Qi Junfeng, Xie Jiarui, et al. Coordinated control strategy of wind turbine generator and energy storage equipment to avoid frequency secondary drop[J]. Proceedings of the CSEE, 2024, 44(10): 3824-3836.
[18] 王德胜, 颜湘武, 贾焦心, 等. 永磁直驱风机基于虚拟同步技术的高、低电压连续故障穿越策略[J]. 中国电机工程学报, 2022, 42(6): 2164-2175.
Wang Desheng, Yan Xiangwu, Jia Jiaoxin, et al. High/ low voltage continuous fault ride through strategy of PMSGs based on virtual synchronization technology [J]. Proceedings of the CSEE, 2022, 42(6): 2164-2175.
[19] 金铭鑫, 王彤, 黄世楼, 等. 含储能型虚拟同步发电机的直驱风机并网系统自适应协调阻尼控制策略[J]. 电力自动化设备, 2021, 41(10): 170-177, 191.
Jin Mingxin, Wang Tong, Huang Shilou, et al. Adaptive coordinated damping control strategy for grid-connected direct-driven wind turbine system with energy storage-based virtual synchronous generators [J]. Electric Power Automation Equipment, 2021, 41(10): 170-177, 191.
[20] 李尚志, 徐泰山, 李英彪, 等. 构网型全功率风机并网系统机电尺度建模及动态稳定性分析[J]. 华中科技大学学报(自然科学版), 2024, 52(7): 12-21.
Li Shangzhi, Xu Taishan, Li Yingbiao, et al. Electromechanical scale modeling and dynamic stability analysis of grid connected full power wind turbine system[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2024, 52(7): 12-21.
[21] Yang Dejian, Wang Xin, Chen Wei, et al. Adaptive frequency droop feedback control-based power tracking operation of a DFIG for temporary frequency regulation[J]. IEEE Transactions on Power Systems, 2024, 39(2): 2682-2692.
[22] 孟志伟, 侯玉强, 方勇杰, 等. 强阻尼电压源型虚拟同步发电机大扰动功角稳定性分析[J]. 电力系统自动化, 2018, 42(9): 44-50.
Meng Zhiwei, Hou Yuqiang, Fang Yongjie, et al. Analysis on large disturbance power-angle stability of strong-damping voltage-source virtual synchronous generators[J]. Automation of Electric Power Systems, 2018, 42(9): 44-50.
[23] 马亦卓, 谭贝斯, 徐晋, 等. 基于虚拟同步控制的构网型直驱风机轴系扭振特性分析[J/OL]. 电网技术, 2024: 1-10[2024-07-22]. https://link.cnki.net/urlid/ 11.2410.tm.20240719.1507.002.
Ma Yizhuo, Tan Beisi, Xu Jin, et al. Torsional oscillation characteristics analysis of grid-forming pmsg-based wind turbine system based on virtual synchronous generator control[J]. Power System Technology, 2024: 1-10[2024-07-22]. https://link. cnki.net/urlid/11.2410.tm.20240719.1507.002.
[24] Sun Kun, Yao Wei, Wen Jinyu, et al. A two-stage simultaneous control scheme for the transient angle stability of VSG considering current limitation and voltage support[J]. IEEE Transactions on Power Systems, 2022, 37(3): 2137-2150.
[25] Luo Cong, Chen Yandong, Xu Yuancan, et al. Two-stage transient control for VSG considering fault current limitation and transient angle stability[J]. IEEE Transactions on Industrial Electronics, 2024, 71(7): 7169-7179.
[26] 国家电网有限公司. 风电机组虚拟同步发电机技术要求和试验方法: Q/GDW 11826—2018[S]. 北京: 国家电网有限公司, 2018.
[27] 国家市场监督管理总局, 国家标准化管理委员会. 并网电源一次调频技术规定及试验导则: GB/T 40595—2021[S]. 北京: 中国标准出版社, 2021.
[28] 颜湘武, 崔森, 宋子君, 等. 基于超级电容储能控制的双馈风电机组惯量与一次调频策略[J]. 电力系统自动化, 2020, 44(14): 111-120.
Yan Xiangwu, Cui Sen, Song Zijun, et al. Inertia and primary frequency regulation strategy of doubly-fed wind turbine based on super-capacitor energy storage control[J]. Automation of Electric Power Systems, 2020, 44(14): 111-120.
Research on the Transient Support Capacity Improvement Strategy of Grid-Forming PMSG Based on Integration of Wind Power and Storage
Abstract After the high proportion of wind power is connected, it brings a series of problems to the stability of the frequency and voltage, and the grid needs wind power to assume the main responsibility for ensuring power supply. Existing studies have shown that the virtual synchronous grid-forming equipment, including grid-forming wind turbines, has good frequency/voltage active temporary and steady-state support capabilities, and has better temporary and steady-state adaptability in weak grid scenarios. Based on these advantages, grid-forming wind turbines are expected to play a greater role in the future grid supported by low inertia and weak voltage. However, the maximum power point tracking (MPPT) operation mode of the wind turbine and its own limited rotational energy lead to the restriction of the transient support capacity of the grid-forming permanent magnet synchronous motor(PMSG), while the grid-forming PMSG based wind-storage generator has an additional energy source due to its access to energy storage, and its transient support performance has been greatly improved, which is an effective solution. At present, the access mode of energy storage is mostly parallel energy storage on the DC side or AC side, in which the energy storage driven by grid-following control adopts the passive mode of responding to the frequency acquisition signal to support the grid frequency, and most of the energy storage driven by virtual synchronous grid-forming control is connected to the AC side of the wind turbine, and the energy storage cannot be incorporated into the virtual synchronous control system. Therefore, this study is dedicated to proposing a transient support capacity improvement strategy for grid-forming PMSG based on wind-storage integration.
Firstly, the power energy storage represented by the supercapacitor was selected to form a grid-forming PMSG based Wind-storage generator with grid-forming PMSG, and the dynamic model of the grid-forming PMSG and grid-forming PMSG based wind-storage generator were established, and the constraints of the wind turbine dynamics on the frequency support capacity and transient stability of the grid-forming PMSG were summarized by analyzing the transient response of the grid-forming PMSG under frequency and voltage drops.
Then, combined with the energy flow characteristics of the grid-forming PMSG based wind-storage generator in the transient support process, the transient response power of the Grid-forming control is decomposed into inertia response power signal and damping response power signal to drive energy storage, and a transient support capacity improvement strategy for grid-forming PMSG based on wind-storage integration is formed, which realizes the flexible allocation and invocation of rotor kinetic energy and energy storage, and incorporates the rotor kinetic energy and energy storage into the active support system of virtual synchronous control to improve the frequency support capacity and transient stability of the grid-forming PMSG based wind-storage generator.
Finally, after simulation verification under various conditions, the strategy can improve the transient support capacity of the grid-forming PMSG based wind-storage generator, including: (1) The frequency support capacity has been improved, which reduces the constraints of MPPT on the frequency support capacity of the wind turbine. (2) The fault ride-through capability is improved, the transient fluctuation of rotor speed and DC bus voltage is effectively suppressed, the redundant energy generated by fault ride-through is effectively absorbed. (3) Combined with the fault ride-through power angle stability control strategy, the redundant energy during the fault period is converted into energy storage energy, so as to avoid the reduction of wind turbine power generation efficiency and reduce energy waste.
Keywords：Grid-forming PMSG, wind-storage integrated generator, virtual synchronous control, supercapacitors, transient support
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.242174
国家自然科学基金资助项目（52207102）。
收稿日期2024-12-03
改稿日期 2025-02-24
蔡 光 男，1996年生，博士研究生，研究方向为并网新能源发电建模、控制和稳定性分析。
E-mail：cai_guang_cg@163.com
颜湘武 男，1965年生，教授，博士生导师，研究方向为新能源电力系统分析与控制、现代电力变换、新型储能与节能技术等。
E-mail：xiangwuy@ncepu.edu.cn（通信作者）
（编辑 赫 蕾）