
图1 双极直流配电网的结构
Fig.1 The structure of a bipolar DC distribution network
摘要 建设供电容量大、灵活性高、对直流型源荷友好的双极直流配电网是构建新型配电网的有效途径之一。然而,电压不平衡问题对双极直流配电网的推广和应用提出了挑战。该文分析电压不平衡的产生机理,并基于灵敏度定义了电压不平衡传递矩阵,该矩阵用于反映电压不平衡因子在双极直流配电网中各节点的传递特性。在此基础上,推导电压不平衡传递矩阵中各元素的解析表达式,提出基于牛顿-拉夫逊法的潮流计算方法来确定电压不平衡传递矩阵,所提方法采用注入功率进行潮流建模,并考虑分布式发电的下垂控制模型和综合负荷模型。最后,采用改造的IEEE 33节点测试系统验证了所提方法的有效性,并分析了电压不平衡传递的影响因素。
关键词:电压不平衡 传递 双极直流配电网 灵敏度 牛顿-拉夫逊法
随着新型电力系统建设进程的推进,配电网中的直流要素愈发突出[1],这给直流配电网的发展和应用注入了强劲动力。直流配电网具有单极和双极两种结构,相较于单极结构,双极直流配电网的供电可靠性更高、传输容量更大、电压等级更灵活[2],上述优势使双极结构成为直流配电网的主要选择。双极直流配电网特有的电压不平衡问题是制约其发展的关键因素。
传递分析及计算是高效治理电压不平衡的基础,其主要目的是揭示网络发生单点或多点扰动时其他节点电压不平衡的变化规律。潮流计算是分析和量化电压不平衡传递特性的核心工具,根据网络的潮流特性可以得到电压电流经线路和源荷组成的阻抗网络在各节点形成约束关系,进而可知电压不平衡的分布规律[3]。现有关于双极直流配电网潮流计算的研究主要聚焦于潮流建模和求解两方面。
双极直流配电网潮流建模的关键在于如何清晰地刻画极间的耦合潮流[4]。在双极直流配电网中,源、荷以类似于三角形的形式接在不同极之间,这不可避免地增强了极间的电气联系与潮流耦合[5]。因此,现有研究倾向于通过基尔霍夫电流定律构建节点注入电流平衡方程[6],该方法能线性地描述双极潮流耦合且无需对网络做任何近似,目前已在潮流分析[7]、电压不平衡抑制[8]等方面得到了广泛应用。然而,该方法需要将功率转换为电流进行建模,当网络中恒功率负荷比例较高时,显著增加了潮流建模难度。针对该问题,有研究提出在系统电压运行点处对1/U进行一阶泰勒展开,从而将恒功率负荷等效为恒电阻负荷并联恒电流负荷的形式[9]。该方法有效地降低了含高比例恒功率负荷的双极直流配电网的潮流建模复杂度,然而该方法依赖系统运行点的稳定性,难以应用于大扰动下电压不平衡传递的计算。
双极直流配电网的潮流计算一般是求解非线性方程组的过程,已有研究采用Banach不动点定理证明了在明确的运行条件下直流网络中潮流解的存在性和唯一性[10]。在已知源荷条件时,可采用牛顿-拉夫逊(Newton-Raphson, N-R)、前推回代等方法准确求解直流潮流。此外,双极直流配电网可将网络潮流分解为定电压控制节点和定功率控制节点两部分[11],或通过文献[12]的方法实现潮流模型的线性表达,从而通过矩阵变换进行求解。
然而,现有研究主要是通过潮流计算结果得到电压不平衡评估指标[13],这仅能呈现电压不平衡的传递结果,而无法反映电压不平衡在网络中的传递过程。此外,在实际工程中已知的节点注入量往往不是节点电流而是节点功率[14],因此现有基于注入电流构建的潮流模型与应用需求不匹配。
为了解决上述问题,本文基于电压灵敏度分析定义了电压不平衡传递矩阵,通过该矩阵揭示扰动激发的电压不平衡在双极直流配电网中的传递过程,矩阵元素的大小能清晰反映各节点对电压不平衡的抑制或增强作用,可为制定合理的电压不平衡治理方案提供依据。此外,本文给出了电压不平衡传递矩阵的确定方法,该方法构建了基于注入功率的潮流模型,分析了电压灵敏度与电压不平衡传递矩阵的关联关系,并联合线性潮流和N-R法进行求解,兼具高求解精度和求解效率。
双极直流配电网具有正极、中线、负极三根配电线,源荷经电力电子变换器连接至正极端口(正极-中线)、双极端口(正极-负极)或负极端口(中线-负极)[15],上层电网经电压平衡器(Voltage Balancer, VB)将电能传输至双极直流配电网,其结构如图1所示。本文主要关注双极直流配电网内部,上层电网可以是交流或直流,但需要特别考虑上、下层电网接口处变换器的影响。

图1 双极直流配电网的结构
Fig.1 The structure of a bipolar DC distribution network
此外,一般需采取适当的接地措施防止保护装置发生故障。目前,主要有直接接地和电阻接地两种方案[16]。第一种接地方案的优势是容易进行故障检测,但容易损坏设备;第二种接地方案能更好地保护设备,但中线电压不为零,增加了网损。
双极直流配电网不平衡电压的定义与接地方案有关。对于中线直接接地的情形,若某节点正极电压与负极电压的绝对值不相等,则该节点会产生不平衡电压;对于中线不接地或经电阻接地的情形,若某节点的正极端口电压与负极端口电压不相等,则该节点会产生不平衡电压。一般用电压不平衡因子(Voltage Unbalance Factor, VUF)来评估某节点不平衡电压的严重程度[17-18],即
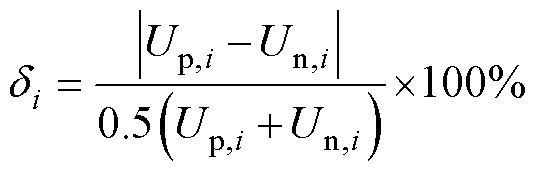 (1)
(1)
式中,di为i节点的电压不平衡因子;Up,i和Un,i分别为i节点正、负极端口的电压,端口电压可由节点电压计算得到,两者的转换关系为
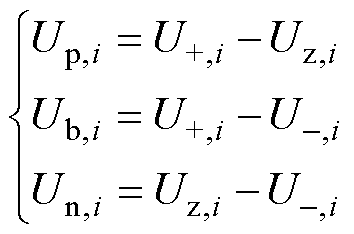 (2)
(2)
式中,U+,i、Uz,i、U-,i分别为i节点的正极、中线、负极电压,U+,i>0、U-,i<0、Uz,i取值在0附近;Ub,i为i节点双极端口的电压。
双极直流配电网两极参数、源荷及换流器的差异化设计或不对称扰动均会产生不平衡电压[17],而电压平衡器对不平衡电压的抑制作用有限。这导致中性线产生不平衡电流,增加馈线及接地导体的损耗,严重时可能导致变压器产生直流偏磁,诱发谐波、振动等一系列问题[3]。
在双极直流配电网的运行阶段,源荷的不对称扰动难以避免,其具有传递性。若N节点的双极直流配电网发生不对称扰动,则在i节点引起的VUF变化量Ddi可表示为
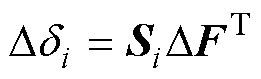 (3)
(3)
式中,Si为i节点的不平衡电压传递向量,如式(4)所示;DF为不平衡电压影响因素的扰动矩阵,如式(5)所示,DF中非零元素的数量反映了双极直流配电网中电压不平衡扰动源的数量。
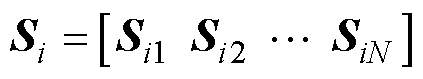 (4)
(4)
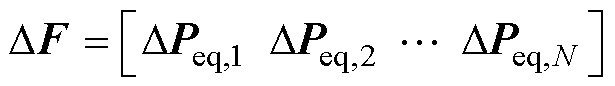 (5)
(5)
式中,Sij=[S+,ij Sz,ij S-,ij];j节点与i节点有电气连接,且1≤j≤N,Sij中任意元素Sj,ij用来衡量j节点j 极不平衡电压影响因素的扰动对i节点VUF的影响,如式(6)所示;DPeq, j为j(1≤j≤N)节点等效净负荷功率的变化量向量,DPeq,j=[DPeq,+,j DPeq,z,j DPeq,-, j],DPeq,j, j(jÎ{+, z, -})如式(7)所示,推导过程见文献[5]。
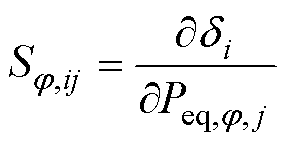 (6)
(6)
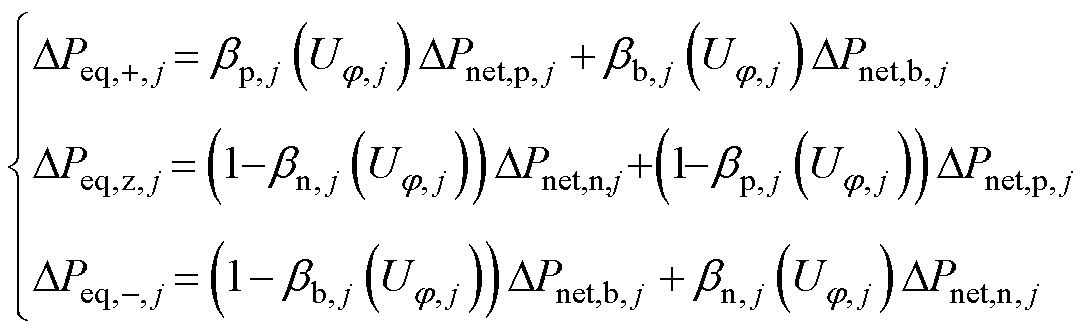 (7)
(7)
式中,DPnet,r, j为j节点r 端口净负荷的变化量,rÎ{p, b, n};br, j(Uj, j)为j节点r 端口的解耦系数,其物理含义为r 端口对j 极有影响的负荷占比,bp, j(Uj, j)= U+, j/(U+, j-Uz, j)、bb, j(Uj, j)=U+, j/(U+, j-U-, j)、bn, j(Uj, j)= U-, j/(U-, j-Uz, j),具体推导见文献[5]。
式(3)可进一步拓展为矩阵形式,即
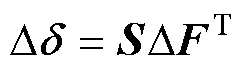 (8)
(8)
其中
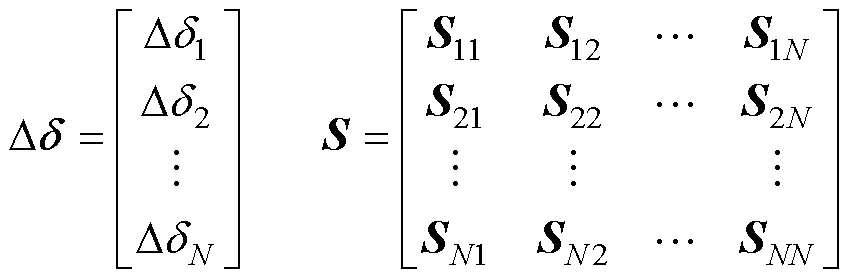
本文将S定义为双极直流配电网不平衡电压的传递矩阵。根据式(1)中VUF的定义,式(6)可进一步表述为
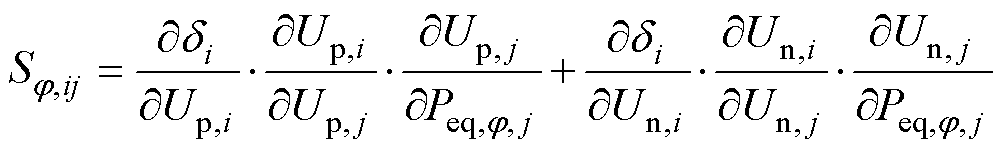 (9)
(9)
将式(2)代入式(1)和式(9),可得
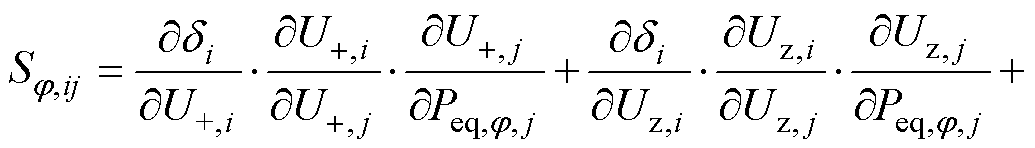
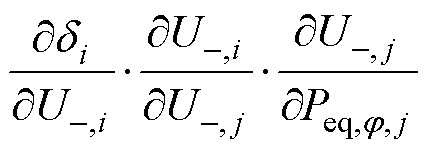 (10)
(10)
通过式(10)即可确定双极直流配电网不平衡电压的传递矩阵S。
本节给出式(10)中3个关键参数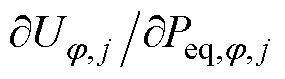 、
、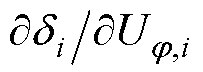 、
、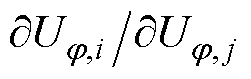 的确定方法。
的确定方法。
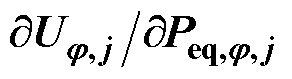 的计算方法
的计算方法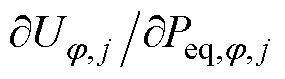 是与节点电压灵敏度相关的参数,采用N-R法进行潮流计算时可获取该参数。
是与节点电压灵敏度相关的参数,采用N-R法进行潮流计算时可获取该参数。
现有研究一般采用节点注入电流方程分析双极直流配电网的潮流[4],节点电压与节点注入电流之间的关系可表示为
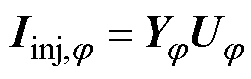 (11)
(11)
式中,Iinj,j为j 极的节点注入电流向量;Yj 为j 极的电导矩阵;Uj 为j 极的节点电压向量。
不平衡电流向量为
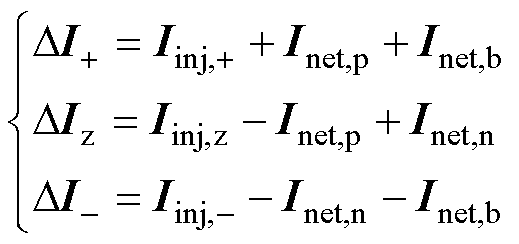 (12)
(12)
式中,DIj 为j 极的不平衡电流向量;Inet,r 为r 端口的净负荷电流,表示为
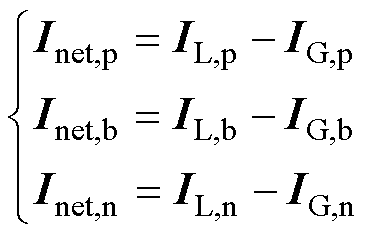 (13)
(13)
式中,IL,r 为r 端口的负荷电流;IG,r 分别为r 端口分布式发电(Distributed Generation, DG)的输出电流。
IL,r 和IG,r 可进一步表示为节点电压的参数方程。计算DIj 对Uj 的偏导得到雅可比矩阵,进而对雅可比矩阵求逆可得各节点的电压灵敏度矩阵。
在式(11)~式(13)基础上,进一步可构建基于注入功率的潮流模型。任意节点i的注入功率与注入电流的关系可表述为
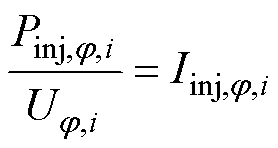 (14)
(14)
将式(11)代入式(14),得到其展开式为
 (15)
(15)
j 极i节点的不平衡功率DPinj,j,i可表示为
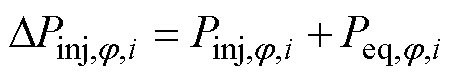 (16)
(16)
DPinj,j,i对j 极任意节点j的电压求偏导可得雅可比矩阵J3N×3N为
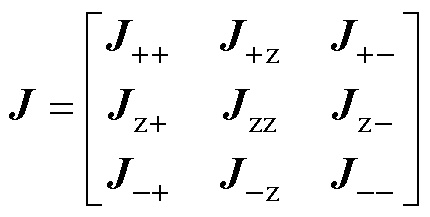 (17)
(17)
式中,J中各子矩阵的任意元素可表示为
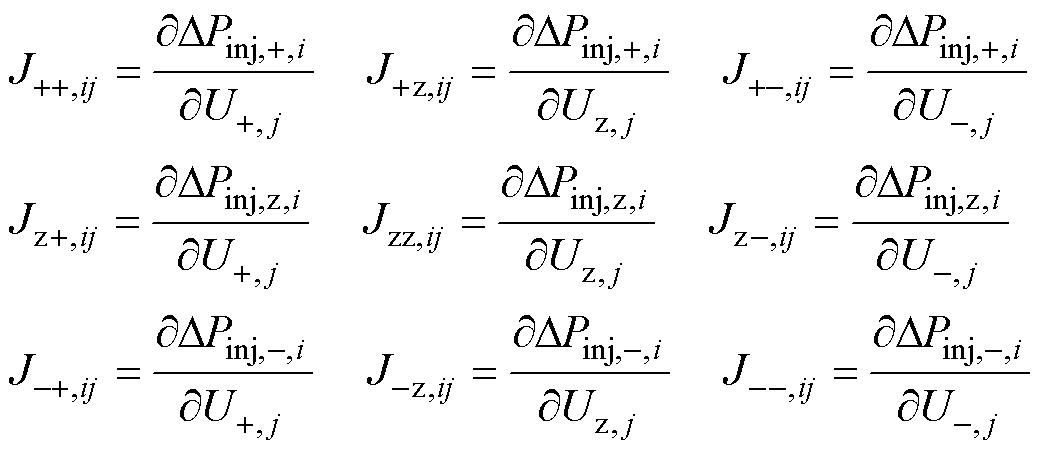
计算节点等效净负荷Peq,j,i[5]表示为
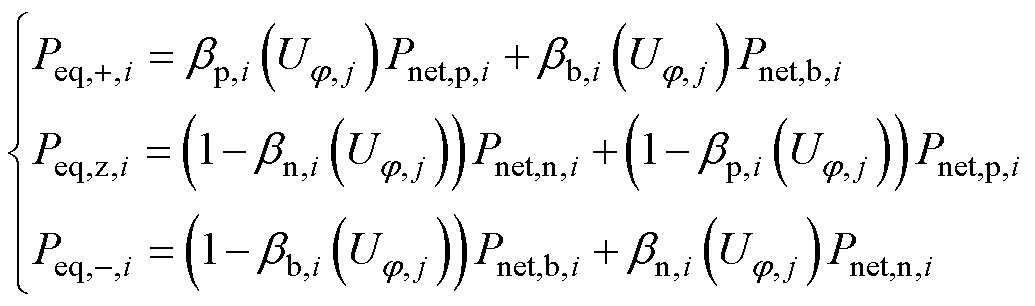 (18)
(18)
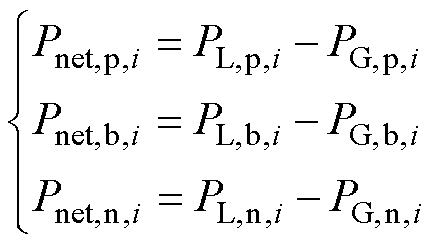 (19)
(19)
式中,PL,r,i为i节点r 端口的负荷功率;PG,r,i为i节点r 端口的DG输出功率。
为了使所提方法具有普适性,采用综合负荷模型,并考虑DG的功率-电压下垂控制,即
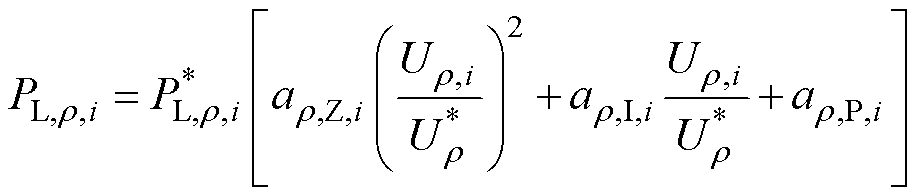 (20)
(20)
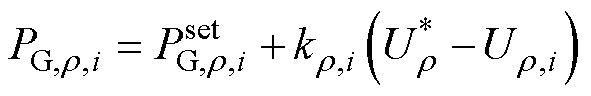 (21)
(21)
式中,ar,Z,i、ar,I,i、ar,P,i分别为i节点r 端口负荷的综合负荷系数,且ar,Z,i+ar,I,i+ar,P,i=1,其值的大小反映i节点r 端口恒电阻(Z)、恒电流(I)、恒功率(P)负荷的占比;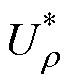 为r 端口电压的标称值;
为r 端口电压的标称值;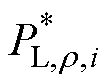 为r 端口负荷的基准值;
为r 端口负荷的基准值;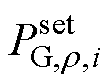 为r 端口DG输出功率的设定值;Ur,i为i节点r 端口的电压;kr,i为i节点r 端口DG输出功率的下垂系数。需要注意的是,VB可被等效为正、负极端口的受控电流源,类似于三线接入的DG[19]。
为r 端口DG输出功率的设定值;Ur,i为i节点r 端口的电压;kr,i为i节点r 端口DG输出功率的下垂系数。需要注意的是,VB可被等效为正、负极端口的受控电流源,类似于三线接入的DG[19]。
将式(2)、式(18)~式(21)代入式(17),可得Ji中各元素的表达式,具体见附录。为了降低Ji中各元素的复杂度,在表达式(18)中将br, j(Uj, j)视为整体予以保留。在实际计算中,br,j(Uj,j)会被提前确定。
若双极直流配电网的雅可比矩阵非奇异,则可计算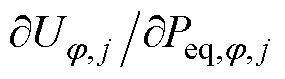 为
为
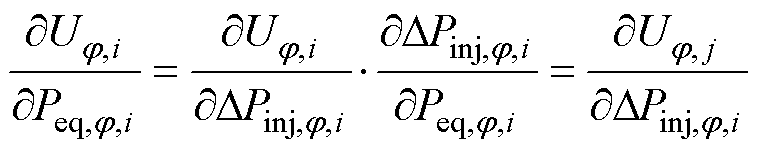 (22)
(22)
因此,对Ji求逆可得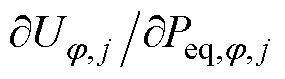 。
。
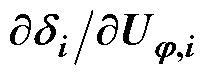 的计算方法
的计算方法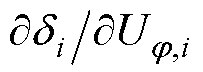 可由式(1)求导得到。需要注意的是,式(1)中含绝对值项,求导时需去掉绝对值符号。对于双极直流配电网的任意节点i,式(1)与式(23)等价。
可由式(1)求导得到。需要注意的是,式(1)中含绝对值项,求导时需去掉绝对值符号。对于双极直流配电网的任意节点i,式(1)与式(23)等价。
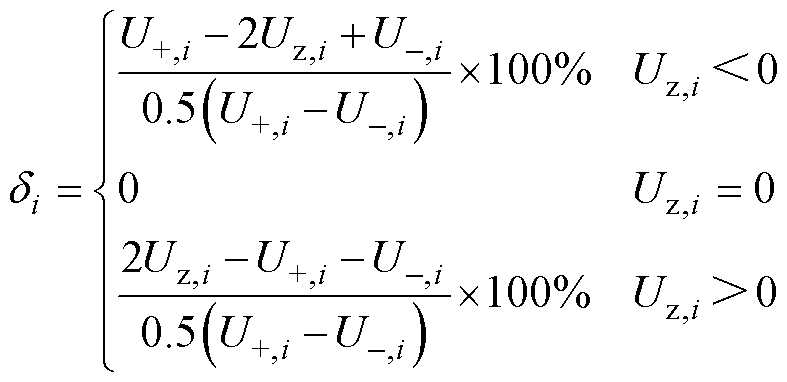 (23)
(23)
式(23)对Uj,i求偏导,可得
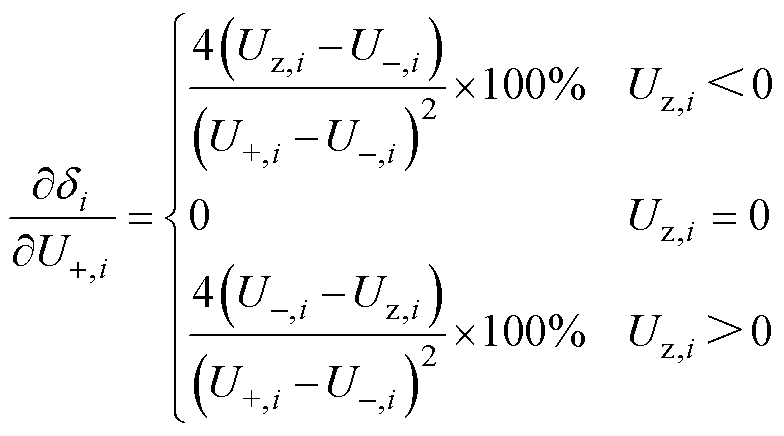 (24)
(24)
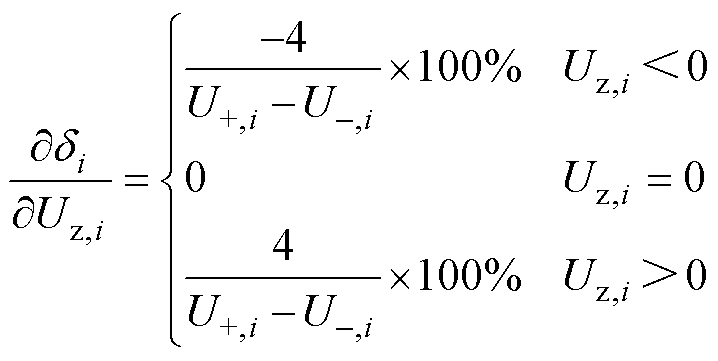 (25)
(25)
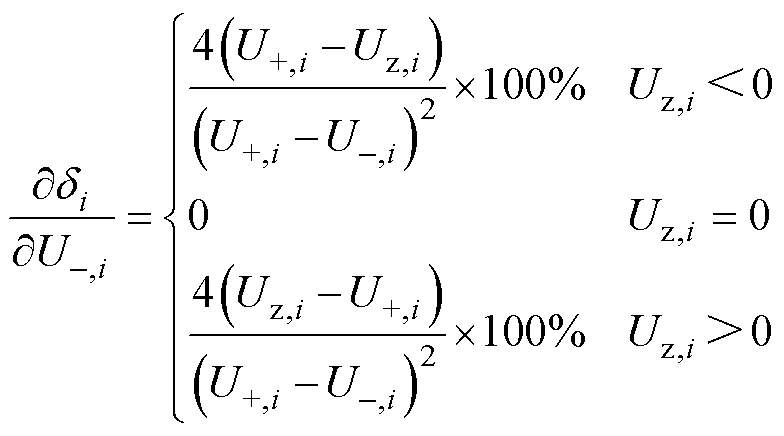 (26)
(26)
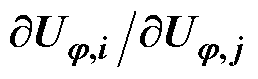 的计算方法
的计算方法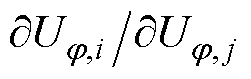 可由i-j支路潮流的电压等式[20]求导得到。任意支路i-j满足欧姆定律[21]为
可由i-j支路潮流的电压等式[20]求导得到。任意支路i-j满足欧姆定律[21]为
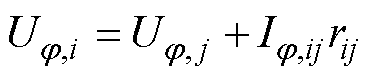 (27)
(27)
式中,rij为i-j支路电阻;Ij,ij为j 极i-j支路电流。由式(27)可得: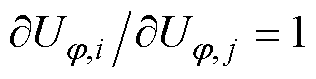 。
。
根据前述分析,将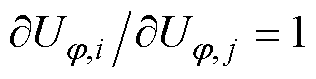 、
、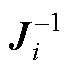 、式(24)~式(26)代入式(10),即可确定不平衡电压传递矩阵S中各元素的值。需要注意的是,式(24)~式(26)由潮流计算结果确定,Ji需根据复合函数求导进一步展开或进行简化。由于在给定源荷条件下br, j(Uj, j)具有唯一值[5],因此可提前确定br, j(Uj, j) 来简化Ji的复杂度,从而提升N-R法的求解效率。
、式(24)~式(26)代入式(10),即可确定不平衡电压传递矩阵S中各元素的值。需要注意的是,式(24)~式(26)由潮流计算结果确定,Ji需根据复合函数求导进一步展开或进行简化。由于在给定源荷条件下br, j(Uj, j)具有唯一值[5],因此可提前确定br, j(Uj, j) 来简化Ji的复杂度,从而提升N-R法的求解效率。
双极直流配电网电压不平衡传递计算流程如图2所示。主要包含以下步骤:

图2 双极直流配电网电压不平衡传递计算流程
Fig.2 Calculation process of voltage unbalance transfer in bipolar DC distribution networks
(1)给定双极直流配电网线路参数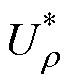 、
、 ,根据线路参数形成电导矩阵Yj。
,根据线路参数形成电导矩阵Yj。
(2)设定迭代次数k=1、误差容忍e,发生扰动之前的源荷参数矩阵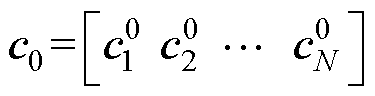 ,其中任意节点i的源荷参数向量
,其中任意节点i的源荷参数向量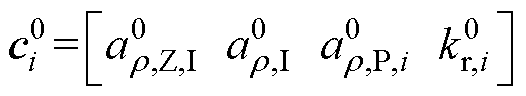 (参数物理意义与前文相同,上标“0”表述扰动前的参数),并根据文献[9]的线性潮流计算方法得到Uj, j。
(参数物理意义与前文相同,上标“0”表述扰动前的参数),并根据文献[9]的线性潮流计算方法得到Uj, j。
(3)将初始电压矩阵设置为U(k)=[U+(k) Uz(k) U-(k)],其中向量Uj(k)=[Uj,1(k) Uj,2(k) …Uj,N(k)]T。根据U(k)确定br, j(Uj, j),并将br, j(Uj, j)和U(k)代入式(A1)~式(A9),得到第k次迭代的雅可比矩阵J(k),将Uj, j和c0代入式(15)、式(16)、式(18)~式(21)得到第k次迭代的不平衡功率矩阵DPinj(k)= [DPinj,+(k) DPinj,z(k) DPinj,-(k)],其中向量DPinj,j(k)= [DPinj,j,1(k) DPinj,j,2(k) …DPinj,j,N(k)]T。
(4)根据式(28)修正电压。
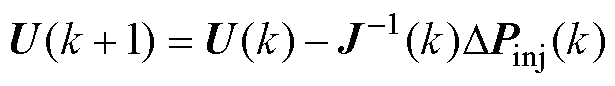 (28)
(28)
(5)重复步骤(3)、步骤(4),直至DPinj(k)的无穷范数不超过e。
(6)得到c0源荷条件下的电压矩阵U0和雅可比矩阵J0,将U0代入式(24)~式(26)确定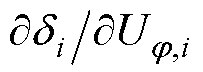 ,进而将(J0)-1、
,进而将(J0)-1、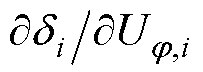 、
、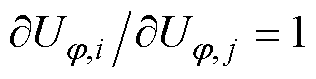 代入式(10)确定不平衡电压传递矩阵S。
代入式(10)确定不平衡电压传递矩阵S。
(7)获取源荷的扰动矩阵Dc,将Dc代入式(7)、式(20)、式(21)确定不平衡电压影响因素的扰动矩阵DF。
(8)根据式(8)计算双极直流配电网在源荷扰动Dc下各节点VUF的变化量。
本节在修改的IEEE 33节点测试系统中验证所提方法的有效性。图3为修改的IEEE 33节点测试系统,需要注意的是,该系统与交流配电网研究中采用的改造系统在电压等级、线路参数、负荷分布等方面均有较大差异。具体而言,该系统的标称电压为±3 kV,额定容量为1 MV·A;各节点负荷分布如图4所示,其中,15、22、25节点(红色节点)仅有双极负荷,负荷基准值为对应节点的总负荷功率(仅保留有功负荷),其余节点正极负极负荷基准值按3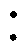 2的比例从对应节点的总负荷功率中分配;考虑到建设成本,VB采用集中式架构[19],安装在1节点,等效为接在正极端口和负极端口的受控电流源[4],控制方式为I-V下垂控制[4],拓扑结构为Buck- Boost或半桥式[19],额定功率为500 kW;节点1为松弛节点,正、负极电压分别固定为1(pu)和-1(pu);ar,Z,i=0.2、ar,I,i=0.7、ar,P,i=0.1、kr,i=0.8;上层电网等效为无穷大电源;由于仅关注稳态网络,因此忽略了标准算例系统的线路电抗,仅保留电阻。
2的比例从对应节点的总负荷功率中分配;考虑到建设成本,VB采用集中式架构[19],安装在1节点,等效为接在正极端口和负极端口的受控电流源[4],控制方式为I-V下垂控制[4],拓扑结构为Buck- Boost或半桥式[19],额定功率为500 kW;节点1为松弛节点,正、负极电压分别固定为1(pu)和-1(pu);ar,Z,i=0.2、ar,I,i=0.7、ar,P,i=0.1、kr,i=0.8;上层电网等效为无穷大电源;由于仅关注稳态网络,因此忽略了标准算例系统的线路电抗,仅保留电阻。
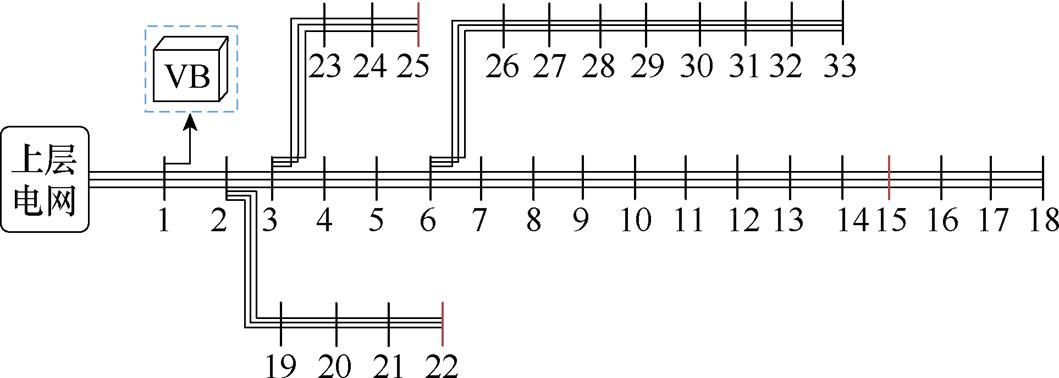
图3 修改的IEEE 33节点测试系统
Fig.3 The modified IEEE 33 node test system
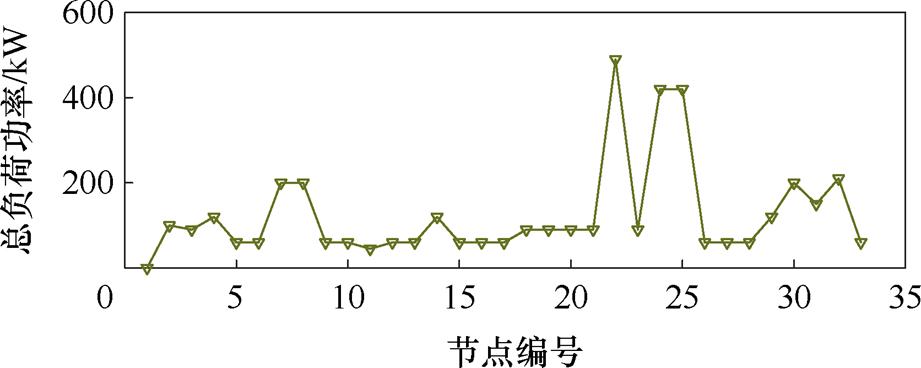
图4 IEEE 33节点测试系统的初始负荷
Fig.4 The initial load of IEEE 33 node test system
在图3测试系统中执行了三个算例,具体如下:
算例1:通过三个方法验证所提潮流计算方法的有效性。方法1(基准方法):基于注入电流方程的潮流计算方法[7];方法2:基于注入功率方程的潮流计算方法,电压初值随机,br, j(Uj, j)迭代;方法3(所提方法):基于注入功率方程的潮流计算方法,电压初值由文献[9]的线性潮流计算方法给定,br, j(Uj, j)固定。
算例2:采用方法3计算六个场景下的电压不平衡传递。场景1:单点正极负荷扰动;场景2:单点负极负荷扰动;场景3:单点正极、负极负荷同向扰动;场景4:多点正极负荷同向扰动;场景5:多点负极负荷同向扰动;场景6:多点正极、负极负荷同向扰动。
算例3:在场景6下采用方法3分析综合负荷系数对电压不平衡的影响。
图5对比了不同方法的潮流计算结果,纵轴表示方法2、3与基准方法计算结果的相对误差。
由图5可见,基于注入功率方程的潮流计算方法能得到精确的计算结果(方法2与基准方法的误差几乎为0)。但该方法需要更新解耦系数br, j(Uj, j),这会影响N-R法的计算效率。方法3的迭代次数比方法2少了44.44%,计算时间降低了47.31%,这说明通过适当方法固定br, j(Uj, j)能提升潮流计算的效率,这种提升效果在大规模网络中会更加显著。
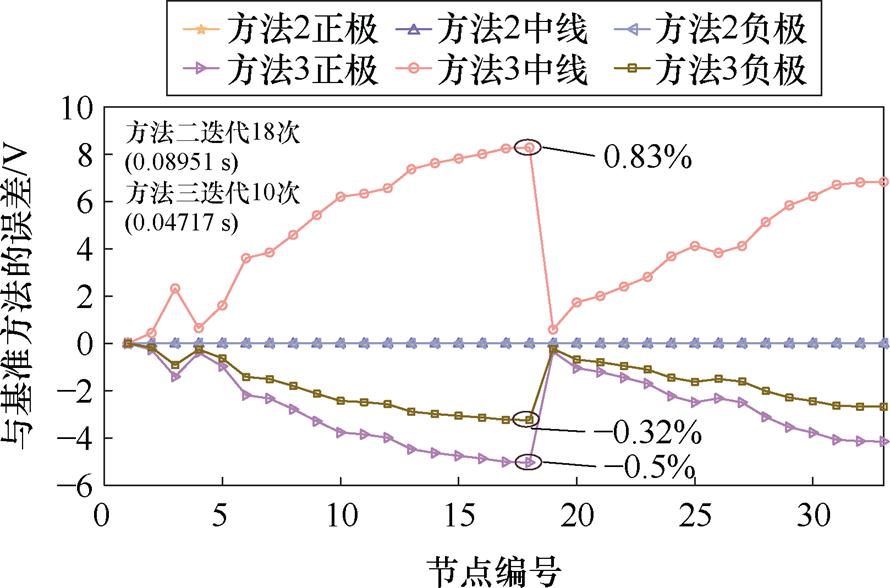
图5 潮流计算结果
Fig.5 The results of power flow calculation
需要注意的是,解耦系数br, j(Uj, j)固定,既可能获得恰当的初值降低迭代次数,也可能增加初始电压的修正过程,但N-R法具有二次方收敛特性[14],增加的修正过程对计算时间的影响较小。br, j(Uj, j)的取值受节点电压影响,而节点电压是迭代变化的(见式(28)),因此方法3对电压初值比方法2更加敏感。方法3得到的正极、中线、负极电压与基准方法计算结果的最大相对误差分别为-0.5%、-0.32%、0.83%,这是可接受的精度,证明了所提潮流计算方法的可行性与精确性。
图6展示了测试系统在六种场景下的VUF与基准方法所得VUF的差值。为了方便,所有场景的负荷总扰动量均为50 kW,单点扰动施加在节点5,多点扰动均匀地施加在所有节点。
由图6可以看出:
(1)负极负荷增加(见图6a场景2、场景5)或正极负荷减少(见图6b场景1、场景4、场景6)能显著降低系统的VUF,这是因为促进两极负荷均衡分布能抑制电压不平衡的产生与传递。
(2)相比单点负荷同向扰动,多点负荷同向扰动对电压不平衡传递的抑制作用更加显著(场景4、场景5),这表明可以通过负荷切换、储能调度等手段促进多点负荷同时向更均衡的方向变化,从而抑制不平衡传递。

图6 电压不平衡传递计算结果
Fig.6 Calculation results of voltage unbalance transfer
(3)单点(节点5)负荷扰动对扰动点下游的影响比上游更大,这表明电压不平衡的传递方向与潮流方向一致,在扰动点下游(节点6~18、26~33)没有DG的情况下,扰动点对电压不平衡的抑制或增强作用会对下游产生一致性影响,因此可在扰动频发的节点配置储能、潮流控制器、电力弹簧等潮流调节设备来抑制电压不平衡传递。
(4)多点扰动对电压不平衡增强作用会随潮流方向累积,将在线路末端(节点18、33)达到最大,这表明有必要通过直流变压器、电压平衡器等调压设备阻隔电压不平衡传递。
式(A1)~式(A9)表明,ar,P,i的取值不影响雅可比矩阵和电压不平衡传递矩阵。故该算例固定ar,P,i=0.1,计算ar,Z,i和ar,I,i取值从0.1~0.9时的电压不平衡传递矩阵和VUF,并以ar,Z,i=0.2、ar,I,i=0.2(算例1方法3)的计算结果为基准,量化了ar,Z,i和ar,I,i取值对电压不平衡传递矩阵和VUF产生的影响,结果如图7和图8所示。
由图7a和图8a可以看出,随着ar,Z,i增大,电压不平衡矩阵的元素逐渐增大且VUF逐步降低,越靠近线路末端节点(18、33),该现象越显著。这表明当系统恒电阻负荷比例较高时,可优先调控靠近线路末端节点的恒电阻负荷。例如,给靠近线路末端的恒电阻负荷串联电力弹簧构建智能负载,提升系统电压不平衡调节的自由度。由图7b和图8b可以看出,随着ar,I,i增大,电压不平衡矩阵的元素逐渐减小且VUF逐步增大,越靠近线路末端节点(18、33),该现象越显著。这表明当系统恒电流负荷比例较高时,电压不平衡易沿阻抗网络传递且在线路末端叠加,因此有必要在电压不平衡传递路径上配置潮流调控设备,阻断或抑制电压不平衡传递。
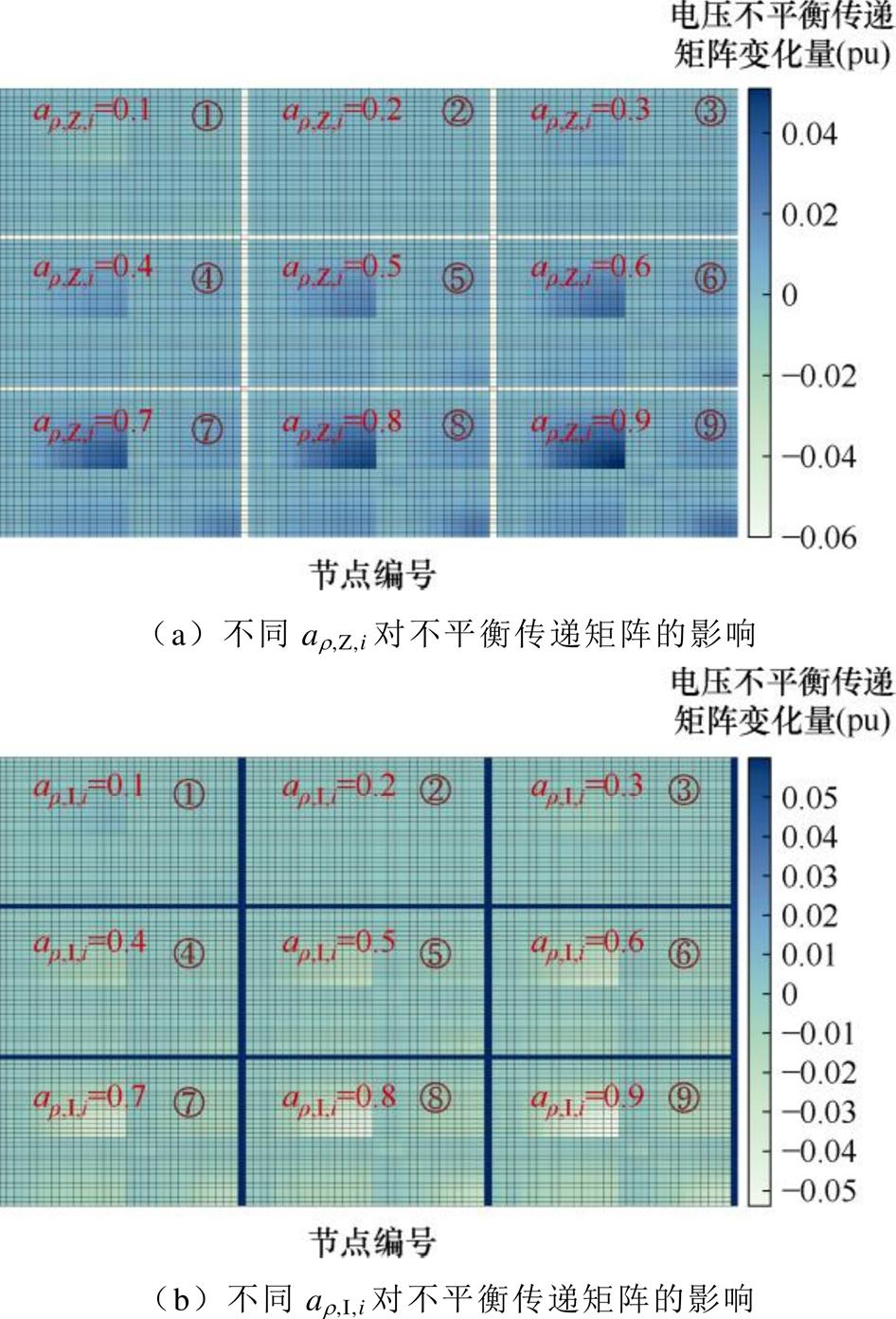
图7 不同综合负荷系数对不平衡传递矩阵的影响
Fig.7 The influence of different ZIP coefficients on voltage unbalance transfer matrix

图8 不同综合负荷系数对VUF的影响
Fig.8 The influence of different ZIP coefficients on VUF
此外,本文还验证了场景6下所提方法在多电压等级双极直流配电网及中的应用效果,见附录。
为了揭示电压不平衡在双极直流配电网中的传递特性和规律,本文定义了电压不平衡传递矩阵,提出了基于潮流计算的电压不平衡传递计算方法,并在IEEE 33节点测试系统中验证了所提方法的应用效果。具体结论如下:
1)所提潮流计算方法具有令人满意的计算效率和求解精度,在含高比例恒功率负荷或注入功率数据易获取的场景中具有应用优势。
2)电压不平衡传递矩阵能反映扰动工况下双极直流配电网中各节点电压不平衡因子的变化和传递情况。具体而言,扰动产生的电压不平衡会随潮流方向在网络中传播,需要在网络关键节点处采取阻断或抑制不平衡传递的措施。
3)所提电压不平衡计算方法适用于多电压等级双极直流配电网。算例结果表明,DCT正、负极的电压比对电压不平衡传递有显著影响。在正、负极源荷分布较均匀的双极直流配电网中,建议一致性控制DCT正、负极电压比;反之,建议适当优化DCT正、负极电压比来抑制电压不平衡的传递。
附 录
式(17)雅可比矩阵中各元素的表达式为
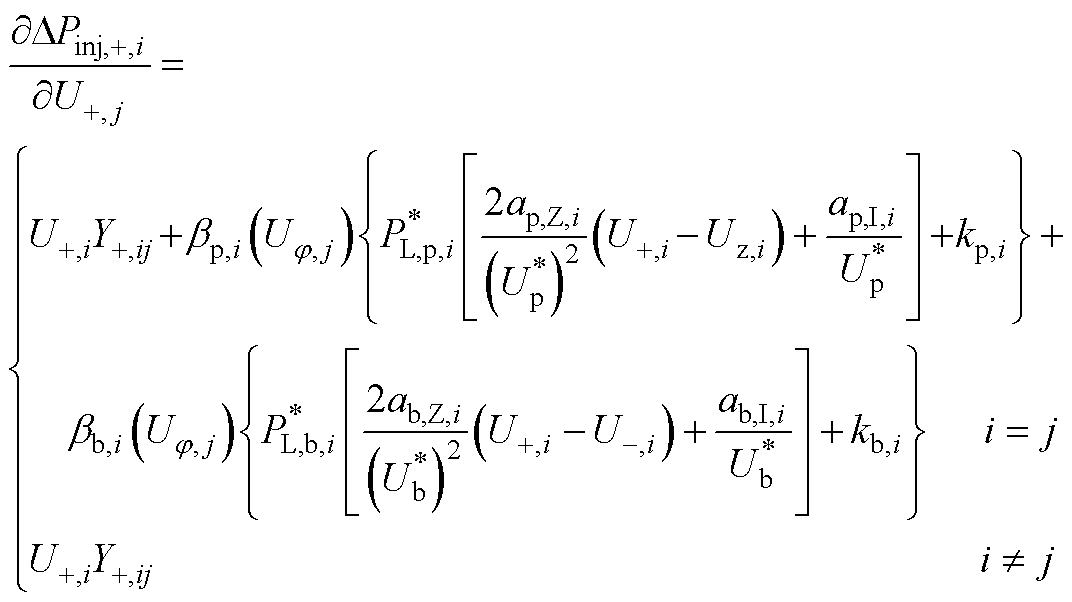 (A1)
(A1)
 (A2)
(A2)
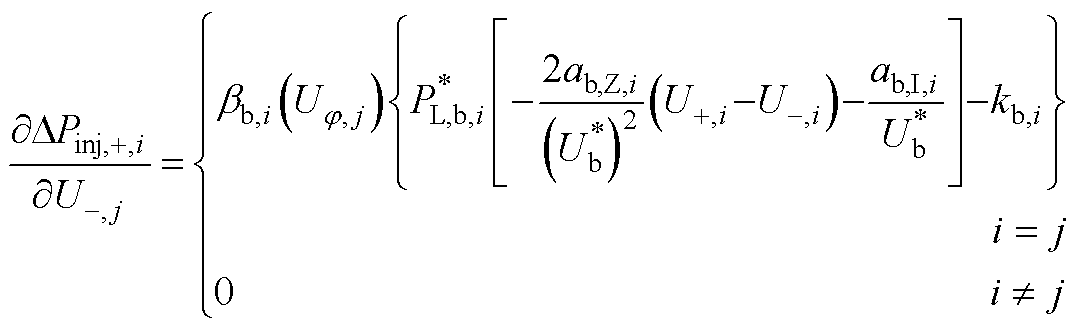 (A3)
(A3)
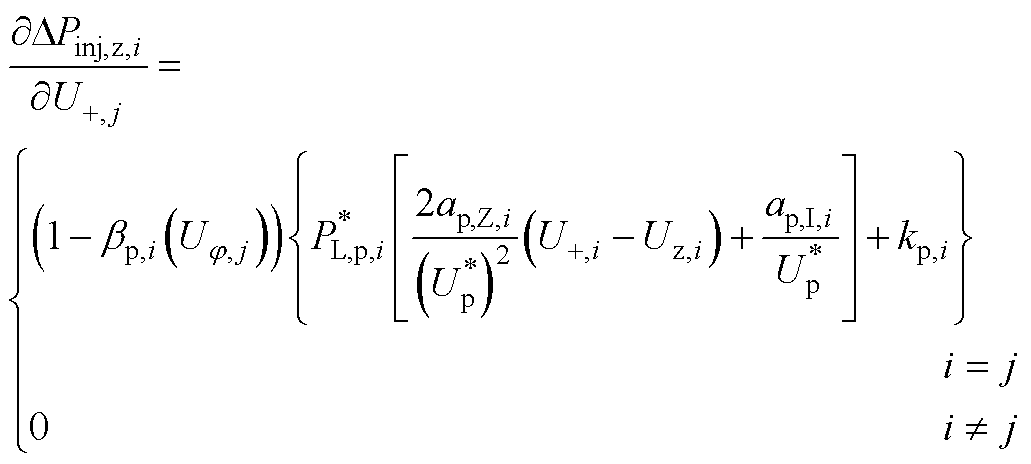 (A4)
(A4)
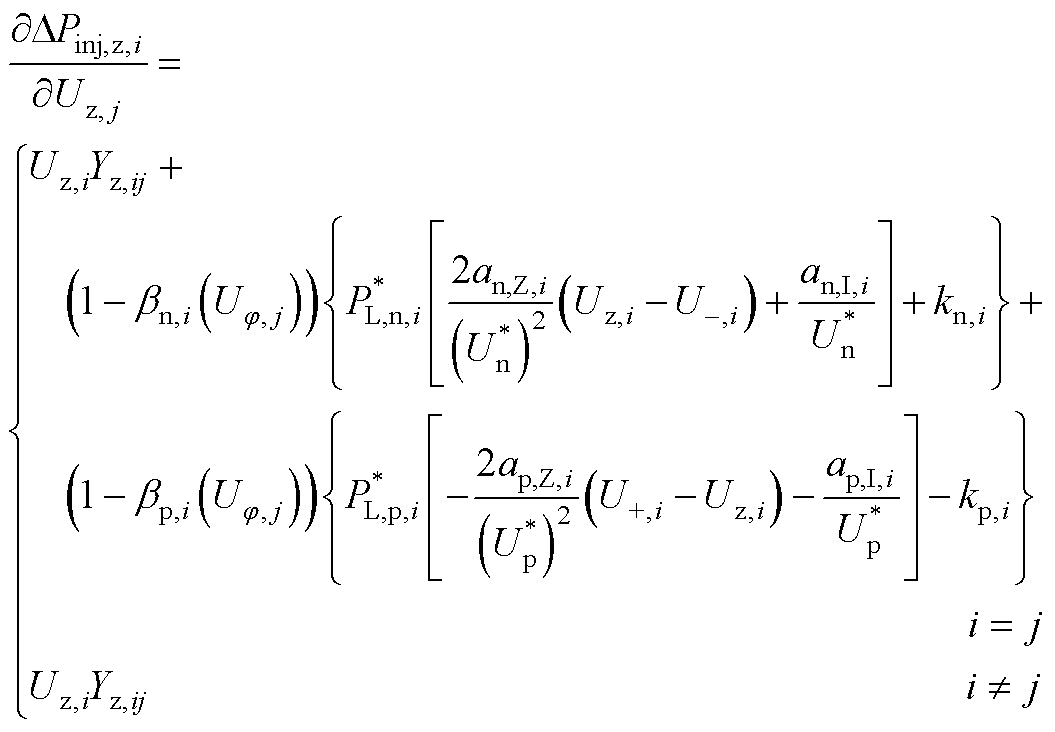 (A5)
(A5)
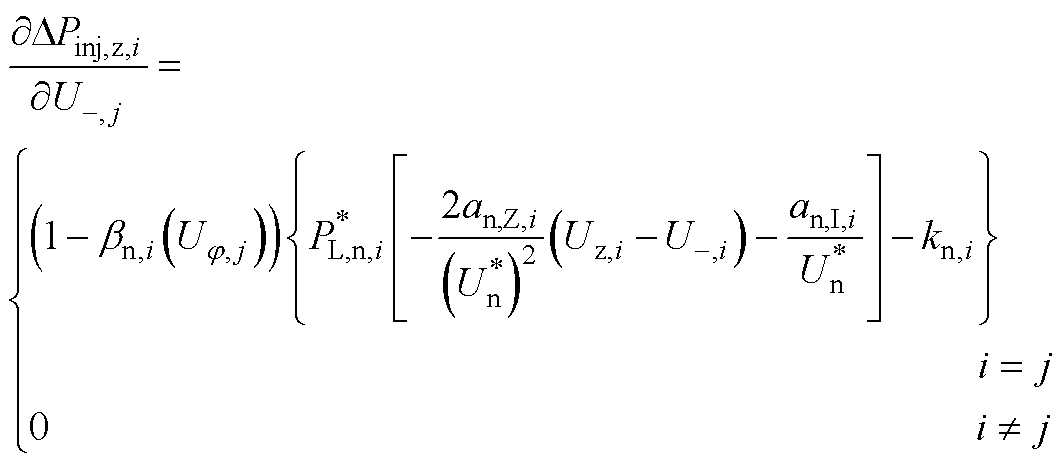 (A6)
(A6)
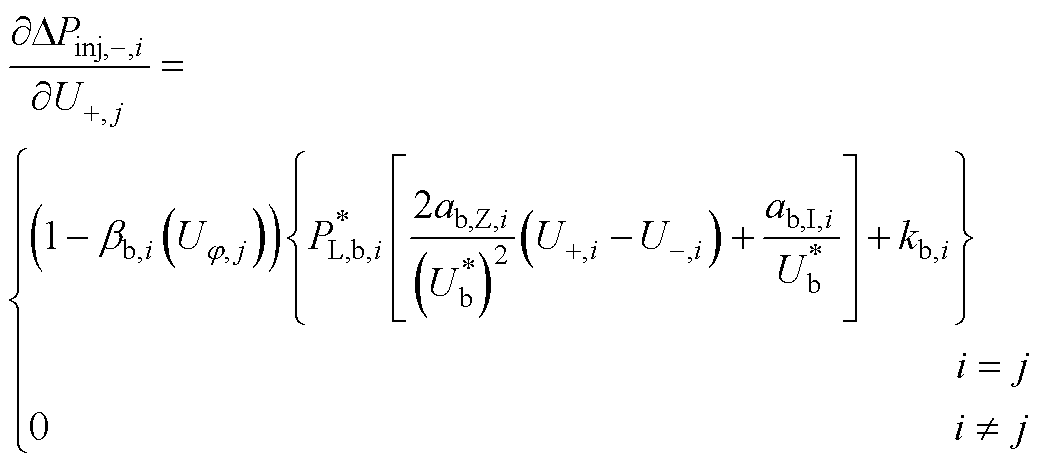 (A7)
(A7)
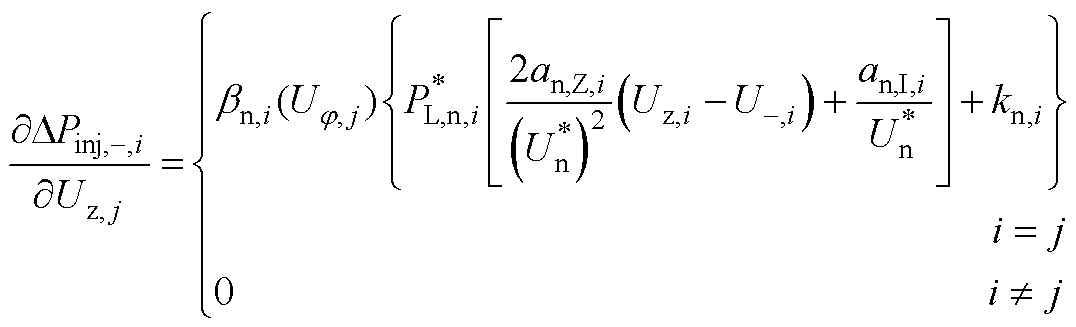 (A8)
(A8)
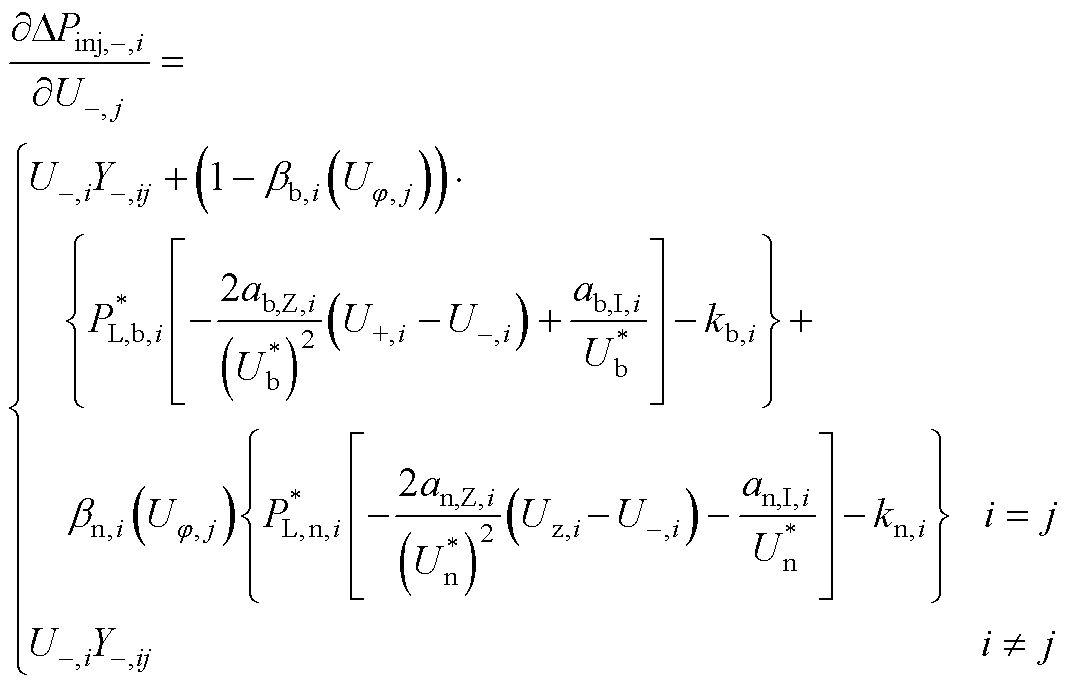 (A9)
(A9)
以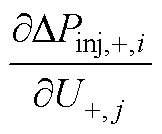 的表达式为例说明式(A1)~式(A9)的推导过程,其余元素表达式的推导过程类似,不再赘述。
的表达式为例说明式(A1)~式(A9)的推导过程,其余元素表达式的推导过程类似,不再赘述。
根据链式法则,可将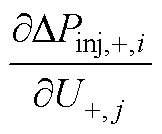 表述为
表述为
 (A10)
(A10)
将式(2)、式(18)~式(21)代入式(A10),可得式(A1)。
场景6下,所提方法在多电压等级双极直流配电网及中的应用效果:
直流变压器(DC Transformer, DCT)是不同电压等级双极直流配电网互联的核心设备,双主动全桥直流变换器(Dual Active Bridge DC-DC converter, DAB)是目前应用较为广泛的DCT拓扑[22]。该算例中:两个DAB型DCT分别位于支路5、6和24、25;DCT一次侧和二次侧的标称电压分别为±3 000 V和±750 V;两个DCT均处于定电压比控制,正负极电压比均为3.85;在应用所提方法时,需要在式(11)的电导矩阵Yj中考虑DCT的附加电导矩阵YT,本文采用文献[12]中给出了DCT稳态模型及定电压控制下的附加电导矩阵。测试系统的其余参数保持不变,负荷扰动设置与算例2一致。DCT的其他参数详见文献[12]。电压不平衡传递计算结果如附图1所示。
附图1比较了多点正极、负极负荷同向扰动下(场景6),多/单电压等级双极直流配电网的电压不平衡传递计算结果。该算例中,电压不平衡的诱因是正、负极负荷分布不均(6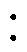 4),算例2表明场景6一定程度能均衡负荷。当正、负极DCT的电压比保持一致(均为3.85)时,DCT二次侧正、负极端口电压的差异进一步减小。因此,含DCT的支路(5、6和24、25)显著抑制了电压不平衡的传递,这有效缓解了电压不平衡在末端节点(18、33)的累积效应。
4),算例2表明场景6一定程度能均衡负荷。当正、负极DCT的电压比保持一致(均为3.85)时,DCT二次侧正、负极端口电压的差异进一步减小。因此,含DCT的支路(5、6和24、25)显著抑制了电压不平衡的传递,这有效缓解了电压不平衡在末端节点(18、33)的累积效应。

附图1 电压不平衡传递计算结果
App.Fig.1 Calculation results of voltage unbalance transfer
进一步分析了DCT电压比对电压不平衡传递的影响。公平起见,规避了负荷分布对不平衡的影响(将正、负极负荷比例调整至1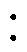 1)。为了配电网安全运行,限定正、负极电压偏差不超过±5%。因此,DCT的电压比取值范围约为[3.62, 4.42]。图6和附图1已经表明了测试系统VUF在节点18处的变化最大。方便起见,本文仅展示了在DCT不同正、负极电压比下节点18的VUF变化,如附图2a所示。此外,采用皮尔逊系数[23]分析了VUF变化与DCT电压比的相关性,该系数越接近1表明正相关性越强,如附图2b所示。
1)。为了配电网安全运行,限定正、负极电压偏差不超过±5%。因此,DCT的电压比取值范围约为[3.62, 4.42]。图6和附图1已经表明了测试系统VUF在节点18处的变化最大。方便起见,本文仅展示了在DCT不同正、负极电压比下节点18的VUF变化,如附图2a所示。此外,采用皮尔逊系数[23]分析了VUF变化与DCT电压比的相关性,该系数越接近1表明正相关性越强,如附图2b所示。
由附图2a可见,在正、负极负荷分布均匀情况下,DCT正、负极电压比的差异越大,VUF的变化越大。这是因为在定电压比控制下,DCT一次侧和二次侧的端口电压呈线性关系[12],一致性电压比不会影响VUF,而差异性电压比会放大甚至激发该情形下的电压不平衡。这意味着,在正、负极源荷分布不均的多电压等级双极直流配电网中,可以通过优化DCT正、负极电压比来抑制电压不平衡传递。由附图2b可见,在DCT正、负极电压比异向变化区域(红色虚线框),DCT正负极电压比与VUF变化呈现较强相关性,这进一步验证了附图2a的现象。

附图2 不同电压比对VUF的影响
App.Fig.2 The influence on VUF of different ratios for voltage
参考文献
[1] 何东, 蒋磊, 兰征, 等. 基于常通型SiC JFET器件的中低压直流固态断路器研究综述[J]. 电工技术学报, 2024, 39(22): 7213-7227.
He Dong, Jiang Lei, Lan Zheng, et al. Review of research on medium and low voltage DC solid-state circuit breakers based on normally-on SiC JFETs[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7213-7227.
[2] 廖建权, 周念成, 王强钢. 辐射型双极直流配电网不平衡电压分析及抑制[J]. 中国电机工程学报, 2019, 39(18): 5380-5388, 5585.
Liao Jianquan, Zhou Niancheng, Wang Qianggang. Analysis and suppression of unbalanced voltage in radiant bipolar DC distribution network[J]. Pro- ceedings of the CSEE, 2019, 39(18): 5380-5388, 5585.
[3] 王强钢, 周亦尧, 廖建权, 等. 直流配电网电能质量研究综述[J]. 电力系统自动化, 2023, 47(7): 193-207.
Wang Qianggang, Zhou Yiyao, Liao Jianquan, et al. Review on power quality in DC distribution network[J]. Automation of Electric Power Systems, 2023, 47(7): 193-207.
[4] Lee J O, Kim Y S, Moon S I. Current injection power flow analysis and optimal generation dispatch for bipolar DC microgrids[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 1918-1928.
[5] Zhou Yiyao, Wang Qianggang, Huang Tao, et al. Convex optimal power flow based on power injection-based equations and its application in bipolar DC distribution network[J]. Electric Power Systems Research, 2024, 230: 110271.
[6] Chew B S H, Xu Yan, Wu Qiuwei. Voltage balancing for bipolar DC distribution grids: a power flow based binary integer multi-objective optimization app- roach[J]. IEEE Transactions on Power Systems, 2019, 34(1): 28-39.
[7] Lee J O, Kim Y S, Jeon J H. Generic power flow algorithm for bipolar DC microgrids based on Newton-Raphson method[J]. International Journal of Electrical Power & Energy Systems, 2022, 142: 108357.
[8] Lee J O, Kim Y S, Jeon J H. Optimal power flow for bipolar DC microgrids[J]. International Journal of Electrical Power & Energy Systems, 2022, 142: 108375.
[9] 周念成, 张渝, 廖建权, 等. 计及直流变压器控制的多电压等级双极直流配电网线性化潮流计算[J]. 中国电机工程学报, 2022, 42(6): 2070-2083.
Zhou Niancheng, Zhang Yu, Liao Jianquan, et al. Linearization formulation based power flow calculation of multiple-voltage grades bipolar DC distribution network considering control modes of DC transformer[J]. Proceedings of the CSEE, 2022, 42(6): 2070-2083.
[10] Montoya O D. On the existence of the power flow solution in DC grids with CPLs through a graph-based method[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(8): 1434-1438.
[11] 许丹, 王斌, 张晓天, 等. 考虑节点控制模式的柔性直流电网潮流线性化计算方法[J]. 电力系统自动化, 2017, 41(19): 54-58, 73.
Xu Dan, Wang Bin, Zhang Xiaotian, et al. Linearized calculating method for power flow of flexible DC power grid considering node control mode[J]. Automation of Electric Power Systems, 2017, 41(19): 54-58, 73.
[12] Wang Hongbin, Zhou Niancheng, Zhang Yu, et al. Linearized power flow calculation of bipolar DC dis- tribution network with multiple flexible equipment[J]. International Journal of Electrical Power & Energy Systems, 2024, 155: 109568.
[13] 何大禄, 廖建权, 王强钢. 基于三有源桥串并联直流潮流控制器的环形双极直流配电网不平衡潮流抑制[J]. 电工技术学报, 2022, 37(11): 2837-2848.
He Dalu, Liao Jianquan, Wang Qianggang. Triple active bridge power flow controller based unbalanced power flow suppression for ring bipolar DC dis- tribution network[J]. Transactions of China Electro- technical Society, 2022, 37(11): 2837-2848.
[14] 陈珩. 电力系统稳态分析[M]. 4版. 北京: 中国电力出版社, 2015.
[15] 李博通, 刘涛, 杨昕陆, 等. 故障自清除型直流配电网新型双极短路故障元件识别方法[J]. 电工技术学报, 2022, 37(17): 4423-4434.
Li Botong, Liu Tao, Yang Xinlu, et al. New fault element identification method of bipolar short-circuit fault in DC distribution network with fault self- clearing[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4423-4434.
[16] 王伟, 帅智康, 李杨, 等. 基于固态断路器主动注入式直流故障测距方法[J]. 电工技术学报, 2024, 39(8): 2360-2370.
Wang Wei, Shuai Zhikang, Li Yang, et al. Active injection DC fault location method base on solid-state circuit breaker[J]. Transactions of China Electro- technical Society, 2024, 39(8): 2360-2370.
[17] Liao Jianquan, Liu Yangtao, Guo Chunsheng, et al. Power quality of DC microgrid: index classification, definition, correlation analysis and cases study[J]. International Journal of Electrical Power & Energy Systems, 2024, 156: 109782.
[18] 周文, 苏灿, 胡雪凯, 等. 直流配电系统电能质量探析[J/OL]. 电源学报, http://kns.cnki.net/kcms/ detail/12.1420.TM.20230224.1111.004.html.
Zhou Wen, Su Can, Hu Xuekai, et al. Analysis of power quality in DC distribution system[J/OL]. Journal of Power Supply, http://kns.cnki.net/kcms/ detail/12.1420.TM.20230224.1111.004.html.
[19] Pires V F, Cordeiro A, Roncero-Clemente C, et al. DC-DC converters for bipolar microgrid voltage balancing: a comprehensive review of architectures and topologies[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(1): 981-998.
[20] Gan Lingwen, Low S H. Optimal power flow in direct current networks[J]. IEEE Transactions on Power Systems, 2014, 29(6): 2892-2904.
[21] Farivar M, Low S H. Branch flow model: relaxations and convexification: part I[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564.
[22] 刘朋, 贾燕冰, 韩肖清. 含双有源全桥变换器多电压等级直流配电网潮流分析与计算[J]. 电网技术, 2021, 45(2): 741-750.
Liu Peng, Jia Yanbing, Han Xiaoqing. DAB-based power flow analysis and calculation for multi-voltage grades DC distribution network[J]. Power System Technology, 2021, 45(2): 741-750.
[23] Li Guanzhi, Zhang Aining, Zhang Qizhi, et al. Pearson correlation coefficient-based performance enhancement of broad learning system for stock price prediction[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(5): 2413-2417.
Abstract The bipolar DC distribution network offers high power supply reliability, extensive transmission capacity, and adaptable voltage levels. Developing a bipolar DC distribution network represents an effective strategy for constructing a new type of distribution network. Voltage unbalance constitutes a distinctive power quality issue within bipolar DC distribution networks. Power flow calculation serves as the fundamental tool for analyzing voltage imbalance. Nevertheless, conventional power flow calculation methods merely illustrate the transfer outcomes of voltage unbalance, failing to depict its transfer process within the network. Furthermore, in practical engineering, power is often the measured electrical quantity rather than current, making the existing power flow model based on injected current unsuitable for meeting the application requirements. Hence, this paper proposes a power-injection equation to analyze and quantify the transfer characteristics associated with voltage unbalance.
Initially, the generation and transfer mechanism of voltage unbalance within the bipolar DC distribution network is studied. The voltage unbalance transfer matrix grounded on sensitivity is established to depict the transfer characteristics of voltage unbalance factors at individual nodes. Furthermore, the analytical formulations for each component of the voltage unbalance transfer matrix are derived, and a power flow calculation technique based on the Newton-Raphson method is proposed for determining the matrix. The suggested method employs a power-injection equation for power flow modeling and integrates droop control and comprehensive load models of distributed generation. Finally, the effectiveness of the proposed approach is validated via the modified IEEE 33-node test system. Three case studies are conducted.
Numerical results reveal the following findings. (1) The proposed power flow calculation method exhibits a negligible sacrifice in accuracy, with no more than a 0.83% deviation and a calculation efficiency enhancement of 44%. Additionally, it offers the advantage of accommodating constant power loads, which is suitable for high prevalence power load or load data readily available scenarios. (2) The voltage unbalance transfer matrix effectively illustrates voltage unbalance factors’ alterations and transfer conditions at each node under disturbance conditions. Disturbances induce voltage unbalances that propagate throughout the network following the direction of power flow. Measures must be implemented to block or suppress it at critical network nodes. For instance, strategies such as load switching and energy storage scheduling encourage multi-point loads to adjust in a more balanced manner simultaneously, curtailing unbalanced transfer. Moreover, incorporating a power spring in series with a constant resistance load near the line's terminus can introduce intelligent load management, affording greater flexibility in system voltage unbalance adjustment. The deployment of voltage-regulating equipment, such as DC transformers and voltage balancers, is instrumental in obstructing unbalanced voltage transfer.
Keywords:Voltage unbalance, transfer, bipolar DC distribution network, sensitivity, Newton-Raphson method
中图分类号:TM744
DOI: 10.19595/j.cnki.1000-6753.tces.240497
国家自然科学基金重点项目(52337007)和中央高校基本科研业务费基金项目(2023CDJYXTD-004)资助。
收稿日期 2024-03-29
改稿日期 2024-05-29
周亦尧 男,1996年生,博士研究生,研究方向直流配电网稳态分析及运行优化。
E-mail: yiyaozhou@cqu.edu.cn
王强钢 男,1987年生,教授,博士生导师,研究方向为电力系统保护与控制、电能质量等。
E-mail: qianggang1987@cqu.edu.cn(通信作者)
(编辑 陈 诚)