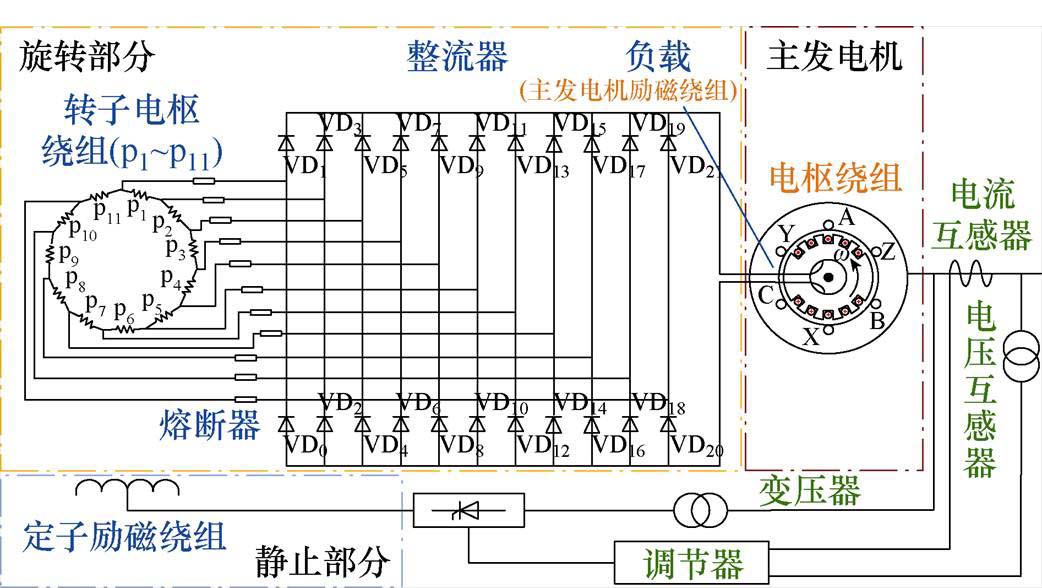
图1 某11相环形无刷励磁系统结构示意图
Fig.1 Structural diagram of 11-phase annular brushless excitation system
摘要 旋转整流器故障诊断对多相环形无刷励磁系统的安全运行具有重要意义。而旋转整流器故障种类繁多且故障特征微弱,机理驱动的诊断方案具有较好的可解释性,但难以实现全故障的准确诊断;数据驱动的诊断方案快速准确,但面向应用时训练和调试难度大。因此,提出一种机理与数据混合驱动的旋转整流器故障诊断方案:首先根据故障机理推导故障后励磁电流的频域特征,利用有限元仿真确定机理诊断模型的阈值;然后引入快速动态时间规整(Fast-DTW)算法计算励磁电流时域波形相似度,结合k近邻(kNN)算法分类器得到数据驱动模型;最后利用集成学习的思想,融合机理与数据诊断方案。实验结果表明,混合驱动的诊断方案能够在降低训练难度的情况下,实现旋转整流器故障的准确诊断。
关键词:旋转整流器故障 机理驱动 数据驱动 快速动态时间规整(Fast-DTW) 集成学习
无刷励磁系统取消了电刷和集电环,可靠性高、维护简单,广泛应用于核能发电[1]、航空航天[2]、船舶动力[3]等场景。近年来出现的多相环形无刷励磁系统具有更大容量、更低输出电流谐波、更低二极管电压,成为大容量核电机组的首选励磁方式[4]。
旋转整流器是无刷励磁系统的核心部件,但现有的二极管不连续导通(Diode Non-Conduction detection, DNC)监测系统经常由于霍尔元件的失灵而失效。根据中国核能协会2010~2020年的统计数据,核电机组DNC系统的误动或拒动多达32次,严重影响励磁系统安全稳定运行。因此,迫切需要准确的旋转整流器故障诊断方案。
现有旋转整流器故障诊断方案主要有基于信号处理的机理驱动法[5-12]和基于人工智能的数据驱动法[13-18]。
机理驱动法通过机理分析得到故障后不同电气量的特征,然后提取相关信号实现故障诊断。用于旋转整流器故障诊断的电信号包括励磁机电枢电流[5-6]、励磁电流[7-10]及感应电动势[11-12]。由于无刷励磁机的电枢绕组和整流器高速旋转,现场难以直接测量电枢电流。测量感应电动势需要在励磁机内部加装探测线圈,增加了安装和维护成本。而励磁机的定子励磁电流可以直接测量,更便于现场应用。文献[7-10]正是基于旋转整流器故障的励磁电流故障机理提出了诊断方案。但文献[10]同时指出,旋转整流器故障模式多且励磁电流机理特征存在重叠现象,难以进行全故障工况的准确诊断。
数据驱动法是利用人工智能学习数据之间的内在联系,实现故障诊断。许多物理量可以用作诊断指标:文献[13]使用二维小波系数能量从无刷电机热图像中提取特征用于整流器故障诊断;文献[14-16]基于励磁电流时域波形,利用不同算法进行旋转整流器故障诊断;文献[17-18]则以励磁电流频域分量作为输入实现旋转整流器故障诊断。但数据驱动法具有黑箱属性[19],其性能依赖训练数据,存在适用性和可解释性挑战。此外,上述文献中诊断方案的训练集数据获取自样机实验,而现场机组不能进行全部旋转整流器故障工况的实验,因此这些方案难以现场应用。
机理驱动和数据驱动具有差异性和互补性,二者有机结合有助于提升故障诊断的准确性、适用性和可解释性[20-22]。为此,本文提出机理与数据混合驱动的旋转整流器故障诊断方案。首先,通过机理分析确定故障励磁电流的频域特征;其次,基于有限元仿真数据确定诊断阈值,建立机理驱动模型;然后,引入快速动态时间规整(Fast Dynamic Time Warping, Fast-DTW)算法计算励磁电流相似度,使用k邻近(k-Nearest Neighbors, kNN)算法建立数据驱动模型;最后,利用集成学习融合机理驱动和数据驱动模型结果,实现旋转整流器故障的准确诊断。
混合驱动的方案融合了机理驱动法和数据驱动法的优势,仅利用仿真数据即可完成诊断模型的训练,大大降低了训练难度。在保证诊断准确率的同时,励磁电流的时频域特征为混合驱动方案提供了较好的可解释性。
为了更清晰地阐述多相环形无刷励磁系统的旋转整流器故障类型,图1以某11相环形无刷励磁系统为例,绘制了其结构示意图。从图中可知,无刷励磁机组的各相电枢绕组环形连接,每相引出端经熔断器与整流器相连,构成了系统的旋转部分。整流器的输出电流给主发电机的励磁绕组提供直流电。主发电机的输出电流经变压、整流后为无刷励磁机的定子励磁绕组提供直流电流。

图1 某11相环形无刷励磁系统结构示意图
Fig.1 Structural diagram of 11-phase annular brushless excitation system
本质上来说,所有旋转整流器故障均由二极管的开路或者短路引起。二极管开路发生的概率较低,因此本文只考虑单个二极管的情况。而实际上并不存在单个二极管的短路故障,因为二极管被击穿短路后,整流回路会出现瞬时过电流,导致熔断器熔断,单个二极管短路会迅速演变成整流器的一相开路故障。对于多相机组而言,一相开路后的整流器输出电流波形质量仍能满足主发电机的需求,系统可以在一相开路的情况下冗余运行。若此时另一相熔断器断开,整流器将发生两相开路。两相开路故障属于严重故障,将导致系统直接停机。所以,旋转二极管故障类型包括一管开路、一相开路和两相开路三种。但两相开路故障包括不同的相对位置,对11相机组而言,两相开路有五种不同相对位置。
多相无刷励磁系统的旋转整流器故障诊断存在诸多困难:①励磁机的电枢绕组和整流二极管处于高速旋转状态,唯一可直接测得的电气量是励磁电流;②旋转整流器相数多,存在带故障运行的情况,故障模式丰富;③故障特征需从定子侧的电枢绕组感应到转子侧的励磁绕组,经电枢反应后励磁电流上反映出的特征微弱。
诊断方案层面,机理分析与数据驱动两条技术路线呈现出不同的特点。基于机理分析的方式能够根据研究对象的物理模型获取用于故障诊断的特征,可解释性强,便于现场应用;而数据驱动的方式依靠人工智能算法学习电气量的内在联系,实现快速故障诊断。但这两种方案也存在各自的局限性:由文献[10]的分析可知,旋转整流器故障在励磁电流的时频特征上出现部分重叠,机理分析的诊断方案难以实现全部整流器故障工况的准确诊断。文献[14-16]采用数据驱动的方式实现了整流器故障的快速诊断,但需要利用实验数据作为训练集,为模型训练带来较大困难。
为此,本文提出一种机理与数据混合驱动的故障诊断方案。该方案仅利用仿真数据完成分类模型的训练,在降低训练难度的同时,实现旋转整流器故障的诊断。
本文提出的机理与数据混合驱动的旋转整流器诊断方案的基本原理如图2所示,包括数据预处理、模型建立和混合决策三个部分。混合驱动模型的数据来源包括有限元仿真和实验数据获取的励磁电流,其中有限元仿真数据用于诊断模型的训练以及参数的调试,实验数据用于测试诊断性能。
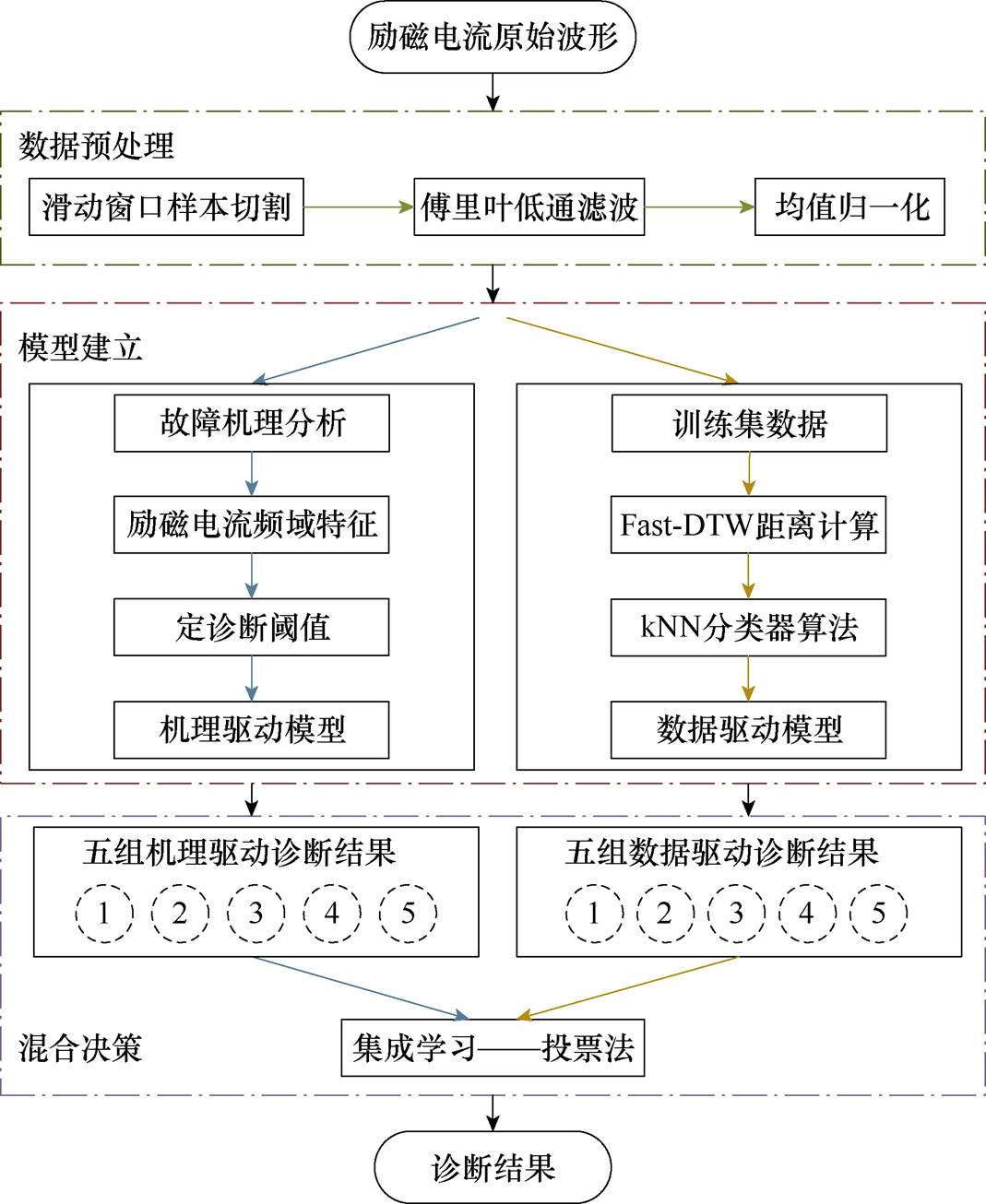
图2 机理与数据混合驱动的诊断方案基本原理
Fig.2 The basic principle of a hybrid physics-driven and data-driven diagnosis method
任意形式获取的励磁电流原始数据均需经过预处理,以规范化样本,增强算法的普适性:
第一步是滑动窗口样本切割。这部分有两个作用:一是保证样本具有合适长度,便于诊断方案学习特征;二是保证样本具有不同起点,以接近真实运行情况。对于5对磁极的11相励磁机,每五个电周期的励磁电流波形呈现较强的周期性[16],因此单个样本的长度选择五个电周期为宜。切割样本的过程中,只要保证相邻两个样本之间的扫描间隔不能被窗口长度除尽即可。
第二步是傅里叶低通滤波。实验波形的采样难免受到环境干扰而产生高次谐波,此举将励磁电流中的高频干扰滤除。滤波的截止频率影响诊断结果的准确率,过高的截止频率导致滤波不彻底,过低的截止频率导致滤波后的励磁电流信息过少。综合考虑,设置截止频率为基波的十倍频,保证每种运行状态下的励磁电流有足够的时频域特征。
第三步是均值归一化。其目的是保证诊断方案能够应用于不同励磁电压等级下的励磁电流波形。不同电压等级下,相同故障模式下的励磁电流波形整体趋势相同,有效值发生等比例变化,傅里叶分解出的频域分量也会等比例变化。针对这一特点,提出均值归一化的方法,即将样本的每一个值都除以时间序列均值,得到一个均值为1的新时间序列。
预处理后,励磁电流原始波形形成一个个长度相同、起点不对齐、无量纲的时间序列样本。
2.2.1 励磁电流的频域故障特征
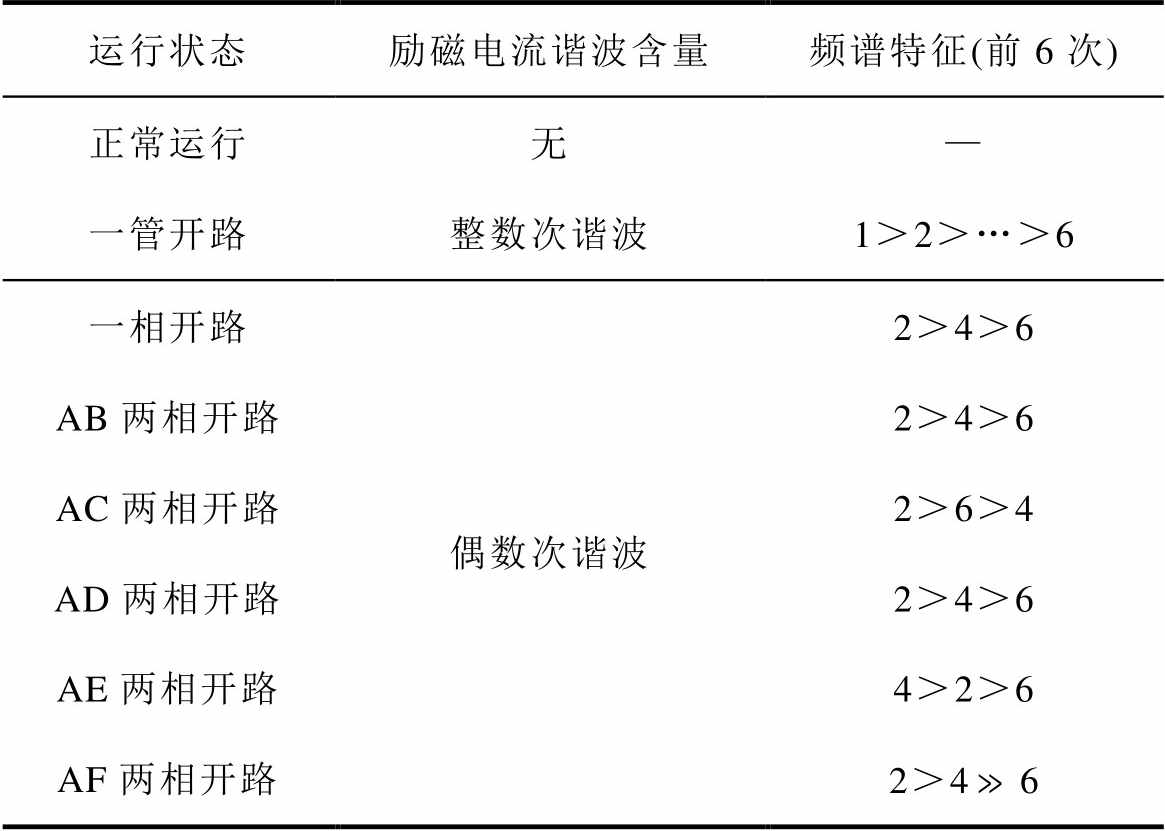
根据文献[10]对11相无刷励磁系统旋转整流器故障的励磁电流频域特征分析,整流器故障对励磁电流的影响可以简单归结如下:无刷励磁系统发生任意旋转整流器故障后,可以等效为对应位置二极管工作状态缺失,这进一步导致电枢电流波形的对称性遭到破坏,出现电枢电流畸变量。畸变量产生的磁动势经电枢反应作用到定子励磁绕组上,使励磁绕组中出现特定次的谐波电动势,即励磁电流中存在特定次谐波。上述过程的严格推导在文献[10]中已经给出,本文不再详细叙述,将结论总结如下:正常运行时励磁电流中几乎只含有直流量;一管开路故障后励磁电流出现整数次谐波;一相开路和两相开路故障后励磁电流中包含偶数次谐波。此外,文献[10]中展示了旋转整流器故障样机实验的励磁电流各次谐波有效值的傅里叶分解结果。根据分解结果,本文进一步总结不同旋转整流器故障发生后励磁电流的频域有效值特征,见表1。表中,AB~AF指五种相对位置的两相开路。
表1 旋转整流器故障的励磁电流频域特征
Tab.1 Frequency-domain characteristics of excitation current in rotating rectifier faults
运行状态励磁电流谐波含量频谱特征(前6次) 正常运行无— 一管开路整数次谐波1>2>…>6 一相开路偶数次谐波2>4>6 AB两相开路2>4>6 AC两相开路2>6>4 AD两相开路2>4>6 AE两相开路4>2>6 AF两相开路2>46
根据表1,正常运行和一管开路故障时的励磁电流频域特征较为独特,而相开路均导致励磁电流出现偶数次谐波,特别是两相开路相对位置较多,区分难度大。但不同相开路之间,励磁电流特征次谐波的有效值并不相同,例如:AE两相开路的4次谐波最大,而AC两相开路的6次谐波大于4次谐波。根据这些励磁电流频域有效值的机理特征,可以设置旋转整流器故障的诊断方案。
2.2.2 基于频域特征机理的诊断方案
频域特征驱动的诊断方案需要选择合适的故障特征。①相比正常运行状态而言,旋转整流器故障发生后,励磁电流中将出现不同的频域特征。这意味着总谐波含量增加,因此总谐波含量能够区分是否发生故障。而实际应用中,应将总谐波含量比直流量,比直流量后,不同励磁电压等级的励磁电流具有相同量纲;②单个二极管的开路故障导致励磁电流中含有各整数次谐波,而相开路故障导致励磁电流中含有偶数次谐波。所以,励磁电流的奇数次谐波与偶数次谐波的比值可以区分旋转整流器的故障是管开路还是相开路。
而所有的相开路故障发生后,励磁电流中均出现偶数次谐波。但观察表1可知,不同相开路故障励磁电流频谱上偶数次谐波的有效值各不相同。因此,可以借助偶数次谐波的比例关系来区分各种相开路故障,如4次与2次比值、6次与4次比值等。
通过上述分析可知,旋转整流器故障后,励磁电流的频域特征可包括如下四种:总谐波与直流量比值、奇数次谐波与偶数次谐波比值、4次谐波与2次谐波比值、6次谐波与4次谐波比值。接下来,需要根据这四种特征,选择合适的阈值实现机理驱动的旋转整流器故障诊断。参照文献[23],基于有限元仿真的励磁电流结果,可以提取四种频域特征值,并在特征值的基础上乘以可靠系数,获得每个频域特征的诊断阈值。最后,当实测的励磁电流数据输入时,能用阈值实现机理驱动的旋转整流器故障诊断。
2.3.1 Fast-DTW算法原理
传统的DTW算法是一种计算两条时间序列相似度的方法,它通过时间序列的拉伸或压缩,使时间序列尽可能对齐。与欧氏距离等距离衡量方式相比,DTW算法在计算不等长、不对齐的时间序列时,具有较大优势[24]。接下来,具体介绍DTW算法的原理。
设存在长度为m的时间序列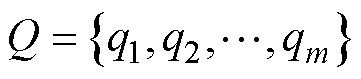 和长度为n的时间序列
和长度为n的时间序列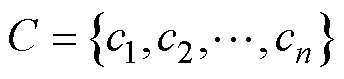 。为了对齐这两个时间序列,需要构造一个m×n的距离矩阵D。矩阵元素D(i, j)表示xi和yj之间的距离,通常用欧氏距离表示。D(i, j)也就是时间序列Q和C每一个点之间的相似度,距离越小则相似度越高。
。为了对齐这两个时间序列,需要构造一个m×n的距离矩阵D。矩阵元素D(i, j)表示xi和yj之间的距离,通常用欧氏距离表示。D(i, j)也就是时间序列Q和C每一个点之间的相似度,距离越小则相似度越高。
从时间序列Q和C的起点到它们的终点之间存在若干条规整路径W,有
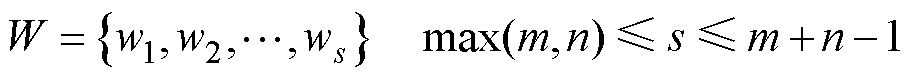 (1)
(1)
式中,W中的第k个元素wk=(a, b)为时间序列Q和C之间产生映射关系的点的坐标。
规整路径W需要满足三个约束条件:
(1)边界条件:w1=(1, 1),ws=(m, n),即W必须经过时间序列X和Y的起始点。
(2)连续性:若wk-1=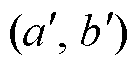 ,则
,则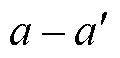 ≤1且
≤1且 ≤1。即W必须包含时间序列X和Y的每一个点。
≤1。即W必须包含时间序列X和Y的每一个点。
(3)单调性:若wk-1=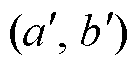 ,则
,则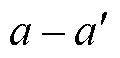 ≥1且
≥1且 ≥1。即时间序列Q和C的坐标点之间只能随着时间单调映射。
≥1。即时间序列Q和C的坐标点之间只能随着时间单调映射。
事实上,满足三条约束条件的W可以有多个,需要通过动态规划的方法求解规整代价最小的路径。设s(i, j)表示从起点D(1, 1)开始到点D(i, j)的最小距离,d(i, j)为从路径起点至(i, j)累积的距离,则s(i, j)可以表示为
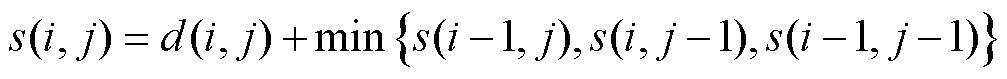 (2)
(2)
由式(2)可得,DTW算法求得的两条时间序列之间的距离为
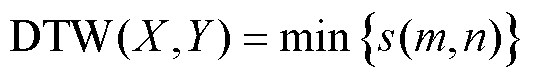 (3)
(3)
为了更好地展示DTW算法的对应关系,图3以两条时间序列为例,给出了DTW和欧式距离的对应关系示意图。其中,蓝色虚线是DTW对应关系,灰色点画线是欧氏距离对应关系。
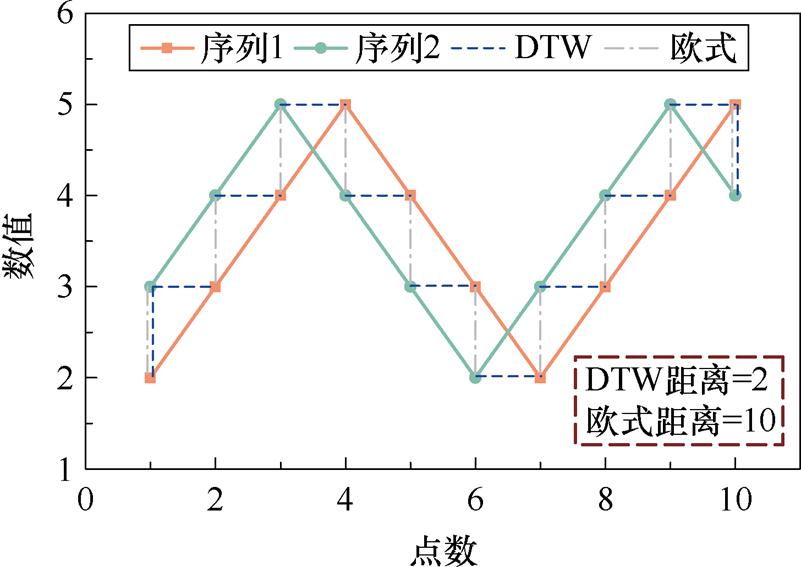
图3 DTW与欧式距离的对应关系
Fig.3 The mapping of DTW and Euclidean distance
从图3中可知,两条时间序列在趋势上相似,在横轴上平移了1个点。但欧氏距离的计算结果远大于DTW距离。这是由于在计算时间序列间的欧氏距离时,各点是一一对应的;而在计算DTW距离时,通过对时间序列的扭曲,各点之间的对应关系被改变:序列2的第一个点和序列1的最后一个点均对应了另一条曲线的两个点,从而计算出一个较小的距离。因此,对于同种类别但不同起点的时间序列,DTW算法可以轻易得出相似度较高的结论。
然而,传统DTW算法的时间复杂度为O(n2),在计算较长时间序列时展现出较高的时间复杂性。而Fast-DTW算法通过简化策略,显著提高了DTW算法的计算效率,使时间复杂度降低为O(n)[25]:
(1)减小搜索范围。Fast-DTW通过缩小式(1)中规整路径边界的形式,减小最优路径的搜索范围,降低计算量。
(2)数据抽象。Fast-DTW通过降低采样率的方式,降低计算量。即计算式(2)时,间隔若干个点计算一次,找到最优路径后再将其映射回全精度矩阵。
(3)索引。索引通过使用下界函数修剪单个任务需要运行DTW的次数,来显著加快许多DTW应用程序的速度,但不会加快单次DTW算法。
需要说明的是,与其他距离度量方式相比,Fast- DTW算法的时间成本仍然较高,特别是当时间序列较长时。因此,在实际应用中应尽可能缩小训练集规模,避免出现诊断时间过长的现象。
2.3.2 数据驱动的诊断方案
在文献[10, 16]中,旋转整流器故障后的励磁电流波形已被证明具有不同的时域特征:根据旋转整流器的故障类型,励磁电流时域波形将出现不同数量和位置的畸变,从而导致不同故障的励磁电流波形形态各异。Fast-DTW算法能够衡量不同起点时间序列的相似性,但需要合适的分类器对计算结果分类。而kNN算法作为一种简单的机器学习算法,能够找到特征空间中距离样本最近的k个样本的类别,从而确定样本的类别,具有对异常值不敏感、可解释性好等优点[26],因而得到广泛应用[27]。由于不需要提前训练,在解决小训练集样本问题时,kNN算法也具有独特优势,这也使得该学习器与DTW算法结合效果较好[28]。
当实测数据输入时,预处理后的样本先与训练集的每个样本计算DTW距离,然后利用kNN算法找到距离最近的k个样本,进而得到实测数据的类别,实现旋转整流器故障的诊断。
机理驱动的故障诊断侧重励磁电流的频域特征,而数据驱动的故障诊断偏向励磁电流的时域波形特征。根据第1节的分析可知,机理驱动和数据驱动的诊断方案均存在局限性。而集成学习能够将机理驱动与数据驱动得到的多个学习器的结果结合,得出最终的诊断结果。这种结合方式能从三个方面带来好处[29]:①多个学习器可减小单分类器因误选而导致的泛化性能不佳的风险;②学习算法往往会陷入局部极小,而多次运行之后进行结合,可降低陷入糟糕局部极小点的风险;③结合多个学习器,相应的假设空间有所扩大,可能学得更好的近似。
因此,本文提出的诊断方案设置五个训练集分别用来训练五个机理驱动模型和五个数据驱动模型,并引入集成学习中的绝对多数投票法,实现励磁电流数据的诊断。绝对多数投票法的原理如下:假设总类别数为N,一个分类任务L(x)由T个分类器li(x)共同决策,每个分类器产生一个预测结果
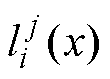 ,则L(x)的结果可以表示为
,则L(x)的结果可以表示为
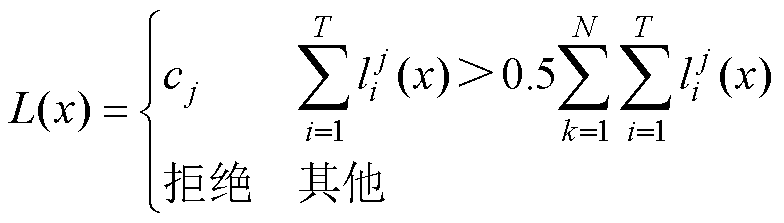 (4)
(4)
根据投票结果,如果有半数以上的分类器得到的标签为cj,则最终输出类别为cj。若没有得票超过半数的标签,则绝对多数投票法拒绝输出标签。
综上所述,当励磁电流原始实验波形输入后,完整的诊断流程如下:首先原始波形需经过预处理步骤,生成标准化的样本;然后该样本需要分别经过五个训练好的机理驱动学习器和五个数据驱动学习器,得到十个分类结果;最后利用集成学习中的绝对多数投票法,得出最终的诊断结果。
本节的全部算例基于Python3.7.3平台并使用Intel i7-13700K 3.40 GHz的CPU进行,所采用的数据源自某11相环形无刷励磁机的Ansys有限元仿真模型与动模样机实验平台,11相环形无刷励磁系统的结构参数见表2。
11相无刷励磁系统的仿真模型示意图和样机实验平台如图4和图5所示。
仿真和实验均需获取正常运行、一管开路、一相开路以及五种相对位置的两相开路下的励磁电流原始数据。原始数据以滑动窗口的形式进行切割,单个窗口的长度为62.5 ms,对应五个电周期。相邻两个样本之间间隔13 ms,保证每个样本的起点不同。接下来,以20 V电压等级的仿真和实验为例,设置截止频率800 Hz对样本进行滤波,如图6所示。为了便于展示,图6中每段波形的长度为25 ms,对应两个电周期长度。
表2 某11相无刷励磁机的参数
Tab.2 Parameters of 11-phase brushless exciter

参 数数 值 额定励磁电压/V60.33 额定视在功率/(kV·A)22.3 功率因数0.9 额定转速/(r/min)960 定子外径/mm327 转子外径/mm227 线圈节距8 电枢电阻/W0.24 额定励磁电流/A12.97 额定相电压/V120 额定频率/Hz80 定子槽数77 定子内径/mm230 转子内径/mm70 励磁绕组每极匝数90 励磁回路电阻/W4.65

图4 Ansys有限元仿真示意图
Fig.4 Diagram of Ansys finite element simulation

图5 实验平台
Fig.5 Experimental platform
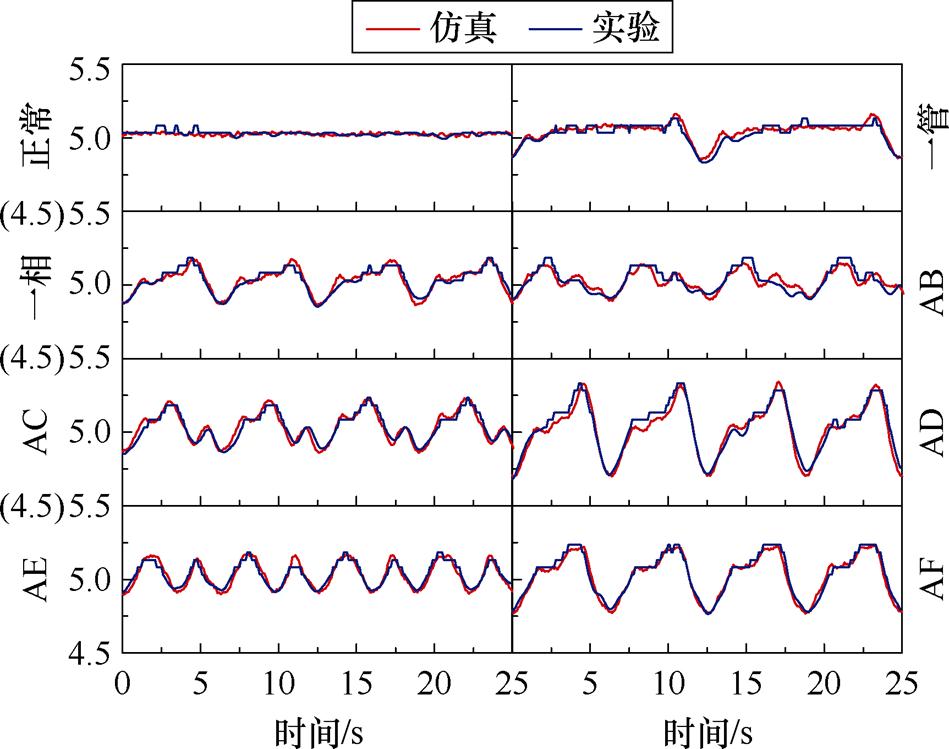
图6 八种工况下的仿真与实验励磁电流波形
Fig.6 Simulation and experimental excitation current waveforms under eight operating conditions
由图6可知,有限元仿真运行在理想条件下,励磁电流波形更平滑;样机实验波形由于磁极不对称和环境干扰,励磁电流波形存在局部失真和不对称的现象,但整体来说,滤波后的仿真与实验励磁电流波形整体趋势一致、形状相近。因此,有望利用仿真数据训练模型,实现测试集上的诊断。
然后,在20 V到26 V四个励磁电压等级上的励磁电流波形上验证均值归一化的效果。以A相开路为例,绘制归一化前后的励磁电流波形如图7所示。
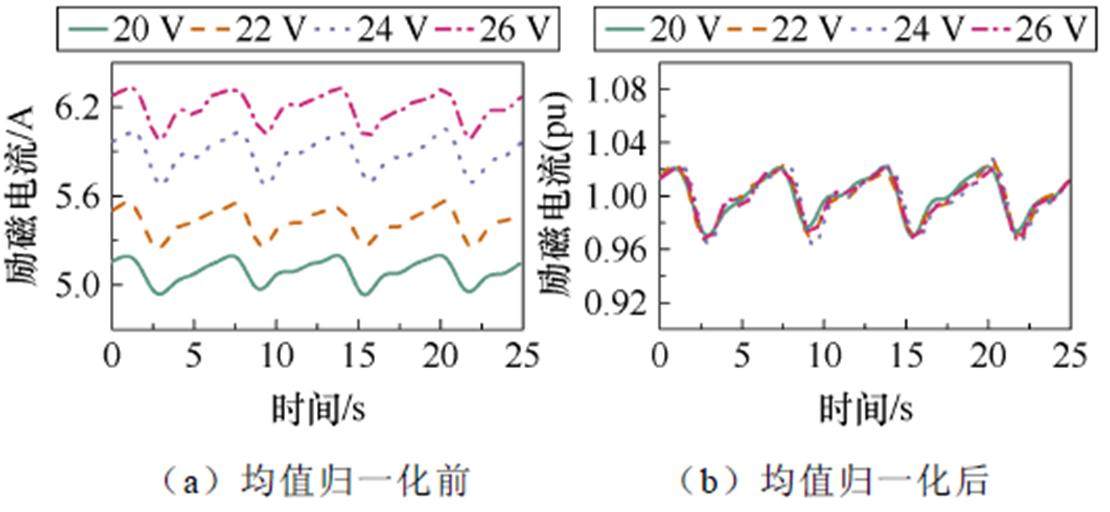
图7 不同电压等级下A相开路的励磁电流实验波形
Fig.7 Experimental waveforms of excitation current for phase-A open circuit at different voltage levels
归一化后,不同励磁电压等级下的电流波形具有相同的幅度和相近的趋势,这使得诊断方案具有更好的适用性。
为更好地接近现场应用情况,本文的训练集和验证集均为20 V电压等级下的仿真数据,测试集为实验数据。由于DTW算法的时间复杂度较高,训练集样本的规模不宜过大,否则诊断时长将大大增加,故本文单个训练集和验证集下每种工况只包含100个样本。而测试集样本来自样机实验数据。为测试泛化能力,测试集包含四个励磁电压等级,每个励磁电压等级每种工况下各50个样本。仿真与实验励磁电流波形生成的训练集、验证集和测试集样本分布见表3。
表3 仿真与实验数据的样本分布
Tab.3 Sample distribution of simulations and experiments
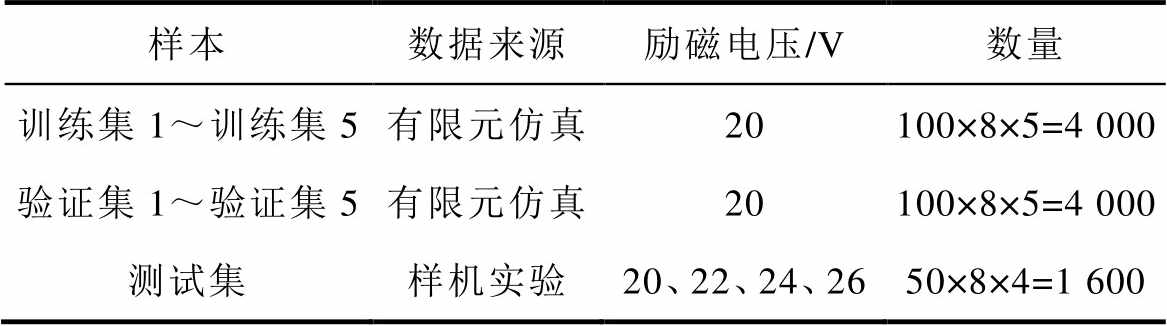
样本数据来源励磁电压/V数量 训练集1~训练集5有限元仿真20100×8×5=4 000 验证集1~验证集5有限元仿真20100×8×5=4 000 测试集样机实验20、22、24、2650×8×4=1 600
进一步地,本文使用准确率、kappa系数和诊断时长来评价各诊断模型的性能。kappa系数用来衡量分类器的预测与实际标签之间的一致性,它的计算依赖故障诊断的混淆矩阵,具体表达式为
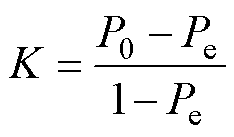 (5)
(5)
式中,P0为预测一致性,即准确率;Pe为偶然一致性。二者的表达式为
 (6)
(6)
 (7)
(7)
kappa系数的取值范围为[-1, 1],但一般在[0, 1]之间。数值越大说明分类一致性较好。
本节将测试纯机理驱动的诊断模型的效果。根据机理分析的结论,旋转整流器故障后,励磁电流的特征包括总谐波与直流量比值、奇数次谐波与偶数次谐波比值、4次谐波与2次谐波比值、6次谐波与4次谐波比值四种。为了进一步确定机理驱动的诊断逻辑,图8绘制了20 V励磁电压等级下,有限元仿真获取的各工况下励磁电流的频谱分布。
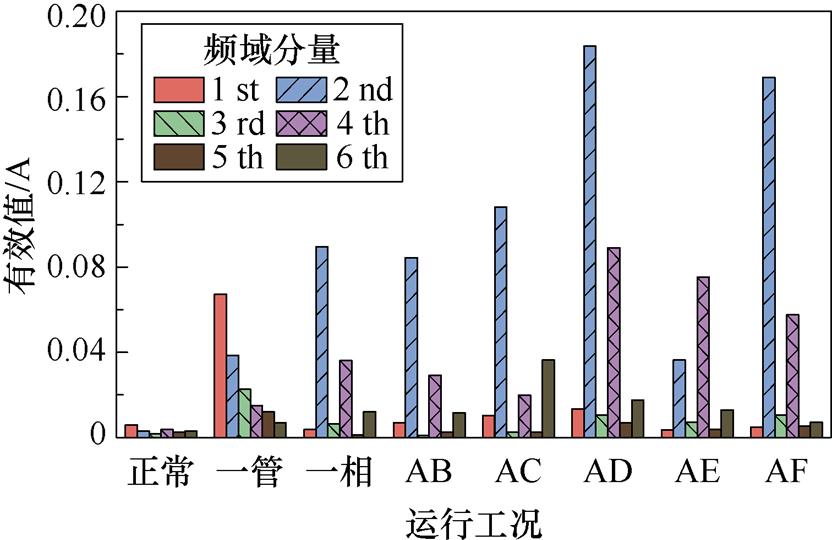
图8 八种工况的频域分布
Fig.8 Frequency domain distribution under eight operation conditions
结合理论分析的结果观察图8,可知最容易区分的是一管开路故障,因为只有一管开路含有奇数次谐波。各种相开路故障均包含偶数次谐波,其中AC两相开路的6次谐波大于4次谐波,AE两相开路的4次谐波最大,特征较明显。至于其他相开路故障,需依据机理分析获取的四个特征来确定最终的诊断阈值。整体的诊断逻辑如图9所示。
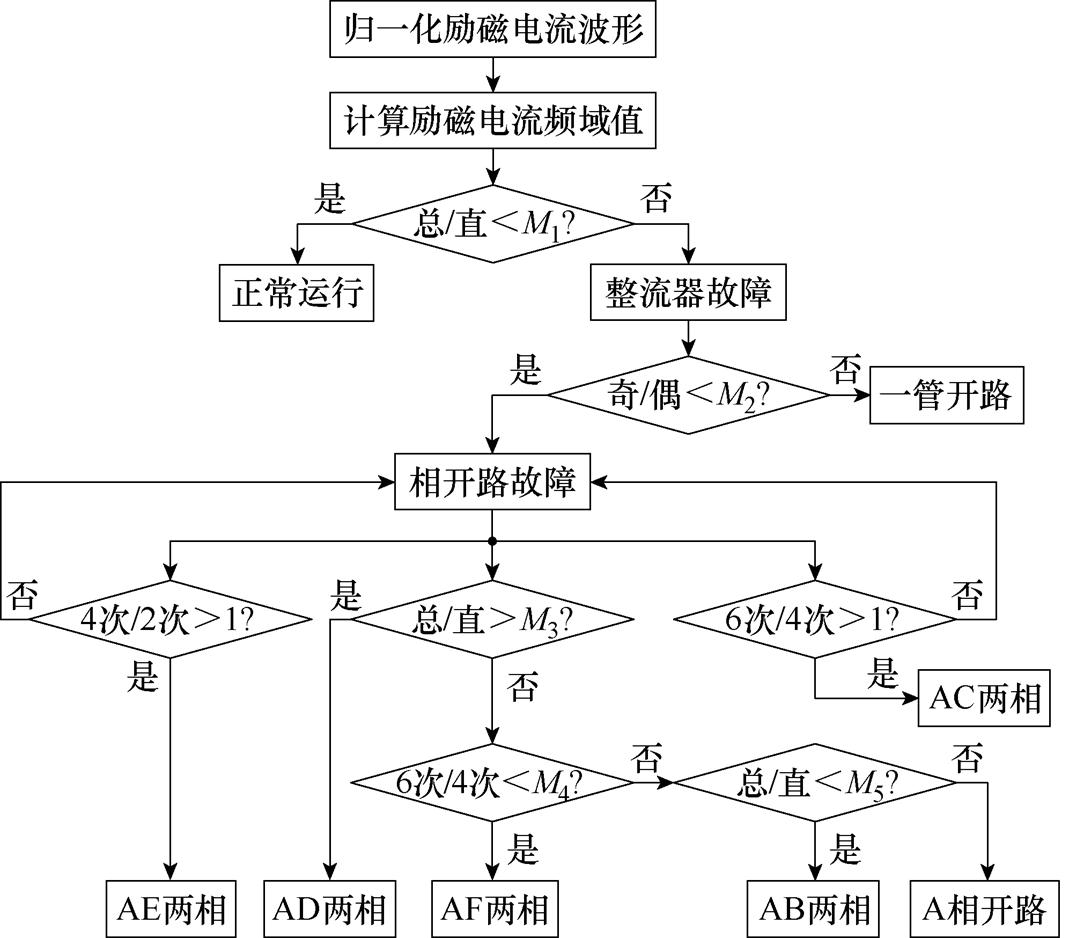
图9 机理驱动的诊断逻辑
Fig.9 Mechanism driven diagnostic logic
根据图9可知,当归一化的励磁电流波形输入后,首先需对励磁电流做频域分解,然后判断总谐波含量与直流量的比值。若总/直小于阈值M1,系统正常运行,否则认为发生旋转整流器故障。进一步确认旋转整流器故障的类别:计算励磁电流中的奇偶次谐波比,若奇/偶小于阈值M2,认为系统有相开路故障发生,否则诊断为一管开路故障。进一步对相开路故障进行区分:若4次谐波比2次谐波大,诊断为AE两相开路故障;若6次谐波比4次谐波大,诊断为AC两相开路故障。接着判断总/直,若大于阈值M3,诊断为AD两相开路故障,否则继续判断6次/4次。若6次/4次小于阈值M4,诊断为AF两相开路故障,否则继续诊断总/直。若总/直小于阈值M5,诊断为AB两相开路,否则诊断为A相开路故障。
综上所述,需要整定五个阈值来完成纯机理的旋转整流器故障诊断。阈值的整定过程与文献[23]类似。本文基于有限元仿真数据完成整定,在五组训练集上,可以整定出五组用于旋转整流器故障诊断的阈值。以下以第一组训练集为例,给出具体整定过程:
对于区分是否发生故障的阈值M1,其表达式为
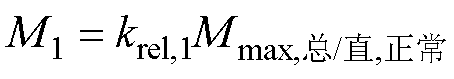 (8)
(8)
式中,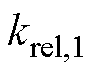 为阈值M1的可靠系数;
为阈值M1的可靠系数;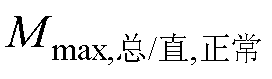 为正常运行时总谐波与直流量比值的最大值。
为正常运行时总谐波与直流量比值的最大值。
根据训练集1的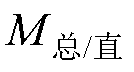 计算结果,正常运行时的
计算结果,正常运行时的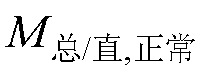 的取值范围为(4.89×10-4, 7.01×10-4),而
的取值范围为(4.89×10-4, 7.01×10-4),而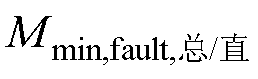 发生在AB两相开路,为3.32×10-2。由于发生故障后励磁电流出现大量谐波,可靠系数
发生在AB两相开路,为3.32×10-2。由于发生故障后励磁电流出现大量谐波,可靠系数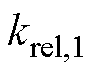 可以取较大值以防正常情况被误判为故障,例如
可以取较大值以防正常情况被误判为故障,例如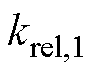 =10,此时M1=7.01×10-3。
=10,此时M1=7.01×10-3。
对于用来区分管开路和相开路的阈值M2,其表达式为
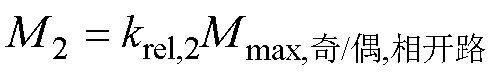 (9)
(9)
式中,krel,2为阈值M2的可靠系数; 为所有相开路故障后奇数次谐波与偶数次谐波比值的最大值。
为所有相开路故障后奇数次谐波与偶数次谐波比值的最大值。
根据训练集1的 计算结果,一管开路时的
计算结果,一管开路时的 的取值范围为(1.30, 2.05),而
的取值范围为(1.30, 2.05),而 发生在AE两相开路,为0.25。由于发生一管开路后励磁电流出现大量奇数次谐波,可靠系数krel,2可以取较大值以防相开路被误诊断为管开路,例如krel,2=3,此时M2=0.75。
发生在AE两相开路,为0.25。由于发生一管开路后励磁电流出现大量奇数次谐波,可靠系数krel,2可以取较大值以防相开路被误诊断为管开路,例如krel,2=3,此时M2=0.75。
由图8可知,AD两相开路总谐波含量最大,因此用来诊断AD两相开路故障的阈值M3的表达式为
 (10)
(10)
式中,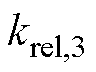 为阈值M3的可靠系数;
为阈值M3的可靠系数; 为除了AD两相开路外其余相开路故障,总/直的最大值。
为除了AD两相开路外其余相开路故障,总/直的最大值。
根据训练集1的计算结果,AD两相开路时的 的取值范围为(6.55×10-2, 7.78×10-2),而
的取值范围为(6.55×10-2, 7.78×10-2),而 发生在AF两相开路,为5.87× 10-2。对用于相开路诊断的阈值而言,可靠系数可以取一较小值,以在诊断可靠性和准确性之间动态平衡。例如,krel,3=1.05,此时M3=6.16×10-2。
发生在AF两相开路,为5.87× 10-2。对用于相开路诊断的阈值而言,可靠系数可以取一较小值,以在诊断可靠性和准确性之间动态平衡。例如,krel,3=1.05,此时M3=6.16×10-2。
由图8可知,AF两相开路的6次谐波极小,因此用来诊断AF两相开路故障的阈值M4的表达式为
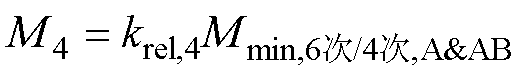 (11)
(11)
式中,krel,4为阈值M4的可靠系数;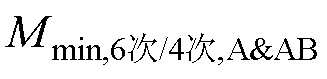 为A相开路和AB两相开路6次谐波与4次谐波之比的最小值。
为A相开路和AB两相开路6次谐波与4次谐波之比的最小值。
根据训练集1的计算结果,AF两相开路时的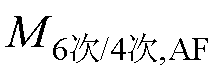 的取值范围为(0.023, 0.13),而
的取值范围为(0.023, 0.13),而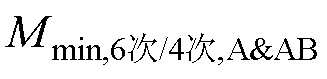 发生在AB两相开路,为0.25。可靠系数krel,4可以取1.5,此时M4=0.20。
发生在AB两相开路,为0.25。可靠系数krel,4可以取1.5,此时M4=0.20。
由图8可知,AB两相开路故障的总谐波含量比A相开路略小,因此用来诊断AB两相开路故障和A相开路的阈值M5的表达式为
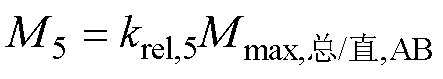 (12)
(12)
式中,krel,5为阈值M5的可靠系数;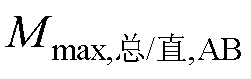 为AB两相开路总谐波与直流量之比的最大值。
为AB两相开路总谐波与直流量之比的最大值。
根据训练集1的计算结果,A相开路时的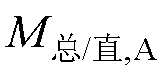 的取值范围为(3.68×10-2, 3.92×10-2),而
的取值范围为(3.68×10-2, 3.92×10-2),而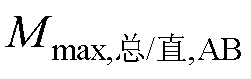 为3.35×10-2。可靠系数krel,5可以取1.05,此时M5= 3.52×10-2。
为3.35×10-2。可靠系数krel,5可以取1.05,此时M5= 3.52×10-2。
五个训练集下可以确定出五组阈值,将测试集数据在这五组阈值下进行测试,得到的五组机理驱动的结果见表4。
表4 五组机理驱动模型的结果
Tab.4 Results of five mechanism driven models
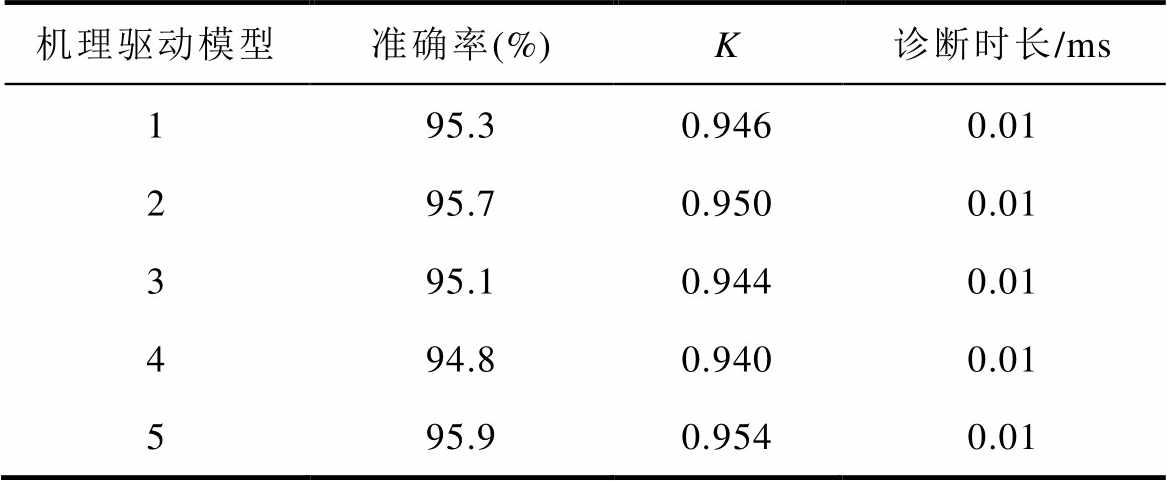
机理驱动模型准确率(%)K诊断时长/ms 195.30.9460.01 295.70.9500.01 395.10.9440.01 494.80.9400.01 595.90.9540.01
由表4可知,五组机理驱动模型的诊断准确率以及kappa系数较为接近,说明机理驱动模型寻找到的频域阈值边界较稳定。虽然机理驱动模型的诊断用时很短,但总体的准确率不够高,难以满足实际运用的准确性需求。
进一步观察错判样本,部分A相开路诊断为AB两相开路。统计这两种工况的总谐波与直流量的比值,可知A相开路的取值范围为(3.08×10-2, 3.99×10-2),平均值为3.54×10-2。AB两相开路的取值范围为(2.69×10-2, 3.06×10-2),平均值为3.06× 10-2。综上所述,在样机实验中,A相开路和AB两相开路的励磁电流总谐波与直流量的比值存在重合的现象,因此出现误判。
纯数据驱动的旋转整流器故障诊断以励磁电流波形的时域特征为诊断依据。实际运行中读取到的励磁电流波形起始点不同,给时域特征的识别和学习带来困难。为了模拟这一情况,预处理过程中的样本切割保证了一定的不对齐性。本文用不对齐的励磁电流仿真数据样本训练数据驱动模型,在不对齐的励磁电流实验数据样本上完成测试。依赖Fast-DTW算法对时间轴的拉伸和扭曲能力处理不对齐数据,结合kNN学习器在小样本条件下的独特优势,实现数据驱动的旋转整流器故障诊断。
首先要确定kNN分类器的近邻k。设置参数k=1~20,在验证集数据上对模型参数寻优。训练集1~训练集5在验证集1~验证集5上的结果相近,为了方便展示,绘制训练集1在验证集1上Fast- DTW-kNN的诊断准确率变化如图10所示。
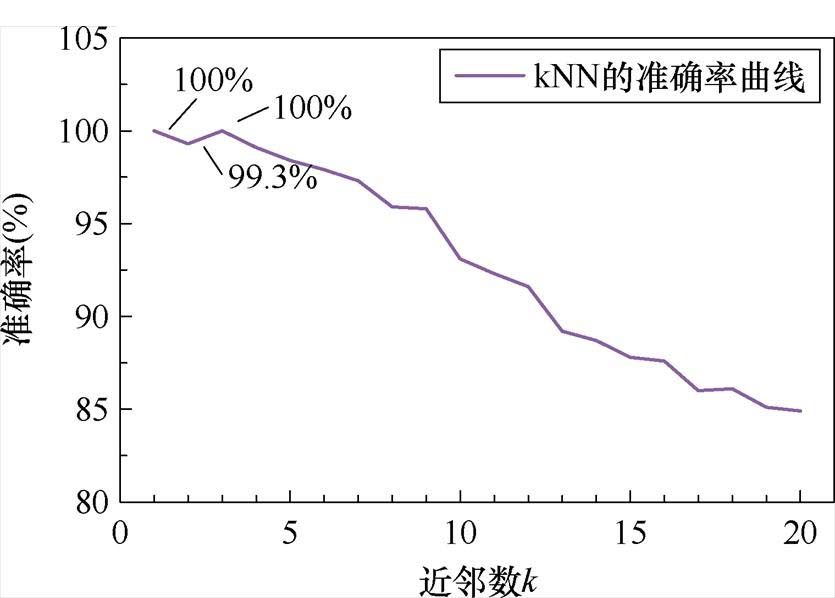
图10 Fast-DTW-kNN的寻优过程
Fig.10 Optimization process of Fast DTW kNN
由图10可知,k=1和k=3时准确率最高,达到了100%。此后,随着k的增大,准确率呈下降趋势。不过k取值过小会导致算法对于噪声或异常数据过于敏感,因此,对于Fast-DTW-kNN的数据驱动算法,k应当取3。
选取最优近邻数k后,接下来将使用Fast-DTW- kNN诊断测试集样本。为了对比Fast-DTW的加速效果,本节分别训练了DTW-kNN诊断模型以及Fast-DTW-kNN诊断模型,结果见表5。
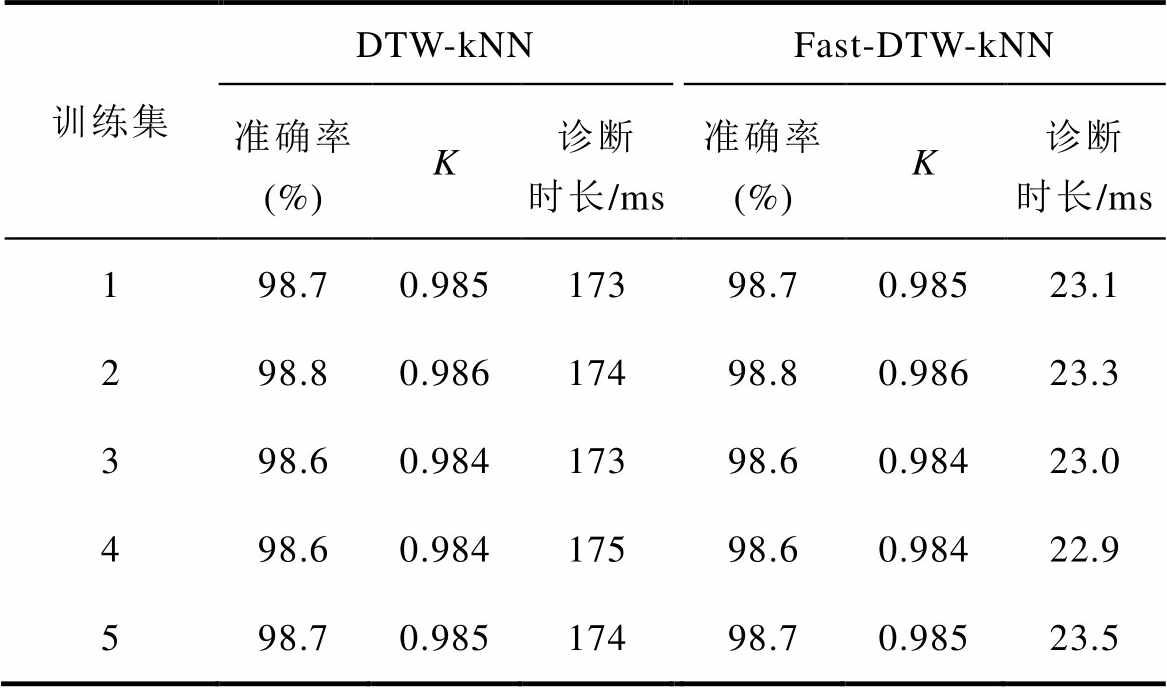
表5 五个训练集下的诊断结果
Tab.5 The diagnostic results under five training sets
训练集DTW-kNNFast-DTW-kNN 准确率 (%)K诊断时长/ms准确率 (%)K诊断时长/ms 198.70.98517398.70.98523.1 298.80.98617498.80.98623.3 398.60.98417398.60.98423.0 498.60.98417598.60.98422.9 598.70.98517498.70.98523.5
由表5易知,不同训练集数据下训练出来的诊断模型准确率接近,说明训练集样本的时域波形特征相近。准确率和kappa系数结果接近,这说明模型在考虑一定随机性的情况下,仍能保持较好的预测结果一致性。而诊断时间主要由计算单个测试样本与训练集样本间的DTW距离引起,kNN学习器的分类时间几乎可以忽略不计。对比DTW算法与Fast-DTW算法的结果,可知Fast-DTW在与DTW的准确率一致的前提下,计算速度大幅提升。虽然单个样本23 ms左右的诊断时长比机理驱动的决策过程要长,但总的来说满足实际运用需求。
为进一步分析数据驱动的错判样本类别及数量,以训练集1上的结果为例,绘制DTW-kNN模型和Fast-DTW-kNN模型诊断结果的混淆矩阵,如图11a和图11b所示。
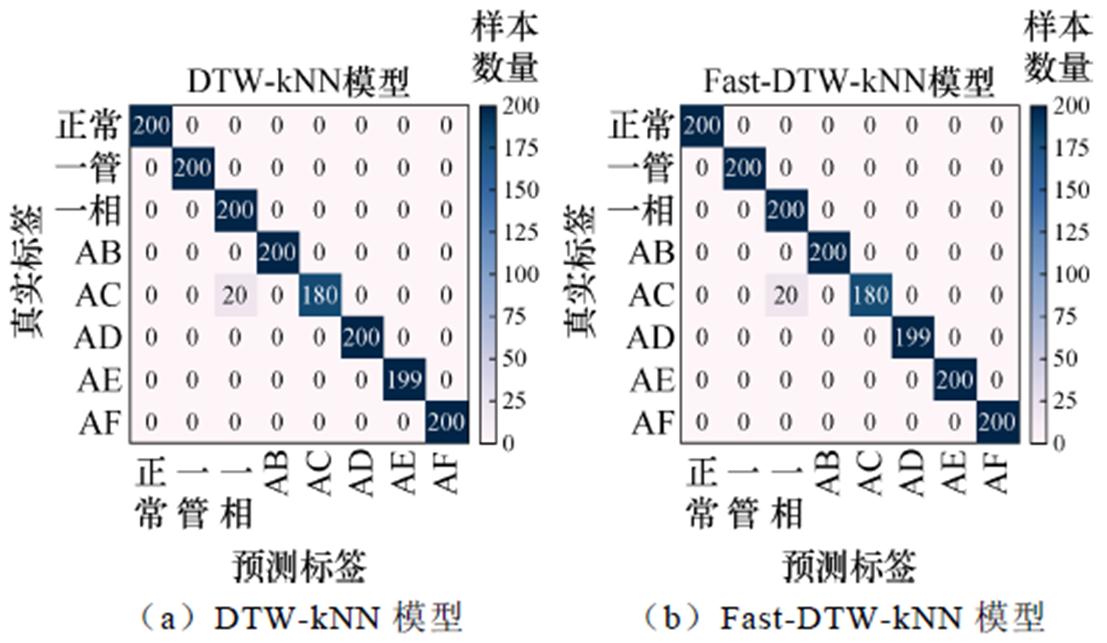
图11 数据驱动模型的混淆矩阵
Fig.11 Confusion matrices of data-driven models
观察图11,可知错判样本集中在AC两相开路故障与一相开路故障之间,而其他类别几乎没有出现错判。这说明,数据驱动的诊断方案能够解决机理驱动中存在的A相开路诊断成AB两相开路的问题。因此,结合机理驱动和数据驱动的结果,有望实现旋转整流器故障的可靠诊断。
根据3.1节的内容,机理驱动的诊断方案利用故障后励磁电流波形的频域特征,实现旋转整流器的故障诊断。但由于励磁电流频谱重叠,机理驱动的方法会将小部分一相开路故障诊断成AB两相开路故障。根据3.2节的内容,数据驱动的诊断方案利用Fast-DTW算法学习励磁电流波形特征,引入kNN分类器实现旋转整流器故障诊断。但机理驱动的方式会将小部分AC两相开路故障诊断成一相开路故障。单纯的机理或数据驱动诊断方案均难以满足实际应用的需求。
进一步分析可知,这两种驱动方式发生误判的种类并不重叠。而在第3.1节和3.2节中,分别得到了五个机理驱动的模型和五个数据驱动的诊断模型。本节以这十个学习器为基础,引入集成学习中的绝对多数投票法思想,将机理驱动与数据驱动诊断方案得到的结果有机融合,实现机理与数据混合驱动的旋转整流器故障诊断。
同时,为了突出混合驱动故障诊断的优势,本文引入了一些单驱动故障诊断模型作为对比。如分类任务常用的决策树算法、随机森林算法、kNN算法、支持向量机算法,以及深度学习领域的多层感知机算法和卷积神经网络算法。单驱动模型均使用训练集1的数据进行训练,在验证集1上寻优,测试集与混合驱动一致。得到的最优参数、诊断准确率、kappa系数和诊断时长见表6。
表6 机理与数据混合驱动的诊断结果
Tab.6 The diagnostic results of mechanism and data hybrid driving models
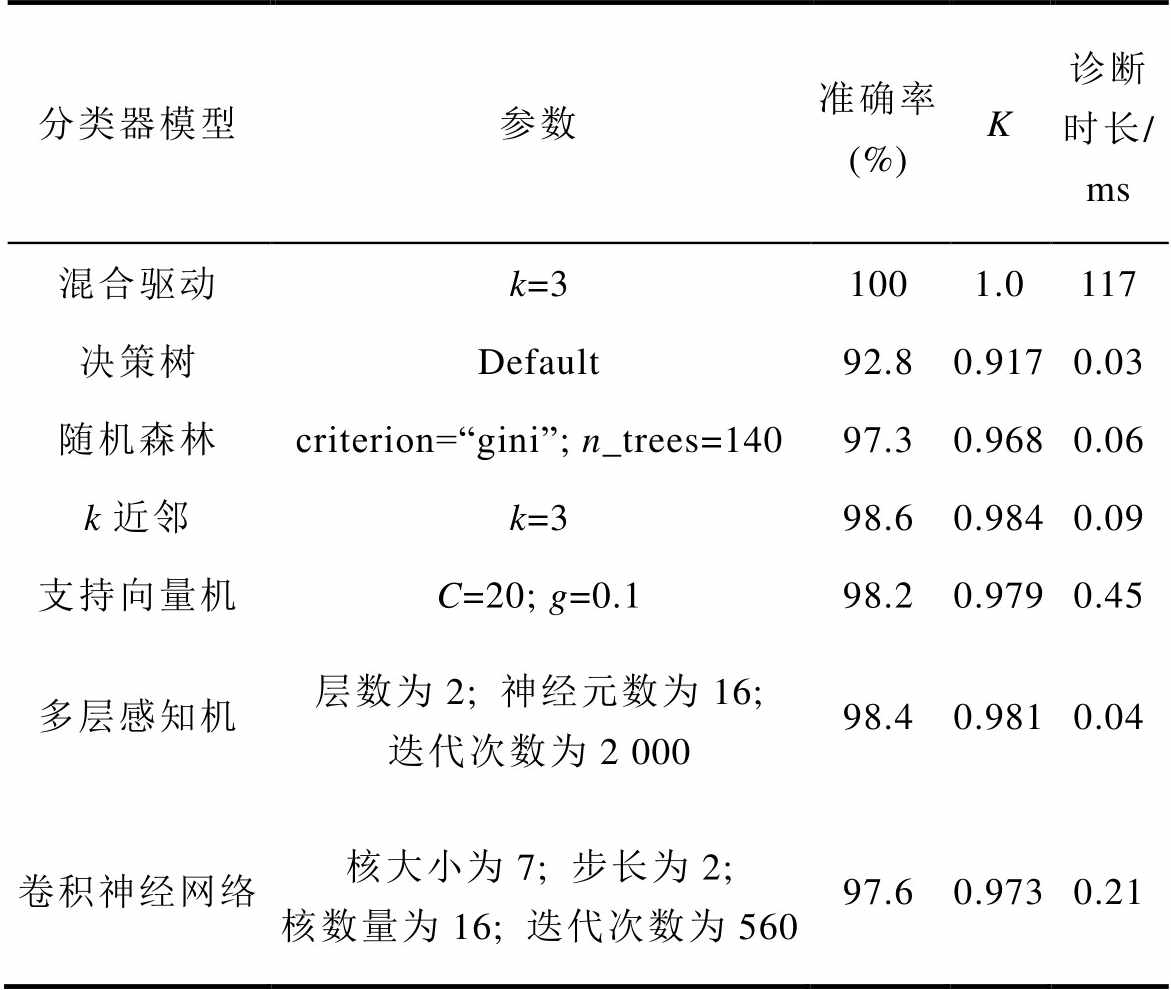
分类器模型参数准确率 (%)K诊断时长/ ms 混合驱动k=31001.0117 决策树Default92.80.9170.03 随机森林criterion=“gini”; n_trees=14097.30.9680.06 k近邻k=398.60.9840.09 支持向量机C=20; g=0.198.20.9790.45 多层感知机层数为2; 神经元数为16; 迭代次数为2 00098.40.9810.04 卷积神经网络核大小为7; 步长为2; 核数量为16; 迭代次数为56097.60.9730.21
机理与数据混合驱动的诊断方案建立了五个机理驱动模型和五个数据驱动模型,导致诊断时间增加至117 ms,但其诊断准确率达到了100%。现场应用时,旋转整流器故障发生后到保护装置动作之间会设置一个2 s左右的延时环节,说明在满足动作时效的基础上诊断可靠性要求远高于快速性。因此,117 ms的诊断时长完全满足实际应用需求。而单驱动模型的准确率和kappa系数都较低,难以达到现场应用的要求。
综合算例分析的结果,机理与数据混合驱动的方式在故障诊断任务中具有诸多优势:①仅利用离线的仿真数据建立混合驱动诊断模型,降低了实际应用的难度;②诊断模型综合考虑旋转整流器故障后励磁电流的频域机理和时域特征两方面的信息,展现出较好的诊断性能;③混合驱动包含机理推导的结论和客观的波形规律,提升了诊断结果的准确性;④机理分析为诊断提供了更好的可解释性,增加了诊断结果的可信度。
本文针对多相环形无刷励磁系统中旋转整流器的故障诊断问题,提出了一种基于仿真数据训练的机理与数据混合驱动诊断方案。通过实验验证,得出以下结论:
1)本文所提方案利用有限元仿真数据训练旋转整流器的故障诊断模型,避免对现场实验数据的依赖,降低训练的难度,同时提高现场应用的可行性。
2)集成学习融合机理驱动模型与数据驱动模型的优势,有效克服单一模型的局限性,实现了高准确率的故障诊断。
3)机理驱动法和数据驱动法的诊断本质上依赖励磁电流的频域和时域特征,这为故障诊断提供了直观依据,增加了可解释性。
未来的工作着眼于将本文提出的机理与数据混合驱动的诊断方案应用于不同相数、不同极对数的机型。此外,应进一步提升诊断速度,降低计算负担。
参考文献
[1] 郝亮亮, 张扬, 屈天龙, 等. 多相多边形无刷励磁机及旋转整流系统的运行状态分析[J]. 电力自动化设备, 2020, 40(4): 159-165.
Hao Liangliang, Zhang Yang, Qu Tianlong, et al. Operating state analysis of multi-phase angular brushless exciter and rotating rectifier system[J]. Electric Power Automation Equipment, 2020, 40(4): 159-165.
[2] 李小宁, 高朝晖, 王爽, 等. 飞机主电源系统关键器件健康状态评估研究[J]. 电气工程学报, 2023, 18(4): 188-198.
Li Xiaoning, Gao Zhaohui, Wang Shuang, et al. Research on health assessment method of key components in aircraft main power system[J]. Journal of Electrical Engineering, 2023, 18(4): 188-198.
[3] 朱威, 马伟明, 阳习党, 等. 基于电压波形相似度测量的十二相不控整流装置故障诊断[J]. 海军工程大学学报, 2018, 30(2): 49-54.
Zhu Wei, Ma Weiming, Yang Xidang, et al. Fault diagnosis method of 12-phase uncontrolled rectifier based on volt waveform similarity measurement[J]. Journal of Naval University of Engineering, 2018, 30(2): 49-54.
[4] Hao Liangliang, Chen Jianlin, He Li, et al. Modeling, analysis, and identification of armature winding interturn fault in multiphase brushless exciters[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 1119-1131.
[5] 刘念, 王贺新, 赵欣. 核电站无刷励磁系统的电枢电流谐波分析研究[J]. 四川电力技术, 2018, 41(1): 17-21.
Liu Nian, Wang Hexin, Zhao Xin. Analysis on harmonic of armature current for brushless excitation system of nuclear plant[J]. Sichuan Electric Power Technology, 2018, 41(1): 17-21.
[6] Pang Ji, Liu Weiguo, Wei Zhihuang, et al. Online diode fault detection in rotating rectifier of the brushless synchronous starter generator[J]. IEEE Transactions on Industrial Informatics, 2020, 16(11): 6943-6951.
[7] 郝亮亮, 陈建林, 段贤稳, 等. 核电多相无刷励磁系统中旋转整流器不同开路故障模式的特征分析及诊断[J]. 电工技术学报, 2023, 38(18): 4932-4946.
Hao Liangliang, Chen Jianlin, Duan Xianwen, et al. Analysis and diagnosis of different open-circuit fault modes of rotating rectifier in multi-phase brushless excitation system at nuclear power plant[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(18): 4932-4946.
[8] 郝亮亮, 李佳慧, 李洪学, 等. 核电多相角形无刷励磁系统旋转二极管开路故障特征分析[J]. 电力系统自动化, 2019, 43(11): 112-120.
Hao Liangliang, Li Jiahui, Li Hongxue, et al. Characteristic analysis of open-circuit fault of rotating diode in nuclear multi-phase angular brushless excitation system[J]. Automation of Electric Power Systems, 2019, 43(11): 112-120.
[9] 蔡波冲, 武玉才, 赵艳军. 基于定子电流谐波法的无刷励磁机旋转二极管开路故障检测[J]. 大电机技术, 2018(4): 61-65.
Cai Bochong, Wu Yucai, Zhao Yanjun. The detection of open-circuit fault of rotary diode in brushless exciter using stator current harmonic method[J]. Large Electric Machine and Hydraulic Turbine, 2018(4): 61-65.
[10] Chen Jianlin, Hao Liangliang, Li Huazhong, et al. Time-frequency characteristics analysis and diagnosis of rotating rectifier faults in multiphase annular brushless system[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3233-3244.
[11] 孙宇光, 杜威, 桂林, 等. 用于多相无刷励磁机开路与短路故障检测的磁极探测线圈设计[J]. 电工技术学报, 2022, 37(14): 3542-3554.
Sun Yuguang, Du Wei, Gui Lin, et al. Design of pole detection coils for open-circuit and short-circuit faults in multiphase brushless exciter[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3542- 3554.
[12] Wu Yucai, Cai Bochong, Ma Qianqian. Research on an online diagnosis for rotating diode faults in three-phase brushless exciter with two coils[J]. IET Electric Power Applications, 2019, 13(1): 101-109.
[13] Mohammad-Alikhani A, Rahnama M, Vahedi A. Neighbors class solidarity feature selection for fault diagnosis of brushless generator using thermal imaging[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(9): 6221-6227.
[14] 胡启昊, 郝亮亮, 周艳真, 等. 基于励磁电流时序特征的核电多相旋转整流器二极管开路故障诊断[J]. 中国电机工程学报, 2023, 43(20): 8082-8094.
Hu Qihao, Hao Liangliang, Zhou Yanzhen, et al. Diode open-circuit fault diagnosis of nuclear multi- phase rotating rectifier based on timing features of field current[J]. Proceedings of the CSEE, 2023, 43(20): 8082-8094.
[15] 梁郑秋, 郝亮亮, 周艳真, 等. 基于卷积神经网络的核电多相无刷励磁系统旋转整流器故障诊断[J]. 电工技术学报, 2023, 38(20): 5458-5472.
Liang Zhengqiu, Hao Liangliang, Zhou Yanzhen, et al. Fault diagnosis of rotating rectifier in nuclear multi- phase brushless excitation system based on con- volutional neural network[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5458-5472.
[16] Cai Yuang, Hao Liangliang, Zhou Yanzhen, et al. Rotating rectifier fault diagnosis of nuclear multiphase brushless excitation system based on DTW metric and kNN classifier[J]. IEEE Transa- ctions on Power Electronics, 2023, 38(8): 10329- 10343.
[17] 崔江, 唐军祥, 张卓然, 等. 基于极限学习机的航空发电机旋转整流器快速故障分类方法研究[J]. 中国电机工程学报, 2018, 38(8): 2458-2466, 2555.
Cui Jiang, Tang Junxiang, Zhang Zhuoran, et al. Fast fault classification method research of aircraft generator rotating rectifier based on extreme learning machine[J]. Proceedings of the CSEE, 2018, 38(8): 2458-2466, 2555.
[18] 崔江, 郭瑞东, 张卓然, 等. 基于改进DBN的发电机旋转整流器故障特征提取技术[J]. 中国电机工程学报, 2020, 40(7): 2369-2376.
Cui Jiang, Guo Ruidong, Zhang Zhuoran, et al. Generator rotating rectifier fault feature extraction technique based on improved DBN[J]. Proceedings of the CSEE, 2020, 40(7): 2369-2376.
[19] Hutson M. Has artificial intelligence become alchemy?[J]. Science, 2018, 360(6388): 478.
[20] 时光, 陈翼喆, 李莹, 等. 基于先验知识的弓网接触电阻预测模型精度提升方法[J]. 电工技术学报, 2024, 39(14): 4535-4546.
Shi Guang, Chen Yizhe, Li Ying, et al. Accuracy improvement method of pantograph contact resistance prediction model based on prior knowledge[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4535-4546.
[21] 王彪, 吕洋, 陈中, 等. 考虑信息时移的分布式光伏机理-数据混合驱动短期功率预测[J]. 电力系统自动化, 2022, 46(11): 67-74.
Wang Biao, Lü Yang, Chen Zhong, et al. Hybrid mechanism-data-driven short-term power forecasting of distributed photovoltaic considering information time shift[J]. Automation of Electric Power Systems, 2022, 46(11): 67-74.
[22] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[23] Cai Yuang, Hao Liangliang, Chen Jianlin, et al. Analysis and monitoring of the fuse conditions in nuclear power multiphase brushless excitation system[J]. IEEE Transactions on Industrial Infor- matics, 2024, 20(6): 8559-8571.
[24] Danielsson P E. Euclidean distance mapping[J]. Computer Graphics and Image Processing, 1980, 14(3): 227-248.
[25] 姬文江, 左元, 黑新宏, 等. 基于FastDTW的道岔故障智能诊断方法[J]. 模式识别与人工智能, 2020, 33(11): 1013-1022.
Ji Wenjiang, Zuo Yuan, Hei Xinhong, et al. An intelligent fault diagnosis method based on FastDTW for railway turnout[J]. Pattern Recognition and Artificial Intelligence, 2020, 33(11): 1013-1022.
[26] 李荣陆, 胡运发. 基于密度的kNN文本分类器训练样本裁剪方法[J]. 计算机研究与发展, 2004, 41(4): 539-545.
Li Ronglu, Hu Yunfa. A density-based method for reducing the amount of training data in kNN text classification[J]. Journal of Computer Research and Development, 2004, 41(4): 539-545.
[27] 张剑, 崔明建, 何怡刚. 结合数据驱动与物理模型的主动配电网双时间尺度电压协调优化控制[J]. 电工技术学报, 2024, 39(5): 1327-1339.
Zhang Jian, Cui Mingjian, He Yigang. Dual timescales coordinated and optimal voltages control in distribution systems using data-driven and physical optimization[J]. Transactions of China Electro- technical Society, 2024, 39(5): 1327-1339.
[28] Cui Langfu, Zhang Qingzhen, Shi Yan, et al. A method for satellite time series anomaly detection based on fast-DTW and improved-kNN[J]. Chinese Journal of Aeronautics, 2023, 36(2): 149-159.
[29] Dietterich T G. Ensemble methods in machine learning[M]//Berlin, Heidelberg: Springer, 2000: 1- 15.
Abstract The rotating rectifier is the key part of multiphase annular brushless excitation systems. Nevertheless, the rectifiers often experience faults caused by diode failures, which brings security risks in practice. Accurately diagnosing faults in the rotating rectifier is pivotal for ensuring the safe operation of multiphase annular brushless excitation systems. However, the types of rotating rectifier faults are diverse, and the characteristics of different faults are inherently weak. Traditional mechanism-driven diagnostic schemes offer interpretability but often struggle with precise fault diagnosis. New data-driven diagnostic schemes exhibit speed and accuracy but encounter challenges in training and debugging in practical applications. This paper proposes a hybrid mechanism-data-driven diagnostic scheme for rotating rectifier faults.
Based on the fault mechanism, the frequency domain characteristics of the excitation current after the fault are derived, and the fault characteristic patterns are summarized. Then, thresholds of the mechanism diagnosis model are calculated using finite element simulation data. Extracting the frequency domain characteristics of the excitation current allows the fault mechanism to be clearly described, thus providing a solid foundation for subsequent fault diagnosis. The current waveform under normal operation and different fault conditions can be simulated by adjusting the models, which allows for determining thresholds for various operating conditions.
Then, the fast dynamic time warping (Fast-DTW) algorithm is introduced to calculate the similarity of excitation current time-domain waveforms, subsequently forming a data-driven model combined with the k-nearest neighbors (kNN) classifier. The fast-DTW algorithm can align waveforms of different time lengths and start points to capture subtle differences between waveforms. By combining the fast-DTW algorithm with the kNN classifier, the data-driven model can realize the diagnosis of rotating rectifier faults.
Mechanism-driven and data-driven diagnostic schemes are integrated based on ensemble learning principles. Ensemble learning significantly enhances the overall performance of the model by combining the results of multiple learners. Five mechanism-driven and five data-driven models are established to obtain a final diagnostic result based on the absolute majority voting method. The hybrid diagnostic scheme exhibits the advantages of mechanism-driven and data-driven models, effectively overcoming the limitations of a single-driven model.
Finally, the verification of prototype experiments indicates that the hybrid scheme’s diagnostic accuracy reaches 100%, significantly surpassing single-driven models. Establishing diagnostic models requires offline simulation data, reducing training difficulty and improving practicality on-site. The hybrid scheme maintains a reasonable diagnostic speed while ensuring high accuracy.
In conclusion, the proposed hybrid mechanism-data-driven fault diagnosis scheme combines mechanism analysis and data-driven methods to enhance the accuracy and robustness of fault diagnosis, demonstrating excellent test performance in prototype experiments. The diagnostic approach based on the time-frequency characteristics of the excitation current demonstrates excellent interpretability, achieving accurate fault diagnosis solely through training with simulation data.
Keywords:Rotating rectifier faults, mechanism-driven, data-driven, fast-dynamic time warping (Fast-DTW), ensemble learning
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.240672
中央高校基本科研业务费专项资金项目(2023YJS162)、中央高校基本科研业务费专项资金项目(2020JBM070)和中广核集团公司科技项目(3100077013)资助。
收稿日期 2024-04-29
改稿日期 2024-07-04
蔡宇昂 男,1998年生,博士研究生,主要研究方向为多相无刷励磁系统故障智能保护、多项无刷励磁机本体分析。
E-mail: 20117019@bjtu.edu.cn
郝亮亮 男,1985年生,副教授,博士生导师,主要研究方向为电力系统主设备故障分析及保护、直流输电控制与保护、励磁 控制。
E-mail: llhao@bjtu.edu.cn(通信作者)
(编辑 崔文静)