 (
(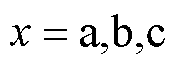 )相逆变器的电流为
)相逆变器的电流为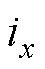 ,流出逆变器时
,流出逆变器时 ;否则,
;否则,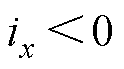 。在理想的PWM信号
。在理想的PWM信号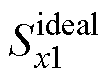 和
和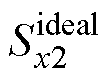 中插入死区时间
中插入死区时间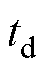 即可得到实际的PWM信号
即可得到实际的PWM信号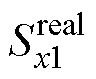 和
和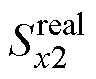 ,该信号用于驱动各桥臂中的功率器件。
,该信号用于驱动各桥臂中的功率器件。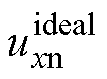 为不考虑VSI死区非线性效应时理想的输出电压。实际输出电压
为不考虑VSI死区非线性效应时理想的输出电压。实际输出电压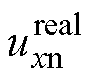 由
由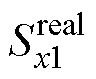 和
和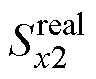 决定,同时还需考虑开关器件开通延迟、关断延迟时间
决定,同时还需考虑开关器件开通延迟、关断延迟时间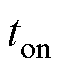 和
和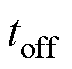 、开关管和二极管的管压降
、开关管和二极管的管压降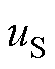 和
和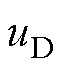 。
。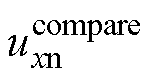 为
为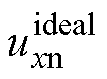 和
和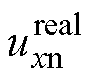 的对比波形。图1中,
的对比波形。图1中, 部分表示实际输出小于理想输出,
部分表示实际输出小于理想输出, 部分表示实际输出大于理想输出。逆变器理想输出电压与实际输出电压之差
部分表示实际输出大于理想输出。逆变器理想输出电压与实际输出电压之差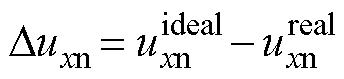 与电流极性相关。
与电流极性相关。摘要 针对伺服系统在高开关频率应用下逆变器死区非线性效应引起的电流谐波畸变问题,提出无死区双调制波脉冲宽度调制(PWM)和逆变器非线性补偿相结合的策略。首先基于反并联二极管的续流特性,在互补驱动脉冲之间加入驱动空缺区以避免死区时间的引入。其次通过向直轴注入斜坡电流来获取逆变器非线性特性所对应的误差电压,采用线性迭代插值法来求解逆变器非线性误差电压与电流幅值之间的关系,最终实现逆变器非线性误差电压的在线补偿。同时阐述了引入死区时间后再进行补偿和无死区双调制波PWM的区别,对两者解除占空比限制的效果进行了分析。最后通过仿真和实验表明,所提策略能够增加输出电压的线性调制区,消除由死区时间导致的输出占空比限制,有效地抑制了高开关频率逆变器死区非线性效应导致的电流谐波畸变。此外所提策略易于实现,无需额外的控制环路计算,可适用于更高开关频率的伺服驱动控制系统。
关键词:永磁同步电机 逆变器死区非线性 死区消除 非线性补偿 误差电压计算
将高开关频率器件应用于伺服系统中显著提升了系统的电流环带宽,但给快速开关和高频调制带来的问题还有待深入研究。在实际应用中,为避免电压源逆变器(Voltage Source Inverter, VSI)桥臂直通,需在脉冲宽度调制(Pulse Width Modulation, PWM)信号中加入死区时间,且开关器件存在固有的非理想特性,如开关延时、寄生电容和导通压降等。死区时间和器件非理想特性统称为VSI死区非线性效应,使得VSI的实际输出与理想输出存在偏差,导致输出电流波形畸变,且VSI的死区非线性效应会随着开关频率的升高而加剧[1]。同时高开关频率对应着更短的环路计算时间,死区非线性补偿策略须更加简单以节省计算时间和资源。因此,简单且能够准确补偿VSI死区非线性的策略对于改善输出电流波形质量,充分发挥高开关频率对于伺服驱动系统性能提升的优势具有重要意义。
现有文献对于VSI死区非线性效应的研究可分为死区非线性补偿和死区消除两类。其中死区非线性补偿基于伏秒等效原理,通过离线测量或在线辨识得到逆变器非线性电压误差(Inverter Nonlinear Voltages Error, INVE)后将其补偿到控制系统。通过增加额外的硬件电路和滤波器来检测逆变器的实际输出电压,与电流控制器输出的理想电压作差可得INVE,但额外的硬件电路使得逆变器结构复杂的同时也增加了其成本[2]。文献[3-4]中,电流谐波被认为是由INVE引起的周期性扰动,通过比例积分(Proportional Integral, PI)调节器来抑制电流谐波,然而这种方法只能补偿INVE中的周期性电压误差。文献[5]提出基于广义比例积分观测器的鲁棒谐振预测电流控制方法,提高系统面对非周期及周期性扰动时的鲁棒性。文献[6]使用分段式饱和函数对VSI死区效应进行补偿,在小电流时补偿电压与电流幅值呈线性关系,但该方法补偿电压的精度有限。文献[7]提出一种高频纹波电流提取和补偿方法,来抑制逆变器非线性引起的位置估算误差。文献[8-10]根据离线实验获得的数据,将误差电压与电流幅值之间的关系拟合为函数。该方法中逆变器非线性模型精确,但需单独测量出不同电流下各种因素造成的误差电压,同时拟合获得的曲线仅适用于特定器件。文献[11]提出基于q轴电流误差的死区时间在线补偿方法。文献[12]对每个PWM周期内的实际作用脉冲进行精确补偿。文献[13]提出一种基于开关脉冲调整的死区补偿策略。以上三种方法均需要对PWM信号进行实时计算和调整,在高频应用中占用的控制器计算资源将会更多。文献[14]提出一种可以同时实现死区时间补偿和电容电压平衡的数字调制方法,可用于高开关频率,但采样频率需为开关频率的数倍。
为了更准确地获取INVE,VSI的死区非线性被建模为与每相电流相关的误差电压源,该方法由于在不需要额外硬件电路的同时也能较为准确地获取INVE而受到了许多学者的关注。通过在电机与VSI连接的回路中使用基尔霍夫电压定律得到不同相电流下的误差电压[15-19]。文献[15]假设A相电流ia和ia/2的电压误差相等,得到梯形波模型中INVE的饱和值,然而该假设在小电流时并不成立。文献[16]中要求控制器至少工作在两个不同的开关频率下,通过消元法才能解算出INVE。文献[17]提出基于迭代线性插值的INVE精确解算方法。文献[18]通过三维线性插值获得INVE,以精确补偿VSI的死区非线性。文献[19]建立了含有4个待定参数和电流的INVE模型。准确建模并求解出INVE在不同电流下的关系是实现精确INVE补偿的关键,但以上方法对于INVE的求解过程相对复杂。随着开关频率的增加,补偿方法也需要更为简单,因此直接对调制波进行补偿更容易被接受[20]。然而加入死区后再对死区进行补偿会直接或间接地增加调制波幅值,调制波幅值在低开关频率下增加较小,但在高开关频率下增加显著,会使线性调制区下降严重[21]。这是一种“先污染后治理”的方案,不可避免地会引入补偿误差。
第二种方法是死区消除法,该方法基于反并联二极管的续流作用,根据负载电流极性屏蔽无效开关的驱动信号,从而避免死区时间的引入[22-23]。然而直接检测电流的过零点对检测电路的要求较高且准确度得不到保证。文献[23-24]在消除死区PWM的基础上增加产生同步整流的额外驱动脉冲,以减轻过零点时的电流跳变。文献[25-26]通过划分电流过零区域,分别处理不同区域内的死区效应。文献[27]提出基于双二阶广义积分器锁频环的死区消除PWM并通过加入延迟补偿来获得准确的电流极性。然而此种方法并未考虑由器件开关延迟、寄生电容和导通压降等造成的非线性误差电压,因此这类方法有一定的局限性。
综上所述,高开关频率下加入死区时间后再进行补偿的方法效果受限,而死区消除方法中并未考虑除死区时间外的非线性因素。针对以上问题,本文首先在分析死区时间和逆变器非理想特性对输出电压影响的基础上,提出无死区双调制波PWM和逆变器非线性补偿相结合的策略;其次阐述了引入死区时间后再进行补偿与无死区双调制波PWM的区别,对两者解除占空比限制的效果进行了分析;最后通过仿真和实验验证了本文所提策略的有效性。
电压型逆变器输出电压畸变示意图如图1所示,规定 (
(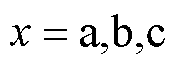 )相逆变器的电流为
)相逆变器的电流为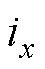 ,流出逆变器时
,流出逆变器时 ;否则,
;否则,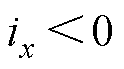 。在理想的PWM信号
。在理想的PWM信号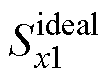 和
和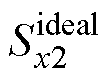 中插入死区时间
中插入死区时间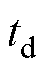 即可得到实际的PWM信号
即可得到实际的PWM信号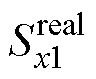 和
和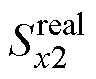 ,该信号用于驱动各桥臂中的功率器件。
,该信号用于驱动各桥臂中的功率器件。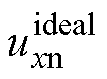 为不考虑VSI死区非线性效应时理想的输出电压。实际输出电压
为不考虑VSI死区非线性效应时理想的输出电压。实际输出电压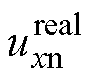 由
由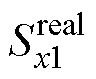 和
和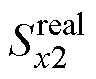 决定,同时还需考虑开关器件开通延迟、关断延迟时间
决定,同时还需考虑开关器件开通延迟、关断延迟时间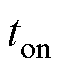 和
和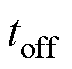 、开关管和二极管的管压降
、开关管和二极管的管压降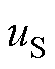 和
和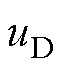 。
。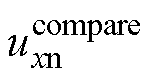 为
为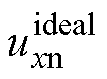 和
和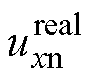 的对比波形。图1中,
的对比波形。图1中, 部分表示实际输出小于理想输出,
部分表示实际输出小于理想输出, 部分表示实际输出大于理想输出。逆变器理想输出电压与实际输出电压之差
部分表示实际输出大于理想输出。逆变器理想输出电压与实际输出电压之差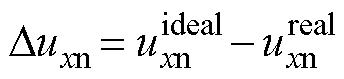 与电流极性相关。
与电流极性相关。
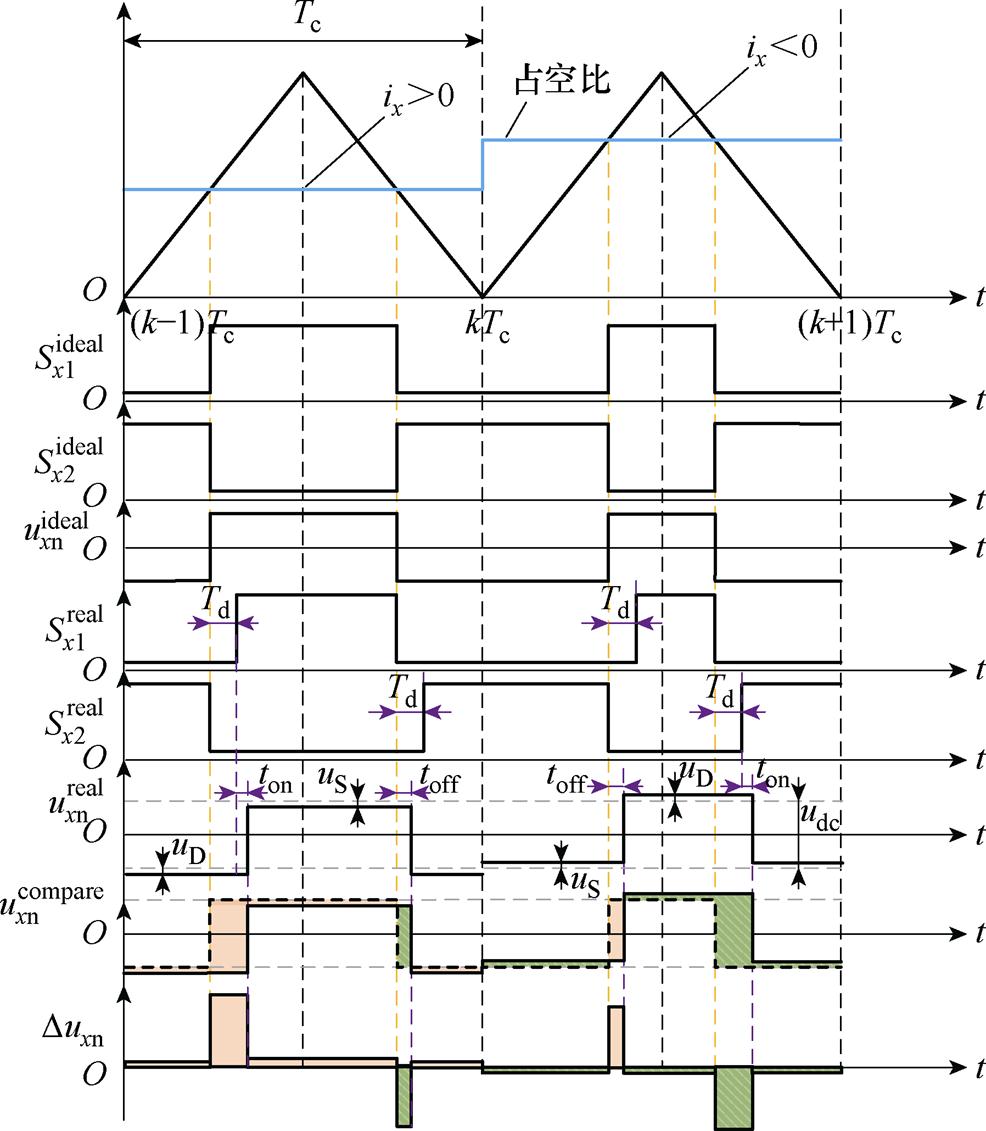
图1 电压型逆变器输出电压畸变示意图
Fig.1 Schematic of the output voltage distortion process of voltage source inverter
考虑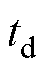 、
、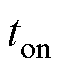 、
、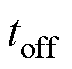 、
、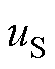 和
和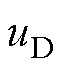 对输出电压的影响,则理想导通时间与实际导通时间之差
对输出电压的影响,则理想导通时间与实际导通时间之差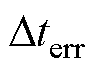 可以表示为
可以表示为
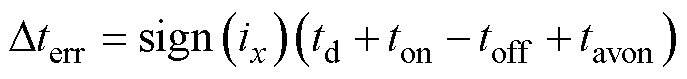 (1)
(1)
式中,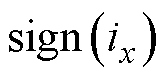 为符号函数,当
为符号函数,当 时,
时,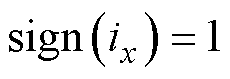 ,当
,当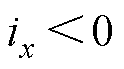 时,
时,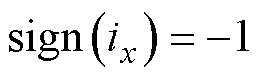 ;
;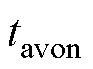 为开关器件和二极管的导通压降对应的等效误差时间。根据伏秒平衡原理,
为开关器件和二极管的导通压降对应的等效误差时间。根据伏秒平衡原理,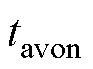 可表示为
可表示为
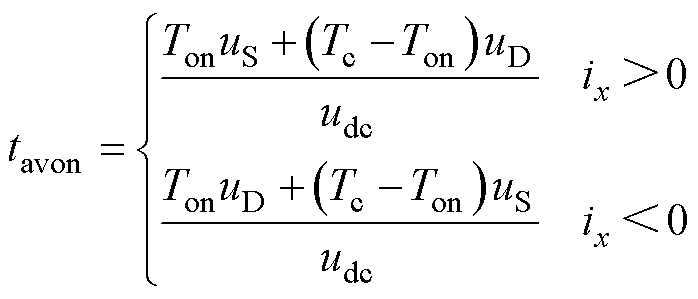 (2)
(2)
式中,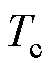 为PWM周期;
为PWM周期;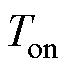 为功率器件导通时间;
为功率器件导通时间;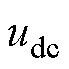 为直流母线电压。
为直流母线电压。
根据以上分析,非线性误差电压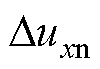 可表示为
可表示为
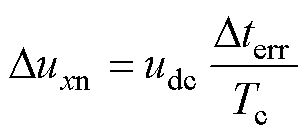 (3)
(3)
综上所述,逆变器死区非线性误差电压的影响因素众多,并且和电流极性相关。通常死区时间可设置为某一确定的值,但是器件的开关延迟、导通压降会随着工作条件变化而不易得到[10]。因此本文将死区时间和逆变器非线性分开考虑。
忽略dq坐标系交叉耦合的影响,电流环的等效控制框图如图2所示。
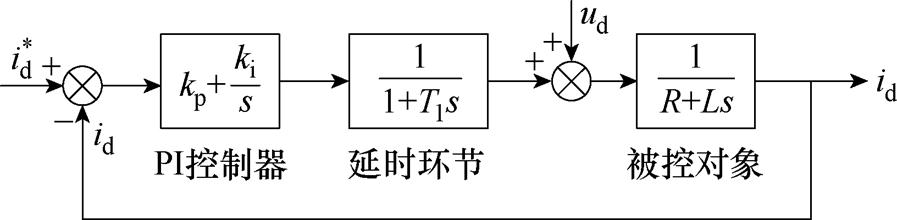
图2 电流环结构框图
Fig.2 Block diagram of current loop structure
图2中,kp、ki分别为PI控制器的比例和积分系数,Tl为控制系统中存在的总延时,R为电机电阻,L为电机电感。由图2可得电流环的开环传递函数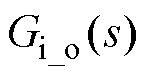 为
为
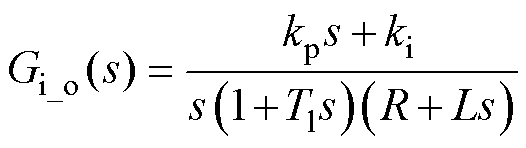 (4)
(4)
采用“零极相消”的方法消除大时间常数极点,选择阻尼比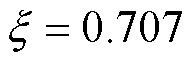 ,PI控制器参数整定[28]为
,PI控制器参数整定[28]为
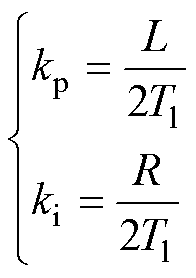 (5)
(5)
化简后可得电流的闭环传递函数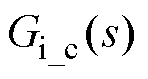 为
为
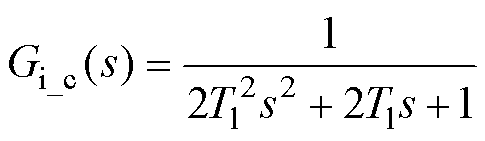 (6)
(6)
电流环闭环幅频特性曲线如图3a所示。将逆变器死区非线性在dq坐标系下引起的谐波畸变视为扰动量ud,从扰动量ud到id的传递函数可表示为
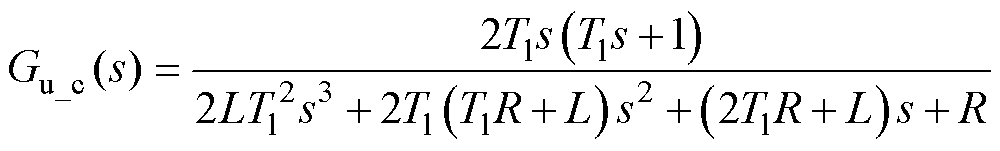 (7)
(7)
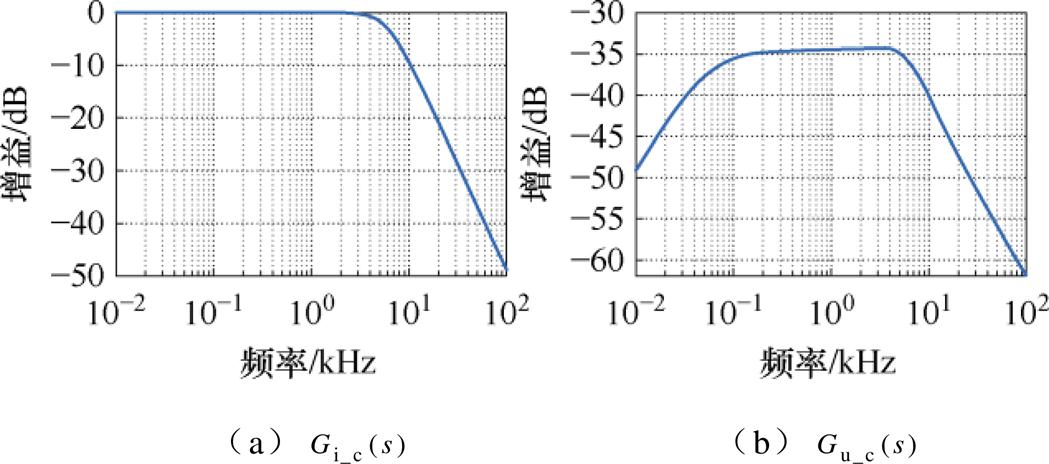
图3 幅频特性曲线
Fig.3 Amplitude-frequency characteristic curves
电压扰动传递函数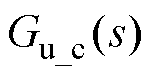 的幅频特性曲线如图3b所示,显然,
的幅频特性曲线如图3b所示,显然,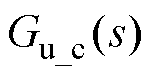 所有的增益均低于-30 dB,这表明高开关频率控制下由VSI死区非线性所引起的电流畸变能够被PI控制器所抑制。
所有的增益均低于-30 dB,这表明高开关频率控制下由VSI死区非线性所引起的电流畸变能够被PI控制器所抑制。
在PWM中理想占空比的取值范围为0~1,采用上升沿延迟的方式设置死区时间后,PWM的输出占空比将会受到限制,如图4所示。当计算出的调制波比较值较大时,设置死区时间后上桥臂驱动信号本该为高电平的时间将保持为低电平;当计算出的调制波比较值较小时,设置死区时间后下桥臂驱动信号本该为高电平的时间也将保持为低电平。即调制波比较值处于较低或较高范围时,将出现驱动脉冲消失的现象。因此理想占空比只能在 的范围内进行连续调节或者保持恒定高低电平。死区时间导致的占空比限制会随着开关频率的升高而加剧,减少了实际的输出电压空间范围,缩小了线性调制区。
的范围内进行连续调节或者保持恒定高低电平。死区时间导致的占空比限制会随着开关频率的升高而加剧,减少了实际的输出电压空间范围,缩小了线性调制区。
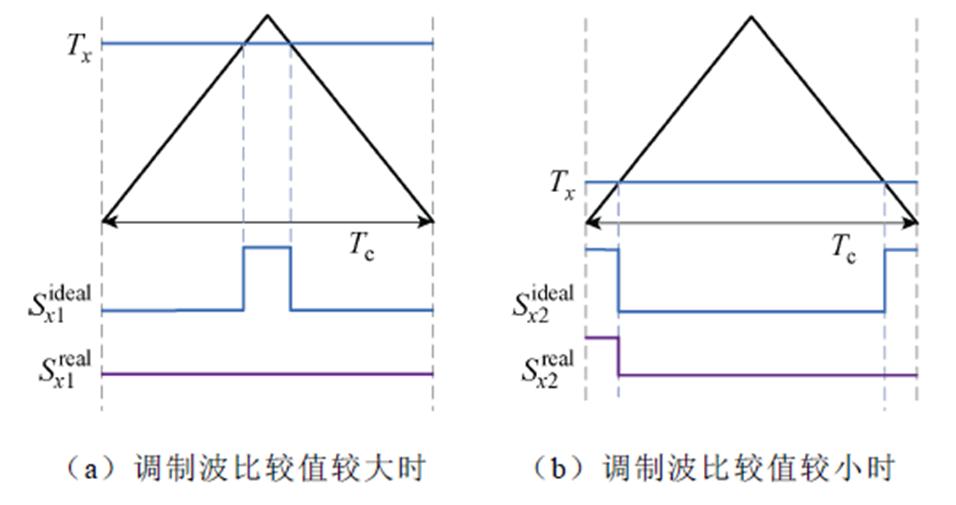
图4 死区时间对输出占空比的限制
Fig.4 Limitation of output duty cycle by dead-time
通过第1节分析,逆变器死区非线性效应具体表现为实际输出电压和理想输出电压存在偏差,且在高开关频率下死区时间会严重限制输出占空比的范围。为此本文提出无死区双调制波PWM和逆变器非线性补偿相结合的策略,以抑制高开关频率下逆变器的死区非线性效应。
基于反并联二极管的续流作用,根据负载电流极性调整上、下开关管驱动信号,在互补驱动脉冲中插入驱动空缺区,从而避免死区时间的加入。具体方法为当电流大于零时,给上开关管理想的驱动信号,在下开关管驱动信号中加入驱动空缺区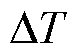 ;电流小于零时,给下开关管理想的驱动信号,在上开关管驱动信号中加入驱动空缺区
;电流小于零时,给下开关管理想的驱动信号,在上开关管驱动信号中加入驱动空缺区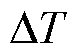 。所提出的无死区双调制波PWM实现方法如图5所示,可以清楚地看出驱动信号的产生过程。与理想的空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)相比,额外添加了一个辅助调制波
。所提出的无死区双调制波PWM实现方法如图5所示,可以清楚地看出驱动信号的产生过程。与理想的空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)相比,额外添加了一个辅助调制波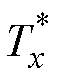 ,其幅值根据电流极性在原始调制波
,其幅值根据电流极性在原始调制波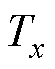 的基础上上移或下移
的基础上上移或下移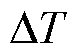 。双调制波和三角载波相比,可在上下开关管驱动信号之间形成驱动空缺区,既避免了桥臂直通现象的发生,也避免了死区时间的加入。此外,依据双调制波与三角载波的比较结果就可直接获得各个开关器件的驱动信号,无需额外的控制环路计算,同时所生成的PWM信号是关于载波中点对称的。
。双调制波和三角载波相比,可在上下开关管驱动信号之间形成驱动空缺区,既避免了桥臂直通现象的发生,也避免了死区时间的加入。此外,依据双调制波与三角载波的比较结果就可直接获得各个开关器件的驱动信号,无需额外的控制环路计算,同时所生成的PWM信号是关于载波中点对称的。
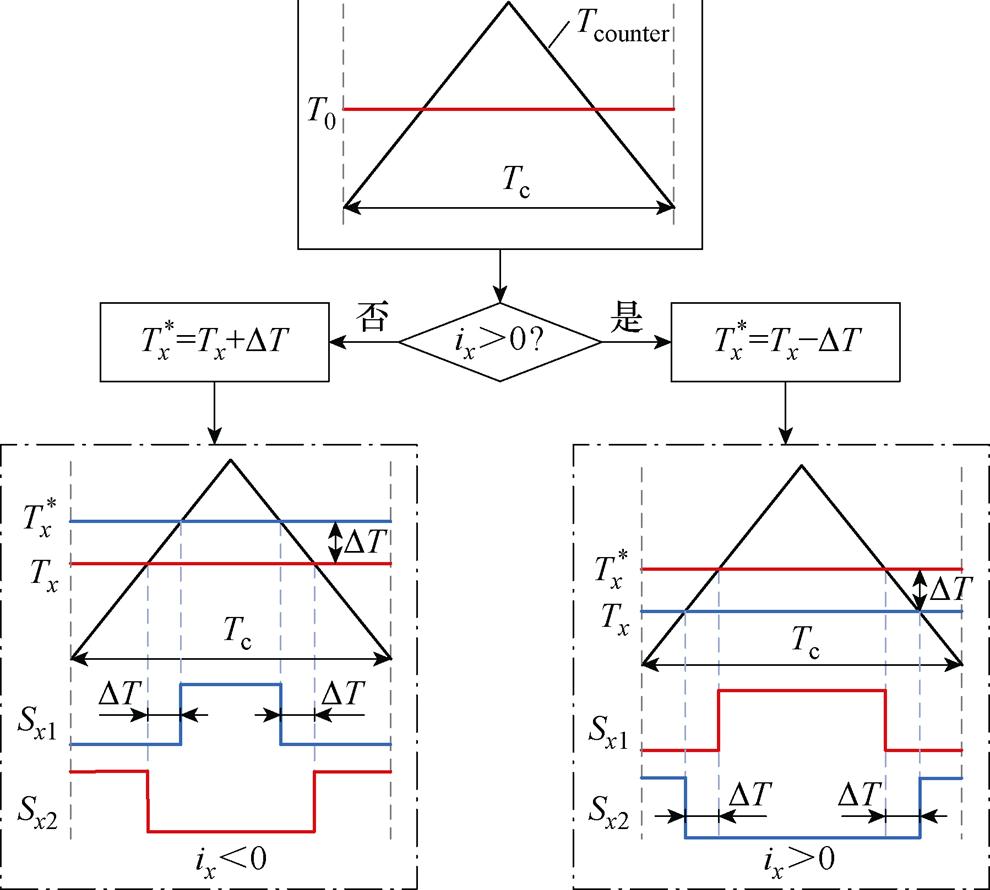
图5 无死区双调制波PWM方法
Fig.5 Schematic of the no-dead-time double- modulation-wave PWM
器件的开关延时、功率管及体二极管的导通压降等多种非线性因素是随着工作条件变化且参数未知的,本文将逆变器的非线性特性建模为与相电流幅值相关的误差电压源 。借助VSI与电机连接的物理模型,采用向d轴注入电流的方式获取逆变器非线性特性所对应的误差电压。
。借助VSI与电机连接的物理模型,采用向d轴注入电流的方式获取逆变器非线性特性所对应的误差电压。
首先,VSI和永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)连接的等效电路如图6所示,图中,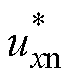 和
和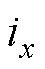 分别为逆变器
分别为逆变器 相桥臂的理想输出电压和电流。自调试过程中,将q轴电流控制为0,保持PMSM的转子位置为0,施加不同幅值的d轴电流。此时A相电流等于d轴电流,负载电流从A相流入,从B相和C相流出[15-16]。
相桥臂的理想输出电压和电流。自调试过程中,将q轴电流控制为0,保持PMSM的转子位置为0,施加不同幅值的d轴电流。此时A相电流等于d轴电流,负载电流从A相流入,从B相和C相流出[15-16]。
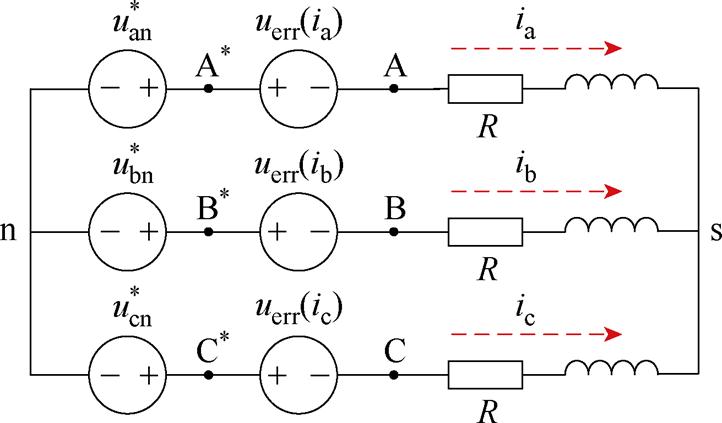
图6 VSI和PMSM等效电路
Fig.6 Equivalent circuit of VSI and PMSM
对于三相对称负载,三相电流有
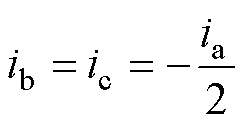 (8)
(8)
此时d轴电流控制器的输出参考电压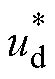 [15]有
[15]有
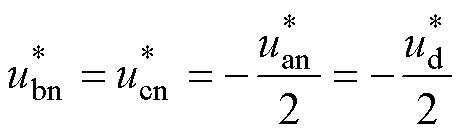 (9)
(9)
图7显示了上述条件下的等效电路。将基尔霍夫电压定律(Kirchhoff Voltage Laws, KVL)应用于图7中虚线所示的由a相和b相组成的回路中,可建立关系为
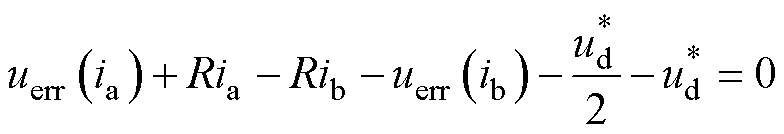 (10)
(10)
可认为非线性误差电压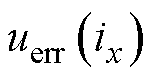 是电流的奇函数[15-16],则式(10)可转换为
是电流的奇函数[15-16],则式(10)可转换为
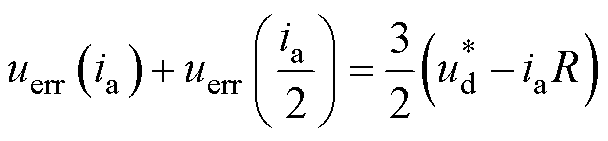 (11)
(11)
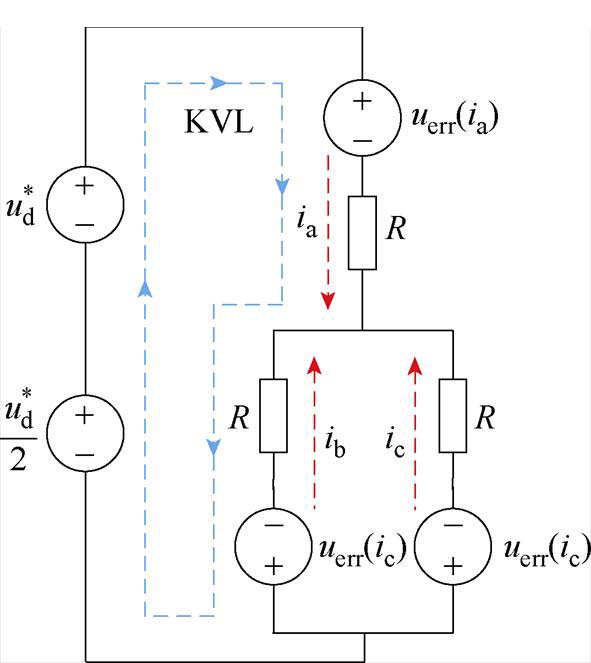
图7 VSI和PMSM等效电路(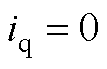 ,
, 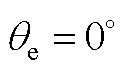 )
)
Fig.7 Equivalent circuit of VSI and PMSM for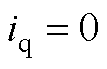 and
and 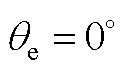
在获得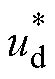 和
和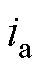 的前提下,可通过式(11)得到
的前提下,可通过式(11)得到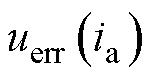 与
与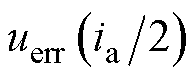 之和。目前对于
之和。目前对于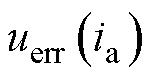 的解算方法都较为复杂和繁琐,本文提出一种基于线性迭代插值的解算方法。
的解算方法都较为复杂和繁琐,本文提出一种基于线性迭代插值的解算方法。
由式(11)可知,若已知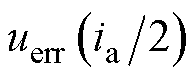 ,
,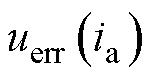 也就能够轻易解算出来。为了获得不同ia值下的
也就能够轻易解算出来。为了获得不同ia值下的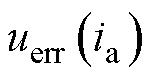 ,在自调试过程中d轴电流增量为
,在自调试过程中d轴电流增量为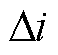 ,上限为电机峰值电流
,上限为电机峰值电流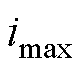 ,进行图8所示的uerr(i)计算流程。求解方法的核心思想是线性迭代插值,即当
,进行图8所示的uerr(i)计算流程。求解方法的核心思想是线性迭代插值,即当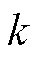
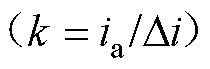 为奇数时近似认为有
为奇数时近似认为有
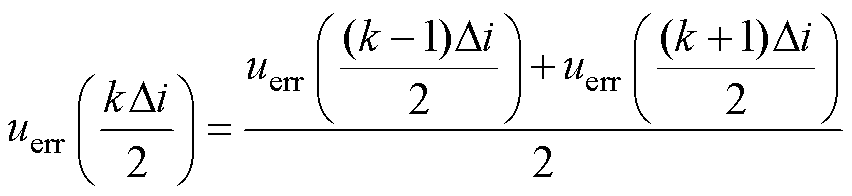 (12)
(12)
根据式(11)和式(12),非线性误差电压表示为
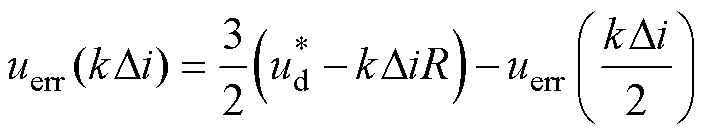 (13)
(13)
在电机控制过程中通过查表获取当前电流下的非线性误差电压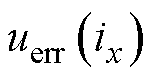 ,通过式(14)将三相非线性误差电压
,通过式(14)将三相非线性误差电压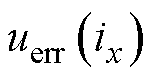 变换至
变换至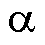 、
、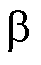 静止坐标系下从而对系统进行补偿。
静止坐标系下从而对系统进行补偿。
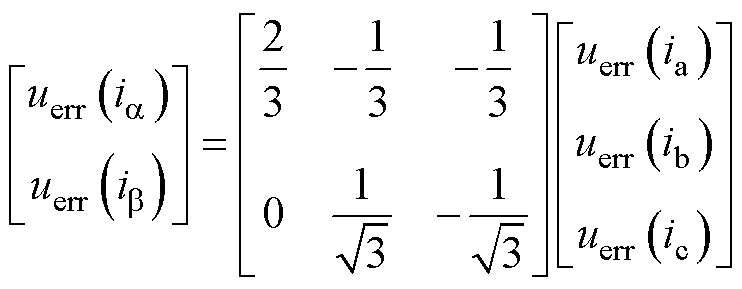 (14)
(14)
式中,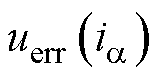 和
和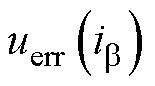 分别为
分别为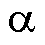 、
、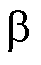 静止坐标系下所对应的非线性误差电压。
静止坐标系下所对应的非线性误差电压。
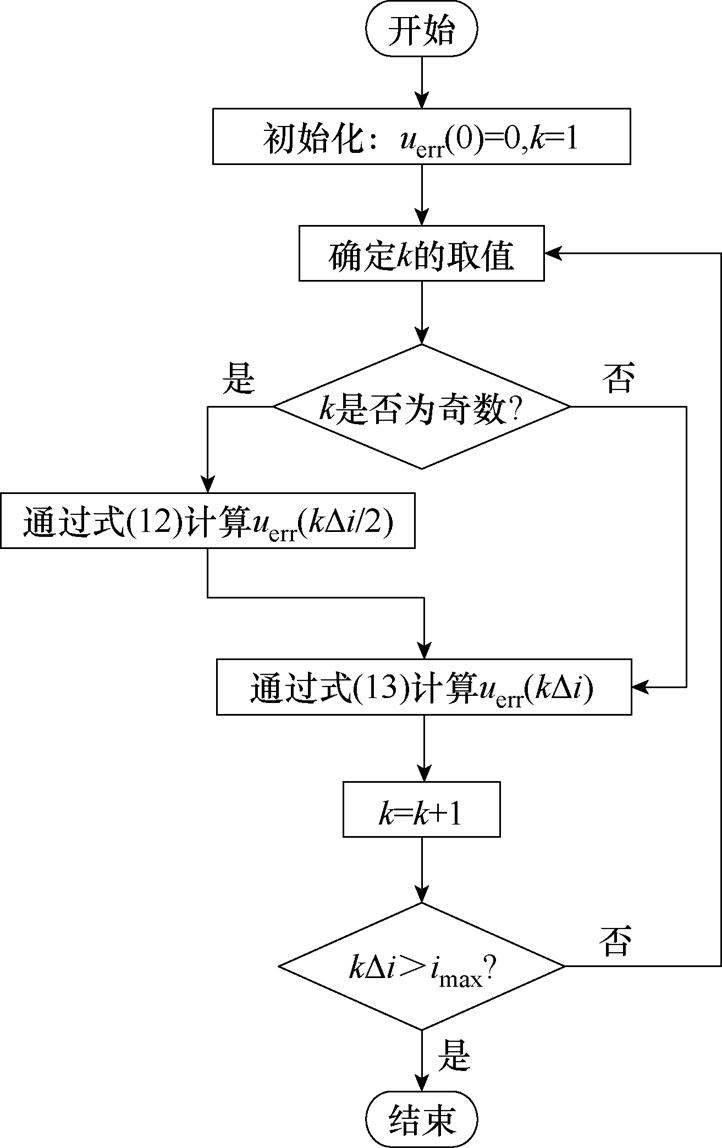
图8 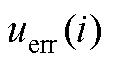 计算流程
计算流程
Fig.8 Flow chart of the 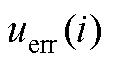 calculation
calculation
设置的死区应与无死区双调制波PWM中的驱动空缺区具有相同的效果,即避免上、下桥臂发生直通,处于该区间内的PWM信号均为低电平,因此本文将两者时长设为一致。死区和驱动空缺区对输出电压的影响有所不同,前者会导致误差电压的产生,而后者则不会造成此类影响。当计算出的调制波比较值处于较低或较高范围时,经过幅值调整后会出现比较值超出三角载波范围的情况。引入死区时间后再进行补偿与无死区双调制波PWM在效果上也存在显著差异,本节将对此进行分析。
脉冲补偿与电压补偿在本质上是一致的。就PWM而言,调整脉冲宽度实际上也就是在调整逆变器的输出电压[29]。因此不论是何种补偿手段,其最终均可归结为调整输出占空比与理想占空比保持一致。引入死区时间后再进行相应补偿,理论上可以实现输出占空比与理想占空比保持一致,但补偿后脉冲波形不再对称于三角载波的中心。因此一个PWM周期内的平均电压误差虽然为零,但仍会存在两个误差电压脉冲,导致补偿效果不够理想[30-31]。
死区补偿示意图如图9所示。在图9所示的阴影三角形中,根据相似三角形原理得
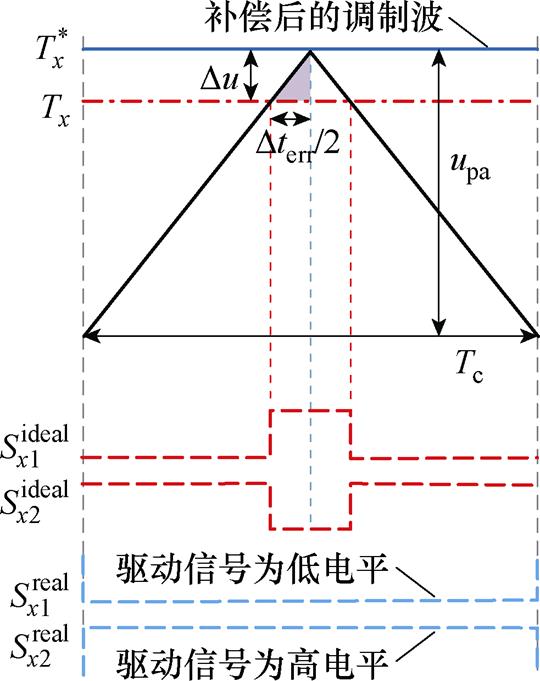
图9 死区补偿示意图(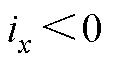 )
)
Fig.9 Schematic of dead time compensation for 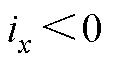
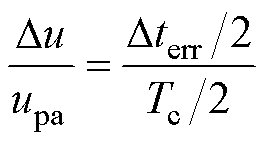 (15)
(15)
式中,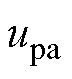 为三角载波的幅值;
为三角载波的幅值;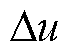 为补偿后调制波改变的值,可表示为
为补偿后调制波改变的值,可表示为
 (16)
(16)
可以看出,补偿后调制波改变的值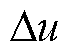 与
与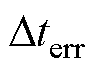 成正比,与PWM周期
成正比,与PWM周期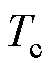 成反比。在式(16)中,假设
成反比。在式(16)中,假设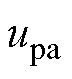 =1,
=1,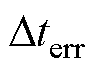 =1 ms,在10 kHz开关频率下,补偿后调制波需要改变的值仅为0.01,而在100 kHz下该值为0.1。这表明死区补偿引起调制波幅值的改变量在低开关频率下很小,而在高开关频率时则相当可观。当计算出的三角载波比较值大于
=1 ms,在10 kHz开关频率下,补偿后调制波需要改变的值仅为0.01,而在100 kHz下该值为0.1。这表明死区补偿引起调制波幅值的改变量在低开关频率下很小,而在高开关频率时则相当可观。当计算出的三角载波比较值大于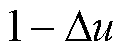 ,并且此时电流
,并且此时电流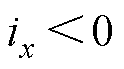 ,死区补偿后调制波的值将大于三角载波的幅值,出现驱动脉冲消失;同样当计算出的三角载波比较值小于
,死区补偿后调制波的值将大于三角载波的幅值,出现驱动脉冲消失;同样当计算出的三角载波比较值小于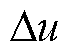 ,并且此时电流
,并且此时电流 ,死区补偿后调制波的值小于三角载波的最小值,也将出现驱动脉冲消失。因此引入死区时间后再进行相应补偿的效果不够理想,从而影响系统的性能。
,死区补偿后调制波的值小于三角载波的最小值,也将出现驱动脉冲消失。因此引入死区时间后再进行相应补偿的效果不够理想,从而影响系统的性能。
无死区双调制波PWM示意图如图10所示。在图10中,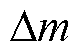 为辅助调制波在原始调制波的基础上改变的值,可表示为
为辅助调制波在原始调制波的基础上改变的值,可表示为
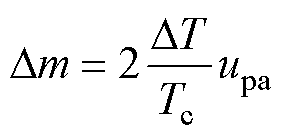 (17)
(17)
对比式(16)和式(17)可知,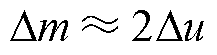 ,这表明辅助调制波相比于死区补偿后的调制波更易出现超过三角载波范围的情况。值得注意的是,无死区双调制波PWM通过双调制波和三角载波进行比较产生上、下开关管的驱动信号。当计算出的三角载波比较值大于
,这表明辅助调制波相比于死区补偿后的调制波更易出现超过三角载波范围的情况。值得注意的是,无死区双调制波PWM通过双调制波和三角载波进行比较产生上、下开关管的驱动信号。当计算出的三角载波比较值大于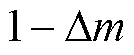 ,并且此时电流
,并且此时电流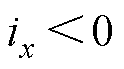 ,辅助调制波将会大于三角载波的幅值,此时上开关管驱动信号在一个PWM周期内保持为低电平,但下开关管实际的驱动信号仍与理想的驱动信号保持一致;当计算出的三角载波比较值小于
,辅助调制波将会大于三角载波的幅值,此时上开关管驱动信号在一个PWM周期内保持为低电平,但下开关管实际的驱动信号仍与理想的驱动信号保持一致;当计算出的三角载波比较值小于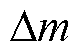 ,并且此时电流
,并且此时电流 ,辅助调制波将会小于三角载波的最小值,此时下开关管驱动信号在一个PWM周期内保持为低电平,但上开关管实际的驱动信号仍与理想的驱动信号保持一致。综上所述,不管计算出的调制波比较值处于较低还是较高范围,无死区双调制波PWM都可以实现理想占空比的输出,从而消除由死区时间导致的占空比限制。
,辅助调制波将会小于三角载波的最小值,此时下开关管驱动信号在一个PWM周期内保持为低电平,但上开关管实际的驱动信号仍与理想的驱动信号保持一致。综上所述,不管计算出的调制波比较值处于较低还是较高范围,无死区双调制波PWM都可以实现理想占空比的输出,从而消除由死区时间导致的占空比限制。
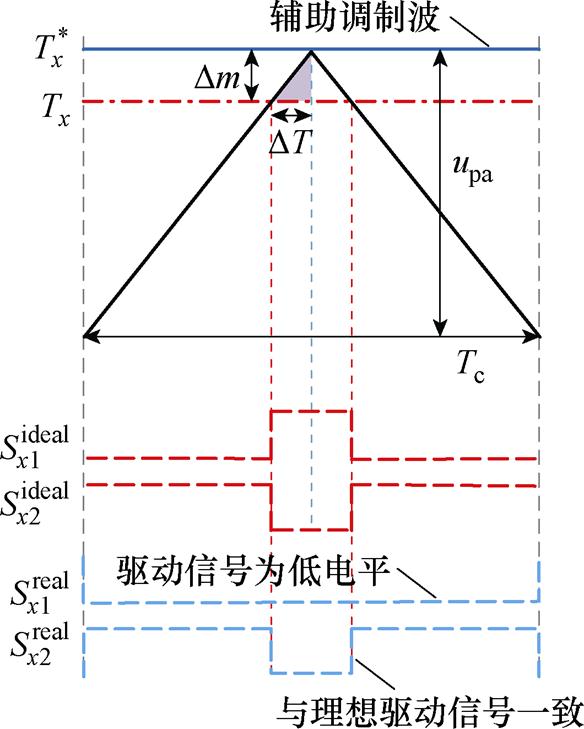
图10 无死区双调制波PWM示意图(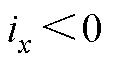 )
)
Fig.10 Schematic of the no-dead-time double- modulation-wave PWM for 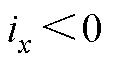
通过Matlab/Simulink软件搭建PMSM速度电流双闭环控制系统仿真模型,具体仿真模型的参数见表1。设定目标转速为1 800 r/min,不同策略下所对应的A相电流及其驱动脉冲仿真结果如图11所示。
图11a为理想开关时刻(即上、下开关管驱动信号互补)下的A相电流波形及其驱动信号。可以看出,电机A相电流波形正弦度较好。图11b为加入死区时间后的A相电流及其驱动信号,此时电流波形畸变明显。这是因为在高开关频率条件下死区时间会引入大量的电压误差脉冲,同时死区时间导致驱动脉冲消失,减小了实际可以达到的输出电压空间范围。图11c为传统平均误差电压补偿方式下A相电流及其驱动信号,其过零点相比于无补偿时更为平滑。然而引入死区时间后再进行相应补偿会使得调制波的值超出三角载波的范围,导致驱动脉冲消失,补偿的效果不够理想。图11d为无死区双调制波PWM下A相电流及其驱动信号,在原始调制波幅值过大或者过小的区域也将会出现驱动脉冲消失的现象。但此时影响输出电压的驱动信号并未消失,消失的驱动脉冲处于反并联二极管续流阶段,不会对输出电压造成影响。表明了所提出的无死区双调制波PWM可以实现理想占空比的输出,消除了由死区时间导致的占空比限制,拓宽了输出电压的线性调制区。
表1 仿真模型的参数
Tab.1 Parameters of simulation model
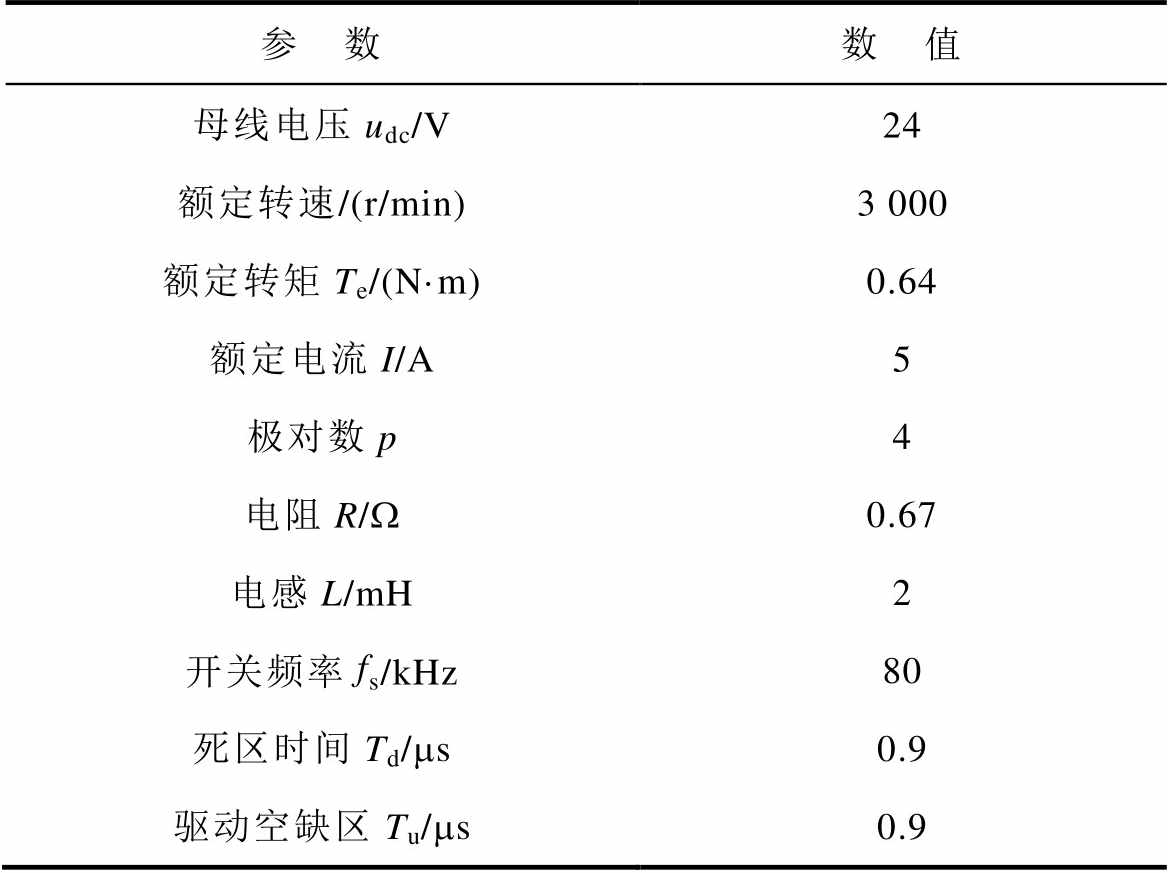
参 数数 值 母线电压udc/V24 额定转速/(r/min)3 000 额定转矩Te/(N·m)0.64 额定电流I/A5 极对数p4 电阻R/W0.67 电感L/mH2 开关频率fs/kHz80 死区时间Td/ms0.9 驱动空缺区Tu/ms0.9
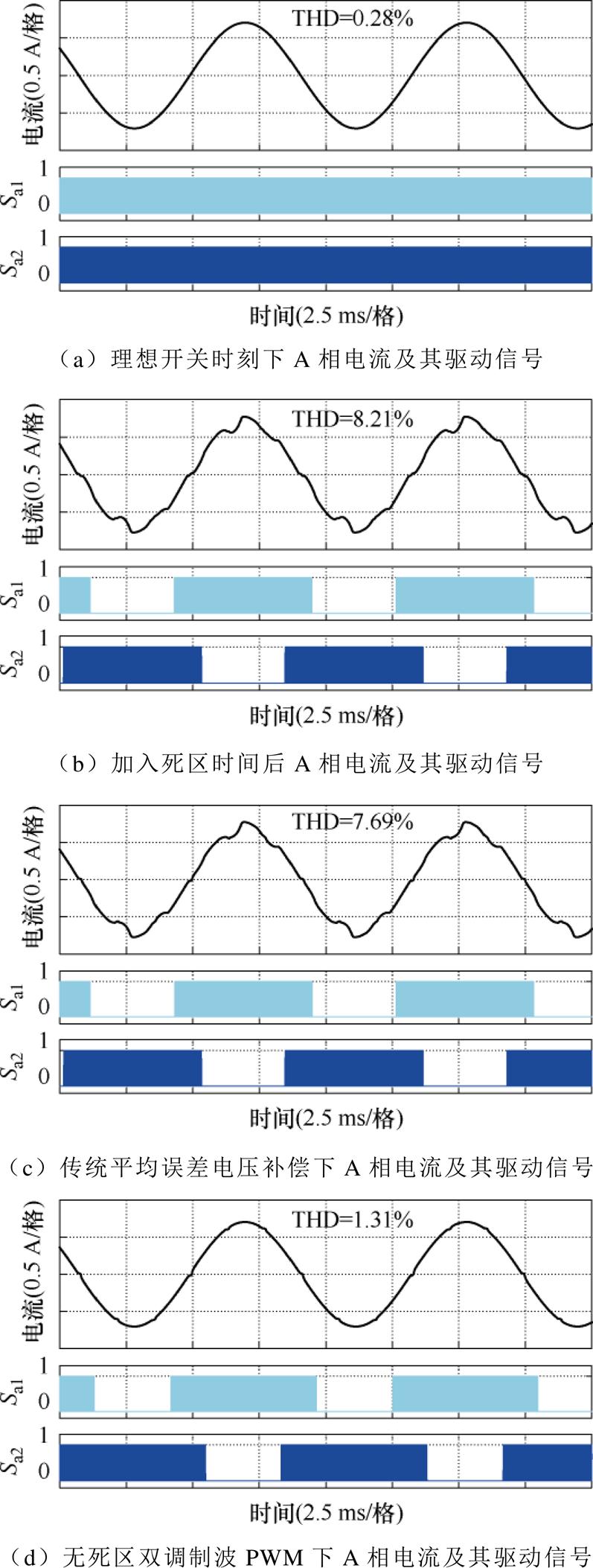
图11 A相电流及其驱动信号波形仿真结果
Fig.11 A-phase current and drive signal waveform simulation results
搭建如图12所示的实验平台对本文所提策略进行实验验证。以Cyclone V 5CEBA4F23C7N作为主控芯片,电机为鸣志公司的SM0601EE2,相关参数与仿真一致,见表1。栅极驱动器型号为2ED2181S06F,驱动电阻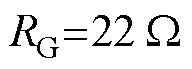 ,功率器件型号为ISC080N10NM6,导通电阻
,功率器件型号为ISC080N10NM6,导通电阻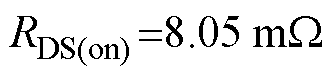 ,二极管压降
,二极管压降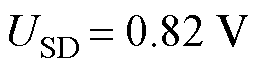 。测试过程中由磁滞制动器模拟电机负载。在实验中,利用电流传感器采集电机的相电流波形,通过示波器获取并显示波形数据,同时将波形数据保存并导入Matlab中进行数据分析。
。测试过程中由磁滞制动器模拟电机负载。在实验中,利用电流传感器采集电机的相电流波形,通过示波器获取并显示波形数据,同时将波形数据保存并导入Matlab中进行数据分析。

图12 实验平台
Fig.12 Experimental platform
死区时间设为0.9 ms,开关频率定为80 kHz,电机带载运行在300、750、1 050和1 500 r/min时的A相电流波形及其总谐波畸变率(Total Harmonic Distortion, THD)如图13所示,电流THD分别为2.95%、2.51%、2.46%和2.15%。电流波形未出现明显畸变,这说明了由VSI死区非线性所引起的电流畸变能够被PI控制器抑制。
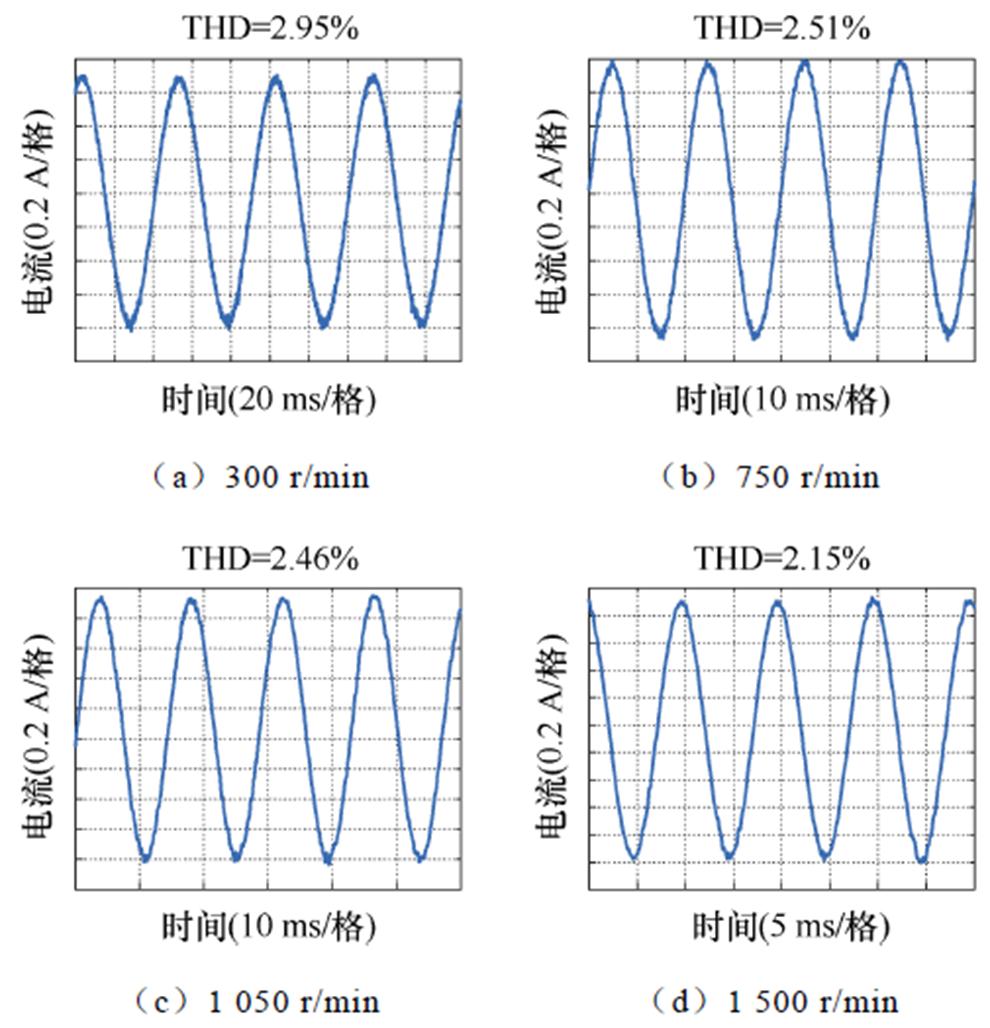
图13 不同速度下A相电流波形
Fig.13 A-phase current waveforms at different speeds
高开关频率控制下电流环带宽较高,低速下由VSI死区非线性引起的电流畸变会被电流控制器所抑制。随着转速的增加,反电动势也会增大。因此选择在1 800 r/min不同带载工况下对本文所提策略进行实验验证。
在开关频率为40 kHz和80 kHz的条件下,电机空载时A相电流实验波形如图14所示,电流THD分别为13.39%和25.58%。可以看出,在80 kHz开关频率下电流波形畸变更严重,在波峰波谷处出现明显的“凹陷”。因此在80 kHz开关频率下对本文所提策略进行实验验证。
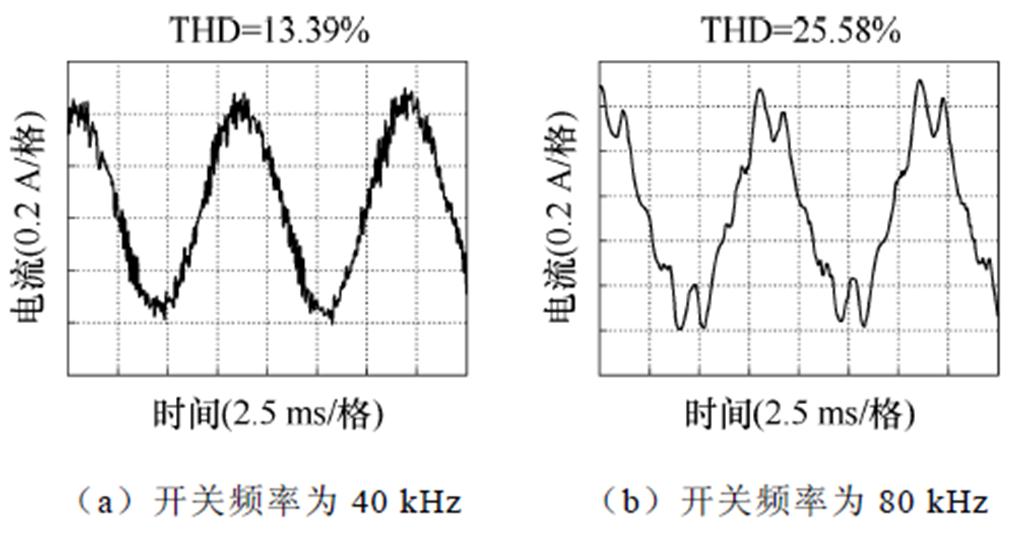
图14 不同工作频率下的A相电流实验波形
Fig.14 Experimental waveforms of A-phase current at different operating frequencies
电机运行在空载,分别采用传统平均误差电压补偿和无死区双调制波PWM时的A相电流实验波形如图15所示。采用传统平均误差电压补偿后电流THD=13.14%,采用本文所提无死区双调制波PWM后电流THD降至5.55%。
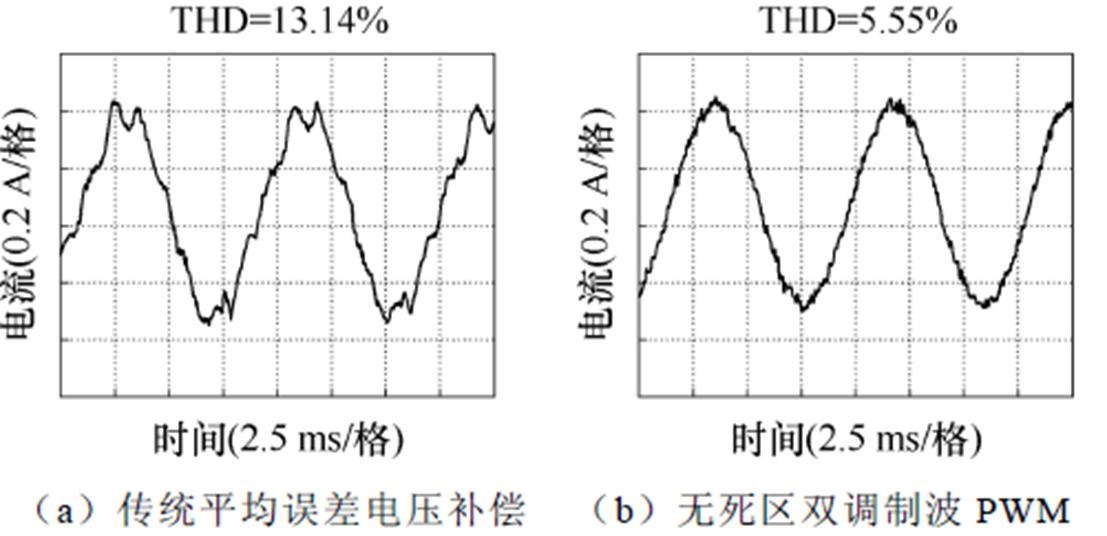
图15 空载下A相电流实验波形
Fig.15 Experimental waveforms of A-phase current under no load
电机带载工况下的A相电流及驱动信号实验波形如图16所示,调制信号的实验波形如图17所示。图16a和图17a为未进行死区补偿时的实验结果,电流THD=10.75%,电流波形畸变严重,在波峰波谷处出现明显的“凹陷”。调制波的幅值存在超出三角载波范围的情况,导致部分区域驱动脉冲消失。这是因为在高开关频率条件下死区时间的存在限制了可调节的占空比范围,减少了实际的输出电压空间范围,同时引起大量的电压误差脉冲,使得电流波形畸变严重。图16b和图17b为进行传统平均误差电压补偿后的实验结果,补偿后电流THD=9.00%,电流波形正弦度得到了一定的改善但效果不明显。引入死区时间后再进行相应补偿会使得调制波的值超出三角载波的范围,导致驱动脉冲消失,补偿后仍存在较为明显的波形畸变。图16c和图17c为采用无死区双调制波PWM后的实验结果,电流THD= 2.56%,波形正弦度得到明显改善,电流“凹陷”现象消失。采用无死区双调制波PWM后,也将会出现辅助调制波超出三角载波范围的情况,仍然存在驱动脉冲消失的现象,但消失的驱动脉冲并没有对输出电压造成影响。实验结果表明,本文所提无死区双调制波PWM能够有效地降低电流THD,消除由死区时间导致的占空比限制。
在电机运行过程中,使用示波器余晖功能捕获A相桥臂在额定电流5 A以内的输出电压波形,输出电压上升沿和下降沿如图18所示,不同电流下输出电压存在严重的非线性特性。

图16 带载下A相电流及驱动信号实验波形
Fig.16 Experimental waveforms of A-phase current and drive signal under load
在实现无死区双调制波PWM的基础上进行VSI非线性误差电压辨识,考虑电流采样精度后电流增量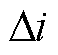 定为0.1 A,电流上限imax为额定电流5 A,d轴电压与d轴电流对应关系如图19a所示,根据图8流程计算可得VSI非线性误差电压与电流的对应关系如图19b所示,VSI非线性误差电压随着电流的增加而减小。
定为0.1 A,电流上限imax为额定电流5 A,d轴电压与d轴电流对应关系如图19a所示,根据图8流程计算可得VSI非线性误差电压与电流的对应关系如图19b所示,VSI非线性误差电压随着电流的增加而减小。
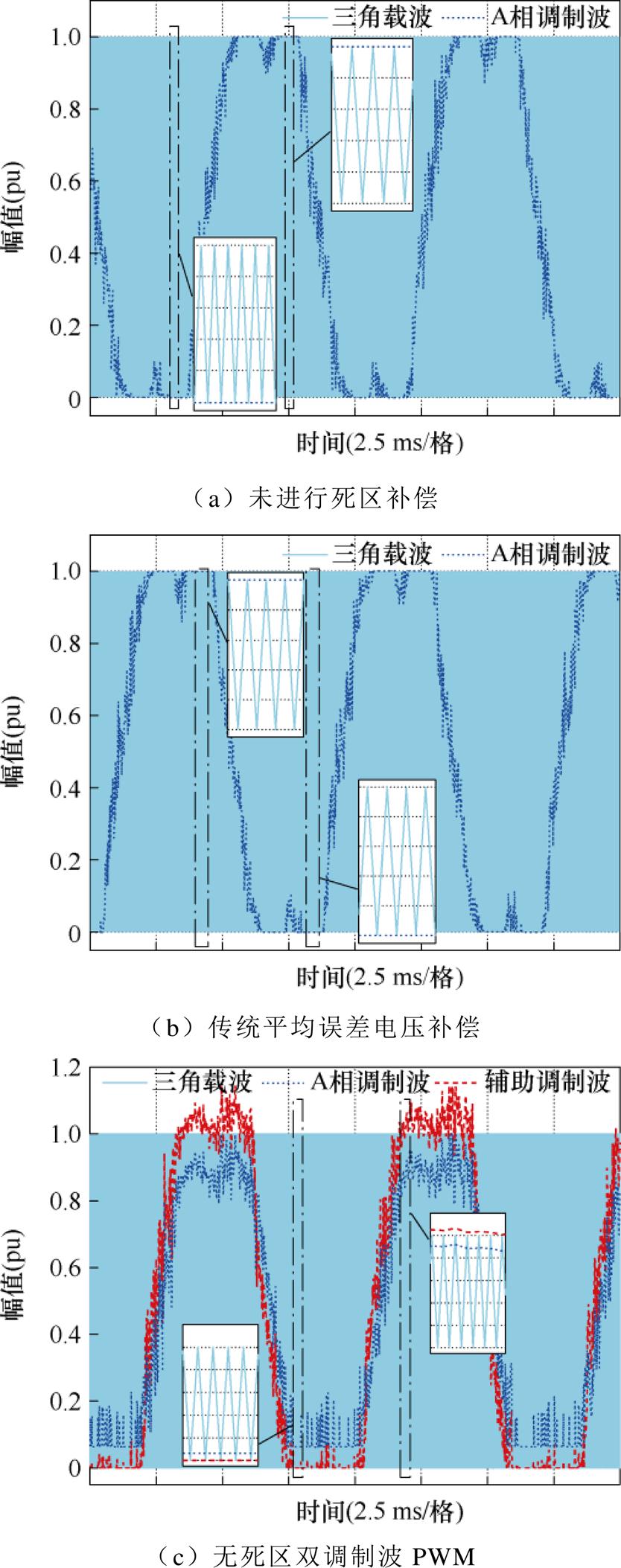
图17 带载下调制信号的实验波形
Fig.17 Experimental waveforms of modulated signals
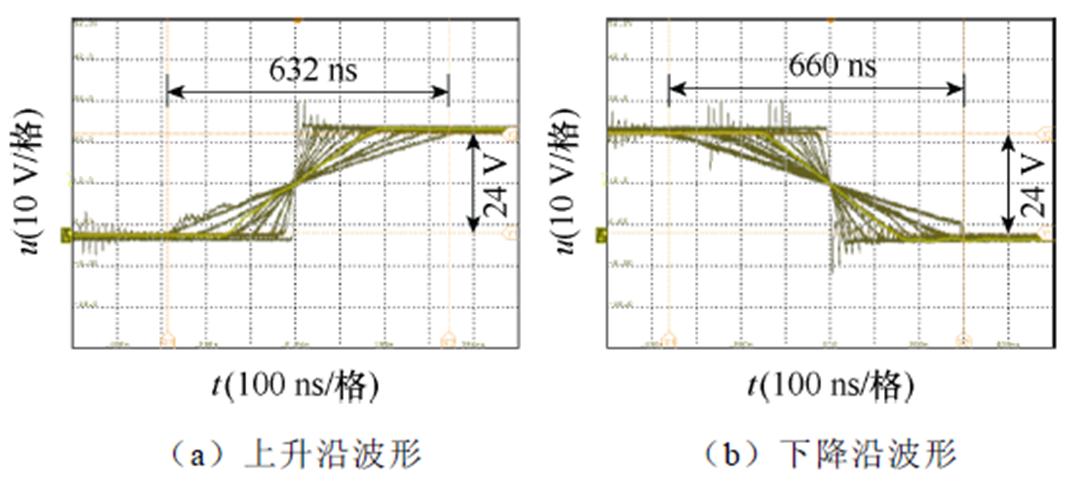
图18 不同电流下的输出电压实验波形
Fig.18 Experimentally measured waveforms of output voltage under different current amplitudes
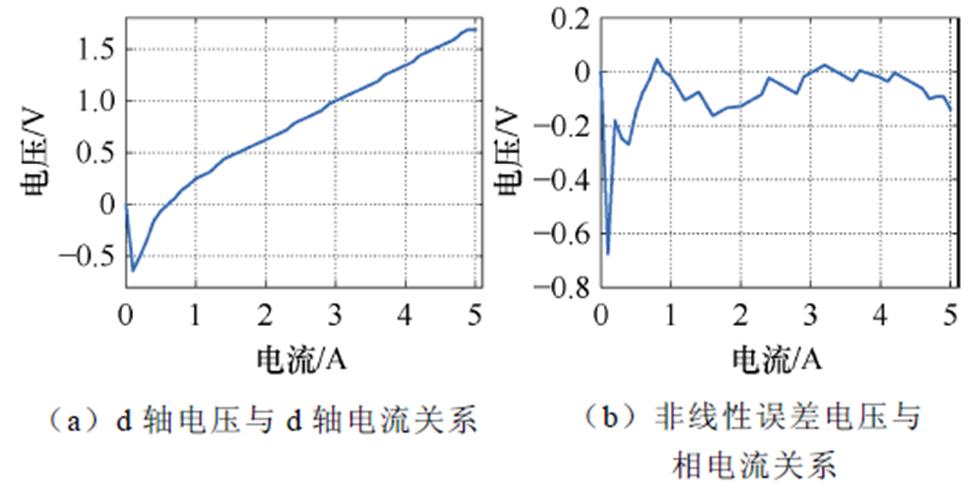
图19 电压与电流的对应关系
Fig.19 Relationship between voltage and current
在空载和带载工况下的实验结果如图20所示,空载条件下电流THD=5.27%,带载条件下电流THD= 2.32%。在无死区双调制波PWM避免死区时间加入的基础上,进行非线性误差电压补偿后,电流THD略低于采用无死区双调制波PWM的电流THD。这表明在高频应用场景中,逆变器的死区非线性效应主要是由死区时间引起的,其中器件的非理想特性影响较小。
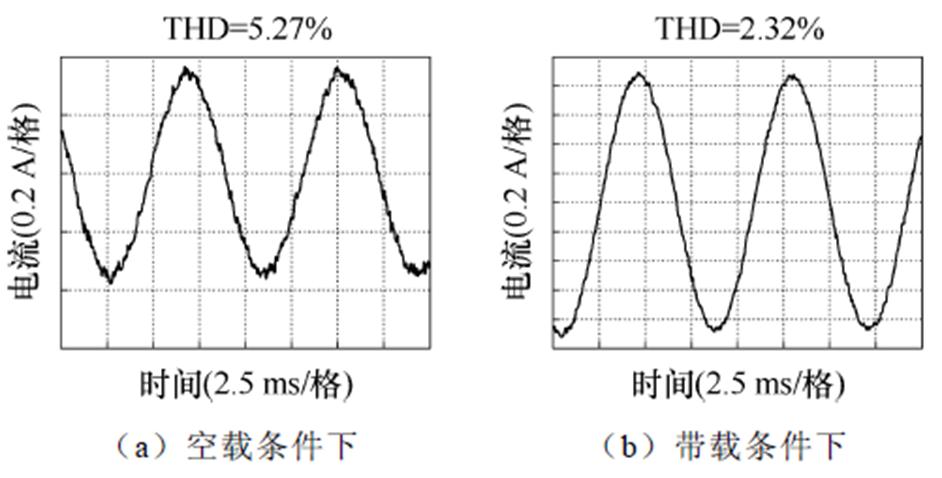
图20 本文所提策略下A相电流及驱动信号实验波形
Fig.20 Experimental waveforms of A-phase current and drive signal under the strategy proposed in this paper
进一步对相电流波形进行幅频分析,A相电流在未进行死区补偿、传统平均误差电压补偿、本文所提策略下的谐波分析结果如图21所示。可以看出,本文所提策略下的谐波幅值远低于含死区不补偿和传统平均误差电压补偿方法,5次、7次等奇次谐波显著降低,本文所提策略有较好的谐波抑制效果。

图21 A相电流频谱
Fig.21 A-phase current spectrum
针对伺服系统在高开关频率应用下VSI死区非线性效应严重问题,本文提出了无死区双调制波PWM和VSI非线性补偿相结合的策略,仿真与实验结果表明,所提策略能够有效地抑制高频VSI死区非线性效应导致的电流谐波畸变。得到结论如下:
1)死区时间和器件非理想特性会在VSI输出电压中产生非线性误差,高频控制下电流环带宽较高,低速下由VSI死区非线性引起的电流畸变能被PI控制器所抑制。
2)死区时间导致的占空比限制会随着开关频率的升高而加剧,缩小线性调制区。在高开关频率控制下引入死区时间后再进行相应补偿无法解除由死区时间导致的占空比限制,补偿效果不够理想。
3)本文所提的无死区双调制波PWM能够实现理想占空比的输出,消除由死区时间导致的占空比限制。该策略无需进行控制环路计算,可用于更高开关频率的伺服驱动控制系统。
4)在高频应用场景中,VSI的死区非线性效应主要是由死区时间引起的,其中器件的非理想特性影响较小。
参考文献
[1] Ren Ren, Zhang Fanghua, Liu Bo, et al. A closed-loop modulation scheme for duty cycle compensation of PWM voltage distortion at high switching frequency inverter[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(2): 1475-1486.
[2] Schubert M, Scharfenstein D, De Doncker R W. A novel online current- and voltage-sensor offset adaption scheme utilizing the effect of inverter voltage distortion[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 6011-6017.
[3] Wu Zhaoqian, Ding Kang, Yang Zhijian, et al. Analytical prediction and minimization of deadtime- related harmonics in permanent magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 7736-7746.
[4] 周世超, 刘侃, 丁荣军, 等. 基于谐波分离的逆变器非线性因素直接提取和补偿方法[J]. 中国电机工程学报, 2021, 41(22): 7763-7771.
Zhou Shichao, Liu Kan, Ding Rongjun, et al. Direct extraction and compensation of inverter nonlinearity based on harmonic separation[J]. Proceedings of the CSEE, 2021, 41(22): 7763-7771.
[5] 杨帆, 赵希梅, 金鸿雁, 等. 基于广义比例积分观测器的永磁同步电机鲁棒谐振预测电流控制[J]. 电工技术学报, 2024, 39(10): 2995-3006.
Yang Fan, Zhao Ximei, Jin Hongyan, et al. Robust resonant predictive current control of permanent magnet synchronous motor based on generalized proportional-integral observer[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2995-3006.
[6] 王高林, 李卓敏, 詹瀚林, 等. 考虑逆变器非线性的内置式永磁同步电机转子位置锁相环观测器[J]. 电工技术学报, 2014, 29(3): 172-179.
Wang Gaolin, Li Zhuomin, Zhan Hanlin, et al. Phase- locked-loop rotor position observer for IPMSM considering inverter nonlinearity[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 172-179.
[7] 徐奇伟, 熊德鑫, 陈杨明, 等. 基于新型高频纹波电流补偿方法的内置式永磁同步电机无传感器控制[J]. 电工技术学报, 2023, 38(3): 680-691.
Xu Qiwei, Xiong Dexin, Chen Yangming, et al. Research on sensorless control strategy of IPMSM based on new high frequency ripple current com- pensation method[J]. Transactions of China Elec- trotechnical Society, 2023, 38(3): 680-691.
[8] 陈斌, 王婷, 吕征宇, 等. 电压型逆变器非线性的分析及补偿[J]. 电工技术学报, 2014, 29(6): 24-30.
Chen Bin, Wang Ting, Lü Zhengyu, et al. The analysis and compensation of voltage source inverter nonlinearity[J]. Transactions of China Electrotech- nical Society, 2014, 29(6): 24-30.
[9] 苏振中, 王东, 聂子玲, 等. 磁轴承用全桥功率放大器死区效应分析与补偿算法设计[J]. 中国电机工程学报, 2018, 38(19): 5829-5837.
Su Zhenzhong, Wang Dong, Nie Ziling, et al. Analysis and compensation algorithm design of the dead-time effect of full-bridge power amplifier for active magnetic bearing[J]. Proceedings of the CSEE, 2018, 38(19): 5829-5837.
[10] 沈泽微, 蒋栋, 陈嘉楠. 一种通用的PWM变流器开关脉冲延时补偿策略[J]. 中国电机工程学报, 2021, 41(9): 2990-2998.
Shen Zewei, Jiang Dong, Chen Jianan. A general switch pulse delay compensation strategy for PWM converter[J]. Proceedings of the CSEE, 2021, 41(9): 2990-2998.
[11] 韩坤, 孙晓, 刘秉, 等. 一种永磁同步电机矢量控制SVPWM死区效应在线补偿方法[J]. 中国电机工程学报, 2018, 38(2): 620-627.
Han Kun, Sun Xiao, Liu Bing, et al. Dead-time on-line compensation scheme of SVPWM for per- manent magnet synchronous motor drive system with vector control[J]. Proceedings of the CSEE, 2018, 38(2): 620-627.
[12] 倪瑞政, 李庭, 陈杰, 等. 一种脉冲式死区补偿方法的研究[J]. 电工技术学报, 2019, 34(增刊2): 553-559.
Ni Ruizheng, Li Ting, Chen Jie, et al. Research on a pulse dead zone compensation method[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(S2): 553-559.
[13] 康薇, 肖飞, 任强, 等. 双有源桥DC-DC变换器三移相调制及其死区效应分析和补偿[J]. 电工技术学报, 2024, 39(6): 1907-1922.
Kang Wei, Xiao Fei, Ren Qiang, et al. Three-phase shift modulation of DC-DC converter with dual active bridges and its dead-time effect analysis and compensation[J]. Transactions of China Electro- technical Society, 2024, 39(6): 1907-1922.
[14] 宁继超, 贲洪奇, 王雪松, 等. 带有死区时间补偿及电容电压平衡功能的二极管钳位型三电平逆变器数字调制方法[J]. 电工技术学报, 2024, 39(20): 6444-6461.
Ning Jichao, Ben Hongqi, Wang Xuesong, et al. A digital modulation method for dead-time com- pensation and capacitor voltage balance in diode clamped three-level inverters[J]. Transactions of China Electrotechnical Society, 2024, 39(20): 6444- 6461.
[15] Park Y, Sul S K. A novel method utilizing trapezoidal voltage to compensate for inverter nonlinearity[J]. IEEE Transactions on Power Electronics, 2012, 27(12): 4837-4846.
[16] Seyyedzadeh S M, Shoulaie A. Accurate modeling of the nonlinear characteristic of a voltage source inver- ter for better performance in near zero currents[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 71-78.
[17] 龙江, 杨明, 陈扬洋, 等. 基于误差电压精确计算的表贴式永磁同步电机逆变器非线性补偿方法[J]. 中国电机工程学报, 2022, 42(17): 6425-6435, 23.
Long Jiang, Yang Ming, Chen Yangyang, et al. Inverter nonlinearity compensation method for SPMSM drives based on accurate voltage error calculation[J]. Proceedings of the CSEE, 2022, 42(17): 6425-6435, 23.
[18] Shang Chaoyi, Yang Ming, Long Jiang, et al. An accurate VSI nonlinearity modeling and compensation method accounting for DC-link voltage variation based on LUT[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 8645-8655.
[19] Chen Zhiwei, Shi Tingna, Cao Yanfei, et al. An accurate inverter nonlinearity compensation method for IPMSM torque estimation based on numerical fitting[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(2): 2126-2138.
[20] Wan Wenchao, Yu Tianbao, Duan Shanxu. Dead-time compensation in active NPC three-level inverters considering current ripple[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 1189-1199.
[21] Yan Qingzeng, Yuan Xibo. A double-modulation- wave PWM for dead-time-effect elimination and synchronous rectification in SiC-device-based high- switching-frequency converters[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13500-13513.
[22] 王勇, 高宁, 罗悦华, 等. 三相三电平并网逆变器无死区SPWM控制研究[J]. 中国电机工程学报, 2011, 31(21): 70-75.
Wang Yong, Gao Ning, Luo Yuehua, et al. SPWM research for dead-time elimination in a three-phase three-level grid-connected inverter[J]. Proceedings of the CSEE, 2011, 31(21): 70-75.
[23] Diao Naizhe, Sun Xianrui, Song Chonghui, et al. A multimodulation times SVPWM for dead-time effect elimination in three-level neutral point clamped converters[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 5476-5485.
[24] Yan Qingzeng, Xiao Langtao, Yuan Xibo, et al. A double-modulation-wave PWM with reduced dependency on current polarities for dead-time-effect elimination in three-level T-type converters[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8413-8427.
[25] 杨波, 吴建德, 李武华, 等. 在线自适应PWM死区消除方法[J]. 电工技术学报, 2011, 26(11): 45-52.
Yang Bo, Wu Jiande, Li Wuhua, et al. Online adaptive dead-time elimination method for PWM voltage source inverters[J]. Transactions of China Electrotechnical Society, 2011, 26(11): 45-52.
[26] 刘和平, 路莹超, 王华斌, 等. 电压型逆变器分段死区补偿调制策略[J]. 电机与控制学报, 2018, 22(3): 25-32.
Liu Heping, Lu Yingchao, Wang Huabin, et al. Dead- time compensation modulation strategy of subsection integrated in voltage source inverter[J]. Electric Machines and Control, 2018, 22(3): 25-32.
[27] Yan Qingzeng, Zhao Rende, Yuan Xibo, et al. A DSOGI-FLL-based dead-time elimination PWM for three-phase power converters[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2805-2818.
[28] 唐小琦, 苏玲宏, 周向东, 等. 基于FPGA的交流伺服系统电流环带宽扩展[J]. 华中科技大学学报(自然科学版), 2014, 42(2): 1-5.
Tang Xiaoqi, Su Linghong, Zhou Xiangdong, et al. Bandwidth expansion of current loop for AC servo system based on FPGA[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(2): 1-5.
[29] 吴茂刚, 赵荣祥, 汤新舟. 正弦和空间矢量PWM逆变器死区效应分析与补偿[J]. 中国电机工程学报, 2006, 26(12): 101-105.
Wu Maogang, Zhao Rongxiang, Tang Xinzhou. Dead-time effects analysis and compensation of SPWM and SVPWM inverter[J]. Proceedings of the CSEE, 2006, 26(12): 101-105.
[30] 梁营玉, 刘建政. 电压源变流器死区效应分析及抑制策略[J]. 电力系统自动化, 2018, 42(24): 135-142.
Liang Yingyu, Liu Jianzheng. Analysis and supper- ssion strategy of dead-time effect for voltage source converter[J]. Automation of Electric Power Systems, 2018, 42(24): 135-142.
[31] 冯婉, 张文娟, 苗轶如, 等. 基于dq坐标系下6次谐波抑制的车用感应电机低频共振削弱方法[J]. 电工技术学报, 2023, 38(24): 6632-6645.
Feng Wan, Zhang Wenjuan, Miao Yiru, et al. Low frequency resonance reduction method of induction motor used by electric vehicle based on sixth harmonic suppression in dq coordinate[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(24): 6632-6645.
Abstract In servo systems, the bandwidth of the current loop is increased by raising the switching frequency. However, the dead-time nonlinearity of the voltage source inverter (VSI) intensifies with the increase of switching frequency, causing the deviation between the actual and the theoretical output voltage, resulting in serious distortion of the inverter output current waveform.
The requirement of computational power constrains the implementation of high switching frequency control. Consequently, the dead-time nonlinearity compensation strategy should be more straightforward to decrease computational time, especially for high switching frequency applications. The amplitude increase is relatively modest at a low switching frequency but significantly surges at a high one, bringing on a severe degradation of the linear modulation region. It is an imperfect solution to compensate after the occurrence of dead-time, which unavoidably introduces compensation errors. Furthermore, the accurate solution of inverter nonlinear voltage error (INVE) under different currents represents a crucial aspect of achieving exact INVE compensation. Nevertheless, the existing methods are complex.
This paper proposes a novel strategy that combines no-dead-time double modulation wave pulse-width modulation (PWM) and inverter nonlinearity compensation for analyzing the dead-time nonlinearity and the nonideal characteristics of the inverter on the output voltage error. Firstly, according to the continuous current characteristics of the anti-parallel diode, the drive vacancy area is added between the complementary drive pulses to avoid the introduction of dead time. Compared with the ideal space vector pulse width modulation (SVPWM), an auxiliary modulating wave is added. Depending on the current polarity, its amplitude is adjusted up or down from the original modulating waveform. The underlap periods are generated between the complementary drive pulse by contrasting the double-modulating and the triangular carrier waves. It is practical to avoid both the bridge arm shoot-through and the introduction of dead time. Most importantly, the actual output voltage of thismethod is identical to the optimal voltage, which directly eliminates the dead-time nonlinearity and removes the limitation of dead time on the output duty cycle at a high switching frequency. Moreover, the control signals of each switching device are obtained based on the comparison between the double-modulating and the carrier wave. No additional control loop calculations are required, while the generated PWM signals are symmetric about the carrier midpoint.
Secondly, the inverter nonlinearity is equated to the INVE, which varies with the current. When the motor is at a standstill of  , by injecting the ramp current signal into the direct axis and applying Kirchhoff's voltage law, the sum of INVE containing the nonlinear factor of the two-phase VSI is obtained. Finally, the relationship between the INVE and the current amplitude is calculated using the linear iterative interpolation approach, and the online compensation of the INVE is achieved.
, by injecting the ramp current signal into the direct axis and applying Kirchhoff's voltage law, the sum of INVE containing the nonlinear factor of the two-phase VSI is obtained. Finally, the relationship between the INVE and the current amplitude is calculated using the linear iterative interpolation approach, and the online compensation of the INVE is achieved.
The results show that the proposed strategy can increase the linear modulation region of the output voltage, eliminate the output duty cycle limitation derived from the dead-time, and effectively suppress the current harmonic distortion phenomenon caused by the dead-time nonlinearity of high switching frequency inverters. In addition, the strategy is easy to implement without additional control loop calculations, which can be applied to servo drive control systems requiring high switching frequencies.
Keywords:Permanent magnet synchronous motor, inverter dead-time nonlinearity, dead-time elimination, nonlinearity compensation, voltage error calculation
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.240687
收稿日期 2024-04-30
改稿日期 2024-07-05
周国祥 男,1999年生,硕士研究生,研究方向为高频逆变器调制与控制。
E-mail: zhouguoxiang@my.swjtu.edu.cn
王邦继 男,1984年生,副教授,博士生导师,研究方向为电机系统及其控制。
E-mail: bangjw@163.com(通信作者)
(编辑 陈 诚)