图1 传统的同步整流驱动策略
Fig.1 Conventional SR driving schemes
摘要 LLC谐振变换器因其高效率、高功率密度和宽范围电压输出的优点，常应用于电动汽车充电装置中。为了进一步提高效率，该变换器的二次侧采用同步整流技术。因传统的同步整流方案受到了一系列限制，包括电流互感器成本高、高压检测困难、工作范围窄、计算负担重或准确度不高等问题。为解决这些问题，提出一种无高频采样的LLC谐振变换器同步整流方案。该方案基于简化的时域分析，在线识别LLC谐振变换器的不同工作模式并实时计算同步整流管的导通或延迟导通占空比。仿真结果表明，所提方法可在全频率范围与各种负载工况下实现同步整流管的精确驱动，且与其他基于模型的无高频采样驱动方案相比，该方案更为精确。最后，通过构建一台6.6 kW的实验样机，验证了该方案的稳态精确性和动态可靠性。
关键词：LLC谐振变换器 时域分析 同步整流 模式识别
LLC谐振变换器作为电动汽车充电器中最常见的拓扑之一，具有多种优势，包括能够实现软开关、高效率、高功率密度以及宽电压增益，已成为研究热点[1-5]。然而，由于二次侧整流二极管较高的导通压降，其导通损耗占总损耗的比重较大[6]。为了进一步提升电能转换效率，通过引入同步整流（Syn- chronous Rectification, SR）技术，利用MOSFET模拟整流二极管的开关行为可以降低变换器损耗[7]。
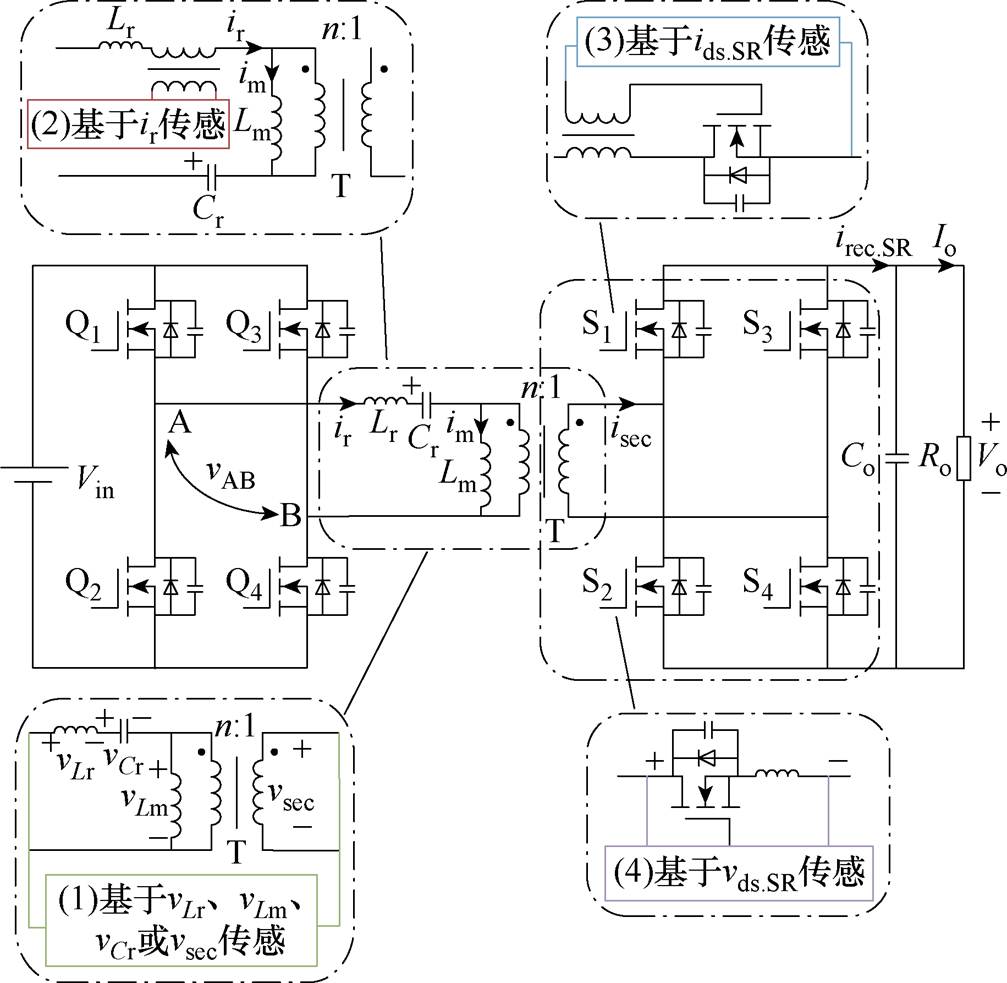
传统的同步整流驱动方案可大致分为三类：基于电流检测、电压检测及无高频采样的方法[8-10]。传统的同步整流驱动策略如图1所示。基于电流检测的同步整流方案采用电流互感器来检测LLC谐振变换器的一次电流ir或SR管漏源电流ids.SR，从而产生同步整流控制信号，该类方案因能够获取同步整流器的实时电流状态而具有较高精度。然而，额外的电流互感器会增加变换器的体积和损耗[11]。
基于电压检测的SR方案根据采样信号的不同，又分为基于谐振腔电压方案和SR MOSFET漏源电压vds.SR方案。前者包括基于谐振电感电压vLr、励磁电感电压vLm、谐振电容电压vCr或二次电压vsec传感器的SR方案，较于电流检测方案，具有效率高、功率密度高等特点。然而，基于谐振腔电压的方案通常需要搭建复杂的分立电路来对信号进行处理[12-13]。而对于SR MOSFET漏源电压方案，由于MOSFET封装自身的寄生电感的影响，容易引起SR驱动的提早关断，影响SR MOSFET性能[14-15]。为了消除寄生电感的影响，文献[16]提出了基于自适应漏源电压检测的SR方案，通过探测SR反向二极管的导通状态控制SR驱动信号时长，然而其稳态精度需要较小的步长，而动态调节过程中需要较大的步长，因此难以兼顾SR控制的稳态精度和动态性能。与此同时，电压检测方案在一定程度上受到应用场景的限制，特别是在电动汽车场合中，最高输出电压一般至少为400 V，而商用SR芯片的最大耐压值为200 V左右。而使用分立电路进行SR控制，又将增加电路成本、提高检测难度。因此，在电动汽车应用场景下通常会采用无高频采样的SR方案。
图1 传统的同步整流驱动策略
Fig.1 Conventional SR driving schemes
无高频采样的SR方案解决了传感器成本高的难题，该方案大多基于LLC谐振变换器的模型分析来调整SR驱动信号[17]。因此，选取合适的建模分析方法尤为重要。目前，常用的LLC谐振变换器建模分析方法是基波分析（Fundamental Harmonic Approximation, FHA）法和时域分析（Time Domain Analysis, TDA）法[18]。FHA法基于频域进行分析，仅考虑一次、二次电压基频分量的等效线性网络，当开关频率偏离谐振频率时分析得到的特性误差较大。TDA法通过求解时域下的LLC谐振电路微分状态方程得到精确的动态模型，建模精度较高，但难以描述动态过程[19-20]。
文献[21-22]根据改进的FHA建模得到了SR导通时序，然而该模型存在控制精度低的问题，导致SR性能下降。文献[23]通过TDA对LLC谐振变换器SR导通时序进行精确计算，并引入查表法实现了精度较高的SR信号驱动，但查表法存在占据存储空间大等问题。文献[24]提出了一种新颖的双重前馈策略，同时优化了LLC谐振变换器逆变和整流控制的动态性能，其中最终的SR控制信号结合了时域分析法得到的准确前馈信号及传统自适应漏源电压检测SR控制信号的阶梯式调节信号，通过查表法简化工作模式识别的过程，但仍存在计算繁琐、控制方案复杂等问题。除此之外，上述的基于模型的无高频采样的SR方案普遍忽略了在轻载情况下额外的电流断续导通模式（Discontinuous Conduction Mode, DCM），这可能使得SR MOSFET过度开通并导致额外的无功环流甚至引起LLC谐振变换器电压增益畸变[18, 25]。
针对以上问题，本文对于脉冲频率调制（Pulse Frequency Modulation, PFM）下的全桥LLC谐振变换器进行研究，提出一种无需高频采样的基于时域模型的同步整流驱动方案。本方案利用简化的时域分析法对全工作区域下LLC谐振变换器的不同运行模式进行建模，从而实现对于不同模式下SR MOSFET开通时的在线计算。同时，根据时域分析，本方案提出了一种LLC谐振变换器工作模式识别算法，从而确保对于额外DCM的识别，使得LLC谐振变换器在轻载工况下也能够实现高效SR控制，提高变换器的可靠性和效率。
图1为同步整流全桥LLC谐振变换器的拓扑结构，它由两个H桥（一次侧为开关管Q1～Q4组成的逆变H桥、二次侧为S1～S4组成的同步整流H桥）、三元件谐振腔（谐振电容Cr、谐振电感Lr、励磁电感Lm）和一个电压比为n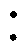
1的单输出绕组变压器T组成。Vin为输入电压，vAB为一次侧逆变开关网络桥臂中点电压，ir为流过Cr和Lr的谐振电流，励磁电流im流经Lm，经过滤波电容Co前的电流为二次电流irec.SR，输出电阻Ro上的电压为输出电压Vo，输出电流用Io表示[26-29]。根据电路规格、开关频率和负载条件的不同，变换器在一个开关周期Ts内可在多个基础工作模态间过渡，可由励磁电感Lm两端电压表征：正钳位vm=nVo（P模态）、负钳位vm=-nVo（N模态），以及励磁电感自由谐振|vm|＜nVo（O模态）。
为了推导的普适性，电路中的状态变量及其归一化基准见表1，三种基本模态的等效电路模型如图2所示。
表1 LLC谐振变换器变量及其归一化基准
Tab.1 LLC converter variables and normalization
参 数公 式 谐振频率fr 最小谐振频率fm 电感比k 谐振阻抗Zr 电压增益M 品质因数Q
（续）
参 数公 式 归一化电压vn 归一化电流in 归一化频率fn
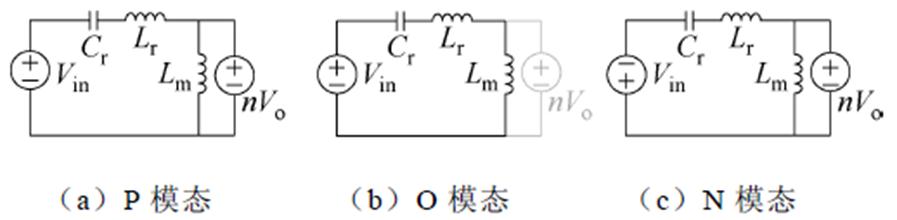
图2 三模态等效电路模型
Fig.2 Equivalent circuit models of three modes
P模态下，仅Cr和Lr参与谐振，谐振腔输出电压钳位至nVo，因此，ir呈正弦变化，im呈线性变化。根据图2中的等效电路模型和基尔霍夫定律，建立求解关键状态变量的微分方程组为
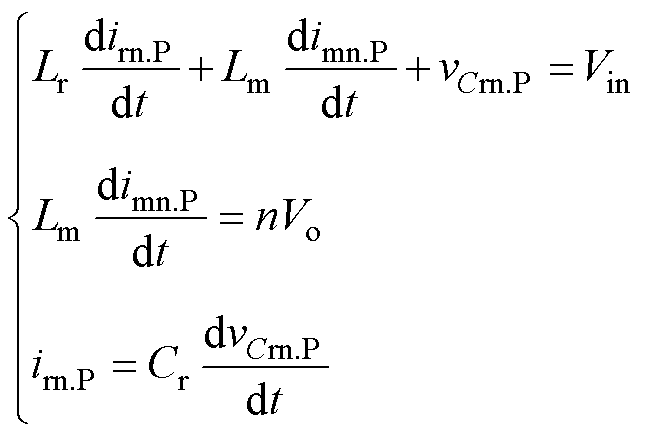（1）
式中，irn.P、imn.P和vCrn.P分别为变换器工作在P模态时的归一化谐振电流、励磁电流和谐振电压。
采用归一化标准求解方程组式（1），可得
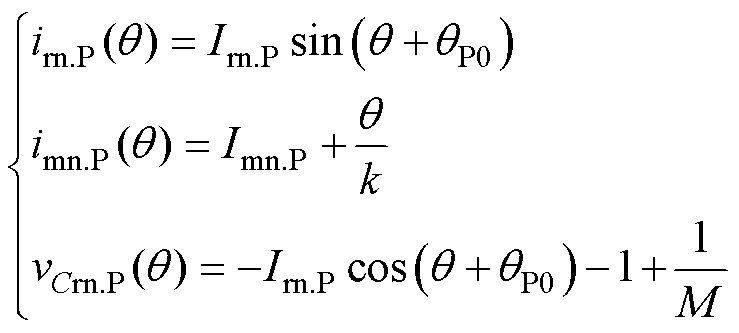（2）
式中，
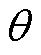为电角度，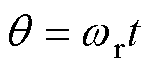
；Irn.P和Imn.P为与谐振腔电感元件电流的初始值相关的未知量；qP0为P模态时的初始电角度。实际上，式（2）是对P模态谐振腔电路工作的精确描述。
O模态下，Lm不再被钳位，因此ir=im并呈正弦变化。利用类似的分析方法，O模态的方程组表示为
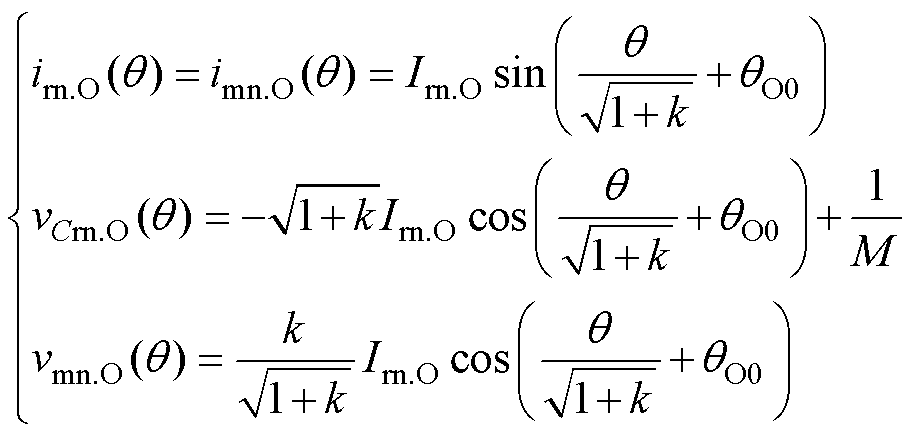（3）
N模态下的ir和im变化趋势与P模态相同，谐振腔输出电压钳位至-nVo。同理可得方程组为
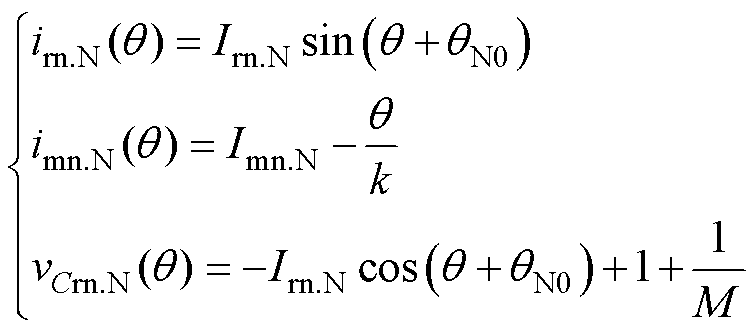（4）
式中，Irn.O、Imn.O、Irn.N和Imn.N分别为O模态和N模态下与谐振腔电感电流初始值相关的未知量；qN0为N模态时的初始电角度。
对于LLC谐振变换器而言，通过组合不同模态可得到LLC谐振变换器的八种主要工作模式：P、O、PO、PON、PN、NP、NOP和OPO。其中，PO、PON和PN模式仅存在于欠谐振区域（Below- Resonance Region, BRR），PO和PON模式都包含O模态，工作在DCM，通过增加负载或降低开关频率，LLC谐振变换器可从PO模式转换为PON模式。继续增加负载，PON模式中的O模态缩短至0，进入PN模式，此时工作在CCM。NP、NOP和OPO工作模式存在于过谐振区域（Above-Resonance Region, ARR），NP模式下，vm达到nVo，足以导通二次侧整流管，在Ts/2结束前便进入P模态。在较轻负载条件下，LLC谐振变换器从NP模式切换为NOP模式，需在O模态获得足够的提升电压后，才可进入P模态。在整个工作频率范围内，LLC谐振变换器的不同模式边界与相应的M-fn关系分布如图3所示。
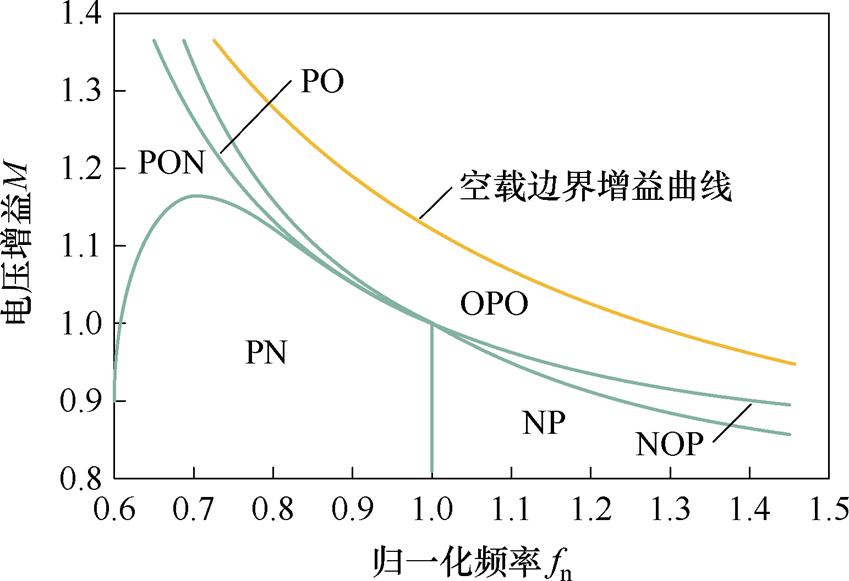
图3 LLC谐振变换器工作模式边界与M-fn分布
Fig.3 LLC resonant converter operating mode boundaries and M-fn distribution
此外，仅在谐振点处工作在P模式。O模式为截止模式，此模式下无任何能量传输到二次侧。特别地，OPO模式存在于全频率范围内。
LLC谐振变换器在不同工作模式下受到若干条件的约束，利用这些约束条件可推导出对应工作模式下的方程组。主要约束条件如下：
（1）连续性：在相邻模态的临界处，电感电流和电容电压均连续。
（2）对称性：电路处于稳态时，电容电压和电感电流的初始值应与其在Ts/2结束处的终值绝对值相同，符号相反。
（3）模态切换：在Ts/2内，相邻模态切换处的输出谐振电流为0。特别地，当电路从O模态切换到P或N模态时，励磁电感的电压是连续的，O模态末的vm被限制为nVo或-nVo。这种额外的约束条件只适用于PON、NOP和OPO模式。例如，NOP模式下，N模态末和P模态初的ir=im，O模态末的vm=nVo。
（4）周期性：一个工作模式下的不同模态总时长为Ts/2。在PFM下Ts可变，因此归一化后表示为p/fn。
（5）负荷条件：由于输出电流在O模态时中断，仅P模态和N模态参与能量传递。归一化后的输出电流表达式为
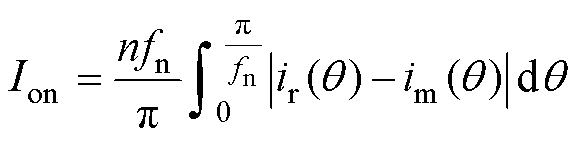（5）
根据1.1节可知，联立特定工作模式的时域方程和约束条件可以得到LLC谐振变换器各状态变量的解析式或计算数值解。其中，通过计算LLC谐振变换器P、O、N三种模态的时长，并根据不同模态控制SR驱动信号即可实现基于时域模型的无高频采样SR方案。然而，LLC谐振变换器在不同工作模式的各模态的表达式是不同的，因此准确识别LLC谐振变换器的不同模式对于精确驱动SR十分重要。
O模式（截止模式）时整流侧开关管全部关断，不需要对其进行SR控制。P模式只存在于谐振点，因此可看作是BRR中的一种特殊PO模式或ARR中特殊的NP模式。研究发现，工作在PON和PN模式很可能失去零电压软开关（Zero Voltage Switching, ZVS）特性，因为在最后一个N模态中，逆变侧的谐振电流会急剧下降，无法满足ZVS要求，因此在设计LLC谐振槽时，通常会避免出现PN和PON工作模式，在模式识别和SR计算分析中忽略这两种模式。
综上所述，PFM下的LLC谐振变换器通常会被设计运行在，PO、OPO、NP和NOP四种模式，其中只需得到两种模式边界，即BRR中PO/OPO模式之间的边界和ARR中NP/NOP模式之间的边界。两种相邻模式的边界可通过求解特定的模式方程组和附加的边界条件得到。
根据第1节分析可以发现，LLC谐振变换器主要工作在PO、OPO、NP和NOP模式。通过将SR MOSFET在对应的开关周期P模态和对称的开关周期N模态开通即可实现SR驱动的精确控制。以Q1和Q4开通的半周期为例：P模态下S1和S4导通，N模态下S2和S3导通，O模态所有整流管均关断。
涉及SR导通计算的工作模式为BRR内的OPO和PO模式，ARR内的NP模式，由于ARR区域内的OPO和NOP模式负载很小，因此无需开通SR。图4为PFM下Ts/2内三种关键模式的谐振腔电流波形及其对应的SR驱动信号。
图4 三种工作模式下的关键波形和SR导通分析
Fig.4 Analysis of critical waveforms and SR conduction in three modes of operation
已知fn和采样计算得到的Ion，通过数值求解时域方程组可得相应模式下各模态持续时间，由图4可知，SR导通时序与其相关。然而，不同模式下的方程求解难度有异，需针对不同模式推导简化而精确的驱动策略。
在PO模式下，P模态上管导通，二次侧二极管VD1导通；O模态上管导通，二次侧二极管均断开，励磁电感电压处于±nVo之间。下列方程中设定P模态开始时刻为0，因为其只影响表达式的初始相移，处于P模态的元件电气量加下标1，处于O模态的元件电气量加下标2，归一化处理过后的变量加下标n。在P模态中，电路中的电压电流方程为
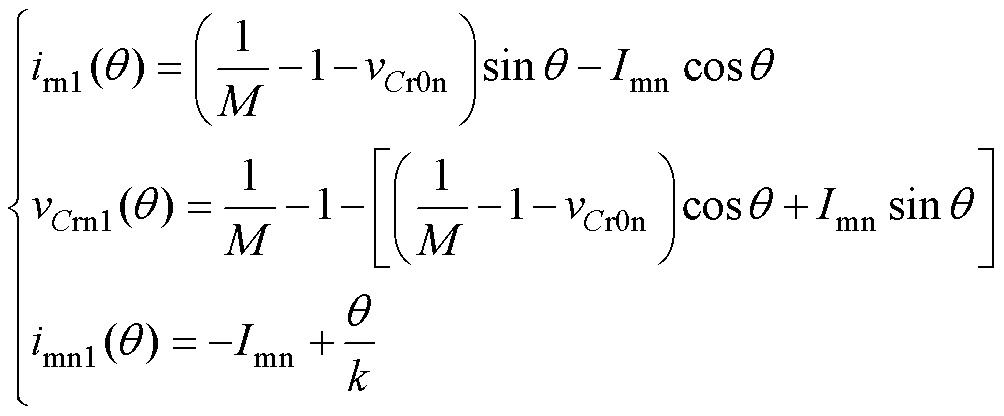（6）
式中，Imn和vCr0n分别为归一化处理过后的励磁电流初始值和谐振电容的初始电压。
电路进入O模态时，变压器一次、二次侧无能量传输，励磁电感Lm不再被输出电压钳位，加入谐振腔，以最小谐振频率fm共同谐振，此时二次侧整流管关断，电路中的电压、电流方程分别为
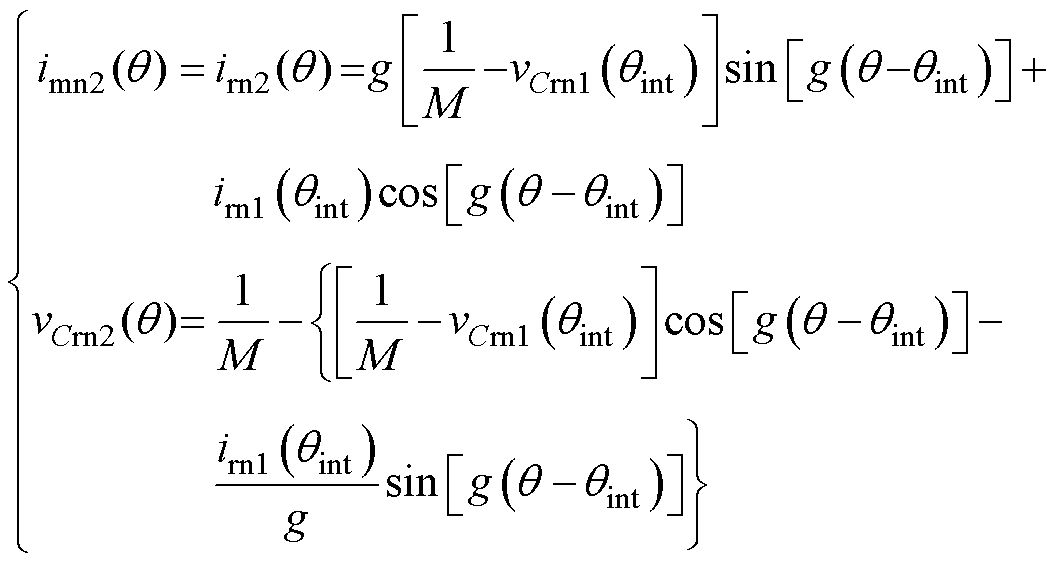（7）
其中
（8）
在PO模式中，两种模态间隔时刻所对应的角度为qint。根据一系列边界条件可联立求得PO模式的时域方程组，其中P模态持续时间对应的电角度为qP，为了简化方程形式，假设F表示为
（9）
则时域方程组可以写为
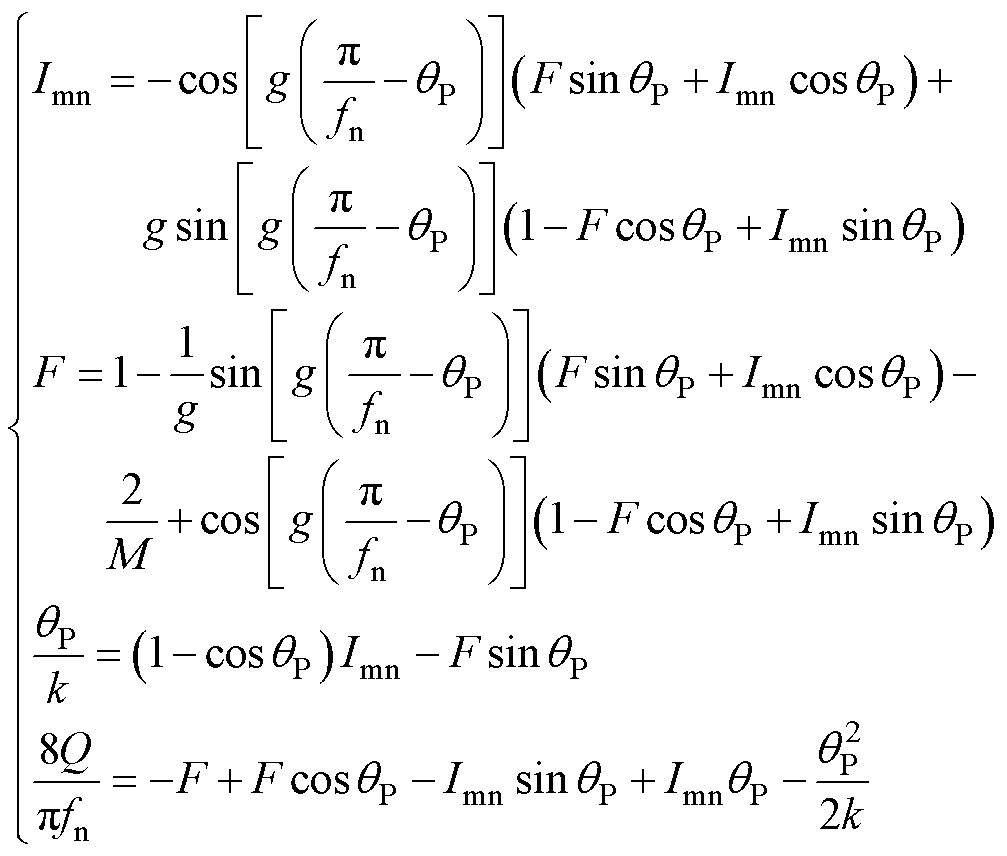（10）
由于方程组中的一项变量表达式近似为零，即
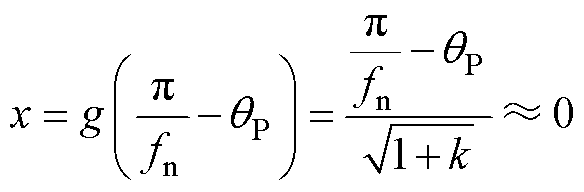（11）
则方程组式（10）中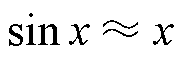
，
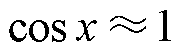。此外，由于ir在O模态近似不变，可得近似条件为
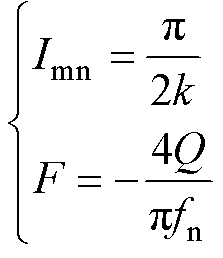（12）
综上所述，可得qP的简单近似解析式为
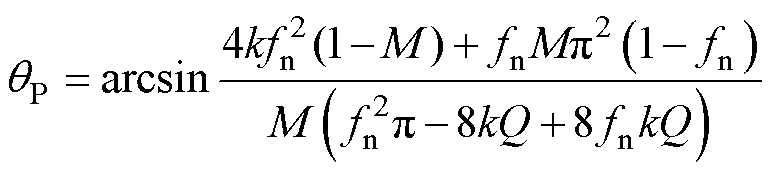（13）
同步整流管的导通时间为谐振电流和励磁电流分离的时间。在PO模式下，同步整流管比一次侧提早关断，P模态的持续时间即为SR导通时间，此时的同步整流导通占空比DSR_on为
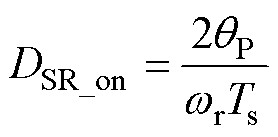（14）
工作在NP模式下，电路工作在CCM，时域方程组存在解析解，其中P模态的电路方程同为式（6），处于P模态的元件电气量加下标1，处于N模态的元件电气量加下标3，进入下一个Ts/2内的N模态的电压电流方程为
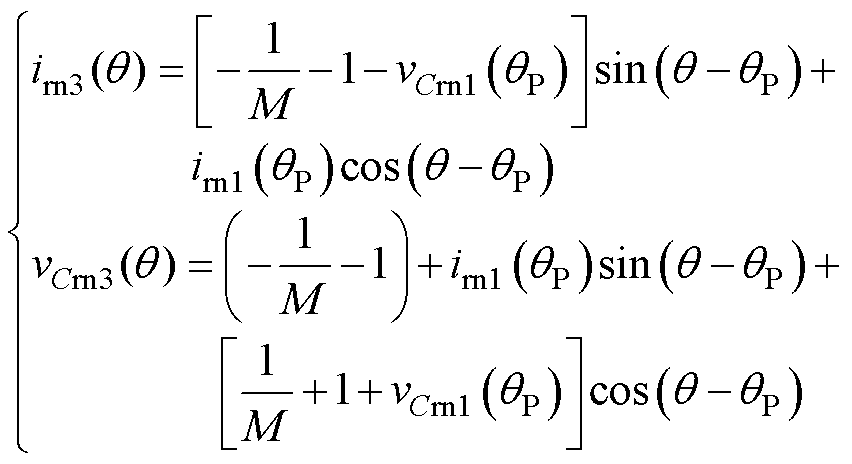（15）
N模态下的励磁电流和P模态保持相同的变化趋势，即
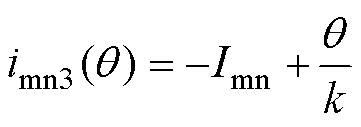（16）
同理可以求得最终的时域方程组为
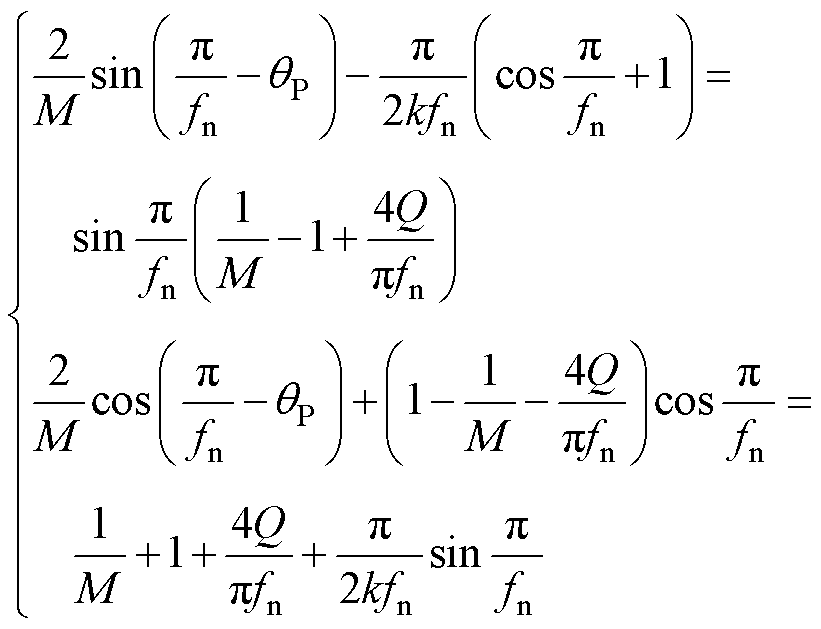（17）
N模态持续时间对应的电角度为qN，根据（17）可求得qN为
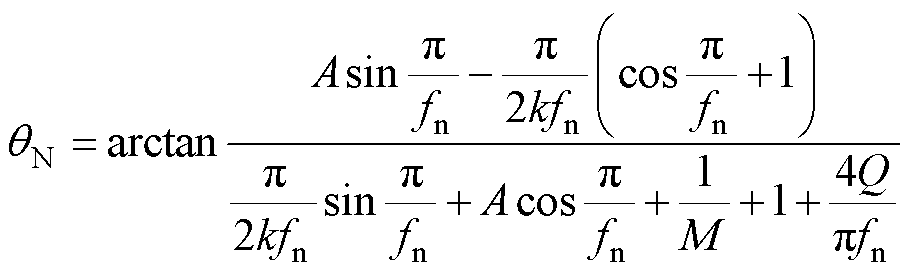（18）
其中
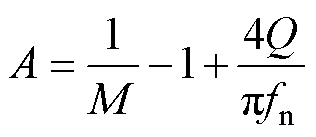（19）
该模式下，二次侧SR延迟开通，N模态的持续时间即延迟导通的时间，因此可通过qN推导得到延迟导通的占空比，此时SR导通时间为当前Ts/2内P模态持续时间与下一Ts/2内N模态持续时间之和。
此时同步整流管延迟导通占空比DSR_delay为
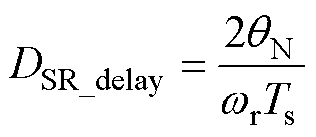（20）
LLC谐振变换器在OPO模式下存在三种工作模态，上述两种模式采用的时域方程求解法更为复杂困难，因此采用Matlab中的cftool工具拟合OPO模式下的SR导通和延迟导通占空比表达式。根据图4c的对应关系可知，O1模态对应二次侧SR管延迟导通时间，P模态对应其导通时间，二次侧SR管比一次侧开关管提早关断，对应O2模态。
图5为OPO模式下的三维拟合曲面，分别表示SR管DSR_on-Ion-fn、DSR_delay-Ion-fn之间的关系。SR导通占空比DSR_on和延迟导通占空比DSR_delay的拟合表达式分别为
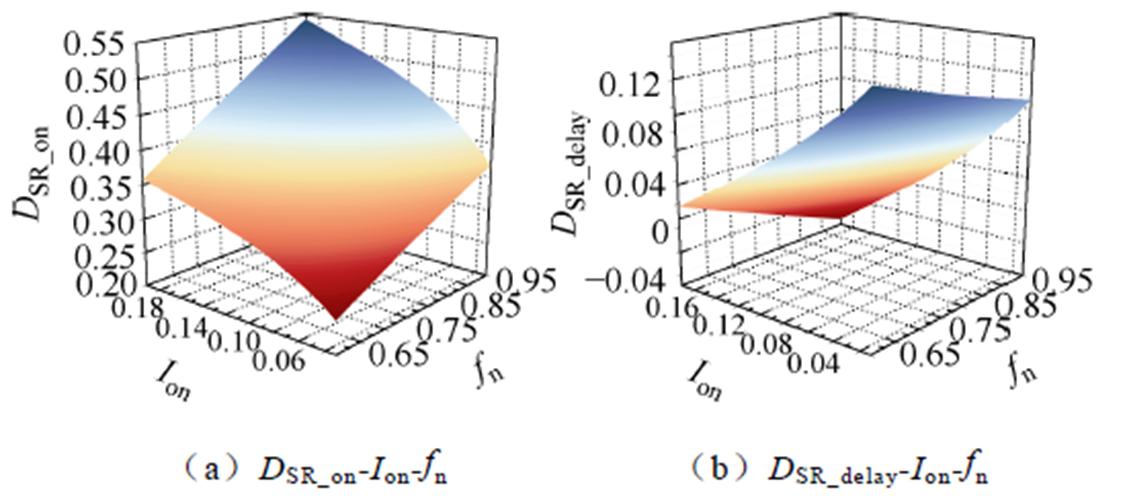
图5 OPO模式下关于SR导通时序的多项式拟合曲面
Fig.5 Three-dimensional polynomial fitting curve of SR on-time sequence in the OPO mode
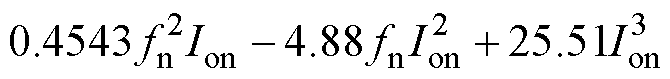（21）
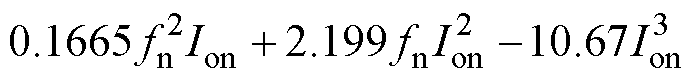（22）
SR导通和延迟导通占空比的平均拟合误差分别为0.067 1%和0.026 13%，保证了SR驱动信号的准确性。因此在PFM下，fn由控制回路计算，Ion是唯一需要采样的信号。
如1.2节所述，基于时域模型的SR方案需要识别LLC谐振变换器的在BRR中PO/OPO模式之间的边界和ARR中NP/NOP模式之间的边界。两种相邻模式的边界可通过求解特定的模式方程组和附加的边界条件得到。
为了易于推导模式边界解析式，令PO和OPO的边界模式为PO模式，NP和NOP的边界模式为NP模式。
对于PO模式，判断P模态前是否出现O模态的依据是ir和im的斜率。如果以PO模式运行而非OPO模式，应使得P模态初始时刻的dir/dt＞dim/dt，同时谐振电感电压的初值应为nVo的1/k，需添加的临界条件为
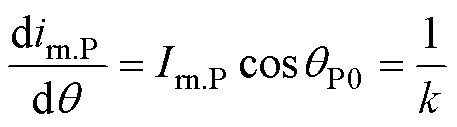（23）
结合1.1节中提到的其他主要约束条件，可得到最终求解边界解析式的方程组为
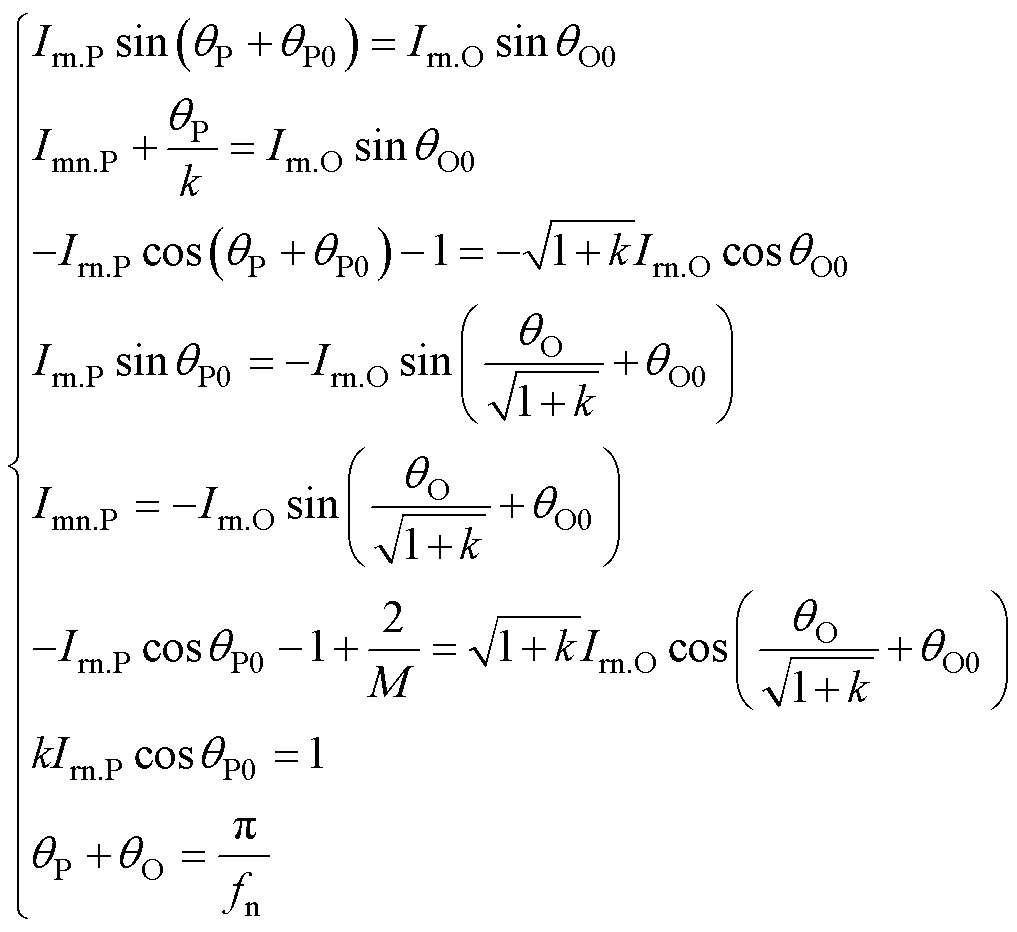（24）
式中，qO0为O模态时的初始电角度。
归一化输出电流表达式为
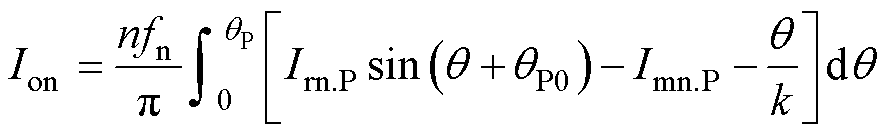（25）
由于仅有O模态中的im波形为正弦，O模态下关于im的方程为超越方程，在P、N模态呈线性变化，因此所有包含O模态的工作模式均处于DCM，时域方程组没有闭合形式的解，因此需要适当的简化条件。参考式（11），利用近似简化条件得
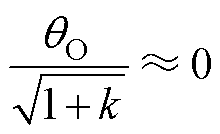（26）
根据LLC谐振变换器的原理可知，上述简化条件会使得输出电流计算值偏高，因此在推导Ion关于fn的表达式时，需在标幺值处理上进行互补简化，使其标幺基准值增大为原来的M倍，即
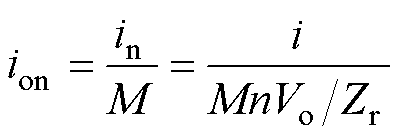（27）
综上所述，基于简化时域分析方法求出PO/OPO模式间的边界解析式为
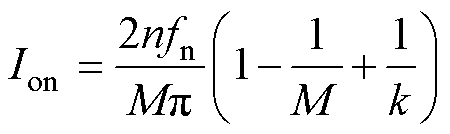（28）
类似地，在NP模式下，P模态开始时的vm瞬时值应大于nVo，Lm输出被钳位。因此，NP模式到NOP模式的临界条件同式（23）。
同理，联立所有边界条件和相关电压电流表达式可通过求解方程组得到边界解析式，由于边界模式为NP模式，不存在O模态，所以无需简化条件即可得到最终的边界解析式为
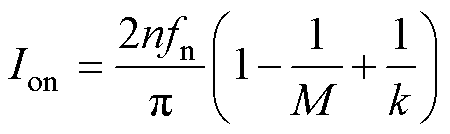（29）
式（28）和式（29）分别作为用于识别PO/OPO和NP/NOP模式的边界解析式，给定参数后，代入实时获得的fn和M即可得到Ion的边界判断值，将其分别设为Ion.b1和Ion.b2。
本文利用PLECS软件，对于两种模式边界曲线，不同工况下工作在三种典型模式的SR开关信号进行仿真分析，并与上述理论推导的结果进行 对比。
基于简化时域分析得出的边界解析式和仿真得到的用于模式识别的边界曲线和工作区域如图6所示，其中最大误差率仅为0.61%，可看出所提方法的准确性和有效性。
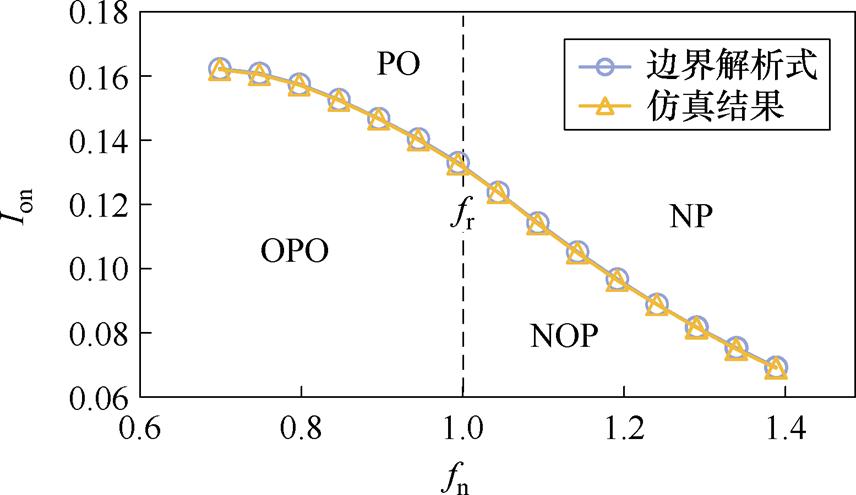
图6 边界解析式和仿真所得模式边界曲线比较
Fig.6 Comparison of model boundary curves from theoretical analysis and simulation
3.2.1 PO模式
如图7所示为PO模式下采用的简化时域分析方程组求得的SR导通占空比与仿真结果的对比。
分析得到，工作在PO模式时，导通占空比较为准确，且随着负载增加误差减小，但在远低于谐振频率的区域内准确性略差，这是因为不再完全符合时域方程组的简化近似条件式（11）和式（12）。
图8为本文所提出方法及文献[22]中所计算的导通占空比与仿真结果的对比，可以看出本文所提出方法的准确度较高，在各种负载情况下的误差均最小。
3.2.2 NP模式
在NP模式下，由于存在精确解析解，因此从图9可看出最大的误差率仅为0.16%，可以精确地生成SR驱动信号，其中DSR_delay=0.5-DSR_on。
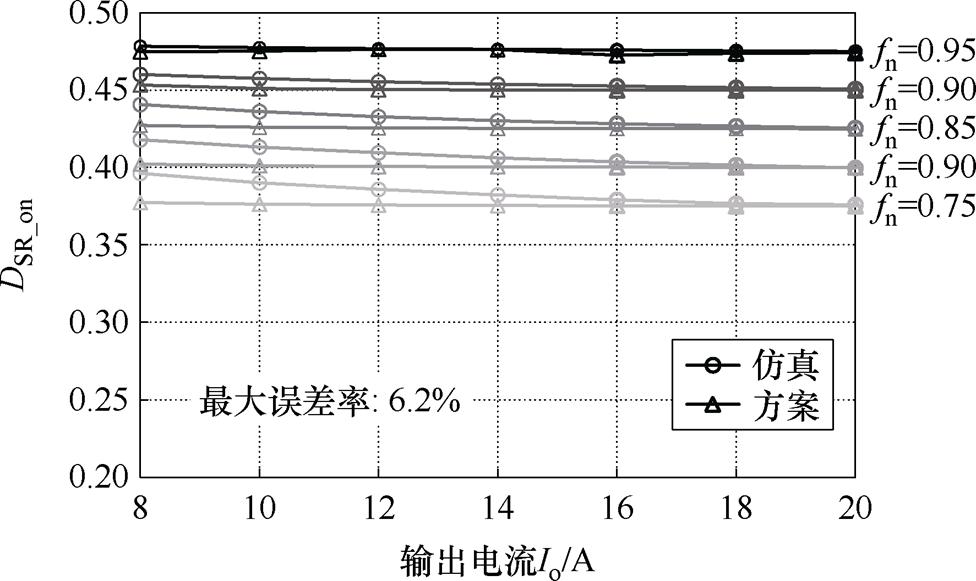
图7 PO模式下所提SR方案的SR导通占空比和仿真结果对比
Fig.7 Comparison of model boundary curves from theoretical analysis and simulation
图8 fn=0.85情况下不同SR方案的SR导通占空比与仿真结果比较
Fig.8 Comparison of the SR-on duty cycle of the different SR scheme and the simulation results when fn=0.85
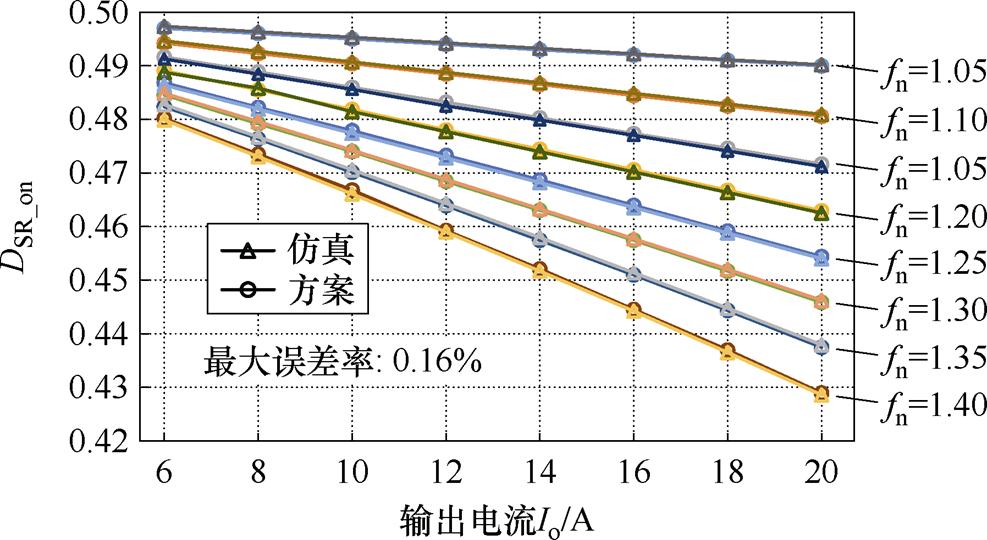
图9 NP模式下所提SR方案的SR导通占空比和仿真结果对比
Fig.9 SR-on duty cycle of the proposed SR scheme and the simulation results in the NP mode
3.2.3 OPO模式
OPO模式下，采用多项式拟合得到的DSR_on和DSR_delay与仿真结果比较如图10、图11所示。从图10可以看出，方案推导得到的SR导通占空比与仿真结果基本一致，但在模式切换的边界处准确性略差，最大误差率仍不超过1%，符合精度要求。
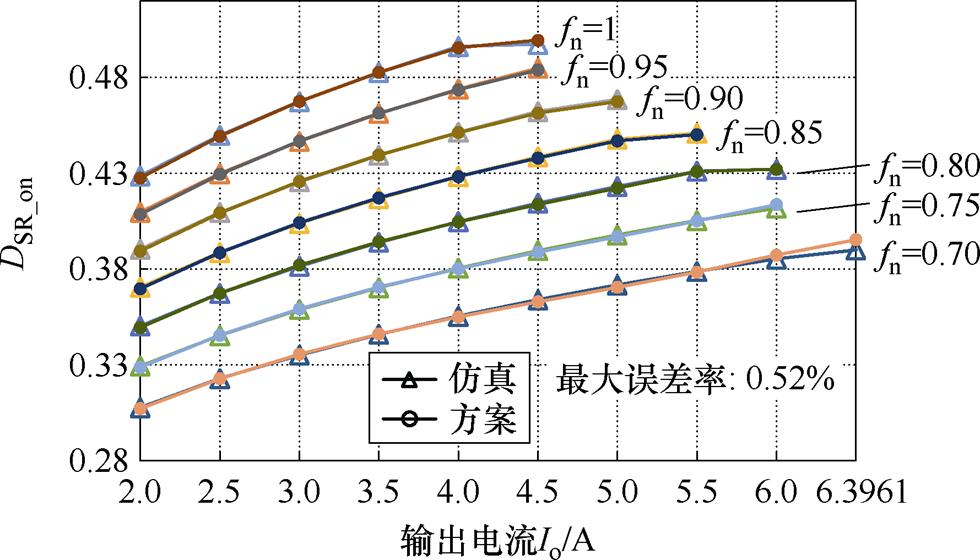
图10 OPO模式下所提SR方案的SR导通占空比和仿真结果对比
Fig.10 SR-on duty cycle of the proposed SR scheme and the simulation results in the OPO mode
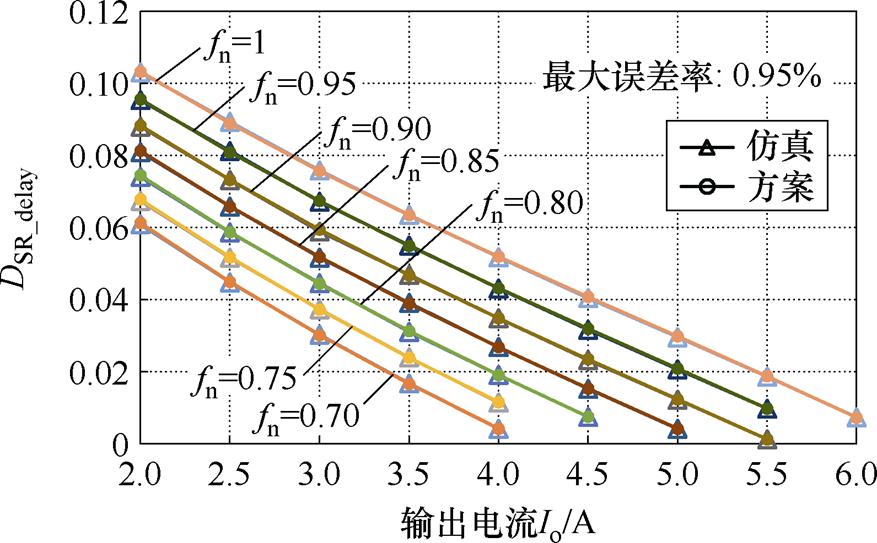
图11 OPO模式下所提SR方案的SR延迟导通占空比和仿真结果对比
Fig.11 SR-delay duty cycle of the proposed SR scheme and the simulation results in the OPO mode
由图11可以看出，方案推导得到的SR延迟导通占空比误差率略高于导通占空比，这是由于OPO模式中O1模态的持续时间占空比很小，一定程度上放大了误差率。
与传统的同步整流驱动方案不同，本设计方案无需高频采样电路，只需输入当前工况下的开关频率和输出电压电流采样即可实现。
本文所提出的基于时域模型的SR控制方案流程如图12所示，首先，根据当前fn和采样计算Ion识别LLC谐振变换器的不同工作模式，并执行对应的计算模块，在其他区域内关断SR。其中，当处于PO工作区域时，代入求解式（14）得到DSR_on；识别出工作模式为NP时，代入式（20）求解得到DSR_delay；当工作在OPO模式下，利用拟合多项式（21）和式（22）计算得到DSR_on和DSR_delay，最终获得较为精确的SR门级驱动信号。
以上控制流程设计旨在通过简化而精确的时域分析，优化SR系统的控制策略，兼顾时域方程组的简单性和准确性，确保在不同工作条件下获得最佳性能。
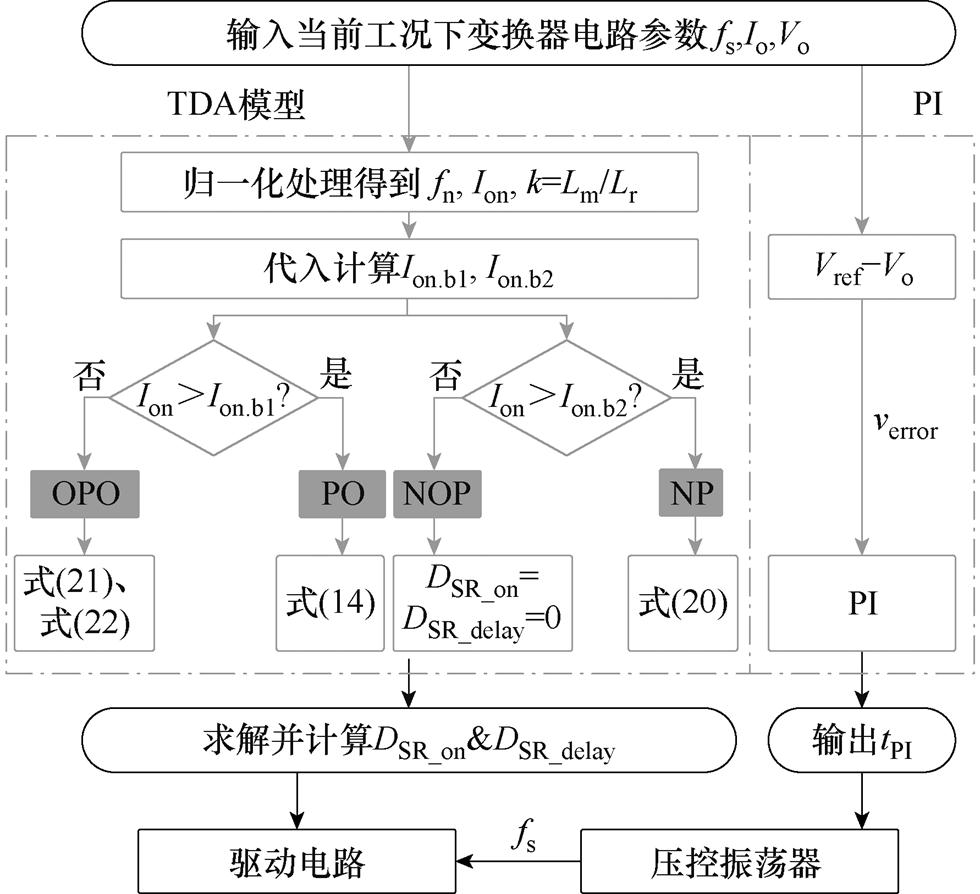
图12 所提出的SR驱动方案控制流程框图
Fig.12 Flow chart of the proposed S&A TDA-based SR control scheme
为了验证所提出的基于时域模型的简化精确SR控制方案的有效性，搭建了如图13所示的实物样机，具体参数见表2。
图13 实物样机
Fig.13 Hardware prototype
表2 实验样机参数
Tab.2 Specifications of prototype
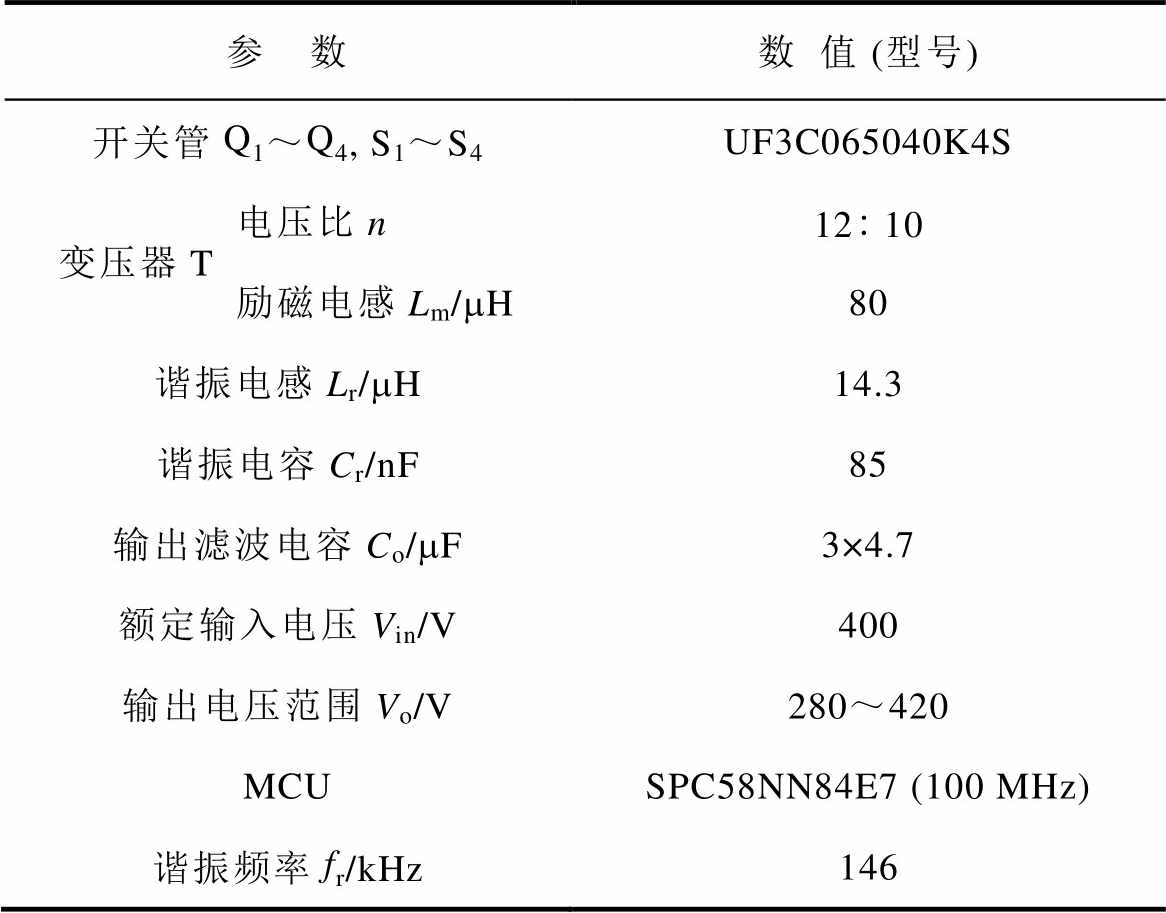
参 数数值 (型号) 开关管Q1～Q4, S1～S4UF3C065040K4S 变压器T 电压比n1210 励磁电感Lm/mH80 谐振电感Lr/mH14.3 谐振电容Cr/nF85 输出滤波电容Co/mF3×4.7 额定输入电压Vin/V400 输出电压范围Vo/V280～420 MCUSPC58NN84E7 (100 MHz) 谐振频率fr/kHz146
图14展示了在fn=0.8的情况下，400 V稳定电压输入时，负载电流从20 A切换至0.8 A时LLC谐振变换器模式切换的暂态关键波形，由PO模式切换至OPO模式，从放大后的波形可以看出，SR驱动信号在瞬态过程中依然有效且稳定，该方法提供了可靠的SR驱动信号，并具有优异的动态响应。
图14 欠谐振区域内负载电流从20 A切换到0.8 A时LLC谐振变换器模式切换瞬态SR实验波形
Fig.14 Experimental waveforms of mode-switching transient SR of LLC converter when the load current is switched from 20 A to 0.8 A in the below resonance region
同样地，在fn=1.2、输入电压为400 V的情况下由20 A切换到0 A，其过程波形如图15所示。其中LLC谐振变换器在输出电流Io=2.8 A时从NP模式切换至NOP工作模式，并关闭SR。由图15可知，在整个暂态过程中，该方法可以实现不同模式的识别，并采用相应的策略精确，有效地驱动二次侧SR，动态响应良好。
图15 过谐振区域内负载电流从20 A切换到0 A时LLC谐振变换器模式切换瞬态SR实验波形
Fig.15 Experimental waveforms of mode-switching transient SR of LLC converter during load current switching from 20 A to 0 A in the above resonance region
图16～图18展示了LLC谐振变换器分别工作在OPO、PO和NP三种典型模式下的两种不同工况稳态实验波形。图16和图17中，SR off对应O模态的持续时间，SR on对应P模态的持续时间。此外，图18中的SR off对应N模态持续时间。可以看出，二次侧SR开通的时序符合理论分析的结果，在三种主要模式下几乎没有额外的二极管导通时间或额外的导通周期，实现了理想的SR精确驱动。
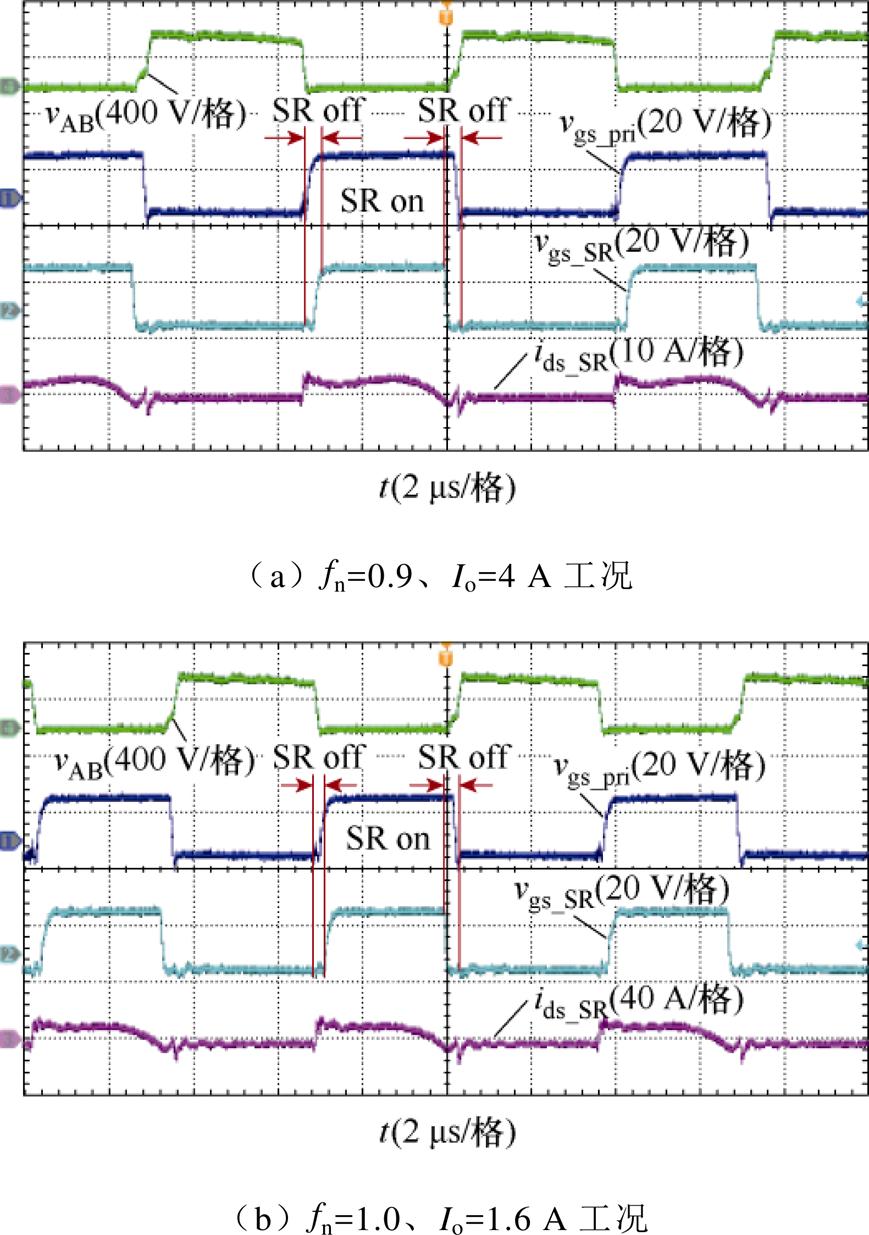
图16 工作在OPO模式下的SR稳态关键波形
Fig.16 SR steady state critical waveforms operating in OPO mode
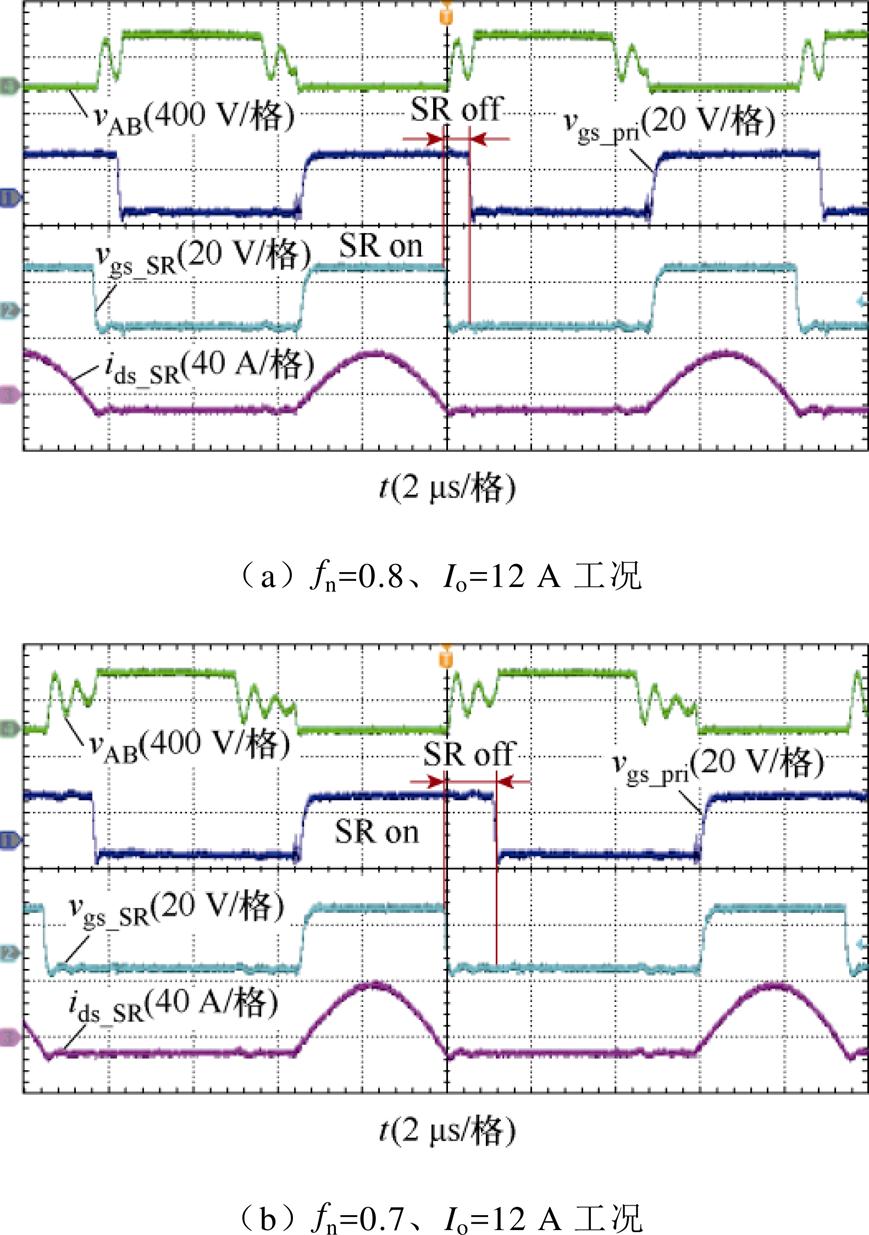
图17 工作在PO模式下的SR稳态关键波形
Fig.17 SR steady state critical waveforms operating in PO mode
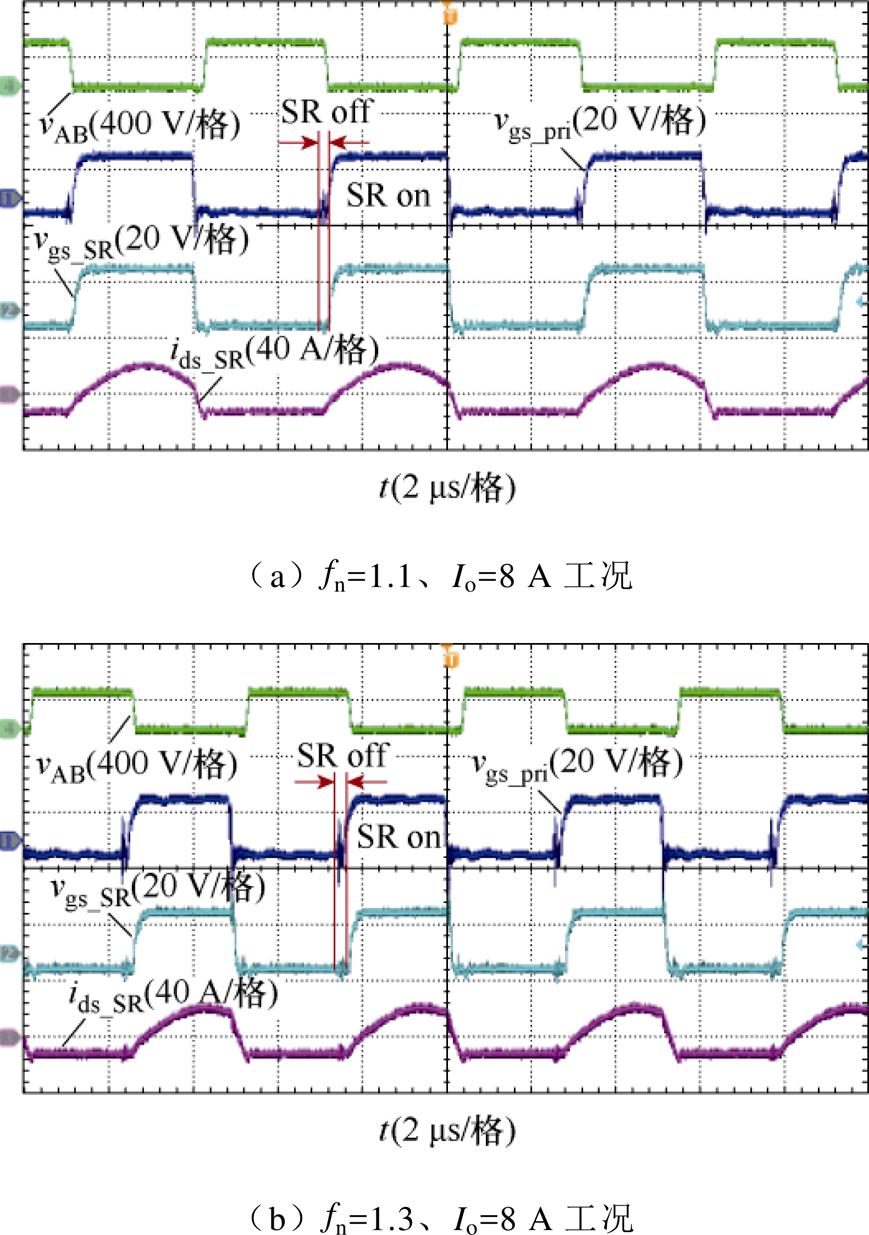
图18 工作在NP模式下的SR稳态关键波形
Fig.18 SR steady state critical waveforms operating in NP mode
图19a、图19b分别为欠谐振区域和过谐振区域内，基于简化精确时域模型的SR驱动方案计算结果与实验得到的SR实际导通或延迟导通时间对比。其中，通过观测实验波形中的二次侧SR漏源电流ids_SR与vAB的时序关系可以确定SR的DSR_on和DSR_delay。
但由于实际电路中的寄生参数等因素的影响，导致实验和仿真结果略有误差，随着负载增加，误差逐渐缩小，平均误差不超过5%，因此所提出的方案适用于各种负载情况，且在重载条件下准确度更高。
图19 所提出策略的计算结果与实验数据的对比
Fig.19 Comparison of computational results of the proposed strategy with experimental data
表3比较了本文所提出的SR控制算法与文献[23, 25]中模型法的运算时间，可以发现本文基于简化精确时域模型方法的计算量较小，算法的运算时间占控制周期的比例很小，约为1%。文献[23]基于曲线拟合查表法，在控制芯片的计算耗时较短，但没有对不同的工作模式进行识别分析，损失了精度。
表3 不同SR控制算法运算时间比较
Tab.3 Comparison of computation time of different SR control algorithms（单位: ns）
算法种类运行时间 文献[23]52 文献[25]92 所提出的方案BRR (PO) 区域94 BRR (OPO) 区域35 ARR区域95
在额定功率下测试了采用本文所提出的数字SR算法、文献[22]中的SR方案和不采用SR策略的LLC谐振变换器效率曲线。变换器的效率测试是通过测试输入电流与电压以及输出电流与电压，并将其分别相乘得到输入功率和输出功率来实现的。其中，输入输出电压分别通过万用表（Fluke 101基本数字万用表）测量变换器输入输出端口电压得到，输入输出电流分别通过可编程电源以及数字负载（IT6000C双向可编程直流电源）的电流读数获得。效率曲线的对比如图20所示，可以看出，效率在全工作区域内得到了提升，采用本文方案后的峰值效率可达到96.26%。与无SR方案相比，在BRR区域和ARR区域的最大效率分别提高了约1%和0.9%，即损耗降低了66 W和59.4 W。与文献[22]中的SR方案相比，随着变换器远离谐振点工作，所提方法的效率不断提高，在BRR和ARR区域的效率分别提升了约0.1%和0.2%，即减少7 W和13 W的损耗。这是由于文献[22]基于FHA模型，所提策略下的SR MOSFET的导通时序过早，使得LLC转换器的工作类似于谐振双有源桥变换器，导致无功功率的产生，进而增加额外的导通损耗、变压器损耗和零电压开关特性的损耗。
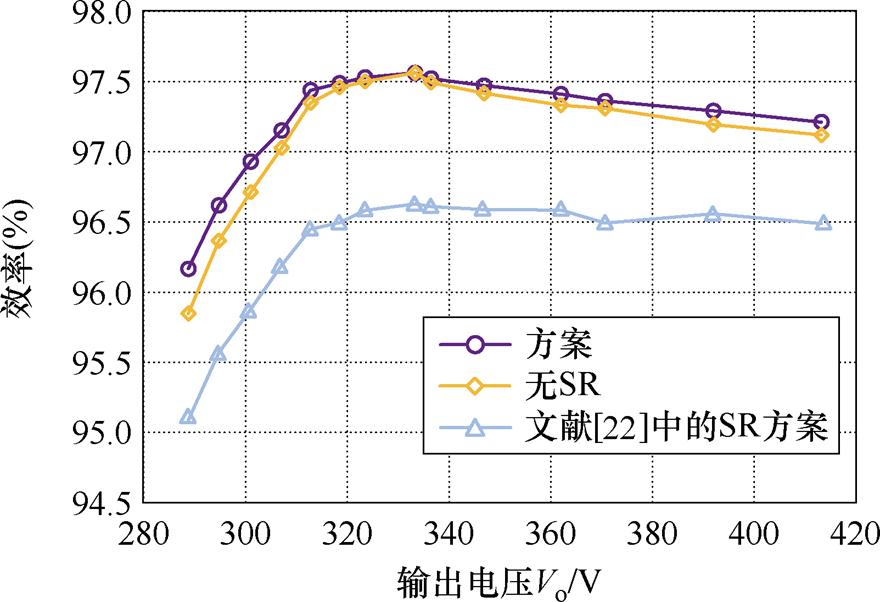
图20 额定功率下不同输出电压情况所提出策略与无同步整流方案的效率曲线对比
Fig.20 Comparison of the efficiency curves of the proposed strategy with and without synchronous rectification scheme for different output voltage cases at rated power
本文基于时域模型研究了一种针对PFM下的全桥LLC谐振变换器的新型无高频采样SR驱动方案。
1）通过简化和推导时域方程，得到了准确的SR导通或延迟占空比表达式，实现了数字控制器对SR导通时序的在线计算，从而有效地驱动SR。
2）采用简化时域分析法推导得到了精确的模式边界解析式，有利于准确识别工作模式并调整SR驱动信号，避免了不必要的损耗，整体平均误差不超过3%。
3）该方法在全频率范围内具有更高的精度，可以适应各种负载情况，通过仿真和实验验证，展示了该方案在稳态准确性和动态可靠性方面的优势。
4）与其他无高频采样方案相比，该方法在BRR区域和ARR区域分别提高了1%和0.9%的效率，最终测试的峰值效率高达96.26%。与其他基于模型的高频采样SR方案相比具有更高的效率，在BRR和ARR区域的效率分别提升了约0.1%和0.2%。
综上所述，这项研究为LLC谐振变换器在电动汽车充电装置中提供了有效的解决方案，有望推动电动汽车技术的进一步发展。
参考文献
[1] Li Haoran, Zhang Zhiliang, Wang Shengdong, et al. A 300-kHz 6.6-kW SiC bidirectional LLC onboard charger[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(2): 1435-1445.
[2] 李彬彬, 王志远, 张丙旭, 等. 采用辅助变压器的可调压谐振零电压零电流开关变换器[J]. 电力系统自动化, 2022, 46(7): 160-169.
Li Binbin, Wang Zhiyuan, Zhang Bingxu, et al. Voltage-regulatable resonant zero-voltage zero- current switching converter with auxiliary trans- former[J]. Automation of Electric Power Systems, 2022, 46(7): 160-169.
[3] 桑汐坤, 王懿杰, 徐殿国. 基于输入并联输出串联的高效高升压比DC-DC变换器[J]. 电工技术学报, 2023, 38(20): 5488-5502.
Sang Xikun, Wang Yijie, Xu Dianguo. High- efficiency high voltage gain DC-DC converter based on input parallel and output series connection[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5488-5502.
[4] 陈梦颖, 陈博, 刘超, 等. 一种应用于移相调制同步整流型谐振变换器的轻载效率优化分析方法[J]. 电工技术学报, 2025, 40(6): 1900-1914.
Chen Mengying, Chen Bo, Liu Chao, et al. A light load efficiency optimal analysis method applied to phase-shift-modulated synchronous rectification[J]. Transactions of China Electrotechnical Society, 2025, 40(6): 1900-1914.
[5] 何晓坤, 胡仁杰, 陈武. 一种适用于新能源中压直流汇集的无环流零电流软开关三电平谐振式复合全桥变换器[J]. 电工技术学报, 2023, 38(19): 5274- 5287.
He Xiaokun, Hu Renjie, Chen Wu. A novel circulating current free zero current switching three- level resonant composite full bridge converter for new energy medium voltage DC collection system[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5274-5287
[6] 鲁静, 同向前, 尹军, 等. L-LLC谐振型双向DC- DC变换器轻载优化控制策略研究[J]. 电工技术学报, 2022, 37(17): 4458-4465.
Lu Jing, Tong Qianqian, Yin Jun, et al. The optimal control strategy for L-LLC bi-directional resonant DC-DC converter under light load[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4458- 4465.
[7] Wei Yuqi, Luo Quanming, Mantooth H A. Syn- chronous rectification for LLC resonant converter: an overview[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 7264-7280.
[8] Yu Haiming, Xie Xiaogao, Xu Sen, et al. A novel synchronous rectifier driving scheme for LLC converter based on secondary rectification current emulation[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(4): 3825-3835.
[9] 吕征宇, 李佳晨, 杨华. 新型LLC谐振变换器数字同步整流驱动方式[J]. 电机与控制学报, 2018, 22(1): 16-22.
Lü Zhengyu, Li Jiachen, Yang Hua. Digital syn- chronous rectification driving method for LLC resonant converter[J]. Electric Machines and Control, 2018, 22(1): 16-22.
[10] 孙城皓, 孙秋野, 王睿, 等. 基于拓展型双曲正切函数的全桥LLC变换器大信号建模方法[J]. 电工技术学报, 2023, 38(1): 234-245.
Sun Chenghao, Sun Qiuye, Wang Rui, et al. Large- signal modeling method of full-bridge LLC converter based on extended hyperbolic tangent function[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 234-245.
[11] Wu Xinke, Hua Guichao, Zhang Junming, et al. A new current-driven synchronous rectifier for series- parallel resonant (LLC) DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1): 289-297.
[12] Xu Shengyou, Qian Qinsong, Tao Tao, et al. Syn- chronous rectification using resonant capacitor voltage for secondary side resonant active clamp flyback converter[C]//2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 2926-2931.
[13] Hsu J D, Ordonez M, Eberle W, et al. LLC syn- chronous rectification using resonant capacitor voltage[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10970-10987.
[14] Mohammadi M, Ordonez M. Synchronous recti- fication of LLC resonant converters using homopolarity cycle modulation[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1781-1790.
[15] 王广旭. 具有寄生电感补偿的LLC同步整流电路设计[D]. 南京: 东南大学, 2021.
Wang Guangxu. Design of LLC synchronous rectifier circuit with parasitic inductance compensation[D]. Nanjing: Southeast University, 2021.
[16] Feng Weiyi, Lee F C, Mattavelli P, et al. A universal adaptive driving scheme for synchronous rectification in LLC resonant converters[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3775-3781.
[17] Ivensky G, Bronshtein S, Abramovitz A. Approximate analysis of resonant LLC DC-DC converter[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3274-3284.
[18] Fang Xiang, Hu Haibing, Shen Z J, et al. Operation mode analysis and peak gain approximation of the LLC resonant converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1985-1995.
[19] 王志刚, 董长城, 侯凯, 等. 全桥LLC电路时域模型及其分析[J]. 电力系统自动化, 2018, 42(20): 138- 143, 164.
Wang Zhigang, Dong Changcheng, Hou Kai, et al. Time domain model of full bridge LLC circuit and its analysis[J]. Automation of Electric Power Systems, 2018, 42(20): 138-143, 164.
[20] 李浩然, 崔超辉, 王生东, 等. 基于二阶拟合模型的SiC双向LLC数字同步整流控制[J]. 电工技术学报, 2022, 37(24): 6191-6203.
Li Haoran, Cui Chaohui, Wang Shengdong, et al. Two-order fitting model-based digital synchronous rectifier control for SiC bidirectional LLC con- verter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6191-6203.
[21] Li Haoran, Wang Shengdong, Zhang Zhiliang, et al. A bidirectional synchronous/asynchronous rectifier control for wide battery voltage range in SiC bidi- rectional LLC chargers[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 6090-6101.
[22] Zhu Xinyi, Li Haoran, Zhang Zhiliang, et al. A sensorless model-based digital driving scheme for synchronous rectification in 1-kV input 1-MHz GaN LLC converters[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8359-8369.
[23] 汪洪亮, 高文勇, 唐伟, 等. 基于时域分析的LLC同步整流控制研究[J]. 电力电子技术, 2023, 57(8): 104-107.
Wang Hongliang, Gao Wenyong, Tang Wei, et al. Research on LLC synchronous rectification control based on time domain analysis[J]. Power Electronics，2023, 57(8): 104-107.
[24] Pei Long, Jia Lixin, Wang Laili, et al. A novel dual-feedforward strategy for both the inverter- control and rectifier-control of LLC converters based on time-domain model[C]//2023 IEEE 14th Inter- national Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 2023: 1103-1108.
[25] Li Haoran, Wang Shengdong, Zhang Zhiliang, et al. Bidirectional synchronous rectification on-line calcu- lation control for high voltage applications in SiC bidirectional LLC portable chargers[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(5): 5557- 5568.
[26] 张朝阳. 基于多变量的全桥LLC谐振变换器混合控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
Zhang Chaoyang. Research on hybrid control strategy of full-bridge LLC resonant converter based on multivariable[D]. Harbin: Harbin Institute of Tech- nology, 2020.
[27] 陈孝莺, 许国, 韩华, 等. 基于脉宽调制的电流断续型谐振变换器[J]. 电工技术学报, 2022, 37(24): 6252-6261.
Chen Xiaoying, Xu Guo, Han Hua, et al. Dis- continuous current mode resonant converter with pulse width modulation control[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6252- 6261.
[28] Chen Jie, Xu Junzhong, Tang Haiguo, et al. Second harmonic voltage suppression for LLC converter in dual-stage single-phase rectifier based on voltage- oriented state plane feedforward control[J]. IEEE Transactions on Power Electronics, 2023, 38(8): 9329-9334.
[29] 程鹤, 徐恺, 李朋圣, 等. 三相CLLC谐振变换器磁集成平面变压器设计与优化[J]. 电工技术学报, 2024, 39(12): 3774-3786.
Cheng He, Xu Kai, Li Pengsheng, et al. Design and optimization of three-phase CLLC resonant converter with magnetic integrated planar transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3774-3786.
Abstract The LLC converter plays a pivotal role in the infrastructure supporting electric vehicles, where efficiency and reliability are paramount. Its ability to efficiently transfer energy between different voltage levels makes it particularly suitable for EV charging stations, where power conversion efficiency directly impacts operational costs and environmental sustainability.
Synchronous rectification has emerged as a promising strategy for optimizing LLC converter performance. By replacing traditional diode rectifiers with active switches that operate synchronously with the converter's switching frequency, synchronous rectification minimizes energy losses and improves overall efficiency. However, existing synchronous rectification methods have faced challenges, such as complex control algorithms, sensitivity to load variations, and the need for high-frequency sampling.
Unlike conventional approaches that rely on high-frequency sampling for precise timing control, the novel synchronous rectification scheme utilizes a streamlined time-domain analysis. This approach dynamically adjusts the timing of the synchronous rectifier based on real-time feedback from the LLC converter's operating modes, ensuring optimal efficiency across a wide range of operating conditions with high-frequency sampling and alleviating the computational burden.
By reducing the complexity of control algorithms and eliminating the need for high-frequency sampling circuits, the scheme not only lowers manufacturing costs but also enhances reliability by reducing potential points of failure. This simplification is particularly advantageous in high-power applications like EV charging stations, where robustness and operational uptime are essential.
Simulation studies have validated the effectiveness of the proposed scheme under different load conditions and frequencies. Simulations have shown significant efficiency improvements compared to traditional methods, highlighting the scheme's potential to reduce energy losses and improve overall system performance.
Furthermore, experimental validation using a 6.6 kW prototype shows that the proposed scheme delivers consistent and efficient operation under steady-state and dynamic conditions, further supporting its potential for commercial EV charging infrastructure integration.
The adoption of the proposed synchronous rectification scheme promises to enhance the efficiency and reliability of LLC converters and accelerate the transition to electric mobility. As governments and industries worldwide prioritize sustainability goals and seek to reduce carbon footprints, improvements in energy conversion technologies play a crucial role in supporting the widespread adoption of electric vehicles.
In conclusion, the synchronous rectification scheme represents a significant step in evolving LLC converters for electric vehicle charging infrastructure. By overcoming traditional limitations and leveraging streamlined control strategies, the scheme enhances performance and contributes to the sustainability of transportation systems. As research continues to refine and optimize power conversion technologies, the ongoing advancements in LLC converter designs underscore their pivotal role in shaping a cleaner, greener future for global transportation.
Keywords：LLC resonant converter, time domain analysis, synchronous rectification, mode recognition
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240671
收稿日期 2024-04-29
改稿日期 2024-06-25
张宇鑫 女，2001年生，硕士研究生，研究方向为 LLC 谐振变换器的分析与控制。
E-mail: zhangyuxin9@sjtu.edu.cn
王 勇 男，1975年生，教授，博士生导师，研究方向为新能源变换控制与汽车电子等。
E-mail: wangyong75@sjtu.edu.cn（通信作者）
（编辑 陈 诚）