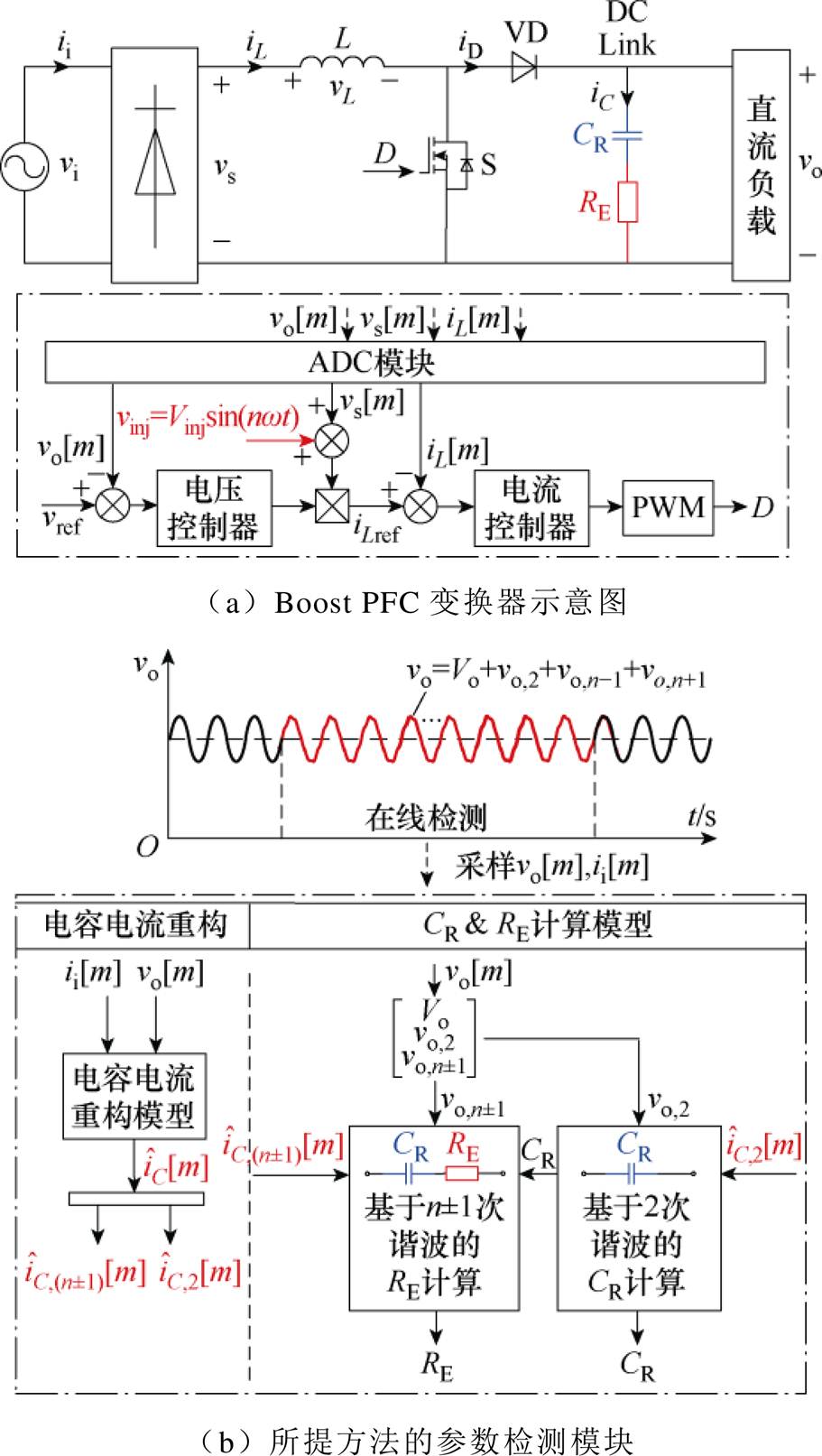
图1 单相Boost PFC变换器的主电路和所提出的谐波注入的检测方案
Fig.1 Main circuit of single-phase Boost PFC converter and the proposed harmonic injection detection scheme
摘要 电解电容是功率变换器系统中最易失效的元件,通过实时检测其电容CR和等效串联电阻RE,明确电容退化状态对于提高系统可靠性至关重要。为此该文提出一种基于“去过零区间”的改进谐波注入电容参数在线检测方法。首先,基于母线电压谐波响应提出谐波电容电流重构方法,构建无电容电流采样的CR和RE参数计算模型。其次,高次谐波引入会带来电流过零畸变问题,直接影响了电容电流重构的准确度,提出“去过零区间”改进谐波注入方式,进一步改进电容参数检测精度。最后,搭建一台48 W/72 W/144 W的单相Boost功率因数校正(PFC)实验样机,不同工况下实验结果表明,改进谐波注入方式的检测误差控制在5%以内,所提电容参数检测法基于交直流功率平衡原理,适用于常见直流母线系统。
关键词:直流母线电容 等效串联电阻RE和电容CR 改进谐波注入 在线检测
Boost功率因数校正(Power Factor Correction, PFC)变换器是在交直流系统中应用最普遍的变换 器[1-4],而其直流母线电解电容易失效性则会引起系统失稳,甚至崩溃[5]。因此实时检测电解电容(Aluminum Electrolytic Capacitor, AEC)的使用寿命,及时更换即将失效的电解电容,对提高PFC电源的可靠性具有重要意义[6]。
特征参数容值CR和等效串联电阻RE是衡量电解电容寿命的重要技术指标[7]。随着电容使用时间变长,其电解液会挥发,表现为CR下降和RE增大,而且RE增加相对于CR变化更为显著[8-9],因此许多关于CR和RE的检测方法被相继提出[10-14]。
根据参数检测方法对变换器的影响程度可将其分为离线检测和在线检测,两种方法都是通过直接或间接计算CR和RE来评估电容的健康状态[10]。对于离线检测方法,文献[11-12]将信号发生器、电容和附加电阻组合成一个回路,然后通过采样电容两端的正弦电压波形,采用牛顿迭代法计算该电容的CR和RE。文献[13]采用阻抗矢量计算基于离线傅里叶变换的CR和RE。文献[14]设计了一种电容充放电电路,并采用最小二乘法进行CR和RE的离线计算。这些方法在操作上相对简单且测试成本较低,但是需要定期将电容从功率变换器系统中移除或在变换器停机时进行测试,给实际操作造成了很大的不便,难以广泛推广。所以在变换器长时间正常工作的情况下,离线检测方法并不适用于电容参数的检测,故现有大多数检测方法为在线检测。
相比离线检测,在线检测无须停止设备运行,能够反映不同工作条件下的电容参数变化情况,适用于变换器长期正常工作时的场合,更具有研究价值。因此,通过在线检测直流母线电容CR和RE的值,可在线准确地评估其健康状况,这对提高功率变换器的稳定性和可靠性至关重要。目前已有学者提出了两大类用于AEC的CR和RE在线检测方法[15-31]:一种是利用系统固有的工作信息进行参数检测[15-23];另一种是利用附加信号注入的高次谐波响应信息进行参数检测[24-31]。一般就交直流系统而言,通常可以利用固有低频信息检测CR参数,通过中高频信息检测RE参数。
文献[15]通过对电路原始的电压电流信号进行采样,利用低频纹波检测CR和RE,但电容的低频阻抗不利于准确检测RE。因此,可以利用高频开关纹波信息对RE进行检测[16-19],但高频纹波的采集需要高精度触发电路和额外的复杂采样电路[20-23]。为实现同步检测CR和RE,学者们提出了利用谐波信号注入的检测方法[24-31],通过谐波信号来构建中频域的谐波模型进而实现CR和RE的同步检测。在此基础上,文献[24-25]利用LMS算法对注入的不同次谐波计算出的CR和RE做了寿命估计分析,结果较为准确,但谐波信号频率较为接近,需要更高要求的带通滤波器。文献[26]提出了基于开关管短路电流的CR和RE估计,然而它需要对短路电流进行采样,RE的估计精度较低。文献[27]通过向电机系统注入谐波信号进而对直流侧电容上的电压及电流纹波信息进行采样,实现对电机驱动系统直流侧电容参数检测,同样的电容器检测方案进一步应用于电容器组的健康评估[28]。以上两种方法都需要对电容所在支路的电压电流进行采样,带来高检测成本的同时复杂性也大幅提高。因此,在线检测方法需要特别关注两个核心问题:一是计算思想是否依赖于电容器所处的电路布局,对其他类型的电路结构是否适用还有待进一步讨论;二是不同环境下对测量结果进行改进时,是否充分考虑被测对象的实际情况。
Boost PFC变换器是一典型的交直流应用对象,在工程中对其AEC检测受到普遍关注。文献[29-30]通过在Boost主电路中注入正弦谐波信号,检测CR和RE参数,得到在不考虑电流畸变的情况下的计算模型,但此时参数检测精度较低,并不能满足行业检测标准。原因是当注入高频谐波信号时,会导致其输入电流无法及时跟踪上参考电流,出现电流过零畸变现象[31]。因此,利用谐波注入法检测CR和RE时需要考虑电流过零畸变对参数检测的影响,但现有的高频谐波注入方式尚无文献关注此问题。
综上所述,本文针对Boost PFC变换器探讨一种基于“去过零区间”改进谐波注入的电容参数在线检测方法。首先为避免对电容电流进行高精度采样,拟基于母线电压谐波响应给出谐波电容电流重构方法,由交直流功率平衡原理进一步推导出无电容电流采样的CR和RE参数计算模型。此外,考虑谐波注入会带来电流过零畸变问题,分析其对电容电流重构准确度的影响,拟提出“去过零区间”改进谐波注入方式,以提高电容参数检测精度。通过仿真讨论明确“去过零区间”注入参数选取,最后搭建一台48 W/72 W/144 W实验样机以验证所提方法的可行性。
图1a为单相Boost PFC变换器的主电路和所提出的谐波注入的检测方案,本文所提变换器的控制方式采用平均电流模式(Average Current Mode, ACM),ACM采用电压电流双闭环结构。图中,vo为直流母线侧的输出电压,vref为参考电压信号;iL为电感电流,iLref为电压外环输出信号和直流侧输入电压vs的乘积,PWM为输出控制的占空比信号,D为开关管S导通占空比,[m]为各变量在不同频率下的信号分量。

图1 单相Boost PFC变换器的主电路和所提出的谐波注入的检测方案
Fig.1 Main circuit of single-phase Boost PFC converter and the proposed harmonic injection detection scheme
在不影响Boost PFC变换器正常工作的前提下,通过在电压外环叠加谐波电压vinj,将谐波电压转换成谐波电流,从而在变换器的电流控制环路中注入奇数n次谐波电流,在谐波响应下输出电压会出现2次、n-1次和n+1次偶次谐波分量,如图1b所示。利用此谐波响应对电容电流进行重构,然后通过低频下2次分量估算CR,通过中频域下n-1次和n+1次分量估算RE,从而同时实现CR和RE的在线检测。这里的电容电压等于输出电压vo,电容电流iC通过功率平衡原理重构获得。图2中,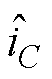 为电容电流重构量,其余参数含义在后续推导时给出,此处不再解释。以下将重点讨论谐波电容电流iC的重构方法以及受电流畸变影响的改进谐波注入的参数计算模型。
为电容电流重构量,其余参数含义在后续推导时给出,此处不再解释。以下将重点讨论谐波电容电流iC的重构方法以及受电流畸变影响的改进谐波注入的参数计算模型。
Boost PFC变换器如图1a所示,右侧蓝色和红色代表的是实际的输出滤波电容器。其阻抗为
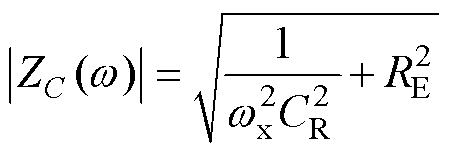 (1)
(1)
式中,wx为电容电流频率。
二极管电流iD为
 (2)
(2)
式中,po为输出瞬时功率;pin为输入瞬时功率;vo为直流母线电容电压。
根据电路的阻抗特性,可以认为二极管电流的交流分量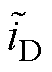 流入电容器,直流分量流入负载。不妨设电容电流重构为
流入电容器,直流分量流入负载。不妨设电容电流重构为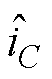 ,则
,则
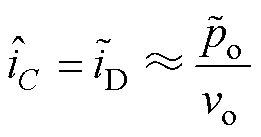 (3)
(3)
输入电压vi为
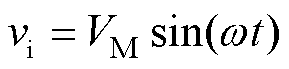 (4)
(4)
式中,VM为输入电压幅值;w 为角频率,w=314 rad/s。
通过电流环在输入电流ii中注入连续谐波,注入后的输入电流表达式为
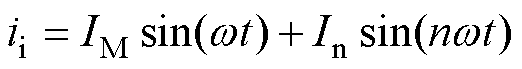 (5)
(5)
式中,IM为输入电流幅值;In为注入电流幅值,根据RE与1/(nwCR) 量值相当来确定注入谐波次数n。则输入功率为
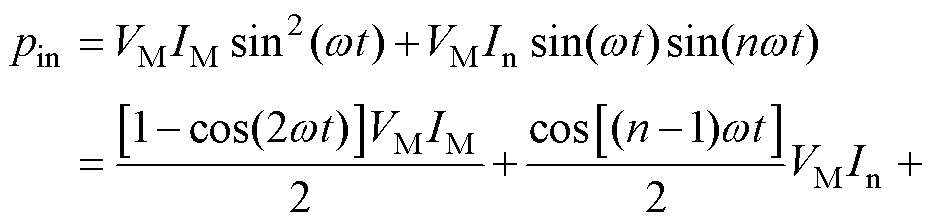
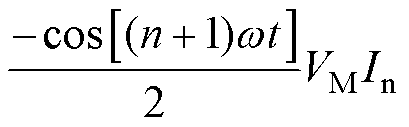 (6)
(6)
不考虑功率损耗,即功率平衡时,存在
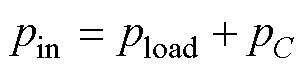 (7)
(7)
式中,pload和pC分别为瞬时直流负载消耗功率和直流母线电容吸收功率。
由式(6)和式(7)得
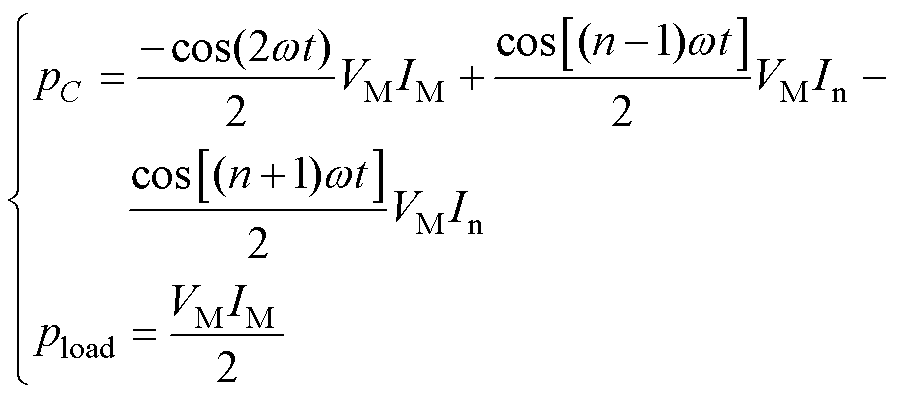 (8)
(8)
则流过二极管的电流iD为
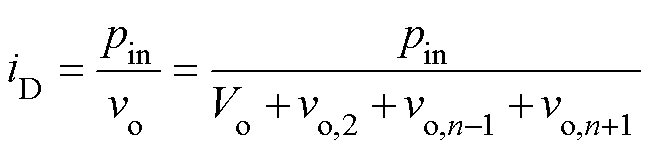 (9)
(9)
式中,vo具体成分包括直流电压Vo、二次工频电压vo,2、n-1次工频电压vo,n-1和n+1次工频电压vo,n+1。
假设所有谐波分量都流经直流母线电容,即重构的电容电流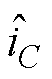 为
为
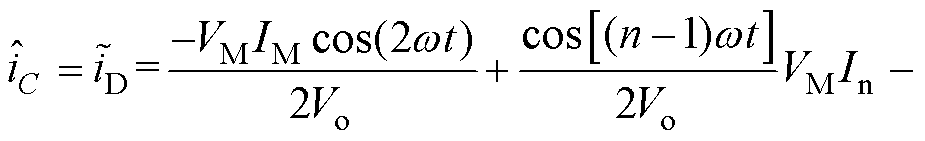
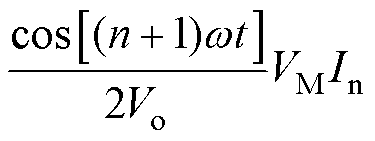 (10)
(10)
则直流母线电容电流重构后的2次、n-1次和n+1次谐波分量可分别表示为
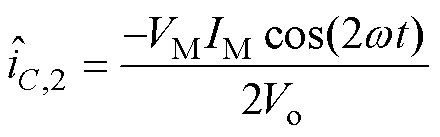 (11)
(11)
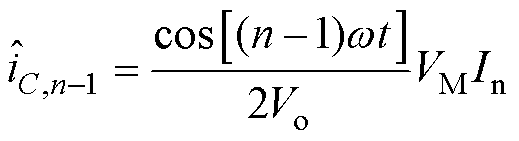 (12)
(12)
 (13)
(13)
由式(1)得,由于CR RE,因此从电容阻抗里很难提取RE,导致检测精度较低。故本文采用电容低频阻抗模型|ZC(2)|估算CR,进一步采用中频域谐波电容阻抗模型|ZC(n-1)|和|ZC(n+1)|估算RE。
RE,因此从电容阻抗里很难提取RE,导致检测精度较低。故本文采用电容低频阻抗模型|ZC(2)|估算CR,进一步采用中频域谐波电容阻抗模型|ZC(n-1)|和|ZC(n+1)|估算RE。
在谐波电流注入Boost PFC系统后,直流母线侧会产生高次谐波电压分裂现象,表现出包含偶数次纹波功率的特征。其中,主要纹波功率集中在2次、n-1次和n+1次工频纹波。基于电容在上述条件下的频域模型,可得出
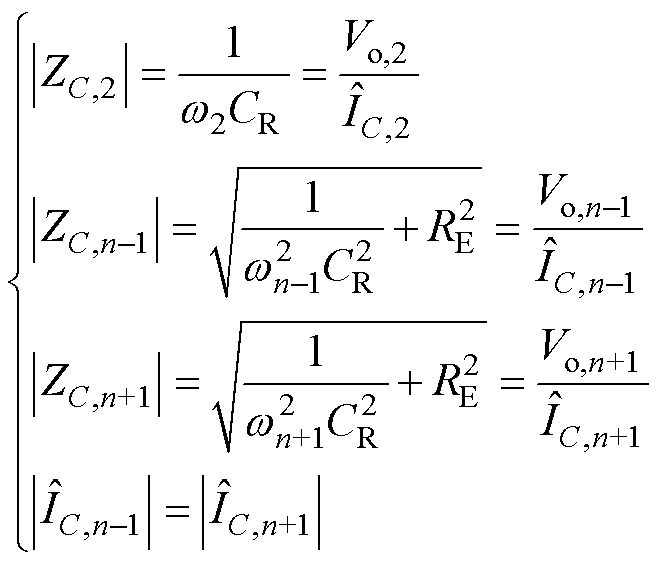 (14)
(14)
式中,Vo,n-1和Vo,n+1分别为n-1和n+1次谐波电压的幅值;wn-1和wn+1分别为n-1和n+1次谐波的角频率。
Vo,2、Vo,n-1和Vo,n+1通过对vo进行离散傅里叶变换(Discrete Fourier Transform, DFT)后得到,方程组式(11)~式(14)联立求解得出CR和RE的计算模型为
 (15)
(15)
谐波电流注入电流环后,会导致电感电流iL无法在过零区间快速跟踪参考电流iLref,电感电流iL的相应波形会发生不对称的过零畸变,过零时刻的不对称畸变如图2所示。另外,高次谐波注入后,电容电流的谐波分量也会受到影响,导致参数计算精度较低。
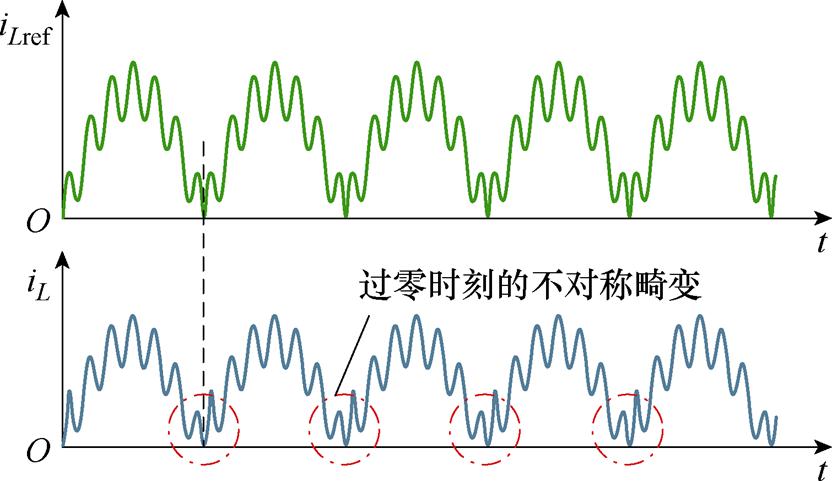
图2 过零时刻的不对称畸变
Fig.2 Asymmetric distortion at zero-crossing moments
考虑在注入n次电流后发生不对称畸变的情况下,输入电流会包含各种奇次谐波(奇对称),表达式为
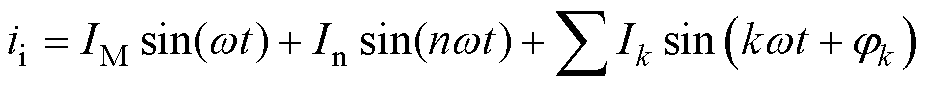
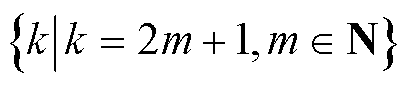 (16)
(16)
式中,Ik为第k次奇次谐波电流的幅值;jk为其相位,k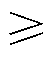 3,且为正整数。
3,且为正整数。
与式(4)~式(9)的处理类似,可得重构的电容电流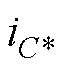 为
为
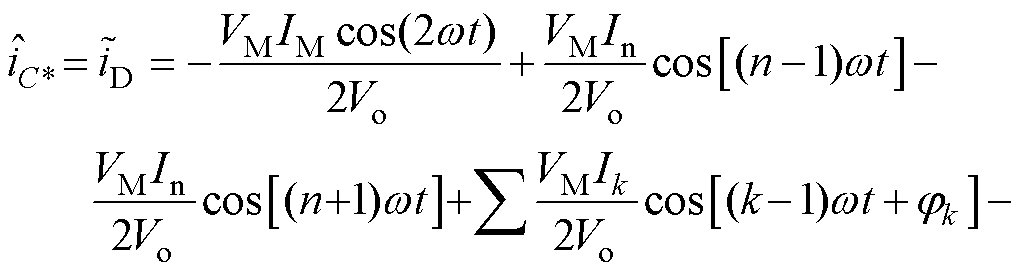
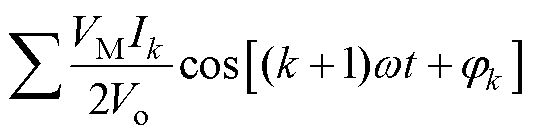 (17)
(17)
由式(17)可得,输入电流的n-2(k=n-2)次谐波影响电容器电流的n-1次谐波分量,电容电流的n-1次谐波分量可表示为
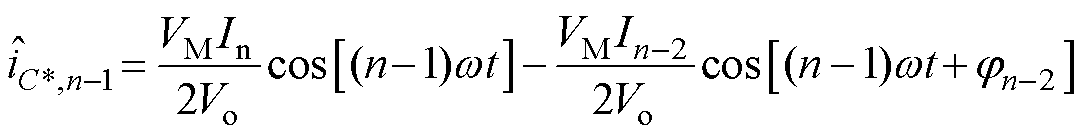 (18)
(18)
同理,电容电流的n+1(k=n+2)次谐波分量可表示为
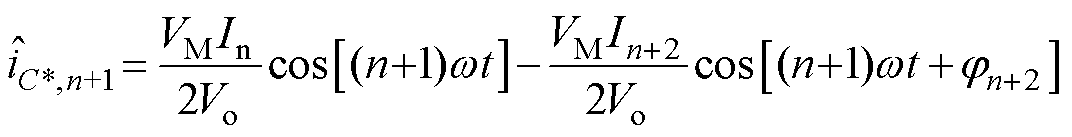 (19)
(19)
可以发现,式(18)的n-1次和式(19)的n+1次涉及到其他次分量,电容电流重构量无法进行直接求解,且无法直观判断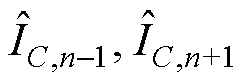 是否相等。因此本节进一步考虑谐波电流注入后,保证其不发生过零畸变的同时实现高精度检测的解决办法。
是否相等。因此本节进一步考虑谐波电流注入后,保证其不发生过零畸变的同时实现高精度检测的解决办法。
为解决谐波注入法带来畸变现象导致参数检测较低的不利影响,本节提出了一种“去过零区间”改进谐波注入的参数检测方法。“去过零区间”注入示意图及宽度e 如图3所示,通过避免在输入电流过零点的区间附近注入谐波信号,可以使输入电流在其他注入区域有效跟踪参考电流信号,从而解决谐波信号全区间注入导致的电流过零畸变问题。
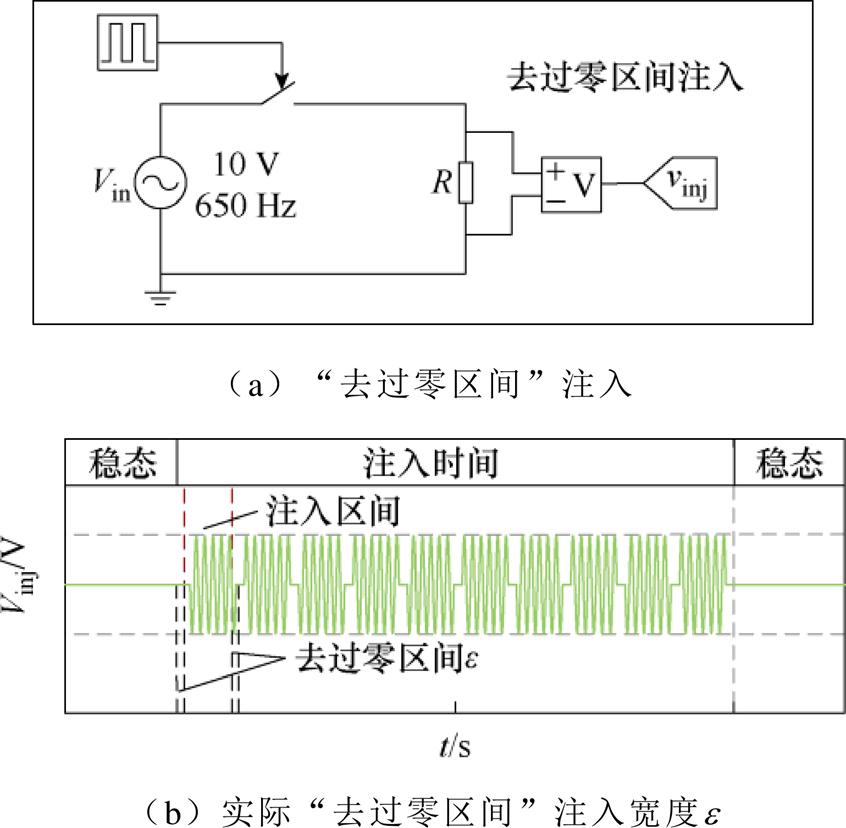
图3 “去过零区间”注入示意图及宽度e
Fig.3 Schematic and width eof zero-crossing removal interval injection
在一个周期 [-p, p] 的区间范围,谐波“去过零区间”注入后的输入电流表达式为
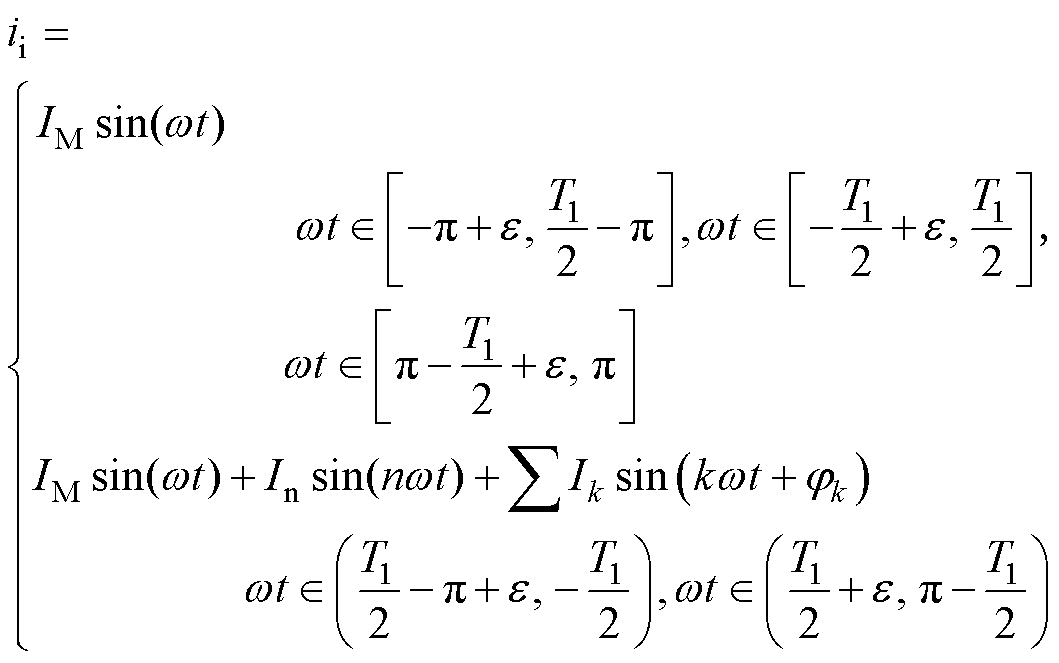 (20)
(20)
式中,e 为“去过零区间”的宽度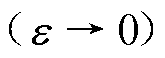 ;T1为注入谐波电流的周期。
;T1为注入谐波电流的周期。
同理按照前面方法,与式(4)~式(9)的处理类似,此时重构的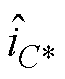 为
为
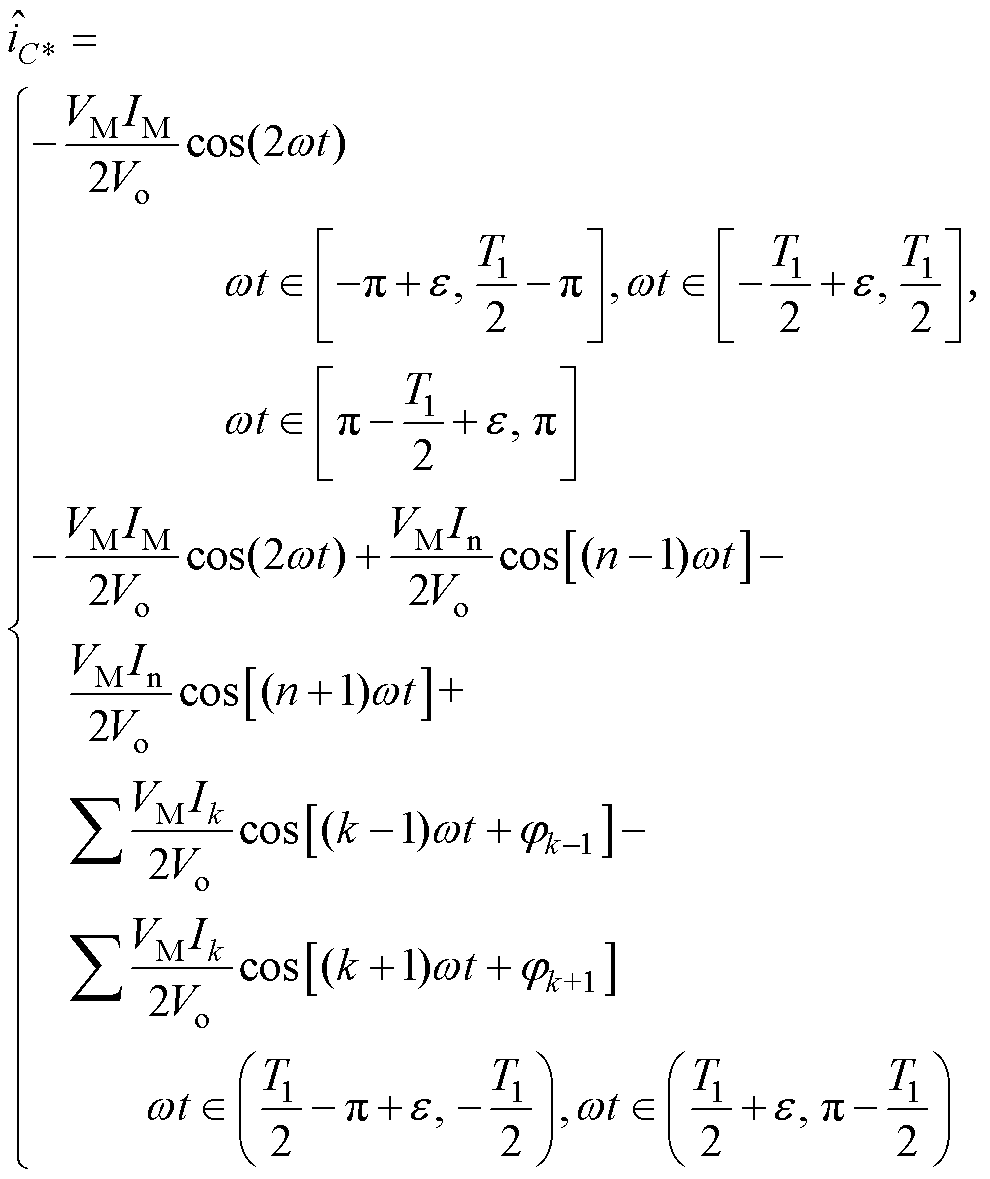 (21)
(21)
将式(21)的电容电流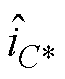 进行傅里叶分解得
进行傅里叶分解得
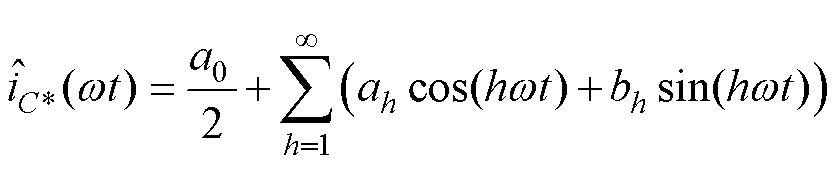 (22)
(22)
其中
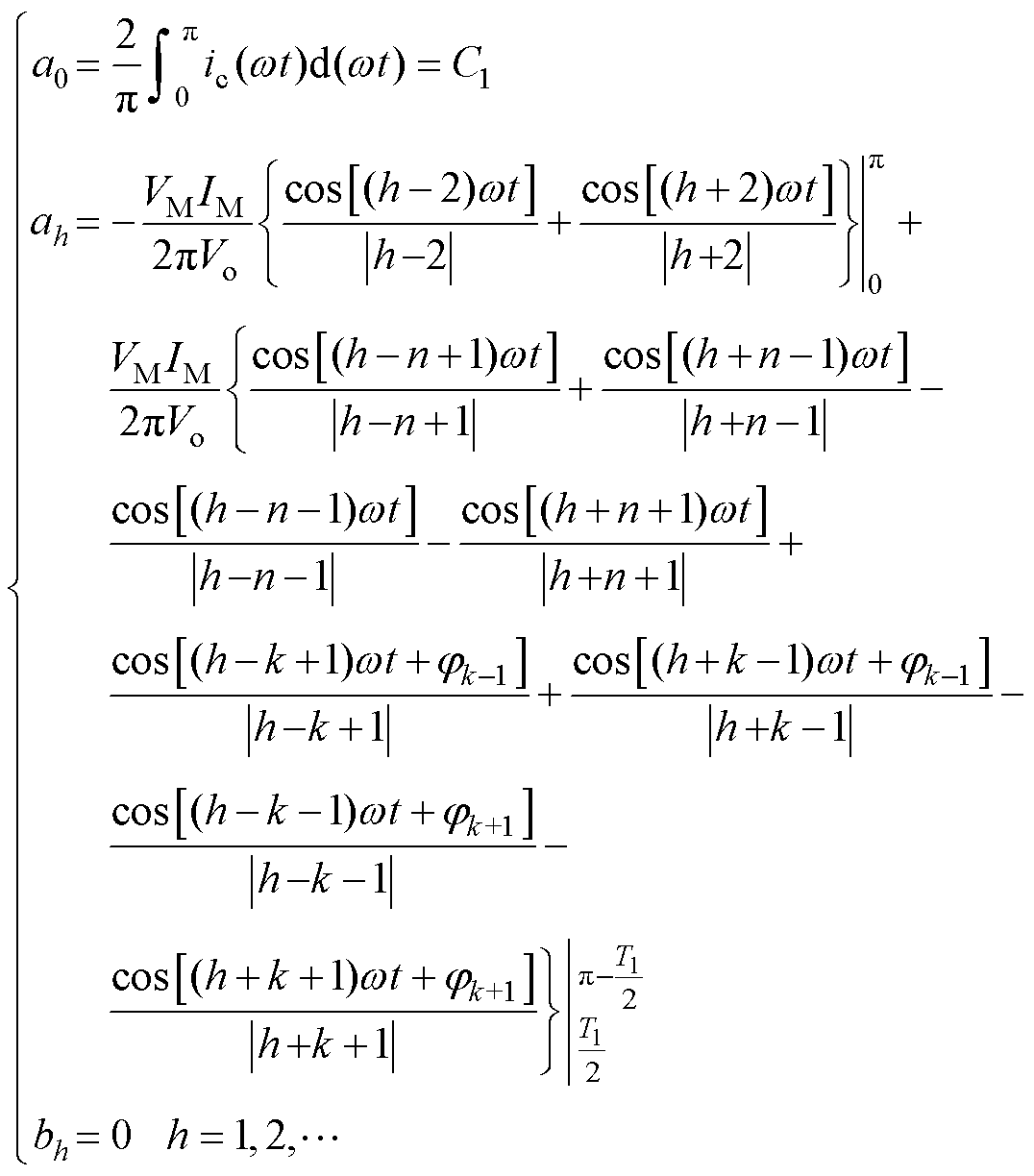
式中,a0为经过分解的直流信号;C1为一个常数;ah为电容电流在谐波注入后经过傅里叶分解后在各个频域中的系数;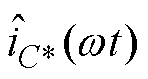 为偶函数,故bh=0。
为偶函数,故bh=0。
可以看出,ah的n-1次和n+1次电容电流信号的系数相等,即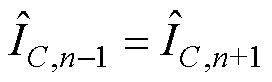 。利用此关系,可以规避重构过零点附近的高次电容电流导致产生的计算误差,保证其不发生过零畸变,完成电容参数CR和RE检测。另外,此关系仍符合1.2节导出的参数计算模型式(15),进一步说明了模型的普适性。
。利用此关系,可以规避重构过零点附近的高次电容电流导致产生的计算误差,保证其不发生过零畸变,完成电容参数CR和RE检测。另外,此关系仍符合1.2节导出的参数计算模型式(15),进一步说明了模型的普适性。
根据第1节“去过零区间”改进谐波注入方式检测原理,本节选取了18种情况来验证所提出的方法,见表1。这里考虑的仿真条件包括“去过零区间”宽度及不对称度(Ⅰ~Ⅷ)、注入电压幅值及频率(Ⅸ~ⅩⅤ)、不同电容(Ⅲ与ⅩⅥ)和不同(包括RE)负载(Ⅲ与ⅩⅦ、ⅩⅥ与ⅩⅧ),通过讨论各项条件结合仿真结果进行量化对比分析。
用于仿真的Boost PFC变换器系统的参数见表2。所使用的电容Ca、Cb分别为470 mF(100 mW)和670 mF(200 mW),在finj=650 Hz时,1/(nwCR) 与RE比例接近。因此本文采用注入电流次数为13次,使电容的12次和14次谐波电容电流幅值相等,完成电容参数CR和RE在线检测。需要注意,仿真中使用的CR和RE都是假设值,以模拟电容参数的变化。
表1 18种情况的仿真参数
Tab.1 Simulation parameters of 18 cases

类别仿真条件去过零区间(%)对称注入 CR/mFRE/mWRL/WVinj/Vfinj/Hz Ⅰ6702001001065060是 Ⅱ6702001001065040是 Ⅲ6702001001065010是 Ⅳ670200100106500是 Ⅴ6702001001065060否 Ⅵ6702001001065040否 Ⅶ6702001001065010否 Ⅷ670200100106500否 Ⅸ670200100865010是 Ⅹ670200100665010是 Ⅺ670200100465010是 Ⅻ6702001001045010是 ⅩⅢ6702001001075010是 ⅩⅣ6702001001095010是 ⅩⅤ670200100101 15010是 ⅩⅥ4702001001065010是 ⅩⅦ6702002001065010是 ⅩⅧ4701001001065010是
表2 Boost PFC变换器仿真参数
Tab.2 The simulation parameters of the Boost PFC converter
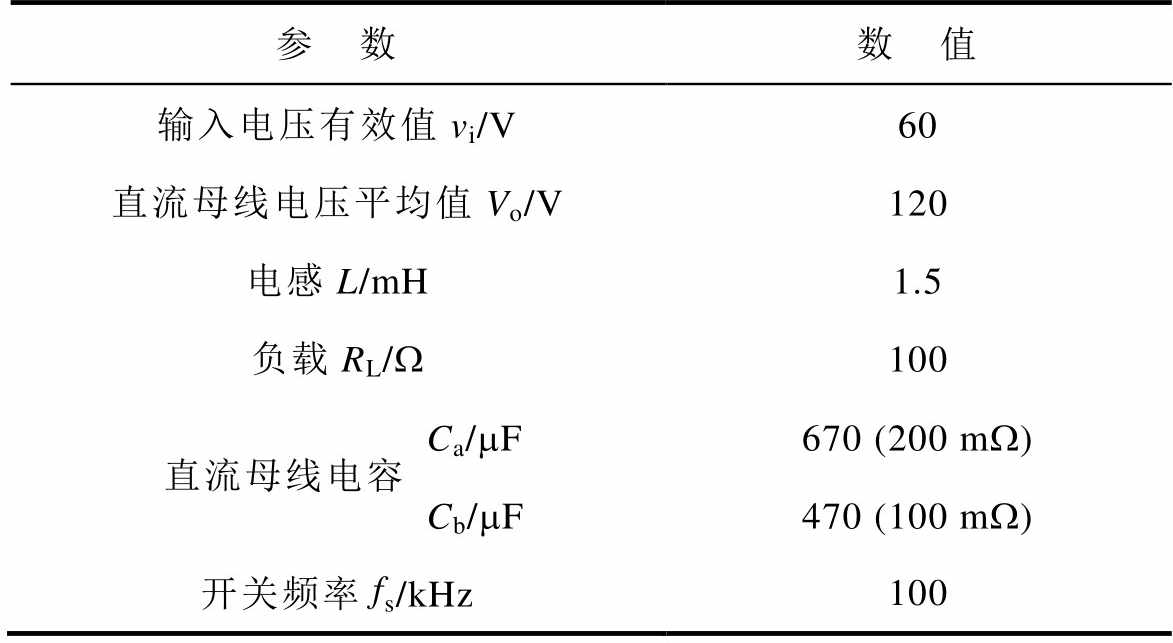
参 数数 值 输入电压有效值vi/V60 直流母线电压平均值Vo/V120 电感L/mH1.5 负载RL/W100 直流母线电容 Ca/mF670 (200 mW) Cb/mF470 (100 mW) 开关频率fs/kHz100
为验证所提“去过零区间”改进谐波注入法的正确性,同时确定如何选择“去过零区间”使检测精度较高,本节针对“去过零区间”的宽度及不对称度进行了8种不同条件下的对比分析,见表1(Ⅰ~Ⅷ)。并给出了Ⅲ对称注入、“去过零区间”10%与Ⅵ不对称注入、“去过零区间”40%的仿真结果。
案例Ⅲ、Ⅵ的仿真结果分别如图4和图5所示。由图4和图5可知,谐波电流注入后,输入电流在过零处未发生畸变,对输入电流ii和输出电压vo的仿真结果进行DFT分析,代入参数计算模型式(15),RE和CR估计结果见表3(Ⅰ~Ⅷ)。由仿真结果可知,“去过零区间”宽度越宽,其谐波注入的含量越少,在输出侧高次谐波分量越低,检测精度越低;同时,不对称注入会加重过零畸变的影响,导致检测精度进一步降低。当采用Ⅲ对称注入、“去过零区间”选取10%时,其RE和CR计算精度在1.1%以内。另外通过表3(Ⅳ、Ⅷ)可知,当“去过零区间”为0%注入时即全区间注入,CR的估算误差增大,其中RE的误差显著增大,可见过零畸变影响下的检测精度较低,说明了所提“去过零区间”改进谐波注入方法的有效性。

图4 案例Ⅲ的仿真结果
Fig.4 Simulation results for the case of Ⅲ
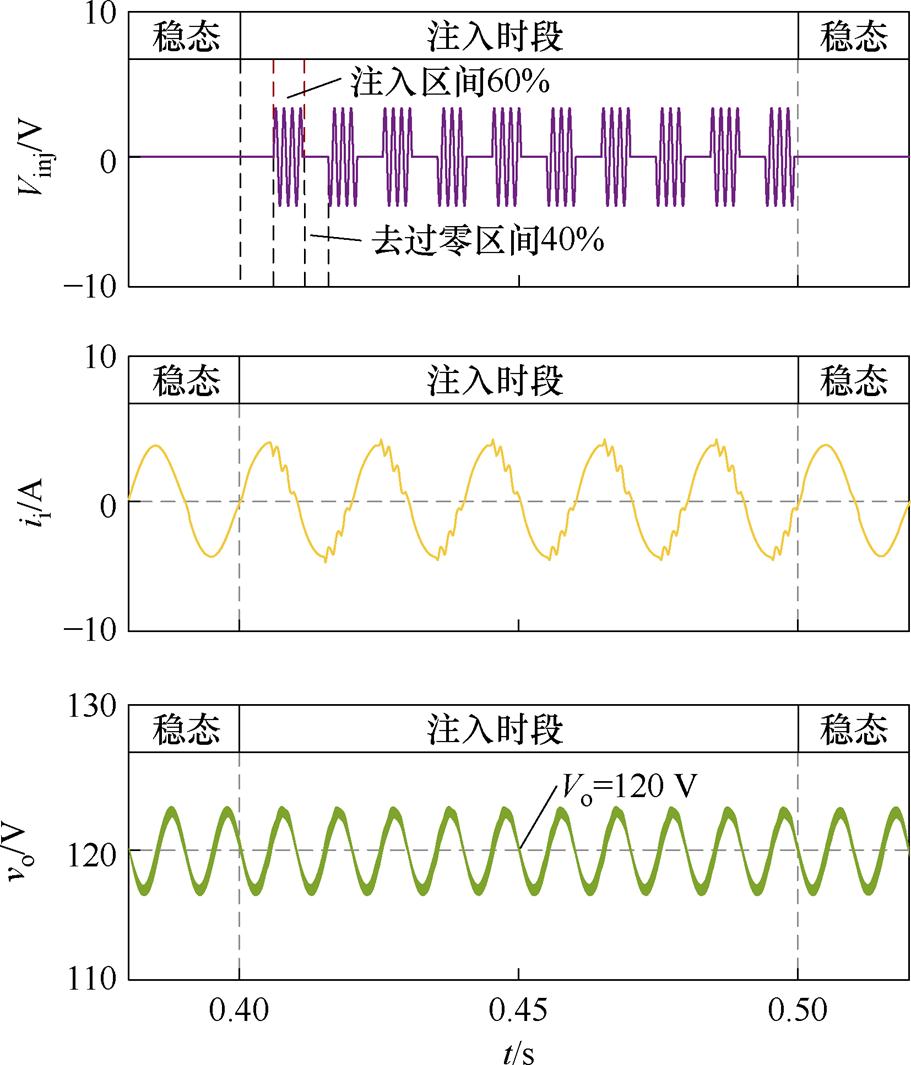
图5 案例Ⅵ的仿真结果
Fig.5 Simulation results for the case of Ⅵ
表3 18种情况下的仿真结果
Tab.3 Simulation results of 18 cases
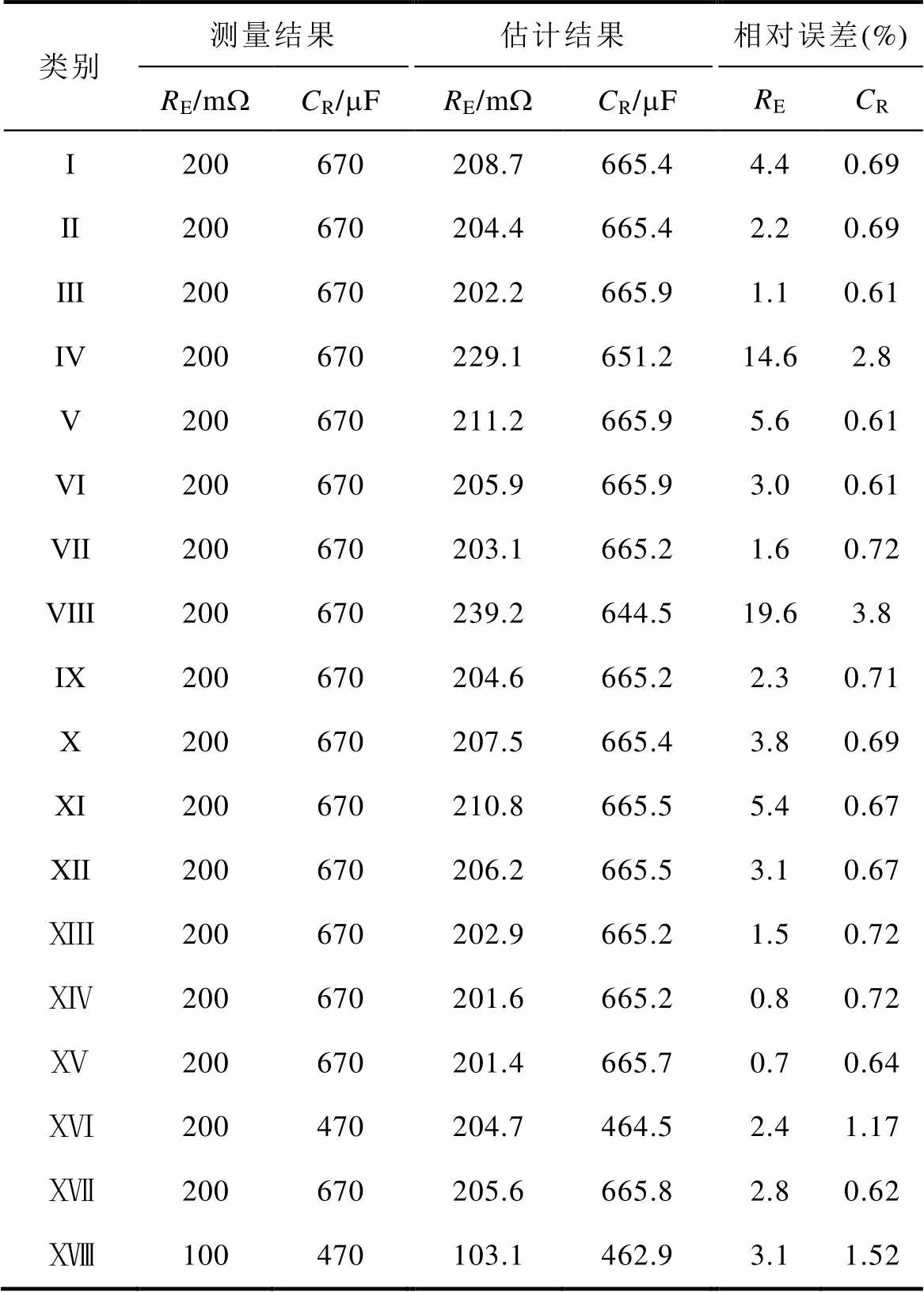
类别测量结果估计结果相对误差(%) RE/mWCR/mFRE/mWCR/mFRECR Ⅰ200670208.7665.44.40.69 Ⅱ200670204.4665.42.20.69 Ⅲ200670202.2665.91.10.61 Ⅳ200670229.1651.214.62.8 Ⅴ200670211.2665.95.60.61 Ⅵ200670205.9665.93.00.61 Ⅶ200670203.1665.21.60.72 Ⅷ200670239.2644.519.63.8 Ⅸ200670204.6665.22.30.71 Ⅹ200670207.5665.43.80.69 Ⅺ200670210.8665.55.40.67 Ⅻ200670206.2665.53.10.67 ⅩⅢ200670202.9665.21.50.72 ⅩⅣ200670201.6665.20.80.72 ⅩⅤ200670201.4665.70.70.64 ⅩⅥ200470204.7464.52.41.17 ⅩⅦ200670205.6665.82.80.62 ⅩⅧ100470103.1462.93.11.52
由2.1节知,在对称注入下且“去过零区间”越窄,检测精度越高,因此本节采用对称注入和“去过零区间”选取10%进行对比分析。
图6为表1(Ⅸ~Ⅺ)不同注入电压幅值的仿真波形。可以看出,谐波分量随着注入幅值的增大而减小,系统功率因数值均大于99%。将输出电压vo和输入电流ii的谐波分量代入参数计算模型式(15),得到相应的估计结果见表3(Ⅸ~Ⅺ)。
当注入电压小于输入电压的5%时,检测误差急剧增大,且输入电流的13次谐波分量小于7%。为了保证检测精度,减少对系统的影响,本方案选择5个工频周期(0.1 s),注入电压为输入电压的10%左右,因此在所选18种情况下注入电压幅值10 V检测精度最佳。
根据工程设计,Boost PFC变换器电流回路的截止频率通常设置为开关频率的1/20,因此注入谐波电压的频率小于5 kHz。同时根据电容的初始参数选择注入频率n,以保证电容器的电容值和阻抗值在n-1次和n+1次频率下占同一数量级。
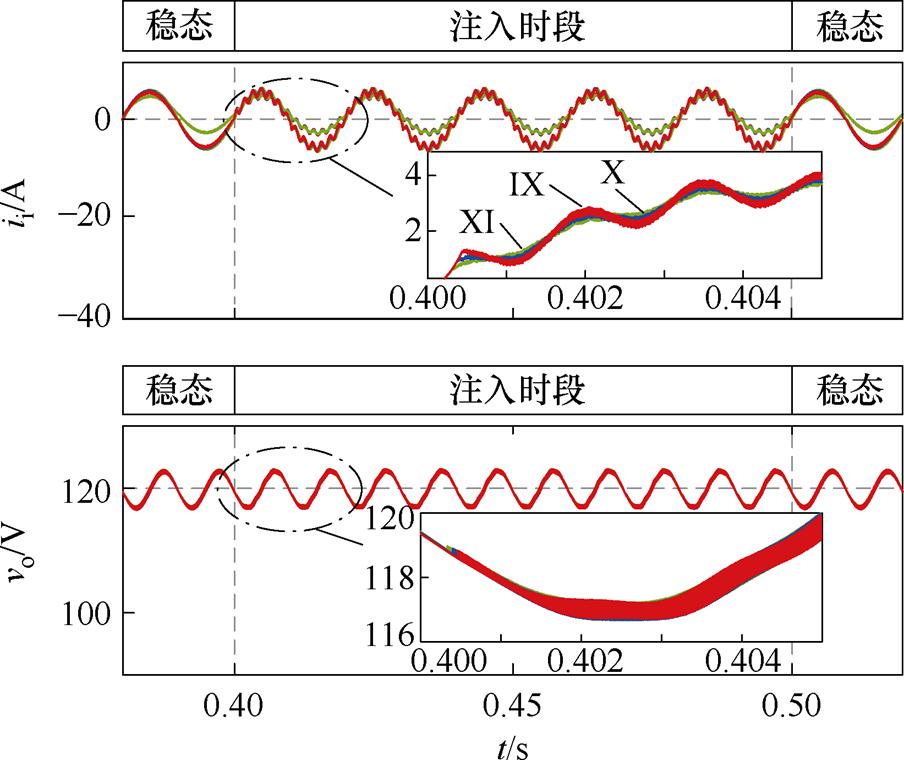
图6 案例Ⅸ~Ⅺ的仿真结果
Fig.6 Simulation results for the case of Ⅸ~Ⅺ
图7为表1(Ⅻ~ⅩⅤ)不同注入电压频率下的仿真波形。以Ca为例,RE=200 mW,不同频率下的阻抗和容抗见表4,容抗和阻抗值逐渐趋近于1。将输入电流ii和输出电压vo的谐波分量代入参数计算模型式(15),得到相应的估计结果见表3(Ⅻ~ ⅩⅤ)。
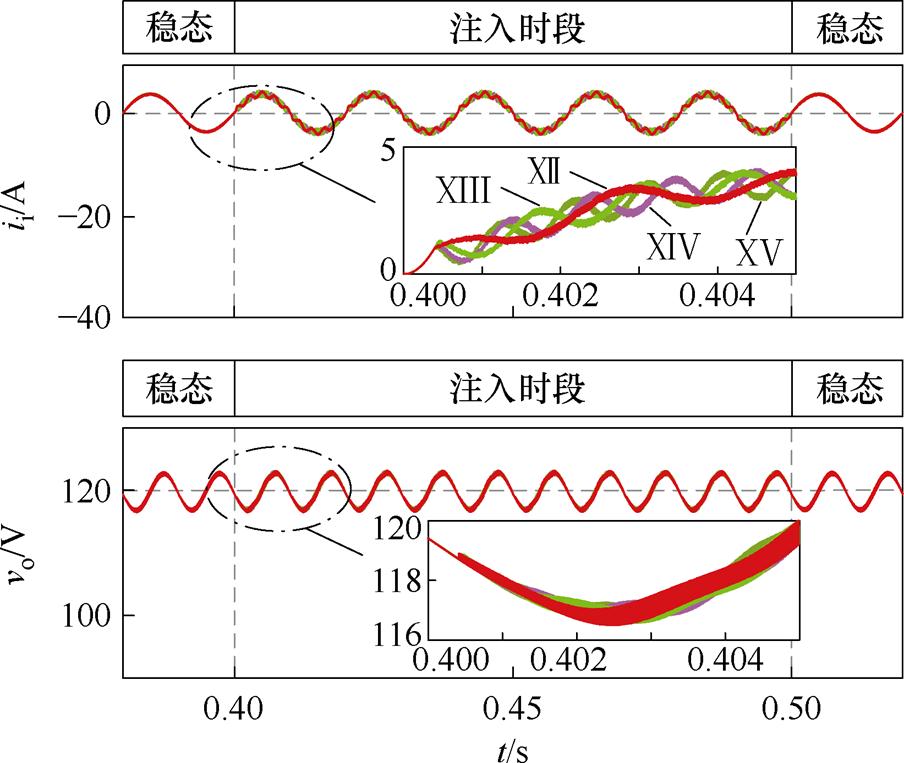
图7 案例Ⅻ~ⅩⅤ的仿真结果
Fig.7 Simulation results for the case of Ⅻ~ⅩⅤ
表4 Ca不同频率下的阻抗和容抗
Tab.4 Impedance and reactance of Ca at different frequencies

频率/Hz1/(wCa)RE1/(wCa) 4000.5940.337 6000.3960.505 8000.2960.675 10000.2380.840 1 2000.1981.01
由于CR依据直流母线电压的2次谐波计算,所以注入信号的频率对CR的估计结果影响较小。然而,RE主要是依据谐波注入信号构建的中频域信号的电压和电流谐波计算的,因此,注入信号的频率对RE的检测精度有较大影响。分析表3的仿真结果得到,当RE 1/(wCa)>0.5时,所提检测方法的检测精度在2%以内,具有较高的检测精度,当RE
1/(wCa)>0.5时,所提检测方法的检测精度在2%以内,具有较高的检测精度,当RE 1/(wCa)<0.5时,检测精度为3.1%,RE的检测误差相对增大。仿真结果验证了注入谐波的频率主要影响RE的估计误差。同时表明设计注入信号的频率时,应保障电容的容抗和阻抗之比大于0.5,在此条件下,仿真的相对误差小于10%检测标准,验证了所提在线检测方案是可行的。
1/(wCa)<0.5时,检测精度为3.1%,RE的检测误差相对增大。仿真结果验证了注入谐波的频率主要影响RE的估计误差。同时表明设计注入信号的频率时,应保障电容的容抗和阻抗之比大于0.5,在此条件下,仿真的相对误差小于10%检测标准,验证了所提在线检测方案是可行的。
由2.1节和2.2节可知,选定对称注入、“去过零区间”选取10%、注入幅值10 V和频率650 Hz进行后续的对比分析。本节对两种电容器Ca和Cb进行测试,证明所提出的RE和CR估计方法的有效性。
以Ⅲ和ⅩⅥ为研究对象,分别选择不同的电容CR。当改进的谐波电流注入后,Ca和Cb的输入电流和输出电压分别如图8和图9所示。由图8和图9知,谐波注入之后,输入电流ii在过零点处并没有出现畸变,而在650 Hz的频率范围内有奇次谐波存在,这与1.3节理论推导相吻合。当变换器功率一定时,随着母线电容值的增大,直流母线电压的基波值逐渐减小。
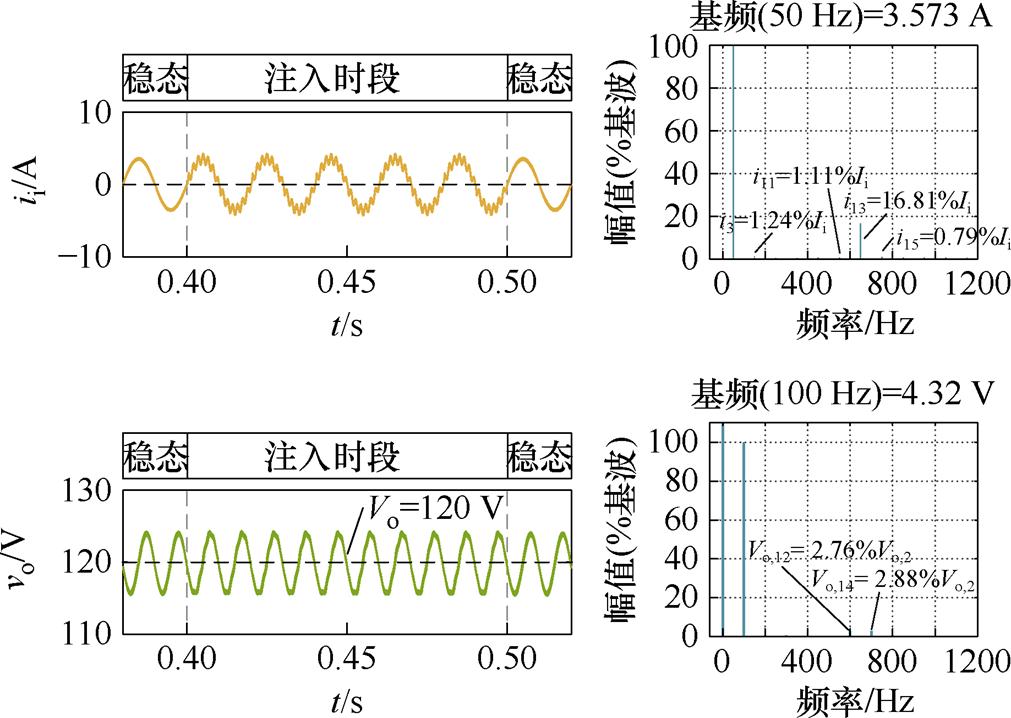
图8 案例Ⅲ的仿真结果
Fig.8 Simulation results for the case of Ⅲ
通过对输入电流ii和输出电压vo的DFT分解仿真结果进行分析,将图8和图9的数据代入参数计算模型式(15),RE和CR的估计结果分别列于表3(Ⅲ、ⅩⅥ)。发现RE的计算精度在3%以内,因此,所提“去过零区间”改进注入方法能在不同的电容条件下保持较高的检测精度。
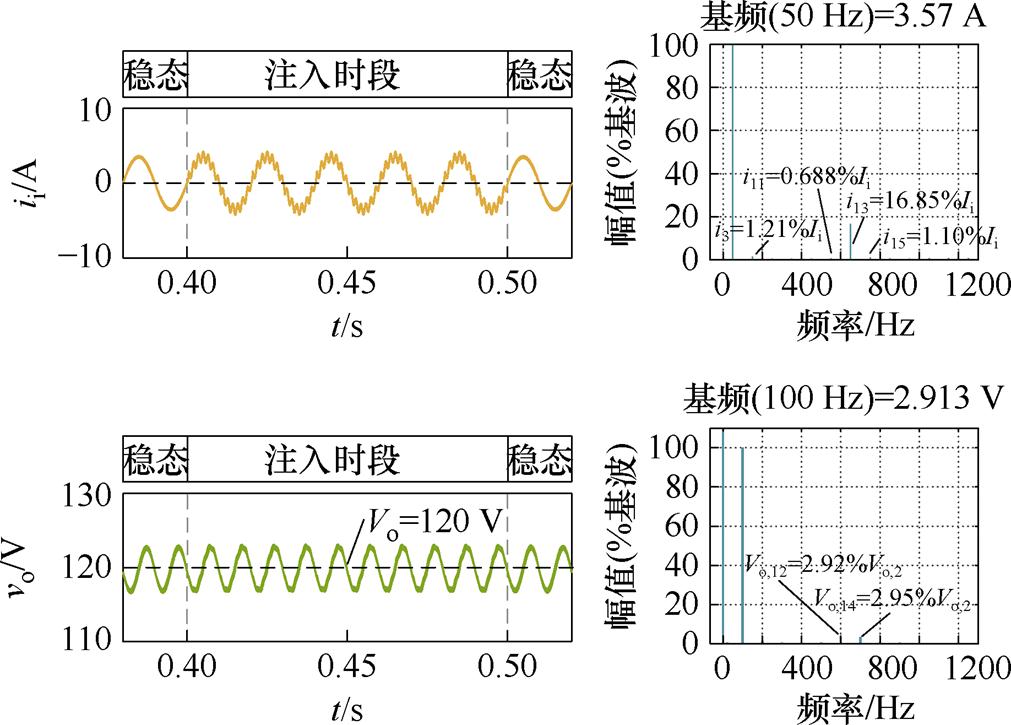
图9 案例ⅩⅥ的仿真结果
Fig.9 Simulation result for the case of ⅩⅥ
本节仍选定对称注入、“去过零区间”选取10%、注入幅值10 V和频率650 Hz进行后续的对比分析。为了验证所提方法的适用性和准确性,本节在不同负载(包括RE)条件下进行了一系列仿真验证。
以Ⅲ和ⅩⅦ为研究对象,分别选择不同的负载RL。图10显示了不同负载下的输入电流ii和输出电压vo波形,可以看出,随着负载的增大,变换器功率下降,由于输入电压不变,导致变换器输入电流和输出电压的2次谐波相应减小,相应的谐波分量也随之增加,检测精度相对变小。
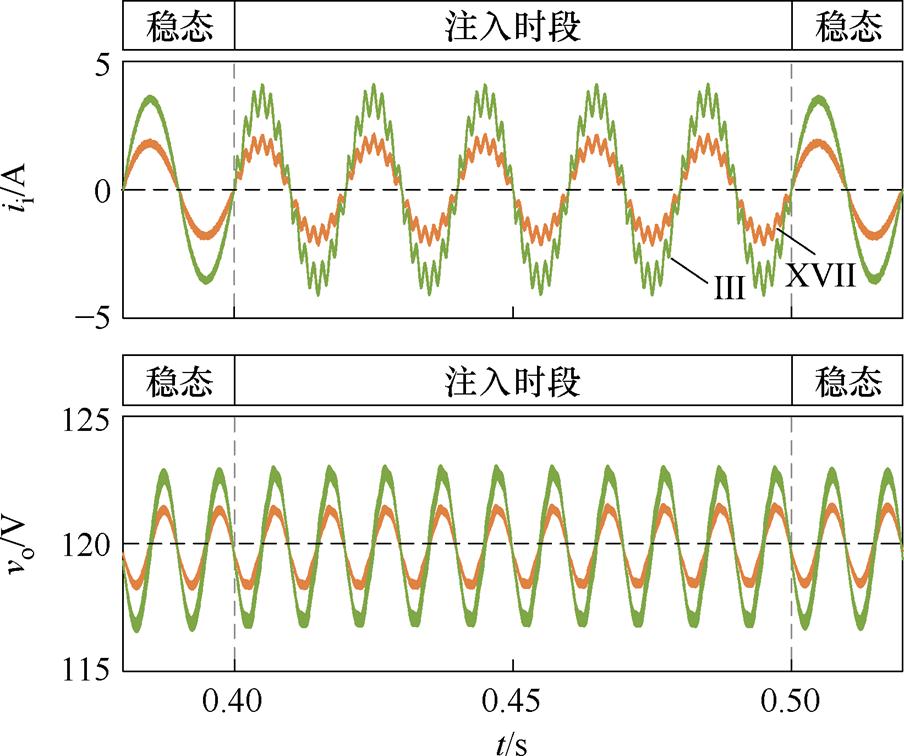
图10 案例Ⅲ和ⅩⅦ的仿真结果
Fig.10 Simulation results for the case of Ⅲ and ⅩⅦ
另外,以ⅩⅥ和ⅩⅧ为研究对象,分别选择不同的RE。图11显示了不同RE条件下的输入电流ii和输出电压vo波形。同样可以看出,输出电压随着RE的增大,输出电压的纹波值会相应增大。因此,在注入电压和电容的等效串联电容CR相同的情况下,估计精度随着RE的减小而减小。

图11 案例ⅩⅥ和ⅩⅧ的仿真结果
Fig.11 Simulation results for the case of ⅩⅥ and ⅩⅧ
对输入电流ii和输出电压vo的DFT分解仿真结果进行分析,RE和CR的估计结果分别列于表3(Ⅲ与ⅩⅦ、ⅩⅥ与ⅩⅧ),相应的估计误差均在3%以内,依旧保持较高的检测精度,说明了所提方法在不同的负载条件下的可行性。
本文实验方案拟针对不同功率等级(48 W/72 W/ 144 W)Boost PFC实验样机展开验证,CR和RE在线检测实验样机如图12所示,样机系统参数为:环境温度T=25℃, vi=60 V, vo=120 V, L=1.5 mH, RL= 100 W, fs=100 kHz, MOSFET: IRFP460, MCU: TMS320F28377。另外,设计制作电路板时着重降低了其寄生参数对检测的影响,因此不再考虑其工作时的寄生参数。谐波信号注入在DSP内实现,CR和RE的计算和显示在上位机上实现。
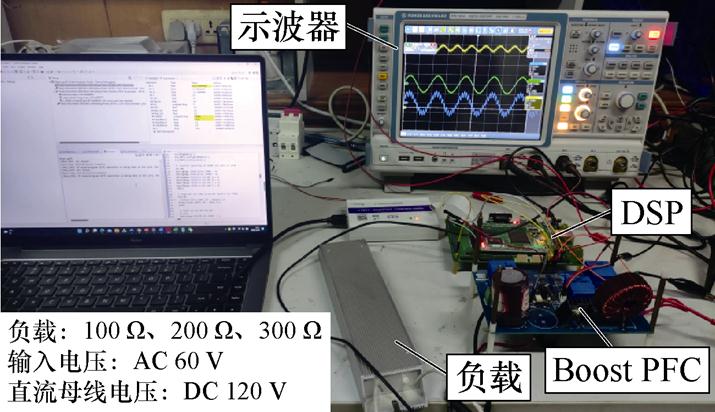
图12 CR和RE在线检测实验样机
Fig.12 CR and RE online detect prototype
DSP中详细的RE和CR在线估计流程如图13所示。利用DSP内部的CLA单元实现对变换器的双环控制。它减少了中断程序的任务,保证了ADC样本的实时读取。当电压vs过零时,将谐波电压注入控制回路,在此期间ADC对输出电压和输入电流进行采样。基于采样数据,在上位机上通过DFT变换得到电容参数。
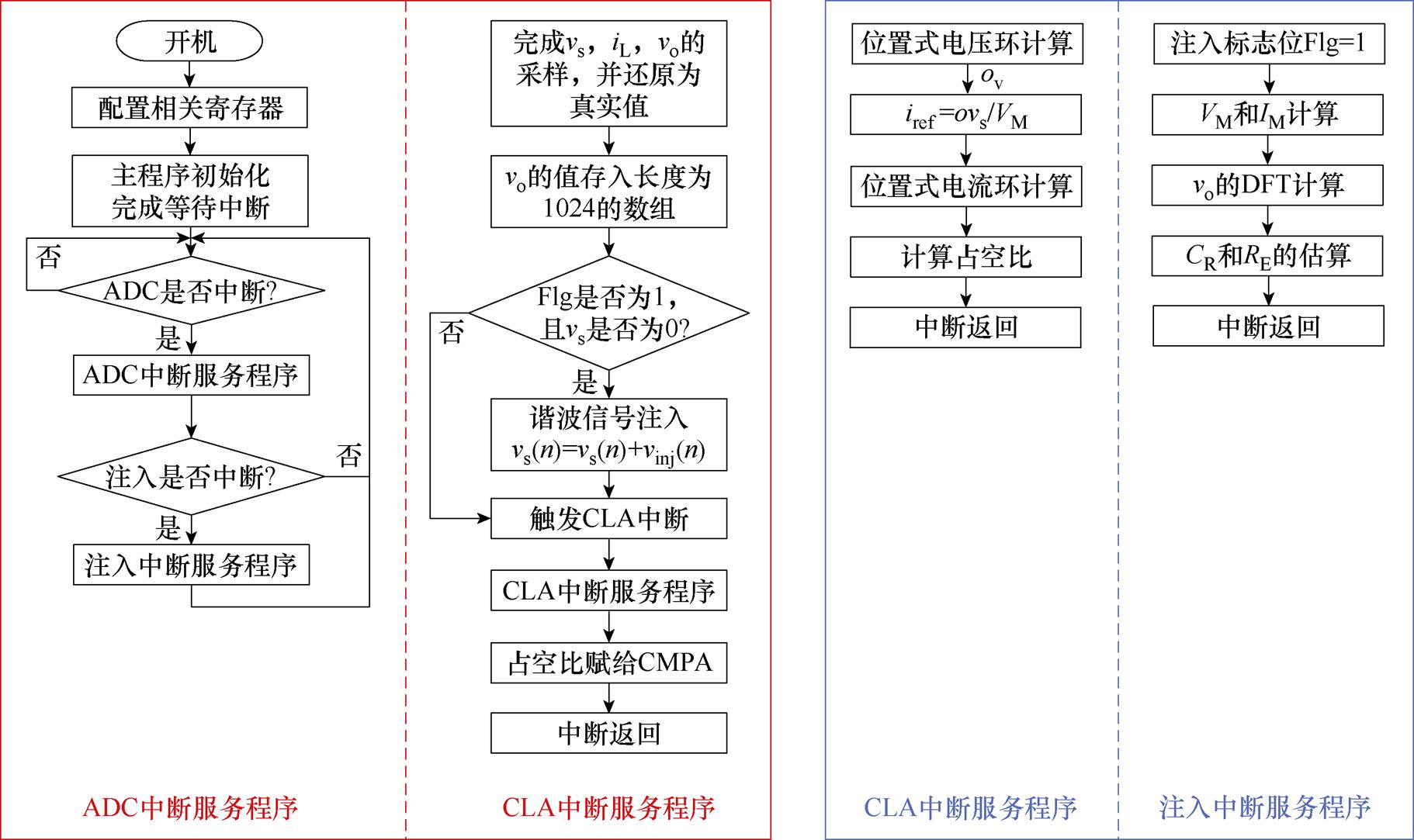
图13 DSP上实现的在线估算系统流程
Fig.13 Flowchart of the online estimation system implemented in DSP
本节在选定对称注入、“去过零区间”选取10%、注入幅值10 V和频率650 Hz条件下,采用了两种电容C1和C2,分别在三种不同负载条件下进行了实验验证。通过对比实验,观察不同电容条件下的检测精度。图14~图16分别显示了负载为100 W、200 W、300 W,电容分别为C1和C2时,谐波“去过零区间”注入的实验波形。
根据图14~图16波形对比可知,谐波电流在经“去过零区间”注入后,输入电流在过零点处未发生畸变现象。将输入电流ii和输出电压vo进一步DFT分解得到各次谐波分量,并代入参数计算模型式(15),得到的RE和CR的估计结果见表5。表5给出了不同电容和负载下的实验结果,检测结果与LCR仪测量结果基本一致,相对误差小于5%,验证了所提“去过零区间”改进谐波注入方法的可行性。
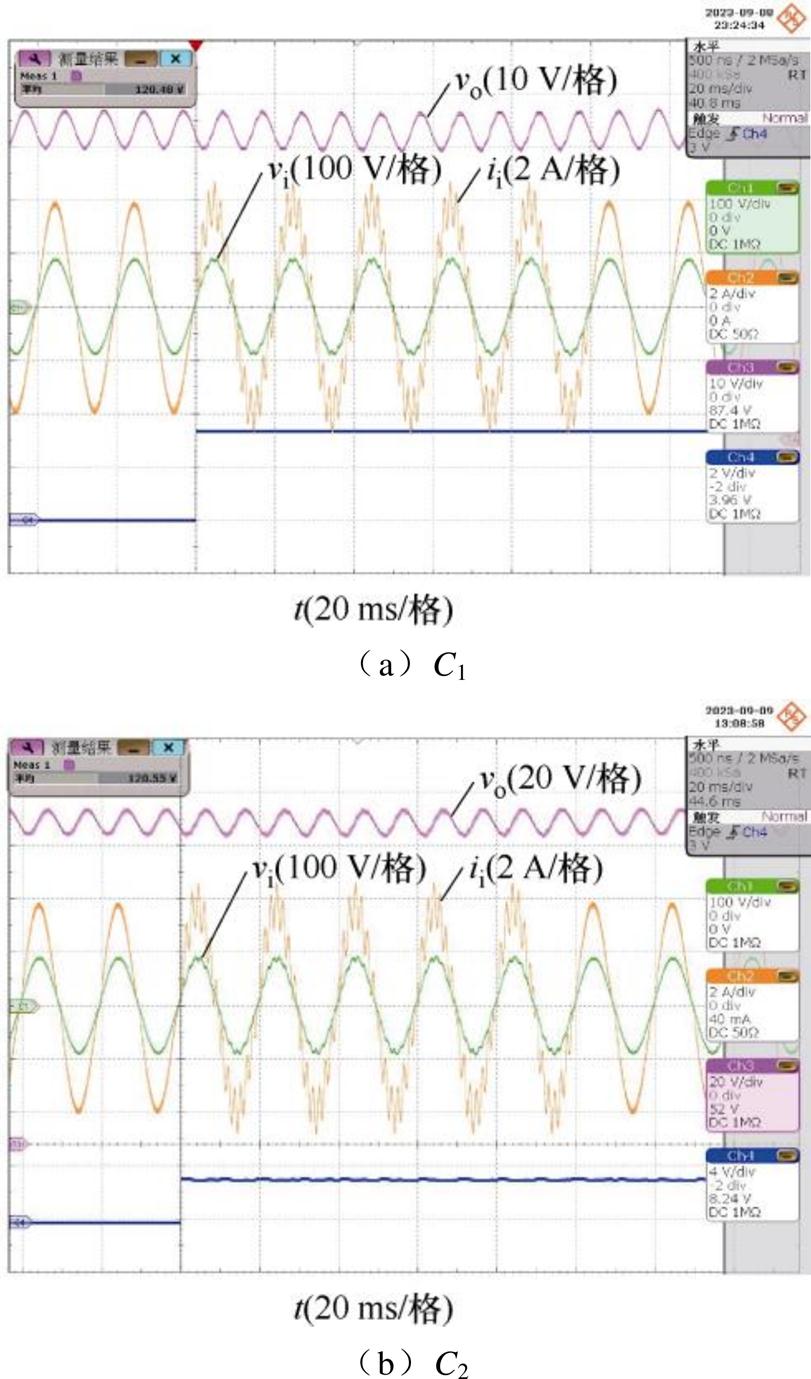
图14 谐波“去过零区间”注入的实验波形(RL=100 W)
Fig.14 Experimental waveforms with harmonic zero-crossing removal interval injection(RL=100 W)
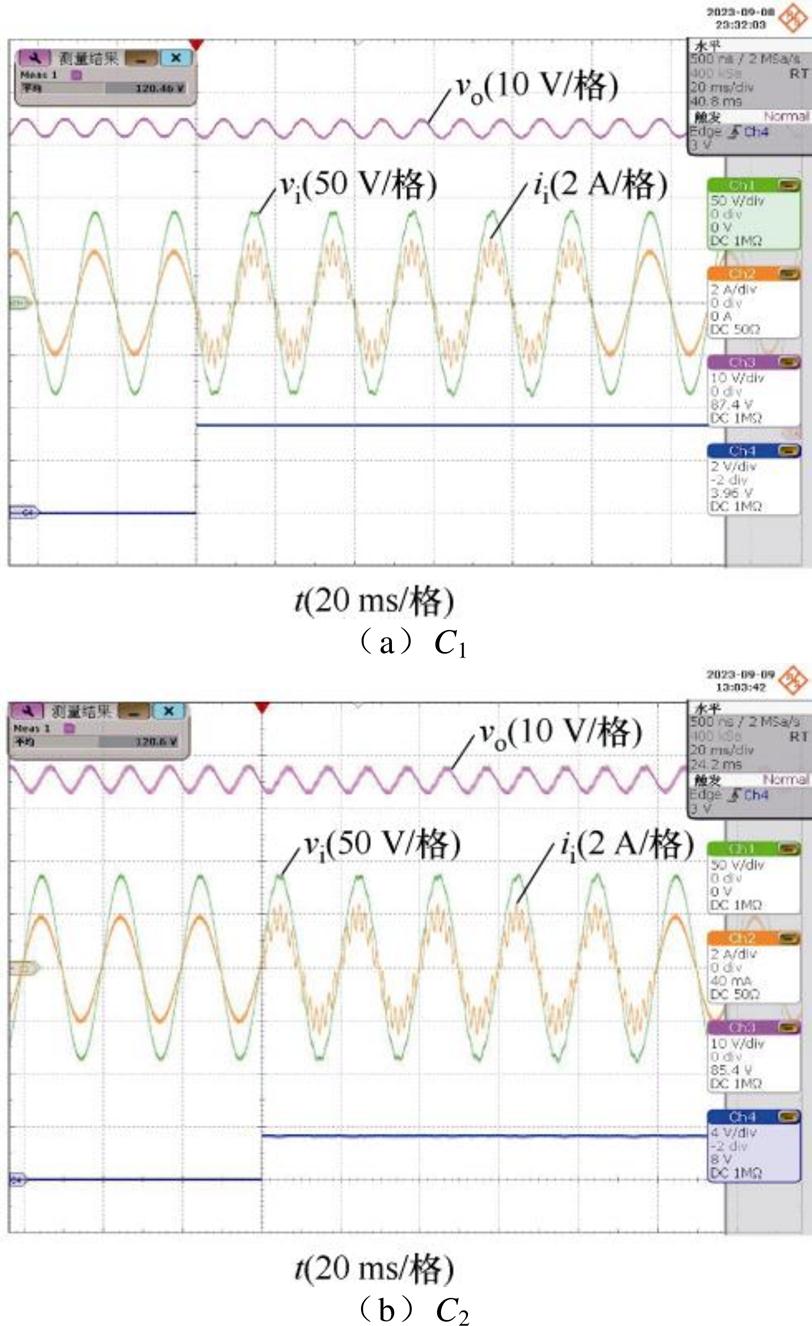
图15 谐波“去过零区间”注入的实验波形(RL=200 W)
Fig.15 Experimental waveforms with harmonic zero-crossing removal interval injection(RL=200 W)
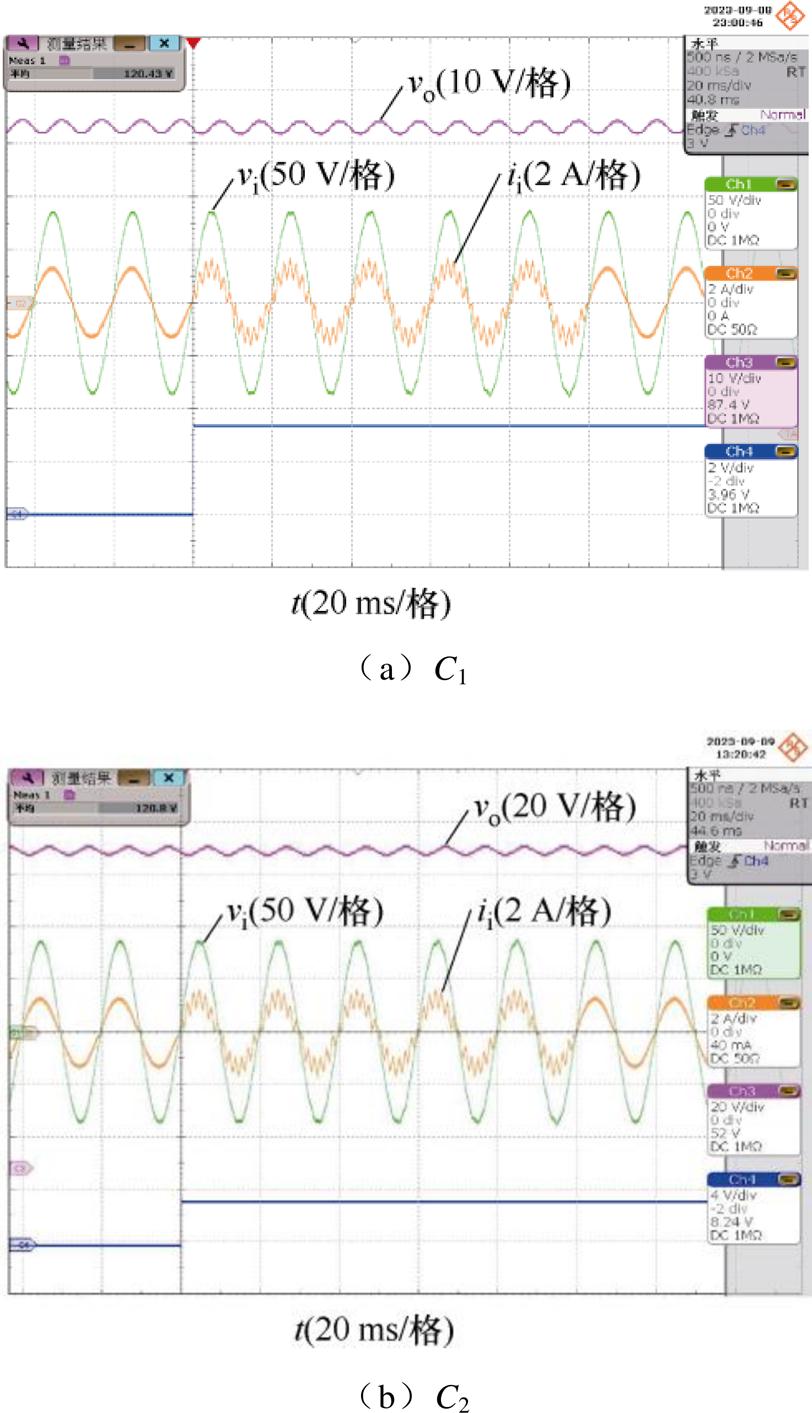
图16 谐波“去过零区间”注入的实验波形(RL=300 W)
Fig.16 Experimental waveforms with harmonic zero-crossing removal interval injection(RL=300 W)
表5 不同阻抗负载下的实验结果
Tab.5 Experimental results under different impedance loads
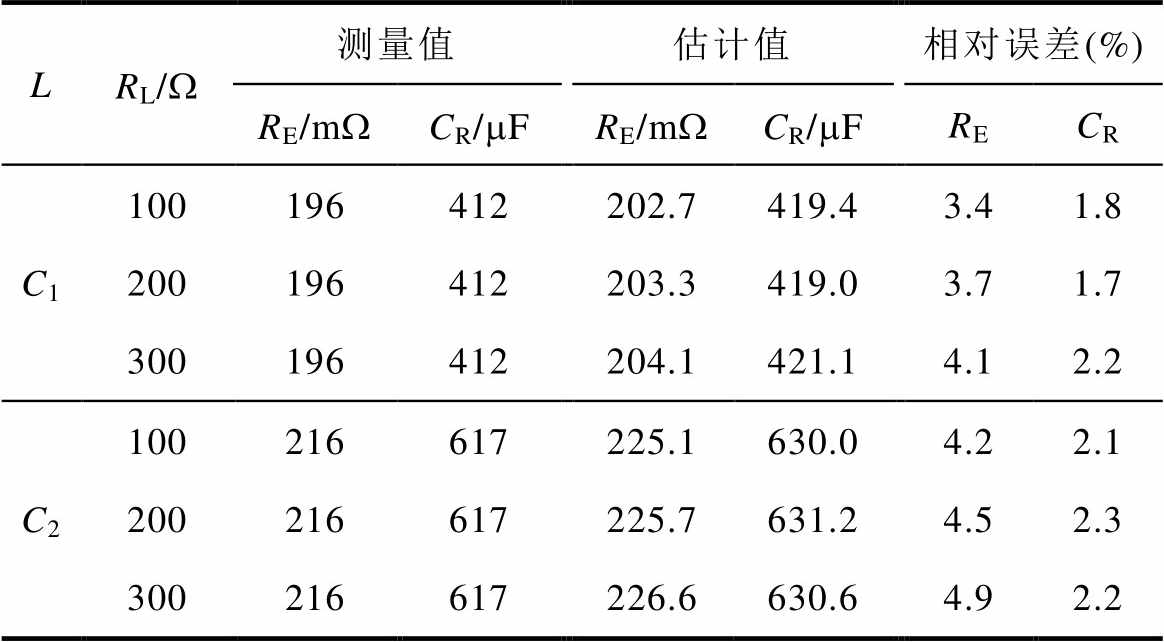
LRL/W测量值估计值相对误差(%) RE/mWCR/mFRE/mWCR/mFRECR C1100196412202.7419.43.41.8 200196412203.3419.03.71.7 300196412204.1421.14.12.2 C2100216617225.1630.04.22.1 200216617225.7631.24.52.3 300216617226.6630.64.92.2
从表5中可以观察到,当功率较低时,误差率会更高;而在电容较大时,误差率也会增加。这主要是由于在功率较低和电容较大的情况下,直流母线端的电压纹波信息减小,导致谐波信号含量降低,从而在数据处理阶段遗失部分关键数据信息。因此在进行滤波处理时应该考虑到这些影响因素。
本文提出了一种“去过零区间”改进谐波注入的直流链路AEC的CR和RE在线检测方法,可以同时对CR和RE进行检测。针对不同负载和电容工况进行了多种仿真和实验验证,实验结果显示,CR和RE的检测误差均在5%以内。该方法基于母线电压谐波响应提出了谐波电容电流重构方法,构建出无电容电流采样的CR和RE参数计算模型,仅通过检测输出电压即可完成RE的检测。同时考虑了谐波注入引起的电流过零畸变现象,提出了“去过零区间”改进谐波注入方式,进一步改进了电容参数检测精度。此外,注入过程是在软件中实现的,不需要额外的硬件设备。最后,该方法是基于交直流功率平衡原理,可扩展到其他AC-DC变换器中应用。
参考文献
[1] 王议锋, 王忠杰, 陈博, 等. 基于耦合电感的交错Boost变换器性能优化[J]. 电工技术学报, 2022, 37(8): 2097-2106.
Wang Yifeng, Wang Zhongjie, Chen Bo, et al. Performance optimization of interleaved Boost based on coupled inductors[J]. Transactions of China Elec- trotechnical Society, 2022, 37(8): 2097-2106.
[2] 林通, 江平, 姚佳. 一种基于耦合电感的零电流纹波功率因数校正变换器[J]. 电工技术学报, 2022, 37(18): 4732-4744.
Lin Tong, Jiang Ping, Yao Jia. A zero current ripple tapped inductor power factor correction converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4732-4744.
[3] 王立乔, 陈建医, 程超然, 等. 单级单相无电解电容Buck-Boost逆变器[J]. 电工技术学报, 2023, 38(24): 6768-6781.
Wang Liqiao, Chen Jianyi, Cheng Chaoran, et al. A single-stage single-phase Buck-Boost inverter without electrolytic capacitor[J]. Transactions of China Elec- trotechnical Society, 2023, 38(24): 6768-6781.
[4] 陶星澳, 王丰, 卓放. 部分功率直流变换器研究综述[J]. 电工技术学报, 2024, 39(10): 3021-3037.
Tao Xing’ao, Wang Feng, Zhuo Fang. Review of partial power DC converter research[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3021-3037.
[5] Lu Weiguo, Lang Shuang, Zhou Luowei, et al. Improvement of stability and power factor in PCM controlled boost PFC converter with hybrid dynamic compensation[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2015, 62(1): 320-328.
[6] 樊靖轩, 施佳楠, 徐子梁, 等. 基于GaN的开关线性复合高速随动脉冲负载直流变换器[J]. 电工技术学报, 2024, 39(6): 1818-1829.
Fan Jingxuan, Shi Jianan, Xu Ziliang, et al. GaN- based switched linear composite high-speed follow-up pulse load DC converter[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1818-1829.
[7] 皇金锋, 李林鸿, 任舒欣, 等. 考虑滤波电容等效串联电阻的输出本质安全型Buck-Boost变换器分析与设计[J]. 电工技术学报, 2021, 36(8): 1658- 1670.
Huang Jinfeng, Li Linhong, Ren Shuxin, et al. Analysis and design of an intrinsically safe Buck- Boost converter on considering of the filter capacitor with equivalent series resistance[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1658- 1670.
[8] Soliman H, Wang Huai, Blaabjerg F. A review of the condition monitoring of capacitors in power elec- tronic converters[J]. IEEE Transactions on Industry Applications, 2016, 52(6): 4976-4989.
[9] 罗天柱. 单相Boost PFC变换器的直流母线电容参数检测方法研究[D]. 重庆: 重庆大学, 2022.
Luo Tianzhu. Research on DC bus capacitance parameter detection method of single-phase Boost PFC converter[D]. Chongqing: Chongqing University, 2022.
[10] Pu Xingsi, Nguyen T H, Lee D C, et al. Fault diagnosis of DC-link capacitors in three-phase AC/DC PWM converters by online estimation of equivalent series resistance[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 4118-4127.
[11] Amaral A M R, Marques Cardoso A J. Using Newton- raphson method to estimate the condition of aluminum electrolytic capacitors[C]//2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 2007: 827-832.
[12] Tsang K M, Chan W L. Simple method for measuring the equivalent series inductance and resistance of electrolytic capacitors[J]. IET Power Electronics, 2010, 3(4): 465.
[13] Amaral A M R, Marques Cardoso A J. A simple offline technique for evaluating the condition of aluminum-electrolytic-capacitors[J]. IEEE Transa- ctions on Industrial Electronics, 2009, 56(8): 3230- 3237.
[14] Amaral A M R, Marques Cardoso A J. An automatic technique to obtain the equivalent circuit of aluminum electrolytic capacitors[C]//2008 34th Annual Con- ference of IEEE Industrial Electronics, Orlando, FL, USA, 2008: 539-544.
[15] Yao Kai, Tang Weijie, Bi Xiaopeng, et al. An online monitoring scheme of DC-link capacitor’s ESR and C for a Boost PFC converter[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5944-5951.
[16] 罗丹, 陈民铀, 赖伟, 等. 基于Haar小波变换重构开关序列的MMC子模块电容值在线监测方法[J]. 电工技术学报, 2022, 37(20): 5278-5289.
Luo Dan, Chen Minyou, Lai Wei, et al. Online monitoring method for sub-module capacitance in modular multilevel converter based on Haar wavelet transform reconstruction switch sequence[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(20): 5278-5289.
[17] 辛熙锴, 马柯, 蔡旭. 工频周期四点电压采样的MMC子模块电容值在线监测方法[J]. 中国电机工程学报, 2021, 41(11): 3896-3904.
Xin Xikai, Ma Ke, Cai Xu. Online monitoring for sub-module capacitance in modular multilevel con- verter with four sampling points of capacitor voltage[J]. Proceedings of the CSEE, 2021, 41(11): 3896-3904.
[18] 林晓婉, 代锋, 刘沈全, 等. 含LCC-HVDC的交直流混联电网统一谐波状态估计方法[J]. 电力系统自动化, 2022, 46(13): 94-103.
Lin Xiaowan, Dai Feng, Liu Shenquan, et al. Unified harmonic state estimation method for AC/DC hybrid power grid with LCC-HVDC[J]. Automation of Electric Power Systems, 2022, 46(13): 94-103.
[19] Laadjal K, Sahraoui M, Cardoso A J M, et al. Online estimation of aluminum electrolytic-capacitor para- meters using a modified prony’s method[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4764-4774.
[20] 蒋兴良, 周文轩, 董莉娜, 等. 基于旋转圆柱三电极阵列的覆冰测量方法[J]. 电工技术学报, 2024, 39(5): 1524-1535.
Jiang Xingliang, Zhou Wenxuan, Dong Lina, et al. Ice coating measurement method based on rotating cylindrical three-electrode array[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1524- 1535.
[21] Zhao Zhaoyang, Lu Weiguo, Davari P, et al. An online parameters monitoring method for output capacitor of buck converter based on large-signal load transient trajectory analysis[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4004-4015.
[22] 孙鹏菊, 龚灿, 杜雄, 等. 一种大功率交流变流器直流母线电容等效串联电阻的在线监测方法[J]. 中国电机工程学报, 2017, 37(17): 5134-5142, 5233.
Sun Pengju, Gong Can, Du Xiong, et al. An online monitoring scheme of equivalent series resistance for DC-link capacitor of high-power AC converter[J]. Proceedings of the CSEE, 2017, 37(17): 5134-5142, 5233.
[23] Lu Weiguo, Lu Xuemei, Han Jinxin, et al. Online estimation of ESR for DC-link capacitor of Boost PFC converter using wavelet transform based time- frequency analysis method[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 7755-7764.
[24] Ahmeid M, Armstrong M, Gadoue S, et al. Real-time parameter estimation of DC-DC converters using a self-tuned Kalman filter[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5666-5674.
[25] Li B X, Low K S. Low sampling rate online para- meters monitoring of DC-DC converters for predictive- maintenance using biogeography-based optimi- zation[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 2870-2879.
[26] Sun Pengju, Gong Can, Du Xiong, et al. Online condition monitoring for both IGBT module and DC-link capacitor of power converter based on short- circuit current simultaneously[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3662-3671.
[27] Kim M, Sul S K, Lee J. Condition monitoring of DC-link capacitors in drive system for electric vehicles[C]//2012 IEEE Vehicle Power and Pro- pulsion Conference, Seoul, Korea (South), 2012: 633-637.
[28] Gupta Y, Ahmad M W, Narale S, et al. Health estimation of individual capacitors in a bank with reduced sensor requirements[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7250-7259.
[29] Ahmad M W, Agarwal N, Kumar P N, et al. Low- frequency impedance monitoring and corresponding failure criteria for aluminum electrolytic capacitors[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5657-5666.
[30] Meng Jinlei, Chen E X, Ge S J. Online E-cap condition monitoring method based on state obser- ver[C]//2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-6.
[31] Sun Jian. On the zero-crossing distortion in single- phase PFC converters[J]. IEEE Transactions on Power Electronics, 2004, 19(3): 685-692.
Abstract Boost PFC converter is commonly utilized in rectifier circuits due to its ability to achieve a high power factor and low input current distortion. For the single-phase boost PFC converter, large-capacity and low-priced aluminum electrolytic capacitors (AECs) are typically employed to balance the instantaneous power deviation between the input and the output. However, the failure-prone nature of electrolytic capacitors may result in system instability or even collapse. Therefore, the real-time detection of electrolytic capacitor status information, assessment of its service life, and timely replacement of the soon-to-be-failed electrolytic capacitor can provide an important technical guarantee for the reliability of PFC power supply operation. This paper proposes an improved "zero-crossing removal interval" harmonic injection method for online detection of capacitance parameters to solve current zero-crossing distortion caused by harmonic injection. Additionally, based on the harmonic response of the bus voltage, the harmonic capacitor current reconstruction is achieved, and a model for calculating the CR and RE parameters without capacitor current sampling is constructed.
Firstly, the AC and DC input-output power action characteristics of the Boost PFC converter are fully utilized, i.e., the high harmonic current injection of the current control loop produces a high harmonic voltage splitting phenomenon on the output voltage. The two split harmonic voltage signals are employed to reconstruct the capacitor current; the capacitor's low-frequency impedance model is used to estimate CR; a mid-frequency domain harmonic capacitor parameter computation model is established to estimate the RE. In addition, the high harmonic current injection in the current loop inevitably results in an asymmetric zero-crossing distortion of the input current, directly affecting the accuracy of the capacitance parameter computation model. Consequently, the zero-crossing removal interval harmonic current injection method is employed to solve zero-crossing distortion caused by inter-area injection. The improved “zero-crossing removal interval” method avoids the reconstructed high-order capacitor current calculation error, enhancing CR and RE accuracy.
Eighteen types of capacitor conditions are selected for simulation calculation, and 48 W/72 W/144 W Boost PFC experimental prototypes are established. The proposed detection method is verified under an input voltage of 60 V, a switching frequency of 100 kHz, and an output voltage of 120 V. The results demonstrated that the method exhibits high detection accuracy under symmetrical injection conditions with a 10% zero-crossing removal interval, a 10 V injection amplitude, and a 650 Hz frequency. Furthermore, the improved “zero-crossing removal interval” method can achieve parameter detection error within 5% under different loads (100 W, 200 W, and 300 W) and capacitor conditions (196 mW/412 mF and 216 mW/617 mF), regardless of light or heavy loads.
This paper presents the following conclusions. (1) The proposed method considers the impact of current on distortion caused by harmonic injection. A “zero-crossing removal interval” harmonic injection method improves the accuracy of capacitance parameter detection. (2) In the “zero-crossing removal interval” method, the capacitor current is obtained through algorithmic reconstruction, which avoids high-precision capacitor current sampling. The harmonic injection is achieved by the control algorithm without additional hardware equipment. (3) The proposed capacitance parameter calculation model is derived based on the AC-DC power balance, making it straightforward to extend to similar AC-DC converters.
Keywords:DC-link capacitance, RE and CR, improved harmonic injection, online detection
中图分类号:TM461
DOI: 10.19595/j.cnki.1000-6753.tces.240600
国家自然科学基金资助项目(52077021)。
收稿日期 2024-04-18
改稿日期 2024-05-06
卢伟国 男,1977年生,博导,教授,研究方向为电能变换系统及控制、无线供能与取能技术等。
E-mail: luweiguo@cqu.edu.cn
曹 琪 男,2000年生,硕士研究生,研究方向为电能变换系统及控制。
E-mail: student_caoqi@163.com(通信作者)
(编辑 陈 诚)