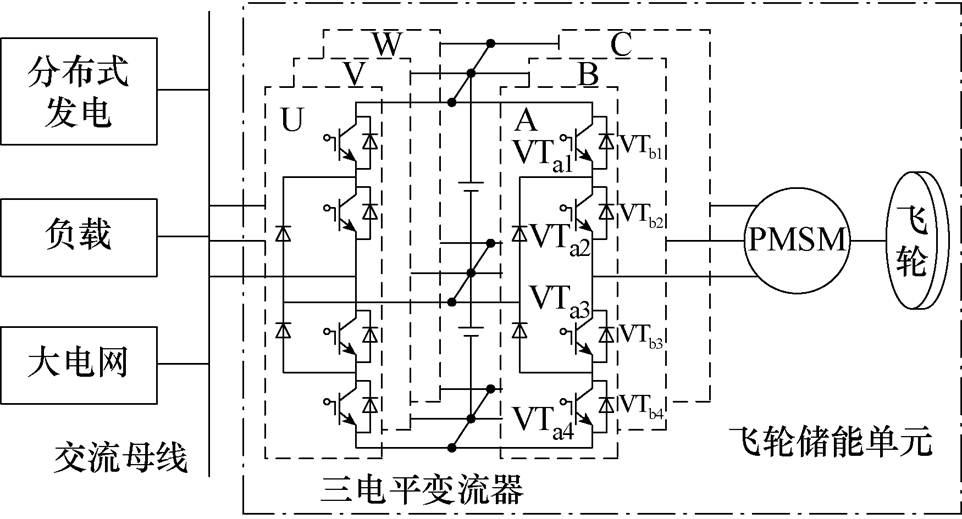
图1 交流并网的飞轮储能单元
Fig.1 AC grid-connected flywheel energy storage unit
摘要 永磁同步电机拖动大惯量飞轮充能过程,三电平变流器长时间处于低调制比状态,经典虚拟空间矢量调制策略会频繁出现窄脉冲,进而导致电压电流波形畸变、功率器件损坏以及电机起动瞬间中点电位失控等问题。针对以上问题,该文提出考虑永磁同步电机控制离散性的窄脉冲分析方法,定量分析经典虚拟空间矢量调制算法在低调制比区域的窄脉冲分布规律。在此基础上,提出一种基于矢量序列优化的混合虚拟空间矢量调制策略,实现了三电平变流器低调制比区域窄脉冲抑制。仿真和实验结果表明,该方法不仅有效抑制了窄脉冲、改善电流波形质量,也降低了三电平变流器开关动作次数,解决了电机起动瞬间中点电位失控的问题。
关键词:数字化电机控制 三电平变流器 低调制比 窄脉冲 中点电位平衡 虚拟空间矢量调制
近年来,随着光伏和风电等新能源大规模并网,微电网成为了研究热点[1-3]。储能技术是保证微电网稳定运行的关键技术手段,也是推动微电网技术在可再生能源中广泛应用的重要措施之一[4]。飞轮储能凭借功率密度高、充放电速度快、寿命长、转化效率高等优势,对改善电网电能质量具有重要意义[5-7]。
图1为并联在交流微电网的飞轮储能单元,它由具有高效率、低谐波等优势[8-10]的三电平变流器、永磁电机和同轴的惯性飞轮构成。在系统从零速开始为飞轮充能过程中,由于飞轮转动惯量大,电机长时间处于中低速运行工况,三电平变流器处于低调制比状态,经典虚拟空间矢量调制算法(Virtual Space Vector Pulse Width Modulation, VSVPWM)会频繁产生窄脉冲。受数字化控制离散性的影响,经典VSVPWM扇区边界发生改变,加剧了窄脉冲问题。在窄脉冲的作用下,变流器输出的电压电流波形发生严重畸变,甚至会导致IGBT反向恢复过程出现强烈的振荡,对器件造成损害。因此,针对三电平变流器窄脉冲进行抑制十分重要。

图1 交流并网的飞轮储能单元
Fig.1 AC grid-connected flywheel energy storage unit
三电平变流器窄脉冲抑制策略的研究包括两个方面,首先是分析窄脉冲出现区域。文献[11-12]分别针对三电平SVPWM和VSVPWM算法窄脉冲分布区域做了定性分析,文献[13]进一步通过构造电压矢量序列最小脉冲宽度与功率器件最小脉宽限制的差值函数,定量分析了VSVPWM算法的窄脉冲分布区域。然而,以上分析方法均是基于载波比无限大的假设,尚未考虑电机数字化控制的离散性带来的影响。
其次,在消除或减少窄脉冲方面,主要包括优化矢量序列设计[12-16]、非最近三矢量调制[17]以及窄脉冲剔除/拓宽[18-20]等方法。文献[17]在低调制比区域选用非最近三矢量增加有效矢量作用时间以抑制窄脉冲,但会增加输出电压电流谐波含量。文献[20]提出一种死区补偿和窄脉冲抑制分区执行的调制策略,解决了死区补偿和窄脉冲消除算法相互干扰的问题。在窄脉冲抑制区域,剔除或拓宽窄脉冲,使其满足功率器件最小脉冲宽度的限制,但会导致电压参考矢量的合成误差。文献[12]提出一种舍弃小矢量的窄脉冲抑制算法,将出现窄脉冲的小矢量作用时间分配至其冗余矢量,但该方法降低了中点电位的平衡能力。文献[13]提出一种零矢量首发的十三段VSVPWM策略,在极低调制比下能够很好地抑制窄脉冲,并实现中点电位的平衡控制。但随着调制比的增加,零矢量作用时间减少,该方法会引入新的窄脉冲,且相对于经典九段式VSVPWM,存在开关次数明显增多的问题。
针对上述问题,本文提出一种考虑电机数字化控制离散性的窄脉冲分析方法和基于矢量序列优化的混合VSVPWM窄脉冲抑制策略。首先,基于永磁同步电机稳态数学模型,分析数字化控制下电压参考矢量变化特性及其对扇区边界的影响;其次,建立电压矢量序列最小脉冲宽度与功率器件最小脉宽限制的差值函数,对经典VSVPWM算法在低调制比区域窄脉冲分布做量化分析;最后,提出一种基于矢量序列优化的混合VSVPWM策略抑制低调制比区域的窄脉冲,并通过仿真和实验进行了验证。
永磁同步电机dq坐标系下的基波数学模型为
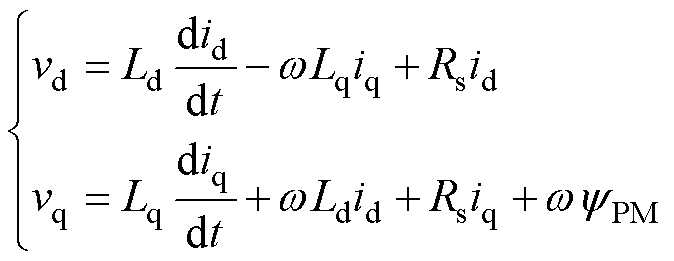 (1)
(1)
式中,vd、vq为电机d、q轴电压;id、iq为电机d、q轴电流;Ld、Lq为电机d、q轴电感;Rs为定子电阻;w 为电气角速度;yPM为电机永磁磁链。
电机稳态运行时,忽略式(1)中的动态变化项,得到其稳态模型为
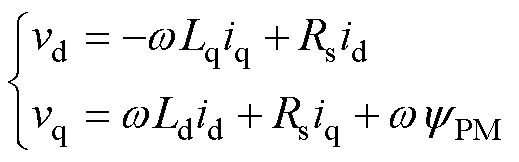 (2)
(2)
定义调制比为
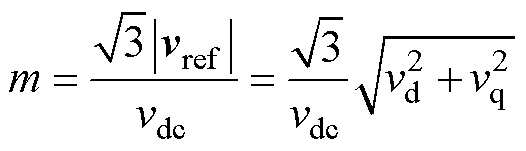 (3)
(3)
在线性调制区域内,调制比mÎ[0, 1],本文规定调制比m<0.5的区域为低调制比区域。将式(2)代入式(3)中,并忽略定子电阻压降,得
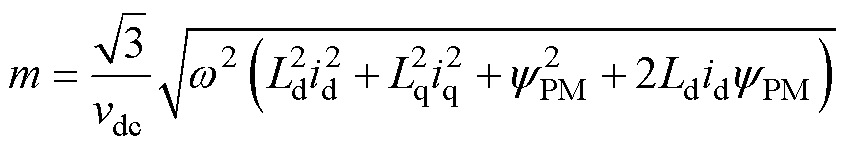 (4)
(4)
对于表贴式永磁同步电机,采用id=0的磁场定向控制(Field-Oriented Control, FOC),式(4)中与id有关的项全部为零,即
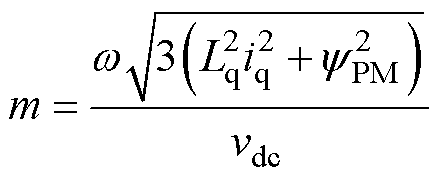 (5)
(5)
式(5)表明,当系统负载和母线电压不变时,电压参考矢量调制比与转速呈线性关系,即当电机从起动到升速过程,调制比m从零逐渐增大。
在数字化电机控制中,由于PWM周期的存在,电压参考矢量是离散变化的,如图2a所示。在PWM周期Ts内,参考矢量相位变化量可表示为
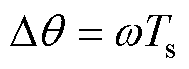 (6)
(6)
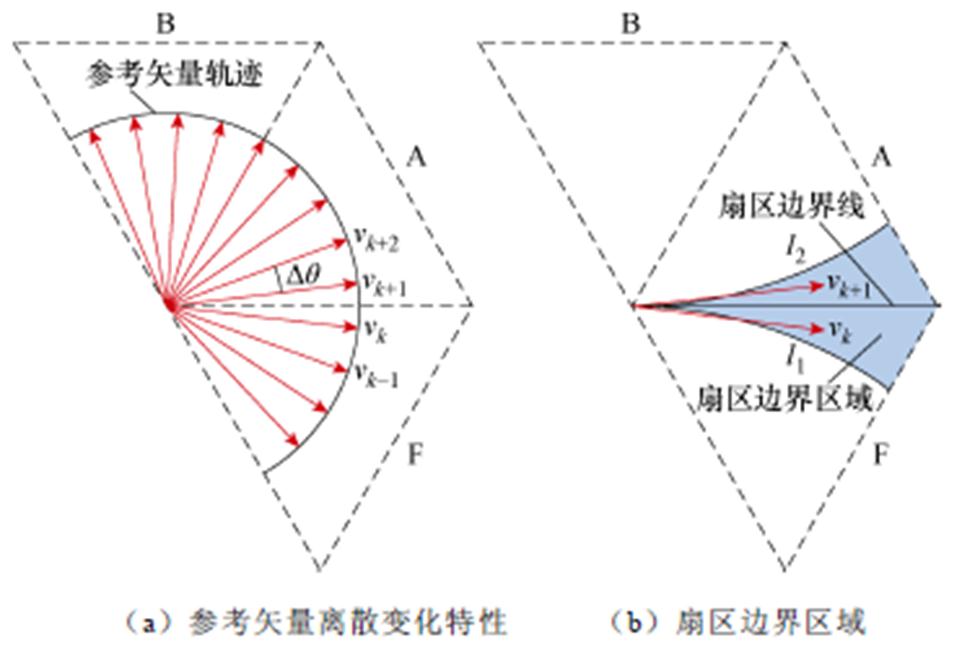
图2 参考矢量离散变化特性及扇区边界区域
Fig.2 Discrete variation characteristics of voltage reference vector and its sector boundary region
将式(6)代入式(5)中,推出Dq 表达式为
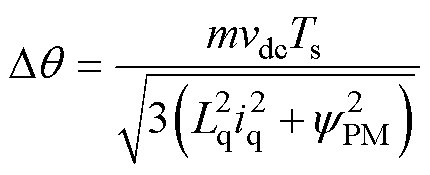 (7)
(7)
式(7)表明,当PWM周期恒定时,电机在升速过程中,电压参考矢量的相位变化量Dq 随调制比m逐渐增大,由数字化控制造成的参考矢量离散变化特性不容忽略。当考虑该离散特性时,电压参考矢量不只在边界线处切换扇区。以图2b所示的F扇区电压参考矢量vk为例,经过一个PWM周期,同样发生扇区切换,运行至A扇区的vk+1处。根据式(7),求出电压参考矢量在F和A扇区发生切换的区域边界线l1和l2,如图2b所示,着色区域表示电压参考矢量在相邻PWM周期发生扇区切换的区域。F1区域切换至A1区域开关序列如图3所示。而在扇区边界区域内,三电平经典VSVPWM策略的电压参考矢量开关序列的首发矢量由POP跳变为PPO,在该处极易产生窄脉冲,如图3所示。
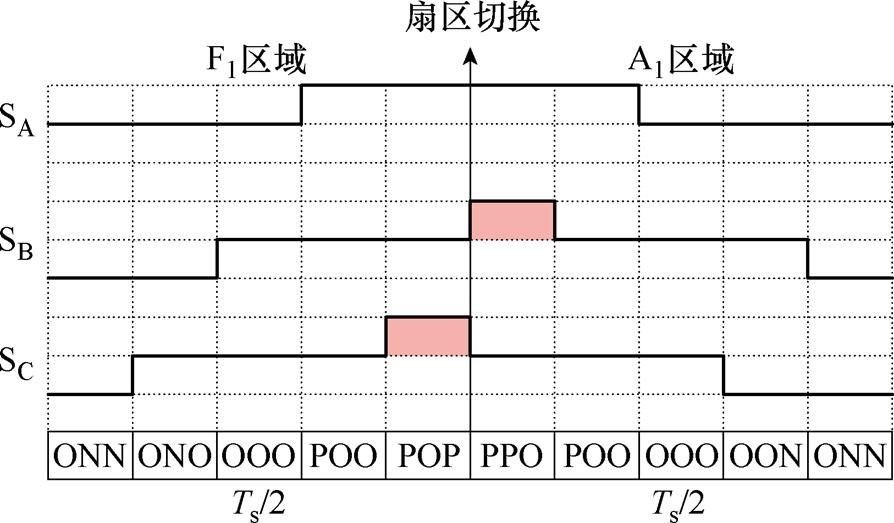
图3 F1区域切换至A1区域开关序列
Fig.3 The switch pattern from region F1 to A1
根据全扇区对称性,考虑控制离散性的全扇区边界区域划分如图4所示。图4可见在相邻两个PWM周期内电压参考矢量发生扇区切换的区域。以A扇区为例,图4中AF区域内电压参考矢量在上一PWM周期由F扇区切换至A扇区;AB区域内电压参考矢量在下一PWM周期将切换至B扇区;AA区域内电压参考矢量在相邻两个PWM周期均未发生扇区切换。
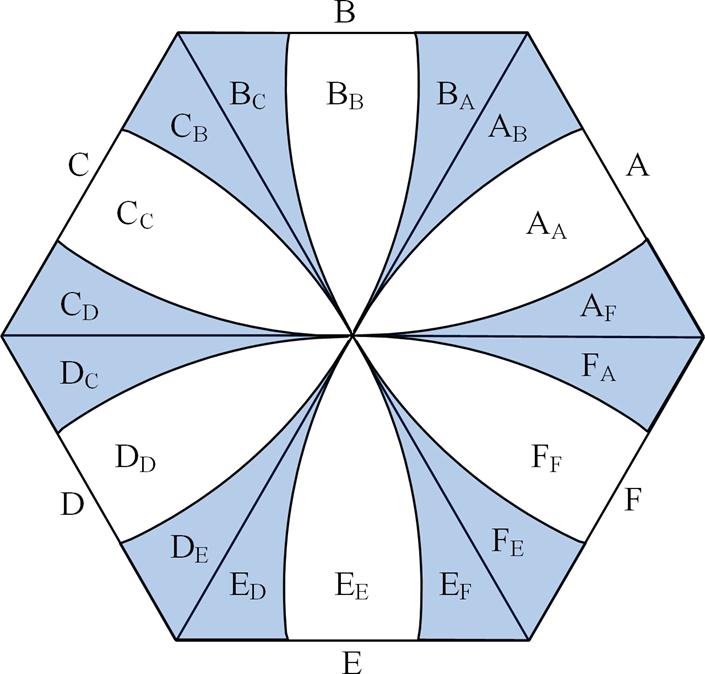
图4 考虑控制离散性的全扇区边界区域划分
Fig.4 Boundary region division of all sectors considering the discreteness of motor control
图5a为A扇区虚拟空间矢量分布图[21],本文重点研究低调制比A1区域的窄脉冲分布规律,如图5b所示,参考矢量vref由最近三虚拟矢量vzS1、vzS2和vz0合成,其作用时间分别为
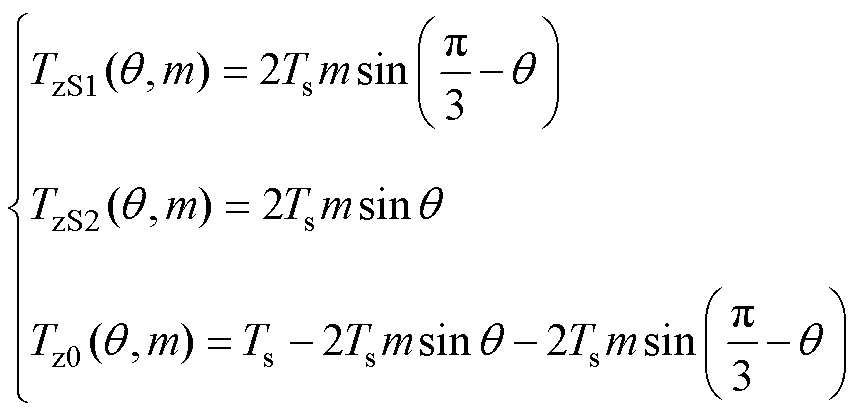 (8)
(8)
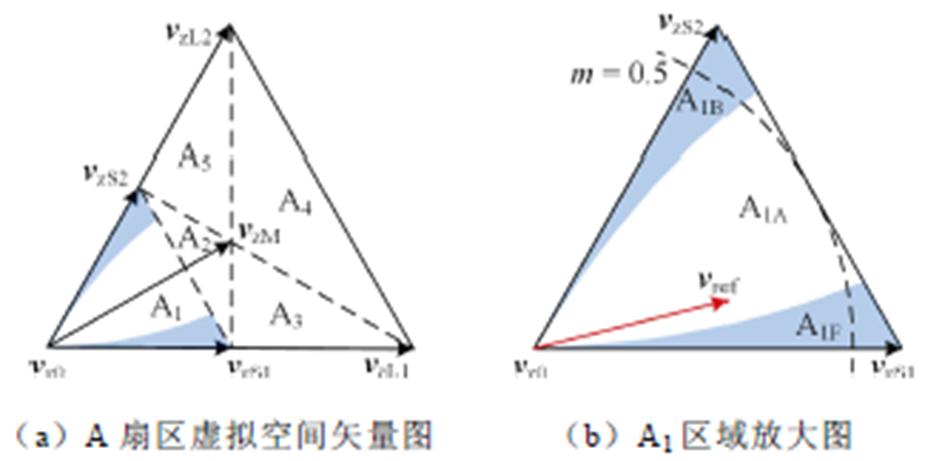
图5 A扇区虚拟空间矢量及A1区域放大图
Fig.5 The virtual space vector in region A and the enlarged map of region A1
对三电平P、O、N状态进行编码分别记为2、1、0,并将三相电平编码之和作为基本矢量的编码,例如PPO(5)的编码为2+2+1=5,OON(2)的编码为1+1+0=2。根据图5b,在分析低调制比区域最大编码矢量PPO(5)窄脉冲时,需考虑三种情况。
A1F区域内的参考矢量在上一PWM周期由F1区域切换至A1区域,其开关序列首发矢量由POP(5)变为PPO(5),如图3所示,这使得A扇区PPO(5)处和F扇区POP(5)处极易产生窄脉冲。由于扇区的对称性,F1A、B1C、C1B、D1E以及E1D区域的窄脉冲分析方法类似。
为了确保功率器件能够有效地开通和关断,需要限制其最小导通时间[22],记作最小脉宽限制Tmin。脉冲宽度与最小脉宽限制Tmin的差值定义为最小脉宽函数(Minimum Pulse Width Function, MPWF),将最小脉宽函数值小于零的区域设定为窄脉冲限制区[13]。因此,A1F区域PPO(5)矢量处的最小脉宽函数可以表示为
 (9)
(9)
以最小脉宽限制Tmin=2 ms、PWM周期Ts=100 ms为例(下同),代入式(9),得到A1F区域窄脉冲分布如图6阴影区域所示。
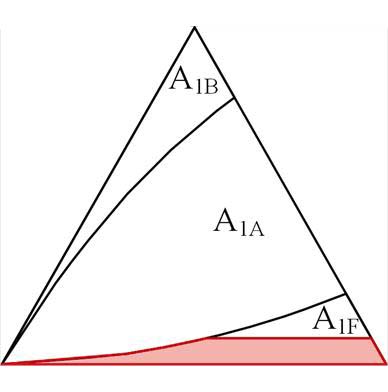
图6 A1F区域窄脉冲限制区
Fig.6 Narrow pulse limited region in A1F
A1A区域内的参考矢量在相邻PWM周期均未发生扇区切换。由于矢量序列的对称性,当前PWM
周期的结尾矢量与下一PWM周期的首发矢量形成接续,而在该位置也可能出现窄脉冲,如图7所示。虽然PPO(5)矢量在序列上形成了接续,但本质上分属于两个PWM周期,因此在分析时需要考虑数字化控制离散性造成的影响。在稳态条件下,认为调制比恒定,下一PWM周期的矢量作用时间可由参考矢量相位的变化量Dq 求出。因此,A1A区域内PPO(5)矢量接续处的最小脉宽函数可表示为
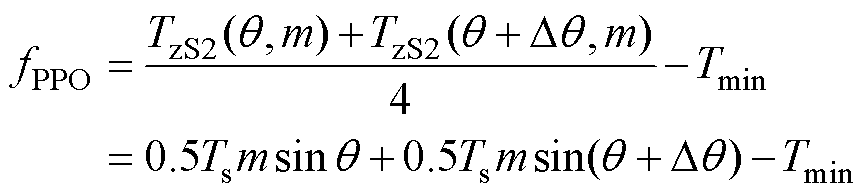 (10)
(10)
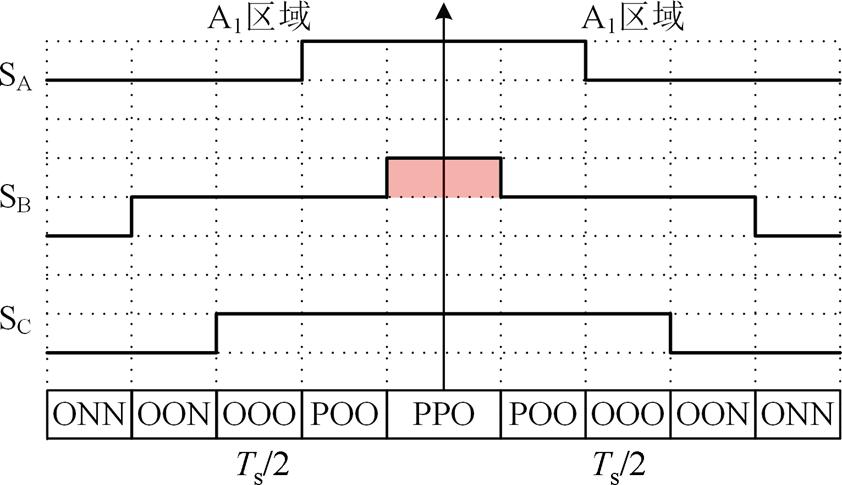
图7 A1A区域相邻周期矢量序列
Fig.7 Switch pattern between adjacent period in region A1A
根据式(10),可得到A1A区域窄脉冲限制区如图8阴影区域所示。同理可分析B1B、C1C、D1D、E1E以及F1F区域的窄脉冲。
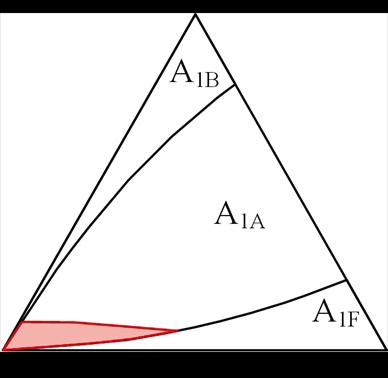
图8 A1A区域窄脉冲限制区
Fig.8 Narrow pulse limited region in A1A
A1B区域内的电压参考矢量虽然在下一PWM周期切换至B1区域,但其序列的首发矢量并未发生变化,如图9所示。此外,由于PPO(5)在A1B区域的作用时间较长,故在该区域内几乎不会产生窄脉冲。
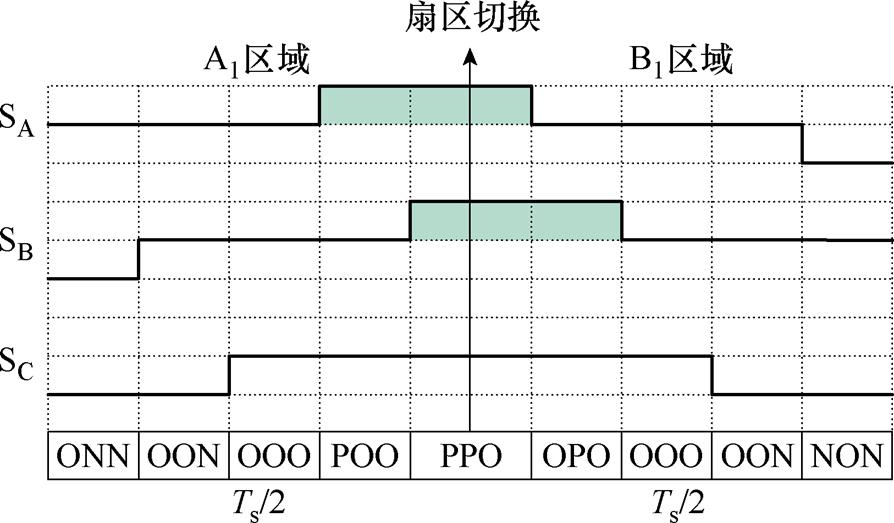
图9 A1区域切换至B1区域矢量序列
Fig.9 The switch pattern from region A1 to B1
综合以上分析,将A1区域最大编码矢量PPO(5)处的窄脉冲限制区总结于图10,并将A1A和A1F两限制区边界线相交处的调制比记为边界调制比mb,该值可通过式(11)解得。对于A1区域,当参考矢量调制比大于mb时,PPO(5)处的窄脉冲主要受扇区切换的影响分布在A1F区域;当调制比小于mb时,有效矢量作用时间短,同时受扇区切换的影响,在A1F和A1A区域均可能出现窄脉冲。根据扇区的对称性,可以得到全扇区低调制比区域最大编码矢量处窄脉冲限制区,如图10所示。当电压参考矢量在FA、BC和DE扇区之间发生切换时,由于开关序列首发矢量发生跳变,在这些扇区边界处最大编码矢量极易出现窄脉冲。
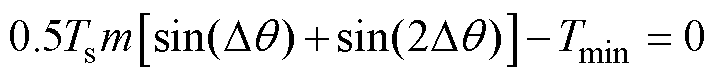 (11)
(11)
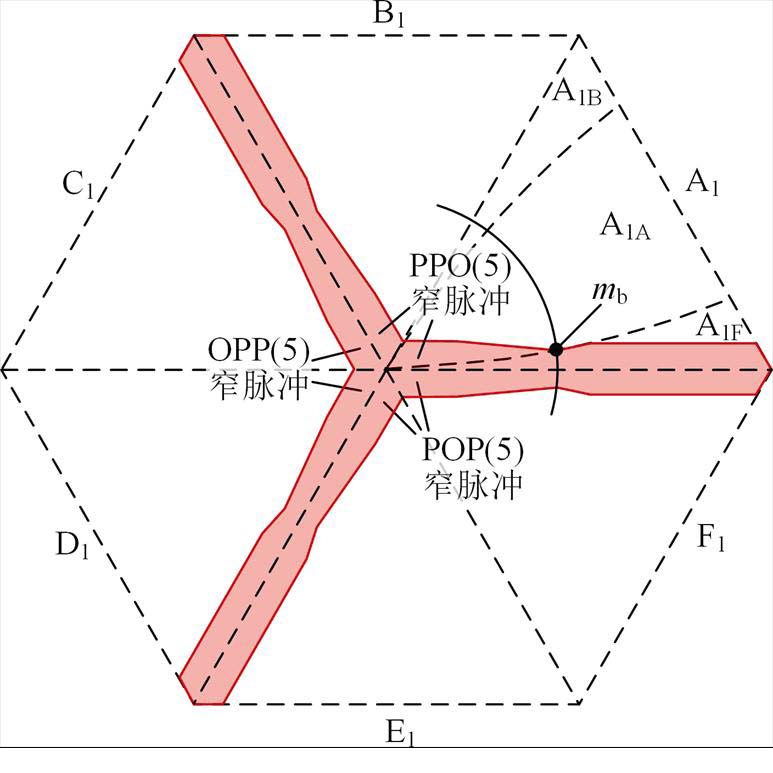
图10 低调制比区域最大编码矢量窄脉冲限制区
Fig.10 Narrow pulse limited region of maximum encoding vector in low modulation index region
针对经典VSVPWM在低调制比区域存在窄脉冲的问题,本文提出一种基于矢量序列优化的低调制比混合VSVPWM(Low modulation index Hybrid VSVPWM, LH_VSVPWM)策略。结合图10所示的窄脉冲分布规律,在小于边界调制比mb的窄脉冲分布区域,增补作用时间较长的冗余零矢量抑制窄脉冲;在大于边界调制比mb的窄脉冲分布区域,舍弃作用时间较短的冗余小矢量抑制窄脉冲。对于无窄脉冲分布的区域,为了兼顾功率器件开关动作次数及中点电位平衡能力,延用经典VSVPWM矢量 序列。
以A1区域为例,进行精细化分区,如图11所示。针对图11各精细化区域,分别优化其矢量序列,如图12所示。在A1-1区域,延用经典VSVPWM矢量序列;在A1-2区域,增补冗余零矢量PPP(6)和NNN(0);在A1-3区域,舍弃冗余小矢量PPO(5),将作用时间增加至其互补矢量OON(2);在A1-4区域,舍弃冗余小矢量ONN(1),将其作用时间增加至矢量POO(4)。
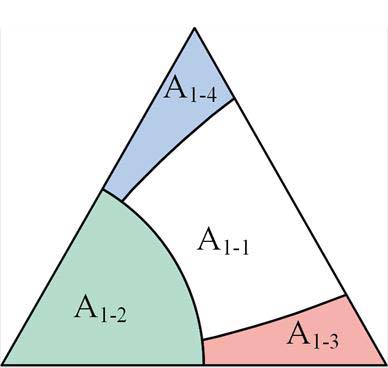
图11 A1区域精细化分区
Fig.11 Fine partition in region A1

图12 A1区LH_VSVPWM矢量序列
Fig.12 Switch pattern of LH_VSVPWM in region A1
图12中红色双向箭头表示LH_VSVPWM各矢量序列最大编码矢量处的脉冲宽度,若满足最小脉冲宽度的限制,则在整个低调制比区域,最大编码矢量处不会产生窄脉冲。A1各精细化区域最小脉宽函数可表示为
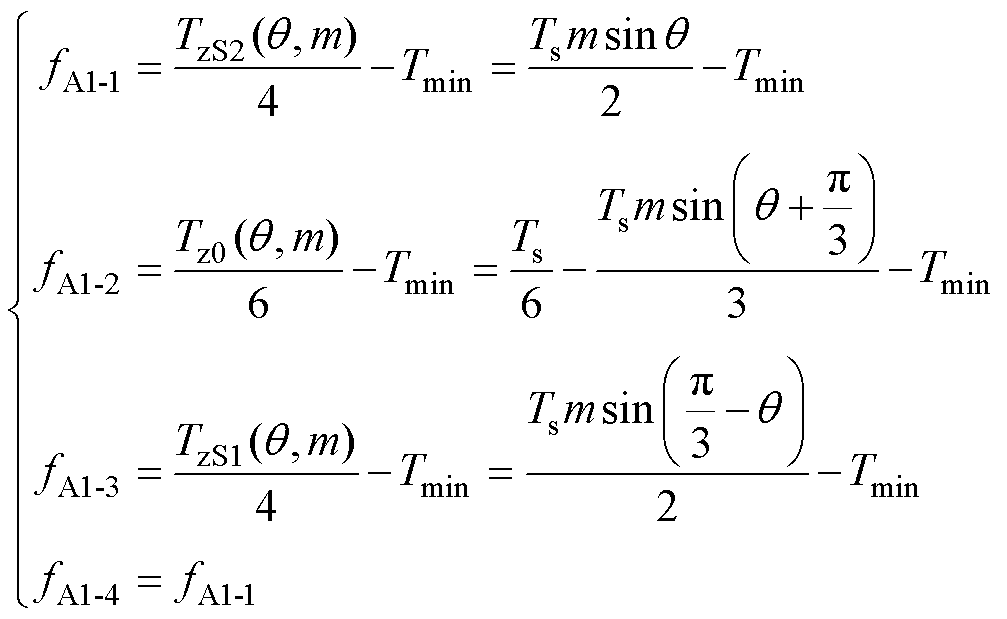 (12)
(12)
图13为式(12)最小脉宽函数在A1各精细化区域的热力图。从图中可以看出,最小脉宽函数在各自作用域内的值均大于零,表明LH_VSVPWM能够有效抑制三电平低调制比区域的窄脉冲。
中点电位偏差DVnp是由流经电容中点的电流在其作用时间内累积形成的[23-24],可表示为
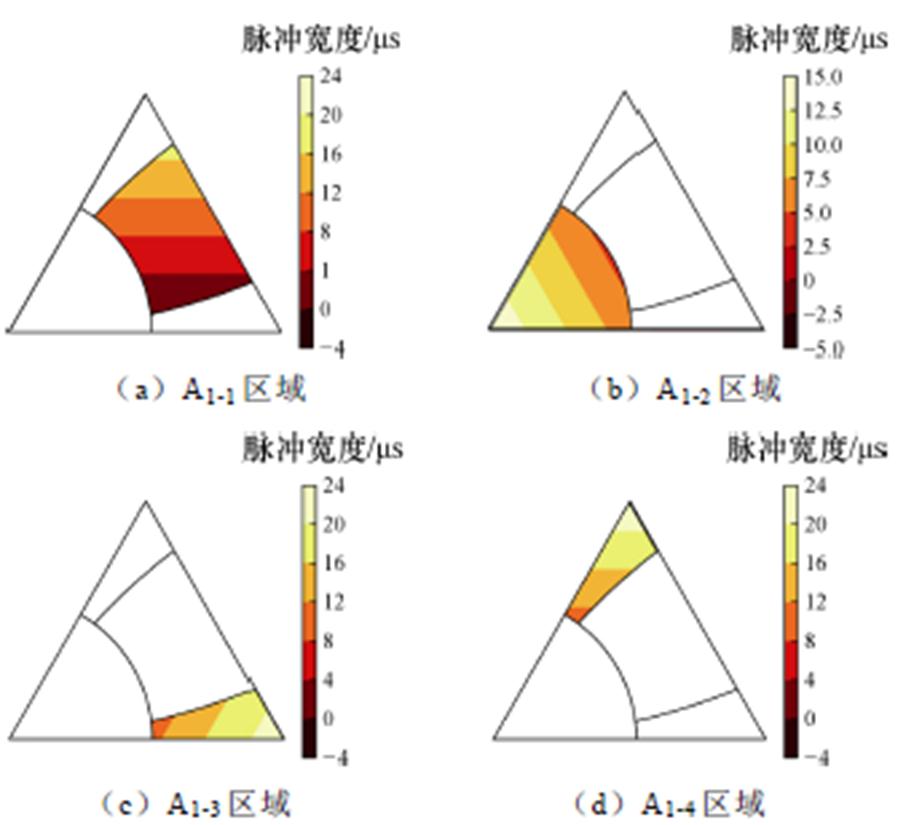
图13 LH_VSVPWM窄脉冲分析
Fig.13 Narrow pulse analysis of LH_VSVPWM strategy
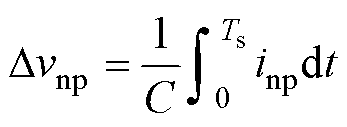 (13)
(13)
式中,C为直流侧电容值;inp为流出电容中点的电流。表1给出了A扇区小矢量作用时对中点电流的影响,其中ia、ic极性为正。
表1 A1区域小矢量作用时中点电流
Tab.1 Neutral-point currents of short vectors in region A1

小矢量inp POO-ia PPOic ONNia OON-ic
在PWM周期内,认为相电流恒定,式(13)中点电位偏差可进一步表示为
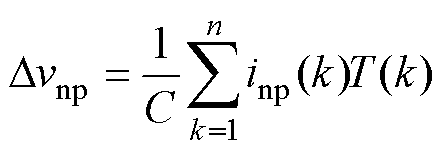 (14)
(14)
式中,n为开关周期内的矢量个数;inp(k)和T(k)分别为第k个矢量的中点电流和作用时间。
根据式(14),分析LH_VSVPWM各矢量序列在PWM周期内中点电位偏差,如图14所示。同理,分析受窄脉冲影响后经典VSVPWM矢量序列中点电位偏差。表2对比了两种策略在PWM周期内的中点电位偏差。在极低调制比区域A1-2,LH_ VSVPWM能够抑制窄脉冲,实现PWM周期内中点电位偏差为零;而经典VSVPWM受窄脉冲的影响,部分小矢量无法由变流器实现,使得中点电位存在偏差,且剩余的有效小矢量作用时间短,中点电位调节能力弱。而对于其他区域,两种调制策略对中点电位偏差的影响效果相似,剩余的有效小矢量对中点电位调节能力相同,但LH_VSVPWM在抑制窄脉冲方面更具优势。

图14 LH_VSVPWM矢量序列中点电位偏差
Fig.14 Neutral-point potential deviation of LH_VSVPWM
表2 考虑窄脉冲影响的中点电位偏差对比
Tab.2 Comparison of neutral-point potential deviation considering the effect of narrow pulse

A1区域LH_VSVPWM经典VSVPWM A1-100 A1-20-icTzS2/2-iaTzS1/2 A1-3-icTzS2-icTzS2/2 A1-4-iaTzS1-iaTzS1/2
为验证本文提出的LH_VSVPWM在永磁同步电机拖动飞轮升速充能过程中三电平变流器窄脉冲抑制效果,在Matlab/Simulink中搭建仿真模型,开关频率设为10kHz,死区时间设为2 ms。对应永磁同步电机升速过程,等间隔选取低调制比0.1、0.3和0.5的工况,对比经典九段式VSVPWM(记作Seg9_VSVPWM)、十三段VSVPWM[12](记作Seg13_VSVPWM)和本文提出的LH_VSVPWM的窄脉冲抑制效果,仿真结果如图15~图18所示。
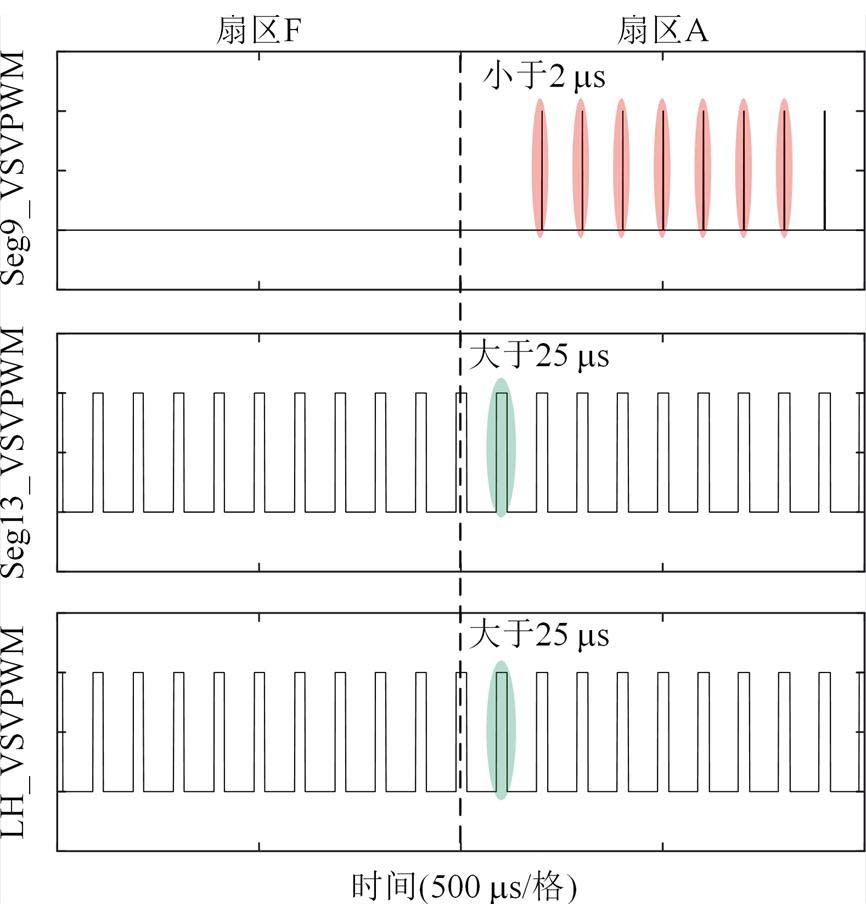
图15 调制比0.1时开关器件VTb1仿真结果
Fig.15 Simulation results under modulation index 0.1
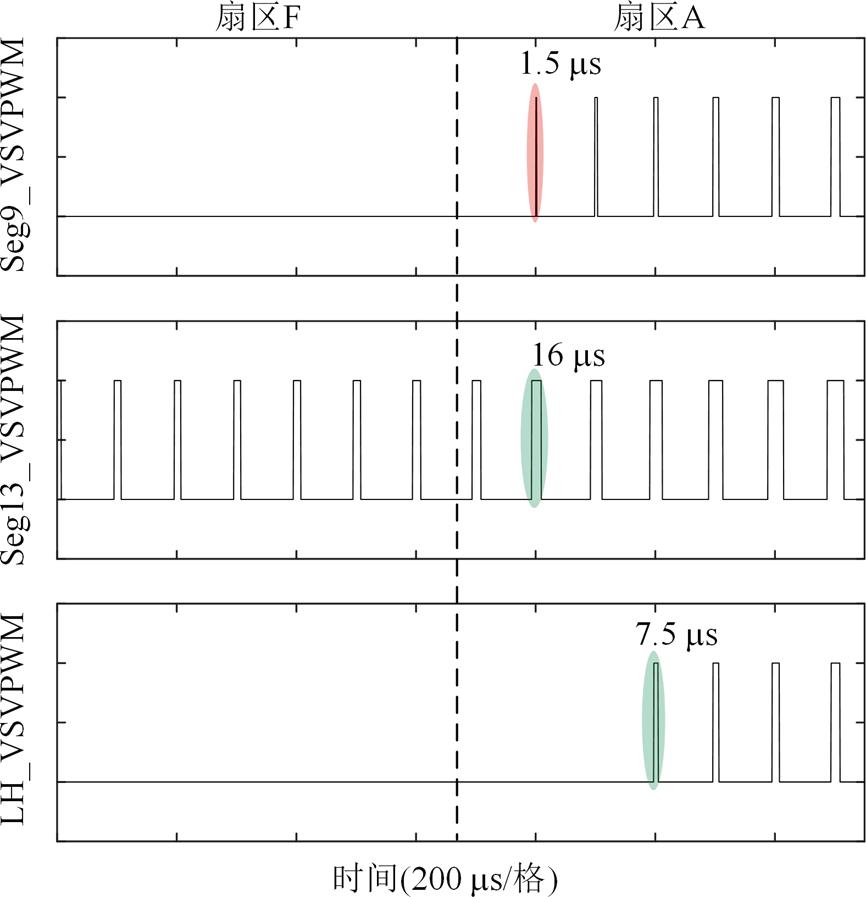
图16 调制比0.3时开关器件VTb1仿真结果
Fig.16 Simulation results under modulation index 0.3
图15表明,当调制比为0.1时,在A扇区边界以及中间区域,Seg9_VSVPWM开关器件PWM波形出现了连续的窄脉冲,宽度均小于2 ms。而LH_VSVPWM通过优化矢量序列,使得功率器件脉冲宽度均在25 ms以上,在极低调制区域完全消除了窄脉冲。
当调制比升至0.3,Seg9_VSVPWM在F和A扇区边界处,脉冲波形出现了宽度为1.5 ms的窄脉冲,如图16所示。Seg13_VSVPWM在该区域仍保持着良好的窄脉冲抑制效果,将最小脉冲宽度保持在16 ms,但该方法开关次数较多,一定程度上增加了系统的损耗。LH_VSVPWM通过合理分配矢量时间,消除了边界区域的窄脉冲,将最小脉冲宽度限制在7.5 ms,同时减少了功率器件动作次数,在降低开关损耗方面更具优势。
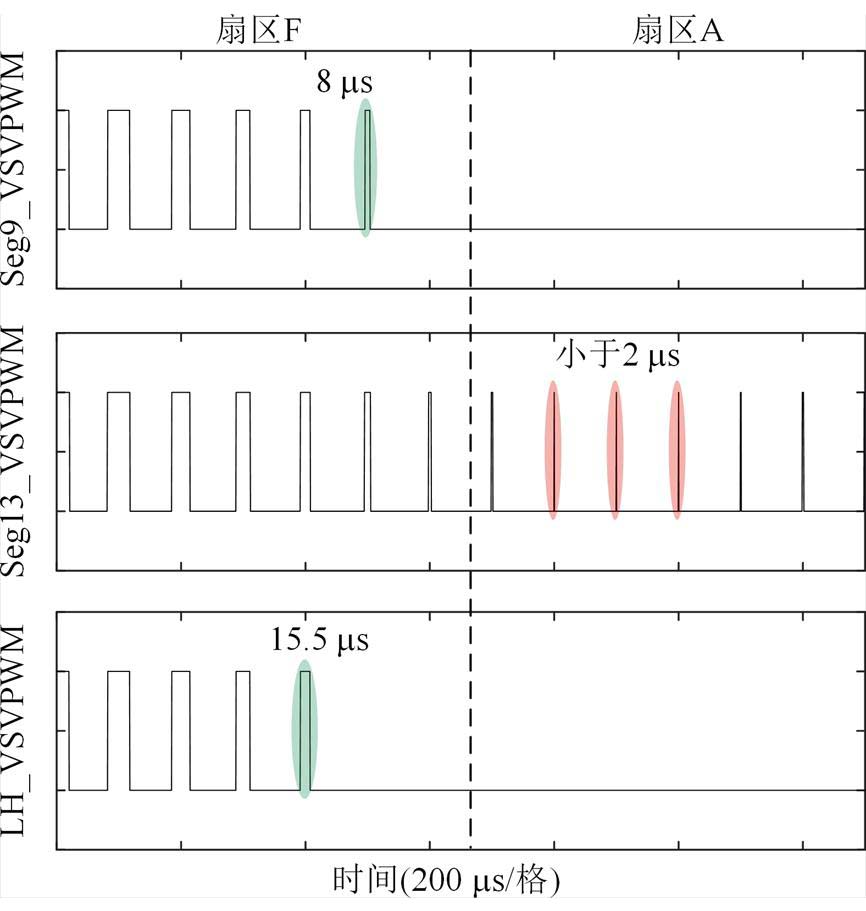
图17 调制比0.5时开关器件VTc1仿真结果
Fig.17 Simulation results under modulation index 0.5
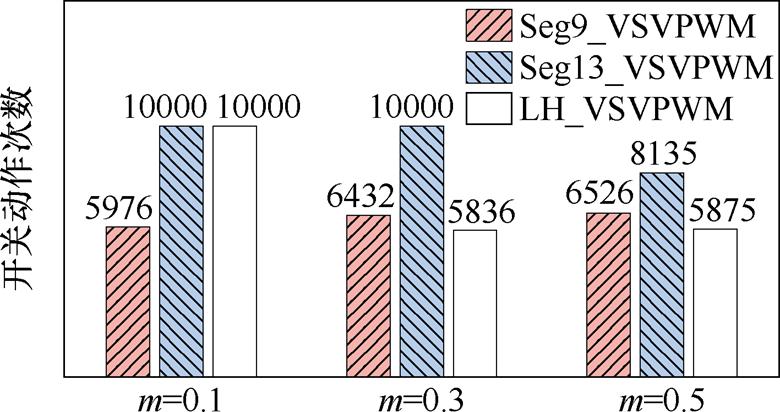
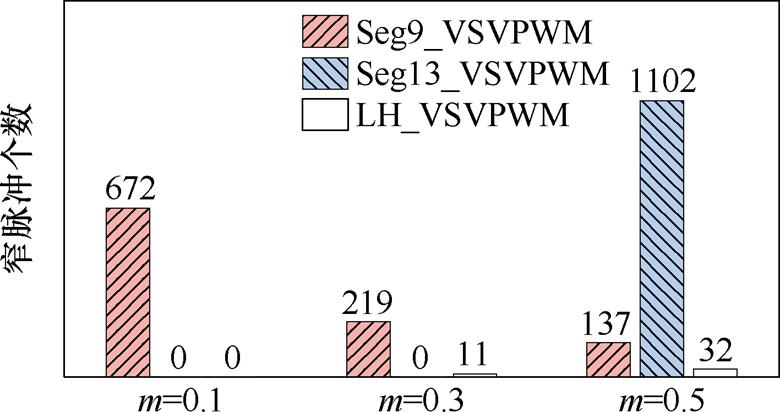
图18 1 s内开关动作次数及窄脉冲个数
Fig.18 The number of switch and narrow pulse in 1 s
图17对比了在调制比为0.5时开关器件Tc1的PWM波形。由于调制比的增加,零矢量的作用时间趋近于零,Seg13_VSVPWM功率器件PWM波形在A扇区中间区域连续出现了宽度小于2 ms的窄脉冲。而Seg9_VSVPWM和LH_VSVPWM在A扇区内开关器件并未动作,限制了窄脉冲的出现。
永磁电机拖动飞轮缓慢升速过程中,低调制比窄脉冲累积问题比较严重。图18对比了三种调制策略在1 s内功率器件动作次数及窄脉冲出现个数。在极低调制比0.1工况下,Seg9_VSVPWM开关动作次数最少,但窄脉冲出现最为频繁,1 s内累积出现672次窄脉冲,Seg13_VSVPWM和LH_VSVPWM能够完全消除该调制比下的窄脉冲。随着调制比增加,Seg9_VSVPWM窄脉冲个数呈下降趋势,但出现仍十分频繁。Seg13_VSVPWM在调制比0.3时能够很好地抑制窄脉冲,而在调制比0.5的区域,该方法窄脉冲个数急剧增加,1 s内累积出现1 102次。相比之下,LH_VSVPWM在调制比0.3和0.5下开关动作次数最少,同时保持良好的窄脉冲抑制效果,1 s内窄脉冲仅出现11和32次。
综合以上仿真结果,LH_VSVPWM在整个低调制比区域都有着较优的窄脉冲抑制能力,而且在抑制窄脉冲方面具有针对性,改善系统性能的同时减少了器件开关次数。因此,LH_VSVPWM在三电平逆变器低调制比区域更具适用性。
为了进一步验证本文LH_VSVPWM算法,在实验室搭建二极管中点钳位(Diode Neutral Point Clamped, DNPC)三电平变流器实验平台,如图19所示。直流电源提供输入电压,三电平变流器输出侧连接对拖永磁同步电机的电动端。对拖电机的发电侧连接不控整流器,将电能提供给负载电阻,实现功率的单向流动。电机控制方式为FOC,实验参数见表3。

图19 DNPC三电平逆变器实验平台
Fig.19 DNPC three-level inverter experimental platform
图20为Seg9_VSVPWM和LH_VSVPWM策略在电机起动瞬间的实验对比结果。在电机起动之前,受窄脉冲的影响,Seg9_VSVPWM相电压出现了连续窄脉冲甚至断续的现象。经过一段时间的累积,直流侧电容电压出现了明显的偏差,并在电机起动瞬间达到峰值。在这种极低调制比的工况下,小矢量的作用时间较短,对中点电位调节能力较弱,使得电容电压恢复过程十分缓慢。而LH_VSVPWM通过优化矢量序列,合理分配作用时间较长的零矢量,剔除了极低调制比下的窄脉冲,在电机起动瞬间中点电位平衡控制上取得了良好的效果。
表3 实验参数
Tab.3 Experimental parameter
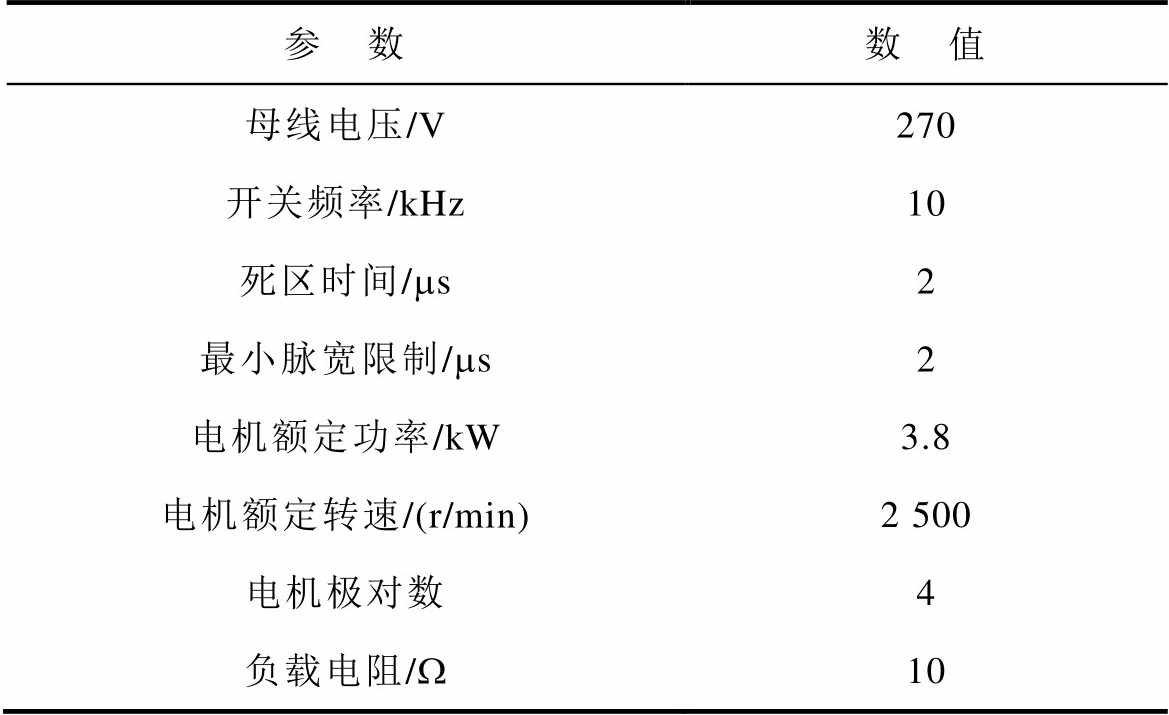
参 数数 值 母线电压/V270 开关频率/kHz10 死区时间/ms2 最小脉宽限制/ms2 电机额定功率/kW3.8 电机额定转速/(r/min)2 500 电机极对数4 负载电阻/W10
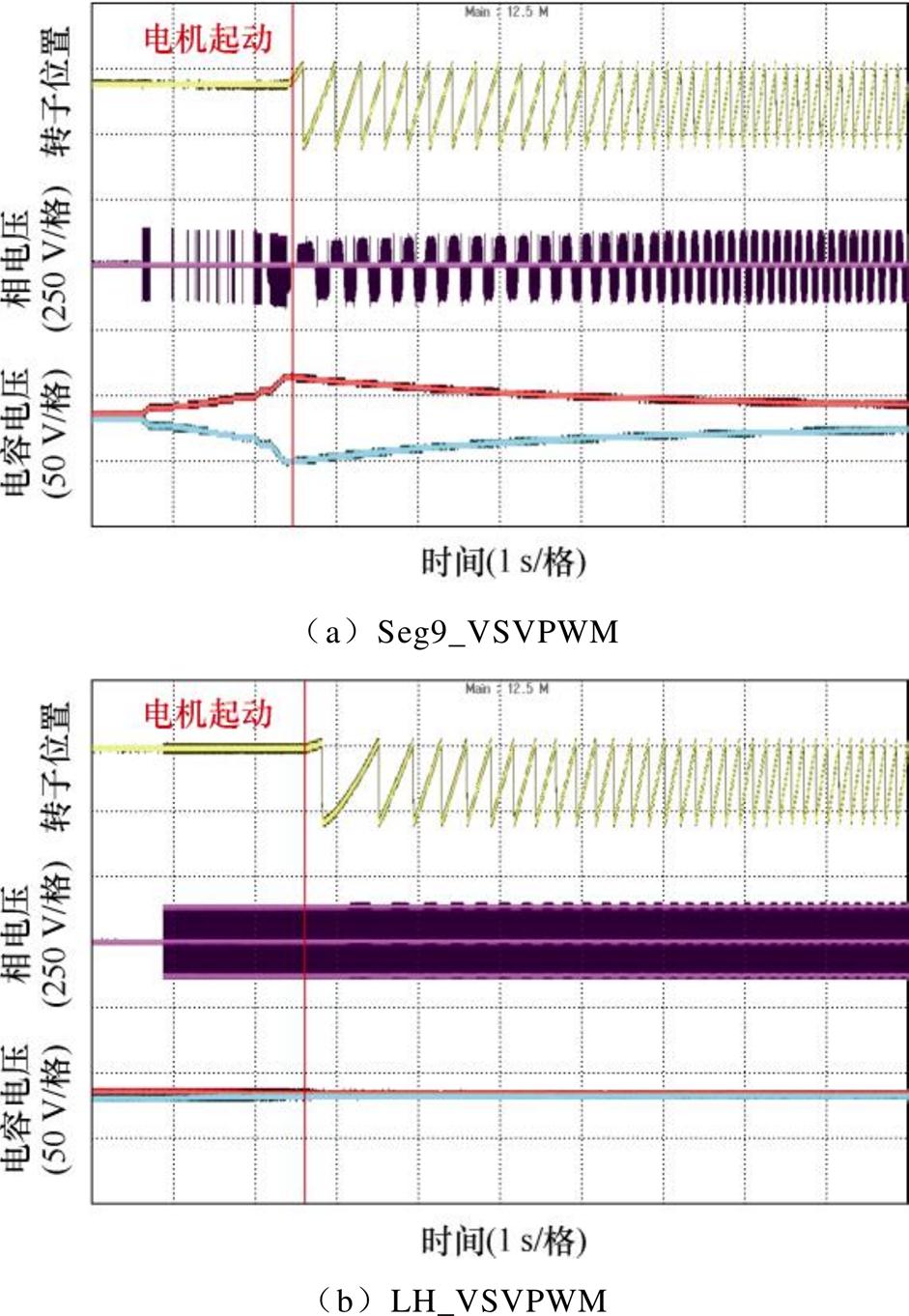
图20 电机起动瞬间实验结果对比
Fig.20 Comparison of experimental results during motor starting process
调制比为0.1时,通过观测功率器件VTb1和VTb4的PWM脉冲、B相电压以及B相和C相电流波形,对比三种调制策略的作用效果,如图21所示。放大PWM脉冲波形发现Seg9_VSVPWM的窄脉冲分布十分密集,在扇区边界处连续出现宽度小于的2 ms的窄脉冲。部分窄脉冲由于作用时间较短,在开通后并不能正常关断,出现了异常脉冲,导致了相电压和相电流发生明显畸变,如图21a放大图C和D所示。相比之下,Seg13_VSVPWM和LH_VSVPWM能够将开关器件最小脉冲宽度增加至30 ms左右,抑制了边界区域的窄脉冲,如图21b和图21c所示。
图22为三种调制策略在调制比0.3工况的实验结果对比。相较于调制比0.1工况,Seg9_VSVPWM在扇区边界处的窄脉冲有所改善,但仍存在小于2 ms的PWM脉冲,导致相电压产生了一定的畸变,电流THD只有15.07%。Seg13_VSVPWM与调制比0.1工况表现一致,保持了很好的脉宽特性,开关器件的PWM脉冲宽度均在10 ms以上,但其开关动作次数较多,电流波形质量相对较差,THD仅为15.84%。而本文提出的LH_VSVPWM,不仅能够有效抑制扇区边界处的窄脉冲,将VTb1和VTb4的最小PWM脉冲宽度分别控制在6.4 ms和7.6 ms,同时减少了功率器件的开关动作次数,电流波形得到改善,THD降低至13.78%。


图21 调制比0.1实验结果对比
Fig.21 Comparison of experimental results under modulation index 0.1
当调制比升至0.5时,三种调制算法的实验结果总结于图23。由图23a可知,调制比0.5工况下Seg9_VSVPWM的窄脉冲问题得到进一步缓解,但其最小脉冲宽度仍然小于3 ms,对系统的相电压造成一定的影响,电流THD为20.25%。但在该工况下,由于零矢量作用时间急剧下降,Seg13_VSVPWM的表现并不理想,出现了宽度小于2 ms的连续窄脉冲以及受窄脉冲影响的异常脉冲,使得相电压和电流产生严重畸变,电流THD高达23.50%,如图23b所示。而LH_VSVPWM在调制比0.5区域具有良好的脉宽特性,最小脉冲宽度保持在12 ms以上。此外,LH_VSVPWM有着更优的谐波性能,电流THD达到17.49%,相比于Seg9_VSVPWM和Seg13_ VSVPWM,分别降低了2.76%和6.01%。
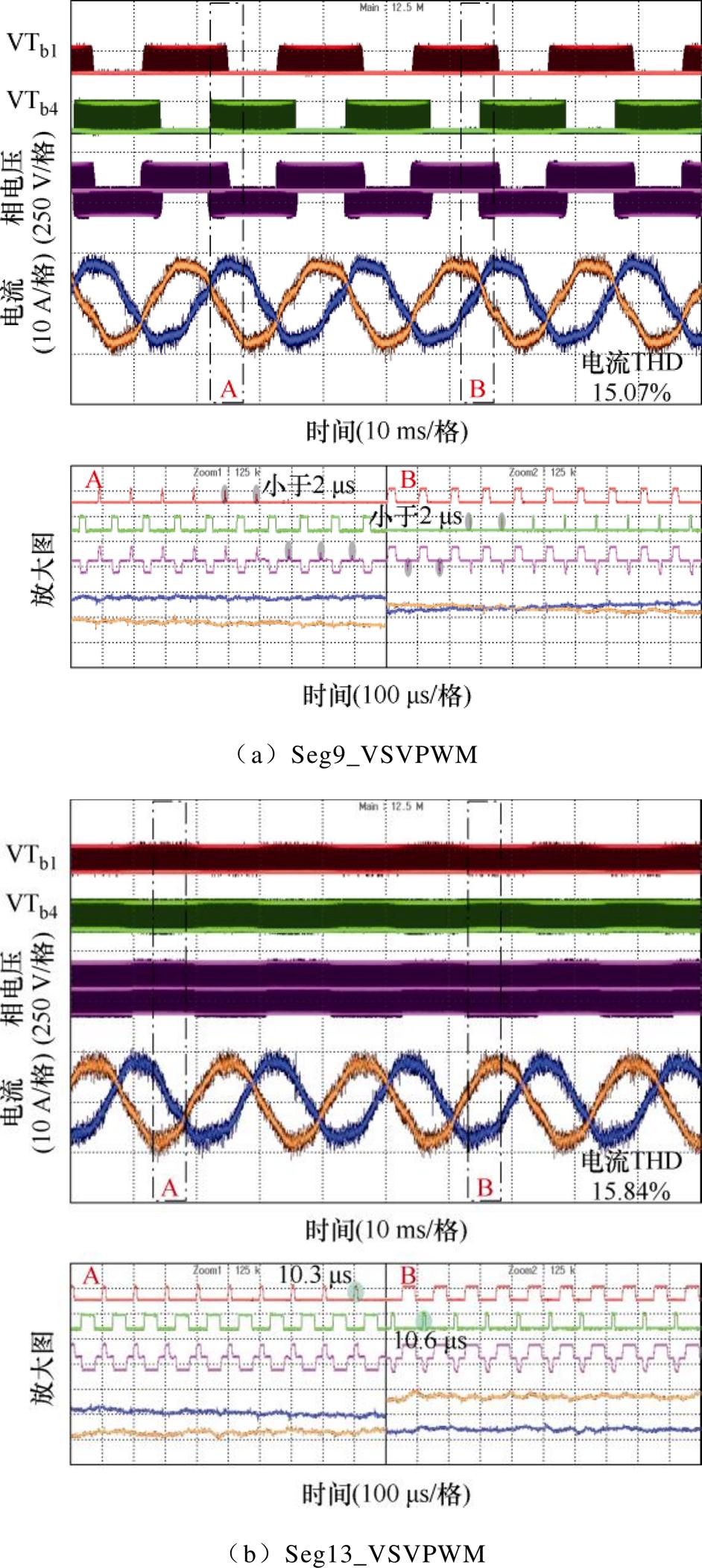

图22 调制比0.3实验结果对比
Fig.22 Comparison of experimental results under modulation index 0.3
综合图20~图23实验结果,进一步证明了LH_VSVPWM算法的有效性。在电机起动瞬间,通过消除窄脉冲,能够维持中点电位的动态平衡。随着调制比的增加,LH_VSVPWM具备更优的脉宽特性和谐波性能,开关动作次数更少,对降低逆变器的开关损耗具有积极作用。不同调制比下实验结果见表4。因此,本文提出的LH_VSVPWM适用于三电平低调制比区域。
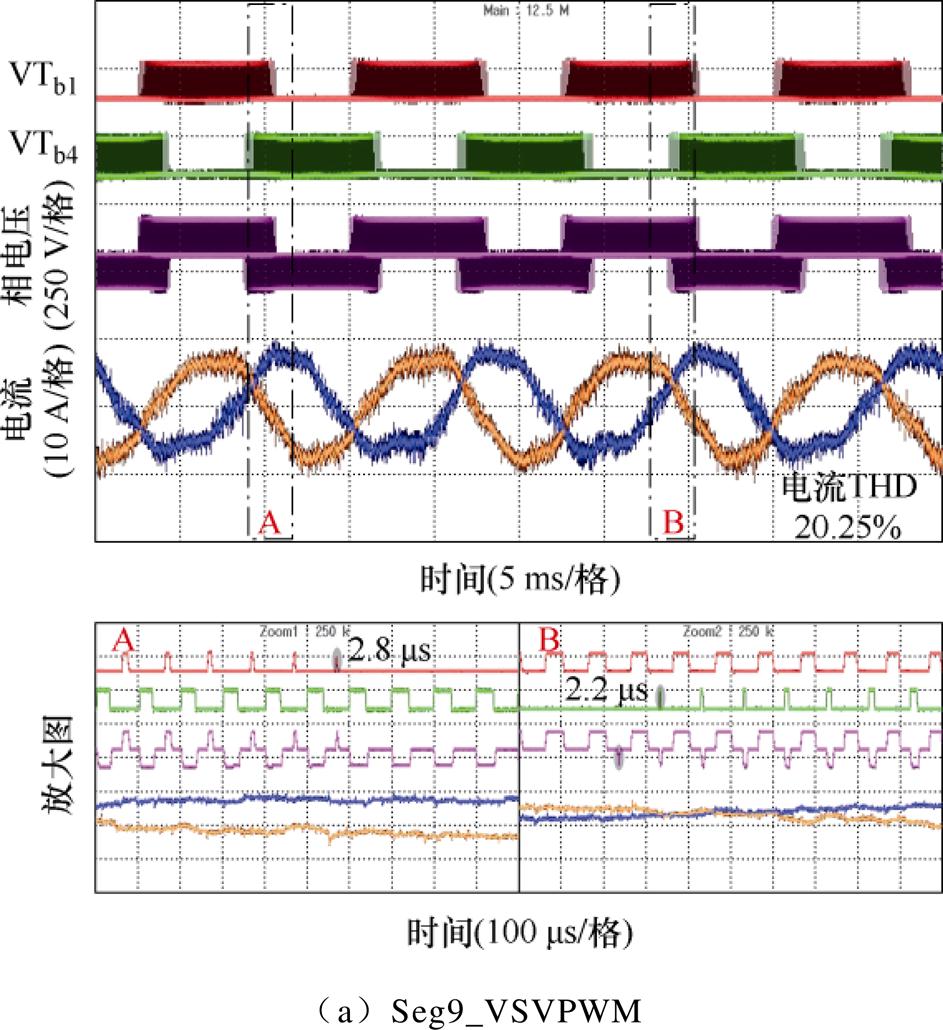
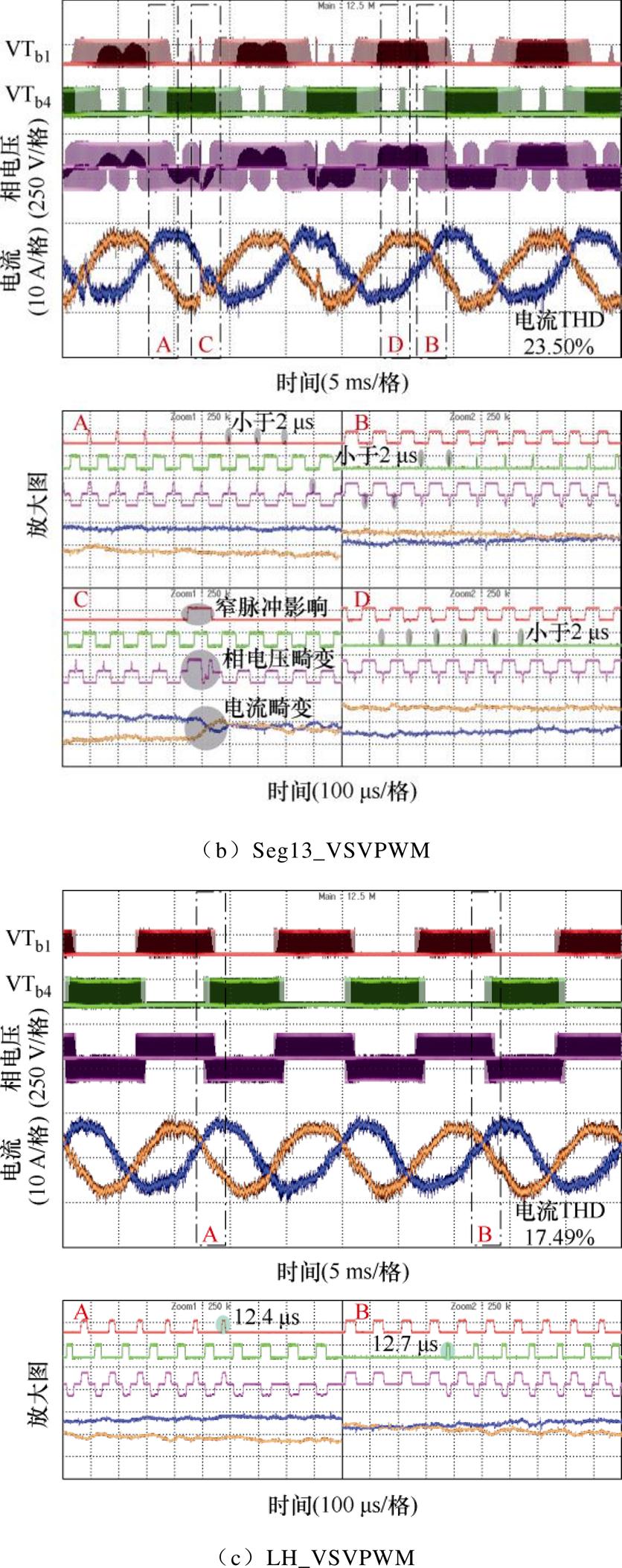
图23 调制比0.5实验结果对比
Fig.23 Comparison of experimental results under modulation index 0.5
表4 实验结果总结
Tab.4 Summary of experimental results
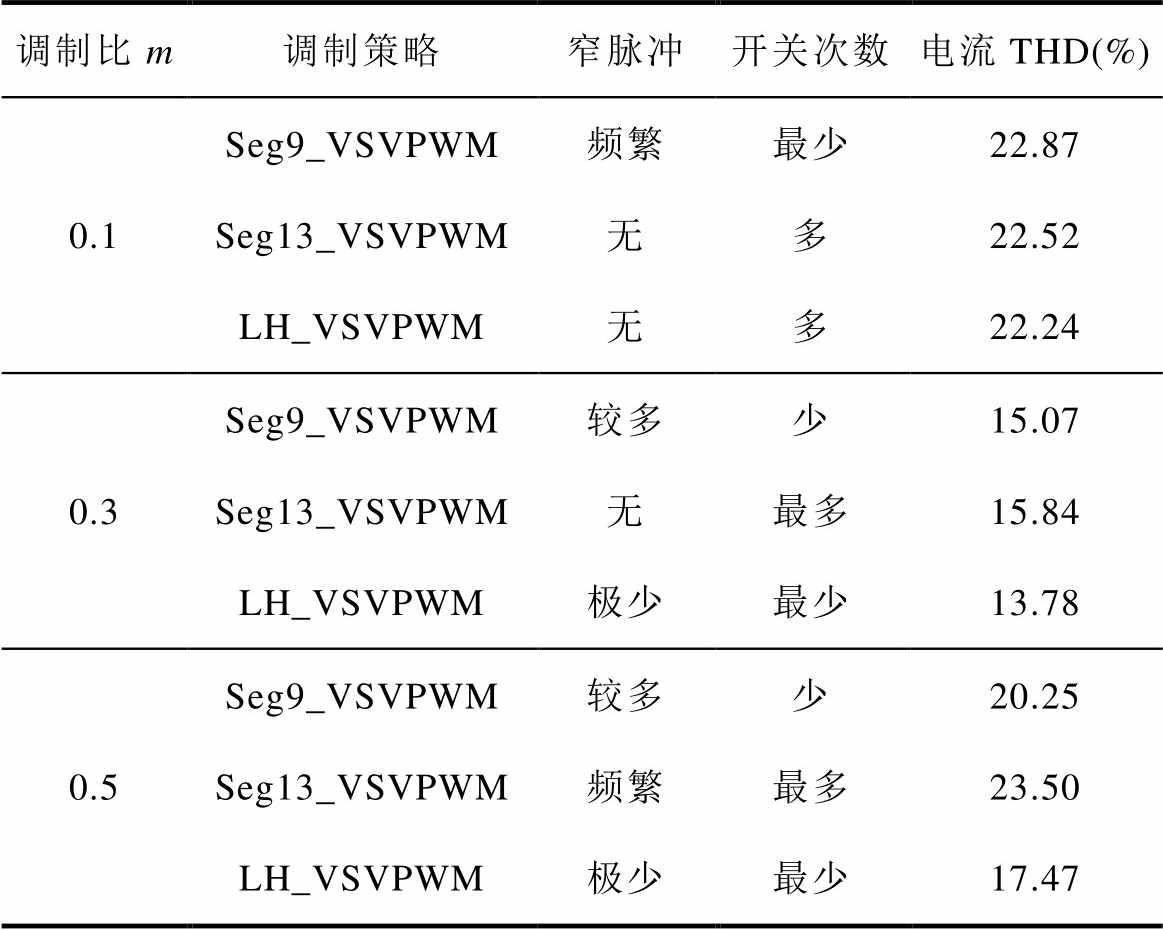
调制比m调制策略窄脉冲开关次数电流THD(%) 0.1Seg9_VSVPWM频繁最少22.87 Seg13_VSVPWM无多22.52 LH_VSVPWM无多22.24 0.3Seg9_VSVPWM较多少15.07 Seg13_VSVPWM无最多15.84 LH_VSVPWM极少最少13.78 0.5Seg9_VSVPWM较多少20.25 Seg13_VSVPWM频繁最多23.50 LH_VSVPWM极少最少17.47
本文针对飞轮充能过程三电平变流器在低调制比区域频繁出现窄脉冲的问题进行研究。通过考虑永磁同步电机数字化控制离散性,建立电压矢量序列最小脉冲宽度与功率器件最小脉宽限制的差值函数,定量分析了经典VSVPWM算法在三电平变流器低调制比区域的窄脉冲分布规律。分析结果表明,在三电平低调制比区域内,受有效矢量作用时间短以及开关序列首发矢量跳变的影响,经典VSVPWM最大编码矢量在FA、BC和DE扇区边界处极易出现窄脉冲。在此基础上提出一种基于矢量序列优化的LH_VSVPWM窄脉冲抑制策略。相比于现有调制算法,LH_VSVPWM在调制比小于0.5的区域内,将PWM最小脉冲宽度限制在6 ms以上,具有良好的窄脉冲抑制效果。在LH_VSVPWM作用下,三电平变流器开关动作次数有所降低,电流波形质量得到改善,同时有效解决电机起动瞬间中点电位失控的问题。
参考文献
[1] 楼冠男, 秦琦, 顾伟, 等. 考虑移动式储能均衡的微电网群分布式动态协同控制策略[J]. 电力系统自动化, 2023, 47(19): 74-85.
Lou Guannan, Qin Qi, Gu Wei, et al. Distributed dynamic cooperative control strategy for microgrid clusters considering equalization of mobile energy storage[J]. Automation of Electric Power Systems, 2023, 47(19): 74-85.
[2] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Elec- trotechnical Society, 2023, 38(5): 1312-1324, 1374.
[3] 王力, 胡佳成, 曾祥君, 等. 基于混合储能的交直流混联微电网功率分级协调控制策略[J]. 电工技术学报, 2024, 39(8): 2311-2324.
Wang Li, Hu Jiacheng, Zeng Xiangjun, et al. Hierarchical coordinated power control strategy for AC-DC hybrid microgrid with hybrid energy storage[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2311-2324.
[4] 郝艺, 周瑀涵, 刘晨曦, 等. 含跟网型储能的新能源多馈入系统小扰动电压支撑强度分析[J]. 电工技术学报, 2024, 39(11): 3569-3580.
Hao Yi, Zhou Yuhan, Liu Chenxi, et al. Small disturbance voltage support strength analysis for renewable multi-infeed system with grid-following energy storage[J]. Transactions of China Elec- trotechnical Society, 2024, 39(11): 3569-3580.
[5] Li Xiaojun, Anvari B, Palazzolo A, et al. A utility- scale flywheel energy storage system with a shaftless, hubless, high-strength steel rotor[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(8): 6667-
6675.
[6] 张玮亚, 王紫钰, 汤文杰, 等. 飞轮储能系统双向准谐振软开关DC-DC变换器的研究[J]. 电气技术, 2016, 17(12): 20-24.
Zhang Weiya, Wang Ziyu, Tang Wenjie, et al. Research on bi-directional quasi-resonant zero voltage switching DC-DC converter for flywheel energy storage system[J]. Electrical Engineering, 2016, 17(12): 20-24.
[7] Takarli Reza, Amini Ali, Khajueezadeh, Moham- madsadegh, et al. A Comprehensive review on flywheel energy storage systems: survey on electrical machine power electronic converters, and control system[J]. IEEE Access, 2023, 11: 81224-81255.
[8] Hu Cungang, Yu Xinghuo, Homels D G, et al. An improved virtual space vector modulation scheme for three-level active neutral-point-clamped inverter[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7419-7434.
[9] 王金平, 刘斌, 董浩, 等. 中点钳位型三电平逆变器基于调制波分解的调制策略[J]. 电工技术学报, 2023, 38(12): 3221-3233.
Wang Jinping, Liu Bin, Dong Hao, et al. A modulation strategy based on modulation wave decomposition for neutral point clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3221-3233.
[10] Qin Changwei, Li Xiaoyan. Improved virtual space vector modulation scheme for the reduced switch count three-level inverter with balanced and unbalanced neutral-point voltage conditions[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 2092-2104.
[11] Lee Y H, Suh B S, Hyun D S. A novel PWM scheme for a three-level voltage source inverter with GTO thyristors[J]. IEEE Transactions on Industry Appli- cations, 1996, 32(2): 260-8.
[12] 李敏裕, 马晓军, 魏曙光, 等. 三电平虚拟空间矢量脉宽调制算法窄脉冲抑制研究[J]. 电工技术学报, 2018, 33(14): 3264-3273.
Li Minyu, Ma Xiaojun, Wei Shuguang, at al. Research on narrow pulse suppression of three-level virtual space vector pulse width modulation algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3264-3273.
[13] 李文善, 温旭辉, 张剑, 等. 高频三电平低调制比区窄脉冲抑制混合调制策略[J]. 电机与控制学报, 2021, 25(12): 116-126.
Li Wenshan, Wen Xuhui, Zhang Jian, et al. Narrow pulse suppression of high frequency three level converter based on hybrid modulation strategy in low modulation index region[J]. Electric Machines and Control, 2021, 25(12): 116-126.
[14] 徐华, 高菊玲, 何礼高. 三电平逆变器SVPWM的死区补偿和窄脉冲处理[J]. 电力电子技术, 2012, 46(1): 26-28.
Xu Hua, Gao Juling, He Ligao. The dead-time and narrow pulse compensation of three-level inverter based on SVPWM[J]. Power Electronics, 2012, 46(1): 26-28.
[15] Gao Zhan, Ge Qiongxuan, Li Yaohua, et al. Hybrid improved carrier-based PWM Strategy for three-level neutral-point-clamped inverter with wide frequency range[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8517-8538.
[16] 高瞻, 王立欣, 周志达, 等. 适用于三电平逆变器低调制比区域的双极性载波脉宽调制策略研究[J]. 中国电机工程学报, 2023, 43(18): 7254-7267.
Gao Zhan, Wang Lixin, Zhou Zhida, et al. Research on bipolar carrier-based PWM strategy suitable for low modulation index region of three-level inverter[J]. Proceedings of the CSEE, 2023, 43(18): 7254-7267.
[17] Liu H L, Cho G H. Three-level space vector PWM in low index modulation region avoiding narrow pulse problem[J]. IEEE Transactions on Power Electronics, 1994, 9(5): 481-486.
[18] 薄保中, 刘卫国, 苏彦民. 三电平逆变器PWM控制窄脉冲补偿技术的研究[J]. 中国电机工程学报, 2005, 25(10): 60-64.
Bo Baozhong, Liu Weiguo, Su Yanmin. Study of compensating technique in PWM control for three- level inverters[J]. Proceedings of the CSEE, 2005, 25(10): 60-64.
[19] Ran Wang, Ma Liang, Lin Feng, et al. Zero-sequence voltage injection for narrow pulse compensation and neutral point potential balancing of NPC inverter[C]// 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, 2009: 887- 891.
[20] 肖宏伟, 何英杰, 刘进军, 等. 基于窄脉冲消除的三电平逆变器矢量不对称死区补偿调制策略研究[J]. 中国电机工程学报, 2021, 41(4): 1386-1397, 1545.
Xiao Hongwei, He Yingjie, Liu Jinjun, et al. Research on vector asymmetric dead-time compensation modu- lation strategy of three-level inverter based on narrow pulse elimination[J] Proceedings of the CSEE, 2021, 41(4): 1386-1397, 1545.
[21] Busquets-Monge S, Bordonau J, Boroyevich D, et al. The nearest three virtual space vector PWM-a modulation for the comprehensive neutral-point balancing in the three-level NPC inverter[J]. IEEE Power Electronics Letters, 2004, 2(1): 11-15.
[22] 白华, 赵争鸣, 张永昌, 等. 最小脉宽特性对高压三电平变频器的影响[J]. 电工技术学报, 2006, 19(12): 60-65.
Bai Hua, Zhao Zhengming, Zhang Yongchang, et al. Effect of minimum pulse width on high voltage three-level inverters[J]. Transactions of China Elec- trotechnical Society, 2006, 19(12): 60-65.
[23] Guo Feng, Yang Tao, Li Chen, et al. Active modu- lation strategy for capacitor voltage balancing of three-level neutral-point-clamped converters in high- speed drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(3): 2276-2287.
[24] 董志强, 王琛琛, 周明磊, 等. 基于SHEPWM的三电平三相逆变器中点电位主动平衡控制[J]. 电工技术学报, 2024, 39(4): 1147-1158.
Dong Zhiqiang, Wang Chenchen, Zhou Minglei, et al. Active NP voltage balance control strategy for three- level three phase inverter under SHEPWM[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(4): 1147-1158.
Abstract During the charging process of flywheel driving by permanent magnet synchronous motor, the three-level converter operates in a low modulation index for a long time, and the traditional virtual space vector pulse width modulation (VSVPWM) strategy frequently generates narrow pulses. Due to the discrete nature of digital control, the sector boundaries in the traditional VSVPWM strategy can shift, exacerbating the narrow pulse issue. These narrow pulses lead to significant distortion in the voltage and current waveforms of the converter and even damage the power devices.
This paper proposed an analysis method considering the discreteness of motor digital control and a hybrid VSVPWM strategy based on vector sequence optimization. Firstly, the variation characteristics of the voltage reference vector and its influence on sector boundary under digital control were studied based on the steady-state mathematical model of the motor. Then, the minimum pulse width function was established to quantitatively analyze the distribution of narrow pulses in the traditional VSVPWM within the low modulation index region. Consequently, according to the narrow pulse distribution law, a hybrid VSVPWM strategy based on vector sequence optimization was proposed.
The traditional VSVPWM (Seg9_VSVPWM), the thirteen-segment VSVPWM (Seg13_VSVPWM), and the proposed hybrid VSVPWM (LH_VSVPWM) were compared. The simulation results show that when the modulation index is 0.1 and 0.3, Seg9_VSVPWM continuously presents narrow pulses less than 2 msat the boundary between sectors F and A with 672 and 219 times within 1 s. When the modulation index is 0.5, Seg13_VSVPWM would produce the narrowest pulses and accumulate 1 102 times within 1s. However, when the modulation index is 0.1, the proposed LH_VSVPWM eliminates the narrow pulse by optimizing the vector sequence. In addition, LH_VSVPWM has the fewest switching action times in the modulation index of 0.3 and 0.5, which is 5 836 and 5 875 times in 1s, respectively. Meanwhile, the proposed strategy performs well in limiting narrow pulses, occurring only 11 and 32 times within 1 s. The experimental results further demonstrate that LH_VSVPWM can effectively suppress the narrow pulse and keep the minimum pulse width above 6 ms in low modulation index region. Moreover, LH_VSVPWM improves the three-level converter’s output current waveform quality, with THD values of 22.24%, 13.78%, and 17.47% in the modulation index of 0.1, 0.3, and 0.5, respectively. It is the lowest among the three modulation strategies. Compared with Seg9_VSVPWM, the proposed LH_VSVPWM keeps the neutral-point potential balanced during motor start.
The following conclusions can be drawn. (1) The discreteness of motor digital control affects the variation characteristics of the voltage reference voltage and sector boundary of VSVPWM, which aggravates the narrow pulse problem. (2) In the low modulation index region of three-level converters, the effective vector durations are short, and the first vector of switching sequence changes between sectors F and A, B and C, and D and E. Therefore, the traditional VSVPWM maximum coding vectors are prone to narrow pulses at the boundary of these sectors. (3) The proposed method effectively suppresses the narrow pulse and reduces the switching times of power devices. Besides, LH_VSVPWM improves output waveform quality and solves the problem of neutral-point potential imbalance during motor startup.
Keywords:Digital motor control, three-level converter, low modulation index, narrow pulse, neutral-point potential balance, virtual space vector pulse width modulation
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.240477
收稿日期 2024-03-26
改稿日期 2024-06-04
陈 凯 男,1998年生,博士研究生,研究方向为电机控制及电力电子。
E-mail: chenkai@mail.iee.ac.cn
温旭辉 女,1963年生,研究员,博士生导师,研究方向为电机控制及电力电子。
E-mail: wxh@mail.iee.ac.cn(通信作者)
(编辑 郭丽军)