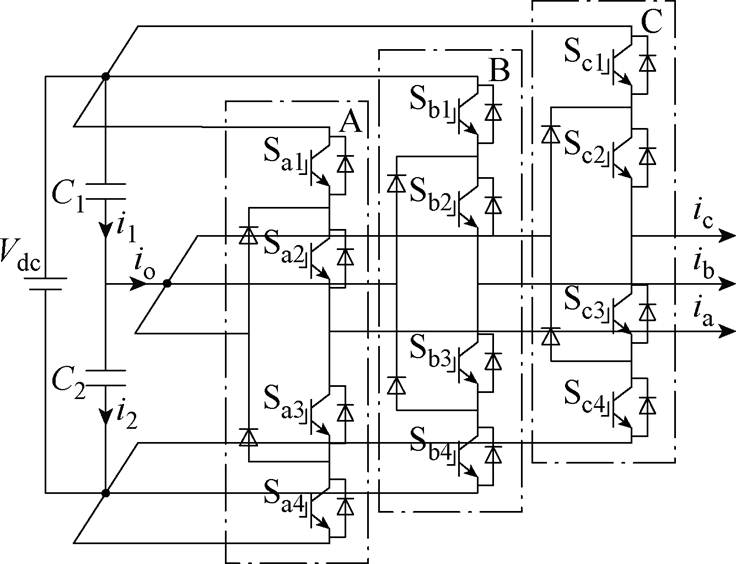
图1 NPC型逆变器拓扑结构
Fig.1 The topology of NPC inverter
摘要 中点钳位（NPC）型三电平逆变器存在直流侧电容中点电压失衡问题，传统虚拟空间矢量脉宽调制（VSVPWM）在中高调制度下中点调节能力较弱。为此，该文提出一种扇区重构型VSVPWM（SR-VSVPWM）。首先，通过引入等效中矢量并重构位于中高调制度的扇区，提高中高调制度下中点调节能力。其次，采用占空比调制法平滑开关切换。再次，对其多种调制度下的中点调节裕度进行分析，揭示影响其中点调节能力的因素。最后，通过Starsim硬件在环实验平台，验证所提方法的正确性和有效性，与传统VSVPWM单一小矢量调节相比，该方法有效地提高了中高调制度下中点偏移平衡速度与中点波动抑制能力。
关键词：中点钳位（NPC）型三电平逆变器 虚拟空间矢量脉宽调制 中点电压平衡 扇区重构 等效中矢量
多电平逆变器适用于大容量、高电压变流场合，可以有效降低电流谐波含量，而中点钳位（Neutral Point Clamped, NPC）型三电平逆变器是其中应用最为广泛的一种拓扑结构，所需电容与独立电源较少，其体积与成本较为均衡，且开关器件电压应力小[1]。由于电容分压的结构特点，NPC型三电平逆变器受器件参数不对称、控制不合理和外部干扰等因素的影响会出现上、下电容分压不均的情况，即中点失衡。中点失衡存在中点偏移和中点波动两种形式，这些都将使逆变器输出畸变，电流谐波增大，甚至导致开关器件因承受电压应力过大而损坏[2]。
国内外学者针对NPC型逆变器的中点失衡问题，提出了许多中点平衡策略。部分中点策略从NPC型逆变器拓扑改进入手，文献[3]提出一种三维坐标系三电平四桥臂逆变器调制方法，简化调制计算的同时利用其冗余矢量调节中点电压。文献[4]提出双三电平逆变器，该拓扑具有更多备选矢量，可在满足共模电压抑制的情况下实现传统虚拟空间矢量脉宽调制（Virtual Space Vector Pulse Width Modulation, VSVPWM）。而大部分中点平衡策略则通过调整逆变器的调制策略实现，常见调制策略有非连续脉宽调制（Discontinuous Pulse Width Modulation, DPWM）、载波脉宽调制（Carrier-Based Pulse Width Modulation, CBPWM）和VSVPWM[5]。
DPWM的优势是开关频率较低，根据钳位方式的不同，DPWM分为许多种类。文献[6]分析了各种DPWM的有效范围，并按照其对中点电压的影响进行分类，在此基础上设计了一种混合调制策略。文献[7]在采用相似方式的同时，进一步优化了调制策略切换时过渡矢量的选择。此类方法有效降低了开关损耗，但中点平衡能力有限，特别是电压偏移产生时，无法完全消除偏移且存在较大波动。
CBPWM与VSVPWM相比具有易于实现的优势，但不具备中点波动抑制能力。文献[8]采用零序电压注入法实现主动中点平衡，其平衡策略在高调制度低功率因数的情况下平衡能力较弱。为结合两种调制策略的优势，文献[9-10]提出将VSVPWM等效为CBPWM的方法，在保留VSVPWM中点波动抑制能力的同时，降低了VSVPWM实现的复杂度。文献[11]在此基础上引入CBPWM的零序电压注入，使其具备主动中点平衡能力。
VSVPWM是以中点波动抑制为目的，由空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）演变而来的一种调制策略[12]。文献[13]基于中点失衡后中小矢量的变化，引入失衡度对虚拟矢量进行修正，提高了VSVPWM的中点波动抑制能力。文献[14-15]选用共模电压较低的矢量构建虚拟矢量组，在抑制中点波动的同时降低共模电压。此类VSVPWM缺乏主动中点平衡能力，难以修正中点偏移。文献[16]在此基础上构建仅由基本中矢量组成的虚拟中矢量，在降低共模电压的同时主动调节中点电压。文献[17]使用成对小矢量调节中点电压，但在平衡系数计算时考虑了不可调节的中矢量造成的影响。文献[18]对采用小矢量调节的VSVPWM中点平衡能力进行研究，分析了各种工况下一个调制周期整体的平衡能力，这种方式有利于评价平衡策略的效果，但不能为进一步提高平衡能力提供方向。文献[19-21]重构传统VSVPWM扇区划分，在高调制区域中点不平衡时采用对应小矢量和两个大矢量进行合成，在避免调节系数计算的同时，对高调制度下的中点平衡能力有一定提升。为进一步提高平衡能力，文献[22-23]在采用小矢量调节的同时，将中矢量引入中点调节，设定三种固定中矢量参与度，根据中点平衡需要进行选择。文献[24]在此基础上将虚拟中矢量中的小矢量也分解为成对小矢量，参与中点调节。此外，为提高中、小矢量中点平衡参与度，部分中点平衡策略采用可变扇区划分。文献[25]仅对虚拟中矢量中的小矢量进行调整，构建幅值变化的虚拟中矢量，采用模糊控制获取其调节系数。文献[26]对涉及中、小矢量的虚拟矢量均引入调节系数，但仅选择其中调节能力较强的虚拟矢量参与中点平衡。此类平衡策略灵活度高，但扇区随中点平衡状况变化，其实现较为复杂。
本文提出一种扇区重构型VSVPWM，通过引入等效中矢量和重构中高调制度扇区，在保留固定扇区划分的同时，使中、小矢量充分参与中点调节。该方法可以有效抑制中点电压波动，加快中点偏移恢复，且每个扇区只存在一个调节系数，易于实现。
NPC型逆变器拓扑结构如图1所示，通过调整开关器件Sx1、Sx2、Sx3、Sx4通断，各相均可输出Vdc/2、0、-Vdc/2三种电平，将三种电平对应的开关状态分别以P、O、N表示。三相开关状态存在27种组合，采用60°坐标系表示其空间矢量，则NPC型逆变器空间矢量分布如图2所示。其中开关状态ONN下的基本矢量以VONN表示，其余开关状态表示类似。
图1 NPC型逆变器拓扑结构
Fig.1 The topology of NPC inverter
图2 NPC型逆变器空间矢量分布
Fig.2 The space vector of NPC inverter
定义VC1、VC2分别为上、下电容电压；i1、i2分别为上、下电容电流；io为中点电流；ia、ib、ic为三相输出电流。对中点失衡原理进行分析，存在
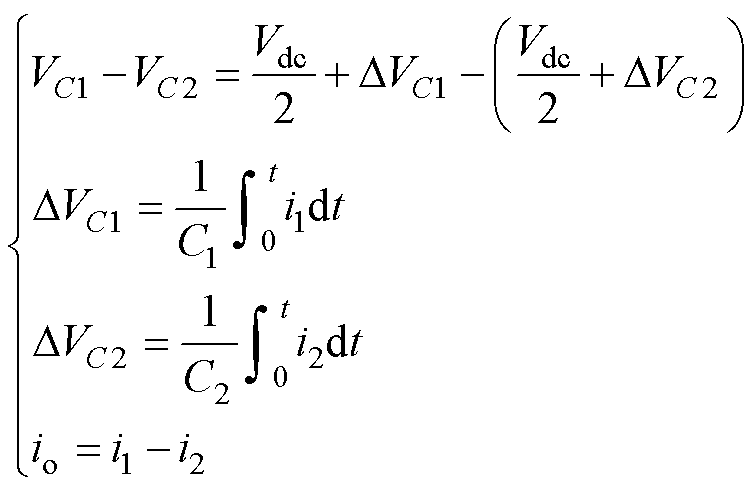（1）
用DV表示中点电压失衡程度，得
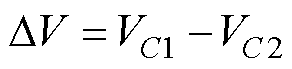（2）
在上、下电容参数相同时，可得
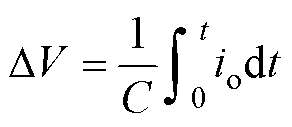（3）
由式（3）可知，中点电流产生的中点电荷造成中点电压失衡，合理控制中点电流可以实现一定程度的中点电压平衡。
虚拟矢量法的基本原理是根据基本矢量构建一组新的虚拟矢量，利用这组虚拟矢量来合成目标矢量，构建的原则是：假设在较短的调制周期内三相电流保持不变，使得一个调制周期内虚拟矢量作用造成的中点电荷变化为零。
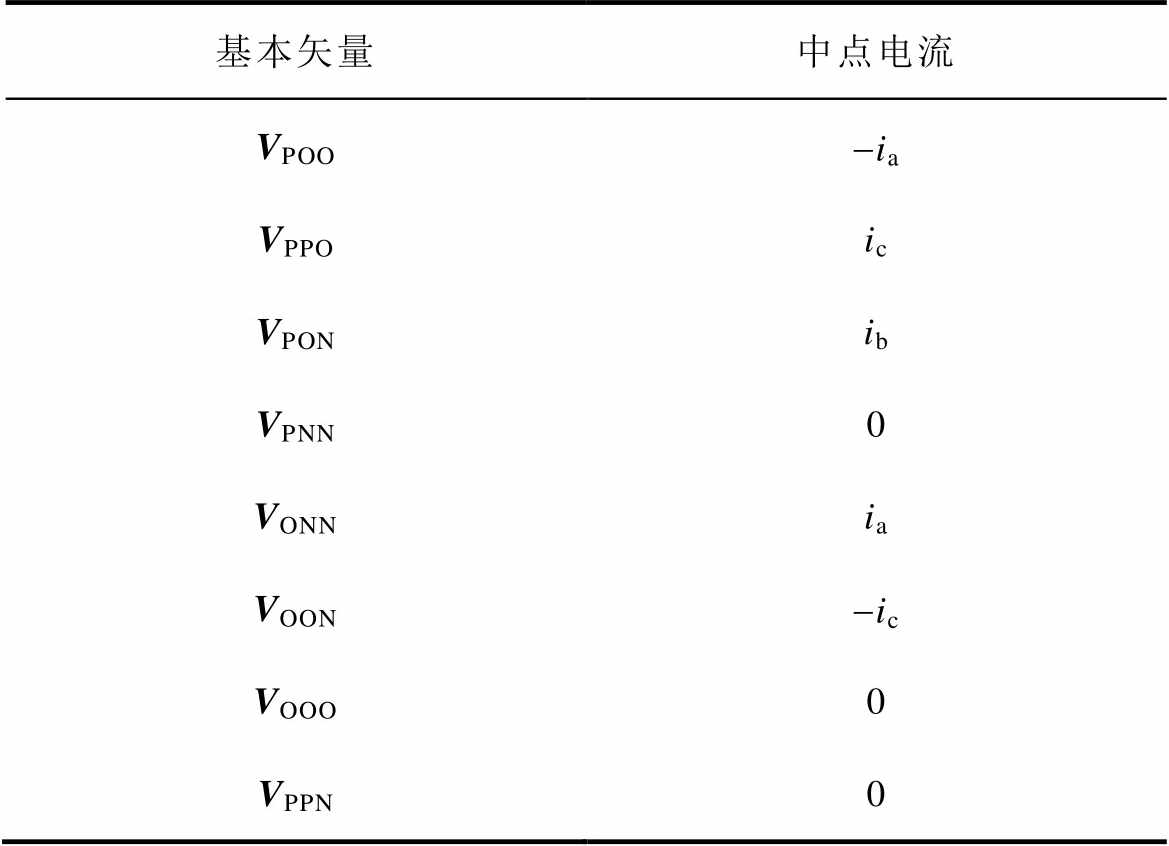
分析各个开关状态下的电路拓扑，可知在三相电流对称的情况下，大矢量和零矢量不产生中点电流，对中点电荷没有影响。小矢量与中矢量根据其开关状态与中点的关系产生中点电流。NPC型逆变器在大扇区Ⅰ内各基本矢量中点电流见表1。
表1 大扇区Ⅰ基本矢量中点电流
Tab.1 Theneutral point current of basic vector in large sector I
基本矢量中点电流 VPOO-ia VPPOic VPONib VPNN0 VONNia VOON-ic VOOO0 VPPN0
对于大扇区Ⅰ，根据虚拟空间矢量法原则构建虚拟矢量组，虚拟矢量Vvx与基本矢量关系为
（4）
采用60°坐标系表示大扇区Ⅰ的小扇区与虚拟矢量分布如图3所示。
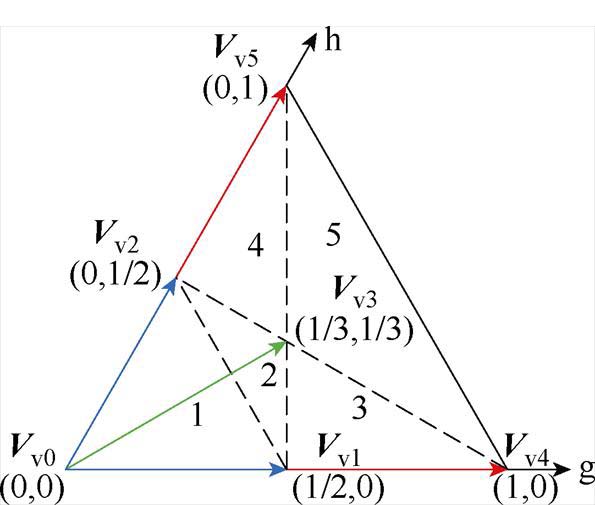
图3 小扇区与虚拟矢量分布
Fig.3 The distribution of small sector and virtual vector
在理想条件下，VSVPWM可以将中点电压平衡在一定范围内。但在实际运行中，调制计算误差以及运行条件变化等原因造成的中点偏移不能被消除。
传统VSVPWM为将所有扇区的小扇区判断、矢量作用时间计算等过程变换到大扇区Ⅰ进行，使各大扇区虚拟矢量位置经过旋转与大扇区Ⅰ完全对应，采用一种非对称小扇区划分，并以此设计矢量序列。本文在此基础上进行一定调整，采用一种对称小扇区划分，两种小扇区分布对比如图4所示。
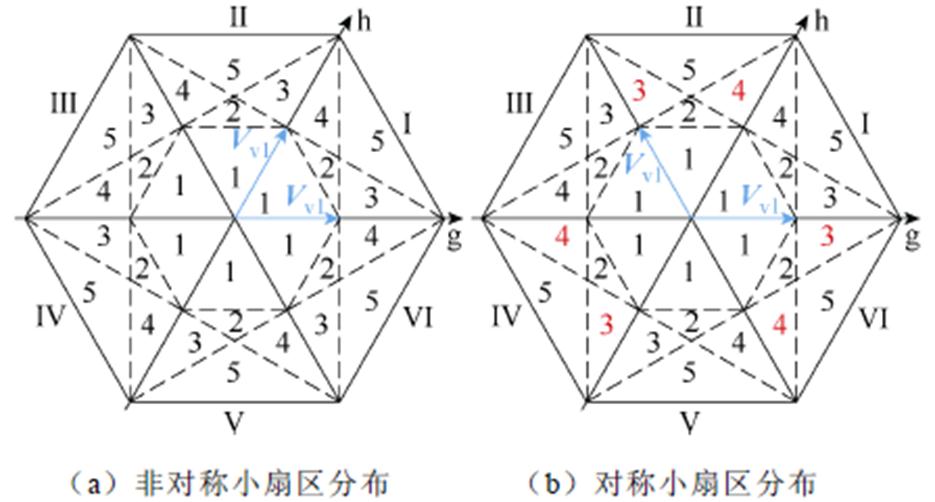
图4 小扇区分布对比
Fig.4 The comparison of small sector distribution
对称于60°坐标轴的小扇区分布如图4b所示，采用此类小扇区分布进行偶数大扇区的扇区归算时，需要交换g、h坐标值。设计九段对称矢量序列，列出部分扇区前半部分矢量序列见表2。
表2中，Ⅱ1-S表示图4b中大扇区Ⅱ的小扇区1，而Ⅱ1-A则表示图4a中大扇区Ⅱ的小扇区1。TA、TB、TC表示矢量序列中三个虚拟矢量的作用时间，作用时间与虚拟矢量的对应关系随扇区变化。在Ⅰ2-S中，虚拟矢量Vv1、Vv2、Vv3的作用时间分别对应TA、TB、TC。Vv2v3PPO表示由虚拟矢量Vv2与Vv3中对应部分共同合成的基本矢量VPPO，且由式（4）可知其作用时间为TB/2+TC/3。表2中其余的扇区、矢量与矢量作用时间的定义与之同理。由图4可知，两种扇区分布在奇数大扇区完全一致，其矢量序列完全相同，在表2中不再重复列出，以偶数大扇区Ⅱ为例讨论其差异。
表2 部分扇区矢量序列
Tab.2 The vector sequence of partial sector
扇区矢量序列 Ⅰ1-STB/2TA/2TCTB/2TA/2 Vv2PPOVv1POOVv0OOOVv2OONVv1ONN Ⅰ2-STB/2+TC/3TA/2TC/3TB/2TA/2+TC/3 Vv2v3PPOVv1POOVv3PONVv2OONVv1v3ONN Ⅰ3-STC/3TA/2TC/3TBTA/2+TC/3 Vv3PPOVv1POOVv3PONVv4PNNVv1v3ONN Ⅰ4-STB/2+TC/3TATC/3TB/2TC/3 Vv2v3PPOVv5PPNVv3PONVv2OONVv3ONN Ⅰ5-STC/3TATC/3TBTC/3 Vv3PPOVv5PPNVv3PONVv4PNNVv3ONN Ⅱ1-STB/2TA/2TCTB/2TA/2 Vv2PPOVv1OPOVv0OOOVv2OONVv1NON Ⅱ1-ATB/2TA/2TCTB/2TA/2 Vv2NONVv1OONVv0OOOVv2OPOVv1PPO TA/2TB/2TCTA/2TB/2 Vv1PPOVv2OPOVv0OOOVv1NONVv2NON
在Ⅱ1-A中，为保持扇区切换平滑和遍历所需矢量，主要存在两种矢量序列，见表2。若采用VNON为起始矢量的序列，则从Ⅰ1到Ⅱ1的大扇区过渡过程不平滑，开关状态越级跳变。若采用VPPO为起始矢量的序列，在非对称扇区分布的定义下，偶数大扇区与奇数大扇区的矢量序列中同列矢量作用时间种类将会有所不同，这不利于中点平衡策略以统一形式在所有扇区实现。
采用表2中Ⅱ1-S对应的序列可以在保证扇区平滑过渡的同时统一奇偶大扇区矢量序列与矢量作用时间形式，简化中点平衡策略实现过程，其余小扇区内此类序列对比也与之同理。
传统VSVPWM可以通过调节矢量序列中成对小矢量的作用时间来主动平衡中点电压，成对小矢量具有相同幅值和相位，但产生相反的中点电流。小扇区1、2、3、4均存在成对小矢量，通过调整成对小矢量作用时间可以在不影响调制结果的情况下控制中点电流，进而实现中点电压调节。小扇区5中没有此类成对小矢量，无法对中点电压进行主动调节。
因此，为实现所有扇区内中点电压主动调节，本节提出一种等效中矢量VSVPWM（Equivalent Medium Vector VSVPWM, EMV-VSVPWM），在传统VSVPWM及其小矢量平衡系数调节的基础上，引入等效中矢量控制中点电流，计算各个扇区相应的平衡系数以调节矢量作用时间。
下面以大扇区Ⅰ为例，介绍各个小扇区中点平衡策略实现过程。对于小扇区5，大扇区Ⅰ内的基本大矢量与基本中矢量存在
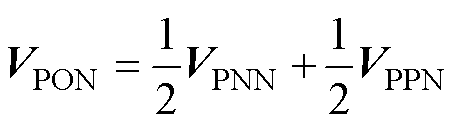（5）
即中矢量可以由同扇区内的两个大矢量合成。因此，在原有VSVPWM小扇区5调制策略的基础上，可以通过引入中点平衡系数调整Vv3中VPON分量、Vv4和Vv5的作用时间，实现主动平衡中点电压的等效调制。
由表2可知，对于小扇区5，虚拟矢量Vv5、Vv4、Vv3的作用时间分别对应TA、TB、TC，根据中点电荷平衡原则，可得关系式为
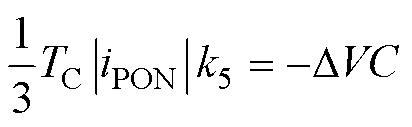（6）
式中，TC/3为虚拟矢量Vv3中VPON的作用时间；k5为小扇区5中点平衡系数；iPON为VPON对应的中点电流，其余电流定义均与此类似。
其他小扇区则直接采用相应的成对小矢量进行中点电荷平衡，将成对小矢量的中点电流统一以正小矢量的中点电流表示。
小扇区1和小扇区2同时包含虚拟矢量Vv1、Vv2，其作用时间分别为TA、TB，可得关系式为
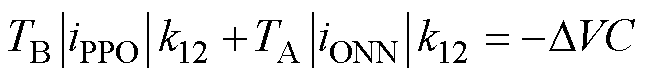（7）
小扇区3包含虚拟矢量Vv1，其关系式为
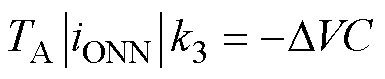（8）
小扇区4包含虚拟矢量Vv2，其关系式为
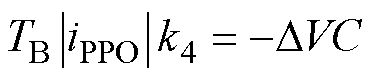（9）
其中小扇区1、2具有相同的中点平衡系数k12，并且此系数同时调整小扇区两组小矢量作用时间。k3、k4分别为小扇区3、4的中点平衡系数。
根据式（6）～式（9），各个小扇区中点平衡系数计算结果如下
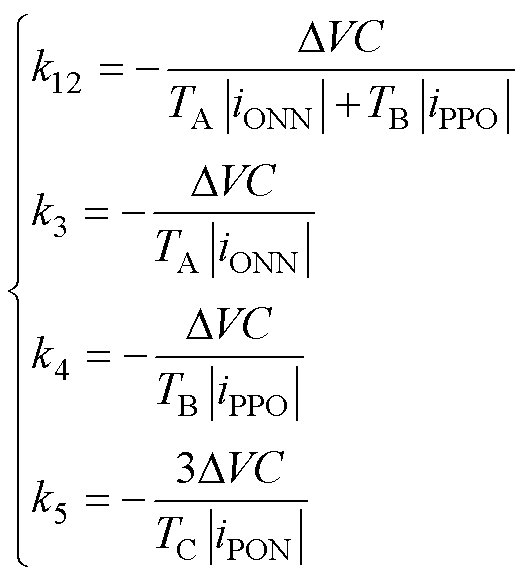（10）
利用中点平衡系数对表2中矢量作用时间进行修正时，还需要考虑对应基本矢量的中点电流方向。采用符号函数sign(x) 来判断电流方向，当x≥0时，sign(x)=1；当x＜0时，sign(x)=-1。小扇区5矢量作用时间修正关系为
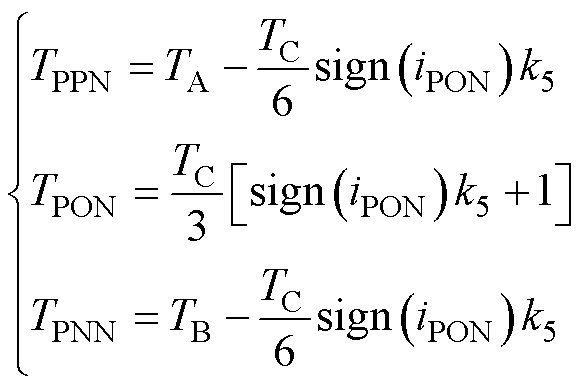（11）
式中，TPPN对应表2中扇区Ⅰ5-S基本矢量VPPN的作用时间，其余矢量作用时间表示与之类似。
其余小扇区矢量作用时间修正关系式形式类似，小扇区1矢量作用时间修正关系为
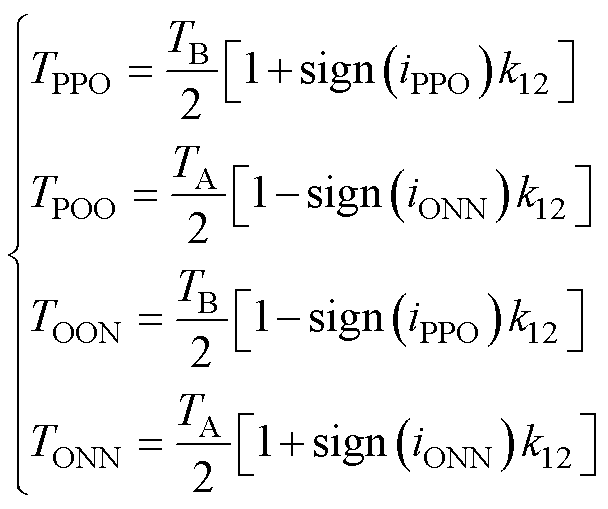（12）
在实际运行过程中，为保证调整后基本矢量作用时间计算不出现负数，需对中点平衡系数的取值加以约束。由式（11）推理可知，中点平衡系数k5的取值受以下条件约束。
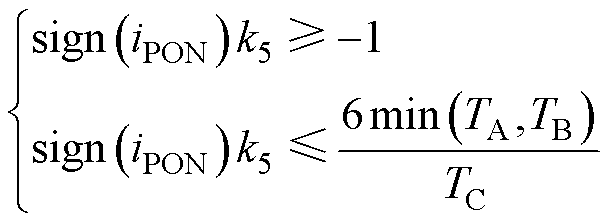（13）
由式（12）推理可知，中点平衡系数k12、k3、k4的取值范围均为[-1, 1]。
对于小扇区5，若中点电流iPON为正电流，当DV=0时，k5=0，中点电流iPON作用时间不变，小扇区5的调制不造成中点电荷变化，其调制结果与传统VSVPWM相同；当DV＞0时，-1≤k5＜0，根据式（11）可知，正中点电流iPON作用时间减小，DV减小；当DV＜0时，0＜k5≤6min(TA, TB)/TC，根据式（11）可知，正中点电流iPON作用时间增大，DV增大。将逆变器输出电压表示为VAO、VBO、VCO，则中点平衡策略实现如图5所示。
对于小扇区1，若中点电流iONN、iPPO为正电流且TA＜TB，当DV＞0时，-1≤k12＜0，正中点电流iONN、iPPO作用时间变短，负中点电流iPOO、iOON作用时间变长，DV减小，中点平衡策略实现如图6所示。
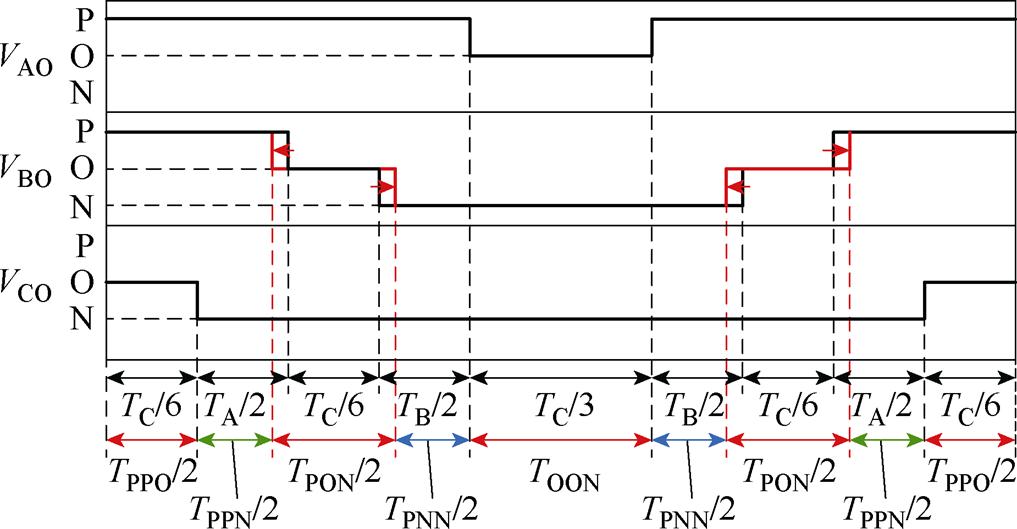
图5 小扇区5中点平衡策略
Fig.5 The neutral point balance strategy for small sector 5
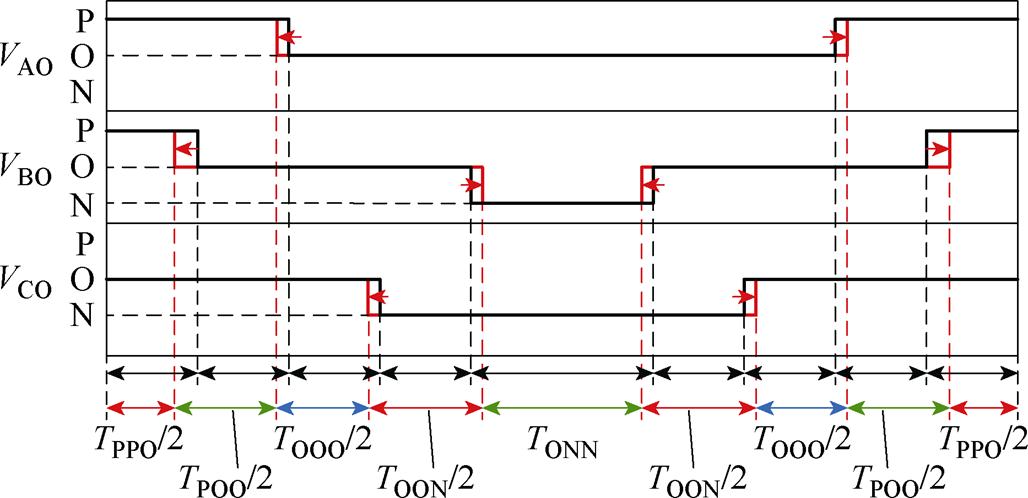
图6 小扇区1中点平衡策略
Fig.6 The neutral point balance strategy for small sector 1
通过调整小扇区分布，各个大扇区的矢量序列在中点电流分布形式上与大扇区Ⅰ完全相同，其中点平衡系数引入过程可以直接推广到其他大扇区的矢量序列中，只需给出虚拟矢量作用时间以及对应的基本矢量中点电流即可以统一形式进行计算。
2.1节提出的中点平衡策略可以在所有小扇区内生效，但其中点调节能力将随工况发生变化。定义中点调节裕度来衡量其调节能力，中点调节裕度越大，可调节的中点电荷量越大，中点收敛速度越快。为验证2.1节所提出的中点平衡策略在多种工况下的有效性，对EMV-VSVPWM中点调节裕度进行分析。其中，以小扇区位置为依据，将调制度m划分为三个等级，低调制度（m∈[0, 
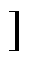
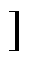
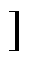下位于小扇区1、2，中调制度（m∈(, 2/3下位于小扇区2、3、4，高调制度（m∈(2/3, 1）下位于小扇区3、4、5。在三个等级内分别取一个调制度进行分析，从低到高依次为0.4、0.6、0.8。
由式（3）可知，一个周期内的中点电荷变化量由中点电流大小及其作用时间决定。影响中点电流大小的主要因素是三相电流的幅值及功率因数角，而中点电流的作用时间由虚拟矢量作用时间以及中点平衡系数决定，为研究其最大调节中点电荷，始终选取中点平衡系数为其最值。以大扇区Ⅰ为例，各个小扇区内的最大调节中点电荷为
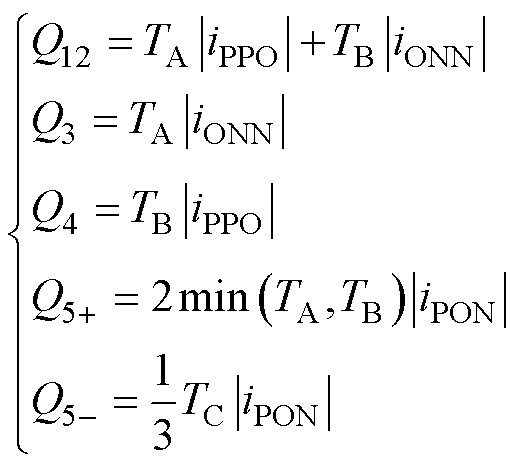（14）
当中矢量的中点电流imid与中点调节方向相同时，大矢量等效为中矢量参与中点调节，则有sign(imidDV)＜0，小扇区5最大调节电荷Q5=Q5+；反之，则中矢量分解为大矢量，sign(imidDV)＞0，Q5=Q5-。
设定三相负载电流对称且幅值标幺化，选取功率因数角j =0°、35°和60°，在开环运行条件下分析多个调制度下的一个周期内中点调节裕度变化。
当调制度m=0.4，调制在小扇区1内进行时，一个周期内中点调节裕度如图7所示。此时，两组小矢量充分参与调节，中点调节裕度相对稳定性高。并且，由于两组小矢量作用时间及其中点电流存在互补性，中点调节裕度在部分工况下保持不变。
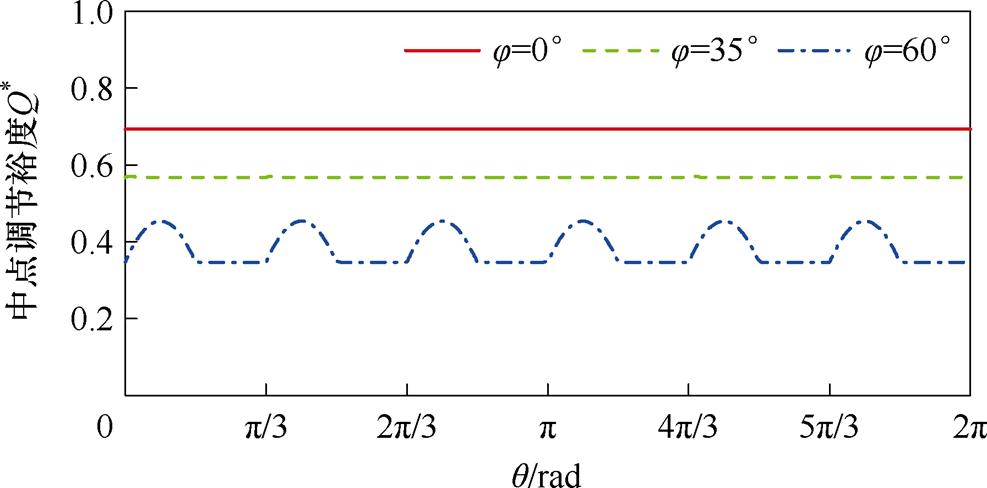
图7 m=0.4，中点调节裕度分析
Fig.7 The margin of neutral point adjustment in m=0.4
当调制度m=0.6时，调制在小扇区2、3、4内进行，一个周期内中点调节裕度如图8所示，随功率因数角的增大，中点调节裕度有一定程度的下降。
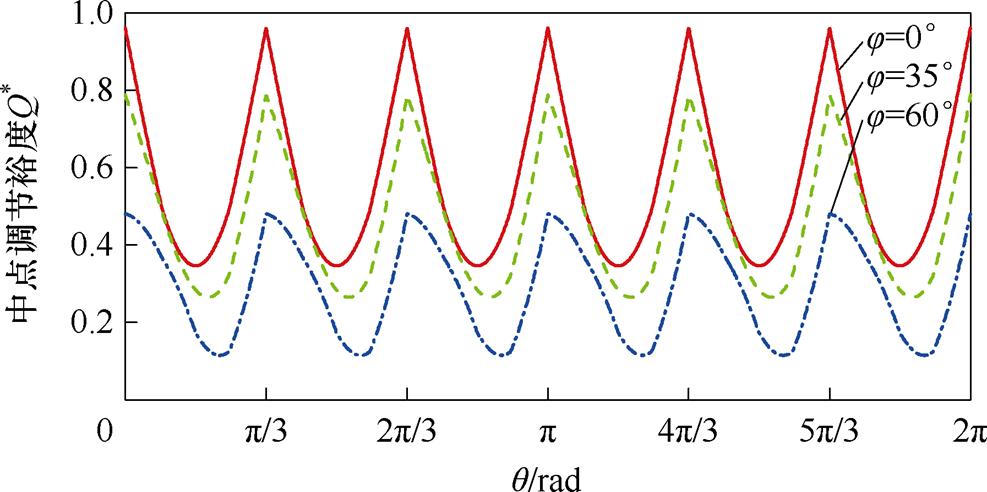
图8 m=0.6，中点调节裕度分析
Fig.8 The margin of neutral point adjustment in m=0.6
当调制度m=0.8时，调制在小扇区3、4、5内进行，且小扇区5存在Q5=Q5+和Q5=Q5-两种情况。由图9可知，在调制过程中，存在部分中点电压调节作用较弱的区域。以功率因数角为0°、大扇区Ⅰ的情况为例，对其产生原因进行分析。这样的区域可以分为两类：第一类区域在小扇区3、4与小扇区5的边界上，目标矢量几乎仅由虚拟大矢量Vv4、Vv5与虚拟中矢量Vv3合成，小矢量参与度较小；第二类区域位于小扇区5的中心，此类区域只能由中矢量中点电流进行调节，但区域内中矢量中点电流整体较小且会过零，过零位置将随功率因数角改变，在此区域附近采用中矢量调节效果较弱。大扇区Ⅰ的中矢量中点电流iPON的过零位置与相应的中点调节裕度较低区域如图9a和图9c所示。
图9 m=0.8，中点调节裕度分析
Fig.9 The margin of neutral point adjustment in m=0.8
根据以上分析，EMV-VSVPWM通过引入中矢量可以实现所有区域的中点电压调节，但是其调节裕度受限于中矢量中点电流方向与幅值，在中高调制度下效果不佳。
针对上文提出调制策略在中高调制度下表现不佳的问题，本节提出扇区重构型VSVPWM（Sector Reconstruction VSVPWM, SR-VSVPWM）。首先在原有VSVPWM扇区划分的基础上，保留原有1、2小扇区划分与平衡策略，而对小扇区3、4、5进行重构，新的小扇区划分如图10所示。
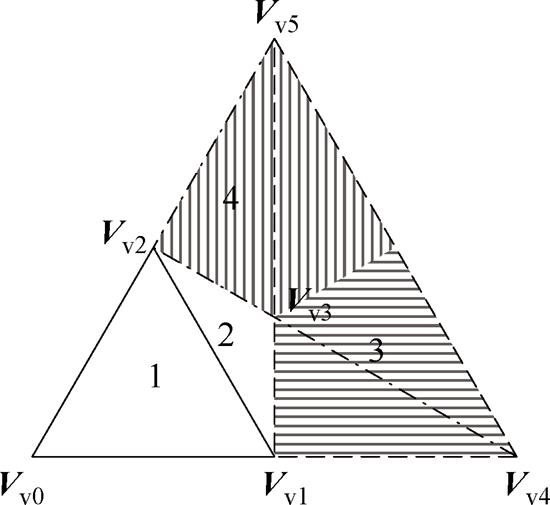
图10 重构小扇区划分
Fig.10 The distribution of reconstructed small sector
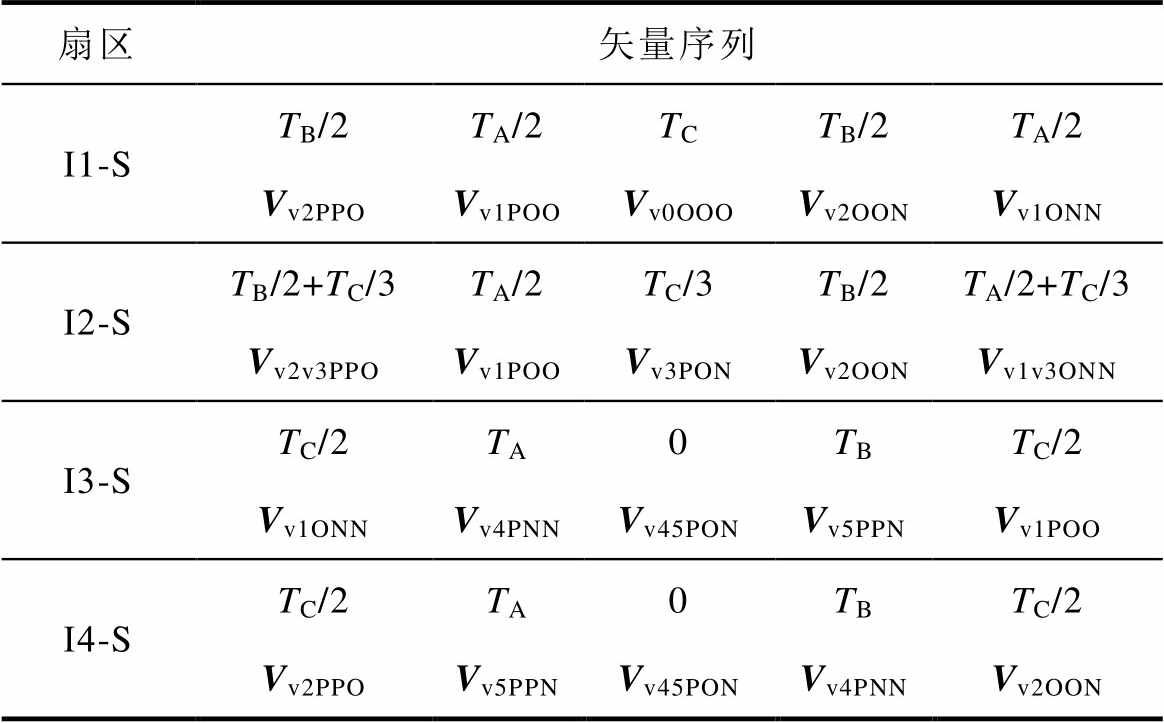
在重构的扇区划分中，原小扇区5被分割，分别并入小扇区3、4中，重构四边形小扇区3以虚拟矢量Vv1、Vv4、Vv5合成目标矢量，重构四边形小扇区4以虚拟矢量Vv2、Vv4、Vv5合成目标矢量。这样划分的优势在于，小扇区3、4的分界线不再与矢量选择三角形边界重合，分界线附近的目标矢量合成将包含更多的小矢量分量。同时，虚拟大矢量Vv4、Vv5也可根据中点平衡需要与基本中矢量进行等效变换。重构小扇区的矢量序列见表3。
对于重构小扇区3，当中矢量中点电流方向与中点调节方向一致时，sign(imidDV)＜0，将虚拟大矢量等效变换为中矢量，并利用成对小矢量进行调节。重构扇区矢量序列的时间表示在列方向上与原小扇区5序列保持一致，即虚拟矢量Vv4、Vv5、Vv1的作用时间为TA、TB、TC，定义重构小扇区3中点平衡系数为kR3，根据中点电荷平衡目标，其关系式为
表3 重构扇区矢量序列
Tab.3 The reconstructed sector vector sequence
扇区矢量序列 Ⅰ1-STB/2TA/2TCTB/2TA/2 Vv2PPOVv1POOVv0OOOVv2OONVv1ONN Ⅰ2-STB/2+TC/3TA/2TC/3TB/2TA/2+TC/3 Vv2v3PPOVv1POOVv3PONVv2OONVv1v3ONN Ⅰ3-STC/2TA0TBTC/2 Vv1ONNVv4PNNVv45PONVv5PPNVv1POO Ⅰ4-STC/2TA0TBTC/2 Vv2PPOVv5PPNVv45PONVv4PNNVv2OON
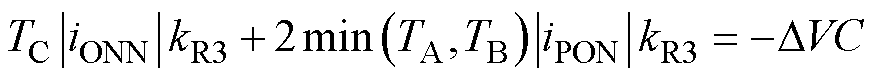（15）
当中矢量中点电流方向与中点调节方向相反时，sign(imidDV)＞0，仅用小矢量进行调节，其关系式为
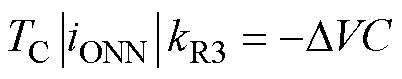（16）
当中矢量中点电流方向与中点调节方向相同时，修正各基本矢量作用时间的关系式为
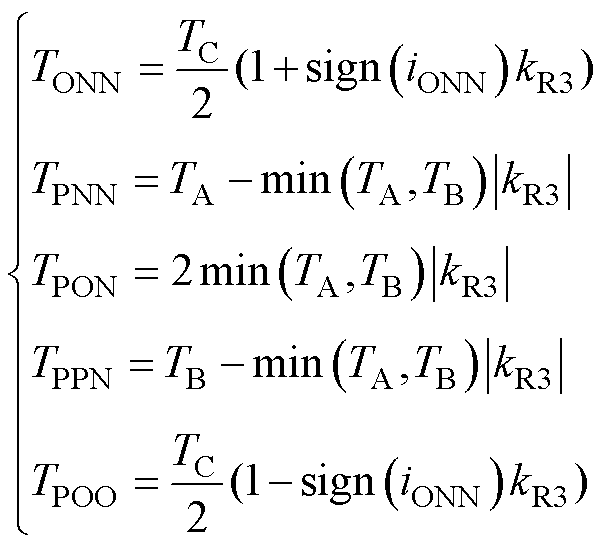（17）
当中矢量中点电流方向与中点调节方向相反时，则使中矢量作用时间为零，TPON=0，TPNN=TA，TPPN=TB，只按式（17）调整TONN和TPOO。其中，平衡系数kR3取值范围仍是[-1, 1]。重构小扇区4的中点平衡策略与重构小扇区3同理。
重构扇区的矢量序列各相开关状态切换次数较多，需要对其进行调整，以便于调制实现。以大扇区Ⅰ重构小扇区3为例，假设原矢量序列内所有矢量作用时间均相等，对其矢量序列调整进行分析。
对于表3中小扇区3的矢量序列，以保持相开关状态作用时间不变为原则对其进行调整，将每相同类开关状态进行合并，矢量序列调整前后状态如图11所示。
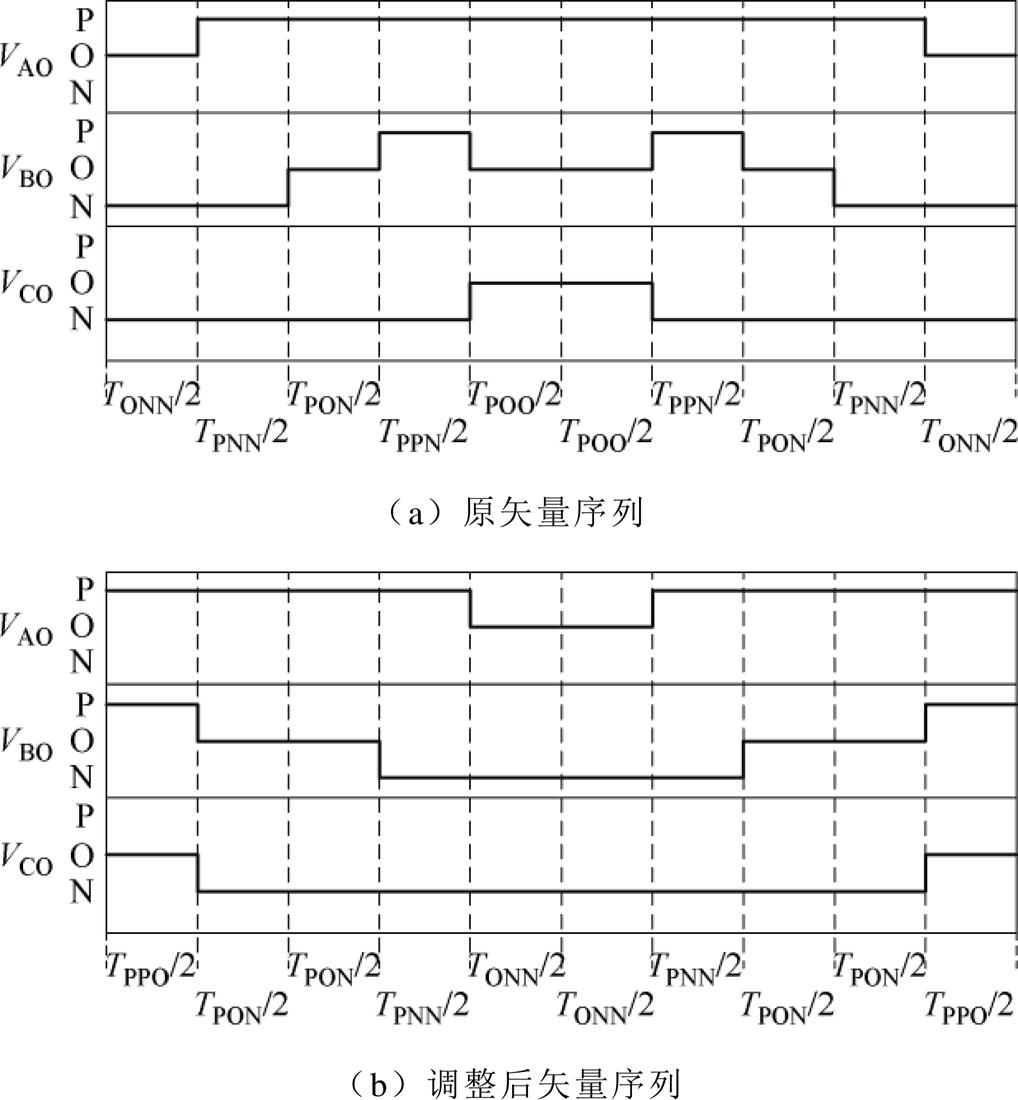
图11 矢量序列调整
Fig.11 The adjustment of vector sequence
对矢量序列调整前后合成矢量等效性进行分析。NPC型逆变器每相均有两组状态互反的开关器件，定义三相（组）开关器件占空比为da1、da2、db1、db2、dc1、dc2。TS为调制周期，对各相开关状态进行统计，则有
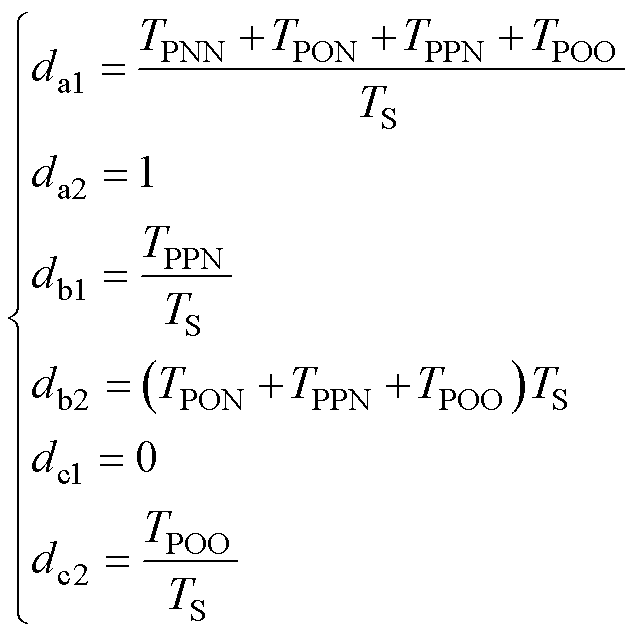（18）
当TPOO＞TPPN时，一个调制周期内合成电压矢量为
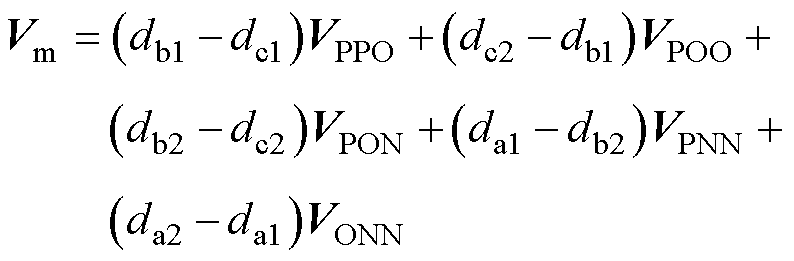（19）
将式（18）代入式（19），则有
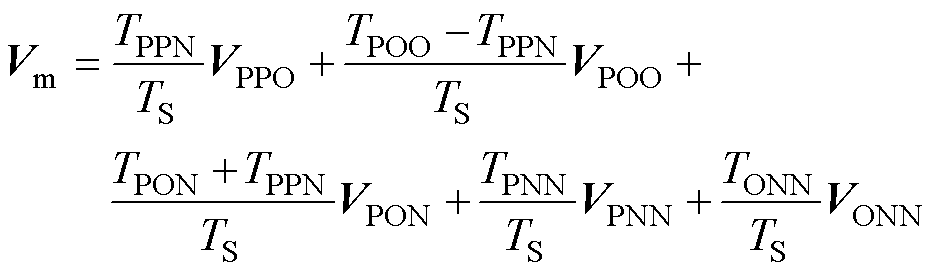（20）
在60°坐标系下，存在
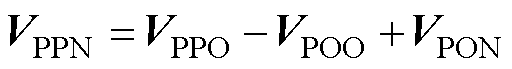（21）
则式（20）可以改写为
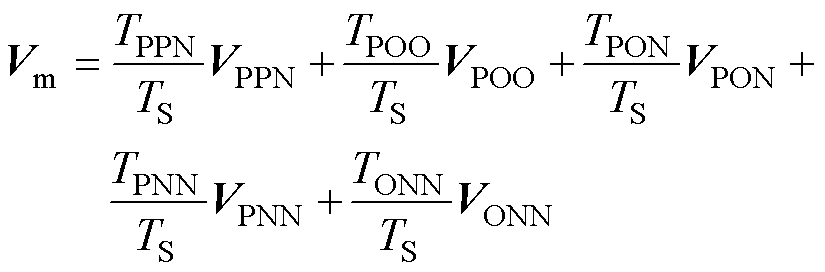（22）
由此可证明调整后的矢量序列最终合成矢量与调整前等效。同时，对式（19）和图11进行分析可知，调整后的矢量序列在特殊条件下会减少开关状态，但不会改变开关频率，也不会使各相开关状态跨级跳变。
分析表1可知，当相开关状态为O时，中点电流包含该相电流分量。在上述调整方式下，一个周期内各相O状态作用总时间不发生变化，在三相电流近似不变条件下，可保证中点平衡策略的有效性。
按照2.2节的方式，在中高调制度下对SR- VSVPWM进行中点平衡裕度分析，并与原有EMV- VSVPWM进行对比，如图12所示。由图12可知，在中高调制度下，SR-VSVPWM的中点调节裕度整体上高于EMV-VSVPWM，有效弥补了2.1节中所提两类区域的不足。此外，与EMV-VSVPWM相比，在中矢量中点电流不能参与调节的情况下，SR- VSVPWM具有更大的调节裕度。
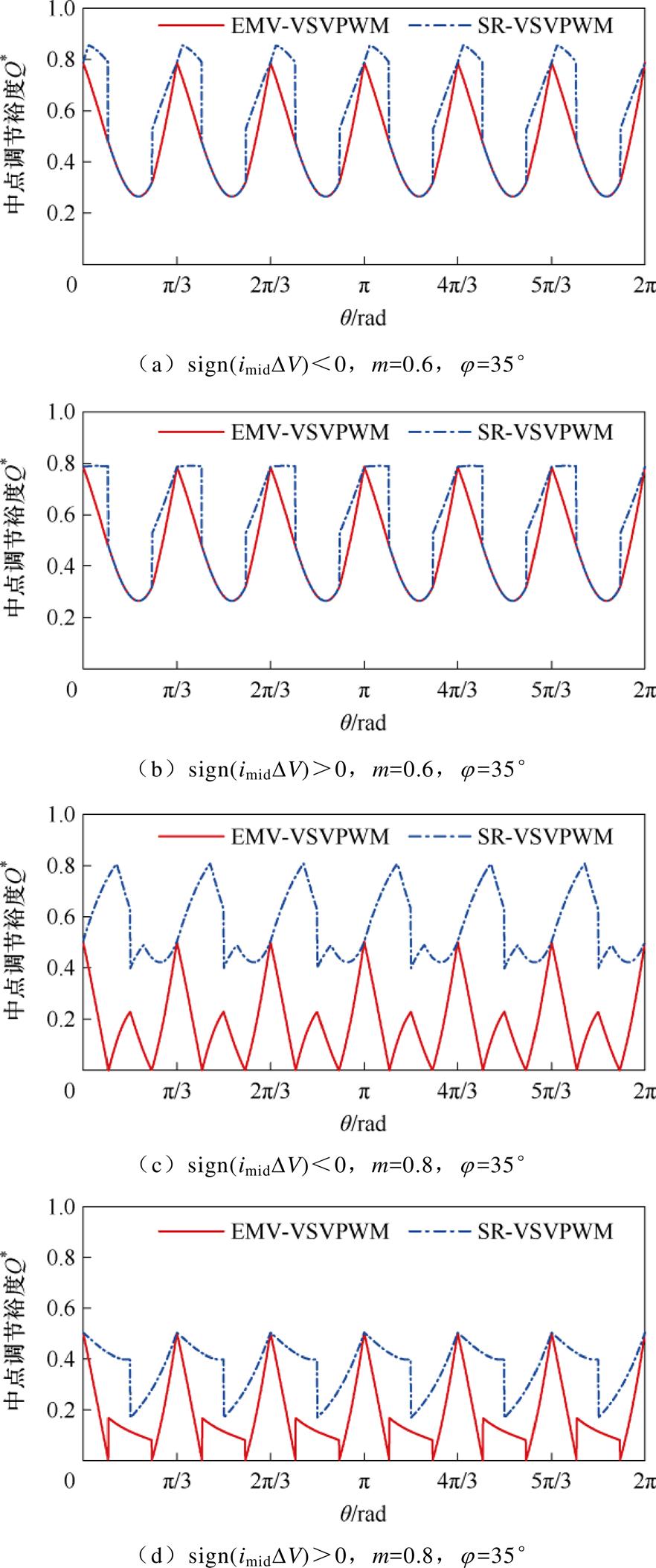
图12 中点调节裕度对比
Fig.12 The neutral point adjustment margin contrast
两种调制策略在低调制度下（m=0.4）基本相同，由2.2节可知，低调制度下其中点平衡裕度相对稳定性高，故在本节分析中不再列出。
为验证本文所提调制策略的有效性，通过StarSim硬件在环（Hardware in the Loop, HIL）实验平台进行验证，实验平台结构如图13所示。
图13 StarSim硬件在环实验平台
Fig.13 The StarSim HIL experiment platform
图13中，HIL仿真器运行三相负载与NPC型逆变器主电路模型，而快速控制原型（Rapid Control Prototyping, RCP）实现控制策略，其采样频率为10 kHz。使用MDO3024型号示波器采集NPC型逆变器上、下电容电压以及负载电流。实验平台主电路关键参数见表4。
设置上、下电容初始电压均偏离平衡点50 V，开关频率fc=10 kHz，在不同工况下，观察采用EMV- VSVPWM与SR-VSVPWM的上、下电容中点电压平衡过程与相电流，并与采用单一小矢量调节的传统VSVPWM进行对比。
表4 实验平台关键参数
Tab.4 The key parameters of the experimental platform
参 数数 值 直流总电压/V200 直流侧电容/mF5 000 开关频率/kHz5/10 基波频率/Hz50 纯阻性负载/W 阻感性负载/W
图14为三种调制策略在纯阻性负载下中点平衡过程，其中ia为A相负载电流。当调制度为0.6时，EMV-VSVPWM和SR-VSVPWM的平衡时间分别为39.0 ms和43.5 ms，两者在中低调制度下调制方式类似，其平衡时间相近且均优于传统VSVPWM的79.6 ms，中点平衡后，EMV-VSVPWM和SR- VSVPWM的A相负载电流总谐波畸变率（Total Harmonic Distortion, THD）均在0.99%左右，低于传统VSVPWM的3.66%，如图14a～图14c所示。
图14 纯阻性负载下中点平衡过程（j=0°）
Fig.14 The neutral point balance process in pure resistive load (j=0°)
当调制度升高到0.8时，由于可参与中点调节的小矢量和中矢量占比减小，EMV-VSVPWM与SR-VSVPWM的平衡时间分别增大到76.6 ms与56.1 ms，仍优于传统VSVPWM的115.7 ms，EMV- VSVPWM与SR-VSVPWM的THD分别为0.93%与0.94%，低于传统VSVPWM的2.38%，如图14d～图14f所示。
图15为三种调制策略在阻感性负载下中点平衡过程。结果表明：与纯阻性负载相比，各种运行条件下的中点平衡速度与电流质量均有不同程度的恶化，但是相较于传统VSVPWM，本文提出的EMV-VSVPWM与SR-VSVPWM仍能保持较大优势，且SR-VSVPWM在高调制度（m=0.8）下中点平衡速度保持最佳。
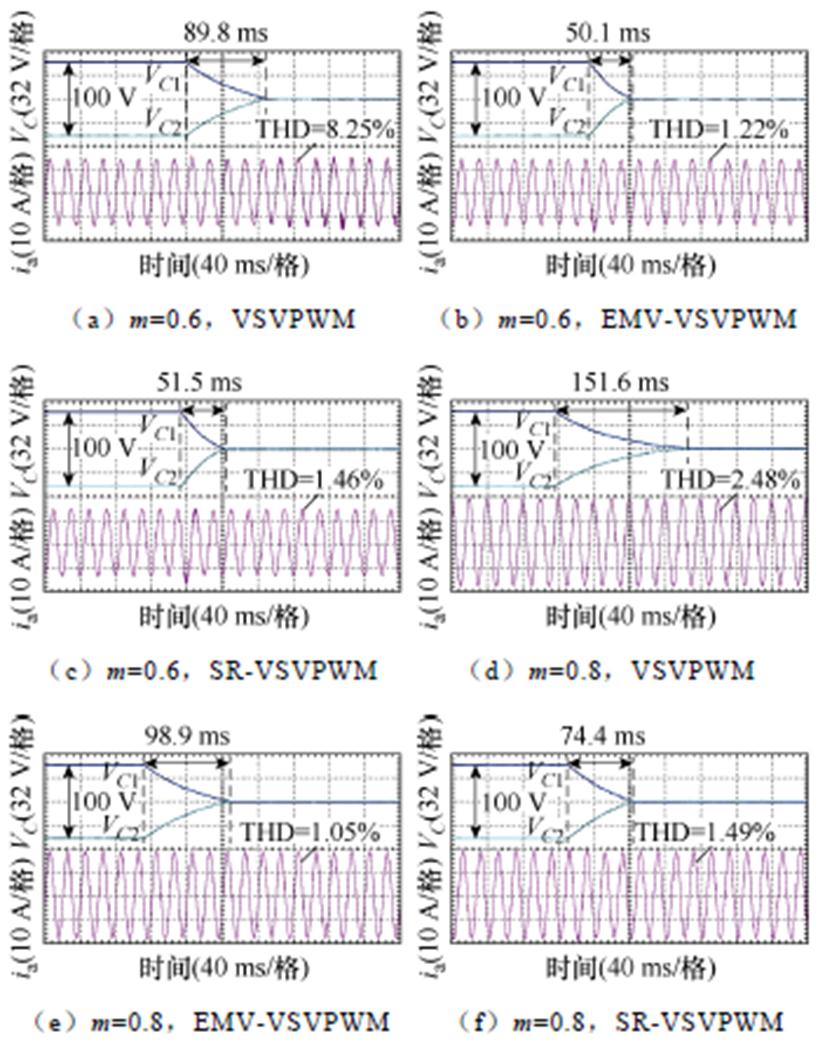
图15 阻感性负载下中点平衡过程（j =35°）
Fig.15 The neutral point balance process in inductive load (j =35°)
综上所述，在中高调制度下，EMV-VSVPWM与SR-VSVPWM的中点平衡速度均优于传统VSVPWM，能更快修正中点电压的偏移，且达到稳态后，可以有效减少负载电流谐波，提高电流质量。在高调制度下，SR-VSVPWM具有最佳的中点调节能力，可充分利用高调制度下较少的中、小矢量分量实现中点电压偏移的迅速修正。这与图12中点调节裕度对比结果一致。
在纯阻性负载下，设置调制度从0.4提高到0.8，观察三种调制策略在调制度提高过程中稳态中点电压波动变化。为便于评价稳态中点电压波动状况，定义中点电压绝对平均值DVMAV，DVMAV越大，表示中点波动程度越大，中点失衡程度DV定义见式（2），则DVMAV表达式为
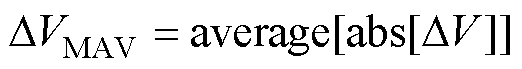（23）
式中，函数
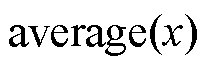与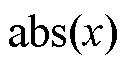
分别为求x的平均值与绝对值函数。
图16为三种调制策略在开关频率为10 kHz时变调制度中点平衡过程。结果表明：三种调制策略下，稳态中点电压均未产生明显偏移，且在调制度提高之后仍能保持稳定，中点电压波动程度较小。在低调制度下，主要由小矢量分量调节中点电压，三种调制策略均能有效调动小矢量参与中点调节，EMV-VSVPWM与SR-VSVPWM的中点波动程度略低于传统VSVPWM，而THD没有太大差别。在高调制度下，由中、小矢量共同调节中点电压，此时中、小矢量分量占比较小，传统VSVPWM仅用小矢量调节，其中点波动抑制能力较差，中点波动程度较大，其DVMAV=49.8 mV。而EMV-VSVPWM与SR-VSVPWM可同时采用中、小矢量调节，中点波动抑制能力较强，中点波动程度较低，其DVMAV分别为26.2 mV与26.5 mV。
将开关频率降低到5 kHz，并重复上述实验。图17为三种调制策略的变调制度中点平衡过程。结果表明：三种调制策略下的稳态中点电压波动仍能稳定在一定水平内且不发生偏移。与开关频率为10 kHz相比，各种运行条件下的中点电压波动程度与THD均有所提高，其中，高调制度下THD恶化最为明显。但在高调制度下，本文提出的EMV- VSVPWM与SR-VSVPWM在稳态中点波动抑制以及电流波形改善方面仍能保持优势。
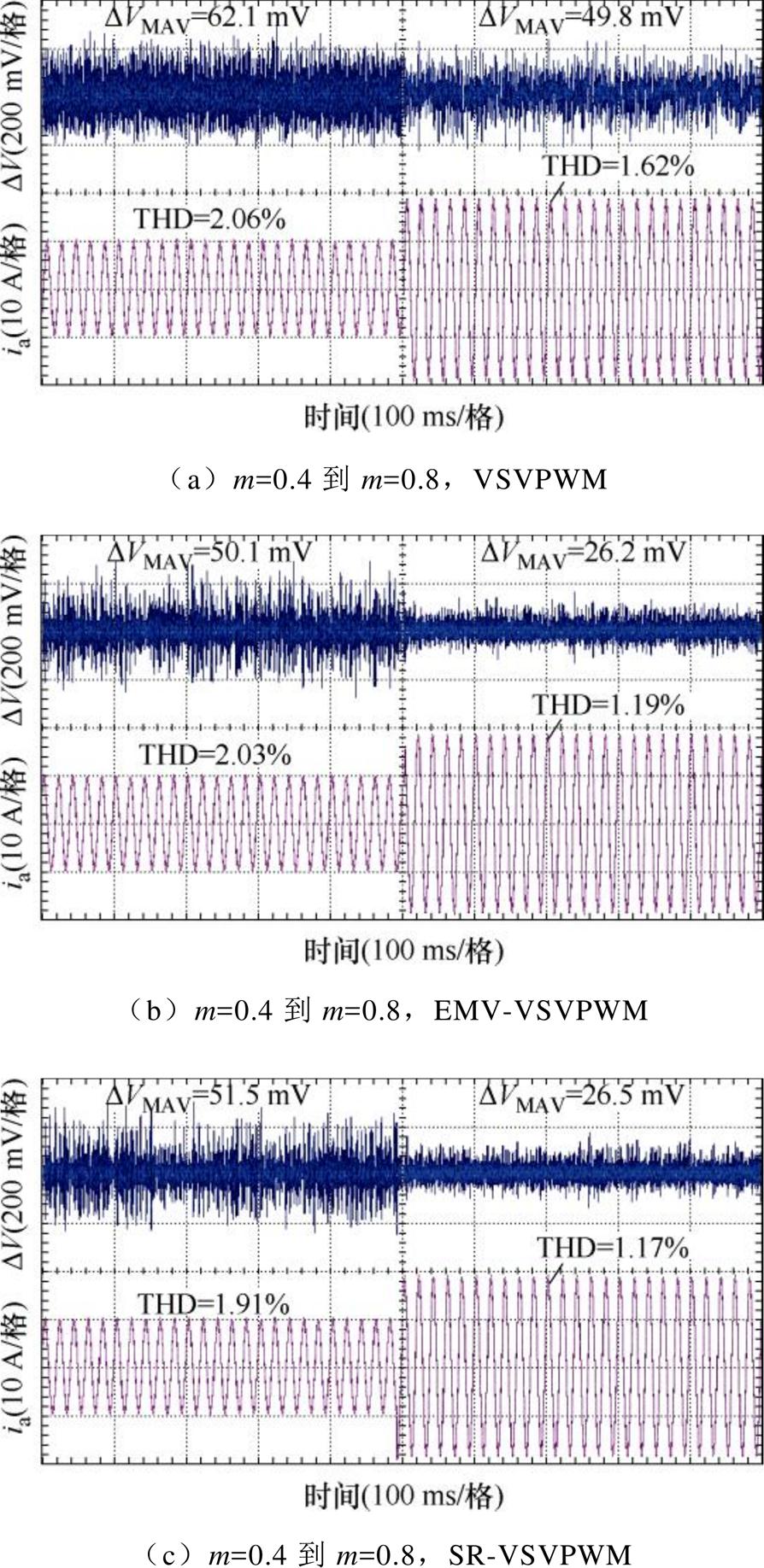
图16 变调制度中点平衡过程（fc=10 kHz）
Fig.16 The neutral point balance process in variable modulation depth ( fc=10 kHz)
图17 变调制度中点平衡过程（fc=5 kHz）
Fig.17 The neutral point balance process in variable modulation depth ( fc=5 kHz)
本文首先针对NPC型逆变器VSVPWM中点平衡问题提出一种EMV-VSVPWM策略，对其多种工况下的中点调节能力进行分析；然后针对原有策略中高调制度下中点调节能力较弱的问题，进一步提出了一种SR-VSVPWM策略；最后通过硬件在环实验验证，得到以下结论：
1）VSVPWM通过调节小矢量和中矢量作用时间主动平衡中点电压的能力有限，在扇区切换以及对应中点电流过零的位置存在调节能力较弱的区域，随着调制度增大与功率因数降低，其调节能力进一步降低甚至消失。
2）在中高调制度扇区，首先将扇区边界与矢量选取边界分离，使任意扇区边界上均存在小矢量分量；然后直接采用小矢量和两个大矢量进行合成并以等效中矢量形式引入中矢量。这些方法可以有效提高中、小矢量的参与度。
3）硬件在环实验验证结果表明，与单一小矢量调节的传统VSVPWM策略相比，本文提出的SR- VSVPWM策略提高了中点偏移的平衡速度，降低了稳态中点波动程度与电流谐波，且在高调制度工况下优势更大。
参考文献
[1] 董志强, 王琛琛, 周明磊, 等. 基于SHEPWM的三电平三相逆变器中点电位主动平衡控制策略[J]. 电工技术学报, 2024, 39(4): 1147-1158.
Dong Zhiqiang, Wang Chenchen, Zhou Minglei, et al. Active neutral-point voltage balance control strategy for three-level three-phase inverter under SHEPWM[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1147-1158.
[2] 陈兮, 黄声华, 李炳璋, 等. 一种零序注入的三电平中点钳位型变换器中点电位平衡控制策略[J]. 电工技术学报, 2019, 34(2): 337-348.
Chen Xi, Huang Shenghua, Li Bingzhang, et al. A novel zero sequence injection scheme for three-level NPC converters considering neutral-point potential balance[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 337-348.
[3] 张志, 陈浩辉, 陈思哲, 等. 一种基于ghg 坐标系的三电平四桥臂逆变器简化空间矢量脉宽调制方法[J]. 电工技术学报, 2023, 38(16): 4324-4338.
Zhang Zhi, Chen Haohui, Chen Sizhe, et al. A simplified space vector pulse width modulation method based on ghg coordinates system for the three-level four-leg inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4324-4338.
[4] 夏帅, 郑京港, 陈瑞成, 等. 低共模电压双三电平变换器中点电位主动控制调制策略[J]. 电工技术学报, 2022, 37(24): 6388-6398.
Xia Shuai, Zheng Jinggang, Chen Ruicheng, et al. Low common mode voltage strategy with active neutral point voltage control of dual three level converters[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6388-6398.
[5] 高瞻, 李耀华, 葛琼璇, 等. 适用于大功率三电平中点钳位整流器的SVPWM和DPWM策略研究[J]. 电工技术学报, 2020, 35(23): 4864-4876.
Gao Zhan, Li Yaohua, Ge Qiongxuan, et al. Research on SVPWM and DPWM strategies suitable for high power three-level neutral point clamped rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4864-4876.
[6] 王金平, 翟飞, 姜卫东, 等. 一种全范围内中点电压平衡的中点钳位型三电平变换器的扩展非连续脉宽调制策略[J]. 中国电机工程学报, 2019, 39(6): 1770-1782, 1873.
Wang Jinping, Zhai Fei, Jiang Weidong, et al. An extended DPWM for neutral point clamped three- level converter with a full range of neutral point voltage balance[J]. Proceedings of the CSEE, 2019, 39(6): 1770-1782, 1873.
[7] 孙青松, 吴学智, 唐芬. 考虑中点电位平衡的三电平逆变器断续脉宽调制策略研究[J]. 中国电机工程学报, 2017, 37(增刊1): 177-185.
Sun Qingsong, Wu Xuezhi, Tang Fen. Three-level inverter discontinuous pulse-width modulation strategy considering neutral point potential balance[J]. Proceedings of the CSEE, 2017, 37(S1): 177-185.
[8] 陈仲, 许亚明, 那显龙. 基于中点电流的三电平NPC逆变器电容电压均衡控制分析[J]. 中国电机工程学报, 2016, 36(19): 5308-5317, 5413.
Chen Zhong, Xu Yaming, Na Xianlong. Analysis of a new voltage balance method for three-level NPC inverters based on neutral-point current[J]. Pro- ceedings of the CSEE, 2016, 36(19): 5308-5317, 5413.
[9] 李宁, 王跃, 蒋应伟, 等. 三电平NPC变流器虚拟空间矢量调制策略与载波调制策略的内在关系研究[J]. 电网技术, 2014, 38(1): 166-174.
Li Ning, Wang Yue, Jiang Yingwei, et al. Research on internal relation between virtual space vector pulse width modulation strategy and carrier sinusoidal pulse width modulation strategy for three-level neutral point clamped converter[J]. Power System Tech- nology, 2014, 38(1): 166-174.
[10] He Yingjie, Lei Chao, Liu Yunfeng, et al. Research on the equivalent virtual space vector modulation output of diode clamped N-level converter under multi-modulation carrier modulation[J]. Energies, 2020, 13(15): 1-18.
[11] 王金平, 刘斌, 董浩, 等. 中点钳位型三电平逆变器基于调制波分解的调制策略[J]. 电工技术学报, 2023, 38(12): 3221-3233.
Wang Jinping, Liu Bin, Dong Hao, et al. A modulation strategy based on modulation wave decomposition for neutral point clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3221-3233.
[12] Guo Feng, Yang Tao, Bozhko S, et al. 3L-NPC AC-DC power converter using virtual space vector PWM with optimal switching sequence based on g-h coordinate[C]//2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Trans- portation Electrification Conference (ESARS-ITEC), Nottingham, UK, 2018: 1-7.
[13] Wu Xiang, Tan Guojun, Ye Zongbin, et al. Virtual- space-vector PWM for a three-level neutral-point- clamped inverter with unbalanced DC-links[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2630-2642.
[14] Jiang Weidong, Wang Peidong, Ma Mingna, et al. A novel virtual space vector modulation with reduced common-mode voltage and eliminated neutral point voltage oscillation for neutral point clamped three- level inverter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 884-894.
[15] Ma Zhixun, Niu Haichuan, Wu Xiang, et al. An improved overmodulation strategy for a three-level NPC inverter considering neutral-point voltage balance and common-mode voltage suppression[J]. Sustainability, 2022, 14(19): 1-16.
[16] Dong Lei, Zang Zetian, Ming Yuanshan, et al. Research on the coordination suppression strategy of neutral point potential and common mode voltage for NPC three-level inverter[J]. Symmetry, 2022, 15(1): 35.
[17] Fan Bo, Fu Zhumu, Fu Jiangtao, et al. Midpoint potential compensation balance control method based on virtual space vector pulse-width modulation for NPC three-level inverter[J]. International Transa- ctions on Electrical Energy Systems, 2019, 29(9): 1-17.
[18] Guo Feng, Yang Tao, Li Chen, et al. Active modulation strategy for capacitor voltage balancing of three-level neutral-point-clamped converters in high- speed drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(3): 2276-2287.
[19] 向超群, 陈春阳, 韩丁, 等. 中点电位不平衡度反馈的三电平虚拟空间矢量调制方法[J]. 电机与控制学报, 2018, 22(3): 50-58.
Xiang Chaoqun, Chen Chunyang, Han Ding, et al. VSVPWM for NPC three-level inverter with neutral point potential unbalance degree feedback[J]. Electric Machines and Control, 2018, 22(3): 50-58.
[20] Fan Bo, Cao Zhe, Wang Chunguang, et al. A novel neutral-point potential balance control method based on voltage feedback for neutral-point clamped three- level inverter[J]. International Journal of Electrical Power & Energy Systems, 2023, 145: 108583.
[21] Xiang Chaoqun, Shu Cheng, Han Ding, et al. Improved virtual space vector modulation for three- level neutral-point-clamped converter with feedback of neutral-point voltage[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5452-5464.
[22] 桂石翁, 吴芳, 万山明, 等. 变虚拟空间矢量的三电平NPC变换器中点电位平衡控制策略[J]. 中国电机工程学报, 2015, 35(19): 5013-5021.
Gui Shiweng, Wu Fang, Wan Shanming, et al. A strategy for considering neutral-point potential balance for three-level NPC inverters with the varied virtual space vector[J]. Proceedings of the CSEE, 2015, 35(19): 5013-5021.
[23] Yuan Qingqing, Li An, Qian Jinyue, et al. DC-link capacitor voltage control for the NPC three-level inverter with a newly MPC-based virtual vector modulation[J]. IET Power Electronics, 2020, 13(5): 1093-1102.
[24] 周冠卿, 张国荣, 解润生, 等. 改进的三电平逆变器变虚拟空间矢量调制策略[J]. 电力系统自动化, 2023, 47(1): 172-182.
Zhou Guanqing, Zhang Guorong, Xie Runsheng, et al. Improved variable virtual-space-vector modulation strategy for three-level inverter[J]. Automation of Electric Power Systems, 2023, 47(1): 172-182.
[25] 杨清, 黄景涛, 关海平, 等. 高调制深度下三电平NPC逆变器中点电位快速均衡控制[J/OL]. 电源学报, 2023, https://kns.cnki.net/kcms2/detail/12.1420. TM.20230524.1732.004.html.
Yang Qing, Huang Jingtao, Guan Haiping, et al. Fast neutral point potential balancing of three-level NPC inverter under high modulation depth[J/OL]. Journal of Power Supply, 2023, https://kns.cnki.net/kcms2/ detail/12.1420.TM.20230524.1732.004.html.
[26] Xia Shuai, Wu Xiaojie, Zheng Jinggang, et al. A virtual space vector PWM with active neutral point voltage control and common mode voltage suppression for three-level NPC converters[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11761-11771.
Abstract As a typical multilevel inverter, a neutral point clamped (NPC) three-level inverter is suitable for large-capacity and high-voltage converters, which can effectively reduce current harmonic content. However, the NPC three-level inverter has the problem of neutral point voltage imbalance due to the structural characteristics of capacitive voltage division. The traditional virtual space-vector pulse width modulation (VSVPWM) has limited ability to suppress neutral point voltage fluctuation. Correcting its offset is challenging, especially in the medium and high modulation depths. Therefore, this paper proposes a sector reconfiguration VSVPWM. By introducing equivalent medium vectors and reconstructing sectors in medium and high modulation depths, small and medium vectors can fully participate in neutral point balance adjustment while retaining fixed sector division. This method can effectively suppress the neutral point voltage fluctuation and accelerate the recovery of the neutral point offset. There is only one balance coefficient for each fixed sector, which is easy to implement.
Firstly, the equivalent relationship between a large vector and a medium vector is analyzed. An equivalent medium vector with constant amplitude is then constructed. The equivalent medium vector can participate in the neutral point balance by adjusting the proportion of medium and large vectors. After that, a virtual vector group, including equivalent medium vectors, is constructed. Furthermore, an equivalent medium vector VSVPWM (EMV-VSVPWM) is proposed, which improves the neutral point adjustment ability in the sector with a medium vector. Secondly, the level of modulation depth is divided based on the operational sector position, and the neutral point margin of the EMV-VSVPWM strategy depths is analyzed in one modulation period. It is found that the regions with weaker capacity of neutral point balance exist in high modulation depth. Therefore, a sector reconstruction VSVPWM (SR-VSVPWM) is then designed. The sector boundary and vector selection boundary in the medium and high modulation depths are separated to increase the proportion of small and medium vectors in such regions, which can enhance the neutral point adjustment margin. Furthermore, the neutral point balance coefficient of small and medium vectors is unified to reduce the computational complexity. Meanwhile, the vector sequence is optimized according to the principle of constant switching state, and the switching loss is reduced.
The initial neutral point voltage offset and modulation depth experiments are carried out on a hardware experimental platform in the loop. The results indicate that the SR-VSVPWM strategy can achieve the fast balance of the middle point in pure resistor load and resistor-inductance load conditions. Compared with the traditional VSVPWM single small vector adjustment, the neutral point voltage offset is eliminated, and the balance time in the high modulation depth is reduced by about 46%. In addition, the current harmonics are also reduced. When the experiment on variable modulation depth is considered, SR-VSVPWM still exhibits strong suppression of neutral point fluctuations and good current quality in high modulation depth. After the switching frequency is reduced to 5 kHz, the neutral point fluctuation level of SR-VSVPWM is 79.1% of the traditional VSVPWM.
Keywords：Neutral point clamped (NPC) three-level inverter, virtual space vector pulse width modulation, neutral point voltage balance, sector reconstruction, equivalent medium vector
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.240520
国家自然科学基金地区科学基金项目（62363030）和新疆维吾尔自治区科学技术厅重大科技专项项目（2022A01004-3）资助。
收稿日期 2024-04-01
改稿日期 2024-05-06
胡瀚林 男，2001年生，硕士研究生，研究方向为电力电子与电力传动。
E-mail: shzu_huhanlin@163.com
赵 咪 女，1980年生，教授，硕士生导师，研究方向为智能电网故障诊断与控制、电力电子与电力传动等。
E-mail: zhaomi530@163.com（通信作者）
（编辑 陈 诚）