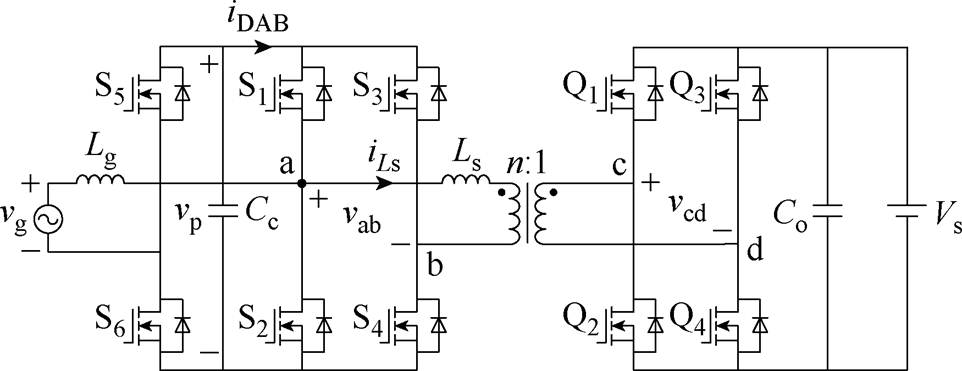
图1 图腾柱DAB AC-DC变换器拓扑结构
Fig.1 Totem-pole DAB AC-DC converter
摘要 单级式图腾柱双有源桥AC-DC变换器具有元件数量少、功率密度高和成本低等优点,在车载充电机等领域具有广阔的应用前景。然而,现有的单移相和扩展移相调制策略由于存在调制自由度不足的问题,而无法对变换器进行多目标的优化,使图腾柱双有源桥AC-DC变换器在并网电流质量和效率等稳态性能方面仍有提升空间,限制了该变换器在车载充电机中的进一步应用。首次,该文在扩展移相调制策略的基础上引入非对称调制,从而提出具有三个自由度的非对称扩展移相调制策略。其次,对变换器在非对称扩展移相调制下所有可能的工作模式进行分析,并借助时域分析法建立各工作模式的时域稳态分析模型。然后,考虑控制传输功率以实现功率因数校正的同时,进行电感电流初值和峰峰值的多目标优化调制策略求解。最后,相比传统的单移相和扩展移相调制策略,所提出的非对称扩展移相优化调制策略大幅度提升了变换器的稳态性能:并网电流的质量显著提升,峰值效率提升超过5%和1.5%。所提理论分析和优化结果都在仿真和实验中得到了验证。
关键词:图腾柱双有源桥 AC-DC变换器 非对称扩展移相调制 功率因数校正 优化调制策略
车载充电机(On-Board Chargers, OBC)作为电动汽车的一个重要组件,它允许在任何可接入交流电源的地方为电动汽车充电[1],因此逐渐成为当前的研究热点。目前,常见的OBC产品大多采用两级式解决方案,即一个前级功率因数校正(Power Factor Correction, PFC)整流器和一个后级隔离 DC-DC 变换器[2-3]。然而,由于采用两级功率变换,使变换器的效率、可靠性和功率密度等受到限制,并且大量的元件和控制回路增加了系统的复杂性和成本[4]。
为此,目前已经提出了几种单级式双有源桥(Dual Active Bridge, DAB)AC-DC变换器[5-8]。单级式DAB AC-DC变换器由于采用单级功率变换,且取消了直流母线上大容量电解电容的使用,因此在效率、可靠性和功率密度等方面更具潜力。特别地,在文献[9]中介绍了一种图腾柱DAB AC-DC变换器,该拓扑在交流侧采用图腾柱无桥整流结构,且将整流器中的高频桥臂和DAB变换器的一次侧桥臂进行复用,从而进一步减少了开关管数量和变换器损耗,使其在众多单级DAB AC-DC变换器拓扑中更具优势。
单级式DAB AC-DC变换器可以在没有电流传感器和电流闭环控制的情况下实现PFC功能[7-9]。这进一步简化了控制器设计,降低了系统成本。且单级式DAB AC-DC变换器在一个开关周期内可以等效为DAB DC-DC变换器,因此,传统的基于DAB DC-DC变换器的移相调制[10]和优化方法[11-12]可以直接应用于DAB AC-DC变换器中。但是对于AC-DC变换器而言,在一个工频周期内的宽电压增益变化与开环PFC的实现,给单级式DAB AC-DC变换器的调制策略及其优化带来了新的挑战。因此目前对单级式DAB AC-DC变换器的研究主要集中在考虑开环PFC实现与宽电压增益范围下的调制策略优化上面[13-14]。
文献[15]中详细分析了由于DAB AC-DC变换器输入电压的工频变化,使相邻开关周期的等效输入电压发生突变,进而导致了相邻开关周期电感电流初值存在耦合,使电感电流的理论值与实际值存在误差。文献[11]对DAB AC-DC变换器在单移相(Single Phase-Shift, SPS)调制下的稳态波形进行了仿真和实验验证,证明了SPS下的电感电流初值耦合问题使并网电流发生畸变,说明了在调制中实现电感电流初值解耦的必要性。针对图腾柱DAB AC-DC变换器,在文献[7-9]中均在扩展移相(Extended Phase-Shift, EPS)调制中进行了优化调制策略的研究,文献[7]为优化开环PFC下的并网电流质量,在EPS内部模式下引入了电感电流初值约束,使各开关周期的电感电流初值为0,从而实现了电感电流初值的解耦。文献[8]在EPS外部模式下以电感电流峰值为优化目标,从而降低导通损耗,提升变换器效率。但是上述研究中两自由度的EPS调制由于存在优化空间不足的问题,不能实现对变换器并网电流质量和效率的同时优化。
为了解决图腾柱DAB AC-DC变换器中传统EPS调制自由度不足的问题。本文通过在EPS调制的基础上引入非对称调制,提出了具有三自由度的非对称扩展移相(Asymmetric Extended Phase-Shift, AEPS)调制策略。首先,对图腾柱DAB AC-DC变换器的拓扑结构和工作原理进行介绍。其次,介绍了AEPS调制的典型波形及其工作模式划分,并借助时域分析法建立了AEPS所有工作模式下的时域稳态分析模型。然后,借助拉格朗日算法和卡鲁什库恩塔克(Karush kuhn tucker, KKT)条件对AEPS优化调制策略进行求解,并进行仿真验证。最后,给出实验结果,验证理论分析与仿真结果的正确性。
图1所示为图腾柱DAB AC-DC变换器拓扑结构。它由前端图腾柱整流器和后端DAB变换器构成。其中,S1、S2既是图腾柱整流器的高频桥臂开关管,也是DAB一次侧的超前桥臂开关管。
对于前端图腾柱整流器,S1和S2工作在高频,S5和S6工作在工频。Lg为网侧电感,其大小与并网电流纹波相关。前端整流器的输出电容Cc用来滤除整流电压中的高频分量,因此其容值非常小。

图1 图腾柱DAB AC-DC变换器拓扑结构
Fig.1 Totem-pole DAB AC-DC converter
后端DAB由4个一次侧高频开关S1~S4、高频变压器和4个二次侧高频开关Q1~Q4构成。变压器匝比为n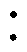 1,漏感用Ls表示。iLs为变压器漏感电流,其在一个开关周期内的平均传输功率电流为iDAB。
1,漏感用Ls表示。iLs为变压器漏感电流,其在一个开关周期内的平均传输功率电流为iDAB。
图2显示了变换器的典型工作波形。在交流侧,S5和S6以工频开关,S1和S2以固定的50%占空比高频互补导通。交流侧输入电压vg和输入电流ig的幅值分别为Vg和Ig,交流电压被整流为以两倍工频波动且幅值为2Vg的直流电压vp,即DAB的输入电压。对于DAB变换器,在EPS调制下,其一次侧开关管S1~S4以50%占空比两两互补导通,因此在桥臂中点产生两电平方波vab。二次侧开关管Q1~Q4通过内移相角及一、二次侧间的外移相角控制DAB变换器的电感电流,从而控制传输功率,因此二次侧为三电平波形vcd,且幅值为输出电压Vo。
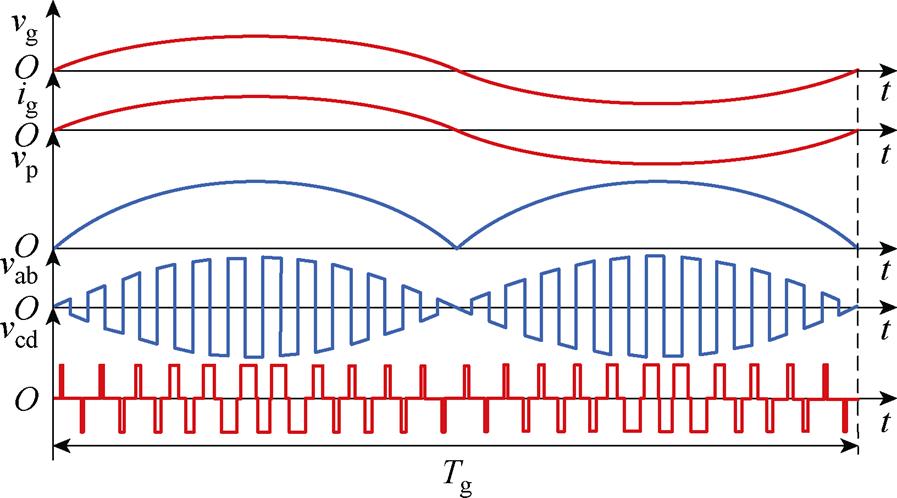
图2 典型工作波形
Fig.2 Typical operating waveforms
由于电容Cc的容值很小,因此可以忽略电容上发出的无功功率。此时认为网侧的瞬时输入功率pin等于后端DAB的传输功率,即
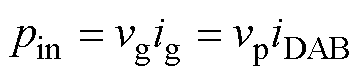 (1)
(1)
因此可以通过控制各开关周期的传输功率电流iDAB来控制并网电流ig的瞬时变化,这意味着PFC可以通过控制DAB变换器每个开关周期的平均传输电流iDAB来实现。
图3所示为实现开环PFC的原理,Tg为工频周期,Ts为开关周期。
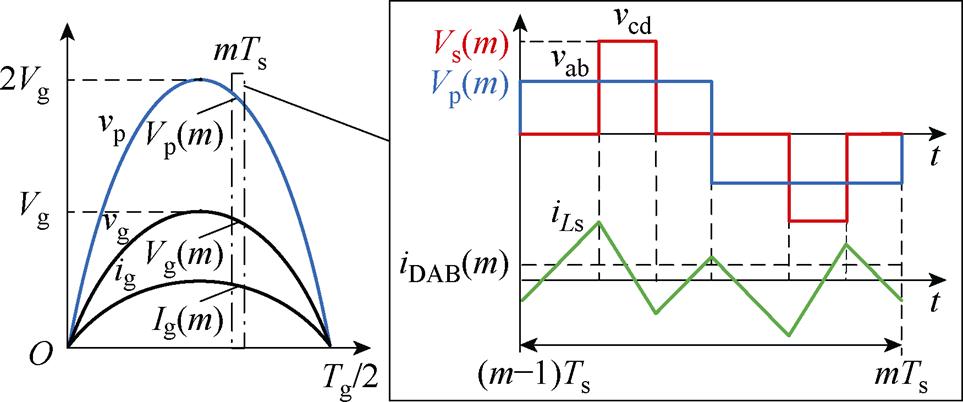
图3 基于开关周期内瞬时功率平衡的开环PFC
Fig.3 Open-loop PFC based on power balancing in Ts
尽管输入电压vp大小在工频周期内变化,但是由于Tg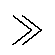 Ts,因此在一个开关周期内可以将输入电压视为恒定值。则在一个工频周期中的第m个开关周期内的等效输入电压Vp(m)为
Ts,因此在一个开关周期内可以将输入电压视为恒定值。则在一个工频周期中的第m个开关周期内的等效输入电压Vp(m)为
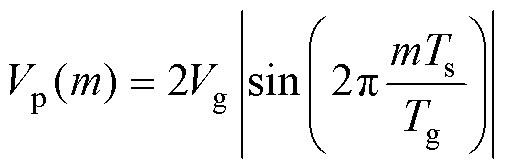 (2)
(2)
由此可知,实现开环PFC的关键是通过移相调制策略精确控制第m个开关周期的平均传输功率电流iDAB(m)大小,满足
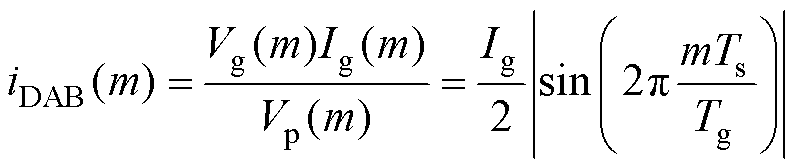 (3)
(3)
根据现有研究,图腾柱DAB AC-DC变换器常用的调制策略为EPS调制[9],如图4a所示为EPS调制的典型波形,其中D0为S1、Q4间的外移相角,用来控制传输功率;D2为Q1、Q3间的内移相角,在文献[9]中用来优化变换器零电压软开关(Zero Voltage Switching, ZVS)范围。为了进一步增加图腾柱DAB AC-DC变换器的调制自由度,在不改变电感一次电压vab波形的前提下,通过在EPS 调制的基础上引入非对称调制,如图4b所示。
此时D1+D2≠0.5,而使原有的两个调制变量D0、D2增加到3个D0、D1和D2。这意味着所提出的AEPS调制拥有更多的优化空间,基于AEPS调制方式的优化调制策略研究是本文的主要内容。
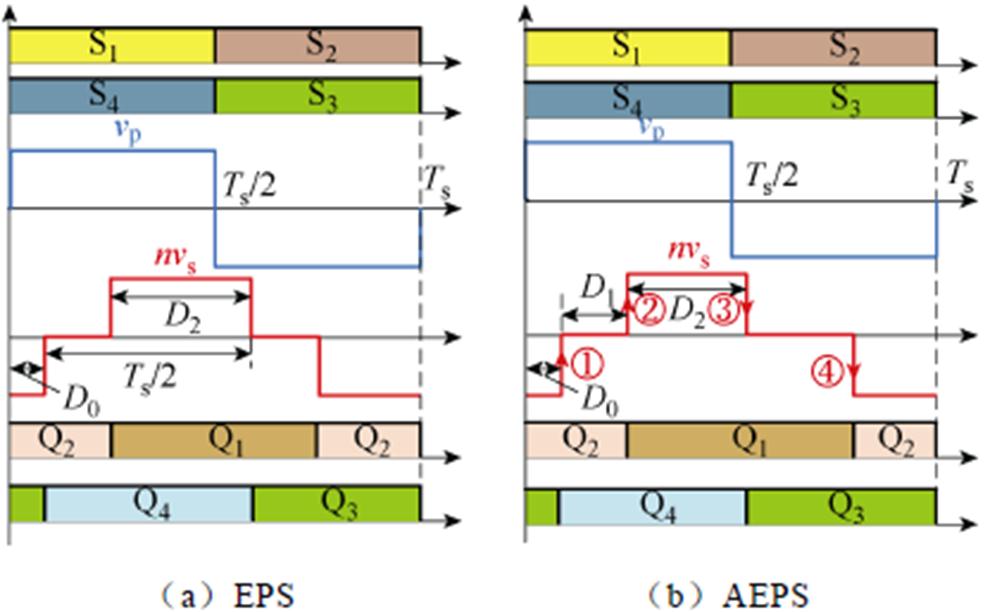
图4 EPS与AEPS调制波形
Fig.4 EPS and AEPS modulated waveforms
建立变换器的稳态分析模型是优化调制策略的基础。本文选择时域分析法来建立AEPS下DAB变换器的时域稳态模型。利用时域分析法建模的第一步就是需要对AEPS调制的工作模式进行划分,从而确定不同工作模式下的电感两端电压波形。AEPS调制正向功率传输下所有工作模式如图5所示,考虑二次电压电平变化时刻①②③④所处区间的排列组合,可以得到在正向功率传输下的九种工作模式。而对于模式3、6、7、8和9,由于电感两端电压乘积vabvcd<0的区间较长,在该区间内功率存储在电感Ls中,而不能直接传输到二次侧,这将增加电感电流峰值,进而增加变换器损耗,因此选择模式1、2、4和5作为AEPS调制的工作模式。
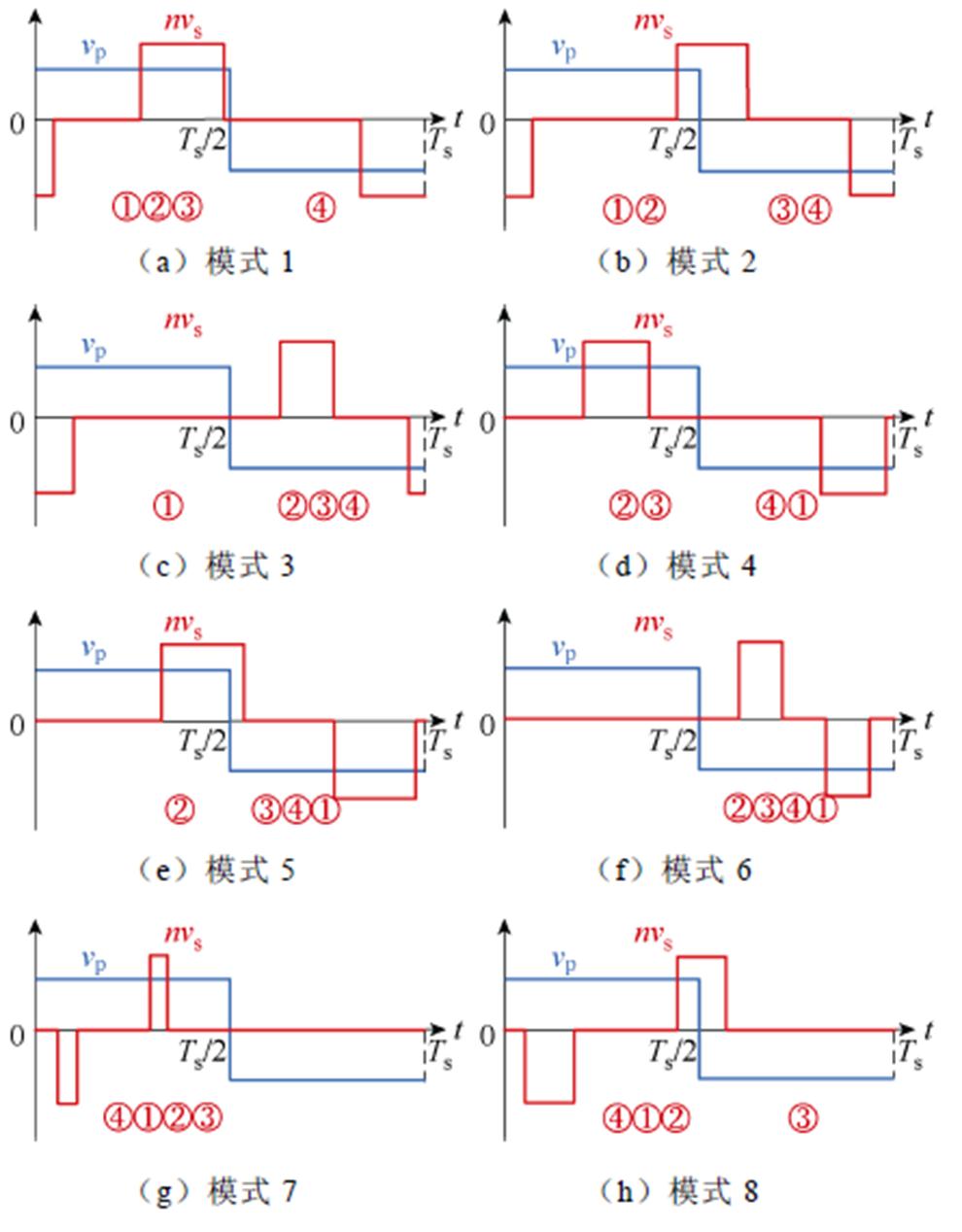
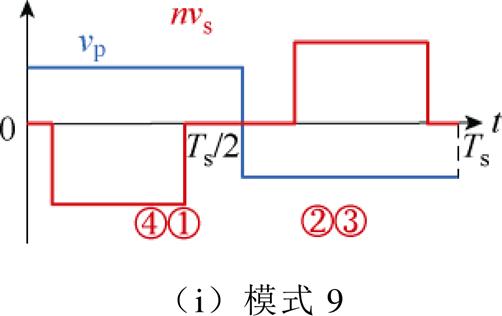
图5 AEPS调制正向功率传输下所有工作模式
Fig.5 All operating modes under AEPS modulated forward power transfer
建立不同工作模式的时域稳态模型过程一致,现以AEPS调制的模式4为例,其典型工作波形如图6所示。建立该模式下的时域稳态分析。
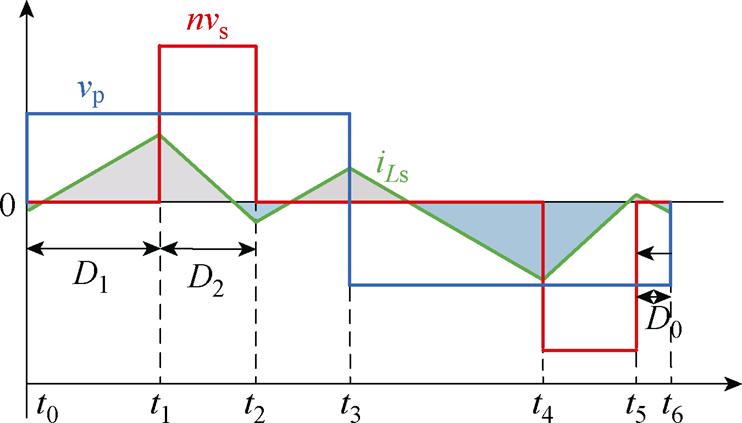
图6 AEPS调制模式4的典型工作波形
Fig.6 Typical waveforms of AEPS modulation mode 4
电感电流iLs(t)表示为
 (4)
(4)
对于移相调制,考虑变压器的偏磁问题,需要引入式(5),即电感电流iLs在一个开关周期内的积分为0。
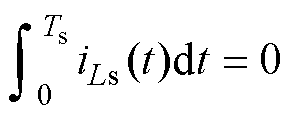 (5)
(5)
将式(5)代入式(4),便可求得一个开关周期内的电感电流初值iLs(t0),进而可以求得各时刻的电感电流值及其在一个开关周期内的平均传输功率电流值iDAB。定义电压增益M及电流基准ibase分别为
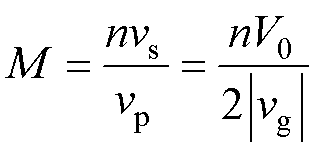 (6)
(6)
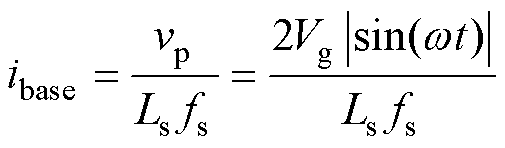 (7)
(7)
则归一化后的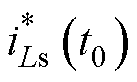 和
和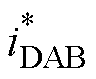 分别为
分别为
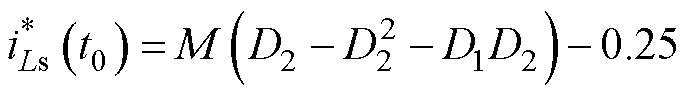 (8)
(8)
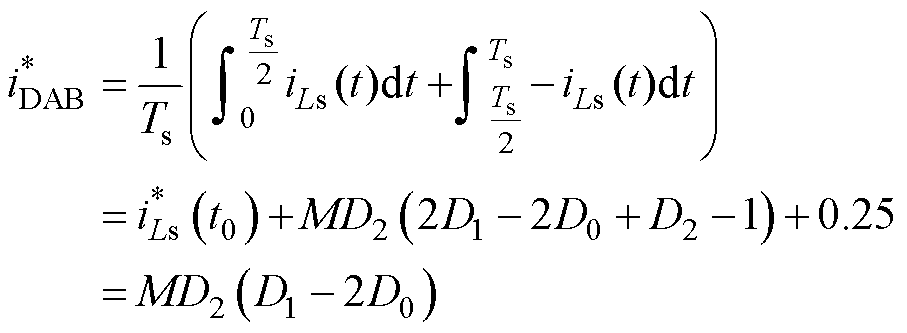 (9)
(9)
由式(9)可知,电感电流初值iLs(t0)会影响一个开关周期内的平均传输功率电流值iDAB大小。而传统移相调制直接应用于DAB AC-DC变换器存在的初值耦合问题,进而影响iDAB的控制精度,以及网侧电流ig的波形质量。因此有必要在所提出的AEPS调制中引入初值约束以实现初值解耦。
另外与EPS调制不同的是,由于AEPS调制的非对称性,造成其电感电流的非对称性。根据电压增益M与移相角之间的关系,在模式4下的电感电流峰峰值满足
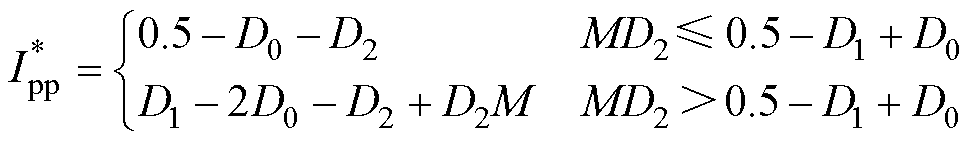 (10)
(10)
同理可以建立其他工作模式的时域稳态模型,结果见表1。由表1中模式1、2、4和5的解析表达式和不同工作模态的移相角范围,可以通过遍历的方法得到AEPS调制各模式全工作域下电感电流峰峰值Ipp的取值,如图7所示。由图7可得,模式4在低功率段的电流峰值最小,而模式2的传输功率范围最大。因此在低功率段选择模式4,在高功率段选择模式2。
对于DAB变换器,损耗一般包括开关损耗、导通损耗和磁心损耗。相同工况下磁心损耗差别不大,因此通常将开关损耗或导通损耗设为优化目标。而对于单级式DAB AC-DC变换器,需要额外引入电感电流初值约束来优化开环PFC下的并网电流质量[13],因此无法以ZVS范围为优化目标。故在本节中,选择导通损耗作为优化目标。导通损耗的优化可以等效为电感电流有效值的优化。然而,电流有效值计算较为复杂,不利于优化求解,考虑到电感电流峰峰值与其有效值的单调性相同[11],本节将电感电流峰峰值作为优化目标。
表1 各工作模式时域稳态模型 Tab.1 Time-domain steady state model for each operating mode

工作模式工作模式约束传输功率电流电感电流峰峰值 模式1 模式2 模式4 模式5
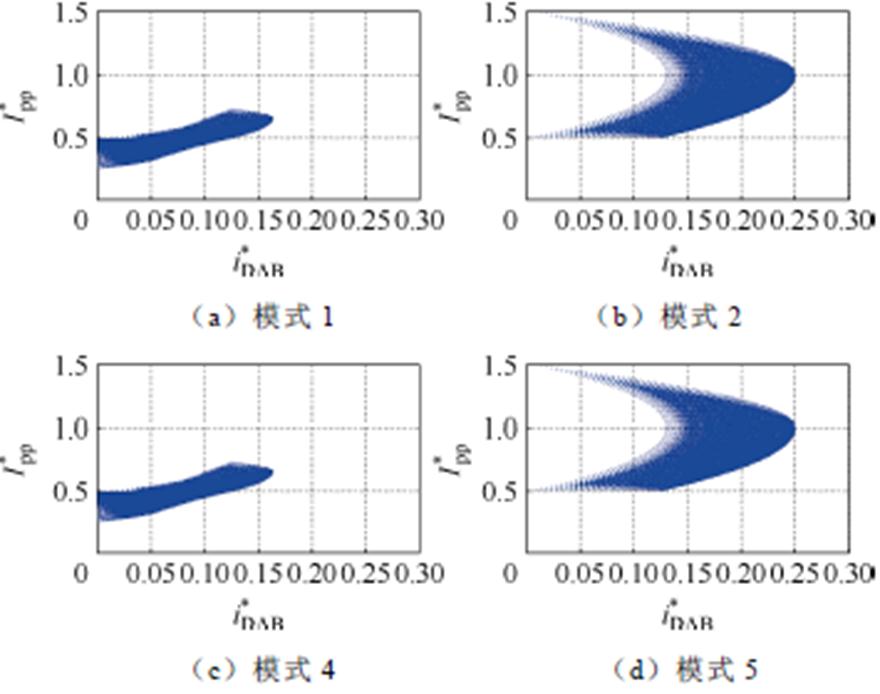
图7 M=2时各模式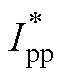 取值
取值
Fig.7 All the 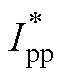 for each mode at M=2
for each mode at M=2
以低功率段的优化调制策略求解为例,由上述分析可知,低功率段的工作模式为AEPS调制模式4。在模式4下以最小电感电流峰峰值为优化目标,引入PFC下的传输功率电流约束,引入电感电流初值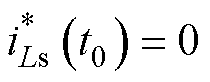 的电流初值解耦约束,同时考虑模式4下工作模式的移相角间的不等式约束。根据模式4的时域稳态分析模型,上述问题可转化为
的电流初值解耦约束,同时考虑模式4下工作模式的移相角间的不等式约束。根据模式4的时域稳态分析模型,上述问题可转化为
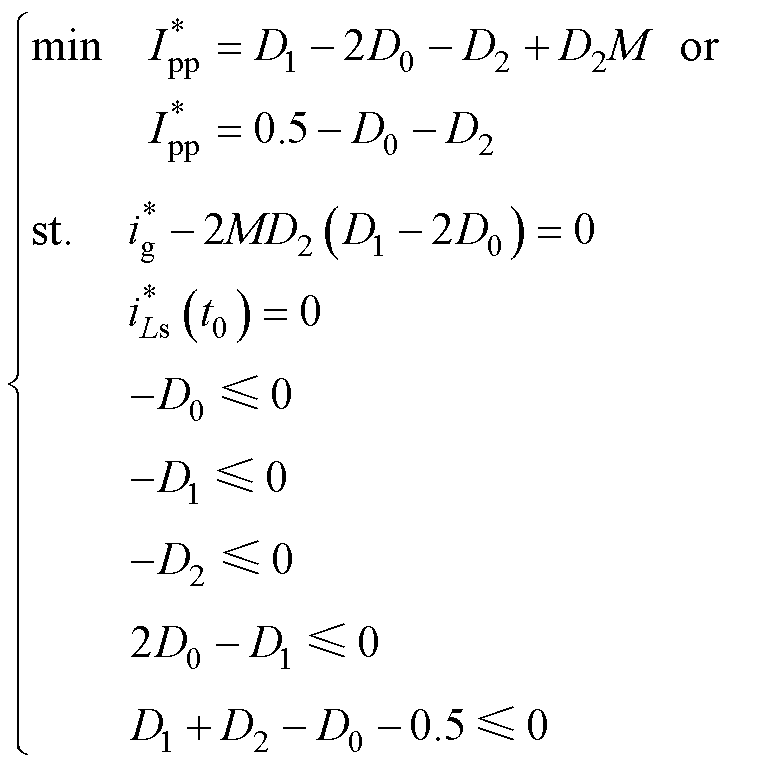 (11)
(11)
拉格朗日算法和KKT条件[12]是求解上述等式约束与不等式约束下最优化问题的常用方法,根据式(11)建立相应的拉格朗日方程,求解得到低功率段下模式4的调制变量D0、D1和D2的优化解析表达式。
当MD2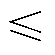 0.5-D1+D0时,有
0.5-D1+D0时,有
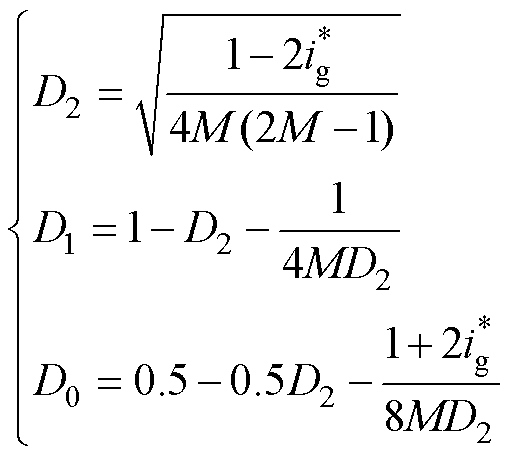 (12)
(12)
当MD2>0.5-D1+D0时,有
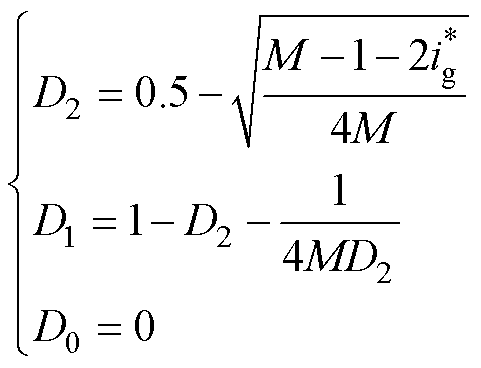 (13)
(13)
同理,在高功率段下AEPS调制模式2的调制变量D0、D1和D2的优化解为
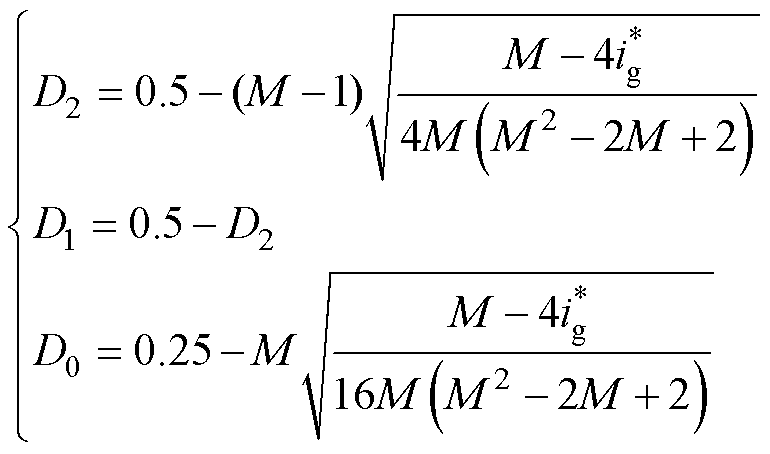 (14)
(14)
此外,根据不同模式切换的临界条件,得到高低功率段切换的临界电流值为
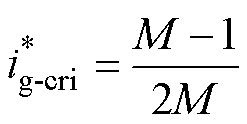 (15)
(15)
上述优化求解得到了调制变量D0、D1和D2解析表达式(12)~式(14)。三个移相角是由一个工频周期内的电压增益M和输入电流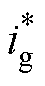 实时计算得到的,而不是电流闭环的输出。因此,可以通过开环
实时计算得到的,而不是电流闭环的输出。因此,可以通过开环
计算实现PFC的功能。图8显示了AEPS移相调制方案下的控制框图和流程。其中,电压增益M可以通过电压采样并计算得到,而输入电流给定为
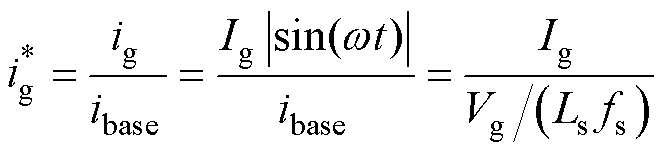 (16)
(16)
变换器输入电流ig幅值的大小由电压闭环的输出给定。
根据图8所示的AEPS优化调制策略流程,可以计算得到不同输入电流幅值给定时的调制变量D0、D1和D2。由于正负半周电压电流的对称性,其在正负半个工频周期内的变化是相同的。图9所示为电流幅值Ig=6 A和Ig=10 A时,在半个工频周期内AEPS优化调制三个移相角的变化曲线。当Ig=6 A时,一直处于低功率段,此时工作在模式4;当Ig=10 A时,随着传输功率电流的增加,由低功率段转向高功率段,此时工作模式发生模式4向模式2的转变。由于不同模式间的移相角是连续变化的,因此可以实现两种工作模式的无缝切换。
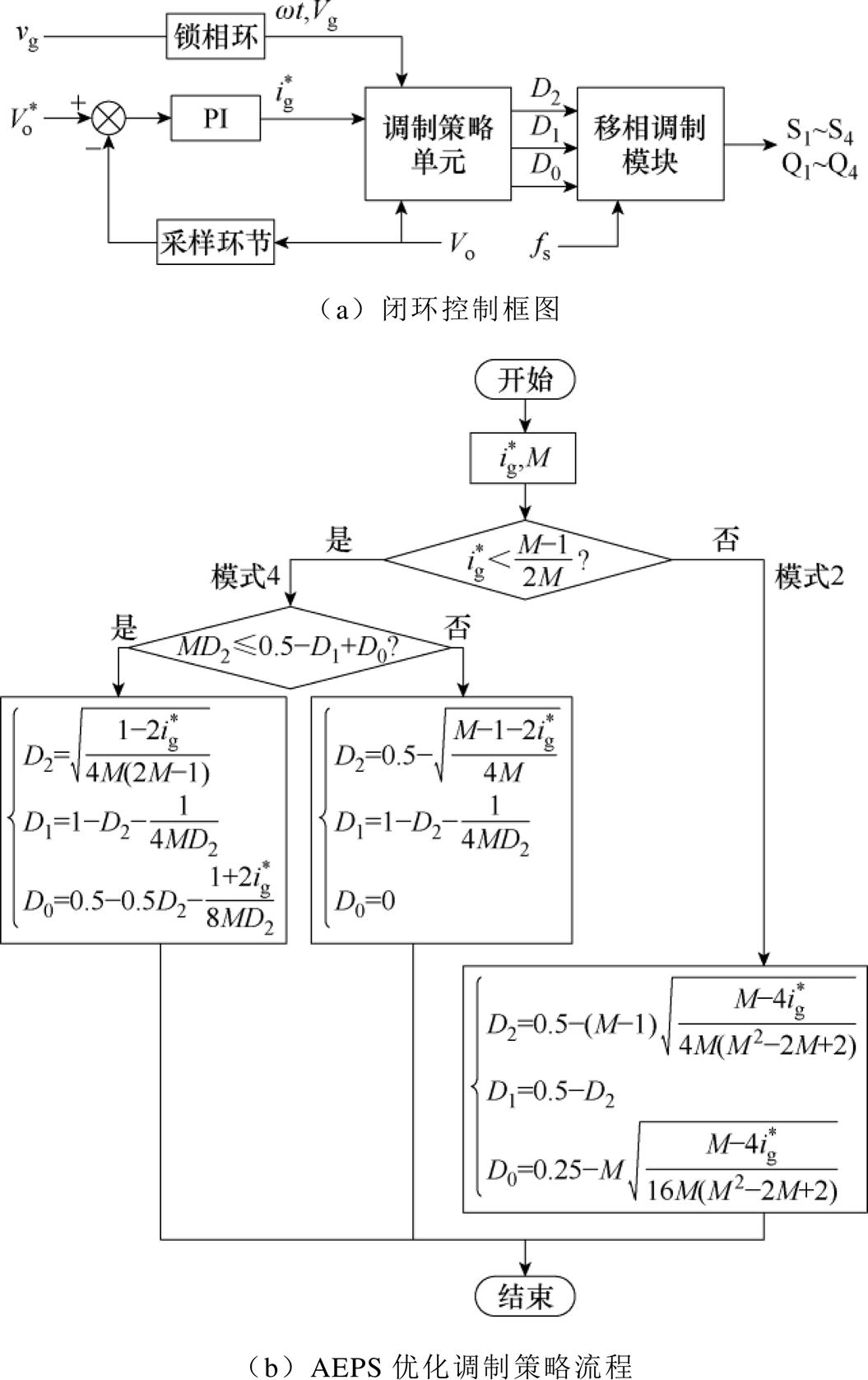
图8 变换器的控制框图及调制策略流程
Fig.8 Control block diagram of the converter

图9 半工频周期下AEPS三移相角曲线
Fig.9 AEPS three phase angle curves at half line cycle
根据表2仿真和实验参数,借助Matlab/Simulink对图腾柱DAB AC-DC变换器进行仿真建模,在该模型下完成了对传统移相调制策略与所提出的AEPS优化调制仿真结果的比较分析。
表2 仿真和实验参数
Tab.2 Simulation and experimental parameters
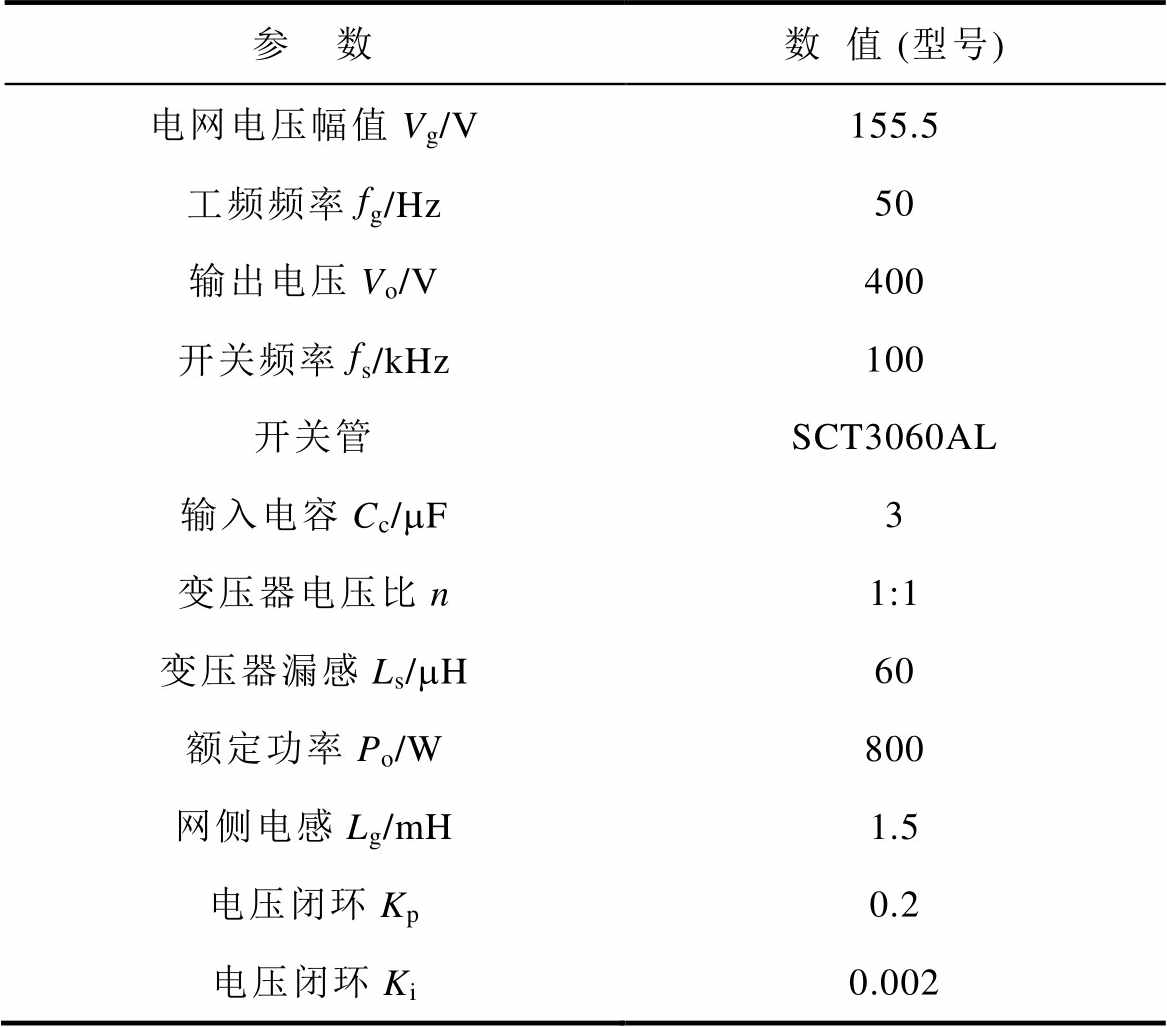
参 数数值 (型号) 电网电压幅值Vg/V155.5 工频频率fg/Hz50 输出电压Vo/V400 开关频率fs/kHz100 开关管SCT3060AL 输入电容Cc/mF3 变压器电压比n1:1 变压器漏感Ls/mH60 额定功率Po/W800 网侧电感Lg/mH1.5 电压闭环Kp0.2 电压闭环Ki0.002
为了验证引入的电感电流初值约束,即约束iLs(t0)=0以优化并网电流质量的可行性,本节在图腾柱DAB AC-DC变换器中分别采用了SPS调制与APES优化调制策略。图10所示为Ig=6 A时在SPS调制下的仿真波形,此时并网电流总谐波失真(Total Harmonic Distortion, THD)为9.15%,电流畸变严重,且实际电流幅值Ig=5.702 A,与给定值之间存在误差。由图10d可知,在SPS调制下由于电感电流初值耦合的问题而使电感电流实际值与理论值之间存在误差,进而影响电感电流控制的精确性从而使并网电流发生畸变。
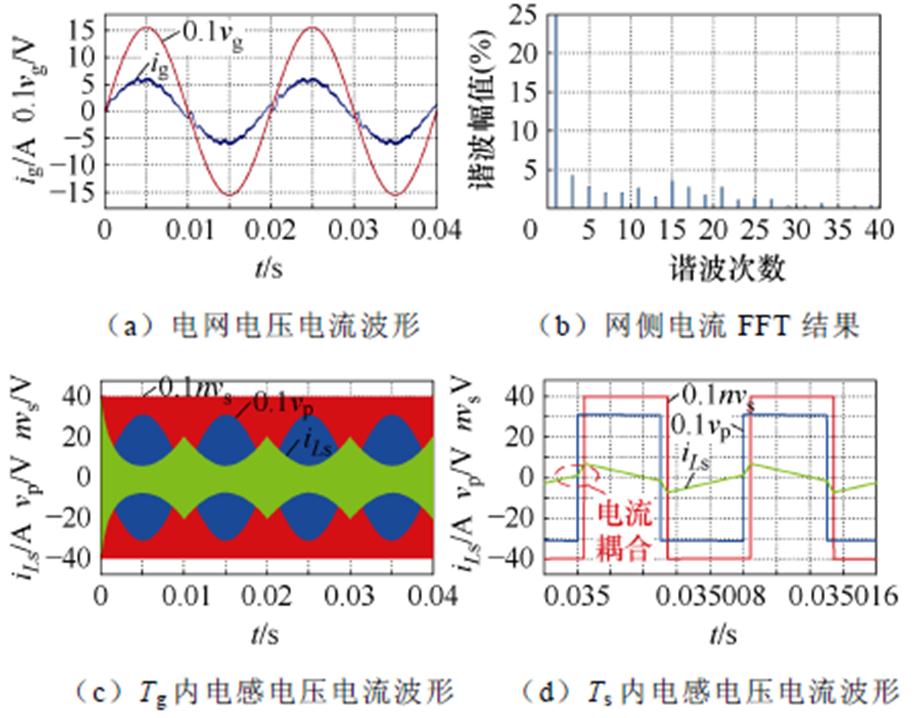
图10 Ig=6 A时SPS调制策略仿真波形
Fig.10 Simulation waveforms of SPS modulation strategy at Ig=6 A
图11所示为Ig=6 A时在AEPS优化调制下的仿真波形,此时并网电流THD=3.42%,实际电流幅值Ig=6.036 A。由图11d所示开关周期内的电感电流波形可知,AEPS调制引入了电感电流初值约束,使每个开关周期的电感电流初值iLs(t0)=0,从而实现了相邻开关周期间的电流解耦,保证了对各开关周期传输平均电流的精确控制,从而提升了并网电流质量。
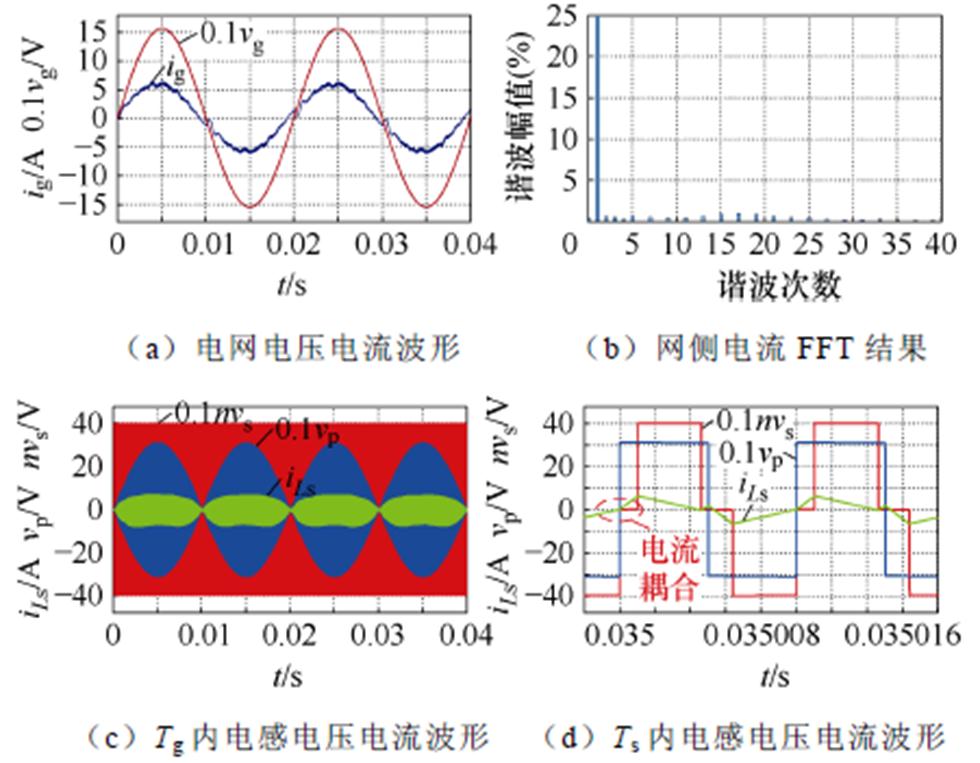
图11 Ig=6 A时AEPS优化调制策略仿真波形
Fig.11 Simulation waveforms of AEPS optimized modulation strategy at Ig=6 A
AEPS优化调制引入初值解耦约束的同时,还进行了电感电流峰峰值优化。如图12所示为各开关周期电感电流峰峰值Ipp在半个工频周期内的变化,相比传统的SPS调制以及EPS调制,所提出的AEPS优化调制策略在全功率段范围内都降低了电感电流的峰峰值。同时为了验证所提出的AEPS优化调制策略对电感电流有效值IRMS的优化,图13给出了相同功率下不同调制策略的IRMS曲线。
由图13可知,虽然在优化求解时以电感电流峰峰值Ipp为优化目标,但是所提出的优化调制策略同样降低了全功率段的电感电流有效值IRMS。
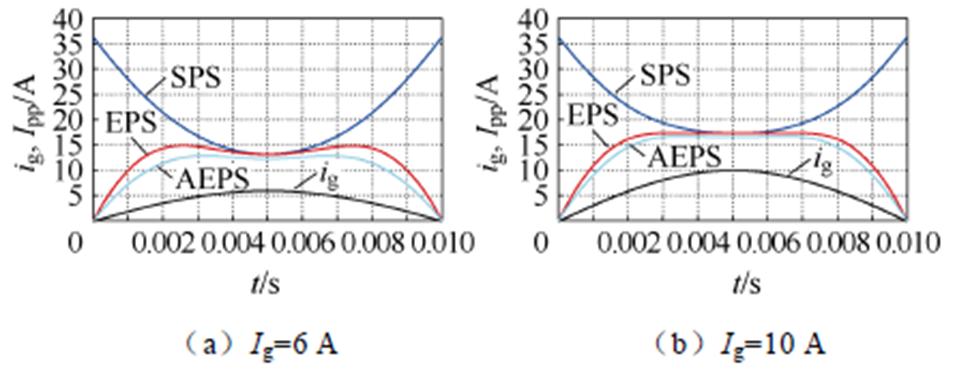
图12 同功率下SPS、EPS[9]与AEPS的Ipp对比
Fig.12 Ipp comparison between SPS、EPS[9] and AEPS under the same power
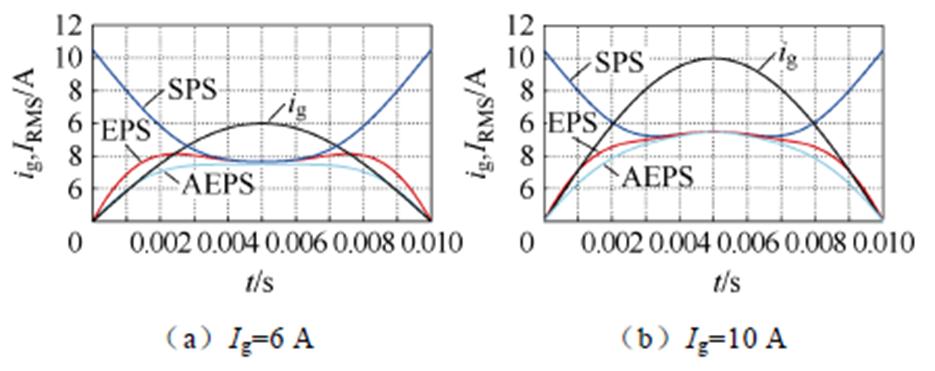
图13 同功率下SPS、EPS[9]与AEPS的IRMS对比
Fig.13 IRMS comparison between SPS、EPS[9] and AEPS under the same power
由上述仿真结果可知,相对传统的移相调制策略,所提出的AEPS优化调制策略可以实现优化并网电流质量的同时,在全功率段降低了电感电流有效值IRMS,从而提升了变换器效率。
为了验证变换器ZVS的实现情况,本节对所提出的AEPS优化调制策略下开关管的ZVS实现进行了分析。为了实现ZVS,电感电流除了方向满足要求外,其大小也必须足够大,以在桥臂开关管开通前对其漏-源极电容Coss进行完全放电。临界ZVS电流IZVS计算式为
 (17)
(17)
式中,VDS为开关管漏-源极电压应力;WCoss为Coss电容完全放电时所释放的能量,其大小可由开关管SCT3060AL数据表中Coss-VDS曲线计算得到,L为换向所涉及的电感。当L=Ls=60 mH时,开关管的临界ZVS电流IZVS和VDS之间的关系可以计算出来并绘制如图14所示。
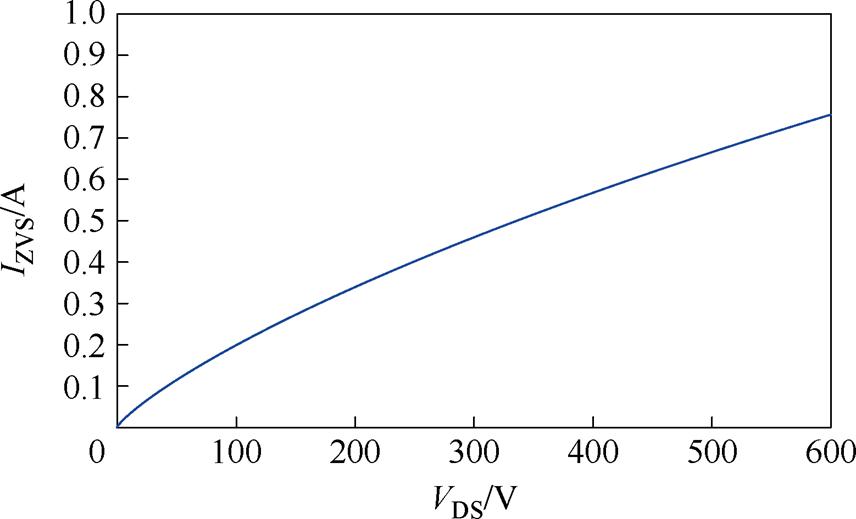
图14 IZVS-VDS变化曲线
Fig.14 IZVS-VDS variation curve
特别地,如果开关管开通时刻电流方向满足ZVS要求但小于IZVS,此时开关管的寄生电容Coss在导通前只能部分放电,那么只能实现部分ZVS。
定义各开关管的电流方向向下,则可以得到AEPS调制下各开关管开通时刻电流见表3。根据表3中表达式可以得到AEPS优化调制策略下变换器ZVS实现情况如图15所示。
表3 各开关管开通时刻电流Tab.3 Current at turn-on time of each switch

工作模式开关管S1~S4开关管Q1~Q4 模式2 模式4
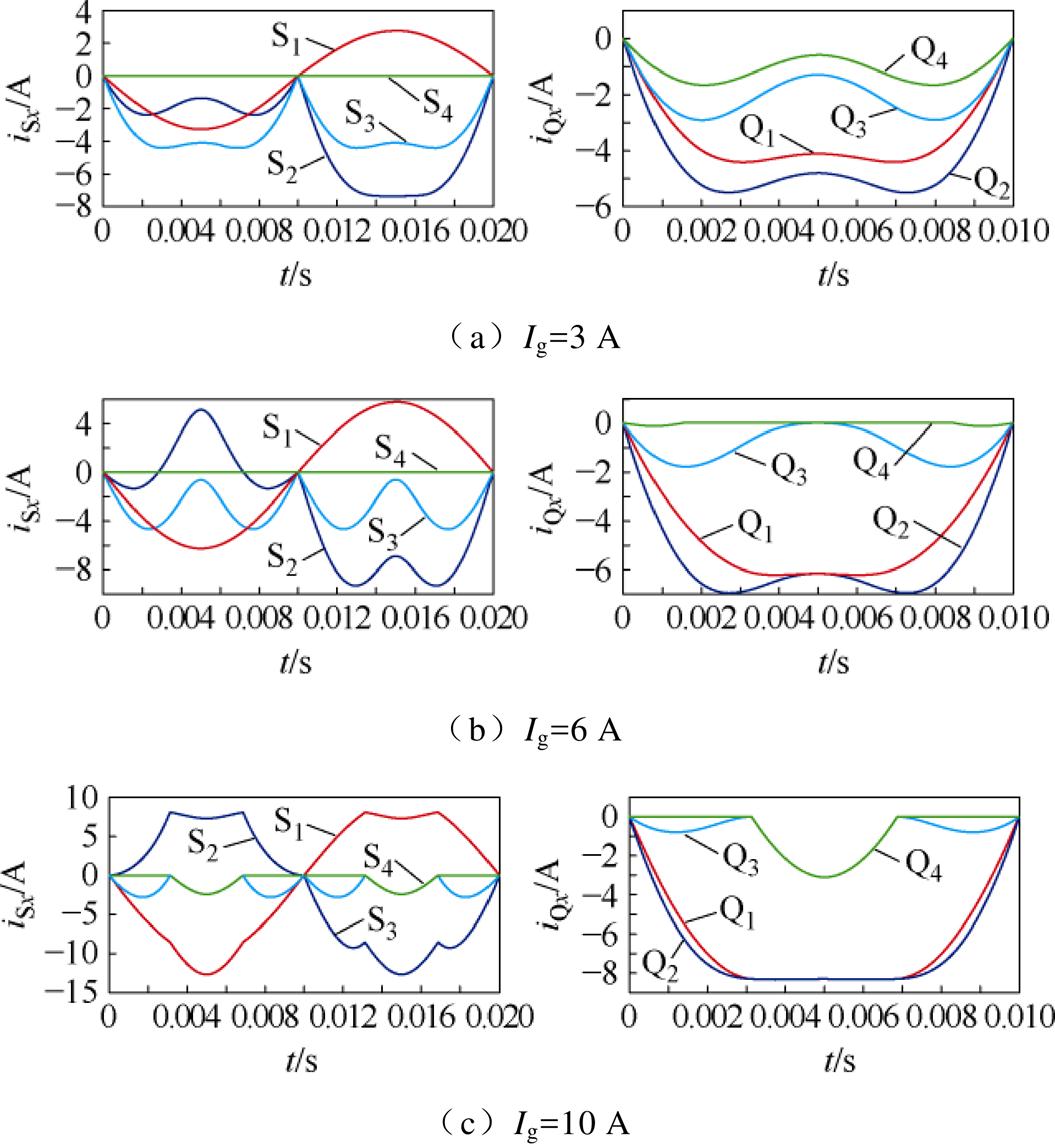
图15 AEPS优化调制策略下变换器ZVS实现情况
Fig.15 Converter ZVS implementation with AEPS
由图15可知,开关管S1、S2的ZVS实现主要取决于网侧电流ig:正半工频周期,S1可以实现ZVS、S2硬开通;在负半工频周期,S2可以实现ZVS、S1硬开通。开关管S3、S4、Q1~Q4在正负半周期的ZVS情况具有对称性,以正半工频周期为例。S3和Q1~Q3在全功率段均可实现ZVS;S4在中低功率段均为硬开通,只有在高功率段可实现ZVS;Q4在中功率段为硬开通,其他工况可实现ZVS。
综上所述,尽管所提出的AEPS优化调制策略没有以ZVS实现范围为优化目标,变换器在AEPS调制下至少5个开关管可以同时实现ZVS或部分ZVS。
为了验证上述提出的AEPS优化调制策略理论分析与仿真结果的正确性。根据表2中所示参数,搭建了一台额定功率800 W的图腾柱DAB AC-DC变换器实验样机,如图16所示。

图16 实验样机
Fig.16 Experimental prototype
该样机由1个工频半桥和DAB一次、二次侧4个高频半桥模块构成的主电路、移相电感、高频变压器、交流侧输入电感、输出电解电容、采样电路、DSP28335控制系统和辅助电源等模块组成。
为了验证变换器在稳态工作时网侧电压电流波形的正确性,测试了变换器在AEPS优化调制下输出功率分别为400 W和800 W时的交流输入电压电流波形,如图17所示。由上向下分别为后端DAB的输入电压vp、交流输入电压vg和输入电流ig。当输出功率为400 W时,电网电流ig的THD=4.87%,功率因数(Power Factor, PF)为0.999;当输出功率为800 W时,电网电流ig的THD=2.63%,PF=0.999。均满足并网电流质量及功率因数要求。由此可知,变换器在AEPS优化调制策略下的开环PFC的电流质量优良。
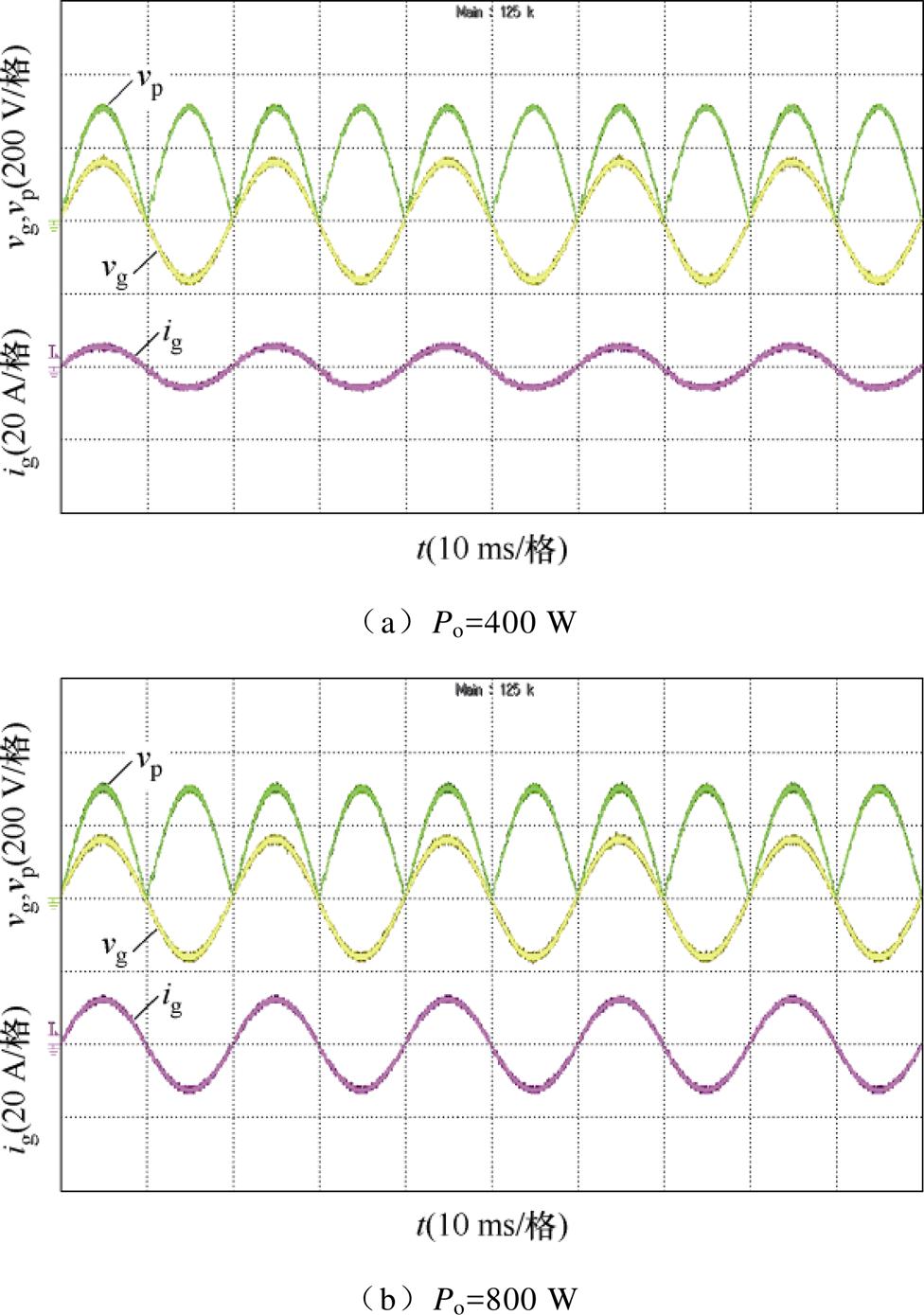
图17 不同功率等级下的变换器电压和电流波形
Fig.17 Steady-state waveforms of converter voltage and current at different output powers
为了对比分析AEPS调制相比传统的SPS、EPS调制在THD和效率等方面的优势。图18和图19分别给出了输出功率Po=400 W和Po=800 W时变换器在SPS、EPS与AEPS调制下工频周期与开关周期内的稳态波形。

图18 Po=400 W时SPS、EPS与AEPS调制下的变换器稳态波形
Fig.18 Steady-state waveforms of the converter under SPS, EPS and AEPS modulation at Po=400 W

图19 Po=800W时SPS、EPS与AEPS调制下的变换器稳态波形
Fig.19 Steady-state waveforms of the converter under SPS, EPS and AEPS modulation at Po=800W
在Po=400 W时,SPS调制下:Ig=6.36 A,THD= 15.98%,PF=0.973;EPS调制下:Ig=5.86 A,THD= 6.35%,PF=0.998;AEPS调制下:Ig=5.7 A,THD= 4.87%,PF=0.999。
在Po=800 W时,SPS调制下:Ig=11.91 A,THD= 9.58%,PF=0.992;EPS调制下:Ig=11.41 A,THD= 3.76%,PF=0.999;AEPS调制下:Ig=11.2 A,THD= 2.63%,PF=0.999。
由电感电流iLs实验波形可知,Po=400 W和800 W时,AEPS调制下的电感电流峰峰值均小于相同功率下的SPS与EPS调制。且由SPS、EPS和AEPS调制开关周期内的电感电流iLs实验波形可知,AEPS调制下各开关周期的电感电流初值iLs(t0)= 0,即实现了相邻开关周期的电流初值解耦。上述实验波形均与理论分析及仿真结果一致。
AEPS调制开关周期内的电感两端电压及电流波形如图20所示,将工频周期内T1、T2区间的稳态波形放大至开关周期,可以得到变换器在AEPS调制模式4和模式2两种工作模式下开关周期内的移相电感一次、二次电压和电流波形,其一次电压vab为两电平方波,二次电压vcd为三电平波形,与理论分析一致。电感电流iLs在两种模式下的波形与理论分析与仿真结果一致,在模式4下,各开关周期内的电感电流波形初值为0,实现了电感电流的初值解耦,从而实现了对电感电流的精确控制,优化了并网电流质量。在模式4与模式2下均引入了电感电流峰峰值优化,使全功率段下电感电流峰峰值最小。且由实验结果可知,由于求解得到的不同工作模式下的移相角表达式是连续的,因此实验中不同模式间实现了无缝且平滑的切换。

图20 AEPS调制开关周期内的电感两端电压及电流波形
Fig.20 Voltage and current waveforms of the inductor during a switching cycle
图21所示为采用所提出的AEPS调制方案下的变换器THD曲线。并与未进行并网电流质量优化的SPS与EPS调制方案的THD结果进行比较。实验结果证明,由于所提出的AEPS调制引入了电感电流初值约束实现电流解耦,相比SPS与EPS调制降低了变换器在全功率范围内的THD,证明了所提出的AEPS调制策略对并网电流质量的提升。
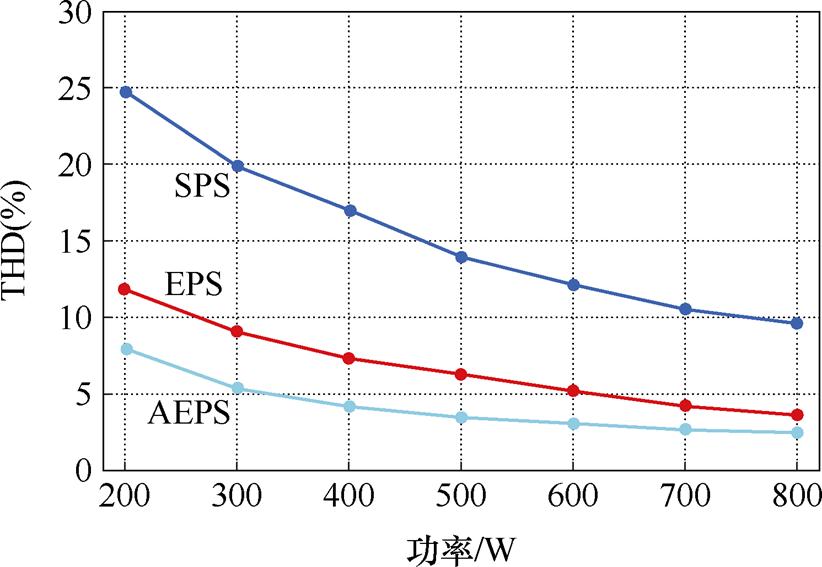
图21 在SPS、EPS[9]与AEPS调制下变换器THD曲线
Fig.21 Converter THD curves under SPS, EPS[9] and AEPS modulation
对变换器在不同调制策略下的效率曲线进行了测试,结果如图22所示。在变换器的功率为满载时,AEPS调制下的变换器峰值效率达到了93.5%。相比传统的SPS与EPS调制,在200 W时效率分别提升了14.7%和4.6%,在满载时分别提升了5%和1.5%。因此,所提出的AEPS优化调制策略提升了变换器在全功率范围内的效率。
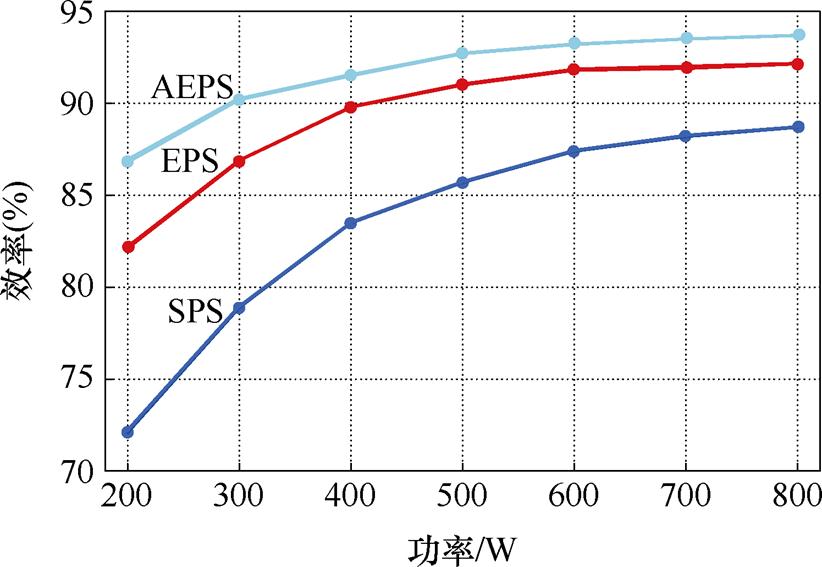
图22 在SPS、EPS[9]与AEPS调制下变换器效率曲线
Fig.22 Converter efficiency curves under SPS, EPS[9] and AEPS modulation
由实验结果可知,所提出的具有三自由度AEPS优化调制策略,相比传统的移相调制策略,实现了对变换器并网电流质量与效率的同步提升。在调制策略研究方面进一步挖掘了移相调制策略的自由度,综合优化了变换器的稳态性能。
本文针对图腾柱DAB AC-DC变换器的特点,在传统EPS调制的基础上引入非对称调制,提出了具有三自由度的AEPS调制。为了解决DAB AC-DC变换器的建模时电感电流初值耦合造成的并网电流畸变问题,在AEPS调制中引入了电感电流初值约束,从而优化了开环PFC下的并网电流质量。同时,在AEPS调制下考虑电感电流峰峰值的优化,对所提出的优化调制策略进行了仿真和实验验证。在AEPS优化调制策略下的800 W实验样机实现了93.5%的峰值效率和2.63%的并网电流THD,证明了所提出的AEPS优化调制策略实现了对变换器并网电流质量和效率的同步提升。说明了AEPS调制在图腾柱DAB AC-DC变换器上的优越性,这有助于推动该拓扑在OBC上的应用。
参考文献
[1] Yilmaz M, Krein P T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2151-2169.
[2] 晏益朋, 余城洋, 熊露婧, 等. 一种基于离散时域模型的单相PWM整流器控制参数多目标优化设计方法[J]. 电工技术学报, 2024, 39(1): 206-216.
Yan Yipeng, Yu Chengyang, Xiong Lujing, et al. A multi-objective controller parameter design optimi- zation method of single-phase PWM rectifierwith discrete-time domain model[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 206-216.
[3] Li Bin, Li Qiang, Lee F C, et al. A high-efficiency high-density wide-bandgap device-based bidirectional on-board charger[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(3): 1627-1636.
[4] Wang Huai, Blaabjerg F. Reliability of capacitors for DC-link applications in power electronic converters- an overview[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3569-3578.
[5] Jeong Y S, Lee S H, Jeong S G, et al. High-efficiency bidirectional grid-tied converter using single power conversion with high-quality grid current[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8504-8513.
[6] Everts J, Krismer F, Van den Keybus J, et al. Optimal ZVS modulation of single-phase single-stage bidire- ctional DAB AC-DC converters[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(8): 3954- 3970.
[7] Weise N D, Castelino G, Basu K, et al. A single-stage dual-active-bridge-based soft switched AC-DC con- verter with open-loop power factor correction and other advanced features[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4007-4016.
[8] Zhang Yun, Yang Gen, Li Jing, et al. A modulation scheme with full range ZVS and natural power factor correction for bridgeless single-stage isolated AC-DC converter[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 195-205.
[9] 刘猛, 孙孝峰, 王洪龙, 等. 一种新型单级隔离型AC-DC变换器研究[J]. 中国电机工程学报, 2023, 43(7): 2802-2814, 28.
Liu Meng, Sun Xiaofeng, Wang Honglong, et al. Research on novel single-stage isolated AC-DC converter[J]. Proceedings of the CSEE, 2023, 43(7): 2802-2814, 28.
[10] 邓丹阳, 陈艳慧. 双有源桥直流变换器三电平扩展移相控制下电感电流有效值最优跟踪控制策略[J]. 电工技术学报, 2024, 39(18): 5800-5815.
Deng Danyang, Chen Yanhui. Optimal tracking control strategy of inductive current RMS for dual active bridge dc converter with three-level extended phase-shift control[J]. Transactions of China Elec- trotechnical Society, 2024, 39(18): 5800-5815.
[11] Mou Di, Luo Quanming, Li Jia, et al. Five-degree- of-freedom modulation scheme for dual active bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10584-10601.
[12] 刘赞, 沙金, 邱高峰, 等. 多级离散扩展移相控制双有源桥DC-DC变换器的原理、参数设计与性能[J]. 电工技术学报, 2024, 39(12): 3761-3773.
Liu Zhan, Sha Jin, Qiu Gaofeng, et al. Principle, parameter design and performance of multistage discrete extended-phase-shift control dual active bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3761-3773.
[13] Sha Deshang, Zhang Debin, Zhang Jiankun. A single- stage dual-active-bridge AC-DC converter employing mode transition based on real-time calculation[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10081-10088.
[14] Li Xiaoguang, Wu Fengjiang, Yang Guijie, et al. Improved modulation strategy for single-phase isolated quasi-single-stage AC-DC converter to improve current characteristics[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4296-4308.
[15] Singh A, Yadav A K, Khaligh A. Steady-state modeling of a dual-active bridge AC-DC converter considering circuit nonidealities and intracycle transient effects[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11276-11287.
Abstract The single-stage Totem pole dual active bridge (DAB) AC-DC converter has the advantages of low component count, high power density, and low cost, which has a broad application prospect in the field of on-board chargers (OBC). However, in the available research, the traditional single phase shift (SPS) and extended phase shift (EPS) modulation strategies are unable to optimize the quality of grid-connected current and efficiency of the Totem pole DAB AC-DC converter at the same time due to the problem of insufficient modulation degrees of freedom, limiting the further application in on-board chargers.
This paper introduces the asymmetric modulation based on the extended phase shift modulation strategy when the duty cycle of the secondary side switching tubes is no longer 50%. An asymmetric extended phase shift (AEPS) modulation strategy with three degrees of freedom is proposed. Accordingly, a multi-objective optimal modulation strategy is solved by considering the simultaneous optimization of the grid-connected current quality and efficiency of the Totem pole DAB AC-DC converter.
Firstly, the steady-state analytical model of AEPS modulation is established by using the time domain analysis method. The initial value decoupling constraint of the inductor current is considered to optimize the quality of grid-connected current, and the peak-to-peak inductor current is taken as the optimization objective. According to the Lagrange algorithm and Karush Kuhn Tucker conditions, the above multi-objective optimization problem is transformed into mathematical equations to solve the optimization solution of modulation variables. Matlab simulations show that the inductor current’s initial value decoupling and peak-to-peak value optimization are realized under the AEPS optimization modulation strategy. Compared with the SPS and EPS modulation, the proposed AEPS optimization modulation strategy reduces the peak-to-peak and RMS levels of the inductor current in the full power band, which reduces the conduction loss of the converter. Moreover, the optimized solutions in different operating modes under APES modulation are continuous, making seamless switching between different operating modes available.
An experimental prototype of a totem pole DAB AC-DC converter with a rated power of 800 W is constructed. Experimental results show that the converter achieves a peak efficiency of 93.5% under the proposed AEPS optimized modulation strategy, 5% and 14.7% higher than the SPS strategy at full load and light load, respectively; 1.5% and 14.7% higher than the EPS modulation strategy at full load and light load, respectively. The converter's grid-connected current THD is significantly reduced in the full power range, improving its grid-connected current quality. Simulation and experimental results verify the effectiveness of the proposed AEPS-optimized modulation strategy.
Keywords:Totem pole dual active bridge (DAB), AC-DC converter, asymmetric extended phase shift (EPS) modulation, power factor correction, modulation strategy optimization
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240510
国家自然科学基金资助项目(52177170)。
收稿日期 2024-04-01
改稿日期 2024-05-24
余城洋 男,1998年生,硕士研究生,研究方向为高效双向AC/DC功率变换器的优化设计。
E-mail: 202111021094t@stu.cqu.edu.cn
罗全明 男,1976年生,教授,博士生导师,研究方向为电力电子拓扑及控制、电力电子数字设计、宽禁带器件特性及应用等。
E-mail: lqm394@126.com(通信作者)
(编辑 陈 诚)