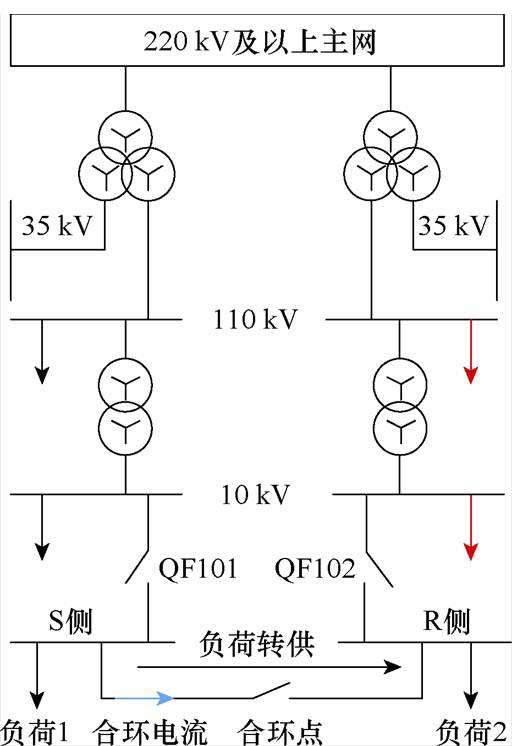
图1 典型合环场景
Fig.1 Typical ring closing scenario
摘要 合环转供电已成为中压配电网转移负荷的重要方式，但计划停电进行合环会降低供电可靠性，直接合环又会产生较大的冲击电流，影响电网稳定运行。基于此，该文首先提出了一种改进型移相变压器（IPST），其在传统移相器的基础上增加了调幅绕组，可以灵活改变电压幅值与相位，实现不停电合环；其次针对负荷转供后，IPST内部阻抗引起的负荷侧电压质量下降问题，通过多端口网络理论建立IPST等效模型，将IPST端口阻抗特性转化为等效解析式，并推导调节电压关于调幅挡位Tm、调相挡位Tp的函数表达式，从而结合电压调节目标预测出IPST的目标挡位，提升电压质量；然后针对IPST退出旁路合闸时产生的冲击电流问题，推导出冲击电流关于IPST挡位的函数关系式，结合电流调节目标及电压质量约束预测出IPST目标挡位，实现在保证电压质量的同时，使得冲击电流下降，安全退出IPST；最后基于PSCAD/EMTDC验证阻抗表达式的正确性和调控策略的有效性。
关键词：配电网 合环转供 移相变压器 等效阻抗 合环电流
我国配电网通常采用“闭环设计，开环运行”的方式[1]，当设备需要检修或者负荷过重时，需要通过转移负荷的方式保证供电可靠性[2-3]。但通过计划停电的方式进行合环会对供电可靠性和用户满意度造成影响[4]，直接合环又会产生较大的冲击电流[5-6]，可能会损坏电网中的设备，造成继电保护装置误动，影响电网的稳定性。因此，不停电合环转供负荷[7-8]是当前热门的研究方向。
目前，国内外对于配电网合环技术进行了大量的研究。文献[9-10]提出了合环前稳态电流和合环冲击电流的计算方法，为合环可行性提供了判断依据，并给出了合环操作判定条件的流程，文献[11]研究合环电流非周期分量衰减时间及合环过程对配电网继电保护的影响，探索简化的合环判断条件。通过优化潮流分布来调节合环点电压可以达到满足合环的条件，文献[12]提出一种基于分布式电源主动控制的配电网合环电压波动抑制方法；文献[13]提出一种配电网合环电压综合调节方法，通过调节分布式电源出力和柔性负荷使合环点电压满足合环开关闭合的条件，但应用场景要求较高，需要系统层面的配合，且分布式电源出力灵活多变，控制算法较为复杂。对于在合环点装设合环装置进行合环也有大量研究；文献[14]提出了一种基于双电压源型换流器（Voltage Source Converter, VSC）实现合环转供的装置，改变合环点电压，实现柔性合环；文献[15]提出了应用于电网合环的蓄电池储能系统，利用储能系统控制合环点电压，保证电网供电连续性；文献[16]提出基于潮流控制器的中压双电源配电环网故障无缝自愈供电系统实现方案，但电力电子设备造价昂贵，维护成本较高，无法得到广泛应用。
传统移相变压器（Phase-Shifting Transformers, PST）具有改变电压相位及幅值的功能，常用于调控电力系统潮流[17]，PST按照铁心类型分为单芯与双芯，双心移相器相对于单心移相器可调范围较大，且有载分接触头位于变压器低压侧，操作相对安全，可靠性更高[18]；按照调节特性分为对称型与非对称型，对称型PST主要用于改变电压相位，非对称型PST的电压幅值及相位均会发生改变，但幅值与相位的耦合度较高，难以做到对电压灵活控制，应用的合环场景具有局限性[19]。晶闸管式可控移相器（Thyristor Controlled Phase Shift Transformer, TCPST）利用晶闸管的开通与关断代替传统PST的有载分接开关[20]，可连续调节控制且响应速度快，但是造价较为昂贵，维护成本高。
本文提出了一种改进型移相变压器（Improved Phase-Shifting Transformer, IPST），在传统双心对称型PST的调相绕组（phase modulation winding of Excitation Transformer, ETp）上增加了调幅绕组（amplitude-modulated winding of Excitation Trans- former, ETm），实现了电压的幅值与相位均可控，通过控制合环点电压，有效减小了冲击电流，实现不停电合环，保证供电可靠性，且成本较低、运行维护简单；针对合环完成后负荷侧的电压质量下降问题，推导出IPST的阻抗特性表达式，并提出了电压调节策略，从而提高负荷侧的电能质量；针对IPST退出合环时产生的冲击电流问题，利用IPST的调节特性及阻抗特性进行挡位调节，减小退出时的冲击电流，有效地保护了合环装置。
配电网通常采用开环运行的方式，典型合环场景如图1所示。
当图1中R侧网络中的设备检修时，需要进行负荷转供，即通过合环操作由S侧提供电能。但由于S侧与R侧的电压存在一定的幅值相位差值，直接合环可能会产生较大的冲击电流，影响电网的稳定性。基于此，本文提出一种改进型移相变压器（IPST），IPST是在传统双心对称移相变压器[21-22]的基础上进行改进，在励磁变压器（Excitation Transformer, ET）二次侧的调相绕组（ETp）基础上增加了调幅绕组（ETm），使得IPST同时具有调幅和调相的功能。在ETm与ETp的协同配合下，实现电压的相位、幅值可控。将IPST装设在合环点，通过调节电压幅值与相位使R侧电压与调节电压接近，从而实现不停电合环。IPST的拓扑结构与工作原理如图2所示。
图1 典型合环场景
Fig.1 Typical ring closing scenario
图2a中，ET为励磁变压器，其中ETm为调幅绕组，ETp为调相绕组，ST为串联变压器；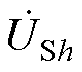
、
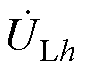为IPST两侧电压，h=a, b, c三相；图2b中，
、
、
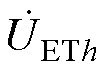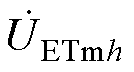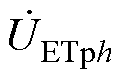分别为ET绕组原侧、调幅侧、调相侧电压，
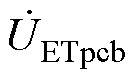为b、c调相绕组之间的电压差；
、
、
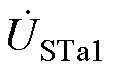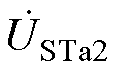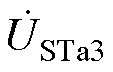为ST三绕组电压；ks为ST一次绕组与二次、三次绕组的匝数比；km、kp分别为Etm、ETp与ET一次绕组的匝数比；图2c中
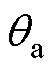为IPST两侧电压
、
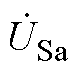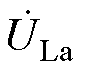相位的差值；在传统PST上增加ETm后与ETp进行协同配合可以实现对电压的幅值与相位灵活调控。
图2 IPST的拓扑结构及工作原理
Fig.2 IPST structure and working principle
由图2c可得，以a相为例，IPST电压之间的关系为
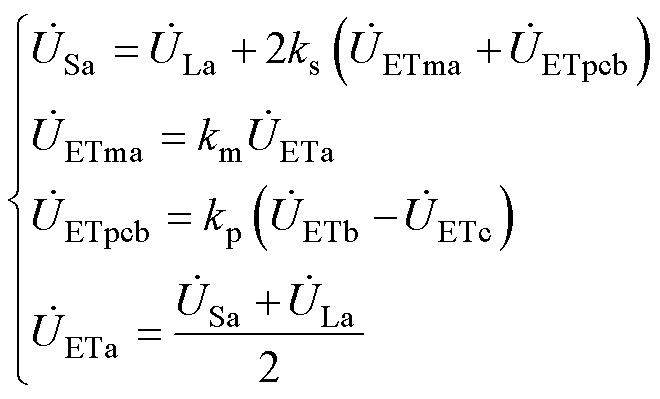（1）
如图2c所示，将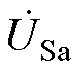
作为基准轴建立旋转笛卡尔坐标系，在笛卡尔坐标系中对图2c和式（1）中的相量进行计算，求解出调节电压与ETm、ETp的电压比km、kp之间的关系式为
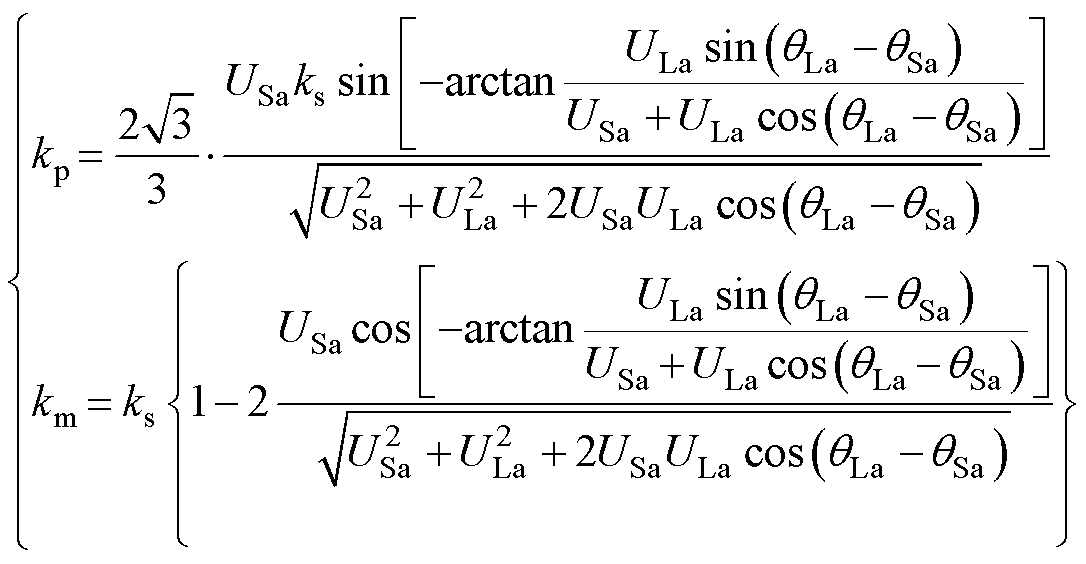（2）
式中，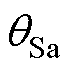
、
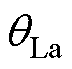为IPST两侧电压相位。通过式（2）可以得到，当IPST获取S侧电压
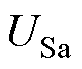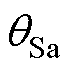、及R侧电压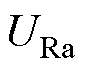
、
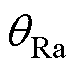时，将R侧电压作为调节电压目标值
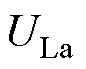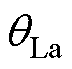、，可以求解出对应的目标绕组的电压比（kmr, kpr）及目标挡位（Tmr, Tpr）。通过空载调节至目标挡位后，IPST调节侧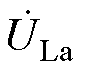电压与R侧电压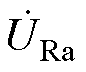
接近，即可完成合环，减小了冲击电流，实现不停电合环。
合环完成后，R侧电源退出，负荷由S侧电源提供，但由于IPST内部存在的阻抗，导致R侧电压下降。为保证电能质量，需要再次调节IPST，由于IPST绕组的复杂耦合关系，其阻抗特性呈现出较强的非线性特征，无法求得需要调节的目标挡位值，因此需要详细分析IPST的阻抗特性，推导出IPST带负载调节时调节电压的解析式。
IPST在合环之前属于空载调节，合环完成后由于IPST内部绕组的耦合关系[23-24]较为复杂，且内部阻抗与IPST的ETm、ETp共同影响着调节侧电压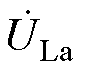，因此需要详细推导出IPST内部的阻抗关系式，得到IPST带负载调节时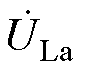与ETm、ETp的档位（Tm, Tp）即电压比（km, kp）之间的函数表达式，为后续带负载调节提供理论基础。
根据IPST的工作原理可将IPST等效成一个调幅的理想变压器、调相的理想PST及内部阻抗串联而成，如图3所示。
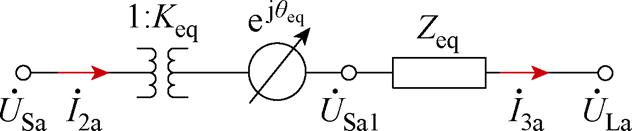
图3 IPST等效模型
Fig.3 IPST equivalent model
图3中，Keq为理想IPST的调幅作用因子，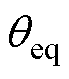
为理想IPST的调相作用因子，Zeq为IPST的等效阻抗，
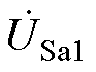为IPST理想状态下的调节电压，
、
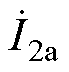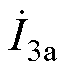分别为S侧、L侧电流，则IPST两侧电压、电流关系为
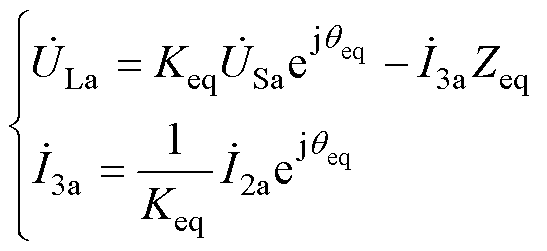（3）
将图2a中的绕组进行“T”型电路等效，IPST等效电路如图4所示。
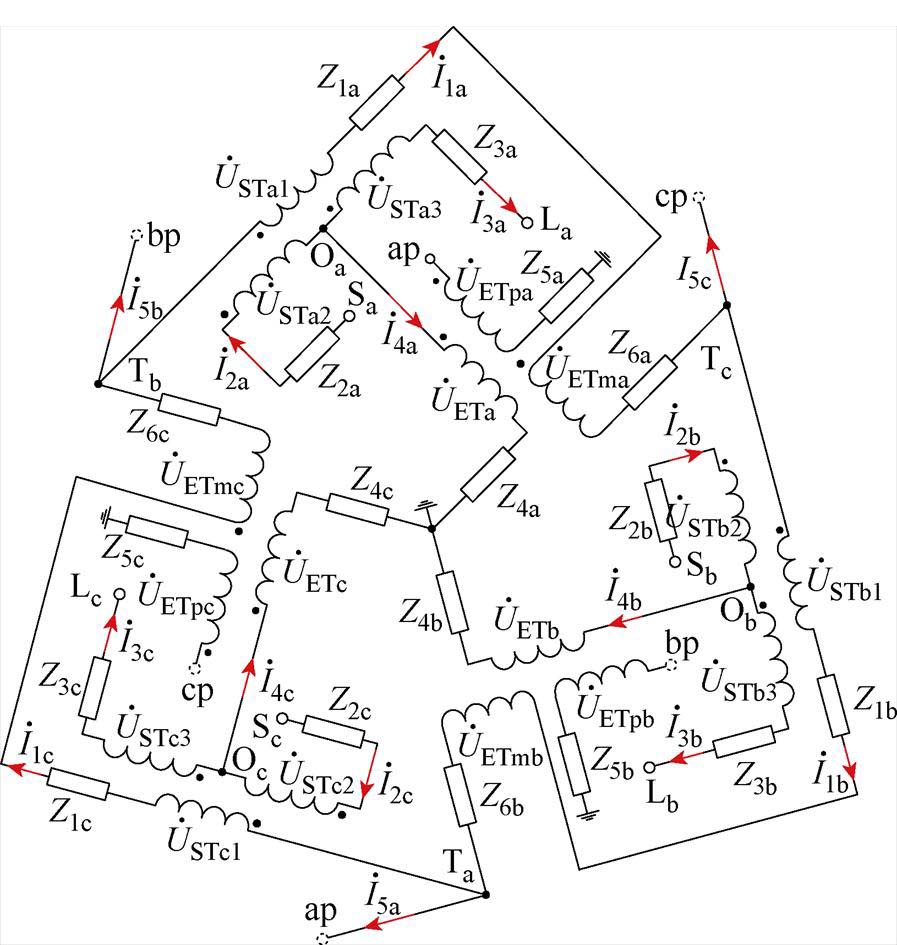
图4 IPST等效电路
Fig.4 IPST equivalent circuit diagram
图4中，Z1h、Z2h、Z3h为ST三侧绕组等效阻抗，I1h、I2h、I3h为ST三侧绕组电流；Z4h、Z5h、Z6h为ET三侧绕组等效阻抗，I4h、I5h、I6h为ET三侧绕组电流。
下面以a相为例对改进移相变压器等效阻抗进行推导，根据附录推导的各绕组电流关系式（A4）可以得到图3中IPST两端电流关系为
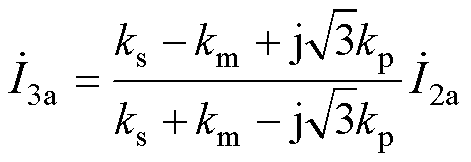（4）
联合式（3）与式（4）可得出Keq、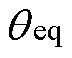
与绕组电压比ks、km、kp之间的函数关系为
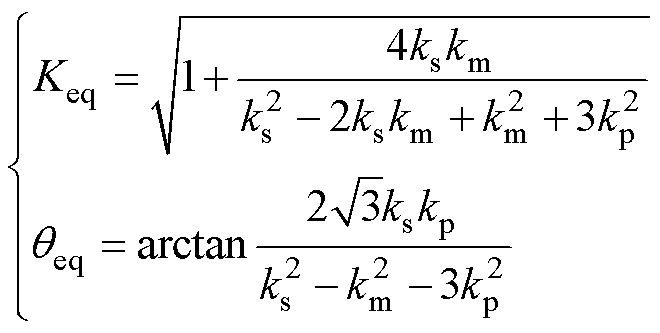（5）
根据附录中的各绕组电压关系式（A5），结合式（A4）消去绕组内部感应电动势可得图3中IPST两侧电压电流表达式为
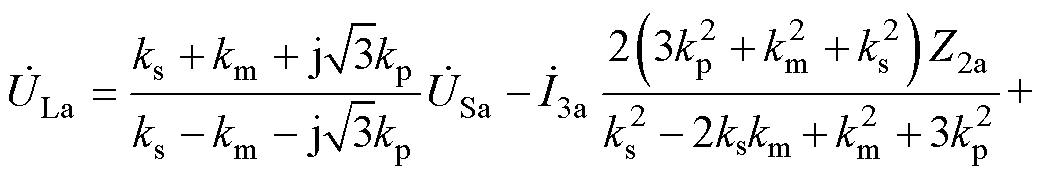
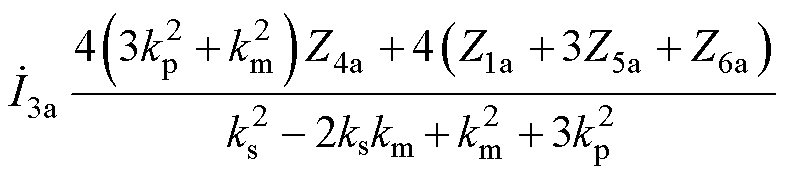（6）
联合式（3）～式（6）可得IPST等效阻抗表达式为
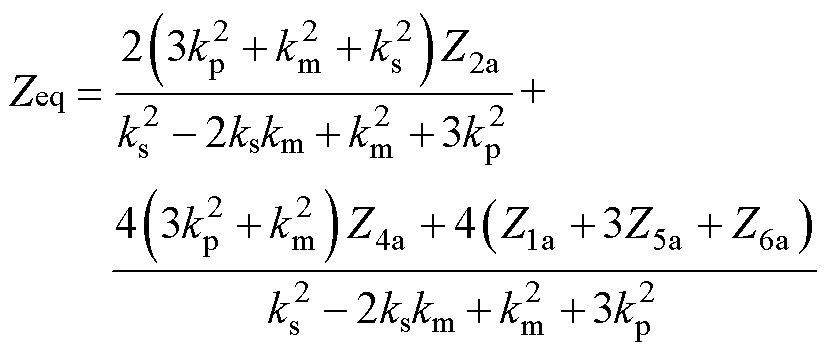（7）
在实际工程中ks一般为固定值，因此根据式（7）可以得到IPST等效阻抗与ETp、ETm电压比/挡位及绕组漏抗有关，且呈现复杂的非线性。
为详细分析IPST的阻抗特性，该文采用控制变量法，分别对ET与ST的短路阻抗百分比进行改变，求解出每组挡位（Tm, Tp）对应的等效阻抗并整理数据绘制成三维视图，如图5所示。
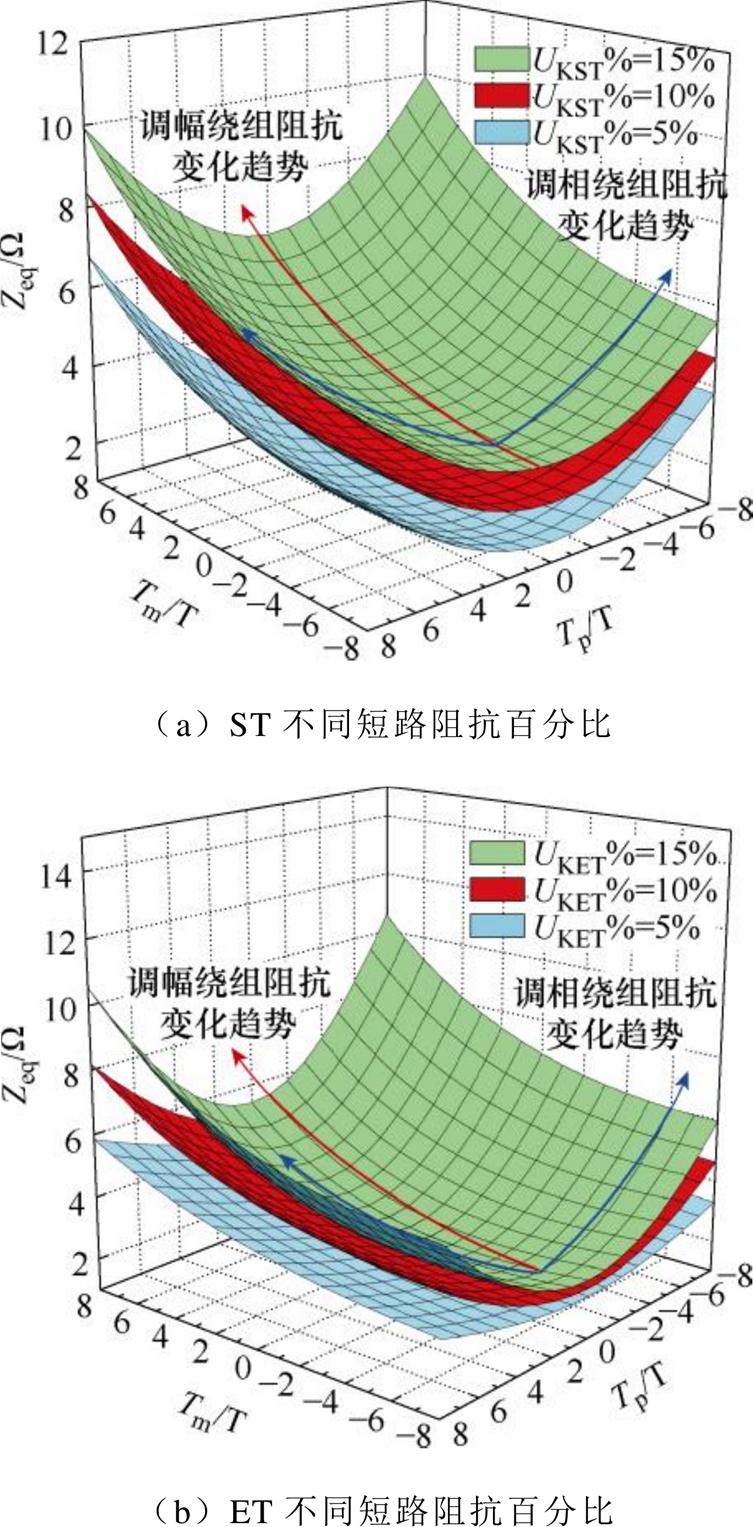
图5 IPST阻抗特性分析
Fig.5 Analysis of IPST impedance characteristics
由图5a可得，当增大ST短路阻抗百分比UKST%时，阻抗曲面呈向上平移的趋势，说明ST短路阻抗主要影响阻抗曲面的整体高度；由图5b可得，当增大ET短路阻抗UKET%时，阻抗曲面呈陡度增大的趋势，说明ET短路阻抗主要影响阻抗曲面的陡度；综合两图看，随着调幅绕组挡位Tm的增大，等效阻抗呈上升的趋势，而调相绕组Tp对应的阻抗具有对称性，0档的时候对应的阻抗最小。
IPST主要应用于10 kV电压等级下的配电网合环场景[25-26]，通过IPST对合环点的电压进行调节，完成合环过程。
图1中合环点的合环装置如图6所示。
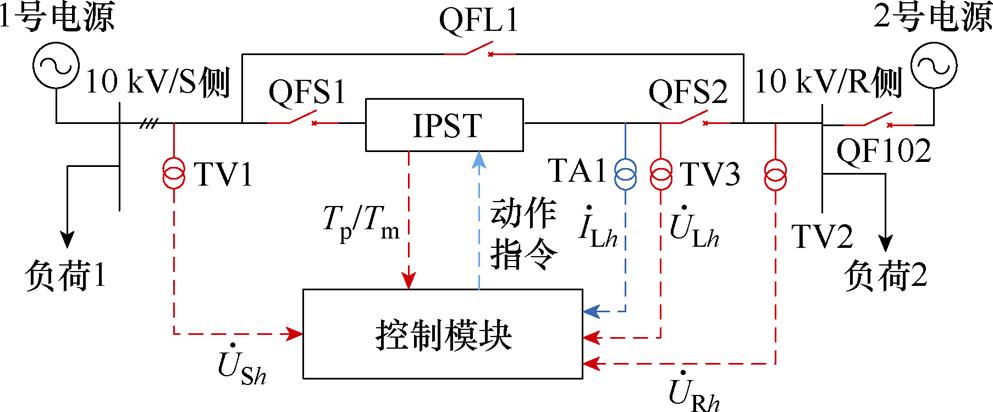
图6 基于IPST的合环装置
Fig.6 IPST ring closing device
QF102为安装在2号电源与10 kV母线之间的合闸开关，QFL1为联络线路的合闸开关，QFS1、QFS2为IPST与线路的合闸开关。
合环过程流程如下：
（1）闭合QFS1将IPST投入，使其带电。
（2）通过TV1、TV2提取S侧及R侧电压、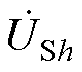
，将
作为调节电压目标，通过式（2）
求解出IPST的目标挡位Tmr与Tpr。
（3）调节IPST挡位至目标挡位后，调节电压接近合环点电压，闭合QFS2，断开QF102，2号电源进行检修，负荷2由1号电源提供。
当负荷转供完成后，由于IPST内部存在的阻抗，由式（3）可得调节电压受到调幅调相绕组及内部阻抗的耦合作用，导致负荷2母线电压质量[27-28]下降。因此，需要继续调节IPST以提高电压质量。将式（3）在笛卡尔坐标系中展开可得
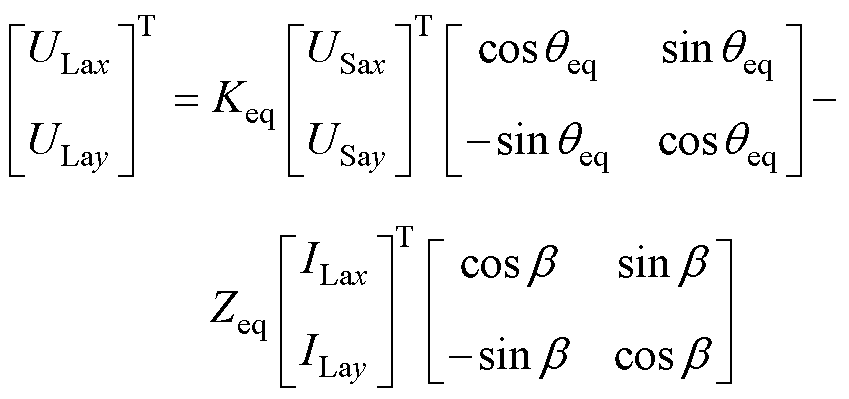（8）
式中，ULax、ULay、USax、USay为IPST两侧电压的向量坐标；ILax、ILay为调节侧电流的向量坐标；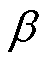
为Zeq的阻抗角。则调节电压的幅值与相位可由式（9）求得。
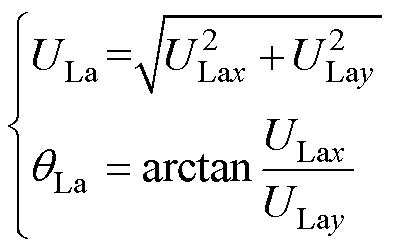（9）
联合式（8）和式（9）可以推导出调节电压幅值及相位与IPST的挡位（Tm, Tp）之间的函数解析式为
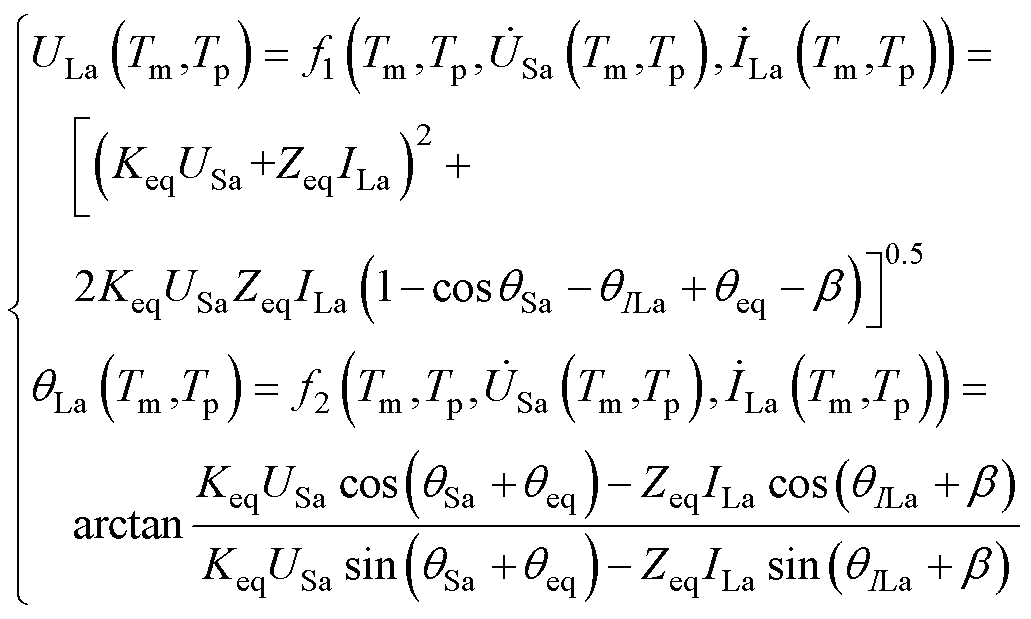（10）
式中，ILa、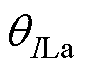
为IPST调节侧电流幅值及相位，由TA1测量得到。
IPST负荷侧电压调控目的是通过调节挡位使得负荷侧电压接近额定值ULN，因此可以设定目标函数Hu为
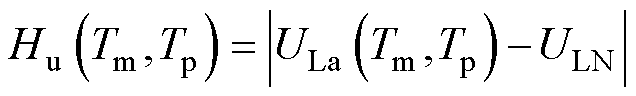（11）
考虑IPST逐级调节挡位的动作逻辑，可以得到IPST局部挡位动作目标集合W，有
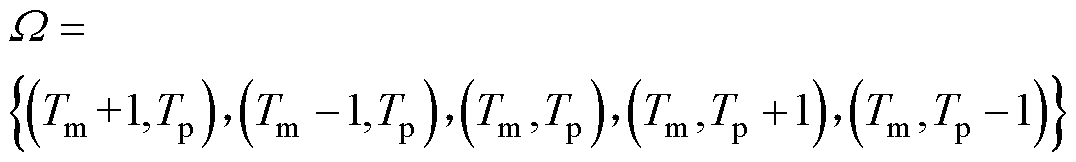（12）
根据式（10）可得，当已知S侧电压、R侧电流、当前挡位（Tm, Tp）信息时可以求解出R侧电压的幅值与相位。由于在IPST调节过程中，S侧电压几乎保持不变，且IPST临近挡位对应的电流相差较小，可近似认为集合内的、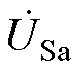
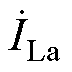为常数，影响IPST的调节电压主要由IPST的调幅因子Keq、调相因子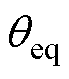及内部阻抗Zeq决定，因此可以预测出集合内挡位（Tmx, Tpy）的调节电压ULa为
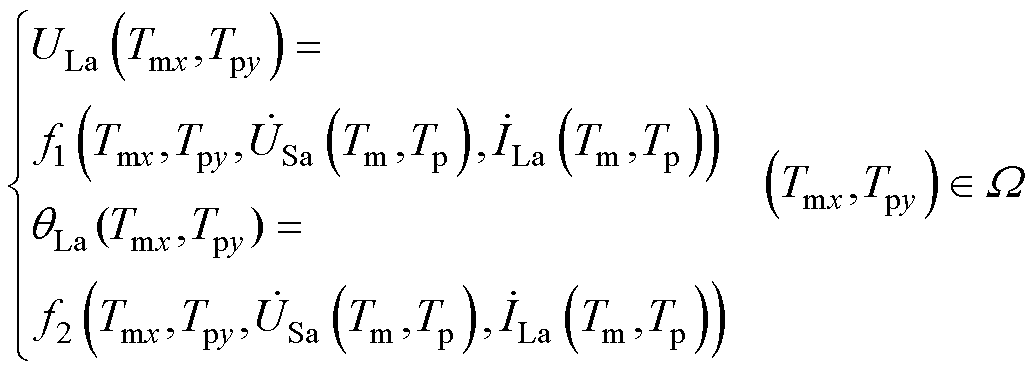（13）
通过采集当前挡位对应的信息，可以预测出临近挡位对应的电压信息及目标函数，具体流程如图7所示。
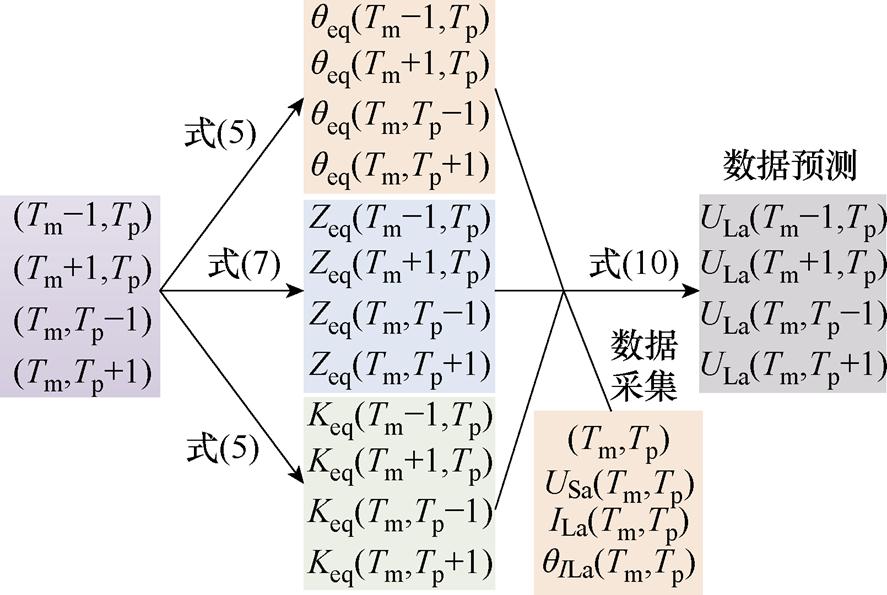
图7 电压预测流程
Fig.7 Voltage prediction process
为减少IPST动作次数，在所预测的电压中选择最接近额定电压即Hu最小时对应的挡位作为目标挡位（Tmr, Tpr）。
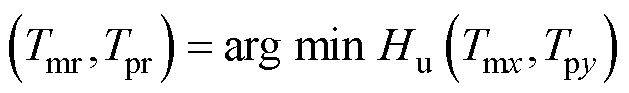（14）
式中，arg为目标函数的自变量。
当IPST完成一次调档时，目标挡位变为当前挡位，即
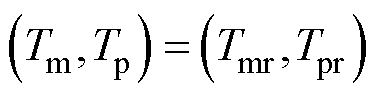（15）
因此，需要重新生成新的集合W，并重复上述步骤，若是目标挡位不再改变，则停止调档。
通过上述步骤可以预测出IPST下一步的调节目标，经过不断的调节最终使R侧电压接近于额定电压值，完成调节目标。
当2号电源供电设备需要进行长时间检修时，IPST长时间运行会增加电能损耗，需要将其退出。此时需要闭合QFL1对IPST进行旁路，以便IPST退出合环，潮流直接由线路传输给R侧。但由于IPST两侧电压幅值及相位存在差异，直接合环时会产生较大的冲击电流Ich，易对合环装置造成损坏，需要再次调节IPST，使得旁路时，产生的冲击电流减小，因此可以设计冲击电流目标函数为
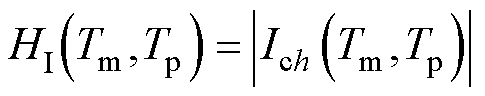（16）
对IPST进行旁路时产生的冲击电流可以利用戴维南定理等效得到，Uoc为QFL1两端压差，则冲击电流表达式为
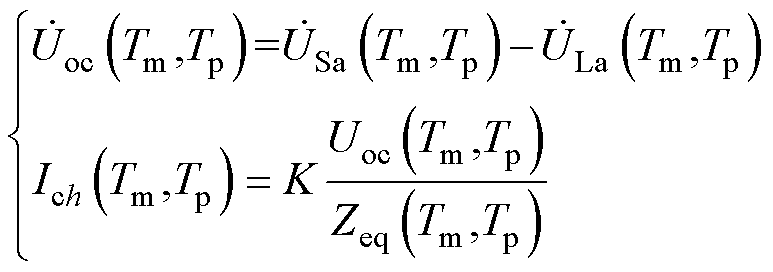（17）
式中，K为冲击系数，一般取1.8～1.9。
由式（13）可以得到临近挡位的电压，结合冲击电流表达式（17），可以预测临近挡位的合环冲击电流为
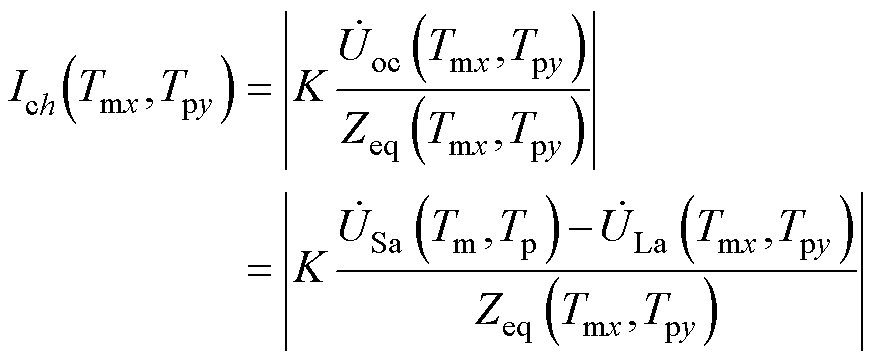
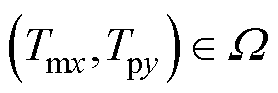（18）
为减少IPST动作次数，选择出目标函数最小的对应挡位作为IPST下一步需要动作的目标，通过反复迭代，直到IPST冲击电流值最小；极端条件下，IPST在调节过程中可能会造成电压的波动，因此需要施加一个电压约束，保证电压平稳的情况下，再选择较小冲击电流对应的挡位，有
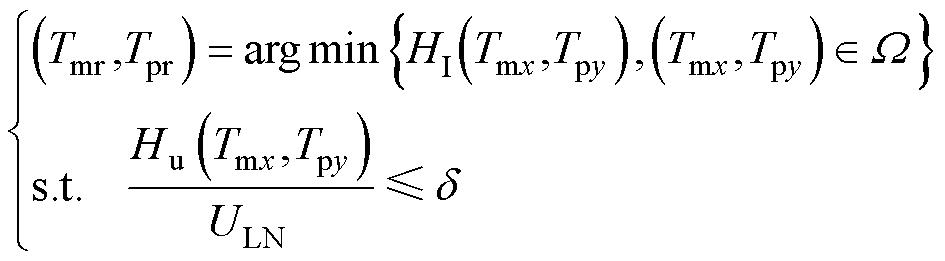（19）
式中，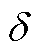
为电压波动范围，一般取7%。
通过式（10）～式（13）、式（16）～式（19）可以预测出IPST下一步的调节目标，经过不断的调节最终使得旁路IPST过程中产生的冲击电流最小，完成调节目标，IPST退出合环。
IPST作为合环装置的三种工作流程如图8所示。
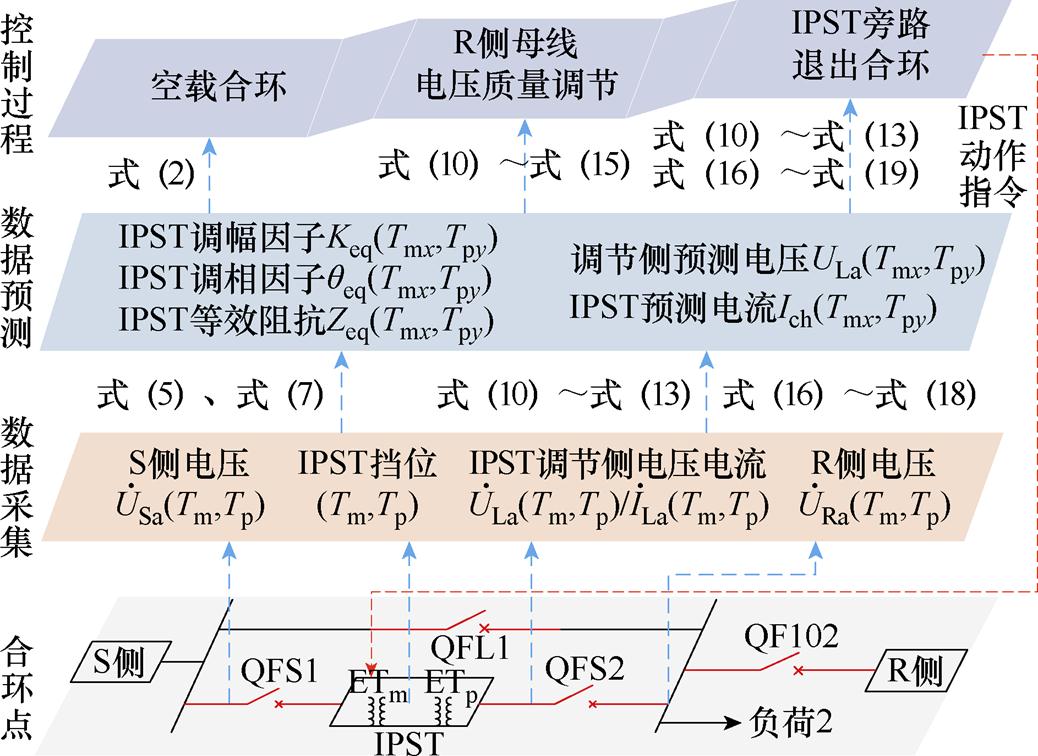
图8 IPST合环装置工作流程
Fig.8 Workflow of the IPST ring closing device
在PSCAD/EMTDC中搭建图1的典型合环场景，合环装置参数见表1。
表1 IPST参数
Tab.1 IPST parameter
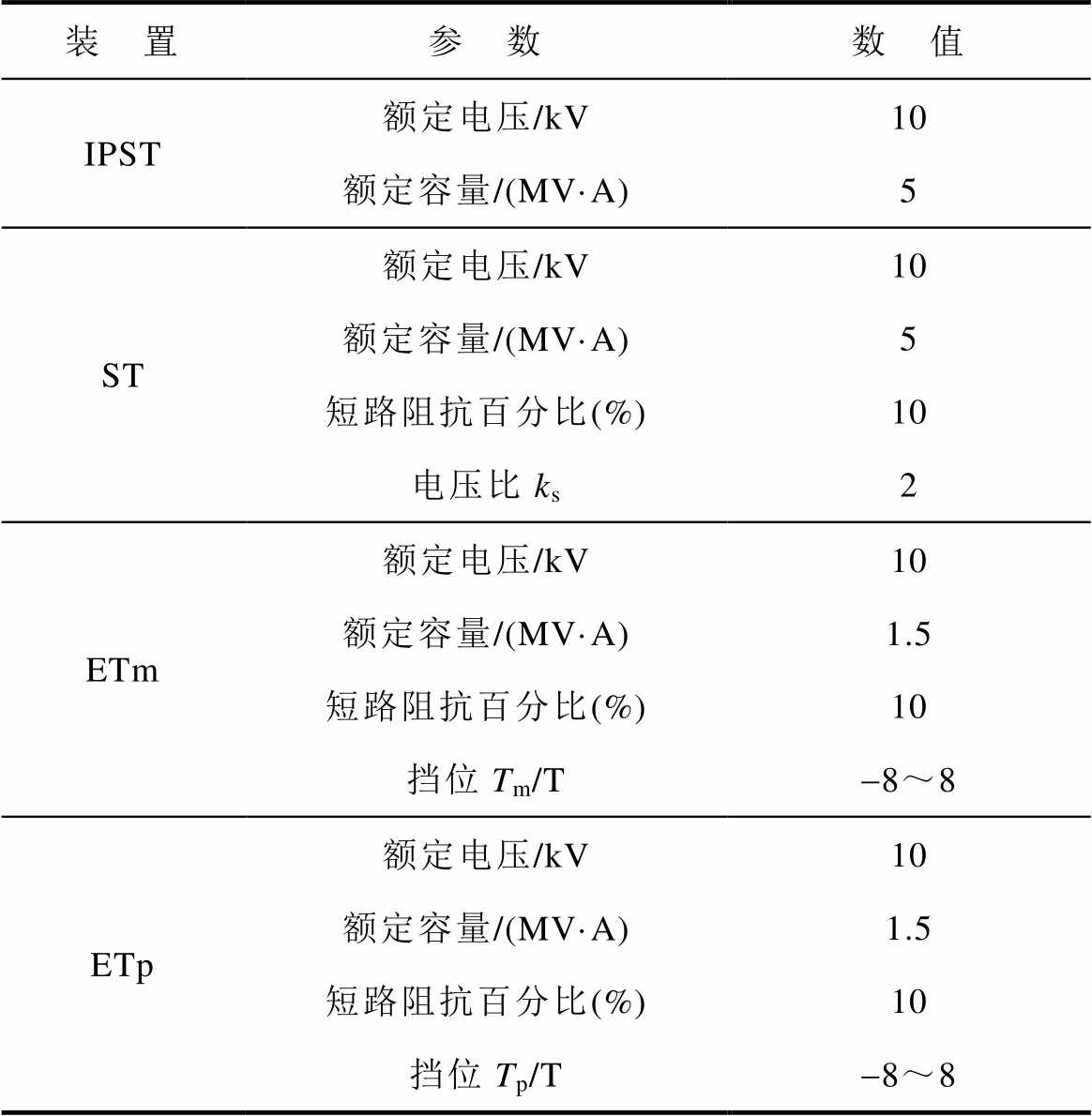
装 置参 数数 值 IPST额定电压/kV10 额定容量/(MV·A)5 ST额定电压/kV10 额定容量/(MV·A)5 短路阻抗百分比(%)10 电压比ks2 ETm额定电压/kV10 额定容量/(MV·A)1.5 短路阻抗百分比(%)10 挡位Tm/T-8～8 ETp额定电压/kV10 额定容量/(MV·A)1.5 短路阻抗百分比(%)10 挡位Tp/T-8～8
为验证式（7）的准确性，本文控制其他参数不变测量出每一个（Tm, Tp）对应的阻抗，并与理论阻抗进行对比，整理数据呈现于图9中。
由图9a可得，IPST调幅调相绕组挡位（Tm, Tp）的测量阻抗与理论阻抗的值基本重合，由图9b可以得到，测量阻抗与实际阻抗之间的误差最大不超过5%。因此，利用多端口网络理论推导出的等效阻抗关系式是较为准确的，为IPST带负载调压计算公式求解提供了理论基础。
对10 kV配电网进行合环操作，将R侧负荷2转移至S侧，10 kV配电网的R侧与S侧的电压数据见表2。
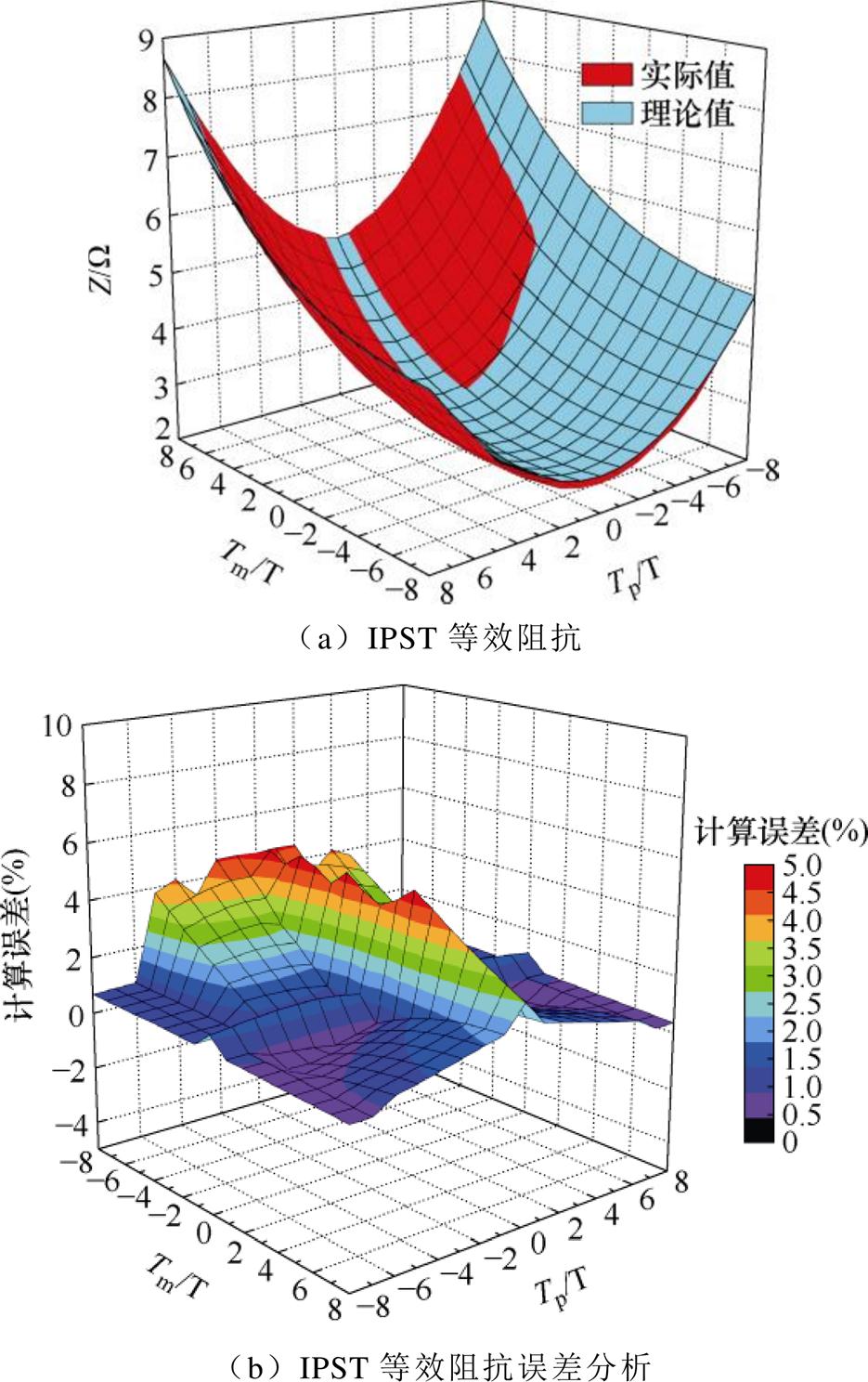
图9 等效阻抗值对比分析
Fig.9 Comparative impedance analysis
表2 合环场景数据
Tab.2 Loop closing scenario data
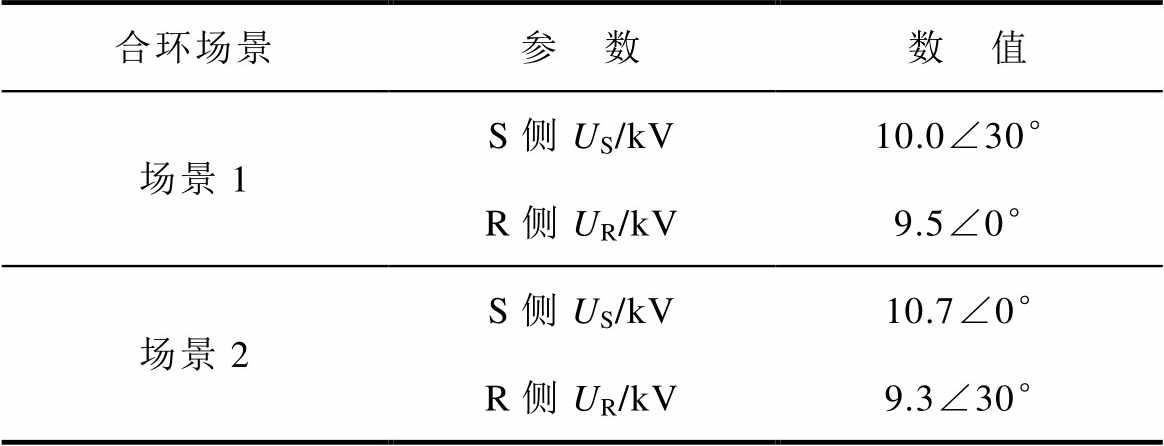
合环场景参 数数 值 场景1S侧US/kV10.0∠30° R侧UR/kV9.5∠0° 场景2S侧US/kV10.7∠0° R侧UR/kV9.3∠30°
首先合QFS1，在合环点投入IPST，使其带电。将合环场景1的数据代入式（2）中求解出目标挡位（Tmr, Tpr）为 (-1, -6) T，调整IPST调幅及调相绕组挡位至目标挡位，仿真波形如图10所示。
图10a为IPST调节电压仿真波形，首先由调幅绕组ETm动作，改变IPST调节侧电压幅值ULa接近合环点电压幅值URa，再由调相绕组ETp动作使调节电压相位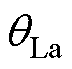接近合环点电压相位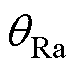，最后QFS2闭合，进行合环。图10b为利用IPST进行合环的电流波形，极值约为46.366 A，IPST的挡位为离散值，无法十分精确地调节电压，因此会存在较小的合环电流。图10c为直接合环时电流的波形，电流极值约为2 165.520 A，通过IPST进行合环可以有效降低合环电流，减小对电网的冲击。
合环完成后，QF102断开，R侧电源退出，负荷由S侧转供。但由于IPST内部存在阻抗，导致R侧母线电压下降，低于安全值。为提升供电可靠性，需要继续调节IPST提升电压质量。
提取当前IPST两侧电压及电流数据，根据图8中提升电压质量流程求解得出挡位动作路径如图11所示。
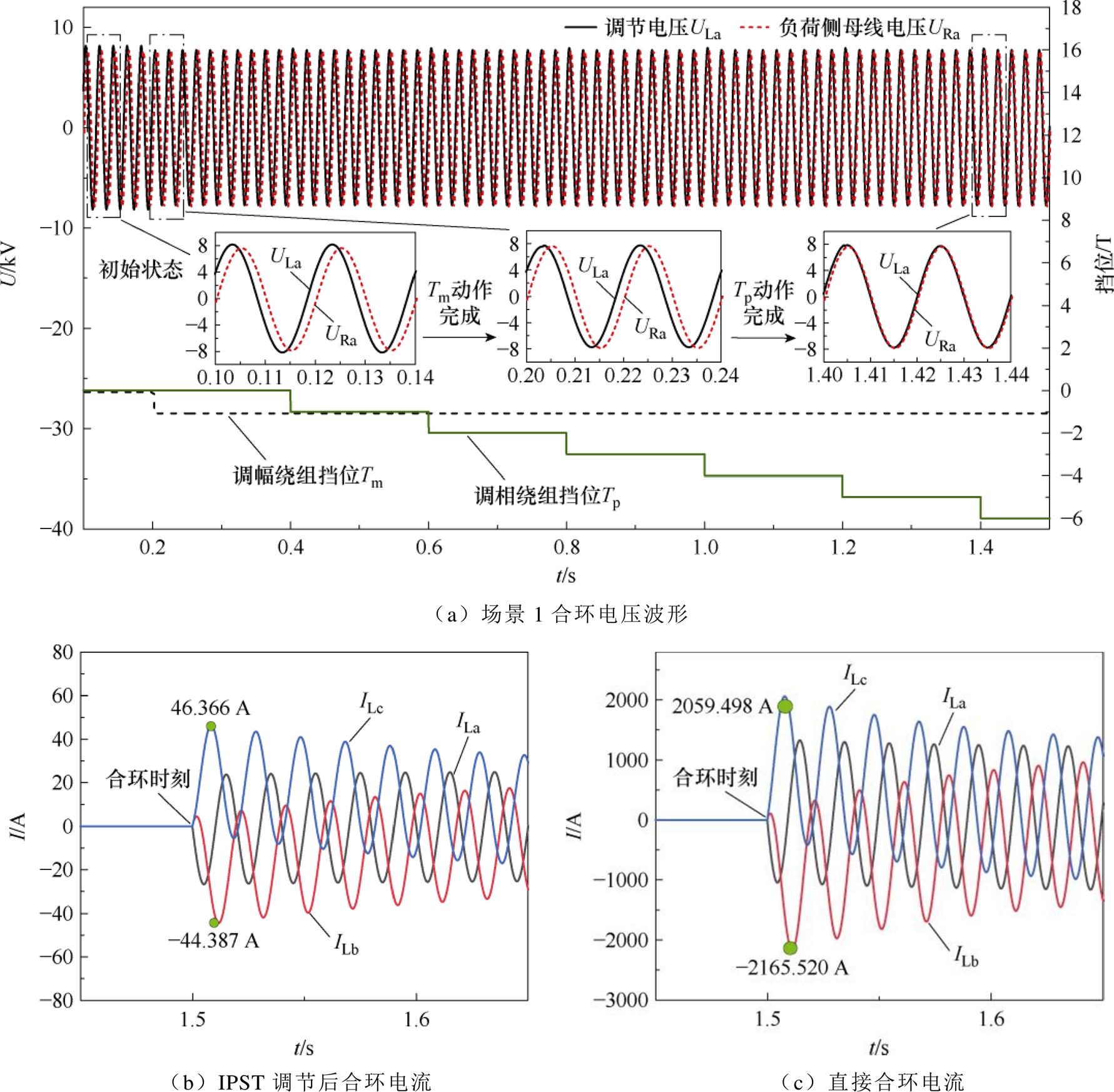
图10 场景1合环仿真波形
Fig.10 Loop closing scenario 1 simulation waveforms
由图11a可得，根据式（13）求解出当前挡位（Tm, Tp）及临近挡位（Tmx, Tpy）的电压相位及幅值，并根据式（14）选择出合适的目标挡位，以此方法进行不断的调节，直到调节至第5步时，再次预测临近挡位的电压，与实际值比较后，发现预测电压10.03 kV与当前电压9.99 kV离额定值较远，不需要再次进行调节，(1, -4) T为最终挡位，具体调节过程如图11b所示。
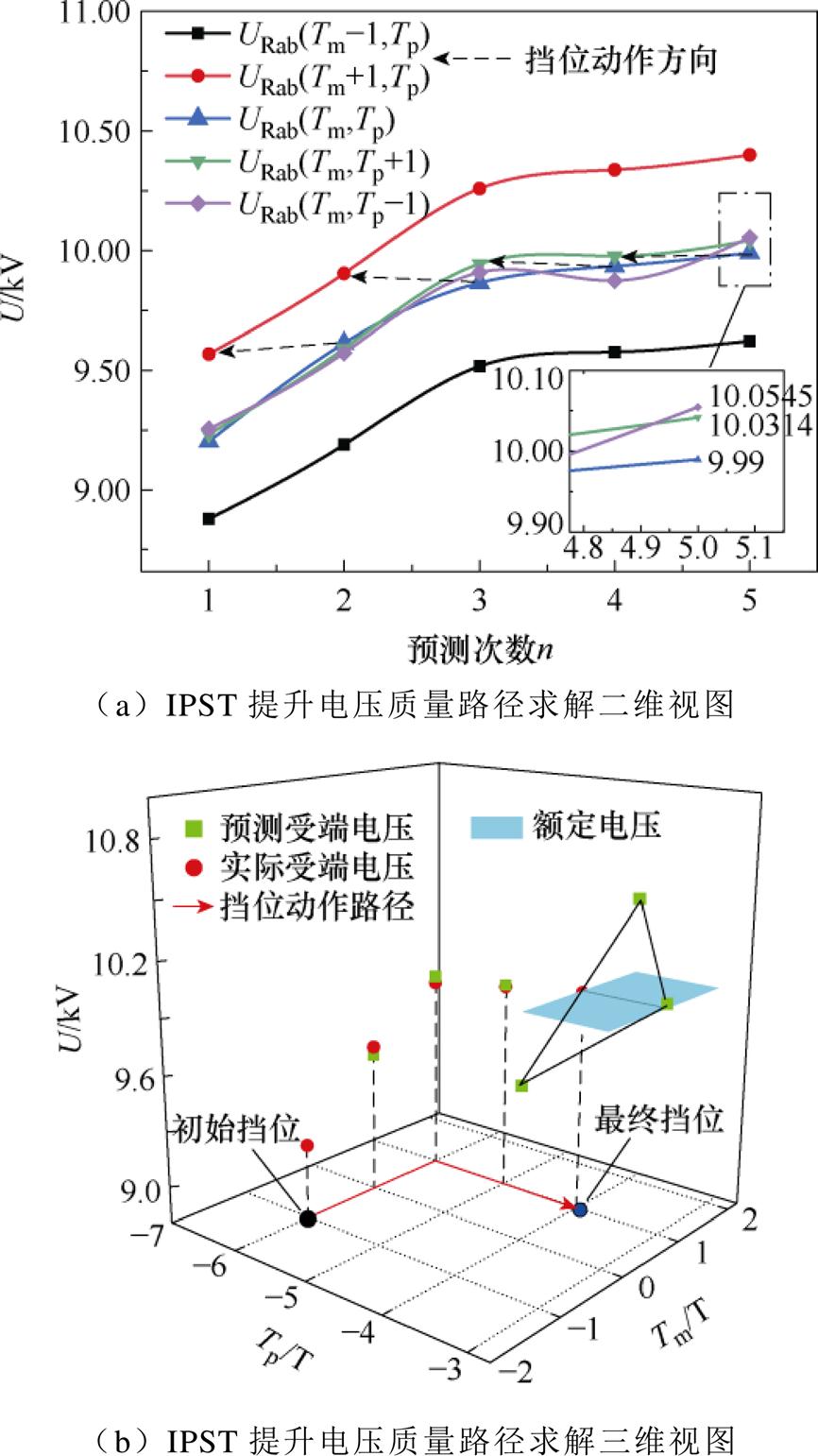
图11 IPST提升电压质量动作路径
Fig.11 The process of solving the IPST to improve the voltage quality
IPST调节电压质量波形如图12所示。
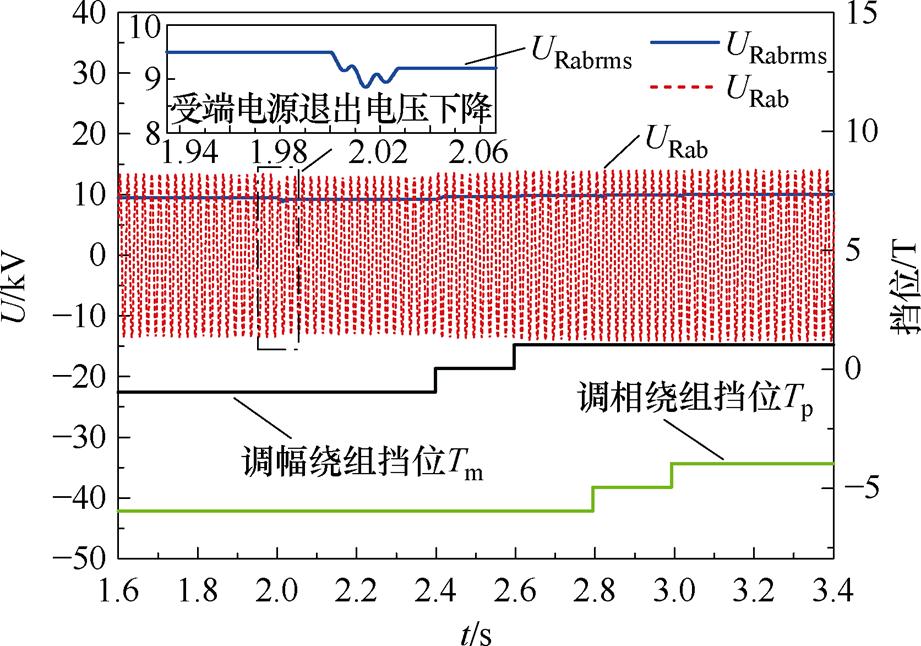
图12 IPST调节电压质量仿真波形
Fig.12 Simulation waveforms of IPST regulation voltage quality
图12为IPST调节过程中的仿真波形，当R侧电源退出后其电压URab及有效值URabrms出现明显的下降，电压质量下降，在IPST的调节下，电压值逐渐增大并接近额定值，从而提升供电可靠性。
当R侧电源需要长时间检修，负荷需要由S侧电源长时间提供，利用IPST长时间供电会产生电能损耗，此时需要合QFL1，对IPST进行旁路退出，由S侧直接通过联络线传输功率至R侧。但由于IPST两侧存在电压差值，直接倒闸会产生较大的环流及冲击电流，对合环装置及电网产生影响，因此需要再次调节IPST，减小冲击电流。
提取当前IPST两侧电压及电流数据，根据图8中IPST退出合环流程求解出挡位动作路径，如图13所示。
由图13可得，初始挡位（Tm, Tp）为 (1, -4) T，根据式（13）、式（17）及式（18）求解出 (1, -4) T临近挡位对应的电压ULa及对应的倒闸产生的冲击电流Ich，由式（19）得到IPST下一步动作方向为Tp+1，即调整至 (1, -3) T，以此类推，当动作至 (0, 2) T时，临近挡位预测冲击电流均小于当前电流，此时停止调节。
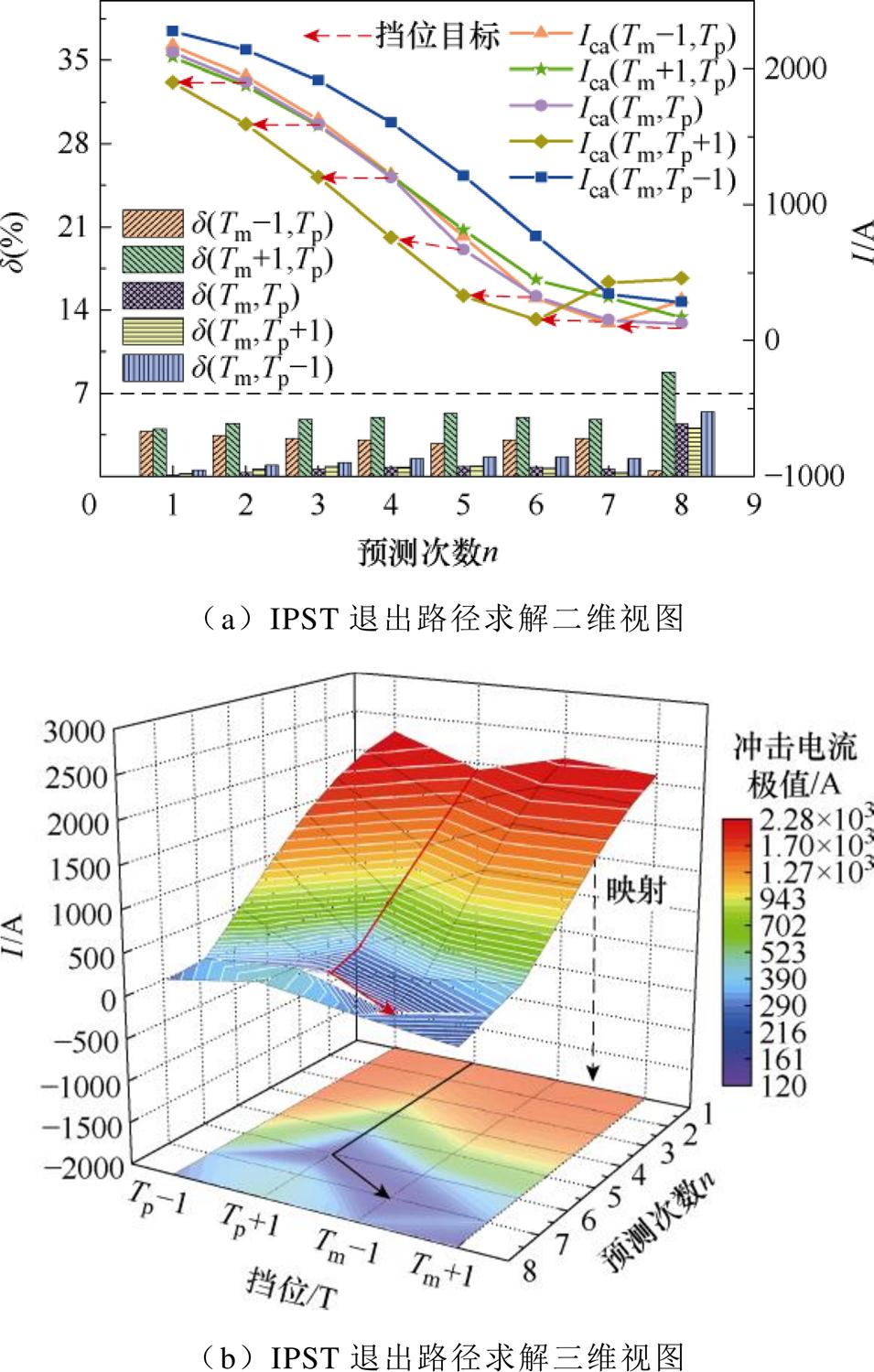
图13 IPST动作路径求解
Fig.13 Solving the IPST action path
IPST调节仿真波形如图14所示。
图14 IPST退出调节波形
Fig.14 IPST exit adjustment waveforms
如图14所示，IPST由 (1, -4) T调节至 (0, 2) T，调节过程中电压保持稳定、波动幅度较小，满足电压质量的要求。
IPST调节完成后，闭合QFL1，对IPST进行旁路，如图15所示为IPST进行调节前后对应的冲击电流仿真波形。
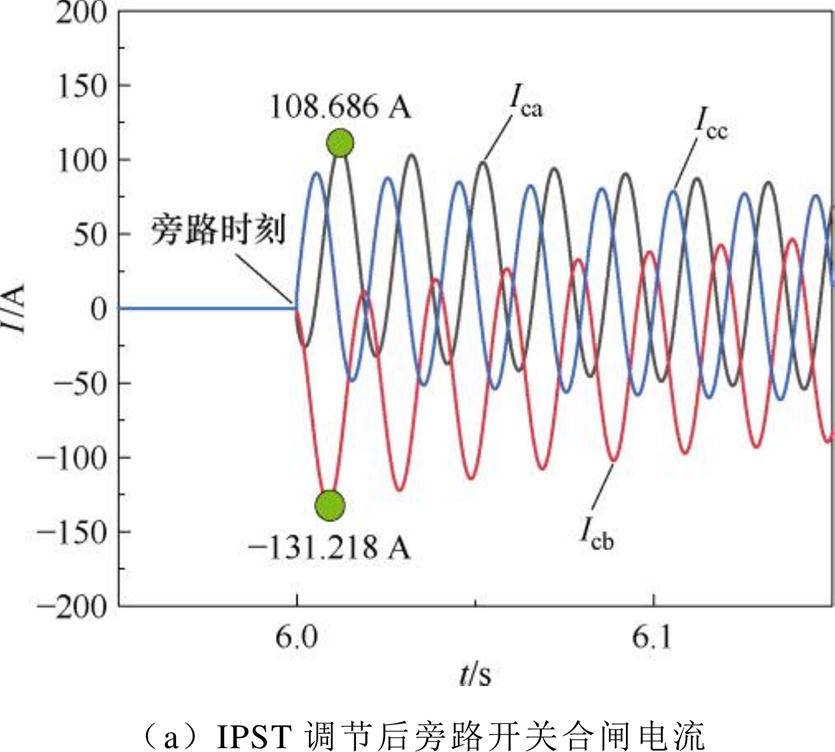
图15 IPST调节前后电流对比
Fig.15 Comparison of the cross-current before and after IPST adjustment
由图15a可得，当IPST调节挡位后进行旁路产生的冲击电流极值为131.218 A，与图15c直接合环形成的冲击电流极值2 148.456 A对比减小了93.89%，图15b为经过IPST调节后环流叠加负荷电流后IPST的穿越电流Ith，极值为525.899 A，对比图15d中直接合环的穿越电流极值1 751.519 A减小了69.97%，有效地保护了IPST合环装置。
为实现不停电合环转供，本文提出了基于IPST的合环装置，在传统移相器上增加了调幅绕组，能够对电压的相位与幅值进行灵活控制，实现了不停电合环，并在合环完成后，通过电流电压预测方法实现了电压质量的调节及IPST的安全退出过程。
1）针对IPST的拓扑结构及工作原理进行详细分析研究，寻找各绕组电压之间的耦合关系，推导出kp、km与调节电压之间的复杂非线性关系式，求解出目标电压对应的（Tpr, Tmr），使IPST调节电压与合环点电压接近，大幅度减小了合环冲击电流，实现不停电合环；建立IPST等效模型，通过多端口网络理论将IPST端口阻抗特性转化为函数解析式，并进行详细分析，为带负载调节控制提供了理论基础。
2）针对负荷侧电源退出后，由于IPST内部存在阻抗，导致电压下降问题，结合IPST阻抗关系式及IPST等效模型，求解出IPST带负载调节侧电压与IPST挡位之间的函数关系式，预测得到IPST下一步的调节目标，通过不断调节，使得负荷侧电压达到额定值，提升了供电可靠性。
3）针对IPST退出合环时，由于IPST两侧电压的差异，导致旁路IPST时产生较大的冲击电流的问题，本文推导出冲击电流表达式，结合IPST预测电压，建立目标函数及电压约束，求解出IPST的目标挡位，保证电压质量的条件下，减小冲击电流，有效地保护了合环装置。
附 录
1. IPST等效阻抗求解过程
下面以a相为例对IPST等效阻抗进行推导，利用KCL定理对图4中节点Oa和节点Ta分析可得
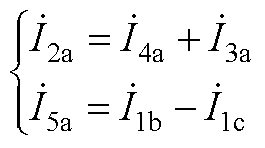（A1）
ST与ET一、二次电流关系为
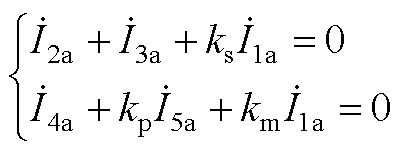（A2）
abc三相电流之间的关系为
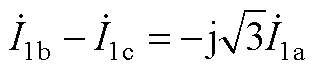（A3）
结合式（A1）～式（A3）可以得到IPST各绕组之间的电流关系式为
（A4）
各绕组电压关系式为
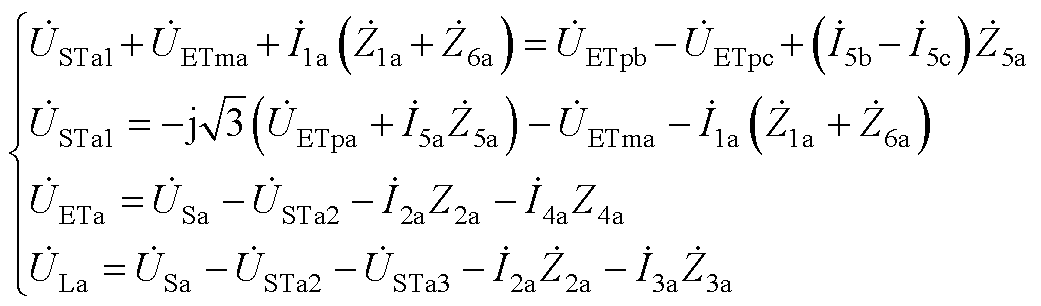（A5）
2. 场景2仿真结果
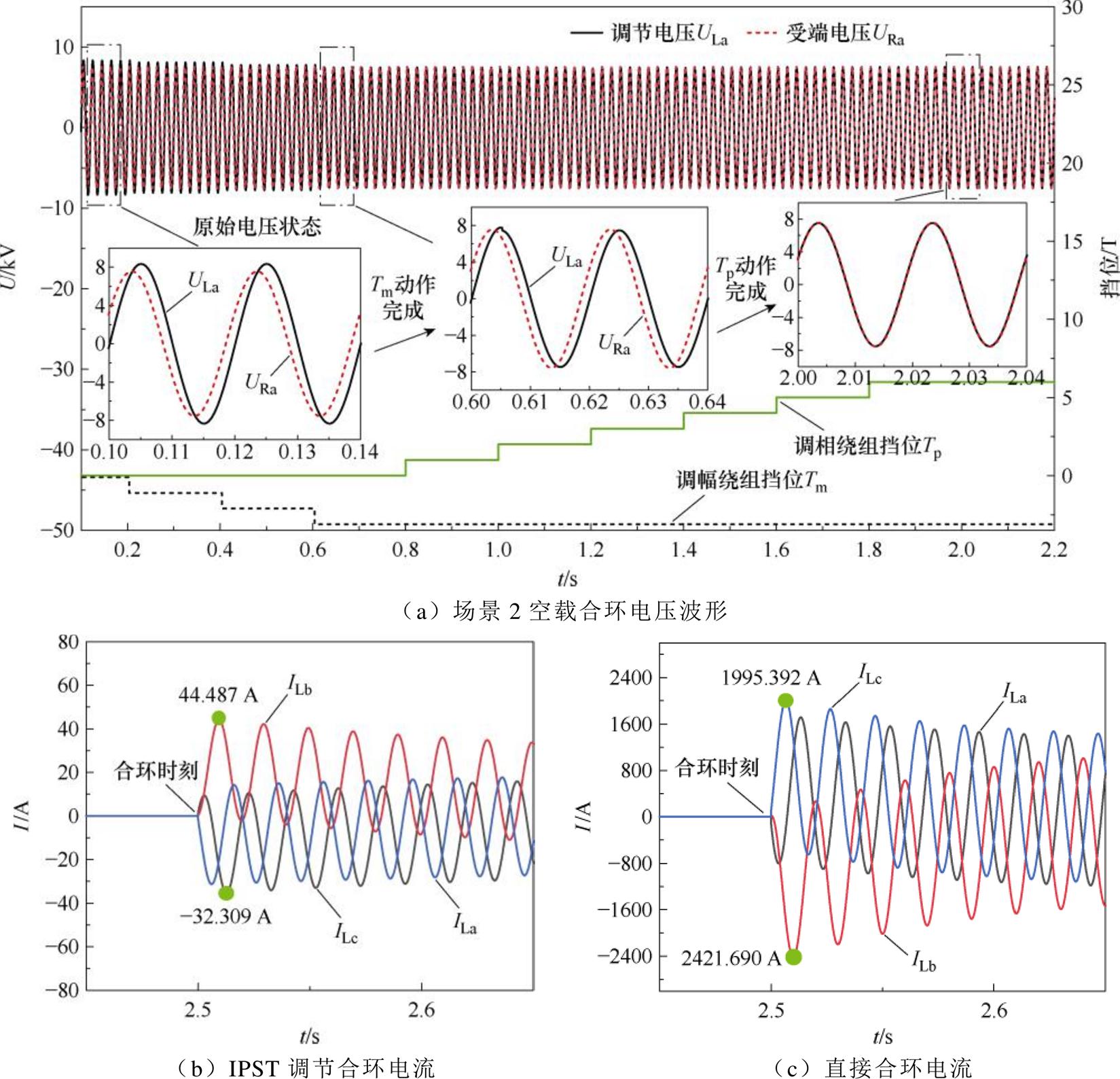
附图1 场景2空载合环仿真波形
App.Fig.1 Simulation waveforms in loop closing scenario 2
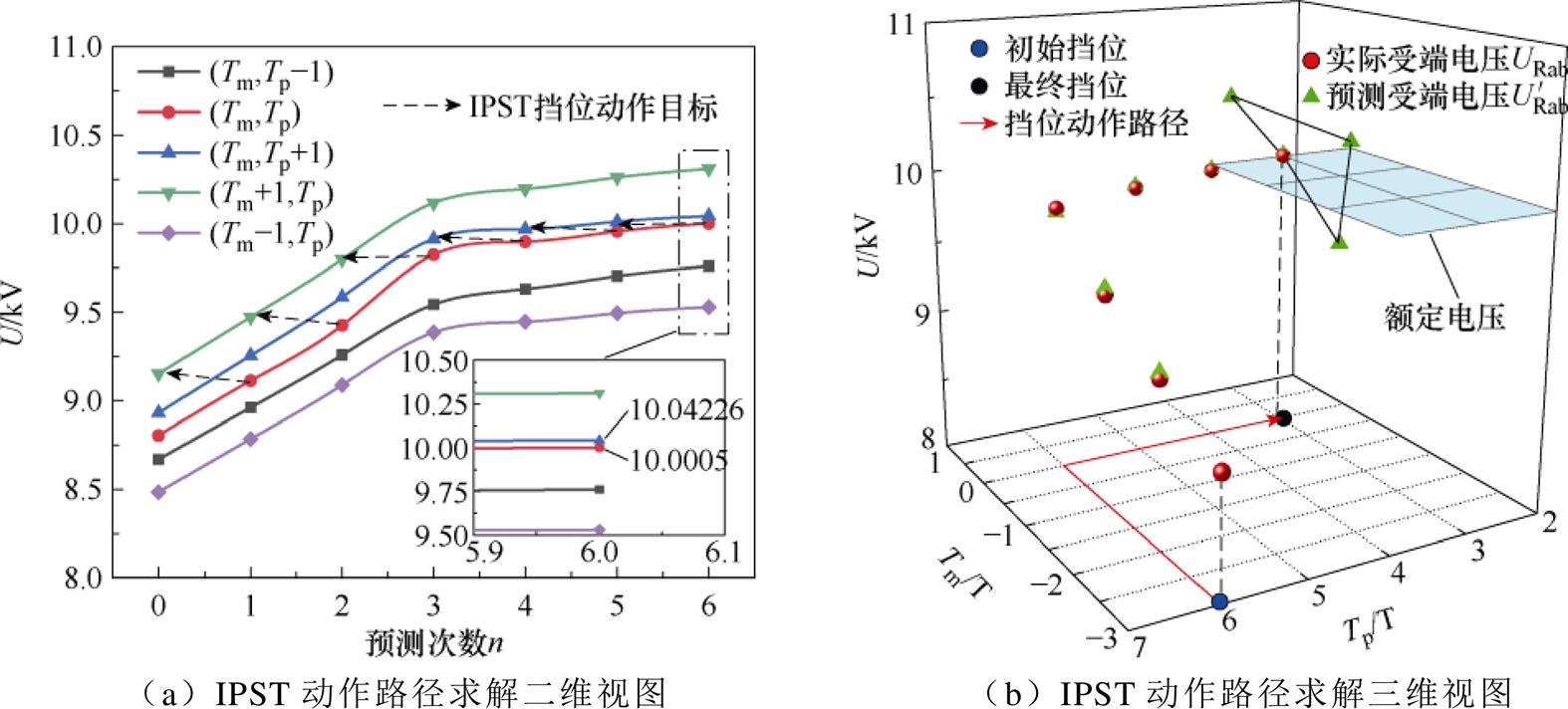
附图2 IPST提升电压质量路径求解过程
App.Fig.2 The process of solving the IPST to improve the voltage quality
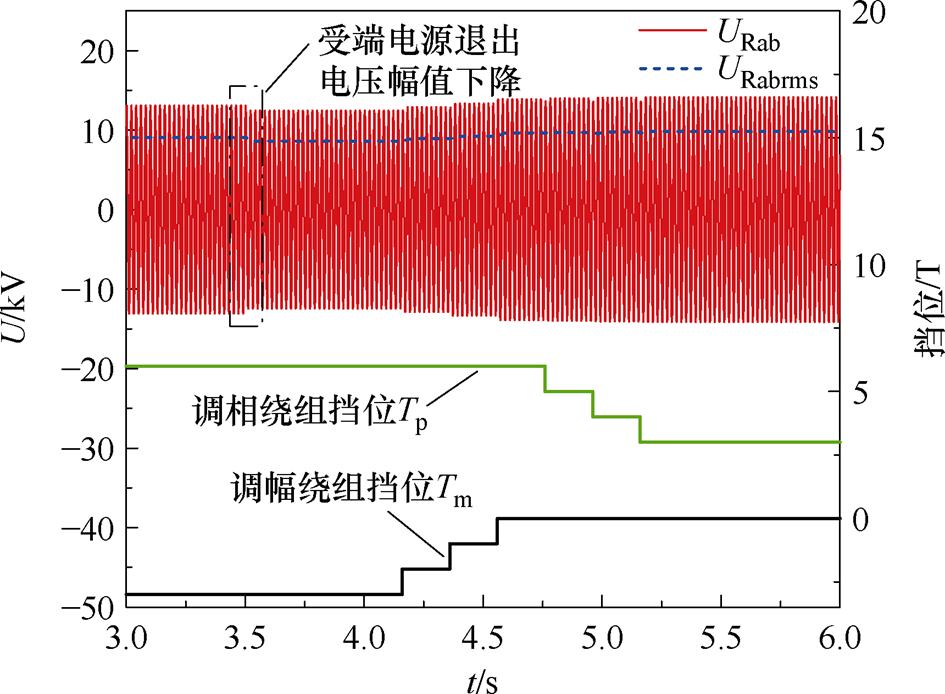
附图3 IPST调节电压质量仿真波形
App.Fig.3 Simulation waveforms of IPST regulation voltage quality
附图4 IPST调节前后冲击电流对比
App.Fig.4 Comparison of the cross-current before and after IPST adjustment
参考文献
[1] 颜湘武, 邵晨, 吴鸣, 等. 基于电磁式旋转潮流控制器的有源配电网多场景控制[J]. 电工技术学报, 2023, 38(增刊1): 44-55.
Yan Xiangwu, Shao Chen, Wu Ming, et al. Multi- scene control method of active distribution network based on electromagnetic rotating power flow con- troller[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 44-55.
[2] 吴振辉, 彭晓涛, 沈阳武, 等. 一种配电网环型供电模型及其合环运行方式的研究[J]. 中国电机工程学报, 2013, 33(10): 57-63.
Wu Zhenhui, Peng Xiaotao, Shen Yangwu, et al. Study on a loop power supply model and its loop- close operation mode for distribution network[J]. Proceedings of the CSEE, 2013, 33(10): 57-63.
[3] 夏翔, 熊军, 胡列翔. 地区电网的合环潮流分析与控制[J]. 电网技术, 2004, 28(22): 76-80.
Xia Xiang, Xiong Jun, Hu Liexiang. Analysis and control of loop power flow in regional power network[J]. Power System Technology, 2004, 28(22): 76-80.
[4] 王怡, 杨知方, 余娟, 等. 考虑可靠性需求的配电网多种设备统一优化配置[J]. 电工技术学报, 2023, 38(24): 6727-6743.
Wang Yi, Yang Zhifang, Yu Juan, et al. A unified optimal placement method for multiple types of devices in distribution networks considering reliabi- lity demand[J]. Transactions of China Electrotech- nical Society, 2023, 38(24): 6727-6743.
[5] 章坚民, 相炜, 罗刚, 等. 配电网30°相角差线路不停电转供的解决方案及关键分析[J]. 电力系统自动化, 2018, 42(1): 74-81.
Zhang Jianmin, Xiang Wei, Luo Gang, et al. Solution and its key issue analysis for load transfer without power interruption of distribution lines with 30°phase angle difference[J]. Automation of Electric Power Systems, 2018, 42(1): 74-81.
[6] 张亮, 章坚民, 金乃正, 等. 配电网30°相角差线路不停电转供的混合顺控方法及试点验证[J]. 电力系统自动化, 2018, 42(2): 128-135, 153.
Zhang Liang, Zhang Jianmin, Jin Naizheng, et al. Hybrid sequence control and pilot project verification for none-electricity-cut load transferring of distri- bution lines with 30 degree phase angle difference[J]. Automation of Electric Power Systems, 2018, 42(2): 128-135, 153.
[7] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685.
Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[8] 杨用春, 唐健雄, 牛超群, 等. 基于移相变压器的灵活合环控制装置及控制策略研究[J]. 华北电力大学学报(自然科学版), 2022, 49(1): 48-57.
Yang Yongchun, Tang Jianxiong, Niu Chaoqun, et al. Research on flexible loop-closing control device and control strategy based on phase shifting transfor- mer[J]. Journal of North China Electric Power Univer- sity (Natural Science Edition), 2022, 49(1): 48-57.
[9] 赖胜杰, 夏成军, 纪焕聪, 等. 计及负荷等值阻抗的配电网合环转供电分析模型[J]. 电工技术学报, 2022, 37(11): 2859-2868.
Lai Shengjie, Xia Chengjun, Ji Huancong, et al. An analysis model for power transfer from loop closing in distribution network considering load equivalent impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2859-2868.
[10] 石钟文, 温辉, 杨利森, 等. 基于改进算法的10 kV配电网合环稳态电流计算[J]. 智慧电力, 2023, 51(3): 111-118.
Shi Zhongwen, Wen Hui, Yang Lisen, et al. Calculation of loop closing steady-state current in 10 kV distribution network based on improved algorithm[J]. Smart Power, 2023, 51(3): 111-118.
[11] 刘健, 孙泉, 张小庆, 等. 配电网合环分析与合环条件判断[J]. 电力系统自动化, 2014, 38(11): 130-135.
Liu Jian, Sun Quan, Zhang Xiaoqing, et al. Analysis on and criteria for loop closing operation for distribution grids[J]. Automation of Electric Power Systems, 2014, 38(11): 130-135.
[12] 欧阳金鑫, 陈纪宇, 袁毅峰, 等. 基于分布式电源主动控制的配电网合环电压波动抑制方法[J]. 电力自动化设备, 2024, 44(1): 49-56.
Ouyang Jinxin, Chen Jiyu, Yuan Yifeng, et al. Suppression method of loop closing voltage fluctuation in distribution network based on active control of distributed generator[J]. Electric Power Automation Equipment, 2024, 44(1): 49-56.
[13] 王旭东. 基于分布式发电和柔性负荷的配电网合环电压综合调节方法研究[J]. 电气应用, 2019, 38(10): 76-83.
Wang Xudong. Comprehensive regulation method study of distribution network closed-loop voltage based on distributed generations and flexible loads[J]. Electrotechnical Application, 2019, 38(10): 76-83.
[14] 杨用春, 牛超群, 唐健雄, 等. 基于双VSC的柔性合环装置的交直流侧合环控制策略研究[J]. 华北电力大学学报(自然科学版), 2023, 50(2): 1-9.
Yang Yongchun, Niu Chaoqun, Tang Jianxiong, et al. Research on the control strategy of AC and DC side loop-closing of flexible loop-closing device based on double VSC[J]. Journal of North China Electric Power University (Natural Science Edition), 2023, 50(2): 1-9.
[15] 邵云峰, 刘永强, 马中静, 等. 基于蓄电池储能系统的电网合环技术研究[J]. 电器与能效管理技术, 2020(10): 27-35, 54.
Shao Yunfeng, Liu Yongqiang, Ma Zhongjing, et al. Research on grid loop closing techniques based on battery energy storage systems[J]. Electrical & Energy Management Technology, 2020(10): 27-35, 54.
[16] 仉志华. 基于UPFC的自愈配电环网及其潮流优化控制技术的研究[D]. 济南: 山东大学, 2012.
Zhang Zhihua. Research on self-healing distribution ring network based on UPFC and its power flow optimization control technology[D]. Jinan: Shandong University, 2012.
[17] Yuan Jiaxin, Zhang Weizhe, Mei Jiajun, et al. Independent fast phase shifting transformer: a flexible and high-precision power flow controller[J]. IEEE Transactions on Power Delivery, 2023, 38(6): 4410- 4421.
[18] 余梦泽, 李峰, 李作红, 等. 移相变压器原理、拓扑、应用及发展[J]. 武汉大学学报(工学版), 2023, 56(10): 1224-1237.
Yu Mengze, Li Feng, Li Zuohong, et al. Principle, topology, application and development of phase- shifting transformer[J]. Geomatics and Engineering Science of Wuhan University, 2023, 56(10): 1224- 1237.
[19] 杨用春, 唐健雄, 牛超群, 等. 基于IPST的合环装置三相不对称下耦合特性及控制策略[J]. 电力系统自动化, 2022, 46(14): 158-168.
Yang Yongchun, Tang Jianxiong, Niu Chaoqun, et al. Coupling characteristic and control strategy for loop closing device based on improved phase shifting transformer under three-phase asymmetry con- dition[J]. Automation of Electric Power Systems, 2022, 46(14): 158-168.
[20] 赵镜红, 周长朵, 王涵铭, 等. 计及边端效应的直线式移相变压器等效电路分析[J]. 电工技术学报, 2024, 39(6): 1792-1805.
Zhao Jinghong, Zhou Changduo, Wang Hanming, et al. Equivalent circuit analysis of linear phase-shifting transformer considering edge effect[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1792- 1805.
[21] 高飞, 刘欣, 王利桐, 等. 对称双芯移相变压器有载分接开关最大级电压计算方法研究[J]. 中国电机工程学报, 2017, 37(7): 2110-2119.
Gao Fei, Liu Xin, Wang Litong, et al. Study on the maximum step voltage calculation method of on-load tap changer in symmetrical two-core phase shifting transformer[J]. Proceedings of the CSEE, 2017, 37(7): 2110-2119.
[22] Liang Guishu, Wang Litong, Gao Fei, et al. A new maximum step voltage calculation method of on-load tap-changer for symmetrical two-core phase-shifting transformer[J]. IEEE Transactions on Power Delivery, 2018, 33(6): 2718-2725.
[23] 卜亮, 韩松, 周超, 等. 基于UMEC的双芯Sen变压器电磁暂态模型[J]. 电网技术, 2021, 45(8): 3283- 3290.
Bu Liang, Han Song, Zhou Chao, et al. Electro- magnetic transient model of two-core Sen transformer based on UMEC[J]. Power System Technology, 2021, 45(8): 3283-3290.
[24] 杨庆, 崔浩楠, 揭青松, 等. 基于对偶性原理的配电变压器高频电磁暂态模型[J]. 高电压技术, 2022, 48(4): 1498-1509.
Yang Qing, Cui Haonan, Jie Qingsong, et al. High frequency electromagnetic transient model of dis- tribution transformer based on duality principle[J]. High Voltage Engineering, 2022, 48(4): 1498-1509.
[25] 徐志, 刘静佳, 蒋羽鹏, 等. 基于移相变压器+调压变压器的10kV配电网合环控制装置及控制方法[J]. 南方电网技术, 2023, 17(3): 85-96.
Xu Zhi, Liu Jingjia, Jiang Yupeng, et al. Loop closing control device and control method of 10kV dis- tribution network based on phase shifting transformer and voltage regulating transformer[J]. Southern Power System Technology, 2023, 17(3): 85-96.
[26] 周自强, 张焰, 郭强, 等. 基于概率潮流的10 kV配电网合环操作安全性评估[J]. 电网技术, 2019, 43(4): 1421-1429.
Zhou Ziqiang, Zhang Yan, Guo Qiang, et al. Security assessment of loop closing operation in 10 kV dis- tribution network based on probabilistic load flow[J]. Power System Technology, 2019, 43(4): 1421-1429.
[27] 刘善伟, 郭建龙, 刘文泽, 等. 10 kV配电网电能质量综合等级评估方法研究[J]. 机电工程技术, 2021, 50(8): 152-156.
Liu Shanwei, Guo Jianlong, Liu Wenze, et al. Study on the method of comprehensive grade evaluation of power quality in 10 kV distribution network[J]. Mechanical & Electrical Engineering Technology, 2021, 50(8): 152-156.
[28] 刘康康. 配电网电能质量综合评估方法研究[D]. 贵阳: 贵州大学, 2022.
Liu Kangkang. Research on comprehensive evaluation method of power quality in distribution network[D]. Guiyang: Guizhou University, 2022.
Abstract Due to the existence of important loads, the new distribution network needs to be supplied with power when the equipment of the original distribution network is overhauled. Two closing types exist when accessing the new distribution network: loop and ring-closing. The distribution network is cut off for loop closing, leading to power supply interruption, or the ring of the distribution network is directly closed, producing a large impulse current due to the large voltage difference between the two distribution networks. As a result, the relay protection malfunction occurs, which affects the reliability and stability of the power grid. Two ways are adopted to avoid the above issues. One is to provide the loop closing condition through theoretical calculation, and the voltage of the loop closing point is similar by controlling the whole distribution network. The loop is directly closed after meeting the ring closing conditions. However, the control process is more complex, and the loop closing current is still large. The second is to use the voltage regulating device to change the voltage of one side of the ring closing point and carry out the ring-closing. Although the control effect of the ring-closing device is better, the price and maintenance costs are high.
This paper proposes an improved phase shifter (IPST) with an amplitude modulation winding (ETm) based on the amplitude modulation winding (ETp) of the traditional phase shifter. It can flexibly change the voltage amplitude and phase by adjusting the gears of ETp and ETm, thereby changing the voltage at the closing point. The voltage between the two distribution networks is similar, and the loop closure is realized. In addition, the voltage quality on the load side is degraded because of the internal impedance of the IPST after the load transfer. An IPST equivalence model is established based on the multi-port network theory. The impedance characteristics of the IPST port are converted into the equivalent analytical formula. The functional expressions of the regulation voltage on the amplitude modulation gear Tm and phase modulation gear Tp are derived. Thus, the target gear of the IPST is predicted, and the voltage quality is improved. Thirdly, to address the problem of the inrush current generated when the IPST exits bypass closing, the functional relationship of the inrush current on the IPST gear is derived. The IPST target gear is predicted by combining the current regulation target and the voltage quality constraint. The voltage quality can be ensured, and the impulse current can drop and safely exit the IPST. Finally, the impedance expression’s correctness and the control strategy’s effectiveness are verified through PSCAD/ EMTDC.
Keywords：Distribution network, loop closing to supply, phase-shifting transformers, equivalent impedance, closing loop current
中图分类号：TM571
DOI: 10.19595/j.cnki.1000-6753.tces.240615
国家自然科学基金（51607068）、中央高校基本科研业务费专项资金（2021MS068）资助项目。
收稿日期 2024-04-22
改稿日期 2024-06-19
杨用春 男，1982年生，博士，讲师，研究方向为柔性交流输电技术、交直流电力变换及电能质量分析与控制。
E-mail: yongchunyang@126.com
杜翔宇 男，2000年生，硕士研究生，研究方向为配电网合环技术、柔性交流输电技术。
E-mail: xiangyudu218@163.com（通信作者）
（编辑 崔文静）