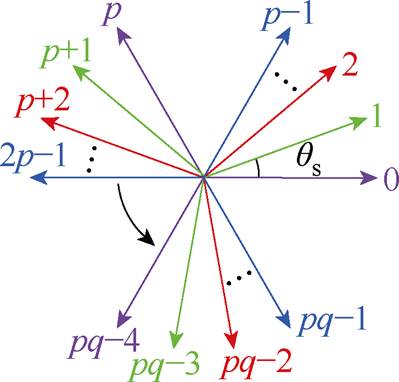
图1 AMM的拓扑结构
Fig.1 The topological structure of AMM
摘要 针对多相电机传统谐波抑制策略往往依赖复杂滤波器或观测器提取谐波,且需要构建大量不同频率的比例谐振控制器(PR),导致谐波抑制复杂且实用性差的问题,提出一种基于谐波映射规律的无滤波器单频率PR谐波抑制策略。首先,基于磁动势等效原则,建立非对称多相电机的通用空间矢量解耦矩阵,创立谐波在子平面的映射通式,推导谐波幅值、相位的映射规律。其次,基于图像化的映射规律获取所有子平面谐波的映射轨迹,优化谐波唯一映射的最少相数非对称多相电机拓扑。再次,基于电流移相方法构造虚拟电机,并通过矢量解耦变换子平面提取谐波。然后,通过线性空间旋转变换整合频率,提出基于单频率PR的谐波统一抑制方法。最后,开展双三相电机稳、暂态工况下的谐波提取及抑制实验,提取谐波的还原度可达92%以上且总谐波畸变率由抑制前的15.36%降至2.86%。理论和实验验证了该文所提谐波映射规律及单频率PR谐波统一抑制策略的有效性。
关键词:非对称多相电机 谐波抑制 虚拟电机 单频率PR控制 谐波映射规律
非对称多相电机(Asymmetric Multiphase Motor, AMM)具有高功率密度、强容错性等优点[1],因此在电动汽车、船舶推进等领域备受关注[2]。然而,AMM中空间谐波电流(奇次和偶次谐波[3])与时间谐波电流(奇次谐波[4])的耦合作用,导致转矩波动增大、效率降低,从而限制了其广泛应用[5]。目前已有一些优化谐波源头的方法,如通过调整矢量占空比来补偿死区[6-7]、构造虚拟矢量来降低控制主动引入谐波[8-9],但这些方法属于被动型谐波抑制策略,仅适用于特定工况。相比之下,基于谐波提取的主动谐波抑制策略是更有效的通用型谐波解决方案,但存在耦合谐波分离困难及谐波控制器设计复杂的问题。因此,针对AMM时空谐波耦合严重的问题,开展准确全面的简化式谐波提取策略以及统一的主动式谐波抑制策略的研究,对推动高性能AMM的实用化具有重要意义。
准确提取谐波是AMM谐波抑制策略的基础。目前,谐波提取方法主要有谐波分离与辨识两大类。文献[10]将双三相电机的5、7次谐波变换到同步坐标系后,再利用低通滤波器分离谐波。文献[11]利用三相电机中5、7次谐波在同步旋转系是6次谐波的特点,设计了单切比雪夫滤波器同时提取两种谐波。上述两种基于滤波器提取谐波的算法,前者在低转速下谐波与基波频率接近,导致提取的谐波与基波混叠;而后者的滤波器设计较为复杂。文献[12]将双三相电机构造成虚拟九相电机,实现了基波与11、13次谐波解耦。然而,该方法仍需依赖同步坐标系下的四组低通滤波器来提取5、7、11和13次谐波电流。文献[13]在此基础上进一步将双三相电机构造成十五相电机,并通过同步旋转坐标变换将交流谐波转换成直流量,实现了无滤波器提取谐波,但构造电机相数的增加导致谐波提取的运算量显著增加。此外,上述两种方法均需要使用四组PI控制器分别对四组谐波进行调控。与通过滤波器分离谐波的思路不同,文献[14-16]分别提出基于矩阵束算法、谐波观测器以及自适应神经网络策略的谐波辨识方法。其中,矩阵速算法和谐波观测器两种算法需要建立系统的数学模型,对参数准确性要求较高。而新兴的人工智能算法依赖前期的大量数据来训练模型,并对训练过程中的算力有较高需求。
谐波抑制控制器设计是谐波抑制策略的核心。目前有较多研究致力于设计能抑制特定频率谐波的控制器。例如,文献[17-19]分别利用谐波前馈控制器、修正型重复控制器和强抗干扰的改进型准比例谐振控制器(Proportional Resonance, PR)来抑制永磁同步电机的整数倍频谐波。上述方法都对谐振频率附近的谐波有着较好的抑制效果,但在抑制多种频率的谐波时需大量不同频率的控制器,导致了算法运算量大且需对谐振频率不同的控制器进行逐一调参。此外,一些学者采用同步旋转坐标变换将交流谐波转换成直流,然后使用PI控制器跟踪谐波指令[20]。该过程本质上和文献[19]中的PR控制器原理相同。另一种主流的谐波抑制策略是将谐波跟踪目标作为子项,加入到模型预测控制(Model Predictive Control, MPC)的代价函数中[21-22]。一方面,主流算法为减少计算量普遍采用有限集MPC,其输出的离散开关状态会引入额外谐波;另一方面,MPC算法通常不会对谐波进行预处理,需要直接跟踪交流信号,因此在低载波比下,控制效果不如矢量控制等其他控制器。
综上所述,现有谐波抑制算法通常依赖复杂的多频次谐波提取器并需要针对每种谐波频率对控制器逐一进行参数优化,显著增加了抑制算法的复杂性。为了简化AMM谐波抑制策略,本文利用矢量空间解耦(Vector Space Decomposition, VSD)能够将不同频率谐波分离到多个子平面的优势,提出一种基于谐波映射规律的无滤波器单频率PR控制器谐波抑制策略。首先,本文建立多相AMM的通用VSD变换矩阵,并推导了谐波在子平面的映射规律。然后,通过映射规律寻找能使谐波映射到唯一子平面的最优AMM拓扑,并确立映射子平面,再基于电流移相构建虚拟AMM来提取谐波。其次,利用所选子平面上谐波成对映射的特征,以及频率阶次数差值相等且相序相反的特性,在通过线性空间旋转变换整合频率后,采用单频率PR控制器实现了谐波的统一调控。最后,基于双三相电机实验平台,验证了所提谐波提取和抑制策略的有 效性。
图1为AMM的通用绕组拓扑结构,因其每p相为一个绕组单元,共有q(q≥2)组互差相移角qs的绕组单元的特性,被简称为相移qs的pq相 电机。

图1 AMM的拓扑结构
Fig.1 The topological structure of AMM
根据磁动势等效原则,通过静止坐标变换式(1),AMM的所有变量被映射到正交子平面ab1上。
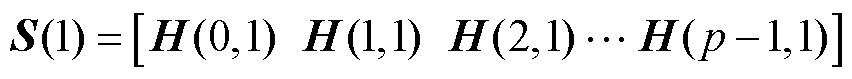 (1)
(1)
其中
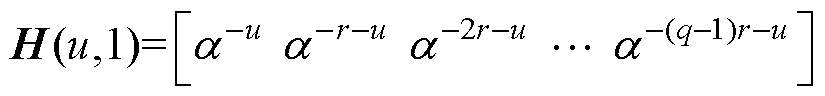
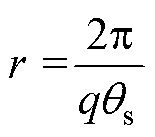
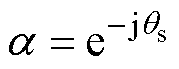 u∈[0, p-1]
u∈[0, p-1]
将式(1)推广到任意正交子平面abx上,得到映射到平面abx的通用坐标变换式为
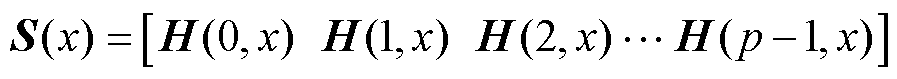 (2)
(2)
其中
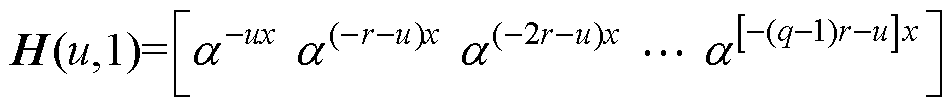
由于变换因子ax=ax+m(m=2p/qs),因此相移qs的AMM只存在m个子平面。将m个平面的映射向量组合,可得多相定子坐标系映射到多个子平面(ab0、ab1、ab2 …ab(m-1))的坐标变换矩阵T,即VSD变换矩阵。为确保变换前后磁动势守恒,矩阵加入了系数2/(pq)。
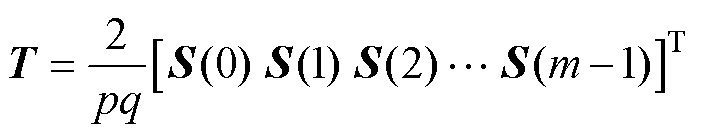 (3)
(3)
以相电流为例,其映射到正交子平面的等式为
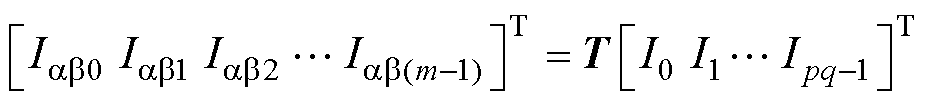 (4)
(4)
式中,[I0I1…Ipq-1]为相电流;[Iab0Iab1 Iab2 … Iab(m-1)]为子平面ab0、ab1、ab22 …ab(m-1)上的电流映射分量。
本节以相电流为研究对象,利用傅里叶分解将相电流分解为不同频率的谐波分量,推导并理论分析各频率分量在子平面的通式,以揭示映射分量的幅值与相序变化规律。傅里叶分解后,相电流的有限级数表达式为
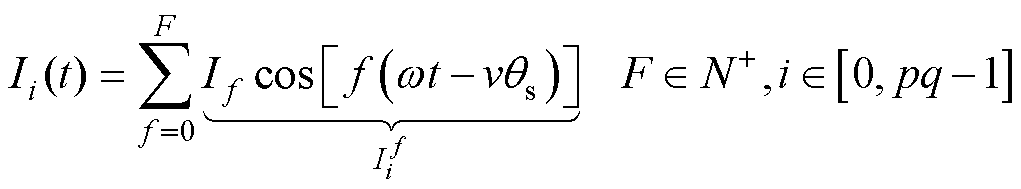 (5)
(5)
式中,i为绕组序号;f和F分别为谐波次数和考虑到的最大谐波次数;w 为基波电角速度;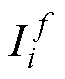 为相电流Ii(t)的f次谐波分量组;If为
为相电流Ii(t)的f次谐波分量组;If为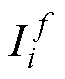 的幅值;v为相位变量。设I0(t)的初相位为0,根据“相电流的相位关系与绕组在空间上的电角度差一致”的特性,得到Ii(t)的相位变量v的计算式为
的幅值;v为相位变量。设I0(t)的初相位为0,根据“相电流的相位关系与绕组在空间上的电角度差一致”的特性,得到Ii(t)的相位变量v的计算式为
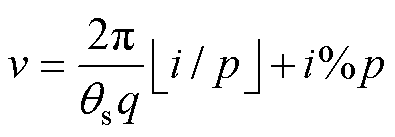 (6)
(6)
将变量i的值域代回式(6)可求出v的值域为
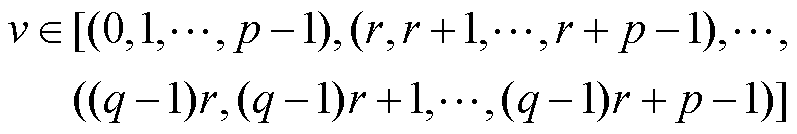 (7)
(7)
将式(4)的相电流组替换为式(5)中的f次谐波分量组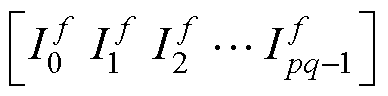 ,得到相电流的f次谐波映射到任意子平面abx上的通式
,得到相电流的f次谐波映射到任意子平面abx上的通式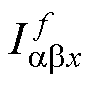 为
为
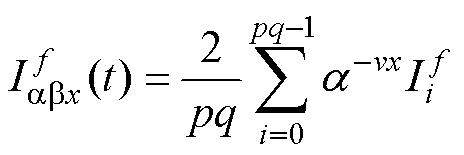 (8)
(8)
再利用欧拉公式将式(8)转换成复数形式为
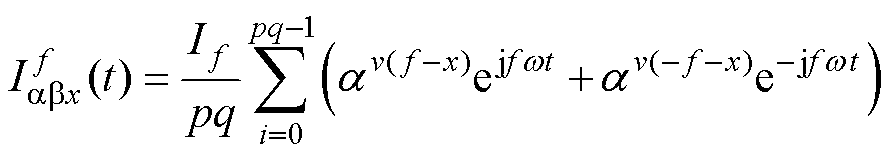 (9)
(9)
为消除式(9)中的复杂变量v,引入一组值域范围与v相同的中间变量表达式zr+y(z∈[0, q-1]),
y∈[0, p-1]),v被替换后的通式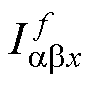 被简化为
被简化为
 (10)
(10)
式中,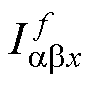 由复数子分量
由复数子分量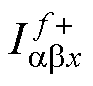 和
和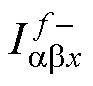 组成。其中,两子分量又分别由影响幅值的实数系数
组成。其中,两子分量又分别由影响幅值的实数系数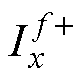 、
、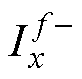 和影响相位的单位旋转因子ejfwt和e-jfwt组成。因此,下文将分别从幅值和相序两方面来阐述通式
和影响相位的单位旋转因子ejfwt和e-jfwt组成。因此,下文将分别从幅值和相序两方面来阐述通式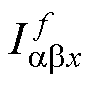 的特性。
的特性。
首先,系数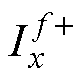 、
、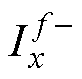 是幅值特性的决定性因素。在式(10)中,系数
是幅值特性的决定性因素。在式(10)中,系数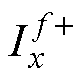 、
、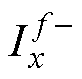 在形式上是一组数列之和,基本单元为
在形式上是一组数列之和,基本单元为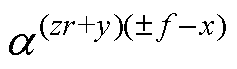 。系数值的分类讨论如下:
。系数值的分类讨论如下:
(1)当ar(±f-x)≠1且a(±f-x)≠1时,正、负序分量可以利用等比数列的求和法则求和,求和法则计算得到的系数表达式为
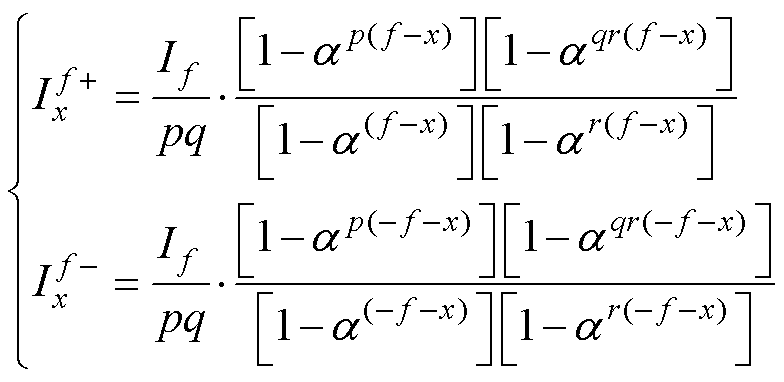 (11)
(11)
式中,子项1-aqr(±f-x)恒为0,因此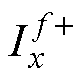 和
和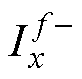 为0,表明f次谐波映射在平面abx上无映射。
为0,表明f次谐波映射在平面abx上无映射。
(2)当ar(±f-x)=1且ap(±f-x)=1时,代回式(10),系数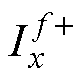 和
和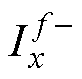 也为0,即f次谐波在abx上无映射。
也为0,即f次谐波在abx上无映射。
(3)当a(±f-x)=1时,即±f-x=2pk/qs(k为整数),代回式(10),系数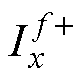 =
=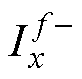 =1,f次谐波映射在平面abx上的分量幅值与映射前相等,将这种映射方式定义为全映射方式。
=1,f次谐波映射在平面abx上的分量幅值与映射前相等,将这种映射方式定义为全映射方式。
(4)当ar(±f-x)=1且ap(±f-x)≠1时,即±f-x=kq且 ±f-x≠2pk/(pqs),系数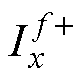 和
和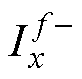 为
为
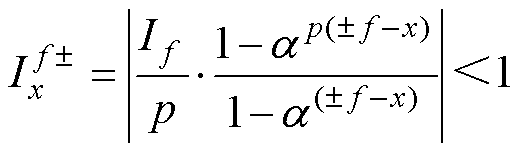 (12)
(12)
表明f次谐波映射在平面abx上的分量幅值小于映射前,将这种映射方式定义为部分映射方式。
然后,式(10)中除系数外的剩余子项ejfwt和e-jfwt是幅值为1的旋转因子,是相序特性的决定性因素。正、负序复数子分量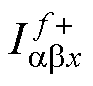 和
和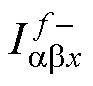 分别包含了旋转因子ejfwt和e-jfwt,而实数系数并不影响相位,因此复数子分量与旋转因子相位特性一致。其中,
分别包含了旋转因子ejfwt和e-jfwt,而实数系数并不影响相位,因此复数子分量与旋转因子相位特性一致。其中,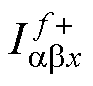 的旋转角频率为fw t,实数部分(a 轴分量)相位上超前虚数部分(b 轴分量)p/2。
的旋转角频率为fw t,实数部分(a 轴分量)相位上超前虚数部分(b 轴分量)p/2。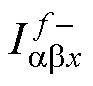 的旋转角频率也为fw t,但相位上是a轴分量滞后b 轴分量p/2。定义a 轴分量超前b 轴分量的
的旋转角频率也为fw t,但相位上是a轴分量滞后b 轴分量p/2。定义a 轴分量超前b 轴分量的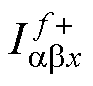 为正序分量,反之为负序分量。
为正序分量,反之为负序分量。
综上所述,f次谐波在子平面abx上的幅值映射规律可归纳如下:
(1)f次谐波满足±f-x=2pk/qs,映射方式为全映射方式,其在子平面abx上的映射分量与映射前的幅值保持一致。
(2)f次谐波满足±f-x=kq且±f-x≠2pk/(pqs),映射方式为部分映射,其在子平面abx上的映射分量与映射前的幅值保持一致。
(3)其余情况下,f次谐波在子平面abx上无映射分量。
相序映射规律体现为幅值映射规律适用于“+f”和“-f”时,映射分量的相序分别是正序和负序分量。基于分析所得幅值映射规律可筛选谐波的唯一映射子平面,基于相序规律可设计相位变换坐标系用来整合谐波频率。
在本节中,基于多谐波映射规律,提出一种针对AMM的单频率PR统一谐波抑制策略,抑制策略的统一控制框图如图2所示。首先,基于谐波映射规律确立最优的AMM拓扑,再通过电流移相构造虚拟AMM,继而实现在VSD子平面提取谐波。然后,设计线性空间旋转坐标变换统一谐波频率后,通过相同谐振频率的准PR控制器统一调控谐波。最后PR控制器输出经过逆变换后再移相,得到真实电机的电压指令值。后文以相移p/6的双中性点双三相电机(Dual Three-Phase Motor, DTPM)的5、7、11和13次谐波为实例,详细阐述了策略的设计步骤。

图2 谐波抑制策略的统一控制框图
Fig.2 General control block diagram of harmonic suppression strateg
绕组相数和相移角qs是确立AMM拓扑的两个核心要素[1]。
随着相数增加,更多低频次谐波被有效映射到独立的子平面中。当相数达到足够大的数值时,如文献[13]所述,1、5、7、11和13次电流映射到独立子平面。然而,实现这一目标是以电机相数增加到15相为代价。与双三相电机相比,电机相数增加了1.5倍,导致VSD矩阵阶数和虚构电流组数量同样增加了1.5倍,进而使得谐波提取策略的运算量增加了5.25倍。虽然高相数AMM能够完全分离目标次谐波,但线性增加的相数会导致二次方倍的运算量增长。因此,设计虚拟AMM的相数时,需在谐波分离效果与运算量之间折衷。
相移角qs会影响谐波的映射方式。合适的相移角下,目标谐波能以全映射方式映射到唯一的子平面,降低控制复杂度。而不当的相移角设计,会使谐波以部分映射方式映射到非唯一子平面,导致谐波无法提取。
基于上述分析,本节围绕电机相数和相移角qs优化两方面展开,提出三点设计准则,并结合图像化的谐波映射轨迹来优化虚拟AMM的拓扑。
2.1.1 相带铺满准则
当相移角满足qs=lp/(pq)(l为正整数)时,电机绕组能够完全铺满相带。例如,相移p/6和p/9的DTPM分别是相带铺满和相带有空缺的六相AMM。
图3为谐波映射轨迹,图中,相同颜色的箭头是同一平面,虚线箭头表示无映射。图3a~图3d展示了两种六相AMM的谐波映射轨迹。其中,谐波全映射方式下轨迹的绘制步骤如下:
(1)全映射方式的条件±f=x+2pk/qs是一周期性函数。选择正2pk/qs边形为框架绘制谐波映射轨迹可以反映映射条件的周期性特性。
(2)以正2p/qs边形的任意顶点为起点,记从起点逆时针跳转x个顶点的位置为平面abx和fx次谐波,其中,fx=2pk/qs+x。
(3)当abx与fx次谐波的顶点重合即满足条件±f=x+2pk/qs。如果fx>0,则该谐波在平面上的映射是全映射的正序分量;如果fx<0,映射是全映射的负序分量。

图3 谐波映射轨迹
Fig.3 Harmonic mapping trajectory
部分映射的条件±f=x+kq≠x+2pk/(pqs)也是周期性函数,其中kq是2pk/(pqs)的因数,选择正2pk/(pqs)边形绘制谐波映射轨迹。但由于正2pk/(pqs)边形与周期kq不匹配,部分映射平面会在正2pk/(pqs)边形上周期性重复。
图3a~图3d中,两类DTPM分别选择正十二边形和正十八边形作为全映射框架,正六边形和正九边形作为部分映射框架。所选的子平面以分离1、3、5次电流,并实现唯一正序映射为目标。相移p/6的DTPM能以等幅值的全映射方式分离谐波,而相移p/9的DTPM只能实现不等幅值的部分映射。这是因为相移p/9的DTPM在空间拓上存在相带空缺,导致其谐波在全映射平面ab1、ab3、ab5上不是唯一映射,谐波无法分离。最终只能选平面ab4、ab6、ab8满足1、3、5次电流的唯一映射需求。
通过对比两类DTPM的谐波映射结果,可以得到相带铺满准则:为了实现奇数次谐波的唯一等幅值全映射,在构造AMM时,应优先选择相移角qs=lp/(pq)的相带铺满型拓扑。
2.1.2 谐波成对映射准则
为了降低虚拟AMM相数,同时确保谐波与基波解耦,提出谐波两两一组映射到同一个子平面的谐波成对映射准则。
如图3a所示,在ab1平面上,-11次和1次谐波的阶次差值与ab5平面-7次和5次谐波的阶次差值相等,均为12。与DTPM类似,在全映射方式下,其他拓扑的AMM在任意子平面上也存在一组阶次数差值为2p/qs,并且具有相反相序的谐波。利用这一特征,将两种阶次数差值是2p/qs的谐波成对映射到同一个子平面,以降低虚拟AMM的相数。相移p/6的DTPM中,5次和13次谐波,7次和11次谐波映射分量具有相反相序时,阶次数差值相等,为18。根据这一映射特征,推导出分离5、7、11和13次谐波的虚拟AMM相移角度qs=p/9。
据此,谐波成对映射准则为:频次数差值Df=2p/qs的谐波成对映射到相同子平面,以此降低虚拟AMM相数,此时AMM的相移角qs=2p/Df。
2.1.3 最小相数准则
为缩小虚拟AMM相数的优化范围,还需知道谐波次数与虚拟AMM相数之间的关系,以确立分离谐波所需的最小相数AMM。
p-q相AMM存在Z个线性无关平面,Z满足
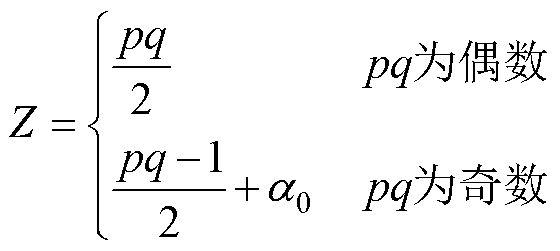 (13)
(13)
式中,a0为广义零序平面ab0的实数轴,奇数相AMM需引入a0单独构成一个实数平面。
根据2.1.2节,DTPM的谐波映射情况为:基波独占一个平面,5次和13次,7次和11次谐波成对映射。由此得出至少需要3个映射子平面,从而推导出虚拟AMM的相数需大于等于6。
据此,最小相数准则为:分离n种不同的谐波,需要1个基波平面以及n/2个谐波平面,虚构电机的相数应大于或等于n+2。
根据上述的三条准则,最优的AMM拓扑选择了相移为p/9的三三相电机(Triple Three-phase Permanent Motor, TTPM),以实现对DTPM的5、7、11和13次谐波的分离,并将这些谐波以全映射方式映射在唯一的子平面上。TTPM对应的映射子平面为a0、ab1、ab3、ab7、ab13。谐波轨迹已在图3e、图3f中给出。
为构造虚拟p-q相AMM,需通过相电流移相操作,获得与虚拟AMM各相绕组在空间上具有相同相位差的虚拟相电流。
对于相移p/6的DTPM,ABC、DEF绕组单元的相位分别为0和-p/6。而TTPM的A1B1C1、A2B2C2、A3B3C3绕组单元,其相位分别为0、-p/9和-2p/9。为降低数据更新的延迟,应选择相位超前最小的真实电流进行移相虚构电流。电流相移过程如图4所示,其中,IA1B1C1用IABC替代,IA2B2c2以IABC移相p/9虚构,IA3B3c3以IDEF移相p/18虚构。
构造虚拟AMM后还需利用VSD将谐波分离到各子平面,本文所选映射平面对应的VSD矩阵为
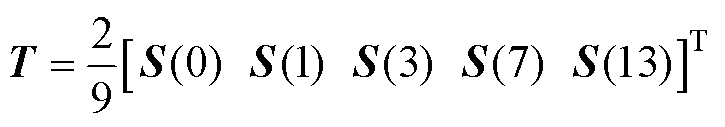 (14)
(14)
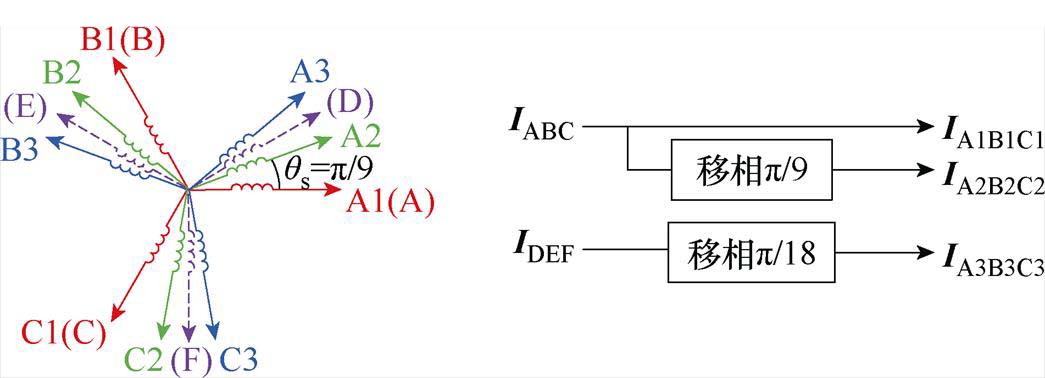
图4 电流移相示意图
Fig.4 Schematic diagram of current phase shift
基于式(14),有TTPM的相电流映射到正交子平面上的坐标变换式为
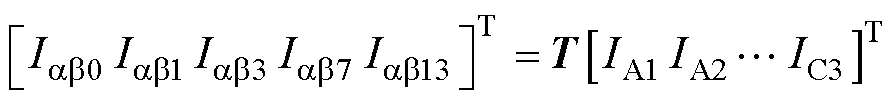 (15)
(15)
在相移qs的AMM中,任意子平面上相反相序的相邻频率谐波分量表达式为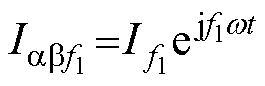 和
和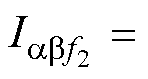
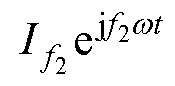 ,根据映射规律可知,两分量的阶次数差值f1- f2=2p/qs。通过式(16),分量的阶次数被整合成±p/qs次。
,根据映射规律可知,两分量的阶次数差值f1- f2=2p/qs。通过式(16),分量的阶次数被整合成±p/qs次。
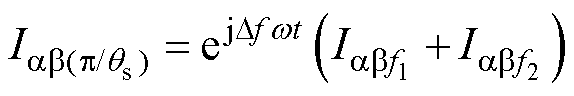 (16)
(16)
其中
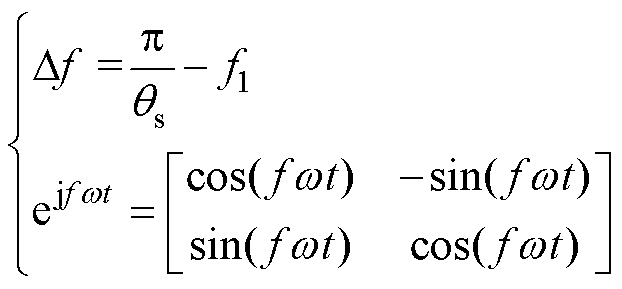 (17)
(17)
式中,ejDfwt为线性空间旋转变换因子。
变换后,正负序分量的频率被统一,用单个谐振阶次数为p/qs的PR控制器即可同时控制一个子平面上的两种谐波。
对于TTPM,利用线性空间旋转变换ej2fwt,子平面ab7上的7次谐波分量I7ej7wt和11次谐波分量I11e-j11wt被整合为±9倍频谐波分量。同样地,ab13上的5次谐波I5ej-5wt和13次谐波I13ej13wt被线性空间旋转变换e-j4fwt也整合为±9倍频谐波分量。最终,用谐振点为9倍基频的PR控制器统一调控谐波。
控制器输出是虚拟AMM的电压指令,这些指令还需还原为真实电机的电压指令值。首先,需要通过线性空间旋转逆变换,使PR控制器输出的指令电压还原成频率整合前的原始频率。然后,再经过逆VSD变换,得到虚拟TTPM的相电压给定指令。最后,通过移相操作,将虚拟TTPM的相电压指令还原成与真实DTPM相位一致的相电压指令值。
综合上述步骤,得到了基于谐波映射规律的DTPM单频率PR谐波抑制策略框图,如图5所示。
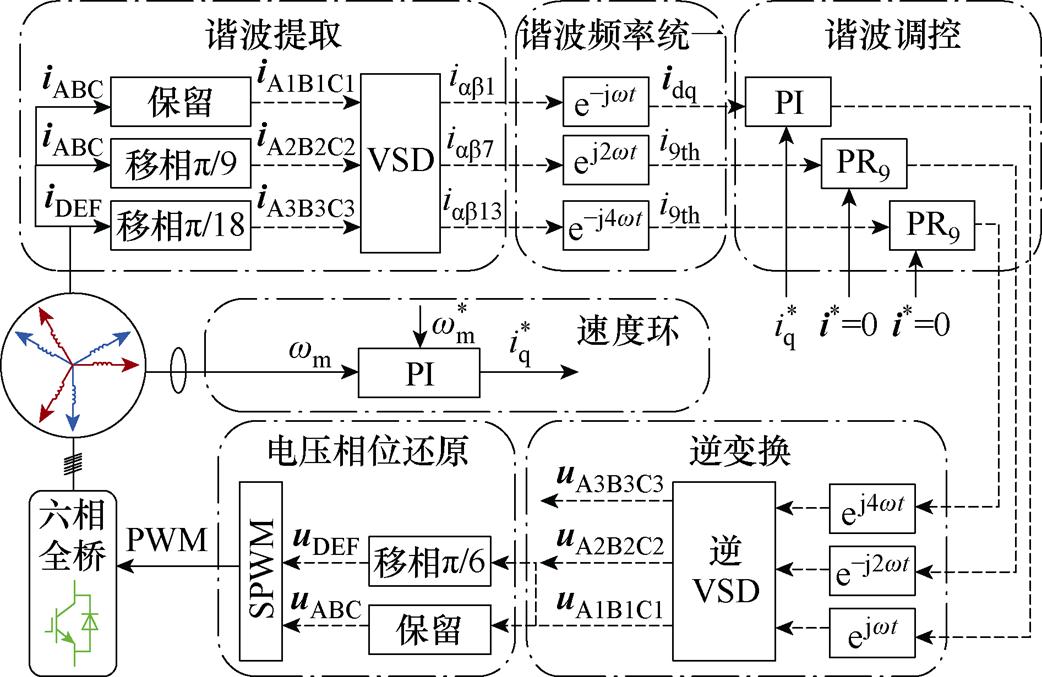
图5 DTPM的谐波抑制策略框图
Fig.5 Diagram of harmonic suppression for DTPM
谐波电流的频率统一为9倍基频后,两组谐波电流环的控制框图相同,如图6所示。图6中,Td为控制周期;Rs、Lz分别为相电阻、漏感;kp、kr分别为比例、谐振增益系数;w、wc分别为谐振角频率、谐振带宽频率;uh为电压扰动信号;j 为相位滞后角。
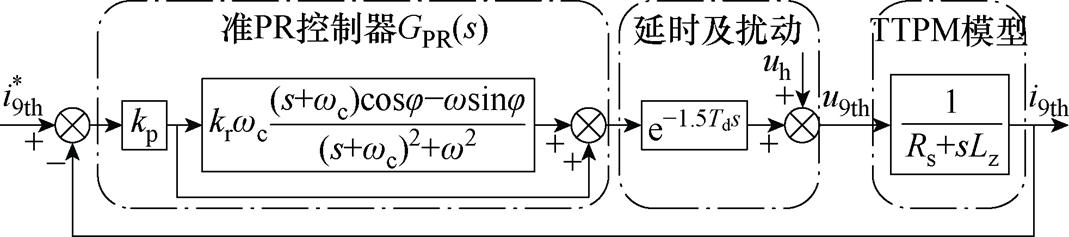
图6 9次谐波电流环控制框图
Fig.6 Diagram of 9th harmonic current loop control
控制框图包括准PR控制器、延时及扰动和TTPM谐波轴电机数学模型三个环节。为降低相位滞后,采用了引入相位补偿的串联型准PR控制器GPR(s)。代入控制器表达式后,谐波电流环的开环传递函数为
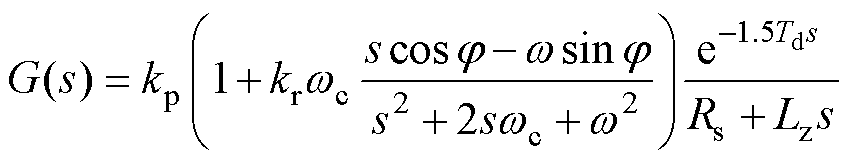 (18)
(18)
电流环动态响应速度远高于反电动势,因此求解电机模型的传递函数时只考虑阻抗模型。
首先对比例增益系数kp进行参数整定。忽略谐振环节和扰动环节,将延时环节等效为一阶惯性环节后整个系统的开环传递函数为
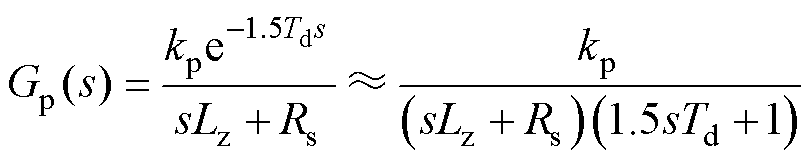 (19)
(19)
电机及其驱动器的相关参数见表1。10 kHz开关频率对应的控制周期Td=100 ms。代入电机参数,由控制系统的截止频率小于1/10开关频率这一限制条件,算得此时kp的极大值kpMax=1.051 1。
表1 电机及其驱动器参数
Tab.1 Motor and its driver parameters
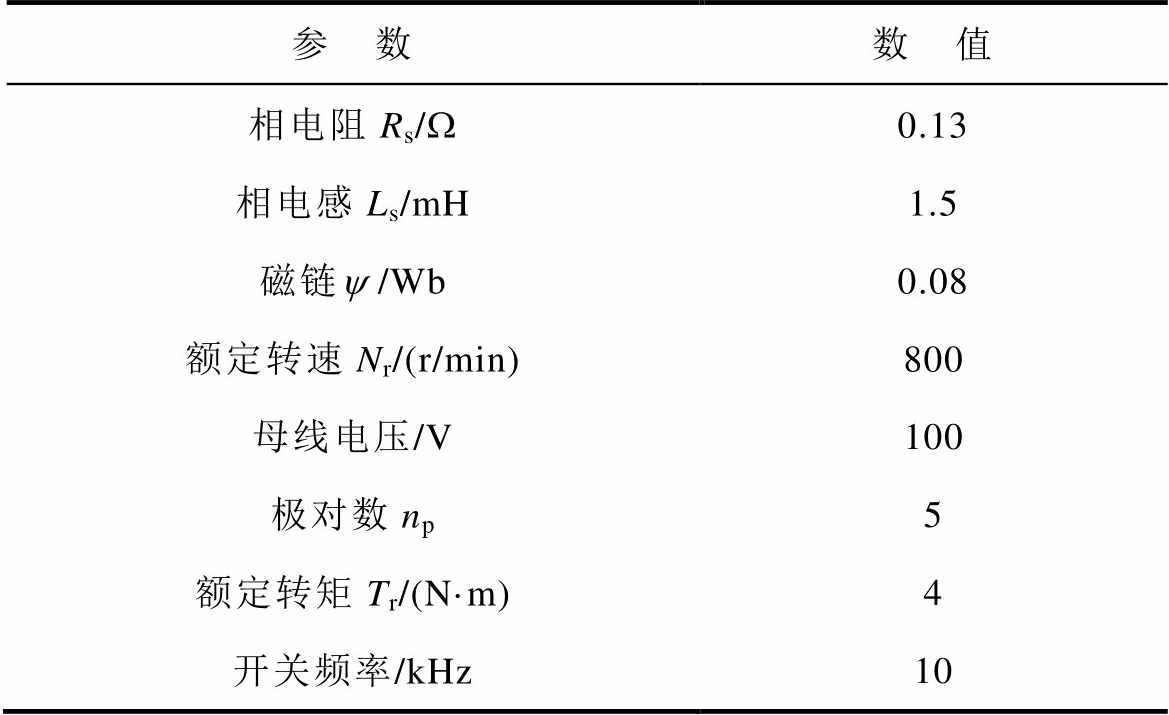
参 数数 值 相电阻Rs/W0.13 相电感Ls/mH1.5 磁链y /Wb0.08 额定转速Nr/(r/min)800 母线电压/V100 极对数np5 额定转矩Tr/(N·m)4 开关频率/kHz10
然后设计谐振增益系数kr。kp=1.051 1,kr=40,wc=5rad/s,增加w 为300p, 600p, 900p, 1 200p。开环传递函数G(s)随各参数变化的Bode图如图7所示。图7a给出了开环传递函数G(s)随着谐振角频率w 变化的Bode图。相同kp和kr,随着w 增加,谐振频率点的幅值减小,相位裕度降低,而非谐振点幅值和相位保持一致。因此,变谐振频率过程整定kr只需要关注电机运行最高转速800 r/min对应9倍基频的谐振角频率1 200p 即可。
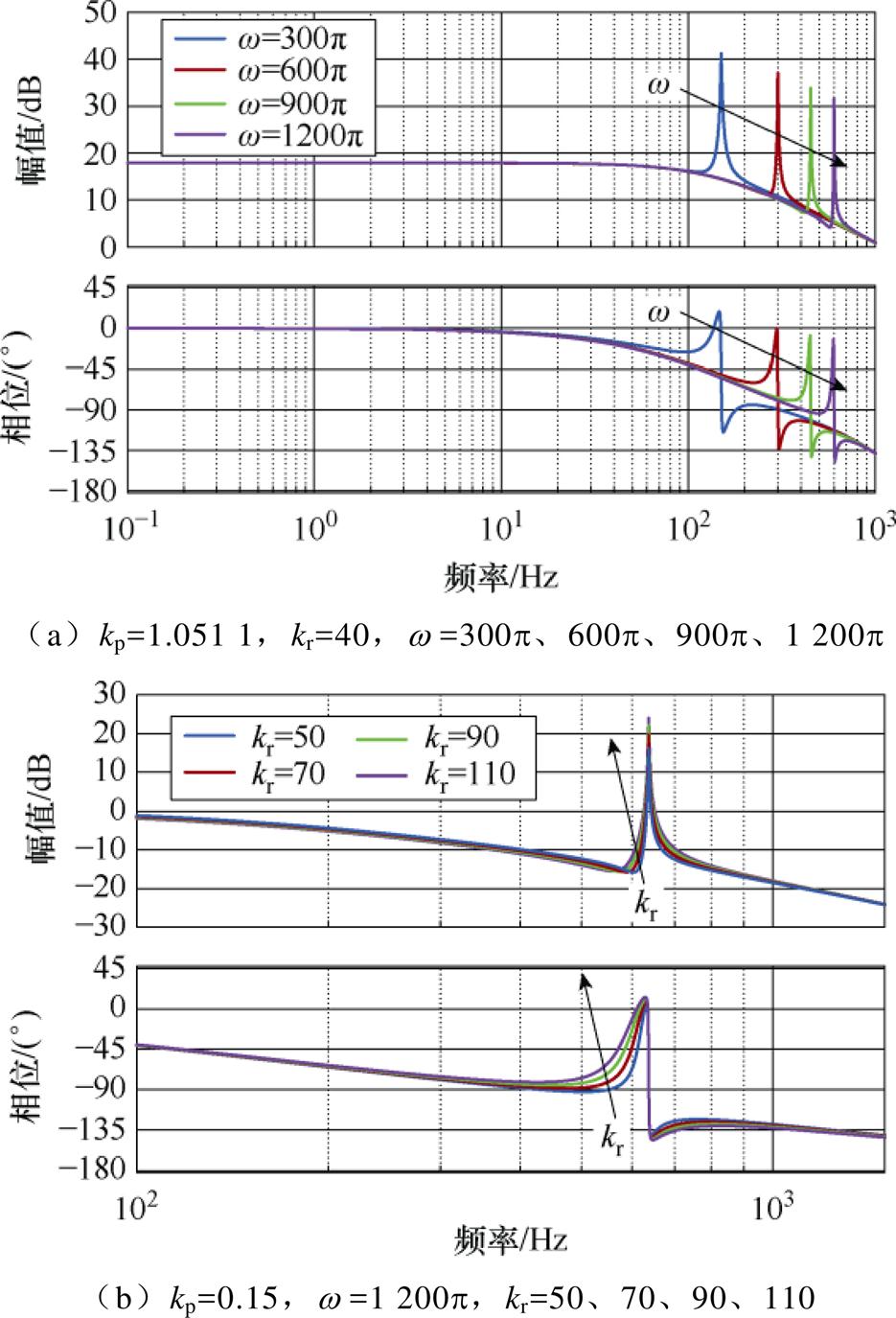
图7 开环传递函数G(s)随各参数变化的Bode图
Fig.7 Bode diagram of transfer function G(s) varying with parameters
若系统跟踪误差要求小于5%,则控制系统闭环传递函数的增益需满足
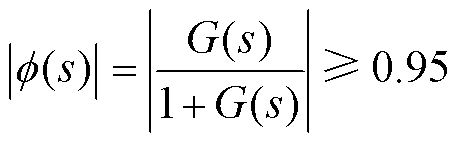 (20)
(20)
此时开环传递函数在谐振频率处的对数幅值需大于25 dB。代入kp最大值以及电机参数计算得到满足等式(20)的最小值krMin=27。
kp只改变开环传递函数的幅值,而不影响相位裕度。在不明显改变截至频率和相位裕度的情况下,应尽可能增大kr,使PR控制器有更好的选频特性。图7a中已满足谐振频率点的幅值和相位要求,但非谐振频率处的对数幅值仍然过大,控制无法滤除非谐振频率谐波。需要进一步减小kp,增大kr,削弱全频段的对数幅值,同时抵消由于kp变小而导致的谐振频率处幅值降低。
图7b为开环传递函数G(s)随着kr变化的Bode图。设置kp=0.15(在图7a基础上减小17 dB全频段的对数幅值),增加kr=50、70、90、110。随着kr增加,谐振频率处的幅值增加,相位裕度几乎没有改变。直至kr增加至110才弥补上因kp降低而减少的幅频响应值。最终,选择kp=0.15,kr=110,此时相位裕度为38°。当kp和kr增加时,电流环带宽会增大,动态性能提高,但同时非谐振点的电流纹波也会增加,因此实际选择参数时需要折衷。
另外,开环传递函数G(s)无右半平面的极点,而在幅值大于0 dB的频率区间内,相频曲线没有穿越-180°,正、负穿越次数是0。因此,根据奈奎斯特对数稳定判据可以判定系统稳定。
为验证所提控制策略的谐波提取性能和谐波抑制效果,分别进行了谐波注入实验和稳、动态低速运行实验。实验基于主控为TMS320F28335的两电平六相驱动器控制的对拖电机平台,如图8所示,主要的实验参数已在表1中列出,实验框图如图5所示。
由于受控电机反电动势呈正弦,并且气隙均匀,实验通过注入谐波电压来产生较大的谐波电流,以验证谐波提取算法的有效性。实验期间,电机空载,采用电压开环控制,死区时间设置为1 ms。为了便于观察相序,谐波注入分两次进行:一次注入5和13次谐波,另一次注入7和11次谐波。两次注入的基波均为16.67 Hz的13 V正弦电压,注入的5和7次,11和13次谐波电压幅值分别为2 V和6 V。提取谐波通过电流移相构造的虚拟TTPM来实现。

图8 实验平台
Fig.8 Experimental platform
4.1.1 5、7次电流提取实验结果
图9为注入5、7次电压后的实验波形,通过快速傅里叶变换(Fast Fourier Transform, FFT)可知,谐波电压主要引入了5、7次谐波电流,幅值分别为1.59 A、1.52 A。图10为5、7次谐波电流的提取波形以及提取谐波的FFT分析结果。观察图10,主动引入的5、7次谐波电流分别被分离到ab13和ab7平面中,其中ab7平面上只含有7次谐波分量,且a分量ia7相位上超前b 分量ib7,ab13平面上只含有5次谐波分量,且a 分量ia7相位上滞后b 分量ib7,与图3a的谐波映射轨迹分析结果一致。表2为整理所得的相电流与提取谐波电流的FFT结果,可发现提取的5、7次谐波电流幅值分别为1.51 A、1.46 A,达到了实际谐波幅值1.59 A、1.52 A的95%和96%。
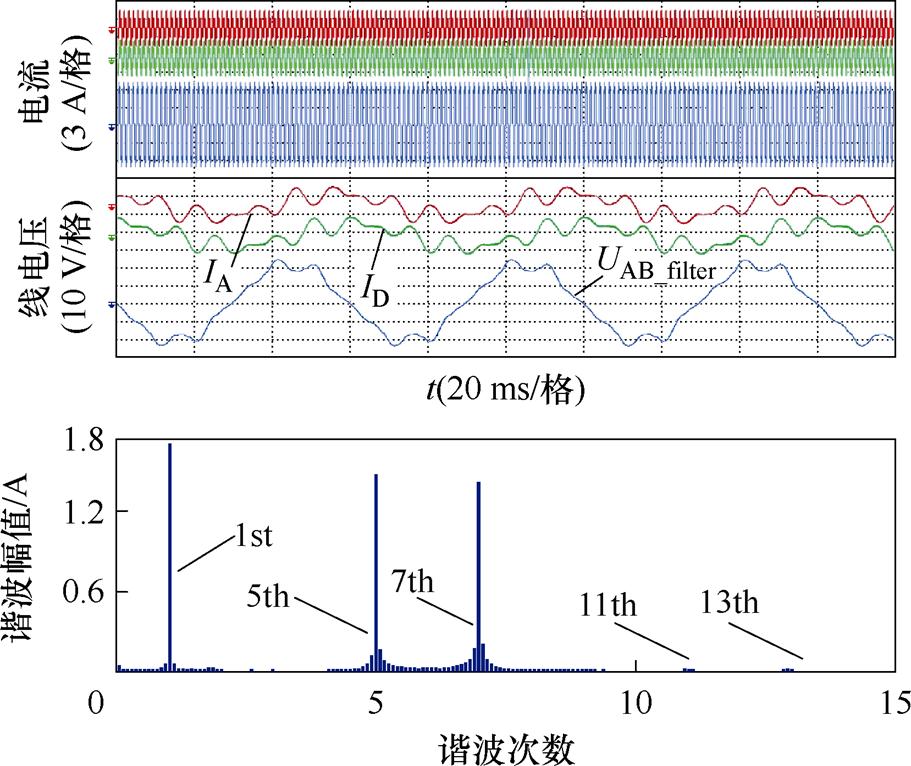
图9 注入5、7次谐波电压后的波形和IA的FFT结果
Fig.9 Waveforms injecting 5th, 7th voltages and FFT of IA
4.1.2 11、13次电流提取实验结果
图11为注入11、13次谐波电压后的实验波形,其中,相电流的5、7、11和13次谐波幅值分别为0.14、0.10、0.51、0.43 A。图12为谐波提取结果,5次、13次和7、11次谐波分别被成对映射到ab13和ab7平面。由于死区的存在,引入了少部分5、7次谐波,但11次和13次谐波占主要部分,从图12中仍可以反映11、13次谐波的相序。其中,11次是负序谐波,13次是正序谐波。注入11、13次谐波后的电流FFT结果见表3。对比发现,本文采用谐波提取算法,实现了5、7、11、13次电流幅值分别达到实际谐波幅值的93%、92%、94%及95%。
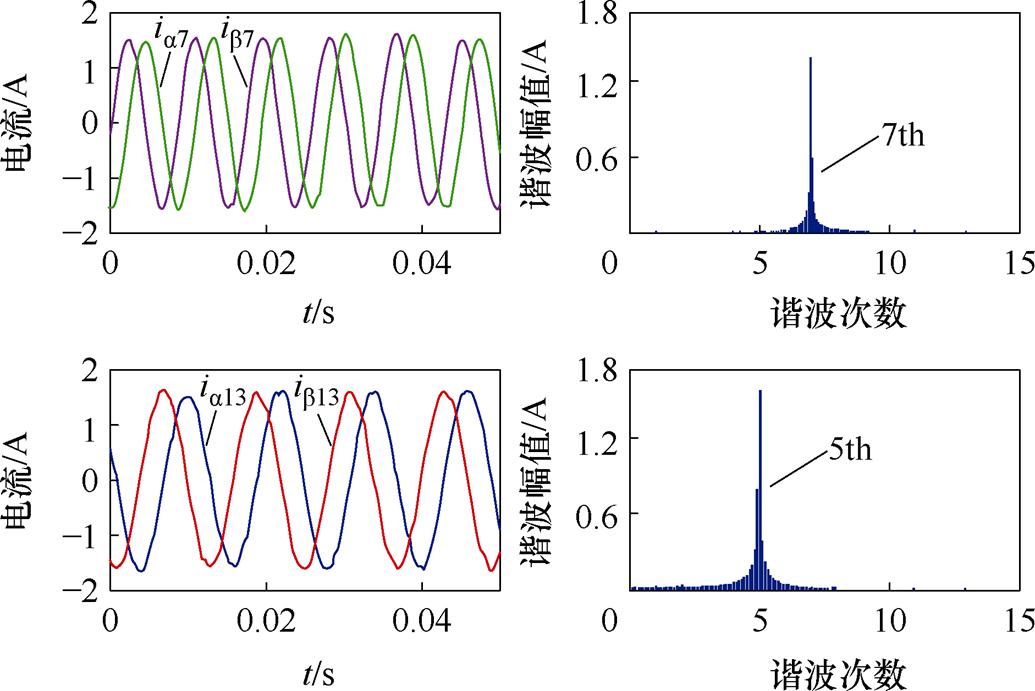
图10 5、7次谐波电流提取结果
Fig.10 Extraction of 5th , 7th harmonic currents
表2 注入5、7次谐波后的电流FFT结果
Tab.2 FFT results of current after 5th and 7th harmonic injection (单位: A)
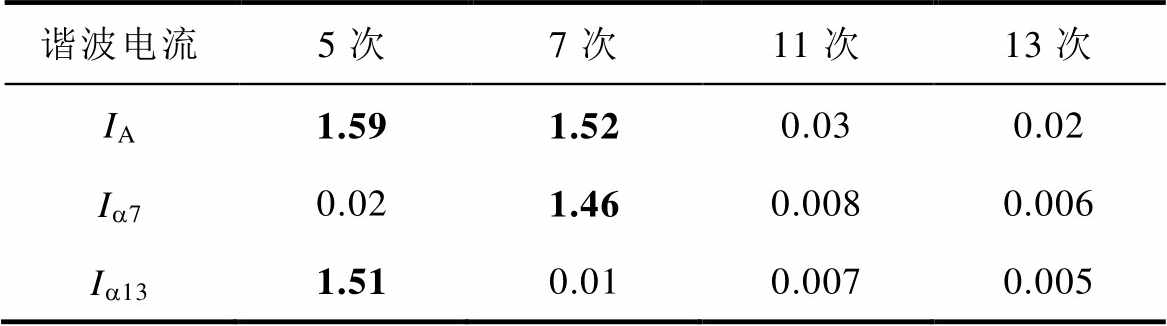
谐波电流5次7次11次13次 IA1.591.520.030.02 Ia70.021.460.0080.006 Ia131.510.010.0070.005

图11 注入11、13次谐波电压后的波形及IA的FFT结果
Fig.11 Waveforms injecting 11,13th voltages and FFT of IA

图12 11、13次谐波电流提取结果
Fig.12 Extraction results of 11th , 13th currents
表3 注入11、13次谐波后的电流FFT结果
Tab.3 FFT results of current after 11th and 13th harmonic injection (单位: A)
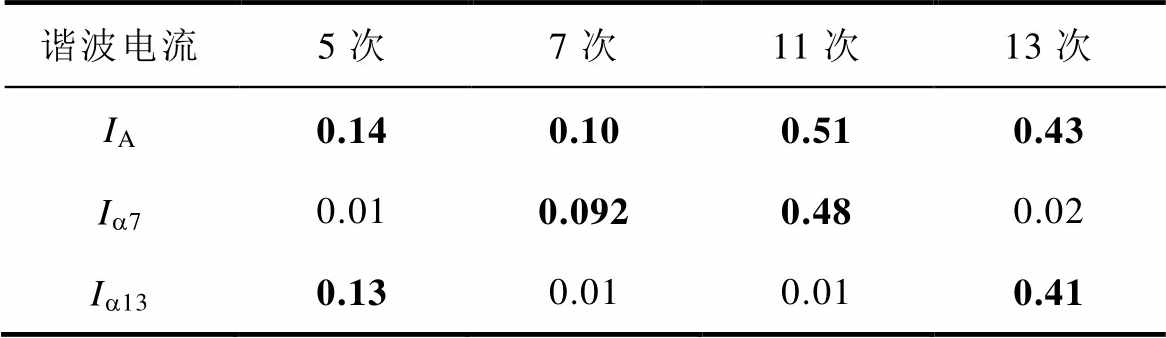
谐波电流5次7次11次13次 IA0.140.100.510.43 Ia70.010.0920.480.02 Ia130.130.010.010.41
综上所述,提取的电流幅值还原度可达原谐波的92%以上,映射谐波相序也与理论一致。
实验中通过设置较大死区(3 ms)产生谐波电流,在不同工况下分别对无谐波抑制策略(纯PI控制)、多同步旋转系下的电流谐波抑制(Multiple Synchronous Reference Frame, MSRF)策略[23]以及本文所提谐波抑制策略进行对比实验。其中,无谐波抑制策略组为对照组,以反映相电流的原始谐波含量。
4.2.1 稳态工况谐波抑制实验
给定恒定4 N·m额定负载,初始速度为200 r/min,依次在第2、5、8 s阶跃至400、600、800 r/min。图13为全速过程下的电流、电压波形。无谐波抑制算法的对照组实验中相电流过零点以及波峰有明显畸变,线电压UAB均较正弦,表明无主动注入电压谐波来抑制电流畸变。稳态下的谐波电流峰值高达0.83 A,且全速工况下的谐波幅值接近。相比于传统PI,MSRF策略控制下的相电流全速工况下正弦度均有所提升,稳态下的谐波电流峰值最高只有0.57 A。采用本文的谐波抑制策略后,在200 r/min低速时能观察到主动注入的线电压谐波,相电流正弦度有明显提升。在额定转速(800 r/min)下,尽管由于控制载波比降低导致谐波抑制效果有所下降,但与对照组和MSRF策略组相比,谐波峰值(0.36 A)更低,相电流仍更正弦,波形抖振更少。
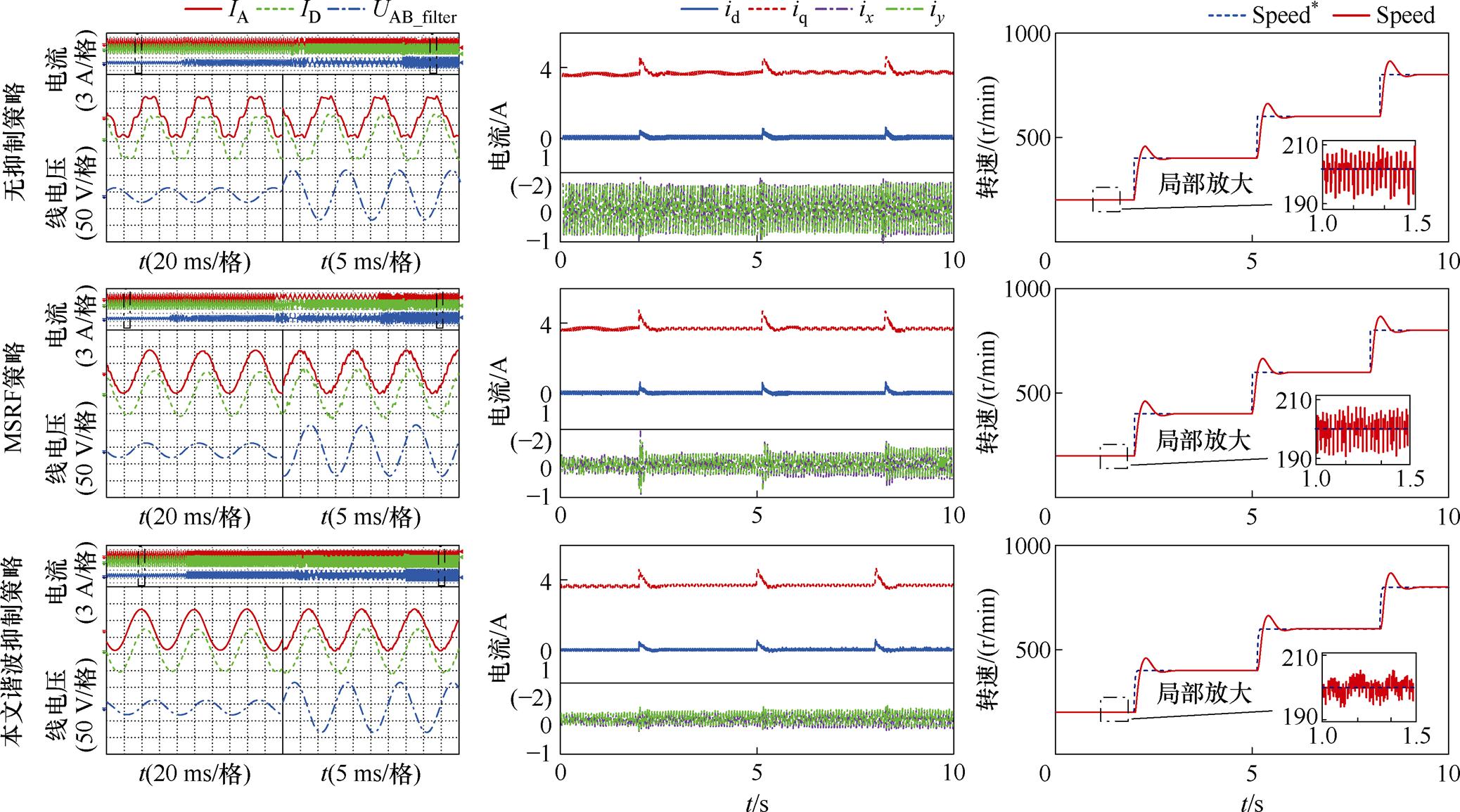
图13 稳态实验波形
Fig.13 Steady state experimental waveforms
谐波在低速下的危害更大,因此将200 r/min下的相电流IA进行FFT分析以对比三种算法的谐波抑制效果,FFT结果在图14中给出。对比FFT结果,采用本文谐波抑制策略后,总谐波畸变率(Total Harmonic Distortion, THD)由对照组的15.68%和MSRF组的7.21%降至3.12%。相比对照组,5、7、11、13次谐波电流占比分别从原始含量的13.92%、5.31%、4.05%、2.96%分别下降至3.02%、0.43%、0.39%、1.19%。与MSRF相比,所提策略不会引入额外的17次电流谐波。此外,转速波动也分别由对照组的±8.6 r/min,MSRF组的±7.2 r/min降低至所提策略组的±3.7 r/min。
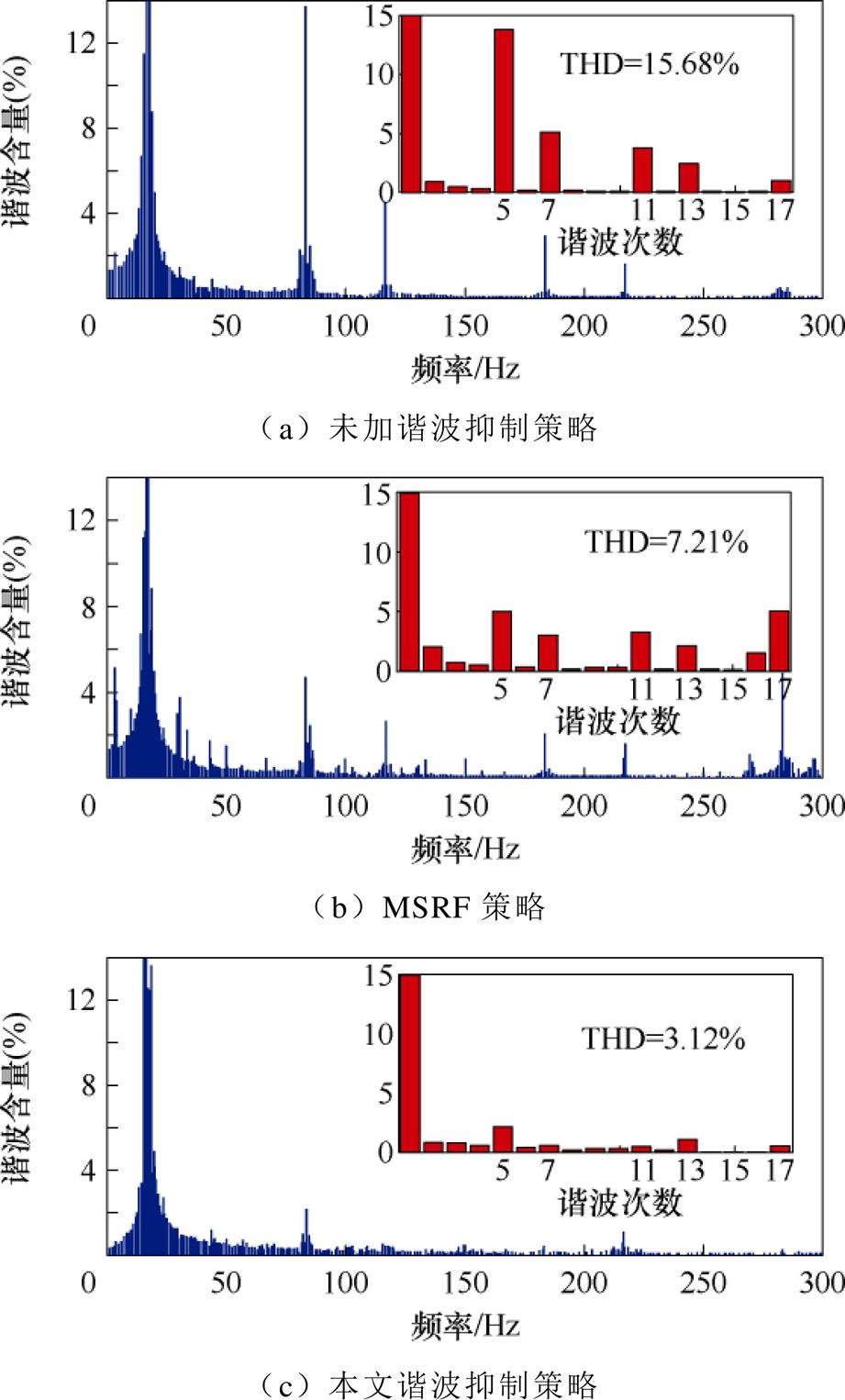
图14 200 r/min工况下,相电流IA的FFT结果
Fig.14 FFT results of IA under 200 r/min
实验结果表明,本文所提抑制策略在全速段具有良好的谐波抑制能力。
4.2.2 动态工况谐波抑制鲁棒性实验
为了验证动态过程中谐波抑制鲁棒性,本文进一步开展了MSRF策略和本文谐波抑制策略在负载和转速突变的动态工况下的鲁棒性对比实验。负载突变实验中,转速保持额定转速800 r/min,由空载阶跃至额定负载4 N·m。而转速突变实验中,保持额定4 N·m负载,转速由200 r/min阶跃至800 r/min。
图15为两种控制策略下的转速阶跃过程的波形,二者的转速响应的上升时间均小于0.2 s。由于本文策略无滤波器,其上升时间由MSRF控制策略组的142 ms下降至128 ms。此外,转速突变过程中的谐波由MSRF控制策略组的1.5 A峰值降低至所提控制策略组的0.6 A。

图15 转速阶跃过程的动态实验波形
Fig.15 Experimental waveforms of speed step dynamic processes
图16为负载突变对比实验的波形。对比MSRF策略,本文所提策略具有更快的负载动态能力,空载至满载过程转速最低值为351 r/min,比MSRF控制策略组高127 r/min。同时,动态过程的谐波峰峰值也由MSRF控制策略组的0.65 A降低至本文抑制策略的0.46 A。
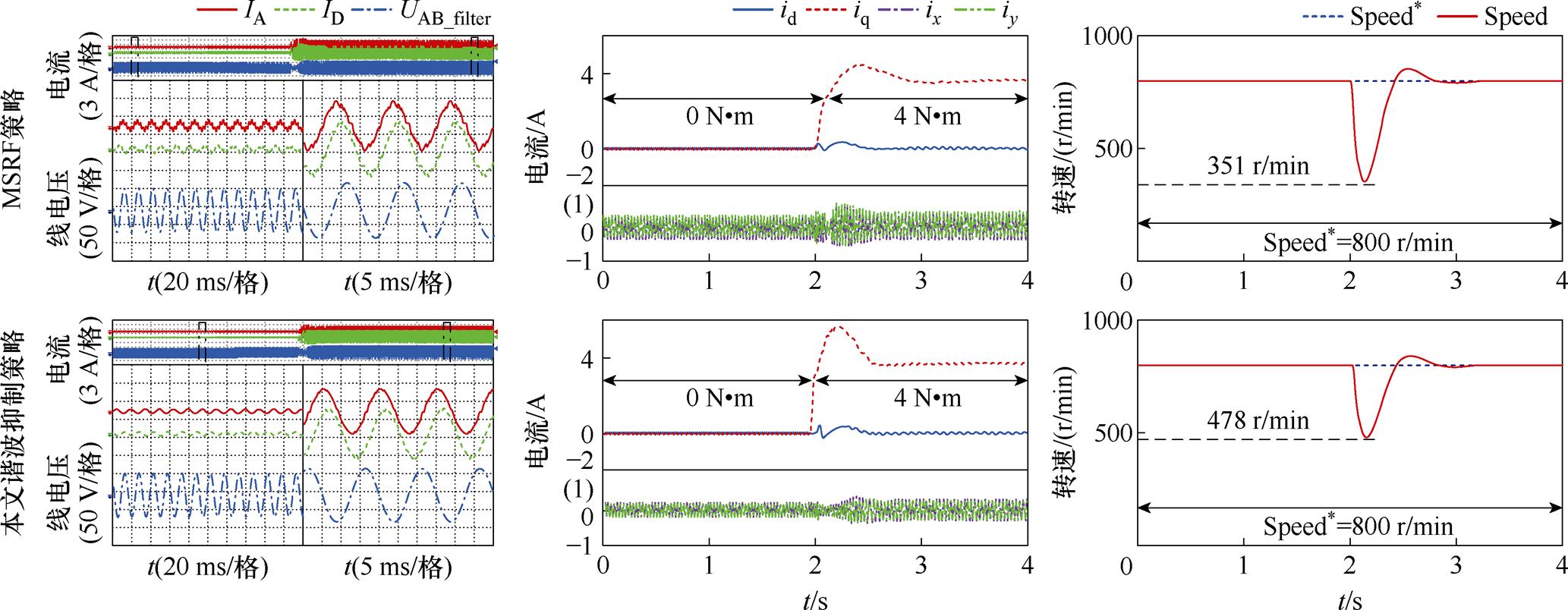
图16 负载阶跃过程的动态实验波形
Fig.16 Experimental waveforms of load step dynamic processes
实验结果表明,所提抑制策略即使在动态响应过程中也能保持良好的谐波抑制鲁棒性,并具有优良的动态跟踪性能。
为降低AMM由谐波提取器以及多种频率PR控制器给谐波抑制算法带来的复杂度,本文提出了一种无滤波器的单频率PR控制器统一谐波抑制算法,并设计双三相电机谐波抑制实验,得出以下结论:
1)谐波的映射方式有等幅值的全映射及幅值变小的部分映射两种。映射分量相序同样有a 分量超前或滞后b 分量p/2两种。幅值和相序由绕组最小单元数、单元之间的相移角和映射子平面共同决定。
2)基于谐波映射规律创立了最优AMM拓扑选取准则,并通过电流移相构造虚拟AMM来提取谐波,有效避免了构造滤波器或谐波观测器带来的谐波提取复杂且不准确的问题。
3)利用所选子平面上的谐波成对映射,且频率阶次数差值相等、相序相反的特征,采用线性空间旋转坐标变换整合谐波频率,使得一半谐波数量的单频率PR控制器即可调控所有谐波,有效解决了传统算法抑制多频次谐波时需要大量PR控制器以及PR控制器谐振频率不同带来的多次调参问题。
4)采用所提策略后,提取谐波的幅值能达到原幅值的92%以上,5、7、11和13次谐波电流的占比分别由抑制前的13.92%、5.31%、4.05%、2.96%降至3.02%、0.43%、0.39%、1.19%,且在全速域运行工况下具有良好的谐波抑制鲁棒性。
参考文献
[1] 孙玉华, 赵文祥, 吉敬华, 等. 高转矩性能多相组永磁电机及其关键技术综述[J]. 电工技术学报, 2023, 38(6): 1403-1420.
Sun Yuhua, Zhao Wenxiang, Ji Jinghua, et al. Overview of multi-star multi-phase permanent magnet machines with high torque performance and its key technologies[J]. Transactions of China Electrotech- nical Society, 2023, 38(6): 1403-1420.
[2] Huang Linsen, Ji Jinghua, Tao Tao, et al. Remedial direct torque control for dual three-phase permanent- magnet motor with harmonic torque suppression[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 11085-11097.
[3] 金石, 朱熙, 金无痕, 等. 基于谐波提取器的永磁同步电机谐波抑制方法[J]. 电气工程学报, 2021, 16(1): 9-15.
Jin Shi, Zhu Xi, Jin Wuhen, et al. Harmonic supper- ssion method of permanent magnet synchronous motor based on harmonic extractor[J]. Journal of Electrical Engineering, 2021, 16(1): 9-15.
[4] 刘伟, 刘磊. 基于电流预测及谐波抑制的双三相永磁同步电动机容错控制研究[J]. 电气技术, 2023, 24(7): 20-25, 33.
Liu Wei, Liu Lei. Research on fault-tolerant control of dual three-phase permanent magnet synchronous motor based on current prediction and harmonic suppression[J]. Electrical Engineering, 2023, 24(7): 20-25, 33.
[5] 李帅, 孙立志, 刘兴亚, 等. 永磁同步电机电流谐波抑制策略[J]. 电工技术学报, 2019, 34(增刊1): 87-96.
Li Shuai, Sun Lizhi, Liu Xingya, et al. Current harmonics suppression strategies of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 87-96.
[6] 宁继超, 贲洪奇, 王雪松, 等. 带有死区时间补偿及电容电压平衡功能的二极管钳位型三电平逆变器数字调制方法[J]. 电工技术学报, 2024, 39(20): 6444-6461.
Ning Jichao, Fen Hongqi, Wang Xuesong. A digital modulation method for dead-time compensation and capacitor voltage balance in diode clamped three- level inverters[J]. Transactions of China Electro- technical Society, 2024, 39(20): 6444-6461.
[7] Zhang Xiaoguang, Cheng Yu, Zhao Zhihao, et al. Optimized model predictive control with dead-time voltage vector for PMSM drives[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(3): 3149- 3158.
[8] Liu Senyi, Liu Chunhua. Virtual-vector-based robust predictive current control for dual three-phase PMSM[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(3): 2048-2058.
[9] 武雪松, 宋文胜, 薛诚. 基于虚拟电压矢量集占空比优化的五相永磁同步电机直接转矩控制算法[J]. 中国电机工程学报, 2019, 39(3): 857-867.
Wu Xuesong, Song Wensheng, Xue Cheng. Direct torque control schemes for five-phase permanent- magnet synchronous machines based on duty ratio optimization of virtual voltage vector sets[J]. Pro- ceedings of the CSEE, 2019, 39(3): 857-867.
[10] 冯婉, 张文娟, 苗轶如, 等. 基于dq坐标系下6次谐波抑制的车用感应电机低频共振削弱方法[J]. 电工技术学报, 2023, 38(24): 6632-6645.
Feng Wan, Zhang Wenjuan, Miao Yiru, et al. Low frequency resonance reduction method of induction motor used by electric vehicle based on sixth harmonic suppression in dq coordinate[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(24): 6632-6645.
[11] Wang Wusen, Liu Chunhua, Liu Senyi, et al. Current harmonic suppression for permanent-magnet syn- chronous motor based on Chebyshev filter and PI controller[J]. IEEE Transactions on Magnetics, 2021, 57(2): 8201406.
[12] Yan Luocheng, Zhu Ziqiang, Qi Ji, et al. Multiple synchronous reference frame current harmonic regulation of dual three phase PMSM with enhanced dynamic performance and system stability[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 8825-8838.
[13] Yan Luocheng, Zhu Ziqiang, Qi Ji, et al. Suppression of major current harmonics for dual three-phase PMSMs by virtual multi three-phase systems[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 5478-5490.
[14] 余洋, 余宗哲, 王孟云, 等. 机械弹性储能用永磁同步电机多源谐波提取及统一抑制[J]. 电工技术学报, 2024, 39(4): 1033-1045, 1073.
Yu Yang, Yu Zongzhe, Wang Mengyun, et al. Multi- source harmonic extraction and unified suppression of permanent magnet synchronous motor for mechanical elastic energy storage[J]. Transactions of China Elec- trotechnical Society, 2024, 39(4): 1033-1045, 1073.
[15] 张剑, 温旭辉, 李文善, 等. 基于谐波观测器的永磁同步电机谐波电流抑制策略研究[J]. 中国电机工程学报, 2020, 40(10): 3336-3349.
Zhang Jian, Wen Xuhui, Li Wenshan, et al. Research on harmonic current suppression strategies of permanent magnet synchronous motor systems based on harmonic observers[J]. Proceedings of the CSEE, 2020, 40(10): 3336-3349.
[16] 王硕, 康劲松. 一种基于自适应线性神经网络算法的永磁同步电机电流谐波提取和抑制方法[J]. 电工技术学报, 2019, 34(4): 654-663.
Wang Shuo, Kang Jinsong. Harmonic extraction and suppression method of permanent magnet syn- chronous motor based on adaptive linear neural network[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 654-663.
[17] 沈宏源, 吴新振, 王海峰, 等. 九相开绕组永磁电机SPWM中的三次谐波抑制[J]. 中国电机工程学报, 2023, 43(5): 1992-2000.
Shen Hongyuan, Wu Xinzhen, Wang Haifeng, et al. Suppression of third harmonic caused by SPWM for a nine-phase open-end winding permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2023, 43(5): 1992-2000.
[18] Xu Jiaqun, Wei Zhenqiang, Wang Shikai. Active disturbance rejection repetitive control for current harmonic suppression of PMSM[J]. IEEE Transa- ctions on Power Electronics, 2023, 38(11): 14423- 14437.
[19] Wang Xiaosheng, Jiang Chaoqiang, Zhuang Feifei, et al. A harmonic injection method equivalent to the resonant controller for speed ripple reduction of PMSM[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(10): 9793-9803.
[20] 孙嘉伟, 郑泽东, 李驰, 等. 对称型多相电机断相容错运行下的电流谐波分析与补偿[J]. 电工技术学报, 2022, 37(21): 5424-5434.
Sun Jiawei, Zheng Zedong, Li Chi, et al. Analysis and compensation of current harmonics in symmetrical multiphase machines in fault-tolerant operation against open-phase faults[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5424-5434.
[21] González-Prieto I, Duran M J, Gonzalez-Prieto A, et al. A simple multistep solution for model predictive control in multiphase electric drives[J]. IEEE Transactions on Industrial Electronics, 2024, 71(2): 1158-1169.
[22] González-Prieto A, González-Prieto I, Duran M J. Smart voltage vectors for model predictive control of six-phase electric drives[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 9024-9035.
[23] Karttunen J, Kallio S, Honkanen J, et al. Partial current harmonic compensation in dual three-phase PMSMs considering the limited available voltage[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1038-1048.
Abstract The coupling between spatial-harmonic and time-harmonic currents in asymmetric multiphase motors (AMM) increases torque ripple and decreases efficiency, limiting their widespread application. Currently, active harmonic suppression strategies rely on complex filters or observers to extract harmonics and require the construction of numerous proportional resonance (PR) controllers at different frequencies, making the complexity and impracticality of harmonic suppression. Therefore, this paper proposes a single-frequency PR harmonic suppression strategy without filters based on the harmonic mapping law.
Firstly, based on the magnetic electromotive force equivalence principle, the universal space vector decoupling matrixes for AMM are established. Then, a mapping formula for harmonics of different frequency components on the subspaces is established. The general formula is decomposed into two independent components: amplitude and phase. The amplitude and phase mapping law of harmonics on the subspaces is derived according to the characteristics of the two components. Secondly, three criteria are proposed to search for the AMM with the minimum number of phases to ensure the unique mapping of harmonics. Based on the graphical representation of the mapping laws, the mapping trajectories of all harmonics are obtained to optimize the AMM topology and establish the subspaces for harmonic mapping. Then, based on the current phase-shifting method, a virtual AMM is constructed, and harmonics are extracted through the vector decoupling transformation subspaces. Finally, after unifying the frequency through linear space rotation transformation, PR controllers with the same resonant frequency are used to regulate harmonics.
Harmonic extraction and suppression experiments under steady-state and transient conditions are conducted using a dual three-phase motor. The extracted harmonic amplitudes can reach over 92% of the actual harmonics, demonstrating that the proposed algorithm can effectively separate harmonics. In the harmonic suppression experiment, the strategies of no harmonic suppression, current harmonic suppression under multiple synchronous rotating frames, and the proposed harmonic suppression strategy are compared. The proposed strategy decreases the proportions of the 5th, 7th, 11th, and 13th harmonic currents from 13.92%, 5.31%, 4.05%, and 2.96% before suppression to 3.02%, 0.43%, 0.39%, and 1.19%, respectively. The total harmonic distortion (THD) is decreased from 15.36% to 2.86%. Moreover, the harmonic suppression exhibited robustness under various operating conditions across the entire speed range.
The following conclusions can be drawn. (1) There are two harmonic mapping methods: full mapping with equal amplitudes and partial mapping with reduced amplitudes. The phase of mapping components can be divided into the a component leads or lags the b component by p/2. (2) Based on the harmonic mapping law, an optimal AMM topology selection criterion is established, and a virtual AMM is constructed, effectively avoiding the complex and inaccurate problem of harmonic extraction caused by constructing filters or harmonic observers. (3) The features of harmonic pair mapping on the selected subspace are that the difference in frequency order is equal, and the phase sequence is opposite. Thus, linear spatial rotation coordinate transformations are applied to unify frequencies, which enables single-frequency PR controllers with half the number of harmonics to regulate all harmonics.
Keywords:Asymmetric multiphase motor, harmonic suppression, virtual motor, single frequency PR control, harmonic mapping law
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240560
国家自然科学基金(52207037)和电磁能技术全国重点实验室课题(61422172220203)资助项目。
收稿日期 2024-04-10
改稿日期 2024-05-10
周 豪 男,1997年生,博士研究生,研究方向为多相电驱系统谐波抑制、故障诊断及其容错控制。
E-mail: zhouhao@cqu.edu.cn
向学位 男,1993年生,副研究员,硕士生导师,研究方向为电机系统设计、控制与故障诊断。
E-mail: xueweixiang@cqu.edu.cn(通信作者)
(编辑 崔文静)