（1）
摘要 在以变频器驱动的永磁同步电机控制系统中，传统的空间矢量脉宽调制（SVPWM）技术会在逆变器开关频率及其倍频处产生高频电流谐波，进而导致永磁同步电机在运行过程中产生较大的高频电磁振动。因此，提出一种随机开关频率与随机零矢量结合的双随机SVPWM控制方法，应用于永磁同步电机高频电流谐波频谱扩展中，该方法可分散集中在开关频率及其倍频处的高频谐波，有效地削弱高频电磁振动。同时，采用改进梅森旋转（MT）算法生成随机数，增强了随机序列的随机性和空间遍历性，保证了双随机SVPWM控制方法的扩频效果。实验结果表明，基于改进MT算法的双随机SVPWM控制方式达到了有效抑制电机高频段电磁振动的目的。
关键词：永磁同步电机 电流谐波 电磁振动 双随机空间矢量脉宽调制（SVPWM）
近年来，电力传动、航空航天等工业领域对永磁同步电机（Permanent Magnet Synchronous Machine, PMSM）驱动系统电磁兼容性的要求越来越高。在以变频器驱动的PMSM控制系统中，常用空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）技术对PMSM进行控制。传统SVPWM控制方式的开关频率和零矢量作用时间是固定的，因此逆变器中功率开关管的导通时刻不变，变频器在工作过程中会产生聚集在开关频率及其倍频处附近的高频谐波。此类谐波会使PMSM电枢反应磁动势发生改变，进而增大PMSM气隙磁场中高频电磁力波幅值，使电机高频段电磁振动加大。
目前，针对PMSM高频振动抑制问题所做的研究主要集中在本体设计[1-2]和控制策略[3-4]两个方面。其中，从控制角度出发来抑制PMSM高频电磁振动具有较强的便捷性。在现有控制策略中，随机空间矢量脉宽调制（Random Space Vector Pulse Width Modulation, RSVPWM）技术[5-10]对开关信号频率、脉冲位置等参数进行随机化处理，在不需要改变系统拓扑的情况下就能实现高频谐波在较宽的频率范围内的良好扩散，有效降低高频谐波峰值，从而抑制振动噪声。文献[11]分析了PMSM在变频器供电方式下产生的电流谐波对径向电磁力和振动加速度的影响，指出采用变频器供电会加剧电机的高频振动，且高频振动加速度随着开关频率的增大而减小。文献[12]通过调节载波移相位改变电机两绕组电流中的高频谐波的角度差，能够有效地抵消电机合成磁动势的高频分量，降低了电机的径向电磁力和高频振动噪声。文献[13]通过选取的零矢量产生共模电压，抵消由非零电压矢量带来的共模电压，有效地减少了相电流3次谐波含量，同时结合单随机开关频率调制技术，使得开关频率及其整数倍处高频谐波幅值大大减少。实验结果表明，该方法能有效降低高低频段电流谐波幅值，实现电机全频段的减振控制。
RSVPWM技术对相电流高频谐波频谱扩散有良好的效果，但RSVPWM技术应用在实际系统中时，其随机数的随机性很大程度上影响RSVPWM技术最终的振动抑制效果。传统的随机数生成方法产生的随机数具有重复性、不均匀性等不利特性，导致RSVPWM技术在实际应用中易造成电机不稳定异动。因此，本文首先推导了PMSM在变频器供电条件下引入的高频径向电磁力的数学模型，分析了变频器供电方式下引入的高频电磁力对电机振动的影响；然后提出了一种基于改进梅森旋转（Mersenne Twister, MT）算法的永磁同步电机双随机SVPWM振动抑制策略，利用改进MT算法生成随机数，提升随机序列的随机性和空间遍历性，输出均匀稳定的随机开关频率和随机零矢量，有效减少了高频谐波含量，抑制了高频段电磁振动；最后搭建电机振动实验平台，验证所提控制方式的有 效性。
在变频器供电方式下，PMSM的转子永磁磁场和定子电枢反应磁场相互作用，使气隙磁场中出现大量成分复杂的谐波，导致电机径向电磁力密度升高，电机定子齿部产生不同阶次的形变，致使PMSM产生高频电磁振动[14-15]。根据麦克斯韦应力张量法可得单位面积上径向电磁力表达式为
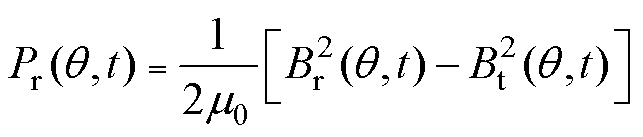（1）
式中，Pr(q, t)为单位面积上径向电磁力；Br(q, t)为气隙磁通密度的径向分量；Bt(q, t)为气隙磁通密度的切向分量；m0为真空磁导率。
由于电机中气隙的切向磁通密度Bt远小于径向磁通密度Br，在分析电机的电磁振动时一般忽略其影响，因此式（1）可化简为
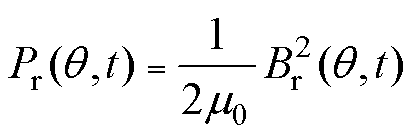（2）
在分析PMSM气隙磁场时，采用磁动势乘以磁导的方法来计算气隙径向磁通密度，表达式为
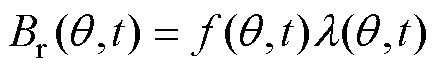（3）
式中，f(q,t)为气隙磁动势；l(q,t)为气隙比磁导。
当PMSM采用正弦波供电时，气隙磁动势可表示为
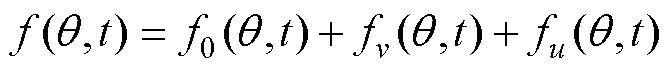（4）
式中，f0(q,t)为基波磁动势；fv(q,t)为定子谐波磁动势；fu(q,t)为转子永磁体等效磁动势。
当PMSM采用变频器供电方式时，电机定子绕组中会产生新的谐波电流成分，fv(q,t)将分为以下两部分：①定子电枢磁动势；②h次时间谐波电流产生的磁动势，即
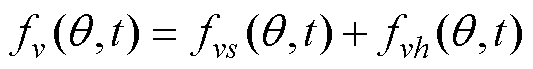（5）
式中，fvs(q,t)为定子电枢磁动势；fvh(q,t)为h次时间谐波电流产生的磁动势。
PMSM中气隙比磁导l(q,t)的表达式为
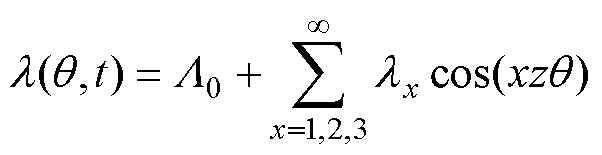（6）
式中，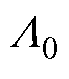
为单位面积气隙磁导的恒定分量；lx为气隙磁导x次谐波幅值；z为定子槽数。
将式（4）～式（6）代入式（3）中，可以得出变频器供电方式下PMSM中气隙磁场的解析表达式为
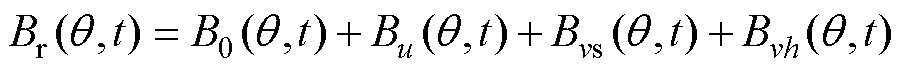（7）
其中，基波气隙磁通密度为
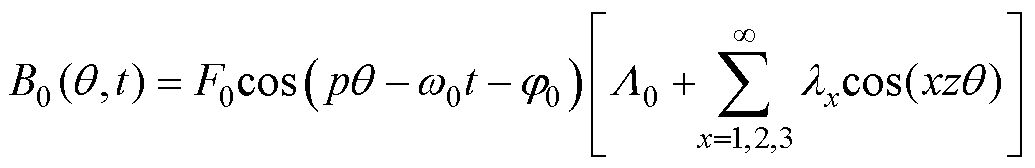（8）
转子永磁体等效磁通密度为
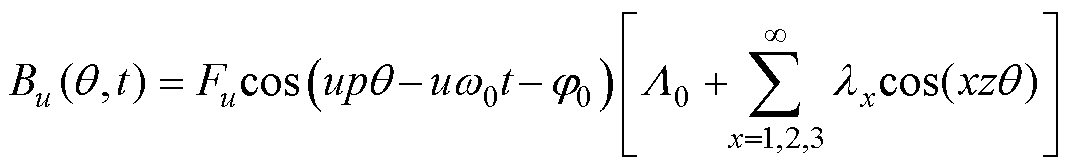（9）
基波电流产生的定子谐波磁通密度为
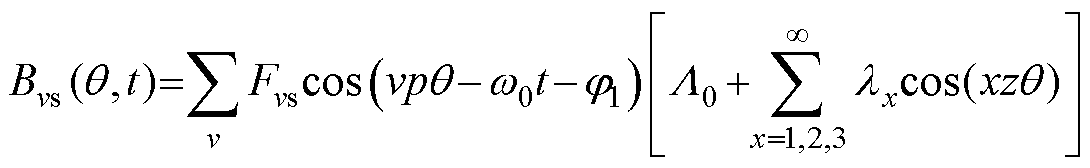（10）
变频器供电引入的附加磁通密度为
（11）
式中，Fu为转子永磁谐波磁动势幅值；u为转子永磁磁场谐波次数，大小为2r+1，r=0, ±1, ±2；Fvs为电枢电流基波产生的v次谐波磁动势幅值；Fvh为h次时间谐波电流产生的v次谐波磁动势幅值；h为变频器供电方式下引入的电流谐波次数；j1为电枢电流基波产生的v次谐波磁动势的相位；j2为采用变频器供电方式下引入的h次电流谐波影响下的v次谐波磁动势的相位；w0为转子基波磁动势角频率；v为电枢谐波磁场次数；p为电机极对数。
在PMSM气隙磁场解析表达式（7）中，第四项Bvh(q,t)与变频器的开关频率密切相关，其表达式为
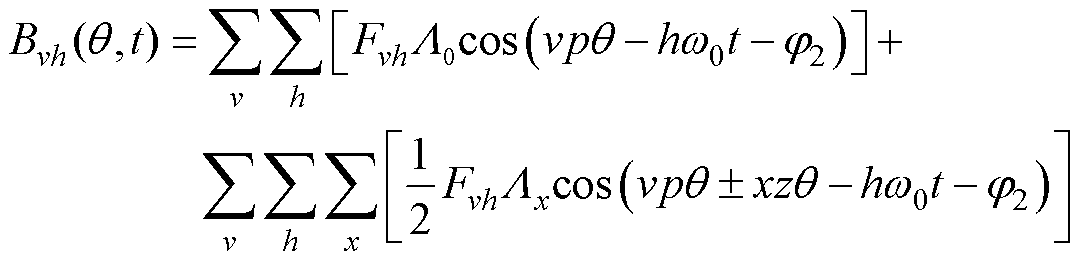（12）
式中，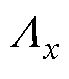
为在x次谐波影响下的气隙磁导。
本文主要分析采用变频器供电方式对电机高频电磁振动的影响，因此只考虑式中由变频器供电引入的高频电流谐波。将式（12）代入式（2），得到作用在电机定子齿上的径向电磁力高频部分，忽略表达式中的高次项，可得出采用变频器供电方式下引起电机产生高频振动的高频电磁力部分，此部分电磁力由高频电流谐波和转子永磁体主磁场相互作用而产生，其表达式为
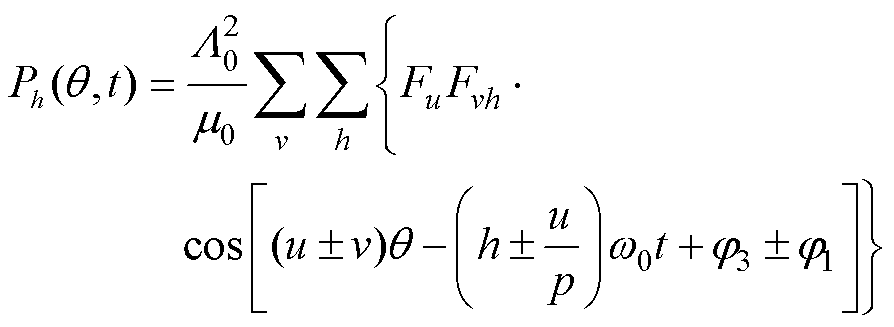（13）
式中，j3为忽略Bvh(q, t)中的高次项后，采用变频器供电方式下引起电机产生高频振动的高频电磁力相位。
采用变频器供电方式时，其主要谐波电流频率fk与开关频率fc的关系式为
（14）
式中，f0为电机的基频；k1和k2为奇偶性相异的正整数。
结合式（13）、式（14），可得变频器供电方式下引入的h次高频谐波与转子u次谐波相互作用而产生的径向电磁力频率为
（15）
式中，r为任意自然数；k1、k3为奇偶性相同的正整数。
结合式（14）、式（15）分析可知，在开关频率处，变频器供电方式下引入的高频谐波频率主要为fk±2f0，fk±4f0，引入的高频径向电磁力波频率主要为fk±f0。此径向电磁力波幅值较大、频率较高，是变频器供电方式下引起PMSM产生高频振动的主要原因。
针对PMSM在变频器供电方式下产生高频段电磁振动这一问题，本文提出一种随机开关频率与随机零矢量相结合的双随机SVPWM控制方法，应用于永磁电机高频电流谐波频谱扩展中[16-24]，有效削弱了高频电磁振动，图1为双随机SVPWM控制方式的示意图。
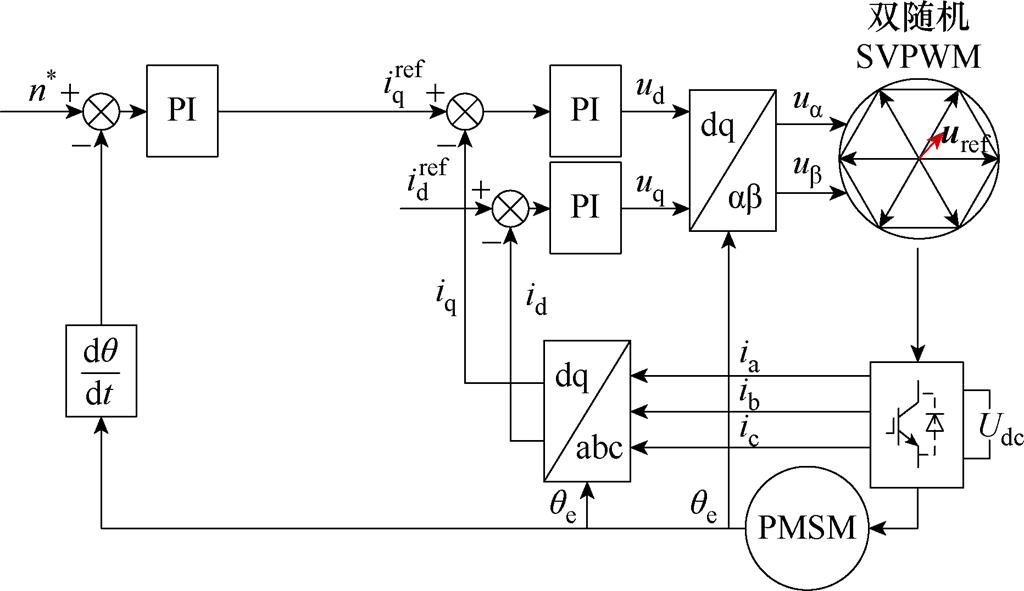
图1 双随机SVPWM控制
Fig.1 Double random SVPWM control
变频器供电方式下，PMSM通常采用SVPWM控制方式进行控制，通过控制逆变器六个开关管的通断来合成逆变器的输出电压。在SVPWM控制方式下，三相逆变器共有八种开关状态，对应着八种电压矢量，其中包括六个有效空间电压矢量（U1(100)，U2(110)，U3(010)，U4(011)，U5(001)，U6(101)）和两个零矢量（U0(000)和U7(111)）。而逆变器输出电压的幅值仅与有效空间电压矢量的作用时间有关，与零矢量的作用时间无关，改变零矢量的作用时间可在一定范围内随机地改变脉冲的导通时刻，从而改变输出相电流的频谱，进而影响电机的振动特性。
采用SVPWM控制方式下电压的空间矢量合成示意图如图2所示。
图2 电压空间矢量合成示意图
Fig.2 Diagram of voltage space vector synthesis
根据“伏-秒平衡”的原则进行合成，可得
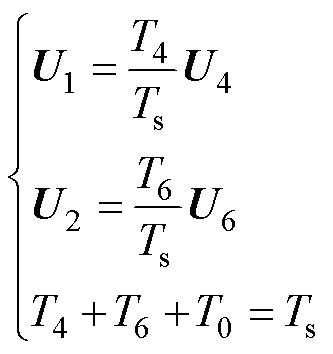（16）
式中，T4、T6、T0分别为U4、U6和零矢量U0(U7)的作用时间；Ts为开关周期。
由式（16）可见，采用SVPWM控制方式时，输出电压Uout的幅值仅与有效电压矢量U4、U6的作用时间有关，而与零矢量U0(U7)的作用时间无关，因此，在保持有效电压矢量U4、U6作用时间不变的前提下，通过对零矢量U0(U7)的作用时间进行随机化处理，就能实现脉冲的导通位置随机，实现输出电压幅值不变情况下的随机零矢量控制。以A相电压波形为例，随机零矢量分配如图3所示。
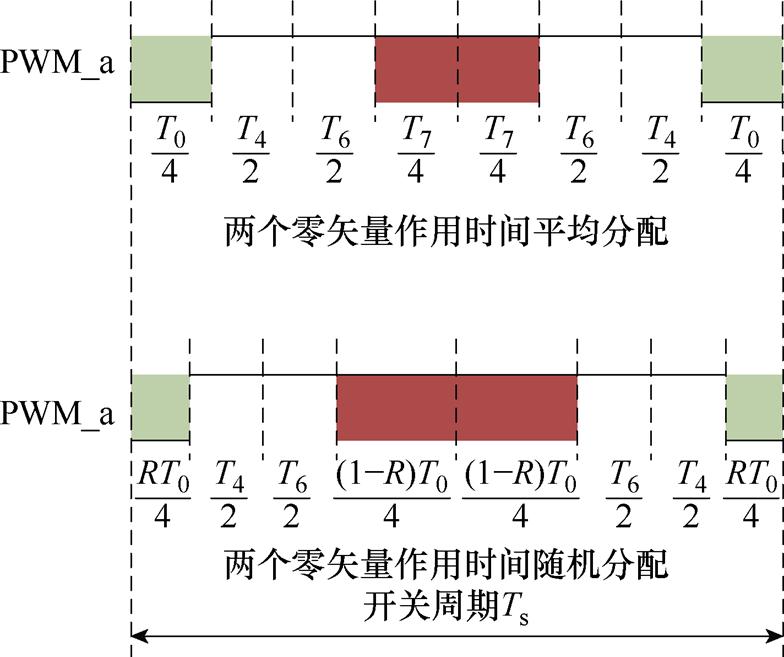
图3 随机零矢量分配
Fig.3 Random zero vector assignment
对两个零矢量作用时间做随机化处理，零矢量的作用时间可表示为
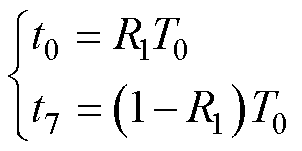（17）
式中，t0、t7分别对应零矢量中U0和U7的时间；R1为一个在区间[0, 1]上均匀分布的随机数。
将随机化处理后的零矢量U0和U7重新分配到空间矢量中，就可以在不改变输出电压幅值的情况下实现频谱扩散的效果。
随机开关频率SVPWM控制方式是在传统SVPWM控制方式的基础上，对开关频率进行随机化处理，将开关频率及其倍频处的谐波分散到指定频域内，以达到抑制电机高频电磁振动的目的。进行随机化处理后的开关频率表达式为
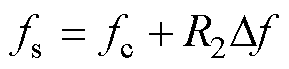（18）
式中，fs为随机化处理后的逆变器开关频率；fc为中心频率；R2为随机数；Df为常数。
给定Df的初值后，通过改变R2的值来改变系统的开关频率。但逆变器开关频率过低，易产生明显的电磁振动；逆变器开关频率过高，会增加逆变器开关管的能量损耗，造成系统运行不稳定。因此，适当选择开关频率的变化范围是保证系统稳定运行的关键。随机开关频率SVPWM如图4所示。
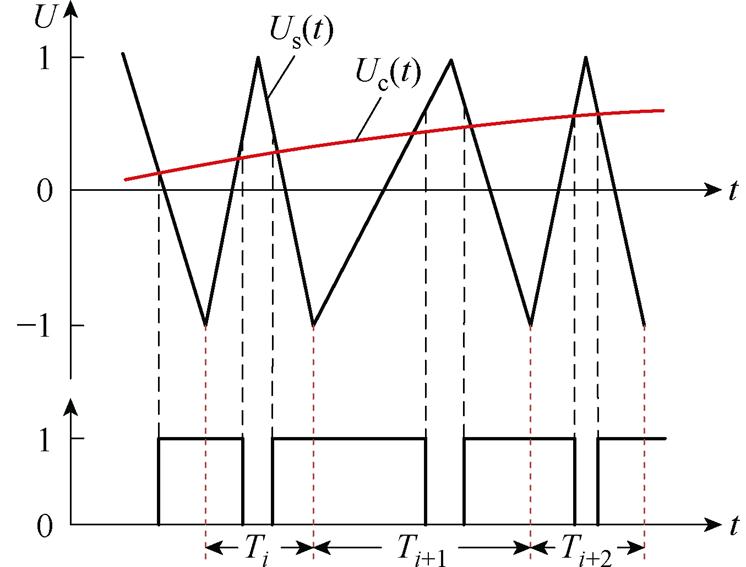
图4 随机开关频率SVPWM
Fig.4 Random switching frequency SVPWM
将双随机SVPWM控制方式引入PMSM控制系统中，可以有效地抑制高频段尖峰谐波，降低高频电磁振动。但在双随机SVPWM控制方式中，传统的随机数生成方法产生的随机数具有重复性、不均匀性等特点，导致双随机SVPWM控制方式在实际应用中易造成电机不稳定异动。因此，对双随机SVPWM控制方式中随机数的生成方法进行研究具有必要性。
PMSM在采用双随机SVPWM控制（Double Random Control, DRC）方式时，随机数的生成是最为关键的步骤，随机度的高低、随机数分布的均匀程度都将直接影响双随机SVPWM控制方法的扩频减振效果，传统的随机数生成方法存在随机数分布不均匀、随机周期不受控、随机数自由度小等问题。因此，本文提出一种结合Logistic与Kent两种混沌映射方式交叉映射的改进MT算法[25-30]（命名为LKMT）来生成随机数，该方法具有实现便捷、产生的随机数自由度高、重复率低等优点，并基于此方法实现电机的双随机SVPWM控制（命名为LKMT-DRC）方式。图5为PMSM采用LKMT-DRC方式的系统控制框图。
Logistic混沌映射是一种非线性的典型映射，生成的是一种离散序列，其表达式为
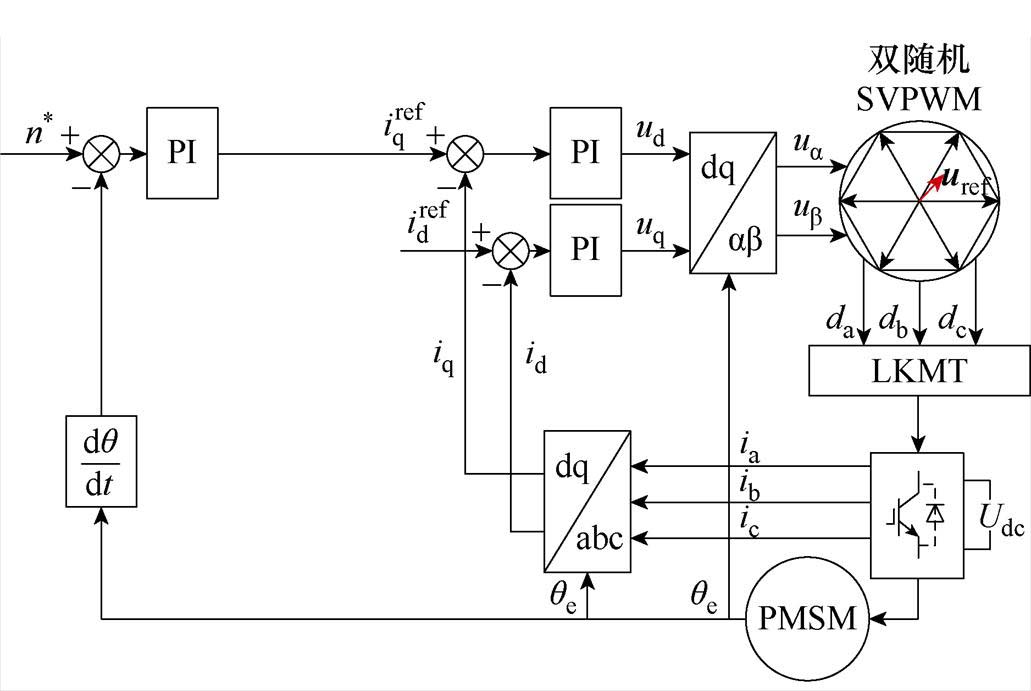
图5 LKMT-DRC控制方式
Fig.5 Control method of LKMT-DRC
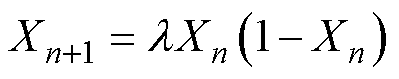（19）
式中，l 为 [0, 4] 之间的可调参数；Xn为序列迭代值，XnÎ[0, 1]；X0为初始值。
在给定X0的初值后，通过改变l 的值，可以把Logistic离散序列划分成三个区间：①当0≤l≤3时，随机序列在 (0, 1) 区间内呈稳定状态；②当3＜ l≤3.6时，随机序列在 (0, 1) 区间内呈周期性序列；③当3.6＜l≤4时，随机序列在 (0, 1) 区间内呈混沌性序列。本文设定l=3.7。
Kent混沌映射是一种离散的混沌系统，其表达式为
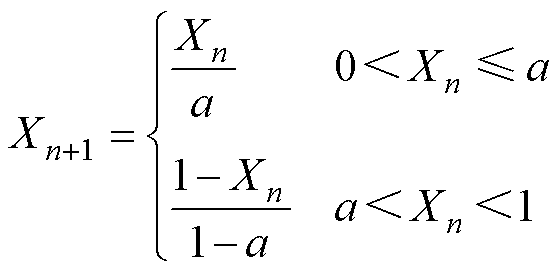（20）
式中，aÎ(0, 1)，文本设定a=0.3。
LKMT方法结合了Logistic与Kent两种混沌映射方式，并基于MT方法产生新的随机数序列。LKMT的框架如图6所示，其流程如下：
1）初始化：生成初始序列
首先设定一个种子，利用MT算法生成初始随机序列，序列中的其余随机数由初始值M[0]生成，其迭代公式为
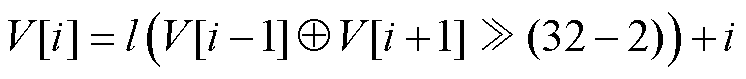（21）
式中，V[i]为第i个随机数；l为算法中设置的常量；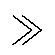
表示右移操作。
2）产生混沌映射序列
应用Logistic映射和Kent映射将初始序列交叉映射到混沌空间中，表达式为
图6 随机数生成步骤流程
Fig.6 Flow chart of random number generation steps
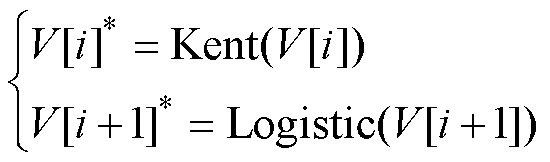（22）
式中，V[i]*为将V[i]进行Kent混沌映射到 (0, 1) 之间的混沌空间中；V[i+1]*为将V[i+1]进行Logistic混沌映射到 (0, 1) 之间的混沌空间中。
3）应用TGFSR扭曲映射
再次应用MT方法进行TGFSR扭曲映射得到新的随机序列，其表达式为
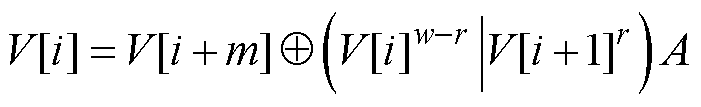（23）
式中，m为 (0, N) 间的整数；V[i]w-r为V[i]的前w-r二进制位；V[i+1]r为V[i]的后r二进制位；ï表示V[i]w-r和V[i+1]r的组合。
假设V[i+m]Å(V[i]w-rïV[i+1]r)为H，则
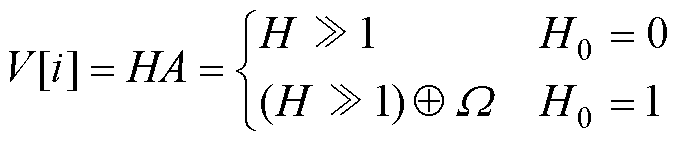（24）
式中，H0为最低位；W为设定的二进制常量。
4）提取随机数
利用Transformsequence函数将LKMT方法生成的随机数序列以二进制形式输出得到最终的随机序列并应用在PMSM控制系统中，对电机进行双随机SVPWM控制。
为了验证本文所提LKMT-DRC控制方式在扩频减振方面的有效性，分别对其进行了仿真和实验分析。
在Simulink仿真环境中搭建传统SVPWM控制方法和双随机SVPWM控制方法的仿真模型，参数设置为：母线电压为311 V，转速为1 500 r/min，开关频率为10 kHz，开关频率变化范围为9～11 kHz。两种控制方式下的电机相电流频谱仿真结果如图7所示。
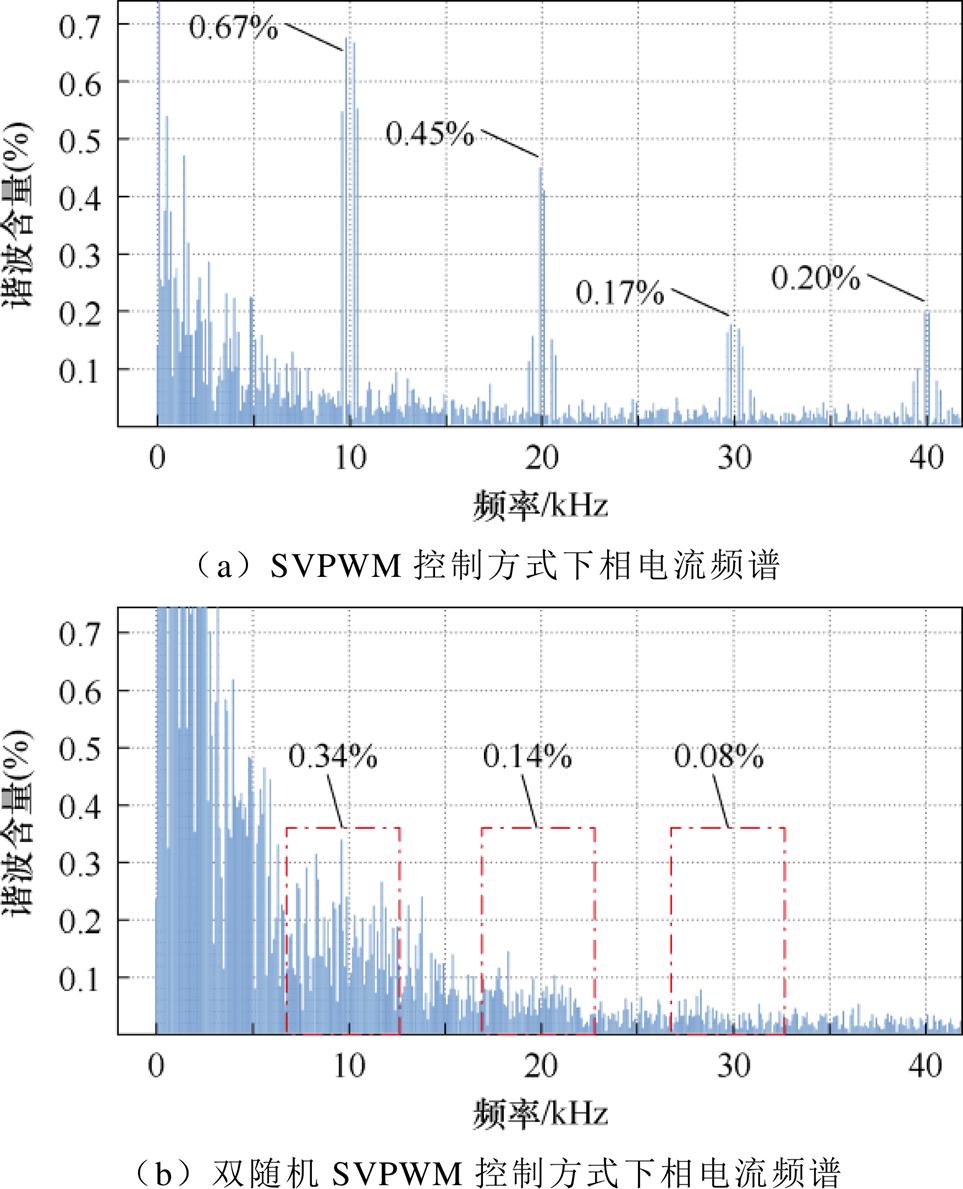
图7 相电流频谱对比分析
Fig.7 Comparative analysis of phase current spectrum
由仿真结果可知，LKMT-DRC控制方法可以有效分散聚集在开关频率及其倍频处的谐波分量，达到抑制PMSM高频谐波幅值的目的。
进一步观察LKMT-DRC控制方法与传统SVPWM控制方法的功率谱仿真结果，如图8所示。
图8 相电流功率谱
Fig.8 Power spectrum of phase current
由图8中仿真结果可以明显看出，相比于传统SVPWM控制方法，LKMT-DRC控制方法有效地将聚集在开关频率及其倍频处的尖峰谐波幅值削弱，分散到更宽频域范围内。
本文以一台4.4 kW分数槽集中绕组永磁同步电机为研究对象，分别对传统SVPWM控制方式及LKMT-DRC控制方式下的PMSM相电流谐波及振动加速度进行实验对比分析，并在LKMT-DRC控制方式下采用不同的扩频范围，分析LKMT-DRC控制方式的振动抑制效果。实验主控制器采用RTU-BOX，实验中电压和电流波形数据通过电压电流钳分别得到，振动加速度数据由振动加速度传感器和振动数据采集器得到。所搭建的PMSM实验平台如图9所示。电机系统实验参数见表1。
图9 PMSM实验平台
Fig.9 Experimental platform of PMSM
表1 实验参数
Tab.1 Experimental parameters
参 数数 值 极对数5 槽数12 d轴电感/mH18 q轴电感/mH22 直流母线电压/V180 基波频率f0/Hz50 固定开关频率fs/kHz10 随机开关频率变化范围/kHz9～11
4.2.1 相电流谐波实验
为了验证所提LKMT-DRC控制方式的扩频效果，对采用传统SVPWM控制方式和LKMT-DRC控制方式下PMSM的相电流频谱进行分析。
图10为采用传统SVPWM控制方式下PMSM的相电流谐波频谱分析结果。如图所示，在开关频率及其倍频处附近存在明显的尖峰谐波，其中，在开关频率10 kHz处的尖峰谐波含量为1.23%，在9.8、9.9、10.1、10.2 kHz处的谐波含量分别为0.234%、0.112%、0.365%、0.099%，与理论结果fk±2f0，fk±4f0均相符。在开关频率整数倍频20、30、40 kHz附近处的尖峰谐波含量分别为0.58%、0.45%、0.42%。
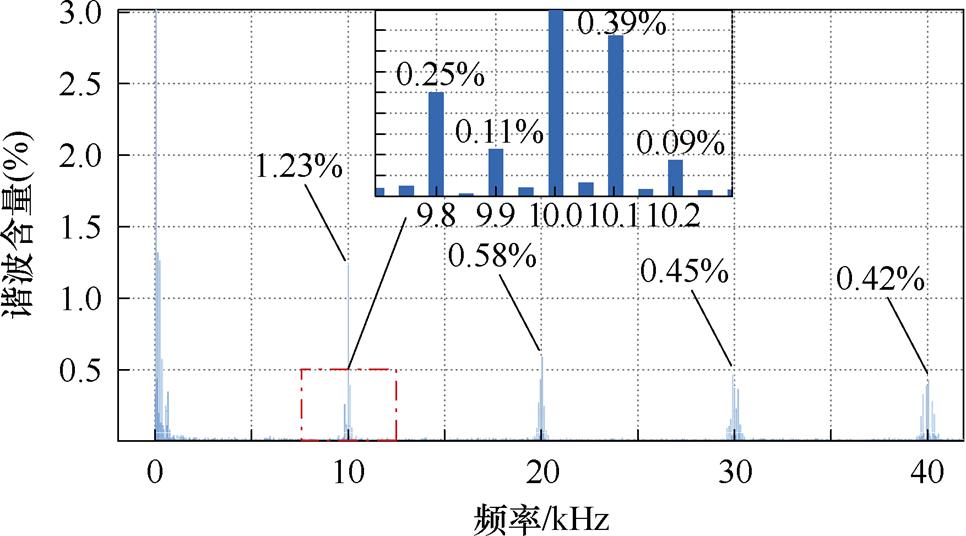
图10 SVPWM控制方式频谱分析
Fig.10 Spectrogram of SVPWM control mode
图11为采用LKMT-DRC控制方式下的相电流傅里叶分析结果。由实验结果可知，采用LKMT- DRC控制方式时，谐波频谱扩展效果良好，集中在开关频率及其倍频处附近的谐波幅值明显降低。其中，开关频率10 kHz处附近的尖峰谐波幅值由1.23%降低至0.14%，在开关频率整数倍频20、30、40 kHz处附近的尖峰谐波幅值分别由0.58%、0.45%、0.42%降低至0.13%、0.12%、0.12%，验证了所提LKMT-DRC控制方式的有效性。
图11 LKMT-DRC控制方式频谱分析
Fig.11 Spectrogram of LKMT-DRC control mode
图12为采用传统SVPWM控制方式和采用LKMT-DRC控制方式下PMSM相电流功率谱分析的对比结果。
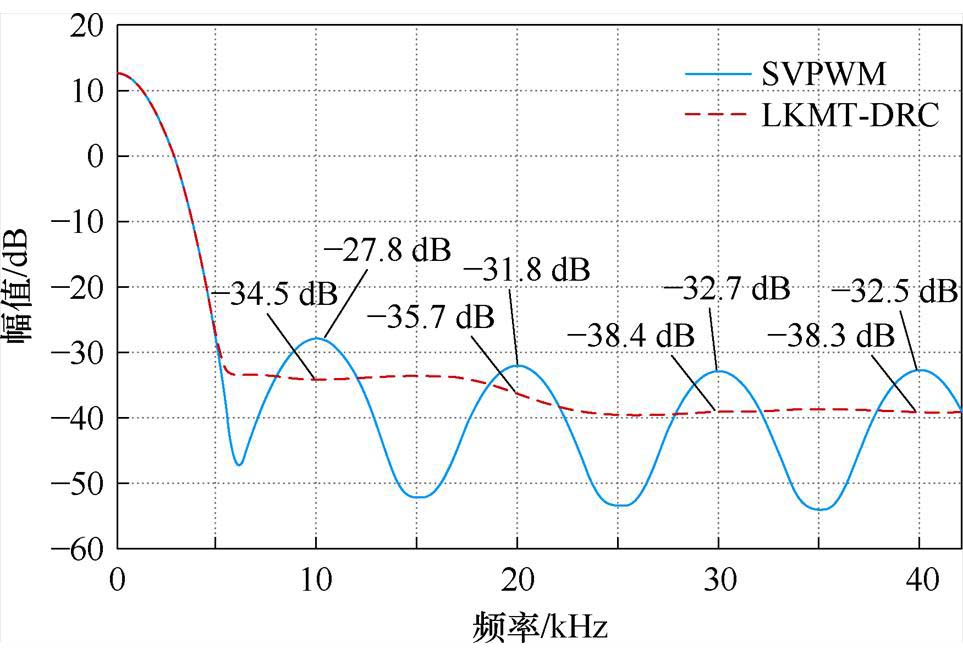
图12 电流功率谱分析
Fig.12 Spectrum analysis of current power
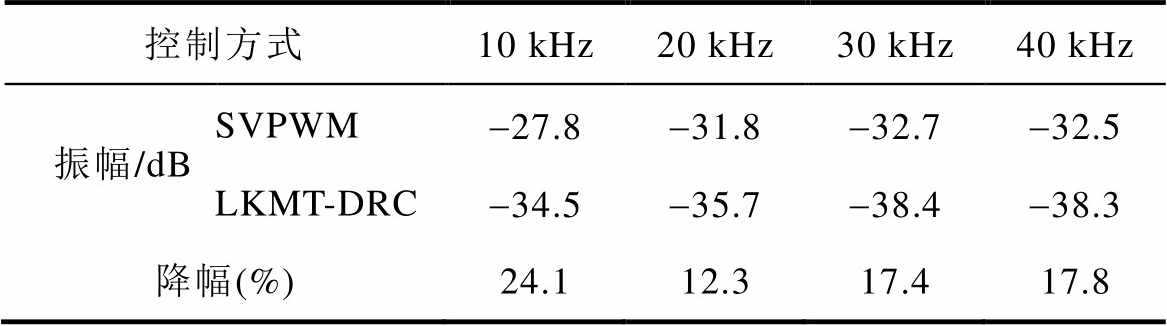
由图12可知，在变频器供电方式下，PMSM在采用传统SVPWM控制方式时的电流功率谱在开关频率及其倍频处附近存在明显的尖峰谐波，此尖峰谐波会导致电机在运行过程中产生明显的高频电磁振动。引入LKMT-DRC控制方式后，PMSM的相电流功率谱变得更加平滑，无明显尖峰，接近白噪声频谱，可有效地降低PMSM在运行过程中的振动和噪声。两种控制方式下的相电流功率谱谐波峰值对比见表2。
表2 两种控制方式下相电流谐波峰值对比
Tab.2 Comparison of phase current harmonic peaks under two control modes
控制方式10 kHz20 kHz30 kHz40 kHz 振幅/dB SVPWM-27.8-31.8-32.7-32.5 LKMT-DRC-34.5-35.7-38.4-38.3 降幅(%)24.112.317.417.8
通过比较结果得知，采用LKMT-DRC控制方式时，相电流扩频效果良好，可有效抑制变频器供电方式下引入的高频谐波。
4.2.2 振动加速度实验
为了验证本文所提LKMT-DRC控制方式对电机高频振动抑制的有效性，分别对采用传统SVPWM控制方式和LKMT-DRC控制方式下电机在高频段的振动加速度进行比对，并分析在双随机SVPWM控制方式下分别采用LKMT算法生成随机数和传统数学公式法生成的随机数的对比结果。
图13为PMSM采用传统SVPWM控制方式和LKMT-DRC控制方式下电机在高频段的振动加速度数据。
由图13可知，采用传统SVPWM控制方式时，在开关频率10 kHz处附近的高频振动加速度峰值坐标为 (9.95, 0.073)，符合理论值fk±f0。引入LKMT- DRC控制方式后，在开关频率10 kHz处附近的高频振动加速度峰值降低为0.052g，降幅达28.8%。两种控制方式下振动加速度峰值对比见表3。
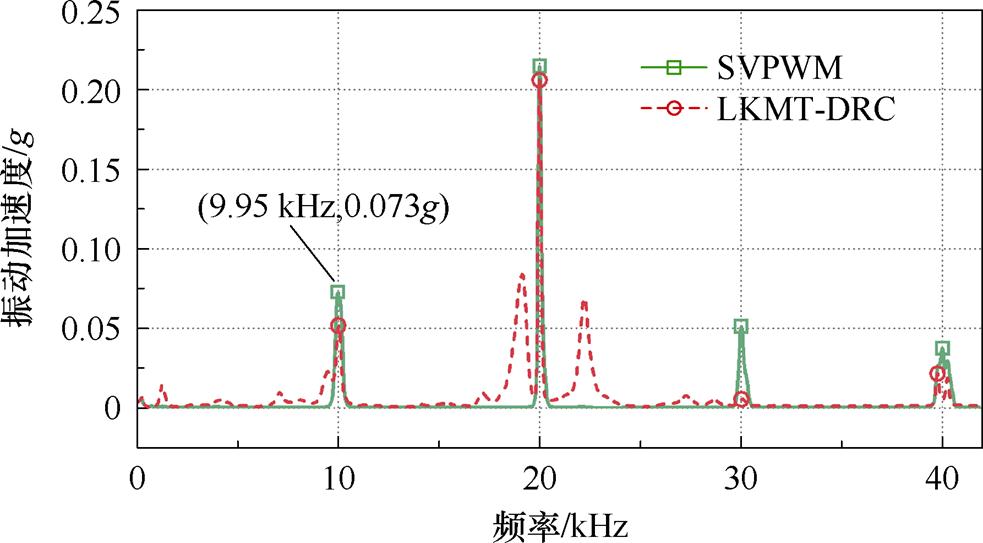
图13 振动加速度对比分析
Fig.13 Comparative analysis of vibration acceleration
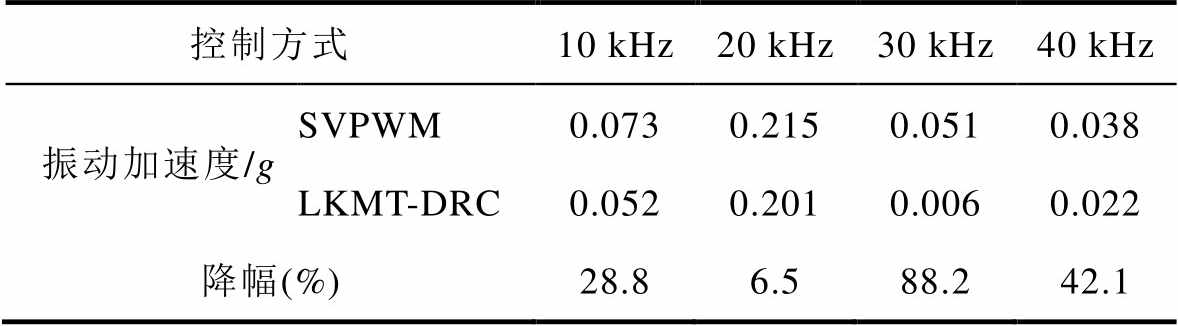
表3 两种控制方式下振动加速度峰值对比
Tab.3 Comparison of peak vibration acceleration under two control modes
控制方式10 kHz20 kHz30 kHz40 kHz 振动加速度/g SVPWM0.0730.2150.0510.038 LKMT-DRC0.0520.2010.0060.022 降幅(%)28.86.588.242.1
上述结果表明，采用LKMT-DRC控制方式可显著抑制PMSM在开关频率及其整数倍频处附近的高频振动加速度，提升电机的运行稳定性。
图14为PMSM在双随机控制方式下分别采用本文所提LKMT算法生成随机数和传统数学公式法生成随机数的振动数据比对结果。
图14 不同随机数算法下振动加速度对比
Fig.14 Comparison of vibration acceleration under different random number algorithms
由实验结果可知，相较于传统数学公式法生成随机数的振动加速度曲线，利用本文所提LKMT算法生成随机数的振动加速度曲线明显降低，可见LKMT算法提升了随机序列的随机性和空间遍历性，能够输出随机且均匀稳定的随机开关频率和随机零矢量，可以提升双随机SVPWM控制方法对电机的高频振动抑制效果。
4.2.3 LKMT-DRC控制方式下扩频范围影响分析
当PMSM采用LKMT-DRC控制方式时，不同的扩频范围也会影响到最终的振动抑制效果，本文进一步对PMSM采用LKMT-DRC控制方式时选取不同的扩频范围下的线电压及振动加速度进行对比分析。
图15为采用四种不同扩频范围时，PMSM在600 r/min下的振动加速度数据。
为了更直观地对比PMSM采用LKMT-DRC控制方式时选取不同的扩频范围对电机高频振动抑制效果的影响，对开关频率及其倍频处的振动加速度的功率谱进行分析，分析结果如图16所示。
由图16可见，更高的扩频范围会提升LKMT- DRC控制方式的高频振动抑制效果，且扩频范围越宽，LKMT-DRC控制方式的高频振动抑制效果越好。但实际工程中不同的扩频范围会影响电机的控制效果。因此，进一步采集过大及过小扩频范围下电机的输出线电压进行分析。
图15 不同扩频范围下振动加速度
Fig.15 Vibration acceleration in different spreading ranges
图16 不同扩频范围下振动加速度功率谱
Fig.16 Power spectrum of vibration acceleration in different spreading ranges
图17为传统SVPWM控制方式下输出线电压的频谱图。由图可见，在SVPWM控制方式下，输出线电压的频谱在开关频率及其倍频处尖峰谐波幅值较高。
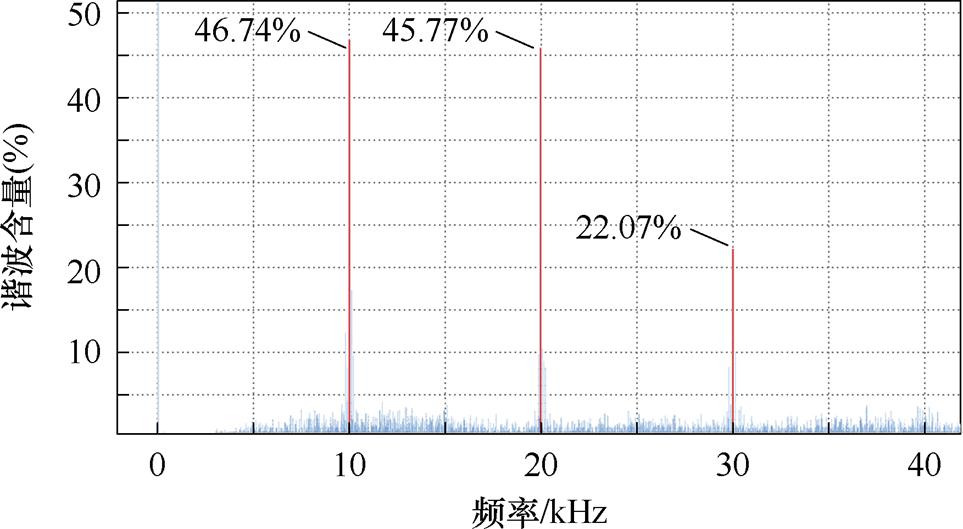
图17 SVPWM控制方式下线电压频谱
Fig.17 Line voltage spectrum under SVPWM control mode
图18为采用LKMT-DRC控制方式时扩频范围过小情况下的线电压频谱，此时LKMT-DRC控制方式的扩频范围为开关频率的5%。其中，开关频率10 kHz处附近的尖峰谐波幅值由46.74%降低至13.35%，在开关频率整数倍频20 kHz、30 kHz处附近的尖峰谐波幅值分别由45.77%、22.07%降低至20.62%、7.37%，尖峰谐波幅值的降幅还不是很大，扩频效果不足。
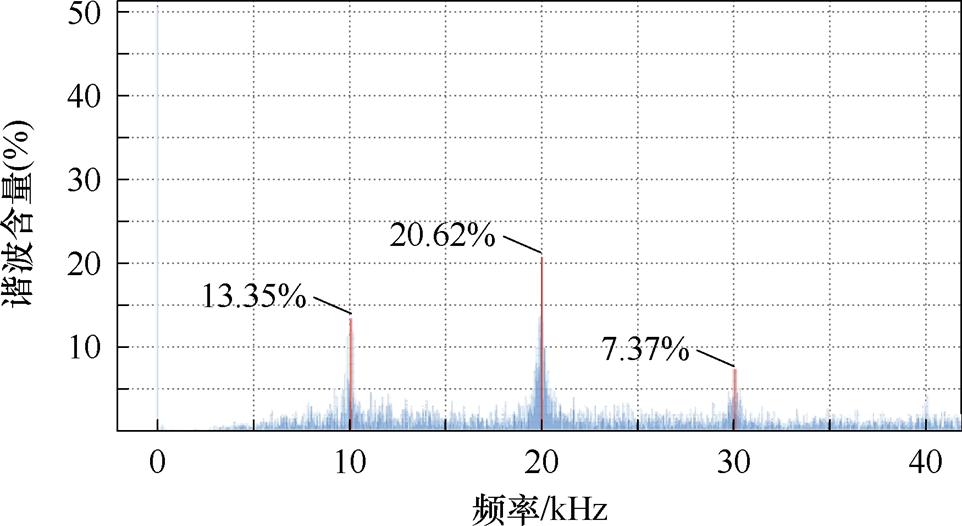
图18 过小扩频范围下线电压频谱图
Fig.18 Spectrogram of line voltage at small spreading range
图19为采用LKMT-DRC控制方式时选取适当扩频范围下的线电压频谱，此时LKMT-DRC控制方式的扩频范围为开关频率的10%和20%，图20为此扩频范围下的输出线电压波形。
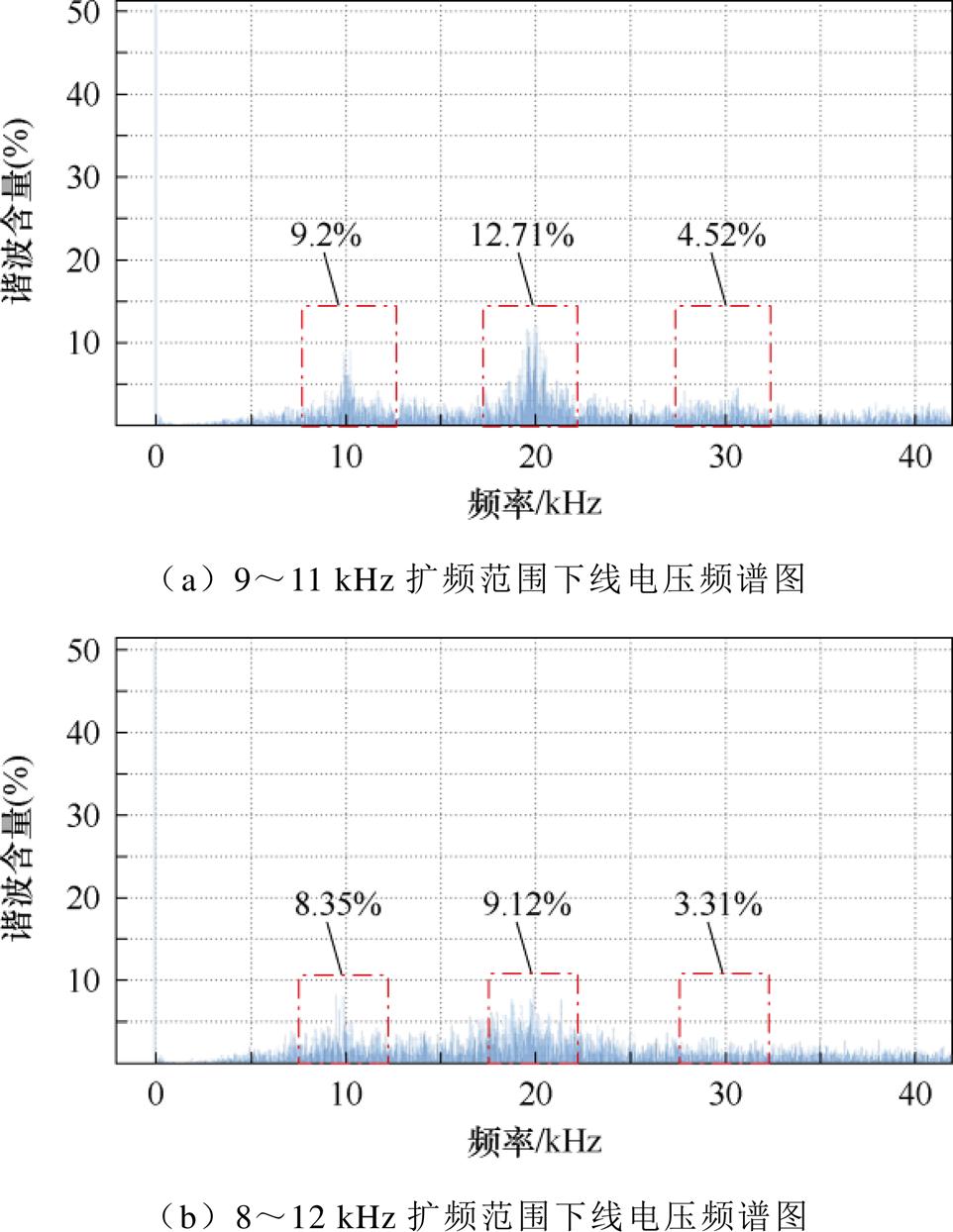
图19 适当扩频范围下线电压频谱图
Fig.19 Spectrogram of line voltage at appropriate spreading range
由图19和图20可以看出，当选取的扩频范围适当时，LKMT-DRC控制方式可以有效地抑制开关频率及其倍频处的尖峰谐波幅值，且输出线电压波形平稳，无明显畸变。
图20 适当扩频范围下线电压波形
Fig.20 Line voltage waveforms at appropriate spreading range
图21为采用LKMT-DRC控制方式时扩频范围过大情况下的线电压频谱，此时LKMT-DRC控制方式的扩频范围为开关频率的90%和100%，图22为此扩频范围下的输出线电压波形。
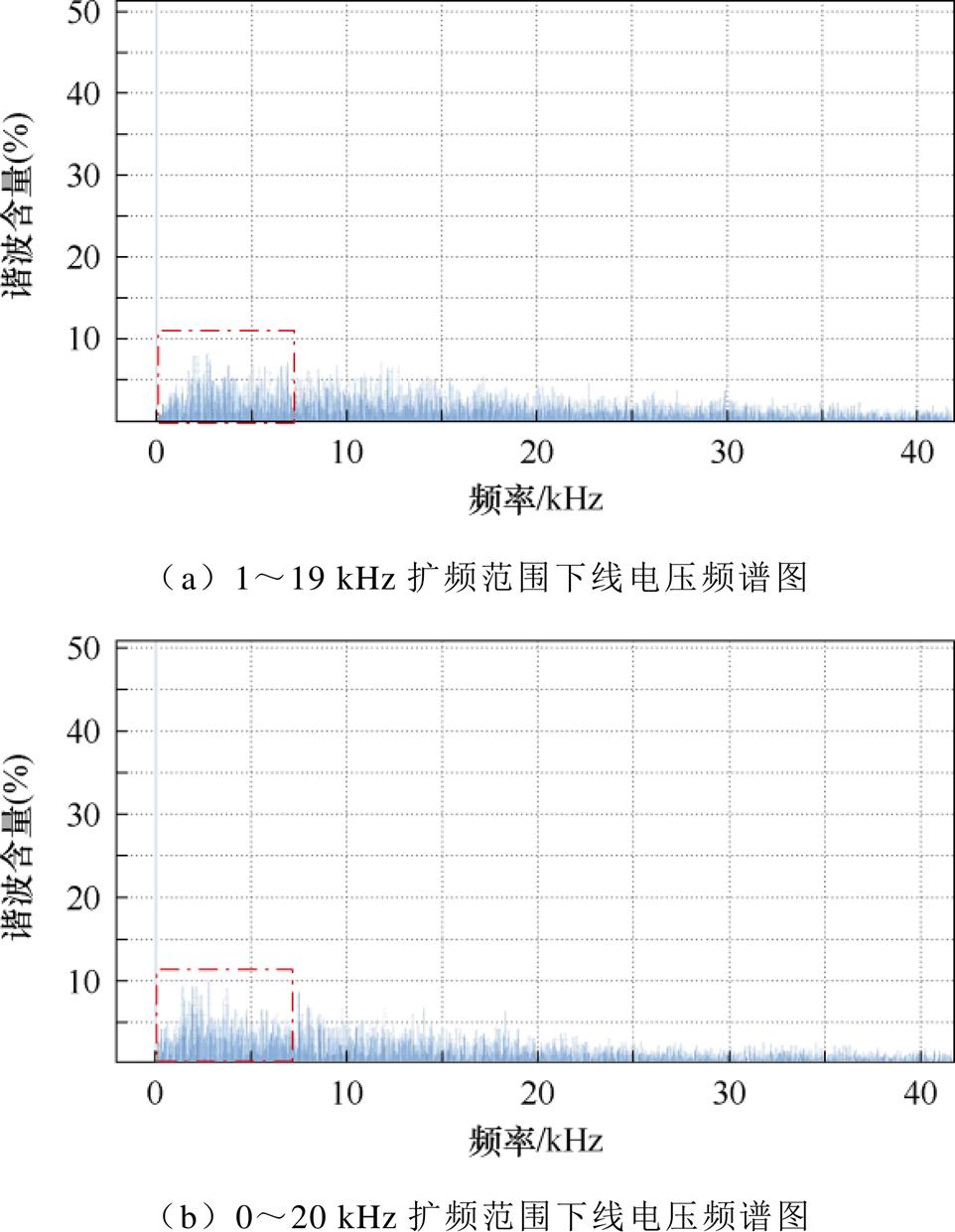
图21 扩频范围过大情况下线电压频谱图
Fig.21 Spectrogram of line voltage at large spreading range
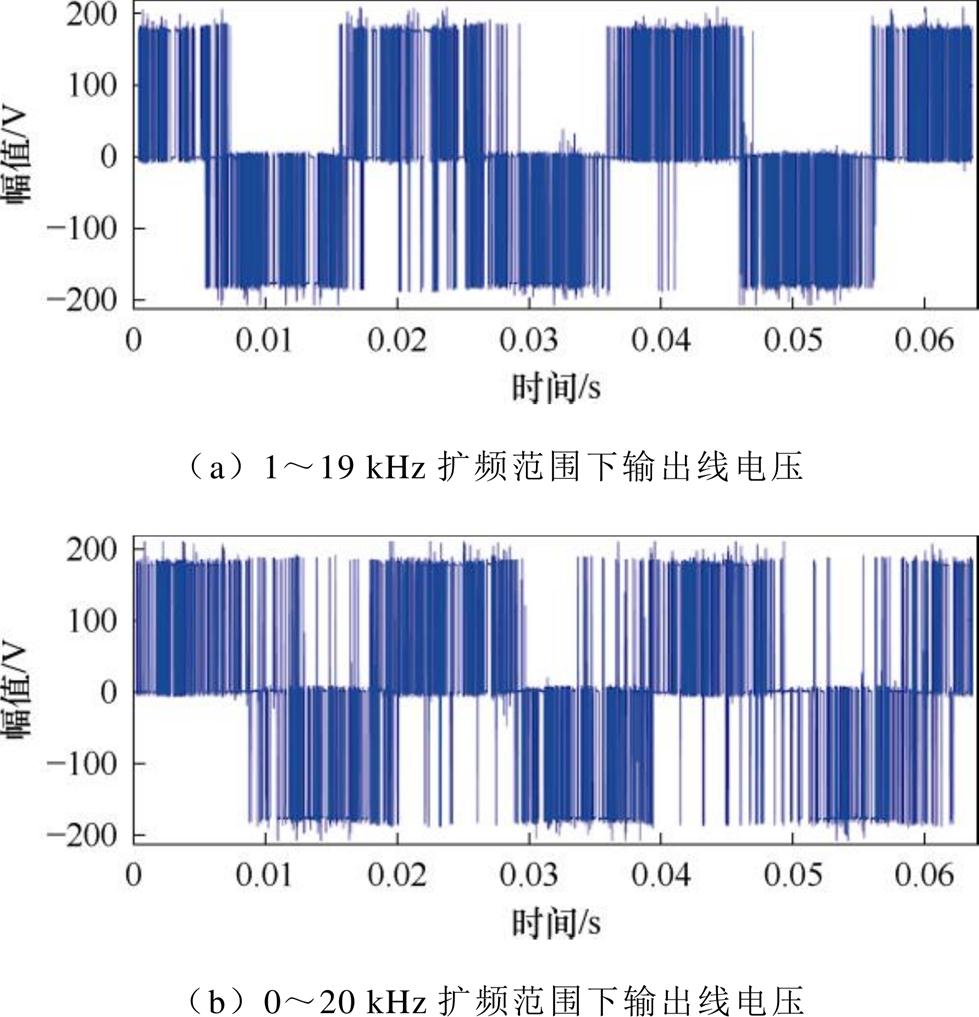
图22 扩频范围过大情况下线电压波形
Fig.22 Line voltage waveforms at large spreading range
由图21和图22可见，虽然开关频率及其倍频处的高频谐波幅值得到有效抑制，但全频段谐波成分复杂，低次谐波含量过多，造成电机低频振动加大，且输出线电压畸变严重。
由上述分析可知，PMSM采用LKMT-DRC控制方式可以有效地达到扩频减振的目的，但在实际工程中应用LKMT-DRC控制方式时应合理选择扩频范围，以达到良好的控制效果。
本文针对PMSM在变频器供电方式下采用SVPWM控制方式时会在开关频率及其倍频处附近产生高频段电磁振动这一问题，提出了一种LKMT- DRC控制方式，并对其控制效果进行了实验验证，结论如下：
1）变频器供电方式下，采用SVPWM控制方式会在开关频率处附近引入幅值较高的高频谐波和径向电磁力波，引入的谐波频率主要为fk±2f0、fk±4f0，引入的高频径向电磁力波频率主要为fk±f0，结合实验结果得到验证。
2）相比于传统SVPWM控制方式，采用LKMT- DRC控制方式可有效分散集中在开关频率及其整数倍处的高频谐波，抑制高频谐波幅值，显著降低由高频电磁力波引起的在开关频率及其整数倍频处附近的高频振动加速度，对于PMSM高频段减振控制具有实际意义。
3）本文所提LKMT算法生成的随机数能够提升随机序列的随机性和空间遍历性，输出随机且均匀稳定的随机开关频率和随机零矢量，保证了双随机SVPWM控制方式的有效性。并且采用LKMT- DRC控制方式时可以有效地达到扩频减振的目的，但在实际工程中应用LKMT-DRC控制方式时应合理选择扩频范围，以达到良好的控制效果。
参考文献
[1] Deng Wenzhe, Zuo Shuguang. Electromagnetic vibration and noise of the permanent-magnet syn- chronous motors for electric vehicles: an overview[J]. IEEE Transactions on Transportation Electrification, 2019, 5(1): 59-70.
[2] 陈永校. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.
[3] 孙明阳, 和阳, 邱先群, 等. 随机频率三角波注入永磁同步电机无位置传感器降噪控制[J]. 电工技术学报, 2023, 38(6): 1460-1471.
Sun Mingyang, He Yang, Qiu Xianqun, et al. Random-frequency triangular wave injection based sensorless control of PMSM drives for audible noise reduction[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1460-1471.
[4] 谷鑫, 鲁金月, 王志强, 等. 基于无差拍电流预测控制的永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2022, 37(24): 6345-6356.
Gu Xin, Lu Jinyue, Wang Zhiqiang, et al. Harmonic current suppression strategy for permanent magnet synchronous motor based on deadbeat current predi- ction control[J]. Transactions of China Electro- technical Society, 2022, 37(24): 6345-6356.
[5] 赵文祥, 李亮, 吉敬华, 等. 双三相PMSM锯齿载波双随机SVPWM策略[J]. 中国电机工程学报, 2022, 42(9): 3412-3422.
Zhao Wenxiang, Li Liang, Ji Jinghua, et al. Sawtooth carrier double random SVPWM strategy for dual three-phase PMSM[J]. Proceedings of the CSEE, 2022, 42(9): 3412-3422.
[6] 许家群, 赵嗣芳, 殷志鹏. 永磁同步电机锯齿载波减振控制[J]. 中国电机工程学报, 2019, 39(14): 4281-4291, 4272.
Xu Jiaqun, Zhao Sifang, Yin Zhipeng. Permanent magnet synchronous motor control for vibration reduction based on sawtooth carrier[J]. Proceedings of the CSEE, 2019, 39(14): 4281-4291, 4272.
[7] 蒋栋, 沈泽微, 刘自程, 等. 电力推进系统电力电子噪声的主动抑制技术进展[J]. 中国电机工程学报, 2020, 40(16): 5291-5302.
Jiang Dong, Shen Zewei, Liu Zicheng, et al. Progress in active mitigation technologies of power electronics noise for electrical propulsion system[J]. Proceedings of the CSEE, 2020, 40(16): 5291-5302.
[8] Huang Yingliang, Xu Yongxiang, Zhang Wentao, et al. PWM frequency noise cancellation in two-segment three-phase motor using parallel interleaved inver- ters[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2515-2525.
[9] 刘和平, 刘庆, 张威, 等. 电动汽车用感应电机削弱振动和噪声的随机PWM控制策略[J]. 电工技术学报, 2019, 34(7): 1488-1495.
Liu Heping, Liu Qing, Zhang Wei, et al. Random PWM technique for acoustic noise and vibration reduction in induction motors used by electric vehicles[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1488-1495.
[10] Lee K, Shen Guangtong, Yao Wenxi, et al. Performance characterization of random pulse width modulation algorithms in industrial and commercial adjustable-speed drives[J]. IEEE Transactions on Industry Applications, 2017, 53(2): 1078-1087.
[11] Zhang Wentao, Xu Yongxiang, Huang Huidong, et al. Vibration reduction for dual-branch three-phase permanent magnet synchronous motor with carrier phase-shift technique[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 607-618.
[12] 吴振兴, 王逸林, 王志伟, 等. 直线电机振动抑制的载波移相策略研究[J]. 电机与控制学报, 2019, 23(12): 16-22, 31.
Wu Zhenxing, Wang Yilin, Wang Zhiwei, et al. Research on carrier phase shifting strategy for linear motor vibration suppression[J]. Electric Machines and Control, 2019, 23(12): 16-22, 31.
[13] 王恒, 赵文祥, 吉敬华, 等. 基于谐波抑制的共母线开绕组永磁同步电机减振控制[J]. 电机与控制应用, 2021, 48(3): 7-15.
Wang Heng, Zhao Wenxiang, Ji Jinghua, et al. Vibration control of open-winding permanent magnet synchronous motor with common bus based on harmonic suppression[J]. Electric Machines & Control Application, 2021, 48(3): 7-15.
[14] 陈少先, 丁树业, 申淑锋, 等. 船舶用表贴式永磁同步电机的电磁振动分析与抑制[J]. 电工技术学报, 2023, 38(5): 1275-1286, 1298.
Chen Shaoxian, Ding Shuye, Shen Shufeng, et al. Analysis and suppression of electromagnetic vibration of surface mounted permanent magnet synchronous motor for ships[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1275-1286, 1298.
[15] 李泽星, 夏加宽, 刘铁法, 等. 基于极间虚齿的表贴式永磁电机六倍频振动噪声的削弱[J]. 电工技术学报, 2023, 38(5): 1287-1298.
Li Zexing, Xia Jiakuan, Liu Tiefa, et al. Reduction of six times frequency vibration and noise of surface- mounted permanent magnet synchronous machines with interpolar virtual teeth[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1287-1298.
[16] 刘琦, 朱劲松, 陈文明, 等. 基于双分频带的新型随机开关频率SVPWM策略[J]. 电力工程技术, 2023, 42(3): 206-216.
Liu Qi, Zhu Jinsong, Chen Wenming, et al. Novel random switching frequency SVPWM strategy based on dual-segregate-frequency band[J]. Electric Power Engineering Technology, 2023, 42(3): 206-216.
[17] 刘洋, 王庆义, 赵金. 基于矢量控制系统的双随机PWM技术研究[J]. 中国电机工程学报, 2010, 30(36): 98-102.
Liu Yang, Wang Qingyi, Zhao Jin. Dual randomized PWM based on vector control system[J]. Proceedings of the CSEE, 2010, 30(36): 98-102.
[18] 卢峥, 欧阳红林, 孟超, 等. 多电平双Y移30°永磁同步电机的矢量控制系统[J]. 电工技术学报, 2016, 31(22): 45-56.
Lu Zheng, Ouyang Honglin, Meng Chao, et al. Vector control system of multilevel inverter double star winding shifted by30° permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 45-56.
[19] 朱琳, 卜飞飞, 黄文新, 等. 五相逆变器非正弦双随机空间矢量脉宽调制策略[J]. 电工技术学报, 2018, 33(20): 4824-4833.
Zhu Lin, Bu Feifei, Huang Wenxin, et al. Non- sinusoidal dual random space vector pulse width modulation strategy for five-phase inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4824-4833.
[20] 周长攀, 苏健勇, 杨贵杰, 等. 基于双零序电压注入PWM策略的双三相永磁同步电机矢量控制[J]. 中国电机工程学报, 2015, 35(10): 2522-2533.
Zhou Changpan, Su Jianyong, Yang Guijie, et al. Vector control of dual three-phase PMSM based on double zero-sequence voltage injection PWM strategy[J]. Proceedings of the CSEE, 2015, 35(10): 2522-2533.
[21] 周立, 苏美霞, 王杰. 永磁同步电机模糊多矢量模型预测控制[J]. 电气工程学报, 2022, 17(4): 181- 192.
Zhou Li, Su Meixia, Wang Jie. Fuzzy multi-vector model predictive control of permanent magnet syn- chronous motor[J]. Journal of Electrical Engineering, 2022, 17(4): 181-192.
[22] 徐奇伟, 熊德鑫, 陈杨明, 等. 基于新型高频纹波电流补偿方法的内置式永磁同步电机无传感器控制[J]. 电工技术学报, 2023, 38(3): 680-691.
Xu Qiwei, Xiong Dexin, Chen Yangming, et al. Research on sensorless control strategy of IPMSM based on new high frequency ripple current com- pensation method[J]. Transactions of China Electro- technical Society, 2023, 38(3): 680-691.
[23] Miyama Y, Ishizuka M, Kometani H, et al. Vibration reduction by applying carrier phase-shift PWM on dual three-phase winding permanent magnet syn- chronous motor[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5998-6004.
[24] 金石, 朱熙, 金无痕, 等. 基于谐波提取器的永磁同步电机谐波抑制方法[J]. 电气工程学报, 2021, 16(1): 9-15.
Jin Shi, Zhu Xi, Jin Wuhen, et al. Harmonic suppression method of permanent magnet syn- chronous motor based on harmonic extractor[J]. Journal of Electrical Engineering, 2021, 16(1): 9-15.
[25] 葛仕杰, 汪烈军, 李永明. 基于混沌的无线传感器网络分组加密算法[J]. 计算机工程与设计, 2022, 43(9): 2456-2463.
Ge Shijie, Wang Liejun, Li Yongming. Block encryption algorithm for wireless sensor networks based on chaotic map[J]. Computer Engineering and Design, 2022, 43(9): 2456-2463.
[26] 孙敏, 陕童, 续森炜. 基于I-SM4和SM2的混合加密算法[J]. 计算机科学, 2023, 50(增刊2): 869-872.
Sun Min, Shan Tong, Xu Senwei. Hybrid encryption algorithm based on I-SM4 and SM2[J]. Computer Science, 2023, 50(S2): 869-872.
[27] 焦然, 王宜敏. 引入梅森旋转算法的三角网格模型部分隐写算法[J]. 电子测量技术, 2017, 40(12): 228-232.
Jiao Ran, Wang Yimin. 3Dtrangle mesh part stegano- graphy algorithm with Mersenne twister[J]. Electronic Measurement Technology, 2017, 40(12): 228-232.
[28] 张良杰, 黎文娟. 结合梅森旋转和Arnold变换的图像加密算法[J]. 信息技术, 2021, 45(11): 49-54.
Zhang Liangjie, Li Wenjuan. Image encryption algorithm combining mersenne twister and Arnold transformation[J]. Information Technology, 2021, 45(11): 49-54.
[29] Morales-Ferre R, Richter P, Falletti E, et al. A survey on coping with intentional interference in satellite navigation for manned and unmanned aircraft[J]. IEEE Communications Surveys & Tutorials, 2020, 22(1): 249-291.
[30] 张琳琳. 一种基于混合映射策略的改进梅森旋转演算法[J]. 信息技术, 2022, 46(10): 12-17, 23.
Zhang Linlin. A improved Mersenne Twister based on hybrid mapping strategy[J]. Information Technology, 2022, 46(10): 12-17, 23.
Abstract In the inverter-driven permanent magnet synchronous machine (PMSM) control system, high-frequency current harmonics near the switching frequency and its multiples are generated using space vector pulse width modulation (SVPWM), which brings high-frequency electromagnetic vibration. Therefore, a double random SVPWM control method combining random switching frequency and random zero vector is applied to the high-frequency current harmonic spectrum expansion. Meanwhile, the random number is generated by the improved Mersenne twister (MT) algorithm, which enhances the random performance of the random sequences and ensures the spreading effect of the double random SVPWM control method.
Firstly, random zero vector control can be achieved by changing the action time of the zero vector and reassigning the randomized zero vectors into the space vectors. Secondly, the switching frequency of the traditional SVPWM control method is fixed, and the random switching frequency control can be achieved by changing the fixed switching frequency of the inverter and dispersing the harmonics at the switching frequency and its multiples into the specified frequency domain. Thirdly, the random number is generated by the improved MT algorithm, which is applied to the double random SVPWM control of the permanent magnet synchronous machine to enhance the degree of freedom and spatial traversal of the random sequence. The new control method proposed is named LKMT-DRC.
Experimental verifications are conducted on a 4.4 kW fractional-slot permanent magnet synchronous machine. The PMSM phase current harmonics and vibration acceleration under the conventional SVPWM control and LKMT-DRC control are compared, and the vibration suppression effect of the LKMT-DRC control is analyzed using different spreading ranges. Under the inverter power supply mode, the harmonic frequencies introduced by the SVPWM control mode are mainly fk±2f0 and fk±4f0, and the frequency of the introduced high-frequency radial electromagnetic force wave is mainly fk±f0. Compared with the traditional SVPWM control mode, the high-frequency harmonics concentrated on the switching frequency. Its integer multiples can be effectively dispersed using LKMT-DRC control mode, and the vibration suppression effect caused by the high-frequency electromagnetic force wave can be significantly reduced. Meanwhile, the random numbers generated by the proposed LKMT algorithm can improve the randomness and spatial traversability of the random sequences, which ensures the effectiveness of the double-random SVPWM control method.
The contributions of the proposed double random SVPWM control method based on the improved MT algorithm are as follows. (1) A mathematical model of the high-frequency radial electromagnetic force introduced by PMSM under inverter power supply conditions is derived, and the effect of the high-frequency electromagnetic force under inverter power supply mode on motor vibration is analyzed. (2) The LKMT-DRC control method is proposed, which effectively reduces high-frequency harmonic content and suppresses high-frequency electromagnetic vibration. (3) The effects of different spreading ranges on the final damping under the LKMT-DRC control mode are analyzed, and the appropriate ranges are indicated.
Keywords：Permanent magnet synchronous machine, current harmonic, electromagnetic vibration, double random space vector pulse width modulation (SVPWM)
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240639
国家自然科学基金资助项目（51907052）。
收稿日期 2024-04-24
改稿日期 2024-05-15
陈浈斐 女，1987年生，博士，副教授，研究方向为永磁电机设计与电磁分析、电力设备故障诊断。
E-mail: chenzhenfei@hhu.edu.cn（通信作者）
万向民 男，2000年生，硕士研究生，研究方向为永磁电机驱动与控制。
E-mail: 1134807310@qq.com
（编辑 崔文静）